Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T20:16:45.204Z Has data issue: false hasContentIssue false
  • English
  • Français

Theorems relating Hankel and Meijer's Bessel transforms

Published online by Cambridge University Press:  18 May 2009

K. C. Sharma
K. C. Sharma
Affiliation:
Department of MathematicsUniversity of RajasthanJaipur
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this note a theorem, giving a relation between the Hankel transform of f(x) and Meijer's Bessel function transform of f(x)g(x), is proved. Some corollaries, obtained by specializing the function g(x), are stated as theorems. These theorems are further illustrated by certain suitable examples in which certain integrals involving products of Bessel functions or of Gauss's hypergeometric function and Appell's hypergeometric function are evaluated. Throughout this note we use the following notations:

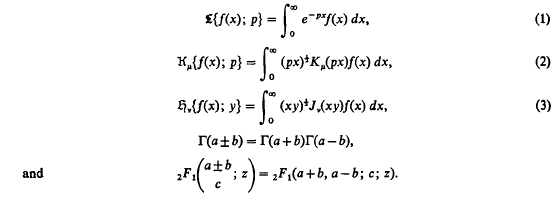
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 6 , Issue 2 , July 1963 , pp. 107 - 112
Copyright
Copyright © Glasgow Mathematical Journal Trust 1963

References

REFERENCES

1.Erdélyi, A., Tables of integral transforms, Vol. II (New York, 1954).Google Scholar
2.Erdélyi, A., Higher transcendental functions, Vol. I (New York, 1953).Google Scholar
3.Erdélyi, A., Higher transcendental functions, Vol. II (New York, 1954).Google Scholar
4.Bhonsle, B. R., A relation between Laplace and Hankel transforms, Proc. Glasgow Math. Assoc. 5 (1962), 114–115.CrossRefGoogle Scholar
5.Bailey, W. N., Some infinite integrals involving Bessel functions, Proc. London Math. Soc. (2) 40 (1935), 37–48.Google Scholar
6.Bailey, W. N., Some infinite integrals involving Bessel functions, II, J. London Math. Soc. 11 (1936), 16–20.CrossRefGoogle Scholar