Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:54:13.036Z Has data issue: false hasContentIssue false
  • English
  • Français

ROOTS OF DEHN TWISTS ABOUT MULTICURVES

Part of: Low-dimensional topology

Published online by Cambridge University Press:  30 October 2017

KASHYAP RAJEEVSARATHY  and
PRAHLAD VAIDYANATHAN
KASHYAP RAJEEVSARATHY
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462066, Madhya Pradesh, India e-mail: [email protected] (https://home.iiserb.ac.in/ekashyap/), [email protected] (https://home.iiserb.ac.in/eprahlad/)
PRAHLAD VAIDYANATHAN
Affiliation:
Department of Mathematics, Indian Institute of Science Education and Research Bhopal, Bhopal Bypass Road, Bhauri, Bhopal 462066, Madhya Pradesh, India e-mail: [email protected] (https://home.iiserb.ac.in/ekashyap/), [email protected] (https://home.iiserb.ac.in/eprahlad/)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A multicurve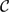${\mathcal{C}}$ in a closed orientable surface Sg of genus g is defined to be a finite collection of disjoint non-isotopic essential simple closed curves. A left-handed Dehn twist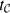$t_{\mathcal{C}}$about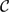${\mathcal{C}}$ is the product of left-handed Dehn twists about the individual curves in 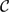${\mathcal{C}}$. In this paper, we derive necessary and sufficient conditions for the existence of a root of 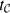$t_{\mathcal{C}}$ in the mapping class group Mod(Sg). Using these conditions, we obtain combinatorial data that correspond to roots, and use it to determine upper bounds on the degree of a root. As an application of our theory, we classify all such roots up to conjugacy in Mod(S4). Finally, we establish that no such root can lie in the level m congruence subgroup of Mod(Sg), for m ≥ 3.

MSC classification

Primary: 57M60: Group actions in low dimensions
Secondary: 57M99: None of the above, but in this section
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 60 , Issue 3 , September 2018 , pp. 555 - 583
Copyright
Copyright © Glasgow Mathematical Journal Trust 2017 

References

REFERENCES

1. Edmonds, Allan L., Surface symmetry. I, Michigan Math. J. 29 (2) (1982), 171–183.CrossRefGoogle Scholar
2. Farb, Benson and Margalit, Dan, A primer on mapping class groups, Princeton Mathematical Series, volume 49 (Princeton University Press, Princeton, NJ, 2012).Google Scholar
3. Harvey, W. J., Cyclic groups of automorphisms of a compact Riemann surface, Quart. J. Math. Oxford Ser. (2) 17 (1966), 86–97.Google Scholar
4. Kerckhoff, Steven P., The Nielsen realization problem, Bull. Amer. Math. Soc. 2 (3) (1980), 452–454.Google Scholar
5. Margalit, Dan and Schleimer, Saul, Dehn twists have roots, Geom. Topol. 13 (3) (2009), 1495–1497.Google Scholar
6. McCullough, Darryl and Rajeevsarathy, Kashyap, Roots of Dehn twists, Geom. Dedic. 151 (2011), 397–409. 10.1007/s10711-010-9541-4.Google Scholar
7. Monden, Naoyuki et al., On roots of dehn twists, Rocky Mt. J. Math. 44 (3) (2014), 987–1001.Google Scholar
8. Nielsen, Jakob, Abbildungsklassen endlicher Ordnung, Acta Math. 75, 23–115.Google Scholar
9. Rajeevsarathy, Kashyap, Roots of dehn twists about separating curves, J. Aust. Math.Soc. 95 (2013), 266–288.CrossRefGoogle Scholar
10. Rajeevsarathy, Kashyap, Fractional powers of Dehn twists about nonseparating curves, Glasg. Math. J. 56 (1) (2014), 197–210.Google Scholar
11. Thurston, William P., The gometry and topology of three-manifolds, Available at: http://www.msri.org/communications/books/gt3m/PDFGoogle Scholar