Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hughes, H. K.
1945.
The asymptotic developments of a class of entire functions.
Bulletin of the American Mathematical Society,
Vol. 51,
Issue. 6,
p.
456.
Riney, T. D.
1959.
Coefficients in certain asymptotic factorial expansions.
Proceedings of the American Mathematical Society,
Vol. 10,
Issue. 4,
p.
511.
1969.
The Special Functions and Their Approximations.
Vol. 53,
Issue. ,
p.
330.
1969.
The Special Functions and their Approximations.
Vol. 53,
Issue. ,
p.
453.
Harris, Bernard
and
Soms, Andrew P.
1973.
The Reliability of Systems of Independent Parallel Components When Some Components are Repeated.
Journal of the American Statistical Association,
Vol. 68,
Issue. 344,
p.
894.
Harris, Bernard
and
Soms, Andrew P.
1974.
Properties of the Generalized Incomplete Modified Bessel Distributions with Applications to Reliability Theory.
Journal of the American Statistical Association,
Vol. 69,
Issue. 345,
p.
259.
Paris, R. B.
1980.
On the asymptotic expansions of solutions of an nth order linear differential equation.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 85,
Issue. 1-2,
p.
15.
Witte, N S
1998.
Exact solution for the reflection and diffraction of atomic de Broglie waves by a travelling evanescent laser wave.
Journal of Physics A: Mathematical and General,
Vol. 31,
Issue. 2,
p.
807.
Kowalenko, Victor
2002.
Exactification of the asymptotics for Bessel and Hankel functions.
Applied Mathematics and Computation,
Vol. 133,
Issue. 2-3,
p.
487.
Paris, R.B.
2010.
Exponentially small expansions in the asymptotics of the Wright function.
Journal of Computational and Applied Mathematics,
Vol. 234,
Issue. 2,
p.
488.
Bennequin, Daniel
2014.
Neuromathematics of Vision.
p.
243.
Karp, D. B.
and
Prilepkina, E. G.
2018.
An Inverse Factorial Series for a General Gamma Ratio and Related Properties of the Nørlund–Bernoulli Polynomials.
Journal of Mathematical Sciences,
Vol. 234,
Issue. 5,
p.
680.


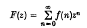
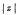 from the behaviour of
from the behaviour of 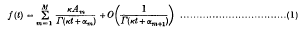
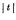 such that
such that