Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-22T21:02:55.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Polynomial Grothendieck properties

Published online by Cambridge University Press:  18 May 2009

Manuel González  and
Joaquí M. Gutiérrez
Manuel González
Affiliation:
Departamento de Matemáticas, Facultad de Ciendcias, Universidad de Cantabria, 39071 Santander, Spain
Joaquí M. Gutiérrez
Affiliation:
Departamento de Matemática Aplicada, ETS de Ingenieros Industriaiales, Universidad Politécnica de Nadrid, C. José Gutiérrez Abascal 2, 28006 Madrid, Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

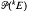A Banach space sE has the Grothendieck property if every (linear bounded) operator from E into c0 is weakly compact. It is proved that, for an integer k > 1, every k-homogeneous polynomial from E into c0 is weakly compact if and only if the space (kE) of scalar valued polynomials on E is reflexive. This is equivalent to the symmetric A>fold projective tensor product of £(i.e., the predual of 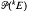(kE)) having the Grothendieck property. The Grothendieck property of the projective tensor product E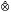F is also characterized. Moreover, the Grothendieck property of E is described in terms of sequences of polynomials. Finally, it is shown that if every operator from E into c0 is completely continuous, then so is every polynomial between these spaces.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 37 , Issue 2 , May 1995 , pp. 211 - 219
Copyright
Copyright © Glasgow Mathematical Journal Trust 1995

References

REFERENCES

1.Alencar, R., Aron, R. M. and Dineen, S., A reflexive space of holomorphic functions in infinitely many variables, Proc. Amer. Math. Soc. 90 (1984), 407–411.CrossRefGoogle Scholar
2.Alencar, R., Aron, R. M. and Fricke, G., Tensor products of Tsirelson's space, Illinois J. Math. 31 (1987), 17–23.CrossRefGoogle Scholar
3.Aron, R. M., Herves, C. and Valdivia, M., Weakly continuous mappings on Banach spaces, J. Fund. Anal. 52 (1983), 189–204.CrossRefGoogle Scholar
4.Astala, K. and Tylli, H. O., On the bounded compact approximation property and measures of noncompactness, J. Fund. Anal. 70 (1987), 388–401.CrossRefGoogle Scholar
5.Casazza, P. G. and Shura, T. J., Tsirelson's Space, Lecture Notes in Math. 1363 (Springer-Verlag 1989).CrossRefGoogle Scholar
6.Davie, A. M. and Gamelin, T. W., A theorem on polynomial-star approximation, Proc. Amer. Math. Soc. 106 (1989), 351–356.CrossRefGoogle Scholar
7.Farmer, J. D., Polynomial reflexivity in Banach spaces, Israel J. Math. 87 (1994), 257–273.CrossRefGoogle Scholar
8.González, M., Remarks on Q-reflexive Banach spaces, preprint.Google Scholar
9.González, M. and Gutiérrez, J. M., Unconditionally converging polynomials on Banach spaces, Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
10.González, M. and Gutiérrez, J. M., Weak compactness in spaces of differentiable mappings, Rocky Mountain J. Math., to appear.Google Scholar
11.González, M. and Gutiérrez, J. M., When every polynomial is unconditionally converging, Arch. Math. 63 (1994), 145–151.CrossRefGoogle Scholar
12.González, M. and Onieva, V., Lifting results for sequences in Banach spaces, Math. Proc. Cambridge Philos. Soc. 105 (1989), 117–121.CrossRefGoogle Scholar
13.Gonzalo, R. and Jaramillo, J. A., Compact polynomials between Banach spaces, preprint.Google Scholar
14.Gutiérrez, J. M., Weakly continuous functions on Banach spaces not containing ℓ1 Proc. Amer. Math. Soc. 119 (1993), 147–152.Google Scholar
15.Holub, J. R., Reflexivity of ℒ(E, F), Proc. Amer. Math. Soc. 39 (1973), 175–177.Google Scholar
16.Kalton, N. J., Spaces of compact operators, Math. Ann. 208 (1974), 267–278.CrossRefGoogle Scholar
17.Khasanov, V., On Banach spaces with Grothendieck property (Russian), in Extremal problems of the theory of functions, Collect. Articles, Tomsk 1984, 85–96.Google Scholar
18.Lotz, H. P., Uniform convergence of operators on L ∞; and similar spaces, Math. Z. 190 (1985), 207–220.CrossRefGoogle Scholar
19.Mujica, J., Complex Analysis in Banach Spaces, Math. Studies 120 (North-Holland 1986).Google Scholar
20.Pelczynski, A., A property of multilinear operations, Studia Math. 16 (1957), 173–182.CrossRefGoogle Scholar
21.Pisier, G., Factorization of Linear Operators and Geometry of Banach Spaces, Reg. Conf. Ser. Math. 60 (American Mathematical Society 1986).CrossRefGoogle Scholar
22.Ryan, R. A., Applications of topological tensor products to infinite dimensional holomorphy, Ph.D. thesis, Trinity College, Dublin 1980.Google Scholar
23.Ryan, R. A., Weakly compact holomorphic mappings on Banach spaces, Pacific J. Math. 131 (1988), 179–190.CrossRefGoogle Scholar
24.Willis, G., The compact approximation property does not imply the approximation property, Studia Math. 103 (1992), 99–108.CrossRefGoogle Scholar