Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-23T05:51:28.359Z Has data issue: false hasContentIssue false
  • English
  • Français

ON GROUPS WITH TWO ISOMORPHISM CLASSES OF DERIVED SUBGROUPS

Published online by Cambridge University Press:  25 February 2013

PATRIZIA LONGOBARDI ,
MERCEDE MAJ ,
DEREK J. S. ROBINSON  and
HOWARD SMITH
PATRIZIA LONGOBARDI
Affiliation:
Dipartimento di Matematica, Università di Salerno84084 Fisciano (Salerno), Italy e-mail: [email protected]
MERCEDE MAJ
Affiliation:
Dipartimento di Matematica, Università di Salerno84084 Fisciano (Salerno), Italy e-mail: [email protected]
DEREK J. S. ROBINSON
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign Urbana, IL 61801, USA e-mail: [email protected]
HOWARD SMITH
Affiliation:
Department of Mathematics, Bucknell University, Lewisburg, PA 17837, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The structure of groups which have at most two isomorphism classes of derived subgroups (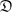$\mathfrak{D}$2-groups) is investigated. A complete description of 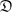$\mathfrak{D}$2-groups is obtained in the case where the derived subgroup is finite: the solution leads an interesting number theoretic problem. In addition, detailed information is obtained about soluble 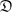$\mathfrak{D}$2-groups, especially those with finite rank, where algebraic number fields play an important role. Also, detailed structural information about insoluble 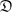$\mathfrak{D}$2-groups is found, and the locally free 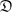$\mathfrak{D}$2-groups are characterized.

Keywords

Primary 20F14
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 655 - 668
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Baer, R., Polyminimaxgruppen, Math. Ann. 175 (1968), 1–43.CrossRefGoogle Scholar
2.de Giovanni, F. and de Mari, F., Groups with finitely many derived subgroups of non-normal subgroups, Arch. Math. (Basel) 86 (2006), 310–316.Google Scholar
3.de Giovanni, F. and Robinson, D. J. S., Groups with finitely many derived subgroups, J. Lond. Math. Soc. 71 (2) (2005), 658–668.Google Scholar
4.Granville, A. and Monagan, M. B., The first case of Fermat's last theorem is true for all prime exponents up to 714, 591, 416, 091, 389, Trans. Amer. Math. Soc. 306 (1988), 329–359.Google Scholar
5.Herzog, M., Longobardi, P. and Maj, M., On the number of commutators in groups. Ischia Group Theory 2004, Contemp. Math. 402 (2006), 181–192 (American Mathematical Society, Providence, RI).Google Scholar
6.Lennox, J. C. and Robinson, D. J. S., The theory of infinite soluble groups (Oxford University Press, Oxford, UK, 2004).CrossRefGoogle Scholar
7.Miller, G. A. and Moreno, H. C., Non-abelian groups in which every subgroup is abelian, Trans. Am. Math. Soc. 4 (1903), 398–404.Google Scholar
8.Robinson, D. J. S., On the cohomology of soluble groups of finite rank, J. Pure Appl. Algebra 6 (1975), 155–164.CrossRefGoogle Scholar
9.Robinson, D. J. S., Splitting theorems for infinite groups, Symposia Math. 17 (1976), 441–470.Google Scholar
10.Tits, J., Free subgroups in linear groups, J. Algebra 20 (1972), 250–270.Google Scholar