In [1], we introduced the notion of multiplicative forms on associative algebras 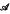of finite rank over integral domains D, and obtained a complete classification when D ⊆, the complex field. We propose here to remove the hypothesis of associativity, using a refinement of the technique of Schafer [2]. In [l], it was noted that multiplicative forms extend uniquely under the adjunction of an identity when 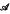is associative but not unitary; this appears difficult to verify in the general case, so that some mild restriction on 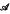is required. We shall assume that 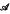is biregular, that is that 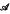contains elements eL, eR such that the linear maps x 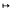eL x and x 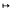xeR, are bijective on 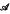We can then (§1) reduce the biregular case to the unitary case, which is handled in §2.