Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-27T03:22:16.773Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple semidirect products of associative systems

Published online by Cambridge University Press:  18 May 2009

Richard Steiner
Richard Steiner
Affiliation:
Department of Mathematics, University of GlasgowUniversity of Gardens, Glasgow G12 8QW
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that a group G is the semidirect product of a subgroup N and a normal subgroup M. Then the elements of G have unique expressions mn (m ∈ M, n ∈ N) and the commutator function

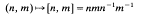
maps N x M into M. In fact there is an action (by automorphisms) of N on M given by

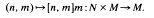
Conversely, if one is given an action of a group N on a group M then one can construct a semidirect product.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 31 , Issue 3 , September 1989 , pp. 353 - 369
Copyright
Copyright © Glasgow Mathematical Journal Trust 1989

References

1.Ellis, G. and Steiner, R., Higher-dimensional crossed modules and the homotopy groups of (n + 1)-ads, J. Pure Appl. Algebra 46 (1987), 117–136.Google Scholar
2.End, W., Groups with projections and applications to homotopy theory, J. Pure Appl. Algebra 18 (1980), 111–123.Google Scholar
3.Giraud, J., Cohomologie non abélienne (Springer, 1971).Google Scholar
4.Neumann, B. H., Embedding theorems for semigroups, J. London Math. Soc. 35 (1960), 184–192.Google Scholar
5.Preston, G. B., Semidirect products of semigroups, Proc. Roy. Soc. Edinburgh Sect. A 102 (1986), 91–102.Google Scholar
6.Usenko, V. M., On semidirect products of monoids, Ukrainian Math. J. 34 (1982), 151–155.Google Scholar