Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shparlinski, Igor E.
2012.
Modular hyperbolas.
Japanese Journal of Mathematics,
Vol. 7,
Issue. 2,
p.
235.
Alsulmi, Badria
Cochrane, Todd
Mossinghoff, Michael J.
Pigno, Vincent
Pinner, Chris
Richardson, C. J.
and
Thompson, Ian
2018.
A Generalization of the Goresky--Klapper Conjecture, Part I.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 4,
p.
2973.
Cochrane, Todd
Mossinghoff, Michael J.
Pinner, Chris
and
Richardson, C. J.
2021.
A Generalization of the Goresky–Klapper Conjecture, Part II.
Experimental Mathematics,
Vol. 30,
Issue. 2,
p.
209.
Song, Yanbo
2021.
On two sums related to the Lehmer problem over short intervals.
AIMS Mathematics,
Vol. 6,
Issue. 11,
p.
11723.
Xiaoqing, Zhao
and
Yuan, Yi
2024.
Square-free numbers in the intersection of Lehmer set and Piatetski-Shapiro sequence.
AIMS Mathematics,
Vol. 9,
Issue. 12,
p.
33591.
Wang, Jiankang
and
Xu, Zhefeng
2025.
Partitions into two Lehmer numbers in ℤq
.
Mathematica Slovaca,
Vol. 75,
Issue. 1,
p.
45.


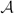 and
and 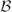 consist of consecutive integers which are coprime to
consist of consecutive integers which are coprime to