All topological spaces here are assumed to be T2. The collection 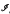F(Y)of all homeomorphisms whose domains and ranges are closed subsets of a topological space Y is an inverse semigroup under the operation of composition. We are interested in the general problem of getting some information about the subsemigroups of 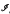F(Y) whenever Y is a compact metric space. Here, we specifically look at the problem of determining those spaces X with the property that 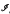F(X) is isomorphic to a subsemigroup of 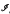F(Y). The main result states that if X is any first countable space with an uncountable number of points, then the semigroup 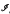F(X) can be embedded into the semigroup 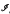F(Y) if and only if either X is compact and Y contains a copy of X, or X is noncompact and locally compact and Y contains a copy of the one-point compactification of X.