Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-20T07:00:07.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Duals of Banach spaces of entire functions

Published online by Cambridge University Press:  18 May 2009

J. M. Anderson  and
J. Duncan
J. M. Anderson
Affiliation:
Mathematics Dept. University College London Wc1e6bt, U.K.
J. Duncan
Affiliation:
Dept. of Math. SciencesUniversity of Arkansas Fayetteville, AR 72701U.S.A.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

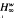Let w be a strictly positive function on ℂ and let , respectively 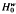denote the Banach spaces of those entire functions φ(z) with ∣φ(z)∣= O(w(z)) and ∣φ(z)∣ = o(w(z)). In this generality, these spaces may contain only constants, but for many functions w(z) these will be interesting Banach spaces with norm

.

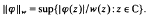We study two specific problems.

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 2 , May 1990 , pp. 215 - 220
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Anderson, J. M., Clunie, J. and Pommerenke, Ch., On Bloch functions and normal functions, J. Reine Angew. Math. 270 (1974), 12–37.Google Scholar
2.Bierstedt, K-D. and Summers, W. H., Biduals of weighted Banach spaces of analytic functions, preprint.Google Scholar
3.Clunie, J. and Kovari, T., On integral functions having prescribed asymptotic growth, II, Canad. J. Math. 20 (1968), 7–30.CrossRefGoogle Scholar
4.Crabb, M. J., Duncan, J. and McGregor, C. M., Some extremal problems in the theory of numerical ranges, Acta Math. 128 (1972), 123–142.CrossRefGoogle Scholar
5.Rubel, L. A. and Shields, A. L., The second duals of certain spaces of analytic functions, J. Austral. Math. Soc. 11 (1970) 276–280.CrossRefGoogle Scholar