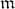Hostname: page-component-f554764f5-68cz6 Total loading time: 0 Render date: 2025-04-10T22:48:37.940Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTRACTED, $\mathfrak{m}$-FULL AND RELATED CLASSES OF IDEALS IN LOCAL RINGS

Published online by Cambridge University Press:  25 February 2013

DAVID E. RUSH
DAVID E. RUSH*
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The class of 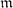$\mathfrak{m}$-full and four related classes of ideals in a local ring (R, 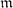$\mathfrak{m}$) are extended by replacing 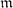$\mathfrak{m}$ with other ideals and the resulting classes of ideals are compared. It is shown that contracted ideals are 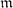$\mathfrak{m}$-full in a local ring with infinite residue field.

Keywords

13H9913E0513B22
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 55 , Issue 3 , September 2013 , pp. 669 - 675
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Conca, A., De Negri, E. and Rossi, M. E., Integrally closed and componentwise linear ideals, Math. Z. 265 (2010), 715–734.CrossRefGoogle Scholar
2.D'Cruz, C., Quadratic transform of complete ideals in regular local rings, Commun. Algebra 28 (2000), 693–698.Google Scholar
3.Epstein, N., A guide to closure operations in commutative algebra, in Progress in commutative algebra 2 (Walter de Gruyter, Berlin, 2012), 1–37.Google Scholar
4.Goto, S., Integral closedness of complete–intersection ideals, J. Algebra 108 (1987), 151–160.CrossRefGoogle Scholar
5.Heinzer, W., Lantz, D. and Shah, K., The Ratliff–Rush ideals in a Noetherian ring, Commun. Algebra 20 (1992), 591–622.Google Scholar
6.Heinzer, W., Ratliff, L. J. Jr. and Rush, D. E., Basically full ideals in local rings, J. Algebra 250 (2002), 371–396.CrossRefGoogle Scholar
7.Hong, J., Lee, H., Noh, S. and Rush, D. E., Full ideals, Commun. Algebra 37 (2009), 2627–2639.CrossRefGoogle Scholar
8.Huneke, C., Complete ideals in two-dimensional regular local rings, Proceedings of the Microprogram in Commutative Algebra, MSRI, Berkeley (1987), Springer, New York (1989), 325–338.Google Scholar
9.Matsumura, H., Commutative ring theory (Cambridge University Press, Cambridge, UK, 1986).Google Scholar
10.Petro, J. W., Some results on the asymptotic completion of an ideal, Proc. Amer. Math. Soc. 15 (1964), 519–524.CrossRefGoogle Scholar
11.Ratliff, L. J. Jr., Δ-closures of ideals and rings, Trans. Amer. Math. Soc. 313 (1) (1989), 221–247.Google Scholar
12.Ratliff, L. J. Jr. and Rush, D. E., Asymptotic primes of Delta-closures of ideals, Commun. Algebra 30 (1) (2002), 1513–1531.Google Scholar
13.Sakuma, M., On prime operations in the theory of ideals, Hiroshima Math. J. 20 (1957), 101–106.CrossRefGoogle Scholar
14.Swanson, I. and Huneke, C., Integral closure of ideals, rings, and modules, London Math. Soc. Lecture Note Series 336 (Cambridge University Press, Cambridge, UK, 2006).Google Scholar
15.Vasconcelos, W., Integral closure, Rees algebras, multiplicity and algorithms (Springer, New York, 2005).Google Scholar
16.Vassilev, J., Structure on the set of closure operations on a commutative ring, J. Algebra 321 (2009), 2737–2753.CrossRefGoogle Scholar
17.Vassilev, J. and Vraciu, A., When is the tight closure determined by the test ideal?, J. Commutative Algebra 1 (2009), 591–602.CrossRefGoogle Scholar
18.Watanabe, J., $\mathfrak{m}$-full ideals, Nagoya Math. J. 106 (1987), 101–111.Google Scholar
19.Yao, Y., Modules with finite F-representation type, J. London Math. Soc. 72 (2005), 53–72.CrossRefGoogle Scholar
20.Zariski, O. and Samuel, P., Commutative algebra, Vol. II (D. Van Nostrand, New York, 1960).CrossRefGoogle Scholar