Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Alías, Luis J.
2003.
An integral formula for compact hypersurfaces in space forms and its applications.
Journal of the Australian Mathematical Society,
Vol. 74,
Issue. 2,
p.
239.
Costa-Filho, Wagner Oliveira
2021.
Remarks on biharmonic hypersurfaces in space forms.
Differential Geometry and its Applications,
Vol. 79,
Issue. ,
p.
101831.


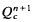 be an
be an 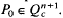 We consider the function
We consider the function 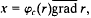 where
where