Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maaß, Hans
1978.
Lineare Relationen für die Fourierkoeffizienten einiger Modulformen zweiten Grades.
Mathematische Annalen,
Vol. 232,
Issue. 2,
p.
163.


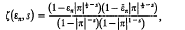
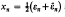 are distributed according to the density function
are distributed according to the density function
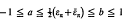 is
is