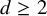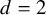1 Overview
The question of whether Ulrich modules exist for complete local domains has been open for over three decades. In the first half of the paper, we construct the first known counterexamples to the existence of Ulrich modules for (complete) local domains. In fact, the construction gives many counterexamples in all dimensions
![]() $d\geq 2$
and with minimal modification; it can also be used to give counterexamples that are essentially of finite type over fields.
$d\geq 2$
and with minimal modification; it can also be used to give counterexamples that are essentially of finite type over fields.
In the second half of the paper, we show that our counterexamples for the existence of Ulrich modules in dimension 2 are counterexamples to the existence of weakly lim Ulrich sequences for (complete) local domains. This is a rather surprising turn of events, given that 1) lim Cohen–Macaulay sequences exist for complete local domains of positive characteristic with F-finite residue fields [Reference Bhatt, Hochster and MaBHM] and 2) weakly lim Ulrich sequences (and, in fact, lim Ulrich sequences) exist for standard graded rings over infinite F-finite fields of positive characteristic [Reference MaM]. Note that our counterexamples are fairly simple affine nonstandard graded algebras.
2 Introduction
Ulrich modules were introduced by Bernd Ulrich in 1984 as a means to study the Gorenstein property of Cohen-Macaulay rings [Reference UlrichU]. Since then, the theory of Ulrich modules has become a very active area of research in both commutative algebra and algebraic geometry. Ulrich modules have many powerful and broad applications, ranging from the original purpose of giving a criteria for when a local Cohen-Macaulay ring is Gorenstein [Reference UlrichU] to new methods of finding Chow forms of a variety [Reference Eisenbud, Schreyer and WeymanES] to longstanding open conjectures in multiplicity theory.
One of the major applications of Ulrich modules is Lech’s conjecture on Hilbert–Samuel multiplicities, where the existence of Ulrich modules or Ulrich-like objects has been the main approach for the majority of established cases. More specifically, the existence of Ulrich modules for complete local domains implies the following conjecture:
Conjecture 2.1 (Lech’s Conjecture [Reference LechL1]).
Let
![]() $\varphi : (R,\mathfrak {m},k) \rightarrow (S,\mathfrak {n},l)$
be a flat local map between local rings. Then
$\varphi : (R,\mathfrak {m},k) \rightarrow (S,\mathfrak {n},l)$
be a flat local map between local rings. Then
![]() $e_{\mathfrak {m}}(R) \leq e_{\mathfrak {n}}(S)$
.
$e_{\mathfrak {m}}(R) \leq e_{\mathfrak {n}}(S)$
.
Historically, the existence of Ulrich modules has been a challenging question. The existing literature is sparse and has mainly explored positive existence results (i.e., classes of rings for which Ulrich modules exist). The major existence results are that Ulrich modules exist for the following classes of rings:
-
1. strict complete intersection rings [Reference Herzog, Ulrich and BackelinHUB]
-
2. generic determinantal rings [Reference Bruns, Römer and WiebeBRW]
-
3. projective
 $1$
-dimensional schemes over arbitrary fields [Reference Eisenbud, Schreyer and WeymanES]
$1$
-dimensional schemes over arbitrary fields [Reference Eisenbud, Schreyer and WeymanES]-
• The subcase of two-dimensional, standard graded Cohen-Macaulay domains was proved earlier in [Reference Brennan, Herzog and UlrichBHU].
-
-
4. some Veronese subrings of degree d of a polynomial ring in n variables:
-
•
 $n=3$
with d arbitrary and
$n=3$
with d arbitrary and
 $n=4$
with
$n=4$
with
 $d = 2^{\ell }$
in arbitrary characteristic [Reference HanesHa99]
$d = 2^{\ell }$
in arbitrary characteristic [Reference HanesHa99] -
• arbitrary n and d in characteristic
 $0$
[Reference Eisenbud, Schreyer and WeymanES]
$0$
[Reference Eisenbud, Schreyer and WeymanES] -
• arbitrary n and d for characteristic
 $p \geq (d-1)n + (n+1)$
[Reference SaccochiSa]
$p \geq (d-1)n + (n+1)$
[Reference SaccochiSa]
-
Beyond these results, there has been limited progress. In particular, for over 30 years, it has been unknown whether complete local domains always have Ulrich modules. In the first half of the paper, we resolve the question of existence of Ulrich modules in the negative.
Theorem A. Ulrich modules do not always exist for complete local domains.
We prove Theorem A by constructing complete local domains R of all dimensions
![]() $d \geq 2$
whose
$d \geq 2$
whose
![]() $S_2$
-ification S is a regular local ring. The key ingredient to proving that our counterexamples do not have Ulrich modules is Lemma 4.1, which states that any MCM module over R is an MCM module over S. This yields the following intermediary theorem:
$S_2$
-ification S is a regular local ring. The key ingredient to proving that our counterexamples do not have Ulrich modules is Lemma 4.1, which states that any MCM module over R is an MCM module over S. This yields the following intermediary theorem:
Theorem B. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain. Suppose R has an
$(R, \mathfrak {m}, k)$
be a local domain. Suppose R has an
![]() $S_2$
-ification S such that S is a regular local ring. Then every MCM module of R has the form
$S_2$
-ification S such that S is a regular local ring. Then every MCM module of R has the form
![]() $S^{\oplus h}$
. Consequently, R has Ulrich modules if and only if S is an Ulrich module of R.
$S^{\oplus h}$
. Consequently, R has Ulrich modules if and only if S is an Ulrich module of R.
In the second half of the paper, we consider the existence of (weakly) lim Ulrich sequences. To give some context, MCM modules (or small Cohen–Macaulay modules) and Ulrich modules (a special type of MCM module) are central to the main approaches to several major conjectures in multiplicity theory such as Serre’s positivity and Lech’s conjecture, respectively. However, existence results for MCM modules and Ulrich modules have been sparse and difficult to obtain. For example, the existence of MCM modules is open in dimension 3. As such, the weaker notions of lim Cohen–Macaulay sequences by Bhatt, Hochster and Ma [Reference Bhatt, Hochster and MaBHM] and (weakly) lim Ulrich sequences by Ma [Reference MaM] were introduced as suitable replacements for small Cohen–Macaulay modules and Ulrich modules in the current approaches to Serre’s positivity and Lech’s conjecture respectively. Lim Cohen–Macaulay sequences and (weakly) lim Ulrich sequences have been shown to exist in much more general contexts.
In an earlier draft of [Reference MaM] (prior to the results of this paper), Ma posed the following question:
Question 2.2 [Reference MaM].
Does every complete local domain of characteristic
![]() $p>0$
with an F-finite residue field admit a lim Ulrich sequence, or at least a weakly lim Ulrich sequence?
$p>0$
with an F-finite residue field admit a lim Ulrich sequence, or at least a weakly lim Ulrich sequence?
Given that lim Cohen–Macaulay sequences exist for completely local domains of positive characteristic with F-finite residue fields [Reference Bhatt, Hochster and MaBHM, Reference MaM], it is reasonable to ask if (weakly) lim Ulrich sequences exist for these rings. However, we answer the question in the negative in this paper.
Theorem C. Weakly lim Ulrich sequences do not always exist for complete local domains.
To prove Theorem C, we establish important characterizations of (weakly) lim Cohen–Macaulay sequences and (weakly) lim Ulrich sequences for local domains of dimension
![]() $2.$
$2.$
3 Preliminaries
In this section, we review the relevant definitions and properties of Ulrich modules and (weakly) lim Ulrich sequences. Throughout this paper, all rings are commutative with a multiplicative identity. All local rings
![]() $(R, \mathfrak {m}, k)$
include the Noetherian condition. For simplicity, we assume that k is infinite unless explicitly stated otherwise. In particular, we assume the existence of a minimal reduction generated by d elements for the maximal ideal
$(R, \mathfrak {m}, k)$
include the Noetherian condition. For simplicity, we assume that k is infinite unless explicitly stated otherwise. In particular, we assume the existence of a minimal reduction generated by d elements for the maximal ideal
![]() $\mathfrak {m}$
of a local ring R of dimension d.
$\mathfrak {m}$
of a local ring R of dimension d.
Notation
Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be a finitely generated module over R. Throughout the paper, we use the following notation:
$(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be a finitely generated module over R. Throughout the paper, we use the following notation:
-
•
 $\underline {x} = x_1, \ldots , x_d$
$\underline {x} = x_1, \ldots , x_d$
-
•
 $\ell _R(M)$
is the length of M as a module over R. We write
$\ell _R(M)$
is the length of M as a module over R. We write
 $\ell (M)$
when it is clear from the context which R is being used.
$\ell (M)$
when it is clear from the context which R is being used. -
•
 $H_i(\underline {x}; M)$
is the i-th Koszul homology of the module M with respect to
$H_i(\underline {x}; M)$
is the i-th Koszul homology of the module M with respect to
 $\underline {x}.$
$\underline {x}.$
-
•
 $h_i^R(\underline {x}; M) = \ell _R(H_i(\underline {x}; M))$
$h_i^R(\underline {x}; M) = \ell _R(H_i(\underline {x}; M))$
-
•
 $\chi (\underline {x};M) = \sum _{i = 0}^{d}(-1)^{i}\ell (H_i(\underline {x}; M)) = \sum _{i=0}^d (-1)^i h_i(\underline {x}; M).$
$\chi (\underline {x};M) = \sum _{i = 0}^{d}(-1)^{i}\ell (H_i(\underline {x}; M)) = \sum _{i=0}^d (-1)^i h_i(\underline {x}; M).$
-
•
 $\chi _1(\underline {x}; M) = \sum _{i = 1}^{d}(-1)^{i-1}\ell (H_i(\underline {x}; M)) = \sum _{i=1}^d (-1)^{i-1} h_i(\underline {x}; M).$
$\chi _1(\underline {x}; M) = \sum _{i = 1}^{d}(-1)^{i-1}\ell (H_i(\underline {x}; M)) = \sum _{i=1}^d (-1)^{i-1} h_i(\underline {x}; M).$
-
•
 $\nu _R(M)$
is the minimal number of generators of M.
$\nu _R(M)$
is the minimal number of generators of M. -
•
 $e_R(M)$
is the multiplicity of M with respect to the maximal ideal
$e_R(M)$
is the multiplicity of M with respect to the maximal ideal
 $\mathfrak {m}.$
When
$\mathfrak {m}.$
When
 $M=R$
, we write
$M=R$
, we write
 $e(R).$
$e(R).$
3.1 Ulrich modules
Definition 3.1 (Hilbert-Samuel Multiplicity).
Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be a finitely generated module over R. The Hilbert-Samuel multiplicity of M with respect to
$(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be a finitely generated module over R. The Hilbert-Samuel multiplicity of M with respect to
![]() $\mathfrak {m}$
is
$\mathfrak {m}$
is
Definition 3.2 (MCM).
Let M be a finitely generated module over
![]() $(R,m,k)$
. Then M is maximal Cohen-Macaulay (or MCM) module of R if
$(R,m,k)$
. Then M is maximal Cohen-Macaulay (or MCM) module of R if
![]() $\text {depth}_R(M) = \text {dim}(R).$
$\text {depth}_R(M) = \text {dim}(R).$
We review some useful facts.
Proposition 3.3. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain of dimension d. Let M be an MCM module over R. Then we have
$(R, \mathfrak {m}, k)$
be a local domain of dimension d. Let M be an MCM module over R. Then we have
-
(a)
 $e_R(M) = \text {rank}_R(M) \cdot e(R),$
$e_R(M) = \text {rank}_R(M) \cdot e(R),$
-
(b)
 $e_R(M) = \ell (M/IM)$
, where
$e_R(M) = \ell (M/IM)$
, where
 $I \subseteq \mathfrak {m}$
is a minimal reduction of
$I \subseteq \mathfrak {m}$
is a minimal reduction of
 $\mathfrak {m}$
, and
$\mathfrak {m}$
, and -
(c)
 $e_R(M) \geq \nu _R(M).$
$e_R(M) \geq \nu _R(M).$
The statements in Proposition 3.3 are standard in the literature. For example, proofs can be found in [Reference HanesHa99] and [Reference UlrichU].
Definition 3.4. Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be an MCM module over R. Then M is an Ulrich module if
$(R, \mathfrak {m}, k)$
be a local ring of dimension d. Let M be an MCM module over R. Then M is an Ulrich module if
![]() $e_R(M) = \nu _R(M).$
Equivalently, M is an Ulrich module if
$e_R(M) = \nu _R(M).$
Equivalently, M is an Ulrich module if
![]() $\mathfrak {m} M = IM$
for any minimal reduction
$\mathfrak {m} M = IM$
for any minimal reduction
![]() $I\subseteq \mathfrak {m}.$
$I\subseteq \mathfrak {m}.$
Lemma 3.5. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain containing k. Let L be a finite algebraic extension of k. Then
$(R, \mathfrak {m}, k)$
be a local domain containing k. Let L be a finite algebraic extension of k. Then
![]() $S = L \otimes _k R$
is a local ring with maximal ideal
$S = L \otimes _k R$
is a local ring with maximal ideal
![]() $\mathfrak {m} S$
, and S has an Ulrich module if and only if R has an Ulrich module.
$\mathfrak {m} S$
, and S has an Ulrich module if and only if R has an Ulrich module.
The proof of Lemma 3.5 is standard. We include it below for completeness.
Proof. Observe that S is a free module-finite extension of R and that
![]() $\mathfrak {m} S$
is the maximal ideal of S. So any system of parameters for R is a system of parameters for S.
$\mathfrak {m} S$
is the maximal ideal of S. So any system of parameters for R is a system of parameters for S.
Now suppose N is an Ulrich module over S. It is clear that any MCM module over S is an MCM module over R. We have
![]() $e(R) = e(S)$
because the length of
$e(R) = e(S)$
because the length of
![]() $S/(\mathfrak {m} S)^t = L \otimes _R (R/\mathfrak {m}^t)$
over S is the same as the length of
$S/(\mathfrak {m} S)^t = L \otimes _R (R/\mathfrak {m}^t)$
over S is the same as the length of
![]() $R/\mathfrak {m}^t$
over R. Let
$R/\mathfrak {m}^t$
over R. Let
![]() $[L:k]$
be the degree of the field extension. Then
$[L:k]$
be the degree of the field extension. Then
![]() $\nu _R(N) = [L:k]\nu _S(N)$
and we have
$\nu _R(N) = [L:k]\nu _S(N)$
and we have
Then
So N is an Ulrich module of R.
Conversely, if M is an MCM module of R, then
![]() $S\otimes _R M$
is an MCM module of S, and we have
$S\otimes _R M$
is an MCM module of S, and we have
![]() $e_R(M) = e_S(S\otimes _R M)$
and
$e_R(M) = e_S(S\otimes _R M)$
and
![]() $\nu _R(M) = \nu _S(S \otimes _R M)$
. So if M is an Ulrich module of R, then
$\nu _R(M) = \nu _S(S \otimes _R M)$
. So if M is an Ulrich module of R, then
![]() $S\otimes _R M$
is an Ulrich module of S.
$S\otimes _R M$
is an Ulrich module of S.
3.2 (Weakly) lim Cohen–Macaulay sequences and (weakly) lim Ulrich sequences
We review the definitions and relevant properties of (weakly) lim Cohen-Macaulay sequences and (weakly) lim Ulrich sequences. (Weakly) lim Cohen-Macaulay sequences were introduced by Bhatt, Hochster and Ma [Reference Bhatt, Hochster and MaBHM]. See [Reference HochsterHoc17]. (Weakly) lim Ulrich sequences were introduced by Ma [Reference MaM].
Definition 3.6. Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d. A sequence of finitely generated nonzero R-modules
$(R, \mathfrak {m}, k)$
be a local ring of dimension d. A sequence of finitely generated nonzero R-modules
![]() $\{M_n\}$
of dimension d is called lim Cohen–Macaulay if there exists a system of parameters
$\{M_n\}$
of dimension d is called lim Cohen–Macaulay if there exists a system of parameters
![]() $\underline {x}$
such that for all
$\underline {x}$
such that for all
![]() $i \geq 1$
, we have
$i \geq 1$
, we have
A sequence of finitely generated R-modules
![]() $\{M_n\}$
of dimension d is called weaky lim Cohen–Macaulay if there exists a system of parameters
$\{M_n\}$
of dimension d is called weaky lim Cohen–Macaulay if there exists a system of parameters
![]() $\underline {x}$
such that
$\underline {x}$
such that
Definition 3.7. Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d. A sequence of finitely generated nonzero R-modules
$(R, \mathfrak {m}, k)$
be a local ring of dimension d. A sequence of finitely generated nonzero R-modules
![]() $\{M_n\}$
of dimension d is called lim Ulrich (respectively, weakly lim Ulrich) if
$\{M_n\}$
of dimension d is called lim Ulrich (respectively, weakly lim Ulrich) if
![]() $\{M_n\}$
is lim Cohen–Macaulay (respectively, weakly lim Cohen–Macaulay) and
$\{M_n\}$
is lim Cohen–Macaulay (respectively, weakly lim Cohen–Macaulay) and
Throughout the paper, we use the following proposition due to [Reference Bhatt, Hochster and MaBHM] and [Reference MaM].
Proposition 3.8 [Reference Bhatt, Hochster and MaBHM][Reference MaM].
Let
![]() $(R, \mathfrak {m}, k)$
be a local ring of dimension d.
$(R, \mathfrak {m}, k)$
be a local ring of dimension d.
-
(a) [Reference Bhatt, Hochster and MaBHM](See [Reference Iyengar, Ma and WalkerIMW, Lemma 5.7]) If
 $\{M_n\}$
is a lim Cohen–Macaulay sequence of R, then for every system of parameters
$\{M_n\}$
is a lim Cohen–Macaulay sequence of R, then for every system of parameters
 $\underline {x} = x_1, \ldots , x_d$
, we have where
$\underline {x} = x_1, \ldots , x_d$
, we have where $$ \begin{align*} \lim_{n \to \infty} \frac {h_i(\underline{x};M_n)}{\nu_R(M_n)} = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac {h_i(\underline{x};M_n)}{\nu_R(M_n)} = 0, \end{align*} $$
 $i\geq 1.$
$i\geq 1.$
-
(b) [Reference MaM, Prop. 2.6] If
 $\{M_n\}$
is a weakly lim Cohen–Macaulay sequence of R, then for every system of parameters
$\{M_n\}$
is a weakly lim Cohen–Macaulay sequence of R, then for every system of parameters
 $\underline {x} = x_1, \ldots , x_d$
, we have
$\underline {x} = x_1, \ldots , x_d$
, we have  $$ \begin{align*} \lim_{n \to \infty} \frac {\chi_1(\underline{x};M_n)}{\nu_R(M_n)} = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac {\chi_1(\underline{x};M_n)}{\nu_R(M_n)} = 0. \end{align*} $$
4 Ulrich modules do not always exist for local domains
Lemma 4.1. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain. If R has an
$(R, \mathfrak {m}, k)$
be a local domain. If R has an
![]() $S_2$
-ification S that is a local ring, then any MCM module M of R is an MCM module of S.
$S_2$
-ification S that is a local ring, then any MCM module M of R is an MCM module of S.
Proof. Let M be an MCM module over R. We want to show that for any
![]() $f \in S - R$
and any
$f \in S - R$
and any
![]() $m \in M$
, there is a well-defined element
$m \in M$
, there is a well-defined element
![]() $f \cdot m \in M$
. Let
$f \cdot m \in M$
. Let
![]() $W = R - \{0\}$
. Since M is MCM, it is torsion-free over R and embeds in
$W = R - \{0\}$
. Since M is MCM, it is torsion-free over R and embeds in
![]() $W^{-1}M$
. It suffices to show that
$W^{-1}M$
. It suffices to show that
![]() $f \cdot (m/1) \in M$
. Since any element in the
$f \cdot (m/1) \in M$
. Since any element in the
![]() $S_2$
-ification of R is multiplied back into R by an ideal in R of height at least
$S_2$
-ification of R is multiplied back into R by an ideal in R of height at least
![]() $2$
(see [Reference Hochster and HunekeHH, (2.3)]), the height of the ideal
$2$
(see [Reference Hochster and HunekeHH, (2.3)]), the height of the ideal
![]() $R :_{R} f$
is at least two. Thus, there exist u and v in
$R :_{R} f$
is at least two. Thus, there exist u and v in
![]() $R :_{R} f$
such that the sequence
$R :_{R} f$
such that the sequence
![]() $u, v$
is a part of a system of parameters for R. Since M is MCM, the sequence
$u, v$
is a part of a system of parameters for R. Since M is MCM, the sequence
![]() $u, v$
is a regular sequence on M. Then
$u, v$
is a regular sequence on M. Then
![]() $v \cdot ((uf) \cdot (m/1)) = u \cdot ((vf) \cdot (m/1)) \in vM$
implies that
$v \cdot ((uf) \cdot (m/1)) = u \cdot ((vf) \cdot (m/1)) \in vM$
implies that
![]() $(vf)\cdot (m/1) \in vM$
. Since M is torsion-free over R, we have
$(vf)\cdot (m/1) \in vM$
. Since M is torsion-free over R, we have
![]() $f\cdot (m/1) \in M.$
$f\cdot (m/1) \in M.$
Theorem 4.2. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain. Suppose R has an
$(R, \mathfrak {m}, k)$
be a local domain. Suppose R has an
![]() $S_2$
-ification S such that S is a regular local ring. Then every MCM module of R has the form
$S_2$
-ification S such that S is a regular local ring. Then every MCM module of R has the form
![]() $S^{\oplus h}$
. Consequently, R has Ulrich modules if and only if S is an Ulrich module of R if and only if
$S^{\oplus h}$
. Consequently, R has Ulrich modules if and only if S is an Ulrich module of R if and only if
![]() $IS = \mathfrak {m} S$
for any minimal reduction I of
$IS = \mathfrak {m} S$
for any minimal reduction I of
![]() $\mathfrak {m}.$
$\mathfrak {m}.$
Proof. By Lemma 4.1, any MCM module M over R is MCM over S. But S is regular. Hence,
![]() $M \cong S^{\oplus h}$
by the Auslander–Buchsbaum formula. The second statement follows immediately because
$M \cong S^{\oplus h}$
by the Auslander–Buchsbaum formula. The second statement follows immediately because
![]() $S^{\oplus h}$
is an Ulrich module of R if and only if S is an Ulrich module of R.
$S^{\oplus h}$
is an Ulrich module of R if and only if S is an Ulrich module of R.
Theorem 4.3. Let
![]() $S = k[\![\underline {x}]\!] = k[\![x_1, \ldots , x_d]\!]$
, where
$S = k[\![\underline {x}]\!] = k[\![x_1, \ldots , x_d]\!]$
, where
![]() $d\geq 2.$
Let
$d\geq 2.$
Let
![]() $\underline {u} = u_1, \ldots , u_d$
be a system for parameters of S such that
$\underline {u} = u_1, \ldots , u_d$
be a system for parameters of S such that
![]() $I = (\underline {u})S$
is not integrally closed. Let
$I = (\underline {u})S$
is not integrally closed. Let
![]() $\overline {I}$
be the integral closure of I in S. Let
$\overline {I}$
be the integral closure of I in S. Let
![]() $\{g_{\lambda }\}_{\lambda \in \Lambda }$
be an arbitrary collection of elements in
$\{g_{\lambda }\}_{\lambda \in \Lambda }$
be an arbitrary collection of elements in
![]() $\overline {I}$
and
$\overline {I}$
and
![]() $f \in \overline {I}-I.$
For
$f \in \overline {I}-I.$
For
![]() $1 \leq j \leq d$
, let
$1 \leq j \leq d$
, let
![]() $v_j, w_j$
be elements of the maximal ideal of
$v_j, w_j$
be elements of the maximal ideal of
![]() $ k[\![\underline {u}]\!]$
that generate a height
$ k[\![\underline {u}]\!]$
that generate a height
![]() $2$
ideal in
$2$
ideal in
![]() $k[\![\underline {u}]\!]$
(e.g., one can take powers of distinct elements in
$k[\![\underline {u}]\!]$
(e.g., one can take powers of distinct elements in
![]() $\{u_1, \ldots , u_d\}).$
Define R to be the domain
$\{u_1, \ldots , u_d\}).$
Define R to be the domain
Then R has no Ulrich modules.
Proof. First, notice that
![]() $k[\![\underline {u}]\!] \subset k[\![\underline {x}]\!]$
is a module-finite extension. Then R is (Noetherian) local and
$k[\![\underline {u}]\!] \subset k[\![\underline {x}]\!]$
is a module-finite extension. Then R is (Noetherian) local and
![]() $R \subset k[\![\underline {x}]\!] $
is a module-finite extension.
$R \subset k[\![\underline {x}]\!] $
is a module-finite extension.
Let
![]() $\mathfrak {m}_R$
be the maximal ideal of R. From the construction of R, it is clear that
$\mathfrak {m}_R$
be the maximal ideal of R. From the construction of R, it is clear that
![]() $\underline {u} = u_1, \ldots , u_d$
is a system for parameters for R and, in fact, a minimal reduction of
$\underline {u} = u_1, \ldots , u_d$
is a system for parameters for R and, in fact, a minimal reduction of
![]() $\mathfrak {m}_R$
because all the other adjoined elements are integral over
$\mathfrak {m}_R$
because all the other adjoined elements are integral over
![]() $(\underline {u}) S$
in S and thus integral over
$(\underline {u}) S$
in S and thus integral over
![]() $(\underline {u}) R$
in R. Then for all
$(\underline {u}) R$
in R. Then for all
![]() $1 \leq j \leq d$
, the element
$1 \leq j \leq d$
, the element
![]() $x_j$
is multiplied into R by
$x_j$
is multiplied into R by
![]() $v_j$
and
$v_j$
and
![]() $w_j$
which generate a height
$w_j$
which generate a height
![]() $2$
ideal in R. Thus
$2$
ideal in R. Thus
![]() $x_j$
is in the
$x_j$
is in the
![]() $S_2$
-ification of R for all
$S_2$
-ification of R for all
![]() $1\leq j \leq d.$
But this means that
$1\leq j \leq d.$
But this means that
![]() $S = k[\![\underline {x}]\!]$
is the
$S = k[\![\underline {x}]\!]$
is the
![]() $S_2$
-ification of
$S_2$
-ification of
![]() $R.$
$R.$
By Theorem 4.2, it suffices to show that S is not an Ulrich module of R. But
![]() $(\underline {u})S \neq \mathfrak {m}_RS$
because
$(\underline {u})S \neq \mathfrak {m}_RS$
because
![]() $f \notin (\underline {u})S.$
Thus, R has no Ulrich modules.
$f \notin (\underline {u})S.$
Thus, R has no Ulrich modules.
Remark 4.4. Similar constructions can be used to generate counterexamples that are essentially of finite type over fields. For example, see Counterexample 4.6.
Remark 4.5. In [Reference Iyengar, Ma and WalkerIMW], Iyengar, Ma and Walker consider rings of the form
![]() $T = k + J$
, where
$T = k + J$
, where
![]() $S = k[\![x, y]\!]$
and
$S = k[\![x, y]\!]$
and
![]() $J \subseteq S$
is an ideal primary to
$J \subseteq S$
is an ideal primary to
![]() $(x, y)S$
. If J has a minimal reduction
$(x, y)S$
. If J has a minimal reduction
![]() $I = (u, v)S$
, then the rings T have the form in Theorem 4.3. Thus,
$I = (u, v)S$
, then the rings T have the form in Theorem 4.3. Thus,
![]() $T = k +J$
has no Ulrich modules if
$T = k +J$
has no Ulrich modules if
![]() $J \neq IS.$
$J \neq IS.$
In the case where J does not have a minimal reduction, we can reduce to the previous case by taking a finite algebraic field extension of k so that J has a minimal reduction and then apply Lemma 3.5.
Counterexample 4.6. This is the first counterexample we found, which led to the general construction in Theorem 4.3. The local domain
where
![]() $\mathfrak {m}$
is the maximal ideal
$\mathfrak {m}$
is the maximal ideal
![]() $(x^n, x^{n+1}, x^ny, y^{n}, y^{n+1}, xy^{n}, xy)$
, and its completion
$(x^n, x^{n+1}, x^ny, y^{n}, y^{n+1}, xy^{n}, xy)$
, and its completion
do not have Ulrich modules for
![]() $n\geq 2.$
$n\geq 2.$
We can show that R and
![]() $\widehat {R}$
do not have Ulrich modules directly. The argument is essentially the same for R and
$\widehat {R}$
do not have Ulrich modules directly. The argument is essentially the same for R and
![]() $\widehat {R}$
. We will work with R. The
$\widehat {R}$
. We will work with R. The
![]() $S_2$
-ification of R is
$S_2$
-ification of R is
![]() $S = k[x,y]_{(x,y)}$
, and the ideal
$S = k[x,y]_{(x,y)}$
, and the ideal
![]() $(xy, x^n-y^n)R$
is a minimal reduction for
$(xy, x^n-y^n)R$
is a minimal reduction for
![]() $\mathfrak {m} R$
. But
$\mathfrak {m} R$
. But
as ideals in S.
We can recover this counterexample from the general construction in Theorem 4.3 by setting
 $$ \begin{align*} \underline{x} &= x, y \\ \underline{u} &= xy, x^n - y^n\\ f &= x^n\\ v_j &= (xy)^n \hspace{1em} \text{and } \hspace{1em} w_j = x^n-y^n \hspace{2em} 1\leq j \leq 2\\ g_1 &= x^{n+1} \hspace{1em} \text{ and } \hspace{1em} g_2 = y^{n+1}. \end{align*} $$
$$ \begin{align*} \underline{x} &= x, y \\ \underline{u} &= xy, x^n - y^n\\ f &= x^n\\ v_j &= (xy)^n \hspace{1em} \text{and } \hspace{1em} w_j = x^n-y^n \hspace{2em} 1\leq j \leq 2\\ g_1 &= x^{n+1} \hspace{1em} \text{ and } \hspace{1em} g_2 = y^{n+1}. \end{align*} $$
Remark 4.7. We can use R in Counterexample 4.6 to give a new counterexample to the localization of Ulrich modules (i.e., a local ring
![]() $(T,\mathfrak {n},\ell )$
that has an Ulrich module M and a prime ideal
$(T,\mathfrak {n},\ell )$
that has an Ulrich module M and a prime ideal
![]() $\mathfrak {p} \subseteq T$
such that
$\mathfrak {p} \subseteq T$
such that
![]() $M_{\mathfrak {p}}$
is not an Ulrich module over
$M_{\mathfrak {p}}$
is not an Ulrich module over
![]() $T_{\mathfrak {p}}$
). Although a counterexample to localization was first given by Hanes in [Reference HanesHa99], the following counterexample is stronger in the sense that T localizes to a ring that has no Ulrich modules, whereas Hanes’s counterexample localizes to a ring that does have an Ulrich module. Note that Ulrich modules are called linear MCM modules in [Reference HanesHa99].
$T_{\mathfrak {p}}$
). Although a counterexample to localization was first given by Hanes in [Reference HanesHa99], the following counterexample is stronger in the sense that T localizes to a ring that has no Ulrich modules, whereas Hanes’s counterexample localizes to a ring that does have an Ulrich module. Note that Ulrich modules are called linear MCM modules in [Reference HanesHa99].
Counterexample 4.8 (Localization).
Consider the ring
where
![]() $\mathfrak {n} = (s^{n+1}, sx^{n}, x^{n+1}, x^ny, sy^n, y^{n+1}, xy^n, s^{n-1}xy)$
and
$\mathfrak {n} = (s^{n+1}, sx^{n}, x^{n+1}, x^ny, sy^n, y^{n+1}, xy^n, s^{n-1}xy)$
and
![]() $n\geq 2$
. Let
$n\geq 2$
. Let
be the inclusion map and
![]() $\mathfrak {p} = \varphi ^{-1}((x,y))$
. Then the localization
$\mathfrak {p} = \varphi ^{-1}((x,y))$
. Then the localization
![]() $T_{\mathfrak {p}}$
is the ring
$T_{\mathfrak {p}}$
is the ring
localized at the obvious maximal ideal. But
![]() $T_{\mathfrak {p}}$
has no Ulrich modules by Counterexample 4.6.
$T_{\mathfrak {p}}$
has no Ulrich modules by Counterexample 4.6.
It remains to show that T has an Ulrich module. Let S be the localization of the
![]() $(n+1)$
th Veronese subring of
$(n+1)$
th Veronese subring of
![]() $k[s, x, y]$
at the homogeneous maximal ideal. One can compute
$k[s, x, y]$
at the homogeneous maximal ideal. One can compute
![]() $e_{T}(T) = (n+1)^2 = e_{S}(S)$
. The rings T and S have the same fraction field and so
$e_{T}(T) = (n+1)^2 = e_{S}(S)$
. The rings T and S have the same fraction field and so
![]() $\text {rank}_T(S) = 1$
. Now S has an Ulrich module M by Proposition 3.6 in [Reference HanesHa04]. Then M is MCM over T and
$\text {rank}_T(S) = 1$
. Now S has an Ulrich module M by Proposition 3.6 in [Reference HanesHa04]. Then M is MCM over T and
![]() $\text {rank}_{T}(M) = \text {rank}_{S}(M)$
. Then
$\text {rank}_{T}(M) = \text {rank}_{S}(M)$
. Then
Thus,
![]() $e_{T}(M) = \nu _{T}(M)$
and M is Ulrich over
$e_{T}(M) = \nu _{T}(M)$
and M is Ulrich over
![]() $T.$
$T.$
5 (Weakly) lim Cohen–Macaulay and (weakly) lim Ulrich sequences over domains of dimension 2
Definition 5.1. Let
![]() $(R, \mathfrak {m}, k)$
be a local ring. Let
$(R, \mathfrak {m}, k)$
be a local ring. Let
![]() $\mathcal {M} = \{M_n\}$
be a sequence of nonzero finitely generated R-modules. Let
$\mathcal {M} = \{M_n\}$
be a sequence of nonzero finitely generated R-modules. Let
![]() $\nu _R(M_n)$
be the minimal number of generators of
$\nu _R(M_n)$
be the minimal number of generators of
![]() $M_n$
. Let
$M_n$
. Let
![]() $\{a_n\}$
and
$\{a_n\}$
and
![]() $\{b_n\}$
be a sequence of positive integers. We define
$\{b_n\}$
be a sequence of positive integers. We define
![]() $\sim _{\mathcal {M}}$
to be the equivalence relation
$\sim _{\mathcal {M}}$
to be the equivalence relation
![]() $\sim _{\mathcal {M}}$
, where
$\sim _{\mathcal {M}}$
, where
![]() $\{a_n\} \sim _{\mathcal {M}} \{b_n\}$
if
$\{a_n\} \sim _{\mathcal {M}} \{b_n\}$
if
For the sake of simplicity, we write
![]() $a_n \sim _{\mathcal {M}} b_n$
instead of
$a_n \sim _{\mathcal {M}} b_n$
instead of
![]() $\{a_n\} \sim _{\mathcal {M}} \{b_n\}$
.
$\{a_n\} \sim _{\mathcal {M}} \{b_n\}$
.
Lemma 5.2. Let
![]() $(R, \mathfrak {m}, k)$
be a local ring. Let
$(R, \mathfrak {m}, k)$
be a local ring. Let
![]() $\mathcal {M} = \{M_n\}$
and
$\mathcal {M} = \{M_n\}$
and
![]() $\mathcal {N} = \{N_n\}$
be two sequences of nonzero finitely generated R-modules. Let
$\mathcal {N} = \{N_n\}$
be two sequences of nonzero finitely generated R-modules. Let
![]() $\{a_n\}$
and
$\{a_n\}$
and
![]() $\{b_n\}$
be a sequence of non-negative integers. Suppose
$\{b_n\}$
be a sequence of non-negative integers. Suppose
![]() $\nu _R(N_n) \sim _{\mathcal {M}} \nu _R(M_n).$
If
$\nu _R(N_n) \sim _{\mathcal {M}} \nu _R(M_n).$
If
![]() $a_n \sim _{\mathcal {M}} b_n$
, then
$a_n \sim _{\mathcal {M}} b_n$
, then
![]() $a_n \sim _{\mathcal {N}} b_n.$
In particular,
$a_n \sim _{\mathcal {N}} b_n.$
In particular,
![]() $\nu _R(M_n) \sim _{\mathcal {N}} \nu _R(N_n).$
$\nu _R(M_n) \sim _{\mathcal {N}} \nu _R(N_n).$
Proof. Since
![]() $\nu _R(N_n) \sim _{\mathcal {M}} \nu _R(M_n)$
, we have
$\nu _R(N_n) \sim _{\mathcal {M}} \nu _R(M_n)$
, we have
![]() $\lim _{n \to \infty } \frac {\nu _R(M_n)}{\nu _R(N_n)} = 1.$
Then
$\lim _{n \to \infty } \frac {\nu _R(M_n)}{\nu _R(N_n)} = 1.$
Then
 $$ \begin{align*} 0 = \lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(M_n)} = \left(\lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(M_n)} \right)\left(\lim_{n \to \infty} \frac{\nu_R(M_n)}{\nu_R(N_n)}\right) &= \lim_{n \to \infty}\left(\frac{a_n-b_n}{\nu_R(M_n)} \cdot \frac{\nu_R(M_n)}{\nu_R(N_n)}\right) \\ &= \lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(N_n)}.\\[-32pt] \end{align*} $$
$$ \begin{align*} 0 = \lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(M_n)} = \left(\lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(M_n)} \right)\left(\lim_{n \to \infty} \frac{\nu_R(M_n)}{\nu_R(N_n)}\right) &= \lim_{n \to \infty}\left(\frac{a_n-b_n}{\nu_R(M_n)} \cdot \frac{\nu_R(M_n)}{\nu_R(N_n)}\right) \\ &= \lim_{n \to \infty} \frac{a_n-b_n}{\nu_R(N_n)}.\\[-32pt] \end{align*} $$
Theorem 5.3. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain of dimension
$(R, \mathfrak {m}, k)$
be a local domain of dimension
![]() $2$
. Let
$2$
. Let
![]() $\{M_n\}$
be a weakly lim Cohen–Macaulay (resp. weakly lim Ulrich) sequence over R. Let
$\{M_n\}$
be a weakly lim Cohen–Macaulay (resp. weakly lim Ulrich) sequence over R. Let
![]() $C_n \subseteq M_n$
be a torsion submodule such that the quotient
$C_n \subseteq M_n$
be a torsion submodule such that the quotient
![]() has no finite length submodules. Then the sequence
has no finite length submodules. Then the sequence
![]() $\{\overline {M}_n\}$
is a lim Cohen–Macaulay (resp. lim Ulrich) sequence over R.
$\{\overline {M}_n\}$
is a lim Cohen–Macaulay (resp. lim Ulrich) sequence over R.
Proof. Let
![]() be a weakly lim Cohen–Macaulay sequence over R. Let
be a weakly lim Cohen–Macaulay sequence over R. Let
![]() $I = (\underline {x})$
be a system of parameters of the maximal ideal
$I = (\underline {x})$
be a system of parameters of the maximal ideal
![]() $\mathfrak {m}$
. Recall that
$\mathfrak {m}$
. Recall that
![]() $\nu _R(M_n)$
denotes the minimal number of generators of
$\nu _R(M_n)$
denotes the minimal number of generators of
![]() $M_n$
. First, we check that
$M_n$
. First, we check that
Consider the short exact sequence
We know that
![]() $\nu _R(\overline {M}_n) \leq \nu _R(M_n) \leq \nu _R(\overline {M}_n) + \nu _R(C_n).$
So it suffices to show that
$\nu _R(\overline {M}_n) \leq \nu _R(M_n) \leq \nu _R(\overline {M}_n) + \nu _R(C_n).$
So it suffices to show that
From the short exact sequence, we get the long exact sequence of Koszul homology
 $$ \begin{align*} 0 &\to H_2(\underline{x};C_n) \to H_2(\underline{x};M_n) \to H_2(\underline{x}; \overline{M}_n)\\ &\to H_1(\underline{x};C_n) \to H_1(\underline{x};M_n) \to H_1(\underline{x}; \overline{M}_n) \to H_0(\underline{x};C_n) \to H_0(\underline{x};M_n) \to H_0(\underline{x}; \overline{M}_n) \to 0. \end{align*} $$
$$ \begin{align*} 0 &\to H_2(\underline{x};C_n) \to H_2(\underline{x};M_n) \to H_2(\underline{x}; \overline{M}_n)\\ &\to H_1(\underline{x};C_n) \to H_1(\underline{x};M_n) \to H_1(\underline{x}; \overline{M}_n) \to H_0(\underline{x};C_n) \to H_0(\underline{x};M_n) \to H_0(\underline{x}; \overline{M}_n) \to 0. \end{align*} $$
Now
![]() $\overline {M}_n$
has no finite length torsion submodules, so
$\overline {M}_n$
has no finite length torsion submodules, so
![]() $H_2(\underline {x};\overline {M}_n) = 0$
. We observe the following:
$H_2(\underline {x};\overline {M}_n) = 0$
. We observe the following:
-
(a)
 $H_2(\underline {x};C_n) \cong H_2(\underline {x};M_n)$
$H_2(\underline {x};C_n) \cong H_2(\underline {x};M_n)$
-
(b)
 $h_1(\underline {x}; C_n) \leq h_1(\underline {x}; M_n)$
$h_1(\underline {x}; C_n) \leq h_1(\underline {x}; M_n)$
-
(c)
 $\chi _1(\underline {x};M) \geq 0$
for any finitely generated R-module M [Reference SerreS, Corollary on pg. 90]
$\chi _1(\underline {x};M) \geq 0$
for any finitely generated R-module M [Reference SerreS, Corollary on pg. 90] -
(d)
 $\chi (\underline {x}; C_n) = e(\underline {x};C_n) = 0$
, where
$\chi (\underline {x}; C_n) = e(\underline {x};C_n) = 0$
, where
 $e(\underline {x};C_n)$
is the multiplicity of
$e(\underline {x};C_n)$
is the multiplicity of
 $C_n$
with respect to
$C_n$
with respect to
 $(\underline {x})$
, and the first equality is by [Reference SerreS, Theorem 1 on pg. 57]
$(\underline {x})$
, and the first equality is by [Reference SerreS, Theorem 1 on pg. 57] -
(e)
 $0 \leq h_0(\underline {x}; M_n) - h_0(\underline {x}; \overline {M}_n) \leq h_0(\underline {x}; C_n)$
$0 \leq h_0(\underline {x}; M_n) - h_0(\underline {x}; \overline {M}_n) \leq h_0(\underline {x}; C_n)$
From (a), (b) and (c), it follows that
and because
![]() $\mathcal {M}$
is weakly lim Cohen–Macaulay, we have
$\mathcal {M}$
is weakly lim Cohen–Macaulay, we have
But
![]() $\chi (\underline {x};C_n) = 0$
and so,
$\chi (\underline {x};C_n) = 0$
and so,
![]() $\chi _1(\underline {x};C_n) = h_0(\underline {x};C_n) = \ell (C_n/(\underline {x})C_n).$
Then the inequality
$\chi _1(\underline {x};C_n) = h_0(\underline {x};C_n) = \ell (C_n/(\underline {x})C_n).$
Then the inequality
yields
Next, we show that
![]() $\{\overline {M}_n\}$
is a lim Cohen-Macaulay sequence over R. We already know that
$\{\overline {M}_n\}$
is a lim Cohen-Macaulay sequence over R. We already know that
![]() $h_2(\underline {x}; \overline {M}_n) = 0.$
It remains to show
$h_2(\underline {x}; \overline {M}_n) = 0.$
It remains to show
 $$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(\overline{M}_n)} = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(\overline{M}_n)} = 0. \end{align*} $$
By Lemma 5.2, it is enough to show that
 $$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(M_n)} = 0 \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(M_n)} = 0 \end{align*} $$
because
![]() $\nu _R(\overline {M}_n) \sim _{\mathcal {M}} \nu _R(M_n)$
. Take the alternating sum of the lengths of the Koszul homology in the exact sequence
$\nu _R(\overline {M}_n) \sim _{\mathcal {M}} \nu _R(M_n)$
. Take the alternating sum of the lengths of the Koszul homology in the exact sequence
This is the sum
Then
 $$ \begin{align*} h_1(\underline{x}; \overline{M}_n)& = -h_1(\underline{x}; C_n) + h_0(\underline{x}; C_n) + h_1(\underline{x}; M_n) - h_0(\underline{x}; M_n) + h_0(\underline{x};\overline{M}_n)\\ & = -h_2(\underline{x};C_n) + h_1(\underline{x};M_n) -h_0(\underline{x};M_n) + h_0(\underline{x};\overline{M}_n) \\ &= -h_2(\underline{x};M_n) + h_1(\underline{x};M_n) -h_0(\underline{x};M_n) + h_0(\underline{x};\overline{M}_n) \\ & = \chi_1(\underline{x};M_n) - (h_0(\underline{x};M_n) - h_0(\underline{x};\overline{M}_n)). \end{align*} $$
$$ \begin{align*} h_1(\underline{x}; \overline{M}_n)& = -h_1(\underline{x}; C_n) + h_0(\underline{x}; C_n) + h_1(\underline{x}; M_n) - h_0(\underline{x}; M_n) + h_0(\underline{x};\overline{M}_n)\\ & = -h_2(\underline{x};C_n) + h_1(\underline{x};M_n) -h_0(\underline{x};M_n) + h_0(\underline{x};\overline{M}_n) \\ &= -h_2(\underline{x};M_n) + h_1(\underline{x};M_n) -h_0(\underline{x};M_n) + h_0(\underline{x};\overline{M}_n) \\ & = \chi_1(\underline{x};M_n) - (h_0(\underline{x};M_n) - h_0(\underline{x};\overline{M}_n)). \end{align*} $$
Now we know that
and by (e) and (1) above, we have
Thus,
 $$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(M_n)} = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{ h_1(\underline{x};\overline{M}_n)}{\nu_R(M_n)} = 0, \end{align*} $$
and the sequence
![]() $\{\overline {M}_n\}$
is lim Cohen–Macaulay.
$\{\overline {M}_n\}$
is lim Cohen–Macaulay.
In the case where
![]() $\{M_n\}$
is a weakly lim Ulrich sequence, it remains to check that
$\{M_n\}$
is a weakly lim Ulrich sequence, it remains to check that
 $$ \begin{align*} \lim_{n \to \infty} \frac{e_R(\overline{M}_n)}{\nu_R(\overline{M}_n)} = 1. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{e_R(\overline{M}_n)}{\nu_R(\overline{M}_n)} = 1. \end{align*} $$
But
![]() $e_R(\overline {M}_n) = e_R(M_n)$
and
$e_R(\overline {M}_n) = e_R(M_n)$
and
![]() $\nu _R(\overline {M}_n) \sim _{\mathcal {M}} \nu _R(M_n)$
, so the condition immediately follows, and thus,
$\nu _R(\overline {M}_n) \sim _{\mathcal {M}} \nu _R(M_n)$
, so the condition immediately follows, and thus,
![]() $\{\overline {M}_n\}$
is a lim Ulrich sequence of R.
$\{\overline {M}_n\}$
is a lim Ulrich sequence of R.
Definition 5.4. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain and let M be finitely generated torsion-free R-module. Let
$(R, \mathfrak {m}, k)$
be a local domain and let M be finitely generated torsion-free R-module. Let
![]() $(S, \mathfrak {n}, \ell )$
be a local module-finite extension domain of R. Suppose
$(S, \mathfrak {n}, \ell )$
be a local module-finite extension domain of R. Suppose
![]() $\mathcal {K} = frac(R) = frac(S).$
Then we define
$\mathcal {K} = frac(R) = frac(S).$
Then we define
![]() $MS$
to be the S-module generated by M in
$MS$
to be the S-module generated by M in
![]() $M \otimes _R \mathcal {K}.$
$M \otimes _R \mathcal {K}.$
Remark 5.5. In the case where R is a local domain with a
![]() $S_2$
-ification S that is local, if M is an MCM module of R, then
$S_2$
-ification S that is local, if M is an MCM module of R, then
![]() $MS = M$
by Lemma 4.1.
$MS = M$
by Lemma 4.1.
Lemma 5.6. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain of dimension
$(R, \mathfrak {m}, k)$
be a local domain of dimension
![]() $2$
and let M be a finitely generated torsion-free R-module. Let
$2$
and let M be a finitely generated torsion-free R-module. Let
![]() $(S, \mathfrak {n}, \ell )$
be a local module-finite extension domain of R. Suppose
$(S, \mathfrak {n}, \ell )$
be a local module-finite extension domain of R. Suppose
![]() $S \subseteq \text {frac}(R)$
and
$S \subseteq \text {frac}(R)$
and
![]() $S/R$
has finite length. Choose a fixed constant t such that
$S/R$
has finite length. Choose a fixed constant t such that
![]() $\mathfrak {m}^tS \subseteq R.$
Let
$\mathfrak {m}^tS \subseteq R.$
Let
![]() $x,y$
be a system of parameters for R. Then
$x,y$
be a system of parameters for R. Then
-
(a)
 $MS \subseteq M:_{\mathcal {K} \otimes _R M}(x^t, y^t)R,$
$MS \subseteq M:_{\mathcal {K} \otimes _R M}(x^t, y^t)R,$
-
(b)
 $(M:_{M \otimes _R \mathcal {K}}(x^t,y^t))/M \cong H_1(x^t,y^t;M),$
$(M:_{M \otimes _R \mathcal {K}}(x^t,y^t))/M \cong H_1(x^t,y^t;M),$
-
(c)
 $\ell _R(MS/M) \leq h_1(x^t, y^t;M).$
$\ell _R(MS/M) \leq h_1(x^t, y^t;M).$
Proof. Part (a) is clear by the choice of t. Part (c) follows immediately from parts (a) and (b). It remains to prove part (b). Define
to be the map
where the equality follows from the relation
![]() $ux^t + vy^t = 0.$
This map is well-defined. If
$ux^t + vy^t = 0.$
This map is well-defined. If
![]() $[(u,v)]$
is trivial, then there exists
$[(u,v)]$
is trivial, then there exists
![]() $w \in M$
such that
$w \in M$
such that
![]() $[(u,v)] = [y^tw, -x^tw]$
. But
$[(u,v)] = [y^tw, -x^tw]$
. But
![]() $[y^tw, -x^tw]$
is mapped to
$[y^tw, -x^tw]$
is mapped to
![]() $[(y^tw)/y^t] = [w/1] =0.$
$[(y^tw)/y^t] = [w/1] =0.$
For the map going the other direction, define
to be the map
This is clearly well-defined. The maps
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are inverses, so we are done.
$\psi $
are inverses, so we are done.
Theorem 5.7. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain of dimension
$(R, \mathfrak {m}, k)$
be a local domain of dimension
![]() $2$
. Let
$2$
. Let
![]() $(S, \mathfrak {n}, \ell )$
be a local module–finite extension domain of R such that
$(S, \mathfrak {n}, \ell )$
be a local module–finite extension domain of R such that
![]() $S \subseteq \text {frac}(R)$
and
$S \subseteq \text {frac}(R)$
and
![]() $S/R$
has finite length. Let
$S/R$
has finite length. Let
![]() $\mathcal {M} = \{M_n\}$
be a lim Cohen–Macaulay (resp. lim Ulrich) sequence of torsion-free R-modules. Then the sequence
$\mathcal {M} = \{M_n\}$
be a lim Cohen–Macaulay (resp. lim Ulrich) sequence of torsion-free R-modules. Then the sequence
![]() $\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay (resp. lim Ulrich) sequence of R-modules and also a lim Cohen–Macaulay sequence of S-modules.
$\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay (resp. lim Ulrich) sequence of R-modules and also a lim Cohen–Macaulay sequence of S-modules.
Proof. We first prove that
Let
![]() $Q_n = M_nS/M_n.$
Note that
$Q_n = M_nS/M_n.$
Note that
![]() $Q_n$
has finite length because
$Q_n$
has finite length because
![]() $S/R$
has finite length. The short exact sequence
$S/R$
has finite length. The short exact sequence
yields the long exact sequence
Then
and so it suffices to show that
Let
![]() $\underline {x} = x_1, x_2$
be a system of parameters for R. By Lemma 5.6, we know that
$\underline {x} = x_1, x_2$
be a system of parameters for R. By Lemma 5.6, we know that
![]() $\ell (Q_n) \leq h_1(x_1^t, x_2^t;M_n)$
for some fixed t. But
$\ell (Q_n) \leq h_1(x_1^t, x_2^t;M_n)$
for some fixed t. But
![]() $\mathcal {M}$
is a lim Cohen-Macaulay sequence, so
$\mathcal {M}$
is a lim Cohen-Macaulay sequence, so
![]() $h_1(x_1^t, x_2^t;M_n) \sim _{\mathcal {M}} 0$
and
$h_1(x_1^t, x_2^t;M_n) \sim _{\mathcal {M}} 0$
and
Then
Next, by taking a prime cyclic filtration of
![]() $Q_n$
, one can observe that
$Q_n$
, one can observe that
Then it immediately follows that
We now show that
![]() $\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence of R-modules. It is enough to show that
$\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence of R-modules. It is enough to show that
Because
![]() $M_n$
and
$M_n$
and
![]() $M_nS$
are torsion-free over R, we have the long exact sequence
$M_nS$
are torsion-free over R, we have the long exact sequence
 $$ \begin{align} \begin{aligned} 0 &\to H_2(\underline{x};Q_n) \to H_1(\underline{x};M_n) \to H_1(\underline{x};M_nS) \to H_1(\underline{x}; Q_n)\\ &\to H_0(\underline{x};M_n) \to H_0(\underline{x};M_nS) \to H_0(\underline{x};Q_n) \to 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 &\to H_2(\underline{x};Q_n) \to H_1(\underline{x};M_n) \to H_1(\underline{x};M_nS) \to H_1(\underline{x}; Q_n)\\ &\to H_0(\underline{x};M_n) \to H_0(\underline{x};M_nS) \to H_0(\underline{x};Q_n) \to 0. \end{aligned} \end{align} $$
Next we show that for all
![]() $i \geq 0$
,
$i \geq 0$
,
We see that
because
![]() $H_2(\underline {x};Q_n)$
injects into
$H_2(\underline {x};Q_n)$
injects into
![]() $H_1(\underline {x};M_n)$
. We already proved that
$H_1(\underline {x};M_n)$
. We already proved that
![]() $\ell (Q_n) \sim _{\mathcal {M}} 0$
. It immediately follows that
$\ell (Q_n) \sim _{\mathcal {M}} 0$
. It immediately follows that
Then it follows from
![]() $\chi (\underline {x}; Q_n) = 0$
that
$\chi (\underline {x}; Q_n) = 0$
that
From the long exact sequence (2), we have
But
![]() $h_1(\underline {x};M_n) \sim _{\mathcal {M}} 0$
and
$h_1(\underline {x};M_n) \sim _{\mathcal {M}} 0$
and
![]() $h_1(\underline {x};Q_n)\sim _{\mathcal {M}} 0.$
Therefore,
$h_1(\underline {x};Q_n)\sim _{\mathcal {M}} 0.$
Therefore,
![]() $\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence over R.
$\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence over R.
If
![]() $\mathcal {M}$
is lim Ulrich, it immediately follows that
$\mathcal {M}$
is lim Ulrich, it immediately follows that
![]() $\mathcal {N}$
is lim Ulrich because
$\mathcal {N}$
is lim Ulrich because
![]() $e_R(M_n) = e_R(M_nS)$
and
$e_R(M_n) = e_R(M_nS)$
and
![]() $\nu _R(M_n) \sim _{\mathcal {M}} \nu _R(M_nS).$
It remains to check that
$\nu _R(M_n) \sim _{\mathcal {M}} \nu _R(M_nS).$
It remains to check that
![]() $\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence for
$\mathcal {N} = \{M_nS\}$
is a lim Cohen–Macaulay sequence for
![]() $S.$
$S.$
For any i, the Koszul homology
![]() $H_i(\underline {x};M_nS)$
does not change whether we think of
$H_i(\underline {x};M_nS)$
does not change whether we think of
![]() $M_nS$
as an R-module or an S-module. We also have
$M_nS$
as an R-module or an S-module. We also have
which yields
Then
 $$ \begin{align*} \lim_{n\to \infty} \frac{h_1^S(\underline{x};M_nS)}{\nu_S(M_nS)} \leq \lim_{n\to \infty} \frac{\nu_R(S)h_1^R(\underline{x};M_nS)}{\nu_R(M_nS)} =\nu_R(S) \lim_{n\to \infty} \frac{h_1^R(\underline{x};M_nS)}{\nu_R(M_nS)} = 0. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \frac{h_1^S(\underline{x};M_nS)}{\nu_S(M_nS)} \leq \lim_{n\to \infty} \frac{\nu_R(S)h_1^R(\underline{x};M_nS)}{\nu_R(M_nS)} =\nu_R(S) \lim_{n\to \infty} \frac{h_1^R(\underline{x};M_nS)}{\nu_R(M_nS)} = 0. \end{align*} $$
Thus,
![]() $\mathcal {N} = \{M_nS\}$
is a lim Cohen-Macaulay sequence over S.
$\mathcal {N} = \{M_nS\}$
is a lim Cohen-Macaulay sequence over S.
Theorem 5.8. A sequence of finitely generated nonzero torsion–free modules
![]() $\{N_n\}$
over a regular local ring S of dimension
$\{N_n\}$
over a regular local ring S of dimension
![]() $2$
is lim Cohen–Macaulay if and only if for the minimal free resolution
$2$
is lim Cohen–Macaulay if and only if for the minimal free resolution
we have
![]() $ \lim _{n \to \infty } b_n/a_n = 0.$
Such a sequence is always lim Ulrich.
$ \lim _{n \to \infty } b_n/a_n = 0.$
Such a sequence is always lim Ulrich.
Proof. Let
![]() $x, y$
be a regular system of parameters for S. We have
$x, y$
be a regular system of parameters for S. We have
and
Then
![]() $\{N_n\}$
is lim Cohen–Macaulay over S if and only if
$\{N_n\}$
is lim Cohen–Macaulay over S if and only if
Moreover, we have
Note that
![]() $e_S(N_n) = a_n-b_n$
by [Reference SerreS, Theorem 1 on pg. 57]. Thus,
$e_S(N_n) = a_n-b_n$
by [Reference SerreS, Theorem 1 on pg. 57]. Thus,
![]() $\{N_n\}$
is a lim Ulrich sequence for
$\{N_n\}$
is a lim Ulrich sequence for
![]() $S.$
$S.$
6 Weakly lim Ulrich sequences do not always exist for local domains
Theorem 6.1. Let
![]() $(R, \mathfrak {m}, k)$
be a local domain of dimension
$(R, \mathfrak {m}, k)$
be a local domain of dimension
![]() $2$
. Suppose R has an
$2$
. Suppose R has an
![]() $S_2$
-ification S that is a regular local ring. The following are equivalent:
$S_2$
-ification S that is a regular local ring. The following are equivalent:
-
(a) R has a weakly lim Ulrich sequence.
-
(b) R has an Ulrich module.
-
(c) S is an Ulrich module of R.
-
(d) For any minimal reduction I of
 $\mathfrak {m}$
, we have
$\mathfrak {m}$
, we have
 $IS = \mathfrak {m} S.$
$IS = \mathfrak {m} S.$
Proof. First, (c) and (d) are equivalent by definition. Next (b) and (c) are equivalent by Theorem 4.2. It is clear that (b) implies (a). It remains to show that (a) implies (b).
Suppose R has a weakly lim Ulrich sequence. Then by Theorems 5.3 and 5.7, there exists a lim Ulrich sequence
![]() $\mathcal {M} = \{M_n\}$
of torsion-free R modules that are also S modules. Consider the minimal free resolution
$\mathcal {M} = \{M_n\}$
of torsion-free R modules that are also S modules. Consider the minimal free resolution
where
![]() $a_n = \nu _S(M_n).$
Now
$a_n = \nu _S(M_n).$
Now
and
Then Theorem 5.8 yields
 $$ \begin{align*} \lim_{n \to \infty} \frac{\nu_R(S^{b_n})}{\nu_R(M_n)} = \lim_{n \to \infty} \frac{\nu_R(S)b_n}{\nu_R(M_n)} \leq \lim_{n \to \infty} \frac{\nu_R(S)b_n}{\nu_S(M_n)} = \lim_{n \to \infty} \frac{\nu_R(S)b_n}{a_n} = 0, \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{\nu_R(S^{b_n})}{\nu_R(M_n)} = \lim_{n \to \infty} \frac{\nu_R(S)b_n}{\nu_R(M_n)} \leq \lim_{n \to \infty} \frac{\nu_R(S)b_n}{\nu_S(M_n)} = \lim_{n \to \infty} \frac{\nu_R(S)b_n}{a_n} = 0, \end{align*} $$
and
 $$ \begin{align*} \lim_{n \to \infty} \frac{e_R(S^{b_n})}{\nu_R(M_n)} = \lim_{n \to \infty} \frac{e_R(S)b_n}{\nu_R(M_n)} \leq \lim_{n \to \infty} \frac{e_R(S)b_n}{\nu_S(M_n)} = \lim_{n \to \infty} \frac{e_R(S)b_n}{a_n} = 0. \end{align*} $$
$$ \begin{align*} \lim_{n \to \infty} \frac{e_R(S^{b_n})}{\nu_R(M_n)} = \lim_{n \to \infty} \frac{e_R(S)b_n}{\nu_R(M_n)} \leq \lim_{n \to \infty} \frac{e_R(S)b_n}{\nu_S(M_n)} = \lim_{n \to \infty} \frac{e_R(S)b_n}{a_n} = 0. \end{align*} $$
Consequently, by the minimal free resolution above, we have
and
Combining equivalences 3 and 4, we have
Thus, S is an Ulrich module of R.
Theorem 6.2. Weakly lim Ulrich sequences do not always exist for (complete) local domains.
Corollary 6.3 (Localization).
Weakly lim Ulrich sequences do not always localize for local domains. More precisely, there exist local domains
![]() $(R, \mathfrak {m}, k)$
that have a weakly lim Ulrich sequence
$(R, \mathfrak {m}, k)$
that have a weakly lim Ulrich sequence
![]() $\{M_n\}$
and a prime ideal
$\{M_n\}$
and a prime ideal
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\{(M_n)_{\mathfrak {p}}\}$
is not a weakly lim Ulrich sequence for
$\{(M_n)_{\mathfrak {p}}\}$
is not a weakly lim Ulrich sequence for
![]() $R_{\mathfrak {p}}.$
Moreover, there exist local domains that have weakly lim Ulrich sequences and a prime ideal
$R_{\mathfrak {p}}.$
Moreover, there exist local domains that have weakly lim Ulrich sequences and a prime ideal
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $R_{\mathfrak {p}}$
has no weakly lim Ulrich sequences.
$R_{\mathfrak {p}}$
has no weakly lim Ulrich sequences.
Acknowledgements
I am deeply grateful to Melvin Hochster for introducing me to the questions in this paper and for the many helpful discussions, advice and support. I would also like to thank Takumi Murayama for helpful conversations and for his comments on this manuscript. Finally, I would like to thank David Eisenbud and Bernd Ulrich for their helpful comments at Bernd Ulrich’s 65th birthday conference.
Competing interest
The authors have no competing interest to declare.
Funding statement
This research was supported by grants from the National Science Foundation, DGE 1841052, DMS-1401384 and DMS-1902116.