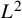1 Introduction
1.1 Introduction
One of the fundamental problems in the natural and social sciences is to explain macroscopic phenomena that we can observe from the rules governing the microscopic system giving rise to the phenomena. Hydrodynamic limit provides a rigorous mathematical method to derive the deterministic partial differential equations describing the time evolution of macroscopic parameters, from the stochastic dynamics of a microscopic large-scale interacting system. The heart of this method is to take the limit with respect to proper space-time scaling, so that the law of large numbers absorbs the large degree of freedom of the microscopic system, allowing us to extract the behavior of the macroscopic parameters which characterize the equilibrium states of the microscopic system. Hence, techniques from probability theory including various estimates on Markov processes and their stationary distributions have played a central role. In this article, we introduce a novel, geometric perspective to the theory of hydrodynamic limits. Instead of using the law of large numbers, we construct a new cohomology theory for microscopic models to identify the macroscopic observables and give interpretations to the mechanism giving the macroscopic partial differential equations. Our main theorem gives an analogue of Varadhan’s decomposition of closed
![]() $L^2$
-forms, which has played a key role in the proofs of the hydrodynamic limits of nongradient systems.
$L^2$
-forms, which has played a key role in the proofs of the hydrodynamic limits of nongradient systems.
Initially, many of the techniques developed in the theory of hydrodynamic limit were specific to the interacting system under consideration. In the seminal article [Reference Guo, Papanicolaou and Varadhan7], Guo, Papanicolaou and Varadhan introduced a widely applicable strategy known as the entropy method for proving the hydrodynamic limit when the interacting system satisfies a certain condition known as the gradient condition. Furthermore, Varadhan in [Reference Varadhan18] introduced a novel, refined strategy for systems which do not necessarily satisfy the gradient condition, relying on proving the so-called decomposition of closed
![]() $L^2$
-forms. Although this strategy has been successful in proving the hydrodynamic limit for a number of nongradient systems [Reference Quastel13, Reference Kipnis, Landim and Olla9, Reference Funaki, Uchiyama and Yau6, Reference Varadhan and Yau19, Reference Sasada15, Reference Sasada16, Reference Olla and Sasada12], the implementation in practice has proven notoriously difficult, requiring arguments with sharp spectral gap estimates specific to the system under consideration (see, for example, [Reference Kipnis and Landim8, Section 7]). Due to the restrictiveness of the gradient condition, many interesting microscopic systems are known or expected to be nongradient. Thus, it is vital to understand the mechanism of Varadhan’s strategy and construct model-independent criteria for implementation applicable to a wide variety of models.
$L^2$
-forms. Although this strategy has been successful in proving the hydrodynamic limit for a number of nongradient systems [Reference Quastel13, Reference Kipnis, Landim and Olla9, Reference Funaki, Uchiyama and Yau6, Reference Varadhan and Yau19, Reference Sasada15, Reference Sasada16, Reference Olla and Sasada12], the implementation in practice has proven notoriously difficult, requiring arguments with sharp spectral gap estimates specific to the system under consideration (see, for example, [Reference Kipnis and Landim8, Section 7]). Due to the restrictiveness of the gradient condition, many interesting microscopic systems are known or expected to be nongradient. Thus, it is vital to understand the mechanism of Varadhan’s strategy and construct model-independent criteria for implementation applicable to a wide variety of models.
The motivation of this article is to systematically investigate various large-scale interacting systems in a unified fashion, especially to understand the mechanism in which similar decompositions seemingly independent of the stochastic data appear in the proofs of the hydrodynamic limits. For this goal, we introduce a general framework encompassing a wide variety of interacting systems, including the different variants of the exclusion processes and the lattice-gas with energy (see Examples 1.3 and 2.10). We let X be a certain infinite graph which we call a locale, generalizing the typical Euclidean lattice modeling the space where the microscopic dynamics takes place. We let S be a set expressing the possible states at each vertex, such as the number of particles or amount of energy, and let ![]() be the configuration space expressing all of the possible configurations of states on X. The dynamics of a microscopic stochastic system are usually expressed by a generator. However, in our framework, we focus on the interaction
be the configuration space expressing all of the possible configurations of states on X. The dynamics of a microscopic stochastic system are usually expressed by a generator. However, in our framework, we focus on the interaction
![]() $\phi $
– a certain map
$\phi $
– a certain map
![]() $\phi \colon S\times S\rightarrow S\times S$
encoding the permitted change in states on adjacent vertices (see Definition 2.4). The interaction gives
$\phi \colon S\times S\rightarrow S\times S$
encoding the permitted change in states on adjacent vertices (see Definition 2.4). The interaction gives
![]() $S^X$
a geometric structure, that of a graph whose edges correspond to the transitions (i.e., all possible change of the configuration at a single instant (see §1.2)). This structure is independent of the transition rate – stochastic data which encodes the expected frequency of the transitions.
$S^X$
a geometric structure, that of a graph whose edges correspond to the transitions (i.e., all possible change of the configuration at a single instant (see §1.2)). This structure is independent of the transition rate – stochastic data which encodes the expected frequency of the transitions.
In this article, we construct the uniform cohomology reflecting the topological property of the geometric structure of
![]() $S^X$
by replacing the space of functions on
$S^X$
by replacing the space of functions on
![]() $S^X$
with a new class of functions called the uniform functions, which considers the distances between the vertices of the locale. Our key result, Theorem 6, states that under general assumptions, the zeroth uniform cohomology is isomorphic to the space of conserved quantities – functions on S whose sums are conserved by
$S^X$
with a new class of functions called the uniform functions, which considers the distances between the vertices of the locale. Our key result, Theorem 6, states that under general assumptions, the zeroth uniform cohomology is isomorphic to the space of conserved quantities – functions on S whose sums are conserved by
![]() $\phi $
. This cohomology is finite dimensional even though
$\phi $
. This cohomology is finite dimensional even though
![]() $S^X$
in general has an infinite number of connected components. For the cases where the hydrodynamic limit is proven, conserved quantities are known to correspond to the macroscopic parameters which characterize the equilibrium (or stationary) measures of the microscopic system. Thus, we believe uniform cohomology gives an alternative justification for the origin of the macroscopic observables. In addition, Theorem 6 also states that the uniform cohomology of
$S^X$
in general has an infinite number of connected components. For the cases where the hydrodynamic limit is proven, conserved quantities are known to correspond to the macroscopic parameters which characterize the equilibrium (or stationary) measures of the microscopic system. Thus, we believe uniform cohomology gives an alternative justification for the origin of the macroscopic observables. In addition, Theorem 6 also states that the uniform cohomology of
![]() $S^X$
for degrees other than zero vanishes. The essential case is for degree one, where we prove that any closed uniform form is the differential of a uniform function.
$S^X$
for degrees other than zero vanishes. The essential case is for degree one, where we prove that any closed uniform form is the differential of a uniform function.
Our main theorem, Theorem 1, gives a certain structure theorem for closed uniform forms that are shift-invariant (i.e., invariant by the action of a group). Here, we assume the existence of a free action of a group on the locale, which ensures a certain homogeneity. The theorem is obtained as a straightforward application of group cohomology to Theorem 6. If we choose a fundamental domain of X for the action of the group, then we obtain a decomposition theorem in the spirit of the decomposition of Varadhan (see Theorems 3, 4 and 5 of §1.3). The closed forms of Varadhan are
![]() $L^2$
-forms for the equilibrium measure arising from the choice of the transition rate. Although uniform functions and forms are defined algebraically without the need for any stochastic data, our shift-invariant forms in fact form a common core of the various spaces of shift-invariant
$L^2$
-forms for the equilibrium measure arising from the choice of the transition rate. Although uniform functions and forms are defined algebraically without the need for any stochastic data, our shift-invariant forms in fact form a common core of the various spaces of shift-invariant
![]() $L^2$
-forms constructed for each choice of the transition rate, and will in subsequent research play a crucial role in proving Varadhan’s decomposition for
$L^2$
-forms constructed for each choice of the transition rate, and will in subsequent research play a crucial role in proving Varadhan’s decomposition for
![]() $L^2$
-forms (see, for example, [Reference Bannai and Sasada3]). Our main theorem indicates that the specification of Varadhan’s decomposition is determined by the underlying geometric structure of the model. Moreover, our theory gives a cohomological interpretation of the dimension of the space of shift-invariant closed forms modulo the exact forms – whose origin up until now had been a mystery. The proof of our main theorem does not require any spectral gap estimates and can be applied universally to a wide variety of systems.
$L^2$
-forms (see, for example, [Reference Bannai and Sasada3]). Our main theorem indicates that the specification of Varadhan’s decomposition is determined by the underlying geometric structure of the model. Moreover, our theory gives a cohomological interpretation of the dimension of the space of shift-invariant closed forms modulo the exact forms – whose origin up until now had been a mystery. The proof of our main theorem does not require any spectral gap estimates and can be applied universally to a wide variety of systems.
Currently, all existing research concerning hydrodynamic limits for nongradient systems deals exclusively with the case when the locale is the Euclidean lattice
![]() $\mathbb {Z}^d$
, with an action of
$\mathbb {Z}^d$
, with an action of
![]() $G=\mathbb {Z}^d$
given by the translation. Our decomposition theorem is valid for far more general infinite locales and groups, including various crystal lattices with their group of translations and Cayley graphs associated to finitely generated infinite groups with natural action of the group. The theorem is also true for systems with multiple linearly independent conserved quantities. Our result provides crucial insight into the formulation of Varadhan’s decomposition in these general settings. One of our goals is to find a more intuitive and universal proof of the hydrodynamic limits for nongradient models. In a subsequent article [Reference Bannai and Sasada3], we prove Varadhan’s decomposition theorem for a general class of models, where the main result of the present article is the key for the generalization. Furthermore, we will use this decomposition theorem to perform scaling limits for the general class of models.
$G=\mathbb {Z}^d$
given by the translation. Our decomposition theorem is valid for far more general infinite locales and groups, including various crystal lattices with their group of translations and Cayley graphs associated to finitely generated infinite groups with natural action of the group. The theorem is also true for systems with multiple linearly independent conserved quantities. Our result provides crucial insight into the formulation of Varadhan’s decomposition in these general settings. One of our goals is to find a more intuitive and universal proof of the hydrodynamic limits for nongradient models. In a subsequent article [Reference Bannai and Sasada3], we prove Varadhan’s decomposition theorem for a general class of models, where the main result of the present article is the key for the generalization. Furthermore, we will use this decomposition theorem to perform scaling limits for the general class of models.
Our theory is constructed from scratch, using only algebraic and combinatorial methods. In particular, no probability theory, measure theory or analytic methods are used. Most importantly, we have taken care to make this article including the proof of our main result self-contained, except for the proof of the well-established long exact sequence arising in group cohomology (see §5.2). Thus, we believe our article should be accessible to mathematicians in a wide range of disciplines. We hope this article would introduce to a broad audience interesting mathematical concepts related to typical large-scale interacting systems, and to researchers in probability theory potentially powerful cohomological techniques that may be relevant in identifying important structures of stochastic models.
The remainder of this section is as follows. In §1.2, we describe our framework and present some examples. Then in §1.3, we state Theorem 1, the main theorem of our article, asserting the decomposition for shift-invariant uniform closed forms. We then explain its relation to the decomposition by Varadhan. Finally, in §1.4, we provide an overview of our article and the outline of the proof of our main theorem.
1.2 The large-scale interacting system
In this subsection, we introduce the various objects in our framework describing large-scale interacting systems and give natural assumptions which ensure our main theorem. The precise mathematical definitions of the objects in the triplet
![]() $(X,S,\phi )$
given in §1.1 are as follows. We define a locale
$(X,S,\phi )$
given in §1.1 are as follows. We define a locale
![]() $(X,E)$
to be any locally finite simple symmetric directed graph which is connected (see §2.1 for details). Here, X denotes the set of vertices, and
$(X,E)$
to be any locally finite simple symmetric directed graph which is connected (see §2.1 for details). Here, X denotes the set of vertices, and
![]() $E\subset X\times X$
denotes the set of directed edges of the locale. We regard a locale
$E\subset X\times X$
denotes the set of directed edges of the locale. We regard a locale
![]() $(X,E)$
as a metric space equipped with the graph distance. By abuse of notation (see Remark 2.8), we will often denote the locale
$(X,E)$
as a metric space equipped with the graph distance. By abuse of notation (see Remark 2.8), we will often denote the locale
![]() $(X,E)$
with the same symbol as its set of vertices X. The condition that X is connected and locally finite implies that the set of vertices of X is countable. If the set of vertices is an infinite set, then we say that X is an infinite locale. We define the set of states S as a nonempty set with a designated element
$(X,E)$
with the same symbol as its set of vertices X. The condition that X is connected and locally finite implies that the set of vertices of X is countable. If the set of vertices is an infinite set, then we say that X is an infinite locale. We define the set of states S as a nonempty set with a designated element
![]() $*\in S$
which we call the base state, and we define the symmetric binary interaction, or simply an interaction
$*\in S$
which we call the base state, and we define the symmetric binary interaction, or simply an interaction
![]() $\phi $
on S, to be a map
$\phi $
on S, to be a map
![]() $\phi \colon S\times S\rightarrow S\times S$
such that for any pair of states
$\phi \colon S\times S\rightarrow S\times S$
such that for any pair of states
![]() $(s_1,s_2)\in S\times S$
satisfying
$(s_1,s_2)\in S\times S$
satisfying
![]() $\phi (s_1,s_2)\neq (s_1,s_2)$
, we have
$\phi (s_1,s_2)\neq (s_1,s_2)$
, we have
![]() $\hat \imath \circ \phi \circ \hat \imath \circ \phi (s_1,s_2)=(s_1,s_2)$
, where
$\hat \imath \circ \phi \circ \hat \imath \circ \phi (s_1,s_2)=(s_1,s_2)$
, where
![]() $\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
$\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
![]() $S\times S$
. The ordering of
$S\times S$
. The ordering of
![]() $S\times S$
determines the direction of the interaction, and the condition intuitively means that if we execute the interaction and if it is nontrivial, then further executing the interaction in the reverse direction takes us back to where we started. To realize the full large-scale interacting system, we also need to choose a transition rate. However, this is outside the scope of the current article.
$S\times S$
determines the direction of the interaction, and the condition intuitively means that if we execute the interaction and if it is nontrivial, then further executing the interaction in the reverse direction takes us back to where we started. To realize the full large-scale interacting system, we also need to choose a transition rate. However, this is outside the scope of the current article.
The most typical example of an infinite locale is given by the Euclidean lattice
![]() $\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for integers
$\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for integers
![]() $d\geq 1$
, where
$d\geq 1$
, where
![]() $\mathbb {Z}^d$
is the d-fold product of the set of integers
$\mathbb {Z}^d$
is the d-fold product of the set of integers
![]() $\mathbb {Z}$
, and
$\mathbb {Z}$
, and
Here, we let ![]() for any
for any
![]() $x=(x_1,\ldots ,x_d)$
,
$x=(x_1,\ldots ,x_d)$
,
![]() $y=(y_1,\ldots ,y_d)$
in
$y=(y_1,\ldots ,y_d)$
in
![]() $\mathbb {Z}^d$
. Crystal lattices such as the triangular and hexagonal lattices as well as Cayley graphs associated to finitely generated infinite groups (see Figure 1) are other examples of infinite locales.
$\mathbb {Z}^d$
. Crystal lattices such as the triangular and hexagonal lattices as well as Cayley graphs associated to finitely generated infinite groups (see Figure 1) are other examples of infinite locales.
We say that a locale is weakly transferable if for any ball
![]() $B\subset X$
, the complement
$B\subset X$
, the complement
![]() $X\setminus B$
is a nonempty finite disjoint union of connected infinite graphs. By definition, a weakly transferable locale is an infinite locale. We will also consider a stronger condition on the locale which we call transferable (see Definition 4.16 for the precise definition). Immediately from the definition, we see that if for any ball
$X\setminus B$
is a nonempty finite disjoint union of connected infinite graphs. By definition, a weakly transferable locale is an infinite locale. We will also consider a stronger condition on the locale which we call transferable (see Definition 4.16 for the precise definition). Immediately from the definition, we see that if for any ball
![]() $B\subset X$
, the complement
$B\subset X$
, the complement
![]() $X\setminus B$
is a connected infinite graph, then X is transferable. The Euclidean lattice
$X\setminus B$
is a connected infinite graph, then X is transferable. The Euclidean lattice
![]() $\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
$\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
![]() $d>1$
, crystal lattices such as the triangular and hexagonal lattices, and the Cayley graph for a finitely generated free group generated by
$d>1$
, crystal lattices such as the triangular and hexagonal lattices, and the Cayley graph for a finitely generated free group generated by
![]() $d>1$
elements give examples of transferable locales (see Remark 4.19). The Euclidean lattice
$d>1$
elements give examples of transferable locales (see Remark 4.19). The Euclidean lattice
![]() $\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
for
$\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
for
![]() $d=1$
, which is also the Cayley graph for a free group generated by one element, gives an example of a weakly transferable locale which is not transferable. See Example 2.2 in §2 for other examples of locales.
$d=1$
, which is also the Cayley graph for a free group generated by one element, gives an example of a weakly transferable locale which is not transferable. See Example 2.2 in §2 for other examples of locales.

Figure 1 The triangular and hexagonal lattices, and the Cayley graph for the free group G generated by
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
(see Example 2.2 (4)).
$\sigma _2$
(see Example 2.2 (4)).
We call the triplet
![]() $(X,S,\phi )$
as above a topological interacting system, or simply a system for short. For the system
$(X,S,\phi )$
as above a topological interacting system, or simply a system for short. For the system
![]() $(X,S,\phi )$
, we define the configuration space
$(X,S,\phi )$
, we define the configuration space
![]() $S^X$
by
$S^X$
by
We call any element
![]() $\eta \in S^X$
a configuration, and we denote by
$\eta \in S^X$
a configuration, and we denote by
![]() $\star $
the base configuration, defined to be the configuration whose components are all at base state. Next, for any
$\star $
the base configuration, defined to be the configuration whose components are all at base state. Next, for any
![]() $\eta \in S^X$
and
$\eta \in S^X$
and
![]() $e=(x_1,x_2)\in E$
, we let
$e=(x_1,x_2)\in E$
, we let
![]() $(\eta ^{\prime }_{x_1}, \eta ^{\prime }_{x_2}) =\phi (\eta _{x_1},\eta _{x_2})$
. We define
$(\eta ^{\prime }_{x_1}, \eta ^{\prime }_{x_2}) =\phi (\eta _{x_1},\eta _{x_2})$
. We define
![]() $\eta ^e=(\eta _x^e)\in S^X$
by
$\eta ^e=(\eta _x^e)\in S^X$
by

The transition structure on
![]() $S^X$
, expressing all possible change of the configuration at a single instant, is defined as
$S^X$
, expressing all possible change of the configuration at a single instant, is defined as ![]() . Then
. Then
![]() $(S^X,\Phi )$
is a symmetric directed graph (see Lemma 2.5 for a proof). Again by abuse of notation, we will often denote the graph
$(S^X,\Phi )$
is a symmetric directed graph (see Lemma 2.5 for a proof). Again by abuse of notation, we will often denote the graph
![]() $(S^X,\Phi )$
by
$(S^X,\Phi )$
by
![]() $S^X$
(see also Remark 2.8). We remark that generally,
$S^X$
(see also Remark 2.8). We remark that generally,
![]() $S^X$
on an infinite locale is not connected, simple nor locally finite as a graph, and the set of vertices is not countable.
$S^X$
on an infinite locale is not connected, simple nor locally finite as a graph, and the set of vertices is not countable.
Next, we introduce the conserved quantity for the interaction
![]() $\phi $
, which we define to be any function
$\phi $
, which we define to be any function
![]() $\xi \colon S\rightarrow \mathbb {R}$
satisfying
$\xi \colon S\rightarrow \mathbb {R}$
satisfying
![]() $\xi (*)=0$
and
$\xi (*)=0$
and
for any
![]() $(s_1,s_2)\in S\times S$
, where
$(s_1,s_2)\in S\times S$
, where ![]() . This function gives values reflecting the state, such as the number of particles or energy depending on the physical context, whose sums are conserved by the interaction. We denote by
. This function gives values reflecting the state, such as the number of particles or energy depending on the physical context, whose sums are conserved by the interaction. We denote by
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
the
${\operatorname {\mathrm {Consv}}}^\phi (S)$
the
![]() $\mathbb {R}$
-linear space of all conserved quantities for the interaction
$\mathbb {R}$
-linear space of all conserved quantities for the interaction
![]() $\phi $
.
$\phi $
.
Denote by
![]() $S^X_*$
the subset of
$S^X_*$
the subset of
![]() $S^X$
consisting of elements
$S^X$
consisting of elements
![]() $\eta =(\eta _x)$
such that
$\eta =(\eta _x)$
such that
![]() $\eta _x=*$
for all but finite
$\eta _x=*$
for all but finite
![]() $x\in X$
. Then
$x\in X$
. Then
![]() $S^X_*$
also has a structure of a graph induced from that of
$S^X_*$
also has a structure of a graph induced from that of
![]() $S^X$
. Note that if X is finite, then
$S^X$
. Note that if X is finite, then
![]() $S^X_*=S^X$
. Any conserved quantity
$S^X_*=S^X$
. Any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
defines a function
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
defines a function
![]() $\xi _X\colon S^X_*\rightarrow \mathbb {R}$
by
$\xi _X\colon S^X_*\rightarrow \mathbb {R}$
by ![]() for any
for any
![]() $\eta \in S^X_*$
. Note that the sum is a finite sum since
$\eta \in S^X_*$
. Note that the sum is a finite sum since
![]() $\eta \in S^X_*$
. We call the value
$\eta \in S^X_*$
. We call the value
![]() $\xi _X(\eta )$
a conserved quantity of the configuration
$\xi _X(\eta )$
a conserved quantity of the configuration
![]() $\eta $
.
$\eta $
.
Throughout this article, we let
![]() $\mathbb {N}=\{0,1,\ldots ,\}$
denote the set of natural numbers. We consider the following properties of an interaction, which will play an important role in our main theorem.
$\mathbb {N}=\{0,1,\ldots ,\}$
denote the set of natural numbers. We consider the following properties of an interaction, which will play an important role in our main theorem.
Definition 1.1. For an interaction
![]() $\phi $
on S, let
$\phi $
on S, let ![]() .
.
-
1. We say that the interaction
 $\phi $
is irreducibly quantified, if for any finite locale X if the configurations
$\phi $
is irreducibly quantified, if for any finite locale X if the configurations
 $\eta ,\eta '\in S^X$
have the same conserved quantities (i.e., if
$\eta ,\eta '\in S^X$
have the same conserved quantities (i.e., if
 $\xi _X(\eta )=\xi _X(\eta ')$
for any
$\xi _X(\eta )=\xi _X(\eta ')$
for any
 $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
), then there exists a finite path (see §2.1) from
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
), then there exists a finite path (see §2.1) from
 $\eta $
to
$\eta $
to
 $\eta '$
in
$\eta '$
in
 $S^X$
.
$S^X$
. -
2. We say that the interaction
 $\phi $
is simple if
$\phi $
is simple if
 $c_\phi =1$
, and for any nonzero conserved quantity
$c_\phi =1$
, and for any nonzero conserved quantity
 $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, the monoid generated by
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, the monoid generated by
 $\xi (S)$
via addition in
$\xi (S)$
via addition in
 $\mathbb {R}$
is isomorphic to
$\mathbb {R}$
is isomorphic to
 $\mathbb {N}$
or
$\mathbb {N}$
or
 $\mathbb {Z}$
.
$\mathbb {Z}$
.
A monoid is defined to be a set with a binary operation that is associative and has an identity element, the first examples being
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $\mathbb {Z}$
or
$\mathbb {Z}$
or
![]() $\mathbb {R}$
with the operation being the usual addition and with identity element
$\mathbb {R}$
with the operation being the usual addition and with identity element
![]() $0$
. Provided
$0$
. Provided
![]() $c_\phi =1$
, the second condition in Definition 1.1 (2) is satisfied, for example, if there exists
$c_\phi =1$
, the second condition in Definition 1.1 (2) is satisfied, for example, if there exists
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
such that
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
such that
![]() $\xi (S)\subset \mathbb {N}$
and
$\xi (S)\subset \mathbb {N}$
and
![]() $1\in \xi (S)$
, or
$1\in \xi (S)$
, or
![]() $\xi (S)\subset \mathbb {Z}$
and
$\xi (S)\subset \mathbb {Z}$
and
![]() $\pm 1\in \xi (S)$
.
$\pm 1\in \xi (S)$
.
Remark 1.2. The second condition of Definition 1.1 (1) implies that any configurations with the same conserved quantities are in the same connected component of the configuration space
![]() $S^X_*$
. The configuration space on an infinite locale X usually has an infinite number of connected components. If the above condition is satisfied, then we may prove that the connected components of
$S^X_*$
. The configuration space on an infinite locale X usually has an infinite number of connected components. If the above condition is satisfied, then we may prove that the connected components of
![]() $S^X_*$
are characterized by its conserved quantities (see Remark 2.25). This condition is equivalent to the condition that the associated stochastic process on the configurations with fixed conserved quantities are irreducible.
$S^X_*$
are characterized by its conserved quantities (see Remark 2.25). This condition is equivalent to the condition that the associated stochastic process on the configurations with fixed conserved quantities are irreducible.
The following are examples of interactions and corresponding conserved quantities.
Example 1.3.
-
1. The most basic situation is when
 $S=\{0,1\}$
with base state
$S=\{0,1\}$
with base state
 $*=0$
. The map
$*=0$
. The map
 $\phi \colon S\times S\rightarrow S\times S$
defined by exchanging the components of
$\phi \colon S\times S\rightarrow S\times S$
defined by exchanging the components of
 $S\times S$
is an interaction (see Figure 2). The conserved quantity
$S\times S$
is an interaction (see Figure 2). The conserved quantity
 $\xi \colon S\rightarrow \mathbb {N}$
given by
$\xi \colon S\rightarrow \mathbb {N}$
given by
 $\xi (s)=s$
gives a basis of the one-dimensional
$\xi (s)=s$
gives a basis of the one-dimensional
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple. The stochastic process induced from this interaction via a choice of a transition rate is called the exclusion process.
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple. The stochastic process induced from this interaction via a choice of a transition rate is called the exclusion process.
Figure 2 Exclusion process.
-
2. Consider the case
 $S=\{0,1,\ldots ,\kappa \}$
with base state
$S=\{0,1,\ldots ,\kappa \}$
with base state
 $*=0$
for some integer
$*=0$
for some integer
 $\kappa>1$
. The map
$\kappa>1$
. The map
 $\phi \colon S\times S\rightarrow S\times S$
defined by exchanging the components of
$\phi \colon S\times S\rightarrow S\times S$
defined by exchanging the components of
 $S\times S$
is an interaction (see Figure 3). For
$S\times S$
is an interaction (see Figure 3). For
 $i=1,\ldots ,\kappa $
, let
$i=1,\ldots ,\kappa $
, let
 $\xi ^{(i)}$
be the conserved quantity given by
$\xi ^{(i)}$
be the conserved quantity given by
 $\xi ^{(i)}(s)=1$
if
$\xi ^{(i)}(s)=1$
if
 $s=i$
and
$s=i$
and
 $\xi ^{(i)}(s)=0$
otherwise. Then
$\xi ^{(i)}(s)=0$
otherwise. Then
 $\xi ^{(1)},\ldots ,\xi ^{(\kappa )}$
gives a basis of the
$\xi ^{(1)},\ldots ,\xi ^{(\kappa )}$
gives a basis of the
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. The stochastic process induced from this interaction via a choice of a transition rate is called the multi-color exclusion process, or more generally, the multi-species exclusion process.
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. The stochastic process induced from this interaction via a choice of a transition rate is called the multi-color exclusion process, or more generally, the multi-species exclusion process.
Figure 3 Multi-species exclusion process.
See Example 2.10 in §2.2 for other examples of interactions covered by our theory. We will prove in Proposition 2.19 that all of the interactions in Examples 1.3 and 2.10 are irreducibly quantified.
Remark 1.4. For
![]() $s\in S$
in the interactions in Example 1.3,
$s\in S$
in the interactions in Example 1.3,
![]() $s=0$
describes the state where there are no particles at the vertex, and
$s=0$
describes the state where there are no particles at the vertex, and
![]() $s=i$
for an integer
$s=i$
for an integer
![]() $i>0$
the state where there exists a particle of type labeled as i (referred to as color i or species i) at the vertex. The exclusion in the exclusion and the multi-species exclusion processes signify that at most one particle is allowed to occupy each vertex. The conserved quantity
$i>0$
the state where there exists a particle of type labeled as i (referred to as color i or species i) at the vertex. The exclusion in the exclusion and the multi-species exclusion processes signify that at most one particle is allowed to occupy each vertex. The conserved quantity
![]() $\xi ^{(i)}$
returns
$\xi ^{(i)}$
returns
![]() $1$
if a particle of species i occupies the vertex and
$1$
if a particle of species i occupies the vertex and
![]() $0$
otherwise. Then
$0$
otherwise. Then ![]() for a configuration
for a configuration
![]() $\eta =(\eta _x)\in S^X_*$
on a locale X expresses the total number of particles of species k in the configuration.
$\eta =(\eta _x)\in S^X_*$
on a locale X expresses the total number of particles of species k in the configuration.
The hydrodynamic limits of the exclusion process for certain choices of transition rates of nongradient type have been studied by Funaki, Uchiyama and Yau [Reference Funaki, Uchiyama and Yau6] and Varadhan and Yau [Reference Varadhan and Yau19] (see also Theorem 3 of §1.3). For the multi-species exclusion process, a variant has been studied by Quastel [Reference Quastel13] and Erignoux [Reference Erignoux5]. See Remark 2.12 for other known cases corresponding to the interactions given in Example 2.10. Up until now, all of the interacting systems of nongradient type whose hydrodynamic limits have been proved are models over the Euclidean lattice.
Typical research in hydrodynamic limit investigates the stochastic process of large-scale interacting systems obtained from a specific interaction with a specific transition rate on a specific locale. One important purpose of this article is to construct a mathematical framework to study many types of models at once and to find specific conditions on the locale and interactions to allow for a suitable theory. The notion of transferable locales and irreducibly quantified interactions, which we believe are new and have not previously appeared in literature, are steps in this direction. The distinctive feature of our framework is the separation of the stochastic data from the geometric data, as well as the separation of the set of states and the interaction from the underlying locale. The theory works best when S is discrete, a case which already covers a wide variety of models. In future research, we hope to generalize our framework to include known models with more general S, such as
![]() $S=\mathbb {R}$
and
$S=\mathbb {R}$
and
![]() $S=\mathbb {R}_{\geq 0}$
, where a more subtle notion of uniform functions incorporating smoothness should be necessary for compatibility with existing models.
$S=\mathbb {R}_{\geq 0}$
, where a more subtle notion of uniform functions incorporating smoothness should be necessary for compatibility with existing models.
1.3 Main theorem and relation to Varadhan’s decomposition
The goal of our article is to study the topological properties of the configuration space
![]() $S^X$
with transition structure via a newly defined class of uniform functions and forms. In this subsection, we introduce Theorem 1, which is the main theorem of this article, giving a decomposition of shift-invariant closed uniform forms. We will then discuss its relation to Varadhan’s decomposition of shift-invariant closed
$S^X$
with transition structure via a newly defined class of uniform functions and forms. In this subsection, we introduce Theorem 1, which is the main theorem of this article, giving a decomposition of shift-invariant closed uniform forms. We will then discuss its relation to Varadhan’s decomposition of shift-invariant closed
![]() $L^2$
-forms.
$L^2$
-forms.
We first introduce notations concerning functions and forms on the configuration space with transition structure. Consider the system
![]() $(X,S,\phi )$
, and let
$(X,S,\phi )$
, and let
![]() $S^X$
be the corresponding configuration space with transition structure. For any set A, we let
$S^X$
be the corresponding configuration space with transition structure. For any set A, we let ![]() be the
be the
![]() $\mathbb {R}$
-linear space of functions from A to
$\mathbb {R}$
-linear space of functions from A to
![]() $\mathbb {R}$
. We say that a function
$\mathbb {R}$
. We say that a function
![]() $f\in C(S^X)$
is local if there exists a finite
$f\in C(S^X)$
is local if there exists a finite
![]() $\Lambda \subset X$
such that f is in the image of
$\Lambda \subset X$
such that f is in the image of
![]() $C(S^\Lambda )$
with respect to the inclusion
$C(S^\Lambda )$
with respect to the inclusion
![]() $C(S^\Lambda )\hookrightarrow C(S^X)$
induced from the projection
$C(S^\Lambda )\hookrightarrow C(S^X)$
induced from the projection
![]() $S^X\rightarrow S^\Lambda $
. In other words, a function is local if it only depends on a configuration through a finite sublocale. Any local function may be regarded as a function in
$S^X\rightarrow S^\Lambda $
. In other words, a function is local if it only depends on a configuration through a finite sublocale. Any local function may be regarded as a function in
![]() $C(S^X_*)$
via the map induced from the projection
$C(S^X_*)$
via the map induced from the projection
![]() $S^X_*\rightarrow S^\Lambda $
. We denote by
$S^X_*\rightarrow S^\Lambda $
. We denote by
![]() $C_{\mathrm {loc}}(S^X)$
the space of local functions on
$C_{\mathrm {loc}}(S^X)$
the space of local functions on
![]() $S^X$
, which is a subspace of both
$S^X$
, which is a subspace of both
![]() $C(S^X)$
and
$C(S^X)$
and
![]() $C(S^X_*)$
. We define the space of uniform functions (see Definition 3.5 for the precise definition) to be a certain
$C(S^X_*)$
. We define the space of uniform functions (see Definition 3.5 for the precise definition) to be a certain
![]() $\mathbb {R}$
-linear subspace
$\mathbb {R}$
-linear subspace
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)$
of
$C_{\operatorname {\mathrm {unif}}}(S^X)$
of
![]() $C(S^X_*)$
containing the space of local functions
$C(S^X_*)$
containing the space of local functions
![]() $C_{\mathrm {loc}}(S^X)$
, and we let
$C_{\mathrm {loc}}(S^X)$
, and we let
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
be the subspace of
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
be the subspace of
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)$
consisting of function f satisfying
$C_{\operatorname {\mathrm {unif}}}(S^X)$
consisting of function f satisfying
![]() $f(\star )=0$
. We define the space of closed uniform forms
$f(\star )=0$
. We define the space of closed uniform forms
![]() $Z_{\operatorname {\mathrm {unif}}}^1(S^X)$
(see Definitions 2.27 and 3.10 for the precise definition) to be a certain
$Z_{\operatorname {\mathrm {unif}}}^1(S^X)$
(see Definitions 2.27 and 3.10 for the precise definition) to be a certain
![]() $\mathbb {R}$
-linear subspace of
$\mathbb {R}$
-linear subspace of
![]() $\prod _{e\in E}C_{\mathrm {loc}}(S^X)$
, and we define the differential
$\prod _{e\in E}C_{\mathrm {loc}}(S^X)$
, and we define the differential
![]() $\partial \colon C^0_{\operatorname {\mathrm {unif}}}(S^X)\rightarrow Z_{\operatorname {\mathrm {unif}}}^1(S^X)$
by
$\partial \colon C^0_{\operatorname {\mathrm {unif}}}(S^X)\rightarrow Z_{\operatorname {\mathrm {unif}}}^1(S^X)$
by ![]() where
where
![]() $\nabla _{\!e} f$
for any
$\nabla _{\!e} f$
for any
![]() $e\in E$
is the function defined by
$e\in E$
is the function defined by
for any
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
and
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
and
![]() $\eta \in S^X_*$
. The differential
$\eta \in S^X_*$
. The differential
![]() $\partial $
is induced from the differential of the standard cochain complex associated with the graph
$\partial $
is induced from the differential of the standard cochain complex associated with the graph
![]() $(S^X,\Phi )$
(see §2.3 and Appendix A).
$(S^X,\Phi )$
(see §2.3 and Appendix A).
For our main theorem, we consider a locale with a free action of a group. Let G be a group, and we assume that the locale X has a free action of a group G. This induces actions of G on various functions and forms. Both the Euclidean lattice and crystal lattices such as the triangular and hexagonal lattices of dimension d have natural free actions of
![]() $G=\mathbb {Z}^d$
. For any
$G=\mathbb {Z}^d$
. For any
![]() $\mathbb {R}$
-linear space with an action of G, we denote by
$\mathbb {R}$
-linear space with an action of G, we denote by
![]() $U^G$
the G-invariant subspace of U. We will often say shift-invariant to mean G-invariant if the group G is understood. We denote by
$U^G$
the G-invariant subspace of U. We will often say shift-invariant to mean G-invariant if the group G is understood. We denote by ![]() the space of shift-invariant closed uniform forms, and by
the space of shift-invariant closed uniform forms, and by ![]() the image by
the image by
![]() $\partial $
of the space of shift-invariant uniform functions.
$\partial $
of the space of shift-invariant uniform functions.
Remark 1.5. The existence of a free action of G ensures that the locale X is homogenous. We understand the quotient
![]() $\mathcal {C}/\mathcal {E}$
to philosophically represent the first uniform cohomology of the quotient space
$\mathcal {C}/\mathcal {E}$
to philosophically represent the first uniform cohomology of the quotient space
![]() $S^X/G$
, a topological space which can be interpreted as a model of an infinitesimal neighborhood of a macroscopic point.
$S^X/G$
, a topological space which can be interpreted as a model of an infinitesimal neighborhood of a macroscopic point.
We denote by
![]() $\operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
the space of group homomorphisms from G to
$\operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
the space of group homomorphisms from G to
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. In other words,
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. In other words,
![]() $\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
is any map
$\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
is any map
![]() $\psi \colon G\rightarrow {\operatorname {\mathrm {Consv}}}^\phi (S)$
satisfying
$\psi \colon G\rightarrow {\operatorname {\mathrm {Consv}}}^\phi (S)$
satisfying
![]() $\psi (\sigma \tau )=\psi (\sigma )+\psi (\tau )$
for any
$\psi (\sigma \tau )=\psi (\sigma )+\psi (\tau )$
for any
![]() $\sigma ,\tau \in G$
. Our decomposition theorem giving the uniform analogue of Varadhan’s decomposition is as follows.
$\sigma ,\tau \in G$
. Our decomposition theorem giving the uniform analogue of Varadhan’s decomposition is as follows.
Theorem 1 (=Theorem 5.17).
For the system
![]() $(X,S,\phi )$
, assume that the interaction
$(X,S,\phi )$
, assume that the interaction
![]() $\phi $
is irreducibly quantified and that X has a free action of a group G. If X is transferable, or if the interaction
$\phi $
is irreducibly quantified and that X has a free action of a group G. If X is transferable, or if the interaction
![]() $\phi $
is simple and X is weakly transferable, then we have a canonical isomorphism
$\phi $
is simple and X is weakly transferable, then we have a canonical isomorphism
Moreover, a choice of a fundamental domain for the action of G on X gives a natural decomposition
of
![]() $\mathbb {R}$
-linear spaces.
$\mathbb {R}$
-linear spaces.
If the rank of the maximal abelian quotient
![]() $G^{\operatorname {\mathrm {ab}}}$
of G is finite, then we have the following.
$G^{\operatorname {\mathrm {ab}}}$
of G is finite, then we have the following.
Corollary 2 (=Corollary 5.19).
Let the assumptions be as in Theorem 1. Moreover, suppose that
![]() $G^{\operatorname {\mathrm {ab}}}$
is of finite rank d. If we fix a generator of the free part of
$G^{\operatorname {\mathrm {ab}}}$
is of finite rank d. If we fix a generator of the free part of
![]() $G^{\operatorname {\mathrm {ab}}}$
, then we have an isomorphism
$G^{\operatorname {\mathrm {ab}}}$
, then we have an isomorphism
![]() $ \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S)) \cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S). $
A choice of a fundamental domain of X for the action of G gives a decomposition
$ \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S)) \cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S). $
A choice of a fundamental domain of X for the action of G gives a decomposition
 $$ \begin{align} \mathcal{C}\cong \mathcal{E}\oplus \bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align} $$
$$ \begin{align} \mathcal{C}\cong \mathcal{E}\oplus \bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align} $$
The decomposition (5) decomposes any shift-invariant closed uniform form in
![]() $\mathcal {C}$
as a unique sum of a form in
$\mathcal {C}$
as a unique sum of a form in
![]() $\mathcal {E}$
, closed forms whose potential are shift-invariant uniform functions, and a form obtained as the image with respect to the isomorphism (5) of elements in
$\mathcal {E}$
, closed forms whose potential are shift-invariant uniform functions, and a form obtained as the image with respect to the isomorphism (5) of elements in
![]() $\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
. The space
$\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
. The space
![]() $\mathcal {E}$
corresponds to the part which averages out to zero when taking a proper space-time scaling limit and so does not appear in the hydrodynamic limit. Hence, the decomposition theorem implies that the macroscopic property of our model may be completely expressed in terms of forms arising from the space
$\mathcal {E}$
corresponds to the part which averages out to zero when taking a proper space-time scaling limit and so does not appear in the hydrodynamic limit. Hence, the decomposition theorem implies that the macroscopic property of our model may be completely expressed in terms of forms arising from the space
![]() $\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
, which are related to the flow of conserved quantities in each of the directions induced by the action of the group G.
$\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
, which are related to the flow of conserved quantities in each of the directions induced by the action of the group G.
In addition to the geometric data
![]() $(X,S,\phi )$
, if we fix a suitable transition rate, then this gives a shift-invariant equilibrium measure on the configuration space and a compatible inner product on the space of forms. If we consider the case when the locale is the Euclidean lattice
$(X,S,\phi )$
, if we fix a suitable transition rate, then this gives a shift-invariant equilibrium measure on the configuration space and a compatible inner product on the space of forms. If we consider the case when the locale is the Euclidean lattice
![]() $X=(\mathbb {Z}^d,\mathbb {E}^d)$
with standard translation by the group
$X=(\mathbb {Z}^d,\mathbb {E}^d)$
with standard translation by the group
![]() $G=\mathbb {Z}^d$
, and if
$G=\mathbb {Z}^d$
, and if
![]() $(S,\phi )$
is the exclusion process of Example 1.3 (1), a typical choice of a transition rate gives rise to the product measure
$(S,\phi )$
is the exclusion process of Example 1.3 (1), a typical choice of a transition rate gives rise to the product measure
![]() $\nu =\mu _p^{\otimes \mathbb {Z}^d}$
on
$\nu =\mu _p^{\otimes \mathbb {Z}^d}$
on
![]() $S^X=\{0,1\}^{\mathbb {Z}^d}$
, where
$S^X=\{0,1\}^{\mathbb {Z}^d}$
, where
![]() $\mu _p$
is the probability measure on
$\mu _p$
is the probability measure on
![]() $S=\{0,1\}$
given by
$S=\{0,1\}$
given by
for some real number
![]() $0<p<1$
. We denote by
$0<p<1$
. We denote by
![]() $L^2(\nu )$
the usual
$L^2(\nu )$
the usual
![]() $L^2$
-space of square integrable functions on
$L^2$
-space of square integrable functions on
![]() $\{0,1\}^{\mathbb {Z}^d}$
with respect to the measure
$\{0,1\}^{\mathbb {Z}^d}$
with respect to the measure
![]() $\nu $
. The space of local functions
$\nu $
. The space of local functions
![]() $C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
is known to be a dense subspace of
$C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
is known to be a dense subspace of
![]() $L^2(\nu )$
. We let
$L^2(\nu )$
. We let
![]() $\xi \colon \{0,1\}\rightarrow \mathbb {N}$
be the conserved quantity given by
$\xi \colon \{0,1\}\rightarrow \mathbb {N}$
be the conserved quantity given by
![]() $\xi (s)=s$
, which gives a basis of
$\xi (s)=s$
, which gives a basis of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (\{0,1\})$
. For any
${\operatorname {\mathrm {Consv}}}^\phi (\{0,1\})$
. For any
![]() $x\in X$
, we let
$x\in X$
, we let
![]() $\xi _x\colon \{0,1\}^{\mathbb {Z}^d}\rightarrow \mathbb {R}$
be the function defined by
$\xi _x\colon \{0,1\}^{\mathbb {Z}^d}\rightarrow \mathbb {R}$
be the function defined by ![]() for any
for any
![]() $\eta =(\eta _x)\in \{0,1\}^{\mathbb {Z}^d}$
. For any
$\eta =(\eta _x)\in \{0,1\}^{\mathbb {Z}^d}$
. For any
![]() $x=(x_j)\in \mathbb {Z}^d$
, denote by
$x=(x_j)\in \mathbb {Z}^d$
, denote by
![]() $\tau _x$
the translation of
$\tau _x$
the translation of
![]() $(\mathbb {Z}^d,\mathbb {E}^d)$
by x. In this case, Varadhan’s decomposition of shift-invariant closed
$(\mathbb {Z}^d,\mathbb {E}^d)$
by x. In this case, Varadhan’s decomposition of shift-invariant closed
![]() $L^2$
-forms proved by Funaki, Uchiyama and Yau is the following.
$L^2$
-forms proved by Funaki, Uchiyama and Yau is the following.
Theorem 3 [Reference Funaki, Uchiyama and Yau6, Theorem 4.1].
Let
![]() $\omega =(\omega _{e})\in \prod _{e\in E} L^2(\nu )$
be a shift-invariant closed
$\omega =(\omega _{e})\in \prod _{e\in E} L^2(\nu )$
be a shift-invariant closed
![]() $L^2$
-form. Then there exists a set of constants
$L^2$
-form. Then there exists a set of constants
![]() $a_1,\ldots ,a_d\in \mathbb {R}$
and a series of local functions
$a_1,\ldots ,a_d\in \mathbb {R}$
and a series of local functions
![]() $(f_n)_{n\in \mathbb {N}}$
in
$(f_n)_{n\in \mathbb {N}}$
in
![]() $C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
such that
$C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
such that
 $$\begin{align*}\omega_e=\lim_{n\rightarrow\infty}\nabla_e\bigg(\sum_{x\in\mathbb{Z}^d}\tau_x(f_n) +\sum_{j=1}^da_j\sum_{x\in\mathbb{Z}^d} x_j\xi_x\bigg) \end{align*}$$
$$\begin{align*}\omega_e=\lim_{n\rightarrow\infty}\nabla_e\bigg(\sum_{x\in\mathbb{Z}^d}\tau_x(f_n) +\sum_{j=1}^da_j\sum_{x\in\mathbb{Z}^d} x_j\xi_x\bigg) \end{align*}$$
in
![]() $L^2(\nu )$
for any
$L^2(\nu )$
for any
![]() $e\in \mathbb {E}$
.
$e\in \mathbb {E}$
.
The same statement for certain transition rates giving non-product measures on
![]() $\{0,1\}^{\mathbb {Z}^d}$
was proved by Varadhan and Yau [Reference Varadhan and Yau19], requiring different spectral gap estimates. The uniform version of Theorem 3, obtained by applying Corollary 2 to the above model for the fundamental domain
$\{0,1\}^{\mathbb {Z}^d}$
was proved by Varadhan and Yau [Reference Varadhan and Yau19], requiring different spectral gap estimates. The uniform version of Theorem 3, obtained by applying Corollary 2 to the above model for the fundamental domain
![]() $\Lambda _0=\{(0,\ldots ,0)\}$
of
$\Lambda _0=\{(0,\ldots ,0)\}$
of
![]() $X=\mathbb {Z}^d$
for the action of
$X=\mathbb {Z}^d$
for the action of
![]() $G=\mathbb {Z}^d$
, is given as follows.
$G=\mathbb {Z}^d$
, is given as follows.
Theorem 4. Let
![]() $\omega =(\omega _{e})\in \prod _{e\in \mathbb {E}}C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
be a shift-invariant closed form. Then there exists a set of constants
$\omega =(\omega _{e})\in \prod _{e\in \mathbb {E}}C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
be a shift-invariant closed form. Then there exists a set of constants
![]() $a_1,\ldots ,a_d\in \mathbb {R}$
and a local function f in
$a_1,\ldots ,a_d\in \mathbb {R}$
and a local function f in
![]() $ C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
satisfying
$ C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
satisfying
![]() $f(\star )=0$
such that
$f(\star )=0$
such that
 $$\begin{align*}\omega_e=\nabla_e\biggl(\sum_{x\in\mathbb{Z}^d}\tau_x(f) +\sum_{j=1}^da_j\sum_{x\in\mathbb{Z}^d} x_j\xi_x\biggr) \end{align*}$$
$$\begin{align*}\omega_e=\nabla_e\biggl(\sum_{x\in\mathbb{Z}^d}\tau_x(f) +\sum_{j=1}^da_j\sum_{x\in\mathbb{Z}^d} x_j\xi_x\biggr) \end{align*}$$
in
![]() $C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
for any
$C_{\mathrm {loc}}(\{0,1\}^{\mathbb {Z}^d})$
for any
![]() $e\in \mathbb {E}$
.
$e\in \mathbb {E}$
.
Our proof does not require a choice of the transition rate, thus completely independent of the measure. We remark that the sums in the brackets on the right-hand side of Theorem 3 and Theorem 4 are uniform functions in
![]() $C^0_{\operatorname {\mathrm {unif}}}(\{0,1\}^{\mathbb {Z}^d})$
.
$C^0_{\operatorname {\mathrm {unif}}}(\{0,1\}^{\mathbb {Z}^d})$
.
Next, consider a general system
![]() $(X,S,\phi )$
satisfying the assumptions of Theorem 1, and suppose that X has a free action of
$(X,S,\phi )$
satisfying the assumptions of Theorem 1, and suppose that X has a free action of
![]() $G=\mathbb {Z}^d$
. We fix the generator of G to be the standard basis of
$G=\mathbb {Z}^d$
. We fix the generator of G to be the standard basis of
![]() $\mathbb {Z}^d$
, and we denote an element of
$\mathbb {Z}^d$
, and we denote an element of
![]() $G=\mathbb {Z}^d$
by
$G=\mathbb {Z}^d$
by
![]() $\tau =(\tau _j)\in \mathbb {Z}^d$
instead of
$\tau =(\tau _j)\in \mathbb {Z}^d$
instead of
![]() $x=(x_j)$
since the locale X in general does not coincide with G. The disassociation of the group G from the locale X is another distinctive feature of our framework. If we fix a fundamental domain
$x=(x_j)$
since the locale X in general does not coincide with G. The disassociation of the group G from the locale X is another distinctive feature of our framework. If we fix a fundamental domain
![]() $\Lambda _0$
of X for the action of G, then Corollary 2 in this case gives the following.
$\Lambda _0$
of X for the action of G, then Corollary 2 in this case gives the following.
Theorem 5. Assume for simplicity that
![]() $c_\phi $
is finite, and fix a basis
$c_\phi $
is finite, and fix a basis
![]() $\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
$\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. Let
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. Let
![]() $\omega =(\omega _{e})\in \prod _{e\in E}C_{\mathrm {loc}}(S^X)$
be a shift-invariant closed uniform form. In other words, let
$\omega =(\omega _{e})\in \prod _{e\in E}C_{\mathrm {loc}}(S^X)$
be a shift-invariant closed uniform form. In other words, let
![]() $\omega \in \mathcal {C}$
. Then there exists
$\omega \in \mathcal {C}$
. Then there exists
![]() $a_{ij}\in \mathbb {R}$
for
$a_{ij}\in \mathbb {R}$
for
![]() $i=1,\ldots ,c_\phi $
and
$i=1,\ldots ,c_\phi $
and
![]() $j=1,\ldots ,d$
and a shift-invariant uniform function F in
$j=1,\ldots ,d$
and a shift-invariant uniform function F in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
 $$ \begin{align} \omega=\partial\biggl(F +\sum_{i=1}^{c_\phi}\sum_{j=1}^da_{ij}\biggl(\sum_{\tau\in G}\tau_j\xi^{(i)}_{\tau(\Lambda_0)}\biggr)\biggr), \end{align} $$
$$ \begin{align} \omega=\partial\biggl(F +\sum_{i=1}^{c_\phi}\sum_{j=1}^da_{ij}\biggl(\sum_{\tau\in G}\tau_j\xi^{(i)}_{\tau(\Lambda_0)}\biggr)\biggr), \end{align} $$
where we let
![]() $\xi _W$
be the function in
$\xi _W$
be the function in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
defined as
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
defined as ![]() for any conserved quantity
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
and
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
and
![]() $W\subset X$
.
$W\subset X$
.
In Theorem 5, we remark that
![]() $\partial F\in \mathcal {E}$
, and by Remark 5.20,
$\partial F\in \mathcal {E}$
, and by Remark 5.20,

is the image of
![]() $ \psi =\bigl (\sum _{i=1}^{c_\phi }a_{i1}\xi ^{(i)},\ldots ,\sum _{i=1}^{c_\phi }a_{id}\xi ^{(i)}\bigr ) \in \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S) $
through the isomorphism (5) for the choice of
$ \psi =\bigl (\sum _{i=1}^{c_\phi }a_{i1}\xi ^{(i)},\ldots ,\sum _{i=1}^{c_\phi }a_{id}\xi ^{(i)}\bigr ) \in \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S) $
through the isomorphism (5) for the choice of
![]() $\Lambda _0$
in Theorem 5. The equality
$\Lambda _0$
in Theorem 5. The equality
![]() $\omega =\partial F + \omega _\psi $
of (6) is precisely the decomposition given by (5).
$\omega =\partial F + \omega _\psi $
of (6) is precisely the decomposition given by (5).
In fact, Theorem 4 is a special case of Theorem 5, as follows. If
![]() $\Lambda _0$
is finite, then we may see from the definition that any
$\Lambda _0$
is finite, then we may see from the definition that any
![]() $\omega \in \prod _{e\in E}C_{\mathrm {loc}}(S^X)$
which is closed and shift-invariant is uniform. In addition, again if
$\omega \in \prod _{e\in E}C_{\mathrm {loc}}(S^X)$
which is closed and shift-invariant is uniform. In addition, again if
![]() $\Lambda _0$
is finite, any shift-invariant uniform function
$\Lambda _0$
is finite, any shift-invariant uniform function
![]() $F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
is of the form
$F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
is of the form
![]() $F=\sum _{\tau \in \mathbb {Z}^d}\tau (f)$
for some local function
$F=\sum _{\tau \in \mathbb {Z}^d}\tau (f)$
for some local function
![]() $f\in C_{\mathrm {loc}}(S^X)$
satisfying
$f\in C_{\mathrm {loc}}(S^X)$
satisfying
![]() $f(\star )=0$
(see Lemma 5.15). Here,
$f(\star )=0$
(see Lemma 5.15). Here,
![]() $\tau (f)$
denotes the image of f with respect to the action of
$\tau (f)$
denotes the image of f with respect to the action of
![]() $\tau \in \mathbb {Z}^d$
. For the case
$\tau \in \mathbb {Z}^d$
. For the case
![]() $X=\mathbb {Z}^d$
with the action of
$X=\mathbb {Z}^d$
with the action of
![]() $G=\mathbb {Z}^d$
given by the standard translation, if we let
$G=\mathbb {Z}^d$
given by the standard translation, if we let
![]() $\Lambda _0=\{(0,\ldots ,0)\}$
, then we have
$\Lambda _0=\{(0,\ldots ,0)\}$
, then we have
![]() $\tau _{x}(\Lambda _0)=\{x\}$
for any
$\tau _{x}(\Lambda _0)=\{x\}$
for any
![]() $x\in \mathbb {Z}^d$
. From these observations and the definition of the differential
$x\in \mathbb {Z}^d$
. From these observations and the definition of the differential
![]() $\partial $
, we see that Theorem 4 follows from Theorem 5.
$\partial $
, we see that Theorem 4 follows from Theorem 5.
In the general setting of Theorem 1, the choice of a transition rate satisfying certain conditions gives an inner product compatible with the norm on the space of
![]() $L^2$
-forms. The existence of Varadhan’s decomposition amounts to the following question. See [Reference Bannai and Sasada2, Conjecture 5.5] for a precise formulation of this question as a conjecture.
$L^2$
-forms. The existence of Varadhan’s decomposition amounts to the following question. See [Reference Bannai and Sasada2, Conjecture 5.5] for a precise formulation of this question as a conjecture.
Question. Assume that the fundamental domain of the action of G on the vertices of X is finite. For a suitable definition of closed
![]() $L^2$
-forms, if
$L^2$
-forms, if
![]() $\omega $
is a shift-invariant closed
$\omega $
is a shift-invariant closed
![]() $L^2$
-form, then does there exist
$L^2$
-form, then does there exist
![]() $\omega _n\in \mathcal {E}$
for
$\omega _n\in \mathcal {E}$
for
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
such that
$\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
such that
Here, we let
![]() $\omega _\psi $
be the element in
$\omega _\psi $
be the element in
![]() $\mathcal {C}$
corresponding to
$\mathcal {C}$
corresponding to
![]() $\psi $
in the decomposition (5) of Corollary 2 given for a choice of a fundamental domain of X for the action of G.
$\psi $
in the decomposition (5) of Corollary 2 given for a choice of a fundamental domain of X for the action of G.
The question is answered affirmatively for the cases that Varadhan’s decomposition are shown. Although our local forms construct the core of the
![]() $L^2$
-space, and local closed forms in our sense are closed forms in the sense of the
$L^2$
-space, and local closed forms in our sense are closed forms in the sense of the
![]() $L^2$
-space, it is currently not generally known whether our local closed forms form a core of closed forms in the sense of
$L^2$
-space, it is currently not generally known whether our local closed forms form a core of closed forms in the sense of
![]() $L^2$
-spaces. Nevertheless, in subsequent research, we prove Varadhan’s decomposition for certain locales using Theorem 1 of this article, when S is finite and
$L^2$
-spaces. Nevertheless, in subsequent research, we prove Varadhan’s decomposition for certain locales using Theorem 1 of this article, when S is finite and
![]() $\mu $
is a product measure, assuming a certain spectral gap estimate pertaining to the interaction (cf. [Reference Bannai and Sasada3]). Through this process, we hope to understand the role played by the sharp spectral gap estimates in the proof of hydrodynamic limits for nongradient systems, a question which has been an important open question for the past thirty years (see, for example, [Reference Kipnis and Landim8, Preface]).
$\mu $
is a product measure, assuming a certain spectral gap estimate pertaining to the interaction (cf. [Reference Bannai and Sasada3]). Through this process, we hope to understand the role played by the sharp spectral gap estimates in the proof of hydrodynamic limits for nongradient systems, a question which has been an important open question for the past thirty years (see, for example, [Reference Kipnis and Landim8, Preface]).
Let
![]() $\mathcal {C}_{L^2}$
and
$\mathcal {C}_{L^2}$
and
![]() $\mathcal {E}_{L^2}$
be the shift-invariant closed and exact forms for the
$\mathcal {E}_{L^2}$
be the shift-invariant closed and exact forms for the
![]() $L^2$
-space. The inner product on the
$L^2$
-space. The inner product on the
![]() $L^2$
-space defines an orthogonal decomposition
$L^2$
-space defines an orthogonal decomposition
which is different from (5). By reinterpreting the method in hydrodynamic limits for obtaining the macroscopic deterministic partial differential equation from the microscopic system, we have come to understand that the diffusion matrix associated with the macroscopic partial differential equation is given precisely by the matrix relating the two decompositions (5) and (8). One critical observation from this fact is that the size of the diffusion matrix of our system should be
![]() $c_\phi d$
, the dimension of
$c_\phi d$
, the dimension of
![]() $\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
.
$\bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
.
Through our investigation, we have come to see the stochastic data consisting of the measure and compatible inner product as a certain analogy of differential geometric data on Riemannian manifolds – the volume form and the metric. Through this analogy, the orthogonal decomposition (8) may be regarded as a differential geometric decomposition given as a certain analogue of the Hodge-Kodaira decomposition in Riemannian geometry, whereas the decomposition (5) is viewed as a more topological decomposition. In light of this analogy, it would be interesting to interpret the diffusion matrix relating the topological and measure theoretic structures of
![]() $\mathcal {C}_{L^2}$
as an analogy of the period matrix in Hodge theory comparing the topological and differential geometric structures of the manifold. Such ideas will be explored in future research.
$\mathcal {C}_{L^2}$
as an analogy of the period matrix in Hodge theory comparing the topological and differential geometric structures of the manifold. Such ideas will be explored in future research.
1.4 Overview
In this subsection, we give an overview of the proof of Theorem 1. The key result for the proof is Theorem 6 below concerning the property of uniform cohomology. Consider the system
![]() $(X,S,\phi )$
. The uniform cohomology is defined for a configuration space with transition structure as follows.
$(X,S,\phi )$
. The uniform cohomology is defined for a configuration space with transition structure as follows.
Definition 1.6. We define the uniform cohomology
![]() $H^m_{\operatorname {\mathrm {unif}}}(S^X)$
for
$H^m_{\operatorname {\mathrm {unif}}}(S^X)$
for
![]() $m\in \mathbb {N}$
of the configuration space
$m\in \mathbb {N}$
of the configuration space
![]() $S^X$
with transition structure to be the cohomology of the cochain complex
$S^X$
with transition structure to be the cohomology of the cochain complex
which is zero in degrees
![]() $m\neq 0,1$
. Concretely, we have
$m\neq 0,1$
. Concretely, we have ![]() ,
, ![]() , and
, and
![]() $H^m_{\operatorname {\mathrm {unif}}}(S^X)=\{0\}$
in degrees
$H^m_{\operatorname {\mathrm {unif}}}(S^X)=\{0\}$
in degrees
![]() $m\neq 0,1$
. The uniform cohomology is philosophically the reduced cohomology in the sense of topology of the pointed space consisting of the configuration space
$m\neq 0,1$
. The uniform cohomology is philosophically the reduced cohomology in the sense of topology of the pointed space consisting of the configuration space
![]() $S^X$
and base configuration
$S^X$
and base configuration
![]() $\star \in S^X$
.
$\star \in S^X$
.
Theorem 6 (=Theorem 5.8).
For the system
![]() $(X,S,\phi )$
, assume that the interaction
$(X,S,\phi )$
, assume that the interaction
![]() $\phi $
is irreducibly quantified. If X is transferable, or if the interaction
$\phi $
is irreducibly quantified. If X is transferable, or if the interaction
![]() $\phi $
is simple and X is weakly transferable, then we have
$\phi $
is simple and X is weakly transferable, then we have
 $$\begin{align*}H^m_{\operatorname{\mathrm{unif}}}(S^X)\cong \begin{cases} {\operatorname{\mathrm{Consv}}}^\phi(S) & m=0\\ \{0\} & m\neq0. \end{cases} \end{align*}$$
$$\begin{align*}H^m_{\operatorname{\mathrm{unif}}}(S^X)\cong \begin{cases} {\operatorname{\mathrm{Consv}}}^\phi(S) & m=0\\ \{0\} & m\neq0. \end{cases} \end{align*}$$
The configuration space
![]() $S^X$
with transition structure viewed geometrically as a graph generally has an infinite number of connected components. Hence, it may be surprising that
$S^X$
with transition structure viewed geometrically as a graph generally has an infinite number of connected components. Hence, it may be surprising that
![]() $H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is finite dimensional. This calculation very beautifully reflects the fact that assuming the conditions of the theorem, the connected components of the graph
$H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is finite dimensional. This calculation very beautifully reflects the fact that assuming the conditions of the theorem, the connected components of the graph
![]() $S^X_*$
can be determined from the values of its conserved quantities (see Remark 2.25). By the definition of
$S^X_*$
can be determined from the values of its conserved quantities (see Remark 2.25). By the definition of
![]() $H^m_{\operatorname {\mathrm {unif}}}(S^X)$
, Theorem 6 is equivalent to the existence of a short exact sequence
$H^m_{\operatorname {\mathrm {unif}}}(S^X)$
, Theorem 6 is equivalent to the existence of a short exact sequence
In other words, (9) is a sequence of
![]() $\mathbb {R}$
-linear maps such that i is injective,
$\mathbb {R}$
-linear maps such that i is injective,
![]() $\partial $
is surjective, and
$\partial $
is surjective, and
![]() $\operatorname {Im} i=\operatorname {\mathrm {Ker}}\partial $
. A large portion of our article is dedicated to the construction of (9), especially the proof that the differential
$\operatorname {Im} i=\operatorname {\mathrm {Ker}}\partial $
. A large portion of our article is dedicated to the construction of (9), especially the proof that the differential
![]() $\partial $
is surjective.
$\partial $
is surjective.
First, in §2.1, we introduce our model and the associated configuration space. In §2.2, we introduce the notion of a conserved quantity. Then in §2.3, we define the usual cohomology for the configuration space with transition structure and the notion of closed forms. We then give the relation between the conserved quantities and the
![]() $H^0$
of the configuration space.
$H^0$
of the configuration space.
In §3.1, we introduce the notion of local functions with exact support and prove that any function
![]() $f\in C(S^X_*)$
may be expanded uniquely as a possibly infinite sum of local functions with exact support. We say that
$f\in C(S^X_*)$
may be expanded uniquely as a possibly infinite sum of local functions with exact support. We say that
![]() $f\in C(S^X_*)$
is uniform if the diameter of support in the expansion of f is uniformly bounded. In §3.2, we first note that the function
$f\in C(S^X_*)$
is uniform if the diameter of support in the expansion of f is uniformly bounded. In §3.2, we first note that the function
![]() $\xi _X=\sum _{x\in X}\xi _x$
for any conserved quantity
$\xi _X=\sum _{x\in X}\xi _x$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
is uniform. Since
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
is uniform. Since
![]() $\xi _X(\star )=0$
, the correspondence
$\xi _X(\star )=0$
, the correspondence
![]() $\xi \mapsto \xi _X$
gives a natural inclusion
$\xi \mapsto \xi _X$
gives a natural inclusion
![]() $i\colon {\operatorname {\mathrm {Consv}}}^\phi (S)\hookrightarrow C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Assume now that the interaction is irreducibly quantified. We prove in Theorem 3.7 that this inclusion gives an isomorphism
$i\colon {\operatorname {\mathrm {Consv}}}^\phi (S)\hookrightarrow C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Assume now that the interaction is irreducibly quantified. We prove in Theorem 3.7 that this inclusion gives an isomorphism
It remains to prove that
![]() $\partial $
is surjective. In Definition 3.10, we define the notion of uniform forms. For the remainder of §3, we assume in addition that X is strongly transferable – that is,
$\partial $
is surjective. In Definition 3.10, we define the notion of uniform forms. For the remainder of §3, we assume in addition that X is strongly transferable – that is,
![]() $X\setminus B$
is an infinite connected graph for any ball B in X. We consider a function
$X\setminus B$
is an infinite connected graph for any ball B in X. We consider a function
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f$
is uniform, and we construct in Proposition 3.18 of §3.3 a symmetric pairing
$\partial f$
is uniform, and we construct in Proposition 3.18 of §3.3 a symmetric pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
on a certain additive submonoid
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
on a certain additive submonoid
![]() $\mathcal {M}\subset {\mathbb {R}}^{c_\phi }$
(see Definition 2.24) satisfying the cocycle condition
$\mathcal {M}\subset {\mathbb {R}}^{c_\phi }$
(see Definition 2.24) satisfying the cocycle condition
for any
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
. We then prove in Proposition 3.19 of §3.4 that if
$\alpha ,\beta ,\gamma \in \mathcal {M}$
. We then prove in Proposition 3.19 of §3.4 that if
![]() $h_f\equiv 0$
, then
$h_f\equiv 0$
, then
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
In §4, we consider the case when X is weakly transferable. This section is technical and can be skipped if the reader is only interested in the strongly transferable case. In §4.2, we again construct a pairing
![]() $h_f$
for any
$h_f$
for any
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f$
is uniform, and we prove in Proposition 4.13 the cocycle condition for
$\partial f$
is uniform, and we prove in Proposition 4.13 the cocycle condition for
![]() $h_f$
. We note that in general, the pairing
$h_f$
. We note that in general, the pairing
![]() $h_f$
may not be symmetric. We prove in Proposition 4.14 of §4.3 a weakly transferable version of Proposition 3.19. Finally, we prove in §4.4 that the pairing
$h_f$
may not be symmetric. We prove in Proposition 4.14 of §4.3 a weakly transferable version of Proposition 3.19. Finally, we prove in §4.4 that the pairing
![]() $h_f$
is symmetric if the locale X is transferable.
$h_f$
is symmetric if the locale X is transferable.
In §5, we complete the proof that
![]() $\partial $
is surjective (see Theorem 5.2 for details). The method of proof is as follows. For any closed uniform form
$\partial $
is surjective (see Theorem 5.2 for details). The method of proof is as follows. For any closed uniform form
![]() $\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
, since
$\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
, since
![]() $\omega $
is closed, by Lemma 2.28, there exists
$\omega $
is closed, by Lemma 2.28, there exists
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f=\omega $
. Note that f may not necessarily be a uniform function. By the previous argument, there exists a pairing
$\partial f=\omega $
. Note that f may not necessarily be a uniform function. By the previous argument, there exists a pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying the cocycle condition. We prove in Lemma 5.5 that if the pairing
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying the cocycle condition. We prove in Lemma 5.5 that if the pairing
![]() $h_f$
is symmetric, or in Lemma 5.5 if the interaction is simple, there exists a function
$h_f$
is symmetric, or in Lemma 5.5 if the interaction is simple, there exists a function
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
for any
![]() $\alpha ,\beta \in \mathcal {M}$
. We modify the function f using h to obtain a function with the same
$\alpha ,\beta \in \mathcal {M}$
. We modify the function f using h to obtain a function with the same
![]() $\partial f$
but satisfies
$\partial f$
but satisfies
![]() $h_f\equiv 0$
. By Proposition 3.19 or Proposition 4.14, we see that
$h_f\equiv 0$
. By Proposition 3.19 or Proposition 4.14, we see that
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. This proves that the differential
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. This proves that the differential
![]() $\partial $
in (9) is surjective, completing the proof of Theorem 6.
$\partial $
in (9) is surjective, completing the proof of Theorem 6.
Now for the proof of Theorem 1, suppose that the locale X has a free action of a group G. This gives a natural action of G on various spaces of functions and forms. Noting that G acts trivially on
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
, the boundary homomorphism of the long exact sequence for group cohomology (49) associated with the short exact sequence (9) immediately gives an inclusion
${\operatorname {\mathrm {Consv}}}^\phi (S)$
, the boundary homomorphism of the long exact sequence for group cohomology (49) associated with the short exact sequence (9) immediately gives an inclusion
For a fixed fundamental domain
![]() $\Lambda _0$
of X for the action of G, we let
$\Lambda _0$
of X for the action of G, we let
for any
![]() $\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
, noting that
$\psi \in \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))$
, noting that
![]() $\psi (\tau )\in {\operatorname {\mathrm {Consv}}}^\phi (S)$
for any
$\psi (\tau )\in {\operatorname {\mathrm {Consv}}}^\phi (S)$
for any
![]() $\tau \in G$
. The relation of
$\tau \in G$
. The relation of
![]() $\omega _\psi $
to the form in (7) is explained in Remark 5.20. By explicit calculation, we see in Proposition 5.18 that
$\omega _\psi $
to the form in (7) is explained in Remark 5.20. By explicit calculation, we see in Proposition 5.18 that
![]() $\delta (\omega _\psi )=\psi $
; hence,
$\delta (\omega _\psi )=\psi $
; hence,
![]() $\delta $
is surjective. The
$\delta $
is surjective. The
![]() $\mathbb {R}$
-linear map
$\mathbb {R}$
-linear map
![]() $\omega \mapsto (\omega -\omega _\psi ,\psi )$
for
$\omega \mapsto (\omega -\omega _\psi ,\psi )$
for ![]() gives a decomposition of
gives a decomposition of
![]() $\mathbb {R}$
-linear spaces
$\mathbb {R}$
-linear spaces
completing the proof of Theorem 1. In Appendix A, we review well-known results concerning cohomology of graphs. In Appendix B, we give some examples. In Appendix B.1, we describe the objects appearing in our article for the exclusion process. Finally, in Appendix B.2, we let
![]() $X=\mathbb {Z}$
and consider the multi-color exclusion process for
$X=\mathbb {Z}$
and consider the multi-color exclusion process for
![]() $S=\{0,1,2\}$
. Then X is not transferable and
$S=\{0,1,2\}$
. Then X is not transferable and
![]() $c_\phi =2$
. We prove that
$c_\phi =2$
. We prove that
![]() $\partial $
of Definition 1.6 is not surjective in this case.
$\partial $
of Definition 1.6 is not surjective in this case.
2 Configuration space and conserved quantities
In this section, we will introduce the configuration space of a large-scale interacting system and the notion of a conserved quantity. We then define and investigate its cohomology.
2.1 Configuration space and transition structure
In this subsection, we will give a graph structure which we call the transition structure on the configuration space of states on a locale. We first review some terminology related to graphs.
A directed graph
![]() $(X,E)$
, or simply a graph, is a pair consisting of a set X, which we call the set of vertices, and a subset
$(X,E)$
, or simply a graph, is a pair consisting of a set X, which we call the set of vertices, and a subset
![]() $E\subset X\times X$
, which we call the set of directed edges, or simply edges. For any
$E\subset X\times X$
, which we call the set of directed edges, or simply edges. For any
![]() $e\in E = X\times X$
, we denote by
$e\in E = X\times X$
, we denote by
![]() $o(e)$
and
$o(e)$
and
![]() $t(e)$
the first and second components of e, which we call the origin and target of e, so that
$t(e)$
the first and second components of e, which we call the origin and target of e, so that
![]() $e = (o(e), t(e))\in X\times X$
. For any
$e = (o(e), t(e))\in X\times X$
. For any
![]() $e\in E$
, we let
$e\in E$
, we let ![]() , which we call the opposite of e. We say that a directed graph
, which we call the opposite of e. We say that a directed graph
![]() $(X,E)$
is symmetric if
$(X,E)$
is symmetric if
![]() $\bar e \in E$
for any
$\bar e \in E$
for any
![]() $e\in E$
, and simple if
$e\in E$
, and simple if
![]() $(x,x)\not \in E$
for any
$(x,x)\not \in E$
for any
![]() $x\in X$
. For any
$x\in X$
. For any
![]() $e=(o(e),t(e))\in E$
, we will often use e to denote the set
$e=(o(e),t(e))\in E$
, we will often use e to denote the set
![]() $e=\{o(e),t(e)\}$
. We say that
$e=\{o(e),t(e)\}$
. We say that
![]() $(X,E)$
is locally finite if for any
$(X,E)$
is locally finite if for any
![]() $x\in X$
, the set
$x\in X$
, the set
![]() $\{ e \in E \mid x \in e\}$
is finite. In this article, by abuse of notation (see Remark 2.8), we will often simply denote the graph
$\{ e \in E \mid x \in e\}$
is finite. In this article, by abuse of notation (see Remark 2.8), we will often simply denote the graph
![]() $(X,E)$
by its set of vertices X.
$(X,E)$
by its set of vertices X.
We define a finite path on the graph X to be a finite sequence ![]() of edges in E such that
of edges in E such that
![]() $t(e^i)=o(e^{i+1})$
for any integer
$t(e^i)=o(e^{i+1})$
for any integer
![]() $0<i<N$
. We denote by
$0<i<N$
. We denote by
![]() $\operatorname {\mathrm {len}}(\vec p)$
the number of elements N in
$\operatorname {\mathrm {len}}(\vec p)$
the number of elements N in
![]() $\vec p$
, which we call the length of
$\vec p$
, which we call the length of
![]() $\vec p$
. We let
$\vec p$
. We let ![]() and
and ![]() , and we say that
, and we say that
![]() $\vec p$
is a path from
$\vec p$
is a path from
![]() $o(\vec p)$
to
$o(\vec p)$
to
![]() $t(\vec p)$
. For paths
$t(\vec p)$
. For paths
![]() $\vec p_1,\vec p_2$
such that
$\vec p_1,\vec p_2$
such that
![]() $t(\vec p_1)=o(\vec p_2)$
, we denote by
$t(\vec p_1)=o(\vec p_2)$
, we denote by
![]() $\vec p_1\vec p_2$
the path from
$\vec p_1\vec p_2$
the path from
![]() $o(\vec p_1)$
to
$o(\vec p_1)$
to
![]() $t(\vec p_2)$
obtained as the composition of the two paths. If a path
$t(\vec p_2)$
obtained as the composition of the two paths. If a path
![]() $\vec p$
satisfies
$\vec p$
satisfies
![]() $o(\vec p)=t(\vec p)$
, then we say that
$o(\vec p)=t(\vec p)$
, then we say that
![]() $\vec p$
is a closed path. For any
$\vec p$
is a closed path. For any
![]() $x,x'\in X$
, we denote by
$x,x'\in X$
, we denote by
![]() $P(x,x')$
the set of paths from x to
$P(x,x')$
the set of paths from x to
![]() $x'$
. We define the graph distance
$x'$
. We define the graph distance
![]() $d_X(x,x')$
between x and
$d_X(x,x')$
between x and
![]() $x'$
by
$x'$
by
if
![]() $P(x,x')\neq \emptyset $
, and
$P(x,x')\neq \emptyset $
, and ![]() otherwise. We say that any subset
otherwise. We say that any subset
![]() $Y\subset X$
is connected if
$Y\subset X$
is connected if
![]() $d_Y(x,x')<\infty $
for any
$d_Y(x,x')<\infty $
for any
![]() $x,x'\in Y$
, where
$x,x'\in Y$
, where
![]() $d_Y$
is the graph distance on the graph
$d_Y$
is the graph distance on the graph
![]() $(Y,E_Y)$
given by
$(Y,E_Y)$
given by ![]() .
.
Definition 2.1. We define the locale to be a locally finite simple symmetric directed graph
![]() $X=(X,E)$
which is connected. If the set of vertices of X is an infinite set, then we say that X is an infinite locale.
$X=(X,E)$
which is connected. If the set of vertices of X is an infinite set, then we say that X is an infinite locale.
We will use the terminology locale to express the discrete object that models the space where the dynamics under question takes place. We understand the connectedness to be an important feature of the locale.
Example 2.2.
-
1. The most typical example of an infinite locale is the Euclidean lattice
 $\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for integers
$\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for integers
 $d\geq 1$
, where
$d\geq 1$
, where
 $\mathbb {Z}^d$
is the d-fold product of
$\mathbb {Z}^d$
is the d-fold product of
 $\mathbb {Z}$
, and Here, we let
$\mathbb {Z}$
, and Here, we let
 for any
for any
 $x=(x_1,\ldots ,x_d)$
,
$x=(x_1,\ldots ,x_d)$
,
 $y=(y_1,\ldots ,y_d)$
in
$y=(y_1,\ldots ,y_d)$
in
 $\mathbb {Z}^d$
.
$\mathbb {Z}^d$
.
-
2. For integers
 $d\geq 1$
and
$d\geq 1$
and
 $n>0$
, a variant of the Euclidean lattice is given by the Euclidean lattice with nearest n-neighbor
$n>0$
, a variant of the Euclidean lattice is given by the Euclidean lattice with nearest n-neighbor
 $\mathbb {Z}^d_n=(\mathbb {Z}^d,\mathbb {E}^d_n)$
(see Figure 4), where
$\mathbb {Z}^d_n=(\mathbb {Z}^d,\mathbb {E}^d_n)$
(see Figure 4), where 

Figure 4 The Euclidean lattices
 $\mathbb {Z}^2$
and with nearest
$\mathbb {Z}^2$
and with nearest
 $2$
-neighbor
$2$
-neighbor
 $\mathbb {Z}^2_2$
.
$\mathbb {Z}^2_2$
. -
3. Many types of crystal lattices such as the triangular, hexagonal and diamond lattices are infinite locales (see, for example, [Reference Sunada17, Example 3.4, Example 8.3] and [Reference Kotani and Sunada10, §5]).
-
4. Let G be a finitely generated group, and let
 $\mathcal {S}\subset G$
be a minimal set of generators. Then the associated Cayley graph
$\mathcal {S}\subset G$
be a minimal set of generators. Then the associated Cayley graph
 $(G,E_{\mathcal {S}})$
given by
$(G,E_{\mathcal {S}})$
given by  is a locale. If G is infinite, then the associated Cayley graph is an infinite locale.
is a locale. If G is infinite, then the associated Cayley graph is an infinite locale. -
5. Let
 $X_1=(X_1,E_1)$
and
$X_1=(X_1,E_1)$
and
 $X_2=(X_2,E_2)$
be locales. If
$X_2=(X_2,E_2)$
be locales. If  and then
and then
 $(X,E)$
is a locale, which we denote
$(X,E)$
is a locale, which we denote
 $X_1\times X_2$
. We say that X is a product of
$X_1\times X_2$
. We say that X is a product of
 $X_1$
and
$X_1$
and
 $X_2$
. Note that
$X_2$
. Note that
 $(\mathbb {Z}^d,\mathbb {E}^d)$
coincides with the d-fold product
$(\mathbb {Z}^d,\mathbb {E}^d)$
coincides with the d-fold product
 $(\mathbb {Z},\mathbb {E}) \times \cdots \times (\mathbb {Z},\mathbb {E})$
.
$(\mathbb {Z},\mathbb {E}) \times \cdots \times (\mathbb {Z},\mathbb {E})$
.
-
6. Suppose
 $X=(X,E)$
is a locale, and let
$X=(X,E)$
is a locale, and let
 $Y\subset X$
be a connected subset. If we let
$Y\subset X$
be a connected subset. If we let  , then
, then
 $Y=(Y,E_Y)$
gives a graph which is a locale. We call Y a sublocale of X.
$Y=(Y,E_Y)$
gives a graph which is a locale. We call Y a sublocale of X.
Next, we introduce the set of states, which is a nonempty set S expressing the possible states the model may take at each vertex, and the configuration space
![]() $S^X$
for S on X.
$S^X$
for S on X.
Definition 2.3. We define the set of states to be a nonempty set S. We call any element of S a state. We will designate an element
![]() $*\in S$
which we call the base state. If
$*\in S$
which we call the base state. If
![]() $S\subset \mathbb {R}$
and
$S\subset \mathbb {R}$
and
![]() $0\in S$
, then we will often take the base state
$0\in S$
, then we will often take the base state
![]() $*$
to be
$*$
to be
![]() $0$
. For any locale
$0$
. For any locale
![]() $X=(X,E)$
, we define the configuration space for S on X by
$X=(X,E)$
, we define the configuration space for S on X by
We call an element
![]() $\eta =(\eta _x)$
of
$\eta =(\eta _x)$
of
![]() $S^X$
a configuration. We denote by
$S^X$
a configuration. We denote by
![]() $\star $
the base configuration, which is the configuration in
$\star $
the base configuration, which is the configuration in
![]() $S^X$
whose components are all at base state.
$S^X$
whose components are all at base state.
Now, we introduce the symmetric binary interaction, which expresses the interaction between states on adjoining vertices.
Definition 2.4. A symmetric binary interaction, which we simply call an interaction on S, is a map
![]() $ \phi \colon S\times S\rightarrow S\times S $
such that
$ \phi \colon S\times S\rightarrow S\times S $
such that
for any
![]() $(s_1,s_2)\in S\times S$
satisfying
$(s_1,s_2)\in S\times S$
satisfying
![]() $\phi (s_1,s_2)\neq (s_1,s_2)$
, where
$\phi (s_1,s_2)\neq (s_1,s_2)$
, where
![]() $\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
$\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
![]() $S\times S$
.
$S\times S$
.
Examples of the set of states S and interactions
![]() $\phi $
are given in Example 2.10 of §2.2. Throughout this article, a system
$\phi $
are given in Example 2.10 of §2.2. Throughout this article, a system
![]() $(X,S,\phi )$
indicates that X is a locale, S is a set of states, and
$(X,S,\phi )$
indicates that X is a locale, S is a set of states, and
![]() $\phi $
is an interaction. We will next define the configuration space with transition structure associated with such a system. We first prepare a lemma.
$\phi $
is an interaction. We will next define the configuration space with transition structure associated with such a system. We first prepare a lemma.
Lemma 2.5. For a locale
![]() $X=(X,E)$
and the set of states S, let
$X=(X,E)$
and the set of states S, let
![]() $S^X$
be the configuration space for S on X. Let
$S^X$
be the configuration space for S on X. Let
![]() $\phi \colon S\times S\rightarrow S\times S$
be an interaction on S. For any
$\phi \colon S\times S\rightarrow S\times S$
be an interaction on S. For any
![]() $e=(o(e),t(e))\in E\subset X\times X$
, we define the map
$e=(o(e),t(e))\in E\subset X\times X$
, we define the map
![]() $\phi _e\colon S^X\rightarrow S^X$
by
$\phi _e\colon S^X\rightarrow S^X$
by ![]() , where
, where
![]() $\eta ^e=(\eta ^e_x)\in S^X$
is defined as in (1). In other words,
$\eta ^e=(\eta ^e_x)\in S^X$
is defined as in (1). In other words,
![]() $\phi _e(\eta )$
is obtained by applying
$\phi _e(\eta )$
is obtained by applying
![]() $\phi $
to the
$\phi $
to the
![]() $o(e)$
and
$o(e)$
and
![]() $t(e)$
components of
$t(e)$
components of
![]() $\eta $
. If we denote by
$\eta $
. If we denote by
![]() $\Phi $
the image of the map
$\Phi $
the image of the map
then the pair
![]() $(S^X, \Phi )$
is a symmetric directed graph.
$(S^X, \Phi )$
is a symmetric directed graph.
Proof. It is sufficient to prove that the directed graph
![]() $(S^X, \Phi )$
is symmetric. By the definition of an interaction, we have
$(S^X, \Phi )$
is symmetric. By the definition of an interaction, we have
![]() $\hat \imath \circ \phi \circ \hat \imath \circ \phi (s_1,s_2)=(s_1,s_2)$
for any
$\hat \imath \circ \phi \circ \hat \imath \circ \phi (s_1,s_2)=(s_1,s_2)$
for any
![]() $(s_1,s_2)\in S\times S$
such that
$(s_1,s_2)\in S\times S$
such that
![]() $\phi (s_1,s_2)\neq (s_1,s_2)$
. This shows that for any
$\phi (s_1,s_2)\neq (s_1,s_2)$
. This shows that for any
![]() $\eta \in S^X$
, if
$\eta \in S^X$
, if
![]() $\phi _e(\eta )\neq \eta $
, then we have
$\phi _e(\eta )\neq \eta $
, then we have
![]() $\phi _{\bar e}\circ \phi _e(\eta )=\eta $
. Consider the element
$\phi _{\bar e}\circ \phi _e(\eta )=\eta $
. Consider the element
![]() $(\eta , \phi _e(\eta )) \in \Phi $
. If
$(\eta , \phi _e(\eta )) \in \Phi $
. If
![]() $\phi _e(\eta )=\eta $
, then
$\phi _e(\eta )=\eta $
, then
![]() $(\phi _e(\eta ), \eta )=(\eta ,\eta )\in \Phi $
. If
$(\phi _e(\eta ), \eta )=(\eta ,\eta )\in \Phi $
. If
![]() $\phi _e(\eta )\neq \eta $
, then
$\phi _e(\eta )\neq \eta $
, then
![]() $(\phi _e(\eta ), \eta ) = ( \phi _e(\eta ), \phi _{\bar e} \circ \phi _e(\eta ))$
, which is an element in
$(\phi _e(\eta ), \eta ) = ( \phi _e(\eta ), \phi _{\bar e} \circ \phi _e(\eta ))$
, which is an element in
![]() $\Phi $
since it is the image of
$\Phi $
since it is the image of
![]() $(\bar e, \phi _e(\eta ))\in E\times S^X$
by the map (11).
$(\bar e, \phi _e(\eta ))\in E\times S^X$
by the map (11).
Remark 2.6. In fact, the condition (10) that we impose on the interaction is simply a sufficient condition and not a necessary condition for our theory. The property that we actually use is that
![]() $(S^X, \Phi )$
is a symmetric directed graph.
$(S^X, \Phi )$
is a symmetric directed graph.
Definition 2.7. For a locale X and a set of states S, if we fix an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
, then Lemma 2.5 implies that
$\phi \colon S\times S\rightarrow S\times S$
, then Lemma 2.5 implies that
![]() $\Phi $
gives a structure of a symmetric directed graph
$\Phi $
gives a structure of a symmetric directed graph
on the configuration space
![]() $S^X$
. We call this structure the transition structure, and we call any element
$S^X$
. We call this structure the transition structure, and we call any element
![]() $\varphi \in \Phi $
a transition. In particular, we say that
$\varphi \in \Phi $
a transition. In particular, we say that
![]() $\varphi = (\eta , \phi _e(\eta ))\in \Phi $
is a transition of
$\varphi = (\eta , \phi _e(\eta ))\in \Phi $
is a transition of
![]() $\eta $
by e. Following the convention in literature, we will often denote
$\eta $
by e. Following the convention in literature, we will often denote
![]() $\phi _e(\eta )$
by
$\phi _e(\eta )$
by
![]() $\eta ^e$
.
$\eta ^e$
.
Remark 2.8. Our convention of denoting the locale
![]() $(X,E)$
by X and the configuration space with transition structure
$(X,E)$
by X and the configuration space with transition structure
![]() $(S^X,\Phi )$
by
$(S^X,\Phi )$
by
![]() $S^X$
follows similar convention as that of topological spaces, where the topological space and its underlying set is denoted by the same symbol. We are interpreting the set of edges of a graph as giving a geometric structure to the set of vertices.
$S^X$
follows similar convention as that of topological spaces, where the topological space and its underlying set is denoted by the same symbol. We are interpreting the set of edges of a graph as giving a geometric structure to the set of vertices.
For the configuration space
![]() $S^X$
with transition structure, the edges
$S^X$
with transition structure, the edges
![]() $\Phi $
expresses all the possible transitions on the configuration space with respect to the interaction
$\Phi $
expresses all the possible transitions on the configuration space with respect to the interaction
![]() $\phi $
. For any element
$\phi $
. For any element
![]() $\eta =(\eta _x)\in S^X$
, we define the support of
$\eta =(\eta _x)\in S^X$
, we define the support of
![]() $\eta $
to be the set
$\eta $
to be the set ![]() . The subset
. The subset
of the configuration space will play an important role in our theory. If we let ![]() , then
, then
![]() $S^X_*=(S^X_*,\Phi _*)$
is again a symmetric directed graph, which we refer to again as a configuration space with transition structure.
$S^X_*=(S^X_*,\Phi _*)$
is again a symmetric directed graph, which we refer to again as a configuration space with transition structure.
For any set A, we let ![]() be the
be the
![]() $\mathbb {R}$
-linear space of functions from A to
$\mathbb {R}$
-linear space of functions from A to
![]() $\mathbb {R}$
. As in §1.2, for any finite
$\mathbb {R}$
. As in §1.2, for any finite
![]() $\Lambda \subset X$
, we let
$\Lambda \subset X$
, we let ![]() . Following standard convention, we let
. Following standard convention, we let
![]() $S^\emptyset =\{\star \}$
if
$S^\emptyset =\{\star \}$
if
![]() $\Lambda =\emptyset $
. The natural projection
$\Lambda =\emptyset $
. The natural projection
![]() $S^X_*\subset S^X\rightarrow S^\Lambda $
given by mapping
$S^X_*\subset S^X\rightarrow S^\Lambda $
given by mapping
![]() $\eta =(\eta _x)_{x\in X}\in S^X$
to
$\eta =(\eta _x)_{x\in X}\in S^X$
to ![]() induces a natural injection
induces a natural injection
![]() $C(S^\Lambda )\hookrightarrow C(S^X_*)$
. From now on, we will identify
$C(S^\Lambda )\hookrightarrow C(S^X_*)$
. From now on, we will identify
![]() $C(S^\Lambda )$
with its image in
$C(S^\Lambda )$
with its image in
![]() $C(S^X_*)$
. Note that any
$C(S^X_*)$
. Note that any
![]() $f\in C(S^X_*)$
is a function in
$f\in C(S^X_*)$
is a function in
![]() $C(S^\Lambda )$
if and only if f as a function for
$C(S^\Lambda )$
if and only if f as a function for
![]() $\eta \in S^X_*$
depends only on
$\eta \in S^X_*$
depends only on
![]() $\eta |_{\Lambda }\in S^\Lambda $
. We call any such function a local function. We denote by
$\eta |_{\Lambda }\in S^\Lambda $
. We call any such function a local function. We denote by
![]() $C_{\mathrm {loc}}(S^X)$
the space of local functions, which is a subspace of both
$C_{\mathrm {loc}}(S^X)$
the space of local functions, which is a subspace of both
![]() $C(S^X)$
and
$C(S^X)$
and
![]() $C(S^X_*)$
. If the set of vertices of X is finite, then we simply have
$C(S^X_*)$
. If the set of vertices of X is finite, then we simply have
![]() $C_{\mathrm {loc}}(S^X)=C(S^X)=C(S^X_*)$
. Our methods are of interest predominantly for the case when X is an infinite locale.
$C_{\mathrm {loc}}(S^X)=C(S^X)=C(S^X_*)$
. Our methods are of interest predominantly for the case when X is an infinite locale.
2.2 Conserved quantities and irreducibly quantified interactions
In this subsection, we introduce the notion of conserved quantities, which are certain invariants of states preserved by the interaction. Using the conserved quantities, we will introduce the important notion for an interaction to be irreducibly quantified. In what follows, let S be a set of states with base state
![]() $*\in S$
, and we fix an interaction
$*\in S$
, and we fix an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
on S.
$\phi \colon S\times S\rightarrow S\times S$
on S.
Definition 2.9. A conserved quantity for the interaction
![]() $\phi $
is a function
$\phi $
is a function
![]() $\xi \colon S\rightarrow \mathbb {R}$
satisfying
$\xi \colon S\rightarrow \mathbb {R}$
satisfying
![]() $\xi (*)=0$
and
$\xi (*)=0$
and
for any
![]() $(s_1,s_2)\in S\times S$
and
$(s_1,s_2)\in S\times S$
and ![]() . We denote by
. We denote by
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
the
${\operatorname {\mathrm {Consv}}}^\phi (S)$
the
![]() $\mathbb {R}$
-linear subspace of
$\mathbb {R}$
-linear subspace of
![]() $\operatorname {\mathrm {Map}}(S,\mathbb {R})$
consisting of the conserved quantities for the interaction
$\operatorname {\mathrm {Map}}(S,\mathbb {R})$
consisting of the conserved quantities for the interaction
![]() $\phi $
. We let
$\phi $
. We let ![]() .
.
Examples of interactions and corresponding conserved quantities are given as follows.
Example 2.10.
-
1. Let
 $S=\{0,1,\ldots ,\kappa \}$
with base state
$S=\{0,1,\ldots ,\kappa \}$
with base state
 $*=0$
for some integer
$*=0$
for some integer
 $\kappa>0$
. For the multi-species exclusion process of Example 1.3 (2), we have
$\kappa>0$
. For the multi-species exclusion process of Example 1.3 (2), we have
 $c_\phi =\kappa $
, and the conserved quantities given by
$c_\phi =\kappa $
, and the conserved quantities given by
 $\xi ^{(i)}(s)=1$
if
$\xi ^{(i)}(s)=1$
if
 $s=i$
and
$s=i$
and
 $\xi ^{(i)}(s)=0$
otherwise for
$\xi ^{(i)}(s)=0$
otherwise for
 $i=1,\ldots ,\kappa $
give a basis of the
$i=1,\ldots ,\kappa $
give a basis of the
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
.
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. -
2. Let
 $S=\mathbb {N}$
or
$S=\mathbb {N}$
or
 $S=\{0,\ldots ,\kappa \}\subset \mathbb {N}$
for some integer
$S=\{0,\ldots ,\kappa \}\subset \mathbb {N}$
for some integer
 $\kappa>0$
. We let
$\kappa>0$
. We let
 $*=0$
be the base state. The map
$*=0$
be the base state. The map
 $\phi \colon S\times S\rightarrow S\times S$
defined by is an interaction. The stochastic process induced from this interaction when S is finite is the generalized exclusion process (see Figure 5). Note that for any
$\phi \colon S\times S\rightarrow S\times S$
defined by is an interaction. The stochastic process induced from this interaction when S is finite is the generalized exclusion process (see Figure 5). Note that for any
 $n>1$
in S, we have
$n>1$
in S, we have
 $\phi (n,0)=(n-1,1)$
; hence, for any conserved quantity
$\phi (n,0)=(n-1,1)$
; hence, for any conserved quantity
 $\xi $
, Equation (2) inductively gives This shows that
$\xi $
, Equation (2) inductively gives This shows that $$\begin{align*}\xi(n) = \xi(n) + \xi(0) = \xi(n-1) + \xi(1) = \xi(n-2) + 2\xi(1) = \cdots = n\xi(1). \end{align*}$$
$$\begin{align*}\xi(n) = \xi(n) + \xi(0) = \xi(n-1) + \xi(1) = \xi(n-2) + 2\xi(1) = \cdots = n\xi(1). \end{align*}$$
 $c_\phi =1$
, and the conserved quantity
$c_\phi =1$
, and the conserved quantity
 $\xi \colon S\rightarrow \mathbb {N}$
given by
$\xi \colon S\rightarrow \mathbb {N}$
given by
 $\xi (s)=s$
gives a basis of the one-dimensional
$\xi (s)=s$
gives a basis of the one-dimensional
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple in the sense of Definition 1.1 (2).
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple in the sense of Definition 1.1 (2).
-
3. Let
 $S=\mathbb {N}$
, or let
$S=\mathbb {N}$
, or let
 $S=\{0,\ldots ,\kappa \}\subset \mathbb {N}$
for some integer
$S=\{0,\ldots ,\kappa \}\subset \mathbb {N}$
for some integer
 $\kappa>1$
, with base state
$\kappa>1$
, with base state
 $*=0$
. The map
$*=0$
. The map
 $\phi \colon S\times S\rightarrow S\times S$
defined by is an interaction. We have
$\phi \colon S\times S\rightarrow S\times S$
defined by is an interaction. We have
 $c_\phi =2$
, and the functions
$c_\phi =2$
, and the functions
 $\xi ^{(1)}(s)=s$
and give a basis of the
$\xi ^{(1)}(s)=s$
and give a basis of the $$\begin{align*}\xi^{(2)}(s)= \begin{cases} 1 & s>0\\ 0 & s=0 \end{cases} \end{align*}$$
$$\begin{align*}\xi^{(2)}(s)= \begin{cases} 1 & s>0\\ 0 & s=0 \end{cases} \end{align*}$$
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is the lattice gas with energy. Intuitively, S represents the amount of energy on the vertex, with
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is the lattice gas with energy. Intuitively, S represents the amount of energy on the vertex, with
 $s=0$
representing the fact that there are no particles.
$s=0$
representing the fact that there are no particles.
-
4. For
 $S=\{-1,0,1\}$
with base state
$S=\{-1,0,1\}$
with base state
 $*=0$
, the map
$*=0$
, the map
 $\phi \colon S\times S\rightarrow S\times S$
defined by and
$\phi \colon S\times S\rightarrow S\times S$
defined by and $$ \begin{align*} \phi((0,0)) &= (-1,1), &\phi((-1,1)) &= (1,-1), &\phi((1,-1)) &= (0,0),& \end{align*} $$
$$ \begin{align*} \phi((0,0)) &= (-1,1), &\phi((-1,1)) &= (1,-1), &\phi((1,-1)) &= (0,0),& \end{align*} $$
 $\phi ((s_1,s_2))=(s_2,s_1)$
for
$\phi ((s_1,s_2))=(s_2,s_1)$
for
 $s_1,s_2\in S$
such that
$s_1,s_2\in S$
such that
 $s_1+s_2\neq 0$
is an interaction. We have
$s_1+s_2\neq 0$
is an interaction. We have
 $c_\phi =1$
, and the conserved quantity
$c_\phi =1$
, and the conserved quantity
 $\xi \colon S\rightarrow \mathbb {Z}$
given by
$\xi \colon S\rightarrow \mathbb {Z}$
given by
 $\xi (s)=s$
gives a basis of the
$\xi (s)=s$
gives a basis of the
 $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
 ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple in the sense of Definition 1.1 (2).
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. This interaction is simple in the sense of Definition 1.1 (2).
-
5. For
 $S=\{0,1\}$
with base state
$S=\{0,1\}$
with base state
 $*=0$
, the map
$*=0$
, the map
 $\phi \colon S\times S\rightarrow S\times S$
defined by for any
$\phi \colon S\times S\rightarrow S\times S$
defined by for any $$ \begin{align*} \phi((0,s)) &= (1,s), &\phi((1,s)) &= (0,s) \end{align*} $$
$$ \begin{align*} \phi((0,s)) &= (1,s), &\phi((1,s)) &= (0,s) \end{align*} $$
 $s\in S$
does not satisfy (10). However,
$s\in S$
does not satisfy (10). However,
 $(S^X,\Phi )$
is a symmetric directed graph for any locale X, and our theory applies also to this case (see also Remark 2.6). This case is known as the Glauber model. Since
$(S^X,\Phi )$
is a symmetric directed graph for any locale X, and our theory applies also to this case (see also Remark 2.6). This case is known as the Glauber model. Since
 $\phi (0,0)=(1,0)$
, Equation (12) gives
$\phi (0,0)=(1,0)$
, Equation (12) gives
 $\xi (1)=\xi (0)=0$
for any conserved quantity
$\xi (1)=\xi (0)=0$
for any conserved quantity
 $\xi $
; hence, we have
$\xi $
; hence, we have
 $c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)=0$
.
$c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)=0$
.
The exclusion process of Example 1.3 (1) is a special case of both the multi-species exclusion process and the generalized exclusion process, with the set of states given by
![]() $S=\{0,1\}$
.
$S=\{0,1\}$
.
Let X be a locale, and let
![]() $S^X_*$
be the configuration space with transition structure associated with our interaction. Note that if
$S^X_*$
be the configuration space with transition structure associated with our interaction. Note that if
![]() $\xi $
is a conserved quantity, then
$\xi $
is a conserved quantity, then
![]() $\xi $
defines a function
$\xi $
defines a function
![]() $\xi _X\colon S^X_*\rightarrow \mathbb {R}$
given by
$\xi _X\colon S^X_*\rightarrow \mathbb {R}$
given by
for any
![]() $\eta =(\eta _x)\in S^X_*$
. The sum is well defined since by definition,
$\eta =(\eta _x)\in S^X_*$
. The sum is well defined since by definition,
![]() $\eta _x=*$
outside a finite number of
$\eta _x=*$
outside a finite number of
![]() $x\in X$
.
$x\in X$
.

Figure 5 Generalized exclusion process.
Remark 2.11. The interactions in Example 2.10 have the following interpretations. See Remark 1.4 for the case of the multi-species exclusion process.
-
(2) For
 $s\in S$
in the process in Example 2.10 (2),
$s\in S$
in the process in Example 2.10 (2),
 $s=0$
describes the state where there are no particles at the vertex, and
$s=0$
describes the state where there are no particles at the vertex, and
 $s=k$
for an integer
$s=k$
for an integer
 $k>0$
the state where there are k indistinguishable particles at the vertex. Then for the conserved quantity given by
$k>0$
the state where there are k indistinguishable particles at the vertex. Then for the conserved quantity given by
 $\xi (s)=s$
for any
$\xi (s)=s$
for any
 $s\in S$
, the value
$s\in S$
, the value
 $\xi _X(\eta )$
for a configuration
$\xi _X(\eta )$
for a configuration
 $\eta \in S^X_*$
expresses the total number of particles in the configuration. If
$\eta \in S^X_*$
expresses the total number of particles in the configuration. If
 $S=\{0,\cdots ,\kappa \}$
for some integer
$S=\{0,\cdots ,\kappa \}$
for some integer
 $\kappa>0$
, then this process is called the generalized exclusion process, since at most
$\kappa>0$
, then this process is called the generalized exclusion process, since at most
 $\kappa $
particles are allowed to occupy the vertex. If
$\kappa $
particles are allowed to occupy the vertex. If
 $S=\mathbb {N}$
, then the process includes the trivial case where the particles evolve as independent random walks with no interactions between the particles, as described in [Reference Kipnis and Landim8, Chapter 1].
$S=\mathbb {N}$
, then the process includes the trivial case where the particles evolve as independent random walks with no interactions between the particles, as described in [Reference Kipnis and Landim8, Chapter 1]. -
(3) For
 $s\in S$
, the process in Example 2.10 (3),
$s\in S$
, the process in Example 2.10 (3),
 $s=0$
describes the state where there are no particles at the vertex, and
$s=0$
describes the state where there are no particles at the vertex, and
 $s=k$
for an integer
$s=k$
for an integer
 $k>0$
the state where there is a particle with energy k at the vertex. Then
$k>0$
the state where there is a particle with energy k at the vertex. Then
 $\xi _X^{(1)}(\eta )$
for a configuration
$\xi _X^{(1)}(\eta )$
for a configuration
 $\eta \in S^X_*$
expresses the total energy of the particles in the configuration, and
$\eta \in S^X_*$
expresses the total energy of the particles in the configuration, and
 $\xi _X^{(2)}(\eta )$
expresses the total number of particles in the configuration.
$\xi _X^{(2)}(\eta )$
expresses the total number of particles in the configuration. -
(4) For the process in Example 2.10 (4), s describes the spin of the particle at the vertex. Then for the conserved quantity given by
 $\xi (s)=s$
for any
$\xi (s)=s$
for any
 $s\in S$
, the value
$s\in S$
, the value
 $\xi _X(\eta )$
for a configuration
$\xi _X(\eta )$
for a configuration
 $\eta \in S^X_*$
expresses the total spin of the configuration.
$\eta \in S^X_*$
expresses the total spin of the configuration. -
(5) For
 $s\in S$
in the Glauber model in Example 2.10 (5), one interpretation is that
$s\in S$
in the Glauber model in Example 2.10 (5), one interpretation is that
 $s=0$
describes the state where there are no particles at the vertex, and
$s=0$
describes the state where there are no particles at the vertex, and
 $s=1$
describes the state where there is a single particle at the vertex. Since the interaction allows for the creation and annihilation of particles, there are no nontrivial conserved quantities. Another interpretation is that s describes the spin of the particle at each vertex.
$s=1$
describes the state where there is a single particle at the vertex. Since the interaction allows for the creation and annihilation of particles, there are no nontrivial conserved quantities. Another interpretation is that s describes the spin of the particle at each vertex.
Remark 2.12. The hydrodynamic limits for the generalized exclusion process have been studied by Kipnis-Landim-Olla [Reference Kipnis, Landim and Olla9]. See also [Reference Kipnis and Landim8, Chapter 7]. The case of lattice gas with energy has been studied by Nagahata [Reference Nagahara11], and the stochastic process induced from the interaction in Example 2.10 (4) was studied by Sasada [Reference Sasada15]. In all of the known cases, the underlying locale is taken to be the Euclidean lattice.
The important notion of irreducibly quantified is defined as follows.
Definition 2.13. We say that an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
is irreducibly quantified if for any finite locale
$\phi \colon S\times S\rightarrow S\times S$
is irreducibly quantified if for any finite locale
![]() $(X,E)$
and configurations
$(X,E)$
and configurations
![]() $\eta ,\eta '\in S^X$
satisfying
$\eta ,\eta '\in S^X$
satisfying
for all conserved quantities
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, there exists a finite path
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, there exists a finite path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
in
$\eta '$
in
![]() $S^X$
.
$S^X$
.
Remark 2.14. If we consider
![]() $S=\{0,1\}$
with base state
$S=\{0,1\}$
with base state
![]() $*=0$
and the interaction
$*=0$
and the interaction
![]() $\phi $
given by
$\phi $
given by
then a function
![]() $\xi \colon S\rightarrow \mathbb {R}$
satisfying
$\xi \colon S\rightarrow \mathbb {R}$
satisfying
![]() $\xi (0)=0$
and (12) would imply that
$\xi (0)=0$
and (12) would imply that
![]() $\xi (1)=0$
; hence,
$\xi (1)=0$
; hence,
![]() $\xi \equiv 0$
. In fact, this interaction is not irreducibly quantified. In order to deal with such a model, it may be necessary to consider conserved quantities with values in
$\xi \equiv 0$
. In fact, this interaction is not irreducibly quantified. In order to deal with such a model, it may be necessary to consider conserved quantities with values in
![]() $\mathbb {Z}/2\mathbb {Z}$
.
$\mathbb {Z}/2\mathbb {Z}$
.
The remainder of this section is devoted to the proof of Proposition 2.19, which asserts that the interactions given in Example 2.10 are all irreducibly quantified. For the proof, we first introduce the notion of exchangeability.
Definition 2.15. We say that an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
is exchangeable if for any
$\phi \colon S\times S\rightarrow S\times S$
is exchangeable if for any
![]() $(s_1,s_2)\in S\times S$
, a suitable composition of maps
$(s_1,s_2)\in S\times S$
, a suitable composition of maps
![]() $\phi $
and
$\phi $
and
![]() $\bar \phi $
such that
$\bar \phi $
such that
![]() $(s_1,s_2)$
maps to
$(s_1,s_2)$
maps to
![]() $(s_2,s_1)\in S\times S$
. Here, if we write
$(s_2,s_1)\in S\times S$
. Here, if we write
![]() $\phi (s_1,s_2)=(\phi _1(s_1,s_2),\phi _2(s_1,s_2))\in S\times S$
, then we let
$\phi (s_1,s_2)=(\phi _1(s_1,s_2),\phi _2(s_1,s_2))\in S\times S$
, then we let ![]() for any
for any
![]() $(s_1,s_2)\in S\times S$
. In other words,
$(s_1,s_2)\in S\times S$
. In other words, ![]() , where
, where
![]() $\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
$\hat \imath \colon S\times S\rightarrow S\times S$
is the bijection obtained by exchanging the components of
![]() $S\times S$
.
$S\times S$
.
It is straightforward to check that the interactions in Example 2.10 are all exchangeable. Since
![]() $\bar \phi \circ \phi (s_1,s_2)=(s_1,s_2)$
if
$\bar \phi \circ \phi (s_1,s_2)=(s_1,s_2)$
if
![]() $\phi (s_1,s_2)\neq (s_1,s_2)$
, the composition of Definition 2.15 is necessarily of the form
$\phi (s_1,s_2)\neq (s_1,s_2)$
, the composition of Definition 2.15 is necessarily of the form
![]() $\phi ^n$
or
$\phi ^n$
or
![]() $\bar \phi ^n$
for some integer
$\bar \phi ^n$
for some integer
![]() $n\geq 0$
. In what follows, consider a system
$n\geq 0$
. In what follows, consider a system
![]() $(X,S,\phi )$
and the associated configuration space
$(X,S,\phi )$
and the associated configuration space
![]() $S^X_*$
with transition structure. We first prepare some notations.
$S^X_*$
with transition structure. We first prepare some notations.
Definition 2.16. Let
![]() $\eta $
be a configuration in
$\eta $
be a configuration in
![]() $S^X_*$
, and let
$S^X_*$
, and let
![]() $x,y$
be vertices in X.
$x,y$
be vertices in X.
-
1. We define
 $\eta ^{x,y}\in S^X_*$
to be the configuration whose component outside
$\eta ^{x,y}\in S^X_*$
to be the configuration whose component outside
 $x,y\in X$
coincides with that of
$x,y\in X$
coincides with that of
 $\eta $
, and the x and y components are given by
$\eta $
, and the x and y components are given by  and
and  .
. -
2. We define
 to be the configuration whose component outside
to be the configuration whose component outside
 $x,y\in X$
coincides with that of
$x,y\in X$
coincides with that of
 $\eta $
, and the x and y components are given by
$\eta $
, and the x and y components are given by  and
and  , where
, where
 $\phi (\eta _x,\eta _y)=(\phi _1(\eta _x,\eta _y),\phi _2(\eta _x,\eta _y))\in S\times S$
for the interaction
$\phi (\eta _x,\eta _y)=(\phi _1(\eta _x,\eta _y),\phi _2(\eta _x,\eta _y))\in S\times S$
for the interaction
 $\phi $
on S.
$\phi $
on S.
A path in
![]() $S^X_*$
is a sequence of transitions, and a transition is induced by an interaction on some edge of the locale. Hence, for a sequence of edges
$S^X_*$
is a sequence of transitions, and a transition is induced by an interaction on some edge of the locale. Hence, for a sequence of edges
![]() $\boldsymbol {e}=(e^1,\ldots ,e^N)$
in E and
$\boldsymbol {e}=(e^1,\ldots ,e^N)$
in E and
![]() $\eta \in S^X_*$
, if we let
$\eta \in S^X_*$
, if we let ![]() and
and ![]() for
for
![]() $i=1,\ldots ,N$
, then
$i=1,\ldots ,N$
, then
![]() $\varphi ^i=(\eta ^i,\eta ^{i+1})$
is a transition and
$\varphi ^i=(\eta ^i,\eta ^{i+1})$
is a transition and ![]() gives a path from
gives a path from
![]() $\eta $
to
$\eta $
to ![]() in
in
![]() $S^X_*$
. We call this path
$S^X_*$
. We call this path
![]() $\vec \gamma _\eta ^{\boldsymbol {e}}$
the path with origin
$\vec \gamma _\eta ^{\boldsymbol {e}}$
the path with origin
![]() $\eta $
induced by
$\eta $
induced by
![]() $\boldsymbol {e}$
, or a path obtained by applying the edges
$\boldsymbol {e}$
, or a path obtained by applying the edges
![]() $\boldsymbol {e}$
to
$\boldsymbol {e}$
to
![]() $\eta $
.
$\eta $
.
We prove some existences of paths between certain configurations, when the interaction is exchangeable.
Lemma 2.17. If an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
is exchangeable, then for any configuration
$\phi \colon S\times S\rightarrow S\times S$
is exchangeable, then for any configuration
![]() $\eta \in S^X_*$
and vertices
$\eta \in S^X_*$
and vertices
![]() $x,y\in X$
, there exists a path
$x,y\in X$
, there exists a path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta ^{x,y}$
in
$\eta ^{x,y}$
in
![]() $S^X_*$
.
$S^X_*$
.
Proof. Since X is connected, there exists a path
![]() $\vec p=(e^1,\ldots ,e^N)$
from x to y. Note that by definition,
$\vec p=(e^1,\ldots ,e^N)$
from x to y. Note that by definition,
![]() $x=o(e^1)$
and
$x=o(e^1)$
and
![]() $y=t(e^N)$
. Since
$y=t(e^N)$
. Since
![]() $\phi $
is exchangeable, applying
$\phi $
is exchangeable, applying
![]() $e^1$
or
$e^1$
or
![]() $\bar e^1$
sufficiently many times to
$\bar e^1$
sufficiently many times to
![]() $\eta $
, we obtain a path from
$\eta $
, we obtain a path from
![]() $\eta $
to
$\eta $
to
![]() $\eta ^{o(e^1),t(e^1)}$
. Repeating this process for
$\eta ^{o(e^1),t(e^1)}$
. Repeating this process for
![]() $e^2,\ldots ,e^{N}$
, we obtain a path
$e^2,\ldots ,e^{N}$
, we obtain a path
![]() $\vec \gamma _1$
from
$\vec \gamma _1$
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
, where
$\eta '$
, where
![]() $\eta '$
is such that the components of
$\eta '$
is such that the components of
![]() $\eta '$
coincides with that of
$\eta '$
coincides with that of
![]() $\eta $
outside the vertices appearing in the edges
$\eta $
outside the vertices appearing in the edges
![]() $e^1,\ldots ,e^{N}$
,
$e^1,\ldots ,e^{N}$
,
![]() $\eta ^{\prime }_{o(e^i)}=\eta _{t(e^i)}$
for
$\eta ^{\prime }_{o(e^i)}=\eta _{t(e^i)}$
for
![]() $i=1,\ldots , N-1$
, and
$i=1,\ldots , N-1$
, and
![]() $\eta ^{\prime }_{y}=\eta _x$
. Then, reversing the above process, first by applying
$\eta ^{\prime }_{y}=\eta _x$
. Then, reversing the above process, first by applying
![]() $e^{N-1}$
or
$e^{N-1}$
or
![]() $\bar e^{N-1}$
sufficiently many times to
$\bar e^{N-1}$
sufficiently many times to
![]() $\eta '$
, we obtain a path from
$\eta '$
, we obtain a path from
![]() $\eta '$
to
$\eta '$
to
![]() $(\eta ')^{o(e^{N-1}),t(e^{N-1})}$
. Repeating this process for
$(\eta ')^{o(e^{N-1}),t(e^{N-1})}$
. Repeating this process for
![]() $e^{N-2},\ldots ,e^{1}$
, we see that we obtain a path
$e^{N-2},\ldots ,e^{1}$
, we see that we obtain a path
![]() $\vec \gamma _2$
from
$\vec \gamma _2$
from
![]() $\eta '$
to
$\eta '$
to
![]() $\eta ^{x.y}$
. Then the composition
$\eta ^{x.y}$
. Then the composition ![]() gives a path from
gives a path from
![]() $\eta $
to
$\eta $
to
![]() $\eta ^{x,y}$
in
$\eta ^{x,y}$
in
![]() $S^X_*$
as desired.
$S^X_*$
as desired.
Lemma 2.18. If an interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
is exchangeable, then for any configuration
$\phi \colon S\times S\rightarrow S\times S$
is exchangeable, then for any configuration
![]() $\eta \in S^X_*$
and vertices
$\eta \in S^X_*$
and vertices
![]() $x,y\in X$
, there exists a path
$x,y\in X$
, there exists a path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to ![]() in
in
![]() $S^X_*$
.
$S^X_*$
.
Proof. Again, since X is connected, there exists a path
![]() $\vec p=(e^1,\ldots ,e^N)$
from
$\vec p=(e^1,\ldots ,e^N)$
from
![]() $x=o(e^1)$
to
$x=o(e^1)$
to
![]() $y=t(e^N)$
. If we let
$y=t(e^N)$
. If we let
![]() $x'=o(e^N)$
, then
$x'=o(e^N)$
, then
![]() $x'$
is a vertex connected to y by the edge
$x'$
is a vertex connected to y by the edge
![]() $e^N$
. Then by construction, if we let
$e^N$
. Then by construction, if we let ![]() , then
, then
![]() $\eta '$
is a configuration whose component outside
$\eta '$
is a configuration whose component outside
![]() $x,x',y\in X$
coincides with that of
$x,x',y\in X$
coincides with that of
![]() $\eta $
, and the
$\eta $
, and the
![]() $x, x'$
and y components are given by
$x, x'$
and y components are given by
![]() $\eta ^{\prime }_x=\eta _{x'}$
,
$\eta ^{\prime }_x=\eta _{x'}$
,
![]() $\eta ^{\prime }_{x'}=\phi _1(\eta _x,\eta _y)$
, and
$\eta ^{\prime }_{x'}=\phi _1(\eta _x,\eta _y)$
, and
![]() $\eta ^{\prime }_y = \phi _2(\eta _x,\eta _y)$
. Thus, we have
$\eta ^{\prime }_y = \phi _2(\eta _x,\eta _y)$
. Thus, we have ![]() . By Lemma 2.17, there exists a path
. By Lemma 2.17, there exists a path
![]() $\vec \gamma _1$
from
$\vec \gamma _1$
from
![]() $\eta $
to
$\eta $
to
![]() $\eta ^{x,x'}$
and a path
$\eta ^{x,x'}$
and a path
![]() $\vec \gamma _2$
from
$\vec \gamma _2$
from
![]() $\eta '$
to
$\eta '$
to ![]() in
in
![]() $S^X_*$
. If we denote by
$S^X_*$
. If we denote by
![]() $\vec \varphi $
the path given by a single transition
$\vec \varphi $
the path given by a single transition
![]() $\varphi =(\eta ^{x,x'},\eta ')$
, then the composition
$\varphi =(\eta ^{x,x'},\eta ')$
, then the composition ![]() gives a path from
gives a path from
![]() $\eta $
to
$\eta $
to ![]() in
in
![]() $S^X_*$
as desired.
$S^X_*$
as desired.
Using the above results, we may prove that various interactions are irreducibly quantified.
Proposition 2.19. The interactions of Example 2.10 are all irreducibly quantified.
Proof. By Example 2.10, we see that
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
are finite dimensional. Let X be a locale and let
${\operatorname {\mathrm {Consv}}}^\phi (S)$
are finite dimensional. Let X be a locale and let
![]() $\eta ,\eta '\in S^X_*$
such that
$\eta ,\eta '\in S^X_*$
such that
![]() $\xi _X(\eta )=\xi _X(\eta ')$
for any conserved quantity
$\xi _X(\eta )=\xi _X(\eta ')$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. We prove the existence of a path
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. We prove the existence of a path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
by induction on the cardinality of the set
$\eta '$
by induction on the cardinality of the set ![]() . Note that
. Note that
![]() $\Delta (\eta ,\eta ')$
is finite since the supports of
$\Delta (\eta ,\eta ')$
is finite since the supports of
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
are finite. If
$\eta '$
are finite. If
![]() $|\Delta (\eta ,\eta ')|=0$
, then
$|\Delta (\eta ,\eta ')|=0$
, then
![]() $\eta =\eta '$
, and there is nothing to prove. Suppose
$\eta =\eta '$
, and there is nothing to prove. Suppose
![]() $|\Delta (\eta ,\eta ')|>0$
and that the assertion is proved for
$|\Delta (\eta ,\eta ')|>0$
and that the assertion is proved for
![]() $\eta ",\eta '$
, where
$\eta ",\eta '$
, where
![]() $\eta "$
is any configuration in
$\eta "$
is any configuration in
![]() $S^X_*$
such that
$S^X_*$
such that
![]() $|\Delta (\eta ",\eta ')|<|\Delta (\eta ,\eta ')|$
and
$|\Delta (\eta ",\eta ')|<|\Delta (\eta ,\eta ')|$
and
![]() $\xi _X(\eta ")=\xi _X(\eta ')$
for any conserved quantity
$\xi _X(\eta ")=\xi _X(\eta ')$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
.
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
.
-
1. Consider the case of the multi-species exclusion process of Example 2.10 (1) with conserved quantity
 $\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
. Let
$\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
. Let
 $x\in \Delta (\eta ,\eta ')$
. If we let
$x\in \Delta (\eta ,\eta ')$
. If we let
 $\eta _x=i\in S$
, then since
$\eta _x=i\in S$
, then since
 $\xi ^{(i)}_X(\eta )=\xi ^{(i)}_X(\eta ')$
, there exists
$\xi ^{(i)}_X(\eta )=\xi ^{(i)}_X(\eta ')$
, there exists
 $y\in \Delta (\eta ,\eta ')$
such that
$y\in \Delta (\eta ,\eta ')$
such that
 $\eta _y^{\prime }=i$
. By Lemma 2.17, there exists a path
$\eta _y^{\prime }=i$
. By Lemma 2.17, there exists a path
 $\vec \gamma _1$
from
$\vec \gamma _1$
from
 $\eta $
to
$\eta $
to
 $\eta ^{x,y}$
. Note that
$\eta ^{x,y}$
. Note that
 $\eta ^{x,y}$
coincides with
$\eta ^{x,y}$
coincides with
 $\eta $
outside
$\eta $
outside
 $x,y$
, and we have
$x,y$
, and we have
 $\eta ^{x,y}_y=\eta _x=i=\eta _y^{\prime }$
, which implies that
$\eta ^{x,y}_y=\eta _x=i=\eta _y^{\prime }$
, which implies that
 $\xi _X(\eta )=\xi _X(\eta ^{x,y})=\xi _X(\eta ')$
for any conserved quantity and
$\xi _X(\eta )=\xi _X(\eta ^{x,y})=\xi _X(\eta ')$
for any conserved quantity and
 $|\Delta (\eta ^{x,y},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
$|\Delta (\eta ^{x,y},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
 $\vec \gamma _2$
from
$\vec \gamma _2$
from
 $\eta ^{x,y}$
to
$\eta ^{x,y}$
to
 $\eta '$
in
$\eta '$
in
 $S^X_*$
. Our assertion is proved by taking
$S^X_*$
. Our assertion is proved by taking  .
. -
2. Consider the case of the generalized exclusion process of Example 2.10 (2) with conserved quantity
 $\xi $
given by
$\xi $
given by
 $\xi (s)=s$
. Again, let
$\xi (s)=s$
. Again, let
 $x\in \Delta (\eta ,\eta ')$
such that
$x\in \Delta (\eta ,\eta ')$
such that
 $\eta _x>\eta ^{\prime }_x$
. Since
$\eta _x>\eta ^{\prime }_x$
. Since
 $\xi _X(\eta )=\xi _X(\eta ')$
, there exists
$\xi _X(\eta )=\xi _X(\eta ')$
, there exists
 $y\in \Delta (\eta ,\eta ')$
such that
$y\in \Delta (\eta ,\eta ')$
such that
 $\eta _y<\eta ^{\prime }_y$
. Let
$\eta _y<\eta ^{\prime }_y$
. Let  , and let
, and let
 $\eta ^0=\eta $
and
$\eta ^0=\eta $
and  for
for
 $i=1,\ldots ,M$
. By Lemma 2.18, there exists a path
$i=1,\ldots ,M$
. By Lemma 2.18, there exists a path
 $\vec \gamma _i$
from
$\vec \gamma _i$
from
 $\eta ^{i-1}$
to
$\eta ^{i-1}$
to
 $\eta ^{i}$
in
$\eta ^{i}$
in
 $S^X_*$
for
$S^X_*$
for
 $1<i<M$
. We have
$1<i<M$
. We have
 $\xi _X(\eta ^M)=\xi _X(\eta )=\xi _X(\eta ')$
, and since
$\xi _X(\eta ^M)=\xi _X(\eta )=\xi _X(\eta ')$
, and since
 $\eta ^M_x=\eta _x-M$
and
$\eta ^M_x=\eta _x-M$
and
 $\eta ^M_y=\eta _y+M$
, we have either
$\eta ^M_y=\eta _y+M$
, we have either
 $\eta ^M_x=\eta ^{\prime }_x$
or
$\eta ^M_x=\eta ^{\prime }_x$
or
 $\eta ^M_y=\eta ^{\prime }_y$
. This shows that
$\eta ^M_y=\eta ^{\prime }_y$
. This shows that
 $|\Delta (\eta ^{M},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
$|\Delta (\eta ^{M},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
 $\vec \gamma '$
from
$\vec \gamma '$
from
 $\eta ^{M}$
to
$\eta ^{M}$
to
 $\eta '$
in
$\eta '$
in
 $S^X_*$
. Our assertion is proved by taking
$S^X_*$
. Our assertion is proved by taking  .
. -
3. Consider the case of the lattice gas with energy of Example 2.10 (3) with conserved quantity
 $\xi ^{(1)}$
and
$\xi ^{(1)}$
and
 $\xi ^{(2)}$
. Suppose there exists
$\xi ^{(2)}$
. Suppose there exists
 $x\in \Delta (\eta ,\eta ')$
such that
$x\in \Delta (\eta ,\eta ')$
such that
 $\eta ^{\prime }_x=0$
. Then, since
$\eta ^{\prime }_x=0$
. Then, since
 $\xi _X^{(2)}(\eta )=\xi _X^{(2)}(\eta ')$
, there exists
$\xi _X^{(2)}(\eta )=\xi _X^{(2)}(\eta ')$
, there exists
 $y\in \Delta (\eta ,\eta ')$
such that
$y\in \Delta (\eta ,\eta ')$
such that
 $\eta _y=0$
. Then
$\eta _y=0$
. Then
 $\eta ^{x,y}$
satisfies
$\eta ^{x,y}$
satisfies
 $\xi _X(\eta ^{x,y})=\xi _X(\eta ')$
for any conserved quantity
$\xi _X(\eta ^{x,y})=\xi _X(\eta ')$
for any conserved quantity
 $\xi $
, and
$\xi $
, and
 $|\Delta (\eta ^{x,y},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
$|\Delta (\eta ^{x,y},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
 $\vec \gamma _2$
from
$\vec \gamma _2$
from
 $\eta ^{x,y}$
to
$\eta ^{x,y}$
to
 $\eta '$
in
$\eta '$
in
 $S^X_*$
. If we let
$S^X_*$
. If we let
 $\vec \gamma _1$
be the path from
$\vec \gamma _1$
be the path from
 $\eta $
to
$\eta $
to
 $\eta ^{x,y}$
given in Lemma 2.17, then
$\eta ^{x,y}$
given in Lemma 2.17, then  satisfies the desired property. Otherwise, we have
satisfies the desired property. Otherwise, we have
 $\eta _x\neq 0$
and
$\eta _x\neq 0$
and
 $\eta ^{\prime }_x\neq 0$
for any
$\eta ^{\prime }_x\neq 0$
for any
 $x\in \Delta (\eta ,\eta ')$
. Since
$x\in \Delta (\eta ,\eta ')$
. Since
 $\xi _X^{(1)}(\eta )=\xi _X^{(1)}(\eta ')$
, there exists
$\xi _X^{(1)}(\eta )=\xi _X^{(1)}(\eta ')$
, there exists
 $x,y\in \Delta (\eta ,\eta ')$
such that
$x,y\in \Delta (\eta ,\eta ')$
such that
 $\eta _x>\eta ^{\prime }_x$
and
$\eta _x>\eta ^{\prime }_x$
and
 $\eta _y<\eta ^{\prime }_y$
. As in (2), let
$\eta _y<\eta ^{\prime }_y$
. As in (2), let  , and let
, and let
 $\eta ^0=\eta $
and
$\eta ^0=\eta $
and  for
for
 $i=1,\ldots ,M$
. By Lemma 2.18, there exists a path
$i=1,\ldots ,M$
. By Lemma 2.18, there exists a path
 $\vec \gamma _i$
from
$\vec \gamma _i$
from
 $\eta ^{i-1}$
to
$\eta ^{i-1}$
to
 $\eta ^{i}$
in
$\eta ^{i}$
in
 $S^X_*$
for
$S^X_*$
for
 $1<i<M$
. We have
$1<i<M$
. We have
 $\xi _X(\eta ^M)=\xi _X(\eta )=\xi _X(\eta ')$
and either
$\xi _X(\eta ^M)=\xi _X(\eta )=\xi _X(\eta ')$
and either
 $s^M_x=\eta ^{\prime }_x$
or
$s^M_x=\eta ^{\prime }_x$
or
 $s^M_y=\eta ^{\prime }_y$
, which shows that
$s^M_y=\eta ^{\prime }_y$
, which shows that
 $|\Delta (\eta ^{M},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
$|\Delta (\eta ^{M},\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
 $\vec \gamma '$
from
$\vec \gamma '$
from
 $\eta ^{M}$
to
$\eta ^{M}$
to
 $\eta '$
in
$\eta '$
in
 $S^X_*$
. Our assertion is proved by taking
$S^X_*$
. Our assertion is proved by taking  .
. -
4. The case of Example 2.10 (4) is proved in a similar fashion as that of (1), but by first using the interaction
 $\phi ((0,0))=(1,-1)$
and
$\phi ((0,0))=(1,-1)$
and
 $\phi ((-1,1))=(0,0)$
to equalize the number of vertices whose states are at
$\phi ((-1,1))=(0,0)$
to equalize the number of vertices whose states are at
 $+1$
and
$+1$
and
 $-1$
.
$-1$
. -
5. Consider the Glauber model of Example 2.10 (5). Since in this case, the only conserved quantity is the zero map, the condition for the conserved quantity is always satisfied. Let
 $x\in \Delta (\eta ,\eta ')$
. If we let
$x\in \Delta (\eta ,\eta ')$
. If we let
 $e\in E$
be any edge such that
$e\in E$
be any edge such that
 $o(e)=x$
, then
$o(e)=x$
, then
 $\eta ^e$
coincides with
$\eta ^e$
coincides with
 $\eta $
outside x and we have
$\eta $
outside x and we have
 $\eta ^e_x=\eta ^{\prime }_x$
. This shows we have
$\eta ^e_x=\eta ^{\prime }_x$
. This shows we have
 $|\Delta (\eta ^e,\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
$|\Delta (\eta ^e,\eta ')|<|\Delta (\eta ,\eta ')|$
. Hence, by the induction hypothesis, there exists a path
 $\vec \gamma '$
from
$\vec \gamma '$
from
 $\eta ^e$
to
$\eta ^e$
to
 $\eta '$
in
$\eta '$
in
 $S^X_*$
. Our assertion is proved by taking
$S^X_*$
. Our assertion is proved by taking  , where
, where
 $\vec \varphi $
is the path given by the transition
$\vec \varphi $
is the path given by the transition
 $\varphi =(\eta ,\eta ^e)$
.
$\varphi =(\eta ,\eta ^e)$
.
2.3 The cohomology of the configuration space
In this subsection, we consider the cohomology as graphs of a configuration space with transition structure. See Appendix A for generalities concerning the homology and cohomology of graphs. Let
![]() $(X,E)$
be a locale, and we let
$(X,E)$
be a locale, and we let
![]() $S^X_*=(S^X_*,\Phi _*)$
be the configuration space with transition structure associated to a system
$S^X_*=(S^X_*,\Phi _*)$
be the configuration space with transition structure associated to a system
![]() $(X,S,\phi )$
. For any
$(X,S,\phi )$
. For any
![]() $\varphi =(o(\varphi ),t(\varphi ))\in \Phi _*$
, we let
$\varphi =(o(\varphi ),t(\varphi ))\in \Phi _*$
, we let ![]() , which we call the opposite transition.
, which we call the opposite transition.
The cohomology defined in Definition A.1 of a configuration space with transition structure is given as follows.
Definition 2.20. Let
![]() $(X,S,\phi )$
be a system. For the graph
$(X,S,\phi )$
be a system. For the graph
![]() $(S^X_*,\Phi _*)$
, let
$(S^X_*,\Phi _*)$
, let
where ![]() . We define the differential
. We define the differential
by ![]() for any
for any
![]() $\varphi =(\eta ,\eta ^e)\in \Phi _*$
. The cohomology of
$\varphi =(\eta ,\eta ^e)\in \Phi _*$
. The cohomology of
![]() $(S^X_*,\Phi _*)$
is given by
$(S^X_*,\Phi _*)$
is given by
and
![]() $H^m(S^X_*)=\{0\}$
for any
$H^m(S^X_*)=\{0\}$
for any
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $m\neq 0,1$
.
$m\neq 0,1$
.
We will often call an element in
![]() $C^1(S^X_*)$
a form. We next show that the differential (15) coincides with the differential given in §1.2. By the definition of
$C^1(S^X_*)$
a form. We next show that the differential (15) coincides with the differential given in §1.2. By the definition of
![]() $\Phi _*$
in (11), we have a surjection
$\Phi _*$
in (11), we have a surjection
![]() $E\times S^X_*\rightarrow \Phi _*$
. This shows that we have natural injections
$E\times S^X_*\rightarrow \Phi _*$
. This shows that we have natural injections
Hence, we may view a form
![]() $\omega \in C^1(S^X_*)$
as a family of functions
$\omega \in C^1(S^X_*)$
as a family of functions
![]() $\omega = (\omega _e)_{e\in E}$
through the identification
$\omega = (\omega _e)_{e\in E}$
through the identification
where
![]() $\omega _e\colon S^X_*\rightarrow \mathbb {R}$
is the function defined as
$\omega _e\colon S^X_*\rightarrow \mathbb {R}$
is the function defined as
Conversely, any family of functions
![]() $(\omega _e) \in \prod _{e\in E} C(S^X_*)$
comes from an element
$(\omega _e) \in \prod _{e\in E} C(S^X_*)$
comes from an element
![]() $\omega $
in
$\omega $
in
![]() $C^1(S^X_*)$
if and only if
$C^1(S^X_*)$
if and only if
![]() $\omega _e(\eta )=\omega _{e'}(\eta )$
if
$\omega _e(\eta )=\omega _{e'}(\eta )$
if
![]() $\eta ^e=\eta ^{e'}$
,
$\eta ^e=\eta ^{e'}$
,
![]() $\omega _e(\eta )=0$
if
$\omega _e(\eta )=0$
if
![]() $\eta ^e=\eta $
, and
$\eta ^e=\eta $
, and
![]() $\omega _e(\eta )=-\omega _{\bar e}(\eta ^e)$
for any
$\omega _e(\eta )=-\omega _{\bar e}(\eta ^e)$
for any
![]() $(e,\eta )\in E\times S^X_*$
. For any
$(e,\eta )\in E\times S^X_*$
. For any
![]() $f\in C(S^X_*)$
, if we view
$f\in C(S^X_*)$
, if we view
![]() $\partial f$
as an element
$\partial f$
as an element
![]() $\partial f = ((\partial f)_e)_{e\in E}$
in
$\partial f = ((\partial f)_e)_{e\in E}$
in
![]() $\prod _{e\in E}C(S^X_*)$
, then we see that
$\prod _{e\in E}C(S^X_*)$
, then we see that
![]() $(\partial f)_e$
is a function satisfying
$(\partial f)_e$
is a function satisfying
![]() $(\partial f)_e(\eta )= f(\eta ^e) - f(\eta )$
for any
$(\partial f)_e(\eta )= f(\eta ^e) - f(\eta )$
for any
![]() $\eta \in S^X_*$
. If we define the function
$\eta \in S^X_*$
. If we define the function
![]() $\nabla _e f\in \operatorname {\mathrm {Map}}(S^X_*,\mathbb {R})$
for any
$\nabla _e f\in \operatorname {\mathrm {Map}}(S^X_*,\mathbb {R})$
for any
![]() $e\in E$
by
$e\in E$
by
for any
![]() $\eta \in S^X_*$
, then we have
$\eta \in S^X_*$
, then we have
![]() $\partial f = (\nabla _e f)_{e\in E}$
by construction. Hence, our differential coincides with the differential
$\partial f = (\nabla _e f)_{e\in E}$
by construction. Hence, our differential coincides with the differential
![]() $\partial $
of §1.2. In what follows, we will often identify a form
$\partial $
of §1.2. In what follows, we will often identify a form
![]() $\omega \in C^1(S^X_*)$
with its representation
$\omega \in C^1(S^X_*)$
with its representation
![]() $\omega = (\omega _e)_{e\in E}$
in
$\omega = (\omega _e)_{e\in E}$
in
![]() $\prod _{e\in E}C(S^X_*)$
.
$\prod _{e\in E}C(S^X_*)$
.
We next use the conserved quantities of §2.2 to investigate the cohomology
![]() $H^0(S^X_*)$
. We say that a function
$H^0(S^X_*)$
. We say that a function
![]() $f\in C(S^X_*)$
is horizontal, if
$f\in C(S^X_*)$
is horizontal, if
![]() $\partial f=0$
. We have the following.
$\partial f=0$
. We have the following.
Lemma 2.21. Suppose
![]() $f\in C(S^X_*)$
is horizontal. Then if
$f\in C(S^X_*)$
is horizontal. Then if
![]() $\eta ,\eta '\in S^X_*$
are in the same connected components of
$\eta ,\eta '\in S^X_*$
are in the same connected components of
![]() $S^X_*$
, then we have
$S^X_*$
, then we have
![]() $f(\eta )=f(\eta ')$
. In particular, the function f is constant on the connected components of
$f(\eta )=f(\eta ')$
. In particular, the function f is constant on the connected components of
![]() $S^X_*$
.
$S^X_*$
.
Proof. This follows from Lemma A.2, applied to the graph
![]() $(S^X_*,\Phi _*)$
.
$(S^X_*,\Phi _*)$
.
Let
![]() $\xi $
be a conserved quantity in
$\xi $
be a conserved quantity in
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. If we associate to
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. If we associate to
![]() $\xi $
the function
$\xi $
the function
![]() $\xi _X\colon S^X_*\rightarrow \mathbb {R}$
of (13), then this induces a homomorphism of
$\xi _X\colon S^X_*\rightarrow \mathbb {R}$
of (13), then this induces a homomorphism of
![]() $\mathbb {R}$
-linear spaces
$\mathbb {R}$
-linear spaces
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)\rightarrow C(S^X_*)$
. This homomorphism is injective since for a fixed
${\operatorname {\mathrm {Consv}}}^\phi (S)\rightarrow C(S^X_*)$
. This homomorphism is injective since for a fixed
![]() $x\in X$
, if we let
$x\in X$
, if we let
![]() $\eta \in S^X_*$
be the configuration with s in the x-component and at base state in the other components, then we have
$\eta \in S^X_*$
be the configuration with s in the x-component and at base state in the other components, then we have
![]() $\xi (s)=\xi _X(\eta )$
; hence,
$\xi (s)=\xi _X(\eta )$
; hence,
![]() $\xi _X=\xi ^{\prime }_X$
implies that
$\xi _X=\xi ^{\prime }_X$
implies that
![]() $\xi =\xi '$
for any
$\xi =\xi '$
for any
![]() $\xi ,\xi '\in {\operatorname {\mathrm {Consv}}}^\phi (S)$
.
$\xi ,\xi '\in {\operatorname {\mathrm {Consv}}}^\phi (S)$
.
Lemma 2.22. Let
![]() $\xi $
be a conserved quantity for the interaction
$\xi $
be a conserved quantity for the interaction
![]() $\phi $
. Then the function
$\phi $
. Then the function
![]() $\xi _X\in C(S^X_*)$
defined by (13) is horizontal. In particular,
$\xi _X\in C(S^X_*)$
defined by (13) is horizontal. In particular,
![]() $\xi _X$
defines a class in
$\xi _X$
defines a class in
![]() $H^0(S^X_*)$
.
$H^0(S^X_*)$
.
Proof. For any
![]() $\varphi =(\eta ,\eta ^e)\in \Phi _*$
, we have
$\varphi =(\eta ,\eta ^e)\in \Phi _*$
, we have
If we let
![]() $e=(x_1, x_2)\in E\subset X\times X$
, then by definition of
$e=(x_1, x_2)\in E\subset X\times X$
, then by definition of
![]() $\phi _e$
given in Lemma 2.5, we have
$\phi _e$
given in Lemma 2.5, we have
![]() $(\eta ^e_{x_1}, \eta ^e_{x_2})=\phi (\eta _{x_1}, \eta _{x_2})$
and
$(\eta ^e_{x_1}, \eta ^e_{x_2})=\phi (\eta _{x_1}, \eta _{x_2})$
and
![]() $\eta ^e_x=\eta _x$
for
$\eta ^e_x=\eta _x$
for
![]() $x\neq x_1,x_2$
. This shows that
$x\neq x_1,x_2$
. This shows that
as desired, where the last equality follows from (2).
Lemma 2.22 shows that (13) induces an injective homomorphism of
![]() $\mathbb {R}$
-linear spaces
$\mathbb {R}$
-linear spaces
Remark 2.23. We remark that
![]() $H^0(S^X_*)$
is in general very large, containing the
$H^0(S^X_*)$
is in general very large, containing the
![]() $\mathbb {R}$
-algebra generated by the image of
$\mathbb {R}$
-algebra generated by the image of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. For example, the function
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. For example, the function
![]() $(\xi _X)^2$
on
$(\xi _X)^2$
on
![]() $S^X_*$
for any conserved quantity
$S^X_*$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
also defines an element of
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
also defines an element of
![]() $H^0(S^X_*)$
. The property (12) ensures that
$H^0(S^X_*)$
. The property (12) ensures that
![]() $\xi _X$
is an extensive quantity (i.e., additive with respect to the size of the system). We will prove in Theorem 5.8 that under suitable conditions, (16) gives an isomorphism between
$\xi _X$
is an extensive quantity (i.e., additive with respect to the size of the system). We will prove in Theorem 5.8 that under suitable conditions, (16) gives an isomorphism between
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
and the
${\operatorname {\mathrm {Consv}}}^\phi (S)$
and the
![]() $0$
-th uniform cohomology of the configuration space with transition structure.
$0$
-th uniform cohomology of the configuration space with transition structure.
Let
![]() $\eta =(\eta _x)$
and
$\eta =(\eta _x)$
and
![]() $\eta '=(\eta ^{\prime }_x)$
be configurations in
$\eta '=(\eta ^{\prime }_x)$
be configurations in
![]() $S^X_*$
, and let
$S^X_*$
, and let
![]() $\vec \gamma $
be a finite path from
$\vec \gamma $
be a finite path from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
. If
$\eta '$
. If
![]() $\xi $
is a conserved quantity for the interaction
$\xi $
is a conserved quantity for the interaction
![]() $\phi $
, then Lemma 2.22 and Lemma 2.21 give the equality
$\phi $
, then Lemma 2.22 and Lemma 2.21 give the equality
This shows that
![]() $\xi _X$
is constant on each of the connected components of
$\xi _X$
is constant on each of the connected components of
![]() $S^X_*$
. From now until the end of this subsection, we assume that X is an infinite locale. We define a monoid to be any set with a binary operation that is associative and has an identity element. We say that a monoid is commutative if the operation is commutative.
$S^X_*$
. From now until the end of this subsection, we assume that X is an infinite locale. We define a monoid to be any set with a binary operation that is associative and has an identity element. We say that a monoid is commutative if the operation is commutative.
Definition 2.24. Assume for simplicity that
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional, and fix an
${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional, and fix an
![]() $\mathbb {R}$
-linear basis
$\mathbb {R}$
-linear basis
![]() $\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
$\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
. We define the map
${\operatorname {\mathrm {Consv}}}^\phi (S)$
. We define the map
by ![]() for any
for any
![]() $\eta =(\eta _x)\in S^X_*$
, where
$\eta =(\eta _x)\in S^X_*$
, where ![]() for any
for any
![]() $i=1,\ldots ,c_\phi $
. Assuming that X is an infinite locale, we let
$i=1,\ldots ,c_\phi $
. Assuming that X is an infinite locale, we let ![]() , which we view as a commutative monoid with operation induced from the addition on
, which we view as a commutative monoid with operation induced from the addition on
![]() ${\mathbb {R}}^{c_\phi }$
. Then the monoid
${\mathbb {R}}^{c_\phi }$
. Then the monoid
![]() $\mathcal {M}$
is determined independently up to a natural isomorphism of the choice of the basis
$\mathcal {M}$
is determined independently up to a natural isomorphism of the choice of the basis
![]() $(\xi ^{(1)},\ldots ,\xi ^{(c_\phi )})$
.
$(\xi ^{(1)},\ldots ,\xi ^{(c_\phi )})$
.
Remark 2.25. We may define the commutative monoid
![]() $\mathcal {M}$
of Definition 2.24 intrinsically as an additive submonoid of
$\mathcal {M}$
of Definition 2.24 intrinsically as an additive submonoid of
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {R}}({\operatorname {\mathrm {Consv}}}^\phi (S),\mathbb {R})$
as follows. We define a map
${\operatorname {\mathrm {Hom}}}_{\mathbb {R}}({\operatorname {\mathrm {Consv}}}^\phi (S),\mathbb {R})$
as follows. We define a map
by
![]() $\eta \mapsto (\xi \mapsto \xi _X(\eta ))$
, and we let
$\eta \mapsto (\xi \mapsto \xi _X(\eta ))$
, and we let ![]() . In fact, the monoid
. In fact, the monoid
![]() $\mathcal {M}$
is defined independently of the choice of the infinite locale X. In what follows, we will denote the map
$\mathcal {M}$
is defined independently of the choice of the infinite locale X. In what follows, we will denote the map
![]() $ {\boldsymbol {\xi }}_{\!X}^{\operatorname {\mathrm {univ}}}\colon S^X_*\rightarrow \mathcal {M} $
simply by
$ {\boldsymbol {\xi }}_{\!X}^{\operatorname {\mathrm {univ}}}\colon S^X_*\rightarrow \mathcal {M} $
simply by
![]() ${\boldsymbol {\xi }}_{\!X}$
. If
${\boldsymbol {\xi }}_{\!X}$
. If
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional, a choice of a basis
${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional, a choice of a basis
![]() $\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
$\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
gives an isomorphism
${\operatorname {\mathrm {Consv}}}^\phi (S)$
gives an isomorphism
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {R}}({\operatorname {\mathrm {Consv}}}^\phi (S),\mathbb {R})\cong {\mathbb {R}}^{c_\phi }$
, and the monoid
${\operatorname {\mathrm {Hom}}}_{\mathbb {R}}({\operatorname {\mathrm {Consv}}}^\phi (S),\mathbb {R})\cong {\mathbb {R}}^{c_\phi }$
, and the monoid
![]() $\mathcal {M}$
maps to the
$\mathcal {M}$
maps to the
![]() $\mathcal {M}$
of Definition 2.24 through this isomorphism.
$\mathcal {M}$
of Definition 2.24 through this isomorphism.
By Lemma 2.22 and Lemma 2.21, if the configurations
![]() $\eta , \eta '\in S^X_*$
are connected by a path, then it is in the same fiber of the map
$\eta , \eta '\in S^X_*$
are connected by a path, then it is in the same fiber of the map
![]() ${\boldsymbol {\xi }}_{\!X}$
. However, the condition that the interaction is irreducibly quantified implies that the fibers of the map
${\boldsymbol {\xi }}_{\!X}$
. However, the condition that the interaction is irreducibly quantified implies that the fibers of the map
![]() ${\boldsymbol {\xi }}_{\!X}$
are connected. Thus, in this case, the connected components of
${\boldsymbol {\xi }}_{\!X}$
are connected. Thus, in this case, the connected components of
![]() $S^X_*$
correspond bijectively with the elements of
$S^X_*$
correspond bijectively with the elements of
![]() $\mathcal {M}$
. The authors thank Hiroyuki Ochiai for suggesting this formulation.
$\mathcal {M}$
. The authors thank Hiroyuki Ochiai for suggesting this formulation.
By Remark 2.25, if the interaction is irreducibly quantified, then the connected components of
![]() $S^X_*$
correspond bijectively with the elements of the image
$S^X_*$
correspond bijectively with the elements of the image
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() ${\boldsymbol {\xi }}_X$
. In particular, if
${\boldsymbol {\xi }}_X$
. In particular, if
![]() $c_\phi =0$
, then
$c_\phi =0$
, then
![]() $S^X_*$
is connected. However, if
$S^X_*$
is connected. However, if
![]() $c_\phi>0$
, then we have
$c_\phi>0$
, then we have
![]() $\dim _{\mathbb {R}} H^0(S^X_*)=\infty $
. Although
$\dim _{\mathbb {R}} H^0(S^X_*)=\infty $
. Although
![]() $H^m(S^X_*)$
is the standard cohomology of
$H^m(S^X_*)$
is the standard cohomology of
![]() $S^X_*$
and reflects the topological structure of the graph
$S^X_*$
and reflects the topological structure of the graph
![]() $(S^X_*,\Phi _*)$
, it is not so useful in the sense that it is in general infinite dimensional over infinite locales. In §3, we will define the notion of uniform functions which gives a certain subspace
$(S^X_*,\Phi _*)$
, it is not so useful in the sense that it is in general infinite dimensional over infinite locales. In §3, we will define the notion of uniform functions which gives a certain subspace
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)\subset C(S^X_*)$
, and we will define in §5 the uniform cohomology
$C_{\operatorname {\mathrm {unif}}}(S^X)\subset C(S^X_*)$
, and we will define in §5 the uniform cohomology
![]() $H^m_{\operatorname {\mathrm {unif}}}(S^X)$
by replacing the functions and forms of (14) with uniform functions and forms. For uniform cohomology, the inclusion of (16) induces an isomorphism
$H^m_{\operatorname {\mathrm {unif}}}(S^X)$
by replacing the functions and forms of (14) with uniform functions and forms. For uniform cohomology, the inclusion of (16) induces an isomorphism
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)\cong H^0_{\operatorname {\mathrm {unif}}}(S^X)$
; hence,
${\operatorname {\mathrm {Consv}}}^\phi (S)\cong H^0_{\operatorname {\mathrm {unif}}}(S^X)$
; hence,
![]() $H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is finite dimensional if
$H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is finite dimensional if
![]() $c_\phi $
is finite.
$c_\phi $
is finite.
For the first cohomology, the group
![]() $H^1(S^X_*)$
is in general also large since there are many linearly independent forms which are not exact. For example,
$H^1(S^X_*)$
is in general also large since there are many linearly independent forms which are not exact. For example,
![]() $H^1$
may be infinite dimensional as follows.
$H^1$
may be infinite dimensional as follows.
Remark 2.26. Let
![]() $X=(\mathbb {Z}^d,\mathbb {E}^d)$
and
$X=(\mathbb {Z}^d,\mathbb {E}^d)$
and
![]() $S=\{0,1,\ldots ,\kappa \}$
for an integer
$S=\{0,1,\ldots ,\kappa \}$
for an integer
![]() $d>1$
and some natural number
$d>1$
and some natural number
![]() $\kappa>0$
. If we let
$\kappa>0$
. If we let
![]() $S^X_*$
be the configuration space for S on X with transition structure for the multi-species exclusion process of Example 1.3, then we have
$S^X_*$
be the configuration space for S on X with transition structure for the multi-species exclusion process of Example 1.3, then we have
![]() $\dim _{\mathbb {R}} H^1(S^X_*)=\infty $
.
$\dim _{\mathbb {R}} H^1(S^X_*)=\infty $
.
This may be seen as follows. For any
![]() $x\in X$
, let
$x\in X$
, let
![]() $1_x\in S^X_*$
be the configuration with
$1_x\in S^X_*$
be the configuration with
![]() $1$
in the x component and
$1$
in the x component and
![]() $0$
in the other components. For any edge
$0$
in the other components. For any edge
![]() $e =(x,x')\in \mathbb {E}$
, the configuration
$e =(x,x')\in \mathbb {E}$
, the configuration
![]() $1_x^e$
is the configuration
$1_x^e$
is the configuration
![]() $1_{x'}$
with
$1_{x'}$
with
![]() $1$
in the
$1$
in the
![]() $x'$
component and
$x'$
component and
![]() $0$
in the other components; hence,
$0$
in the other components; hence, ![]() is a transition of
is a transition of
![]() $S^X_*$
. If we let
$S^X_*$
. If we let
![]() $\omega \in C^1(S^X_*)= \operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(\Phi _*,\mathbb {R})$
be the form given by
$\omega \in C^1(S^X_*)= \operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(\Phi _*,\mathbb {R})$
be the form given by
![]() $\omega (1_e) =-\omega (1_{\bar e})=1$
and
$\omega (1_e) =-\omega (1_{\bar e})=1$
and
![]() $\omega (\varphi )=0$
for
$\omega (\varphi )=0$
for
![]() $\varphi \neq 1_e, 1_{\bar e}$
, then we may prove that
$\varphi \neq 1_e, 1_{\bar e}$
, then we may prove that
![]() $\omega $
gives a nonzero element in
$\omega $
gives a nonzero element in
![]() $H^1(S^X_*)$
. In addition, we may prove that such
$H^1(S^X_*)$
. In addition, we may prove that such
![]() $\omega $
for a finite set of edges in E which do not share common vertices give linearly independent elements of
$\omega $
for a finite set of edges in E which do not share common vertices give linearly independent elements of
![]() $H^1(S^X_*)$
, giving our assertion.
$H^1(S^X_*)$
, giving our assertion.
In considering uniform cohomology, we will consider a class of forms called closed forms, which are in fact always exact. We recall that a finite path on a graph
![]() $S^X_*$
is a finite sequence
$S^X_*$
is a finite sequence
![]() $(\varphi ^1,\ldots ,\varphi ^N)$
of transitions of
$(\varphi ^1,\ldots ,\varphi ^N)$
of transitions of
![]() $S^X_*$
such that
$S^X_*$
such that
![]() $t(\varphi ^i)=o(\varphi ^{i+1})$
for any integer
$t(\varphi ^i)=o(\varphi ^{i+1})$
for any integer
![]() $0<i<N$
. As in (54), for a form
$0<i<N$
. As in (54), for a form
![]() $\omega \in C^1(S^X_*)$
on
$\omega \in C^1(S^X_*)$
on
![]() $S^X_*$
, we define the integral of
$S^X_*$
, we define the integral of
![]() $\omega $
with respect to the path
$\omega $
with respect to the path
![]() $\vec \gamma =(\varphi ^1,\ldots ,\varphi ^N)$
by
$\vec \gamma =(\varphi ^1,\ldots ,\varphi ^N)$
by

As in Definition A.3, we define a closed form as follows.
Definition 2.27. We say that a form
![]() $\omega \in C^1(S^X_*)=\operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(\Phi _*,\mathbb {R})$
is closed if for any closed path
$\omega \in C^1(S^X_*)=\operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(\Phi _*,\mathbb {R})$
is closed if for any closed path
![]() $\vec \gamma $
in
$\vec \gamma $
in
![]() $S^X_*$
, we have
$S^X_*$
, we have
 $$\begin{align*}\int_{\vec\gamma}\omega=0. \end{align*}$$
$$\begin{align*}\int_{\vec\gamma}\omega=0. \end{align*}$$
We say that a form
![]() $\omega \in C^1(S^X_*)$
is exact if there exists a function
$\omega \in C^1(S^X_*)$
is exact if there exists a function
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f = \omega $
. By Lemma A.4, a form is exact if and only if it is closed.
$\partial f = \omega $
. By Lemma A.4, a form is exact if and only if it is closed.
Lemma 2.28. A form
![]() $\omega \in C^1(S^X_*)$
is exact if and only if it is closed.
$\omega \in C^1(S^X_*)$
is exact if and only if it is closed.
Proof. This follows from Lemma A.4 applied to the graph
![]() $(S^X_*,\Phi _*)$
.
$(S^X_*,\Phi _*)$
.
We will denote by
![]() $Z^1(S^X_*)$
the space of closed forms on
$Z^1(S^X_*)$
the space of closed forms on
![]() $(S^X_*,\Phi _*)$
. Closed forms will play a role in the definition of uniform cohomology.
$(S^X_*,\Phi _*)$
. Closed forms will play a role in the definition of uniform cohomology.
3 Uniform functions and uniform forms
In this section, we will define the notion of uniform functions and uniform forms, which are functions and forms which reflect the geometry of the underlying locale. We will then investigate its properties, including a criterion for a function to be uniform.
3.1 Uniform functions on the configuration space
For any system
![]() $(X,S,\phi )$
, let
$(X,S,\phi )$
, let
![]() $S^X = \prod _{x\in X}S$
be the configuration space for S on X. We let
$S^X = \prod _{x\in X}S$
be the configuration space for S on X. We let
![]() $S^X_* \subset S^X$
be the subset consisting of configurations with finite support. In this subsection, we will prove the existence of a canonical expansion of functions in
$S^X_* \subset S^X$
be the subset consisting of configurations with finite support. In this subsection, we will prove the existence of a canonical expansion of functions in
![]() $C(S^X_*)$
in terms of local functions with exact support (see Definition 3.1), and we will introduce the notion of uniform functions, which are functions which reflect the geometry of the underlying locale.
$C(S^X_*)$
in terms of local functions with exact support (see Definition 3.1), and we will introduce the notion of uniform functions, which are functions which reflect the geometry of the underlying locale.
For a finite
![]() $\Lambda \subset X$
, there exists a natural inclusion
$\Lambda \subset X$
, there exists a natural inclusion
![]() $ \iota ^\Lambda \colon S^\Lambda \hookrightarrow S^\Lambda \times S^{X\setminus \Lambda }_* = S^X_* $
given by
$ \iota ^\Lambda \colon S^\Lambda \hookrightarrow S^\Lambda \times S^{X\setminus \Lambda }_* = S^X_* $
given by
![]() $\eta _\Lambda \mapsto (\eta _\Lambda ,\star )$
for any
$\eta _\Lambda \mapsto (\eta _\Lambda ,\star )$
for any
![]() $\eta _\Lambda \in S^\Lambda $
, where
$\eta _\Lambda \in S^\Lambda $
, where
![]() $\star \in S^{X\setminus \Lambda }$
is the element whose components are all at base state. By abuse of notation, we will often denote
$\star \in S^{X\setminus \Lambda }$
is the element whose components are all at base state. By abuse of notation, we will often denote
![]() $\iota ^\Lambda (\eta |_\Lambda )$
by
$\iota ^\Lambda (\eta |_\Lambda )$
by
![]() $\eta |_\Lambda $
. This inclusion induces a homomorphism
$\eta |_\Lambda $
. This inclusion induces a homomorphism
which may be regarded as an
![]() $\mathbb {R}$
-linear operator on the set of functions
$\mathbb {R}$
-linear operator on the set of functions
![]() $C(S^X_*)$
. Note that we have
$C(S^X_*)$
. Note that we have
![]() $\iota ^\Lambda f(\eta )=f(\eta |_\Lambda )$
for any
$\iota ^\Lambda f(\eta )=f(\eta |_\Lambda )$
for any
![]() $f\in C(S^X_*)$
and
$f\in C(S^X_*)$
and
![]() $\eta \in S^X$
. By definition, if
$\eta \in S^X$
. By definition, if
![]() $f\in C(S^\Lambda )$
, then we have
$f\in C(S^\Lambda )$
, then we have
![]() $\iota ^{\Lambda } f=f$
. For any
$\iota ^{\Lambda } f=f$
. For any
![]() $\Lambda ,\Lambda '\subset X$
, we have
$\Lambda ,\Lambda '\subset X$
, we have
![]() $\iota ^{\Lambda }\iota ^{\Lambda '} = \iota ^{\Lambda '}\iota ^{\Lambda } =\iota ^{\Lambda \cap \Lambda '}$
.
$\iota ^{\Lambda }\iota ^{\Lambda '} = \iota ^{\Lambda '}\iota ^{\Lambda } =\iota ^{\Lambda \cap \Lambda '}$
.
Definition 3.1. For any finite
![]() $\Lambda \subset X$
, we let
$\Lambda \subset X$
, we let
We call any function
![]() $f\in C_\Lambda (S^X)$
a local function with exact support
$f\in C_\Lambda (S^X)$
a local function with exact support
![]() $\Lambda $
.
$\Lambda $
.
Any function in
![]() $C(S^X_*)$
has a unique expansion in terms of local functions with exact support, as will be shown in Proposition 3.3. We first start with the following lemma.
$C(S^X_*)$
has a unique expansion in terms of local functions with exact support, as will be shown in Proposition 3.3. We first start with the following lemma.
Lemma 3.2. Let
![]() $(f_\Lambda )$
be a set of functions such that
$(f_\Lambda )$
be a set of functions such that
![]() $f_\Lambda \in C_\Lambda (S^X)$
for any finite
$f_\Lambda \in C_\Lambda (S^X)$
for any finite
![]() $\Lambda \subset X$
. Then the sum
$\Lambda \subset X$
. Then the sum
defines a function in
![]() $C(S^X_*)$
.
$C(S^X_*)$
.
Proof. By definition, for any
![]() $\eta =(\eta _x)\in S^X_*$
, the support
$\eta =(\eta _x)\in S^X_*$
, the support
![]() $\operatorname {\mathrm {Supp}}(\eta )\subset X$
satisfies
$\operatorname {\mathrm {Supp}}(\eta )\subset X$
satisfies
![]() $|\operatorname {\mathrm {Supp}}(\eta )|<\infty $
. Then we have
$|\operatorname {\mathrm {Supp}}(\eta )|<\infty $
. Then we have

where the last sum is defined since it is a finite sum. We see that the sum defines a function
![]() $f\colon S^X\rightarrow \mathbb {R}$
, as desired.
$f\colon S^X\rightarrow \mathbb {R}$
, as desired.
The expansion of functions in
![]() $C(S^X_*)$
in terms of local functions with exact support is given as follows.
$C(S^X_*)$
in terms of local functions with exact support is given as follows.
Proposition 3.3. For any
![]() $f\in C(S^X_*)$
, there exists a unique expansion
$f\in C(S^X_*)$
, there exists a unique expansion
in terms of local functions with exact support
![]() $f_\Lambda \in C_\Lambda (S^X)$
for finite
$f_\Lambda \in C_\Lambda (S^X)$
for finite
![]() $\Lambda \subset X$
.
$\Lambda \subset X$
.
Proof. We construct
![]() $f_\Lambda $
by induction on the cardinality of
$f_\Lambda $
by induction on the cardinality of
![]() $\Lambda $
. Suppose an expansion of the form (18) exists. Note that for any
$\Lambda $
. Suppose an expansion of the form (18) exists. Note that for any
![]() $\Lambda , \Lambda '\subset X$
such that
$\Lambda , \Lambda '\subset X$
such that
![]() $\Lambda '\not \subset \Lambda $
, we have
$\Lambda '\not \subset \Lambda $
, we have
![]() $\iota ^{\Lambda } f_{\Lambda '}=0$
since
$\iota ^{\Lambda } f_{\Lambda '}=0$
since
![]() $f_{\Lambda '}\in C_{\Lambda '}(S^X)$
; hence, if we apply the
$f_{\Lambda '}\in C_{\Lambda '}(S^X)$
; hence, if we apply the
![]() $\mathbb {R}$
-linear operator
$\mathbb {R}$
-linear operator
![]() $\iota ^{\Lambda }$
of (17) on (18), then we obtain the equality
$\iota ^{\Lambda }$
of (17) on (18), then we obtain the equality
Hence, this shows that assuming the existence of the expansion,
![]() $f_\Lambda $
is uniquely given inductively for the set
$f_\Lambda $
is uniquely given inductively for the set
![]() $\Lambda $
by
$\Lambda $
by
We will prove by induction on the cardinality of
![]() $\Lambda $
that the function
$\Lambda $
that the function
![]() $f_\Lambda $
inductively given by (19) is a function in
$f_\Lambda $
inductively given by (19) is a function in
![]() $C_\Lambda (S^X)$
. We let
$C_\Lambda (S^X)$
. We let
![]() $\star \in S^X$
be the base state. For
$\star \in S^X$
be the base state. For
![]() $\Lambda =\emptyset $
, equation (19) gives
$\Lambda =\emptyset $
, equation (19) gives
![]() $ f_\emptyset =\iota ^\emptyset f, $
which shows that
$ f_\emptyset =\iota ^\emptyset f, $
which shows that
![]() $f_\emptyset $
is an element in
$f_\emptyset $
is an element in
![]() $C_\emptyset (S^X)$
. Note that
$C_\emptyset (S^X)$
. Note that
![]() $f_\emptyset $
is the constant function given by
$f_\emptyset $
is the constant function given by
![]() $f_\emptyset (\eta )=f(\star )$
for any
$f_\emptyset (\eta )=f(\star )$
for any
![]() $\eta \in S^X$
. For
$\eta \in S^X$
. For
![]() $|\Lambda |>0$
, suppose
$|\Lambda |>0$
, suppose
![]() $f_{\Lambda '}\in C_{\Lambda '}(S^X)$
for any
$f_{\Lambda '}\in C_{\Lambda '}(S^X)$
for any
![]() $\Lambda '\subsetneq \Lambda $
. Then by (19), the function
$\Lambda '\subsetneq \Lambda $
. Then by (19), the function
![]() $f_\Lambda $
is a function in
$f_\Lambda $
is a function in
![]() $C(S^\Lambda )$
. Next, we prove that
$C(S^\Lambda )$
. Next, we prove that
![]() $f\in C_\Lambda (S^X)$
. Suppose
$f\in C_\Lambda (S^X)$
. Suppose
![]() $\eta =(\eta _x)\in S^X$
satisfies
$\eta =(\eta _x)\in S^X$
satisfies
![]() $\eta _x=*$
for some
$\eta _x=*$
for some
![]() $x\in \Lambda $
. If
$x\in \Lambda $
. If
![]() $\Lambda '\subsetneq \Lambda $
and
$\Lambda '\subsetneq \Lambda $
and
![]() $x\in \Lambda '$
, then we have
$x\in \Lambda '$
, then we have
![]() $f_{\Lambda '}(\eta )=0$
since
$f_{\Lambda '}(\eta )=0$
since
![]() $f_{\Lambda '}\in C_{\Lambda '}(S^X)$
. Hence, by (19), we have
$f_{\Lambda '}\in C_{\Lambda '}(S^X)$
. Hence, by (19), we have
Note that since
![]() $\eta _x=*$
, we have
$\eta _x=*$
, we have
![]() $\iota ^\Lambda f(\eta ) =\iota ^{\Lambda \setminus \{x\}}f(\eta )$
by definition of
$\iota ^\Lambda f(\eta ) =\iota ^{\Lambda \setminus \{x\}}f(\eta )$
by definition of
![]() $\iota ^\Lambda $
; hence, we have
$\iota ^\Lambda $
; hence, we have
 $$ \begin{align*} f_\Lambda(\eta) &=\iota^{\Lambda\setminus\{x\}} f(\eta) - \sum_{\Lambda'\subset\Lambda\setminus\{x\}} f_{\Lambda'}(\eta) =\biggl(\iota^{\Lambda\setminus\{x\}} f(\eta) - \sum_{\Lambda'\subsetneq\Lambda\setminus\{x\}} f_{\Lambda'}(\eta)\biggr) - f_{\Lambda\setminus\{x\}}(\eta)\\ &= f_{\Lambda\setminus\{x\}}(\eta)- f_{\Lambda\setminus\{x\}}(\eta)=0. \end{align*} $$
$$ \begin{align*} f_\Lambda(\eta) &=\iota^{\Lambda\setminus\{x\}} f(\eta) - \sum_{\Lambda'\subset\Lambda\setminus\{x\}} f_{\Lambda'}(\eta) =\biggl(\iota^{\Lambda\setminus\{x\}} f(\eta) - \sum_{\Lambda'\subsetneq\Lambda\setminus\{x\}} f_{\Lambda'}(\eta)\biggr) - f_{\Lambda\setminus\{x\}}(\eta)\\ &= f_{\Lambda\setminus\{x\}}(\eta)- f_{\Lambda\setminus\{x\}}(\eta)=0. \end{align*} $$
This proves that
![]() $f_\Lambda \in C_\Lambda (S^X)$
, as desired. The sum (18) gives the function f in
$f_\Lambda \in C_\Lambda (S^X)$
, as desired. The sum (18) gives the function f in
![]() $C(S^X_*)$
since for any
$C(S^X_*)$
since for any
![]() $\eta \in S^X$
, we have
$\eta \in S^X$
, we have
![]() $f(\eta )=\iota ^{\operatorname {\mathrm {Supp}}(\eta )}f(\eta )=\sum _{\Lambda \subset \operatorname {\mathrm {Supp}}(\eta )} f_{\Lambda }(\eta )$
.
$f(\eta )=\iota ^{\operatorname {\mathrm {Supp}}(\eta )}f(\eta )=\sum _{\Lambda \subset \operatorname {\mathrm {Supp}}(\eta )} f_{\Lambda }(\eta )$
.
Corollary 3.4. If
![]() $f\in C(S^\Lambda )$
for some finite
$f\in C(S^\Lambda )$
for some finite
![]() $\Lambda \subset X$
, then we have a unique expansion
$\Lambda \subset X$
, then we have a unique expansion
in terms of local functions with exact support
![]() $f_{\Lambda '}\in C_{\Lambda '}(S^X)$
for
$f_{\Lambda '}\in C_{\Lambda '}(S^X)$
for
![]() $\Lambda '\subset \Lambda $
.
$\Lambda '\subset \Lambda $
.
Proof. Our statement follows by applying the
![]() $\mathbb {R}$
-linear operator
$\mathbb {R}$
-linear operator
![]() $\iota ^\Lambda $
to the expansion (18) of Proposition 3.3, noting that
$\iota ^\Lambda $
to the expansion (18) of Proposition 3.3, noting that
![]() $\iota ^\Lambda f=f$
and
$\iota ^\Lambda f=f$
and
![]() $\iota ^\Lambda f_{\Lambda '}=0$
if
$\iota ^\Lambda f_{\Lambda '}=0$
if
![]() $\Lambda '\not \subset \Lambda $
.
$\Lambda '\not \subset \Lambda $
.
For any
![]() $\Lambda \subset X$
, we define the diameter
$\Lambda \subset X$
, we define the diameter
![]() $\operatorname {diam}(\Lambda )$
of
$\operatorname {diam}(\Lambda )$
of
![]() $\Lambda $
by
$\Lambda $
by
Since X is connected, if
![]() $\Lambda \subset X$
is finite, then we have
$\Lambda \subset X$
is finite, then we have
![]() $\operatorname {diam}(\Lambda )<\infty $
. Uniform functions are defined as follows.
$\operatorname {diam}(\Lambda )<\infty $
. Uniform functions are defined as follows.
Definition 3.5. We say that a function
![]() $f\in C(S^X_*)$
is uniform if there exists
$f\in C(S^X_*)$
is uniform if there exists
![]() $R>0$
such that the canonical expansion of (18) is given by
$R>0$
such that the canonical expansion of (18) is given by
 $$\begin{align*}f=\sum_{\substack{\Lambda\subset X\\\operatorname{diam}(\Lambda)\leq R}} f_\Lambda. \end{align*}$$
$$\begin{align*}f=\sum_{\substack{\Lambda\subset X\\\operatorname{diam}(\Lambda)\leq R}} f_\Lambda. \end{align*}$$
In other words,
![]() $f_\Lambda =0$
in the expansion (18) if
$f_\Lambda =0$
in the expansion (18) if
![]() $\operatorname {diam}(\Lambda )>R$
. We denote by
$\operatorname {diam}(\Lambda )>R$
. We denote by
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)$
the
$C_{\operatorname {\mathrm {unif}}}(S^X)$
the
![]() $\mathbb {R}$
-linear subspace of
$\mathbb {R}$
-linear subspace of
![]() $C(S^X_*)$
consisting of uniform functions, and by
$C(S^X_*)$
consisting of uniform functions, and by
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
the subspace of
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
the subspace of
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)$
consisting of functions satisfying
$C_{\operatorname {\mathrm {unif}}}(S^X)$
consisting of functions satisfying
![]() $f(\star )=0$
.
$f(\star )=0$
.
For any
![]() $x\in X$
and
$x\in X$
and
![]() $\Lambda \subset X$
, we let
$\Lambda \subset X$
, we let ![]() and for
and for
![]() $\Lambda ,\Lambda '\subset X$
, we let
$\Lambda ,\Lambda '\subset X$
, we let ![]()
Remark 3.6. Suppose
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
so that there exists some
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
so that there exists some
![]() $R>0$
such that
$R>0$
such that
![]() $f_\Lambda \equiv 0$
in the expansion (18) if
$f_\Lambda \equiv 0$
in the expansion (18) if
![]() $\operatorname {diam}(\Lambda )>R$
. Let
$\operatorname {diam}(\Lambda )>R$
. Let
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
be subsets of X such that
$\Lambda '$
be subsets of X such that
![]() $d_X(\Lambda ,\Lambda ')>R$
. By Corollary 3.4, we have
$d_X(\Lambda ,\Lambda ')>R$
. By Corollary 3.4, we have
![]() $\iota ^{\Lambda \cup \Lambda '} f =\sum _{\Lambda "\subset \Lambda \cup \Lambda '}f_{\Lambda "}$
,
$\iota ^{\Lambda \cup \Lambda '} f =\sum _{\Lambda "\subset \Lambda \cup \Lambda '}f_{\Lambda "}$
,
![]() $\iota ^{\Lambda } f =\sum _{\Lambda "\subset \Lambda }f_{\Lambda "}$
and
$\iota ^{\Lambda } f =\sum _{\Lambda "\subset \Lambda }f_{\Lambda "}$
and
![]() $\iota ^{\Lambda '} f =\sum _{\Lambda "\subset \Lambda '}f_{\Lambda "}$
. Note that if
$\iota ^{\Lambda '} f =\sum _{\Lambda "\subset \Lambda '}f_{\Lambda "}$
. Note that if
![]() $\Lambda "\subset \Lambda \cup \Lambda '$
satisfies
$\Lambda "\subset \Lambda \cup \Lambda '$
satisfies
![]() $\Lambda "\cap \Lambda \neq \emptyset $
and
$\Lambda "\cap \Lambda \neq \emptyset $
and
![]() $\Lambda "\cap \Lambda '\neq \emptyset $
, then we have
$\Lambda "\cap \Lambda '\neq \emptyset $
, then we have
![]() $\operatorname {diam}(\Lambda ")>R$
; hence,
$\operatorname {diam}(\Lambda ")>R$
; hence,
![]() $f_{\Lambda "}=0$
from our choice of R. This shows that we have
$f_{\Lambda "}=0$
from our choice of R. This shows that we have
![]() $ \iota ^{\Lambda \cup \Lambda '}f=\iota ^{\Lambda } f+\iota ^{\Lambda '}f, $
where we have used the fact that
$ \iota ^{\Lambda \cup \Lambda '}f=\iota ^{\Lambda } f+\iota ^{\Lambda '}f, $
where we have used the fact that
![]() $f(\star )=\iota ^\emptyset f=0$
.
$f(\star )=\iota ^\emptyset f=0$
.
3.2 Horizontal uniform functions
Consider the system
![]() $(X,S,\phi )$
. From now until the end of §3, we assume that the interaction
$(X,S,\phi )$
. From now until the end of §3, we assume that the interaction
![]() $\phi $
is irreducibly quantified in the sense of Definition 2.13. The purpose of this subsection is to prove the following theorem.
$\phi $
is irreducibly quantified in the sense of Definition 2.13. The purpose of this subsection is to prove the following theorem.
Theorem 3.7. For the system
![]() $(X,S,\phi $
), assume that X is an infinite locale and the interaction
$(X,S,\phi $
), assume that X is an infinite locale and the interaction
![]() $\phi $
is irreducibly quantified. Let f be a uniform function in
$\phi $
is irreducibly quantified. Let f be a uniform function in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. If f is horizontal (i.e., if
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. If f is horizontal (i.e., if
![]() $\partial f=0$
), then there exists a conserved quantity
$\partial f=0$
), then there exists a conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
such that
$\xi \colon S\rightarrow \mathbb {R}$
such that
for any
![]() $\eta =(\eta _x)\in S^X$
.
$\eta =(\eta _x)\in S^X$
.
Theorem 3.7 implies that assuming that X is infinite and
![]() $\phi $
is irreducibly quantified, any uniform function which is constant on the connected components of
$\phi $
is irreducibly quantified, any uniform function which is constant on the connected components of
![]() $S^X_*$
coincides with
$S^X_*$
coincides with
![]() $\xi _X$
for some conserved quantity
$\xi _X$
for some conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. We will give the proof of Theorem 3.7 at the end of this subsection. We first prove the following lemma.
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. We will give the proof of Theorem 3.7 at the end of this subsection. We first prove the following lemma.
Lemma 3.8. Suppose
![]() $f\in C(S^X_*)$
, and for any
$f\in C(S^X_*)$
, and for any
![]() $x\in X$
, let
$x\in X$
, let
![]() $f_{\{x\}}$
be the function with exact support
$f_{\{x\}}$
be the function with exact support
![]() $\Lambda =\{x\}$
in the canonical expansion (18). If f is horizontal, then the functions
$\Lambda =\{x\}$
in the canonical expansion (18). If f is horizontal, then the functions
are all equal as x varies over X.
Proof. Consider the expansion
of (18). We let s be any element in S. For
![]() $x,x'\in X$
, we let
$x,x'\in X$
, we let ![]() and
and ![]() be the configuration in
be the configuration in
![]() $S^X_*$
with s respectively in the x and
$S^X_*$
with s respectively in the x and
![]() $x'$
components, and base state
$x'$
components, and base state
![]() $*$
in the other components. This implies that
$*$
in the other components. This implies that
in other words, that
![]() $\xi _X(\eta )=\xi _X(\eta ')$
for any conserved quantity
$\xi _X(\eta )=\xi _X(\eta ')$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. Hence, from the fact that the interaction is irreducibly quantified, there exists a finite path
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. Hence, from the fact that the interaction is irreducibly quantified, there exists a finite path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
in
$\eta '$
in
![]() $S^X_*$
. By Lemma 2.21, noting that
$S^X_*$
. By Lemma 2.21, noting that
![]() $\partial f=0$
, we have
$\partial f=0$
, we have
which shows that
![]() $\iota ^{\{x\}}f_{\{x\}}\colon S\rightarrow \mathbb {R}$
is independent of the choice of
$\iota ^{\{x\}}f_{\{x\}}\colon S\rightarrow \mathbb {R}$
is independent of the choice of
![]() $x\in X$
as desired.
$x\in X$
as desired.
Next, we prove the following lemma.
Lemma 3.9. Assume that X is an infinite locale, and suppose f is a uniform function in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. If f is horizontal, then we have
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. If f is horizontal, then we have
where
![]() $f_{\{x\}}$
is the function with exact support
$f_{\{x\}}$
is the function with exact support
![]() $\Lambda =\{x\}$
in the canonical expansion (18).
$\Lambda =\{x\}$
in the canonical expansion (18).
Proof. Since f is uniform, there exists an
![]() $R>0$
such that
$R>0$
such that
![]() $f_\Lambda \equiv 0$
if
$f_\Lambda \equiv 0$
if
![]() $\operatorname {diam}(\Lambda )>R$
. By Proposition 3.3, it is sufficient to prove that for any finite
$\operatorname {diam}(\Lambda )>R$
. By Proposition 3.3, it is sufficient to prove that for any finite
![]() $\Lambda \subset X$
satisfying
$\Lambda \subset X$
satisfying
![]() $|\Lambda |>1$
, we have
$|\Lambda |>1$
, we have
![]() $f_\Lambda \equiv 0$
in the expansion of (18). We will prove this by induction on the cardinality of
$f_\Lambda \equiv 0$
in the expansion of (18). We will prove this by induction on the cardinality of
![]() $\Lambda \subset X$
. We consider a finite
$\Lambda \subset X$
. We consider a finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that ![]() , and assume that
, and assume that
![]() $f_{\Lambda '}\equiv 0$
for any
$f_{\Lambda '}\equiv 0$
for any
![]() $\Lambda '\subset X$
such that
$\Lambda '\subset X$
such that
![]() $1<|\Lambda '|<n$
. Note that this condition is trivially true for
$1<|\Lambda '|<n$
. Note that this condition is trivially true for
![]() $n=2$
. We let
$n=2$
. We let
![]() $\Lambda _n\subset X$
be a subset of X with n elements such that
$\Lambda _n\subset X$
be a subset of X with n elements such that
![]() $\operatorname {diam}(\Lambda _n)>R$
. Such
$\operatorname {diam}(\Lambda _n)>R$
. Such
![]() $\Lambda _n$
exists since X is a locally finite infinite graph that is connected. Then by construction, we have
$\Lambda _n$
exists since X is a locally finite infinite graph that is connected. Then by construction, we have
![]() $f_{\Lambda _n}\equiv 0$
. We fix a bijection between the set
$f_{\Lambda _n}\equiv 0$
. We fix a bijection between the set
![]() $\{1,\cdots ,n\}$
and the sets
$\{1,\cdots ,n\}$
and the sets
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda _n$
, which induces bijections
$\Lambda _n$
, which induces bijections
![]() $S^n \cong S^\Lambda $
and
$S^n \cong S^\Lambda $
and
![]() $S^n\cong S^{\Lambda _n}$
. For any
$S^n\cong S^{\Lambda _n}$
. For any
![]() $(\eta _i) \in S^n$
, which we view as an element in
$(\eta _i) \in S^n$
, which we view as an element in
![]() $S^\Lambda $
and
$S^\Lambda $
and
![]() $S^{\Lambda _n}$
, we let
$S^{\Lambda _n}$
, we let ![]() and
and ![]() . Then for any conserved quantity
. Then for any conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
, we have
$\xi \colon S\rightarrow \mathbb {R}$
, we have
 $$\begin{align*}\sum_{x\in X}\xi(\eta_x)=\sum_{x\in X}\xi(\eta^{\prime}_x)=\sum_{i=1}^n \xi(\eta_i). \end{align*}$$
$$\begin{align*}\sum_{x\in X}\xi(\eta_x)=\sum_{x\in X}\xi(\eta^{\prime}_x)=\sum_{i=1}^n \xi(\eta_i). \end{align*}$$
In other words,
![]() $\xi _X(\eta )=\xi _X(\eta ')$
. Since the interaction is irreducibly quantified, there exists a finite path
$\xi _X(\eta )=\xi _X(\eta ')$
. Since the interaction is irreducibly quantified, there exists a finite path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
in
$\eta '$
in
![]() $S^X_*$
. By Lemma 2.21 and our condition that
$S^X_*$
. By Lemma 2.21 and our condition that
![]() $\partial f=0$
, we have
$\partial f=0$
, we have
![]() $f(\eta ) = f(\eta ')$
. Note that by Lemma 3.8, if we let
$f(\eta ) = f(\eta ')$
. Note that by Lemma 3.8, if we let ![]() , then
, then
![]() $\zeta $
is independent of the choice of
$\zeta $
is independent of the choice of
![]() $x\in X$
. Corollary 3.4 implies that we have
$x\in X$
. Corollary 3.4 implies that we have
 $$ \begin{align*} f(\eta) &= \iota^{\Lambda} f(\eta) = f_{\Lambda}(\eta) + \sum_{\Lambda'\subsetneq\Lambda} f_{\Lambda'}(\eta) = f_{\Lambda}(\eta) + \sum_{x\in\Lambda} f_{\{x\}}(\eta)= f_{\Lambda}(\eta) + \sum_{i=1}^n \zeta(\eta_i)\\ f(\eta') &= \iota^{\Lambda_n} f(\eta') = f_{\Lambda_n}(\eta') + \sum_{\Lambda'\subsetneq\Lambda_n} f_{\Lambda'}(\eta') = \sum_{x\in\Lambda_n}f_{\{x\}}(\eta')= \sum_{i=1}^n \zeta(\eta_i). \end{align*} $$
$$ \begin{align*} f(\eta) &= \iota^{\Lambda} f(\eta) = f_{\Lambda}(\eta) + \sum_{\Lambda'\subsetneq\Lambda} f_{\Lambda'}(\eta) = f_{\Lambda}(\eta) + \sum_{x\in\Lambda} f_{\{x\}}(\eta)= f_{\Lambda}(\eta) + \sum_{i=1}^n \zeta(\eta_i)\\ f(\eta') &= \iota^{\Lambda_n} f(\eta') = f_{\Lambda_n}(\eta') + \sum_{\Lambda'\subsetneq\Lambda_n} f_{\Lambda'}(\eta') = \sum_{x\in\Lambda_n}f_{\{x\}}(\eta')= \sum_{i=1}^n \zeta(\eta_i). \end{align*} $$
Hence, we have
![]() $f_{\Lambda }(\eta )=0$
. Since this was true for any
$f_{\Lambda }(\eta )=0$
. Since this was true for any
![]() $(\eta _i)\in S^n$
, we have
$(\eta _i)\in S^n$
, we have
![]() $f_\Lambda \equiv 0$
, as desired. Our assertion now follows by induction on n.
$f_\Lambda \equiv 0$
, as desired. Our assertion now follows by induction on n.
We may now prove Theorem 3.7.
Proof of Theorem 3.7.
Let ![]() , which by Lemma 3.8 is independent of the choice of
, which by Lemma 3.8 is independent of the choice of
![]() $x\in X$
. Then by Lemma 3.9 and the definition of
$x\in X$
. Then by Lemma 3.9 and the definition of
![]() $\iota ^{\{x\}}f_{\{x\}}$
, we have
$\iota ^{\{x\}}f_{\{x\}}$
, we have
for any
![]() $\eta =(\eta _x)\in S^X_*$
. It is sufficient to show that
$\eta =(\eta _x)\in S^X_*$
. It is sufficient to show that
![]() $\xi $
is a conserved quantity. First, note that we have
$\xi $
is a conserved quantity. First, note that we have
![]() $\xi (*)=f_{\{x\}}(*)=0$
for any
$\xi (*)=f_{\{x\}}(*)=0$
for any
![]() $x\in X$
since
$x\in X$
since
![]() $f_{\{x\}}$
has exact support
$f_{\{x\}}$
has exact support
![]() $\{x\}$
. Consider an edge
$\{x\}$
. Consider an edge
![]() $e=(o(e),t(e))\in E\subset X\times X$
, and for
$e=(o(e),t(e))\in E\subset X\times X$
, and for
![]() $(s_1,s_2)\in S\times S$
, let
$(s_1,s_2)\in S\times S$
, let
![]() $\eta \in S^X_*$
be the configuration with
$\eta \in S^X_*$
be the configuration with
![]() $s_1$
in the
$s_1$
in the
![]() $o(e)$
component,
$o(e)$
component,
![]() $s_2$
in the
$s_2$
in the
![]() $t(e)$
component, and base states
$t(e)$
component, and base states
![]() $*$
at the other components. Then
$*$
at the other components. Then
![]() $\eta ^e$
is the configuration with
$\eta ^e$
is the configuration with
![]() $s^{\prime }_1$
in the
$s^{\prime }_1$
in the
![]() $o(e)$
component,
$o(e)$
component,
![]() $s^{\prime }_2$
in the
$s^{\prime }_2$
in the
![]() $t(e)$
component, and base states at the other components, where
$t(e)$
component, and base states at the other components, where
![]() $(s_1^{\prime },s_2^{\prime })=\phi (s_1,s_2)$
. If we let
$(s_1^{\prime },s_2^{\prime })=\phi (s_1,s_2)$
. If we let
![]() $\varphi =(\eta ,\eta ^e)$
be the transition from
$\varphi =(\eta ,\eta ^e)$
be the transition from
![]() $\eta $
to
$\eta $
to
![]() $\eta ^e$
, then
$\eta ^e$
, then
![]() $\partial f=0$
implies that
$\partial f=0$
implies that
This shows that
![]() $\xi $
satisfies (12); hence, it is a conserved quantity as desired.
$\xi $
satisfies (12); hence, it is a conserved quantity as desired.
3.3 Pairings for functions with uniform differentials
Let X be an infinite locale and assume that the interaction is irreducibly quantified. In this subsection, we first define the notion of uniform forms. Next, we will prove Proposition 3.18, which associates a certain pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
to any function
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
to any function
![]() $f\in C(S^X_*)$
whose differential
$f\in C(S^X_*)$
whose differential
![]() $\partial f\in C^1(S^X_*)$
is a uniform form, where
$\partial f\in C^1(S^X_*)$
is a uniform form, where
![]() $\mathcal {M}$
is the commutative monoid given in Definition 2.24 (see also Remark 2.25).
$\mathcal {M}$
is the commutative monoid given in Definition 2.24 (see also Remark 2.25).
A ball in X is a set of the form ![]() for some
for some
![]() $x\in X$
and constant
$x\in X$
and constant
![]() $R>0$
. We say that x is the center and
$R>0$
. We say that x is the center and
![]() $R>0$
is the radius of
$R>0$
is the radius of
![]() $ B(x,R)$
. If B is a ball in X, then we denote by
$ B(x,R)$
. If B is a ball in X, then we denote by
![]() $r(B)$
the radius of B. For any
$r(B)$
the radius of B. For any
![]() $\Lambda \subset X$
, we let
$\Lambda \subset X$
, we let ![]() , which we call the R-thickening of
, which we call the R-thickening of
![]() $\Lambda $
. In particular, for any edge
$\Lambda $
. In particular, for any edge
![]() $e=(o(e),t(e))\in E \subset X\times X$
, we let
$e=(o(e),t(e))\in E \subset X\times X$
, we let ![]() . For any
. For any
![]() $R>0$
, we define the set of R-uniform forms
$R>0$
, we define the set of R-uniform forms
![]() $C^1_R(S^X) \subset C^1(S^X_*)\subset \prod _{e\in E}\operatorname {\mathrm {Map}}(S^X_*,\mathbb {R})$
by
$C^1_R(S^X) \subset C^1(S^X_*)\subset \prod _{e\in E}\operatorname {\mathrm {Map}}(S^X_*,\mathbb {R})$
by
Definition 3.10. We define the space of uniform forms on
![]() $S^X$
to be the
$S^X$
to be the
![]() $\mathbb {R}$
-linear space
$\mathbb {R}$
-linear space
We define a closed uniform form to be a uniform form which is closed in the sense of Definition 2.27. We will denote by
![]() $Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
the space of closed uniform forms.
$Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
the space of closed uniform forms.
For any subset
![]() $Y\subset X$
, we denote by
$Y\subset X$
, we denote by
![]() $\operatorname {\mathrm {pr}}_{Y}$
the map of sets
$\operatorname {\mathrm {pr}}_{Y}$
the map of sets
![]() $\operatorname {\mathrm {pr}}_{Y}\colon S^X_*\rightarrow S^Y_*$
induced from the natural projection
$\operatorname {\mathrm {pr}}_{Y}\colon S^X_*\rightarrow S^Y_*$
induced from the natural projection
![]() $\operatorname {\mathrm {pr}}_{Y}\colon S^X\rightarrow S^Y$
. For any
$\operatorname {\mathrm {pr}}_{Y}\colon S^X\rightarrow S^Y$
. For any
![]() $\eta \in S^X_*$
, we will often denote
$\eta \in S^X_*$
, we will often denote
![]() $\operatorname {\mathrm {pr}}_Y(\eta )$
by
$\operatorname {\mathrm {pr}}_Y(\eta )$
by
![]() $\eta |_Y$
. By abuse of notation, we often write
$\eta |_Y$
. By abuse of notation, we often write
![]() $\eta |_Y$
for the configuration
$\eta |_Y$
for the configuration
![]() $\iota _Y(\eta |_Y)$
in
$\iota _Y(\eta |_Y)$
in
![]() $S^X_*$
. We say that the configurations
$S^X_*$
. We say that the configurations
![]() $\eta ,\eta '\in S^X_*$
coincide outside Y if
$\eta ,\eta '\in S^X_*$
coincide outside Y if
![]() $\eta |_{Y^c}=\eta '|_{Y^c}$
for
$\eta |_{Y^c}=\eta '|_{Y^c}$
for ![]() .
.
For any conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
and
$\xi \colon S\rightarrow \mathbb {R}$
and
![]() $W\subset X$
, we define the function
$W\subset X$
, we define the function
![]() $\xi _W\colon S^X_*\rightarrow \mathbb {R}$
by
$\xi _W\colon S^X_*\rightarrow \mathbb {R}$
by ![]() for any
for any
![]() $\eta \in S^X_*$
. The following result concerns the values of functions whose differentials are uniform.
$\eta \in S^X_*$
. The following result concerns the values of functions whose differentials are uniform.
Lemma 3.11. Let
![]() $f\in C(S^X_*)$
, and assume that
$f\in C(S^X_*)$
, and assume that
![]() $\partial f\in C^1_R(S^X)$
for some
$\partial f\in C^1_R(S^X)$
for some
![]() $R>0$
. Let
$R>0$
. Let
![]() $Y\subset X$
be a sublocale, and suppose
$Y\subset X$
be a sublocale, and suppose
![]() $\eta ,\eta '\in S^X_*$
are configurations which coincide outside Y and satisfy
$\eta ,\eta '\in S^X_*$
are configurations which coincide outside Y and satisfy
![]() $\xi _Y(\eta )=\xi _Y(\eta ')$
for any conserved quantity
$\xi _Y(\eta )=\xi _Y(\eta ')$
for any conserved quantity
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. Suppose that the interaction is irreducibly quantified. If
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
. Suppose that the interaction is irreducibly quantified. If
![]() $\widetilde {Y}$
is any subset of X such that
$\widetilde {Y}$
is any subset of X such that
![]() $ B(Y,R)\subset \widetilde {Y}$
, then we have
$ B(Y,R)\subset \widetilde {Y}$
, then we have
Proof. Since
![]() $\partial f\in C^1_R(S^X)$
, we have
$\partial f\in C^1_R(S^X)$
, we have
![]() $\nabla _{\!e} f\in C\bigl (S^{ B(e,R)}\bigr )$
. Hence, since
$\nabla _{\!e} f\in C\bigl (S^{ B(e,R)}\bigr )$
. Hence, since
![]() $ B(Y,R)\subset \widetilde {Y}$
, we have
$ B(Y,R)\subset \widetilde {Y}$
, we have
for any
![]() $e\subset Y$
. The condition
$e\subset Y$
. The condition
![]() $\xi _Y(\eta )=\xi _Y(\eta ')$
implies that
$\xi _Y(\eta )=\xi _Y(\eta ')$
implies that
![]() $\xi _Y(\eta |_Y)=\xi _Y(\eta '|_Y)$
for any conserved quantity
$\xi _Y(\eta |_Y)=\xi _Y(\eta '|_Y)$
for any conserved quantity
![]() $\xi $
. Since the interaction is irreducibly quantified, there exists a path
$\xi $
. Since the interaction is irreducibly quantified, there exists a path
![]() $\vec \gamma |_Y$
from
$\vec \gamma |_Y$
from
![]() $\eta |_Y$
to
$\eta |_Y$
to
![]() $\eta '|_Y$
in
$\eta '|_Y$
in
![]() $S^Y_*$
. If we let
$S^Y_*$
. If we let
![]() $\boldsymbol {e}=(e^1,\ldots ,e^N)$
be the sequence of edges in Y such that
$\boldsymbol {e}=(e^1,\ldots ,e^N)$
be the sequence of edges in Y such that
![]() $\vec \gamma |_Y=\vec \gamma _{\eta |_Y}^{\boldsymbol {e}}$
, then since
$\vec \gamma |_Y=\vec \gamma _{\eta |_Y}^{\boldsymbol {e}}$
, then since
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
coincide outside Y, the path
$\eta '$
coincide outside Y, the path ![]() gives a path from
gives a path from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
and the path
$\eta '$
and the path ![]() gives a path from
gives a path from
![]() $\eta |_{\widetilde {Y}}$
to
$\eta |_{\widetilde {Y}}$
to
![]() $\eta '|_{\widetilde {Y}}$
. Note that for any
$\eta '|_{\widetilde {Y}}$
. Note that for any
![]() $e\in E$
, by definition,
$e\in E$
, by definition,
![]() $\nabla _{\!e} f(\eta )= f(\eta ^e)-f(\eta )$
. Hence,
$\nabla _{\!e} f(\eta )= f(\eta ^e)-f(\eta )$
. Hence,
 $$ \begin{align*} f(\eta')&-f(\eta)=\sum_{i=1}^N \nabla_{\!e^i} f(\eta^{{i-1}}),& f(\eta'|_{\widetilde{Y}})&-f(\eta|_{\widetilde{Y}}) =\sum_{i=1}^N \nabla_{\!e^i} f(\eta^{{i-1}}|_{\widetilde{Y}}), \end{align*} $$
$$ \begin{align*} f(\eta')&-f(\eta)=\sum_{i=1}^N \nabla_{\!e^i} f(\eta^{{i-1}}),& f(\eta'|_{\widetilde{Y}})&-f(\eta|_{\widetilde{Y}}) =\sum_{i=1}^N \nabla_{\!e^i} f(\eta^{{i-1}}|_{\widetilde{Y}}), \end{align*} $$
where we let ![]() and
and ![]() for
for
![]() $i=1,\ldots , N$
. Our assertion now follows from (20).
$i=1,\ldots , N$
. Our assertion now follows from (20).
For the remainder of this article, we consider the map
given in Remark 2.25. For finite
![]() $\Lambda $
, we denote by
$\Lambda $
, we denote by ![]() the image of
the image of
![]() $S^X_*$
with respect to the map
$S^X_*$
with respect to the map
![]() ${\boldsymbol {\xi }}_\Lambda $
. As the notation suggests, the set
${\boldsymbol {\xi }}_\Lambda $
. As the notation suggests, the set
![]() $\mathcal {M}_{|\Lambda |}$
as a subset of
$\mathcal {M}_{|\Lambda |}$
as a subset of
![]() $\mathcal {M}$
depends only on the cardinality of
$\mathcal {M}$
depends only on the cardinality of
![]() $\Lambda $
. We have the following.
$\Lambda $
. We have the following.
Proposition 3.12. Let
![]() $f\in C(S^X_*)$
, and suppose
$f\in C(S^X_*)$
, and suppose
![]() $\partial f\in C^1_R(S^X)$
for some
$\partial f\in C^1_R(S^X)$
for some
![]() $R>0$
. Then for any finite connected
$R>0$
. Then for any finite connected
![]() $\Lambda ,\Lambda '\subset X$
such that
$\Lambda ,\Lambda '\subset X$
such that
![]() $d_X(\Lambda ,\Lambda ')>R$
, there exists a function
$d_X(\Lambda ,\Lambda ')>R$
, there exists a function
![]() $h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
such that
$h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
such that
for all
![]() $\eta \in S^X_*$
.
$\eta \in S^X_*$
.
Proof. Let
![]() $\Lambda ,\Lambda '$
be finite connected subsets of X such that
$\Lambda ,\Lambda '$
be finite connected subsets of X such that
![]() $d_X(\Lambda ,\Lambda ')>R$
. Noting that
$d_X(\Lambda ,\Lambda ')>R$
. Noting that
![]() $\iota ^W f(\eta )=f(\eta |_W)$
for any
$\iota ^W f(\eta )=f(\eta |_W)$
for any
![]() $W\subset X$
, it is sufficient to prove the statement for
$W\subset X$
, it is sufficient to prove the statement for
![]() $\eta \in S^X_*$
with support in
$\eta \in S^X_*$
with support in
![]() $\Lambda \cup \Lambda '$
. Consider configurations
$\Lambda \cup \Lambda '$
. Consider configurations
![]() $\eta ,\eta '\in S^X_*$
such that
$\eta ,\eta '\in S^X_*$
such that
![]() $\operatorname {\mathrm {Supp}}(\eta ),\operatorname {\mathrm {Supp}}(\eta ')\subset \Lambda \cup \Lambda '$
, and satisfying
$\operatorname {\mathrm {Supp}}(\eta ),\operatorname {\mathrm {Supp}}(\eta ')\subset \Lambda \cup \Lambda '$
, and satisfying
![]() ${\boldsymbol {\xi }}_\Lambda (\eta )={\boldsymbol {\xi }}_\Lambda (\eta ')$
and
${\boldsymbol {\xi }}_\Lambda (\eta )={\boldsymbol {\xi }}_\Lambda (\eta ')$
and
![]() $\eta |_{\Lambda '}=\eta '|_{\Lambda '}$
. Then by construction, we have
$\eta |_{\Lambda '}=\eta '|_{\Lambda '}$
. Then by construction, we have
![]() ${\boldsymbol {\xi }}_{\!X}(\eta )={\boldsymbol {\xi }}_{\!X}(\eta ')$
. Since the interaction is irreducibly quantified and the configurations
${\boldsymbol {\xi }}_{\!X}(\eta )={\boldsymbol {\xi }}_{\!X}(\eta ')$
. Since the interaction is irreducibly quantified and the configurations
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
coincide outside
$\eta '$
coincide outside
![]() $\Lambda $
, by Lemma 3.11 applied to
$\Lambda $
, by Lemma 3.11 applied to ![]() , which is a locale, and
, which is a locale, and ![]() , we have
, we have
Since
![]() $\eta '=\eta '|_{\Lambda \cup \Lambda '}$
and
$\eta '=\eta '|_{\Lambda \cup \Lambda '}$
and
![]() $\eta =\eta |_{\Lambda \cup \Lambda '}$
, noting that
$\eta =\eta |_{\Lambda \cup \Lambda '}$
, noting that
![]() $(\Lambda \cup \Lambda ') \cap B(\Lambda ,R) =\Lambda $
, we have
$(\Lambda \cup \Lambda ') \cap B(\Lambda ,R) =\Lambda $
, we have
This shows that the function
![]() $ \iota ^{\Lambda \cup \Lambda '}f(\eta ) -\iota ^{\Lambda }f(\eta ) $
depends only on
$ \iota ^{\Lambda \cup \Lambda '}f(\eta ) -\iota ^{\Lambda }f(\eta ) $
depends only on
![]() ${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
![]() $\eta |_{\Lambda '}$
if
$\eta |_{\Lambda '}$
if
![]() $d_X(\Lambda ,\Lambda ')>R$
. Since
$d_X(\Lambda ,\Lambda ')>R$
. Since
![]() $\iota ^{\Lambda '}f(\eta )$
also depends only on
$\iota ^{\Lambda '}f(\eta )$
also depends only on
![]() $\eta |_{\Lambda '}$
, we see that
$\eta |_{\Lambda '}$
, we see that
is a function which depends only on
![]() ${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
![]() $\eta |_{\Lambda '}$
. Due to symmetry, we can also see that (21) depends only on
$\eta |_{\Lambda '}$
. Due to symmetry, we can also see that (21) depends only on
![]() ${\boldsymbol {\xi }}_{\!\Lambda '}(\eta )$
and
${\boldsymbol {\xi }}_{\!\Lambda '}(\eta )$
and
![]() $\eta |_{\Lambda }$
. This implies that (21) only depends on
$\eta |_{\Lambda }$
. This implies that (21) only depends on
![]() ${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
${\boldsymbol {\xi }}_{\!\Lambda }(\eta )$
and
![]() ${\boldsymbol {\xi }}_{\!\Lambda '}(\eta )$
; hence, there exists a function
${\boldsymbol {\xi }}_{\!\Lambda '}(\eta )$
; hence, there exists a function
![]() $h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{\!|\Lambda |}\times \mathcal {M}_{\!|\Lambda '|}\rightarrow \mathbb {R}$
such that
$h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{\!|\Lambda |}\times \mathcal {M}_{\!|\Lambda '|}\rightarrow \mathbb {R}$
such that
for any
![]() $\eta \in S^X_*$
, as desired.
$\eta \in S^X_*$
, as desired.
Lemma 3.13. Let
![]() $f\in C(S^X_*)$
and
$f\in C(S^X_*)$
and
![]() $\partial f\in C^1_R(S^X)$
for some
$\partial f\in C^1_R(S^X)$
for some
![]() $R>0$
. For finite connected subsets
$R>0$
. For finite connected subsets
![]() $\Lambda ,\Lambda ',\Lambda "$
in X, suppose
$\Lambda ,\Lambda ',\Lambda "$
in X, suppose
![]() $\Lambda '$
and
$\Lambda '$
and
![]() $\Lambda "$
are in the same connected component of
$\Lambda "$
are in the same connected component of
![]() $X\setminus B(\Lambda ,R)$
. Then the functions
$X\setminus B(\Lambda ,R)$
. Then the functions
![]() $h_f^{\Lambda ,\Lambda '}$
and
$h_f^{\Lambda ,\Lambda '}$
and
![]() $h_f^{\Lambda ,\Lambda "}$
of Proposition 3.12 satisfy
$h_f^{\Lambda ,\Lambda "}$
of Proposition 3.12 satisfy
for any
![]() $\alpha \in \mathcal {M}_{|\Lambda |}$
and
$\alpha \in \mathcal {M}_{|\Lambda |}$
and
![]() $\beta \in \mathcal {M}_{|\Lambda '|}\cap \mathcal {M}_{|\Lambda "|}$
.
$\beta \in \mathcal {M}_{|\Lambda '|}\cap \mathcal {M}_{|\Lambda "|}$
.
Proof. Let
![]() $\alpha \in \mathcal {M}_{|\Lambda |}$
and
$\alpha \in \mathcal {M}_{|\Lambda |}$
and
![]() $\beta \in \mathcal {M}_{|\Lambda '|}\cap \mathcal {M}_{|\Lambda "|}$
. Then since
$\beta \in \mathcal {M}_{|\Lambda '|}\cap \mathcal {M}_{|\Lambda "|}$
. Then since
![]() $\Lambda \cap \Lambda '=\Lambda \cap \Lambda "=\emptyset $
, there exist states
$\Lambda \cap \Lambda '=\Lambda \cap \Lambda "=\emptyset $
, there exist states
![]() $\eta '$
and
$\eta '$
and
![]() $\eta "\in S^X$
at base state outside
$\eta "\in S^X$
at base state outside
![]() $\Lambda \cup \Lambda '$
and
$\Lambda \cup \Lambda '$
and
![]() $\Lambda \cup \Lambda "$
, respectively, satisfying
$\Lambda \cup \Lambda "$
, respectively, satisfying
![]() ${\boldsymbol {\xi }}_{\!\Lambda }(\eta ')={\boldsymbol {\xi }}_{\!\Lambda }(\eta ")=\alpha $
and
${\boldsymbol {\xi }}_{\!\Lambda }(\eta ')={\boldsymbol {\xi }}_{\!\Lambda }(\eta ")=\alpha $
and
![]() ${\boldsymbol {\xi }}_{\!\Lambda '}(\eta ')= {\boldsymbol {\xi }}_{\!\Lambda "}(\eta ")=\beta $
. Moreover, we may choose
${\boldsymbol {\xi }}_{\!\Lambda '}(\eta ')= {\boldsymbol {\xi }}_{\!\Lambda "}(\eta ")=\beta $
. Moreover, we may choose
![]() $\eta '$
and
$\eta '$
and
![]() $\eta "$
so that they coincide on
$\eta "$
so that they coincide on
![]() $\Lambda $
. Let Y be a sublocale of X containing
$\Lambda $
. Let Y be a sublocale of X containing
![]() $\Lambda '\cup \Lambda "$
such that
$\Lambda '\cup \Lambda "$
such that
![]() $d_X(Y,\Lambda )>R$
. By our choice of
$d_X(Y,\Lambda )>R$
. By our choice of
![]() $\eta '$
and
$\eta '$
and
![]() $\eta "$
, we have
$\eta "$
, we have
![]() ${\boldsymbol {\xi }}_{\!X}(\eta ')={\boldsymbol {\xi }}_{\!X}(\eta ")=\alpha +\beta $
. Since the interaction is irreducibly quantified, by Lemma 3.11 applied to Y and
${\boldsymbol {\xi }}_{\!X}(\eta ')={\boldsymbol {\xi }}_{\!X}(\eta ")=\alpha +\beta $
. Since the interaction is irreducibly quantified, by Lemma 3.11 applied to Y and
![]() $\widetilde {Y}= B(Y,R)$
, we have
$\widetilde {Y}= B(Y,R)$
, we have
Since
![]() $\eta '$
and
$\eta '$
and
![]() $\eta "$
are at base state outside
$\eta "$
are at base state outside
![]() $\Lambda \cup \Lambda '$
and
$\Lambda \cup \Lambda '$
and
![]() $\Lambda \cup \Lambda "$
and
$\Lambda \cup \Lambda "$
and
![]() $\Lambda \cap B(Y,R)=\emptyset $
, we have
$\Lambda \cap B(Y,R)=\emptyset $
, we have
![]() $\eta '=\eta '|_{\Lambda \cup \Lambda '}$
,
$\eta '=\eta '|_{\Lambda \cup \Lambda '}$
,
![]() $\eta "=\eta "|_{\Lambda \cup \Lambda "}$
,
$\eta "=\eta "|_{\Lambda \cup \Lambda "}$
,
![]() $\eta '|_{ B(Y,R)}=\eta '|_{\Lambda '}$
, and
$\eta '|_{ B(Y,R)}=\eta '|_{\Lambda '}$
, and
![]() $\eta "|_{ B(Y,R)}=\eta "|_{\Lambda "}$
. Noting that
$\eta "|_{ B(Y,R)}=\eta "|_{\Lambda "}$
. Noting that
![]() $\iota ^W f(\eta )=f(\eta |_W)$
for any
$\iota ^W f(\eta )=f(\eta |_W)$
for any
![]() $W\subset X$
, Equation (22) gives
$W\subset X$
, Equation (22) gives
Noting also that
![]() $\iota ^{\Lambda }f(\eta ')=\iota ^{\Lambda }f(\eta ")$
since
$\iota ^{\Lambda }f(\eta ')=\iota ^{\Lambda }f(\eta ")$
since
![]() $\eta '$
and
$\eta '$
and
![]() $\eta "$
coincide on
$\eta "$
coincide on
![]() $\Lambda $
, by the definition of
$\Lambda $
, by the definition of
![]() $h_f^{\Lambda ,\Lambda '}$
and
$h_f^{\Lambda ,\Lambda '}$
and
![]() $h_f^{\Lambda ,\Lambda "}$
, we have
$h_f^{\Lambda ,\Lambda "}$
, we have

as desired.
Let
![]() $\mathcal {M}$
be the commutative monoid defined in Definition 2.24. We will next construct a well-defined pairing
$\mathcal {M}$
be the commutative monoid defined in Definition 2.24. We will next construct a well-defined pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. We first consider some conditions on the locale.
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. We first consider some conditions on the locale.
Definition 3.14. We say that a locale X is weakly transferable if for any ball
![]() $B\subset X$
, the complement
$B\subset X$
, the complement
![]() $X\setminus B$
is a nonempty finite disjoint union of connected infinite graphs. In particular, if
$X\setminus B$
is a nonempty finite disjoint union of connected infinite graphs. In particular, if
![]() $X\setminus B$
is a connected infinite graph for any ball
$X\setminus B$
is a connected infinite graph for any ball
![]() $B\subset X$
, then we say that X is strongly transferable.
$B\subset X$
, then we say that X is strongly transferable.
Immediate from the definition, weakly transferable locales are infinite locales.
Remark 3.15. Consider the Euclidean lattice given in Example 2.2 (1). Then
![]() $\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
$\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
![]() $d>1$
is strongly transferable. The Euclidean lattice
$d>1$
is strongly transferable. The Euclidean lattice
![]() $\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
is weakly transferable, but not strongly transferable.
$\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
is weakly transferable, but not strongly transferable.
For any
![]() $R>0$
, consider the set
$R>0$
, consider the set
For any
![]() $(\Lambda _1,\Lambda ^{\prime }_1),(\Lambda _2,\Lambda _2^{\prime })\in \mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
, we denote
$(\Lambda _1,\Lambda ^{\prime }_1),(\Lambda _2,\Lambda _2^{\prime })\in \mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
, we denote
![]() $(\Lambda _1,\Lambda ^{\prime }_1)\leftrightarrow (\Lambda _2,\Lambda _2^{\prime })$
if
$(\Lambda _1,\Lambda ^{\prime }_1)\leftrightarrow (\Lambda _2,\Lambda _2^{\prime })$
if
![]() $\Lambda _1=\Lambda _2$
and
$\Lambda _1=\Lambda _2$
and
![]() $\Lambda ^{\prime }_1$
and
$\Lambda ^{\prime }_1$
and
![]() $\Lambda _2^{\prime }$
are in the same connected component of
$\Lambda _2^{\prime }$
are in the same connected component of
![]() $X\setminus B(\Lambda _1,R)=X\setminus B(\Lambda _2,R)$
, or
$X\setminus B(\Lambda _1,R)=X\setminus B(\Lambda _2,R)$
, or
![]() $\Lambda ^{\prime }_1=\Lambda ^{\prime }_2$
and
$\Lambda ^{\prime }_1=\Lambda ^{\prime }_2$
and
![]() $\Lambda _1$
and
$\Lambda _1$
and
![]() $\Lambda _2$
are in the same connected component of
$\Lambda _2$
are in the same connected component of
![]() $X\setminus B(\Lambda ^{\prime }_1,R)=X\setminus B(\Lambda ^{\prime }_2,R)$
. Note that we have
$X\setminus B(\Lambda ^{\prime }_1,R)=X\setminus B(\Lambda ^{\prime }_2,R)$
. Note that we have
![]() $(\Lambda _1,\Lambda ^{\prime }_1)\leftrightarrow (\Lambda _2,\Lambda _2^{\prime })$
if and only if
$(\Lambda _1,\Lambda ^{\prime }_1)\leftrightarrow (\Lambda _2,\Lambda _2^{\prime })$
if and only if
![]() $(\Lambda ^{\prime }_1,\Lambda _1)\leftrightarrow (\Lambda ^{\prime }_2,\Lambda _2)$
.
$(\Lambda ^{\prime }_1,\Lambda _1)\leftrightarrow (\Lambda ^{\prime }_2,\Lambda _2)$
.
Definition 3.16. We denote by
![]() ${\mathscr {A}}_R$
the subset of
${\mathscr {A}}_R$
the subset of
![]() $\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
consisting of pairs
$\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
consisting of pairs
![]() $(\Lambda ,\Lambda ')$
such that at least one of
$(\Lambda ,\Lambda ')$
such that at least one of
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
are balls.
$\Lambda '$
are balls.
From now until the end of this subsection, we assume that X is strongly transferable. In this case, we will prove that the pairing
![]() $h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
of Proposition 3.12 associated with f is independent of the choice of
$h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
of Proposition 3.12 associated with f is independent of the choice of
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and defines a well-defined pairing
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and defines a well-defined pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying a certain cocycle condition. We will address the weakly transferable case in §4.
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying a certain cocycle condition. We will address the weakly transferable case in §4.
Lemma 3.17. Suppose X is strongly transferable. Then for any
![]() $(\Lambda _1,\Lambda ^{\prime }_1), (\Lambda _2,\Lambda ^{\prime }_2)\in {\mathscr {A}}_R$
, we have
$(\Lambda _1,\Lambda ^{\prime }_1), (\Lambda _2,\Lambda ^{\prime }_2)\in {\mathscr {A}}_R$
, we have
for any
![]() $\alpha \in \mathcal {M}_{|\Lambda _1|}\cap \mathcal {M}_{|\Lambda _2|}$
and
$\alpha \in \mathcal {M}_{|\Lambda _1|}\cap \mathcal {M}_{|\Lambda _2|}$
and
![]() $\beta \in \mathcal {M}_{|\Lambda ^{\prime }_1|}\cap \mathcal {M}_{|\Lambda ^{\prime }_2|}$
.
$\beta \in \mathcal {M}_{|\Lambda ^{\prime }_1|}\cap \mathcal {M}_{|\Lambda ^{\prime }_2|}$
.
Proof. We first consider the case when
![]() $\Lambda _1,\Lambda ^{\prime }_1, \Lambda _2,\Lambda ^{\prime }_2$
are all balls. Note that for a ball B, the R-thickening
$\Lambda _1,\Lambda ^{\prime }_1, \Lambda _2,\Lambda ^{\prime }_2$
are all balls. Note that for a ball B, the R-thickening
![]() $ B(B,R)$
is also a ball. Let B be a ball such that
$ B(B,R)$
is also a ball. Let B be a ball such that
![]() $|B|\geq |\Lambda _i|$
and
$|B|\geq |\Lambda _i|$
and
![]() $d_X(\Lambda _i,B)>R$
for
$d_X(\Lambda _i,B)>R$
for
![]() $i=1,2$
. Then since X is strongly transferable, the sets
$i=1,2$
. Then since X is strongly transferable, the sets
![]() $X\setminus B(\Lambda _1,R)$
,
$X\setminus B(\Lambda _1,R)$
,
![]() $X\setminus B(\Lambda _2,R)$
and
$X\setminus B(\Lambda _2,R)$
and
![]() $X\setminus B(B,R)$
are all sublocales; hence, we have
$X\setminus B(B,R)$
are all sublocales; hence, we have
Our assertion follows from Lemma 3.13. Now, consider the case for general
![]() $(\Lambda _i,\Lambda ^{\prime }_i)\in {\mathscr {A}}_R$
. By replacing the component which is not a ball with a ball of sufficiently large size in the complement, we see that there exists a pair of balls
$(\Lambda _i,\Lambda ^{\prime }_i)\in {\mathscr {A}}_R$
. By replacing the component which is not a ball with a ball of sufficiently large size in the complement, we see that there exists a pair of balls
![]() $(B_i,B^{\prime }_i)\in {\mathscr {A}}_R$
such that
$(B_i,B^{\prime }_i)\in {\mathscr {A}}_R$
such that
![]() $|B_i|\geq |\Lambda _i|$
,
$|B_i|\geq |\Lambda _i|$
,
![]() $|B^{\prime }_i|\geq |\Lambda ^{\prime }_i|$
for
$|B^{\prime }_i|\geq |\Lambda ^{\prime }_i|$
for
![]() $i=1,2$
satisfying
$i=1,2$
satisfying
![]() $(\Lambda _i,\Lambda ^{\prime }_i)\leftrightarrow (B_i,B^{\prime }_i)$
. Again by Lemma 3.13, we see that
$(\Lambda _i,\Lambda ^{\prime }_i)\leftrightarrow (B_i,B^{\prime }_i)$
. Again by Lemma 3.13, we see that
![]() $h_f^{\Lambda _i,\Lambda ^{\prime }_i}(\alpha ,\beta )=h_f^{B_i,B^{\prime }_i}(\alpha ,\beta )$
for any
$h_f^{\Lambda _i,\Lambda ^{\prime }_i}(\alpha ,\beta )=h_f^{B_i,B^{\prime }_i}(\alpha ,\beta )$
for any
![]() $\alpha \in \mathcal {M}_{|\Lambda _i|}$
and
$\alpha \in \mathcal {M}_{|\Lambda _i|}$
and
![]() $\beta \in \mathcal {M}_{|\Lambda ^{\prime }_i|}$
. Our assertion now follows from our assertion for balls.
$\beta \in \mathcal {M}_{|\Lambda ^{\prime }_i|}$
. Our assertion now follows from our assertion for balls.
Proposition 3.18. For the system
![]() $(X,S,\phi $
), assume that X is strongly transferable and that the interaction
$(X,S,\phi $
), assume that X is strongly transferable and that the interaction
![]() $\phi $
is irreducibly quantified. Let
$\phi $
is irreducibly quantified. Let
![]() $f\in C(S^X_*)$
be a function such that
$f\in C(S^X_*)$
be a function such that
![]() $\partial f\in C^1_R(S^X)$
for some constant
$\partial f\in C^1_R(S^X)$
for some constant
![]() $R>0$
. Then there exists a pairing
$R>0$
. Then there exists a pairing
such that for any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
for any
![]() $\eta \in S^X$
. Moreover, the pairing
$\eta \in S^X$
. Moreover, the pairing
![]() $h_f$
is symmetric – in other words,
$h_f$
is symmetric – in other words,
![]() $h_f(\alpha ,\beta )=h_f(\beta ,\alpha )$
for any
$h_f(\alpha ,\beta )=h_f(\beta ,\alpha )$
for any
![]() $\alpha ,\beta \in \mathcal {M}$
– and satisfies the cocycle condition
$\alpha ,\beta \in \mathcal {M}$
– and satisfies the cocycle condition
for any
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
.
$\alpha ,\beta ,\gamma \in \mathcal {M}$
.
Proof. Note that for any
![]() $\alpha ,\beta \in \mathcal {M}$
, there exists
$\alpha ,\beta \in \mathcal {M}$
, there exists
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\alpha ,\beta \in \mathcal {M}_k$
. By Lemma 3.17, the pairing
$\alpha ,\beta \in \mathcal {M}_k$
. By Lemma 3.17, the pairing
![]() $h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
of Proposition 3.12 associated with f is independent of the choice of
$h_f^{\Lambda ,\Lambda '}\colon \mathcal {M}_{|\Lambda |}\times \mathcal {M}_{|\Lambda '|}\rightarrow \mathbb {R}$
of Proposition 3.12 associated with f is independent of the choice of
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
; hence, we have a pairing
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
; hence, we have a pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. The equality of (23) follows from Proposition 3.12. In addition, for
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. The equality of (23) follows from Proposition 3.12. In addition, for
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
![]() $(\Lambda ',\Lambda )\in {\mathscr {A}}_R$
, which by (23) implies that
$(\Lambda ',\Lambda )\in {\mathscr {A}}_R$
, which by (23) implies that
![]() $h_f$
is symmetric. In order to prove the cocycle condition, fix an arbitrary
$h_f$
is symmetric. In order to prove the cocycle condition, fix an arbitrary
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
, and let
$\alpha ,\beta ,\gamma \in \mathcal {M}$
, and let
![]() $k\in \mathbb {N}$
be such that
$k\in \mathbb {N}$
be such that
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}_k$
. Let
$\alpha ,\beta ,\gamma \in \mathcal {M}_k$
. Let
![]() $B_1$
be any ball with
$B_1$
be any ball with
![]() $|B_1|>k$
. Since X is strongly transferable,
$|B_1|>k$
. Since X is strongly transferable,
![]() $X\setminus B(B_1,R)$
is a locale. Take any ball
$X\setminus B(B_1,R)$
is a locale. Take any ball
![]() $B_2$
with
$B_2$
with
![]() $|B_2|>k$
in
$|B_2|>k$
in
![]() $X\setminus B(B_1,R)$
. Let B be a ball sufficiently large containing both
$X\setminus B(B_1,R)$
. Let B be a ball sufficiently large containing both
![]() $B_1$
and
$B_1$
and
![]() $B_2$
. Then again, since X is strongly transferable,
$B_2$
. Then again, since X is strongly transferable,
![]() $X\setminus B(B,R)$
is a locale. Take any ball
$X\setminus B(B,R)$
is a locale. Take any ball
![]() $B_3$
with
$B_3$
with
![]() $|B_3|>k$
in
$|B_3|>k$
in
![]() $X\setminus B(B,R)$
. Then the balls
$X\setminus B(B,R)$
. Then the balls
![]() $B_1,B_2,B_3\subset X$
satisfy
$B_1,B_2,B_3\subset X$
satisfy
![]() $|B_i|\geq k$
and
$|B_i|\geq k$
and
![]() $d_X(B_i,B_j)>R$
for
$d_X(B_i,B_j)>R$
for
![]() $i\neq j$
. Since
$i\neq j$
. Since
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}_k$
, there exists
$\alpha ,\beta ,\gamma \in \mathcal {M}_k$
, there exists
![]() $\eta \in S^X$
such that
$\eta \in S^X$
such that
![]() $\xi ^{B_1}(\eta )=\alpha $
,
$\xi ^{B_1}(\eta )=\alpha $
,
![]() $\xi ^{B_2}(\eta )=\beta $
,
$\xi ^{B_2}(\eta )=\beta $
,
![]() $\xi ^{B_3}(\eta )=\gamma $
and is at base state outside
$\xi ^{B_3}(\eta )=\gamma $
and is at base state outside
![]() $B_1\cup B_2\cup B_3$
. We let
$B_1\cup B_2\cup B_3$
. We let
![]() $\Lambda \subset X\setminus B(B_3,R)$
be a finite connected subset of X such that
$\Lambda \subset X\setminus B(B_3,R)$
be a finite connected subset of X such that
![]() $B_1\cup B_2\subset \Lambda $
, and let
$B_1\cup B_2\subset \Lambda $
, and let
![]() $\Lambda ' \subset X\setminus B(B_1,R)$
be a finite connected subset of X such that
$\Lambda ' \subset X\setminus B(B_1,R)$
be a finite connected subset of X such that
![]() $B_2\cup B_3\subset \Lambda '$
. For example, we may take
$B_2\cup B_3\subset \Lambda '$
. For example, we may take
![]() $\Lambda $
to be the union of
$\Lambda $
to be the union of
![]() $B_1,B_2$
and points on a path in
$B_1,B_2$
and points on a path in
![]() $X\setminus B(B_3,R)$
from the center of
$X\setminus B(B_3,R)$
from the center of
![]() $B_1$
to the center of
$B_1$
to the center of
![]() $B_2$
, and similarly for
$B_2$
, and similarly for
![]() $\Lambda '$
. Note by construction, we have
$\Lambda '$
. Note by construction, we have
![]() $(B_1,\Lambda ')$
,
$(B_1,\Lambda ')$
,
![]() $(\Lambda ,B_3)\in {\mathscr {A}}_R$
. Then by Lemma 3.13 and the definition of h, we have
$(\Lambda ,B_3)\in {\mathscr {A}}_R$
. Then by Lemma 3.13 and the definition of h, we have
 $$ \begin{align*} h_f(\alpha,\beta)&=h_f^{B_1,B_2}(\alpha,\beta)=\iota^{B_1\cup B_2}f(\eta) -\iota^{B_1}f(\eta)-\iota^{B_2}f(\eta)\\ h_f(\alpha+\beta,\gamma)&=h_f^{\Lambda,B_3}(\alpha+\beta,\gamma) =\iota^{\Lambda\cup B_3}f(\eta) -\iota^{\Lambda}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\beta,\gamma)&=h_f^{B_2,B_3}(\alpha,\beta)=\iota^{B_2\cup B_3}f(\eta) -\iota^{B_2}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\alpha,\beta+\gamma)&=h_f^{B_1,\Lambda'}(\alpha,\beta+\gamma)=\iota^{B_1\cup\Lambda'}f(\eta) -\iota^{B_1}f(\eta)-\iota^{\Lambda'}f(\eta). \end{align*} $$
$$ \begin{align*} h_f(\alpha,\beta)&=h_f^{B_1,B_2}(\alpha,\beta)=\iota^{B_1\cup B_2}f(\eta) -\iota^{B_1}f(\eta)-\iota^{B_2}f(\eta)\\ h_f(\alpha+\beta,\gamma)&=h_f^{\Lambda,B_3}(\alpha+\beta,\gamma) =\iota^{\Lambda\cup B_3}f(\eta) -\iota^{\Lambda}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\beta,\gamma)&=h_f^{B_2,B_3}(\alpha,\beta)=\iota^{B_2\cup B_3}f(\eta) -\iota^{B_2}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\alpha,\beta+\gamma)&=h_f^{B_1,\Lambda'}(\alpha,\beta+\gamma)=\iota^{B_1\cup\Lambda'}f(\eta) -\iota^{B_1}f(\eta)-\iota^{\Lambda'}f(\eta). \end{align*} $$
Since
![]() $\eta $
is at base state outside
$\eta $
is at base state outside
![]() $B_1\cup B_2\cup B_3$
, we have
$B_1\cup B_2\cup B_3$
, we have
which proves our assertion.
3.4 Criterion for uniformity
In this subsection, we prove Proposition 3.19, which gives a criterion for a function
![]() $f\in C(S^X_*)$
to be uniform when X is strongly transferable. The weakly transferable case will be addressed in Proposition 4.14. This result will play an essential role in the proof of Theorem 5.2. As in §3.3, we assume here that the interaction is irreducibly quantified.
$f\in C(S^X_*)$
to be uniform when X is strongly transferable. The weakly transferable case will be addressed in Proposition 4.14. This result will play an essential role in the proof of Theorem 5.2. As in §3.3, we assume here that the interaction is irreducibly quantified.
Proposition 3.19. For the system
![]() $(X,S,\phi )$
, assume that X is strongly transferable and that the interaction
$(X,S,\phi )$
, assume that X is strongly transferable and that the interaction
![]() $\phi $
is irreducibly quantified. Let
$\phi $
is irreducibly quantified. Let
![]() $f\in C(S^X_*)$
be a function such that
$f\in C(S^X_*)$
be a function such that
![]() $\partial f\in C^1_R(S^X)$
for some
$\partial f\in C^1_R(S^X)$
for some
![]() $R>0$
, and let
$R>0$
, and let
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing given in Proposition 3.18. If
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing given in Proposition 3.18. If
![]() $h_f\equiv 0$
, then we have
$h_f\equiv 0$
, then we have
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
We first prove a lemma to characterize the functions in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, which does not require X to be strongly transferable. For any ball
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, which does not require X to be strongly transferable. For any ball
![]() $ B(x,R)$
, we denote by
$ B(x,R)$
, we denote by ![]() the punctured ball.
the punctured ball.
Lemma 3.20. Suppose
![]() $f\in C(S^X_*)$
. Then
$f\in C(S^X_*)$
. Then
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
if and only if there exists
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
if and only if there exists
![]() $R>0$
such that for any finite
$R>0$
such that for any finite
![]() $\Lambda \subset X$
and
$\Lambda \subset X$
and
![]() $x\in \Lambda $
, we have
$x\in \Lambda $
, we have
Proof. First observe that for any
![]() $f\in C(S^X_*)$
, we have
$f\in C(S^X_*)$
, we have
where
![]() $f_\Lambda $
is the local function with exact support in the canonical expansion (18).
$f_\Lambda $
is the local function with exact support in the canonical expansion (18).
Suppose
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Then there exists
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Then there exists
![]() $R>0$
such that
$R>0$
such that
![]() $f_{\Lambda '}\equiv 0$
for any finite
$f_{\Lambda '}\equiv 0$
for any finite
![]() $\Lambda '\subset X$
safisfying
$\Lambda '\subset X$
safisfying
![]() $\operatorname {diam}(\Lambda ')>R$
. Then for any finite
$\operatorname {diam}(\Lambda ')>R$
. Then for any finite
![]() $\Lambda \subset X$
and
$\Lambda \subset X$
and
![]() $x\in \Lambda $
, we have
$x\in \Lambda $
, we have
 $$ \begin{align*} \sum_{\Lambda'\subset\Lambda,x\in\Lambda'}f_{\Lambda'}&=\sum_{\Lambda'\subset\Lambda\cap B(x,R),x\in\Lambda'}f_{\Lambda'} =\sum_{\Lambda'\subset\Lambda\cap B(x,R)}f_{\Lambda'} -\sum_{\Lambda'\subset\Lambda\cap \mathcal{B}^*(x,R)}f_{\Lambda'}\\ &=\iota^{\Lambda\cap B(x,R)}f-\iota^{\Lambda\cap \mathcal{B}^*(x,R)} f. \end{align*} $$
$$ \begin{align*} \sum_{\Lambda'\subset\Lambda,x\in\Lambda'}f_{\Lambda'}&=\sum_{\Lambda'\subset\Lambda\cap B(x,R),x\in\Lambda'}f_{\Lambda'} =\sum_{\Lambda'\subset\Lambda\cap B(x,R)}f_{\Lambda'} -\sum_{\Lambda'\subset\Lambda\cap \mathcal{B}^*(x,R)}f_{\Lambda'}\\ &=\iota^{\Lambda\cap B(x,R)}f-\iota^{\Lambda\cap \mathcal{B}^*(x,R)} f. \end{align*} $$
This gives (25). Next, we prove the converse. By the same argument, if (25) holds, then we have
for any finite
![]() $\Lambda \subset X$
and
$\Lambda \subset X$
and
![]() $x\in \Lambda $
. Suppose there exists finite
$x\in \Lambda $
. Suppose there exists finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $\operatorname {diam}(\Lambda )>R$
and
$\operatorname {diam}(\Lambda )>R$
and
![]() $f_\Lambda \not \equiv 0$
. By iteratively replacing
$f_\Lambda \not \equiv 0$
. By iteratively replacing
![]() $\Lambda '\subset \Lambda $
by
$\Lambda '\subset \Lambda $
by
![]() $\Lambda $
if necessary, we may assume that for any
$\Lambda $
if necessary, we may assume that for any
![]() $\Lambda '\subsetneq \Lambda $
, we have
$\Lambda '\subsetneq \Lambda $
, we have
![]() $f_{\Lambda '}\equiv 0$
or
$f_{\Lambda '}\equiv 0$
or
![]() $\operatorname {diam}(\Lambda ')\leq R$
. However, for this
$\operatorname {diam}(\Lambda ')\leq R$
. However, for this
![]() $\Lambda $
and any
$\Lambda $
and any
![]() $x\in \Lambda $
such that there exists
$x\in \Lambda $
such that there exists
![]() $y\in \Lambda $
with
$y\in \Lambda $
with
![]() $d_X(x,y)>R$
, we have
$d_X(x,y)>R$
, we have
Comparing with the previous equality, we see that
![]() $f_\Lambda \equiv 0$
. This contradicts our hypothesis that
$f_\Lambda \equiv 0$
. This contradicts our hypothesis that
![]() $f_\Lambda \not \equiv 0$
; hence, our assertion is proved.
$f_\Lambda \not \equiv 0$
; hence, our assertion is proved.
Before the proof of Proposition 3.19, we prepare an additional lemma. Here, we will assume that X is strongly transferable. The weakly transferable case will be treated in §4.
Lemma 3.21. For the system
![]() $(X,S,\phi )$
, assume that X is strongly transferable and that the interaction
$(X,S,\phi )$
, assume that X is strongly transferable and that the interaction
![]() $\phi $
is irreducibly quantified. Suppose
$\phi $
is irreducibly quantified. Suppose
![]() $f\in C(S^X_*)$
and
$f\in C(S^X_*)$
and
![]() $\partial f\in C^1_R(S^X)$
for some
$\partial f\in C^1_R(S^X)$
for some
![]() $R>0$
, and let
$R>0$
, and let
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing given in Proposition 3.18. If
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing given in Proposition 3.18. If
![]() $h_f\equiv 0$
, then for any
$h_f\equiv 0$
, then for any
![]() $x\in X$
and finite
$x\in X$
and finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $d_X(x,\Lambda )>R$
, we have
$d_X(x,\Lambda )>R$
, we have
Proof. Note that by the definition of the pairing
![]() $h_f$
given in (23), we have
$h_f$
given in (23), we have
for any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. If
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. If
![]() $\Lambda $
is a ball, then
$\Lambda $
is a ball, then
![]() $(\Lambda , B(x,R))$
and
$(\Lambda , B(x,R))$
and
![]() $(\Lambda ,\mathcal {B}^*(x,R))$
are both pairs in
$(\Lambda ,\mathcal {B}^*(x,R))$
are both pairs in
![]() ${\mathscr {A}}_R$
; hence, our assertion immediately follows by applying (26) to the left-hand side. Consider a general finite
${\mathscr {A}}_R$
; hence, our assertion immediately follows by applying (26) to the left-hand side. Consider a general finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $d_X(x,\Lambda )>R$
. It is sufficient to prove that
$d_X(x,\Lambda )>R$
. It is sufficient to prove that
for any
![]() $\eta \in S^X_*$
such that
$\eta \in S^X_*$
such that
![]() $\operatorname {\mathrm {Supp}}(\eta )\subset \Lambda \cup B(x,R)$
. Since X is strongly transferable,
$\operatorname {\mathrm {Supp}}(\eta )\subset \Lambda \cup B(x,R)$
. Since X is strongly transferable,
![]() $X\setminus B(x,2R)$
is a locale. Let
$X\setminus B(x,2R)$
is a locale. Let
![]() $B\subset X\setminus B(x,2R)$
be a ball whose cardinality is greater than that of
$B\subset X\setminus B(x,2R)$
be a ball whose cardinality is greater than that of
![]() $\Lambda $
and satisfying
$\Lambda $
and satisfying
![]() $d_X(\Lambda ,B)>R$
. Such a set B exists since
$d_X(\Lambda ,B)>R$
. Such a set B exists since
![]() $X\setminus B(x,2R)$
is infinite. Now choose a
$X\setminus B(x,2R)$
is infinite. Now choose a
![]() $\eta '\in S^X_*$
such that
$\eta '\in S^X_*$
such that
![]() $\eta '$
coincides with
$\eta '$
coincides with
![]() $\eta $
outside
$\eta $
outside
![]() $\Lambda \cup B$
, is at base state on
$\Lambda \cup B$
, is at base state on
![]() $\Lambda $
, and
$\Lambda $
, and
![]() ${\boldsymbol {\xi }}_{B}(\eta ')={\boldsymbol {\xi }}_{\Lambda }(\eta )$
. This implies that
${\boldsymbol {\xi }}_{B}(\eta ')={\boldsymbol {\xi }}_{\Lambda }(\eta )$
. This implies that
![]() ${\boldsymbol {\xi }}_{X}(\eta ')={\boldsymbol {\xi }}_{X}(\eta )$
. Since X is strongly transferable, the complement
${\boldsymbol {\xi }}_{X}(\eta ')={\boldsymbol {\xi }}_{X}(\eta )$
. Since X is strongly transferable, the complement ![]() is a locale. From our condition that the interaction is irreducibly quantified, by Lemma 3.11 applied to
is a locale. From our condition that the interaction is irreducibly quantified, by Lemma 3.11 applied to
![]() $Y=X\setminus B(x,R)$
and
$Y=X\setminus B(x,R)$
and
![]() $\widetilde {Y}= X\setminus \{x\}$
, we have
$\widetilde {Y}= X\setminus \{x\}$
, we have
Noting that
![]() $\eta '=\eta '|_{B\cup B(x,R)}$
and
$\eta '=\eta '|_{B\cup B(x,R)}$
and
![]() $\eta =\eta |_{\Lambda \cup B(x,R)}$
, we see that
$\eta =\eta |_{\Lambda \cup B(x,R)}$
, we see that
Since
![]() $B\subset X\setminus B(x,2R)$
, we have
$B\subset X\setminus B(x,2R)$
, we have
![]() $d_X(B, B(x,R))>R$
; hence,
$d_X(B, B(x,R))>R$
; hence,
![]() $(B, B(x,R))$
and
$(B, B(x,R))$
and
![]() $(B,\mathcal {B}^*(x,R))$
are both pairs in
$(B,\mathcal {B}^*(x,R))$
are both pairs in
![]() ${\mathscr {A}}_R$
. Our condition (26) on f applied to this pair implies that
${\mathscr {A}}_R$
. Our condition (26) on f applied to this pair implies that
Hence, (28) gives
Our assertion (27) follows from the fact that
![]() $\eta $
and
$\eta $
and
![]() $\eta '$
coincide on
$\eta '$
coincide on
![]() $ B(x,R)$
.
$ B(x,R)$
.
We may now prove Proposition 3.19.
Proof of Proposition 3.19.
Suppose
![]() $f\in C(S^X_*)$
and
$f\in C(S^X_*)$
and
![]() $\partial f\in C^1_R(S^X)$
, and that
$\partial f\in C^1_R(S^X)$
, and that
![]() $ h_f\equiv 0 $
for the pairing
$ h_f\equiv 0 $
for the pairing
![]() $h_f$
of Proposition 3.18. By Lemma 3.20, it is sufficient to check that for any fixed finite subset
$h_f$
of Proposition 3.18. By Lemma 3.20, it is sufficient to check that for any fixed finite subset
![]() $\Lambda \subset X$
and
$\Lambda \subset X$
and
![]() $x\in \Lambda $
, we have
$x\in \Lambda $
, we have
We let ![]() . Then the above equation may be written as
. Then the above equation may be written as
In order to prove this, it is sufficient to prove that
since (29) may be obtained by applying
![]() $\iota ^{\Lambda '\cup (\Lambda \cap B(x,R))}$
to both sides of (30). Hence, it is sufficient to prove that for any finite
$\iota ^{\Lambda '\cup (\Lambda \cap B(x,R))}$
to both sides of (30). Hence, it is sufficient to prove that for any finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $\Lambda \cap B(x,R)=\emptyset $
, we have
$\Lambda \cap B(x,R)=\emptyset $
, we have
which is precisely Lemma 3.21.
4 Pairing and criterion in the weakly transferable case
In this section, we will extend Proposition 3.18 concerning the construction of the pairing
![]() $h_f$
and Proposition 3.19 concerning the criterion for uniformity to the case when the locale X is weakly transferable. The reader interested only in the strongly transferable case may skip to §5. We first start with the classification of objects in
$h_f$
and Proposition 3.19 concerning the criterion for uniformity to the case when the locale X is weakly transferable. The reader interested only in the strongly transferable case may skip to §5. We first start with the classification of objects in
![]() ${\mathscr {B}}_R$
which generalizes the set of pairs
${\mathscr {B}}_R$
which generalizes the set of pairs
![]() ${\mathscr {A}}_R$
given in Definition 3.16
${\mathscr {A}}_R$
given in Definition 3.16
4.1 Equivalence relation for pairs
Let
![]() $R>0$
. In this subsection, we investigate a certain equivalence relation for certain pairs
$R>0$
. In this subsection, we investigate a certain equivalence relation for certain pairs
![]() $(B,B')$
in a subset of
$(B,B')$
in a subset of
![]() $\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
. The result of this subsection is concerned only with the underlying graph structure of the locale X. We define a variant of
$\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
. The result of this subsection is concerned only with the underlying graph structure of the locale X. We define a variant of
![]() ${\mathscr {A}}_R$
of Definition 3.16 as follows.
${\mathscr {A}}_R$
of Definition 3.16 as follows.
Definition 4.1. For any
![]() $r\in \mathbb {N}$
, we denote by
$r\in \mathbb {N}$
, we denote by
![]() ${\mathscr {B}}^r_R$
the subset of
${\mathscr {B}}^r_R$
the subset of
![]() $\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
consisting of pairs of balls
$\mathscr {F}\kern -0.5mm{\mathscr {C}}_R$
consisting of pairs of balls
![]() $(B,B')$
such that the radii of B and
$(B,B')$
such that the radii of B and
![]() $B'$
are at least r. Furthermore, we let
$B'$
are at least r. Furthermore, we let ![]() .
.
We define the relation
![]() $\sim _{r}$
to be the equivalence relation in
$\sim _{r}$
to be the equivalence relation in
![]() ${\mathscr {B}}^r_R$
generated by the relations
${\mathscr {B}}^r_R$
generated by the relations
![]() $(B,B')\leftrightarrow (B,B")$
and
$(B,B')\leftrightarrow (B,B")$
and
![]() $(B',B)\leftrightarrow (B",B)$
. In this subsection, we first study the equivalence relation
$(B',B)\leftrightarrow (B",B)$
. In this subsection, we first study the equivalence relation
![]() $\sim _{r}$
on
$\sim _{r}$
on
![]() ${\mathscr {B}}^r_R$
. In particular, we have the following.
${\mathscr {B}}^r_R$
. In particular, we have the following.
Proposition 4.2. For any
![]() $r\in \mathbb {N}$
, there are at most two equivalence classes with respect to the equivalence relation
$r\in \mathbb {N}$
, there are at most two equivalence classes with respect to the equivalence relation
![]() $\sim _{r}$
in
$\sim _{r}$
in
![]() ${\mathscr {B}}^r_R$
. Moreover, there is only one equivalence class if
${\mathscr {B}}^r_R$
. Moreover, there is only one equivalence class if
![]() $(B,B')\sim _{r}(B',B)$
for some
$(B,B')\sim _{r}(B',B)$
for some
![]() $(B,B')\in {\mathscr {B}}^r_R$
.
$(B,B')\in {\mathscr {B}}^r_R$
.
The following observation will be used throughout this section.
Remark 4.3. Let X be a weakly transferable locale, and let
![]() $B\subset X$
be a ball.
$B\subset X$
be a ball.
-
1. For any finite set
 $\Lambda \subset X$
and
$\Lambda \subset X$
and
 $r,R>0$
, there exists a ball
$r,R>0$
, there exists a ball
 $B'$
of radius at least r such that
$B'$
of radius at least r such that
 $d_X(\Lambda ,B')>R$
and
$d_X(\Lambda ,B')>R$
and
 $B'\subset (X\setminus B)$
.
$B'\subset (X\setminus B)$
. -
2. For any finite connected set
 $\Lambda \subset X\setminus B$
and
$\Lambda \subset X\setminus B$
and
 $r,R>0$
, there exists a ball
$r,R>0$
, there exists a ball
 $B'$
of radius at least r such that
$B'$
of radius at least r such that
 $d_X(B,B')>R$
and
$d_X(B,B')>R$
and
 $B'$
and
$B'$
and
 $\Lambda $
are in the same connected component of
$\Lambda $
are in the same connected component of
 $X\setminus B$
.
$X\setminus B$
.
In order to prove Proposition 4.2, we first prove Lemma 4.4 and Lemma 4.5.
Lemma 4.4. For any
![]() $r\in \mathbb {N}$
, suppose there exists three balls
$r\in \mathbb {N}$
, suppose there exists three balls
![]() $B_1,B_2,B_3$
of radii at least r in X such that
$B_1,B_2,B_3$
of radii at least r in X such that
![]() $d_X(B_i,B_j)>2R$
for
$d_X(B_i,B_j)>2R$
for
![]() $i\neq j$
. Then either
$i\neq j$
. Then either
![]() $(B_1,B_2)\leftrightarrow (B_1,B_3)$
or
$(B_1,B_2)\leftrightarrow (B_1,B_3)$
or
![]() $(B_1,B_2)\leftrightarrow (B_3,B_2)$
holds.
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
holds.
Proof. Suppose
![]() $B_2$
and
$B_2$
and
![]() $B_3$
are not in the same connected component of
$B_3$
are not in the same connected component of
![]() $X\setminus B(B_1,R)$
. Since X is connected, there exists a path
$X\setminus B(B_1,R)$
. Since X is connected, there exists a path
![]() $\vec p=(e^1,\ldots ,e^N)$
such that
$\vec p=(e^1,\ldots ,e^N)$
such that
![]() $o(\vec \gamma )\in B_2$
and
$o(\vec \gamma )\in B_2$
and
![]() $t(\vec \gamma )\in B_3$
. We take the shortest among such paths, and let
$t(\vec \gamma )\in B_3$
. We take the shortest among such paths, and let
![]() $p^i=t(e^i)$
for
$p^i=t(e^i)$
for
![]() $i=1,\ldots ,N$
. Since
$i=1,\ldots ,N$
. Since
![]() $B_2$
and
$B_2$
and
![]() $B_3$
are not in the same connected component of
$B_3$
are not in the same connected component of
![]() $X\setminus B(B_1,R)$
, there exists j such that
$X\setminus B(B_1,R)$
, there exists j such that
![]() $p^j\in B(B_1,R)$
. Since
$p^j\in B(B_1,R)$
. Since
![]() $d_X(B_1,B_2)>2R$
, we have
$d_X(B_1,B_2)>2R$
, we have
![]() $p^j\not \in B(B_2,R)$
; hence,
$p^j\not \in B(B_2,R)$
; hence,
![]() $j>R$
. Then for any
$j>R$
. Then for any
![]() $i\geq j$
, we have
$i\geq j$
, we have
![]() $p^i\in X\setminus B(B_2,R)$
since we have taken
$p^i\in X\setminus B(B_2,R)$
since we have taken
![]() $\vec p$
to be the shortest path from a vertex in
$\vec p$
to be the shortest path from a vertex in
![]() $B_2$
to a vertex in
$B_2$
to a vertex in
![]() $B_3$
. Then
$B_3$
. Then
![]() $\vec p'=(p^j,p^{j+1},\ldots ,p^N)$
gives a path in
$\vec p'=(p^j,p^{j+1},\ldots ,p^N)$
gives a path in
![]() $X\setminus B(B_2,R)$
from
$X\setminus B(B_2,R)$
from
![]() $p^j$
to a vertex in
$p^j$
to a vertex in
![]() $B_3$
. Since
$B_3$
. Since
![]() $p^j\in B(B_1,R)$
, there exists a path in
$p^j\in B(B_1,R)$
, there exists a path in
![]() $X\setminus B(B_2,R)$
from an element in
$X\setminus B(B_2,R)$
from an element in
![]() $B_1$
to the vertex
$B_1$
to the vertex
![]() $p^j$
. The combination of this path with
$p^j$
. The combination of this path with
![]() $\vec p'$
gives a path in
$\vec p'$
gives a path in
![]() $X\setminus B(B_2,R)$
from a vertex in
$X\setminus B(B_2,R)$
from a vertex in
![]() $B_1$
to a vertex in
$B_1$
to a vertex in
![]() $B_3$
; hence,
$B_3$
; hence,
![]() $B_1$
and
$B_1$
and
![]() $B_3$
are in the same connected component of
$B_3$
are in the same connected component of
![]() $X\setminus B(B_2,R)$
, as desired.
$X\setminus B(B_2,R)$
, as desired.
Lemma 4.5. For any
![]() $r\in \mathbb {N}$
, suppose there exists three balls
$r\in \mathbb {N}$
, suppose there exists three balls
![]() $B_1,B_2,B_3$
of radii at least r in X such that
$B_1,B_2,B_3$
of radii at least r in X such that
![]() $d_X(B_i,B_j)>2R$
for
$d_X(B_i,B_j)>2R$
for
![]() $i\neq j$
. Then
$i\neq j$
. Then
![]() $(B_1,B_2)\sim _{r}(B_1,B_3)$
or
$(B_1,B_2)\sim _{r}(B_1,B_3)$
or
![]() $(B_1,B_2)\sim _{r} (B_3,B_1)$
holds.
$(B_1,B_2)\sim _{r} (B_3,B_1)$
holds.
Proof. By Lemma 4.4, at least one of
![]() $(B_1,B_2)\sim _{r}(B_1,B_3)$
or
$(B_1,B_2)\sim _{r}(B_1,B_3)$
or
![]() $(B_1,B_2)\sim _{r}(B_3,B_2)$
holds. Also, by reversing the roles of
$(B_1,B_2)\sim _{r}(B_3,B_2)$
holds. Also, by reversing the roles of
![]() $B_2$
and
$B_2$
and
![]() $B_3$
, we see that at least one of
$B_3$
, we see that at least one of
![]() $(B_1,B_3)\sim _{r}(B_1,B_2)$
or
$(B_1,B_3)\sim _{r}(B_1,B_2)$
or
![]() $(B_1,B_3)\sim _{r}(B_2,B_3)$
holds. Hence, if
$(B_1,B_3)\sim _{r}(B_2,B_3)$
holds. Hence, if
![]() $(B_1,B_2)\not \sim _{r}(B_1,B_3)$
, then we have
$(B_1,B_2)\not \sim _{r}(B_1,B_3)$
, then we have
![]() $(B_1,B_2)\sim _{r}(B_3,B_2)$
and
$(B_1,B_2)\sim _{r}(B_3,B_2)$
and
![]() $(B_1,B_3)\sim _{r}(B_2,B_3)$
, where the last equivalence implies that
$(B_1,B_3)\sim _{r}(B_2,B_3)$
, where the last equivalence implies that
![]() $(B_3,B_2)\sim _{r}(B_3,B_1)$
by symmetry. This implies that
$(B_3,B_2)\sim _{r}(B_3,B_1)$
by symmetry. This implies that
![]() $(B_1,B_2)\sim _{r}(B_3,B_2)\sim _{r}(B_3,B_1)$
, as desired.
$(B_1,B_2)\sim _{r}(B_3,B_2)\sim _{r}(B_3,B_1)$
, as desired.
We may now prove Proposition 4.2.
Proof of Proposition 4.2.
We fix a pair
![]() $(B_1,B^{\prime }_1)\in {\mathscr {B}}^r_R$
. We let
$(B_1,B^{\prime }_1)\in {\mathscr {B}}^r_R$
. We let
![]() $B^{\prime \prime }_1\subset X\setminus B(B_1,2R)$
be a ball of radius at least r which is in the same connected component as
$B^{\prime \prime }_1\subset X\setminus B(B_1,2R)$
be a ball of radius at least r which is in the same connected component as
![]() $B^{\prime }_1$
in
$B^{\prime }_1$
in
![]() $X\setminus B(B_1,R)$
. Then we have
$X\setminus B(B_1,R)$
. Then we have
![]() $(B_1,B^{\prime }_1)\sim _{r} (B_1,B^{\prime \prime }_1)$
. Consider any
$(B_1,B^{\prime }_1)\sim _{r} (B_1,B^{\prime \prime }_1)$
. Consider any
![]() $(B_2,B^{\prime }_2)\in {\mathscr {B}}^r_R$
. We let B be a ball sufficiently large containing
$(B_2,B^{\prime }_2)\in {\mathscr {B}}^r_R$
. We let B be a ball sufficiently large containing
![]() $B_1\cup B^{\prime \prime }_1$
. Then
$B_1\cup B^{\prime \prime }_1$
. Then
![]() $ B(B,2R)$
is also a ball, and
$ B(B,2R)$
is also a ball, and
![]() $X\setminus B(B,2R)$
decomposes into a finite sum of locales. We let
$X\setminus B(B,2R)$
decomposes into a finite sum of locales. We let
![]() $B_3 \subset X\setminus B(B,2R)$
be a close ball of radius at least r which is in the same connected component as
$B_3 \subset X\setminus B(B,2R)$
be a close ball of radius at least r which is in the same connected component as
![]() $B_2$
in
$B_2$
in
![]() $X\setminus B(B^{\prime }_2,R)$
. Then by definition, we have
$X\setminus B(B^{\prime }_2,R)$
. Then by definition, we have
![]() $(B_2,B^{\prime }_2)\sim _{r}(B_3,B^{\prime }_2)$
. Finally, we let
$(B_2,B^{\prime }_2)\sim _{r}(B_3,B^{\prime }_2)$
. Finally, we let
![]() $B'$
be the ball sufficiently large containing
$B'$
be the ball sufficiently large containing
![]() $B_1\cup B^{\prime \prime }_1\cup B_3$
, and we let
$B_1\cup B^{\prime \prime }_1\cup B_3$
, and we let
![]() $B^{\prime \prime }_3 \subset X\setminus B(B',2R)$
be a ball of radius at least r which is in the same connected component of
$B^{\prime \prime }_3 \subset X\setminus B(B',2R)$
be a ball of radius at least r which is in the same connected component of
![]() $X\setminus B(B_3,R)$
as
$X\setminus B(B_3,R)$
as
![]() $B^{\prime }_2$
. Then by construction, we have
$B^{\prime }_2$
. Then by construction, we have
![]() $(B_2,B^{\prime }_2)\sim _{r} (B_3,B^{\prime }_2)\sim _{r} (B_3,B^{\prime \prime }_3)$
.
$(B_2,B^{\prime }_2)\sim _{r} (B_3,B^{\prime }_2)\sim _{r} (B_3,B^{\prime \prime }_3)$
.
By our construction of
![]() $B^{\prime \prime }_1$
and
$B^{\prime \prime }_1$
and
![]() $B^{\prime \prime }_3$
and Lemma 4.5, either
$B^{\prime \prime }_3$
and Lemma 4.5, either
![]() $(B_1,B^{\prime \prime }_1)\sim _{r}(B_1,B^{\prime \prime }_3)$
or
$(B_1,B^{\prime \prime }_1)\sim _{r}(B_1,B^{\prime \prime }_3)$
or
![]() $(B_1,B^{\prime \prime }_1)\sim _{r}(B^{\prime \prime }_3,B_1)$
holds. Furthermore, either
$(B_1,B^{\prime \prime }_1)\sim _{r}(B^{\prime \prime }_3,B_1)$
holds. Furthermore, either
![]() $(B_1,B^{\prime \prime }_3)\sim _{r}(B_3,B^{\prime \prime }_3)$
or
$(B_1,B^{\prime \prime }_3)\sim _{r}(B_3,B^{\prime \prime }_3)$
or
![]() $(B^{\prime \prime }_3,B_1)\sim _{r}(B^{\prime \prime }_3,B_3)$
. Combining the two, noting that
$(B^{\prime \prime }_3,B_1)\sim _{r}(B^{\prime \prime }_3,B_3)$
. Combining the two, noting that
![]() $(B_2,B^{\prime }_2)\sim _{r} (B_3,B^{\prime \prime }_3)$
, we obtain our assertion.
$(B_2,B^{\prime }_2)\sim _{r} (B_3,B^{\prime \prime }_3)$
, we obtain our assertion.
As a consequence of Proposition 4.2, we have the following.
Proposition 4.6. Let
![]() $X=(X,E)$
be a weakly transferable locale, and let
$X=(X,E)$
be a weakly transferable locale, and let
![]() $R>0$
. For any integer
$R>0$
. For any integer
![]() $r\in \mathbb {N}$
, we choose an equivalence
$r\in \mathbb {N}$
, we choose an equivalence
![]() ${\mathscr {C}}^r_R$
in
${\mathscr {C}}^r_R$
in
![]() ${\mathscr {B}}^r_R$
with respect to the equivalence relation
${\mathscr {B}}^r_R$
with respect to the equivalence relation
![]() $\sim _{r}$
. Then one of the following holds.
$\sim _{r}$
. Then one of the following holds.
-
1. For any
 $r\in \mathbb {N}$
, we have
$r\in \mathbb {N}$
, we have
 ${\mathscr {B}}^r_R={\mathscr {C}}^r_R$
.
${\mathscr {B}}^r_R={\mathscr {C}}^r_R$
. -
2. There exists
 $r_0\in \mathbb {N}$
such that for any
$r_0\in \mathbb {N}$
such that for any
 $r<r_0$
, we have
$r<r_0$
, we have
 ${\mathscr {B}}^r_R={\mathscr {C}}^r_R$
, and for
${\mathscr {B}}^r_R={\mathscr {C}}^r_R$
, and for
 $r\geq r_0$
, we have (31)where
$r\geq r_0$
, we have (31)where $$ \begin{align} {\mathscr{B}}^r_R={\mathscr{C}}^r_R\cup\overline{{\mathscr{C}}}^r_R, \end{align} $$
$$ \begin{align} {\mathscr{B}}^r_R={\mathscr{C}}^r_R\cup\overline{{\mathscr{C}}}^r_R, \end{align} $$
 .
.
Moreover, we may choose
![]() ${\mathscr {C}}^r_R$
so that
${\mathscr {C}}^r_R$
so that
![]() ${\mathscr {C}}^r_R={\mathscr {C}}^{r_0}_R \cap {\mathscr {B}}^r_R$
for any
${\mathscr {C}}^r_R={\mathscr {C}}^{r_0}_R \cap {\mathscr {B}}^r_R$
for any
![]() $r\geq r_0$
, where we let
$r\geq r_0$
, where we let
![]() $r_0=0$
when (1) holds.
$r_0=0$
when (1) holds.
Proof. Suppose (1) does not hold. Then by Proposition 4.2, there exists
![]() $r\in \mathbb {N}$
such that for any
$r\in \mathbb {N}$
such that for any
![]() $(B,B')\in {\mathscr {B}}^r_R$
, we have
$(B,B')\in {\mathscr {B}}^r_R$
, we have
![]() $(B,B')\not \sim _r(B',B)$
. Then for any
$(B,B')\not \sim _r(B',B)$
. Then for any
![]() $r'\geq r$
and
$r'\geq r$
and
![]() $(B,B')\in {\mathscr {B}}^{r'}_R$
, if
$(B,B')\in {\mathscr {B}}^{r'}_R$
, if
![]() $(B,B')\sim _{k'}(B',B)$
, then this would imply that
$(B,B')\sim _{k'}(B',B)$
, then this would imply that
![]() $(B,B')\sim _r(B',B)$
. Hence, our assumption implies that
$(B,B')\sim _r(B',B)$
. Hence, our assumption implies that
![]() $(B,B')\not \sim _{r'}(B',B)$
. We take
$(B,B')\not \sim _{r'}(B',B)$
. We take
![]() $r_0$
to be the minimum of such r. Then (31) follows from Proposition 4.2.
$r_0$
to be the minimum of such r. Then (31) follows from Proposition 4.2.
Note that for any
![]() $r\geq r_0$
and
$r\geq r_0$
and
![]() $(B_1,B^{\prime }_1)$
and
$(B_1,B^{\prime }_1)$
and
![]() $(B_2,B^{\prime }_2)$
in
$(B_2,B^{\prime }_2)$
in
![]() ${\mathscr {B}}^r_R$
, we have
${\mathscr {B}}^r_R$
, we have
![]() $(B_1,B^{\prime }_1)\sim _{r_0}(B_2,B^{\prime }_2)$
if and only if
$(B_1,B^{\prime }_1)\sim _{r_0}(B_2,B^{\prime }_2)$
if and only if
![]() $(B_1,B^{\prime }_1)\sim _{r}(B_2,B^{\prime }_2)$
. This may be proved as follows. It is immediate from the definition that if
$(B_1,B^{\prime }_1)\sim _{r}(B_2,B^{\prime }_2)$
. This may be proved as follows. It is immediate from the definition that if
![]() $\sim _{r}$
holds, then
$\sim _{r}$
holds, then
![]() $\sim _{r_0}$
holds. However, if
$\sim _{r_0}$
holds. However, if
![]() $(B_1,B^{\prime }_1)\sim _{r_0}(B_2,B^{\prime }_2)$
and if
$(B_1,B^{\prime }_1)\sim _{r_0}(B_2,B^{\prime }_2)$
and if
![]() $(B_1,B^{\prime }_1)\not \sim _{r}(B_2,B^{\prime }_2)$
, then we would have
$(B_1,B^{\prime }_1)\not \sim _{r}(B_2,B^{\prime }_2)$
, then we would have
![]() $(B_1,B^{\prime }_1)\sim _{r}(B^{\prime }_2,B_2)$
, which would imply that
$(B_1,B^{\prime }_1)\sim _{r}(B^{\prime }_2,B_2)$
, which would imply that
![]() $(B_1,B^{\prime }_1)\sim _{r_0}(B^{\prime }_2,B_2)$
. Then we would have
$(B_1,B^{\prime }_1)\sim _{r_0}(B^{\prime }_2,B_2)$
. Then we would have
![]() $(B_2,B^{\prime }_2)\sim _{r_0}(B^{\prime }_2,B_2)$
, contradicting our choice of
$(B_2,B^{\prime }_2)\sim _{r_0}(B^{\prime }_2,B_2)$
, contradicting our choice of
![]() $r_0$
.
$r_0$
.
If we choose an equivalence class
![]() ${\mathscr {C}}^{r_0}_R$
of
${\mathscr {C}}^{r_0}_R$
of
![]() ${\mathscr {B}}^{r_0}_R$
with respect to the equivalence
${\mathscr {B}}^{r_0}_R$
with respect to the equivalence
![]() $\sim _{r_0}$
, then we may take
$\sim _{r_0}$
, then we may take ![]() for any
for any
![]() $r\geq r_0$
, which gives an equivalence class of
$r\geq r_0$
, which gives an equivalence class of
![]() ${\mathscr {B}}^r_R$
with respect to the equivalence
${\mathscr {B}}^r_R$
with respect to the equivalence
![]() $\sim _{r}$
satisfying the condition of our assertion.
$\sim _{r}$
satisfying the condition of our assertion.
Definition 4.7. Let
![]() $X=(X,E)$
be a weakly transferable locale, and let
$X=(X,E)$
be a weakly transferable locale, and let
![]() $R>0$
. If (1) of Proposition 4.6 holds, then we say that
$R>0$
. If (1) of Proposition 4.6 holds, then we say that
![]() ${\mathscr {B}}_R$
has a unique class, and we define the integer
${\mathscr {B}}_R$
has a unique class, and we define the integer
![]() $r_0$
to be one. If (2) of Proposition 4.6 holds, then we say that
$r_0$
to be one. If (2) of Proposition 4.6 holds, then we say that
![]() ${\mathscr {B}}_R$
is split, and we define
${\mathscr {B}}_R$
is split, and we define
![]() $r_0$
to be the minimum integer satisfying (31). Moreover, we will fix an equivalence class
$r_0$
to be the minimum integer satisfying (31). Moreover, we will fix an equivalence class
![]() ${\mathscr {C}}^r_R$
of
${\mathscr {C}}^r_R$
of
![]() ${\mathscr {B}}^r_R$
with respect to the equivalence relation
${\mathscr {B}}^r_R$
with respect to the equivalence relation
![]() $\sim _{r}$
so that
$\sim _{r}$
so that
![]() ${\mathscr {C}}^r_R= {\mathscr {C}}^{r_0}_R\cap {\mathscr {B}}^r_R$
for
${\mathscr {C}}^r_R= {\mathscr {C}}^{r_0}_R\cap {\mathscr {B}}^r_R$
for
![]() $r\geq r_0$
.
$r\geq r_0$
.
4.2 Pairing for functions in the weakly transferable case
In this subsection, we will construct and prove the cocycle condition for the pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. We let X be a weakly transferable locale. We let
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
. We let X be a weakly transferable locale. We let
![]() ${\mathscr {B}}^r_R$
as in Definition 4.1, and we fix an equivalence class
${\mathscr {B}}^r_R$
as in Definition 4.1, and we fix an equivalence class
![]() ${\mathscr {C}}^r_R$
of
${\mathscr {C}}^r_R$
of
![]() ${\mathscr {B}}^r_R$
with respect to the equivalence relation
${\mathscr {B}}^r_R$
with respect to the equivalence relation
![]() $\sim _{r}$
as in Definition 4.7. We define the pairing
$\sim _{r}$
as in Definition 4.7. We define the pairing
![]() $h_f$
as follows.
$h_f$
as follows.
Definition 4.8. Let
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f \in C^1_R(S^X)$
for some
$\partial f \in C^1_R(S^X)$
for some
![]() $R>0$
. We define the pairing
$R>0$
. We define the pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
as follows. For any
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
as follows. For any
![]() $\alpha ,\beta \in \mathcal {M}$
, we let
$\alpha ,\beta \in \mathcal {M}$
, we let
![]() $k\geq r_0$
such that
$k\geq r_0$
such that
![]() $\alpha ,\beta \in \mathcal {M}_k$
. By taking an arbitrary
$\alpha ,\beta \in \mathcal {M}_k$
. By taking an arbitrary
![]() $(B,B')\in {\mathscr {C}}^k_R$
, we let
$(B,B')\in {\mathscr {C}}^k_R$
, we let
where
![]() $h_f^{B,B'}$
is the pairing
$h_f^{B,B'}$
is the pairing
![]() $h_f^{\Lambda ,\Lambda '}$
defined in Proposition 3.12 for
$h_f^{\Lambda ,\Lambda '}$
defined in Proposition 3.12 for
![]() $(\Lambda ,\Lambda ')=(B,B')$
. Note that we have
$(\Lambda ,\Lambda ')=(B,B')$
. Note that we have
![]() $|B|\geq r(B)$
and
$|B|\geq r(B)$
and
![]() $|B'|\geq r(B')$
; hence,
$|B'|\geq r(B')$
; hence,
![]() $|B|, |B'|\geq k$
.
$|B|, |B'|\geq k$
.
For the remainder of this subsection, we let
![]() $R>0$
, and we fix a
$R>0$
, and we fix a
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f\in C^1_R(S^X)$
. If
$\partial f\in C^1_R(S^X)$
. If
![]() $(B_1,B^{\prime }_1),(B_2,B^{\prime }_2)\in {\mathscr {C}}^k_R$
, then we have
$(B_1,B^{\prime }_1),(B_2,B^{\prime }_2)\in {\mathscr {C}}^k_R$
, then we have
![]() $(B_1,B^{\prime }_1)\sim _{k}(B_2,B^{\prime }_2)$
; hence, by Lemma 3.13, we see that
$(B_1,B^{\prime }_1)\sim _{k}(B_2,B^{\prime }_2)$
; hence, by Lemma 3.13, we see that
for any
![]() $\alpha ,\beta \in \mathcal {M}_k$
. Since
$\alpha ,\beta \in \mathcal {M}_k$
. Since
![]() ${\mathscr {C}}^k_R={\mathscr {C}}^{r_0}_R\cap {\mathscr {B}}^k_R$
, this shows that
${\mathscr {C}}^k_R={\mathscr {C}}^{r_0}_R\cap {\mathscr {B}}^k_R$
, this shows that
![]() $h_f$
is independent of the choices of
$h_f$
is independent of the choices of
![]() $k\geq r_0$
satisfying
$k\geq r_0$
satisfying
![]() $\alpha ,\beta \in \mathcal {M}_k$
and the pair
$\alpha ,\beta \in \mathcal {M}_k$
and the pair
![]() $(B,B')\in {\mathscr {C}}^k_R$
.
$(B,B')\in {\mathscr {C}}^k_R$
.
When X is weakly transferable, the pairing
![]() $h_f$
may not be symmetric.
$h_f$
may not be symmetric.
Lemma 4.9. If
![]() ${\mathscr {B}}_R$
has a unique class, then the pairing
${\mathscr {B}}_R$
has a unique class, then the pairing
![]() $h_f$
is symmetric.
$h_f$
is symmetric.
Proof. If
![]() ${\mathscr {B}}_R$
has a unique class, then
${\mathscr {B}}_R$
has a unique class, then
![]() $(B,B')\in {\mathscr {C}}^k_R$
implies that
$(B,B')\in {\mathscr {C}}^k_R$
implies that
![]() $(B',B)\in {\mathscr {C}}^k_R$
. This shows that for any
$(B',B)\in {\mathscr {C}}^k_R$
. This shows that for any
![]() $k\geq r_0$
and
$k\geq r_0$
and
![]() $\alpha ,\beta \in \mathcal {M}_k$
, we have
$\alpha ,\beta \in \mathcal {M}_k$
, we have
as desired.
Remark 4.10. If
![]() ${\mathscr {B}}_R$
is split, then
${\mathscr {B}}_R$
is split, then
![]() $h_f$
may not necessarily be symmetric.
$h_f$
may not necessarily be symmetric.
The pairing
![]() $h_f$
may be calculated as follows.
$h_f$
may be calculated as follows.
Proposition 4.11. For any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and for any
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and for any
![]() $\alpha \in \mathcal {M}_{|\Lambda |}$
and
$\alpha \in \mathcal {M}_{|\Lambda |}$
and
![]() $\beta \in \mathcal {M}_{|\Lambda '|}$
, we have
$\beta \in \mathcal {M}_{|\Lambda '|}$
, we have
In particular, if
![]() $h_f$
is symmetric, then we have
$h_f$
is symmetric, then we have
Proof. Fix an arbitrary
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
![]() $\alpha \in \mathcal {M}_{|\Lambda |}$
,
$\alpha \in \mathcal {M}_{|\Lambda |}$
,
![]() $\beta \in \mathcal {M}_{|\Lambda '|}$
. Let
$\beta \in \mathcal {M}_{|\Lambda '|}$
. Let
![]() $k\geq r_0$
such that
$k\geq r_0$
such that
![]() $k\geq \max \{|\Lambda |,|\Lambda '|\}$
. Assume without loss of generality that
$k\geq \max \{|\Lambda |,|\Lambda '|\}$
. Assume without loss of generality that
![]() $\Lambda $
is a ball. Since X is weakly transferable, the connected component of
$\Lambda $
is a ball. Since X is weakly transferable, the connected component of
![]() $X\setminus B(\Lambda ,R)$
containing
$X\setminus B(\Lambda ,R)$
containing
![]() $\Lambda '$
is infinite and hence contains a closed ball
$\Lambda '$
is infinite and hence contains a closed ball
![]() $B'$
such that
$B'$
such that
![]() $r(B')\geq k$
. Then
$r(B')\geq k$
. Then
![]() $(\Lambda ,\Lambda ')\leftrightarrow (\Lambda ,B')$
. Again, the connected component of
$(\Lambda ,\Lambda ')\leftrightarrow (\Lambda ,B')$
. Again, the connected component of
![]() $X\setminus B(B',R)$
containing
$X\setminus B(B',R)$
containing
![]() $\Lambda $
is infinite and hence contains a ball B such that
$\Lambda $
is infinite and hence contains a ball B such that
![]() $r(B)\geq k$
. Then
$r(B)\geq k$
. Then
![]() $(\Lambda ,B')\leftrightarrow (B,B')$
. By construction,
$(\Lambda ,B')\leftrightarrow (B,B')$
. By construction,
![]() $(B,B')\in {\mathscr {B}}^k_R$
. If
$(B,B')\in {\mathscr {B}}^k_R$
. If
![]() $(B,B')\in {\mathscr {C}}^k_R$
, then by Lemma 3.13, noting that
$(B,B')\in {\mathscr {C}}^k_R$
, then by Lemma 3.13, noting that
![]() $|B|,|B'|\geq k$
, we have
$|B|,|B'|\geq k$
, we have
If
![]() $(B,B')\not \in {\mathscr {C}}^k_R$
, then
$(B,B')\not \in {\mathscr {C}}^k_R$
, then
![]() $(B',B)\in {\mathscr {C}}^k_R$
; hence, we have
$(B',B)\in {\mathscr {C}}^k_R$
; hence, we have
as desired.
In order to prove the cocycle condition of
![]() $h_f$
, we will prepare the following lemma concerning the existence of a triplet of balls
$h_f$
, we will prepare the following lemma concerning the existence of a triplet of balls
![]() $B_1,B_2,B_3$
sufficiently large and sufficiently apart satisfying the condition
$B_1,B_2,B_3$
sufficiently large and sufficiently apart satisfying the condition
![]() $(B_1,B_2)\leftrightarrow (B_1,B_3)\leftrightarrow (B_2,B_3)$
. Note that if X is strongly transferable, then this condition is automatically satisfied if
$(B_1,B_2)\leftrightarrow (B_1,B_3)\leftrightarrow (B_2,B_3)$
. Note that if X is strongly transferable, then this condition is automatically satisfied if
![]() $d_X(B_i,B_j)>R$
for
$d_X(B_i,B_j)>R$
for
![]() $i\neq j$
.
$i\neq j$
.
Lemma 4.12. For any
![]() $r\in \mathbb {N}$
, there exists balls
$r\in \mathbb {N}$
, there exists balls
![]() $B_1,B_2,B_3$
of radii at least r in X such that
$B_1,B_2,B_3$
of radii at least r in X such that
![]() $d_X(B_i,B_j)>R$
for
$d_X(B_i,B_j)>R$
for
![]() $i\neq j$
and
$i\neq j$
and
Moreover, we may take
![]() $B_1,B_2,B_3$
so that
$B_1,B_2,B_3$
so that
![]() $(B_1,B_2)$
,
$(B_1,B_2)$
,
![]() $(B_1,B_3)$
,
$(B_1,B_3)$
,
![]() $(B_2,B_3)\in {\mathscr {C}}^r_R$
.
$(B_2,B_3)\in {\mathscr {C}}^r_R$
.
Proof. Take
![]() $B_1$
to be a ball in X such that
$B_1$
to be a ball in X such that
![]() $r(B_1)\geq r$
. We then take
$r(B_1)\geq r$
. We then take
![]() $B_2$
to be an arbitrary ball in
$B_2$
to be an arbitrary ball in
![]() $X\setminus B(B_1,2R)$
such that
$X\setminus B(B_1,2R)$
such that
![]() $r(B_2)\geq r$
. Finally, we take a ball
$r(B_2)\geq r$
. Finally, we take a ball
![]() $\Lambda $
containing
$\Lambda $
containing
![]() $B_1$
and
$B_1$
and
![]() $B_2$
, and let
$B_2$
, and let
![]() $B_3$
be a ball in
$B_3$
be a ball in
![]() $X\setminus B(\Lambda ,2R)$
with
$X\setminus B(\Lambda ,2R)$
with
![]() $r(B_3)\geq r$
. By construction, we have
$r(B_3)\geq r$
. By construction, we have
![]() $d_X(B_i,B_j)>2R$
for
$d_X(B_i,B_j)>2R$
for
![]() $i\neq j$
. By Lemma 4.5, the following holds.
$i\neq j$
. By Lemma 4.5, the following holds.
-
1. Either
 $(B_1,B_2)\leftrightarrow (B_1,B_3)$
or
$(B_1,B_2)\leftrightarrow (B_1,B_3)$
or
 $(B_1,B_2)\leftrightarrow (B_3,B_2)$
.
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
. -
2. Either
 $(B_1,B_3)\leftrightarrow (B_1,B_2)$
or
$(B_1,B_3)\leftrightarrow (B_1,B_2)$
or
 $(B_1,B_3)\leftrightarrow (B_2,B_3)$
.
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
. -
3. Either
 $(B_2,B_3)\leftrightarrow (B_2,B_1)$
or
$(B_2,B_3)\leftrightarrow (B_2,B_1)$
or
 $(B_2,B_3)\leftrightarrow (B_1,B_3)$
.
$(B_2,B_3)\leftrightarrow (B_1,B_3)$
.
From this observation, we see that at least one of the following holds.
-
(a)
 $(B_1,B_2)\leftrightarrow (B_1,B_3)$
and
$(B_1,B_2)\leftrightarrow (B_1,B_3)$
and
 $(B_1,B_3)\leftrightarrow (B_2,B_3)$
.
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
. -
(b)
 $(B_1,B_2)\leftrightarrow (B_3,B_2)$
and
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
and
 $(B_1,B_3)\leftrightarrow (B_2,B_3)$
.
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
. -
(c)
 $(B_1,B_3)\leftrightarrow (B_1,B_2)$
and
$(B_1,B_3)\leftrightarrow (B_1,B_2)$
and
 $(B_2,B_3)\leftrightarrow (B_2,B_1)$
.
$(B_2,B_3)\leftrightarrow (B_2,B_1)$
.
In fact, if (a) does not hold, then either
![]() $(B_1,B_2)\not \leftrightarrow (B_1,B_3)$
or
$(B_1,B_2)\not \leftrightarrow (B_1,B_3)$
or
![]() $(B_1,B_3)\not \leftrightarrow (B_2,B_3)$
holds. If
$(B_1,B_3)\not \leftrightarrow (B_2,B_3)$
holds. If
![]() $(B_1,B_2)\not \leftrightarrow (B_1,B_3)$
, then by (1), we have
$(B_1,B_2)\not \leftrightarrow (B_1,B_3)$
, then by (1), we have
![]() $(B_1,B_2)\leftrightarrow (B_3,B_2)$
, and by (2), we have
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
, and by (2), we have
![]() $(B_1,B_3)\leftrightarrow (B_2,B_3)$
; hence, (b) holds. If
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
; hence, (b) holds. If
![]() $(B_1,B_3)\not \leftrightarrow (B_2,B_3)$
, then by (2), we have
$(B_1,B_3)\not \leftrightarrow (B_2,B_3)$
, then by (2), we have
![]() $(B_1,B_2)\leftrightarrow (B_3,B_2)$
, and by (3), we have
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
, and by (3), we have
![]() $(B_2,B_3)\leftrightarrow (B_2,B_1)$
; hence, (c) holds.
$(B_2,B_3)\leftrightarrow (B_2,B_1)$
; hence, (c) holds.
If (a) holds, then we have (32). If (b) holds, then we obtain (32) by taking
![]() $B_1$
to be
$B_1$
to be
![]() $B_2$
and
$B_2$
and
![]() $B_2$
to be
$B_2$
to be
![]() $B_1$
, If (c) holds, then we obtain (32) by taking
$B_1$
, If (c) holds, then we obtain (32) by taking
![]() $B_2$
to be
$B_2$
to be
![]() $B_3$
and
$B_3$
and
![]() $B_3$
to be
$B_3$
to be
![]() $B_2$
. Our last assertion is proved if
$B_2$
. Our last assertion is proved if
![]() $(B_1,B_2)\in {\mathscr {C}}^r_R$
. If
$(B_1,B_2)\in {\mathscr {C}}^r_R$
. If
![]() $(B_1,B_2)\not \in {\mathscr {C}}^r_R$
, our assertion is proved by taking
$(B_1,B_2)\not \in {\mathscr {C}}^r_R$
, our assertion is proved by taking
![]() $B_1$
to be
$B_1$
to be
![]() $B_3$
and
$B_3$
and
![]() $B_3$
to be
$B_3$
to be
![]() $B_1$
.
$B_1$
.
We are now ready to prove the cocycle condition for our
![]() $h_f$
.
$h_f$
.
Proposition 4.13. Assume that X is a weakly transferable locale. Let
![]() $R>0$
, and let
$R>0$
, and let
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f\in C^1_R(S^X)$
. Then the pairing
$\partial f\in C^1_R(S^X)$
. Then the pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfies
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfies
for any
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
.
$\alpha ,\beta ,\gamma \in \mathcal {M}$
.
Proof. For an arbitrary
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
, there exists
$\alpha ,\beta ,\gamma \in \mathcal {M}$
, there exists
![]() $k\geq r_0$
such that
$k\geq r_0$
such that
![]() $\alpha ,\beta ,\gamma ,\in \mathcal {M}_k$
. Let
$\alpha ,\beta ,\gamma ,\in \mathcal {M}_k$
. Let
![]() $B_1,B_2,B_3$
be balls in X satisfying the condition of Lemma 4.12 for
$B_1,B_2,B_3$
be balls in X satisfying the condition of Lemma 4.12 for
![]() $r=k$
. Then since
$r=k$
. Then since
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}_k$
, there exists
$\alpha ,\beta ,\gamma \in \mathcal {M}_k$
, there exists
![]() $\eta \in S^X$
such that
$\eta \in S^X$
such that
![]() $\xi ^{B_1}(\eta )=\alpha $
,
$\xi ^{B_1}(\eta )=\alpha $
,
![]() $\xi ^{B_2}(\eta )=\beta $
,
$\xi ^{B_2}(\eta )=\beta $
,
![]() $\xi ^{B_3}(\eta )=\gamma $
and is at base state outside
$\xi ^{B_3}(\eta )=\gamma $
and is at base state outside
![]() $B_1\cup B_2\cup B_3$
. Then since
$B_1\cup B_2\cup B_3$
. Then since
![]() $(B_1,B_3)\leftrightarrow (B_2,B_3)$
, there exists a finite connected subset
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
, there exists a finite connected subset
![]() $\Lambda \subset X\setminus B(B_3,R)$
such that
$\Lambda \subset X\setminus B(B_3,R)$
such that
![]() $B_1\cup B_2\subset \Lambda $
, and since
$B_1\cup B_2\subset \Lambda $
, and since
![]() $(B_1,B_2)\leftrightarrow (B_1,B_3)$
, there exists a finite connected subset
$(B_1,B_2)\leftrightarrow (B_1,B_3)$
, there exists a finite connected subset
![]() $\Lambda ' \subset X\setminus B(B_1,R)$
such that
$\Lambda ' \subset X\setminus B(B_1,R)$
such that
![]() $B_2\cup B_3\subset \Lambda '$
. Note by construction, we have
$B_2\cup B_3\subset \Lambda '$
. Note by construction, we have
![]() $(B_1,\Lambda ')$
,
$(B_1,\Lambda ')$
,
![]() $(\Lambda ,B_3)\in {\mathscr {A}}_R$
and
$(\Lambda ,B_3)\in {\mathscr {A}}_R$
and
![]() $(B_1,B_2), (B_2,B_3)\in {\mathscr {C}}^k_R$
. Then by Lemma 3.13 and the definition of h, we have
$(B_1,B_2), (B_2,B_3)\in {\mathscr {C}}^k_R$
. Then by Lemma 3.13 and the definition of h, we have
 $$ \begin{align*} h_f(\alpha,\beta)&=h_f^{B_1,B_2}(\alpha,\beta)=\iota^{B_1\cup B_2}f(\eta) -\iota^{B_1}f(\eta)-\iota^{B_2}f(\eta)\\ h_f(\alpha+\beta,\gamma)&=h_f^{\Lambda,B_3}(\alpha+\beta,\gamma) =\iota^{\Lambda\cup B_3}f(\eta) -\iota^{\Lambda}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\beta,\gamma)&=h_f^{B_2,B_3}(\alpha,\beta)=\iota^{B_2\cup B_3}f(\eta) -\iota^{B_2}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\alpha,\beta+\gamma)&=h_f^{B_1,\Lambda'}(\alpha,\beta+\gamma)=\iota^{B_1\cup\Lambda'}f(\eta) -\iota^{B_1}f(\eta)-\iota^{\Lambda'}f(\eta). \end{align*} $$
$$ \begin{align*} h_f(\alpha,\beta)&=h_f^{B_1,B_2}(\alpha,\beta)=\iota^{B_1\cup B_2}f(\eta) -\iota^{B_1}f(\eta)-\iota^{B_2}f(\eta)\\ h_f(\alpha+\beta,\gamma)&=h_f^{\Lambda,B_3}(\alpha+\beta,\gamma) =\iota^{\Lambda\cup B_3}f(\eta) -\iota^{\Lambda}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\beta,\gamma)&=h_f^{B_2,B_3}(\alpha,\beta)=\iota^{B_2\cup B_3}f(\eta) -\iota^{B_2}f(\eta)-\iota^{B_3}f(\eta)\\ h_f(\alpha,\beta+\gamma)&=h_f^{B_1,\Lambda'}(\alpha,\beta+\gamma)=\iota^{B_1\cup\Lambda'}f(\eta) -\iota^{B_1}f(\eta)-\iota^{\Lambda'}f(\eta). \end{align*} $$
Since
![]() $\eta $
is at base state outside
$\eta $
is at base state outside
![]() $B_1\cup B_2\cup B_3$
, we have
$B_1\cup B_2\cup B_3$
, we have
which proves our assertion.
4.3 Criterion for uniformity in the weakly transferable case
In this subsection, we will prove Proposition 4.14, which is a weakly transferable version of Proposition 3.19.
Proposition 4.14. Assume that the locale X is weakly transferable. Suppose
![]() $f\in C(S^X_*)$
satisfies
$f\in C(S^X_*)$
satisfies
![]() $\partial f\in C^1_R(S^X)$
for
$\partial f\in C^1_R(S^X)$
for
![]() $R>0$
, and let
$R>0$
, and let
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing defined in Definition 4.8. If
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing defined in Definition 4.8. If
![]() $h_f\equiv 0$
, then we have
$h_f\equiv 0$
, then we have
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
The proof of Proposition 4.14 is the same as that of Proposition 3.19, but by using Lemma 4.15 below which is valid even when X is weakly transferable, instead of Lemma 3.21, which assumed that X is strongly transferable.
Lemma 4.15. Assume that X is weakly transferable. Suppose
![]() $f\in C(S^X_*)$
and
$f\in C(S^X_*)$
and
![]() $\partial f\in C^1_R(S^X)$
, and let
$\partial f\in C^1_R(S^X)$
, and let
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing defined in Definition 4.8. If
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be the pairing defined in Definition 4.8. If
![]() $h_f\equiv 0$
, then for any
$h_f\equiv 0$
, then for any
![]() $x\in X$
and finite
$x\in X$
and finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $d_X(x,\Lambda )>R$
, we have
$d_X(x,\Lambda )>R$
, we have
where ![]() is the punctured ball.
is the punctured ball.
Proof. Since
![]() $h_f\equiv 0$
, by the definition of the pairing
$h_f\equiv 0$
, by the definition of the pairing
![]() $h_f$
given in Definition 4.8 and Proposition 3.12, we have
$h_f$
given in Definition 4.8 and Proposition 3.12, we have
for any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. Again, if B is a ball, then
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. Again, if B is a ball, then
![]() $(B, B(x,R))$
and
$(B, B(x,R))$
and
![]() $(B,\mathcal {B}^*(x,R))$
are both pairs in
$(B,\mathcal {B}^*(x,R))$
are both pairs in
![]() ${\mathscr {A}}_R$
; hence, our assertion immediately follows by applying (33) to the left-hand side. Consider a general finite
${\mathscr {A}}_R$
; hence, our assertion immediately follows by applying (33) to the left-hand side. Consider a general finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $d_X(x,\Lambda )>R$
. It is sufficient to prove that
$d_X(x,\Lambda )>R$
. It is sufficient to prove that
for any
![]() $\eta \in S^X_*$
such that
$\eta \in S^X_*$
such that
![]() $\operatorname {\mathrm {Supp}}(\eta )\subset \Lambda \cup B(x,R)$
. Since X is weakly transferable,
$\operatorname {\mathrm {Supp}}(\eta )\subset \Lambda \cup B(x,R)$
. Since X is weakly transferable, ![]() decomposes into a finite number of locales
decomposes into a finite number of locales
![]() $Y=Y_1\cup \cdots \cup Y_K$
. We may reorder the
$Y=Y_1\cup \cdots \cup Y_K$
. We may reorder the
![]() $Y_i$
so that there exists integer k such that
$Y_i$
so that there exists integer k such that
![]() $Y_i\cap \Lambda \neq \emptyset $
for
$Y_i\cap \Lambda \neq \emptyset $
for
![]() $i\leq k$
and
$i\leq k$
and
![]() $Y_i\cap \Lambda =\emptyset $
for
$Y_i\cap \Lambda =\emptyset $
for
![]() $i>k$
. Let
$i>k$
. Let ![]() . Then we have
. Then we have
![]() $\Lambda =\Lambda _1\cup \cdots \cup \Lambda _k$
.
$\Lambda =\Lambda _1\cup \cdots \cup \Lambda _k$
.
Let
![]() $B^{\prime }_1$
be a ball such that
$B^{\prime }_1$
be a ball such that
![]() $ B(\Lambda ,R)\cup B(x,R)\subset B^{\prime }_1$
. Let
$ B(\Lambda ,R)\cup B(x,R)\subset B^{\prime }_1$
. Let
![]() $B_1\subset (X\setminus B(B^{\prime }_1,R))\cap Y_1$
,
$B_1\subset (X\setminus B(B^{\prime }_1,R))\cap Y_1$
,
![]() $d_X(\Lambda ,B_1)>R$
be a ball whose cardinality is greater than that of
$d_X(\Lambda ,B_1)>R$
be a ball whose cardinality is greater than that of
![]() $\Lambda _1$
. Such a set
$\Lambda _1$
. Such a set
![]() $B_1$
exists since
$B_1$
exists since
![]() $Y_1$
is an infinite set. Now choose a
$Y_1$
is an infinite set. Now choose a
![]() $\eta '\in S^X_*$
such that
$\eta '\in S^X_*$
such that
![]() $\eta '$
coincides with
$\eta '$
coincides with
![]() $\eta $
outside
$\eta $
outside
![]() $\Lambda _1\cup B_1$
, is as base state on
$\Lambda _1\cup B_1$
, is as base state on
![]() $\Lambda _1$
, and
$\Lambda _1$
, and
![]() ${\boldsymbol {\xi }}_{B_1}(\eta ')={\boldsymbol {\xi }}_{\Lambda _1}(\eta )$
. This implies that
${\boldsymbol {\xi }}_{B_1}(\eta ')={\boldsymbol {\xi }}_{\Lambda _1}(\eta )$
. This implies that
![]() ${\boldsymbol {\xi }}_{X}(\eta ')={\boldsymbol {\xi }}_{X}(\eta )$
. Since the transition is irreducibly quantified, by Lemma 3.11 applied to
${\boldsymbol {\xi }}_{X}(\eta ')={\boldsymbol {\xi }}_{X}(\eta )$
. Since the transition is irreducibly quantified, by Lemma 3.11 applied to
![]() $Y_1$
and
$Y_1$
and ![]() , we have
, we have
Noting that
![]() $\eta '=\eta '|_{B_1\cup B^{\prime }_1}$
and
$\eta '=\eta '|_{B_1\cup B^{\prime }_1}$
and
![]() $\eta =\eta |_{B^{\prime }_1}$
, we see that
$\eta =\eta |_{B^{\prime }_1}$
, we see that
By our choice of
![]() $B_1$
, we have
$B_1$
, we have
![]() $d_X(B_1,B^{\prime }_1)>R$
; hence,
$d_X(B_1,B^{\prime }_1)>R$
; hence,
![]() $(B_1, B^{\prime }_1)$
and
$(B_1, B^{\prime }_1)$
and
![]() $(B_1,B^{\prime }_1\setminus \{x\})$
are both pairs in
$(B_1,B^{\prime }_1\setminus \{x\})$
are both pairs in
![]() ${\mathscr {A}}_R$
. Our condition (33) on f applied to this pair implies that
${\mathscr {A}}_R$
. Our condition (33) on f applied to this pair implies that
Hence, (35) gives
![]() $ f(\eta '|_{B^{\prime }_1})-f(\eta |_{B^{\prime }_1}) =f(\eta '|_{B^{\prime }_1\setminus \{x\}})-f(\eta |_{B^{\prime }_1\setminus \{x\}}). $
In particular, since
$ f(\eta '|_{B^{\prime }_1})-f(\eta |_{B^{\prime }_1}) =f(\eta '|_{B^{\prime }_1\setminus \{x\}})-f(\eta |_{B^{\prime }_1\setminus \{x\}}). $
In particular, since
![]() $\eta '$
is at base state outside
$\eta '$
is at base state outside
![]() $B_1\cup \Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)$
and
$B_1\cup \Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)$
and
![]() $\eta $
is at base state outside
$\eta $
is at base state outside
![]() $\Lambda \cup B(x,R)$
, we have
$\Lambda \cup B(x,R)$
, we have
Note that
![]() $\eta '|_{\Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)} =\eta |_{\Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)}$
since
$\eta '|_{\Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)} =\eta |_{\Lambda _2\cup \cdots \cup \Lambda _k\cup B(x,R)}$
since
![]() $\eta '$
and
$\eta '$
and
![]() $\eta $
coincides outside
$\eta $
coincides outside
![]() $\Lambda _1\cup B^{\prime \prime }_1$
. Hence, we see that
$\Lambda _1\cup B^{\prime \prime }_1$
. Hence, we see that
By applying the same argument with
![]() $\Lambda $
replaced by
$\Lambda $
replaced by
![]() $\Lambda _2\cup \cdots \cup \Lambda _k$
and
$\Lambda _2\cup \cdots \cup \Lambda _k$
and
![]() $\Lambda _1$
replaced by
$\Lambda _1$
replaced by
![]() $\Lambda _2$
, we have
$\Lambda _2$
, we have
By repeating this process, we see that
Our assertion (34) follows from the fact that
![]() $\eta $
is supported on
$\eta $
is supported on
![]() $\Lambda \cup B(x,R)$
and the fact that
$\Lambda \cup B(x,R)$
and the fact that
![]() $\iota ^W f(\eta )=f(\eta |_W)$
for any
$\iota ^W f(\eta )=f(\eta |_W)$
for any
![]() $W\subset X$
.
$W\subset X$
.
4.4 Transferability
In this subsection, we will introduce the notion of transferability for a locale X, which ensures that the pairing
![]() $h_f$
defined in Definition 4.8 is symmetric.
$h_f$
defined in Definition 4.8 is symmetric.
Definition 4.16. Let X be a locale. We say that X is transferable if X is weakly transferable and satisfies either one of the following conditions.
-
(a) There exists a ball B such that
 $X\setminus B$
has three or more disjoint connected components (which are all infinite since X is weakly transferable).
$X\setminus B$
has three or more disjoint connected components (which are all infinite since X is weakly transferable). -
(b) For any
 $r\in \mathbb {N}$
, there exists a ball B of radius at least r such that
$r\in \mathbb {N}$
, there exists a ball B of radius at least r such that
 $X\setminus B$
is connected.
$X\setminus B$
is connected.
Note that by (b), if X is strongly transferable, then it is transferable.
Example 4.17. The following subgraphs
![]() $X=(X,E)$
of the Euclidean lattice
$X=(X,E)$
of the Euclidean lattice
![]() $\mathbb {Z}^2=(\mathbb {Z}^2,\mathbb {E})$
give examples of locales which are transferable but not strongly transferable (see Figure 6).
$\mathbb {Z}^2=(\mathbb {Z}^2,\mathbb {E})$
give examples of locales which are transferable but not strongly transferable (see Figure 6).
Remark 4.18. The locale
![]() $\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
is weakly transferable but not transferable since the complements of balls always have exactly two connected components. The locale
$\mathbb {Z}=(\mathbb {Z},\mathbb {E})$
is weakly transferable but not transferable since the complements of balls always have exactly two connected components. The locale
![]() $\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
$\mathbb {Z}^d=(\mathbb {Z}^d,\mathbb {E}^d)$
for
![]() $d>1$
is transferable since it is strongly transferable.
$d>1$
is transferable since it is strongly transferable.
Remark 4.19. Let G be a finitely generated free group G with set of generators
![]() $\mathcal {S}$
, and let
$\mathcal {S}$
, and let
![]() $(G,E_{\mathcal {S}})$
be the Cayley graph given in Example 2.2 (4). If the number of free generators of G is equal to one, then
$(G,E_{\mathcal {S}})$
be the Cayley graph given in Example 2.2 (4). If the number of free generators of G is equal to one, then
![]() $G=\mathbb {Z}$
; hence,
$G=\mathbb {Z}$
; hence,
![]() $(G,E_{\mathcal {S}})$
is weakly transferable but not transferable. If the number of free generators of G is
$(G,E_{\mathcal {S}})$
is weakly transferable but not transferable. If the number of free generators of G is
![]() $d>1$
, then
$d>1$
, then
![]() $(G,E_{\mathcal {S}})$
is transferable. This follows from Definition 4.16 (a) and the fact that
$(G,E_{\mathcal {S}})$
is transferable. This follows from Definition 4.16 (a) and the fact that
![]() $G\setminus \{{\operatorname {\mathrm {id}}}_G\}$
has exactly
$G\setminus \{{\operatorname {\mathrm {id}}}_G\}$
has exactly
![]() $2d$
connected components (see Figure 1 for the case
$2d$
connected components (see Figure 1 for the case
![]() $d=2$
).
$d=2$
).
More generally, for a finitely generated infinite group G, it is known that the number of ends of a Cayley graph
![]() $(G,E_{\mathcal {S}})$
is either
$(G,E_{\mathcal {S}})$
is either
![]() $1$
,
$1$
,
![]() $2$
or infinity, and the number of ends is
$2$
or infinity, and the number of ends is
![]() $2$
if and only if it has an infinite cyclic subgroup of finite index (see [Reference Cohen4, (1.6) Theorem]). In the case that
$2$
if and only if it has an infinite cyclic subgroup of finite index (see [Reference Cohen4, (1.6) Theorem]). In the case that
![]() $(G,E_{\mathcal {S}})$
is weakly transferable, then it is strongly transferable, not transferable, or transferable if and only if the number of ends is respectively
$(G,E_{\mathcal {S}})$
is weakly transferable, then it is strongly transferable, not transferable, or transferable if and only if the number of ends is respectively
![]() $1$
,
$1$
,
![]() $2$
, or infinity.
$2$
, or infinity.
Proposition 4.20. Suppose X is weakly transferable. Then X is transferable if an only if
![]() ${\mathscr {B}}_R$
has a unique equivalence class for any
${\mathscr {B}}_R$
has a unique equivalence class for any
![]() $R>0$
in the sense of Definition 4.7.
$R>0$
in the sense of Definition 4.7.
Proof. Suppose (a) of Definition 4.16 holds for the ball B. Let
![]() $Y_1$
,
$Y_1$
,
![]() $Y_2$
,
$Y_2$
,
![]() $Y_3$
be three distinct connected components (there may be more) of
$Y_3$
be three distinct connected components (there may be more) of
![]() $X\setminus B$
. For any
$X\setminus B$
. For any
![]() $r\in \mathbb {N}$
, there exists balls
$r\in \mathbb {N}$
, there exists balls
![]() $B_1$
,
$B_1$
,
![]() $B_2$
,
$B_2$
,
![]() $B_3$
of radii at least r such that
$B_3$
of radii at least r such that
![]() $ B(B_i,R)\subset Y_i$
for
$ B(B_i,R)\subset Y_i$
for
![]() $i=1,2,3$
and
$i=1,2,3$
and
![]() $d_X(B_i,B_j)>R$
for any
$d_X(B_i,B_j)>R$
for any
![]() $i\neq j$
. In particular, by exchanging the numberings
$i\neq j$
. In particular, by exchanging the numberings
![]() $i=1,2$
if necessary, we may assume that
$i=1,2$
if necessary, we may assume that
![]() $(B_1,B_2)\in {\mathscr {C}}^r_R$
. By construction, there exists paths from B to
$(B_1,B_2)\in {\mathscr {C}}^r_R$
. By construction, there exists paths from B to
![]() $Y_1$
and B to
$Y_1$
and B to
![]() $Y_3$
which do not pass through
$Y_3$
which do not pass through
![]() $Y_2$
; hence,
$Y_2$
; hence,
![]() $Y_1$
and
$Y_1$
and
![]() $Y_3$
are in the same connected component of
$Y_3$
are in the same connected component of
![]() $X\setminus Y_2$
. Hence, in particular,
$X\setminus Y_2$
. Hence, in particular,
![]() $B_1$
and
$B_1$
and
![]() $B_3$
are in the same connected component of
$B_3$
are in the same connected component of
![]() $X\setminus B(B_2,R)$
, and we have
$X\setminus B(B_2,R)$
, and we have
![]() $(B_1,B_2)\leftrightarrow (B_3,B_2)$
. In the same manner, we may prove that
$(B_1,B_2)\leftrightarrow (B_3,B_2)$
. In the same manner, we may prove that
![]() $(B_1,B_3)\leftrightarrow (B_1,B_2)$
, and
$(B_1,B_3)\leftrightarrow (B_1,B_2)$
, and
![]() $(B_1,B_3)\leftrightarrow (B_2,B_3)$
. This shows that we have
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
. This shows that we have
![]() $(B_1,B_2)\sim _{r}(B_3,B_2)\sim _{r} (B_3,B_1)\sim _{r} (B_2,B_1)$
. By Proposition 4.2, we see that
$(B_1,B_2)\sim _{r}(B_3,B_2)\sim _{r} (B_3,B_1)\sim _{r} (B_2,B_1)$
. By Proposition 4.2, we see that
![]() ${\mathscr {B}}^r_R$
has a unique equivalence class with respect to the equivalence relation
${\mathscr {B}}^r_R$
has a unique equivalence class with respect to the equivalence relation
![]() $\sim _{r}$
$\sim _{r}$
Next, suppose (b) of Definition 4.16 holds. Fix a
![]() $r\in \mathbb {N}$
and
$r\in \mathbb {N}$
and
![]() $R>0$
, and let
$R>0$
, and let
![]() $ B(x,R')$
be the ball given by (2) of radius
$ B(x,R')$
be the ball given by (2) of radius
![]() $R'\geq k+R$
such that
$R'\geq k+R$
such that
![]() $X\setminus B(x,R')$
is connected. If we let
$X\setminus B(x,R')$
is connected. If we let ![]() , then
, then
![]() $B_1$
is a ball of radius at least r such that
$B_1$
is a ball of radius at least r such that
![]() $X\setminus B(B_1,R)$
is connected. Take a ball
$X\setminus B(B_1,R)$
is connected. Take a ball
![]() $B_2$
of radius at least r and
$B_2$
of radius at least r and
![]() $d_X(B_1,B_2)>R$
, and a finite connected
$d_X(B_1,B_2)>R$
, and a finite connected
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $B_1\cup B_2\subset \Lambda $
. Since X is weakly transferable,
$B_1\cup B_2\subset \Lambda $
. Since X is weakly transferable,
![]() $X\setminus B(B_2,R)$
decomposes into a finite number of locales. We let Y be the connected component of
$X\setminus B(B_2,R)$
decomposes into a finite number of locales. We let Y be the connected component of
![]() $X\setminus B(B_2,R)$
containing
$X\setminus B(B_2,R)$
containing
![]() $B_1$
, and we take
$B_1$
, and we take
![]() $B_3$
to be a ball of radius at least r satisfying
$B_3$
to be a ball of radius at least r satisfying
![]() $B_3\subset Y\setminus B(B_1,R)$
and
$B_3\subset Y\setminus B(B_1,R)$
and
![]() $d_X(\Lambda ,B_3)>R$
. Since
$d_X(\Lambda ,B_3)>R$
. Since
![]() $X\setminus B(B_1,R)$
is connected by our construction of
$X\setminus B(B_1,R)$
is connected by our construction of
![]() $B_1$
, we have
$B_1$
, we have
![]() $(B_1,B_2)\leftrightarrow (B_1,B_3)$
. Also since
$(B_1,B_2)\leftrightarrow (B_1,B_3)$
. Also since
![]() $B_1, B_3\subset Y$
, we have
$B_1, B_3\subset Y$
, we have
![]() $(B_2,B_1)\leftrightarrow (B_2,B_3)$
. Moreover, since
$(B_2,B_1)\leftrightarrow (B_2,B_3)$
. Moreover, since
![]() $ B(B_3,R)\cap \Lambda =\emptyset $
and
$ B(B_3,R)\cap \Lambda =\emptyset $
and
![]() $\Lambda $
is connected, we have
$\Lambda $
is connected, we have
![]() $(B_1,B_3)\leftrightarrow (B_2,B_3)$
. This shows that
$(B_1,B_3)\leftrightarrow (B_2,B_3)$
. This shows that
![]() $(B_1,B_2)\sim _{r} (B_1,B_3)\sim _{r}(B_2,B_3)\sim _{r}(B_2,B_1)$
, which by Proposition 4.2 shows that
$(B_1,B_2)\sim _{r} (B_1,B_3)\sim _{r}(B_2,B_3)\sim _{r}(B_2,B_1)$
, which by Proposition 4.2 shows that
![]() ${\mathscr {B}}^r_R$
has a unique equivalence class with respect to the equivalence relation
${\mathscr {B}}^r_R$
has a unique equivalence class with respect to the equivalence relation
![]() $\sim _{r}$
.
$\sim _{r}$
.
Finally, we prove that if there exists
![]() $r\in \mathbb {N}$
such that for any ball B of radius at least r, the set
$r\in \mathbb {N}$
such that for any ball B of radius at least r, the set
![]() $X\setminus B$
has exactly two connected components, then for any
$X\setminus B$
has exactly two connected components, then for any
![]() $R>0$
, there are two equivalence classes in
$R>0$
, there are two equivalence classes in
![]() ${\mathscr {B}}^r_R$
with respect to
${\mathscr {B}}^r_R$
with respect to
![]() $\sim _{r}$
. We first prove that in this situation, for any ball B of radius at least r, there exists a decomposition
$\sim _{r}$
. We first prove that in this situation, for any ball B of radius at least r, there exists a decomposition
![]() $X\setminus B=Y^+_B\cup Y^-_B$
into infinite locales, where
$X\setminus B=Y^+_B\cup Y^-_B$
into infinite locales, where
![]() $Y^{\pm }_{B}\cap Y^{\pm }_{B'}$
are infinite sets and
$Y^{\pm }_{B}\cap Y^{\pm }_{B'}$
are infinite sets and
![]() $Y^{\pm }_{B}\cap Y^{\mp }_{B'}$
are finite sets for any balls
$Y^{\pm }_{B}\cap Y^{\mp }_{B'}$
are finite sets for any balls
![]() $B,B'$
of radius at least r. This follows from the fact that one of
$B,B'$
of radius at least r. This follows from the fact that one of
![]() $Y^+_{B}\cap Y^+_{B'}$
or
$Y^+_{B}\cap Y^+_{B'}$
or
![]() $Y^+_{B}\cap Y^-_{B'}$
must be infinite since
$Y^+_{B}\cap Y^-_{B'}$
must be infinite since
![]() $Y^+_{B}$
is infinite. If both are infinite, then there exists a ball B satisfying
$Y^+_{B}$
is infinite. If both are infinite, then there exists a ball B satisfying
![]() $B\cup B'\subset B$
and
$B\cup B'\subset B$
and
![]() $X\setminus B$
has at least three disjoint connected components in
$X\setminus B$
has at least three disjoint connected components in
![]() $Y^+_{B}\cap Y^+_{B'}$
,
$Y^+_{B}\cap Y^+_{B'}$
,
![]() $Y^+_{B}\cap Y^-_{B'}$
and
$Y^+_{B}\cap Y^-_{B'}$
and
![]() $Y^-_{B}$
, contradicting our assertion. Hence, exactly one of
$Y^-_{B}$
, contradicting our assertion. Hence, exactly one of
![]() $Y^+_{B}\cap Y^+_{B'}$
and
$Y^+_{B}\cap Y^+_{B'}$
and
![]() $Y^+_{B}\cap Y^-_{B'}$
is infinite and the other is finite. So we choose the
$Y^+_{B}\cap Y^-_{B'}$
is infinite and the other is finite. So we choose the
![]() $\pm $
label of
$\pm $
label of
![]() $B'$
so that
$B'$
so that
![]() $Y^+_{B}\cap Y^+_{B'}$
is infinite and
$Y^+_{B}\cap Y^+_{B'}$
is infinite and
![]() $Y^+_{B}\cap Y^-_{B'}$
is finite.
$Y^+_{B}\cap Y^-_{B'}$
is finite.
Consider any
![]() $R>0$
. For each
$R>0$
. For each
![]() $(B,B')\in {\mathscr {B}}^r_R$
, we denote
$(B,B')\in {\mathscr {B}}^r_R$
, we denote
![]() $B<B'$
if
$B<B'$
if
![]() $B'\subset Y_{B}^+$
. This is equivalent to the condition that
$B'\subset Y_{B}^+$
. This is equivalent to the condition that
![]() $B\subset Y_{B'}^-$
for the following reason. Consider
$B\subset Y_{B'}^-$
for the following reason. Consider
![]() $x\in Y_{B}^-\cap Y_{B'}^-$
and
$x\in Y_{B}^-\cap Y_{B'}^-$
and
![]() $y\in B'\subset Y_{B}^+$
. Since X is connected, there exists a path
$y\in B'\subset Y_{B}^+$
. Since X is connected, there exists a path
![]() $\vec p$
from x to y, which must go through B since
$\vec p$
from x to y, which must go through B since
![]() $Y_{B}^-$
and
$Y_{B}^-$
and
![]() $ Y_{B}^+$
are disjoint and connected by B. This shows that x hence
$ Y_{B}^+$
are disjoint and connected by B. This shows that x hence
![]() $Y^-_{B'}$
is connected to B in
$Y^-_{B'}$
is connected to B in
![]() $X\setminus B'$
. Hence, for any
$X\setminus B'$
. Hence, for any
![]() $(B,B')\in {\mathscr {B}}^r_R$
, either one of
$(B,B')\in {\mathscr {B}}^r_R$
, either one of
![]() $B<B'$
or
$B<B'$
or
![]() $B>B'$
hold. Moreover, if
$B>B'$
hold. Moreover, if
![]() $B<B'$
, then
$B<B'$
, then
![]() $B'\subset Y^+_{ B(B,R)}$
and
$B'\subset Y^+_{ B(B,R)}$
and
![]() $B\subset Y^-_{ B(B',R)}$
. This shows that for any
$B\subset Y^-_{ B(B',R)}$
. This shows that for any
![]() $(B_1,B^{\prime }_1), (B_2,B^{\prime }_2)\in {\mathscr {B}}^r_R$
, we have
$(B_1,B^{\prime }_1), (B_2,B^{\prime }_2)\in {\mathscr {B}}^r_R$
, we have
![]() $(B_1,B^{\prime }_1)\leftrightarrow (B_2,B^{\prime }_2)$
if and only if we have
$(B_1,B^{\prime }_1)\leftrightarrow (B_2,B^{\prime }_2)$
if and only if we have
![]() $B_1<B^{\prime }_1$
and
$B_1<B^{\prime }_1$
and
![]() $B_2<B^{\prime }_2$
, or
$B_2<B^{\prime }_2$
, or
![]() $B_1>B^{\prime }_1$
and
$B_1>B^{\prime }_1$
and
![]() $B_2>B^{\prime }_2$
. In other words, pairs are in the same equivalence class if and only if their order is preserved. This proves that
$B_2>B^{\prime }_2$
. In other words, pairs are in the same equivalence class if and only if their order is preserved. This proves that
![]() ${\mathscr {B}}^r_R$
has exactly two equivalence classes as desired.
${\mathscr {B}}^r_R$
has exactly two equivalence classes as desired.
Corollary 4.21. If X is transferable, then for any
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f\in C^1_{\operatorname {\mathrm {unif}}}(S^X)$
, the pairing
$\partial f\in C^1_{\operatorname {\mathrm {unif}}}(S^X)$
, the pairing
![]() $h_f$
defined in Definition 4.8 is symmetric.
$h_f$
defined in Definition 4.8 is symmetric.
5 Uniform cohomology and the main theorem
In this section, we will introduce and calculate the uniform cohomology of a configuration space with transition structure satisfying certain conditions. We will then consider a free action of a group G on the locale and prove our main theorem, Theorem 5.17, which coincides with Theorem 1 of §1.3.
5.1 Uniform cohomology of the configuration space
In this subsection, we will define the uniform cohomology of a configuration space with transition structure. We will then prove our key theorem, Theorem 5.2, which states that under certain conditions, any closed uniform form is integrable by a uniform function. This result is central to the proof of our main theorem.
Consider the system
![]() $(S,X,\phi )$
and the associated configuration space with transition structure. In what follows, we denote by
$(S,X,\phi )$
and the associated configuration space with transition structure. In what follows, we denote by
![]() $Z^1(S^X_*)$
be the set of closed forms of
$Z^1(S^X_*)$
be the set of closed forms of
![]() $S^X_*$
, and
$S^X_*$
, and ![]() the set of uniform closed forms. We first prove the following.
the set of uniform closed forms. We first prove the following.
Lemma 5.1. Let
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Then we have
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Then we have
![]() $\partial f\in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
.
$\partial f\in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
.
Proof. By the definition of
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
![]() $R>0$
such that
$R>0$
such that
for
![]() $f_\Lambda \in C_\Lambda (S^X)\subset C(S^\Lambda )$
. Then for any
$f_\Lambda \in C_\Lambda (S^X)\subset C(S^\Lambda )$
. Then for any
![]() $e\in E$
, we have
$e\in E$
, we have
![]() $\nabla _{\!e} f_\Lambda \in C(S^{\Lambda \cup e})$
and
$\nabla _{\!e} f_\Lambda \in C(S^{\Lambda \cup e})$
and
![]() $\nabla _{\!e} f_\Lambda \equiv 0$
if
$\nabla _{\!e} f_\Lambda \equiv 0$
if
![]() $\Lambda \cap e=\emptyset $
; hence,
$\Lambda \cap e=\emptyset $
; hence,
![]() $\partial f\in C^1_{R+1}(S^X)\subset C^1_{\operatorname {\mathrm {unif}}}(S^X)$
. The fact that
$\partial f\in C^1_{R+1}(S^X)\subset C^1_{\operatorname {\mathrm {unif}}}(S^X)$
. The fact that
![]() $\partial f\in Z^1(S^X_*)$
follows from Lemma 2.28, which states that exact forms are closed.
$\partial f\in Z^1(S^X_*)$
follows from Lemma 2.28, which states that exact forms are closed.
Lemma 5.1 shows that the differential
![]() $\partial $
induces an homomorphism
$\partial $
induces an homomorphism
As in Definition 1.6, we define the uniform cohomology
![]() $H^m_{\operatorname {\mathrm {unif}}}(S^X)$
of the configuration space
$H^m_{\operatorname {\mathrm {unif}}}(S^X)$
of the configuration space
![]() $S^X$
with transition structure to be the cohomology of the complex (36). Our choice for
$S^X$
with transition structure to be the cohomology of the complex (36). Our choice for
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
of restricting to functions satisfying
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
of restricting to functions satisfying
![]() $f(\star )=0$
implies that uniform cohomology is philosophically the reduced cohomology in the sense of topology of the pointed space consisting of the configuration space
$f(\star )=0$
implies that uniform cohomology is philosophically the reduced cohomology in the sense of topology of the pointed space consisting of the configuration space
![]() $S^X$
and base configuration
$S^X$
and base configuration
![]() $\star \in S^X$
.
$\star \in S^X$
.
Now, let X be a locale which is weakly transferable in the sense of Definition 4.16, and assume that the interaction is irreducibly quantified. Let
![]() $c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
. Our theorem concerning the integration of uniform forms is as follows.
$c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
. Our theorem concerning the integration of uniform forms is as follows.
Theorem 5.2. Let
![]() $(X,S,\phi )$
be a system such that the interaction
$(X,S,\phi )$
be a system such that the interaction
![]() $\phi $
is irreducibly quantified. If the locale X is transferable, or the interaction
$\phi $
is irreducibly quantified. If the locale X is transferable, or the interaction
![]() $\phi $
is simple and X is weakly transferable, then for any
$\phi $
is simple and X is weakly transferable, then for any
![]() $\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
$\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
![]() $\partial f=\omega $
.
$\partial f=\omega $
.
The proof of Theorem 5.2 is based on Lemma 5.5 and Lemma 5.6 below. A homomorphism of monoids is a map of sets preserving the binary operation and the identity element. We say that a monoid
![]() ${\mathscr {E}}$
with operation
${\mathscr {E}}$
with operation
![]() $+_{{\mathscr {E}}}$
satisfies the (right)-cancellation property if
$+_{{\mathscr {E}}}$
satisfies the (right)-cancellation property if
![]() $a+_{{\mathscr {E}}} b=a'+_{{\mathscr {E}}} b$
implies that
$a+_{{\mathscr {E}}} b=a'+_{{\mathscr {E}}} b$
implies that
![]() $a=a'$
for any
$a=a'$
for any
![]() $a,a',b\in {\mathscr {E}}$
. Note that any monoid obtained as a submonoid of a group satisfies the cancellation property. We will first prove the following lemma concerning commutative monoids satisfying the cancellation property.
$a,a',b\in {\mathscr {E}}$
. Note that any monoid obtained as a submonoid of a group satisfies the cancellation property. We will first prove the following lemma concerning commutative monoids satisfying the cancellation property.
Lemma 5.3. Assume that
![]() ${\mathscr {E}}$
is a commutative monoid with operation
${\mathscr {E}}$
is a commutative monoid with operation
![]() $+_{{\mathscr {E}}}$
satisfying the cancellation property. If there exists an injective homomorphism of monoids
$+_{{\mathscr {E}}}$
satisfying the cancellation property. If there exists an injective homomorphism of monoids
where we view
![]() $\mathbb {R}$
as a an abelian group via the usual addition, then there exists a homomorphism of monoids
$\mathbb {R}$
as a an abelian group via the usual addition, then there exists a homomorphism of monoids
![]() $\pi \colon {\mathscr {E}}\rightarrow \mathbb {R}$
such that
$\pi \colon {\mathscr {E}}\rightarrow \mathbb {R}$
such that
![]() $\pi \circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
.
$\pi \circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
.
Proof. The statement follows from the fact that
![]() $\mathbb {R}$
is a divisible abelian group (see Remark 5.4). We will give a proof for the sake of completeness. We consider the set of pairs
$\mathbb {R}$
is a divisible abelian group (see Remark 5.4). We will give a proof for the sake of completeness. We consider the set of pairs
![]() $({\mathscr {N}}, \pi _{\!{\mathscr {N}}})$
, where
$({\mathscr {N}}, \pi _{\!{\mathscr {N}}})$
, where
![]() ${\mathscr {N}}$
is a submonoid of
${\mathscr {N}}$
is a submonoid of
![]() ${\mathscr {E}}$
containing
${\mathscr {E}}$
containing
![]() $i(\mathbb {R})$
and
$i(\mathbb {R})$
and
![]() $\pi _{\!{\mathscr {N}}}\colon {\mathscr {N}}\rightarrow \mathbb {R}$
is an homomorphism of monoids such that
$\pi _{\!{\mathscr {N}}}\colon {\mathscr {N}}\rightarrow \mathbb {R}$
is an homomorphism of monoids such that
![]() $\pi _{\!{\mathscr {N}}}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
.
$\pi _{\!{\mathscr {N}}}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
.
We consider an order on the set of such pairs such that
![]() $({\mathscr {N}}, \pi _{\!{\mathscr {N}}})\leq ({\mathscr {N}}', \pi _{\!{\mathscr {N}}'})$
if and only if
$({\mathscr {N}}, \pi _{\!{\mathscr {N}}})\leq ({\mathscr {N}}', \pi _{\!{\mathscr {N}}'})$
if and only if
![]() ${\mathscr {N}}\subset {\mathscr {N}}'$
and
${\mathscr {N}}\subset {\mathscr {N}}'$
and
![]() $\pi _{\!{\mathscr {N}}'}\big |_{\!{\mathscr {N}}}=\pi _{\!{\mathscr {N}}}$
. Let
$\pi _{\!{\mathscr {N}}'}\big |_{\!{\mathscr {N}}}=\pi _{\!{\mathscr {N}}}$
. Let
![]() $(({\mathscr {N}}_i,\pi _{\!{\mathscr {N}}_i}))_{i\in I}$
be a totally ordered set of such pairs. If we let
$(({\mathscr {N}}_i,\pi _{\!{\mathscr {N}}_i}))_{i\in I}$
be a totally ordered set of such pairs. If we let ![]() and if we let
and if we let
![]() $\pi _{\!{\mathscr {N}}}\colon {\mathscr {N}}\rightarrow \mathbb {R}$
be a homomorphism of monoids obtained as the collection of
$\pi _{\!{\mathscr {N}}}\colon {\mathscr {N}}\rightarrow \mathbb {R}$
be a homomorphism of monoids obtained as the collection of
![]() $\pi _{\!{\mathscr {N}}_i}$
, then we have
$\pi _{\!{\mathscr {N}}_i}$
, then we have
![]() $\pi _{\!{\mathscr {N}}}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
. Hence,
$\pi _{\!{\mathscr {N}}}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
. Hence,
![]() $({\mathscr {N}},\pi _{\!{\mathscr {N}}})$
is a maximal element of the totally ordered set
$({\mathscr {N}},\pi _{\!{\mathscr {N}}})$
is a maximal element of the totally ordered set
![]() $(({\mathscr {N}}_i,\pi _{\!{\mathscr {N}}_i}))_{i\in I}$
. By Zorn’s lemma, there exists a maximal pair
$(({\mathscr {N}}_i,\pi _{\!{\mathscr {N}}_i}))_{i\in I}$
. By Zorn’s lemma, there exists a maximal pair
![]() $({\mathscr {M}},\pi _{\!{\mathscr {M}}})$
in the set of all such pairs.
$({\mathscr {M}},\pi _{\!{\mathscr {M}}})$
in the set of all such pairs.
We will prove by contradiction that
![]() ${\mathscr {M}}={\mathscr {E}}$
. Suppose
${\mathscr {M}}={\mathscr {E}}$
. Suppose
![]() ${\mathscr {M}}\subsetneq {\mathscr {E}}$
. Let
${\mathscr {M}}\subsetneq {\mathscr {E}}$
. Let
![]() $w\in {\mathscr {E}}$
such that
$w\in {\mathscr {E}}$
such that
![]() $w\not \in {\mathscr {M}}$
, and let
$w\not \in {\mathscr {M}}$
, and let ![]() . Note that since
. Note that since
![]() ${\mathscr {E}}$
is commutative if there exists a nontrivial algebraic relation between elements of
${\mathscr {E}}$
is commutative if there exists a nontrivial algebraic relation between elements of
![]() ${\mathscr {M}}$
and
${\mathscr {M}}$
and
![]() $\mathbb {N} w$
, then there would exist
$\mathbb {N} w$
, then there would exist
![]() $a,b\in {\mathscr {M}}$
such that
$a,b\in {\mathscr {M}}$
such that
![]() $a+_{\!{\mathscr {E}}} mw=b+_{\!{\mathscr {E}}}nw$
for some
$a+_{\!{\mathscr {E}}} mw=b+_{\!{\mathscr {E}}}nw$
for some
![]() $m,n\in \mathbb {N}$
. By the cancellation property of
$m,n\in \mathbb {N}$
. By the cancellation property of
![]() ${\mathscr {E}}$
, this implies that
${\mathscr {E}}$
, this implies that
![]() $a+_{\!{\mathscr {E}}} nw=b$
for some
$a+_{\!{\mathscr {E}}} nw=b$
for some
![]() $a,b\in {\mathscr {M}}$
and integer
$a,b\in {\mathscr {M}}$
and integer
![]() $n>0$
. In the case that there exists an integer
$n>0$
. In the case that there exists an integer
![]() $n>0$
and
$n>0$
and
![]() $a,b\in {\mathscr {M}}$
such that
$a,b\in {\mathscr {M}}$
such that
![]() $a+_{\!{\mathscr {E}}} nw=b$
, we define u be an element in
$a+_{\!{\mathscr {E}}} nw=b$
, we define u be an element in
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
If
![]() $n',a',b'$
satisfies the same condition, then we have
$n',a',b'$
satisfies the same condition, then we have
![]() $n' a+_{\!{\mathscr {E}}} n'nw=n'b$
and
$n' a+_{\!{\mathscr {E}}} n'nw=n'b$
and
![]() $n a'+_{\!{\mathscr {E}}} nn'w=nb'$
. Combining this equality, we have
$n a'+_{\!{\mathscr {E}}} nn'w=nb'$
. Combining this equality, we have
Hence,
![]() $n' a+_{\!{\mathscr {E}}} nb'=n'a+_{\!{\mathscr {E}}} n b'$
since
$n' a+_{\!{\mathscr {E}}} nb'=n'a+_{\!{\mathscr {E}}} n b'$
since
![]() ${\mathscr {E}}$
is commutative and satisfies the cancellation property. This shows that we have
${\mathscr {E}}$
is commutative and satisfies the cancellation property. This shows that we have
which implies that u is independent of the choice of
![]() $a,b\in {\mathscr {M}}$
and
$a,b\in {\mathscr {M}}$
and
![]() $n>0$
. However, if for any integer
$n>0$
. However, if for any integer
![]() $n>0$
and
$n>0$
and
![]() $a,b\in {\mathscr {M}}$
, we have
$a,b\in {\mathscr {M}}$
, we have
![]() $a+_{\!{\mathscr {E}}} nw\neq b$
, then we let
$a+_{\!{\mathscr {E}}} nw\neq b$
, then we let
![]() $u=0$
. In both cases, we define the function
$u=0$
. In both cases, we define the function
![]() $\pi _{\!{\mathscr {M}}'}\colon {\mathscr {M}}'\rightarrow \mathbb {R}$
by
$\pi _{\!{\mathscr {M}}'}\colon {\mathscr {M}}'\rightarrow \mathbb {R}$
by
![]() $\pi _{{\mathscr {M}}'}(a+nw)=\pi _{\!{\mathscr {M}}}(a)+nu$
for any
$\pi _{{\mathscr {M}}'}(a+nw)=\pi _{\!{\mathscr {M}}}(a)+nu$
for any
![]() $a\in {\mathscr {M}}$
and
$a\in {\mathscr {M}}$
and
![]() $n\in \mathbb {N}$
. This gives a homomorphism of monoids satisfying
$n\in \mathbb {N}$
. This gives a homomorphism of monoids satisfying
![]() $\pi _{{\mathscr {M}}'}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
; hence, we have
$\pi _{{\mathscr {M}}'}\circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
; hence, we have
![]() $({\mathscr {M}},\pi _{\!{\mathscr {M}}})<({\mathscr {M}}',\pi _{\!{\mathscr {M}}'})$
, which contradicts the fact that
$({\mathscr {M}},\pi _{\!{\mathscr {M}}})<({\mathscr {M}}',\pi _{\!{\mathscr {M}}'})$
, which contradicts the fact that
![]() $({\mathscr {M}},\pi _{\!{\mathscr {M}}})$
is maximal for such pairs.
$({\mathscr {M}},\pi _{\!{\mathscr {M}}})$
is maximal for such pairs.
This shows that we have
![]() ${\mathscr {M}}={\mathscr {E}}$
. Then
${\mathscr {M}}={\mathscr {E}}$
. Then ![]() is a homomorphism of monoids satisfying
is a homomorphism of monoids satisfying
![]() $\pi \circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
, as desired.
$\pi \circ \iota ={\operatorname {\mathrm {id}}}_{\mathbb {R}}$
, as desired.
Remark 5.4. Assume that D is a divisible abelian group; that is, for any
![]() $v\in D$
and integer
$v\in D$
and integer
![]() $n>0$
, there exists
$n>0$
, there exists
![]() $u\in D$
such that
$u\in D$
such that
![]() $un=v$
. Then we may prove that if
$un=v$
. Then we may prove that if
![]() $\iota \colon D\hookrightarrow {\mathscr {E}}$
is an injective homomorphism into a commutative monoid
$\iota \colon D\hookrightarrow {\mathscr {E}}$
is an injective homomorphism into a commutative monoid
![]() ${\mathscr {E}}$
satisfying the cancellation property, then there exists a homomorphism of monoids
${\mathscr {E}}$
satisfying the cancellation property, then there exists a homomorphism of monoids
![]() $\pi \colon {\mathscr {E}}\rightarrow D$
such that
$\pi \colon {\mathscr {E}}\rightarrow D$
such that
![]() $\pi \circ \iota ={\operatorname {\mathrm {id}}}_D$
. Indeed, by the Grothendieck construction, the monoid
$\pi \circ \iota ={\operatorname {\mathrm {id}}}_D$
. Indeed, by the Grothendieck construction, the monoid ![]() defined via the equivalence relation
defined via the equivalence relation
![]() $(a,b)\sim (a',b')$
if
$(a,b)\sim (a',b')$
if
![]() $a+_{{\mathscr {E}}} b'=a'+_{{\mathscr {E}}} b$
for any
$a+_{{\mathscr {E}}} b'=a'+_{{\mathscr {E}}} b$
for any
![]() $(a,b), (a',b')\in {\mathscr {E}}\times {\mathscr {E}}$
is an abelian group since
$(a,b), (a',b')\in {\mathscr {E}}\times {\mathscr {E}}$
is an abelian group since
![]() ${\mathscr {E}}$
satisfies the cancellation property. In addition, we have an injective homomorphism
${\mathscr {E}}$
satisfies the cancellation property. In addition, we have an injective homomorphism
![]() ${\mathscr {E}}\hookrightarrow A$
given by mapping
${\mathscr {E}}\hookrightarrow A$
given by mapping
![]() $a\in {\mathscr {E}}$
to the class of
$a\in {\mathscr {E}}$
to the class of
![]() $(a,0)$
in A. Since the composition
$(a,0)$
in A. Since the composition
![]() $\iota _A\colon D\hookrightarrow {\mathscr {E}}\hookrightarrow A$
is an injective homomorphism of abelian groups, from the fact that D is divisible and hence an injective object in the category of abelian groups (see [Reference Robinson14, 4.1.2]), there exists a homomorphism
$\iota _A\colon D\hookrightarrow {\mathscr {E}}\hookrightarrow A$
is an injective homomorphism of abelian groups, from the fact that D is divisible and hence an injective object in the category of abelian groups (see [Reference Robinson14, 4.1.2]), there exists a homomorphism
![]() $\pi _A\colon A\rightarrow D$
such that
$\pi _A\colon A\rightarrow D$
such that
![]() $\pi _A\circ \iota _A={\operatorname {\mathrm {id}}}_D$
. Then
$\pi _A\circ \iota _A={\operatorname {\mathrm {id}}}_D$
. Then ![]() satisfies
satisfies
![]() $\pi \circ \iota ={\operatorname {\mathrm {id}}}_D$
as desired. The authors thank Kei Hagihara and Shuji Yamamoto for discussion concerning this remark as well as the proof of Lemma 5.3.
$\pi \circ \iota ={\operatorname {\mathrm {id}}}_D$
as desired. The authors thank Kei Hagihara and Shuji Yamamoto for discussion concerning this remark as well as the proof of Lemma 5.3.
Next, let
![]() $\mathcal {M}$
be a commutative monoid with operation
$\mathcal {M}$
be a commutative monoid with operation
![]() $+$
and identity element
$+$
and identity element
![]() $0$
. We first give a construction of extensions of monoids arising from a pairing
$0$
. We first give a construction of extensions of monoids arising from a pairing
![]() $H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying
$H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying
![]() $H(0,0)=0$
and
$H(0,0)=0$
and
for any
![]() $\alpha ,\beta ,\gamma \in \mathcal {M}$
. We let
$\alpha ,\beta ,\gamma \in \mathcal {M}$
. We let ![]() , and we denote an element of
, and we denote an element of
![]() ${\mathscr {E}}$
by
${\mathscr {E}}$
by
![]() $[\alpha , u]$
for
$[\alpha , u]$
for
![]() $\alpha \in \mathcal {M}$
and
$\alpha \in \mathcal {M}$
and
![]() $u\in \mathbb {R}$
. Define the binary operation
$u\in \mathbb {R}$
. Define the binary operation
![]() $+_{{\mathscr {E}}}$
on
$+_{{\mathscr {E}}}$
on
![]() ${\mathscr {E}}$
by
${\mathscr {E}}$
by
for any
![]() $\alpha ,\beta \in \mathcal {M}$
and
$\alpha ,\beta \in \mathcal {M}$
and
![]() $u,v\in \mathbb {R}$
. The element
$u,v\in \mathbb {R}$
. The element
![]() $[0,0]$
is an identity element with respect to
$[0,0]$
is an identity element with respect to
![]() $+_{{\mathscr {E}}}$
, and the cocycle condition (37) ensures that
$+_{{\mathscr {E}}}$
, and the cocycle condition (37) ensures that
![]() $+_{{\mathscr {E}}}$
is associative. Hence,
$+_{{\mathscr {E}}}$
is associative. Hence,
![]() ${\mathscr {E}}$
is a monoid with respect to the operation
${\mathscr {E}}$
is a monoid with respect to the operation
![]() $+_{{\mathscr {E}}}$
, which fits into the exact sequence of monoids
$+_{{\mathscr {E}}}$
, which fits into the exact sequence of monoids
Here, the arrows are homomorphisms of monoids with the injection
![]() $\mathbb {R}\rightarrow {\mathscr {E}}$
given by
$\mathbb {R}\rightarrow {\mathscr {E}}$
given by
![]() $u\mapsto [0,u]$
, and the surjection
$u\mapsto [0,u]$
, and the surjection
![]() ${\mathscr {E}}\rightarrow \mathcal {M}$
given by
${\mathscr {E}}\rightarrow \mathcal {M}$
given by
![]() $[\alpha ,u]\mapsto \alpha $
. If the pairing H is symmetric, then we see that
$[\alpha ,u]\mapsto \alpha $
. If the pairing H is symmetric, then we see that
![]() ${\mathscr {E}}$
is a commutative monoid. Note that if
${\mathscr {E}}$
is a commutative monoid. Note that if
![]() $\mathcal {M}$
satisfies the right cancellation property, then
$\mathcal {M}$
satisfies the right cancellation property, then
![]() ${\mathscr {E}}$
also satisfies the right cancellation property. In fact, if
${\mathscr {E}}$
also satisfies the right cancellation property. In fact, if
![]() $[\alpha ,u]+_{{\mathscr {E}}}[\beta ,v]=[\alpha ',u]+_{{\mathscr {E}}}[\beta ,w]$
for some
$[\alpha ,u]+_{{\mathscr {E}}}[\beta ,v]=[\alpha ',u]+_{{\mathscr {E}}}[\beta ,w]$
for some
![]() $\alpha ,\alpha ',\beta \in \mathcal {M}$
and
$\alpha ,\alpha ',\beta \in \mathcal {M}$
and
![]() $u,u',v\in \mathbb {R}$
, then we have
$u,u',v\in \mathbb {R}$
, then we have
This shows that
![]() $\alpha +\beta =\alpha '+\beta $
; hence,
$\alpha +\beta =\alpha '+\beta $
; hence,
![]() $\alpha =\alpha '$
since
$\alpha =\alpha '$
since
![]() $\mathcal {M}$
satisfies the right cancellation property. Then we have
$\mathcal {M}$
satisfies the right cancellation property. Then we have
![]() $u+v-H(\alpha ,\beta ) =u'+v-H(\alpha ',\beta )= u'+v-H(\alpha ,\beta )$
in
$u+v-H(\alpha ,\beta ) =u'+v-H(\alpha ',\beta )= u'+v-H(\alpha ,\beta )$
in
![]() $\mathbb {R}$
; hence,
$\mathbb {R}$
; hence,
![]() $u=u'$
. This shows that
$u=u'$
. This shows that
![]() $[\alpha ,u]=[\alpha ',u']$
, proving that the monoid
$[\alpha ,u]=[\alpha ',u']$
, proving that the monoid
![]() ${\mathscr {E}}$
satisfies the right cancellation property.
${\mathscr {E}}$
satisfies the right cancellation property.
Lemma 5.5. Let
![]() $\mathcal {M}$
be a commutative monoid satisfying the cancellation property, and let
$\mathcal {M}$
be a commutative monoid satisfying the cancellation property, and let
![]() $H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be a symmetric pairing satisfying the cocycle condition (37). Then there exists a function
$H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be a symmetric pairing satisfying the cocycle condition (37). Then there exists a function
such that
![]() $H(\alpha ,\beta )=h(\alpha )+h(\beta ) - h(\alpha +\beta )$
for any
$H(\alpha ,\beta )=h(\alpha )+h(\beta ) - h(\alpha +\beta )$
for any
![]() $\alpha ,\beta \in \mathcal {M}$
.
$\alpha ,\beta \in \mathcal {M}$
.
Proof. If we prove our assertion for the pairing ![]() and show that there exists a function
and show that there exists a function
![]() $\widetilde {h}\colon \mathcal {M}\rightarrow \mathbb {R}$
satisfying our condition, then our assertion is proved also for
$\widetilde {h}\colon \mathcal {M}\rightarrow \mathbb {R}$
satisfying our condition, then our assertion is proved also for
![]() $H(\alpha ,\beta )$
by taking
$H(\alpha ,\beta )$
by taking ![]() . Hence, by replacing H by
. Hence, by replacing H by
![]() $\widetilde {H}$
, we may assume that
$\widetilde {H}$
, we may assume that
![]() $H(0,0)=0$
. Consider the extension
$H(0,0)=0$
. Consider the extension
![]() ${\mathscr {E}}$
given in (38) corresponding to the pairing H. Then
${\mathscr {E}}$
given in (38) corresponding to the pairing H. Then
![]() ${\mathscr {E}}$
is a commutative monoid since H is symmetric. Hence by Lemma 5.3, there exists a homomorphism of monoids
${\mathscr {E}}$
is a commutative monoid since H is symmetric. Hence by Lemma 5.3, there exists a homomorphism of monoids
![]() $\pi \colon {\mathscr {E}}\rightarrow \mathbb {R}$
such that
$\pi \colon {\mathscr {E}}\rightarrow \mathbb {R}$
such that
![]() $\pi ([0,u])=u$
for any
$\pi ([0,u])=u$
for any
![]() $u\in \mathbb {R}$
. For any
$u\in \mathbb {R}$
. For any
![]() $\alpha \in \mathcal {M}$
, choose an arbitrary
$\alpha \in \mathcal {M}$
, choose an arbitrary
![]() $u\in \mathbb {R}$
, and let
$u\in \mathbb {R}$
, and let
If
![]() $v\in \mathbb {R}$
, then we have
$v\in \mathbb {R}$
, then we have
![]() $[\alpha ,v]=[\alpha ,u]+_{{\mathscr {E}}} [0,w]$
for some
$[\alpha ,v]=[\alpha ,u]+_{{\mathscr {E}}} [0,w]$
for some
![]() $w\in \mathbb {R}$
since the classes of
$w\in \mathbb {R}$
since the classes of
![]() $[\alpha ,v]$
and
$[\alpha ,v]$
and
![]() $[\alpha ,u]$
coincide on
$[\alpha ,u]$
coincide on
![]() $\mathcal {M}\cong {\mathscr {E}}/\mathbb {R}$
; hence,
$\mathcal {M}\cong {\mathscr {E}}/\mathbb {R}$
; hence,
 $$ \begin{align*} [\alpha,v]+_{{\mathscr{E}}}[0,-\pi([\alpha,v])]&=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u]+_{{\mathscr{E}}} [0,w])]\\ &=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[0,-\pi([0,w])]\\ &=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[0,-w]\\ &=[\alpha,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]=\widetilde{\alpha}. \end{align*} $$
$$ \begin{align*} [\alpha,v]+_{{\mathscr{E}}}[0,-\pi([\alpha,v])]&=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u]+_{{\mathscr{E}}} [0,w])]\\ &=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[0,-\pi([0,w])]\\ &=[\alpha,u]+_{{\mathscr{E}}} [0,w]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[0,-w]\\ &=[\alpha,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]=\widetilde{\alpha}. \end{align*} $$
Hence,
![]() $\widetilde {\alpha }$
is independent of the choice of
$\widetilde {\alpha }$
is independent of the choice of
![]() $u\in \mathbb {R}$
. We define
$u\in \mathbb {R}$
. We define
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
to be the function defined by
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
to be the function defined by
Note that by (39), for any
![]() $\alpha ,\beta \in \mathcal {M}$
, we have
$\alpha ,\beta \in \mathcal {M}$
, we have
 $$ \begin{align*} \widetilde{\alpha}+_{{\mathscr{E}}}\widetilde{\beta}&=[\alpha,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[\beta,H(\alpha,\beta)] +_{{\mathscr{E}}}[0,-\pi([\beta,H(\alpha,\beta)])]\\ &=[\alpha+\beta,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])-\pi([\beta,H(\alpha,\beta)])]\\ &=[\alpha+\beta,u]+_{{\mathscr{E}}}[0,-\pi([\alpha+_{{\mathscr{E}}}\beta,u])]=\widetilde{\alpha+\beta}. \end{align*} $$
$$ \begin{align*} \widetilde{\alpha}+_{{\mathscr{E}}}\widetilde{\beta}&=[\alpha,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])]+_{{\mathscr{E}}}[\beta,H(\alpha,\beta)] +_{{\mathscr{E}}}[0,-\pi([\beta,H(\alpha,\beta)])]\\ &=[\alpha+\beta,u]+_{{\mathscr{E}}}[0,-\pi([\alpha,u])-\pi([\beta,H(\alpha,\beta)])]\\ &=[\alpha+\beta,u]+_{{\mathscr{E}}}[0,-\pi([\alpha+_{{\mathscr{E}}}\beta,u])]=\widetilde{\alpha+\beta}. \end{align*} $$
This shows that
 $$ \begin{align*} [\alpha+\beta,h(\alpha+\beta)]&=\widetilde{\alpha+\beta}=\widetilde{\alpha}+_{{\mathscr{E}}}\widetilde{\beta}\\ &=[\alpha,h(\alpha)]+_{{\mathscr{E}}}[\beta,h(\beta)]=[\alpha+\beta,h(\alpha)+h(\beta)-H(\alpha,\beta)]. \end{align*} $$
$$ \begin{align*} [\alpha+\beta,h(\alpha+\beta)]&=\widetilde{\alpha+\beta}=\widetilde{\alpha}+_{{\mathscr{E}}}\widetilde{\beta}\\ &=[\alpha,h(\alpha)]+_{{\mathscr{E}}}[\beta,h(\beta)]=[\alpha+\beta,h(\alpha)+h(\beta)-H(\alpha,\beta)]. \end{align*} $$
Hence, we have
![]() $ h(\alpha +\beta )=h(\alpha )+h(\beta )-H(\alpha ,\beta ) $
for any
$ h(\alpha +\beta )=h(\alpha )+h(\beta )-H(\alpha ,\beta ) $
for any
![]() $\alpha ,\beta \in \mathcal {M}$
, as desired.
$\alpha ,\beta \in \mathcal {M}$
, as desired.
Next, we consider the case when
![]() $\mathcal {M}\cong \mathbb {N}$
or
$\mathcal {M}\cong \mathbb {N}$
or
![]() $\mathcal {M}\cong \mathbb {Z}$
.
$\mathcal {M}\cong \mathbb {Z}$
.
Lemma 5.6. Assume that
![]() $\mathcal {M}\cong \mathbb {N}$
or
$\mathcal {M}\cong \mathbb {N}$
or
![]() $\mathcal {M}\cong \mathbb {Z}$
, viewed as a commutative monoid with respect to addition, and let
$\mathcal {M}\cong \mathbb {Z}$
, viewed as a commutative monoid with respect to addition, and let
![]() $H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be a pairing satisfying the cocycle condition (37). Then there exists a function
$H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
be a pairing satisfying the cocycle condition (37). Then there exists a function
such that
![]() $H(\alpha ,\beta )=h(\alpha )+h(\beta ) - h(\alpha +\beta )$
for any
$H(\alpha ,\beta )=h(\alpha )+h(\beta ) - h(\alpha +\beta )$
for any
![]() $\alpha ,\beta \in \mathcal {M}$
.
$\alpha ,\beta \in \mathcal {M}$
.
Proof. Again, as in the proof of Lemma 5.6, by replacing the pairing H by
![]() $H-H(0,0)$
, we may assume that
$H-H(0,0)$
, we may assume that
![]() $H(0,0)=0$
. We first treat the case
$H(0,0)=0$
. We first treat the case
![]() $\mathcal {M}\cong \mathbb {N}$
, which we regard as a commutative monoid with respect to the usual addition. Consider the extension
$\mathcal {M}\cong \mathbb {N}$
, which we regard as a commutative monoid with respect to the usual addition. Consider the extension
![]() ${\mathscr {E}}$
given in (38) corresponding to the pairing H. Note that
${\mathscr {E}}$
given in (38) corresponding to the pairing H. Note that
![]() $[1,0]$
gives an element in
$[1,0]$
gives an element in
![]() ${\mathscr {E}}$
. For any
${\mathscr {E}}$
. For any
![]() $\alpha \in \mathcal {M}$
corresponding to
$\alpha \in \mathcal {M}$
corresponding to
![]() $n\in \mathbb {N}$
, we define
$n\in \mathbb {N}$
, we define
![]() $h(\alpha )$
to be the element in
$h(\alpha )$
to be the element in
![]() $\mathbb {R}$
given by the formula
$\mathbb {R}$
given by the formula
where
![]() $n[1,0]$
is the n-fold sum of
$n[1,0]$
is the n-fold sum of
![]() $[1,0]$
with respect to the operator
$[1,0]$
with respect to the operator
![]() $+_{{\mathscr {E}}}$
. Then for
$+_{{\mathscr {E}}}$
. Then for
![]() $\beta \in \mathcal {M}$
corresponding to
$\beta \in \mathcal {M}$
corresponding to
![]() $n'\in \mathbb {N}$
, we have
$n'\in \mathbb {N}$
, we have
![]() $ n'[1,0] = [ \beta , h(\beta )] $
and
$ n'[1,0] = [ \beta , h(\beta )] $
and
By the definition of the operation
![]() $+_{{\mathscr {E}}}$
, we have
$+_{{\mathscr {E}}}$
, we have
Since the operation
![]() $+_{{\mathscr {E}}}$
is associative, comparing this equality with (40), we have
$+_{{\mathscr {E}}}$
is associative, comparing this equality with (40), we have
![]() $ h(\alpha +\beta )=h(\alpha )+h(\beta )-H(\alpha ,\beta )$
for any
$ h(\alpha +\beta )=h(\alpha )+h(\beta )-H(\alpha ,\beta )$
for any
![]() $\alpha ,\beta \in \mathcal {M}$
. Hence, we see that
$\alpha ,\beta \in \mathcal {M}$
. Hence, we see that
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
satisfies the requirement of our assertion. The case for
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
satisfies the requirement of our assertion. The case for
![]() $\mathcal {M}\cong \mathbb {Z}$
may be proved precisely in the same manner. In this case, we regard
$\mathcal {M}\cong \mathbb {Z}$
may be proved precisely in the same manner. In this case, we regard
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() ${\mathscr {E}}$
as abelian groups instead of commutative monoids.
${\mathscr {E}}$
as abelian groups instead of commutative monoids.
Remark 5.7. For the case that
![]() $\mathcal {M}$
is an abelian group, the extension
$\mathcal {M}$
is an abelian group, the extension
![]() ${\mathscr {E}}$
in Lemma 5.5 corresponding to the symmetric cocycle
${\mathscr {E}}$
in Lemma 5.5 corresponding to the symmetric cocycle
![]() $H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
is a commutative group. The existence of
$H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
is a commutative group. The existence of
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
for this case corresponds to the well-known fact that such an extension
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
for this case corresponds to the well-known fact that such an extension
![]() ${\mathscr {E}}$
splits since the additive group of
${\mathscr {E}}$
splits since the additive group of
![]() $\mathbb {R}$
is divisible and hence an injective object in the category of abelian groups (see [Reference Robinson14, 4.1.2]). The statement for Lemma 5.6 corresponds to the fact that the group cohomology
$\mathbb {R}$
is divisible and hence an injective object in the category of abelian groups (see [Reference Robinson14, 4.1.2]). The statement for Lemma 5.6 corresponds to the fact that the group cohomology
![]() $H^2(\mathbb {Z},\mathbb {R})=\{0\}$
. The existence of
$H^2(\mathbb {Z},\mathbb {R})=\{0\}$
. The existence of
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
ensures that the cocycle
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
ensures that the cocycle
![]() $H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
is in fact symmetric in this case.
$H\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
is in fact symmetric in this case.
We are now ready to prove Theorem 5.2.
Proof of Theorem 5.2.
Suppose
![]() $\omega \in Z_{\operatorname {\mathrm {unif}}}(S^X) = C^1_{\operatorname {\mathrm {unif}}}(S^X)\cap Z^1(S^X_*)$
. Since
$\omega \in Z_{\operatorname {\mathrm {unif}}}(S^X) = C^1_{\operatorname {\mathrm {unif}}}(S^X)\cap Z^1(S^X_*)$
. Since
![]() $\omega \in Z^1(S^X_*)$
, by Lemma 2.28, there exists
$\omega \in Z^1(S^X_*)$
, by Lemma 2.28, there exists
![]() $f\in C(S^X_*)$
such that
$f\in C(S^X_*)$
such that
![]() $\partial f=\omega $
. Furthermore, since
$\partial f=\omega $
. Furthermore, since
![]() $\omega \in C^1_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
$\omega \in C^1_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists
![]() $R>0$
such that
$R>0$
such that
![]() $\partial f=\omega \in C^1_R(S^X)$
. Hence, by Definition 4.8 and Proposition 4.13 (see also Proposition 3.18), there exists a pairing
$\partial f=\omega \in C^1_R(S^X)$
. Hence, by Definition 4.8 and Proposition 4.13 (see also Proposition 3.18), there exists a pairing
![]() $h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying the cocycle condition (24). By Lemma 4.9, if X is transferable (see also Proposition 3.18) and by Remark 5.7 if the interaction is simple, we see that
$h_f\colon \mathcal {M}\times \mathcal {M}\rightarrow \mathbb {R}$
satisfying the cocycle condition (24). By Lemma 4.9, if X is transferable (see also Proposition 3.18) and by Remark 5.7 if the interaction is simple, we see that
![]() $h_f$
is symmetric. Note that here we have used the fact that
$h_f$
is symmetric. Note that here we have used the fact that
![]() $\mathcal {M}\cong \mathbb {N}$
or
$\mathcal {M}\cong \mathbb {N}$
or
![]() $\mathcal {M}\cong \mathbb {Z}$
if the interaction is simple. Hence, by Proposition 4.11 (see also Proposition 3.18), we have
$\mathcal {M}\cong \mathbb {Z}$
if the interaction is simple. Hence, by Proposition 4.11 (see also Proposition 3.18), we have
for any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
![]() $\eta \in S^X$
. Note that
$\eta \in S^X$
. Note that
![]() $\mathcal {M}$
satisfies the cancellation property since it is a submonoid of an abelian group. Hence, by Lemma 5.5, there exists
$\mathcal {M}$
satisfies the cancellation property since it is a submonoid of an abelian group. Hence, by Lemma 5.5, there exists
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
for any
![]() $\alpha ,\beta \in \mathcal {M}$
. We define the function
$\alpha ,\beta \in \mathcal {M}$
. We define the function
![]() $g\in C(S^X_*)$
by
$g\in C(S^X_*)$
by
We will prove that g is uniform. By Lemma 2.22, for any conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
, the function
$\xi \colon S\rightarrow \mathbb {R}$
, the function
![]() $\xi _X\in C(S^X_*)$
is horizontal. This implies that
$\xi _X\in C(S^X_*)$
is horizontal. This implies that
![]() $\nabla _{\!e}\xi _X=0$
; hence,
$\nabla _{\!e}\xi _X=0$
; hence,
![]() $\xi _X(\eta ^e)=\xi _X(\eta )$
for any
$\xi _X(\eta ^e)=\xi _X(\eta )$
for any
![]() $e\in E$
. This shows that
$e\in E$
. This shows that
![]() $h\circ {\boldsymbol {\xi }}_{\!X}(\eta ^e)= h\circ {\boldsymbol {\xi }}_{\!X}(\eta )$
for any
$h\circ {\boldsymbol {\xi }}_{\!X}(\eta ^e)= h\circ {\boldsymbol {\xi }}_{\!X}(\eta )$
for any
![]() $e\in E$
; hence,
$e\in E$
; hence,
![]() $\nabla _{\!e}(h\circ {\boldsymbol {\xi }}_{\!X})=0$
, which implies that
$\nabla _{\!e}(h\circ {\boldsymbol {\xi }}_{\!X})=0$
, which implies that
![]() $\partial (h\circ {\boldsymbol {\xi }}_{\!X})=0$
. This gives the formula
$\partial (h\circ {\boldsymbol {\xi }}_{\!X})=0$
. This gives the formula
![]() $\partial g=\partial f=\omega $
. Furthermore, noting that
$\partial g=\partial f=\omega $
. Furthermore, noting that
![]() $\iota ^{\Lambda } (h\circ {\boldsymbol {\xi }}_{\!X}(\eta ))=h\circ {\boldsymbol {\xi }}_\Lambda (\eta )$
for any
$\iota ^{\Lambda } (h\circ {\boldsymbol {\xi }}_{\!X}(\eta ))=h\circ {\boldsymbol {\xi }}_\Lambda (\eta )$
for any
![]() $\Lambda \subset X$
, we have
$\Lambda \subset X$
, we have
 $$ \begin{align*} \iota^{\Lambda\cup\Lambda'}g(\eta)-\iota^{\Lambda} g(\eta)-\iota^{\Lambda'}g(\eta) &=\iota^{\Lambda\cup\Lambda'} f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) \\ &\qquad+h\circ {\boldsymbol{\xi}}_{\Lambda\cup\Lambda'}(\eta)- h\circ {\boldsymbol{\xi}}_\Lambda(\eta)-h\circ {\boldsymbol{\xi}}_{\Lambda'}(\eta)=0 \end{align*} $$
$$ \begin{align*} \iota^{\Lambda\cup\Lambda'}g(\eta)-\iota^{\Lambda} g(\eta)-\iota^{\Lambda'}g(\eta) &=\iota^{\Lambda\cup\Lambda'} f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) \\ &\qquad+h\circ {\boldsymbol{\xi}}_{\Lambda\cup\Lambda'}(\eta)- h\circ {\boldsymbol{\xi}}_\Lambda(\eta)-h\circ {\boldsymbol{\xi}}_{\Lambda'}(\eta)=0 \end{align*} $$
for any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
and
![]() $\eta \in S^X$
, where we have used the coboundary condition (41) and the fact that
$\eta \in S^X$
, where we have used the coboundary condition (41) and the fact that
![]() ${\boldsymbol {\xi }}_{\Lambda \cup \Lambda '}(\eta ) = {\boldsymbol {\xi }}_{\Lambda }(\eta )+{\boldsymbol {\xi }}_{\Lambda '}(\eta )$
. From the definition of the pairing given in Definition 4.8, we see that
${\boldsymbol {\xi }}_{\Lambda \cup \Lambda '}(\eta ) = {\boldsymbol {\xi }}_{\Lambda }(\eta )+{\boldsymbol {\xi }}_{\Lambda '}(\eta )$
. From the definition of the pairing given in Definition 4.8, we see that
![]() $h_g\equiv 0$
. Hence, by Proposition 4.14, we see that
$h_g\equiv 0$
. Hence, by Proposition 4.14, we see that
![]() $g\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Our assertion is now proved by replacing f by g.
$g\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. Our assertion is now proved by replacing f by g.
By using Theorem 5.2, we may calculate the uniform cohomology of
![]() $S^X$
as follows.
$S^X$
as follows.
Theorem 5.8. Let X be a locale, and assume that the interaction is irreducibly quantified. If either X is transferable, or the interaction is simple and X is weakly transferable, then we have
 $$ \begin{align*} H^m_{\operatorname{\mathrm{unif}}}(S^X) \cong \begin{cases} {\operatorname{\mathrm{Consv}}}^\phi(S) &m=0,\\ \{0\} & m\neq0. \end{cases} \end{align*} $$
$$ \begin{align*} H^m_{\operatorname{\mathrm{unif}}}(S^X) \cong \begin{cases} {\operatorname{\mathrm{Consv}}}^\phi(S) &m=0,\\ \{0\} & m\neq0. \end{cases} \end{align*} $$
In particular, we have
![]() $\dim _{\mathbb {R}} H^0_{\operatorname {\mathrm {unif}}}(S^X)=\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
.
$\dim _{\mathbb {R}} H^0_{\operatorname {\mathrm {unif}}}(S^X)=\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
.
Proof. As stated in §1.4, Theorem 5.8 is equivalent to the fact that the sequence
is exact. A conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
defines a uniform function
$\xi \colon S\rightarrow \mathbb {R}$
defines a uniform function
![]() $\xi _X\colon S^X\rightarrow \mathbb {R}$
whose definition
$\xi _X\colon S^X\rightarrow \mathbb {R}$
whose definition ![]() is the canonical expansion (18) with each
is the canonical expansion (18) with each
![]() $\xi _x\in C_{\{x\}}(S^X)$
. This shows that
$\xi _x\in C_{\{x\}}(S^X)$
. This shows that
![]() $\xi _X$
is uniform satisfying
$\xi _X$
is uniform satisfying
![]() $\xi _X(\star )=0$
; hence, (16) induces an inclusion
$\xi _X(\star )=0$
; hence, (16) induces an inclusion
However, if
![]() $f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
satisfies
$f\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
satisfies
![]() $\partial f=0$
, then by Theorem 3.7, there exists a conserved quantity
$\partial f=0$
, then by Theorem 3.7, there exists a conserved quantity
![]() $\xi \colon S\rightarrow \mathbb {R}$
such that
$\xi \colon S\rightarrow \mathbb {R}$
such that
![]() $f(\eta )=\xi _X(\eta )$
, which shows that f is in the image of (43). This proves that we have an isomorphism
$f(\eta )=\xi _X(\eta )$
, which shows that f is in the image of (43). This proves that we have an isomorphism
From Theorem 5.2, we see that the differential
![]() $\partial $
is surjective; hence, the short exact sequence (42) is exact. Our assertion now follows from the definition of uniform cohomology given in Definition 1.6.
$\partial $
is surjective; hence, the short exact sequence (42) is exact. Our assertion now follows from the definition of uniform cohomology given in Definition 1.6.
Remark 5.9. The fact that
![]() $H^m_{\operatorname {\mathrm {unif}}}=\{0\}$
for
$H^m_{\operatorname {\mathrm {unif}}}=\{0\}$
for
![]() $m\neq 0$
reflects the fact that we are viewing the configuration space as modeling a space with a simple topological structure whose only topological feature is its connected components. The
$m\neq 0$
reflects the fact that we are viewing the configuration space as modeling a space with a simple topological structure whose only topological feature is its connected components. The
![]() $H^0_{\operatorname {\mathrm {unif}}}$
is expressed in terms of the conserved quantities and is finite dimensional if
$H^0_{\operatorname {\mathrm {unif}}}$
is expressed in terms of the conserved quantities and is finite dimensional if
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional.
${\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite dimensional.
Example 5.10. In each of the examples of Example 2.10, we have the following.
-
1. In the case of the multi-species exclusion process, we have
 $H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong {\mathbb {R}}^{\kappa }$
, where
$H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong {\mathbb {R}}^{\kappa }$
, where
 $\kappa>0$
is such that
$\kappa>0$
is such that
 $S=\{0,\ldots ,\kappa \}$
.
$S=\{0,\ldots ,\kappa \}$
. -
2. In the case of the generalized exclusion process, we have
 $H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \mathbb {R}$
.
$H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \mathbb {R}$
. -
3. In the case of the lattice gas with energy process, we have
 $H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong {\mathbb {R}}^2$
.
$H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong {\mathbb {R}}^2$
. -
4. For the interaction of Example 2.10 (4), we have
 $H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \mathbb {R}$
.
$H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \mathbb {R}$
. -
5. For the Glauber Model of Example 2.10 (5), we have
 $H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \{0\}$
.
$H^0_{\operatorname {\mathrm {unif}}}(S^X)\cong \{0\}$
.
5.2 Group action on the configuration space
In this subsection, we first review basic definitions and results concerning group cohomology of a group G acting on an
![]() $\mathbb {R}$
-linear space V. We will then consider the action of a group G on the locale X.
$\mathbb {R}$
-linear space V. We will then consider the action of a group G on the locale X.
We say that an
![]() $\mathbb {R}$
-linear space V is a G-module if any
$\mathbb {R}$
-linear space V is a G-module if any
![]() $\sigma \in G$
gives an
$\sigma \in G$
gives an
![]() $\mathbb {R}$
-linear homomorphism
$\mathbb {R}$
-linear homomorphism
![]() $\sigma \colon V\rightarrow V$
such that
$\sigma \colon V\rightarrow V$
such that
![]() $(\tau \sigma )(v)=\tau (\sigma (v)) =\tau \circ \sigma (v)$
for any
$(\tau \sigma )(v)=\tau (\sigma (v)) =\tau \circ \sigma (v)$
for any
![]() $\sigma ,\tau \in G$
and
$\sigma ,\tau \in G$
and
![]() $v\in V$
. In what follows, we will often simply denote
$v\in V$
. In what follows, we will often simply denote
![]() $\sigma (v)$
by
$\sigma (v)$
by
![]() $\sigma v$
. For any G-module V, we denote by
$\sigma v$
. For any G-module V, we denote by
![]() $V^G$
the G-invariant subspace of V, defined by
$V^G$
the G-invariant subspace of V, defined by ![]() .
.
Definition 5.11. Let V be a G-module. The zeroth group cohomology
![]() $H^0(G,V)$
of G with coefficients in V is given as
$H^0(G,V)$
of G with coefficients in V is given as
Furthermore, we let

where
![]() $1$
is the identity element of G. Then the first group cohomology
$1$
is the identity element of G. Then the first group cohomology
![]() $H^1(G,V)$
of G with coefficients in V is given as
$H^1(G,V)$
of G with coefficients in V is given as
In particular, if the action of G on V is trivial – in other words, if
![]() $\sigma v=v$
for any
$\sigma v=v$
for any
![]() $v\in V$
and
$v\in V$
and
![]() $\sigma \in G$
– then we have
$\sigma \in G$
– then we have
![]() $H^0(G,V)=V$
and
$H^0(G,V)=V$
and
where
![]() $\operatorname {\mathrm {Hom}}(G,V)$
denotes the set of homomorphisms of groups from G to V.
$\operatorname {\mathrm {Hom}}(G,V)$
denotes the set of homomorphisms of groups from G to V.
Remark 5.12. The group cohomology of G with coefficients in V is usually defined using the right derived functor of the functor
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}[G]}(\mathbb {Z},-)$
applied to V. In other words,
${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}[G]}(\mathbb {Z},-)$
applied to V. In other words, ![]() for any integer
for any integer
![]() $m\in \mathbb {Z}$
(see, for example, [Reference Atiyah and Wall1, §1]). Definition 5.11 is the well-known description of this cohomology group in terms of explicit cocycles (see [Reference Atiyah and Wall1, §2]).
$m\in \mathbb {Z}$
(see, for example, [Reference Atiyah and Wall1, §1]). Definition 5.11 is the well-known description of this cohomology group in terms of explicit cocycles (see [Reference Atiyah and Wall1, §2]).
Let V and
![]() $V'$
be G-modules. We say that an
$V'$
be G-modules. We say that an
![]() $\mathbb {R}$
-linear homomorphism
$\mathbb {R}$
-linear homomorphism
is a G-homomorphism if
![]() $\pi (\sigma v)=\sigma \pi (v)$
for any
$\pi (\sigma v)=\sigma \pi (v)$
for any
![]() $\sigma \in G$
and
$\sigma \in G$
and
![]() $v\in V$
. By definition, we have
$v\in V$
. By definition, we have
![]() $\pi (V^G)\subset \pi (V)^G$
, where
$\pi (V^G)\subset \pi (V)^G$
, where
![]() $\pi (V)$
is the G-submodule of V defined to be the image of V with respect to
$\pi (V)$
is the G-submodule of V defined to be the image of V with respect to
![]() $\pi $
. Note that
$\pi $
. Note that
![]() $\pi $
gives an exact sequence
$\pi $
gives an exact sequence
of G-modules, which by the standard theory of cohomology of groups (see, for example, [Reference Atiyah and Wall1, (1.3)]) gives rise to the long exact sequence
The homomorphism
![]() $\delta $
is given explicitly as follows. For any
$\delta $
is given explicitly as follows. For any
![]() $\omega \in \pi (V)^G$
, choose a
$\omega \in \pi (V)^G$
, choose a
![]() $v\in V$
such that
$v\in V$
such that
![]() $\pi (v)=\omega $
. Then
$\pi (v)=\omega $
. Then
![]() $\delta (\omega )\in H^1(G,\operatorname {\mathrm {Ker}}\pi )$
is the class given by the cocycle satisfying
$\delta (\omega )\in H^1(G,\operatorname {\mathrm {Ker}}\pi )$
is the class given by the cocycle satisfying
for any
![]() $\sigma \in G$
(see [Reference Atiyah and Wall1, §2 p.97]). Note that since
$\sigma \in G$
(see [Reference Atiyah and Wall1, §2 p.97]). Note that since
![]() $\omega =\pi (v)$
is invariant under the action of G, we have
$\omega =\pi (v)$
is invariant under the action of G, we have
![]() $\pi (\delta (\omega )(\sigma ))=(1-\sigma )\pi (v)=0$
; hence,
$\pi (\delta (\omega )(\sigma ))=(1-\sigma )\pi (v)=0$
; hence,
![]() $\delta (\omega )(\sigma )\in \operatorname {\mathrm {Ker}}\pi $
for any
$\delta (\omega )(\sigma )\in \operatorname {\mathrm {Ker}}\pi $
for any
![]() $\sigma \in G$
. Our choice of the sign of the homomorphism
$\sigma \in G$
. Our choice of the sign of the homomorphism
![]() $\delta $
in (47) is to ensure compatibility with standard sign conventions used in probability theory.
$\delta $
in (47) is to ensure compatibility with standard sign conventions used in probability theory.
In what follows, let X be a locale, and let G be a group.
Definition 5.13. An automorphism of a locale X is a bijective map of sets
![]() $\sigma \colon X\rightarrow X$
such that
$\sigma \colon X\rightarrow X$
such that
![]() $\sigma (E)=E\subset X\times X$
. The set
$\sigma (E)=E\subset X\times X$
. The set
![]() $\operatorname {\mathrm {Aut}}(X)$
of all automorphisms of X form a group with respect to the operation given by composition of automorphisms. We say that X has an action of G if there exists a homomorphism of groups
$\operatorname {\mathrm {Aut}}(X)$
of all automorphisms of X form a group with respect to the operation given by composition of automorphisms. We say that X has an action of G if there exists a homomorphism of groups
![]() $G\rightarrow \operatorname {\mathrm {Aut}}(X)$
so that any
$G\rightarrow \operatorname {\mathrm {Aut}}(X)$
so that any
![]() $\sigma \in G$
induces an automorphism
$\sigma \in G$
induces an automorphism
![]() $\sigma \colon X\rightarrow X$
.
$\sigma \colon X\rightarrow X$
.
Example 5.14.
-
1. Let d be an integer
 $>0$
. Consider the Euclidean lattice
$>0$
. Consider the Euclidean lattice
 $X=(\mathbb {Z}^d,\mathbb {E}^d)$
, and let
$X=(\mathbb {Z}^d,\mathbb {E}^d)$
, and let
 $G=\mathbb {Z}^d$
. For any
$G=\mathbb {Z}^d$
. For any
 $\tau \in G$
, if we define the automorphism
$\tau \in G$
, if we define the automorphism
 $\tau \colon X\rightarrow X$
by
$\tau \colon X\rightarrow X$
by  for any
for any
 $x\in X$
, then this gives an action of G on X.
$x\in X$
, then this gives an action of G on X. -
2. The group
 $G=\mathbb {Z}^2$
acts on the triangular and hexagonal lattices via translation. The group
$G=\mathbb {Z}^2$
acts on the triangular and hexagonal lattices via translation. The group
 $G=\mathbb {Z}^3$
acts on the diamond lattice also via translation.
$G=\mathbb {Z}^3$
acts on the diamond lattice also via translation. -
3. If G is a finitely generated group with set of minimal generators
 $\mathcal {S}$
, then left multiplication by elements of G gives an action of the group G on the Cayley graph
$\mathcal {S}$
, then left multiplication by elements of G gives an action of the group G on the Cayley graph
 $(G,E_{\mathcal {S}})$
.
$(G,E_{\mathcal {S}})$
.
From now until the end of §5.3, we assume that X has an action of a group G. If we denote the group action from the left, then
![]() $S^X_*=(S^X_*,\Phi _*)$
has a natural G-action given by
$S^X_*=(S^X_*,\Phi _*)$
has a natural G-action given by ![]() for any
for any
![]() $\eta =(\eta _x)$
and
$\eta =(\eta _x)$
and
![]() $\sigma \in G$
. Then
$\sigma \in G$
. Then
![]() $C^0(S^X_*)=C(S^X_*)$
and
$C^0(S^X_*)=C(S^X_*)$
and
![]() $C^1(S^X_*)$
have natural G-actions given for any
$C^1(S^X_*)$
have natural G-actions given for any
![]() $\sigma \in G$
by
$\sigma \in G$
by
![]() $\sigma (f)=f\circ \sigma $
for any function
$\sigma (f)=f\circ \sigma $
for any function
![]() $f\in C(S^X_*)$
, and
$f\in C(S^X_*)$
, and
![]() $\sigma (\omega )=\omega \circ \sigma $
for any form
$\sigma (\omega )=\omega \circ \sigma $
for any form
![]() $\omega \in C^1(S^X_*)$
. Since the action of G preserves the distance on the locale X and preserves closed forms on
$\omega \in C^1(S^X_*)$
. Since the action of G preserves the distance on the locale X and preserves closed forms on
![]() $C^1(S^X_*)$
, the groups
$C^1(S^X_*)$
, the groups
![]() $C_{\operatorname {\mathrm {unif}}}(S^X)$
and
$C_{\operatorname {\mathrm {unif}}}(S^X)$
and
![]() $Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
have induced G-module structures.
$Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
have induced G-module structures.
In case of functions and forms, we will use the term shift-invariant interchangeably with the term G-invariant when the group G is understood. We say that a subset
![]() $\Lambda _0\subset X$
is a fundamental domain of X for the action of G if it represents the set of orbits of the vertices of X for the action of G.
$\Lambda _0\subset X$
is a fundamental domain of X for the action of G if it represents the set of orbits of the vertices of X for the action of G.
Lemma 5.15. Suppose X has an action of a group G, and assume that the set of orbits of the vertices of X for the action of G is finite. Then for any shift-invariant uniform function
![]() $F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists a local function
$F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
, there exists a local function
![]() $f\in C_{\mathrm {loc}}(S^X)$
satisfying
$f\in C_{\mathrm {loc}}(S^X)$
satisfying
![]() $f(\star )=0$
such that
$f(\star )=0$
such that
in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
.
Proof. By definition,
![]() $F(\star )=0$
. Since F is uniform, there exists
$F(\star )=0$
. Since F is uniform, there exists
![]() $R>0$
such that the expansion (18) of F in terms of local functions with exact support is given by
$R>0$
such that the expansion (18) of F in terms of local functions with exact support is given by
Since F is shift-invariant, we have
![]() $\tau (F_\Lambda )=\tau (F)_{\tau (\Lambda )}=F_{\tau (\Lambda )}$
for any
$\tau (F_\Lambda )=\tau (F)_{\tau (\Lambda )}=F_{\tau (\Lambda )}$
for any
![]() $\tau \in G$
. Let
$\tau \in G$
. Let
![]() ${\mathscr {I}}^*_{\!R}$
be the set of nonempty finite
${\mathscr {I}}^*_{\!R}$
be the set of nonempty finite
![]() $\Lambda \subset X$
such that
$\Lambda \subset X$
such that
![]() $\operatorname {diam}(\Lambda )\leq R$
. Then
$\operatorname {diam}(\Lambda )\leq R$
. Then
![]() ${\mathscr {I}}^*_{\!R}$
has a natural action of G. We denote by
${\mathscr {I}}^*_{\!R}$
has a natural action of G. We denote by
![]() $\sim $
the equivalence relation on
$\sim $
the equivalence relation on
![]() ${\mathscr {I}}^*_{\!R}$
given by
${\mathscr {I}}^*_{\!R}$
given by
![]() $\Lambda \sim \Lambda '$
if
$\Lambda \sim \Lambda '$
if
![]() $\Lambda '=\tau (\Lambda )$
for some
$\Lambda '=\tau (\Lambda )$
for some
![]() $\tau \in G$
. Let
$\tau \in G$
. Let
![]() $\Lambda _0\subset X$
be a fundamental domain of X for the action of G. Then any equivalence class of
$\Lambda _0\subset X$
be a fundamental domain of X for the action of G. Then any equivalence class of
![]() ${\mathscr {I}}^*_{\!R}$
with respect to the relation
${\mathscr {I}}^*_{\!R}$
with respect to the relation
![]() $\sim $
contains a representative that intersects with
$\sim $
contains a representative that intersects with
![]() $\Lambda _0$
. Since
$\Lambda _0$
. Since
![]() $\Lambda _0$
is finite, and the diameters of the sets in
$\Lambda _0$
is finite, and the diameters of the sets in
![]() ${\mathscr {I}}^*_{\!R}$
are bounded, this implies that
${\mathscr {I}}^*_{\!R}$
are bounded, this implies that
![]() ${\mathscr {I}}^*_{\!R}/\sim $
is finite. For each equivalence class C of
${\mathscr {I}}^*_{\!R}/\sim $
is finite. For each equivalence class C of
![]() ${\mathscr {I}}^*_{\!R}/\sim $
, let
${\mathscr {I}}^*_{\!R}/\sim $
, let ![]() , which is again finite. If we let
, which is again finite. If we let

then it is a finite sum and hence gives a local function in
![]() $C_{\mathrm {loc}}(S^X)$
. Then since
$C_{\mathrm {loc}}(S^X)$
. Then since
![]() ${\mathscr {I}}^*_{\!R}/\sim $
is finite,
${\mathscr {I}}^*_{\!R}/\sim $
is finite,

again defines a local function in
![]() $C_{\mathrm {loc}}(S^X)$
, which by construction satisfies (48) as desired.
$C_{\mathrm {loc}}(S^X)$
, which by construction satisfies (48) as desired.
The action of G on
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
viewed as a subspace of
${\operatorname {\mathrm {Consv}}}^\phi (S)$
viewed as a subspace of
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
is given by the trivial action. Applying (46) to the short exact sequence (42), we obtain the long exact sequence
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
is given by the trivial action. Applying (46) to the short exact sequence (42), we obtain the long exact sequence

Moreover, since G acts trivially on
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
, by (45), we have
${\operatorname {\mathrm {Consv}}}^\phi (S)$
, by (45), we have
Remark 5.16. We may view the cohomology group
![]() $H^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
as a group which philosophically reflects the first reduced cohomology group of the quotient space
$H^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
as a group which philosophically reflects the first reduced cohomology group of the quotient space
![]() $S^X/G$
with fixed base point
$S^X/G$
with fixed base point
![]() $\star /G$
. Intuitively, we are viewing
$\star /G$
. Intuitively, we are viewing
![]() $S^X$
as a model of the configuration space on X which we view as an infinitely magnified version of a point in a macroscopic space. In this context, the cohomology
$S^X$
as a model of the configuration space on X which we view as an infinitely magnified version of a point in a macroscopic space. In this context, the cohomology
![]() $H^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
is regarded as representing the flow of the conserved quantities at this point induced from the action of G. More generally, for
$H^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
is regarded as representing the flow of the conserved quantities at this point induced from the action of G. More generally, for
![]() $m\in \mathbb {Z}$
, we may view the m-th group cohomology
$m\in \mathbb {Z}$
, we may view the m-th group cohomology
![]() $H^m\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
as a group philosophically reflecting the m-th reduced cohomology group of the quotient space
$H^m\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
as a group philosophically reflecting the m-th reduced cohomology group of the quotient space
![]() $S^X/G$
with fixed base point
$S^X/G$
with fixed base point
![]() $\star /G$
.
$\star /G$
.
5.3 Group cohomology of the configuration space
In this subsection, we will prove Theorem 5.17, which is the main theorem of this article. We say that an action of a group G on a locale X is free if
![]() $\sigma (x)=\tau (x)$
implies that
$\sigma (x)=\tau (x)$
implies that
![]() $\sigma =\tau $
for any
$\sigma =\tau $
for any
![]() $x\in X$
and
$x\in X$
and
![]() $\sigma ,\tau \in G$
. Throughout this subsection, we assume that X has a free action of a group G.
$\sigma ,\tau \in G$
. Throughout this subsection, we assume that X has a free action of a group G.
As in §1.2, denote by
![]() $\mathcal {C}=\bigl (Z^1_{\operatorname {\mathrm {unif}}}(S^X)\bigr )^G$
the space of shift-invariant closed uniform forms, and by
$\mathcal {C}=\bigl (Z^1_{\operatorname {\mathrm {unif}}}(S^X)\bigr )^G$
the space of shift-invariant closed uniform forms, and by
![]() $\mathcal {E} = \partial \bigl (C^0_{\operatorname {\mathrm {unif}}}(S^X)^G\bigr )$
the image by
$\mathcal {E} = \partial \bigl (C^0_{\operatorname {\mathrm {unif}}}(S^X)^G\bigr )$
the image by
![]() $\partial $
of the space of shift-invariant uniform functions. The main theorem of this article is the following, given as Theorem 1 in §1.3.
$\partial $
of the space of shift-invariant uniform functions. The main theorem of this article is the following, given as Theorem 1 in §1.3.
Theorem 5.17. Let the system
![]() $(X,S,\phi )$
be as in Theorem 5.8, and assume that the action of G on the locale X is free. Then the boundary morphism
$(X,S,\phi )$
be as in Theorem 5.8, and assume that the action of G on the locale X is free. Then the boundary morphism
![]() $\delta $
of (49) gives a canonical isomorphism
$\delta $
of (49) gives a canonical isomorphism
Moreover, a choice of a fundamental domain for the action of G on X gives an
![]() $\mathbb {R}$
-linear homomorphism
$\mathbb {R}$
-linear homomorphism
![]() $\lambda \colon \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))\rightarrow \mathcal {C}$
such that
$\lambda \colon \operatorname {\mathrm {Hom}}(G,{\operatorname {\mathrm {Consv}}}^\phi (S))\rightarrow \mathcal {C}$
such that
![]() $\delta \circ \lambda ={\operatorname {\mathrm {id}}}$
, which gives a decomposition
$\delta \circ \lambda ={\operatorname {\mathrm {id}}}$
, which gives a decomposition
In order to prove Theorem 5.17, we first prove Proposition 5.18 concerning the existence of a section of
![]() $\delta $
. Let
$\delta $
. Let
![]() $\Lambda _0$
be a fundamental domain of X for the action of G. Since the action of G on X is free, any
$\Lambda _0$
be a fundamental domain of X for the action of G. Since the action of G on X is free, any
![]() $x\in X$
may be uniquely written as
$x\in X$
may be uniquely written as
![]() $\sigma (x_0)$
for some
$\sigma (x_0)$
for some
![]() $x_0\in \Lambda _0$
and
$x_0\in \Lambda _0$
and
![]() $\sigma \in G$
. Then for
$\sigma \in G$
. Then for
![]() $\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, we have
$\xi \in {\operatorname {\mathrm {Consv}}}^\phi (S)$
, we have
where ![]() for any
for any
![]() $W\subset X$
.
$W\subset X$
.
Proposition 5.18. Let X be a locale with a free action of a group G, and let
![]() $\Lambda _0 \subset X$
be a fundamental domain of X for the action of G. For any
$\Lambda _0 \subset X$
be a fundamental domain of X for the action of G. For any
![]() $\psi \in Z^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
, we let
$\psi \in Z^1\bigl (G, {\operatorname {\mathrm {Consv}}}^\phi (S)\bigr )$
, we let ![]() , where
, where
Then we have
![]() $\delta (\omega _\psi )=\psi $
.
$\delta (\omega _\psi )=\psi $
.
Proof. By definition, the map is
![]() $\mathbb {R}$
-linear. Since
$\mathbb {R}$
-linear. Since
![]() $\psi $
is a cocycle with values in
$\psi $
is a cocycle with values in
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
and the group G acts trivially on
${\operatorname {\mathrm {Consv}}}^\phi (S)$
and the group G acts trivially on
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
, we have
${\operatorname {\mathrm {Consv}}}^\phi (S)$
, we have
![]() $\psi (\sigma \tau )=\psi (\tau )+\psi (\sigma )$
for any
$\psi (\sigma \tau )=\psi (\tau )+\psi (\sigma )$
for any
![]() $\sigma ,\tau \in G$
. Note that
$\sigma ,\tau \in G$
. Note that
 $$ \begin{align*} \sigma(\theta_\psi)=\sum_{\tau\in G} &\sigma\bigl(\psi(\tau)_{\tau(\Lambda_0)}\bigr) = \sum_{\tau\in G} \psi(\tau)_{\sigma\tau(\Lambda_0)}\\ &= \sum_{\tau\in G} \bigl(\psi(\sigma\tau)_{\sigma\tau(x_0)}-\psi(\sigma)_{\sigma\tau(\Lambda_0)}\bigr) = \sum_{\tau\in G} \bigl(\psi(\tau)_{\tau(\Lambda_0)}-\psi(\sigma)_{\tau(\Lambda_0)}\bigr) =\theta_\psi-\psi(\sigma)_X. \end{align*} $$
$$ \begin{align*} \sigma(\theta_\psi)=\sum_{\tau\in G} &\sigma\bigl(\psi(\tau)_{\tau(\Lambda_0)}\bigr) = \sum_{\tau\in G} \psi(\tau)_{\sigma\tau(\Lambda_0)}\\ &= \sum_{\tau\in G} \bigl(\psi(\sigma\tau)_{\sigma\tau(x_0)}-\psi(\sigma)_{\sigma\tau(\Lambda_0)}\bigr) = \sum_{\tau\in G} \bigl(\psi(\tau)_{\tau(\Lambda_0)}-\psi(\sigma)_{\tau(\Lambda_0)}\bigr) =\theta_\psi-\psi(\sigma)_X. \end{align*} $$
Hence, we have
![]() $(1-\sigma )\theta _\psi =\psi (\sigma )_X$
for any
$(1-\sigma )\theta _\psi =\psi (\sigma )_X$
for any
![]() $\sigma \in G$
. Since
$\sigma \in G$
. Since
![]() $\psi (\sigma )$
is a conserved quantity,
$\psi (\sigma )$
is a conserved quantity,
![]() $\psi (\sigma )_X$
is horizontal by Lemma 2.22; hence, we have
$\psi (\sigma )_X$
is horizontal by Lemma 2.22; hence, we have
![]() $(1-\sigma )\omega _\psi = (1-\sigma )\partial \theta _\psi = \partial \psi (\sigma )_X=0$
for any
$(1-\sigma )\omega _\psi = (1-\sigma )\partial \theta _\psi = \partial \psi (\sigma )_X=0$
for any
![]() $\sigma \in G$
. This implies that we have
$\sigma \in G$
. This implies that we have
![]() $\omega _\psi \in \mathcal {C}$
. By the explicit description of the homomorphism
$\omega _\psi \in \mathcal {C}$
. By the explicit description of the homomorphism
![]() $\delta $
in (47), we see that
$\delta $
in (47), we see that
![]() $\delta (\omega _\psi )=\psi $
, as desired.
$\delta (\omega _\psi )=\psi $
, as desired.
We may now prove Theorem 5.17.
Proof of Theorem 5.17.
By the definition of
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $\mathcal {E}$
, the long exact sequence (49) gives the exact sequence
$\mathcal {E}$
, the long exact sequence (49) gives the exact sequence
By Proposition 5.18, for any
![]() $\psi \in \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
, there exists
$\psi \in \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
, there exists
![]() $\omega _\psi \in \mathcal {C}$
such that
$\omega _\psi \in \mathcal {C}$
such that
![]() $\delta (\omega _\psi )=\psi $
. This implies that
$\delta (\omega _\psi )=\psi $
. This implies that
![]() $\delta $
is surjective. By construction, the map
$\delta $
is surjective. By construction, the map
![]() $\psi \mapsto \omega _\psi $
is
$\psi \mapsto \omega _\psi $
is
![]() $\mathbb {R}$
-linear; hence, we have a decomposition
$\mathbb {R}$
-linear; hence, we have a decomposition
![]() $ \mathcal {C}\cong \mathcal {E}\oplus \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S)), $
given explicitly by mapping any
$ \mathcal {C}\cong \mathcal {E}\oplus \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S)), $
given explicitly by mapping any
![]() $\omega \in \mathcal {C}$
to the element
$\omega \in \mathcal {C}$
to the element
![]() $( \omega -\omega _\psi , \psi )\in \mathcal {E}\oplus \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
, where
$( \omega -\omega _\psi , \psi )\in \mathcal {E}\oplus \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
, where ![]() .
.
As a corollary of Theorem 5.17, we have the following result, which coincides with Corollary 2 of the introduction.
Corollary 5.19. Let the system
![]() $(X,S,\phi )$
and the G-action be as in Theorem 5.17. Assume in addition that the abelian quotient
$(X,S,\phi )$
and the G-action be as in Theorem 5.17. Assume in addition that the abelian quotient
![]() $G^{\operatorname {\mathrm {ab}}}$
of G is of finite rank d. If we choose a generator of the free part of
$G^{\operatorname {\mathrm {ab}}}$
of G is of finite rank d. If we choose a generator of the free part of
![]() $G^{\operatorname {\mathrm {ab}}}$
, then we have an isomorphism
$G^{\operatorname {\mathrm {ab}}}$
, then we have an isomorphism
![]() $ \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S)) \cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S). $
A choice of a fundamental domain of X for the action of G gives a decomposition
$ \operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S)) \cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S). $
A choice of a fundamental domain of X for the action of G gives a decomposition
 $$ \begin{align} \mathcal{C}\cong \mathcal{E}\oplus \bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align} $$
$$ \begin{align} \mathcal{C}\cong \mathcal{E}\oplus \bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align} $$
Proof. We have
where
![]() $G^{\operatorname {\mathrm {ab}}}_{\operatorname {\mathrm {tors}}}$
is the torsion subgroup of
$G^{\operatorname {\mathrm {ab}}}_{\operatorname {\mathrm {tors}}}$
is the torsion subgroup of
![]() $G^{\operatorname {\mathrm {ab}}}$
, and the equality follows from the fact that
$G^{\operatorname {\mathrm {ab}}}$
, and the equality follows from the fact that
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
is abelian and torsion free. This implies that any element in
${\operatorname {\mathrm {Consv}}}^\phi (S)$
is abelian and torsion free. This implies that any element in
![]() $\operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
is determined by the image of the generators of the free part of
$\operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))$
is determined by the image of the generators of the free part of
![]() $G^{\operatorname {\mathrm {ab}}}$
; hence, if we fix such a set of generators, then we have an isomorphism
$G^{\operatorname {\mathrm {ab}}}$
; hence, if we fix such a set of generators, then we have an isomorphism
 $$\begin{align*}\operatorname{\mathrm{Hom}}(G, {\operatorname{\mathrm{Consv}}}^\phi(S))\cong\bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}(G, {\operatorname{\mathrm{Consv}}}^\phi(S))\cong\bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S). \end{align*}$$
Our assertion now follows from Theorem 5.17.
Remark 5.20. Let the system
![]() $(X,S,\phi )$
be as in Theorem 5.8, and assume that
$(X,S,\phi )$
be as in Theorem 5.8, and assume that
![]() $G=\mathbb {Z}^d$
and that the action of G on X is free. The standard basis of
$G=\mathbb {Z}^d$
and that the action of G on X is free. The standard basis of
![]() $G=\mathbb {Z}^d$
gives an isomorphism
$G=\mathbb {Z}^d$
gives an isomorphism
![]() $\operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))\cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
, by associating to the element
$\operatorname {\mathrm {Hom}}(G, {\operatorname {\mathrm {Consv}}}^\phi (S))\cong \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
, by associating to the element
 $$\begin{align*}\psi=(\zeta^{(1)},\ldots,\zeta^{(d)}) \in\bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S) \end{align*}$$
$$\begin{align*}\psi=(\zeta^{(1)},\ldots,\zeta^{(d)}) \in\bigoplus_{j=1}^d{\operatorname{\mathrm{Consv}}}^\phi(S) \end{align*}$$
the cocycle
![]() $\psi \colon G\rightarrow {\operatorname {\mathrm {Consv}}}^\phi (S)$
given by
$\psi \colon G\rightarrow {\operatorname {\mathrm {Consv}}}^\phi (S)$
given by ![]() for any
for any
![]() $\tau =(\tau _j)\in \mathbb {Z}^d$
. If we fix a fundamental domain
$\tau =(\tau _j)\in \mathbb {Z}^d$
. If we fix a fundamental domain
![]() $\Lambda _0$
of X for the action of G, then the map
$\Lambda _0$
of X for the action of G, then the map
![]() $\theta _\psi $
in Proposition 5.18 is given by
$\theta _\psi $
in Proposition 5.18 is given by
 $$\begin{align*}\theta_{\psi}=\sum_{j=1}^d\Bigl(\sum_{\tau\in G}\tau_j\zeta_{\tau(\Lambda_0)}^{(j)}\Bigr). \end{align*}$$
$$\begin{align*}\theta_{\psi}=\sum_{j=1}^d\Bigl(\sum_{\tau\in G}\tau_j\zeta_{\tau(\Lambda_0)}^{(j)}\Bigr). \end{align*}$$
Hence, the form in
![]() $\mathcal {C}$
corresponding to
$\mathcal {C}$
corresponding to
![]() $\psi =(\zeta ^{(1)},\ldots ,\zeta ^{(d)})$
is given by the form
$\psi =(\zeta ^{(1)},\ldots ,\zeta ^{(d)})$
is given by the form
![]() $\omega _\psi =\partial \bigl (\sum _{j=1}^d\sum _{\tau \in G}\tau _j\zeta _{\tau (\Lambda _0)}^{(j)}\bigr )$
as stated in (7) of §1.4. Then Corollary 5.19 implies that any shift-invariant closed local form
$\omega _\psi =\partial \bigl (\sum _{j=1}^d\sum _{\tau \in G}\tau _j\zeta _{\tau (\Lambda _0)}^{(j)}\bigr )$
as stated in (7) of §1.4. Then Corollary 5.19 implies that any shift-invariant closed local form
![]() $\omega $
decomposes as
$\omega $
decomposes as
for some shift-invariant uniform function F in
![]() $C^0_{\operatorname {\mathrm {unif}}}(S^X)$
and
$C^0_{\operatorname {\mathrm {unif}}}(S^X)$
and
![]() $\psi \in \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
. For the case when
$\psi \in \bigoplus _{j=1}^d{\operatorname {\mathrm {Consv}}}^\phi (S)$
. For the case when
![]() $c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite, if we fix a basis
$c_\phi =\dim _{\mathbb {R}}{\operatorname {\mathrm {Consv}}}^\phi (S)$
is finite, if we fix a basis
![]() $\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
$\xi ^{(1)},\ldots ,\xi ^{(c_\phi )}$
of
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)$
, then we have
${\operatorname {\mathrm {Consv}}}^\phi (S)$
, then we have
![]() $ \zeta ^{(j)}=\sum _{i=1}^{c_\phi }a_{ij}\xi ^{(i)} $
for some
$ \zeta ^{(j)}=\sum _{i=1}^{c_\phi }a_{ij}\xi ^{(i)} $
for some
![]() $a_{ij}\in \mathbb {R}$
,
$a_{ij}\in \mathbb {R}$
,
![]() $i=1,\ldots ,c_{\phi }$
,
$i=1,\ldots ,c_{\phi }$
,
![]() $j=1,\ldots ,d$
. This shows that
$j=1,\ldots ,d$
. This shows that
 $$\begin{align*}\theta_{\psi}=\sum_{i=1}^{c_\phi}\sum_{j=1}^d a_{ij}\Bigl(\sum_{\tau\in G}\tau_j\xi^{(i)}_{\tau(\Lambda_0)}\Bigr), \end{align*}$$
$$\begin{align*}\theta_{\psi}=\sum_{i=1}^{c_\phi}\sum_{j=1}^d a_{ij}\Bigl(\sum_{\tau\in G}\tau_j\xi^{(i)}_{\tau(\Lambda_0)}\Bigr), \end{align*}$$
which with (52) gives the representation of Theorem 5 of the introduction.
A The cohomology of graphs
In this section, we review well-known facts concerning the definition of the cohomology of a graph. A cohomology is an algebraic method to extract invariants of a mathematical object. Let
![]() $(X,E)$
be any symmetric directed graph. Following [Reference Sunada17, §4.6], we define the cohomology of
$(X,E)$
be any symmetric directed graph. Following [Reference Sunada17, §4.6], we define the cohomology of
![]() $(X,E)$
as follows.
$(X,E)$
as follows.
Definition A.1. For any symmetric directed graph
![]() $(X,E)$
, we let
$(X,E)$
, we let
where ![]() . Furthermore, we define the differential
. Furthermore, we define the differential
by ![]() for any
for any
![]() $e\in E$
. We define the cohomology of
$e\in E$
. We define the cohomology of
![]() $(X,E)$
by
$(X,E)$
by
and ![]() for any
for any
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $m\neq 0,1$
.
$m\neq 0,1$
.
We call any
![]() $\omega $
in
$\omega $
in
![]() $C^1(X)$
a form on
$C^1(X)$
a form on
![]() $(X,E)$
. A form is the analogue of a differential form. We say that a form
$(X,E)$
. A form is the analogue of a differential form. We say that a form
![]() $\omega $
is exact if there exists
$\omega $
is exact if there exists
![]() $f\in C(X)$
such that
$f\in C(X)$
such that
![]() $\omega =\partial f$
. Then the cohomology
$\omega =\partial f$
. Then the cohomology
![]() $H^1(X)$
is the quotient space of the space of forms by the space of exact forms.
$H^1(X)$
is the quotient space of the space of forms by the space of exact forms.
The cohomology
![]() $H^m(X)$
reflects the topology of the graph
$H^m(X)$
reflects the topology of the graph
![]() $(X,E)$
. In fact, classes of the
$(X,E)$
. In fact, classes of the
![]() $0$
-th cohomology
$0$
-th cohomology
![]() $H^0(X)$
correspond to functions constant on each connected components of
$H^0(X)$
correspond to functions constant on each connected components of
![]() $(X,E)$
, and the classes of the
$(X,E)$
, and the classes of the
![]() $1$
-st cohomology
$1$
-st cohomology
![]() $H^1(X)$
correspond to functions on closed paths in
$H^1(X)$
correspond to functions on closed paths in
![]() $(X,E)$
. In what follows, we will make these statements precise.
$(X,E)$
. In what follows, we will make these statements precise.
The statement for
![]() $H^0(X)$
may be given as follows.
$H^0(X)$
may be given as follows.
Lemma A.2. For any
![]() $f\in C(X)$
, the function f is horizontal (i.e.,
$f\in C(X)$
, the function f is horizontal (i.e.,
![]() $\partial f=0$
) if and only if f is constant on the connected components of
$\partial f=0$
) if and only if f is constant on the connected components of
![]() $(X,E)$
.
$(X,E)$
.
Proof. Let
![]() $f\in H^0(X)=\ker \partial $
so that
$f\in H^0(X)=\ker \partial $
so that
![]() $\partial f=0$
. Suppose
$\partial f=0$
. Suppose
![]() $x,x'\in X$
are in the same connected components of
$x,x'\in X$
are in the same connected components of
![]() $(X,E)$
. Then there exists a path
$(X,E)$
. Then there exists a path
![]() $\vec p=(e^1,\ldots ,e^N)$
from x to
$\vec p=(e^1,\ldots ,e^N)$
from x to
![]() $x'$
such that
$x'$
such that
![]() $o(e^1)=x$
,
$o(e^1)=x$
,
![]() $t(e^N)=x'$
, and
$t(e^N)=x'$
, and
![]() $t(e^i)=o(e^{i+1})$
for
$t(e^i)=o(e^{i+1})$
for
![]() $0<i<N$
. Then
$0<i<N$
. Then
 $$\begin{align*}f(x')-f(x)=\sum_{i=1}^N (f(t(e^i))-f(o(e^i))). \end{align*}$$
$$\begin{align*}f(x')-f(x)=\sum_{i=1}^N (f(t(e^i))-f(o(e^i))). \end{align*}$$
Since
![]() $\partial f=0$
, we have
$\partial f=0$
, we have
![]() $f(t(e^i))-f(o(e^i))=0$
for any
$f(t(e^i))-f(o(e^i))=0$
for any
![]() $0<i<N$
; hence, this implies that
$0<i<N$
; hence, this implies that
![]() $f(x')=f(x)$
. This shows that f is constant on the connected components of
$f(x')=f(x)$
. This shows that f is constant on the connected components of
![]() $(X,E)$
. Conversely, if f is constant on the connected components of
$(X,E)$
. Conversely, if f is constant on the connected components of
![]() $(X,E)$
, then we have
$(X,E)$
, then we have
![]() $\partial f=0$
. This shows that
$\partial f=0$
. This shows that
![]() $H^0(X)=\operatorname {\mathrm {Ker}}\partial $
corresponds to the
$H^0(X)=\operatorname {\mathrm {Ker}}\partial $
corresponds to the
![]() $\mathbb {R}$
-linear space of functions on X which are constant on the connected components.
$\mathbb {R}$
-linear space of functions on X which are constant on the connected components.
As an analogy of the line integral of differential forms, we may define an integration of forms along a path in
![]() $(X,E)$
. For any path
$(X,E)$
. For any path
![]() $\vec p=(e^1,\ldots ,e^N)$
in
$\vec p=(e^1,\ldots ,e^N)$
in
![]() $(X,E)$
and form
$(X,E)$
and form
![]() $\omega \in C^1(X)$
, we define the integral of
$\omega \in C^1(X)$
, we define the integral of
![]() $\omega $
along
$\omega $
along
![]() $\vec p$
by
$\vec p$
by

We say that a path
![]() $\vec p$
in
$\vec p$
in
![]() $(X,E)$
is closed if
$(X,E)$
is closed if
![]() $o(\vec p)=t(\vec p)$
.
$o(\vec p)=t(\vec p)$
.
Definition A.3. We say that a form
![]() $\omega \in C^1(X)$
is closed if
$\omega \in C^1(X)$
is closed if
![]() $\int _{\vec p}\omega =0$
for any closed path
$\int _{\vec p}\omega =0$
for any closed path
![]() $\vec p$
in
$\vec p$
in
![]() $(X,E)$
.
$(X,E)$
.
Lemma A.4. A form
![]() $\omega \in C^1(X)$
is exact if and only if it is closed.
$\omega \in C^1(X)$
is exact if and only if it is closed.
Proof. Suppose
![]() $\omega =\partial f$
for some
$\omega =\partial f$
for some
![]() $f\in C(X)$
. Then for any closed path
$f\in C(X)$
. Then for any closed path
![]() $\vec p=(e^1,\ldots ,e^N)$
, we have
$\vec p=(e^1,\ldots ,e^N)$
, we have
 $$\begin{align*}\int_{\vec p}\omega=\sum_{i=1}^N\omega(e^i)=\sum_{i=1}^N (f(t(e^i))-f(o(e^i)))=f(t(\vec p))-f(o(\vec p))=0. \end{align*}$$
$$\begin{align*}\int_{\vec p}\omega=\sum_{i=1}^N\omega(e^i)=\sum_{i=1}^N (f(t(e^i))-f(o(e^i)))=f(t(\vec p))-f(o(\vec p))=0. \end{align*}$$
This shows that
![]() $\omega $
is closed. Conversely, suppose
$\omega $
is closed. Conversely, suppose
![]() $\omega $
is closed. Fix
$\omega $
is closed. Fix
![]() $x_0\in X$
for each connected component of X. For any
$x_0\in X$
for each connected component of X. For any
![]() $x\in X$
, let
$x\in X$
, let
![]() $\vec p_{x_0,x}$
be the path from
$\vec p_{x_0,x}$
be the path from
![]() $x_0$
to x, where
$x_0$
to x, where
![]() $x_0$
is the fixed point in the connected component containing x. Let
$x_0$
is the fixed point in the connected component containing x. Let

Since
![]() $\omega $
is closed, the integral is independent of the choice of the path
$\omega $
is closed, the integral is independent of the choice of the path
![]() $\vec p_{x_0,x}$
. By construction, for any
$\vec p_{x_0,x}$
. By construction, for any
![]() $e\in E$
, we have
$e\in E$
, we have
 $$\begin{align*}\partial f(e)=f(t(e))-f(o(e))= \int_{\vec p_{x_0,t(e)}}\omega-\int_{\vec p_{x_0,o(e)}}\omega= \int_{\vec p_{o(e),t(e)}}\omega=\omega(e), \end{align*}$$
$$\begin{align*}\partial f(e)=f(t(e))-f(o(e))= \int_{\vec p_{x_0,t(e)}}\omega-\int_{\vec p_{x_0,o(e)}}\omega= \int_{\vec p_{o(e),t(e)}}\omega=\omega(e), \end{align*}$$
where
![]() $\vec p_{o(e),t(e)}=(e)$
is the path of length
$\vec p_{o(e),t(e)}=(e)$
is the path of length
![]() $1$
from
$1$
from
![]() $o(e)$
to
$o(e)$
to
![]() $t(e)$
. This shows that
$t(e)$
. This shows that
![]() $\omega =\partial f\in C^1(X)$
; hence,
$\omega =\partial f\in C^1(X)$
; hence,
![]() $\omega $
is exact as desired.
$\omega $
is exact as desired.
Let
![]() $Z^1(X)\subset C^1(X)$
be the space of closed forms on X. By Lemma A.4, we have
$Z^1(X)\subset C^1(X)$
be the space of closed forms on X. By Lemma A.4, we have
![]() $Z^1(X)=\partial C(X)$
; hence,
$Z^1(X)=\partial C(X)$
; hence,
![]() $H^1(X)=C^1(X)/Z^1(X)$
. For any closed path
$H^1(X)=C^1(X)/Z^1(X)$
. For any closed path
![]() $\vec p$
in
$\vec p$
in
![]() $(X,E)$
, the integration along
$(X,E)$
, the integration along
![]() $\vec p$
gives a well-defined homomorphism
$\vec p$
gives a well-defined homomorphism
In fact, the first homology
![]() $H_1(X,\mathbb {Z})$
consists of finite formal sums of closed paths of
$H_1(X,\mathbb {Z})$
consists of finite formal sums of closed paths of
![]() $(X,E)$
, and we have
$(X,E)$
, and we have
where
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(H_1(X,\mathbb {Z}),\mathbb {R})$
denotes the space of group homomorphisms from
${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(H_1(X,\mathbb {Z}),\mathbb {R})$
denotes the space of group homomorphisms from
![]() $H_1(X,\mathbb {Z})$
to
$H_1(X,\mathbb {Z})$
to
![]() $\mathbb {R}$
. In the equality (56), a class of a form
$\mathbb {R}$
. In the equality (56), a class of a form
![]() $\omega \in H^1(X)$
maps to a a homomorphism
$\omega \in H^1(X)$
maps to a a homomorphism
![]() $H_1(X,\mathbb {Z})\rightarrow \mathbb {R}$
mapping a closed path
$H_1(X,\mathbb {Z})\rightarrow \mathbb {R}$
mapping a closed path
![]() $\vec p$
to
$\vec p$
to
![]() $\int _{\vec p}\omega $
. To further make this statement precise, we next review the construction of the homology groups
$\int _{\vec p}\omega $
. To further make this statement precise, we next review the construction of the homology groups
![]() $H_0(X,\mathbb {Z})$
and
$H_0(X,\mathbb {Z})$
and
![]() $H_1(X,\mathbb {Z})$
of the graph
$H_1(X,\mathbb {Z})$
of the graph
![]() $(X,E)$
.
$(X,E)$
.
Following [Reference Sunada17, §4.1], let

where
![]() $\sim $
is the equivalence relation given by
$\sim $
is the equivalence relation given by
![]() $e \sim -\bar e$
for any
$e \sim -\bar e$
for any
![]() $e\in E$
. In other words,
$e\in E$
. In other words,
![]() $C_0(X,\mathbb {Z})$
and
$C_0(X,\mathbb {Z})$
and
![]() $C_1(X,\mathbb {Z})$
are free abelian groups generated by the set of vertices and edges of
$C_1(X,\mathbb {Z})$
are free abelian groups generated by the set of vertices and edges of
![]() $(X,E)$
(i.e., certain sets of finite formal sums over the set of vertices and edges of
$(X,E)$
(i.e., certain sets of finite formal sums over the set of vertices and edges of
![]() $(X,E)$
). We call any element of
$(X,E)$
). We call any element of
![]() $C_0(X,\mathbb {Z})$
or
$C_0(X,\mathbb {Z})$
or
![]() $C_1(X,\mathbb {Z})$
a chain. We define the boundary morphism
$C_1(X,\mathbb {Z})$
a chain. We define the boundary morphism
to be the group homomorphism given by ![]() . In other words,
. In other words,
for any
![]() $\sum _{e\in E}b_e e\in C_1(X,\mathbb {Z})$
.
$\sum _{e\in E}b_e e\in C_1(X,\mathbb {Z})$
.
Definition A.5. We define the homology of
![]() $(X,E)$
by
$(X,E)$
by
and
![]() $H_m(X,\mathbb {Z})=\{0\}$
for
$H_m(X,\mathbb {Z})=\{0\}$
for
![]() $m\neq 0,1$
.
$m\neq 0,1$
.
Note that lower numberings (as in
![]() $H_0$
,
$H_0$
,
![]() $H_1,\ldots $
) are used for objects pertaining to homology, in contrast with upper numberings (as in
$H_1,\ldots $
) are used for objects pertaining to homology, in contrast with upper numberings (as in
![]() $H^0$
,
$H^0$
,
![]() $H^1,\ldots $
) for objects pertaining to cohomology. The homology
$H^1,\ldots $
) for objects pertaining to cohomology. The homology
![]() $H_0(X,\mathbb {Z})$
is related to the connected components of
$H_0(X,\mathbb {Z})$
is related to the connected components of
![]() $(X,E)$
as follows.
$(X,E)$
as follows.
Lemma A.6. If we denote by
![]() $\pi _0(X)$
the set of connected components of the graph
$\pi _0(X)$
the set of connected components of the graph
![]() $(X,E)$
, then we have
$(X,E)$
, then we have
![]() $H_0(X,\mathbb {Z})\cong \bigoplus _{C\in \pi _0(X)}\mathbb {Z} C$
.
$H_0(X,\mathbb {Z})\cong \bigoplus _{C\in \pi _0(X)}\mathbb {Z} C$
.
Proof. Our assertion follows from the fact that the classes in
![]() $H_0(X,\mathbb {Z})$
corresponding to vertices
$H_0(X,\mathbb {Z})$
corresponding to vertices
![]() $x,x'\in X$
coincide if and only if there exists a path
$x,x'\in X$
coincide if and only if there exists a path
![]() $\vec p=(e^1,\ldots ,e^N)$
from x to
$\vec p=(e^1,\ldots ,e^N)$
from x to
![]() $x'$
– in other words, if and only if x and
$x'$
– in other words, if and only if x and
![]() $x'$
are in the same connected component of
$x'$
are in the same connected component of
![]() $(X,E)$
.
$(X,E)$
.
The first homology
![]() $H_1(X,\mathbb {Z})$
is related to closed paths as follows. A path
$H_1(X,\mathbb {Z})$
is related to closed paths as follows. A path
![]() $\vec p=(e^1,\ldots ,e^N)$
in
$\vec p=(e^1,\ldots ,e^N)$
in
![]() $(X,E)$
defines a chain
$(X,E)$
defines a chain ![]() in
in
![]() $C_1(X,\mathbb {Z})$
. Then
$C_1(X,\mathbb {Z})$
. Then
 $$\begin{align*}d(\alpha)=\sum_{i=1}^N (t(e^i)-o(e^i))=t(\vec p)-o(\vec p)\in C_0(X,\mathbb{Z}), \end{align*}$$
$$\begin{align*}d(\alpha)=\sum_{i=1}^N (t(e^i)-o(e^i))=t(\vec p)-o(\vec p)\in C_0(X,\mathbb{Z}), \end{align*}$$
where
![]() $t(\vec p)=t(e^N)$
and
$t(\vec p)=t(e^N)$
and
![]() $o(\vec p)=o(e^1)$
. In particular, if the path
$o(\vec p)=o(e^1)$
. In particular, if the path
![]() $\vec p$
is closed, then we have
$\vec p$
is closed, then we have
![]() $d(\alpha )=0$
. This shows that any closed path
$d(\alpha )=0$
. This shows that any closed path
![]() $\vec p$
in
$\vec p$
in
![]() $(X,E)$
defines a homology class
$(X,E)$
defines a homology class
![]() $\alpha \in H_1(X,\mathbb {Z})=\operatorname {\mathrm {Ker}} d$
. Moreover, we have the following.
$\alpha \in H_1(X,\mathbb {Z})=\operatorname {\mathrm {Ker}} d$
. Moreover, we have the following.
Lemma A.7. Any chain
![]() $\alpha \in H_1(X,\mathbb {Z})$
may be expressed as a sum of closed paths.
$\alpha \in H_1(X,\mathbb {Z})$
may be expressed as a sum of closed paths.
Proof. This fact is proved in [Reference Sunada17, §4.2].
In the example of Figure 7, let
![]() $X=\{x_1,\ldots ,x_7\}$
and
$X=\{x_1,\ldots ,x_7\}$
and
![]() $E=\{e_1,\ldots ,e_7\}\cup \{\bar e_1,\ldots , \bar e_7\}$
. Then the pair
$E=\{e_1,\ldots ,e_7\}\cup \{\bar e_1,\ldots , \bar e_7\}$
. Then the pair
![]() $(X,E)$
for a symmetric directed graph. Then
$(X,E)$
for a symmetric directed graph. Then
![]() $\vec p_1=(e_1,e_2,e_3)$
and
$\vec p_1=(e_1,e_2,e_3)$
and
![]() $\vec p_2=(e_4,e_5,e_6)$
are closed paths of
$\vec p_2=(e_4,e_5,e_6)$
are closed paths of
![]() $(X,E)$
. The vertices
$(X,E)$
. The vertices
![]() $x_1,x_2,x_3$
are in one connected component, and
$x_1,x_2,x_3$
are in one connected component, and
![]() $x_4,x_5,x_6,x_7$
are in a different connected component. Hence,
$x_4,x_5,x_6,x_7$
are in a different connected component. Hence,
![]() $\pi _0(X)=\{ C(x_1), C(x_4)\}$
, where
$\pi _0(X)=\{ C(x_1), C(x_4)\}$
, where
![]() $C(x)$
denotes the connected component of X containing
$C(x)$
denotes the connected component of X containing
![]() $x\in X$
. This shows that
$x\in X$
. This shows that
If we let ![]() , then
, then
Hence,
![]() $\alpha _1\in H_1(X)$
. Similarly,
$\alpha _1\in H_1(X)$
. Similarly, ![]() . In fact, we have
. In fact, we have

Figure 7 Example of calculation of homology.
The relation between homology and cohomology is given as follows.
Proposition A.8. Let
![]() $(X,E)$
be a symmetric directed graph. We have
$(X,E)$
be a symmetric directed graph. We have
Proof. Note that a homomorphism
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_0(X,\mathbb {Z}),\mathbb {R})$
is determined by the image of
${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_0(X,\mathbb {Z}),\mathbb {R})$
is determined by the image of
![]() $x\in X$
, and we have
$x\in X$
, and we have
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_0(X,\mathbb {Z}),\mathbb {R})=\operatorname {\mathrm {Map}}(X,\mathbb {R})$
. Similarly, we have
${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_0(X,\mathbb {Z}),\mathbb {R})=\operatorname {\mathrm {Map}}(X,\mathbb {R})$
. Similarly, we have
![]() ${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_1(X,\mathbb {Z}),\mathbb {R})=\operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(E,\mathbb {R})$
. Thus, by (14), we have
${\operatorname {\mathrm {Hom}}}_{\mathbb {Z}}(C_1(X,\mathbb {Z}),\mathbb {R})=\operatorname {\mathrm {Map}}^{\operatorname {\mathrm {alt}}}(E,\mathbb {R})$
. Thus, by (14), we have
The differential
![]() $\partial \colon C^0(X)\rightarrow C^1(X)$
of (53) is the homomorphism induced via pull-back of the differential
$\partial \colon C^0(X)\rightarrow C^1(X)$
of (53) is the homomorphism induced via pull-back of the differential
![]() $d\colon C_1(X,\mathbb {Z})\rightarrow C_0(X,\mathbb {Z})$
of (57). Hence, by duality, we have
$d\colon C_1(X,\mathbb {Z})\rightarrow C_0(X,\mathbb {Z})$
of (57). Hence, by duality, we have
 $$ \begin{align*} H^0(X)&=\operatorname{\mathrm{Ker}}\bigl(\partial\colon {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_0(X,\mathbb{Z}),\mathbb{R})\rightarrow {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R})\bigr)\\ &= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}\bigl(C_0(X,\mathbb{Z})/d C_1(X,\mathbb{Z}),\mathbb{R}\bigr)= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(H_0(X,\mathbb{Z}),\mathbb{R}),\\ H^1(X)&= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R})/\partial {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R}))\\ &= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(\operatorname{\mathrm{Ker}} d,\mathbb{R})= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(H_1(X,\mathbb{Z}),\mathbb{R}). \end{align*} $$
$$ \begin{align*} H^0(X)&=\operatorname{\mathrm{Ker}}\bigl(\partial\colon {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_0(X,\mathbb{Z}),\mathbb{R})\rightarrow {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R})\bigr)\\ &= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}\bigl(C_0(X,\mathbb{Z})/d C_1(X,\mathbb{Z}),\mathbb{R}\bigr)= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(H_0(X,\mathbb{Z}),\mathbb{R}),\\ H^1(X)&= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R})/\partial {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(C_1(X,\mathbb{Z}),\mathbb{R}))\\ &= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(\operatorname{\mathrm{Ker}} d,\mathbb{R})= {\operatorname{\mathrm{Hom}}}_{\mathbb{Z}}(H_1(X,\mathbb{Z}),\mathbb{R}). \end{align*} $$
This proves our assertion.
By Proposition A.8, we see that Lemma A.2 is in fact a consequence of Lemma A.6. In particular,
![]() $\dim _{\mathbb {R}} H^0(X)$
corresponds to the number of connected components of
$\dim _{\mathbb {R}} H^0(X)$
corresponds to the number of connected components of
![]() $(X,E)$
. Moreover, by Proposition A.8 and Lemma A.7, we see that a class in
$(X,E)$
. Moreover, by Proposition A.8 and Lemma A.7, we see that a class in
![]() $H^1(X)$
corresponds to the space of functions on closed paths of
$H^1(X)$
corresponds to the space of functions on closed paths of
![]() $(X,E)$
given by integration as in (55).
$(X,E)$
given by integration as in (55).
B Examples
B.1 The exclusion process
In this subsection, we focus on the exclusion process and give explicit descriptions of objects newly introduced in this article, such as the uniform functions, uniform forms and uniform cohomology.
Consider
![]() $S=\{0,1\}$
with the base state
$S=\{0,1\}$
with the base state
![]() $*=0$
and
$*=0$
and
![]() $\phi (s,s')=(s',s)$
. We consider any locale
$\phi (s,s')=(s',s)$
. We consider any locale
![]() $X=(X,E)$
. For this setting,
$X=(X,E)$
. For this setting,
![]() ${\operatorname {\mathrm {Consv}}}^\phi (S)=\{\xi : \{0,1\} \to \mathbb {R}; \xi (0)=0\}$
and so
${\operatorname {\mathrm {Consv}}}^\phi (S)=\{\xi : \{0,1\} \to \mathbb {R}; \xi (0)=0\}$
and so
![]() $c_{\phi }=1$
. The class of functions with exact support
$c_{\phi }=1$
. The class of functions with exact support
![]() $\Lambda $
, which is defined in 3.1 and denoted by
$\Lambda $
, which is defined in 3.1 and denoted by
![]() $C_{\Lambda }(S^X)$
, is explicitly given as
$C_{\Lambda }(S^X)$
, is explicitly given as
Namely, it is a one-dimensional space. Then, Proposition 3.3 implies that any function
![]() $f \in C(S^X_*)$
is uniquely given as
$f \in C(S^X_*)$
is uniquely given as
for some
![]() $a_{\Lambda } \in \mathbb {R}$
for each
$a_{\Lambda } \in \mathbb {R}$
for each
![]() $\Lambda $
. In particular, the space of uniform functions for this case is given as the set of functions of the form
$\Lambda $
. In particular, the space of uniform functions for this case is given as the set of functions of the form
 $$\begin{align*}f = \sum_{\substack{\Lambda\subset X\\\operatorname{diam}(\Lambda)\leq R}} a_{\Lambda} \Pi_{x \in \Lambda}\eta_x \end{align*}$$
$$\begin{align*}f = \sum_{\substack{\Lambda\subset X\\\operatorname{diam}(\Lambda)\leq R}} a_{\Lambda} \Pi_{x \in \Lambda}\eta_x \end{align*}$$
for some
![]() $R>0$
. In particular,
$R>0$
. In particular,
![]() $\sum _{x \in X} \eta _x$
is a uniform function. Also, if
$\sum _{x \in X} \eta _x$
is a uniform function. Also, if
![]() $X=\mathbb {Z}^d$
, then
$X=\mathbb {Z}^d$
, then
![]() $\sum _{x \in \mathbb {Z}^d}x_j \eta _x$
is a uniform function for
$\sum _{x \in \mathbb {Z}^d}x_j \eta _x$
is a uniform function for
![]() $j=1,2,\dots ,d$
.
$j=1,2,\dots ,d$
.
The zeroth cohomology
![]() $H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is the space of functions
$H^0_{\operatorname {\mathrm {unif}}}(S^X)$
is the space of functions
![]() $f \in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
$f \in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
![]() $\nabla _e f=0$
for any
$\nabla _e f=0$
for any
![]() $e \in E$
. Theorem 3.7 claims that
$e \in E$
. Theorem 3.7 claims that
![]() $H^0_{\operatorname {\mathrm {unif}}}(S^X)$
coincides with the one-dimensional space
$H^0_{\operatorname {\mathrm {unif}}}(S^X)$
coincides with the one-dimensional space
![]() $\{a \sum _{x \in X} \eta _x \ | \ a \in \mathbb {R}\}$
.
$\{a \sum _{x \in X} \eta _x \ | \ a \in \mathbb {R}\}$
.
Next, we give some examples of the pairing
![]() $h_f$
in Proposition 3.18. First note that
$h_f$
in Proposition 3.18. First note that
![]() $\mathcal {M}= \{0,1,2,\dots \}$
for this setting. Let
$\mathcal {M}= \{0,1,2,\dots \}$
for this setting. Let
![]() $f=(\sum _{x \in X} \eta _x)^2=\sum _{x,y \in X}\eta _x \eta _y \in C(S^X_*)$
. Then
$f=(\sum _{x \in X} \eta _x)^2=\sum _{x,y \in X}\eta _x \eta _y \in C(S^X_*)$
. Then
![]() $\partial f =0 \in C^1_R(S^X)$
for any
$\partial f =0 \in C^1_R(S^X)$
for any
![]() $R>0$
. For any
$R>0$
. For any
![]() $\Lambda , \Lambda '$
such that
$\Lambda , \Lambda '$
such that
![]() $d_X(\Lambda ,\Lambda ')>0$
, we have
$d_X(\Lambda ,\Lambda ')>0$
, we have
 $$ \begin{align*} \iota^{\Lambda\cup\Lambda'} f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) &=\Bigl(\sum_{x \in \Lambda\cup\Lambda'}\eta_x\Bigr)^2 -\Bigl(\sum_{x \in \Lambda}\eta_x\Bigr)^2 - \Bigl(\sum_{x \in \Lambda'}\eta_x\Bigr)^2 = 2 \sum_{x \in \Lambda}\eta_x \sum_{y \in \Lambda'}\eta_y \\ &= 2 \xi_{\Lambda}(\eta)\xi_{\Lambda'}(\eta). \end{align*} $$
$$ \begin{align*} \iota^{\Lambda\cup\Lambda'} f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) &=\Bigl(\sum_{x \in \Lambda\cup\Lambda'}\eta_x\Bigr)^2 -\Bigl(\sum_{x \in \Lambda}\eta_x\Bigr)^2 - \Bigl(\sum_{x \in \Lambda'}\eta_x\Bigr)^2 = 2 \sum_{x \in \Lambda}\eta_x \sum_{y \in \Lambda'}\eta_y \\ &= 2 \xi_{\Lambda}(\eta)\xi_{\Lambda'}(\eta). \end{align*} $$
Namely,
![]() $h_f(\alpha , \beta )=2\alpha \beta $
for any
$h_f(\alpha , \beta )=2\alpha \beta $
for any
![]() $\alpha ,\beta \in \mathcal {M}$
. Note that
$\alpha ,\beta \in \mathcal {M}$
. Note that
![]() $h_f \neq 0$
in this case.
$h_f \neq 0$
in this case.
B.2 Counterexample for the case when
 $X=(\mathbb {Z},\mathbb {E})$
and
$X=(\mathbb {Z},\mathbb {E})$
and
 $c_\phi =2$
.
$c_\phi =2$
.
In Theorem 5.2, we assumed that the interaction is simple in the weakly transferable case. In this subsection, we give an example of a weakly transferable locale X and an interaction
![]() $\phi $
that is irreducibly quantified and satisfies
$\phi $
that is irreducibly quantified and satisfies
![]() $c_\phi>1$
, but the uniform cohomology
$c_\phi>1$
, but the uniform cohomology
![]() $H^1_{\operatorname {\mathrm {unif}}}(S^X)$
does not satisfy the conclusion of Theorem 5.2. More precisely, we prove the following.
$H^1_{\operatorname {\mathrm {unif}}}(S^X)$
does not satisfy the conclusion of Theorem 5.2. More precisely, we prove the following.
Proposition B.1. Suppose
![]() $\kappa =2$
so that
$\kappa =2$
so that
![]() $S=\{0,1,2\}$
, and let
$S=\{0,1,2\}$
, and let
![]() $X=(\mathbb {Z},\mathbb {E})$
, which is weakly transferable. If we consider the configuration with transition structure
$X=(\mathbb {Z},\mathbb {E})$
, which is weakly transferable. If we consider the configuration with transition structure
![]() $S^X$
for the interaction
$S^X$
for the interaction
![]() $\phi \colon S\times S\rightarrow S\times S$
given in Example 1.3 (2), then we have
$\phi \colon S\times S\rightarrow S\times S$
given in Example 1.3 (2), then we have
![]() $H^1_{\operatorname {\mathrm {unif}}}(S^X)\neq 0$
.
$H^1_{\operatorname {\mathrm {unif}}}(S^X)\neq 0$
.
Proof. We will explicitly construct a form
![]() $\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
which is not integrable by a function
$\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
which is not integrable by a function
![]() $F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. For any
$F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
. For any
![]() $W\subset S^X_*$
, let
$W\subset S^X_*$
, let
![]() $\boldsymbol {1}_W$
be the characteristic function of W on
$\boldsymbol {1}_W$
be the characteristic function of W on
![]() $S^X_*$
. Let
$S^X_*$
. Let
![]() $\omega =(\omega _e)_{e\in E}\in \operatorname {\mathrm {Map}}(\Phi ,\mathbb {R})$
such that
$\omega =(\omega _e)_{e\in E}\in \operatorname {\mathrm {Map}}(\Phi ,\mathbb {R})$
such that
if
![]() $t(e)\geq o(e)$
and
$t(e)\geq o(e)$
and ![]() otherwise. We let
otherwise. We let
![]() $f\in C(S^X_*)$
be the function
$f\in C(S^X_*)$
be the function
Then for any
![]() $\eta \in S^X_*$
and
$\eta \in S^X_*$
and
![]() $e\in \mathbb {E}$
, we have
$e\in \mathbb {E}$
, we have
If we suppose
![]() $t(e)\geq o(e)$
, then the sum of
$t(e)\geq o(e)$
, then the sum of
![]() $\nabla _{\!e} f(\eta )$
cancels outside
$\nabla _{\!e} f(\eta )$
cancels outside
![]() $e=(x,y)$
, and we have
$e=(x,y)$
, and we have
Furthermore, we have
![]() $\nabla _{\bar e}f(\eta )=\omega _e=\omega _{\bar e}$
; hence,
$\nabla _{\bar e}f(\eta )=\omega _e=\omega _{\bar e}$
; hence,
![]() $\partial f=\omega $
, which by Lemma 2.28 shows that
$\partial f=\omega $
, which by Lemma 2.28 shows that
![]() $\omega \in Z^1(S^X_*)$
. By definition, we have
$\omega \in Z^1(S^X_*)$
. By definition, we have
![]() $\omega \in C^1_0(S^X)\subset C^1_{\operatorname {\mathrm {unif}}}(S^X)$
; hence,
$\omega \in C^1_0(S^X)\subset C^1_{\operatorname {\mathrm {unif}}}(S^X)$
; hence,
![]() $\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
.
$\omega \in Z^1_{\operatorname {\mathrm {unif}}}(S^X)$
.
We prove our assertion by contradiction. Suppose there exists
![]() $F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
$F\in C^0_{\operatorname {\mathrm {unif}}}(S^X)$
such that
![]() $\partial F=\omega $
. By taking
$\partial F=\omega $
. By taking
![]() $F-F(*)$
if necessary, we may assume that
$F-F(*)$
if necessary, we may assume that
![]() $F(*)=0$
. For any
$F(*)=0$
. For any
![]() $\eta ,\eta '\in S^X_*$
, if
$\eta ,\eta '\in S^X_*$
, if
![]() ${\boldsymbol {\xi }}_{\!X}(\eta )={\boldsymbol {\xi }}_{\!X}(\eta ')$
, then since the interaction is irreducibly quantified by Proposition 2.19, there exists a path
${\boldsymbol {\xi }}_{\!X}(\eta )={\boldsymbol {\xi }}_{\!X}(\eta ')$
, then since the interaction is irreducibly quantified by Proposition 2.19, there exists a path
![]() $\vec \gamma $
from
$\vec \gamma $
from
![]() $\eta $
to
$\eta $
to
![]() $\eta '$
. Since
$\eta '$
. Since
![]() $\partial (f-F)=0$
, by Lemma 2.21, we have
$\partial (f-F)=0$
, by Lemma 2.21, we have
![]() $(f-F)(\eta )=(f-F)(\eta ')$
. This shows that there exists
$(f-F)(\eta )=(f-F)(\eta ')$
. This shows that there exists
![]() $h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
$h\colon \mathcal {M}\rightarrow \mathbb {R}$
such that
![]() $ f(\eta )-F(\eta )=h\circ {\boldsymbol {\xi }}_{\!X}(\eta ) $
for any
$ f(\eta )-F(\eta )=h\circ {\boldsymbol {\xi }}_{\!X}(\eta ) $
for any
![]() $\eta \in S^X_*$
. By Remark 3.6, we have
$\eta \in S^X_*$
. By Remark 3.6, we have
![]() $ \iota ^{\Lambda \cup \Lambda '}F=\iota ^{\Lambda } F+\iota ^{\Lambda '}F $
for any pair
$ \iota ^{\Lambda \cup \Lambda '}F=\iota ^{\Lambda } F+\iota ^{\Lambda '}F $
for any pair
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. Hence,
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
. Hence,
 $$ \begin{align*} \iota^{\Lambda\cup\Lambda'}f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) &= \iota^{\Lambda\cup\Lambda'}(f-F)(\eta)-\iota^{\Lambda} (f-F)(\eta)-\iota^{\Lambda'}(f-F)(\eta)\\ &= h\circ{\boldsymbol{\xi}}_{\Lambda\cup\Lambda'}(\eta)-h\circ{\boldsymbol{\xi}}_\Lambda(\eta)-h\circ{\boldsymbol{\xi}}_{\Lambda'}(\eta)\\ &= h\circ({\boldsymbol{\xi}}_\Lambda(\eta)+{\boldsymbol{\xi}}_{\Lambda'}(\eta))-h\circ{\boldsymbol{\xi}}_\Lambda(\eta)-h\circ{\boldsymbol{\xi}}_{\Lambda'}(\eta). \end{align*} $$
$$ \begin{align*} \iota^{\Lambda\cup\Lambda'}f(\eta)-\iota^{\Lambda} f(\eta)-\iota^{\Lambda'}f(\eta) &= \iota^{\Lambda\cup\Lambda'}(f-F)(\eta)-\iota^{\Lambda} (f-F)(\eta)-\iota^{\Lambda'}(f-F)(\eta)\\ &= h\circ{\boldsymbol{\xi}}_{\Lambda\cup\Lambda'}(\eta)-h\circ{\boldsymbol{\xi}}_\Lambda(\eta)-h\circ{\boldsymbol{\xi}}_{\Lambda'}(\eta)\\ &= h\circ({\boldsymbol{\xi}}_\Lambda(\eta)+{\boldsymbol{\xi}}_{\Lambda'}(\eta))-h\circ{\boldsymbol{\xi}}_\Lambda(\eta)-h\circ{\boldsymbol{\xi}}_{\Lambda'}(\eta). \end{align*} $$
In particular, for
![]() $\eta ,\eta '\in S^X_*$
, if
$\eta ,\eta '\in S^X_*$
, if
![]() ${\boldsymbol {\xi }}_\Lambda (\eta )={\boldsymbol {\xi }}_{\Lambda '}(\eta ')$
and
${\boldsymbol {\xi }}_\Lambda (\eta )={\boldsymbol {\xi }}_{\Lambda '}(\eta ')$
and
![]() ${\boldsymbol {\xi }}_\Lambda (\eta ')={\boldsymbol {\xi }}_{\Lambda '}(\eta )$
, then we have
${\boldsymbol {\xi }}_\Lambda (\eta ')={\boldsymbol {\xi }}_{\Lambda '}(\eta )$
, then we have
In what follows, we prove that this it not the case. For any
![]() $(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
$(\Lambda ,\Lambda ')\in {\mathscr {A}}_R$
, we have
 $$ \begin{align*} \iota^{\Lambda\cup\Lambda'}f-\iota^{\Lambda} f-\iota^{\Lambda'}f &=\sum_{\substack{y>x\\x,y\in\Lambda\cup\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}} -\sum_{\substack{y>x\\x,y\in\Lambda}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}-\sum_{\substack{y>x\\x,y\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}\\ &=\sum_{\substack{y>x\\ y\in\Lambda,x\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}} +\sum_{\substack{y>x\\ x\in\Lambda,y\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}. \end{align*} $$
$$ \begin{align*} \iota^{\Lambda\cup\Lambda'}f-\iota^{\Lambda} f-\iota^{\Lambda'}f &=\sum_{\substack{y>x\\x,y\in\Lambda\cup\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}} -\sum_{\substack{y>x\\x,y\in\Lambda}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}-\sum_{\substack{y>x\\x,y\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}\\ &=\sum_{\substack{y>x\\ y\in\Lambda,x\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}} +\sum_{\substack{y>x\\ x\in\Lambda,y\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}. \end{align*} $$
Since
![]() $\Lambda $
and
$\Lambda $
and
![]() $\Lambda '$
are connected, replacing
$\Lambda '$
are connected, replacing
![]() $\Lambda $
by
$\Lambda $
by
![]() $\Lambda '$
if necessary, we may assume that
$\Lambda '$
if necessary, we may assume that
![]() $y>x$
for any
$y>x$
for any
![]() $y\in \Lambda $
and
$y\in \Lambda $
and
![]() $x\in \Lambda '$
. Then we have
$x\in \Lambda '$
. Then we have
 $$\begin{align*}\iota^{\Lambda\cup\Lambda'}f-\iota^{\Lambda} f-\iota^{\Lambda'}f =\sum_{\substack{y>x\\y\in\Lambda,x\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}=\xi_{\Lambda'}^{(1)}\xi_{\Lambda}^{(2)}, \end{align*}$$
$$\begin{align*}\iota^{\Lambda\cup\Lambda'}f-\iota^{\Lambda} f-\iota^{\Lambda'}f =\sum_{\substack{y>x\\y\in\Lambda,x\in\Lambda'}}\boldsymbol{1}_{\{\eta_x=1,\eta_y=2\}}=\xi_{\Lambda'}^{(1)}\xi_{\Lambda}^{(2)}, \end{align*}$$
where
![]() $\xi ^{(1)}$
and
$\xi ^{(1)}$
and
![]() $\xi ^{(2)}$
are the conserved quantities defined in Example 1.3 (2). Fix
$\xi ^{(2)}$
are the conserved quantities defined in Example 1.3 (2). Fix
![]() $y\in \Lambda $
and
$y\in \Lambda $
and
![]() $y'\in \Lambda '$
. We let
$y'\in \Lambda '$
. We let
![]() $\eta =(\eta _x)\in S^X_*$
be an element such that
$\eta =(\eta _x)\in S^X_*$
be an element such that
![]() $\eta _{y'}=1$
,
$\eta _{y'}=1$
,
![]() $\eta _y=2$
and is at base state outside y and
$\eta _y=2$
and is at base state outside y and
![]() $y'$
, and we let
$y'$
, and we let
![]() $\eta '=(\eta ^{\prime }_x)\in S^X_*$
be an element such that
$\eta '=(\eta ^{\prime }_x)\in S^X_*$
be an element such that
![]() $\eta ^{\prime }_{y'}=2$
,
$\eta ^{\prime }_{y'}=2$
,
![]() $\eta ^{\prime }_y=1$
and is at base state outside y and
$\eta ^{\prime }_y=1$
and is at base state outside y and
![]() $y'$
. Then we have
$y'$
. Then we have
![]() $\xi _{\Lambda '}^{(1)}(\eta )\xi _{\Lambda '}^{(2)}(\eta )=1$
, but
$\xi _{\Lambda '}^{(1)}(\eta )\xi _{\Lambda '}^{(2)}(\eta )=1$
, but
![]() $\xi _{\Lambda '}^{(1)}(\eta ')\xi _{\Lambda '}^{(2)}(\eta ')=0$
; hence, we have
$\xi _{\Lambda '}^{(1)}(\eta ')\xi _{\Lambda '}^{(2)}(\eta ')=0$
; hence, we have
which gives a contradiction, as desired.
Acknowledgements
The authors would like to sincerely thank Megumi Harada and Hiroyuki Ochiai for carefully reading a preliminary version of this article and pointing out important improvements. The authors would also like to thank Kei Hagihara and Shuji Yamamoto for detailed discussions, especially concerning the definition of irreducibly quantified interactions. We are grateful to David Croydon for pointing out that Cayley graphs also fit into our formalism. The authors also thank Takeshi Katsura, Asuka Takatsu, Ryokichi Tanaka and Kazuki Yamada for comments and discussion. The first and third authors would like to thank the Department of Mathematics at Columbia University, where part of this research was conducted. The authors are very grateful to the referee for carefully reading the article and giving helpful comments which helped to improve the article.
Author contributions
The topic of the article arose from a discussion between Sasada and Kametani. Bannai and Sasada wrote the first draft. All authors contributed to the revision of the manuscript and approved the final version.
Competing interest
The authors have no competing interest to declare.
Funding statement
This work was supported in part by JST CREST Grant Number JPMJCR1913, KAKENHI 18H05233, and the UTokyo Global Activity Support Program for Young Researchers.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.