1 Introduction
Spaces of Bridgeland stability on a triangulated category
![]() $\mathcal {D}$
have been introduced in [Reference BridgelandBri07]. By definition, these spaces
$\mathcal {D}$
have been introduced in [Reference BridgelandBri07]. By definition, these spaces ![]() are non-compact; in fact, they admit a
are non-compact; in fact, they admit a
![]() $\mathbb {C}$
-action that allows to rescale the central charges. The projectivizations
$\mathbb {C}$
-action that allows to rescale the central charges. The projectivizations ![]() are still non-compact, since the ratio of masses of some objects may go to zero. Recently, several partial compactifications have been proposed ([Reference Bapat, Deopurkar and LicataBDL20; Reference BologneseBol20; Reference Kikuta, Koseki and OuchiKKO22; Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22]), whose merits we compare at the end of the introduction. Our goal is to provide a generalized notion of stability conditions that could provide a smooth compactification in the sense of orbifolds of the quotient
are still non-compact, since the ratio of masses of some objects may go to zero. Recently, several partial compactifications have been proposed ([Reference Bapat, Deopurkar and LicataBDL20; Reference BologneseBol20; Reference Kikuta, Koseki and OuchiKKO22; Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22]), whose merits we compare at the end of the introduction. Our goal is to provide a generalized notion of stability conditions that could provide a smooth compactification in the sense of orbifolds of the quotient ![]() . In this paper, we achieve this goal for the
. In this paper, we achieve this goal for the
![]() $CY_3$
-categories
$CY_3$
-categories
![]() $\mathcal {D}^{3}_{Q}$
where Q is a quiver of
$\mathcal {D}^{3}_{Q}$
where Q is a quiver of
![]() $A_n$
-type.
$A_n$
-type.
Our approach is motivated by the isomorphism of Bridgeland-Smith [Reference Bridgeland and SmithBS15] of ![]() with spaces of quadratic differentials with simple zeros and the generalization of this isomorphism to differentials with higher order zeros constructed in our previous paper [Reference Barbieri, Möller, Qiu and SoBMQS22]. Its main result states that these are isomorphic to spaces of stability conditions on quotient categories
with spaces of quadratic differentials with simple zeros and the generalization of this isomorphism to differentials with higher order zeros constructed in our previous paper [Reference Barbieri, Möller, Qiu and SoBMQS22]. Its main result states that these are isomorphic to spaces of stability conditions on quotient categories
![]() $\mathcal {D}^{3}_{Q} /\mathcal {D}^3_{Q_I}$
for some subquivers
$\mathcal {D}^{3}_{Q} /\mathcal {D}^3_{Q_I}$
for some subquivers
![]() $Q_I \subset Q$
. In both contexts, simple and higher order zeroes, part of the isomorphism is given by identifying central charges of (simple and stable) objects with the distance between zeroes with respect to the metric induced by a quadratic differential. A first and naive idea would be to interpret collision of zeroes of a quadratic differential as the vanishing of central charges. To get a smooth compactification, this idea has to be refined.
$Q_I \subset Q$
. In both contexts, simple and higher order zeroes, part of the isomorphism is given by identifying central charges of (simple and stable) objects with the distance between zeroes with respect to the metric induced by a quadratic differential. A first and naive idea would be to interpret collision of zeroes of a quadratic differential as the vanishing of central charges. To get a smooth compactification, this idea has to be refined.
Our approach is also motivated by the smooth compactification [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3] of strata of differentials by multi-scale differentials. From there, we take the idea that if central charges go to zero, we ‘zoom in’ (i.e., we rescale and get another nonzero ‘central charge’ on a subcategory). This ‘central charge’, in turn, might vanish on some simple objects and forces us to rescale again, thus arriving at a filtration of subcategories. From multi-scale differentials, we also borrow the observation that the result of the rescaling process is only well defined up to multiplication by a common scalar factor, resulting in the definition of equivalence below.
Combining these ideas, we can now paraphrase our main notion; see Definition 4.1 for the precise formulation. A non-split multi-scale stability condition
![]() $(\mathcal {A}_\bullet , Z_\bullet )$
on a triangulated category consists of
$(\mathcal {A}_\bullet , Z_\bullet )$
on a triangulated category consists of
-
○ a multi-scale heart
 $\mathcal {A}_\bullet = (\mathcal {A}_i)$
(i.e., a collection
$\mathcal {A}_\bullet = (\mathcal {A}_i)$
(i.e., a collection
 $\mathcal {A}_L \subset \cdots \mathcal {A}_1 \subset \mathcal {A}_0$
of abelian categories), and
$\mathcal {A}_L \subset \cdots \mathcal {A}_1 \subset \mathcal {A}_0$
of abelian categories), and -
○ a multi-scale central charge (i.e., a collection
 $Z_\bullet = (Z_i)_{i=0}^L$
of nonzero
$Z_\bullet = (Z_i)_{i=0}^L$
of nonzero  -linear maps on the Grothendieck groups
-linear maps on the Grothendieck groups
 $Z_i: K(\mathcal {A}_i) \to \mathbb {C}$
, where
$Z_i: K(\mathcal {A}_i) \to \mathbb {C}$
, where
 $Z_i$
factors through
$Z_i$
factors through
 $\operatorname {Ker}(Z_{i-1})$
),
$\operatorname {Ker}(Z_{i-1})$
),
with the following properties. First, the categories
![]() $\mathcal {A}_i$
are hearts of the ‘vanishing’ triangulated subcategories
$\mathcal {A}_i$
are hearts of the ‘vanishing’ triangulated subcategories
![]() $\mathcal {V}^Z_i \subset \mathcal {D}$
generated by objects
$\mathcal {V}^Z_i \subset \mathcal {D}$
generated by objects
![]() $E \in \mathcal {A}_{i-1}$
such that the central charge of the previous filtration step vanishes (i.e.,
$E \in \mathcal {A}_{i-1}$
such that the central charge of the previous filtration step vanishes (i.e.,
![]() $Z_{i-1}(E) = 0$
). Second, the central charges
$Z_{i-1}(E) = 0$
). Second, the central charges
![]() $Z_i$
map simples in
$Z_i$
map simples in
![]() $\mathcal {A}_i \setminus \mathcal {A}_{i+1}$
to the semi-closed upper half-plane
$\mathcal {A}_i \setminus \mathcal {A}_{i+1}$
to the semi-closed upper half-plane
![]() $\overline {\mathbb {H}}$
. (This implies that
$\overline {\mathbb {H}}$
. (This implies that
![]() $\mathcal {V}^Z_{i+1} \cap \mathcal {A}_i$
is a Serre subcategory of
$\mathcal {V}^Z_{i+1} \cap \mathcal {A}_i$
is a Serre subcategory of
![]() $\mathcal {A}_{i}$
.) Third, the induced quotient heart with quotient central charge
$\mathcal {A}_{i}$
.) Third, the induced quotient heart with quotient central charge
![]() $(\overline {\mathcal {A}}_i, \overline {Z}_i)$
is a stability condition in the usual sense of [Reference BridgelandBri07] on the quotient category
$(\overline {\mathcal {A}}_i, \overline {Z}_i)$
is a stability condition in the usual sense of [Reference BridgelandBri07] on the quotient category
![]() $\mathcal {V}^Z_i/\mathcal {V}^Z_{i+1}$
. We say that two non-split multi-scale stability conditions are equivalent if the induced quotients
$\mathcal {V}^Z_i/\mathcal {V}^Z_{i+1}$
. We say that two non-split multi-scale stability conditions are equivalent if the induced quotients
![]() $(\overline {\mathcal {A}}_i, \overline {Z}_i)$
are projectively equivalent for all
$(\overline {\mathcal {A}}_i, \overline {Z}_i)$
are projectively equivalent for all
![]() $i \geq 1$
. We denote by
$i \geq 1$
. We denote by
![]() $\operatorname {MStab}(\mathcal {D})$
the set of equivalence classes of those multi-scale stability conditions and add a circle (e.g.,
$\operatorname {MStab}(\mathcal {D})$
the set of equivalence classes of those multi-scale stability conditions and add a circle (e.g.,
![]() $\operatorname {MStab}^\circ (\mathcal {D})$
) to denote a specific connected component or a set of reachable stability conditions.
$\operatorname {MStab}^\circ (\mathcal {D})$
) to denote a specific connected component or a set of reachable stability conditions.
In this paper, we only consider multi-scale stability conditions that are non-split and thus drop this adjective from now on. In Section 1.2 below, we will explain why this notion needs refinements to provide compactifications for more general categories
![]() $\mathcal {D}$
, even for other
$\mathcal {D}$
, even for other
![]() $CY_3$
quiver categories
$CY_3$
quiver categories
![]() $\mathcal {D}^{3}_{Q}$
.
$\mathcal {D}^{3}_{Q}$
.
We recall that for
![]() $\mathcal {D}^{3}_{Q}$
of type
$\mathcal {D}^{3}_{Q}$
of type
![]() $A_n$
, the group of autoequivalences
$A_n$
, the group of autoequivalences ![]() preserving a connected component of
preserving a connected component of ![]() (modulo those acting trivially) is an extension of
(modulo those acting trivially) is an extension of
![]() $\mathbb {Z}/(n+3)\mathbb {Z}$
by the spherical twist group
$\mathbb {Z}/(n+3)\mathbb {Z}$
by the spherical twist group
![]() $\operatorname {ST}(A_n)$
, which is isomorphic to a braid group; see Section 3.3.
$\operatorname {ST}(A_n)$
, which is isomorphic to a braid group; see Section 3.3.
Theorem 1.1. The quotient ![]() of the space of multi-scale stability conditions has a structure of a complex orbifold. The projectivization of this orbifold
of the space of multi-scale stability conditions has a structure of a complex orbifold. The projectivization of this orbifold ![]() is a compactification of the space of projectivized stability conditions up to autoequivalence
is a compactification of the space of projectivized stability conditions up to autoequivalence ![]()
As a complex orbifold, the space ![]() is simply the moduli space of curves
is simply the moduli space of curves
![]() $\mathcal {M}_{0,n+2}$
. The compactification
$\mathcal {M}_{0,n+2}$
. The compactification ![]() is, however, not equal to the Deligne-Mumford compactification
is, however, not equal to the Deligne-Mumford compactification
![]() ${\overline {\mathcal M}}_{0,n+2}$
. It is rather a blowup of the latter, as we explain in Section 6.
${\overline {\mathcal M}}_{0,n+2}$
. It is rather a blowup of the latter, as we explain in Section 6.
1.1 Techniques
One important technique is the plumbing of a multi-scale stability condition, depending on complex numbers
![]() $\tau _i$
for
$\tau _i$
for
![]() $i=0,\ldots ,L$
, that builds a usual stability condition. If
$i=0,\ldots ,L$
, that builds a usual stability condition. If
![]() $\tau _i \in i\mathbb {R}_{-}$
is purely imaginary for all i, the result is just the top level heart
$\tau _i \in i\mathbb {R}_{-}$
is purely imaginary for all i, the result is just the top level heart
![]() ${\mathcal A}_0$
together with a central charge that is a rescaled linear combination of the
${\mathcal A}_0$
together with a central charge that is a rescaled linear combination of the
![]() $Z_i$
. One should envision that the size of
$Z_i$
. One should envision that the size of
![]() $Z_i$
is
$Z_i$
is
![]() $e^{- \pi i \tau _i}$
, thus very small for
$e^{- \pi i \tau _i}$
, thus very small for
![]() $\tau _i$
close to
$\tau _i$
close to
![]() $-i\infty $
, and this is continuously completed by declaring that
$-i\infty $
, and this is continuously completed by declaring that
![]() $\tau _i = -i\infty $
means no plumbing at all. The process of plumbing becomes interesting for
$\tau _i = -i\infty $
means no plumbing at all. The process of plumbing becomes interesting for
![]() $\tau _i$
not purely imaginary. This involves rotating
$\tau _i$
not purely imaginary. This involves rotating
![]() ${\mathcal A}_i$
. The higher level hearts
${\mathcal A}_i$
. The higher level hearts
![]() ${\mathcal A}_{i-1}$
etc. then have to be modified to still contain the rotated heart while still providing the same quotient heart. This modification of the representative, however, causes that the plumbing action of
${\mathcal A}_{i-1}$
etc. then have to be modified to still contain the rotated heart while still providing the same quotient heart. This modification of the representative, however, causes that the plumbing action of
![]() $(\tau _1,\ldots ,\tau _L) \in -\mathbb {H}^L$
is not the action of a semigroup: the semigroup addition and the action only almost commute, with an error that goes to zero as
$(\tau _1,\ldots ,\tau _L) \in -\mathbb {H}^L$
is not the action of a semigroup: the semigroup addition and the action only almost commute, with an error that goes to zero as
![]() $\tau _i \to -i\infty $
.
$\tau _i \to -i\infty $
.
In this way, we give
![]() $\operatorname {MStab}^\circ (\mathcal {D}^3_{A_n})$
a topology by declaring neighborhoods of a multi-scale stability conditions to be plumbings with
$\operatorname {MStab}^\circ (\mathcal {D}^3_{A_n})$
a topology by declaring neighborhoods of a multi-scale stability conditions to be plumbings with
![]() $t_i := e^{-\pi i \tau _i}$
small composed with a small deformation of the stability condition. However, this space is not locally compact. In fact, for
$t_i := e^{-\pi i \tau _i}$
small composed with a small deformation of the stability condition. However, this space is not locally compact. In fact, for
![]() $n=2$
, the space is isomorphic to
$n=2$
, the space is isomorphic to
![]() ${\mathbb H} \cup \mathbb {P}^1(\mathbb {Q})$
with the horoball topology, as we will explain in Section 6.4.
${\mathbb H} \cup \mathbb {P}^1(\mathbb {Q})$
with the horoball topology, as we will explain in Section 6.4.
The complex orbifold structure on the quotient ![]() is locally given by the functions
is locally given by the functions
![]() $t_i$
together with the central charges
$t_i$
together with the central charges
![]() $Z_i$
. This statement requires to control the stabilizer of a neighborhood of the multi-scale stability condition. We show that this stabilizer contains a finite index subgroup isomorphic to
$Z_i$
. This statement requires to control the stabilizer of a neighborhood of the multi-scale stability condition. We show that this stabilizer contains a finite index subgroup isomorphic to
![]() $\mathbb {Z}^L$
.
$\mathbb {Z}^L$
.

Figure 1 Quadratic differential illustrating a degenerating sequence in ![]() and a rotated situation.
and a rotated situation.
For compactness of ![]() , the obvious idea is to normalize in a given sequence of multi-scale stability conditions the mass of the largest simple to be one, and then define an order on the set of simples corresponding to the speed in which their central charges go to zero. The level sets for this order will then correspond to the index set of the limiting multi-scale stability condition. The challenge for this idea arises if the central charge of a stable but nonsimple object tends to zero despite the normalization while the central charge of its simple factors do not. This forces the central charge of some simple object to tend to the positive real axis.
, the obvious idea is to normalize in a given sequence of multi-scale stability conditions the mass of the largest simple to be one, and then define an order on the set of simples corresponding to the speed in which their central charges go to zero. The level sets for this order will then correspond to the index set of the limiting multi-scale stability condition. The challenge for this idea arises if the central charge of a stable but nonsimple object tends to zero despite the normalization while the central charge of its simple factors do not. This forces the central charge of some simple object to tend to the positive real axis.
Consider, for example, the sequence
![]() $\sigma _n = (\mathcal {A}, Z_n)$
of stability conditions on
$\sigma _n = (\mathcal {A}, Z_n)$
of stability conditions on
![]() $\mathcal {D}^3_{A_2}$
, all supported on a fixed heart
$\mathcal {D}^3_{A_2}$
, all supported on a fixed heart
![]() $\mathcal {A}$
and with
$\mathcal {A}$
and with
See Figure 1 for the picture of the corresponding quadratic differential. In the limit
![]() $n\to \infty $
, the central charge vanishes precisely on the subcategory generated by the nontrivial extension E of
$n\to \infty $
, the central charge vanishes precisely on the subcategory generated by the nontrivial extension E of
![]() $S_1$
by
$S_1$
by
![]() $S_2$
. Since E is not simple, it does not define a nontrivial Serre subcategory of
$S_2$
. Since E is not simple, it does not define a nontrivial Serre subcategory of
![]() ${\mathcal A}$
, contradicting a consequence of our definition of multi-scale stability condition.
${\mathcal A}$
, contradicting a consequence of our definition of multi-scale stability condition.
The solution to find the limiting object is to rotate the sequence by
![]() $\lambda _n$
so that
$\lambda _n$
so that
![]() $Z_{\lambda _n \sigma _n}(S_2) \in {\mathbb H}^-$
; see Figure 1 on the right. The heart
$Z_{\lambda _n \sigma _n}(S_2) \in {\mathbb H}^-$
; see Figure 1 on the right. The heart
![]() $\mathcal {A}$
is replaced by
$\mathcal {A}$
is replaced by
![]() ${\mathcal A}_0:=\mu _{S_2}{\mathcal A}$
, the tilt one would usually perform also inside
${\mathcal A}_0:=\mu _{S_2}{\mathcal A}$
, the tilt one would usually perform also inside ![]() if the central charge of the simple
if the central charge of the simple
![]() $S_2$
approaches the positive real axis. Now E is simple, and the vanishing category
$S_2$
approaches the positive real axis. Now E is simple, and the vanishing category
![]() ${\mathcal V}^Z_1$
generated by E has the property that
${\mathcal V}^Z_1$
generated by E has the property that
![]() ${\mathcal V}^Z_1 \cap {\mathcal A}_0$
is Serre in
${\mathcal V}^Z_1 \cap {\mathcal A}_0$
is Serre in
![]() ${\mathcal A}_0$
. The limiting multi-scale stability condition consists of the filtration
${\mathcal A}_0$
. The limiting multi-scale stability condition consists of the filtration
![]() ${\mathcal A}_0\supset {\mathcal A}_1=\langle E\rangle $
together with
${\mathcal A}_0\supset {\mathcal A}_1=\langle E\rangle $
together with
![]() $Z_0(S_2[1]) = -1$
and
$Z_0(S_2[1]) = -1$
and
![]() $Z_0(E)=0$
as well as
$Z_0(E)=0$
as well as
![]() $Z_1(E)$
arbitrary nonzero in view of the notion of equivalence.
$Z_1(E)$
arbitrary nonzero in view of the notion of equivalence.
1.2 Obstructions to generalization
Continuing the idea of proof for compactness, we consider one of the simplest cases beyond
![]() $A_n$
-type quivers, stability conditions on the
$A_n$
-type quivers, stability conditions on the
![]() $CY_3$
-category of the Kronecker quiver, or, in the language of quadratic differentials (see [Reference Bridgeland and SmithBS15, Example 12.5]), the stratum
$CY_3$
-category of the Kronecker quiver, or, in the language of quadratic differentials (see [Reference Bridgeland and SmithBS15, Example 12.5]), the stratum
![]() $\mathcal Q(-3,-3,1,1)$
with two triple poles and two simple zeros. We again consider a situation where the central charge of a stable but nonsimple object tends to zero within the normalization that the mass of the largest simple is approximately one. Now using a small rotation does not seem to help. The compactification of strata of differentials ([Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3; Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2]) that we recall in Section 6 hints to the reason for this problem.
$\mathcal Q(-3,-3,1,1)$
with two triple poles and two simple zeros. We again consider a situation where the central charge of a stable but nonsimple object tends to zero within the normalization that the mass of the largest simple is approximately one. Now using a small rotation does not seem to help. The compactification of strata of differentials ([Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3; Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2]) that we recall in Section 6 hints to the reason for this problem.
The boundary strata of the compactification are encoded by level graphs, whose vertices correspond to components of stable curves and where a vertex
![]() $v_1$
is above a vertex
$v_1$
is above a vertex
![]() $v_2$
if the differential tends to zero on
$v_2$
if the differential tends to zero on
![]() $v_2$
more quickly than on
$v_2$
more quickly than on
![]() $v_1$
. In terms of multi-scale stability conditions, we find the same level structure (given by index of
$v_1$
. In terms of multi-scale stability conditions, we find the same level structure (given by index of
![]() ${\mathcal A}_i$
) and components (given by the components of the ext-quiver on the simples in
${\mathcal A}_i$
) and components (given by the components of the ext-quiver on the simples in
![]() ${\mathcal A}_i$
). However, for differentials, we allow for horizontal degenerations (i.e., edges between vertices on the same level). In this degeneration of the Kronecker quiver alluded to above (with central charge as in (1)), we should normalize the sequence to keep the length of the “short” stable object E (i.e., the extension of
${\mathcal A}_i$
). However, for differentials, we allow for horizontal degenerations (i.e., edges between vertices on the same level). In this degeneration of the Kronecker quiver alluded to above (with central charge as in (1)), we should normalize the sequence to keep the length of the “short” stable object E (i.e., the extension of
![]() $S_1$
by
$S_1$
by
![]() $S_2$
or geometrically the length of the core curve of the cylinder) constant. This happens at the expense of letting the mass of both simples go to infinity. In the geometric picture, the surface splits into two subsurfaces with quadratic differentials of type
$S_2$
or geometrically the length of the core curve of the cylinder) constant. This happens at the expense of letting the mass of both simples go to infinity. In the geometric picture, the surface splits into two subsurfaces with quadratic differentials of type
![]() $(-3,-2,1)$
. It would be interesting to enlarge the concept of non-split multi-scale differentials so as to include this ‘splitting’ of the category.
$(-3,-2,1)$
. It would be interesting to enlarge the concept of non-split multi-scale differentials so as to include this ‘splitting’ of the category.
It seems quite plausible that the current definition of (non-split) multi-scale stability condition provides a partial compactification of ![]() to a complex orbifold for general quiver categories (or whenever
to a complex orbifold for general quiver categories (or whenever ![]() is of tame type). This requires to overcome several technical problems that we highlight along with the definition of the topology in Section 4. Currently, we rely on the fact that hearts in
is of tame type). This requires to overcome several technical problems that we highlight along with the definition of the topology in Section 4. Currently, we rely on the fact that hearts in
![]() ${\mathcal D}_{A_n}^3$
have finitely many indecomposables.
${\mathcal D}_{A_n}^3$
have finitely many indecomposables.
1.3 Comparison to other compactifications
We are aware of four other papers aiming to compactify spaces of stability conditions. Bolognese [Reference BologneseBol20] uses a metric completion to give a partial compactification. The Thurston-type compactifications of Bapat, Deopukar and Licata [Reference Bapat, Deopurkar and LicataBDL20] and Kikuta-Koseki-Ouchi [Reference Kikuta, Koseki and OuchiKKO22] use the tuple of all masses to get a map from the space of projectivized stability conditions to some projective space and take the closure there. The space of lax stability conditions of Broomhead, Pauksztello, Ploog, Woolf [Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22] allows some of the masses of semistable objects to be zero but requires a modified support property and zero being an isolated point of the set of all masses.
Common to all these approaches is that they aim to (partially) compactify the space ![]() of projectivized stability conditions, whereas we compactify its quotient by
of projectivized stability conditions, whereas we compactify its quotient by ![]() . Moreover, in all these four papers, the boundary or boundary strata are real codimension one, whereas in our approach, the boundary has complex codimension one since we construct a complex orbifold. We mention that [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 15] proposes a real-oriented blowup of the complex orbifold, thus a real manifold with corners, to which the
. Moreover, in all these four papers, the boundary or boundary strata are real codimension one, whereas in our approach, the boundary has complex codimension one since we construct a complex orbifold. We mention that [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 15] proposes a real-oriented blowup of the complex orbifold, thus a real manifold with corners, to which the
![]() $\operatorname{GL} _2^+(\mathbb {R})$
-action extends. This real-oriented blowup construction can certainly also be incorporated into a modified definition of multi-scale stability conditions. In this real blowup, there are real codimension one boundary strata, which parametrize stability conditions on a quotient category by a rank one subcategory together – this is an effect of the real blowup – with the phase of the simple with vanishing mass. This seems to agree with the codimension one boundary strata of [Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22]. Since both approaches, ours and [Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22], use stability conditions on quotient categories and the difficulties often stem from lifting problems, it would be interesting to compare or combine them. However, this does not seem to solve the problem of getting a compact space in a more general setting, as we see no subsitute for the missing ‘horizontal degenerations’.
$\operatorname{GL} _2^+(\mathbb {R})$
-action extends. This real-oriented blowup construction can certainly also be incorporated into a modified definition of multi-scale stability conditions. In this real blowup, there are real codimension one boundary strata, which parametrize stability conditions on a quotient category by a rank one subcategory together – this is an effect of the real blowup – with the phase of the simple with vanishing mass. This seems to agree with the codimension one boundary strata of [Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22]. Since both approaches, ours and [Reference Broomhead, Pauksztello, Ploog and WoolfBPPW22], use stability conditions on quotient categories and the difficulties often stem from lifting problems, it would be interesting to compare or combine them. However, this does not seem to solve the problem of getting a compact space in a more general setting, as we see no subsitute for the missing ‘horizontal degenerations’.
2 Background and notation
In this section, we recall basic material about stability conditions, quivers and their
![]() $CY_3$
-categories
$CY_3$
-categories
![]() ${\mathcal D}_Q^3$
. References for this include [Reference Happel, Reiten and SmaløHRS96; Reference Gelfand and ManinGM03; Reference Beilinson, Bernstein and DeligneBBD82; Reference BridgelandBri07; Reference BridgelandBri09; Reference NeemanNee14; Reference Derksen, Weyman and ZelevinskyDWZ08; Reference KellerKel11].
${\mathcal D}_Q^3$
. References for this include [Reference Happel, Reiten and SmaløHRS96; Reference Gelfand and ManinGM03; Reference Beilinson, Bernstein and DeligneBBD82; Reference BridgelandBri07; Reference BridgelandBri09; Reference NeemanNee14; Reference Derksen, Weyman and ZelevinskyDWZ08; Reference KellerKel11].
2.1 Notation and fundamental assumptions
We fix some notation that will be used throughout. Let k denote an algebraically closed field, and any category is additive, k-linear and essentially small. We deal with finite-dimensional abelian and triangulated categories of modules (resp., dg modules) over a finite-dimensional algebra (resp., a dg algebra). Whenever we define a subcategory, we mean that there is a fully faithful functor that we assume to be the embedding.
Given subcategories
![]() ${\mathcal A}_1,{\mathcal A}_2$
of an abelian or a triangulated category
${\mathcal A}_1,{\mathcal A}_2$
of an abelian or a triangulated category
![]() $\mathcal C$
, and a set of objects
$\mathcal C$
, and a set of objects
![]() $\mathcal B$
, we define (usually omitting the subscript
$\mathcal B$
, we define (usually omitting the subscript
![]() $\mathcal C$
)
$\mathcal C$
)

We define
![]() $\langle \mathcal B\rangle $
depending on the context to be the abelian category generated by
$\langle \mathcal B\rangle $
depending on the context to be the abelian category generated by
![]() $\mathcal B$
, the thick triangulated category generated by
$\mathcal B$
, the thick triangulated category generated by
![]() $\mathcal B$
, the torsion-free class or the torsion class generated by
$\mathcal B$
, the torsion-free class or the torsion class generated by
![]() $\mathcal B$
.
$\mathcal B$
.
Let
![]() ${\mathcal A}$
be an abelian category. It is called a (finite) length category if any object
${\mathcal A}$
be an abelian category. It is called a (finite) length category if any object
![]() $E\in {\mathcal A}$
admits a finite sequence of subobjects
$E\in {\mathcal A}$
admits a finite sequence of subobjects
such that all
![]() $E_i/E_{i-1}$
are simple. It is called finite if, moreover, it has finitely many simple objects. If an abelian category is finite, its Grothendieck group is generated by the isomorphism classes of its simples.
$E_i/E_{i-1}$
are simple. It is called finite if, moreover, it has finitely many simple objects. If an abelian category is finite, its Grothendieck group is generated by the isomorphism classes of its simples.
Let
![]() ${\mathcal D}$
be a triangulated category. For simplicity, we make the strong assumption that its Grothendieck group is a finite rank lattice
${\mathcal D}$
be a triangulated category. For simplicity, we make the strong assumption that its Grothendieck group is a finite rank lattice
![]() $K({\mathcal D})\simeq \mathbb {Z}^{\oplus n}$
. This is not the general situation, though it will hold for the most relevant categories considered later. The main reason for such an hypothesis is to simplify the definition of a (multi-scale) stability condition.
$K({\mathcal D})\simeq \mathbb {Z}^{\oplus n}$
. This is not the general situation, though it will hold for the most relevant categories considered later. The main reason for such an hypothesis is to simplify the definition of a (multi-scale) stability condition.
Definition 2.1. A bounded t-structure on a triangulated category
![]() ${\mathcal D}$
is the datum of a full additive subcategory
${\mathcal D}$
is the datum of a full additive subcategory
![]() $\mathcal P\subset {\mathcal D}$
stable under positive shift such that
$\mathcal P\subset {\mathcal D}$
stable under positive shift such that
![]() $\mathcal P\perp \mathcal P^\perp ={\mathcal D}$
, and moreover,
$\mathcal P\perp \mathcal P^\perp ={\mathcal D}$
, and moreover,
![]() ${\mathcal D}$
is generated by
${\mathcal D}$
is generated by
![]() $\cup _{m\in \mathbb {Z}}\big (\mathcal P[m]\cap \mathcal P^\perp [-m]\big )$
. The heart of a bounded t-structure is the subcategory
$\cup _{m\in \mathbb {Z}}\big (\mathcal P[m]\cap \mathcal P^\perp [-m]\big )$
. The heart of a bounded t-structure is the subcategory
![]() $\mathcal P \cap \mathcal P^\perp [1]$
.
$\mathcal P \cap \mathcal P^\perp [1]$
.
The heart
![]() ${\mathcal A}$
of a bounded t-structure is an abelian category. The cohomological functor
${\mathcal A}$
of a bounded t-structure is an abelian category. The cohomological functor
![]() $H^0:{\mathcal D}\to {\mathcal A}$
realizes an isomorphism at the level of Grothendieck groups
$H^0:{\mathcal D}\to {\mathcal A}$
realizes an isomorphism at the level of Grothendieck groups
Moreover, a bounded t-structure is uniquely determined by its heart as
![]() $\mathcal P= \langle \mathcal {H}[i],i\geq 0\rangle $
. For this reason, we will speak about a t-structure or its heart interchangeably.
$\mathcal P= \langle \mathcal {H}[i],i\geq 0\rangle $
. For this reason, we will speak about a t-structure or its heart interchangeably.
There is a partial order on hearts
![]() ${\mathcal A}_1\le {\mathcal A}_2$
defined by
${\mathcal A}_1\le {\mathcal A}_2$
defined by
![]() $\mathcal P_1\supset \mathcal P_2$
, or equivalently,
$\mathcal P_1\supset \mathcal P_2$
, or equivalently,
![]() $\mathcal P_1^\perp \supset \mathcal P_2^\perp $
. A heart
$\mathcal P_1^\perp \supset \mathcal P_2^\perp $
. A heart
![]() $\mathcal {H}$
will be called intermediate with respect to a fixed heart
$\mathcal {H}$
will be called intermediate with respect to a fixed heart
![]() ${\mathcal A}$
if
${\mathcal A}$
if
![]() ${\mathcal A} \leq \mathcal {H} \leq {\mathcal A}[1]$
.
${\mathcal A} \leq \mathcal {H} \leq {\mathcal A}[1]$
.
2.2 Torsion pairs and tilting
A torsion pair for an abelian category
![]() ${\mathcal A}$
consists of a pair
${\mathcal A}$
consists of a pair
![]() $(\mathcal {T},\mathcal {F})$
of full additive subcategories of
$(\mathcal {T},\mathcal {F})$
of full additive subcategories of
![]() ${\mathcal A}$
called torsion class and torsion-free class, such that
${\mathcal A}$
called torsion class and torsion-free class, such that
![]() ${\mathcal A}=\mathcal {T}\perp \mathcal {F}$
. In other words, a torsion pair mimics a bounded t-structure at abelian level. In fact, a torsion pair in the heart of a bounded t-structure
${\mathcal A}=\mathcal {T}\perp \mathcal {F}$
. In other words, a torsion pair mimics a bounded t-structure at abelian level. In fact, a torsion pair in the heart of a bounded t-structure
![]() ${\mathcal A}$
in a
${\mathcal A}$
in a
![]() ${\mathcal D}$
defines new bounded t-structures with hearts
${\mathcal D}$
defines new bounded t-structures with hearts
They are called, respectively, the forward tilt at
![]() $\mathcal {F}$
(resp. backward tilt at
$\mathcal {F}$
(resp. backward tilt at
![]() $\mathcal {T}$
), [Reference Happel, Reiten and SmaløHRS96]. They are related by
$\mathcal {T}$
), [Reference Happel, Reiten and SmaløHRS96]. They are related by
![]() $\mu ^\sharp _{\mathcal {T}[-1]} \mu ^\flat _{\mathcal {T}}{\mathcal A}={\mathcal A}$
and
$\mu ^\sharp _{\mathcal {T}[-1]} \mu ^\flat _{\mathcal {T}}{\mathcal A}={\mathcal A}$
and
![]() $\mu ^\flat _{\mathcal {F}[1]}\mu ^\sharp _{\mathcal {F}}{\mathcal A} = {\mathcal A}$
. The forward tilt of
$\mu ^\flat _{\mathcal {F}[1]}\mu ^\sharp _{\mathcal {F}}{\mathcal A} = {\mathcal A}$
. The forward tilt of
![]() ${\mathcal A}$
at a torsion-free class is intermediate with respect to
${\mathcal A}$
at a torsion-free class is intermediate with respect to
![]() ${\mathcal A}$
; the backward tilt of
${\mathcal A}$
; the backward tilt of
![]() ${\mathcal A}$
at a torsion class is intermediate with respect to
${\mathcal A}$
at a torsion class is intermediate with respect to
![]() ${\mathcal A}[-1]$
.
${\mathcal A}[-1]$
.
In a finite abelian category, torsion and torsion-free classes are closed under extensions and are characterized by being closed under quotients and subobjects, respectively. This implies that any Serre subcategory is both torsion and torsion-free class. When we tilt at a torsion(-free) class
![]() $\langle S\rangle $
generated by a simple object S, we speak about a simple tilt, and we simplify the notation to
$\langle S\rangle $
generated by a simple object S, we speak about a simple tilt, and we simplify the notation to
![]() $\mu ^\sharp _S{\mathcal A}$
and
$\mu ^\sharp _S{\mathcal A}$
and
![]() $\mu ^\flat _S{\mathcal A}$
. Suppose
$\mu ^\flat _S{\mathcal A}$
. Suppose
![]() ${\mathcal A}$
is a finite heart with simple objects
${\mathcal A}$
is a finite heart with simple objects
![]() $\operatorname {Sim}({\mathcal A}):=\{S_1,\dots , S_n\}$
, which are rigid (i.e., have no nontrivial self-extensions), and let
$\operatorname {Sim}({\mathcal A}):=\{S_1,\dots , S_n\}$
, which are rigid (i.e., have no nontrivial self-extensions), and let
![]() $S\in \operatorname {Sim}({\mathcal A})$
. Then
$S\in \operatorname {Sim}({\mathcal A})$
. Then
 $$\begin{align*}\begin{aligned} \operatorname{Sim} \mu^\sharp{\mathcal A} &= \{S[1]\}\cup \{\operatorname{Cone}\big(S\stackrel{ev}{\to}S[1]\otimes \operatorname{Ext}^1(T,S)^*\big)[-1], \ S\neq T \in\operatorname{Sim}{\mathcal A}\}\\ \operatorname{Sim} \mu^\flat{\mathcal A} &= \{S[-1]\}\cup \{\operatorname{Cone}\big(S[-1]\otimes \operatorname{Ext}^1(S,T)\stackrel{ev}{\to} T), \ S\neq T \in\operatorname{Sim}{\mathcal A}\}.\, \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \operatorname{Sim} \mu^\sharp{\mathcal A} &= \{S[1]\}\cup \{\operatorname{Cone}\big(S\stackrel{ev}{\to}S[1]\otimes \operatorname{Ext}^1(T,S)^*\big)[-1], \ S\neq T \in\operatorname{Sim}{\mathcal A}\}\\ \operatorname{Sim} \mu^\flat{\mathcal A} &= \{S[-1]\}\cup \{\operatorname{Cone}\big(S[-1]\otimes \operatorname{Ext}^1(S,T)\stackrel{ev}{\to} T), \ S\neq T \in\operatorname{Sim}{\mathcal A}\}.\, \end{aligned}\end{align*}$$
See, for example, [Reference King and QiuKQ15]. Note also that the simple tilting of a finite heart in
![]() ${\mathcal D}$
is another finite heart. In some cases, tilting at a torsion (or torsion-free) class can be decomposed into a finite sequence of simple tilts.
${\mathcal D}$
is another finite heart. In some cases, tilting at a torsion (or torsion-free) class can be decomposed into a finite sequence of simple tilts.
Proposition 2.2. Suppose that
![]() ${\mathcal A}$
is a finite heart.
${\mathcal A}$
is a finite heart.
-
1. Tilting at a torsion-free class in
 ${\mathcal A}$
containing only finitely many indecomposables is equivalent to performing a sequence of simple forward tilts.
${\mathcal A}$
containing only finitely many indecomposables is equivalent to performing a sequence of simple forward tilts. -
2. Conversely, suppose
 $a_1, \dots , a_{k}$
is a finite sequence of objects in
$a_1, \dots , a_{k}$
is a finite sequence of objects in
 ${\mathcal A}$
such that
${\mathcal A}$
such that
 $a_i \in {\mathcal A}$
is simple in
$a_i \in {\mathcal A}$
is simple in
 $\mu ^\sharp _{a_{i-1}}\dots \mu ^\sharp _{a_1}{\mathcal A}$
. Then
$\mu ^\sharp _{a_{i-1}}\dots \mu ^\sharp _{a_1}{\mathcal A}$
. Then
 $\mu ^\sharp _{a_{k}}\dots \mu ^\sharp _{a_1}{\mathcal A} = \mu ^\sharp _{\mathcal {F}}{\mathcal A}$
, where
$\mu ^\sharp _{a_{k}}\dots \mu ^\sharp _{a_1}{\mathcal A} = \mu ^\sharp _{\mathcal {F}}{\mathcal A}$
, where
 $\mathcal {F} = \langle a_0,\dots , a_k \rangle $
.
$\mathcal {F} = \langle a_0,\dots , a_k \rangle $
. -
3. More generally, for any two torsion-free classes
 $\mathcal {F}_1\subset \mathcal {F}_2$
with
$\mathcal {F}_1\subset \mathcal {F}_2$
with
 $\mathcal F_2$
having finitely many indecomposables, there is a sequence of simple tilts at objects
$\mathcal F_2$
having finitely many indecomposables, there is a sequence of simple tilts at objects
 $a_i$
such that
$a_i$
such that
 $\mu _{\mathcal {F}_2}^\sharp =\mu ^\sharp _{a_k}\cdots \mu ^\sharp _{a_1} \mu ^\sharp _{\mathcal {F}_1}$
and
$\mu _{\mathcal {F}_2}^\sharp =\mu ^\sharp _{a_k}\cdots \mu ^\sharp _{a_1} \mu ^\sharp _{\mathcal {F}_1}$
and
 $\mathcal {F}_2=\langle \mathcal {F}_1,a_1,\cdots , a_k\rangle $
.
$\mathcal {F}_2=\langle \mathcal {F}_1,a_1,\cdots , a_k\rangle $
.
Proof. For the proof of the first two items, see [Reference WoolfWoo10, Proof of Proposition 2.4] and use the relation
![]() $\mu ^\sharp _{\mathcal {T}[-1]}(\mu ^\flat _{\mathcal {T}}{\mathcal A}) = {\mathcal A}$
to convert the statement about backward tilts in loc. cit. to the given version. The last statement follows from [Reference Hügel, Laking, Št’ovíček and VitóriaHLŠV22, Section 7.1] (see, in particular, Proposition 7.5).
$\mu ^\sharp _{\mathcal {T}[-1]}(\mu ^\flat _{\mathcal {T}}{\mathcal A}) = {\mathcal A}$
to convert the statement about backward tilts in loc. cit. to the given version. The last statement follows from [Reference Hügel, Laking, Št’ovíček and VitóriaHLŠV22, Section 7.1] (see, in particular, Proposition 7.5).
2.3 Bridgeland stability conditions
Recall from [Reference BridgelandBri07] that a stability condition
![]() $\sigma $
on a triangulated category
$\sigma $
on a triangulated category
![]() ${\mathcal D}$
is a pair
${\mathcal D}$
is a pair
![]() $\sigma = ({\mathcal A},Z)$
, consisting of the heart of a bounded t-structure
$\sigma = ({\mathcal A},Z)$
, consisting of the heart of a bounded t-structure
![]() ${\mathcal A}$
, together with a central charge
${\mathcal A}$
, together with a central charge ![]() (i.e., a group homomorphism that maps the class of nonzero elements in
(i.e., a group homomorphism that maps the class of nonzero elements in
![]() ${\mathcal A}$
to the semi-closed half plane
${\mathcal A}$
to the semi-closed half plane
![]() $\overline {\mathbb {H}}:=\{re^{\pi i \theta }\in {\mathbb R} | r\in {\mathbb R}_{>0},\ 0<\theta \leq 1\}$
and that satisfies the support property and Harder-Narasimhan condition of loc. cit). We fix a finite rank lattice K and a surjective morphism
$\overline {\mathbb {H}}:=\{re^{\pi i \theta }\in {\mathbb R} | r\in {\mathbb R}_{>0},\ 0<\theta \leq 1\}$
and that satisfies the support property and Harder-Narasimhan condition of loc. cit). We fix a finite rank lattice K and a surjective morphism
![]() $\nu : K({\mathcal A})\to K$
and require that Z factors through
$\nu : K({\mathcal A})\to K$
and require that Z factors through
![]() $\nu $
. In the case
$\nu $
. In the case ![]() , we require that
, we require that
![]() $K = K({\mathcal A})$
and
$K = K({\mathcal A})$
and ![]() .
.
We use that stability conditions can equivalently be specified as a
![]() $\sigma = (\mathcal {P}, Z)$
using a central charge and a slicing, compatible in the sense that
$\sigma = (\mathcal {P}, Z)$
using a central charge and a slicing, compatible in the sense that
![]() $E\in \mathcal P(\phi )$
implies
$E\in \mathcal P(\phi )$
implies
![]() $Z([E])=m\exp (\pi i \phi )$
for some positive
$Z([E])=m\exp (\pi i \phi )$
for some positive
![]() $m\in \mathbb {R}$
.
$m\in \mathbb {R}$
.
An object
![]() $E\in {\mathcal D}$
is called
$E\in {\mathcal D}$
is called
![]() $\sigma $
-semistable if
$\sigma $
-semistable if
![]() $E\in \mathcal P(\phi )$
for some
$E\in \mathcal P(\phi )$
for some
![]() $\phi \in \mathbb {R}$
. It is called
$\phi \in \mathbb {R}$
. It is called
![]() $\sigma $
-stable if it is simple in
$\sigma $
-stable if it is simple in
![]() $\mathcal P(\phi )$
. This notion makes sense because any subcategory
$\mathcal P(\phi )$
. This notion makes sense because any subcategory
![]() $\mathcal P(\phi )$
is abelian if
$\mathcal P(\phi )$
is abelian if
![]() $\mathcal P=\{\mathcal P(\phi )\}_{\phi \in \mathbb {R}}$
is a slicing compatible with
$\mathcal P=\{\mathcal P(\phi )\}_{\phi \in \mathbb {R}}$
is a slicing compatible with ![]() .
.
Let
![]() $\lambda \in \mathbb {C}$
, and suppose
$\lambda \in \mathbb {C}$
, and suppose
![]() $0 < \epsilon = \Re (\lambda ) \leq 1$
. We observe, and will use later, that
$0 < \epsilon = \Re (\lambda ) \leq 1$
. We observe, and will use later, that
![]() $\sigma $
-semistable objects X in the heart
$\sigma $
-semistable objects X in the heart
![]() ${\mathcal A}$
(equivalently Z-semistable objects) with
${\mathcal A}$
(equivalently Z-semistable objects) with
![]() $1-\epsilon \leq \phi (X) <(\leq ) 1$
and those with
$1-\epsilon \leq \phi (X) <(\leq ) 1$
and those with
![]() $0<\phi (X)\leq (<)1-\epsilon $
, for
$0<\phi (X)\leq (<)1-\epsilon $
, for
![]() $\epsilon \in (0,1)$
, form a torsion pair
$\epsilon \in (0,1)$
, form a torsion pair
![]() $(\mathcal {T}_\lambda ,\mathcal {F}_\lambda )$
in
$(\mathcal {T}_\lambda ,\mathcal {F}_\lambda )$
in
![]() ${\mathcal A}$
due to the Harder-Narasimhan condition.
${\mathcal A}$
due to the Harder-Narasimhan condition.
The space of stability conditions is a complex manifold ![]() . There are two natural commuting actions:
. There are two natural commuting actions:
-
○ a left action by
 $\mathbb {C}$
, by rescaling the central charge and tilting the heart, if
$\mathbb {C}$
, by rescaling the central charge and tilting the heart, if
 $0 < \Re (\lambda ) \leq 1$
,
$0 < \Re (\lambda ) \leq 1$
,  $$\begin{align*}\lambda \cdot ({\mathcal A},Z) \;=\;(\mu^\sharp_{\mathcal{F}_\lambda} {\mathcal A},e^{-\pi i \lambda} Z)\,,\end{align*}$$
$$\begin{align*}\lambda \cdot ({\mathcal A},Z) \;=\;(\mu^\sharp_{\mathcal{F}_\lambda} {\mathcal A},e^{-\pi i \lambda} Z)\,,\end{align*}$$
-
○ and a right action by
 via pullback, where
via pullback, where $$\begin{align*}\Phi.({\mathcal A},Z) \;=\;\big(\Phi {\mathcal A},Z\circ [\Phi]^{-1})\big),\end{align*}$$
$$\begin{align*}\Phi.({\mathcal A},Z) \;=\;\big(\Phi {\mathcal A},Z\circ [\Phi]^{-1})\big),\end{align*}$$
 $[\Phi ]$
is the map induced by
$[\Phi ]$
is the map induced by
 $\Phi $
on
$\Phi $
on
 $K({\mathcal D})$
.
$K({\mathcal D})$
.
In particular, the shift
![]() $[1]$
acts as
$[1]$
acts as
![]() $\lambda =1$
. Note that the
$\lambda =1$
. Note that the
![]() $\mathbb {C}$
-action does not change the notion of semistability and stability.
$\mathbb {C}$
-action does not change the notion of semistability and stability.
We denote by ![]() a connected component, specified by the context. The stability manifold
a connected component, specified by the context. The stability manifold ![]() is tiled into subsets
is tiled into subsets ![]() of stability conditions supported on the heart
of stability conditions supported on the heart
![]() ${\mathcal A}$
. The component
${\mathcal A}$
. The component ![]() is called finite type if it is the union of
is called finite type if it is the union of ![]() over finite hearts. It is called of tame type if the
over finite hearts. It is called of tame type if the
![]() $\mathbb {C}$
-orbits of
$\mathbb {C}$
-orbits of ![]() for all finite type hearts cover
for all finite type hearts cover ![]() .
.
We let ![]() be the subgroup of
be the subgroup of ![]() consisting on autoequivalences of
consisting on autoequivalences of
![]() $\mathcal {D}$
that preserve the component
$\mathcal {D}$
that preserve the component ![]() , and we define
, and we define ![]() the subgroup of negligible autoequivalences (i.e., those that act trivially on
the subgroup of negligible autoequivalences (i.e., those that act trivially on ![]() ). We use fancy fonts like
). We use fancy fonts like
to denote the quotient groups by negligible autoequivalences. It is the quotient spaces ![]() by these actions that we want to compactify.
by these actions that we want to compactify.
2.4 Quivers with potential, module and Ginzburg categories
In this paper,
![]() $(Q,W)$
is a quiver
$(Q,W)$
is a quiver
![]() $Q=(Q_0,Q_1,s,t)$
with potential W (i.e., a formal sum of cycles) up to right-equivalence; see [Reference Derksen, Weyman and ZelevinskyDWZ08; Reference Keller and YangKY11] for standard results. We assume that
$Q=(Q_0,Q_1,s,t)$
with potential W (i.e., a formal sum of cycles) up to right-equivalence; see [Reference Derksen, Weyman and ZelevinskyDWZ08; Reference Keller and YangKY11] for standard results. We assume that
![]() $(Q,W)$
has no loops and no 2-cycles, that the set of vertices
$(Q,W)$
has no loops and no 2-cycles, that the set of vertices
![]() $Q_0$
and the set of arrows
$Q_0$
and the set of arrows
![]() $Q_1$
are finite, and that the potential defines a bilateral ideal
$Q_1$
are finite, and that the potential defines a bilateral ideal
![]() $\partial W=\langle \partial _a W \mid a\in Q_1\rangle \subset k Q$
such that the Jacobian algebra,
$\partial W=\langle \partial _a W \mid a\in Q_1\rangle \subset k Q$
such that the Jacobian algebra,
obtained by quotienting the completed path algebra by the ideal defined by the potential, is finite dimensional. Note that in our case of interest,
![]() $\widehat {k Q}/\partial W =k Q/\partial W$
. For a ring
$\widehat {k Q}/\partial W =k Q/\partial W$
. For a ring
![]() $\mathcal J$
, we denote by
$\mathcal J$
, we denote by
![]() $\operatorname {Mod} \mathcal J$
the abelian category of left modules and by
$\operatorname {Mod} \mathcal J$
the abelian category of left modules and by
![]() $\operatorname {mod} \mathcal J$
the abelian category of finitely generated left modules. The category
$\operatorname {mod} \mathcal J$
the abelian category of finitely generated left modules. The category
![]() $\operatorname {mod} \mathcal J(Q,W)$
is finite with simple objects
$\operatorname {mod} \mathcal J(Q,W)$
is finite with simple objects
![]() $\operatorname {Sim}(\operatorname {mod} \mathcal J(Q,W))=\{S_1,\dots , S_n\}$
, where
$\operatorname {Sim}(\operatorname {mod} \mathcal J(Q,W))=\{S_1,\dots , S_n\}$
, where
![]() $n=|Q_0|$
.
$n=|Q_0|$
.
If
![]() $I\subset Q_0$
is a collection of vertices of
$I\subset Q_0$
is a collection of vertices of
![]() $(Q,W)$
, by
$(Q,W)$
, by
![]() $(Q_I,W_I)$
, we mean the restriction of
$(Q_I,W_I)$
, we mean the restriction of
![]() $(Q,W)$
to I. It is another finite quiver with potential, possibly disconnected, defined by
$(Q,W)$
to I. It is another finite quiver with potential, possibly disconnected, defined by
![]() $(Q_I)_0=I$
,
$(Q_I)_0=I$
,
![]() $(Q_I)_1=\left \{a:i\to j\in Q_1\mid i,j\in I\right \}$
, and with source, tail functions and potential obtained by restriction from
$(Q_I)_1=\left \{a:i\to j\in Q_1\mid i,j\in I\right \}$
, and with source, tail functions and potential obtained by restriction from
![]() $(Q,W)$
to I. We call it a (full) subquiver. The complement of I in
$(Q,W)$
to I. We call it a (full) subquiver. The complement of I in
![]() $Q_0$
will be denoted
$Q_0$
will be denoted
![]() $I^c$
.
$I^c$
.
The mutation of a quiver with potential
![]() $(Q,W)$
at a vertex i is an operation that produces another quiver with the same set of vertices and a new set of arrows and a new potential, defined as follows. From
$(Q,W)$
at a vertex i is an operation that produces another quiver with the same set of vertices and a new set of arrows and a new potential, defined as follows. From
![]() $Q_1$
, keep all arrows not incident to i; replace any arrow a with either
$Q_1$
, keep all arrows not incident to i; replace any arrow a with either
![]() $s(a)$
or
$s(a)$
or
![]() $t(a)$
equal to i with its opposite; add an arrow
$t(a)$
equal to i with its opposite; add an arrow
![]() $[ab]:k_1\to k_2$
for any pair of consecutive arrows
$[ab]:k_1\to k_2$
for any pair of consecutive arrows
![]() $a:k_1\to i$
and
$a:k_1\to i$
and
![]() $b:i\to k_2$
; finally, remove any two-cycles. The new potential is the formal sum of W and
$b:i\to k_2$
; finally, remove any two-cycles. The new potential is the formal sum of W and
![]() $\sum _{a,b\in Q_1}[ab]b^*a^*$
.
$\sum _{a,b\in Q_1}[ab]b^*a^*$
.
The Ginzburg algebra of
![]() $(Q,W)$
is a dg algebra denoted
$(Q,W)$
is a dg algebra denoted
![]() $\Gamma (Q,W)$
and introduced in [Reference GinzburgGin06; Reference Keller and YangKY11]. It does not depend on the mutation class of a quiver with potential.
$\Gamma (Q,W)$
and introduced in [Reference GinzburgGin06; Reference Keller and YangKY11]. It does not depend on the mutation class of a quiver with potential.
Definition 2.3. The perfectly-valued derived category
![]() $\operatorname {pvd}(\Gamma )$
associated with a dg algebra
$\operatorname {pvd}(\Gamma )$
associated with a dg algebra
![]() $\Gamma $
is the subcategory of the derived category
$\Gamma $
is the subcategory of the derived category
![]() ${\mathcal D}(\Gamma )$
consisting on dg modules with finite dimensional total cohomology.
${\mathcal D}(\Gamma )$
consisting on dg modules with finite dimensional total cohomology.
Once we fixed
![]() $(Q,W)$
and
$(Q,W)$
and
![]() $I\subset Q_0$
, we write
$I\subset Q_0$
, we write
![]() $\mathcal J=\mathcal J(Q,W)$
,
$\mathcal J=\mathcal J(Q,W)$
,
![]() $\Gamma =\Gamma (Q,W)$
, and
$\Gamma =\Gamma (Q,W)$
, and
![]() $\mathcal J_I=\mathcal J(Q_I,W_I)$
,
$\mathcal J_I=\mathcal J(Q_I,W_I)$
,
![]() $\Gamma _I=\Gamma (Q_I,W_I)$
. We have the following inclusion of triangulated categories, [Reference Keller and YangKY11]
$\Gamma _I=\Gamma (Q_I,W_I)$
. We have the following inclusion of triangulated categories, [Reference Keller and YangKY11]
It is proven in [Reference Keller and YangKY11] that the standard t-structure with heart
![]() $\operatorname {Mod}\mathcal J$
in the derived category
$\operatorname {Mod}\mathcal J$
in the derived category
![]() ${\mathcal D}(\Gamma )$
restricts to
${\mathcal D}(\Gamma )$
restricts to
![]() $\operatorname {per}(\Gamma )$
and
$\operatorname {per}(\Gamma )$
and
![]() $\operatorname {pvd}(\Gamma )$
, on which it defines a bounded t-structure with heart
$\operatorname {pvd}(\Gamma )$
, on which it defines a bounded t-structure with heart
![]() $\mod \mathcal J$
, that we call standard as well.
$\mod \mathcal J$
, that we call standard as well.
The perfectly valued derived category of the Ginzburg algebra of a quiver with potential is 3-Calabi-Yau, which means that for any objects
![]() $E,F\in \operatorname {pvd}(\Gamma )$
, there is a natural isomorphism of k-vector spaces
$E,F\in \operatorname {pvd}(\Gamma )$
, there is a natural isomorphism of k-vector spaces ![]() . Moreover, the simple objects in the standard heart
. Moreover, the simple objects in the standard heart
![]() $\mod \mathcal J$
are spherical in
$\mod \mathcal J$
are spherical in
![]() $\operatorname {pvd}(\Gamma )$
; see [Reference KellerKel11, Lemma 4.4] and [Reference King and QiuKQ15, Corollary 8.5].
$\operatorname {pvd}(\Gamma )$
; see [Reference KellerKel11, Lemma 4.4] and [Reference King and QiuKQ15, Corollary 8.5].
If two quivers with potential
![]() $(Q,W)$
and
$(Q,W)$
and
![]() $(Q',W')$
are related by mutations, then
$(Q',W')$
are related by mutations, then
![]() ${\mathcal D}(\Gamma (Q,W))\simeq {\mathcal D}(\Gamma (Q',W'))$
and
${\mathcal D}(\Gamma (Q,W))\simeq {\mathcal D}(\Gamma (Q',W'))$
and
![]() $\operatorname {pvd}(\Gamma (Q,W))\simeq \operatorname {pvd}(\Gamma (Q',W'))$
. Therefore,
$\operatorname {pvd}(\Gamma (Q,W))\simeq \operatorname {pvd}(\Gamma (Q',W'))$
. Therefore,
![]() $\operatorname {mod}\mathcal J(Q',W')$
is viewed as another heart of bounded t-structure of
$\operatorname {mod}\mathcal J(Q',W')$
is viewed as another heart of bounded t-structure of
![]() $\operatorname {pvd}\Gamma (Q,W)$
. We recall that, in general, not all bounded t-structures have this shape.
$\operatorname {pvd}\Gamma (Q,W)$
. We recall that, in general, not all bounded t-structures have this shape.
It is clear that any property of
![]() $\operatorname {pvd}(\Gamma )$
and
$\operatorname {pvd}(\Gamma )$
and
![]() $\operatorname {mod}(\mathcal J)$
also holds for
$\operatorname {mod}(\mathcal J)$
also holds for
![]() $\operatorname {pvd}(\Gamma _I)$
and
$\operatorname {pvd}(\Gamma _I)$
and
![]() $\operatorname {mod} \mathcal J_I$
.
$\operatorname {mod} \mathcal J_I$
.
As explained in [Reference Kalck and YangKY18], the Ginzburg algebra
![]() $\Gamma _I$
is isomorphic to
$\Gamma _I$
is isomorphic to
![]() $\Gamma /\Gamma e \Gamma $
, where
$\Gamma /\Gamma e \Gamma $
, where
![]() $e=\sum _{i\in I^c}e_i$
is the idempotent in
$e=\sum _{i\in I^c}e_i$
is the idempotent in
![]() $\Gamma $
associated to the complement
$\Gamma $
associated to the complement
![]() $I^c= Q_0\setminus I$
. However, the dg algebra
$I^c= Q_0\setminus I$
. However, the dg algebra
![]() $e\Gamma e$
is the endomorphism algebra of the projective module
$e\Gamma e$
is the endomorphism algebra of the projective module
![]() $\Gamma e = \sum _{i\in I^c}\Gamma e_i$
in
$\Gamma e = \sum _{i\in I^c}\Gamma e_i$
in
![]() ${\mathcal D}(\Gamma )$
, and the Verdier quotient
${\mathcal D}(\Gamma )$
, and the Verdier quotient
![]() ${\mathcal D}(\Gamma )/{\mathcal D}(\Gamma _I)$
coincides with
${\mathcal D}(\Gamma )/{\mathcal D}(\Gamma _I)$
coincides with
![]() ${\mathcal D}(e\Gamma e)$
. Similarly,
${\mathcal D}(e\Gamma e)$
. Similarly,
![]() $\mathcal J_I=\mathcal J/\mathcal J e \mathcal J$
and the quotient perfectly valued and abelian categories that will be relevant in the rest of the paper are
$\mathcal J_I=\mathcal J/\mathcal J e \mathcal J$
and the quotient perfectly valued and abelian categories that will be relevant in the rest of the paper are
![]() $\operatorname {pvd} e\Gamma e$
and
$\operatorname {pvd} e\Gamma e$
and
![]() $\operatorname {mod} e\mathcal J e$
:
$\operatorname {mod} e\mathcal J e$
:

The last line is part of a recollement of abelian categories, described, for instance, in [Reference PsaroudakisPsa18].
In the rest of the paper, we let
-
○
 ${\mathcal D}_Q^3$
be the 3-Calabi-Yau triangulated category
${\mathcal D}_Q^3$
be the 3-Calabi-Yau triangulated category
 $\operatorname {pvd}\Gamma (Q,W)$
.
$\operatorname {pvd}\Gamma (Q,W)$
.
The case of primary interest will be quivers of type
![]() $A_n$
– that is, that can be obtained with by finite sequence of mutations from the quiver
$A_n$
– that is, that can be obtained with by finite sequence of mutations from the quiver
Any restriction of a quiver of type
![]() $A_n$
is a union of quivers of type
$A_n$
is a union of quivers of type
![]() $A_m$
’s.
$A_m$
’s.
Given an
![]() $A_n$
-configuration, and the abelian category
$A_n$
-configuration, and the abelian category
![]() $\operatorname {mod} \mathcal J(A_n)$
, we denote by
$\operatorname {mod} \mathcal J(A_n)$
, we denote by
![]() $S_i$
the simple module associated with the vertex i. For
$S_i$
the simple module associated with the vertex i. For
![]() $i\leq k$
, we denote by
$i\leq k$
, we denote by
![]() $S_{i...k}$
the
$S_{i...k}$
the
![]() $\mathcal J(A_n)$
-module defined inductively as the indecomposable fitting into the short exact sequence
$\mathcal J(A_n)$
-module defined inductively as the indecomposable fitting into the short exact sequence
The
![]() $S_{i\dots k}$
, are the projective resolutions
$S_{i\dots k}$
, are the projective resolutions
![]() $P_i$
of
$P_i$
of
![]() $S_i$
in the abelian subcategory
$S_i$
in the abelian subcategory
![]() $\langle S_i,\dots , S_{k}\rangle $
which is of
$\langle S_i,\dots , S_{k}\rangle $
which is of
![]() $A_{(k-i)}$
-type by construction.
$A_{(k-i)}$
-type by construction.
3 Stability manifolds for marked surfaces
Decorated marked surfaces are one of the natural sources for quiver categories. They are well studied thanks also to the Bridgeland-Smith isomomorphism [Reference Bridgeland and SmithBS15] to spaces of quadratic differentials with simple zeros. We recall this result here, together with the generalization in our previous paper [Reference Barbieri, Möller, Qiu and SoBMQS22]. This setup contains our main case study, the
![]() $A_n$
-quiver, and serves as motivation for the use of quotient categories. Triangulations of decorated marked surfaces will serve as reference points to pick out the right connected components of stability manifolds needed in the later sections.
$A_n$
-quiver, and serves as motivation for the use of quotient categories. Triangulations of decorated marked surfaces will serve as reference points to pick out the right connected components of stability manifolds needed in the later sections.
3.1 The stability manifold of a decorated marked surface
A natural way to construct quivers is from triangulations of surfaces, and we will use this formalism to keep track of connected components of stability spaces and later the multi-scale stabilty conditions.
A marked surface
![]() $\mathbf {S}=(\mathbf {S},{\mathbb M},\mathbb P)$
consists of a connected bordered differentiable surface with a fixed orientation, with a finite set
$\mathbf {S}=(\mathbf {S},{\mathbb M},\mathbb P)$
consists of a connected bordered differentiable surface with a fixed orientation, with a finite set
![]() ${\mathbb M}=\{M_i\}_{i=1}^b$
of marked points on the boundary
${\mathbb M}=\{M_i\}_{i=1}^b$
of marked points on the boundary
![]() $\partial \mathbf {S}=\bigcup _{i=1}^b \partial _i$
, and with a finite set
$\partial \mathbf {S}=\bigcup _{i=1}^b \partial _i$
, and with a finite set
![]() $\mathbb P=\{p_j\}_{j=1}^p$
of punctures in its interior
$\mathbb P=\{p_j\}_{j=1}^p$
of punctures in its interior
![]() $\mathbf {S}^\circ =\mathbf {S}-\partial \mathbf {S}$
, such that each connected component of
$\mathbf {S}^\circ =\mathbf {S}-\partial \mathbf {S}$
, such that each connected component of
![]() $\partial \mathbf {S}$
contains at least one marked point.
$\partial \mathbf {S}$
contains at least one marked point.
A decorated marked surface
![]() ${\mathbf {S}}_\Delta $
(abbreviated as DMS) is obtained from a marked surface
${\mathbf {S}}_\Delta $
(abbreviated as DMS) is obtained from a marked surface
![]() $\mathbf {S}$
by decorating it with a set
$\mathbf {S}$
by decorating it with a set
![]() $\Delta = \{z_i\}_{i=1}^r$
of points in the surface interior
$\Delta = \{z_i\}_{i=1}^r$
of points in the surface interior
![]() $\mathbf {S}^\circ $
. These points are called finite critical points or finite singularities.
$\mathbf {S}^\circ $
. These points are called finite critical points or finite singularities.
An open arc is an (isotopty class of) curve
![]() $\gamma \colon I\to {\mathbf {S}}_\Delta $
such that its interior is in
$\gamma \colon I\to {\mathbf {S}}_\Delta $
such that its interior is in
![]() ${\mathbf {S}}_\Delta ^\circ \setminus \Delta $
and its endpoints are in the set of marked points
${\mathbf {S}}_\Delta ^\circ \setminus \Delta $
and its endpoints are in the set of marked points
![]() ${\mathbb M}$
. An (open) arc system
${\mathbb M}$
. An (open) arc system
![]() $\{\gamma _i\}$
is a collection of open arcs on
$\{\gamma _i\}$
is a collection of open arcs on
![]() ${\mathbf {S}}_\Delta $
such that there is no (self-)intersection between any of them in
${\mathbf {S}}_\Delta $
such that there is no (self-)intersection between any of them in
![]() ${\mathbf {S}}_\Delta ^\circ \setminus \Delta $
. A triangulation
${\mathbf {S}}_\Delta ^\circ \setminus \Delta $
. A triangulation
![]() ${\mathbb T}$
of
${\mathbb T}$
of
![]() ${\mathbf {S}}_\Delta $
is a maximal arc system of open arcs, which, in fact, divide
${\mathbf {S}}_\Delta $
is a maximal arc system of open arcs, which, in fact, divide
![]() ${\mathbf {S}}_\Delta $
into triangles.
${\mathbf {S}}_\Delta $
into triangles.
The quiver
![]() $Q_{\mathbb T}$
with potential
$Q_{\mathbb T}$
with potential
![]() $W_{\mathbb T}$
associated to a triangulation
$W_{\mathbb T}$
associated to a triangulation
![]() ${\mathbb T}$
is constructed as follows. The vertices correspond to the open arcs in
${\mathbb T}$
is constructed as follows. The vertices correspond to the open arcs in
![]() ${\mathbb T}$
, the arrows of
${\mathbb T}$
, the arrows of
![]() $Q_{\mathbb T}$
correspond to oriented intersection between open arcs in
$Q_{\mathbb T}$
correspond to oriented intersection between open arcs in
![]() ${\mathbb T}$
, so that there is a 3-cycle in
${\mathbb T}$
, so that there is a 3-cycle in
![]() $Q_{\mathbb T}$
locally in each triangle, and the potential
$Q_{\mathbb T}$
locally in each triangle, and the potential
![]() $W_{\mathbb T}$
is the sum of all such
$W_{\mathbb T}$
is the sum of all such
![]() $3$
-cycles.
$3$
-cycles.
For a fixed initial triangulation
![]() ${\mathbb T}_0$
, we denote by
${\mathbb T}_0$
, we denote by
![]() $\Gamma _{{\mathbb T}_0} = \Gamma (Q_{{\mathbb T}_0}, W_{{\mathbb T}_0})$
the Ginzburg algebra associated with the quiver associated with
$\Gamma _{{\mathbb T}_0} = \Gamma (Q_{{\mathbb T}_0}, W_{{\mathbb T}_0})$
the Ginzburg algebra associated with the quiver associated with
![]() ${\mathbb T}_0$
we let
${\mathbb T}_0$
we let
![]() ${\mathcal D}^3_{Q_{{\mathbb T}_0}} = \operatorname {pvd}(\Gamma _{{\mathbb T}_0})$
or simply
${\mathcal D}^3_{Q_{{\mathbb T}_0}} = \operatorname {pvd}(\Gamma _{{\mathbb T}_0})$
or simply
![]() $\mathcal {D}^{3}_{Q}$
the corresponding
$\mathcal {D}^{3}_{Q}$
the corresponding
![]() $CY_3$
-category. Finally, we define
$CY_3$
-category. Finally, we define ![]() to be the connected component of the space of Bridgeland stability conditions on
to be the connected component of the space of Bridgeland stability conditions on
![]() $\mathcal {D}^{3}_{Q}$
containing stability conditions supported on the standard heart
$\mathcal {D}^{3}_{Q}$
containing stability conditions supported on the standard heart
![]() ${\mathcal H}_0$
of
${\mathcal H}_0$
of
![]() $Q_{{\mathbb T}_0}$
.
$Q_{{\mathbb T}_0}$
.
In this paper, we fix throughout a DMS
![]() $\mathbf {S}$
of type
$\mathbf {S}$
of type
![]() $A_n$
. It is a disc with
$A_n$
. It is a disc with
![]() $b=1$
boundary component, which has
$b=1$
boundary component, which has
![]() $n+3$
marked points,
$n+3$
marked points,
![]() $r= n+1$
finite critical points in its interior, and no punctures. We use this reference surface and a reference triangulation on it to define the component
$r= n+1$
finite critical points in its interior, and no punctures. We use this reference surface and a reference triangulation on it to define the component ![]() . Recall from [Reference Bridgeland and SmithBS15, Theorem 9.9 and Section 12.1] that the subgroup
. Recall from [Reference Bridgeland and SmithBS15, Theorem 9.9 and Section 12.1] that the subgroup ![]() preserving a connected component of
preserving a connected component of ![]() is an extension of
is an extension of
![]() $\mathbb {Z}/(n+3)\mathbb {Z}$
by the spherical twist group
$\mathbb {Z}/(n+3)\mathbb {Z}$
by the spherical twist group
![]() $\operatorname {ST}(A_n)$
.
$\operatorname {ST}(A_n)$
.
In this language, the main theorem of Bridgeland-Smith (for a general
![]() $CY_3$
-quiver category
$CY_3$
-quiver category
![]() $\mathcal {D}^{3}_{Q}$
associated with a triangulation of
$\mathcal {D}^{3}_{Q}$
associated with a triangulation of
![]() ${\mathbf {S}}_\Delta $
, see [Reference Bridgeland and SmithBS15] for the excluded cases) reads:
${\mathbf {S}}_\Delta $
, see [Reference Bridgeland and SmithBS15] for the excluded cases) reads:
Theorem 3.1 [Reference Bridgeland and SmithBS15; Reference King and QiuKQ20]
There is an isomorphism of complex manifolds
This map K is equivariant with respect to the action of the mapping class group
![]() $\operatorname {MCG}(\mathbf {S}_{\Delta })$
on the domain and of the automorphism group
$\operatorname {MCG}(\mathbf {S}_{\Delta })$
on the domain and of the automorphism group ![]() on the range. These groups act properly discontinuously on domain, resp. range.
on the range. These groups act properly discontinuously on domain, resp. range.
Here,
![]() $\operatorname {FQuad}^\circ (\mathbf {S}_{\Delta })$
is a space of framed quadratic differentials with simple zeros at
$\operatorname {FQuad}^\circ (\mathbf {S}_{\Delta })$
is a space of framed quadratic differentials with simple zeros at
![]() $\Delta $
, whose definition we recall along with the examples in Section 6. Its generalization to nonsimple zeros motivates the notion of collapse and the use of quotient categories, which we recall in Section 3.2.
$\Delta $
, whose definition we recall along with the examples in Section 6. Its generalization to nonsimple zeros motivates the notion of collapse and the use of quotient categories, which we recall in Section 3.2.
As a technical tool, we introduce the exchange graph
![]() $\operatorname {EG}({\mathbf {S}}_\Delta )$
, the directed graph whose vertices are the triangulations of
$\operatorname {EG}({\mathbf {S}}_\Delta )$
, the directed graph whose vertices are the triangulations of
![]() ${\mathbf {S}}_\Delta $
and whose edges are given by (forward) flips of the triangulation. The exchange graph
${\mathbf {S}}_\Delta $
and whose edges are given by (forward) flips of the triangulation. The exchange graph
![]() $\operatorname {EG}({\mathcal D})$
of a triangulated category is the directed graph whose vertices are the finite hearts and whose edges are given by forward tilts at simples in the heart. We denote by
$\operatorname {EG}({\mathcal D})$
of a triangulated category is the directed graph whose vertices are the finite hearts and whose edges are given by forward tilts at simples in the heart. We denote by
![]() $\operatorname {EG}^\circ ({\mathbf {S}}_\Delta )$
the connected component containing the initial triangulation
$\operatorname {EG}^\circ ({\mathbf {S}}_\Delta )$
the connected component containing the initial triangulation
![]() ${\mathbb T}_0$
and by
${\mathbb T}_0$
and by
![]() $\operatorname {EG}^\circ (\mathcal {D}^{3}_{Q})$
the connected component corresponding to the standard heart
$\operatorname {EG}^\circ (\mathcal {D}^{3}_{Q})$
the connected component corresponding to the standard heart
![]() $\mod \mathcal J(Q_{{\mathbb T}_0}, W_{{\mathbb T}_0})$
. A key step in the proof of Theorem 3.1 is the isomorphism
$\mod \mathcal J(Q_{{\mathbb T}_0}, W_{{\mathbb T}_0})$
. A key step in the proof of Theorem 3.1 is the isomorphism
of exchange graphs.
3.2 Stability manifolds of certain quotient categories
Higher order zeros are modeled by the collapse of a subsurface
![]() $\Sigma \subset {\mathbf {S}}_\Delta $
in a DMS. We use this to deduce information on certain components of the stability manifold of the quotient categories
$\Sigma \subset {\mathbf {S}}_\Delta $
in a DMS. We use this to deduce information on certain components of the stability manifold of the quotient categories
![]() $\mathcal {D}^{3}_{Q} / {\mathcal {D}^3_{Q_I}}$
. We decompose
$\mathcal {D}^{3}_{Q} / {\mathcal {D}^3_{Q_I}}$
. We decompose
![]() $\Sigma $
into connected components
$\Sigma $
into connected components
![]() $\Sigma _i$
, and we provide each boundary component of
$\Sigma _i$
, and we provide each boundary component of
![]() $\Sigma _i$
with an integer enhancement
$\Sigma _i$
with an integer enhancement
![]() $\kappa _{ij}$
. To match the hypothesis with [Reference Barbieri, Möller, Qiu and SoBMQS22], we suppose throughout that
$\kappa _{ij}$
. To match the hypothesis with [Reference Barbieri, Möller, Qiu and SoBMQS22], we suppose throughout that
![]() $\kappa _{ij} \geq 3$
and consider
$\kappa _{ij} \geq 3$
and consider
![]() $\Sigma $
as a marked surface with
$\Sigma $
as a marked surface with
![]() $\kappa _{ij}$
points on each boundary component.
$\kappa _{ij}$
points on each boundary component.
To topologically formalize the collapse of
![]() $\Sigma $
, we define a weighted DMS (wDMS for short) to be a DMS with a weight function
$\Sigma $
, we define a weighted DMS (wDMS for short) to be a DMS with a weight function
![]() $\mathbf {w}: \Delta \to \mathbb {Z}_{\geq -1}$
, where the total weight is required to be
$\mathbf {w}: \Delta \to \mathbb {Z}_{\geq -1}$
, where the total weight is required to be
![]() $||\mathbf {w}|| = 4g-4 + |{\mathbb M}|+2b$
. Contracting
$||\mathbf {w}|| = 4g-4 + |{\mathbb M}|+2b$
. Contracting
![]() $\Sigma \subset {\mathbf {S}}_\Delta $
and replacing each boundary component by a decoration point in
$\Sigma \subset {\mathbf {S}}_\Delta $
and replacing each boundary component by a decoration point in
![]() $\Delta $
with weight
$\Delta $
with weight
![]() $\mathbf {w}_{ij} = \kappa _{ij}-2$
defines a wDMS that we usually denote by
$\mathbf {w}_{ij} = \kappa _{ij}-2$
defines a wDMS that we usually denote by
![]() $\overline {{\mathbf {S}}}_{\mathbf {w}}$
. In the sequel (as in [Reference Barbieri, Möller, Qiu and SoBMQS22]), we restrict to the case of no punctures
$\overline {{\mathbf {S}}}_{\mathbf {w}}$
. In the sequel (as in [Reference Barbieri, Möller, Qiu and SoBMQS22]), we restrict to the case of no punctures
![]() $p=0$
, no unmarked boundary components and
$p=0$
, no unmarked boundary components and
![]() $\mathbf {w}: \Delta \to \mathbb {Z}_{\geq 1}$
.
$\mathbf {w}: \Delta \to \mathbb {Z}_{\geq 1}$
.
To categorify the collapse, we homotope the initial triangulation
![]() ${\mathbb T}_0$
such that the arcs intersect the boundary of
${\mathbb T}_0$
such that the arcs intersect the boundary of
![]() $\Sigma $
in the marked points and such that
$\Sigma $
in the marked points and such that
![]() ${\mathbb T}_0|_\Sigma $
is a triangulation of this subsurface. In this way,
${\mathbb T}_0|_\Sigma $
is a triangulation of this subsurface. In this way,
![]() $\Sigma $
becomes a DMS with a triangulation, and we may form the
$\Sigma $
becomes a DMS with a triangulation, and we may form the
![]() $CY_3$
-category
$CY_3$
-category
![]() ${\mathcal D}_3(\Sigma )$
. We define the Verdier quotient category
${\mathcal D}_3(\Sigma )$
. We define the Verdier quotient category
As in Section 3.1, there are two exchange graphs associated with this situation, one based on ‘flips’ and topology and the other based on tilts of hearts. The isomorphism (7) below between these graphs is one of reasons to work with the quotient categories.
A partial triangulation
![]() $\mathbb {A}$
of
$\mathbb {A}$
of
![]() $\overline {{\mathbf {S}}}_{\mathbf {w}}$
is a collection of open arcs that triangulates the subsurface of
$\overline {{\mathbf {S}}}_{\mathbf {w}}$
is a collection of open arcs that triangulates the subsurface of
![]() ${\mathbf {S}}_\Delta $
whose complement is homeomorphic to
${\mathbf {S}}_\Delta $
whose complement is homeomorphic to
![]() $\Sigma $
, and such that each boundary component
$\Sigma $
, and such that each boundary component
![]() $c_{ij}$
of
$c_{ij}$
of
![]() $\Sigma $
is homeomorphic in
$\Sigma $
is homeomorphic in
![]() $\overline {{\mathbf {S}}}_{\mathbf {w}} \setminus \mathbb {A}$
to a
$\overline {{\mathbf {S}}}_{\mathbf {w}} \setminus \mathbb {A}$
to a
![]() $(\kappa _{ij} = w_{ij}+2)$
-gon, possibly with ends points identified.
$(\kappa _{ij} = w_{ij}+2)$
-gon, possibly with ends points identified.
On the set of partial triangulation
![]() $\mathbb {A}$
, there is an operation of forward flip of an arc
$\mathbb {A}$
, there is an operation of forward flip of an arc
![]() $\gamma \in \mathbb {A}$
, defined by moving both endpoints counterclockwise one edge bounding the subsurface of
$\gamma \in \mathbb {A}$
, defined by moving both endpoints counterclockwise one edge bounding the subsurface of
![]() ${\mathbf {S}}_\Delta \setminus (\mathbb {A} \setminus \{\gamma \})$
that contains
${\mathbf {S}}_\Delta \setminus (\mathbb {A} \setminus \{\gamma \})$
that contains
![]() $\gamma $
. This generalizes the usual notion of flip of triangulations; see [Reference Barbieri, Möller, Qiu and SoBMQS22, Figure 2]. We define the exchange graph
$\gamma $
. This generalizes the usual notion of flip of triangulations; see [Reference Barbieri, Möller, Qiu and SoBMQS22, Figure 2]. We define the exchange graph
![]() $\operatorname {EG}(\overline {{\mathbf {S}}}_{\mathbf {w}})$
to be the (infinite) directed graph whose vertices are the partial triangulations of the decorated surface
$\operatorname {EG}(\overline {{\mathbf {S}}}_{\mathbf {w}})$
to be the (infinite) directed graph whose vertices are the partial triangulations of the decorated surface
![]() $\overline {{\mathbf {S}}}_{\mathbf {w}}$
and whose edges are given by forward flips.
$\overline {{\mathbf {S}}}_{\mathbf {w}}$
and whose edges are given by forward flips.
Definition 3.2. Let
![]() ${\mathcal V} \subset {\mathcal D}$
be a thick triangulated subcategory. We say that a heart
${\mathcal V} \subset {\mathcal D}$
be a thick triangulated subcategory. We say that a heart
![]() ${\mathcal A}$
of
${\mathcal A}$
of
![]() ${\mathcal D}$
is
${\mathcal D}$
is
![]() ${\mathcal V}$
-compatible if
${\mathcal V}$
-compatible if
![]() ${\mathcal A} \cap {\mathcal V}$
is a Serre subcategory of
${\mathcal A} \cap {\mathcal V}$
is a Serre subcategory of
![]() ${\mathcal A}$
.
${\mathcal A}$
.
We call a heart
![]() $\overline {{\mathcal A}}$
of
$\overline {{\mathcal A}}$
of
![]() ${\mathcal D}/{\mathcal V}$
of quotient type if there is a
${\mathcal D}/{\mathcal V}$
of quotient type if there is a
![]() ${\mathcal V}$
-compatible heart
${\mathcal V}$
-compatible heart
![]() ${\mathcal A}$
of
${\mathcal A}$
of
![]() ${\mathcal D}$
whose essential image in
${\mathcal D}$
whose essential image in
![]() ${\mathcal D}/{\mathcal V}$
is
${\mathcal D}/{\mathcal V}$
is
![]() $\overline {{\mathcal A}}$
.
$\overline {{\mathcal A}}$
.
We define the principal component
![]() $\operatorname {EG}^\bullet (\overline {{\mathbf {S}}}_{\mathbf {w}})$
to be the full subgraph of partial triangulations that admit a refinement to a triangulation in
$\operatorname {EG}^\bullet (\overline {{\mathbf {S}}}_{\mathbf {w}})$
to be the full subgraph of partial triangulations that admit a refinement to a triangulation in
![]() $\operatorname {EG}^\circ ({\mathbf {S}}_\Delta $
) (i.e., the full subgraph given by triangulations reachable by a finite number of flips from
$\operatorname {EG}^\circ ({\mathbf {S}}_\Delta $
) (i.e., the full subgraph given by triangulations reachable by a finite number of flips from
![]() ${\mathbb T}_0$
). We define the principal component
${\mathbb T}_0$
). We define the principal component
![]() $\operatorname {EG}^\bullet ({\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}}))$
to be the full subgraph of
$\operatorname {EG}^\bullet ({\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}}))$
to be the full subgraph of
![]() $\operatorname {EG}({\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}}))$
consisting of hearts of quotient type that admit a representative in the distiguished component
$\operatorname {EG}({\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}}))$
consisting of hearts of quotient type that admit a representative in the distiguished component
![]() $\operatorname {EG}^\circ ({\mathcal D}({\mathbf {S}}_\Delta ))$
. It is a priori not clear that these definitions yield connected components. This is proven along with [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 5.9], which moreover states that
$\operatorname {EG}^\circ ({\mathcal D}({\mathbf {S}}_\Delta ))$
. It is a priori not clear that these definitions yield connected components. This is proven along with [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 5.9], which moreover states that
and that both graphs are
![]() $(m,m)$
-regular.
$(m,m)$
-regular.
We now define the principal component of the stability manifold ![]() to be
to be

The terminology is justified by the following results:
Proposition 3.3 [Reference Barbieri, Möller, Qiu and SoBMQS22]
The space ![]() is union of connected components of
is union of connected components of ![]() .
.
Referring to Section 6 for the definition of framed quadratic differentials, we recall here the generalization of the Bridgeland-Smith isomorphism that serves as motivation for definition of multi-scale stability conditions using the comparison to compactification of strata; see Section 6.
Theorem 3.4 (Theorem 1.1 of [Reference Barbieri, Möller, Qiu and SoBMQS22])
There is an isomorphism of complex manifolds
between the principal part of the space of Teichmüller-framed quadratic differentials and the principal part of the space of stability conditions on
![]() ${\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}})$
.
${\mathcal D}(\overline {{\mathbf {S}}}_{\mathbf {w}})$
.
3.3 Braid groups and spherical twists
Motivated by the relation to groups of autoequivalences given in (17) and (18) below, we recall a few basic properties of the braid groups
![]() $B_{n+1}$
on
$B_{n+1}$
on
![]() $n+1$
strands; see, for example, [Reference Farb and MargalitFM12, Section 9]. The standard generators are the
$n+1$
strands; see, for example, [Reference Farb and MargalitFM12, Section 9]. The standard generators are the
![]() $\tau _i$
twisting the strands i and
$\tau _i$
twisting the strands i and
![]() $i+1$
. They satisfy the defining standard braid relations.
$i+1$
. They satisfy the defining standard braid relations.
The pure braid group is the kernel of the homomorphism recording the strand permutation – that is, sits in the exact sequence
The center of
![]() $B_{n+1}$
is cyclic, generated by the element
$B_{n+1}$
is cyclic, generated by the element
except for the case where of
![]() $n=1$
, since
$n=1$
, since
![]() $B_2$
is cyclic where thus
$B_2$
is cyclic where thus
![]() $\theta _2$
is the square of the generator. In all cases, the element
$\theta _2$
is the square of the generator. In all cases, the element
![]() $\theta _n$
as defined above also belongs to the pure braid group
$\theta _n$
as defined above also belongs to the pure braid group ![]() . As a special case of the Birman exact sequence, we obtain
. As a special case of the Birman exact sequence, we obtain
where
![]() $F_{n+1}$
is the free group on
$F_{n+1}$
is the free group on
![]() $n+1$
generators. This exact sequence is split by adding the extra strand. Iterating this, we obtain for each r consecutive integers a natural homomorphism
$n+1$
generators. This exact sequence is split by adding the extra strand. Iterating this, we obtain for each r consecutive integers a natural homomorphism
Via this homomorphism, we define for
![]() $I = \{1,\ldots ,r\}$
the elements
$I = \{1,\ldots ,r\}$
the elements
![]() $\theta _{I,n} := \varphi _{r,n} (\theta _r) \in B_{n+1}$
. These correspond to a full rotation of a disc encircling precisely the points in I.
$\theta _{I,n} := \varphi _{r,n} (\theta _r) \in B_{n+1}$
. These correspond to a full rotation of a disc encircling precisely the points in I.
More generally, we will define the braid group
![]() $B_Q$
associated with a quiver Q; see [Reference QiuQiu16, Definition 10.1 and Proposition 10.4]. It is generated by an element
$B_Q$
associated with a quiver Q; see [Reference QiuQiu16, Definition 10.1 and Proposition 10.4]. It is generated by an element
![]() $\widetilde \tau _i$
for each vertex of the quiver and defined by the relations
$\widetilde \tau _i$
for each vertex of the quiver and defined by the relations
 $$ \begin{align}\begin{aligned} \widetilde\tau_i\widetilde\tau_j\widetilde\tau_i\;=\;\widetilde\tau_j\widetilde\tau_i\widetilde\tau_j & \quad\text{if}\quad |i-j|=1\\ \widetilde\tau_i\widetilde\tau_j\;=\; \widetilde\tau_j\widetilde\tau_i &\quad \text{if}\quad |i-j|\geq 2, \\ R_i = R_j &\quad\text{for each cycle } 1 \to 2 \to \cdots \to m \to 1\,, \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \widetilde\tau_i\widetilde\tau_j\widetilde\tau_i\;=\;\widetilde\tau_j\widetilde\tau_i\widetilde\tau_j & \quad\text{if}\quad |i-j|=1\\ \widetilde\tau_i\widetilde\tau_j\;=\; \widetilde\tau_j\widetilde\tau_i &\quad \text{if}\quad |i-j|\geq 2, \\ R_i = R_j &\quad\text{for each cycle } 1 \to 2 \to \cdots \to m \to 1\,, \end{aligned}\end{align} $$
where
![]() $R_i = \widetilde \tau _i \widetilde \tau _{i+1} \cdots \widetilde \tau _m\widetilde \tau _1 \cdots \widetilde \tau _{i-1}$
. In the case
$R_i = \widetilde \tau _i \widetilde \tau _{i+1} \cdots \widetilde \tau _m\widetilde \tau _1 \cdots \widetilde \tau _{i-1}$
. In the case
![]() $Q=A_n$
, we retrieve the above definition of
$Q=A_n$
, we retrieve the above definition of
![]() $B_{A_n} = B_{n+1}$
. We will be most interested in the case that Q is of type
$B_{A_n} = B_{n+1}$
. We will be most interested in the case that Q is of type
![]() $A_n$
though not necessarily equal to
$A_n$
though not necessarily equal to
![]() $A_n$
. Suppose the vertices in the index set I form a subquiver of type
$A_n$
. Suppose the vertices in the index set I form a subquiver of type
![]() $A_r$
. Then the braid group of the restricted quiver
$A_r$
. Then the braid group of the restricted quiver
![]() $B_{Q_I} \cong B_{r+1}$
, and we let
$B_{Q_I} \cong B_{r+1}$
, and we let
![]() $\theta _r$
be its central element. Inclusion of strands again defines a natural homomorphism
$\theta _r$
be its central element. Inclusion of strands again defines a natural homomorphism
![]() $\varphi _{I,n}: B_{Q_I} \to B_{n+1}$
, and we define in this more general context
$\varphi _{I,n}: B_{Q_I} \to B_{n+1}$
, and we define in this more general context
![]() $\theta _{I,n} := \varphi _{I} (\theta _r)$
.
$\theta _{I,n} := \varphi _{I} (\theta _r)$
.
Given a quiver
![]() $(Q,W)$
and its Ginzburg algebra
$(Q,W)$
and its Ginzburg algebra
![]() $\Gamma $
, we let
$\Gamma $
, we let ![]() be the spherical twist group (see Seidel-Thomas [Reference Seidel and ThomasST01]) of
be the spherical twist group (see Seidel-Thomas [Reference Seidel and ThomasST01]) of
![]() $\operatorname {pvd}(\Gamma )$
– that is, the subgroup generated by the set of spherical twists
$\operatorname {pvd}(\Gamma )$
– that is, the subgroup generated by the set of spherical twists
![]() $\Phi _{S}$
for all simples S of
$\Phi _{S}$
for all simples S of
![]() $\Gamma $
, where the twist functor
$\Gamma $
, where the twist functor
![]() $\Phi _S$
is defined by
$\Phi _S$
is defined by
This uses that in the case
![]() ${\mathcal D} = \mathcal {D}^{3}_{Q}$
, as a consequence of [Reference King and QiuKQ15, Corollary 8.5], all the simples in any heart of
${\mathcal D} = \mathcal {D}^{3}_{Q}$
, as a consequence of [Reference King and QiuKQ15, Corollary 8.5], all the simples in any heart of
![]() ${\mathcal D}$
are spherical.
${\mathcal D}$
are spherical.
Remark 3.5. For a heart
![]() ${\mathcal A}$
with simples
${\mathcal A}$
with simples
![]() $S_1,...,S_n$
listed in an order such that
$S_1,...,S_n$
listed in an order such that
![]() $\dim (\operatorname {Ext}^1(S_j,S_i)) = 0$
for
$\dim (\operatorname {Ext}^1(S_j,S_i)) = 0$
for
![]() $j<i$
and
$j<i$
and
![]() $\dim (\operatorname {Ext}^1(S_i,S_j)) = 0$
for
$\dim (\operatorname {Ext}^1(S_i,S_j)) = 0$
for
![]() $j>i$
, the mutated heart
$j>i$
, the mutated heart
![]() $\mu _{S_i}^\sharp ({\mathcal A})$
has simples
$\mu _{S_i}^\sharp ({\mathcal A})$
has simples
compare [Reference Bridgeland and SmithBS15, Proof of Proposition 7.1]. Moreover,
We write
![]() $\operatorname {ST}(A_n)$
for spherical twist group of a quiver of type
$\operatorname {ST}(A_n)$
for spherical twist group of a quiver of type
![]() $A_n$
.
$A_n$
.
Proposition 3.6 [Reference Seidel and ThomasST01; Reference QiuQiu16; Reference QiuQiu18]
There is an isomorphism
![]() $\operatorname {ST}(\Gamma )\cong B_Q$
between the twist groups, sending the standard generators
$\operatorname {ST}(\Gamma )\cong B_Q$
between the twist groups, sending the standard generators
![]() $\tau _i \to \Phi _{S_i}$
to the standard generators. In particular, the group
$\tau _i \to \Phi _{S_i}$
to the standard generators. In particular, the group
![]() $\operatorname {ST}(A_n)$
is isomorphic to the braid group
$\operatorname {ST}(A_n)$
is isomorphic to the braid group
![]() $B_{n+1}$
.
$B_{n+1}$
.
We now apply this to understand the groups of autoequivalences for
![]() ${\mathcal D} = \operatorname {pvd}(\Gamma )$
. By [Reference Bridgeland and SmithBS15, Theorem 9.9], there is an exact sequence
${\mathcal D} = \operatorname {pvd}(\Gamma )$
. By [Reference Bridgeland and SmithBS15, Theorem 9.9], there is an exact sequence
where ![]() is the quotient of
is the quotient of
![]() $\operatorname {ST}(\mathcal {D}^{3}_{Q})$
by its subgroup of negligible automorphisms. In the special case
$\operatorname {ST}(\mathcal {D}^{3}_{Q})$
by its subgroup of negligible automorphisms. In the special case
![]() $\mathcal {D}^{3}_{Q} = D^3_{A_n}$
, the mapping class group is
$\mathcal {D}^{3}_{Q} = D^3_{A_n}$
, the mapping class group is
![]() $\operatorname {MCG}(\overline {\Delta },{\mathbb M}_{n+3}) \cong \mathbb {Z}/(n+3)$
, so there is an exact sequence
$\operatorname {MCG}(\overline {\Delta },{\mathbb M}_{n+3}) \cong \mathbb {Z}/(n+3)$
, so there is an exact sequence
See, for example, [Reference Bridgeland and SmithBS15, Section 12.1].
In Section 5.3, we need the following action on Grothedieck groups to control the effect of the action of
![]() $\theta _{I,n}$
.
$\theta _{I,n}$
.
Lemma 3.7 [Reference IkedaIke17, Section 4]
On
![]() $K(\mathcal {D}^{3}_{Q})$
, a spherical twist
$K(\mathcal {D}^{3}_{Q})$
, a spherical twist
![]() $\Phi _{S_i}$
induces a group homomorphism
$\Phi _{S_i}$
induces a group homomorphism
![]() $[\Phi _i]$
defined by
$[\Phi _i]$
defined by
where
![]() $\chi (\cdot ,\cdot )$
denotes the Euler pairing.
$\chi (\cdot ,\cdot )$
denotes the Euler pairing.
4 Multi-scale stability conditions
We start with a definition that makes sense for general triangulated categories with finite rank Grothendieck group. We will then define a
![]() $\mathbb {C}$
-action and a notion of plumbing stability conditions that will be used to give a topology on the set of multi-scale stability conditions. In all these steps, we have to be much more restrictive, essentially restricting to
$\mathbb {C}$
-action and a notion of plumbing stability conditions that will be used to give a topology on the set of multi-scale stability conditions. In all these steps, we have to be much more restrictive, essentially restricting to
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
. We indicate the technical difficulties needed to overcome in order to generalize to
${\mathcal D} = {\mathcal D}^3_{A_n}$
. We indicate the technical difficulties needed to overcome in order to generalize to
![]() $CY_3$
-quiver categories or beyond.
$CY_3$
-quiver categories or beyond.
Definition 4.1. Let
![]() ${\mathcal D}$
a triangulated category with
${\mathcal D}$
a triangulated category with
![]() $\mathrm {rank}(K({\mathcal D})) < \infty $
. A multi-scale stability condition on
$\mathrm {rank}(K({\mathcal D})) < \infty $
. A multi-scale stability condition on
![]() ${\mathcal D}$
consists of an equivalence class of the following data:
${\mathcal D}$
consists of an equivalence class of the following data:
-
○ a multi-scale heart
 $\mathcal {A}_\bullet = (\mathcal {A}_i)$
– that is, a collection
$\mathcal {A}_\bullet = (\mathcal {A}_i)$
– that is, a collection
 $\mathcal {A}_L \subset \cdots \mathcal {A}_1 \subset \mathcal {A}_0$
of abelian categories), and
$\mathcal {A}_L \subset \cdots \mathcal {A}_1 \subset \mathcal {A}_0$
of abelian categories), and -
○ a multi-scale central charge – that is, a collection
 $Z_\bullet = (Z_i)_{i=0}^L$
of nonzero
$Z_\bullet = (Z_i)_{i=0}^L$
of nonzero  -linear maps on the Grothendieck groups
-linear maps on the Grothendieck groups
 $Z_i: K(\mathcal {A}_i) \to \mathbb {C}$
,
$Z_i: K(\mathcal {A}_i) \to \mathbb {C}$
,
with the property that
-
○ the abelian category
 $\mathcal {A}_i$
is generated by the nonzero objects E in
$\mathcal {A}_i$
is generated by the nonzero objects E in
 $\mathcal {A}_{i-1}$
with
$\mathcal {A}_{i-1}$
with
 $Z_{i-1}(E)=0$
for all
$Z_{i-1}(E)=0$
for all
 $i \geq 1$
,
$i \geq 1$
, -
○ the abelian category
 $\mathcal {A}_i$
is a heart of
$\mathcal {A}_i$
is a heart of
 ${\mathcal V}_i$
, which is defined as
${\mathcal V}_i$
, which is defined as
 ${\mathcal V}_0 = {\mathcal D}$
and for all
${\mathcal V}_0 = {\mathcal D}$
and for all
 $i \geq 1$
as the thick triangulated subcategory of
$i \geq 1$
as the thick triangulated subcategory of
 ${\mathcal V}_{i-1}$
generated by
${\mathcal V}_{i-1}$
generated by
 ${\mathcal A}_i$
,
${\mathcal A}_i$
, -
○ the map
 $Z_i$
factors through
$Z_i$
factors through
 $K_{i-1} := \operatorname {Ker}(Z_{i-1})$
,
$K_{i-1} := \operatorname {Ker}(Z_{i-1})$
, -
○ the induced heart
 $\overline {\mathcal {A}}_i = \mathcal {A}_i/\mathcal {A}_{i+1}$
together with the induced central charge
$\overline {\mathcal {A}}_i = \mathcal {A}_i/\mathcal {A}_{i+1}$
together with the induced central charge
 $\overline {Z_i}: K({\mathcal V}_i/{\mathcal V}_{i+1}) \to \mathbb {C}$
form a stability condition in the usual sense on
$\overline {Z_i}: K({\mathcal V}_i/{\mathcal V}_{i+1}) \to \mathbb {C}$
form a stability condition in the usual sense on
 ${\mathcal V}_i/{\mathcal V}_{i+1}$
for all
${\mathcal V}_i/{\mathcal V}_{i+1}$
for all
 $i=0,\ldots ,L$
.
$i=0,\ldots ,L$
.
Two multi-scale stability conditions
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
and
$(\mathcal {A}_\bullet ,Z_\bullet )$
and
![]() $(\mathcal {A}_\bullet ^{\prime },Z_\bullet ^{\prime })$
are equivalent if
$(\mathcal {A}_\bullet ^{\prime },Z_\bullet ^{\prime })$
are equivalent if
-
i) there is equality of triangulated categories
 $\mathcal {V}_i = \mathcal {V}_i^{\prime }$
for
$\mathcal {V}_i = \mathcal {V}_i^{\prime }$
for
 $i=0,\ldots L$
,
$i=0,\ldots L$
, -
ii) the induced stability conditions
 $(\overline {A_i},\overline {Z}_i)$
and
$(\overline {A_i},\overline {Z}_i)$
and
 $(\overline {A_i}',\overline {Z}_i^{\prime })$
are projectively equivalent for
$(\overline {A_i}',\overline {Z}_i^{\prime })$
are projectively equivalent for
 $i=1,\ldots ,L$
, and are equal for
$i=1,\ldots ,L$
, and are equal for
 $i=0$
.
$i=0$
.
Two multi-scale stability conditions
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
and
$(\mathcal {A}_\bullet ,Z_\bullet )$
and
![]() $(\mathcal {A}_\bullet ^{\prime },Z_\bullet ^{\prime })$
are projectively equivalent if the projective equivalence in ii) above holds for
$(\mathcal {A}_\bullet ^{\prime },Z_\bullet ^{\prime })$
are projectively equivalent if the projective equivalence in ii) above holds for
![]() $i=0,\ldots ,L$
.
$i=0,\ldots ,L$
.
We write
![]() $[{\mathcal A}_\bullet ,Z_\bullet ]$
for an equivalence class, and
$[{\mathcal A}_\bullet ,Z_\bullet ]$
for an equivalence class, and
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
for a representative of a multi-scale stability condition. Moreover, we denote by
$({\mathcal A}_\bullet ,Z_\bullet )$
for a representative of a multi-scale stability condition. Moreover, we denote by
![]() ${\mathcal V}_\bullet $
the collection of nested triangulated subcategories
${\mathcal V}_\bullet $
the collection of nested triangulated subcategories
![]() $({\mathcal V}_i)$
defined by
$({\mathcal V}_i)$
defined by
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
. Sometimes write
$({\mathcal A}_\bullet ,Z_\bullet )$
. Sometimes write
![]() ${\mathcal V}_i^Z$
for the categories
${\mathcal V}_i^Z$
for the categories
![]() ${\mathcal V}_i$
defined above to indicate the dependence on
${\mathcal V}_i$
defined above to indicate the dependence on
![]() $Z_\bullet $
.
$Z_\bullet $
.
The definition relies on the following lemma for the quotient hearts to be meaningful.
Lemma 4.2. The subcategory
![]() ${\mathcal A}_{i+1}$
is Serre in
${\mathcal A}_{i+1}$
is Serre in
![]() ${\mathcal A}_i$
and
${\mathcal A}_i$
and
![]() ${\mathcal A}_{i+1} = {\mathcal V}_{i+1} \cap \mathcal {A}_i$
for all i (i.e.,
${\mathcal A}_{i+1} = {\mathcal V}_{i+1} \cap \mathcal {A}_i$
for all i (i.e.,
![]() ${\mathcal A}_{i+1}$
is
${\mathcal A}_{i+1}$
is
![]() ${\mathcal V}_{i+1}$
-compatible in the sense of Definition 3.2). In particular, the inclusion
${\mathcal V}_{i+1}$
-compatible in the sense of Definition 3.2). In particular, the inclusion
![]() $\iota : {\mathcal V}_{i+1}\to {\mathcal V}_i$
is t-exact with respect to
$\iota : {\mathcal V}_{i+1}\to {\mathcal V}_i$
is t-exact with respect to
![]() ${\mathcal A}_{i+1}$
and
${\mathcal A}_{i+1}$
and
![]() ${\mathcal A}_i$
, and
${\mathcal A}_i$
, and
![]() ${\mathcal A}_i$
induces a quotient heart in
${\mathcal A}_i$
induces a quotient heart in
![]() ${\mathcal V}_i /{\mathcal V}_{i+1}$
. Moreover,
${\mathcal V}_i /{\mathcal V}_{i+1}$
. Moreover,
![]() $K({\mathcal V}_i/{\mathcal V}_{i+1})=K_i/K_{i+1}$
so that
$K({\mathcal V}_i/{\mathcal V}_{i+1})=K_i/K_{i+1}$
so that
![]() $Z_i$
descends to
$Z_i$
descends to
![]() $\overline {Z_i}$
, as required.
$\overline {Z_i}$
, as required.
Proof. Serreness of
![]() ${\mathcal A}_{i+1}\subset {\mathcal A}_i$
follows from the additivity of
${\mathcal A}_{i+1}\subset {\mathcal A}_i$
follows from the additivity of
![]() $Z_i$
on short exact sequences and the fact that
$Z_i$
on short exact sequences and the fact that
![]() $Z_i$
takes values in a strictly convex sector in
$Z_i$
takes values in a strictly convex sector in
![]() ${\mathbb C}$
. The second statement follows from the observation that
${\mathbb C}$
. The second statement follows from the observation that
![]() $Z_i(X) = 0$
for any
$Z_i(X) = 0$
for any
![]() $X \in {\mathcal V}_{i+1}$
. Serreness of
$X \in {\mathcal V}_{i+1}$
. Serreness of
![]() ${\mathcal A}_{i+1}\subset {\mathcal A}_i$
guarantees that
${\mathcal A}_{i+1}\subset {\mathcal A}_i$
guarantees that
![]() ${\mathcal V}_{i+1}$
consists on objects of
${\mathcal V}_{i+1}$
consists on objects of
![]() ${\mathcal V}_i$
whose cohomology with respect to
${\mathcal V}_i$
whose cohomology with respect to
![]() ${\mathcal A}_i$
is concentrated in
${\mathcal A}_i$
is concentrated in
![]() ${\mathcal A}_{i+1}$
, and that the t-structure restricts, so the next claim follows from [Reference Antieau, Gepner and HellerAGH19, Proposition 2.20] or [Reference Chuang and RouquierCR17, Lemma 3.3]. For the last, observe that
${\mathcal A}_{i+1}$
, and that the t-structure restricts, so the next claim follows from [Reference Antieau, Gepner and HellerAGH19, Proposition 2.20] or [Reference Chuang and RouquierCR17, Lemma 3.3]. For the last, observe that
![]() $K_{i+1}$
is the image of
$K_{i+1}$
is the image of
![]() $\iota _*:K({\mathcal A}_{i+1})\to K_i$
and that the right exact sequence
$\iota _*:K({\mathcal A}_{i+1})\to K_i$
and that the right exact sequence
![]() $K({\mathcal A}_{i+1})\to K({\mathcal A}_i)\to K({\mathcal A}_i/{\mathcal A}_{i+1}) \to 0$
is used to compute the Grothendieck group of the quotient category.
$K({\mathcal A}_{i+1})\to K({\mathcal A}_i)\to K({\mathcal A}_i/{\mathcal A}_{i+1}) \to 0$
is used to compute the Grothendieck group of the quotient category.
Let
![]() $\operatorname {MStab}({\mathcal D})$
be the set of all multi-scale stability conditions on
$\operatorname {MStab}({\mathcal D})$
be the set of all multi-scale stability conditions on
![]() ${\mathcal D}$
. The integer L in Definition 4.1 will be referred to as the number of levels below zero of the stability condition. A usual stability condition has
${\mathcal D}$
. The integer L in Definition 4.1 will be referred to as the number of levels below zero of the stability condition. A usual stability condition has
![]() $L=0$
.
$L=0$
.
Reachability
We now fix a component ![]() of the stability manifold of
of the stability manifold of
![]() ${\mathcal D}$
. If
${\mathcal D}$
. If
![]() ${\mathcal D} = \mathcal {D}^{3}_{Q_{3}}$
is a quiver category, we use an initial triangulation
${\mathcal D} = \mathcal {D}^{3}_{Q_{3}}$
is a quiver category, we use an initial triangulation
![]() ${\mathbb T}_0$
of a DMS as in Section 3.1 to single out this components.
${\mathbb T}_0$
of a DMS as in Section 3.1 to single out this components.
A multi-scale stability condition
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
is called reachable if the top level heart
$(\mathcal {A}_\bullet ,Z_\bullet )$
is called reachable if the top level heart
![]() ${\mathcal A}_0$
supports stability conditions in
${\mathcal A}_0$
supports stability conditions in ![]() . We denote the set of all reachable multi-scale stability conditions on
. We denote the set of all reachable multi-scale stability conditions on
![]() ${\mathcal D}$
by
${\mathcal D}$
by
![]() $\operatorname {MStab}^\circ ({\mathcal D})$
, and the set of reachable multi-scale stability conditions with the same
$\operatorname {MStab}^\circ ({\mathcal D})$
, and the set of reachable multi-scale stability conditions with the same
![]() ${\mathcal V}_\bullet $
by
${\mathcal V}_\bullet $
by
![]() $\operatorname {MStab}^\circ ({\mathcal D}, {\mathcal V}_\bullet )$
.
$\operatorname {MStab}^\circ ({\mathcal D}, {\mathcal V}_\bullet )$
.
In the next section, we will informally call a multi-scaled stability conditions with at least one level below zero a boundary point, and finally prove this is actually the case.
Groups of autoequivalences
For general
![]() ${\mathcal D}$
, we define the group
${\mathcal D}$
, we define the group ![]() to be the autoequivalences that stabilize
to be the autoequivalences that stabilize
![]() ${\mathcal V}$
. For
${\mathcal V}$
. For
![]() ${\mathcal D} = \mathcal {D}^{3}_{Q}$
, we use bullets to denote those autoequivalences that moreover stabilize the principal components defined in Section 3.2.
${\mathcal D} = \mathcal {D}^{3}_{Q}$
, we use bullets to denote those autoequivalences that moreover stabilize the principal components defined in Section 3.2.
Lemma 4.3. The factor group
acts properly discontinuously on ![]() .
.
The stabilizer ![]() of a projectivized stability condition
of a projectivized stability condition
![]() $[\sigma ]$
is a finite extension of a subgroup Z in the center of
$[\sigma ]$
is a finite extension of a subgroup Z in the center of ![]() . In case
. In case
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
, the group Z is the center, generated by
${\mathcal D} = {\mathcal D}^3_{A_n}$
, the group Z is the center, generated by
![]() $\theta _n$
defined in (11).
$\theta _n$
defined in (11).
Proof. The first statement is shown in the proof of [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorems 8.1, 8.2], summarized here in Theorem 3.4 (see, in particular, the part about the orbifold structure, together with Equation (5.7)).
For the second statement we may pass, thanks to the first statement, to the finite index subgroup of the stabilizer
![]() $H_{[\sigma ]}$
of a projective stability condition that acts trivially on a neighborhood of the unprojectivized
$H_{[\sigma ]}$
of a projective stability condition that acts trivially on a neighborhood of the unprojectivized
![]() $\sigma $
. As in the proof of [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorems 8.2], since the action of
$\sigma $
. As in the proof of [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorems 8.2], since the action of
![]() $\mathbb {C}$
and
$\mathbb {C}$
and ![]() commute, the second statement follows. The last claim is a restatement of braid group properties from Section 3.3.
commute, the second statement follows. The last claim is a restatement of braid group properties from Section 3.3.
4.1 Numerical data of multi-scale stability conditions of type
 $A_n$
$A_n$
From here on, we restrict to the case
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
. In this case, we can completely describe the subcategories and hearts that appear in a multi-scale stability condition.
${\mathcal D} = {\mathcal D}^3_{A_n}$
. In this case, we can completely describe the subcategories and hearts that appear in a multi-scale stability condition.
Lemma 4.4. If
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
is a multi-scale stability condition and
$(\mathcal {A}_\bullet ,Z_\bullet )$
is a multi-scale stability condition and
![]() ${\mathcal A}_0=\operatorname {mod} \mathcal J_Q$
, then
${\mathcal A}_0=\operatorname {mod} \mathcal J_Q$
, then
![]() ${\mathcal A}_{1}=\operatorname {mod} \mathcal J_{Q_{I}}$
, where I is a subset of the vertices of
${\mathcal A}_{1}=\operatorname {mod} \mathcal J_{Q_{I}}$
, where I is a subset of the vertices of
![]() $\mathcal Q$
, and
$\mathcal Q$
, and
![]() ${\mathcal V}_1 = \operatorname {pvd} \Gamma _I$
.
${\mathcal V}_1 = \operatorname {pvd} \Gamma _I$
.
Moreover, there is a bijection of the subcategories
![]() ${\mathcal V}_1^Z$
with homotopy classes of decorated marked subsurfaces
${\mathcal V}_1^Z$
with homotopy classes of decorated marked subsurfaces
![]() $\Sigma \subset {\mathbf {S}}_\Delta $
, such that each component
$\Sigma \subset {\mathbf {S}}_\Delta $
, such that each component
![]() $\Sigma _j$
for
$\Sigma _j$
for
![]() $j \in J$
is of type
$j \in J$
is of type
![]() $A_{n_j}$
(i.e., a disc with
$A_{n_j}$
(i.e., a disc with
![]() $n_j+1$
decoration points in its interior and
$n_j+1$
decoration points in its interior and
![]() $n_j+3$
marked points at its boundary). Here,
$n_j+3$
marked points at its boundary). Here,
![]() $n_j \geq 1$
and the decomposition is constrained precisely by
$n_j \geq 1$
and the decomposition is constrained precisely by
![]() $\sum _{j \in J} (n_j+1) \leq n + 1$
, where equality is allowed if and only if
$\sum _{j \in J} (n_j+1) \leq n + 1$
, where equality is allowed if and only if
![]() $|J| \geq 2$
.
$|J| \geq 2$
.
Using this notation, we say that
![]() ${\mathcal V}_1^Z$
is a subcategory of type
${\mathcal V}_1^Z$
is a subcategory of type
![]() $\rho := (n_1,\ldots ,n_{|J|})$
. Iterating this over all
$\rho := (n_1,\ldots ,n_{|J|})$
. Iterating this over all
![]() ${\mathcal V}_i$
appearing in a multi-scale stability condition, we say that
${\mathcal V}_i$
appearing in a multi-scale stability condition, we say that
![]() $[{\mathcal A}_\bullet ,Z_\bullet ]$
is of type
$[{\mathcal A}_\bullet ,Z_\bullet ]$
is of type
![]() ${\boldsymbol {\rho }} = (\rho _i)_{i=1}^L$
, where
${\boldsymbol {\rho }} = (\rho _i)_{i=1}^L$
, where
![]() $\rho _i$
is the type of
$\rho _i$
is the type of
![]() ${\mathcal V}_i$
.
${\mathcal V}_i$
.
Proof. Consider
![]() ${\mathcal A}_1 \subset {\mathcal V}_1^{Z}$
. Since
${\mathcal A}_1 \subset {\mathcal V}_1^{Z}$
. Since
![]() ${\mathcal A}_1 \subset {\mathcal A}_0$
is Serre, it is generated by a subset
${\mathcal A}_1 \subset {\mathcal A}_0$
is Serre, it is generated by a subset
![]() $\mathcal S_1 \subset \operatorname {Sim}({\mathcal A}_0)$
of the simples of
$\mathcal S_1 \subset \operatorname {Sim}({\mathcal A}_0)$
of the simples of
![]() ${\mathcal A}_0$
, those whose
${\mathcal A}_0$
, those whose
![]() $Z_0$
-image is zero. By the correspondence summarized in Section 2.4, this defines the subquiver
$Z_0$
-image is zero. By the correspondence summarized in Section 2.4, this defines the subquiver
![]() $Q_I$
and shows
$Q_I$
and shows
![]() ${\mathcal A}_{1}=\operatorname {mod} \mathcal J_{I}$
.
${\mathcal A}_{1}=\operatorname {mod} \mathcal J_{I}$
.
For the second claim, we show the chain of equalities
where
![]() $\operatorname {pvd}_R({\mathcal D}) \subset \operatorname {pvd} ({\mathcal D})$
is the full subcategory with cohomologies in
$\operatorname {pvd}_R({\mathcal D}) \subset \operatorname {pvd} ({\mathcal D})$
is the full subcategory with cohomologies in
![]() $\operatorname {mod} R$
. The first follows using the characterization of
$\operatorname {mod} R$
. The first follows using the characterization of
![]() ${\mathcal A}_0$
as a heart in terms of a decomposition of objects in
${\mathcal A}_0$
as a heart in terms of a decomposition of objects in
![]() $\operatorname {pvd}_{J_I}(\Gamma )$
into triangles and Serreness of
$\operatorname {pvd}_{J_I}(\Gamma )$
into triangles and Serreness of
![]() $\operatorname {mod} \mathcal J_I$
in
$\operatorname {mod} \mathcal J_I$
in
![]() ${\mathcal A}_0$
, as in Lemma 4.2. For the second, we just intersect
${\mathcal A}_0$
, as in Lemma 4.2. For the second, we just intersect
![]() $\Gamma _I=\Gamma /\Gamma e \Gamma $
with
$\Gamma _I=\Gamma /\Gamma e \Gamma $
with
![]() $H^0\Gamma =\mathcal J$
. The last equality follows from [Reference Kalck and YangKY18, Corollary 6.4 (b)], where we can take
$H^0\Gamma =\mathcal J$
. The last equality follows from [Reference Kalck and YangKY18, Corollary 6.4 (b)], where we can take
![]() $B=\Gamma /\Gamma e \Gamma =\Gamma _I$
thanks to Theorem 7.1 in loc. cit.
$B=\Gamma /\Gamma e \Gamma =\Gamma _I$
thanks to Theorem 7.1 in loc. cit.
Conversely, choosing
![]() $Z_0$
to be zero for any subset of the simples and
$Z_0$
to be zero for any subset of the simples and
![]() $\overline {\mathbb {H}}$
-valued for the complementary set of simples defines a subcategory
$\overline {\mathbb {H}}$
-valued for the complementary set of simples defines a subcategory
![]() ${\mathcal V}_1^Z$
that can be be completed to a multi-scale stability condition.
${\mathcal V}_1^Z$
that can be be completed to a multi-scale stability condition.
We now translate into the language of Section 3. Let
![]() ${\mathbb T}$
be the triangulation of the DMS
${\mathbb T}$
be the triangulation of the DMS
![]() ${\mathbf {S}}_\Delta $
corresponding to
${\mathbf {S}}_\Delta $
corresponding to
![]() ${\mathcal A}_0$
. Dual to the open arcs forming the triangulation, there are closed arcs connecting the decorating points. These are in canonical bijection to the simples in
${\mathcal A}_0$
. Dual to the open arcs forming the triangulation, there are closed arcs connecting the decorating points. These are in canonical bijection to the simples in
![]() ${\mathcal A}_0$
, see, for example, the summary in [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 7.2]. Let
${\mathcal A}_0$
, see, for example, the summary in [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 7.2]. Let
![]() $\mathbb {A}_1^\vee = \{\eta _S, S \in \mathcal S_1\}$
be the closed arcs corresponding to
$\mathbb {A}_1^\vee = \{\eta _S, S \in \mathcal S_1\}$
be the closed arcs corresponding to
![]() ${\mathcal A}_1$
and
${\mathcal A}_1$
and
![]() $\mathbb {A}_1$
the set of dual closed arcs. Let
$\mathbb {A}_1$
the set of dual closed arcs. Let
![]() $\Sigma = \Sigma _1$
be the subsurface consisting of a tubular neighborhood of
$\Sigma = \Sigma _1$
be the subsurface consisting of a tubular neighborhood of
![]() $\mathbb {A}_1^\vee $
, and let
$\mathbb {A}_1^\vee $
, and let
![]() $\Sigma ^{(j)}$
denote its connected components. They are all homotopic to a disc containing a certain number, say
$\Sigma ^{(j)}$
denote its connected components. They are all homotopic to a disc containing a certain number, say
![]() $n_j+1$
, of simple zeros with one boundary component. Homotoping the open arcs in
$n_j+1$
, of simple zeros with one boundary component. Homotoping the open arcs in
![]() $\mathbb {A}_0$
so that they intersect
$\mathbb {A}_0$
so that they intersect
![]() $\Sigma $
minimally, we deduce from duality that precisely those in
$\Sigma $
minimally, we deduce from duality that precisely those in
![]() $\mathbb {A}_1$
have nontrivial intersection with
$\mathbb {A}_1$
have nontrivial intersection with
![]() $\Sigma $
. We may thus mark
$\Sigma $
. We may thus mark
![]() $\kappa ^{(j)} = n_j+3$
points on the boundary of
$\kappa ^{(j)} = n_j+3$
points on the boundary of
![]() $\Sigma ^{(j)}$
and restrict the arcs in
$\Sigma ^{(j)}$
and restrict the arcs in
![]() $\mathbb {A}_1$
to arcs in
$\mathbb {A}_1$
to arcs in
![]() $\Sigma $
connecting these boundary points so that
$\Sigma $
connecting these boundary points so that
![]() $\mathbb {A}_1|_\Sigma $
is a triangulation of
$\mathbb {A}_1|_\Sigma $
is a triangulation of
![]() $\Sigma $
. In fact, the quiver associated with each subsurface
$\Sigma $
. In fact, the quiver associated with each subsurface
![]() $\Sigma ^{(j)}$
is of type
$\Sigma ^{(j)}$
is of type
![]() $A_{n_j}$
.
$A_{n_j}$
.
The constraints for
![]() $n_j$
reflect that the total number of decoration points in
$n_j$
reflect that the total number of decoration points in
![]() ${\mathbf {S}}_\Delta $
has to be at least two and the fact that there is at least one simple outside
${\mathbf {S}}_\Delta $
has to be at least two and the fact that there is at least one simple outside
![]() ${\mathcal A}_1$
(i.e., a closed arc not contained in
${\mathcal A}_1$
(i.e., a closed arc not contained in
![]() $\Sigma $
). This arc has to connect
$\Sigma $
). This arc has to connect
![]() $\Sigma $
with a decoration point outside
$\Sigma $
with a decoration point outside
![]() $\Sigma $
(the case of strict inequality) or connects two components (the case
$\Sigma $
(the case of strict inequality) or connects two components (the case
![]() $|J| \geq 2$
).
$|J| \geq 2$
).
As a consequence, we may associate with each subsurface
![]() $\Sigma _j^{(i)}$
a subcategory
$\Sigma _j^{(i)}$
a subcategory
![]() ${\mathcal V}_i^{(j)}$
of
${\mathcal V}_i^{(j)}$
of
![]() ${\mathcal V}_i$
, that jointly gives an orthogonal decomposition of
${\mathcal V}_i$
, that jointly gives an orthogonal decomposition of
![]() ${\mathcal V}_i$
. We refer to
${\mathcal V}_i$
. We refer to
![]() ${\mathcal V}_i^{(j)}$
as the components of
${\mathcal V}_i^{(j)}$
as the components of
![]() ${\mathcal V}_i$
.
${\mathcal V}_i$
.
Recall the notion of principal components from Section 3.2.
Corollary 4.5. Suppose that
![]() $({\mathcal A}_\bullet , Z_\bullet ) \in \operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. Then the quotient hearts
$({\mathcal A}_\bullet , Z_\bullet ) \in \operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. Then the quotient hearts
![]() $\overline {{\mathcal A}}_i \subset {\mathcal V}_{i}/{\mathcal V}_{i+1}$
support a stability condition in the principal component
$\overline {{\mathcal A}}_i \subset {\mathcal V}_{i}/{\mathcal V}_{i+1}$
support a stability condition in the principal component ![]() of the stability manifold of
of the stability manifold of
![]() ${\mathcal V}_{i}/{\mathcal V}_{i+1}$
for all
${\mathcal V}_{i}/{\mathcal V}_{i+1}$
for all
![]() $i=0,\ldots ,L$
.
$i=0,\ldots ,L$
.
Proof. In fact, they belong to the one corresponding to the triangulation
![]() $\mathbb {A}_i|_{\Sigma _i}$
, extending the notation of the previous proof in the obvious way.
$\mathbb {A}_i|_{\Sigma _i}$
, extending the notation of the previous proof in the obvious way.
4.2 The
 $\mathbb {C}$
-action
$\mathbb {C}$
-action
Extending the
![]() $\mathbb {C}$
-action from usual stability conditions to multi-scale stability conditions is a crucial ingredient for the subsequent plumbing construction.
$\mathbb {C}$
-action from usual stability conditions to multi-scale stability conditions is a crucial ingredient for the subsequent plumbing construction.
Proposition 4.6. Recall that we suppose
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
. Then there is an action of
${\mathcal D} = {\mathcal D}^3_{A_n}$
. Then there is an action of
![]() $\mathbb {C}$
denoted by
$\mathbb {C}$
denoted by
![]() $(\lambda ,[{\mathcal A}_\bullet ,Z_\bullet ]) \mapsto \lambda \cdot [{\mathcal A}_\bullet ,Z_\bullet ] =: [{\mathcal A}_\bullet ^{\prime },Z_\bullet ^{\prime }]$
on
$(\lambda ,[{\mathcal A}_\bullet ,Z_\bullet ]) \mapsto \lambda \cdot [{\mathcal A}_\bullet ,Z_\bullet ] =: [{\mathcal A}_\bullet ^{\prime },Z_\bullet ^{\prime }]$
on
![]() $\operatorname {MStab}^\circ (\mathcal {D})$
, such that
$\operatorname {MStab}^\circ (\mathcal {D})$
, such that
-
(i) the collection of subcategories
 ${\mathcal V}_i^{Z} = {\mathcal V}_i^{Z'} =: {\mathcal V}_i$
is preserved,
${\mathcal V}_i^{Z} = {\mathcal V}_i^{Z'} =: {\mathcal V}_i$
is preserved, -
(ii)
 $Z_i^{\prime } \;=\; e^{-\sqrt {-1}\pi \lambda } Z_i$
, and
$Z_i^{\prime } \;=\; e^{-\sqrt {-1}\pi \lambda } Z_i$
, and -
(iii)
 $\lambda \cdot (\overline {{\mathcal A}}_i,\overline {Z}_i) = (\overline {{\mathcal A}}^{\prime }_i,\overline {Z}^{\prime }_i)$
is the usual
$\lambda \cdot (\overline {{\mathcal A}}_i,\overline {Z}_i) = (\overline {{\mathcal A}}^{\prime }_i,\overline {Z}^{\prime }_i)$
is the usual
 $\mathbb {C}$
-action on
$\mathbb {C}$
-action on  .
.
Thanks to Proposition 4.6, proven below, we define the projectivized space of multi-scale stability conditions
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}) = \operatorname {MStab}^\circ ({\mathcal D})/\mathbb {C}$
. In this language, note that retaining just the filtration steps from a level j onward (i.e., the datum of tuples
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}) = \operatorname {MStab}^\circ ({\mathcal D})/\mathbb {C}$
. In this language, note that retaining just the filtration steps from a level j onward (i.e., the datum of tuples
![]() $({\mathcal A}_{\geq j}, Z_{\geq j})$
together with the ambient triangulated category
$({\mathcal A}_{\geq j}, Z_{\geq j})$
together with the ambient triangulated category
![]() ${\mathcal V}^Z_{j-1}$
) gives by definition an element in
${\mathcal V}^Z_{j-1}$
) gives by definition an element in
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal V}^Z_{j-1})$
with
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal V}^Z_{j-1})$
with
![]() $L-j+1$
levels below zero.
$L-j+1$
levels below zero.
The restriction
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
stems from two requirements in the proof. First, we need finite type. Second, we need a way to lift tilts from quotient categories to
${\mathcal D} = {\mathcal D}^3_{A_n}$
stems from two requirements in the proof. First, we need finite type. Second, we need a way to lift tilts from quotient categories to
![]() ${\mathcal D}$
itself. We have shown this for quiver categories in [Reference Barbieri, Möller, Qiu and SoBMQS22] and isolate this step in the following notion.
${\mathcal D}$
itself. We have shown this for quiver categories in [Reference Barbieri, Möller, Qiu and SoBMQS22] and isolate this step in the following notion.
Definition 4.7. Given a thick triangulated subcategory
![]() ${\mathcal V} \subset {\mathcal D}$
, a heart
${\mathcal V} \subset {\mathcal D}$
, a heart
![]() ${\mathcal A}$
of
${\mathcal A}$
of
![]() ${\mathcal D}$
and a simple object S in
${\mathcal D}$
and a simple object S in
![]() ${\mathcal A} \setminus ({\mathcal V}\cap {\mathcal A})$
, we call a heart
${\mathcal A} \setminus ({\mathcal V}\cap {\mathcal A})$
, we call a heart
![]() ${\mathcal A}'$
with
${\mathcal A}'$
with
![]() $\overline {{\mathcal A}} = \overline {{\mathcal A}'} := {\mathcal A}'/({\mathcal V} \cap {\mathcal A}')$
a convenient representative with respect to (the forward tilt at) S if
$\overline {{\mathcal A}} = \overline {{\mathcal A}'} := {\mathcal A}'/({\mathcal V} \cap {\mathcal A}')$
a convenient representative with respect to (the forward tilt at) S if
![]() ${\mathcal A}'$
is
${\mathcal A}'$
is
![]() ${\mathcal V}$
-compatible and if
${\mathcal V}$
-compatible and if
It means that a simple tilt of
![]() ${\mathcal A}$
at S induces a simple tilt of
${\mathcal A}$
at S induces a simple tilt of
![]() $\overline {{\mathcal A}}$
at
$\overline {{\mathcal A}}$
at
![]() $\overline {S}$
.
$\overline {S}$
.
Lemma 4.8. Suppose
![]() ${\mathcal D} = \mathcal {D}^{3}_{Q}$
. For every
${\mathcal D} = \mathcal {D}^{3}_{Q}$
. For every
![]() ${\mathcal V}$
-compatible finite heart
${\mathcal V}$
-compatible finite heart
![]() ${\mathcal A}$
and every simple S, there exists a convenient representative
${\mathcal A}$
and every simple S, there exists a convenient representative
![]() ${\mathcal A}'$
, which can be obtained from
${\mathcal A}'$
, which can be obtained from
![]() ${\mathcal A}$
by a finite sequence of simple tilts at simples in
${\mathcal A}$
by a finite sequence of simple tilts at simples in
![]() ${\mathcal A} \cap {\mathcal V}$
.
${\mathcal A} \cap {\mathcal V}$
.
If
![]() ${\mathcal A}'$
is a convenient representative for S, then
${\mathcal A}'$
is a convenient representative for S, then
![]() $\mu _S^\sharp {\mathcal A}'$
is
$\mu _S^\sharp {\mathcal A}'$
is
![]() ${\mathcal V}$
-compatible and
${\mathcal V}$
-compatible and
Proof. See [Reference Barbieri, Möller, Qiu and SoBMQS22, Proposition 5.8].
In the following, we will give an explicit procedure for finding a convenient representative if
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
, that will be useful later.
${\mathcal D} = {\mathcal D}^3_{A_n}$
, that will be useful later.
Lemma 4.9. Recall that we suppose
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
. Let
${\mathcal D} = {\mathcal D}^3_{A_n}$
. Let
![]() ${\mathcal A}$
be a heart compatible with
${\mathcal A}$
be a heart compatible with
![]() ${\mathcal V}$
, and let
${\mathcal V}$
, and let
![]() $S_0 \in {\mathcal A} \backslash {\mathcal A}\cap {\mathcal V}$
be simple. Then there exist a (possibly empty) set of indecomposables
$S_0 \in {\mathcal A} \backslash {\mathcal A}\cap {\mathcal V}$
be simple. Then there exist a (possibly empty) set of indecomposables
![]() $\{S_1,\dots , S_{1\dots m}, S^{\prime }_1,\dots , S^{\prime }_{1\dots m'}\}\subset {\mathcal A}\cap {\mathcal V}$
explicitly defined in the proof below, such that
$\{S_1,\dots , S_{1\dots m}, S^{\prime }_1,\dots , S^{\prime }_{1\dots m'}\}\subset {\mathcal A}\cap {\mathcal V}$
explicitly defined in the proof below, such that
![]() $(\mu ^\sharp _{S^{\prime }_{1\dots m'}}\cdots \mu ^\sharp _{S^{\prime }_1})(\mu ^\sharp _{S_{1\dots m}}\cdots \mu ^\sharp _{S_1})({\mathcal A})$
is a convenient representative of
$(\mu ^\sharp _{S^{\prime }_{1\dots m'}}\cdots \mu ^\sharp _{S^{\prime }_1})(\mu ^\sharp _{S_{1\dots m}}\cdots \mu ^\sharp _{S_1})({\mathcal A})$
is a convenient representative of
![]() $\overline {{\mathcal A}}$
with respect to
$\overline {{\mathcal A}}$
with respect to
![]() $S_0$
.
$S_0$
.
Proof. Observe that for any simple
![]() $S \in {\mathcal A}$
, the number of (isomorphism classes of) simples T in
$S \in {\mathcal A}$
, the number of (isomorphism classes of) simples T in
![]() ${\mathcal A}$
satisfying
${\mathcal A}$
satisfying
![]() $\operatorname {ext}^1(T, S) = 1$
is at most
$\operatorname {ext}^1(T, S) = 1$
is at most
![]() $2$
, since
$2$
, since
![]() ${\mathcal A}=\operatorname {rep}(Q,W)$
with
${\mathcal A}=\operatorname {rep}(Q,W)$
with
![]() $(Q,W)$
a quiver of
$(Q,W)$
a quiver of
![]() $A_n$
-type or, more generally, since it comes from a triangulation of a surface. If there are no simples in
$A_n$
-type or, more generally, since it comes from a triangulation of a surface. If there are no simples in
![]() ${\mathcal A}\cap {\mathcal V}$
with this property, then
${\mathcal A}\cap {\mathcal V}$
with this property, then
![]() ${\mathcal A}$
is convenient with respect to
${\mathcal A}$
is convenient with respect to
![]() $S_0$
, and we are done. Otherwise, we fix a simple
$S_0$
, and we are done. Otherwise, we fix a simple
![]() $S_1\in {\mathcal A}\cap {\mathcal V}$
with
$S_1\in {\mathcal A}\cap {\mathcal V}$
with
and we define
![]() $S_1,\dots , S_m$
as the maximal collection of simples in
$S_1,\dots , S_m$
as the maximal collection of simples in
![]() ${\mathcal A}\cap {\mathcal V}$
, with
${\mathcal A}\cap {\mathcal V}$
, with
for
![]() $i\geq 1$
. Note that the second condition in (24) singles out exactly one among the two possible objects with nontrivial extension with
$i\geq 1$
. Note that the second condition in (24) singles out exactly one among the two possible objects with nontrivial extension with
![]() $S_i$
. Consequently, the collection is uniquely specified for a given
$S_i$
. Consequently, the collection is uniquely specified for a given
![]() ${\mathcal A}$
, and the definition is well posed. See Figure 2 for an example of the corresponding ext-quiver.
${\mathcal A}$
, and the definition is well posed. See Figure 2 for an example of the corresponding ext-quiver.

Figure 2 (Partial) ext-quiver containing the
![]() $A_{m+1}$
-configuration of
$A_{m+1}$
-configuration of
![]() $S_0,S_1,\dots , S_m$
defined in the text. The small red dots correspond to simples in
$S_0,S_1,\dots , S_m$
defined in the text. The small red dots correspond to simples in
![]() ${\mathcal A} \cap {\mathcal V}$
, while the big blue dots correspond to simples of
${\mathcal A} \cap {\mathcal V}$
, while the big blue dots correspond to simples of
![]() ${\mathcal A}$
not in
${\mathcal A}$
not in
![]() ${\mathcal V}$
.
${\mathcal V}$
.
Tilting
![]() ${\mathcal A}$
at
${\mathcal A}$
at
![]() $S_1$
produces a configuration of simples in
$S_1$
produces a configuration of simples in
![]() $\mu ^\sharp _{S_1}{\mathcal A}\ni S_0$
such that the sequence of objects defined by (23),(24) in
$\mu ^\sharp _{S_1}{\mathcal A}\ni S_0$
such that the sequence of objects defined by (23),(24) in
![]() $\mu ^\sharp _{S_1}{\mathcal A}$
has length
$\mu ^\sharp _{S_1}{\mathcal A}$
has length
![]() $m-1$
and consists of
$m-1$
and consists of
![]() $S_{12},S_3,\dots , S_m$
, as displayed in Figure 3 using the correspondence between simple tilts and mutations.
$S_{12},S_3,\dots , S_m$
, as displayed in Figure 3 using the correspondence between simple tilts and mutations.
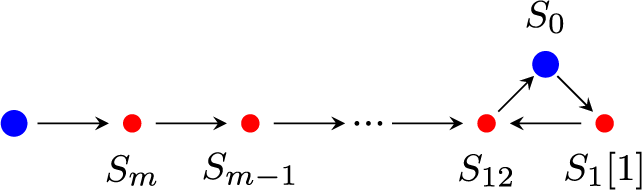
Figure 3 Mutation at
![]() $S_1$
of the ext-quiver of Figure 2.
$S_1$
of the ext-quiver of Figure 2.
Tilting inductively at
![]() $S_{1\dots i}$
(recall the notation from (3)), the procedure leads to a configuration where such a sequence has length
$S_{1\dots i}$
(recall the notation from (3)), the procedure leads to a configuration where such a sequence has length
![]() $0$
, as desired, see Figure 4. We define
$0$
, as desired, see Figure 4. We define
![]() $\mathcal X = \langle S_{1\dots m},\ldots , S_1\rangle $
so that
$\mathcal X = \langle S_{1\dots m},\ldots , S_1\rangle $
so that
![]() $\mu ^\sharp _{\mathcal {X}}:=\mu ^\sharp _{S_{1\dots m}}\cdots \mu ^\sharp _{S_1}$
by Proposition 2.2. By construction,
$\mu ^\sharp _{\mathcal {X}}:=\mu ^\sharp _{S_{1\dots m}}\cdots \mu ^\sharp _{S_1}$
by Proposition 2.2. By construction,
![]() $\mathcal {X} \subset {\mathcal A}\cap {\mathcal V}$
and
$\mathcal {X} \subset {\mathcal A}\cap {\mathcal V}$
and
![]() $\overline {\mu ^\sharp _{\mathcal {X}}{\mathcal A}}= \overline {{\mathcal A}}\subset {\mathcal D}/{\mathcal V}$
.
$\overline {\mu ^\sharp _{\mathcal {X}}{\mathcal A}}= \overline {{\mathcal A}}\subset {\mathcal D}/{\mathcal V}$
.
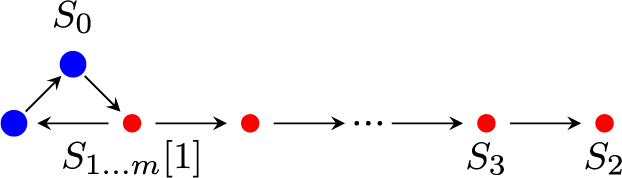
Figure 4 The result of mutating at
![]() $S_1, S_{12},\dots , S_{1\dots m}$
the ext-quiver of Figure 2.
$S_1, S_{12},\dots , S_{1\dots m}$
the ext-quiver of Figure 2.
Suppose now that there exists another simple
![]() $S_1^{\prime }\neq S_1$
satisfying (23). Proceeding in the same way, we define
$S_1^{\prime }\neq S_1$
satisfying (23). Proceeding in the same way, we define
![]() $S_i^{\prime }$
using (23) and (24) and define inductively
$S_i^{\prime }$
using (23) and (24) and define inductively
![]() $S^{\prime }_{1\dots i}$
for
$S^{\prime }_{1\dots i}$
for
![]() $i=1,\dots ,m'$
as above. They are not in
$i=1,\dots ,m'$
as above. They are not in
![]() $\langle S_1,\dots , S_{m+1}\rangle $
, due to the second condition in (24). Then, with
$\langle S_1,\dots , S_{m+1}\rangle $
, due to the second condition in (24). Then, with
![]() $\mathcal X' = \langle S^{\prime }_{1\dots m},\ldots , S^{\prime }_1\rangle $
,
$\mathcal X' = \langle S^{\prime }_{1\dots m},\ldots , S^{\prime }_1\rangle $
,
is a convenient representative of
![]() $\overline {{\mathcal A}}$
with respect to
$\overline {{\mathcal A}}$
with respect to
![]() $S_0$
.
$S_0$
.
Proof of Proposition 4.6
Here and in many cases in the sequel, all aspects of the proof are visible in the situation with just two levels (i.e.,
![]() $L=1$
), and for expository simplicity, we restrict to this case and if needed we mention briefly in the end how to proceed by induction. Suppose
$L=1$
), and for expository simplicity, we restrict to this case and if needed we mention briefly in the end how to proceed by induction. Suppose
![]() $\Re \lambda \geq 0$
; the other case is analogous.
$\Re \lambda \geq 0$
; the other case is analogous.
For a rescaling by
![]() $e^{-\pi i\lambda }$
with
$e^{-\pi i\lambda }$
with
![]() $\lambda \in i\mathbb {R}$
and for a rotation (
$\lambda \in i\mathbb {R}$
and for a rotation (
![]() $\lambda \in \mathbb {R}$
) so that the phase of no simple in
$\lambda \in \mathbb {R}$
) so that the phase of no simple in
![]() ${\mathcal A}_0$
with nonzero central charge exceeds
${\mathcal A}_0$
with nonzero central charge exceeds
![]() $(0,1]$
, we just apply (ii) to the multi-scale central charge, and all the other conditions still hold. It thus suffices to consider general rotations (i.e.,
$(0,1]$
, we just apply (ii) to the multi-scale central charge, and all the other conditions still hold. It thus suffices to consider general rotations (i.e.,
![]() $\lambda \in (0,1]$
), repeating the process
$\lambda \in (0,1]$
), repeating the process
![]() $\lfloor \lambda \rfloor $
many times.
$\lfloor \lambda \rfloor $
many times.
We denote by
![]() $\mathcal {F}^1_\lambda \subset {\mathcal A}_1$
the torsion-free class induced by the action of
$\mathcal {F}^1_\lambda \subset {\mathcal A}_1$
the torsion-free class induced by the action of
![]() $\lambda $
on
$\lambda $
on
![]() $({\mathcal A}_1,Z_1)$
. Similarly, we let
$({\mathcal A}_1,Z_1)$
. Similarly, we let
![]() $\overline {\mathcal {F}}_\lambda \subset \overline {{\mathcal A}_0}$
be the analogous torsion-free class for the
$\overline {\mathcal {F}}_\lambda \subset \overline {{\mathcal A}_0}$
be the analogous torsion-free class for the
![]() $\lambda $
-action on
$\lambda $
-action on
![]() $(\overline {{\mathcal A}_0}, \overline {Z_0})$
. We can decompose the tilt at
$(\overline {{\mathcal A}_0}, \overline {Z_0})$
. We can decompose the tilt at
![]() $\overline {\mathcal {F}}_\lambda $
as a composition of tilts at finitely many simple torsion-free classes
$\overline {\mathcal {F}}_\lambda $
as a composition of tilts at finitely many simple torsion-free classes
![]() $\overline {\mathcal {F}}_i=\langle \overline {X_i}\rangle \subset \overline {{\mathcal A}_0}$
according to Proposition 2.2.
$\overline {\mathcal {F}}_i=\langle \overline {X_i}\rangle \subset \overline {{\mathcal A}_0}$
according to Proposition 2.2.
The subcategory
![]() $\mathcal {F}^1_\lambda $
is a torsion-free class in
$\mathcal {F}^1_\lambda $
is a torsion-free class in
![]() ${\mathcal A}_0$
, and we first forward-tilt
${\mathcal A}_0$
, and we first forward-tilt
![]() ${\mathcal A}_0$
and
${\mathcal A}_0$
and
![]() ${\mathcal A}_1$
at
${\mathcal A}_1$
at
![]() $\mathcal {F}^1_\lambda $
. Then we inductively ‘lift’ the simple tilt at
$\mathcal {F}^1_\lambda $
. Then we inductively ‘lift’ the simple tilt at
![]() $\overline {X_i}$
at
$\overline {X_i}$
at
![]() $\mu ^\sharp _{\overline {\mathcal {F}}_{i-1}}\overline {{\mathcal A}_0}^{(i-1)}$
(with
$\mu ^\sharp _{\overline {\mathcal {F}}_{i-1}}\overline {{\mathcal A}_0}^{(i-1)}$
(with
![]() $\overline {{\mathcal A}_0}^{(0)} =\overline {{\mathcal A}_0}$
) to the upper level in the following way. If
$\overline {{\mathcal A}_0}^{(0)} =\overline {{\mathcal A}_0}$
) to the upper level in the following way. If
![]() $S=X_1$
, we apply Lemma 4.8 and forward tilt
$S=X_1$
, we apply Lemma 4.8 and forward tilt
![]() ${\mathcal A}_0$
to arrive at a convenient representative
${\mathcal A}_0$
to arrive at a convenient representative
![]() ${\mathcal A}^{\prime }_0=\mu ^\sharp _{\mathcal X}{\mathcal A}_0$
for S. Second, we tilt forward at S, and third, we perform the backward tilt at
${\mathcal A}^{\prime }_0=\mu ^\sharp _{\mathcal X}{\mathcal A}_0$
for S. Second, we tilt forward at S, and third, we perform the backward tilt at
![]() $\mathcal X[1]$
. At the end, we arrive at a heart
$\mathcal X[1]$
. At the end, we arrive at a heart
![]() ${\mathcal A}_0^{\prime \prime }$
on which
${\mathcal A}_0^{\prime \prime }$
on which
![]() $Z_0$
is still well defined, and with the following properties:
$Z_0$
is still well defined, and with the following properties:
-
(1)
 ${\mathcal V}_0^{\prime \prime } = {\mathcal V}_0$
, since after each of the three steps, the simples annihilated by
${\mathcal V}_0^{\prime \prime } = {\mathcal V}_0$
, since after each of the three steps, the simples annihilated by
 $Z_0$
generate the same category;
$Z_0$
generate the same category; -
(2) the quotient heart
 $\overline {{\mathcal A}}_0^{\prime \prime }$
coincides with
$\overline {{\mathcal A}}_0^{\prime \prime }$
coincides with
 $\mu _S^\sharp \overline {{\mathcal A}_0}$
, thanks to (22);
$\mu _S^\sharp \overline {{\mathcal A}_0}$
, thanks to (22); -
(3) the intersection
 ${\mathcal A}^{\prime \prime }_0 \cap {\mathcal V}_0 = {\mathcal A}_1$
, since the forward and backward tilts cancel on
${\mathcal A}^{\prime \prime }_0 \cap {\mathcal V}_0 = {\mathcal A}_1$
, since the forward and backward tilts cancel on
 ${\mathcal A}_1$
.
${\mathcal A}_1$
.
Repeating this process for all i, in the end, we change the central charge as required by (ii). Using (1) at each step ensures (i), and (2) together with (3) at each step ensure (iii). This procedure indeed defines an action of
![]() $\mathbb {C}$
, since the equivalence class of the multi-scale stability condition is uniquely determined by the conditions (i)–(iii). It obviously agrees with the
$\mathbb {C}$
, since the equivalence class of the multi-scale stability condition is uniquely determined by the conditions (i)–(iii). It obviously agrees with the
![]() $\mathbb {C}$
-action on
$\mathbb {C}$
-action on
![]() $\operatorname {Stab}({\mathcal V}_0/{\mathcal V}_1)$
.
$\operatorname {Stab}({\mathcal V}_0/{\mathcal V}_1)$
.
For later use, we record that the ‘lifts’ of the tilts at
![]() ${\overline {\mathcal {F}}_{i}}$
used in the previous proof are actually tilts at explicit torsion-free classes
${\overline {\mathcal {F}}_{i}}$
used in the previous proof are actually tilts at explicit torsion-free classes
![]() $\mathcal F_i$
.
$\mathcal F_i$
.
Lemma 4.10. Recall that
![]() ${\mathcal D} = {\mathcal D}_{A_n}$
, and let
${\mathcal D} = {\mathcal D}_{A_n}$
, and let
![]() ${\mathcal A}_\bullet =({\mathcal A}_0,{\mathcal A}_1)$
and
${\mathcal A}_\bullet =({\mathcal A}_0,{\mathcal A}_1)$
and
![]() $Z_\bullet = (Z_0,Z_1)$
. For
$Z_\bullet = (Z_0,Z_1)$
. For
![]() $\lambda \in \mathbb {R}_{\geq 0}$
such that
$\lambda \in \mathbb {R}_{\geq 0}$
such that
-
○
 $\lambda \cdot (\overline {{\mathcal A}_0},\overline {Z_0})=(\mu ^\sharp _{S_0}\overline {{\mathcal A}_0}, e^{-\pi \lambda }\overline {Z_0})$
in
$\lambda \cdot (\overline {{\mathcal A}_0},\overline {Z_0})=(\mu ^\sharp _{S_0}\overline {{\mathcal A}_0}, e^{-\pi \lambda }\overline {Z_0})$
in
 $\operatorname {Stab}^\circ ({\mathcal D}/{\mathcal V})$
, and
$\operatorname {Stab}^\circ ({\mathcal D}/{\mathcal V})$
, and -
○ there are no indecomposables in
 ${\mathcal A}_1$
with phase
${\mathcal A}_1$
with phase
 $\phi _{\overline {Z_1}}$
less than or equal to
$\phi _{\overline {Z_1}}$
less than or equal to
 $\lambda $
,
$\lambda $
,
the action by
![]() $\lambda $
on
$\lambda $
on
![]() $[{\mathcal A}_\bullet ,Z_\bullet ]$
gives
$[{\mathcal A}_\bullet ,Z_\bullet ]$
gives
![]() $[{\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ]$
with nested hearts
$[{\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ]$
with nested hearts
for
![]() $\mathcal {F}=\langle S^{\prime }_{01\dots m'}, \dots S^{\prime }_{01},S_{01\dots m}, \dots S_{01}, S_0\rangle $
, using the same notation as in proof of Lemma 4.9. Moreover,
$\mathcal {F}=\langle S^{\prime }_{01\dots m'}, \dots S^{\prime }_{01},S_{01\dots m}, \dots S_{01}, S_0\rangle $
, using the same notation as in proof of Lemma 4.9. Moreover,
![]() $\mathcal {F}\subset \langle S_0,{\mathcal A}_1\rangle \setminus {\mathcal A}_1$
.
$\mathcal {F}\subset \langle S_0,{\mathcal A}_1\rangle \setminus {\mathcal A}_1$
.
Proof. Suppose for simplicity
![]() $m>0$
,
$m>0$
,
![]() $m'=0$
in the notation of Lemma 4.9. We know that
$m'=0$
in the notation of Lemma 4.9. We know that
![]() ${\mathcal A}^{\prime }_0=\mu ^\flat _{\mathcal X[1]} \mu ^\sharp _{S_0}\mu ^\sharp _{\mathcal X}{\mathcal A}_0$
by the procedure described in the proof of Proposition 4.6. Since
${\mathcal A}^{\prime }_0=\mu ^\flat _{\mathcal X[1]} \mu ^\sharp _{S_0}\mu ^\sharp _{\mathcal X}{\mathcal A}_0$
by the procedure described in the proof of Proposition 4.6. Since
we deduce that
and hence,
![]() $\mu ^\sharp _{\mathcal {F}} ({\mathcal A})= \mu ^\flat _{\mathcal X[1]} \mu ^\sharp _{S_0} \mu ^\sharp _{\mathcal X}({\mathcal A}).$
$\mu ^\sharp _{\mathcal {F}} ({\mathcal A})= \mu ^\flat _{\mathcal X[1]} \mu ^\sharp _{S_0} \mu ^\sharp _{\mathcal X}({\mathcal A}).$
We use the subsequent lemma as a preparation for Proposition 5.2 below.
Lemma 4.11. Let
![]() $\mathcal {F}_i$
for
$\mathcal {F}_i$
for
![]() $i=1,\ldots ,r$
be the torsion-free classes lifting the classes
$i=1,\ldots ,r$
be the torsion-free classes lifting the classes
![]() $\overline {\mathcal {F}}_i \subset \overline {{\mathcal A}_0}^{(i-1)}$
appearing in the proof of Proposition 4.6 and explicitly described by Lemma 4.10. Then
$\overline {\mathcal {F}}_i \subset \overline {{\mathcal A}_0}^{(i-1)}$
appearing in the proof of Proposition 4.6 and explicitly described by Lemma 4.10. Then
![]() $\mathcal {F}_j \cap \mathcal {F}_{i}[1] =\{0\}$
for any
$\mathcal {F}_j \cap \mathcal {F}_{i}[1] =\{0\}$
for any
![]() $j>i$
. Moreover, for any
$j>i$
. Moreover, for any
![]() $r' \leq r$
, the result of the sequence of forward-tilts at
$r' \leq r$
, the result of the sequence of forward-tilts at
![]() $\mathcal {F}_i$
of
$\mathcal {F}_i$
of
![]() ${\mathcal A}_0$
for
${\mathcal A}_0$
for
![]() $i=1,\ldots , r'$
is intermediate with respect to
$i=1,\ldots , r'$
is intermediate with respect to
![]() ${\mathcal A}_0$
.
${\mathcal A}_0$
.
Proof. By Lemma 4.10, the class
![]() $\mathcal {F}_i$
is generated by a simple object X in
$\mathcal {F}_i$
is generated by a simple object X in
![]() ${\mathcal A}^{(i-1)}$
together possibly with extensions of X with
${\mathcal A}^{(i-1)}$
together possibly with extensions of X with
![]() ${\mathcal A}^{(i-1)}\cap {\mathcal V}_1$
. Similarly is
${\mathcal A}^{(i-1)}\cap {\mathcal V}_1$
. Similarly is
![]() $\mathcal {F}_{i-1}$
for an object Y, with
$\mathcal {F}_{i-1}$
for an object Y, with
![]() $\pi (X)\neq \pi (Y)$
in
$\pi (X)\neq \pi (Y)$
in
![]() ${\mathcal D}/{\mathcal V}_1$
; hence
${\mathcal D}/{\mathcal V}_1$
; hence
![]() $X\neq Y$
, and also
$X\neq Y$
, and also
![]() $X\neq Y[1]$
(since the central charge defines a stability condition on the quotient). None of the extensions of X with
$X\neq Y[1]$
(since the central charge defines a stability condition on the quotient). None of the extensions of X with
![]() ${\mathcal A}_1$
can be in
${\mathcal A}_1$
can be in
![]() ${\mathcal V}_1$
, nor they can just be extensions of
${\mathcal V}_1$
, nor they can just be extensions of
![]() $Y[1]$
with
$Y[1]$
with
![]() ${\mathcal V}_1$
. Hence,
${\mathcal V}_1$
. Hence,
![]() $\mathcal {F}_i \cap \mathcal {F}_{i-1}[1] =\{0\}$
and
$\mathcal {F}_i \cap \mathcal {F}_{i-1}[1] =\{0\}$
and
![]() $\mathcal {F}_{i-1}[1]\subset {^\perp {\mathcal {F}_i}}$
. This is the start for an inductive argument. In fact, we deduce that
$\mathcal {F}_{i-1}[1]\subset {^\perp {\mathcal {F}_i}}$
. This is the start for an inductive argument. In fact, we deduce that
![]() $\mu ^\sharp _{\mathcal {F}_2} \mu ^\sharp _{\mathcal {F}_1}{\mathcal A}_0\supset \mathcal {F}_2[1],\mathcal {F}_1[1]$
. Now the previous argument shows that
$\mu ^\sharp _{\mathcal {F}_2} \mu ^\sharp _{\mathcal {F}_1}{\mathcal A}_0\supset \mathcal {F}_2[1],\mathcal {F}_1[1]$
. Now the previous argument shows that
![]() $\mathcal {F}_3$
does not intersect
$\mathcal {F}_3$
does not intersect
![]() $\mathcal {F}_2[1]$
and
$\mathcal {F}_2[1]$
and
![]() $\mathcal {F}_1[1]$
nontrivially, and we may proceed with the induction.
$\mathcal {F}_1[1]$
nontrivially, and we may proceed with the induction.
The last part of the statement then follows from standard facts in tilting theory.
5 The topology on the space of multi-scale stability conditions
The goal of this section is to provide the space of multi-scale stability conditions
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
with a natural topology so that the quotient by autoequivalences acquires a complex structure (Section 5.3) and so that the further taking the quotient by the
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
with a natural topology so that the quotient by autoequivalences acquires a complex structure (Section 5.3) and so that the further taking the quotient by the
![]() $\mathbb {C}$
-action gives a compact space (Section 5.4). The definition of neighborhoods is based on the plumbing construction of Section 5.1 and explicitly given in Section 5.2. The name of the construction is derived from [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3]; see also Section 6 where a plumbing construction is performed on Riemann surfaces and where we will see that the constructions are analogous.
$\mathbb {C}$
-action gives a compact space (Section 5.4). The definition of neighborhoods is based on the plumbing construction of Section 5.1 and explicitly given in Section 5.2. The name of the construction is derived from [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3]; see also Section 6 where a plumbing construction is performed on Riemann surfaces and where we will see that the constructions are analogous.
5.1 Plumbing of stability conditions
The plumbing construction takes as input a multi-scale stability condition
![]() $(\mathcal {A}_\bullet , Z_\bullet )$
and a collection
$(\mathcal {A}_\bullet , Z_\bullet )$
and a collection
![]() ${\boldsymbol {\tau }}=(\tau _1,\ldots ,\tau _L) \in -\mathbb {H}^L$
and outputs an honest stability condition. More generally, we will allow
${\boldsymbol {\tau }}=(\tau _1,\ldots ,\tau _L) \in -\mathbb {H}^L$
and outputs an honest stability condition. More generally, we will allow
![]() ${\boldsymbol {\tau }}$
to take the formal value
${\boldsymbol {\tau }}$
to take the formal value
![]() $\tau _j = -i\infty $
for j in any fixed subset
$\tau _j = -i\infty $
for j in any fixed subset
![]() $J \subset \{1,\ldots L\}$
and let
$J \subset \{1,\ldots L\}$
and let
![]() $-\mathbb {H}_\infty = -\mathbb {H} \cup \{-i\infty \}$
. The result of the plumbing construction will then be a multi-scale stability condition with
$-\mathbb {H}_\infty = -\mathbb {H} \cup \{-i\infty \}$
. The result of the plumbing construction will then be a multi-scale stability condition with
![]() $|J|$
levels below zero, the extreme case
$|J|$
levels below zero, the extreme case
![]() ${\boldsymbol {\tau }} = (-i\infty )^L$
being the identity, no plumbing at all. Using all tuples
${\boldsymbol {\tau }} = (-i\infty )^L$
being the identity, no plumbing at all. Using all tuples
![]() ${\boldsymbol {\tau }}$
with each entry of large (or infinite) imaginary part and then allowing small deformations of the resulting generalized stability conditions at each level will provide a neighborhood of
${\boldsymbol {\tau }}$
with each entry of large (or infinite) imaginary part and then allowing small deformations of the resulting generalized stability conditions at each level will provide a neighborhood of
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
.
$(\mathcal {A}_\bullet ,Z_\bullet )$
.
For simplicity, we start with a multi-scale stability conditions
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
with
$(\mathcal {A}_\bullet ,Z_\bullet )$
with
![]() $L=1$
and let
$L=1$
and let
![]() ${\mathcal V} = {\mathcal V}_1^Z$
.
${\mathcal V} = {\mathcal V}_1^Z$
.
Proposition 5.1. Suppose that the representative
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition has precisely one level below zero. For
$(\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition has precisely one level below zero. For
![]() $\tau \in -\mathbb {H}$
, there is a (honest) stability condition
$\tau \in -\mathbb {H}$
, there is a (honest) stability condition
![]() $({\mathcal A}',Z') = \tau \ast (\mathcal {A}_\bullet ,Z_\bullet )$
, the plumbing of
$({\mathcal A}',Z') = \tau \ast (\mathcal {A}_\bullet ,Z_\bullet )$
, the plumbing of
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
with
$(\mathcal {A}_\bullet ,Z_\bullet )$
with
![]() $\tau $
, uniquely determined by the conditions
$\tau $
, uniquely determined by the conditions
-
○
 $({\mathcal A}' \cap {\mathcal V},Z'|_{K({\mathcal V})}) = \tau \cdot ({\mathcal A}_1,Z_1)$
for the usual
$({\mathcal A}' \cap {\mathcal V},Z'|_{K({\mathcal V})}) = \tau \cdot ({\mathcal A}_1,Z_1)$
for the usual
 $\mathbb {C}$
-action,
$\mathbb {C}$
-action, -
○ the quotient central charges agree
 ,
, -
○ the hearts
 $\overline {{\mathcal A}'} = \overline {{\mathcal A}}_0$
coincide in
$\overline {{\mathcal A}'} = \overline {{\mathcal A}}_0$
coincide in
 ${\mathcal D}/{\mathcal V}$
.
${\mathcal D}/{\mathcal V}$
.
Note that the plumbing procedure depends on a chosen representative. For the definition of the topology, we will use that the set
![]() $\{ \tau \ast (\mathcal {A}_\bullet ,Z_\bullet ), \, -\Im (\tau )> C\}$
for any fixed C does not depend on this representative, since the change of representative results in translation of the corresponding
$\{ \tau \ast (\mathcal {A}_\bullet ,Z_\bullet ), \, -\Im (\tau )> C\}$
for any fixed C does not depend on this representative, since the change of representative results in translation of the corresponding
![]() $\tau $
by a real number. We use that
$\tau $
by a real number. We use that
(see, for example, the survey [Reference PsaroudakisPsa18, Proposition 2.9]) to define two projections
Using these projections, we combine central charges as
Proof. The heart of
![]() $\tau \cdot ({\mathcal A}_1, Z_1)$
equals
$\tau \cdot ({\mathcal A}_1, Z_1)$
equals
![]() $\mu ^\sharp _{\mathcal F} {\mathcal A}_1$
for some torsion-free class
$\mu ^\sharp _{\mathcal F} {\mathcal A}_1$
for some torsion-free class
![]() $\mathcal F \subset {\mathcal A}_1\subset {\mathcal A}_0$
. We take
$\mathcal F \subset {\mathcal A}_1\subset {\mathcal A}_0$
. We take
![]() ${\mathcal A}' = \mu ^\sharp _{\mathcal F} {\mathcal A}_0$
, and by [Reference Barbieri, Möller, Qiu and SoBMQS22, Lemma 5.6], the last condition holds. Since
${\mathcal A}' = \mu ^\sharp _{\mathcal F} {\mathcal A}_0$
, and by [Reference Barbieri, Möller, Qiu and SoBMQS22, Lemma 5.6], the last condition holds. Since
![]() $\mu ^\sharp _{\mathcal F} {\mathcal A}_1 \subset {\mathcal A}'$
and since
$\mu ^\sharp _{\mathcal F} {\mathcal A}_1 \subset {\mathcal A}'$
and since
![]() ${\mathcal A}'$
is a finite heart thanks to
${\mathcal A}'$
is a finite heart thanks to
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
, we can use the observation (25) to get the decomposition
${\mathcal D} = {\mathcal D}^3_{A_n}$
, we can use the observation (25) to get the decomposition
![]() $K({\mathcal A}'/ \mu ^\sharp _{\mathcal F} {\mathcal A}_1) \oplus K(\mu ^\sharp _{\mathcal F} {\mathcal A}_1)$
and define
$K({\mathcal A}'/ \mu ^\sharp _{\mathcal F} {\mathcal A}_1) \oplus K(\mu ^\sharp _{\mathcal F} {\mathcal A}_1)$
and define
![]() $Z = Z_0 \oplus e^{-\pi i \tau } Z_1$
. This is indeed a central charge, since
$Z = Z_0 \oplus e^{-\pi i \tau } Z_1$
. This is indeed a central charge, since
![]() $Z(S) \in \overline {\mathbb {H}}$
for all simples
$Z(S) \in \overline {\mathbb {H}}$
for all simples
![]() $S \in {\mathcal A}_1$
by the hypothesis on
$S \in {\mathcal A}_1$
by the hypothesis on
![]() $Z_0$
and
$Z_0$
and
![]() $Z_1$
.
$Z_1$
.
Next, we generalize to the action of
![]() ${\boldsymbol {\tau }} = (\tau , -i\infty , \ldots , -i\infty )$
on a multi-scale stability condition
${\boldsymbol {\tau }} = (\tau , -i\infty , \ldots , -i\infty )$
on a multi-scale stability condition
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
. In this case, we apply Proposition 5.1 to the first two levels
$(\mathcal {A}_\bullet ,Z_\bullet )$
. In this case, we apply Proposition 5.1 to the first two levels
![]() $( ({\mathcal A}_0, {\mathcal A}_1),(Z_0,Z_1))$
and record as
$( ({\mathcal A}_0, {\mathcal A}_1),(Z_0,Z_1))$
and record as
![]() ${\boldsymbol {\tau }}$
-image the tuple
${\boldsymbol {\tau }}$
-image the tuple
(i.e., the top two levels have been merged to obtain a multi-scale stability condition with
![]() $L-1$
levels below zero).
$L-1$
levels below zero).
This construction also gives a recipe for the plumbing
![]() ${\boldsymbol {\tau }} \ast (\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition
${\boldsymbol {\tau }} \ast (\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
by a general
$(\mathcal {A}_\bullet ,Z_\bullet )$
by a general
![]() ${\boldsymbol {\tau }} \in -\mathbb {H}_\infty ^L$
. We take j to be the highest index with
${\boldsymbol {\tau }} \in -\mathbb {H}_\infty ^L$
. We take j to be the highest index with
![]() $\tau _j \neq -i\infty $
. Then we apply the preceding construction to the multi-scale stability condition
$\tau _j \neq -i\infty $
. Then we apply the preceding construction to the multi-scale stability condition
![]() $( {\mathcal A}_{\geq j},Z_{\geq j})$
on
$( {\mathcal A}_{\geq j},Z_{\geq j})$
on
![]() ${\mathcal V}_j^Z$
and iterate with the action of the remaining coordinates
${\mathcal V}_j^Z$
and iterate with the action of the remaining coordinates
![]() ${\boldsymbol {\tau }}' = (\tau _1, \cdots , \widehat {\tau _j}, \cdots )$
. It will turn out that the plumbing procedure is not quite independent of the order of the levels at which we perform the plumbing step, only nearly so. The reason is that already one-level plumbing and rotation are only nearly compatible. We need a quantitative version of this fact.
${\boldsymbol {\tau }}' = (\tau _1, \cdots , \widehat {\tau _j}, \cdots )$
. It will turn out that the plumbing procedure is not quite independent of the order of the levels at which we perform the plumbing step, only nearly so. The reason is that already one-level plumbing and rotation are only nearly compatible. We need a quantitative version of this fact.
Proposition 5.2. Let
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
be a fixed representative of a multi-scale stability condition with
$(\mathcal {A}_\bullet ,Z_\bullet )$
be a fixed representative of a multi-scale stability condition with
![]() $L=1$
. Let
$L=1$
. Let
![]() $\tau \in -{\mathbb H}$
,
$\tau \in -{\mathbb H}$
,
![]() $\lambda \in \mathbb {C}$
, with
$\lambda \in \mathbb {C}$
, with
Then the hearts of the two stability conditions
are intermediate hearts with respect to
![]() ${\mathcal A}_0$
, and the difference of the central charges may be coarsely estimated by
${\mathcal A}_0$
, and the difference of the central charges may be coarsely estimated by
 $$ \begin{align} \left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \,\leq \, \ell \cdot |e^{-\pi i (\lambda+\tau)}| \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)| \end{align} $$
$$ \begin{align} \left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \,\leq \, \ell \cdot |e^{-\pi i (\lambda+\tau)}| \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)| \end{align} $$
for any simple
![]() $S_j \in \operatorname {Sim}({\mathcal A}_0)$
, where
$S_j \in \operatorname {Sim}({\mathcal A}_0)$
, where
![]() $\ell $
is the number of classes of indecomposables in
$\ell $
is the number of classes of indecomposables in
![]() $K(\overline {{\mathcal A}_0})$
.
$K(\overline {{\mathcal A}_0})$
.
We recall from [Reference BridgelandBri16, Proposition 7.4] that the local homeomorphism given by the forgetful map ![]() is actually injective when restricted to all hearts that are intermediate with respect to a given heart
is actually injective when restricted to all hearts that are intermediate with respect to a given heart
![]() ${\mathcal A}_0$
(i.e., in
${\mathcal A}_0$
(i.e., in
![]() $[{\mathcal A}_0,{\mathcal A}_0[1]]$
). Consequently, to show that
$[{\mathcal A}_0,{\mathcal A}_0[1]]$
). Consequently, to show that
![]() $\widetilde {\sigma }$
and
$\widetilde {\sigma }$
and
![]() $\widehat {\sigma }$
are nearby, it suffices to estimate the differences of the central charges if
$\widehat {\sigma }$
are nearby, it suffices to estimate the differences of the central charges if
![]() $\widetilde {{\mathcal A}}, \widehat {{\mathcal A}} \in [{\mathcal A}_0,{\mathcal A}_0[1]]$
.
$\widetilde {{\mathcal A}}, \widehat {{\mathcal A}} \in [{\mathcal A}_0,{\mathcal A}_0[1]]$
.
Proof. The result of plumbing is given by definition as
![]() $({\mathcal A}, Z):=\tau \ast (\mathcal {A}_\bullet ,Z_\bullet )$
with
$({\mathcal A}, Z):=\tau \ast (\mathcal {A}_\bullet ,Z_\bullet )$
with
 $$\begin{align*}\begin{aligned} &{\mathcal A}=\mu_{\mathcal{F}_\tau}^\sharp{\mathcal A}_0\supset\mu_{\mathcal{F}_\tau}^\sharp{\mathcal A}_1,\quad \mathcal{F}_\tau=\langle E\in {\mathcal A}_1,\, Z_1\text{-semistable s.t. }\phi_{Z_1}(E)\leq \Re\tau\rangle\\ &Z := \overline{Z_0} \oplus e^{-i\pi\tau} \cdot Z_1\,. \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} &{\mathcal A}=\mu_{\mathcal{F}_\tau}^\sharp{\mathcal A}_0\supset\mu_{\mathcal{F}_\tau}^\sharp{\mathcal A}_1,\quad \mathcal{F}_\tau=\langle E\in {\mathcal A}_1,\, Z_1\text{-semistable s.t. }\phi_{Z_1}(E)\leq \Re\tau\rangle\\ &Z := \overline{Z_0} \oplus e^{-i\pi\tau} \cdot Z_1\,. \end{aligned}\end{align*}$$
We first consider the case where
-
(
 $\star $
) there is exactly one isomorphism class
$\star $
) there is exactly one isomorphism class
 $[S_0]\in K({\mathcal A})$
of a Z-stable object in
$[S_0]\in K({\mathcal A})$
of a Z-stable object in
 ${\mathcal A}$
with phase
${\mathcal A}$
with phase
 ${0<\phi _Z(S_0)\leq \Re \lambda }$
, and moreover,
${0<\phi _Z(S_0)\leq \Re \lambda }$
, and moreover,
 $[S_0] \not \in K({\mathcal V})$
.
$[S_0] \not \in K({\mathcal V})$
.
(Note that
![]() $S_0$
must be simple in
$S_0$
must be simple in
![]() ${\mathcal A}$
.) In this case, the stability condition
${\mathcal A}$
.) In this case, the stability condition
![]() $\widetilde {\sigma }$
is given by
$\widetilde {\sigma }$
is given by
![]() $\widetilde {Z} =e^{-i\pi \lambda }Z$
and
$\widetilde {Z} =e^{-i\pi \lambda }Z$
and
![]() $\widetilde {{\mathcal A}} =\mu ^\sharp _{S_0}{\mathcal A} = \mu ^\sharp _{\widetilde {\mathcal F}}{\mathcal A}_0$
with
$\widetilde {{\mathcal A}} =\mu ^\sharp _{S_0}{\mathcal A} = \mu ^\sharp _{\widetilde {\mathcal F}}{\mathcal A}_0$
with
![]() $\widetilde {\mathcal F} = \langle \mathcal F_\tau , S_0 \rangle $
. In particular,
$\widetilde {\mathcal F} = \langle \mathcal F_\tau , S_0 \rangle $
. In particular,
![]() $\widetilde {{\mathcal A}} \in [{\mathcal A}_0,{\mathcal A}_0[1]]$
.
$\widetilde {{\mathcal A}} \in [{\mathcal A}_0,{\mathcal A}_0[1]]$
.
However, the heart
![]() $\widehat {{\mathcal A}}$
is obtained by
$\widehat {{\mathcal A}}$
is obtained by
![]() $\tau $
-plumbing the multi-scale heart
$\tau $
-plumbing the multi-scale heart
![]() $({\mathcal A}_1 \subset \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0)$
, where
$({\mathcal A}_1 \subset \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0)$
, where
![]() ${\mathcal {F}=\langle S_0,S_{01},\dots \rangle \subset {\mathcal A}_0}$
is explicitly described in Lemma 4.10, since assumption
${\mathcal {F}=\langle S_0,S_{01},\dots \rangle \subset {\mathcal A}_0}$
is explicitly described in Lemma 4.10, since assumption
![]() $(\star )$
implies that the torsion-free class in
$(\star )$
implies that the torsion-free class in
![]() $\overline {{\mathcal A}_0}$
of objects with phase
$\overline {{\mathcal A}_0}$
of objects with phase
![]() $0<\phi _{\overline {Z_0}}\leq \Re \lambda $
is generated by
$0<\phi _{\overline {Z_0}}\leq \Re \lambda $
is generated by
![]() $\overline {S_0}$
. Consequently,
$\overline {S_0}$
. Consequently,
Since
![]() $\mathcal {G} \subset \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0\cap {\mathcal V}_1$
and
$\mathcal {G} \subset \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0\cap {\mathcal V}_1$
and
![]() $\mu ^\sharp _{\mathcal {F}}{\mathcal A}_1 = {\mathcal A}_1$
, we deduce
$\mu ^\sharp _{\mathcal {F}}{\mathcal A}_1 = {\mathcal A}_1$
, we deduce
![]() $\mathcal {G} \cap \mathcal {F}[1] =\{0\}$
, and consequently (by the same arguments as in Lemma 4.11), we deduce
$\mathcal {G} \cap \mathcal {F}[1] =\{0\}$
, and consequently (by the same arguments as in Lemma 4.11), we deduce
![]() ${\mathcal A}_0\leq \mu ^\sharp _{\mathcal {F}}{\mathcal A}\leq \widehat {{\mathcal A}} = \mu ^\sharp _{\mathcal {G}} \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0 \leq {\mathcal A}_0[1]$
in the partial order from Section 2.1.
${\mathcal A}_0\leq \mu ^\sharp _{\mathcal {F}}{\mathcal A}\leq \widehat {{\mathcal A}} = \mu ^\sharp _{\mathcal {G}} \mu ^\sharp _{\mathcal {F}}{\mathcal A}_0 \leq {\mathcal A}_0[1]$
in the partial order from Section 2.1.
To compare central charges, note that the plumbing procedure happens over two different decompositions of
![]() $K({\mathcal D})$
: one induced by
$K({\mathcal D})$
: one induced by
![]() $K({\mathcal A}_0/{\mathcal A}_1) \oplus K({\mathcal A}_1)$
, and the other induced by
$K({\mathcal A}_0/{\mathcal A}_1) \oplus K({\mathcal A}_1)$
, and the other induced by
![]() $K(\mu _{\mathcal {F}}^\sharp {\mathcal A}_0/{\mathcal A}_1) \oplus K({\mathcal A}_1)$
. The change of basis
$K(\mu _{\mathcal {F}}^\sharp {\mathcal A}_0/{\mathcal A}_1) \oplus K({\mathcal A}_1)$
. The change of basis
![]() $K(\mu ^\sharp _{\mathcal {F}}{\mathcal A}_0) \simeq K({\mathcal A}_0)=K({\mathcal A}_0/{\mathcal A}_1)\oplus K({\mathcal A}_1)$
has the form of a block lower-triangular matrix
$K(\mu ^\sharp _{\mathcal {F}}{\mathcal A}_0) \simeq K({\mathcal A}_0)=K({\mathcal A}_0/{\mathcal A}_1)\oplus K({\mathcal A}_1)$
has the form of a block lower-triangular matrix
 $$\begin{align*}\left[\mu_{\mathcal{F}}\right]^{-1}=\begin{pmatrix} C_{n-k} & 0 \\ B_{1\overline{0}} & \mathbf{1}_k\end{pmatrix}, \end{align*}$$
$$\begin{align*}\left[\mu_{\mathcal{F}}\right]^{-1}=\begin{pmatrix} C_{n-k} & 0 \\ B_{1\overline{0}} & \mathbf{1}_k\end{pmatrix}, \end{align*}$$
where the entries of
![]() $B_{1\overline {0}}=(b_{ij})_{ij}$
have absolute value at most
$B_{1\overline {0}}=(b_{ij})_{ij}$
have absolute value at most
![]() $1$
, where we hardly control the block
$1$
, where we hardly control the block
![]() $C_{n-k}$
, and where the block
$C_{n-k}$
, and where the block
![]() $\mathbf {1}_k$
expresses that
$\mathbf {1}_k$
expresses that
![]() ${\mathcal V}$
is preserved. Using the projections
${\mathcal V}$
is preserved. Using the projections
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
onto the summands
$\pi _1$
onto the summands
![]() $K({\mathcal A}_0/{\mathcal A}_1)\oplus K({\mathcal A}_1)$
, we find
$K({\mathcal A}_0/{\mathcal A}_1)\oplus K({\mathcal A}_1)$
, we find
and
 $$ \begin{align}\begin{aligned} \widehat{Z}&\;=\; e^{-\pi i \lambda}Z_0\circ\widehat{\pi}_0 + e^{-\pi i (\tau+\lambda)}Z_1\circ\widehat{\pi}_1\\ &\ =e^{-\pi i \lambda}Z_0\circ\pi_0 + e^{-\pi i (\tau+\lambda)}Z_1\circ(\pi_1+B_{1\overline{0}}\pi_0), \end{aligned}\end{align} $$
$$ \begin{align}\begin{aligned} \widehat{Z}&\;=\; e^{-\pi i \lambda}Z_0\circ\widehat{\pi}_0 + e^{-\pi i (\tau+\lambda)}Z_1\circ\widehat{\pi}_1\\ &\ =e^{-\pi i \lambda}Z_0\circ\pi_0 + e^{-\pi i (\tau+\lambda)}Z_1\circ(\pi_1+B_{1\overline{0}}\pi_0), \end{aligned}\end{align} $$
where we see
![]() $B_{1\overline {0}}$
as a map
$B_{1\overline {0}}$
as a map
![]() $K({\mathcal A}_0/{\mathcal A}_1)\to K({\mathcal A}_1)$
. Now consider the simples in
$K({\mathcal A}_0/{\mathcal A}_1)\to K({\mathcal A}_1)$
. Now consider the simples in
![]() ${\mathcal A}_0$
. For
${\mathcal A}_0$
. For
![]() $S_j\in {\mathcal A}_1$
, the two expressions agree. For
$S_j\in {\mathcal A}_1$
, the two expressions agree. For
![]() $S_j$
a simple of
$S_j$
a simple of
![]() ${\mathcal A}_0$
not in
${\mathcal A}_0$
not in
![]() ${\mathcal A}_1$
, we find
${\mathcal A}_1$
, we find
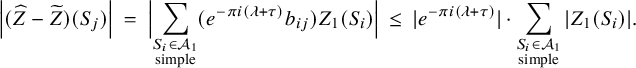 $$ \begin{align*} \left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \;=\; \Bigl|\sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}}(e^{-\pi i (\lambda+\tau)}b_{ij})Z_1(S_i)\Bigr| \,\leq\, |e^{-\pi i (\lambda+\tau)}| \cdot \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)|. \end{align*} $$
$$ \begin{align*} \left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \;=\; \Bigl|\sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}}(e^{-\pi i (\lambda+\tau)}b_{ij})Z_1(S_i)\Bigr| \,\leq\, |e^{-\pi i (\lambda+\tau)}| \cdot \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)|. \end{align*} $$
We now drop the assumption (
![]() $\star $
) and allow for multiple indecomposables
$\star $
) and allow for multiple indecomposables
![]() $X\in {\mathcal A}$
with
$X\in {\mathcal A}$
with
![]() $0<\phi _Z(X)\leq \Re \lambda $
.
$0<\phi _Z(X)\leq \Re \lambda $
.
The assumption (28) still guarantees that
![]() $\widetilde {{\mathcal A}}\in \left [{\mathcal A}_0,{\mathcal A}_0[1]\right ]$
, and
$\widetilde {{\mathcal A}}\in \left [{\mathcal A}_0,{\mathcal A}_0[1]\right ]$
, and
![]() $\widetilde {Z}=e^{-\pi i \lambda }\overline {Z_0}\circ \pi _0 + e^{-\pi i (\lambda +\tau )}Z_1 \circ \pi _1$
, as before.
$\widetilde {Z}=e^{-\pi i \lambda }\overline {Z_0}\circ \pi _0 + e^{-\pi i (\lambda +\tau )}Z_1 \circ \pi _1$
, as before.
The result of
![]() $\lambda \cdot ({\mathcal A}_\bullet , Z_\bullet )$
is a multi-scale stability condition
$\lambda \cdot ({\mathcal A}_\bullet , Z_\bullet )$
is a multi-scale stability condition
![]() $\sigma '$
with nested hearts
$\sigma '$
with nested hearts
![]() ${\mathcal A}_1^{\prime } \subset {\mathcal A}_0^{\prime }$
that can be explicitly obtained as in the proof of Proposition 4.6 by performing a forward-tilt at
${\mathcal A}_1^{\prime } \subset {\mathcal A}_0^{\prime }$
that can be explicitly obtained as in the proof of Proposition 4.6 by performing a forward-tilt at
![]() $\mathcal {F}_\lambda ^1$
and a sequence of forward-tilts at torsion-free classes
$\mathcal {F}_\lambda ^1$
and a sequence of forward-tilts at torsion-free classes
![]() $\mathcal {F}_i$
described in Lemma 4.10 and Lemma 4.11. At each step, at the 0 level, the matrix of the change of basis has the form of a block lower triangular matrix, with a block
$\mathcal {F}_i$
described in Lemma 4.10 and Lemma 4.11. At each step, at the 0 level, the matrix of the change of basis has the form of a block lower triangular matrix, with a block
![]() $B_{1\bar {0}}= \prod _i B_{1\bar {0}}^{(i)}$
, whose entries have absolute value
$B_{1\bar {0}}= \prod _i B_{1\bar {0}}^{(i)}$
, whose entries have absolute value
![]() $\leq \ell ^{\prime }_i$
, bounded by the number
$\leq \ell ^{\prime }_i$
, bounded by the number
![]() $\ell ^{\prime }_i$
of classes of indecomposables in
$\ell ^{\prime }_i$
of classes of indecomposables in
![]() $\mathcal {F}^1_\lambda $
or
$\mathcal {F}^1_\lambda $
or
![]() $\mathcal {F}_i$
. Lemma 4.11 guarantees that the heart
$\mathcal {F}_i$
. Lemma 4.11 guarantees that the heart
![]() ${\mathcal A}_0^{\prime }$
is intermediate with respect to
${\mathcal A}_0^{\prime }$
is intermediate with respect to
![]() ${\mathcal A}_0$
, and so is the heart of
${\mathcal A}_0$
, and so is the heart of
![]() $\tau *\sigma '$
thanks to assumption 28. Similarly to (5.1), we obtain
$\tau *\sigma '$
thanks to assumption 28. Similarly to (5.1), we obtain
 $$\begin{align*}\left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \leq |e^{-\pi i (\lambda+\tau)}| \cdot \ell\sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)|, \end{align*}$$
$$\begin{align*}\left|(\widehat{Z}-\widetilde{Z})(S_j)\right| \leq |e^{-\pi i (\lambda+\tau)}| \cdot \ell\sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)|, \end{align*}$$
where
![]() $\ell $
is the number of classes of indecomposables in
$\ell $
is the number of classes of indecomposables in
![]() $K({\mathcal A}_0)$
. Last, the case
$K({\mathcal A}_0)$
. Last, the case
![]() $\Re \lambda =0$
is just easier, and the argument above shows that in such a case,
$\Re \lambda =0$
is just easier, and the argument above shows that in such a case,
![]() $\lambda \cdot (\tau \ast ({\mathcal A}_\bullet ,Z_\bullet )) =\tau \ast (\lambda \cdot ({\mathcal A}_\bullet ,Z_\bullet ))$
.
$\lambda \cdot (\tau \ast ({\mathcal A}_\bullet ,Z_\bullet )) =\tau \ast (\lambda \cdot ({\mathcal A}_\bullet ,Z_\bullet ))$
.
Remark 5.3. The same observation shows that the plumbing (with fixed parameter
![]() $\tau \in -\mathbb {H}$
) of a path
$\tau \in -\mathbb {H}$
) of a path ![]() is not continuous. Discontinuities occur when some simple (not at bottom level) is tilted. However, the size of the jumps decreases with
is not continuous. Discontinuities occur when some simple (not at bottom level) is tilted. However, the size of the jumps decreases with
![]() $|e^{-\pi i \tau }|$
. More precisely, suppose that
$|e^{-\pi i \tau }|$
. More precisely, suppose that
![]() $L=1$
and that
$L=1$
and that
![]() $\gamma $
is a path for which at precisely one value
$\gamma $
is a path for which at precisely one value
![]() $t_0 \in [0,1]$
, such a tilt occurs. Then the hearts of the two stability conditions
$t_0 \in [0,1]$
, such a tilt occurs. Then the hearts of the two stability conditions
are intermediate hearts with respect to the top level heart
![]() ${\mathcal A}_0$
of
${\mathcal A}_0$
of
![]() $\lim _{t \to t_0^-}\gamma (t_0)$
, and the difference of the central charges may be coarsely estimated by
$\lim _{t \to t_0^-}\gamma (t_0)$
, and the difference of the central charges may be coarsely estimated by
 $$ \begin{align} \left|({Z}^+-{Z}^-)(S_j)\right| \,\leq \, \ell \cdot |e^{-\pi i \tau}| \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)| \end{align} $$
$$ \begin{align} \left|({Z}^+-{Z}^-)(S_j)\right| \,\leq \, \ell \cdot |e^{-\pi i \tau}| \sum_{\substack{S_i\in{\mathcal A}_1\\\text{simple}}} |Z_1(S_i)| \end{align} $$
for any simple
![]() $S_j \in \operatorname {Sim}({\mathcal A}_0)$
, where
$S_j \in \operatorname {Sim}({\mathcal A}_0)$
, where
![]() $\ell $
is the number of classes of indecomposables in
$\ell $
is the number of classes of indecomposables in
![]() $K(\overline {{\mathcal A}_0})$
. The proof is exactly the same as for the previous proposition.
$K(\overline {{\mathcal A}_0})$
. The proof is exactly the same as for the previous proposition.
Let again
![]() $0 \leq \Re (\tau ) < 1$
, and decompose
$0 \leq \Re (\tau ) < 1$
, and decompose
![]() $\tau = \tau _R + i \tau _I$
into its real and imaginary part. We observe that the plumbing in Proposition 4.6 can be viewed a composition of three steps: First, we apply the action of
$\tau = \tau _R + i \tau _I$
into its real and imaginary part. We observe that the plumbing in Proposition 4.6 can be viewed a composition of three steps: First, we apply the action of
![]() $\tau _R$
, resulting in a tilt at a torsion-free class
$\tau _R$
, resulting in a tilt at a torsion-free class
![]() $\mathcal F \subset {\mathcal A}_1$
and turning
$\mathcal F \subset {\mathcal A}_1$
and turning
![]() $Z_1$
by
$Z_1$
by
![]() $e^{-\pi i \tau _R}$
resulting in some other representative
$e^{-\pi i \tau _R}$
resulting in some other representative
![]() $({\mathcal A}_\bullet ^{\Re (\tau )}, Z_\bullet ^{\Re (\tau )})$
of the multi-scale stability condition. Second, we rescale
$({\mathcal A}_\bullet ^{\Re (\tau )}, Z_\bullet ^{\Re (\tau )})$
of the multi-scale stability condition. Second, we rescale
![]() $e^{-\pi i \tau _R}Z_1$
by
$e^{-\pi i \tau _R}Z_1$
by
![]() $e^{\pi \tau _I}$
, and finally, we form the direct sum Z and drop the lower levels to get an honest stability condition. The observation that
$e^{\pi \tau _I}$
, and finally, we form the direct sum Z and drop the lower levels to get an honest stability condition. The observation that
![]() $[\mu ^\sharp _{\mathcal {F}}]^{-1}$
in the previous proof preserves
$[\mu ^\sharp _{\mathcal {F}}]^{-1}$
in the previous proof preserves
![]() ${\mathcal V}_1$
and the first step just described does preserve
${\mathcal V}_1$
and the first step just described does preserve
![]() ${\mathcal V}_1$
as well, together imply the following corollary where we relax the bound for
${\mathcal V}_1$
as well, together imply the following corollary where we relax the bound for
![]() $\Re (\tau )$
appearing in Proposition 5.2.
$\Re (\tau )$
appearing in Proposition 5.2.
Corollary 5.4. Let
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
be a fixed representative of a multi-scale stability condition with
$(\mathcal {A}_\bullet ,Z_\bullet )$
be a fixed representative of a multi-scale stability condition with
![]() $L=1$
. Let
$L=1$
. Let
![]() $\tau \in -{\mathbb H}$
,
$\tau \in -{\mathbb H}$
,
![]() $\lambda \in \mathbb {C}$
, with
$\lambda \in \mathbb {C}$
, with
![]() $0 \leq \Re (\lambda ) < 1$
. Then the hearts of the two stability conditions
$0 \leq \Re (\lambda ) < 1$
. Then the hearts of the two stability conditions
are intermediate hearts with respect to
![]() ${\mathcal A}_0^{\Re (\tau )}$
, and the difference of the central charges may be coarsely estimated as in (30).
${\mathcal A}_0^{\Re (\tau )}$
, and the difference of the central charges may be coarsely estimated as in (30).
Remark 5.5. For
![]() $\lambda \in 2\mathbb {Z}$
and any
$\lambda \in 2\mathbb {Z}$
and any
![]() $\tau \in -\mathbb {H}$
, plumbing and the
$\tau \in -\mathbb {H}$
, plumbing and the
![]() $\lambda $
-action commute (i.e., the hearts
$\lambda $
-action commute (i.e., the hearts
![]() $\widetilde {\sigma }$
and
$\widetilde {\sigma }$
and
![]() $\widehat {\sigma }$
from (29) agree).
$\widehat {\sigma }$
from (29) agree).
5.2 Neighborhoods in the space
 $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
We work here with a representative
![]() $(\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition and let
$(\mathcal {A}_\bullet ,Z_\bullet )$
of a multi-scale stability condition and let
be a tuple of (small) positive real numbers where
![]() $\delta _j$
will control the size of plumbing of level j. Moreover, we fix a collection of positive real numbers
$\delta _j$
will control the size of plumbing of level j. Moreover, we fix a collection of positive real numbers
The following Definition 5.6 captures the idea that neighborhoods of boundary points consist of the multi-scale stability conditions, described heuristically as follows. Suppose
![]() $L=1$
for simplicity. We write
$L=1$
for simplicity. We write
![]() $\epsilon _0,\epsilon _1,\epsilon _{01}$
for
$\epsilon _0,\epsilon _1,\epsilon _{01}$
for
![]() $J=\{0\},\{1\},\{0,1\}$
, respectively. Then
$J=\{0\},\{1\},\{0,1\}$
, respectively. Then
-
○ we may plumb by
 $\tau $
with large negative imaginary part (so that the lower level stability condition
$\tau $
with large negative imaginary part (so that the lower level stability condition
 $({\mathcal A}_1,e^{-\pi i \tau } Z_1)$
stays small in size) and wiggle the result in
$({\mathcal A}_1,e^{-\pi i \tau } Z_1)$
stays small in size) and wiggle the result in  by a small amount (by a size controlled by
by a small amount (by a size controlled by
 $\varepsilon _{01}$
);
$\varepsilon _{01}$
); -
○ alternatively, we may not plumb (i.e.,
 $\tau = -i\infty $
) and wiggle in
$\tau = -i\infty $
) and wiggle in  and
and  a bit (by sizes controlled by
a bit (by sizes controlled by
 $\varepsilon _i$
) on level i, for
$\varepsilon _i$
) on level i, for
 $i=0,1$
.
$i=0,1$
.
We say that a stability condition
![]() $(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
with
$(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
with
![]() $L' \leq L$
levels below zero arises by plumbing of size at most
$L' \leq L$
levels below zero arises by plumbing of size at most
![]() ${\boldsymbol {\delta }}$
from
${\boldsymbol {\delta }}$
from
![]() $(\mathcal {A}_\bullet , Z_\bullet )$
if there is
$(\mathcal {A}_\bullet , Z_\bullet )$
if there is
![]() $\tau \in (-\mathbb {H}_\infty )^L$
) with
$\tau \in (-\mathbb {H}_\infty )^L$
) with
![]() $|e^{-\pi i \tau _j}| < \delta _j $
for
$|e^{-\pi i \tau _j}| < \delta _j $
for
![]() $j=1,\ldots ,L$
and
$j=1,\ldots ,L$
and
![]() $({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) = \tau \ast ({\mathcal A}_\bullet ,Z_\bullet )$
. For a such a stability condition, we denote the new vanishing categories by
$({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) = \tau \ast ({\mathcal A}_\bullet ,Z_\bullet )$
. For a such a stability condition, we denote the new vanishing categories by
![]() ${\mathcal V}^{\prime }_i$
. Say levels in the interval
${\mathcal V}^{\prime }_i$
. Say levels in the interval
![]() $J_i = \{j_1,\ldots \} \subset \{0,\ldots ,L\}$
have been plumbed to form the new level i. (This implies by definition that
$J_i = \{j_1,\ldots \} \subset \{0,\ldots ,L\}$
have been plumbed to form the new level i. (This implies by definition that
![]() $\tau _{j_1} = -i\infty $
.)
$\tau _{j_1} = -i\infty $
.)
We define the natural inner product on ![]() by using as an orthonormal basis the basis
by using as an orthonormal basis the basis
![]() $Z_{S_i}$
dual to the simples of
$Z_{S_i}$
dual to the simples of
![]() ${\mathcal A}_0$
. (Note that this norm depends on the heart
${\mathcal A}_0$
. (Note that this norm depends on the heart
![]() ${\mathcal A}_0$
and its simples, but the norm around any other multi-scale stability condition
${\mathcal A}_0$
and its simples, but the norm around any other multi-scale stability condition
![]() $\sigma ^\dagger = (\mathcal {A}_\bullet ^\dagger ,Z^\dagger _\bullet )$
is comparable, scaling by a factor
$\sigma ^\dagger = (\mathcal {A}_\bullet ^\dagger ,Z^\dagger _\bullet )$
is comparable, scaling by a factor
![]() $C = C(\sigma ,\sigma ^\dagger )$
given by the operator norm of the identity map with respect to the to norms.)
$C = C(\sigma ,\sigma ^\dagger )$
given by the operator norm of the identity map with respect to the to norms.)
Definition 5.6. We define the set
![]() $V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}(\mathcal {A}_\bullet ,Z_\bullet )$
to be the set of all multi-scale stability conditions
$V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}(\mathcal {A}_\bullet ,Z_\bullet )$
to be the set of all multi-scale stability conditions
![]() $(\mathcal {A}_\bullet ^{\prime \prime },Z^{\prime \prime }_\bullet )$
with
$(\mathcal {A}_\bullet ^{\prime \prime },Z^{\prime \prime }_\bullet )$
with
![]() $L'$
levels below zero such that
$L'$
levels below zero such that
-
(1) there is a multi-scale stability condition
 $(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
with
$(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
with
 $L' \leq L$
levels that arises by plumbing of size at most
$L' \leq L$
levels that arises by plumbing of size at most
 ${\boldsymbol {\delta }}$
from
${\boldsymbol {\delta }}$
from
 $(\mathcal {A}_\bullet ,Z_\bullet )$
, and
$(\mathcal {A}_\bullet ,Z_\bullet )$
, and -
(2) the multi-scale stability condition
 $(\mathcal {A}_\bullet ^{\prime \prime },Z^{\prime \prime }_\bullet )$
is in a neighborhood of
$(\mathcal {A}_\bullet ^{\prime \prime },Z^{\prime \prime }_\bullet )$
is in a neighborhood of
 $(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
in
$(\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet )$
in
 $\prod \operatorname {Stab}^\circ ({\mathcal V}^{\prime }_i/{\mathcal V}^{\prime }_{i+1})$
which maps to the product of
$\prod \operatorname {Stab}^\circ ({\mathcal V}^{\prime }_i/{\mathcal V}^{\prime }_{i+1})$
which maps to the product of
 $\varepsilon _J$
-balls on
$\varepsilon _J$
-balls on
 $K({\mathcal V}^{\prime }_i/{\mathcal V}^{\prime }_{i+1})^\vee $
under the forgetful map retaining just the quotients of the multi-scale central charges. Here, J is the interval that is plumbed to produce level i.
$K({\mathcal V}^{\prime }_i/{\mathcal V}^{\prime }_{i+1})^\vee $
under the forgetful map retaining just the quotients of the multi-scale central charges. Here, J is the interval that is plumbed to produce level i.
A neighborhood of
![]() $(\mathcal {A}_\bullet ,Z_\bullet ,)$
is a set in
$(\mathcal {A}_\bullet ,Z_\bullet ,)$
is a set in
![]() $\operatorname {MStab}^\circ ({\mathcal D}_{A_n})$
that contains
$\operatorname {MStab}^\circ ({\mathcal D}_{A_n})$
that contains
![]() $V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}(\mathcal {A}_\bullet ,Z_\bullet ,)$
for some
$V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}(\mathcal {A}_\bullet ,Z_\bullet ,)$
for some
![]() ${\boldsymbol {\varepsilon }}$
and
${\boldsymbol {\varepsilon }}$
and
![]() ${\boldsymbol {\delta }}$
.
${\boldsymbol {\delta }}$
.
This definition includes the case that
![]() $L=0$
and that
$L=0$
and that
![]() $(\mathcal {A}, Z)$
is an honest stability condition, in which case, the neighborhoods have to contain the
$(\mathcal {A}, Z)$
is an honest stability condition, in which case, the neighborhoods have to contain the
![]() $\varepsilon $
-balls in the norm with orthonormal bases given by the simples of
$\varepsilon $
-balls in the norm with orthonormal bases given by the simples of
![]() $\mathcal {A}$
, since the deformation of stability conditions is locally controlled by the deformation of the central charge. This gives the second part of the following lemma.
$\mathcal {A}$
, since the deformation of stability conditions is locally controlled by the deformation of the central charge. This gives the second part of the following lemma.
Lemma 5.7. The system of neighborhoods given in Definition 5.6 defines a topology on
![]() $\operatorname {MStab}({\mathcal D}^3_{A_n})$
whose restriction to
$\operatorname {MStab}({\mathcal D}^3_{A_n})$
whose restriction to ![]() is the usual topology where the forgetful map retaining the central charge is a local homeomorphism.
is the usual topology where the forgetful map retaining the central charge is a local homeomorphism.
Proof. The only axiom whose verification is nontrivial is the following. Let U be a neighborhood of
![]() $\sigma =[A_\bullet ,Z_\bullet ]$
, in the sense of Definition 5.6. Then there is a smaller neighborhood V of this point, such that U is a neighborhood of each
$\sigma =[A_\bullet ,Z_\bullet ]$
, in the sense of Definition 5.6. Then there is a smaller neighborhood V of this point, such that U is a neighborhood of each
![]() $\sigma ^\dagger =[{\mathcal A}^\dagger _\bullet ,Z^\dagger _\bullet ]$
in V. We continue with the case
$\sigma ^\dagger =[{\mathcal A}^\dagger _\bullet ,Z^\dagger _\bullet ]$
in V. We continue with the case
![]() $L = 1$
; the general case works with the same argument. By definition, U contains some
$L = 1$
; the general case works with the same argument. By definition, U contains some
![]() $V_{{\boldsymbol {\varepsilon }},\delta }(A_\bullet ,Z_\bullet )$
. The rough idea is to take
$V_{{\boldsymbol {\varepsilon }},\delta }(A_\bullet ,Z_\bullet )$
. The rough idea is to take
![]() $V = V_{{\boldsymbol {\varepsilon }}^*,\delta ^*}(A_\bullet ,Z_\bullet )$
for some
$V = V_{{\boldsymbol {\varepsilon }}^*,\delta ^*}(A_\bullet ,Z_\bullet )$
for some
![]() $({\boldsymbol {\varepsilon }}^*,\delta ^*)$
smaller than
$({\boldsymbol {\varepsilon }}^*,\delta ^*)$
smaller than
![]() $({\boldsymbol {\varepsilon }}, \delta )$
in each entry, so that U contains
$({\boldsymbol {\varepsilon }}, \delta )$
in each entry, so that U contains
![]() $V_{({\boldsymbol {\varepsilon }}-{\boldsymbol {\varepsilon }}^*)/C, \delta -\delta ^*}(\sigma ^\dagger )$
, just as if we would be working plainly in vector spaces, where
$V_{({\boldsymbol {\varepsilon }}-{\boldsymbol {\varepsilon }}^*)/C, \delta -\delta ^*}(\sigma ^\dagger )$
, just as if we would be working plainly in vector spaces, where
![]() $C = C(\sigma ,\sigma ^\dagger )\geq 1$
accounts for the change of basis in the definition of the norms. We will prove that
$C = C(\sigma ,\sigma ^\dagger )\geq 1$
accounts for the change of basis in the definition of the norms. We will prove that
![]() $V_{({\boldsymbol {\varepsilon }}-{\boldsymbol {\varepsilon }}^*)/C, \delta -\delta ^*}(\sigma ^\dagger )$
is indeed contained in
$V_{({\boldsymbol {\varepsilon }}-{\boldsymbol {\varepsilon }}^*)/C, \delta -\delta ^*}(\sigma ^\dagger )$
is indeed contained in
![]() $V_{{\boldsymbol {\varepsilon }},\delta }(\sigma )$
for
$V_{{\boldsymbol {\varepsilon }},\delta }(\sigma )$
for
![]() ${\boldsymbol {\varepsilon }}^*$
carefully chosen. We have to avoid that
${\boldsymbol {\varepsilon }}^*$
carefully chosen. We have to avoid that
![]() $\varepsilon _0^*$
,
$\varepsilon _0^*$
,
![]() $\varepsilon _1^*$
are large compared to
$\varepsilon _1^*$
are large compared to
![]() $\varepsilon _{01}^*$
so that any plumbing after deforming
$\varepsilon _{01}^*$
so that any plumbing after deforming
![]() $({\mathcal A}^\dagger _\bullet ,Z^\dagger _\bullet )$
of the order of
$({\mathcal A}^\dagger _\bullet ,Z^\dagger _\bullet )$
of the order of
![]() $\varepsilon _0$
,
$\varepsilon _0$
,
![]() $\varepsilon _1$
does not fail of being near
$\varepsilon _1$
does not fail of being near
![]() $\sigma $
.
$\sigma $
.
We may thus first take the pair
![]() $(\varepsilon _0^*, \varepsilon _1^*)$
so small that any point in the
$(\varepsilon _0^*, \varepsilon _1^*)$
so small that any point in the
![]() $(\varepsilon _0^*, \varepsilon _1^*)$
-ball in
$(\varepsilon _0^*, \varepsilon _1^*)$
-ball in ![]() can be reached from
can be reached from
![]() $\sigma $
by a path
$\sigma $
by a path
![]() $\gamma (t)$
involving at most one tilt, at
$\gamma (t)$
involving at most one tilt, at
![]() $t=0$
. Suppose the chosen
$t=0$
. Suppose the chosen
![]() $\sigma ^\dagger =(A_\bullet ^\dagger , Z_\bullet ^\dagger )\in V_{{\boldsymbol {\varepsilon }}^*,\delta ^*}(\sigma )$
has also
$\sigma ^\dagger =(A_\bullet ^\dagger , Z_\bullet ^\dagger )\in V_{{\boldsymbol {\varepsilon }}^*,\delta ^*}(\sigma )$
has also
![]() $L = 1$
levels below zero, and let
$L = 1$
levels below zero, and let
![]() $\gamma ^\dagger (t)$
be the straight path connecting
$\gamma ^\dagger (t)$
be the straight path connecting
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma ^\dagger $
. Let
$\sigma ^\dagger $
. Let
![]() $\tau $
in
$\tau $
in
![]() $-{\mathbb {H}}$
of magnitude at most
$-{\mathbb {H}}$
of magnitude at most
![]() $\delta ^*$
, and
$\delta ^*$
, and
![]() $\hat \sigma =\tau *\sigma ^\dagger $
,
$\hat \sigma =\tau *\sigma ^\dagger $
,
![]() $\sigma '=\tau *\sigma $
. By the argument in Proposition 5.2 and the one-tilt hypothesis, the hearts
$\sigma '=\tau *\sigma $
. By the argument in Proposition 5.2 and the one-tilt hypothesis, the hearts
![]() $\hat {\mathcal {A}}$
and
$\hat {\mathcal {A}}$
and
![]() ${\mathcal A}'$
are intermediate with respect to
${\mathcal A}'$
are intermediate with respect to
![]() ${\mathcal A}_0$
, so the distance between
${\mathcal A}_0$
, so the distance between
![]() $\hat \sigma $
and
$\hat \sigma $
and
![]() $\sigma '$
is controlled by their central charges. If the plumbing of the path
$\sigma '$
is controlled by their central charges. If the plumbing of the path
![]() $\gamma ^\dagger $
is continuous, then
$\gamma ^\dagger $
is continuous, then
In the general case of a single tilt, use Remark 5.3 and compare
![]() $\sigma ' = \sigma ^-$
with
$\sigma ' = \sigma ^-$
with
![]() $\sigma ^+ := ({\mathcal A}^+,Z^+) = \lim _{t \to 0^+} \tau *\gamma ^\dagger (t)$
. Now (32) and the previous estimate in the new notation give the rough estimate
$\sigma ^+ := ({\mathcal A}^+,Z^+) = \lim _{t \to 0^+} \tau *\gamma ^\dagger (t)$
. Now (32) and the previous estimate in the new notation give the rough estimate
The triangle inequality shows that requiring, moreover,
![]() $\varepsilon _{01}^* \leq \varepsilon _0^* + \delta _1^*(\varepsilon _1^* + \ell n)$
does the job.
$\varepsilon _{01}^* \leq \varepsilon _0^* + \delta _1^*(\varepsilon _1^* + \ell n)$
does the job.
The next lemma will be used in the proofs at the end of this section. We consider a sequence
![]() $\{\sigma _j\}_j$
of multi-scale stability conditions in
$\{\sigma _j\}_j$
of multi-scale stability conditions in
![]() $\operatorname {MStab}^\circ ({\mathcal D}_{A_n}^3)$
.
$\operatorname {MStab}^\circ ({\mathcal D}_{A_n}^3)$
.
Lemma 5.8. Fix
![]() $\lambda \in \mathbb {C}$
with
$\lambda \in \mathbb {C}$
with
![]() $0<\Re (\lambda )<1$
, and consider the
$0<\Re (\lambda )<1$
, and consider the
![]() $\mathbb {C}$
-action given in Proposition 4.6. Then a sequence
$\mathbb {C}$
-action given in Proposition 4.6. Then a sequence
![]() $\{\sigma _j\}_j$
converges to
$\{\sigma _j\}_j$
converges to
![]() $\sigma $
in
$\sigma $
in
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
if and only if
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
if and only if
![]() $\{\lambda \cdot \sigma _j\}_j$
converges to
$\{\lambda \cdot \sigma _j\}_j$
converges to
![]() $\lambda \cdot \sigma $
.
$\lambda \cdot \sigma $
.
Proof. Again, we give the details in the case that
![]() $\sigma $
has
$\sigma $
has
![]() $L=1$
levels below zero. Extracting subsequences, we may assume that all
$L=1$
levels below zero. Extracting subsequences, we may assume that all
![]() $\sigma _j$
have the same number of levels below zero. If they are strict multi-scale stability conditions, the claim follows from the corresponding statement in
$\sigma _j$
have the same number of levels below zero. If they are strict multi-scale stability conditions, the claim follows from the corresponding statement in ![]() . The interesting case is that
. The interesting case is that ![]() for all j.
for all j.
Convergence and the definition of neighborhoods implies that
![]() $\sigma _j$
is in an open set
$\sigma _j$
is in an open set
![]() $V_{\varepsilon _j,\delta _j}(\sigma ^{\prime }_j)$
, where
$V_{\varepsilon _j,\delta _j}(\sigma ^{\prime }_j)$
, where
![]() $\sigma ^{\prime }_j = \tau _j * \sigma $
for some fixed representative of
$\sigma ^{\prime }_j = \tau _j * \sigma $
for some fixed representative of
![]() $\sigma $
and for both
$\sigma $
and for both
![]() $\varepsilon _j \to 0$
and
$\varepsilon _j \to 0$
and
![]() $\delta _j = |e^{-\pi i \tau _j}| \to 0$
as
$\delta _j = |e^{-\pi i \tau _j}| \to 0$
as
![]() $j \to \infty $
. We apply the action of
$j \to \infty $
. We apply the action of
![]() $\lambda $
to this sequence and use Corollary 5.4 to see that
$\lambda $
to this sequence and use Corollary 5.4 to see that
![]() $\lambda \cdot (\tau _j * \sigma )$
is close to
$\lambda \cdot (\tau _j * \sigma )$
is close to
![]() $\tau _j * (\lambda \cdot \sigma )$
in a way controlled by (30). We conclude that
$\tau _j * (\lambda \cdot \sigma )$
in a way controlled by (30). We conclude that
![]() $\lambda \cdot \sigma _j$
is in an
$\lambda \cdot \sigma _j$
is in an
![]() $\varepsilon ^{\prime }_j$
-ball of
$\varepsilon ^{\prime }_j$
-ball of
![]() $\lambda \cdot (\tau _j * \sigma )$
for
$\lambda \cdot (\tau _j * \sigma )$
for
![]() $\varepsilon ^{\prime }_j = \varepsilon _j + \ell \delta _j$
, which certifies convergence.
$\varepsilon ^{\prime }_j = \varepsilon _j + \ell \delta _j$
, which certifies convergence.
The Hausdorff property
We now start proving that
![]() $\operatorname {MStab}^\circ (D^3_{A_n})$
is a nice topological space.
$\operatorname {MStab}^\circ (D^3_{A_n})$
is a nice topological space.
Lemma 5.9. The space
![]() $\operatorname {MStab}^\circ (D^3_{A_n})$
is second countable.
$\operatorname {MStab}^\circ (D^3_{A_n})$
is second countable.
Proof. The basis of neighborhoods consisting of
![]() $V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}( {\mathcal A}_\bullet ,Z_\bullet )$
with
$V_{{\boldsymbol {\varepsilon }},{\boldsymbol {\delta }}}( {\mathcal A}_\bullet ,Z_\bullet )$
with
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
such that the
$({\mathcal A}_\bullet ,Z_\bullet )$
such that the
![]() $Z_i$
’s map the collection of simples to a (projectivized) tuple of rational numbers, and with all entries of
$Z_i$
’s map the collection of simples to a (projectivized) tuple of rational numbers, and with all entries of
![]() $({\boldsymbol {\varepsilon }},{\boldsymbol {\delta }})$
being rational, obviously generates the same topology as the one using real numbers.
$({\boldsymbol {\varepsilon }},{\boldsymbol {\delta }})$
being rational, obviously generates the same topology as the one using real numbers.
Theorem 5.10. For any subgroup ![]() , the quotient
, the quotient
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
and the projectivized version
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
and the projectivized version
![]() $\mathbb {P}\mathrm {MStab}^\circ ( {\mathcal D}^3_{A_n})/G$
are Hausdorff topological spaces.
$\mathbb {P}\mathrm {MStab}^\circ ( {\mathcal D}^3_{A_n})/G$
are Hausdorff topological spaces.
Proof. Since the relevant (quotient) spaces are second countable, being Hausdorff is equivalent to uniqueness of limits, which we now show. Suppose that the sequence
![]() $\sigma _j = [\mathcal {A}_{\bullet ,j},Z_{\bullet ,j}]$
of multi-scale stability condition converges to
$\sigma _j = [\mathcal {A}_{\bullet ,j},Z_{\bullet ,j}]$
of multi-scale stability condition converges to
![]() $\sigma = [\mathcal {A}_\bullet ,Z_\bullet ]$
and that the sequence
$\sigma = [\mathcal {A}_\bullet ,Z_\bullet ]$
and that the sequence
![]() $\sigma _j^{\prime } = \Phi _j [\mathcal {A}_{\bullet ,j},Z_{\bullet ,j}]$
, with
$\sigma _j^{\prime } = \Phi _j [\mathcal {A}_{\bullet ,j},Z_{\bullet ,j}]$
, with
![]() $\Phi _j \in G$
, converges to
$\Phi _j \in G$
, converges to
![]() $\sigma ' = [\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet ]$
in
$\sigma ' = [\mathcal {A}_\bullet ^{\prime },Z^{\prime }_\bullet ]$
in
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. We need to show that
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. We need to show that
![]() $[\mathcal {A}^{\prime }_\bullet ,Z^{\prime }_\bullet ] = \Phi [\mathcal {A}_\bullet ,Z_\bullet ]$
for some
$[\mathcal {A}^{\prime }_\bullet ,Z^{\prime }_\bullet ] = \Phi [\mathcal {A}_\bullet ,Z_\bullet ]$
for some
![]() $\Phi \in G$
. We restrict our argument to the cases that all the
$\Phi \in G$
. We restrict our argument to the cases that all the
![]() $\sigma _j$
are honest stability conditions, that
$\sigma _j$
are honest stability conditions, that
![]() $[ \mathcal {A}_\bullet ,Z_\bullet ]$
has
$[ \mathcal {A}_\bullet ,Z_\bullet ]$
has
![]() $L=1$
level below zero and that
$L=1$
level below zero and that
![]() $[\mathcal {A}^{\prime }_\bullet ,Z^{\prime }_\bullet ]$
has
$[\mathcal {A}^{\prime }_\bullet ,Z^{\prime }_\bullet ]$
has
![]() $L' \in \{0,1\}$
, leaving the inductive arguments to treat the general case to the reader. Note that the mass
$L' \in \{0,1\}$
, leaving the inductive arguments to treat the general case to the reader. Note that the mass
![]() $M_{\max }(\sigma _j)$
of the longest and the mass
$M_{\max }(\sigma _j)$
of the longest and the mass
![]() $M_{\min }(\sigma _j)$
of the shortest stable object in
$M_{\min }(\sigma _j)$
of the shortest stable object in
![]() $\sigma _j$
is a notion that is invariant under the action of
$\sigma _j$
is a notion that is invariant under the action of ![]() .
.
The case
![]() $L'=0$
is absurd, since this implies that
$L'=0$
is absurd, since this implies that
![]() $M_{\min }(\sigma _j)/ M_{\max }(\sigma _j)$
is bounded below, while the convergence to
$M_{\min }(\sigma _j)/ M_{\max }(\sigma _j)$
is bounded below, while the convergence to
![]() $\sigma $
implies that this ratio tends to zero.
$\sigma $
implies that this ratio tends to zero.
In general, for a sequence
![]() $\sigma _j$
converging to
$\sigma _j$
converging to
![]() $\sigma $
with
$\sigma $
with
![]() $L=1$
and for some cut-off parameter
$L=1$
and for some cut-off parameter
![]() $M>1$
, we say that a simple S is ‘short’ if its mass is less that
$M>1$
, we say that a simple S is ‘short’ if its mass is less that
![]() $1/M$
times the largest mass of a simple, and ‘long’ otherwise.
$1/M$
times the largest mass of a simple, and ‘long’ otherwise.
In the case
![]() $L'=1$
, consider the set of short stable objects in the sequences
$L'=1$
, consider the set of short stable objects in the sequences
![]() $\sigma _j$
and
$\sigma _j$
and
![]() $\sigma ^{\prime }_j$
, respectively. By definition of the topology, these short stable objects eventually (as
$\sigma ^{\prime }_j$
, respectively. By definition of the topology, these short stable objects eventually (as
![]() $C \to \infty $
) generate the vanishing subcategories
$C \to \infty $
) generate the vanishing subcategories
![]() ${\mathcal V}$
and
${\mathcal V}$
and
![]() ${\mathcal V}'$
. Consequently,
${\mathcal V}'$
. Consequently,
![]() $\Phi _j {\mathcal V} = {\mathcal V}'$
for
$\Phi _j {\mathcal V} = {\mathcal V}'$
for
![]() $j \geq N$
for some N large enough. Replacing
$j \geq N$
for some N large enough. Replacing
![]() $\Phi _j$
by
$\Phi _j$
by
![]() $\Phi _N^{-1} \circ \Phi _j$
, we may suppose from now on that
$\Phi _N^{-1} \circ \Phi _j$
, we may suppose from now on that
![]() ${\mathcal V} = {\mathcal V}'$
and
${\mathcal V} = {\mathcal V}'$
and ![]() for all
for all
![]() $j\geq N$
. Using the triangle inequality and the definition of the metric, it is easy to show that also the sequence
$j\geq N$
. Using the triangle inequality and the definition of the metric, it is easy to show that also the sequence
![]() $\Phi _j (\sigma )$
converges to
$\Phi _j (\sigma )$
converges to
![]() $\sigma '$
in
$\sigma '$
in
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. Since all these objects are now, in fact, in
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
. Since all these objects are now, in fact, in
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n},{\mathcal V})$
, this implies that
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n},{\mathcal V})$
, this implies that
![]() $\Phi _j ({\mathcal A}_0,Z_0) \to ({\mathcal A}_0^{\prime },Z_0^{\prime })$
in
$\Phi _j ({\mathcal A}_0,Z_0) \to ({\mathcal A}_0^{\prime },Z_0^{\prime })$
in ![]() and
and
![]() $\Phi _j [{\mathcal A}_1,Z_1] \to [{\mathcal A}_1^{\prime },Z_1^{\prime }]$
as projectivized stability conditions in
$\Phi _j [{\mathcal A}_1,Z_1] \to [{\mathcal A}_1^{\prime },Z_1^{\prime }]$
as projectivized stability conditions in ![]() . Since
. Since ![]() acts on
acts on ![]() via
via ![]() , by Lemma 4.3, the image
, by Lemma 4.3, the image ![]() acts properly discontinuously on
acts properly discontinuously on ![]() . By definition, the stabilizer in a neighborhood of
. By definition, the stabilizer in a neighborhood of
![]() $(\overline {{\mathcal A}_0},\overline {Z_0})$
is finite; hence, after passing to a sub-sequence, we may assume (again for
$(\overline {{\mathcal A}_0},\overline {Z_0})$
is finite; hence, after passing to a sub-sequence, we may assume (again for
![]() $j\geq N$
, which we assume now throughout) that
$j\geq N$
, which we assume now throughout) that ![]() with
with
![]() $\overline {\Phi }^{(N)} (\overline {{\mathcal A}_0},\overline {Z_0}) = (\overline {{\mathcal A}_0^{\prime }},\overline {Z_0^{\prime }})$
.
$\overline {\Phi }^{(N)} (\overline {{\mathcal A}_0},\overline {Z_0}) = (\overline {{\mathcal A}_0^{\prime }},\overline {Z_0^{\prime }})$
.
On lower level, the stabilizer of
![]() $[{\mathcal A}_1,Z_1]$
is not finite. Let H be the stabilizer of the un-projectivized
$[{\mathcal A}_1,Z_1]$
is not finite. Let H be the stabilizer of the un-projectivized
![]() $({\mathcal A}_1,Z_1)$
. We recall that, by Lemma 4.3, the group H is a finite extension of
$({\mathcal A}_1,Z_1)$
. We recall that, by Lemma 4.3, the group H is a finite extension of
![]() $Z(B_{\operatorname {rk}(K({\mathcal V}))})$
, which, in turn, acts trivially on the projectivized
$Z(B_{\operatorname {rk}(K({\mathcal V}))})$
, which, in turn, acts trivially on the projectivized
![]() $[{\mathcal A}_1,Z_1]$
. This implies that, at the cost of passing to a sub-sequence, there are
$[{\mathcal A}_1,Z_1]$
. This implies that, at the cost of passing to a sub-sequence, there are
![]() $z_j\in Z(B_{\operatorname {rk}(K({\mathcal V}))})$
such that
$z_j\in Z(B_{\operatorname {rk}(K({\mathcal V}))})$
such that
![]() $\overline \Phi _j\big (z_j[{\mathcal A}_1,Z_1]\big )$
is, in fact, the same converging sequence, but we can now work with their representatives in
$\overline \Phi _j\big (z_j[{\mathcal A}_1,Z_1]\big )$
is, in fact, the same converging sequence, but we can now work with their representatives in ![]() that have finite stabilizer. We can extract a convergent subsequence with
that have finite stabilizer. We can extract a convergent subsequence with
![]() ${\Phi _j}_{|{\mathcal V}}({\mathcal A}_1,Z_1) \equiv ({\mathcal A}_1^{\prime },Z_1^{\prime })$
. Taken together, this means that there is N large enough so that
${\Phi _j}_{|{\mathcal V}}({\mathcal A}_1,Z_1) \equiv ({\mathcal A}_1^{\prime },Z_1^{\prime })$
. Taken together, this means that there is N large enough so that
![]() $\Phi _{N}\sigma _\bullet =\sigma ^{\prime }_\bullet $
.
$\Phi _{N}\sigma _\bullet =\sigma ^{\prime }_\bullet $
.
The case
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})$
is similar: one then has to correct also the top level by a central element to ensure convergence to some
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})$
is similar: one then has to correct also the top level by a central element to ensure convergence to some
![]() $\overline {\Phi ^{(0)}}$
.
$\overline {\Phi ^{(0)}}$
.
5.3 The complex structure on quotients of boundary neighborhoods in
 $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
Next, we upgrade from a topology to a structure of complex orbifold. This will not be possible on
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
, but only the quotient by the group of autoequivalences; see Section 6.4 for an illustration in the case of the
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
, but only the quotient by the group of autoequivalences; see Section 6.4 for an illustration in the case of the
![]() $A_2$
-quiver. The first step in this direction is to exhibit a subgroup
$A_2$
-quiver. The first step in this direction is to exhibit a subgroup
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
in the stabilizer of the boundary such that the quotient
${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
in the stabilizer of the boundary such that the quotient
![]() $\operatorname {MStab}^\circ ({\mathcal D},{\mathcal V}_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
is a complex manifold. We then determine the full stabilizer of these boundary neighborhoods and exhibit the orbifold structure.
$\operatorname {MStab}^\circ ({\mathcal D},{\mathcal V}_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
is a complex manifold. We then determine the full stabilizer of these boundary neighborhoods and exhibit the orbifold structure.
We fix once for all a multi-scale stability condition
![]() $\sigma _\bullet =[{\mathcal A}_\bullet ,Z_\bullet ]$
with L levels below zero, and let
$\sigma _\bullet =[{\mathcal A}_\bullet ,Z_\bullet ]$
with L levels below zero, and let
![]() ${\mathcal V}_\bullet $
be the associated sequence of nested vanishing subcategories of
${\mathcal V}_\bullet $
be the associated sequence of nested vanishing subcategories of
![]() ${\mathcal D}={\mathcal D}^3_{A_n}$
.
${\mathcal D}={\mathcal D}^3_{A_n}$
.
The simple twist group
 $\mathit {Tw}^{s}({\mathcal V}_{\bullet})$
$\mathit {Tw}^{s}({\mathcal V}_{\bullet})$
Recall the numerical data associated with a multi-scaled stability conditions of type
![]() $A_n$
from Section 4.1, and suppose
$A_n$
from Section 4.1, and suppose
![]() $\sigma _\bullet $
is of type
$\sigma _\bullet $
is of type
![]() ${\boldsymbol {\rho }}$
. We focus at a level i, and let
${\boldsymbol {\rho }}$
. We focus at a level i, and let
![]() ${\mathcal V}_i^{(j)}$
be the components of
${\mathcal V}_i^{(j)}$
be the components of
![]() ${\mathcal V}_i$
. Suppose that
${\mathcal V}_i$
. Suppose that
![]() ${\mathcal V}_i^{(j)}$
has type
${\mathcal V}_i^{(j)}$
has type
![]() $n_{i}^{(j)}$
(i.e., the heart
$n_{i}^{(j)}$
(i.e., the heart
![]() ${\mathcal V}_i^{(j)}\cap {\mathcal A}_i$
has
${\mathcal V}_i^{(j)}\cap {\mathcal A}_i$
has
![]() $n_{i}^{(j)}$
simples
$n_{i}^{(j)}$
simples
![]() $S_1,\ldots ,S_{n_{i}^{(j)}}$
in the subset
$S_1,\ldots ,S_{n_{i}^{(j)}}$
in the subset
![]() $\mathcal S = \mathcal S(i,j)$
of
$\mathcal S = \mathcal S(i,j)$
of
![]() $\operatorname {Sim}({\mathcal A}_0)$
). We recall the definition in Section 3.3 of the group elements
$\operatorname {Sim}({\mathcal A}_0)$
). We recall the definition in Section 3.3 of the group elements
![]() $\theta _{I,n}$
.
$\theta _{I,n}$
.
For I denoting the closed arcs in the subsurface
![]() $\Sigma _i^{(j)}$
, we let
$\Sigma _i^{(j)}$
, we let
 $$ \begin{align} \mathfrak{c}_{i,j} = \begin{cases} \theta_{I,n} & \text{if } n_i^{(j)} \text{ is odd}\\ \theta_{I,n}^2 & \text{if } n_i^{(j)} \text{ is even.} \end{cases} \end{align} $$
$$ \begin{align} \mathfrak{c}_{i,j} = \begin{cases} \theta_{I,n} & \text{if } n_i^{(j)} \text{ is odd}\\ \theta_{I,n}^2 & \text{if } n_i^{(j)} \text{ is even.} \end{cases} \end{align} $$
From
![]() ${\boldsymbol {\rho }}$
, we derive another collection of integers
${\boldsymbol {\rho }}$
, we derive another collection of integers
![]() $(\ell _i)_{i=1}^L$
. Recall that we define
$(\ell _i)_{i=1}^L$
. Recall that we define
![]() $\kappa _i^{(j)} = n_i^{(j)} + 3$
to be the number of marked points on the boundary of
$\kappa _i^{(j)} = n_i^{(j)} + 3$
to be the number of marked points on the boundary of
![]() $\Sigma _i^{(j)}$
. We let
$\Sigma _i^{(j)}$
. We let
 $$ \begin{align} \widehat{\kappa}_i^{(j)} \;=\; \begin{cases} (n_i^{(j)} + 3)/2 & \text{if } n_i^{(j)} \text{ is odd} \\ (n_i^{(j)} + 3) & \text{if } n_i^{(j)} \text{ is even.} \\ \end{cases} \end{align} $$
$$ \begin{align} \widehat{\kappa}_i^{(j)} \;=\; \begin{cases} (n_i^{(j)} + 3)/2 & \text{if } n_i^{(j)} \text{ is odd} \\ (n_i^{(j)} + 3) & \text{if } n_i^{(j)} \text{ is even.} \\ \end{cases} \end{align} $$
(This notation is consistent with the enhancements in Section 6.) We define
For each level i and each j, we now define the elements
 $$ \begin{align} \mathfrak{c}_i := \prod_j \mathfrak{c}_{i,j}^{\ell_i/\widehat{\kappa}_{i}^{(j)}} := \prod_j \theta_{I(i,j),n}^{\ell_i/\kappa_i^{(j)}}. \end{align} $$
$$ \begin{align} \mathfrak{c}_i := \prod_j \mathfrak{c}_{i,j}^{\ell_i/\widehat{\kappa}_{i}^{(j)}} := \prod_j \theta_{I(i,j),n}^{\ell_i/\kappa_i^{(j)}}. \end{align} $$
and we define the simple twist group to be
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet ) :=\langle \mathfrak {c}_1,\dots , \mathfrak {c}_L\rangle $
.
${\operatorname {Tw}}^s({\mathcal V}_\bullet ) :=\langle \mathfrak {c}_1,\dots , \mathfrak {c}_L\rangle $
.
Proposition 5.11. For each level i, the element ![]() preserves the neighborhoods
preserves the neighborhoods
![]() $V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
for all
$V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
for all
![]() $({\boldsymbol {\varepsilon }},\delta )$
small enough.
$({\boldsymbol {\varepsilon }},\delta )$
small enough.
Implicit in the notation is that the elements
![]() $\mathfrak {c}_{i,j}$
for fixed j commute. In fact, we have the following:
$\mathfrak {c}_{i,j}$
for fixed j commute. In fact, we have the following:
Lemma 5.12. The elements
![]() $\mathfrak {c}_{i,j}$
for all
$\mathfrak {c}_{i,j}$
for all
![]() $(i,j)$
commute. In particular, the simple twist group
$(i,j)$
commute. In particular, the simple twist group
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet ) = \langle \mathfrak {c}_1,\dots , \mathfrak {c}_L\rangle $
is a free abelian group of rank L.
${\operatorname {Tw}}^s({\mathcal V}_\bullet ) = \langle \mathfrak {c}_1,\dots , \mathfrak {c}_L\rangle $
is a free abelian group of rank L.
Proof. For fixed i, the elements
![]() $\mathfrak {c}_{i,j}$
and
$\mathfrak {c}_{i,j}$
and
![]() $\mathfrak {c}_{i,j'}$
commute by (14) since they correspond to disjoint subsurfaces, and hence, any two vertices, one in
$\mathfrak {c}_{i,j'}$
commute by (14) since they correspond to disjoint subsurfaces, and hence, any two vertices, one in
![]() $I(i,j)$
and one in
$I(i,j)$
and one in
![]() $I(i,j')$
, cannot be connected by an edge in the corresponding quiver. For different level indices
$I(i,j')$
, cannot be connected by an edge in the corresponding quiver. For different level indices
![]() $i < i'$
, the elements
$i < i'$
, the elements
![]() $\mathfrak {c}_{i,j}$
and
$\mathfrak {c}_{i,j}$
and
![]() $\mathfrak {c}_{i',j'}$
commute for the same reason if
$\mathfrak {c}_{i',j'}$
commute for the same reason if
![]() $Q_{I(i',j')}$
is not a subquiver of
$Q_{I(i',j')}$
is not a subquiver of
![]() $Q_{I(i,j)}$
. If it is a subquiver, the elements commute since
$Q_{I(i,j)}$
. If it is a subquiver, the elements commute since
![]() $\theta _{I,n}$
is (the image of) the central element in the braid group corresponding to
$\theta _{I,n}$
is (the image of) the central element in the braid group corresponding to
![]() $Q_{I(i,j)}$
.
$Q_{I(i,j)}$
.
Proof of Proposition 5.11
Focusing on the subcategories above and below i, we may reduce to the case that
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
has
$({\mathcal A}_\bullet ,Z_\bullet )$
has
![]() $L=1$
and we consider
$L=1$
and we consider
![]() $i=1$
, thus writing
$i=1$
, thus writing
![]() ${\mathcal V} = {\mathcal V}_1$
. Suppose the connected components
${\mathcal V} = {\mathcal V}_1$
. Suppose the connected components
![]() ${\mathcal V}^{(j)}$
have type
${\mathcal V}^{(j)}$
have type
![]() $n_j$
and correspond to the subsurfaces
$n_j$
and correspond to the subsurfaces
![]() $\Sigma ^{(j)}$
. We claim that
$\Sigma ^{(j)}$
. We claim that

Granting the claim, we conclude that
![]() $\mathfrak {c}_{1}$
acts like the shift by
$\mathfrak {c}_{1}$
acts like the shift by
![]() $\ell _1$
on
$\ell _1$
on
![]() ${\mathcal A}_1 \cap {\mathcal V}^{(j)}$
for every j, and thus on the whole
${\mathcal A}_1 \cap {\mathcal V}^{(j)}$
for every j, and thus on the whole
![]() $({\mathcal A}_1,Z_1)$
. Since adding
$({\mathcal A}_1,Z_1)$
. Since adding
![]() $\widehat {\kappa }_{1}^{(j)}$
to
$\widehat {\kappa }_{1}^{(j)}$
to
![]() $\tau $
does not change the norm used in (1) of the topology definition, the elements stabilize the neighborhoods, as claimed. Since
$\tau $
does not change the norm used in (1) of the topology definition, the elements stabilize the neighborhoods, as claimed. Since
![]() $\tau +\widehat {\kappa }_{1}^{(j)}$
realizes a plumbing of size at most
$\tau +\widehat {\kappa }_{1}^{(j)}$
realizes a plumbing of size at most
![]() $\delta $
, if
$\delta $
, if
![]() $\tau $
does so, the elements stabilize the neighborhoods (as defined by (1)–(2) in Definition 5.6), as claimed.
$\tau $
does so, the elements stabilize the neighborhoods (as defined by (1)–(2) in Definition 5.6), as claimed.
The first equality of (39) is [Reference Seidel and ThomasST01, Lemma 4.14] applied to the subquiver
![]() $Q_{I(1,j)}$
. The second equality holds by definition of the induced actions on Grothendieck groups; see (19). For the third equality, we write each spherical twist appearing in the definition of
$Q_{I(1,j)}$
. The second equality holds by definition of the induced actions on Grothendieck groups; see (19). For the third equality, we write each spherical twist appearing in the definition of
![]() $\mathfrak {c}_{1,j}$
as a composition of tilts at simples in
$\mathfrak {c}_{1,j}$
as a composition of tilts at simples in
![]() ${\mathcal V}$
using (16). The claim then follows since such tilts do not change the quotient heart; see [Reference Barbieri, Möller, Qiu and SoBMQS22, Lemma 5.6].
${\mathcal V}$
using (16). The claim then follows since such tilts do not change the quotient heart; see [Reference Barbieri, Möller, Qiu and SoBMQS22, Lemma 5.6].
The complex structure on boundary neighborhoods
Consider a neighborhood
![]() $V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
as given in Definition 5.6. As we stated after (39), the element
$V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
as given in Definition 5.6. As we stated after (39), the element
![]() $\mathfrak {c}_i$
acts as the shift by
$\mathfrak {c}_i$
acts as the shift by
![]() $\ell _i$
on the i-th level of
$\ell _i$
on the i-th level of
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
. Consequently, plumbing by
$({\mathcal A}_\bullet ,Z_\bullet )$
. Consequently, plumbing by
![]() ${\boldsymbol {\tau }}$
and plumbing by
${\boldsymbol {\tau }}$
and plumbing by
![]() ${\boldsymbol {\tau }} + \ell _i e_i$
(where
${\boldsymbol {\tau }} + \ell _i e_i$
(where
![]() $e_i$
is the i-th unit vector) give the same stability condition in the quotient
$e_i$
is the i-th unit vector) give the same stability condition in the quotient
![]() $V_{{\boldsymbol {\varepsilon }},\delta }( {\mathcal A}_\bullet ,Z_\bullet )/ {\operatorname {Tw}}^s({\mathcal V}_\bullet )$
. Therefore, on this quotient space, the parameters
$V_{{\boldsymbol {\varepsilon }},\delta }( {\mathcal A}_\bullet ,Z_\bullet )/ {\operatorname {Tw}}^s({\mathcal V}_\bullet )$
. Therefore, on this quotient space, the parameters
-
○
 $t_i = \exp \{2 \pi \sqrt {-1} \frac {\tau _i}{\ell _i}\}$
for
$t_i = \exp \{2 \pi \sqrt {-1} \frac {\tau _i}{\ell _i}\}$
for
 $i=1,\ldots , L$
,
$i=1,\ldots , L$
, -
○ the ratios of central charges of simples on
 for
for
 $j>0$
,
$j>0$
, -
○ the central charges of the simples on

all together give a complex chart.
Instead of using ratios of central charges, we may equivalently fix a representative
![]() $({\mathcal A}_\bullet ,Z_\bullet )$
of the multi-scale stability condition such that a (‘pivot’) simple
$({\mathcal A}_\bullet ,Z_\bullet )$
of the multi-scale stability condition such that a (‘pivot’) simple
![]() $S_i$
in each
$S_i$
in each
![]() ${\mathcal A}_i$
for
${\mathcal A}_i$
for
![]() $i>0$
has
$i>0$
has
![]() $Z(S_i) = 1$
, and use central charges of the remaining (non-pivot) simples in
$Z(S_i) = 1$
, and use central charges of the remaining (non-pivot) simples in
![]() $\operatorname {Sim}({\mathcal A}_i) \setminus \operatorname {Sim}({\mathcal A}_{i+1})$
together with the
$\operatorname {Sim}({\mathcal A}_i) \setminus \operatorname {Sim}({\mathcal A}_{i+1})$
together with the
![]() $t_i$
as coordinates.
$t_i$
as coordinates.
Next, we check compatibility (i.e., we compare two charts defined around points in
![]() $V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
and
$V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
and
![]() $V^{\prime }_{{\boldsymbol {\varepsilon }}',\delta '} ({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet )/{\operatorname {Tw}}^s({\mathcal V}^{\prime }_\bullet )$
with
$V^{\prime }_{{\boldsymbol {\varepsilon }}',\delta '} ({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet )/{\operatorname {Tw}}^s({\mathcal V}^{\prime }_\bullet )$
with
![]() $L\neq L'$
) in the case of nontrivial intersection of the neighborhoods. In particular, we check compatibility with the existing complex structure on
$L\neq L'$
) in the case of nontrivial intersection of the neighborhoods. In particular, we check compatibility with the existing complex structure on ![]() . Fix
. Fix
![]() $\sigma =({\mathcal A}_\bullet ,Z_\bullet )$
with
$\sigma =({\mathcal A}_\bullet ,Z_\bullet )$
with
![]() $L=1$
, consider a point
$L=1$
, consider a point
![]() $\sigma ' = ({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) \in V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
, and suppose first that
$\sigma ' = ({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) \in V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
, and suppose first that
![]() $L=1$
and
$L=1$
and
![]() $\sigma ' = ({\mathcal A},Z)$
is actually an honest stability condition. We now use the definition of the plumbed central charge according to Proposition 5.1 and the ‘pivot’ viewpoint for coordinates. We find that the central charge
$\sigma ' = ({\mathcal A},Z)$
is actually an honest stability condition. We now use the definition of the plumbed central charge according to Proposition 5.1 and the ‘pivot’ viewpoint for coordinates. We find that the central charge
![]() $Z_0^{\prime }(S)$
of a simple
$Z_0^{\prime }(S)$
of a simple
![]() $S \in \operatorname {Sim}({\mathcal A})$
is equal to
$S \in \operatorname {Sim}({\mathcal A})$
is equal to
![]() $Z_0(S)$
if
$Z_0(S)$
if
![]() $S \not \in \operatorname {Sim}({\mathcal A}_1)$
or equal to
$S \not \in \operatorname {Sim}({\mathcal A}_1)$
or equal to
![]() $t_1 Z_1(S)$
if
$t_1 Z_1(S)$
if
![]() $S \in \operatorname {Sim}({\mathcal A}_i)$
. Since
$S \in \operatorname {Sim}({\mathcal A}_i)$
. Since
![]() $t_1 \neq 0$
near
$t_1 \neq 0$
near
![]() $\sigma '$
, this coordinate change is a biholomorphism. Similarly, the compatibility holds if
$\sigma '$
, this coordinate change is a biholomorphism. Similarly, the compatibility holds if
![]() $L>1$
and if the neighboring point
$L>1$
and if the neighboring point
![]() $\sigma '$
has
$\sigma '$
has
![]() $L'>0$
below zero, the coordinate change map being given by a product of
$L'>0$
below zero, the coordinate change map being given by a product of
![]() $t_j$
’s times
$t_j$
’s times
![]() $Z_i(S)$
for
$Z_i(S)$
for
![]() $S \in \operatorname {Sim}({\mathcal A}_i) \setminus \operatorname {Sim}({\mathcal A}_{i+1})$
. We summarize this discussion:
$S \in \operatorname {Sim}({\mathcal A}_i) \setminus \operatorname {Sim}({\mathcal A}_{i+1})$
. We summarize this discussion:
Proposition 5.13. The quotients of the boundary neighborhoods
![]() $V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
by the simple twist group
$V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
by the simple twist group
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
admit a complex structure compatible with the complex structure around any point
${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
admit a complex structure compatible with the complex structure around any point
![]() $({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) \in V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
with less that L levels below zero.
$({\mathcal A}^{\prime }_\bullet ,Z^{\prime }_\bullet ) \in V_{{\boldsymbol {\varepsilon }},\delta }({\mathcal A}_\bullet ,Z_\bullet )$
with less that L levels below zero.
The orbifold structure
The following proposition ensures that the complex structure on
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
-quotients of neighborhoods actually gives the structure of an orbifold on the quotient space
${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
-quotients of neighborhoods actually gives the structure of an orbifold on the quotient space ![]() .
.
Proposition 5.14. The stabilizer in ![]() of a multi-scale stability condition
of a multi-scale stability condition
![]() $\sigma _\bullet =( {\mathcal A}_\bullet ,Z_\bullet )$
contains
$\sigma _\bullet =( {\mathcal A}_\bullet ,Z_\bullet )$
contains
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
as a finite index subgroup.
${\operatorname {Tw}}^s({\mathcal V}_\bullet )$
as a finite index subgroup.
Proof. For the intended finiteness assertion, we may restrict attention from ![]() to the group of spherical twists
to the group of spherical twists
![]() $\operatorname {ST}(A_n) \cong B_{n+1}$
thanks to (18).
$\operatorname {ST}(A_n) \cong B_{n+1}$
thanks to (18).
Suppose that
![]() $L=1$
, and suppose, moreover, that the lower level is connected. Consider the intersection G of the stabilizer
$L=1$
, and suppose, moreover, that the lower level is connected. Consider the intersection G of the stabilizer
![]() $H_{\sigma _\bullet }$
with
$H_{\sigma _\bullet }$
with
![]() $\operatorname {ST}(A_n)$
. We know that any
$\operatorname {ST}(A_n)$
. We know that any
![]() $\rho \in G$
stabilizes
$\rho \in G$
stabilizes
![]() ${\mathcal V}$
and fixes the (lower level) stability condition on
${\mathcal V}$
and fixes the (lower level) stability condition on
![]() ${\mathcal V}$
projectively. This implies as in the proof of Lemma 4.3 that after passing to a finite index subgroup of
${\mathcal V}$
projectively. This implies as in the proof of Lemma 4.3 that after passing to a finite index subgroup of
![]() $G=H_{\sigma _\bullet }\cap \operatorname {ST}(A_n)$
, we may assume that
$G=H_{\sigma _\bullet }\cap \operatorname {ST}(A_n)$
, we may assume that
![]() $\rho |_{\mathcal V}$
as an element of
$\rho |_{\mathcal V}$
as an element of ![]() is central (i.e., a power of
is central (i.e., a power of
![]() $\theta _{I,n}$
) since the
$\theta _{I,n}$
) since the
![]() $\mathbb {C}$
-action and the action of autoequivalences commute. Consequently,
$\mathbb {C}$
-action and the action of autoequivalences commute. Consequently,
![]() $\langle \mathfrak {c}_1 \rangle = {\operatorname {Tw}}^s({\mathcal V}_\bullet ) \subset G$
of finite index.
$\langle \mathfrak {c}_1 \rangle = {\operatorname {Tw}}^s({\mathcal V}_\bullet ) \subset G$
of finite index.
Suppose still
![]() $L=1$
but now that the lower level has, say, k connected components
$L=1$
but now that the lower level has, say, k connected components
![]() ${\mathcal V}^{(j)}$
. Now the preceding argument implies that after passing to a finite index subgroup G of the stabilizer (thereby getting rid of potential nontrivial pointwise stabilizers of
${\mathcal V}^{(j)}$
. Now the preceding argument implies that after passing to a finite index subgroup G of the stabilizer (thereby getting rid of potential nontrivial pointwise stabilizers of
![]() $({\mathcal V}_1, Z_1)$
), any
$({\mathcal V}_1, Z_1)$
), any
![]() $\rho |_{{\mathcal V}^{(j)}}$
for
$\rho |_{{\mathcal V}^{(j)}}$
for
![]() $\rho \in G$
is central in the autoequivalence group of each component of
$\rho \in G$
is central in the autoequivalence group of each component of
![]() ${\mathcal V}^{(j)}$
(i.e., a power of the
${\mathcal V}^{(j)}$
(i.e., a power of the
![]() $\mathfrak {c}_{1,j}$
). We now use that, moreover, the elements in G act by simultaneously rescaling the restrictions of
$\mathfrak {c}_{1,j}$
). We now use that, moreover, the elements in G act by simultaneously rescaling the restrictions of
![]() $({\mathcal V}_1, Z_1)$
to the components
$({\mathcal V}_1, Z_1)$
to the components
![]() ${\mathcal V}^{(j)}$
by definition of the equivalence relation of multi-scale stability condition. We deduce that G is a cyclic group. Since the exponents in the definition of
${\mathcal V}^{(j)}$
by definition of the equivalence relation of multi-scale stability condition. We deduce that G is a cyclic group. Since the exponents in the definition of
![]() $\mathfrak {c}_1$
were chosen to projectivize simultaneously (raise the first equation of (39) to the right power), the claim follows in this case.
$\mathfrak {c}_1$
were chosen to projectivize simultaneously (raise the first equation of (39) to the right power), the claim follows in this case.
For
![]() $L>1$
, a new phenomenon occurs: Suppose
$L>1$
, a new phenomenon occurs: Suppose
![]() ${\mathcal A}_i \cap {\mathcal V}_i^{(j)} = {\mathcal A}_{i+1} \cap {\mathcal V}_{i+1}^{(j')}$
for certain components
${\mathcal A}_i \cap {\mathcal V}_i^{(j)} = {\mathcal A}_{i+1} \cap {\mathcal V}_{i+1}^{(j')}$
for certain components
![]() ${\mathcal V}_i^{(j)}$
and
${\mathcal V}_i^{(j)}$
and
![]() ${\mathcal V}_{i+1}^{(j')}$
of the vanishing subcategories at level i and
${\mathcal V}_{i+1}^{(j')}$
of the vanishing subcategories at level i and
![]() $i+1$
. This is possible if
$i+1$
. This is possible if
![]() $Z_i|_{{\mathcal A}_i \cap {\mathcal V}_i^{(j)}} = 0$
and the required non-vanishing of
$Z_i|_{{\mathcal A}_i \cap {\mathcal V}_i^{(j)}} = 0$
and the required non-vanishing of
![]() $Z_i$
is ensured on some other component
$Z_i$
is ensured on some other component
![]() ${\mathcal V}_i^{({k})}$
of
${\mathcal V}_i^{({k})}$
of
![]() ${\mathcal V}$
. Then the condition ‘projectively equivalent’ in the definition of a multi-scale stability condition imposes no constraint relating the action on
${\mathcal V}$
. Then the condition ‘projectively equivalent’ in the definition of a multi-scale stability condition imposes no constraint relating the action on
![]() $({\mathcal A}_i \cap {\mathcal V}_i^{(j)},Z_i|_{{\mathcal V}_i^{(j)}})$
and
$({\mathcal A}_i \cap {\mathcal V}_i^{(j)},Z_i|_{{\mathcal V}_i^{(j)}})$
and
![]() $({\mathcal A}_i \cap {\mathcal V}_i^{({k})}, Z_i|_{{\mathcal V}_i^{(k)}})$
. We capture this problem as follows:
$({\mathcal A}_i \cap {\mathcal V}_i^{({k})}, Z_i|_{{\mathcal V}_i^{(k)}})$
. We capture this problem as follows:
We write G for the finite index subgroup of the stabilizer that acts trivially on each
![]() $({\mathcal V}_i,Z_i)$
. Let E be the set of (homotopy classes of) seams of the subsurfaces corresponding to the components
$({\mathcal V}_i,Z_i)$
. Let E be the set of (homotopy classes of) seams of the subsurfaces corresponding to the components
![]() ${\mathcal V}_i^{(j)}$
, and identify
${\mathcal V}_i^{(j)}$
, and identify
![]() $\mathbb {Z}^E$
with the group generated by the
$\mathbb {Z}^E$
with the group generated by the
![]() $\theta _{I(i,j),n}$
(i.e., the group generated by the twist around these seams). Then there is a natural embedding
$\theta _{I(i,j),n}$
(i.e., the group generated by the twist around these seams). Then there is a natural embedding
![]() $G \to \mathbb {Z}^E$
. The image is contained for each level i by
$G \to \mathbb {Z}^E$
. The image is contained for each level i by
![]() $C_i-1$
constraints due to simultaneous projectivization, where
$C_i-1$
constraints due to simultaneous projectivization, where
![]() $C_i$
is the number of components where
$C_i$
is the number of components where
![]() ${\mathcal A}_i \cap {\mathcal V}_i^{(j)} \neq {\mathcal A}_{i+1} \cap {\mathcal V}_{i+1}^{(j')}$
(i.e., where the seam of the subsurface at level i does not agree with the seam of the subsurface at level
${\mathcal A}_i \cap {\mathcal V}_i^{(j)} \neq {\mathcal A}_{i+1} \cap {\mathcal V}_{i+1}^{(j')}$
(i.e., where the seam of the subsurface at level i does not agree with the seam of the subsurface at level
![]() $i+1$
). Since
$i+1$
). Since
![]() $\sum _{i=1}^L C_i = E$
and since these constraints are obviously independent, we conclude that G is a free group of rank L. Since
$\sum _{i=1}^L C_i = E$
and since these constraints are obviously independent, we conclude that G is a free group of rank L. Since
![]() ${\operatorname {Tw}}^s({\mathcal V}_\bullet ) \subset G$
is also free group of rank L, this must be an inclusion of finite index.
${\operatorname {Tw}}^s({\mathcal V}_\bullet ) \subset G$
is also free group of rank L, this must be an inclusion of finite index.
The group G appearing in the last paragraph of the proof should be called the full twist group
![]() ${\operatorname {Tw}}({\mathcal V}_\bullet )$
in analogy with the full twist group of level graphs appearing in [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6]; see also Section 6. The factor group
${\operatorname {Tw}}({\mathcal V}_\bullet )$
in analogy with the full twist group of level graphs appearing in [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6]; see also Section 6. The factor group
![]() ${\operatorname {Tw}}({\mathcal V}_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
is thus responsible for the orbifold structure of
${\operatorname {Tw}}({\mathcal V}_\bullet )/{\operatorname {Tw}}^s({\mathcal V}_\bullet )$
is thus responsible for the orbifold structure of ![]() .
.
5.4 Compactness
Our goal is the following:
Theorem 5.15. For any finite index subgroup ![]() the quotient space
the quotient space
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
is compact.
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
is compact.
Proof. Since
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
is second countable, because G is countable, compactness is equivalent to being sequentially compact. Given a sequence
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
is second countable, because G is countable, compactness is equivalent to being sequentially compact. Given a sequence
![]() $\sigma _m$
of stability conditions, we want to extract a convergent sub-sequence after rescaling the family appropriately. Since the quotient space
$\sigma _m$
of stability conditions, we want to extract a convergent sub-sequence after rescaling the family appropriately. Since the quotient space ![]() has finitely many chambers (given by undecorated triangulations of the disc) and since the stability spaces of quotient categories involved in
has finitely many chambers (given by undecorated triangulations of the disc) and since the stability spaces of quotient categories involved in
![]() $\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
have the same property (corresponding to partial triangulations; see [Reference Barbieri, Möller, Qiu and SoBMQS22]), we may modify
$\mathbb {P}\mathrm {MStab}^\circ ({\mathcal D}^3_{A_n})/G$
have the same property (corresponding to partial triangulations; see [Reference Barbieri, Möller, Qiu and SoBMQS22]), we may modify
![]() $\sigma _m$
by suitable elements of G and pass to a subsequence and assume that all elements of
$\sigma _m$
by suitable elements of G and pass to a subsequence and assume that all elements of
![]() $\sigma _m$
belongs to a single chamber. We will, moreover, assume that
$\sigma _m$
belongs to a single chamber. We will, moreover, assume that ![]() are honest stability conditions. At the end of the proof, it will be clear that the general case follows by the same argument, just using an extra index for the levels of the initial multi-scale stability conditions.
are honest stability conditions. At the end of the proof, it will be clear that the general case follows by the same argument, just using an extra index for the levels of the initial multi-scale stability conditions.
We define a (weak) full order
![]() $\succcurlyeq $
on
$\succcurlyeq $
on
![]() $\operatorname {Sim}({\mathcal A})$
by
$\operatorname {Sim}({\mathcal A})$
by
Equivalently,
![]() $S_1$
is strictly smaller than
$S_1$
is strictly smaller than
![]() $S_2$
if the ratio of central charges tends to zero. Since there are finitely many simples, we may index the level sets of this order by integers
$S_2$
if the ratio of central charges tends to zero. Since there are finitely many simples, we may index the level sets of this order by integers
![]() $0,1,\ldots ,L$
and use these to generate Serre subcategories of
$0,1,\ldots ,L$
and use these to generate Serre subcategories of
![]() ${\mathcal A}$
. For consistence of indexing, we assume that
${\mathcal A}$
. For consistence of indexing, we assume that
![]() ${\mathcal A}_L$
is generated by the set of smallest simples (with respect to
${\mathcal A}_L$
is generated by the set of smallest simples (with respect to
![]() $\succcurlyeq $
), that
$\succcurlyeq $
), that
![]() ${\mathcal A}_{L-1}$
is generated by
${\mathcal A}_{L-1}$
is generated by
![]() $\operatorname {Sim}(A_L)$
and the set of second smallest simples, etc., thus arriving at a nested sequence
$\operatorname {Sim}(A_L)$
and the set of second smallest simples, etc., thus arriving at a nested sequence
Let’s order the simples of
![]() ${\mathcal A}$
so that
${\mathcal A}$
so that
![]() $(S_1,\ldots ,S_{r_0}) \not \in \operatorname {Sim}({\mathcal A}_1)$
, using implicitly the definition
$(S_1,\ldots ,S_{r_0}) \not \in \operatorname {Sim}({\mathcal A}_1)$
, using implicitly the definition
![]() ${r_0 = \operatorname {rk}(K({\mathcal A}_0)) - \operatorname {rk}(K({\mathcal A}_1)) \geq 1}$
. Since
${r_0 = \operatorname {rk}(K({\mathcal A}_0)) - \operatorname {rk}(K({\mathcal A}_1)) \geq 1}$
. Since
![]() $\mathbb {P}^{n-1}$
is compact, we may assume after passing to a sub sequence and choosing appropriated representatives
$\mathbb {P}^{n-1}$
is compact, we may assume after passing to a sub sequence and choosing appropriated representatives
![]() $({\mathcal A}, Z^{(m)})$
of the projectivized stability conditions that the sequence
$({\mathcal A}, Z^{(m)})$
of the projectivized stability conditions that the sequence
![]() $(Z^{(m)}(S_1),\ldots , Z^{(m)}(S_n))$
converges – in fact, to a point
$(Z^{(m)}(S_1),\ldots , Z^{(m)}(S_n))$
converges – in fact, to a point
![]() $Z_0$
where precisely the first
$Z_0$
where precisely the first
![]() $r_0$
entries are different from zero by definition of
$r_0$
entries are different from zero by definition of
![]() $\succcurlyeq $
. Since
$\succcurlyeq $
. Since
![]() $Z^{(m)}(S_i) \in \overline {\mathbb {H}}$
, we know that
$Z^{(m)}(S_i) \in \overline {\mathbb {H}}$
, we know that
![]() $Z_0(S_i) \in \overline {\mathbb {H}} \cup \mathbb {R}_{>0} \cup \{0\}$
. Suppose that
$Z_0(S_i) \in \overline {\mathbb {H}} \cup \mathbb {R}_{>0} \cup \{0\}$
. Suppose that
![]() $Z_0(S_i) \in \mathbb {R}_{>0}$
for none of the
$Z_0(S_i) \in \mathbb {R}_{>0}$
for none of the
![]() $S_i$
. Then we iterate the construction: We consider
$S_i$
. Then we iterate the construction: We consider
![]() $(Z^{(m)}(S_{r_0+1}),\ldots , Z^{(m)}(S_n)) \in \mathbb {P}^{n-r_0-1}$
and use rescaling by real numbers and passage to a subsequence so that this converges to a point
$(Z^{(m)}(S_{r_0+1}),\ldots , Z^{(m)}(S_n)) \in \mathbb {P}^{n-r_0-1}$
and use rescaling by real numbers and passage to a subsequence so that this converges to a point
![]() $Z_1$
. If again,
$Z_1$
. If again,
![]() $Z_1(S_i) \in \mathbb {R}_{>0}$
holds for none of the
$Z_1(S_i) \in \mathbb {R}_{>0}$
holds for none of the
![]() $S_i \in \operatorname {Sim}({\mathcal A}_i)$
, we continue to construct
$S_i \in \operatorname {Sim}({\mathcal A}_i)$
, we continue to construct
![]() $Z_2, \ldots Z_L$
, which we consider as functions
$Z_2, \ldots Z_L$
, which we consider as functions
![]() $Z_i: K({\mathcal A}_i) \to \mathbb {C}$
. It is now obvious that the tuple
$Z_i: K({\mathcal A}_i) \to \mathbb {C}$
. It is now obvious that the tuple
![]() $\sigma := ({\mathcal A}_\bullet ,Z_\bullet )$
is a multi-scale stability condition and that
$\sigma := ({\mathcal A}_\bullet ,Z_\bullet )$
is a multi-scale stability condition and that
![]() $\sigma _n \to \sigma $
by definition of the plumbing procedure (in fact, plumbing with
$\sigma _n \to \sigma $
by definition of the plumbing procedure (in fact, plumbing with
![]() $\tau _i \in -i\mathbb {R}$
purely imaginary suffices as the lower levels just need to be rescaled appropriately).
$\tau _i \in -i\mathbb {R}$
purely imaginary suffices as the lower levels just need to be rescaled appropriately).
Finally, we have to deal with the case that
![]() $Z_i(S) \in \mathbb {R}_{>0}$
for some S we excluded so far. We would like to rotate by some
$Z_i(S) \in \mathbb {R}_{>0}$
for some S we excluded so far. We would like to rotate by some
![]() $\lambda \in S^1$
and apply Lemma 5.8. We have to be careful since this rotation has to be applied to
$\lambda \in S^1$
and apply Lemma 5.8. We have to be careful since this rotation has to be applied to
![]() $({\mathcal A},Z^{(m)})$
(not just the central charge) and might change the heart and alter our basic assumption. To circumvent this problem, we use that for
$({\mathcal A},Z^{(m)})$
(not just the central charge) and might change the heart and alter our basic assumption. To circumvent this problem, we use that for
![]() ${\mathcal D} = {\mathcal D}^3_{A_n}$
, the heart
${\mathcal D} = {\mathcal D}^3_{A_n}$
, the heart
![]() ${\mathcal A}$
has only finitely many stables. Passing to a subsequence, we may assume that there are only finitely many problematic phases
${\mathcal A}$
has only finitely many stables. Passing to a subsequence, we may assume that there are only finitely many problematic phases
![]() $P \in S^1$
that arise as limits of phases
$P \in S^1$
that arise as limits of phases
![]() $\phi $
such
$\phi $
such
![]() $\mathcal P_m(\phi ) \neq \emptyset $
for the slicing
$\mathcal P_m(\phi ) \neq \emptyset $
for the slicing
![]() $\mathcal P_m$
associated with
$\mathcal P_m$
associated with
![]() $\sigma _m$
and that (possibly iteratively) tilting at the torsion pairs defined by those slices, we stay in the same fundamental domain of
$\sigma _m$
and that (possibly iteratively) tilting at the torsion pairs defined by those slices, we stay in the same fundamental domain of
![]() $\mathbb {P}\mathrm {MStab}({\mathcal D}^3_{A_n})$
with respect to the action of G. Now we just apply the
$\mathbb {P}\mathrm {MStab}({\mathcal D}^3_{A_n})$
with respect to the action of G. Now we just apply the
![]() ${\mathbb C}$
-action to the initial sequence for some
${\mathbb C}$
-action to the initial sequence for some
![]() $\lambda $
such that
$\lambda $
such that
![]() $1 \not \in e^{i\lambda } P$
and run the argument of the previous paragraph.
$1 \not \in e^{i\lambda } P$
and run the argument of the previous paragraph.
Theorem 5.10, Propositions 5.13 and 5.14 together with Theorem 5.15 complete the proof of Theorem 1.1 .
6 The BCGGM-compactification and examples
In this section, we recall the main features and notions of the smooth compactification (as orbifold or DM-stack) of the strata of abelian differentials and quadratic differentials by multi-scale differentials, as constructed in [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3] together with [Reference Costantini, Möller and ZachhuberCMZ19] (see also [Reference Chen, Grushevsky, Holmes, Möller and SchmittCGHMS23] for the log geometry viewpoint on this compactification). We focus on the case of the stratum
![]() $Q_n$
corresponding to the
$Q_n$
corresponding to the
![]() $A_n$
-quiver and denote the multi-scale compactification by
$A_n$
-quiver and denote the multi-scale compactification by
![]() $\overline {Q}_n$
and its projectivization by
$\overline {Q}_n$
and its projectivization by
![]() $\mathbb {P}\overline {Q}_n$
. At the end of this section, we will assert an isomorphism
$\mathbb {P}\overline {Q}_n$
. At the end of this section, we will assert an isomorphism
of complex orbifolds and give a sketch of proof.
As complex variety, the labeled version of the projectivized stratum
![]() $\mathbb {P} Q_n$
is isomorphic to the moduli space
$\mathbb {P} Q_n$
is isomorphic to the moduli space
![]() ${\mathcal M}_{0,n+2}$
of pointed genus zero surfaces and, as such, comes with its Deligne-Mumford compactification
${\mathcal M}_{0,n+2}$
of pointed genus zero surfaces and, as such, comes with its Deligne-Mumford compactification
![]() ${\overline {\mathcal M}}_{0,n+2}$
. This kind of compactification of quadratic differential strata is available only for genus zero differentials. One of the goals in this section is to explain why
${\overline {\mathcal M}}_{0,n+2}$
. This kind of compactification of quadratic differential strata is available only for genus zero differentials. One of the goals in this section is to explain why
![]() $\mathbb {P}\overline {Q}_n$
is not isomorphic to
$\mathbb {P}\overline {Q}_n$
is not isomorphic to
![]() ${\overline {\mathcal M}}_{0,n+2}$
.
${\overline {\mathcal M}}_{0,n+2}$
.
Spaces of quadratic differentials
Let
![]() $\mathbf {w} = (w_1,\ldots , w_r)$
be a tuple of integers
$\mathbf {w} = (w_1,\ldots , w_r)$
be a tuple of integers
![]() $\geq -1$
, and let
$\geq -1$
, and let
![]() $\mathbf {w}^- = (w_{r+1}, \ldots , w_{r+b}) $
be a tuple of integers
$\mathbf {w}^- = (w_{r+1}, \ldots , w_{r+b}) $
be a tuple of integers
![]() $\leq -2$
in the quadratic case. Let
$\leq -2$
in the quadratic case. Let
![]() ${{\mathrm {Quad}_{g,r+b}}} (\mathbf {w},\mathbf {w}^-)$
be the moduli space of quadratic differentials
${{\mathrm {Quad}_{g,r+b}}} (\mathbf {w},\mathbf {w}^-)$
be the moduli space of quadratic differentials
![]() $(X,\mathbf {z},q)$
on a pointed curve
$(X,\mathbf {z},q)$
on a pointed curve
![]() $(X,\mathbf {z})$
, where
$(X,\mathbf {z})$
, where
![]() $\mathbf {z} = (z_1,\ldots ,z_{r+b})$
such that q has signature
$\mathbf {z} = (z_1,\ldots ,z_{r+b})$
such that q has signature
![]() $(\mathbf {w},\mathbf {w}^-)$
. In this space, the critical points are labeled. The unlabeled version is denoted by
$(\mathbf {w},\mathbf {w}^-)$
. In this space, the critical points are labeled. The unlabeled version is denoted by
![]() ${{\mathrm {Quad}_{g}}}(\mathbf {w},\mathbf {w}^-)$
(i.e., without the subscript). We abbreviate
${{\mathrm {Quad}_{g}}}(\mathbf {w},\mathbf {w}^-)$
(i.e., without the subscript). We abbreviate
All these spaces come with their projectivized versions, the quotient by the
![]() $\mathbb {C}^*$
-action, denoted by a letter
$\mathbb {C}^*$
-action, denoted by a letter
![]() $\mathbb {P}$
in front. Occasionally, we will compare with spaces of abelian differentials, denoted by
$\mathbb {P}$
in front. Occasionally, we will compare with spaces of abelian differentials, denoted by
![]() ${\Omega \mathcal M}_{g}(\mathbf {w},\mathbf {w}^-)$
. For a fixed weighted DMS
${\Omega \mathcal M}_{g}(\mathbf {w},\mathbf {w}^-)$
. For a fixed weighted DMS
![]() ${\mathbf {S}}_{\mathbf {w}}$
as in Section 3.2, we denote by
${\mathbf {S}}_{\mathbf {w}}$
as in Section 3.2, we denote by
![]() $\operatorname {FQuad}({\mathbf {S}}_{\mathbf {w}})$
the moduli space of framed quadratic differentials
$\operatorname {FQuad}({\mathbf {S}}_{\mathbf {w}})$
the moduli space of framed quadratic differentials
![]() $(X,\mathbf {z},q,\psi )$
of signature
$(X,\mathbf {z},q,\psi )$
of signature
![]() $(\mathbf {w},\mathbf {w}^-)$
with a (Teichmüller) marking
$(\mathbf {w},\mathbf {w}^-)$
with a (Teichmüller) marking
![]() $\psi $
of the real oriented blowup of X at the poles by the surface
$\psi $
of the real oriented blowup of X at the poles by the surface
![]() ${\mathbf {S}}_{\mathbf {w}}$
. (We suppressed
${\mathbf {S}}_{\mathbf {w}}$
. (We suppressed
![]() $\mathbf {w}^-$
in the notation.)
$\mathbf {w}^-$
in the notation.)
6.1 Enhanced level graphs
Recall (e.g., from [Reference Arbarello, Cornalba and GriffithsACG11]) that boundary strata of the Deligne-Mumford compactification
![]() ${\overline {\mathcal M}}_{g}$
are indexed by the dual graphs of the corresponding stable curves.
${\overline {\mathcal M}}_{g}$
are indexed by the dual graphs of the corresponding stable curves.
Abelian case
The first datum to characterize points in a boundary stratum of the multi-scale compactification of
![]() ${\Omega \mathcal M}_{g}(\mathbf {w},\mathbf {w}^-)$
is the following. An enhanced level graph
${\Omega \mathcal M}_{g}(\mathbf {w},\mathbf {w}^-)$
is the following. An enhanced level graph
![]() $\widehat {\Gamma }$
(for abelian differentials) is the dual graph of a pointed stable curve
$\widehat {\Gamma }$
(for abelian differentials) is the dual graph of a pointed stable curve
![]() $(\widehat {X},\widehat {\mathbf {z}})$
, with a weak total order on the vertices and a natural number
$(\widehat {X},\widehat {\mathbf {z}})$
, with a weak total order on the vertices and a natural number
![]() $\kappa _e$
, the enhancement, assigned with each edge. In particular,
$\kappa _e$
, the enhancement, assigned with each edge. In particular,
![]() $\widehat {\Gamma }$
is connected, unless specified otherwise. The weak total order is usually given arranging the vertices in levels, indexed by non-positive integers, the top level being level zero. We call an edge horizontal if it starts and ends at the same level, and vertical otherwise. We write
$\widehat {\Gamma }$
is connected, unless specified otherwise. The weak total order is usually given arranging the vertices in levels, indexed by non-positive integers, the top level being level zero. We call an edge horizontal if it starts and ends at the same level, and vertical otherwise. We write
![]() $E = E(\widehat {\Gamma }) = E^h \cup E^v$
for this decomposition of the set of edges. We require that
$E = E(\widehat {\Gamma }) = E^h \cup E^v$
for this decomposition of the set of edges. We require that
![]() $\widehat {\kappa }_e = 0$
if and only if e is horizontal.
$\widehat {\kappa }_e = 0$
if and only if e is horizontal.
The enhancement encodes the orders of zeros and poles of the collection of differentials
![]() $\omega _v$
on the pointed stable curve
$\omega _v$
on the pointed stable curve
![]() $(\widehat {X},\widehat {\mathbf {z}})$
. On the vertex
$(\widehat {X},\widehat {\mathbf {z}})$
. On the vertex
![]() $v \in \widehat {\Gamma }$
, the differential
$v \in \widehat {\Gamma }$
, the differential
![]() $\omega _v$
is required to have order
$\omega _v$
is required to have order
![]() $w_i$
if the i-th marked point (
$w_i$
if the i-th marked point (
![]() $i=1,\ldots , r+b$
) is adjacent to v. At (the node corresponding to) a horizontal edge e adjacent to v, the differential has a simple pole, and the residues at the two ends of e match (i.e., they add up to zero). At the upper end of a vertical edge e, the differential has a zero of order
$i=1,\ldots , r+b$
) is adjacent to v. At (the node corresponding to) a horizontal edge e adjacent to v, the differential has a simple pole, and the residues at the two ends of e match (i.e., they add up to zero). At the upper end of a vertical edge e, the differential has a zero of order
![]() $\widehat {\kappa }_e-1$
, at the lower end a pole of order
$\widehat {\kappa }_e-1$
, at the lower end a pole of order
![]() $-\widehat {\kappa }_e-1$
. In particular, at each edge, the orders add up to
$-\widehat {\kappa }_e-1$
. In particular, at each edge, the orders add up to
![]() $-2$
. Such a collection of differentials
$-2$
. Such a collection of differentials
![]() ${\boldsymbol {\omega }} = (\omega _v)$
is called a twisted differential (of signature
${\boldsymbol {\omega }} = (\omega _v)$
is called a twisted differential (of signature
![]() $(\mathbf {w},\mathbf {w}^-)$
) compatible with
$(\mathbf {w},\mathbf {w}^-)$
) compatible with
![]() $\widehat {\Gamma }$
if, moreover, the global residue condition (GRC) from [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM1] holds. An enhanced level graph comes with a vertex genus
$\widehat {\Gamma }$
if, moreover, the global residue condition (GRC) from [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM1] holds. An enhanced level graph comes with a vertex genus
![]() $g_v$
for each
$g_v$
for each
![]() $v \in V$
, defined by the requirement that
$v \in V$
, defined by the requirement that
![]() $2g_v-2$
is the sum of the adjacent zero and pole orders. For each signature, there is only a finite number of enhanced level graphs (in particular, a finite number of enhancements) for which the space of twisted differentials on each vertex is nonempty.
$2g_v-2$
is the sum of the adjacent zero and pole orders. For each signature, there is only a finite number of enhanced level graphs (in particular, a finite number of enhancements) for which the space of twisted differentials on each vertex is nonempty.
Quadratic differentials
We can view the space of quadratic differentials inside the space of abelian differentials (via the canonical cover construction) as a subspace of surfaces with an involution; see, for example, [Reference Costantini, Möller and ZachhuberCMZ19]. Due to the involutions, only some of the (abelian) enhanced level graphs appear, encoded as follows. An enhanced level graph
![]() $\Gamma $
(for quadratic differentials) is the dual graph of a stable curve
$\Gamma $
(for quadratic differentials) is the dual graph of a stable curve
![]() $(X,\mathbf {z})$
with a level structure as above and enhancements
$(X,\mathbf {z})$
with a level structure as above and enhancements
![]() $\kappa _e$
associated with the edges
$\kappa _e$
associated with the edges
![]() $e \in E(\Gamma )$
with the only difference that we now aim for twisted quadratic differentials
$e \in E(\Gamma )$
with the only difference that we now aim for twisted quadratic differentials
![]() $\mathbf {q} = (q_v)$
compatible with
$\mathbf {q} = (q_v)$
compatible with
![]() $\Gamma $
, which comprises the vanishing according to the signature
$\Gamma $
, which comprises the vanishing according to the signature
![]() $(\mathbf {w},\mathbf {w}^-)$
at the points of
$(\mathbf {w},\mathbf {w}^-)$
at the points of
![]() $\mathbf {z}$
and the following three conditions: at horizontal edges,
$\mathbf {z}$
and the following three conditions: at horizontal edges,
![]() $q_v$
should have a double pole with matching
$q_v$
should have a double pole with matching
![]() $2$
-residues, at vertical edges the orders are
$2$
-residues, at vertical edges the orders are
![]() $\kappa _e-2$
at the upper end and
$\kappa _e-2$
at the upper end and
![]() $-\kappa _e-2$
at the lower end, and the collection
$-\kappa _e-2$
at the lower end, and the collection
![]() $\mathbf {q}$
satisfies the global residue condition. This condition (see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2] depends on a double cover of enhanced level graphs
$\mathbf {q}$
satisfies the global residue condition. This condition (see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2] depends on a double cover of enhanced level graphs
![]() $\widehat {\pi }: \widehat {\Gamma } \to \Gamma $
, which is a graph morphism with the following conditions. Edges with even
$\widehat {\pi }: \widehat {\Gamma } \to \Gamma $
, which is a graph morphism with the following conditions. Edges with even
![]() $\kappa _e$
have two preimages with enhancement
$\kappa _e$
have two preimages with enhancement
![]() $\widehat {\kappa }_e = \kappa _e/2$
. Edges with odd
$\widehat {\kappa }_e = \kappa _e/2$
. Edges with odd
![]() $\kappa _e$
have one preimage with enhancement
$\kappa _e$
have one preimage with enhancement
![]() $\widehat {\kappa }_e = \kappa _e$
. The preimage of a vertex with an adjacent leg (marked point or edge) that carries an odd label is a single vertex. The preimage of a vertex without such an adjacent leg consists of two vertices if the vertex genus is zero, and one or two vertices otherwise. Here, the vertex genus
$\widehat {\kappa }_e = \kappa _e$
. The preimage of a vertex with an adjacent leg (marked point or edge) that carries an odd label is a single vertex. The preimage of a vertex without such an adjacent leg consists of two vertices if the vertex genus is zero, and one or two vertices otherwise. Here, the vertex genus
![]() $g_v$
is defined by the requirement that
$g_v$
is defined by the requirement that
![]() $2(2g-2)$
equals the sum of the adjacent zero and pole orders. (All these conditions are necessary for
$2(2g-2)$
equals the sum of the adjacent zero and pole orders. (All these conditions are necessary for
![]() $\widehat {\Gamma }$
to be an enhanced level graph compatible with a twisted differential
$\widehat {\Gamma }$
to be an enhanced level graph compatible with a twisted differential
![]() ${\boldsymbol {\omega }} = (\omega _v)$
on a cover, abusively also denoted by
${\boldsymbol {\omega }} = (\omega _v)$
on a cover, abusively also denoted by
![]() $\widehat {\pi }: \widehat {X} \to X$
which is on each vertex v the canonical cover corresponding to
$\widehat {\pi }: \widehat {X} \to X$
which is on each vertex v the canonical cover corresponding to
![]() $q_v$
and such that
$q_v$
and such that
![]() $\widehat {\pi }^* q_v = \omega _v^2$
.) See [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2] for an example where the double cover is not uniquely determined by
$\widehat {\pi }^* q_v = \omega _v^2$
.) See [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2] for an example where the double cover is not uniquely determined by
![]() $\Gamma $
. Again, for given
$\Gamma $
. Again, for given
![]() $\rho $
, the number of enhanced level graphs that allow a compatible
$\rho $
, the number of enhanced level graphs that allow a compatible
![]() $\mathbf {q}$
is finite. Figure 5 shows the double covers of enhanced level graphs for the boundary divisors where two resp. three simple zeros have come together.
$\mathbf {q}$
is finite. Figure 5 shows the double covers of enhanced level graphs for the boundary divisors where two resp. three simple zeros have come together.

Figure 5 Level graphs of two (left) resp. three (right) zeros coming together and their double covers. Simple zeros and the pole of order
![]() $-n-5$
on top level are omitted. The boxed numbers are the
$-n-5$
on top level are omitted. The boxed numbers are the
![]() $\kappa _e$
.
$\kappa _e$
.
Adjacency of boundary strata
For an enhanced level graph
![]() $\widehat {\Gamma }$
, we denote by
$\widehat {\Gamma }$
, we denote by
![]() $D_{\widehat {\Gamma }}^\circ $
the open boundary stratum of multi-scale differentials (defined below) compatible with
$D_{\widehat {\Gamma }}^\circ $
the open boundary stratum of multi-scale differentials (defined below) compatible with
![]() $\widehat {\Gamma }$
. The boundary strata contained in the closure
$\widehat {\Gamma }$
. The boundary strata contained in the closure
![]() $D_{\widehat {\Gamma }}$
of
$D_{\widehat {\Gamma }}$
of
![]() $D_{\widehat {\Gamma }}^\circ $
can be described by the process of degeneration, or more easily starting with the converse process of undegeneration. Note that
$D_{\widehat {\Gamma }}^\circ $
can be described by the process of degeneration, or more easily starting with the converse process of undegeneration. Note that
![]() $D_{\widehat {\Gamma }}$
is, in general, not irreducible: the connected components of strata of meromorphic differentials that make up the twisted differential, or more generally components of strata with residue conditions, are one source that can create irreducible components
$D_{\widehat {\Gamma }}$
is, in general, not irreducible: the connected components of strata of meromorphic differentials that make up the twisted differential, or more generally components of strata with residue conditions, are one source that can create irreducible components
A horizontal undegeneration selects a subset H of the horizontal edges and contracts them. This results in a morphism
![]() $\delta ^H$
of enhanced level graphs. To define the i-th vertical undegeneration, view the i-th level passage as a line in the level graph just above level
$\delta ^H$
of enhanced level graphs. To define the i-th vertical undegeneration, view the i-th level passage as a line in the level graph just above level
![]() $-i$
and contract all the edges crossing that level passage. Again, this results in a morphism
$-i$
and contract all the edges crossing that level passage. Again, this results in a morphism
![]() $\delta _i$
of enhanced level graphs. This can obviously be generalized for any subset
$\delta _i$
of enhanced level graphs. This can obviously be generalized for any subset
![]() $I = \{i_1,\ldots ,i_n\}$
of the set of levels to yield a graph contraction map
$I = \{i_1,\ldots ,i_n\}$
of the set of levels to yield a graph contraction map
![]() $\delta _I$
. These two notions of undegeneration commute, and a general undegeneration is a composition of the two. A degeneration of level graphs is the inverse procedure.
$\delta _I$
. These two notions of undegeneration commute, and a general undegeneration is a composition of the two. A degeneration of level graphs is the inverse procedure.
The complex codimension of a boundary stratum given by a level graph
![]() $\widehat {\Gamma }$
with L levels below zero and h horizontal edges is
$\widehat {\Gamma }$
with L levels below zero and h horizontal edges is
![]() $h+L$
.
$h+L$
.
Boundary strata of
 ${Q}_{n}$
${Q}_{n}$
For these type of strata, the level graphs are strongly constrained.
Lemma 6.1. For the spaces
![]() $Q_n$
(i.e., with type
$Q_n$
(i.e., with type
![]() $(\mathbf {w},\mathbf {w}^-) = (1^{n+1}, -n-3)$
), the level graphs are trees without horizontal edges and with all vertex genera
$(\mathbf {w},\mathbf {w}^-) = (1^{n+1}, -n-3)$
), the level graphs are trees without horizontal edges and with all vertex genera
![]() $g_v = 0$
. In particular, for boundary strata of
$g_v = 0$
. In particular, for boundary strata of
![]() $Q_n$
, the graph
$Q_n$
, the graph
![]() $\Gamma $
determines the double cover
$\Gamma $
determines the double cover
![]() $\widehat {\Gamma }$
.
$\widehat {\Gamma }$
.
Proof. For the statement about horizontal edges, undegenerate all but one horizontal edge and all levels. Now note that each top level vertex must have at least one pole of order
![]() $\geq 2$
or positive genus. For the second statement, the only ambiguity for
$\geq 2$
or positive genus. For the second statement, the only ambiguity for
![]() $\widehat {\Gamma }$
given
$\widehat {\Gamma }$
given
![]() $\Gamma $
is the ‘criss-cross’ ([Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2, Example 4.3]), which requires
$\Gamma $
is the ‘criss-cross’ ([Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM2, Example 4.3]), which requires
![]() $\pi _1(\Gamma ) \neq \{e\}$
.
$\pi _1(\Gamma ) \neq \{e\}$
.
6.2 Examples
We list the boundary components of
![]() $\mathbb {P}\overline {Q}_n$
and their adjacency in the two examples of lowest complexity.
$\mathbb {P}\overline {Q}_n$
and their adjacency in the two examples of lowest complexity.
The
 ${A_2}$
-quiver
${A_2}$
-quiver
The projectivized space
![]() $\mathbb {P}\overline {Q}_2$
is a smooth compactification of
$\mathbb {P}\overline {Q}_2$
is a smooth compactification of
![]() ${\mathcal M}_{0,4}$
. Since the construction introduces no orbifold structure in codimension one (see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6]), it agrees with
${\mathcal M}_{0,4}$
. Since the construction introduces no orbifold structure in codimension one (see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6]), it agrees with
![]() ${\overline {\mathcal M}}_{0,4}$
. The three boundary points correspond to the two-level graph with one edge, two vertices, and the pole together with one of the three simple zeros on top level. The action of
${\overline {\mathcal M}}_{0,4}$
. The three boundary points correspond to the two-level graph with one edge, two vertices, and the pole together with one of the three simple zeros on top level. The action of
![]() $S_3$
permutes the three boundary points.
$S_3$
permutes the three boundary points.
The
 ${A_3}$
-quiver
${A_3}$
-quiver
In this case, the projectivized labeled space
![]() $\mathbb {P}\overline {Q}_3$
is a surface, the largest dimension that can be visualized on a piece of paper. There are three types of boundary divisors – namely,
$\mathbb {P}\overline {Q}_3$
is a surface, the largest dimension that can be visualized on a piece of paper. There are three types of boundary divisors – namely,

The dual graphs are associated with labeled stable curves, and this requires labeling the simple zeros. We distinguish the enhanced graph further by remembering the one (case
![]() $D_1$
) or two (case
$D_1$
) or two (case
![]() $D_2$
) simple zeros on top level, or the grouping in pairs at the end of each cherry (case
$D_2$
) simple zeros on top level, or the grouping in pairs at the end of each cherry (case
![]() $D_3)$
; see also Figure 6 where each of these boundary divisors occurs.
$D_3)$
; see also Figure 6 where each of these boundary divisors occurs.

Figure 6 The boundary of the stratum
![]() $\mathbb {P}\overline {Q}_3 = \mathbb {P} {{\mathrm {Quad}_{0,5}}}(1^4,-8).$
$\mathbb {P}\overline {Q}_3 = \mathbb {P} {{\mathrm {Quad}_{0,5}}}(1^4,-8).$
The codimension two strata are thus given by ‘slanted cherries’ (one of the lower ends of the level graph
![]() $D_3$
pushed down further to level
$D_3$
pushed down further to level
![]() $-2$
), which are the intersection point of a
$-2$
), which are the intersection point of a
![]() $D_3$
-divisor and a
$D_3$
-divisor and a
![]() $D_2$
-divisor, and a chain over three levels, with the pole and one zero on top, one on middle and two on bottom level, giving an intersection point of
$D_2$
-divisor, and a chain over three levels, with the pole and one zero on top, one on middle and two on bottom level, giving an intersection point of
![]() $D_1$
and
$D_1$
and
![]() $D_2$
. It is easy to check that the boundary strata are all irreducible here, as depicted in Figure 6.
$D_2$
. It is easy to check that the boundary strata are all irreducible here, as depicted in Figure 6.
The action of
![]() $S_4$
is by permutation of the marked zeros and thus on boundary strata by the natural permutation action on the additional indices of each boundary divisor type
$S_4$
is by permutation of the marked zeros and thus on boundary strata by the natural permutation action on the additional indices of each boundary divisor type
![]() $D_i$
.
$D_i$
.
The Deligne-Mumford compactification
For comparison, recall that boundary divisors of
![]() ${\overline {\mathcal M}}_{0,5}$
are in bijection with
${\overline {\mathcal M}}_{0,5}$
are in bijection with
![]() $2$
-element subsets of
$2$
-element subsets of
![]() $\{1,\ldots ,5\}$
. This shows that for the
$\{1,\ldots ,5\}$
. This shows that for the
![]() $A_3$
-quiver, the boundary divisors of
$A_3$
-quiver, the boundary divisors of
![]() ${\overline {\mathcal M}}_{0,n+2}$
are in bijection with those of type
${\overline {\mathcal M}}_{0,n+2}$
are in bijection with those of type
![]() $D_1$
and
$D_1$
and
![]() $D_2$
. There is a natural forgetful map
$D_2$
. There is a natural forgetful map
![]() $\mathbb {P}\overline {Q}_3 \to {\overline {\mathcal M}}_{0,5}$
that contracts the divisors of type
$\mathbb {P}\overline {Q}_3 \to {\overline {\mathcal M}}_{0,5}$
that contracts the divisors of type
![]() $D_3$
. The existence of ‘cherry shaped’ divisors like
$D_3$
. The existence of ‘cherry shaped’ divisors like
![]() $D_3$
shows that
$D_3$
shows that
![]() $\mathbb {P}\overline {Q}_n$
is not isomorphic to
$\mathbb {P}\overline {Q}_n$
is not isomorphic to
![]() ${\overline {\mathcal M}}_{0,n+2}$
for any
${\overline {\mathcal M}}_{0,n+2}$
for any
![]() $n \geq 3$
. See [Reference Chen, Grushevsky, Holmes, Möller and SchmittCGHMS23, Section 7] for more on this birational map.
$n \geq 3$
. See [Reference Chen, Grushevsky, Holmes, Möller and SchmittCGHMS23, Section 7] for more on this birational map.
6.3 Multi-scale differentials
We now give the key definition and explain the remaining terminology subsequently. A quadratic multi-scale differential of type
![]() $(\mathbf {w},\mathbf {w}^-)$
on a stable pointed curve
$(\mathbf {w},\mathbf {w}^-)$
on a stable pointed curve
![]() $(X,\mathbf {z})$
consists of
$(X,\mathbf {z})$
consists of
-
(i) an enhanced level structure on the dual graph
 $\Gamma $
of
$\Gamma $
of
 $(X,\mathbf {z})$
,
$(X,\mathbf {z})$
, -
(ii) a twisted quadratic differential
 $\mathbf {q} = (q_v)_{v \in V(\Gamma )}$
of type
$\mathbf {q} = (q_v)_{v \in V(\Gamma )}$
of type
 $(\mathbf {w},\mathbf {w}^-)$
compatible with the enhanced level structure,
$(\mathbf {w},\mathbf {w}^-)$
compatible with the enhanced level structure, -
(iii) and a prong-matching
 $\wp $
for each node of X joining components of non-equal level.
$\wp $
for each node of X joining components of non-equal level.
Two quadratic multi-scale differentials are considered equivalent if they differ by the action of the level rotation torus.
We make the same definition for abelian multi-scale differentials, skipping the word ‘quadratic’ everywhere, replacing
![]() $\mathbf {q}$
by
$\mathbf {q}$
by
![]() ${\boldsymbol {\omega }} = (\omega _v)$
and applying the abelian conventions for enhanced level graphs. To motivate the notion of ‘prong-matching’ and ‘level rotation torus’, we start with the following:
${\boldsymbol {\omega }} = (\omega _v)$
and applying the abelian conventions for enhanced level graphs. To motivate the notion of ‘prong-matching’ and ‘level rotation torus’, we start with the following:
Proof of the isomorphism (40), Part I
Our main goal is to define
![]() $\overline {K}_n^{-1}$
as a map of sets, starting with a multi-scale stability condition. If
$\overline {K}_n^{-1}$
as a map of sets, starting with a multi-scale stability condition. If
![]() $\sigma = [{\mathcal A}_\bullet , Z_\bullet ]$
is an honest stability condition, we associate with it a quadratic differential using the Bridgeland-Smith isomorphism recalled in Theorem 3.1.
$\sigma = [{\mathcal A}_\bullet , Z_\bullet ]$
is an honest stability condition, we associate with it a quadratic differential using the Bridgeland-Smith isomorphism recalled in Theorem 3.1.
Suppose from now on that
![]() $\sigma $
is a strict multi-scale stability condition, and suppose that the number of levels below zero is
$\sigma $
is a strict multi-scale stability condition, and suppose that the number of levels below zero is
![]() $L=1$
, leaving the bookkeeping for larger L to the reader. By Lemma 4.4, we may associate with
$L=1$
, leaving the bookkeeping for larger L to the reader. By Lemma 4.4, we may associate with
![]() ${\mathcal V} = {\mathcal V}_1^Z$
a type
${\mathcal V} = {\mathcal V}_1^Z$
a type
![]() $\rho = (n_1,\ldots ,n_{|J|})$
, where J is an index set for the components of
$\rho = (n_1,\ldots ,n_{|J|})$
, where J is an index set for the components of
![]() ${\mathcal V}$
. We associate with
${\mathcal V}$
. We associate with
![]() $\sigma $
the level graph
$\sigma $
the level graph
![]() $\Gamma $
consisting of a tree with one vertex on top level (carrying the unique pole) and
$\Gamma $
consisting of a tree with one vertex on top level (carrying the unique pole) and
![]() $|J|$
vertices on bottom level, each of them carrying
$|J|$
vertices on bottom level, each of them carrying
![]() $n_j+1$
markings for simple zeros and enhancement
$n_j+1$
markings for simple zeros and enhancement
![]() $\kappa _j = n_j+3$
. As part of the bijectivity claim for the map
$\kappa _j = n_j+3$
. As part of the bijectivity claim for the map
![]() $\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q}, \wp )$
we are about to construct, we observe that all possible level graphs with
$\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q}, \wp )$
we are about to construct, we observe that all possible level graphs with
![]() $L=1$
for quadratic differentials of type
$L=1$
for quadratic differentials of type
![]() $A_n$
arise in this way. We now apply the isomorphism from Theorem 3.4 (for the quotient category
$A_n$
arise in this way. We now apply the isomorphism from Theorem 3.4 (for the quotient category
![]() ${\mathcal D}/{\mathcal V}$
) to the stability condition
${\mathcal D}/{\mathcal V}$
) to the stability condition
![]() $(\overline {{\mathcal A}}_0,\overline {Z_0})$
on top level. We get the complex structure of the irreducible component of
$(\overline {{\mathcal A}}_0,\overline {Z_0})$
on top level. We get the complex structure of the irreducible component of
![]() $(X,\mathbf {z})$
corresponding to the top level vertex
$(X,\mathbf {z})$
corresponding to the top level vertex
![]() $v_0$
together with the quadratic differential
$v_0$
together with the quadratic differential
![]() $q_{v_0}$
on these components. Similarly, we apply this isomorphism (for each
$q_{v_0}$
on these components. Similarly, we apply this isomorphism (for each
![]() ${\mathcal V}^j)$
to each stability condition
${\mathcal V}^j)$
to each stability condition
![]() $( {\mathcal A}_1 \cap {\mathcal V}^{j}, Z_1|_{{\mathcal V}^j})$
on lower level to get the complex structure and the quadratic differential corresponding to the vertices
$( {\mathcal A}_1 \cap {\mathcal V}^{j}, Z_1|_{{\mathcal V}^j})$
on lower level to get the complex structure and the quadratic differential corresponding to the vertices
![]() $v_j$
of
$v_j$
of
![]() $\Gamma $
on lower level. (For
$\Gamma $
on lower level. (For
![]() $L=1$
, there is no further quotient, so we can as well apply Theorem 3.1 on lower level.) The enhancements of
$L=1$
, there is no further quotient, so we can as well apply Theorem 3.1 on lower level.) The enhancements of
![]() $\Gamma $
were chosen so that the collection
$\Gamma $
were chosen so that the collection
![]() $\mathbf {q} = (q_v)_{v \in V(\Gamma )}$
is indeed a twisted differential compatible with the enhanced level structure. We let
$\mathbf {q} = (q_v)_{v \in V(\Gamma )}$
is indeed a twisted differential compatible with the enhanced level structure. We let
![]() $\mathbf {z}$
be the unordered tuple of zeros and poles (different from the nodes of X) of the various differentials
$\mathbf {z}$
be the unordered tuple of zeros and poles (different from the nodes of X) of the various differentials
![]() $q_v$
. (We have no canonical way to label the points
$q_v$
. (We have no canonical way to label the points
![]() $\mathbf {z}$
, and this fits with our target being the
$\mathbf {z}$
, and this fits with our target being the
![]() $S_{n+1}$
-quotient of
$S_{n+1}$
-quotient of
![]() $\overline {Q}_n$
.)
$\overline {Q}_n$
.)
We need to be more precise about automorphisms in the application of Theorem 3.4 (or Bridgeland-Smith) at each level. In fact, above we were using that this isomorphism is equivariant with respect to the action of the mapping class group
![]() $\operatorname {MCG}(\mathbf {S}_{\Delta })$
on the domain and of the group
$\operatorname {MCG}(\mathbf {S}_{\Delta })$
on the domain and of the group ![]() on the range (see [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 7.2]). So far, we have given a well-defined map
on the range (see [Reference Barbieri, Möller, Qiu and SoBMQS22, Theorem 7.2]). So far, we have given a well-defined map
![]() $\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q})$
with
$\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q})$
with
![]() $\mathbf {z}$
considered up to the
$\mathbf {z}$
considered up to the
![]() $S_{n+1}$
-action.
$S_{n+1}$
-action.
The missing notions will be motivated by making this map bijective thanks to the prong
![]() $\wp $
and well defined on equivalence classes. First, observe that the above assignment depended on the stability conditions up to
$\wp $
and well defined on equivalence classes. First, observe that the above assignment depended on the stability conditions up to ![]() . However, the group fixing the boundary stratum of
. However, the group fixing the boundary stratum of
![]() $\sigma $
is
$\sigma $
is ![]() , and its natural map
, and its natural map
![]() $\varphi : A \to G$
is not surjective. In fact, each
$\varphi : A \to G$
is not surjective. In fact, each ![]() has an exact sequence (18), and the braid groups
has an exact sequence (18), and the braid groups
![]() $B_{n_j+1}$
for each j as well as
$B_{n_j+1}$
for each j as well as ![]() are in the image of
are in the image of
![]() $\varphi $
, but the product of cokernels (each isomorphic to
$\varphi $
, but the product of cokernels (each isomorphic to
![]() $\mathbb {Z}/(n_j+3)\mathbb {Z}$
) is not hit surjectively. (Apply (18) to
$\mathbb {Z}/(n_j+3)\mathbb {Z}$
) is not hit surjectively. (Apply (18) to ![]() and use that the cokernel is generated by the shift to prove this.) As a conclusion, the equivalence relation generated by autoequivalences on multi-scale stability conditions is coarser than what is expected for Theorem 3.4 to be a bijection. We thus need an additional datum. To motivate the following definition, recall that the shift acts (via the correspondence to framed quadratic differentials) by cyclically shifting the marked points at each pole.
and use that the cokernel is generated by the shift to prove this.) As a conclusion, the equivalence relation generated by autoequivalences on multi-scale stability conditions is coarser than what is expected for Theorem 3.4 to be a bijection. We thus need an additional datum. To motivate the following definition, recall that the shift acts (via the correspondence to framed quadratic differentials) by cyclically shifting the marked points at each pole.
Prong matchings in the abelian case
A prong at a zero of order m of an abelian differential is a tangent vector that coincides with one of its
![]() $\kappa = m+1$
outgoing horizontal directions. A prong at a pole of order
$\kappa = m+1$
outgoing horizontal directions. A prong at a pole of order
![]() $|m|$
is a tangent vector that coincides with one of its
$|m|$
is a tangent vector that coincides with one of its
![]() $\kappa = |m|-1$
incoming horizontal directions. (For poles, this is the same as choosing one of the marked points in
$\kappa = |m|-1$
incoming horizontal directions. (For poles, this is the same as choosing one of the marked points in
![]() $M_i$
as defined in Section 3.1.) The prongs are labelled cyclically (by embedding in the plane) in clockwise order in the case of zeros (resp. counterclockwise order in the case of poles). Given an enhanced level graph
$M_i$
as defined in Section 3.1.) The prongs are labelled cyclically (by embedding in the plane) in clockwise order in the case of zeros (resp. counterclockwise order in the case of poles). Given an enhanced level graph
![]() $\widehat {\Gamma }$
, a prong-matching
$\widehat {\Gamma }$
, a prong-matching
![]() $\widehat {\wp } = (\widehat {\wp }_e)_{e \in E^v}$
is a bijection of the prongs at the upper and lower even of each edge that reverses the cyclic order. Consequently, there are
$\widehat {\wp } = (\widehat {\wp }_e)_{e \in E^v}$
is a bijection of the prongs at the upper and lower even of each edge that reverses the cyclic order. Consequently, there are
![]() $\widehat {K}_{\widehat {\Gamma }} = \prod _{e \in E^v} \widehat {\kappa }_e$
different prong matchings for
$\widehat {K}_{\widehat {\Gamma }} = \prod _{e \in E^v} \widehat {\kappa }_e$
different prong matchings for
![]() $\widehat {\Gamma }$
.
$\widehat {\Gamma }$
.
The level rotation torus
The lower level differential should be projectivized, since only in this way limits are well defined (compare with the proof of Theorem 5.15) and since only in this way the
![]() $\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q})$
will pass to the equivalence class of
$\sigma \mapsto (X,\mathbf {z},\Gamma , \mathbf {q})$
will pass to the equivalence class of
![]() $\sigma $
. However, just rescaling the lower level by
$\sigma $
. However, just rescaling the lower level by
![]() $\mathbb {C}^*$
is no longer well defined, as this comprises rotation and changes the horizontal direction that the notion of prong relies on. There is a finite unramified cover of
$\mathbb {C}^*$
is no longer well defined, as this comprises rotation and changes the horizontal direction that the notion of prong relies on. There is a finite unramified cover of
![]() $\mathbb {C}^*$
(of course, still abstractly isomorphic to
$\mathbb {C}^*$
(of course, still abstractly isomorphic to
![]() $\mathbb {C}^*$
) that naturally acts by rotation on the differentials
$\mathbb {C}^*$
) that naturally acts by rotation on the differentials
![]() ${\boldsymbol {\omega }}$
and on
${\boldsymbol {\omega }}$
and on
![]() $\wp $
simultaneously so that the preimages of
$\wp $
simultaneously so that the preimages of
![]() $1 \in \mathbb {C}^*$
fix the differential and permute cyclically each
$1 \in \mathbb {C}^*$
fix the differential and permute cyclically each
![]() $\wp _e$
. This algebraic torus (for general
$\wp _e$
. This algebraic torus (for general
![]() $\sigma $
isomorphic to
$\sigma $
isomorphic to
![]() $(\mathbb {C}^*)^L$
) is called level rotation torus; see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6] for the full definition.
$(\mathbb {C}^*)^L$
) is called level rotation torus; see [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 6] for the full definition.
Prong matchings and level rotation torus in the quadratic case
Prongs and their matchings are defined as in the abelian case, noting that a zero order m of a quadratic differential has
![]() $\kappa _e = m+2$
outgoing horizontal directions (to be counted on a local square root!), and a pole of order
$\kappa _e = m+2$
outgoing horizontal directions (to be counted on a local square root!), and a pole of order
![]() $|m|$
has
$|m|$
has
![]() $\kappa _e = |m|-2$
incoming horizontal directions. There are
$\kappa _e = |m|-2$
incoming horizontal directions. There are
![]() ${K}_{\Gamma } = \prod _{e \in E^v} \kappa _e$
prong matchings.
${K}_{\Gamma } = \prod _{e \in E^v} \kappa _e$
prong matchings.
To understand the action of the level rotation torus, the easiest way is to pass to the canonical cover and use that a prong-matching of the quadratic differential induces a prong-matching of an abelian differential. Now the equivalence relation given by the level rotation torus is just defined as in the abelian case, restricted to those abelian multi-scale differentials that actually arise as double covers. See [Reference Costantini, Möller and SchwabCMS23, Section 7] for full details.
Proof of the isomorphism (40), Part II
Finally, we show how to associate with
![]() $\sigma $
a prong-matching
$\sigma $
a prong-matching
![]() $\wp $
. We continue with the setting above – in particular,
$\wp $
. We continue with the setting above – in particular,
![]() $L=1$
. Consider the ray obtained by plumbing
$L=1$
. Consider the ray obtained by plumbing ![]() with a purely imaginary parameter (i.e., without rotation). The limit
with a purely imaginary parameter (i.e., without rotation). The limit
![]() $t \to \infty $
of the Bridgeland-Smith preimages
$t \to \infty $
of the Bridgeland-Smith preimages
![]() $K^{-1}(it * \sigma )$
is a multi-scale differential with underlying
$K^{-1}(it * \sigma )$
is a multi-scale differential with underlying
![]() $(X,\mathbf {z},\Gamma ,\mathbf {q})$
as above, by definition of plumbing and of the topology on
$(X,\mathbf {z},\Gamma ,\mathbf {q})$
as above, by definition of plumbing and of the topology on
![]() $\overline {Q}_n$
. It thus comes with a prong-matching
$\overline {Q}_n$
. It thus comes with a prong-matching
![]() $\wp $
, and we now set
$\wp $
, and we now set
![]() $\overline {K}_n^{-1}(\sigma ) = (X,\mathbf {z},\Gamma , \mathbf {q}, \wp )$
. (We remark that this
$\overline {K}_n^{-1}(\sigma ) = (X,\mathbf {z},\Gamma , \mathbf {q}, \wp )$
. (We remark that this
![]() $\wp $
is the only choice if we want
$\wp $
is the only choice if we want
![]() $\overline {K}_n^{-1}$
to be continuous. Formally, in the language of [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 7], this is the only prong-matching so that the comparison diffeomorphisms between the welding of the limiting stable curve and the nearby plumbed curves is almost turning-number preserving. Informally, when
$\overline {K}_n^{-1}$
to be continuous. Formally, in the language of [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 7], this is the only prong-matching so that the comparison diffeomorphisms between the welding of the limiting stable curve and the nearby plumbed curves is almost turning-number preserving. Informally, when
![]() $|J| \geq 2$
, the right choice of
$|J| \geq 2$
, the right choice of
![]() $\wp $
differs from a wrong choice of
$\wp $
differs from a wrong choice of
![]() $\wp '$
by rotating say one prong for the subsurface
$\wp '$
by rotating say one prong for the subsurface
![]() $j=1$
on lower level. With the wrong
$j=1$
on lower level. With the wrong
![]() $\wp '$
, the turning numbers near the subsurface
$\wp '$
, the turning numbers near the subsurface
![]() $j=1$
do not work out. By rotating the whole lower level using the
$j=1$
do not work out. By rotating the whole lower level using the
![]() $\mathbb {C}$
-action, turning numbers can be fixed for
$\mathbb {C}$
-action, turning numbers can be fixed for
![]() $j=1$
, but then since
$j=1$
, but then since
![]() $|J| \geq 2$
, the turning numbers will not work out at some other subsurface of lower level.)
$|J| \geq 2$
, the turning numbers will not work out at some other subsurface of lower level.)
To see that
![]() $\overline {K}_n^{-1}$
is bijective, note that both the initial failure (due to the cokernel of
$\overline {K}_n^{-1}$
is bijective, note that both the initial failure (due to the cokernel of
![]() $\varphi :A \to G$
) and the additional datum
$\varphi :A \to G$
) and the additional datum
![]() $\wp $
capture the possibility of rotating a lower level component independently of other components. We leave the details to the reader.
$\wp $
capture the possibility of rotating a lower level component independently of other components. We leave the details to the reader.
To show continuity (and well-definedness mod ![]() ), it is best to first lift the map
), it is best to first lift the map
![]() $\overline {K}_n^{-1}$
to a map from
$\overline {K}_n^{-1}$
to a map from
![]() $\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
to the Teichmüller-framed version of
$\operatorname {MStab}^\circ ({\mathcal D}^3_{A_n})$
to the Teichmüller-framed version of
![]() $\overline {Q}_n$
, the augmented Teichmüller space in the sense of [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 7]. This is a bordification of
$\overline {Q}_n$
, the augmented Teichmüller space in the sense of [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 7]. This is a bordification of
![]() $\operatorname {FQuad}({\mathbf {S}}_{\mathbf {w}})$
on which the mapping class group acts. One now needs to check that this lifted
$\operatorname {FQuad}({\mathbf {S}}_{\mathbf {w}})$
on which the mapping class group acts. One now needs to check that this lifted
![]() $\overline {K}_n^{-1}$
is a homeomorphism using the respective definition of topologies and the equivariance with respect to the mapping class group and
$\overline {K}_n^{-1}$
is a homeomorphism using the respective definition of topologies and the equivariance with respect to the mapping class group and ![]() -action.
-action.
To show compatibility with the complex structure, one needs to recall that the complex structure on
![]() $\overline {Q}_n$
is defined using plumbing (in the sense of complex geometry). This gives a collection of periods that defines local coordinates (the perturbed period coordinates in [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 9]; in fact, no modification of the differential is needed for
$\overline {Q}_n$
is defined using plumbing (in the sense of complex geometry). This gives a collection of periods that defines local coordinates (the perturbed period coordinates in [Reference Bainbridge, Chen, Gendron, Grushevsky and MöllerBCGGM3, Section 9]; in fact, no modification of the differential is needed for
![]() $A_n$
-type since all the residues are zero), and one only needs to check that they correspond to the coordinates defined in Section 5.3. We leave again the details to the reader.
$A_n$
-type since all the residues are zero), and one only needs to check that they correspond to the coordinates defined in Section 5.3. We leave again the details to the reader.
6.4 Why taking  -quotients? The
-quotients? The
 $A_2$
-quiver revisited
$A_2$
-quiver revisited
In this subsection, we revisit
![]() $\mathbb {P}\mathrm {MStab}({{\mathcal {D}^{3}_{A_2}}})$
to show that prior to taking the
$\mathbb {P}\mathrm {MStab}({{\mathcal {D}^{3}_{A_2}}})$
to show that prior to taking the ![]() -quotient is neither a compact space (contrary to the Thurston-type compactifications in [Reference Bapat, Deopurkar and LicataBDL20]) nor carries a complex structure.
-quotient is neither a compact space (contrary to the Thurston-type compactifications in [Reference Bapat, Deopurkar and LicataBDL20]) nor carries a complex structure.
In fact,
![]() $\mathbb {P}\mathrm {MStab}({{\mathcal {D}^{3}_{A_2}}})$
coincides with the upper half plane with cusps
$\mathbb {P}\mathrm {MStab}({{\mathcal {D}^{3}_{A_2}}})$
coincides with the upper half plane with cusps
![]() $\widetilde {\mathbb {H}} = \mathbb {H} \cup \mathbb {P}^1_{\mathbb {Q}}$
provided with the horoball topology where a neighborhood basis of
$\widetilde {\mathbb {H}} = \mathbb {H} \cup \mathbb {P}^1_{\mathbb {Q}}$
provided with the horoball topology where a neighborhood basis of
![]() $\infty $
consists of the sets
$\infty $
consists of the sets
![]() $U_C = \{\tau : \Im (\tau )> C\}$
and a neighborhood basis of
$U_C = \{\tau : \Im (\tau )> C\}$
and a neighborhood basis of
![]() $z \in \mathbb {Q}$
are the images of
$z \in \mathbb {Q}$
are the images of
![]() $U_C$
under a Möbius transformation mapping
$U_C$
under a Möbius transformation mapping
![]() $\infty $
to z. Here,
$\infty $
to z. Here,
![]() $\mathbb {P}^1_{\mathbb {Q}}=\mathbb {Q}\cup \{\infty \}$
, and it is known that
$\mathbb {P}^1_{\mathbb {Q}}=\mathbb {Q}\cup \{\infty \}$
, and it is known that ![]() see, for example, [Reference SutherlandSut11].
see, for example, [Reference SutherlandSut11].
To prove this, we start with a classification of the boundary strata. In this case, necessarily
![]() $L=1$
. Since the Grothendieck group of a vanishing subcategory
$L=1$
. Since the Grothendieck group of a vanishing subcategory
![]() ${\mathcal V}$
of
${\mathcal V}$
of
![]() ${\mathcal D}:={\mathcal D}^3_{A_2}$
has rank
${\mathcal D}:={\mathcal D}^3_{A_2}$
has rank
![]() $1$
, all stability conditions on it are projectively equivalent.
$1$
, all stability conditions on it are projectively equivalent.
Next we list the possible
![]() ${\mathcal V}$
. Recall that a heart suporting a stability condition on the space
${\mathcal V}$
. Recall that a heart suporting a stability condition on the space
![]() $\operatorname {Stab}({\mathcal D})/\operatorname {sph}({\mathcal D})$
can be identified with one of the following: the standard heart
$\operatorname {Stab}({\mathcal D})/\operatorname {sph}({\mathcal D})$
can be identified with one of the following: the standard heart
![]() ${\mathcal H}_0=\langle S_1,S_2\rangle $
or its shift
${\mathcal H}_0=\langle S_1,S_2\rangle $
or its shift
![]() ${\mathcal H}_0[1]$
, or
${\mathcal H}_0[1]$
, or
![]() $\langle S_1[1], E\rangle $
,
$\langle S_1[1], E\rangle $
,
![]() $\langle S_1,S_2[1]\rangle $
,
$\langle S_1,S_2[1]\rangle $
,
![]() $\langle S_2, E[1]\rangle $
, where
$\langle S_2, E[1]\rangle $
, where
![]() $S_2\to E\to S_1$
is a short exact sequence. In fact, the vanishing category
$S_2\to E\to S_1$
is a short exact sequence. In fact, the vanishing category
![]() ${\mathcal A}_1$
arising from one of the hearts above is generated by one of the indecomposables
${\mathcal A}_1$
arising from one of the hearts above is generated by one of the indecomposables
![]() $S_1,S_2,E$
of
$S_1,S_2,E$
of
![]() ${\mathcal H}_0$
, those appearing in Figure 1. Therefore, in
${\mathcal H}_0$
, those appearing in Figure 1. Therefore, in
![]() $\operatorname {Stab}({\mathcal D})$
, we associate with any such
$\operatorname {Stab}({\mathcal D})$
, we associate with any such
![]() ${\mathcal V}$
the image of a generating simple in
${\mathcal V}$
the image of a generating simple in
![]() $\mathbb {P}^1(K({\mathcal D})) \cong \mathbb {P}^1_{\mathbb {Q}}$
and call this map c. We let
$\mathbb {P}^1(K({\mathcal D})) \cong \mathbb {P}^1_{\mathbb {Q}}$
and call this map c. We let
![]() ${\mathcal H}_0$
be the standard heart of the
${\mathcal H}_0$
be the standard heart of the
![]() $A_2$
-quiver and let
$A_2$
-quiver and let
![]() ${\mathcal V}_1 = \langle S_2 \rangle $
, corresponding to
${\mathcal V}_1 = \langle S_2 \rangle $
, corresponding to
![]() $c({\mathcal V}_1) = \bigl (\begin {smallmatrix} 0 \\ 1 \end {smallmatrix} \bigr ) \in K({\mathcal D})$
. This subcategory obviously corresponds to any central charge with
$c({\mathcal V}_1) = \bigl (\begin {smallmatrix} 0 \\ 1 \end {smallmatrix} \bigr ) \in K({\mathcal D})$
. This subcategory obviously corresponds to any central charge with
![]() $Z_0(S_1) \in \pm \mathbb {H}$
and
$Z_0(S_1) \in \pm \mathbb {H}$
and
![]() $Z_0(S_2) = 0$
.
$Z_0(S_2) = 0$
.
We first consider the action of the Seidel-Thomas group
![]() $\operatorname {sph}({\mathcal D}) \cong B_3$
on
$\operatorname {sph}({\mathcal D}) \cong B_3$
on
![]() ${\mathcal H}_0$
and
${\mathcal H}_0$
and
![]() ${\mathcal V}_1$
. The element
${\mathcal V}_1$
. The element
![]() $\tau _2$
stabilizes
$\tau _2$
stabilizes
![]() ${\mathcal V}_1$
. The generator of center
${\mathcal V}_1$
. The generator of center
![]() $\theta _2$
of
$\theta _2$
of
![]() $B_3$
acts by the shift by
$B_3$
acts by the shift by
![]() $[\pm 5]$
and thus trivially on
$[\pm 5]$
and thus trivially on
![]() ${\mathcal V}_1$
. Given that
${\mathcal V}_1$
. Given that
![]() $B_3/\langle \theta _2\rangle \simeq \operatorname{PSL} _2(\mathbb {Z})$
[Reference Farb and MargalitFM12] and that
$B_3/\langle \theta _2\rangle \simeq \operatorname{PSL} _2(\mathbb {Z})$
[Reference Farb and MargalitFM12] and that
![]() $\tau _2$
acts as
$\tau _2$
acts as
![]() $\bigl (\begin {smallmatrix} 1 & 1 \\ 0& 1 \end {smallmatrix} \bigr )$
on
$\bigl (\begin {smallmatrix} 1 & 1 \\ 0& 1 \end {smallmatrix} \bigr )$
on
![]() $K({\mathcal D}^3_{A_2})$
, the orbits of the action
$K({\mathcal D}^3_{A_2})$
, the orbits of the action
![]() $\operatorname {sph}({\mathcal D})$
on
$\operatorname {sph}({\mathcal D})$
on
![]() ${\mathcal V}_1$
are in bijection (of cosets) with
${\mathcal V}_1$
are in bijection (of cosets) with
The quotient ![]() is generated by
is generated by
![]() $[-1]$
, which also acts trivially on any
$[-1]$
, which also acts trivially on any
![]() ${\mathcal V}$
. To summarize, the orbit
${\mathcal V}$
. To summarize, the orbit ![]() is in natural bijection with
is in natural bijection with
![]() $\mathbb {P}^1_{\mathbb {Q}}$
via the map c. The resulting space
$\mathbb {P}^1_{\mathbb {Q}}$
via the map c. The resulting space ![]() is the compact orbifold
is the compact orbifold
![]() $\widetilde {{\mathbb {H}}}/\operatorname{PSL} _2(\mathbb {Z})$
.
$\widetilde {{\mathbb {H}}}/\operatorname{PSL} _2(\mathbb {Z})$
.
Acknowledgements
We thank Dawei Chen and Yu Qiu for inspiring discussions.
Competing interest
The authors have no competing interest to declare.
Funding statement
Research of A.B. was partially supported by the project REDCOM: Reducing complexity in algebra, logic, combinatorics, financed by the programme Ricerca Scientifica di Eccellenza 2018 of the Fondazione Cariverona. Research of M.M. and J.S. is supported by the DFG-project MO 1884/2-1, and by the Collaborative Research Centre TRR 326 ‘Geometry and Arithmetic of Uniformized Structures’.