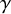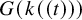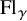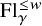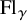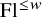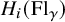Introduction
Let k be an algebraically closed field,
![]() $K:=k((t))$
the field of Laurent power series over k, and
$K:=k((t))$
the field of Laurent power series over k, and
![]() $\mathcal {O}=\mathcal {O}_K=k[[t]]$
the ring of integers of K. Let G be a connected reductive group over k, and let
$\mathcal {O}=\mathcal {O}_K=k[[t]]$
the ring of integers of K. Let G be a connected reductive group over k, and let
![]() $G^{\operatorname {sc}}$
be the simply-connected covering of the derived group of G. For an algebraic group H over K (resp.
$G^{\operatorname {sc}}$
be the simply-connected covering of the derived group of G. For an algebraic group H over K (resp.
![]() $\mathcal {O}$
), we denote by
$\mathcal {O}$
), we denote by
![]() $LH$
(resp.
$LH$
(resp.
![]() $L^+(H)$
) the corresponding loop (resp. arc) group.
$L^+(H)$
) the corresponding loop (resp. arc) group.
We fix a maximal torus
![]() $T\subseteq G$
and an Iwahori subgroup scheme
$T\subseteq G$
and an Iwahori subgroup scheme
![]() $I\subseteq L^+(G)$
such that
$I\subseteq L^+(G)$
such that
![]() $I\cap LT=L^+(T)$
, and let
$I\cap LT=L^+(T)$
, and let
![]() $T_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
and
$T_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
and
![]() $I^{\operatorname {sc}}\subseteq L^+(G^{\operatorname {sc}})$
be the corresponding maximal torus and the Iwahori subgroups of
$I^{\operatorname {sc}}\subseteq L^+(G^{\operatorname {sc}})$
be the corresponding maximal torus and the Iwahori subgroups of
![]() $G^{\operatorname {sc}}$
, respectively. Let
$G^{\operatorname {sc}}$
, respectively. Let
![]() $W=W_G$
be the Weyl group of G, let
$W=W_G$
be the Weyl group of G, let
![]() $\Lambda =X_*(T_{G^{\operatorname {sc}}})$
be the group of cocharacters, and let
$\Lambda =X_*(T_{G^{\operatorname {sc}}})$
be the group of cocharacters, and let
![]() $\widetilde {W}:=W\ltimes \Lambda $
be the affine Weyl group of G.
$\widetilde {W}:=W\ltimes \Lambda $
be the affine Weyl group of G.
Denote by
![]() $\operatorname {Fl}=L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
the affine flag variety of
$\operatorname {Fl}=L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
the affine flag variety of
![]() $G^{\operatorname {sc}}$
. Then we have a natural embedding
$G^{\operatorname {sc}}$
. Then we have a natural embedding
![]() $\widetilde {W}\hookrightarrow \operatorname {Fl}$
. For every
$\widetilde {W}\hookrightarrow \operatorname {Fl}$
. For every
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
the closure of the
$\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
the closure of the
![]() $I^{\operatorname {sc}}$
-orbit
$I^{\operatorname {sc}}$
-orbit
![]() $I^{\operatorname {sc}}w\subseteq \operatorname {Fl}$
. Then each
$I^{\operatorname {sc}}w\subseteq \operatorname {Fl}$
. Then each
![]() $\operatorname {Fl}^{\leq w}$
is a closed projective subscheme of
$\operatorname {Fl}^{\leq w}$
is a closed projective subscheme of
![]() $\operatorname {Fl}$
, usually referred to as the affine Schubert variety, while
$\operatorname {Fl}$
, usually referred to as the affine Schubert variety, while
![]() $\operatorname {Fl}$
is an inductive limit of the
$\operatorname {Fl}$
is an inductive limit of the
![]() $\operatorname {Fl}^{\leq w}$
’s.
$\operatorname {Fl}^{\leq w}$
’s.
For a regular semi-simple element
![]() $\gamma \in G(K)$
, we denote by
$\gamma \in G(K)$
, we denote by
![]() $\operatorname {Fl}_{\gamma }\subseteq \operatorname {Fl}$
the corresponding affine Springer fiber (i.e., the closed ind-subscheme of points
$\operatorname {Fl}_{\gamma }\subseteq \operatorname {Fl}$
the corresponding affine Springer fiber (i.e., the closed ind-subscheme of points
![]() $gI^{\operatorname {sc}}\in \operatorname {Fl}$
such that
$gI^{\operatorname {sc}}\in \operatorname {Fl}$
such that
![]() $g^{-1}\gamma g\in I$
).
$g^{-1}\gamma g\in I$
).
Let
![]() $G_{\gamma }$
be the centralizer of
$G_{\gamma }$
be the centralizer of
![]() $\gamma $
in G. It is a torus defined over K. Let
$\gamma $
in G. It is a torus defined over K. Let
![]() $S_{\gamma }\subseteq G_{\gamma }$
be the maximal K-split torus. We will always assume that
$S_{\gamma }\subseteq G_{\gamma }$
be the maximal K-split torus. We will always assume that
![]() $S_{\gamma }$
is contained in
$S_{\gamma }$
is contained in
![]() $T_K$
, where
$T_K$
, where
![]() $T_K$
denote the extension of scalars of T to K.
$T_K$
denote the extension of scalars of T to K.
For every ind-subscheme
![]() $Z\subseteq \operatorname {Fl}_G$
, we denote by
$Z\subseteq \operatorname {Fl}_G$
, we denote by
![]() $Z_{\gamma }$
the intersection
$Z_{\gamma }$
the intersection
![]() $Z\cap \operatorname {Fl}_{\gamma }$
. Then
$Z\cap \operatorname {Fl}_{\gamma }$
. Then
![]() $\operatorname {Fl}_{\gamma }$
is a union of the
$\operatorname {Fl}_{\gamma }$
is a union of the
![]() $\operatorname {Fl}^{\leq w}_{\gamma }$
; hence, each homology group
$\operatorname {Fl}^{\leq w}_{\gamma }$
; hence, each homology group
![]() $H_i(\operatorname {Fl}_{\gamma })$
is by definition the direct limit of the
$H_i(\operatorname {Fl}_{\gamma })$
is by definition the direct limit of the
![]() $H_i(\operatorname {Fl}_{\gamma }^{\leq w})$
’s. The main result of this paper implies that the canonical map
$H_i(\operatorname {Fl}_{\gamma }^{\leq w})$
’s. The main result of this paper implies that the canonical map
![]() $H_i(\operatorname {Fl}_{\gamma }^{\leq w})\to H_i(\operatorname {Fl}_{\gamma })$
is injective if w is sufficiently regular.
$H_i(\operatorname {Fl}_{\gamma }^{\leq w})\to H_i(\operatorname {Fl}_{\gamma })$
is injective if w is sufficiently regular.
More precisely, let
![]() $\pi :\widetilde {W}\to \widetilde {W}/W=\Lambda $
be the projection. For
$\pi :\widetilde {W}\to \widetilde {W}/W=\Lambda $
be the projection. For
![]() $m\in \mathbb N$
, we say that
$m\in \mathbb N$
, we say that
![]() $w\in \widetilde {W}$
is m-regular if
$w\in \widetilde {W}$
is m-regular if
![]() $|\langle \alpha ,\pi (w)\rangle |\geq m$
for every root
$|\langle \alpha ,\pi (w)\rangle |\geq m$
for every root
![]() $\alpha $
of
$\alpha $
of
![]() $(G,T)$
. The main goal of this paper is to prove the following result used in our companion work [Reference Bezrukavnikov and VarshavskyBV].
$(G,T)$
. The main goal of this paper is to prove the following result used in our companion work [Reference Bezrukavnikov and VarshavskyBV].
Theorem 0.1. There exists
![]() $m\in \mathbb N$
(depending on
$m\in \mathbb N$
(depending on
![]() $\gamma $
) such that for every finite set
$\gamma $
) such that for every finite set
![]() $w_1,\ldots ,w_n$
of m-regular elements of
$w_1,\ldots ,w_n$
of m-regular elements of
![]() $\widetilde {W}$
, the natural map
$\widetilde {W}$
, the natural map
![]() $H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq w_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for every
$H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq w_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for every
![]() $i\in \mathbb Z$
.
$i\in \mathbb Z$
.
If the group G and element
![]() $\gamma $
are defined over
$\gamma $
are defined over
![]() ${\mathbb F}_q$
, the expression
${\mathbb F}_q$
, the expression
 $$\begin{align*}\left| \left(\bigcup_{j=1}^n \operatorname{Fl}^{\leq w_j}_{\gamma}\right)({\mathbb F}_q)\right|=\operatorname{Tr}\left(\operatorname{Fr},H_*\left(\bigcup_{j=1}^n \operatorname{Fl}^{\leq w_j}_{\gamma}\right)\right) \end{align*}$$
$$\begin{align*}\left| \left(\bigcup_{j=1}^n \operatorname{Fl}^{\leq w_j}_{\gamma}\right)({\mathbb F}_q)\right|=\operatorname{Tr}\left(\operatorname{Fr},H_*\left(\bigcup_{j=1}^n \operatorname{Fl}^{\leq w_j}_{\gamma}\right)\right) \end{align*}$$
appears in computation of truncated orbital integrals.
As explained in [Reference Bezrukavnikov and VarshavskyBV], Theorem 0.1 allows one to interpret
![]() $H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq w_j}_{\gamma })$
as a term of a filtration on
$H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq w_j}_{\gamma })$
as a term of a filtration on
![]() $H_i(\operatorname {Fl}_{\gamma })$
, which turns out to have favorable properties with respect to the affine Springer action: it is a good filtration compatible with a natural filtration on the group ring of the affine Weyl group. This provides a way to interpret a certain weighted orbital integral (or rather the closely related value of the averaging of a distribution) in terms of
$H_i(\operatorname {Fl}_{\gamma })$
, which turns out to have favorable properties with respect to the affine Springer action: it is a good filtration compatible with a natural filtration on the group ring of the affine Weyl group. This provides a way to interpret a certain weighted orbital integral (or rather the closely related value of the averaging of a distribution) in terms of
![]() $H_*(\operatorname {Fl}_{\gamma })$
equipped with an action of Frobenius and affine Springer action.
$H_*(\operatorname {Fl}_{\gamma })$
equipped with an action of Frobenius and affine Springer action.
Theorem 0.1 will be deduced from a more general result. For each Borel subgroup
![]() $B\supseteq T$
of G, we denote its unipotent radical by
$B\supseteq T$
of G, we denote its unipotent radical by
![]() $U_{B}\subseteq G$
. For every
$U_{B}\subseteq G$
. For every
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\operatorname {Fl}^{\leq _{B}w}\subseteq \operatorname {Fl}$
the closure of the
$\operatorname {Fl}^{\leq _{B}w}\subseteq \operatorname {Fl}$
the closure of the
![]() $U_{B}(K)$
-orbit
$U_{B}(K)$
-orbit
![]() $U_{B}(K)w\subseteq \operatorname {Fl}$
, which is called the semi-infinite orbit. Then
$U_{B}(K)w\subseteq \operatorname {Fl}$
, which is called the semi-infinite orbit. Then
![]() $\operatorname {Fl}^{\leq _{B}w}$
is a closed ind-subscheme of
$\operatorname {Fl}^{\leq _{B}w}$
is a closed ind-subscheme of
![]() $\operatorname {Fl}$
.
$\operatorname {Fl}$
.
We consider tuples
![]() $\overline {w}=\{w_B\}_B$
of elements of
$\overline {w}=\{w_B\}_B$
of elements of
![]() $\widetilde {W}$
, where B runs over the set of all Borel subgroups
$\widetilde {W}$
, where B runs over the set of all Borel subgroups
![]() $B\supseteq T$
of G. Most of the time will restrict ourselves to tuples, which are admissible (see Definition 1.3.1) and m-regular (see Notation 1.3.9). In particular, the last assumption implies that each
$B\supseteq T$
of G. Most of the time will restrict ourselves to tuples, which are admissible (see Definition 1.3.1) and m-regular (see Notation 1.3.9). In particular, the last assumption implies that each
![]() $w_B$
is m-regular.
$w_B$
is m-regular.
For each tuple
![]() $\overline {w}$
, we denote by
$\overline {w}$
, we denote by
![]() $\operatorname {Fl}^{\leq \overline {w}}$
the reduced intersection
$\operatorname {Fl}^{\leq \overline {w}}$
the reduced intersection
![]() $\bigcap _{B}\operatorname {Fl}^{\leq _{B}w_{B}}$
. Each
$\bigcap _{B}\operatorname {Fl}^{\leq _{B}w_{B}}$
. Each
![]() $\operatorname {Fl}^{\leq \overline {w}}$
is a projective scheme (see Corollary 2.1.7(c)).
$\operatorname {Fl}^{\leq \overline {w}}$
is a projective scheme (see Corollary 2.1.7(c)).
Theorem 0.1 follows from the following two results:
Theorem 0.2. For every
![]() $w\in \widetilde {W}$
, there exists a unique admissible tuple
$w\in \widetilde {W}$
, there exists a unique admissible tuple
![]() $\overline {w}$
such that
$\overline {w}$
such that
![]() $\operatorname {Fl}^{\leq w}=\operatorname {Fl}^{\leq \overline {w}}$
. Moreover, there exists
$\operatorname {Fl}^{\leq w}=\operatorname {Fl}^{\leq \overline {w}}$
. Moreover, there exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $m\in \mathbb N$
and every
$m\in \mathbb N$
and every
![]() $(m+r)$
-regular
$(m+r)$
-regular
![]() $w\in \widetilde {W}$
, the tuple
$w\in \widetilde {W}$
, the tuple
![]() $\overline {w}$
is m-regular.
$\overline {w}$
is m-regular.
Theorem 0.3. There exists
![]() $m\in \mathbb N$
(depending on
$m\in \mathbb N$
(depending on
![]() $\gamma $
) such that for every finite set
$\gamma $
) such that for every finite set
![]() $\overline {w}_1,\ldots ,\overline {w}_n$
of m-regular admissible tuples, the natural map
$\overline {w}_1,\ldots ,\overline {w}_n$
of m-regular admissible tuples, the natural map
![]() $H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all i.
$H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all i.
Notice that Theorem 0.3 is vacuous if
![]() $\gamma $
is elliptic. Indeed, in this case, the affine Springer fiber
$\gamma $
is elliptic. Indeed, in this case, the affine Springer fiber
![]() $\operatorname {Fl}_{\gamma }$
is of finite type, so there exists an integer m such that for every m-regular admissible tuple
$\operatorname {Fl}_{\gamma }$
is of finite type, so there exists an integer m such that for every m-regular admissible tuple
![]() $\overline {w}$
, we have an equality
$\overline {w}$
, we have an equality
![]() $\operatorname {Fl}_{\gamma }^{\leq \overline {w}}=\operatorname {Fl}_{\gamma }$
.
$\operatorname {Fl}_{\gamma }^{\leq \overline {w}}=\operatorname {Fl}_{\gamma }$
.
To show the assertion in general, we use induction on the semisimple rank of G. Namely, if
![]() $\gamma $
is not elliptic, then
$\gamma $
is not elliptic, then
![]() $\operatorname {Fl}_{\gamma }$
is equipped with an action of a nontrivial torus S, and the scheme of fixed points
$\operatorname {Fl}_{\gamma }$
is equipped with an action of a nontrivial torus S, and the scheme of fixed points
![]() $\operatorname {Fl}_{\gamma }^S$
is naturally isomorphic to a disjoint union of affine Springer fibers corresponding to a proper Levi subgroup M of G. Thus, an analog of Theorem 0.3 for
$\operatorname {Fl}_{\gamma }^S$
is naturally isomorphic to a disjoint union of affine Springer fibers corresponding to a proper Levi subgroup M of G. Thus, an analog of Theorem 0.3 for
![]() $\operatorname {Fl}_{\gamma }^S$
holds by induction hypothesis, and we use finiteness properties of
$\operatorname {Fl}_{\gamma }^S$
holds by induction hypothesis, and we use finiteness properties of
![]() $H_i(\operatorname {Fl}_{\gamma })$
and localization theorem in equivariant cohomology to relate homology of
$H_i(\operatorname {Fl}_{\gamma })$
and localization theorem in equivariant cohomology to relate homology of
![]() $\operatorname {Fl}_{\gamma }$
with that of
$\operatorname {Fl}_{\gamma }$
with that of
![]() $\operatorname {Fl}_{\gamma }^S$
.
$\operatorname {Fl}_{\gamma }^S$
.
The paper is organized as follows. In Section 1, we study orderings on affine Weyl groups and introduce admissible tuples, which play a central role later. In Section 2, we study semi-infinite orbits in affine flag varieties and their intersections, establish Theorem 0.2, and show technical results needed later. In Section 3, we study geometric properties of the affine Springer fibers and establish a finiteness property of its homology.
Finally, in Section 4, we prove Theorem 0.3 using results of the previous sections. Namely, we review the localization theorem in the equivariant cohomology with compact support in subsection 4.1, give a criterion of an injectivity of the map on homology in subsection 4.2, and complete the proof in subsection 4.3.
The authors thank the anonymous referee for numerous corrections and suggestions that helped us to improve the exposition.
1 Combinatorics of affine Weyl groups
1.1 Preliminaries
1.1.1. Roots
(a) Let V be a finite dimensional vector space over
![]() $\mathbb R$
,
$\mathbb R$
,
![]() $V^*$
the dual space, and let
$V^*$
the dual space, and let
![]() $\Phi \subseteq V^*$
be a (reduced) root system (see, for example, [Reference BehrendBe] or [Reference BourbakiBo, Section VI]).
$\Phi \subseteq V^*$
be a (reduced) root system (see, for example, [Reference BehrendBe] or [Reference BourbakiBo, Section VI]).
(b) We denote by
![]() $\mathcal {C}=\mathcal {C}_{\Phi }$
the set of all Weyl chambers
$\mathcal {C}=\mathcal {C}_{\Phi }$
the set of all Weyl chambers
![]() $C\subseteq V$
of
$C\subseteq V$
of
![]() $\Phi $
. For each
$\Phi $
. For each
![]() $C\in \mathcal {C}$
, we denote by
$C\in \mathcal {C}$
, we denote by
![]() $\Phi _{C}\subseteq \Phi $
the set of C-positive roots, by
$\Phi _{C}\subseteq \Phi $
the set of C-positive roots, by
![]() $\Delta _{C}\subseteq \Phi _C$
the set of C-simple roots, and by
$\Delta _{C}\subseteq \Phi _C$
the set of C-simple roots, and by
![]() $\Psi _C\subseteq V^*$
the set of C-fundamental weights.
$\Psi _C\subseteq V^*$
the set of C-fundamental weights.
(c) We set
![]() $\widetilde {\Phi }:=\Phi \times \mathbb Z$
and call it the set of affine roots. Every
$\widetilde {\Phi }:=\Phi \times \mathbb Z$
and call it the set of affine roots. Every
![]() $\widetilde {\alpha }=(\alpha ,n)$
is identified with an affine function
$\widetilde {\alpha }=(\alpha ,n)$
is identified with an affine function
![]() $\widetilde {\alpha }:V\to \mathbb R$
, given by the rule
$\widetilde {\alpha }:V\to \mathbb R$
, given by the rule
![]() $\widetilde {\alpha }(x)=\alpha (x)+n$
. In particular, we identify each root
$\widetilde {\alpha }(x)=\alpha (x)+n$
. In particular, we identify each root
![]() $\alpha \in \Phi $
with affine root
$\alpha \in \Phi $
with affine root
![]() $(\alpha ,0)\in \widetilde {\Phi }$
. For a subset
$(\alpha ,0)\in \widetilde {\Phi }$
. For a subset
![]() $\Phi '\subseteq \Phi $
(resp. a Weyl chamber
$\Phi '\subseteq \Phi $
(resp. a Weyl chamber
![]() $C\in \mathcal {C}$
), we denote by
$C\in \mathcal {C}$
), we denote by
![]() $\widetilde {\Phi '}$
(resp.
$\widetilde {\Phi '}$
(resp.
![]() $\widetilde {\Phi }_C$
), the set of all
$\widetilde {\Phi }_C$
), the set of all
![]() $\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
such that
$\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
such that
![]() $\alpha \in \Phi '$
(resp.
$\alpha \in \Phi '$
(resp.
![]() $\alpha \in \Phi _C$
).
$\alpha \in \Phi _C$
).
(d) Let
![]() $W=W_{\Phi }\subseteq \operatorname {Aut} (V)$
be the Weyl group of
$W=W_{\Phi }\subseteq \operatorname {Aut} (V)$
be the Weyl group of
![]() $\Phi $
, let
$\Phi $
, let
![]() $\Lambda \subseteq V$
be the subgroup generated by coroots
$\Lambda \subseteq V$
be the subgroup generated by coroots
![]() $\{\check {\alpha }\}_{\alpha \in \Phi }$
, and let
$\{\check {\alpha }\}_{\alpha \in \Phi }$
, and let
![]() $\widetilde {W}:=W\ltimes \Lambda $
be the affine Weyl group of
$\widetilde {W}:=W\ltimes \Lambda $
be the affine Weyl group of
![]() $\Phi $
. We will denote by
$\Phi $
. We will denote by
![]() $\pi $
the natural projection
$\pi $
the natural projection
![]() $\widetilde {W}\to \widetilde {W}/W=\Lambda $
.
$\widetilde {W}\to \widetilde {W}/W=\Lambda $
.
(e) The lattice
![]() $\Lambda $
acts on V by translations. Then the group
$\Lambda $
acts on V by translations. Then the group
![]() $\widetilde {W}$
acts on V by affine transformations; hence, it acts on
$\widetilde {W}$
acts on V by affine transformations; hence, it acts on
![]() $\widetilde {\Phi }$
by the rule
$\widetilde {\Phi }$
by the rule
![]() $w(\widetilde {\alpha })(x)=\widetilde {\alpha }(w^{-1}(x))$
for all
$w(\widetilde {\alpha })(x)=\widetilde {\alpha }(w^{-1}(x))$
for all
![]() $x\in V$
. In particular, for each
$x\in V$
. In particular, for each
![]() $\mu \in \Lambda $
and
$\mu \in \Lambda $
and
![]() $(\alpha ,n)\in \widetilde {\Phi }$
, we have
$(\alpha ,n)\in \widetilde {\Phi }$
, we have
![]() $\mu (\alpha ,n)=(\alpha ,n-\langle \alpha ,\mu \rangle )$
.
$\mu (\alpha ,n)=(\alpha ,n-\langle \alpha ,\mu \rangle )$
.
(f) For each
![]() $\widetilde {\alpha }\in \widetilde {\Phi }$
, the affine reflection
$\widetilde {\alpha }\in \widetilde {\Phi }$
, the affine reflection
![]() $s_{\widetilde {\alpha }}$
satisfies
$s_{\widetilde {\alpha }}$
satisfies
![]() $s_{\widetilde {\alpha }}(x)=x-\widetilde {\alpha }(x)\check {\alpha }$
for all
$s_{\widetilde {\alpha }}(x)=x-\widetilde {\alpha }(x)\check {\alpha }$
for all
![]() $x\in V$
. In particular, for all
$x\in V$
. In particular, for all
![]() $(\alpha ,n)\in \widetilde {\Phi }$
, we have equality
$(\alpha ,n)\in \widetilde {\Phi }$
, we have equality
![]() $s_{\alpha ,n}=(-n\check {\alpha })s_{\alpha }\in \widetilde {W}$
.
$s_{\alpha ,n}=(-n\check {\alpha })s_{\alpha }\in \widetilde {W}$
.
(g) For each
![]() $\alpha \in \Phi $
, we denote by
$\alpha \in \Phi $
, we denote by
![]() $\widetilde {W}_{\alpha }\subseteq \widetilde {W}$
the subgroup generated by reflections
$\widetilde {W}_{\alpha }\subseteq \widetilde {W}$
the subgroup generated by reflections
![]() $s_{\widetilde {\alpha }}$
, with
$s_{\widetilde {\alpha }}$
, with
![]() $\widetilde {\alpha }=(\alpha ,n), n\in \mathbb Z$
.
$\widetilde {\alpha }=(\alpha ,n), n\in \mathbb Z$
.
1.1.2. The fundamental Weyl chamber
(a) We fix a Weyl chamber
![]() $C_0\in \mathcal {C}$
and denote by
$C_0\in \mathcal {C}$
and denote by
![]() $A_0$
the fundamental alcove such that
$A_0$
the fundamental alcove such that
![]() $A_0\subseteq C_0$
and such that
$A_0\subseteq C_0$
and such that
![]() $0\in V$
lies in the closure of
$0\in V$
lies in the closure of
![]() $A_0$
.
$A_0$
.
(b) The choice of
![]() $C_0$
defines the set of positive roots
$C_0$
defines the set of positive roots
![]() $\Phi _{>0}=\Phi _{C_0}\subseteq \Phi $
and the set of positive affine roots
$\Phi _{>0}=\Phi _{C_0}\subseteq \Phi $
and the set of positive affine roots
![]() $\widetilde {\Phi }_{>0}\subseteq \widetilde {\Phi }$
. Explicitly,
$\widetilde {\Phi }_{>0}\subseteq \widetilde {\Phi }$
. Explicitly,
![]() $\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
is positive if and only if either
$\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
is positive if and only if either
![]() $n>0$
, or
$n>0$
, or
![]() $n=0$
and
$n=0$
and
![]() $\alpha>0$
.
$\alpha>0$
.
(c) Then
![]() $C_0$
defines a set of simple reflection
$C_0$
defines a set of simple reflection
![]() $S\subseteq W$
, and
$S\subseteq W$
, and
![]() $A_0$
defines a set of simple affine reflections
$A_0$
defines a set of simple affine reflections
![]() $\widetilde {S}\subseteq \widetilde {W}$
. In particular, a choice of
$\widetilde {S}\subseteq \widetilde {W}$
. In particular, a choice of
![]() $C_0$
defines length functions and Bruhat orders
$C_0$
defines length functions and Bruhat orders
![]() $\leq $
on both W and
$\leq $
on both W and
![]() $\widetilde {W}$
.
$\widetilde {W}$
.
(d) Using
![]() $A_0$
, we identify each
$A_0$
, we identify each
![]() $w\in \widetilde {W}$
with the corresponding alcove
$w\in \widetilde {W}$
with the corresponding alcove
![]() $w(A_0)\subseteq V$
. In particular, we will say that
$w(A_0)\subseteq V$
. In particular, we will say that
![]() $w\in \widetilde {W}$
belongs to
$w\in \widetilde {W}$
belongs to
![]() $C\in \mathcal {C}$
, or
$C\in \mathcal {C}$
, or
![]() $w\in C$
, if
$w\in C$
, if
![]() $w(A_0)\subseteq C$
. Explicitly, this means that
$w(A_0)\subseteq C$
. Explicitly, this means that
![]() $\langle \alpha ,w(A_0)\rangle =\langle w^{-1}(\alpha ),A_0\rangle \geq 0$
for each
$\langle \alpha ,w(A_0)\rangle =\langle w^{-1}(\alpha ),A_0\rangle \geq 0$
for each
![]() $\alpha \in \Phi _{C}$
, or, what is the same,
$\alpha \in \Phi _{C}$
, or, what is the same,
![]() $w^{-1}(\Phi _{C})\subseteq \widetilde {\Phi }_{>0}$
.
$w^{-1}(\Phi _{C})\subseteq \widetilde {\Phi }_{>0}$
.
1.1.3. Fundamental weights
(a) We set
![]() $\Psi :=\bigcup _{C\in \mathcal {C}}\Psi _C\subseteq V^*$
. For
$\Psi :=\bigcup _{C\in \mathcal {C}}\Psi _C\subseteq V^*$
. For
![]() $\psi \in \Psi $
and
$\psi \in \Psi $
and
![]() $C\in \mathcal {C}$
, we write
$C\in \mathcal {C}$
, we write
![]() $C\owns \psi $
, if
$C\owns \psi $
, if
![]() $\psi \in \Psi _C$
.
$\psi \in \Psi _C$
.
(b) Every
![]() $\psi \in \Psi $
gives rise to a fundamental coweight
$\psi \in \Psi $
gives rise to a fundamental coweight
![]() $\check {\psi }\in \Lambda _{\mathbb Q}:=\Lambda \otimes _{\mathbb Z}\mathbb Q\subseteq V$
. Namely,
$\check {\psi }\in \Lambda _{\mathbb Q}:=\Lambda \otimes _{\mathbb Z}\mathbb Q\subseteq V$
. Namely,
![]() $\check {\psi }$
is characterized by condition that for every
$\check {\psi }$
is characterized by condition that for every
![]() $C\in \mathcal {C}$
such that
$C\in \mathcal {C}$
such that
![]() $\psi \in \Psi _C$
and every
$\psi \in \Psi _C$
and every
![]() $\alpha \in \Delta _C$
, we have
$\alpha \in \Delta _C$
, we have
![]() $\langle \alpha ,\check {\psi }\rangle =\langle \psi ,\check {\alpha }\rangle $
. In particular, for every
$\langle \alpha ,\check {\psi }\rangle =\langle \psi ,\check {\alpha }\rangle $
. In particular, for every
![]() $C\in \mathcal {C}$
, we have
$C\in \mathcal {C}$
, we have
![]() $\psi \in \Psi _C$
if and only if
$\psi \in \Psi _C$
if and only if
![]() $\check {\psi }$
lies in the closure of C.
$\check {\psi }$
lies in the closure of C.
(c) For every
![]() $\psi \in \Psi $
, we denote by
$\psi \in \Psi $
, we denote by
![]() $\Phi (\psi )$
(resp.
$\Phi (\psi )$
(resp.
![]() $\Phi ^{\psi }$
) the set of
$\Phi ^{\psi }$
) the set of
![]() $\alpha \in \Phi $
such that
$\alpha \in \Phi $
such that
![]() $\langle \alpha ,\check {\psi }\rangle \geq 0$
(resp.
$\langle \alpha ,\check {\psi }\rangle \geq 0$
(resp.
![]() $\langle \alpha ,\check {\psi }\rangle =0$
). Notice that
$\langle \alpha ,\check {\psi }\rangle =0$
). Notice that
![]() $\Phi ^{\psi }$
is a root system, and there is a bijection
$\Phi ^{\psi }$
is a root system, and there is a bijection
![]() $C\mapsto C^{\psi }$
between Weyl chambers
$C\mapsto C^{\psi }$
between Weyl chambers
![]() $C\owns \psi $
of
$C\owns \psi $
of
![]() $\Phi $
and Weyl chambers of
$\Phi $
and Weyl chambers of
![]() $\Phi ^{\psi }$
. This bijection satisfies the property that
$\Phi ^{\psi }$
. This bijection satisfies the property that
![]() $(\Phi ^{\psi })_{C^{\psi }}=\Phi _{C}\cap \Phi ^{\psi }$
. We denote by
$(\Phi ^{\psi })_{C^{\psi }}=\Phi _{C}\cap \Phi ^{\psi }$
. We denote by
![]() $W^{\psi }\subseteq W$
and
$W^{\psi }\subseteq W$
and
![]() $\widetilde {W}^{\psi }\subseteq \widetilde {W}$
the Weyl group and the affine Weyl group of
$\widetilde {W}^{\psi }\subseteq \widetilde {W}$
the Weyl group and the affine Weyl group of
![]() $\Phi ^{\psi }$
, respectively.
$\Phi ^{\psi }$
, respectively.
(d) For every
![]() $\psi \in \Psi $
, we fix a Weyl chamber
$\psi \in \Psi $
, we fix a Weyl chamber
![]() $C^{\psi }_0$
of
$C^{\psi }_0$
of
![]() $\Phi ^{\psi }$
. As in Section 1.1.2(b), this choice defines the set of positive affine roots
$\Phi ^{\psi }$
. As in Section 1.1.2(b), this choice defines the set of positive affine roots
![]() $\widetilde {\Phi }^{\psi }_{>0}\subseteq \widetilde {\Phi }^{\psi }$
, and we denote by
$\widetilde {\Phi }^{\psi }_{>0}\subseteq \widetilde {\Phi }^{\psi }$
, and we denote by
![]() $\widetilde {W}_{\psi }\subseteq \widetilde {W}$
the set of all
$\widetilde {W}_{\psi }\subseteq \widetilde {W}$
the set of all
![]() $w\in \widetilde {W}$
such that
$w\in \widetilde {W}$
such that
![]() $w^{-1}(\widetilde {\Phi }^{\psi }_{>0})\subseteq \widetilde {\Phi }_{>0}$
. Then for every
$w^{-1}(\widetilde {\Phi }^{\psi }_{>0})\subseteq \widetilde {\Phi }_{>0}$
. Then for every
![]() $w\in \widetilde {W}$
, there exists a unique decomposition
$w\in \widetilde {W}$
, there exists a unique decomposition
![]() $w=w^{\psi }w_{\psi }$
, where
$w=w^{\psi }w_{\psi }$
, where
![]() $w^{\psi }\in \widetilde {W}^{\psi }$
and
$w^{\psi }\in \widetilde {W}^{\psi }$
and
![]() $w_{\psi }\in \widetilde {W}_{\psi }$
(compare, for example, [Reference Bezrukavnikov and VarshavskyBV, Lemma B.1.7(b)]). In other words,
$w_{\psi }\in \widetilde {W}_{\psi }$
(compare, for example, [Reference Bezrukavnikov and VarshavskyBV, Lemma B.1.7(b)]). In other words,
![]() $\widetilde {W}_{\psi }\subseteq \widetilde {W}$
is a set of representatives of the set of left cosets
$\widetilde {W}_{\psi }\subseteq \widetilde {W}$
is a set of representatives of the set of left cosets
![]() $\widetilde {W}^{\psi }\backslash \widetilde {W}$
.
$\widetilde {W}^{\psi }\backslash \widetilde {W}$
.
1.1.4. Properties of the Bruhat order
(a) Let
![]() $w',w"\in \widetilde {W}$
and
$w',w"\in \widetilde {W}$
and
![]() $s\in \widetilde {S}$
be such that
$s\in \widetilde {S}$
be such that
![]() $w'\leq w"$
. Then we have either
$w'\leq w"$
. Then we have either
![]() $w's\leq w"s$
(resp.
$w's\leq w"s$
(resp.
![]() $sw'\leq sw"$
) or
$sw'\leq sw"$
) or
![]() $w's\leq w"$
and
$w's\leq w"$
and
![]() $w'\leq w"s$
(resp.
$w'\leq w"s$
(resp.
![]() $sw'\leq w"$
and
$sw'\leq w"$
and
![]() $w'\leq sw"$
) or both (see, for example, [Reference Björner and BrentiBB, Proposition 2.2.7]).
$w'\leq sw"$
) or both (see, for example, [Reference Björner and BrentiBB, Proposition 2.2.7]).
(b) Let
![]() $w',w"\in \widetilde {W}$
and
$w',w"\in \widetilde {W}$
and
![]() $s\in \widetilde {S}$
be such that
$s\in \widetilde {S}$
be such that
![]() $sw'<w'$
and
$sw'<w'$
and
![]() $sw"<w"$
. Then, by part (a), we have
$sw"<w"$
. Then, by part (a), we have
![]() $w'\leq w"$
if and only if
$w'\leq w"$
if and only if
![]() $sw'\leq sw"$
.
$sw'\leq sw"$
.
(c) Let
![]() $w,w'$
and
$w,w'$
and
![]() $w"$
be elements of
$w"$
be elements of
![]() $\widetilde {W}$
such that
$\widetilde {W}$
such that
![]() $l(ww')=l(w)+l(w')$
and
$l(ww')=l(w)+l(w')$
and
![]() $ww'\leq ww"$
. Then
$ww'\leq ww"$
. Then
![]() $w'\leq w"$
. Indeed, if
$w'\leq w"$
. Indeed, if
![]() $w=s\in \widetilde {S}$
, then the assertion follows from part (a). The general case follows by induction on
$w=s\in \widetilde {S}$
, then the assertion follows from part (a). The general case follows by induction on
![]() $l(w)$
. By a similar argument, if
$l(w)$
. By a similar argument, if
![]() $l(ww")=l(w)+l(w")$
and
$l(ww")=l(w)+l(w")$
and
![]() $w'\leq w"$
, then
$w'\leq w"$
, then
![]() $ww'\leq ww"$
.
$ww'\leq ww"$
.
(d) For every
![]() $\mu \in \Lambda $
and
$\mu \in \Lambda $
and
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $l(u\mu u^{-1})=l(\mu )$
. Indeed, it is enough to show the assertion in the case
$l(u\mu u^{-1})=l(\mu )$
. Indeed, it is enough to show the assertion in the case
![]() $u=s=s_{\alpha }$
for a simple root
$u=s=s_{\alpha }$
for a simple root
![]() $\alpha $
. In this case, we have
$\alpha $
. In this case, we have
![]() $s\mu s=\mu $
, if
$s\mu s=\mu $
, if
![]() $\langle \alpha ,\mu \rangle =0$
;
$\langle \alpha ,\mu \rangle =0$
;
![]() $s\mu>\mu >\mu s$
if
$s\mu>\mu >\mu s$
if
![]() $\langle \alpha ,\mu \rangle>0$
; and
$\langle \alpha ,\mu \rangle>0$
; and
![]() $s\mu <\mu <\mu s$
if
$s\mu <\mu <\mu s$
if
![]() $\langle \alpha ,\mu \rangle <0$
.
$\langle \alpha ,\mu \rangle <0$
.
(e) Note that
![]() $w\in \widetilde {W}$
belongs to
$w\in \widetilde {W}$
belongs to
![]() $C_0$
if and only if
$C_0$
if and only if
![]() $l(sw)>l(w)$
for every
$l(sw)>l(w)$
for every
![]() $s\in S$
. In other words,
$s\in S$
. In other words,
![]() $\widetilde {W}\cap C_0$
is the set of the shortest representatives of cosets
$\widetilde {W}\cap C_0$
is the set of the shortest representatives of cosets
![]() $W\backslash \widetilde {W}$
. In particular, for every
$W\backslash \widetilde {W}$
. In particular, for every
![]() $w\in \widetilde {W}\cap C_0$
and
$w\in \widetilde {W}\cap C_0$
and
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $l(uw)=l(u)+l(w)$
, and for every
$l(uw)=l(u)+l(w)$
, and for every
![]() $u\leq u'$
in W, we have
$u\leq u'$
in W, we have
![]() $uw\leq u'w$
.
$uw\leq u'w$
.
(f) The characterization of
![]() $C_0$
given in part (e) implies that for every
$C_0$
given in part (e) implies that for every
![]() $w\in \widetilde {W}\cap C_0$
and
$w\in \widetilde {W}\cap C_0$
and
![]() $s\in \widetilde {S}$
with
$s\in \widetilde {S}$
with
![]() $ws<w$
, we have
$ws<w$
, we have
![]() $ws\in C_0$
.
$ws\in C_0$
.
(g) For every
![]() $u\in W$
and every
$u\in W$
and every
![]() $\mu \in \Lambda \cap C_0$
, we have
$\mu \in \Lambda \cap C_0$
, we have
![]() $u\leq \mu $
. Indeed, it is enough to show that
$u\leq \mu $
. Indeed, it is enough to show that
![]() $u\leq _R\mu $
(see [Reference Björner and BrentiBB, Definition 3.1.1]). Hence, by [Reference Björner and BrentiBB, Proposition 3.1.3], it is enough to show that for every affine root
$u\leq _R\mu $
(see [Reference Björner and BrentiBB, Definition 3.1.1]). Hence, by [Reference Björner and BrentiBB, Proposition 3.1.3], it is enough to show that for every affine root
![]() $\widetilde {\alpha }>0$
such that
$\widetilde {\alpha }>0$
such that
![]() $u(\widetilde {\alpha })<0$
, we have
$u(\widetilde {\alpha })<0$
, we have
![]() $\mu (\widetilde {\alpha })<0$
. If
$\mu (\widetilde {\alpha })<0$
. If
![]() $\widetilde {\alpha }=(\alpha ,n)>0$
satisfies
$\widetilde {\alpha }=(\alpha ,n)>0$
satisfies
![]() $u(\widetilde {\alpha })=(u(\alpha ),n)<0$
, then
$u(\widetilde {\alpha })=(u(\alpha ),n)<0$
, then
![]() $n=0$
, and
$n=0$
, and
![]() $\alpha>0$
. Hence,
$\alpha>0$
. Hence,
![]() $\mu (\widetilde {\alpha })=(\alpha ,-\langle \alpha ,\mu \rangle )<0$
because
$\mu (\widetilde {\alpha })=(\alpha ,-\langle \alpha ,\mu \rangle )<0$
because
![]() $\mu \in C_0$
is regular; thus,
$\mu \in C_0$
is regular; thus,
![]() $\langle \alpha ,\mu \rangle>0$
.
$\langle \alpha ,\mu \rangle>0$
.
Lemma 1.1.5. Assume that
![]() $w',w"\in C\cap \widetilde {W}$
for some
$w',w"\in C\cap \widetilde {W}$
for some
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $w'<w"$
. Then
$w'<w"$
. Then
(a) for every
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $uw'<uw"$
;
$uw'<uw"$
;
(b) there exists a sequence
![]() $w'<w_1<\ldots <w_n=w"$
such that
$w'<w_1<\ldots <w_n=w"$
such that
![]() $w_i\in C$
and
$w_i\in C$
and
![]() $l(w_i)=l(w')+i$
for each i;
$l(w_i)=l(w')+i$
for each i;
(c) for every
![]() $\mu \in \Lambda \cap C$
and
$\mu \in \Lambda \cap C$
and
![]() $w\in \widetilde {W}\cap C$
, we have
$w\in \widetilde {W}\cap C$
, we have
![]() $l(\mu w)=l(\mu )+ l(w)$
.
$l(\mu w)=l(\mu )+ l(w)$
.
Proof. (a) By induction, it is enough to show that for every element
![]() $s\in S$
, we have
$s\in S$
, we have
![]() $sw'<sw"$
. By Section 1.1.4(b), it is enough to show that
$sw'<sw"$
. By Section 1.1.4(b), it is enough to show that
![]() $w'<sw'$
if and only if
$w'<sw'$
if and only if
![]() $w"<sw"$
. Let
$w"<sw"$
. Let
![]() $u\in W$
be such that
$u\in W$
be such that
![]() $C=u(C_0)$
. Then it follows from Section 1.1.4(e) that each condition
$C=u(C_0)$
. Then it follows from Section 1.1.4(e) that each condition
![]() $w'<sw'$
and
$w'<sw'$
and
![]() $w"<sw"$
is equivalent to
$w"<sw"$
is equivalent to
![]() $u<su$
.
$u<su$
.
(b) Using part (a) and Section 1.1.4(e), we may assume that
![]() $C=C_0$
. If
$C=C_0$
. If
![]() $l(w")-l(w')=1$
, there is nothing to prove, so we can assume that
$l(w")-l(w')=1$
, there is nothing to prove, so we can assume that
![]() $l(w")-l(w')>1$
. By induction, it is enough to show the existence of
$l(w")-l(w')>1$
. By induction, it is enough to show the existence of
![]() $w\in C_0$
such that
$w\in C_0$
such that
![]() $w'<w<w"$
.
$w'<w<w"$
.
Choose
![]() $s\in \widetilde {S}$
such that
$s\in \widetilde {S}$
such that
![]() $w"s<w"$
. Then
$w"s<w"$
. Then
![]() $w"s\in C_0$
by Section 1.1.4(f). If
$w"s\in C_0$
by Section 1.1.4(f). If
![]() $w'<w"s$
, then
$w'<w"s$
, then
![]() $w:=w"s$
does the job. If not, then by Section 1.1.4(a) we get
$w:=w"s$
does the job. If not, then by Section 1.1.4(a) we get
![]() $w's<w'$
and
$w's<w'$
and
![]() $w's<w"s$
. Then by Section 1.1.4(f), we have
$w's<w"s$
. Then by Section 1.1.4(f), we have
![]() $w's\in C_0$
, so by induction on
$w's\in C_0$
, so by induction on
![]() $l(w")$
, there exist
$l(w")$
, there exist
![]() $w\in C_0$
such that
$w\in C_0$
such that
![]() $w's<w<w"s$
.
$w's<w<w"s$
.
If
![]() $ws<w$
, then it follows from Section 1.1.4(a) that
$ws<w$
, then it follows from Section 1.1.4(a) that
![]() $w'\leq w<w"s$
, contradicting our assumption. Hence, we may assume that
$w'\leq w<w"s$
, contradicting our assumption. Hence, we may assume that
![]() $ws>w$
, in which case by Section 1.1.4(a) we have
$ws>w$
, in which case by Section 1.1.4(a) we have
![]() $w'<ws<w"$
; thus, it is enough to show that
$w'<ws<w"$
; thus, it is enough to show that
![]() $ws\in C_0$
.
$ws\in C_0$
.
Assume that
![]() $ws\notin C_0$
. Since
$ws\notin C_0$
. Since
![]() $w\in C_0$
, this would imply that there exists a simple root
$w\in C_0$
, this would imply that there exists a simple root
![]() $\alpha $
of
$\alpha $
of
![]() $C_0$
such that
$C_0$
such that
![]() $ws=s_{\alpha }w$
. Then we have
$ws=s_{\alpha }w$
. Then we have
![]() $w'<s_{\alpha }w$
and
$w'<s_{\alpha }w$
and
![]() $w'\in C_0$
and therefore by Section 1.1.4(c) that
$w'\in C_0$
and therefore by Section 1.1.4(c) that
![]() $w'\leq w<w"s$
, contradicting the assumption.
$w'\leq w<w"s$
, contradicting the assumption.
(c) Using Sections 1.1.4(d),(e), we can assume that
![]() $C=C_0$
. Now the proof goes by induction on
$C=C_0$
. Now the proof goes by induction on
![]() $l(w)$
. Choose
$l(w)$
. Choose
![]() $s\in \widetilde {S}$
such that
$s\in \widetilde {S}$
such that
![]() $ws<w$
. Then
$ws<w$
. Then
![]() $ws\in C_0$
by Section 1.1.4(f); hence, by the induction hypothesis, we have
$ws\in C_0$
by Section 1.1.4(f); hence, by the induction hypothesis, we have
Thus, it is enough to show that
![]() $\mu ws<\mu w$
.
$\mu ws<\mu w$
.
Let
![]() $\alpha $
be a simple affine root such that
$\alpha $
be a simple affine root such that
![]() $s=s_{\alpha }$
. Then
$s=s_{\alpha }$
. Then
![]() $\widetilde {\beta }:=w(\alpha )<0$
because
$\widetilde {\beta }:=w(\alpha )<0$
because
![]() $ws<w$
, and we want to show that
$ws<w$
, and we want to show that
![]() $\mu (\widetilde {\beta })=\mu w(\alpha )<0$
. Write
$\mu (\widetilde {\beta })=\mu w(\alpha )<0$
. Write
![]() $\widetilde {\beta }$
in the form
$\widetilde {\beta }$
in the form
![]() $(\beta ,n)$
, where
$(\beta ,n)$
, where
![]() $\beta \in \Phi $
. Then
$\beta \in \Phi $
. Then
![]() $\mu (\widetilde {\beta })=\widetilde {\beta }-\langle \beta ,\mu \rangle $
, so it remains to show that
$\mu (\widetilde {\beta })=\widetilde {\beta }-\langle \beta ,\mu \rangle $
, so it remains to show that
![]() $\langle \beta ,\mu \rangle \geq 0$
.
$\langle \beta ,\mu \rangle \geq 0$
.
Since
![]() $\widetilde {\beta }<0$
, we get
$\widetilde {\beta }<0$
, we get
![]() $n\leq 0$
; therefore,
$n\leq 0$
; therefore,
![]() $w^{-1}(\beta )=\alpha -n>0$
. This implies that
$w^{-1}(\beta )=\alpha -n>0$
. This implies that
![]() $\beta \in \Phi _{C_0}$
because
$\beta \in \Phi _{C_0}$
because
![]() $w\in C_0$
; hence,
$w\in C_0$
; hence,
![]() $\langle \beta ,\mu \rangle \geq 0$
because
$\langle \beta ,\mu \rangle \geq 0$
because
![]() $\mu \in C_0$
.
$\mu \in C_0$
.
1.2 Orderings on affine Weyl groups
Notation 1.2.1. (a) Let
![]() $\widetilde {\alpha }\in \widetilde {\Phi }$
and
$\widetilde {\alpha }\in \widetilde {\Phi }$
and
![]() $w\in \widetilde {W}$
. We say that
$w\in \widetilde {W}$
. We say that
![]() $s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
if
$s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
if
![]() $w^{-1}(\widetilde {\alpha })>0$
.
$w^{-1}(\widetilde {\alpha })>0$
.
(b) Let
![]() $\Phi '\subseteq \Phi $
be a subset, and
$\Phi '\subseteq \Phi $
be a subset, and
![]() $w',w"\in \widetilde {W}$
. We say that
$w',w"\in \widetilde {W}$
. We say that
![]() $w"<_{\Phi '} w'$
if there exist affine roots
$w"<_{\Phi '} w'$
if there exist affine roots
![]() $\widetilde {\alpha }_1,\ldots ,\widetilde {\alpha }_n\in \widetilde {\Phi '}$
such that
$\widetilde {\alpha }_1,\ldots ,\widetilde {\alpha }_n\in \widetilde {\Phi '}$
such that
![]() $s_{\widetilde {\alpha }_i}\ldots s_{\widetilde {\alpha }_1}w'<_{\widetilde {\alpha }_i}s_{\widetilde {\alpha }_{i-1}}\ldots s_{\widetilde {\alpha }_1}w'$
for all i, and
$s_{\widetilde {\alpha }_i}\ldots s_{\widetilde {\alpha }_1}w'<_{\widetilde {\alpha }_i}s_{\widetilde {\alpha }_{i-1}}\ldots s_{\widetilde {\alpha }_1}w'$
for all i, and
![]() $w"=s_{\widetilde {\alpha }_n}\ldots s_{\widetilde {\alpha }_1}w'$
. For
$w"=s_{\widetilde {\alpha }_n}\ldots s_{\widetilde {\alpha }_1}w'$
. For
![]() $\alpha \in \Phi $
, we write
$\alpha \in \Phi $
, we write
![]() $w"<_{\alpha } w'$
instead of
$w"<_{\alpha } w'$
instead of
![]() $w"<_{\{\alpha \}} w'$
.
$w"<_{\{\alpha \}} w'$
.
(c) Let
![]() $\Phi '\subseteq \Phi $
, and
$\Phi '\subseteq \Phi $
, and
![]() $x',x"\in V$
. We say that
$x',x"\in V$
. We say that
![]() $x"<_{\Phi '} x'$
if the difference
$x"<_{\Phi '} x'$
if the difference
![]() $x'-x"$
is a positive linear combination of elements
$x'-x"$
is a positive linear combination of elements
![]() $\check {\alpha }$
with
$\check {\alpha }$
with
![]() $\alpha \in \Phi '$
. For
$\alpha \in \Phi '$
. For
![]() $\alpha \in \Phi $
, we write
$\alpha \in \Phi $
, we write
![]() $x"<_{\alpha } x'$
instead of
$x"<_{\alpha } x'$
instead of
![]() $x"<_{\{\alpha \}} x'$
.
$x"<_{\{\alpha \}} x'$
.
(d) For each
![]() $C\in \mathcal {C}$
,
$C\in \mathcal {C}$
,
![]() $\psi \in \Psi $
(and
$\psi \in \Psi $
(and
![]() $\psi \in C$
), we write
$\psi \in C$
), we write
![]() $<_C$
(resp.
$<_C$
(resp.
![]() $<_{\psi }$
, resp.
$<_{\psi }$
, resp.
![]() $<_{C^{\psi }}$
) instead of
$<_{C^{\psi }}$
) instead of
![]() $<_{\Phi _C}$
(resp.
$<_{\Phi _C}$
(resp.
![]() $<_{\Phi (\psi )}$
, resp.
$<_{\Phi (\psi )}$
, resp.
![]() $<_{\Phi ^{\psi }(C^{\psi })}$
).
$<_{\Phi ^{\psi }(C^{\psi })}$
).
Lemma 1.2.2.
(a) For each
![]() $\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
and
$\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
and
![]() $w\in \widetilde {W}$
, we have
$w\in \widetilde {W}$
, we have
![]() $s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
(see Section 1.2.1(a)) if and only if
$s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
(see Section 1.2.1(a)) if and only if
![]() $s_{\widetilde {\alpha }}w(x)<_{\alpha }w(x)$
(see Section 1.2.1 (c)) for all
$s_{\widetilde {\alpha }}w(x)<_{\alpha }w(x)$
(see Section 1.2.1 (c)) for all
![]() $x\in A_0$
.
$x\in A_0$
.
(b) For each
![]() $\alpha \in \Phi $
and
$\alpha \in \Phi $
and
![]() $w\in \widetilde {W}$
, we have
$w\in \widetilde {W}$
, we have
![]() $w<_{\alpha }\check {\alpha }w$
(see Section 1.2.1(b)).
$w<_{\alpha }\check {\alpha }w$
(see Section 1.2.1(b)).
(c) For each
![]() $x',x"\in V$
and
$x',x"\in V$
and
![]() $\psi \in \Psi $
, we have
$\psi \in \Psi $
, we have
![]() $x'\leq _{\psi } x"$
(see Section 1.2.1(c)) if and only if
$x'\leq _{\psi } x"$
(see Section 1.2.1(c)) if and only if
![]() $\langle \psi ,x'\rangle \leq \langle \psi ,x"\rangle $
.
$\langle \psi ,x'\rangle \leq \langle \psi ,x"\rangle $
.
Proof. (a) Fix
![]() $x\in A_0$
. Then
$x\in A_0$
. Then
![]() $w^{-1}(\widetilde {\alpha })>0$
if and only if
$w^{-1}(\widetilde {\alpha })>0$
if and only if
![]() $w^{-1}(\widetilde {\alpha })(x)=\widetilde {\alpha }(w(x))>0$
. Thus,
$w^{-1}(\widetilde {\alpha })(x)=\widetilde {\alpha }(w(x))>0$
. Thus,
![]() $s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
if and only if
$s_{\widetilde {\alpha }}w<_{\widetilde {\alpha }}w$
if and only if
![]() $s_{\widetilde {\alpha }}w(x)=w(x)-\widetilde {\alpha }(w(x))\check {\alpha }<_{\alpha }w(x)$
.
$s_{\widetilde {\alpha }}w(x)=w(x)-\widetilde {\alpha }(w(x))\check {\alpha }<_{\alpha }w(x)$
.
(b) Let
![]() $r\in \mathbb Z$
such that the affine root
$r\in \mathbb Z$
such that the affine root
![]() $\widetilde {\alpha }=(\alpha ,r)$
satisfies
$\widetilde {\alpha }=(\alpha ,r)$
satisfies
![]() $0<\widetilde {\alpha }(\check {\alpha }w(x))<1$
. Using identity
$0<\widetilde {\alpha }(\check {\alpha }w(x))<1$
. Using identity
![]() $\widetilde {\alpha }(s_{\widetilde {\alpha }}(\check {\alpha }w(x)))=- \widetilde {\alpha }(\check {\alpha }w(x))$
, we get
$\widetilde {\alpha }(s_{\widetilde {\alpha }}(\check {\alpha }w(x)))=- \widetilde {\alpha }(\check {\alpha }w(x))$
, we get
![]() $0<(\widetilde {\alpha }+1)(s_{\widetilde {\alpha }}(\check {\alpha }w(x)))<1$
. Thus, by the observation of part (a), we have
$0<(\widetilde {\alpha }+1)(s_{\widetilde {\alpha }}(\check {\alpha }w(x)))<1$
. Thus, by the observation of part (a), we have
![]() $w=s_{\widetilde {\alpha }+1}s_{\widetilde {\alpha }}(\check {\alpha }w)<_{\widetilde {\alpha }+1}s_{\widetilde {\alpha }}(\check {\alpha }w)<_{\widetilde {\alpha }}\check {\alpha }w$
; hence,
$w=s_{\widetilde {\alpha }+1}s_{\widetilde {\alpha }}(\check {\alpha }w)<_{\widetilde {\alpha }+1}s_{\widetilde {\alpha }}(\check {\alpha }w)<_{\widetilde {\alpha }}\check {\alpha }w$
; hence,
![]() $w<_{\alpha }\check {\alpha }w$
.
$w<_{\alpha }\check {\alpha }w$
.
(c) The ‘only if’ assertion follows from definitions. To see the ‘if’ assertion, we choose a Weyl chamber
![]() $C\ni \psi $
, and let
$C\ni \psi $
, and let
![]() $\alpha _{\psi }\in \Delta _C$
be the simple root, corresponding to
$\alpha _{\psi }\in \Delta _C$
be the simple root, corresponding to
![]() $\psi $
. Then the difference
$\psi $
. Then the difference
![]() $x"-x'$
can be (uniquely) written in the form
$x"-x'$
can be (uniquely) written in the form
![]() $\sum _{\alpha \in \Delta _C} c_{\alpha }\check {\alpha }$
with
$\sum _{\alpha \in \Delta _C} c_{\alpha }\check {\alpha }$
with
![]() $c_{\alpha }\in \mathbb R$
, and the assumption that
$c_{\alpha }\in \mathbb R$
, and the assumption that
![]() $\langle \psi ,x'\rangle \leq \langle \psi ,x"\rangle $
implies that
$\langle \psi ,x'\rangle \leq \langle \psi ,x"\rangle $
implies that
![]() $c_{\alpha _{\psi }}\geq 0$
. Now the assertion follows from the observation that for every
$c_{\alpha _{\psi }}\geq 0$
. Now the assertion follows from the observation that for every
![]() $\alpha \in \Delta _C\smallsetminus \{\alpha _{\psi }\}$
, we have
$\alpha \in \Delta _C\smallsetminus \{\alpha _{\psi }\}$
, we have
![]() $\alpha \in \Phi (\psi )$
and
$\alpha \in \Phi (\psi )$
and
![]() $-\alpha \in \Phi (\psi )$
.
$-\alpha \in \Phi (\psi )$
.
Corollary 1.2.3.
(a) For each
![]() $w,w'\in \widetilde {W}$
and
$w,w'\in \widetilde {W}$
and
![]() $\alpha \in \Phi $
, we have
$\alpha \in \Phi $
, we have
![]() $w<_{\alpha }w'$
if and only if we have
$w<_{\alpha }w'$
if and only if we have
![]() $w\in \widetilde {W}_{\alpha }w'$
and
$w\in \widetilde {W}_{\alpha }w'$
and
![]() $w(x)<_{\alpha }w'(x)$
for all
$w(x)<_{\alpha }w'(x)$
for all
![]() $x\in A_0$
.
$x\in A_0$
.
(b) For each
![]() $\Phi '\subseteq \Phi $
and
$\Phi '\subseteq \Phi $
and
![]() $w,w'\in \widetilde {W}$
with
$w,w'\in \widetilde {W}$
with
![]() $w<_{\Phi '} w'$
, we have
$w<_{\Phi '} w'$
, we have
![]() $w(x)<_{\Phi '} w'(x)$
for each
$w(x)<_{\Phi '} w'(x)$
for each
![]() $x\in A_0$
; hence,
$x\in A_0$
; hence,
![]() $\pi (w)\leq _{\Phi '} \pi (w')$
in the sense of Section 1.2.1(c).
$\pi (w)\leq _{\Phi '} \pi (w')$
in the sense of Section 1.2.1(c).
(c) Let
![]() $\Phi '\subseteq \Phi $
have a property that if
$\Phi '\subseteq \Phi $
have a property that if
![]() $\mu \in \Lambda $
is a positive linear combination of elements
$\mu \in \Lambda $
is a positive linear combination of elements
![]() $\check {\alpha }$
with
$\check {\alpha }$
with
![]() $\alpha \in \Phi '$
, then
$\alpha \in \Phi '$
, then
![]() $\mu $
is a finite sum of elements
$\mu $
is a finite sum of elements
![]() $\check {\alpha }$
with
$\check {\alpha }$
with
![]() $\alpha \in \Phi '$
. Then for every
$\alpha \in \Phi '$
. Then for every
![]() $\mu ,\mu '\in \Lambda $
, we have
$\mu ,\mu '\in \Lambda $
, we have
![]() $\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(b) if and only if
$\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(b) if and only if
![]() $\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(c).
$\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(c).
Proof. (a) If
![]() $w<_{\alpha }w'$
, then
$w<_{\alpha }w'$
, then
![]() $w\in \widetilde {W}_{\alpha }w'$
(by definition), and
$w\in \widetilde {W}_{\alpha }w'$
(by definition), and
![]() $w(x)<_{\alpha }w'(x)$
for all
$w(x)<_{\alpha }w'(x)$
for all
![]() $x\in A_0$
(by Lemma 1.2.2(a)). Conversely, assume that
$x\in A_0$
(by Lemma 1.2.2(a)). Conversely, assume that
![]() $w=uw'$
with
$w=uw'$
with
![]() $u\in \widetilde {W}_{\alpha }$
such that
$u\in \widetilde {W}_{\alpha }$
such that
![]() $w(x)<_{\alpha }w'(x)$
for all
$w(x)<_{\alpha }w'(x)$
for all
![]() $x\in A_0$
. Then we have either
$x\in A_0$
. Then we have either
![]() $u=s_{\widetilde {\alpha }}$
or
$u=s_{\widetilde {\alpha }}$
or
![]() $u=\check {\alpha }^m$
for some
$u=\check {\alpha }^m$
for some
![]() $m\in \mathbb Z_{<0}$
. In the first case, we have
$m\in \mathbb Z_{<0}$
. In the first case, we have
![]() $w<_{\alpha }w'$
by Lemma 1.2.2(a), while in the second one, we have
$w<_{\alpha }w'$
by Lemma 1.2.2(a), while in the second one, we have
![]() $w<_{\alpha }w'$
by Lemma 1.2.2(b).
$w<_{\alpha }w'$
by Lemma 1.2.2(b).
(b) By definition, it is enough to assume that
![]() $w=s_{\widetilde {\alpha }}w'<_{\widetilde {\alpha }}w'$
. In this case, the first assertion follows from Lemma 1.2.2(a). Next, since
$w=s_{\widetilde {\alpha }}w'<_{\widetilde {\alpha }}w'$
. In this case, the first assertion follows from Lemma 1.2.2(a). Next, since
![]() $0\in V$
lies in the closure of
$0\in V$
lies in the closure of
![]() $A_0\subseteq V$
, the second one follows from the equality
$A_0\subseteq V$
, the second one follows from the equality
![]() $\pi (w)=w(0)$
.
$\pi (w)=w(0)$
.
(c) Assume that
![]() $\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(c). By our assumption of
$\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(c). By our assumption of
![]() $\Phi '$
, we may assume that
$\Phi '$
, we may assume that
![]() $\mu =\mu '-\check {\alpha }$
for some
$\mu =\mu '-\check {\alpha }$
for some
![]() $\alpha \in \Phi '$
. In this case, it follows from Lemma 1.2.2(b) that
$\alpha \in \Phi '$
. In this case, it follows from Lemma 1.2.2(b) that
![]() $\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(b). The converse assertion follows from part (b).
$\mu <_{\Phi '}\mu '$
in the sense of Section 1.2.1(b). The converse assertion follows from part (b).
Remarks 1.2.4. (a) Let
![]() $\Phi '\subseteq \Phi $
, let
$\Phi '\subseteq \Phi $
, let
![]() $w\in \widetilde {W}$
, and let
$w\in \widetilde {W}$
, and let
![]() $w_{\operatorname {fin}}\in W$
be the image of
$w_{\operatorname {fin}}\in W$
be the image of
![]() $w\in \widetilde {W}$
under the projection
$w\in \widetilde {W}$
under the projection
![]() $\widetilde {W}\to W$
. Then it follows from definition that for every
$\widetilde {W}\to W$
. Then it follows from definition that for every
![]() $w'\leq _{\Phi '} w"$
, we have
$w'\leq _{\Phi '} w"$
, we have
![]() $w w'\leq _{w_{\operatorname {fin}}(\Phi ')} ww"$
. In particular,
$w w'\leq _{w_{\operatorname {fin}}(\Phi ')} ww"$
. In particular,
(i) for every
![]() $\mu \in \Lambda $
, we have
$\mu \in \Lambda $
, we have
![]() $w'\leq _{\Phi '} w"$
if and only if
$w'\leq _{\Phi '} w"$
if and only if
![]() $\mu w'\leq _{\Phi '} \mu w"$
;
$\mu w'\leq _{\Phi '} \mu w"$
;
(ii) for every
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $w'\leq _{\Phi '} w"$
if and only if
$w'\leq _{\Phi '} w"$
if and only if
![]() $uw'\leq _{u(\Phi ')} uw"$
.
$uw'\leq _{u(\Phi ')} uw"$
.
(b) Note that for each
![]() $\alpha \in \Phi $
, the subset
$\alpha \in \Phi $
, the subset
![]() $\Phi ':=\{\alpha \}$
satisfies the assumption of Corollary 1.2.3(c).
$\Phi ':=\{\alpha \}$
satisfies the assumption of Corollary 1.2.3(c).
(c) Arguing as in Lemma 1.2.2(c), we see that for each
![]() $\psi \in \Psi $
, the subset
$\psi \in \Psi $
, the subset
![]() $\Phi ':=\Phi (\psi )$
satisfies the assumption of Corollary 1.2.3(c).
$\Phi ':=\Phi (\psi )$
satisfies the assumption of Corollary 1.2.3(c).
Proposition 1.2.5. Let
![]() $w',w"\in \widetilde {W}$
, and let C be a Weyl chamber.
$w',w"\in \widetilde {W}$
, and let C be a Weyl chamber.
Then
![]() $w'\leq _C w"$
if and only if for every sufficiently regular
$w'\leq _C w"$
if and only if for every sufficiently regular
![]() $\mu \in \Lambda \cap C$
, we have
$\mu \in \Lambda \cap C$
, we have
![]() $\mu w'\leq \mu w"$
; that is, there exists
$\mu w'\leq \mu w"$
; that is, there exists
![]() $\mu \in \Lambda \cap C$
such that
$\mu \in \Lambda \cap C$
such that
![]() $\mu '\mu w'\leq \mu '\mu w"$
for every
$\mu '\mu w'\leq \mu '\mu w"$
for every
![]() $\mu '\in \Lambda \cap C$
.
$\mu '\in \Lambda \cap C$
.
Proof. First, we claim that for every
![]() $w',w"\in \widetilde {W}\cap C$
and
$w',w"\in \widetilde {W}\cap C$
and
![]() $\widetilde {\alpha }\in \widetilde {\Phi }$
such that
$\widetilde {\alpha }\in \widetilde {\Phi }$
such that
![]() $w'=s_{\widetilde {\alpha }}w"$
, we have
$w'=s_{\widetilde {\alpha }}w"$
, we have
![]() $w'<_C w"$
if and only if
$w'<_C w"$
if and only if
![]() $w'< w"$
.
$w'< w"$
.
Replacing
![]() $\widetilde {\alpha }$
by
$\widetilde {\alpha }$
by
![]() $-\widetilde {\alpha }$
, if necessary, we may assume that
$-\widetilde {\alpha }$
, if necessary, we may assume that
![]() $\widetilde {\alpha }=\alpha +n$
with
$\widetilde {\alpha }=\alpha +n$
with
![]() $\alpha \in \Phi _C$
. Then
$\alpha \in \Phi _C$
. Then
![]() $w'<_C w"$
holds if and only if
$w'<_C w"$
holds if and only if
![]() $w^{\prime \prime -1}(\widetilde {\alpha })>0$
. However, since
$w^{\prime \prime -1}(\widetilde {\alpha })>0$
. However, since
![]() $w',w"\in C$
, we get that
$w',w"\in C$
, we get that
![]() $(w")^{-1}(\alpha )>0$
and
$(w")^{-1}(\alpha )>0$
and
![]() $(w')^{-1}(\alpha )>0$
. Since
$(w')^{-1}(\alpha )>0$
. Since
![]() $s_{\widetilde {\alpha }}(\widetilde {\alpha })=-\widetilde {\alpha }$
, we get
$s_{\widetilde {\alpha }}(\widetilde {\alpha })=-\widetilde {\alpha }$
, we get
![]() $s_{\widetilde {\alpha }}(\alpha )=-\alpha -2n$
; therefore,
$s_{\widetilde {\alpha }}(\alpha )=-\alpha -2n$
; therefore,
This together with
![]() $(w")^{-1}(\alpha )>0$
implies that
$(w")^{-1}(\alpha )>0$
implies that
![]() $n<0$
; thus,
$n<0$
; thus,
![]() $\widetilde {\alpha }<0$
. Therefore,
$\widetilde {\alpha }<0$
. Therefore,
![]() $w'< w"$
holds if and only if
$w'< w"$
holds if and only if
![]() $w^{\prime \prime -1}(\widetilde {\alpha })>0$
.
$w^{\prime \prime -1}(\widetilde {\alpha })>0$
.
Now we are ready to show our assertion. Assume that
![]() $w'\leq _C w"$
, and we are going to show that for each sufficiently regular
$w'\leq _C w"$
, and we are going to show that for each sufficiently regular
![]() $\mu \in \Lambda \cap C$
, we have
$\mu \in \Lambda \cap C$
, we have
![]() $\mu w'\leq \mu w"$
. By induction, we can assume that
$\mu w'\leq \mu w"$
. By induction, we can assume that
![]() $w'=s_{\widetilde {\alpha }}w"$
for some
$w'=s_{\widetilde {\alpha }}w"$
for some
![]() $\widetilde {\alpha }\in \widetilde {\Phi }$
. Choose
$\widetilde {\alpha }\in \widetilde {\Phi }$
. Choose
![]() $\mu \in \Lambda \cap C$
sufficiently regular so that
$\mu \in \Lambda \cap C$
sufficiently regular so that
![]() $\mu w',\mu w"\in C$
. Then
$\mu w',\mu w"\in C$
. Then
![]() $\mu w'\leq _C \mu w"$
(by Remark 1.2.4(a)(i)), and
$\mu w'\leq _C \mu w"$
(by Remark 1.2.4(a)(i)), and
![]() $\mu w'=s_{\mu (\widetilde {\alpha })}\mu w"$
. Hence, by what is shown above,
$\mu w'=s_{\mu (\widetilde {\alpha })}\mu w"$
. Hence, by what is shown above,
![]() $\mu w'\leq \mu w"$
.
$\mu w'\leq \mu w"$
.
Conversely, assume that for every sufficiently regular element
![]() $\mu \in \Lambda \cap C$
, we have
$\mu \in \Lambda \cap C$
, we have
![]() $\mu w'\leq \mu w"$
, and we want to show that
$\mu w'\leq \mu w"$
, and we want to show that
![]() $w'\leq _C w"$
. Replacing
$w'\leq _C w"$
. Replacing
![]() $w'$
and
$w'$
and
![]() $w"$
by
$w"$
by
![]() $\mu w'$
and
$\mu w'$
and
![]() $\mu w"$
, respectively, and using Remark 1.2.4(a)(i), we may assume that
$\mu w"$
, respectively, and using Remark 1.2.4(a)(i), we may assume that
![]() $w',w"\in C$
and
$w',w"\in C$
and
![]() $w'\leq w"$
. Then using Lemma 1.1.5(b), we may assume in addition that
$w'\leq w"$
. Then using Lemma 1.1.5(b), we may assume in addition that
![]() $w'=s_{\widetilde {\alpha }}w"$
. Then, by what is shown above,
$w'=s_{\widetilde {\alpha }}w"$
. Then, by what is shown above,
![]() $w'\leq _C w"$
.
$w'\leq _C w"$
.
Corollary 1.2.6. Let
![]() $w',w"\in \widetilde {W}$
, and let C be a Weyl chamber.
$w',w"\in \widetilde {W}$
, and let C be a Weyl chamber.
(a) If
![]() $w'\leq _C w"$
and
$w'\leq _C w"$
and
![]() $w'\in C$
, then
$w'\in C$
, then
![]() $w'\leq w"$
.
$w'\leq w"$
.
(b) If
![]() $w'\leq w"$
and
$w'\leq w"$
and
![]() $w"\in C$
, then
$w"\in C$
, then
![]() $w'\leq _C w"$
.
$w'\leq _C w"$
.
(c) If
![]() $w',w"\in C$
, then
$w',w"\in C$
, then
![]() $w'\leq _C w"$
if and only if
$w'\leq _C w"$
if and only if
![]() $w'\leq w"$
.
$w'\leq w"$
.
Proof.
(a) By Proposition 1.2.5, there exists
![]() $\mu \in \Lambda \cap C$
such that
$\mu \in \Lambda \cap C$
such that
![]() $\mu w'\leq \mu w"$
. Since
$\mu w'\leq \mu w"$
. Since
![]() $\mu , w'\in C$
, the assertion follows from Lemma 1.1.5(c) and Section 1.1.4(c).
$\mu , w'\in C$
, the assertion follows from Lemma 1.1.5(c) and Section 1.1.4(c).
(b) Using Lemma 1.1.5(c) and Section 1.1.4(c), we conclude that
![]() $\mu w'\leq \mu w"$
for every
$\mu w'\leq \mu w"$
for every
![]() $\mu \in \Lambda \cap C$
. Therefore, we get
$\mu \in \Lambda \cap C$
. Therefore, we get
![]() $w'\leq _C w"$
by Proposition 1.2.5.
$w'\leq _C w"$
by Proposition 1.2.5.
(c) follows from parts (a) and (b).
Lemma 1.2.7. Let
![]() $\psi \in \Psi $
,
$\psi \in \Psi $
,
![]() $w',w"\in \widetilde {W}^{\psi }$
,
$w',w"\in \widetilde {W}^{\psi }$
,
![]() $C\owns \psi $
and
$C\owns \psi $
and
![]() $w\in \widetilde {W}$
.
$w\in \widetilde {W}$
.
(a) We have
![]() $w"w\leq _{C} w'w$
if and only if
$w"w\leq _{C} w'w$
if and only if
![]() $w"w\leq _{C^{\psi }} w'w$
.
$w"w\leq _{C^{\psi }} w'w$
.
(b) If
![]() $w\in \widetilde {W}_{\psi }$
, then
$w\in \widetilde {W}_{\psi }$
, then
![]() $w"w\leq _{C} w'w$
if and only if
$w"w\leq _{C} w'w$
if and only if
![]() $w"\leq _{C^{\psi }} w'$
.
$w"\leq _{C^{\psi }} w'$
.
Proof.
(a) Since
![]() $(\Phi ^{\psi })_{C^{\psi }}\subseteq \Phi _C$
, the ‘if’ assertion is obvious. Conversely, assume that
$(\Phi ^{\psi })_{C^{\psi }}\subseteq \Phi _C$
, the ‘if’ assertion is obvious. Conversely, assume that
![]() $w"w\leq _C w'w$
. Then there exist affine roots
$w"w\leq _C w'w$
. Then there exist affine roots
such that
![]() $w"w=s_{\widetilde {\beta }_n}\ldots s_{\widetilde {\beta }_1}w'w$
, and
$w"w=s_{\widetilde {\beta }_n}\ldots s_{\widetilde {\beta }_1}w'w$
, and
![]() $s_{\widetilde {\beta }_i}\ldots s_{\widetilde {\beta }_1}w'w<_{\widetilde {\beta }_i} s_{\widetilde {\beta }_{i-1}}\ldots s_{\widetilde {\beta }_1}w'w$
for all i. Then for every
$s_{\widetilde {\beta }_i}\ldots s_{\widetilde {\beta }_1}w'w<_{\widetilde {\beta }_i} s_{\widetilde {\beta }_{i-1}}\ldots s_{\widetilde {\beta }_1}w'w$
for all i. Then for every
![]() $x\in A_0$
, the difference
$x\in A_0$
, the difference
![]() $w'w(x)-w"w(x)$
is a positive linear combination of the
$w'w(x)-w"w(x)$
is a positive linear combination of the
![]() $\check {\beta }_i$
’s (by Lemma 1.2.2(a)).
$\check {\beta }_i$
’s (by Lemma 1.2.2(a)).
Since
![]() $w"w\in \widetilde {W}^{\psi }w'w$
, we conclude that
$w"w\in \widetilde {W}^{\psi }w'w$
, we conclude that
![]() $w'w(x)-w"w(x)$
is a linear combination of coroots of
$w'w(x)-w"w(x)$
is a linear combination of coroots of
![]() $\Phi ^{\psi }$
. Therefore, each
$\Phi ^{\psi }$
. Therefore, each
![]() $\beta _i$
is a root of
$\beta _i$
is a root of
![]() $\Phi ^{\psi }$
; thus,
$\Phi ^{\psi }$
; thus,
![]() $\beta _i\in (\Phi ^{\psi })_{C^{\psi }}$
. But this implies that
$\beta _i\in (\Phi ^{\psi })_{C^{\psi }}$
. But this implies that
![]() $w"w\leq _{C^{\psi }} w'w$
.
$w"w\leq _{C^{\psi }} w'w$
.
(b) By part (a), we have to show that
![]() $w"w\leq _{C^{\psi }} w'w$
if and only if
$w"w\leq _{C^{\psi }} w'w$
if and only if
![]() $w"\leq _{C^{\psi }} w'$
. Thus, we can assume that
$w"\leq _{C^{\psi }} w'$
. Thus, we can assume that
![]() $w"=s_{\widetilde {\beta }}w'$
for some
$w"=s_{\widetilde {\beta }}w'$
for some
![]() $\widetilde {\beta }\in \widetilde {\Phi }^{\psi }$
. In other words, we have to show that
$\widetilde {\beta }\in \widetilde {\Phi }^{\psi }$
. In other words, we have to show that
![]() $w^{\prime -1}(\widetilde {\beta })\in \widetilde {\Phi }^{\psi }_{>0}$
if and only if
$w^{\prime -1}(\widetilde {\beta })\in \widetilde {\Phi }^{\psi }_{>0}$
if and only if
![]() $w^{-1}(w^{\prime -1}(\widetilde {\beta }))\in \widetilde {\Phi }_{>0}$
. But this follows from the assumption that
$w^{-1}(w^{\prime -1}(\widetilde {\beta }))\in \widetilde {\Phi }_{>0}$
. But this follows from the assumption that
![]() $w\in \widetilde {W}_{\psi }$
.
$w\in \widetilde {W}_{\psi }$
.
1.3 Admissible tuples
Definition 1.3.1.
(a) We say that a tuple
![]() $\overline {\mu }=\{\mu _C\}_{C\in \mathcal {C}}\in V^{\mathcal {C}}$
is admissible (resp. quasi-admissible, resp. strictly admissible) if for every
$\overline {\mu }=\{\mu _C\}_{C\in \mathcal {C}}\in V^{\mathcal {C}}$
is admissible (resp. quasi-admissible, resp. strictly admissible) if for every
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $\alpha \in \Delta _{C}$
, the difference
$\alpha \in \Delta _{C}$
, the difference
![]() $\mu _C-\mu _{s_{\alpha }(C)}$
belongs to
$\mu _C-\mu _{s_{\alpha }(C)}$
belongs to
![]() $\mathbb R_{\geq 0}\check {\alpha }$
(resp.
$\mathbb R_{\geq 0}\check {\alpha }$
(resp.
![]() $\mathbb R\check {\alpha }$
, resp.
$\mathbb R\check {\alpha }$
, resp.
![]() $\mathbb R_{>0}\check {\alpha }$
).
$\mathbb R_{>0}\check {\alpha }$
).
(b) A tuple
![]() $\overline {w}=\{w_C\}_C\in \widetilde {W}^{\mathcal {C}}$
is called admissible (resp. quasi-admissible, resp. strictly admissible) if for every
$\overline {w}=\{w_C\}_C\in \widetilde {W}^{\mathcal {C}}$
is called admissible (resp. quasi-admissible, resp. strictly admissible) if for every
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $\alpha \in \Delta _{C}$
, we have
$\alpha \in \Delta _{C}$
, we have
![]() $w_{s_{\alpha }(C)}\leq _{\alpha }w_C$
(resp.
$w_{s_{\alpha }(C)}\leq _{\alpha }w_C$
(resp.
![]() $w_{s_{\alpha }(C)}\in \widetilde {W}_{\alpha }w_C$
, resp.
$w_{s_{\alpha }(C)}\in \widetilde {W}_{\alpha }w_C$
, resp.
![]() $w_{s_{\alpha }(C)}<_{\alpha }w_C$
).
$w_{s_{\alpha }(C)}<_{\alpha }w_C$
).
Remarks 1.3.2.
(a) It follows from Corollary 1.2.3(b) that if
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is (quasi)-admissible, then the tuple
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is (quasi)-admissible, then the tuple
![]() $\pi (\overline {w})\in \Lambda ^{\mathcal {C}}\subseteq V^{\mathcal {C}}$
is (quasi)-admissible as well.
$\pi (\overline {w})\in \Lambda ^{\mathcal {C}}\subseteq V^{\mathcal {C}}$
is (quasi)-admissible as well.
(b) Moreover, it follows from Corollary 1.2.3(c) and Section 1.2.4(b) that a tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
is (quasi)-admissible as an element of
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
is (quasi)-admissible as an element of
![]() $\widetilde {W}^{\mathcal {C}}$
if and only if it is such as an element of
$\widetilde {W}^{\mathcal {C}}$
if and only if it is such as an element of
![]() $V^{\mathcal {C}}$
.
$V^{\mathcal {C}}$
.
(c) The notion of an admissible tuple in
![]() $V^{\mathcal {C}}$
is not new. For example, it is called complementary polyhedron in [Reference BehrendBe, Definition 2.1]. However, we do not know whether admissible tuples in
$V^{\mathcal {C}}$
is not new. For example, it is called complementary polyhedron in [Reference BehrendBe, Definition 2.1]. However, we do not know whether admissible tuples in
![]() $\widetilde {W}^{\mathcal {C}}$
were studied earlier.
$\widetilde {W}^{\mathcal {C}}$
were studied earlier.
Notation 1.3.3.
(a) For
![]() $\overline {\mu },\overline {\mu }'\in V^{\mathcal {C}}$
(resp.
$\overline {\mu },\overline {\mu }'\in V^{\mathcal {C}}$
(resp.
![]() $\overline {w},\overline {w}'\in \widetilde {W}^{\mathcal {C}}$
), we will say that
$\overline {w},\overline {w}'\in \widetilde {W}^{\mathcal {C}}$
), we will say that
![]() $\overline {\mu }\leq \overline {\mu }'$
(resp.
$\overline {\mu }\leq \overline {\mu }'$
(resp.
![]() $\overline {w}\leq \overline {w}'$
) if
$\overline {w}\leq \overline {w}'$
) if
![]() $\mu _C\leq _C\mu ^{\prime }_C$
(resp.
$\mu _C\leq _C\mu ^{\prime }_C$
(resp.
![]() $w_C\leq _C w^{\prime }_C$
) for all
$w_C\leq _C w^{\prime }_C$
) for all
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
(b) For
![]() $\overline {\mu }\in V^{\mathcal {C}}$
, we define by
$\overline {\mu }\in V^{\mathcal {C}}$
, we define by
![]() $V^{\leq \overline {\mu }}$
the set of all
$V^{\leq \overline {\mu }}$
the set of all
![]() $x\in V$
such that
$x\in V$
such that
![]() $x\leq _C\mu _C$
for all
$x\leq _C\mu _C$
for all
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
1.3.4.
Quasi-admissible tuples in
![]() $V^{\mathcal {C}}$
. (a) The set of quasi-admissible tuples in
$V^{\mathcal {C}}$
. (a) The set of quasi-admissible tuples in
![]() $V^{\mathcal {C}}$
(resp.
$V^{\mathcal {C}}$
(resp.
![]() $\Lambda ^{\mathcal {C}}$
) can be naturally identified with
$\Lambda ^{\mathcal {C}}$
) can be naturally identified with
![]() $\mathbb R^{\Psi }$
(resp.
$\mathbb R^{\Psi }$
(resp.
![]() $\mathbb Z^{\Psi }$
).
$\mathbb Z^{\Psi }$
).
Indeed, for each quasi-admissible tuple
![]() $\overline {\mu }\in V^{\mathcal {C}}$
and every
$\overline {\mu }\in V^{\mathcal {C}}$
and every
![]() $\psi \in \Psi $
, the element
$\psi \in \Psi $
, the element
![]() $\overline {\mu }(\psi ):=\langle \psi ,\mu _C\rangle $
does not depend on
$\overline {\mu }(\psi ):=\langle \psi ,\mu _C\rangle $
does not depend on
![]() $C\owns \psi $
. To see this, we observe that for every pair of Weyl chambers
$C\owns \psi $
. To see this, we observe that for every pair of Weyl chambers
![]() $C,C'\owns \psi $
, there exists
$C,C'\owns \psi $
, there exists
![]() $w\in W_{\Phi ^{\psi }}$
such that
$w\in W_{\Phi ^{\psi }}$
such that
![]() $C'=w(C)$
. Therefore,
$C'=w(C)$
. Therefore,
![]() $\overline {\mu }$
defines a tuple
$\overline {\mu }$
defines a tuple
![]() $\{\overline {\mu }(\psi )\}_{\psi \in \Psi }\in \mathbb R^{\Psi }$
.
$\{\overline {\mu }(\psi )\}_{\psi \in \Psi }\in \mathbb R^{\Psi }$
.
Conversely, every tuple
![]() $\{\overline {\mu }(\psi )\}\in \mathbb R^{\Psi }$
gives rise to a quasi-admissible tuple
$\{\overline {\mu }(\psi )\}\in \mathbb R^{\Psi }$
gives rise to a quasi-admissible tuple
![]() $\overline {\mu }\in V^{\mathcal {C}}$
defined by the rule
$\overline {\mu }\in V^{\mathcal {C}}$
defined by the rule
![]() $\mu _C:=\sum _{\alpha _i\in \Delta _C}\overline {\mu }(\psi _i)\check {\alpha }_i$
, where
$\mu _C:=\sum _{\alpha _i\in \Delta _C}\overline {\mu }(\psi _i)\check {\alpha }_i$
, where
![]() $\psi _i\in \Psi _C$
is the fundamental weight corresponding to
$\psi _i\in \Psi _C$
is the fundamental weight corresponding to
![]() $\alpha _i\in \Delta _C$
.
$\alpha _i\in \Delta _C$
.
(b) The set of quasi-admissible tuples in
![]() $V^{\mathcal {C}}$
(resp.
$V^{\mathcal {C}}$
(resp.
![]() $\Lambda ^{\mathcal {C}}$
) is a group with respect to the coordinatewise addition in V (resp.
$\Lambda ^{\mathcal {C}}$
) is a group with respect to the coordinatewise addition in V (resp.
![]() $\Lambda $
). Moreover, the identification of part (a) identifies this group with
$\Lambda $
). Moreover, the identification of part (a) identifies this group with
![]() $\mathbb R^{\Psi }$
(resp.
$\mathbb R^{\Psi }$
(resp.
![]() $\mathbb Z^{\Psi }$
). Also, the set of admissible tuples in
$\mathbb Z^{\Psi }$
). Also, the set of admissible tuples in
![]() $V^{\mathcal {C}}$
(resp.
$V^{\mathcal {C}}$
(resp.
![]() $\Lambda ^{\mathcal {C}}$
) is a submonoid.
$\Lambda ^{\mathcal {C}}$
) is a submonoid.
(c) The identification of part (a) preserves coordinatewise ordering. In other words, for every two quasi-admissible tuples
![]() $\overline {\mu },\overline {\mu }'\in V^{\mathcal {C}}$
, we have
$\overline {\mu },\overline {\mu }'\in V^{\mathcal {C}}$
, we have
![]() $\mu _C\leq _C\mu ^{\prime }_C$
for all
$\mu _C\leq _C\mu ^{\prime }_C$
for all
![]() $C\in \mathcal {C}$
if and only if
$C\in \mathcal {C}$
if and only if
![]() $\overline {\mu }(\psi )\leq \overline {\mu }'(\psi )$
for all
$\overline {\mu }(\psi )\leq \overline {\mu }'(\psi )$
for all
![]() $\psi \in \Psi $
. In particular, for every quasi-admissible tuples
$\psi \in \Psi $
. In particular, for every quasi-admissible tuples
![]() $\overline {\mu }\in V^{\mathcal {C}}$
, the subset
$\overline {\mu }\in V^{\mathcal {C}}$
, the subset
![]() $V^{\leq \overline {\mu }}\subseteq V$
(see Section 1.3.3(b)) consists of all
$V^{\leq \overline {\mu }}\subseteq V$
(see Section 1.3.3(b)) consists of all
![]() $x\in V$
such that
$x\in V$
such that
![]() $\langle \psi ,x\rangle \leq \overline {\mu }(\psi )$
for all
$\langle \psi ,x\rangle \leq \overline {\mu }(\psi )$
for all
![]() $\psi \in \Psi $
.
$\psi \in \Psi $
.
(d) From now on, we will not distinguish between a quasi-admissible tuple
![]() $\{\mu _C\}_C$
in
$\{\mu _C\}_C$
in
![]() $V^{\mathcal {C}}$
(resp.
$V^{\mathcal {C}}$
(resp.
![]() $\Lambda ^{\mathcal {C}}$
) and the corresponding tuple
$\Lambda ^{\mathcal {C}}$
) and the corresponding tuple
![]() $\{\overline {\mu }(\psi )\}_{\psi }$
in
$\{\overline {\mu }(\psi )\}_{\psi }$
in
![]() $\mathbb R^{\Psi }$
(resp.
$\mathbb R^{\Psi }$
(resp.
![]() $\mathbb Z^{\Psi }$
). In particular, for every
$\mathbb Z^{\Psi }$
). In particular, for every
![]() $\psi \in \Psi $
, we denote by
$\psi \in \Psi $
, we denote by
![]() $\overline {e}_{\psi }\in \Lambda ^{\mathcal {C}}$
the quasi-admissible tuple, corresponding to the standard vector
$\overline {e}_{\psi }\in \Lambda ^{\mathcal {C}}$
the quasi-admissible tuple, corresponding to the standard vector
![]() $\overline {e}_{\psi }\in \mathbb Z^{\Psi }$
, given by the rule
$\overline {e}_{\psi }\in \mathbb Z^{\Psi }$
, given by the rule
![]() $\overline {e}_{\psi }(\psi ')=\delta _{\psi ,\psi '}$
.
$\overline {e}_{\psi }(\psi ')=\delta _{\psi ,\psi '}$
.
Examples 1.3.5.
(a) Every
![]() $\mu \in C_0\subseteq V$
gives rise to an admissible tuple
$\mu \in C_0\subseteq V$
gives rise to an admissible tuple
![]() $\overline {\mu }\in V^{\mathcal {C}}$
defined by the rule
$\overline {\mu }\in V^{\mathcal {C}}$
defined by the rule
![]() $\mu _{u(C_0)}:=u(\mu )$
for all
$\mu _{u(C_0)}:=u(\mu )$
for all
![]() $u\in W$
.
$u\in W$
.
(b) Consider the tuple
![]() $\overline {w}_{\operatorname {st}}\in W^{\mathcal {C}}\subseteq \widetilde {W}^{\mathcal {C}}$
, defined by the rule
$\overline {w}_{\operatorname {st}}\in W^{\mathcal {C}}\subseteq \widetilde {W}^{\mathcal {C}}$
, defined by the rule
![]() $(w_{\operatorname {st}})_{u(C_0)}=u$
. Then
$(w_{\operatorname {st}})_{u(C_0)}=u$
. Then
![]() $\overline {w}_{\operatorname {st}}$
is admissible. Indeed, by definition, we have to show that for every
$\overline {w}_{\operatorname {st}}$
is admissible. Indeed, by definition, we have to show that for every
![]() $u\in W$
and
$u\in W$
and
![]() $\alpha \in \Phi _{u(C_0)}$
, we have
$\alpha \in \Phi _{u(C_0)}$
, we have
![]() $s_{\alpha }u<_{\alpha }u$
; that is,
$s_{\alpha }u<_{\alpha }u$
; that is,
![]() $u^{-1}(\alpha )>0$
. Since
$u^{-1}(\alpha )>0$
. Since
![]() $u^{-1}(\alpha )\in \Phi _{C_0}$
, we are done.
$u^{-1}(\alpha )\in \Phi _{C_0}$
, we are done.
(c) Using Remark 1.2.4(a)(i) and Lemma 1.2.2(b), for every (quasi)-admissible tuples
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
and
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
and
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, the tuple
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, the tuple ![]() is (quasi)-admissible as well. In particular, for every
is (quasi)-admissible as well. In particular, for every
![]() $\mu \in \Lambda $
and (quasi)-admissible tuple
$\mu \in \Lambda $
and (quasi)-admissible tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, the tuple
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, the tuple
![]() $\mu \overline {w}:=\{\mu w_C\}_C$
is (quasi)-admissible.
$\mu \overline {w}:=\{\mu w_C\}_C$
is (quasi)-admissible.
Notation 1.3.6. Arguing as in Section 1.3.4(a), for each quasi-admissible
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
![]() $\psi \in \Psi $
, the class
$\psi \in \Psi $
, the class
![]() $[w_C]\in \widetilde {W}^{\psi }\backslash \widetilde {W}$
and hence also element
$[w_C]\in \widetilde {W}^{\psi }\backslash \widetilde {W}$
and hence also element
![]() $(w_C)_{\psi }\in \widetilde {W}_{\psi }$
(see Section 1.1.3(d)) does not depend on
$(w_C)_{\psi }\in \widetilde {W}_{\psi }$
(see Section 1.1.3(d)) does not depend on
![]() $C\owns \psi $
. We will denote this element by
$C\owns \psi $
. We will denote this element by
![]() $\overline {w}_{\psi }$
.
$\overline {w}_{\psi }$
.
The following characterization of admissible tuples will be crucial for the rest of the paper.
Lemma 1.3.7. A tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
![]() $\overline {\mu }\in V^{\mathcal {C}}$
) is admissible if and only if for all
$\overline {\mu }\in V^{\mathcal {C}}$
) is admissible if and only if for all
![]() $C,C'\in \mathcal {C}$
, we have
$C,C'\in \mathcal {C}$
, we have
![]() $w_{C}\leq _{C'} w_{C'}$
(resp.
$w_{C}\leq _{C'} w_{C'}$
(resp.
![]() $\mu _{C}\leq _{C'}\mu _{C'}$
).
$\mu _{C}\leq _{C'}\mu _{C'}$
).
Proof. We will only prove the assertion for
![]() $\overline {w}$
, while the other case is similar, but easier. Assume first that
$\overline {w}$
, while the other case is similar, but easier. Assume first that
![]() $\overline {w}$
is admissible, and we want to show that for every two Weyl chambers C and
$\overline {w}$
is admissible, and we want to show that for every two Weyl chambers C and
![]() $C'$
, we have
$C'$
, we have
![]() $w_{C}\leq _{C'} w_{C'}$
. Using Remark 1.2.4(a)(ii), we may assume that
$w_{C}\leq _{C'} w_{C'}$
. Using Remark 1.2.4(a)(ii), we may assume that
![]() $C'=C_0$
. Let
$C'=C_0$
. Let
![]() $u\in W$
be such that
$u\in W$
be such that
![]() $C=u(C_0)$
, choose a reduced decomposition
$C=u(C_0)$
, choose a reduced decomposition
![]() $u=s_1\ldots s_n$
of u, and for each
$u=s_1\ldots s_n$
of u, and for each
![]() $j=1,\ldots ,n$
, we set
$j=1,\ldots ,n$
, we set
![]() $u_j:=s_1\ldots s_j$
and
$u_j:=s_1\ldots s_j$
and
![]() $C_j:=u_j(C_0)$
. It is enough to show that
$C_j:=u_j(C_0)$
. It is enough to show that
![]() $w_{C_{j+1}}\leq _{C_0} w_{C_j}$
for each
$w_{C_{j+1}}\leq _{C_0} w_{C_j}$
for each
![]() $j=0,\ldots ,n-1$
.
$j=0,\ldots ,n-1$
.
Let
![]() $\alpha _{j+1}\in \Delta _{C_0}$
be such that
$\alpha _{j+1}\in \Delta _{C_0}$
be such that
![]() $s_{j+1}=s_{\alpha _{j+1}}$
. By construction, we obtain that
$s_{j+1}=s_{\alpha _{j+1}}$
. By construction, we obtain that
![]() $u_{j+1}=u_j s_{j+1}>u_j$
; hence,
$u_{j+1}=u_j s_{j+1}>u_j$
; hence,
![]() $u_j(\alpha _{j+1})\in \Phi _{C_0}$
. Also since
$u_j(\alpha _{j+1})\in \Phi _{C_0}$
. Also since
![]() $\alpha _{j+1}\in \Delta _{C_0}$
, we get that
$\alpha _{j+1}\in \Delta _{C_0}$
, we get that
![]() $u_j(\alpha _{j+1})\in \Delta _{C_j}$
. Since
$u_j(\alpha _{j+1})\in \Delta _{C_j}$
. Since
![]() $C_{j+1}=s_{u_j(\alpha _{j+1})}(C_j)$
, the admissibility assumption implies that
$C_{j+1}=s_{u_j(\alpha _{j+1})}(C_j)$
, the admissibility assumption implies that
![]() $w_{C_{j+1}}\leq _{u_j(\alpha _{j+1})}w_{C_j}$
; thus, we have
$w_{C_{j+1}}\leq _{u_j(\alpha _{j+1})}w_{C_j}$
; thus, we have
![]() $w_{C_{j+1}}\leq _{C_0} w_{C_j}$
because
$w_{C_{j+1}}\leq _{C_0} w_{C_j}$
because
![]() $u_j(\alpha _{j+1})\in \Phi _{C_0}$
.
$u_j(\alpha _{j+1})\in \Phi _{C_0}$
.
Conversely, assume that
![]() $w_{C}\leq _{C'} w_{C'}$
for all
$w_{C}\leq _{C'} w_{C'}$
for all
![]() $C,C'\in \mathcal {C}$
. Choose
$C,C'\in \mathcal {C}$
. Choose
![]() $C\in \mathcal {C}$
,
$C\in \mathcal {C}$
,
![]() $\alpha \in \Delta _C$
, and set
$\alpha \in \Delta _C$
, and set
![]() $C'=s_{\alpha }(C)$
. Since
$C'=s_{\alpha }(C)$
. Since
![]() $w_{C'}\leq _C w_C$
, there exist a tuple of affine roots
$w_{C'}\leq _C w_C$
, there exist a tuple of affine roots
![]() $\widetilde {\beta }_1=(\beta _i,n_i),\ldots ,\widetilde {\beta }_r=(\beta _r,n_r)\in \widetilde {\Phi }_{C}$
such that
$\widetilde {\beta }_1=(\beta _i,n_i),\ldots ,\widetilde {\beta }_r=(\beta _r,n_r)\in \widetilde {\Phi }_{C}$
such that
![]() $w_{C'}=s_{\widetilde {\beta }_r}\ldots s_{\widetilde {\beta }_1} w_C$
, and
$w_{C'}=s_{\widetilde {\beta }_r}\ldots s_{\widetilde {\beta }_1} w_C$
, and
![]() $s_{\widetilde {\beta }_i}\ldots s_{\widetilde {\beta }_1}w_C<_{\widetilde {\beta }_i} s_{\widetilde {\beta }_{i-1}}\ldots s_{\widetilde {\beta }_1}w_C$
for all i. Therefore, for each
$s_{\widetilde {\beta }_i}\ldots s_{\widetilde {\beta }_1}w_C<_{\widetilde {\beta }_i} s_{\widetilde {\beta }_{i-1}}\ldots s_{\widetilde {\beta }_1}w_C$
for all i. Therefore, for each
![]() $x\in A_0$
, the difference
$x\in A_0$
, the difference
![]() $w_C(x)-w_{C'}(x)$
is a positive linear combination of the
$w_C(x)-w_{C'}(x)$
is a positive linear combination of the
![]() $\check {\beta }_i$
’s (by Lemma 1.2.2(a)), and hence a positive linear combination of C-simple coroots.
$\check {\beta }_i$
’s (by Lemma 1.2.2(a)), and hence a positive linear combination of C-simple coroots.
However, since
![]() $w_C\leq _{C'}w_{C'}$
, the difference
$w_C\leq _{C'}w_{C'}$
, the difference
![]() $w_C(x)-w_{C'}(x)$
is also a negative linear combination of
$w_C(x)-w_{C'}(x)$
is also a negative linear combination of
![]() $C'$
-simple coroots. Combining these two statements, we conclude that
$C'$
-simple coroots. Combining these two statements, we conclude that
![]() $w_C(x)-w_{C'}(x)$
has to be a positive multiple of
$w_C(x)-w_{C'}(x)$
has to be a positive multiple of
![]() $\check {\alpha }$
. Hence, all the
$\check {\alpha }$
. Hence, all the
![]() $\beta _i$
’s have to be
$\beta _i$
’s have to be
![]() $\alpha $
; thus,
$\alpha $
; thus,
![]() $w_{C'}\leq _{\alpha } w_C$
.
$w_{C'}\leq _{\alpha } w_C$
.
The following corollary seems to be known to specialists.
Corollary 1.3.8. Let
![]() $\overline {\mu }$
be an admissible tuple in
$\overline {\mu }$
be an admissible tuple in
![]() $V^{\mathcal {C}}$
, and let
$V^{\mathcal {C}}$
, and let
![]() $\psi \in \Psi $
.
$\psi \in \Psi $
.
(a) The subset
![]() $V^{\leq \overline {\mu }}\subseteq V$
equals the convex hull of
$V^{\leq \overline {\mu }}\subseteq V$
equals the convex hull of
![]() $\{\mu _C\}_{C\in \mathcal {C}}$
.
$\{\mu _C\}_{C\in \mathcal {C}}$
.
(b) If
![]() $\overline {\mu }$
is strictly admissible, then for every
$\overline {\mu }$
is strictly admissible, then for every
![]() $C\not \ni \psi $
, we have
$C\not \ni \psi $
, we have
![]() $\langle \psi ,\mu _C\rangle <\overline {\mu }(\psi )$
.
$\langle \psi ,\mu _C\rangle <\overline {\mu }(\psi )$
.
(c) If
![]() $\overline {\mu }$
is strictly admissible, then the intersection of
$\overline {\mu }$
is strictly admissible, then the intersection of
![]() $V^{\leq \overline {\mu }}$
and the set of
$V^{\leq \overline {\mu }}$
and the set of
![]() $x\in V$
such that
$x\in V$
such that
![]() $\langle \psi, x \rangle =\overline {\mu }(\psi )$
equals the convex hull of
$\langle \psi, x \rangle =\overline {\mu }(\psi )$
equals the convex hull of
![]() $\{\mu _C\}_{C\ni \psi }$
.
$\{\mu _C\}_{C\ni \psi }$
.
Proof.
(a) For every
![]() $C\in \mathcal {C}$
, we have
$C\in \mathcal {C}$
, we have
![]() $\mu _C\leq _{C'}\mu _{C'}$
for every
$\mu _C\leq _{C'}\mu _{C'}$
for every
![]() $C'\in \mathcal {C}$
(by Lemma 1.3.7); thus,
$C'\in \mathcal {C}$
(by Lemma 1.3.7); thus,
![]() $\mu _C\in V^{\leq \overline {\mu }}$
. Since subset
$\mu _C\in V^{\leq \overline {\mu }}$
. Since subset
![]() $V^{\leq \overline {\mu }}\subseteq V$
is convex, this implies that the convex hull of
$V^{\leq \overline {\mu }}\subseteq V$
is convex, this implies that the convex hull of
![]() $\{\mu _C\}_{C\in \mathcal {C}}$
is contained in
$\{\mu _C\}_{C\in \mathcal {C}}$
is contained in
![]() $V^{\leq \overline {\mu }}$
.
$V^{\leq \overline {\mu }}$
.
To show the opposite inclusion, it suffices to show that for every affine function l on V such that
![]() $l(\mu _{C'})\leq 0$
for all
$l(\mu _{C'})\leq 0$
for all
![]() $C'\in \mathcal {C}$
and every
$C'\in \mathcal {C}$
and every
![]() $x\in V^{\leq \overline {\mu }}$
, we have
$x\in V^{\leq \overline {\mu }}$
, we have
![]() $l(x)\leq 0$
. Let
$l(x)\leq 0$
. Let
![]() $\lambda \in V^*$
be the vector part of l and choose
$\lambda \in V^*$
be the vector part of l and choose
![]() $C\in \mathcal {C}$
such that
$C\in \mathcal {C}$
such that
![]() $\alpha \in \overline {C}$
. Since
$\alpha \in \overline {C}$
. Since
![]() $x\leq _C\mu _C$
, we get
$x\leq _C\mu _C$
, we get
![]() $l(\mu _C)-l(x)=\langle \lambda ,\mu _C\rangle -\langle \lambda ,x\rangle \geq 0$
; therefore,
$l(\mu _C)-l(x)=\langle \lambda ,\mu _C\rangle -\langle \lambda ,x\rangle \geq 0$
; therefore,
![]() $l(x)\leq l(\mu _C)\leq 0$
.
$l(x)\leq l(\mu _C)\leq 0$
.
(b) Since
![]() $\langle \psi ,\mu _C\rangle \leq \overline {\mu }(\psi )$
for every
$\langle \psi ,\mu _C\rangle \leq \overline {\mu }(\psi )$
for every
![]() $C\in \mathcal {C}$
, it suffices to show that for every
$C\in \mathcal {C}$
, it suffices to show that for every
![]() $C\in \mathcal {C}$
such that
$C\in \mathcal {C}$
such that
![]() $\langle \psi ,\mu _C\rangle =\overline {\mu }(\psi )$
, we have
$\langle \psi ,\mu _C\rangle =\overline {\mu }(\psi )$
, we have
![]() $\psi \in \Psi _C$
. To show the result, we essentially repeat the first part of the proof of Lemma 1.3.7.
$\psi \in \Psi _C$
. To show the result, we essentially repeat the first part of the proof of Lemma 1.3.7.
Using Remark 1.2.4(a)(ii), we may assume that
![]() $\psi \in \Psi _{C_0}$
, and let
$\psi \in \Psi _{C_0}$
, and let
![]() $u\in W$
be such that
$u\in W$
be such that
![]() $C=u(C_0)$
. It suffices to show that
$C=u(C_0)$
. It suffices to show that
![]() $u\in W^{\psi }$
. Let
$u\in W^{\psi }$
. Let
![]() $u_j$
,
$u_j$
,
![]() $C_j$
and
$C_j$
and
![]() $\alpha _{j+1}$
be as in the proof of Lemma 1.3.7. Since
$\alpha _{j+1}$
be as in the proof of Lemma 1.3.7. Since
![]() $\overline {\mu }$
is strictly admissible, we get
$\overline {\mu }$
is strictly admissible, we get
![]() $\mu _{C_{j+1}}<_{u_j(\alpha _{j+1})}\mu _{C_j}$
for every
$\mu _{C_{j+1}}<_{u_j(\alpha _{j+1})}\mu _{C_j}$
for every
![]() $j=0,\ldots ,n-1$
. Moreover, since
$j=0,\ldots ,n-1$
. Moreover, since
![]() $\psi \in \Psi _{C_0}$
and
$\psi \in \Psi _{C_0}$
and
![]() $u_j(\alpha _{j+1})\in \Phi _{C_0}$
, we conclude that
$u_j(\alpha _{j+1})\in \Phi _{C_0}$
, we conclude that
![]() $\langle \psi ,u_j(\alpha _{j+1})\rangle \geq 0$
. So the assumption that
$\langle \psi ,u_j(\alpha _{j+1})\rangle \geq 0$
. So the assumption that
![]() $\langle \psi ,\mu _C\rangle =\overline {\mu }(\psi )=\langle \psi ,\mu _{C_0}\rangle $
implies that for every j, we have
$\langle \psi ,\mu _C\rangle =\overline {\mu }(\psi )=\langle \psi ,\mu _{C_0}\rangle $
implies that for every j, we have
![]() $\langle \psi ,u_j(\alpha _{j+1})\rangle =0$
; hence,
$\langle \psi ,u_j(\alpha _{j+1})\rangle =0$
; hence,
![]() $u_j(\alpha _{j+1})\in \Phi ^{\psi }$
and thus
$u_j(\alpha _{j+1})\in \Phi ^{\psi }$
and thus
![]() $s_{u_j(\alpha _{j+1})}\in W^{\psi }$
. Therefore,
$s_{u_j(\alpha _{j+1})}\in W^{\psi }$
. Therefore, ![]() , as claimed.
, as claimed.
(c) is an immediate consequence of parts (a) and (b).
Notation 1.3.9.
(a) Let
![]() $m\in \mathbb R$
and
$m\in \mathbb R$
and
![]() $C\in \mathcal {C}$
. We say that
$C\in \mathcal {C}$
. We say that
![]() $\mu \in V$
is
$\mu \in V$
is
![]() $(C,m)$
-regular if
$(C,m)$
-regular if
![]() $\langle \alpha ,\mu \rangle \geq m$
for every
$\langle \alpha ,\mu \rangle \geq m$
for every
![]() $\alpha \in \Phi _{C}$
. We say that
$\alpha \in \Phi _{C}$
. We say that
![]() $w\in \widetilde {W}$
is
$w\in \widetilde {W}$
is
![]() $(C,m)$
-regular if
$(C,m)$
-regular if
![]() $\pi (w)=w(0)\in \Lambda $
is
$\pi (w)=w(0)\in \Lambda $
is
![]() $(C,m)$
-regular.
$(C,m)$
-regular.
(b) Let
![]() $m\in \mathbb R$
. We say that a tuple
$m\in \mathbb R$
. We say that a tuple
![]() $\overline {\mu }\in V^{\mathcal {C}}$
is m-regular if
$\overline {\mu }\in V^{\mathcal {C}}$
is m-regular if
![]() $\mu _C$
is
$\mu _C$
is
![]() $(C,m)$
-regular for every
$(C,m)$
-regular for every
![]() $C\in \mathcal {C}$
. We say that a tuple
$C\in \mathcal {C}$
. We say that a tuple
![]() $\overline {\mu }\in V^{\mathcal {C}}$
is regular if it is m-regular for some
$\overline {\mu }\in V^{\mathcal {C}}$
is regular if it is m-regular for some
![]() $m>0$
. A tuple
$m>0$
. A tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is called m-regular (resp. regular) if
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is called m-regular (resp. regular) if
![]() $\pi (\overline {w})\in \Lambda ^{\mathcal {C}}\subseteq V^{\mathcal {C}}$
is m-regular (resp. regular).
$\pi (\overline {w})\in \Lambda ^{\mathcal {C}}\subseteq V^{\mathcal {C}}$
is m-regular (resp. regular).
(c) For every
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
![]() $\psi \in \Psi $
, we define
$\psi \in \Psi $
, we define
![]() $\overline {w}^{\psi }\in (\widetilde {W}^{\psi })^{\mathcal {C}^{\psi }}$
by the rule
$\overline {w}^{\psi }\in (\widetilde {W}^{\psi })^{\mathcal {C}^{\psi }}$
by the rule
![]() $(w^{\psi })_{C^{\psi }}=(w_C)^{\psi }$
for each
$(w^{\psi })_{C^{\psi }}=(w_C)^{\psi }$
for each
![]() $C\owns \psi $
(see Section 1.1.3).
$C\owns \psi $
(see Section 1.1.3).
Lemma 1.3.10.
(a) If
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
![]() $\overline {\mu }\in V^{\mathcal {C}}$
) is quasi-admissible and regular, then it is strictly admissible.
$\overline {\mu }\in V^{\mathcal {C}}$
) is quasi-admissible and regular, then it is strictly admissible.
(b) If
![]() $\overline {\mu }\in V^{\mathcal {C}}$
is quasi-admissible and regular, then for every
$\overline {\mu }\in V^{\mathcal {C}}$
is quasi-admissible and regular, then for every
![]() $\psi \in \Psi $
, we have
$\psi \in \Psi $
, we have
![]() $\overline {\mu }(\psi )>0$
(see Section 1.3.4(a)).
$\overline {\mu }(\psi )>0$
(see Section 1.3.4(a)).
(c) If the tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible, then the tuple
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible, then the tuple
![]() $\overline {w}^{\psi }$
is admissible as well.
$\overline {w}^{\psi }$
is admissible as well.
(d) If
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is
![]() $(m+1)$
-regular, then
$(m+1)$
-regular, then
![]() $\overline {w}^{\psi }$
is m-regular.
$\overline {w}^{\psi }$
is m-regular.
Proof.
(a) We will only show the assertion for
![]() $\overline {w}$
. Fix
$\overline {w}$
. Fix
![]() $C\in \mathcal {C}$
, let
$C\in \mathcal {C}$
, let
![]() $\alpha \in \Phi _C$
, and set
$\alpha \in \Phi _C$
, and set
![]() $C'=s_{\alpha }(C)$
. We want to show that
$C'=s_{\alpha }(C)$
. We want to show that
![]() $w_{C'}\leq _{\alpha } w_C$
. Since
$w_{C'}\leq _{\alpha } w_C$
. Since
![]() $\overline {w}$
is quasi-admissible, we get
$\overline {w}$
is quasi-admissible, we get
![]() $w_{C'}\in \widetilde {W}_{\alpha }w_{C}$
. Therefore, for every
$w_{C'}\in \widetilde {W}_{\alpha }w_{C}$
. Therefore, for every
![]() $x\in A_0$
, we have
$x\in A_0$
, we have
![]() $w_{C'}(x)=w_C(x)-a\check {\alpha }$
for some
$w_{C'}(x)=w_C(x)-a\check {\alpha }$
for some
![]() $a\in \mathbb R$
. Since
$a\in \mathbb R$
. Since
![]() $\overline {w}$
is regular, we conclude
$\overline {w}$
is regular, we conclude
![]() $\langle \alpha ,w_C(x)\rangle>0$
and
$\langle \alpha ,w_C(x)\rangle>0$
and
![]() $\langle \alpha ,w_{C'}(x)\rangle <0$
. Thus,
$\langle \alpha ,w_{C'}(x)\rangle <0$
. Thus,
![]() $a>0$
, and hence,
$a>0$
, and hence,
![]() $w_{C'}<_{\alpha } w_C$
(by Corollary 1.2.3(a)).
$w_{C'}<_{\alpha } w_C$
(by Corollary 1.2.3(a)).
(b) Since
![]() $\overline {\mu }(\psi )=\langle \psi ,\mu _C\rangle $
for every Weyl chamber
$\overline {\mu }(\psi )=\langle \psi ,\mu _C\rangle $
for every Weyl chamber
![]() $C\owns \psi $
(by definition), we have
$C\owns \psi $
(by definition), we have
![]() $\langle \alpha ,\mu _C\rangle>0$
for every
$\langle \alpha ,\mu _C\rangle>0$
for every
![]() $\alpha \in \Delta _C$
(since
$\alpha \in \Delta _C$
(since
![]() $\overline {\mu }$
is regular), and
$\overline {\mu }$
is regular), and
![]() $\psi =\sum _{\alpha \in \Delta _C} c_{\alpha }\alpha $
with
$\psi =\sum _{\alpha \in \Delta _C} c_{\alpha }\alpha $
with
![]() $c_{\alpha }\geq 0$
for all
$c_{\alpha }\geq 0$
for all
![]() $\alpha \in \Delta _C$
, the assertion follows.
$\alpha \in \Delta _C$
, the assertion follows.
(c) follows from Lemma 1.2.7(b) and Lemma 1.3.7.
(d) Let
![]() $C\owns \psi $
be a Weyl chamber. We have to show that if w is
$C\owns \psi $
be a Weyl chamber. We have to show that if w is
![]() $(C,m+1)$
-regular, and
$(C,m+1)$
-regular, and
![]() $\psi \in C$
, then
$\psi \in C$
, then
![]() $w^{\psi }$
is
$w^{\psi }$
is
![]() $(C^{\psi },m)$
-regular.
$(C^{\psi },m)$
-regular.
Notice that if w is
![]() $(C,m+1)$
-regular, then for all
$(C,m+1)$
-regular, then for all
![]() $\alpha \in \Phi _C$
and
$\alpha \in \Phi _C$
and
![]() $x\in A_0$
, we have
$x\in A_0$
, we have
![]() $\langle w^{-1}(\alpha ),x\rangle =\langle \alpha ,w(x)\rangle>m$
, or equivalently,
$\langle w^{-1}(\alpha ),x\rangle =\langle \alpha ,w(x)\rangle>m$
, or equivalently,
![]() $w^{-1}(\alpha )-m\in \widetilde {\Phi }_{>0}$
. Conversely, if
$w^{-1}(\alpha )-m\in \widetilde {\Phi }_{>0}$
. Conversely, if
![]() $\langle \alpha ,w(x)\rangle>m$
for all
$\langle \alpha ,w(x)\rangle>m$
for all
![]() $\alpha \in \Phi _C$
, then
$\alpha \in \Phi _C$
, then
![]() $\langle \alpha ,w(0)\rangle \geq m$
for all
$\langle \alpha ,w(0)\rangle \geq m$
for all
![]() $\alpha \in \Phi _C$
; thus, w is
$\alpha \in \Phi _C$
; thus, w is
![]() $(C,m)$
-regular.
$(C,m)$
-regular.
Thus, it suffices to show that for every
![]() $\alpha \in (\Phi ^{\psi })_{C^{\psi }}$
, we have
$\alpha \in (\Phi ^{\psi })_{C^{\psi }}$
, we have
![]() $w^{-1}(\alpha )-m\in \widetilde {\Phi }_{>0}$
if and only if
$w^{-1}(\alpha )-m\in \widetilde {\Phi }_{>0}$
if and only if
![]() $(w^{\psi })^{-1}(\alpha )-m\in \widetilde {\Phi }^{\psi }_{>0}$
. Since
$(w^{\psi })^{-1}(\alpha )-m\in \widetilde {\Phi }^{\psi }_{>0}$
. Since
![]() $w=w^{\psi }w_{\psi }$
, the assertion follows from the fact that
$w=w^{\psi }w_{\psi }$
, the assertion follows from the fact that
![]() $w_{\psi }\in \widetilde {W}_{\psi }$
.
$w_{\psi }\in \widetilde {W}_{\psi }$
.
The following lemma will be used in Lemma 3.2.10.
Lemma 1.3.11. Let
![]() $\overline {\mu }\in V^{\mathcal {C}}$
be regular and quasi-admissible. Then for every
$\overline {\mu }\in V^{\mathcal {C}}$
be regular and quasi-admissible. Then for every
![]() $x\in V^{\leq \overline {\mu }}$
,
$x\in V^{\leq \overline {\mu }}$
,
![]() $\psi \in \Psi $
and
$\psi \in \Psi $
and
![]() $\alpha \in \Phi $
such that
$\alpha \in \Phi $
such that
![]() $\langle \alpha ,\check {\psi }\rangle>0$
and
$\langle \alpha ,\check {\psi }\rangle>0$
and
![]() $\langle \psi ,x\rangle =\overline {\mu }(\psi )$
, we have
$\langle \psi ,x\rangle =\overline {\mu }(\psi )$
, we have
![]() $\langle \alpha ,x\rangle>0$
.
$\langle \alpha ,x\rangle>0$
.
Proof. By Lemma 1.3.10(a), the tuple
![]() $\overline {\mu }$
is strictly admissible. Then, by Corollary 1.3.8(c), the intersection of
$\overline {\mu }$
is strictly admissible. Then, by Corollary 1.3.8(c), the intersection of
![]() $V^{\leq \overline {\mu }}$
with the set of
$V^{\leq \overline {\mu }}$
with the set of
![]() $x\in V$
such that
$x\in V$
such that
![]() $\langle \psi ,x\rangle =\overline {\mu }(\psi )$
is equal to the convex hull of
$\langle \psi ,x\rangle =\overline {\mu }(\psi )$
is equal to the convex hull of
![]() $\{\mu _C\}_{C\owns \psi }$
.
$\{\mu _C\}_{C\owns \psi }$
.
Therefore, it is enough to show that for every Weyl chamber
![]() $C\owns \psi $
, we have
$C\owns \psi $
, we have
![]() $\langle \alpha ,\mu _C\rangle>0$
. Since tuple
$\langle \alpha ,\mu _C\rangle>0$
. Since tuple
![]() $\overline {\mu }$
is regular, it is enough to show that
$\overline {\mu }$
is regular, it is enough to show that
![]() $\langle \alpha ,y\rangle>0$
for some
$\langle \alpha ,y\rangle>0$
for some
![]() $y\in C\subseteq V^*$
. But this follows from our assumption
$y\in C\subseteq V^*$
. But this follows from our assumption
![]() $\langle \alpha ,\check {\psi }\rangle>0$
together with observation that
$\langle \alpha ,\check {\psi }\rangle>0$
together with observation that
![]() $\check {\psi }\in \overline {C}$
(see Section 1.1.3(b)).
$\check {\psi }\in \overline {C}$
(see Section 1.1.3(b)).
The following very important technical result will be used in Proposition 3.1.8.
Lemma 1.3.12. Let
![]() $\overline {u}\in \widetilde {W}^{\mathcal {C}}$
be admissible, and
$\overline {u}\in \widetilde {W}^{\mathcal {C}}$
be admissible, and
![]() $\psi \in \Psi $
. Then there exists
$\psi \in \Psi $
. Then there exists
![]() $m\in \mathbb N$
such that for every m-regular admissible tuple
$m\in \mathbb N$
such that for every m-regular admissible tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
![]() $\mu \in \Lambda $
such that
$\mu \in \Lambda $
such that
![]() $\mu u_C\leq _{C^{\psi }} w_C$
for each
$\mu u_C\leq _{C^{\psi }} w_C$
for each
![]() $C\owns \psi $
, we have
$C\owns \psi $
, we have
![]() $\mu u_C\leq _C w_C$
for each C.
$\mu u_C\leq _C w_C$
for each C.
Proof. First, we claim that there exists an admissible tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
such that
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
such that
![]() $\mu _C^{-1}u_C\leq _C \mu ^{-1}_{C'}u_{C'}$
for every
$\mu _C^{-1}u_C\leq _C \mu ^{-1}_{C'}u_{C'}$
for every
![]() $C,C'\in \mathcal {C}$
. Indeed,
$C,C'\in \mathcal {C}$
. Indeed,
![]() $\overline {u}$
is admissible; hence, for each
$\overline {u}$
is admissible; hence, for each
![]() $C\in \mathcal {C}$
,
$C\in \mathcal {C}$
,
![]() $\alpha \in \Delta _C$
and
$\alpha \in \Delta _C$
and
![]() $x\in A_0$
, we have
$x\in A_0$
, we have
![]() $u_C(x)-u_{s_{\alpha }(C)}(x)=m_{C,\alpha ,x}\check {\alpha }$
for some constant
$u_C(x)-u_{s_{\alpha }(C)}(x)=m_{C,\alpha ,x}\check {\alpha }$
for some constant
![]() $m_{C,\alpha ,x}\geq 0$
(use Lemma 1.2.2(a)). Let
$m_{C,\alpha ,x}\geq 0$
(use Lemma 1.2.2(a)). Let
![]() $m'$
be the supremum of the
$m'$
be the supremum of the
![]() $m_{C,\alpha ,x}$
’s, choose
$m_{C,\alpha ,x}$
’s, choose
![]() $\mu \in C_0\cap \Lambda $
such that
$\mu \in C_0\cap \Lambda $
such that
![]() $\langle \alpha ,\mu \rangle \geq m'$
for all
$\langle \alpha ,\mu \rangle \geq m'$
for all
![]() $\alpha \in \Delta _{C_0}$
, and let
$\alpha \in \Delta _{C_0}$
, and let
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the tuple, corresponding to
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the tuple, corresponding to
![]() $\mu $
as in Section 1.3.5(a).
$\mu $
as in Section 1.3.5(a).
We claim that
![]() $\mu _C^{-1}u_C\leq _C \mu ^{-1}_{C'}u_{C'}$
for every
$\mu _C^{-1}u_C\leq _C \mu ^{-1}_{C'}u_{C'}$
for every
![]() $C,C'\in \mathcal {C}$
. Indeed, arguing as in Lemma 1.3.7 word-by-word, it is enough to check that
$C,C'\in \mathcal {C}$
. Indeed, arguing as in Lemma 1.3.7 word-by-word, it is enough to check that
![]() $\mu _C^{-1}u_C\leq _{\alpha } \mu ^{-1}_{C'}u_{C'}$
for all
$\mu _C^{-1}u_C\leq _{\alpha } \mu ^{-1}_{C'}u_{C'}$
for all
![]() $C\in \mathcal {C},\alpha \in \Delta _C$
and
$C\in \mathcal {C},\alpha \in \Delta _C$
and
![]() $C'=s_{\alpha }(C)$
. Then by Corollary 1.2.3(a), it is enough to check that
$C'=s_{\alpha }(C)$
. Then by Corollary 1.2.3(a), it is enough to check that
![]() $\mu _C^{-1}u_C(x)\leq _{\alpha } \mu ^{-1}_{C'}u_{C'}(x)$
for each
$\mu _C^{-1}u_C(x)\leq _{\alpha } \mu ^{-1}_{C'}u_{C'}(x)$
for each
![]() $x\in A_0$
. By construction, we have
$x\in A_0$
. By construction, we have
![]() $\mu ^{-1}_{C'}u_{C'}(x)-\mu _C^{-1}u_C(x)= (\langle \alpha ,\mu _C\rangle -m_{C,\alpha ,x})\check {\alpha }$
, so the assertion follows from the fact that
$\mu ^{-1}_{C'}u_{C'}(x)-\mu _C^{-1}u_C(x)= (\langle \alpha ,\mu _C\rangle -m_{C,\alpha ,x})\check {\alpha }$
, so the assertion follows from the fact that
![]() $m_{C,\alpha ,x}<m'\leq \langle \alpha ,\mu _C\rangle $
.
$m_{C,\alpha ,x}<m'\leq \langle \alpha ,\mu _C\rangle $
.
Denote m to be the maximum of the
![]() $\langle \alpha ,\mu _C\rangle +1$
’s, taken over all
$\langle \alpha ,\mu _C\rangle +1$
’s, taken over all
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $\alpha \in \Delta _{C}$
. We claim that such an m satisfies the required property.
$\alpha \in \Delta _{C}$
. We claim that such an m satisfies the required property.
To see this, we choose any m-regular admissible tuple
![]() $\overline {w}$
, and we claim that tuple
$\overline {w}$
, and we claim that tuple ![]() is admissible. By Section 1.3.5(c), it is quasi-admissible, so by Lemma 1.3.10(a), it is enough to show that it is regular. For every
is admissible. By Section 1.3.5(c), it is quasi-admissible, so by Lemma 1.3.10(a), it is enough to show that it is regular. For every
![]() $C\in \mathcal {C}$
,
$C\in \mathcal {C}$
,
![]() $\alpha \in \Delta _C$
, we have
$\alpha \in \Delta _C$
, we have
![]() $\langle \alpha ,\mu _C^{-1}\pi (w_C)\rangle = \langle \alpha ,\pi (w_C)\rangle -\langle \alpha ,\mu _C\rangle>0$
because
$\langle \alpha ,\mu _C^{-1}\pi (w_C)\rangle = \langle \alpha ,\pi (w_C)\rangle -\langle \alpha ,\mu _C\rangle>0$
because
![]() $\langle \alpha ,\pi (w_C)\rangle \geq m$
by m-regularity of
$\langle \alpha ,\pi (w_C)\rangle \geq m$
by m-regularity of
![]() $\overline {w}$
, and
$\overline {w}$
, and
![]() $\langle \alpha ,\mu _C\rangle \leq m-1$
, by construction.
$\langle \alpha ,\mu _C\rangle \leq m-1$
, by construction.
Let
![]() $\mu \in \Lambda $
be such that
$\mu \in \Lambda $
be such that
![]() $\mu u_C\leq _{C^{\psi }} w_C$
for each
$\mu u_C\leq _{C^{\psi }} w_C$
for each
![]() $C\owns \psi $
, and let
$C\owns \psi $
, and let
![]() $C'\in \mathcal {C}$
be arbitrary. We want to show that
$C'\in \mathcal {C}$
be arbitrary. We want to show that
![]() $\mu u_{C'}\leq _{C'} w_{C'}$
. Using Remark 1.2.4(a)(ii), it is enough to do it in the case
$\mu u_{C'}\leq _{C'} w_{C'}$
. Using Remark 1.2.4(a)(ii), it is enough to do it in the case
![]() $C'=C_0$
, so using Remark 1.2.4(a)(i), we have to show that
$C'=C_0$
, so using Remark 1.2.4(a)(i), we have to show that
![]() $\mu _{C_0}^{-1}\mu u_{C_0}\leq _{C_0}\mu _{C_0}^{-1}w_{C_0}$
.
$\mu _{C_0}^{-1}\mu u_{C_0}\leq _{C_0}\mu _{C_0}^{-1}w_{C_0}$
.
Choose
![]() $u\in W$
of minimal length such that
$u\in W$
of minimal length such that
![]() $\psi _0:=u^{-1}(\psi )$
belongs to
$\psi _0:=u^{-1}(\psi )$
belongs to
![]() $\Psi _{C_0}$
, and set
$\Psi _{C_0}$
, and set
![]() $C:=u(C_0)$
. Since
$C:=u(C_0)$
. Since ![]() is admissible, we conclude from Lemma 1.3.7 that
is admissible, we conclude from Lemma 1.3.7 that
![]() $\mu _{C}^{-1}w_{C}\leq _{C_0}\mu _{C_0}^{-1}w_{C_0}$
, while by our construction, we get
$\mu _{C}^{-1}w_{C}\leq _{C_0}\mu _{C_0}^{-1}w_{C_0}$
, while by our construction, we get
![]() $\mu _{C_0}^{-1}u_{C_0}\leq _{C_0} \mu _{C}^{-1}u_{C}$
; hence,
$\mu _{C_0}^{-1}u_{C_0}\leq _{C_0} \mu _{C}^{-1}u_{C}$
; hence,
![]() $\mu _{C_0}^{-1}\mu u_{C_0}\leq _{C_0} \mu _{C}^{-1}\mu u_{C}$
(by Remark 1.2.4(a)(i)). Thus, it is enough to show that
$\mu _{C_0}^{-1}\mu u_{C_0}\leq _{C_0} \mu _{C}^{-1}\mu u_{C}$
(by Remark 1.2.4(a)(i)). Thus, it is enough to show that
![]() $\mu _C^{-1}\mu u_C\leq _{C_0} \mu _C^{-1}w_{C}$
, or, equivalently, that
$\mu _C^{-1}\mu u_C\leq _{C_0} \mu _C^{-1}w_{C}$
, or, equivalently, that
![]() $\mu u_C\leq _{C_0} w_{C}$
.
$\mu u_C\leq _{C_0} w_{C}$
.
Since
![]() $\psi _0\in C_0$
, we get that
$\psi _0\in C_0$
, we get that
![]() $\psi \in C$
. Hence, by our assumption,
$\psi \in C$
. Hence, by our assumption,
![]() $\mu u_C\leq _{C^{\psi }} w_{C}$
. Therefore, to show that
$\mu u_C\leq _{C^{\psi }} w_{C}$
. Therefore, to show that
![]() $\mu u_C\leq _{C_0} w_{C}$
, it suffices to check that
$\mu u_C\leq _{C_0} w_{C}$
, it suffices to check that
![]() $(\Phi ^{\psi })_{C^{\psi }}\subseteq \Phi _{C_0}$
.
$(\Phi ^{\psi })_{C^{\psi }}\subseteq \Phi _{C_0}$
.
If
![]() $\beta \in (\Phi ^{\psi })_{C^{\psi }}$
, then
$\beta \in (\Phi ^{\psi })_{C^{\psi }}$
, then
![]() $u^{-1}(\beta )\in (\Phi ^{\psi _0})_{C_0^{\psi _0}}$
. Since
$u^{-1}(\beta )\in (\Phi ^{\psi _0})_{C_0^{\psi _0}}$
. Since
![]() $u\in W$
is an element of minimal length such that
$u\in W$
is an element of minimal length such that
![]() $\psi =u(\psi _0)$
, we get that
$\psi =u(\psi _0)$
, we get that
![]() $u((\Phi ^{\psi _0})_{C_0^{\psi _0}})\subseteq \Phi _{C_0}$
. In particular, we have
$u((\Phi ^{\psi _0})_{C_0^{\psi _0}})\subseteq \Phi _{C_0}$
. In particular, we have
![]() $\beta =u(u^{-1}(\beta ))\in \Phi _{C_0}$
.
$\beta =u(u^{-1}(\beta ))\in \Phi _{C_0}$
.
2 Semi-infinite orbits in affine flag varieties
2.1 Definitions and basic properties
Notation 2.1.1.
(a) Let k be an algebraically closed field,
![]() $K:=k((t))$
the field of Laurent power series over k, and
$K:=k((t))$
the field of Laurent power series over k, and
![]() $\mathcal {O}=\mathcal {O}_K=k[[t]]$
the ring of integers of K. For every affine scheme X over
$\mathcal {O}=\mathcal {O}_K=k[[t]]$
the ring of integers of K. For every affine scheme X over
![]() $\mathcal {O}$
(resp. K), we denote by
$\mathcal {O}$
(resp. K), we denote by
![]() $L^+X$
(resp.
$L^+X$
(resp.
![]() $LX$
) the corresponding arc- (resp. loop-) space.
$LX$
) the corresponding arc- (resp. loop-) space.
(b) Let G be a semi-simple and simply connected group over k. Fix a maximal torus
![]() $T\subseteq G$
, let
$T\subseteq G$
, let
![]() $\Phi =\Phi (G,T)$
be the root system of
$\Phi =\Phi (G,T)$
be the root system of
![]() $(G,T)$
, let
$(G,T)$
, let
![]() $W=W_{G}$
be the Weyl group of G, and
$W=W_{G}$
be the Weyl group of G, and
![]() $\widetilde {W}=N_{LG}(LT)/L^+T$
the affine Weyl group of G. Then, in the notation of Section 1.1.1, we have natural isomorphisms
$\widetilde {W}=N_{LG}(LT)/L^+T$
the affine Weyl group of G. Then, in the notation of Section 1.1.1, we have natural isomorphisms
![]() $\Lambda \overset {\thicksim }{\to } X_*(T)$
and
$\Lambda \overset {\thicksim }{\to } X_*(T)$
and
![]() $W_{\Phi }\overset {\thicksim }{\to } W$
. Moreover, the map
$W_{\Phi }\overset {\thicksim }{\to } W$
. Moreover, the map
![]() $\mu \mapsto \mu (t)$
defines an embedding
$\mu \mapsto \mu (t)$
defines an embedding
![]() $\Lambda \hookrightarrow LT$
, which in turn induces isomorphisms of groups
$\Lambda \hookrightarrow LT$
, which in turn induces isomorphisms of groups
![]() $\Lambda \overset {\thicksim }{\to } LT/L^+T$
and
$\Lambda \overset {\thicksim }{\to } LT/L^+T$
and
![]() $\widetilde {W}_{\Phi }\overset {\thicksim }{\to }\widetilde {W}$
.
$\widetilde {W}_{\Phi }\overset {\thicksim }{\to }\widetilde {W}$
.
Notation 2.1.2.
(a) For every
![]() $C\in \mathcal {C}$
, let
$C\in \mathcal {C}$
, let
![]() $B_C\subseteq G$
be the Borel subgroup containing T such that
$B_C\subseteq G$
be the Borel subgroup containing T such that
![]() $\Phi (B_C,T)=\Phi _C$
, and let
$\Phi (B_C,T)=\Phi _C$
, and let
![]() $U_C\subseteq B_C$
be the unipotent radical.
$U_C\subseteq B_C$
be the unipotent radical.
(b) Choose
![]() $C_0\in \mathcal {C}_{\Phi }$
as in Section 1.1.2, let
$C_0\in \mathcal {C}_{\Phi }$
as in Section 1.1.2, let
![]() $T\subseteq B_0=B_{C_0}\subseteq G$
be the corresponding Borel subgroup, let
$T\subseteq B_0=B_{C_0}\subseteq G$
be the corresponding Borel subgroup, let
![]() $B_0^{-}\supseteq T$
be the opposite Borel subgroup, and let
$B_0^{-}\supseteq T$
be the opposite Borel subgroup, and let
![]() $I\subseteq L^+G$
be the Iwahori subgroup, defined as the preimage of
$I\subseteq L^+G$
be the Iwahori subgroup, defined as the preimage of
![]() $B_0^{-}\subseteq G$
under the projection
$B_0^{-}\subseteq G$
under the projection
![]() $L^+G\to G$
.
$L^+G\to G$
.
(c) For every
![]() $\alpha \in \Phi $
, we have a natural isomorphism
$\alpha \in \Phi $
, we have a natural isomorphism
![]() $\exp _{\alpha }:\operatorname {Lie} U_{\alpha }\overset {\thicksim }{\to } U_{\alpha }$
. For
$\exp _{\alpha }:\operatorname {Lie} U_{\alpha }\overset {\thicksim }{\to } U_{\alpha }$
. For
![]() $\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
, we set
$\widetilde {\alpha }=(\alpha ,n)\in \widetilde {\Phi }$
, we set
![]() $U_{\widetilde {\alpha }}:=\exp _{\alpha }(t^n \operatorname {Lie} U_{\alpha })\subseteq L(U_{\alpha })$
, and
$U_{\widetilde {\alpha }}:=\exp _{\alpha }(t^n \operatorname {Lie} U_{\alpha })\subseteq L(U_{\alpha })$
, and
![]() $\widetilde {\alpha }':=(-\alpha ,n)$
.
$\widetilde {\alpha }':=(-\alpha ,n)$
.
(d) In the conventions of parts (b), (c), we get the equality ![]() .
.
2.1.3. Affine flag varieties
(a) Denote by
![]() $\operatorname {Fl}=\operatorname {Fl}_G$
the affine flag variety
$\operatorname {Fl}=\operatorname {Fl}_G$
the affine flag variety
![]() $LG/I$
of G over k, and by
$LG/I$
of G over k, and by
![]() $\operatorname {Gr}=\operatorname {Gr}_G$
the affine Grassmannian
$\operatorname {Gr}=\operatorname {Gr}_G$
the affine Grassmannian
![]() $LG/L^+G$
. We have a natural projection
$LG/L^+G$
. We have a natural projection
![]() $\operatorname {pr}:\operatorname {Fl}\to \operatorname {Gr}$
. Note that both
$\operatorname {pr}:\operatorname {Fl}\to \operatorname {Gr}$
. Note that both
![]() $\operatorname {Fl}$
and
$\operatorname {Fl}$
and
![]() $\operatorname {Gr}$
are equipped with an action of the ind-group scheme
$\operatorname {Gr}$
are equipped with an action of the ind-group scheme
![]() $LG$
, and that projection
$LG$
, and that projection
![]() $\operatorname {pr}$
is
$\operatorname {pr}$
is
![]() $LG$
-equivariant.
$LG$
-equivariant.
(b) The embedding
![]() $N_{LG}(LT)\hookrightarrow LG$
induces embeddings
$N_{LG}(LT)\hookrightarrow LG$
induces embeddings
![]() $\widetilde {W}\hookrightarrow \operatorname {Fl}$
and
$\widetilde {W}\hookrightarrow \operatorname {Fl}$
and
![]() $\Lambda \hookrightarrow \operatorname {Gr}$
, and we identify
$\Lambda \hookrightarrow \operatorname {Gr}$
, and we identify
![]() $\widetilde {W}$
(resp.
$\widetilde {W}$
(resp.
![]() $\Lambda $
) with its image in
$\Lambda $
) with its image in
![]() $\operatorname {Fl}$
(resp.
$\operatorname {Fl}$
(resp.
![]() $\operatorname {Gr}$
). Furthermore, both
$\operatorname {Gr}$
). Furthermore, both
![]() $\operatorname {Fl}$
and
$\operatorname {Fl}$
and
![]() $\operatorname {Gr}$
are equipped with the action of
$\operatorname {Gr}$
are equipped with the action of
![]() $T\subseteq L^+(T)\subseteq LG$
, and these identifications identify
$T\subseteq L^+(T)\subseteq LG$
, and these identifications identify
![]() $\widetilde {W}$
(resp.
$\widetilde {W}$
(resp.
![]() $\Lambda $
) with the locus of T-fixed points
$\Lambda $
) with the locus of T-fixed points
![]() $\operatorname {Fl}^T$
(resp.
$\operatorname {Fl}^T$
(resp.
![]() $\operatorname {Gr}^T$
).
$\operatorname {Gr}^T$
).
(c) Note that
![]() $\operatorname {Fl}$
decompose as a union
$\operatorname {Fl}$
decompose as a union
![]() $\operatorname {Fl}=\bigcup _{w\in \widetilde {W}}Iw$
of I-orbits, and for every
$\operatorname {Fl}=\bigcup _{w\in \widetilde {W}}Iw$
of I-orbits, and for every
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
the closure of the I-orbit
$\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
the closure of the I-orbit
![]() $Iw\subseteq \operatorname {Fl}$
. Then
$Iw\subseteq \operatorname {Fl}$
. Then
![]() $\operatorname {Fl}^{\leq w}$
is a reduced projective subscheme of
$\operatorname {Fl}^{\leq w}$
is a reduced projective subscheme of
![]() $\operatorname {Fl}$
called the affine Schubert variety.
$\operatorname {Fl}$
called the affine Schubert variety.
(d) Fix any
![]() $C\in \mathcal {C}$
. Then we have decompositions
$C\in \mathcal {C}$
. Then we have decompositions
![]() $\operatorname {Fl}=\bigcup _{w\in \widetilde {W}}L(U_C)w$
and
$\operatorname {Fl}=\bigcup _{w\in \widetilde {W}}L(U_C)w$
and
![]() $\operatorname {Gr}=\bigcup _{\mu \in \Lambda }L(U_C)\mu $
by
$\operatorname {Gr}=\bigcup _{\mu \in \Lambda }L(U_C)\mu $
by
![]() $L(U_C)$
-orbits. For every
$L(U_C)$
-orbits. For every
![]() $w\in \widetilde {W}$
(resp.
$w\in \widetilde {W}$
(resp.
![]() $\mu \in \Lambda $
), we denote by
$\mu \in \Lambda $
), we denote by
![]() $\operatorname {Fl}^{\leq _{C}w}\subseteq \operatorname {Fl}$
(resp.
$\operatorname {Fl}^{\leq _{C}w}\subseteq \operatorname {Fl}$
(resp.
![]() $\operatorname {Gr}^{\leq _{C}\mu }\subseteq \operatorname {Gr}$
) the closure of the
$\operatorname {Gr}^{\leq _{C}\mu }\subseteq \operatorname {Gr}$
) the closure of the
![]() $L(U_C)$
-orbit
$L(U_C)$
-orbit
![]() $L(U_C)w\subseteq \operatorname {Fl}$
(resp.
$L(U_C)w\subseteq \operatorname {Fl}$
(resp.
![]() $L(U_C)\mu \subseteq \operatorname {Gr}$
). We also set
$L(U_C)\mu \subseteq \operatorname {Gr}$
). We also set
![]() $\operatorname {Fl}^{\leq ^{\prime }_{C}\mu }:=\operatorname {pr}^{-1}( \operatorname {Gr}^{\leq _{C}\mu })\subseteq \operatorname {Fl}$
. Notice that
$\operatorname {Fl}^{\leq ^{\prime }_{C}\mu }:=\operatorname {pr}^{-1}( \operatorname {Gr}^{\leq _{C}\mu })\subseteq \operatorname {Fl}$
. Notice that
![]() $\operatorname {Fl}^{\leq _{C}w}$
,
$\operatorname {Fl}^{\leq _{C}w}$
,
![]() $\operatorname {Gr}^{\leq _{C}\mu }$
and
$\operatorname {Gr}^{\leq _{C}\mu }$
and
![]() $\operatorname {Fl}^{\leq ^{\prime }_{C}w}$
are closed reduced ind-subschemes.
$\operatorname {Fl}^{\leq ^{\prime }_{C}w}$
are closed reduced ind-subschemes.
(e) For every tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
(resp.
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
), we denote by
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
), we denote by
![]() $\operatorname {Fl}^{\leq \overline {w}}$
(resp.
$\operatorname {Fl}^{\leq \overline {w}}$
(resp.
![]() $\operatorname {Gr}^{\leq \overline {\mu }}$
) the reduced intersection
$\operatorname {Gr}^{\leq \overline {\mu }}$
) the reduced intersection
![]() $\bigcap _C \operatorname {Fl}^{\leq _C w_C}$
(resp.
$\bigcap _C \operatorname {Fl}^{\leq _C w_C}$
(resp.
![]() $\bigcap _C \operatorname {Gr}^{\leq _C \mu _C}$
), and set
$\bigcap _C \operatorname {Gr}^{\leq _C \mu _C}$
), and set
![]() $\operatorname {Fl}^{\leq ' \overline {\mu }}:=\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq \overline {\mu }})$
.
$\operatorname {Fl}^{\leq ' \overline {\mu }}:=\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq \overline {\mu }})$
.
The following simple lemma will play a central role later.
Lemma 2.1.4. Let
![]() $Z\subseteq \operatorname {Fl}$
(resp.
$Z\subseteq \operatorname {Fl}$
(resp.
![]() $Z\subseteq \operatorname {Gr}$
) be a closed reduced T-invariant ind-subscheme, C a Weyl chamber, and
$Z\subseteq \operatorname {Gr}$
) be a closed reduced T-invariant ind-subscheme, C a Weyl chamber, and
![]() $w\in \widetilde {W}$
(resp.
$w\in \widetilde {W}$
(resp.
![]() $\mu \in \Lambda $
). Then
$\mu \in \Lambda $
). Then
![]() $Z\cap L(U_C)w\neq \emptyset $
if and only if
$Z\cap L(U_C)w\neq \emptyset $
if and only if
![]() $w\in Z$
(resp.
$w\in Z$
(resp.
![]() $\mu \in Z$
).
$\mu \in Z$
).
Proof. We will show the assertion for
![]() $Z\subseteq \operatorname {Fl}$
and
$Z\subseteq \operatorname {Fl}$
and
![]() $w\in \widetilde {W}$
, while the proof of the second assertion is identical.
$w\in \widetilde {W}$
, while the proof of the second assertion is identical.
Clearly, if
![]() $w\in Z$
, then
$w\in Z$
, then
![]() $Z\cap L(U_C)w\neq \emptyset $
. Conversely, let z be an element of
$Z\cap L(U_C)w\neq \emptyset $
. Conversely, let z be an element of
![]() $Z\cap L(U_C)w$
, and pick
$Z\cap L(U_C)w$
, and pick
![]() $u\in L(U_C)$
such that
$u\in L(U_C)$
such that
![]() $z=uw$
. For any
$z=uw$
. For any
![]() $\nu \in \Lambda =\operatorname {Hom}(\mathbb G_m,T)$
and
$\nu \in \Lambda =\operatorname {Hom}(\mathbb G_m,T)$
and
![]() $a\in \mathbb G_m$
, we have
$a\in \mathbb G_m$
, we have
![]() $\nu (a)(z)=(\nu (a)u\nu (a)^{-1})(w)$
because
$\nu (a)(z)=(\nu (a)u\nu (a)^{-1})(w)$
because
![]() $w\in \operatorname {Fl}$
is T-invariant; hence,
$w\in \operatorname {Fl}$
is T-invariant; hence,
![]() $(\nu (a)u\nu (a)^{-1})(w)\in Z$
because Z is T-invariant. Next, for
$(\nu (a)u\nu (a)^{-1})(w)\in Z$
because Z is T-invariant. Next, for
![]() $\nu \in \Lambda \cap C$
, the morphism
$\nu \in \Lambda \cap C$
, the morphism
![]() $a\mapsto (\nu (a)u\nu (a)^{-1})(w):\mathbb G_m\to Z\subseteq \operatorname {Fl}$
extends to the morphism
$a\mapsto (\nu (a)u\nu (a)^{-1})(w):\mathbb G_m\to Z\subseteq \operatorname {Fl}$
extends to the morphism
![]() $\mathbb A^1\to \operatorname {Fl}$
, which sends
$\mathbb A^1\to \operatorname {Fl}$
, which sends
![]() $0$
to w. Since
$0$
to w. Since
![]() $Z\subseteq \operatorname {Fl}$
is closed, we conclude that
$Z\subseteq \operatorname {Fl}$
is closed, we conclude that
![]() $w\in Z$
.
$w\in Z$
.
Lemma 2.1.5. Let
![]() $w,w'\in \widetilde {W}$
, and let C be a Weyl chamber.
$w,w'\in \widetilde {W}$
, and let C be a Weyl chamber.
(a) We have
![]() $w'\in \operatorname {Fl}^{\leq w}$
if and only if
$w'\in \operatorname {Fl}^{\leq w}$
if and only if
![]() $w'\leq w$
.
$w'\leq w$
.
(b) If
![]() $w\in C$
, then
$w\in C$
, then
![]() $I w\subseteq \operatorname {Fl}$
is contained in
$I w\subseteq \operatorname {Fl}$
is contained in
![]() $L(U_C)w\subseteq \operatorname {Fl}$
.
$L(U_C)w\subseteq \operatorname {Fl}$
.
(c) If
![]() $Iw\cap L(U_C)w'\neq \emptyset $
, then
$Iw\cap L(U_C)w'\neq \emptyset $
, then
![]() $w'\leq w$
.
$w'\leq w$
.
Proof. (a) is a standard.
(b) In the notation of Section 2.1.2(c), for every
![]() $\widetilde {\alpha }\in \widetilde {\Phi }$
and
$\widetilde {\alpha }\in \widetilde {\Phi }$
and
![]() $w\in \widetilde {W}$
, we have
$w\in \widetilde {W}$
, we have
![]() $wU_{\widetilde {\alpha }}w^{-1}=U_{w(\widetilde {\alpha })}$
and
$wU_{\widetilde {\alpha }}w^{-1}=U_{w(\widetilde {\alpha })}$
and
![]() $w(\widetilde {\alpha }')=w(\widetilde {\alpha })'$
. Combining this with Section 2.1.2(d), we see that for every
$w(\widetilde {\alpha }')=w(\widetilde {\alpha })'$
. Combining this with Section 2.1.2(d), we see that for every
![]() $w\in \widetilde {W}$
, we have
$w\in \widetilde {W}$
, we have
 $$ \begin{align} Iw=\left(\prod_{\widetilde{\alpha}>0,w^{-1}(\widetilde{\alpha})<0}U_{\widetilde{\alpha}'}\right)w. \end{align} $$
$$ \begin{align} Iw=\left(\prod_{\widetilde{\alpha}>0,w^{-1}(\widetilde{\alpha})<0}U_{\widetilde{\alpha}'}\right)w. \end{align} $$
Using formula (2.1), it remains to check that every
![]() $\widetilde {\alpha }=(\alpha ,n)>0$
such that
$\widetilde {\alpha }=(\alpha ,n)>0$
such that
![]() $w^{-1}(\widetilde {\alpha })<0$
satisfies
$w^{-1}(\widetilde {\alpha })<0$
satisfies
![]() $U_{\widetilde {\alpha }'}\subseteq L(U_C)$
; that is,
$U_{\widetilde {\alpha }'}\subseteq L(U_C)$
; that is,
![]() $-\alpha \in \Phi _C$
. However,
$-\alpha \in \Phi _C$
. However,
![]() $n\geq 0$
because
$n\geq 0$
because
![]() $\widetilde {\alpha }>0$
. Therefore,
$\widetilde {\alpha }>0$
. Therefore,
![]() $w^{-1}(\alpha )=w^{-1}(\widetilde {\alpha })-n<0$
. Thus,
$w^{-1}(\alpha )=w^{-1}(\widetilde {\alpha })-n<0$
. Thus,
![]() $w^{-1}(-\alpha )>0$
; hence,
$w^{-1}(-\alpha )>0$
; hence,
![]() $-\alpha \in \Phi _C$
because
$-\alpha \in \Phi _C$
because
![]() $w\in C$
.
$w\in C$
.
(c) If
![]() $Iw\cap L(U_C)w'\neq \emptyset $
, then
$Iw\cap L(U_C)w'\neq \emptyset $
, then
![]() $\operatorname {Fl}^{\leq w}\cap L(U_C)w'\neq \emptyset $
. Since
$\operatorname {Fl}^{\leq w}\cap L(U_C)w'\neq \emptyset $
. Since
![]() $\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
is closed and T-invariant, we get
$\operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}$
is closed and T-invariant, we get
![]() $w'\in \operatorname {Fl}^{\leq w}$
(by Lemma 2.1.4); thus,
$w'\in \operatorname {Fl}^{\leq w}$
(by Lemma 2.1.4); thus,
![]() $w'\leq w$
(by part (a)).
$w'\leq w$
(by part (a)).
The following proposition gives a geometric interpretation of the ordering
![]() $\leq _C$
, generalizing the well-known result (see, for example, [Reference Mirkovic and VilonenMV, Proposition 3.1]) for the affine Grassmannian.
$\leq _C$
, generalizing the well-known result (see, for example, [Reference Mirkovic and VilonenMV, Proposition 3.1]) for the affine Grassmannian.
Proposition 2.1.6. For each
![]() $w',w"\in \widetilde {W}$
and every Weyl chamber
$w',w"\in \widetilde {W}$
and every Weyl chamber
![]() $C\in \mathcal {C}$
, we have
$C\in \mathcal {C}$
, we have
![]() $w'\leq _C w"$
if and only if
$w'\leq _C w"$
if and only if
![]() $w'\in \operatorname {Fl}^{\leq _C w"}$
.
$w'\in \operatorname {Fl}^{\leq _C w"}$
.
Proof. Assume that
![]() $w'\leq _C w"$
. Then by Proposition 1.2.5, there exists
$w'\leq _C w"$
. Then by Proposition 1.2.5, there exists
![]() $\mu \in \Lambda \cap C$
such that
$\mu \in \Lambda \cap C$
such that
![]() $\mu w'\leq \mu w"$
and
$\mu w'\leq \mu w"$
and
![]() $\mu w"\in C$
. Then
$\mu w"\in C$
. Then
![]() $\mu w'\in \operatorname {Fl}$
lies in the closure of
$\mu w'\in \operatorname {Fl}$
lies in the closure of
![]() $I\mu w"\subseteq \operatorname {Fl}$
(by Lemma 2.1.5(a)), and thus in the closure of
$I\mu w"\subseteq \operatorname {Fl}$
(by Lemma 2.1.5(a)), and thus in the closure of
![]() $L(U_C)\mu w"\subseteq \operatorname {Fl}$
(by Lemma 2.1.5(b)). Since
$L(U_C)\mu w"\subseteq \operatorname {Fl}$
(by Lemma 2.1.5(b)). Since
![]() $U_C$
is normalized by T, this implies that
$U_C$
is normalized by T, this implies that
![]() $w'\in \operatorname {Fl}$
lies in the closure of
$w'\in \operatorname {Fl}$
lies in the closure of
![]() $\mu ^{-1} L(U_C)\mu w" =L(U_C)w"\subseteq \operatorname {Fl}$
; that is,
$\mu ^{-1} L(U_C)\mu w" =L(U_C)w"\subseteq \operatorname {Fl}$
; that is,
![]() $w'\in \operatorname {Fl}^{\leq _C w"}$
.
$w'\in \operatorname {Fl}^{\leq _C w"}$
.
Conversely, assume that
![]() $w'\in \operatorname {Fl}$
lies in the closure of
$w'\in \operatorname {Fl}$
lies in the closure of
![]() $L(U_C) w"\subseteq \operatorname {Fl}$
. Then there exists a closed subgroup scheme
$L(U_C) w"\subseteq \operatorname {Fl}$
. Then there exists a closed subgroup scheme
![]() $U'\subseteq L(U_C)$
such that
$U'\subseteq L(U_C)$
such that
![]() $w'\in \operatorname {Fl}$
lies in the closure of
$w'\in \operatorname {Fl}$
lies in the closure of
![]() $U' w"\subseteq \operatorname {Fl}$
. Then
$U' w"\subseteq \operatorname {Fl}$
. Then
![]() $\mu w'\in \operatorname {Fl}$
lies in the closure of
$\mu w'\in \operatorname {Fl}$
lies in the closure of
![]() $\mu U' w"=(\mu U'\mu ^{-1})\mu w"$
for every
$\mu U' w"=(\mu U'\mu ^{-1})\mu w"$
for every
![]() $\mu \in \Lambda $
. However, if
$\mu \in \Lambda $
. However, if
![]() $\mu \in \Lambda \cap C$
is sufficiently regular, then
$\mu \in \Lambda \cap C$
is sufficiently regular, then
![]() $\mu U'\mu ^{-1}\subseteq I$
; thus,
$\mu U'\mu ^{-1}\subseteq I$
; thus,
![]() $\mu w'\in \operatorname {Fl}$
lies in the closure of
$\mu w'\in \operatorname {Fl}$
lies in the closure of
![]() $I\mu w"\subseteq \operatorname {Fl}$
. This implies that
$I\mu w"\subseteq \operatorname {Fl}$
. This implies that
![]() $\mu w'\leq \mu w"$
(by Lemma 2.1.5(a)); thus,
$\mu w'\leq \mu w"$
(by Lemma 2.1.5(a)); thus,
![]() $w'\leq _C w"$
(by Proposition 1.2.5).
$w'\leq _C w"$
(by Proposition 1.2.5).
Corollary 2.1.7.
(a) A tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible if and only if for every
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible if and only if for every
![]() $C\in \mathcal {C}$
the intersection
$C\in \mathcal {C}$
the intersection
![]() $L(U_C)w_C\cap \operatorname {Fl}^{\leq \overline {w}}$
is nonempty.
$L(U_C)w_C\cap \operatorname {Fl}^{\leq \overline {w}}$
is nonempty.
(b) For a tuple
![]() $\overline {u}$
and an admissible tuple
$\overline {u}$
and an admissible tuple
![]() $\overline {w}$
, we have
$\overline {w}$
, we have
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
if and only if
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
if and only if
![]() $\overline {w}\leq \overline {u}$
.
$\overline {w}\leq \overline {u}$
.
(c) For a tuple
![]() $\overline {w}$
, we have an inclusion
$\overline {w}$
, we have an inclusion
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \bigcup _C \operatorname {Fl}^{\leq w_C}$
. In particular, each
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \bigcup _C \operatorname {Fl}^{\leq w_C}$
. In particular, each
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}$
is a closed subscheme of finite type.
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}$
is a closed subscheme of finite type.
(d) Let
![]() $Z\subseteq \operatorname {Fl}$
be a closed T-invariant ind-subscheme. For every
$Z\subseteq \operatorname {Fl}$
be a closed T-invariant ind-subscheme. For every
![]() $z\in Z$
, consider tuple
$z\in Z$
, consider tuple
![]() $\overline {u}=\overline {u}(z)\in \widetilde {W}^{\mathcal {C}}$
defined by the rule that
$\overline {u}=\overline {u}(z)\in \widetilde {W}^{\mathcal {C}}$
defined by the rule that
![]() $z\in L(U_C)u_C$
for all
$z\in L(U_C)u_C$
for all
![]() $C\in \mathcal {C}$
. Then the tuple
$C\in \mathcal {C}$
. Then the tuple
![]() $\overline {u}$
is admissible, and
$\overline {u}$
is admissible, and
![]() $u_C\in \widetilde {W}\cap Z$
for all
$u_C\in \widetilde {W}\cap Z$
for all
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
(e) In the situation of part (d), we have an inclusion
![]() $Z\subseteq \bigcap _C(\bigcup _{w\in \widetilde {W}\cap Z}\operatorname {Fl}^{\leq _C w})$
.
$Z\subseteq \bigcap _C(\bigcup _{w\in \widetilde {W}\cap Z}\operatorname {Fl}^{\leq _C w})$
.
(f) For every tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, we have an equality
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, we have an equality ![]() (compare Sections 1.3.5(b),(c)).
(compare Sections 1.3.5(b),(c)).
Proof.
(a) By Lemma 1.3.7 and Proposition 2.1.6, a tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible if and only if
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is admissible if and only if
![]() $w_{C}\in \operatorname {Fl}^{\leq \overline {w}}=\bigcap _{C'\in \mathcal {C}}\operatorname {Fl}^{\leq _{C'} w_{C'}}$
for each
$w_{C}\in \operatorname {Fl}^{\leq \overline {w}}=\bigcap _{C'\in \mathcal {C}}\operatorname {Fl}^{\leq _{C'} w_{C'}}$
for each
![]() $C\in \mathcal {C}$
. Since
$C\in \mathcal {C}$
. Since
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}$
is closed and T-invariant, the assertion now follows from Lemma 2.1.4.
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}$
is closed and T-invariant, the assertion now follows from Lemma 2.1.4.
(b) The ‘if’ assertion follows from Proposition 2.1.6. Conversely, if
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
, then
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
, then
![]() $w_C\in \operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
(as in part (a)); hence,
$w_C\in \operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq \overline {u}}$
(as in part (a)); hence,
![]() $w_C\in \operatorname {Fl}^{\leq _C u_C}$
for every C. Therefore,
$w_C\in \operatorname {Fl}^{\leq _C u_C}$
for every C. Therefore,
![]() $w_C\leq _C u_C$
by Proposition 2.1.6.
$w_C\leq _C u_C$
by Proposition 2.1.6.
(c) Let z be any element of
![]() $\operatorname {Fl}^{\leq \overline {w}}$
, let
$\operatorname {Fl}^{\leq \overline {w}}$
, let
![]() $u\in \widetilde {W}$
be such that
$u\in \widetilde {W}$
be such that
![]() $z\in Iu$
, and let
$z\in Iu$
, and let
![]() $C\in \mathcal {C}$
be such that
$C\in \mathcal {C}$
be such that
![]() $u\in C$
. We want to show that
$u\in C$
. We want to show that
![]() $u\leq w_C$
, and thus
$u\leq w_C$
, and thus
![]() $z\in \operatorname {Fl}^{\leq w_C}$
.
$z\in \operatorname {Fl}^{\leq w_C}$
.
By Lemma 2.1.5(b), we get
![]() $z\in Iu\subseteq L(U_C)u$
. However, we have
$z\in Iu\subseteq L(U_C)u$
. However, we have
![]() $z\in \operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _C w_C}$
. Therefore, by Proposition 2.1.6, we get that
$z\in \operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _C w_C}$
. Therefore, by Proposition 2.1.6, we get that
![]() $u\leq _C w_C$
, which by Corollary 1.2.6(a) implies that
$u\leq _C w_C$
, which by Corollary 1.2.6(a) implies that
![]() $u\leq w_C$
.
$u\leq w_C$
.
(d) By construction,
![]() $z\in \operatorname {Fl}^{\leq \overline {u}}\cap L(U_C)u_C$
for all
$z\in \operatorname {Fl}^{\leq \overline {u}}\cap L(U_C)u_C$
for all
![]() $C\in \mathcal {C}$
; hence,
$C\in \mathcal {C}$
; hence,
![]() $\overline {u}$
is admissible by part (a). Since
$\overline {u}$
is admissible by part (a). Since
![]() $z\in L(U_C)u_C\cap Z$
, we get
$z\in L(U_C)u_C\cap Z$
, we get
![]() $u_C\in Z$
by Lemma 2.1.4.
$u_C\in Z$
by Lemma 2.1.4.
(e) follows immediately from part (d).
(f) It is enough to show that for every
![]() $C\in \mathcal {C}$
, the preimage
$C\in \mathcal {C}$
, the preimage
![]() $\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq _C\mu _C})$
equals
$\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq _C\mu _C})$
equals
![]() $\operatorname {Fl}^{\leq _C (\mu _C (w_{\operatorname {st}})_C)}$
. Using Proposition 2.1.6, we have to check that for every
$\operatorname {Fl}^{\leq _C (\mu _C (w_{\operatorname {st}})_C)}$
. Using Proposition 2.1.6, we have to check that for every
![]() $\mu \in \Lambda $
and
$\mu \in \Lambda $
and
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $\mu \leq _C \mu _C$
if and only if
$\mu \leq _C \mu _C$
if and only if
![]() $\mu u\leq _C\mu _C (w_{\operatorname {st}})_C$
.
$\mu u\leq _C\mu _C (w_{\operatorname {st}})_C$
.
The ‘only if’ assertion follows from Corollary 1.2.3(b). Conversely, if
![]() $\mu \leq _C \mu _C$
, then
$\mu \leq _C \mu _C$
, then
![]() $\mu u\leq _C \mu _C u$
by Lemma 1.2.2(b). So by Remark 1.2.4(a)(i), it is enough to show that
$\mu u\leq _C \mu _C u$
by Lemma 1.2.2(b). So by Remark 1.2.4(a)(i), it is enough to show that
![]() $u\leq _C (w_{\operatorname {st}})_C$
. Since
$u\leq _C (w_{\operatorname {st}})_C$
. Since
![]() $\overline {w}_{\operatorname {st}}$
is admissible and
$\overline {w}_{\operatorname {st}}$
is admissible and
![]() $u=(w_{\operatorname {st}})_{u(C_0)}$
, the assertion follows from Lemma 1.3.7.
$u=(w_{\operatorname {st}})_{u(C_0)}$
, the assertion follows from Lemma 1.3.7.
2.2 Proof of Theorem 0.2
2.2.1. Let
![]() $m\in \mathbb N$
. Recall that
$m\in \mathbb N$
. Recall that
![]() $w\in \widetilde {W}$
is called m-regular if
$w\in \widetilde {W}$
is called m-regular if
![]() $\pi (w)\in \Lambda $
is m-regular; that is, we have
$\pi (w)\in \Lambda $
is m-regular; that is, we have
![]() $|\langle \alpha ,\pi (w)\rangle |\geq m$
for all
$|\langle \alpha ,\pi (w)\rangle |\geq m$
for all
![]() $\alpha \in \Phi $
. For each
$\alpha \in \Phi $
. For each
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\widetilde {W}^{\leq w}$
the set of
$\widetilde {W}^{\leq w}$
the set of
![]() $w'\in \widetilde {W}$
such that
$w'\in \widetilde {W}$
such that
![]() $w'\leq w$
.
$w'\leq w$
.
The following result is a more precise version of Theorem 0.2.
Theorem 2.2.2.
(a) For each
![]() $w\in \widetilde {W}$
, there exists a unique admissible tuple
$w\in \widetilde {W}$
, there exists a unique admissible tuple
![]() $\overline {w}$
such that the Schubert variety
$\overline {w}$
such that the Schubert variety
![]() $\operatorname {Fl}^{\leq w}$
equals
$\operatorname {Fl}^{\leq w}$
equals
![]() $\operatorname {Fl}^{\leq \overline {w}}$
.
$\operatorname {Fl}^{\leq \overline {w}}$
.
Moreover,
![]() $\overline {w}=\{w_C\}_C$
is characterized by the condition that
$\overline {w}=\{w_C\}_C$
is characterized by the condition that
![]() $w_C$
is a unique maximal element of
$w_C$
is a unique maximal element of
![]() $\widetilde {W}^{\leq w}$
with respect to the ordering
$\widetilde {W}^{\leq w}$
with respect to the ordering
![]() $\leq _C$
.
$\leq _C$
.
(b) Furthermore, there exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $m\in \mathbb N$
and every
$m\in \mathbb N$
and every
![]() $(m+r)$
-regular
$(m+r)$
-regular
![]() $w\in \widetilde {W}$
, the tuple
$w\in \widetilde {W}$
, the tuple
![]() $\overline {w}$
is m-regular.
$\overline {w}$
is m-regular.
Proof.
(a) Denote by
![]() $X(w)$
the closed ind-subscheme
$X(w)$
the closed ind-subscheme
![]() $\bigcap _C(\bigcup _{w'\leq w} \operatorname {Fl}^{\leq _C w'})\subseteq \operatorname {Fl}$
(compare Corollary 2.1.7(c)), and we claim that
$\bigcap _C(\bigcup _{w'\leq w} \operatorname {Fl}^{\leq _C w'})\subseteq \operatorname {Fl}$
(compare Corollary 2.1.7(c)), and we claim that
![]() $X(w)$
equals
$X(w)$
equals
![]() $\operatorname {Fl}^{\leq w}$
. Indeed, the inclusion
$\operatorname {Fl}^{\leq w}$
. Indeed, the inclusion
![]() $\operatorname {Fl}^{\leq w}\subseteq X(w)$
follows from Corollary 2.1.7(e), while the opposite inclusion
$\operatorname {Fl}^{\leq w}\subseteq X(w)$
follows from Corollary 2.1.7(e), while the opposite inclusion
![]() $X(w)\subseteq \operatorname {Fl}^{\leq w}$
follows from identity
$X(w)\subseteq \operatorname {Fl}^{\leq w}$
follows from identity
![]() $X(w)=\bigcup _{\overline {w}'\in (\widetilde {W}^{\leq w})^{\mathcal {C}}}\operatorname {Fl}^{\leq \overline {w}'}$
and Corollary 2.1.7(c).
$X(w)=\bigcup _{\overline {w}'\in (\widetilde {W}^{\leq w})^{\mathcal {C}}}\operatorname {Fl}^{\leq \overline {w}'}$
and Corollary 2.1.7(c).
Next, since
![]() $\operatorname {Fl}^{\leq w}=\bigcup _{\overline {w}'\in (\widetilde {W}^{\leq w})^{\mathcal {C}}}\operatorname {Fl}^{\leq \overline {w}'}$
is irreducible, there exists a tuple
$\operatorname {Fl}^{\leq w}=\bigcup _{\overline {w}'\in (\widetilde {W}^{\leq w})^{\mathcal {C}}}\operatorname {Fl}^{\leq \overline {w}'}$
is irreducible, there exists a tuple
![]() $\overline {w}=\{w_C\}_C\in (\widetilde {W}^{\leq w})^{\mathcal {C}}$
such that
$\overline {w}=\{w_C\}_C\in (\widetilde {W}^{\leq w})^{\mathcal {C}}$
such that
![]() $\operatorname {Fl}^{\leq w}=\operatorname {Fl}^{\leq \overline {w}}$
.
$\operatorname {Fl}^{\leq w}=\operatorname {Fl}^{\leq \overline {w}}$
.
Then for each
![]() $w'\leq w$
and
$w'\leq w$
and
![]() $C\in \mathcal {C}$
, we have
$C\in \mathcal {C}$
, we have
![]() $w'\in \operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}^{\leq _C w_C}$
. Thus, by Proposition 2.1.6, we have
$w'\in \operatorname {Fl}^{\leq w}\subseteq \operatorname {Fl}^{\leq _C w_C}$
. Thus, by Proposition 2.1.6, we have
![]() $w'\leq _C w_C$
; that is,
$w'\leq _C w_C$
; that is,
![]() $w_C$
is the biggest element of
$w_C$
is the biggest element of
![]() $\widetilde {W}^{\leq w}$
with respect to ordering
$\widetilde {W}^{\leq w}$
with respect to ordering
![]() $\leq _C$
. In particular, for every other Weyl chamber
$\leq _C$
. In particular, for every other Weyl chamber
![]() $C'$
, we have
$C'$
, we have
![]() $w_{C'}\leq _C w_C$
. Thus, by Lemma 1.3.7, we conclude that
$w_{C'}\leq _C w_C$
. Thus, by Lemma 1.3.7, we conclude that
![]() $\overline {w}$
is admissible.
$\overline {w}$
is admissible.
The uniqueness of
![]() $\overline {w}$
follows immediately from Corollary 2.1.7(b).
$\overline {w}$
follows immediately from Corollary 2.1.7(b).
(b) Choose any
![]() $\mu \in \Lambda \cap C_0$
, and let r be the maximum of the
$\mu \in \Lambda \cap C_0$
, and let r be the maximum of the
![]() $2\langle \psi ,\mu \rangle $
’s, taken over
$2\langle \psi ,\mu \rangle $
’s, taken over
![]() $\psi \in \Psi _{C_0}$
. We claim this r satisfies the required property; that is, for every
$\psi \in \Psi _{C_0}$
. We claim this r satisfies the required property; that is, for every
![]() $m\in \mathbb N$
and every
$m\in \mathbb N$
and every
![]() $(m+r)$
-regular
$(m+r)$
-regular
![]() $w\in \widetilde {W}$
, the tuple
$w\in \widetilde {W}$
, the tuple
![]() $\overline {w}$
is m-regular. In other words, we claim that
$\overline {w}$
is m-regular. In other words, we claim that
![]() $w_{u(C_0)}$
is
$w_{u(C_0)}$
is
![]() $(u(C_0),m)$
-regular or, equivalently, that
$(u(C_0),m)$
-regular or, equivalently, that
![]() $u^{-1}w_{u(C_0)}$
is
$u^{-1}w_{u(C_0)}$
is
![]() $(C_0,m)$
-regular for all
$(C_0,m)$
-regular for all
![]() $u\in W$
.
$u\in W$
.
Claim 2.2.3. Let
![]() $w\in \widetilde {W}$
, and let
$w\in \widetilde {W}$
, and let
![]() $\overline {w}:=\{w_C\}_{C\in \mathcal {C}}$
be the tuple from Theorem 2.2.2(a).
$\overline {w}:=\{w_C\}_{C\in \mathcal {C}}$
be the tuple from Theorem 2.2.2(a).
(a) If
![]() $w=w_0w_+$
, where
$w=w_0w_+$
, where
![]() $w_0\in W$
is the longest element, and
$w_0\in W$
is the longest element, and
![]() $w_+\in \widetilde {W}\cap C_0$
, then
$w_+\in \widetilde {W}\cap C_0$
, then
![]() $w_{u(C_0)}=uw_+$
for all
$w_{u(C_0)}=uw_+$
for all
![]() $u\in W$
.
$u\in W$
.
(b) If
![]() $w\in Ww_+$
with
$w\in Ww_+$
with
![]() $w_+\in \widetilde {W}\cap C_0$
, then for all
$w_+\in \widetilde {W}\cap C_0$
, then for all
![]() $u\in W$
, we have inequalities
$u\in W$
, we have inequalities
Proof.
(a) Fix
![]() $u\in W$
. We will show that
$u\in W$
. We will show that
![]() $w\leq w_0u^{-1} w_{u(C_0)}\leq w$
, which will imply that
$w\leq w_0u^{-1} w_{u(C_0)}\leq w$
, which will imply that
![]() $w_0u^{-1} w_{u(C_0)}=w_0w_+$
, and thus
$w_0u^{-1} w_{u(C_0)}=w_0w_+$
, and thus
![]() $w_{u(C_0)}=uw_+$
.
$w_{u(C_0)}=uw_+$
.
Since
![]() $u\leq w_0$
, we get
$u\leq w_0$
, we get
![]() $uw_+\leq w_0w_+=w$
(use Section 1.1.4(e)). Therefore, by the characterization of
$uw_+\leq w_0w_+=w$
(use Section 1.1.4(e)). Therefore, by the characterization of
![]() $\overline {w}$
, given Theorem 2.2.2(a), we get
$\overline {w}$
, given Theorem 2.2.2(a), we get
![]() $uw_+\leq _{u(C_0)} w_{u(C_0)}$
. Hence,
$uw_+\leq _{u(C_0)} w_{u(C_0)}$
. Hence,
![]() $w=w_0w_+\leq _{w_0(C_0)}w_0u^{-1} w_{u(C_0)}$
(by Remark 1.2.4(a)(ii)); thus,
$w=w_0w_+\leq _{w_0(C_0)}w_0u^{-1} w_{u(C_0)}$
(by Remark 1.2.4(a)(ii)); thus,
![]() $w\leq w_0u^{-1} w_{u(C_0)}$
(by Corollary 1.2.6(a)). However,
$w\leq w_0u^{-1} w_{u(C_0)}$
(by Corollary 1.2.6(a)). However,
![]() $w_{u(C_0)}\leq w=w_0w_+$
; thus, using Section 1.1.4(e), we conclude that
$w_{u(C_0)}\leq w=w_0w_+$
; thus, using Section 1.1.4(e), we conclude that
![]() $w_0u^{-1} w_{u(C_0)}\leq w$
.
$w_0u^{-1} w_{u(C_0)}\leq w$
.
(b) By Remark 1.2.4(a)(ii), it is enough to show that
Consider element
![]() $w':=w_0w_+$
. Then
$w':=w_0w_+$
. Then
![]() $w\leq w'$
(use Section 1.1.4(e)), and thus, we have
$w\leq w'$
(use Section 1.1.4(e)), and thus, we have
![]() $w_{u(C_0)}\leq w'$
. Hence,
$w_{u(C_0)}\leq w'$
. Hence,
![]() $w_{u(C_0)}\leq _{u(C_0)} w^{\prime }_{u(C_0)}$
(by the characterization of
$w_{u(C_0)}\leq _{u(C_0)} w^{\prime }_{u(C_0)}$
(by the characterization of
![]() $w^{\prime }_{u(C_0)}$
, given in Theorem 2.2.2(a)); thus,
$w^{\prime }_{u(C_0)}$
, given in Theorem 2.2.2(a)); thus,
![]() $w_{u(C_0)}\leq _{u(C_0)}uw_+$
(by part (a)). To show the other inequality, it is enough to show that
$w_{u(C_0)}\leq _{u(C_0)}uw_+$
(by part (a)). To show the other inequality, it is enough to show that
![]() $u\mu ^{-1}w_+\leq w$
. Since w and hence also
$u\mu ^{-1}w_+\leq w$
. Since w and hence also
![]() $w_+$
is
$w_+$
is
![]() $(m+r)$
-regular, our definition of r implies that
$(m+r)$
-regular, our definition of r implies that
![]() $\mu ^{-1}w_+\in \widetilde {W}\cap C_0$
. Since
$\mu ^{-1}w_+\in \widetilde {W}\cap C_0$
. Since
![]() $u\leq \mu $
(by Section 1.1.4(g)), and
$u\leq \mu $
(by Section 1.1.4(g)), and
![]() $l(w_+)=l(\mu )+l(\mu ^{-1}w_+)$
(by Lemma 1.1.5(c)), we conclude from Section 1.1.4(c) and part (e) that
$l(w_+)=l(\mu )+l(\mu ^{-1}w_+)$
(by Lemma 1.1.5(c)), we conclude from Section 1.1.4(c) and part (e) that
![]() $u(\mu ^{-1}w_+)\leq w_+\leq w$
.
$u(\mu ^{-1}w_+)\leq w_+\leq w$
.
Let us come back to the proof of the Theorem. By Claim 2.2.3(b) and Corollary 1.2.3(b), we have
Hence, we have
![]() $\pi (u^{-1}w_{u(C_0)})=\pi (w_+)- \sum _{\alpha \in \Delta _{C_0}}m_{\alpha }\check {\alpha }$
, such that
$\pi (u^{-1}w_{u(C_0)})=\pi (w_+)- \sum _{\alpha \in \Delta _{C_0}}m_{\alpha }\check {\alpha }$
, such that
![]() $0\leq m_{\alpha }\leq \langle \psi _{\alpha },\mu \rangle $
, where
$0\leq m_{\alpha }\leq \langle \psi _{\alpha },\mu \rangle $
, where
![]() $\psi _{\alpha }\in \Psi _{C_0}$
is the fundamental weight corresponding to
$\psi _{\alpha }\in \Psi _{C_0}$
is the fundamental weight corresponding to
![]() $\alpha $
for each
$\alpha $
for each
![]() $\alpha \in \Delta _{C_0}$
. In particular, for each
$\alpha \in \Delta _{C_0}$
. In particular, for each
![]() $\alpha \in \Delta _{C_0}$
, we have
$\alpha \in \Delta _{C_0}$
, we have
because
![]() $w_+$
is
$w_+$
is
![]() $(m+r)$
-regular, and
$(m+r)$
-regular, and
![]() $2m_{\alpha }\leq 2\langle \psi _{\alpha },\mu \rangle \leq r$
.
$2m_{\alpha }\leq 2\langle \psi _{\alpha },\mu \rangle \leq r$
.
2.3 Technical lemmas
Notation 2.3.1. Fix
![]() $\psi \in \Psi $
.
$\psi \in \Psi $
.
(a) Denote by
![]() $P_{\psi }\supseteq T$
the parabolic subgroup of G such that
$P_{\psi }\supseteq T$
the parabolic subgroup of G such that
![]() $\Phi (P_{\psi },T)=\Phi (\psi )$
(see Section 1.1.3(c)), by
$\Phi (P_{\psi },T)=\Phi (\psi )$
(see Section 1.1.3(c)), by
![]() $M_{\psi }\supseteq T$
the Levi subgroup of
$M_{\psi }\supseteq T$
the Levi subgroup of
![]() $P_{\psi }$
, by
$P_{\psi }$
, by
![]() $U_{\psi }\subseteq P_{\psi }$
the unipotent radical, by
$U_{\psi }\subseteq P_{\psi }$
the unipotent radical, by
![]() $M^{\operatorname {sc}}_{\psi }$
the simply connected covering of the derived (=commutator) group of
$M^{\operatorname {sc}}_{\psi }$
the simply connected covering of the derived (=commutator) group of
![]() $M_{\psi }$
. Let
$M_{\psi }$
. Let
![]() $P_{\psi }\to M_{\psi }$
be the natural projection, and set
$P_{\psi }\to M_{\psi }$
be the natural projection, and set
![]() $P^{\operatorname {sc}}_{\psi }:=P_{\psi }\times _{M_{\psi }}M^{\operatorname {sc}}_{\psi }$
.
$P^{\operatorname {sc}}_{\psi }:=P_{\psi }\times _{M_{\psi }}M^{\operatorname {sc}}_{\psi }$
.
(b) Note that we have a natural homomorphism
![]() $P^{\operatorname {sc}}_{\psi }\to P_{\psi }\subseteq G$
; thus, the loop group
$P^{\operatorname {sc}}_{\psi }\to P_{\psi }\subseteq G$
; thus, the loop group
![]() $L(P^{\operatorname {sc}}_{\psi })$
acts on
$L(P^{\operatorname {sc}}_{\psi })$
acts on
![]() $\operatorname {Fl}$
. For every
$\operatorname {Fl}$
. For every
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\operatorname {Fl}^{\leq _{\psi }w}\subseteq \operatorname {Fl}$
the closure of the
$\operatorname {Fl}^{\leq _{\psi }w}\subseteq \operatorname {Fl}$
the closure of the
![]() $L(P^{\operatorname {sc}}_{\psi })$
-orbit
$L(P^{\operatorname {sc}}_{\psi })$
-orbit
![]() $L(P^{\operatorname {sc}}_{\psi })w\subseteq \operatorname {Fl}$
. For every
$L(P^{\operatorname {sc}}_{\psi })w\subseteq \operatorname {Fl}$
. For every
![]() $\mu \in \Lambda $
, we denote by
$\mu \in \Lambda $
, we denote by
![]() $\operatorname {Gr}^{\leq _{\psi }\mu }\subseteq \operatorname {Gr}$
the closure of the
$\operatorname {Gr}^{\leq _{\psi }\mu }\subseteq \operatorname {Gr}$
the closure of the
![]() $L(P^{\operatorname {sc}}_{\psi })$
-orbit
$L(P^{\operatorname {sc}}_{\psi })$
-orbit
![]() $L(P^{\operatorname {sc}}_{\psi })\mu \subseteq \operatorname {Gr}$
.
$L(P^{\operatorname {sc}}_{\psi })\mu \subseteq \operatorname {Gr}$
.
Lemma 2.3.2.
(a) For
![]() $w',w"\in \widetilde {W}$
and
$w',w"\in \widetilde {W}$
and
![]() $\psi \in \Psi $
, we have
$\psi \in \Psi $
, we have
![]() $w'\leq _{\psi } w"$
if and only if
$w'\leq _{\psi } w"$
if and only if
![]() $w'\in \operatorname {Fl}^{\leq _{\psi } w"}$
.
$w'\in \operatorname {Fl}^{\leq _{\psi } w"}$
.
(b) For
![]() $u\in \widetilde {W}$
,
$u\in \widetilde {W}$
,
![]() $\psi \in \Psi $
and an admissible tuple
$\psi \in \Psi $
and an admissible tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, we have
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, we have
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
if and only if
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
if and only if
![]() $\overline {w}_{\psi }\leq _{\psi } u$
(compare Section 1.3.6).
$\overline {w}_{\psi }\leq _{\psi } u$
(compare Section 1.3.6).
Proof.
(a) Assume first that
![]() $w'\leq _{\psi } w"$
, and we want to prove that
$w'\leq _{\psi } w"$
, and we want to prove that
![]() $L(P^{\operatorname {sc}}_{\psi })w'\subseteq \operatorname {Fl}$
is contained in the closure of
$L(P^{\operatorname {sc}}_{\psi })w'\subseteq \operatorname {Fl}$
is contained in the closure of
![]() $L(P^{\operatorname {sc}}_{\psi })w"\subseteq \operatorname {Fl}$
. By definition, we can assume that
$L(P^{\operatorname {sc}}_{\psi })w"\subseteq \operatorname {Fl}$
. By definition, we can assume that
![]() $w'=s_{\widetilde {\beta }}w"<_{\widetilde {\beta }}w"$
, where
$w'=s_{\widetilde {\beta }}w"<_{\widetilde {\beta }}w"$
, where
![]() $\widetilde {\beta }=(\beta ,m)$
, and
$\widetilde {\beta }=(\beta ,m)$
, and
![]() $\langle \beta ,\psi \rangle \geq 0$
. Then there exists a Weyl chamber
$\langle \beta ,\psi \rangle \geq 0$
. Then there exists a Weyl chamber
![]() $C\owns \psi $
such that
$C\owns \psi $
such that
![]() $\beta \in \Phi _{C}$
. Then
$\beta \in \Phi _{C}$
. Then
![]() $w'<_C w"$
; hence, by Proposition 2.1.6,
$w'<_C w"$
; hence, by Proposition 2.1.6,
![]() $w'$
lies in the closure of
$w'$
lies in the closure of
![]() $L(U_C)w"\subseteq \operatorname {Fl}$
. Since
$L(U_C)w"\subseteq \operatorname {Fl}$
. Since
![]() $L(U_C)\subseteq L(P^{\operatorname {sc}}_{\psi })$
, the assertion follows.
$L(U_C)\subseteq L(P^{\operatorname {sc}}_{\psi })$
, the assertion follows.
Conversely, assume that
![]() $w'$
belongs to the closure of
$w'$
belongs to the closure of
![]() $L(P^{\operatorname {sc}}_{\psi })w"\subseteq \operatorname {Fl}$
. Choose any Weyl chamber
$L(P^{\operatorname {sc}}_{\psi })w"\subseteq \operatorname {Fl}$
. Choose any Weyl chamber
![]() $C\owns \psi $
. Then
$C\owns \psi $
. Then
![]() $L(P^{\operatorname {sc}}_{\psi })w"$
is a union of orbits
$L(P^{\operatorname {sc}}_{\psi })w"$
is a union of orbits
![]() $\bigcup _{w\in \widetilde {W}^{\psi }}L(U_C)ww"$
. Therefore,
$\bigcup _{w\in \widetilde {W}^{\psi }}L(U_C)ww"$
. Therefore,
![]() $w'$
belongs to the closure of
$w'$
belongs to the closure of
![]() $L(U_C)ww"\subseteq \operatorname {Fl}$
for some
$L(U_C)ww"\subseteq \operatorname {Fl}$
for some
![]() $w\in \widetilde {W}^{\psi }$
. Hence, by Proposition 2.1.6, we get
$w\in \widetilde {W}^{\psi }$
. Hence, by Proposition 2.1.6, we get
![]() $w'\leq _C ww"$
, and thus
$w'\leq _C ww"$
, and thus
![]() $w'\leq _{\psi }ww"$
. However, since
$w'\leq _{\psi }ww"$
. However, since
![]() $w\in \widetilde {W}^{\psi }$
, we also get
$w\in \widetilde {W}^{\psi }$
, we also get
![]() $ww"\leq _{\psi } w"$
.
$ww"\leq _{\psi } w"$
.
(b) Choose any Weyl chamber
![]() $C\owns \psi $
. Then
$C\owns \psi $
. Then
![]() $w_C\in \widetilde {W}^{\psi }\overline {w}_{\psi }$
; hence, we have
$w_C\in \widetilde {W}^{\psi }\overline {w}_{\psi }$
; hence, we have
![]() $\overline {w}_{\psi }\leq _{\psi } u$
if and only if
$\overline {w}_{\psi }\leq _{\psi } u$
if and only if
![]() $w_C\leq _{\psi } u$
.
$w_C\leq _{\psi } u$
.
Assume first that
![]() $w_C\leq _{\psi } u$
. Then by part (a) we have
$w_C\leq _{\psi } u$
. Then by part (a) we have
![]() $\operatorname {Fl}^{\leq _{\psi } w_C}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
. However, we always have inclusions
$\operatorname {Fl}^{\leq _{\psi } w_C}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
. However, we always have inclusions
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _C w_C}\subseteq \operatorname {Fl}^{\leq _{\psi } w_C}$
, which imply that
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _C w_C}\subseteq \operatorname {Fl}^{\leq _{\psi } w_C}$
, which imply that
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
. Conversely, since
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
. Conversely, since
![]() $\overline {w}$
is admissible, we get
$\overline {w}$
is admissible, we get
![]() $w_C\in \operatorname {Fl}^{\leq \overline {w}}$
by Lemma 1.3.7. Therefore, if
$w_C\in \operatorname {Fl}^{\leq \overline {w}}$
by Lemma 1.3.7. Therefore, if
![]() $\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
, we get
$\operatorname {Fl}^{\leq \overline {w}}\subseteq \operatorname {Fl}^{\leq _{\psi } u}$
, we get
![]() $w_C\in \operatorname {Fl}^{\leq _{\psi } u}$
. Hence, by part (a), we have
$w_C\in \operatorname {Fl}^{\leq _{\psi } u}$
. Hence, by part (a), we have
![]() $w_C\leq _{\psi } u$
.
$w_C\leq _{\psi } u$
.
The remaining results of this subsection will be only used in Section 4.3.
Corollary 2.3.3.
(a) For
![]() $\mu ',\mu "\in \Lambda $
and
$\mu ',\mu "\in \Lambda $
and
![]() $\psi \in \Psi $
, we have
$\psi \in \Psi $
, we have
![]() $\mu '\in \operatorname {Gr}^{\leq _{\psi } \mu "}$
if and only if
$\mu '\in \operatorname {Gr}^{\leq _{\psi } \mu "}$
if and only if
![]() $\langle \psi ,\mu '\rangle \leq \langle \psi ,\mu "\rangle $
.
$\langle \psi ,\mu '\rangle \leq \langle \psi ,\mu "\rangle $
.
(b) For
![]() $m\in \mathbb Z$
and
$m\in \mathbb Z$
and
![]() $\psi \in \Psi $
, there exists a unique closed reduced ind-subscheme
$\psi \in \Psi $
, there exists a unique closed reduced ind-subscheme
![]() $\operatorname {Gr}^{\leq _{\psi } m}\subseteq \operatorname {Gr}$
such that
$\operatorname {Gr}^{\leq _{\psi } m}\subseteq \operatorname {Gr}$
such that
![]() $\operatorname {Gr}^{\leq _{\psi } m}=\operatorname {Gr}^{\leq _{\psi } \mu }$
for every
$\operatorname {Gr}^{\leq _{\psi } m}=\operatorname {Gr}^{\leq _{\psi } \mu }$
for every
![]() $\mu \in \Lambda $
and
$\mu \in \Lambda $
and
![]() $\psi \in \Psi $
such that
$\psi \in \Psi $
such that
![]() $\langle \psi ,\mu \rangle =m$
.
$\langle \psi ,\mu \rangle =m$
.
(c) For every admissible tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, we have an equality of reduced subschemes
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, we have an equality of reduced subschemes
![]() $\operatorname {Gr}^{\leq \overline {\mu }}=\bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}\subseteq \operatorname {Gr}$
(compare Section 1.3.4(a)).
$\operatorname {Gr}^{\leq \overline {\mu }}=\bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}\subseteq \operatorname {Gr}$
(compare Section 1.3.4(a)).
Proof.
(a) Using equality
![]() $\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq _{\psi }\mu "})=\bigcup _{w\in W} \operatorname {Fl}^{\leq _{\psi }\mu "w}$
, we see that
$\operatorname {pr}^{-1}(\operatorname {Gr}^{\leq _{\psi }\mu "})=\bigcup _{w\in W} \operatorname {Fl}^{\leq _{\psi }\mu "w}$
, we see that
![]() $\mu '\in \operatorname {Gr}^{\leq _{\psi } \mu "}$
if and only if
$\mu '\in \operatorname {Gr}^{\leq _{\psi } \mu "}$
if and only if
![]() $\mu '\in \operatorname {Fl}^{\leq _{\psi } \mu " w}$
for some
$\mu '\in \operatorname {Fl}^{\leq _{\psi } \mu " w}$
for some
![]() $w\in W$
. Hence, by Lemma 2.3.2(a), this happens if and only if we have
$w\in W$
. Hence, by Lemma 2.3.2(a), this happens if and only if we have
![]() $\mu '\leq _{\psi }\mu "w$
for some
$\mu '\leq _{\psi }\mu "w$
for some
![]() $w\in W$
. Since
$w\in W$
. Since
![]() $\pi (\mu "w)=\mu "$
, it thus follows from Corollary 1.2.3(b),(c) and Section 1.2.4(c) that this happens if and only if
$\pi (\mu "w)=\mu "$
, it thus follows from Corollary 1.2.3(b),(c) and Section 1.2.4(c) that this happens if and only if
![]() $\mu '\leq _{\psi }\mu "$
in the sense of Section 1.2.1(c). Now the assertion follows from Lemma 1.2.2(c).
$\mu '\leq _{\psi }\mu "$
in the sense of Section 1.2.1(c). Now the assertion follows from Lemma 1.2.2(c).
(b) follows immediately from part (a).
(c) Notice that for every
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $\psi \in \Psi _C$
, the inclusion
$\psi \in \Psi _C$
, the inclusion
![]() $U_C\subseteq P^{\operatorname {sc}}_{\psi }$
implies the inclusion
$U_C\subseteq P^{\operatorname {sc}}_{\psi }$
implies the inclusion
![]() $\operatorname {Gr}^{\leq _{C}\mu _C}\subseteq \operatorname {Gr}^{\leq _{\psi }\mu _C}=\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
, from which the inclusion ‘
$\operatorname {Gr}^{\leq _{C}\mu _C}\subseteq \operatorname {Gr}^{\leq _{\psi }\mu _C}=\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
, from which the inclusion ‘
![]() $\subseteq $
’ follows.
$\subseteq $
’ follows.
Conversely, for every
![]() $y\in \bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
and
$y\in \bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
and
![]() $C\in \mathcal {C}$
, let
$C\in \mathcal {C}$
, let
![]() $\nu \in \Lambda $
be such that
$\nu \in \Lambda $
be such that
![]() $y\in L(U_C)\nu $
, and we want to show that
$y\in L(U_C)\nu $
, and we want to show that
![]() $\nu \leq _C\mu _C$
. Since the ind-subscheme
$\nu \leq _C\mu _C$
. Since the ind-subscheme
![]() $\bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}\subseteq \operatorname {Gr}$
is closed and T-invariant, it follows from Lemma 2.1.4 that
$\bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}\subseteq \operatorname {Gr}$
is closed and T-invariant, it follows from Lemma 2.1.4 that
![]() $\nu \in \bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
. Hence, by part (a), we have
$\nu \in \bigcap _{\psi \in \Psi }\operatorname {Gr}^{\leq _{\psi }\overline {\mu }(\psi )}$
. Hence, by part (a), we have
![]() $\langle \psi ,\nu \rangle \leq \overline {\mu }(\psi )$
for each
$\langle \psi ,\nu \rangle \leq \overline {\mu }(\psi )$
for each
![]() $\psi \in \Psi $
, from which inequality
$\psi \in \Psi $
, from which inequality
![]() $\nu \leq _C\mu _C$
follows from Section 1.3.4(c).
$\nu \leq _C\mu _C$
follows from Section 1.3.4(c).
Lemma 2.3.4.
(a) For all
![]() $\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
, there exist admissible tuples
$\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
, there exist admissible tuples
![]() $\overline {w}_1\ldots ,\overline {w}_n$
from
$\overline {w}_1\ldots ,\overline {w}_n$
from
![]() $\widetilde {W}^{\mathcal {C}} $
such that the reduced intersection
$\widetilde {W}^{\mathcal {C}} $
such that the reduced intersection
![]() $\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}$
equals
$\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}$
equals
![]() $\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
$\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
(b) For all
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
,
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
,
![]() $\psi \in \Psi $
and
$\psi \in \Psi $
and
![]() $u\in \widetilde {W}$
, there exist admissible tuples
$u\in \widetilde {W}$
, there exist admissible tuples
![]() $\overline {w}_1\ldots ,\overline {w}_n$
from
$\overline {w}_1\ldots ,\overline {w}_n$
from
![]() $\widetilde {W}^{\mathcal {C}}$
such that the reduced intersection
$\widetilde {W}^{\mathcal {C}}$
such that the reduced intersection
![]() $\operatorname {Fl}^{\leq \overline {w}}\cap \operatorname {Fl}^{\leq _{\psi } u}$
equals
$\operatorname {Fl}^{\leq \overline {w}}\cap \operatorname {Fl}^{\leq _{\psi } u}$
equals
![]() $\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
$\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
Proof. We denote by Z the reduced intersection
![]() $\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}$
in the case (a), and
$\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}$
in the case (a), and
![]() $\operatorname {Fl}^{\leq \overline {w}}\cap \operatorname {Fl}^{\leq _{\psi } u}$
in the case (b). Then, by Corollary 2.1.7(c), in both cases, Z is a closed T-invariant subscheme of
$\operatorname {Fl}^{\leq \overline {w}}\cap \operatorname {Fl}^{\leq _{\psi } u}$
in the case (b). Then, by Corollary 2.1.7(c), in both cases, Z is a closed T-invariant subscheme of
![]() $\operatorname {Fl}$
of finite type; thus, the intersection
$\operatorname {Fl}$
of finite type; thus, the intersection
![]() $\widetilde {W}\cap Z$
is finite.
$\widetilde {W}\cap Z$
is finite.
By Corollary 2.1.7(d), each
![]() $z\in Z$
defines an admissible tuple
$z\in Z$
defines an admissible tuple
![]() $\overline {u}=\overline {u}(z)\in \widetilde {W}^{\mathcal {C}}$
satisfying
$\overline {u}=\overline {u}(z)\in \widetilde {W}^{\mathcal {C}}$
satisfying
![]() $u_C\in \widetilde {W}\cap Z$
for each
$u_C\in \widetilde {W}\cap Z$
for each
![]() $C\in \mathcal {C}$
. It follows that the set of tuples
$C\in \mathcal {C}$
. It follows that the set of tuples
![]() $\{\overline {u}(z)\}_{z\in Z}$
is finite, so it will suffice to show the equality
$\{\overline {u}(z)\}_{z\in Z}$
is finite, so it will suffice to show the equality
One inclusion follows from the fact that
![]() $z\in \operatorname {Fl}^{\leq \overline {u}(z)}$
for every
$z\in \operatorname {Fl}^{\leq \overline {u}(z)}$
for every
![]() $z\in Z$
. To show the converse, it is enough to show that if
$z\in Z$
. To show the converse, it is enough to show that if
![]() $\overline {u}\in \widetilde {W}^{\mathcal {C}}$
satisfies
$\overline {u}\in \widetilde {W}^{\mathcal {C}}$
satisfies
![]() $u_C\in Z$
for all
$u_C\in Z$
for all
![]() $C\in \mathcal {C}$
, then
$C\in \mathcal {C}$
, then
![]() $\operatorname {Fl}^{\leq \overline {u}}\subseteq Z$
. Using definition of Z, it remains to show the corresponding assertion in the cases
$\operatorname {Fl}^{\leq \overline {u}}\subseteq Z$
. Using definition of Z, it remains to show the corresponding assertion in the cases
![]() $Z=\operatorname {Fl}^{\leq \overline {w}}$
and
$Z=\operatorname {Fl}^{\leq \overline {w}}$
and
![]() $Z=\operatorname {Fl}^{\leq _{\psi }u}$
. In the first case, we have
$Z=\operatorname {Fl}^{\leq _{\psi }u}$
. In the first case, we have
![]() $u_C\in \operatorname {Fl}^{\leq _C w_C}$
; hence,
$u_C\in \operatorname {Fl}^{\leq _C w_C}$
; hence,
![]() $\operatorname {Fl}^{\leq _C u_C}\subseteq \operatorname {Fl}^{\leq _C w_C}$
for all
$\operatorname {Fl}^{\leq _C u_C}\subseteq \operatorname {Fl}^{\leq _C w_C}$
for all
![]() $C\in \mathcal {C}$
, and thus,
$C\in \mathcal {C}$
, and thus,
![]() $\operatorname {Fl}^{\leq \overline {u}}\subseteq \operatorname {Fl}^{\leq \overline {w}} $
. In the second case, the assertion follows from Lemma 2.3.2(b).
$\operatorname {Fl}^{\leq \overline {u}}\subseteq \operatorname {Fl}^{\leq \overline {w}} $
. In the second case, the assertion follows from Lemma 2.3.2(b).
We will need the following ‘effective’ version of Lemma 2.3.4.
Lemma 2.3.5.
(a) There exists
![]() $r'\in \mathbb N$
such that for every
$r'\in \mathbb N$
such that for every
![]() $m\in \mathbb N$
and every two
$m\in \mathbb N$
and every two
![]() $(m+r')$
-regular admissible tuples
$(m+r')$
-regular admissible tuples
![]() $\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
, there exist m-regular admissible tuples
$\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
, there exist m-regular admissible tuples
![]() $\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
$\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
![]() $\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}=\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
$\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}=\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
(b) There exists
![]() $r'\in \mathbb N$
such that for every
$r'\in \mathbb N$
such that for every
![]() $m,d\in \mathbb N$
, every
$m,d\in \mathbb N$
, every
![]() $(m+2d+r')$
-regular admissible tuple
$(m+2d+r')$
-regular admissible tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
and every
![]() $u\in \widetilde {W}$
, satisfying
$u\in \widetilde {W}$
, satisfying
![]() $\langle \psi ,\pi (u)\rangle =\pi (\overline {w})(\psi )-d$
, there exist m-regular admissible tuples
$\langle \psi ,\pi (u)\rangle =\pi (\overline {w})(\psi )-d$
, there exist m-regular admissible tuples
![]() $\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
$\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
 $$\begin{align*}\operatorname{Fl}^{\leq\overline{w}}\cap \operatorname{Fl}^{\leq_{\psi} u}=\bigcup_{t=1}^n \operatorname{Fl}^{\leq\overline{w}_t}. \end{align*}$$
$$\begin{align*}\operatorname{Fl}^{\leq\overline{w}}\cap \operatorname{Fl}^{\leq_{\psi} u}=\bigcup_{t=1}^n \operatorname{Fl}^{\leq\overline{w}_t}. \end{align*}$$
The proof is based on the following two claims:
Claim 2.3.6.
(a) For every two quasi-admissible tuples
![]() $\overline {\mu }',\overline {\mu }"\in \Lambda ^{\mathcal {C}}$
, there exists a unique maximal quasi-admissible tuple
$\overline {\mu }',\overline {\mu }"\in \Lambda ^{\mathcal {C}}$
, there exists a unique maximal quasi-admissible tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
such that
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
such that
![]() $\overline {\mu }\leq \overline {\mu }'$
and
$\overline {\mu }\leq \overline {\mu }'$
and
![]() $\overline {\mu }\leq \overline {\mu }"$
. Moreover,
$\overline {\mu }\leq \overline {\mu }"$
. Moreover,
![]() $\overline {\mu }$
is m-regular if both
$\overline {\mu }$
is m-regular if both
![]() $\overline {\mu }'$
and
$\overline {\mu }'$
and
![]() $\overline {\mu }"$
are m-regular.
$\overline {\mu }"$
are m-regular.
(b) For every
![]() $\psi \in \Psi $
,
$\psi \in \Psi $
,
![]() $m,d\in \mathbb N$
and every
$m,d\in \mathbb N$
and every
![]() $(m+2d)$
-regular quasi-admissible tuple
$(m+2d)$
-regular quasi-admissible tuple
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, the tuple
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
, the tuple
![]() $\overline {\nu }:=\overline {\mu }-d\overline {e}_{\psi }$
is m-regular.
$\overline {\nu }:=\overline {\mu }-d\overline {e}_{\psi }$
is m-regular.
Proof.
(a) Notice that
![]() $\overline {\mu }\leq \overline {\mu }'$
if and only if
$\overline {\mu }\leq \overline {\mu }'$
if and only if
![]() $\overline {\mu }(\psi )\leq \overline {\mu }'(\psi )$
for all
$\overline {\mu }(\psi )\leq \overline {\mu }'(\psi )$
for all
![]() $\psi \in \Psi $
. Thus, a maximal
$\psi \in \Psi $
. Thus, a maximal
![]() $\overline {\mu }$
satisfies
$\overline {\mu }$
satisfies
![]() $\overline {\mu }(\psi )=\min \{\overline {\mu }'(\psi ),\overline {\mu }"(\psi )\}$
for all
$\overline {\mu }(\psi )=\min \{\overline {\mu }'(\psi ),\overline {\mu }"(\psi )\}$
for all
![]() $\psi \in \Psi $
. This shows the first assertion.
$\psi \in \Psi $
. This shows the first assertion.
For the second one, choose
![]() $C\in \mathcal {C}$
, let
$C\in \mathcal {C}$
, let
![]() $\alpha _1,\ldots ,\alpha _r$
be the simple roots of C, and let
$\alpha _1,\ldots ,\alpha _r$
be the simple roots of C, and let
![]() $\psi _1,\ldots ,\psi _r$
be the corresponding fundamental weights. We want to show that
$\psi _1,\ldots ,\psi _r$
be the corresponding fundamental weights. We want to show that
![]() $\langle \alpha _j, \mu _C\rangle \geq m$
for all j. Without loss of generality, we may assume that
$\langle \alpha _j, \mu _C\rangle \geq m$
for all j. Without loss of generality, we may assume that
![]() $\overline {\mu }(\psi _j)=\overline {\mu }'(\psi _j)$
. Recall that we have
$\overline {\mu }(\psi _j)=\overline {\mu }'(\psi _j)$
. Recall that we have
![]() $\mu _C=\sum _{i=1}^r\overline {\mu }(\psi _i)\check {\alpha }_i$
and
$\mu _C=\sum _{i=1}^r\overline {\mu }(\psi _i)\check {\alpha }_i$
and
![]() $\mu ^{\prime }_C=\sum _{i=1}^r\overline {\mu }'(\psi _i)\check {\alpha }_i$
. Since
$\mu ^{\prime }_C=\sum _{i=1}^r\overline {\mu }'(\psi _i)\check {\alpha }_i$
. Since
![]() $\langle \alpha _j,\check {\alpha }_j\rangle =2>0, \overline {\mu }(\psi _j)=\overline {\mu }'(\psi _j)$
and
$\langle \alpha _j,\check {\alpha }_j\rangle =2>0, \overline {\mu }(\psi _j)=\overline {\mu }'(\psi _j)$
and
![]() $\langle \alpha _j,\check {\alpha }_i\rangle \leq 0, \overline {\mu }(\psi _i)\leq \overline {\mu }'(\psi _i)$
for all
$\langle \alpha _j,\check {\alpha }_i\rangle \leq 0, \overline {\mu }(\psi _i)\leq \overline {\mu }'(\psi _i)$
for all
![]() $i\neq j$
, we conclude that
$i\neq j$
, we conclude that
![]() $\langle \alpha _j,\mu _C\rangle \geq \langle \alpha _j,\mu ^{\prime }_C\rangle \geq m$
.
$\langle \alpha _j,\mu _C\rangle \geq \langle \alpha _j,\mu ^{\prime }_C\rangle \geq m$
.
(b) Let
![]() $C, \alpha _i$
and
$C, \alpha _i$
and
![]() $\psi _i$
be as in the proof of part (a). Then for every j, the pairing
$\psi _i$
be as in the proof of part (a). Then for every j, the pairing
![]() $\langle \alpha _j, \mu _C\rangle $
equals
$\langle \alpha _j, \mu _C\rangle $
equals
![]() $\langle \alpha _j, \mu _C\rangle -d\langle \alpha _j,\check {\alpha }_i\rangle \geq (m+2d)-2d=m$
, if
$\langle \alpha _j, \mu _C\rangle -d\langle \alpha _j,\check {\alpha }_i\rangle \geq (m+2d)-2d=m$
, if
![]() $\psi =\psi _i$
, and equals
$\psi =\psi _i$
, and equals
![]() $\langle \alpha _j, \mu _C\rangle \geq m+2d\geq m$
, otherwise.
$\langle \alpha _j, \mu _C\rangle \geq m+2d\geq m$
, otherwise.
Claim 2.3.7.
(a) There exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $C\in \mathcal {C}$
, every root
$C\in \mathcal {C}$
, every root
![]() $\alpha \in \Phi _C$
with corresponding fundamental weight
$\alpha \in \Phi _C$
with corresponding fundamental weight
![]() $\psi \in \Psi _C$
, and every elements
$\psi \in \Psi _C$
, and every elements
![]() $w,w'\in \widetilde {W}$
with
$w,w'\in \widetilde {W}$
with
![]() $w\leq _C w'$
, we have either
$w\leq _C w'$
, we have either
![]() $\check {\alpha }w\leq _{C}w'$
or
$\check {\alpha }w\leq _{C}w'$
or
![]() $\langle \psi ,\pi (w')-\pi (w)\rangle \leq r$
.
$\langle \psi ,\pi (w')-\pi (w)\rangle \leq r$
.
(b) There exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $\psi \in \Psi $
,
$\psi \in \Psi $
,
![]() $\alpha \in \Phi $
and
$\alpha \in \Phi $
and
![]() $w,w'\in \widetilde {W}$
such that
$w,w'\in \widetilde {W}$
such that
![]() $w\leq _{\psi } w'$
and
$w\leq _{\psi } w'$
and
![]() $\langle \psi ,\alpha \rangle =1$
, we have either
$\langle \psi ,\alpha \rangle =1$
, we have either
![]() $\check {\alpha }w\leq _{\psi }w'$
or
$\check {\alpha }w\leq _{\psi }w'$
or
![]() $\langle \psi ,\pi (w')-\pi (w)\rangle \leq r$
.
$\langle \psi ,\pi (w')-\pi (w)\rangle \leq r$
.
Proof. Since W is finite, in both cases (a) and (b), it will be enough to find r to satisfy the condition for
![]() $w\in \Lambda u$
and
$w\in \Lambda u$
and
![]() $w'\in \Lambda u'$
, where
$w'\in \Lambda u'$
, where
![]() $u,u'\in W$
are fixed. Moreover, using Remark 1.2.4(a)(ii), we may assume that
$u,u'\in W$
are fixed. Moreover, using Remark 1.2.4(a)(ii), we may assume that
![]() $w'=u'$
. Similarly, we fix
$w'=u'$
. Similarly, we fix
![]() $C\in \mathcal {C}$
, and
$C\in \mathcal {C}$
, and
![]() $\alpha \in \Phi _C$
with corresponding
$\alpha \in \Phi _C$
with corresponding
![]() $\psi \in \Psi _C$
.
$\psi \in \Psi _C$
.
In the case (a), we consider the set
![]() $S_C$
of all
$S_C$
of all
![]() $\mu \in \Lambda $
such that
$\mu \in \Lambda $
such that
![]() $\mu u\leq _C u'$
. Then, by Corollary 1.2.3(b), every
$\mu u\leq _C u'$
. Then, by Corollary 1.2.3(b), every
![]() $\mu \in S_C$
satisfies
$\mu \in S_C$
satisfies
![]() $\mu =\pi (\mu u)\leq _C \pi (u')=0$
; hence, the set
$\mu =\pi (\mu u)\leq _C \pi (u')=0$
; hence, the set
![]() $S_C^{\max }$
of all maximal elements of
$S_C^{\max }$
of all maximal elements of
![]() $S_C$
with respect to the ordering
$S_C$
with respect to the ordering
![]() $\leq _C$
is finite and nonempty. We take
$\leq _C$
is finite and nonempty. We take
![]() $r\in \mathbb N$
to be the maximum of all
$r\in \mathbb N$
to be the maximum of all
![]() $-\langle \psi ,\mu \rangle $
taken over all
$-\langle \psi ,\mu \rangle $
taken over all
![]() $\mu \in S_{C}^{\max }$
.
$\mu \in S_{C}^{\max }$
.
In the case (b), we consider the set
![]() $S_{\psi }$
of all
$S_{\psi }$
of all
![]() $\mu '\in \Lambda $
such that
$\mu '\in \Lambda $
such that
![]() $\mu ' u\leq _{\psi } u'$
. Then every
$\mu ' u\leq _{\psi } u'$
. Then every
![]() $\mu '\in S_{\psi }$
satisfies
$\mu '\in S_{\psi }$
satisfies
![]() $\mu '\leq _{\psi }0$
; hence, the set
$\mu '\leq _{\psi }0$
; hence, the set
![]() $S_{\psi }^{\max }$
of all maximal elements of
$S_{\psi }^{\max }$
of all maximal elements of
![]() $S_{\psi }$
with respect to the ordering
$S_{\psi }$
with respect to the ordering
![]() $\leq _{\psi }$
is a finite and nonempty union of cosets of
$\leq _{\psi }$
is a finite and nonempty union of cosets of
![]() $\Lambda ^{\psi }:=\{\mu \in \Lambda \,|\,\langle \psi ,\mu \rangle =0\}$
. We take
$\Lambda ^{\psi }:=\{\mu \in \Lambda \,|\,\langle \psi ,\mu \rangle =0\}$
. We take
![]() $r\in \mathbb N$
to be the maximum of all
$r\in \mathbb N$
to be the maximum of all
![]() $-\langle \psi ,\mu '\rangle $
, taken over all
$-\langle \psi ,\mu '\rangle $
, taken over all
![]() $\mu '\in S^{\max }_{\psi }$
.
$\mu '\in S^{\max }_{\psi }$
.
Then in both cases, r satisfies the required property. Indeed, assume that
![]() $\mu \in S_C$
(resp.
$\mu \in S_C$
(resp.
![]() $\mu \in S_{\psi }$
) while
$\mu \in S_{\psi }$
) while
![]() $\check {\alpha }\mu \notin S_C$
, (resp.
$\check {\alpha }\mu \notin S_C$
, (resp.
![]() $\check {\alpha }\mu \notin S_C$
), and we want to check that
$\check {\alpha }\mu \notin S_C$
), and we want to check that
![]() $\langle \psi ,\mu \rangle \geq -r$
. Choose any
$\langle \psi ,\mu \rangle \geq -r$
. Choose any
![]() $\mu '\in S_C^{\max }$
(resp.
$\mu '\in S_C^{\max }$
(resp.
![]() $\mu '\in S_{\psi }^{\max }$
) to be such that
$\mu '\in S_{\psi }^{\max }$
) to be such that
![]() $\mu '\geq _C\mu $
(resp.
$\mu '\geq _C\mu $
(resp.
![]() $\mu '\geq _{\psi }\mu $
.) Then
$\mu '\geq _{\psi }\mu $
.) Then
![]() $\mu '-\mu =\sum _{\beta \in \Delta _C}m_{\beta }\check {\beta }$
and
$\mu '-\mu =\sum _{\beta \in \Delta _C}m_{\beta }\check {\beta }$
and
![]() $m_{\alpha }\geq 0$
. Since
$m_{\alpha }\geq 0$
. Since
![]() $\check {\alpha }\mu \notin S_C$
(resp.
$\check {\alpha }\mu \notin S_C$
(resp.
![]() $\check {\alpha }\mu \notin S_{\psi }$
), we have
$\check {\alpha }\mu \notin S_{\psi }$
), we have
![]() $m_{\alpha }=0$
; thus,
$m_{\alpha }=0$
; thus,
![]() $\langle \psi ,\mu \rangle =\langle \psi ,\mu '\rangle \geq -r$
.
$\langle \psi ,\mu \rangle =\langle \psi ,\mu '\rangle \geq -r$
.
Now we are ready to prove Lemma 2.3.5.
2.3.8.
Proof of Lemma 2.3.5.
(a) Let
![]() $r\in \mathbb N$
be as in Claim 2.3.7(a). We will show that
$r\in \mathbb N$
be as in Claim 2.3.7(a). We will show that
![]() $r':=2r$
satisfies the required property. Let
$r':=2r$
satisfies the required property. Let
![]() $\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
be
$\overline {w}',\overline {w}"\in \widetilde {W}^{\mathcal {C}}$
be
![]() $(m+r')$
-regular admissible tuples. Then, by Lemma 2.3.4, there exist admissible tuples
$(m+r')$
-regular admissible tuples. Then, by Lemma 2.3.4, there exist admissible tuples
![]() $\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
$\overline {w}_1\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}} $
such that
![]() $\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}=\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
$\operatorname {Fl}^{\leq \overline {w}'}\cap \operatorname {Fl}^{\leq \overline {w}"}=\bigcup _{t=1}^n \operatorname {Fl}^{\leq \overline {w}_t}$
.
Using Corollary 2.1.7(b), one can assume that each
![]() $\overline {w}_t$
is a maximal admissible tuple, satisfying
$\overline {w}_t$
is a maximal admissible tuple, satisfying
![]() $\overline {w}_t\leq \overline {w}',\overline {w}"$
, and we have to show that each
$\overline {w}_t\leq \overline {w}',\overline {w}"$
, and we have to show that each
![]() $\overline {w}_t$
is m-regular.
$\overline {w}_t$
is m-regular.
Let
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
be a maximal quasi-admissible tuple, satisfying
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
be a maximal quasi-admissible tuple, satisfying
![]() $\overline {w}\leq \overline {w}',\overline {w}"$
. It is enough to show that such a
$\overline {w}\leq \overline {w}',\overline {w}"$
. It is enough to show that such a
![]() $\overline {w}$
is m-regular. Indeed, Lemma 1.3.10(a) then would imply that
$\overline {w}$
is m-regular. Indeed, Lemma 1.3.10(a) then would imply that
![]() $\overline {w}$
is admissible.
$\overline {w}$
is admissible.
Set
![]() $\overline {\mu }':=\pi (\overline {w}')$
, and
$\overline {\mu }':=\pi (\overline {w}')$
, and
![]() $\overline {\mu }":=\pi (\overline {w}")$
, and let
$\overline {\mu }":=\pi (\overline {w}")$
, and let
![]() $\overline {\mu }$
be the maximal tuple such that
$\overline {\mu }$
be the maximal tuple such that
![]() $\overline {\mu }\leq \overline {\mu }'$
and
$\overline {\mu }\leq \overline {\mu }'$
and
![]() $\overline {\mu }\leq \overline {\mu }"$
. Then
$\overline {\mu }\leq \overline {\mu }"$
. Then
![]() $\overline {\mu }$
is
$\overline {\mu }$
is
![]() $(m+r')$
-regular by Claim 2.3.6(a), and
$(m+r')$
-regular by Claim 2.3.6(a), and
![]() $\pi (\overline {w})\leq \overline {\mu }$
by Corollary 1.2.3(b).
$\pi (\overline {w})\leq \overline {\mu }$
by Corollary 1.2.3(b).
It is enough to show that
![]() $\pi (\overline {w})(\psi )\geq \overline {\mu }(\psi )-r$
for every
$\pi (\overline {w})(\psi )\geq \overline {\mu }(\psi )-r$
for every
![]() $\psi \in \Psi $
. Indeed, if this is shown, then for every
$\psi \in \Psi $
. Indeed, if this is shown, then for every
![]() $C\in \mathcal {C}$
with simple roots
$C\in \mathcal {C}$
with simple roots
![]() $\alpha _1,\ldots ,\alpha _r$
, we have
$\alpha _1,\ldots ,\alpha _r$
, we have
![]() $\pi (w_C)=\mu _C-\sum _i r_i\check {\alpha }_i$
and
$\pi (w_C)=\mu _C-\sum _i r_i\check {\alpha }_i$
and
![]() $0\leq r_i\leq r$
for all i. Then
$0\leq r_i\leq r$
for all i. Then
![]() $\langle \alpha _i,\pi (w_C)\rangle \geq \langle \alpha _i,\mu _C\rangle -2r_i\geq (m+2r)-2r=m$
. Thus,
$\langle \alpha _i,\pi (w_C)\rangle \geq \langle \alpha _i,\mu _C\rangle -2r_i\geq (m+2r)-2r=m$
. Thus,
![]() $\overline {w}$
is m-regular.
$\overline {w}$
is m-regular.
Assume that there exists
![]() $\psi \in \Psi $
such that
$\psi \in \Psi $
such that
![]() $\pi (\overline {w})(\psi )<\overline {\mu }(\psi )-r$
. Consider the quasi-admissible tuple
$\pi (\overline {w})(\psi )<\overline {\mu }(\psi )-r$
. Consider the quasi-admissible tuple
![]() $\overline {e}_{\psi }$
defined by
$\overline {e}_{\psi }$
defined by
![]() $\overline {e}_{\psi }(\psi '):=\delta _{\psi ,\psi '}$
(see Section 1.3.4(d)). Then the quasi-admissible tuple
$\overline {e}_{\psi }(\psi '):=\delta _{\psi ,\psi '}$
(see Section 1.3.4(d)). Then the quasi-admissible tuple
![]() $\overline {e}_{\psi }\overline {w}$
(see Section 1.3.5(c)) satisfies identities
$\overline {e}_{\psi }\overline {w}$
(see Section 1.3.5(c)) satisfies identities
![]() $(\overline {e}_{\psi }\overline {w})_C=w_C$
if
$(\overline {e}_{\psi }\overline {w})_C=w_C$
if
![]() $\psi \notin \Psi _C$
, and
$\psi \notin \Psi _C$
, and
![]() $(\overline {e}_{\psi }\overline {w})_C=\check {\alpha }\overline {w}_C$
if
$(\overline {e}_{\psi }\overline {w})_C=\check {\alpha }\overline {w}_C$
if
![]() $\psi \in \Psi _C$
and
$\psi \in \Psi _C$
and
![]() $\alpha \in \Delta _C$
corresponds to
$\alpha \in \Delta _C$
corresponds to
![]() $\psi $
.
$\psi $
.
Since
![]() $\overline {w}\leq \overline {w}'$
and
$\overline {w}\leq \overline {w}'$
and
![]() $\overline {w}\leq \overline {w}"$
, the assumption
$\overline {w}\leq \overline {w}"$
, the assumption
![]() $\pi (\overline {w})(\psi )<\overline {\mu }(\psi )-r$
together with Claim 2.3.7(a) implies that
$\pi (\overline {w})(\psi )<\overline {\mu }(\psi )-r$
together with Claim 2.3.7(a) implies that
![]() $\overline {e}_{\psi }\overline {w}\leq \overline {w}'$
and
$\overline {e}_{\psi }\overline {w}\leq \overline {w}'$
and
![]() $\overline {e}_{\psi }\overline {w}\leq \overline {w}"$
. Since
$\overline {e}_{\psi }\overline {w}\leq \overline {w}"$
. Since
![]() $\overline {w}<\overline {e}_{\psi }\overline {w}$
, this contradicts the maximality of
$\overline {w}<\overline {e}_{\psi }\overline {w}$
, this contradicts the maximality of
![]() $\overline {w}$
.
$\overline {w}$
.
(b) The proof is similar to that of part (a). Let
![]() $r\in \mathbb N$
to satisfy both Claim 2.3.7(a),(b), and set
$r\in \mathbb N$
to satisfy both Claim 2.3.7(a),(b), and set
![]() $r':=2r$
. Assume that
$r':=2r$
. Assume that
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
is
![]() $(m+2d+r')$
-regular,
$(m+2d+r')$
-regular,
![]() $u\in \widetilde {W}$
satisfies
$u\in \widetilde {W}$
satisfies
![]() $\langle \psi ,\pi (u)\rangle =\pi (\overline {w})(\psi )-d$
, and let
$\langle \psi ,\pi (u)\rangle =\pi (\overline {w})(\psi )-d$
, and let
![]() $\overline {w}'$
be a maximal quasi-admissible tuple satisfying
$\overline {w}'$
be a maximal quasi-admissible tuple satisfying
![]() $\overline {w}'\leq \overline {w}$
and
$\overline {w}'\leq \overline {w}$
and
![]() $\overline {w}^{\prime }_{\psi }\leq _{\psi }u$
.
$\overline {w}^{\prime }_{\psi }\leq _{\psi }u$
.
Using Lemma 2.3.4(b) and Lemma 2.3.2(b), and arguing as in part (a), it is enough to show that
![]() $\pi (\overline {w})(\psi ')\geq \overline {\mu }(\psi ')-r$
for every
$\pi (\overline {w})(\psi ')\geq \overline {\mu }(\psi ')-r$
for every
![]() $\psi '\in \Psi $
.
$\psi '\in \Psi $
.
Assume that there exists
![]() $\psi '\in \Psi $
such that
$\psi '\in \Psi $
such that
![]() $\pi (\overline {w})(\psi ')<\overline {\mu }(\psi ')-r$
, and let
$\pi (\overline {w})(\psi ')<\overline {\mu }(\psi ')-r$
, and let
![]() $\overline {e}_{\psi '}\overline {w}$
be as in part (a). Again, to get a contradiction, it is enough to show that
$\overline {e}_{\psi '}\overline {w}$
be as in part (a). Again, to get a contradiction, it is enough to show that
![]() $\overline {e}_{\psi '}\overline {w}\leq \overline {w}'$
and
$\overline {e}_{\psi '}\overline {w}\leq \overline {w}'$
and
![]() $(\overline {e}_{\psi '}\overline {w})_{\psi }\leq _{\psi } u$
. The proof of the first inequality is identical to that of part (a). Next, if
$(\overline {e}_{\psi '}\overline {w})_{\psi }\leq _{\psi } u$
. The proof of the first inequality is identical to that of part (a). Next, if
![]() $\psi '\neq \psi $
, then
$\psi '\neq \psi $
, then
![]() $(\overline {e}_{\psi '}\overline {w})_{\psi }=\overline {w}_{\psi }\leq _{\psi } u$
by assumption. Finally, if
$(\overline {e}_{\psi '}\overline {w})_{\psi }=\overline {w}_{\psi }\leq _{\psi } u$
by assumption. Finally, if
![]() $\psi '=\psi $
, the inequality
$\psi '=\psi $
, the inequality
![]() $(\overline {e}_{\psi '}\overline {w})_{\psi }\leq _{\psi } u$
follows from Claim 2.3.7(b).
$(\overline {e}_{\psi '}\overline {w})_{\psi }\leq _{\psi } u$
follows from Claim 2.3.7(b).
Lemma 2.3.9. There exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $m\in \mathbb N$
and every
$m\in \mathbb N$
and every
![]() $(m+r)$
-regular
$(m+r)$
-regular
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, there exists an m-regular
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, there exists an m-regular
![]() $\overline {x}\in \Lambda ^{\mathcal {C}}$
such that
$\overline {x}\in \Lambda ^{\mathcal {C}}$
such that
![]() $\operatorname {Fl}^{\leq '\overline {x}}\subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
$\operatorname {Fl}^{\leq '\overline {x}}\subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
Proof. Choose any
![]() $\mu \in \Lambda \cap C_0$
, let
$\mu \in \Lambda \cap C_0$
, let
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the admissible tuple defined by
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the admissible tuple defined by
![]() $\mu _{u(C_0)}:=u(\mu )$
(see Section 1.3.5(a)), and let r be the maximum of the
$\mu _{u(C_0)}:=u(\mu )$
(see Section 1.3.5(a)), and let r be the maximum of the
![]() $\langle \alpha ,\mu \rangle $
’s, where
$\langle \alpha ,\mu \rangle $
’s, where
![]() $\alpha $
runs over all of
$\alpha $
runs over all of
![]() $\Delta _{C_0}$
. We claim that this r satisfies the required property.
$\Delta _{C_0}$
. We claim that this r satisfies the required property.
Namely, to every
![]() $(m+r)$
-regular admissible tuple
$(m+r)$
-regular admissible tuple
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, we associate a quasi-admissible tuple
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
, we associate a quasi-admissible tuple
![]() $\overline {x}:=\overline {\mu }^{-1}\pi (\overline {w})$
(see Section 1.3.4(b)). We claim that
$\overline {x}:=\overline {\mu }^{-1}\pi (\overline {w})$
(see Section 1.3.4(b)). We claim that
![]() $\overline {x}$
is m-regular, and
$\overline {x}$
is m-regular, and
![]() $\operatorname {Fl}^{\leq '\overline {x}}\subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
$\operatorname {Fl}^{\leq '\overline {x}}\subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
To show that
![]() $\overline {x}$
is m-regular, we note that for every
$\overline {x}$
is m-regular, we note that for every
![]() $u\in W$
,
$u\in W$
,
![]() $C=u(C_0)\in \mathcal {C}$
and
$C=u(C_0)\in \mathcal {C}$
and
![]() $\alpha \in \Delta _C$
, we have
$\alpha \in \Delta _C$
, we have
![]() $\langle \alpha ,x_C\rangle =\langle \alpha ,\pi (w_C)\rangle -\langle \alpha ,u(\mu )\rangle \geq (m+r)-r=m$
.
$\langle \alpha ,x_C\rangle =\langle \alpha ,\pi (w_C)\rangle -\langle \alpha ,u(\mu )\rangle \geq (m+r)-r=m$
.
Next, we observe that ![]() (use Corollary 2.1.7(f)). So it remains to show that
(use Corollary 2.1.7(f)). So it remains to show that ![]() or, what is the same,
or, what is the same,
![]() $x_C u\leq _C w_C$
for each
$x_C u\leq _C w_C$
for each
![]() $C=u(C_0)\in \mathcal {C}$
. Unwinding the definitions and using Section 1.2.4(a), it is enough to show that for every
$C=u(C_0)\in \mathcal {C}$
. Unwinding the definitions and using Section 1.2.4(a), it is enough to show that for every
![]() $u\in W$
, we have
$u\in W$
, we have
![]() $1\leq _{C_0}\mu u$
. By Corollary 1.2.6, it remains to show that
$1\leq _{C_0}\mu u$
. By Corollary 1.2.6, it remains to show that
![]() $\mu u\in \widetilde {W}\cap C_0$
; that is, for every
$\mu u\in \widetilde {W}\cap C_0$
; that is, for every
![]() $\alpha \in \Phi _{C_0}$
we have
$\alpha \in \Phi _{C_0}$
we have
![]() $(\mu u)^{-1}(\alpha )>0$
. But
$(\mu u)^{-1}(\alpha )>0$
. But
![]() $(\mu u)^{-1}(\alpha )=u^{-1}(\mu ^{-1}(\alpha ))=(u^{-1}(\alpha ),\langle \alpha ,\mu \rangle )>0$
because
$(\mu u)^{-1}(\alpha )=u^{-1}(\mu ^{-1}(\alpha ))=(u^{-1}(\alpha ),\langle \alpha ,\mu \rangle )>0$
because
![]() $\langle \alpha ,\mu \rangle>0$
.
$\langle \alpha ,\mu \rangle>0$
.
Lemma 2.3.10. There exists
![]() $r\in \mathbb N$
such that for every
$r\in \mathbb N$
such that for every
![]() $m\in \mathbb Z$
and every
$m\in \mathbb Z$
and every
![]() $(m+r)$
-regular tuple
$(m+r)$
-regular tuple
![]() $\overline {x}\in \Lambda ^{\mathcal {C}}$
, there exists a sequence
$\overline {x}\in \Lambda ^{\mathcal {C}}$
, there exists a sequence
![]() $\overline {x}=\overline {x}_0\leq \overline {x}_1\leq \ldots $
in
$\overline {x}=\overline {x}_0\leq \overline {x}_1\leq \ldots $
in
![]() $\Lambda ^{\mathcal {C}}$
such that sequence
$\Lambda ^{\mathcal {C}}$
such that sequence
![]() $\{\overline {x}_i(\psi )\}_i$
tends to infinity for all
$\{\overline {x}_i(\psi )\}_i$
tends to infinity for all
![]() $\psi \in \Psi $
, each
$\psi \in \Psi $
, each
![]() $\overline {x}_i$
is m-regular, and
$\overline {x}_i$
is m-regular, and
![]() $\overline {x}_i=\overline {x}_{i-1}+\overline {e}_{\psi _{i}}$
for some
$\overline {x}_i=\overline {x}_{i-1}+\overline {e}_{\psi _{i}}$
for some
![]() $\psi _i\in \Psi $
and all i.
$\psi _i\in \Psi $
and all i.
Proof. Choose
![]() $\mu \in \Lambda \cap C_0$
, and let
$\mu \in \Lambda \cap C_0$
, and let
![]() $\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the tuple
$\overline {\mu }\in \Lambda ^{\mathcal {C}}$
be the tuple
![]() $\mu _{u(C_0)}:=u(\mu )$
from Section 1.3.5(a). Then
$\mu _{u(C_0)}:=u(\mu )$
from Section 1.3.5(a). Then
![]() $\overline {\mu }$
is regular and admissible. Let
$\overline {\mu }$
is regular and admissible. Let
![]() $\overline {y}\in \mathbb N^{\Psi }$
be the corresponding tuple (see Section 1.3.4(a) and Lemma 1.3.10(b)). Choose a sequence
$\overline {y}\in \mathbb N^{\Psi }$
be the corresponding tuple (see Section 1.3.4(a) and Lemma 1.3.10(b)). Choose a sequence
![]() $\overline {y}_0=0,\overline {y}_1,\ldots ,\overline {y}_n=\overline {y}$
in
$\overline {y}_0=0,\overline {y}_1,\ldots ,\overline {y}_n=\overline {y}$
in
![]() $\mathbb N^{\Psi }$
such that
$\mathbb N^{\Psi }$
such that
![]() $\overline {y}_i-\overline {y}_{i-1}=\overline {e}_{\psi _i}$
for all i and some
$\overline {y}_i-\overline {y}_{i-1}=\overline {e}_{\psi _i}$
for all i and some
![]() $\psi _i\in \Psi $
, and continue it to all i by the rule
$\psi _i\in \Psi $
, and continue it to all i by the rule
![]() $ \overline {y}_{i+n}:=\overline {y}_i+\overline {y}$
.
$ \overline {y}_{i+n}:=\overline {y}_i+\overline {y}$
.
Define r to be the maximum of the
![]() $-\langle (y_i)_C,\alpha \rangle $
’s, taken over
$-\langle (y_i)_C,\alpha \rangle $
’s, taken over
![]() $i=1,\ldots ,n$
,
$i=1,\ldots ,n$
,
![]() $C\in \mathcal {C}$
and
$C\in \mathcal {C}$
and
![]() $\alpha \in \Delta _C$
. Then the sequence
$\alpha \in \Delta _C$
. Then the sequence
![]() $\overline {x}_i:=\overline {x}+\overline {y}_i$
satisfies the required property.
$\overline {x}_i:=\overline {x}+\overline {y}_i$
satisfies the required property.
2.4 Stratification of the affine flag variety
Notation 2.4.1.
(a) Let k, K and
![]() $\mathcal {O}$
be as in Section 2.1.1, let G be a connected reductive group over k, and let
$\mathcal {O}$
be as in Section 2.1.1, let G be a connected reductive group over k, and let
![]() $T\subseteq G$
be a maximal torus.
$T\subseteq G$
be a maximal torus.
(b) Let
![]() $G^{\operatorname {sc}}$
be the simply connected covering of the derived group of G, and let
$G^{\operatorname {sc}}$
be the simply connected covering of the derived group of G, and let
![]() $T_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
be the corresponding maximal torus – that is, the pullback of
$T_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
be the corresponding maximal torus – that is, the pullback of
![]() $T\subseteq G$
. Let
$T\subseteq G$
. Let
![]() $\Phi $
be the root system
$\Phi $
be the root system
![]() $\Phi (G,T)=\Phi (G^{\operatorname {sc}},T_{G^{\operatorname {sc}}})$
of
$\Phi (G,T)=\Phi (G^{\operatorname {sc}},T_{G^{\operatorname {sc}}})$
of
![]() $G^{\operatorname {sc}}$
, let
$G^{\operatorname {sc}}$
, let
![]() $\Psi $
be the set of fundamental weights of
$\Psi $
be the set of fundamental weights of
![]() $G^{\operatorname {sc}}$
, and let
$G^{\operatorname {sc}}$
, and let
![]() $\widetilde {W}$
be the affine Weyl group of
$\widetilde {W}$
be the affine Weyl group of
![]() $G^{\operatorname {sc}}$
.
$G^{\operatorname {sc}}$
.
(c) Choose an Iwahori subgroup scheme
![]() $I\subseteq LG$
as in Section 2.1.2, set
$I\subseteq LG$
as in Section 2.1.2, set
![]() $I^{\operatorname {sc}}:=I\cap L(G^{\operatorname {sc}})\subseteq L(G^{\operatorname {sc}})$
, and let
$I^{\operatorname {sc}}:=I\cap L(G^{\operatorname {sc}})\subseteq L(G^{\operatorname {sc}})$
, and let
![]() $\operatorname {Fl}=\operatorname {Fl}_{G^{\operatorname {sc}}}:=L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
be the affine flag variety of
$\operatorname {Fl}=\operatorname {Fl}_{G^{\operatorname {sc}}}:=L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
be the affine flag variety of
![]() $G^{\operatorname {sc}}$
.
$G^{\operatorname {sc}}$
.
Notation 2.4.2. In the situation of Section 2.4.1, fix
![]() $\psi \in \Psi \subseteq X^*(T_{G^{\operatorname {sc}}})$
.
$\psi \in \Psi \subseteq X^*(T_{G^{\operatorname {sc}}})$
.
(a) Let
![]() $P_{\psi }, M_{\psi }, U_{\psi }, M^{\operatorname {sc}}_{\psi }$
and
$P_{\psi }, M_{\psi }, U_{\psi }, M^{\operatorname {sc}}_{\psi }$
and
![]() $P^{\operatorname {sc}}_{\psi }$
be as in Section 2.3.1(b). Notice that groups
$P^{\operatorname {sc}}_{\psi }$
be as in Section 2.3.1(b). Notice that groups
![]() $M^{\operatorname {sc}}_{\psi }, U_{\psi }$
and
$M^{\operatorname {sc}}_{\psi }, U_{\psi }$
and
![]() $P^{\operatorname {sc}}_{\psi }$
would not change if we replace group G by
$P^{\operatorname {sc}}_{\psi }$
would not change if we replace group G by
![]() $G^{\operatorname {sc}}$
.
$G^{\operatorname {sc}}$
.
(b) Note that
![]() $I_{M_{\psi }}:=I\cap L(M_{\psi })\subseteq L(M_{\psi })$
is an Iwahori subgroup scheme, let
$I_{M_{\psi }}:=I\cap L(M_{\psi })\subseteq L(M_{\psi })$
is an Iwahori subgroup scheme, let
![]() $I_{M^{\operatorname {sc}}_{\psi }}\subseteq L(M^{\operatorname {sc}}_{\psi })$
be the preimage of
$I_{M^{\operatorname {sc}}_{\psi }}\subseteq L(M^{\operatorname {sc}}_{\psi })$
be the preimage of
![]() $I_{M_{\psi }}\subseteq L(M_{\psi })$
, and set
$I_{M_{\psi }}\subseteq L(M_{\psi })$
, and set
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}:=L(M^{\operatorname {sc}}_{\psi })/I_{M^{\operatorname {sc}}_{\psi }}$
.
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}:=L(M^{\operatorname {sc}}_{\psi })/I_{M^{\operatorname {sc}}_{\psi }}$
.
(c) As in Section 2.3.1(b), we have a natural homomorphism
![]() $P^{\operatorname {sc}}_{\psi }\to G^{\operatorname {sc}}$
; thus, the loop group
$P^{\operatorname {sc}}_{\psi }\to G^{\operatorname {sc}}$
; thus, the loop group
![]() $L(P^{\operatorname {sc}}_{\psi })$
acts on
$L(P^{\operatorname {sc}}_{\psi })$
acts on
![]() $\operatorname {Fl}$
. For every
$\operatorname {Fl}$
. For every
![]() $w\in \widetilde {W}$
, we denote by
$w\in \widetilde {W}$
, we denote by
![]() $\operatorname {Fl}^{\leq _{\psi }w}\subseteq \operatorname {Fl}$
the closure of the
$\operatorname {Fl}^{\leq _{\psi }w}\subseteq \operatorname {Fl}$
the closure of the
![]() $L(P^{\operatorname {sc}}_{\psi })$
-orbit
$L(P^{\operatorname {sc}}_{\psi })$
-orbit
![]() $L(P^{\operatorname {sc}}_{\psi })w\subseteq \operatorname {Fl}$
.
$L(P^{\operatorname {sc}}_{\psi })w\subseteq \operatorname {Fl}$
.
(d) As in Section 2.1.1, we have an equality
![]() $\Lambda =X_*(T_{G^{\operatorname {sc}}})$
. As in Section 1.1.3(b), the coweight
$\Lambda =X_*(T_{G^{\operatorname {sc}}})$
. As in Section 1.1.3(b), the coweight
![]() $\check {\psi }$
belongs to
$\check {\psi }$
belongs to
![]() $\Lambda _{\mathbb Q}$
. We denote by
$\Lambda _{\mathbb Q}$
. We denote by
![]() $T_{\psi }\subseteq T_{G^{\operatorname {sc}}}$
the one-dimensional subtorus such that
$T_{\psi }\subseteq T_{G^{\operatorname {sc}}}$
the one-dimensional subtorus such that
![]() $X_*(T_{\psi })\subseteq \Lambda $
equals
$X_*(T_{\psi })\subseteq \Lambda $
equals
![]() $(\mathbb Z\check {\psi })\cap \Lambda \subseteq \Lambda _{\mathbb Q}$
.
$(\mathbb Z\check {\psi })\cap \Lambda \subseteq \Lambda _{\mathbb Q}$
.
(e) Alternatively,
![]() $T_{\psi }$
can be defined as the connected center of the Levi subgroup
$T_{\psi }$
can be defined as the connected center of the Levi subgroup
![]() $(M_{\psi })_{G^{\operatorname {sc}}}$
of
$(M_{\psi })_{G^{\operatorname {sc}}}$
of
![]() $G^{\operatorname {sc}}$
, where
$G^{\operatorname {sc}}$
, where
![]() $(M_{\psi })_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
is the pullback of
$(M_{\psi })_{G^{\operatorname {sc}}}\subseteq G^{\operatorname {sc}}$
is the pullback of
![]() $M_{\psi }\subseteq G$
.
$M_{\psi }\subseteq G$
.
2.4.3. Stratification
(a) For each
![]() $\nu \in \widetilde {W}_{\psi }$
, we set
$\nu \in \widetilde {W}_{\psi }$
, we set
![]() $Z_{\nu }:=\operatorname {Fl}^{\leq _{\psi }\nu }\smallsetminus \bigcup _{\nu '<_{\psi }\nu }\operatorname {Fl}^{\leq _{\psi }\nu '}$
. Then each
$Z_{\nu }:=\operatorname {Fl}^{\leq _{\psi }\nu }\smallsetminus \bigcup _{\nu '<_{\psi }\nu }\operatorname {Fl}^{\leq _{\psi }\nu '}$
. Then each
![]() $Z_{\nu }\subseteq \operatorname {Fl}$
is a reduced locally closed
$Z_{\nu }\subseteq \operatorname {Fl}$
is a reduced locally closed
![]() $L(P^{\operatorname {sc}}_{\psi })$
-invariant ind-subscheme. Moreover, since
$L(P^{\operatorname {sc}}_{\psi })$
-invariant ind-subscheme. Moreover, since
![]() $\widetilde {W}_{\psi }$
is a set of representatives of the set of cosets
$\widetilde {W}_{\psi }$
is a set of representatives of the set of cosets
![]() $\widetilde {W}^{\psi }\backslash \widetilde {W}$
(see Section 1.1.3(d)), the set
$\widetilde {W}^{\psi }\backslash \widetilde {W}$
(see Section 1.1.3(d)), the set
![]() $\{Z_{\nu }\}_{\nu \in \widetilde {W}_{\psi }}$
forms a stratification of
$\{Z_{\nu }\}_{\nu \in \widetilde {W}_{\psi }}$
forms a stratification of
![]() $\operatorname {Fl}$
.
$\operatorname {Fl}$
.
(b) For each
![]() $\nu \in \widetilde {W}_{\psi }$
, we consider
$\nu \in \widetilde {W}_{\psi }$
, we consider
![]() $I_{\nu }:=\nu I\nu ^{-1}\subseteq LG$
,
$I_{\nu }:=\nu I\nu ^{-1}\subseteq LG$
,
![]() $I_{P_{\psi },\nu }:=I_{\nu }\cap L(P_{\psi })\subseteq L(P_{\psi })$
and
$I_{P_{\psi },\nu }:=I_{\nu }\cap L(P_{\psi })\subseteq L(P_{\psi })$
and
![]() $I_{U_{\psi },\nu }:=I_{\nu }\cap L(U_{\psi })\subseteq L(U_{\psi })$
. Let
$I_{U_{\psi },\nu }:=I_{\nu }\cap L(U_{\psi })\subseteq L(U_{\psi })$
. Let
![]() $I_{P^{\operatorname {sc}}_{\psi },\nu }\subseteq L(P^{\operatorname {sc}}_{\psi })$
be the preimage of
$I_{P^{\operatorname {sc}}_{\psi },\nu }\subseteq L(P^{\operatorname {sc}}_{\psi })$
be the preimage of
![]() $I_{P_{\psi },\nu }\subseteq L(P_{\psi })$
, and set
$I_{P_{\psi },\nu }\subseteq L(P_{\psi })$
, and set
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }:=L(P^{\operatorname {sc}}_{\psi })/I_{P^{\operatorname {sc}}_{\psi },\nu }$
.
$\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }:=L(P^{\operatorname {sc}}_{\psi })/I_{P^{\operatorname {sc}}_{\psi },\nu }$
.
(c) Note that for each
![]() $\nu \in \widetilde {W}_{\psi }$
, we have an equality
$\nu \in \widetilde {W}_{\psi }$
, we have an equality
![]() $I_{M_{\psi }}=I_{\nu }\cap L(M_{\psi })\subseteq L(M_{\psi })$
. Therefore, isomorphism
$I_{M_{\psi }}=I_{\nu }\cap L(M_{\psi })\subseteq L(M_{\psi })$
. Therefore, isomorphism
![]() $U_{\psi }\times M_{\psi }\overset {\thicksim }{\to } P_{\psi }:(u,m)\mapsto um$
induces isomorphisms
$U_{\psi }\times M_{\psi }\overset {\thicksim }{\to } P_{\psi }:(u,m)\mapsto um$
induces isomorphisms
Moreover, the embedding and the projection
![]() $M^{\operatorname {sc}}_{\psi }\to P^{\operatorname {sc}}_{\psi }\to M^{\operatorname {sc}}_{\psi }$
induce morphisms
$M^{\operatorname {sc}}_{\psi }\to P^{\operatorname {sc}}_{\psi }\to M^{\operatorname {sc}}_{\psi }$
induce morphisms
(d) By Lemma 2.3.2(a), each
![]() $Z_{\nu }\subseteq \operatorname {Fl}$
is an
$Z_{\nu }\subseteq \operatorname {Fl}$
is an
![]() $L(P^{\operatorname {sc}}_{\psi })$
-orbit of
$L(P^{\operatorname {sc}}_{\psi })$
-orbit of
![]() $\nu \in \operatorname {Fl}$
. Moreover, the group ind-scheme
$\nu \in \operatorname {Fl}$
. Moreover, the group ind-scheme
![]() $L(P^{\operatorname {sc}}_{\psi })\simeq L(M^{\operatorname {sc}}_{\psi })\times L(U_{\psi })$
is reduced (see [Reference Beilinson and DrinfeldBD] if k is of characteristic zero, and [Reference FaltingsFa] in general), so the morphism
$L(P^{\operatorname {sc}}_{\psi })\simeq L(M^{\operatorname {sc}}_{\psi })\times L(U_{\psi })$
is reduced (see [Reference Beilinson and DrinfeldBD] if k is of characteristic zero, and [Reference FaltingsFa] in general), so the morphism
![]() $[h]\mapsto h\nu $
induces an isomorphism
$[h]\mapsto h\nu $
induces an isomorphism
![]() $\iota _{\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z_{\nu }$
.
$\iota _{\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z_{\nu }$
.
(e) Since
![]() $T_{G^{\operatorname {sc}}}$
normalizes
$T_{G^{\operatorname {sc}}}$
normalizes
![]() $P^{\operatorname {sc}}_{\psi }$
and fixes
$P^{\operatorname {sc}}_{\psi }$
and fixes
![]() $\nu \in \operatorname {Fl}$
, the orbit
$\nu \in \operatorname {Fl}$
, the orbit
![]() $Z_{\nu }\subseteq \operatorname {Fl}$
is
$Z_{\nu }\subseteq \operatorname {Fl}$
is
![]() $T_{G^{\operatorname {sc}}}$
-invariant; hence,
$T_{G^{\operatorname {sc}}}$
-invariant; hence,
![]() $Z_{\nu}$
is
$Z_{\nu}$
is
![]() $T_{\psi }$
-equivariant. Furthermore, the isomorphism
$T_{\psi }$
-equivariant. Furthermore, the isomorphism
![]() $\iota _{\nu }$
of part (d) identifies the
$\iota _{\nu }$
of part (d) identifies the
![]() $T_{\psi }$
-action on
$T_{\psi }$
-action on
![]() $Z_{\nu }$
with the
$Z_{\nu }$
with the
![]() $T_{\psi }$
-action on
$T_{\psi }$
-action on
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
given by the formula
$\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
given by the formula
![]() $t[um]=[tut^{-1}m]$
for
$t[um]=[tut^{-1}m]$
for
![]() $u\in L(U_{\psi })$
and
$u\in L(U_{\psi })$
and
![]() $m\in L(M^{\operatorname {sc}}_{\psi })$
. In particular, the isomorphism
$m\in L(M^{\operatorname {sc}}_{\psi })$
. In particular, the isomorphism
![]() $\iota _{\nu }$
induces an isomorphism
$\iota _{\nu }$
induces an isomorphism
![]() $\iota ^{T_{\psi }}_{\nu }:\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu }:[m]\mapsto m\nu $
, where
$\iota ^{T_{\psi }}_{\nu }:\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu }:[m]\mapsto m\nu $
, where
![]() $Z_{\nu }^{T_{\psi }}$
denotes the locus of
$Z_{\nu }^{T_{\psi }}$
denotes the locus of
![]() $T_{\psi }$
-fixed points.
$T_{\psi }$
-fixed points.
(f) Since
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
is ind-proper, we conclude that
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
is ind-proper, we conclude that
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\subseteq \operatorname {Fl}$
is closed. So it follows from part (e) that each ind-subscheme
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\subseteq \operatorname {Fl}$
is closed. So it follows from part (e) that each ind-subscheme
![]() $Z^{T_{\psi }}_{\nu }\subseteq \operatorname {Fl}^{T_{\psi }}$
is closed. Moreover,
$Z^{T_{\psi }}_{\nu }\subseteq \operatorname {Fl}^{T_{\psi }}$
is closed. Moreover,
![]() $\operatorname {Fl}^{T_{\psi }}$
is reduced because
$\operatorname {Fl}^{T_{\psi }}$
is reduced because
![]() $\operatorname {Fl}$
is such. Since set-theoretically
$\operatorname {Fl}$
is such. Since set-theoretically
![]() $\operatorname {Fl}^{T_{\psi }}$
decomposes as a disjoint union
$\operatorname {Fl}^{T_{\psi }}$
decomposes as a disjoint union
![]() $\bigsqcup _{\nu \in \widetilde {W}_{\psi }}Z^{T_{\psi }}_{\nu }$
, we conclude that each
$\bigsqcup _{\nu \in \widetilde {W}_{\psi }}Z^{T_{\psi }}_{\nu }$
, we conclude that each
![]() $Z^{T_{\psi }}_{\nu }\subseteq \operatorname {Fl}^{T_{\psi }}$
is open and closed.
$Z^{T_{\psi }}_{\nu }\subseteq \operatorname {Fl}^{T_{\psi }}$
is open and closed.
2.4.4.
Retraction. Let Y be an ind-scheme, and let
![]() $Z\subseteq Y$
be a locally closed ind-subscheme. A morphism
$Z\subseteq Y$
be a locally closed ind-subscheme. A morphism
![]() $p:Y\to Z$
is called a retraction if the restriction
$p:Y\to Z$
is called a retraction if the restriction
![]() $p|_Z$
is the identity.
$p|_Z$
is the identity.
Lemma 2.4.5. For every
![]() $\nu \in \widetilde {W}_{\psi }$
, there is a unique
$\nu \in \widetilde {W}_{\psi }$
, there is a unique
![]() $T_{\psi }$
-equivariant retraction
$T_{\psi }$
-equivariant retraction
![]() $p_{\nu }:Z_{\nu }\to Z_{\nu }^{T_{\psi }}$
. Moreover, under an isomorphisms of Sections 2.4.3(d)–(f), the retraction
$p_{\nu }:Z_{\nu }\to Z_{\nu }^{T_{\psi }}$
. Moreover, under an isomorphisms of Sections 2.4.3(d)–(f), the retraction
![]() $p_{\nu }$
corresponds to the projection
$p_{\nu }$
corresponds to the projection
![]() $p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}:[um]\mapsto [m]$
.
$p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}:[um]\mapsto [m]$
.
Proof. To see the existence of a retraction and its relation to
![]() $p_{\psi ,\nu }$
, we note that
$p_{\psi ,\nu }$
, we note that
![]() $\iota _{\nu }$
induces an isomorphism
$\iota _{\nu }$
induces an isomorphism
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\nu }=\operatorname {Fl}^{T_{\psi }}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu }$
, and that
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\nu }=\operatorname {Fl}^{T_{\psi }}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu }$
, and that
![]() $p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\nu }$
is a
$p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\nu }$
is a
![]() $T_{\psi }$
-equivariant retract. To see the uniqueness, we note that for every S-point
$T_{\psi }$
-equivariant retract. To see the uniqueness, we note that for every S-point
![]() $\eta :S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, the morphism
$\eta :S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, the morphism
![]() $\eta _{\mathbb G_m}: \mathbb G_m\times S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, defined by
$\eta _{\mathbb G_m}: \mathbb G_m\times S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, defined by
![]() $(a,x)\mapsto \psi (a)\eta (s)$
, extends uniquely to the morphism
$(a,x)\mapsto \psi (a)\eta (s)$
, extends uniquely to the morphism
![]() $\eta _{\mathbb A^1}:\mathbb A^1\times S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, and we have an equality
$\eta _{\mathbb A^1}:\mathbb A^1\times S\to \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
, and we have an equality
![]() $p_{\psi ,\nu }(\eta )=\eta _{\mathbb A^1}|_{\{0\}\times S}$
.
$p_{\psi ,\nu }(\eta )=\eta _{\mathbb A^1}|_{\{0\}\times S}$
.
3 Affine Springer fibers
3.1 Geometric properties
Assume that we are in the situation Section 2.4.1.
3.1.1.
Set-up. (a) Let
![]() $\gamma \in G(K)$
be a compact regular semi-simple element, and let
$\gamma \in G(K)$
be a compact regular semi-simple element, and let
![]() $G^{\operatorname {sc}}_{\gamma }\subseteq G^{\operatorname {sc}}$
be the centralizer of
$G^{\operatorname {sc}}_{\gamma }\subseteq G^{\operatorname {sc}}$
be the centralizer of
![]() $\gamma $
inside
$\gamma $
inside
![]() $G^{\operatorname {sc}}$
. In particular,
$G^{\operatorname {sc}}$
. In particular,
![]() $(G^{\operatorname {sc}}_{\gamma })^0\subseteq G^{\operatorname {sc}}$
is a maximal torus defined over K.
$(G^{\operatorname {sc}}_{\gamma })^0\subseteq G^{\operatorname {sc}}$
is a maximal torus defined over K.
(b) Let
![]() $S_{\gamma }\subseteq G^{\operatorname {sc}}_{\gamma }$
be the maximal K-split torus of
$S_{\gamma }\subseteq G^{\operatorname {sc}}_{\gamma }$
be the maximal K-split torus of
![]() $G^{\operatorname {sc}}_{\gamma }$
, and let
$G^{\operatorname {sc}}_{\gamma }$
, and let
![]() $\Lambda _{\gamma }:=X_*(S_{\gamma })$
be the group of cocharacters. The map
$\Lambda _{\gamma }:=X_*(S_{\gamma })$
be the group of cocharacters. The map
![]() $\mu \mapsto \mu (t)$
identifies
$\mu \mapsto \mu (t)$
identifies
![]() $\Lambda _{\gamma }$
with a subgroup of
$\Lambda _{\gamma }$
with a subgroup of
![]() $S_{\gamma }(K)$
.
$S_{\gamma }(K)$
.
(c) Let
![]() $\operatorname {Fl}_{\gamma }\subseteq \operatorname {Fl}$
be the affine Springer fiber. Explicitly,
$\operatorname {Fl}_{\gamma }\subseteq \operatorname {Fl}$
be the affine Springer fiber. Explicitly,
![]() $\operatorname {Fl}_{\gamma }$
consists of cosets
$\operatorname {Fl}_{\gamma }$
consists of cosets
![]() $gI^{\operatorname {sc}}\in L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
such that
$gI^{\operatorname {sc}}\in L(G^{\operatorname {sc}})/I^{\operatorname {sc}}$
such that
![]() $g^{-1}\gamma g\in I$
. Then the group
$g^{-1}\gamma g\in I$
. Then the group
![]() $\Lambda _{\gamma }$
acts on
$\Lambda _{\gamma }$
acts on
![]() $\operatorname {Fl}_{\gamma }$
. Moreover, it is known that the reduced ind-scheme
$\operatorname {Fl}_{\gamma }$
. Moreover, it is known that the reduced ind-scheme
![]() $\operatorname {Fl}_{\gamma ,\operatorname {red}}$
is a scheme of finite type over k, and there exists a closed reduced subscheme
$\operatorname {Fl}_{\gamma ,\operatorname {red}}$
is a scheme of finite type over k, and there exists a closed reduced subscheme
![]() $Y\subseteq \operatorname {Fl}_{\gamma }$
of finite type over k such that
$Y\subseteq \operatorname {Fl}_{\gamma }$
of finite type over k such that
![]() $\operatorname {Fl}_{\gamma ,\operatorname {red}}=\Lambda _{\gamma }(Y)$
.
$\operatorname {Fl}_{\gamma ,\operatorname {red}}=\Lambda _{\gamma }(Y)$
.
(d) For every ind-subscheme
![]() $Z\subseteq \operatorname {Fl}$
, we set
$Z\subseteq \operatorname {Fl}$
, we set
![]() $Z_{\gamma }:=Z\cap \operatorname {Fl}_{\gamma }$
.
$Z_{\gamma }:=Z\cap \operatorname {Fl}_{\gamma }$
.
(e) Main assumption: We always assume that we have an inclusion
![]() $S_{\gamma }\subseteq T_{G^{\operatorname {sc}}}$
, and hence an inclusion
$S_{\gamma }\subseteq T_{G^{\operatorname {sc}}}$
, and hence an inclusion
![]() $\Lambda _{\gamma }\subseteq \Lambda =X_*(T_{G^{\operatorname {sc}}})$
.
$\Lambda _{\gamma }\subseteq \Lambda =X_*(T_{G^{\operatorname {sc}}})$
.
Remark 3.1.2. Note that it follows from [Reference SteinbergSt, Theorem 8.2] (or its particular case [Reference SteinbergSt, Corollary 8.5]) that the centralizer
![]() $G^{\operatorname {sc}}_{\gamma }$
is connected. However, we do not need this fact.
$G^{\operatorname {sc}}_{\gamma }$
is connected. However, we do not need this fact.
Lemma 3.1.3. Suppose that we are in the situation of Section 3.1.1. Then the centralizer
![]() $G^{\operatorname {sc}}_{S_{\gamma }}\subseteq G^{\operatorname {sc}}$
is a Levi subgroup, and
$G^{\operatorname {sc}}_{S_{\gamma }}\subseteq G^{\operatorname {sc}}$
is a Levi subgroup, and
![]() $S_{\gamma }$
is the connected center of
$S_{\gamma }$
is the connected center of
![]() $G^{\operatorname {sc}}_{S_{\gamma }}$
.
$G^{\operatorname {sc}}_{S_{\gamma }}$
.
Proof. Indeed, the centralizer
![]() $G^{\operatorname {sc}}_{S_{\gamma }}$
is split over K because
$G^{\operatorname {sc}}_{S_{\gamma }}$
is split over K because
![]() $G^{\operatorname {sc}}$
and
$G^{\operatorname {sc}}$
and
![]() $S_{\gamma }$
are split over K; therefore, the connected center
$S_{\gamma }$
are split over K; therefore, the connected center
![]() $Z(G^{\operatorname {sc}}_{S_{\gamma }})^0$
of
$Z(G^{\operatorname {sc}}_{S_{\gamma }})^0$
of
![]() $G^{\operatorname {sc}}_{S_{\gamma }}$
is split over K as well. Moreover, since
$G^{\operatorname {sc}}_{S_{\gamma }}$
is split over K as well. Moreover, since
![]() $(G^{\operatorname {sc}}_{\gamma })^0$
is a maximal torus of
$(G^{\operatorname {sc}}_{\gamma })^0$
is a maximal torus of
![]() $G^{\operatorname {sc}}$
, it is a maximal torus of
$G^{\operatorname {sc}}$
, it is a maximal torus of
![]() $G^{\operatorname {sc}}_{S_{\gamma }}$
, and hence contains
$G^{\operatorname {sc}}_{S_{\gamma }}$
, and hence contains
![]() $Z(G^{\operatorname {sc}}_{S_{\gamma }})^0$
. Therefore, the assertion follows from the assumption that
$Z(G^{\operatorname {sc}}_{S_{\gamma }})^0$
. Therefore, the assertion follows from the assumption that
![]() $S_{\gamma }\subseteq (G^{\operatorname {sc}}_{\gamma })^0$
is the maximal K-split torus.
$S_{\gamma }\subseteq (G^{\operatorname {sc}}_{\gamma })^0$
is the maximal K-split torus.
3.1.4.
Observations. Fix
![]() $\psi \in \Psi $
.
$\psi \in \Psi $
.
(a) An inclusion
![]() $(G_{\gamma })^0\subseteq M_{\psi }$
is equivalent to the inclusion
$(G_{\gamma })^0\subseteq M_{\psi }$
is equivalent to the inclusion
![]() $(G^{\operatorname {sc}}_{\gamma })^0\subseteq (M_{\psi })_{G^{\operatorname {sc}}}$
, hence to the inclusion
$(G^{\operatorname {sc}}_{\gamma })^0\subseteq (M_{\psi })_{G^{\operatorname {sc}}}$
, hence to the inclusion
![]() $T_{\psi }\subseteq (G^{\operatorname {sc}}_{\gamma })^0$
(by Section 2.4.2(e)), and thus to the inclusion
$T_{\psi }\subseteq (G^{\operatorname {sc}}_{\gamma })^0$
(by Section 2.4.2(e)), and thus to the inclusion
![]() $T_{\psi }\subseteq S_{\gamma }$
.
$T_{\psi }\subseteq S_{\gamma }$
.
(b) Set
![]() $(\Lambda _{\gamma })_{\mathbb Q}:=\Lambda _{\gamma }\otimes _{\mathbb Z}\mathbb Q$
. By Section 2.4.2(d), an inclusion
$(\Lambda _{\gamma })_{\mathbb Q}:=\Lambda _{\gamma }\otimes _{\mathbb Z}\mathbb Q$
. By Section 2.4.2(d), an inclusion
![]() $T_{\psi }\subseteq S_{\gamma }$
holds if and only if
$T_{\psi }\subseteq S_{\gamma }$
holds if and only if
![]() $\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
.
$\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
.
(c) It follows from parts (a) and (b) that if
![]() $\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
, then element
$\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
, then element
![]() $\gamma $
belongs to
$\gamma $
belongs to
(d) It follows from Lemma 3.1.3 that if
![]() $\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, then there exists a root
$\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, then there exists a root
![]() $\alpha \in \Phi $
such that
$\alpha \in \Phi $
such that
![]() $\alpha \in (\Lambda _{\gamma })^{\perp }$
, but
$\alpha \in (\Lambda _{\gamma })^{\perp }$
, but
![]() $\langle \alpha ,\check {\psi }\rangle \neq 0$
.
$\langle \alpha ,\check {\psi }\rangle \neq 0$
.
Notation 3.1.5. Assume that
![]() $\psi \in \Psi $
satisfies
$\psi \in \Psi $
satisfies
![]() $\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
.
$\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
.
(a) By Section 3.1.4(c), we have
![]() $\gamma \in M_{\psi }(K)\subseteq P_{\psi }(K)$
, and thus, we can consider the affine Springer fibers
$\gamma \in M_{\psi }(K)\subseteq P_{\psi }(K)$
, and thus, we can consider the affine Springer fibers
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
and
$\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }$
and
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }\subseteq \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
. Explicitly,
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }\subseteq \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
. Explicitly,
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }$
(resp.
$\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }$
(resp.
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }$
) consists of all elements
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }$
) consists of all elements
![]() $gI_{P^{\operatorname {sc}}_{\psi },\nu }\in L(P^{\operatorname {sc}}_{\psi })/I_{P^{\operatorname {sc}}_{\psi },\nu }$
(resp.
$gI_{P^{\operatorname {sc}}_{\psi },\nu }\in L(P^{\operatorname {sc}}_{\psi })/I_{P^{\operatorname {sc}}_{\psi },\nu }$
(resp.
![]() $gI_{M^{\operatorname {sc}}_{\psi }}\in L(M^{\operatorname {sc}}_{\psi })/I_{M^{\operatorname {sc}}_{\psi }}$
) such that
$gI_{M^{\operatorname {sc}}_{\psi }}\in L(M^{\operatorname {sc}}_{\psi })/I_{M^{\operatorname {sc}}_{\psi }}$
) such that
![]() $g^{-1}\gamma g\in I_{P_{\psi },\nu }$
(resp.
$g^{-1}\gamma g\in I_{P_{\psi },\nu }$
(resp.
![]() $g^{-1}\gamma g\in I_{M_{\psi }}$
).
$g^{-1}\gamma g\in I_{M_{\psi }}$
).
(b) By construction, the isomorphism
![]() $\iota _{\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z_{\nu }$
from Section 2.4.3(e) restricts to isomorphisms
$\iota _{\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\overset {\thicksim }{\to } Z_{\nu }$
from Section 2.4.3(e) restricts to isomorphisms
![]() $\iota _{\nu ,\gamma }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }\overset {\thicksim }{\to } Z_{\nu ,\gamma }$
and
$\iota _{\nu ,\gamma }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu ,\gamma }\overset {\thicksim }{\to } Z_{\nu ,\gamma }$
and
![]() $\iota ^{T_{\psi }}_{\nu ,\gamma }:\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu ,\gamma }$
.
$\iota ^{T_{\psi }}_{\nu ,\gamma }:\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}\overset {\thicksim }{\to } Z^{T_{\psi }}_{\nu ,\gamma }$
.
3.1.6.
Affine bundle. A morphism
![]() $f:X\to Y$
of (ind-)schemes is called an affine bundle if locally étale on Y it is isomorphic to the projection
$f:X\to Y$
of (ind-)schemes is called an affine bundle if locally étale on Y it is isomorphic to the projection
![]() $Y\times \mathbb A^n\to Y$
and all transition maps are affine.
$Y\times \mathbb A^n\to Y$
and all transition maps are affine.
Proposition 3.1.7. Assume that we are in the situation of Section 3.1.5. Then for every
![]() $\nu \in \widetilde {W}_{\psi }$
, the
$\nu \in \widetilde {W}_{\psi }$
, the
![]() $T_{\psi }$
-equivariant retraction
$T_{\psi }$
-equivariant retraction
![]() $p_{\nu }:Z_{\nu }\to Z_{\nu }^{T_{\psi }}$
of Lemma 2.4.5 induces a retraction
$p_{\nu }:Z_{\nu }\to Z_{\nu }^{T_{\psi }}$
of Lemma 2.4.5 induces a retraction
![]() $p_{\nu ,\gamma }:Z_{\nu ,\gamma }\to Z_{\nu ,\gamma }^{T_{\psi }}$
. Furthermore,
$p_{\nu ,\gamma }:Z_{\nu ,\gamma }\to Z_{\nu ,\gamma }^{T_{\psi }}$
. Furthermore,
![]() $p_{\nu ,\gamma }$
is a composition of affine bundles.
$p_{\nu ,\gamma }$
is a composition of affine bundles.
Proof. To make the argument more structural, we will divide it into steps.
Step 1. By Lemma 2.4.5 and the observations of Section 3.1.5, it suffices to show that the projection
![]() $p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
restricts to the projection
$p_{\psi ,\nu }:\operatorname {Fl}_{P^{\operatorname {sc}}_{\psi },\nu }\to \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
restricts to the projection
and that
![]() $p_{\psi ,\nu ,\gamma }$
is a composition of affine bundles.
$p_{\psi ,\nu ,\gamma }$
is a composition of affine bundles.
Step 2. Let
![]() $U_{\psi }=U_0\supseteq U_1\supseteq \ldots \supseteq U_{n-1}\supseteq U_n=\{1\}$
be the lower central series of
$U_{\psi }=U_0\supseteq U_1\supseteq \ldots \supseteq U_{n-1}\supseteq U_n=\{1\}$
be the lower central series of
![]() $U_{\psi }$
. Then each
$U_{\psi }$
. Then each
![]() $U_i$
is a normal subgroup of
$U_i$
is a normal subgroup of
![]() $P_{\psi }$
, and we set
$P_{\psi }$
, and we set
![]() $P_i:=P_{\psi }/U_i$
and
$P_i:=P_{\psi }/U_i$
and
![]() $P^{\operatorname {sc}}_i:=P^{\operatorname {sc}}_{\psi }/U_i$
. In particular,
$P^{\operatorname {sc}}_i:=P^{\operatorname {sc}}_{\psi }/U_i$
. In particular,
![]() $P_0=M_{\psi }$
and
$P_0=M_{\psi }$
and
![]() $P_n=P_{\psi }$
.
$P_n=P_{\psi }$
.
For every
![]() $i=0,\ldots ,n$
, let
$i=0,\ldots ,n$
, let
![]() $\gamma _i\in L(P_i)$
be the image of
$\gamma _i\in L(P_i)$
be the image of
![]() $\gamma \in L(P_{\psi })$
, and denote by
$\gamma \in L(P_{\psi })$
, and denote by
![]() $I_{P_i,\nu }\subseteq L(P_i)$
(resp.
$I_{P_i,\nu }\subseteq L(P_i)$
(resp.
![]() $I_{P^{\operatorname {sc}}_i,\nu }\subseteq L(P^{\operatorname {sc}}_i)$
) the image of
$I_{P^{\operatorname {sc}}_i,\nu }\subseteq L(P^{\operatorname {sc}}_i)$
) the image of
![]() $I_{P_{\psi },\nu }$
(resp.
$I_{P_{\psi },\nu }$
(resp.
![]() $I_{P^{\operatorname {sc}}_{\psi },\nu }$
). We set
$I_{P^{\operatorname {sc}}_{\psi },\nu }$
). We set
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_i,\nu }:=L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
, and denote by
$\operatorname {Fl}_{P^{\operatorname {sc}}_i,\nu }:=L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
, and denote by
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu ,\gamma }\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_i,\nu }$
the corresponding affine Springer fiber – that is, the collection of all
$\operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu ,\gamma }\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_i,\nu }$
the corresponding affine Springer fiber – that is, the collection of all
![]() $g\in L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
such that
$g\in L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
such that
![]() $g^{-1}\gamma _i g\in I_{P_i,\nu }$
.
$g^{-1}\gamma _i g\in I_{P_i,\nu }$
.
For every
![]() $i=0,\ldots ,n-1$
, we have a natural projection
$i=0,\ldots ,n-1$
, we have a natural projection
and it remains to show that each
![]() $p_{i,\gamma }$
is an affine bundle.
$p_{i,\gamma }$
is an affine bundle.
Step 3. Let
![]() $\widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq L(P^{\operatorname {sc}}_i)$
be the preimage of
$\widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq L(P^{\operatorname {sc}}_i)$
be the preimage of
![]() $\operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu }$
under the natural projection
$\operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq \operatorname {Fl}_{P^{\operatorname {sc}}_{i},\nu }$
under the natural projection
![]() $L(P^{\operatorname {sc}}_i)\to L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
, and set
$L(P^{\operatorname {sc}}_i)\to L(P^{\operatorname {sc}}_i)/I_{P^{\operatorname {sc}}_i,\nu }$
, and set
It is enough to show that each projection
![]() $\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}\to \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _{i}}$
is an affine bundle.
$\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}\to \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _{i}}$
is an affine bundle.
We set
![]() $\overline {U}_{i}:=U_{i}/U_{i+1}$
. Then
$\overline {U}_{i}:=U_{i}/U_{i+1}$
. Then
![]() $\overline {U}_i\subseteq P_{i+1}=P_{\psi }/U_{i+1}$
is a normal subgroup, and we have
$\overline {U}_i\subseteq P_{i+1}=P_{\psi }/U_{i+1}$
is a normal subgroup, and we have
![]() $P_i\cong P_{i+1}/\overline {U}_i$
. Set
$P_i\cong P_{i+1}/\overline {U}_i$
. Set
![]() $I_{\overline {U}_i,\nu }:=I_{P_{i+1},\nu }\cap L(\overline {U}_i)$
. Then
$I_{\overline {U}_i,\nu }:=I_{P_{i+1},\nu }\cap L(\overline {U}_i)$
. Then
![]() $\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
can be identified with the locus of all
$\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
can be identified with the locus of all
![]() $g\in L(P^{\operatorname {sc}}_{i+1})/I_{\overline {U}_i,\nu }$
such that
$g\in L(P^{\operatorname {sc}}_{i+1})/I_{\overline {U}_i,\nu }$
such that
![]() $g^{-1}\gamma _{i+1} g\in I_{P_{i+1},\nu }$
.
$g^{-1}\gamma _{i+1} g\in I_{P_{i+1},\nu }$
.
Step 4. Recall that the projection
![]() $p_i:P_{i+1}\to P_i$
, viewed as a morphism of algebraic varieties, has a section s. Indeed, the isomorphism
$p_i:P_{i+1}\to P_i$
, viewed as a morphism of algebraic varieties, has a section s. Indeed, the isomorphism
![]() $P_{\psi }\overset {\thicksim }{\to } M_{\psi }\times U_{\psi }$
from Section 2.4.3(c) induces an isomorphism
$P_{\psi }\overset {\thicksim }{\to } M_{\psi }\times U_{\psi }$
from Section 2.4.3(c) induces an isomorphism
![]() $P_i\overset {\thicksim }{\to } M_{\psi }\times (U_0/U_i)$
. Choose an ordering of the all roots of G lying in
$P_i\overset {\thicksim }{\to } M_{\psi }\times (U_0/U_i)$
. Choose an ordering of the all roots of G lying in
![]() $\operatorname {Lie} U_0/\operatorname {Lie} U_i$
. Then the map
$\operatorname {Lie} U_0/\operatorname {Lie} U_i$
. Then the map
![]() $(x_{\alpha })_{\alpha }\mapsto \prod _{\alpha }x_{\alpha }$
defines an isomorphism
$(x_{\alpha })_{\alpha }\mapsto \prod _{\alpha }x_{\alpha }$
defines an isomorphism
![]() $\prod _{\alpha } U_{\alpha }\overset {\thicksim }{\to } U_0/U_i$
, where
$\prod _{\alpha } U_{\alpha }\overset {\thicksim }{\to } U_0/U_i$
, where
![]() $U_{\alpha }$
is the root space of
$U_{\alpha }$
is the root space of
![]() $\alpha $
. We define s to be the composition
$\alpha $
. We define s to be the composition
By construction, we have
![]() $s(P^{\operatorname {sc}}_i)\subseteq P^{\operatorname {sc}}_{i+1}$
, so using s, we identify
$s(P^{\operatorname {sc}}_i)\subseteq P^{\operatorname {sc}}_{i+1}$
, so using s, we identify
![]() $\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
with the space of pairs
$\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
with the space of pairs
![]() $(g,u)$
, where
$(g,u)$
, where
![]() $g\in L(P^{\operatorname {sc}}_i)$
and
$g\in L(P^{\operatorname {sc}}_i)$
and
![]() $u\in L(\overline {U}_{i})/I_{\overline {U}_i,\nu }$
, satisfying
$u\in L(\overline {U}_{i})/I_{\overline {U}_i,\nu }$
, satisfying
Moreover, equation (3.1) implies that
![]() $g^{-1}\gamma _i g\in I_{P_i,\nu }$
, and thus
$g^{-1}\gamma _i g\in I_{P_i,\nu }$
, and thus
![]() $g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq L(P^{\operatorname {sc}}_i)$
.
$g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\subseteq L(P^{\operatorname {sc}}_i)$
.
Step 5. For each
![]() $g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
, we set
$g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
, we set
![]() $\widetilde {g}:=s(g)^{-1}\gamma _{i+1}s(g)\in L(P^{\operatorname {sc}}_{i+1})$
. Then
$\widetilde {g}:=s(g)^{-1}\gamma _{i+1}s(g)\in L(P^{\operatorname {sc}}_{i+1})$
. Then
![]() $p_i(\widetilde {g})=g^{-1}\gamma _i g\in I_{P_i,\nu }$
, so there exists a unique
$p_i(\widetilde {g})=g^{-1}\gamma _i g\in I_{P_i,\nu }$
, so there exists a unique
![]() $u_g\in L(\overline {U}_i)$
such that
$u_g\in L(\overline {U}_i)$
such that
![]() $\widetilde {g}=u^{-1}_g s(g^{-1}\gamma _{i}g)$
. Hence, we have an equality
$\widetilde {g}=u^{-1}_g s(g^{-1}\gamma _{i}g)$
. Hence, we have an equality
Let
![]() $\widetilde {m}\in I_{M_{\psi },\nu }\subseteq L(M_{\psi })$
be the image of
$\widetilde {m}\in I_{M_{\psi },\nu }\subseteq L(M_{\psi })$
be the image of
![]() $g^{-1}\gamma _i g\in I_{P_i,\nu }$
. Since
$g^{-1}\gamma _i g\in I_{P_i,\nu }$
. Since
![]() $\overline {U}_{i}$
lies in the center of
$\overline {U}_{i}$
lies in the center of
![]() $U_0/U_{i+1}$
, we have
$U_0/U_{i+1}$
, we have
![]() $\widetilde {g}u\widetilde {g}^{-1}=\widetilde {m}u\widetilde {m}^{-1}$
. Moreover, since
$\widetilde {g}u\widetilde {g}^{-1}=\widetilde {m}u\widetilde {m}^{-1}$
. Moreover, since
![]() $g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
, we get that
$g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
, we get that
![]() $g^{-1}\gamma _i g\in I_{P_i,\nu }$
. Hence, by our construction of s, we have
$g^{-1}\gamma _i g\in I_{P_i,\nu }$
. Hence, by our construction of s, we have
![]() $s(g^{-1}\gamma _i g)\in I_{P_{i+1},\nu }$
, and thus, our condition (3.1) can be rewritten as
$s(g^{-1}\gamma _i g)\in I_{P_{i+1},\nu }$
, and thus, our condition (3.1) can be rewritten as
Step 6. Since
![]() $\overline {U}_i$
is abelian, we have a canonical isomorphism
$\overline {U}_i$
is abelian, we have a canonical isomorphism
![]() $\overline {U}_i\overset {\thicksim }{\to } \operatorname {Lie}\overline {U}_i$
. Therefore, each
$\overline {U}_i\overset {\thicksim }{\to } \operatorname {Lie}\overline {U}_i$
. Therefore, each
![]() $u_g\in L(\overline {U}_i)$
gives rise to an element
$u_g\in L(\overline {U}_i)$
gives rise to an element
![]() $n_g\in \operatorname {Lie} L(\overline {U}_i)$
, and
$n_g\in \operatorname {Lie} L(\overline {U}_i)$
, and
![]() $\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
is identified with the moduli space of pairs
$\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
is identified with the moduli space of pairs
![]() $(g,n)$
, consisting of
$(g,n)$
, consisting of
![]() $g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
and
$g\in \widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}$
and
![]() $n\in \operatorname {Lie} L(\overline {U}_{i})/\operatorname {Lie} I_{\overline {U}_i,\nu }$
such that
$n\in \operatorname {Lie} L(\overline {U}_{i})/\operatorname {Lie} I_{\overline {U}_i,\nu }$
such that
Step 7. Since
![]() $\gamma \in M_{\psi }(K)\subseteq G(K)$
is regular semisimple, the operator
$\gamma \in M_{\psi }(K)\subseteq G(K)$
is regular semisimple, the operator
![]() $\operatorname {Ad}\gamma -1$
is invertible on
$\operatorname {Ad}\gamma -1$
is invertible on
![]() $\operatorname {Lie}\overline {U}_{i}(K)$
, and we set
$\operatorname {Lie}\overline {U}_{i}(K)$
, and we set
![]() $d:=\operatorname {val}\det (\operatorname {Ad}\gamma -1,\operatorname {Lie}\overline {U}_{i}(K))$
. Since each
$d:=\operatorname {val}\det (\operatorname {Ad}\gamma -1,\operatorname {Lie}\overline {U}_{i}(K))$
. Since each
![]() $\widetilde {m}$
is an
$\widetilde {m}$
is an
![]() $M_{\psi }(K)$
-conjugate of
$M_{\psi }(K)$
-conjugate of
![]() $\gamma $
, we conclude that the valuation of determinant of
$\gamma $
, we conclude that the valuation of determinant of
![]() $\operatorname {Ad}\widetilde {m}-1$
on
$\operatorname {Ad}\widetilde {m}-1$
on
![]() $\operatorname {Lie}\overline {U}_{i}(K)$
is d; thus, the linear transformation of
$\operatorname {Lie}\overline {U}_{i}(K)$
is d; thus, the linear transformation of
![]() $\operatorname {Lie} L(\overline {U}_{i})/ \operatorname {Lie}{I}_{\overline {U}_i,\nu }$
, induced by
$\operatorname {Lie} L(\overline {U}_{i})/ \operatorname {Lie}{I}_{\overline {U}_i,\nu }$
, induced by
![]() $\operatorname {Ad}\widetilde {m}-1$
, has a kernel of dimension d. Hence, equation (3.2) implies that
$\operatorname {Ad}\widetilde {m}-1$
, has a kernel of dimension d. Hence, equation (3.2) implies that
![]() $\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
is an affine subbundle of
$\widetilde {\operatorname {Fl}}^{\prime }_{P^{\operatorname {sc}}_{i+1},\nu ,\gamma _{i+1}}$
is an affine subbundle of
![]() $\widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\times (\operatorname {Lie} L(\overline {U}_{i})/\operatorname {Lie} {I}_{\overline {U}_i,\nu })$
of dimension d.
$\widetilde {\operatorname {Fl}}_{P^{\operatorname {sc}}_{i},\nu ,\gamma _i}\times (\operatorname {Lie} L(\overline {U}_{i})/\operatorname {Lie} {I}_{\overline {U}_i,\nu })$
of dimension d.
Proposition 3.1.8. Assume that we are in the situation of Section 3.1.5. Let
![]() $\overline {w}\in \widetilde {W}^{\mathcal {C}}$
be an admissible tuple,
$\overline {w}\in \widetilde {W}^{\mathcal {C}}$
be an admissible tuple,
![]() $\psi \in \Psi $
,
$\psi \in \Psi $
,
![]() $\nu :=\overline {w}_{\psi }\in \widetilde {W}_{\psi }$
, and let
$\nu :=\overline {w}_{\psi }\in \widetilde {W}_{\psi }$
, and let
![]() $Z_{\nu }\subseteq \operatorname {Fl}$
as in Section 2.4.3(a). Then exists
$Z_{\nu }\subseteq \operatorname {Fl}$
as in Section 2.4.3(a). Then exists
![]() $m\in \mathbb N$
such that if
$m\in \mathbb N$
such that if
![]() $\overline {w}$
is m-regular, then
$\overline {w}$
is m-regular, then
(a) the reduced intersections
![]() $Z_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
$Z_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
![]() $Z_{\nu }\cap \left (\bigcap _{\psi \in C}\operatorname {Fl}_{\gamma }^{\leq _{C}w_{C}}\right )$
are equal;
$Z_{\nu }\cap \left (\bigcap _{\psi \in C}\operatorname {Fl}_{\gamma }^{\leq _{C}w_{C}}\right )$
are equal;
(b) the isomorphism
![]() $Z_{\nu }^{T_{\psi }}\overset {\thicksim }{\to } \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
from Sections 2.4.3(e),(f) induces an isomorphism between the reduced intersection
$Z_{\nu }^{T_{\psi }}\overset {\thicksim }{\to } \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
from Sections 2.4.3(e),(f) induces an isomorphism between the reduced intersection
![]() $Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
$Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }^{\leq \overline {w}^{\psi }}$
(see Section 1.3.9(e));
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }^{\leq \overline {w}^{\psi }}$
(see Section 1.3.9(e));
(c) we have an inclusion of sets
![]() $p_{\nu }^{-1}(p_{\nu }(\operatorname {Fl}^{\leq \overline {w}}\cap Z_{\nu ,\gamma })) \subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
$p_{\nu }^{-1}(p_{\nu }(\operatorname {Fl}^{\leq \overline {w}}\cap Z_{\nu ,\gamma })) \subseteq \operatorname {Fl}^{\leq \overline {w}}$
.
Proof.
(a) Let
![]() $Y\subseteq \operatorname {Fl}_{\gamma }$
be a closed subscheme of finite type such that
$Y\subseteq \operatorname {Fl}_{\gamma }$
be a closed subscheme of finite type such that
![]() $\operatorname {Fl}_{\gamma }=\Lambda _{\gamma }(Y)$
(see Section 3.1.1(c)). Then using, for example, Corollary 2.1.7(d),(e), there exists a finite stratification
$\operatorname {Fl}_{\gamma }=\Lambda _{\gamma }(Y)$
(see Section 3.1.1(c)). Then using, for example, Corollary 2.1.7(d),(e), there exists a finite stratification
![]() $Y=\bigcup _{j} Y_{j}$
such that for every j, there exists a tuple
$Y=\bigcup _{j} Y_{j}$
such that for every j, there exists a tuple
![]() $\overline {u}\in \widetilde {W}^{\mathcal {C}}$
such that
$\overline {u}\in \widetilde {W}^{\mathcal {C}}$
such that
![]() $Y_j\subseteq L(U_C)u_C$
for each
$Y_j\subseteq L(U_C)u_C$
for each
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
Thus, it is enough to show that
![]() $Z_{\nu }\cap (\Lambda _{\gamma }(Y_j))^{\leq \overline {w}}$
equals
$Z_{\nu }\cap (\Lambda _{\gamma }(Y_j))^{\leq \overline {w}}$
equals
![]() $Z_{\nu }\cap \left (\bigcap _{C\owns \psi }\Lambda _{\gamma }(Y_j)^{\leq _C w_C}\right )$
for each j. In other words, we have to show that for every
$Z_{\nu }\cap \left (\bigcap _{C\owns \psi }\Lambda _{\gamma }(Y_j)^{\leq _C w_C}\right )$
for each j. In other words, we have to show that for every
![]() $\mu \in \Lambda _{\gamma }\subseteq \Lambda $
and
$\mu \in \Lambda _{\gamma }\subseteq \Lambda $
and
![]() $y\in Y_j$
such that
$y\in Y_j$
such that
![]() $\mu (y)\in \operatorname {Fl}^{\leq _{C} w_C}$
for every
$\mu (y)\in \operatorname {Fl}^{\leq _{C} w_C}$
for every
![]() $C\owns \psi $
and
$C\owns \psi $
and
![]() $\mu (y)\in Z_{\nu }$
, we have
$\mu (y)\in Z_{\nu }$
, we have
![]() $\mu (y)\in \operatorname {Fl}^{\leq _{C} w_C}$
for every
$\mu (y)\in \operatorname {Fl}^{\leq _{C} w_C}$
for every
![]() $C\in \mathcal {C}$
.
$C\in \mathcal {C}$
.
Let
![]() $\overline {u}$
be a tuple of elements of
$\overline {u}$
be a tuple of elements of
![]() $\widetilde {W}$
such that
$\widetilde {W}$
such that
![]() $y\in L(U_C)u_C$
for every C. Then
$y\in L(U_C)u_C$
for every C. Then
![]() $y\in \operatorname {Fl}^{\leq \overline {u}}$
, and it follows from Corollary 2.1.7(d) that
$y\in \operatorname {Fl}^{\leq \overline {u}}$
, and it follows from Corollary 2.1.7(d) that
![]() $\overline {u}$
is admissible. By the assumption, for every
$\overline {u}$
is admissible. By the assumption, for every
![]() $C\owns \psi $
, we have
$C\owns \psi $
, we have
![]() $\mu u_C\leq _C w_C$
and also
$\mu u_C\leq _C w_C$
and also
![]() $(\mu \overline {u})_{\psi }=\nu =\overline {w}_{\psi }$
.
$(\mu \overline {u})_{\psi }=\nu =\overline {w}_{\psi }$
.
By Lemma 1.2.7(a), this implies that
![]() $\mu u_C\leq _{C^{\psi }} w_C$
for every
$\mu u_C\leq _{C^{\psi }} w_C$
for every
![]() $C\owns \psi $
. Hence, it follows from Lemma 1.3.12 that if
$C\owns \psi $
. Hence, it follows from Lemma 1.3.12 that if
![]() $\overline {w}$
is sufficiently regular, then
$\overline {w}$
is sufficiently regular, then
![]() $\mu u_C\leq _{C} w_C$
for every
$\mu u_C\leq _{C} w_C$
for every
![]() $C\in \mathcal {C}$
; thus,
$C\in \mathcal {C}$
; thus,
![]() $\mu (y)\in \bigcap _{C\in \mathcal {C}}\operatorname {Fl}^{\leq _{C} w_C}$
, as claimed.
$\mu (y)\in \bigcap _{C\in \mathcal {C}}\operatorname {Fl}^{\leq _{C} w_C}$
, as claimed.
(b) By part (a), the reduced intersections
![]() $Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
$Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}_{\gamma }^{\leq \overline {w}}$
and
![]() $Z^{T_{\psi }}_{\nu }\cap \left (\bigcap _{C\owns \psi }\operatorname {Fl}_{\gamma }^{\leq _{C}w_{C}}\right )$
are equal. Therefore, it suffices to show that the isomorphism
$Z^{T_{\psi }}_{\nu }\cap \left (\bigcap _{C\owns \psi }\operatorname {Fl}_{\gamma }^{\leq _{C}w_{C}}\right )$
are equal. Therefore, it suffices to show that the isomorphism
![]() $Z_{\nu }^{T_{\psi }}\overset {\thicksim }{\to } \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
induces an isomorphism between the reduced intersection
$Z_{\nu }^{T_{\psi }}\overset {\thicksim }{\to } \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
induces an isomorphism between the reduced intersection
![]() $Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}^{\leq _{C}w_{C}}$
and
$Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}^{\leq _{C}w_{C}}$
and
![]() $\operatorname {Fl}^{\leq _{C^{\psi }}w_{C^{\psi }}}_{M^{\operatorname {sc}}_{\psi }}$
for all
$\operatorname {Fl}^{\leq _{C^{\psi }}w_{C^{\psi }}}_{M^{\operatorname {sc}}_{\psi }}$
for all
![]() $C\owns \psi $
. Since
$C\owns \psi $
. Since
![]() $\operatorname {Fl}^{\leq _{C} w_C}$
is a closed
$\operatorname {Fl}^{\leq _{C} w_C}$
is a closed
![]() $L(U_C)$
-invariant ind-subscheme of
$L(U_C)$
-invariant ind-subscheme of
![]() $\operatorname {Fl}$
, we conclude that a closed ind-subscheme
$\operatorname {Fl}$
, we conclude that a closed ind-subscheme
![]() $Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}^{\leq _{C}w_{C}}$
of
$Z^{T_{\psi }}_{\nu }\cap \operatorname {Fl}^{\leq _{C}w_{C}}$
of
![]() $Z_{\nu}^{T_{\psi}}$
corresponds to a closed
$Z_{\nu}^{T_{\psi}}$
corresponds to a closed
![]() $L(U_C)\cap L(M^{\operatorname {sc}}_{\psi })=L(U_{C^{\psi }})$
-invariant ind-subscheme of
$L(U_C)\cap L(M^{\operatorname {sc}}_{\psi })=L(U_{C^{\psi }})$
-invariant ind-subscheme of
![]() $\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
. Using Proposition 2.1.6, the question is equivalent to the assertion that if
$\operatorname {Fl}_{M^{\operatorname {sc}}_{\psi }}$
. Using Proposition 2.1.6, the question is equivalent to the assertion that if
![]() $w'\in \widetilde {W}^{\psi }$
, then
$w'\in \widetilde {W}^{\psi }$
, then
![]() $w'w_{\psi }\leq _C w^{\psi }w_{\psi }$
if and only if
$w'w_{\psi }\leq _C w^{\psi }w_{\psi }$
if and only if
![]() $w'\leq _{C^{\psi }} w^{\psi }$
. But this was shown in Lemma 1.2.7(b).
$w'\leq _{C^{\psi }} w^{\psi }$
. But this was shown in Lemma 1.2.7(b).
(c) By part (a), it is enough to show that
![]() $p_{\nu }^{-1}(p_{\nu }(\operatorname {Fl}^{\leq _C w_C}\cap Z_{\nu ,\gamma }))\subseteq \operatorname {Fl}^{\leq _C w_C}$
for each
$p_{\nu }^{-1}(p_{\nu }(\operatorname {Fl}^{\leq _C w_C}\cap Z_{\nu ,\gamma }))\subseteq \operatorname {Fl}^{\leq _C w_C}$
for each
![]() $C\owns \psi $
. Since every fiber of
$C\owns \psi $
. Since every fiber of
![]() $p_{\nu }$
lies in a single
$p_{\nu }$
lies in a single
![]() $L(U_{\psi })$
-orbit, the assertion follows from the inclusion
$L(U_{\psi })$
-orbit, the assertion follows from the inclusion
![]() $U_{\psi }\subseteq U_C$
.
$U_{\psi }\subseteq U_C$
.
3.2 Finiteness of homology
3.2.1.
Homology. We fix a prime number
![]() $\ell $
different from the characteristic of k.
$\ell $
different from the characteristic of k.
(a) For a scheme Y of finite type over k and
![]() $\mathcal {F}\in D_c^b(Y,\overline {\mathbb Q}_{\ell })$
, one can form the homology groups
$\mathcal {F}\in D_c^b(Y,\overline {\mathbb Q}_{\ell })$
, one can form the homology groups
![]() $H_i(Y,\mathcal {F}):=(H^i(Y,\mathcal {F}))^*$
. We also set
$H_i(Y,\mathcal {F}):=(H^i(Y,\mathcal {F}))^*$
. We also set
![]() $H_i(Y):=H_i(Y,\overline {\mathbb Q}_{\ell })$
.
$H_i(Y):=H_i(Y,\overline {\mathbb Q}_{\ell })$
.
(b) A closed embedding
![]() $\iota :X\hookrightarrow Y$
induces a morphism
$\iota :X\hookrightarrow Y$
induces a morphism
and hence a morphism
![]() $\iota _*:H_i(X,\mathcal {F}|_X)\to H_i(Y,\mathcal {F})$
.
$\iota _*:H_i(X,\mathcal {F}|_X)\to H_i(Y,\mathcal {F})$
.
(c) By part (b), a closed embedding
![]() $\iota :X\hookrightarrow Y$
induces a morphism
$\iota :X\hookrightarrow Y$
induces a morphism
![]() $\iota _*:H_i(X)\to H_i(Y)$
. Therefore, for every ind-scheme
$\iota _*:H_i(X)\to H_i(Y)$
. Therefore, for every ind-scheme
![]() $Y=\operatorname {colim}_i Y_i$
over k, one can form a homology
$Y=\operatorname {colim}_i Y_i$
over k, one can form a homology
![]() $H_i(Y):=\operatorname {colim}_i H_i(Y_i)$
.
$H_i(Y):=\operatorname {colim}_i H_i(Y_i)$
.
The main goal of this section is to show the following finiteness property of homology of affine Springer fibers:
Proposition 3.2.2. In the situation of Section 3.1.1(e), there exists an integer r such that for every tuple
![]() $\overline {x}\in \mathbb Z^{\Psi }$
and every
$\overline {x}\in \mathbb Z^{\Psi }$
and every
![]() $\psi \in \Psi $
, we have an equality of kernels
$\psi \in \Psi $
, we have an equality of kernels
In order to prove this, we need to introduce certain notation, generalizing [Reference Bezrukavnikov and VarshavskyBV, Sections A.4.2 and 3.1.2].
3.2.3.
Filtrations. Let
![]() $\Gamma $
be an ordered monoid – that is, a monoid and a partially ordered set such that
$\Gamma $
be an ordered monoid – that is, a monoid and a partially ordered set such that
![]() $\sigma \tau \leq \sigma '\tau '$
for each
$\sigma \tau \leq \sigma '\tau '$
for each
![]() $\sigma \leq \sigma '$
and
$\sigma \leq \sigma '$
and
![]() $\tau \leq \tau '$
.
$\tau \leq \tau '$
.
(a) By a
![]() $\Gamma $
-filtered set (or a set with a
$\Gamma $
-filtered set (or a set with a
![]() $\Gamma $
-filtration), we mean a set X together with collections of subsets
$\Gamma $
-filtration), we mean a set X together with collections of subsets
![]() $\{X_{\sigma }\}_{\sigma \in \Gamma }$
such that
$\{X_{\sigma }\}_{\sigma \in \Gamma }$
such that
![]() $X_{\sigma }\subseteq X_{\tau }$
for all
$X_{\sigma }\subseteq X_{\tau }$
for all
![]() $\sigma \leq \tau $
, and
$\sigma \leq \tau $
, and
![]() $X=\bigcup _{\sigma } X_{\sigma }$
.
$X=\bigcup _{\sigma } X_{\sigma }$
.
(b) By a
![]() $\Gamma $
-filtered group we mean a group A with a
$\Gamma $
-filtered group we mean a group A with a
![]() $\Gamma $
-filtration such that
$\Gamma $
-filtration such that
![]() $1\in A_1$
and
$1\in A_1$
and ![]() .
.
(c) Let A be a
![]() $\Gamma $
-filtered group, and X is a set equipped with an A-action and a
$\Gamma $
-filtered group, and X is a set equipped with an A-action and a
![]() $\Gamma $
-filtration. We say that
$\Gamma $
-filtration. We say that
![]() $\Gamma $
-filtration on X is compatible with a filtration of A if for every
$\Gamma $
-filtration on X is compatible with a filtration of A if for every
![]() $\sigma ,\tau \in \Gamma $
we have
$\sigma ,\tau \in \Gamma $
we have
![]() $A_{\sigma }(X_{\tau })\subseteq X_{\sigma \tau }$
.
$A_{\sigma }(X_{\tau })\subseteq X_{\sigma \tau }$
.
(d) In the situation of (c), we will say that the
![]() $\Gamma $
-filtration on X is finitely generated over A if there exists a finite subset
$\Gamma $
-filtration on X is finitely generated over A if there exists a finite subset
![]() $\Gamma _0\subseteq \Gamma $
such that
$\Gamma _0\subseteq \Gamma $
such that
![]() $\{X_{\sigma }\}_{\sigma \in \Gamma }$
is generated by
$\{X_{\sigma }\}_{\sigma \in \Gamma }$
is generated by
![]() $\{X_{\sigma }\}_{\sigma \in \Gamma _0}$
; that is, for every
$\{X_{\sigma }\}_{\sigma \in \Gamma _0}$
; that is, for every
![]() $\sigma \in \Gamma $
, we have
$\sigma \in \Gamma $
, we have
![]() $X_{\sigma }=\bigcup _{\{(\tau ,\sigma ')\in \Gamma \times \Gamma _0\,|\,\tau \sigma '=\sigma \}} A_{\tau }(X_{\sigma '})$
.
$X_{\sigma }=\bigcup _{\{(\tau ,\sigma ')\in \Gamma \times \Gamma _0\,|\,\tau \sigma '=\sigma \}} A_{\tau }(X_{\sigma '})$
.
3.2.4. Rees algebras and modules. Let L be a field, and assume that we are in the situation of Section 3.2.3.
(a) For a
![]() $\Gamma $
-filtered group A, the group algebra
$\Gamma $
-filtered group A, the group algebra
![]() $L[A]$
is also equipped with a
$L[A]$
is also equipped with a
![]() $\Gamma $
-filtration
$\Gamma $
-filtration
![]() $L[A]_{\sigma }:=\operatorname {Span}_L(A_{\sigma })$
, and we denote by
$L[A]_{\sigma }:=\operatorname {Span}_L(A_{\sigma })$
, and we denote by
![]() $R(L[A]):=\bigoplus _{\sigma \in \Gamma } L[A]_{\sigma }$
the corresponding Rees algebra. Note that
$R(L[A]):=\bigoplus _{\sigma \in \Gamma } L[A]_{\sigma }$
the corresponding Rees algebra. Note that
![]() $R(L[A])$
is the monoid algebra of the monoid
$R(L[A])$
is the monoid algebra of the monoid
![]() $R(A):=\{(a,\sigma )\in A\times \Gamma \,|\, a\in A_{\sigma }\}$
.
$R(A):=\{(a,\sigma )\in A\times \Gamma \,|\, a\in A_{\sigma }\}$
.
(b) Let X be a scheme locally of finite type over k equipped with an action of A. Assume that A is a
![]() $\Gamma $
-filtered group, and that X is equipped with a
$\Gamma $
-filtered group, and that X is equipped with a
![]() $\Gamma $
-filtration compatible with
$\Gamma $
-filtration compatible with
![]() $\Gamma $
-filtration on A and such that
$\Gamma $
-filtration on A and such that
![]() $X_{\sigma }\subseteq X$
is a closed subscheme of finite type over k for each
$X_{\sigma }\subseteq X$
is a closed subscheme of finite type over k for each
![]() $\sigma \in \Gamma $
.
$\sigma \in \Gamma $
.
(c) For every A-equivariant element
![]() $\mathcal {F}\in D_c^b(X,\overline {\mathbb Q}_{\ell })$
, we can form a
$\mathcal {F}\in D_c^b(X,\overline {\mathbb Q}_{\ell })$
, we can form a
![]() $\Gamma $
-graded
$\Gamma $
-graded
![]() $R(\overline {\mathbb Q}_{\ell }[A])$
-module
$R(\overline {\mathbb Q}_{\ell }[A])$
-module
![]() $R(H_i(X,\mathcal {F})):=\bigoplus _{\sigma } H_i(X_{\sigma },\mathcal {F}\,|_{X_{\sigma }})$
for every
$R(H_i(X,\mathcal {F})):=\bigoplus _{\sigma } H_i(X_{\sigma },\mathcal {F}\,|_{X_{\sigma }})$
for every
![]() $i\in \mathbb Z$
. Explicitly, the action of
$i\in \mathbb Z$
. Explicitly, the action of
![]() $a\in A_{\tau }$
on X defines a closed embedding
$a\in A_{\tau }$
on X defines a closed embedding
![]() $a:X_{\sigma }\hookrightarrow X_{\tau \sigma }$
, and hence a homomorphism
$a:X_{\sigma }\hookrightarrow X_{\tau \sigma }$
, and hence a homomorphism
![]() $H_i(X_{\sigma },\mathcal {F}\,|_{X_{\sigma }})\to H_i(X_{\tau \sigma },\mathcal {F}\,|_{X_{\tau \sigma }})$
(see Section 3.2.1(b)).
$H_i(X_{\sigma },\mathcal {F}\,|_{X_{\sigma }})\to H_i(X_{\tau \sigma },\mathcal {F}\,|_{X_{\tau \sigma }})$
(see Section 3.2.1(b)).
In particular, we form a
![]() $\Gamma $
-graded
$\Gamma $
-graded
![]() $R(\overline {\mathbb Q}_{\ell }[A])$
-module
$R(\overline {\mathbb Q}_{\ell }[A])$
-module
![]() $R(H_i(X)):=R(H_i(X,\overline {\mathbb Q}_{\ell }))$
.
$R(H_i(X)):=R(H_i(X,\overline {\mathbb Q}_{\ell }))$
.
Lemma 3.2.5. In the situation of Section 3.2.4(b), assume that
![]() $\mathrm{(i)} $
the group A acts on the set of irreducible components of X with finite stabilizers;
$\mathrm{(i)} $
the group A acts on the set of irreducible components of X with finite stabilizers;
![]() $\mathrm{(ii)} $
the filtration
$\mathrm{(ii)} $
the filtration
![]() $\{X_{\sigma }\}_{\sigma }$
is finitely generated over A;
$\{X_{\sigma }\}_{\sigma }$
is finitely generated over A;
![]() $\mathrm{(iii)} $
the Rees algebra
$\mathrm{(iii)} $
the Rees algebra
![]() $R(\overline {\mathbb Q}_{\ell }[A])$
is Noetherian.
$R(\overline {\mathbb Q}_{\ell }[A])$
is Noetherian.
Then for every A-equivariant object
![]() $\mathcal {F}\in D_c^b(X,\overline {\mathbb Q}_{\ell })$
and
$\mathcal {F}\in D_c^b(X,\overline {\mathbb Q}_{\ell })$
and
![]() $i\in \mathbb Z$
, the
$i\in \mathbb Z$
, the
![]() $R(\overline {\mathbb Q}_{\ell }[A])$
-module
$R(\overline {\mathbb Q}_{\ell }[A])$
-module
![]() $R(H_i(X,\mathcal {F}))$
is finitely generated.
$R(H_i(X,\mathcal {F}))$
is finitely generated.
Proof. The argument is identical to that of [Reference Bezrukavnikov and VarshavskyBV, Lemma 3.1.3], where the case of
![]() $\Gamma =\mathbb Z_{\geq 0}$
is treated.
$\Gamma =\mathbb Z_{\geq 0}$
is treated.
Example 3.2.6.
(a) Let
![]() $\Gamma $
be an ordered monoid
$\Gamma $
be an ordered monoid
![]() $\mathbb Z_{\geq 0}^{\Psi }$
, which we identify with a corresponding submonoid of the group of quasi-admissible tuples in
$\mathbb Z_{\geq 0}^{\Psi }$
, which we identify with a corresponding submonoid of the group of quasi-admissible tuples in
![]() $\Lambda $
via the correspondence of Section 1.3.4(a),(b).
$\Lambda $
via the correspondence of Section 1.3.4(a),(b).
(b) Let
![]() $\Lambda '\subseteq \Lambda $
be a subgroup. Consider a
$\Lambda '\subseteq \Lambda $
be a subgroup. Consider a
![]() $\Gamma $
-filtration on
$\Gamma $
-filtration on
![]() $\Lambda '$
, where for every
$\Lambda '$
, where for every
![]() $\overline {x}\in \Gamma $
, we set
$\overline {x}\in \Gamma $
, we set
![]() $\Lambda ^{\prime }_{\overline {x}}:=\Lambda '\cap V^{\leq \overline {x}}$
, where
$\Lambda ^{\prime }_{\overline {x}}:=\Lambda '\cap V^{\leq \overline {x}}$
, where
![]() $V^{\leq \overline {x}}$
is defined in Section 1.3.9(d). Then
$V^{\leq \overline {x}}$
is defined in Section 1.3.9(d). Then
![]() $\{\Lambda ^{\prime }_{\overline {x}}\}_{\overline {x}}$
is a
$\{\Lambda ^{\prime }_{\overline {x}}\}_{\overline {x}}$
is a
![]() $\Gamma $
-filtered semigroup.
$\Gamma $
-filtered semigroup.
(c) Note that
![]() $R(\Lambda ')=\{(\mu ,\overline {x})\in \Lambda '\times \mathbb Z_{\geq 0}^{\Psi }\,|\,\langle \psi ,\mu \rangle \leq \overline {x}(\psi )\text { for every }\psi \in \Psi \}$
. Therefore, by Gordan’s lemma (see, for example, [Reference EwaldEw, Lemma 3.4, page 154]),
$R(\Lambda ')=\{(\mu ,\overline {x})\in \Lambda '\times \mathbb Z_{\geq 0}^{\Psi }\,|\,\langle \psi ,\mu \rangle \leq \overline {x}(\psi )\text { for every }\psi \in \Psi \}$
. Therefore, by Gordan’s lemma (see, for example, [Reference EwaldEw, Lemma 3.4, page 154]),
![]() $R(\Lambda ')$
is a finitely generated commutative monoid. Therefore, the Rees algebra
$R(\Lambda ')$
is a finitely generated commutative monoid. Therefore, the Rees algebra
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda '])=\overline {\mathbb Q}_{\ell }[R(\Lambda ')]$
is a finitely generated commutative algebra over
$R(\overline {\mathbb Q}_{\ell }[\Lambda '])=\overline {\mathbb Q}_{\ell }[R(\Lambda ')]$
is a finitely generated commutative algebra over
![]() $\overline {\mathbb Q}_{\ell }$
; hence, it is Noetherian.
$\overline {\mathbb Q}_{\ell }$
; hence, it is Noetherian.
(d) We apply the construction of part (b) to
![]() $\Lambda ':=\Lambda _{\gamma }$
, and equip the ind-scheme
$\Lambda ':=\Lambda _{\gamma }$
, and equip the ind-scheme
![]() $X=\operatorname {Fl}_{\gamma }$
(resp.
$X=\operatorname {Fl}_{\gamma }$
(resp.
![]() $X=\operatorname {Gr}_{\gamma }$
) with a
$X=\operatorname {Gr}_{\gamma }$
) with a
![]() $\Gamma $
-filtration
$\Gamma $
-filtration
![]() $\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }$
(resp.
$\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }$
(resp.
![]() $\operatorname {Gr}^{\leq \overline {x}}_{\gamma }$
). Then it follows from definitions that this filtration is compatible with a
$\operatorname {Gr}^{\leq \overline {x}}_{\gamma }$
). Then it follows from definitions that this filtration is compatible with a
![]() $\Gamma $
-filtration on
$\Gamma $
-filtration on
![]() $\Lambda _{\gamma }$
.
$\Lambda _{\gamma }$
.
Lemma 3.2.7. The
![]() $\Gamma $
-filtrations
$\Gamma $
-filtrations
![]() $\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
on
$\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
on
![]() $\operatorname {Gr}_{\gamma }$
and
$\operatorname {Gr}_{\gamma }$
and
![]() $\{\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }\}_{\overline {x}}$
on
$\{\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }\}_{\overline {x}}$
on
![]() $\operatorname {Fl}_{\gamma }$
are finitely generated over
$\operatorname {Fl}_{\gamma }$
are finitely generated over
![]() $\Lambda _{\gamma }$
.
$\Lambda _{\gamma }$
.
Proof. Since the filtration
![]() $\{\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }\}_{\overline {x}}$
on
$\{\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }\}_{\overline {x}}$
on
![]() $\operatorname {Fl}_{\gamma }$
is defined to be the preimage of the filtration
$\operatorname {Fl}_{\gamma }$
is defined to be the preimage of the filtration
![]() $\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
on
$\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
on
![]() $\operatorname {Gr}_{\gamma }$
, it will suffice to show the assertion for
$\operatorname {Gr}_{\gamma }$
, it will suffice to show the assertion for
![]() $\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
.
$\{\operatorname {Gr}^{\leq \overline {x}}_{\gamma }\}_{\overline {x}}$
.
Notice that for every
![]() $\Lambda _{\gamma }$
-invariant subset of
$\Lambda _{\gamma }$
-invariant subset of
![]() $X\subseteq \operatorname {Gr}_{\gamma }$
, the
$X\subseteq \operatorname {Gr}_{\gamma }$
, the
![]() $\Gamma $
-filtration on
$\Gamma $
-filtration on
![]() $\operatorname {Gr}_{\gamma }$
induces a
$\operatorname {Gr}_{\gamma }$
induces a
![]() $\Gamma $
-filtration on X. Moreover, if
$\Gamma $
-filtration on X. Moreover, if
![]() $\operatorname {Gr}_{\gamma }$
is a finite union
$\operatorname {Gr}_{\gamma }$
is a finite union
![]() $\bigcup _j X_j$
of
$\bigcup _j X_j$
of
![]() $\Lambda _{\gamma }$
-invariant subsets, then the filtration on
$\Lambda _{\gamma }$
-invariant subsets, then the filtration on
![]() $\operatorname {Gr}_{\gamma }$
is finitely generated if and only if the corresponding filtration on each
$\operatorname {Gr}_{\gamma }$
is finitely generated if and only if the corresponding filtration on each
![]() $X_j$
is finitely generated.
$X_j$
is finitely generated.
Recall that there exists a closed subscheme of finite type
![]() $Y\subseteq \operatorname {Gr}_{\gamma }$
such that
$Y\subseteq \operatorname {Gr}_{\gamma }$
such that
![]() $\operatorname {Gr}_{\gamma }=\Lambda _{\gamma }(Y)$
. Moreover, using Corollary 2.1.7(d), there exists a finite decomposition
$\operatorname {Gr}_{\gamma }=\Lambda _{\gamma }(Y)$
. Moreover, using Corollary 2.1.7(d), there exists a finite decomposition
![]() $Y=\bigcup _j Y_j$
such that for each j, there exists a tuple
$Y=\bigcup _j Y_j$
such that for each j, there exists a tuple
![]() $\overline {y}=\overline {y}_j$
such that
$\overline {y}=\overline {y}_j$
such that
![]() $Y_j\subseteq L(U_C)y_C$
for all
$Y_j\subseteq L(U_C)y_C$
for all
![]() $C\in \mathcal {C}$
. Then
$C\in \mathcal {C}$
. Then
![]() $\operatorname {Gr}_{\gamma }=\bigcup _j \Lambda _{\gamma }(Y_j)$
, and it suffices to show that the filtration
$\operatorname {Gr}_{\gamma }=\bigcup _j \Lambda _{\gamma }(Y_j)$
, and it suffices to show that the filtration
![]() $\{\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}\}_{\overline {x}}$
on each
$\{\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}\}_{\overline {x}}$
on each
![]() $\Lambda _{\gamma }(Y_j)$
is finitely generated over
$\Lambda _{\gamma }(Y_j)$
is finitely generated over
![]() $\Lambda _{\gamma }$
.
$\Lambda _{\gamma }$
.
Note that for every
![]() $\overline {x}\in \Gamma $
, we have an equality
$\overline {x}\in \Gamma $
, we have an equality
![]() $\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}=\Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}(Y_j)$
. Indeed, it follows from [Reference Mirkovic and VilonenMV, Proposition 3.1] (or can be deduced from Proposition 2.1.6) that for every
$\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}=\Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}(Y_j)$
. Indeed, it follows from [Reference Mirkovic and VilonenMV, Proposition 3.1] (or can be deduced from Proposition 2.1.6) that for every
![]() $\mu \in \Lambda _{\gamma }$
and
$\mu \in \Lambda _{\gamma }$
and
![]() $z\in Y_j$
, we have
$z\in Y_j$
, we have
![]() $\mu z\in \Lambda _{\gamma }(Y_j)^{\leq \overline {x}}$
if and only if
$\mu z\in \Lambda _{\gamma }(Y_j)^{\leq \overline {x}}$
if and only if
![]() $\mu y_C\leq _C x_C$
for all
$\mu y_C\leq _C x_C$
for all
![]() $C\in \mathcal {C}$
. Hence,
$C\in \mathcal {C}$
. Hence,
![]() $\mu z\in \Lambda _{\gamma }(Y_j)^{\leq \overline {x}}$
if and only if
$\mu z\in \Lambda _{\gamma }(Y_j)^{\leq \overline {x}}$
if and only if
![]() $\mu \in \Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}$
, as claimed.
$\mu \in \Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}$
, as claimed.
Therefore, it is enough to show that the
![]() $\Gamma $
-filtration
$\Gamma $
-filtration
![]() $\{(\Lambda _{\gamma })_{\overline {x}-\overline {y}_j}\}_{\overline {x}}$
is finitely generated over
$\{(\Lambda _{\gamma })_{\overline {x}-\overline {y}_j}\}_{\overline {x}}$
is finitely generated over
![]() $\Lambda _{\gamma }$
. Since
$\Lambda _{\gamma }$
. Since
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is a finitely generated
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is a finitely generated
![]() $\overline {\mathbb Q}_{\ell }$
-algebra (by Section 3.2.6(c)), the assertion follows.
$\overline {\mathbb Q}_{\ell }$
-algebra (by Section 3.2.6(c)), the assertion follows.
Corollary 3.2.8. The Rees module
![]() $R(H_i(\operatorname {Fl}_{\gamma }))$
is a finitely generated
$R(H_i(\operatorname {Fl}_{\gamma }))$
is a finitely generated
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-module.
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-module.
Proof. Since Rees algebra
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is Noetherian (see Section 3.2.6(c)), the assertion follows from Lemmas 3.2.5 and 3.2.7.
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is Noetherian (see Section 3.2.6(c)), the assertion follows from Lemmas 3.2.5 and 3.2.7.
Now we are ready to prove Proposition 3.2.2.
3.2.9.
Proof of Proposition 3.2.2.
Since
![]() $\Psi $
is finite, it will suffice to show the existence of r for a fixed
$\Psi $
is finite, it will suffice to show the existence of r for a fixed
![]() $\psi $
. For every
$\psi $
. For every
![]() $r\in \mathbb N$
, the embeddings
$r\in \mathbb N$
, the embeddings
![]() $\operatorname {Fl}^{\leq '\overline {x}}\hookrightarrow \operatorname {Fl}^{\leq '\overline {x}+r\overline {e}_{\psi }}$
for all
$\operatorname {Fl}^{\leq '\overline {x}}\hookrightarrow \operatorname {Fl}^{\leq '\overline {x}+r\overline {e}_{\psi }}$
for all
![]() $\overline {x}$
induce a homomorphism of
$\overline {x}$
induce a homomorphism of
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-modules
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-modules
![]() $\iota _{r\overline {e}_{\psi }}:R(H_i(\operatorname {Fl}_{\gamma }))\to R(H_i(\operatorname {Fl}_{\gamma }))$
, and Proposition 3.2.2 asserts that
$\iota _{r\overline {e}_{\psi }}:R(H_i(\operatorname {Fl}_{\gamma }))\to R(H_i(\operatorname {Fl}_{\gamma }))$
, and Proposition 3.2.2 asserts that
![]() $\operatorname {Ker}\iota _{r\overline {e}_{\psi }}=\operatorname {Ker}\iota _{(r+1)\overline {e}_{\psi }}$
for some r.
$\operatorname {Ker}\iota _{r\overline {e}_{\psi }}=\operatorname {Ker}\iota _{(r+1)\overline {e}_{\psi }}$
for some r.
Since
![]() $\{\operatorname {Ker}\iota _{r\overline {e}_{\psi }}\}_r$
is an increasing sequence of
$\{\operatorname {Ker}\iota _{r\overline {e}_{\psi }}\}_r$
is an increasing sequence of
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-submodules of
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
-submodules of
![]() $R(H_i(\operatorname {Fl}_{\gamma }))$
, the Rees algebra
$R(H_i(\operatorname {Fl}_{\gamma }))$
, the Rees algebra
![]() $R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is Noetherian (by Section 3.2.6(c)), while
$R(\overline {\mathbb Q}_{\ell }[\Lambda _{\gamma }])$
is Noetherian (by Section 3.2.6(c)), while
![]() $R(H_i(\operatorname {Fl}_{\gamma }))$
is finitely generated (by Corollary 3.2.8), this sequence stabilizes.
$R(H_i(\operatorname {Fl}_{\gamma }))$
is finitely generated (by Corollary 3.2.8), this sequence stabilizes.
The following lemma will be used in the proof of Theorem 0.3.
Lemma 3.2.10. There exists
![]() $m\in \mathbb N$
such that for every m-regular tuple
$m\in \mathbb N$
such that for every m-regular tuple
![]() $\overline {x}\in \mathbb Z^{\Psi }$
and every
$\overline {x}\in \mathbb Z^{\Psi }$
and every
![]() $\psi \in \Psi $
such that
$\psi \in \Psi $
such that
![]() $\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, we have
$\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, we have
![]() $\operatorname {Fl}_{\gamma }^{\leq '\overline {x}}=\operatorname {Fl}_{\gamma }^{\leq '\overline {x}+\overline {e}_{\psi }}$
.
$\operatorname {Fl}_{\gamma }^{\leq '\overline {x}}=\operatorname {Fl}_{\gamma }^{\leq '\overline {x}+\overline {e}_{\psi }}$
.
Proof. Our argument is similar to that of Lemma 3.2.7. It is enough to show that
![]() $\operatorname {Gr}_{\gamma }^{\leq \overline {x}}=\operatorname {Gr}_{\gamma }^{\leq \overline {x}+\overline {e}_{\psi }}$
. Let
$\operatorname {Gr}_{\gamma }^{\leq \overline {x}}=\operatorname {Gr}_{\gamma }^{\leq \overline {x}+\overline {e}_{\psi }}$
. Let
![]() $Y, Y_j$
and
$Y, Y_j$
and
![]() $\overline {y}_j$
be as in the proof of Lemma 3.2.7, and choose
$\overline {y}_j$
be as in the proof of Lemma 3.2.7, and choose
![]() $m\in \mathbb N$
such that for every m-regular
$m\in \mathbb N$
such that for every m-regular
![]() $\overline {x}$
, the tuples
$\overline {x}$
, the tuples
![]() $\overline {x}-\overline {y}_j+\overline {e}_{\psi }$
is regular. We claim that this m satisfies the required property.
$\overline {x}-\overline {y}_j+\overline {e}_{\psi }$
is regular. We claim that this m satisfies the required property.
It suffices to show that
![]() $\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}=\Lambda _{\gamma }(Y_j)^{\leq \overline {x}+\overline {e}_{\psi }}$
for each j. For this, it suffices to show that
$\Lambda _{\gamma }(Y_j)^{\leq \overline {x}}=\Lambda _{\gamma }(Y_j)^{\leq \overline {x}+\overline {e}_{\psi }}$
for each j. For this, it suffices to show that
![]() $\Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}= \Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j+\overline {e}_{\psi }}$
. In other words, we have to show that every
$\Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j}= \Lambda _{\gamma }^{\leq \overline {x}-\overline {y}_j+\overline {e}_{\psi }}$
. In other words, we have to show that every
![]() $\mu \in \Lambda ^{\leq \overline {x}-\overline {y}_j+\overline {e}_{\psi }}\smallsetminus \Lambda ^{\leq \overline {x}-\overline {y}_j}$
does not belong to
$\mu \in \Lambda ^{\leq \overline {x}-\overline {y}_j+\overline {e}_{\psi }}\smallsetminus \Lambda ^{\leq \overline {x}-\overline {y}_j}$
does not belong to
![]() $\Lambda _{\gamma }$
.
$\Lambda _{\gamma }$
.
We are going to deduce the assertion from Lemma 1.3.11(b). Since
![]() $\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, it follows from Section 3.1.4(d) that there exists a root
$\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, it follows from Section 3.1.4(d) that there exists a root
![]() $\alpha \in \Phi $
such that
$\alpha \in \Phi $
such that
![]() $\alpha \in (\Lambda _{\gamma })^{\perp }$
and
$\alpha \in (\Lambda _{\gamma })^{\perp }$
and
![]() $\langle \alpha ,\check {\psi }\rangle>0$
. Since
$\langle \alpha ,\check {\psi }\rangle>0$
. Since
![]() $\langle \psi ,\mu \rangle =(\overline {x}-\overline {y}_j+\overline {e}_{\psi })_{\psi }$
, and the tuple
$\langle \psi ,\mu \rangle =(\overline {x}-\overline {y}_j+\overline {e}_{\psi })_{\psi }$
, and the tuple
![]() $\overline {x}-\overline {y}_j+\overline {e}_{\psi }$
is regular by assumption, we conclude from Lemma 1.3.11(b) that
$\overline {x}-\overline {y}_j+\overline {e}_{\psi }$
is regular by assumption, we conclude from Lemma 1.3.11(b) that
![]() $\langle \alpha ,\mu \rangle>0$
. Therefore,
$\langle \alpha ,\mu \rangle>0$
. Therefore,
![]() $\mu \notin \Lambda _{\gamma }$
because
$\mu \notin \Lambda _{\gamma }$
because
![]() $\alpha \in (\Lambda _{\gamma })^{\perp }$
.
$\alpha \in (\Lambda _{\gamma })^{\perp }$
.
4 Proof of Theorem 0.3
4.1 Localization theorem for equivariant cohomology
In this section we will review basic facts about equivariant cohomology (with compact support), including a version of a localization theorem.
4.1.1.
Total cohomology of Artin stacks. For an Artin stack
![]() $\mathcal {X}$
of finite type over k and
$\mathcal {X}$
of finite type over k and
![]() $\mathcal {F}\in D^b_c(\mathcal {X},\overline {\mathbb Q}_{\ell })$
, we denote by
$\mathcal {F}\in D^b_c(\mathcal {X},\overline {\mathbb Q}_{\ell })$
, we denote by
![]() $H^{\bullet }(\mathcal {X},\mathcal {F}):=\bigoplus _i H^i(\mathcal {X},\mathcal {F})$
its total cohomology, and set
$H^{\bullet }(\mathcal {X},\mathcal {F}):=\bigoplus _i H^i(\mathcal {X},\mathcal {F})$
its total cohomology, and set
![]() $H^{\bullet }(\mathcal {X}):= H^{\bullet }(\mathcal {X},\overline {\mathbb Q}_{\ell })$
.
$H^{\bullet }(\mathcal {X}):= H^{\bullet }(\mathcal {X},\overline {\mathbb Q}_{\ell })$
.
(a) Note that
![]() $H^{\bullet }(\mathcal {X})=\operatorname {Ext}^{\bullet }_{\mathcal {X}}(\overline {\mathbb Q}_{\ell },\overline {\mathbb Q}_{\ell })$
is a graded
$H^{\bullet }(\mathcal {X})=\operatorname {Ext}^{\bullet }_{\mathcal {X}}(\overline {\mathbb Q}_{\ell },\overline {\mathbb Q}_{\ell })$
is a graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebra, and identification
$\overline {\mathbb Q}_{\ell }$
-algebra, and identification
![]() $\mathcal {F}[\bullet ]=\overline {\mathbb Q}_{\ell }[\bullet ]\otimes _{\overline {\mathbb Q}_{\ell }}\mathcal {F}$
give to
$\mathcal {F}[\bullet ]=\overline {\mathbb Q}_{\ell }[\bullet ]\otimes _{\overline {\mathbb Q}_{\ell }}\mathcal {F}$
give to
![]() $H^{\bullet }(\mathcal {X},\mathcal {F})$
a natural structure of a graded
$H^{\bullet }(\mathcal {X},\mathcal {F})$
a natural structure of a graded
![]() $H^{\bullet }(\mathcal {X})$
-module.
$H^{\bullet }(\mathcal {X})$
-module.
(b) Every morphism
![]() $\mathcal {F}_1\to \mathcal {F}_2$
in
$\mathcal {F}_1\to \mathcal {F}_2$
in
![]() $D^b_c(\mathcal {X},\overline {\mathbb Q}_{\ell })$
induces a homomorphism
$D^b_c(\mathcal {X},\overline {\mathbb Q}_{\ell })$
induces a homomorphism
![]() $H^{\bullet }(\mathcal {X},\mathcal {F}_1)\to H^{\bullet }(\mathcal {X},\mathcal {F}_2)$
of graded
$H^{\bullet }(\mathcal {X},\mathcal {F}_1)\to H^{\bullet }(\mathcal {X},\mathcal {F}_2)$
of graded
![]() $H^{\bullet }(\mathcal {X})$
-modules.
$H^{\bullet }(\mathcal {X})$
-modules.
(c) For every homomorphism
![]() $f:\mathcal {X}\to \mathcal {Y}$
of Artin stacks of finite type over k, the pullback
$f:\mathcal {X}\to \mathcal {Y}$
of Artin stacks of finite type over k, the pullback
![]() $f^*:H^{\bullet }(\mathcal {Y})\to H^{\bullet }(\mathcal {X})$
is a homomorphism of graded
$f^*:H^{\bullet }(\mathcal {Y})\to H^{\bullet }(\mathcal {X})$
is a homomorphism of graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebras. Moreover, for every
$\overline {\mathbb Q}_{\ell }$
-algebras. Moreover, for every
![]() $\mathcal {F}\in D^b_c(\mathcal {Y},\overline {\mathbb Q}_{\ell })$
the pullback
$\mathcal {F}\in D^b_c(\mathcal {Y},\overline {\mathbb Q}_{\ell })$
the pullback
![]() $f^*$
gives rise to a homomorphism
$f^*$
gives rise to a homomorphism
of graded
![]() $H^{\bullet }(\mathcal {X})$
-modules.
$H^{\bullet }(\mathcal {X})$
-modules.
4.1.2.
Equivariant cohomology (compare [Reference Bernstein and LuntsBL, Reference Goresky, Kottwitz and MacPhersonGKM, Reference AcharAc, Reference Anderson and FultonAF]). Let G be an algebraic group over k, let X be a separated scheme of finite type over k equipped with a G-action, set
![]() $\operatorname {pt}:=\operatorname {Spec} k$
, let
$\operatorname {pt}:=\operatorname {Spec} k$
, let
![]() $[\operatorname {pt}/G]$
be the classifying stack of G, and let
$[\operatorname {pt}/G]$
be the classifying stack of G, and let
![]() $\operatorname {pr}_X:[X/G]\to [\operatorname {pt}/G]$
be the natural projection.
$\operatorname {pr}_X:[X/G]\to [\operatorname {pt}/G]$
be the natural projection.
(a) For every
![]() $\mathcal {F}\in D^b_c([X/G],\overline {\mathbb Q}_{\ell })$
, we define its equivariant cohomology
$\mathcal {F}\in D^b_c([X/G],\overline {\mathbb Q}_{\ell })$
, we define its equivariant cohomology
equivariant cohomology with compact support
and set
![]() $H^{\bullet }_{G}(X):=H^{\bullet }_{G}(X,\overline {\mathbb Q}_{\ell })$
and
$H^{\bullet }_{G}(X):=H^{\bullet }_{G}(X,\overline {\mathbb Q}_{\ell })$
and
![]() $H^{\bullet }_{c,G}(X):=H^{\bullet }_{c,G}(X,\overline {\mathbb Q}_{\ell })$
.
$H^{\bullet }_{c,G}(X):=H^{\bullet }_{c,G}(X,\overline {\mathbb Q}_{\ell })$
.
(b) By Section 4.1.1(a),
![]() $H^{\bullet }_G(\operatorname {pt})$
is a graded
$H^{\bullet }_G(\operatorname {pt})$
is a graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebra, while both
$\overline {\mathbb Q}_{\ell }$
-algebra, while both
![]() $H^{\bullet }_{G}(X,\mathcal {F})$
and
$H^{\bullet }_{G}(X,\mathcal {F})$
and
![]() $H^{\bullet }_{c,G}(X,\mathcal {F})$
have natural structures of graded
$H^{\bullet }_{c,G}(X,\mathcal {F})$
have natural structures of graded
![]() $H^{\bullet }_G(\operatorname {pt})$
-modules.
$H^{\bullet }_G(\operatorname {pt})$
-modules.
(c) Note that
![]() $H^{\bullet }_G(X)=\operatorname {Ext}^{\bullet }_{[X/G]}(\overline {\mathbb Q}_{\ell },\overline {\mathbb Q}_{\ell })$
is a graded
$H^{\bullet }_G(X)=\operatorname {Ext}^{\bullet }_{[X/G]}(\overline {\mathbb Q}_{\ell },\overline {\mathbb Q}_{\ell })$
is a graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebra; hence, both
$\overline {\mathbb Q}_{\ell }$
-algebra; hence, both
![]() $H^{\bullet }_{G}(X,\mathcal {F})$
and
$H^{\bullet }_{G}(X,\mathcal {F})$
and
![]() $H^{\bullet }_{c,G}(X,\mathcal {F})$
have natural structures of graded
$H^{\bullet }_{c,G}(X,\mathcal {F})$
have natural structures of graded
![]() $H^{\bullet }_G(X)$
-modules.
$H^{\bullet }_G(X)$
-modules.
(d) Note that the structures of
![]() $H^{\bullet }_{G}(X,\mathcal {F})$
and
$H^{\bullet }_{G}(X,\mathcal {F})$
and
![]() $H^{\bullet }_{c,G}(X,\mathcal {F})$
of graded
$H^{\bullet }_{c,G}(X,\mathcal {F})$
of graded
![]() $H^{\bullet }_G(\operatorname {pt})$
-modules from part (b) are obtained from structures of graded
$H^{\bullet }_G(\operatorname {pt})$
-modules from part (b) are obtained from structures of graded
![]() $H^{\bullet }_G(X)$
-modules from part (c) by the homomorphism
$H^{\bullet }_G(X)$
-modules from part (c) by the homomorphism
of graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebras from Section 4.1.1(c).
$\overline {\mathbb Q}_{\ell }$
-algebras from Section 4.1.1(c).
4.1.3.
Simple properties. Let G, X and
![]() $\mathcal {F}$
be as in Section 4.1.2.
$\mathcal {F}$
be as in Section 4.1.2.
(a) Using Section 4.1.1(b), for each closed G-invariant subscheme
![]() $Z\subseteq X$
, the long exact sequence for cohomology with compact support naturally upgrades to an exact sequence
$Z\subseteq X$
, the long exact sequence for cohomology with compact support naturally upgrades to an exact sequence
of graded
![]() $H^{\bullet }_G(\operatorname {pt})$
-modules, functorial in
$H^{\bullet }_G(\operatorname {pt})$
-modules, functorial in
![]() $(X,Z)$
.
$(X,Z)$
.
(b) If G acts trivially on X, then we have canonical isomorphism
of graded
![]() $H^{\bullet }_G(\operatorname {pt})$
-modules, functorial in X. Indeed, since
$H^{\bullet }_G(\operatorname {pt})$
-modules, functorial in X. Indeed, since
![]() $[X/G]\simeq X\times [\operatorname {pt}/G]$
, the assertion follows from Künneth formula. Alternatively, choose a compactification
$[X/G]\simeq X\times [\operatorname {pt}/G]$
, the assertion follows from Künneth formula. Alternatively, choose a compactification
![]() $j:X\hookrightarrow \overline {X}$
of X, and apply [Reference AcharAc, Proposition 6.7.5] for
$j:X\hookrightarrow \overline {X}$
of X, and apply [Reference AcharAc, Proposition 6.7.5] for
![]() $H^{\bullet }_{\{1\}\times G}(\overline {X}\times \operatorname {pt},(j_!\overline {\mathbb Q}_{\ell })\boxtimes \overline {\mathbb Q}_{\ell })$
.
$H^{\bullet }_{\{1\}\times G}(\overline {X}\times \operatorname {pt},(j_!\overline {\mathbb Q}_{\ell })\boxtimes \overline {\mathbb Q}_{\ell })$
.
(c) Using observation of Section 4.1.1(c) applied to the projection
![]() $\pi :\operatorname {pt}\to [\operatorname {pt}/G]$
and an object
$\pi :\operatorname {pt}\to [\operatorname {pt}/G]$
and an object
![]() $R(p_X)_!(\mathcal {F})\in D^b_c([\operatorname {pt}/G],\overline {\mathbb Q}_{\ell })$
, we have a homomorphism
$R(p_X)_!(\mathcal {F})\in D^b_c([\operatorname {pt}/G],\overline {\mathbb Q}_{\ell })$
, we have a homomorphism
![]() $\pi ^*:H^{\bullet }_G(\operatorname {pt})\to H^{\bullet }(\operatorname {pt})=\overline {\mathbb Q}_{\ell }$
of graded
$\pi ^*:H^{\bullet }_G(\operatorname {pt})\to H^{\bullet }(\operatorname {pt})=\overline {\mathbb Q}_{\ell }$
of graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebras and a homomorphism
$\overline {\mathbb Q}_{\ell }$
-algebras and a homomorphism
of graded vector spaces (compare [Reference AcharAc, equation (6.7.2)]).
Moreover, if
![]() $H^{\bullet }_{c,S}(X,\mathcal {F})$
is a free graded
$H^{\bullet }_{c,S}(X,\mathcal {F})$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module, then morphism (4.1) is an isomorphism. Indeed, as in the proof of [Reference AcharAc, Lemma 6.7.4], one first reduces to the case
$H^{\bullet }_S(\operatorname {pt})$
-module, then morphism (4.1) is an isomorphism. Indeed, as in the proof of [Reference AcharAc, Lemma 6.7.4], one first reduces to the case
![]() $X=\operatorname {pt}$
in which case the assertion follows from [Reference AcharAc, Lemma 6.7.3].
$X=\operatorname {pt}$
in which case the assertion follows from [Reference AcharAc, Lemma 6.7.3].
4.1.4. Localization theorem (compare [Reference Goresky, Kottwitz and MacPhersonGKM, Reference Anderson and FultonAF]). Let S be an algebraic torus acting on a separated scheme X of finite type over k.
(a) Recall that graded
![]() $\overline {\mathbb Q}_{\ell }$
-algebra
$\overline {\mathbb Q}_{\ell }$
-algebra
![]() $H^{\bullet }_S(\operatorname {pt})$
is canonically isomorphic with the symmetric algebra
$H^{\bullet }_S(\operatorname {pt})$
is canonically isomorphic with the symmetric algebra
![]() $\operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1)[-2])$
, where
$\operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1)[-2])$
, where
![]() $X^*(S)$
denote the group of characters of S, while
$X^*(S)$
denote the group of characters of S, while
![]() $[-2]$
indicates that the vector space
$[-2]$
indicates that the vector space
![]() $X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1)$
is placed in degree
$X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1)$
is placed in degree
![]() $2$
(see, for example, [Reference AcharAc, Theorem 6.7.7]).
$2$
(see, for example, [Reference AcharAc, Theorem 6.7.7]).
We fix an isomorphism of
![]() $\overline {\mathbb Q}_{\ell }$
-vector spaces
$\overline {\mathbb Q}_{\ell }$
-vector spaces
![]() $\overline {\mathbb Q}_{\ell }(-1)\simeq \overline {\mathbb Q}_{\ell }$
; thus, we can view
$\overline {\mathbb Q}_{\ell }(-1)\simeq \overline {\mathbb Q}_{\ell }$
; thus, we can view
![]() $X^*(S)$
as a subset of
$X^*(S)$
as a subset of
![]() $\operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell })\simeq \operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1))\simeq H^{\bullet }_S(\operatorname {pt})$
.
$\operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell })\simeq \operatorname {Sym}^{\bullet }_{\overline {\mathbb Q}_{\ell }}(X^*(S)\otimes _{\mathbb Z}\overline {\mathbb Q}_{\ell }(-1))\simeq H^{\bullet }_S(\operatorname {pt})$
.
(b) By Section 4.1.2(b), both
![]() $H_{c,S}^{\bullet }(X,\mathcal {F})$
and
$H_{c,S}^{\bullet }(X,\mathcal {F})$
and
![]() $H_{S}^{\bullet }(X,\mathcal {F})$
are graded
$H_{S}^{\bullet }(X,\mathcal {F})$
are graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules for every
$H^{\bullet }_S(\operatorname {pt})$
-modules for every
![]() $\mathcal {F}\in D^b_c([X/S],\overline {\mathbb Q}_{\ell })$
. We claim that if
$\mathcal {F}\in D^b_c([X/S],\overline {\mathbb Q}_{\ell })$
. We claim that if
![]() $X^S=\emptyset $
, then there exists
$X^S=\emptyset $
, then there exists
![]() $\lambda \in X^*(S)\subseteq H^{\bullet }_S(\operatorname {pt})$
, which acts on each
$\lambda \in X^*(S)\subseteq H^{\bullet }_S(\operatorname {pt})$
, which acts on each
![]() $H_{c,S}^{\bullet }(X,\mathcal {F})$
and
$H_{c,S}^{\bullet }(X,\mathcal {F})$
and
![]() $H_{S}^{\bullet }(X,\mathcal {F})$
as zero.
$H_{S}^{\bullet }(X,\mathcal {F})$
as zero.
Indeed, by a particular case of the localization theorem (see, for example, [Reference Anderson and FultonAF, Chapter 7, Theorem 1.1]), there exists
![]() $\lambda \in X^*(S)$
such that the image of
$\lambda \in X^*(S)$
such that the image of
![]() $\lambda $
under the pullback
$\lambda $
under the pullback
![]() $(p_X)^*:H^{\bullet }_S(\operatorname {pt})\to H_S^{\bullet }(X)$
is zero, so the assertion follows by the observation of Section 4.1.2(d).
$(p_X)^*:H^{\bullet }_S(\operatorname {pt})\to H_S^{\bullet }(X)$
is zero, so the assertion follows by the observation of Section 4.1.2(d).
(c) The pullback
![]() $H^{\bullet }_{c,S}(X,\mathcal {F})\to H^{\bullet }_{c,S}(X^S,\mathcal {F}|_{X^S})$
induces an isomorphism of localizations
$H^{\bullet }_{c,S}(X,\mathcal {F})\to H^{\bullet }_{c,S}(X^S,\mathcal {F}|_{X^S})$
induces an isomorphism of localizations
Indeed, by part (b), we have
![]() $(X^*(S))^{-1} H^{\bullet }_{c,S}(X\smallsetminus X^S,\mathcal {F})=0$
, so the assertion follows from the exact sequence of Section 4.1.3(a).
$(X^*(S))^{-1} H^{\bullet }_{c,S}(X\smallsetminus X^S,\mathcal {F})=0$
, so the assertion follows from the exact sequence of Section 4.1.3(a).
(d) If
![]() $H^{\bullet }_{c,S}(X,\mathcal {F})$
is a free (or, more generally, torsion free)
$H^{\bullet }_{c,S}(X,\mathcal {F})$
is a free (or, more generally, torsion free)
![]() $H^{\bullet }_S(\operatorname {pt})$
-module, then the restriction map
$H^{\bullet }_S(\operatorname {pt})$
-module, then the restriction map
![]() $H^{\bullet }_{c,S}(X,\mathcal {F})\to H^{\bullet }_{c,S}(X^S,\mathcal {F}|_{X^S})$
is injective. Indeed, our assumption implies that the canonical map
$H^{\bullet }_{c,S}(X,\mathcal {F})\to H^{\bullet }_{c,S}(X^S,\mathcal {F}|_{X^S})$
is injective. Indeed, our assumption implies that the canonical map
![]() $H^{\bullet }_{c,S}(X,\mathcal {F})\to (X^*(S))^{-1} H^{\bullet }_{c,S}(X,\mathcal {F})$
is injective, so the assertion follows from part (c) and Section 4.1.3(b).
$H^{\bullet }_{c,S}(X,\mathcal {F})\to (X^*(S))^{-1} H^{\bullet }_{c,S}(X,\mathcal {F})$
is injective, so the assertion follows from part (c) and Section 4.1.3(b).
4.2 Criterion of injectivity
4.2.1.
Borel–Moore homology. To every scheme X of finite type over k, one associates the Borel-Moore homology groups
![]() $H_{i,BM}(X):=H^i_c(X,\overline {\mathbb Q}_{\ell })^*$
. In particular, we have
$H_{i,BM}(X):=H^i_c(X,\overline {\mathbb Q}_{\ell })^*$
. In particular, we have
![]() $H_{i,BM}(X)=H_i(X)$
if X is proper over k. Also for every closed subscheme
$H_{i,BM}(X)=H_i(X)$
if X is proper over k. Also for every closed subscheme
![]() $Z\subseteq X$
, we have a long exact sequence
$Z\subseteq X$
, we have a long exact sequence
Lemma 4.2.2. Let X be a closed subscheme of Y, and let
![]() $\iota :H_{i,BM}(X)\to H_{i,BM}(Y)$
be the natural map.
$\iota :H_{i,BM}(X)\to H_{i,BM}(Y)$
be the natural map.
(a) The map
![]() $\iota $
is injective if there exists a closed subscheme
$\iota $
is injective if there exists a closed subscheme
![]() $Z\subseteq X$
such that
$Z\subseteq X$
such that
and the map
![]() $H_{i,BM}(X\smallsetminus Z)\to H_{i,BM}(Y\smallsetminus Z)$
is injective.
$H_{i,BM}(X\smallsetminus Z)\to H_{i,BM}(Y\smallsetminus Z)$
is injective.
(b) The map
![]() $\iota $
is injective if there exists a closed subscheme
$\iota $
is injective if there exists a closed subscheme
![]() $Z\subseteq Y$
containing
$Z\subseteq Y$
containing
![]() $Y\smallsetminus X$
such that the natural map
$Y\smallsetminus X$
such that the natural map
![]() $H_{i,BM}(Z\cap X)\to H_{i,BM}(Z)$
is injective.
$H_{i,BM}(Z\cap X)\to H_{i,BM}(Z)$
is injective.
Proof. Both assertions follow from a straightforward diagram chase. Namely, assertion (a) follows from the commutative diagram

with an exact first row, while assertion (b) follows from the commutative diagram with exact rows

4.2.3.
Acyclic morphisms. (a) We say that a scheme X of finite type over k is acyclic if the canonical morphism
![]() $\overline {\mathbb Q}_{\ell }\to R\Gamma (X,\overline {\mathbb Q}_{\ell })$
is an isomorphism.
$\overline {\mathbb Q}_{\ell }\to R\Gamma (X,\overline {\mathbb Q}_{\ell })$
is an isomorphism.
(b) We say that a morphism
![]() $f:X\to Y$
between schemes of finite type over k is acyclic if it is smooth and all geometric fibers of f are acyclic.Footnote
1
$f:X\to Y$
between schemes of finite type over k is acyclic if it is smooth and all geometric fibers of f are acyclic.Footnote
1
(c) Note that if
![]() $f:X\to Y$
is acyclic, then for every connected component
$f:X\to Y$
is acyclic, then for every connected component
![]() $Y'$
of Y, the restriction
$Y'$
of Y, the restriction
![]() $f|_{Y'}:f^{-1}(Y')\to Y'$
is smooth of some relative dimension N, and we have
$f|_{Y'}:f^{-1}(Y')\to Y'$
is smooth of some relative dimension N, and we have
![]() $Rf_!(\overline {\mathbb Q}_{\ell })|_{Y'}\simeq \overline {\mathbb Q}_{\ell }[2N](N)$
(use, for example, [Reference Bezrukavnikov, Kazhdan and VarshavskyBKV, Lemma 1.1.3]).
$Rf_!(\overline {\mathbb Q}_{\ell })|_{Y'}\simeq \overline {\mathbb Q}_{\ell }[2N](N)$
(use, for example, [Reference Bezrukavnikov, Kazhdan and VarshavskyBKV, Lemma 1.1.3]).
The following result uses notation of Section 4.1.
Lemma 4.2.4.
(a) Let S be a torus, let Y be an S-equivariant scheme of finite type over k, and let
![]() $X\subseteq Y$
be a closed S-invariant subscheme. Assume that
$X\subseteq Y$
be a closed S-invariant subscheme. Assume that
(i) the restriction map
![]() $H^{\bullet }_c(Y^S)\to H^{\bullet }_c(X^S)$
is surjective and
$H^{\bullet }_c(Y^S)\to H^{\bullet }_c(X^S)$
is surjective and
(ii) both
![]() $H^{\bullet }_{c,S}(X)$
and
$H^{\bullet }_{c,S}(X)$
and
![]() $H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
$H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules.
$H^{\bullet }_S(\operatorname {pt})$
-modules.
Then
![]() $H^{\bullet }_{c,S}(Y)$
is a free graded
$H^{\bullet }_{c,S}(Y)$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module, and the restriction map
$H^{\bullet }_S(\operatorname {pt})$
-module, and the restriction map
![]() $H^{\bullet }_c(Y)\to H^{\bullet }_c(X)$
is surjective.
$H^{\bullet }_c(Y)\to H^{\bullet }_c(X)$
is surjective.
(b) Assume that Y has a finite S-invariant filtration
![]() $\emptyset =Y_0\subseteq Y_1\subseteq \ldots \subseteq Y_n=Y$
by closed reduced subschemes such that for each
$\emptyset =Y_0\subseteq Y_1\subseteq \ldots \subseteq Y_n=Y$
by closed reduced subschemes such that for each
![]() $j=1,\ldots ,n-1$
,
$j=1,\ldots ,n-1$
,
(i) the restriction map
![]() $H^{\bullet }_c(Y_j^S)\to H^{\bullet }_c(Y_{j-1}^S)$
is surjective and
$H^{\bullet }_c(Y_j^S)\to H^{\bullet }_c(Y_{j-1}^S)$
is surjective and
(ii) there exists an S-equivariant acyclic morphism
![]() $\pi _j:Y_j\smallsetminus Y_{j-1}\to (Y_j\smallsetminus Y_{j-1})^S$
.
$\pi _j:Y_j\smallsetminus Y_{j-1}\to (Y_j\smallsetminus Y_{j-1})^S$
.
Then
![]() $H^{\bullet }_{c,S}(Y)$
is a free graded
$H^{\bullet }_{c,S}(Y)$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module.
$H^{\bullet }_S(\operatorname {pt})$
-module.
Proof. (a) By Section 4.1.3(a), we have a commutative diagram

of graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules with exact bottom row, where vertical arrows are induced by the inclusion
$H^{\bullet }_S(\operatorname {pt})$
-modules with exact bottom row, where vertical arrows are induced by the inclusion
![]() $Y^S\hookrightarrow Y$
. By Section 4.1.3(b), we have canonical isomorphisms
$Y^S\hookrightarrow Y$
. By Section 4.1.3(b), we have canonical isomorphisms
of
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules. Hence, by assumption (i), the map
$H^{\bullet }_S(\operatorname {pt})$
-modules. Hence, by assumption (i), the map
![]() $H^{\bullet }_{c,S}(Y^S)\to H^{\bullet }_{c,S}(X^S)$
is surjective; therefore, the connecting homomorphism
$H^{\bullet }_{c,S}(Y^S)\to H^{\bullet }_{c,S}(X^S)$
is surjective; therefore, the connecting homomorphism
![]() $\delta _2$
is zero.
$\delta _2$
is zero.
By assumption (ii) and the localization theorem (see Section 4.1.4(d)), the right vertical map is injective; hence, the connecting homomorphism
![]() $\delta _1$
is zero as well. Thus, by Section 4.1.3(a), we get a short exact sequence
$\delta _1$
is zero as well. Thus, by Section 4.1.3(a), we get a short exact sequence
of graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules; hence,
$H^{\bullet }_S(\operatorname {pt})$
-modules; hence,
![]() $H^{\bullet }_{c,S}(Y)$
is a free graded
$H^{\bullet }_{c,S}(Y)$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module by assumption (ii). In this case, we have canonical isomorphisms
$H^{\bullet }_S(\operatorname {pt})$
-module by assumption (ii). In this case, we have canonical isomorphisms
of graded vector spaces (see Section 4.1.3(c)); therefore, surjectivity of the map
![]() $H^{\bullet }_{c}(Y)\to H^{\bullet }_{c}(X)$
follows from the surjectivity of
$H^{\bullet }_{c}(Y)\to H^{\bullet }_{c}(X)$
follows from the surjectivity of
![]() $H^{\bullet }_{c,S}(Y)\to H^{\bullet }_{c,S}(X)$
.
$H^{\bullet }_{c,S}(Y)\to H^{\bullet }_{c,S}(X)$
.
(b) We are going to show the assertion by induction on n. Assume first that
![]() $n=1$
. Then
$n=1$
. Then
![]() $\pi :=\pi _1:Y\to Y^S$
is an S-equivariant acyclic morphism, so we conclude from Sections 4.1.3(b) and 4.2.3(c) that
$\pi :=\pi _1:Y\to Y^S$
is an S-equivariant acyclic morphism, so we conclude from Sections 4.1.3(b) and 4.2.3(c) that
![]() $H^{\bullet }_{c,S}(Y,\overline {\mathbb Q}_{\ell })\cong H^{\bullet }_{c,S}(Y^S,R\pi _!\overline {\mathbb Q}_{\ell })$
is a free graded
$H^{\bullet }_{c,S}(Y,\overline {\mathbb Q}_{\ell })\cong H^{\bullet }_{c,S}(Y^S,R\pi _!\overline {\mathbb Q}_{\ell })$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module.
$H^{\bullet }_S(\operatorname {pt})$
-module.
Now assume that
![]() $n>1$
, and set
$n>1$
, and set
![]() $X:=Y_{n-1}$
. By the induction hypothesis, both
$X:=Y_{n-1}$
. By the induction hypothesis, both
![]() $H^{\bullet }_{c,S}(X)$
and
$H^{\bullet }_{c,S}(X)$
and
![]() $H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
$H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-modules. Therefore, by assumption (i), all assumptions of part (a) are satisfied; thus,
$H^{\bullet }_S(\operatorname {pt})$
-modules. Therefore, by assumption (i), all assumptions of part (a) are satisfied; thus,
![]() $H^{\bullet }_{c,S}(Y)$
is a free graded
$H^{\bullet }_{c,S}(Y)$
is a free graded
![]() $H^{\bullet }_S(\operatorname {pt})$
-module.
$H^{\bullet }_S(\operatorname {pt})$
-module.
Lemma 4.2.5. Let Y be an ind-scheme of ind-finite type over k equipped with an action of a torus S, let
![]() $p:Y\to Y^S$
be an S-equivariant acyclic morphism such that its restriction
$p:Y\to Y^S$
be an S-equivariant acyclic morphism such that its restriction
![]() $p|_{Y^S}$
is the identity, and let
$p|_{Y^S}$
is the identity, and let
![]() $X\subseteq Y$
be a reduced locally closed ind-subscheme such that we have an inclusion of sets
$X\subseteq Y$
be a reduced locally closed ind-subscheme such that we have an inclusion of sets
![]() $p^{-1}(p(X))\subseteq X$
.
$p^{-1}(p(X))\subseteq X$
.
Then X is equal to the schematic preimage
![]() $p^{-1}(X^S)\subseteq Y$
. In particular, X is S-invariant, and p induces an S-equivariant acyclic morphism
$p^{-1}(X^S)\subseteq Y$
. In particular, X is S-invariant, and p induces an S-equivariant acyclic morphism
![]() $p_X:X\to X^S$
such that
$p_X:X\to X^S$
such that
![]() $p_X|_{X^S}$
is the identity.
$p_X|_{X^S}$
is the identity.
Proof. Notice that since the inclusion
![]() $p^{-1}(p(X))\supseteq X$
always holds, we have an equality of sets
$p^{-1}(p(X))\supseteq X$
always holds, we have an equality of sets
![]() $p^{-1}(p(X))=X$
; thus, the ind-subscheme
$p^{-1}(p(X))=X$
; thus, the ind-subscheme
![]() $X\subseteq Y$
is S-invariant.
$X\subseteq Y$
is S-invariant.
Next, we claim that we have an equality of sets
![]() $p(X)=X^S$
. Indeed,
$p(X)=X^S$
. Indeed,
![]() $p|_{Y^S}$
is the identity, we get
$p|_{Y^S}$
is the identity, we get
![]() $p(X^S)=X^S$
and
$p(X^S)=X^S$
and
![]() $p(X)\subseteq p^{-1}(p(X))$
. Therefore, we have inclusions
$p(X)\subseteq p^{-1}(p(X))$
. Therefore, we have inclusions
By the proven above, we have an equality of sets
![]() $p^{-1}(X^S)=p^{-1}(p(X))=X$
, and from this, the assertion follows: Indeed, since X is reduced and S is a torus, we conclude that
$p^{-1}(X^S)=p^{-1}(p(X))=X$
, and from this, the assertion follows: Indeed, since X is reduced and S is a torus, we conclude that
![]() $X^S$
is reduced. Since p is smooth, the schematic preimage
$X^S$
is reduced. Since p is smooth, the schematic preimage
![]() $p^{-1}(X^S)$
is reduced, so the equality of reduced ind-subschemes
$p^{-1}(X^S)$
is reduced, so the equality of reduced ind-subschemes
![]() $p^{-1}(X^S)=X$
follows from the corresponding equality of the underlying sets.
$p^{-1}(X^S)=X$
follows from the corresponding equality of the underlying sets.
Corollary 4.2.6. Let Z be an S-equivariant ind-scheme of ind-finite type over k,
![]() $\{Z_{\nu }\}_{\nu \in \Xi }$
an S-invariant stratification of Z,
$\{Z_{\nu }\}_{\nu \in \Xi }$
an S-invariant stratification of Z,
![]() $Y\subseteq Z$
an S-invariant locally closed subscheme of finite type over k, and
$Y\subseteq Z$
an S-invariant locally closed subscheme of finite type over k, and
![]() $X\subseteq Y$
an S-invariant closed subscheme.
$X\subseteq Y$
an S-invariant closed subscheme.
Assume that for each
![]() $\nu \in \Xi $
,
$\nu \in \Xi $
,
(a) the stratum
![]() $Z_{\nu }^S$
is an open and closed ind-subscheme of
$Z_{\nu }^S$
is an open and closed ind-subscheme of
![]() $Z^S$
;
$Z^S$
;
(b) the map
![]() $H_{i,BM}(X\cap Z_{\nu }^S)\to H_{i,BM}(Y\cap Z_{\nu }^S)$
is injective for all i;
$H_{i,BM}(X\cap Z_{\nu }^S)\to H_{i,BM}(Y\cap Z_{\nu }^S)$
is injective for all i;
(c) there exists an S-equivariant acyclic morphism
![]() $p_{\nu }:Y\cap Z_{\nu }\to Y\cap Z_{\nu }^S$
between reduced intersections such that
$p_{\nu }:Y\cap Z_{\nu }\to Y\cap Z_{\nu }^S$
between reduced intersections such that
![]() $p_{\nu }|_{Y\cap Z_{\nu }^S}$
is the identity, and we have an inclusion of sets
$p_{\nu }|_{Y\cap Z_{\nu }^S}$
is the identity, and we have an inclusion of sets
![]() $p_{\nu }^{-1}(p_{\nu }(X\cap Z_{\nu }))\subseteq X$
.
$p_{\nu }^{-1}(p_{\nu }(X\cap Z_{\nu }))\subseteq X$
.
Then the map
![]() $H_{i,BM}(X)\to H_{i,BM}(Y)$
is injective for all i.
$H_{i,BM}(X)\to H_{i,BM}(Y)$
is injective for all i.
Proof. We are going to apply the criterion of Lemma 4.2.4(a).
It follows from assumption (a) that
![]() $Y^S$
(resp.
$Y^S$
(resp.
![]() $X^S$
) is a disjoint union of the
$X^S$
) is a disjoint union of the
![]() $Y\cap Z_{\nu }^S$
’s (resp.
$Y\cap Z_{\nu }^S$
’s (resp.
![]() $X\cap Z_{\nu }^S$
’s). This observation together with assumption (b) implies that the map
$X\cap Z_{\nu }^S$
’s). This observation together with assumption (b) implies that the map
![]() $H_{i,BM}(X^S)\to H_{i,BM}(Y^S)$
is injective for all i, which by duality implies that the map
$H_{i,BM}(X^S)\to H_{i,BM}(Y^S)$
is injective for all i, which by duality implies that the map
![]() $H^{\bullet }_c(Y^S)\to H^{\bullet }_c(X^S)$
is surjective.
$H^{\bullet }_c(Y^S)\to H^{\bullet }_c(X^S)$
is surjective.
It thus suffices to show that both
![]() $H^{\bullet }_{c,S}(X)$
and
$H^{\bullet }_{c,S}(X)$
and
![]() $H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
$H^{\bullet }_{c,S}(Y\smallsetminus X)$
are free graded
![]() $H^{\bullet }(S)$
-modules. Indeed, Lemma 4.2.4(a) then would imply that the restriction map
$H^{\bullet }(S)$
-modules. Indeed, Lemma 4.2.4(a) then would imply that the restriction map
![]() $H^{\bullet }_c(Y)\to H^{\bullet }_c(X)$
is surjective, from which our assertion would follow by duality.
$H^{\bullet }_c(Y)\to H^{\bullet }_c(X)$
is surjective, from which our assertion would follow by duality.
We are going to apply the criterion of Lemma 4.2.4(b):
By assumption (a), the disjoint union
![]() $Y^S=\coprod _{\nu }(Y\cap Z^S_{\nu })$
is of finite type; hence, the set
$Y^S=\coprod _{\nu }(Y\cap Z^S_{\nu })$
is of finite type; hence, the set
![]() $\Xi _0:=\{\nu \in \Xi \,|\,Y\cap Z_{\nu }^S\neq \emptyset \}$
is finite. However, by assumption (c), we have
$\Xi _0:=\{\nu \in \Xi \,|\,Y\cap Z_{\nu }^S\neq \emptyset \}$
is finite. However, by assumption (c), we have
![]() $\Xi _0=\{\nu \in \Xi \,|\,Y\cap Z_{\nu }\neq \emptyset \}$
. Define a standard partial order on
$\Xi _0=\{\nu \in \Xi \,|\,Y\cap Z_{\nu }\neq \emptyset \}$
. Define a standard partial order on
![]() $\Xi _0$
requiring that
$\Xi _0$
requiring that
![]() $\alpha \leq \beta $
if and only if
$\alpha \leq \beta $
if and only if
![]() $Z_{\alpha }\subseteq \overline {Z}_{\beta }$
. Denote the cardinality of
$Z_{\alpha }\subseteq \overline {Z}_{\beta }$
. Denote the cardinality of
![]() $\Xi _0$
by n, and write
$\Xi _0$
by n, and write
![]() $\Xi _0$
in the form
$\Xi _0$
in the form
![]() $\Xi _0=\{\nu _1,\ldots ,\nu _n\}$
such that
$\Xi _0=\{\nu _1,\ldots ,\nu _n\}$
such that
![]() $\nu _j$
is a minimal element of the set
$\nu _j$
is a minimal element of the set
![]() $\{\nu _j,\ldots ,\nu _n\}$
for all
$\{\nu _j,\ldots ,\nu _n\}$
for all
![]() $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
.
For each
![]() $j=1,\ldots , n$
, we denote by
$j=1,\ldots , n$
, we denote by
![]() $Y_j$
the reduced intersection
$Y_j$
the reduced intersection
![]() $Y\cap (\bigcup _{t=1}^j Z_{\nu _t})$
. Then by construction, each
$Y\cap (\bigcup _{t=1}^j Z_{\nu _t})$
. Then by construction, each
![]() $Y_j\subseteq Y$
is closed,
$Y_j\subseteq Y$
is closed,
![]() $Y_n=Y$
, and
$Y_n=Y$
, and
![]() $Y_j\smallsetminus Y_{j-1}=Y\cap Z_{\nu _j}$
. It suffices to show that the induced filtrations
$Y_j\smallsetminus Y_{j-1}=Y\cap Z_{\nu _j}$
. It suffices to show that the induced filtrations
![]() $X_j:=X\cap Y_j$
of X and
$X_j:=X\cap Y_j$
of X and
![]() $(Y\smallsetminus X)_j:=Y_j\cap (Y\smallsetminus X)$
of
$(Y\smallsetminus X)_j:=Y_j\cap (Y\smallsetminus X)$
of
![]() $Y\setminus X$
satisfy the assumptions of Lemma 4.2.4(b).
$Y\setminus X$
satisfy the assumptions of Lemma 4.2.4(b).
Since
![]() $Y^S$
is a disjoint union of the
$Y^S$
is a disjoint union of the
![]() $(Y_j\smallsetminus Y_{j-1})^S$
’s (by assumption (a)), assumption (i) of Lemma 4.2.4(b) follows. Next, since
$(Y_j\smallsetminus Y_{j-1})^S$
’s (by assumption (a)), assumption (i) of Lemma 4.2.4(b) follows. Next, since
![]() $Y_j\smallsetminus Y_{j-1}=Y\cap Z_{\nu _j}$
, we get
$Y_j\smallsetminus Y_{j-1}=Y\cap Z_{\nu _j}$
, we get
![]() $X_j\smallsetminus X_{j-1}=X\cap Z_{\nu _j}$
and
$X_j\smallsetminus X_{j-1}=X\cap Z_{\nu _j}$
and
![]() $(Y\smallsetminus X)_j\smallsetminus (Y\smallsetminus X)_{j-1}=(Y\smallsetminus X)\cap Z_{\nu _j}$
. Hence, it remains to construct S-equivariant acyclic morphisms
$(Y\smallsetminus X)_j\smallsetminus (Y\smallsetminus X)_{j-1}=(Y\smallsetminus X)\cap Z_{\nu _j}$
. Hence, it remains to construct S-equivariant acyclic morphisms
![]() $X\cap Z_{\nu _j}\to X\cap Z^S_{\nu _j}$
and
$X\cap Z_{\nu _j}\to X\cap Z^S_{\nu _j}$
and
![]() $(Y\smallsetminus X)\cap Z_{\nu _j}\to (Y\smallsetminus X)\cap Z^S_{\nu _j}$
. But both morphisms are induced from acyclic morphism
$(Y\smallsetminus X)\cap Z_{\nu _j}\to (Y\smallsetminus X)\cap Z^S_{\nu _j}$
. But both morphisms are induced from acyclic morphism
![]() $p_{\nu _j}:Y\cap Z_{\nu _j}\to Y\cap Z^S_{\nu _j}$
from assumption (c) using Lemma 4.2.5.
$p_{\nu _j}:Y\cap Z_{\nu _j}\to Y\cap Z^S_{\nu _j}$
from assumption (c) using Lemma 4.2.5.
4.3 The proof
Now we are ready to prove our main result (Theorem 0.3).
Theorem 4.3.1. There exists
![]() $m\in \mathbb N$
(depending on
$m\in \mathbb N$
(depending on
![]() $\gamma $
) such that for all m-regular admissible tuples
$\gamma $
) such that for all m-regular admissible tuples
![]() $\overline {w}_1,\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}}$
, the natural map
$\overline {w}_1,\ldots ,\overline {w}_n\in \widetilde {W}^{\mathcal {C}}$
, the natural map
![]() $H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all
$H_i(\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all
![]() $i\in \mathbb Z$
.
$i\in \mathbb Z$
.
Proof. Set
![]() $Z':=\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}\subseteq \operatorname {Fl}$
. We want to show that if each
$Z':=\bigcup _{j=1}^n \operatorname {Fl}^{\leq \overline {w}_j}\subseteq \operatorname {Fl}$
. We want to show that if each
![]() $\overline {w}_j$
is sufficiently regular, then the natural map
$\overline {w}_j$
is sufficiently regular, then the natural map
![]() $H_i(Z^{\prime }_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all
$H_i(Z^{\prime }_{\gamma })\to H_i(\operatorname {Fl}_{\gamma })$
is injective for all
![]() $i\in \mathbb Z$
. To make the proof more structural, we will divide it into steps.
$i\in \mathbb Z$
. To make the proof more structural, we will divide it into steps.
Step 1. Let
![]() $\overline {x}_0\in \Lambda ^{\mathcal {C}}$
be an admissible tuple constructed in Lemma 2.3.9 and such that
$\overline {x}_0\in \Lambda ^{\mathcal {C}}$
be an admissible tuple constructed in Lemma 2.3.9 and such that
![]() $\operatorname {Fl}^{\leq '\bar {x}_0}\subseteq \operatorname {Fl}^{\leq \overline {w}_1}$
, and let
$\operatorname {Fl}^{\leq '\bar {x}_0}\subseteq \operatorname {Fl}^{\leq \overline {w}_1}$
, and let
![]() $\{\overline {x}_l\}_{l\geq 0}$
be a sequence of admissible tuples from Lemma 2.3.10. Moreover, it follows from Lemmas 2.3.9 and 2.3.10 that each
$\{\overline {x}_l\}_{l\geq 0}$
be a sequence of admissible tuples from Lemma 2.3.10. Moreover, it follows from Lemmas 2.3.9 and 2.3.10 that each
![]() $\overline {x}_l$
is sufficiently regular if
$\overline {x}_l$
is sufficiently regular if
![]() $\overline {w}_1$
is sufficiently regular.
$\overline {w}_1$
is sufficiently regular.
Notice that
![]() $\{\operatorname {Fl}^{\leq '\overline {x}_{l}}_{\gamma }\}_{l\geq 0}$
form an exhausting increasing union of closed subsets of
$\{\operatorname {Fl}^{\leq '\overline {x}_{l}}_{\gamma }\}_{l\geq 0}$
form an exhausting increasing union of closed subsets of
![]() $\operatorname {Fl}_{\gamma }$
; hence, it is enough to show that for every
$\operatorname {Fl}_{\gamma }$
; hence, it is enough to show that for every
![]() $l>0$
, the map
$l>0$
, the map
is injective for all l. Using inclusion
we conclude from Lemma 4.2.2(b) that it suffices to show that the map
is injective. We set
![]() $\overline {x}:=\overline {x}_{l-1}$
. Then
$\overline {x}:=\overline {x}_{l-1}$
. Then
![]() $\overline {x}_{l}=\overline {x}+\overline {e}_{\psi }$
for some
$\overline {x}_{l}=\overline {x}+\overline {e}_{\psi }$
for some
![]() $\psi \in \Psi $
, and we want to show that the map
$\psi \in \Psi $
, and we want to show that the map
is injective.
Step 2. If
![]() $\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, then we have an equality
$\check {\psi }\notin (\Lambda _{\gamma })_{\mathbb Q}$
, then we have an equality
![]() $\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }=\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}_{\gamma }$
(by Lemma 3.2.10), so the assertion is tautological.
$\operatorname {Fl}^{\leq '\overline {x}}_{\gamma }=\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}_{\gamma }$
(by Lemma 3.2.10), so the assertion is tautological.
From now on, assume that
![]() $\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
. Let
$\check {\psi }\in (\Lambda _{\gamma })_{\mathbb Q}$
. Let
![]() $r\in \mathbb N$
be as in Proposition 3.2.2. Then, by Lemma 4.2.2(a), it is enough to show that the map
$r\in \mathbb N$
be as in Proposition 3.2.2. Then, by Lemma 4.2.2(a), it is enough to show that the map
is injective.
Step 3. We are going to apply the criterion of Corollary 4.2.6 in the case
![]() $Z=\operatorname {Fl}$
,
$Z=\operatorname {Fl}$
,
![]() $S=T_{\psi }$
,
$S=T_{\psi }$
,
![]() $Y=\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}_{\gamma }\smallsetminus \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}_{\gamma }$
, and
$Y=\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}_{\gamma }\smallsetminus \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}_{\gamma }$
, and
![]() $\{Z_{\nu }\}_{\nu \in \widetilde {W}_{\psi }}$
is the stratification of
$\{Z_{\nu }\}_{\nu \in \widetilde {W}_{\psi }}$
is the stratification of
![]() $\operatorname {Fl}$
by
$\operatorname {Fl}$
by
![]() $L(P^{\operatorname {sc}}_{\psi })$
-orbits, considered in Section 2.4.3.
$L(P^{\operatorname {sc}}_{\psi })$
-orbits, considered in Section 2.4.3.
Since X and Y are locally closed subschemes of Z of finite type over k, it remains to show that X and Y are S-invariant and properties (a)–(c) of Corollary 4.2.6 are satisfied. Property (a) was mentioned in Section 2.4.3(g).
Step 4. We claim that the reduced intersections
![]() $Y\cap Z_{\nu }$
and
$Y\cap Z_{\nu }$
and
![]() $X\cap Z_{\nu }$
are either empty or are of the form
$X\cap Z_{\nu }$
are either empty or are of the form
![]() $\bigcup _{t=1}^m (\operatorname {Fl}_{\gamma }^{\leq \overline {u}_t}\cap Z_{\nu })$
, where each
$\bigcup _{t=1}^m (\operatorname {Fl}_{\gamma }^{\leq \overline {u}_t}\cap Z_{\nu })$
, where each
![]() $\overline {u}_t$
is sufficiently regular, and
$\overline {u}_t$
is sufficiently regular, and
![]() $(\overline {u}_t)_{\psi }=\nu $
.
$(\overline {u}_t)_{\psi }=\nu $
.
First, we claim that it follows from Corollary 2.3.3 that for every stratum
![]() $Z_{\nu }$
such that
$Z_{\nu }$
such that
![]() $Y\cap Z_{\nu }\neq \emptyset $
, we have
$Y\cap Z_{\nu }\neq \emptyset $
, we have
Indeed, our assumption implies that
![]() $\operatorname {pr}(Z_{\nu })\cap (\operatorname {Gr}^{\leq \overline {x}+\overline {e}_{\psi }}\smallsetminus \operatorname {Gr}^{\leq \overline {x}-r\overline {e}_{\psi }})\neq \emptyset $
. Then, using equality
$\operatorname {pr}(Z_{\nu })\cap (\operatorname {Gr}^{\leq \overline {x}+\overline {e}_{\psi }}\smallsetminus \operatorname {Gr}^{\leq \overline {x}-r\overline {e}_{\psi }})\neq \emptyset $
. Then, using equality
![]() $\operatorname {pr}(Z_{\nu })=L(P^{\operatorname {sc}}_{\psi })(\pi (\nu ))\subseteq \operatorname {Gr}$
, we conclude from Corollary 2.3.3(c) that
$\operatorname {pr}(Z_{\nu })=L(P^{\operatorname {sc}}_{\psi })(\pi (\nu ))\subseteq \operatorname {Gr}$
, we conclude from Corollary 2.3.3(c) that
![]() $\pi (\nu ) \text{ belongs to } \operatorname {Gr}^{\leq _{\psi }\overline {x}(\psi )+1}\smallsetminus \operatorname {Gr}^{\leq _{\psi }\overline {x}(\psi )-r}$
, from which inequalities (4.2) follow from Corollary 2.3.3(a),(b).
$\pi (\nu ) \text{ belongs to } \operatorname {Gr}^{\leq _{\psi }\overline {x}(\psi )+1}\smallsetminus \operatorname {Gr}^{\leq _{\psi }\overline {x}(\psi )-r}$
, from which inequalities (4.2) follow from Corollary 2.3.3(a),(b).
Similarly, we claim that we have equalities
For this, we have to show that our assumption on
![]() $\nu $
in (4.3) (resp. (4.4), resp. (4.5)) implies that
$\nu $
in (4.3) (resp. (4.4), resp. (4.5)) implies that
![]() $Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}=\emptyset $
(resp.
$Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}=\emptyset $
(resp.
![]() $Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}=Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}}$
and
$Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}=Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}}$
and
![]() $Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}=\emptyset $
, resp.
$Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}-r\overline {e}_{\psi }}=\emptyset $
, resp.
![]() $Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}}=\emptyset $
). But this follows from Corollary (a),(c).
$Z_{\nu }\cap \operatorname {Fl}^{\leq '\overline {x}}=\emptyset $
). But this follows from Corollary (a),(c).
Next, using inequalities (4.2), we deduce from a combination of Lemma 2.3.5(a),(b) and Corollary 2.1.7(f), that the reduced intersections
![]() $\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
,
$\operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
,
![]() $\operatorname {Fl}^{\leq '\overline {x}}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
and
$\operatorname {Fl}^{\leq '\overline {x}}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
and
![]() $Z'\cap \operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
decompose as finite unions
$Z'\cap \operatorname {Fl}^{\leq '\overline {x}+\overline {e}_{\psi }}\cap \operatorname {Fl}^{\leq _{\psi }\nu }$
decompose as finite unions
![]() $\bigcup _t \operatorname {Fl}^{\leq \overline {u}_t}$
, where each
$\bigcup _t \operatorname {Fl}^{\leq \overline {u}_t}$
, where each
![]() $\overline {u}_t$
is sufficiently regular. Therefore, using formulas (4.3)-(4.5) and Lemma 2.3.2(a), we see that the reduced intersections
$\overline {u}_t$
is sufficiently regular. Therefore, using formulas (4.3)-(4.5) and Lemma 2.3.2(a), we see that the reduced intersections
![]() $X\cap Z_{\nu }$
and
$X\cap Z_{\nu }$
and
![]() $Y\cap Z_{\nu }$
are of the form
$Y\cap Z_{\nu }$
are of the form
![]() $\bigcup _t (\operatorname {Fl}_{\gamma }^{\leq \overline {u}_t}\cap Z_{\nu })$
, where each
$\bigcup _t (\operatorname {Fl}_{\gamma }^{\leq \overline {u}_t}\cap Z_{\nu })$
, where each
![]() $\overline {u}_t$
is sufficiently regular, and
$\overline {u}_t$
is sufficiently regular, and
![]() $(\overline {u}_t)_{\psi }=\nu $
.
$(\overline {u}_t)_{\psi }=\nu $
.
Step 5. Now we are going to show property (b) of Corollary 4.2.6. It is enough to show that the composition
is injective.
By a combination of Step 4 and Proposition 3.1.8(b), the reduced intersection
![]() $X\cap Z^{S}_{\nu }$
is of the form
$X\cap Z^{S}_{\nu }$
is of the form
![]() $\bigcup _t \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }^{\leq \overline {u}^{\psi }_t}$
, and each
$\bigcup _t \operatorname {Fl}_{M^{\operatorname {sc}}_{\psi },\gamma }^{\leq \overline {u}^{\psi }_t}$
, and each
![]() $\overline {u}^{\psi }_t\in \widetilde {W}^{\psi }$
is sufficiently regular (by Lemma 1.3.10(d)).
$\overline {u}^{\psi }_t\in \widetilde {W}^{\psi }$
is sufficiently regular (by Lemma 1.3.10(d)).
By induction on the semisimple rank of G, we can assume that Theorem 4.3.1 holds for the Levi subgroup
![]() $M_{\psi }$
. Therefore, the map
$M_{\psi }$
. Therefore, the map
 $$\begin{align*}H_{i,BM}(\bigcup_t \operatorname{Fl}_{M^{\operatorname{sc}}_{\psi},\gamma}^{\leq\overline{u}^{\psi}_t})\to H_{i,BM}(\operatorname{Fl}_{M^{\operatorname{sc}}_{\psi},\gamma}) \end{align*}$$
$$\begin{align*}H_{i,BM}(\bigcup_t \operatorname{Fl}_{M^{\operatorname{sc}}_{\psi},\gamma}^{\leq\overline{u}^{\psi}_t})\to H_{i,BM}(\operatorname{Fl}_{M^{\operatorname{sc}}_{\psi},\gamma}) \end{align*}$$
is injective, from which the injectivity of (4.6) and hence property (b) of Corollary 4.2.6 follows.
Step 6. It remains to show X and Y are S-invariant and satisfy property (c) of Corollary 4.2.6. Recall that in Proposition 3.1.7, we constructed an S-equivariant retraction
![]() $p_{\nu ,\gamma }:Z_{\nu ,\gamma }\to Z_{\nu ,\gamma }^{S}$
, which is a composition of affine bundles; hence, it is acyclic.
$p_{\nu ,\gamma }:Z_{\nu ,\gamma }\to Z_{\nu ,\gamma }^{S}$
, which is a composition of affine bundles; hence, it is acyclic.
By Lemma 4.2.5, it is enough to show that
![]() $p_{\nu ,\gamma }$
satisfies inclusions of sets
$p_{\nu ,\gamma }$
satisfies inclusions of sets
By Step 4, it suffices to show that for every sufficiently regular admissible tuple
![]() $\overline {u}_t$
such that
$\overline {u}_t$
such that
![]() $(\overline {u}_t)_{\psi }=\nu $
, we have an inclusion of sets
$(\overline {u}_t)_{\psi }=\nu $
, we have an inclusion of sets
![]() $p_{\nu ,\gamma }^{-1}(p_{\nu ,\gamma }(\operatorname {Fl}^{\leq \overline {u}_t}\cap Z_{\nu ,\gamma }))\subseteq \operatorname {Fl}^{\leq \overline {u}_t}$
. But this follows from Proposition 3.1.8(c).
$p_{\nu ,\gamma }^{-1}(p_{\nu ,\gamma }(\operatorname {Fl}^{\leq \overline {u}_t}\cap Z_{\nu ,\gamma }))\subseteq \operatorname {Fl}^{\leq \overline {u}_t}$
. But this follows from Proposition 3.1.8(c).