Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T04:03:44.587Z Has data issue: false hasContentIssue false
  • English
  • Français

PRESENTATIONS OF AFFINE KAC–MOODY GROUPS

Part of: Special aspects of infinite or finite groups Linear algebraic groups and related topics

Published online by Cambridge University Press:  26 October 2018

INNA CAPDEBOSCQ ,
KARINA KIRKINA  and
DMITRIY RUMYNIN
INNA CAPDEBOSCQ
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK; [email protected], [email protected]
KARINA KIRKINA
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK; [email protected], [email protected]
DMITRIY RUMYNIN
Affiliation:
Department of Mathematics, University of Warwick, Coventry CV4 7AL, UK; [email protected], [email protected] Associated member of Laboratory of Algebraic Geometry, National Research University Higher School of Economics, Russia; [email protected]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

How many generators and relations does 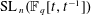$\text{SL}\,_{n}(\mathbb{F}_{q}[t,t^{-1}])$ need? In this paper we exhibit its explicit presentation with 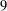$9$ generators and 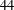$44$ relations. We investigate presentations of affine Kac–Moody groups over finite fields. Our goal is to derive finite presentations, independent of the field and with as few generators and relations as we can achieve. It turns out that any simply connected affine Kac–Moody group over a finite field has a presentation with at most 11 generators and 70 relations. We describe these presentations explicitly type by type. As a consequence, we derive explicit presentations of Chevalley groups 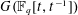$G(\mathbb{F}_{q}[t,t^{-1}])$ and explicit profinite presentations of profinite Chevalley groups 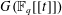$G(\mathbb{F}_{q}[[t]])$.

MSC classification

Primary: 20G44: Kac-Moody groups
Secondary: 20F05: Generators, relations, and presentations
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 6 , 2018 , e21
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2018

References

Abramenko, P. and Mühlherr, B., ‘Presentations de certaines BN -paires jumelees comme sommes amalgamee’, C. R. Math. Acad. Sci. Paris I 325 (1997), 701–706.Google Scholar
Aschbacher, M. and Guralnick, R., ‘Some applications of the first cohomology group’, J. Algebra 90 (1984), 446–460.Google Scholar
Capdeboscq, I., ‘Bounded presentations of Kac–Moody groups’, J. Group Theory 16 (2013), 899–905.Google Scholar
Capdeboscq, I., ‘On the generation of discrete and topological Kac–Moody groups’, C. R. Math. Acad. Sci. Paris 353 (2015), 695–699.Google Scholar
Capdeboscq, I., Lubotzky, A. and Rémy, B., ‘Presentations: from Kac–Moody groups to profinite and back’, Transform. Groups 21 (2016), 929–951.Google Scholar
Capdeboscq, I. and Rémy, B., ‘Uniform finite generation of split non-archimedean simple groups and Frattini subgroups’, Preprint.Google Scholar
Caprace, P.-E., ‘On 2-spherical Kac–Moody groups and their central extensions’, Forum Math. 19 (2007), 763–781.Google Scholar
Carter, R., ‘Kac–Moody groups and their automorphisms’, inGroups, Combinatorics and Geometry (Durham, 1990), LMS Lecture Note Series, 165 (Cambridge University Press, Cambridge, 1992), 218–228.Google Scholar
Carter, R., Lie Algebras of Finite and Affine Type, Cambridge Studies in Advanced Mathematics, 96 (Cambridge University Press, Cambridge, 2005).Google Scholar
Guralnick, R. and Kantor, W., ‘Probabilistic generation of finite simple groups’, J. Algebra 234 (2000), 743–792.Google Scholar
Guralnick, R., Kantor, W., Kassabov, M. and Lubotzky, A., ‘Presentations of finite simple groups: profinite and cohomological approaches’, Groups Geom. Dyn. 1 (2007), 469–523.Google Scholar
Guralnick, R., Kantor, W., Kassabov, M. and Lubotzky, A., ‘Presentations of finite simple groups: A quantitative approach’, J. Amer. Math. Soc. 21 (2008), 711–774.Google Scholar
Guralnick, R., Kantor, W., Kassabov, M. and Lubotzky, A., ‘Presentations of finite simple groups: A computational approach’, J. Eur. Math. Soc. (JEMS) 13 (2011), 391–458.Google Scholar
Kantor, W. and Lubotzky, A., ‘The probability of generating a finite classical group’, Geom. Dedicata 36 (1990), 67–87.Google Scholar
Maróti, A. and Tamburini Bellani, M., ‘A solution to a problem of Wiegold’, Comm. Algebra 41 (2013), 34–49.Google Scholar
Morita, J. and Rehmann, U., ‘Symplectic K2 of Laurent polynomials, associated Kac–Moody groups and Witt rings’, Math. Z. 206 (1991), 57–66.Google Scholar
Tits, J., ‘Uniqueness and presentation of Kac–Moody groups over fields’, J. Algebra 105 (1987), 542–573.Google Scholar