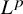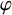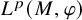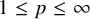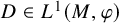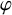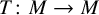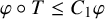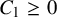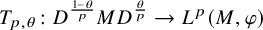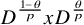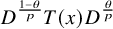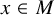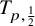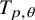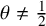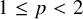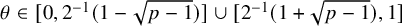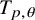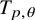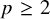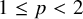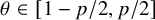1 Introduction
Let M be a von Neumann algebra equipped with a normal faithful state
![]() $\varphi $
. Let
$\varphi $
. Let
![]() $T\colon M\to M$
be a positive map such that
$T\colon M\to M$
be a positive map such that
![]() $\varphi \circ T\leq C_1\varphi $
on the positive cone
$\varphi \circ T\leq C_1\varphi $
on the positive cone
![]() $M^+$
, for some constant
$M^+$
, for some constant
![]() $C_1\geq 0$
. Assume first that
$C_1\geq 0$
. Assume first that
![]() $\varphi $
is a trace (that is,
$\varphi $
is a trace (that is,
![]() $\varphi (xy)=\varphi (yx)$
for all
$\varphi (xy)=\varphi (yx)$
for all
![]() $x,y\in M$
) and consider the associated noncommutative
$x,y\in M$
) and consider the associated noncommutative
![]() $L^p$
-spaces
$L^p$
-spaces
![]() ${\mathcal L}^p(M,\varphi )$
(see, e.g., [Reference Dodds, Dodds and de Pagter6, Reference Pisier and Xu19] or [Reference Hiai10, Chapter 4]). Let
${\mathcal L}^p(M,\varphi )$
(see, e.g., [Reference Dodds, Dodds and de Pagter6, Reference Pisier and Xu19] or [Reference Hiai10, Chapter 4]). Let
![]() $C_\infty =\Vert T\Vert $
. Then for all
$C_\infty =\Vert T\Vert $
. Then for all
![]() $1\leq p<\infty $
, T extends to a bounded map on
$1\leq p<\infty $
, T extends to a bounded map on
![]() ${\mathcal L}^p(M,\varphi )$
, with
${\mathcal L}^p(M,\varphi )$
, with
see [Reference Junge and Xu16, Lemma 1.1]. This extension result plays a significant role in various aspects of operator theory on noncommutative
![]() $L^p$
-spaces, in particular for the study of diffusion operators or semigroups on those spaces; see, for example, [Reference Arhancet1, Reference Duquet and Le Merdy7, Reference Hong, Ray and Wang11] or [Reference Junge, Le Merdy and Xu14, Chapter 5].
$L^p$
-spaces, in particular for the study of diffusion operators or semigroups on those spaces; see, for example, [Reference Arhancet1, Reference Duquet and Le Merdy7, Reference Hong, Ray and Wang11] or [Reference Junge, Le Merdy and Xu14, Chapter 5].
Let us now drop the tracial assumption on
![]() $\varphi $
. For any
$\varphi $
. For any
![]() $1\leq p\leq \infty $
, let
$1\leq p\leq \infty $
, let
![]() $L^p(M,\varphi )$
denote the Haagerup noncommutative
$L^p(M,\varphi )$
denote the Haagerup noncommutative
![]() $L^p$
-space
$L^p$
-space
![]() $L^p(M,\varphi )$
associated with
$L^p(M,\varphi )$
associated with
![]() $\varphi $
[Reference Haagerup8, Reference Haagerup, Junge and Xu9, Reference Hiai10, Reference Terp22]. These spaces extend the tracial noncommutative
$\varphi $
[Reference Haagerup8, Reference Haagerup, Junge and Xu9, Reference Hiai10, Reference Terp22]. These spaces extend the tracial noncommutative
![]() $L^p$
-spaces
$L^p$
-spaces
![]() ${\mathcal L}^p(\cdots )$
in a very beautiful way and many topics in operator theory which had been first studied on tracial noncommutative
${\mathcal L}^p(\cdots )$
in a very beautiful way and many topics in operator theory which had been first studied on tracial noncommutative
![]() $L^p$
-spaces were/are investigated on Haagerup noncommutative
$L^p$
-spaces were/are investigated on Haagerup noncommutative
![]() $L^p$
-spaces. This has led to several major advances; see in particular [Reference Haagerup, Junge and Xu9], [Reference Junge and Xu16, Section 7], [Reference Caspers and de la Salle4], [Reference Arhancet2] and [Reference Junge and LaRacuente13].
$L^p$
-spaces. This has led to several major advances; see in particular [Reference Haagerup, Junge and Xu9], [Reference Junge and Xu16, Section 7], [Reference Caspers and de la Salle4], [Reference Arhancet2] and [Reference Junge and LaRacuente13].
The question of extending a positive map
![]() $T\colon M\to M$
to
$T\colon M\to M$
to
![]() $L^p(M,\varphi )$
was first considered in [Reference Junge and Xu16, Section 7] and [Reference Haagerup, Junge and Xu9, Section 5]. Let
$L^p(M,\varphi )$
was first considered in [Reference Junge and Xu16, Section 7] and [Reference Haagerup, Junge and Xu9, Section 5]. Let
![]() $D\in L^1(M,\varphi )$
be the density of
$D\in L^1(M,\varphi )$
be the density of
![]() $\varphi $
, let
$\varphi $
, let
![]() $1\leq p<\infty $
and let
$1\leq p<\infty $
and let
![]() $\theta \in [0,1]$
. Let
$\theta \in [0,1]$
. Let
![]() $T_{p,\theta }\colon D^{\frac {1-\theta }{p}} MD^{\frac {\theta }{p}}\to L^p(M,\varphi )$
be defined by
$T_{p,\theta }\colon D^{\frac {1-\theta }{p}} MD^{\frac {\theta }{p}}\to L^p(M,\varphi )$
be defined by
(See Section 2 for the necessary background on D and the above definition.) Then [Reference Haagerup, Junge and Xu9, Theorem 5.1] shows that if
![]() $\varphi \circ T\leq C_1\varphi $
, then
$\varphi \circ T\leq C_1\varphi $
, then
![]() $T_{p,{\frac {1}{2}}}$
extends to a bounded map on
$T_{p,{\frac {1}{2}}}$
extends to a bounded map on
![]() $L^p(M,\varphi )$
, with
$L^p(M,\varphi )$
, with
This extends the tracial case (1.1); see Remark 2.5. Furthermore, [Reference Haagerup, Junge and Xu9, Proposition 5.5] shows that if T commutes with the modular automorphism group of
![]() $\varphi $
, then
$\varphi $
, then
![]() $T_{p,\theta }=T_{p,{\frac {1}{2}}}$
for all
$T_{p,\theta }=T_{p,{\frac {1}{2}}}$
for all
![]() $\theta \in [0,1]$
.
$\theta \in [0,1]$
.
In addition to the above results, Haagerup–Junge–Xu stated as an open problem the question whether
![]() $T_{p,\theta }$
is always bounded for
$T_{p,\theta }$
is always bounded for
![]() $\theta \not ={\frac {1}{2}}$
(see [Reference Haagerup, Junge and Xu9, Section 5]). The main result of the present paper is a negative answer to this question. More precisely, we show that if
$\theta \not ={\frac {1}{2}}$
(see [Reference Haagerup, Junge and Xu9, Section 5]). The main result of the present paper is a negative answer to this question. More precisely, we show that if
![]() $1\leq p<2$
and if either
$1\leq p<2$
and if either
![]() $0\leq \theta < 2^{-1}(1-\sqrt {p-1})$
or
$0\leq \theta < 2^{-1}(1-\sqrt {p-1})$
or
![]() $2^{-1}(1+\sqrt {p-1})<\theta \leq 1$
, then there exists
$2^{-1}(1+\sqrt {p-1})<\theta \leq 1$
, then there exists
![]() $M,\varphi $
as above and a unital completely positive map
$M,\varphi $
as above and a unital completely positive map
![]() $T\colon M\to M$
such that
$T\colon M\to M$
such that
![]() $\varphi \circ T=\varphi $
and
$\varphi \circ T=\varphi $
and
![]() $T_{p,\theta }$
is unbounded; see Theorem 6.1.
$T_{p,\theta }$
is unbounded; see Theorem 6.1.
We also show that for any
![]() $M,\varphi $
as above and for any
$M,\varphi $
as above and for any
![]() $2$
-positive map
$2$
-positive map
![]() $T\colon M\to M$
such that
$T\colon M\to M$
such that
![]() $\varphi \circ T\leq C_1\varphi $
for some
$\varphi \circ T\leq C_1\varphi $
for some
![]() $C_1\geq 0$
, then
$C_1\geq 0$
, then
![]() $T_{p,\theta }$
is bounded for all
$T_{p,\theta }$
is bounded for all
![]() $p\geq 2$
and all
$p\geq 2$
and all
![]() $\theta \in [0,1]$
; see Theorem 4.1. In other words, the Haagerup–Junge–Xu problem has a positive solution for
$\theta \in [0,1]$
; see Theorem 4.1. In other words, the Haagerup–Junge–Xu problem has a positive solution for
![]() $p\geq 2$
, provided that we restrict to
$p\geq 2$
, provided that we restrict to
![]() $2$
-positive maps. We also show, under the same assumptions, that
$2$
-positive maps. We also show, under the same assumptions, that
![]() $T_{p,\theta }$
is bounded for all
$T_{p,\theta }$
is bounded for all
![]() $1\leq p\leq 2$
and all
$1\leq p\leq 2$
and all
![]() $\theta \in [1-p/2,p/2]$
; see Theorem 4.3.
$\theta \in [1-p/2,p/2]$
; see Theorem 4.3.
Section 2 contains preliminaries on the
![]() $L^p(M,\varphi )$
and on the question whether
$L^p(M,\varphi )$
and on the question whether
![]() $T_{p,\theta }$
is bounded. Section 3 presents a way to compute
$T_{p,\theta }$
is bounded. Section 3 presents a way to compute
![]() $\Vert T_{p,\theta }\Vert $
in the case when
$\Vert T_{p,\theta }\Vert $
in the case when
![]() $M=M_n$
is a matrix algebra, which plays a key role in the last part of the paper. Section 4 contains the extension results stated in the previous paragraph. Finally, Sections 5 and 6 are devoted to the construction of examples for which
$M=M_n$
is a matrix algebra, which plays a key role in the last part of the paper. Section 4 contains the extension results stated in the previous paragraph. Finally, Sections 5 and 6 are devoted to the construction of examples for which
![]() $T_{p,\theta }$
is unbounded.
$T_{p,\theta }$
is unbounded.
2 The extension problem
Throughout we consider a von Neumann algebra M and we let
![]() $M_*$
denote its predual. We let
$M_*$
denote its predual. We let
![]() $M^+$
and
$M^+$
and
![]() $M_{*}^+$
denote the positive cones of M and
$M_{*}^+$
denote the positive cones of M and
![]() $M_*$
, respectively.
$M_*$
, respectively.
2.1 Haagerup noncommutative
 $L^p$
-spaces
$L^p$
-spaces
Assume that M is
![]() $\sigma $
-finite, and let
$\sigma $
-finite, and let
![]() $\varphi $
be a normal faithful state on M. We shall briefly recall the definition of the Haagerup noncommutative
$\varphi $
be a normal faithful state on M. We shall briefly recall the definition of the Haagerup noncommutative
![]() $L^p$
-spaces
$L^p$
-spaces
![]() $L^p(M,\varphi )$
associated with
$L^p(M,\varphi )$
associated with
![]() $\varphi $
, as well as some of their main features. We refer the reader to [Reference Haagerup8], [Reference Haagerup, Junge and Xu9, Section 1], [Reference Hiai10, Chapter 9], [Reference Pisier and Xu19, Section 3] and [Reference Terp22] for details and complements. We note that
$\varphi $
, as well as some of their main features. We refer the reader to [Reference Haagerup8], [Reference Haagerup, Junge and Xu9, Section 1], [Reference Hiai10, Chapter 9], [Reference Pisier and Xu19, Section 3] and [Reference Terp22] for details and complements. We note that
![]() $L^p(M,\varphi )$
can actually be defined when
$L^p(M,\varphi )$
can actually be defined when
![]() $\varphi $
is any normal faithful weight on M. The assumption that
$\varphi $
is any normal faithful weight on M. The assumption that
![]() $\varphi $
is a state makes the description below a little simpler.
$\varphi $
is a state makes the description below a little simpler.
Let
![]() $(\sigma ^\varphi _t)_{t\in {\mathbb R}}$
be the modular automorphism group of
$(\sigma ^\varphi _t)_{t\in {\mathbb R}}$
be the modular automorphism group of
![]() $\varphi $
[Reference Takesaki20, Chapter VIII], and let
$\varphi $
[Reference Takesaki20, Chapter VIII], and let
be the resulting crossed product; see, for example, [Reference Takesaki20, Chapter X]. If
![]() $M\subset B(H)$
for some Hilbert space H, then we have
$M\subset B(H)$
for some Hilbert space H, then we have
![]() $\mathcal R \subset B(L^2(\mathbb {R};H))$
. Let us regard M as a sub-von Neumann algebra of
$\mathcal R \subset B(L^2(\mathbb {R};H))$
. Let us regard M as a sub-von Neumann algebra of
![]() ${{\mathcal R}}$
in the natural way. Then
${{\mathcal R}}$
in the natural way. Then
![]() $(\sigma ^\varphi _t)_{t\in {\mathbb R}}$
is given by
$(\sigma ^\varphi _t)_{t\in {\mathbb R}}$
is given by
where
![]() $\lambda (t)\in B(L^2(\mathbb {R};H))$
is defined by
$\lambda (t)\in B(L^2(\mathbb {R};H))$
is defined by
![]() $[\lambda (t)\xi ](s)=\xi (s - t)$
for all
$[\lambda (t)\xi ](s)=\xi (s - t)$
for all
![]() $\xi \in L^2(\mathbb {R};H)$
. This is a unitary. For any
$\xi \in L^2(\mathbb {R};H)$
. This is a unitary. For any
![]() $t\in \mathbb {R}$
, define
$t\in \mathbb {R}$
, define
![]() $W(t) \in B(L^2(\mathbb {R};H))$
by
$W(t) \in B(L^2(\mathbb {R};H))$
by
![]() $[W(t)\xi ](s) =e^{-its}\xi (s)$
for all
$[W(t)\xi ](s) =e^{-its}\xi (s)$
for all
![]() $\xi \in L^2(\mathbb {R};H)$
. Then the dual action
$\xi \in L^2(\mathbb {R};H)$
. Then the dual action
![]() $\widehat {\sigma }^\varphi \colon \mathbb {R} \to \mathrm {Aut}({{\mathcal R}})$
of
$\widehat {\sigma }^\varphi \colon \mathbb {R} \to \mathrm {Aut}({{\mathcal R}})$
of
![]() $\sigma ^\varphi $
is defined by
$\sigma ^\varphi $
is defined by
(See [Reference Takesaki20, § VIII.2].) A remarkable fact is that for any
![]() $x\in {{\mathcal R}}$
,
$x\in {{\mathcal R}}$
,
![]() $\widehat {\sigma }^\varphi _t(x)=x$
for all
$\widehat {\sigma }^\varphi _t(x)=x$
for all
![]() $t\in \mathbb {R}$
if and only if
$t\in \mathbb {R}$
if and only if
![]() $x\in M$
.
$x\in M$
.
There exists a unique normal semifinite trace
![]() $\tau _0$
on
$\tau _0$
on
![]() ${{\mathcal R}}$
such that
${{\mathcal R}}$
such that
see, for example, [Reference Hiai10, Theorem 8.15]. This trace gives rise to the
![]() $*$
-algebra
$*$
-algebra
![]() $L^{0}({{\mathcal R}},\tau _0)$
of
$L^{0}({{\mathcal R}},\tau _0)$
of
![]() $\tau _0$
-measurable operators [Reference Hiai10, Chapter 4]. Then for any
$\tau _0$
-measurable operators [Reference Hiai10, Chapter 4]. Then for any
![]() $1\leq p\leq \infty $
, the Haagerup
$1\leq p\leq \infty $
, the Haagerup
![]() $L^p$
-space
$L^p$
-space
![]() $L^p(M,\varphi )$
is defined as
$L^p(M,\varphi )$
is defined as
At this stage, this is just a
![]() $*$
-subspace of
$*$
-subspace of
![]() $L^0({{\mathcal R}},\tau _0)$
(with no norm). One defines its positive cone as
$L^0({{\mathcal R}},\tau _0)$
(with no norm). One defines its positive cone as
It follows from above that
![]() $L^\infty (M,\varphi )=M.$
$L^\infty (M,\varphi )=M.$
Let
![]() $\psi \in M_{*}^+$
, that we regard as a normal weight on M, and let
$\psi \in M_{*}^+$
, that we regard as a normal weight on M, and let
![]() $\widehat {\psi }$
be its dual weight on
$\widehat {\psi }$
be its dual weight on
![]() ${{\mathcal R}}$
[Reference Takesaki20, § VIII.1]. Let
${{\mathcal R}}$
[Reference Takesaki20, § VIII.1]. Let
![]() $h_\psi $
be the Radon–Nikodym derivative of
$h_\psi $
be the Radon–Nikodym derivative of
![]() $\widehat {\psi }$
with respect to
$\widehat {\psi }$
with respect to
![]() $\tau _0$
. That is,
$\tau _0$
. That is,
![]() $h_\psi $
is the unique positive operator affiliated with
$h_\psi $
is the unique positive operator affiliated with
![]() ${{\mathcal R}}$
such that
${{\mathcal R}}$
such that
It turns out that
![]() $h_\psi $
belongs to
$h_\psi $
belongs to
![]() $L^1(M,\varphi )^+$
for all
$L^1(M,\varphi )^+$
for all
![]() $\psi \in M_{*}^+$
and that the mapping
$\psi \in M_{*}^+$
and that the mapping
![]() $\psi \mapsto h_\psi $
is a bijection from
$\psi \mapsto h_\psi $
is a bijection from
![]() $M_{*}^+$
onto
$M_{*}^+$
onto
![]() $L^1(M,\varphi )^+$
. This bijection readily extends to a linear isomorphism
$L^1(M,\varphi )^+$
. This bijection readily extends to a linear isomorphism
![]() $ M_* \longrightarrow L^1(M,\varphi )$
, still denoted by
$ M_* \longrightarrow L^1(M,\varphi )$
, still denoted by
![]() $\psi \mapsto h_\psi $
. Then
$\psi \mapsto h_\psi $
. Then
![]() $L^1(M,\varphi )$
is equipped with the norm
$L^1(M,\varphi )$
is equipped with the norm
![]() $\Vert \,\cdotp \Vert _1$
inherited from
$\Vert \,\cdotp \Vert _1$
inherited from
![]() $M_*$
, that is,
$M_*$
, that is,
![]() $\Vert h_\psi \Vert _{1}=\Vert \psi \Vert _{M_*}$
for all
$\Vert h_\psi \Vert _{1}=\Vert \psi \Vert _{M_*}$
for all
![]() $\psi \in M_*$
. Next, for any
$\psi \in M_*$
. Next, for any
![]() $1\leq p<\infty $
and any
$1\leq p<\infty $
and any
![]() $y\in L^p(M,\varphi )$
, the positive operator
$y\in L^p(M,\varphi )$
, the positive operator
![]() $\vert y\vert $
belongs to
$\vert y\vert $
belongs to
![]() $L^p(M,\varphi )$
as well (thanks to the polar decomposition) and hence
$L^p(M,\varphi )$
as well (thanks to the polar decomposition) and hence
![]() $\vert y\vert ^p$
belongs to
$\vert y\vert ^p$
belongs to
![]() $L^1(M,\varphi )$
. This allows to define
$L^1(M,\varphi )$
. This allows to define
![]() $\Vert y\Vert _p=\Vert \vert y\vert ^p\Vert ^{\frac {1}{p}}$
for all
$\Vert y\Vert _p=\Vert \vert y\vert ^p\Vert ^{\frac {1}{p}}$
for all
![]() $y\in L^p(M,\varphi )$
. Then
$y\in L^p(M,\varphi )$
. Then
![]() $\Vert \,\cdotp \Vert _p$
is a complete norm on
$\Vert \,\cdotp \Vert _p$
is a complete norm on
![]() $L^p(M,\varphi )$
.
$L^p(M,\varphi )$
.
The Banach spaces
![]() $L^p(M,\varphi )$
,
$L^p(M,\varphi )$
,
![]() $1\leq p\leq \infty $
, satisfy the following version of Hölder’s inequality (see, e.g., [Reference Hiai10, Proposition 9.17]).
$1\leq p\leq \infty $
, satisfy the following version of Hölder’s inequality (see, e.g., [Reference Hiai10, Proposition 9.17]).
Lemma 2.1. Let
![]() $1\leq p,q,r\leq \infty $
such that
$1\leq p,q,r\leq \infty $
such that
![]() $p^{-1}+q^{-1} =r^{-1}$
. Then for all
$p^{-1}+q^{-1} =r^{-1}$
. Then for all
![]() $x\in L^p(M,\varphi )$
and all
$x\in L^p(M,\varphi )$
and all
![]() $y\in L^q(M,\varphi )$
, the product
$y\in L^q(M,\varphi )$
, the product
![]() $xy$
belongs to
$xy$
belongs to
![]() $L^r(M,\varphi )$
and
$L^r(M,\varphi )$
and
![]() $\Vert xy\Vert _r\leq \Vert x\Vert _p\Vert y\Vert _q$
.
$\Vert xy\Vert _r\leq \Vert x\Vert _p\Vert y\Vert _q$
.
Let D be the Radon–Nikodym derivative of
![]() $\widehat {\varphi }$
with respect to
$\widehat {\varphi }$
with respect to
![]() $\tau _0$
, and recall that
$\tau _0$
, and recall that
![]() $D\in L^1(M,\varphi )^+$
. This operator is called the density of
$D\in L^1(M,\varphi )^+$
. This operator is called the density of
![]() $\varphi $
. Recall that we regard M as a sub-von Neumann algebra of
$\varphi $
. Recall that we regard M as a sub-von Neumann algebra of
![]() ${{\mathcal R}}$
. Then
${{\mathcal R}}$
. Then
![]() $D^{it}=\lambda (t)$
is a unitary of
$D^{it}=\lambda (t)$
is a unitary of
![]() ${{\mathcal R}}$
for all
${{\mathcal R}}$
for all
![]() $t\in \mathbb {R}$
and
$t\in \mathbb {R}$
and
Let
![]() $\mathrm {Tr}\colon L^1(M,\varphi )\to \mathbb {C}$
be defined by
$\mathrm {Tr}\colon L^1(M,\varphi )\to \mathbb {C}$
be defined by
![]() $\mathrm {Tr}(h_\psi )=\psi (1)$
for all
$\mathrm {Tr}(h_\psi )=\psi (1)$
for all
![]() $\psi \in M_*$
. This functional has two remarkable properties. First, for all
$\psi \in M_*$
. This functional has two remarkable properties. First, for all
![]() $x\in M$
and all
$x\in M$
and all
![]() $\psi \in M_*$
, we have
$\psi \in M_*$
, we have
Second if
![]() $1\leq p,q\leq \infty $
are such that
$1\leq p,q\leq \infty $
are such that
![]() $p^{-1}+q^{-1} =1$
, then for all
$p^{-1}+q^{-1} =1$
, then for all
![]() $x\in L^p(M,\varphi )$
and all
$x\in L^p(M,\varphi )$
and all
![]() $y\in L^q(M,\varphi )$
, we have
$y\in L^q(M,\varphi )$
, we have
This tracial property will be used without any further comment in the paper.
It follows from the definition of
![]() $\Vert \,\cdotp \Vert _1$
and equation (2.3) that the duality pairing
$\Vert \,\cdotp \Vert _1$
and equation (2.3) that the duality pairing
![]() $\langle x,y\rangle =\mathrm {Tr}(xy)$
for
$\langle x,y\rangle =\mathrm {Tr}(xy)$
for
![]() $x\in M$
and
$x\in M$
and
![]() $y\in L^1(M,\varphi )$
yields an isometric isomorphism
$y\in L^1(M,\varphi )$
yields an isometric isomorphism
As a special case of equation (2.3), we have
We note that
![]() $L^2(M,\varphi )$
is a space for the inner product
$L^2(M,\varphi )$
is a space for the inner product
![]() $(x\vert y)=\mathrm {Tr}(y^*x)$
. Moreover, by equation (2.5), we have
$(x\vert y)=\mathrm {Tr}(y^*x)$
. Moreover, by equation (2.5), we have
We finally mention a useful tool. Let
![]() $M_a\subset M$
be the subset of all
$M_a\subset M$
be the subset of all
![]() $x\in M$
such that
$x\in M$
such that
![]() $t\mapsto \sigma ^\varphi _t(x)$
extends to an entire function
$t\mapsto \sigma ^\varphi _t(x)$
extends to an entire function
![]() $z\in \mathbb {C}\mapsto \sigma _z^\varphi (x) \in M$
. (Such elements are called analytic). It is well known that
$z\in \mathbb {C}\mapsto \sigma _z^\varphi (x) \in M$
. (Such elements are called analytic). It is well known that
![]() $M_a$
is a
$M_a$
is a
![]() $w^*$
-dense
$w^*$
-dense
![]() $*$
-subalgebra of M [Reference Takesaki20, Section VIII.2]. Furthermore,
$*$
-subalgebra of M [Reference Takesaki20, Section VIII.2]. Furthermore,
for all
![]() $x\in M_a$
and all
$x\in M_a$
and all
![]() $\theta \in [0,1]$
, and
$\theta \in [0,1]$
, and
![]() $M_aD^{\frac {1}{p}} = D^{\frac {1}{p}}M_a$
is dense in
$M_aD^{\frac {1}{p}} = D^{\frac {1}{p}}M_a$
is dense in
![]() $L^p(M,\varphi )$
, for all
$L^p(M,\varphi )$
, for all
![]() $1\leq p<\infty $
. See [Reference Junge and Xu15, Lemma 1.1] and its proof for these properties.
$1\leq p<\infty $
. See [Reference Junge and Xu15, Lemma 1.1] and its proof for these properties.
2.2 Extension of maps
 $M\to M$
$M\to M$
Given any linear map
![]() $T\colon M\to M$
, we say that T is positive if
$T\colon M\to M$
, we say that T is positive if
![]() $T(M^+)\subset M^+$
. This implies that T is bounded. For any
$T(M^+)\subset M^+$
. This implies that T is bounded. For any
![]() $n\geq 1$
, we say that T is n-positive if the tensor extension map
$n\geq 1$
, we say that T is n-positive if the tensor extension map
![]() $I_{M_n}\otimes T\colon M_n\overline {\otimes } M \to M_n\overline {\otimes }M$
is positive. (Here,
$I_{M_n}\otimes T\colon M_n\overline {\otimes } M \to M_n\overline {\otimes }M$
is positive. (Here,
![]() $M_n$
is the algebra of
$M_n$
is the algebra of
![]() $n\times n$
matrices.) Next, we say that T is completely positive if T is n-positive for all
$n\times n$
matrices.) Next, we say that T is completely positive if T is n-positive for all
![]() $n\geq 1$
. See, for example, [Reference Paulsen18] for basics on these notions.
$n\geq 1$
. See, for example, [Reference Paulsen18] for basics on these notions.
Consider any
![]() $\theta \in [0,1]$
and
$\theta \in [0,1]$
and
![]() $1\leq p<\infty $
. It follows from Lemma 2.1 that
$1\leq p<\infty $
. It follows from Lemma 2.1 that
![]() $D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$
belongs to
$D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$
belongs to
![]() $L^p(M,\varphi )$
for all
$L^p(M,\varphi )$
for all
![]() $x\in M$
. We set
$x\in M$
. We set
It turns out that this is a dense subspace; see [Reference Junge and Xu15, Lemma 1.1].
Let
![]() $T\colon M\to M$
be any bounded linear map. For any
$T\colon M\to M$
be any bounded linear map. For any
![]() $(p,\theta )$
as above, define a linear map
$(p,\theta )$
as above, define a linear map
![]() $T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
by equation (1.2). The question we consider in this paper is whether
$T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
by equation (1.2). The question we consider in this paper is whether
![]() $T_{p,\theta }$
extends to a bounded map
$T_{p,\theta }$
extends to a bounded map
![]() $L^p(M,\varphi )\to L^p(M,\varphi )$
in the case when T is
$L^p(M,\varphi )\to L^p(M,\varphi )$
in the case when T is
![]() $2$
-positive and
$2$
-positive and
![]() $\varphi \circ T\leq \varphi $
on
$\varphi \circ T\leq \varphi $
on
![]() $M_+$
. More precisely, we consider the following:
$M_+$
. More precisely, we consider the following:
Question 2.2. Determine the pairs
![]() $(p,\theta )\in [1,\infty )\times [0,1]$
such that
$(p,\theta )\in [1,\infty )\times [0,1]$
such that
is bounded for all
![]() $(M,\varphi )$
as above and all
$(M,\varphi )$
as above and all
![]() $2$
-positive maps
$2$
-positive maps
![]() $T\colon M\to M$
satisfying
$T\colon M\to M$
satisfying
![]() $\varphi \circ T\leq \varphi $
on
$\varphi \circ T\leq \varphi $
on
![]() $M_+$
.
$M_+$
.
As in the introduction, we could consider maps such that
![]() $\varphi \circ T\leq C_1\varphi $
for some
$\varphi \circ T\leq C_1\varphi $
for some
![]() $C_1\geq 0$
. However, by an obvious scaling, there is no loss in considering
$C_1\geq 0$
. However, by an obvious scaling, there is no loss in considering
![]() $C_1=1$
only.
$C_1=1$
only.
Remark 2.3. Question 2.2 originates from the Haagerup–Junge–Xu paper [Reference Haagerup, Junge and Xu9]. In Section 5 of the latter paper, the authors consider two von Neumann algebras
![]() $M,N$
, and normal faithful states
$M,N$
, and normal faithful states
![]() $\varphi \in M_*$
and
$\varphi \in M_*$
and
![]() $\psi \in N_*$
with respective densities
$\psi \in N_*$
with respective densities
![]() $D_\varphi \in L^1(M,\varphi )$
and
$D_\varphi \in L^1(M,\varphi )$
and
![]() $D_\psi \in L^1(N,\psi )$
. Then they consider a positive map
$D_\psi \in L^1(N,\psi )$
. Then they consider a positive map
![]() $T\colon M\to N$
such that
$T\colon M\to N$
such that
![]() $\psi \circ T\leq C_1\varphi $
for some
$\psi \circ T\leq C_1\varphi $
for some
![]() $C_1>0$
. Given any
$C_1>0$
. Given any
![]() $(p,\theta )\in [1,\infty )\times [0,1]$
, they define
$(p,\theta )\in [1,\infty )\times [0,1]$
, they define
![]() $T_{p,\theta }\colon D_\varphi ^{\frac {1-\theta }{p}} M D_\varphi ^{\frac {\theta }{p}}\to L^p(N,\psi )$
by
$T_{p,\theta }\colon D_\varphi ^{\frac {1-\theta }{p}} M D_\varphi ^{\frac {\theta }{p}}\to L^p(N,\psi )$
by
In [Reference Haagerup, Junge and Xu9, Theorem 5.1], they show that
![]() $T_{p,{\frac {1}{2}}}$
is bounded and that setting
$T_{p,{\frac {1}{2}}}$
is bounded and that setting
![]() $C_\infty =\Vert T\Vert $
, we have
$C_\infty =\Vert T\Vert $
, we have
![]() $\Vert T_{p,{\frac {1}{2}}}\colon L^p(M,\varphi )\to L^p(N,\psi )\Vert \leq C_{\infty }^{1-\frac {1}{p}} C_{1}^{\frac {1}{p}}$
. Then after the statement of [Reference Haagerup, Junge and Xu9, Proposition 5.4], they mention that the boundedness of
$\Vert T_{p,{\frac {1}{2}}}\colon L^p(M,\varphi )\to L^p(N,\psi )\Vert \leq C_{\infty }^{1-\frac {1}{p}} C_{1}^{\frac {1}{p}}$
. Then after the statement of [Reference Haagerup, Junge and Xu9, Proposition 5.4], they mention that the boundedness of
![]() $T_{p,\theta }$
for
$T_{p,\theta }$
for
![]() $\theta \not ={\frac {1}{2}}$
is an open question.
$\theta \not ={\frac {1}{2}}$
is an open question.
Remark 2.4. We wish to point out a special case which will be used in Section 5. Let B be a von Neumman algebra equipped with a normal faithful state
![]() $\psi $
. Let
$\psi $
. Let
![]() $A\subset B$
be a sub-von Neumann algebra which is stable under the modular automorphism group of
$A\subset B$
be a sub-von Neumann algebra which is stable under the modular automorphism group of
![]() $\psi $
(i.e.,
$\psi $
(i.e.,
![]() $\sigma ^\psi _t(A)\subset A$
for all
$\sigma ^\psi _t(A)\subset A$
for all
![]() $t\in \mathbb {R}$
). Let
$t\in \mathbb {R}$
). Let
![]() $\varphi =\psi _{\vert A}$
be the restriction of
$\varphi =\psi _{\vert A}$
be the restriction of
![]() $\psi $
to A. Let
$\psi $
to A. Let
![]() $D\in L^1(A,\varphi )$
and
$D\in L^1(A,\varphi )$
and
![]() $\Delta \in L^1(B,\psi )$
be the densities of
$\Delta \in L^1(B,\psi )$
be the densities of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, respectively. On the one hand, it follows from [Reference Haagerup, Junge and Xu9, Theorem 5.1] (see Remark 2.3) that there exists, for every
$\psi $
, respectively. On the one hand, it follows from [Reference Haagerup, Junge and Xu9, Theorem 5.1] (see Remark 2.3) that there exists, for every
![]() $1\leq p<\infty $
, a contraction
$1\leq p<\infty $
, a contraction
such that
![]() $[\Lambda (p)](D^{\frac {1}{2p}}xD^{\frac {1}{2p}}) = \Delta ^{\frac {1}{2p}}x \Delta ^{\frac {1}{2p}}$
for all
$[\Lambda (p)](D^{\frac {1}{2p}}xD^{\frac {1}{2p}}) = \Delta ^{\frac {1}{2p}}x \Delta ^{\frac {1}{2p}}$
for all
![]() $x\in A$
.
$x\in A$
.
On the other hand, there exists a unique normal conditional expectation
![]() $E\colon B\to A$
such that
$E\colon B\to A$
such that
![]() $\psi =\varphi \circ E$
on B by [Reference Takesaki20, Theorem IX.4.2]. Moreover, it is easy to check that under the natural identifications
$\psi =\varphi \circ E$
on B by [Reference Takesaki20, Theorem IX.4.2]. Moreover, it is easy to check that under the natural identifications
![]() $L^1(A,\varphi )^*\simeq A$
and
$L^1(A,\varphi )^*\simeq A$
and
![]() $L^1(B,\psi )^*\simeq B$
(see equation (2.4) and the discussion preceding it), we have
$L^1(B,\psi )^*\simeq B$
(see equation (2.4) and the discussion preceding it), we have
Now, using [Reference Haagerup, Junge and Xu9, Theorem 5.1] again, there exists, for every
![]() $1\leq p<\infty $
, a contraction
$1\leq p<\infty $
, a contraction
![]() $E(p)\colon L^p(B,\psi )\to L^p(A,\varphi )$
such that
$E(p)\colon L^p(B,\psi )\to L^p(A,\varphi )$
such that
![]() $[E(p)](\Delta ^{\frac {1}{2p}}y \Delta ^{\frac {1}{2p}}) = D^{\frac {1}{2p}}E(y)D^{\frac {1}{2p}}$
for all
$[E(p)](\Delta ^{\frac {1}{2p}}y \Delta ^{\frac {1}{2p}}) = D^{\frac {1}{2p}}E(y)D^{\frac {1}{2p}}$
for all
![]() $y\in B$
. It is clear that
$y\in B$
. It is clear that
![]() $E(p)\circ \Lambda (p)=I_{L^p(A,\varphi )}$
. Consequently,
$E(p)\circ \Lambda (p)=I_{L^p(A,\varphi )}$
. Consequently,
![]() $\Lambda (p)$
is an isometry.
$\Lambda (p)$
is an isometry.
We refer to [Reference Junge and Xu15, Section 2] for more on this.
Remark 2.5. Let
![]() $T\colon M\to M$
be a positive map, and let
$T\colon M\to M$
be a positive map, and let
![]() $\varphi ,D$
as in Subsection 2.1. Assume that
$\varphi ,D$
as in Subsection 2.1. Assume that
![]() $\varphi $
is tracial and for any
$\varphi $
is tracial and for any
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() ${\mathcal L}^p(M,\varphi )$
be the (classical) noncommutative
${\mathcal L}^p(M,\varphi )$
be the (classical) noncommutative
![]() $L^p$
-space with respect to the trace
$L^p$
-space with respect to the trace
![]() $\varphi $
[Reference Hiai10, Section 4.3]. That is,
$\varphi $
[Reference Hiai10, Section 4.3]. That is,
![]() ${\mathcal L}^p(M,\varphi )$
is the completion of M for the norm
${\mathcal L}^p(M,\varphi )$
is the completion of M for the norm
In this case, D commutes with M and
see, for example, [Reference Hiai10, Example 9.11]. Hence,
![]() $T_{p,\theta }=T_{p,0}$
for all
$T_{p,\theta }=T_{p,0}$
for all
![]() $1\leq p<\infty $
and all
$1\leq p<\infty $
and all
![]() $\theta \in [0,1]$
and moreover,
$\theta \in [0,1]$
and moreover,
![]() $T_{p,0}$
is bounded if and only if T extends to a bounded map
$T_{p,0}$
is bounded if and only if T extends to a bounded map
![]() ${\mathcal L}^p(M,\varphi )\to {\mathcal L}^p(M,\varphi )$
. Thus, in the tracial case, the fact that
${\mathcal L}^p(M,\varphi )\to {\mathcal L}^p(M,\varphi )$
. Thus, in the tracial case, the fact that
![]() $T_{p,0}$
is bounded under the assumption
$T_{p,0}$
is bounded under the assumption
![]() $\varphi \circ T\leq C_1\varphi $
is equivalent to the result mentionned in the first paragraph of Section 1; see (equation 1.1).
$\varphi \circ T\leq C_1\varphi $
is equivalent to the result mentionned in the first paragraph of Section 1; see (equation 1.1).
3 Computing
 $\Vert T_{p,\theta }\Vert $
on semifinite von Neumann algebras
$\Vert T_{p,\theta }\Vert $
on semifinite von Neumann algebras
As in the previous section, we let M be a von Neumann algebra equipped with a normal faithful state
![]() $\varphi $
and we let
$\varphi $
and we let
![]() $D\in L^1(M,\varphi )^+$
be the density of
$D\in L^1(M,\varphi )^+$
be the density of
![]() $\varphi $
. We assume further that M is semifinite, and we let
$\varphi $
. We assume further that M is semifinite, and we let
![]() $\tau $
be a distinguished normal semifinite faithful trace on M. For any
$\tau $
be a distinguished normal semifinite faithful trace on M. For any
![]() $1\leq p\leq \infty $
, we let
$1\leq p\leq \infty $
, we let
![]() ${\mathcal L}^p(M,\tau )$
be the noncommutative
${\mathcal L}^p(M,\tau )$
be the noncommutative
![]() $L^p$
-space with respect to
$L^p$
-space with respect to
![]() $\tau $
. Although
$\tau $
. Although
![]() ${\mathcal L}^p(M,\tau )$
is isometrically isomorphic to the Haagerup
${\mathcal L}^p(M,\tau )$
is isometrically isomorphic to the Haagerup
![]() $L^p$
-space
$L^p$
-space
![]() $L^p(M,\tau )$
, it is necessary for our purpose to consider
$L^p(M,\tau )$
, it is necessary for our purpose to consider
![]() ${\mathcal L}^p(M,\tau )$
as such.
${\mathcal L}^p(M,\tau )$
as such.
Let us give a brief account, for which we refer, for example, to [Reference Hiai10, Section 4.3]. Let
![]() ${\mathcal L}^0(M,\tau )$
be the
${\mathcal L}^0(M,\tau )$
be the
![]() $*$
-algebra of all
$*$
-algebra of all
![]() $\tau $
-measurable operators on M. For any
$\tau $
-measurable operators on M. For any
![]() $p<\infty $
,
$p<\infty $
,
![]() ${\mathcal L}^p(M,\tau )$
is the Banach space of all
${\mathcal L}^p(M,\tau )$
is the Banach space of all
![]() $x\in {\mathcal L}^0(M,\tau )$
such that
$x\in {\mathcal L}^0(M,\tau )$
such that
![]() $\tau (\vert x\vert ^p)<\infty $
, equipped with the norm
$\tau (\vert x\vert ^p)<\infty $
, equipped with the norm
Moreover,
![]() ${\mathcal L}^\infty (M,\tau )=M$
. The following analogue of Lemma 2.1 holds true: Whenever
${\mathcal L}^\infty (M,\tau )=M$
. The following analogue of Lemma 2.1 holds true: Whenever
![]() $1\leq p,q,r\leq \infty $
are such that
$1\leq p,q,r\leq \infty $
are such that
![]() $p^{-1}+q^{-1}=r^{-1}$
, then for all
$p^{-1}+q^{-1}=r^{-1}$
, then for all
![]() $x\in {\mathcal L}^p(M,\tau )$
and
$x\in {\mathcal L}^p(M,\tau )$
and
![]() $y\in {\mathcal L}^q(M,\tau )$
,
$y\in {\mathcal L}^q(M,\tau )$
,
![]() $xy$
belongs to
$xy$
belongs to
![]() ${\mathcal L}^r(M,\tau )$
, with
${\mathcal L}^r(M,\tau )$
, with
![]() $\Vert xy\Vert _r\leq \Vert x\Vert _p\Vert x\Vert _q$
(Hölder’s inequality). Furthermore, we have an isometric identification
$\Vert xy\Vert _r\leq \Vert x\Vert _p\Vert x\Vert _q$
(Hölder’s inequality). Furthermore, we have an isometric identification
for the duality pairing given by
![]() $\langle x,y\rangle =\tau (yx)$
for all
$\langle x,y\rangle =\tau (yx)$
for all
![]() $x\in M$
and
$x\in M$
and
![]() $y\in {\mathcal L}^1(M,\tau )$
.
$y\in {\mathcal L}^1(M,\tau )$
.
Let
![]() $\gamma \in {\mathcal L}^1(M,\tau )$
be associated with
$\gamma \in {\mathcal L}^1(M,\tau )$
be associated with
![]() $\varphi $
in the identification (3.1), that is,
$\varphi $
in the identification (3.1), that is,
Then
![]() $\gamma $
is positive and it is clear from Hölder’s inequality that for any
$\gamma $
is positive and it is clear from Hölder’s inequality that for any
![]() $1\leq p<\infty $
,
$1\leq p<\infty $
,
![]() $\theta \in [0,1]$
and
$\theta \in [0,1]$
and
![]() $x\in M$
, the product
$x\in M$
, the product
![]() $\gamma ^{\frac {1-\theta }{p}} x \gamma ^{\frac {\theta }{p}}$
belongs to
$\gamma ^{\frac {1-\theta }{p}} x \gamma ^{\frac {\theta }{p}}$
belongs to
![]() ${\mathcal L}^p(M,\tau )$
.
${\mathcal L}^p(M,\tau )$
.
It is well known that
![]() ${\mathcal L}^p(M,\tau )$
and
${\mathcal L}^p(M,\tau )$
and
![]() $L^p(M,\varphi )$
are isometrically isomorphic (apply Remark 9.10 and Example 9.11 in [Reference Hiai10]). The following lemma provides concrete isometric isomorphisms between these two spaces.
$L^p(M,\varphi )$
are isometrically isomorphic (apply Remark 9.10 and Example 9.11 in [Reference Hiai10]). The following lemma provides concrete isometric isomorphisms between these two spaces.
Lemma 3.1. Let
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $\theta \in [0,1]$
. Then for all
$\theta \in [0,1]$
. Then for all
![]() $x\in M$
, we have
$x\in M$
, we have
Before giving the proof of this lemma, we recall a classical tool. For any
![]() $\theta \in [0,1]$
, define an embedding
$\theta \in [0,1]$
, define an embedding
![]() $J_\theta \colon M\to L^1(M,\varphi )$
by letting
$J_\theta \colon M\to L^1(M,\varphi )$
by letting
Consider
![]() $(J_\theta (M), L^1(M,\varphi ))$
as an interpolation couple, the norm on
$(J_\theta (M), L^1(M,\varphi ))$
as an interpolation couple, the norm on
![]() $J_\theta (M)$
being given by the norm on M, that is,
$J_\theta (M)$
being given by the norm on M, that is,
For any
![]() $1\leq p\leq \infty $
, let
$1\leq p\leq \infty $
, let
be the resulting interpolation space provided by the complex interpolation method [Reference Bergh and Löfström3, Chapter 4]. Regard
![]() $C(p,\theta )$
as a subspace of
$C(p,\theta )$
as a subspace of
![]() $L^1(M,\varphi )$
in the natural way. Then Kosaki’s theorem [Reference Kosaki17, Theorem 9.1] (see also [Reference Hiai10, Theorem 9.36]) asserts that
$L^1(M,\varphi )$
in the natural way. Then Kosaki’s theorem [Reference Kosaki17, Theorem 9.1] (see also [Reference Hiai10, Theorem 9.36]) asserts that
![]() $C(p,\theta )$
is equal to
$C(p,\theta )$
is equal to
![]() $D^{\frac {1-\theta }{p'}}L^{p}(M,\varphi )D^{\frac {\theta }{p'}}$
and that
$D^{\frac {1-\theta }{p'}}L^{p}(M,\varphi )D^{\frac {\theta }{p'}}$
and that
Here,
![]() $p'$
is the conjugate index of p so that
$p'$
is the conjugate index of p so that
![]() $D^{\frac {1-\theta }{p'}}y D^{\frac {\theta }{p'}}$
belongs to
$D^{\frac {1-\theta }{p'}}y D^{\frac {\theta }{p'}}$
belongs to
![]() $L^1(M,\varphi )$
provided that y belongs to
$L^1(M,\varphi )$
provided that y belongs to
![]() $L^p(M,\varphi )$
.
$L^p(M,\varphi )$
.
Likewise, let
![]() $j_\theta \colon M\to {\mathcal L}^1(M,\tau )$
be defined by
$j_\theta \colon M\to {\mathcal L}^1(M,\tau )$
be defined by
![]() $j_\theta (x)=\gamma ^{1-\theta }x\gamma ^\theta $
for all
$j_\theta (x)=\gamma ^{1-\theta }x\gamma ^\theta $
for all
![]() $x\in M$
. Consider
$x\in M$
. Consider
![]() $(j_\theta (M), {\mathcal L}^1(M,\tau ))$
as an interpolation couple, the norm on
$(j_\theta (M), {\mathcal L}^1(M,\tau ))$
as an interpolation couple, the norm on
![]() $j_\theta (M)$
being given by the norm on M, and set
$j_\theta (M)$
being given by the norm on M, and set
regarded as a subspace of
![]() ${\mathcal L}^1(M,\tau )$
. Then arguing as in the proof of [Reference Kosaki17, Theorem 9.1], one obtains that
${\mathcal L}^1(M,\tau )$
. Then arguing as in the proof of [Reference Kosaki17, Theorem 9.1], one obtains that
![]() $c(p,\theta )$
is equal to
$c(p,\theta )$
is equal to
![]() $\gamma ^{\frac {1-\theta }{p'}} {\mathcal L}^{p}(M,\tau )\gamma ^{\frac {\theta }{p'}}$
and that
$\gamma ^{\frac {1-\theta }{p'}} {\mathcal L}^{p}(M,\tau )\gamma ^{\frac {\theta }{p'}}$
and that
Proof of Lemma 3.1.
We fix some
![]() $\theta \in [0,1]$
. We start with the case
$\theta \in [0,1]$
. We start with the case
![]() $p=1$
. Let
$p=1$
. Let
![]() $x\in M$
. For any
$x\in M$
. For any
![]() $x'\in M$
, we have
$x'\in M$
, we have
![]() $\tau (\gamma xx')=\mathrm {Tr}(Dxx')$
and hence
$\tau (\gamma xx')=\mathrm {Tr}(Dxx')$
and hence
![]() $\vert \tau (\gamma xx')\vert =\vert \mathrm {Tr}(Dxx')\vert $
, by equations (2.5) and (3.2). Taking the supremum over all
$\vert \tau (\gamma xx')\vert =\vert \mathrm {Tr}(Dxx')\vert $
, by equations (2.5) and (3.2). Taking the supremum over all
![]() $x'\in M$
with
$x'\in M$
with
![]() $\Vert x'\Vert _M\leq 1$
, it therefore follows from equations (2.4) and (3.1) that
$\Vert x'\Vert _M\leq 1$
, it therefore follows from equations (2.4) and (3.1) that
Now, assume that
![]() $x\in M_a$
(the space of analytic elements of M). According to equation (2.7), we have
$x\in M_a$
(the space of analytic elements of M). According to equation (2.7), we have
![]() $D\sigma ^\varphi _{i\theta }(x)=D^{1-\theta }xD^{\theta }$
. Likewise,
$D\sigma ^\varphi _{i\theta }(x)=D^{1-\theta }xD^{\theta }$
. Likewise,
![]() $\sigma ^\varphi _t(x)=\gamma ^{it}x\gamma ^{-it}$
for all
$\sigma ^\varphi _t(x)=\gamma ^{it}x\gamma ^{-it}$
for all
![]() $t\in \mathbb {R}$
, by [Reference Takesaki20, Theorem VIII.2.11], hence
$t\in \mathbb {R}$
, by [Reference Takesaki20, Theorem VIII.2.11], hence
![]() $\sigma ^\varphi _{i\theta }(x)=\gamma ^{-\theta }x\gamma ^\theta $
. Hence, we have
$\sigma ^\varphi _{i\theta }(x)=\gamma ^{-\theta }x\gamma ^\theta $
. Hence, we have
![]() $\gamma \sigma ^\varphi _{i\theta }(x)=\gamma ^{1-\theta }x\gamma ^{\theta }$
. Applying equation (3.8) with
$\gamma \sigma ^\varphi _{i\theta }(x)=\gamma ^{1-\theta }x\gamma ^{\theta }$
. Applying equation (3.8) with
![]() $\sigma ^\varphi _{i\theta }(x)$
in place of x, we deduce that
$\sigma ^\varphi _{i\theta }(x)$
in place of x, we deduce that
Consider the standard representation
![]() $M\hookrightarrow B(L^2(M,\varphi ))$
, and consider an arbitrary
$M\hookrightarrow B(L^2(M,\varphi ))$
, and consider an arbitrary
![]() $x\in M$
. Assume that
$x\in M$
. Assume that
![]() $\theta \geq {\frac {1}{2}}$
. There exists a net
$\theta \geq {\frac {1}{2}}$
. There exists a net
![]() $(x_i)_i$
in
$(x_i)_i$
in
![]() $M_a$
such that
$M_a$
such that
![]() $x_i\to x$
strongly. Then
$x_i\to x$
strongly. Then
![]() $x_iD^{\frac {1}{2}}\to xD^{\frac {1}{2}}$
in
$x_iD^{\frac {1}{2}}\to xD^{\frac {1}{2}}$
in
![]() $L^2(M,\varphi )$
. Applying Lemma 2.1 (Hölder’s inequality), we deduce that
$L^2(M,\varphi )$
. Applying Lemma 2.1 (Hölder’s inequality), we deduce that
![]() $D^{1-\theta }x_iD^{\theta }=D^{1-\theta }(x_iD^{\frac {1}{2}})D^{\theta -{\frac {1}{2}}}$
converges to
$D^{1-\theta }x_iD^{\theta }=D^{1-\theta }(x_iD^{\frac {1}{2}})D^{\theta -{\frac {1}{2}}}$
converges to
![]() $D^{1-\theta } xD^{\theta }$
in
$D^{1-\theta } xD^{\theta }$
in
![]() $L^{1}(M,\varphi )$
. (This result can also be formally deduced from [Reference Junge12, Lemma 2.3].) Likewise,
$L^{1}(M,\varphi )$
. (This result can also be formally deduced from [Reference Junge12, Lemma 2.3].) Likewise,
![]() $\gamma ^{1-\theta }x_i\gamma ^{\theta }$
converges to
$\gamma ^{1-\theta }x_i\gamma ^{\theta }$
converges to
![]() $\gamma ^{1-\theta } x\gamma ^{\theta }$
in
$\gamma ^{1-\theta } x\gamma ^{\theta }$
in
![]() ${\mathcal L}^{1}(M,\tau )$
. Consequently, equation (3.9) holds true for x. Changing x into
${\mathcal L}^{1}(M,\tau )$
. Consequently, equation (3.9) holds true for x. Changing x into
![]() $x^*$
, we obtain this result as well if
$x^*$
, we obtain this result as well if
![]() $\theta <{\frac {1}{2}}$
. This proves the result when
$\theta <{\frac {1}{2}}$
. This proves the result when
![]() $p=1$
.
$p=1$
.
We further note that the proof that
![]() ${{\mathcal A}}_{1,\theta }=D^{(1-\theta )} M D^{\theta }$
is dense in
${{\mathcal A}}_{1,\theta }=D^{(1-\theta )} M D^{\theta }$
is dense in
![]() $L^1(M,\varphi )$
shows as well that the space
$L^1(M,\varphi )$
shows as well that the space
![]() $\gamma ^{1-\theta } M \gamma ^{\theta }$
is dense in
$\gamma ^{1-\theta } M \gamma ^{\theta }$
is dense in
![]() ${\mathcal L}^1(M,\tau )$
. Thus, equation (3.9) provides an isometric isomorphism
${\mathcal L}^1(M,\tau )$
. Thus, equation (3.9) provides an isometric isomorphism
such that
Now, let
![]() $p>1$
and consider the interpolation spaces
$p>1$
and consider the interpolation spaces
![]() $C(p,\theta )$
and
$C(p,\theta )$
and
![]() $c(p,\theta )$
defined by equations (3.4) and (3.6). Since
$c(p,\theta )$
defined by equations (3.4) and (3.6). Since
![]() $j_\theta =\Phi \circ J_\theta $
, the mapping
$j_\theta =\Phi \circ J_\theta $
, the mapping
![]() $\Phi $
restricts to an isometric isomorphism from
$\Phi $
restricts to an isometric isomorphism from
![]() $C(p,\theta )$
onto
$C(p,\theta )$
onto
![]() $c(p,\theta )$
. Let
$c(p,\theta )$
. Let
![]() $x\in M$
. Applying equations (3.7) and (3.5), we deduce that
$x\in M$
. Applying equations (3.7) and (3.5), we deduce that
 $$ \begin{align*} \big\Vert\gamma^{\frac{1-\theta}{p}} x \gamma^{\frac{\theta}{p}}\big\Vert_{{\mathcal L}^p(M,\tau)} & = \big\Vert\gamma^{1-\theta}x\gamma^\theta\big\Vert_{c(p,\theta)}\\ & = \big\Vert D^{1-\theta}x D^\theta\big\Vert_{C(p,\theta)}\\ &= \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)}, \end{align*} $$
$$ \begin{align*} \big\Vert\gamma^{\frac{1-\theta}{p}} x \gamma^{\frac{\theta}{p}}\big\Vert_{{\mathcal L}^p(M,\tau)} & = \big\Vert\gamma^{1-\theta}x\gamma^\theta\big\Vert_{c(p,\theta)}\\ & = \big\Vert D^{1-\theta}x D^\theta\big\Vert_{C(p,\theta)}\\ &= \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)}, \end{align*} $$
which proves the result.
The following is a straightforward consequence of Lemma 3.1. Given any
![]() $T\colon M\to M$
, it provides a concrete way to compute the norm of the operator
$T\colon M\to M$
, it provides a concrete way to compute the norm of the operator
![]() $T_{p,\theta }$
associated with
$T_{p,\theta }$
associated with
![]() $\varphi $
. Note that in this statement, this norm may be infinite.
$\varphi $
. Note that in this statement, this norm may be infinite.
Corollary 3.2. Let
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() $\theta \in [0,1]$
, and let
$\theta \in [0,1]$
, and let
![]() $T\colon M\to M$
be any bounded map. Then
$T\colon M\to M$
be any bounded map. Then
Let
![]() $n\geq 1$
be an integer, and consider the special case when
$n\geq 1$
be an integer, and consider the special case when
![]() $M=M_n$
, equipped with its usual trace
$M=M_n$
, equipped with its usual trace
![]() $\mathrm {tr}$
. For any
$\mathrm {tr}$
. For any
![]() $\varphi $
and
$\varphi $
and
![]() $T\colon M_n\to M_n$
as above,
$T\colon M_n\to M_n$
as above,
![]() $T_{p,\theta }$
is trivially bounded for all
$T_{p,\theta }$
is trivially bounded for all
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $\theta $
since
$\theta $
since
![]() $L^p(M_n,\varphi )$
is finite-dimensional. However, we will see in Sections 5 and 6 that finding (lower) estimates of the norm of
$L^p(M_n,\varphi )$
is finite-dimensional. However, we will see in Sections 5 and 6 that finding (lower) estimates of the norm of
![]() $T_{p,\theta }$
in this setting will be instrumental to devise counterexamples on infinite dimensional von Neumann algebras. This is why we give a version of the preceding corollary in this specific case.
$T_{p,\theta }$
in this setting will be instrumental to devise counterexamples on infinite dimensional von Neumann algebras. This is why we give a version of the preceding corollary in this specific case.
For any
![]() $1\leq p<\infty $
, let
$1\leq p<\infty $
, let
![]() $S^p_n={\mathcal L}^p(M_n,\mathrm {tr})$
denote the p-Schatten class over
$S^p_n={\mathcal L}^p(M_n,\mathrm {tr})$
denote the p-Schatten class over
![]() $M_n$
.
$M_n$
.
Proposition 3.3. Let
![]() $\Gamma \in M_n$
be a positive definite matrix such that
$\Gamma \in M_n$
be a positive definite matrix such that
![]() $\mathrm {tr}(\Gamma )=1$
and let
$\mathrm {tr}(\Gamma )=1$
and let
![]() $\varphi $
be the faithful state on
$\varphi $
be the faithful state on
![]() $M_n$
associated with
$M_n$
associated with
![]() $\Gamma $
, that is,
$\Gamma $
, that is,
![]() $\varphi (X)=\mathrm {tr}(\Gamma X)$
for all
$\varphi (X)=\mathrm {tr}(\Gamma X)$
for all
![]() $X\in M_n$
. Let
$X\in M_n$
. Let
![]() $T\colon M_n\to M_n$
be any linear map. For any
$T\colon M_n\to M_n$
be any linear map. For any
![]() $p\in [1,\infty )$
and
$p\in [1,\infty )$
and
![]() $\theta \in [0,1]$
, let
$\theta \in [0,1]$
, let
![]() $U_{p,\theta }\colon S^p_n\to S^p_n$
be defined by
$U_{p,\theta }\colon S^p_n\to S^p_n$
be defined by
Then
4 Extension results
This section is devoted to two cases for which Question 2.2 has a positive answer. Let M be a von Neumann algebra equipped with a faithful normal state
![]() $\varphi $
, and let
$\varphi $
, and let
![]() $D\in L^1(M,\varphi )^+$
denote its density.
$D\in L^1(M,\varphi )^+$
denote its density.
Theorem 4.1. Let
![]() $T\colon M\to M$
be a
$T\colon M\to M$
be a
![]() $2$
-positive map such that
$2$
-positive map such that
![]() $\varphi \circ T\leq \varphi $
. For any
$\varphi \circ T\leq \varphi $
. For any
![]() $p\geq 2$
and for any
$p\geq 2$
and for any
![]() $\theta \in [0,1]$
, the mapping
$\theta \in [0,1]$
, the mapping
![]() $T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
defined by equation (1.2) extends to a bounded map
$T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
defined by equation (1.2) extends to a bounded map
![]() $L^p(M,\varphi )\to L^p(M,\varphi )$
.
$L^p(M,\varphi )\to L^p(M,\varphi )$
.
Proof. Consider a
![]() $2$
-positive map
$2$
-positive map
![]() $T\colon M\to M$
such that
$T\colon M\to M$
such that
![]() $\varphi \circ T\leq \varphi $
. We start with the case
$\varphi \circ T\leq \varphi $
. We start with the case
![]() $p=2$
. For any
$p=2$
. For any
![]() $x\in M$
, we have
$x\in M$
, we have
by the Kadison–Schwarz inequality [Reference Choi5]. By equation (2.6), we have
This shows that
![]() $T_{2,1}$
is bounded. The proof that
$T_{2,1}$
is bounded. The proof that
![]() $T_{2,0}$
is bounded is similar.
$T_{2,0}$
is bounded is similar.
Now, let
![]() $\theta \in (0,1)$
and let us show that
$\theta \in (0,1)$
and let us show that
![]() $T_{2,\theta }$
is bounded. Consider the open strip
$T_{2,\theta }$
is bounded. Consider the open strip
Let
![]() $x,a\in M_a$
, and define
$x,a\in M_a$
, and define
![]() $F\colon \overline {{{\mathcal S}}}\to \mathbb {C}$
by
$F\colon \overline {{{\mathcal S}}}\to \mathbb {C}$
by
This is a well-defined function which is actually the restriction to
![]() $\overline {{{\mathcal S}}}$
of an entire function. For all
$\overline {{{\mathcal S}}}$
of an entire function. For all
![]() $t\in \mathbb {R}$
, we have
$t\in \mathbb {R}$
, we have
 $$ \begin{align*} F(it) & = \mathrm{Tr}\Big(D^{\frac{1}{2}}\,T \Big(\sigma^{\varphi}_{\frac{i}{2}}\big(\sigma^{\varphi}_{\frac{t}{2}}(x) \big) \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big)\\ & = \mathrm{Tr}\Big(D^{\frac{1}{2}}\,T \Big(D^{-{\frac{1}{2}}}\sigma^{\varphi}_{\frac{t}{2}}(x) D^{\frac{1}{2}} \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a) \Big)\\ &= \mathrm{Tr}\Big(T_{2,0} \Big(\sigma^{\varphi}_{\frac{t}{2}}(x) D^{\frac{1}{2}} \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big), \end{align*} $$
$$ \begin{align*} F(it) & = \mathrm{Tr}\Big(D^{\frac{1}{2}}\,T \Big(\sigma^{\varphi}_{\frac{i}{2}}\big(\sigma^{\varphi}_{\frac{t}{2}}(x) \big) \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big)\\ & = \mathrm{Tr}\Big(D^{\frac{1}{2}}\,T \Big(D^{-{\frac{1}{2}}}\sigma^{\varphi}_{\frac{t}{2}}(x) D^{\frac{1}{2}} \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a) \Big)\\ &= \mathrm{Tr}\Big(T_{2,0} \Big(\sigma^{\varphi}_{\frac{t}{2}}(x) D^{\frac{1}{2}} \Big) D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big), \end{align*} $$
by equation (2.7). Hence, by equation (2.2),
 $$ \begin{align*} \vert F(it)\vert &\leq \Big\Vert T_{2,0} \Big(\sigma^{\varphi}_{\frac{t}{2}}(x)D^{\frac{1}{2}}\Big)\Big\Vert_2 \Big\Vert D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big\Vert_2\\ &\leq \big\Vert T_{2,0}\big\Vert \big\Vert D^{\frac{it}{2}}(xD^{\frac{1}{2}})D^{-\frac{it}{2}}\big\Vert_2 \big\Vert D^{\frac{it}{2}}(D^{\frac{1}{2}} a)D^{-\frac{it}{2}}\big\Vert_2\\ &= \big\Vert T_{2,0}\big\Vert \big\Vert xD^{\frac{1}{2}}\big\Vert_2 \big\Vert D^{\frac{1}{2}} a\big\Vert_2. \end{align*} $$
$$ \begin{align*} \vert F(it)\vert &\leq \Big\Vert T_{2,0} \Big(\sigma^{\varphi}_{\frac{t}{2}}(x)D^{\frac{1}{2}}\Big)\Big\Vert_2 \Big\Vert D^{\frac{1}{2}} \sigma^{\varphi}_{\frac{t}{2}}(a)\Big\Vert_2\\ &\leq \big\Vert T_{2,0}\big\Vert \big\Vert D^{\frac{it}{2}}(xD^{\frac{1}{2}})D^{-\frac{it}{2}}\big\Vert_2 \big\Vert D^{\frac{it}{2}}(D^{\frac{1}{2}} a)D^{-\frac{it}{2}}\big\Vert_2\\ &= \big\Vert T_{2,0}\big\Vert \big\Vert xD^{\frac{1}{2}}\big\Vert_2 \big\Vert D^{\frac{1}{2}} a\big\Vert_2. \end{align*} $$
Likewise,
hence
By the three lines lemma, we deduce that
To calculate
![]() $F(\theta )$
, we apply equation (2.7) again and we obtain
$F(\theta )$
, we apply equation (2.7) again and we obtain
 $$ \begin{align*} F(\theta) & = \mathrm{Tr}\Big(T \big(D^{-\frac{1-\theta}{2}} x D^{\frac{1-\theta}{2}}\big) D^{\frac{1}{2}} D^{\frac{\theta}{2}} a D^{-\frac{\theta}{2}}D^{\frac{1}{2}}\Big)\\ & = \mathrm{Tr}\Big( D^{\frac{1-\theta}{2}}\,T \big(D^{-\frac{1-\theta}{2}} x D^{\frac{1}{2}} D^{-\frac{\theta}{2}}\big) D^{\frac{\theta}{2}} D^{\frac{1}{2}} a \Big)\\ & = \mathrm{Tr}\Big(T_{2,\theta}\big(xD^{\frac{1}{2}}\big) D^{\frac{1}{2}} a\Big). \end{align*} $$
$$ \begin{align*} F(\theta) & = \mathrm{Tr}\Big(T \big(D^{-\frac{1-\theta}{2}} x D^{\frac{1-\theta}{2}}\big) D^{\frac{1}{2}} D^{\frac{\theta}{2}} a D^{-\frac{\theta}{2}}D^{\frac{1}{2}}\Big)\\ & = \mathrm{Tr}\Big( D^{\frac{1-\theta}{2}}\,T \big(D^{-\frac{1-\theta}{2}} x D^{\frac{1}{2}} D^{-\frac{\theta}{2}}\big) D^{\frac{\theta}{2}} D^{\frac{1}{2}} a \Big)\\ & = \mathrm{Tr}\Big(T_{2,\theta}\big(xD^{\frac{1}{2}}\big) D^{\frac{1}{2}} a\Big). \end{align*} $$
Thus,
Since
![]() $M_aD^{\frac {1}{2}}$
and
$M_aD^{\frac {1}{2}}$
and
![]() $D^{\frac {1}{2}}M_a$
are both dense in
$D^{\frac {1}{2}}M_a$
are both dense in
![]() $L^2(M,\varphi )$
, this estimate shows that
$L^2(M,\varphi )$
, this estimate shows that
![]() $T_{2,\theta }$
is bounded, with
$T_{2,\theta }$
is bounded, with
![]() $\Vert T_{2,\theta }\Vert \leq \big \Vert T_{2,0}\big \Vert ^{1-\theta } \big \Vert T_{2,1}\big \Vert ^\theta $
.
$\Vert T_{2,\theta }\Vert \leq \big \Vert T_{2,0}\big \Vert ^{1-\theta } \big \Vert T_{2,1}\big \Vert ^\theta $
.
We now let
![]() $p\in (2,\infty )$
. The proof in this case is a variant of the proof of [Reference Haagerup, Junge and Xu9, Theorem 5.1]. We use Kosaki’s theorem which is presented after Lemma 3.1; see equations (3.4) and (3.5). Let
$p\in (2,\infty )$
. The proof in this case is a variant of the proof of [Reference Haagerup, Junge and Xu9, Theorem 5.1]. We use Kosaki’s theorem which is presented after Lemma 3.1; see equations (3.4) and (3.5). Let
![]() $\theta \in [0,1]$
. Let
$\theta \in [0,1]$
. Let
![]() ${\mathfrak J}_\theta \colon M\to L^2(M,\varphi )$
be defined by
${\mathfrak J}_\theta \colon M\to L^2(M,\varphi )$
be defined by
![]() ${\mathfrak J}_\theta (x)=D^{\frac {1-\theta }{2}} xD^{\frac {\theta }{2}}$
for all
${\mathfrak J}_\theta (x)=D^{\frac {1-\theta }{2}} xD^{\frac {\theta }{2}}$
for all
![]() $x\in M$
. Equip
$x\in M$
. Equip
![]() ${\mathfrak J}_\theta (M)$
with
${\mathfrak J}_\theta (M)$
with
Consider
![]() $({\mathfrak J}_\theta (M),L^2(M,\varphi ))$
as an interpolation couple. In analogy with equation (3.4), we set
$({\mathfrak J}_\theta (M),L^2(M,\varphi ))$
as an interpolation couple. In analogy with equation (3.4), we set
subspace of
![]() $L^2(M,\varphi )$
given by the complex interpolation method. Let
$L^2(M,\varphi )$
given by the complex interpolation method. Let
![]() $q\in (2,\infty )$
such that
$q\in (2,\infty )$
such that
We introduce one more mapping
![]() $U_\theta \colon L^2(M,\varphi )\to L^1(M,\varphi )$
defined by
$U_\theta \colon L^2(M,\varphi )\to L^1(M,\varphi )$
defined by
By equation (3.5),
![]() $U_\theta $
is an isometric isomorphism from
$U_\theta $
is an isometric isomorphism from
![]() $L^2(M,\varphi )$
onto
$L^2(M,\varphi )$
onto
![]() $C(2,\theta )$
. Since
$C(2,\theta )$
. Since
![]() $U_\theta $
restricts to an isometric isomorphism from
$U_\theta $
restricts to an isometric isomorphism from
![]() ${\mathfrak J}_\theta (M)$
onto
${\mathfrak J}_\theta (M)$
onto
![]() $J_\theta (M)$
, by equations (3.3) and (4.1), it induces an isometric isomorphism from
$J_\theta (M)$
, by equations (3.3) and (4.1), it induces an isometric isomorphism from
![]() $E(p,\theta )$
onto
$E(p,\theta )$
onto
![]() $\big [J_\theta (M),C(2,\theta )\big ]_{\frac {2}{p}}$
. By equation (3.4) and the reiteration theorem for complex interpolation (see [Reference Bergh and Löfström3, Theorem 4.6.1]), the latter is equal to
$\big [J_\theta (M),C(2,\theta )\big ]_{\frac {2}{p}}$
. By equation (3.4) and the reiteration theorem for complex interpolation (see [Reference Bergh and Löfström3, Theorem 4.6.1]), the latter is equal to
![]() $C(p,\theta )$
. Hence,
$C(p,\theta )$
. Hence,
![]() $U_\theta $
actually induces an isometric isomorphism
$U_\theta $
actually induces an isometric isomorphism
Since
![]() $\frac {1}{p'}={\frac {1}{2}}+\frac {1}{q}\,$
, we have
$\frac {1}{p'}={\frac {1}{2}}+\frac {1}{q}\,$
, we have
for all
![]() $y\in L^p(M,\varphi )$
. Applying equations (3.5) and (4.2), we deduce that
$y\in L^p(M,\varphi )$
. Applying equations (3.5) and (4.2), we deduce that
with
Now, let
be given by the first part of the proof (boundedness of
![]() $T_{2,\theta }$
). By equation (4.1), S is bounded on
$T_{2,\theta }$
). By equation (4.1), S is bounded on
![]() ${\mathfrak J}_\theta (M)$
. Hence, by the interpolation theorem, S is bounded on
${\mathfrak J}_\theta (M)$
. Hence, by the interpolation theorem, S is bounded on
![]() $E(p,\theta )$
.
$E(p,\theta )$
.
Using equation (4.3), we deduce that for all
![]() $x\in M$
,
$x\in M$
,
 $$ \begin{align*} \big\Vert D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)} & = \big\Vert D^{\frac{1-\theta}{2}} T(x) D^{\frac{\theta}{2}}\big\Vert_{E(p,\theta)}\\ & \leq \big\Vert S\colon E(p,\theta)\to E(p,\theta)\big\Vert \big\Vert D^{\frac{1-\theta}{2}}x D^{\frac{\theta}{2}}\big\Vert_{E(p,\theta)}\\ & = \big\Vert S\colon E(p,\theta)\to E(p,\theta)\big\Vert \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)}. \end{align*} $$
$$ \begin{align*} \big\Vert D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)} & = \big\Vert D^{\frac{1-\theta}{2}} T(x) D^{\frac{\theta}{2}}\big\Vert_{E(p,\theta)}\\ & \leq \big\Vert S\colon E(p,\theta)\to E(p,\theta)\big\Vert \big\Vert D^{\frac{1-\theta}{2}}x D^{\frac{\theta}{2}}\big\Vert_{E(p,\theta)}\\ & = \big\Vert S\colon E(p,\theta)\to E(p,\theta)\big\Vert \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)}. \end{align*} $$
This proves that
![]() $T_{p,\theta }$
is bounded and completes the proof.
$T_{p,\theta }$
is bounded and completes the proof.
Remark 4.2. Let
![]() $T\colon M\to M$
be a
$T\colon M\to M$
be a
![]() $2$
-positive map such that
$2$
-positive map such that
![]() $\varphi \circ T\leq C_1 T$
for some
$\varphi \circ T\leq C_1 T$
for some
![]() $C_1\geq 0$
, and let
$C_1\geq 0$
, and let
![]() $C_\infty =\Vert T\Vert $
. It follows from the above proof and an obvious scaling that for any
$C_\infty =\Vert T\Vert $
. It follows from the above proof and an obvious scaling that for any
![]() $p\geq 2$
and any
$p\geq 2$
and any
![]() $\theta \in [0,1]$
, we have
$\theta \in [0,1]$
, we have
Theorem 4.3. Let
![]() $T\colon M\to M$
be a
$T\colon M\to M$
be a
![]() $2$
-positive map such that
$2$
-positive map such that
![]() $\varphi \circ T\leq \varphi $
, and let
$\varphi \circ T\leq \varphi $
, and let
![]() $1\leq p\leq 2$
. If
$1\leq p\leq 2$
. If
then
![]() $T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
extends to a bounded map
$T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
extends to a bounded map
![]() $L^p(M,\varphi )\to L^p(M,\varphi )$
.
$L^p(M,\varphi )\to L^p(M,\varphi )$
.
Proof. We will use Theorem 4.1 on
![]() $L^2(M,\varphi )$
, as well as the fact that
$L^2(M,\varphi )$
, as well as the fact that
![]() $T_{1,{\frac {1}{2}}}$
is bounded; see [Reference Haagerup, Junge and Xu9, Lemma 5.3] or Remark 2.3. Let
$T_{1,{\frac {1}{2}}}$
is bounded; see [Reference Haagerup, Junge and Xu9, Lemma 5.3] or Remark 2.3. Let
![]() $p\in (1,2)$
, let
$p\in (1,2)$
, let
![]() $\theta $
satisfying equation (4.4), and let
$\theta $
satisfying equation (4.4), and let
 $$ \begin{align*}\eta= \frac{\theta -\big(1-\frac{p}{2}\big)}{p-1}. \end{align*} $$
$$ \begin{align*}\eta= \frac{\theta -\big(1-\frac{p}{2}\big)}{p-1}. \end{align*} $$
Then
![]() $\eta \in [0,1]$
. This interpolation number is chosen in such a way that
$\eta \in [0,1]$
. This interpolation number is chosen in such a way that
where
![]() $p'$
is the conjugate number of p.
$p'$
is the conjugate number of p.
We set
Let
![]() $V\colon L^2(M,\varphi )\to L^1(M,\varphi )$
defined by
$V\colon L^2(M,\varphi )\to L^1(M,\varphi )$
defined by
![]() $V(y)=D^{\frac {\eta }{2}} y D^{\frac {1-\eta }{2}}$
for all
$V(y)=D^{\frac {\eta }{2}} y D^{\frac {1-\eta }{2}}$
for all
![]() $y\in L^2(M,\varphi )$
. According to equation (3.5), V is an isometric isomorphism from
$y\in L^2(M,\varphi )$
. According to equation (3.5), V is an isometric isomorphism from
![]() $L^2(M,\varphi )$
onto
$L^2(M,\varphi )$
onto
![]() $C(2,1-\eta )$
. Hence, for all
$C(2,1-\eta )$
. Hence, for all
![]() $x\in M$
, we have
$x\in M$
, we have
 $$ \begin{align*} \big\Vert S(D^{\frac{1}{2}} x D^{\frac{1}{2}})\big\Vert_{C(2,1-\eta)} & = \big\Vert D^{\frac{\eta}{2}} D^{\frac{1-\eta}{2}} T(x) D^{\frac{\eta}{2}} D^{\frac{1-\eta}{2}} \big\Vert_{C(2,1-\eta)}\\ & = \big\Vert D^{\frac{1-\eta}{2}} T(x) D^{\frac{\eta}{2}}\big\Vert_{L^2(M,\varphi)}\\ &\leq \big\Vert T_{2,\eta}\big\Vert\big\Vert D^{\frac{1-\eta}{2}} x D^{\frac{\eta}{2}}\big\Vert_{L^2(M,\varphi)}\\ & = \big\Vert T_{2,\eta}\big\Vert\big\Vert D^{\frac{1}{2}} xD^{\frac{1}{2}} \big\Vert_{C(2,1-\eta)}. \end{align*} $$
$$ \begin{align*} \big\Vert S(D^{\frac{1}{2}} x D^{\frac{1}{2}})\big\Vert_{C(2,1-\eta)} & = \big\Vert D^{\frac{\eta}{2}} D^{\frac{1-\eta}{2}} T(x) D^{\frac{\eta}{2}} D^{\frac{1-\eta}{2}} \big\Vert_{C(2,1-\eta)}\\ & = \big\Vert D^{\frac{1-\eta}{2}} T(x) D^{\frac{\eta}{2}}\big\Vert_{L^2(M,\varphi)}\\ &\leq \big\Vert T_{2,\eta}\big\Vert\big\Vert D^{\frac{1-\eta}{2}} x D^{\frac{\eta}{2}}\big\Vert_{L^2(M,\varphi)}\\ & = \big\Vert T_{2,\eta}\big\Vert\big\Vert D^{\frac{1}{2}} xD^{\frac{1}{2}} \big\Vert_{C(2,1-\eta)}. \end{align*} $$
Here, the boundedness of
![]() $T_{2,\eta }$
is provided by Theorem 4.1. This proves that S is bounded on
$T_{2,\eta }$
is provided by Theorem 4.1. This proves that S is bounded on
![]() $C(2,1-\eta )$
.
$C(2,1-\eta )$
.
By equation (3.4) and the reiteration theorem, we have
Therefore, S is bounded on
![]() $C(p,1-\eta )$
. Using equation (3.5) again, as well as equation (4.5), we deduce that for any
$C(p,1-\eta )$
. Using equation (3.5) again, as well as equation (4.5), we deduce that for any
![]() $x\in M$
,
$x\in M$
,
 $$ \begin{align*} \big\Vert D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)} & = \big\Vert D^{\frac{\eta}{p'}} D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}} D^{\frac{1- \eta}{p'}}\big\Vert_{C(p,1-\eta)}\\ &= \big\Vert D^{\frac{1}{2}} T(x) D^{{\frac{1}{2}}}\big\Vert_{C(p,1-\eta)}\\ & \leq \big\Vert S\colon C(p,1-\eta)\to C(p,1-\eta)\big\Vert \big\Vert D^{\frac{1}{2}} x D^{{\frac{1}{2}}}\big\Vert_{C(p,1-\eta)}\\ & = \big\Vert S\colon C(p,1-\eta)\to C(p,1-\eta)\big\Vert \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}} \big\Vert_{L^p(M,\varphi)}. \end{align*} $$
$$ \begin{align*} \big\Vert D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}}\big\Vert_{L^p(M,\varphi)} & = \big\Vert D^{\frac{\eta}{p'}} D^{\frac{1-\theta}{p}} T(x) D^{\frac{\theta}{p}} D^{\frac{1- \eta}{p'}}\big\Vert_{C(p,1-\eta)}\\ &= \big\Vert D^{\frac{1}{2}} T(x) D^{{\frac{1}{2}}}\big\Vert_{C(p,1-\eta)}\\ & \leq \big\Vert S\colon C(p,1-\eta)\to C(p,1-\eta)\big\Vert \big\Vert D^{\frac{1}{2}} x D^{{\frac{1}{2}}}\big\Vert_{C(p,1-\eta)}\\ & = \big\Vert S\colon C(p,1-\eta)\to C(p,1-\eta)\big\Vert \big\Vert D^{\frac{1-\theta}{p}} x D^{\frac{\theta}{p}} \big\Vert_{L^p(M,\varphi)}. \end{align*} $$
This shows that
![]() $T_{p,\theta }$
is bounded.
$T_{p,\theta }$
is bounded.
5 The use of infinite tensor products
In this section, we show how to reduce the problem of constructing a unital completely positive map
![]() $T\colon (M,\varphi )\to (M,\varphi )$
such that
$T\colon (M,\varphi )\to (M,\varphi )$
such that
![]() $\varphi \circ T=\varphi $
and
$\varphi \circ T=\varphi $
and
![]() $T_{p,\theta }$
is unbounded, for a certain pair
$T_{p,\theta }$
is unbounded, for a certain pair
![]() $(p,\theta )$
, to a finite-dimensional question. In the sequel, by a matrix algebra A, we mean an algebra
$(p,\theta )$
, to a finite-dimensional question. In the sequel, by a matrix algebra A, we mean an algebra
![]() $A=M_n$
for some
$A=M_n$
for some
![]() $n\geq 1$
.
$n\geq 1$
.
Lemma 5.1. Let
![]() $A_1,A_2$
be two matrix algebras, and for
$A_1,A_2$
be two matrix algebras, and for
![]() $i=1,2$
, consider a faithful state
$i=1,2$
, consider a faithful state
![]() $\varphi _i$
on
$\varphi _i$
on
![]() $A_i$
. Let
$A_i$
. Let
![]() $B=A_1\otimes _{\mathrm {min}} A_2$
and consider the faithful state
$B=A_1\otimes _{\mathrm {min}} A_2$
and consider the faithful state
![]() $\psi =\varphi _1\otimes \varphi _2$
on B. Let
$\psi =\varphi _1\otimes \varphi _2$
on B. Let
![]() $T_i\colon A_i\to A_i$
be a linear map, for
$T_i\colon A_i\to A_i$
be a linear map, for
![]() $i=1,2$
, and consider
$i=1,2$
, and consider
![]() $T=T_1\otimes T_2\colon B\to B$
. Then for any
$T=T_1\otimes T_2\colon B\to B$
. Then for any
![]() $1\leq p<\infty $
and any
$1\leq p<\infty $
and any
![]() $\theta \in [0,1]$
, we have
$\theta \in [0,1]$
, we have
 $$ \begin{align*} \big\Vert T_{p,\theta}\colon L^p(B,\psi) &\to L^p(B,\psi)\big\Vert \geq \\ &\big\Vert\{T_1\}_{p,\theta}\colon L^p(A_1,\varphi_1)\to L^p(A_1,\varphi_1)\big\Vert \big\Vert\{T_2\}_{p,\theta}\colon L^p(A_2,\varphi_2)\to L^p(A_2,\varphi_2)\big\Vert. \end{align*} $$
$$ \begin{align*} \big\Vert T_{p,\theta}\colon L^p(B,\psi) &\to L^p(B,\psi)\big\Vert \geq \\ &\big\Vert\{T_1\}_{p,\theta}\colon L^p(A_1,\varphi_1)\to L^p(A_1,\varphi_1)\big\Vert \big\Vert\{T_2\}_{p,\theta}\colon L^p(A_2,\varphi_2)\to L^p(A_2,\varphi_2)\big\Vert. \end{align*} $$
Proof. Let
![]() $n_1,n_2\geq 1$
such that
$n_1,n_2\geq 1$
such that
![]() $A_1=M_{n_1}$
and
$A_1=M_{n_1}$
and
![]() $A_2=M_{n_2}$
and let
$A_2=M_{n_2}$
and let
![]() $n=n_1n_2$
. For
$n=n_1n_2$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\Gamma _i\in M_{n_i}$
such that
$\Gamma _i\in M_{n_i}$
such that
![]() $\varphi _i(X_i)=\mathrm {tr}(\Gamma _iX_i)$
for all
$\varphi _i(X_i)=\mathrm {tr}(\Gamma _iX_i)$
for all
![]() $X_i\in M_{n_i}$
. As in Proposition 3.3, consider the mapping
$X_i\in M_{n_i}$
. As in Proposition 3.3, consider the mapping
![]() $\{U_i\}_{p,\theta }\colon S^p_{n_i}\to S^p_{n_i}$
defined by
$\{U_i\}_{p,\theta }\colon S^p_{n_i}\to S^p_{n_i}$
defined by
![]() $\{U_i\}_{p,\theta }(Y_i)= \Gamma _i^{\frac {1-\theta }{p}} T_i\big (\Gamma _i^{-\frac {1-\theta }{p}} Y_i\Gamma _i^{-\frac {\theta }{p}}\big )\Gamma _i^{\frac {\theta }{p}}$
for all
$\{U_i\}_{p,\theta }(Y_i)= \Gamma _i^{\frac {1-\theta }{p}} T_i\big (\Gamma _i^{-\frac {1-\theta }{p}} Y_i\Gamma _i^{-\frac {\theta }{p}}\big )\Gamma _i^{\frac {\theta }{p}}$
for all
![]() $Y_i\in S^p_{n_i}$
. Using the standard identification
$Y_i\in S^p_{n_i}$
. Using the standard identification
we observe that
![]() $\psi (X) =\mathrm {tr}\big ((\Gamma _1\otimes \Gamma _2)X)\big )$
for all
$\psi (X) =\mathrm {tr}\big ((\Gamma _1\otimes \Gamma _2)X)\big )$
for all
![]() $X\in M_n$
. Hence, using the identification
$X\in M_n$
. Hence, using the identification
![]() $S^p_n=S^p_{n_1}\otimes S^p_{n_2}$
inherited from equation (5.1), we obtain the the mapping
$S^p_n=S^p_{n_1}\otimes S^p_{n_2}$
inherited from equation (5.1), we obtain the the mapping
![]() $U_{p,\theta }$
defined by equation (3.10) is actually given by
$U_{p,\theta }$
defined by equation (3.10) is actually given by
For any
![]() $Y_1\in S^p_{n_1}$
and
$Y_1\in S^p_{n_1}$
and
![]() $Y_2\in S^p_{n_2}$
, we have
$Y_2\in S^p_{n_2}$
, we have
![]() $\Vert Y_1\otimes Y_2\Vert _p = \Vert Y_1\Vert _p \Vert Y_2\Vert _p$
. Hence, we deduce
$\Vert Y_1\otimes Y_2\Vert _p = \Vert Y_1\Vert _p \Vert Y_2\Vert _p$
. Hence, we deduce
 $$ \begin{align*} \Vert\{U_1\}_{p,\theta}(Y_1)\Vert \Vert\{U_2\}_{p,\theta}(Y_2)\Vert & =\Vert\{U_1\}_{p,\theta}(Y_1)\otimes \{U_2\}_{p,\theta}(Y_2)\Vert\\ & =\Vert U_{p,\theta}(Y_1\otimes Y_2)\Vert\\ & \leq \Vert U_{p,\theta}\Vert \Vert Y_1\Vert_p\Vert Y_2\Vert_p. \end{align*} $$
$$ \begin{align*} \Vert\{U_1\}_{p,\theta}(Y_1)\Vert \Vert\{U_2\}_{p,\theta}(Y_2)\Vert & =\Vert\{U_1\}_{p,\theta}(Y_1)\otimes \{U_2\}_{p,\theta}(Y_2)\Vert\\ & =\Vert U_{p,\theta}(Y_1\otimes Y_2)\Vert\\ & \leq \Vert U_{p,\theta}\Vert \Vert Y_1\Vert_p\Vert Y_2\Vert_p. \end{align*} $$
This implies that
![]() $\Vert \{U_1\}_{p,\theta }\Vert \Vert \{U_2\}_{p,\theta }\Vert \leq \Vert U_{p,\theta }\Vert $
Applying Proposition 3.3, we obtain the requested inequality.
$\Vert \{U_1\}_{p,\theta }\Vert \Vert \{U_2\}_{p,\theta }\Vert \leq \Vert U_{p,\theta }\Vert $
Applying Proposition 3.3, we obtain the requested inequality.
Throughout the rest of this section, we let
![]() $(A_k)_{k\geq 1}$
be a sequence of matrix algebras. For any
$(A_k)_{k\geq 1}$
be a sequence of matrix algebras. For any
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $\varphi _k$
be a faithful state on
$\varphi _k$
be a faithful state on
![]() $A_k$
. Let
$A_k$
. Let
be the infinite tensor product associated with the
![]() $(A_k,\varphi _k).$
We refer to [Reference Takesaki21, Section XIV.1] for the construction and the properties of this tensor product. We merely recall that if we regard
$(A_k,\varphi _k).$
We refer to [Reference Takesaki21, Section XIV.1] for the construction and the properties of this tensor product. We merely recall that if we regard
![]() $(A_1\otimes \cdots \otimes A_n)_{n\geq 1}$
as an increasing sequence of (finite-dimensional) algebras in the natural way, then
$(A_1\otimes \cdots \otimes A_n)_{n\geq 1}$
as an increasing sequence of (finite-dimensional) algebras in the natural way, then
is
![]() $w^*$
-dense in M. Further,
$w^*$
-dense in M. Further,
![]() $\varphi $
is a normal faithful state on M such that
$\varphi $
is a normal faithful state on M such that
for all
![]() $n\geq 1$
.
$n\geq 1$
.
Proposition 5.2. Let
![]() $1\leq p<\infty $
and
$1\leq p<\infty $
and
![]() $\theta \in [0,1]$
. For any
$\theta \in [0,1]$
. For any
![]() $k\geq 1$
, let
$k\geq 1$
, let
![]() $T_k\colon A_k\to A_k$
be a unital completely positive map such that
$T_k\colon A_k\to A_k$
be a unital completely positive map such that
![]() $\varphi _k\circ T_k=\varphi _k$
. Assume that
$\varphi _k\circ T_k=\varphi _k$
. Assume that
 $$ \begin{align*}\prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\colon L^p(A_k,\varphi_k)\to L^p(A_k,\varphi_k)\big\Vert \longrightarrow\infty\qquad\text{when}\ n\to\infty. \end{align*} $$
$$ \begin{align*}\prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\colon L^p(A_k,\varphi_k)\to L^p(A_k,\varphi_k)\big\Vert \longrightarrow\infty\qquad\text{when}\ n\to\infty. \end{align*} $$
Then there exists a unital completely positive map
![]() $T\colon M\to M$
such that
$T\colon M\to M$
such that
![]() $\varphi \circ T=\varphi $
and
$\varphi \circ T=\varphi $
and
![]() $T_{p,\theta }$
is unbounded.
$T_{p,\theta }$
is unbounded.
Proof. For any
![]() $n\geq 1$
, we introduce
$n\geq 1$
, we introduce
![]() $B_n=A_1\otimes _{\mathrm {min}}\cdots \otimes _{\mathrm {min}} A_n$
and the faithful state
$B_n=A_1\otimes _{\mathrm {min}}\cdots \otimes _{\mathrm {min}} A_n$
and the faithful state
on
![]() $B_n$
. According to [Reference Takesaki21, Proposition XIV.1.11], the modular automorphism group of
$B_n$
. According to [Reference Takesaki21, Proposition XIV.1.11], the modular automorphism group of
![]() $\varphi $
preserves
$\varphi $
preserves
![]() $B_n$
. Consequently (see Remark 2.4), there exists a unique normal conditional expectation
$B_n$
. Consequently (see Remark 2.4), there exists a unique normal conditional expectation
![]() $E_n \colon M\to B_n$
such that
$E_n \colon M\to B_n$
such that
![]() $\varphi =\psi _n\circ E_n$
, and the preadjoint of
$\varphi =\psi _n\circ E_n$
, and the preadjoint of
![]() $E_n$
yields an isometric embedding
$E_n$
yields an isometric embedding
Likewise, let
![]() $F_n\colon B_{n+1}\to B_n$
be the conditional expectation defined by
$F_n\colon B_{n+1}\to B_n$
be the conditional expectation defined by
for all
![]() $a_1\in A_1,\ldots , a_n\in A_n, a_{n+1}\in A_{n+1}$
. Then the preadjoint of
$a_1\in A_1,\ldots , a_n\in A_n, a_{n+1}\in A_{n+1}$
. Then the preadjoint of
![]() $F_n$
yields an isometric embedding
$F_n$
yields an isometric embedding
We can therefore consider
![]() $\big (L^1(B_n,\psi _n)\big )_{n\geq 1}$
as an increasing sequence of subspaces of
$\big (L^1(B_n,\psi _n)\big )_{n\geq 1}$
as an increasing sequence of subspaces of
![]() $L^1(M,\varphi )$
. We introduce
$L^1(M,\varphi )$
. We introduce
Let
![]() $D\in L^1(M,\varphi )$
be the density of
$D\in L^1(M,\varphi )$
be the density of
![]() $\varphi $
. It follows from Remark 2.4 that
$\varphi $
. It follows from Remark 2.4 that
where
![]() ${{\mathcal B}}$
is defined by equation (5.2). Since
${{\mathcal B}}$
is defined by equation (5.2). Since
![]() ${{\mathcal B}}$
is
${{\mathcal B}}$
is
![]() $w^*$
-dense, it is dense in M for the strong operator topology given by the standard representation
$w^*$
-dense, it is dense in M for the strong operator topology given by the standard representation
![]() $M\hookrightarrow B(L^2(M,\varphi ))$
. Hence, by [Reference Junge12, Lemma 2.2],
$M\hookrightarrow B(L^2(M,\varphi ))$
. Hence, by [Reference Junge12, Lemma 2.2],
![]() ${{\mathcal B}} D^{\frac {1}{2}}$
is dense in
${{\mathcal B}} D^{\frac {1}{2}}$
is dense in
![]() $L^2(M,\varphi )$
. This implies that
$L^2(M,\varphi )$
. This implies that
![]() $\mathcal L$
is dense in
$\mathcal L$
is dense in
![]() $L^1(M,\varphi )$
.
$L^1(M,\varphi )$
.
For any
![]() $n\geq 1$
, let
$n\geq 1$
, let
This is a unital completely positive map. Hence, its norm is equal to 1. Let
be the preadjoint of
![]() $V(n)$
. Then
$V(n)$
. Then
![]() $\Vert S_n\Vert =1$
. We observe that
$\Vert S_n\Vert =1$
. We observe that
Indeed by duality, this amounts to show that
![]() $V(n)\circ F_n=F_n\circ V(n+1)$
, where
$V(n)\circ F_n=F_n\circ V(n+1)$
, where
![]() $F_n$
is given by equation (5.3). The latter is true because
$F_n$
is given by equation (5.3). The latter is true because
![]() $\varphi _{n+1}\circ T_{n+1}=\varphi _{n+1}$
.
$\varphi _{n+1}\circ T_{n+1}=\varphi _{n+1}$
.
Thanks to equation (5.4), one may define
by letting
![]() ${\mathcal S}(\eta )=S_n(\eta )$
if
${\mathcal S}(\eta )=S_n(\eta )$
if
![]() $\eta \in L^1(B_n,\psi _n)$
. Then
$\eta \in L^1(B_n,\psi _n)$
. Then
![]() ${{\mathcal S}}$
is bounded, with
${{\mathcal S}}$
is bounded, with
![]() $\Vert {{\mathcal S}}\Vert =1$
. Owing to the density of
$\Vert {{\mathcal S}}\Vert =1$
. Owing to the density of
![]() $\mathcal L$
, there exists a unique bounded
$\mathcal L$
, there exists a unique bounded
![]() $S\colon L^1(M,\varphi )\to L^1(M,\varphi )$
extending
$S\colon L^1(M,\varphi )\to L^1(M,\varphi )$
extending
![]() ${{\mathcal S}}$
. Using the duality (2.4), we set
${{\mathcal S}}$
. Using the duality (2.4), we set
By construction, T is a contraction. Furthermore, for each
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $S_n^*=V(n)$
is a unital completely positive map and
$S_n^*=V(n)$
is a unital completely positive map and
![]() $\psi _{n}\circ S_n^*=\psi _n$
. We deduce that T is unital and completely positive and that
$\psi _{n}\circ S_n^*=\psi _n$
. We deduce that T is unital and completely positive and that
Let
![]() $1\leq p<\infty $
, and let
$1\leq p<\infty $
, and let
![]() $\theta \in [0,1]$
. Let us use the isometric embedding
$\theta \in [0,1]$
. Let us use the isometric embedding
as explained in Remark 2.4. If
![]() $D_n$
denotes the density of
$D_n$
denotes the density of
![]() $\psi _n$
, then it follows from [Reference Haagerup, Junge and Xu9, Proposition 5.5] that the embedding (5.5) maps
$\psi _n$
, then it follows from [Reference Haagerup, Junge and Xu9, Proposition 5.5] that the embedding (5.5) maps
![]() $D_n^{\frac {1-\theta }{p}} x D_n^{\frac {\theta }{p}}$
to
$D_n^{\frac {1-\theta }{p}} x D_n^{\frac {\theta }{p}}$
to
![]() $D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$
for all
$D^{\frac {1-\theta }{p}} x D^{\frac {\theta }{p}}$
for all
![]() $x\in B_n$
. Then the restriction of
$x\in B_n$
. Then the restriction of
![]() $T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to L^p(M,\varphi )$
coincides with
$T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to L^p(M,\varphi )$
coincides with
Finally we observe that by a simple iteration of Lemma 5.1, we have
 $$ \begin{align*}\Vert V(n)_{p,\theta}\Vert\geq \prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\colon L^p(A_k,\varphi_k)\to L^p(A_k,\varphi_k)\big\Vert. \end{align*} $$
$$ \begin{align*}\Vert V(n)_{p,\theta}\Vert\geq \prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\colon L^p(A_k,\varphi_k)\to L^p(A_k,\varphi_k)\big\Vert. \end{align*} $$
The assumption that this product of norms tends to
![]() $\infty $
therefore implies that the operator
$\infty $
therefore implies that the operator
![]() $T_{p,\theta }$
is unbounded.
$T_{p,\theta }$
is unbounded.
6 Nonextension results
The aim of this section is to show the following.
Theorem 6.1. Let
![]() $1\leq p<2$
. If either
$1\leq p<2$
. If either
then there exist a von Neumann algebra M equipped with a normal faithful state
![]() $\varphi $
, as well as a unital completely positive map
$\varphi $
, as well as a unital completely positive map
![]() $T\colon M\to M$
such that
$T\colon M\to M$
such that
![]() $\varphi \circ T=\varphi $
and the mapping
$\varphi \circ T=\varphi $
and the mapping
![]() $T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
defined by equation (1.2) is unbounded.
$T_{p,\theta }\colon {{\mathcal A}}_{p,\theta }\to {{\mathcal A}}_{p,\theta }$
defined by equation (1.2) is unbounded.
This result will be proved at the end of this section, as a simple combination of Proposition 5.2 and the following key result. Recall that
![]() $M_2$
denotes the space of
$M_2$
denotes the space of
![]() $2\times 2$
matrices.
$2\times 2$
matrices.
Proposition 6.2. Let
![]() $1\leq p<2$
, and let
$1\leq p<2$
, and let
![]() $\theta \in [0,1]$
be satisfying equation (6.1). Then there exist a unital completely positive map
$\theta \in [0,1]$
be satisfying equation (6.1). Then there exist a unital completely positive map
![]() $T\colon M_2\to M_2$
and a faithful state
$T\colon M_2\to M_2$
and a faithful state
![]() $\varphi $
on
$\varphi $
on
![]() $M_2$
such that
$M_2$
such that
![]() $\varphi \circ T=\varphi $
and
$\varphi \circ T=\varphi $
and
![]() $\Vert T_{p,\theta }\Vert>1$
.
$\Vert T_{p,\theta }\Vert>1$
.
Proof. Let
![]() $c\in (0,1)$
, and consider
$c\in (0,1)$
, and consider
 $$ \begin{align*}\Gamma =\begin{pmatrix} 1-c & 0 \\ 0 & c\end{pmatrix}. \end{align*} $$
$$ \begin{align*}\Gamma =\begin{pmatrix} 1-c & 0 \\ 0 & c\end{pmatrix}. \end{align*} $$
This is a positive invertible matrix with trace equal to
![]() $1$
. We let
$1$
. We let
![]() $\varphi $
denote its associated faithful state on
$\varphi $
denote its associated faithful state on
![]() $M_2$
, that is,
$M_2$
, that is,
![]() $\varphi (X)=\mathrm {tr}(\Gamma X)=(1-c)x_{11} +cx_{22}$
, for all
$\varphi (X)=\mathrm {tr}(\Gamma X)=(1-c)x_{11} +cx_{22}$
, for all
 $X=\begin {pmatrix} x_{11} & x_{12} \\ x_{21} & x_{22}\end {pmatrix}$
in
$X=\begin {pmatrix} x_{11} & x_{12} \\ x_{21} & x_{22}\end {pmatrix}$
in
![]() $M_2$
.
$M_2$
.
Let
![]() $E_{i,j}$
,
$E_{i,j}$
,
![]() $1\leq i,j\leq 2$
, denote the standard matrix units of
$1\leq i,j\leq 2$
, denote the standard matrix units of
![]() $M_2$
. Let
$M_2$
. Let
![]() $T\colon M_2\to M_2$
be the linear map defined by
$T\colon M_2\to M_2$
be the linear map defined by
Let
![]() $A=\big [T(E_{ij})\big ]_{1\leq i,j\leq 2}\in M_2(M_2)$
. If we regard A as an element of
$A=\big [T(E_{ij})\big ]_{1\leq i,j\leq 2}\in M_2(M_2)$
. If we regard A as an element of
![]() $M_4$
, we have
$M_4$
, we have
 $$ \begin{align*}A=\begin{pmatrix} 1-c & 0 & 0 & (c(1-c))^{\frac{1}{2}} \\ 0 &1-c & (c(1-c))^{\frac{1}{2}} & 0\\ 0 & (c(1-c))^{\frac{1}{2}} & c & 0 \\ (c(1-c))^{\frac{1}{2}} & 0 & 0 & c\end{pmatrix}. \end{align*} $$
$$ \begin{align*}A=\begin{pmatrix} 1-c & 0 & 0 & (c(1-c))^{\frac{1}{2}} \\ 0 &1-c & (c(1-c))^{\frac{1}{2}} & 0\\ 0 & (c(1-c))^{\frac{1}{2}} & c & 0 \\ (c(1-c))^{\frac{1}{2}} & 0 & 0 & c\end{pmatrix}. \end{align*} $$
Clearly, A is unitarily equivalent to
![]() $B\otimes I_2$
, with
$B\otimes I_2$
, with
 $$ \begin{align*}B= \begin{pmatrix} 1-c & (c(1-c))^{\frac{1}{2}} \\ (c(1-c))^{\frac{1}{2}} & c\end{pmatrix}. \end{align*} $$
$$ \begin{align*}B= \begin{pmatrix} 1-c & (c(1-c))^{\frac{1}{2}} \\ (c(1-c))^{\frac{1}{2}} & c\end{pmatrix}. \end{align*} $$
It is plain that B is positive. Consequently, A is positive. Hence, T is completely positive, by Choi’s theorem (see, for example, [Reference Paulsen18, Theorem 3.14]). Furthermore, T is unital. We note that
![]() $\varphi (T(E_{11}))= \varphi (E_{11})=1-c$
,
$\varphi (T(E_{11}))= \varphi (E_{11})=1-c$
,
![]() $\varphi (T(E_{22}))= \varphi (E_{22})=c$
,
$\varphi (T(E_{22}))= \varphi (E_{22})=c$
,
![]() $\varphi (T(E_{12}))= \varphi (E_{12})=0$
and
$\varphi (T(E_{12}))= \varphi (E_{12})=0$
and
![]() $\varphi (T(E_{21}))= \varphi (E_{21})=0$
. Thus,
$\varphi (T(E_{21}))= \varphi (E_{21})=0$
. Thus,
Our aim is now to estimate
![]() $\Vert T_{p,\theta }\Vert $
, using Proposition 3.3. We let
$\Vert T_{p,\theta }\Vert $
, using Proposition 3.3. We let
![]() $U_{p,\theta }\colon S^p_2\to S^p_2$
be defined by equation (3.10). We shall focus on the action of
$U_{p,\theta }\colon S^p_2\to S^p_2$
be defined by equation (3.10). We shall focus on the action of
![]() $U_{p,\theta }$
on the antidiagonal part of
$U_{p,\theta }$
on the antidiagonal part of
![]() $S^p_2$
. First, we have
$S^p_2$
. First, we have
Hence
 $$ \begin{align*} T\big(\Gamma^{-\frac{1-\theta}{p}}E_{12}\Gamma^{-\frac{\theta}{p}}\big) & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} T(E_{12})\\ & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\big(E_{12}+E_{21}\big). \end{align*} $$
$$ \begin{align*} T\big(\Gamma^{-\frac{1-\theta}{p}}E_{12}\Gamma^{-\frac{\theta}{p}}\big) & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} T(E_{12})\\ & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\big(E_{12}+E_{21}\big). \end{align*} $$
Hence,
 $$ \begin{align*} U_{p,\theta}(E_{12}) & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\Big(\Gamma^{\frac{1-\theta}{p}}E_{12} \Gamma^{\frac{\theta}{p}} +\Gamma^{\frac{1-\theta}{p}}E_{21} \Gamma^{\frac{\theta}{p}}\Big)\\ & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\Big( (1-c)^{\frac{1-\theta}{p}} c^{\frac{\theta}{p}} E_{12} + c^{\frac{1-\theta}{p}} (1-c)^{\frac{\theta}{p}} E_{21}\Big)\\ & = (c(1-c))^{\frac{1}{2}}\biggl( E_{12} + \Big(\frac{1-c}{c}\Big)^{\frac{2\theta-1}{p}}E_{21}\biggr). \end{align*} $$
$$ \begin{align*} U_{p,\theta}(E_{12}) & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\Big(\Gamma^{\frac{1-\theta}{p}}E_{12} \Gamma^{\frac{\theta}{p}} +\Gamma^{\frac{1-\theta}{p}}E_{21} \Gamma^{\frac{\theta}{p}}\Big)\\ & = (1-c)^{-\frac{1-\theta}{p}} c^{-\frac{\theta}{p}} (c(1-c))^{\frac{1}{2}}\Big( (1-c)^{\frac{1-\theta}{p}} c^{\frac{\theta}{p}} E_{12} + c^{\frac{1-\theta}{p}} (1-c)^{\frac{\theta}{p}} E_{21}\Big)\\ & = (c(1-c))^{\frac{1}{2}}\biggl( E_{12} + \Big(\frac{1-c}{c}\Big)^{\frac{2\theta-1}{p}}E_{21}\biggr). \end{align*} $$
Likewise, we have
 $$ \begin{align*}U_{p,\theta}(E_{21}) = (c(1-c))^{\frac{1}{2}}\biggl(\Big(\frac{c}{1-c}\Big)^{\frac{2\theta-1}{p}}E_{12} + E_{21}\biggr). \end{align*} $$
$$ \begin{align*}U_{p,\theta}(E_{21}) = (c(1-c))^{\frac{1}{2}}\biggl(\Big(\frac{c}{1-c}\Big)^{\frac{2\theta-1}{p}}E_{12} + E_{21}\biggr). \end{align*} $$
Set
Consider
 $$ \begin{align*}Y=\begin{pmatrix} 0 & a \\ b & 0\end{pmatrix} \qquad\text{with}\quad \vert a\vert^p+\vert b\vert^p=1 \end{align*} $$
$$ \begin{align*}Y=\begin{pmatrix} 0 & a \\ b & 0\end{pmatrix} \qquad\text{with}\quad \vert a\vert^p+\vert b\vert^p=1 \end{align*} $$
so that
![]() $\Vert Y\Vert _p=1$
. Then
$\Vert Y\Vert _p=1$
. Then
 $$ \begin{align*} U_{p,\theta}(Y) & = (c(1-c))^{\frac{1}{2}}\big(aE_{12} +a\delta E_{21} + b\delta^{-1} E_{12} + b E_{21}\big)\\ & = (c(1-c))^{\frac{1}{2}}\big((a+b\delta^{-1}) E_{12} + (a\delta +b)E_{21}\big). \end{align*} $$
$$ \begin{align*} U_{p,\theta}(Y) & = (c(1-c))^{\frac{1}{2}}\big(aE_{12} +a\delta E_{21} + b\delta^{-1} E_{12} + b E_{21}\big)\\ & = (c(1-c))^{\frac{1}{2}}\big((a+b\delta^{-1}) E_{12} + (a\delta +b)E_{21}\big). \end{align*} $$
Hence,
To prove Proposition 6.2, it therefore suffices to show that for any
![]() $1\leq p<2$
and
$1\leq p<2$
and
![]() $\theta \in [0,1]$
satisfying equation (6.1), there exist
$\theta \in [0,1]$
satisfying equation (6.1), there exist
![]() $a,b>0$
and
$a,b>0$
and
![]() $c\in (0,1)$
such that
$c\in (0,1)$
such that
where
![]() $\delta $
is given by equation (6.2).
$\delta $
is given by equation (6.2).
We first assume that
p > 1. We let
![]() $q=\frac {p}{p-1}$
denote its conjugate exponent. Given
$q=\frac {p}{p-1}$
denote its conjugate exponent. Given
![]() $c\in (0,1)$
and
$c\in (0,1)$
and
![]() $\delta $
as above, we define
$\delta $
as above, we define
 $$ \begin{align} a=\biggl(\frac{\delta^q}{1+\delta^{q}}\biggr)^{\frac{1}{p}} \qquad\text{and}\qquad b=\biggl(\frac{1}{1+\delta^{q}}\biggr)^{\frac{1}{p}}. \end{align} $$
$$ \begin{align} a=\biggl(\frac{\delta^q}{1+\delta^{q}}\biggr)^{\frac{1}{p}} \qquad\text{and}\qquad b=\biggl(\frac{1}{1+\delta^{q}}\biggr)^{\frac{1}{p}}. \end{align} $$
They satisfy
![]() $a^p+b^p=1$
as required. Note that these values of
$a^p+b^p=1$
as required. Note that these values of
![]() $(a,b)$
are chosen in order to maximize the quantity
$(a,b)$
are chosen in order to maximize the quantity
![]() $(c(1-c))^{\frac {p}{2}}\big ( (a+b\delta ^{-1})^p +(a\delta +b)^p\big )$
, according to the Lagrange multiplier method.
$(c(1-c))^{\frac {p}{2}}\big ( (a+b\delta ^{-1})^p +(a\delta +b)^p\big )$
, according to the Lagrange multiplier method.
We set
Then we denote by
![]() $\delta _t,a_t,b_t$
the real numbers
$\delta _t,a_t,b_t$
the real numbers
![]() $\delta ,a,b$
defined by equations (6.2) and (6.4) when
$\delta ,a,b$
defined by equations (6.2) and (6.4) when
![]() $c=c_t$
. Also, we set
$c=c_t$
. Also, we set
It follows from above that it suffices to show that
![]() ${\mathfrak m}_t>1$
for some
${\mathfrak m}_t>1$
for some
![]() $t\in \big (0,{\frac {1}{2}}\big )$
. We will prove this property by writing the second-order Taylor expansion of
$t\in \big (0,{\frac {1}{2}}\big )$
. We will prove this property by writing the second-order Taylor expansion of
![]() ${\mathfrak m}_t$
.
${\mathfrak m}_t$
.
We have
Moreover,
 $$ \begin{align*}a_t\delta_t = \frac{\delta_t^{\frac{q}{p} +1}}{(1+\delta_t^q)^{\frac{1}{p}}}\, =\frac{\delta_t^{q}}{(1+\delta_t^q)^{\frac{1}{p}}}\,. \end{align*} $$
$$ \begin{align*}a_t\delta_t = \frac{\delta_t^{\frac{q}{p} +1}}{(1+\delta_t^q)^{\frac{1}{p}}}\, =\frac{\delta_t^{q}}{(1+\delta_t^q)^{\frac{1}{p}}}\,. \end{align*} $$
Hence,
Consequently,
In the sequel, we write
when
![]() $f_t=g_t+o(t^2)$
when
$f_t=g_t+o(t^2)$
when
![]() $t\to 0$
.
$t\to 0$
.
We note that
![]() $c_t(1-c_t)=\big ({\frac {1}{2}}+t\big )\big ({\frac {1}{2}}-t\big ) =\frac 14\big (1-4t^2\big )$
. We deduce that
$c_t(1-c_t)=\big ({\frac {1}{2}}+t\big )\big ({\frac {1}{2}}-t\big ) =\frac 14\big (1-4t^2\big )$
. We deduce that
We set
![]() $\lambda =2\theta -1$
for convenience. Then we have
$\lambda =2\theta -1$
for convenience. Then we have
 $$ \begin{align*} \delta_t & =\Big(\frac{1-2t}{1+2t}\Big)^{\frac{\lambda}{p}} \\ &\equiv \big((1-2t)(1-2t+4t^2)\big)^{\frac{\lambda}{p}} \\ &\equiv (1-4t +8t^2)^{\frac{\lambda}{p}} \\ &\equiv 1 -\frac{4\lambda}{p} t + \frac{8\lambda}{p}t^2 + {\frac{1}{2}}\,\frac{\lambda}{p}\Big(\frac{\lambda}{p}-1\Big)(4t)^2\\ &\equiv 1 -\frac{4\lambda}{p} t + \frac{8\lambda^2}{p^2}t^2. \end{align*} $$
$$ \begin{align*} \delta_t & =\Big(\frac{1-2t}{1+2t}\Big)^{\frac{\lambda}{p}} \\ &\equiv \big((1-2t)(1-2t+4t^2)\big)^{\frac{\lambda}{p}} \\ &\equiv (1-4t +8t^2)^{\frac{\lambda}{p}} \\ &\equiv 1 -\frac{4\lambda}{p} t + \frac{8\lambda}{p}t^2 + {\frac{1}{2}}\,\frac{\lambda}{p}\Big(\frac{\lambda}{p}-1\Big)(4t)^2\\ &\equiv 1 -\frac{4\lambda}{p} t + \frac{8\lambda^2}{p^2}t^2. \end{align*} $$
This implies that
 $$ \begin{align*} \delta_t^q & \equiv 1 -\frac{4\lambda q}{p} t + \frac{8\lambda^2 q}{p^2}t^2 +{\frac{1}{2}}\,q(q-1)\Big(\frac{4\lambda}{p}\Big)^2 t^2\\ &\equiv 1 -\frac{4\lambda q}{p} t + \frac{8\lambda^2 q^2}{p^2}t^2. \end{align*} $$
$$ \begin{align*} \delta_t^q & \equiv 1 -\frac{4\lambda q}{p} t + \frac{8\lambda^2 q}{p^2}t^2 +{\frac{1}{2}}\,q(q-1)\Big(\frac{4\lambda}{p}\Big)^2 t^2\\ &\equiv 1 -\frac{4\lambda q}{p} t + \frac{8\lambda^2 q^2}{p^2}t^2. \end{align*} $$
Likewise,
Since
![]() $p-1=\frac {p}{q}$
, we have
$p-1=\frac {p}{q}$
, we have
 $$ \begin{align*} (1+\delta_t^q)^{p-1} & \equiv 2^{\frac{p}{q}}\Big( 1 -\frac{2\lambda q}{p} t + \frac{4\lambda^2 q^2}{p^2} t^2\Big)^{\frac{p}{q}}\\ & \equiv 2^{\frac{p}{q}}\Big(1 -2\lambda t+\frac{4\lambda^2 q}{p} t^2 +{\frac{1}{2}}\,\frac{p}{q}\Big(\frac{p}{q}-1\Big) \Big(\frac{2\lambda q}{p}\Big)^2 t^2\Big)\\ &\equiv 2^{\frac{p}{q}}\big(1-2\lambda t + 2 \lambda^2 qt^2\big). \end{align*} $$
$$ \begin{align*} (1+\delta_t^q)^{p-1} & \equiv 2^{\frac{p}{q}}\Big( 1 -\frac{2\lambda q}{p} t + \frac{4\lambda^2 q^2}{p^2} t^2\Big)^{\frac{p}{q}}\\ & \equiv 2^{\frac{p}{q}}\Big(1 -2\lambda t+\frac{4\lambda^2 q}{p} t^2 +{\frac{1}{2}}\,\frac{p}{q}\Big(\frac{p}{q}-1\Big) \Big(\frac{2\lambda q}{p}\Big)^2 t^2\Big)\\ &\equiv 2^{\frac{p}{q}}\big(1-2\lambda t + 2 \lambda^2 qt^2\big). \end{align*} $$
Combining this expansion with equations (6.5) and (6.6), we deduce that
 $$ \begin{align*} {\mathfrak m}_t &\equiv \frac{1}{2^p} (1-2pt^2)\,\cdotp 2(1 +2\lambda t + 4\lambda^2t^2) \,\cdotp 2^{\frac{p}{q}}(1-2\lambda t + 2 \lambda^2 qt^2)\\ &\equiv (1-2pt^2)(1+2\lambda^2 qt^2). \end{align*} $$
$$ \begin{align*} {\mathfrak m}_t &\equiv \frac{1}{2^p} (1-2pt^2)\,\cdotp 2(1 +2\lambda t + 4\lambda^2t^2) \,\cdotp 2^{\frac{p}{q}}(1-2\lambda t + 2 \lambda^2 qt^2)\\ &\equiv (1-2pt^2)(1+2\lambda^2 qt^2). \end{align*} $$
Consequently,
The second-order coefficient
![]() $\alpha $
can be written as
$\alpha $
can be written as
 $$ \begin{align*} \alpha & = 2q \Big((2\theta -1)^2 -\frac{p}{q}\Big)\\ & =8q\Big(\theta^2-\theta +\frac{q-p}{4q}\Big)\\ & =8q(\theta-\theta_0)(\theta-\theta_1), \end{align*} $$
$$ \begin{align*} \alpha & = 2q \Big((2\theta -1)^2 -\frac{p}{q}\Big)\\ & =8q\Big(\theta^2-\theta +\frac{q-p}{4q}\Big)\\ & =8q(\theta-\theta_0)(\theta-\theta_1), \end{align*} $$
with
Now, assume equation (6.1). Then
![]() $\alpha>0$
. Hence, equation (6.7) ensures the existence of
$\alpha>0$
. Hence, equation (6.7) ensures the existence of
![]() $t>0$
such that
$t>0$
such that
![]() ${\mathfrak m}_t>1$
, which concludes the proof (in the case
${\mathfrak m}_t>1$
, which concludes the proof (in the case
![]() $p>1$
).
$p>1$
).
We now consider the case p = 1. We apply the same method as before, with
According to equation (6.3), it will suffice to show that whenever
![]() $\theta \not ={\frac {1}{2}}$
, there exists
$\theta \not ={\frac {1}{2}}$
, there exists
![]() $c\in (0,1)$
such that
$c\in (0,1)$
such that
![]() $(c(1-c))^{\frac {1}{2}}(1+\delta )>1$
.
$(c(1-c))^{\frac {1}{2}}(1+\delta )>1$
.
Again, we set
![]() $c_t={\frac {1}{2}}+t$
, for
$c_t={\frac {1}{2}}+t$
, for
![]() $-{\frac {1}{2}}<t<{\frac {1}{2}}$
, we define
$-{\frac {1}{2}}<t<{\frac {1}{2}}$
, we define
![]() $\delta _t$
accordingly, and we set
$\delta _t$
accordingly, and we set
It follows from the previous calculations that
Consequently,
This order one expansion ensures that if
![]() $\theta \not ={\frac {1}{2}}$
, then there exists
$\theta \not ={\frac {1}{2}}$
, then there exists
![]() $t\in \big (-{\frac {1}{2}},{\frac {1}{2}}\big )$
such that
$t\in \big (-{\frac {1}{2}},{\frac {1}{2}}\big )$
such that
![]() ${\mathfrak m}(t)>1$
, which concludes the proof (in the case
${\mathfrak m}(t)>1$
, which concludes the proof (in the case
![]() $p=1$
).
$p=1$
).
Proof of Theorem 6.1.
Let
![]() $(p,\theta )$
satisfying equation (6.1). Thanks to Proposition 6.2, let
$(p,\theta )$
satisfying equation (6.1). Thanks to Proposition 6.2, let
![]() $T_0\colon M_2\to M_2$
and let
$T_0\colon M_2\to M_2$
and let
![]() $\varphi _0$
be a faithful state on
$\varphi _0$
be a faithful state on
![]() $M_2$
such that
$M_2$
such that
![]() $\varphi _0\circ T_0=\varphi _0$
and
$\varphi _0\circ T_0=\varphi _0$
and
![]() $\Vert \{T_0\}_{p,\theta }\Vert>1$
. We apply Proposition 5.2 with
$\Vert \{T_0\}_{p,\theta }\Vert>1$
. We apply Proposition 5.2 with
![]() $(A_k,\varphi _k,T_k)=(M_2,\varphi _0,T_0)$
for all
$(A_k,\varphi _k,T_k)=(M_2,\varphi _0,T_0)$
for all
![]() $k\geq 1$
. In this case,
$k\geq 1$
. In this case,
 $$ \begin{align*}\prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\big\Vert = \Vert\{T_0\}_{p,\theta}\Vert^n, \end{align*} $$
$$ \begin{align*}\prod_{k=1}^n\big\Vert\{T_k\}_{p,\theta}\big\Vert = \Vert\{T_0\}_{p,\theta}\Vert^n, \end{align*} $$
and the latter goes to
![]() $\infty $
when
$\infty $
when
![]() $n\to \infty $
. Hence,
$n\to \infty $
. Hence,
![]() $T_{p,\theta }$
is unbounded.
$T_{p,\theta }$
is unbounded.
Remark 6.3. With Theorem 4.1, Theorem 4.3 and Theorem 6.1, we have solved Question 2.2 in the following cases: (i)
![]() $p\geq 2$
and
$p\geq 2$
and
![]() $\theta \in [0,1]$
; (ii)
$\theta \in [0,1]$
; (ii)
![]() $1\leq p<2$
and
$1\leq p<2$
and
![]() $\theta \in \big [1-p/2,p/2\big ]$
; (iii)
$\theta \in \big [1-p/2,p/2\big ]$
; (iii)
![]() $1\leq p<2$
and
$1\leq p<2$
and
![]() $\theta \in \big [0,2^{-1}(1-\sqrt {p-1})\big )$
; (iv)
$\theta \in \big [0,2^{-1}(1-\sqrt {p-1})\big )$
; (iv)
![]() $1\leq p<2$
and
$1\leq p<2$
and
![]() $\theta \in \big (2^{-1}(1+\sqrt {p-1}),1\Big ]$
.
$\theta \in \big (2^{-1}(1+\sqrt {p-1}),1\Big ]$
.
However, we do not know the answer to Question 2.2 when
![]() $1\leq p<2$
and
$1\leq p<2$
and
Writing a
![]() $(+)$
when Question 2.2 has a positive answer, a
$(+)$
when Question 2.2 has a positive answer, a
![]() $(-)$
when it has a negative answer and a
$(-)$
when it has a negative answer and a
![]() $(?)$
when we do not know the answer, we obtain the following diagram:
$(?)$
when we do not know the answer, we obtain the following diagram:

Acknowledgements
We thank Éric Ricard for several stimulating discussions.
Competing interest
The authors have no competing interest to declare.
Financial support
The first author was supported by the ANR project noncommutative analysis on groups and quantum groups (No./ANR-19-CE40-0002). The authors gratefully thank the support of the Heilbronn Institute for Mathematical Research and the UKRI/EPSRC Additional Funding Program.