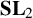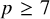1 Introduction
1.1 Klein’s classification and McKay’s correspondence
Felix Klein [Reference KleinKl84] classified finite subgroups G of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
: up to conjugation, there are two infinite series and three isolated cases.
${\mathbf {SL}}_2({\mathbb {C}})$
: up to conjugation, there are two infinite series and three isolated cases.
-
1. The associated quotient singularity
 ${\mathbb {C}}^2/G$
is called a Klein singularity and the singularities arising this way are precisely the rational double point singularities. Its minimal resolution of singularities is a union of
${\mathbb {C}}^2/G$
is called a Klein singularity and the singularities arising this way are precisely the rational double point singularities. Its minimal resolution of singularities is a union of
 ${\mathbb {P}}^1$
’s, whose dual intersection graph
${\mathbb {P}}^1$
’s, whose dual intersection graph
 $\Gamma $
is a simply-laced Dynkin diagram of finite type, that is, of type
$\Gamma $
is a simply-laced Dynkin diagram of finite type, that is, of type
 $A_n$
,
$A_n$
,
 $D_n$
,
$D_n$
,
 $E_6$
,
$E_6$
,
 $E_7$
or
$E_7$
or
 $E_8$
.
$E_8$
. -
2. John McKay [Reference McKayMc80] associated a finite graph
 $\widehat {\Gamma }$
to
$\widehat {\Gamma }$
to
 $G \subset {\mathbf {SL}}_2({\mathbb {C}})$
, whose vertices correspond to the isomorphism classes of the simple representations of G. This graph is a Dynkin diagram of affine type
$G \subset {\mathbf {SL}}_2({\mathbb {C}})$
, whose vertices correspond to the isomorphism classes of the simple representations of G. This graph is a Dynkin diagram of affine type
 $\widehat {A}_n$
,
$\widehat {A}_n$
,
 $\widehat {D}_n$
,
$\widehat {D}_n$
,
 $\widehat {E}_6$
,
$\widehat {E}_6$
,
 $\widehat {E}_7$
or
$\widehat {E}_7$
or
 $\widehat {E}_8$
.
$\widehat {E}_8$
. -
3. After these preparations, the classical McKay correspondence consists of the following observations:
-
(a) The graph
 $\Gamma $
is obtained from
$\Gamma $
is obtained from
 $\widehat {\Gamma }$
by removing the vertex corresponding to the trivial representation.
$\widehat {\Gamma }$
by removing the vertex corresponding to the trivial representation. -
(b) There exists a bijection between conjugacy classes of G, vertices of
 $\widehat {\Gamma }$
and isomorphism classes of simple representations of G.
$\widehat {\Gamma }$
and isomorphism classes of simple representations of G. -
(c) There exists a bijection between finite subgroups of
 ${\mathbf {SL}}_2({\mathbb {C}})$
up to conjugacy, the above Dynkin diagrams of affine type, Klein singularities and the above Dynkin diagrams of finite type.
${\mathbf {SL}}_2({\mathbb {C}})$
up to conjugacy, the above Dynkin diagrams of affine type, Klein singularities and the above Dynkin diagrams of finite type.
-
By now, there are various approaches to and a vast literature on this subject, such as [Reference KnörrerKn85, Reference KostantKo85, Reference McKayMc80, Reference McKayMc81, Reference SteinbergSt85] and many more. Also, there are now generalisations into very different directions: higher dimensional algebraic geometry [Reference ReidRe02], K-theory [Reference Gonzalez-Sprinberg and VerdierGV83], derived categories of coherent sheaves [Reference Bridgeland, King and ReidBKR01, Reference Kapranov and VasserotKV00], representations of quivers [Reference KirillovKi16], non-commutative geometry and Hopf algebras [Reference Chan, Kirkman, Walton and ZhangCKWZ16] and string theory [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and WilsonAetal09] - just to mention a few.
1.2 Positive characteristic
Now, let k be an algebraically closed field of characteristic
![]() $p>0$
.
$p>0$
.
1.2.1 Wild McKay correspondence
The classical McKay correspondence as sketched above is still partially available over k if G is assumed to be a finite subgroup of
![]() ${\mathbf {SL}}_2(k)$
of order prime to p - this is the tame case. If p divides the order of G - this is the modular or wild case - then this correspondence breaks down. We refer to Yasuda’s surveys [Reference YasudaYa22, Reference YasudaYa23] about conjectures and partial results concerning such wild McKay correspondences.
${\mathbf {SL}}_2(k)$
of order prime to p - this is the tame case. If p divides the order of G - this is the modular or wild case - then this correspondence breaks down. We refer to Yasuda’s surveys [Reference YasudaYa22, Reference YasudaYa23] about conjectures and partial results concerning such wild McKay correspondences.
1.2.2 Linearly reductive McKay correspondence
In this article, we show that if G is a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
, then there is a reasonable version of the classical McKay correspondence. For example, we obtain a McKay correspondence for all rational double point singularities if
${\mathbf {SL}}_{2,k}$
, then there is a reasonable version of the classical McKay correspondence. For example, we obtain a McKay correspondence for all rational double point singularities if
![]() $p\geq 7$
. Instead of considering groups, we allow non-reduced group schemes over k, but we require their categories of k-linear and finite-dimensional representations to be semi-simple. We refer to [Reference Tonini and YasudaTY20] about conjectures and partial results concerning a McKay correspondence for the group scheme
$p\geq 7$
. Instead of considering groups, we allow non-reduced group schemes over k, but we require their categories of k-linear and finite-dimensional representations to be semi-simple. We refer to [Reference Tonini and YasudaTY20] about conjectures and partial results concerning a McKay correspondence for the group scheme
![]() $\boldsymbol {\alpha }_p$
, which is not linearly reductive.
$\boldsymbol {\alpha }_p$
, which is not linearly reductive.
Thus, let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
with
${\mathbf {SL}}_{2,k}$
with
![]() $p\geq 7$
. (In this introduction, we will exclude small characteristics whenever this is makes our discussion easier.) Let
$p\geq 7$
. (In this introduction, we will exclude small characteristics whenever this is makes our discussion easier.) Let
![]() $x\in X:=U/G$
with
$x\in X:=U/G$
with
![]() $U={\mathbb {A}}_k^2$
or
$U={\mathbb {A}}_k^2$
or
![]() $U=\widehat {{\mathbb {A}}}_k^2$
be the associated Klein singularity, which is a rational double point. One goal of this article is to define a notion of conjugacy class for G, to construct graphs
$U=\widehat {{\mathbb {A}}}_k^2$
be the associated Klein singularity, which is a rational double point. One goal of this article is to define a notion of conjugacy class for G, to construct graphs
![]() $\Gamma $
and
$\Gamma $
and
![]() $\widehat {\Gamma }$
and to establish bijections as above.
$\widehat {\Gamma }$
and to establish bijections as above.
Let us make three comments:
-
1. It is interesting in its own that a McKay correspondence can be extended from finite group schemes of length prime to p, that is, the tame case, to linearly reductive group schemes.
-
2. What makes this linearly reductive McKay correspondence really interesting is that the bijection in Theorem 1.1 is not true when considering finite groups of order prime to p only, see Example 1.2.
-
3. Probably, many more aspects of the classical McKay correspondence can be carried over to the linearly reductive setting, but rather than writing a whole monograph, we decided to establish only some basic bijections.
1.3 Linearly reductive group schemes
Let G be a finite and linearly reductive group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. By definition, this means that the category
$p\geq 0$
. By definition, this means that the category
![]() $\mathrm {Rep}_k(G)$
of k-linear and finite-dimensional representations of G is semi-simple.
$\mathrm {Rep}_k(G)$
of k-linear and finite-dimensional representations of G is semi-simple.
If
![]() $p=0$
, then every finite group scheme over k is étale and linearly reductive. and in fact, it is the constant group scheme associated to a finite group. In fact, the functor
$p=0$
, then every finite group scheme over k is étale and linearly reductive. and in fact, it is the constant group scheme associated to a finite group. In fact, the functor
![]() $G\mapsto G_{\mathrm {abs}}:=G(k)$
induces an equivalence of categories between finite group schemes over k and finite groups.
$G\mapsto G_{\mathrm {abs}}:=G(k)$
induces an equivalence of categories between finite group schemes over k and finite groups.
If
![]() $p>0$
, then every linearly reductive group scheme admits a canonical semi-direct product decomposition
$p>0$
, then every linearly reductive group scheme admits a canonical semi-direct product decomposition
where
![]() $G^{\mathrm {\acute {e}t}}$
is a group scheme of length prime to p (and thus, the constant group scheme associated to a finite group of order prime to p) and where
$G^{\mathrm {\acute {e}t}}$
is a group scheme of length prime to p (and thus, the constant group scheme associated to a finite group of order prime to p) and where
![]() $G^\circ $
is infinitesimal and diagonalisable. The latter implies that
$G^\circ $
is infinitesimal and diagonalisable. The latter implies that
![]() $G^\circ $
is a product of group schemes of the form
$G^\circ $
is a product of group schemes of the form
![]() $\boldsymbol {\mu }_{p^n}$
. Conversely, every such semi-direct product of a diagonalisable group scheme with the constant group scheme associated to a finite group of order prime to p is linearly reductive. This structure result is usually attributed to Nagata [Reference NagataNa61], but see also [Reference Abramovich, Olsson and VistoliAOV08], [Reference ChinCh92] and [Reference HashimotoHa15]. Linearly reductive group schemes over k strictly contains the class of constant group schemes associated to finite groups of order prime to p.
$\boldsymbol {\mu }_{p^n}$
. Conversely, every such semi-direct product of a diagonalisable group scheme with the constant group scheme associated to a finite group of order prime to p is linearly reductive. This structure result is usually attributed to Nagata [Reference NagataNa61], but see also [Reference Abramovich, Olsson and VistoliAOV08], [Reference ChinCh92] and [Reference HashimotoHa15]. Linearly reductive group schemes over k strictly contains the class of constant group schemes associated to finite groups of order prime to p.
1.3.1 Abstract groups
Associated to G, there is an abstract finite group
![]() $G_{\mathrm {abs}}$
and we refer for the slightly technical definition to Section 2.2. The order of
$G_{\mathrm {abs}}$
and we refer for the slightly technical definition to Section 2.2. The order of
![]() $G_{\mathrm {abs}}$
is equal to the length of G. For example, if G is étale over k, then we have
$G_{\mathrm {abs}}$
is equal to the length of G. For example, if G is étale over k, then we have
![]() $G_{\mathrm {abs}}\cong G(k)$
. The assignment
$G_{\mathrm {abs}}\cong G(k)$
. The assignment
![]() $G\mapsto G_{\mathrm {abs}}$
establishes an equivalence of categories
$G\mapsto G_{\mathrm {abs}}$
establishes an equivalence of categories
 $$ \begin{align} \left\{ \begin{array}{l} \mbox{finite linearly reductive}\\ \mbox{group schemes over }k \end{array}\right\} \quad\leftrightarrow\quad \left\{ \begin{array}{l} \mbox{finite groups with a}\\ \mbox{unique }p\mbox{-Sylow subgroup} \end{array}\right\}, \end{align} $$
$$ \begin{align} \left\{ \begin{array}{l} \mbox{finite linearly reductive}\\ \mbox{group schemes over }k \end{array}\right\} \quad\leftrightarrow\quad \left\{ \begin{array}{l} \mbox{finite groups with a}\\ \mbox{unique }p\mbox{-Sylow subgroup} \end{array}\right\}, \end{align} $$
see [Reference Liedtke, Martin and MatsumotoLMM21] and Lemma 2.2.
1.3.2 Canonical lifts
In [Reference Liedtke, Martin and MatsumotoLMM21], we showed that if G is a finite and linearly reductive group scheme, then there exists a lift of G over the ring of Witt vectors
![]() $W(k)$
. We note that
$W(k)$
. We note that
![]() $G^\circ $
and
$G^\circ $
and
![]() $G^{\mathrm {\acute {e}t}}$
even lift uniquely to
$G^{\mathrm {\acute {e}t}}$
even lift uniquely to
![]() $W(k)$
and we define the canonical lift
$W(k)$
and we define the canonical lift
![]() $G_{\mathrm {can}}\to \mathrm {Spec}\: K$
of G to be the unique lift that is a semi-direct product of the lifts of
$G_{\mathrm {can}}\to \mathrm {Spec}\: K$
of G to be the unique lift that is a semi-direct product of the lifts of
![]() $G^\circ $
and
$G^\circ $
and
![]() $G^{\mathrm {\acute {e}t}}$
. Any lift of G to some extension field of K becomes isomorphic to
$G^{\mathrm {\acute {e}t}}$
. Any lift of G to some extension field of K becomes isomorphic to
![]() $G_{\mathrm {can}}$
after possibly passing to some further field extension. Moreover, the finite group
$G_{\mathrm {can}}$
after possibly passing to some further field extension. Moreover, the finite group
![]() $G_{\mathrm {can}}(\overline {K})$
is isomorphic to
$G_{\mathrm {can}}(\overline {K})$
is isomorphic to
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
1.3.3 Representation theory
By [Reference Liedtke, Martin and MatsumotoLMM21] and Proposition 2.6, there exist canonical equivalences of representation categories
that are compatible with degrees, direct sums, tensor products, duals and simplicity. These equivalences induce isomorphisms of rings
see Corollary 2.8. Here,
![]() $K_F(G)$
denotes the K-group associated to F-linear and finite-dimensional G-representations.
$K_F(G)$
denotes the K-group associated to F-linear and finite-dimensional G-representations.
1.3.4 Hopf algebras
If G is a finite group scheme over k, then the multiplication map turns
![]() $H^0(G,{\mathcal O}_G)$
into a finite-dimensional Hopf algebra over k. We discuss finite group schemes and among them the linearly reductive ones from the point of Hopf algebras in Appendix A.
$H^0(G,{\mathcal O}_G)$
into a finite-dimensional Hopf algebra over k. We discuss finite group schemes and among them the linearly reductive ones from the point of Hopf algebras in Appendix A.
1.4 Linearly reductive subgroup schemes of
 ${\mathbf {SL}}_{2,k}$
${\mathbf {SL}}_{2,k}$
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. Hashimoto [Reference HashimotoHa15] extended Klein’s classification [Reference KleinKl84] of finite subgroups of
$p\geq 0$
. Hashimoto [Reference HashimotoHa15] extended Klein’s classification [Reference KleinKl84] of finite subgroups of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
up to conjugation to the setting of finite and linearly reductive subgroup schemes of
${\mathbf {SL}}_2({\mathbb {C}})$
up to conjugation to the setting of finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
. If
${\mathbf {SL}}_{2,k}$
. If
![]() $p\geq 7$
, then one obtains a list analogous to Klein’s classical list. If
$p\geq 7$
, then one obtains a list analogous to Klein’s classical list. If
![]() $p\in \{2,3,5\}$
, then some classical cases are missing, but there are no new cases.
$p\in \{2,3,5\}$
, then some classical cases are missing, but there are no new cases.
1.5 McKay graph and McKay correspondence
Let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
. As in McKay’s original construction [Reference McKayMc80], we associate an affine Dynkin diagram
${\mathbf {SL}}_{2,k}$
. As in McKay’s original construction [Reference McKayMc80], we associate an affine Dynkin diagram
![]() $\widehat {\Gamma }$
to G, its embedding into
$\widehat {\Gamma }$
to G, its embedding into
![]() ${\mathbf {SL}}_{2,k}$
and the set of isomorphism classes of simple representations of G. This is the McKay graph associated to this data. In fact, we will see that it is compatible with the equivalences induced by (1.1) and (1.2) and we refer to Section 3.1 for details. We establish the following version of McKay’s theorem [Reference McKayMc80] in positive characteristic.
${\mathbf {SL}}_{2,k}$
and the set of isomorphism classes of simple representations of G. This is the McKay graph associated to this data. In fact, we will see that it is compatible with the equivalences induced by (1.1) and (1.2) and we refer to Section 3.1 for details. We establish the following version of McKay’s theorem [Reference McKayMc80] in positive characteristic.
Theorem 1.1 (Theorem 3.6)
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. There exists a bijection between non-trivial, finite and linearly reductive subgroup schemes of
$p\geq 0$
. There exists a bijection between non-trivial, finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
up to conjugation and affine Dynkin graphs of type
${\mathbf {SL}}_{2,k}$
up to conjugation and affine Dynkin graphs of type
 $$ \begin{align*}\begin{array}{lcl} \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7, \widehat{E}_8 &\quad \mbox{if} \quad & p=0\quad \mbox{or} \quad p\geq7, \\ \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7 &\quad \mbox{if} \quad & p=5,\\ \widehat{A}_n, \widehat{D}_n &\quad \mbox{if} \quad & p=3, \\ \widehat{A}_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{lcl} \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7, \widehat{E}_8 &\quad \mbox{if} \quad & p=0\quad \mbox{or} \quad p\geq7, \\ \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7 &\quad \mbox{if} \quad & p=5,\\ \widehat{A}_n, \widehat{D}_n &\quad \mbox{if} \quad & p=3, \\ \widehat{A}_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
By construction, this bijection is compatible with the classical McKay correspondence via the lifting results and the equivalences (1.1), (1.2).
Example 1.2. The linearly reductive group scheme corresponding to
![]() $\widehat {A}_n$
is
$\widehat {A}_n$
is
![]() $\boldsymbol {\mu }_{n+1}$
. This group scheme is reduced, that is, étale, if and only if p does not divide
$\boldsymbol {\mu }_{n+1}$
. This group scheme is reduced, that is, étale, if and only if p does not divide
![]() $n+1$
. In particular, it is crucial to allow non-reduced group schemes in order to obtain a bijection as in characteristic zero.
$n+1$
. In particular, it is crucial to allow non-reduced group schemes in order to obtain a bijection as in characteristic zero.
1.6 Linearly reductive quotient singularities
Consider
![]() ${\mathbf {GL}}_{2,k}$
with its usual linear action on
${\mathbf {GL}}_{2,k}$
with its usual linear action on
![]() $U={\mathbb {A}}^2_k$
or
$U={\mathbb {A}}^2_k$
or
![]() $U=\widehat {{\mathbb {A}}}_k^2$
. If G is a finite, linearly reductive and very small (see Definition 4.1) subgroup scheme of
$U=\widehat {{\mathbb {A}}}_k^2$
. If G is a finite, linearly reductive and very small (see Definition 4.1) subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
, then the associated quotient singularity
${\mathbf {GL}}_{2,k}$
, then the associated quotient singularity
![]() $x\in X:=U/G$
is a two-dimensional linearly reductive quotient singularity in the sense of [Reference Liedtke, Martin and MatsumotoLMM21]. By loc.cit., such a singularity determines G together with its embedding
$x\in X:=U/G$
is a two-dimensional linearly reductive quotient singularity in the sense of [Reference Liedtke, Martin and MatsumotoLMM21]. By loc.cit., such a singularity determines G together with its embedding
![]() $G\to {\mathbf {GL}}_{2,k}$
up to isomorphism and conjugation, respectively.
$G\to {\mathbf {GL}}_{2,k}$
up to isomorphism and conjugation, respectively.
In Section 4.3, we will see that a minimal resolution of singularities of a two-dimensional linearly reductive quotient singularity
![]() $x\in X=U/G$
is provided by the G-Hilbert scheme
$x\in X=U/G$
is provided by the G-Hilbert scheme
which generalises work of Ishii, Ito and Nakamura [Reference Ishii and NakamuraIN19, Reference Ito and NakamuraIN99].
Remark 1.3. In dimension two, a linearly reductive quotient singularity is the same as an F-regular singularity [Reference Liedtke, Martin and MatsumotoLMM21]. Thus, every two-dimensional F-regular singularity can be resolved by a suitable G-Hilbert scheme, see also Remark 4.6.
If moreover G is a subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
, then
${\mathbf {SL}}_{2,k}$
, then
![]() $x\in X=U/G$
is called a Klein singularity. Klein singularities are rational double point singularities. If
$x\in X=U/G$
is called a Klein singularity. Klein singularities are rational double point singularities. If
![]() $p=0$
or
$p=0$
or
![]() $p\geq 7$
, then conversely every rational double point is a Klein singularity by Hashimoto [Reference HashimotoHa15] and, independently, by [Reference Liedtke and SatrianoLS14]. If
$p\geq 7$
, then conversely every rational double point is a Klein singularity by Hashimoto [Reference HashimotoHa15] and, independently, by [Reference Liedtke and SatrianoLS14]. If
![]() $p\in \{2,3,5\}$
, then not every rational double point is a Klein singularity.
$p\in \{2,3,5\}$
, then not every rational double point is a Klein singularity.
1.7 Canonical lifts and simultaneous resolutions
Let G be a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
and let
${\mathbf {GL}}_{2,k}$
and let
![]() $x\in X=U/G$
be the associated linearly reductive quotient singularity. Assume
$x\in X=U/G$
be the associated linearly reductive quotient singularity. Assume
![]() $p>0$
and let
$p>0$
and let
![]() $W(k)$
be the ring of Witt vectors of k. In Section 4.4, we will establish the existence of a canonical lift
$W(k)$
be the ring of Witt vectors of k. In Section 4.4, we will establish the existence of a canonical lift
of
![]() $x\in X=U/G$
. Using G-Hilbert schemes in families, we will see in Section 4.5 that it admits a simultaneous and minimal resolution of singularities
$x\in X=U/G$
. Using G-Hilbert schemes in families, we will see in Section 4.5 that it admits a simultaneous and minimal resolution of singularities
We will prove this resolution to be unique, see Theorem 4.10.
1.8 McKay correspondence for Klein singularities
Let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
and let
${\mathbf {SL}}_{2,k}$
and let
![]() $x\in X=U/G$
be the associated Klein singularity.
$x\in X=U/G$
be the associated Klein singularity.
As discussed in Section 1.5, we have the McKay graph
![]() $\widehat {\Gamma }$
associated to G, its embedding into
$\widehat {\Gamma }$
associated to G, its embedding into
![]() ${\mathbf {SL}}_{2,k}$
and the set of isomorphism classes of simple representations of G.
${\mathbf {SL}}_{2,k}$
and the set of isomorphism classes of simple representations of G.
Let
![]() $\pi :Y\to X$
be a minimal resolution of singularities. Since
$\pi :Y\to X$
be a minimal resolution of singularities. Since
![]() $x\in X$
is a rational double point, the exceptional divisor
$x\in X$
is a rational double point, the exceptional divisor
![]() $\mathrm {Exc}(\pi )$
of
$\mathrm {Exc}(\pi )$
of
![]() $\pi $
is a configuration of
$\pi $
is a configuration of
![]() ${\mathbb {P}}^1$
’s, whose dual intersection graph
${\mathbb {P}}^1$
’s, whose dual intersection graph
![]() $\Gamma $
is a simply-laced Dynkin diagram.
$\Gamma $
is a simply-laced Dynkin diagram.
Theorem 1.4 (Theorem 5.3)
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. Let G be a finite and linearly reductive subgroup scheme of
$p\geq 0$
. Let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
and let
${\mathbf {SL}}_{2,k}$
and let
![]() $x\in X=U/G$
be the associated Klein singularity. Then, there exists a natural bijection of the graph
$x\in X=U/G$
be the associated Klein singularity. Then, there exists a natural bijection of the graph
![]() $\Gamma $
with the graph obtained from
$\Gamma $
with the graph obtained from
![]() $\widehat {\Gamma }$
by removing the vertex corresponding to the trivial representation.
$\widehat {\Gamma }$
by removing the vertex corresponding to the trivial representation.
Since every rational double point in characteristic
![]() $p\geq 7$
is a Klein singularity, we obtain the following.
$p\geq 7$
is a Klein singularity, we obtain the following.
Corollary 1.5. There exists a linearly reductive McKay correspondence for rational double point singularities in every characteristic
![]() $p\geq 7$
.
$p\geq 7$
.
To establish this theorem, we use the Ishii-Ito-Nakamura resolution of singularities (1.3), as well as Hecke correspondences as in the work of Ito and Nakamura [Reference Ito and NakamuraIN99] and Nakajima [Reference NakajimaNa96, Reference NakajimaNa01].
1.9 Generalisations and variants
Let G be a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
and let
${\mathbf {GL}}_{2,k}$
and let
![]() $x\in X=U/G$
be the associated two-dimensional linearly reductive quotient singularity. Let
$x\in X=U/G$
be the associated two-dimensional linearly reductive quotient singularity. Let
![]() $\pi :Y\to X$
be the minimal resolution of singularities and let
$\pi :Y\to X$
be the minimal resolution of singularities and let
![]() $\mathrm {Exc}(\pi )$
be the exceptional divisor of
$\mathrm {Exc}(\pi )$
be the exceptional divisor of
![]() $\pi $
.
$\pi $
.
-
1. In Theorem 5.4, we associate a representation of G to each point of
 $\mathrm {Exc}(\pi )$
. This generalises results of Ishii and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19].
$\mathrm {Exc}(\pi )$
. This generalises results of Ishii and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19]. -
2. In Theorem 5.6, we establish a bijection between the components of
 $\textrm {Exc}(\pi )$
and reflexive
$\textrm {Exc}(\pi )$
and reflexive
 ${\mathcal O}_X$
-modules. Probably, this result should be viewed as a theorem on two-dimensional F-regular singularities, see Remark 5.7. It generalises work of Artin and Verdier [Reference Artin and VerdierAV85], Wunram [Reference WunramWu88] and Ishii and Nakamura [Reference Ishii and NakamuraIN19].
${\mathcal O}_X$
-modules. Probably, this result should be viewed as a theorem on two-dimensional F-regular singularities, see Remark 5.7. It generalises work of Artin and Verdier [Reference Artin and VerdierAV85], Wunram [Reference WunramWu88] and Ishii and Nakamura [Reference Ishii and NakamuraIN19]. -
3. In Theorem 7.1, we establish an equivalence of derived categories of coherent sheaves
 ${\mathcal {D}}(Y)$
and
${\mathcal {D}}(Y)$
and
 ${\mathcal {D}}^G(U)$
(G-equivariant sheaves on U). This generalises work of Kapranov and Vasserot [Reference Kapranov and VasserotKV00], Bridgeland, King and Reid [Reference Bridgeland, King and ReidBKR01] and Ishii, Nakamura and Ueda [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ishii and UedaIU15]. Of course, these articles themselves generalise work of Gonzalez-Sprinberg and Verdier [Reference Gonzalez-Sprinberg and VerdierGV83] from K-theory to derived categories of coherent sheaves.
${\mathcal {D}}^G(U)$
(G-equivariant sheaves on U). This generalises work of Kapranov and Vasserot [Reference Kapranov and VasserotKV00], Bridgeland, King and Reid [Reference Bridgeland, King and ReidBKR01] and Ishii, Nakamura and Ueda [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ishii and UedaIU15]. Of course, these articles themselves generalise work of Gonzalez-Sprinberg and Verdier [Reference Gonzalez-Sprinberg and VerdierGV83] from K-theory to derived categories of coherent sheaves.
1.10 Ito-Reid correspondence
If G is a finite subgroup of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
, then Ito and Reid [Reference Ito and ReidIR96] found a natural bijection, the Ito-Reid correspondence, between the conjugacy classes of G and the vertices of the McKay graph
${\mathbf {SL}}_2({\mathbb {C}})$
, then Ito and Reid [Reference Ito and ReidIR96] found a natural bijection, the Ito-Reid correspondence, between the conjugacy classes of G and the vertices of the McKay graph
![]() $\widehat {\Gamma }$
.
$\widehat {\Gamma }$
.
Theorem 1.6. Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. There exists an Ito-Reid correspondence for finite and linearly reductive subgroup schemes of
$p\geq 0$
. There exists an Ito-Reid correspondence for finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
This can be proven using lifting results and the Ito-Reid correspondence over
![]() ${\mathbb {C}}$
, see Section 6.3 for details.
${\mathbb {C}}$
, see Section 6.3 for details.
The main difficulty is to define a notion of conjugacy class for finite and linearly reductive group schemes that makes such a correspondence work: Let us recall the ring
![]() $K_k(G)$
from Section 1.3.3. If G is a finite and linearly reductive group scheme over k, then we define the set of conjugacy classes of G to be
$K_k(G)$
from Section 1.3.3. If G is a finite and linearly reductive group scheme over k, then we define the set of conjugacy classes of G to be
At first sight, this might look rather artificial. One should think of it as defining conjugacy classes to be “dual” to simple representations. Moreover, our definition is compatible with lifting over
![]() $W(k)$
and it induces a bijection of the conjugacy classes of G with the conjugacy classes of
$W(k)$
and it induces a bijection of the conjugacy classes of G with the conjugacy classes of
![]() $G_{\mathrm {abs}}$
. We refer to Section 6.1 and Appendix B.2 for details.
$G_{\mathrm {abs}}$
. We refer to Section 6.1 and Appendix B.2 for details.
1.11 Conjugacy classes
In Theorem 1.6, we had to find a definition of conjugacy classes that makes this theorem true. This begs for the question whether there are other definitions or approaches, which is a question that is interesting in its own.
Let G be a finite group scheme (not necessarily linearly reductive) over an algebraically closed field k. In Appendix B, we study the following approaches to the notion of the set of conjugacy classes of G:
-
1. The set of conjugacy classes
 $G(k)/\sim $
of the group of k-rational points of G.
$G(k)/\sim $
of the group of k-rational points of G. -
2. The spectrum of
 $F\otimes K_k(G)$
, where F is a field of characteristic zero that contains “sufficiently many” roots of unity.
$F\otimes K_k(G)$
, where F is a field of characteristic zero that contains “sufficiently many” roots of unity. -
3. The scheme that represents the functor of conjugacy classes from schemes over k to sets defined by
 $S\mapsto G(S)/\sim $
,
$S\mapsto G(S)/\sim $
, -
4. the isotypical component of the trivial representation of the adjoint representation of G.
-
5. The simple subrepresentations of the extended adjoint representations
 $^{\mathrm {Ad}}A$
and
$^{\mathrm {Ad}}A$
and
 $^{\mathrm {Ad}}(A^*)$
, which are defined using the quantum doubles of the Hopf algebra
$^{\mathrm {Ad}}(A^*)$
, which are defined using the quantum doubles of the Hopf algebra
 $A:=H^0(G,{\mathcal O}_G)$
and its dual
$A:=H^0(G,{\mathcal O}_G)$
and its dual
 $A^*$
.
$A^*$
.
All approaches lead essentially to the “same answer” in characteristic zero. However, they usually lead to very different notions in positive characteristic. On the other hand, all approaches have their merits and drawbacks. For linearly reductive group schemes, the approach (2) leads to a definition that is compatible with lifting and that leads to an Ito-Reid correspondence.
1.12 Organisation of this article
-
- In Section 2, we recall basic facts about finite and linearly reductive group schemes over algebraically closed fields.
-
- In Section 3, we construct the McKay graph
 $\widehat {\Gamma }$
. The main result is Theorem 3.6, a McKay correspondence.
$\widehat {\Gamma }$
. The main result is Theorem 3.6, a McKay correspondence. -
- In Section 4, we recall basic facts about linearly reductive quotient singularities. We establish an Ishii-Ito-Nakamura-type resolution of singularities, the canonical lift of such a singularity and a unique simultaneous resolution of singularities of the canonical lift.
-
- In Section 5, we revisit the Ishii-Ito-Nakamura-type resolution
 $\pi $
of singularities of
$\pi $
of singularities of
 $x\in X=U/G$
and we introduce Hecke correspondences, which leads to Theorem 5.3, a bijection between simple and non-trivial representations of G and components of
$x\in X=U/G$
and we introduce Hecke correspondences, which leads to Theorem 5.3, a bijection between simple and non-trivial representations of G and components of
 $\pi $
. We also study generalisations of this result to two-dimensional linearly reductive quotient singularities.
$\pi $
. We also study generalisations of this result to two-dimensional linearly reductive quotient singularities. -
- In Section 6, we establish an Ito-Reid correspondence between conjugacy classes of G and exceptional divisors in the minimal resolution of singularities of
 $x\in X=U/G$
.
$x\in X=U/G$
. -
- In Section 7, we study derived categories of G-equivariant sheaves on U and on the minimal resolution
 $\pi :Y\to X=U/G$
.
$\pi :Y\to X=U/G$
. -
- In Appendix A, we recall results on finite group schemes from the point of view of Hopf algebras. We recall the adjoint representation, quantum doubles and the extended adjoint representation.
-
- In Appendix B, we study several approaches toward the notion of a conjugacy class for finite group schemes.
2 Linearly reductive group schemes
In this section, we recall a couple of general facts about finite and linearly reductive group schemes over algebraically closed fields. We discuss the close relationship between such a group scheme G and a certain abstracted group
![]() $G_{\mathrm {abs}}$
associated to it. For the relationship to Hopf algebras, we refer to Appendix A.
$G_{\mathrm {abs}}$
associated to it. For the relationship to Hopf algebras, we refer to Appendix A.
2.1 Group schemes
Let G be a finite group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. Since k is perfect, there is a short exact sequence of finite group schemes over k
$p\geq 0$
. Since k is perfect, there is a short exact sequence of finite group schemes over k
where
![]() $G^\circ $
is the connected component of the identity and where
$G^\circ $
is the connected component of the identity and where
![]() $G^{\mathrm {\acute {e}t}}$
is an étale group scheme over k. The reduction
$G^{\mathrm {\acute {e}t}}$
is an étale group scheme over k. The reduction
![]() $G_{\mathrm {red}}\to G$
provides a canonical splitting of (2.1) and we obtain a canonical semi-direct product decomposition
$G_{\mathrm {red}}\to G$
provides a canonical splitting of (2.1) and we obtain a canonical semi-direct product decomposition
![]() $G\cong G^\circ \rtimes G^{\mathrm {\acute {e}t}}$
. Since k is algebraically closed,
$G\cong G^\circ \rtimes G^{\mathrm {\acute {e}t}}$
. Since k is algebraically closed,
![]() $G^{\mathrm {\acute {e}t}}$
is the constant group scheme associated to the finite group
$G^{\mathrm {\acute {e}t}}$
is the constant group scheme associated to the finite group
![]() $G(k)=G^{\mathrm {\acute {e}t}}(k)$
of k-rational points. Moreover,
$G(k)=G^{\mathrm {\acute {e}t}}(k)$
of k-rational points. Moreover,
![]() $G^\circ $
is an infinitesimal group scheme of length equal to some power of p. In particular, if
$G^\circ $
is an infinitesimal group scheme of length equal to some power of p. In particular, if
![]() $p=0$
or if the length of G is prime to p, then
$p=0$
or if the length of G is prime to p, then
![]() $G^\circ $
is trivial and then, G is étale.
$G^\circ $
is trivial and then, G is étale.
If M is a finitely generated abelian group, then the group algebra
![]() $k[M]$
carries a Hopf algebra structure and the associated commutative group scheme is denoted
$k[M]$
carries a Hopf algebra structure and the associated commutative group scheme is denoted
![]() $D(M):=\mathrm {Spec}\: k[M]$
. By definition, such group schemes are called diagonalisable. For example, we have
$D(M):=\mathrm {Spec}\: k[M]$
. By definition, such group schemes are called diagonalisable. For example, we have
![]() $D({\mathbf {C}}_n)\cong \boldsymbol {\mu }_n$
, where
$D({\mathbf {C}}_n)\cong \boldsymbol {\mu }_n$
, where
![]() ${\mathbf {C}}_n$
denotes the cyclic group of order n. We have that
${\mathbf {C}}_n$
denotes the cyclic group of order n. We have that
![]() $\boldsymbol {\mu }_n$
is étale over k if and only if
$\boldsymbol {\mu }_n$
is étale over k if and only if
![]() $p\nmid n$
.
$p\nmid n$
.
A finite group scheme G over k is said to be linearly reductive if every k-linear and finite-dimensional representation of G is semi-simple. If
![]() $p=0$
, then all finite group schemes over k are étale and linearly reductive. If
$p=0$
, then all finite group schemes over k are étale and linearly reductive. If
![]() $p>0$
, then, by a theorem that is often attributed to Nagata [Reference NagataNa61, Theorem 2] (but see also [Reference Abramovich, Olsson and VistoliAOV08, Proposition 2.10], [Reference ChinCh92] and [Reference HashimotoHa15, Section 2]), a finite group scheme over k is linearly reductive if and only if it is an extension of a finite and étale group scheme, whose length is prime to p, by a diagonalisable group scheme.
$p>0$
, then, by a theorem that is often attributed to Nagata [Reference NagataNa61, Theorem 2] (but see also [Reference Abramovich, Olsson and VistoliAOV08, Proposition 2.10], [Reference ChinCh92] and [Reference HashimotoHa15, Section 2]), a finite group scheme over k is linearly reductive if and only if it is an extension of a finite and étale group scheme, whose length is prime to p, by a diagonalisable group scheme.
2.2 Abstract groups and canonical lifts
Let G be a finite and linearly reductive group scheme over an algebraically closed field k of characteristic
![]() $p>0$
. Following [Reference Liedtke, Martin and MatsumotoLMM21, Section 2], we study the finite group
$p>0$
. Following [Reference Liedtke, Martin and MatsumotoLMM21, Section 2], we study the finite group
Here,
![]() $-^D$
denotes
$-^D$
denotes
![]() $\underline {\mbox {Hom}}(-,{\mathbb {G}}_m)$
, the Cartier dual, of a commutative and finite group scheme. If G is étale, then
$\underline {\mbox {Hom}}(-,{\mathbb {G}}_m)$
, the Cartier dual, of a commutative and finite group scheme. If G is étale, then
![]() $G_{\mathrm {abs}}=G(k)$
and if
$G_{\mathrm {abs}}=G(k)$
and if
![]() $G=\boldsymbol {\mu }_{p^n}$
, then
$G=\boldsymbol {\mu }_{p^n}$
, then
![]() $G_{\mathrm {abs}}={\mathbf {C}}_{p^n}$
. In any case, the order of
$G_{\mathrm {abs}}={\mathbf {C}}_{p^n}$
. In any case, the order of
![]() $G_{\mathrm {abs}}$
is equal to the length of G.
$G_{\mathrm {abs}}$
is equal to the length of G.
Definition 2.1. The finite group
![]() $G_{\mathrm {abs}}$
is called the abstract finite group associated to G.
$G_{\mathrm {abs}}$
is called the abstract finite group associated to G.
Lemma 2.2. The functor
establishes an equivalence of categories between the category of finite and linearly reductive group schemes over k and the category of finite groups with a normal and abelian p-Sylow subgroup.
Proof. [Reference Liedtke, Martin and MatsumotoLMM21, Lemma 2.1].
Remark 2.3. A finite group G with a normal and abelian p-Sylow subgroup P is the same as a finite group with a unique and abelian p-Sylow subgroup. In this case, the Schur-Zassenhaus theorem implies that G is isomorphic to a semi-direct product
![]() $P\rtimes G/P$
.
$P\rtimes G/P$
.
Next, we study lifts to characteristic zero: let
![]() $W(k)$
be the ring of Witt vectors of k, let K be its field of fractions and let
$W(k)$
be the ring of Witt vectors of k, let K be its field of fractions and let
![]() $\overline {K}$
be an algebraic closure of K. By [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 2.4], there exist lifts of G as finite and flat group scheme over
$\overline {K}$
be an algebraic closure of K. By [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 2.4], there exist lifts of G as finite and flat group scheme over
![]() $W(k)$
. More precisely,
$W(k)$
. More precisely,
![]() $G^\circ $
and
$G^\circ $
and
![]() $G^{\mathrm {\acute {e}t}}$
even lift uniquely to
$G^{\mathrm {\acute {e}t}}$
even lift uniquely to
![]() $W(k)$
, but their extension class usually does not, see also [Reference Liedtke, Martin and MatsumotoLMM21, Example 2.6]. However, there is a unique lift
$W(k)$
, but their extension class usually does not, see also [Reference Liedtke, Martin and MatsumotoLMM21, Example 2.6]. However, there is a unique lift
![]() ${\mathcal G}_{\mathrm {can}}$
of G to
${\mathcal G}_{\mathrm {can}}$
of G to
![]() $W(k)$
that is characterised by being a semi-direct product of the unique lift of
$W(k)$
that is characterised by being a semi-direct product of the unique lift of
![]() $G^\circ $
with the unique lift of
$G^\circ $
with the unique lift of
![]() $G^{\mathrm {\acute {e}t}}$
.
$G^{\mathrm {\acute {e}t}}$
.
Definition 2.4. The lift
![]() $\mathcal {G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
is called the canonical lift of G. We set
$\mathcal {G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
is called the canonical lift of G. We set
![]() $G_{\mathrm {can}}:=\mathcal {G}_K\to \mathrm {Spec}\: K$
and also call it canonical lift.
$G_{\mathrm {can}}:=\mathcal {G}_K\to \mathrm {Spec}\: K$
and also call it canonical lift.
Every other lift of G to some extension of
![]() $R\supseteq W(k)$
differs from
$R\supseteq W(k)$
differs from
![]() ${\mathcal G}_{\mathrm {can},R}$
by a twist and thus, there is only one geometric lift of G to
${\mathcal G}_{\mathrm {can},R}$
by a twist and thus, there is only one geometric lift of G to
![]() $\overline {K}$
up to isomorphism, namely
$\overline {K}$
up to isomorphism, namely
![]() $G_{\mathrm {can},\overline {K}}$
, see [Reference Liedtke, Martin and MatsumotoLMM21, Section 2.2].
$G_{\mathrm {can},\overline {K}}$
, see [Reference Liedtke, Martin and MatsumotoLMM21, Section 2.2].
Since
![]() $\overline {K}$
is algebraically closed and of characteristic zero,
$\overline {K}$
is algebraically closed and of characteristic zero,
![]() $G_{\mathrm {can},\overline {K}}$
is the constant group scheme associated to the finite group
$G_{\mathrm {can},\overline {K}}$
is the constant group scheme associated to the finite group
![]() $G_{\mathrm {can}}(\overline {K})$
. In fact, we have
$G_{\mathrm {can}}(\overline {K})$
. In fact, we have
![]() $G^\circ \cong \prod _i \boldsymbol {\mu }_{p^{n_i}}$
for some
$G^\circ \cong \prod _i \boldsymbol {\mu }_{p^{n_i}}$
for some
![]() $n_i$
’s and if we set
$n_i$
’s and if we set
![]() $N:=\max \{n_i\}_i$
, fix a primitive
$N:=\max \{n_i\}_i$
, fix a primitive
![]() $p^N$
.th root of unity
$p^N$
.th root of unity
![]() $\zeta _{p^N}$
and set
$\zeta _{p^N}$
and set
![]() $K_N:=K(\zeta _{p^N})$
, then
$K_N:=K(\zeta _{p^N})$
, then
![]() $G_{\mathrm {can},K_N}$
is the constant group scheme associated to the finite group
$G_{\mathrm {can},K_N}$
is the constant group scheme associated to the finite group
![]() $G_{\mathrm {can}}(K_N)$
and we have
$G_{\mathrm {can}}(K_N)$
and we have
![]() $G_{\mathrm {can}}(K_N)=G_{\mathrm {can}}(\overline {K})$
.
$G_{\mathrm {can}}(K_N)=G_{\mathrm {can}}(\overline {K})$
.
Lemma 2.5. There exist isomorphisms of finite groups
In particular, there exist isomorphisms
of finite group schemes over
![]() $K_N$
and
$K_N$
and
![]() $\overline {K}$
, respectively.
$\overline {K}$
, respectively.
2.3 Representation theory
Let k be an algebraically closed field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $W(k)$
, K and
$W(k)$
, K and
![]() $\overline {K}$
be as in the previous section. The equivalence of Lemma 2.2 can be extended to representations and K-theory. If G is a finite group or a finite group scheme over k, we denote by
$\overline {K}$
be as in the previous section. The equivalence of Lemma 2.2 can be extended to representations and K-theory. If G is a finite group or a finite group scheme over k, we denote by
![]() $\mathrm {Rep}_k(G)$
the category of its k-linear and finite-dimensional representations. Let us first recall [Reference Liedtke, Martin and MatsumotoLMM21, Corollary 2.11].
$\mathrm {Rep}_k(G)$
the category of its k-linear and finite-dimensional representations. Let us first recall [Reference Liedtke, Martin and MatsumotoLMM21, Corollary 2.11].
Proposition 2.6. Let G be a finite and linearly reductive group scheme over k. Then, there exist canonical equivalences of categories
which are compatible with degrees, direct sums, tensor products, duals and simplicity.
Remark 2.7. In particular, this allows us to define characters or even a character table of G via Proposition 2.6 and
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
Let
![]() $K_k(G)$
be the K-group associated to
$K_k(G)$
be the K-group associated to
![]() $\mathrm {Rep}_k(G)$
. In fact,
$\mathrm {Rep}_k(G)$
. In fact,
![]() $K_k(G)$
has a natural structure of a commutative ring with one, where the sum (resp. product) structure comes from direct sums (resp. tensor products) of representations. A straightforward application of Proposition 2.6 is the following.
$K_k(G)$
has a natural structure of a commutative ring with one, where the sum (resp. product) structure comes from direct sums (resp. tensor products) of representations. A straightforward application of Proposition 2.6 is the following.
Corollary 2.8. There exist isomorphisms of rings
3 McKay graph and McKay correspondence
In this section, we introduce the McKay graph associated to a finite and linearly reductive subgroup scheme G over an algebraically closed field k of characteristic
![]() $p\geq 0$
and a representation
$p\geq 0$
and a representation
![]() $\rho :G\to {\mathbf {GL}}_{n,k}$
. This induces a bijection between certain affine Dynkin diagrams and finite and linearly reductive subgroup schemes of
$\rho :G\to {\mathbf {GL}}_{n,k}$
. This induces a bijection between certain affine Dynkin diagrams and finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
. As an application, we establish a linearly reductive McKay correspondence.
${\mathbf {SL}}_{2,k}$
. As an application, we establish a linearly reductive McKay correspondence.
3.1 McKay graph
Let G be a finite and linearly reductive group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. Let
$p\geq 0$
. Let
![]() $\{\rho _i\}_i$
be the finite set of isomorphism classes of k-linear and simple representations of G. Following tradition, we assume that
$\{\rho _i\}_i$
be the finite set of isomorphism classes of k-linear and simple representations of G. Following tradition, we assume that
![]() $\rho _0$
is the trivial representation. We fix a representation
$\rho _0$
is the trivial representation. We fix a representation
![]() $\rho :G\to {\mathbf {GL}}(V)$
. If G is a subgroup scheme of
$\rho :G\to {\mathbf {GL}}(V)$
. If G is a subgroup scheme of
![]() ${\mathbf {SL}}_{n,k}$
or
${\mathbf {SL}}_{n,k}$
or
![]() ${\mathbf {GL}}_{n,k}$
, then
${\mathbf {GL}}_{n,k}$
, then
![]() $\rho $
is usually the linear representation corresponding to the embedding of G into this linear algebraic group. By assumption,
$\rho $
is usually the linear representation corresponding to the embedding of G into this linear algebraic group. By assumption,
![]() $\mathrm {Rep}_k(G)$
is semi-simple. Therefore, there exist unique integers
$\mathrm {Rep}_k(G)$
is semi-simple. Therefore, there exist unique integers
![]() $a_{ij}\in {\mathbb {Z}}_{\geq 0}$
for each i, such that we have isomorphisms of k-linear representations
$a_{ij}\in {\mathbb {Z}}_{\geq 0}$
for each i, such that we have isomorphisms of k-linear representations
Associated to this data, we define the McKay graph, denoted
![]() $\Gamma (G,\{\rho _i\},\rho )$
:
$\Gamma (G,\{\rho _i\},\rho )$
:
-
- The vertices are the
 $\{\rho _{i}\}_i$
. (Some sources exclude the the trivial representation
$\{\rho _{i}\}_i$
. (Some sources exclude the the trivial representation
 $\rho _0$
.)
$\rho _0$
.) -
- There are
 $a_{ij}$
edges from the vertex corresponding to
$a_{ij}$
edges from the vertex corresponding to
 $\rho _i$
to the vertex corresponding to
$\rho _i$
to the vertex corresponding to
 $\rho _j$
.
$\rho _j$
.
We now establish a couple of elementary properties of this graph, which are well-known in the classical case and which immediately carry over to the linearly reductive situation. We leave the proof of the first lemma to the reader.
Lemma 3.1. We have
In particular, if
![]() $\rho $
is self-dual, that is,
$\rho $
is self-dual, that is,
![]() $\rho \cong \rho ^\vee $
, then
$\rho \cong \rho ^\vee $
, then
![]() $a_{ij}=a_{ji}$
for all
$a_{ij}=a_{ji}$
for all
![]() $i,j$
. In this case, we can consider
$i,j$
. In this case, we can consider
![]() $\Gamma (G,\{\rho _i\},\rho )$
as an undirected graph.
$\Gamma (G,\{\rho _i\},\rho )$
as an undirected graph.
Lemma 3.2. Let
![]() $\rho :G\to {\mathbf {SL}}_{2,k}$
be a homomorphism of group schemes over k, considered as a 2-dimensional representation. Then,
$\rho :G\to {\mathbf {SL}}_{2,k}$
be a homomorphism of group schemes over k, considered as a 2-dimensional representation. Then,
![]() $\rho $
is self-dual.
$\rho $
is self-dual.
Proof. Being a 2-dimensional representation,
![]() $\rho ^\vee $
is isomorphic to
$\rho ^\vee $
is isomorphic to
![]() $\rho \otimes \det (\rho )$
and the lemma follows.
$\rho \otimes \det (\rho )$
and the lemma follows.
Lemma 3.3. Let
![]() $\rho :G\to {\mathbf {GL}}_{n,k}$
be a faithful representation. Then, every irreducible representation of G occurs as subrepresentation of
$\rho :G\to {\mathbf {GL}}_{n,k}$
be a faithful representation. Then, every irreducible representation of G occurs as subrepresentation of
![]() $\rho ^{\otimes m}$
for some suitable m.
$\rho ^{\otimes m}$
for some suitable m.
Proof. This is well-known for finite groups. Using Proposition 2.6, it carries over to finite and linearly reductive group schemes.
Corollary 3.4. If
![]() $\rho $
is a faithful representation, then the graph
$\rho $
is a faithful representation, then the graph
![]() $\Gamma (G,\{\rho _i\},\rho )$
is connected.
$\Gamma (G,\{\rho _i\},\rho )$
is connected.
Proof. It suffices to note that the number of paths in
![]() $\Gamma $
of length m that connect the vertices corresponding to
$\Gamma $
of length m that connect the vertices corresponding to
![]() $\rho _i$
and
$\rho _i$
and
![]() $\rho _j$
is equal to the multiplicity of
$\rho _j$
is equal to the multiplicity of
![]() $\rho _i$
in
$\rho _i$
in
![]() $\rho _j\otimes \rho ^{\otimes m}$
, see, for example, the proof of [Reference KirillovKi16, Theorem 8.13].
$\rho _j\otimes \rho ^{\otimes m}$
, see, for example, the proof of [Reference KirillovKi16, Theorem 8.13].
Let k be an algebraically closed field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() $W(k)$
, K and
$W(k)$
, K and
![]() $\overline {K}$
be as in Section 2.2. There, we also discussed the canonical lift
$\overline {K}$
be as in Section 2.2. There, we also discussed the canonical lift
![]() $G_{\mathrm {can}}$
of G over K and we saw that there exists an isomorphism of finite groups
$G_{\mathrm {can}}$
of G over K and we saw that there exists an isomorphism of finite groups
![]() $G_{\mathrm {abs}}\cong G_{\mathrm {can}}(\overline {K})$
. Proposition 2.6 implies the following result.
$G_{\mathrm {abs}}\cong G_{\mathrm {can}}(\overline {K})$
. Proposition 2.6 implies the following result.
Proposition 3.5. Let G be a finite and linearly reductive group scheme over k. Let
![]() $\{\rho _i\}_i$
be the set of isomorphism classes of simple representations of G. Let
$\{\rho _i\}_i$
be the set of isomorphism classes of simple representations of G. Let
![]() $\rho $
be a finite-dimensional representation of G.
$\rho $
be a finite-dimensional representation of G.
-
1. Proposition 2.6 yields sets of representations
 $\{\rho _{\mathrm {can},i}\}_i$
and
$\{\rho _{\mathrm {can},i}\}_i$
and
 $\{\rho _{\mathrm {abs},i}\}_i$
of
$\{\rho _{\mathrm {abs},i}\}_i$
of
 $G_{\mathrm {can}}$
and
$G_{\mathrm {can}}$
and
 $G_{\mathrm {abs}}$
, respectively, which are the sets of isomorphism classes of simple representations of
$G_{\mathrm {abs}}$
, respectively, which are the sets of isomorphism classes of simple representations of
 $G_{\mathrm {can}}$
and
$G_{\mathrm {can}}$
and
 $G_{\mathrm {abs}}$
, respectively.
$G_{\mathrm {abs}}$
, respectively. -
2. Proposition 2.6 yields representations
 $\rho _{\mathrm {can}}$
and
$\rho _{\mathrm {can}}$
and
 $\rho _{\mathrm {abs}}$
of
$\rho _{\mathrm {abs}}$
of
 $G_{\mathrm {can}}$
and
$G_{\mathrm {can}}$
and
 $G_{\mathrm {abs}}$
, respectively.
$G_{\mathrm {abs}}$
, respectively.
This data leads to a bijection of the three McKay graphs
3.2 McKay correspondence
We now run through the classical McKay correspondence [Reference McKayMc80] in our setting, where we follow [Reference KirillovKi16, Section 8.3]. Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
and let G be a finite and linearly reductive subgroup scheme of
$p\geq 0$
and let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
-
1. The K-group
 $K_k(G)$
carries a symmetric bilinear form
$K_k(G)$
carries a symmetric bilinear form  $$ \begin{align*}([V],[W])_0 \,:=\, \dim_k\,\mathrm{Hom}_G(V,W). \end{align*} $$
$$ \begin{align*}([V],[W])_0 \,:=\, \dim_k\,\mathrm{Hom}_G(V,W). \end{align*} $$
-
2. We consider the closed embedding
 $G\to {\mathbf {SL}}_{2,k}$
as a 2-dimensional representation
$G\to {\mathbf {SL}}_{2,k}$
as a 2-dimensional representation
 $\rho :G\to {\mathbf {SL}}_{2,k}\to {\mathbf {GL}}_{2,k}$
and define an operator
$\rho :G\to {\mathbf {SL}}_{2,k}\to {\mathbf {GL}}_{2,k}$
and define an operator  $$ \begin{align*}A\,:\,K_k(G)\,\to\, K_k(G),\qquad [V]\mapsto [V]\otimes\rho\,. \end{align*} $$
$$ \begin{align*}A\,:\,K_k(G)\,\to\, K_k(G),\qquad [V]\mapsto [V]\otimes\rho\,. \end{align*} $$
Since
 $\rho $
is self-dual by Lemma 3.2, it follows that A is symmetric with respect to
$\rho $
is self-dual by Lemma 3.2, it follows that A is symmetric with respect to
 $(-,-)_0$
, see [Reference KirillovKi16, Lemma 8.12].
$(-,-)_0$
, see [Reference KirillovKi16, Lemma 8.12]. -
3. Using
 $\rho $
, we define a symmetric bilinear form on
$\rho $
, we define a symmetric bilinear form on
 $K_k(G)\otimes _{\mathbb {Z}}{\mathbb {R}}$
by which is positive semi-definite. The class
$K_k(G)\otimes _{\mathbb {Z}}{\mathbb {R}}$
by which is positive semi-definite. The class $$ \begin{align*}([V],[W]) \,:=\, \left([V],\, (2-A)[W]\right)_0, \end{align*} $$
$$ \begin{align*}([V],[W]) \,:=\, \left([V],\, (2-A)[W]\right)_0, \end{align*} $$
 $\delta \in K_k(G)$
of the regular representation of G generates the radical of
$\delta \in K_k(G)$
of the regular representation of G generates the radical of
 $(-,-)$
.
$(-,-)$
.
-
4. Let
 $\{\rho _i\}$
be the set of isomorphism classes of simple representations of G.
$\{\rho _i\}$
be the set of isomorphism classes of simple representations of G.-
(a) The McKay graph
 $\widehat {\Gamma }=\Gamma (G,\{\rho _i\}_i,\rho )$
is an affine Dynkin diagram of type
$\widehat {\Gamma }=\Gamma (G,\{\rho _i\}_i,\rho )$
is an affine Dynkin diagram of type
 $\widehat {A}_n$
,
$\widehat {A}_n$
,
 $\widehat {D}_n$
with
$\widehat {D}_n$
with
 $n\geq 4$
,
$n\geq 4$
,
 $\widehat {E}_6$
,
$\widehat {E}_6$
,
 $\widehat {E}_7$
or
$\widehat {E}_7$
or
 $\widehat {E}_8$
.
$\widehat {E}_8$
. -
(b) After removing the vertex corresponding to the trivial representation
 $\rho _0$
from
$\rho _0$
from
 $\widehat {\Gamma }$
, we obtain a finite Dynkin diagram of type
$\widehat {\Gamma }$
, we obtain a finite Dynkin diagram of type
 $A_n$
,
$A_n$
,
 $D_n$
with
$D_n$
with
 $n\geq 4$
,
$n\geq 4$
,
 $E_6$
,
$E_6$
,
 $E_7$
or
$E_7$
or
 $E_8$
, respectively.
$E_8$
, respectively.
-
If G is a finite subgroup of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
, then these statements are part of the classical McKay correspondence, see [Reference McKayMc80] or [Reference KirillovKi16, Section 8.3]. In our setting of finite and linearly reductive subgroup schemes of
${\mathbf {SL}}_2({\mathbb {C}})$
, then these statements are part of the classical McKay correspondence, see [Reference McKayMc80] or [Reference KirillovKi16, Section 8.3]. In our setting of finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
, the above claims immediately follow from the classical McKay correspondence together with the lifting results Proposition 2.6 and Proposition 3.5. We then obtain the following analog of McKay’s theorem [Reference McKayMc80].
${\mathbf {SL}}_{2,k}$
, the above claims immediately follow from the classical McKay correspondence together with the lifting results Proposition 2.6 and Proposition 3.5. We then obtain the following analog of McKay’s theorem [Reference McKayMc80].
Theorem 3.6. Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. There exists a bijection between finite, non-trivial and linearly reductive subgroup schemes of
$p\geq 0$
. There exists a bijection between finite, non-trivial and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
up to conjugation and affine Dynkin diagrams of type
${\mathbf {SL}}_{2,k}$
up to conjugation and affine Dynkin diagrams of type
 $$ \begin{align*}\begin{array}{lcl} \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7, \widehat{E}_8 &\quad \mbox{if} \quad & p=0 \quad \mbox{or} \quad p\geq7, \\ \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7 &\quad \mbox{if} \quad & p=5,\\ \widehat{A}_n, \widehat{D}_n &\quad \mbox{if} \quad & p=3 \mbox{ and} \\ \widehat{A}_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{lcl} \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7, \widehat{E}_8 &\quad \mbox{if} \quad & p=0 \quad \mbox{or} \quad p\geq7, \\ \widehat{A}_n, \widehat{D}_n, \widehat{E}_6, \widehat{E}_7 &\quad \mbox{if} \quad & p=5,\\ \widehat{A}_n, \widehat{D}_n &\quad \mbox{if} \quad & p=3 \mbox{ and} \\ \widehat{A}_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
Proof. If
![]() $p=0$
, then this is part of the classical McKay correspondence. If
$p=0$
, then this is part of the classical McKay correspondence. If
![]() $p>0$
, then this follows from the linearly reductive McKay correspondence just discussed together with Hashimoto’s classification [Reference HashimotoHa15, Theorem 3.8] of finite and linearly reductive subgroup schemes of
$p>0$
, then this follows from the linearly reductive McKay correspondence just discussed together with Hashimoto’s classification [Reference HashimotoHa15, Theorem 3.8] of finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
Remark 3.7. The linearly reductive group schemes corresponding to
![]() $\widehat {E}_6$
,
$\widehat {E}_6$
,
![]() $\widehat {E}_7$
and
$\widehat {E}_7$
and
![]() $\widehat {E}_8$
are étale and correspond to finite groups of order prime to p. The linearly reductive group scheme corresponding to
$\widehat {E}_8$
are étale and correspond to finite groups of order prime to p. The linearly reductive group scheme corresponding to
![]() $\widehat {A}_n$
(resp.
$\widehat {A}_n$
(resp.
![]() $\widehat {D}_n$
) is étale if and only if
$\widehat {D}_n$
) is étale if and only if
![]() $p\nmid (n+1)$
(resp.
$p\nmid (n+1)$
(resp.
![]() $p\nmid (n-2)$
). We refer to [Reference Liedtke and SatrianoLS14, Proposition 4.2] for details. Thus, even if p is sufficiently large, then one does not obtain a bijection in Theorem 3.6 with finite groups of order to prime to p only.
$p\nmid (n-2)$
). We refer to [Reference Liedtke and SatrianoLS14, Proposition 4.2] for details. Thus, even if p is sufficiently large, then one does not obtain a bijection in Theorem 3.6 with finite groups of order to prime to p only.
Remark 3.8. Steinberg [Reference SteinbergSt85] established many properties of the McKay graph and the McKay correspondence for finite subgroups of
![]() ${\mathbf {SU}}_2({\mathbb {C}})$
without using classification lists. It seems plausible to obtain a proof of Theorem 3.6 along these lines without using lifting results or classification lists.
${\mathbf {SU}}_2({\mathbb {C}})$
without using classification lists. It seems plausible to obtain a proof of Theorem 3.6 along these lines without using lifting results or classification lists.
4 Linearly reductive quotient singularities
In this section, we recall linearly reductive quotient singularities in the sense of [Reference Liedtke, Martin and MatsumotoLMM21] and some general results, including the canonical lift of such a singularity over the ring of Witt vectors. In dimension two, we establish a minimal resolution of singularities using G-Hilbert schemes as in the work of Ishii, Ito and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ito and NakamuraIN99]. We also show that the canonical lift admits a unique minimal and simultaneous resolution of singularities. Finally, we discuss Klein singularities and their relation to rational double point singularities.
4.1 Quotient singularities
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. If G is a finite and linearly reductive group scheme over k, if V is a finite-dimensional k-vector space and if
$p\geq 0$
. If G is a finite and linearly reductive group scheme over k, if V is a finite-dimensional k-vector space and if
![]() $\rho :G\to {\mathbf {GL}}(V)$
is a linear representation, then we define the
$\rho :G\to {\mathbf {GL}}(V)$
is a linear representation, then we define the
![]() $\lambda $
-invariant of
$\lambda $
-invariant of
![]() $\rho $
as in [Reference Liedtke, Martin and MatsumotoLMM21, Definition 2.7] to be
$\rho $
as in [Reference Liedtke, Martin and MatsumotoLMM21, Definition 2.7] to be
where
![]() $V^{\boldsymbol {\mu }_n}$
denotes the subspace of
$V^{\boldsymbol {\mu }_n}$
denotes the subspace of
![]() $\boldsymbol {\mu }_n$
-invariants. As explained in [Reference Liedtke, Martin and MatsumotoLMM21, Remark 2.8], the representation
$\boldsymbol {\mu }_n$
-invariants. As explained in [Reference Liedtke, Martin and MatsumotoLMM21, Remark 2.8], the representation
![]() $\rho $
is faithful if and only if
$\rho $
is faithful if and only if
![]() $\lambda (\rho )\neq \dim V$
. Moreover,
$\lambda (\rho )\neq \dim V$
. Moreover,
![]() $\rho $
contains no pseudo-reflections if and only if
$\rho $
contains no pseudo-reflections if and only if
![]() $\lambda (\rho )\leq \dim V-2$
and in this case, the representation
$\lambda (\rho )\leq \dim V-2$
and in this case, the representation
![]() $\rho $
is said to be small.
$\rho $
is said to be small.
Definition 4.1. The representation
![]() $\rho $
is called very small if
$\rho $
is called very small if
![]() $\lambda (\rho )=0$
.
$\lambda (\rho )=0$
.
Note that in dimension two the notions of small and very small coincide. We refer to [Reference Liedtke, Martin and MatsumotoLMM21, Section 3] for the classification of finite and linearly reductive group schemes that admit a very small representation. By [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 6.5],
![]() $\lambda (\rho )$
is equal to the dimension of the non-free locus of the induced G-action on the spectrum of the formal power series ring
$\lambda (\rho )$
is equal to the dimension of the non-free locus of the induced G-action on the spectrum of the formal power series ring
![]() $k[[V^\vee ]]=(k[V^\vee ])^\wedge $
. Following [Reference Liedtke, Martin and MatsumotoLMM21, Definition 6.4] and using the linearisation result [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 6.3], we define:
$k[[V^\vee ]]=(k[V^\vee ])^\wedge $
. Following [Reference Liedtke, Martin and MatsumotoLMM21, Definition 6.4] and using the linearisation result [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 6.3], we define:
Definition 4.2. A linearly reductive quotient singularity over k is an isolated singularity that is analytically isomorphic to
![]() $\mathrm {Spec}\: k[[V^\vee ]]^G$
, where G is a finite and linearly reductive group scheme over k and where
$\mathrm {Spec}\: k[[V^\vee ]]^G$
, where G is a finite and linearly reductive group scheme over k and where
![]() $\rho :G\to {\mathbf {GL}}(V)$
is a very small representation.
$\rho :G\to {\mathbf {GL}}(V)$
is a very small representation.
Remark 4.3. We set
![]() $U:=\mathrm {Spec}\: k[V^\vee ]$
or
$U:=\mathrm {Spec}\: k[V^\vee ]$
or
![]() $U:=\mathrm {Spec}\: k[[V^\vee ]]$
and simply write
$U:=\mathrm {Spec}\: k[[V^\vee ]]$
and simply write
![]() $x\in X=U/G$
with the assumptions of Definition 4.2 implicitly understood.
$x\in X=U/G$
with the assumptions of Definition 4.2 implicitly understood.
Properties of these singularities have been studied in [Reference Liedtke, Martin and MatsumotoLMM21]: for their local étale fundamental groups, class groups and F-signatures, we refer to [Reference Liedtke, Martin and MatsumotoLMM21, Section 7].
By [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 8.1], a linearly reductive quotient singularity determines the finite and linearly reductive group scheme G together with the very small representation
![]() $\rho :G\to {\mathbf {GL}}(V)$
uniquely up to isomorphism and conjugacy, respectively. It thus makes sense to refer to
$\rho :G\to {\mathbf {GL}}(V)$
uniquely up to isomorphism and conjugacy, respectively. It thus makes sense to refer to
![]() $\rho (G)\subset {\mathbf {GL}}(V)$
as the finite and linearly reductive subgroup scheme of
$\rho (G)\subset {\mathbf {GL}}(V)$
as the finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}(V)$
associated to the linearly reductive quotient singularity
${\mathbf {GL}}(V)$
associated to the linearly reductive quotient singularity
![]() $x\in X=U/G$
. In particular, the classification of linearly reductive quotient singularities in dimension d is “the same” as the classification of very small, finite and linearly reductive subgroup schemes of
$x\in X=U/G$
. In particular, the classification of linearly reductive quotient singularities in dimension d is “the same” as the classification of very small, finite and linearly reductive subgroup schemes of
![]() ${\mathbf {GL}}_{d,k}$
up to conjugacy. We refer to [Reference Liedtke, Martin and MatsumotoLMM21, Section 3] for details and this classification.
${\mathbf {GL}}_{d,k}$
up to conjugacy. We refer to [Reference Liedtke, Martin and MatsumotoLMM21, Section 3] for details and this classification.
4.2 Minimal resolution of singularities
If
![]() $x\in X$
is a normal surface singularity, then it admits a unique minimal resolution of singularities
$x\in X$
is a normal surface singularity, then it admits a unique minimal resolution of singularities
If
![]() $x\in X$
is moreover a rational singularity, then the exceptional locus of
$x\in X$
is moreover a rational singularity, then the exceptional locus of
![]() $\pi $
is a union of
$\pi $
is a union of
![]() ${\mathbb {P}}^1$
’s, whose dual intersection graph
${\mathbb {P}}^1$
’s, whose dual intersection graph
![]() $\Gamma $
contains no cycles. The graph
$\Gamma $
contains no cycles. The graph
![]() $\Gamma $
is called the type of
$\Gamma $
is called the type of
![]() $x\in X$
. If the type determines the singularity up to analytic isomorphism, then the singularity is said to be taut.
$x\in X$
. If the type determines the singularity up to analytic isomorphism, then the singularity is said to be taut.
Over
![]() ${\mathbb {C}}$
, taut singularities have been classified by Laufer [Reference LauferLa73]. For example, two-dimensional finite quotient singularities over
${\mathbb {C}}$
, taut singularities have been classified by Laufer [Reference LauferLa73]. For example, two-dimensional finite quotient singularities over
![]() ${\mathbb {C}}$
are taut. Since two-dimensional linearly reductive quotient singularities over algebraically closed fields of positive characteristic are F-regular (see [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 7.1]), they are taut by Tanaka’s theorem [Reference TanakaTa15].
${\mathbb {C}}$
are taut. Since two-dimensional linearly reductive quotient singularities over algebraically closed fields of positive characteristic are F-regular (see [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 7.1]), they are taut by Tanaka’s theorem [Reference TanakaTa15].
Remark 4.4. Very small, finite and linearly reductive subgroup schemes of
![]() ${\mathbf {GL}}_{2,k}$
have been classified in [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 3.4], extending Brieskorn’s classification [Reference BrieskornBr67, Satz 2.9] of small subgroups of
${\mathbf {GL}}_{2,k}$
have been classified in [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 3.4], extending Brieskorn’s classification [Reference BrieskornBr67, Satz 2.9] of small subgroups of
![]() ${\mathbf {GL}}_2({\mathbb {C}})$
. The types of the associated quotient singularities in terms of this classification are given by [Reference BrieskornBr67, Satz 2.11].
${\mathbf {GL}}_2({\mathbb {C}})$
. The types of the associated quotient singularities in terms of this classification are given by [Reference BrieskornBr67, Satz 2.11].
Finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
are automatically very small and they have been classified by Hashimoto [Reference HashimotoHa15, Theorem 3.8], extending Klein’s classification [Reference KleinKl84] of finite subgroups of
${\mathbf {SL}}_{2,k}$
are automatically very small and they have been classified by Hashimoto [Reference HashimotoHa15, Theorem 3.8], extending Klein’s classification [Reference KleinKl84] of finite subgroups of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
and we refer to [Reference HashimotoHa15, Reference Liedtke and SatrianoLS14] for the types of the associated quotient singularities (see also Theorem 4.12 below).
${\mathbf {SL}}_2({\mathbb {C}})$
and we refer to [Reference HashimotoHa15, Reference Liedtke and SatrianoLS14] for the types of the associated quotient singularities (see also Theorem 4.12 below).
4.3 The Ishii-Ito-Nakamura resolution
In [Reference Ito and NakamuraIN99], Ito and Nakamura showed that if G is a finite subgroup of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
, then a minimal resolution of singularities of
${\mathbf {SL}}_2({\mathbb {C}})$
, then a minimal resolution of singularities of
![]() ${\mathbb {C}}^2/G$
is provided by the G-Hilbert scheme
${\mathbb {C}}^2/G$
is provided by the G-Hilbert scheme
![]() $G\text{-}\mathrm {Hilb}({\mathbb {C}}^2)$
. Ishii [Reference IshiiIs02] extended this to quotient singularities
$G\text{-}\mathrm {Hilb}({\mathbb {C}}^2)$
. Ishii [Reference IshiiIs02] extended this to quotient singularities
![]() ${\mathbb {C}}^2/G$
for G a finite and very small subgroup of
${\mathbb {C}}^2/G$
for G a finite and very small subgroup of
![]() ${\mathbf {GL}}_2({\mathbb {C}})$
and Ishii and Nakamura [Reference Ishii and NakamuraIN19] extended this to quotient singularities
${\mathbf {GL}}_2({\mathbb {C}})$
and Ishii and Nakamura [Reference Ishii and NakamuraIN19] extended this to quotient singularities
![]() $U/G$
for G a finite and very small subgroup of
$U/G$
for G a finite and very small subgroup of
![]() ${\mathbf {GL}}_2(k)$
of order prime to p.
${\mathbf {GL}}_2(k)$
of order prime to p.
Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. Let G be a very small, finite and linearly reductive subgroup scheme of
$p\geq 0$
. Let G be a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
. Set
${\mathbf {GL}}_{2,k}$
. Set
![]() $U:={\mathbb {A}}^2_k$
or
$U:={\mathbb {A}}^2_k$
or
![]() $\widehat {{\mathbb {A}}}_k^2$
and let
$\widehat {{\mathbb {A}}}_k^2$
and let
![]() $x\in X:=U/G$
be the associated linearly reductive quotient singularity. By [Reference BlumeBl11], there exists a G-Hilbert scheme
$x\in X:=U/G$
be the associated linearly reductive quotient singularity. By [Reference BlumeBl11], there exists a G-Hilbert scheme
![]() $G\text{-}\mathrm {Hilb}(U)$
over k that parametrises zero-dimensional G-invariant subschemes
$G\text{-}\mathrm {Hilb}(U)$
over k that parametrises zero-dimensional G-invariant subschemes
![]() $Z\subset U$
(so-called clusters), such that the G-representation on
$Z\subset U$
(so-called clusters), such that the G-representation on
![]() $H^0(Z,{\mathcal O}_Z)$
is the regular representation. Taking a cluster Z to its G-orbit (see, for example, [Reference BlumeBl11, Remark 3.3]) induces a morphism
$H^0(Z,{\mathcal O}_Z)$
is the regular representation. Taking a cluster Z to its G-orbit (see, for example, [Reference BlumeBl11, Remark 3.3]) induces a morphism
over k.
Theorem 4.5. The morphism
![]() $\pi $
is a minimal resolution of singularities.
$\pi $
is a minimal resolution of singularities.
Proof. If
![]() $p=0$
, then this is shown in [Reference Ishii and NakamuraIN19], extending [Reference Ito and NakamuraIN99]. If
$p=0$
, then this is shown in [Reference Ishii and NakamuraIN19], extending [Reference Ito and NakamuraIN99]. If
![]() $p>0$
and G is of length prime to p, then this is shown in [Reference Ishii and NakamuraIN19]. However, this proof also works if G is linearly reductive and p divides the length of G.
$p>0$
and G is of length prime to p, then this is shown in [Reference Ishii and NakamuraIN19]. However, this proof also works if G is linearly reductive and p divides the length of G.
Remark 4.6. By [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 11.5], every two-dimensional F-regular singularity
![]() $x\in X$
is a linearly reductive quotient singularity, say
$x\in X$
is a linearly reductive quotient singularity, say
![]() $x\in X=U/G$
for some finite and linearly reductive subgroup scheme G of
$x\in X=U/G$
for some finite and linearly reductive subgroup scheme G of
![]() ${\mathbf {GL}}_{2,k}$
. By [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 8.1], G and its embedding into
${\mathbf {GL}}_{2,k}$
. By [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 8.1], G and its embedding into
![]() ${\mathbf {GL}}_{2,k}$
are unique up to isomorphism and conjugacy, respectively. By Theorem 4.5,
${\mathbf {GL}}_{2,k}$
are unique up to isomorphism and conjugacy, respectively. By Theorem 4.5,
![]() $G\text{-}\mathrm {Hilb}(U)\to U/G=X\ni x$
is the minimal resolution of singularities. In particular, every two-dimensional F-regular singularity can be resolved by a suitable G-Hilbert scheme.
$G\text{-}\mathrm {Hilb}(U)\to U/G=X\ni x$
is the minimal resolution of singularities. In particular, every two-dimensional F-regular singularity can be resolved by a suitable G-Hilbert scheme.
4.4 Canonical lifts
Let k be an algebraically closed field of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $W(k)$
be the ring of Witt vectors, let K be its field of fractions and let
$W(k)$
be the ring of Witt vectors, let K be its field of fractions and let
![]() $\overline {K}$
be an algebraic closure. Let
$\overline {K}$
be an algebraic closure. Let
![]() $x\in X=U/G$
be a d-dimensional linearly reductive singularity, where
$x\in X=U/G$
be a d-dimensional linearly reductive singularity, where
![]() $U={\mathbb {A}}^d_k$
or
$U={\mathbb {A}}^d_k$
or
![]() $U=\widehat {{\mathbb {A}}}_k^d$
. Next, we set
$U=\widehat {{\mathbb {A}}}_k^d$
. Next, we set
![]() ${\mathcal U}:={\mathbb {A}}^d_{W(k)}$
or
${\mathcal U}:={\mathbb {A}}^d_{W(k)}$
or
![]() $\widehat {{\mathbb {A}}}^d_{W(k)}$
, respectively. In Section 2.2, we recalled the canonical lift
$\widehat {{\mathbb {A}}}^d_{W(k)}$
, respectively. In Section 2.2, we recalled the canonical lift
![]() ${\mathcal G}_{\mathrm {can}}$
of G over
${\mathcal G}_{\mathrm {can}}$
of G over
![]() $W(k)$
. By [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 2.9], there exists a unique lift of the G-action from U to
$W(k)$
. By [Reference Liedtke, Martin and MatsumotoLMM21, Proposition 2.9], there exists a unique lift of the G-action from U to
![]() ${\mathcal U}$
. From this, we obtain a flat family
${\mathcal U}$
. From this, we obtain a flat family
of linearly reductive quotient singularities over
![]() $W(k)$
, whose special fibre over k is
$W(k)$
, whose special fibre over k is
![]() $x\in X=U/G$
.
$x\in X=U/G$
.
Definition 4.7. The family (4.1) is called the canonical lift of the linearly reductive quotient singularity
![]() $x\in X=U/G$
.
$x\in X=U/G$
.
By the Lefschetz principle, the geometric generic fibre of
![]() $\mathcal {X}_{\mathrm {can}}$
can be identified with a finite quotient singularity of the form
$\mathcal {X}_{\mathrm {can}}$
can be identified with a finite quotient singularity of the form
![]() ${\mathbb {C}}^d/G_{\mathrm {abs}}$
, where
${\mathbb {C}}^d/G_{\mathrm {abs}}$
, where
![]() $G_{\mathrm {abs}}$
is the abstract group associated to G and the embedding of
$G_{\mathrm {abs}}$
is the abstract group associated to G and the embedding of
![]() $G_{\mathrm {abs}}\to {\mathbf {GL}}_d({\mathbb {C}})$
corresponds to the embedding
$G_{\mathrm {abs}}\to {\mathbf {GL}}_d({\mathbb {C}})$
corresponds to the embedding
![]() $G\to {\mathbf {GL}}_{d,k}$
provided by Proposition 2.6. The canonical lift is unique in the following sense:
$G\to {\mathbf {GL}}_{d,k}$
provided by Proposition 2.6. The canonical lift is unique in the following sense:
Proposition 4.8. We keep the notations and assumptions. Let
![]() $W(k)\subseteq R$
be a finite extension of complete DVRs and let
$W(k)\subseteq R$
be a finite extension of complete DVRs and let
![]() $\mathcal {X}\to \mathrm {Spec}\: R$
be a lift of
$\mathcal {X}\to \mathrm {Spec}\: R$
be a lift of
![]() $x\in X$
that is of the form
$x\in X$
that is of the form
![]() ${\mathcal V}/{\mathcal G}\to \mathrm {Spec}\: R$
for some flat lift
${\mathcal V}/{\mathcal G}\to \mathrm {Spec}\: R$
for some flat lift
![]() ${\mathcal G}$
of G to R and
${\mathcal G}$
of G to R and
![]() ${\mathcal V}\cong {\mathcal U}\times _RS$
. Then, there exists a finite extension
${\mathcal V}\cong {\mathcal U}\times _RS$
. Then, there exists a finite extension
![]() $R\subseteq S$
of complete DVRs, such that
$R\subseteq S$
of complete DVRs, such that
-
1. There exists an isomorphism
of group schemes over S. $$ \begin{align*}{\mathcal G}_{\mathrm{can}} \times_{W(k)}S \,\cong\, {\mathcal G}\times_RS \end{align*} $$
$$ \begin{align*}{\mathcal G}_{\mathrm{can}} \times_{W(k)}S \,\cong\, {\mathcal G}\times_RS \end{align*} $$
-
2. The very small representation
 $\rho :G\to {\mathbf {GL}}_{d,k}$
corresponding to the G-action on U lifts uniquely to
$\rho :G\to {\mathbf {GL}}_{d,k}$
corresponding to the G-action on U lifts uniquely to
 ${\mathcal G}_{\mathrm {can}}$
and
${\mathcal G}_{\mathrm {can}}$
and
 ${\mathcal G}$
, respectively, and they become conjugate over S.
${\mathcal G}$
, respectively, and they become conjugate over S. -
3. There is an isomorphism
of deformations of $$ \begin{align*}\mathcal{X}_{\mathrm{can}}\times_{W(k)}S \,\cong\, \mathcal{X}\times_RS \end{align*} $$
$$ \begin{align*}\mathcal{X}_{\mathrm{can}}\times_{W(k)}S \,\cong\, \mathcal{X}\times_RS \end{align*} $$
 $x\in X$
over S.
$x\in X$
over S.
Proof. Since
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() ${\mathcal G}_{\mathrm {can},R}$
are lifts of G to R, they become isomorphic after passing to a finite extension
${\mathcal G}_{\mathrm {can},R}$
are lifts of G to R, they become isomorphic after passing to a finite extension
![]() $R\subseteq S$
, see also the discussion in Section 2.2. There, we also saw that the linear representation
$R\subseteq S$
, see also the discussion in Section 2.2. There, we also saw that the linear representation
![]() $\rho :G\to {\mathbf {GL}}_{d,k}$
lifts uniquely to
$\rho :G\to {\mathbf {GL}}_{d,k}$
lifts uniquely to
![]() ${\mathcal G}$
and
${\mathcal G}$
and
![]() ${\mathcal G}_{\mathrm {can}}$
, respectively, and that they become conjugate over S. From this, we deduce an isomorphism
${\mathcal G}_{\mathrm {can}}$
, respectively, and that they become conjugate over S. From this, we deduce an isomorphism
![]() $\mathcal {X}_{\mathrm {can}}\times _{W(k)}S\cong \mathcal {X}\times _RS$
.
$\mathcal {X}_{\mathrm {can}}\times _{W(k)}S\cong \mathcal {X}\times _RS$
.
Remark 4.9. If
![]() $d\geq 3$
, then [Reference Liedtke, Martin and MatsumotoLMM21, Corollary 10.10] shows that a d-dimensional linearly reductive quotient singularity
$d\geq 3$
, then [Reference Liedtke, Martin and MatsumotoLMM21, Corollary 10.10] shows that a d-dimensional linearly reductive quotient singularity
![]() $x\in X$
admits precisely one lift over
$x\in X$
admits precisely one lift over
![]() $W(k)$
, namely the canonical lift. If
$W(k)$
, namely the canonical lift. If
![]() $d=2$
, then linearly reductive quotient singularities usually have positive dimensional deformation spaces and admit many non-isomorphic lifts to
$d=2$
, then linearly reductive quotient singularities usually have positive dimensional deformation spaces and admit many non-isomorphic lifts to
![]() $W(k)$
, see [Reference Liedtke, Martin and MatsumotoLMM21, Section 12].
$W(k)$
, see [Reference Liedtke, Martin and MatsumotoLMM21, Section 12].
4.5 Simultaneous resolution of singularities
If
![]() $\mathcal {X}\to S$
is a deformation of a rational double point singularity
$\mathcal {X}\to S$
is a deformation of a rational double point singularity
![]() $x\in X$
, then it admits a simultaneous resolution of singularities, but usually only after some finite base-change
$x\in X$
, then it admits a simultaneous resolution of singularities, but usually only after some finite base-change
![]() $S'\to S$
, see [Reference ArtinAr74]. In the case where
$S'\to S$
, see [Reference ArtinAr74]. In the case where
![]() $\mathcal {X}\to S$
is a family of rational surface singularities, then such a finite
$\mathcal {X}\to S$
is a family of rational surface singularities, then such a finite
![]() $S'\to S$
exists if S maps to the so-called Artin component inside the versal deformation space of
$S'\to S$
exists if S maps to the so-called Artin component inside the versal deformation space of
![]() $x\in X$
. Moreover, due to the existence of flops, these simultaneous resolutions (if they exist) are not unique in general.
$x\in X$
. Moreover, due to the existence of flops, these simultaneous resolutions (if they exist) are not unique in general.
In the special case where
![]() $x\in X$
is a two-dimensional linearly reductive quotient singularity over some algebraically closed field k of characteristic
$x\in X$
is a two-dimensional linearly reductive quotient singularity over some algebraically closed field k of characteristic
![]() $p>0$
and where
$p>0$
and where
![]() $\mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
is the canonical lift of
$\mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
is the canonical lift of
![]() $x\in X$
, we will now show that there exists a simultaneous and minimal resolution of singularities over
$x\in X$
, we will now show that there exists a simultaneous and minimal resolution of singularities over
![]() $W(k)$
and that it is unique. This simultaneous resolution can be most elegantly constructed using the Ishii-Ito-Nakamura resolution from Section 4.3 in families.
$W(k)$
and that it is unique. This simultaneous resolution can be most elegantly constructed using the Ishii-Ito-Nakamura resolution from Section 4.3 in families.
Let k be an algebraically closed field of characteristic
![]() $p>0$
. Let G be a finite and linearly reductive group scheme over k and let
$p>0$
. Let G be a finite and linearly reductive group scheme over k and let
![]() $\rho :G\to {\mathbf {GL}}_{2,k}$
be a very small representation. Let
$\rho :G\to {\mathbf {GL}}_{2,k}$
be a very small representation. Let
![]() ${\mathcal G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the canonical lift of G and let
${\mathcal G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the canonical lift of G and let
![]() $\widetilde {\rho }:{\mathcal G}_{\mathrm {can}}\to {\mathbf {GL}}_{2,W(k)}$
be the lift of
$\widetilde {\rho }:{\mathcal G}_{\mathrm {can}}\to {\mathbf {GL}}_{2,W(k)}$
be the lift of
![]() $\rho $
to
$\rho $
to
![]() $W(k)$
. Let
$W(k)$
. Let
![]() ${\mathcal U}:={\mathbb {A}}^2_{W(k)}$
and let
${\mathcal U}:={\mathbb {A}}^2_{W(k)}$
and let
be the canonical lift of
![]() $x\in X$
. By [Reference BlumeBl11], there exists a
$x\in X$
. By [Reference BlumeBl11], there exists a
![]() ${\mathcal G}_{\mathrm {can}}$
-Hilbert scheme
${\mathcal G}_{\mathrm {can}}$
-Hilbert scheme
that parametrises
![]() ${\mathcal G}_{\mathrm {can}}$
-invariant subschemes
${\mathcal G}_{\mathrm {can}}$
-invariant subschemes
![]() $Z\subset {\mathcal U}$
that are finite and flat over
$Z\subset {\mathcal U}$
that are finite and flat over
![]() $W(k)$
(so-called
$W(k)$
(so-called
![]() ${\mathcal G}_{\mathrm {can}}-$
clusters) and such that the
${\mathcal G}_{\mathrm {can}}-$
clusters) and such that the
![]() ${\mathcal G}_{\mathrm {can}}$
-representation on
${\mathcal G}_{\mathrm {can}}$
-representation on
![]() $H^0(Z,{\mathcal O}_Z)$
is the regular representation. Taking such a cluster Z to its
$H^0(Z,{\mathcal O}_Z)$
is the regular representation. Taking such a cluster Z to its
![]() ${\mathcal G}_{\mathrm {can}}$
-orbit (see, for example, [Reference BlumeBl11, Remark 3.3]) induces a morphism
${\mathcal G}_{\mathrm {can}}$
-orbit (see, for example, [Reference BlumeBl11, Remark 3.3]) induces a morphism
over
![]() $W(k)$
.
$W(k)$
.
Theorem 4.10. Keeping the assumptions and notations
is a simultaneous minimal resolution of singularities of the canonical lift
![]() $\mathcal {X}\to \mathrm {Spec}\: W(k)$
of the linearly reductive quotient singularity
$\mathcal {X}\to \mathrm {Spec}\: W(k)$
of the linearly reductive quotient singularity
![]() $x\in X=U/G$
.
$x\in X=U/G$
.
-
1. The simultaneous resolution
 $\widetilde {\pi }$
is unique up to isomorphism.
$\widetilde {\pi }$
is unique up to isomorphism. -
2. The exceptional locus of
 $\widetilde {\pi }$
is a union of
$\widetilde {\pi }$
is a union of
 ${\mathbb {P}}^1_{W(k)}$
’s meeting transversally and we denote by
${\mathbb {P}}^1_{W(k)}$
’s meeting transversally and we denote by
 $\Gamma $
its dual intersection graph.
$\Gamma $
its dual intersection graph. -
3. The special fibre and the generic fibre are linearly reductive quotient singularities of type
 $\Gamma $
and
$\Gamma $
and
 $\widetilde {\pi }$
identifies the components of the exceptional loci of
$\widetilde {\pi }$
identifies the components of the exceptional loci of
 $\widetilde {\pi }_k$
and
$\widetilde {\pi }_k$
and
 $\widetilde {\pi }_K$
.
$\widetilde {\pi }_K$
.
Proof. We recall that we defined
![]() $G_{\mathrm {can}}:={\mathcal G}_{\mathrm {can},K}$
, which will simplify the notation in the following. The generic and special fibre of (4.2) over K and k are isomorphic to
$G_{\mathrm {can}}:={\mathcal G}_{\mathrm {can},K}$
, which will simplify the notation in the following. The generic and special fibre of (4.2) over K and k are isomorphic to
respectively, by [Reference BlumeBl11, Remark 3.1]. Now,
![]() $G_{\mathrm {can},\overline {K}}\text{-}\mathrm {Hilb}({\mathcal U}_{\overline {K}}) \to {\mathcal U}_{\overline {K}}/G_{\mathrm {can},\overline {K}}$
and
$G_{\mathrm {can},\overline {K}}\text{-}\mathrm {Hilb}({\mathcal U}_{\overline {K}}) \to {\mathcal U}_{\overline {K}}/G_{\mathrm {can},\overline {K}}$
and
![]() $G\text{-}\mathrm {Hilb}(U) \to U/G$
, are minimal resolutions of singularities by Theorem 4.5. Thus,
$G\text{-}\mathrm {Hilb}(U) \to U/G$
, are minimal resolutions of singularities by Theorem 4.5. Thus,
![]() $G_{\mathrm {can}}\text{-}\mathrm {Hilb}({\mathcal U}_K) \to {\mathcal U}_K/G_{\mathrm {can}}$
is a resolution of singularities, which is minimal since it is minimal over
$G_{\mathrm {can}}\text{-}\mathrm {Hilb}({\mathcal U}_K) \to {\mathcal U}_K/G_{\mathrm {can}}$
is a resolution of singularities, which is minimal since it is minimal over
![]() $\overline {K}$
. Thus,
$\overline {K}$
. Thus,
![]() $\mathcal {Y}\to \mathcal {X}\to \mathrm {Spec}\: W(k)$
is a simultaneous minimal resolution of singularities.
$\mathcal {Y}\to \mathcal {X}\to \mathrm {Spec}\: W(k)$
is a simultaneous minimal resolution of singularities.
The exceptional fibres
![]() $\widetilde {\pi }_K$
and
$\widetilde {\pi }_K$
and
![]() $\widetilde {\pi }_k$
of
$\widetilde {\pi }_k$
of
![]() $\widetilde {\pi }$
over K and k are unions of
$\widetilde {\pi }$
over K and k are unions of
![]() ${\mathbb {P}}^1$
’s that intersect transversally. The types, that is dual resolution graphs, associated to
${\mathbb {P}}^1$
’s that intersect transversally. The types, that is dual resolution graphs, associated to
![]() $\widetilde {\pi }_K$
and
$\widetilde {\pi }_K$
and
![]() $\widetilde {\pi }_k$
are the same (see also Remark 4.4) and we denote this graph by
$\widetilde {\pi }_k$
are the same (see also Remark 4.4) and we denote this graph by
![]() $\Gamma $
. In particular, the exceptional fibres of
$\Gamma $
. In particular, the exceptional fibres of
![]() $\widetilde {\pi }_K$
and
$\widetilde {\pi }_K$
and
![]() $\widetilde {\pi }_k$
have the same numbers of irreducible components. In particular, the specialisation maps of Néron-Severi lattices
$\widetilde {\pi }_k$
have the same numbers of irreducible components. In particular, the specialisation maps of Néron-Severi lattices
are isometries of lattices. These identify the components of the exceptional loci of
![]() $\widetilde {\pi }_K$
and
$\widetilde {\pi }_K$
and
![]() $\widetilde {\pi }_k$
. Moreover, given such a component of the exceptional locus of
$\widetilde {\pi }_k$
. Moreover, given such a component of the exceptional locus of
![]() $\widetilde {\pi }_k$
, it is isomorphic to
$\widetilde {\pi }_k$
, it is isomorphic to
![]() ${\mathbb {P}}^1_k$
and it extends uniquely to a
${\mathbb {P}}^1_k$
and it extends uniquely to a
![]() ${\mathbb {P}}^1_{W(k)}$
in the exceptional locus of
${\mathbb {P}}^1_{W(k)}$
in the exceptional locus of
![]() $\widetilde {\pi }$
. This establishes claims (2) and (3).
$\widetilde {\pi }$
. This establishes claims (2) and (3).
It remains to prove claim (1): Let
![]() $\mathcal {Y}'\to \mathcal {X}\to \mathrm {Spec}\: W(k)$
be a simultaneous resolution of singularities that coincides with the minimal resolution on special and generic fibres, respectively. Let
$\mathcal {Y}'\to \mathcal {X}\to \mathrm {Spec}\: W(k)$
be a simultaneous resolution of singularities that coincides with the minimal resolution on special and generic fibres, respectively. Let
![]() $\alpha :\mathcal {Y}^{\prime }_K\,\to \,\mathcal {Y}_K$
be an isomorphism over
$\alpha :\mathcal {Y}^{\prime }_K\,\to \,\mathcal {Y}_K$
be an isomorphism over
![]() $\mathcal {X}_K$
and choose a relatively (to
$\mathcal {X}_K$
and choose a relatively (to
![]() $\mathcal {X}$
) ample invertible sheaf
$\mathcal {X}$
) ample invertible sheaf
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() $\mathcal {Y}_K$
. Then,
$\mathcal {Y}_K$
. Then,
![]() $\alpha ^*\mathcal {L}$
is relatively ample on
$\alpha ^*\mathcal {L}$
is relatively ample on
![]() $\mathcal {Y}_K$
. Since the types of the singularities of
$\mathcal {Y}_K$
. Since the types of the singularities of
![]() $\mathcal {X}_K$
and
$\mathcal {X}_K$
and
![]() $\mathcal {X}_k$
are the same, the fibres of
$\mathcal {X}_k$
are the same, the fibres of
![]() $\mathcal {Y}^{\prime }_K\to \mathcal {X}_K$
and
$\mathcal {Y}^{\prime }_K\to \mathcal {X}_K$
and
![]() $\mathcal {Y}^{\prime }_k\to \mathcal {Y}_k$
contain the same number of exceptional divisors. Thus, the specialisation map of Néron-Severi lattices
$\mathcal {Y}^{\prime }_k\to \mathcal {Y}_k$
contain the same number of exceptional divisors. Thus, the specialisation map of Néron-Severi lattices
![]() $\mathrm {NS}(\mathcal {Y}^{\prime }_K)\to \mathrm {NS}(\mathcal {Y}^{\prime }_k)$
is an injective map between two lattices of the same rank and the same discriminant, whence an isometry. Similarly, the specialisation map of Néron-Severi lattices
$\mathrm {NS}(\mathcal {Y}^{\prime }_K)\to \mathrm {NS}(\mathcal {Y}^{\prime }_k)$
is an injective map between two lattices of the same rank and the same discriminant, whence an isometry. Similarly, the specialisation map of Néron-Severi lattices
![]() $\mathrm {NS}(\mathcal {Y}_K)\to \mathrm {NS}(\mathcal {Y}_k)$
is an isometry. In particular, we can identify the components of the exceptional loci of
$\mathrm {NS}(\mathcal {Y}_K)\to \mathrm {NS}(\mathcal {Y}_k)$
is an isometry. In particular, we can identify the components of the exceptional loci of
![]() $\mathcal {Y}_K$
and
$\mathcal {Y}_K$
and
![]() $\mathcal {Y}_k$
. (If the types of
$\mathcal {Y}_k$
. (If the types of
![]() $\mathcal {X}_k$
and
$\mathcal {X}_k$
and
![]() $\mathcal {X}_K$
differ, then this specialisation map is usually only injective, there are usually more
$\mathcal {X}_K$
differ, then this specialisation map is usually only injective, there are usually more
![]() $(-2)$
-curves in the special fibre and this is also the place where the difficulties with flops begin.) In particular,
$(-2)$
-curves in the special fibre and this is also the place where the difficulties with flops begin.) In particular,
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\alpha ^*\mathcal {L}$
extend to relative ample invertible sheaves on
$\alpha ^*\mathcal {L}$
extend to relative ample invertible sheaves on
![]() $\mathcal {Y}$
and
$\mathcal {Y}$
and
![]() $\mathcal {Y}'$
, respectively. By [Reference KovacsKo09, Theorem 5.14], the isomorphism
$\mathcal {Y}'$
, respectively. By [Reference KovacsKo09, Theorem 5.14], the isomorphism
![]() $\alpha $
extends to an isomorphism
$\alpha $
extends to an isomorphism
![]() $\mathcal {Y}'\to \mathcal {Y}$
over
$\mathcal {Y}'\to \mathcal {Y}$
over
![]() $\mathcal {X}$
and the claimed uniqueness follows.
$\mathcal {X}$
and the claimed uniqueness follows.
4.6 Rational double point singularities and Klein singularities
We specialise Definition 4.2 to the following case.
Definition 4.11. A Klein singularity is a linearly reductive quotient singularity as in Definition 4.2 with
![]() $\dim V=2$
and
$\dim V=2$
and
![]() $\det \rho =1$
, that is,
$\det \rho =1$
, that is,
![]() $\rho $
is a homomorphism of G to
$\rho $
is a homomorphism of G to
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
In particular, a Klein singularity is a two-dimensional and linearly reductive quotient singularity, it is a rational surface singularity, and since
![]() $\det (\rho )=1$
, it is Gorenstein. Quite generally, rational and Gorenstein surface singularities are precisely the rational double point singularities [Reference ArtinAr66]. We refer to [Reference DurfeeDu79] or [Reference DemazureSSS] for more background on surface singularities and rational double point singularities.
$\det (\rho )=1$
, it is Gorenstein. Quite generally, rational and Gorenstein surface singularities are precisely the rational double point singularities [Reference ArtinAr66]. We refer to [Reference DurfeeDu79] or [Reference DemazureSSS] for more background on surface singularities and rational double point singularities.
If
![]() $x\in X$
is a rational double point, then its type
$x\in X$
is a rational double point, then its type
![]() $\Gamma $
is a simply-laced finite Dynkin graph. In characteristic zero, every rational double point singularity is taut. In positive characteristic, a Klein singularity is F-regular and thus, taut. In the case of rational double points, this also follows from Artin’s explicit classification [Reference ArtinAr77]. On the other hand, rational double point singularities that are not F-regular need not be taut. We have the following relation between rational double point singularities and Klein singularities in positive characteristic, see [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 11.2].
$\Gamma $
is a simply-laced finite Dynkin graph. In characteristic zero, every rational double point singularity is taut. In positive characteristic, a Klein singularity is F-regular and thus, taut. In the case of rational double points, this also follows from Artin’s explicit classification [Reference ArtinAr77]. On the other hand, rational double point singularities that are not F-regular need not be taut. We have the following relation between rational double point singularities and Klein singularities in positive characteristic, see [Reference Liedtke, Martin and MatsumotoLMM21, Theorem 11.2].
Theorem 4.12. Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. Let
$p\geq 0$
. Let
![]() $x\in X$
be a normal surface singularity over k.
$x\in X$
be a normal surface singularity over k.
-
1. If
 $p=0$
or
$p=0$
or
 $p\geq 7$
, then
$p\geq 7$
, then
 $x\in X$
is a Klein singularity if and only if
$x\in X$
is a Klein singularity if and only if
 $x\in X$
is a rational double point singularity.
$x\in X$
is a rational double point singularity. -
2. If
 $p>0$
, then
$p>0$
, then
 $x\in X$
is a Klein singularity if and only if
$x\in X$
is a Klein singularity if and only if
 $x\in X$
is a rational double point singularity and F-regular. The finite Dynkin graphs of these singularities are of type
$x\in X$
is a rational double point singularity and F-regular. The finite Dynkin graphs of these singularities are of type  $$ \begin{align*}\begin{array}{lcl} A_n, D_n, E_6, E_7, E_8 &\quad \mbox{if} \quad & p\geq7, \\ A_n, D_n, E_6, E_7 &\quad \mbox{if} \quad & p=5,\\ A_n, D_n &\quad \mbox{if} \quad & p=3, \\ A_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{lcl} A_n, D_n, E_6, E_7, E_8 &\quad \mbox{if} \quad & p\geq7, \\ A_n, D_n, E_6, E_7 &\quad \mbox{if} \quad & p=5,\\ A_n, D_n &\quad \mbox{if} \quad & p=3, \\ A_n &\quad \mbox{if} \quad &p=2. \end{array} \end{align*} $$
A Klein singularity
![]() $x\in X=U/G$
is a linearly reductive quotient singularity and thus, determines G and
$x\in X=U/G$
is a linearly reductive quotient singularity and thus, determines G and
![]() $\rho :G\to {\mathbf {SL}}_{2,k}$
up to isomorphism and conjugacy, respectively. Thus, the classification of Klein singularities boils down to the classification of finite and linearly reductive subgroup schemes of
$\rho :G\to {\mathbf {SL}}_{2,k}$
up to isomorphism and conjugacy, respectively. Thus, the classification of Klein singularities boils down to the classification of finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
and we refer to Remark 4.4 for this classification.
${\mathbf {SL}}_{2,k}$
and we refer to Remark 4.4 for this classification.
5 Hecke correspondences
Let
![]() $x\in X=U/G$
be a Klein singularity over an algebraically closed field k of characteristic
$x\in X=U/G$
be a Klein singularity over an algebraically closed field k of characteristic
![]() $p>0$
. In Section 2.2, we discussed the canonical lift
$p>0$
. In Section 2.2, we discussed the canonical lift
![]() $\mathcal {X}\to \mathrm {Spec}\: W(k)$
of
$\mathcal {X}\to \mathrm {Spec}\: W(k)$
of
![]() $x\in X$
and in Section 4.5 we established a simultaneous minimal resolution of singularities of the canonical lift. More precisely, this simultaneous resolution was constructed using G-Hilbert schemes extending previous work of Ishii, Ito and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ito and NakamuraIN99].
$x\in X$
and in Section 4.5 we established a simultaneous minimal resolution of singularities of the canonical lift. More precisely, this simultaneous resolution was constructed using G-Hilbert schemes extending previous work of Ishii, Ito and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ito and NakamuraIN99].
In this section, we refine this resolution of singularities as in the work of Ito and Nakamura [Reference Ito and NakamuraIN99] and Nakajima [Reference NakajimaNa96, Reference NakajimaNa01]: we eventually obtain a bijection between the components of the minimal resolution of singularities of the Klein singularity
![]() $x\in X=U/G$
and the simple and non-trivial representations of G using special Hecke correspondences.
$x\in X=U/G$
and the simple and non-trivial representations of G using special Hecke correspondences.
5.1 The Ito-Nakamura resolution revisited
We first slightly extend the setup of Section 4.3. Let k be an algebraically closed field of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $x\in X=U/G$
be a Klein singularity as in Definition 4.11, that is, we have
$x\in X=U/G$
be a Klein singularity as in Definition 4.11, that is, we have
![]() $U={\mathbb {A}}^2_k$
and G a very small, finite and linearly reductive subgroup scheme of
$U={\mathbb {A}}^2_k$
and G a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
Let
![]() $\{\rho _i\}_{i\in I}$
be the set of isomorphism classes of simple representations of G. Given a finite-dimensional representation
$\{\rho _i\}_{i\in I}$
be the set of isomorphism classes of simple representations of G. Given a finite-dimensional representation
![]() $\rho $
of G, there exist non-negative integers
$\rho $
of G, there exist non-negative integers
![]() $\nu _i\in {\mathbb {Z}}_+$
, such that
$\nu _i\in {\mathbb {Z}}_+$
, such that
![]() $\rho $
is isomorphic to
$\rho $
is isomorphic to
![]() $\bigoplus _i\rho _i^{\oplus \nu _i}$
and we combine these into a multi-index
$\bigoplus _i\rho _i^{\oplus \nu _i}$
and we combine these into a multi-index
![]() $\nu =(\{\nu _i\})\in {\mathbb {Z}}_{\geq 0}^I$
. We set
$\nu =(\{\nu _i\})\in {\mathbb {Z}}_{\geq 0}^I$
. We set
![]() $\dim (\nu ):=\sum _i\nu _i\dim \rho _i$
, which is the dimension of the representation associated to
$\dim (\nu ):=\sum _i\nu _i\dim \rho _i$
, which is the dimension of the representation associated to
![]() $\nu $
.
$\nu $
.
For any integer
![]() $n\geq 1$
, the G-action on U induces a G-action on the Hilbert scheme
$n\geq 1$
, the G-action on U induces a G-action on the Hilbert scheme
![]() $\mathrm {Hilb}^n(U)$
, which parametrises zero-dimensional subschemes of length n of U. We consider the fixed point scheme
$\mathrm {Hilb}^n(U)$
, which parametrises zero-dimensional subschemes of length n of U. We consider the fixed point scheme
that is, the largest subscheme of
![]() $\mathrm {Hilb}^n(U)$
on which G acts trivially. It parametrises G-invariant and zero-dimensional subschemes of length n of U. Given
$\mathrm {Hilb}^n(U)$
on which G acts trivially. It parametrises G-invariant and zero-dimensional subschemes of length n of U. Given
![]() $\nu =(\{\nu _i\})_i\in {\mathbb {Z}}_{\geq 0}^I$
with
$\nu =(\{\nu _i\})_i\in {\mathbb {Z}}_{\geq 0}^I$
with
![]() $\dim (\nu )=n$
, we define
$\dim (\nu )=n$
, we define
which defines a subscheme of
![]() $\mathrm {Hilb}^{n,G}(U)$
. Adapting [Reference KirillovKi16, Lemma 12.4], which follows [Reference Ito and NakamuraIN99, Section 9], to our situation, we have the following.
$\mathrm {Hilb}^{n,G}(U)$
. Adapting [Reference KirillovKi16, Lemma 12.4], which follows [Reference Ito and NakamuraIN99, Section 9], to our situation, we have the following.
Lemma 5.1. We keep the assumptions and notations and let
![]() $n\geq 1$
be an integer.
$n\geq 1$
be an integer.
-
1. The scheme
 $\mathrm {Hilb}^{n,G}(U)$
is smooth over k.
$\mathrm {Hilb}^{n,G}(U)$
is smooth over k. -
2. We have a decomposition
where the disjoint union runs over all multi-indices $$ \begin{align*}\mathrm{Hilb}^{n,G}(U) \,=\, \bigsqcup_{\nu}\, H^\nu, \end{align*} $$
$$ \begin{align*}\mathrm{Hilb}^{n,G}(U) \,=\, \bigsqcup_{\nu}\, H^\nu, \end{align*} $$
 $\nu \in {\mathbb {Z}}_{\geq 0}^I$
of dimension n. Each
$\nu \in {\mathbb {Z}}_{\geq 0}^I$
of dimension n. Each
 $H^\nu $
is a smooth subscheme of
$H^\nu $
is a smooth subscheme of
 $\mathrm {Hilb}^{n,G}(U)$
.
$\mathrm {Hilb}^{n,G}(U)$
.
Proof. Since U is two-dimensional,
![]() $\mathrm {Hilb}^n(U)$
is smooth over k by [Reference FogartyFo68, Theorem 2.4]. To show Claim (1), it remains to show that the fixed point scheme for the G-action is also smooth, which follows from Lemma 5.2 below. Then, Claim (2) is obvious.
$\mathrm {Hilb}^n(U)$
is smooth over k by [Reference FogartyFo68, Theorem 2.4]. To show Claim (1), it remains to show that the fixed point scheme for the G-action is also smooth, which follows from Lemma 5.2 below. Then, Claim (2) is obvious.
Lemma 5.2. Let k be an algebraically closed field, let X be a scheme that is smooth over k, let G be a finite and linearly reductive group scheme over k and assume that G acts on X. Then, the fixed point scheme
![]() $X^G\subseteq X$
is smooth over k.
$X^G\subseteq X$
is smooth over k.
Proof. Let
![]() $x\in X^G$
. Passing to the completion of the local ring
$x\in X^G$
. Passing to the completion of the local ring
![]() ${\mathcal O}_{X,x}$
, using that X is smooth over k and passing to coordinates such that the G-action is linear (this is always possible by [Reference SatrianoSa12, proof of Corollary 1.8]), we may assume that
${\mathcal O}_{X,x}$
, using that X is smooth over k and passing to coordinates such that the G-action is linear (this is always possible by [Reference SatrianoSa12, proof of Corollary 1.8]), we may assume that
and that the G-action is linear. In this description it is easy to see that the G-invariant subscheme of
![]() $\mathrm {Spec}\:\widehat {{\mathcal O}}_{X,x}$
is smooth (see also the proof of [Reference Ito and NakamuraIN99, Lemma 9.1]), which implies that
$\mathrm {Spec}\:\widehat {{\mathcal O}}_{X,x}$
is smooth (see also the proof of [Reference Ito and NakamuraIN99, Lemma 9.1]), which implies that
![]() $X^G$
is smooth near x.
$X^G$
is smooth near x.
An important special case is the regular representation of G, where we have
![]() $\nu _i=\dim \rho _i$
for all i and in this case, we will write
$\nu _i=\dim \rho _i$
for all i and in this case, we will write
![]() $\delta $
for the corresponding multi-index. The dimension of
$\delta $
for the corresponding multi-index. The dimension of
![]() $\delta $
is equal to the length of G. In this case, we have
$\delta $
is equal to the length of G. In this case, we have
which we already studied in Section 4.3. There, we saw that
![]() $\pi $
is a minimal resolution of singularities of the Klein singularity
$\pi $
is a minimal resolution of singularities of the Klein singularity
![]() $x\in X=U/G$
.
$x\in X=U/G$
.
5.2 Hecke correspondences
We keep the assumptions and notations of the previous section. We let n be the length of G and let
![]() $\delta $
be the multi-index corresponding to the regular representation. For
$\delta $
be the multi-index corresponding to the regular representation. For
![]() $i\in I$
, we set
$i\in I$
, we set
![]() $\alpha _i:=(0,...,0,1,0...)$
with the non-zero entry in the i.th position. We define
$\alpha _i:=(0,...,0,1,0...)$
with the non-zero entry in the i.th position. We define
which is a Hecke correspondence, see [Reference NakajimaNa96], [Reference NakajimaNa01, Section 6.1] or [Reference KirillovKi16, Section 12.4]. We let
be the image under the projection
![]() $\mathrm {pr}_2$
onto the second factor.
$\mathrm {pr}_2$
onto the second factor.
In characteristic zero, the following result is due to Nakajima [Reference NakajimaNa96] and independently to Ito and Nakamura [Reference Ito and NakamuraIN99], see also [Reference KirillovKi16, Section 12.4].
Theorem 5.3. Let k be an algebraically closed field of characteristic
![]() $p\geq 0$
. Let G be a finite and linearly reductive subgroup scheme of
$p\geq 0$
. Let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
, let
${\mathbf {SL}}_{2,k}$
, let
![]() $x\in X:=U/G$
be the associated Klein singularity, and let
$x\in X:=U/G$
be the associated Klein singularity, and let
![]() $\pi :H^\delta \to X$
be the Ito-Nakamura resolution.
$\pi :H^\delta \to X$
be the Ito-Nakamura resolution.
-
1. The assignment
 $i\mapsto E_i$
defines a bijection between the set
$i\mapsto E_i$
defines a bijection between the set
 $\{\rho _i\}_i$
of isomorphism classes of non-trivial simple representations of G and the set of irreducible components of the exceptional divisor
$\{\rho _i\}_i$
of isomorphism classes of non-trivial simple representations of G and the set of irreducible components of the exceptional divisor
 $\mathrm {Exc}(\pi )$
of
$\mathrm {Exc}(\pi )$
of
 $\pi $
.
$\pi $
. -
2. If
 $i\neq j$
, then where the numbering of the
$i\neq j$
, then where the numbering of the $$ \begin{align*}B_i\cdot B_j \,=\, A_{ij} \end{align*} $$
$$ \begin{align*}B_i\cdot B_j \,=\, A_{ij} \end{align*} $$
 $\{\rho _i\}_i$
is as in [Reference Ito and NakamuraIN99, Section 10].
$\{\rho _i\}_i$
is as in [Reference Ito and NakamuraIN99, Section 10].
We thus obtain a bijection between the dual resolution graph of
![]() $\pi $
and the graph obtained by removing the vertex
$\pi $
and the graph obtained by removing the vertex
![]() $\rho _0$
from the McKay graph of G with respect to the embedding
$\rho _0$
from the McKay graph of G with respect to the embedding
![]() $G\to {\mathbf {SL}}_{2,k}\to {\mathbf {GL}}_{2,k}$
.
$G\to {\mathbf {SL}}_{2,k}\to {\mathbf {GL}}_{2,k}$
.
Proof. The case-by-case analysis of [Reference Ito and NakamuraIN99, Section 12] carries directly over from finite subgroups of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
to finite and linearly reductive subgroup schemes of
${\mathbf {SL}}_2({\mathbb {C}})$
to finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
Here is a second proof of this theorem that uses our lifting results:
Proof. If
![]() $p=0$
, then the Lefschetz principle allows to reduce to
$p=0$
, then the Lefschetz principle allows to reduce to
![]() $k={\mathbb {C}}$
, where the theorem is due to Ito, Nakajima and Nakamura [Reference Ito and NakamuraIN99, Reference NakajimaNa96].
$k={\mathbb {C}}$
, where the theorem is due to Ito, Nakajima and Nakamura [Reference Ito and NakamuraIN99, Reference NakajimaNa96].
We now assume
![]() $p>0$
. Let
$p>0$
. Let
![]() $\mathcal {X}_{\mathrm {can}}={\mathcal U}/{\mathcal G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the canonical lift of
$\mathcal {X}_{\mathrm {can}}={\mathcal U}/{\mathcal G}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the canonical lift of
![]() $x\in X=U/G$
(see Section 4.4) and let
$x\in X=U/G$
(see Section 4.4) and let
![]() $\widetilde {\pi }:\mathcal {Y}\to \mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the simultaneous resolution of singularities (see Section 4.5). Moreover, we have the abstract group
$\widetilde {\pi }:\mathcal {Y}\to \mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
be the simultaneous resolution of singularities (see Section 4.5). Moreover, we have the abstract group
![]() $G_{\mathrm {abs}}$
and the canonical lift
$G_{\mathrm {abs}}$
and the canonical lift
![]() $G_{\mathrm {can}}$
associated to G (see Section 2.2) and we have a bijection of simple representations of
$G_{\mathrm {can}}$
associated to G (see Section 2.2) and we have a bijection of simple representations of
![]() $G_{\mathrm {abs}}$
,
$G_{\mathrm {abs}}$
,
![]() $G_{\mathrm {can}}$
and G by Proposition 2.6.
$G_{\mathrm {can}}$
and G by Proposition 2.6.
The generic fibre
![]() $\mathcal {X}_K$
is isomorphic to
$\mathcal {X}_K$
is isomorphic to
![]() ${\mathcal U}_K/G_{\mathrm {can}}$
and using the Lefschetz principle, the geometric generic fibre can be identified with
${\mathcal U}_K/G_{\mathrm {can}}$
and using the Lefschetz principle, the geometric generic fibre can be identified with
![]() ${\mathbb {C}}^2/G_{\mathrm {abs}}$
. Over
${\mathbb {C}}^2/G_{\mathrm {abs}}$
. Over
![]() ${\mathbb {C}}$
, we have Theorem 5.3 for
${\mathbb {C}}$
, we have Theorem 5.3 for
![]() $G_{\mathrm {abs}}$
$G_{\mathrm {abs}}$
![]() ${\mathbb {C}}^2/G_{\mathrm {abs}}$
and its minimal resolution of singularities by [Reference Ito and NakamuraIN99, Reference NakajimaNa96].
${\mathbb {C}}^2/G_{\mathrm {abs}}$
and its minimal resolution of singularities by [Reference Ito and NakamuraIN99, Reference NakajimaNa96].
By the Lefschetz principle, we have it for
![]() $G_{\mathrm {can}}$
,
$G_{\mathrm {can}}$
,
![]() $\mathcal {X}_K={\mathcal U}_{K}/G_{\mathrm {can}}$
and
$\mathcal {X}_K={\mathcal U}_{K}/G_{\mathrm {can}}$
and
![]() $\widetilde {\pi }_K$
. Using the comparison results Proposition 2.6 and Theorem 4.10, we obtain it for
$\widetilde {\pi }_K$
. Using the comparison results Proposition 2.6 and Theorem 4.10, we obtain it for
![]() $\mathcal {X}_k={\mathcal U}_k/{\mathcal G}_{\mathrm {can},k}$
and
$\mathcal {X}_k={\mathcal U}_k/{\mathcal G}_{\mathrm {can},k}$
and
![]() $\widetilde {\pi }_k$
, that is, for
$\widetilde {\pi }_k$
, that is, for
![]() $X=U/G$
, G and
$X=U/G$
, G and
![]() $\pi $
.
$\pi $
.
5.3 Local McKay correspondence
We now extend work of Ishii and Nakamura [Reference IshiiIs02, Reference Ishii and NakamuraIN19] to our linearly reductive setting. Let G be a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
and let
${\mathbf {GL}}_{2,k}$
and let
![]() $x\in X=U/G$
be the associated two-dimensional linearly reductive quotient singularity. Until the end of this section, we do not require it to be a Klein singularity. Note that in dimension two, linearly reductive quotient singularities are the same as F-regular singularities, see Remark 4.6.
$x\in X=U/G$
be the associated two-dimensional linearly reductive quotient singularity. Until the end of this section, we do not require it to be a Klein singularity. Note that in dimension two, linearly reductive quotient singularities are the same as F-regular singularities, see Remark 4.6.
Let
![]() $\{\rho _i\}_i$
be the set of simple representations of G. Let
$\{\rho _i\}_i$
be the set of simple representations of G. Let
![]() $\rho _0$
be the trivial representation and we choose our numbering of the
$\rho _0$
be the trivial representation and we choose our numbering of the
![]() $\rho _i$
’s to be the one of [Reference Ishii and NakamuraIN19, Theorem 3.6]. Let
$\rho _i$
’s to be the one of [Reference Ishii and NakamuraIN19, Theorem 3.6]. Let
![]() $\pi :Y\to X$
be its minimal resolution of singularities and let
$\pi :Y\to X$
be its minimal resolution of singularities and let
![]() $\{E_i\}$
be the irreducible components of the exceptional divisor
$\{E_i\}$
be the irreducible components of the exceptional divisor
![]() $\textrm {Exc}(\pi )$
of
$\textrm {Exc}(\pi )$
of
![]() $\pi $
. Then, there is exists a connection between the
$\pi $
. Then, there is exists a connection between the
![]() $\{\rho _i\}$
and the exceptional divisors of
$\{\rho _i\}$
and the exceptional divisors of
![]() $\pi $
as follows - this is yet another version of the McKay correspondence.
$\pi $
as follows - this is yet another version of the McKay correspondence.
Theorem 5.4. Keeping assumptions and notations, let
![]() ${\mathfrak m}\subset {\mathcal O}_U$
be the maximal ideal corresponding to the origin, let
${\mathfrak m}\subset {\mathcal O}_U$
be the maximal ideal corresponding to the origin, let
![]() $y\in Y$
be a closed point, let
$y\in Y$
be a closed point, let
![]() $Z_y$
be the G-invariant cluster of U corresponding to y and let
$Z_y$
be the G-invariant cluster of U corresponding to y and let
![]() ${\mathcal I}_{Z_y}\subset {\mathcal O}_U$
be its ideal sheaf. Then, the G-representation on
${\mathcal I}_{Z_y}\subset {\mathcal O}_U$
be its ideal sheaf. Then, the G-representation on
![]() ${\mathcal I}_{Z_y}/{\mathfrak m}{\mathcal I}_{Z_y}$
is given by
${\mathcal I}_{Z_y}/{\mathfrak m}{\mathcal I}_{Z_y}$
is given by
 $$ \begin{align*}\left\{ \begin{array}{ll} \rho_i\,\oplus\,\rho_0 &\quad \mbox{if }y\in E_i\,\backslash\,\bigcup_{j\neq i}E_j\\ \rho_i\,\oplus\,\rho_j\,\oplus\,\rho_0 & \quad \mbox{if }y\in E_i\cap E_j \quad \mbox{with} \quad i\neq j. \end{array} \right. \end{align*} $$
$$ \begin{align*}\left\{ \begin{array}{ll} \rho_i\,\oplus\,\rho_0 &\quad \mbox{if }y\in E_i\,\backslash\,\bigcup_{j\neq i}E_j\\ \rho_i\,\oplus\,\rho_j\,\oplus\,\rho_0 & \quad \mbox{if }y\in E_i\cap E_j \quad \mbox{with} \quad i\neq j. \end{array} \right. \end{align*} $$
Proof. For
![]() $k={\mathbb {C}}$
, this is [Reference IshiiIs02, Theorem 7.1]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
$k={\mathbb {C}}$
, this is [Reference IshiiIs02, Theorem 7.1]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
![]() ${\mathbf {GL}}_{2}(k)$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 3.6]. However, these proofs also work if G is a very small and finite and linearly reductive subgroup scheme of
${\mathbf {GL}}_{2}(k)$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 3.6]. However, these proofs also work if G is a very small and finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
.
${\mathbf {GL}}_{2,k}$
.
Remark 5.5. In [Reference Ishii and NakamuraIN19], the G-quiver structure of
![]() $G\text{-}\mathrm {Hilb}(U)$
was studied in the case where G is a very small and finite subgroup of
$G\text{-}\mathrm {Hilb}(U)$
was studied in the case where G is a very small and finite subgroup of
![]() ${\mathbf {GL}}_{2}(k)$
. We leave the extension of these results to the linearly reductive case to the reader.
${\mathbf {GL}}_{2}(k)$
. We leave the extension of these results to the linearly reductive case to the reader.
5.4 Reflexive sheaves on the minimal resolution
We end this section by shortly digressing on work of Wunram [Reference WunramWu88], Ishii and Nakamura [Reference Ishii and NakamuraIN19], which generalises work of Artin and Verdier [Reference Artin and VerdierAV85]. We keep the assumptions and notations from Section 5.3. Let
![]() $F\subset Y$
be the fundamental divisor of
$F\subset Y$
be the fundamental divisor of
![]() $\pi $
, see [Reference ArtinAr66].
$\pi $
, see [Reference ArtinAr66].
Theorem 5.6. Keeping assumptions and notations, there exists a bijection between
-
1. the set of irreducible components
 $\{E_i\}$
of
$\{E_i\}$
of
 $\mathrm {Exc}(\pi )$
and
$\mathrm {Exc}(\pi )$
and -
2. the set of non-trivial indecomposable full
 ${\mathcal O}_Y$
-modules
${\mathcal O}_Y$
-modules
 $\{{\mathcal M}_i\}$
, special in the sense that
$\{{\mathcal M}_i\}$
, special in the sense that
 $H^1(Y,{\mathcal M}_i^{\vee })=0$
$H^1(Y,{\mathcal M}_i^{\vee })=0$
This correspondence
![]() ${\mathcal M}_i\mapsto E_i$
is defined by
${\mathcal M}_i\mapsto E_i$
is defined by
The rank of
![]() ${\mathcal M}_i$
is equal to
${\mathcal M}_i$
is equal to
![]() $c_1({\mathcal M}_i)\cdot F$
, the multiplicity of
$c_1({\mathcal M}_i)\cdot F$
, the multiplicity of
![]() $E_i$
in F.
$E_i$
in F.
Proof. For
![]() $k={\mathbb {C}}$
, this is [Reference WunramWu88]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
$k={\mathbb {C}}$
, this is [Reference WunramWu88]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
![]() ${\mathbf {GL}}_{2,k}$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 2.8]. However, these proofs also work if G is a very small, finite and linearly reductive subgroup scheme of
${\mathbf {GL}}_{2,k}$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 2.8]. However, these proofs also work if G is a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
.
${\mathbf {GL}}_{2,k}$
.
Here, a full
![]() ${\mathcal O}_Y$
-module is as defined in [Reference Ishii and NakamuraIN19, Definition 2.4]. By [Reference Ishii and NakamuraIN19, Corollary 2.5], the assignment
${\mathcal O}_Y$
-module is as defined in [Reference Ishii and NakamuraIN19, Definition 2.4]. By [Reference Ishii and NakamuraIN19, Corollary 2.5], the assignment
![]() ${\mathcal M}\mapsto \pi _*{\mathcal M}$
sets up a bijection between the set of (indecomposable) full
${\mathcal M}\mapsto \pi _*{\mathcal M}$
sets up a bijection between the set of (indecomposable) full
![]() ${\mathcal O}_Y$
-modules with the set of (indecomposable) reflexive
${\mathcal O}_Y$
-modules with the set of (indecomposable) reflexive
![]() ${\mathcal O}_X$
-modules. In particular, the above theorem yields a bijection between the set of irreducible components of
${\mathcal O}_X$
-modules. In particular, the above theorem yields a bijection between the set of irreducible components of
![]() $\mathrm {Exc}(\pi )$
and the set of non-trivial, indecomposable and reflexive
$\mathrm {Exc}(\pi )$
and the set of non-trivial, indecomposable and reflexive
![]() ${\mathcal O}_X$
-modules.
${\mathcal O}_X$
-modules.
Remark 5.7. The group scheme G plays no rôle in this theorem and the discussion thereafter. Probably, these results should be viewed as results on two-dimensional F-regular singularities (see Remark 4.6).
6 Conjugacy classes and Ito-Reid correspondence
For a finite group, the number of isomorphism classes of complex simple representations is equal to the number of conjugacy classes. Thus, one can choose a bijection between these two sets. In particular, for a finite subgroup of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
one can choose a bijection between the vertices of its McKay graph and the conjugacy classes of G. In [Reference Ito and ReidIR96], Ito and Reid gave a canonical bijection between these two sets. In this section, we extend this Ito-Reid correspondence to finite and linearly reductive subgroup schemes of
${\mathbf {SL}}_2({\mathbb {C}})$
one can choose a bijection between the vertices of its McKay graph and the conjugacy classes of G. In [Reference Ito and ReidIR96], Ito and Reid gave a canonical bijection between these two sets. In this section, we extend this Ito-Reid correspondence to finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{2,k}$
. The main difficulty is to define a suitable notion of conjugacy classes for finite and linearly reductive group schemes.
${\mathbf {SL}}_{2,k}$
. The main difficulty is to define a suitable notion of conjugacy classes for finite and linearly reductive group schemes.
6.1 Conjugacy classes
Given a finite group
![]() $G_{\mathrm {abs}}$
, a representation
$G_{\mathrm {abs}}$
, a representation
![]() $\rho :G_{\mathrm {abs}}\to {\mathbf {GL}}_n({\mathbb {C}})$
and an element
$\rho :G_{\mathrm {abs}}\to {\mathbf {GL}}_n({\mathbb {C}})$
and an element
![]() $g\in G_{\mathrm {abs}}$
, we have the trace
$g\in G_{\mathrm {abs}}$
, we have the trace
![]() $\mathrm {tr}(\rho (g))\in {\mathbb {C}}$
. This pairing
$\mathrm {tr}(\rho (g))\in {\mathbb {C}}$
. This pairing
![]() $(\rho ,g)\mapsto \mathrm {tr}(\rho (g))$
induces a non-degenerate pairing between isomorphism classes of simple representations of
$(\rho ,g)\mapsto \mathrm {tr}(\rho (g))$
induces a non-degenerate pairing between isomorphism classes of simple representations of
![]() $G_{\mathrm {abs}}$
and conjugacy classes. Thus, conjugacy classes can be thought of as being “dual” to semi-simple representations, which can be used to give an unusual definition of conjugacy classes. This definition generalises to finite and linearly reductive group schemes. More precisely, we make the following definition, which is inspired by a result of Serre [Reference SerreSe77, Section 11.4] and which we discuss in detail in Appendix B.2.
$G_{\mathrm {abs}}$
and conjugacy classes. Thus, conjugacy classes can be thought of as being “dual” to semi-simple representations, which can be used to give an unusual definition of conjugacy classes. This definition generalises to finite and linearly reductive group schemes. More precisely, we make the following definition, which is inspired by a result of Serre [Reference SerreSe77, Section 11.4] and which we discuss in detail in Appendix B.2.
Definition 6.1. Let G be a finite and linearly reductive group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. Then, the set of conjugacy classes is defined to be
$p\geq 0$
. Then, the set of conjugacy classes is defined to be
![]() $\mathrm {Spec}\: {\mathbb {C}}\otimes K_k(G)$
.
$\mathrm {Spec}\: {\mathbb {C}}\otimes K_k(G)$
.
We discuss several approaches to conjugacy classes for finite group schemes in Appendix B - there, we hope to convince the reader that Definition 6.1 is the best for the purposes of this article. For example, by Proposition B.2 it is compatible with canonical lifts and there is a natural bijection with the set of conjugacy classes of the abstract group
![]() $G_{\mathrm {abs}}$
associated to G. Concerning the choice of field
$G_{\mathrm {abs}}$
associated to G. Concerning the choice of field
![]() ${\mathbb {C}}$
in Definition 6.1, we refer to Remarks B.3.
${\mathbb {C}}$
in Definition 6.1, we refer to Remarks B.3.
6.2 An explicit bijection
For a finite and linearly reductive subgroup scheme G of
![]() ${\mathbf {SL}}_{2,k}$
, we have an associated embedding of the finite group
${\mathbf {SL}}_{2,k}$
, we have an associated embedding of the finite group
![]() $G_{\mathrm {abs}}$
into
$G_{\mathrm {abs}}$
into
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
. Let
${\mathbf {SL}}_2({\mathbb {C}})$
. Let
![]() $\{\rho _i\}_i$
be the set of isomorphism classes of semi-simple representations of G and let
$\{\rho _i\}_i$
be the set of isomorphism classes of semi-simple representations of G and let
![]() $\{\rho _{\mathrm {abs},i}\}_i$
be the corresponding set for
$\{\rho _{\mathrm {abs},i}\}_i$
be the corresponding set for
![]() $G_{\mathrm {abs}}$
obtained by Proposition 2.6. The associated McKay graphs
$G_{\mathrm {abs}}$
obtained by Proposition 2.6. The associated McKay graphs
![]() $\Gamma (G,\rho ,\{\rho _i\}_i)$
and
$\Gamma (G,\rho ,\{\rho _i\}_i)$
and
![]() $\Gamma (G_{\mathrm {abs}},\rho _{\mathrm {abs}}, \{\rho _{\mathrm {abs},i}\}_i)$
coincide by Proposition 3.5 and we denote both by
$\Gamma (G_{\mathrm {abs}},\rho _{\mathrm {abs}}, \{\rho _{\mathrm {abs},i}\}_i)$
coincide by Proposition 3.5 and we denote both by
![]() $\widehat {\Gamma }$
. Next, the group
$\widehat {\Gamma }$
. Next, the group
![]() $G_{\mathrm {abs}}$
admits a presentation of the form
$G_{\mathrm {abs}}$
admits a presentation of the form
for suitable non-negative integers
![]() $r,s,t$
. The non-trivial conjugacy classes of
$r,s,t$
. The non-trivial conjugacy classes of
![]() $G_{\mathrm {abs}}$
can be uniquely represented by the following elements
$G_{\mathrm {abs}}$
can be uniquely represented by the following elements
This allows to give an explicit bijection between the conjugacy classes of
![]() $G_{\mathrm {abs}}$
and the vertices of
$G_{\mathrm {abs}}$
and the vertices of
![]() $\widehat {\Gamma }$
. We refer to [Reference KirillovKi16, Section 2] for details. Using Proposition B.2, we obtain an explicit bijection between the conjugacy classes of G and the vertices of
$\widehat {\Gamma }$
. We refer to [Reference KirillovKi16, Section 2] for details. Using Proposition B.2, we obtain an explicit bijection between the conjugacy classes of G and the vertices of
![]() $\widehat {\Gamma }$
.
$\widehat {\Gamma }$
.
6.3 The Ito-Reid correspondence
If G is a finite subgroup of
![]() ${\mathbf {SL}}_2({\mathbb {C}})$
, then Ito and Reid [Reference Ito and ReidIR96] (see also [Reference ReidRe02]) constructed a canonical bijection. Let us run through [Reference ReidRe02, Section 2] and show that this can be carried over to our linearly reductive setting: let k be an algebraically closed field of characteristic
${\mathbf {SL}}_2({\mathbb {C}})$
, then Ito and Reid [Reference Ito and ReidIR96] (see also [Reference ReidRe02]) constructed a canonical bijection. Let us run through [Reference ReidRe02, Section 2] and show that this can be carried over to our linearly reductive setting: let k be an algebraically closed field of characteristic
![]() $p>0$
and let G be a finite and linearly reductive subgroup scheme of
$p>0$
and let G be a finite and linearly reductive subgroup scheme of
![]() ${\mathbf {SL}}_{2,k}$
.
${\mathbf {SL}}_{2,k}$
.
-
1. Associated to G, we have the abstract group
 $G_{\mathrm {abs}}$
. By Proposition 2.6, an embedding
$G_{\mathrm {abs}}$
. By Proposition 2.6, an embedding
 $G\to {\mathbf {SL}}_{n,k}$
yields an embedding
$G\to {\mathbf {SL}}_{n,k}$
yields an embedding
 $G_{\mathrm {abs}}\to {\mathbf {SL}}_n({\mathbb {C}})$
. By Proposition B.2, we can identify conjugacy classes of G (in the sense of Definition 6.1) and conjugacy classes of
$G_{\mathrm {abs}}\to {\mathbf {SL}}_n({\mathbb {C}})$
. By Proposition B.2, we can identify conjugacy classes of G (in the sense of Definition 6.1) and conjugacy classes of
 $G_{\mathrm {abs}}$
, which allows us to define the age of a conjugacy class of G via the corresponding notion for
$G_{\mathrm {abs}}$
, which allows us to define the age of a conjugacy class of G via the corresponding notion for
 $G_{\mathrm {abs}}$
as, for example, in [Reference ReidRe02, Section 2]. A conjugacy class of age 1 is called junior and if
$G_{\mathrm {abs}}$
as, for example, in [Reference ReidRe02, Section 2]. A conjugacy class of age 1 is called junior and if
 $n=2$
, then all conjugacy classes are junior.
$n=2$
, then all conjugacy classes are junior.
Remark 6.2. Using the “toric mechanism” mentioned in [Reference ReidRe02, Section 2], one can define the age directly and without referring to lifts, but we will not pursue this here.
-
2. Let
 $x\in X:=U/G$
be the associated Klein singularity. We have the canonical lift
$x\in X:=U/G$
be the associated Klein singularity. We have the canonical lift
 $\mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
and the simultaneous resolution of singularities
$\mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
and the simultaneous resolution of singularities
 $\widetilde {\pi }:\mathcal {Y}\to \mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
by Theorem 4.10. Passing to geometric generic fibres and using the Lefschetz principle, we obtain the minimal resolution of singularities of
$\widetilde {\pi }:\mathcal {Y}\to \mathcal {X}_{\mathrm {can}}\to \mathrm {Spec}\: W(k)$
by Theorem 4.10. Passing to geometric generic fibres and using the Lefschetz principle, we obtain the minimal resolution of singularities of
 ${\mathbb {C}}^2/G_{\mathrm {abs}}$
. The special fibre of
${\mathbb {C}}^2/G_{\mathrm {abs}}$
. The special fibre of
 $\widetilde {\pi }$
, the geometric generic fibre of
$\widetilde {\pi }$
, the geometric generic fibre of
 $\widetilde {\pi }$
and the minimal resolution of
$\widetilde {\pi }$
and the minimal resolution of
 ${\mathbb {C}}^2/G_{\mathrm {abs}}$
are crepant in the sense of [Reference ReidRe87] and we can identify the exceptional divisors of these three resolutions with each other, see Theorem 4.10. This way, we obtain an Ito-Reid correspondence between junior conjugacy classes of G and crepant divisors of the resolution [Reference ReidRe02, Theorem 2.1].
${\mathbb {C}}^2/G_{\mathrm {abs}}$
are crepant in the sense of [Reference ReidRe87] and we can identify the exceptional divisors of these three resolutions with each other, see Theorem 4.10. This way, we obtain an Ito-Reid correspondence between junior conjugacy classes of G and crepant divisors of the resolution [Reference ReidRe02, Theorem 2.1].
Remark 6.3. It seems reasonable that one can extend this correspondence to finite and linearly reductive subgroup schemes of
![]() ${\mathbf {SL}}_{n,k}$
with
${\mathbf {SL}}_{n,k}$
with
![]() $n\geq 3$
, but we will not pursue this here.
$n\geq 3$
, but we will not pursue this here.
7 Derived categories
Let G be a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
, let
${\mathbf {GL}}_{2,k}$
, let
![]() $x\in X:=U/G$
be the associated linearly reductive quotient singularity and let
$x\in X:=U/G$
be the associated linearly reductive quotient singularity and let
![]() $\pi :Y\to X$
be its minimal resolution of singularities. Gonzalez-Sprinberg and Verdier [Reference Gonzalez-Sprinberg and VerdierGV83] gave an interpretation of the McKay correspondence as an isomorphism between the K-groups
$\pi :Y\to X$
be its minimal resolution of singularities. Gonzalez-Sprinberg and Verdier [Reference Gonzalez-Sprinberg and VerdierGV83] gave an interpretation of the McKay correspondence as an isomorphism between the K-groups
![]() $K^G(U)$
and
$K^G(U)$
and
![]() $K(Y)$
. Kapranov and Vasserot [Reference Kapranov and VasserotKV00] and Bridgeland, King and Reid [Reference Bridgeland, King and ReidBKR01] generalised this to an equivalence of derived categories
$K(Y)$
. Kapranov and Vasserot [Reference Kapranov and VasserotKV00] and Bridgeland, King and Reid [Reference Bridgeland, King and ReidBKR01] generalised this to an equivalence of derived categories
![]() ${\mathcal {D}}^G(U)$
and
${\mathcal {D}}^G(U)$
and
![]() ${\mathcal {D}}(Y)$
. In this section, we extend this to our setting, following Ishii, Ito, Nakamura and Ueda [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ishii and UedaIU15].
${\mathcal {D}}(Y)$
. In this section, we extend this to our setting, following Ishii, Ito, Nakamura and Ueda [Reference IshiiIs02, Reference Ishii and NakamuraIN19, Reference Ishii and UedaIU15].
We have a commutative diagram

By Theorem 4.5, the minimal resolution
![]() $\pi $
can be constructed by the Ishii-Ito-Nakamura resolution
$\pi $
can be constructed by the Ishii-Ito-Nakamura resolution
We let
![]() ${\mathcal {Z}}$
be the universal cluster over
${\mathcal {Z}}$
be the universal cluster over
![]() $G\text{-}\mathrm {Hilb}(U)$
, we identify
$G\text{-}\mathrm {Hilb}(U)$
, we identify
![]() $G\text{-}\mathrm {Hilb}(U)$
with Y and then, we have a commutative diagram
$G\text{-}\mathrm {Hilb}(U)$
with Y and then, we have a commutative diagram

Let
![]() ${\mathcal {D}}(Y)$
be the derived category of coherent sheaves on Y. Let
${\mathcal {D}}(Y)$
be the derived category of coherent sheaves on Y. Let
![]() ${\mathcal {D}}^G(U)$
be the derived category of G-equivariant coherent sheaves on U. Following [Reference IshiiIs02] and [Reference Ishii and NakamuraIN19], we define two functors
${\mathcal {D}}^G(U)$
be the derived category of G-equivariant coherent sheaves on U. Following [Reference IshiiIs02] and [Reference Ishii and NakamuraIN19], we define two functors
by
and
where
![]() ${\mathcal O}_{{\mathcal {Z}}}^\vee :=\mathbf {R}Hom({\mathcal O}_{{\mathcal {Z}}},{\mathcal O}_{Y\times U})$
denotes the dual of
${\mathcal O}_{{\mathcal {Z}}}^\vee :=\mathbf {R}Hom({\mathcal O}_{{\mathcal {Z}}},{\mathcal O}_{Y\times U})$
denotes the dual of
![]() ${\mathcal O}_{{\mathcal {Z}}}$
, where
${\mathcal O}_{{\mathcal {Z}}}$
, where
![]() $-\otimes \rho _0:{\mathcal {D}}(Y)\to {\mathcal {D}}^G(Y)$
denotes the functor that attaches the trivial G-action and where
$-\otimes \rho _0:{\mathcal {D}}(Y)\to {\mathcal {D}}^G(Y)$
denotes the functor that attaches the trivial G-action and where
![]() $K_U$
denotes the canonical sheaf of U. We refer to [Reference Ishii and NakamuraIN19, Section 3.1] for details, conventions and notations.
$K_U$
denotes the canonical sheaf of U. We refer to [Reference Ishii and NakamuraIN19, Section 3.1] for details, conventions and notations.
Theorem 7.1. Keeping assumptions and notations,
![]() $\Phi $
is fully faithful and
$\Phi $
is fully faithful and
![]() $\Psi $
is a left adjoint of
$\Psi $
is a left adjoint of
![]() $\Phi $
.
$\Phi $
.
Proof. For G is a very small subgroup of
![]() ${\mathbf {GL}}_2({\mathbb {C}})$
, this is [Reference IshiiIs02, Section 6] and [Reference Ishii and UedaIU15, Proposition 1.1 and Lemma 2.9]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
${\mathbf {GL}}_2({\mathbb {C}})$
, this is [Reference IshiiIs02, Section 6] and [Reference Ishii and UedaIU15, Proposition 1.1 and Lemma 2.9]. For k algebraically closed of arbitrary characteristic and G a very small and finite subgroup of
![]() ${\mathbf {GL}}_{2}(k)$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 3.2]. However, these proofs also work if G is a very small, finite and linearly reductive subgroup scheme of
${\mathbf {GL}}_{2}(k)$
of order prime to p, this is [Reference Ishii and NakamuraIN19, Theorem 3.2]. However, these proofs also work if G is a very small, finite and linearly reductive subgroup scheme of
![]() ${\mathbf {GL}}_{2,k}$
.
${\mathbf {GL}}_{2,k}$
.
A Hopf algebras
In the first section of the appendix, we study finite group schemes from the point of view of finite-dimensional Hopf algebras. We also recall the quantum double of a Hopf algebra, as well as the adjoint and the extended adjoint representation. Many results of this section should be well-known to the experts, but are somewhat scattered over the literature - especially, since many sources (sometimes implicitly) assume characteristic zero or work even over the complex numbers.
A.1 Generalities
If G is a finite group scheme over a field k, then the k-algebra
![]() $A:=H^0(G,{\mathcal O}_G)$
is commutative and finite-dimensional as k-vector space. The multiplication
$A:=H^0(G,{\mathcal O}_G)$
is commutative and finite-dimensional as k-vector space. The multiplication
![]() $m:G\times G\to G$
the inverse
$m:G\times G\to G$
the inverse
![]() $i:G\to G$
and the neutral element
$i:G\to G$
and the neutral element
![]() $e:\mathrm {Spec}\: k\to G$
induce k-algebra homomorphisms
$e:\mathrm {Spec}\: k\to G$
induce k-algebra homomorphisms
![]() $m^*:A\to A\otimes _k A$
,
$m^*:A\to A\otimes _k A$
,
![]() $i^*:A\to A$
and
$i^*:A\to A$
and
![]() $e^*:A\to k$
, which turn A into a co-algebra over k with co-multiplication
$e^*:A\to k$
, which turn A into a co-algebra over k with co-multiplication
![]() $m^*$
and antipode
$m^*$
and antipode
![]() $S:=i^*$
, and thus, into a Hopf algebra over k. Since i is the inverse of G, the antipode S satisfies
$S:=i^*$
, and thus, into a Hopf algebra over k. Since i is the inverse of G, the antipode S satisfies
![]() $S^2=\mathrm {id}_A$
, that is, A is an involutive Hopf algebra.
$S^2=\mathrm {id}_A$
, that is, A is an involutive Hopf algebra.
Conversely, if A is a finite-dimensional and commutative Hopf algebra over k, then it is involutive and
![]() $\mathrm {Spec}\: A$
is a finite group scheme over k. Moreover, A is a co-commutative Hopf algebra if and only if G is a commutative group scheme.
$\mathrm {Spec}\: A$
is a finite group scheme over k. Moreover, A is a co-commutative Hopf algebra if and only if G is a commutative group scheme.
Example A.1. Let
![]() $G_{\mathrm {abs}}$
be a finite group. The group algebra
$G_{\mathrm {abs}}$
be a finite group. The group algebra
![]() $k[G_{\mathrm {abs}}]$
becomes a Hopf algebra by defining the co-multiplication to be
$k[G_{\mathrm {abs}}]$
becomes a Hopf algebra by defining the co-multiplication to be
![]() $\Delta (g)=g\otimes g$
and the antipode to be
$\Delta (g)=g\otimes g$
and the antipode to be
![]() $S(g)=g^{-1}$
.
$S(g)=g^{-1}$
.
-
1. Clearly,
 $k[G_{\mathrm {abs}}]$
is an involutive and co-commutative Hopf algebra. Moreover,
$k[G_{\mathrm {abs}}]$
is an involutive and co-commutative Hopf algebra. Moreover,
 $k[G_{\mathrm {abs}}]$
is commutative if and only if
$k[G_{\mathrm {abs}}]$
is commutative if and only if
 $G_{\mathrm {abs}}$
is commutative.
$G_{\mathrm {abs}}$
is commutative. -
2. There exist examples of non-isomorphic finite groups
 $H_{\mathrm {abs}}$
and
$H_{\mathrm {abs}}$
and
 $G_{\mathrm {abs}}$
, whose group rings
$G_{\mathrm {abs}}$
, whose group rings
 $k[H_{\mathrm {abs}}]$
and
$k[H_{\mathrm {abs}}]$
and
 $k[G_{\mathrm {abs}}]$
are isomorphic as k-algebras.
$k[G_{\mathrm {abs}}]$
are isomorphic as k-algebras.However, they are not isomorphic as Hopf algebras: Recall that an element
 $x\in B$
in a Hopf algebra B is called group-like if
$x\in B$
in a Hopf algebra B is called group-like if
 $\Delta (x)=x\otimes x$
. The set of group-like elements of B form a group. If
$\Delta (x)=x\otimes x$
. The set of group-like elements of B form a group. If
 $B=k[G_{\mathrm {abs}}]$
, then the group of group-like elements of B is isomorphic to
$B=k[G_{\mathrm {abs}}]$
, then the group of group-like elements of B is isomorphic to
 $G_{\mathrm {abs}}$
and thus, recovers the group.
$G_{\mathrm {abs}}$
and thus, recovers the group. -
3. There exists an isomorphism of finite group schemes over k
where $$ \begin{align*}G\,\cong\,\mathrm{Spec}\: k[G_{\mathrm{abs}}]^*, \end{align*} $$
$$ \begin{align*}G\,\cong\,\mathrm{Spec}\: k[G_{\mathrm{abs}}]^*, \end{align*} $$
 $k[G_{\mathrm {abs}}]^*$
denotes the dual Hopf algebra and where G denotes the constant group scheme over k associated to
$k[G_{\mathrm {abs}}]^*$
denotes the dual Hopf algebra and where G denotes the constant group scheme over k associated to
 $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
A.2 Simplicity
A Hopf algebra A is co-semi-simple if its dual Hopf algebra
![]() $A^*$
is semi-simple and A is bi-semi-simple if both A and
$A^*$
is semi-simple and A is bi-semi-simple if both A and
![]() $A^*$
are semi-simple.
$A^*$
are semi-simple.
Let G be a finite group scheme over k and let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. To give a finite-dimensional and k-linear representation
$A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. To give a finite-dimensional and k-linear representation
![]() $\rho :G\to \mathrm {GL}(V)$
is the same as to give an A-co-module
$\rho :G\to \mathrm {GL}(V)$
is the same as to give an A-co-module
![]() $V\to V\otimes _k A$
, see [Reference WaterhouseWa79, Section 3.2] for details. Using this equivalence, we see that G is linearly reductive if and only if A is co-semi-simple. For the classification of linearly reductive group schemes (see Section 2) in the language of Hopf algebras we refer to [Reference ChinCh92].
$V\to V\otimes _k A$
, see [Reference WaterhouseWa79, Section 3.2] for details. Using this equivalence, we see that G is linearly reductive if and only if A is co-semi-simple. For the classification of linearly reductive group schemes (see Section 2) in the language of Hopf algebras we refer to [Reference ChinCh92].
The following equivalences are probably well-known to the experts.
Proposition A.2. Let G be a finite group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. Let
$p\geq 0$
. Let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the Hopf algebra associated to G.
$A:=H^0(G,{\mathcal O}_G)$
be the Hopf algebra associated to G.
-
1. A is semi-simple if and only if G is étale.
-
2. A is co-semi-simple if and only if G is linearly reductive.
-
3. A is bi-semi-simple if and only if G is of length prime to p.
Proof. We already established Claim (2) above.
If G is étale, then
![]() $A\cong k[G_{\mathrm {abs}}]^*$
, where
$A\cong k[G_{\mathrm {abs}}]^*$
, where
![]() $G_{\mathrm {abs}}:=G(k)$
is the abstract group associated to G. Since group rings are co-semi-simple, A is semi-simple. Conversely, if A is semi-simple, then
$G_{\mathrm {abs}}:=G(k)$
is the abstract group associated to G. Since group rings are co-semi-simple, A is semi-simple. Conversely, if A is semi-simple, then
![]() $\langle \varepsilon ,\int _H^r\rangle \neq 0$
by Maschke’s theorem for Hopf algebras (see, for example, [Reference LorenzLo18, Section 12.3.1] for notation, statement and proof), which implies that A is a separable k-algebra, which implies that G is étale over k. This establishes Claim (1).
$\langle \varepsilon ,\int _H^r\rangle \neq 0$
by Maschke’s theorem for Hopf algebras (see, for example, [Reference LorenzLo18, Section 12.3.1] for notation, statement and proof), which implies that A is a separable k-algebra, which implies that G is étale over k. This establishes Claim (1).
Of course, (3) follows immediately from (1) and (2), but we can also give an independent proof: Being an involutive Hopf algebra, A is bi-semi-simple if and only if p does not divide
![]() $\dim _k A$
, see [Reference Etingof and GelakiEG98, Corollary 3.2] or [Reference Larson and RadfordLR88, Corollary 2.6]. The latter is equivalent to G being of length prime to p. This establishes Claim (3).
$\dim _k A$
, see [Reference Etingof and GelakiEG98, Corollary 3.2] or [Reference Larson and RadfordLR88, Corollary 2.6]. The latter is equivalent to G being of length prime to p. This establishes Claim (3).
A.3 Adjoint representation
Let
![]() $G_{\mathrm {abs}}$
be a finite group and let k be an algebraically closed field of characteristic
$G_{\mathrm {abs}}$
be a finite group and let k be an algebraically closed field of characteristic
![]() $p\geq 0$
(p may or may not divide the order of
$p\geq 0$
(p may or may not divide the order of
![]() $G_{\mathrm {abs}}$
). Then, the action of
$G_{\mathrm {abs}}$
). Then, the action of
![]() $G_{\mathrm {abs}}$
on itself by conjugation is a permutation representation and we denote by
$G_{\mathrm {abs}}$
on itself by conjugation is a permutation representation and we denote by
the associated k-linear representation.
Remark A.3. To be more precise: Depending on whether one considers
![]() $x\mapsto gxg^{-1}$
or
$x\mapsto gxg^{-1}$
or
![]() $x\mapsto g^{-1}xg$
, one should speak about left or right adjoint actions and representations. For our discussion, this is not important, as long as one chooses one of them and stays with it.
$x\mapsto g^{-1}xg$
, one should speak about left or right adjoint actions and representations. For our discussion, this is not important, as long as one chooses one of them and stays with it.
Remark A.4. Let us recall a couple of general results about
![]() $\rho _{\mathrm {ad}}$
, which are well-known (I thank Frank Himstedt for explaining them to me):
$\rho _{\mathrm {ad}}$
, which are well-known (I thank Frank Himstedt for explaining them to me):
-
1. Let C be the set of conjugacy classes of
 $G_{\mathrm {abs}}$
and let
$G_{\mathrm {abs}}$
and let
 $\{g_c\}_{c\in C}$
be a system of representatives. Then, we have an isomorphism of k-linear representations where
$\{g_c\}_{c\in C}$
be a system of representatives. Then, we have an isomorphism of k-linear representations where
 $C(g_c)$
denotes the centraliser of
$C(g_c)$
denotes the centraliser of
 $g_c\in G_{\mathrm {abs}}$
, where
$g_c\in G_{\mathrm {abs}}$
, where  denotes the one-dimensional trivial representation and where
denotes the one-dimensional trivial representation and where
 $\mathrm {Ind}$
denotes induction from a subgroup. See, for example, [Reference Nagao and TsushimaNT89, page 171 and Exercise 1.5].
$\mathrm {Ind}$
denotes induction from a subgroup. See, for example, [Reference Nagao and TsushimaNT89, page 171 and Exercise 1.5].
-
2. Let
 $g\in G_{\mathrm {abs}}$
and let be a decomposition into indecomposable representations, which is unique up to isomorphism and numbering.
$g\in G_{\mathrm {abs}}$
and let be a decomposition into indecomposable representations, which is unique up to isomorphism and numbering.
There is precisely one summand, say
 $V_{i_1}$
, that has a subrepresentation that is isomorphic to
$V_{i_1}$
, that has a subrepresentation that is isomorphic to  . Moreover, this subrepresentation is unique. Also, there is precisely one summand, say
. Moreover, this subrepresentation is unique. Also, there is precisely one summand, say
 $V_{i_2}$
, that has a quotient representation that is isomorphic to
$V_{i_2}$
, that has a quotient representation that is isomorphic to  . Moreover, this quotient representation is unique. Then, we have
. Moreover, this quotient representation is unique. Then, we have
 $i_1=i_2$
and set which is called the Scott representation of V. See, for example, [Reference Nagao and TsushimaNT89, page 296 and Theorem 8.4].
$i_1=i_2$
and set which is called the Scott representation of V. See, for example, [Reference Nagao and TsushimaNT89, page 296 and Theorem 8.4]. $$ \begin{align*}S(V) \,:=\, V_{i_1}\,=\, V_{i_2}, \end{align*} $$
$$ \begin{align*}S(V) \,:=\, V_{i_1}\,=\, V_{i_2}, \end{align*} $$
In particular, the dimension of the largest trivial subrepresentation (resp. quotient representation) of
![]() $\rho _{\mathrm {ad}}$
is equal to the number of conjugacy classes of
$\rho _{\mathrm {ad}}$
is equal to the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
If A is a finite dimensional Hopf algebra over k, then there is an adjoint action of A on itself (in fact, a left adjoint action and a right adjoint action), see, for example, [Reference MontgomeryMo93, Definition 3.4.1]. We will write
or simply
![]() ${}^{\mathrm {ad}} A$
for this representation.
${}^{\mathrm {ad}} A$
for this representation.
Remarks A.5.
-
1. If
 $G_{\mathrm {abs}}$
is a finite group, then the adjoint representation of
$G_{\mathrm {abs}}$
is a finite group, then the adjoint representation of
 $H:=k[G_{\mathrm {abs}}]$
can be identified with the k-linear extension from
$H:=k[G_{\mathrm {abs}}]$
can be identified with the k-linear extension from
 $G_{\mathrm {abs}}$
to H of the conjugation action of
$G_{\mathrm {abs}}$
to H of the conjugation action of
 $G_{\mathrm {abs}}$
on itself.
$G_{\mathrm {abs}}$
on itself. -
2. Let G be a finite group scheme over k and let
 $A:=H^0(G,{\mathcal O}_G)$
be the
$A:=H^0(G,{\mathcal O}_G)$
be the
 $A:=H^0(G,{\mathcal O}_G)$
. There is an adjoint representation which corresponds to the adjoint representation of the dual Hopf algebra
$A:=H^0(G,{\mathcal O}_G)$
. There is an adjoint representation which corresponds to the adjoint representation of the dual Hopf algebra $$ \begin{align*}\rho_{\mathrm{ad}} \,:\,G\,\to\,{\mathbf{GL}}(V_{\mathrm{ad}}), \end{align*} $$
$$ \begin{align*}\rho_{\mathrm{ad}} \,:\,G\,\to\,{\mathbf{GL}}(V_{\mathrm{ad}}), \end{align*} $$
 $A^*$
.
$A^*$
.
-
(a) If
 $G_{\mathrm {abs}}$
is a finite group and G is the constant group scheme associated to it, then A is isomorphic to the dual of
$G_{\mathrm {abs}}$
is a finite group and G is the constant group scheme associated to it, then A is isomorphic to the dual of
 $k[G_{\mathrm {abs}}]$
equipped with its usual Hopf algebra structure. This shows that
$k[G_{\mathrm {abs}}]$
equipped with its usual Hopf algebra structure. This shows that
 $\rho _{\mathrm {ad}}$
should be defined via the adjoint representation of
$\rho _{\mathrm {ad}}$
should be defined via the adjoint representation of
 $A^*$
rather than A.
$A^*$
rather than A. -
(b) The representation
 $\rho _{\mathrm {ad}}$
should not be confused with the adjoint representation of G on its Lie algebra, see for example, [Reference WaterhouseWa79, page 100, Exercise 13]. The latter can be identified with a subquotient of
$\rho _{\mathrm {ad}}$
should not be confused with the adjoint representation of G on its Lie algebra, see for example, [Reference WaterhouseWa79, page 100, Exercise 13]. The latter can be identified with a subquotient of
 $\rho _{\mathrm {ad}}$
.
$\rho _{\mathrm {ad}}$
.
-
A.4 Quantum doubles
If A is a finite-dimensional Hopf algebra over a field k, then Drinfeld [Reference DrinfeldDr87] defined a Hopf algebra
![]() $D(A):=(A^{\mathrm {op}})^* \bowtie A$
, called the quantum double or Drinfeld double, where the bicrossed product structure is defined using the co-adjoint representation of A on
$D(A):=(A^{\mathrm {op}})^* \bowtie A$
, called the quantum double or Drinfeld double, where the bicrossed product structure is defined using the co-adjoint representation of A on
![]() $A^*$
and the co-adjoint representation of
$A^*$
and the co-adjoint representation of
![]() $A^*$
on A, see also [Reference MontgomeryMo93, Definition 10.3.1].
$A^*$
on A, see also [Reference MontgomeryMo93, Definition 10.3.1].
Remarks A.6. Let A be a finite-dimensional Hopf algebra over k and let
![]() $D(A):=(A^{\mathrm {op}})^* \bowtie A$
be its quantum double.
$D(A):=(A^{\mathrm {op}})^* \bowtie A$
be its quantum double.
-
1. As k-vector space,
 $D(A)$
is of dimension
$D(A)$
is of dimension
 $(\dim _kA)^2$
.
$(\dim _kA)^2$
. -
2. A is a Hopf subalgebra of
 $D(A)$
via
$D(A)$
via
 $\varepsilon \bowtie A$
and
$\varepsilon \bowtie A$
and
 $(A^{\mathrm {op}})^*$
is a Hopf subalgebra of
$(A^{\mathrm {op}})^*$
is a Hopf subalgebra of
 $D(A)$
via
$D(A)$
via
 $(A^{\mathrm {op}})^*\bowtie 1$
.
$(A^{\mathrm {op}})^*\bowtie 1$
. -
3. If A is commutative and co-commutative, then we have
 $A^{\mathrm {op}}=A$
and using the definition of the quantum double, we obtain isomorphisms of Hopf algebras over k, where the tensor product is the trivial tensor product of Hopf algebras. If we set
$A^{\mathrm {op}}=A$
and using the definition of the quantum double, we obtain isomorphisms of Hopf algebras over k, where the tensor product is the trivial tensor product of Hopf algebras. If we set $$ \begin{align*}D(A)\,\cong\,A^*\otimes_k A \,\cong\, D(A^*) \end{align*} $$
$$ \begin{align*}D(A)\,\cong\,A^*\otimes_k A \,\cong\, D(A^*) \end{align*} $$
 $G:=\mathrm {Spec}\: A$
, then we have
$G:=\mathrm {Spec}\: A$
, then we have
 $G^D\cong \mathrm {Spec}\: A^*$
, where
$G^D\cong \mathrm {Spec}\: A^*$
, where
 $-^D$
denotes the Cartier dual group scheme, and we have an isomorphism of finite and commutative group schemes over k.
$-^D$
denotes the Cartier dual group scheme, and we have an isomorphism of finite and commutative group schemes over k. $$ \begin{align*}\mathrm{Spec}\: D(A) \,\cong\, G\times_{\mathrm{Spec}\: k} G^D \end{align*} $$
$$ \begin{align*}\mathrm{Spec}\: D(A) \,\cong\, G\times_{\mathrm{Spec}\: k} G^D \end{align*} $$
-
4. In particular,
 $D(A)$
is commutative if and only if A is commutative and co-commutative.
$D(A)$
is commutative if and only if A is commutative and co-commutative.
The assertions on simplicity in the next proposition extend results of Witherspoon [Reference WitherspoonWi96, Proposition 1.2] from groups to group schemes. They are also related to general semi-simplicity results of quasi-triangular Hopf algebras in positive characteristic due to Etingof and Gelaki [Reference Etingof and GelakiEG98] and in this form, they might be known to the experts.
Proposition A.7. Let G be a finite group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
and let
$p\geq 0$
and let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. Then, the following are equivalent
$A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. Then, the following are equivalent
 $$ \begin{align*} \begin{array}{llll} (1) & D(A)\ \text{is semi-simple} & (1') & D(A^*)\ \text{is semi-simple} \\ (2) & D(A)\ \text{is co-semi-simple} \qquad \qquad \ & (2') & D(A^*)\ \text{is co-semi-simple} \\ (3) & A\ \text{is bi-semi-simple} & (3') & A^*\ \text{is bi-semi-simple} \\ (4) & G\ \text{is of length prime to}\ p \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{llll} (1) & D(A)\ \text{is semi-simple} & (1') & D(A^*)\ \text{is semi-simple} \\ (2) & D(A)\ \text{is co-semi-simple} \qquad \qquad \ & (2') & D(A^*)\ \text{is co-semi-simple} \\ (3) & A\ \text{is bi-semi-simple} & (3') & A^*\ \text{is bi-semi-simple} \\ (4) & G\ \text{is of length prime to}\ p \end{array} \end{align*} $$
Proof. The equivalences (1)
![]() $\Leftrightarrow $
(2)
$\Leftrightarrow $
(2)
![]() $\Leftrightarrow $
(3) and (1’)
$\Leftrightarrow $
(3) and (1’)
![]() $\Leftrightarrow $
(2’)
$\Leftrightarrow $
(2’)
![]() $\Leftrightarrow $
(3’) are shown in [Reference MontgomeryMo93, Corollary 10.3.13]. The equivalence (3)
$\Leftrightarrow $
(3’) are shown in [Reference MontgomeryMo93, Corollary 10.3.13]. The equivalence (3)
![]() $\Leftrightarrow $
(3’) is trivial and finally, the equivalence (3)
$\Leftrightarrow $
(3’) is trivial and finally, the equivalence (3)
![]() $\Leftrightarrow $
(4) was shown in Proposition A.2.
$\Leftrightarrow $
(4) was shown in Proposition A.2.
A.5 Extended adjoint representation
Given a Hopf algebra A, we defined the adjoint representation
![]() ${}^{\mathrm {ad}}A$
in Section A.3 above. There is a way to extend this to a representation
${}^{\mathrm {ad}}A$
in Section A.3 above. There is a way to extend this to a representation
the extended adjoint representation of A, which is denoted by
![]() ${}^{\mathrm {Ad}} A$
. For its definition, we refer to Zhu’s article [Reference ZhuZhu97], as well as [Reference Cohen and WestreichCW11] for subsequent work on this representation. We note that it can be described as an induced representation
${}^{\mathrm {Ad}} A$
. For its definition, we refer to Zhu’s article [Reference ZhuZhu97], as well as [Reference Cohen and WestreichCW11] for subsequent work on this representation. We note that it can be described as an induced representation
where ![]() denotes the trivial one-dimensional representation and where we consider A as a subalgebra of
denotes the trivial one-dimensional representation and where we consider A as a subalgebra of
![]() $D(A)$
via
$D(A)$
via
![]() $\varepsilon \bowtie A$
, see [Reference BurciuBu06] or [Reference JacobyJa17, Section 4.3.4].
$\varepsilon \bowtie A$
, see [Reference BurciuBu06] or [Reference JacobyJa17, Section 4.3.4].
Example A.8. Let
![]() $G_{\mathrm {abs}}$
be a finite group and let
$G_{\mathrm {abs}}$
be a finite group and let
![]() $H:=k[G_{\mathrm {abs}}]$
be the group algebra equipped with its usual Hopf algebra structure. The elements
$H:=k[G_{\mathrm {abs}}]$
be the group algebra equipped with its usual Hopf algebra structure. The elements
![]() $g\in G_{\mathrm {abs}}$
form a basis of H as k-vector space and we denote by
$g\in G_{\mathrm {abs}}$
form a basis of H as k-vector space and we denote by
![]() $\rho _g\in H^*$
the dual basis elements.
$\rho _g\in H^*$
the dual basis elements.
-
1. The multiplication of
 $D(H)$
is given by see, for example, [Reference JacobyJa17, Example 2.4.2].
$D(H)$
is given by see, for example, [Reference JacobyJa17, Example 2.4.2]. $$ \begin{align*}(\rho_h\bowtie g)\cdot(\rho_k\bowtie \ell) \,=\, \delta_{h,gkg^{-1}}\cdot \rho_h\bowtie g\ell, \end{align*} $$
$$ \begin{align*}(\rho_h\bowtie g)\cdot(\rho_k\bowtie \ell) \,=\, \delta_{h,gkg^{-1}}\cdot \rho_h\bowtie g\ell, \end{align*} $$
-
(a) The extended adjoint representation
 ${}^{\mathrm {Ad}} H$
is given by see, for example, [Reference JacobyJa17, Example 2.5.3].
${}^{\mathrm {Ad}} H$
is given by see, for example, [Reference JacobyJa17, Example 2.5.3]. $$ \begin{align*}(\rho_h\bowtie k)\,\mapsto\, (g\,\mapsto\, \delta_{h^{-1},kgk^{-1}}\,\cdot\, kgk^{-1} ) \end{align*} $$
$$ \begin{align*}(\rho_h\bowtie k)\,\mapsto\, (g\,\mapsto\, \delta_{h^{-1},kgk^{-1}}\,\cdot\, kgk^{-1} ) \end{align*} $$
-
(b) The unit of
 $H^*$
is
$H^*$
is
 $\varepsilon :=\sum _{g\in G_{\mathrm {abs}}}\rho _g$
and the restriction of
$\varepsilon :=\sum _{g\in G_{\mathrm {abs}}}\rho _g$
and the restriction of
 ${}^{\mathrm {Ad}}H$
to
${}^{\mathrm {Ad}}H$
to
 $\varepsilon \bowtie H$
is
$\varepsilon \bowtie H$
is
 ${}^{\mathrm {ad}}H$
. Thus, the extended adjoint representation extends the adjoint representation from an A-representation to a
${}^{\mathrm {ad}}H$
. Thus, the extended adjoint representation extends the adjoint representation from an A-representation to a
 $D(A)$
-representation, whence the name.
$D(A)$
-representation, whence the name. -
(c) The extended adjoint representation
 ${}^{\mathrm {Ad}}H$
is semi-simple. More precisely, the k-subvector space of H generated by the elements of a conjugacy class of
${}^{\mathrm {Ad}}H$
is semi-simple. More precisely, the k-subvector space of H generated by the elements of a conjugacy class of
 $G_{\mathrm {abs}}$
is a simple
$G_{\mathrm {abs}}$
is a simple
 $D(H)$
-subrepresentation of
$D(H)$
-subrepresentation of
 ${}^{\mathrm {Ad}}H$
. This gives a bijection between conjugacy classes of
${}^{\mathrm {Ad}}H$
. This gives a bijection between conjugacy classes of
 $G_{\mathrm {abs}}$
and simple subrepresentations of
$G_{\mathrm {abs}}$
and simple subrepresentations of
 ${}^{\mathrm {Ad}}H$
. By [Reference JacobyJa17, Lemma 4.3.2], this is also true if p divides the order of
${}^{\mathrm {Ad}}H$
. By [Reference JacobyJa17, Lemma 4.3.2], this is also true if p divides the order of
 $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
We refer to [Reference BurciuBu06, Reference Dijkgraaf, Pasquier and RocheDPR91, Reference GouldGo93, Reference WitherspoonWi96] for more results about the representation theory of
 $D(H)$
and
$D(H)$
and
 ${}^{\mathrm {Ad}}H$
.
${}^{\mathrm {Ad}}H$
. -
-
2. If we identify
 $H^{**}$
with H, then the multiplication of
$H^{**}$
with H, then the multiplication of
 $D(H^*)$
is given by and the extended adjoint representation
$D(H^*)$
is given by and the extended adjoint representation $$ \begin{align*}(g\bowtie \rho_h)\cdot(\ell\bowtie\rho_k) \,=\, \delta_{h,k} \,\cdot\, (g\cdot \ell) \bowtie \rho_h \end{align*} $$
$$ \begin{align*}(g\bowtie \rho_h)\cdot(\ell\bowtie\rho_k) \,=\, \delta_{h,k} \,\cdot\, (g\cdot \ell) \bowtie \rho_h \end{align*} $$
 ${}^{\mathrm {Ad}} (H^*)$
is given by which can be identified with the dual of the regular representation of
${}^{\mathrm {Ad}} (H^*)$
is given by which can be identified with the dual of the regular representation of $$ \begin{align*}(h\bowtie \rho_k)\,\mapsto\, (\rho_g\,\mapsto\, \rho_{gh^{-1}}), \end{align*} $$
$$ \begin{align*}(h\bowtie \rho_k)\,\mapsto\, (\rho_g\,\mapsto\, \rho_{gh^{-1}}), \end{align*} $$
 $G_{\mathrm {abs}}$
. The restriction of
$G_{\mathrm {abs}}$
. The restriction of
 ${}^{\mathrm {Ad}}(H^*)$
to
${}^{\mathrm {Ad}}(H^*)$
to
 $1\bowtie H^*$
is trivial, which is equal to the adjoint representation
$1\bowtie H^*$
is trivial, which is equal to the adjoint representation
 $^{\mathrm {ad}}(H^*)$
, which is also trivial.
$^{\mathrm {ad}}(H^*)$
, which is also trivial.
Example A.9. Let A be a finite-dimensional Hopf algebra over k that is commutative and co-commutative.
-
1. The adjoint representations
 ${}^{\mathrm {ad}}A$
and
${}^{\mathrm {ad}}A$
and
 ${}^{\mathrm {ad}}(A^*)$
are trivial.
${}^{\mathrm {ad}}(A^*)$
are trivial.
By Remark A.6, we have isomorphisms
of Hopf algebras over k, where the tensor product is the trivial tensor product of Hopf algebras. Thus, to give a representation
![]() $\rho :D(A)\to \mathrm {End}(V)$
is equivalent to giving two representations
$\rho :D(A)\to \mathrm {End}(V)$
is equivalent to giving two representations
![]() $\rho _1:A\to \mathrm {End}(V)$
and
$\rho _1:A\to \mathrm {End}(V)$
and
![]() $\rho _2:A^*\to \mathrm {End}(V)$
, whose actions on V commute.
$\rho _2:A^*\to \mathrm {End}(V)$
, whose actions on V commute.
-
2. Using the description (A.1) of
 ${}^{\mathrm {Ad}}A$
as induced representation, we obtain
${}^{\mathrm {Ad}}A$
as induced representation, we obtain
 ${}^{\mathrm {Ad}}A$
from the the trivial A-action on A (this is
${}^{\mathrm {Ad}}A$
from the the trivial A-action on A (this is
 $\rho _1$
) and the dual of the regular representation of
$\rho _1$
) and the dual of the regular representation of
 $A^*$
(this is
$A^*$
(this is
 $\rho _2$
).
$\rho _2$
). -
3. Similarly, we obtain
 ${}^{\mathrm {Ad}}(A^*)$
from the trivial
${}^{\mathrm {Ad}}(A^*)$
from the trivial
 $A^*$
-action on
$A^*$
-action on
 $A^*$
and the dual of the regular representation of A.
$A^*$
and the dual of the regular representation of A.
B Conjugacy classes for finite group schemes
Let G be a finite group scheme over an algebraically closed field k of characteristic
![]() $p\geq 0$
. In the second section of the appendix, we discuss several approaches towards the notion of a conjugacy class for G. If
$p\geq 0$
. In the second section of the appendix, we discuss several approaches towards the notion of a conjugacy class for G. If
![]() $p=0$
, then all of them lead to the same notion, namely, the familiar one. All approaches look reasonable at first sight if
$p=0$
, then all of them lead to the same notion, namely, the familiar one. All approaches look reasonable at first sight if
![]() $p>0$
and they lead to essentially “the same” answer if G is of length prime to p. In general however, they lead to different notions, all of which have their merits and drawbacks. This appendix serves as a motivation for Definition 6.1, but the discussion and results may be interesting in themselves.
$p>0$
and they lead to essentially “the same” answer if G is of length prime to p. In general however, they lead to different notions, all of which have their merits and drawbacks. This appendix serves as a motivation for Definition 6.1, but the discussion and results may be interesting in themselves.
B.1 First approach: via rational points
Let
![]() $G(k)$
be the group of k-rational points. We obtain an equivalence relation
$G(k)$
be the group of k-rational points. We obtain an equivalence relation
![]() $\sim $
on this set by defining
$\sim $
on this set by defining
![]() $g_1\sim g_2$
if and only if there exists
$g_1\sim g_2$
if and only if there exists
![]() $h\in G(k)$
such that
$h\in G(k)$
such that
![]() $g_1=hg_2h^{-1}$
. The quotient
$g_1=hg_2h^{-1}$
. The quotient
![]() $G(k)/\sim $
is the first candidate for the set of conjugacy classes.
$G(k)/\sim $
is the first candidate for the set of conjugacy classes.
Example B.1. If G is étale over k, then it is the constant group scheme associated to the finite group
![]() $G_{\mathrm {abs}}:=G(k)$
. In this case,
$G_{\mathrm {abs}}:=G(k)$
. In this case,
![]() $G(k)/\sim $
coincides with the set of conjugacy classes of
$G(k)/\sim $
coincides with the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
If G is étale, which is automatic if
![]() $p=0$
, then this approach is satisfactory. However, if
$p=0$
, then this approach is satisfactory. However, if
![]() $p>0$
, then the connected-étale sequence (2.1) induces a bijection
$p>0$
, then the connected-étale sequence (2.1) induces a bijection
which is an isomorphism of finite groups. In particular,
![]() $G(k)/\sim $
depends on the maximal étale quotient
$G(k)/\sim $
depends on the maximal étale quotient
![]() $G^{\mathrm {\acute {e}t}}$
of G only. For example, in the extremal case where G is connected, we have
$G^{\mathrm {\acute {e}t}}$
of G only. For example, in the extremal case where G is connected, we have
![]() $G(k)=\{1\}$
and then,
$G(k)=\{1\}$
and then,
![]() $G(k)/\sim $
consists of one element, and we do not gain much information about G.
$G(k)/\sim $
consists of one element, and we do not gain much information about G.
Concerning functoriality: if
![]() $\varphi :G\to H$
is a homomorphism of finite group schemes over k, then we have induced morphisms
$\varphi :G\to H$
is a homomorphism of finite group schemes over k, then we have induced morphisms
![]() $G(k)\to H(k)$
,
$G(k)\to H(k)$
,
![]() $G^{\mathrm {\acute {e}t}}\to H^{\mathrm {\acute {e}t}}$
and
$G^{\mathrm {\acute {e}t}}\to H^{\mathrm {\acute {e}t}}$
and
![]() $G(k)/\sim \to H(k)/\sim $
.
$G(k)/\sim \to H(k)/\sim $
.
B.2 Second approach: via representations and K-theory
If
![]() $G_{\mathrm {abs}}$
is a finite group of order prime to p, then the category
$G_{\mathrm {abs}}$
is a finite group of order prime to p, then the category
![]() $\operatorname {\mathrm {Rep}}_k(G)$
of k-linear and finite-dimensional
$\operatorname {\mathrm {Rep}}_k(G)$
of k-linear and finite-dimensional
![]() $G_{\mathrm {abs}}$
-representations is semi-simple. In this case, the number of isomorphism classes of simple representations is equal to the number of conjugacy classes. More precisely, if
$G_{\mathrm {abs}}$
-representations is semi-simple. In this case, the number of isomorphism classes of simple representations is equal to the number of conjugacy classes. More precisely, if
![]() $\rho $
is a k-linear and finite-dimensional representation of
$\rho $
is a k-linear and finite-dimensional representation of
![]() $G_{\mathrm {abs}}$
and
$G_{\mathrm {abs}}$
and
![]() $g\in G_{\mathrm {abs}}$
is an element, then
$g\in G_{\mathrm {abs}}$
is an element, then
induces a pairing between representations and conjugacy classes. Since the character table of a finite group is a quadratic and invertible matrix (see, for example, [Reference SerreSe77, Proposition I.7]), this pairing is non-degenerate and one can think of conjugacy classes as being “dual” to simple representations.
This idea can be made precise as follows: Let F be a field, let
![]() $\mathrm {Cl}(G_{\mathrm {abs}})$
be the set of conjugacy classes of
$\mathrm {Cl}(G_{\mathrm {abs}})$
be the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
and let
$G_{\mathrm {abs}}$
and let
![]() $F^{\mathrm {Cl}(G_{\mathrm {abs}})}$
be the ring of class functions on
$F^{\mathrm {Cl}(G_{\mathrm {abs}})}$
be the ring of class functions on
![]() $G_{\mathrm {abs}}$
with values in F. Let g be the order of
$G_{\mathrm {abs}}$
with values in F. Let g be the order of
![]() $G_{\mathrm {abs}}$
, let
$G_{\mathrm {abs}}$
, let
![]() $\zeta _g\in {\mathbb {C}}$
be a primitive g.th primitive root of unity and assume that F contains
$\zeta _g\in {\mathbb {C}}$
be a primitive g.th primitive root of unity and assume that F contains
![]() ${\mathbb {Q}}(\zeta _g)$
. Since the characters of
${\mathbb {Q}}(\zeta _g)$
. Since the characters of
![]() $G_{\mathrm {abs}}$
take values in F (here, we use
$G_{\mathrm {abs}}$
take values in F (here, we use
![]() ${\mathbb {Q}}(\zeta _g)\subseteq F$
), we have injective ring homomorphisms
${\mathbb {Q}}(\zeta _g)\subseteq F$
), we have injective ring homomorphisms
and
![]() $\gamma $
is an isomorphism, see [Reference SerreSe77, Section 11.4] and the first paragraph of [Reference SerreSe77, Section 9.1]. In particular,
$\gamma $
is an isomorphism, see [Reference SerreSe77, Section 11.4] and the first paragraph of [Reference SerreSe77, Section 9.1]. In particular,
is a finite set consisting of maximal ideals only and the topology is discrete. Since
![]() $\gamma $
is an isomorphism, the cardinality of this set is equal to that of
$\gamma $
is an isomorphism, the cardinality of this set is equal to that of
![]() $\mathrm {Cl}(G_{\mathrm {abs}})$
. This carries over to finite and linearly reductive schemes as follows.
$\mathrm {Cl}(G_{\mathrm {abs}})$
. This carries over to finite and linearly reductive schemes as follows.
Proposition B.2. Let G be a finite and linearly reductive group scheme over k and let
![]() $G_{\mathrm {abs}}$
be the associated abstract group. Let g be the length of G, fix a g.th root of unity
$G_{\mathrm {abs}}$
be the associated abstract group. Let g be the length of G, fix a g.th root of unity
![]() $\zeta _g\in {\mathbb {C}}$
and let F be a field that contains
$\zeta _g\in {\mathbb {C}}$
and let F be a field that contains
![]() ${\mathbb {Q}}(\zeta _{g})$
. Then, there exista canonical bijection of sets
${\mathbb {Q}}(\zeta _{g})$
. Then, there exista canonical bijection of sets
and homeomorphisms
Proof. If c is a conjugacy class of
![]() $G_{\mathrm {abs}}$
, then
$G_{\mathrm {abs}}$
, then
![]() $P_{0,c}$
(notation as in [Reference SerreSe77, Section 11.4, Proposition 30]) is an element of
$P_{0,c}$
(notation as in [Reference SerreSe77, Section 11.4, Proposition 30]) is an element of
![]() $\mathrm {Spec}\: F\otimes K_k(G_{\mathrm {abs}})$
and by loc. cit. this defines a bijection. The isomorphisms of Corollary 2.8 induce homeomorphisms and thus, bijections of spectra as stated.
$\mathrm {Spec}\: F\otimes K_k(G_{\mathrm {abs}})$
and by loc. cit. this defines a bijection. The isomorphisms of Corollary 2.8 induce homeomorphisms and thus, bijections of spectra as stated.
Remarks B.3.
-
1. The maximal abelian extension
 ${\mathbb {Q}}\subset {\mathbb {Q}}^{\mathrm {ab}}$
is generated by all roots of unity by the Kronecker-Weber theorem. Thus, if we have
${\mathbb {Q}}\subset {\mathbb {Q}}^{\mathrm {ab}}$
is generated by all roots of unity by the Kronecker-Weber theorem. Thus, if we have
 ${\mathbb {Q}}^{\mathrm {ab}}\subseteq F$
, then we have a field that works independent of the length of G. In Definition 6.1, we have chosen
${\mathbb {Q}}^{\mathrm {ab}}\subseteq F$
, then we have a field that works independent of the length of G. In Definition 6.1, we have chosen
 $F={\mathbb {C}}$
as this field may be more familiar than
$F={\mathbb {C}}$
as this field may be more familiar than
 ${\mathbb {Q}}^{\mathrm {ab}}$
.
${\mathbb {Q}}^{\mathrm {ab}}$
. -
2. In [Reference SerreSe77, Section 11.4], Serre described
 $\mathrm {Spec}\: A\otimes _{\mathbb {Z}} K_k(G_{\mathrm {abs}})$
, where
$\mathrm {Spec}\: A\otimes _{\mathbb {Z}} K_k(G_{\mathrm {abs}})$
, where
 $A={\mathbb {Z}}[\zeta _g]$
. Using Corollary 2.8, we obtain a homeomorphism
$A={\mathbb {Z}}[\zeta _g]$
. Using Corollary 2.8, we obtain a homeomorphism  $$ \begin{align*}\mathrm{Spec}\: A\otimes_{\mathbb{Z}} K_k(G) \,\to\,\mathrm{Spec}\: A\otimes_{\mathbb{Z}} K_k(G_{\mathrm{abs}}). \end{align*} $$
$$ \begin{align*}\mathrm{Spec}\: A\otimes_{\mathbb{Z}} K_k(G) \,\to\,\mathrm{Spec}\: A\otimes_{\mathbb{Z}} K_k(G_{\mathrm{abs}}). \end{align*} $$
In particular, Serre’s results from loc.cit. carry over to
 $A\otimes _{\mathbb {Z}} K_k(G)$
. For the purposes of this article, we are only interested in the fibre over
$A\otimes _{\mathbb {Z}} K_k(G)$
. For the purposes of this article, we are only interested in the fibre over
 $0\in \mathrm {Spec}\: F$
with
$0\in \mathrm {Spec}\: F$
with
 $F=\mathrm {Frac}(A)={\mathbb {Q}}(\zeta _g)$
, that is, the Zariski open subset
$F=\mathrm {Frac}(A)={\mathbb {Q}}(\zeta _g)$
, that is, the Zariski open subset
 $\mathrm {Spec}\: F\otimes K_k(G)\subset \mathrm {Spec}\: A\otimes K_k(G)$
.
$\mathrm {Spec}\: F\otimes K_k(G)\subset \mathrm {Spec}\: A\otimes K_k(G)$
.
Example B.4. Let G be the group scheme
![]() $\boldsymbol {\alpha }_p$
or
$\boldsymbol {\alpha }_p$
or
![]() ${\mathbf {C}}_p$
over the algebraically closed field k of characteristic
${\mathbf {C}}_p$
over the algebraically closed field k of characteristic
![]() $p>0$
. Then,
$p>0$
. Then,
![]() $\operatorname {\mathrm {Rep}}_k(G)$
is not semi-simple: the only simple k-linear representation of G is the trivial one-dimensional representation
$\operatorname {\mathrm {Rep}}_k(G)$
is not semi-simple: the only simple k-linear representation of G is the trivial one-dimensional representation ![]() . Thus,
. Thus, ![]() induces an isomorphism of rings
induces an isomorphism of rings
![]() $K_k(G)\cong {\mathbb {Z}}$
and
$K_k(G)\cong {\mathbb {Z}}$
and
![]() $\mathrm {Spec}\: F\otimes _{\mathbb {Z}} K_k(G)$
consists of one point only. The approach to conjugacy classes in this subsection may therefore lead to somewhat unexpected results if G is not linearly reductive.
$\mathrm {Spec}\: F\otimes _{\mathbb {Z}} K_k(G)$
consists of one point only. The approach to conjugacy classes in this subsection may therefore lead to somewhat unexpected results if G is not linearly reductive.
Proposition B.5. Let
![]() $\varphi :G\to H$
be a morphism of finite and linearly reductive group schemes over k. Let
$\varphi :G\to H$
be a morphism of finite and linearly reductive group schemes over k. Let
![]() $\varphi _{\mathrm {abs}}:G_{\mathrm {abs}}\to H_{\mathrm {abs}}$
be the induced homomorphism of their associated abstract groups. Let F be a field that contains
$\varphi _{\mathrm {abs}}:G_{\mathrm {abs}}\to H_{\mathrm {abs}}$
be the induced homomorphism of their associated abstract groups. Let F be a field that contains
![]() ${\mathbb {Q}}(\zeta _g,\zeta _h)$
, where g (resp. h) denotes the length of G (resp. H).
${\mathbb {Q}}(\zeta _g,\zeta _h)$
, where g (resp. h) denotes the length of G (resp. H).
-
1. There maps
 $\varphi $
and
$\varphi $
and
 $\varphi _{\mathrm {abs}}$
induce ring homomorphisms
$\varphi _{\mathrm {abs}}$
induce ring homomorphisms
 $K_k(H)\to K_k(G)$
and
$K_k(H)\to K_k(G)$
and
 $K_{\overline {K}}(H_{\mathrm {abs}})\to K_{\overline {K}}(G_{\mathrm {abs}})$
, respectively. We obtain a commutative diagram of continuous maps whose vertical arrows are the homeomorphisms from Proposition B.2.
$K_{\overline {K}}(H_{\mathrm {abs}})\to K_{\overline {K}}(G_{\mathrm {abs}})$
, respectively. We obtain a commutative diagram of continuous maps whose vertical arrows are the homeomorphisms from Proposition B.2.
-
2. Let
 $G_{\mathrm {abs}}/\sim \to H_{\mathrm {abs}}/\sim $
be the map on conjugacy classes induced by
$G_{\mathrm {abs}}/\sim \to H_{\mathrm {abs}}/\sim $
be the map on conjugacy classes induced by
 $\varphi _{\mathrm {abs}}$
. We obtain a commutative diagram of maps of sets whose vertical maps are the bijections from Proposition B.2.
$\varphi _{\mathrm {abs}}$
. We obtain a commutative diagram of maps of sets whose vertical maps are the bijections from Proposition B.2.
Proof. Clearly,
![]() $\varphi $
induces a morphism
$\varphi $
induces a morphism
![]() $K_k(H)\to K_k(G)$
of rings since every H-representation becomes a G-representation via
$K_k(H)\to K_k(G)$
of rings since every H-representation becomes a G-representation via
![]() $\varphi $
. Similarly,
$\varphi $
. Similarly,
![]() $\varphi _{\mathrm {abs}}$
induces a ring homomorphism
$\varphi _{\mathrm {abs}}$
induces a ring homomorphism
![]() $\varphi _{K,\mathrm {abs}}\,:\,K_{\overline {K}}(H_{\mathrm {abs}})\to K_{\overline {K}}(G_{\mathrm {abs}})$
. We leave it to the reader to check the compatibility of these maps with the homeomorphisms of Proposition B.2.
$\varphi _{K,\mathrm {abs}}\,:\,K_{\overline {K}}(H_{\mathrm {abs}})\to K_{\overline {K}}(G_{\mathrm {abs}})$
. We leave it to the reader to check the compatibility of these maps with the homeomorphisms of Proposition B.2.
To check commutativity of the second diagram, let
![]() $g\in G_{\mathrm {abs}}$
. With the notations and definitions of [Reference SerreSe77, Section 11.4], it is easy to see that we have
$g\in G_{\mathrm {abs}}$
. With the notations and definitions of [Reference SerreSe77, Section 11.4], it is easy to see that we have
where
is the induced map on spectra. Since the image of the conjugacy class
![]() $[g]$
of
$[g]$
of
![]() $G_{\mathrm {abs}}$
is the conjugacy class
$G_{\mathrm {abs}}$
is the conjugacy class
![]() $[\varphi _{\mathrm {abs}}(g)]$
of
$[\varphi _{\mathrm {abs}}(g)]$
of
![]() $H_{\mathrm {abs}}$
, the assertion follows.
$H_{\mathrm {abs}}$
, the assertion follows.
B.3 Third approach: the scheme of conjugacy classes
Just as group schemes generalise the notion of a group, one could try to replace the set of conjugacy classes by a suitable notion of scheme of conjugacy classes. More precisely, let G be a finite group scheme over k and let
![]() $\underline {\mathrm {Aut}}(G)$
be the automorphism group scheme of G. For every scheme
$\underline {\mathrm {Aut}}(G)$
be the automorphism group scheme of G. For every scheme
![]() $T\to \mathrm {Spec}\: k$
, we have the set
$T\to \mathrm {Spec}\: k$
, we have the set
![]() $G(T)$
of T-valued points of G and a conjugation action of
$G(T)$
of T-valued points of G and a conjugation action of
![]() $G(T)$
on
$G(T)$
on
![]() $G(T)$
. This induces a morphism of schemes
$G(T)$
. This induces a morphism of schemes
![]() $G\to \underline {\mathrm {Aut}}(G)$
. We will say that two elements of
$G\to \underline {\mathrm {Aut}}(G)$
. We will say that two elements of
![]() $G(T)$
are equivalent if they differ by such an automorphism and we denote the resulting equivalence relation by
$G(T)$
are equivalent if they differ by such an automorphism and we denote the resulting equivalence relation by
![]() $\sim $
.
$\sim $
.
We obtain a functor from the category of schemes over k to sets
This functor should somehow represent the conjugacy classes of G in the sense of schemes.
Proposition B.6. Let G be a finite group scheme over k. Then, the functor
![]() $\underline {\mathrm {Conj}}_G$
is representable by a scheme
$\underline {\mathrm {Conj}}_G$
is representable by a scheme
![]() $\mathrm {Conj}_G$
, which is finite over
$\mathrm {Conj}_G$
, which is finite over
![]() $\mathrm {Spec}\: k$
.
$\mathrm {Spec}\: k$
.
Proof. Set
![]() $V:=H^0(G,{\mathcal O}_G)$
and let
$V:=H^0(G,{\mathcal O}_G)$
and let
![]() $\rho _{\mathrm {ad}}:G\to {\mathbf {GL}}(V)$
be the adjoint representation of G (see Appendix A.3). Then, the functor
$\rho _{\mathrm {ad}}:G\to {\mathbf {GL}}(V)$
be the adjoint representation of G (see Appendix A.3). Then, the functor
![]() $\underline {\mathrm {Conj}}_G$
can be rephrased as the functor that associates to each
$\underline {\mathrm {Conj}}_G$
can be rephrased as the functor that associates to each
![]() $T\to \mathrm {Spec}\: k$
the quotient of
$T\to \mathrm {Spec}\: k$
the quotient of
![]() $V\times {\mathcal O}_T$
modulo
$V\times {\mathcal O}_T$
modulo
![]() $G(T)$
. This amounts to representing the quotient
$G(T)$
. This amounts to representing the quotient
![]() $V/G$
by a scheme. Since V is a vector space and thus, can be identified with an affine scheme, and since G is a finite group scheme, this quotient is representable by a scheme. In fact, it is representable by the spectrum of the invariant ring
$V/G$
by a scheme. Since V is a vector space and thus, can be identified with an affine scheme, and since G is a finite group scheme, this quotient is representable by a scheme. In fact, it is representable by the spectrum of the invariant ring
![]() $\mathrm {Spec}\: V^G$
.
$\mathrm {Spec}\: V^G$
.
Definition B.7.
![]() $\mathrm {Conj}_G$
is called the scheme of conjugacy classes of G.
$\mathrm {Conj}_G$
is called the scheme of conjugacy classes of G.
Remark B.8. If
![]() $\rho _{\mathrm {ad}}:G\to {\mathbf {GL}}(H^0(G,{\mathcal O}_G))$
is the adjoint representation, then the previous proof shows that the length of
$\rho _{\mathrm {ad}}:G\to {\mathbf {GL}}(H^0(G,{\mathcal O}_G))$
is the adjoint representation, then the previous proof shows that the length of
![]() $\mathrm {Conj}_G$
over
$\mathrm {Conj}_G$
over
![]() $\mathrm {Spec}\: k$
is equal to the dimension of the maximal trivial subrepresentation of
$\mathrm {Spec}\: k$
is equal to the dimension of the maximal trivial subrepresentation of
![]() $\rho _{\mathrm {ad}}$
. If
$\rho _{\mathrm {ad}}$
. If
![]() $G_{\mathrm {abs}}$
is a finite group or if G is a finite and étale group scheme over
$G_{\mathrm {abs}}$
is a finite group or if G is a finite and étale group scheme over
![]() $\mathrm {Spec}\: k$
, then we gave an explicit description of this maximal trivial subrepresentation of
$\mathrm {Spec}\: k$
, then we gave an explicit description of this maximal trivial subrepresentation of
![]() $\rho _{\mathrm {ad}}$
in Remark A.4.
$\rho _{\mathrm {ad}}$
in Remark A.4.
Examples B.9.
-
1. If G is étale over k, then G is isomorphic to the constant group scheme associated to
 $G_{\mathrm {abs}}:=G(k)$
. In this case,
$G_{\mathrm {abs}}:=G(k)$
. In this case,
 $\mathrm {Conj}_G$
is a disjoint union of copies of
$\mathrm {Conj}_G$
is a disjoint union of copies of
 $\mathrm {Spec}\: k$
, one copy for each conjugacy class of the abstract group
$\mathrm {Spec}\: k$
, one copy for each conjugacy class of the abstract group
 $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
. -
2. If G is commutative, then the adjoint representation is trivial and thus,
 $\mathrm {Conj}_G$
is isomorphic to the scheme underlying G. For example, if
$\mathrm {Conj}_G$
is isomorphic to the scheme underlying G. For example, if
 $G=\boldsymbol {\alpha }_p$
or
$G=\boldsymbol {\alpha }_p$
or
 $G=\boldsymbol {\mu }_p$
, then
$G=\boldsymbol {\mu }_p$
, then
 $\mathrm {Conj}_G$
is a non-reduced scheme of length p with reduction
$\mathrm {Conj}_G$
is a non-reduced scheme of length p with reduction
 $(\mathrm {Conj}_G)_{\mathrm {red}}\cong \mathrm {Spec}\: k$
.
$(\mathrm {Conj}_G)_{\mathrm {red}}\cong \mathrm {Spec}\: k$
.
In characteristic zero, all finite group schemes are étale and Case (1) applies. However, in characteristic
![]() $p>0$
, the second example shows that for non-reduced group schemes
$p>0$
, the second example shows that for non-reduced group schemes
![]() $\mathrm {Conj}_G$
may also be non-reduced. The reduction
$\mathrm {Conj}_G$
may also be non-reduced. The reduction
![]() $(\mathrm {Conj}_G)_{\mathrm {red}}$
is related to our first approach to conjugacy classes:
$(\mathrm {Conj}_G)_{\mathrm {red}}$
is related to our first approach to conjugacy classes:
Proposition B.10.
-
1. A morphism
 $G\to H$
of finite group schemes over k induces a morphism
$G\to H$
of finite group schemes over k induces a morphism
 $\mathrm {Conj}_G\to \mathrm {Conj}_H$
of schemes over k.
$\mathrm {Conj}_G\to \mathrm {Conj}_H$
of schemes over k. -
2. Assume
 $p>0$
and let
$p>0$
and let
 $G\to G^{\mathrm {\acute {e}t}}$
be the maximal étale quotient of the finite group scheme G over k. Then, reduction identifies
$G\to G^{\mathrm {\acute {e}t}}$
be the maximal étale quotient of the finite group scheme G over k. Then, reduction identifies
 $G_{\mathrm {red}}$
with
$G_{\mathrm {red}}$
with
 $G^{\mathrm {\acute {e}t}}$
and the induced natural inclusion
$G^{\mathrm {\acute {e}t}}$
and the induced natural inclusion
 $G^{\mathrm {\acute {e}t}}\to G$
induces an isomorphism of schemes over k. In particular,
$G^{\mathrm {\acute {e}t}}\to G$
induces an isomorphism of schemes over k. In particular, $$ \begin{align*}\mathrm{Conj}_{G^{\mathrm{\acute{e}t}}} \,\to\, \left( \mathrm{Conj}_G \right)_{\mathrm{red}} \end{align*} $$
$$ \begin{align*}\mathrm{Conj}_{G^{\mathrm{\acute{e}t}}} \,\to\, \left( \mathrm{Conj}_G \right)_{\mathrm{red}} \end{align*} $$
 $(\mathrm {Conj}_G)_{\mathrm {red}}$
is a disjoint union of copies of
$(\mathrm {Conj}_G)_{\mathrm {red}}$
is a disjoint union of copies of
 $\mathrm {Spec}\: k$
with one copy for each conjugacy class of the abstract group
$\mathrm {Spec}\: k$
with one copy for each conjugacy class of the abstract group
 $G_{\mathrm {abs}}:=G(k)=G^{\mathrm {\acute {e}t}}(k)$
.
$G_{\mathrm {abs}}:=G(k)=G^{\mathrm {\acute {e}t}}(k)$
.
Proof. We first prove Claim (1). If
![]() $G_{\mathrm {abs}}\to H_{\mathrm {abs}}$
is a homomorphism of groups, then we get a well-defined induced map of conjugacy classes. Thus, if
$G_{\mathrm {abs}}\to H_{\mathrm {abs}}$
is a homomorphism of groups, then we get a well-defined induced map of conjugacy classes. Thus, if
![]() $G\to H$
is as in (1) and if T is a scheme over k, then we get a well-defined map
$G\to H$
is as in (1) and if T is a scheme over k, then we get a well-defined map
![]() $(G(T)/\sim )\to (H(T)/\sim )$
. This induces a morphism of functors
$(G(T)/\sim )\to (H(T)/\sim )$
. This induces a morphism of functors
![]() $\underline {\mathrm {Conj}}_G\to \underline {\mathrm {Conj}}_H$
and thus, a morphism of schemes
$\underline {\mathrm {Conj}}_G\to \underline {\mathrm {Conj}}_H$
and thus, a morphism of schemes
![]() $\mathrm {Conj}_G\to \mathrm {Conj}_H$
.
$\mathrm {Conj}_G\to \mathrm {Conj}_H$
.
Let G be as in Claim (2). Let
![]() $G_{\mathrm {red}}\to G$
be the reduction, which is a morphism of group schemes. We thus obtain canonical homomorphisms
$G_{\mathrm {red}}\to G$
be the reduction, which is a morphism of group schemes. We thus obtain canonical homomorphisms
![]() $G^{\mathrm {\acute {e}t}}\to G\to G^{\mathrm {\acute {e}t}}$
of group schemes over k, which (by Claim (1)) induce morphisms of their associated schemes of conjugacy classes
$G^{\mathrm {\acute {e}t}}\to G\to G^{\mathrm {\acute {e}t}}$
of group schemes over k, which (by Claim (1)) induce morphisms of their associated schemes of conjugacy classes
The composition is the identity. Since
![]() $\mathrm {Conj}_{G^{\mathrm {\acute {e}t}}}$
is reduced, we obtain a factorisation
$\mathrm {Conj}_{G^{\mathrm {\acute {e}t}}}$
is reduced, we obtain a factorisation
All these schemes are reduced and finite over the algebraically closed field k. Thus, all of them are finite disoint unions of copies of
![]() $\mathrm {Spec}\: k$
. To prove that the morphisms in (B.1) are isomorphisms, it suffices to check that the induced maps on k-rational points are bijections. This follows easily from the fact that the maps
$\mathrm {Spec}\: k$
. To prove that the morphisms in (B.1) are isomorphisms, it suffices to check that the induced maps on k-rational points are bijections. This follows easily from the fact that the maps
![]() $G_{\mathrm {red}}(k)\to G(k)\to G^{\mathrm {\acute {e}t}}(k)$
are bijections.
$G_{\mathrm {red}}(k)\to G(k)\to G^{\mathrm {\acute {e}t}}(k)$
are bijections.
If G is moreover linearly reductive, then the length of
![]() $\mathrm {Conj}_G$
is related to the approach to conjugacy classes from Section B.2.
$\mathrm {Conj}_G$
is related to the approach to conjugacy classes from Section B.2.
Proposition B.11. Let G be a finite and linearly reductive group scheme over k, let
![]() $G_{\mathrm {abs}}$
be the abstract group associated to G and let F be a field as in Proposition B.2. Then,
$G_{\mathrm {abs}}$
be the abstract group associated to G and let F be a field as in Proposition B.2. Then,
and this length agrees with the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
Proof. By Remark B.8, the length of
![]() $\mathrm {Conj}_k(G)$
is equal to the dimension of the largest trivial subrepresentation of
$\mathrm {Conj}_k(G)$
is equal to the dimension of the largest trivial subrepresentation of
![]() $\rho _{\mathrm {ad}}$
. Since
$\rho _{\mathrm {ad}}$
. Since
![]() $\mathrm {Rep}_k(G)$
is semi-simple, this is the same as the multiplicity of
$\mathrm {Rep}_k(G)$
is semi-simple, this is the same as the multiplicity of ![]() in
in
![]() $\rho _{\mathrm {ad}}$
. Using the isomorphism from Prop 2.6, this multiplicity is the same as the multiplicity of
$\rho _{\mathrm {ad}}$
. Using the isomorphism from Prop 2.6, this multiplicity is the same as the multiplicity of ![]() in the adjoint representation of
in the adjoint representation of
![]() $G_{\mathrm {abs}}$
. This latter multiplicity is equal to the number of conjugacy classes of
$G_{\mathrm {abs}}$
. This latter multiplicity is equal to the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
, see, for example, Remark A.4. By Proposition B.2, this number is equal to the cardinality of
$G_{\mathrm {abs}}$
, see, for example, Remark A.4. By Proposition B.2, this number is equal to the cardinality of
![]() $\mathrm {Spec}\: F\otimes _{\mathbb {Z}} K_k(G)$
.
$\mathrm {Spec}\: F\otimes _{\mathbb {Z}} K_k(G)$
.
B.4 Fourth approach: via lifting to characteristic zero
Another idea might be to use lifting to characteristic zero: Let k be an algebraically closed field of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $W(k)$
be the ring of Witt vectors of k and let K be field of fractions of
$W(k)$
be the ring of Witt vectors of k and let K be field of fractions of
![]() $W(k)$
.
$W(k)$
.
Example B.12 (Mumford–Oort)
Let
![]() $\varphi :\boldsymbol {\mu }_p\to \underline {\mathrm {Aut}}(\boldsymbol {\alpha }_p)\cong {\mathbb {G}}_m$
be a non-trivial homomorphism and let
$\varphi :\boldsymbol {\mu }_p\to \underline {\mathrm {Aut}}(\boldsymbol {\alpha }_p)\cong {\mathbb {G}}_m$
be a non-trivial homomorphism and let
![]() $G:=\boldsymbol {\alpha }_p\rtimes _\varphi \boldsymbol {\mu }_p$
be the corresponding semi-direct product group scheme. Then, G is a non-commutative group scheme of length
$G:=\boldsymbol {\alpha }_p\rtimes _\varphi \boldsymbol {\mu }_p$
be the corresponding semi-direct product group scheme. Then, G is a non-commutative group scheme of length
![]() $p^2$
over k. Oort and Mumford [Reference Mumford and OortMO68, Introduction, Example (-B)] (but see also [Reference OortOo71, page 266]) showed that there does not exist a lift of G to any extension of
$p^2$
over k. Oort and Mumford [Reference Mumford and OortMO68, Introduction, Example (-B)] (but see also [Reference OortOo71, page 266]) showed that there does not exist a lift of G to any extension of
![]() $W(k)$
.
$W(k)$
.
In particular, one cannot define conjugacy classes by first lifting G over some possibly ramified extension of
![]() $W(k)$
, then passing to the geometric generic fibre of the lift, which would be the constant group associated to an abstract finite group
$W(k)$
, then passing to the geometric generic fibre of the lift, which would be the constant group associated to an abstract finite group
![]() $G_{\mathrm {abs}}$
, and finally use the conjugacy classes of
$G_{\mathrm {abs}}$
, and finally use the conjugacy classes of
![]() $G_{\mathrm {abs}}$
as a replacement for the conjugacy classes of G. The reason is simply that lifts may not exist to start with.
$G_{\mathrm {abs}}$
as a replacement for the conjugacy classes of G. The reason is simply that lifts may not exist to start with.
In the following two cases, lifts do exist and we leave the straightforward proofs of our assertions to the reader:
Remark B.13. Assume that G is étale over k. Then, there exists a unique flat lift of G over
![]() $W(k)$
, which is the constant group scheme associated to
$W(k)$
, which is the constant group scheme associated to
![]() $G_{\mathrm {abs}}:=G(k)$
over
$G_{\mathrm {abs}}:=G(k)$
over
![]() $W(k)$
. The constant scheme associated to the set of conjugacy classes of
$W(k)$
. The constant scheme associated to the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
is the unique a flat lift of the scheme
$G_{\mathrm {abs}}$
is the unique a flat lift of the scheme
![]() $\mathrm {Conj}_G$
over
$\mathrm {Conj}_G$
over
![]() $W(k)$
, which is étale over
$W(k)$
, which is étale over
![]() $W(k)$
. More precisely, it is the constant scheme associated to the set of conjugacy classes of
$W(k)$
. More precisely, it is the constant scheme associated to the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
over
$G_{\mathrm {abs}}$
over
![]() $W(k)$
.
$W(k)$
.
Remark B.14. Assume that G is linearly reductive. Let
![]() $G_{\mathrm {abs}}$
abstract group associated to G and recall that their representation categories are equivalent by Proposition 2.6. Proposition B.2 shows that Definition 6.1 is compatible with
$G_{\mathrm {abs}}$
abstract group associated to G and recall that their representation categories are equivalent by Proposition 2.6. Proposition B.2 shows that Definition 6.1 is compatible with
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
If
![]() ${\mathcal G}\to \mathrm {Spec}\: W(k)$
is a flat lift of G over
${\mathcal G}\to \mathrm {Spec}\: W(k)$
is a flat lift of G over
![]() $W(k)$
, for example, the canonical lift
$W(k)$
, for example, the canonical lift
![]() ${\mathcal G}_{\mathrm {can}}$
, then
${\mathcal G}_{\mathrm {can}}$
, then
where the invariants are taken with respect to the adjoint representation, is a flat lift of
![]() $\mathrm {Conj}_G$
over
$\mathrm {Conj}_G$
over
![]() $W(k)$
, whose geometric generic fibre is the constant scheme associated to the set of conjugacy classes of
$W(k)$
, whose geometric generic fibre is the constant scheme associated to the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
. (Flatness follows from the fact that the special and the geometric generic fibre have the same length by Remark B.8.)
$G_{\mathrm {abs}}$
. (Flatness follows from the fact that the special and the geometric generic fibre have the same length by Remark B.8.)
The length of
![]() $\mathrm {Conj}_G$
is equal to the number of conjugacy classes of
$\mathrm {Conj}_G$
is equal to the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
. The length of
$G_{\mathrm {abs}}$
. The length of
![]() $\mathrm {Conj}_G$
is at least the number of k-rational points
$\mathrm {Conj}_G$
is at least the number of k-rational points
![]() $\mathrm {Conj}_G(k)$
and in general not equal, since
$\mathrm {Conj}_G(k)$
and in general not equal, since
![]() $\mathrm {Conj}_G$
may not be étale over k.
$\mathrm {Conj}_G$
may not be étale over k.
If G is of length prime to p, then it is étale and linearly reductive and in this case, all previous approaches yield essentially the same notion of conjugacy class. On the other hand, the examples of the above subsections show that if G is étale of length divisible by p or if G is linearly reductive but not étale, then the various approaches of the above subsections usually lead to different notions of conjugacy classes.
B.5 Fifth approach: via adjoint representation
Let
![]() $G_{\mathrm {abs}}$
be a finite group and let
$G_{\mathrm {abs}}$
be a finite group and let
![]() $\rho _{\mathrm {ad}}:G_{\mathrm {abs}}\to {\mathbf {GL}}(V_{\mathrm {ad}})$
be its adjoint representation over k. By Remark A.4, the dimension of the largest trivial subrepresentation of
$\rho _{\mathrm {ad}}:G_{\mathrm {abs}}\to {\mathbf {GL}}(V_{\mathrm {ad}})$
be its adjoint representation over k. By Remark A.4, the dimension of the largest trivial subrepresentation of
![]() $\rho _{\mathrm {ad}}$
is equal to the dimension of largest trivial quotient representation of
$\rho _{\mathrm {ad}}$
is equal to the dimension of largest trivial quotient representation of
![]() $\rho _{\mathrm {ad}}$
(even if p divides the order of
$\rho _{\mathrm {ad}}$
(even if p divides the order of
![]() $G_{\mathrm {abs}}$
) and these dimensions are equal to the number of conjugacy classes of
$G_{\mathrm {abs}}$
) and these dimensions are equal to the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
. Unfortunately, these trivial sub- or quotient representations do not admit canonical decompositions into one-dimensional subspaces. Thus, there is no canonical bijection between the conjugacy classes of
$G_{\mathrm {abs}}$
. Unfortunately, these trivial sub- or quotient representations do not admit canonical decompositions into one-dimensional subspaces. Thus, there is no canonical bijection between the conjugacy classes of
![]() $G_{\mathrm {abs}}$
with trivial sub- or quotient representations of
$G_{\mathrm {abs}}$
with trivial sub- or quotient representations of
![]() $\rho _{\mathrm {ad}}$
.
$\rho _{\mathrm {ad}}$
.
Remark B.15. Let
![]() $H:=k[G_{\mathrm {abs}}]$
be the group algebra with its usual Hopf algebra structure. The set of group-like elements of H recovers the group
$H:=k[G_{\mathrm {abs}}]$
be the group algebra with its usual Hopf algebra structure. The set of group-like elements of H recovers the group
![]() $G_{\mathrm {abs}}$
, see Example A.1. This suggests to use the adjoint representation
$G_{\mathrm {abs}}$
, see Example A.1. This suggests to use the adjoint representation
![]() ${}^{\mathrm {ad}}H$
together with the Hopf algebra structure of H - in particular, its co-algebra structure - to define a useful notion of conjugacy class.
${}^{\mathrm {ad}}H$
together with the Hopf algebra structure of H - in particular, its co-algebra structure - to define a useful notion of conjugacy class.
As we have seen (somewhat implicitly) in Section B.3 above, this works: Let
![]() $G:=\mathrm {Spec}\: H^*$
be the constant group scheme associated to
$G:=\mathrm {Spec}\: H^*$
be the constant group scheme associated to
![]() $G_{\mathrm {abs}}$
. Then, the topological space underlying
$G_{\mathrm {abs}}$
. Then, the topological space underlying
![]() $\mathrm {Conj}_G$
is the set of group-like elements of the Hopf algebra H modulo the adjoint representation. This set can be identified with the set of conjugacy classes of
$\mathrm {Conj}_G$
is the set of group-like elements of the Hopf algebra H modulo the adjoint representation. This set can be identified with the set of conjugacy classes of
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
Unfortunately, the previous remark does not carry over to finite group schemes that are not étale, as the following example shows.
Example B.16. Let
![]() $G=\boldsymbol {\mu }_p$
or
$G=\boldsymbol {\mu }_p$
or
![]() $G=\boldsymbol {\alpha }_p$
over the algebraically closed field k of characteristic
$G=\boldsymbol {\alpha }_p$
over the algebraically closed field k of characteristic
![]() $p>0$
.
$p>0$
.
-
1. The adjoint representation
 $\rho _{\mathrm {ad}}$
of G is trivial of dimension p, but there is no canonical way to decompose it into one-dimensional subspaces. This would suggest to have p conjugacy classes, but without being able to distinguish them.
$\rho _{\mathrm {ad}}$
of G is trivial of dimension p, but there is no canonical way to decompose it into one-dimensional subspaces. This would suggest to have p conjugacy classes, but without being able to distinguish them. -
2. Moreover, there is only one group-like element in the Hopf algebra
 $H^0(G,{\mathcal O}_G)^*$
and the adjoint representation on this element is trivial as well. This would suggest to have one conjugacy class only, see also Example B.9.(2).
$H^0(G,{\mathcal O}_G)^*$
and the adjoint representation on this element is trivial as well. This would suggest to have one conjugacy class only, see also Example B.9.(2).
B.6 Sixth approach: via extended adjoint representation
Given a finite-dimensional Hopf algebra A over a field k, we have the adjoint representation
![]() ${}^{\mathrm {ad}}A$
, see Appendix A.3. In Appendix A.4, we recalled the quantum double
${}^{\mathrm {ad}}A$
, see Appendix A.3. In Appendix A.4, we recalled the quantum double
![]() $D(A)=(A^{\mathrm {op}})^*\bowtie A$
. In Appendix A.5, we recalled that
$D(A)=(A^{\mathrm {op}})^*\bowtie A$
. In Appendix A.5, we recalled that
![]() ${}^{\mathrm {ad}}A$
can be extended to a representation of
${}^{\mathrm {ad}}A$
can be extended to a representation of
![]() $D(A)$
on A, the extended adjoint representation
$D(A)$
on A, the extended adjoint representation
![]() ${}^{\mathrm {Ad}}A$
.
${}^{\mathrm {Ad}}A$
.
Generalising work of Witherspoon [Reference WitherspoonWi99], Cohen and Westreich [Reference Cohen and WestreichCW11] defined the set of conjugacy classes of A for a finite-dimensional semi-simple Hopf algebra over
![]() ${\mathbb {C}}$
to be the set of simple subrepresentations of
${\mathbb {C}}$
to be the set of simple subrepresentations of
![]() ${}^{\mathrm {Ad}}A$
. In this context, we also refer to the work of Jacoby [Reference JacobyJa17] and Zhu [Reference ZhuZhu97].
${}^{\mathrm {Ad}}A$
. In this context, we also refer to the work of Jacoby [Reference JacobyJa17] and Zhu [Reference ZhuZhu97].
If G is a finite group scheme over k with Hopf algebra
![]() $A:=H^0(G,{\mathcal O}_G)$
, then
$A:=H^0(G,{\mathcal O}_G)$
, then
![]() $D(A)$
is semi-simple if and only if
$D(A)$
is semi-simple if and only if
![]() $D(A^*)$
is semi-simple if and only if G is of length prime to p, see Proposition A.7. In particular, the (extended) adjoint representations of A or
$D(A^*)$
is semi-simple if and only if G is of length prime to p, see Proposition A.7. In particular, the (extended) adjoint representations of A or
![]() $A^*$
may not be semi-simple. We will now study these representations and their relation to conjugacy classes.
$A^*$
may not be semi-simple. We will now study these representations and their relation to conjugacy classes.
Example B.17. Let G be étale over k. Then it is the constant group scheme associated to
![]() $G_{\mathrm {abs}}:=G(k)$
. If
$G_{\mathrm {abs}}:=G(k)$
. If
![]() $A:=H^0(G,{\mathcal O}_G)$
is the associated Hopf algebra, then we have
$A:=H^0(G,{\mathcal O}_G)$
is the associated Hopf algebra, then we have
![]() $A^*\cong k[G_{\mathrm {abs}}]$
. As seen in Example A.8, the extended adjoint representation
$A^*\cong k[G_{\mathrm {abs}}]$
. As seen in Example A.8, the extended adjoint representation
![]() ${}^{\mathrm {Ad}}(A^*)$
is semi-simple and there is a natural bijection between conjugacy classes of
${}^{\mathrm {Ad}}(A^*)$
is semi-simple and there is a natural bijection between conjugacy classes of
![]() $G_{\mathrm {abs}}$
and simple subrepresentations of
$G_{\mathrm {abs}}$
and simple subrepresentations of
![]() ${}^{\mathrm {Ad}}(A^*)$
. We stress that this is also true if p divides the order of
${}^{\mathrm {Ad}}(A^*)$
. We stress that this is also true if p divides the order of
![]() $G_{\mathrm {abs}}$
.
$G_{\mathrm {abs}}$
.
Example B.18. Let G be a finite and linearly reductive group scheme over k, let
![]() $G_{\mathrm {abs}}$
be the associated abstract finite group and let
$G_{\mathrm {abs}}$
be the associated abstract finite group and let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. Since A is commutative,
$A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. Since A is commutative,
![]() ${}^{\mathrm {ad}}A$
is trivial. Using the description (A.1) of
${}^{\mathrm {ad}}A$
is trivial. Using the description (A.1) of
![]() ${}^{\mathrm {Ad}}A$
as an induced representation, we can identify it with the dual of the regular representation
${}^{\mathrm {Ad}}A$
as an induced representation, we can identify it with the dual of the regular representation
together with the trivial representation of A. By Proposition 2.6, representations of
![]() $A^*$
can be identified with representations of
$A^*$
can be identified with representations of
![]() ${\mathbb {C}}[G_{\mathrm {abs}}]$
and thus, representations of
${\mathbb {C}}[G_{\mathrm {abs}}]$
and thus, representations of
![]() $G_{\mathrm {abs}}$
. Thus, we can decompose
$G_{\mathrm {abs}}$
. Thus, we can decompose
![]() ${}^{\mathrm {Ad}}A$
like the dual of the regular representation of
${}^{\mathrm {Ad}}A$
like the dual of the regular representation of
![]() $G_{\mathrm {abs}}$
: the number of isotypical components of this representation is equal to the number of conjugacy classes of
$G_{\mathrm {abs}}$
: the number of isotypical components of this representation is equal to the number of conjugacy classes of
![]() $G_{\mathrm {abs}}$
. Thus, one can think of the conjugacy classes of
$G_{\mathrm {abs}}$
. Thus, one can think of the conjugacy classes of
![]() $G_{\mathrm {abs}}$
as being “dual” to these isotypical components similarly to Appendix B.2.
$G_{\mathrm {abs}}$
as being “dual” to these isotypical components similarly to Appendix B.2.
The upshot of this discussion is the following: Let G be a finite group scheme over k and let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra.
$A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra.
-
1. If G is étale over k, then simple subrepresentations of
 ${}^{\mathrm {Ad}}(A^*)$
are in bijection with conjugacy classes of
${}^{\mathrm {Ad}}(A^*)$
are in bijection with conjugacy classes of
 $G_{\mathrm {abs}}:=G(k)$
.
$G_{\mathrm {abs}}:=G(k)$
. -
2. If G is linearly reductive, then the isotypical components of
 ${}^{\mathrm {Ad}}A$
give a reasonably good definition for the “dual” of a conjugacy class.
${}^{\mathrm {Ad}}A$
give a reasonably good definition for the “dual” of a conjugacy class.
The following example shows that in general, neither
![]() ${}^{\mathrm {Ad}}A$
nor
${}^{\mathrm {Ad}}A$
nor
![]() ${}^{\mathrm {Ad}}(A^*)$
leads to a good approach toward the notion of a conjugacy class - at least none that is better than the ones already discussed.
${}^{\mathrm {Ad}}(A^*)$
leads to a good approach toward the notion of a conjugacy class - at least none that is better than the ones already discussed.
Example B.19. Let G be a finite and commutative group scheme over k and let
![]() $A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. As a consequence of Example A.9, we have the following.
$A:=H^0(G,{\mathcal O}_G)$
be the associated Hopf algebra. As a consequence of Example A.9, we have the following.
-
1. If
 $G=\boldsymbol {\mu }_p$
, then we have
$G=\boldsymbol {\mu }_p$
, then we have
 $A=k[{\mathbf {C}}_p]$
. Thus,
$A=k[{\mathbf {C}}_p]$
. Thus,
 ${}^{\mathrm {Ad}}A$
splits into the direct sum of p pairwise non-isomorphic one-dimensional representations, which correspond to the characters of G. On the other hand,
${}^{\mathrm {Ad}}A$
splits into the direct sum of p pairwise non-isomorphic one-dimensional representations, which correspond to the characters of G. On the other hand,
 ${}^{\mathrm {Ad}}(A^*)$
is a non-trivial successive p-fold and non-split extension of the trivial representation
${}^{\mathrm {Ad}}(A^*)$
is a non-trivial successive p-fold and non-split extension of the trivial representation  , whose semi-simplification is trivial of dimension p.
, whose semi-simplification is trivial of dimension p. -
2. If
 $G={\mathbf {C}}_p$
, then we obtain the same as before with the rôles of A and
$G={\mathbf {C}}_p$
, then we obtain the same as before with the rôles of A and
 $A^*$
interchanged.
$A^*$
interchanged. -
3. If
 $G=\boldsymbol {\alpha }_p$
, then
$G=\boldsymbol {\alpha }_p$
, then
 $A\cong A^*$
and
$A\cong A^*$
and
 ${}^{\mathrm {Ad}}A\cong {}^{\mathrm {Ad}}(A^*)$
is a successive p-fold and non-split extension of the trivial representation
${}^{\mathrm {Ad}}A\cong {}^{\mathrm {Ad}}(A^*)$
is a successive p-fold and non-split extension of the trivial representation  .
.
Acknowledgements
I thank Frank Himstedt, Martin Lorenz, Yuya Matsumoto, Frans Oort, Matt Satriano, Takehiko Yasuda and the referees for discussions and comments.