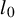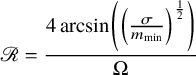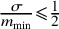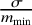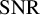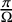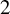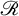1 Introduction
Since the first report of the use of microscopes for observation in the 17th century, optical microscopes have played a central role in helping to untangle complex biological mysteries. Numerous scientific advancements and manufacturing innovations over the past three centuries have led to advanced optical microscope designs with significantly improved image quality. However, due to the physical nature of wave propagation and diffraction, there is a fundamental diffraction barrier in optical imaging systems, which is called the resolution limit. This resolution limit is one of the most important characteristics of an imaging system. In the 19th century, Rayleigh [Reference Rayleigh35] gave a well-known criterion for determining the resolution limit (Rayleigh’s diffraction limit) for distinguishing two point sources, which is extensively used in optical microscopes for analyzing the resolution. The problem to resolve point sources separated below the Rayleigh diffraction limit is then called super-resolution and is commonly known to be very challenging for single snapshot. However, Rayleigh’s criterion is based on intuitive notions and is more applicable to observations with the human eye. It also neglects the effect of the noise in the measurements and the aberrations in the modeling. Due to the rapid advancement of technologies, modern imaging data is generally captured using intricate imaging techniques and sensitive cameras, and may also be subject to analysis by complex processing algorithms. Thus, Rayleigh’s deterministic resolution criterion is not well adapted to current quantitative imaging techniques, necessitating new and more rigorous definitions of resolution limit with respect to the noise, model and imaging methods [Reference Ram, Ward and Ober34].
Our previous works [Reference Liu and Zhang27, Reference Liu and Zhang26, Reference Liu and Zhang25, Reference Liu and Ammari22] have achieved certain success in this respect and enable us to understand the performance of some super-resolution algorithms. Nevertheless, the derived estimates are still lacking enough guiding significance in practice on the possibility of super-resolution.
In this paper, we introduce new and direct insights into the stability of super-resolution problems and significantly enhance many estimates to have practical significance. Our findings reveal several new facts; for example, we theoretically demonstrate that super-resolution from a single snapshot is indeed feasible in practice.
1.1 Resolution limit, super-resolution and diffraction limit
1.1.1 Classical criteria for the resolution limit
The resolution of an optical microscope is usually defined as the shortest distance between two points on a specimen that can still be distinguished by the observer or camera system as separate entities, but it is in some sense ambiguous. In fact, it does not explicitly require that just the source number should be detected or the source locations should be stably reconstructed. From the mathematical perspective, recovering the source number and stably reconstructing the source locations are actually two different tasks [Reference Liu and Zhang26] demanding different separation distances.
Historically, the resolution of optical microscopy focuses mainly on correctly detecting the number of sources, rather than on stably recovering the locations. This can be seen from the below discussions for the classical and semi-classical results on the resolution.
In the 18th and 19th centuries, many classical criteria were proposed to determine the resolution limit. For example, Rayleigh thought that two point sources observed are regarded as just resolved when the principal diffraction maximum of one Airy disk coincides with the first minimum of the other, as is shown by Figure 1. Since the separation of sources is still relatively large, not only the source number can be detected, but also the source locations can be stably recovered.

Figure 1 Rayleigh’s criterion and Rayleigh’s diffraction limit.
However, Rayleigh’s choice of resolution limit is based on the presumed resolving ability of human visual system, which at first glance seems arbitrary. In fact, Rayleigh said about his criterion that
‘This rule is convenient on account of its simplicity and it is sufficiently accurate in view of the necessary uncertainty as to what exactly is meant by resolution.’
As is shown in Figure 1, the Rayleigh diffraction limit results in an
![]() $\sim 20\%$
dip in intensity between the two peaks of Airy disks [Reference Demmerle, Wegel, Schermelleh and Dobbie9]. Schuster pointed out in 1904 [Reference Schuster38] that the dip in intensity necessary to indicate resolution is a physiological phenomenon and there are other forms of spectroscopic investigation besides that of eye observation. Many alternative criteria were proposed by other physicists as illustrated in Figure 2.
$\sim 20\%$
dip in intensity between the two peaks of Airy disks [Reference Demmerle, Wegel, Schermelleh and Dobbie9]. Schuster pointed out in 1904 [Reference Schuster38] that the dip in intensity necessary to indicate resolution is a physiological phenomenon and there are other forms of spectroscopic investigation besides that of eye observation. Many alternative criteria were proposed by other physicists as illustrated in Figure 2.

Figure 2 Different resolution limits.
A more mathematically rigorous criterion was proposed by Sparrow [Reference Sparrow42], who advocates that the resolution limit should be the distance between two point sources where the images no longer have a dip between the central peaks of each Airy disk (as illustrated by Figure 2). Based on Sparrow’s criterion, the two point sources are so close that the source locations may not be stably resolved although the source number is detected. Indeed, the Sparrow resolution limit is less relevant with practical use [Reference Chen and Moitra6, Reference Demmerle, Wegel, Schermelleh and Dobbie9] because it is very signal-to-noise dependent and has no easy comparison to a readily measured value in real images. Therefore, these classical resolution criteria focus on the smallest distance between two sources above which we can be sure that there are two sources, regardless of whether their locations can be resolved stably or not.
The classical resolution criteria mentioned above deal with calculated images that are described by a known and exact mathematical model of the intensity distribution. However, if one has perfect access to the intensity profile of the diffraction image of two point sources, one could locate the exact source despite the diffraction. There would be no resolution limit for the reconstruction. This simple fact has been noticed by many researchers in the field [Reference Toraldo Di Francia12, Reference Den Dekker and van den Bos10, Reference Chen and Moitra6]. Moreover, an imaging system constructed without any aberration or irregularity is not practical because the shape of the point-spread function is never known exactly and the measurement noise is inevitable [Reference Ronchi36, Reference Den Dekker and van den Bos10]. Therefore, a rigorous and practically meaningful resolution limit could only be set when taking into account the aberrations and measurement noises [Reference Ronchi36, Reference Goodman16]. In this setting, the images (detected by detectors in practice) were categorized as detected images by Ronchi [Reference Ronchi36], and their resolution was advocated to be more important to investigate than the resolution defined by those classical criteria. Inspired by this, many researchers have analyzed the two-point resolution from the perspective of statistical inference [Reference Helstrom18, Reference Helstrom19, Reference Lucy29, Reference Lucy28, Reference Goodman16, Reference Shahram and Milanfar39, Reference Shahram and Milanfar40, Reference Shahram and Milanfar41]. For instance, in [Reference Helstrom19], Helstrom has shown that the resolution of two identical objects depends on deciding whether they are both present in the field of view or only one of them is there, and their resolvability is measured by the probability of making this decision correctly. In all the papers mentioned above, the authors have derived quasi-explicit formulas or estimations for the minimum SNR that is required to discriminate two point sources or for the possibility of a correct decision. Although the resolutions (or the requirement) in this respect were thoroughly explored in these works which spanned the course of several decades, these results are rarely (even never) utilized in practical applications due to their complexity.
1.1.2 Concept of super-resolution
We next introduce the concept of super-resolution. Super-resolution microscopy is a series of techniques in optical microscopy that allow such images to have resolutions higher than those imposed by the diffraction limit (Rayleigh resolution limit). Due to the breakthrough in super-resolution techniques in recent years, this topic becomes increasingly popular in various fields, and the concept of super-resolution becomes very general. Some literature claims super-resolution, although theoretically, the sources should be separated by a distance above the Rayleigh limit. Bounds on the recovery of the amplitudes (or intensities) of the sources have been derived. Nevertheless, the original concept of super-resolution actually focuses mainly on both detecting the source number and recovering the source locations.
To the best of our knowledge, there is no unique and mathematically rigorous definition of super-resolution. As we have said, the number detection and location recovery are two inherently different [Reference Liu and Zhang26] but important tasks in the super-resolution; thus, we consider two different super-resolutions in the current paper. One is achieving resolution better than the Rayleigh diffraction limit in detecting the correct source number and is named ‘super-resolution in number detection’. The other is achieving resolution better than the Rayleigh diffraction limit in stably recovering the source locations and is named ‘super-resolution in location recovery’.
1.2 Previous mathematical contributions
Before introducing the mathematical contributions of this work, let us first introduce the mathematical model for the imaging problem in k-dimensional space. We consider the collection of point sources as a discrete measure
![]() $\mu =\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j}$
, where
$\mu =\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j}$
, where
![]() $\mathbf{y}_j \in \mathbb R^k,j=1,\cdots ,n$
represent the location of the point sources and the
$\mathbf{y}_j \in \mathbb R^k,j=1,\cdots ,n$
represent the location of the point sources and the
![]() $a_j$
’s their amplitudes. The imaging problem is to recover the sources
$a_j$
’s their amplitudes. The imaging problem is to recover the sources
![]() $\mu $
from its noisy Fourier data,
$\mu $
from its noisy Fourier data,
 $$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})= \sum_{j=1}^{n}a_j e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
$$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})= \sum_{j=1}^{n}a_j e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
where
![]() $\mathscr F[\cdot ]$
denotes the Fourier transform in the k-dimensional space,
$\mathscr F[\cdot ]$
denotes the Fourier transform in the k-dimensional space,
![]() $\Omega $
is the cut-off frequency, and
$\Omega $
is the cut-off frequency, and
![]() $\mathbf W$
represents the total effect of noise and aberrations. We assume that
$\mathbf W$
represents the total effect of noise and aberrations. We assume that
with
![]() $\sigma $
being the noise level. We denote, respectively, the magnitude of the signal and the minimum separation distance between sources by
$\sigma $
being the noise level. We denote, respectively, the magnitude of the signal and the minimum separation distance between sources by
As most of our analyses are on a one-dimensional space, throughout the paper, we use
![]() $y_j, \omega $
to denote the one-dimensional source locations and frequencies and reserve
$y_j, \omega $
to denote the one-dimensional source locations and frequencies and reserve
![]() $\mathbf{y}_j, \boldsymbol {{\omega }}$
for the problem in spaces of general dimensionality. Especially, we denote the one-dimensional sources as
$\mathbf{y}_j, \boldsymbol {{\omega }}$
for the problem in spaces of general dimensionality. Especially, we denote the one-dimensional sources as
![]() $\mu =\sum _{j=1}^{n}a_{j}\delta _{y_j}$
and the noisy measurement as
$\mu =\sum _{j=1}^{n}a_{j}\delta _{y_j}$
and the noisy measurement as
 $$\begin{align*}\mathbf Y(\omega) = \sum_{j=1}^{n}a_j e^{i y_j\omega} + \mathbf W(\omega),\quad \omega \in [-\Omega, \Omega]. \end{align*}$$
$$\begin{align*}\mathbf Y(\omega) = \sum_{j=1}^{n}a_j e^{i y_j\omega} + \mathbf W(\omega),\quad \omega \in [-\Omega, \Omega]. \end{align*}$$
Model (1) is commonly used in the field of applied mathematics for theoretically analyzing the imaging problem [Reference Donoho13, Reference Candès and Fernandez-Granda5, Reference Batenkov, Goldman and Yomdin3]. It is directly the model in the frequency domain for the imaging modalities with
![]() $\mathrm {sinc}(||\mathbf{x} ||_2)$
being the point spread function [Reference Den Dekker and van den Bos10]. Its discrete form is also a standard model in array signal processing. Moreover, even for imaging with general point spread functions or optical transfer functions, some of the imaging enhancements such as inverse filtering method [Reference Frieden15] will modify the measurements in the frequency domain to (1). These ensure the generality of the model (1) in the fields of imaging and array signal processing.
$\mathrm {sinc}(||\mathbf{x} ||_2)$
being the point spread function [Reference Den Dekker and van den Bos10]. Its discrete form is also a standard model in array signal processing. Moreover, even for imaging with general point spread functions or optical transfer functions, some of the imaging enhancements such as inverse filtering method [Reference Frieden15] will modify the measurements in the frequency domain to (1). These ensure the generality of the model (1) in the fields of imaging and array signal processing.
Based on Rayleigh’s criterion, the corresponding resolution limit for imaging with the point spread function
![]() $\mathrm {sinc}(||\mathbf{x}||_2)^2$
is
$\mathrm {sinc}(||\mathbf{x}||_2)^2$
is
![]() $\frac {\pi }{\Omega }$
. It was shown by many mathematical studies that
$\frac {\pi }{\Omega }$
. It was shown by many mathematical studies that
![]() $\frac {\pi }{\Omega }$
is also the critical limit for the imaging model (1). To be more specific, in [Reference Donoho13], Donoho demonstrated that for sources on grid points spacing by
$\frac {\pi }{\Omega }$
is also the critical limit for the imaging model (1). To be more specific, in [Reference Donoho13], Donoho demonstrated that for sources on grid points spacing by
![]() $\Delta \geqslant \frac {\pi }{\Omega }$
, the stable recovery is possible from (1) in dimension one, but the stability becomes much worse in the case when
$\Delta \geqslant \frac {\pi }{\Omega }$
, the stable recovery is possible from (1) in dimension one, but the stability becomes much worse in the case when
![]() $\Delta < \frac {\pi }{\Omega }$
. Therefore, in the same way as [Reference Donoho13], we regard
$\Delta < \frac {\pi }{\Omega }$
. Therefore, in the same way as [Reference Donoho13], we regard
![]() $\frac {\pi }{\Omega }$
as the Rayleigh limit in this paper, and super-resolution refers to obtaining a better resolution than
$\frac {\pi }{\Omega }$
as the Rayleigh limit in this paper, and super-resolution refers to obtaining a better resolution than
![]() $\frac {\pi }{\Omega }$
.
$\frac {\pi }{\Omega }$
.
For the mathematical theory of super-resolving n point sources or infinity point sources, to the best of our knowledge, the first result was derived by Donoho in 1992 [Reference Donoho13]. He developed a theory from the optimal recovery point of view to explain the possibility and difficulties of super-resolution via sparsity constraint. He considered discrete measures
![]() $\mu $
supported on a lattice
$\mu $
supported on a lattice
![]() $\{k\Delta \}_{k=-\infty }^{\infty }$
and regularized by a so-called ‘Rayleigh index’ R. The available measurement is the noisy Fourier data of
$\{k\Delta \}_{k=-\infty }^{\infty }$
and regularized by a so-called ‘Rayleigh index’ R. The available measurement is the noisy Fourier data of
![]() $\mu $
like model (1) in a one-dimensional space. He showed that the minimax error
$\mu $
like model (1) in a one-dimensional space. He showed that the minimax error
![]() $E^*$
for the amplitude recovery with noise level
$E^*$
for the amplitude recovery with noise level
![]() $\sigma $
was bounded as
$\sigma $
was bounded as
 $$ \begin{align*} \beta_1(R,\Omega)\left(\frac{1}{\Delta}\right)^{2R-1}\sigma\leqslant E^* \leqslant \beta_2(R,\Omega) \left(\frac{1}{\Delta}\right)^{4R+1}\sigma \end{align*} $$
$$ \begin{align*} \beta_1(R,\Omega)\left(\frac{1}{\Delta}\right)^{2R-1}\sigma\leqslant E^* \leqslant \beta_2(R,\Omega) \left(\frac{1}{\Delta}\right)^{4R+1}\sigma \end{align*} $$
for certain small
![]() $\Delta $
. His results emphasize the importance of sparsity in the super-resolution. In recent years, due to the impressive development of super-resolution modalities in biological imaging [Reference Hell and Wichmann17, Reference Westphal, Rizzoli, Lauterbach, Kamin, Jahn and Hell47, Reference Hess, Girirajan and Mason20, Reference Betzig, Patterson, Sougrat, Lindwasser, Olenych, Bonifacino, Davidson, Lippincott-Schwartz and Hess4, Reference Rust, Bates and Zhuang37] and super-resolution algorithms in applied mathematics [Reference Candès and Fernandez-Granda5, Reference Duval and Peyré14, Reference Poon and Peyré33, Reference Tang, Bhaskar, Shah and Recht45, Reference Tang, Bhaskar and Recht44, Reference Morgenshtern and Candes32, Reference Morgenshtern31, Reference Denoyelle, Duval and Peyré11], the inherent super-resolving capacity of the imaging problem becomes increasingly popular and the one-dimensional case was well-studied. In [Reference Demanet and Nguyen8], the authors considered resolving the amplitudes of n-sparse point sources supported on a grid and improved the results of Donoho. Concretely, they showed that the scaling of the noise level for the minimax error should be
$\Delta $
. His results emphasize the importance of sparsity in the super-resolution. In recent years, due to the impressive development of super-resolution modalities in biological imaging [Reference Hell and Wichmann17, Reference Westphal, Rizzoli, Lauterbach, Kamin, Jahn and Hell47, Reference Hess, Girirajan and Mason20, Reference Betzig, Patterson, Sougrat, Lindwasser, Olenych, Bonifacino, Davidson, Lippincott-Schwartz and Hess4, Reference Rust, Bates and Zhuang37] and super-resolution algorithms in applied mathematics [Reference Candès and Fernandez-Granda5, Reference Duval and Peyré14, Reference Poon and Peyré33, Reference Tang, Bhaskar, Shah and Recht45, Reference Tang, Bhaskar and Recht44, Reference Morgenshtern and Candes32, Reference Morgenshtern31, Reference Denoyelle, Duval and Peyré11], the inherent super-resolving capacity of the imaging problem becomes increasingly popular and the one-dimensional case was well-studied. In [Reference Demanet and Nguyen8], the authors considered resolving the amplitudes of n-sparse point sources supported on a grid and improved the results of Donoho. Concretely, they showed that the scaling of the noise level for the minimax error should be
![]() $\mathrm {SRF}^{2n-1}$
, where
$\mathrm {SRF}^{2n-1}$
, where
![]() $\mathrm {SRF}:= \frac {1}{\Delta \Omega }$
is the super-resolution factor. Similar results for multi-clumps cases were also derived in [Reference Batenkov, Demanet, Goldman and Yomdin2, Reference Li and Liao21]. Recently in [Reference Batenkov, Goldman and Yomdin3], the authors derived sharp minimax errors for the location and the amplitude recovery of off-the-grid sources. They showed that for
$\mathrm {SRF}:= \frac {1}{\Delta \Omega }$
is the super-resolution factor. Similar results for multi-clumps cases were also derived in [Reference Batenkov, Demanet, Goldman and Yomdin2, Reference Li and Liao21]. Recently in [Reference Batenkov, Goldman and Yomdin3], the authors derived sharp minimax errors for the location and the amplitude recovery of off-the-grid sources. They showed that for
![]() $\sigma \lesssim (\mathrm {SRF})^{-2p+1}$
, where p is the number of nodes that form a cluster of certain type, the minimax error rate for reconstruction of the clustered nodes is of the order
$\sigma \lesssim (\mathrm {SRF})^{-2p+1}$
, where p is the number of nodes that form a cluster of certain type, the minimax error rate for reconstruction of the clustered nodes is of the order
![]() $(\mathrm {SRF})^{2p-2} \frac {\sigma }{\Omega }$
, while for recovering the corresponding amplitudes, the rate is of the order
$(\mathrm {SRF})^{2p-2} \frac {\sigma }{\Omega }$
, while for recovering the corresponding amplitudes, the rate is of the order
![]() $(\mathrm {SRF})^{2p-1}\sigma $
. Moreover, the corresponding minimax rates for the recovery of the non-clustered nodes and amplitudes are
$(\mathrm {SRF})^{2p-1}\sigma $
. Moreover, the corresponding minimax rates for the recovery of the non-clustered nodes and amplitudes are
![]() $\frac {\sigma }{\Omega }$
and
$\frac {\sigma }{\Omega }$
and
![]() $\sigma $
, respectively. This was generalized to the case of resolving positive sources in [Reference Liu and Ammari23] recently. We also refer the readers to [Reference Moitra30, Reference Chen and Moitra6] for understanding the resolution limit from the perceptive of sample complexity and to [Reference Tang43, Reference Ferreira Da Costa and Chi7] for the resolving limit of some algorithms.
$\sigma $
, respectively. This was generalized to the case of resolving positive sources in [Reference Liu and Ammari23] recently. We also refer the readers to [Reference Moitra30, Reference Chen and Moitra6] for understanding the resolution limit from the perceptive of sample complexity and to [Reference Tang43, Reference Ferreira Da Costa and Chi7] for the resolving limit of some algorithms.
In order to characterize the exact resolution rather than the minimax error in recovering multiple point sources, in the earlier works [Reference Liu and Zhang27, Reference Liu and Zhang26, Reference Liu and Zhang25, Reference Liu and Ammari22, Reference Liu, He and Ammari24], we have defined the so-called ‘computational resolution limits’, which characterize the minimum required distance between point sources so that their number and locations can be stably resolved under certain noise level. By developing a nonlinear approximation theory in so-called Vandermonde spaces, we have derived sharp bounds for computational resolution limits in the one-dimensional super-resolution problem (1). In particular, we have shown in [Reference Liu and Zhang26] that the computational resolution limits for the number and location recoveries should be bounded above by, respectively,
![]() $\frac {4.4e\pi }{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2 n-2}}$
and
$\frac {4.4e\pi }{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2 n-2}}$
and
![]() $\frac {5.88 e\pi }{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2 n-1}}$
, where the noise level
$\frac {5.88 e\pi }{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2 n-1}}$
, where the noise level
![]() $\sigma $
and signal magnitude
$\sigma $
and signal magnitude
![]() $m_{\min }$
are defined as in (2) and (3), respectively. In the present paper, we substantially improve these estimates to have practical significance.
$m_{\min }$
are defined as in (2) and (3), respectively. In the present paper, we substantially improve these estimates to have practical significance.
1.3 Our main contributions in this paper
Our first contribution is two location-amplitude identities characterizing the relations between locations and amplitudes of true and recovered sources in the one-dimensional super-resolution problem. These identities allow us to directly derive the super-resolution capability for number, location and amplitude recovery in the super-resolution problem and improve state-of-the-art estimations to an unprecedented level to have practical significance. Although these nonlinear inverse problems are known to be very challenging, we now have a clear and simple picture of all of them, which allows us to solve them in a unified way in just a few pages. To be more specific, we prove that, under model (1) in dimension one, it is definitely possible to detect the correct source number when the sources are separated by
where
![]() $\frac {\sigma }{m_{\min }}$
represents the inverse of the signal-to-noise ratio (
$\frac {\sigma }{m_{\min }}$
represents the inverse of the signal-to-noise ratio (
![]() $\mathrm {SNR}$
). This substantially improves the estimate in [Reference Liu and Zhang26] and indicates that super-resolution in detecting correct source number (i.e., surpassing the diffraction limit
$\mathrm {SNR}$
). This substantially improves the estimate in [Reference Liu and Zhang26] and indicates that super-resolution in detecting correct source number (i.e., surpassing the diffraction limit
![]() $\frac {\pi }{\Omega }$
) is definitely possible when
$\frac {\pi }{\Omega }$
) is definitely possible when
![]() $\frac {m_{\min }}{\sigma }\geqslant (2e)^{2n-2}$
. Moreover, for the case when resolving two sources, the requirement for the separation is improved to
$\frac {m_{\min }}{\sigma }\geqslant (2e)^{2n-2}$
. Moreover, for the case when resolving two sources, the requirement for the separation is improved to
 $$\begin{align*}d_{\min}\geqslant \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
$$\begin{align*}d_{\min}\geqslant \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
indicating that surpassing the Rayleigh limit in distinguishing two sources is possible when
![]() $\mathrm {SNR}>4$
. This is the first time where it is demonstrated theoretically that super-resolution (‘in number detection’) is actually possible in practice. For the stable location recovery, the estimate is improved to
$\mathrm {SNR}>4$
. This is the first time where it is demonstrated theoretically that super-resolution (‘in number detection’) is actually possible in practice. For the stable location recovery, the estimate is improved to
as compared to the previous result in [Reference Liu and Zhang26], indicating that the location recovery is stable when
![]() $\frac {m_{\min }}{\sigma }\geqslant (2.36 e)^{2n-1}$
. Moreover, under the same separation condition, we also obtain stability results for amplitude recovery and a certain
$\frac {m_{\min }}{\sigma }\geqslant (2.36 e)^{2n-1}$
. Moreover, under the same separation condition, we also obtain stability results for amplitude recovery and a certain
![]() $l_0$
minimization algorithm in the super-resolution problem. These results provide us with a quantitative understanding of the super-resolution of multiple sources. Since our method is rather direct, it is very hard to substantially improve the estimates now, and we even roughly know to what extent the constant factor in the estimates can be improved.
$l_0$
minimization algorithm in the super-resolution problem. These results provide us with a quantitative understanding of the super-resolution of multiple sources. Since our method is rather direct, it is very hard to substantially improve the estimates now, and we even roughly know to what extent the constant factor in the estimates can be improved.
Our second crucial result is the theoretical proof of a two-point resolution limit in multi-dimensional spaces under only an assumption on the noise level. It is given by
 $$ \begin{align} \frac{4\arcsin \left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}} \right)}{\Omega} \end{align} $$
$$ \begin{align} \frac{4\arcsin \left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}} \right)}{\Omega} \end{align} $$
for
![]() $\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
. In the case when
$\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
. In the case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, there is no super-resolution under certain circumstances. Our results show that, for resolving any two point sources, the resolution can exceed the Rayleigh limit when
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, there is no super-resolution under certain circumstances. Our results show that, for resolving any two point sources, the resolution can exceed the Rayleigh limit when
![]() $\mathrm {SNR}>2$
. When
$\mathrm {SNR}>2$
. When
![]() $\mathrm {SNR}>4$
, one can achieve
$\mathrm {SNR}>4$
, one can achieve
![]() $1.5$
times improvement of the Rayleigh limit. This finding indicates that obtaining a resolution far better than the Rayleigh limit in practical imaging and direction-of-arrival problems is possible with refined sensors. As a comparison, former works for the two-point resolution [Reference Helstrom18, Reference Helstrom19, Reference Lucy29, Reference Lucy28, Reference Goodman16, Reference Shahram and Milanfar39, Reference Shahram and Milanfar40, Reference Shahram and Milanfar41] consider the model in the physical domain with the imaging process or the noise being random. In addition, the derived estimate is relatively complicated as the model considered is more complex than (1). For example, the
$1.5$
times improvement of the Rayleigh limit. This finding indicates that obtaining a resolution far better than the Rayleigh limit in practical imaging and direction-of-arrival problems is possible with refined sensors. As a comparison, former works for the two-point resolution [Reference Helstrom18, Reference Helstrom19, Reference Lucy29, Reference Lucy28, Reference Goodman16, Reference Shahram and Milanfar39, Reference Shahram and Milanfar40, Reference Shahram and Milanfar41] consider the model in the physical domain with the imaging process or the noise being random. In addition, the derived estimate is relatively complicated as the model considered is more complex than (1). For example, the
![]() $\mathrm {SNR}$
governing object detectability in [Reference Helstrom19] is given by
$\mathrm {SNR}$
governing object detectability in [Reference Helstrom19] is given by
 $$\begin{align*}\mathrm{SNR} = (E/N)(TW)^{-\frac{1}{2}} \left|\int_A \phi_s(\mathbf{r}, \mathbf{r}) d^2 \mathbf{r}\right|{}^{-1}\times\left[\int_A \int_A\left|\phi_s\left(\mathbf{r}_1, \mathbf{r}_2\right)\right|{}^2 d^2 \mathbf{r}_1 d^2 \mathbf{r}_2\right]^{\frac{1}{2}}, \end{align*}$$
$$\begin{align*}\mathrm{SNR} = (E/N)(TW)^{-\frac{1}{2}} \left|\int_A \phi_s(\mathbf{r}, \mathbf{r}) d^2 \mathbf{r}\right|{}^{-1}\times\left[\int_A \int_A\left|\phi_s\left(\mathbf{r}_1, \mathbf{r}_2\right)\right|{}^2 d^2 \mathbf{r}_1 d^2 \mathbf{r}_2\right]^{\frac{1}{2}}, \end{align*}$$
where
![]() $\phi _s(\cdot )$
denotes the autocovariance function of the field in the aperture plane and
$\phi _s(\cdot )$
denotes the autocovariance function of the field in the aperture plane and
![]() $E, N, T, W, A$
represent other factors.
$E, N, T, W, A$
represent other factors.
The estimate of two-point resolution can be directly extended to the following more general setting:
 $$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \chi(\boldsymbol{{\omega}})\mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})= \sum_{j=1}^{n}a_j \chi(\boldsymbol{{\omega}}) e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
$$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \chi(\boldsymbol{{\omega}})\mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})= \sum_{j=1}^{n}a_j \chi(\boldsymbol{{\omega}}) e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
where
![]() $\chi (\boldsymbol {{\omega }})=0$
or
$\chi (\boldsymbol {{\omega }})=0$
or
![]() $1$
,
$1$
,
![]() $\chi (\mathbf{0})=1$
and
$\chi (\mathbf{0})=1$
and
![]() $\chi (\boldsymbol {{\omega }})=1, ||\boldsymbol {{\omega }}||_2 =\Omega $
. This enables the application of our results to line spectral estimations and directional-of-arrival in signal processing. Moreover, our findings can be applied to imaging systems with general optical transfer functions. A new fact revealed in this paper is that the two-point resolution is actually determined by the boundary points of the transfer function and is not that dependent on the interior frequency information. Also, as revealed in Section 5, the measurements at
$\chi (\boldsymbol {{\omega }})=1, ||\boldsymbol {{\omega }}||_2 =\Omega $
. This enables the application of our results to line spectral estimations and directional-of-arrival in signal processing. Moreover, our findings can be applied to imaging systems with general optical transfer functions. A new fact revealed in this paper is that the two-point resolution is actually determined by the boundary points of the transfer function and is not that dependent on the interior frequency information. Also, as revealed in Section 5, the measurements at
![]() $\boldsymbol {{\omega }} =\mathbf{0}$
and
$\boldsymbol {{\omega }} =\mathbf{0}$
and
![]() $\left |\left |{\boldsymbol {{\omega }}}\right |\right |=\Omega $
are already enough for the algorithm which provably achieves the resolution limit.
$\left |\left |{\boldsymbol {{\omega }}}\right |\right |=\Omega $
are already enough for the algorithm which provably achieves the resolution limit.
In the last part of the paper, we find an algorithm that achieves the optimal resolution when distinguishing two sources and conducts many numerical experiments to manifest its optimal performance and phase transition. Although the noise and the aberration are inevitable and the point source is not an exact delta point, our results still indicate that super-resolving two sources in practice is possible for general imaging modalities, due to the excellent noise tolerance. We plan to examine the practical feasibility of our method in the near future.
To summarize, by this paper, we have shed light on understanding quantitatively when super-resolution is definitely possible and when it is not. It has been disclosed by our results that super-resolution when distinguishing two sources is far more possible than what was commonly recognized.
1.4 Organization of the paper
The paper is organized in the following way. In Section 2, we present the theory of location-amplitude identities. In Section 3, we derive stability results for recovering the number, locations and amplitudes of sources in the one-dimensional super-resolution problem. In Section 4, we derive the exact formula of the two-point resolution limit, and, in Section 5, we devise algorithms achieving exactly the optimal resolution in distinguishing images from one and two sources. The Appendix consists of some useful inequalities.
2 Location-amplitude identities
In this section, we intend to derive two location-amplitude identities that characterize the relations between source locations and amplitudes in the one-dimensional super-resolution problem. We start from the following elementary model in dimension one:
where
![]() $\widehat \mu , \mu $
are discrete measures,
$\widehat \mu , \mu $
are discrete measures,
![]() $\mathscr F[f]=\int _{\mathbb R} e^{iy\omega } f(y)dy$
denotes the Fourier transform, and
$\mathscr F[f]=\int _{\mathbb R} e^{iy\omega } f(y)dy$
denotes the Fourier transform, and
![]() $\mathbf{w}(\omega ) = \mathscr F[\widehat \mu ](\omega ) - \mathscr F[\mu ](\omega )$
. To be more specific, we set
$\mathbf{w}(\omega ) = \mathscr F[\widehat \mu ](\omega ) - \mathscr F[\mu ](\omega )$
. To be more specific, we set
![]() $\mu =\sum _{j=1}^na_j\delta _{y_j}$
and
$\mu =\sum _{j=1}^na_j\delta _{y_j}$
and
![]() $\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
with
$\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
with
![]() $a_j, \widehat a_j$
being the source amplitudes and
$a_j, \widehat a_j$
being the source amplitudes and
![]() $y_j, \widehat y_j$
the source locations.
$y_j, \widehat y_j$
the source locations.
2.1 Statement of the identities
Based on the above model, we have the following location-amplitude identities.
Theorem 2.1 (Location-amplitude identities).
Consider the model
where
![]() $\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
and
$\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
and
![]() $\mu =\sum _{j=1}^na_j\delta _{y_j}$
. For any fixed
$\mu =\sum _{j=1}^na_j\delta _{y_j}$
. For any fixed
![]() $y_t$
and
$y_t$
and
![]() $\widehat y_{t^{\prime }}$
, define the set
$\widehat y_{t^{\prime }}$
, define the set
![]() $S_t$
containing all
$S_t$
containing all
![]() $y_j$
’s and
$y_j$
’s and
![]() $\widehat y_j$
’s except
$\widehat y_j$
’s except
![]() $y_t, \widehat y_{t^{\prime }}$
that
$y_t, \widehat y_{t^{\prime }}$
that
Let
![]() $\# S_t$
be the number of elements in
$\# S_t$
be the number of elements in
![]() $S_t$
(i.e.,
$S_t$
(i.e.,
![]() $n+d-2$
). Then, for any
$n+d-2$
). Then, for any
![]() $0< \omega ^{*\leqslant } \frac {\Omega }{\#S_t}$
, we have the following relations:
$0< \omega ^{*\leqslant } \frac {\Omega }{\#S_t}$
, we have the following relations:
 $$ \begin{align} &\widehat {a}_{t^{\prime}}\prod_{q\in S_t}\left(e^{i\widehat y_{t^{\prime}}\omega^*}-e^{i q\omega^*}\right)- a_t \prod_{q\in S_t} \left(e^{i y_t\omega^*}- e^{i q\omega^*} \right)= \mathbf{w}_1^{\top}\mathbf{v}. \end{align} $$
$$ \begin{align} &\widehat {a}_{t^{\prime}}\prod_{q\in S_t}\left(e^{i\widehat y_{t^{\prime}}\omega^*}-e^{i q\omega^*}\right)- a_t \prod_{q\in S_t} \left(e^{i y_t\omega^*}- e^{i q\omega^*} \right)= \mathbf{w}_1^{\top}\mathbf{v}. \end{align} $$
Moreover, for any
![]() $0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
, we have
$0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
, we have
 $$ \begin{align} a_t \prod_{q\in S_t\cup \{\widehat y_{t^{\prime}}\}}\left(e^{iy_t\omega^*} - e^{iq\omega^*}\right) = \left(e^{i \widehat y_{t^{\prime}}\omega^*}\mathbf{w}_1- \mathbf{w}_2\right)^{\top}\mathbf{v}. \end{align} $$
$$ \begin{align} a_t \prod_{q\in S_t\cup \{\widehat y_{t^{\prime}}\}}\left(e^{iy_t\omega^*} - e^{iq\omega^*}\right) = \left(e^{i \widehat y_{t^{\prime}}\omega^*}\mathbf{w}_1- \mathbf{w}_2\right)^{\top}\mathbf{v}. \end{align} $$
Here,
![]() $\mathbf{w}_1 = (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}(\#S_t\omega ^*))^{\top }$
,
$\mathbf{w}_1 = (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}(\#S_t\omega ^*))^{\top }$
,
![]() $\mathbf{w}_2 = (\mathbf{w}(1), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*))^{\top }$
and the vector
$\mathbf{w}_2 = (\mathbf{w}(1), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*))^{\top }$
and the vector
![]() $\mathbf{v}$
is given by
$\mathbf{v}$
is given by
 $$\begin{align*}\left((-1)^{\# S_t}\sum_{\{q_1,\cdots, q_{\#S_t}\}\in S_{j, \# S_t}} e^{iq_1\omega^*}\cdots e^{iq_{\#S_t}\omega^*}, \ \cdots,\ (-1)^2\sum_{\{q_1, q_2\}\in S_{t,2}} e^{iq_1\omega^*}e^{iq_2\omega^*}, \ (-1)\sum_{\{q_1\}\in S_{t,1}} e^{iq_1\omega^*}, 1 \right)^{\top}, \end{align*}$$
$$\begin{align*}\left((-1)^{\# S_t}\sum_{\{q_1,\cdots, q_{\#S_t}\}\in S_{j, \# S_t}} e^{iq_1\omega^*}\cdots e^{iq_{\#S_t}\omega^*}, \ \cdots,\ (-1)^2\sum_{\{q_1, q_2\}\in S_{t,2}} e^{iq_1\omega^*}e^{iq_2\omega^*}, \ (-1)\sum_{\{q_1\}\in S_{t,1}} e^{iq_1\omega^*}, 1 \right)^{\top}, \end{align*}$$
where
 $S_{t,p}:=\left \{\{q_1, \cdots , q_p\}\bigg | q_j\in S_t, 1\leqslant j\leqslant p, q_{j^{\prime }} \ \text{and}\ q_{j^{\prime \prime }}\ \text {are different elements in}\ S_t \text {when} j^{\prime }\neq j^{\prime \prime } \right \}, p=1,\cdots , \#S_t$
.
$S_{t,p}:=\left \{\{q_1, \cdots , q_p\}\bigg | q_j\in S_t, 1\leqslant j\leqslant p, q_{j^{\prime }} \ \text{and}\ q_{j^{\prime \prime }}\ \text {are different elements in}\ S_t \text {when} j^{\prime }\neq j^{\prime \prime } \right \}, p=1,\cdots , \#S_t$
.
For the convenience of the applications of our location-amplitude identities, we derive the following corollary, as a direct consequence of Theorem 2.1.
Corollary 2.2. Consider the model
where
![]() $\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
and
$\widehat \mu = \sum _{j=1}^d\widehat a_j\delta _{\widehat y_j}$
and
![]() $\mu =\sum _{j=1}^na_j\delta _{y_j}$
and assume that
$\mu =\sum _{j=1}^na_j\delta _{y_j}$
and assume that
![]() $|\mathbf{w}(\omega )|< \sigma , \omega \in [0, \Omega ]$
. For any fixed
$|\mathbf{w}(\omega )|< \sigma , \omega \in [0, \Omega ]$
. For any fixed
![]() $y_t$
and
$y_t$
and
![]() $\widehat y_{t'}$
, define the set
$\widehat y_{t'}$
, define the set
![]() $S_t$
as
$S_t$
as
Let
![]() $\# S_t$
be the number of elements in
$\# S_t$
be the number of elements in
![]() $S_t$
(i.e.,
$S_t$
(i.e.,
![]() $n+d-2$
). Then, for any
$n+d-2$
). Then, for any
![]() $0< \omega ^*\leqslant \frac {\Omega }{\#S_t}$
, we have
$0< \omega ^*\leqslant \frac {\Omega }{\#S_t}$
, we have
 $$ \begin{align} \left|\widehat {a}_{t'}\prod_{q\in S_t}\left(e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}\right)- a_t \prod_{q\in S_t} \left(e^{i y_t\omega^*}- e^{i q\omega^*} \right)\right| < 2^{\#S_t}\sigma. \end{align} $$
$$ \begin{align} \left|\widehat {a}_{t'}\prod_{q\in S_t}\left(e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}\right)- a_t \prod_{q\in S_t} \left(e^{i y_t\omega^*}- e^{i q\omega^*} \right)\right| < 2^{\#S_t}\sigma. \end{align} $$
Moreover, for any
![]() $0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
, we have
$0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
, we have
 $$ \begin{align} \left|a_t \prod_{q\in S_t\cup \{\widehat y_{t'}\}}\left(e^{iy_t\omega^*} - e^{iq\omega^*}\right) \right|< 2^{\#S_t+1}\sigma. \end{align} $$
$$ \begin{align} \left|a_t \prod_{q\in S_t\cup \{\widehat y_{t'}\}}\left(e^{iy_t\omega^*} - e^{iq\omega^*}\right) \right|< 2^{\#S_t+1}\sigma. \end{align} $$
Proof. This is a direct consequence of Theorem 2.1 in view of
2.2 Proof of Theorem 2.1
Before starting the proof, we first introduce some notation and lemmas. Denote by
The following lemma on the inverse of the Vandermonde matrix is standard.
Lemma 2.3. Let
![]() $V_k$
be the Vandermonde matrix
$V_k$
be the Vandermonde matrix
![]() $\left (\phi _{0, k-1}(t_1), \cdots , \phi _{0, k-1}(t_k)\right )$
. Then its inverse
$\left (\phi _{0, k-1}(t_1), \cdots , \phi _{0, k-1}(t_k)\right )$
. Then its inverse
![]() $V_k^{-1}=B$
can be specified as follows:
$V_k^{-1}=B$
can be specified as follows:
 $$\begin{align*}B_{j q}=\left\{\begin{array}{cc}(-1)^{k-q}\left(\frac{\sum_{\substack{1 \leqslant m_1<\ldots<m_{k-q} \leqslant k \\ m_1, \ldots, m_{k-q} \neq j}} t_{m_1} \cdots t_{m_{k-q}}}{\prod_{\substack{1 \leqslant m \leqslant k \\ m \neq j}}\left(t_j-t_m\right)}\right), & \quad 1 \leqslant q<k, \\ \frac{1}{\prod_{\substack{1 \leqslant m \leqslant k \\ m \neq j}}\left(t_j-t_m\right)}, & \quad q=k. \end{array}\right. \end{align*}$$
$$\begin{align*}B_{j q}=\left\{\begin{array}{cc}(-1)^{k-q}\left(\frac{\sum_{\substack{1 \leqslant m_1<\ldots<m_{k-q} \leqslant k \\ m_1, \ldots, m_{k-q} \neq j}} t_{m_1} \cdots t_{m_{k-q}}}{\prod_{\substack{1 \leqslant m \leqslant k \\ m \neq j}}\left(t_j-t_m\right)}\right), & \quad 1 \leqslant q<k, \\ \frac{1}{\prod_{\substack{1 \leqslant m \leqslant k \\ m \neq j}}\left(t_j-t_m\right)}, & \quad q=k. \end{array}\right. \end{align*}$$
The following lemma can be deduced from the inverse of the Vandermonde matrix, and the readers can check Lemma 5 in [Reference Liu and Zhang26] for a simple proof, although the numbers there are real numbers.
Lemma 2.4. Let
![]() $t_1, \cdots , t_k$
be k different complex numbers. For
$t_1, \cdots , t_k$
be k different complex numbers. For
![]() $t\in \mathbb C$
, we have
$t\in \mathbb C$
, we have
 $$\begin{align*}\left(V_k^{-1}\phi_{0,k-1}(t)\right)_{j}=\prod_{1\leqslant q\leqslant k,q\neq j}\frac{t- t_q}{t_j- t_q}, \end{align*}$$
$$\begin{align*}\left(V_k^{-1}\phi_{0,k-1}(t)\right)_{j}=\prod_{1\leqslant q\leqslant k,q\neq j}\frac{t- t_q}{t_j- t_q}, \end{align*}$$
where
![]() $V_k:= \big (\phi _{0,k-1}(t_1),\cdots ,\phi _{0,k-1}(t_k)\big )$
with
$V_k:= \big (\phi _{0,k-1}(t_1),\cdots ,\phi _{0,k-1}(t_k)\big )$
with
![]() $\phi _{0, k-1}(\cdot )$
being defined by (12).
$\phi _{0, k-1}(\cdot )$
being defined by (12).
Now we start the main proof.
Proof. We only prove the theorem for
![]() $\omega ^* \leqslant \frac {\Omega }{\#S_t+1}$
. The case when
$\omega ^* \leqslant \frac {\Omega }{\#S_t+1}$
. The case when
![]() $\omega ^* \leqslant \frac {\Omega }{\#S_t}$
for (7) is obvious afterwards. We fix
$\omega ^* \leqslant \frac {\Omega }{\#S_t}$
for (7) is obvious afterwards. We fix
![]() $t\in \{1,\cdots , n\}$
in the following derivations. From (6), we can write
$t\in \{1,\cdots , n\}$
in the following derivations. From (6), we can write
where
![]() $\widehat a = (\widehat a_1, \cdots , \widehat a_d)^{\top }$
,
$\widehat a = (\widehat a_1, \cdots , \widehat a_d)^{\top }$
,
![]() $a = (a_1, \cdots , a_n)^{\top }, W =\left (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*)\right )^{\top }$
and
$a = (a_1, \cdots , a_n)^{\top }, W =\left (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*)\right )^{\top }$
and
 $$ \begin{align*} &\widehat A = \left( \phi_{0,\#S_t+1}(e^{i \widehat y_1 \omega^*}), \ \phi_{0, \#S_t+1}(e^{i \widehat y_2 \omega^*}), \ \cdots, \ \phi_{0,\#S_t+1}(e^{i \widehat y_d \omega^*})\right), \\ & A = \left( \phi_{0,\#S_t+1}(e^{i y_1 \omega^*}), \ \phi_{0,\#S_t+1}(e^{i y_2 \omega^*}), \ \cdots, \ \phi_{0,\#S_t+1}(e^{i y_n \omega^*})\right), \end{align*} $$
$$ \begin{align*} &\widehat A = \left( \phi_{0,\#S_t+1}(e^{i \widehat y_1 \omega^*}), \ \phi_{0, \#S_t+1}(e^{i \widehat y_2 \omega^*}), \ \cdots, \ \phi_{0,\#S_t+1}(e^{i \widehat y_d \omega^*})\right), \\ & A = \left( \phi_{0,\#S_t+1}(e^{i y_1 \omega^*}), \ \phi_{0,\#S_t+1}(e^{i y_2 \omega^*}), \ \cdots, \ \phi_{0,\#S_t+1}(e^{i y_n \omega^*})\right), \end{align*} $$
with
![]() $0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
. We further decompose (13) into the following two equations:
$0< \omega ^*\leqslant \frac {\Omega }{\#S_t+1}$
. We further decompose (13) into the following two equations:
where
![]() $\mathbf{w}_1 = (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}(\#S_t \omega ^*))^{\top }$
,
$\mathbf{w}_1 = (\mathbf{w}(0), \mathbf{w}(\omega ^*), \cdots , \mathbf{w}(\#S_t \omega ^*))^{\top }$
,
![]() $\mathbf{w}_2 = (\mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*))^{\top }$
and
$\mathbf{w}_2 = (\mathbf{w}(\omega ^*), \cdots , \mathbf{w}((\#S_t+1)\omega ^*))^{\top }$
and
 $$ \begin{align*} B_1 &= \left( \phi_{0, \#S_t}(e^{i y_{1}\omega^*}),\ \cdots,\ \phi_{0, \#S_t}(e^{i y_{n}\omega^*}),\ \phi_{0, \#S_t}(e^{i\widehat y_{1}\omega^*}),\ \cdots, \phi_{0, \#S_t}(e^{i\widehat y_{t'-1}\omega^*}),\right. \\ & \qquad \qquad \ \left. \phi_{0, \#S_t}(e^{i\widehat y_{t'+1}\omega^*}),\ \cdots, \ \phi_{0, \#S_t}(e^{i \widehat y_{d}\omega^*}) \right),\\ B_2 &= \left( \phi_{1, \#S_t+1}(e^{i y_{1}\omega^*}),\ \cdots,\ \phi_{1, \#S_t+1}(e^{i y_{n}\omega^*}),\ \phi_{1, \#S_t+1}(e^{i\widehat y_{1}\omega^*}),\ \cdots, \phi_{1, \#S_t+1}(e^{i\widehat y_{t'-1}\omega^*}),\right. \\ & \qquad \qquad \ \left. \phi_{1, \#S_t+1}(e^{i\widehat y_{t'+1}\omega^*}),\ \cdots, \ \phi_{1, \#S_t+1}(e^{i \widehat y_{d}\omega^*}) \right). \end{align*} $$
$$ \begin{align*} B_1 &= \left( \phi_{0, \#S_t}(e^{i y_{1}\omega^*}),\ \cdots,\ \phi_{0, \#S_t}(e^{i y_{n}\omega^*}),\ \phi_{0, \#S_t}(e^{i\widehat y_{1}\omega^*}),\ \cdots, \phi_{0, \#S_t}(e^{i\widehat y_{t'-1}\omega^*}),\right. \\ & \qquad \qquad \ \left. \phi_{0, \#S_t}(e^{i\widehat y_{t'+1}\omega^*}),\ \cdots, \ \phi_{0, \#S_t}(e^{i \widehat y_{d}\omega^*}) \right),\\ B_2 &= \left( \phi_{1, \#S_t+1}(e^{i y_{1}\omega^*}),\ \cdots,\ \phi_{1, \#S_t+1}(e^{i y_{n}\omega^*}),\ \phi_{1, \#S_t+1}(e^{i\widehat y_{1}\omega^*}),\ \cdots, \phi_{1, \#S_t+1}(e^{i\widehat y_{t'-1}\omega^*}),\right. \\ & \qquad \qquad \ \left. \phi_{1, \#S_t+1}(e^{i\widehat y_{t'+1}\omega^*}),\ \cdots, \ \phi_{1, \#S_t+1}(e^{i \widehat y_{d}\omega^*}) \right). \end{align*} $$
We first consider the case when all the
![]() $e^{y_j \omega ^*}$
’s and
$e^{y_j \omega ^*}$
’s and
![]() $e^{\widehat y_j\omega ^*}$
’s are distinct. Thus,
$e^{\widehat y_j\omega ^*}$
’s are distinct. Thus,
![]() $b=(b_1, \cdots , b_{\#S_t+1})$
in (14) is such that
$b=(b_1, \cdots , b_{\#S_t+1})$
in (14) is such that
 $$\begin{align*}b_{l} = \left\{\begin{array}{ll} a_l, & 1\leqslant l\leqslant n, \\ - \widehat a_{l-n}, & n<l\leqslant n+t'-1,\\ - \widehat a_{l-n+1}, & n+t'-1<l. \end{array}\right. \end{align*}$$
$$\begin{align*}b_{l} = \left\{\begin{array}{ll} a_l, & 1\leqslant l\leqslant n, \\ - \widehat a_{l-n}, & n<l\leqslant n+t'-1,\\ - \widehat a_{l-n+1}, & n+t'-1<l. \end{array}\right. \end{align*}$$
Observe that
 $$ \begin{align*} &B_2 = B_1 \mathrm{diag}\left(e^{iy_1\omega^*} ,\cdots, e^{i y_n \omega^*}, e^{i \widehat y_{1} \omega^*}, \cdots, e^{i \widehat y_{t'-1} \omega^*}, e^{i \widehat y_{t'+1} \omega^*},\cdots, e^{i \widehat y_{d} \omega^*}\right),\\ & \phi_{1, \#S_t+1}(e^{i y_{l}\omega^*}) = e^{i y_{l}\omega^*}\phi_{0, \#S_t}(e^{i y_{l}\omega^*}). \end{align*} $$
$$ \begin{align*} &B_2 = B_1 \mathrm{diag}\left(e^{iy_1\omega^*} ,\cdots, e^{i y_n \omega^*}, e^{i \widehat y_{1} \omega^*}, \cdots, e^{i \widehat y_{t'-1} \omega^*}, e^{i \widehat y_{t'+1} \omega^*},\cdots, e^{i \widehat y_{d} \omega^*}\right),\\ & \phi_{1, \#S_t+1}(e^{i y_{l}\omega^*}) = e^{i y_{l}\omega^*}\phi_{0, \#S_t}(e^{i y_{l}\omega^*}). \end{align*} $$
We rewrite (14) as
 $$ \begin{align} \begin{aligned} &\widehat {a}_{t'} \phi_{0, \#S_t}(e^{i \widehat y_{t'}\omega^*}) = B_1 b + \mathbf{w}_1,\\ &e^{i \widehat y_{t'}\omega^*}\widehat {a}_{t'} \phi_{0, \#S_t}(e^{i \widehat y_{t'}\omega^*}) = B_1\mathrm{diag}\left(e^{i y_1\omega^*} ,\cdots, e^{i y_n \omega^*}, e^{i \widehat y_{1} \omega^*}, \cdots, e^{i \widehat y_{t'-1} \omega^*}, e^{i \widehat y_{t'+1} \omega^*},\cdots, e^{i \widehat y_{d} \omega^*}\right)b + \mathbf{w}_2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\widehat {a}_{t'} \phi_{0, \#S_t}(e^{i \widehat y_{t'}\omega^*}) = B_1 b + \mathbf{w}_1,\\ &e^{i \widehat y_{t'}\omega^*}\widehat {a}_{t'} \phi_{0, \#S_t}(e^{i \widehat y_{t'}\omega^*}) = B_1\mathrm{diag}\left(e^{i y_1\omega^*} ,\cdots, e^{i y_n \omega^*}, e^{i \widehat y_{1} \omega^*}, \cdots, e^{i \widehat y_{t'-1} \omega^*}, e^{i \widehat y_{t'+1} \omega^*},\cdots, e^{i \widehat y_{d} \omega^*}\right)b + \mathbf{w}_2. \end{aligned} \end{align} $$
Since all the
![]() $e^{iy_j\omega ^*}$
’s and
$e^{iy_j\omega ^*}$
’s and
![]() $e^{i\widehat y_j \omega ^*}$
’s are pairwise distinct,
$e^{i\widehat y_j \omega ^*}$
’s are pairwise distinct,
![]() $B_1$
is a regular matrix. We multiply both sides of the above equations by the inverse of
$B_1$
is a regular matrix. We multiply both sides of the above equations by the inverse of
![]() $B_1$
to get from Lemma 2.4 that
$B_1$
to get from Lemma 2.4 that
 $$ \begin{align} \widehat {a}_{t'}\prod_{q\in S_t}\frac{e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}}{e^{i y_t\omega^*}- e^{i q\omega^*}} &= a_t + (B_1^{-1})_{t} \mathbf{w}_1, \end{align} $$
$$ \begin{align} \widehat {a}_{t'}\prod_{q\in S_t}\frac{e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}}{e^{i y_t\omega^*}- e^{i q\omega^*}} &= a_t + (B_1^{-1})_{t} \mathbf{w}_1, \end{align} $$
 $$ \begin{align} e^{i \widehat y_{t'}\omega^*} \widehat {a}_{t'}\prod_{q\in S_t}\frac{e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}}{e^{i y_t\omega^*}- e^{i q\omega^*}} &= e^{i y_{t}\omega^*} a_t + (B_1^{-1})_{t} \mathbf{w}_2, \end{align} $$
$$ \begin{align} e^{i \widehat y_{t'}\omega^*} \widehat {a}_{t'}\prod_{q\in S_t}\frac{e^{i\widehat y_{t'}\omega^*}-e^{i q\omega^*}}{e^{i y_t\omega^*}- e^{i q\omega^*}} &= e^{i y_{t}\omega^*} a_t + (B_1^{-1})_{t} \mathbf{w}_2, \end{align} $$
where
![]() $(B_1^{-1})_{t}$
is the t-th row of
$(B_1^{-1})_{t}$
is the t-th row of
![]() $B_1^{-1}$
. By Lemma 2.3, it follows that
$B_1^{-1}$
. By Lemma 2.3, it follows that
 $$ \begin{align} (B_1^{-1})_{t}\mathbf{w}_1 = \frac{\sum_{p=0}^{\#S_t-1}\left(\mathbf{w}(p \omega^*) (-1)^{\#S_t-p}\sum_{\{q_1,\cdots, q_{\#S_{t}-p}\}\in S_{t, \#S_t-p}} e^{iq_1\omega^*}\cdots e^{iq_{\#S_t-p}\omega^*}\right)+ \mathbf{w}(\#S_t \omega^*)}{\prod_{q\in S_t}(e^{iy_t\omega^*} - e^{i q \omega^*})}. \end{align} $$
$$ \begin{align} (B_1^{-1})_{t}\mathbf{w}_1 = \frac{\sum_{p=0}^{\#S_t-1}\left(\mathbf{w}(p \omega^*) (-1)^{\#S_t-p}\sum_{\{q_1,\cdots, q_{\#S_{t}-p}\}\in S_{t, \#S_t-p}} e^{iq_1\omega^*}\cdots e^{iq_{\#S_t-p}\omega^*}\right)+ \mathbf{w}(\#S_t \omega^*)}{\prod_{q\in S_t}(e^{iy_t\omega^*} - e^{i q \omega^*})}. \end{align} $$
Thus, multiplying
![]() $\prod _{q\in S_t}\left (e^{i y_t\omega ^*}- e^{i q\omega ^*}\right )$
in both sides of (16) proves (7) in the case when all the
$\prod _{q\in S_t}\left (e^{i y_t\omega ^*}- e^{i q\omega ^*}\right )$
in both sides of (16) proves (7) in the case when all the
![]() $e^{iy_j\omega ^*}$
’s and
$e^{iy_j\omega ^*}$
’s and
![]() $e^{i\widehat y_j \omega ^*}$
’s are pairwise distinct. Furthermore, equation (16) times
$e^{i\widehat y_j \omega ^*}$
’s are pairwise distinct. Furthermore, equation (16) times
![]() $e^{i \widehat y_{t'} \omega ^*}$
minus (17) yields
$e^{i \widehat y_{t'} \omega ^*}$
minus (17) yields
Similarly, further expanding
![]() $(B_1^{-1})_{t}\left (e^{i \widehat y_{t'} \omega ^*}\mathbf{w}_1-\mathbf{w}_2\right )$
explicitly by Lemma 2.3 and multiplying
$(B_1^{-1})_{t}\left (e^{i \widehat y_{t'} \omega ^*}\mathbf{w}_1-\mathbf{w}_2\right )$
explicitly by Lemma 2.3 and multiplying
![]() $\prod _{q\in S_t}\left (e^{i y_t\omega ^*}- e^{i q\omega ^*}\right )$
in both sides above yields (8).
$\prod _{q\in S_t}\left (e^{i y_t\omega ^*}- e^{i q\omega ^*}\right )$
in both sides above yields (8).
Finally, we consider the case when the
![]() $e^{iy_j\omega ^*}$
’s and
$e^{iy_j\omega ^*}$
’s and
![]() $e^{i\widehat y_j \omega ^*}$
’s are not pairwise distinct. Since it is a limiting case of the above cases, (7) and (8) still hold in this case. This completes the proof.
$e^{i\widehat y_j \omega ^*}$
’s are not pairwise distinct. Since it is a limiting case of the above cases, (7) and (8) still hold in this case. This completes the proof.
3 Stability of super-resolution in dimension one
In this section, based on our location-amplitude identities, we analyze the super-resolution capability of the reconstruction of the numbers, locations and amplitudes of off-the-grid sources in the one-dimensional super-resolution problem. Note that these problems have been analyzed in [Reference Liu and Zhang26, Reference Batenkov, Goldman and Yomdin3] from different perspectives, but the proofs are over several tens of pages. Now, by our method, we have a direct and clear picture of all these problems, which allows us to prove them in a unified way and in less than ten pages.
We consider the imaging model (1) and focus on the one-dimensional case in this section. Since the source locations
![]() $\mathbf{y}_j$
’s are the supports of the Dirac masses in
$\mathbf{y}_j$
’s are the supports of the Dirac masses in
![]() $\mu $
, we use the support recovery for a substitution of the location reconstruction throughout the paper.
$\mu $
, we use the support recovery for a substitution of the location reconstruction throughout the paper.
Since we focus on the resolution limit case, we consider the case when the point sources are tightly spaced and form a cluster. To be more specific, we denote the ball in the k-dimensional space by
 $$ \begin{align} B_\delta^k(\mathbf{x}):=\left\{\mathbf{y} \ \bigg| \mathbf{y} \in \mathbb{R}^k,\|\mathbf{y}-\mathbf{x}\|_2<\delta\right\}, \end{align} $$
$$ \begin{align} B_\delta^k(\mathbf{x}):=\left\{\mathbf{y} \ \bigg| \mathbf{y} \in \mathbb{R}^k,\|\mathbf{y}-\mathbf{x}\|_2<\delta\right\}, \end{align} $$
and assume
![]() $\mathbf {y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0}), j=1, \ldots , n$
, or equivalently
$\mathbf {y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0}), j=1, \ldots , n$
, or equivalently
![]() $\left \|\mathbf {y}_j\right \|_2<\frac {(n-1) \pi }{2 \Omega }$
. This assumption is a common assumption for super-resolving the off-the-grid sources [Reference Liu and Zhang26, Reference Batenkov, Goldman and Yomdin3] and is necessary for the analysis. Since we are interested in resolving closely-spaced sources, it is also reasonable. We remark that our results for sources in
$\left \|\mathbf {y}_j\right \|_2<\frac {(n-1) \pi }{2 \Omega }$
. This assumption is a common assumption for super-resolving the off-the-grid sources [Reference Liu and Zhang26, Reference Batenkov, Goldman and Yomdin3] and is necessary for the analysis. Since we are interested in resolving closely-spaced sources, it is also reasonable. We remark that our results for sources in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
can be directly generalized to sources in
$B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
can be directly generalized to sources in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {x}),\ \mathbf{x}\in \mathbb R^k$
.
$B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {x}),\ \mathbf{x}\in \mathbb R^k$
.
The reconstruction process is usually targeting at some specific solutions in a so-called admissible set, which comprises discrete measures whose Fourier data are sufficiently close to
![]() $\mathbf{Y}$
. In general, every admissible measure is possibly the ground truth, and it is impossible to distinguish which one is closer to the ground truth without any additional prior information. In our problem, we introduce the following concept of
$\mathbf{Y}$
. In general, every admissible measure is possibly the ground truth, and it is impossible to distinguish which one is closer to the ground truth without any additional prior information. In our problem, we introduce the following concept of
![]() $\sigma $
-admissible discrete measures. For simplicity, we also call them
$\sigma $
-admissible discrete measures. For simplicity, we also call them
![]() $\sigma $
-admissible measures.
$\sigma $
-admissible measures.
Definition 3.1. Given the measurement
![]() $\mathbf Y$
in (1),
$\mathbf Y$
in (1),
![]() $\widehat \mu =\sum _{j=1}^{d} \widehat a_j \delta _{\mathbf {\widehat y}_j}$
is said to be a
$\widehat \mu =\sum _{j=1}^{d} \widehat a_j \delta _{\mathbf {\widehat y}_j}$
is said to be a
![]() $\sigma $
-admissible discrete measure of
$\sigma $
-admissible discrete measure of
![]() $\mathbf Y$
if
$\mathbf Y$
if
If further
![]() $\widehat a_j>0, j=1, \cdots , d$
, then
$\widehat a_j>0, j=1, \cdots , d$
, then
![]() $\widehat \mu $
is said to be a positive
$\widehat \mu $
is said to be a positive
![]() $\sigma $
-admissible discrete measure of
$\sigma $
-admissible discrete measure of
![]() $\mathbf Y$
.
$\mathbf Y$
.
3.1 Stability of number detection
In this section, we estimate the super-resolving capability of number detection in the super-resolution problem. We introduce the concept of computational resolution limit for number detection [Reference Liu and Zhang27, Reference Liu and Zhang26, Reference Liu and Zhang25] and present a sharp bound for it.
Note the set of
![]() $\sigma $
-admissible measures of
$\sigma $
-admissible measures of
![]() $\mathbf Y$
characterizes all possible solutions to our super-resolution problem with the given measurement
$\mathbf Y$
characterizes all possible solutions to our super-resolution problem with the given measurement
![]() $\mathbf Y$
. Detecting the source number n is possible only if all of the admissible measures have at least n supports; otherwise, it is impossible to detect the correct source number without additional a priori information. Thus, following definitions similar to those in [Reference Liu and Zhang26, Reference Liu and Zhang27, Reference Liu and Zhang25], we define the computational resolution limit for the number detection problem as follows.
$\mathbf Y$
. Detecting the source number n is possible only if all of the admissible measures have at least n supports; otherwise, it is impossible to detect the correct source number without additional a priori information. Thus, following definitions similar to those in [Reference Liu and Zhang26, Reference Liu and Zhang27, Reference Liu and Zhang25], we define the computational resolution limit for the number detection problem as follows.
Definition 3.2. The computational resolution limit to the number detection problem in the super-resolution of sources in
![]() $\mathbb R^k$
is defined as the smallest nonnegative number
$\mathbb R^k$
is defined as the smallest nonnegative number
![]() $\mathscr D_{num}(k, n)$
such that for all n-sparse measures
$\mathscr D_{num}(k, n)$
such that for all n-sparse measures
![]() $\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j}, a_j\in \mathbb C,\mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the associated measurement
$\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j}, a_j\in \mathbb C,\mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the associated measurement
![]() $\mathbf{Y}$
in (1), if
$\mathbf{Y}$
in (1), if
then there does not exist any
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf Y$
with less than n supports. In particular, when considering positive sources and positive
$\mathbf Y$
with less than n supports. In particular, when considering positive sources and positive
![]() $\sigma $
-admissible measures, the corresponding computational resolution limit is denoted by
$\sigma $
-admissible measures, the corresponding computational resolution limit is denoted by
![]() $\mathscr D_{num}^+(k, n)$
.
$\mathscr D_{num}^+(k, n)$
.
The definition of ‘computational resolution limit’ emphasizes the impossibility of correctly detecting the number of very close sources by any means. It depends crucially on the signal-to-noise ratio and the sparsity of the sources, which is fundamentally different from all the classical resolution limits [Reference Abbe1, Reference Volkmann46, Reference Rayleigh35, Reference Schuster38, Reference Sparrow42] that depend only on the cutoff frequency.
Our first result is a sharp estimate for the upper bound of the computational resolution limit in the one-dimensional super-resolution problem. As we have said, we will use
![]() $y_j$
’s to denote the one-dimensional source locations.
$y_j$
’s to denote the one-dimensional source locations.
Theorem 3.3. Let the measurement
![]() $\mathbf Y$
in (1) be generated by any one-dimensional source
$\mathbf Y$
in (1) be generated by any one-dimensional source
![]() $\mu =\sum _{j=1}^{n}a_j\delta _{y_j}$
with
$\mu =\sum _{j=1}^{n}a_j\delta _{y_j}$
with
![]() $y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0), j=1,\cdots , n$
. Let
$y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0), j=1,\cdots , n$
. Let
![]() $n\geqslant 2$
and assume that the following separation condition is satisfied:
$n\geqslant 2$
and assume that the following separation condition is satisfied:
where
![]() $\sigma , m_{\min }$
are defined as in (2), (3), respectively. Then there does not exist any
$\sigma , m_{\min }$
are defined as in (2), (3), respectively. Then there does not exist any
![]() $\sigma $
-admissible measures of
$\sigma $
-admissible measures of
![]() $\mathbf Y$
with less than n supports. Moreover, for the cases when
$\mathbf Y$
with less than n supports. Moreover, for the cases when
![]() $n=2$
and
$n=2$
and
![]() $n=3$
, if
$n=3$
, if
 $$\begin{align*}\min_{p\neq j}\Bigg|y_p-y_j\Bigg|\geqslant \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \quad \min_{p\neq j}\Bigg|y_p-y_j\Bigg|\geqslant \frac{2\pi}{\Omega }\Big(\frac{8\sigma}{m_{\min}}\Big)^{\frac{1}{4}}, \quad \text{respectively}, \end{align*}$$
$$\begin{align*}\min_{p\neq j}\Bigg|y_p-y_j\Bigg|\geqslant \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \quad \min_{p\neq j}\Bigg|y_p-y_j\Bigg|\geqslant \frac{2\pi}{\Omega }\Big(\frac{8\sigma}{m_{\min}}\Big)^{\frac{1}{4}}, \quad \text{respectively}, \end{align*}$$
then there does not exist any
![]() $\sigma $
-admissible measures of
$\sigma $
-admissible measures of
![]() $\mathbf Y$
with less than n supports.
$\mathbf Y$
with less than n supports.
Theorem 3.3 gives a sharper upper bound for the computational resolution limit
![]() $\mathscr D_{num}(1, n)$
compared to the one in [Reference Liu and Zhang26]. By the new estimate (3.3), it is already possible to surpass the Rayleigh limit
$\mathscr D_{num}(1, n)$
compared to the one in [Reference Liu and Zhang26]. By the new estimate (3.3), it is already possible to surpass the Rayleigh limit
![]() $\frac {\pi }{\Omega }$
in detecting source number when
$\frac {\pi }{\Omega }$
in detecting source number when
![]() $\frac {m_{\min }}{\sigma }\geqslant (2e)^{2n-2}$
. Moreover, this upper bound is shown to be sharp by a lower bound provided in [Reference Liu, He and Ammari24]. Thus, we can conclude that
$\frac {m_{\min }}{\sigma }\geqslant (2e)^{2n-2}$
. Moreover, this upper bound is shown to be sharp by a lower bound provided in [Reference Liu, He and Ammari24]. Thus, we can conclude that
 $$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}< \mathscr D_{num}(1, n) \leqslant \frac{2e\pi}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}. \end{align*}$$
$$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}< \mathscr D_{num}(1, n) \leqslant \frac{2e\pi}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}. \end{align*}$$
It is also easy to generalize the estimates in Theorem 3.3 to high-dimensional spaces by methods in [Reference Liu and Zhang25, Reference Liu and Ammari22], whereby we can obtain that
 $$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}< \mathscr D_{num}(k, n) \leqslant \frac{C_1(k,n)}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}} \end{align*}$$
$$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}}< \mathscr D_{num}(k, n) \leqslant \frac{C_1(k,n)}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-2}} \end{align*}$$
for a constant
![]() $C_1(k,n)$
.
$C_1(k,n)$
.
In particular, for the case when
![]() $n=2$
, our estimate demonstrates that when the signal-to-noise ratio
$n=2$
, our estimate demonstrates that when the signal-to-noise ratio
![]() $\mathrm {SNR}>4$
, then the resolution is better than the Rayleigh limit and the ‘super-resolution in number detection’ can be achieved thusly. This result is already practically important. As we will see later, our estimate is very sharp and close to the true two-point resolution limit.
$\mathrm {SNR}>4$
, then the resolution is better than the Rayleigh limit and the ‘super-resolution in number detection’ can be achieved thusly. This result is already practically important. As we will see later, our estimate is very sharp and close to the true two-point resolution limit.
Remark. We remark that our new techniques also provide a way to analyze the stability of number detection for sources with multi-cluster patterns. Our former method (also the only one we know of) for analyzing the stability of number detection cannot handle such cases. The technique here is the first known method that can tackle the issue. But since the current paper focuses on understanding the resolution limits in the super-resolution, the multi-cluster case is out of scope and we leave it as a future work.
We now present the proof of Theorem 3.3. The problem is essentially a nonlinear approximation problem where we have to optimize the approximation over the coupled factors: source number d, source locations
![]() $\widehat y_j$
’s and amplitudes
$\widehat y_j$
’s and amplitudes
![]() $\widehat a_j$
’s. Here, by leveraging the location-amplitude identities, we prove it in a rather simple and direct way.
$\widehat a_j$
’s. Here, by leveraging the location-amplitude identities, we prove it in a rather simple and direct way.
We first denote for an integer
![]() $k\geqslant 1$
,
$k\geqslant 1$
,
 $$ \begin{align} \begin{aligned} &\zeta(k)= \left\{ \begin{array}{cc} (\frac{k-1}{2}!)^2,& \text{if } k \text{ is odd,}\\ (\frac{k}{2})!(\frac{k-2}{2})!,& \text{if } k \text{ is even,} \end{array} \right. \quad \xi(k)=\left\{ \begin{array}{cc} \frac{1}{2}, & \text{if } k=1,\\ \frac{(\frac{k-1}{2})!(\frac{k-3}{2})!}{4},& \text{if } k \text{ is odd},\,\, k\geqslant 3,\\ \frac{(\frac{k-2}{2}!)^2}{4},& \text{if } k \text{ is even}. \end{array} \right. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\zeta(k)= \left\{ \begin{array}{cc} (\frac{k-1}{2}!)^2,& \text{if } k \text{ is odd,}\\ (\frac{k}{2})!(\frac{k-2}{2})!,& \text{if } k \text{ is even,} \end{array} \right. \quad \xi(k)=\left\{ \begin{array}{cc} \frac{1}{2}, & \text{if } k=1,\\ \frac{(\frac{k-1}{2})!(\frac{k-3}{2})!}{4},& \text{if } k \text{ is odd},\,\, k\geqslant 3,\\ \frac{(\frac{k-2}{2}!)^2}{4},& \text{if } k \text{ is even}. \end{array} \right. \end{aligned} \end{align} $$
We also define for positive integers
![]() $p, q$
, and
$p, q$
, and
![]() $z_1, \cdots , z_p, \widehat z_1, \cdots , \widehat z_q \in \mathbb C$
, the following vector in
$z_1, \cdots , z_p, \widehat z_1, \cdots , \widehat z_q \in \mathbb C$
, the following vector in
![]() $\mathbb {R}^p$
:
$\mathbb {R}^p$
:
 $$ \begin{align} \eta_{p,q}(z_1,\cdots,z_{p}, \widehat z_1,\cdots,\widehat z_q)=\left(\begin{array}{c} |(z_1-\widehat z_1)|\cdots|(z_1-\widehat z_q)|\\ |(z_2-\widehat z_1)|\cdots|(z_2-\widehat z_q)|\\ \vdots\\ |(z_{p}-\widehat z_1)|\cdots|(z_{p}-\widehat z_q)| \end{array}\right). \end{align} $$
$$ \begin{align} \eta_{p,q}(z_1,\cdots,z_{p}, \widehat z_1,\cdots,\widehat z_q)=\left(\begin{array}{c} |(z_1-\widehat z_1)|\cdots|(z_1-\widehat z_q)|\\ |(z_2-\widehat z_1)|\cdots|(z_2-\widehat z_q)|\\ \vdots\\ |(z_{p}-\widehat z_1)|\cdots|(z_{p}-\widehat z_q)| \end{array}\right). \end{align} $$
We recall the following useful lemmas.
Lemma 3.4. Let
![]() $-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _{k} \leqslant \frac {\pi }{2}$
with
$-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _{k} \leqslant \frac {\pi }{2}$
with
![]() $\min _{p\neq j}|\theta _p-\theta _j|=\theta _{\min }$
. We have the estimate
$\min _{p\neq j}|\theta _p-\theta _j|=\theta _{\min }$
. We have the estimate
 $$\begin{align*}\prod_{1\leqslant p\leqslant k,p\neq j}{\left|e^{i\theta_j}-e^{i\theta_p}\right|}\geqslant \zeta(k)\left(\frac{2\theta_{\min}}{\pi}\right)^{k-1},\ j=1,\cdots, k, \end{align*}$$
$$\begin{align*}\prod_{1\leqslant p\leqslant k,p\neq j}{\left|e^{i\theta_j}-e^{i\theta_p}\right|}\geqslant \zeta(k)\left(\frac{2\theta_{\min}}{\pi}\right)^{k-1},\ j=1,\cdots, k, \end{align*}$$
where
![]() $\zeta (k)$
is defined in (21).
$\zeta (k)$
is defined in (21).
Proof. Note that
Then we have
 $$ \begin{align*} \prod_{1\leqslant p\leqslant k,p\neq j}{\left|e^{i\theta_j}-e^{i\theta_p}\right|}\ \geqslant \left(\frac{2}{\pi}\right)^{k-1} \prod_{1\leqslant p\leqslant k,p\neq j}{\left|\theta_j-\theta_p\right|} \geqslant \zeta(k)\left(\frac{2\theta_{\min}}{\pi}\right)^{k-1}.\\[-40pt] \end{align*} $$
$$ \begin{align*} \prod_{1\leqslant p\leqslant k,p\neq j}{\left|e^{i\theta_j}-e^{i\theta_p}\right|}\ \geqslant \left(\frac{2}{\pi}\right)^{k-1} \prod_{1\leqslant p\leqslant k,p\neq j}{\left|\theta_j-\theta_p\right|} \geqslant \zeta(k)\left(\frac{2\theta_{\min}}{\pi}\right)^{k-1}.\\[-40pt] \end{align*} $$
Lemma 3.5. Let
![]() $-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _{k+1} \leqslant \frac {\pi }{2}$
. Assume that
$-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _{k+1} \leqslant \frac {\pi }{2}$
. Assume that
![]() $\min _{p\neq j}|\theta _p-\theta _j|=\theta _{\min }$
. Then for any
$\min _{p\neq j}|\theta _p-\theta _j|=\theta _{\min }$
. Then for any
![]() $\widehat \theta _1,\cdots , \widehat \theta _k\in \mathbb R$
, we have the following estimate:
$\widehat \theta _1,\cdots , \widehat \theta _k\in \mathbb R$
, we have the following estimate:
 $$\begin{align*}\left|\left|{\eta_{k+1,k}(e^{i\theta_1},\cdots,e^{i\theta_{k+1}},e^{i \widehat \theta_1},\cdots,e^{i\widehat \theta_k})}\right|\right|{}_{\infty}\geqslant \xi(k)\left(\frac{2\theta_{\min}}{\pi}\right)^k, \end{align*}$$
$$\begin{align*}\left|\left|{\eta_{k+1,k}(e^{i\theta_1},\cdots,e^{i\theta_{k+1}},e^{i \widehat \theta_1},\cdots,e^{i\widehat \theta_k})}\right|\right|{}_{\infty}\geqslant \xi(k)\left(\frac{2\theta_{\min}}{\pi}\right)^k, \end{align*}$$
where
![]() $\eta _{k+1,k}$
is defined as in (22).
$\eta _{k+1,k}$
is defined as in (22).
Proof. See Corollary 7 in [Reference Liu and Zhang26].
Proof. We are now ready to prove Theorem 3.3. Suppose that
![]() $\widehat \mu =\sum _{j=1}^{d}\widehat a_j \delta _{\widehat y_j}, d\leqslant n-1$
is a
$\widehat \mu =\sum _{j=1}^{d}\widehat a_j \delta _{\widehat y_j}, d\leqslant n-1$
is a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
. By the Definition 3.1 and the model (1), we have
$\mathbf{Y}$
. By the Definition 3.1 and the model (1), we have
for some
![]() $\mathbf{W}_1$
with
$\mathbf{W}_1$
with
![]() $|\mathbf{W}_1(\omega )|<2\sigma $
. Note that by adding some point sources in
$|\mathbf{W}_1(\omega )|<2\sigma $
. Note that by adding some point sources in
![]() $\widehat \mu $
, from above we can actually construct
$\widehat \mu $
, from above we can actually construct
![]() $\widehat \mu =\sum _{j=1}^{n-1}\widehat a_j \delta _{\widehat y_j}$
such that
$\widehat \mu =\sum _{j=1}^{n-1}\widehat a_j \delta _{\widehat y_j}$
such that
for some
![]() $\mathbf{W}_2$
with
$\mathbf{W}_2$
with
![]() $|\mathbf{W}_2(\omega )|<2\sigma $
. For ease of exposition, we consider in the following that the measure
$|\mathbf{W}_2(\omega )|<2\sigma $
. For ease of exposition, we consider in the following that the measure
![]() $\widehat \mu $
is with
$\widehat \mu $
is with
![]() $n-1$
point sources. The above equation implies that
$n-1$
point sources. The above equation implies that
![]() $\widehat \rho = \sum _{j=1}^{n-1}e^{-\widehat y_j \Omega }\widehat a_{j} \delta _{\widehat y_j}$
and
$\widehat \rho = \sum _{j=1}^{n-1}e^{-\widehat y_j \Omega }\widehat a_{j} \delta _{\widehat y_j}$
and
![]() $\rho = \sum _{j=1}^ne^{-y_j \Omega }a_{j} \delta _{y_j}$
satisfy
$\rho = \sum _{j=1}^ne^{-y_j \Omega }a_{j} \delta _{y_j}$
satisfy
for some
![]() $\mathbf{W}_3$
with
$\mathbf{W}_3$
with
![]() $|\mathbf{W}_3(\omega )|<2\sigma , \omega \in [0,2\Omega ]$
. For any
$|\mathbf{W}_3(\omega )|<2\sigma , \omega \in [0,2\Omega ]$
. For any
![]() $y_t$
and
$y_t$
and
![]() $\widehat y_{t'}$
, define
$\widehat y_{t'}$
, define
![]() $S_t$
as
$S_t$
as
Then
![]() $\#S_t = 2n-3$
. Let
$\#S_t = 2n-3$
. Let
![]() $\omega ^*=\frac {2\Omega }{2n-2}$
. Applying (11) to (24), we obtain that
$\omega ^*=\frac {2\Omega }{2n-2}$
. Applying (11) to (24), we obtain that
 $$\begin{align*}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|\left|a_t \right|< 2^{\#S_t+2}\sigma, \ t=1,\cdots, n. \end{align*}$$
$$\begin{align*}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|\left|a_t \right|< 2^{\#S_t+2}\sigma, \ t=1,\cdots, n. \end{align*}$$
This gives
 $$\begin{align*}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< 2^{2n-1}\frac{\sigma}{m_{\min}}, \ t=1,\cdots, n. \end{align*}$$
$$\begin{align*}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< 2^{2n-1}\frac{\sigma}{m_{\min}}, \ t=1,\cdots, n. \end{align*}$$
Therefore, it follows that
 $$\begin{align*}\min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\max_{t=1,\cdots, n}\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< 2^{2n-1}\frac{\sigma}{m_{\min}}. \end{align*}$$
$$\begin{align*}\min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\max_{t=1,\cdots, n}\prod_{q=1,\cdots, n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< 2^{2n-1}\frac{\sigma}{m_{\min}}. \end{align*}$$
Denote
![]() $y_q \omega ^*$
by
$y_q \omega ^*$
by
![]() $\theta _q$
and
$\theta _q$
and
![]() $\theta _{\min } = \min _{p\neq q}|\theta _p-\theta _q|$
. Since the
$\theta _{\min } = \min _{p\neq q}|\theta _p-\theta _q|$
. Since the
![]() $y_j$
’s are in
$y_j$
’s are in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and
![]() $\omega ^* = \frac {2\Omega }{2n-2}$
, we have that the
$\omega ^* = \frac {2\Omega }{2n-2}$
, we have that the
![]() $\theta _j$
’s are in
$\theta _j$
’s are in
![]() $\left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
. Thus, by Lemma 3.4, we get
$\left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
. Thus, by Lemma 3.4, we get
 $$ \begin{align} \min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\geqslant \zeta(n)\left(\frac{2\theta_{\min}}{\pi}\right)^{n-1}. \end{align} $$
$$ \begin{align} \min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\geqslant \zeta(n)\left(\frac{2\theta_{\min}}{\pi}\right)^{n-1}. \end{align} $$
Moreover, using Lemma 3.5 yields
 $$ \begin{align} \max_{t=1, \cdots, n}\prod_{q=1,\cdots,n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|\geqslant \xi(n-1) \left(\frac{2\theta_{\min}}{\pi}\right)^{n-1}. \end{align} $$
$$ \begin{align} \max_{t=1, \cdots, n}\prod_{q=1,\cdots,n-1}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|\geqslant \xi(n-1) \left(\frac{2\theta_{\min}}{\pi}\right)^{n-1}. \end{align} $$
Combining the above estimates, it follows that
 $$ \begin{align} \zeta(n)\xi(n-1) \left(\frac{2\theta_{\min}}{\pi}\right)^{2n-2}< \frac{2^{2n-1}\sigma}{m_{\min}}. \end{align} $$
$$ \begin{align} \zeta(n)\xi(n-1) \left(\frac{2\theta_{\min}}{\pi}\right)^{2n-2}< \frac{2^{2n-1}\sigma}{m_{\min}}. \end{align} $$
Thus,
 $$\begin{align*}\theta_{\min} < \pi\left( \frac{2}{\zeta(n)\xi(n-1)}\right)^{\frac{1}{2n-2}}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}, \end{align*}$$
$$\begin{align*}\theta_{\min} < \pi\left( \frac{2}{\zeta(n)\xi(n-1)}\right)^{\frac{1}{2n-2}}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}, \end{align*}$$
and consequently,
 $$ \begin{align} d_{\min}= \frac{\theta_{\min}}{\omega^*}< \frac{(2n-2)\pi}{2\Omega}\left( \frac{2}{\zeta(n)\xi(n-1)}\right)^{\frac{1}{2n-2}}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}\leqslant \frac{2\pi e}{\Omega}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}, \end{align} $$
$$ \begin{align} d_{\min}= \frac{\theta_{\min}}{\omega^*}< \frac{(2n-2)\pi}{2\Omega}\left( \frac{2}{\zeta(n)\xi(n-1)}\right)^{\frac{1}{2n-2}}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}\leqslant \frac{2\pi e}{\Omega}\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2n-2}}, \end{align} $$
where
![]() $d_{\min }:=\min _{p\neq q}|y_p-y_q|$
and the last inequality is from Lemma A.1. Therefore, if
$d_{\min }:=\min _{p\neq q}|y_p-y_q|$
and the last inequality is from Lemma A.1. Therefore, if
![]() $d_{\min }\geqslant \frac {2\pi e}{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2n-2}}$
, then there is no
$d_{\min }\geqslant \frac {2\pi e}{\Omega }\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2n-2}}$
, then there is no
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
with less than n supports.
$\mathbf{Y}$
with less than n supports.
The last part consists in proving the cases when
![]() $n=2,3$
. When
$n=2,3$
. When
![]() $n=3$
, the result is enhanced by noting that
$n=3$
, the result is enhanced by noting that
![]() $\frac {2}{\zeta (n)\xi (n-1)}=8$
in (28). When
$\frac {2}{\zeta (n)\xi (n-1)}=8$
in (28). When
![]() $n=2$
, the result is enhanced by improving the estimates (25) and (26). For (25), we now have
$n=2$
, the result is enhanced by improving the estimates (25) and (26). For (25), we now have
 $$\begin{align*}\left|{e^{iy_1\omega^*} - e^{iy_2\omega^*}}\right|\geqslant 2\sin \left(\frac{\theta_{\min}}{2}\right), \end{align*}$$
$$\begin{align*}\left|{e^{iy_1\omega^*} - e^{iy_2\omega^*}}\right|\geqslant 2\sin \left(\frac{\theta_{\min}}{2}\right), \end{align*}$$
where
![]() $\theta _{\min } = |y_1\omega ^*-y_2\omega ^*|$
and
$\theta _{\min } = |y_1\omega ^*-y_2\omega ^*|$
and
![]() $\omega ^*= \Omega $
. For (26), we have
$\omega ^*= \Omega $
. For (26), we have
 $$\begin{align*}\max_{j=1,2}\left|e^{iy_{j}\omega^*} - e^{i\widehat y_1\omega^*}\right|\geqslant 2\sin\left(\frac{\theta_{\min}}{4}\right). \end{align*}$$
$$\begin{align*}\max_{j=1,2}\left|e^{iy_{j}\omega^*} - e^{i\widehat y_1\omega^*}\right|\geqslant 2\sin\left(\frac{\theta_{\min}}{4}\right). \end{align*}$$
Thus, similarly to (27), we obtain that
 $$\begin{align*}2\sin \left(\frac{\theta_{\min}}{2}\right)2\sin\left(\frac{\theta_{\min}}{4}\right)<\frac{2^{3}\sigma}{m_{\min}}, \end{align*}$$
$$\begin{align*}2\sin \left(\frac{\theta_{\min}}{2}\right)2\sin\left(\frac{\theta_{\min}}{4}\right)<\frac{2^{3}\sigma}{m_{\min}}, \end{align*}$$
which gives
 $$\begin{align*}\sin^2 \left(\frac{\theta_{\min}}{2}\right)<\frac{4\sigma}{m_{\min}}. \end{align*}$$
$$\begin{align*}\sin^2 \left(\frac{\theta_{\min}}{2}\right)<\frac{4\sigma}{m_{\min}}. \end{align*}$$
It then follows that
 $$\begin{align*}d_{\min} = \frac{\theta_{\min}}{\omega^*} < \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
$$\begin{align*}d_{\min} = \frac{\theta_{\min}}{\omega^*} < \frac{2\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
which completes the proof.
Comparison with results in [Reference Liu and Zhang26]: Considering that the results in this section are closely related to results in our previous work [Reference Liu and Zhang26], we highlight the major difference between them. Note first that Theorem 3.3 gives a sharper upper bound for
![]() $\mathscr D_{num}(1, n)$
than the previous estimate in [Reference Liu and Zhang26]. It also significantly improves the resolution estimate for resolving two sources, enhancing their practical relevance. These improvements stem from employing location-amplitude identities, a more essential and powerful method than the one used in [Reference Liu and Zhang26, Reference Liu and Zhang27]. In particular, [Reference Liu and Zhang26, Reference Liu and Zhang27] established the approximation theory in the Vandermonde space by some algebraic manipulations, while the derived location-amplitude identities here reveal in depth the essence of the super-resolution problem. For example, identities (7) and (8) (or inequalities (10) and (11)) reveal directly the relation between the amplitudes and locations of the true sources and the recovered ones, demonstrating that the stabilities of the recoveries are determined by
$\mathscr D_{num}(1, n)$
than the previous estimate in [Reference Liu and Zhang26]. It also significantly improves the resolution estimate for resolving two sources, enhancing their practical relevance. These improvements stem from employing location-amplitude identities, a more essential and powerful method than the one used in [Reference Liu and Zhang26, Reference Liu and Zhang27]. In particular, [Reference Liu and Zhang26, Reference Liu and Zhang27] established the approximation theory in the Vandermonde space by some algebraic manipulations, while the derived location-amplitude identities here reveal in depth the essence of the super-resolution problem. For example, identities (7) and (8) (or inequalities (10) and (11)) reveal directly the relation between the amplitudes and locations of the true sources and the recovered ones, demonstrating that the stabilities of the recoveries are determined by
![]() $\frac {\sigma }{\prod _{q\in S_t}(e^{iy_t\omega ^*} - e^{iq\omega ^*})}$
. This analytical perspective transforms the super-resolution problem into analyzing the distribution of the locations of true and recovered sources, leading to optimal stability results for the recovery of source numbers, locations and amplitudes as substantiated in Theorems 3.3, 3.8 and 3.10. As a comparison, the method in [Reference Liu and Zhang26, Reference Liu and Zhang27] deals with only the number detection and location recovery problem, since the algebraic manipulation incurs non-necessary noise amplifications when analyzing the amplitude reconstruction. The method in [Reference Batenkov, Goldman and Yomdin3] is only applicable for recovering the location and amplitude of sources due to the ‘quantitative inverse function theorem’ necessitating an equal number of true and recovered sources. Furthermore, our method is capable of analyzing the stability of super-resolving multi-cluster sources under very general settings, making it highly effective.
$\frac {\sigma }{\prod _{q\in S_t}(e^{iy_t\omega ^*} - e^{iq\omega ^*})}$
. This analytical perspective transforms the super-resolution problem into analyzing the distribution of the locations of true and recovered sources, leading to optimal stability results for the recovery of source numbers, locations and amplitudes as substantiated in Theorems 3.3, 3.8 and 3.10. As a comparison, the method in [Reference Liu and Zhang26, Reference Liu and Zhang27] deals with only the number detection and location recovery problem, since the algebraic manipulation incurs non-necessary noise amplifications when analyzing the amplitude reconstruction. The method in [Reference Batenkov, Goldman and Yomdin3] is only applicable for recovering the location and amplitude of sources due to the ‘quantitative inverse function theorem’ necessitating an equal number of true and recovered sources. Furthermore, our method is capable of analyzing the stability of super-resolving multi-cluster sources under very general settings, making it highly effective.
Due to the simplicity and directness of our method, the bounds derived here are nearly optimal and hard to improve. The only parts in the proof deteriorating the resolution estimate are the noise amplification in Corollary 2.2 and inequality (27), which also indicate the path for future improvement.
3.2 Stability of location reconstruction
We now consider the location (support) recovery problem in the super-resolution. We first introduce the following concept of
![]() $\delta $
-neighborhood of a discrete measure.
$\delta $
-neighborhood of a discrete measure.
Definition 3.6. Let
![]() $\mu =\sum _{j=1}^n a_j \delta _{\mathbf {y}_j}, \mathbf {y}_j \in \mathbb {R}^k$
be a discrete measure and let
$\mu =\sum _{j=1}^n a_j \delta _{\mathbf {y}_j}, \mathbf {y}_j \in \mathbb {R}^k$
be a discrete measure and let
![]() $\delta>0$
be such that the n balls
$\delta>0$
be such that the n balls
![]() $B_\delta ^k\left (\mathbf {y}_j\right ), 1 \leqslant j \leqslant n$
are pairwise disjoint. We say that
$B_\delta ^k\left (\mathbf {y}_j\right ), 1 \leqslant j \leqslant n$
are pairwise disjoint. We say that
![]() $\widehat {\mu }=\sum _{j=1}^n \widehat {a}_j \delta _{\widehat {\mathbf {y}}_j}$
is within
$\widehat {\mu }=\sum _{j=1}^n \widehat {a}_j \delta _{\widehat {\mathbf {y}}_j}$
is within
![]() $\delta $
neighborhood of
$\delta $
neighborhood of
![]() $\mu $
if each
$\mu $
if each
![]() $\widehat {\mathbf {y}}_j$
is contained in one and only one of the n balls
$\widehat {\mathbf {y}}_j$
is contained in one and only one of the n balls
![]() $B_\delta ^k\left (\mathbf {y}_j\right ), 1 \leqslant j \leqslant n$
.
$B_\delta ^k\left (\mathbf {y}_j\right ), 1 \leqslant j \leqslant n$
.
According to the above definition, a measure in a
![]() $\delta $
-neighborhood preserves the inner structure of the true set of sources. For any stable support recovery algorithm, the output should be a measure in some
$\delta $
-neighborhood preserves the inner structure of the true set of sources. For any stable support recovery algorithm, the output should be a measure in some
![]() $\delta $
-neighborhood; otherwise, it is impossible to distinguish which is the reconstructed location of some
$\delta $
-neighborhood; otherwise, it is impossible to distinguish which is the reconstructed location of some
![]() $\mathbf{y}_j$
’s. We now introduce the computational resolution limit for stable support recoveries. For ease of exposition, we only consider measures supported in
$\mathbf{y}_j$
’s. We now introduce the computational resolution limit for stable support recoveries. For ease of exposition, we only consider measures supported in
![]() $B_{\frac {(n-1)\pi }{2\Omega }}^{k}(\mathbf{0})$
.
$B_{\frac {(n-1)\pi }{2\Omega }}^{k}(\mathbf{0})$
.
Definition 3.7. The computational resolution limit to the stable support recovery problem in the super-resolution of sources in
![]() $\mathbb R^{k}$
is defined as the smallest nonnegative number
$\mathbb R^{k}$
is defined as the smallest nonnegative number
![]() $\mathscr D_{supp}(k, n)$
such that for all n-sparse measure
$\mathscr D_{supp}(k, n)$
such that for all n-sparse measure
![]() $\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j},\mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the associated measurement
$\sum _{j=1}^{n}a_{j}\delta _{\mathbf{y}_j},\mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the associated measurement
![]() $\mathbf{Y}$
in (1), if
$\mathbf{Y}$
in (1), if
then there exists
![]() $\delta>0$
such that any
$\delta>0$
such that any
![]() $\sigma $
-admissible measure for
$\sigma $
-admissible measure for
![]() $\mathbf Y$
with n supports in
$\mathbf Y$
with n supports in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
is within a
$B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
is within a
![]() $\delta $
-neighborhood of
$\delta $
-neighborhood of
![]() $\mu $
. In particular, when considering positive sources and positive
$\mu $
. In particular, when considering positive sources and positive
![]() $\sigma $
-admissible measures, the corresponding computational resolution limit is denoted by
$\sigma $
-admissible measures, the corresponding computational resolution limit is denoted by
![]() $\mathscr D_{supp}^+(k, n)$
.
$\mathscr D_{supp}^+(k, n)$
.
Leveraging the location-amplitude identities, we derive the following theorem for stably recovering the source locations in the one-dimensional super-resolution problem.
Theorem 3.8. Let
![]() $n\geqslant 2$
, and consider the measurement
$n\geqslant 2$
, and consider the measurement
![]() $\mathbf{Y}$
in (1) generated by any one-dimensional source
$\mathbf{Y}$
in (1) generated by any one-dimensional source
![]() $\mu =\sum _{j=1}^{n}a_j \delta _{y_j}$
supported on
$\mu =\sum _{j=1}^{n}a_j \delta _{y_j}$
supported on
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
satisfying
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
satisfying
If
![]() $\widehat \mu =\sum _{j=1}^{n}\widehat a_{j}\delta _{\widehat y_j}$
supported on
$\widehat \mu =\sum _{j=1}^{n}\widehat a_{j}\delta _{\widehat y_j}$
supported on
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
![]() $\sigma $
-admissible measure of the measurement
$\sigma $
-admissible measure of the measurement
![]() $\mathbf{Y}$
, then
$\mathbf{Y}$
, then
![]() $\widehat \mu $
is within the
$\widehat \mu $
is within the
![]() $\frac {d_{\min }}{2}$
-neighborhood of
$\frac {d_{\min }}{2}$
-neighborhood of
![]() $\mu $
. After reordering the
$\mu $
. After reordering the
![]() $\widehat y_j$
’s, we have
$\widehat y_j$
’s, we have
where
![]() $C(n)=\sqrt {n-0.5}\ 2^{2n-\frac {3}{2}}e^{2n}4.5^{-1}$
and
$C(n)=\sqrt {n-0.5}\ 2^{2n-\frac {3}{2}}e^{2n}4.5^{-1}$
and
![]() $\mathrm {SRF}:= \frac {\pi }{\Omega d_{\min }}$
is the super-resolution factor. Moreover, for the case when
$\mathrm {SRF}:= \frac {\pi }{\Omega d_{\min }}$
is the super-resolution factor. Moreover, for the case when
![]() $n=2$
, the minimum separation can be improved to
$n=2$
, the minimum separation can be improved to
 $$\begin{align*}d_{\min}\geqslant \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right). \end{align*}$$
$$\begin{align*}d_{\min}\geqslant \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right). \end{align*}$$
Theorem 3.8 gives an upper bound for the computational resolution limit
![]() $\mathscr D_{supp}(1, n)$
that is better than the one in [Reference Liu and Zhang26]. It shows that surpassing the Rayleigh limit in the location recovery is possible when
$\mathscr D_{supp}(1, n)$
that is better than the one in [Reference Liu and Zhang26]. It shows that surpassing the Rayleigh limit in the location recovery is possible when
![]() $\frac {m_{\min }}{\sigma }\geqslant (2.36e)^{2n-1}$
. This upper bound is shown to be sharp by a lower bound provided in [Reference Liu, He and Ammari24], by which we can conclude now that
$\frac {m_{\min }}{\sigma }\geqslant (2.36e)^{2n-1}$
. This upper bound is shown to be sharp by a lower bound provided in [Reference Liu, He and Ammari24], by which we can conclude now that
 $$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}< \mathscr D_{supp}(1, n) \leqslant \frac{2.36e\pi}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}. \end{align*}$$
$$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}< \mathscr D_{supp}(1, n) \leqslant \frac{2.36e\pi}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}. \end{align*}$$
It is also easy to generalize the estimates in Theorem 3.8 to high-dimensional spaces by methods in [Reference Liu and Zhang25, Reference Liu and Ammari22], whereby we can obtain that
 $$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}< \mathscr D_{supp}(k, n) \leqslant \frac{C_2(k,n)}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}, \end{align*}$$
$$\begin{align*}\frac{2e^{-1}}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}< \mathscr D_{supp}(k, n) \leqslant \frac{C_2(k,n)}{\Omega }\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}, \end{align*}$$
for a constant
![]() $C_2(k,n)$
.
$C_2(k,n)$
.
Especially, for the case when
![]() $n=2$
, our estimate demonstrates that when the signal-to-noise ratio
$n=2$
, our estimate demonstrates that when the signal-to-noise ratio
![]() $\mathrm {SNR}>12.5$
, then the resolution is definitely better than the Rayleigh limit, and the ‘super-resolution in location recovery’ can be achieved.
$\mathrm {SNR}>12.5$
, then the resolution is definitely better than the Rayleigh limit, and the ‘super-resolution in location recovery’ can be achieved.
We now present the proof of Theorem 3.8. It follows in a straightforward manner after employing the location-amplitude identities.
We first recall the following auxiliary lemma.
Lemma 3.9. For
![]() $-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _k \leqslant \frac {\pi }{2}$
and
$-\frac {\pi }{2}\leqslant \theta _1<\theta _2<\cdots <\theta _k \leqslant \frac {\pi }{2}$
and
![]() $ \widehat \theta _1, \widehat \theta _2, \cdots , \widehat \theta _k \in \left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
, if
$ \widehat \theta _1, \widehat \theta _2, \cdots , \widehat \theta _k \in \left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
, if
 $$ \begin{align*} \left|\left|{\eta_{k,k}(e^{i \theta_1},\cdots,e^{i \theta_k}, e^{i \widehat \theta_1},\cdots, e^{i \widehat \theta_k})}\right|\right|{}_{\infty}< \left(\frac{2}{\pi}\right)^{k}\epsilon, \text{ and } \theta_{\min} =\min_{q\neq j}\left|{\theta_q-\theta_j}\right|\geqslant \Big(\frac{4\epsilon}{\lambda(k)}\Big)^{\frac{1}{k}}, \end{align*} $$
$$ \begin{align*} \left|\left|{\eta_{k,k}(e^{i \theta_1},\cdots,e^{i \theta_k}, e^{i \widehat \theta_1},\cdots, e^{i \widehat \theta_k})}\right|\right|{}_{\infty}< \left(\frac{2}{\pi}\right)^{k}\epsilon, \text{ and } \theta_{\min} =\min_{q\neq j}\left|{\theta_q-\theta_j}\right|\geqslant \Big(\frac{4\epsilon}{\lambda(k)}\Big)^{\frac{1}{k}}, \end{align*} $$
where
![]() $\eta _{k,k}$
is defined by (22) and
$\eta _{k,k}$
is defined by (22) and
![]() $\lambda (k)$
is given by
$\lambda (k)$
is given by
 $$ \begin{align} \lambda(k)=\left\{ \begin{array}{ll} 1, & k=2,\\ \xi(k-2),& k\geqslant 3, \end{array} \right. \end{align} $$
$$ \begin{align} \lambda(k)=\left\{ \begin{array}{ll} 1, & k=2,\\ \xi(k-2),& k\geqslant 3, \end{array} \right. \end{align} $$
with
![]() $\xi (\cdot )$
being defined in (21), then after reordering
$\xi (\cdot )$
being defined in (21), then after reordering
![]() $\widehat \theta _j$
’s, we have
$\widehat \theta _j$
’s, we have
 $$ \begin{align} \left|\widehat \theta_j -\theta_j\right|< \frac{\theta_{\min}}{2} \text{ and } \left|\widehat \theta_j -\theta_j\right|\leqslant \frac{2^{k-1}\epsilon}{(k-2)!(\theta_{\min})^{k-1}}, \quad j=1,\cdots, k. \end{align} $$
$$ \begin{align} \left|\widehat \theta_j -\theta_j\right|< \frac{\theta_{\min}}{2} \text{ and } \left|\widehat \theta_j -\theta_j\right|\leqslant \frac{2^{k-1}\epsilon}{(k-2)!(\theta_{\min})^{k-1}}, \quad j=1,\cdots, k. \end{align} $$
Proof. See Corollary 9 in [Reference Liu and Zhang26].
Now we start the main proof.
Proof. Since
![]() $\widehat \mu =\sum _{j=1}^{n}\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
$\widehat \mu =\sum _{j=1}^{n}\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
, from the model (1), we have
$\mathbf{Y}$
, from the model (1), we have
for some
![]() $\mathbf{W}_1$
with
$\mathbf{W}_1$
with
![]() $|\mathbf{W}_1(\omega )|<2\sigma , \omega \in [-\Omega ,\Omega ] $
. This implies that
$|\mathbf{W}_1(\omega )|<2\sigma , \omega \in [-\Omega ,\Omega ] $
. This implies that
![]() $\widehat \rho = \sum _{j=1}^{n}e^{-\widehat y_j \Omega }\widehat a_{j} \delta _{\widehat y_j}$
and
$\widehat \rho = \sum _{j=1}^{n}e^{-\widehat y_j \Omega }\widehat a_{j} \delta _{\widehat y_j}$
and
![]() $\rho = \sum _{j=1}^ne^{-y_j \Omega } a_{j} \delta _{y_j}$
satisfy
$\rho = \sum _{j=1}^ne^{-y_j \Omega } a_{j} \delta _{y_j}$
satisfy
for some
![]() $\mathbf{W}_2$
with
$\mathbf{W}_2$
with
![]() $|\mathbf{W}_2(\omega )|<2\sigma , \omega \in [0,2\Omega ]$
. For any
$|\mathbf{W}_2(\omega )|<2\sigma , \omega \in [0,2\Omega ]$
. For any
![]() $y_t$
, let
$y_t$
, let
![]() $\widehat y_{t'}$
be the one in
$\widehat y_{t'}$
be the one in
![]() $\widehat y_j$
’s that is the closest to
$\widehat y_j$
’s that is the closest to
![]() $y_{t}$
and define
$y_{t}$
and define
![]() $S_t$
as
$S_t$
as
Then
![]() $\#S_t = 2n-2$
. Let
$\#S_t = 2n-2$
. Let
![]() $\omega ^*=\frac {2\Omega }{2n-1}$
. Since (33) holds, by (11), we have
$\omega ^*=\frac {2\Omega }{2n-1}$
. Since (33) holds, by (11), we have
 $$ \begin{align} \prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< \frac{2^{2n}\sigma}{m_{\min}}, \ t=1,\cdots, n. \end{align} $$
$$ \begin{align} \prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\prod_{q=1,\cdots, n}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< \frac{2^{2n}\sigma}{m_{\min}}, \ t=1,\cdots, n. \end{align} $$
Therefore, it follows that
 $$\begin{align*}\min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\max_{t=1,\cdots, n}\prod_{q=1,\cdots, n}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< \frac{2^{2n}\sigma}{m_{\min}}. \end{align*}$$
$$\begin{align*}\min_{t=1,\cdots, n}\prod_{q=1,\cdots, n, q\neq t} \left|e^{i y_{t}\omega^*} - e^{i y_{q}\omega^*} \right|\max_{t=1,\cdots, n}\prod_{q=1,\cdots, n}\left|e^{iy_{t}\omega^*} - e^{i\widehat y_q\omega^*}\right|< \frac{2^{2n}\sigma}{m_{\min}}. \end{align*}$$
Denote
![]() $y_q \omega ^*, \widehat y_q\omega ^*$
by, respectively,
$y_q \omega ^*, \widehat y_q\omega ^*$
by, respectively,
![]() $\theta _q, \widehat \theta _q$
and
$\theta _q, \widehat \theta _q$
and
![]() $\theta _{\min } = \min _{p\neq q}|\theta _p-\theta _q|$
. Since
$\theta _{\min } = \min _{p\neq q}|\theta _p-\theta _q|$
. Since
![]() $y_j$
’s in
$y_j$
’s in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and
![]() $\omega ^* = \frac {2\Omega }{2n-1}$
, we have
$\omega ^* = \frac {2\Omega }{2n-1}$
, we have
![]() $\theta _j, \widehat \theta _{j}$
’s in
$\theta _j, \widehat \theta _{j}$
’s in
![]() $\left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
. By Lemma 3.4, we further get
$\left [-\frac {\pi }{2}, \frac {\pi }{2}\right ]$
. By Lemma 3.4, we further get
 $$ \begin{align} \max_{j=1, \cdots, n}\prod_{q=1,\cdots,n}\left|e^{iy_{j}\omega^*} - e^{i \widehat y_q\omega^*}\right|<\frac{1}{\zeta(n)}\left(\frac{\pi}{2\theta_{\min}}\right)^{n-1} \frac{2^{2n}\sigma}{m_{\min}}. \end{align} $$
$$ \begin{align} \max_{j=1, \cdots, n}\prod_{q=1,\cdots,n}\left|e^{iy_{j}\omega^*} - e^{i \widehat y_q\omega^*}\right|<\frac{1}{\zeta(n)}\left(\frac{\pi}{2\theta_{\min}}\right)^{n-1} \frac{2^{2n}\sigma}{m_{\min}}. \end{align} $$
We then utilize Lemma 3.9 to estimate the recovery of the locations. For this purpose, let
![]() $\epsilon = \frac {\pi ^{2n-1}}{\zeta (n)(\theta _{\min })^{n-1}} \frac {2\sigma }{m_{\min }}$
. Then (35) is equivalent to
$\epsilon = \frac {\pi ^{2n-1}}{\zeta (n)(\theta _{\min })^{n-1}} \frac {2\sigma }{m_{\min }}$
. Then (35) is equivalent to
 $$ \begin{align*}\left|\left|{\eta_{n ,n}(e^{i \theta_1},\cdots,e^{i \theta_n}, e^{i \widehat \theta_1},\cdots, e^{i \widehat \theta_n})}\right|\right|{}_{\infty}<\left(\frac{2}{\pi}\right)^n\epsilon.\end{align*} $$
$$ \begin{align*}\left|\left|{\eta_{n ,n}(e^{i \theta_1},\cdots,e^{i \theta_n}, e^{i \widehat \theta_1},\cdots, e^{i \widehat \theta_n})}\right|\right|{}_{\infty}<\left(\frac{2}{\pi}\right)^n\epsilon.\end{align*} $$
We thus only need to check the following condition:
 $$ \begin{align} \theta_{\min}\geqslant \Big(\frac{4\epsilon}{\lambda(n)}\Big)^{\frac{1}{n}}, \quad \text{or equivalently}\,\,\, (\theta_{\min})^n \geqslant \frac{4\epsilon}{\lambda(n)}. \end{align} $$
$$ \begin{align} \theta_{\min}\geqslant \Big(\frac{4\epsilon}{\lambda(n)}\Big)^{\frac{1}{n}}, \quad \text{or equivalently}\,\,\, (\theta_{\min})^n \geqslant \frac{4\epsilon}{\lambda(n)}. \end{align} $$
Indeed, by the separation condition (29),
 $$ \begin{align} \theta_{\min}= d_{\min}\omega^*\geqslant \frac{2.36\pi e}{n-\frac{1}{2}}\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}\geqslant \pi \Big(\frac{4}{\lambda(n)\zeta(n)}\frac{2\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}, \end{align} $$
$$ \begin{align} \theta_{\min}= d_{\min}\omega^*\geqslant \frac{2.36\pi e}{n-\frac{1}{2}}\Big(\frac{\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}\geqslant \pi \Big(\frac{4}{\lambda(n)\zeta(n)}\frac{2\sigma}{m_{\min}}\Big)^{\frac{1}{2n-1}}, \end{align} $$
where we have used Lemma A.2 in the last inequality. Then
 $$\begin{align*}(\theta_{\min})^{2n-1}\geqslant \frac{4\pi^{2n-1}}{\lambda(n)\zeta(n)}\frac{2\sigma}{m_{\min}}, \end{align*}$$
$$\begin{align*}(\theta_{\min})^{2n-1}\geqslant \frac{4\pi^{2n-1}}{\lambda(n)\zeta(n)}\frac{2\sigma}{m_{\min}}, \end{align*}$$
whence we get (36). Therefore, we can apply Lemma 3.9 to get that, after reordering
![]() $\widehat \theta _j$
’s,
$\widehat \theta _j$
’s,
 $$ \begin{align} \begin{aligned} &\left|\widehat \theta_{j}-\theta_j\right|< \frac{\theta_{\min}}{2},\\ &\left|\widehat \theta_{j}-\theta_j\right|< \frac{2^{n}\pi^{2n-1}}{\zeta(n)(n-2)!(\theta_{\min})^{2n-2}}\frac{\sigma}{m_{\min}} , 1\leqslant j\leqslant n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} &\left|\widehat \theta_{j}-\theta_j\right|< \frac{\theta_{\min}}{2},\\ &\left|\widehat \theta_{j}-\theta_j\right|< \frac{2^{n}\pi^{2n-1}}{\zeta(n)(n-2)!(\theta_{\min})^{2n-2}}\frac{\sigma}{m_{\min}} , 1\leqslant j\leqslant n. \end{aligned} \end{align} $$
Finally, we estimate
![]() $\left |\widehat y_j - y_j\right |$
. Since
$\left |\widehat y_j - y_j\right |$
. Since
![]() $\left |\widehat \theta _{j}-\theta _j\right |< \frac {\theta _{\min }}{2}$
, it is clear that
$\left |\widehat \theta _{j}-\theta _j\right |< \frac {\theta _{\min }}{2}$
, it is clear that
![]() $\left |\widehat y_j-y_j\right |< \frac {d_{\min }}{2}.$
Thus,
$\left |\widehat y_j-y_j\right |< \frac {d_{\min }}{2}.$
Thus,
![]() $\widehat \mu $
is within the
$\widehat \mu $
is within the
![]() $\frac {d_{\min }}{2}$
-neighborhood of
$\frac {d_{\min }}{2}$
-neighborhood of
![]() $\mu $
. Moreover,
$\mu $
. Moreover,
Using (38) and Lemma A.3, a direct calculation shows that
 $$ \begin{align} \left|\widehat y_j-y_j\right|< \frac{C(n)}{\Omega} \left(\frac{\pi}{\Omega d_{\min}}\right)^{2n-2} \frac{\sigma}{m_{\min}}, \end{align} $$
$$ \begin{align} \left|\widehat y_j-y_j\right|< \frac{C(n)}{\Omega} \left(\frac{\pi}{\Omega d_{\min}}\right)^{2n-2} \frac{\sigma}{m_{\min}}, \end{align} $$
where
![]() $C(n)=\sqrt {n-0.5}\ 2^{2n-\frac {3}{2}}e^{2n}4.5^{-1}$
.
$C(n)=\sqrt {n-0.5}\ 2^{2n-\frac {3}{2}}e^{2n}4.5^{-1}$
.
The last part is to prove the case when
![]() $n=2$
. When
$n=2$
. When
![]() $n=2$
, by (34), we have
$n=2$
, by (34), we have
 $$ \begin{align} \left|e^{i y_{1}\omega^*} - e^{i \widehat y_{1}\omega^*} \right| \left|e^{iy_{1}\omega^*} - e^{i\widehat y_2\omega^*}\right| \left|e^{iy_{1}\omega^*} - e^{iy_2\omega^*}\right| < \frac{2^{4}\sigma}{m_{\min}}. \end{align} $$
$$ \begin{align} \left|e^{i y_{1}\omega^*} - e^{i \widehat y_{1}\omega^*} \right| \left|e^{iy_{1}\omega^*} - e^{i\widehat y_2\omega^*}\right| \left|e^{iy_{1}\omega^*} - e^{iy_2\omega^*}\right| < \frac{2^{4}\sigma}{m_{\min}}. \end{align} $$
Denote
![]() $\omega ^*|y_1-y_2|=\theta _{\min }$
. Reordering
$\omega ^*|y_1-y_2|=\theta _{\min }$
. Reordering
![]() $\hat y_j$
’s so that
$\hat y_j$
’s so that
![]() $|\widehat y_1- y_1|\leqslant |\widehat y_2- y_1|$
. Thus, if
$|\widehat y_1- y_1|\leqslant |\widehat y_2- y_1|$
. Thus, if
![]() $|\widehat y_{1}-y_1|\omega ^*\geqslant \frac {\theta _{\min }}{2}$
, we have
$|\widehat y_{1}-y_1|\omega ^*\geqslant \frac {\theta _{\min }}{2}$
, we have
![]() $|\widehat y_{2}-y_1|\omega ^*\geqslant \frac {\theta _{\min }}{2}$
. Recall also that
$|\widehat y_{2}-y_1|\omega ^*\geqslant \frac {\theta _{\min }}{2}$
. Recall also that
![]() $\widehat y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0), j=1,2$
. Then (40) yields
$\widehat y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0), j=1,2$
. Then (40) yields
 $$\begin{align*}\left(2\sin\left(\frac{\theta_{\min}}{4}\right)\right)^2 2\sin\left(\frac{\theta_{\min}}{2}\right) < \frac{2^4\sigma}{m_{\min}}, \end{align*}$$
$$\begin{align*}\left(2\sin\left(\frac{\theta_{\min}}{4}\right)\right)^2 2\sin\left(\frac{\theta_{\min}}{2}\right) < \frac{2^4\sigma}{m_{\min}}, \end{align*}$$
which gives
 $$\begin{align*}\sin^3\left(\frac{\theta_{\min}}{2}\right)< \frac{2^3\sigma}{m_{\min}}. \end{align*}$$
$$\begin{align*}\sin^3\left(\frac{\theta_{\min}}{2}\right)< \frac{2^3\sigma}{m_{\min}}. \end{align*}$$
It then follows that
 $$\begin{align*}\theta_{\min}< 2\arcsin\left(\frac{8\sigma}{m_{\min}}\right)^{\frac{1}{3}} \end{align*}$$
$$\begin{align*}\theta_{\min}< 2\arcsin\left(\frac{8\sigma}{m_{\min}}\right)^{\frac{1}{3}} \end{align*}$$
and
 $$\begin{align*}d_{\min}=\frac{\theta_{\min}}{\omega^*}< \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right), \end{align*}$$
$$\begin{align*}d_{\min}=\frac{\theta_{\min}}{\omega^*}< \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right), \end{align*}$$
where we have set
![]() $\omega ^* = \frac {2\Omega }{3}$
. Therefore, if
$\omega ^* = \frac {2\Omega }{3}$
. Therefore, if
 $$\begin{align*}d_{\min}\geqslant \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right), \end{align*}$$
$$\begin{align*}d_{\min}\geqslant \frac{3}{\Omega}\arcsin\left(2\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{3}}\right), \end{align*}$$
then we must have
![]() $|\widehat y_{1}-y_1|\omega ^*<\frac {\theta _{\min }}{2}$
and consequently,
$|\widehat y_{1}-y_1|\omega ^*<\frac {\theta _{\min }}{2}$
and consequently,
![]() $|\widehat y_{1}-y_1|< \frac {d_{\min }}{2}$
. In the same manner, we also have
$|\widehat y_{1}-y_1|< \frac {d_{\min }}{2}$
. In the same manner, we also have
![]() $|\widehat y_{2}-y_2|< \frac {d_{\min }}{2}$
. This completes the proof.
$|\widehat y_{2}-y_2|< \frac {d_{\min }}{2}$
. This completes the proof.
3.3 Stability of amplitude reconstruction
We now consider the stability of the amplitude reconstruction. Note that for the off-the-grid case, it takes several tens pages in [Reference Batenkov, Goldman and Yomdin3] to prove the stability of the reconstruction of each amplitude
![]() $a_j$
. Here, we can take two pages to have a stronger understanding for the amplitude reconstruction.
$a_j$
. Here, we can take two pages to have a stronger understanding for the amplitude reconstruction.
Theorem 3.10. Let
![]() $n\geqslant 2$
and let the measurement
$n\geqslant 2$
and let the measurement
![]() $\mathbf{Y}$
be generated from any one-dimensional source
$\mathbf{Y}$
be generated from any one-dimensional source
![]() $\mu =\sum _{j=1}^{n}a_j \delta _{y_j}$
supported on
$\mu =\sum _{j=1}^{n}a_j \delta _{y_j}$
supported on
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and satisfying the separation condition
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and satisfying the separation condition
For any
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
,
$\mathbf{Y}$
,
![]() $\widehat \mu = \sum _{j=1}^n\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
, after reordering the
$\widehat \mu = \sum _{j=1}^n\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
, after reordering the
![]() $\widehat y_j$
’s, we have
$\widehat y_j$
’s, we have
for a certain constant
![]() $C_1(n)$
. Moreover, if
$C_1(n)$
. Moreover, if
![]() $\widehat y_j = y_j$
, we have
$\widehat y_j = y_j$
, we have
for a certain constant
![]() $C_2(n)$
.
$C_2(n)$
.
Proof. By Theorem 3.8, the separation condition (41) implies
 $$ \begin{align} \Big|\widehat y_j-y_j\Big|<\frac{\sqrt{n-0.5}\ 2^{2n-\frac{3}{2}}e^{2n}4.5^{-1}}{\Omega}\left(\frac{\pi}{\Omega d_{\min}}\right)^{2n-2}\frac{\sigma}{m_{\min}}, \quad 1\leqslant j\leqslant n. \end{align} $$
$$ \begin{align} \Big|\widehat y_j-y_j\Big|<\frac{\sqrt{n-0.5}\ 2^{2n-\frac{3}{2}}e^{2n}4.5^{-1}}{\Omega}\left(\frac{\pi}{\Omega d_{\min}}\right)^{2n-2}\frac{\sigma}{m_{\min}}, \quad 1\leqslant j\leqslant n. \end{align} $$
Together with (41), this gives
![]() $|\widehat y_j-y_j|<\frac {d_{\min }}{9}, j=1,\cdots , n$
. Hence, among
$|\widehat y_j-y_j|<\frac {d_{\min }}{9}, j=1,\cdots , n$
. Hence, among
![]() $\{\widehat y_q\}_{q=1}^n$
,
$\{\widehat y_q\}_{q=1}^n$
,
![]() $\widehat y_j$
is the closest point to
$\widehat y_j$
is the closest point to
![]() $y_j$
. We write
$y_j$
. We write
![]() $y_{j} = \widehat y_j+\epsilon _j$
with
$y_{j} = \widehat y_j+\epsilon _j$
with
![]() $0\leqslant \left |{\epsilon _{j}}\right |< \frac {d_{\min }}{9}$
. Since
$0\leqslant \left |{\epsilon _{j}}\right |< \frac {d_{\min }}{9}$
. Since
![]() $\widehat \mu =\sum _{j=1}^{n}\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
$\widehat \mu =\sum _{j=1}^{n}\widehat a_j \delta _{\widehat y_j}, \widehat y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
is a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
, from the model (1), we have
$\mathbf{Y}$
, from the model (1), we have
for some
![]() $\mathbf{W}_1$
with
$\mathbf{W}_1$
with
![]() $|\mathbf{W}_1(\omega )|<2\sigma , \omega \in [0,\Omega ] $
. For each
$|\mathbf{W}_1(\omega )|<2\sigma , \omega \in [0,\Omega ] $
. For each
![]() $j\in \{1,\cdots , n\}$
, denote by
$j\in \{1,\cdots , n\}$
, denote by
![]() $S_j$
the set containing all
$S_j$
the set containing all
![]() $y_p$
’s and
$y_p$
’s and
![]() $\widehat y_p$
’s except
$\widehat y_p$
’s except
![]() $y_j, \widehat y_{j}$
. By
$y_j, \widehat y_{j}$
. By
![]() $\left |{\widehat y_p - y_p}\right |<\frac {d_{\min }}{9}, 1\leqslant p\leqslant n$
, for all
$\left |{\widehat y_p - y_p}\right |<\frac {d_{\min }}{9}, 1\leqslant p\leqslant n$
, for all
![]() $q\in S_j$
we have
$q\in S_j$
we have
![]() $q\neq y_j$
and
$q\neq y_j$
and
![]() $q\neq \widehat y_j$
. Let
$q\neq \widehat y_j$
. Let
![]() $\omega ^* = \frac {\Omega }{2n-1}$
. As
$\omega ^* = \frac {\Omega }{2n-1}$
. As
![]() $y_p$
’s and
$y_p$
’s and
![]() $\widehat y_p$
’s are in
$\widehat y_p$
’s are in
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
, we also have
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
, we also have
![]() $e^{iq\omega ^*}\neq e^{iy_j\omega ^*}, e^{iq\omega ^*}\neq e^{i\widehat y_j\omega ^*}, q\in S_j$
. Thus, by (10), we can have
$e^{iq\omega ^*}\neq e^{iy_j\omega ^*}, e^{iq\omega ^*}\neq e^{i\widehat y_j\omega ^*}, q\in S_j$
. Thus, by (10), we can have
 $$ \begin{align} \left|\widehat {a}_{j}\prod_{q\in S_j}\frac{e^{i\widehat y_{j}\omega^*}-e^{i q\omega^*}}{e^{i y_j\omega^*}- e^{i q\omega^*}}-a_j\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
$$ \begin{align} \left|\widehat {a}_{j}\prod_{q\in S_j}\frac{e^{i\widehat y_{j}\omega^*}-e^{i q\omega^*}}{e^{i y_j\omega^*}- e^{i q\omega^*}}-a_j\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
Equivalently, we have
 $$ \begin{align} \left|\widehat {a}_{j}-a_j\prod_{q\in S_j}\frac{e^{iy_{j}\omega^*}-e^{i q\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
$$ \begin{align} \left|\widehat {a}_{j}-a_j\prod_{q\in S_j}\frac{e^{iy_{j}\omega^*}-e^{i q\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
We rewrite its LHS as
 $$ \begin{align} \left|\widehat {a}_{j}-a_j\prod_{q\in S_j}\left(\frac{e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}+1\right)\right|, \end{align} $$
$$ \begin{align} \left|\widehat {a}_{j}-a_j\prod_{q\in S_j}\left(\frac{e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}+1\right)\right|, \end{align} $$
and expand that
 $$ \begin{align} \prod_{q\in S_j}\left(\frac{e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}+1\right) = 1+ (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*})g(\epsilon_j, S_j, \widehat y_j, y_j, \omega^*) \end{align} $$
$$ \begin{align} \prod_{q\in S_j}\left(\frac{e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}}{e^{i \widehat y_j\omega^*}- e^{i q\omega^*}}+1\right) = 1+ (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*})g(\epsilon_j, S_j, \widehat y_j, y_j, \omega^*) \end{align} $$
where
for a certain constant
![]() $C_{3}(n)$
. Thus, combining (46), (47) and (48) yields that
$C_{3}(n)$
. Thus, combining (46), (47) and (48) yields that
 $$ \begin{align} \left|\widehat {a}_{j}-a_j\right| < \left|a_j (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}) g(\epsilon_j, S_j, \widehat y_j, y_j, \omega^*)\right| + \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
$$ \begin{align} \left|\widehat {a}_{j}-a_j\right| < \left|a_j (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*}) g(\epsilon_j, S_j, \widehat y_j, y_j, \omega^*)\right| + \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
Now we estimate the two terms in the RHS of the above equation. First, by (11), we have
 $$ \begin{align} \left|a_j (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*})\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
$$ \begin{align} \left|a_j (e^{i y_{j}\omega^*}- e^{i \widehat y_{j}\omega^*})\right| < \frac{2^{2n-1}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align} $$
Second, based on the estimate
![]() $|\widehat y_p -y_p|< \frac {d_{\min }}{9}, p=1,\cdots , n$
, it is easy to prove that
$|\widehat y_p -y_p|< \frac {d_{\min }}{9}, p=1,\cdots , n$
, it is easy to prove that
 $$ \begin{align} \frac{\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}\leqslant \frac{C_4(n)\sigma}{d_{\min}^{2n-2}} \end{align} $$
$$ \begin{align} \frac{\sigma}{\prod_{q\in S_j}\left|e^{i\widehat y_j\omega^*} - e^{iq\omega^*}\right|}\leqslant \frac{C_4(n)\sigma}{d_{\min}^{2n-2}} \end{align} $$
holds for some constant
![]() $C_4(n)$
. Combining estimates (49), (50), (51) and (52) yields
$C_4(n)$
. Combining estimates (49), (50), (51) and (52) yields
 $$\begin{align*}\left|\widehat {a}_{j}-a_j\right|< \frac{C_5(n)}{d_{\min}^{2n-1}}\sigma \end{align*}$$
$$\begin{align*}\left|\widehat {a}_{j}-a_j\right|< \frac{C_5(n)}{d_{\min}^{2n-1}}\sigma \end{align*}$$
for some constant
![]() $C_5(n)$
. Now we consider the case when
$C_5(n)$
. Now we consider the case when
![]() $\widehat y_j = y_j$
. This time, by (45), we have
$\widehat y_j = y_j$
. This time, by (45), we have
 $$\begin{align*}\left|{\widehat a_j - a_j}\right|<\frac{2^{\#S_j}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align*}$$
$$\begin{align*}\left|{\widehat a_j - a_j}\right|<\frac{2^{\#S_j}\sigma}{\prod_{q\in S_j}\left|e^{iy_j\omega^*} - e^{iq\omega^*}\right|}. \end{align*}$$
Together with (52), we demonstrate (43) and complete the proof.
3.4 Stability of a sparsity-promoting algorithm
Nowadays, sparsity-promoting algorithms are popular methods in image processing, signal processing and many other fields. As a direct consequence of results in the above sections, we derive a sharp stability result for the following
![]() $l_0$
-minimization problem in the one-dimensional super-resolution:
$l_0$
-minimization problem in the one-dimensional super-resolution:
where
![]() $||\rho ||_{0}$
is the number of Dirac masses representing the discrete measure
$||\rho ||_{0}$
is the number of Dirac masses representing the discrete measure
![]() $\rho $
.
$\rho $
.
Theorem 3.11. Let
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $\sigma \leqslant m_{\min }$
. Let the measurement
$\sigma \leqslant m_{\min }$
. Let the measurement
![]() $\mathbf{Y}$
in (1) be generated by a one-dimensional source
$\mathbf{Y}$
in (1) be generated by a one-dimensional source
![]() $\mu =\sum _{j=1}^{n}a_j \delta _{y_j}, a_j \in \mathbb C, y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
. Assume that
$\mu =\sum _{j=1}^{n}a_j \delta _{y_j}, a_j \in \mathbb C, y_j \in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
. Assume that
Let
![]() $\mathscr O$
in the minimization problem (53) be (or be included in)
$\mathscr O$
in the minimization problem (53) be (or be included in)
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
. Then the solution to (53) contains exactly n point sources. For any solution
$B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
. Then the solution to (53) contains exactly n point sources. For any solution
![]() $\widehat \mu =\sum _{j=1}^{n}\widehat a_{j}\delta _{\widehat y_j}$
, it is in a
$\widehat \mu =\sum _{j=1}^{n}\widehat a_{j}\delta _{\widehat y_j}$
, it is in a
![]() $\frac {d_{\min }}{9}$
-neighborhood of
$\frac {d_{\min }}{9}$
-neighborhood of
![]() $\mu $
. Moreover, after reordering the
$\mu $
. Moreover, after reordering the
![]() ${\widehat y}_j$
’s, we have
${\widehat y}_j$
’s, we have
for certain constants
![]() $C_1(n)$
and
$C_1(n)$
and
![]() $C_2(n)$
.
$C_2(n)$
.
Theorem 3.11 reveals that sparsity promoting over admissible solutions can resolve the source locations to the resolution limit level. Particularly, under the separation condition (54), any tractable sparsity-promoting algorithms (such as total variation minimization algorithms [Reference Candès and Fernandez-Granda5]) rendering the sparsest solution could stably reconstruct all the source locations and amplitudes.
4 Two-point resolution in the multi-dimensional super-resolution
Now we have understood the stability of super-resolving multiple point sources. Specifically, we have shown that with a
![]() $\mathrm {SNR}$
greater than 4, super-resolution is definitively achievable for resolving two point sources. However, we are not merely interested in estimations; we aim to determine the precise resolution limit for distinguishing two sources. In this section, we will develop the exact formula for this two-point resolution limit. We will particularly address the multi-dimensional imaging problem as described by (1), focusing on super-resolving two point sources, represented as
$\mathrm {SNR}$
greater than 4, super-resolution is definitively achievable for resolving two point sources. However, we are not merely interested in estimations; we aim to determine the precise resolution limit for distinguishing two sources. In this section, we will develop the exact formula for this two-point resolution limit. We will particularly address the multi-dimensional imaging problem as described by (1), focusing on super-resolving two point sources, represented as
![]() $\mu =\sum _{j=1}^{2}a_{j}\delta _{\mathbf{y}_j}, \mathbf{y}_j \in \mathbb R^k$
.
$\mu =\sum _{j=1}^{2}a_{j}\delta _{\mathbf{y}_j}, \mathbf{y}_j \in \mathbb R^k$
.
4.1 Two-point resolution for resolving sources with identical amplitudes
Inspired by the classic diffraction limit problem, we derived the following lemma for the resolution limit when resolving two point sources with identical amplitudes.
Lemma 4.1. Let
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
. For all measures
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
. For all measures
![]() $\mu =\sum _{j=1}^{2}a_j\delta _{\mathbf{y}_j}, \mathbf{y}_j\in \mathbb R^{k}$
with
$\mu =\sum _{j=1}^{2}a_j\delta _{\mathbf{y}_j}, \mathbf{y}_j\in \mathbb R^{k}$
with
![]() $m_{\min }=a_1=a_2>0$
, if
$m_{\min }=a_1=a_2>0$
, if
 $$ \begin{align} \min_{p\neq j} \left|\left|{\mathbf{y}_j-\mathbf{y}_p}\right|\right|{}_2 \geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align} $$
$$ \begin{align} \min_{p\neq j} \left|\left|{\mathbf{y}_j-\mathbf{y}_p}\right|\right|{}_2 \geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align} $$
then there does not exist any
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf Y$
with less than two supports. However, when (56) fails to hold, there exists a
$\mathbf Y$
with less than two supports. However, when (56) fails to hold, there exists a
![]() $\sigma $
-admissible measure of some
$\sigma $
-admissible measure of some
![]() $\mathbf{Y}$
with only one point source. When
$\mathbf{Y}$
with only one point source. When
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
![]() $\sigma $
-admissible measures of some
$\sigma $
-admissible measures of some
![]() $\mathbf{Y}$
with only one point source.
$\mathbf{Y}$
with only one point source.
Proof.
Step 1. We first prove the one-dimensional case. Let
![]() $\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
$\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
![]() $\widehat \mu = a \delta _{\widehat y}$
. A crucial relation is
$\widehat \mu = a \delta _{\widehat y}$
. A crucial relation is
Note that if (57) holds,
![]() $\widehat \mu $
can be a
$\widehat \mu $
can be a
![]() $\sigma $
-admissible measure of some
$\sigma $
-admissible measure of some
![]() $\mathbf{Y}$
generated by model (1). This time, resolving two point sources is impossible. Conversely, if (57) does not hold,
$\mathbf{Y}$
generated by model (1). This time, resolving two point sources is impossible. Conversely, if (57) does not hold,
![]() $\widehat \mu $
cannot be any
$\widehat \mu $
cannot be any
![]() $\sigma $
-admissible measure of some
$\sigma $
-admissible measure of some
![]() $\mathbf{Y}$
generated by
$\mathbf{Y}$
generated by
![]() $\mu $
as in model (1). Let
$\mu $
as in model (1). Let
![]() $\mathscr R$
be the constant such that (57) holds when
$\mathscr R$
be the constant such that (57) holds when
![]() $|y_1-y_2|< \mathscr R$
and fails to hold in the opposite case. Based on the above discussions, proving Lemma 4.1 is to show
$|y_1-y_2|< \mathscr R$
and fails to hold in the opposite case. Based on the above discussions, proving Lemma 4.1 is to show
 $\mathscr R = \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
.
$\mathscr R = \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
.
Instead of considering all the
![]() $\omega \in [-\Omega ,\Omega ]$
directly, we consider
$\omega \in [-\Omega ,\Omega ]$
directly, we consider
In the sequel, we intend to find
![]() $\mathscr R$
so that (58) holds when
$\mathscr R$
so that (58) holds when
![]() $|y_1-y_2|< \mathscr R$
and does not hold in the opposite case. Afterward, we will show that (57) holds as well under some circumstances when
$|y_1-y_2|< \mathscr R$
and does not hold in the opposite case. Afterward, we will show that (57) holds as well under some circumstances when
![]() $|y_1-y_2|< \mathscr R$
.
$|y_1-y_2|< \mathscr R$
.
Step 2. Note that for the general source locations
![]() $y_1, y_2$
, shifting them by x and getting that
$y_1, y_2$
, shifting them by x and getting that
we can transform the problem into the case when
![]() $y_1=-y_2$
. Thus, we consider that the true source is
$y_1=-y_2$
. Thus, we consider that the true source is
![]() $\mu = m_{\min } \delta _{y_1}+ m_{\min } \delta _{y_2}$
with
$\mu = m_{\min } \delta _{y_1}+ m_{\min } \delta _{y_2}$
with
![]() $y_1>0, y_1 = -y_2$
. The measure
$y_1>0, y_1 = -y_2$
. The measure
![]() $\widehat \mu $
is
$\widehat \mu $
is
![]() $a\delta _{\widehat y}$
with a and
$a\delta _{\widehat y}$
with a and
![]() $\widehat y$
to be determined.
$\widehat y$
to be determined.
Then the existence of
![]() $\widehat \mu $
satisfying (58) is equivalent to solving the condition on
$\widehat \mu $
satisfying (58) is equivalent to solving the condition on
![]() $y_1$
so that
$y_1$
so that
where we have used
We denote
![]() $d_{\min }:=|y_1-y_2|$
and first consider the case when
$d_{\min }:=|y_1-y_2|$
and first consider the case when
![]() $0<d_{\min }<\frac {\pi }{\Omega }$
. Note that for two nonnegative values
$0<d_{\min }<\frac {\pi }{\Omega }$
. Note that for two nonnegative values
![]() $x,y$
, we have
$x,y$
, we have
and the equality is attained when
![]() $\theta =0$
. Since
$\theta =0$
. Since
![]() $0<d_{\min }\leqslant \frac {\pi }{\Omega } \left (0<y_1\leqslant \frac {\pi }{2\Omega }\right )$
, we have
$0<d_{\min }\leqslant \frac {\pi }{\Omega } \left (0<y_1\leqslant \frac {\pi }{2\Omega }\right )$
, we have
![]() $\cos (y_1\omega )\geqslant 0, \omega \in [0,\Omega ]$
. Thus, for every
$\cos (y_1\omega )\geqslant 0, \omega \in [0,\Omega ]$
. Thus, for every
![]() $\omega $
,
$\omega $
,
and the minimum is attained when
![]() $\widehat y=0$
and a is a positive number. We now try to find the condition on
$\widehat y=0$
and a is a positive number. We now try to find the condition on
![]() $y_1$
so that there exists
$y_1$
so that there exists
![]() $a\in \mathbb R^+$
satisfying
$a\in \mathbb R^+$
satisfying
This is equivalent to
since the existence of
![]() $\omega _1, \omega _2 \in [0,\Omega ]$
so that
$\omega _1, \omega _2 \in [0,\Omega ]$
so that
results in
If
![]() $d_{\min }=2y_1\leqslant \frac {\pi }{\Omega }$
, then
$d_{\min }=2y_1\leqslant \frac {\pi }{\Omega }$
, then
![]() $0\leqslant y_1\omega \leqslant \frac {\pi }{2}, \omega \in [0,\Omega ]$
. Then problem (59) becomes
$0\leqslant y_1\omega \leqslant \frac {\pi }{2}, \omega \in [0,\Omega ]$
. Then problem (59) becomes
 $$\begin{align*}2m_{\min}\left|1-\cos\left(\frac{d_{\min}}{2}\Omega\right)\right|< 4\sigma. \end{align*}$$
$$\begin{align*}2m_{\min}\left|1-\cos\left(\frac{d_{\min}}{2}\Omega\right)\right|< 4\sigma. \end{align*}$$
Thus,
![]() $4\sin ^2\left (\frac {d_{\min }\Omega }{4}\right )<\frac {4\sigma }{m_{\min }}$
, and equivalently,
$4\sin ^2\left (\frac {d_{\min }\Omega }{4}\right )<\frac {4\sigma }{m_{\min }}$
, and equivalently,
 $$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
$$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
Note that when
 $d_{\min } < \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
, choosing
$d_{\min } < \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
, choosing
![]() $a= \frac {m_{\min }+m_{\min }\cos (y_1\Omega )}{2}$
and
$a= \frac {m_{\min }+m_{\min }\cos (y_1\Omega )}{2}$
and
![]() $\widehat y=0$
makes
$\widehat y=0$
makes
As
![]() $\mathscr F[\widehat \mu ](-\omega )-\mathscr F[\mu ](-\omega ) = \mathscr F[\widehat \mu ](\omega )-\mathscr F[\mu ](\omega )$
this time, the solution makes
$\mathscr F[\widehat \mu ](-\omega )-\mathscr F[\mu ](-\omega ) = \mathscr F[\widehat \mu ](\omega )-\mathscr F[\mu ](\omega )$
this time, the solution makes
Thus, this is exactly the resolution limit
![]() $\mathscr R$
when
$\mathscr R$
when
![]() $0<d_{\min }\leqslant \frac {\pi }{\Omega }$
for the case when
$0<d_{\min }\leqslant \frac {\pi }{\Omega }$
for the case when
![]() $\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
. For the case when
$\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
. For the case when
![]() $d_{\min }> \frac {\pi }{\Omega }$
, by
$d_{\min }> \frac {\pi }{\Omega }$
, by
 $\frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }\leqslant \frac {\pi }{\Omega }$
when
$\frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }\leqslant \frac {\pi }{\Omega }$
when
![]() $\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
and above discussions, we have
$\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
and above discussions, we have
Thus, there does not exist any
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf Y$
with less than two supports. This proves the statements for the case when
$\mathbf Y$
with less than two supports. This proves the statements for the case when
![]() $\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
in the lemma.
$\frac {\sigma }{m_{\min }}\leqslant \frac {1}{2}$
in the lemma.
Now, we consider the case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. We choose a specific case where
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. We choose a specific case where
![]() $a=m_{\min }$
and
$a=m_{\min }$
and
![]() $\widehat y =y_1$
. Then
$\widehat y =y_1$
. Then
gives
Thus, the case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is meaningless. There are always some
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is meaningless. There are always some
![]() $\sigma $
-admissible measures for some images with only one point source.
$\sigma $
-admissible measures for some images with only one point source.
Step 3. Now we consider the case when the sources
![]() $\mathbf{y}_j$
’s are in
$\mathbf{y}_j$
’s are in
![]() $\mathbb R^k$
. We still consider the crucial relation that
$\mathbb R^k$
. We still consider the crucial relation that
By a similar argument as the one in step 1, we need to compute constant
![]() $\mathscr R$
such that (60) holds when
$\mathscr R$
such that (60) holds when
![]() $\left |\left |{\mathbf{y}_1-\mathbf{y}_2}\right |\right |{}_2< \mathscr R$
and fails to hold in the opposite case. Note that by choosing suitable axes or transforming the problem, we can make
$\left |\left |{\mathbf{y}_1-\mathbf{y}_2}\right |\right |{}_2< \mathscr R$
and fails to hold in the opposite case. Note that by choosing suitable axes or transforming the problem, we can make
![]() $\mathbf{y}_1= (y_1, 0, \cdots , 0)^\top , \mathbf{y}_2= (y_2, 0, \cdots , 0)^\top $
. Consider
$\mathbf{y}_1= (y_1, 0, \cdots , 0)^\top , \mathbf{y}_2= (y_2, 0, \cdots , 0)^\top $
. Consider
![]() $\widehat \mu = a \delta _{\mathbf {\widehat y}}, \mathbf {\widehat y} \in \mathbb R^k$
with a and
$\widehat \mu = a \delta _{\mathbf {\widehat y}}, \mathbf {\widehat y} \in \mathbb R^k$
with a and
![]() $\mathbf {\widehat y}$
to be determined. We now have
$\mathbf {\widehat y}$
to be determined. We now have
 $$\begin{align*}\mathscr F[\widehat \mu](\boldsymbol{{\omega}})- \mathscr F[\mu](\boldsymbol{{\omega}}) = ae^{i \mathbf{\widehat y} \cdot \boldsymbol{{\omega}}} - \sum_{j=1}^{2}a_j e^{i \mathbf{y}_j \cdot \boldsymbol{{\omega}}}= ae^{i \mathbf{\widehat y}_{2:k}\cdot \boldsymbol{{\omega}}_{2:k}} e^{\mathbf{\widehat y}_1 \boldsymbol{{\omega}}_1} - \sum_{j=1}^{2}a_j e^{i {y}_j \boldsymbol{{\omega}}_1}, \end{align*}$$
$$\begin{align*}\mathscr F[\widehat \mu](\boldsymbol{{\omega}})- \mathscr F[\mu](\boldsymbol{{\omega}}) = ae^{i \mathbf{\widehat y} \cdot \boldsymbol{{\omega}}} - \sum_{j=1}^{2}a_j e^{i \mathbf{y}_j \cdot \boldsymbol{{\omega}}}= ae^{i \mathbf{\widehat y}_{2:k}\cdot \boldsymbol{{\omega}}_{2:k}} e^{\mathbf{\widehat y}_1 \boldsymbol{{\omega}}_1} - \sum_{j=1}^{2}a_j e^{i {y}_j \boldsymbol{{\omega}}_1}, \end{align*}$$
where
![]() $\mathbf{x}_1$
is the first vector element and
$\mathbf{x}_1$
is the first vector element and
![]() $\mathbf{x}_{2:k}$
is the vector consisting of the
$\mathbf{x}_{2:k}$
is the vector consisting of the
![]() $2$
-nd to the k-th elements of
$2$
-nd to the k-th elements of
![]() $\mathbf{x}$
. Thus, analyzing when (60) holds can be reduced to the one-dimensional case, and it is not hard to see that the result for the one-dimensional space still holds for multi-dimensional spaces.
$\mathbf{x}$
. Thus, analyzing when (60) holds can be reduced to the one-dimensional case, and it is not hard to see that the result for the one-dimensional space still holds for multi-dimensional spaces.
4.2 Resolution limit for detecting two positive sources
Now, we compute the computational resolution limit for detecting two positive sources. We have the following theorem showing that the resolution limit is the one in Lemma 4.1.
Theorem 4.2. For
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the computational resolution limit
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the computational resolution limit
![]() $\mathscr D_{num}^+(k,2)$
for resolving two positive sources in
$\mathscr D_{num}^+(k,2)$
for resolving two positive sources in
![]() $\mathbb R^k$
is given by
$\mathbb R^k$
is given by
 $$\begin{align*}\mathscr D_{num}^+(k,2) = \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
$$\begin{align*}\mathscr D_{num}^+(k,2) = \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
It can be attained if
![]() $a_1=a_2$
. When
$a_1=a_2$
. When
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
![]() $\sigma $
-admissible measures of some
$\sigma $
-admissible measures of some
![]() $\mathbf{Y}$
with only one point source.
$\mathbf{Y}$
with only one point source.
When
![]() $\frac {\sigma }{m_{\min }}<\frac {1}{2}$
, the two-point resolution
$\frac {\sigma }{m_{\min }}<\frac {1}{2}$
, the two-point resolution
![]() $\mathscr D_{num}^+(k,2)$
is already less than the Rayleigh limit
$\mathscr D_{num}^+(k,2)$
is already less than the Rayleigh limit
![]() $\frac {\pi }{\Omega }$
, which far exceeds all expectations. This indicates that, in contrast to what was commonly supposed, super-resolution from a single snapshot is, in fact, very possible.
$\frac {\pi }{\Omega }$
, which far exceeds all expectations. This indicates that, in contrast to what was commonly supposed, super-resolution from a single snapshot is, in fact, very possible.
Remark. Although
![]() $\mathscr D_{num}^{+}(k,2)$
is defined for measures on
$\mathscr D_{num}^{+}(k,2)$
is defined for measures on
![]() $B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
, similar arguments as those in the proof of Lemma 4.1 can generalize the resolution estimate to measures on
$B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
, similar arguments as those in the proof of Lemma 4.1 can generalize the resolution estimate to measures on
![]() $\mathbb R^k$
.
$\mathbb R^k$
.
Now we introduce the proof.
Proof.
Step 1. We only need to consider the case when
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, as the case when
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, as the case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is trivial. Also, we only consider the one-dimensional case since the treatment for multi-dimensional spaces is similar to the one in the proof of Theorem 4.1.
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is trivial. Also, we only consider the one-dimensional case since the treatment for multi-dimensional spaces is similar to the one in the proof of Theorem 4.1.
Let
![]() $\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
$\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
![]() $\widehat \mu = a \delta _{\widehat y}$
. Similarly to step 1 in the proof of Theorem 4.1, the computational resolution limit
$\widehat \mu = a \delta _{\widehat y}$
. Similarly to step 1 in the proof of Theorem 4.1, the computational resolution limit
![]() $\mathscr D_{num}^+(k, 2)$
should be the constant such that
$\mathscr D_{num}^+(k, 2)$
should be the constant such that
holds when
![]() $|y_1-y_2|< \mathscr D_{num}^+(k, 2)$
and fails to hold in the opposite case. Choosing a suitable axis, we assume that the true source is
$|y_1-y_2|< \mathscr D_{num}^+(k, 2)$
and fails to hold in the opposite case. Choosing a suitable axis, we assume that the true source is
![]() $\mu = m_{\min }\alpha \delta _{y_1}+ m_{\min } \delta _{y_2}$
with
$\mu = m_{\min }\alpha \delta _{y_1}+ m_{\min } \delta _{y_2}$
with
![]() $y_1 = -y_2$
,
$y_1 = -y_2$
,
![]() $\alpha \geqslant 1$
. We consider
$\alpha \geqslant 1$
. We consider
![]() $\widehat \mu = a\delta _{\widehat y}$
with
$\widehat \mu = a\delta _{\widehat y}$
with
![]() $a>0$
and
$a>0$
and
![]() $\widehat y$
to be determined. We shall prove that if
$\widehat y$
to be determined. We shall prove that if
 $$\begin{align*}\left|y_1-y_2\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
$$\begin{align*}\left|y_1-y_2\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
then (61) does not hold for any
![]() $\widehat \mu $
consisting of only one positive source. In the opposite case, Theorem 4.1 already ensures the existence of such
$\widehat \mu $
consisting of only one positive source. In the opposite case, Theorem 4.1 already ensures the existence of such
![]() $\widehat \mu , \mu $
, making (61) hold. By the above two results, we prove the theorem.
$\widehat \mu , \mu $
, making (61) hold. By the above two results, we prove the theorem.
In the following proof, we will find a necessary condition for
By the definition of
![]() $\mathscr D_{num}^+(k, 2)$
in Definition 3.2, we only consider the case when
$\mathscr D_{num}^+(k, 2)$
in Definition 3.2, we only consider the case when
![]() $d_{\min }\leqslant \frac {\pi }{\Omega }$
.
$d_{\min }\leqslant \frac {\pi }{\Omega }$
.
Step 2. We analyze a necessary condition – that is,
Since from (61) and the assumption for
![]() $\mu $
,
$\mu $
,
we thus consider
Let
![]() $\alpha = 1+h, h\geqslant 0$
, and rewrite the above formula as
$\alpha = 1+h, h\geqslant 0$
, and rewrite the above formula as
A key observation is that if
![]() $2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a \leqslant 2m_{\min }+hm_{\min }$
, then we have
$2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a \leqslant 2m_{\min }+hm_{\min }$
, then we have
 $$ \begin{align} & \min_{a>0, h\geqslant 0, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\\geqslant &\min_{a>0, h\geqslant 0, \widehat y\in \mathbb R, \widehat x\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{i\widehat x \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{a> 0, h\geqslant 0}\left|a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{2m_{\min}\cos(y_1\Omega)\leqslant b \leqslant 2 m_{\min}}\left|b- 2m_{\min} \cos(y_1 \Omega)\right|+|2m_{\min}-b| \nonumber\\= &\ 2m_{\min} - 2m_{\min} \cos(y_1 \Omega), \end{align} $$
$$ \begin{align} & \min_{a>0, h\geqslant 0, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\\geqslant &\min_{a>0, h\geqslant 0, \widehat y\in \mathbb R, \widehat x\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{i\widehat x \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{a> 0, h\geqslant 0}\left|a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{2m_{\min}\cos(y_1\Omega)\leqslant b \leqslant 2 m_{\min}}\left|b- 2m_{\min} \cos(y_1 \Omega)\right|+|2m_{\min}-b| \nonumber\\= &\ 2m_{\min} - 2m_{\min} \cos(y_1 \Omega), \end{align} $$
where the second equality is because
![]() $a\geqslant 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
,
$a\geqslant 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
,
![]() $hm_{\min }\geqslant 0$
and
$hm_{\min }\geqslant 0$
and
![]() $2m_{\min }\cos (y_1\Omega )= 2m_{\min }\cos (\frac {d_{\min }}{2}\Omega )\geqslant 0$
for
$2m_{\min }\cos (y_1\Omega )= 2m_{\min }\cos (\frac {d_{\min }}{2}\Omega )\geqslant 0$
for
![]() $d_{\min }\leqslant \frac {\pi }{\Omega }$
.
$d_{\min }\leqslant \frac {\pi }{\Omega }$
.
However, letting
![]() $h=0, \widehat y =0$
, we obtain that
$h=0, \widehat y =0$
, we obtain that
 $$ \begin{align*} &\min_{a>0}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0}\left|a - 2m_{\min} \cos(y_1 \Omega)\right|+|a-2m_{\min}|\\=&\ \min_{a>0}(a - 2m_{\min} \cos(y_1 \Omega))+2m_{\min}-a \quad \big(\text{choose } 2m_{\min} \cos(y_1 \Omega)\leqslant a\leqslant 2m_{\min}\big)\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0}\left|a - 2m_{\min} \cos(y_1 \Omega)\right|+|a-2m_{\min}|\\=&\ \min_{a>0}(a - 2m_{\min} \cos(y_1 \Omega))+2m_{\min}-a \quad \big(\text{choose } 2m_{\min} \cos(y_1 \Omega)\leqslant a\leqslant 2m_{\min}\big)\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
Together with (65), this yields
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \widehat y\in \mathbb R}\left|a e^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega) \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \widehat y\in \mathbb R}\left|a e^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega) \end{align*} $$
in the case when
![]() $2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a \leqslant 2m_{\min }+hm_{\min }$
.
$2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a \leqslant 2m_{\min }+hm_{\min }$
.
Now we consider the case when
![]() $a< 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
. In this case, we have
$a< 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
. In this case, we have
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\\geqslant & \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}2m_{\min}+hm_{\min}-a\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\\geqslant & \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}2m_{\min}+hm_{\min}-a\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
Last, we consider the case when
![]() $a>2m_{\min }+hm_{\min }$
. This time, we have
$a>2m_{\min }+hm_{\min }$
. This time, we have
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\\geqslant &\ \min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}, \widehat y \in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}}a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\\geqslant &\ \min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}, \widehat y \in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, a>2m_{\min}+hm_{\min}}a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
Therefore, combining the above discussions yields
 $$ \begin{align*} &\min_{a\geqslant 0, h\geqslant 0, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
$$ \begin{align*} &\min_{a\geqslant 0, h\geqslant 0, \widehat y\in \mathbb R}\left|ae^{i\widehat y\Omega} -h m_{\min} e^{iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
and that is,
 $$ \begin{align*} &\min_{a\geqslant 0, \alpha\geqslant 1, \widehat y\in \mathbb R}\left|a e^{\widehat y\Omega}-m_{\min}\left(\alpha e^{iy_1\Omega}+ e^{-i y_1 \Omega}\right)\right|+\left|a -m_{\min}\left(\alpha+1\right)\right|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a\geqslant 0, \alpha\geqslant 1, \widehat y\in \mathbb R}\left|a e^{\widehat y\Omega}-m_{\min}\left(\alpha e^{iy_1\Omega}+ e^{-i y_1 \Omega}\right)\right|+\left|a -m_{\min}\left(\alpha+1\right)\right|\\ =&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
Thus, (62) is equivalent to
Similarly to the proof of Theorem 4.1, this shows that
 $$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega} \end{align*}$$
$$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega} \end{align*}$$
and completes the proof.
4.3 Resolution limit for detecting two complex sources
Now we consider super-resolving complex sources and have the following theorem.
Theorem 4.3. For
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the computational resolution limit
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the computational resolution limit
![]() $\mathscr D_{num}(k, 2)$
for resolving two sources in
$\mathscr D_{num}(k, 2)$
for resolving two sources in
![]() $\mathbb R^k$
is given by
$\mathbb R^k$
is given by
 $$ \begin{align} \mathscr D_{num}(k, 2) = \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align} $$
$$ \begin{align} \mathscr D_{num}(k, 2) = \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align} $$
It can be attained if
![]() $a_1=a_2$
. When
$a_1=a_2$
. When
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
![]() $\sigma $
-admissible measures of some
$\sigma $
-admissible measures of some
![]() $\mathbf{Y}$
with only one point source.
$\mathbf{Y}$
with only one point source.
Theorem 4.3 demonstrates that when
![]() $\frac {\sigma }{m_{\min }}<\frac {1}{2}$
, the two-point resolution for distinguishing general sources is already better than the Rayleigh limit.
$\frac {\sigma }{m_{\min }}<\frac {1}{2}$
, the two-point resolution for distinguishing general sources is already better than the Rayleigh limit.
We now prove the theorem.
Proof.
Step 1. We only need to analyze the case when
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, as the case when
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, as the case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is trivial. Also, we only consider the one-dimensional case since the treatment for multi-dimensional spaces is similar to the one in the proof of Theorem 4.1.
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
is trivial. Also, we only consider the one-dimensional case since the treatment for multi-dimensional spaces is similar to the one in the proof of Theorem 4.1.
Let
![]() $\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
$\mu = \sum _{j=1}^2a_j \delta _{y_j}$
and
![]() $\widehat \mu = a \delta _{\widehat y}$
. Similarly to step 1 in the proof of Theorem 4.1, the resolution limit
$\widehat \mu = a \delta _{\widehat y}$
. Similarly to step 1 in the proof of Theorem 4.1, the resolution limit
![]() $\mathscr D_{num}(k, 2)$
should be the constant such that the estimate
$\mathscr D_{num}(k, 2)$
should be the constant such that the estimate
holds when
![]() $|y_1-y_2|< \mathscr D_{num}(k,2)$
and fails to hold in the opposite case.
$|y_1-y_2|< \mathscr D_{num}(k,2)$
and fails to hold in the opposite case.
Step 2. Without loss of generality, we assume the true source is
with
![]() $y_1 = -y_2$
,
$y_1 = -y_2$
,
![]() $0< y_1\leqslant \frac {\pi }{2\Omega }$
,
$0< y_1\leqslant \frac {\pi }{2\Omega }$
,
![]() $\alpha \geqslant 1$
and
$\alpha \geqslant 1$
and
![]() $0\leqslant \beta \leqslant \frac {\pi }{2}$
. It is not hard to see that the other cases can all be transformed to the above setting. We consider
$0\leqslant \beta \leqslant \frac {\pi }{2}$
. It is not hard to see that the other cases can all be transformed to the above setting. We consider
![]() $\widehat \mu = ae^{i\gamma }\delta _{\widehat y}$
with
$\widehat \mu = ae^{i\gamma }\delta _{\widehat y}$
with
![]() $a>0$
,
$a>0$
,
![]() $\gamma $
and
$\gamma $
and
![]() $\widehat y$
to be determined. We shall prove that if
$\widehat y$
to be determined. We shall prove that if
 $$\begin{align*}\left|y_1-y_2\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
$$\begin{align*}\left|y_1-y_2\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
then (67) does not hold for any
![]() $\widehat \mu $
consisting of only one source. In the opposite case, Theorem 4.1 already ensures the existence of such
$\widehat \mu $
consisting of only one source. In the opposite case, Theorem 4.1 already ensures the existence of such
![]() $\widehat \mu , \mu $
satisfying (67). By the two results, we prove the theorem.
$\widehat \mu , \mu $
satisfying (67). By the two results, we prove the theorem.
From (67), we have
We rewrite it as
and analyze it by considering the two cases: (1)
![]() $y_1\Omega \geqslant \beta $
; (2)
$y_1\Omega \geqslant \beta $
; (2)
![]() $y_1\Omega <\beta $
.
$y_1\Omega <\beta $
.
Part 1: (
![]() $y_1\Omega \geqslant \beta $
)
$y_1\Omega \geqslant \beta $
)
In the first case, when
![]() $y_1\Omega \geqslant \beta $
, we define
$y_1\Omega \geqslant \beta $
, we define
![]() $\omega ^*=\frac {\beta }{y_1}\in [0,\Omega ]$
. Considering
$\omega ^*=\frac {\beta }{y_1}\in [0,\Omega ]$
. Considering
 $$ \begin{align} \mathscr F[\widehat \mu](\omega+\omega^*)- \mathscr F[\mu](\omega+\omega^*)&= ae^{i\gamma}e^{i \widehat y (\omega+\omega^*)}-m_{\min}\left(\alpha e^{i(y_1 \omega-\beta+y_1\omega^*)}+ e^{i(\beta-y_1\omega^*-y_1 \omega)}\right)\nonumber \\&= ae^{i\gamma+\widehat y\omega^*}e^{i \widehat y \omega}-m_{\min}\left(\alpha e^{i(y_1 \omega)}+ e^{i(-y_1 \omega)}\right), \end{align} $$
$$ \begin{align} \mathscr F[\widehat \mu](\omega+\omega^*)- \mathscr F[\mu](\omega+\omega^*)&= ae^{i\gamma}e^{i \widehat y (\omega+\omega^*)}-m_{\min}\left(\alpha e^{i(y_1 \omega-\beta+y_1\omega^*)}+ e^{i(\beta-y_1\omega^*-y_1 \omega)}\right)\nonumber \\&= ae^{i\gamma+\widehat y\omega^*}e^{i \widehat y \omega}-m_{\min}\left(\alpha e^{i(y_1 \omega)}+ e^{i(-y_1 \omega)}\right), \end{align} $$
(67) is equivalent to
Note that this reduces the problem to a case similar to the one for positive sources. Since the interval
![]() $[-\Omega -\omega ^*, \Omega -\omega ^*]$
includes the interval
$[-\Omega -\omega ^*, \Omega -\omega ^*]$
includes the interval
![]() $[-\Omega , 0]$
, in the same fashion as the proof for positive sources, we consider the necessary condition that
$[-\Omega , 0]$
, in the same fashion as the proof for positive sources, we consider the necessary condition that
Note that minimizing over
![]() $0\leqslant \beta \leqslant y_1\Omega $
is now equivalent to minimizing over
$0\leqslant \beta \leqslant y_1\Omega $
is now equivalent to minimizing over
![]() $0\leqslant \omega ^*\leqslant \Omega $
. We thus consider
$0\leqslant \omega ^*\leqslant \Omega $
. We thus consider
Let
![]() $\alpha = 1+h, h\geqslant 0$
, and rewrite the above formula as
$\alpha = 1+h, h\geqslant 0$
, and rewrite the above formula as
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\ &\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|. \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\ &\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|. \end{align*} $$
A key observation is that if
![]() $2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
, we have
$2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
, we have
 $$ \begin{align} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y\Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\nonumber \\&\qquad \qquad \qquad \qquad \qquad +\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\nonumber \\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \widehat x\in \mathbb R}\left|ae^{-i\widehat y\Omega} -h m_{\min} e^{-i\widehat x \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|ae^{i\gamma}-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{a> 0, h\geqslant 0}\left|a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\right|+\left|a-(2m_{\min}+hm_{\min})\right|\nonumber \\= &\ \min_{2m_{\min}\cos(y_1\Omega)\leqslant b\leqslant 2m_{\min}}\left|b- 2m_{\min} \cos(y_1 \Omega)\right|+|2m_{\min}-b|\nonumber \\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align} $$
$$ \begin{align} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y\Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\nonumber \\&\qquad \qquad \qquad \qquad \qquad +\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\nonumber \\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \widehat x\in \mathbb R}\left|ae^{-i\widehat y\Omega} -h m_{\min} e^{-i\widehat x \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+|ae^{i\gamma}-(2m_{\min}+hm_{\min})|\nonumber \\= &\ \min_{a> 0, h\geqslant 0}\left|a -h m_{\min}- 2m_{\min} \cos(y_1 \Omega)\right|+\left|a-(2m_{\min}+hm_{\min})\right|\nonumber \\= &\ \min_{2m_{\min}\cos(y_1\Omega)\leqslant b\leqslant 2m_{\min}}\left|b- 2m_{\min} \cos(y_1 \Omega)\right|+|2m_{\min}-b|\nonumber \\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align} $$
where the second equality is because
![]() $2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
and
$2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
and
![]() $2m_{\min }\cos (y_1\Omega )= 2m_{\min }\cos (\frac {d_{\min }}{2}\Omega )\geqslant 0$
for
$2m_{\min }\cos (y_1\Omega )= 2m_{\min }\cos (\frac {d_{\min }}{2}\Omega )\geqslant 0$
for
![]() $d_{\min }\leqslant \frac {\pi }{\Omega }$
.
$d_{\min }\leqslant \frac {\pi }{\Omega }$
.
However, letting
![]() $h=0, \widehat y =0, \gamma =0, \omega ^*=0$
, we have
$h=0, \widehat y =0, \gamma =0, \omega ^*=0$
, we have
 $$ \begin{align*} &\min_{a>0}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|.\\=&\ \min_{a>0}\left|a - 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0}(a - 2m_{\min} \cos(y_1 \Omega))+2m_{\min}-a \quad \big(\text{choose} 2m_{\min} \cos(y_1 \Omega)\leqslant a\leqslant 2m_{\min}\big)\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|.\\=&\ \min_{a>0}\left|a - 2m_{\min} \cos(y_1 \Omega)\right|+|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0}(a - 2m_{\min} \cos(y_1 \Omega))+2m_{\min}-a \quad \big(\text{choose} 2m_{\min} \cos(y_1 \Omega)\leqslant a\leqslant 2m_{\min}\big)\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
Together with (71), this yields
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
in the case when
![]() $2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
.
$2m_{\min }\cos (y_1\Omega )+hm_{\min }\leqslant a\leqslant 2m_{\min }+hm_{\min }$
.
Now, we consider the case when
![]() $a< 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
. In this case, we have
$a< 2m_{\min }\cos (y_1\Omega )+hm_{\min }$
. In this case, we have
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \omega^*\in [0,\Omega], a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})|\\\geqslant&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}2m_{\min}+hm_{\min}-a\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \omega^*\in [0,\Omega], a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})|\\\geqslant&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}|a-(2m_{\min}+hm_{\min})|\\=&\ \min_{a>0, h\geqslant 0, a< 2m_{\min}\cos(y_1\Omega)+hm_{\min}}2m_{\min}+hm_{\min}-a\\>&\ 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
Finally, we consider the case when
![]() $a> 2m_{\min }+hm_{\min }$
. In this case, we have
$a> 2m_{\min }+hm_{\min }$
. In this case, we have
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega], a> 2m_{\min}+hm_{\min}}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\\geqslant&\ \min_{a>0, h\geqslant 0, a> 2m_{\min}+hm_{\min}}a-(2m_{\min}\cos(y_1 \Omega)+hm_{\min})\\ >& 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\\geqslant &\ \min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega], a> 2m_{\min}+hm_{\min}}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\\geqslant&\ \min_{a>0, h\geqslant 0, a> 2m_{\min}+hm_{\min}}a-(2m_{\min}\cos(y_1 \Omega)+hm_{\min})\\ >& 2m_{\min} -2m_{\min}\cos(y_1 \Omega). \end{align*} $$
Therefore, combining all the above discussions, we arrive at
 $$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
$$ \begin{align*} &\min_{a>0, h\geqslant 0, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -h m_{\min} e^{-iy_1 \Omega}- 2m_{\min} \cos(y_1 \Omega)\right|\\&\qquad \qquad \qquad \qquad \qquad+\left|ae^{i\gamma+\widehat y\omega^*}-(2m_{\min}+hm_{\min})\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega), \end{align*} $$
or equivalently,
 $$ \begin{align*} &\min_{a>0, \alpha\geqslant 1, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -m_{\min}\left(\alpha e^{-iy_1 \Omega}+ e^{i y_1\Omega}\right)\right|+\left|ae^{i\gamma+\widehat y\omega^*} -m_{\min}\left(\alpha+1\right)\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
$$ \begin{align*} &\min_{a>0, \alpha\geqslant 1, \gamma \in \mathbb R, \widehat y\in \mathbb R, \omega^*\in [0,\Omega]}\left|ae^{i\gamma+\widehat y\omega^*}e^{-i\widehat y \Omega} -m_{\min}\left(\alpha e^{-iy_1 \Omega}+ e^{i y_1\Omega}\right)\right|+\left|ae^{i\gamma+\widehat y\omega^*} -m_{\min}\left(\alpha+1\right)\right|\\=&\ 2m_{\min}-2m_{\min} \cos(y_1 \Omega). \end{align*} $$
Thus, (70) is equivalent to
Similar to the proof of Theorem 4.1, this yields
 $$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
$$\begin{align*}d_{\min} < \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
Part 2: (
![]() $y_1\Omega <\beta $
)
$y_1\Omega <\beta $
)
In part 2, because
![]() $y_1\Omega <\beta $
, the trick used in the former proof does not work now. We utilize another finding for the proof. Suppose
$y_1\Omega <\beta $
, the trick used in the former proof does not work now. We utilize another finding for the proof. Suppose
 $d_{\min }\geqslant \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
and there exists some measure
$d_{\min }\geqslant \frac {4\arcsin \left (\left (\frac {\sigma }{m_{\min }}\right )^{\frac {1}{2}}\right )}{\Omega }$
and there exists some measure
![]() $\widehat \mu =a\delta _{\widehat y}$
so that
$\widehat \mu =a\delta _{\widehat y}$
so that
Then, this is in contradiction with (76) and (77) in Theorem 5.1. Thus, we have proved that
 $$\begin{align*}d_{\min}< \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
$$\begin{align*}d_{\min}< \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
Note that this new finding can also be used to prove the first part, but we keep the first part for a stronger understanding of the optimization problem and its underlying difficulty. The new finding comes from an optimal algorithm described in the next section. Now we have completed the proof.
Remark. We remark that the objectives of Section 3 and Section 4 are different. Section 3 provides estimates for the computational resolution limits in super-resolving n-sparse sources. In contrast, Section 4 focuses on deriving the exact formula for the computational resolution limit when super-resolving two point sources. Regarding the methods of proof, directly addressing the optimization problem (62) and (70) yields optimal estimates for two-point resolution. However, this approach does not extend to the case of super-resolving n-sources. Conversely, location-amplitude identities offer a robust framework for analyzing the resolution of super-resolving n-sparse sources. Moreover, according to Theorem 4.3, the resolution estimate in Theorem 3.3 is already very sharp, demonstrating the effectiveness of location-amplitude identities in delivering precise insights into super-resolution problems.
4.4 Two-point resolution for general imaging models
The two-point resolution estimate in previous sections can actually be generalized to very general imaging problems as we shall discuss next. We assume that the available measurement is
 $$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \chi(\boldsymbol{{\omega}})\left(\mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})\right)= \sum_{j=1}^{n}a_j \chi(\boldsymbol{{\omega}}) e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \chi(\boldsymbol{{\omega}}) \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
$$ \begin{align} \mathbf Y(\boldsymbol{{\omega}}) = \chi(\boldsymbol{{\omega}})\left(\mathscr F[\mu] (\boldsymbol{{\omega}}) + \mathbf W(\boldsymbol{{\omega}})\right)= \sum_{j=1}^{n}a_j \chi(\boldsymbol{{\omega}}) e^{i \mathbf{y}_j\cdot \boldsymbol{{\omega}}} + \chi(\boldsymbol{{\omega}}) \mathbf W(\boldsymbol{{\omega}}), \ \boldsymbol{{\omega}} \in \mathbb R^k, \ ||\boldsymbol{{\omega}}||_2\leqslant \Omega, \end{align} $$
where
![]() $\chi (\boldsymbol {{\omega }})=0$
or
$\chi (\boldsymbol {{\omega }})=0$
or
![]() $1$
,
$1$
,
![]() $\chi (\mathbf{0})=1$
and
$\chi (\mathbf{0})=1$
and
![]() $\chi (\boldsymbol {{\omega }})=1, ||\boldsymbol {{\omega }}||_2 =\Omega $
. Moreover, the noise
$\chi (\boldsymbol {{\omega }})=1, ||\boldsymbol {{\omega }}||_2 =\Omega $
. Moreover, the noise
![]() $\mathbf{W}$
is assumed to be bounded as
$\mathbf{W}$
is assumed to be bounded as
For the imaging model (72), consider similar definitions to the previous ones for
![]() $\sigma $
-admissible measures and the computational resolution limit. It is not hard to see that the estimates in the previous sections still hold, and we have the following theorem.
$\sigma $
-admissible measures and the computational resolution limit. It is not hard to see that the estimates in the previous sections still hold, and we have the following theorem.
Theorem 4.4. Consider the imaging model (72). For
![]() $\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the resolution limits
$\frac {\sigma }{m_{\min }} \leqslant \frac {1}{2}$
, the resolution limits
![]() $\mathscr D_{num}^+(k, 2)$
,
$\mathscr D_{num}^+(k, 2)$
,
![]() $\mathscr D_{num}(k, 2)$
for resolving two sources in
$\mathscr D_{num}(k, 2)$
for resolving two sources in
![]() $\mathbb R^k$
are
$\mathbb R^k$
are
 $$ \begin{align} \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align} $$
$$ \begin{align} \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align} $$
These resolution limits can be attained if
![]() $a_1=a_2$
. When
$a_1=a_2$
. When
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
, no matter what the separation distance is, there are always some
![]() $\sigma $
-admissible measures of some
$\sigma $
-admissible measures of some
![]() $\mathbf{Y}$
corresponding to one point source.
$\mathbf{Y}$
corresponding to one point source.
Compared to (1), the model (72) is more general – for instance, super-resolution from discrete measurements can be modeled by (72). Thus, Theorem 4.4 can be applied directly to super-resolution in practice, line spectral estimation and direction-of-arrival. Moreover, by the inverse filtering methods, our results can be applied to imaging problems with very general optical transfer functions, such as the one shown in Figure 3. We believe that this will inspire new understandings for the resolution of a number of imaging modalities. We remark that it is more appropriate to apply Theorem 4.4 to imaging problems where the noise level at
![]() $0$
and
$0$
and
![]() $||\boldsymbol {{\omega }}||_2=\Omega $
are close or comparable after modifying the model to (72).
$||\boldsymbol {{\omega }}||_2=\Omega $
are close or comparable after modifying the model to (72).

Figure 3 Optical transfer function.
In fact, Theorem 4.4 reveals the fact that the two-point resolution is actually not that related to the continuous band of frequencies but rather mostly determined by the boundary points. In particular, in the one-dimensional case, if we have only measurements in
![]() $[-\Omega +\epsilon , \Omega -\epsilon ]$
for
$[-\Omega +\epsilon , \Omega -\epsilon ]$
for
![]() $\epsilon>0$
, then the resolution in (73) does not hold anymore. In the multi-dimensional cases, similar conclusions hold as well. Thus, the condition
$\epsilon>0$
, then the resolution in (73) does not hold anymore. In the multi-dimensional cases, similar conclusions hold as well. Thus, the condition
![]() $\left |\left |{\boldsymbol {{\omega }}}\right |\right |{}_2=\Omega $
is nearly a necessary condition for Theorem 4.4 to hold.
$\left |\left |{\boldsymbol {{\omega }}}\right |\right |{}_2=\Omega $
is nearly a necessary condition for Theorem 4.4 to hold.
5 Optimal Algorithms
We now have the exact resolution limit for determining whether the image is generated by one or two sources. This is a new benchmark for super-resolution and model order detection algorithms. A natural question is whether we can find the optimal algorithm to distinguish between one and two sources in the image. Note that, according to our theoretical results, when the two sources are separated by more than
 $$\begin{align*}\left|{y_1-y_2}\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
$$\begin{align*}\left|{y_1-y_2}\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align*}$$
any algorithm targeting certain solutions in the set of admissible measures provides a solution with more than one source. But we still cannot confirm that there is more than one source inside. Only by considering the sparest solution in the set of admissible measures can we confirm this fact. However, since
![]() $l_0$
minimization is intractable, this direction is still unrealistic, and we resort to other means. In [Reference Liu and Zhang26], a simple singular value thresholding-based algorithm was proposed to detect the source number. In this section, we consider a variant of it and theoretically demonstrate that the algorithm exactly attains the resolution limit. We remark that the optimality of our algorithm refers to achieving the two-point resolution limit in Theorems 4.2 and 4.3 under the imaging model (1). Algorithms leveraging specific noise patterns may outperform this one.
$l_0$
minimization is intractable, this direction is still unrealistic, and we resort to other means. In [Reference Liu and Zhang26], a simple singular value thresholding-based algorithm was proposed to detect the source number. In this section, we consider a variant of it and theoretically demonstrate that the algorithm exactly attains the resolution limit. We remark that the optimality of our algorithm refers to achieving the two-point resolution limit in Theorems 4.2 and 4.3 under the imaging model (1). Algorithms leveraging specific noise patterns may outperform this one.
5.1 An optimal algorithm for detecting two sources in dimension one
In [Reference Liu and Zhang26], the authors proposed a number detection algorithm called sweeping singular value thresholding number detection algorithm. It determines the number of sources by thresholding the singular value of a Hankel matrix formulated from the measurement data. Here, we consider a simple variant of it.
To be more specific, we first assemble the following Hankel matrix from the measurements (1) – that is,
 $$ \begin{align} \mathbf H=\left(\begin{array}{cc} \mathbf Y(-\Omega)& \mathbf Y(0)\\ \mathbf Y(0)&\mathbf Y(\Omega) \end{array} \right).\end{align} $$
$$ \begin{align} \mathbf H=\left(\begin{array}{cc} \mathbf Y(-\Omega)& \mathbf Y(0)\\ \mathbf Y(0)&\mathbf Y(\Omega) \end{array} \right).\end{align} $$
We denote the singular value decomposition of
![]() $\mathbf H$
as
$\mathbf H$
as
where
![]() $\widehat \Sigma =\text {diag}(\widehat \sigma _1, \widehat \sigma _2)$
with the singular values
$\widehat \Sigma =\text {diag}(\widehat \sigma _1, \widehat \sigma _2)$
with the singular values
![]() $\widehat \sigma _1, \widehat \sigma _2$
ordered in a decreasing manner. We then determine the source number by a thresholding of the singular values. We derive the following Theorem 5.1 for the threshold and the resolution of the algorithm.
$\widehat \sigma _1, \widehat \sigma _2$
ordered in a decreasing manner. We then determine the source number by a thresholding of the singular values. We derive the following Theorem 5.1 for the threshold and the resolution of the algorithm.
Theorem 5.1. Consider
![]() $\mu =\sum _{j=1}^{2}a_j \delta _{y_j},y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and the measurement
$\mu =\sum _{j=1}^{2}a_j \delta _{y_j},y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0)$
and the measurement
![]() $\mathbf{Y}$
in (1) that is generated from
$\mathbf{Y}$
in (1) that is generated from
![]() $\mu $
. If the following separation condition is satisfied
$\mu $
. If the following separation condition is satisfied
 $$ \begin{align} \left|{y_1-y_2}\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align} $$
$$ \begin{align} \left|{y_1-y_2}\right|\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}, \end{align} $$
then we have
for
![]() $\widehat \sigma _2$
being the minimum singular value of the matrix
$\widehat \sigma _2$
being the minimum singular value of the matrix
![]() $\mathbf{H}$
in (74). However, if there exists
$\mathbf{H}$
in (74). However, if there exists
![]() $\widehat \mu $
consisting of only one source being a
$\widehat \mu $
consisting of only one source being a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
, then
$\mathbf{Y}$
, then
Proof. Observe that
![]() $\mathbf H$
has the decomposition
$\mathbf H$
has the decomposition
where
![]() $A=\text {diag}(e^{-iy_1\Omega }a_1, e^{-iy_2\Omega }a_2)$
and
$A=\text {diag}(e^{-iy_1\Omega }a_1, e^{-iy_2\Omega }a_2)$
and
![]() $D=\big (\phi _{1}(e^{i y_1 \Omega }), \phi _{1}(e^{i y_2\Omega })\big )$
with
$D=\big (\phi _{1}(e^{i y_1 \Omega }), \phi _{1}(e^{i y_2\Omega })\big )$
with
![]() $\phi _{1}(\omega )$
being defined as
$\phi _{1}(\omega )$
being defined as
![]() $(1, \omega )^\top $
and
$(1, \omega )^\top $
and
 $$ \begin{align*} \Delta = \left(\begin{array}{cc} \mathbf {W}(-\Omega)& \mathbf {W}(0)\\ \mathbf {W}(0)&\mathbf {W}(\Omega) \end{array} \right). \end{align*} $$
$$ \begin{align*} \Delta = \left(\begin{array}{cc} \mathbf {W}(-\Omega)& \mathbf {W}(0)\\ \mathbf {W}(0)&\mathbf {W}(\Omega) \end{array} \right). \end{align*} $$
We denote the singular values of
![]() $DAD^{\top }$
by
$DAD^{\top }$
by
![]() $\sigma _1, \sigma _2$
.
$\sigma _1, \sigma _2$
.
We first estimate
![]() $\left |\left |{\Delta }\right |\right |{}_2$
. We have
$\left |\left |{\Delta }\right |\right |{}_2$
. We have
 $$ \begin{align*} &\max_{x_1^2+x_2^2=1}\left|\left|{\Delta(x_1, x_2)^{\top}}\right|\right|{}_2\\ = &\max_{x_1^2+x_2^2=1}\sqrt{(x_1\mathbf{W}(-\Omega) +x_2 \mathbf{W}(0))^2+ (x_1\mathbf{W}(0) +x_2 \mathbf{W}(\Omega))^2}\\ = &\max_{x_1^2+x_2^2=1}\sqrt{\mathbf{W}(0)^2+ 2x_1x_2\mathbf{W}(0)(\mathbf{W}(-\Omega)+\mathbf{W}(\Omega))+x_1^2\mathbf{W}(-\Omega)^2+x_2^2\mathbf{W}(\Omega)^2}\\ <&\max_{x_1^2+x_2^2=1}\sqrt{\sigma^2+ 4 \sigma^2 x_1x_2+ (x_1^2+x_2^2)\sigma^2} \quad \Big(\text{by the condition on the noise}\Big)\\ =&2\sigma. \end{align*} $$
$$ \begin{align*} &\max_{x_1^2+x_2^2=1}\left|\left|{\Delta(x_1, x_2)^{\top}}\right|\right|{}_2\\ = &\max_{x_1^2+x_2^2=1}\sqrt{(x_1\mathbf{W}(-\Omega) +x_2 \mathbf{W}(0))^2+ (x_1\mathbf{W}(0) +x_2 \mathbf{W}(\Omega))^2}\\ = &\max_{x_1^2+x_2^2=1}\sqrt{\mathbf{W}(0)^2+ 2x_1x_2\mathbf{W}(0)(\mathbf{W}(-\Omega)+\mathbf{W}(\Omega))+x_1^2\mathbf{W}(-\Omega)^2+x_2^2\mathbf{W}(\Omega)^2}\\ <&\max_{x_1^2+x_2^2=1}\sqrt{\sigma^2+ 4 \sigma^2 x_1x_2+ (x_1^2+x_2^2)\sigma^2} \quad \Big(\text{by the condition on the noise}\Big)\\ =&2\sigma. \end{align*} $$
Thus, we have
![]() $||\Delta ||_2<2\sigma $
. By Weyl’s theorem, we have
$||\Delta ||_2<2\sigma $
. By Weyl’s theorem, we have
Now we estimate the minimum singular value of
![]() $DAD^{\top }$
in the presence of two sources. Denote
$DAD^{\top }$
in the presence of two sources. Denote
![]() $\sigma _{\min }(M)$
and
$\sigma _{\min }(M)$
and
![]() $\lambda _{\min }(M)$
as, respectively, the minimum singular value and eigenvalue of matrix M. We have
$\lambda _{\min }(M)$
as, respectively, the minimum singular value and eigenvalue of matrix M. We have
Therefore, when
![]() $y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0),j=1,2,$
and (75) holds,
$y_j\in B_{\frac {(n-1) \pi }{2\Omega }}^1(0),j=1,2,$
and (75) holds,
![]() $\sigma _{\min }(DAD^{\top })\geqslant 4\sigma $
. This is
$\sigma _{\min }(DAD^{\top })\geqslant 4\sigma $
. This is
![]() $\sigma _2 \geqslant 4\sigma $
. Similarly, by Weyl’s theorem,
$\sigma _2 \geqslant 4\sigma $
. Similarly, by Weyl’s theorem,
![]() $|\widehat \sigma _2-\sigma _2|\leqslant ||\Delta ||_2$
. Thus,
$|\widehat \sigma _2-\sigma _2|\leqslant ||\Delta ||_2$
. Thus,
![]() $\widehat \sigma _2\geqslant 4\sigma -||\Delta ||_2>2\sigma $
. Conclusion (76) follows.
$\widehat \sigma _2\geqslant 4\sigma -||\Delta ||_2>2\sigma $
. Conclusion (76) follows.
However, note that if there exists
![]() $\widehat \mu = \widehat a_1\delta _{\widehat y_1}$
consisting of one source being a
$\widehat \mu = \widehat a_1\delta _{\widehat y_1}$
consisting of one source being a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
, we can substitute the D in (78) by
$\mathbf{Y}$
, we can substitute the D in (78) by
![]() $\big (\phi _{1}(e^{i \widehat y_1 \Omega })\big )$
with the
$\big (\phi _{1}(e^{i \widehat y_1 \Omega })\big )$
with the
![]() $\mathbf{W}$
and
$\mathbf{W}$
and
![]() $\Delta $
being modified. Now we have
$\Delta $
being modified. Now we have
![]() $\sigma _2=0$
and also
$\sigma _2=0$
and also
![]() $||\Delta ||_2< 2\sigma $
. Thus, by (79), we get
$||\Delta ||_2< 2\sigma $
. Thus, by (79), we get
![]() $|\widehat \sigma _2|\leqslant ||\Delta ||_2< 2\sigma $
and prove (77).
$|\widehat \sigma _2|\leqslant ||\Delta ||_2< 2\sigma $
and prove (77).
We summarize the algorithm in the following Algorithm 1
. Note that in practical applications, one can estimate a noise level although not tight and utilize our algorithm to detect the source number. By Theorem 5.1, for all estimated
![]() $\sigma $
’s less than
$\sigma $
’s less than
![]() $\frac {m_{\min }}{2}$
, our algorithm can achieve super-resolution.
$\frac {m_{\min }}{2}$
, our algorithm can achieve super-resolution.

Numerical experiments:
We conduct many numerical experiments to elucidate the performance of Algorithm 1
. We consider
![]() $\Omega =1$
and measurements
$\Omega =1$
and measurements
![]() $\mathbf{Y}$
generated by two sources. The noise level is
$\mathbf{Y}$
generated by two sources. The noise level is
![]() $\sigma $
, and the minimum separation distance between sources is
$\sigma $
, and the minimum separation distance between sources is
![]() $d_{\min }$
. We first perform
$d_{\min }$
. We first perform
![]() $100,000$
random experiments (the randomness is in the choice of
$100,000$
random experiments (the randomness is in the choice of
![]() $(d_{\min },\sigma , y_j, a_j)$
), and the results are shown in Figure 4 (a)–(c). The green points and red points represent, respectively, the cases of successful detection and failed detection. It is indicated that in many cases, our Algorithm 1
can surpass the two-point resolution limit. We also conduct
$(d_{\min },\sigma , y_j, a_j)$
), and the results are shown in Figure 4 (a)–(c). The green points and red points represent, respectively, the cases of successful detection and failed detection. It is indicated that in many cases, our Algorithm 1
can surpass the two-point resolution limit. We also conduct
![]() $100,000$
experiments for the worst-case scenario; see results in Figure 4 (d)–(f). As shown numerically, our algorithm successfully detects the source number when
$100,000$
experiments for the worst-case scenario; see results in Figure 4 (d)–(f). As shown numerically, our algorithm successfully detects the source number when
![]() $d_{\min }$
is above the two-point resolution limit and fails in exactly the opposite cases. Last, we consider the worst cases when detecting the source number is impossible when
$d_{\min }$
is above the two-point resolution limit and fails in exactly the opposite cases. Last, we consider the worst cases when detecting the source number is impossible when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. The results were presented in Figure 4 (g)–(i), and there is no successful case when
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. The results were presented in Figure 4 (g)–(i), and there is no successful case when
![]() $\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. Note that the failed cases when
$\frac {\sigma }{m_{\min }}>\frac {1}{2}$
. Note that the failed cases when
![]() $\frac {\sigma }{m_{\min }}<\frac {1}{2}$
and
$\frac {\sigma }{m_{\min }}<\frac {1}{2}$
and
![]() $d_{\min }$
above the two-point resolution limit is due to the fact that
$d_{\min }$
above the two-point resolution limit is due to the fact that
![]() $|e^{iy_1\Omega }-e^{iy_2\Omega }|$
becomes small when
$|e^{iy_1\Omega }-e^{iy_2\Omega }|$
becomes small when
![]() $|y_1-y_2|\Omega $
approaching
$|y_1-y_2|\Omega $
approaching
![]() $2\pi $
.
$2\pi $
.

Figure 4 Plots of the successful and the unsuccessful number detections by Algorithm 1
depending on the relation between
![]() $\frac {\sigma }{m_{\min }}$
and
$\frac {\sigma }{m_{\min }}$
and
![]() $d_{\min }$
. The green points and red points represent, respectively, the cases of successful detection and failed detection. The black line is the two-point resolution limit
$d_{\min }$
. The green points and red points represent, respectively, the cases of successful detection and failed detection. The black line is the two-point resolution limit
![]() $\mathscr D_{num}(k, 2)$
derived in Theorem 4.3.
$\mathscr D_{num}(k, 2)$
derived in Theorem 4.3.
We also conduct several experiments to illustrate that our algorithm can detect the correct source number even if it seems very unlikely to distinguish the two sources by other methods. We consider
![]() $5$
cases where the source number is correctly detected by our algorithm; see Figure 5 (a). However, as shown by Figure 5 (b)–(f), their MUSIC images only have one peak.
$5$
cases where the source number is correctly detected by our algorithm; see Figure 5 (a). However, as shown by Figure 5 (b)–(f), their MUSIC images only have one peak.

Figure 5 Plot (a) is the relation between
![]() $\frac {\sigma }{m_{\min }}$
and
$\frac {\sigma }{m_{\min }}$
and
![]() $d_{\min }$
for several cases. Plots (b)–(f) are MUSIC images of these cases. Note that it is impossible to detect the correct source number from these MUSIC images.
$d_{\min }$
for several cases. Plots (b)–(f) are MUSIC images of these cases. Note that it is impossible to detect the correct source number from these MUSIC images.
5.2 An optimal algorithm for detecting two sources in multi-dimensional spaces
For detecting two sources in multi-dimensional spaces, we can first apply Algorithm 1
to the measurement in several one-dimensional subspaces
![]() $V_j$
’s and save the outputs, and then determine the source number as the maximum value among these outputs. If some of the
$V_j$
’s and save the outputs, and then determine the source number as the maximum value among these outputs. If some of the
![]() $V_j$
’s are sufficiently close to the space spanned by
$V_j$
’s are sufficiently close to the space spanned by
![]() $\mathbf{y}_2-\mathbf{y}_1$
, it actually achieves similar resolution to the one in Theorem 5.1.
$\mathbf{y}_2-\mathbf{y}_1$
, it actually achieves similar resolution to the one in Theorem 5.1.
To be specific, let
![]() $\mu =\sum _{j=1}^{2}a_j \delta _{\mathbf{y}_j}, \mathbf{y}_j\in \mathbb R^k$
and
$\mu =\sum _{j=1}^{2}a_j \delta _{\mathbf{y}_j}, \mathbf{y}_j\in \mathbb R^k$
and
![]() $\mathbf{Y}(\boldsymbol {{\omega }}), \boldsymbol {{\omega }}\in \mathbb R^k, ||\boldsymbol {{\omega }}||_2\leqslant \Omega $
be the associated measurement in (1). We choose N unit vectors
$\mathbf{Y}(\boldsymbol {{\omega }}), \boldsymbol {{\omega }}\in \mathbb R^k, ||\boldsymbol {{\omega }}||_2\leqslant \Omega $
be the associated measurement in (1). We choose N unit vectors
![]() $\mathbf{v}_j$
’s in
$\mathbf{v}_j$
’s in
![]() $\mathbb R^k$
and formulate the corresponding Hankel matrices
$\mathbb R^k$
and formulate the corresponding Hankel matrices
![]() $\mathbf{H}_{q}$
’s as
$\mathbf{H}_{q}$
’s as
 $$ \begin{align} \mathbf H_q=\left(\begin{array}{cc} \mathbf Y(-\Omega\mathbf{v}_q)& \mathbf Y(0)\\ \mathbf Y(0)&\mathbf Y(\Omega\mathbf{v}_q) \end{array}\right), \quad q=1, \cdots, N. \end{align} $$
$$ \begin{align} \mathbf H_q=\left(\begin{array}{cc} \mathbf Y(-\Omega\mathbf{v}_q)& \mathbf Y(0)\\ \mathbf Y(0)&\mathbf Y(\Omega\mathbf{v}_q) \end{array}\right), \quad q=1, \cdots, N. \end{align} $$
Denoting
![]() $\widehat \sigma _{q,j}$
the j-th singular value of
$\widehat \sigma _{q,j}$
the j-th singular value of
![]() $\mathbf{H}_{q}$
, we can detect the source number by thresholding on
$\mathbf{H}_{q}$
, we can detect the source number by thresholding on
![]() $\widehat \sigma _{q,j}$
’s. Moreover, we have the following theorem on the resolution and the threshold.
$\widehat \sigma _{q,j}$
’s. Moreover, we have the following theorem on the resolution and the threshold.
Theorem 5.2. Consider
![]() $\mu =\sum _{j=1}^{2}a_j \delta _{\mathbf{y}_j}, \mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the measurement
$\mu =\sum _{j=1}^{2}a_j \delta _{\mathbf{y}_j}, \mathbf{y}_j \in B_{\frac {(n-1) \pi }{2\Omega }}^k(\mathbf {0})$
and the measurement
![]() $\mathbf{Y}$
in (1) that is generated from
$\mathbf{Y}$
in (1) that is generated from
![]() $\mu $
. If
$\mu $
. If
with
![]() $\angle (\cdot , \cdot )$
denoting the angle between vectors, and the following separation condition is satisfied
$\angle (\cdot , \cdot )$
denoting the angle between vectors, and the following separation condition is satisfied
 $$ \begin{align} \left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega\cos{\theta_{\min}}}, \end{align} $$
$$ \begin{align} \left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega\cos{\theta_{\min}}}, \end{align} $$
then we have
for
![]() $\widehat \sigma _{q,2}$
being the minimum singular value of the Hankel matrix
$\widehat \sigma _{q,2}$
being the minimum singular value of the Hankel matrix
![]() $\mathbf{H}_q$
that defined in (80). However, if there exists
$\mathbf{H}_q$
that defined in (80). However, if there exists
![]() $\widehat \mu $
consisting of only one source being a
$\widehat \mu $
consisting of only one source being a
![]() $\sigma $
-admissible measure of
$\sigma $
-admissible measure of
![]() $\mathbf{Y}$
, then
$\mathbf{Y}$
, then
Proof. By (81), there exists
![]() $\mathbf{v}_{q^*}$
such that
$\mathbf{v}_{q^*}$
such that
 $$\begin{align*}\left|{\mathbf{y}_1\cdot \mathbf{v}_{q^*}- \mathbf{y}_2\cdot \mathbf{v}_{q^*}}\right|= \cos\theta_{\min}\left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
$$\begin{align*}\left|{\mathbf{y}_1\cdot \mathbf{v}_{q^*}- \mathbf{y}_2\cdot \mathbf{v}_{q^*}}\right|= \cos\theta_{\min}\left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega}. \end{align*}$$
Hence, similar to the proof of Theorem 5.1, we can show that
![]() $\widehat \sigma _{q^*, 2}> 2\sigma $
. This proves (82). Also, we can show (84) in the same way as the one in the proof of Theorem 5.1.
$\widehat \sigma _{q^*, 2}> 2\sigma $
. This proves (82). Also, we can show (84) in the same way as the one in the proof of Theorem 5.1.
We summarize the algorithm as the following Algorithm 2 .

Numerical experiments:
We consider detecting two sources in two-dimensional spaces. For large enough N, we consider
Input
![]() $\mathbf{v}_q$
’s to Algorithm 2
, we then determine the source number by Algorithm 2
from measurements
$\mathbf{v}_q$
’s to Algorithm 2
, we then determine the source number by Algorithm 2
from measurements
![]() $\mathbf{Y}(\boldsymbol {{\omega }})$
. By Theorem 5.2, we can determine the correct number when
$\mathbf{Y}(\boldsymbol {{\omega }})$
. By Theorem 5.2, we can determine the correct number when
 $$\begin{align*}\left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega\cos\left({\frac{\pi}{2N}}\right)}. \end{align*}$$
$$\begin{align*}\left|\left|{\mathbf{y}_1-\mathbf{y}_2}\right|\right|{}_2\geqslant \frac{4\arcsin\left(\left(\frac{\sigma}{m_{\min}}\right)^{\frac{1}{2}}\right)}{\Omega\cos\left({\frac{\pi}{2N}}\right)}. \end{align*}$$
This indicates that we already have an excellent resolution by leveraging only a few
![]() $\mathbf{v}_q$
’s. We use
$\mathbf{v}_q$
’s. We use
![]() $N=10$
unit vectors in the experiments and conduct
$N=10$
unit vectors in the experiments and conduct
![]() $100,000$
random experiments for both the general and worst cases. As shown in Figure 6 (a) and (c), our algorithm successfully detects the source number when
$100,000$
random experiments for both the general and worst cases. As shown in Figure 6 (a) and (c), our algorithm successfully detects the source number when
![]() $d_{\min }$
is above nearly the computational resolution limit
$d_{\min }$
is above nearly the computational resolution limit
![]() $\mathscr D_{num}(k,2)$
and fails to detect the source number on some cases when
$\mathscr D_{num}(k,2)$
and fails to detect the source number on some cases when
![]() $d_{\min }$
is below
$d_{\min }$
is below
![]() $\mathscr D_{num}(k,2)$
. A very interesting phenomenon is that, as shown in Figure 6 (b), there are many cases in which our algorithm detects the correct source number even when
$\mathscr D_{num}(k,2)$
. A very interesting phenomenon is that, as shown in Figure 6 (b), there are many cases in which our algorithm detects the correct source number even when
![]() $d_{\min }$
is much lower than the
$d_{\min }$
is much lower than the
![]() $\mathscr D_{num}(k,2)$
. This indicates that the tolerance of the noise of the algorithm is, in fact, excellent. The reason is that the worst cases or nearly worst cases actually only happen when the noise satisfies certain patterns. Because we use the measurements in N one-dimensional subspaces, it becomes more difficult for the noises in all the subspaces to satisfy these patterns. Thus, the noise tolerance becomes better in the two-dimensional case.
$\mathscr D_{num}(k,2)$
. This indicates that the tolerance of the noise of the algorithm is, in fact, excellent. The reason is that the worst cases or nearly worst cases actually only happen when the noise satisfies certain patterns. Because we use the measurements in N one-dimensional subspaces, it becomes more difficult for the noises in all the subspaces to satisfy these patterns. Thus, the noise tolerance becomes better in the two-dimensional case.

Figure 6 Plots of the successful and the unsuccessful number detections by Algorithm 2
depending on the relation between
![]() $\frac {\sigma }{m_{\min }}$
and
$\frac {\sigma }{m_{\min }}$
and
![]() $d_{\min }$
. The green points and red points represent respectively the cases of successful detection and failed detection. The black line is the derived two-point resolution limit
$d_{\min }$
. The green points and red points represent respectively the cases of successful detection and failed detection. The black line is the derived two-point resolution limit
![]() $\mathscr D_{num}(k, 2)$
.
$\mathscr D_{num}(k, 2)$
.
Note that our theoretical results and algorithms are potentially of great importance in practical applications. We will examine the super-resolving ability of our algorithm in practical examples in future work.
A Some inequalities
In this Appendix, we present some inequalities that are used in this paper. We first recall the following Stirling approximation of factorial
which will be used frequently in the subsequent derivations.
Lemma A.1. Let
![]() $\zeta (n)$
and
$\zeta (n)$
and
![]() $\xi (n-1)$
be defined as in (21). For
$\xi (n-1)$
be defined as in (21). For
![]() $n\geqslant 2$
, we have
$n\geqslant 2$
, we have
 $$\begin{align*}\Big(\frac{2}{\zeta(n)\xi(n-1)}\Big)^{\frac{1}{2n-2}}\leqslant \frac{ 2e}{n-1}. \end{align*}$$
$$\begin{align*}\Big(\frac{2}{\zeta(n)\xi(n-1)}\Big)^{\frac{1}{2n-2}}\leqslant \frac{ 2e}{n-1}. \end{align*}$$
Proof. For
![]() $n=2,3,4$
, it is easy to check that the above inequality holds. Using (86), we have for odd
$n=2,3,4$
, it is easy to check that the above inequality holds. Using (86), we have for odd
![]() $n\geqslant 5$
,
$n\geqslant 5$
,
 $$ \begin{align*} &\zeta(n)\xi(n-1)= (\frac{n-1}{2}!)^2\frac{(\frac{n-3}{2}!)^2}{4}\geqslant \pi^2(\frac{n-1}{2})^n(\frac{n-3}{2})^{n-2}e^{-(2n-4)}\\=&\ (n-1)^{n-2}\frac{\pi^2(\frac{n-1}{2})^n(\frac{n-3}{2})^{n-2}e^{-(2n-4)}}{(n-1)^{n-2}}\\=&\ \pi^2e^2\left(\frac{n-1}{2e}\right)^{2n-2} \frac{(n-3)^{n-2}}{(n-2)^{n-2}}\\\geqslant&\ 0.29 \pi^2e^2\left(\frac{n-1}{2e}\right)^{2n-2} \quad \Big(\text{since} n\geqslant 5\Big), \end{align*} $$
$$ \begin{align*} &\zeta(n)\xi(n-1)= (\frac{n-1}{2}!)^2\frac{(\frac{n-3}{2}!)^2}{4}\geqslant \pi^2(\frac{n-1}{2})^n(\frac{n-3}{2})^{n-2}e^{-(2n-4)}\\=&\ (n-1)^{n-2}\frac{\pi^2(\frac{n-1}{2})^n(\frac{n-3}{2})^{n-2}e^{-(2n-4)}}{(n-1)^{n-2}}\\=&\ \pi^2e^2\left(\frac{n-1}{2e}\right)^{2n-2} \frac{(n-3)^{n-2}}{(n-2)^{n-2}}\\\geqslant&\ 0.29 \pi^2e^2\left(\frac{n-1}{2e}\right)^{2n-2} \quad \Big(\text{since} n\geqslant 5\Big), \end{align*} $$
and for even
![]() $n\geqslant 6$
,
$n\geqslant 6$
,
 $$ \begin{align*} &\zeta(n)\xi(n-1)= (\frac{n}{2})!(\frac{n-2}{2})!\frac{(\frac{n-2}{2})!(\frac{n-4}{2})!}{4}\\\geqslant&\ \pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{n-1}(\frac{n-4}{2})^{\frac{n-3}{2}}e^{-(2n-4)}\\=&\ (n-1)^{2n-2}\frac{\pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{n-1}(\frac{n-4}{2})^{\frac{n-3}{2}}e^{-(2n-4)}}{(n-1)^{2n-2}}\\=&\ \pi^2 e^2 \left(\frac{n-1}{2e}\right)^{2n-2}\frac{n^{\frac{n+1}{2}}(n-2)^{n-1}(n-4)^{\frac{n-3}{2}}}{(n-1)^{2n-2}}\\>&\ \pi^2 \left(\frac{n-1}{2e}\right)^{2n-2}. \end{align*} $$
$$ \begin{align*} &\zeta(n)\xi(n-1)= (\frac{n}{2})!(\frac{n-2}{2})!\frac{(\frac{n-2}{2})!(\frac{n-4}{2})!}{4}\\\geqslant&\ \pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{n-1}(\frac{n-4}{2})^{\frac{n-3}{2}}e^{-(2n-4)}\\=&\ (n-1)^{2n-2}\frac{\pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{n-1}(\frac{n-4}{2})^{\frac{n-3}{2}}e^{-(2n-4)}}{(n-1)^{2n-2}}\\=&\ \pi^2 e^2 \left(\frac{n-1}{2e}\right)^{2n-2}\frac{n^{\frac{n+1}{2}}(n-2)^{n-1}(n-4)^{\frac{n-3}{2}}}{(n-1)^{2n-2}}\\>&\ \pi^2 \left(\frac{n-1}{2e}\right)^{2n-2}. \end{align*} $$
Therefore, for all
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
 $$\begin{align*}\Big(\frac{2}{\zeta(n)\xi(n-1)}\Big)^{\frac{1}{2n-2}}\leqslant \frac{2e}{n-1} \Big(\frac{2}{\pi^2}\Big)^{\frac{1}{2n-2}}\leqslant \frac{2e}{n-1}.\\[-44pt]\end{align*}$$
$$\begin{align*}\Big(\frac{2}{\zeta(n)\xi(n-1)}\Big)^{\frac{1}{2n-2}}\leqslant \frac{2e}{n-1} \Big(\frac{2}{\pi^2}\Big)^{\frac{1}{2n-2}}\leqslant \frac{2e}{n-1}.\\[-44pt]\end{align*}$$
Lemma A.2. Let
![]() $\zeta (n)$
and
$\zeta (n)$
and
![]() $\lambda (n)$
be defined as in (21) and (31), respectively. For
$\lambda (n)$
be defined as in (21) and (31), respectively. For
![]() $n\geqslant 2$
, we have
$n\geqslant 2$
, we have
 $$\begin{align*}\Big(\frac{8}{\zeta(n)\lambda(n)}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2.36e}{n-\frac{1}{2}}. \end{align*}$$
$$\begin{align*}\Big(\frac{8}{\zeta(n)\lambda(n)}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2.36e}{n-\frac{1}{2}}. \end{align*}$$
Proof. For
![]() $n=2,3,4,5$
, the inequality follows from direct calculation. By the Stirling approximation (86), we have for even
$n=2,3,4,5$
, the inequality follows from direct calculation. By the Stirling approximation (86), we have for even
![]() $n\geqslant 6$
,
$n\geqslant 6$
,
 $$ \begin{align*} &\zeta(n)\lambda(n)=\zeta(n)\xi(n-2)=(\frac{n}{2})!(\frac{n-2}{2})!\frac{(\frac{n-4}{2}!)^2}{4}\\\geqslant&\ \pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(\frac{n-4}{2})^{n-3}e^{-(2n-5)}\\= &\ (n-\frac{1}{2})^{2n-1}\frac{\pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(\frac{n-4}{2})^{n-3}e^{-(2n-5)}}{(n-\frac{1}{2})^{2n-1}}\\=&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{\pi^2e^42^2}{(n-\frac{1}{2})^2} \frac{n^{\frac{n+1}{2}}(n-2)^{\frac{n-1}{2}}(n-4)^{n-3}}{(n-\frac{1}{2})^{2n-3}}\\\geqslant&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{4\pi^2}{(n-\frac{1}{2})^2}, \end{align*} $$
$$ \begin{align*} &\zeta(n)\lambda(n)=\zeta(n)\xi(n-2)=(\frac{n}{2})!(\frac{n-2}{2})!\frac{(\frac{n-4}{2}!)^2}{4}\\\geqslant&\ \pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(\frac{n-4}{2})^{n-3}e^{-(2n-5)}\\= &\ (n-\frac{1}{2})^{2n-1}\frac{\pi^2(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(\frac{n-4}{2})^{n-3}e^{-(2n-5)}}{(n-\frac{1}{2})^{2n-1}}\\=&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{\pi^2e^42^2}{(n-\frac{1}{2})^2} \frac{n^{\frac{n+1}{2}}(n-2)^{\frac{n-1}{2}}(n-4)^{n-3}}{(n-\frac{1}{2})^{2n-3}}\\\geqslant&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{4\pi^2}{(n-\frac{1}{2})^2}, \end{align*} $$
and for odd
![]() $n\geqslant 7$
,
$n\geqslant 7$
,
 $$ \begin{align*} &\zeta(n)\lambda(n)=\zeta(n)\xi(n-2)=(\frac{n-1}{2}!)^2\frac{(\frac{n-3}{2})!(\frac{n-5}{2})!}{4}\\\geqslant&\ \pi^2(\frac{n-1}{2})^{n}(\frac{n-3}{2})^{\frac{n-2}{2}}(\frac{n-5}{2})^{\frac{n-4}{2}}e^{-(2n-5)}\\= &\ (n-\frac{1}{2})^{2n-1}\frac{\pi^2(\frac{n-1}{2})^{n}(\frac{n-3}{2})^{\frac{n-2}{2}}(\frac{n-5}{2})^{\frac{n-4}{2}}e^{-(2n-5)}}{(n-\frac{1}{2})^{2n-1}}\\= &\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{\pi^2e^42^2}{(n-\frac{1}{2})^2} \frac{(n-1)^{n}(n-3)^{\frac{n-2}{2}}(n-5)^{\frac{n-4}{2}}}{(n-\frac{1}{2})^{2n-3}}\\\geqslant&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{4\pi^2}{(n-\frac{1}{2})^2}. \end{align*} $$
$$ \begin{align*} &\zeta(n)\lambda(n)=\zeta(n)\xi(n-2)=(\frac{n-1}{2}!)^2\frac{(\frac{n-3}{2})!(\frac{n-5}{2})!}{4}\\\geqslant&\ \pi^2(\frac{n-1}{2})^{n}(\frac{n-3}{2})^{\frac{n-2}{2}}(\frac{n-5}{2})^{\frac{n-4}{2}}e^{-(2n-5)}\\= &\ (n-\frac{1}{2})^{2n-1}\frac{\pi^2(\frac{n-1}{2})^{n}(\frac{n-3}{2})^{\frac{n-2}{2}}(\frac{n-5}{2})^{\frac{n-4}{2}}e^{-(2n-5)}}{(n-\frac{1}{2})^{2n-1}}\\= &\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{\pi^2e^42^2}{(n-\frac{1}{2})^2} \frac{(n-1)^{n}(n-3)^{\frac{n-2}{2}}(n-5)^{\frac{n-4}{2}}}{(n-\frac{1}{2})^{2n-3}}\\\geqslant&\ (\frac{n-\frac{1}{2}}{2e})^{2n-1}\frac{4\pi^2}{(n-\frac{1}{2})^2}. \end{align*} $$
Therefore, for all
![]() $n\geqslant 2$
,
$n\geqslant 2$
,
 $$\begin{align*}\Big(\frac{8}{\zeta(n)\lambda(n)}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2e}{n-\frac{1}{2}}\Big(\frac{(n-\frac{1}{2})^28}{4\pi^2}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2.36e}{n-\frac{1}{2}}.\\[-44pt] \end{align*}$$
$$\begin{align*}\Big(\frac{8}{\zeta(n)\lambda(n)}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2e}{n-\frac{1}{2}}\Big(\frac{(n-\frac{1}{2})^28}{4\pi^2}\Big)^{\frac{1}{2n-1}}\leqslant \frac{2.36e}{n-\frac{1}{2}}.\\[-44pt] \end{align*}$$
Lemma A.3. Let
![]() $\zeta (n)$
be defined as in (21). For
$\zeta (n)$
be defined as in (21). For
![]() $n\geqslant 2$
, we have
$n\geqslant 2$
, we have
 $$\begin{align*}\frac{(n-\frac{1}{2})^{2n-1}}{\zeta(n)(n-2)!}\leqslant 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-0.5}(4.5\pi)^{-1}. \end{align*}$$
$$\begin{align*}\frac{(n-\frac{1}{2})^{2n-1}}{\zeta(n)(n-2)!}\leqslant 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-0.5}(4.5\pi)^{-1}. \end{align*}$$
Proof: By the Stirling approximation formula (86), when n is odd and
![]() $n\geqslant 3$
, we have
$n\geqslant 3$
, we have
 $$ \begin{align*} &\frac{(n-\frac{1}{2})^{2n-1}}{\zeta(n)(n-2)!}=\frac{(n-\frac{1}{2})^{2n-1}}{(\frac{n-1}{2}!)^2(n-2)!}\\\leqslant&\ \frac{(n-\frac{1}{2})^{2n-1}}{(\sqrt{2\pi})^3(\frac{n-1}{2})^{n}(n-2)^{n-2+\frac{1}{2}}e^{-(2n-3)}}\\\leqslant &\ \frac{2^{n}e^{2n}\sqrt{n-\frac{1}{2}}}{(e\sqrt{2\pi})^3}\frac{(n-\frac{1}{2})^{2n-\frac{3}{2}}}{(n-1)^n (n-2)^{n-\frac{3}{2}}}\leqslant\frac{2^{n-\frac{3}{2}}e^{2n-0.95}\sqrt{n-\frac{1}{2}}}{(\sqrt{\pi})^3}\\<&\ 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-\frac{1}{2}}(4.5\pi)^{-1}. \end{align*} $$
$$ \begin{align*} &\frac{(n-\frac{1}{2})^{2n-1}}{\zeta(n)(n-2)!}=\frac{(n-\frac{1}{2})^{2n-1}}{(\frac{n-1}{2}!)^2(n-2)!}\\\leqslant&\ \frac{(n-\frac{1}{2})^{2n-1}}{(\sqrt{2\pi})^3(\frac{n-1}{2})^{n}(n-2)^{n-2+\frac{1}{2}}e^{-(2n-3)}}\\\leqslant &\ \frac{2^{n}e^{2n}\sqrt{n-\frac{1}{2}}}{(e\sqrt{2\pi})^3}\frac{(n-\frac{1}{2})^{2n-\frac{3}{2}}}{(n-1)^n (n-2)^{n-\frac{3}{2}}}\leqslant\frac{2^{n-\frac{3}{2}}e^{2n-0.95}\sqrt{n-\frac{1}{2}}}{(\sqrt{\pi})^3}\\<&\ 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-\frac{1}{2}}(4.5\pi)^{-1}. \end{align*} $$
When n is even and
![]() $n\geqslant 4$
, we have
$n\geqslant 4$
, we have
 $$ \begin{align*} &\frac{(n-\frac{1}{2})^{2n-{1}}}{\zeta(n)(n-2)!}=\frac{(n-\frac{1}{2})^{2n-{1}}}{(\frac{n}{2})!(\frac{n-2}{2})!(n-2)!}\\\leqslant&\ \frac{(n-\frac{1}{2})^{2n-{1}}}{(\sqrt{2\pi})^3(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(n-2)^{n-2+\frac{1}{2}}e^{-(2n-3)}}\\\leqslant &\ \frac{2^{n}e^{2n}\sqrt{n-\frac{1}{2}}}{(e\sqrt{2\pi})^3}\frac{(n-\frac{1}{2})^{2n-{1.5}}}{n^{\frac{n+1}{2}}(n-2)^{\frac{n-1}{2}} (n-2)^{n-{1.5}}}\leqslant \frac{2^{n-\frac{3}{2}}e^{2n-0.95}\sqrt{n-\frac{1}{2}}}{(\sqrt{\pi})^3}\\<&\ 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-\frac{1}{2}}(4.5\pi)^{-1}. \end{align*} $$
$$ \begin{align*} &\frac{(n-\frac{1}{2})^{2n-{1}}}{\zeta(n)(n-2)!}=\frac{(n-\frac{1}{2})^{2n-{1}}}{(\frac{n}{2})!(\frac{n-2}{2})!(n-2)!}\\\leqslant&\ \frac{(n-\frac{1}{2})^{2n-{1}}}{(\sqrt{2\pi})^3(\frac{n}{2})^{\frac{n+1}{2}}(\frac{n-2}{2})^{\frac{n-1}{2}}(n-2)^{n-2+\frac{1}{2}}e^{-(2n-3)}}\\\leqslant &\ \frac{2^{n}e^{2n}\sqrt{n-\frac{1}{2}}}{(e\sqrt{2\pi})^3}\frac{(n-\frac{1}{2})^{2n-{1.5}}}{n^{\frac{n+1}{2}}(n-2)^{\frac{n-1}{2}} (n-2)^{n-{1.5}}}\leqslant \frac{2^{n-\frac{3}{2}}e^{2n-0.95}\sqrt{n-\frac{1}{2}}}{(\sqrt{\pi})^3}\\<&\ 2^{n-\frac{3}{2}}e^{2n}\sqrt{n-\frac{1}{2}}(4.5\pi)^{-1}. \end{align*} $$
For
![]() $n=2$
, the inequality follows from a direct calculation.
$n=2$
, the inequality follows from a direct calculation.
Financial support
The work was supported in part by Swiss National Science Foundation grant number 200021–200307.
Competing interests
The authors have no competing interest to declare.