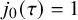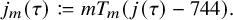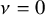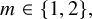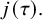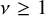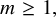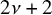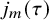1 Introduction and statement of results
Let
![]() $j(\tau )$
be the usual modular function for
$j(\tau )$
be the usual modular function for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
with Fourier expansion
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
with Fourier expansion
where ![]() Its values at imaginary quadratic arguments in the upper-half of the complex plane are examples of singular moduli [Reference Zagier34]. They are algebraic integers that generate Hilbert class fields of imaginary quadratic fields, in addition to serving as isomorphism class invariants of elliptic curves with complex multiplication. Well-known examples of these values include
Its values at imaginary quadratic arguments in the upper-half of the complex plane are examples of singular moduli [Reference Zagier34]. They are algebraic integers that generate Hilbert class fields of imaginary quadratic fields, in addition to serving as isomorphism class invariants of elliptic curves with complex multiplication. Well-known examples of these values include
 $$ \begin{align*}j\kern1pt\left(\frac{1+\sqrt{-3}}{2}\right)=0,\ \ j(i)=1728, \ \ {\mathrm{and}}\ \ j\kern1pt\left(\frac{1+\sqrt{-15}}{2}\right)=\frac{-191025-85995\sqrt{5}}{2}. \end{align*} $$
$$ \begin{align*}j\kern1pt\left(\frac{1+\sqrt{-3}}{2}\right)=0,\ \ j(i)=1728, \ \ {\mathrm{and}}\ \ j\kern1pt\left(\frac{1+\sqrt{-15}}{2}\right)=\frac{-191025-85995\sqrt{5}}{2}. \end{align*} $$
We consider the sequence of modular functions ![]() that satisfy
that satisfy
Each
![]() $j_m(\tau )$
is a monic degree m polynomial in
$j_m(\tau )$
is a monic degree m polynomial in
![]() $\mathbb {Z}[j(\tau )],$
and the set
$\mathbb {Z}[j(\tau )],$
and the set
![]() $\{j_m(\tau ) : m \ge 0\}$
is a basis of
$\{j_m(\tau ) : m \ge 0\}$
is a basis of
![]() $M^!_0$
, the space of weakly holomorphic modular functions on
$M^!_0$
, the space of weakly holomorphic modular functions on
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. The first examples are
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. The first examples are
![]() $j_0(\tau ) = 1$
and
$j_0(\tau ) = 1$
and
 $$ \begin{align*} j_1(\tau) &= j(\tau) - 744 = q^{-1} + 196884q + \cdots,\\ j_2(\tau) &= j(\tau)^2 - 1488j(\tau) + 159768 = q^{-2} + 42987520q + \cdots,\\ j_3(\tau) &= j(\tau)^3 - 2232 j(\tau)^2 + 1069956 j(\tau) - 36866976 = q^{-3} + 2592899910q + \cdots. \end{align*} $$
$$ \begin{align*} j_1(\tau) &= j(\tau) - 744 = q^{-1} + 196884q + \cdots,\\ j_2(\tau) &= j(\tau)^2 - 1488j(\tau) + 159768 = q^{-2} + 42987520q + \cdots,\\ j_3(\tau) &= j(\tau)^3 - 2232 j(\tau)^2 + 1069956 j(\tau) - 36866976 = q^{-3} + 2592899910q + \cdots. \end{align*} $$
In terms of the Hecke operators
![]() $T_m$
(see [Reference Serre28, Ch. VII] and [Reference Zagier34]), for positive integers m, we have
$T_m$
(see [Reference Serre28, Ch. VII] and [Reference Zagier34]), for positive integers m, we have
 $$ \begin{align} j_m(\tau)=q^{-m}+\sum_{n=1}^{\infty}c_m(n)q^n= mT_m\left(j(\tau)-744\right). \end{align} $$
$$ \begin{align} j_m(\tau)=q^{-m}+\sum_{n=1}^{\infty}c_m(n)q^n= mT_m\left(j(\tau)-744\right). \end{align} $$
We shall derive infinitely many relations for the singular moduli of these functions. To make this precise, for positive integers d with
![]() $-d\equiv 0,1\ \pmod 4$
, we let
$-d\equiv 0,1\ \pmod 4$
, we let
![]() $\mathcal {Q}_d$
be the set of integral positive definite binary quadratic forms
$\mathcal {Q}_d$
be the set of integral positive definite binary quadratic forms ![]() with discriminant
with discriminant
![]() $-d=B^2-4AC$
. The group
$-d=B^2-4AC$
. The group ![]() acts on
acts on
![]() $\mathcal {Q}_d$
by
$\mathcal {Q}_d$
by

and does so with finitely many orbits, the number of which is the discriminant
![]() $-d$
class number. For each
$-d$
class number. For each
![]() $Q \in \mathcal {Q}_d$
, we let
$Q \in \mathcal {Q}_d$
, we let
![]() $\alpha _Q \in \mathbb {H}$
be a root of
$\alpha _Q \in \mathbb {H}$
be a root of
![]() $Q(\tau ,1) = 0.$
The numbers
$Q(\tau ,1) = 0.$
The numbers
![]() $j_m(\alpha _Q)$
are its singular moduli.
$j_m(\alpha _Q)$
are its singular moduli.
We study the weighted traces of these values which are defined as follows. If we let
![]() $\Gamma _Q$
be the stabilizer of Q in
$\Gamma _Q$
be the stabilizer of Q in
![]() $\Gamma $
, then it is well known that
$\Gamma $
, then it is well known that
 $$\begin{align*}\#\Gamma_Q = \begin{cases} 3 &\text{if } Q \sim a(X^2 + XY + Y^2),\\ 2 &\text{if } Q \sim a(X^2 + Y^2),\\ 1 &\text{if otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\#\Gamma_Q = \begin{cases} 3 &\text{if } Q \sim a(X^2 + XY + Y^2),\\ 2 &\text{if } Q \sim a(X^2 + Y^2),\\ 1 &\text{if otherwise}. \end{cases} \end{align*}$$
Following Zagier [Reference Zagier34], the trace functions we consider are

For
![]() $m = 0$
, where
$m = 0$
, where
![]() $j_0(\tau )=1,$
we obtain the Hurwitz–Kronecker class numbers
$j_0(\tau )=1,$
we obtain the Hurwitz–Kronecker class numbers ![]() These numbers are prominent in the Eichler–Selberg trace formula (for example, see [Reference Zagier32]) for the trace
These numbers are prominent in the Eichler–Selberg trace formula (for example, see [Reference Zagier32]) for the trace
![]() $\mathrm {Tr}(n;2k)$
of the action of the Hecke operators
$\mathrm {Tr}(n;2k)$
of the action of the Hecke operators
![]() $T_n$
on
$T_n$
on
![]() $S_{2k},$
the complex vector space of weight
$S_{2k},$
the complex vector space of weight
![]() $2k$
cusp forms on
$2k$
cusp forms on
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
$\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
Theorem (The Eichler–Selberg trace formula).
For integers
![]() $k \ge 2$
, we have
$k \ge 2$
, we have
 $$ \begin{align} \mathrm{Tr}(n; 2k) = -\frac{1}{2} \sum_{r \in \mathbb{Z}} p_{2k} (r,n) \mathbf{t}_0(4n-r^2) - \lambda_{2k-1}(n), \end{align} $$
$$ \begin{align} \mathrm{Tr}(n; 2k) = -\frac{1}{2} \sum_{r \in \mathbb{Z}} p_{2k} (r,n) \mathbf{t}_0(4n-r^2) - \lambda_{2k-1}(n), \end{align} $$
where ![]() and
and
 $$ \begin{align} p_k(r,n) = \sum_{0 \le j \le \frac{k}{2}-1} (-1)^j \binom{k-2-j}{j} n^j r^{k-2-2j} = \mathrm{Coeff}_{X^{k-2}} \left(\frac{1}{1-rX+nX^2}\right). \end{align} $$
$$ \begin{align} p_k(r,n) = \sum_{0 \le j \le \frac{k}{2}-1} (-1)^j \binom{k-2-j}{j} n^j r^{k-2-2j} = \mathrm{Coeff}_{X^{k-2}} \left(\frac{1}{1-rX+nX^2}\right). \end{align} $$
We generalize these formulas to traces of singular moduli, where (1.3) are the
![]() $m=0$
cases of a doubly infinite suite of formulas in
$m=0$
cases of a doubly infinite suite of formulas in
![]() $m\geq 0$
and
$m\geq 0$
and
![]() $\nu \geq 0.$
The general formulas involve the trace functions
$\nu \geq 0.$
The general formulas involve the trace functions
![]() $\mathbf {t}_m(4n-r^2)$
. To make this precise, for every
$\mathbf {t}_m(4n-r^2)$
. To make this precise, for every
![]() $\nu \geq 0$
and
$\nu \geq 0$
and
![]() $m\geq 0,$
we define the generating function
$m\geq 0,$
we define the generating function

where for
![]() $d\le 0$
, we let
$d\le 0$
, we let

By (1.3), each
![]() $\mathrm {Tr}(n;2k)$
is essentially the nth coefficient of
$\mathrm {Tr}(n;2k)$
is essentially the nth coefficient of
![]() $\mathcal {G}_{0,k-1}(\tau ).$
Therefore, we refer to any explicit formula for
$\mathcal {G}_{0,k-1}(\tau ).$
Therefore, we refer to any explicit formula for
![]() $\mathcal {G}_{m,\nu }(\tau )$
as an Eichler–Selberg relation for m and
$\mathcal {G}_{m,\nu }(\tau )$
as an Eichler–Selberg relation for m and
![]() $\nu .$
$\nu .$
Our first result establishes that these generating functions are weakly holomorphic modular forms, meromorphic modular forms whose poles (if any) are supported at cusps. For convenience, we let
![]() $M^!_k$
denote the space of such weight k forms on
$M^!_k$
denote the space of such weight k forms on
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
$\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
Theorem 1.1. If
![]() $\nu \geq 0$
and
$\nu \geq 0$
and
![]() $m\geq 1,$
then we have that
$m\geq 1,$
then we have that
![]() $\mathcal {G}_{m,\nu }(\tau )\in M^!_{2\nu +2}.$
$\mathcal {G}_{m,\nu }(\tau )\in M^!_{2\nu +2}.$
The
![]() $\nu =0$
Eichler–Selberg relations only involve derivatives of the
$\nu =0$
Eichler–Selberg relations only involve derivatives of the
![]() $j_m(\tau )$
, as they generate
$j_m(\tau )$
, as they generate
![]() $M^!_2$
due to the absence of holomorphic modular forms. For convenience, we let
$M^!_2$
due to the absence of holomorphic modular forms. For convenience, we let ![]() .
.
Theorem 1.2. For positive integers
![]() $m,$
the following are true.
$m,$
the following are true.
1) We have
 $$\begin{align*}\mathcal{G}_{m,0}(\tau) = -\frac{1}{2}\sum_{\kappa \mid m} \sum_{0 < r < \kappa} \frac{\kappa}{r(\kappa-r)} \cdot Dj_{r(\kappa-r)}(\tau). \end{align*}$$
$$\begin{align*}\mathcal{G}_{m,0}(\tau) = -\frac{1}{2}\sum_{\kappa \mid m} \sum_{0 < r < \kappa} \frac{\kappa}{r(\kappa-r)} \cdot Dj_{r(\kappa-r)}(\tau). \end{align*}$$
2) If n is a positive integer, then we have
 $$\begin{align*}\sum_{r \in \mathbb{Z}} \mathbf{t}_m(4n-r^2) = n \sum_{\kappa \mid m} \sum_{0 < r < \kappa} \frac{\kappa}{r(\kappa-r)} c_{r(\kappa-r)}(n). \end{align*}$$
$$\begin{align*}\sum_{r \in \mathbb{Z}} \mathbf{t}_m(4n-r^2) = n \sum_{\kappa \mid m} \sum_{0 < r < \kappa} \frac{\kappa}{r(\kappa-r)} c_{r(\kappa-r)}(n). \end{align*}$$
Example. Theorem 1.2, with
![]() $m\in \{1, 2\}$
, gives Kaneko’s identities [Reference Kaneko16]
$m\in \{1, 2\}$
, gives Kaneko’s identities [Reference Kaneko16]
which he used to derive his well-known singular moduli formula for the coefficients of
![]() $j(\tau )$
$j(\tau )$
 $$ \begin{align*} c_1(n)=\frac{1}{n}\left \{ \sum_{r \in \mathbb{Z}} \mathbf{t}_1(n-r^2)+\sum_{r\geq 1\ odd}\left( (-1)^n \mathbf{t}_1(4n-r^2)-\mathbf{t}_1(16n-r^2)\right)\right\}. \end{align*} $$
$$ \begin{align*} c_1(n)=\frac{1}{n}\left \{ \sum_{r \in \mathbb{Z}} \mathbf{t}_1(n-r^2)+\sum_{r\geq 1\ odd}\left( (-1)^n \mathbf{t}_1(4n-r^2)-\mathbf{t}_1(16n-r^2)\right)\right\}. \end{align*} $$
Such formulas have been extended to higher levels N in subsequent works [Reference Matsusaka18, Reference Matsusaka and Osanai19, Reference Ohta25]. Finally, as a different kind of generalization, Theorem 1.2 (2) shows how to express the coefficients of each
![]() $j_m(\tau )$
in terms of traces of singular moduli.
$j_m(\tau )$
in terms of traces of singular moduli.
For
![]() $\nu> 0$
, there are holomorphic modular forms, and so the relations have richer structure. To make this precise, we recall the weight
$\nu> 0$
, there are holomorphic modular forms, and so the relations have richer structure. To make this precise, we recall the weight
![]() $2k$
modular Poincaré series [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 6.3]
$2k$
modular Poincaré series [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 6.3]

where
![]() $|_{2k}$
is the slash operator,
$|_{2k}$
is the slash operator,
![]() $\Gamma =\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
, and
$\Gamma =\operatorname {\mathrm {PSL}}_2(\mathbb {Z})$
, and
![]() $\Gamma _{\infty }$
is the stabilizer for the cusp infinity. The usual Eisenstein series is
$\Gamma _{\infty }$
is the stabilizer for the cusp infinity. The usual Eisenstein series is
![]() $P_{2k,0}(\tau ) = E_{2k}(\tau ),$
and for negative integers
$P_{2k,0}(\tau ) = E_{2k}(\tau ),$
and for negative integers
![]() $-h$
, we have the weakly holomorphic
$-h$
, we have the weakly holomorphic
 $$ \begin{align} P_{2k,-h}(\tau)=q^{-h}+\sum_{n=1}^{\infty}c_{2k,-h}(n)q^n. \end{align} $$
$$ \begin{align} P_{2k,-h}(\tau)=q^{-h}+\sum_{n=1}^{\infty}c_{2k,-h}(n)q^n. \end{align} $$
For small
![]() $\nu ,$
when there are no cusp forms, we obtain the following Eichler–Selberg relations.
$\nu ,$
when there are no cusp forms, we obtain the following Eichler–Selberg relations.
Theorem 1.3. If
![]() $\nu \in \{1, 2, 3, 4, 6\},$
then for every positive integer m, the following are true.
$\nu \in \{1, 2, 3, 4, 6\},$
then for every positive integer m, the following are true.
1) We have that
2) If n is a positive integer, then we have
Remark. The Poincaré series in Theorem 1.3 are easily described in terms of the Eisenstein series
 $$ \begin{align*}E_4(\tau)=1+240\sum_{n=1}^{\infty}\sigma_3(n)q^n \ \ \ {\mathrm{and}}\ \ \ E_6(\tau)=1-504\sum_{n=1}^{\infty} \sigma_5(n)q^n. \end{align*} $$
$$ \begin{align*}E_4(\tau)=1+240\sum_{n=1}^{\infty}\sigma_3(n)q^n \ \ \ {\mathrm{and}}\ \ \ E_6(\tau)=1-504\sum_{n=1}^{\infty} \sigma_5(n)q^n. \end{align*} $$
For
![]() $k\in \{4, 6, 8, 10, 14\},$
we have
$k\in \{4, 6, 8, 10, 14\},$
we have
 $$ \begin{align*}P_{k,-1}(\tau) = \begin{cases} E_4(\tau)\cdot (j(\tau)-984) &\mathrm{if}\ k=4,\\ E_6(\tau)\cdot (j(\tau)-240) &\mathrm{if}\ k=6,\\ E_4^2(\tau)\cdot (j(\tau)-1224) &\mathrm{if}\ k=8,\\ E_4(\tau)E_6(\tau)\cdot (j(\tau)-480) &\mathrm{if}\ k=10,\\ E_4^2(\tau)E_6(\tau)\cdot (j(\tau)-720) &\mathrm{if}\ k=14. \end{cases} \end{align*} $$
$$ \begin{align*}P_{k,-1}(\tau) = \begin{cases} E_4(\tau)\cdot (j(\tau)-984) &\mathrm{if}\ k=4,\\ E_6(\tau)\cdot (j(\tau)-240) &\mathrm{if}\ k=6,\\ E_4^2(\tau)\cdot (j(\tau)-1224) &\mathrm{if}\ k=8,\\ E_4(\tau)E_6(\tau)\cdot (j(\tau)-480) &\mathrm{if}\ k=10,\\ E_4^2(\tau)E_6(\tau)\cdot (j(\tau)-720) &\mathrm{if}\ k=14. \end{cases} \end{align*} $$
Generalizing (1.1), for
![]() $m>1,$
we have the Hecke formula
$m>1,$
we have the Hecke formula
Example. For positive integers
![]() $n,$
Theorem 1.3 with
$n,$
Theorem 1.3 with
![]() $\nu = 1$
and
$\nu = 1$
and
![]() $m=1$
implies that
$m=1$
implies that
Cusp forms arise in the general case. Special values of symmetrized shifted convolution L-functions, and Petersson norms control these cusp forms in these Eichler–Selberg relations. Throughout, we let
![]() $d_{2k}$
denote the dimension of
$d_{2k}$
denote the dimension of
![]() $S_{2k}$
, the space of weight
$S_{2k}$
, the space of weight
![]() $2k$
cusp forms on
$2k$
cusp forms on
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
$\operatorname {\mathrm {SL}}_2(\mathbb {Z}).$
Theorem 1.4. If
![]() $\nu \geq 1$
and
$\nu \geq 1$
and
![]() $m \ge 1$
, then we have
$m \ge 1$
, then we have
 $$ \begin{align*} \mathcal{G}_{m,\nu}(\tau)= &\sum_{\kappa \mid m} \sum_{0 < r \le \kappa} r^{2\nu+1} P_{2\nu+2, -r(\kappa-r)}(\tau) -\sum_{j=1}^{d_{2\nu+2}} \left(24\sigma_1(m) - \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu+1}} \frac{\widehat{L}(f_j, m; 2\nu+1)}{\|f_j\|^2} \right) f_j, \end{align*} $$
$$ \begin{align*} \mathcal{G}_{m,\nu}(\tau)= &\sum_{\kappa \mid m} \sum_{0 < r \le \kappa} r^{2\nu+1} P_{2\nu+2, -r(\kappa-r)}(\tau) -\sum_{j=1}^{d_{2\nu+2}} \left(24\sigma_1(m) - \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu+1}} \frac{\widehat{L}(f_j, m; 2\nu+1)}{\|f_j\|^2} \right) f_j, \end{align*} $$
where the
![]() $f_j$
’s are normalized Hecke eigenforms of
$f_j$
’s are normalized Hecke eigenforms of
![]() $S_{2\nu +2}$
and
$S_{2\nu +2}$
and

Example. Example 1 of [Reference Mertens and Ono22] gives
![]() $\widehat {L}(\Delta , 1; 11)=-33.383\dots $
and
$\widehat {L}(\Delta , 1; 11)=-33.383\dots $
and
![]() $\widehat {L}(\Delta , 2; 11)=266.439\dots ,$
which arise in Theorem 1.4 when
$\widehat {L}(\Delta , 2; 11)=266.439\dots ,$
which arise in Theorem 1.4 when
![]() $\nu = 5$
and
$\nu = 5$
and
![]() $m\in \{1, 2\}.$
By brute force computation, we have
$m\in \{1, 2\}.$
By brute force computation, we have
 $$ \begin{align*} \mathcal{G}_{1,5}(\tau) &= E_{12}(\tau) -\frac{82104}{691} \Delta(\tau),\\ \mathcal{G}_{2,5}(\tau) &= P_{12,-1}(\tau) + 2049 E_{12}(\tau) - \left(\alpha - \frac{1746612}{691} \right) \Delta(\tau), \end{align*} $$
$$ \begin{align*} \mathcal{G}_{1,5}(\tau) &= E_{12}(\tau) -\frac{82104}{691} \Delta(\tau),\\ \mathcal{G}_{2,5}(\tau) &= P_{12,-1}(\tau) + 2049 E_{12}(\tau) - \left(\alpha - \frac{1746612}{691} \right) \Delta(\tau), \end{align*} $$
where
with
![]() $\alpha = 1842.894\ldots $
. Using
$\alpha = 1842.894\ldots $
. Using
![]() $\|\Delta \|^2 = \langle \Delta , \Delta \rangle = 0.0000010353\ldots ,$
these numerics illustrate Theorem 1.4
$\|\Delta \|^2 = \langle \Delta , \Delta \rangle = 0.0000010353\ldots ,$
these numerics illustrate Theorem 1.4
 $$ \begin{align*} \frac{82104}{691} &= 24 + \frac{65520}{691} = 24 - \frac{\Gamma(11)}{(4\pi)^{11}} \frac{(-33.383\ldots)}{\|\Delta\|^2},\\ \alpha - \frac{1746612}{691} &= 24 \cdot 3 - \frac{\Gamma(11)}{(4\pi)^{11}} \frac{(266.439\ldots)}{\|\Delta\|^2}. \end{align*} $$
$$ \begin{align*} \frac{82104}{691} &= 24 + \frac{65520}{691} = 24 - \frac{\Gamma(11)}{(4\pi)^{11}} \frac{(-33.383\ldots)}{\|\Delta\|^2},\\ \alpha - \frac{1746612}{691} &= 24 \cdot 3 - \frac{\Gamma(11)}{(4\pi)^{11}} \frac{(266.439\ldots)}{\|\Delta\|^2}. \end{align*} $$
Theorem 1.4 gives a doubly infinite family of modified Eichler–Selberg trace formulas, where Hecke eigenvalues are weighted by shifted convolution L-values and where traces of singular moduli
![]() $\mathbf {t}_m(4n-r^2)$
replace the Hurwitz–Kronecker class numbers
$\mathbf {t}_m(4n-r^2)$
replace the Hurwitz–Kronecker class numbers
![]() $\mathbf {t}_0(4n-r^2)=H(4n-r^2).$
To make this precise, we let
$\mathbf {t}_0(4n-r^2)=H(4n-r^2).$
To make this precise, we let

where, as above,
![]() $c_{f_j}(n)$
is the eigenvalue of
$c_{f_j}(n)$
is the eigenvalue of
![]() $T_n$
for the Hecke eigenform
$T_n$
for the Hecke eigenform
![]() $f_j\in S_{2k}.$
$f_j\in S_{2k}.$
Corollary 1.5. If
![]() $2k \in 2\mathbb {Z}^+\setminus \{2, 4, 6, 8, 10, 14\}$
and m is a positive integer, then we have
$2k \in 2\mathbb {Z}^+\setminus \{2, 4, 6, 8, 10, 14\}$
and m is a positive integer, then we have
 $$ \begin{align*}\mathrm{Tr}(n; 2k) =\frac{1}{ 24 \sigma_1(m)}\cdot\left( \mathrm{Tr}_m(n; 2k) +\frac{1}{2} \sum_{r \in \mathbb{Z}} p_{2k}(r,n) \mathbf{t}_m(4n-r^2) + \sum_{\kappa \mid m} \sum_{0 < r \le \kappa} r^{2k-1} c_{2k, -r(\kappa-r)}(n)\right). \end{align*} $$
$$ \begin{align*}\mathrm{Tr}(n; 2k) =\frac{1}{ 24 \sigma_1(m)}\cdot\left( \mathrm{Tr}_m(n; 2k) +\frac{1}{2} \sum_{r \in \mathbb{Z}} p_{2k}(r,n) \mathbf{t}_m(4n-r^2) + \sum_{\kappa \mid m} \sum_{0 < r \le \kappa} r^{2k-1} c_{2k, -r(\kappa-r)}(n)\right). \end{align*} $$
To obtain these results, we adapt Zagier’s novel (unpublished) proof [Reference Zagier32] of the Eichler–Selberg trace formula. In Section 2, we recall his proof and his work on traces of singular moduli, and we prove Theorems 1.1–1.3. The proof of Theorem 1.4 is more involved, as we make use of the theory of vector-valued Poincaré series, the arithmetic of half-integral weight Kloosterman sums, Rankin–Cohen bracket operators and symmetrized shifted convolution L-functions. In Section 3, we recall important formalities regarding vector-valued modular forms that transform according to the Weil representation. In Section 4, we relate the Fourier coefficients of half-integral weight Maass–Poincaré series to traces of singular moduli, and finally, in Section 5, we assemble these facts to prove Theorem 1.4.
2 Zagier’s work and the proofs of Theorems 1.1–1.3
In unpublished notes [Reference Zagier32], Zagier gave a novel proof of the Eichler–Selberg trace formula using harmonic Maass forms (see [Reference Bruinier and Funke7] or [Reference Bringmann, Folsom, Ono and Rolen4] for background on harmonic Maass forms). Saad and the third author [Reference Ono and Saad26] obtained further such formulas by modifying his argument. We adapt his argument in a different aspect.
2.1 Zagier’s Proof
We begin by sketching his proof, which relies on the following theorem.
Theorem (Zagier [Reference Zagier33]).
We have that

is a harmonic Maass form of weight
![]() $3/2$
on
$3/2$
on
![]() $\Gamma _0(4)$
, where
$\Gamma _0(4)$
, where ![]() and
and
![]() $\Gamma (s; x)$
is the incomplete Gamma function. Its holomorphic part is the Fourier series
$\Gamma (s; x)$
is the incomplete Gamma function. Its holomorphic part is the Fourier series

Zagier uses a sequence of modular forms he constructs from
![]() $\mathcal {H}(\tau )$
and Jacobi’s weight 1/2 theta function
$\mathcal {H}(\tau )$
and Jacobi’s weight 1/2 theta function
To define these modular forms, he requires Atkin’s U-operator defined by

and the Rankin–Cohen bracket differential operators. For modular forms f and g (possibly non-holomorphic), with weights k and l, respectively, these operators are defined by

where ![]() . These functions are weight
. These functions are weight
![]() $2\nu +k+l$
(possibly non-holomorphic) modular forms, which one can project to obtain a holomorphic modular form via an integral map
$2\nu +k+l$
(possibly non-holomorphic) modular forms, which one can project to obtain a holomorphic modular form via an integral map
![]() $\pi _{\mathrm {hol}}.$
$\pi _{\mathrm {hol}}.$
Zagier studies the resulting sequence of modular forms
![]() $\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
, where
$\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
, where
![]() $\nu \geq 1$
. He computes them in two ways. The first method is combinatorial, and it uses the identity (for example, see [Reference Mertens20, Reference Mertens21])
$\nu \geq 1$
. He computes them in two ways. The first method is combinatorial, and it uses the identity (for example, see [Reference Mertens20, Reference Mertens21])
 $$\begin{align*}\pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu|U_4) = [\mathcal{H}^+, \theta]_\nu|U_4 + 2 \binom{2\nu}{\nu} \sum_{n=1}^\infty \lambda_{2\nu+1}(n) q^n. \end{align*}$$
$$\begin{align*}\pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu|U_4) = [\mathcal{H}^+, \theta]_\nu|U_4 + 2 \binom{2\nu}{\nu} \sum_{n=1}^\infty \lambda_{2\nu+1}(n) q^n. \end{align*}$$
A straightforward brute force calculation with (2.3) gives
 $$ \begin{align} [\mathcal{H}^+, \theta]_\nu |U_4 = \binom{2\nu}{\nu} \sum_{n=0}^\infty \left(\sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) H(4n-r^2) \right) q^n. \end{align} $$
$$ \begin{align} [\mathcal{H}^+, \theta]_\nu |U_4 = \binom{2\nu}{\nu} \sum_{n=0}^\infty \left(\sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) H(4n-r^2) \right) q^n. \end{align} $$
Therefore, the nth coefficient of
![]() $\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is
$\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is
 $$ \begin{align} \binom{2\nu}{\nu} \left(\sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) H(4n-r^2) + 2\lambda_{2\nu+1}(n) \right). \end{align} $$
$$ \begin{align} \binom{2\nu}{\nu} \left(\sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) H(4n-r^2) + 2\lambda_{2\nu+1}(n) \right). \end{align} $$
As an alternate calculation, Zagier combines (for example, see [Reference Eichler and Zagier13, Theorem 5.5]) the Rankin–Cohen bracket operators with Hecke–Petersson theory. As each
![]() $\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is a cusp form, we have
$\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is a cusp form, we have
 $$ \begin{align*} \pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu |U_4) = \sum_{j=1}^{d_{2\nu+2}} a_j f_j, \end{align*} $$
$$ \begin{align*} \pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu |U_4) = \sum_{j=1}^{d_{2\nu+2}} a_j f_j, \end{align*} $$
where the
![]() $f_j$
’s form a basis of Hecke eigenforms for
$f_j$
’s form a basis of Hecke eigenforms for
![]() $S_{2\nu +2}$
. In particular, we have
$S_{2\nu +2}$
. In particular, we have
![]() $T_n f_j = c_{f_j}(n) f_j,$
where
$T_n f_j = c_{f_j}(n) f_j,$
where
To compute the
![]() $a_j,$
he expresses
$a_j,$
he expresses
![]() $\mathcal {H}(\tau )$
in terms of Eisenstein series (see [Reference Ono and Saad26, Section 2.2] or [Reference Hirzebruch and Zagier14, Ch. 2]), which allows him to use the method of unfolding and the Rankin–Selberg method to derive the Petersson inner product identity (for example, see [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 6.3])
$\mathcal {H}(\tau )$
in terms of Eisenstein series (see [Reference Ono and Saad26, Section 2.2] or [Reference Hirzebruch and Zagier14, Ch. 2]), which allows him to use the method of unfolding and the Rankin–Selberg method to derive the Petersson inner product identity (for example, see [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 6.3])
 $$ \begin{align*} a_j \langle f_j, f_j \rangle = \langle \pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu |U_4), f_j \rangle = -2 \binom{2\nu}{\nu} \langle f_j, f_j \rangle. \end{align*} $$
$$ \begin{align*} a_j \langle f_j, f_j \rangle = \langle \pi_{\mathrm{hol}}([\mathcal{H}, \theta]_\nu |U_4), f_j \rangle = -2 \binom{2\nu}{\nu} \langle f_j, f_j \rangle. \end{align*} $$
For each j, this gives
![]() $a_j=-2\binom {2\nu }{\nu }.$
Therefore, the nth coefficient of
$a_j=-2\binom {2\nu }{\nu }.$
Therefore, the nth coefficient of
![]() $\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is
$\pi _{\mathrm {hol}}([\mathcal {H}, \theta ]_\nu |U_4)$
is
![]() $-2 \binom {2\nu }{\nu }\cdot \mathrm {Tr}(n; 2\nu +2),$
which when equated with (2.5) gives the Eichler–Selberg trace formula.
$-2 \binom {2\nu }{\nu }\cdot \mathrm {Tr}(n; 2\nu +2),$
which when equated with (2.5) gives the Eichler–Selberg trace formula.
2.2 Proofs of Theorems 1.1–1.3
Zagier’s proof begins with the fact that
![]() $\mathcal {H}^+(\tau )$
is the holomorphic part of a weight 3/2 harmonic Maass form. In 2002, Zagier [Reference Zagier34] greatly generalized this fact.
$\mathcal {H}^+(\tau )$
is the holomorphic part of a weight 3/2 harmonic Maass form. In 2002, Zagier [Reference Zagier34] greatly generalized this fact.
Theorem 5 of [Reference Zagier34].
For positive integers m, we have that

is a weakly holomorphic modular form of weight
![]() $3/2$
on
$3/2$
on
![]() $\Gamma _0(4)$
.
$\Gamma _0(4)$
.
Proof of Theorem 1.1.
Emulating Zagier’s proof of the Eichler–Selberg trace formula, we replace
![]() $\mathcal {H}^+(\tau )$
in (2.4) with the
$\mathcal {H}^+(\tau )$
in (2.4) with the
![]() $g_m(\tau )$
. Namely, we define
$g_m(\tau )$
. Namely, we define

By the combinatorial calculation that gave (2.4), we obtain the earlier definition (1.5)
 $$ \begin{align*} \mathcal{G}_{m,\nu}(\tau) = -\frac{1}{2} \sum_{n \gg -\infty} \sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) \mathbf{t}_m(4n-r^2) q^n. \end{align*} $$
$$ \begin{align*} \mathcal{G}_{m,\nu}(\tau) = -\frac{1}{2} \sum_{n \gg -\infty} \sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) \mathbf{t}_m(4n-r^2) q^n. \end{align*} $$
Furthermore, the theory of Rankin–Cohen brackets in this setting (see [Reference Eichler and Zagier13, Theorem 5.5]) implies that
![]() $\mathcal {G}_{m,\nu }(\tau )$
is a weakly holomorphic modular form in
$\mathcal {G}_{m,\nu }(\tau )$
is a weakly holomorphic modular form in
![]() $M_{2\nu +2}^!.$
$M_{2\nu +2}^!.$
Proof of Theorem 1.2.
The space of weight 2 holomorphic modular forms is
![]() $M_2 = \{0\}$
and
$M_2 = \{0\}$
and
Therefore, we have
 $$ \begin{align*} \mathcal{G}_{m,0}(\tau) +\frac{1}{2} \sum_{-\frac{m^2}{4} \le n < 0} \frac{1}{n} \left(\sum_{r \in \mathbb{Z}} \mathbf{t}_m(4n-r^2)\right) Dj_{-n}(\tau) = 0. \end{align*} $$
$$ \begin{align*} \mathcal{G}_{m,0}(\tau) +\frac{1}{2} \sum_{-\frac{m^2}{4} \le n < 0} \frac{1}{n} \left(\sum_{r \in \mathbb{Z}} \mathbf{t}_m(4n-r^2)\right) Dj_{-n}(\tau) = 0. \end{align*} $$
The first claim follows from (1.6). By comparing the nth coefficients, the second claim is obtained.
Proof of Theorem 1.3.
For
![]() $\nu> 0$
, we note that
$\nu> 0$
, we note that
 $$ \begin{align} \mathcal{G}_{m,\nu}(\tau) + \frac{1}{2} \sum_{-\frac{m^2}{4} \le n \le 0} \sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) \mathbf{t}_m(4n-r^2) P_{2\nu+2, n}(\tau) \end{align} $$
$$ \begin{align} \mathcal{G}_{m,\nu}(\tau) + \frac{1}{2} \sum_{-\frac{m^2}{4} \le n \le 0} \sum_{r \in \mathbb{Z}} p_{2\nu+2}(r,n) \mathbf{t}_m(4n-r^2) P_{2\nu+2, n}(\tau) \end{align} $$
is a cusp form. We are merely cancelling the poles at infinity with Poincaré series that satisfy (1.8), and we capture the constant term with Eisenstein series
![]() $P_{2\nu +2,0}(\tau )=E_{2\nu +2}(\tau )=1+\cdots .$
For
$P_{2\nu +2,0}(\tau )=E_{2\nu +2}(\tau )=1+\cdots .$
For
![]() $\nu \in \{1, 2, 3, 4, 6\}$
, the space of cusp forms
$\nu \in \{1, 2, 3, 4, 6\}$
, the space of cusp forms
![]() $S_{2\nu +2}=\{0\}$
is trivial. Therefore, the theorem follows from the identity
$S_{2\nu +2}=\{0\}$
is trivial. Therefore, the theorem follows from the identity
 $$ \begin{align} p_{2\nu+2} \left(r, \frac{r^2-\kappa^2}{4}\right) = \frac{(\kappa - r)^{2\nu+1} + (\kappa + r)^{2\nu+1}}{2^{2\nu+1} \kappa}. \end{align} $$
$$ \begin{align} p_{2\nu+2} \left(r, \frac{r^2-\kappa^2}{4}\right) = \frac{(\kappa - r)^{2\nu+1} + (\kappa + r)^{2\nu+1}}{2^{2\nu+1} \kappa}. \end{align} $$
3 Vector-valued modular forms
The proof of Theorem 1.4 is much more involved than the proofs of Theorems 1.2 and 1.3. Nevertheless, its proof is still based on Theorem 1.1, and the aim is to understand the Fourier expansion of
![]() $\mathcal {G}_{m,\nu }(\tau )$
arithmetically in terms of traces of Hecke operators and shifted convolution L-functions. These calculations shall depend on the arithmetic of half-integral weight vector-valued modular forms that transform with respect to the Weil representation. To this end, here we recall essential preliminaries.
$\mathcal {G}_{m,\nu }(\tau )$
arithmetically in terms of traces of Hecke operators and shifted convolution L-functions. These calculations shall depend on the arithmetic of half-integral weight vector-valued modular forms that transform with respect to the Weil representation. To this end, here we recall essential preliminaries.
3.1 The Weil representation
Let
![]() $\mathcal {O}(\mathbb {H})$
be the set of all holomorphic functions
$\mathcal {O}(\mathbb {H})$
be the set of all holomorphic functions
![]() $\phi : \mathbb {H} \to \mathbb {C}$
. For
$\phi : \mathbb {H} \to \mathbb {C}$
. For
![]() $z \in \mathbb {C} \setminus \{0\}$
, we take the principal branch of
$z \in \mathbb {C} \setminus \{0\}$
, we take the principal branch of
![]() $z^{1/2}$
as
$z^{1/2}$
as
![]() $\arg (z^{1/2}) \in (-\pi /2, \pi /2]$
. For an integer
$\arg (z^{1/2}) \in (-\pi /2, \pi /2]$
. For an integer
![]() $k \in \mathbb {Z}$
, we put
$k \in \mathbb {Z}$
, we put
![]() $z^{k/2} = (z^{1/2})^k$
. For
$z^{k/2} = (z^{1/2})^k$
. For
![]() $n \in \mathbb {Z}_{\ge 0}$
, we put
$n \in \mathbb {Z}_{\ge 0}$
, we put ![]() , and
, and ![]() .
.
The metaplectic group
![]() $\operatorname {\mathrm {Mp}}_2(\mathbb {R})$
is a group defined by
$\operatorname {\mathrm {Mp}}_2(\mathbb {R})$
is a group defined by

where the group operation is ![]()
As usual, we have ![]() , and for any
, and for any
![]() $\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {R})$
, we define
$\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {R})$
, we define
![]() $j(\gamma , \tau ) = c\tau +d$
and
$j(\gamma , \tau ) = c\tau +d$
and
![]() $\widetilde {\gamma } = \left (\bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ), j(\gamma , \tau )^{1/2} \right ) \in \operatorname {\mathrm {Mp}}_2(\mathbb {R})$
. Let
$\widetilde {\gamma } = \left (\bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ), j(\gamma , \tau )^{1/2} \right ) \in \operatorname {\mathrm {Mp}}_2(\mathbb {R})$
. Let
![]() $\operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
be the inverse image of
$\operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
be the inverse image of
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
under the projection
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
under the projection
![]() $\operatorname {\mathrm {Mp}}_2(\mathbb {R}) \to \operatorname {\mathrm {SL}}_2(\mathbb {R})$
. As usual, we let
$\operatorname {\mathrm {Mp}}_2(\mathbb {R}) \to \operatorname {\mathrm {SL}}_2(\mathbb {R})$
. As usual, we let ![]() and
and ![]() It is well known that
It is well known that
![]() $\operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
is generated by
$\operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
is generated by
![]() $\widetilde {T}$
and
$\widetilde {T}$
and
![]() $\widetilde {S}$
, (see [Reference Bruinier6, p.16]) and its center is generated by
$\widetilde {S}$
, (see [Reference Bruinier6, p.16]) and its center is generated by
 $$\begin{align*}\widetilde{-I} = \widetilde{S}^2 = (\widetilde{S} \widetilde{T})^3 = \left(\begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}, i \right). \end{align*}$$
$$\begin{align*}\widetilde{-I} = \widetilde{S}^2 = (\widetilde{S} \widetilde{T})^3 = \left(\begin{pmatrix}-1 & 0 \\ 0 & -1\end{pmatrix}, i \right). \end{align*}$$
Moreover, we let ![]() , representing the metaplectic stabilizer for the cusp at infinity.
, representing the metaplectic stabilizer for the cusp at infinity.
We recall the Weil representation,Footnote 1 the unitary representation
![]() $\rho : \operatorname {\mathrm {Mp}}_2(\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {C})$
defined by
$\rho : \operatorname {\mathrm {Mp}}_2(\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {C})$
defined by

We note that
![]() $\rho (\widetilde {-I}) = \rho (\widetilde {S}^2) = -i I$
. We let
$\rho (\widetilde {-I}) = \rho (\widetilde {S}^2) = -i I$
. We let
![]() $\rho ^* : \operatorname {\mathrm {Mp}}_2(\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {C})$
be the dual representation of
$\rho ^* : \operatorname {\mathrm {Mp}}_2(\mathbb {Z}) \to \operatorname {\mathrm {GL}}_2(\mathbb {C})$
be the dual representation of
![]() $\rho $
$\rho $
We recall an explicit formula for
![]() $\rho (\widetilde {\gamma })$
, which is easily derived from work of both Shintani [Reference Shintani29, Proposition 1.6] and Bruinier [Reference Bruinier6, Proposition 1.1], where for odd integers d, we let
$\rho (\widetilde {\gamma })$
, which is easily derived from work of both Shintani [Reference Shintani29, Proposition 1.6] and Bruinier [Reference Bruinier6, Proposition 1.1], where for odd integers d, we let

Proposition 3.1. For
![]() $c \ge 0$
, we have
$c \ge 0$
, we have
 $$ \begin{align*} \rho(\widetilde{\gamma}) = \begin{cases} \displaystyle{\frac{\epsilon_c}{1+i} \left(\frac{a}{c}\right) \begin{pmatrix}1 & i^{cd} \\ i^{ac} & -i^{(a+d)c}\end{pmatrix}} &\text{if } c \equiv 1\quad \pmod{2},\\ \displaystyle{\epsilon_a^{-1} \left(\frac{c}{a}\right) \begin{pmatrix}0 & i^{ab} \\ 1 & 0\end{pmatrix}} &\text{if } c \equiv 2\quad \pmod{4},\\ \displaystyle{\epsilon_a^{-1} \left(\frac{c}{a}\right) \begin{pmatrix}1 & 0 \\ 0 & i^{ab}\end{pmatrix}} &\text{if } c \equiv 0\quad \pmod{4}. \end{cases} \end{align*} $$
$$ \begin{align*} \rho(\widetilde{\gamma}) = \begin{cases} \displaystyle{\frac{\epsilon_c}{1+i} \left(\frac{a}{c}\right) \begin{pmatrix}1 & i^{cd} \\ i^{ac} & -i^{(a+d)c}\end{pmatrix}} &\text{if } c \equiv 1\quad \pmod{2},\\ \displaystyle{\epsilon_a^{-1} \left(\frac{c}{a}\right) \begin{pmatrix}0 & i^{ab} \\ 1 & 0\end{pmatrix}} &\text{if } c \equiv 2\quad \pmod{4},\\ \displaystyle{\epsilon_a^{-1} \left(\frac{c}{a}\right) \begin{pmatrix}1 & 0 \\ 0 & i^{ab}\end{pmatrix}} &\text{if } c \equiv 0\quad \pmod{4}. \end{cases} \end{align*} $$
We now give the definition of a vector-valued modular form that transforms under the Weil representation. If
![]() $k \in \frac {1}{2} \mathbb {Z}$
and
$k \in \frac {1}{2} \mathbb {Z}$
and
![]() $f: \mathbb {H} \to \mathbb {C}^2$
. For
$f: \mathbb {H} \to \mathbb {C}^2$
. For
![]() $(\gamma , \phi (\tau )) \in \operatorname {\mathrm {Mp}}_2(\mathbb {Z}),$
then we define the slash operator
$(\gamma , \phi (\tau )) \in \operatorname {\mathrm {Mp}}_2(\mathbb {Z}),$
then we define the slash operator
We say that
![]() $f: \mathbb {H} \to \mathbb {C}^2$
is a weight k (vector-valued) modular form with respect to
$f: \mathbb {H} \to \mathbb {C}^2$
is a weight k (vector-valued) modular form with respect to
![]() $\rho $
if
$\rho $
if
for every
![]() $(\gamma , \phi ) \in \operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
. We define them for
$(\gamma , \phi ) \in \operatorname {\mathrm {Mp}}_2(\mathbb {Z})$
. We define them for
![]() $\rho ^*$
in a similar manner.
$\rho ^*$
in a similar manner.
3.2 Jacobi’s theta functions
For later use, we recall the Jacobi theta functions (for example, see [Reference Eichler and Zagier13, Section 5]) in this context. If we set ![]() , where
, where ![]() we have
we have

and ![]() The specialization
The specialization
![]() $\Theta (\tau , 0)$
is a weight 1/2 vector-valued modular form with respect to
$\Theta (\tau , 0)$
is a weight 1/2 vector-valued modular form with respect to
![]() $\rho $
, and in general is a (vector-valued) Jacobi form, which for
$\rho $
, and in general is a (vector-valued) Jacobi form, which for
![]() $(\gamma , \phi )\in \operatorname {\mathrm {Mp}}_2(\mathbb {Z}),$
in this case, means that
$(\gamma , \phi )\in \operatorname {\mathrm {Mp}}_2(\mathbb {Z}),$
in this case, means that

4 Maass–Poincaré series and traces of singular moduli
The proof of Theorem 1.4 relies on Maass–Poincaré series that transform with respect to the Weil representation. We construct these series following [Reference Bruinier6], and we relate them to traces of singular moduli. The goal of this section, Theorem 4.5, can be immediately derived as a special case of Alfes’ result [Reference Alfes1, Theorem 4.3], which applies the Kudla–Millson theta lift ([Reference Bruinier and Funke7]) to integer weight Poincaré series. However, we will also provide a direct proof that requires minimal advanced prior knowledge below.
4.1 The Whittaker functions
Let
![]() $M_{\mu , \nu }(z)$
and
$M_{\mu , \nu }(z)$
and
![]() $W_{\mu , \nu }(z)$
be the Whittaker functions (for example, see [Reference Whittaker and Watson30, Ch. 16] and [Reference Magnus, Oberhettinger and Soni17, 24]). The next two lemmas are crucial for constructing Maass–Poincaré series.
$W_{\mu , \nu }(z)$
be the Whittaker functions (for example, see [Reference Whittaker and Watson30, Ch. 16] and [Reference Magnus, Oberhettinger and Soni17, 24]). The next two lemmas are crucial for constructing Maass–Poincaré series.
Lemma 4.1 [Reference Magnus, Oberhettinger and Soni17, 7.2.1], [24, 13.15.19].
For positive integers
![]() $n,$
we have
$n,$
we have
 $$\begin{align*}\frac{\mathrm{d}^n}{\mathrm{d} z^n} \left(e^{-z/2} z^{-\nu-1/2} M_{\mu, \nu}(z) \right) = (-1)^n \frac{(\mu + \nu + 1/2)^{\overline{n}}}{(2\nu+1)^{\overline{n}}} e^{-z/2} z^{-\nu - n/2-1/2} M_{\mu+n/2, \nu+n/2}(z). \end{align*}$$
$$\begin{align*}\frac{\mathrm{d}^n}{\mathrm{d} z^n} \left(e^{-z/2} z^{-\nu-1/2} M_{\mu, \nu}(z) \right) = (-1)^n \frac{(\mu + \nu + 1/2)^{\overline{n}}}{(2\nu+1)^{\overline{n}}} e^{-z/2} z^{-\nu - n/2-1/2} M_{\mu+n/2, \nu+n/2}(z). \end{align*}$$
Lemma 4.2 [Reference Magnus, Oberhettinger and Soni17, 7.5.1], [24, 13.23.1].
For
![]() $\operatorname {\mathrm {Re}}(\nu + \alpha + 1/2)> 0$
and
$\operatorname {\mathrm {Re}}(\nu + \alpha + 1/2)> 0$
and
![]() $2\operatorname {\mathrm {Re}}(z)> \beta > 0$
, we have
$2\operatorname {\mathrm {Re}}(z)> \beta > 0$
, we have
 $$ \begin{align*} \int_0^\infty e^{-zt} t^{\alpha-1} M_{\mu, \nu}(\beta t) \mathrm{d} t &= \frac{\beta^{\nu+1/2} \Gamma\left(\nu+\alpha+\frac{1}{2}\right)}{\left(z+\frac{\beta}{2}\right)^{\nu+\alpha+1/2}}\cdot {}_2F_1 \left(\nu-\mu+\frac{1}{2}, \nu+\alpha+\frac{1}{2}; 2\nu+1; \frac{2\beta}{\beta+2z}\right), \end{align*} $$
$$ \begin{align*} \int_0^\infty e^{-zt} t^{\alpha-1} M_{\mu, \nu}(\beta t) \mathrm{d} t &= \frac{\beta^{\nu+1/2} \Gamma\left(\nu+\alpha+\frac{1}{2}\right)}{\left(z+\frac{\beta}{2}\right)^{\nu+\alpha+1/2}}\cdot {}_2F_1 \left(\nu-\mu+\frac{1}{2}, \nu+\alpha+\frac{1}{2}; 2\nu+1; \frac{2\beta}{\beta+2z}\right), \end{align*} $$
where
![]() ${}_2F_1(a,b; c; z)$
is the Gaussian hypergeometric function.
${}_2F_1(a,b; c; z)$
is the Gaussian hypergeometric function.
For
![]() $n \in \mathbb {Z}$
,
$n \in \mathbb {Z}$
,
![]() $k \in \frac {1}{2} \mathbb {Z}$
,
$k \in \frac {1}{2} \mathbb {Z}$
,
![]() $y> 0$
, and
$y> 0$
, and
![]() $s \in \mathbb {C}$
, we define the modified Whittaker functions
$s \in \mathbb {C}$
, we define the modified Whittaker functions


The special values of these functions at
![]() $s = k/2$
play a crucial role in the construction of the Maass–Poincaré series. To this end, for
$s = k/2$
play a crucial role in the construction of the Maass–Poincaré series. To this end, for
![]() $n < 0$
, we have
$n < 0$
, we have
 $$ \begin{align} \mathcal{M}_{k,n} \left(y, \frac{k}{2}\right) &= \Gamma(k)^{-1} e^{-2\pi ny}. \end{align} $$
$$ \begin{align} \mathcal{M}_{k,n} \left(y, \frac{k}{2}\right) &= \Gamma(k)^{-1} e^{-2\pi ny}. \end{align} $$
As for the
![]() $\mathcal {W}$
-function, we have
$\mathcal {W}$
-function, we have
 $$ \begin{align} \mathcal{W}_{k,n} \left(y, \frac{k}{2}\right) = \begin{cases} \Gamma(k)^{-1} n^{k-1} e^{-2\pi ny} &\text{if } n> 0,\\ 0 &\text{if } n \le 0 \end{cases} \end{align} $$
$$ \begin{align} \mathcal{W}_{k,n} \left(y, \frac{k}{2}\right) = \begin{cases} \Gamma(k)^{-1} n^{k-1} e^{-2\pi ny} &\text{if } n> 0,\\ 0 &\text{if } n \le 0 \end{cases} \end{align} $$
(see [Reference Magnus, Oberhettinger and Soni17, 7.2.4]). Moreover, we note that, ([Reference Magnus, Oberhettinger and Soni17, 7.6.1], [24, 13.14]),
 $$ \begin{align} \begin{split} W_{\mu, \nu}(y) &\sim e^{-y/2} y^\mu \quad (y \to \infty),\\ M_{\mu, \nu}(y) &= y^{\nu+1/2} (1+ O(y)) \quad (y \to 0). \end{split} \end{align} $$
$$ \begin{align} \begin{split} W_{\mu, \nu}(y) &\sim e^{-y/2} y^\mu \quad (y \to \infty),\\ M_{\mu, \nu}(y) &= y^{\nu+1/2} (1+ O(y)) \quad (y \to 0). \end{split} \end{align} $$
4.2 Kloosterman sums
The Fourier expansions of the Maass–Poincaré series require Kloosterman sums, which we recall here. For
![]() $k \in \frac {1}{2}\mathbb {Z} \setminus \mathbb {Z}$
,
$k \in \frac {1}{2}\mathbb {Z} \setminus \mathbb {Z}$
,
![]() $m, n \in \mathbb {Z}$
, and
$m, n \in \mathbb {Z}$
, and
![]() $c>0$
with
$c>0$
with
![]() $c \equiv 0\ \pmod {4}$
, we define the half-integral weight Kloosterman sum by
$c \equiv 0\ \pmod {4}$
, we define the half-integral weight Kloosterman sum by

where
![]() $\overline {d} \in \mathbb {Z}/c\mathbb {Z}$
satisfies that
$\overline {d} \in \mathbb {Z}/c\mathbb {Z}$
satisfies that
![]() $d \overline {d} \equiv 1\ \pmod {c}$
. The condition
$d \overline {d} \equiv 1\ \pmod {c}$
. The condition
![]() $d\ (c)^*$
means that d runs over
$d\ (c)^*$
means that d runs over
![]() $d \in \mathbb {Z}/c\mathbb {Z}$
such that
$d \in \mathbb {Z}/c\mathbb {Z}$
such that
![]() $(c,d) = 1$
. We note that the Kloosterman sums satisfy
$(c,d) = 1$
. We note that the Kloosterman sums satisfy
We now relate the Weil representation to such Kloosterman sums. For notational convenience, we let
 $$\begin{align*}\rho(\widetilde{\gamma}) = \begin{pmatrix}\rho(\widetilde{\gamma})_{00} & \rho(\widetilde{\gamma})_{01} \\ \rho(\widetilde{\gamma})_{10} & \rho(\widetilde{\gamma})_{11}\end{pmatrix}. \end{align*}$$
$$\begin{align*}\rho(\widetilde{\gamma}) = \begin{pmatrix}\rho(\widetilde{\gamma})_{00} & \rho(\widetilde{\gamma})_{01} \\ \rho(\widetilde{\gamma})_{10} & \rho(\widetilde{\gamma})_{11}\end{pmatrix}. \end{align*}$$
Then the following sum formula holds for each entry of
![]() $\rho (\widetilde {\gamma })$
.
$\rho (\widetilde {\gamma })$
.
Proposition 4.3. If
![]() $\alpha , \beta \in \{0,1\}$
and m and n satisfy
$\alpha , \beta \in \{0,1\}$
and m and n satisfy
![]() $m \equiv -\alpha\ \pmod {4}$
and
$m \equiv -\alpha\ \pmod {4}$
and
![]() $n \equiv -\beta\ \pmod {4},$
then for every positive integer c, we have
$n \equiv -\beta\ \pmod {4},$
then for every positive integer c, we have
 $$ \begin{align*} \frac{1}{4} \left(1 + \left(\frac{4}{c}\right) \right) K_{3/2}(m,n,4c)= \sum_{d\ (c)^*} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e}\left(\frac{ma + nd}{4c}\right), \end{align*} $$
$$ \begin{align*} \frac{1}{4} \left(1 + \left(\frac{4}{c}\right) \right) K_{3/2}(m,n,4c)= \sum_{d\ (c)^*} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e}\left(\frac{ma + nd}{4c}\right), \end{align*} $$
where we take any
![]() $\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
for which
$\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
for which
![]() $(c,d)$
forms its bottom row.
$(c,d)$
forms its bottom row.
Proof. First, we check that the right-hand side is well defined. Let
![]() $R_{\alpha \beta }(\gamma )$
denote its summand. It suffices to show that
$R_{\alpha \beta }(\gamma )$
denote its summand. It suffices to show that
![]() $R_{\alpha \beta }(T^j \gamma T^l) = R_{\alpha \beta }(\gamma )$
holds for any
$R_{\alpha \beta }(T^j \gamma T^l) = R_{\alpha \beta }(\gamma )$
holds for any
![]() $j, l \in \mathbb {Z}$
. Since
$j, l \in \mathbb {Z}$
. Since
![]() $\widetilde {T^j \gamma T^l} = \widetilde {T}^j \widetilde {\gamma } \widetilde {T}^l$
holds, we have
$\widetilde {T^j \gamma T^l} = \widetilde {T}^j \widetilde {\gamma } \widetilde {T}^l$
holds, we have
 $$\begin{align*}R_{\alpha \beta}(T^j \gamma T^l) = i^{\alpha j + \beta l} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e} \left(\frac{ma+nd}{4c}\right) \mathbf{e} \left(\frac{mj+nl}{4}\right) = R_{\alpha \beta}(\gamma). \end{align*}$$
$$\begin{align*}R_{\alpha \beta}(T^j \gamma T^l) = i^{\alpha j + \beta l} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e} \left(\frac{ma+nd}{4c}\right) \mathbf{e} \left(\frac{mj+nl}{4}\right) = R_{\alpha \beta}(\gamma). \end{align*}$$
Next, for each
![]() $\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
with
$\gamma = \bigl (\begin {smallmatrix}a & b \\ c & d\end {smallmatrix}\bigr ) \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
with
![]() $c> 0$
, we prove the refined equation
$c> 0$
, we prove the refined equation
 $$ \begin{align} \rho(\widetilde{\gamma})_{\alpha \beta} = \frac{1}{4} \left(1 + \left(\frac{4}{c}\right) \right) \sum_{\substack{\delta\ (4c) \\ \delta \equiv d\ (c) \\ \delta \equiv 1\ (2)}} \left(\frac{c}{\delta}\right) \epsilon_{\delta}^{-1} \mathbf{e} \left(\frac{a - \overline{\delta}}{4c}\right)^\alpha \mathbf{e} \left(\frac{d-\delta}{4c}\right)^\beta, \end{align} $$
$$ \begin{align} \rho(\widetilde{\gamma})_{\alpha \beta} = \frac{1}{4} \left(1 + \left(\frac{4}{c}\right) \right) \sum_{\substack{\delta\ (4c) \\ \delta \equiv d\ (c) \\ \delta \equiv 1\ (2)}} \left(\frac{c}{\delta}\right) \epsilon_{\delta}^{-1} \mathbf{e} \left(\frac{a - \overline{\delta}}{4c}\right)^\alpha \mathbf{e} \left(\frac{d-\delta}{4c}\right)^\beta, \end{align} $$
where
![]() $\overline {\delta }$
is the inverse of
$\overline {\delta }$
is the inverse of
![]() $\delta $
in
$\delta $
in
![]() $(\mathbb {Z}/4c\mathbb {Z})^\times $
. This immediately implies the proposition.
$(\mathbb {Z}/4c\mathbb {Z})^\times $
. This immediately implies the proposition.
To confirm (4.8), let ![]() and
and ![]() (
(
![]() $j = 0,1,2,3$
). For simplicity, let
$j = 0,1,2,3$
). For simplicity, let
![]() $\rho "(\gamma )_{\alpha \beta }$
denote the right-hand side of (4.8) and show that
$\rho "(\gamma )_{\alpha \beta }$
denote the right-hand side of (4.8) and show that
![]() $\rho "(\gamma )_{\alpha \beta } = \rho (\widetilde {\gamma })_{\alpha \beta }$
. If
$\rho "(\gamma )_{\alpha \beta } = \rho (\widetilde {\gamma })_{\alpha \beta }$
. If
![]() $\delta $
is odd, then we can easily check that
$\delta $
is odd, then we can easily check that
 $$\begin{align*}\overline{\delta} = \begin{cases} a(1+b_j c) &\text{if } c \equiv 1\quad \pmod{2} \text{ and } a \equiv 1\quad \pmod{2},\\ (a+c)(1+(b_j+d_j)c) &\text{if } c \equiv 1\quad \pmod{2} \text{ and } a \equiv 0\quad \pmod{2},\\ a(1-ab_j cd_j) &\text{if } c \equiv 2\quad \pmod{4},\\ a(1-b_jc) &\text{if } c \equiv 0\quad \pmod{4}. \end{cases} \end{align*}$$
$$\begin{align*}\overline{\delta} = \begin{cases} a(1+b_j c) &\text{if } c \equiv 1\quad \pmod{2} \text{ and } a \equiv 1\quad \pmod{2},\\ (a+c)(1+(b_j+d_j)c) &\text{if } c \equiv 1\quad \pmod{2} \text{ and } a \equiv 0\quad \pmod{2},\\ a(1-ab_j cd_j) &\text{if } c \equiv 2\quad \pmod{4},\\ a(1-b_jc) &\text{if } c \equiv 0\quad \pmod{4}. \end{cases} \end{align*}$$
We prove the case where
![]() $c \equiv 1\ \pmod {2}$
and
$c \equiv 1\ \pmod {2}$
and
![]() $a \equiv 1\ \pmod {2}$
, leaving the others to the reader. We have
$a \equiv 1\ \pmod {2}$
, leaving the others to the reader. We have
 $$ \begin{align*} \rho"(\gamma)_{\alpha \beta} &= \frac{1}{2} \sum_{\substack{0 \le j \le 3 \\ d_j \equiv 1\ (2)}} \left(\frac{c}{d_j}\right) \epsilon_{d_j}^{-1} \mathbf{e} \left(\frac{-ab_j}{4}\right)^\alpha \mathbf{e} \left(\frac{-j}{4}\right)^\beta = \frac{i^{-ab \alpha}}{2} \left(\frac{d}{c}\right) \sum_{\substack{0 \le j \le 3 \\ d_j \equiv 1\ (2)}} (-1)^{\frac{(c-1)(d_j-1)}{4}} \epsilon_{d_j}^{-1} i^{-j(\alpha+\beta)}. \end{align*} $$
$$ \begin{align*} \rho"(\gamma)_{\alpha \beta} &= \frac{1}{2} \sum_{\substack{0 \le j \le 3 \\ d_j \equiv 1\ (2)}} \left(\frac{c}{d_j}\right) \epsilon_{d_j}^{-1} \mathbf{e} \left(\frac{-ab_j}{4}\right)^\alpha \mathbf{e} \left(\frac{-j}{4}\right)^\beta = \frac{i^{-ab \alpha}}{2} \left(\frac{d}{c}\right) \sum_{\substack{0 \le j \le 3 \\ d_j \equiv 1\ (2)}} (-1)^{\frac{(c-1)(d_j-1)}{4}} \epsilon_{d_j}^{-1} i^{-j(\alpha+\beta)}. \end{align*} $$
Since the value of the sum depends only on
![]() $c, d\ \pmod {4}$
, a direct calculation yields
$c, d\ \pmod {4}$
, a direct calculation yields
 $$\begin{align*}\rho"(\gamma)_{\alpha \beta} = \frac{i^{-ab \alpha}}{2} \left(\frac{d}{c}\right) \frac{2\epsilon_c}{1+i} \times \begin{cases} 1 &\text{if } (\alpha, \beta) = (0,0),\\ i^{cd} &\text{if } (\alpha, \beta) = (0,1), (1,0),\\ (-1)^{d-1} &\text{if } (\alpha, \beta) = (1,1). \end{cases} \end{align*}$$
$$\begin{align*}\rho"(\gamma)_{\alpha \beta} = \frac{i^{-ab \alpha}}{2} \left(\frac{d}{c}\right) \frac{2\epsilon_c}{1+i} \times \begin{cases} 1 &\text{if } (\alpha, \beta) = (0,0),\\ i^{cd} &\text{if } (\alpha, \beta) = (0,1), (1,0),\\ (-1)^{d-1} &\text{if } (\alpha, \beta) = (1,1). \end{cases} \end{align*}$$
Combining simple calculations with Proposition 3.1, one obtains
![]() $\rho (\widetilde {\gamma })_{\alpha \beta }$
.
$\rho (\widetilde {\gamma })_{\alpha \beta }$
.
4.3 The Maass–Poincaré series
Using the two previous subsections, we now construct the Maass–Poincaré series. We let ![]() and
and ![]() . Assume that
. Assume that
![]() $k \in \frac {1}{2} \mathbb {Z}$
satisfies
$k \in \frac {1}{2} \mathbb {Z}$
satisfies
![]() $2k \equiv 3\ \pmod {4}$
. For
$2k \equiv 3\ \pmod {4}$
. For
![]() $\alpha \in \{0, 1\}$
and
$\alpha \in \{0, 1\}$
and
![]() $m \equiv -\alpha\ \pmod {4}$
, we define the Maass–Poincaré series of weight k with respect to
$m \equiv -\alpha\ \pmod {4}$
, we define the Maass–Poincaré series of weight k with respect to
![]() $\rho ^*$
by
$\rho ^*$
by

This series converges absolutely and uniformly on compact subsets in
![]() $\operatorname {\mathrm {Re}}(s)> 1$
[Reference Bruinier6, p.29], and we note that
$\operatorname {\mathrm {Re}}(s)> 1$
[Reference Bruinier6, p.29], and we note that ![]() is invariant under
is invariant under
![]() $|_{k,\rho ^*} (\gamma , \phi )$
for any
$|_{k,\rho ^*} (\gamma , \phi )$
for any
![]() $(\gamma , \phi ) \in \widetilde {\Gamma }_\infty $
as
$(\gamma , \phi ) \in \widetilde {\Gamma }_\infty $
as
![]() $2k \equiv 3\ \pmod {4}$
.
$2k \equiv 3\ \pmod {4}$
.
The Fourier expansions of the functions involve the Bessel functions (see [Reference Magnus, Oberhettinger and Soni17, Ch. 3] and [Reference Whittaker and Watson30, Ch. 17])

Proposition 4.4. For
![]() $\operatorname {\mathrm {Re}}(s)> 1$
, we have
$\operatorname {\mathrm {Re}}(s)> 1$
, we have

where
 $$ \begin{align*} b_{m,k}^{(\beta)}(n, s) &= 2\pi i^{-k} \sum_{c> 0} \left(1+\left(\frac{4}{c}\right)\right) \frac{K_{3/2}(m,n,4c)}{4c}\\ &\qquad \qquad \times \begin{cases} \displaystyle{|mn|^{\frac{1-k}{2}} J_{2s-1} \left(\frac{\pi \sqrt{|mn|}}{c}\right)} &\text{if } mn > 0,\\ \displaystyle{|mn|^{\frac{1-k}{2}} I_{2s-1} \left(\frac{\pi \sqrt{|mn|}}{c}\right)} &\text{if } mn < 0,\\ \displaystyle{2^{k-1} \pi^{s+k/2-1} |m+n|^{s-k/2} (4c)^{1-2s}} &\text{if } mn=0, m+n \neq 0,\\ \displaystyle{2^{2k-2} \pi^{k-1} \Gamma(2s) (8c)^{1-2s}} &\text{if } m = n = 0. \end{cases} \end{align*} $$
$$ \begin{align*} b_{m,k}^{(\beta)}(n, s) &= 2\pi i^{-k} \sum_{c> 0} \left(1+\left(\frac{4}{c}\right)\right) \frac{K_{3/2}(m,n,4c)}{4c}\\ &\qquad \qquad \times \begin{cases} \displaystyle{|mn|^{\frac{1-k}{2}} J_{2s-1} \left(\frac{\pi \sqrt{|mn|}}{c}\right)} &\text{if } mn > 0,\\ \displaystyle{|mn|^{\frac{1-k}{2}} I_{2s-1} \left(\frac{\pi \sqrt{|mn|}}{c}\right)} &\text{if } mn < 0,\\ \displaystyle{2^{k-1} \pi^{s+k/2-1} |m+n|^{s-k/2} (4c)^{1-2s}} &\text{if } mn=0, m+n \neq 0,\\ \displaystyle{2^{2k-2} \pi^{k-1} \Gamma(2s) (8c)^{1-2s}} &\text{if } m = n = 0. \end{cases} \end{align*} $$
Proof. Dividing the sum of the Poincaré series into the identity class and the remaining part, we have

Let
![]() $H_{k, \rho ^*}^{(\alpha , m)}(\tau , s)$
denote the sum of the second term. By following the exact same argument as in the proof of Theorem 1.9 in Bruinier’s book [Reference Bruinier6], we obtain the Fourier expansion,
$H_{k, \rho ^*}^{(\alpha , m)}(\tau , s)$
denote the sum of the second term. By following the exact same argument as in the proof of Theorem 1.9 in Bruinier’s book [Reference Bruinier6], we obtain the Fourier expansion,
 $$\begin{align*}H_{k,\rho^*}^{(\alpha, m)}(\tau,s) = \sum_{\beta \in \{0,1\}} \sum_{n \in \mathbb{Z}} \left( \sum_{c> 0} \sum_{d \in (\mathbb{Z}/c\mathbb{Z})^\times} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e}\left(\frac{ma+nd}{4c}\right) I_m(n) \right) \mathbf{e} \left(\frac{nu}{4}\right) \mathfrak{e}_\beta, \end{align*}$$
$$\begin{align*}H_{k,\rho^*}^{(\alpha, m)}(\tau,s) = \sum_{\beta \in \{0,1\}} \sum_{n \in \mathbb{Z}} \left( \sum_{c> 0} \sum_{d \in (\mathbb{Z}/c\mathbb{Z})^\times} \rho(\widetilde{\gamma})_{\alpha \beta} \mathbf{e}\left(\frac{ma+nd}{4c}\right) I_m(n) \right) \mathbf{e} \left(\frac{nu}{4}\right) \mathfrak{e}_\beta, \end{align*}$$
where
![]() $I_m(n)$
is given by
$I_m(n)$
is given by

By combining this with Proposition 4.3, we obtain Proposition 4.4.
4.4 Traces of singular moduli
The coefficients of these functions are related to traces of singular moduli, as shown in several previous works (for example, see [Reference Bringmann and Ono5, Reference Bruinier, Jenkins and Ono8, Reference Duke, Imamoḡlu and Tóth12]). To make this precise, we consider weight 3/2 modular forms h on
![]() $\Gamma _0(4)$
satisfying
$\Gamma _0(4)$
satisfying
We define ![]() for
for
![]() $i \in \{0, 1\}$
, and then we have that
$i \in \{0, 1\}$
, and then we have that

is a weight 3/2 vector-valued modular form with respect to
![]() $\rho ^*$
(see [Reference Eichler and Zagier13, Section 5] and [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 2]).
$\rho ^*$
(see [Reference Eichler and Zagier13, Section 5] and [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 2]).
We relate the
![]() $g_m(\tau )$
in (2.6) and
$g_m(\tau )$
in (2.6) and ![]() to the Maass–Poincaré expressions
to the Maass–Poincaré expressions

where
![]() $\alpha \equiv n^2\ \pmod {4}$
for each n. To be precise, we have the following theorem.
$\alpha \equiv n^2\ \pmod {4}$
for each n. To be precise, we have the following theorem.
Theorem 4.5. If m is a nonnegative integer, then we have
 $$\begin{align*}\lim_{s \to 3/4} G_m(\tau, s) = \begin{pmatrix}g_{m,0}(\tau) \\ g_{m,1}(\tau)\end{pmatrix}. \end{align*}$$
$$\begin{align*}\lim_{s \to 3/4} G_m(\tau, s) = \begin{pmatrix}g_{m,0}(\tau) \\ g_{m,1}(\tau)\end{pmatrix}. \end{align*}$$
Remark. We note that the case of
![]() $m=0$
was stated by Williams [Reference Williams31, Example 5.1].
$m=0$
was stated by Williams [Reference Williams31, Example 5.1].
Sketch of the Proof. This result is standard, and so we sketch the proof. We first recall facts about Niebur–Poincaré series
![]() $F_m(\tau , s)$
(see [Reference Niebur23] or [Reference Duke, Imamoḡlu and Tóth12, Section 4]), which are defined for
$F_m(\tau , s)$
(see [Reference Niebur23] or [Reference Duke, Imamoḡlu and Tóth12, Section 4]), which are defined for
![]() $\operatorname {\mathrm {Re}}(s)> 1,$
and give alternative expressions for the
$\operatorname {\mathrm {Re}}(s)> 1,$
and give alternative expressions for the
![]() $j_m(\tau )$
. Specifically, as described in [Reference Duke, Imamoḡlu and Tóth12, (4.10)], it is known that
$j_m(\tau )$
. Specifically, as described in [Reference Duke, Imamoḡlu and Tóth12, (4.10)], it is known that
and
For nonnegative integers m, the trace functions

have a direct connection to the coefficients of the earlier Maass–Poincaré series. Indeed, by combining the result of Duke, Imamoḡlu and Tóth in [Reference Duke, Imamoḡlu and Tóth12, Proposition 4] with our Proposition 4.4, for
![]() $\operatorname {\mathrm {Re}}(s)> 1$
,
$\operatorname {\mathrm {Re}}(s)> 1$
,
![]() $m \ge 0$
, and
$m \ge 0$
, and
![]() $d> 0$
with
$d> 0$
with
![]() $d \equiv 0, 3\ \pmod {4}$
, we obtain that
$d \equiv 0, 3\ \pmod {4}$
, we obtain that
 $$\begin{align*}\mathrm{Tr}_d(F_{-m}(\cdot, s)) = \begin{cases} \displaystyle{- d^{1/2} \sum_{n|m} n b_{-n^2, 3/2}^{(\beta)} \left(d, \frac{s}{2} + \frac{1}{4}\right)} &\text{if } m> 0,\\ \displaystyle{-2^{s-2} \pi^{-s/2-1} d^{1/2} \zeta(s) b_{0, 3/2}^{(\beta)} \left(d, \frac{s}{2} + \frac{1}{4}\right)} &\text{if } m = 0. \end{cases} \end{align*}$$
$$\begin{align*}\mathrm{Tr}_d(F_{-m}(\cdot, s)) = \begin{cases} \displaystyle{- d^{1/2} \sum_{n|m} n b_{-n^2, 3/2}^{(\beta)} \left(d, \frac{s}{2} + \frac{1}{4}\right)} &\text{if } m> 0,\\ \displaystyle{-2^{s-2} \pi^{-s/2-1} d^{1/2} \zeta(s) b_{0, 3/2}^{(\beta)} \left(d, \frac{s}{2} + \frac{1}{4}\right)} &\text{if } m = 0. \end{cases} \end{align*}$$
Therefore, (4.13) implies that
 $$ \begin{align} \mathbf{t}_m(d) = \lim_{s \to 3/4} \begin{cases} \displaystyle{- d^{1/2} \sum_{n|m} n b_{-n^2, 3/2}^{(\beta)} (d, s) + \frac{4d^{1/2}}{\sqrt{\pi}} \sigma_1(m) b_{0, 3/2}^{(\beta)}(d,s)} &\text{if } m> 0,\\ \displaystyle{- \frac{d^{1/2}}{6 \sqrt{\pi}} b_{0, 3/2}^{(\beta)} (d, s)} &\text{if } m = 0. \end{cases} \end{align} $$
$$ \begin{align} \mathbf{t}_m(d) = \lim_{s \to 3/4} \begin{cases} \displaystyle{- d^{1/2} \sum_{n|m} n b_{-n^2, 3/2}^{(\beta)} (d, s) + \frac{4d^{1/2}}{\sqrt{\pi}} \sigma_1(m) b_{0, 3/2}^{(\beta)}(d,s)} &\text{if } m> 0,\\ \displaystyle{- \frac{d^{1/2}}{6 \sqrt{\pi}} b_{0, 3/2}^{(\beta)} (d, s)} &\text{if } m = 0. \end{cases} \end{align} $$
By applying (4.3) and (4.4), we thereby conclude the proof of the theorem.
Remark. We note that subtle technicalities arise in the proof of Theorem 4.5, which have been addressed in the aforementioned works but deserve commentary. The
![]() $G_m(\tau , s)$
are defined for
$G_m(\tau , s)$
are defined for
![]() $\operatorname {\mathrm {Re}}(s)> 1$
, where they enjoy the Fourier series expansion in Proposition 4.4. As we can only be analytically continued up to
$\operatorname {\mathrm {Re}}(s)> 1$
, where they enjoy the Fourier series expansion in Proposition 4.4. As we can only be analytically continued up to
![]() $\operatorname {\mathrm {Re}}(s)> 3/4$
, care is required when letting
$\operatorname {\mathrm {Re}}(s)> 3/4$
, care is required when letting
![]() $s \to 3/4$
. In fact, the Fourier coefficients
$s \to 3/4$
. In fact, the Fourier coefficients
![]() $b_{-m^2, 3/2}^{(\beta )}(-n^2, s)$
have a simple pole at
$b_{-m^2, 3/2}^{(\beta )}(-n^2, s)$
have a simple pole at
![]() $s = 3/4$
, which cancels out with a zero from
$s = 3/4$
, which cancels out with a zero from ![]() , (for example, see [Reference Duke, Imamoḡlu and Tóth12, Lemma 3]). This issue is addressed by examining the growth of the Fourier coefficients of
, (for example, see [Reference Duke, Imamoḡlu and Tóth12, Lemma 3]). This issue is addressed by examining the growth of the Fourier coefficients of
![]() $G_m(\tau , s)$
, including
$G_m(\tau , s)$
, including
![]() $\mathrm {Tr}_d(F_{-m}(\cdot , s))$
, as
$\mathrm {Tr}_d(F_{-m}(\cdot , s))$
, as
![]() $d \to \infty $
and the behavior as
$d \to \infty $
and the behavior as
![]() $s \to 3/4$
. We refer the reader to [Reference Bruinier, Jenkins and Ono8, Reference Duke11, Reference Duke, Imamoḡlu and Tóth12] for these details.
$s \to 3/4$
. We refer the reader to [Reference Bruinier, Jenkins and Ono8, Reference Duke11, Reference Duke, Imamoḡlu and Tóth12] for these details.
5 Proof of Theorem 1.4
We have constructed the Poincaré series
![]() $G_m(\tau , s)$
whose Fourier coefficients give the traces of singular moduli. We turn to the problem of providing the Hecke decomposition of
$G_m(\tau , s)$
whose Fourier coefficients give the traces of singular moduli. We turn to the problem of providing the Hecke decomposition of
![]() $\mathcal {G}_{m,\nu }(\tau )$
. Specifically, we compute the Petersson inner product
$\mathcal {G}_{m,\nu }(\tau )$
. Specifically, we compute the Petersson inner product
![]() $\langle \mathcal {G}_{m,\nu }, f \rangle $
with a normalized Hecke eigenform f of
$\langle \mathcal {G}_{m,\nu }, f \rangle $
with a normalized Hecke eigenform f of
![]() $S_{2\nu +2}$
. We first recall useful facts about Jacobi forms to relate the Rankin–Cohen brackets to these Poincaré series.
$S_{2\nu +2}$
. We first recall useful facts about Jacobi forms to relate the Rankin–Cohen brackets to these Poincaré series.
5.1 Jacobi forms and the modified heat operator
For a function
![]() $\varphi : \mathbb {H} \times \mathbb {C} \to \mathbb {C}$
,
$\varphi : \mathbb {H} \times \mathbb {C} \to \mathbb {C}$
,
![]() $\gamma \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
, and positive integers
$\gamma \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
, and positive integers
![]() $k, m \in \mathbb {Z}_{>0}$
, we define the slash operator
$k, m \in \mathbb {Z}_{>0}$
, we define the slash operator

and the weighted heat operator

where ![]() . Then, we have
. Then, we have
for any
![]() $\gamma \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
(see [Reference Eichler and Zagier13, (11) in Section 3]). For simplicity, we put
$\gamma \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
(see [Reference Eichler and Zagier13, (11) in Section 3]). For simplicity, we put ![]() .
.
Lemma 5.1. For a Poincaré series defined by
 $$\begin{align*}G(\tau) = \sum_{(\gamma, \phi) \in \widetilde{\Gamma}_\infty \backslash \operatorname{\mathrm{Mp}}_2(\mathbb{Z})} \begin{pmatrix}\psi_0(\tau) \\ \psi_1(\tau)\end{pmatrix} \bigg|_{3/2, \rho^*} (\gamma, \phi), \end{align*}$$
$$\begin{align*}G(\tau) = \sum_{(\gamma, \phi) \in \widetilde{\Gamma}_\infty \backslash \operatorname{\mathrm{Mp}}_2(\mathbb{Z})} \begin{pmatrix}\psi_0(\tau) \\ \psi_1(\tau)\end{pmatrix} \bigg|_{3/2, \rho^*} (\gamma, \phi), \end{align*}$$
with test functions
![]() $\psi _0, \psi _1: \mathbb {H} \to \mathbb {C}$
, we have
$\psi _0, \psi _1: \mathbb {H} \to \mathbb {C}$
, we have
 $$\begin{align*}{}^t \Theta(\tau, z) G(\tau) = \sum_{\gamma \in \Gamma_\infty \backslash \Gamma} (\theta_0(\tau, z) \psi_0(\tau) + \theta_1(\tau, z) \psi_1(\tau)) |_{2,1} \gamma. \end{align*}$$
$$\begin{align*}{}^t \Theta(\tau, z) G(\tau) = \sum_{\gamma \in \Gamma_\infty \backslash \Gamma} (\theta_0(\tau, z) \psi_0(\tau) + \theta_1(\tau, z) \psi_1(\tau)) |_{2,1} \gamma. \end{align*}$$
Proof. By a direct calculation with (3.4), we have
 $$ \begin{align*} {}^t \Theta(\tau, z) G(\tau) = \sum_{(\gamma, \phi) \in \widetilde{\Gamma}_\infty \backslash \operatorname{\mathrm{Mp}}_2(\mathbb{Z})} \phi(\tau)^{-4} \mathbf{e} \left(\frac{-cz^2}{c\tau+d}\right) {}^t \Theta\left(\gamma \tau, \frac{z}{c\tau+d}\right) {}^t \rho((\gamma, \phi))^{-1} \rho^*((\gamma, \phi))^{-1} \begin{pmatrix}\psi_0(\gamma\tau) \\ \psi_1(\gamma \tau)\end{pmatrix}. \end{align*} $$
$$ \begin{align*} {}^t \Theta(\tau, z) G(\tau) = \sum_{(\gamma, \phi) \in \widetilde{\Gamma}_\infty \backslash \operatorname{\mathrm{Mp}}_2(\mathbb{Z})} \phi(\tau)^{-4} \mathbf{e} \left(\frac{-cz^2}{c\tau+d}\right) {}^t \Theta\left(\gamma \tau, \frac{z}{c\tau+d}\right) {}^t \rho((\gamma, \phi))^{-1} \rho^*((\gamma, \phi))^{-1} \begin{pmatrix}\psi_0(\gamma\tau) \\ \psi_1(\gamma \tau)\end{pmatrix}. \end{align*} $$
Since
![]() ${}^t \rho ((\gamma , \phi ))^{-1} \rho ^*((\gamma , \phi ))^{-1} = I$
and
${}^t \rho ((\gamma , \phi ))^{-1} \rho ^*((\gamma , \phi ))^{-1} = I$
and
![]() $\phi (\tau )^{-4} = (c\tau +d)^{-2}$
, we obtain the result.
$\phi (\tau )^{-4} = (c\tau +d)^{-2}$
, we obtain the result.
We require the following proposition for the
![]() $p_k(r,n)$
in the Eichler–Selberg trace formula.
$p_k(r,n)$
in the Eichler–Selberg trace formula.
Proposition 5.2. For
![]() $\nu , l \in \mathbb {Z}_{\ge 0}$
and
$\nu , l \in \mathbb {Z}_{\ge 0}$
and
![]() $r \in \mathbb {Z}$
, we define the differential operator by
$r \in \mathbb {Z}$
, we define the differential operator by

Then, for a function
![]() $: \mathbb {H} \to \mathbb {C}$
, we have the Taylor expansion
$: \mathbb {H} \to \mathbb {C}$
, we have the Taylor expansion
 $$\begin{align*}L_{2\nu} \circ \cdots \circ L_2 f(\tau)(\zeta^r + \zeta^{-r}) = 2 \sum_{l=0}^\infty p_{2\nu+2}(r,D,l) f(\tau) \frac{(2\pi irz)^{2l}}{(2l)!}. \end{align*}$$
$$\begin{align*}L_{2\nu} \circ \cdots \circ L_2 f(\tau)(\zeta^r + \zeta^{-r}) = 2 \sum_{l=0}^\infty p_{2\nu+2}(r,D,l) f(\tau) \frac{(2\pi irz)^{2l}}{(2l)!}. \end{align*}$$
In particular, letting
![]() $p_k(r,n)$
as in (1.4), we have that
$p_k(r,n)$
as in (1.4), we have that
![]() $p_{2\nu +2}(r,D,0) = p_{2\nu +2}(r,D)$
and
$p_{2\nu +2}(r,D,0) = p_{2\nu +2}(r,D)$
and
Proof. We check that the Taylor coefficients of
![]() $L_{2\nu } \circ \cdots \circ L_2 f(\tau ) (\zeta ^r + \zeta ^{-r})$
and the sequence (5.2) satisfy the same recursion. The claim is clear for
$L_{2\nu } \circ \cdots \circ L_2 f(\tau ) (\zeta ^r + \zeta ^{-r})$
and the sequence (5.2) satisfy the same recursion. The claim is clear for
![]() $\nu = 0$
. For
$\nu = 0$
. For
![]() $\nu> 0$
, let
$\nu> 0$
, let

Then
![]() $S_{\nu , l, j}$
satisfies the recursion
$S_{\nu , l, j}$
satisfies the recursion
 $$\begin{align*}S_{\nu, l, j} = -D S_{\nu-1, l, j-1} + \frac{r^2}{4} \left(1 + \frac{4\nu-1}{2l+1}\right) S_{\nu-1, l+1, j}, \end{align*}$$
$$\begin{align*}S_{\nu, l, j} = -D S_{\nu-1, l, j-1} + \frac{r^2}{4} \left(1 + \frac{4\nu-1}{2l+1}\right) S_{\nu-1, l+1, j}, \end{align*}$$
for
![]() $\nu \ge 1$
and
$\nu \ge 1$
and
![]() $0 \le j \le \nu $
with
$0 \le j \le \nu $
with
![]() $S_{\nu , l, -1} = 0$
, which implies that
$S_{\nu , l, -1} = 0$
, which implies that
 $$\begin{align*}p_{2\nu+2}(r,D,l) = -D p_{2\nu}(r,D,l) + \frac{r^2}{4} \left(1 + \frac{4\nu-1}{2l+1}\right) p_{2\nu} (r,D,l+1). \end{align*}$$
$$\begin{align*}p_{2\nu+2}(r,D,l) = -D p_{2\nu}(r,D,l) + \frac{r^2}{4} \left(1 + \frac{4\nu-1}{2l+1}\right) p_{2\nu} (r,D,l+1). \end{align*}$$
One can check that the Taylor coefficients also satisfy this recursion.
We use this proposition to understand the combinatorial properties of the Rankin–Cohen bracket operators, which is a slight generalization of [Reference Eichler and Zagier13, Theorem 5.5].
Proposition 5.3. Let
![]() $\nu \ge 0$
be a nonnegative integer. For a modular form h of weight
$\nu \ge 0$
be a nonnegative integer. For a modular form h of weight
![]() $3/2$
on
$3/2$
on
![]() $\Gamma _0(4)$
of the form (4.10), we have
$\Gamma _0(4)$
of the form (4.10), we have

Proof. By definition, we have

A direct calculation implies that

and
 $$ \begin{align*} \sum_{\substack{r, s \ge 0\\ r+s = \nu}} (-1)^r \frac{\Gamma(3/2+\nu) \Gamma(1/2+\nu)}{s! \Gamma(3/2+r) r! \Gamma(1/2+s)} m^{2s} (4D-m^2)^r = \binom{2\nu}{\nu} p_{2\nu+2}(m,D). \end{align*} $$
$$ \begin{align*} \sum_{\substack{r, s \ge 0\\ r+s = \nu}} (-1)^r \frac{\Gamma(3/2+\nu) \Gamma(1/2+\nu)}{s! \Gamma(3/2+r) r! \Gamma(1/2+s)} m^{2s} (4D-m^2)^r = \binom{2\nu}{\nu} p_{2\nu+2}(m,D). \end{align*} $$
The last equation immediately follows from Proposition 5.2.
For each
![]() $n \ge 0$
and
$n \ge 0$
and
![]() $\nu \ge 0$
, we define
$\nu \ge 0$
, we define
Combining Theorem 4.5 and Lemma 5.3, for
![]() $m\geq 1,$
we obtain the following key expressions:
$m\geq 1,$
we obtain the following key expressions:
 $$ \begin{align} \mathcal{G}_{m,\nu}(\tau) = -\frac{1}{2\binom{2\nu}{\nu}} \cdot [g_m, \theta]_\nu |U_4 = -\frac{1}{2} \lim_{s \to 3/4} \left( -\frac{\sqrt{\pi}}{2} \sum_{n \mid m} n \Phi_{n, \nu}(\tau, s) + 2\sigma_1(m) \Phi_{0,\nu}(\tau, s)\right). \end{align} $$
$$ \begin{align} \mathcal{G}_{m,\nu}(\tau) = -\frac{1}{2\binom{2\nu}{\nu}} \cdot [g_m, \theta]_\nu |U_4 = -\frac{1}{2} \lim_{s \to 3/4} \left( -\frac{\sqrt{\pi}}{2} \sum_{n \mid m} n \Phi_{n, \nu}(\tau, s) + 2\sigma_1(m) \Phi_{0,\nu}(\tau, s)\right). \end{align} $$
The order of limits of s and z is interchanged, which is justified by the Remark at the end of Section 4.4.
5.2 The Selberg–Poincaré series
To prove Theorem 1.4 using (5.4), we must calculate
![]() $\Phi _{n,\nu }(\tau , s)$
and
$\Phi _{n,\nu }(\tau , s)$
and
![]() $\langle \Phi _{n, \nu }(\cdot , s), f\rangle $
at
$\langle \Phi _{n, \nu }(\cdot , s), f\rangle $
at
![]() $s = 3/4$
for Hecke eigenforms f. To this end, we use Selberg’s generalization [Reference Selberg27] of the Poincaré series in (1.7). For integers
$s = 3/4$
for Hecke eigenforms f. To this end, we use Selberg’s generalization [Reference Selberg27] of the Poincaré series in (1.7). For integers
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $m\in \mathbb {Z},$
they are defined by
$m\in \mathbb {Z},$
they are defined by

This series converges absolutely and uniformly on compact subsets for
![]() $\operatorname {\mathrm {Re}}(s)> 1-k/2$
and admits meromorphic continuation. In particular, it is known that
$\operatorname {\mathrm {Re}}(s)> 1-k/2$
and admits meromorphic continuation. In particular, it is known that
![]() $P_{k,m}(\tau , s)$
is holomorphic at
$P_{k,m}(\tau , s)$
is holomorphic at
![]() $s = 1-k/2$
. This fact follows from comparing it with the Maass–Poincaré series defined by
$s = 1-k/2$
. This fact follows from comparing it with the Maass–Poincaré series defined by

Indeed, from (4.5), we have
Thus, for
![]() $\operatorname {\mathrm {Re}}(s)> -k/2$
, the poles of these two types of Poincaré series agree. However, the Fourier expansion of the Maass–Poincaré series (see [Reference Jeon, Kang and Kim15, Theorem 3.2]) and the Weil bound for the Kloosterman sums imply its holomorphy at
$\operatorname {\mathrm {Re}}(s)> -k/2$
, the poles of these two types of Poincaré series agree. However, the Fourier expansion of the Maass–Poincaré series (see [Reference Jeon, Kang and Kim15, Theorem 3.2]) and the Weil bound for the Kloosterman sums imply its holomorphy at
![]() $s = 1-k/2$
.
$s = 1-k/2$
.
The next lemma describes the Petersson inner product of cusp forms with these series.
Lemma 5.4. For
![]() $f \in S_k$
and
$f \in S_k$
and
![]() $m> 0$
, we have
$m> 0$
, we have

Proof. It follows from the classical unfolding argument (see [Reference Bringmann, Folsom, Ono and Rolen4, Ch. 10.1], for instance).
5.3 The case of
 $n=0$
$n=0$
Here, we calculate
![]() $\langle \Phi _{0, \nu }(\cdot , s), f\rangle $
at
$\langle \Phi _{0, \nu }(\cdot , s), f\rangle $
at
![]() $s = 3/4$
for a normalized Hecke eigenform f. To this end, we decompose
$s = 3/4$
for a normalized Hecke eigenform f. To this end, we decompose
![]() $\Phi _{0,\nu }(\tau ,s)$
in terms of the Selberg–Poincaré series.
$\Phi _{0,\nu }(\tau ,s)$
in terms of the Selberg–Poincaré series.
Proposition 5.5. We have that
 $$\begin{align*}\Phi_{0,\nu}(\tau, s) = 4^{-s+3/4} \sum_{0 \le l \le \nu} \frac{(s-3/4)^{\underline{l}}}{(4\pi)^l} \binom{2\nu+1}{2l+1} \sum_{r \in \mathbb{Z}} r^{2\nu-2l} P_{2\nu+2, r^2} \left(\tau, s-\frac{3}{4}-l\right). \end{align*}$$
$$\begin{align*}\Phi_{0,\nu}(\tau, s) = 4^{-s+3/4} \sum_{0 \le l \le \nu} \frac{(s-3/4)^{\underline{l}}}{(4\pi)^l} \binom{2\nu+1}{2l+1} \sum_{r \in \mathbb{Z}} r^{2\nu-2l} P_{2\nu+2, r^2} \left(\tau, s-\frac{3}{4}-l\right). \end{align*}$$
Proof. By applying (5.1), Lemma 5.1 and Proposition 5.2,

The summand is calculated as

Then the claim follows from the Leibniz rule, where ![]() , and the fact that
, and the fact that
 $$\begin{align*}\sum_{l \le j \le \nu} (-1)^j 2^{2(\nu-j)} \binom{2\nu-j}{j} \binom{j}{l} = (-1)^l \binom{2\nu+1}{2l+1}. \end{align*}$$
$$\begin{align*}\sum_{l \le j \le \nu} (-1)^j 2^{2(\nu-j)} \binom{2\nu-j}{j} \binom{j}{l} = (-1)^l \binom{2\nu+1}{2l+1}. \end{align*}$$
The next result provides a formula for the Petersson norm of a cusp form f.
Theorem 5.6. For a normalized Hecke eigenform
![]() $f \in S_{2\nu +2}$
, we have
$f \in S_{2\nu +2}$
, we have
Proof. First, we note that the Fourier coefficients of a normalized Hecke eigenform are real. By Lemma 5.4 and Proposition 5.5, we find that
 $$ \begin{align*} \langle \Phi_{0,\nu}(\cdot, s), f \rangle &= 4^{-s+3/4} \sum_{0 \le l \le \nu} \frac{(s-3/4)^{\underline{l}}}{(4\pi)^l} \frac{\Gamma(2\nu+s+1/4-l)}{(4\pi)^{2\nu+s+1/4-l}} \binom{2\nu+1}{2l+1} \cdot 2 \sum_{r =1}^\infty \frac{c_f(r^2)}{r^{2s+2\nu+1/2}}. \end{align*} $$
$$ \begin{align*} \langle \Phi_{0,\nu}(\cdot, s), f \rangle &= 4^{-s+3/4} \sum_{0 \le l \le \nu} \frac{(s-3/4)^{\underline{l}}}{(4\pi)^l} \frac{\Gamma(2\nu+s+1/4-l)}{(4\pi)^{2\nu+s+1/4-l}} \binom{2\nu+1}{2l+1} \cdot 2 \sum_{r =1}^\infty \frac{c_f(r^2)}{r^{2s+2\nu+1/2}}. \end{align*} $$
As in [Reference Cohen and Strömberg10, Lemma 11.12.6], let

for
![]() $f \in S_{2\nu +2}$
. Then, it is known that
$f \in S_{2\nu +2}$
. Then, it is known that
![]() $B(f,s)$
admits the meromorphic continuation to the whole
$B(f,s)$
admits the meromorphic continuation to the whole
![]() $\mathbb {C}$
-plane, and
$\mathbb {C}$
-plane, and
![]() $L(\mathrm {Sym}^2(f), s)$
has no poles (see [Reference Cohen and Strömberg10, Remark 11.12.8]). In particular,
$L(\mathrm {Sym}^2(f), s)$
has no poles (see [Reference Cohen and Strömberg10, Remark 11.12.8]). In particular,
![]() $B(f, 2s+2\nu +1/2)$
has no pole at
$B(f, 2s+2\nu +1/2)$
has no pole at
![]() $s = 3/4$
. Therefore, by [Reference Cohen and Strömberg10, Corollary 11.12.7], we have
$s = 3/4$
. Therefore, by [Reference Cohen and Strömberg10, Corollary 11.12.7], we have
 $$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{0,\nu}(\cdot, s), f\rangle &= \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu+1}} (2\nu+1) 2B(f, 2\nu+2)\\ &= \frac{2(2\nu+1)!}{(4\pi)^{2\nu+1}} \frac{6}{\pi^2} \frac{\pi}{2} \frac{(4\pi)^{2\nu+2}}{(2\nu+1)!} \langle f, f \rangle\\ &=24 \|f\|^2.\\[-47pt] \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{0,\nu}(\cdot, s), f\rangle &= \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu+1}} (2\nu+1) 2B(f, 2\nu+2)\\ &= \frac{2(2\nu+1)!}{(4\pi)^{2\nu+1}} \frac{6}{\pi^2} \frac{\pi}{2} \frac{(4\pi)^{2\nu+2}}{(2\nu+1)!} \langle f, f \rangle\\ &=24 \|f\|^2.\\[-47pt] \end{align*} $$
5.4 The cases of
 $n> 0$
$n> 0$
We turn to the case of positive
![]() $n.$
Again, we first decompose
$n.$
Again, we first decompose
![]() $\Phi _{n,\nu }(\tau ,s).$
$\Phi _{n,\nu }(\tau ,s).$
Proposition 5.7. For
![]() $n> 0$
, we have
$n> 0$
, we have
 $$ \begin{align*} \Phi_{n, \nu}(\tau, s) &= \frac{1}{\Gamma(2s)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2)}} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} Q_{\nu, i_1+i_2} (n,r) \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}}\widetilde{P}_{n,r}^{i_1, i_2} (\tau, s), \end{align*} $$
$$ \begin{align*} \Phi_{n, \nu}(\tau, s) &= \frac{1}{\Gamma(2s)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2)}} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} Q_{\nu, i_1+i_2} (n,r) \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}}\widetilde{P}_{n,r}^{i_1, i_2} (\tau, s), \end{align*} $$
where we let

Proof. Arguing as above, by applying (5.1), Lemma 5.1 and Proposition 5.2, we obtain

The summand is calculated as

Similar to the case of
![]() $n=0$
, direct calculation utilizing
$n=0$
, direct calculation utilizing ![]() yields
yields

For the second term, by Lemma 4.1, we find that

The claim follows by combining these results.
We split the sum defining
![]() $\Phi _{n, \nu }(\tau , s)$
into
$\Phi _{n, \nu }(\tau , s)$
into
![]() $\Phi _{n, \nu }^+(\tau , s)$
and
$\Phi _{n, \nu }^+(\tau , s)$
and
![]() $\Phi _{n, \nu }^-(\tau , s),$
based on the inequalities
$\Phi _{n, \nu }^-(\tau , s),$
based on the inequalities
![]() $r^2> n^2$
or
$r^2> n^2$
or
![]() $r^2 \le n^2.$
We consider them as
$r^2 \le n^2.$
We consider them as
![]() $s \to 3/4$
. By (4.5), the summand of the Poincaré series
$s \to 3/4$
. By (4.5), the summand of the Poincaré series
![]() $\widetilde {P}_{n,r}^{i_1, i_2} (\tau , s)$
satisfies
$\widetilde {P}_{n,r}^{i_1, i_2} (\tau , s)$
satisfies

as ![]() . Therefore, for
. Therefore, for
![]() $\operatorname {\mathrm {Re}}(s)> -\nu +i_1 + 3/4$
, the Poincaré series is holomorphic (in s). In particular,
$\operatorname {\mathrm {Re}}(s)> -\nu +i_1 + 3/4$
, the Poincaré series is holomorphic (in s). In particular,
![]() $\widetilde {P}_{n,r}^{i_1, i_2} (\tau , s)$
is holomorphic at
$\widetilde {P}_{n,r}^{i_1, i_2} (\tau , s)$
is holomorphic at
![]() $s = 3/4$
for
$s = 3/4$
for
![]() $0 \le i_1 < \nu $
. Regarding the case of
$0 \le i_1 < \nu $
. Regarding the case of
![]() $i_1 = \nu $
, by a similar argument as in Section 5.2 – that is, by comparing it with the Selberg–Poincaré series or the Maass–Poincaré series – we see that it is also holomorphic at
$i_1 = \nu $
, by a similar argument as in Section 5.2 – that is, by comparing it with the Selberg–Poincaré series or the Maass–Poincaré series – we see that it is also holomorphic at
![]() $s=3/4$
. Therefore, we have
$s=3/4$
. Therefore, we have
 $$ \begin{align*} \lim_{s \to 3/4} \Phi_{n, \nu}^-(\tau, s) &= \frac{1}{\Gamma(3/2)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2)\\r^2 \le n^2}} Q_{\nu,0} (n,r) \widetilde{P}_{n,r}^{0,0}(\tau, 3/4). \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \Phi_{n, \nu}^-(\tau, s) &= \frac{1}{\Gamma(3/2)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2)\\r^2 \le n^2}} Q_{\nu,0} (n,r) \widetilde{P}_{n,r}^{0,0}(\tau, 3/4). \end{align*} $$
Since
![]() $Q_{\nu ,0}(n,r) = p_{2\nu +2}(r, (r^2-n^2)/4)$
and
$Q_{\nu ,0}(n,r) = p_{2\nu +2}(r, (r^2-n^2)/4)$
and
![]() $\widetilde {P}_{n,r}^{0,0}(\tau , 3/4) = P_{2\nu +2, \frac {r^2-n^2}{4}}(\tau )$
, by (2.8), we have
$\widetilde {P}_{n,r}^{0,0}(\tau , 3/4) = P_{2\nu +2, \frac {r^2-n^2}{4}}(\tau )$
, by (2.8), we have
 $$ \begin{align} \lim_{s \to 3/4} \Phi_{n, \nu}^-(\tau, s) = \frac{4}{n \sqrt{\pi}} \sum_{0 < r \le n} r^{2\nu+1} P_{2\nu+2, -r(n-r)}(\tau). \end{align} $$
$$ \begin{align} \lim_{s \to 3/4} \Phi_{n, \nu}^-(\tau, s) = \frac{4}{n \sqrt{\pi}} \sum_{0 < r \le n} r^{2\nu+1} P_{2\nu+2, -r(n-r)}(\tau). \end{align} $$
As a counterpart to Theorem 5.6, the Petersson inner product of
![]() $\Phi _{n, \nu }^+(\tau , s)$
with a Hecke eigenform is expressed in terms of the symmetrized shifted convolution L-functions.
$\Phi _{n, \nu }^+(\tau , s)$
with a Hecke eigenform is expressed in terms of the symmetrized shifted convolution L-functions.
Theorem 5.8. For a normalized Hecke eigenform
![]() $f \in S_{2\nu +2}$
, we have
$f \in S_{2\nu +2}$
, we have
 $$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f \rangle = \frac{4}{n \sqrt{\pi}} \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \widehat{L}(f, n/d; 2\nu+1). \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f \rangle = \frac{4}{n \sqrt{\pi}} \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \widehat{L}(f, n/d; 2\nu+1). \end{align*} $$
Proof. By Proposition 5.7, we have
 $$ \begin{align*} &\langle \Phi_{n, \nu}^+(\cdot, s), f \rangle\\ &= \frac{1}{\Gamma(2s)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2) \\ r^2> n^2}} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} Q_{\nu, i_1+i_2} (n,r) \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}} \langle \widetilde{P}_{n,r}^{i_1, i_2} (\cdot, s), f \rangle. \end{align*} $$
$$ \begin{align*} &\langle \Phi_{n, \nu}^+(\cdot, s), f \rangle\\ &= \frac{1}{\Gamma(2s)} \sum_{\substack{r \in \mathbb{Z} \\ r \equiv n\ (2) \\ r^2> n^2}} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} Q_{\nu, i_1+i_2} (n,r) \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}} \langle \widetilde{P}_{n,r}^{i_1, i_2} (\cdot, s), f \rangle. \end{align*} $$
The unfolding argument, combined with Lemma 4.2, gives

By changing variables
![]() $r = 2m+n$
for
$r = 2m+n$
for
![]() $r> n$
and
$r> n$
and
![]() $r = -2m-n$
for
$r = -2m-n$
for
![]() $r < -n$
, we have
$r < -n$
, we have
 $$ \begin{align*} &\langle \Phi_{n,\nu}^+(\cdot, s), f\rangle\\ &= \frac{2}{\Gamma(2s)} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}} (\pi n^2)^{s -\frac{3}{4}-i_1} \Gamma \left(s + 2\nu + \frac{1}{4} - i_1 \right)\\ &\times \sum_{m=1}^\infty \frac{Q_{\nu, i_1+i_2} (n,2m+n) c_f (m(m+n))}{(\pi (2m+n)^2)^{s + 2\nu + \frac{1}{4} - i_1}} {}_2 F_1 \left(s+\frac{3}{4}, s + 2\nu + \frac{1}{4} - i_1; 2s+i_2; \frac{n^2}{(2m+n)^2}\right), \end{align*} $$
$$ \begin{align*} &\langle \Phi_{n,\nu}^+(\cdot, s), f\rangle\\ &= \frac{2}{\Gamma(2s)} \sum_{\substack{i_1, i_2 \ge 0 \\ i_1 + i_2 \le \nu}} \frac{(-1)^{i_1}}{i_1! i_2!} \left(\frac{n^2}{4} \right)^{i_1+i_2} \frac{(s-3/4)^{\underline{i_1}} (s-3/4)^{\overline{i_2}}}{(2s)^{\overline{i_2}}} (\pi n^2)^{s -\frac{3}{4}-i_1} \Gamma \left(s + 2\nu + \frac{1}{4} - i_1 \right)\\ &\times \sum_{m=1}^\infty \frac{Q_{\nu, i_1+i_2} (n,2m+n) c_f (m(m+n))}{(\pi (2m+n)^2)^{s + 2\nu + \frac{1}{4} - i_1}} {}_2 F_1 \left(s+\frac{3}{4}, s + 2\nu + \frac{1}{4} - i_1; 2s+i_2; \frac{n^2}{(2m+n)^2}\right), \end{align*} $$
where we note that
![]() $Q_{\nu ,i}(n,-r) = Q_{\nu ,i}(n,r)$
holds. For a normalized Hecke eigenform
$Q_{\nu ,i}(n,-r) = Q_{\nu ,i}(n,r)$
holds. For a normalized Hecke eigenform
![]() $f \in S_{2\nu +2}$
, since
$f \in S_{2\nu +2}$
, since
 $$\begin{align*}c_f(m(m+n)) = \sum_{d \mid (m, m+n)} \mu(d) d^{2\nu+1} c_f\left(\frac{m}{d}\right) c_f\left(\frac{m+n}{d}\right), \end{align*}$$
$$\begin{align*}c_f(m(m+n)) = \sum_{d \mid (m, m+n)} \mu(d) d^{2\nu+1} c_f\left(\frac{m}{d}\right) c_f\left(\frac{m+n}{d}\right), \end{align*}$$
the last sum becomes
 $$ \begin{align*} &\sum_{d \mid n} \mu(d) d^{2\nu+1} \sum_{m=1}^\infty \frac{Q_{\nu, i_1+i_2} (n,2dm+n) c_f(m) c_f(m+n/d)}{(\pi (2dm+n)^2)^{s + 2\nu + \frac{1}{4} - i_1}}\\ &\quad \times {}_2 F_1 \left(s+\frac{3}{4}, s + 2\nu + \frac{1}{4} - i_1; 2s+i_2; \frac{n^2}{(2dm+n)^2}\right).\end{align*} $$
$$ \begin{align*} &\sum_{d \mid n} \mu(d) d^{2\nu+1} \sum_{m=1}^\infty \frac{Q_{\nu, i_1+i_2} (n,2dm+n) c_f(m) c_f(m+n/d)}{(\pi (2dm+n)^2)^{s + 2\nu + \frac{1}{4} - i_1}}\\ &\quad \times {}_2 F_1 \left(s+\frac{3}{4}, s + 2\nu + \frac{1}{4} - i_1; 2s+i_2; \frac{n^2}{(2dm+n)^2}\right).\end{align*} $$
Then, this Dirichlet series is holomorphic at
![]() $s = 3/4$
. Indeed, since
$s = 3/4$
. Indeed, since
![]() $Q_{\nu , i_1+i_2} (n,2dm+n)$
has degree
$Q_{\nu , i_1+i_2} (n,2dm+n)$
has degree
![]() $2(\nu -i_1-i_2)$
in m, it suffices to show that
$2(\nu -i_1-i_2)$
in m, it suffices to show that
 $$\begin{align*}\sum_{m=1}^\infty \frac{c_f(m) c_f(m+n/d)}{m^{2(s+\nu+1/4+i_2)}} \end{align*}$$
$$\begin{align*}\sum_{m=1}^\infty \frac{c_f(m) c_f(m+n/d)}{m^{2(s+\nu+1/4+i_2)}} \end{align*}$$
(conditionally) converges at
![]() $s = 3/4$
. This can be seen by partial summation using the estimate
$s = 3/4$
. This can be seen by partial summation using the estimate
with some
![]() $\delta> 0$
, (see [Reference Blomer2, Corollary 1.4]). Therefore, all terms corresponding to nonzero
$\delta> 0$
, (see [Reference Blomer2, Corollary 1.4]). Therefore, all terms corresponding to nonzero
![]() $(i_1, i_2)$
vanish as
$(i_1, i_2)$
vanish as
![]() $s \to 3/4$
, and we obtain
$s \to 3/4$
, and we obtain
 $$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f\rangle &= \frac{4}{\sqrt{\pi}} \Gamma(2\nu+1) \sum_{d \mid n} \mu(d) d^{2\nu+1} \\ &\quad \times \sum_{m=1}^\infty \frac{Q_{\nu, 0} (n,2dm+n) c_f(m) c_f(m+n/d)}{(\pi (2dm+n)^2)^{2\nu + 1}} {}_2 F_1 \left(\frac{3}{2}, 2\nu + 1; \frac{3}{2}; \frac{n^2}{(2dm+n)^2}\right). \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f\rangle &= \frac{4}{\sqrt{\pi}} \Gamma(2\nu+1) \sum_{d \mid n} \mu(d) d^{2\nu+1} \\ &\quad \times \sum_{m=1}^\infty \frac{Q_{\nu, 0} (n,2dm+n) c_f(m) c_f(m+n/d)}{(\pi (2dm+n)^2)^{2\nu + 1}} {}_2 F_1 \left(\frac{3}{2}, 2\nu + 1; \frac{3}{2}; \frac{n^2}{(2dm+n)^2}\right). \end{align*} $$
Since we have
 $$\begin{align*}\frac{1}{r^{2(2\nu+1)}} {}_2 F_1 \left(\frac{3}{2}, 2\nu + 1; \frac{3}{2}; \frac{n^2}{r^2}\right) = \frac{1}{(r^2-n^2)^{2\nu+1}} \end{align*}$$
$$\begin{align*}\frac{1}{r^{2(2\nu+1)}} {}_2 F_1 \left(\frac{3}{2}, 2\nu + 1; \frac{3}{2}; \frac{n^2}{r^2}\right) = \frac{1}{(r^2-n^2)^{2\nu+1}} \end{align*}$$
and
![]() $Q_{\nu ,0}(n,r) = p_{2\nu +2}(r, (r^2-n^2)/4)$
with (2.8) again, the proof is complete as
$Q_{\nu ,0}(n,r) = p_{2\nu +2}(r, (r^2-n^2)/4)$
with (2.8) again, the proof is complete as
 $$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f\rangle &= \frac{4}{n \sqrt{\pi}} \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \sum_{m=1}^\infty c_f(m) c_f(m+n/d) \left(\frac{1}{m^{2\nu+1}} - \frac{1}{(m+n/d)^{2\nu+1}}\right). \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \langle \Phi_{n,\nu}^+(\cdot, s), f\rangle &= \frac{4}{n \sqrt{\pi}} \frac{\Gamma(2\nu+1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \sum_{m=1}^\infty c_f(m) c_f(m+n/d) \left(\frac{1}{m^{2\nu+1}} - \frac{1}{(m+n/d)^{2\nu+1}}\right). \end{align*} $$
5.5 Proof of Theorem 1.4
We apply the results from the two previous subsections. For
![]() $m> 0$
and
$m> 0$
and
![]() $\nu \ge 0$
, let
$\nu \ge 0$
, let

As stated in (5.4), we have
However, from (5.6), the minus part

For the plus part, by Theorem 5.6 and Theorem 5.8 and the Möbius inversion formula, we have
 $$ \begin{align*} \lim_{s \to 3/4} \langle \Phi^+(\cdot, s), f \rangle &= \sum_{n \mid m} \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \widehat{L}(f, n/d; 2\nu+1) - 24\sigma_1(m) \|f\|^2\\ &= \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \widehat{L}(f, m; 2\nu+1) - 24 \sigma_1(m) \|f\|^2. \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \langle \Phi^+(\cdot, s), f \rangle &= \sum_{n \mid m} \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \sum_{d \mid n} \mu(d) \widehat{L}(f, n/d; 2\nu+1) - 24\sigma_1(m) \|f\|^2\\ &= \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \widehat{L}(f, m; 2\nu+1) - 24 \sigma_1(m) \|f\|^2. \end{align*} $$
Combining these facts, we are pleased to obtain the conclusion of the theorem
 $$ \begin{align*} \lim_{s \to 3/4} \Phi(\tau, s) &= \sum_{n \mid m} \sum_{0 < r \le n} r^{2\nu+1} P_{2\nu+2, -r(n-r)}(\tau) - \sum_{j=1}^{d_{2\nu+2}} \left(24 \sigma_1(m) - \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \frac{\widehat{L}(f, m; 2\nu+1)}{\|f_j\|^2} \right) f_j. \end{align*} $$
$$ \begin{align*} \lim_{s \to 3/4} \Phi(\tau, s) &= \sum_{n \mid m} \sum_{0 < r \le n} r^{2\nu+1} P_{2\nu+2, -r(n-r)}(\tau) - \sum_{j=1}^{d_{2\nu+2}} \left(24 \sigma_1(m) - \frac{\Gamma (2\nu + 1)}{(4\pi)^{2\nu + 1}} \frac{\widehat{L}(f, m; 2\nu+1)}{\|f_j\|^2} \right) f_j. \end{align*} $$
Acknowledgements
The authors thank Masanobu Kaneko and Gyucheol Shin for comments that improved this paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
This work was supported by the MEXT Initiative for Realizing Diversity in the Research Environment through Kyushu University’s Diversity and Super Global Training Program for Female and Young Faculty (SENTAN-Q). The second author was supported by JSPS KAKENHI (JP20K14292, JP21K18141 and JP24K16901). The third author thanks the Thomas Jefferson Fund and grants from the NSF (DMS-2002265 and DMS-2055118).