It is a classical fact that the deformation-obstruction theory of a coherent sheaf E on a projective variety X is governed by the groups
![]() $\operatorname {\mathrm {Ext}}^i_X(E,E)$
for
$\operatorname {\mathrm {Ext}}^i_X(E,E)$
for
![]() $i=1,2$
[Reference Hartshorne5, Section 7]. The Atiyah class, as defined in [Reference Illusie7] in the algebraic setting, globalizes and generalizes this correspondence – roughly speaking, it measures how much a family of sheaves varies over a base. When working over a moduli space, these self-
$i=1,2$
[Reference Hartshorne5, Section 7]. The Atiyah class, as defined in [Reference Illusie7] in the algebraic setting, globalizes and generalizes this correspondence – roughly speaking, it measures how much a family of sheaves varies over a base. When working over a moduli space, these self-
![]() $\operatorname {\mathrm {Ext}}$
groups often give an important extra structure in the form of an obstruction theory (often with additional properties), which is the foundational ingredient in enumerative sheaf theories. Examples are the famous Donaldson–Thomas theory [Reference Thomas23], PT-theory [Reference Pandharipande and Thomas18], [Reference Huybrechts and Thomas6], moduli spaces of stable sheaves on surfaces [Reference Mochizuki14] and, more recently, CY4 theory [Reference Oh and Thomas15]. In each of these cases, the technical tool used to obtain the obstruction theory is the Atiyah class.
$\operatorname {\mathrm {Ext}}$
groups often give an important extra structure in the form of an obstruction theory (often with additional properties), which is the foundational ingredient in enumerative sheaf theories. Examples are the famous Donaldson–Thomas theory [Reference Thomas23], PT-theory [Reference Pandharipande and Thomas18], [Reference Huybrechts and Thomas6], moduli spaces of stable sheaves on surfaces [Reference Mochizuki14] and, more recently, CY4 theory [Reference Oh and Thomas15]. In each of these cases, the technical tool used to obtain the obstruction theory is the Atiyah class.
In many cases, particularly for wall-crossing arguments as in [Reference Mochizuki14], [Reference Joyce8], [Reference Kuhn and Tanaka9], it is necessary to consider moduli stacks that include properly semi-stable objects which may have positive-dimensional stabilizers. To work with these, one would like an obstruction theory on the stack. This is constructed in [Reference Mochizuki14] for moduli stacks of objects with a two-term resolution, and in [Reference Joyce8] by using derived moduli stacks of perfect complexes.
The main result of this paper is to generalize Illusie’s construction of the Atiyah class to algebraic stacks, using Olsson’s definition of the cotangent complex [Reference Olsson16]. We also treat some variants, such as Gillam’s reduced Atiyah class [Reference Gillam3], and a version of the Atiyah class for exact sequences. We then show various compatibility properties for the Atiyah class and its variants.
As a second main result, we show that the Atiyah class indeed gives an obstruction theory for moduli stacks of perfect complexes (Theorem 1.4). The main new part here is that it captures the infinitesimal automorphisms. For simplicity, we only treat the absolute case of a proper scheme over a field, although the relative case follows along the same lines.
Roughly, our construction of the Atiyah class proceeds by presenting a given algebraic stack
![]() $\mathcal {X}$
as a groupoid
$\mathcal {X}$
as a groupoid
![]() $W\rightrightarrows X$
in algebraic spaces.
$W\rightrightarrows X$
in algebraic spaces.
Then, up to descent, the Atiyah class of a sheaf E on
![]() $\mathcal {X}$
should morally be obtained by taking mapping cones of a commutative square involving the Atiyah classes of the pullback of E to X and W, respectively. Since taking mapping cones in the derived category is not functorial, some work is needed to make this into a definition. For this purpose, in §2.3, we introduce a topos
$\mathcal {X}$
should morally be obtained by taking mapping cones of a commutative square involving the Atiyah classes of the pullback of E to X and W, respectively. Since taking mapping cones in the derived category is not functorial, some work is needed to make this into a definition. For this purpose, in §2.3, we introduce a topos
![]() ${W}_{\parallel }$
associated to the groupoid
${W}_{\parallel }$
associated to the groupoid
![]() $W\rightrightarrows X$
, whose objects are certain diagrams involving sheaves of W and X. Then the desired mapping cone operation can be encoded as a functor that takes a complex of sheaves of modules on
$W\rightrightarrows X$
, whose objects are certain diagrams involving sheaves of W and X. Then the desired mapping cone operation can be encoded as a functor that takes a complex of sheaves of modules on
![]() ${W}_{\parallel }$
and yields a complex on W. With this technical tool, the strategy to define the Atiyah class goes through. (From a higher categorical viewpoint, the use of
${W}_{\parallel }$
and yields a complex on W. With this technical tool, the strategy to define the Atiyah class goes through. (From a higher categorical viewpoint, the use of
![]() ${W}_{\parallel }$
allows us to keep track of the necessary coherence data used in the pushout operation.)
${W}_{\parallel }$
allows us to keep track of the necessary coherence data used in the pushout operation.)
Relation to existing work
Throughout, we build on the constructions and results of [Reference Huybrechts and Thomas6], [Reference Illusie7] and [Reference Gillam3], which we generalize to algebraic stacks. Our construction also recovers the G-equivariant Atiyah class considered by Ricolfi [Reference Ricolfi20]. Throughout, we use Olsson’s definition of the quasi-coherent derived category and the cotangent complex for algebraic stacks developed in [Reference Olsson16] and [Reference Laszlo and Olsson10]; see also the excellent discussion in [Reference Hall and Rydh4, §1].
Generalizations of the Atiyah class to the theory of algebraic stacks have appeared before in different contexts: In the setting of derived algebraic geometry of Schürg, Toën and Vezzosi [Reference Schürg, Toën and Vezzosi21], a perfect complex E on a derived geometry stack
![]() $\mathcal {Y}$
with a perfect cotangent complex gives rise to a map from
$\mathcal {Y}$
with a perfect cotangent complex gives rise to a map from
![]() $\mathcal {Y}$
to the (derived) moduli stack of perfect complexes. In ([Reference Schürg, Toën and Vezzosi21], Appendix A), they define the Atiyah class as the induced pullback map on cotangent complexes and argue that it recovers Illusie’s definition in the case of schemes. Moreover, Lurie has constructed the Atiyah class in the context of spectral algebraic geometry [Reference Lurie12, §19.2.2]. In the purely classical setting, our definition goes beyond these, as we do not require the perfectness assumptions made in [Reference Schürg, Toën and Vezzosi21], and since the current version of [Reference Lurie12] presently only deals with Deligne–Mumford stacks.Footnote
1
$\mathcal {Y}$
to the (derived) moduli stack of perfect complexes. In ([Reference Schürg, Toën and Vezzosi21], Appendix A), they define the Atiyah class as the induced pullback map on cotangent complexes and argue that it recovers Illusie’s definition in the case of schemes. Moreover, Lurie has constructed the Atiyah class in the context of spectral algebraic geometry [Reference Lurie12, §19.2.2]. In the purely classical setting, our definition goes beyond these, as we do not require the perfectness assumptions made in [Reference Schürg, Toën and Vezzosi21], and since the current version of [Reference Lurie12] presently only deals with Deligne–Mumford stacks.Footnote
1
Finally, the paper [Reference Aranha and Pstragowski1] shows how to construct virtual cycles from perfect obstruction theories on algebraic stacks and thus fits in neatly with the viewpoint taken here, that it is often advantageous to consider fundamental constructions directly on the moduli stack.
Notations and conventions
For a Grothendieck topos T and a ring R in T, we let
![]() $\operatorname {\mathrm {Mod}}(R)$
denote the category of R-modules and
$\operatorname {\mathrm {Mod}}(R)$
denote the category of R-modules and
![]() $D(R)$
its derived category. We identify
$D(R)$
its derived category. We identify
![]() $\operatorname {\mathrm {Mod}}(R)$
with the subcategory of
$\operatorname {\mathrm {Mod}}(R)$
with the subcategory of
![]() $D(R)$
generated by complexes concentrated in degree zero.
$D(R)$
generated by complexes concentrated in degree zero.
For any abelian category
![]() $\mathcal {A}$
, write
$\mathcal {A}$
, write
![]() $C(\mathcal {A})$
for the category of complexes of objects in
$C(\mathcal {A})$
for the category of complexes of objects in
![]() $\mathcal {A}$
. Write
$\mathcal {A}$
. Write
![]() $C^{\leq 0}(\mathcal {A})$
and
$C^{\leq 0}(\mathcal {A})$
and
![]() $C^{[-1,0]}(\mathcal {A})$
for the full sub-category of complexes bounded in degrees
$C^{[-1,0]}(\mathcal {A})$
for the full sub-category of complexes bounded in degrees
![]() $\leq 0$
and in degrees
$\leq 0$
and in degrees
![]() $-1,0$
, respectively. When
$-1,0$
, respectively. When
![]() $\mathcal {A}= \operatorname {\mathrm {Mod}}(R)$
, we simply write
$\mathcal {A}= \operatorname {\mathrm {Mod}}(R)$
, we simply write
![]() $C(R)$
and
$C(R)$
and
![]() $C^{\leq 0}(R)$
,
$C^{\leq 0}(R)$
,
![]() $C^{[-1,0]}(R)$
, respectively.
$C^{[-1,0]}(R)$
, respectively.
We will use the following convention regarding shift functors: For any complex E of R-modules, we have a natural isomorphism
If
![]() $E,F$
are complexes, then by
$E,F$
are complexes, then by
![]() $E\otimes F[1]$
we mean
$E\otimes F[1]$
we mean
![]() $(E\otimes F)[1]$
rather than
$(E\otimes F)[1]$
rather than
![]() $E\otimes (F[1])$
.
$E\otimes (F[1])$
.
All tensor products, pullbacks and duals of objects in a derived category be in the derived sense. For modules and complexes, we will consider the underived tensor products and pullbacks but will point out when these do not necessarily compute the derived operation.
We use the definition of algebraic stacks as in the Stacks project [22, Tag 026N].
1 Statements of results
In this section, we introduce the Atiyah class on an algebraic stack and several variants, and we state their basic properties and mutual relations. The proofs will be given in the following sections.
1.1 The Atiyah class
The Atiyah class of a vector bundle E on a smooth scheme X is a linear map that turns a vector field v on X into a class
![]() $\alpha _{v}\in \operatorname {\mathrm {Ext}}^1(E,E)$
that measures how E varies in the directions of v and is compatible with any pullbacks of schemes. Via the cup product, it also gives rise to a map
$\alpha _{v}\in \operatorname {\mathrm {Ext}}^1(E,E)$
that measures how E varies in the directions of v and is compatible with any pullbacks of schemes. Via the cup product, it also gives rise to a map
![]() $H^1(T_X)\to \operatorname {\mathrm {Ext}}^2(E,E)$
– here, the source is naturally identified with the collection of infinitesimal deformations of X via the Kodaira–Spencer map. This provides an obstruction class to extending E over infinitesimal deformations
$H^1(T_X)\to \operatorname {\mathrm {Ext}}^2(E,E)$
– here, the source is naturally identified with the collection of infinitesimal deformations of X via the Kodaira–Spencer map. This provides an obstruction class to extending E over infinitesimal deformations
![]() $X'$
of X: One can extend E to a vector bundle on
$X'$
of X: One can extend E to a vector bundle on
![]() $X'$
if and only if the class in
$X'$
if and only if the class in
![]() $\operatorname {\mathrm {Ext}}^2(E,E)$
obtained from
$\operatorname {\mathrm {Ext}}^2(E,E)$
obtained from
![]() $X'$
is zero. An appropriate way to write the Atiyah class that generalizes beyond the case of smooth schemes is as a map
$X'$
is zero. An appropriate way to write the Atiyah class that generalizes beyond the case of smooth schemes is as a map
in the derived category of X, where
![]() $L_X$
denotes the cotangent complex of X as defined by Illusie [Reference Illusie7].Footnote
2
If one further replaces X by an algebraic stack
$L_X$
denotes the cotangent complex of X as defined by Illusie [Reference Illusie7].Footnote
2
If one further replaces X by an algebraic stack
![]() $\mathcal {X}$
, one would like that the Atiyah class also captures how the (infinitesimal) stabilizer groups of
$\mathcal {X}$
, one would like that the Atiyah class also captures how the (infinitesimal) stabilizer groups of
![]() $\mathcal {X}$
act on E. This is where we pick up.
$\mathcal {X}$
act on E. This is where we pick up.
Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
$f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
![]() $E\in D^-_{qcoh}(\mathcal {X})$
. In §4.1, we define the Atiyah class of E over
$E\in D^-_{qcoh}(\mathcal {X})$
. In §4.1, we define the Atiyah class of E over
![]() $\mathcal {Y}$
, which is a natural map
$\mathcal {Y}$
, which is a natural map
Here,
![]() $L_{\mathcal {X}/\mathcal {Y}}$
denotes Olsson’s generalization of the relative cotangent complex to algebraic stacks [Reference Olsson16], which we review in §2.1. We also use the notation
$L_{\mathcal {X}/\mathcal {Y}}$
denotes Olsson’s generalization of the relative cotangent complex to algebraic stacks [Reference Olsson16], which we review in §2.1. We also use the notation
![]() $\operatorname {\mathrm {at}}_{E,\mathcal {X}/\mathcal {Y}}$
when we want to emphasize the dependence on f. If E is dualizable in the derived category (equivalently, a perfect complex; see [Reference Hall and Rydh4, Lemma 4.3]), then the data of
$\operatorname {\mathrm {at}}_{E,\mathcal {X}/\mathcal {Y}}$
when we want to emphasize the dependence on f. If E is dualizable in the derived category (equivalently, a perfect complex; see [Reference Hall and Rydh4, Lemma 4.3]), then the data of
![]() $\operatorname {\mathrm {at}}_E$
is equivalent to that of a map
$\operatorname {\mathrm {at}}_E$
is equivalent to that of a map
which we also call the Atiyah class.
We now list a series of fundamental properties of the Atiyah class. The proofs will be given in §5: Let
![]() $F,E$
be objects of
$F,E$
be objects of
![]() $D^-_{qcoh}(\mathcal {X})$
.
$D^-_{qcoh}(\mathcal {X})$
.
Functoriality
Given a map
![]() $F\to E$
in
$F\to E$
in
![]() $D^-_{qcoh}(\mathcal {X})$
, the induced diagram
$D^-_{qcoh}(\mathcal {X})$
, the induced diagram
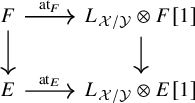
commutes.
Pullback
Given another morphism
![]() $f':\mathcal {X}'\to \mathcal {Y}'$
together with maps
$f':\mathcal {X}'\to \mathcal {Y}'$
together with maps
![]() $A:\mathcal {X}'\to \mathcal {X}$
and
$A:\mathcal {X}'\to \mathcal {X}$
and
![]() $B:\mathcal {Y}'\to \mathcal {Y}$
, and a
$B:\mathcal {Y}'\to \mathcal {Y}$
, and a
![]() $2$
-isomorphism
$2$
-isomorphism
![]() $B\circ f'\Rightarrow f\circ A$
, the induced diagram
$B\circ f'\Rightarrow f\circ A$
, the induced diagram

commutes. If E is perfect, then equivalently, the diagram
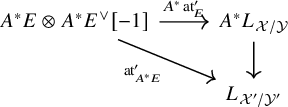
commutes.
Tensor products
Identify
![]() $E\otimes L_{\mathcal {X}/\mathcal {Y}}[1]\otimes F\simeq L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E\otimes F$
using the standard symmetry isomorphism of the derived tensor product. Then, up to this identification, we have an equality
$E\otimes L_{\mathcal {X}/\mathcal {Y}}[1]\otimes F\simeq L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E\otimes F$
using the standard symmetry isomorphism of the derived tensor product. Then, up to this identification, we have an equality
As a special case of this, if E and F are perfect and
![]() $\operatorname {\mathrm {at}}_F$
is trivial (e.g., if F is pulled back from
$\operatorname {\mathrm {at}}_F$
is trivial (e.g., if F is pulled back from
![]() $\mathcal {Y}$
), then the following diagram commutes:
$\mathcal {Y}$
), then the following diagram commutes:
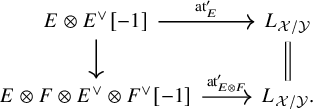
Here, the left vertical map is induced by the diagonal map
![]() $\mathcal {O}_X\to F\otimes F^{\vee }$
and the symmetry isomorphisms of the tensor product.
$\mathcal {O}_X\to F\otimes F^{\vee }$
and the symmetry isomorphisms of the tensor product.
Determinants
Suppose that E is perfect and consider the natural trace map
![]() $\operatorname {tr}:\operatorname {\mathrm {Hom}}(E,L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E)\to \operatorname {\mathrm {Hom}}(\mathcal {O}_{\mathcal {X}}, L_{\mathcal {X}/\mathcal {Y}}[1])$
. Then we have
$\operatorname {tr}:\operatorname {\mathrm {Hom}}(E,L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E)\to \operatorname {\mathrm {Hom}}(\mathcal {O}_{\mathcal {X}}, L_{\mathcal {X}/\mathcal {Y}}[1])$
. Then we have
![]() $\operatorname {\mathrm {at}}_{\det (E)} = \operatorname {tr}(\operatorname {\mathrm {at}}_E)\otimes \det (E)$
as morphisms
$\operatorname {\mathrm {at}}_{\det (E)} = \operatorname {tr}(\operatorname {\mathrm {at}}_E)\otimes \det (E)$
as morphisms
![]() $\det E\to L_{\mathcal {X}/\mathcal {Y}}\otimes \det E[1]$
, at least when E has a global finite length resolution by locally free sheaves. In particular, if the latter condition holds, the following diagram commutes
$\det E\to L_{\mathcal {X}/\mathcal {Y}}\otimes \det E[1]$
, at least when E has a global finite length resolution by locally free sheaves. In particular, if the latter condition holds, the following diagram commutes
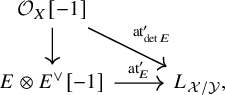
where the left vertical map is induced by the natural diagonal map
![]() $\mathcal {O}_X\to E\otimes E^{\vee }$
.
$\mathcal {O}_X\to E\otimes E^{\vee }$
.
Pushforward
Consider a cartesian diagram
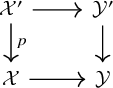
and suppose that
![]() $\mathcal {X}'\to \mathcal {X}$
is concentrated [Reference Hall and Rydh4, Definition 2.4]. Let
$\mathcal {X}'\to \mathcal {X}$
is concentrated [Reference Hall and Rydh4, Definition 2.4]. Let
![]() $E\in D^-_{qcoh}(\mathcal {X}')$
. Then we have a commutative diagram
$E\in D^-_{qcoh}(\mathcal {X}')$
. Then we have a commutative diagram
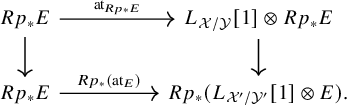
Suppose that, moreover, the diagram is Cartesian and that the morphisms
![]() $\mathcal {X}\to \mathcal {Y}$
and
$\mathcal {X}\to \mathcal {Y}$
and
![]() $\mathcal {Y}'\to \mathcal {X}$
are Tor-independent, and that E is a perfect complex. Then the right vertical morphism in (1.1) is an isomorphism, and this gives a natural identification
$\mathcal {Y}'\to \mathcal {X}$
are Tor-independent, and that E is a perfect complex. Then the right vertical morphism in (1.1) is an isomorphism, and this gives a natural identification
![]() $Rp_*(\operatorname {\mathrm {at}}_E)=\operatorname {\mathrm {at}}_{Rp_*E}$
as morphisms
$Rp_*(\operatorname {\mathrm {at}}_E)=\operatorname {\mathrm {at}}_{Rp_*E}$
as morphisms
![]() $Rp_*E\to L_{\mathcal {X}/\mathcal {Y}}[1]\otimes Rp_*E$
. If, moreover,
$Rp_*E\to L_{\mathcal {X}/\mathcal {Y}}[1]\otimes Rp_*E$
. If, moreover,
![]() $Rp_*E$
is perfect, this can be restated as commutativity of the following diagram:
$Rp_*E$
is perfect, this can be restated as commutativity of the following diagram:
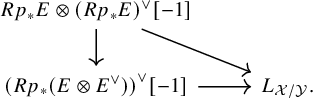
1.2 The reduced Atiyah class
Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a map of algebraic stacks and let
$f:\mathcal {X}\to \mathcal {Y}$
be a map of algebraic stacks and let
![]() $E\in D^-_{qcoh}(\mathcal {Y})$
. Let
$E\in D^-_{qcoh}(\mathcal {Y})$
. Let
be an exact triangle in
![]() $D^-_{qcoh}(\mathcal {X})$
such that
$D^-_{qcoh}(\mathcal {X})$
such that
![]() $R\operatorname {\mathrm {Hom}}^{-1}(F,G)=0$
. For example, this applies if E is a sheaf and G is a quotient of the ordinary pullback of E as a quasi-coherent sheaf.
$R\operatorname {\mathrm {Hom}}^{-1}(F,G)=0$
. For example, this applies if E is a sheaf and G is a quotient of the ordinary pullback of E as a quasi-coherent sheaf.
Then the reduced Atiyah class associated to this data is a natural map
If G is dualizable, this corresponds to a map
We also write
![]() $\overline {\operatorname {\mathrm {at}}}_{E}$
and
$\overline {\operatorname {\mathrm {at}}}_{E}$
and
![]() $\overline {\operatorname {\mathrm {at}}}^{\prime }_{E}$
if the rest of the data is understood.
$\overline {\operatorname {\mathrm {at}}}^{\prime }_{E}$
if the rest of the data is understood.
Proposition 1.1. Assume that
![]() $E, F$
and G are dualizable. We have the following compatibility between the reduced Atiyah class and the ordinary Atiyah class of
$E, F$
and G are dualizable. We have the following compatibility between the reduced Atiyah class and the ordinary Atiyah class of
![]() $f^{*}E$
: The diagram
$f^{*}E$
: The diagram
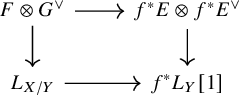
anti-commutes.
1.3 Atiyah class of an exact sequence
Let
![]() $\mathcal {X}\to \mathcal {Y}$
be a map of algebraic stacks and let
$\mathcal {X}\to \mathcal {Y}$
be a map of algebraic stacks and let
be an exact sequence of bounded above complexes of
![]() $\mathcal {O}_{\mathcal {X}}$
modules with quasi-coherent cohomology sheaves. Assume that the images of
$\mathcal {O}_{\mathcal {X}}$
modules with quasi-coherent cohomology sheaves. Assume that the images of
![]() $F,E,G$
in
$F,E,G$
in
![]() $D^-_{qcoh}(\mathcal {X})$
are perfect complexes and that their duals lie again in
$D^-_{qcoh}(\mathcal {X})$
are perfect complexes and that their duals lie again in
![]() $D^-_{qcoh}(\mathcal {X})$
(the latter is automatic if, for example,
$D^-_{qcoh}(\mathcal {X})$
(the latter is automatic if, for example,
![]() $\mathcal {X}$
is quasi-compact). Then there is a canonical way to complete the natural map
$\mathcal {X}$
is quasi-compact). Then there is a canonical way to complete the natural map
![]() $F\otimes G^{\vee }\to E\otimes E^{\vee }$
in
$F\otimes G^{\vee }\to E\otimes E^{\vee }$
in
![]() $D^-_{qcoh}(\mathcal {X})$
to a triangle
$D^-_{qcoh}(\mathcal {X})$
to a triangle
Moreover, there exists a natural mophism
which we call the Atiyah class of the exact sequence
![]() $\underline {E}$
.
$\underline {E}$
.
Proposition 1.2. We have a natural commutative diagram
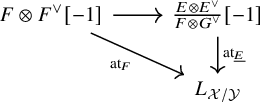
where the horizontal map is the shift of the morphism
Proposition 1.3. Let
![]() $\mathcal {X}\xrightarrow {f}\mathcal {Y} \to \mathcal {Z}$
be maps of algebraic stacks with f flat and let E be a bounded above complex of
$\mathcal {X}\xrightarrow {f}\mathcal {Y} \to \mathcal {Z}$
be maps of algebraic stacks with f flat and let E be a bounded above complex of
![]() $\mathcal {O}_{\mathcal {Y}}$
-modules with quasi-coherent cohomology. Let
$\mathcal {O}_{\mathcal {Y}}$
-modules with quasi-coherent cohomology. Let
![]() $E_{\mathcal {X}}:=f^{*}E$
and suppose we are given an exact sequence
$E_{\mathcal {X}}:=f^{*}E$
and suppose we are given an exact sequence
![]() $\underline {E}_{\mathcal {X}}$
of the form
$\underline {E}_{\mathcal {X}}$
of the form
Then we have a natural morphism of distinguished triangles
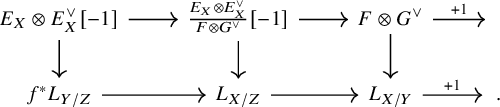
Here, the morphisms in the upper row are shifts of the ones in (1.2), except for the last one which is minus the map
![]() $F\otimes G^{\vee }\to E_X\otimes E_X^{\vee }$
provided there.Footnote
3
$F\otimes G^{\vee }\to E_X\otimes E_X^{\vee }$
provided there.Footnote
3
1.4 Deformation theoretic properties
We present two important examples of how the Atiyah class can be used to construct obstruction theories. For simplicity, we work over a base field k and let X be a smooth and proper scheme of dimension d over k.
Obstruction theory on moduli spaces of sheaves
Let
![]() $\mathcal {M}$
be a stack over
$\mathcal {M}$
be a stack over
![]() $\operatorname {\mathrm {Spec}} k$
and let
$\operatorname {\mathrm {Spec}} k$
and let
![]() $E\in D^-_{qcoh}(X\times \mathcal {M})$
be perfect. Consider the Atiyah class map of E relative to X:
$E\in D^-_{qcoh}(X\times \mathcal {M})$
be perfect. Consider the Atiyah class map of E relative to X:
Since E is dualizable, and by the projection formula, this data is equivalent to a map
Using dualizability again, we obtain a morphism
Theorem 1.4. Suppose that
![]() $\mathcal {M}$
is an open substack of the moduli stack of coherent sheaves on X. Then
$\mathcal {M}$
is an open substack of the moduli stack of coherent sheaves on X. Then
![]() $\operatorname {\mathrm {At}}_E$
is an obstruction theory. More generally, this holds when
$\operatorname {\mathrm {At}}_E$
is an obstruction theory. More generally, this holds when
![]() $\mathcal {M}$
is an open substack of a moduli space of universally gluable perfect complexes on X.
$\mathcal {M}$
is an open substack of a moduli space of universally gluable perfect complexes on X.
This is proven in §§6.3–6.5 for moduli of sheaves. The statement for complexes is addressed in Remark 6.16. Recall that an obstruction theory on an algebraic stack
![]() $\mathcal {Y}$
consists of a map
$\mathcal {Y}$
consists of a map
![]() $g:\mathbb {E}\to L_{\mathcal {Y}}$
in
$g:\mathbb {E}\to L_{\mathcal {Y}}$
in
![]() $D_{qcoh}(\mathcal {Y})$
, so that
$D_{qcoh}(\mathcal {Y})$
, so that
![]() $h^i(g)$
is an isomorphism for
$h^i(g)$
is an isomorphism for
![]() $i\geq 0$
, and so that
$i\geq 0$
, and so that
![]() $h^{-1}(g)$
is surjective [Reference Mochizuki14, Definition 2.4.1].
$h^{-1}(g)$
is surjective [Reference Mochizuki14, Definition 2.4.1].
Obstruction theory on Quot-schemes
Let
![]() $\mathcal {Y}$
be an algebraic stack and let E be a
$\mathcal {Y}$
be an algebraic stack and let E be a
![]() $\mathcal {Y}$
-flat coherent sheaf on
$\mathcal {Y}$
-flat coherent sheaf on
![]() $X\times \mathcal {Y}$
. Let
$X\times \mathcal {Y}$
. Let
![]() $f:\mathcal {Q}\to \mathcal {Y}$
be an open substack of the relative Quot-scheme of E over
$f:\mathcal {Q}\to \mathcal {Y}$
be an open substack of the relative Quot-scheme of E over
![]() $\mathcal {Y}$
and let
$\mathcal {Y}$
and let
be the universal exact sequence on
![]() $X\times \mathcal {Q}$
. We consider the associated reduced Atiyah class
$X\times \mathcal {Q}$
. We consider the associated reduced Atiyah class
![]() $\overline {\operatorname {\mathrm {at}}}_{E}:=\overline {\operatorname {\mathrm {at}}}_{E,V\times \mathcal {X}/V\times \mathcal {Y},G}$
as a map
$\overline {\operatorname {\mathrm {at}}}_{E}:=\overline {\operatorname {\mathrm {at}}}_{E,V\times \mathcal {X}/V\times \mathcal {Y},G}$
as a map
![]() $\overline {\operatorname {\mathrm {at}}}_E:F\to \pi _{\mathcal {X}}^{*} L_{\mathcal {X}/\mathcal {Y}}\otimes G$
in the derived category. As before, this data is equivalent to a morphism
$\overline {\operatorname {\mathrm {at}}}_E:F\to \pi _{\mathcal {X}}^{*} L_{\mathcal {X}/\mathcal {Y}}\otimes G$
in the derived category. As before, this data is equivalent to a morphism
Proposition 1.5. The map
![]() $\overline {\operatorname {\mathrm {At}}}_E$
is a relative obstruction theory for
$\overline {\operatorname {\mathrm {At}}}_E$
is a relative obstruction theory for
![]() $f:\mathcal {Q}\to \mathcal {Y}$
.
$f:\mathcal {Q}\to \mathcal {Y}$
.
2 Preliminaries
2.1 Derived category and cotangent complex of an algebraic stack
Let
![]() $\mathcal {X}$
be an algebraic stack and let
$\mathcal {X}$
be an algebraic stack and let
![]() $\mathcal {O}_{\mathcal {X}}$
denote its structure sheaf in the lisse-étale topos on
$\mathcal {O}_{\mathcal {X}}$
denote its structure sheaf in the lisse-étale topos on
![]() $\mathcal {X}$
. Given a smooth cover
$\mathcal {X}$
. Given a smooth cover
![]() $X\to \mathcal {X}$
, where X is an algebraic space, one can form the strictly simplicial algebraic space
$X\to \mathcal {X}$
, where X is an algebraic space, one can form the strictly simplicial algebraic space
![]() $X_{\bullet } = X_{\bullet , \operatorname {et}}$
, which we consider as a strictly simplicial topos with respect to the étale topology on every component. We write
$X_{\bullet } = X_{\bullet , \operatorname {et}}$
, which we consider as a strictly simplicial topos with respect to the étale topology on every component. We write
![]() $X_{\bullet , \operatorname {lis-et}}$
for the strictly simplicial topos obtained by taking the corresponding lisse-étale topos in place of each
$X_{\bullet , \operatorname {lis-et}}$
for the strictly simplicial topos obtained by taking the corresponding lisse-étale topos in place of each
![]() $X_n$
. It is shown in [Reference Olsson16, 4.6] that we have flat morphisms of topoi
$X_n$
. It is shown in [Reference Olsson16, 4.6] that we have flat morphisms of topoi
Moreover, the functor
![]() $\epsilon _*$
is exact and preserves flatness. We define
$\epsilon _*$
is exact and preserves flatness. We define
![]() $\eta _X^{*}$
to be the composition
$\eta _X^{*}$
to be the composition
![]() $\epsilon _*\circ \pi ^{*}:\operatorname {\mathrm {Mod}}(\mathcal {O}_{\mathcal {X}})\to \operatorname {\mathrm {Mod}}(\mathcal {O}_{X_{\bullet }})$
. It defines a functor on the categories of chain complexes and due to exactness also on the derived categories, both of which we also denote by
$\epsilon _*\circ \pi ^{*}:\operatorname {\mathrm {Mod}}(\mathcal {O}_{\mathcal {X}})\to \operatorname {\mathrm {Mod}}(\mathcal {O}_{X_{\bullet }})$
. It defines a functor on the categories of chain complexes and due to exactness also on the derived categories, both of which we also denote by
![]() $\eta _X^{*}$
. Let
$\eta _X^{*}$
. Let
![]() $\eta _{X_*}:=R\pi _*\circ \epsilon ^{*}:D(\mathcal {O}_{X_{\bullet }})\to D(\mathcal {O}_{\mathcal {X}})$
. By ([Reference Laszlo and Olsson10], Example 2.2.5), the functors
$\eta _{X_*}:=R\pi _*\circ \epsilon ^{*}:D(\mathcal {O}_{X_{\bullet }})\to D(\mathcal {O}_{\mathcal {X}})$
. By ([Reference Laszlo and Olsson10], Example 2.2.5), the functors
![]() $\eta _X^{*}$
and
$\eta _X^{*}$
and
![]() $\eta _{X_*}$
restrict to mutually inverse equivalences on the derived categories with quasi-coherent cohomology sheaves
$\eta _{X_*}$
restrict to mutually inverse equivalences on the derived categories with quasi-coherent cohomology sheaves
Given a smooth surjective map of algebraic spaces
![]() $g:W\to X$
over
$g:W\to X$
over
![]() $\mathcal {X}$
, let
$\mathcal {X}$
, let
![]() $W_{\bullet }$
be the induced hypercover for the map
$W_{\bullet }$
be the induced hypercover for the map
![]() $W\to \mathcal {X}$
and let
$W\to \mathcal {X}$
and let
![]() $g_{\bullet }:W_{\bullet }\to X_{\bullet }$
be the map induced by g. Then there is a canonical natural isomorphism between the functors
$g_{\bullet }:W_{\bullet }\to X_{\bullet }$
be the map induced by g. Then there is a canonical natural isomorphism between the functors
![]() $g^{*}\eta _X^{*}$
and
$g^{*}\eta _X^{*}$
and
![]() $\eta _W^{*}$
on the levels of sheaves, which induces isomorphisms between the induced functors on complexes and derived categories, respectively. We recall the notion of the cotangent complex of algebraic stacks as given in [Reference Olsson16, §8]: Given a morphism of algebraic stacks
$\eta _W^{*}$
on the levels of sheaves, which induces isomorphisms between the induced functors on complexes and derived categories, respectively. We recall the notion of the cotangent complex of algebraic stacks as given in [Reference Olsson16, §8]: Given a morphism of algebraic stacks
![]() $f:\mathcal {X}\to \mathcal {Y}$
, choose a
$f:\mathcal {X}\to \mathcal {Y}$
, choose a
![]() $2$
-commutative diagram
$2$
-commutative diagram
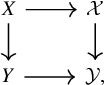
where
![]() $X,Y$
are algebraic spaces and where the maps
$X,Y$
are algebraic spaces and where the maps
![]() $Y\to \mathcal {Y}$
and
$Y\to \mathcal {Y}$
and
![]() $X\to \mathcal {X}_Y:= Y\times _{\mathcal {Y}} \mathcal {X}$
are smooth and surjective. Let
$X\to \mathcal {X}_Y:= Y\times _{\mathcal {Y}} \mathcal {X}$
are smooth and surjective. Let
![]() $X_{\bullet }$
and
$X_{\bullet }$
and
![]() $Y_{\bullet }$
be the strictly simplicial algebraic spaces associated to
$Y_{\bullet }$
be the strictly simplicial algebraic spaces associated to
![]() $X\to \mathcal {X}$
and
$X\to \mathcal {X}$
and
![]() $Y\to \mathcal {Y}$
, respectively. One defines a complex
$Y\to \mathcal {Y}$
, respectively. One defines a complex
![]() $L_{\mathcal {X}/\mathcal {Y},X/Y}$
on
$L_{\mathcal {X}/\mathcal {Y},X/Y}$
on
![]() $X_{\bullet }$
whose restriction to
$X_{\bullet }$
whose restriction to
![]() $X_n$
is given by the complex
$X_n$
is given by the complex
where
![]() $\Omega _{X_n/\mathcal {X}_{Y_n}}$
is placed in degree one, and the map is induced from the natural map of differentials
$\Omega _{X_n/\mathcal {X}_{Y_n}}$
is placed in degree one, and the map is induced from the natural map of differentials
![]() $h^0(L_{X_n/Y_n})\simeq \Omega _{X_n/Y_n}\to \Omega _{X_n/\mathcal {X}_{Y_n}}$
. It is shown in [Reference Olsson16] that this defines an element of
$h^0(L_{X_n/Y_n})\simeq \Omega _{X_n/Y_n}\to \Omega _{X_n/\mathcal {X}_{Y_n}}$
. It is shown in [Reference Olsson16] that this defines an element of
![]() $D_{qcoh}^{\leq 1}(X_{\bullet })$
and that the element
$D_{qcoh}^{\leq 1}(X_{\bullet })$
and that the element
![]() $\eta _* L_{\mathcal {X}/\mathcal {Y},X/Y}\in D^{\leq 1}_{qcoh}(\mathcal {X})$
is independent of the choice of diagram (2.3) up to canonical isomorphisms. This is used to define
$\eta _* L_{\mathcal {X}/\mathcal {Y},X/Y}\in D^{\leq 1}_{qcoh}(\mathcal {X})$
is independent of the choice of diagram (2.3) up to canonical isomorphisms. This is used to define
![]() $L_{\mathcal {X}/\mathcal {Y}}$
, so that one has a canonical isomorphism
$L_{\mathcal {X}/\mathcal {Y}}$
, so that one has a canonical isomorphism
![]() $\eta ^{*}L_{\mathcal {X}/\mathcal {Y}} \simeq L_{\mathcal {X}/\mathcal {Y},X/Y}$
for any choice of diagram (2.3).
$\eta ^{*}L_{\mathcal {X}/\mathcal {Y}} \simeq L_{\mathcal {X}/\mathcal {Y},X/Y}$
for any choice of diagram (2.3).
Remark 2.1. Define
![]() $\Omega _{X_{\bullet }/\mathcal {X}_{Y_{\bullet }}}$
to be the
$\Omega _{X_{\bullet }/\mathcal {X}_{Y_{\bullet }}}$
to be the
![]() $\mathcal {O}_{X_{\bullet }}$
-module which on
$\mathcal {O}_{X_{\bullet }}$
-module which on
![]() $X_n$
is given by
$X_n$
is given by
![]() $\Omega _{X_n/\mathcal {X}_{Y_n}}$
with the obvious pullback maps. Then we may restate
$\Omega _{X_n/\mathcal {X}_{Y_n}}$
with the obvious pullback maps. Then we may restate
Here,
![]() $L_{X_{\bullet }/Y_{\bullet }}$
is the usual cotangent complex for the map of topoi
$L_{X_{\bullet }/Y_{\bullet }}$
is the usual cotangent complex for the map of topoi
![]() $X_{\bullet }\to Y_{\bullet }$
, and the map indicated by ‘
$X_{\bullet }\to Y_{\bullet }$
, and the map indicated by ‘
![]() $-$
’ is minus the natural map whose restriction to the n-th simplicial degree is given by the composition
$-$
’ is minus the natural map whose restriction to the n-th simplicial degree is given by the composition
![]() $L_{X_n/Y_n}\xrightarrow {\tau _{\geq 0}} \Omega _{X_n/Y_n}\to \Omega _{X_n/\mathcal {X}_{Y_n}} $
.
$L_{X_n/Y_n}\xrightarrow {\tau _{\geq 0}} \Omega _{X_n/Y_n}\to \Omega _{X_n/\mathcal {X}_{Y_n}} $
.
2.2 Simplicial methods
We recall some notation and basic facts about simplicial rings and simplicial sheaves of modules in general topoi. For a general reference, see Illusie’s book [Reference Illusie7]. Throughout this subsection, let T denote a topos.
Simplicial modules
For a simplicial ring A in T, we denote by
![]() $A-\operatorname {\mathrm {Mods}}$
the category of A-modules. When A is an ordinary, we regard it as a constant simplicial ring, so that
$A-\operatorname {\mathrm {Mods}}$
the category of A-modules. When A is an ordinary, we regard it as a constant simplicial ring, so that
![]() $A-\operatorname {\mathrm {Mods}}$
denotes the category of simplicial A-modules. In either case, we denote by
$A-\operatorname {\mathrm {Mods}}$
denotes the category of simplicial A-modules. In either case, we denote by
![]() $D^{\Delta }(A)$
the derived category obtained by localizing
$D^{\Delta }(A)$
the derived category obtained by localizing
![]() $A-\operatorname {\mathrm {Mods}}$
at the class of quasi-isomorphisms.
$A-\operatorname {\mathrm {Mods}}$
at the class of quasi-isomorphisms.
Dold–Kan correspondence
Let A be an ordinary ring in T. The normalized chain functor induces an equivalence of abelian categories
![]() $N:A-\operatorname {\mathrm {Mods}} \to C^{\leq 0}(A)$
; see [Reference Illusie7, I 1.3]. It sends homotopic maps to homotopic maps and there are natural identifications
$N:A-\operatorname {\mathrm {Mods}} \to C^{\leq 0}(A)$
; see [Reference Illusie7, I 1.3]. It sends homotopic maps to homotopic maps and there are natural identifications
![]() $\pi _i(M)\simeq h^{-i}(NM)$
for a simplicial A-module M. In particular, N preserves quasi-isomorphisms and induces an equivalence
$\pi _i(M)\simeq h^{-i}(NM)$
for a simplicial A-module M. In particular, N preserves quasi-isomorphisms and induces an equivalence
![]() $N:D^{\Delta }(A)\to D^{\leq 0}(A)$
.
$N:D^{\Delta }(A)\to D^{\leq 0}(A)$
.
Cones and distinguished triangles
As in [Reference Illusie7, I 3.2.1], let
![]() $\sigma $
denote the simplicial
$\sigma $
denote the simplicial
![]() ${\mathbb {Z}}$
-module satisfying
${\mathbb {Z}}$
-module satisfying
![]() $N\sigma ={\mathbb {Z}}[1]$
and let
$N\sigma ={\mathbb {Z}}[1]$
and let
![]() $\gamma $
be the simplicial
$\gamma $
be the simplicial
![]() ${\mathbb {Z}}$
-module such that
${\mathbb {Z}}$
-module such that
![]() $N\gamma $
is the complex
$N\gamma $
is the complex
![]() ${\mathbb {Z}}\to {\mathbb {Z}}$
concentrated in degrees
${\mathbb {Z}}\to {\mathbb {Z}}$
concentrated in degrees
![]() $[-1,0]$
. Let A be a simplicial ring in the topos T and let E be an A-module. We write
$[-1,0]$
. Let A be a simplicial ring in the topos T and let E be an A-module. We write
![]() $\sigma E:=\sigma \otimes _{\mathbb {Z}} E$
and
$\sigma E:=\sigma \otimes _{\mathbb {Z}} E$
and
![]() $\gamma E:=\gamma \otimes _{\mathbb {Z}} E$
. One has canonical isomorphisms
$\gamma E:=\gamma \otimes _{\mathbb {Z}} E$
. One has canonical isomorphisms
![]() $\pi _i(E) = \pi _{i+1}(\sigma E)$
for any
$\pi _i(E) = \pi _{i+1}(\sigma E)$
for any
![]() $i\geq 0$
. We have a natural exact sequence of A-modules
$i\geq 0$
. We have a natural exact sequence of A-modules
For a map
![]() $\alpha :E\to F$
of A-modules, we define
$\alpha :E\to F$
of A-modules, we define
We have the sequence of natural maps
and the induced maps on homotopy groups fit into a long exact sequence. One declares a sequence
![]() $E\to F\to G\to \sigma E$
in
$E\to F\to G\to \sigma E$
in
![]() $D^{\Delta }(A)$
to be a distinguished triangle if it is isomorphic in
$D^{\Delta }(A)$
to be a distinguished triangle if it is isomorphic in
![]() $D^{\Delta }(A)$
to a sequence of the form (2.4); see [Reference Illusie7, I 3.2.2]. If A is an ordinary ring in T, and E a simplicial A-module, then in
$D^{\Delta }(A)$
to a sequence of the form (2.4); see [Reference Illusie7, I 3.2.2]. If A is an ordinary ring in T, and E a simplicial A-module, then in
![]() $D^{\leq 0}(A)$
, we have natural isomorphisms
$D^{\leq 0}(A)$
, we have natural isomorphisms
![]() $N\sigma E\simeq (NE)[1]$
, and the Dold–Kan correspondence preserves the notions of distinguished triangle.
$N\sigma E\simeq (NE)[1]$
, and the Dold–Kan correspondence preserves the notions of distinguished triangle.
Derived tensor product
Let A be a simplicial ring in T. The derived tensor product defines a functor
![]() $D^{\Delta }(A)\times D^{\Delta }(A)\to D^{\Delta }(A), (E,F)\mapsto E\otimes _A F$
, which can be computed as follows: For any quasi-isomorphism
$D^{\Delta }(A)\times D^{\Delta }(A)\to D^{\Delta }(A), (E,F)\mapsto E\otimes _A F$
, which can be computed as follows: For any quasi-isomorphism
![]() $L\to E$
where L is a flat (i.e., degreewise flat) A-module, the derived tensor product is computed by the (usual) tensor product
$L\to E$
where L is a flat (i.e., degreewise flat) A-module, the derived tensor product is computed by the (usual) tensor product
![]() $L\otimes _A F$
of A-modules (taken degree-wise). The analogous statement holds with a flat replacement of F. For fixed E, the functor
$L\otimes _A F$
of A-modules (taken degree-wise). The analogous statement holds with a flat replacement of F. For fixed E, the functor
![]() $E\otimes -:D^{\Delta }(A)\to D^{\Delta }(A)$
is naturally triangulated, and similarly for
$E\otimes -:D^{\Delta }(A)\to D^{\Delta }(A)$
is naturally triangulated, and similarly for
![]() $-\otimes E$
. If A is an ordinary ring and E, F are simplicial A-modules, then we have canonical natural isomorphisms
$-\otimes E$
. If A is an ordinary ring and E, F are simplicial A-modules, then we have canonical natural isomorphisms
![]() $N(E\otimes ^{\ell } F) \simeq NE\otimes ^{L} NF$
in
$N(E\otimes ^{\ell } F) \simeq NE\otimes ^{L} NF$
in
![]() $D^{\leq 0}(A)$
, which are compatible with the symmetry isomorphism of the tensor product.
$D^{\leq 0}(A)$
, which are compatible with the symmetry isomorphism of the tensor product.
Now let
![]() $P\to B$
be a morphism of A-algebras. Then, the derived tensor product
$P\to B$
be a morphism of A-algebras. Then, the derived tensor product
![]() $B\otimes _{P} -$
induces a triangulated functor
$B\otimes _{P} -$
induces a triangulated functor
![]() $D^{\Delta }(P)\to D^{\Delta }(B)$
, which is left-adjoint to the functor
$D^{\Delta }(P)\to D^{\Delta }(B)$
, which is left-adjoint to the functor
![]() $D^{\Delta }(B)\to D^{\Delta }(P), N\mapsto N_P$
given by restriction of scalars.
$D^{\Delta }(B)\to D^{\Delta }(P), N\mapsto N_P$
given by restriction of scalars.
We have the following:
Lemma 2.2. Suppose that
![]() $P\to B$
is a quasi-isomorphism of A-algebras. Then the derived tensor product and restriction of scalars are mutually inverse equivalences of categories. In other words, the natural adjunction maps
$P\to B$
is a quasi-isomorphism of A-algebras. Then the derived tensor product and restriction of scalars are mutually inverse equivalences of categories. In other words, the natural adjunction maps
![]() $M\to B\otimes _P M$
for M in
$M\to B\otimes _P M$
for M in
![]() $D^{\Delta }(P)$
and
$D^{\Delta }(P)$
and
![]() $B\otimes _P N_P\to N_P$
for N in
$B\otimes _P N_P\to N_P$
for N in
![]() $D^{\Delta }(B)$
are isomorphisms.
$D^{\Delta }(B)$
are isomorphisms.
Proof. This is [Reference Illusie7, I Corollaire 3.3.4.6].
Simplicial resolutions
Let
![]() $A\to B$
be a map of ordinary rings in a topos T. We denote by
$A\to B$
be a map of ordinary rings in a topos T. We denote by
the standard simplicial resolution of B over A [Reference Illusie7, I 1.5]. It is a simplicial A-algebra and flat over A in each degree. There is a natural quasi-isomorphism
![]() $P_A(B)\to B$
, where we regard B as a constant simplicial A-algebra in T.
$P_A(B)\to B$
, where we regard B as a constant simplicial A-algebra in T.
We will use the following result.
Lemma 2.3. Let
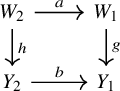
be a commutative diagram of locally ringed topoi with enough points. Assume that a and b are flat. Then the natural map
![]() $a^{-1}P_{g^{-1}\mathcal {O}_{Y_1}}(\mathcal {O}_{W_1})\to P_{h^{-1}\mathcal {O}_{Y_2}}(\mathcal {O}_{W_2})$
of simplicial sheaves of rings on
$a^{-1}P_{g^{-1}\mathcal {O}_{Y_1}}(\mathcal {O}_{W_1})\to P_{h^{-1}\mathcal {O}_{Y_2}}(\mathcal {O}_{W_2})$
of simplicial sheaves of rings on
![]() $W_2$
is flat in each degree.
$W_2$
is flat in each degree.
Proof. This can be checked on stalks of
![]() $W_2$
. Since taking the standard simplicial resolution commutes with pullback of topoi and with filtered direct limits, we are reduced to the following setting: We have a diagram in the category of local rings
$W_2$
. Since taking the standard simplicial resolution commutes with pullback of topoi and with filtered direct limits, we are reduced to the following setting: We have a diagram in the category of local rings
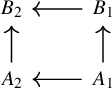
with
![]() $B_2$
flat over
$B_2$
flat over
![]() $B_1$
and
$B_1$
and
![]() $A_2$
flat over
$A_2$
flat over
![]() $A_1$
, and we need to show that the natural map
$A_1$
, and we need to show that the natural map
![]() $P_{A_1}(B_1)\to P_{A_2}(B_2)$
is degreewise flat. Denote this map by
$P_{A_1}(B_1)\to P_{A_2}(B_2)$
is degreewise flat. Denote this map by
![]() $F:P\to R$
with n-th part
$F:P\to R$
with n-th part
![]() $F_n:P_n\to R_n$
for
$F_n:P_n\to R_n$
for
![]() $n\geq 0$
. We also define
$n\geq 0$
. We also define
![]() $F_{-1}: B_1\to B_2$
. We show by induction on
$F_{-1}: B_1\to B_2$
. We show by induction on
![]() $n\geq -1$
that
$n\geq -1$
that
![]() $F_n$
is flat and injective. The base case follows from the fact that a flat morphism of local rings is faithfully flat and therefore injective. By the construction of the standard simplicial resolution, we have that
$F_n$
is flat and injective. The base case follows from the fact that a flat morphism of local rings is faithfully flat and therefore injective. By the construction of the standard simplicial resolution, we have that
![]() $P_{n+1}$
is the free polynomial algebra
$P_{n+1}$
is the free polynomial algebra
![]() $A_1[P_n]$
over the set of elements of
$A_1[P_n]$
over the set of elements of
![]() $P_n$
. The analogue is true for
$P_n$
. The analogue is true for
![]() $R_{n+1}$
, and the map
$R_{n+1}$
, and the map
![]() $F_{n+1}$
is the map
$F_{n+1}$
is the map
![]() $P_{n+1}=A_1[P_n]\to A_2[R_n]=R_{n+1}$
obtained by functoriality of this construction. The induction step then follows from Lemma 2.4 (note that
$P_{n+1}=A_1[P_n]\to A_2[R_n]=R_{n+1}$
obtained by functoriality of this construction. The induction step then follows from Lemma 2.4 (note that
![]() $A_1\to A_2$
is injective since it is a flat map of local rings).
$A_1\to A_2$
is injective since it is a flat map of local rings).
Lemma 2.4. Consider a commutative diagram of rings

where the map
![]() $A_1\to A_2$
is flat and injective and
$A_1\to A_2$
is flat and injective and
![]() $B_1\to B_2$
is injective. Then the induced map between polynomial algebras
$B_1\to B_2$
is injective. Then the induced map between polynomial algebras
![]() $A_1[B_1]\to A_2[B_2]$
is flat and injective.
$A_1[B_1]\to A_2[B_2]$
is flat and injective.
Proof. The injectivity is clear. The map
![]() $A_1[B_1]\to A_2[B_1]=A_2\otimes _{A_1} A_1[B_1]$
is a base change of a flat map, hence flat, and
$A_1[B_1]\to A_2[B_1]=A_2\otimes _{A_1} A_1[B_1]$
is a base change of a flat map, hence flat, and
![]() $A_2[B_1]\to A_2[B_2]$
is a free algebra by injectivity, hence also flat. Since a composition of flat morphisms is flat, the result follows.
$A_2[B_1]\to A_2[B_2]$
is a free algebra by injectivity, hence also flat. Since a composition of flat morphisms is flat, the result follows.
Module of principal parts
Let
![]() $A\to B$
be a map of rings in T. The (first) module of principal parts for the ring map
$A\to B$
be a map of rings in T. The (first) module of principal parts for the ring map
![]() $A\to B$
is given by
$A\to B$
is given by
![]() $P_{B/A}^1:= (B\otimes _A B)/I_{\Delta }^2$
, where
$P_{B/A}^1:= (B\otimes _A B)/I_{\Delta }^2$
, where
![]() $I_{\Delta }$
is the kernel of the multiplication map
$I_{\Delta }$
is the kernel of the multiplication map
![]() $B\otimes _AB\to B$
. (Here, the tensor product is in general not a derived one). The A-module
$B\otimes _AB\to B$
. (Here, the tensor product is in general not a derived one). The A-module
![]() $P_{B/A}^1$
is naturally a
$P_{B/A}^1$
is naturally a
![]() $(B,B)$
-bimodule. Recall that
$(B,B)$
-bimodule. Recall that
![]() $\Omega ^1_{B/A}=I_{\Delta }/I_{\Delta }^2$
, so that we have an exact sequence of
$\Omega ^1_{B/A}=I_{\Delta }/I_{\Delta }^2$
, so that we have an exact sequence of
![]() $(B,B)$
-bimodules called the exact sequence of principal parts
$(B,B)$
-bimodules called the exact sequence of principal parts
Here, for each of the outer terms, the two B-module structures agree. We will denote this sequence by
![]() $\underline {P}^1_{B/A}$
. The map
$\underline {P}^1_{B/A}$
. The map
![]() $b\mapsto b\otimes 1$
gives a splitting of this sequence for the left B-module structures, and
$b\mapsto b\otimes 1$
gives a splitting of this sequence for the left B-module structures, and
![]() $b\to 1\otimes b$
gives a splitting for the right B-module structures. Now let E be a B-module. Then we set
$b\to 1\otimes b$
gives a splitting for the right B-module structures. Now let E be a B-module. Then we set
![]() $P^1_{B/A}(E):=P^1_{B/A}\otimes _B E$
, where we take the tensor product with respect to the right B-module structure on
$P^1_{B/A}(E):=P^1_{B/A}\otimes _B E$
, where we take the tensor product with respect to the right B-module structure on
![]() $P^1_{B/A}$
. Equivalently,
$P^1_{B/A}$
. Equivalently,
![]() $P_{B/A}^1(E)=B\otimes _A E/(I_{\Delta }^2 B\otimes _A E)$
. Then the sequence of principal parts for E is
$P_{B/A}^1(E)=B\otimes _A E/(I_{\Delta }^2 B\otimes _A E)$
. Then the sequence of principal parts for E is
![]() $\underline {P}^1_{B/A}(E):=\underline {P}^1_{B/A}\otimes _B E$
, or explicitly,
$\underline {P}^1_{B/A}(E):=\underline {P}^1_{B/A}\otimes _B E$
, or explicitly,
We usually regard this as a sequence of B-modules with respect to the left B-module structure. Note that it is in general not split.
Illusie’s Atiyah class
With these ingredients, we recall Illusie’s definition of Atiyah class: Let
![]() $f:X\to Y$
be a morphism of ringed topoi and let
$f:X\to Y$
be a morphism of ringed topoi and let
![]() $E\in D^{\leq 0}(X)$
. Let
$E\in D^{\leq 0}(X)$
. Let
![]() $P:= P_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
be the standard simplicial resolution. By the Dold–Kan correspondence, we may regard E as an object of
$P:= P_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
be the standard simplicial resolution. By the Dold–Kan correspondence, we may regard E as an object of
![]() $D^{\Delta }(\mathcal {O}_X)$
and thus of
$D^{\Delta }(\mathcal {O}_X)$
and thus of
![]() $D^{\Delta }(P)$
by restriction of scalars. We have the exact sequence of principal parts associated to
$D^{\Delta }(P)$
by restriction of scalars. We have the exact sequence of principal parts associated to
![]() $E_P$
, which is an exact sequence of P-modules:
$E_P$
, which is an exact sequence of P-modules:
Note that the leftmost term here computes the derived tensor product since
![]() $\Omega _{P/f^{-1}\mathcal {O}_Y}$
is flat over P. Moreover, it is canonically quasi-isomorphic to the restriction of scalars of
$\Omega _{P/f^{-1}\mathcal {O}_Y}$
is flat over P. Moreover, it is canonically quasi-isomorphic to the restriction of scalars of
![]() $L_{X/Y}\otimes _{\mathcal {O}_X} E$
. From the sequence
$L_{X/Y}\otimes _{\mathcal {O}_X} E$
. From the sequence
![]() $\underline {P}_{P/f^{-1}\mathcal {O}_Y}(E_P)$
, we obtain a morphism
$\underline {P}_{P/f^{-1}\mathcal {O}_Y}(E_P)$
, we obtain a morphism
![]() $E_P\to \sigma (L_{X/Y}\otimes _{\mathcal {O}_X} E)_P$
in
$E_P\to \sigma (L_{X/Y}\otimes _{\mathcal {O}_X} E)_P$
in
![]() $D^{\Delta }(P)$
. Extending scalars to
$D^{\Delta }(P)$
. Extending scalars to
![]() $\mathcal {O}_X$
, this defines a canonical morphism
$\mathcal {O}_X$
, this defines a canonical morphism
![]() $E\to \sigma L_{X/Y}\otimes _{\mathcal {O}_X} E$
in
$E\to \sigma L_{X/Y}\otimes _{\mathcal {O}_X} E$
in
![]() $D^{\Delta }(\mathcal {O}_X)$
. The Atiyah class is the corresponding morphism
$D^{\Delta }(\mathcal {O}_X)$
. The Atiyah class is the corresponding morphism
in
![]() $D^{\leq 0}(\mathcal {O}_X)$
obtained via the Dold–Kan correspondence.
$D^{\leq 0}(\mathcal {O}_X)$
obtained via the Dold–Kan correspondence.
2.3 The parallel arrow category.
Let
be a diagram of topoi. We obtain an induced topos
![]() ${W}_{\parallel }$
whose objects are tuples
${W}_{\parallel }$
whose objects are tuples
![]() $(A_X,A_W,s^{\sharp },t^{\sharp })$
, where
$(A_X,A_W,s^{\sharp },t^{\sharp })$
, where
![]() $A_X$
and
$A_X$
and
![]() $A_W$
are objects of X and W, respectively, and
$A_W$
are objects of X and W, respectively, and
![]() $s^\sharp :s^{-1}A_X\to A_W$
and
$s^\sharp :s^{-1}A_X\to A_W$
and
![]() $t^{\sharp }:t^{-1}A_X\to A_W$
are morphisms in W. Giving a ring
$t^{\sharp }:t^{-1}A_X\to A_W$
are morphisms in W. Giving a ring
![]() $R=(R_X,R_W,s^{\sharp },t^{\sharp })$
in
$R=(R_X,R_W,s^{\sharp },t^{\sharp })$
in
![]() ${W}_{\parallel }$
is equivalent to giving rings on X and W, and giving
${W}_{\parallel }$
is equivalent to giving rings on X and W, and giving
![]() $s,t$
the structure of morphism of ringed topoi. Given such an R, we use the following notation: For an
$s,t$
the structure of morphism of ringed topoi. Given such an R, we use the following notation: For an
![]() $R_X$
-module
$R_X$
-module
![]() $M_X$
, we write
$M_X$
, we write
![]() $s_R^{*}M_X:=s^{-1}M_X\otimes _{s^{-1}R_X} R_W$
and
$s_R^{*}M_X:=s^{-1}M_X\otimes _{s^{-1}R_X} R_W$
and
![]() $t_R^{*}M_X:=t^{-1}M_X\otimes _{t^{-1}R_X} R_W$
for the respective (in general un-derived) base change of
$t_R^{*}M_X:=t^{-1}M_X\otimes _{t^{-1}R_X} R_W$
for the respective (in general un-derived) base change of
![]() $M_X$
. Then an R-module is given by a tuple
$M_X$
. Then an R-module is given by a tuple
![]() $M=(M_X,M_W, s^{*}, t^{*})$
, where
$M=(M_X,M_W, s^{*}, t^{*})$
, where
![]() $M_X$
and
$M_X$
and
![]() $M_W$
are
$M_W$
are
![]() $R_X$
and
$R_X$
and
![]() $R_W$
-modules, respectively, and where
$R_W$
-modules, respectively, and where
![]() $s^{*}:s_R^{*}M_X\to M_W$
and
$s^{*}:s_R^{*}M_X\to M_W$
and
![]() $t^{*}:t_R^{*}M_X\to M_W$
are morphisms of
$t^{*}:t_R^{*}M_X\to M_W$
are morphisms of
![]() $R_W$
-modules.
$R_W$
-modules.
We define a functor
![]() $\operatorname {\mathrm {Cone}}_R:C(R) \to C(R_W)$
by
$\operatorname {\mathrm {Cone}}_R:C(R) \to C(R_W)$
by
If R is a simplicial ring in
![]() ${W}_{\parallel }$
, the analogous discussion holds for R-modules, and we get a functor
${W}_{\parallel }$
, the analogous discussion holds for R-modules, and we get a functor
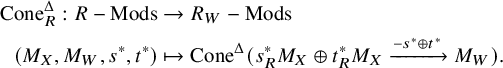 $$ \begin{align*} \operatorname{\mathrm{Cone}}_R^{\Delta}: R-\operatorname{\mathrm{Mods}}&\to R_W-\operatorname{\mathrm{Mods}} \\ (M_X,M_W,s^{*},t^{*})&\mapsto \operatorname{Cone}^{\Delta}(s_R^{*}M_X\oplus t_R^{*}M_X\xrightarrow{-s^{*}\oplus t^{*}} M_W). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Cone}}_R^{\Delta}: R-\operatorname{\mathrm{Mods}}&\to R_W-\operatorname{\mathrm{Mods}} \\ (M_X,M_W,s^{*},t^{*})&\mapsto \operatorname{Cone}^{\Delta}(s_R^{*}M_X\oplus t_R^{*}M_X\xrightarrow{-s^{*}\oplus t^{*}} M_W). \end{align*} $$
Under some natural flatness assumptions, we have induced functors on the derived categories:
Lemma 2.5.
-
i) Let R be a ring on
 ${W}_{\parallel }$
with
${W}_{\parallel }$
with
 $s^{\sharp }:s^{-1}R_X\to R_W$
and
$s^{\sharp }:s^{-1}R_X\to R_W$
and
 $t^{\sharp }:t^{-1}R_X\to R_W$
flat. Then
$t^{\sharp }:t^{-1}R_X\to R_W$
flat. Then
 $\operatorname {\mathrm {Cone}}_R$
descends to a triangulated functor of derived categories
$\operatorname {\mathrm {Cone}}_R$
descends to a triangulated functor of derived categories
 $D(R)\to D(R_W)$
(also denoted
$D(R)\to D(R_W)$
(also denoted
 $\operatorname {\mathrm {Cone}}_R$
).
$\operatorname {\mathrm {Cone}}_R$
). -
ii) Let R be a simplicial ring on
 ${W}_{\parallel }$
with
${W}_{\parallel }$
with
 $s^{\sharp }:s^{-1}R_X\to R_W$
and
$s^{\sharp }:s^{-1}R_X\to R_W$
and
 $t^{\sharp }:t^{-1}R_X\to R_W$
flat. Then
$t^{\sharp }:t^{-1}R_X\to R_W$
flat. Then
 $\operatorname {\mathrm {Cone}}_R^{\Delta }$
descends to a triangulated functor
$\operatorname {\mathrm {Cone}}_R^{\Delta }$
descends to a triangulated functor
 $D^{\Delta }(R)\to D^{\Delta }(R_W)$
(also denoted
$D^{\Delta }(R)\to D^{\Delta }(R_W)$
(also denoted
 $\operatorname {\mathrm {Cone}}_R^{\Delta }$
).
$\operatorname {\mathrm {Cone}}_R^{\Delta }$
). -
iii) Let R be an ordinary ring
 ${W}_{\parallel }$
, viewed as a constant simplicial ring, and assume that
${W}_{\parallel }$
, viewed as a constant simplicial ring, and assume that
 $s^{\sharp }$
and
$s^{\sharp }$
and
 $t^{\sharp }$
are flat. Then the two constructions in i) and ii) are compatible with the Dold–Kan correspondence, in the sense that the two functors obtained by traversing the outer edges of the diagram are related by a canonical natural isomorphism.
$t^{\sharp }$
are flat. Then the two constructions in i) and ii) are compatible with the Dold–Kan correspondence, in the sense that the two functors obtained by traversing the outer edges of the diagram are related by a canonical natural isomorphism.
Proof. We prove 2.5. For any ring S, the abelian category of complexes
![]() $C^{[-1,0]}(S)$
concentrated in degrees
$C^{[-1,0]}(S)$
concentrated in degrees
![]() $-1$
and
$-1$
and
![]() $0$
is canonically identified with the category of maps of S-modules.
$0$
is canonically identified with the category of maps of S-modules.
The functor
![]() $\operatorname {\mathrm {Cone}}_R:C(R)\to C(R_W)$
factors as
$\operatorname {\mathrm {Cone}}_R:C(R)\to C(R_W)$
factors as
![]() $C(R)\to C(C^{[-1,0]}(R_W))\to C(R_W)$
, where the first map is induced from the functor
$C(R)\to C(C^{[-1,0]}(R_W))\to C(R_W)$
, where the first map is induced from the functor
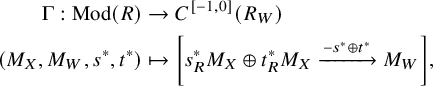 $$ \begin{align*} \Gamma: \operatorname{\mathrm{Mod}}(R) &\to C^{[-1,0]}(R_W) \\ (M_X,M_W,s^{*},t^{*}) & \mapsto \left[s_R^{*}M_X\oplus t_R^{*}M_X\xrightarrow{-s^{*}\oplus t^{*}}M_W\right], \end{align*} $$
$$ \begin{align*} \Gamma: \operatorname{\mathrm{Mod}}(R) &\to C^{[-1,0]}(R_W) \\ (M_X,M_W,s^{*},t^{*}) & \mapsto \left[s_R^{*}M_X\oplus t_R^{*}M_X\xrightarrow{-s^{*}\oplus t^{*}}M_W\right], \end{align*} $$
and the second map is taking the mapping cone. By the flatness assumption,
![]() $\Gamma $
is exact and therefore induces a triangulated functor
$\Gamma $
is exact and therefore induces a triangulated functor
![]() $D(R)\to D(C^{[-1,0]}(R_W))$
.
$D(R)\to D(C^{[-1,0]}(R_W))$
.
Therefore, it is enough to show that for any ring S, the mapping cone functor
![]() $C(C^{[-1,0]}(S))\to C(S)$
descends to a triangulated functor of derived categories. We may regard
$C(C^{[-1,0]}(S))\to C(S)$
descends to a triangulated functor of derived categories. We may regard
![]() $C(C^{[-1,0]}(S))$
as a category of double complexes
$C(C^{[-1,0]}(S))$
as a category of double complexes
![]() $A^{i,j}$
with nonzero entries only for
$A^{i,j}$
with nonzero entries only for
![]() $i\in \{-1,0\}$
. Then the mapping cone is exactly given by taking the associated double complex with the sign conventions of [22, Remark 0G6A]. By [22, Remark 0G6A and Remark 0G6D], taking the total complex defines a triangulated functor of the homotopy categories
$i\in \{-1,0\}$
. Then the mapping cone is exactly given by taking the associated double complex with the sign conventions of [22, Remark 0G6A]. By [22, Remark 0G6A and Remark 0G6D], taking the total complex defines a triangulated functor of the homotopy categories
![]() $K(C^{[-1,0]}(S))\to K(S)$
. To see that this preserves quasi-isomorphisms, one can use that the spectral sequence for the double complex converges; see [22, Lemma 0132]. Hence, it descends to a functor
$K(C^{[-1,0]}(S))\to K(S)$
. To see that this preserves quasi-isomorphisms, one can use that the spectral sequence for the double complex converges; see [22, Lemma 0132]. Hence, it descends to a functor
![]() $D(C^{[-1,0]}(S))\to D(S)$
. This finishes the proof of 2.5.
$D(C^{[-1,0]}(S))\to D(S)$
. This finishes the proof of 2.5.
Part ii) follows from an analogous argument with simplicial modules. Here, one uses additionally that base change along a degree-wise flat map of simplicial rings preserves quasi-isomorphism of modules. For S any simplicial ring, and
![]() $[A_{-1}\xrightarrow {\alpha } A_0]\in C^{[-1,0]}(S)$
, we describe the triangulated structure on the mapping cone functor: We have
$[A_{-1}\xrightarrow {\alpha } A_0]\in C^{[-1,0]}(S)$
, we describe the triangulated structure on the mapping cone functor: We have
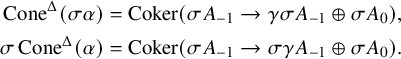 $$ \begin{align*} \operatorname{\mathrm{Cone}}^{\Delta}(\sigma \alpha) &= \operatorname{Coker}(\sigma A_{-1}\to \gamma \sigma A_{-1} \oplus \sigma A_0),\\ \sigma \operatorname{\mathrm{Cone}}^{\Delta}(\alpha) &= \operatorname{Coker}(\sigma A_{-1}\to \sigma \gamma A_{-1}\oplus \sigma A_0). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Cone}}^{\Delta}(\sigma \alpha) &= \operatorname{Coker}(\sigma A_{-1}\to \gamma \sigma A_{-1} \oplus \sigma A_0),\\ \sigma \operatorname{\mathrm{Cone}}^{\Delta}(\alpha) &= \operatorname{Coker}(\sigma A_{-1}\to \sigma \gamma A_{-1}\oplus \sigma A_0). \end{align*} $$
We take the canonical isomorphism between them induced by the symmetry isomorphism of the tensor product
![]() $\gamma \sigma A_{-1}\simeq \sigma \gamma A_{-1}$
.
$\gamma \sigma A_{-1}\simeq \sigma \gamma A_{-1}$
.
The compatibility (iii) follows from the constructions by using the basic compatibilities of the Dold–Kan correspondence, in particular, that it is compatible with the symmetry isomorphisms of tensor products on the level of derived categories.
Lemma 2.6. Let R be a ring in
![]() ${W}_{\parallel }$
. For any complex of R-modules E, we have a natural morphism
${W}_{\parallel }$
. For any complex of R-modules E, we have a natural morphism
![]() $c_E:\operatorname {\mathrm {Cone}}_R(E)\to E_{W}[1]$
. If the pullback maps
$c_E:\operatorname {\mathrm {Cone}}_R(E)\to E_{W}[1]$
. If the pullback maps
![]() $s^{*}:s_R^{*}E_X\to E_W$
and
$s^{*}:s_R^{*}E_X\to E_W$
and
![]() $t^{*}:t_R^{*}E_X\to E_W$
are quasi-isomorphisms, then so is
$t^{*}:t_R^{*}E_X\to E_W$
are quasi-isomorphisms, then so is
![]() $c_E$
. The same picture holds in the category of simplicial
$c_E$
. The same picture holds in the category of simplicial
![]() $\mathcal {O}_{\mathcal {X}}$
modules with the obvious modifications, and the two situations are compatible via the Dold–Kan correspondence.
$\mathcal {O}_{\mathcal {X}}$
modules with the obvious modifications, and the two situations are compatible via the Dold–Kan correspondence.
Proof. We define
![]() $c_E$
as the composition
$c_E$
as the composition
(the alternative choice of second map
![]() $(0\oplus t^{*})$
gives the same map up to chain-homotopy). One checks directly that this is a quasi-isomorphism when
$(0\oplus t^{*})$
gives the same map up to chain-homotopy). One checks directly that this is a quasi-isomorphism when
![]() $s^{*}$
and
$s^{*}$
and
![]() $t^{*}$
are quasi-isomorphisms. The proofs of the remaining statements are left to the reader.
$t^{*}$
are quasi-isomorphisms. The proofs of the remaining statements are left to the reader.
We have the following result regarding tensor products:
Lemma 2.7.
-
i) Let R be a simplicial ring on
 ${W}_{\parallel }$
with flat pullback maps
${W}_{\parallel }$
with flat pullback maps
 $s^{\sharp }, t^{\sharp }$
and let
$s^{\sharp }, t^{\sharp }$
and let
 $L,E$
be R-modules. Then there is a natural map
$L,E$
be R-modules. Then there is a natural map
 $\operatorname {\mathrm {Cone}}_R^{\Delta }(L\otimes _R E)\to \operatorname {\mathrm {Cone}}_R^{\Delta }(L)\otimes _{R_W} E_W$
. If either of L and E are flat and if
$\operatorname {\mathrm {Cone}}_R^{\Delta }(L\otimes _R E)\to \operatorname {\mathrm {Cone}}_R^{\Delta }(L)\otimes _{R_W} E_W$
. If either of L and E are flat and if
 $s^{*}:s_R^{*}E_X\to E_W$
and
$s^{*}:s_R^{*}E_X\to E_W$
and
 $t^{*}:t_R^{*}E_X\to E_W$
are quasi-isomorphisms, then
$t^{*}:t_R^{*}E_X\to E_W$
are quasi-isomorphisms, then
 $\operatorname {\mathrm {Cone}}_R^{\Delta }(L\otimes _R E)\to \operatorname {\mathrm {Cone}}_R^{\Delta }(L)\otimes _{R_W} E_W$
is a quasi-isomorphism. In particular, for any
$\operatorname {\mathrm {Cone}}_R^{\Delta }(L\otimes _R E)\to \operatorname {\mathrm {Cone}}_R^{\Delta }(L)\otimes _{R_W} E_W$
is a quasi-isomorphism. In particular, for any
 $E\in D^{\Delta }(R)$
, we have a canonical
$E\in D^{\Delta }(R)$
, we have a canonical
 $2$
-morphism which is an isomorphism if the pullback maps
$2$
-morphism which is an isomorphism if the pullback maps
 $s^{*}$
,
$s^{*}$
,
 $t^{*}$
of E are isomorphisms in
$t^{*}$
of E are isomorphisms in
 $D^{\Delta }(R_W)$
.
$D^{\Delta }(R_W)$
.
-
ii) The analogous statement holds if R is an ordinary ring and
 $L,E$
are bounded above complexes of R-modules.
$L,E$
are bounded above complexes of R-modules. -
iii) The natural isomorphisms in the derived category in i) and ii) are compatible via the Dold–Kan correspondence.
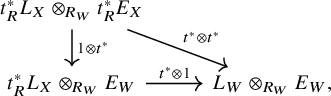
Proof. We only address i). Part ii) is analogous, and iii) can be seen by tracing through the argument and using the compatibilites of the Dold–Kan correspondence. Note that for any R-module F, we have
where the map in the outer cone is the composition of
![]() $-s^{*}$
with the inclusion
$-s^{*}$
with the inclusion
![]() $F_Z\to \operatorname {\mathrm {Cone}}^{\Delta }(t^{*})$
. For any commutative triangle
$F_Z\to \operatorname {\mathrm {Cone}}^{\Delta }(t^{*})$
. For any commutative triangle
in
![]() $R_W-\operatorname {\mathrm {Mods}}$
, we obtain induced maps
$R_W-\operatorname {\mathrm {Mods}}$
, we obtain induced maps
which form the first three terms of an exact triangle. In particular, if u is a quasi-isomorphism, then
![]() $\operatorname {Cone}^{\Delta }(u)$
is acyclic, so
$\operatorname {Cone}^{\Delta }(u)$
is acyclic, so
![]() $\alpha $
is also a quasi-isomorphism. Applying this to the triangle
$\alpha $
is also a quasi-isomorphism. Applying this to the triangle
we get a natural map,
which is a quasi-isomorphism if
![]() $t^{*}:t_R^{*}E_X\to E_W$
is one and if additionally either one of L or E is flat.
$t^{*}:t_R^{*}E_X\to E_W$
is one and if additionally either one of L or E is flat.
Similarly, we have the triangle
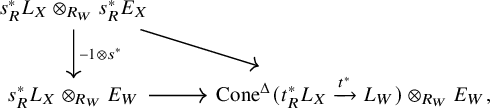
where the horizontal map is obtained by applying
![]() $-\otimes _{R_W} E_W$
to the composition
$-\otimes _{R_W} E_W$
to the composition
We get an induced morphism
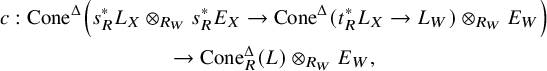 $$ \begin{gather*} c: \operatorname{Cone}^{\Delta}\left(s^{*}_RL_X \otimes_{R_W} s^{*}_RE_X \to \operatorname{Cone}^{\Delta}(t^{*}_RL_X\to L_W) \otimes_{R_W} E_W\right) \\ \to \operatorname{\mathrm{Cone}}_R^{\Delta}(L)\otimes_{R_W} E_W, \end{gather*} $$
$$ \begin{gather*} c: \operatorname{Cone}^{\Delta}\left(s^{*}_RL_X \otimes_{R_W} s^{*}_RE_X \to \operatorname{Cone}^{\Delta}(t^{*}_RL_X\to L_W) \otimes_{R_W} E_W\right) \\ \to \operatorname{\mathrm{Cone}}_R^{\Delta}(L)\otimes_{R_W} E_W, \end{gather*} $$
which again is a quasi-isomorphism if
![]() $s^{*}:s_R^{*}E_X\to E_W$
is and if one of L or E is flat. Putting together b and c, we get a natural morphism
$s^{*}:s_R^{*}E_X\to E_W$
is and if one of L or E is flat. Putting together b and c, we get a natural morphism
which is a quasi-isomorphism if L (resp. E) is flat and that both pullback maps of E are quasi-isomorphisms.
Variant 2.8. Let
![]() $W_{\wedge }$
denote the topos associated to the diagram
$W_{\wedge }$
denote the topos associated to the diagram
Its objects are tuples
![]() $(A^{\prime }_{X},A^{\prime \prime }_{X}, A_W,s^{\sharp }, t^{\sharp })$
, where
$(A^{\prime }_{X},A^{\prime \prime }_{X}, A_W,s^{\sharp }, t^{\sharp })$
, where
![]() $A^{\prime }_{X}, A^{\prime \prime }_X$
are objects of X, where
$A^{\prime }_{X}, A^{\prime \prime }_X$
are objects of X, where
![]() $A_W$
is an object of W and where
$A_W$
is an object of W and where
![]() $s^{\sharp }:s^{-1}A^{\prime }_X\to A_W$
and
$s^{\sharp }:s^{-1}A^{\prime }_X\to A_W$
and
![]() $t^{\sharp }:t^{-1} A^{\prime \prime }_X\to A_W$
are morphisms in W. Then everything in the preceding subsection goes through with
$t^{\sharp }:t^{-1} A^{\prime \prime }_X\to A_W$
are morphisms in W. Then everything in the preceding subsection goes through with
![]() $W_{\wedge }$
in place of
$W_{\wedge }$
in place of
![]() ${W}_{\parallel }$
and straightforward modifications. Note also that we have an exact pullback functor
${W}_{\parallel }$
and straightforward modifications. Note also that we have an exact pullback functor
![]() $\operatorname {Sh}({W}_{\parallel })\to \operatorname {Sh}(W_{\wedge })$
given on objects by
$\operatorname {Sh}({W}_{\parallel })\to \operatorname {Sh}(W_{\wedge })$
given on objects by
If
![]() ${R}_{\parallel }$
is a ring on
${R}_{\parallel }$
is a ring on
![]() ${W}_{\parallel }$
and
${W}_{\parallel }$
and
![]() $R_{\wedge }$
its restriction to
$R_{\wedge }$
its restriction to
![]() $W_{\wedge }$
, then
$W_{\wedge }$
, then
![]() $\operatorname {\mathrm {Cone}}_{{R}_{\parallel }}$
factors as
$\operatorname {\mathrm {Cone}}_{{R}_{\parallel }}$
factors as
The analogous picture holds for the simplicial versions.
Application to algebraic stacks
We apply the preceding discussion to the derived categories of algebraic stacks and the cotangent complex. This lays the groundwork for our definition of the Atiyah class on a stack using the modules of principal parts.
Situation 2.9. Consider the diagram (2.3) with the associated strictly simplicial algebraic spaces
![]() $X_{\bullet }$
and
$X_{\bullet }$
and
![]() $Y_{\bullet }$
. Let
$Y_{\bullet }$
. Let
![]() $W:=X\times _{\mathcal {X}_Y} X$
, with associated projections
$W:=X\times _{\mathcal {X}_Y} X$
, with associated projections
![]() $s,t:W\to X$
on the first and second factor, respectively, and let
$s,t:W\to X$
on the first and second factor, respectively, and let
![]() $h:W\to Y$
be the induced map. Let
$h:W\to Y$
be the induced map. Let
![]() $W_{\bullet }$
be the strictly simplicial algebraic space associated to the covering
$W_{\bullet }$
be the strictly simplicial algebraic space associated to the covering
![]() $W\xrightarrow {s} X\to \mathcal {X}$
. One has canonical isomorphisms
$W\xrightarrow {s} X\to \mathcal {X}$
. One has canonical isomorphisms
![]() $W_n\simeq X_n\times _{\mathcal {X}_{Y_n}}X_n$
and maps
$W_n\simeq X_n\times _{\mathcal {X}_{Y_n}}X_n$
and maps
![]() $h_n:W_n\to Y_n$
. We denote by
$h_n:W_n\to Y_n$
. We denote by
![]() ${W}_{\parallel }$
the topos associated to the diagram
${W}_{\parallel }$
the topos associated to the diagram
It has a natural structure of ringed topos with flat pullback maps
![]() $s_{\bullet }^{\sharp }, t_{\bullet }^{\sharp }$
, and we write
$s_{\bullet }^{\sharp }, t_{\bullet }^{\sharp }$
, and we write
![]() $\mathcal {O}_{{W}_{\parallel }}$
for the structure sheaf.
$\mathcal {O}_{{W}_{\parallel }}$
for the structure sheaf.
We denote by
![]() $({Y}_{\parallel },\mathcal {O}_{{Y}_{\parallel }})$
the ringed topos associated to the diagram
$({Y}_{\parallel },\mathcal {O}_{{Y}_{\parallel }})$
the ringed topos associated to the diagram
with both arrows the identity. There is a natural map of topoi
![]() ${h}_{\parallel }:{W}_{\parallel }\to {Y}_{\parallel }$
.
${h}_{\parallel }:{W}_{\parallel }\to {Y}_{\parallel }$
.
For E a complex of
![]() $\mathcal {O}_{\mathcal {X}}$
-modules, we write
$\mathcal {O}_{\mathcal {X}}$
-modules, we write
![]() $E_{X_{\bullet }}:=\eta _X^{*}E$
and
$E_{X_{\bullet }}:=\eta _X^{*}E$
and
![]() $E_{W_{\bullet }}:=\eta _W^{*}E$
. We have natural morphisms
$E_{W_{\bullet }}:=\eta _W^{*}E$
. We have natural morphisms
![]() $s_{\bullet }^{*}E_{X_{\bullet }}\to E_{W_{\bullet }}$
and
$s_{\bullet }^{*}E_{X_{\bullet }}\to E_{W_{\bullet }}$
and
![]() $t_{\bullet }^{*}E_{X_{\bullet }}\to E_{W_{\bullet }}$
. Thus, we get naturally a complex of
$t_{\bullet }^{*}E_{X_{\bullet }}\to E_{W_{\bullet }}$
. Thus, we get naturally a complex of
![]() $\mathcal {O}_{{W}_{\parallel }}$
-modules, which we denote
$\mathcal {O}_{{W}_{\parallel }}$
-modules, which we denote
![]() $E_{{W}_{\parallel }}$
.
$E_{{W}_{\parallel }}$
.
In Situation 2.9, we have the following properties:
Lemma 2.10. For any a complex of
![]() $\mathcal {O}_{\mathcal {X}}$
-modules E, we have a natural morphism
$\mathcal {O}_{\mathcal {X}}$
-modules E, we have a natural morphism
![]() $ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(E_{{W}_{\parallel }})\to E_{W_{\bullet }}[1]$
. If E has quasi-coherent (or more generally, Cartesian) cohomology sheaves, this map is a quasi-isomorphism. The same picture holds in the category of simplicial
$ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(E_{{W}_{\parallel }})\to E_{W_{\bullet }}[1]$
. If E has quasi-coherent (or more generally, Cartesian) cohomology sheaves, this map is a quasi-isomorphism. The same picture holds in the category of simplicial
![]() $\mathcal {O}_{\mathcal {X}}$
modules with the obvious modifications, and the two situations are compatible via the Dold–Kan correspondence.
$\mathcal {O}_{\mathcal {X}}$
modules with the obvious modifications, and the two situations are compatible via the Dold–Kan correspondence.
Proof. This is a restatement of Lemma 2.6, using that the pullback maps
![]() $s^{*}$
and
$s^{*}$
and
![]() $t^{*}$
are quasi-isomorphisms whenever E has quasi-coherent cohomology sheaves.
$t^{*}$
are quasi-isomorphisms whenever E has quasi-coherent cohomology sheaves.
Lemma 2.11. In
![]() $D_{qcoh}(W_{\bullet })$
, the object
$D_{qcoh}(W_{\bullet })$
, the object
![]() $\eta _{W}^{*}L_{\mathcal {X}/\mathcal {Y}}$
is naturally isomorphic to
$\eta _{W}^{*}L_{\mathcal {X}/\mathcal {Y}}$
is naturally isomorphic to
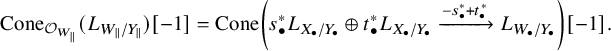 $$\begin{align*}\operatorname{\mathrm{Cone}}_{\mathcal{O}_{{W}_{\parallel}}}(L_{{W}_{\parallel}/{Y}_{\parallel}})[-1]=\operatorname{Cone} \left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\oplus t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-s^{*}_{\bullet}+t_{\bullet}^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)[-1].\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Cone}}_{\mathcal{O}_{{W}_{\parallel}}}(L_{{W}_{\parallel}/{Y}_{\parallel}})[-1]=\operatorname{Cone} \left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\oplus t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-s^{*}_{\bullet}+t_{\bullet}^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)[-1].\end{align*}$$
This isomorphism is functorial in the diagram (2.3).
Proof. The displayed equality is immediate from the definition of
![]() ${W}_{\parallel }$
and the definition of cotangent complex for a morphism of topoi. By the construction of the cotangent complex and Remark 2.1, we have a canonical isomorphism
${W}_{\parallel }$
and the definition of cotangent complex for a morphism of topoi. By the construction of the cotangent complex and Remark 2.1, we have a canonical isomorphism
We pull this isomorphism back via
![]() $s_{\bullet }$
. Due to the diagram
$s_{\bullet }$
. Due to the diagram
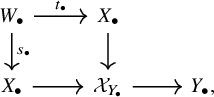
we have natural quasi-isomorphisms of complexes
We claim that the following diagram commutes:
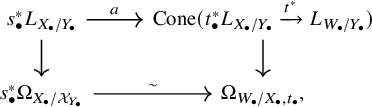
where the upper horizontal map is given by the pullback
![]() $s^{*}:s_{\bullet }^{*}L_{X_{\bullet }/Y_{\bullet }}\to L_{W_{\bullet }/Y_{\bullet }}$
followed by the inclusion of
$s^{*}:s_{\bullet }^{*}L_{X_{\bullet }/Y_{\bullet }}\to L_{W_{\bullet }/Y_{\bullet }}$
followed by the inclusion of
![]() $L_{W_{\bullet }/Y_{\bullet }}$
into the cone. Indeed, this follows from the observation that the map
$L_{W_{\bullet }/Y_{\bullet }}$
into the cone. Indeed, this follows from the observation that the map
![]() $s^{*}_{\bullet }L_{X_{\bullet }/Y_{\bullet }}\to \Omega _{W_{\bullet }/X_{\bullet },t_{\bullet }}$
factors through
$s^{*}_{\bullet }L_{X_{\bullet }/Y_{\bullet }}\to \Omega _{W_{\bullet }/X_{\bullet },t_{\bullet }}$
factors through
![]() $L_{W_{\bullet }/Y_{\bullet }}$
. It follows from this that, after pulling back the right-hand side of (2.5) along
$L_{W_{\bullet }/Y_{\bullet }}$
. It follows from this that, after pulling back the right-hand side of (2.5) along
![]() $s_{\bullet }$
, the result is naturally quasi-isomorphic to
$s_{\bullet }$
, the result is naturally quasi-isomorphic to
 $$\begin{align*}\operatorname{Cone}\left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-a} \operatorname{Cone}\left(t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{t^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)\right)[-1].\end{align*}$$
$$\begin{align*}\operatorname{Cone}\left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-a} \operatorname{Cone}\left(t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{t^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)\right)[-1].\end{align*}$$
An easy calculation shows that this iterated cone is identical to
 $$\begin{align*}\operatorname{Cone} \left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\oplus t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-s^{*}_{\bullet}+t_{\bullet}^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)[-1],\end{align*}$$
$$\begin{align*}\operatorname{Cone} \left(s_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\oplus t_{\bullet}^{*}L_{X_{\bullet}/Y_{\bullet}}\xrightarrow{-s^{*}_{\bullet}+t_{\bullet}^{*}} L_{W_{\bullet}/Y_{\bullet}}\right)[-1],\end{align*}$$
as desired. The compatibility with pullback follows from the compatibility of (2.5) and the usual pullback compatibilities of the cotangent complex for algebraic spaces.
Remark 2.12. In Situation 2.9, suppose that R is a simplicial ring on
![]() ${W}_{\parallel }$
with a given map
${W}_{\parallel }$
with a given map
![]() $R\to \mathcal {O}_{{W}_{\parallel }}$
. Then we have the following diagram of functors, which commutes up to canonical natural isomorphisms:
$R\to \mathcal {O}_{{W}_{\parallel }}$
. Then we have the following diagram of functors, which commutes up to canonical natural isomorphisms:
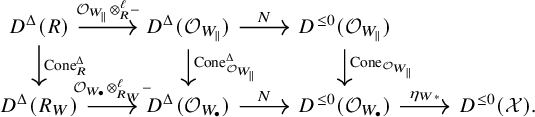
For the following lemma, let
![]() $W_{\wedge }$
be the ringed topos associated to the diagram
$W_{\wedge }$
be the ringed topos associated to the diagram
![]() $X_{\bullet }\xleftarrow {s_{\bullet }} W_{\bullet }\xrightarrow {t_{\bullet }} X_{\bullet }$
. Recall that we have a natural restriction functor
$X_{\bullet }\xleftarrow {s_{\bullet }} W_{\bullet }\xrightarrow {t_{\bullet }} X_{\bullet }$
. Recall that we have a natural restriction functor
![]() $D({W}_{\parallel })\to D(W_{\wedge })$
. The following will be used in the proof of Lemma 4.4.
$D({W}_{\parallel })\to D(W_{\wedge })$
. The following will be used in the proof of Lemma 4.4.
Lemma 2.13. Let
![]() $E_{{W}_{\parallel }}=(E_{X_{\bullet }},E_{W_{\bullet }}, s^{*},t^{*})$
be a complex of
$E_{{W}_{\parallel }}=(E_{X_{\bullet }},E_{W_{\bullet }}, s^{*},t^{*})$
be a complex of
![]() $\mathcal {O}_{{W}_{\parallel }}$
-modules such that
$\mathcal {O}_{{W}_{\parallel }}$
-modules such that
![]() $E_{X_{\bullet }}$
has quasi-coherent cohomology sheaves and such that the pullback maps
$E_{X_{\bullet }}$
has quasi-coherent cohomology sheaves and such that the pullback maps
![]() $s^{*}$
and
$s^{*}$
and
![]() $t^{*}$
are quasi-isomorphisms. Let
$t^{*}$
are quasi-isomorphisms. Let
![]() $F:=\eta _{W*}E_{W_{\bullet }}\in D_{qcoh}(\mathcal {X})$
, and let
$F:=\eta _{W*}E_{W_{\bullet }}\in D_{qcoh}(\mathcal {X})$
, and let
![]() $F_{{W}_{\parallel }}=(\eta _X^{*}F, \eta _W^{*}F)$
denote the induced object of
$F_{{W}_{\parallel }}=(\eta _X^{*}F, \eta _W^{*}F)$
denote the induced object of
![]() $D({W}_{\parallel })$
. Let
$D({W}_{\parallel })$
. Let
![]() $E_{W_{\wedge }}$
and
$E_{W_{\wedge }}$
and
![]() $F_{W_\wedge }$
denote the images of
$F_{W_\wedge }$
denote the images of
![]() $E_{{W}_{\parallel }}$
and
$E_{{W}_{\parallel }}$
and
![]() $F_{{W}_{\parallel }}$
in
$F_{{W}_{\parallel }}$
in
![]() $D(W_{\wedge })$
, respectively. Then there is a natural isomorphism
$D(W_{\wedge })$
, respectively. Then there is a natural isomorphism
![]() $F_{W_{\wedge }}\to E_{W_{\wedge }}$
in
$F_{W_{\wedge }}\to E_{W_{\wedge }}$
in
![]() $D(W_{\wedge })$
.
$D(W_{\wedge })$
.
Proof. Let
![]() $W_{\wedge ,lis-et}$
be the ringed topos associated to the diagram
$W_{\wedge ,lis-et}$
be the ringed topos associated to the diagram
From the diagram of ringed topoi
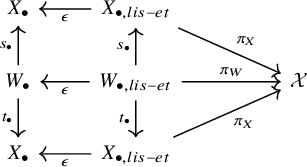
we see that there is an induced morphism
![]() $\epsilon _{\wedge }: {W}_{\wedge ,lis-et} \to W_{\wedge }$
. Let
$\epsilon _{\wedge }: {W}_{\wedge ,lis-et} \to W_{\wedge }$
. Let
![]() $F_{\wedge ,lis-et}=(\pi _X^{*}F,\pi _W^{*}F, \pi _X^{*}F)$
, with pullback maps induced by the identifications
$F_{\wedge ,lis-et}=(\pi _X^{*}F,\pi _W^{*}F, \pi _X^{*}F)$
, with pullback maps induced by the identifications
![]() $\pi _W^{*}=s^{*}\pi _X^{*}$
and
$\pi _W^{*}=s^{*}\pi _X^{*}$
and
![]() $\pi _W^{*}=t^{*}\pi _X^{*}$
, respectively. Since the functors
$\pi _W^{*}=t^{*}\pi _X^{*}$
, respectively. Since the functors
![]() $\epsilon _*$
are exact, we have
$\epsilon _*$
are exact, we have
![]() $F_{\wedge }={\epsilon }_{\wedge *}F_{\wedge , lis-et}$
. In particular, since
$F_{\wedge }={\epsilon }_{\wedge *}F_{\wedge , lis-et}$
. In particular, since
![]() $\epsilon _*\epsilon ^{*}$
is naturally isomorphic to the identity, it is enough to show that there is a natural quasi-isomorphism
$\epsilon _*\epsilon ^{*}$
is naturally isomorphic to the identity, it is enough to show that there is a natural quasi-isomorphism
![]() $\epsilon _{\wedge }^{*}E_{W_{\wedge }}\to F_{\wedge ,lis-et}$
.
$\epsilon _{\wedge }^{*}E_{W_{\wedge }}\to F_{\wedge ,lis-et}$
.
We are reduced to the following situation: Let
![]() $G=(G_{X},G_W,G_{X},s^{*},t^{*})$
be a complex of
$G=(G_{X},G_W,G_{X},s^{*},t^{*})$
be a complex of
![]() $\mathcal {O}_{W_{\wedge , lis-et}}$
-modules such that
$\mathcal {O}_{W_{\wedge , lis-et}}$
-modules such that
![]() $G_X$
has quasicoherent cohomology sheaves, and such that
$G_X$
has quasicoherent cohomology sheaves, and such that
![]() $s^{*}$
,
$s^{*}$
,
![]() $t^{*}$
are quasi-isomorphisms, and suppose that
$t^{*}$
are quasi-isomorphisms, and suppose that
![]() $F=R(\pi _W)_*G_W$
. Then we need to show that G is naturally isomorphic to
$F=R(\pi _W)_*G_W$
. Then we need to show that G is naturally isomorphic to
![]() $F_{\wedge ,lis-et}$
. Without loss of generality, we may assume that G is K-injective. Then
$F_{\wedge ,lis-et}$
. Without loss of generality, we may assume that G is K-injective. Then
![]() $G_W$
and
$G_W$
and
![]() $G_X$
are themselves K-injective. We can therefore assume that
$G_X$
are themselves K-injective. We can therefore assume that
![]() $F=\pi _{W*}G_W$
. Let also
$F=\pi _{W*}G_W$
. Let also
![]() $F':=\pi _{X*}G_X$
. The morphism
$F':=\pi _{X*}G_X$
. The morphism
![]() $s^{*}:s^{*}G_X\to G_W$
corresponds to a morphism
$s^{*}:s^{*}G_X\to G_W$
corresponds to a morphism
![]() $G_X\to s_*G_W$
, and by applying
$G_X\to s_*G_W$
, and by applying
![]() $\pi _{W*}$
we obtain a map
$\pi _{W*}$
we obtain a map
![]() $\sigma :F'\to F$
. Similarly, we obtain
$\sigma :F'\to F$
. Similarly, we obtain
![]() $\tau :F'\to F$
from
$\tau :F'\to F$
from
![]() $t^{*}:t^{*}G_X\to G_W$
. The maps
$t^{*}:t^{*}G_X\to G_W$
. The maps
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are quasi-isomorphisms, as one can check after applying
$\tau $
are quasi-isomorphisms, as one can check after applying
![]() $\pi _W^{*}$
, since
$\pi _W^{*}$
, since
![]() $F'$
and F have quasi-coherent comohology.
$F'$
and F have quasi-coherent comohology.
Then we have the following commutative diagram of complexes of
![]() $\mathcal {O}_{W_{\bullet ,lis-et}}$
-modules:
$\mathcal {O}_{W_{\bullet ,lis-et}}$
-modules:

The horizontal maps going to the right are the quasi-isomorphisms coming from the push-pull adjunctions associated to
![]() $\pi _X$
and
$\pi _X$
and
![]() $\pi _W$
, respectively. Setting
$\pi _W$
, respectively. Setting
![]() $\widetilde {F}_{\wedge , lis-et}= (\pi _X^{*}F', \pi _W^{*}F, \pi _X^{*}F', s^{*}\pi _X^{*}\sigma , t^{*}\pi _X^{*}\tau )$
, it follows that we have quasi-isomorphisms
$\widetilde {F}_{\wedge , lis-et}= (\pi _X^{*}F', \pi _W^{*}F, \pi _X^{*}F', s^{*}\pi _X^{*}\sigma , t^{*}\pi _X^{*}\tau )$
, it follows that we have quasi-isomorphisms
as desired.
2.4 Tensor triangulated categories and additivity of traces
Traces in a closed symmetric monoidal category
Let
![]() $\mathcal {C}$
be a symmetric closed monoidal category with product
$\mathcal {C}$
be a symmetric closed monoidal category with product
![]() $-\otimes -$
, unit
$-\otimes -$
, unit
![]() $\mathcal {O}$
, and internal Hom-functor
$\mathcal {O}$
, and internal Hom-functor
![]() $\mathcal {H}om(-,-)$
. Let
$\mathcal {H}om(-,-)$
. Let
![]() $\tau $
denote the symmetry morphism of the tensor product. We let
$\tau $
denote the symmetry morphism of the tensor product. We let
![]() $E,F,G$
denote arbitrary elements of
$E,F,G$
denote arbitrary elements of
![]() $\mathcal {C}$
and write
$\mathcal {C}$
and write
![]() $E^{\vee }:=\mathcal {H}om(E,\mathcal {O})$
. Recall that we have an adjunction between
$E^{\vee }:=\mathcal {H}om(E,\mathcal {O})$
. Recall that we have an adjunction between
![]() $-\otimes E$
and
$-\otimes E$
and
![]() $\mathcal {H}om(E,-)$
. We have various natural maps in
$\mathcal {H}om(E,-)$
. We have various natural maps in
![]() $\mathcal {C}$
:
$\mathcal {C}$
:
-
(1) Evaluation. We have a natural map
 $ev: \mathcal {H}om(E,F)\otimes E\to F$
, corresponding to the identity on
$ev: \mathcal {H}om(E,F)\otimes E\to F$
, corresponding to the identity on
 $\mathcal {H}om(E,F)$
under adjunction.
$\mathcal {H}om(E,F)$
under adjunction. -
(2) As a special case, we get the evaluation map
 $ev:E^{\vee }\otimes E\to \mathcal {O}$
.
$ev:E^{\vee }\otimes E\to \mathcal {O}$
. -
(3) Composition. We have a natural map
 $comp: \mathcal {H}om(F,G)\otimes \mathcal {H}om(E,F)\to \mathcal {H}om(E,G)$
. This map is adjoint to the map
$comp: \mathcal {H}om(F,G)\otimes \mathcal {H}om(E,F)\to \mathcal {H}om(E,G)$
. This map is adjoint to the map
 $\mathcal {H}om(F,G)\otimes \mathcal {H}om(E,F)\otimes E\to G$
which is obtained from composing two evaluation maps.
$\mathcal {H}om(F,G)\otimes \mathcal {H}om(E,F)\otimes E\to G$
which is obtained from composing two evaluation maps. -
(4) As a special case, we get the composition map
 $comp:F\otimes E^{\vee }\to \mathcal {H}om(E,F)$
, where we use the canonical isomorphism
$comp:F\otimes E^{\vee }\to \mathcal {H}om(E,F)$
, where we use the canonical isomorphism
 $F\simeq \mathcal {H}om(\mathcal {O},F)$
.
$F\simeq \mathcal {H}om(\mathcal {O},F)$
. -
(5) Diagonal. We have a diagonal map
 $s:\mathcal {O}\to \mathcal {H}om(E,E)$
which corresponds to
$s:\mathcal {O}\to \mathcal {H}om(E,E)$
which corresponds to
 $\operatorname {id}_{E}$
under adjunction.
$\operatorname {id}_{E}$
under adjunction.
We recall the notion of dualizable object:
Definition 2.14. The object E is called dualizable if the composition map
![]() $comp:E\otimes E^{\vee }\to \mathcal {H}om(E,E)$
is an isomorphism. See the discussion preceding Definition 2.2 in [Reference Ponto and Shulman19].
$comp:E\otimes E^{\vee }\to \mathcal {H}om(E,E)$
is an isomorphism. See the discussion preceding Definition 2.2 in [Reference Ponto and Shulman19].
For dualizable E and arbitrary F, the canonical map
![]() $comp: F\otimes E^{\vee }\to \mathcal {H}om(E,F)$
is an isomorphism, and we will often use this isomorphism to identify the source and target.
$comp: F\otimes E^{\vee }\to \mathcal {H}om(E,F)$
is an isomorphism, and we will often use this isomorphism to identify the source and target.
Let E be a dualizable object of
![]() $\mathcal {C}$
. Then we have further natural maps
$\mathcal {C}$
. Then we have further natural maps
-
(1) Trace I. We define the trace map
 $\operatorname {tr}:\mathcal {H}om({E},{E})\to \mathcal {O}$
as the composition
$\operatorname {tr}:\mathcal {H}om({E},{E})\to \mathcal {O}$
as the composition
 $\mathcal {H}om(E,E)\simeq {E}\otimes {E}^{\vee }\xrightarrow {\tau } E^{\vee }\otimes {E}\xrightarrow {ev} \mathcal {O}$
.
$\mathcal {H}om(E,E)\simeq {E}\otimes {E}^{\vee }\xrightarrow {\tau } E^{\vee }\otimes {E}\xrightarrow {ev} \mathcal {O}$
. -
(2) Trace II. We have a map
 $\operatorname {tr}:\mathcal {H}om({E}, {F} \otimes {E})\to {F}$
given by the composition
$\operatorname {tr}:\mathcal {H}om({E}, {F} \otimes {E})\to {F}$
given by the composition
 $\mathcal {H}om({E}, {F}\otimes {E})\simeq {F}\otimes {E}\otimes {E}^{\vee }\xrightarrow {{F}\otimes tr}{F}$
. By abuse of language, we call this also the trace map.
$\mathcal {H}om({E}, {F}\otimes {E})\simeq {F}\otimes {E}\otimes {E}^{\vee }\xrightarrow {{F}\otimes tr}{F}$
. By abuse of language, we call this also the trace map. -
(3) Diagonal II. We have the composition
 $\eta :=comp^{-1}\circ s:\mathcal {O}\to {E}\otimes {E}^{\vee }$
, which we will also call diagonal.
$\eta :=comp^{-1}\circ s:\mathcal {O}\to {E}\otimes {E}^{\vee }$
, which we will also call diagonal.
A morphism
![]() $f:{E}\to {F}\otimes {E}$
corresponds by adjunction to a map
$f:{E}\to {F}\otimes {E}$
corresponds by adjunction to a map
![]() $\mathcal {O}\to \mathcal {H}om({E},{F}\otimes {E})$
. When E is dualizable, we define
$\mathcal {O}\to \mathcal {H}om({E},{F}\otimes {E})$
. When E is dualizable, we define
![]() $\operatorname {tr}_{f}$
as the composition
$\operatorname {tr}_{f}$
as the composition
![]() $\mathcal {O}\to \mathcal {H}om({E},{F}\otimes {E})\xrightarrow {\operatorname {tr}} {F}.$
$\mathcal {O}\to \mathcal {H}om({E},{F}\otimes {E})\xrightarrow {\operatorname {tr}} {F}.$
As a consequence of the definition and the naturality of adjunction, we have the following:
Lemma 2.15. For
![]() $f:{E}\to {F}\otimes {E}$
, the map
$f:{E}\to {F}\otimes {E}$
, the map
![]() $tr_{f}$
is equal to the composition
$tr_{f}$
is equal to the composition
where
![]() $\tau $
denotes the symmetry isomorphism of the tensor product.
$\tau $
denotes the symmetry isomorphism of the tensor product.
Proof. The composition of the final two maps is by definition equal to
![]() $\operatorname {id}_F\otimes \operatorname {tr}$
. Now consider the following diagram:
$\operatorname {id}_F\otimes \operatorname {tr}$
. Now consider the following diagram:
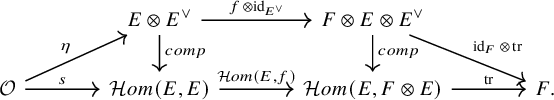
The left and right triangles commute by definition, while the square commutes by naturality of the composition map. By naturality of adjunction, the first two arrows in the lower row compose to the map adjoint to f. Thus, by definition, the lower row composes to
![]() $\operatorname {tr}_f$
, and the same must be true for the composition along the top.
$\operatorname {tr}_f$
, and the same must be true for the composition along the top.
We will need the following compatibility of traces with tensor products
Lemma 2.16. Let
![]() $f:E\to F\otimes E$
be a morphism in
$f:E\to F\otimes E$
be a morphism in
![]() $\mathcal {C}$
with E dualizable and let V be another dualizable object of
$\mathcal {C}$
with E dualizable and let V be another dualizable object of
![]() $\mathcal {C}$
. Then
$\mathcal {C}$
. Then
Proof. This follows by applying Corollary 5.9 of [Reference Ponto and Shulman19].
Criterion for additivity of traces
We now assume that, say,
![]() $\mathcal {C}=D(R)$
is the derived category of a category of sheaves of modules over a ring R in a topos T. In particular, it is closed monoidal with a compatible triangulated structure. Let
$\mathcal {C}=D(R)$
is the derived category of a category of sheaves of modules over a ring R in a topos T. In particular, it is closed monoidal with a compatible triangulated structure. Let
![]() ${F}, {E}, {G}$
be dualizable objects of
${F}, {E}, {G}$
be dualizable objects of
![]() $D(R)$
that are part of an exact triangle
$D(R)$
that are part of an exact triangle
Suppose that we have a commutative diagram for some element
![]() $L\in D(R)$
:
$L\in D(R)$
:
where the lower row is obtained from the upper by tensoring with L. We want a criterion that allows us to conclude that
![]() $tr(f)=tr(g)+tr(h)$
. We follow the strategy in [Reference May13, §8].
$tr(f)=tr(g)+tr(h)$
. We follow the strategy in [Reference May13, §8].
We will make the following
Assumption 2.17. The objects
![]() $F,E,G$
are elements of the bounded above derived category
$F,E,G$
are elements of the bounded above derived category
![]() $D^-(R)$
.
$D^-(R)$
.
Situation 2.18. Suppose Assumption 2.17 holds. (This is likely unnecessary if one works with K-flat complexes in what follows.) Choose a representation of (2.7) by a short exact sequence
![]() $0\to {F}\to {E}\to {G}\to 0$
of bounded above complexes of flat R-modules (or suppose one is given). Further, choose an injective resolution J of R, so that the derived dual of a complex is explicitly realized by
$0\to {F}\to {E}\to {G}\to 0$
of bounded above complexes of flat R-modules (or suppose one is given). Further, choose an injective resolution J of R, so that the derived dual of a complex is explicitly realized by
![]() $(-)^{\vee }:=\mathcal {H}om_R(-,J)$
. Then we have again an exact sequence
$(-)^{\vee }:=\mathcal {H}om_R(-,J)$
. Then we have again an exact sequence
![]() $0\to G^{\vee }\to {E}^\vee \to {F}^{\vee }\to 0$
. We define complexes W and
$0\to G^{\vee }\to {E}^\vee \to {F}^{\vee }\to 0$
. We define complexes W and
![]() $\overline {W}$
via
$\overline {W}$
via
 $$ \begin{align*} W&:= {E}\otimes {E}^{\vee}/{F}\otimes {G}^{\vee}\\ \overline{W}&:= {E}^{\vee}\otimes {E}/{G}^\vee \otimes {F}. \end{align*} $$
$$ \begin{align*} W&:= {E}\otimes {E}^{\vee}/{F}\otimes {G}^{\vee}\\ \overline{W}&:= {E}^{\vee}\otimes {E}/{G}^\vee \otimes {F}. \end{align*} $$
The tensor product here is the ordinary tensor product of complexes, which represents the derived tensor product due to the choice of
![]() ${F}$
and
${F}$
and
![]() ${E}$
. We have a natural isomorphism
${E}$
. We have a natural isomorphism
![]() $W\to \overline {W}$
coming from the symmetry isomorphism of the tensor product. Moreover, we have natural inclusions of complexes
$W\to \overline {W}$
coming from the symmetry isomorphism of the tensor product. Moreover, we have natural inclusions of complexes
and
The inclusions into W are given by
and
respectively, and analogously for the inclusions into
![]() $\overline {W}$
.
$\overline {W}$
.
Lemma 2.19. Let the notation be as in Situation 2.18.
-
(i) Let
 $\overline {\eta }$
be the composition
$\overline {\eta }$
be the composition
 $\mathcal {O}\xrightarrow {\eta } {E}\otimes {E}^{\vee }\to W$
in
$\mathcal {O}\xrightarrow {\eta } {E}\otimes {E}^{\vee }\to W$
in
 $D(R)$
. Then the following diagram commutes:
$D(R)$
. Then the following diagram commutes: 
-
(ii) There exists a natural map of complexes
 $\overline {\operatorname {ev}}:\overline {W}\to J$
whose image in
$\overline {\operatorname {ev}}:\overline {W}\to J$
whose image in
 $D(R)$
makes the following diagram commute:
$D(R)$
makes the following diagram commute: 
Proof. The map in (ii) is the natural quotient map of
![]() $ev:E^{\vee }\otimes E\to J$
, which vanishes on the subcomplex
$ev:E^{\vee }\otimes E\to J$
, which vanishes on the subcomplex
![]() $G^{\vee }\otimes F$
. The commutativity of the right triangle follows by unwinding the definitions.
$G^{\vee }\otimes F$
. The commutativity of the right triangle follows by unwinding the definitions.
-
(i) We let
 $V:=({F}\otimes {E}^{\vee }\oplus {E}\otimes {G}^{\vee })/({F}\otimes {G}^{\vee })$
, where the quotient is with respect to the antidiagonal inclusion. Then we have a natural exact sequence of complexes
$V:=({F}\otimes {E}^{\vee }\oplus {E}\otimes {G}^{\vee })/({F}\otimes {G}^{\vee })$
, where the quotient is with respect to the antidiagonal inclusion. Then we have a natural exact sequence of complexes  $$\begin{align*}0\to V \xrightarrow{j_1} {E}\otimes {E}^{\vee}\to {G}\otimes {F}^{\vee}\to 0.\end{align*}$$
$$\begin{align*}0\to V \xrightarrow{j_1} {E}\otimes {E}^{\vee}\to {G}\otimes {F}^{\vee}\to 0.\end{align*}$$
Moreover, we have natural maps
 $j_2:V\to {F}\otimes {F}^{\vee }$
and
$j_2:V\to {F}\otimes {F}^{\vee }$
and
 $j_3:V\to {G}\otimes {G}^{\vee }$
obtained by composing projection onto a factor with a respective quotient map. We claim that the following diagram of complexes commutes:
$j_3:V\to {G}\otimes {G}^{\vee }$
obtained by composing projection onto a factor with a respective quotient map. We claim that the following diagram of complexes commutes: 
By precomposing with the surjection
 ${F}\otimes {E}^{\vee }\oplus {E}\otimes {G}^{\vee }\to V$
, this reduces to the commutativity of the following two diagrams, which one can see directly. Now the problem is reduced to finding a map
${F}\otimes {E}^{\vee }\oplus {E}\otimes {G}^{\vee }\to V$
, this reduces to the commutativity of the following two diagrams, which one can see directly. Now the problem is reduced to finding a map
 $\eta _V:\mathcal {O}\to V$
in the derived category such that commutes. After dualizing in the derived category, this follows from (ii).
$\eta _V:\mathcal {O}\to V$
in the derived category such that commutes. After dualizing in the derived category, this follows from (ii).
Now we have the following result:
Proposition 2.20 [Reference May13, §8].
Suppose there exists a dotted arrow making its two adjacent squares in the following diagram commute. Then
![]() $tr(f)=tr(g)+tr(h)$
.
$tr(f)=tr(g)+tr(h)$
.
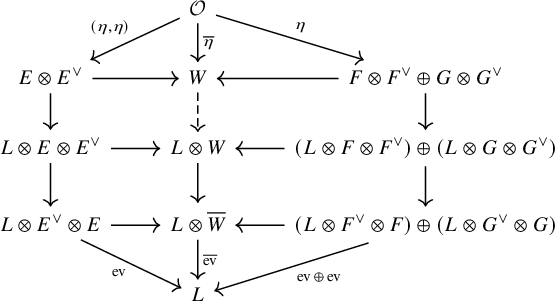
3 Constructions for topoi
3.1 Construction of the reduced Atiyah class
We review the construction of the reduced Atiyah class for a map of ringed topoi, following the ideas in [Reference Gillam3].
A diagram of exact sequences
Let
![]() $\mathcal {A}$
be an abelian category and consider the following diagram in
$\mathcal {A}$
be an abelian category and consider the following diagram in
![]() $\mathcal {A}$
in which the solid arrows commute:
$\mathcal {A}$
in which the solid arrows commute:
Assume that s is a section of e (i.e.,
![]() $e\circ s =\operatorname {\mathrm {id}}_{E"}$
). Then, the composition
$e\circ s =\operatorname {\mathrm {id}}_{E"}$
). Then, the composition
![]() $q\circ s$
induces a morphism
$q\circ s$
induces a morphism
![]() $\delta :\operatorname {\mathrm {Ker}}(q")\to \operatorname {\mathrm {Ker}}(f)$
.
$\delta :\operatorname {\mathrm {Ker}}(q")\to \operatorname {\mathrm {Ker}}(f)$
.
Now suppose this diagram extends to a commutative diagram in which all solid rows and columns are exact and where the dotted arrows give a spliting of the middle exact sequence
Then we have the morphism
![]() $\delta : F"\to G'$
as described above. From the composition
$\delta : F"\to G'$
as described above. From the composition
![]() $r\circ j: F\to E'$
, we get an induced map
$r\circ j: F\to E'$
, we get an induced map
![]() $\operatorname {Coker}(a)\to \operatorname {Coker}(j')$
and thus another map
$\operatorname {Coker}(a)\to \operatorname {Coker}(j')$
and thus another map
![]() $F"\to G'$
. By a diagram chase, one checks this to be equal to
$F"\to G'$
. By a diagram chase, one checks this to be equal to
![]() $-\delta $
.
$-\delta $
.
Now assume that, further,
![]() $\mathcal {A}$
is the category of modules over a simplicial ring A in a topos. Then, the above morphisms fit into the following diagrams of triangles in
$\mathcal {A}$
is the category of modules over a simplicial ring A in a topos. Then, the above morphisms fit into the following diagrams of triangles in
![]() $D^{\Delta }(A)$
:
$D^{\Delta }(A)$
:
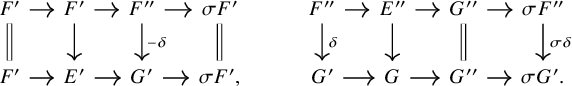
This shows that composing
![]() $\delta $
with the connecting map
$\delta $
with the connecting map
![]() $G'\to \sigma F'$
yields minus the connecting map associated to the exact sequence of the F’s, while composing
$G'\to \sigma F'$
yields minus the connecting map associated to the exact sequence of the F’s, while composing
![]() $\sigma \delta $
with the connecting map
$\sigma \delta $
with the connecting map
![]() $G"\to \sigma F"$
yields the connecting map associated to the exact sequence of the G’s.
$G"\to \sigma F"$
yields the connecting map associated to the exact sequence of the G’s.
The reduced Atiyah class
Now let
![]() $f:X\to Y$
be a morphism of ringed topoi. Let
$f:X\to Y$
be a morphism of ringed topoi. Let
![]() $E\in C^{\leq 0}(\mathcal {O}_Y)$
be a complex whose components are Tor-independent to f, so that, in particular, the component-wise pullback
$E\in C^{\leq 0}(\mathcal {O}_Y)$
be a complex whose components are Tor-independent to f, so that, in particular, the component-wise pullback
![]() $E_X:=f^{*}E$
equals the derived pullback. Let
$E_X:=f^{*}E$
equals the derived pullback. Let
be an exact sequence in
![]() $C^{\leq 0}(\mathcal {O}_X)$
, which we also view as a sequence of simplicial
$C^{\leq 0}(\mathcal {O}_X)$
, which we also view as a sequence of simplicial
![]() $\mathcal {O}_X$
-modules via the Dold–Kan correspondence. Let
$\mathcal {O}_X$
-modules via the Dold–Kan correspondence. Let
![]() $R:=P_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
be the standard simplicial resolution and let
$R:=P_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
be the standard simplicial resolution and let
![]() $E_R:=f^{-1}E\otimes _{f^{-1}\mathcal {O}_Y} R$
. Denote by
$E_R:=f^{-1}E\otimes _{f^{-1}\mathcal {O}_Y} R$
. Denote by
![]() $\cdot \mid _R$
restriction of scalars from
$\cdot \mid _R$
restriction of scalars from
![]() $\mathcal {O}_X$
to R. Since R is flat, the natural morphism
$\mathcal {O}_X$
to R. Since R is flat, the natural morphism
![]() $E_R\to E_X|_R$
is a quasi-isomorphism, and it is termwise surjective, since
$E_R\to E_X|_R$
is a quasi-isomorphism, and it is termwise surjective, since
![]() $R\to \mathcal {O}_X$
is. Let
$R\to \mathcal {O}_X$
is. Let
![]() $G_R:=G|_R$
and let
$G_R:=G|_R$
and let
![]() $F_R$
be the kernel of the induced map
$F_R$
be the kernel of the induced map
![]() $E_R\to G_R$
. We have an induced map of exact sequences of R-modules, in which the vertical arrows are quasi-isomorphisms
$E_R\to G_R$
. We have an induced map of exact sequences of R-modules, in which the vertical arrows are quasi-isomorphisms
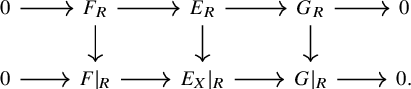
We now take the exact sequence of principal parts with respect to the upper row. This gives the following commutative diagram of solid arrows with exact rows and columns:
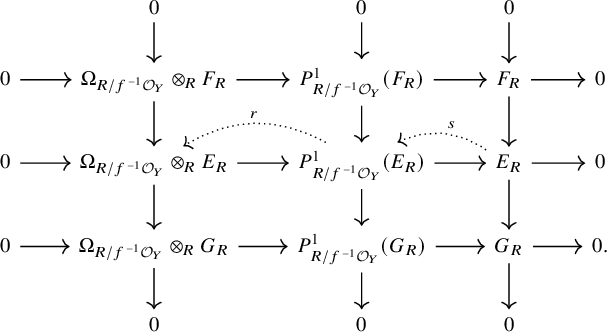
Here, the arrows denoted by s and r come from a splitting of the middle exact sequence, which is defined as follows: Since
![]() $E_R = R\otimes _{f^{-1}\mathcal {O}_Y}f^{-1}E$
, we have by definition
$E_R = R\otimes _{f^{-1}\mathcal {O}_Y}f^{-1}E$
, we have by definition
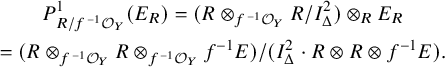 $$ \begin{gather*} P^1_{R/f^{-1}\mathcal{O}_Y}(E_R) = (R\otimes_{f^{-1}\mathcal{O}_Y} R/I_{\Delta}^2)\otimes_R E_R \\ = (R\otimes_{f^{-1}\mathcal{O}_Y} R \otimes_{f^{-1}\mathcal{O}_Y} f^{-1}E)/(I_{\Delta}^{2}\cdot R\otimes R\otimes f^{-1}E). \end{gather*} $$
$$ \begin{gather*} P^1_{R/f^{-1}\mathcal{O}_Y}(E_R) = (R\otimes_{f^{-1}\mathcal{O}_Y} R/I_{\Delta}^2)\otimes_R E_R \\ = (R\otimes_{f^{-1}\mathcal{O}_Y} R \otimes_{f^{-1}\mathcal{O}_Y} f^{-1}E)/(I_{\Delta}^{2}\cdot R\otimes R\otimes f^{-1}E). \end{gather*} $$
Then s is given on local sections by
![]() $a\otimes m\mapsto a\otimes 1 \otimes m$
, which one checks to be a morphism of left R-modules. We see that the lower right square of (3.4) is of the form (3.1). In particular, we get the induced morphism
$a\otimes m\mapsto a\otimes 1 \otimes m$
, which one checks to be a morphism of left R-modules. We see that the lower right square of (3.4) is of the form (3.1). In particular, we get the induced morphism
By passing to derived categories, and taking extensions of scalars along
![]() $R\to \mathcal {O}_X$
, this corresponds to a morphism
$R\to \mathcal {O}_X$
, this corresponds to a morphism
in
![]() $D^{\Delta }(\mathcal {O}_X)$
, or equivalently
$D^{\Delta }(\mathcal {O}_X)$
, or equivalently
![]() $D^{\leq 0}(\mathcal {O}_X)$
, which we call the reduced Atiyah class of E over Y with respect to the sequence (3.3) on X. We also write
$D^{\leq 0}(\mathcal {O}_X)$
, which we call the reduced Atiyah class of E over Y with respect to the sequence (3.3) on X. We also write
![]() $\overline {\operatorname {\mathrm {at}}}_E$
if the remaining data is understood.
$\overline {\operatorname {\mathrm {at}}}_E$
if the remaining data is understood.
Remark 3.1. The morphism
![]() $\delta :F_R\to \Omega _{R/f^{-1}\mathcal {O}_Y}\otimes _R G_R$
obtained by using the lower right corner of (3.4) is explicitly given as follows: For a local section
$\delta :F_R\to \Omega _{R/f^{-1}\mathcal {O}_Y}\otimes _R G_R$
obtained by using the lower right corner of (3.4) is explicitly given as follows: For a local section
![]() $f=\sum r_i\otimes f^{-1}e_i$
, where
$f=\sum r_i\otimes f^{-1}e_i$
, where
![]() $r_i$
are sections of R and
$r_i$
are sections of R and
![]() $e_i$
are sections of E (over Y), we have
$e_i$
are sections of E (over Y), we have
Remark 3.2. The following triangles commute:
-
1)

-
2)

In both cases, the vertical morphisms are induced from the connecting map
![]() $G\to F[1]$
of the given exact sequence. This follows from the morphisms of triangles (3.2).
$G\to F[1]$
of the given exact sequence. This follows from the morphisms of triangles (3.2).
Remark 3.3. In general, the reduced Atiyah class depends on slightly more than a map
![]() $\varphi :f^{*}E\to G$
in the derived category
$\varphi :f^{*}E\to G$
in the derived category
![]() $D(\mathcal {O}_X)$
, analogously to how cones in the derived category are unique only up to non-unique isomorphism. However, for any given
$D(\mathcal {O}_X)$
, analogously to how cones in the derived category are unique only up to non-unique isomorphism. However, for any given
![]() $\varphi $
, by a variation of the above using cocones/cones instead of kernels/cokernels, one can define a reduced Atiyah class
$\varphi $
, by a variation of the above using cocones/cones instead of kernels/cokernels, one can define a reduced Atiyah class
![]() $F:=\operatorname {cocone}(\varphi )\to L_{X/Y}\otimes G$
, which is well defined up to an element of
$F:=\operatorname {cocone}(\varphi )\to L_{X/Y}\otimes G$
, which is well defined up to an element of
![]() $\operatorname {\mathrm {Ext}}^{-1}(F,G)$
.
$\operatorname {\mathrm {Ext}}^{-1}(F,G)$
.
Lemma 3.4 (Shift invariance).
Consider the reduced Atiyah class
![]() $\overline {\operatorname {\mathrm {at}}}_{E[1]}$
associated to the shift of the sequence (3.3). Then, the following diagram commutes:
$\overline {\operatorname {\mathrm {at}}}_{E[1]}$
associated to the shift of the sequence (3.3). Then, the following diagram commutes:
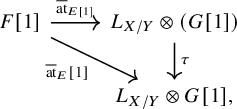
where
![]() $\tau $
denotes the compatibility morphism making the tensor product
$\tau $
denotes the compatibility morphism making the tensor product
![]() $L_{X/Y}\otimes -$
into a triangulated functor.
$L_{X/Y}\otimes -$
into a triangulated functor.
Proof. On the level of simplicial modules, the shift functor corresponds to taking a tensor product
![]() $\sigma \otimes _{\mathbb {Z}}- $
, where
$\sigma \otimes _{\mathbb {Z}}- $
, where
![]() $\sigma $
is the simplicial
$\sigma $
is the simplicial
![]() ${\mathbb {Z}}$
-module defined in §2.2. The statement then follows from the fact that for any R-module M, we have canonical isomorphisms of exact sequences, functorial in M, which are induced by the properties of the tensor product:
${\mathbb {Z}}$
-module defined in §2.2. The statement then follows from the fact that for any R-module M, we have canonical isomorphisms of exact sequences, functorial in M, which are induced by the properties of the tensor product:
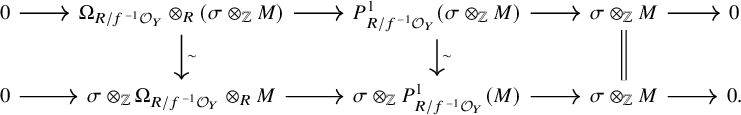
We extend the definition of the reduced Atiyah class to objects in
![]() $D^-(X)$
(cf. Construction 5.6 for the analogue for the usual Atiyah class):
$D^-(X)$
(cf. Construction 5.6 for the analogue for the usual Atiyah class):
Construction 3.5. Let
![]() $f:X\to Y$
be a morphism of ringed topoi, let
$f:X\to Y$
be a morphism of ringed topoi, let
![]() $E\in D^{-}(Y)$
, with
$E\in D^{-}(Y)$
, with
![]() $E_X:=f^{*}E$
and let
$E_X:=f^{*}E$
and let
be an exact triangle in
![]() $D^-(X)$
. Assume that
$D^-(X)$
. Assume that
![]() $\operatorname {\mathrm {Ext}}^{-1}(F,G) = 0$
. Choose
$\operatorname {\mathrm {Ext}}^{-1}(F,G) = 0$
. Choose
![]() $N>0$
so that the
$N>0$
so that the
![]() $E[N],F[N]$
and
$E[N],F[N]$
and
![]() $G[N]$
all lie in
$G[N]$
all lie in
![]() $D^{\leq 0}(X)$
. By Remark 3.3, we obtain a well-defined map
$D^{\leq 0}(X)$
. By Remark 3.3, we obtain a well-defined map
We define
where
![]() $\tau ^{(N)}: L_{X/Y}\otimes (G[N])\to L_{X/Y}\otimes G [N]$
is the N-fold application of the compatibility map of tensor product with the shift functor. This is independent of choice of N by Lemma 3.4.
$\tau ^{(N)}: L_{X/Y}\otimes (G[N])\to L_{X/Y}\otimes G [N]$
is the N-fold application of the compatibility map of tensor product with the shift functor. This is independent of choice of N by Lemma 3.4.
3.2 The reduced Atiyah class via the graded cotangent complex
Let
![]() $f:X\to Y$
be a morphism of ringed topoi and let E be an
$f:X\to Y$
be a morphism of ringed topoi and let E be an
![]() $\mathcal {O}_Y$
-module, Tor-independent to f. Let
$\mathcal {O}_Y$
-module, Tor-independent to f. Let
![]() $E_X:=f^{*}E$
and let
$E_X:=f^{*}E$
and let
be an exact sequence of
![]() $\mathcal {O}_X$
-modules. We will use the
$\mathcal {O}_X$
-modules. We will use the
![]() ${\mathbb {Z}}$
-graded cotangent complex as defined in [Reference Illusie7, IV 2]. For a
${\mathbb {Z}}$
-graded cotangent complex as defined in [Reference Illusie7, IV 2]. For a
![]() ${\mathbb {Z}}$
-graded ring
${\mathbb {Z}}$
-graded ring
![]() $A=\oplus A_i$
, we let
$A=\oplus A_i$
, we let
![]() $k^i$
denote the functor that sends a graded A-module
$k^i$
denote the functor that sends a graded A-module
![]() $M=\oplus M_i$
to the
$M=\oplus M_i$
to the
![]() $A_0$
-module given by its i-th graded piece
$A_0$
-module given by its i-th graded piece
![]() $M_i$
.
$M_i$
.
Let
![]() $X[E_X]$
denote the graded ringed topos whose underlying site is the étale site of X and whose sheaf of rings is given by
$X[E_X]$
denote the graded ringed topos whose underlying site is the étale site of X and whose sheaf of rings is given by
![]() $\mathcal {O}_X\oplus E$
, where E is placed in degree
$\mathcal {O}_X\oplus E$
, where E is placed in degree
![]() $1$
, and similarly for
$1$
, and similarly for
![]() $Y[E],X[G]$
. Let
$Y[E],X[G]$
. Let
![]() $q:X[G]\to X$
be the morphism induced by the inclusion
$q:X[G]\to X$
be the morphism induced by the inclusion
![]() $\mathcal {O}_X\to \mathcal {O}_X\oplus G$
and, similarly,
$\mathcal {O}_X\to \mathcal {O}_X\oplus G$
and, similarly,
![]() $r:X[E_X]\to X$
.
$r:X[E_X]\to X$
.
Proposition 3.6.
-
(i) We have a canonical natural isomorphism
of objects of $$\begin{align*}k^1q_*L^{gr}_{X[E_X]/X}\simeq E_X\end{align*}$$
$$\begin{align*}k^1q_*L^{gr}_{X[E_X]/X}\simeq E_X\end{align*}$$
 $D(\mathcal {O}_X)$
.
$D(\mathcal {O}_X)$
.
-
(ii) We have a canonical natural isomorphism
of objects of $$\begin{align*}k^1q_*L^{gr}_{X[G]/X[E_X]}\simeq F[1]\end{align*}$$
$$\begin{align*}k^1q_*L^{gr}_{X[G]/X[E_X]}\simeq F[1]\end{align*}$$
 $D(\mathcal {O}_X)$
.
$D(\mathcal {O}_X)$
.
-
(iii) Up to the isomorphisms in 3.6 and 3.6, applying
 $k^1\circ q_*$
to the connecting homomorphism of graded cotangent complexes associated to the composition
$k^1\circ q_*$
to the connecting homomorphism of graded cotangent complexes associated to the composition
 $X[G]\to X[E_X]\to X[F]$
recovers the inclusion
$X[G]\to X[E_X]\to X[F]$
recovers the inclusion
 $F\to E$
up to a shift.
$F\to E$
up to a shift.
Proof. Statement 3.6 is [Reference Illusie7, IV (2.2.5)], the other parts can be deduced from that as in [Reference Gillam3, §1.8]: Consider the distinguished triangle in
![]() $D^{gr}(X[G])$
$D^{gr}(X[G])$
Applying
![]() $k^1\circ q_*$
and the isomorphisms of 3.6, we obtain a distinguished triangle in
$k^1\circ q_*$
and the isomorphisms of 3.6, we obtain a distinguished triangle in
![]() $D(X)$
:
$D(X)$
:
It follows that there is a unique isomorphism
![]() $k^1 \circ q_* L^{gr}_{X[E_X]/X[G]}\simeq F$
that identifies the connecting map on cohomology sheaves with the inclusion
$k^1 \circ q_* L^{gr}_{X[E_X]/X[G]}\simeq F$
that identifies the connecting map on cohomology sheaves with the inclusion
![]() $F\to E$
.
$F\to E$
.
Consider the transitivity triangle of graded cotangent complexes associated to the morphism of graded ringed topoi
![]() $X[G]\to X[E_X]\to Y[E]$
and let
$X[G]\to X[E_X]\to Y[E]$
and let
be the connecting map. Applying
![]() $k^1\circ q_*$
and the isomorphisms of Proposition 3.6, we obtain a map
$k^1\circ q_*$
and the isomorphisms of Proposition 3.6, we obtain a map
Proposition 3.7. The map (3.7) agrees with the shift
![]() $\overline {\operatorname {\mathrm {at}}}_{E,X/Y,G}[1]$
of the reduced Atiyah class.
$\overline {\operatorname {\mathrm {at}}}_{E,X/Y,G}[1]$
of the reduced Atiyah class.
Proof. The definition in [Reference Gillam3, 2.3] goes through in our setting and gives the same resulting notion of reduced Atiyah class. By Theorem 2.6 there, the map defined in this way agrees with (3.7) up to a shift.
Corollary 3.8. The reduced Atiyah class is preserved under Tor-independent pullback: Consider a commutative diagram of ringed topoi
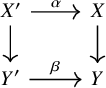
such that
![]() $\beta $
is Tor-independent to E and such that
$\beta $
is Tor-independent to E and such that
![]() $\alpha $
is Tor-independent to
$\alpha $
is Tor-independent to
![]() $E_X$
and G. Then the diagram
$E_X$
and G. Then the diagram
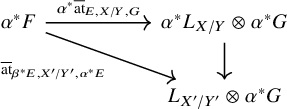
commutes.
Proof. This follows directly from Proposition 3.7 and the functoriality of the transitivity triangle for graded cotangent complexes.
Lemma 3.9. Consider a commutative diagram of ringed topoi
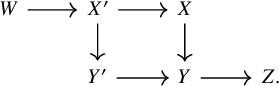
We assume further that X and
![]() $Y'$
are Tor-independent over Y and that the induced square of rings on
$Y'$
are Tor-independent over Y and that the induced square of rings on
![]() $X'$
obtained by pulling back the structure sheaves of
$X'$
obtained by pulling back the structure sheaves of
![]() $Y,Y'$
and X is cocartesian. Then the diagram of (shifted) connecting maps
$Y,Y'$
and X is cocartesian. Then the diagram of (shifted) connecting maps

on W anti-commutes. Here,
![]() $\cdot \mid _W$
denotes pullback to W.
$\cdot \mid _W$
denotes pullback to W.
Proof. By taking suitable simplicial resolutions, we are reduced to the setting that we have a diagram
of simplicial rings in a topos T, in which the square is cocartesian and in which all maps are free in each simplicial degree.
We then get a diagram of D-modules
It is now a basic exercise in homological algebra to show that the following induced diagram of connecting maps in
![]() $D^{\Delta }(D)$
anti-commutes:
$D^{\Delta }(D)$
anti-commutes:
Proposition 3.10. Let
![]() $E,F,G$
and
$E,F,G$
and
![]() $f:X\to Y$
be as before and let
$f:X\to Y$
be as before and let
![]() $Y\to Z$
be a morphism of ringed topoi. Then the following diagram anti-commutes:
$Y\to Z$
be a morphism of ringed topoi. Then the following diagram anti-commutes:
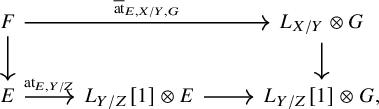
where the right vertical map is obtained from the connecting homomorphism of cotangent complexes by tensoring with G.
3.3 The Atiyah class for an exact sequence
Let
![]() $f:X\to Y$
be a morphism of ringed topoi and let
$f:X\to Y$
be a morphism of ringed topoi and let
![]() $0\to F\to E\to G\to 0$
be an exact sequence of bounded above complexes of
$0\to F\to E\to G\to 0$
be an exact sequence of bounded above complexes of
![]() $\mathcal {O}_X$
-modules, such that
$\mathcal {O}_X$
-modules, such that
![]() $F,E$
and G are dualizable and such that their duals lie again in
$F,E$
and G are dualizable and such that their duals lie again in
![]() $D^-(X)$
. After taking appropriate resolutions and up to shifting, we may assume that
$D^-(X)$
. After taking appropriate resolutions and up to shifting, we may assume that
![]() $E,F$
and G are concentrated in degrees
$E,F$
and G are concentrated in degrees
![]() $\leq 0$
and that they have flat components. Let
$\leq 0$
and that they have flat components. Let
![]() $\mathcal {O}_X\to J$
be an injective resolution and let
$\mathcal {O}_X\to J$
be an injective resolution and let
![]() $F^{\vee }, E^{\vee }$
and
$F^{\vee }, E^{\vee }$
and
![]() $G^{\vee }$
be the complexes obtained by applying
$G^{\vee }$
be the complexes obtained by applying
![]() $\mathcal {H}om_{X}(-,J)$
to
$\mathcal {H}om_{X}(-,J)$
to
![]() $F,E$
and G, respectively. Let N be large enough so that
$F,E$
and G, respectively. Let N be large enough so that
![]() $E^{\vee },F^{\vee } $
and
$E^{\vee },F^{\vee } $
and
![]() $G^{\vee }$
have no nonzero cohomology in degrees
$G^{\vee }$
have no nonzero cohomology in degrees
![]() $\geq N$
and set
$\geq N$
and set
![]() $\overline {E}:=(\tau ^{\leq N} E)[N]$
, and similarly for
$\overline {E}:=(\tau ^{\leq N} E)[N]$
, and similarly for
![]() $\overline {F}$
,
$\overline {F}$
,
![]() $\overline {G}$
. We let
$\overline {G}$
. We let
![]() $J':=\tau ^{\leq N}J[N]$
. Then the sequence
$J':=\tau ^{\leq N}J[N]$
. Then the sequence
![]() $0\to \overline {G}\to \overline {E}\to \overline {F}\to 0$
is exact, and we have the natural commutative diagram of complexes
$0\to \overline {G}\to \overline {E}\to \overline {F}\to 0$
is exact, and we have the natural commutative diagram of complexes
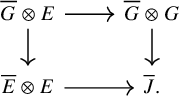
Using the Alexander–Whitney map of the Dold–Kan correspondence, we get such a diagram in the category of simplicial
![]() $\mathcal {O}_X$
-modules.
$\mathcal {O}_X$
-modules.
Now let
![]() $R=P^1_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
. Then we have the following commutative diagram of R-modules in which the rows are exact sequences
$R=P^1_{f^{-1}\mathcal {O}_Y}(\mathcal {O}_X)$
. Then we have the following commutative diagram of R-modules in which the rows are exact sequences
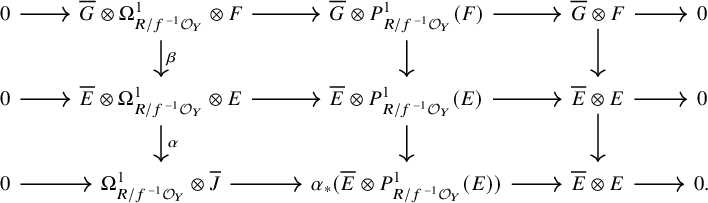
Here, the last row is obtained from the second by pushout along the map
![]() $\alpha $
, and
$\alpha $
, and
![]() $\alpha $
is induced from the evaluation map
$\alpha $
is induced from the evaluation map
![]() $\overline {E}\otimes E\to J$
. Abbreviate
$\overline {E}\otimes E\to J$
. Abbreviate
![]() $P(E):=P^1_{R/f^{-1}\mathcal {O}_Y}$
. Since the composition
$P(E):=P^1_{R/f^{-1}\mathcal {O}_Y}$
. Since the composition
![]() $\alpha \circ \beta $
is zero, we can quotient out
$\alpha \circ \beta $
is zero, we can quotient out
![]() $\overline {G}\otimes \Omega ^1_{R/f^{-1}\mathcal {O}_Y}\otimes F$
to obtain a diagram:
$\overline {G}\otimes \Omega ^1_{R/f^{-1}\mathcal {O}_Y}\otimes F$
to obtain a diagram:
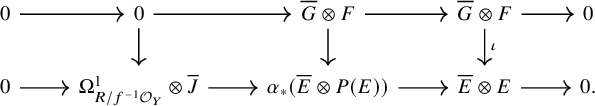
Here, the vertical maps are injections of R-modules, so we can take the quotient exact sequence
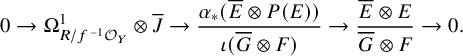 $$\begin{align*}0\to \Omega^1_{R/f^{-1}\mathcal{O}_Y}\otimes \overline{J} \to \frac{\alpha_*(\overline{E}\otimes P(E))}{\iota(\overline{G}\otimes F)}\to \frac{\overline{E}\otimes E}{\overline{G}\otimes F} \to 0. \end{align*}$$
$$\begin{align*}0\to \Omega^1_{R/f^{-1}\mathcal{O}_Y}\otimes \overline{J} \to \frac{\alpha_*(\overline{E}\otimes P(E))}{\iota(\overline{G}\otimes F)}\to \frac{\overline{E}\otimes E}{\overline{G}\otimes F} \to 0. \end{align*}$$
The induced connecting map defines (after extending scalars to
![]() $\mathcal {O}_X$
, applying the Dold–Kan correspondence, and shifting) a morphism in
$\mathcal {O}_X$
, applying the Dold–Kan correspondence, and shifting) a morphism in
![]() $D^-(\mathcal {O}_X)$
$D^-(\mathcal {O}_X)$
which we call the Atiyah class
![]() $\operatorname {\mathrm {at}}_{\underline {E}}=\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
of the exact sequence
$\operatorname {\mathrm {at}}_{\underline {E}}=\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
of the exact sequence
![]() $0\to F\to E\to G \to 0$
.
$0\to F\to E\to G \to 0$
.
Remark 3.11. It is easy to see by standard arguments that the result of the construction is independent of the choice of J. The dependence on N is not addressed here.
We observe the following directly from the construction.
Corollary 3.12. The morphism
![]() $\operatorname {\mathrm {at}}_{\underline {E}}$
is compatible with the usual Atiyah class (i.e., the diagram
$\operatorname {\mathrm {at}}_{\underline {E}}$
is compatible with the usual Atiyah class (i.e., the diagram
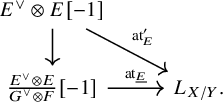
commutes).
Corollary 3.13. The map
![]() $\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
is functorial in Y (i.e., given a map
$\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
is functorial in Y (i.e., given a map
![]() $Y\to Y'$
, the composition
$Y\to Y'$
, the composition
equals
![]() $\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
(assuming we make the same choices of N in each construction)).
$\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
(assuming we make the same choices of N in each construction)).
Lemma 3.14. The map
![]() $\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
is functorial for morphisms
$\operatorname {\mathrm {at}}_{\underline {E},X/Y}$
is functorial for morphisms
![]() $a:X'\to X$
. More precisely, given such a morphism, the diagram
$a:X'\to X$
. More precisely, given such a morphism, the diagram
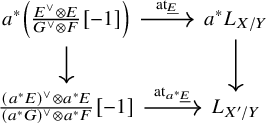
commutes (assuming we make the same choices of N in the construction). Here, we assume that
![]() $E,F,G$
are already given by bounded above complexes with flat components.
$E,F,G$
are already given by bounded above complexes with flat components.
Proof. The main point is that to compute the derived pullback of
![]() $\overline {E}$
(and similarly
$\overline {E}$
(and similarly
![]() $\overline {G}, \overline {F}$
), we may use either a flat resolution of
$\overline {G}, \overline {F}$
), we may use either a flat resolution of
![]() $\overline {E}$
– denote this
$\overline {E}$
– denote this
![]() $La^{*}\overline {E}$
by abuse of notation – or repeat the construction with
$La^{*}\overline {E}$
by abuse of notation – or repeat the construction with
![]() $a^{*}E$
in place of E, which we denote
$a^{*}E$
in place of E, which we denote
![]() $\overline {a^{*}E}$
. The two are related by a natural map
$\overline {a^{*}E}$
. The two are related by a natural map
![]() $La^{*}E\to \overline {a^{*}E}$
, which is a quasi-isomorphism, as can be checked locally where it follows from the assumption that E is a perfect complex. The details are left to the reader.
$La^{*}E\to \overline {a^{*}E}$
, which is a quasi-isomorphism, as can be checked locally where it follows from the assumption that E is a perfect complex. The details are left to the reader.
Now suppose that we have an exact sequence
![]() $0\to F\to E_X\to G\to 0$
as in (3.3). Then the Atiyah class for the exact sequence is related to the reduced Atiyah class.
$0\to F\to E_X\to G\to 0$
as in (3.3). Then the Atiyah class for the exact sequence is related to the reduced Atiyah class.
Proposition 3.15. We have a commutative diagram
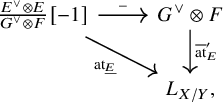
where the horizontal map is minus the natural connecting homomorphism.
Proof. We may work with the sequence
instead of
![]() $F,E,G$
as in the construction of the reduced Atiyah class. We need to show that we have a commutative diagram
$F,E,G$
as in the construction of the reduced Atiyah class. We need to show that we have a commutative diagram
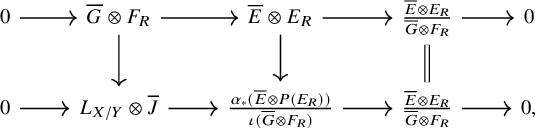
where the left vertical arrow is obtained from the composition
and therefore induces the reduced Atiyah class (up to a shift) when passing to
![]() $D(X)$
. The proposition then clearly follows. To construct the diagram, let
$D(X)$
. The proposition then clearly follows. To construct the diagram, let
![]() $s:E_R\to P(E_R)$
denote the section in the construction of the reduced Atiyah class. Then the middle vertical map is the composition
$s:E_R\to P(E_R)$
denote the section in the construction of the reduced Atiyah class. Then the middle vertical map is the composition
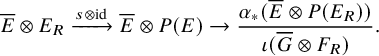 $$\begin{align*}\overline{E}\otimes E_R\xrightarrow{s\otimes \operatorname{id}} \overline{E}\otimes P(E)\to \frac{\alpha_*(\overline{E}\otimes P(E_R))}{\iota(\overline{G}\otimes F_R)}.\end{align*}$$
$$\begin{align*}\overline{E}\otimes E_R\xrightarrow{s\otimes \operatorname{id}} \overline{E}\otimes P(E)\to \frac{\alpha_*(\overline{E}\otimes P(E_R))}{\iota(\overline{G}\otimes F_R)}.\end{align*}$$
Since the composition
![]() $\overline {E}\otimes E_R\to \overline {E}\otimes P(E_R)\to \overline {E}\otimes E_R$
is the identity, we naturally obtain a commutative diagram of the desired form, and it remains only to show that the left vertical map is as desired. But in fact, we have a subdiagram
$\overline {E}\otimes E_R\to \overline {E}\otimes P(E_R)\to \overline {E}\otimes E_R$
is the identity, we naturally obtain a commutative diagram of the desired form, and it remains only to show that the left vertical map is as desired. But in fact, we have a subdiagram
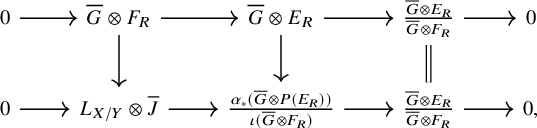
the lower row of which is identified with the row
Under this identification, the middle map factors as
and it follows that the left vertical map indeed factors through the reduced Atiyah class, as desired.
4 Definitions
We construct the Atiyah class for an algebraic stack and show that it is independent of various choices made in the construction. We then address the case of the reduced Atiyah class and of the Atiyah class of an exact sequence.
4.1 Construction of the Atiyah class
We define the Atiyah class for an object
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
with vanishing cohomology groups in positive degree. In Construction 5.6, we generalize this to arbitrary bounded above complexes, which uses the invariance of the Atiyah class under shifts (Corollary 5.5).
$E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
with vanishing cohomology groups in positive degree. In Construction 5.6, we generalize this to arbitrary bounded above complexes, which uses the invariance of the Atiyah class under shifts (Corollary 5.5).
Construction 4.1. Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
$f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
. By truncating, we may assume that E is represented by a complex with nonzero terms only in negative degrees. We let
$E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
. By truncating, we may assume that E is represented by a complex with nonzero terms only in negative degrees. We let
![]() $E_{{W}_{\parallel }}$
be the induced
$E_{{W}_{\parallel }}$
be the induced
![]() $\mathcal {O}_{{W}_{\parallel }}$
-module, which we also regard as a simplicial module. Choose a diagram as in (2.3) and consider the setup of Situation 2.9. We let
$\mathcal {O}_{{W}_{\parallel }}$
-module, which we also regard as a simplicial module. Choose a diagram as in (2.3) and consider the setup of Situation 2.9. We let
![]() $R:=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}({W}_{\parallel })$
be the free simplicial resolution. This is a simplicial ring on
$R:=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}({W}_{\parallel })$
be the free simplicial resolution. This is a simplicial ring on
![]() ${W}_{\parallel }$
with components
${W}_{\parallel }$
with components
![]() $R_X=P_{g^{-1}\mathcal {O}_{Y_{\bullet }}}(\mathcal {O}_{X_{\bullet }})$
and
$R_X=P_{g^{-1}\mathcal {O}_{Y_{\bullet }}}(\mathcal {O}_{X_{\bullet }})$
and
![]() $R_W=P_{h^{-1}\mathcal {O}_{Y_{\bullet }}}(\mathcal {O}_{W_{\bullet }})$
. We regard
$R_W=P_{h^{-1}\mathcal {O}_{Y_{\bullet }}}(\mathcal {O}_{W_{\bullet }})$
. We regard
![]() $E_{{W}_{\parallel }}$
as an R-module via restriction of scalars. Consider the exact sequence of principal parts
$E_{{W}_{\parallel }}$
as an R-module via restriction of scalars. Consider the exact sequence of principal parts
![]() $ \underline {P}_{R/\mathcal {O}_{{Y}_{\parallel }}}^1(E_{{W}_{\parallel }})$
associated to
$ \underline {P}_{R/\mathcal {O}_{{Y}_{\parallel }}}^1(E_{{W}_{\parallel }})$
associated to
![]() $E_{{W}_{\parallel }}$
and the ring map
$E_{{W}_{\parallel }}$
and the ring map
![]() ${h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}\to R$
.
${h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}\to R$
.
It induces a map
in
![]() $D^{\Delta }(R)$
. By Lemma 2.2, this is just the restriction of a morphism in
$D^{\Delta }(R)$
. By Lemma 2.2, this is just the restriction of a morphism in
![]() $D^{\Delta }({W}_{\parallel })$
and thus corresponds to a unique morphism
$D^{\Delta }({W}_{\parallel })$
and thus corresponds to a unique morphism
![]() $E_{{W}_{\parallel }} \to L_{{W}_{\parallel }/{Y}_{\parallel }}\otimes _{\mathcal {O}_{{W}_{\parallel }}} E_{{W}_{\parallel }}[1]$
in
$E_{{W}_{\parallel }} \to L_{{W}_{\parallel }/{Y}_{\parallel }}\otimes _{\mathcal {O}_{{W}_{\parallel }}} E_{{W}_{\parallel }}[1]$
in
![]() $D(\mathcal {O}_{{W}_{\parallel }})$
by the Dold–Kan correspondence. We have canonical natural isomorphisms
$D(\mathcal {O}_{{W}_{\parallel }})$
by the Dold–Kan correspondence. We have canonical natural isomorphisms
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(E)\xrightarrow {\sim } E_{W_{\bullet }}[1]$
and
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(E)\xrightarrow {\sim } E_{W_{\bullet }}[1]$
and
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(L_{{W}_{\parallel }/{Y}_{\parallel }})\xrightarrow {\sim } \eta _W^{*}L_{\mathcal {X}/\mathcal {Y}}[1]$
by Lemmas 2.10 and 2.11, respectively. Since E has quasi-coherent cohomology sheaves, the assumptions of Lemma 2.7 i) are satisfied, so that we obtain a morphism
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(L_{{W}_{\parallel }/{Y}_{\parallel }})\xrightarrow {\sim } \eta _W^{*}L_{\mathcal {X}/\mathcal {Y}}[1]$
by Lemmas 2.10 and 2.11, respectively. Since E has quasi-coherent cohomology sheaves, the assumptions of Lemma 2.7 i) are satisfied, so that we obtain a morphism
Applying
![]() $\eta _{W*}$
and the shift
$\eta _{W*}$
and the shift
![]() $[-1]$
and multiplying by
$[-1]$
and multiplying by
![]() $-1$
(the sign is obtained from commuting two shift functors and is needed for compatibility with the usual Atiyah class), we obtain a morphism
$-1$
(the sign is obtained from commuting two shift functors and is needed for compatibility with the usual Atiyah class), we obtain a morphism
This is the Atiyah class of E over
![]() $\mathcal {Y}$
. We will also write
$\mathcal {Y}$
. We will also write
![]() $\operatorname {\mathrm {at}}_E$
if the morphism
$\operatorname {\mathrm {at}}_E$
if the morphism
![]() $f:\mathcal {X}\to \mathcal {Y}$
is understood. In Corollary 4.6, we show that the Atiyah class is independent of choice of diagram (2.3).
$f:\mathcal {X}\to \mathcal {Y}$
is understood. In Corollary 4.6, we show that the Atiyah class is independent of choice of diagram (2.3).
As a consequence of the construction, we have the following:
Lemma 4.2. The morphism (4.3) is functorial in
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
for a fixed choice of diagram (2.3).
$E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
for a fixed choice of diagram (2.3).
Remark 4.3.
-
i) In Construction 4.1, let F be an R-module together with an isomorphism
 $F\to E_{{W}_{\parallel }}$
in
$F\to E_{{W}_{\parallel }}$
in
 $D^{\Delta }(R)$
. Then we may instead work with the exact sequence
$D^{\Delta }(R)$
. Then we may instead work with the exact sequence
 $\underline {P}_{R/{h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}}(F)$
and define (4.1) equivalently as the map obtained as the composition
$\underline {P}_{R/{h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}}(F)$
and define (4.1) equivalently as the map obtained as the composition  $$\begin{align*}E_{{W}_{\parallel}}\xrightarrow{\sim}F \to \sigma \underline{P}_{R/\mathcal{O}_{{Y}_{\parallel}}}^1(F_{{W}_{\parallel}}) \xrightarrow{\sim} \sigma L_{{W}_{\parallel}/{Y}_{\parallel}}\otimes_{\mathcal{O}_{{W}_{\parallel}}} E_{{W}_{\parallel}}.\end{align*}$$
$$\begin{align*}E_{{W}_{\parallel}}\xrightarrow{\sim}F \to \sigma \underline{P}_{R/\mathcal{O}_{{Y}_{\parallel}}}^1(F_{{W}_{\parallel}}) \xrightarrow{\sim} \sigma L_{{W}_{\parallel}/{Y}_{\parallel}}\otimes_{\mathcal{O}_{{W}_{\parallel}}} E_{{W}_{\parallel}}.\end{align*}$$
-
ii) We may also replace
 ${W}_{\parallel }$
and
${W}_{\parallel }$
and
 ${Y}_{\parallel }$
by their analogues
${Y}_{\parallel }$
by their analogues
 $W_{\wedge }$
and
$W_{\wedge }$
and
 $Y_{\wedge }$
, associated to the respective diagrams throughout Construction 4.1.
$Y_{\wedge }$
, associated to the respective diagrams throughout Construction 4.1. $$\begin{align*}X_{\bullet}\xleftarrow{s_{\bullet}} W_{\bullet} \xrightarrow{t_{\bullet}} X_{\bullet}, \mbox{ and } Y_{\bullet} \xleftarrow{=}Y_{\bullet}\xrightarrow{=}Y_{\bullet}\end{align*}$$
$$\begin{align*}X_{\bullet}\xleftarrow{s_{\bullet}} W_{\bullet} \xrightarrow{t_{\bullet}} X_{\bullet}, \mbox{ and } Y_{\bullet} \xleftarrow{=}Y_{\bullet}\xrightarrow{=}Y_{\bullet}\end{align*}$$
Well-definedness and compatibility with pullback
Suppose that we are given a map of diagrams (2.3) – that is, that we have a
![]() $2$
-commuting cube
$2$
-commuting cube
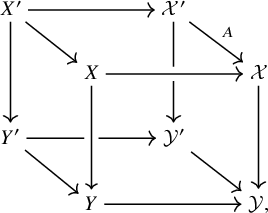
whose front and back faces are as in (2.3). (This means, in particular, that for any two maps
![]() $X'\to \mathcal {Y}$
obtained by traveling along the edges of the cube, the two two-isomorphisms relating them by traversing the faces are identical.)
$X'\to \mathcal {Y}$
obtained by traveling along the edges of the cube, the two two-isomorphisms relating them by traversing the faces are identical.)
Lemma 4.4. Let
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
. Let
$E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
. Let
Then the diagram
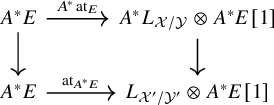
commutes.
Proof. By using the setup of Situation 2.9 and Construction 4.1 for the primed objects, we obtain a commutative cube of simplicial algebraic spaces
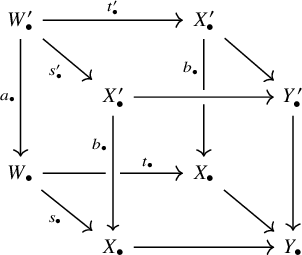
as well as morphisms of topoi
![]() ${a}_{\parallel }:{W}_{\parallel }^{\prime }\to {W}_{\parallel }$
and
${a}_{\parallel }:{W}_{\parallel }^{\prime }\to {W}_{\parallel }$
and
![]() ${Y}_{\parallel }^{\prime }\to {Y}_{\parallel }$
, which fit in a
${Y}_{\parallel }^{\prime }\to {Y}_{\parallel }$
, which fit in a
![]() $2$
-commutative square
$2$
-commutative square
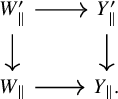
By construction, the Atiyah class
![]() $\operatorname {\mathrm {at}}_E$
corresponds via
$\operatorname {\mathrm {at}}_E$
corresponds via
![]() $\eta _W^{*}$
to a map
$\eta _W^{*}$
to a map
![]() $\alpha :E_{W_{\bullet }}\to \eta _W^{*}L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E_{W_{\bullet }}$
, obtained as the shift of the map (4.2). Since the pullback
$\alpha :E_{W_{\bullet }}\to \eta _W^{*}L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E_{W_{\bullet }}$
, obtained as the shift of the map (4.2). Since the pullback
![]() $A^{*}$
can be computed as
$A^{*}$
can be computed as
![]() $\eta _{W'*}a_{\bullet }^{*}\eta _W^{*}$
, we have a natural commutative diagram
$\eta _{W'*}a_{\bullet }^{*}\eta _W^{*}$
, we have a natural commutative diagram
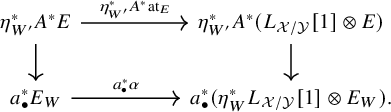
Let
![]() $E':=\eta _{W'*}(a_{\bullet }^{*}E_W)$
. We apply Construction 4.1 to the primed objects (i.e., with respect to the backside of (4.4) and
$E':=\eta _{W'*}(a_{\bullet }^{*}E_W)$
. We apply Construction 4.1 to the primed objects (i.e., with respect to the backside of (4.4) and
![]() $E'$
). We obtain the ring
$E'$
). We obtain the ring
![]() $R'=P_{{h}_{\parallel }^{\prime -1}\mathcal {O}_{{Y}_{\parallel }^{\prime }}}(\mathcal {O}_{{W}_{\parallel }^{\prime }})$
and the map
$R'=P_{{h}_{\parallel }^{\prime -1}\mathcal {O}_{{Y}_{\parallel }^{\prime }}}(\mathcal {O}_{{W}_{\parallel }^{\prime }})$
and the map
as the shift of the map (4.2). By functoriality of simplicial resolutions, we have a natural map
![]() ${a}_{\parallel }^{-1}R\to R'$
of rings on
${a}_{\parallel }^{-1}R\to R'$
of rings on
![]() ${W}_{\parallel }^{\prime }$
. Now the statement of the lemma is equivalent to the following:
${W}_{\parallel }^{\prime }$
. Now the statement of the lemma is equivalent to the following:
Claim 4.5. The diagram
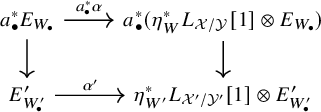
in
![]() $D(W^{\prime }_{\bullet })$
commutes, where the vertical maps are induced by the natural isomorphism
$D(W^{\prime }_{\bullet })$
commutes, where the vertical maps are induced by the natural isomorphism
![]() $a_{\bullet }^{*}E_{W_{\bullet }}\xrightarrow {\sim } E^{\prime }_{W'}$
and the pullback map on cotangent complexes.
$a_{\bullet }^{*}E_{W_{\bullet }}\xrightarrow {\sim } E^{\prime }_{W'}$
and the pullback map on cotangent complexes.
Proof. We may assume that E is represented by a complex of flat modules concentrated in degrees
![]() $\leq 0$
, so that we have an induced representative with flat terms for
$\leq 0$
, so that we have an induced representative with flat terms for
![]() $E_{{W}_{\parallel }}$
. Then the pullback
$E_{{W}_{\parallel }}$
. Then the pullback
![]() ${a}_{\parallel }^{*}E_{{W}_{\parallel }}={a}_{\parallel }^{*}E_{{W}_{\parallel }}$
can be computed termwise, and its components are given by
${a}_{\parallel }^{*}E_{{W}_{\parallel }}={a}_{\parallel }^{*}E_{{W}_{\parallel }}$
can be computed termwise, and its components are given by
![]() $b_{\bullet }^{*}E_X$
and
$b_{\bullet }^{*}E_X$
and
![]() $a_{\bullet }^{*}E_W$
, respectively.
$a_{\bullet }^{*}E_W$
, respectively.
By functoriality of the principal parts construction, we have a morphism of exact sequences of
![]() ${a}_{\parallel }^{-1}R$
-modules
${a}_{\parallel }^{-1}R$
-modules
![]() ${a}_{\parallel }^{-1}\underline {P}^1_{\mathcal {O}_{{W}_{\parallel }}/{h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}}(E_{{W}_{\parallel }})\to \underline {P}^1_{\mathcal {O}_{{W}_{\parallel }^{\prime }}/{h'}_{\parallel }^{-1}\mathcal {O}_{{Y'}_{\parallel }}}({a}_{\parallel }^{*}E_{{W}_{\parallel }}).$
We get the induced diagram of connecting maps in
${a}_{\parallel }^{-1}\underline {P}^1_{\mathcal {O}_{{W}_{\parallel }}/{h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}}(E_{{W}_{\parallel }})\to \underline {P}^1_{\mathcal {O}_{{W}_{\parallel }^{\prime }}/{h'}_{\parallel }^{-1}\mathcal {O}_{{Y'}_{\parallel }}}({a}_{\parallel }^{*}E_{{W}_{\parallel }}).$
We get the induced diagram of connecting maps in
![]() $D^{\Delta }({a}_{\parallel }^{-1}R)$
$D^{\Delta }({a}_{\parallel }^{-1}R)$
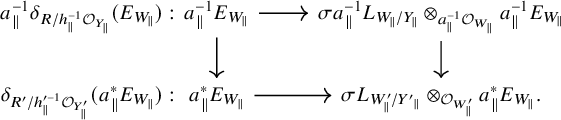
By adjunction, this corresponds to a diagram in
![]() $D^{\Delta }(R')$
, which in turn corresponds to a diagram in
$D^{\Delta }(R')$
, which in turn corresponds to a diagram in
![]() $D(\mathcal {O}_{{W}_{\parallel }})$
:
$D(\mathcal {O}_{{W}_{\parallel }})$
:
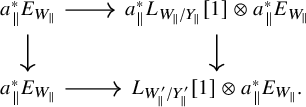
After applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W'}_{\parallel }}}$
and shifting, the upper line is canonically identified with
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W'}_{\parallel }}}$
and shifting, the upper line is canonically identified with
![]() $a_{\bullet }^{*}\alpha $
(this uses that we have a natural isomorphism
$a_{\bullet }^{*}\alpha $
(this uses that we have a natural isomorphism
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W'}_{\parallel }}}\circ {a}_{\parallel }^{*}\simeq a_{\bullet }^{*}\circ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
, which one can check by computing with K-flat complexes of
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W'}_{\parallel }}}\circ {a}_{\parallel }^{*}\simeq a_{\bullet }^{*}\circ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
, which one can check by computing with K-flat complexes of
![]() $\mathcal {O}_{{W}_{\parallel }}$
modules). The lower line yields a map
$\mathcal {O}_{{W}_{\parallel }}$
modules). The lower line yields a map
To finish the proof of the claim, we need to show that under the isomorphism
![]() $a^{*}E_{W}\to E^{\prime }_{W'}$
, the maps
$a^{*}E_{W}\to E^{\prime }_{W'}$
, the maps
![]() $\alpha "$
and
$\alpha "$
and
![]() $\alpha $
get identified. This follows from Lemma 2.13 and Remark 4.3 ii).
$\alpha $
get identified. This follows from Lemma 2.13 and Remark 4.3 ii).
Corollary 4.6. The map
![]() $\operatorname {\mathrm {at}}_{E}:E\to L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E$
obtained from Construction 4.1 is independent of choice of diagram (2.3).
$\operatorname {\mathrm {at}}_{E}:E\to L_{\mathcal {X}/\mathcal {Y}}[1]\otimes E$
obtained from Construction 4.1 is independent of choice of diagram (2.3).
Proof. Suppose we are given two choices

We need to show that
![]() $\operatorname {\mathrm {at}}_{E,\mathcal {X}/\mathcal {Y},X_1/Y_1}$
and
$\operatorname {\mathrm {at}}_{E,\mathcal {X}/\mathcal {Y},X_1/Y_1}$
and
![]() $\operatorname {\mathrm {at}}_{E,\mathcal {X}/{\mathcal {Y}},X_2/Y_2}$
agree. By replacing
$\operatorname {\mathrm {at}}_{E,\mathcal {X}/{\mathcal {Y}},X_2/Y_2}$
agree. By replacing
![]() $X_2\to Y_2$
with the fiber product
$X_2\to Y_2$
with the fiber product
![]() $X_{1}\times _{\mathcal {X}}X_2\to Y_1\times _{\mathcal {Y}}Y_2$
, we may without loss of generality assume that we have a
$X_{1}\times _{\mathcal {X}}X_2\to Y_1\times _{\mathcal {Y}}Y_2$
, we may without loss of generality assume that we have a
![]() $2$
-commuting diagram
$2$
-commuting diagram
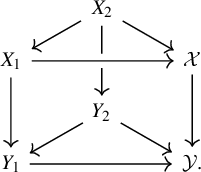
By adding in the identity morphisms on
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
, this gives a
$\mathcal {Y}$
, this gives a
![]() $2$
-commuting cube (4.4), and we obtain the desired equality from Lemma 4.4.
$2$
-commuting cube (4.4), and we obtain the desired equality from Lemma 4.4.
Corollary 4.7. The Atiyah class is compatible with pullback. More precisely, given a
![]() $2$
-commutative square
$2$
-commutative square
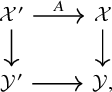
the natural diagram
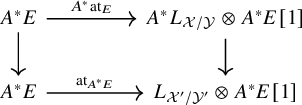
commutes.
Compatibility with Illusie’s definition
Proposition 4.8. If
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are in fact algebraic spaces, then the morphism
$\mathcal {Y}$
are in fact algebraic spaces, then the morphism
![]() $\operatorname {\mathrm {at}}_E$
agrees with Illusie’s Atiyah class for E with respect to the map of ringed étale topoi
$\operatorname {\mathrm {at}}_E$
agrees with Illusie’s Atiyah class for E with respect to the map of ringed étale topoi
![]() $\mathcal {X}_{\operatorname {et}}\to \mathcal {Y}_{\operatorname {et}}$
.
$\mathcal {X}_{\operatorname {et}}\to \mathcal {Y}_{\operatorname {et}}$
.
Proof. In this case, we may choose
![]() $X=\mathcal {X}$
and
$X=\mathcal {X}$
and
![]() $Y=\mathcal {Y}$
in diagram (2.3), so that we get
$Y=\mathcal {Y}$
in diagram (2.3), so that we get
![]() $W=X$
. Then
$W=X$
. Then
![]() $X_{\bullet }$
and
$X_{\bullet }$
and
![]() $W_{\bullet }$
are constant strictly simplicial algebraic spaces with value X, and
$W_{\bullet }$
are constant strictly simplicial algebraic spaces with value X, and
![]() $Y_{\bullet }$
is the constant strictly simplicial algebraic space with value Y. In this case, we have the morphism of topoi
$Y_{\bullet }$
is the constant strictly simplicial algebraic space with value Y. In this case, we have the morphism of topoi
![]() $\Delta :{W}_{\parallel }\to X_{\bullet }$
, where
$\Delta :{W}_{\parallel }\to X_{\bullet }$
, where
![]() $\Delta ^{*}M_X = (M_X,M_X,\operatorname {id},\operatorname {id})$
. The morphism
$\Delta ^{*}M_X = (M_X,M_X,\operatorname {id},\operatorname {id})$
. The morphism
![]() $c_E$
of Lemma 2.6 gives a natural transformation of functors
$c_E$
of Lemma 2.6 gives a natural transformation of functors
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}\circ \Delta ^{*}\Rightarrow [-1]$
, which induces to a natural isomorphism of functors from
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}\circ \Delta ^{*}\Rightarrow [-1]$
, which induces to a natural isomorphism of functors from
![]() $D(\mathcal {O}_{X_{\bullet }})$
to itself. It follows from Construction 4.1 that the morphism
$D(\mathcal {O}_{X_{\bullet }})$
to itself. It follows from Construction 4.1 that the morphism
![]() $E_{{W}_{\parallel }} \to L_{{W}_{\parallel }/{Y}_{\parallel }}[1]\otimes _{\mathcal {O}_{{W}_{\parallel }}} E_{{W}_{\parallel }}$
obtained from (4.1) by applying the functors
$E_{{W}_{\parallel }} \to L_{{W}_{\parallel }/{Y}_{\parallel }}[1]\otimes _{\mathcal {O}_{{W}_{\parallel }}} E_{{W}_{\parallel }}$
obtained from (4.1) by applying the functors
![]() $D^{\Delta }(R)\to D^{\Delta }(\mathcal {O}_{{W}_{\parallel }})\to D({W}_{\parallel })$
is naturally identified with the pullback
$D^{\Delta }(R)\to D^{\Delta }(\mathcal {O}_{{W}_{\parallel }})\to D({W}_{\parallel })$
is naturally identified with the pullback
![]() $\Delta ^{*}\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}$
of the Atiyah class for the map of topoi
$\Delta ^{*}\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}$
of the Atiyah class for the map of topoi
![]() $X_{\bullet }\to Y_{\bullet }$
. Thus, taking the cone, we see that (4.2) is identified with
$X_{\bullet }\to Y_{\bullet }$
. Thus, taking the cone, we see that (4.2) is identified with
![]() $\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}[1]$
. From the commutative diagram of topoi
$\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}[1]$
. From the commutative diagram of topoi
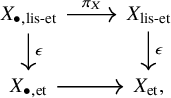
we see that
![]() $\eta _{X*}\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}$
is naturally identified with the pullback to the lisse-étale site of the usual Atiyah class for the map
$\eta _{X*}\operatorname {\mathrm {at}}_{E_{X_{\bullet }}, X_{\bullet }/Y_{\bullet }}$
is naturally identified with the pullback to the lisse-étale site of the usual Atiyah class for the map
![]() $X_{\operatorname {et}}\to Y_{\operatorname {et}}$
, from which the result follows.
$X_{\operatorname {et}}\to Y_{\operatorname {et}}$
, from which the result follows.
As a first application of our definition, we compute the Atiyah class of the universal vector bundle on
![]() $BGL_n$
over a chosen base field k.
$BGL_n$
over a chosen base field k.
Example 4.9. Let
![]() $\mathcal {V}$
denote the universal rank n locally free sheaf on
$\mathcal {V}$
denote the universal rank n locally free sheaf on
![]() $BGL_n$
, which is the sheaf of sections of the vector bundle associated to the universal principal
$BGL_n$
, which is the sheaf of sections of the vector bundle associated to the universal principal
![]() $GL_n$
-bundle. We have the
$GL_n$
-bundle. We have the
![]() $2$
-cartesian diagram, where the map x from
$2$
-cartesian diagram, where the map x from
![]() $\operatorname {\mathrm {Spec}} k$
is the one corresponding to the trivial
$\operatorname {\mathrm {Spec}} k$
is the one corresponding to the trivial
![]() $GL_n$
-torsor
$GL_n$
-torsor
There is a natural trivialization of the pullback
![]() $\mathcal {V}_{\operatorname {\mathrm {Spec}} k}$
. Then for every T-valued point
$\mathcal {V}_{\operatorname {\mathrm {Spec}} k}$
. Then for every T-valued point
![]() $g=(g_{i,j})$
on
$g=(g_{i,j})$
on
![]() $GL_n$
, the
$GL_n$
, the
![]() $2$
-morphism
$2$
-morphism
![]() $\rho $
indicated in the diagram induces a natural pullback map
$\rho $
indicated in the diagram induces a natural pullback map
![]() $\rho ^{*}: t^{*}\mathcal {V}_{\operatorname {\mathrm {Spec}} k}|_T\xrightarrow {\sim }s^{*}\mathcal {V}_{\operatorname {\mathrm {Spec}} k}|_T$
. With respect to the given trivialization of
$\rho ^{*}: t^{*}\mathcal {V}_{\operatorname {\mathrm {Spec}} k}|_T\xrightarrow {\sim }s^{*}\mathcal {V}_{\operatorname {\mathrm {Spec}} k}|_T$
. With respect to the given trivialization of
![]() $\mathcal {V}$
over
$\mathcal {V}$
over
![]() $\operatorname {\mathrm {Spec}} k$
, this morphism is just given by
$\operatorname {\mathrm {Spec}} k$
, this morphism is just given by
![]() $g^{-1}:\mathcal {O}_T^{\oplus n} \to \mathcal {O}_T^{\oplus n}$
.
$g^{-1}:\mathcal {O}_T^{\oplus n} \to \mathcal {O}_T^{\oplus n}$
.
We now compute the Atiyah class of
![]() $\mathcal {V}$
using Construction 4.1, where we chose
$\mathcal {V}$
using Construction 4.1, where we chose
![]() $X=Y=\operatorname {\mathrm {Spec}} k$
, so that we get
$X=Y=\operatorname {\mathrm {Spec}} k$
, so that we get
![]() $W=GL_n$
. More precisely, we will calculate the restriction of
$W=GL_n$
. More precisely, we will calculate the restriction of
![]() $\operatorname {\mathrm {at}}_{\mathcal {V}}$
to the etale site of W, so that we do not have to consider the associated strictly simplicial algebraic spaces. Thus, here we let
$\operatorname {\mathrm {at}}_{\mathcal {V}}$
to the etale site of W, so that we do not have to consider the associated strictly simplicial algebraic spaces. Thus, here we let
![]() ${W}_{\parallel }$
and
${W}_{\parallel }$
and
![]() ${Y}_{\parallel }$
be the topos associated to the diagrams
${Y}_{\parallel }$
be the topos associated to the diagrams
respectively, and
![]() ${h}_{\parallel }:{W}_{\parallel }\to {Y}_{\parallel }$
the natural map, and we let
${h}_{\parallel }:{W}_{\parallel }\to {Y}_{\parallel }$
the natural map, and we let
![]() $\mathcal {V}_{{W}_{\parallel }}$
denote the locally free sheaf on
$\mathcal {V}_{{W}_{\parallel }}$
denote the locally free sheaf on
![]() ${W}_{\parallel }$
obtained by pullback. First, to calculate
${W}_{\parallel }$
obtained by pullback. First, to calculate
![]() $\operatorname {\mathrm {at}}_{\mathcal {V}_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel }}$
, we do not need to take a simplicial resolution of
$\operatorname {\mathrm {at}}_{\mathcal {V}_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel }}$
, we do not need to take a simplicial resolution of
![]() $\mathcal {O}_{{W}_{\parallel }}$
over
$\mathcal {O}_{{W}_{\parallel }}$
over
![]() ${h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}$
since the map
${h}_{\parallel }^{-1}\mathcal {O}_{{Y}_{\parallel }}$
since the map
![]() ${W}_{\parallel }\to {Y}_{\parallel }$
is composed of smooth maps of algebraic spaces. Moreover, since
${W}_{\parallel }\to {Y}_{\parallel }$
is composed of smooth maps of algebraic spaces. Moreover, since
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
preserves mapping cones of complexes, we may calculate
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
preserves mapping cones of complexes, we may calculate
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(\operatorname {\mathrm {at}}_{\mathcal {V}_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel }})$
by first applying
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(\operatorname {\mathrm {at}}_{\mathcal {V}_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel }})$
by first applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
to the sequence of principal parts
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
to the sequence of principal parts
![]() $P_{{W}_{\parallel }/{Y}_{\parallel }}(\mathcal {V}_{{W}_{\parallel }})$
and only then taking connecting homomorphisms. Writing out the pullback maps in the sequence of principal parts
$P_{{W}_{\parallel }/{Y}_{\parallel }}(\mathcal {V}_{{W}_{\parallel }})$
and only then taking connecting homomorphisms. Writing out the pullback maps in the sequence of principal parts
![]() $P_{{W}_{\parallel }/{Y}_{\parallel }}(\mathcal {V}_{{W}_{\parallel }})$
gives the following diagram on W, where we use that
$P_{{W}_{\parallel }/{Y}_{\parallel }}(\mathcal {V}_{{W}_{\parallel }})$
gives the following diagram on W, where we use that
![]() $\Omega _{X/Y}=0$
:
$\Omega _{X/Y}=0$
:
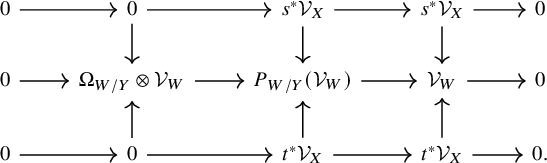
Since
![]() $\mathcal {V}_W$
is pulled back from
$\mathcal {V}_W$
is pulled back from
![]() $X=Y=\operatorname {\mathrm {Spec}} k$
via s, we have a natural splitting
$X=Y=\operatorname {\mathrm {Spec}} k$
via s, we have a natural splitting
![]() $P_{W/Y}(\mathcal {V}_W)=\Omega _{W/Y}\otimes s^{*}\mathcal {V}_{X}\oplus s^{*}\mathcal {V}_X$
. With respect to this splitting, one calculates that the induced pullback map along t is given by
$P_{W/Y}(\mathcal {V}_W)=\Omega _{W/Y}\otimes s^{*}\mathcal {V}_{X}\oplus s^{*}\mathcal {V}_X$
. With respect to this splitting, one calculates that the induced pullback map along t is given by
It follows, that after applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
, the resulting exact sequence has the following exact subsequence, and the termwise inclusions give quasi-isomorphisms:
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
, the resulting exact sequence has the following exact subsequence, and the termwise inclusions give quasi-isomorphisms:
It is a general fact that for an exact sequence of this form, the connecting map is canonically quasi-isomorphic to minus the shift of the map the cone is taken over for the middle term – that is, in our case, this gives
In particular, we find that there is a natural isomorphism
![]() $s^{*}x^{*}L_{BGL_n}[1]\simeq \Omega _{W/Y}$
and that using this identification and the trivialization of
$s^{*}x^{*}L_{BGL_n}[1]\simeq \Omega _{W/Y}$
and that using this identification and the trivialization of
![]() $\mathcal {V}_X$
, we have that
$\mathcal {V}_X$
, we have that
![]() $s^{*}x^{*}\operatorname {\mathrm {at}}_{\mathcal {V}}$
is given by
$s^{*}x^{*}\operatorname {\mathrm {at}}_{\mathcal {V}}$
is given by
where
![]() $T=(T_{ij})$
is the universal matrix on
$T=(T_{ij})$
is the universal matrix on
![]() $GL_n$
. In particular, for
$GL_n$
. In particular, for
![]() $n=1$
, we have the following:
$n=1$
, we have the following:
Example 4.10. By taking the trace in (4.5), we obtain the section
given by
![]() $\operatorname {tr}(d(T^{-1})T)$
. This is equal to
$\operatorname {tr}(d(T^{-1})T)$
. This is equal to
In particular, for
![]() $n=1$
, we have
$n=1$
, we have
![]() $T=(t)$
as a
$T=(t)$
as a
![]() $1\times 1$
matrix, and the pullback of
$1\times 1$
matrix, and the pullback of
![]() $\operatorname {\mathrm {at}}_{\mathcal {L}}\otimes \mathcal {L}^{-1}$
– with
$\operatorname {\mathrm {at}}_{\mathcal {L}}\otimes \mathcal {L}^{-1}$
– with
![]() $\mathcal {L}$
the universal rank
$\mathcal {L}$
the universal rank
![]() $1$
sheaf – to
$1$
sheaf – to
![]() $\mathbb {G}_m=GL_1$
is given by
$\mathbb {G}_m=GL_1$
is given by
sending
![]() $1$
to
$1$
to
![]() $d(1/t) t=-dt/t$
. We have the natural map
$d(1/t) t=-dt/t$
. We have the natural map
![]() $DET:BGL_n\to B\mathbb {G}_m$
given by associating to a locally free sheaf its determinant line bundle. By taking fiber products with a point, this induces a map
$DET:BGL_n\to B\mathbb {G}_m$
given by associating to a locally free sheaf its determinant line bundle. By taking fiber products with a point, this induces a map
![]() $GL_n\to \mathbb {G}_m$
, (which is again just the determinant) whose pullback map on differentials is given by
$GL_n\to \mathbb {G}_m$
, (which is again just the determinant) whose pullback map on differentials is given by
![]() $dt\mapsto d(\det T)$
. In particular, we have
$dt\mapsto d(\det T)$
. In particular, we have
![]() $td(1/t)\mapsto \det T d(\det T^{-1})$
. This shows that we have a natural identification
$td(1/t)\mapsto \det T d(\det T^{-1})$
. This shows that we have a natural identification
![]() $\operatorname {tr}(s^{*}x^{*}\operatorname {\mathrm {at}}_{\mathcal {V}})= s^{*}x^{*}(\operatorname {\mathrm {at}}_{\det \mathcal {V}}\otimes \det \mathcal {V}^{-1})$
. One can show that this isomorphism is part of a descent datum, and thus we have
$\operatorname {tr}(s^{*}x^{*}\operatorname {\mathrm {at}}_{\mathcal {V}})= s^{*}x^{*}(\operatorname {\mathrm {at}}_{\det \mathcal {V}}\otimes \det \mathcal {V}^{-1})$
. One can show that this isomorphism is part of a descent datum, and thus we have
4.2 Construction of the reduced Atiyah class
Construction 4.11. Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks. Let
$f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks. Let
![]() $E\in D^-_{qcoh}(\mathcal {Y})$
and let
$E\in D^-_{qcoh}(\mathcal {Y})$
and let
![]() $E_{\mathcal {X}}:= f^{*}E$
. Let
$E_{\mathcal {X}}:= f^{*}E$
. Let
![]() $F \to E_{\mathcal {X}}\to G \xrightarrow {+1}$
be a distinguished triangle in
$F \to E_{\mathcal {X}}\to G \xrightarrow {+1}$
be a distinguished triangle in
![]() $D^-_{qcoh}(\mathcal {X})$
such that
$D^-_{qcoh}(\mathcal {X})$
such that
![]() $R\operatorname {\mathrm {Hom}}^{-1}(F, G) = 0$
. We let
$R\operatorname {\mathrm {Hom}}^{-1}(F, G) = 0$
. We let
![]() $X_{\bullet }, Y_{\bullet }$
and
$X_{\bullet }, Y_{\bullet }$
and
![]() $W_{\bullet }$
be as in Situation 2.9 and let
$W_{\bullet }$
be as in Situation 2.9 and let
![]() $R=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}(\mathcal {O}_{{W}_{\parallel }})$
. Let
$R=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}(\mathcal {O}_{{W}_{\parallel }})$
. Let
![]() $F_{{W}_{\parallel }}, E_{{W}_{\parallel }}$
and
$F_{{W}_{\parallel }}, E_{{W}_{\parallel }}$
and
![]() $G_{{W}_{\parallel }}$
denote the
$G_{{W}_{\parallel }}$
denote the
![]() $\mathcal {O}_{{W}_{\parallel }}$
-modules induced by
$\mathcal {O}_{{W}_{\parallel }}$
-modules induced by
![]() $E_{\mathcal {X}}$
and G, respectively, and let
$E_{\mathcal {X}}$
and G, respectively, and let
![]() $E_{{Y}_{\parallel }}$
denote the
$E_{{Y}_{\parallel }}$
denote the
![]() $\mathcal {O}_{{Y}_{\parallel }}$
-module induced by E. From Construction 3.5, we obtain a morphism
$\mathcal {O}_{{Y}_{\parallel }}$
-module induced by E. From Construction 3.5, we obtain a morphism
Applying the sequence of maps of (2.6), we get
We also write
![]() $\overline {\operatorname {\mathrm {at}}}_E$
if the rest of the data is clear.
$\overline {\operatorname {\mathrm {at}}}_E$
if the rest of the data is clear.
Proposition 4.12. The reduced Atiyah class is independent of the choice of cover
![]() $X/Y$
.
$X/Y$
.
Proof. This is similar to Lemma 4.4 and left to the reader (and slightly simpler since E and G are assumed to be quasicoherent sheaves, rather than more general complexes).
Proposition 4.13. If
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are algebraic spaces, the reduced Atiyah class of Construction 4.11 agrees with the one for ringed topoi defined in §3.1.
$\mathcal {Y}$
are algebraic spaces, the reduced Atiyah class of Construction 4.11 agrees with the one for ringed topoi defined in §3.1.
Proof. The proof is analogous to the proof of Proposition 4.8 and left to the reader.
Corollary 4.14. The following triangles commute:
-
1)

-
2)

In both cases, the vertical morphisms are induced from the connecting map
![]() $G\to F[1]$
of the given exact sequence.
$G\to F[1]$
of the given exact sequence.
Proof. From Remark 3.2, we get commutative triangles for the classical Atiyah classes
![]() $\operatorname {\mathrm {at}}_{E_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel },G_{{W}_{\parallel }} }$
and
$\operatorname {\mathrm {at}}_{E_{{W}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel },G_{{W}_{\parallel }} }$
and
![]() $\overline {\operatorname {\mathrm {at}}}_{E_{{Y}_{\parallel }}, {W}_{\parallel }/{Y}_{\parallel },G_{{W}_{\parallel }}}$
. The result follows by passing to
$\overline {\operatorname {\mathrm {at}}}_{E_{{Y}_{\parallel }}, {W}_{\parallel }/{Y}_{\parallel },G_{{W}_{\parallel }}}$
. The result follows by passing to
![]() $D(\mathcal {X})$
.
$D(\mathcal {X})$
.
4.3 Construction of the Atiyah class for an exact sequence
Let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
$f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and let
![]() $0\to F\to E\to G\to 0$
be an exact sequence of quasicoherent sheaves on
$0\to F\to E\to G\to 0$
be an exact sequence of quasicoherent sheaves on
![]() $\mathcal {X}$
, which we denote by
$\mathcal {X}$
, which we denote by
![]() $\underline {E}$
. Assume that
$\underline {E}$
. Assume that
![]() $F,E$
and G are dualizable as objects of the derived category of
$F,E$
and G are dualizable as objects of the derived category of
![]() $\mathcal {X}$
. We let
$\mathcal {X}$
. We let
![]() ${X}_{\parallel }$
,
${X}_{\parallel }$
,
![]() ${Y}_{\parallel }$
and
${Y}_{\parallel }$
and
![]() ${W}_{\parallel }$
be as in Situation 2.9. We also let
${W}_{\parallel }$
be as in Situation 2.9. We also let
![]() $R=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}\mathcal {O}_{{W}_{\parallel }}$
, and we let
$R=P_{h^{-1}\mathcal {O}_{{Y}_{\parallel }}}\mathcal {O}_{{W}_{\parallel }}$
, and we let
![]() $F_{{W}_{\parallel }}, E_{{W}_{\parallel }}$
and
$F_{{W}_{\parallel }}, E_{{W}_{\parallel }}$
and
![]() $G_{{W}_{\parallel }}$
denote the sheaves on
$G_{{W}_{\parallel }}$
denote the sheaves on
![]() ${W}_{\parallel }$
induced by
${W}_{\parallel }$
induced by
![]() $F,E,G$
, respectively. Let
$F,E,G$
, respectively. Let
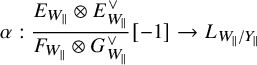 $$\begin{align*}\alpha:\frac{E_{{W}_{\parallel}}\otimes E_{{W}_{\parallel}}^{\vee}}{F_{{W}_{\parallel}}\otimes G^{\vee}_{{W}_{\parallel}}}[-1]\to L_{{W}_{\parallel}/{Y }_{\parallel}} \end{align*}$$
$$\begin{align*}\alpha:\frac{E_{{W}_{\parallel}}\otimes E_{{W}_{\parallel}}^{\vee}}{F_{{W}_{\parallel}}\otimes G^{\vee}_{{W}_{\parallel}}}[-1]\to L_{{W}_{\parallel}/{Y }_{\parallel}} \end{align*}$$
be the Atiyah class of the exact sequence
![]() $\underline {E}_{{W}_{\parallel }}$
with respect to the morphism of topoi
$\underline {E}_{{W}_{\parallel }}$
with respect to the morphism of topoi
![]() ${W}_{\parallel }\to {Y}_{\parallel }$
. This is a morphism in
${W}_{\parallel }\to {Y}_{\parallel }$
. This is a morphism in
![]() $D({W}_{\parallel })$
. By taking cones, shifting, and applying
$D({W}_{\parallel })$
. By taking cones, shifting, and applying
![]() $\eta _{W*}$
, we obtain a morphism
$\eta _{W*}$
, we obtain a morphism
which we call the Atiyah class of the exact sequence
![]() $\underline {E}$
. We also write
$\underline {E}$
. We also write
![]() $\operatorname {\mathrm {at}}_{\underline {E}}$
if the morphism
$\operatorname {\mathrm {at}}_{\underline {E}}$
if the morphism
![]() $f:\mathcal {X}\to \mathcal {Y}$
is understood.
$f:\mathcal {X}\to \mathcal {Y}$
is understood.
From the construction and Corollary 3.12, we conclude the following:
Corollary 4.15. The morphism
![]() $\operatorname {\mathrm {at}}_{\underline {E}}$
is compatible with the usual Atiyah class (i.e., the diagram
$\operatorname {\mathrm {at}}_{\underline {E}}$
is compatible with the usual Atiyah class (i.e., the diagram
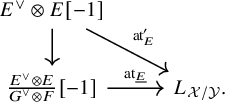
commutes).
Similarly, we conclude immediately from Proposition 3.15:
Corollary 4.16. We have a commutative diagram
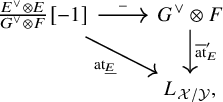
where the horizontal map is the natural connecting homomorphism.
5 Properties
5.1 Tensor compatibility of the Atiyah class
Let A be a ring, and B an A-algebra. For a B-module M, let
![]() $\underline {P}^1_{B/A}(M)$
denote the exact sequence
$\underline {P}^1_{B/A}(M)$
denote the exact sequence
We will also write
![]() $\underline {P}^1_{B/A}(M)$
to denote the corresponding element of
$\underline {P}^1_{B/A}(M)$
to denote the corresponding element of
![]() $\operatorname {\mathrm {Ext}}^1_B(M,\Omega _{B/A}\otimes _B M)$
.
$\operatorname {\mathrm {Ext}}^1_B(M,\Omega _{B/A}\otimes _B M)$
.
Lemma 5.1. Let M and N be B-modules and suppose that M is flat. Then in
![]() $\operatorname {\mathrm {Ext}}^1_B(M\otimes _B N, \Omega _{B/A}\otimes _B M\otimes _B N)$
we have the following equality:
$\operatorname {\mathrm {Ext}}^1_B(M\otimes _B N, \Omega _{B/A}\otimes _B M\otimes _B N)$
we have the following equality:
Here, we regard
![]() $M\otimes _B \underline {P}_{B/A}(N)$
as an extension of
$M\otimes _B \underline {P}_{B/A}(N)$
as an extension of
![]() $M\otimes N$
by
$M\otimes N$
by
![]() $ \Omega _{B/A}\otimes _B M\otimes _B N$
via the symmetry isomorphism of the tensor product.
$ \Omega _{B/A}\otimes _B M\otimes _B N$
via the symmetry isomorphism of the tensor product.
Proof. Recall that
![]() $P^1_{B/A}(M) = B\otimes _A M/(I_{\Delta }^{2}B\otimes _A M)$
, where
$P^1_{B/A}(M) = B\otimes _A M/(I_{\Delta }^{2}B\otimes _A M)$
, where
![]() $I_{\Delta }$
is the kernel of the map of A-algebras
$I_{\Delta }$
is the kernel of the map of A-algebras
![]() $B\otimes _A B\to B$
; the B-module structure on
$B\otimes _A B\to B$
; the B-module structure on
![]() $P^1_{B/A}(M)$
is given by action on the left side of the tensor product. Therefore, we have natural isomorphisms
$P^1_{B/A}(M)$
is given by action on the left side of the tensor product. Therefore, we have natural isomorphisms
![]() $P_{B/A}(M)\otimes _B N \simeq N\otimes _B P_{B/A}(M)\simeq N\otimes _A M/I_{N,M}$
, where
$P_{B/A}(M)\otimes _B N \simeq N\otimes _B P_{B/A}(M)\simeq N\otimes _A M/I_{N,M}$
, where
![]() $I_{N,M}:=I_{\Delta }^2 (N\otimes _A M)$
, and similarly with N and M reversed.
$I_{N,M}:=I_{\Delta }^2 (N\otimes _A M)$
, and similarly with N and M reversed.
We then have that the left-hand side of the equality in the lemma is represented by the Baer sum of the following two exact sequences:
where
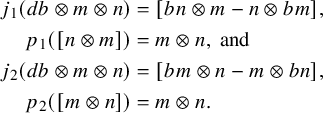 $$ \begin{align*} j_1(db\otimes m\otimes n) &= [bn\otimes m - n\otimes bm],\\ p_1([n\otimes m])&=m\otimes n, \mbox{ and }\\ j_2(db\otimes m\otimes n) &= [bm\otimes n- m\otimes bn],\\ p_2([m\otimes n])&= m\otimes n. \end{align*} $$
$$ \begin{align*} j_1(db\otimes m\otimes n) &= [bn\otimes m - n\otimes bm],\\ p_1([n\otimes m])&=m\otimes n, \mbox{ and }\\ j_2(db\otimes m\otimes n) &= [bm\otimes n- m\otimes bn],\\ p_2([m\otimes n])&= m\otimes n. \end{align*} $$
We make the definition of the Baer sum explicit: We have submodules
given by
Then the Baer sum of (5.1) and (5.2) is given by
where the maps are defined by
![]() $p_3((a,b)+ Q)=p_1(a)$
, and
$p_3((a,b)+ Q)=p_1(a)$
, and
![]() $j_3(x)= (j_1(x),0)+Q$
.
$j_3(x)= (j_1(x),0)+Q$
.
Note that we also have (by exactness of the sequences (5.1) and (5.2))
We claim that this extension is isomorphic to
![]() $\underline {P}^1_{B/A}(M\otimes _B N)$
. We first construct a map of B-modules
$\underline {P}^1_{B/A}(M\otimes _B N)$
. We first construct a map of B-modules
![]() $P_{B/A}^1(M\otimes _B N)\to R/Q$
. By the universal property of the module of principal parts, this is equivalent to giving an A-linear degree one differential operator
$P_{B/A}^1(M\otimes _B N)\to R/Q$
. By the universal property of the module of principal parts, this is equivalent to giving an A-linear degree one differential operator
![]() $M\otimes _B N\to R/Q$
. We define
$M\otimes _B N\to R/Q$
. We define
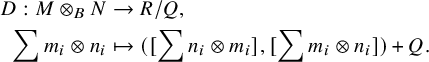 $$ \begin{align*} D: M\otimes_B N &\to R/Q,\\ \sum m_i\otimes n_i &\mapsto ([\sum n_i\otimes m_i], [\sum m_i\otimes n_i])+Q. \end{align*} $$
$$ \begin{align*} D: M\otimes_B N &\to R/Q,\\ \sum m_i\otimes n_i &\mapsto ([\sum n_i\otimes m_i], [\sum m_i\otimes n_i])+Q. \end{align*} $$
This is well defined since if
![]() $\sum m_i\otimes n_i=\sum m_j^{\prime }\otimes n_j^{\prime }$
in
$\sum m_i\otimes n_i=\sum m_j^{\prime }\otimes n_j^{\prime }$
in
![]() $M\otimes _B N$
, then the difference
$M\otimes _B N$
, then the difference
lies in Q due to (5.3). The map D is clearly A-linear, and a first order differential operator, since for any
![]() $b\in B$
, we have
$b\in B$
, we have
and thus, the map
![]() $x\mapsto D(bx)-bD(x)$
is B-linear. Thus, we have the corresponding map of B-modules
$x\mapsto D(bx)-bD(x)$
is B-linear. Thus, we have the corresponding map of B-modules
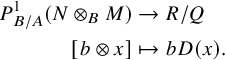 $$ \begin{align*} P^1_{B/A}(N\otimes_B M)&\to R/Q\\ [b\otimes x]&\mapsto b D(x). \end{align*} $$
$$ \begin{align*} P^1_{B/A}(N\otimes_B M)&\to R/Q\\ [b\otimes x]&\mapsto b D(x). \end{align*} $$
A straightforward explicit computation shows that the diagram

commutes, which finishes the proof.
Since taking tensor products, Kähler differentials, modules of principal parts and Baer sums commute with sheafification and are suitably functorial, we have as a consequence the following:
Corollary 5.2. Lemma 5.1 holds when A and B are rings in a topos.
Using Lemma 5.1, we can prove the tensor compatibility of the Atiyah class. Regard
![]() $E\otimes {\operatorname {\mathrm {at}}}_F$
as a map
$E\otimes {\operatorname {\mathrm {at}}}_F$
as a map
![]() $E\otimes F\to L_{\mathcal {X}/\mathcal {Y}}\otimes E\otimes F [1]$
via the composition
$E\otimes F\to L_{\mathcal {X}/\mathcal {Y}}\otimes E\otimes F [1]$
via the composition
Here, the second map is the map defining the triangulated structure on
![]() $E\otimes -$
, and the third map is the symmetry isomorphism exchanging E and
$E\otimes -$
, and the third map is the symmetry isomorphism exchanging E and
![]() $L_{\mathcal {X}/\mathcal {Y}}$
.
$L_{\mathcal {X}/\mathcal {Y}}$
.
Proposition 5.3. Let
![]() $\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks, and
$\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks, and
![]() $E,F\in D^{\leq 0}_{qcoh}(\mathcal {O}_{\mathcal {X}})$
. Then we have the equality
$E,F\in D^{\leq 0}_{qcoh}(\mathcal {O}_{\mathcal {X}})$
. Then we have the equality
Proof. We use the setup of Construction 4.1. Without loss of generality, we may assume that E is represented by a complex of flat
![]() $\mathcal {O}_{\mathcal {X}}$
-modules, so in particular, we may choose
$\mathcal {O}_{\mathcal {X}}$
-modules, so in particular, we may choose
![]() $E\otimes F\in D^{\leq 0}_{qcoh}(\mathcal {O}_{\mathcal {X}})$
to be represented by the usual tensor product of the complexes E and F. Let
$E\otimes F\in D^{\leq 0}_{qcoh}(\mathcal {O}_{\mathcal {X}})$
to be represented by the usual tensor product of the complexes E and F. Let
![]() $E_R\to E_{{W}_{\parallel }}$
be a flat resolution of the R-module
$E_R\to E_{{W}_{\parallel }}$
be a flat resolution of the R-module
![]() $E_{{W}_{\parallel }}$
. By the construction of the Atiyah class in 4.1, we may use the exact sequences
$E_{{W}_{\parallel }}$
. By the construction of the Atiyah class in 4.1, we may use the exact sequences
to compute
![]() $\operatorname {\mathrm {at}}_{E}$
and
$\operatorname {\mathrm {at}}_{E}$
and
![]() $\operatorname {\mathrm {at}}_{E\otimes F}$
, respectively. By Corollary 5.2, we have an equality of extensions of R-modules
$\operatorname {\mathrm {at}}_{E\otimes F}$
, respectively. By Corollary 5.2, we have an equality of extensions of R-modules
After taking connecting maps in
![]() $D^{\Delta }(R)$
and using that extensions of scalars and the Dold-Kan correspondence are compatible with the symmetry isomorphisms of the derived tensor product, we get an equality of maps
$D^{\Delta }(R)$
and using that extensions of scalars and the Dold-Kan correspondence are compatible with the symmetry isomorphisms of the derived tensor product, we get an equality of maps
By Lemma 2.7, this implies the result after passing to
![]() $D^{\leq 0}(\mathcal {O}_{W_{\bullet }})$
and then to
$D^{\leq 0}(\mathcal {O}_{W_{\bullet }})$
and then to
![]() $D^{\leq 0}(\mathcal {X})$
.
$D^{\leq 0}(\mathcal {X})$
.
If we assume that one of the Atiyah classes of E or F vanish, this simplifies to the following:
Corollary 5.4. Suppose that
![]() $\operatorname {\mathrm {at}}_F=0$
(respectively that
$\operatorname {\mathrm {at}}_F=0$
(respectively that
![]() $\operatorname {\mathrm {at}}_E=0$
), then we have
$\operatorname {\mathrm {at}}_E=0$
), then we have
![]() $\operatorname {\mathrm {at}}_{E\otimes F}=\operatorname {\mathrm {at}}_E\otimes F$
(respectively
$\operatorname {\mathrm {at}}_{E\otimes F}=\operatorname {\mathrm {at}}_E\otimes F$
(respectively
![]() $\operatorname {\mathrm {at}}_{E\otimes F}=E\otimes {\operatorname {\mathrm {at}}_F}$
) after identifying the targets using symmetry of the tensor product.
$\operatorname {\mathrm {at}}_{E\otimes F}=E\otimes {\operatorname {\mathrm {at}}_F}$
) after identifying the targets using symmetry of the tensor product.
Corollary 5.5 (Shift invariance).
For
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
, the following diagram commutes:
$E\in D^{\leq 0}_{qcoh}(\mathcal {X})$
, the following diagram commutes:
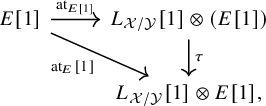
where
![]() $\tau $
is the map defining the triangulated structure on the tensor product functor
$\tau $
is the map defining the triangulated structure on the tensor product functor
![]() $L_{\mathcal {X}/\mathcal {Y}}[1]\otimes -$
(see [22, Tag 0G6A and Tag 0G6E]).
$L_{\mathcal {X}/\mathcal {Y}}[1]\otimes -$
(see [22, Tag 0G6A and Tag 0G6E]).
Proof. This follows from Proposition 5.3 applied to
![]() $F\otimes E$
with
$F\otimes E$
with
![]() $F=\mathcal {O}_{\mathcal {X}}[1]$
and noting that
$F=\mathcal {O}_{\mathcal {X}}[1]$
and noting that
![]() $\operatorname {\mathrm {at}}_{F}=0$
, since F is pulled back from
$\operatorname {\mathrm {at}}_{F}=0$
, since F is pulled back from
![]() $\mathcal {Y}$
.
$\mathcal {Y}$
.
Construction 5.6. Using Corollary 5.5, we extend the definition of
![]() $\operatorname {\mathrm {at}}_E$
to any
$\operatorname {\mathrm {at}}_E$
to any
![]() $E\in D^-_{qcoh}(\mathcal {X})$
: Choose some large enough integer
$E\in D^-_{qcoh}(\mathcal {X})$
: Choose some large enough integer
![]() $N\geq 0$
, so that
$N\geq 0$
, so that
![]() $E[N]\in D^{\leq 0}_{qcoh}(\mathcal {X})$
, so that
$E[N]\in D^{\leq 0}_{qcoh}(\mathcal {X})$
, so that
![]() $\operatorname {\mathrm {at}}_{E[N]}$
is defined. Then define
$\operatorname {\mathrm {at}}_{E[N]}$
is defined. Then define
![]() $\operatorname {\mathrm {at}}_E$
via the commutative diagram
$\operatorname {\mathrm {at}}_E$
via the commutative diagram
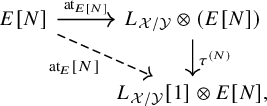
where we take
![]() $\tau ^{(N)}:= \tau [N]\circ \cdots \circ \tau $
. Explicitly, we have
$\tau ^{(N)}:= \tau [N]\circ \cdots \circ \tau $
. Explicitly, we have
Corollary 5.5 guarantees that this is independent of the choice of N.
Remark 5.7. In what follows, we will generally check properties of the Atiyah class for objects
![]() $E\in D^{\leq 0}$
. In each case, one may check that the statement is appropriately invariant under shifts.
$E\in D^{\leq 0}$
. In each case, one may check that the statement is appropriately invariant under shifts.
Another consequence is the following:
Corollary 5.8. The following diagram is a morphism of exact triangles:
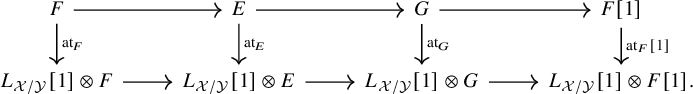
Here, the lower row is obtained by applying the triangulated functor
![]() $L_{\mathcal {X}/\mathcal {Y}}[1]\otimes -$
to the upper row.
$L_{\mathcal {X}/\mathcal {Y}}[1]\otimes -$
to the upper row.
5.2 Compatibility with traces
We let
![]() $f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and consider Atiyah classes with respect to this morphism. In Proposition 5.9 and Corollary 5.10, we make global boundedness assumptions, but the results likely hold for arbitrary perfect complexes; cf. [Reference Lieblich and Olsson11].
$f:\mathcal {X}\to \mathcal {Y}$
be a morphism of algebraic stacks and consider Atiyah classes with respect to this morphism. In Proposition 5.9 and Corollary 5.10, we make global boundedness assumptions, but the results likely hold for arbitrary perfect complexes; cf. [Reference Lieblich and Olsson11].
Proposition 5.9. Let
![]() $F\to E\to G\to F[1]$
be a distinguished triangle of perfect complexes in
$F\to E\to G\to F[1]$
be a distinguished triangle of perfect complexes in
![]() $D^b_{qcoh}(\mathcal {X})$
and assume each of
$D^b_{qcoh}(\mathcal {X})$
and assume each of
![]() $E,F,G$
has finite Tor-amplitude. Then
$E,F,G$
has finite Tor-amplitude. Then
Proof. By the shift invariance of the Atiyah class and Lemma 2.16, we may assume that the given distinguished triangle is represented by a short exact sequence of complexes
where
![]() $F,E,G$
have flat components and lie in
$F,E,G$
have flat components and lie in
![]() $C^{\leq 0}(\mathcal {X})$
.
$C^{\leq 0}(\mathcal {X})$
.
We then use the setup of Situation 2.18 with
![]() $L=L_{\mathcal {X}/\mathcal {Y}}[1]$
and
$L=L_{\mathcal {X}/\mathcal {Y}}[1]$
and
![]() $R=\mathcal {O}_{\mathcal {X}}$
(this is justified by Corollary 5.8). Then by Proposition 2.20, we need to find a morphism
$R=\mathcal {O}_{\mathcal {X}}$
(this is justified by Corollary 5.8). Then by Proposition 2.20, we need to find a morphism
making the diagram there commute. By the assumption on Tor-dimension, each term of the sequence
lies in
![]() $D^-_{qcoh}(\mathcal {X})$
. We can therefore find an integer N, such that the natural maps from the good truncation
$D^-_{qcoh}(\mathcal {X})$
. We can therefore find an integer N, such that the natural maps from the good truncation
![]() $\tau _{\leq N}$
are quasi-isomorphisms for each term. Set
$\tau _{\leq N}$
are quasi-isomorphisms for each term. Set
![]() $\overline {E}:=(\tau _{\leq N}E)[N]$
and define
$\overline {E}:=(\tau _{\leq N}E)[N]$
and define
![]() $\overline {F},\overline {G}$
in the same way, so that we obtain an exact sequence in
$\overline {F},\overline {G}$
in the same way, so that we obtain an exact sequence in
![]() $C^{\leq 0}(\mathcal {O}_{\mathcal {X}})$
. We also let
$C^{\leq 0}(\mathcal {O}_{\mathcal {X}})$
. We also let
![]() $\overline {E}_{{W}_{\parallel }}, \overline {F}_{{W}_{\parallel }}$
and
$\overline {E}_{{W}_{\parallel }}, \overline {F}_{{W}_{\parallel }}$
and
![]() $\overline {{G}}_{{W}_{\parallel }}$
denote the induced complexes of
$\overline {{G}}_{{W}_{\parallel }}$
denote the induced complexes of
![]() $\mathcal {O}_{{W}_{\parallel }}$
-modules, which we regard as simplicial modules via the Dold–Kan correspondence and as R-modules by restriction of scalars. Choose resolutions of
$\mathcal {O}_{{W}_{\parallel }}$
-modules, which we regard as simplicial modules via the Dold–Kan correspondence and as R-modules by restriction of scalars. Choose resolutions of
![]() $F_{{W}_{\parallel }},E_{{W}_{\parallel }}$
and
$F_{{W}_{\parallel }},E_{{W}_{\parallel }}$
and
![]() $G_{{W}_{\parallel }}$
by termwise flat R-modules, so that we have a morphism of exact sequences
$G_{{W}_{\parallel }}$
by termwise flat R-modules, so that we have a morphism of exact sequences

We then obtain a natural morphism of exact sequences of R-modules
This is termwise an injection of complexes, so we get a quotient exact sequence
![]() $\underline {S}$
of the form
$\underline {S}$
of the form
 $$\begin{align*}0\to \Omega^1_{R/h^{-1}\mathcal{O}_{{Y}_{\parallel}}}\otimes_R \frac{E_{R}\otimes_R \overline{E}_{{W}_{\parallel}}}{F_R\otimes_R\overline{G}_{{W}_{\parallel}}}\to ***\to \frac{E_R\otimes \overline{E}_{{W}_{\parallel}}}{F_R\otimes \overline{G}_{{W}_{\parallel}}}\to 0.\end{align*}$$
$$\begin{align*}0\to \Omega^1_{R/h^{-1}\mathcal{O}_{{Y}_{\parallel}}}\otimes_R \frac{E_{R}\otimes_R \overline{E}_{{W}_{\parallel}}}{F_R\otimes_R\overline{G}_{{W}_{\parallel}}}\to ***\to \frac{E_R\otimes \overline{E}_{{W}_{\parallel}}}{F_R\otimes \overline{G}_{{W}_{\parallel}}}\to 0.\end{align*}$$
Taking the connecting map of this sequence and passing back to
![]() $D({W}_{\parallel })$
, we obtain a morphism
$D({W}_{\parallel })$
, we obtain a morphism
![]() $\alpha $
making the following square commute:
$\alpha $
making the following square commute:
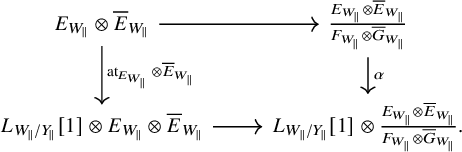
We claim that the diagram
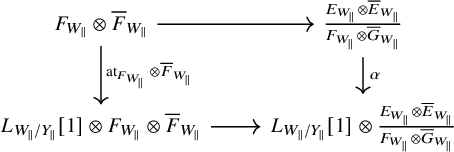
also commutes (and similarly with G in place of F in the left column). This follows from the observation that the exact sequence
![]() $\underline {P}^1_{R/{h}_{\parallel }^{-1}\mathcal {O}({Y}_{\parallel })}(F_R)\otimes \overline {F}_{{W}_{\parallel }}$
is isomorphic to the termwise cokernel of the map of exact sequences
$\underline {P}^1_{R/{h}_{\parallel }^{-1}\mathcal {O}({Y}_{\parallel })}(F_R)\otimes \overline {F}_{{W}_{\parallel }}$
is isomorphic to the termwise cokernel of the map of exact sequences
and thus includes into
![]() $\underline {S}$
. Then we get the commutativity (5.4) by taking connecting morphisms and passing to
$\underline {S}$
. Then we get the commutativity (5.4) by taking connecting morphisms and passing to
![]() $D({W}_{\parallel })$
. The argument for G in place of F goes similarly. Taking
$D({W}_{\parallel })$
. The argument for G in place of F goes similarly. Taking
![]() $\eta _{W*}\circ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(\alpha ) \circ [-1]$
then gives a morphism
$\eta _{W*}\circ \operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}(\alpha ) \circ [-1]$
then gives a morphism
Shifting by
![]() $-N$
gives the desired map in Proposition 2.20.
$-N$
gives the desired map in Proposition 2.20.
Corollary 5.10. Let
![]() $E\in D^-_{qcoh}(\mathcal {O}_{\mathcal {X}})$
be an object that can be represented by a finite length complex of locally free sheaves. Then we have an equality of maps
$E\in D^-_{qcoh}(\mathcal {O}_{\mathcal {X}})$
be an object that can be represented by a finite length complex of locally free sheaves. Then we have an equality of maps
![]() $\mathcal {O}_{\mathcal {X}}\to L_{\mathcal {X}/\mathcal {Y}}[1]$
:
$\mathcal {O}_{\mathcal {X}}\to L_{\mathcal {X}/\mathcal {Y}}[1]$
:
Proof. We argue by induction on the number k of nonzero components in a resolution by locally free sheaves. Without loss of generality, we may assume that E is given by such a resolution. If
![]() $k=1$
, the result follows from Example 4.10. If
$k=1$
, the result follows from Example 4.10. If
![]() $k>1$
, we may write
$k>1$
, we may write
![]() $k=k_1+k_2$
for positive integers
$k=k_1+k_2$
for positive integers
![]() $k_1,k_2$
and can take bad truncations of E to get an exact sequence of complexes
$k_1,k_2$
and can take bad truncations of E to get an exact sequence of complexes
where F has
![]() $k_1$
nonzero components and G has
$k_1$
nonzero components and G has
![]() $k_2$
, and they are all locally free. Then by Proposition 5.9 and the induction hypothesis, on one hand, we have
$k_2$
, and they are all locally free. Then by Proposition 5.9 and the induction hypothesis, on one hand, we have
On the other hand, the determinant is multiplicative in exact sequences of perfect complexes, which gives
![]() $\det E=\det F\otimes \det G$
. Using the tensor compatibility Proposition 5.3, we find
$\det E=\det F\otimes \det G$
. Using the tensor compatibility Proposition 5.3, we find
5.3 Compatibility of Atiyah class and reduced Atiyah class
We prove Proposition 1.1. Consider the setup of Construction 4.11 and let
![]() $\mathcal {Y}\to \mathcal {Z}$
be a further morphism of algebraic stacks. Choose a diagram
$\mathcal {Y}\to \mathcal {Z}$
be a further morphism of algebraic stacks. Choose a diagram
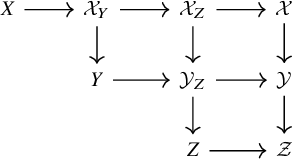
in which all squares are cartesian, the horizontal morphisms are smooth and surjective, and
![]() $X,Y$
and Z are algebraic spaces. We let
$X,Y$
and Z are algebraic spaces. We let
![]() $X_{\bullet }$
,
$X_{\bullet }$
,
![]() $Y_{\bullet }$
and
$Y_{\bullet }$
and
![]() $Z_{\bullet }$
be the strictly simplicial algebraic spaces associated to compositions along the horizontal rows, respectively. We also let
$Z_{\bullet }$
be the strictly simplicial algebraic spaces associated to compositions along the horizontal rows, respectively. We also let
![]() $V:=Y\times _{\mathcal {Y}_Z}Y$
with strictly simplicial algebraic space
$V:=Y\times _{\mathcal {Y}_Z}Y$
with strictly simplicial algebraic space
![]() $V_{\bullet }$
associated to the morphism
$V_{\bullet }$
associated to the morphism
![]() $V\to \mathcal {Y}$
, and further
$V\to \mathcal {Y}$
, and further
![]() $W:=X\times _{\mathcal {X}_Y} X$
and
$W:=X\times _{\mathcal {X}_Y} X$
and
![]() $\widetilde {W}:=X\times _{\mathcal {X}_Z} X$
with strictly simplicial algebraic spaces
$\widetilde {W}:=X\times _{\mathcal {X}_Z} X$
with strictly simplicial algebraic spaces
![]() $W_{\bullet }$
and
$W_{\bullet }$
and
![]() $\widetilde {W}_{\bullet }$
associated to the morphisms to
$\widetilde {W}_{\bullet }$
associated to the morphisms to
![]() $\mathcal {X}$
. We have the following natural commutative diagram:
$\mathcal {X}$
. We have the following natural commutative diagram:
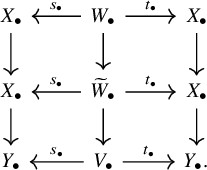
Here, by abuse of notation, we use
![]() $s_{\bullet }$
and
$s_{\bullet }$
and
![]() $t_{\bullet }$
to denote the morphisms given by (degreewise) projection to the first and second factor, respectively. We define diagrammatic topoi
$t_{\bullet }$
to denote the morphisms given by (degreewise) projection to the first and second factor, respectively. We define diagrammatic topoi
![]() ${W}_{\parallel }$
,
${W}_{\parallel }$
,
![]() ${\widetilde {W}}_{\parallel }$
and
${\widetilde {W}}_{\parallel }$
and
![]() ${V}_{\parallel }$
by the rows of this diagram and
${V}_{\parallel }$
by the rows of this diagram and
![]() ${Y}_{\parallel }$
and
${Y}_{\parallel }$
and
![]() ${Z}_{\parallel }$
associated to the constant diagram with values
${Z}_{\parallel }$
associated to the constant diagram with values
![]() $Y_{\bullet }$
and
$Y_{\bullet }$
and
![]() $Z_{\bullet }$
, respectively. Then we have morphisms
$Z_{\bullet }$
, respectively. Then we have morphisms
Denote the sheaves on either of these obtained by pulling back
![]() $E, F$
or G, respectively, by a corresponding subscript. In particular, we have
$E, F$
or G, respectively, by a corresponding subscript. In particular, we have
![]() $E_{{Y}_{\parallel }}$
on Y, which is Tor-independent with the morphism
$E_{{Y}_{\parallel }}$
on Y, which is Tor-independent with the morphism
![]() ${W}_{\parallel }\to {Y}_{\parallel }$
, and we have an exact sequence
${W}_{\parallel }\to {Y}_{\parallel }$
, and we have an exact sequence
By construction, the reduced Atiyah class
![]() $\overline {\operatorname {\mathrm {at}}}_{E,\mathcal {X}/\mathcal {Y},G}$
is obtained from
$\overline {\operatorname {\mathrm {at}}}_{E,\mathcal {X}/\mathcal {Y},G}$
is obtained from
![]() $\overline {\operatorname {\mathrm {at}}}_{E_{{Y}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel },{G}_{\parallel }}$
by applying
$\overline {\operatorname {\mathrm {at}}}_{E_{{Y}_{\parallel }},{W}_{\parallel }/{Y}_{\parallel },{G}_{\parallel }}$
by applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
and descent to
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
and descent to
![]() $D(\mathcal {X})$
. Similarly, the Atiyah class
$D(\mathcal {X})$
. Similarly, the Atiyah class
![]() $\operatorname {\mathrm {at}}_{E,\mathcal {Y}/\mathcal {Z}}$
is obtained from
$\operatorname {\mathrm {at}}_{E,\mathcal {Y}/\mathcal {Z}}$
is obtained from
![]() $\operatorname {\mathrm {at}}_{E_{{V}_{\parallel }},{V}_{\parallel }/{Z }_{\parallel }}$
by applying
$\operatorname {\mathrm {at}}_{E_{{V}_{\parallel }},{V}_{\parallel }/{Z }_{\parallel }}$
by applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{V}_{\parallel }}}$
and passing to
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{V}_{\parallel }}}$
and passing to
![]() $D(\mathcal {Y})$
.
$D(\mathcal {Y})$
.
Let
![]() ${\widetilde {f}}_{\parallel }$
denote the morphism
${\widetilde {f}}_{\parallel }$
denote the morphism
![]() ${\widetilde {W}}_{\parallel }\to {V}_{\parallel }$
. By Proposition 3.10, we have the anti-commutative diagram
${\widetilde {W}}_{\parallel }\to {V}_{\parallel }$
. By Proposition 3.10, we have the anti-commutative diagram
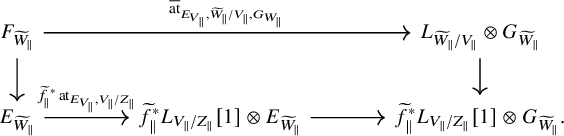
We also have a morphism
![]() ${Y}_{\parallel }\to {V}_{\parallel }$
induced by the morphism
${Y}_{\parallel }\to {V}_{\parallel }$
induced by the morphism
![]() $Y_{\bullet }\to V_{\bullet }$
, given by the diagonal of
$Y_{\bullet }\to V_{\bullet }$
, given by the diagonal of
![]() $Y_n\times _{\mathcal {Y}_{Z_n}}Y_n$
in degree n. This fits into the commutative diagram
$Y_n\times _{\mathcal {Y}_{Z_n}}Y_n$
in degree n. This fits into the commutative diagram
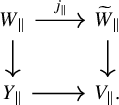
Here, the horizontal maps are Tor-independent to
![]() $E_{{V}_{\parallel }}$
and to
$E_{{V}_{\parallel }}$
and to
![]() $E_{{\widetilde {W}}_{\parallel }}$
and
$E_{{\widetilde {W}}_{\parallel }}$
and
![]() $G_{{\widetilde {W}}_{\parallel }}$
, respectively; thus, we can apply Corollary 3.8. Moreover, the pullback
$G_{{\widetilde {W}}_{\parallel }}$
, respectively; thus, we can apply Corollary 3.8. Moreover, the pullback
![]() ${j}_{\parallel }^{*}L_{{\widetilde {W}}_{\parallel }/{V}_{\parallel }}\to L_{{W}_{\parallel }/{Y}_{\parallel }}$
is a quasi-isomorphism (this follows, since the morphisms
${j}_{\parallel }^{*}L_{{\widetilde {W}}_{\parallel }/{V}_{\parallel }}\to L_{{W}_{\parallel }/{Y}_{\parallel }}$
is a quasi-isomorphism (this follows, since the morphisms
![]() $Y_{\bullet }\to V_{\bullet }\leftarrow \widetilde {W}_{\bullet }$
are Tor-independent, which can be checked degreewise). In conclusion, by pulling back along
$Y_{\bullet }\to V_{\bullet }\leftarrow \widetilde {W}_{\bullet }$
are Tor-independent, which can be checked degreewise). In conclusion, by pulling back along
![]() ${j}_{\parallel }$
, we obtain an anti-commutative diagram in
${j}_{\parallel }$
, we obtain an anti-commutative diagram in
![]() $D({W}_{\parallel })$
:
$D({W}_{\parallel })$
:
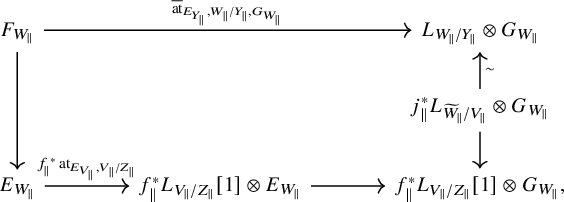
where
![]() ${f}_{\parallel }$
is the morphism
${f}_{\parallel }$
is the morphism
![]() ${W}_{\parallel }\to {V}_{\parallel }$
. By applying
${W}_{\parallel }\to {V}_{\parallel }$
. By applying
![]() $\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
and passing to
$\operatorname {\mathrm {Cone}}_{\mathcal {O}_{{W}_{\parallel }}}$
and passing to
![]() $D(\mathcal {X})$
, we conclude the following:
$D(\mathcal {X})$
, we conclude the following:
Proposition 5.11. The diagram
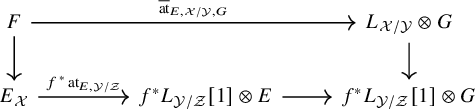
anti-commutes.
If
![]() $E,F,G$
are perfect complexes, this directly implies Proposition 1.1.
$E,F,G$
are perfect complexes, this directly implies Proposition 1.1.
5.4 Compatibilities of the Atiyah class for an exact sequence
Proposition 5.12. The map
![]() $\operatorname {\mathrm {at}}_{\underline {E},\mathcal {X}/\mathcal {Y}}$
is functorial in
$\operatorname {\mathrm {at}}_{\underline {E},\mathcal {X}/\mathcal {Y}}$
is functorial in
![]() $\mathcal {Y}$
– that is, given a map
$\mathcal {Y}$
– that is, given a map
![]() $\mathcal {Y}\to \mathcal {Z}$
, the composition
$\mathcal {Y}\to \mathcal {Z}$
, the composition
equals
![]() $\operatorname {\mathrm {at}}_{\underline {E},\mathcal {X}/\mathcal {Y}}$
(at least assuming we make the same choices of N in the construction).
$\operatorname {\mathrm {at}}_{\underline {E},\mathcal {X}/\mathcal {Y}}$
(at least assuming we make the same choices of N in the construction).
Proof. We use the setup of §5.3. There we had the topoi
and the following morphisms of maps of topoi
whose cotangent complexes represent (after taking cones and shifting)
![]() $L_{\mathcal {X}/\mathcal {Y}}$
,
$L_{\mathcal {X}/\mathcal {Y}}$
,
![]() $L_{\mathcal {X}/\mathcal {Y}}$
and
$L_{\mathcal {X}/\mathcal {Y}}$
and
![]() $L_{\mathcal {X}/\mathcal {Z}}$
, respectively. The result now follows from Corollary 3.13 and Lemma 3.14.
$L_{\mathcal {X}/\mathcal {Z}}$
, respectively. The result now follows from Corollary 3.13 and Lemma 3.14.
Proof of Proposition 1.3.
The commutativity of the first square follows from the functoriality of the usual Atiyah class and Corollary 4.15. Commutativity of the second square follows from Proposition 5.12 and Corollary 4.16. Finally, the commutativity of the square involving connecting morphisms is Proposition 5.11.
6 Deformation theoretic properties
In this section, we prove Theorem 1.4. The proof of Proposition 1.5 is similar, but not addressed here. For details see [Reference Gillam3, §4]. In §§6.3–6.5, we use the following notation: X is a smooth projective variety over a base field k, and
![]() $\mathcal {M}$
is an open substack of the moduli stack of coherent sheaves on X.Footnote
4
$\mathcal {M}$
is an open substack of the moduli stack of coherent sheaves on X.Footnote
4
6.1 Deformations of morphisms to algebraic stacks
Let
![]() $\mathcal {Y}$
be an algebraic stack over a base scheme S and let T be a scheme over S. Here, we consider the problem of deforming maps from the scheme T to
$\mathcal {Y}$
be an algebraic stack over a base scheme S and let T be a scheme over S. Here, we consider the problem of deforming maps from the scheme T to
![]() $\mathcal {Y}$
. As a special case of [Reference Olsson17, Theorem 1.5], we have the following:
$\mathcal {Y}$
. As a special case of [Reference Olsson17, Theorem 1.5], we have the following:
Theorem 6.1. Let
![]() $g:T\to \mathcal {Y}$
be a morphism and let
$g:T\to \mathcal {Y}$
be a morphism and let
![]() $j:T\hookrightarrow \overline {T}$
be a square zero extension of T by a quasicoherent sheaf I. Then,
$j:T\hookrightarrow \overline {T}$
be a square zero extension of T by a quasicoherent sheaf I. Then,
-
1) there is a natural obstruction class
 $\omega (g,\overline {T})\in \operatorname {\mathrm {Ext}}^1(g^{*}L_{\mathcal {Y}},I)$
which vanishes if and only if there is an extension of g to a morphism
$\omega (g,\overline {T})\in \operatorname {\mathrm {Ext}}^1(g^{*}L_{\mathcal {Y}},I)$
which vanishes if and only if there is an extension of g to a morphism
 $\overline {g}:\overline {T}\to \mathcal {Y}$
.
$\overline {g}:\overline {T}\to \mathcal {Y}$
. -
2) if an extension of g to
 $\overline {T}$
exists, then the set of isomorphism classes of extensions naturally forms a torsor under
$\overline {T}$
exists, then the set of isomorphism classes of extensions naturally forms a torsor under
 $\operatorname {\mathrm {Ext}}^0(g^{*}L_{\mathcal {Y}},I)$
.
$\operatorname {\mathrm {Ext}}^0(g^{*}L_{\mathcal {Y}},I)$
. -
3) for a fixed extension
 $\overline {g}$
of g, the set of automorphisms of
$\overline {g}$
of g, the set of automorphisms of
 $\overline {g}$
as an extension of g is canonically isomorphic to
$\overline {g}$
as an extension of g is canonically isomorphic to
 $\operatorname {\mathrm {Ext}}^{-1}(g^{*}L_{\mathcal {Y}}, I)$
.
$\operatorname {\mathrm {Ext}}^{-1}(g^{*}L_{\mathcal {Y}}, I)$
.
One can describe the characterizations in Theorem 6.1 explicitly.
Remark 6.2 (Obstructions).
The morphism g induces a natural map
![]() $g^{*}L_{\mathcal {Y}}\to L_T$
. Similarly, j induces a natural map
$g^{*}L_{\mathcal {Y}}\to L_T$
. Similarly, j induces a natural map
![]() $L_T\to L_{T/\overline {T}}$
, and
$L_T\to L_{T/\overline {T}}$
, and
![]() $L_{T/\overline {T}}$
is concentrated in degrees
$L_{T/\overline {T}}$
is concentrated in degrees
![]() $\leq -1$
with
$\leq -1$
with
![]() $h^{-1}(L_{T/\overline {T}})$
naturally isomorphic to I. The obstruction class
$h^{-1}(L_{T/\overline {T}})$
naturally isomorphic to I. The obstruction class
![]() $\omega (g,\overline {T})$
is then given by the composition
$\omega (g,\overline {T})$
is then given by the composition
This follows from the construction in [Reference Olsson17, 4.8] and the construction of the obstruction class for topoi in [Reference Illusie7, III 2.2].
Remark 6.3 (Deformations).
For a given
![]() $g:T\to \mathcal {Y}$
, let
$g:T\to \mathcal {Y}$
, let
![]() $\overline {T}$
be the trivial extension of T by I, given by taking the structure sheaf
$\overline {T}$
be the trivial extension of T by I, given by taking the structure sheaf
![]() $\mathcal {O}_T\oplus I$
on T. Then there is a natural morphism
$\mathcal {O}_T\oplus I$
on T. Then there is a natural morphism
![]() $\overline {T}\to T$
corresponding to the inclusion
$\overline {T}\to T$
corresponding to the inclusion
![]() $\mathcal {O}_T\oplus \{0\}\subset \mathcal {O}_T\oplus I$
, giving rise to a canonical extension of g as the composition
$\mathcal {O}_T\oplus \{0\}\subset \mathcal {O}_T\oplus I$
, giving rise to a canonical extension of g as the composition
![]() $\overline {T}\to T\to \mathcal {Y}$
. Taking this as a base point, the torsor structure in Theorem 6.1 (2) induces a bijection between the set of isomorphism classes of extensions of g and the group
$\overline {T}\to T\to \mathcal {Y}$
. Taking this as a base point, the torsor structure in Theorem 6.1 (2) induces a bijection between the set of isomorphism classes of extensions of g and the group
![]() $\operatorname {\mathrm {Ext}}^0(g^{*}L_{\mathcal {Y}},I)$
. To describe this bijection explicitly, note that we have a natural isomorphism
$\operatorname {\mathrm {Ext}}^0(g^{*}L_{\mathcal {Y}},I)$
. To describe this bijection explicitly, note that we have a natural isomorphism
![]() $h^0(i^{*}L_{\overline {T}/T})\simeq I$
. Now, for a given extension
$h^0(i^{*}L_{\overline {T}/T})\simeq I$
. Now, for a given extension
![]() $\overline {g}:\overline {T}\to \mathcal {Y}$
, consider the composition
$\overline {g}:\overline {T}\to \mathcal {Y}$
, consider the composition
![]() $\overline {g}^{*}L_{\mathcal {Y}}\to L_{\overline {T}}\to L_{\overline {T}/T}$
. Up to given isomorphisms, this restricts to a map
$\overline {g}^{*}L_{\mathcal {Y}}\to L_{\overline {T}}\to L_{\overline {T}/T}$
. Up to given isomorphisms, this restricts to a map
![]() $\alpha _{\overline {g}}:g^{*}L_{\mathcal {Y}}\to I$
on T. The association
$\alpha _{\overline {g}}:g^{*}L_{\mathcal {Y}}\to I$
on T. The association
![]() $\overline {g}\mapsto \alpha _{\overline {g}}$
is the bijection in question. This follows from [Reference Olsson17, 4.8] and the construction in [Reference Illusie7, III 2.2].
$\overline {g}\mapsto \alpha _{\overline {g}}$
is the bijection in question. This follows from [Reference Olsson17, 4.8] and the construction in [Reference Illusie7, III 2.2].
Remark 6.4 (Automorphisms).
Consider a fixed square zero extension
![]() $j:T\hookrightarrow \overline {T}$
with sheaf of ideals I, and an extension
$j:T\hookrightarrow \overline {T}$
with sheaf of ideals I, and an extension
![]() $\overline {g}:\overline {T}\to \mathcal {Y}$
of g. Let
$\overline {g}:\overline {T}\to \mathcal {Y}$
of g. Let
![]() $\operatorname {Aut}(\overline {g})$
denote the automorphism group of
$\operatorname {Aut}(\overline {g})$
denote the automorphism group of
![]() $\overline {g}$
as an extension of g (i.e., the group of
$\overline {g}$
as an extension of g (i.e., the group of
![]() $2$
-isomorphisms of
$2$
-isomorphisms of
![]() $\overline {g}:\overline {T}\to \mathcal {Y}$
that restrict to the identity
$\overline {g}:\overline {T}\to \mathcal {Y}$
that restrict to the identity
![]() $2$
-isomorphism when restricted to T). Let
$2$
-isomorphism when restricted to T). Let
![]() $\operatorname {Aut}_{\mathcal {Y}}(\overline {T})$
denote the group of automorphisms of
$\operatorname {Aut}_{\mathcal {Y}}(\overline {T})$
denote the group of automorphisms of
![]() $\overline {T}$
as an extension of T over
$\overline {T}$
as an extension of T over
![]() $\mathcal {Y}$
whose elements are pairs
$\mathcal {Y}$
whose elements are pairs
![]() $(a,\phi )$
, where
$(a,\phi )$
, where
![]() $a:\overline {T}\to \overline {T}$
is an automorphism satisfying
$a:\overline {T}\to \overline {T}$
is an automorphism satisfying
![]() $a\circ j = j$
, and where
$a\circ j = j$
, and where
![]() $\phi $
is a
$\phi $
is a
![]() $2$
-isomorphism
$2$
-isomorphism
![]() $\phi :\overline {g}\circ a \Rightarrow \overline {g}$
. Similarly, we let
$\phi :\overline {g}\circ a \Rightarrow \overline {g}$
. Similarly, we let
![]() $\operatorname {Aut}_{S}(\overline {T})$
denote the group of automorphisms of
$\operatorname {Aut}_{S}(\overline {T})$
denote the group of automorphisms of
![]() $\overline {T}$
as an extension of T over S. Then we have a natural forgetful map
$\overline {T}$
as an extension of T over S. Then we have a natural forgetful map
![]() $\operatorname {Aut}_{\mathcal {Y}}(\overline {T})\to \operatorname {Aut}_S(\overline {T})$
whose Kernel is
$\operatorname {Aut}_{\mathcal {Y}}(\overline {T})\to \operatorname {Aut}_S(\overline {T})$
whose Kernel is
![]() $\operatorname {Aut}(\overline {g})$
. We have identifications
$\operatorname {Aut}(\overline {g})$
. We have identifications
![]() $\operatorname {\mathrm {Ext}}^0(L_{X/\mathcal {Y}},I)\simeq \operatorname {Aut}_{\mathcal {Y}}(\overline {T})$
, which are natural in
$\operatorname {\mathrm {Ext}}^0(L_{X/\mathcal {Y}},I)\simeq \operatorname {Aut}_{\mathcal {Y}}(\overline {T})$
, which are natural in
![]() $\mathcal {Y}$
(and, in particular, hold for S in place of
$\mathcal {Y}$
(and, in particular, hold for S in place of
![]() $\mathcal {Y}$
), and via the exact triangle
$\mathcal {Y}$
), and via the exact triangle
![]() $g^{*}L_{\mathcal {Y}/S}\to L_{T/S}\to L_{T/\mathcal {Y}}\xrightarrow {+1}$
, we obtain the exact sequence
$g^{*}L_{\mathcal {Y}/S}\to L_{T/S}\to L_{T/\mathcal {Y}}\xrightarrow {+1}$
, we obtain the exact sequence
By what is said above, this gives an identification
For our purposes, a different characterization of the bijection
![]() $\operatorname {\mathrm {Ext}}^{-1}(g^{*}L_{\mathcal {Y}/S},I)\simeq \operatorname {Aut}(\overline {g})$
than the one given in Remark 6.4 will be needed. For the rest of this subsection, we consider the case where
$\operatorname {\mathrm {Ext}}^{-1}(g^{*}L_{\mathcal {Y}/S},I)\simeq \operatorname {Aut}(\overline {g})$
than the one given in Remark 6.4 will be needed. For the rest of this subsection, we consider the case where
![]() $\overline {T}$
is the trivial square zero extension of T by I and where
$\overline {T}$
is the trivial square zero extension of T by I and where
![]() $\overline {g}$
is the trivial extension of g. Let
$\overline {g}$
is the trivial extension of g. Let
![]() $y:Y\to \mathcal {Y}$
be a smooth cover by an algebraic space and assume that
$y:Y\to \mathcal {Y}$
be a smooth cover by an algebraic space and assume that
![]() $g:T\to \mathcal {Y}$
factors through Y (this can always be arranged by passing to an étale cover of T, which is enough for our later application). We fix such a factorization
$g:T\to \mathcal {Y}$
factors through Y (this can always be arranged by passing to an étale cover of T, which is enough for our later application). We fix such a factorization
![]() $g_Y:T\to Y$
(with an implicit choice of
$g_Y:T\to Y$
(with an implicit choice of
![]() $2$
-isomorphism
$2$
-isomorphism
![]() $y\circ g_Y\Rightarrow g)$
. Form the Cartesian diagram
$y\circ g_Y\Rightarrow g)$
. Form the Cartesian diagram

We observe that Y naturally has the structure of a groupoid algebraic space with the space of morphisms given by Z and that we have a natural equivalence
![]() $[Y/Z]\xrightarrow {\sim }\mathcal {Y}$
. Moreover, by definition of the
$[Y/Z]\xrightarrow {\sim }\mathcal {Y}$
. Moreover, by definition of the
![]() $2$
-cartesian product, the set of automorphisms of the morphism
$2$
-cartesian product, the set of automorphisms of the morphism
![]() $g:T\to \mathcal {Y}$
is in natural bijection to the set of maps
$g:T\to \mathcal {Y}$
is in natural bijection to the set of maps
![]() $f:T\to Z$
satisfying
$f:T\to Z$
satisfying
![]() $s\circ f=t\circ f = g_Y$
. In particular, there is a morphism
$s\circ f=t\circ f = g_Y$
. In particular, there is a morphism
![]() $e:T\to Z$
corresponding to the identity automorphism of
$e:T\to Z$
corresponding to the identity automorphism of
![]() $g_Y$
.
$g_Y$
.
Now let
![]() $\overline {g}_Y$
denote the composition
$\overline {g}_Y$
denote the composition
![]() $\overline {T}\to T\xrightarrow {g_Y} Y$
, which is a lift of
$\overline {T}\to T\xrightarrow {g_Y} Y$
, which is a lift of
![]() $\overline {g}$
. Then we observe the following:
$\overline {g}$
. Then we observe the following:
Lemma 6.5. We have a natural bijection between
![]() $\operatorname {Aut}(\overline {g})$
and the set of morphisms
$\operatorname {Aut}(\overline {g})$
and the set of morphisms
![]() $\overline {f}:\overline {T}\to Z$
satisfying
$\overline {f}:\overline {T}\to Z$
satisfying
![]() $s\circ \overline {f}= t\circ \overline {f} =\overline {g}_Y$
and
$s\circ \overline {f}= t\circ \overline {f} =\overline {g}_Y$
and
![]() $\overline {f}\circ j = e$
. In other words, the group of infinitesimal automorphisms of
$\overline {f}\circ j = e$
. In other words, the group of infinitesimal automorphisms of
![]() $\overline {g}$
is in bijection with the group of deformations of e to
$\overline {g}$
is in bijection with the group of deformations of e to
![]() $\overline {T}$
that induce the trivial deformation of
$\overline {T}$
that induce the trivial deformation of
![]() $g_Y$
upon composition with either s or t.
$g_Y$
upon composition with either s or t.
As a consequence of this Lemma, we have a canonical isomorphism
 $$\begin{align*}\operatorname{Aut}(g)\simeq \operatorname{\mathrm{Ker}}\left(\operatorname{\mathrm{Hom}}(e^{*}L_Z,I)\xrightarrow{(-s^{*},t^{*})} \operatorname{\mathrm{Hom}}(e^{*}s^{*}L_Y,I)\oplus \operatorname{\mathrm{Hom}}(e^{*}t^{*}L_Y,I)\right).\end{align*}$$
$$\begin{align*}\operatorname{Aut}(g)\simeq \operatorname{\mathrm{Ker}}\left(\operatorname{\mathrm{Hom}}(e^{*}L_Z,I)\xrightarrow{(-s^{*},t^{*})} \operatorname{\mathrm{Hom}}(e^{*}s^{*}L_Y,I)\oplus \operatorname{\mathrm{Hom}}(e^{*}t^{*}L_Y,I)\right).\end{align*}$$
Let
![]() $z:=y\circ s:Z\to \mathcal {Y}$
. By Lemma 2.11, we have the natural isomorphism
$z:=y\circ s:Z\to \mathcal {Y}$
. By Lemma 2.11, we have the natural isomorphism
Using this, we get an identification
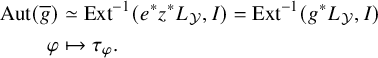 $$ \begin{align} \begin{aligned} \operatorname{Aut}(\overline{g})&\simeq \operatorname{\mathrm{Ext}}^{-1}(e^{*}z^{*}L_{\mathcal{Y}},I)=\operatorname{\mathrm{Ext}}^{-1}(g^{*}L_{\mathcal{Y}},I)\\ \varphi&\mapsto \tau_{\varphi}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{Aut}(\overline{g})&\simeq \operatorname{\mathrm{Ext}}^{-1}(e^{*}z^{*}L_{\mathcal{Y}},I)=\operatorname{\mathrm{Ext}}^{-1}(g^{*}L_{\mathcal{Y}},I)\\ \varphi&\mapsto \tau_{\varphi}. \end{aligned} \end{align} $$
6.2 Deformations of sheaves
Let
![]() $X, T$
be schemes over a common base field k. Let
$X, T$
be schemes over a common base field k. Let
![]() $T\hookrightarrow \overline {T}$
be a square zero extension defined by an ideal sheaf I. Let also E be a T-flat quasicoherent sheaf on
$T\hookrightarrow \overline {T}$
be a square zero extension defined by an ideal sheaf I. Let also E be a T-flat quasicoherent sheaf on
![]() $X\times T$
. We consider the problem of extending E to a
$X\times T$
. We consider the problem of extending E to a
![]() $\overline {T}$
-flat coherent sheaf on
$\overline {T}$
-flat coherent sheaf on
![]() $X\times \overline {T}$
. Let
$X\times \overline {T}$
. Let
![]() $\pi :X\times T\to T$
denote the projection. By [Reference Illusie7, IV Proposition 3.1.8], we have the following:
$\pi :X\times T\to T$
denote the projection. By [Reference Illusie7, IV Proposition 3.1.8], we have the following:
Theorem 6.6.
-
1) There is a natural obstruction class
 $\omega ^{sh}(E, \overline {T})\in \operatorname {\mathrm {Ext}}^2_{X\times T}(E,\pi ^{*}I\otimes E )$
which vanishes if and only if there is an extension of E to a
$\omega ^{sh}(E, \overline {T})\in \operatorname {\mathrm {Ext}}^2_{X\times T}(E,\pi ^{*}I\otimes E )$
which vanishes if and only if there is an extension of E to a
 $\overline {T}$
-flat sheaf on
$\overline {T}$
-flat sheaf on
 $X\times \overline {T}$
.
$X\times \overline {T}$
. -
2) If a
 $\overline {T}$
-flat extension of E to
$\overline {T}$
-flat extension of E to
 $X\times \overline {T}$
exists, then the set of isomorphism classes of such extensions naturally forms a torsor under
$X\times \overline {T}$
exists, then the set of isomorphism classes of such extensions naturally forms a torsor under
 $\operatorname {\mathrm {Ext}}^1_{X\times T}(E,\pi ^{*}I\otimes E)$
.
$\operatorname {\mathrm {Ext}}^1_{X\times T}(E,\pi ^{*}I\otimes E)$
. -
3) For a fixed
 $\overline {T}$
-flat extension
$\overline {T}$
-flat extension
 $\overline {E}$
, the set of automorphisms of
$\overline {E}$
, the set of automorphisms of
 $\overline {E}$
which restrict to the identity on E is canonically isomorphic to
$\overline {E}$
which restrict to the identity on E is canonically isomorphic to
 $\operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
.
$\operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
.
We make some of the natural maps implied in this theorem explicit.
Remark 6.7 (Obstructions).
For a given
![]() $\overline {T}$
, the obstruction class
$\overline {T}$
, the obstruction class
![]() $\omega ^{sh}(E,\overline {T})$
is given by the composition
$\omega ^{sh}(E,\overline {T})$
is given by the composition
Here, the first map is the Atiyah class, the second map is induced from the naturality of cotangent complexes, and the last map is induced from the natural identification
![]() $\tau _{\geq 1}L_{T/\overline {T}}\simeq I[1]$
. This is proven in [Reference Illusie7, IV Proposition 3.1.8].
$\tau _{\geq 1}L_{T/\overline {T}}\simeq I[1]$
. This is proven in [Reference Illusie7, IV Proposition 3.1.8].
Remark 6.8 (Deformations).
Let
![]() $\overline {T}$
be the trivial extension of T by I. Then there is a canonical flat extension of E to
$\overline {T}$
be the trivial extension of T by I. Then there is a canonical flat extension of E to
![]() $X\times \overline {T}$
given by
$X\times \overline {T}$
given by
![]() $E\oplus \pi ^{*}I\otimes E$
, with multiplication by I given by
$E\oplus \pi ^{*}I\otimes E$
, with multiplication by I given by
![]() $j(e,0)=(0,je)$
for local sections. The torsor structure on the space of extensions therefore gives rise to a bijection between
$j(e,0)=(0,je)$
for local sections. The torsor structure on the space of extensions therefore gives rise to a bijection between
![]() $\operatorname {\mathrm {Ext}}^1_{X\times T}(E,I\otimes E)$
and the set of extensions of E to
$\operatorname {\mathrm {Ext}}^1_{X\times T}(E,I\otimes E)$
and the set of extensions of E to
![]() $\overline {T}$
. To describe this bijection, let
$\overline {T}$
. To describe this bijection, let
![]() ${\nu \in \operatorname {\mathrm {Ext}}^1_{X\times T}(E,\pi ^{*}I\otimes E)}$
, corresponding to an extension
${\nu \in \operatorname {\mathrm {Ext}}^1_{X\times T}(E,\pi ^{*}I\otimes E)}$
, corresponding to an extension
We make this into an
![]() $\mathcal {O}_{X\times T}\oplus \pi ^{*}I$
-module, by defining the action of I on
$\mathcal {O}_{X\times T}\oplus \pi ^{*}I$
-module, by defining the action of I on
![]() $\overline {E}$
on local sections as
$\overline {E}$
on local sections as
![]() $jx:=\mu (j\otimes \rho (x))$
. One checks that this defines a
$jx:=\mu (j\otimes \rho (x))$
. One checks that this defines a
![]() $\overline {T}$
-flat coherent sheaf on
$\overline {T}$
-flat coherent sheaf on
![]() $X\times \overline {T}$
extending E. It is straightforward to see that this construction is invertible.
$X\times \overline {T}$
extending E. It is straightforward to see that this construction is invertible.
Remark 6.9 (Automorphisms).
Let
![]() $\overline {T}$
be the trivial extension of T by I and let
$\overline {T}$
be the trivial extension of T by I and let
![]() $\overline {E}=E\oplus \pi ^{*}I\otimes E$
be the canonical flat extension of E to
$\overline {E}=E\oplus \pi ^{*}I\otimes E$
be the canonical flat extension of E to
![]() $\overline {T}$
. For an element
$\overline {T}$
. For an element
![]() $a\in \operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
, the map
$a\in \operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
, the map
![]() $\psi _a:\overline {E}\to \overline {E}$
given locally by
$\psi _a:\overline {E}\to \overline {E}$
given locally by
![]() $(x_1,j\otimes x_2)\mapsto (x_1,j\otimes x_2 +\varphi (x_1))$
is an automorphism of
$(x_1,j\otimes x_2)\mapsto (x_1,j\otimes x_2 +\varphi (x_1))$
is an automorphism of
![]() $\overline {E}$
which restricts to the identity on E. This gives the claimed bijection of automorphism groups for this choice of
$\overline {E}$
which restricts to the identity on E. This gives the claimed bijection of automorphism groups for this choice of
![]() $\overline {E}$
.
$\overline {E}$
.
Remark 6.10. Suppose that X is a smooth projective variety and that T is of finite type over k. Then in particular, E has a finite length resolution by locally free sheaves. Then we have natural isomorphisms
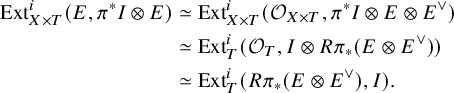 $$ \begin{align*} \operatorname{\mathrm{Ext}}^i_{X\times T}(E,\pi^{*}I\otimes E)&\simeq \operatorname{\mathrm{Ext}}^i_{X\times T}(\mathcal{O}_{X\times T}, \pi^{*}I \otimes E\otimes E^{\vee})\\ &\simeq \operatorname{\mathrm{Ext}}^i_T(\mathcal{O}_T, I\otimes R\pi_*(E\otimes E^{\vee}))\\ &\simeq \operatorname{\mathrm{Ext}}^i_T(R\pi_*(E\otimes E^{\vee}), I). \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{Ext}}^i_{X\times T}(E,\pi^{*}I\otimes E)&\simeq \operatorname{\mathrm{Ext}}^i_{X\times T}(\mathcal{O}_{X\times T}, \pi^{*}I \otimes E\otimes E^{\vee})\\ &\simeq \operatorname{\mathrm{Ext}}^i_T(\mathcal{O}_T, I\otimes R\pi_*(E\otimes E^{\vee}))\\ &\simeq \operatorname{\mathrm{Ext}}^i_T(R\pi_*(E\otimes E^{\vee}), I). \end{align*} $$
Here, all tensor products and duals are taken in the derived sense. The first isomorphism is due to the fact that E is dualizable, the second one is push-pull adjunction and the projection formula, and the third one uses that
![]() $R\pi _*(E\otimes E^{\vee })$
is dualizable.
$R\pi _*(E\otimes E^{\vee })$
is dualizable.
6.3 Comparison of obstruction classes
Now let
![]() $X,\mathcal {M}$
be as specified in the beginning of the section with universal sheaf
$X,\mathcal {M}$
be as specified in the beginning of the section with universal sheaf
![]() $\mathcal {E}$
on
$\mathcal {E}$
on
![]() $\mathcal {M}\times X$
. Our goal is to show that the map
$\mathcal {M}\times X$
. Our goal is to show that the map
![]() $\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
is surjective on
$\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
is surjective on
![]() $h^{-1}$
. By the arguments of [Reference Behrend and Fantechi2, §4],Footnote
5
it is enough to show that for every map from an affine scheme
$h^{-1}$
. By the arguments of [Reference Behrend and Fantechi2, §4],Footnote
5
it is enough to show that for every map from an affine scheme
![]() $g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
$g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
given by composition with the Atiyah class is injective. In fact, it is enough to show that for any such g and I and any square zero extension
![]() $T\hookrightarrow \overline {T}$
, there exists an extension of g to
$T\hookrightarrow \overline {T}$
, there exists an extension of g to
![]() $\overline {T}$
if and only if the image of the obstruction class
$\overline {T}$
if and only if the image of the obstruction class
![]() $\omega (g,\overline {T})$
under this map vanishes. By Remark 6.2, the obstruction class
$\omega (g,\overline {T})$
under this map vanishes. By Remark 6.2, the obstruction class
![]() $\omega (g,\overline {T})$
is obtained as the composition of the natural maps
$\omega (g,\overline {T})$
is obtained as the composition of the natural maps
However, let
![]() $E=g^{*}\mathcal {E}$
, so that we have a commutative diagram
$E=g^{*}\mathcal {E}$
, so that we have a commutative diagram
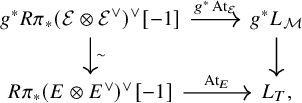
where the left vertical map is the canonical base change isomorphism. We find that the image of
![]() $\omega (g,\overline {T})$
under
$\omega (g,\overline {T})$
under
![]() $(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}$
is up to the given isomorphism equal to the composition
$(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}$
is up to the given isomorphism equal to the composition
By the definition of
![]() $\operatorname {\mathrm {At}}_E$
, this corresponds to the morphism
$\operatorname {\mathrm {At}}_E$
, this corresponds to the morphism
By Remark 6.7, this is exactly the obstruction to the existence of a
![]() $\overline {T}$
-flat extension of E to
$\overline {T}$
-flat extension of E to
![]() $\overline {T}\times X$
and therefore an obstruction to the existence of an extension of
$\overline {T}\times X$
and therefore an obstruction to the existence of an extension of
![]() $\overline {g}$
by the universal property of
$\overline {g}$
by the universal property of
![]() $\mathcal {M}$
. This shows what we needed.
$\mathcal {M}$
. This shows what we needed.
6.4 Comparison of deformation spaces
We show that the map
![]() $\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
is an isomorphism on
$\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
is an isomorphism on
![]() $h^0$
. By the arguments of [Reference Behrend and Fantechi2, §4], it is enough to show that for every map from an affine scheme
$h^0$
. By the arguments of [Reference Behrend and Fantechi2, §4], it is enough to show that for every map from an affine scheme
![]() $g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
$g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
given by composition with the Atiyah class is an isomorphism. This follows from the following stronger statement:
Lemma 6.11. Let
![]() $\overline {T}$
be the trivial extension of T by I and let
$\overline {T}$
be the trivial extension of T by I and let
![]() $\overline {g}:\overline {T}\to \mathcal {M}$
be any extension of g. Let
$\overline {g}:\overline {T}\to \mathcal {M}$
be any extension of g. Let
![]() $\overline {E}$
be the corresponding extension of E. Then the class
$\overline {E}$
be the corresponding extension of E. Then the class
![]() $\alpha _{\overline {g}}$
of Remark 6.3 is mapped by
$\alpha _{\overline {g}}$
of Remark 6.3 is mapped by
![]() $(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}$
to the class of
$(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}$
to the class of
corresponding to the extension
![]() $\overline {E}$
via Remark 6.8.
$\overline {E}$
via Remark 6.8.
Proof. By Remark 6.3, we have that
![]() $(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}\alpha _{\overline {g}}$
is equal to the composition
$(g^{*}\operatorname {\mathrm {At}}_{\mathcal {E}})^{*}\alpha _{\overline {g}}$
is equal to the composition
The composition of the first two maps is just
![]() $j^{*}\operatorname {\mathrm {At}}_{\overline {E}}$
. Therefore, by definition of
$j^{*}\operatorname {\mathrm {At}}_{\overline {E}}$
. Therefore, by definition of
![]() $\operatorname {\mathrm {At}}$
, this corresponds under adjunction to the morphism
$\operatorname {\mathrm {At}}$
, this corresponds under adjunction to the morphism
Thus, we are reduced to showing that this morphism agrees with the class
![]() $\beta _{\overline {E}}$
in
$\beta _{\overline {E}}$
in
![]() $\operatorname {\mathrm {Ext}}^1(E,\pi ^{*}I\otimes E)$
. This is shown in Lemma 6.12 below.
$\operatorname {\mathrm {Ext}}^1(E,\pi ^{*}I\otimes E)$
. This is shown in Lemma 6.12 below.
Lemma 6.12. Let T be an affine scheme and I a quasicoherent sheaf on T and let
![]() $j:T\to \overline {T}$
be the trivial square zero thickening of T with ideal sheaf I. Let E be a coherent sheaf on
$j:T\to \overline {T}$
be the trivial square zero thickening of T with ideal sheaf I. Let E be a coherent sheaf on
![]() $T\times X$
and
$T\times X$
and
![]() $\overline {E}$
an extension of E to
$\overline {E}$
an extension of E to
![]() $\overline {T}$
such that the induced map
$\overline {T}$
such that the induced map
![]() $I\otimes _{T} E\to I\overline {E}\subset \overline {E}$
is an isomorphism (see [Reference Illusie7, IV 3.1]). Let
$I\otimes _{T} E\to I\overline {E}\subset \overline {E}$
is an isomorphism (see [Reference Illusie7, IV 3.1]). Let
![]() $\beta \in \operatorname {\mathrm {Ext}}^1_{T\times X}(E,\pi ^{*}I\otimes E)$
be the corresponding extension class. Then the composition
$\beta \in \operatorname {\mathrm {Ext}}^1_{T\times X}(E,\pi ^{*}I\otimes E)$
be the corresponding extension class. Then the composition
equals
![]() $\beta $
.
$\beta $
.
Proof. Let
![]() $r:\overline {T}\to T$
be the projection coming from the inclusion
$r:\overline {T}\to T$
be the projection coming from the inclusion
![]() $\mathcal {O}_T=\mathcal {O}_T\oplus \{0\}\subset \mathcal {O}_T\oplus I$
. Let
$\mathcal {O}_T=\mathcal {O}_T\oplus \{0\}\subset \mathcal {O}_T\oplus I$
. Let
![]() $R=P_{r^{-1}\mathcal {O}_T}(\mathcal {O}_{\overline {T}})$
be the standard simplicial resolution. Then we have the following commutative diagram of R-modules with exact rows:
$R=P_{r^{-1}\mathcal {O}_T}(\mathcal {O}_{\overline {T}})$
be the standard simplicial resolution. Then we have the following commutative diagram of R-modules with exact rows:
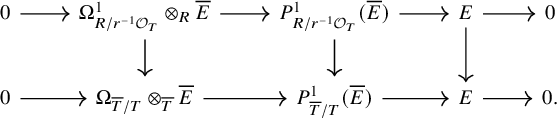
The upper row is used to define the Atiyah class, so by taking connecting map in
![]() $D^{\Delta }(R)$
and passing to
$D^{\Delta }(R)$
and passing to
![]() $D(\overline {T})$
, we get the commutative diagram
$D(\overline {T})$
, we get the commutative diagram
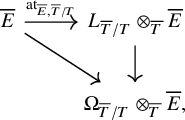
where the diagonal map is the connecting map associated to the sequence of principal parts
![]() $\underline {P}_{\overline {T}/T}(\overline {E})$
. This reduces us to showing that the restriction of
$\underline {P}_{\overline {T}/T}(\overline {E})$
. This reduces us to showing that the restriction of
![]() $\underline {P}_{\overline {T}/T}(\overline {E})$
along j is equal to the extension
$\underline {P}_{\overline {T}/T}(\overline {E})$
along j is equal to the extension
![]() $\beta $
corresponding to E via the identification
$\beta $
corresponding to E via the identification
![]() $j^{*}\Omega ^1_{\overline {T}/T}=I$
. This follows from a straightforward calculation using that
$j^{*}\Omega ^1_{\overline {T}/T}=I$
. This follows from a straightforward calculation using that
![]() $P^1_{\overline {T}/T}(E)=(\mathcal {O}_T\oplus I)\otimes _{\mathcal {O}_T}\overline {E}$
.
$P^1_{\overline {T}/T}(E)=(\mathcal {O}_T\oplus I)\otimes _{\mathcal {O}_T}\overline {E}$
.
6.5 Comparison of automorphism groups
We show that the map
![]() $\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
induces an isomorpism on
$\operatorname {\mathrm {At}}_{\mathcal {E}}:R\pi _*(\mathcal {E}\otimes \mathcal {E}^{\vee })^{\vee }[-1]\to L_{\mathcal {M}}$
induces an isomorpism on
![]() $h^{-1}$
. It is enough to show that for every map from an affine scheme
$h^{-1}$
. It is enough to show that for every map from an affine scheme
![]() $g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
$g:T\to \mathcal {M}$
and any quasicoherent sheaf I on T, the map
given by composition with the Atiyah class is an isomorphism. This follows from the following more precise statement:
Lemma 6.13. Let
![]() $\overline {T}$
be the trivial extension of T by I and let
$\overline {T}$
be the trivial extension of T by I and let
![]() $\overline {g}:\overline {T}\to \mathcal {M}$
be the trivial extension of g to
$\overline {g}:\overline {T}\to \mathcal {M}$
be the trivial extension of g to
![]() $\overline {T}$
. Let
$\overline {T}$
. Let
![]() $\overline {E}$
be the corresponding extension of E. Let
$\overline {E}$
be the corresponding extension of E. Let
![]() $\varphi $
be an automorphism of
$\varphi $
be an automorphism of
![]() $\overline {g}$
extending
$\overline {g}$
extending
![]() $\operatorname {\mathrm {id}}_g$
, which we view as an automorphism
$\operatorname {\mathrm {id}}_g$
, which we view as an automorphism
![]() $\gamma _{\varphi }$
of
$\gamma _{\varphi }$
of
![]() $\overline {E}$
via the universal property of
$\overline {E}$
via the universal property of
![]() $\mathcal {M}$
. Then the element
$\mathcal {M}$
. Then the element
![]() $\tau _{\varphi }$
corresponding to
$\tau _{\varphi }$
corresponding to
![]() $\varphi $
via (6.1) is mapped to the element of
$\varphi $
via (6.1) is mapped to the element of
![]() $\operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
corresponding to
$\operatorname {\mathrm {Hom}}_{X\times T}(E,\pi ^{*}I\otimes E)$
corresponding to
![]() $\varphi $
via Remark 6.9.
$\varphi $
via Remark 6.9.
Proof. We will first make two reductions: First, the statement can be checked étale locally on T; therefore, we can choose a smooth cover Y and assume that g factors through Y, so that we are in the situation of Lemma 6.5. Then, in particular,
![]() $\varphi $
corresponds to a morphism
$\varphi $
corresponds to a morphism
![]() $f:\overline {T}\to Z$
which is the image of
$f:\overline {T}\to Z$
which is the image of
![]() $\tau _{\varphi }$
in
$\tau _{\varphi }$
in
![]() $\operatorname {\mathrm {Hom}}(e^{*}L_{Z},I) $
Second, the image of
$\operatorname {\mathrm {Hom}}(e^{*}L_{Z},I) $
Second, the image of
![]() $\tau _{\varphi }$
is via adjunction identified with the composition
$\tau _{\varphi }$
is via adjunction identified with the composition
where the first morphism is just
![]() $\operatorname {\mathrm {At}}_E$
, and the second morphism is the one induced by the infinitesimal automorphism
$\operatorname {\mathrm {At}}_E$
, and the second morphism is the one induced by the infinitesimal automorphism
![]() $\varphi \times \operatorname {\mathrm {id}}$
of the extension
$\varphi \times \operatorname {\mathrm {id}}$
of the extension
![]() $\overline {g}\times \operatorname {\mathrm {id}}_X$
of
$\overline {g}\times \operatorname {\mathrm {id}}_X$
of
![]() $g\times \operatorname {\mathrm {id}}_X$
. Since
$g\times \operatorname {\mathrm {id}}_X$
. Since
![]() $\tau _{\varphi }$
factors through a map
$\tau _{\varphi }$
factors through a map
![]() $\tau _{\varphi }^{\prime }:h^1(e^{*}L_{\mathcal {M}})\to I$
, we can rewrite this composition as
$\tau _{\varphi }^{\prime }:h^1(e^{*}L_{\mathcal {M}})\to I$
, we can rewrite this composition as
This reduces the problem to understanding the maps
![]() $(\tau _{\geq 0}\otimes id_E)\circ g^{*}\operatorname {\mathrm {at}}_{\mathcal {E}}$
and
$(\tau _{\geq 0}\otimes id_E)\circ g^{*}\operatorname {\mathrm {at}}_{\mathcal {E}}$
and
![]() $g^{*}\tau _{\varphi }^{\prime }\otimes \operatorname {\mathrm {id}}_E$
. By Lemma 6.14 below, the former is given as follows: For a section m of
$g^{*}\tau _{\varphi }^{\prime }\otimes \operatorname {\mathrm {id}}_E$
. By Lemma 6.14 below, the former is given as follows: For a section m of
![]() $E_Z$
, write
$E_Z$
, write
![]() $m=\sum x_i s^{*}n_i=\sum x_j^{\prime } t^{*}n_j^{\prime }$
using the isomorphisms
$m=\sum x_i s^{*}n_i=\sum x_j^{\prime } t^{*}n_j^{\prime }$
using the isomorphisms
![]() $s^{*}E_Y\simeq E_Z\simeq t^{*}E_Y$
. Then
$s^{*}E_Y\simeq E_Z\simeq t^{*}E_Y$
. Then
![]() $e\mapsto \sum dx_i\otimes s^{*}e_i-\sum dx_j^{\prime }\otimes \varphi (t^{*}e_j^{\prime })$
in
$e\mapsto \sum dx_i\otimes s^{*}e_i-\sum dx_j^{\prime }\otimes \varphi (t^{*}e_j^{\prime })$
in
![]() $\Omega _Z\otimes E_Z/(s^{*}(\Omega _Y\otimes _Y E_Y)+t^{*}(\Omega _Y\otimes _Y E_Y))$
. In particular, if
$\Omega _Z\otimes E_Z/(s^{*}(\Omega _Y\otimes _Y E_Y)+t^{*}(\Omega _Y\otimes _Y E_Y))$
. In particular, if
![]() $m=s^{*}n = \sum x_j^{\prime }t^{*}n_j^{\prime }$
, then
$m=s^{*}n = \sum x_j^{\prime }t^{*}n_j^{\prime }$
, then
![]() $s^{*}y^{*}h^0(\operatorname {\mathrm {at}}_{\mathcal {E}})(m) = -\sum dx_j^{\prime }\otimes \varphi (t^{*}n_j^{\prime })$
. Pulling back along g gives
$s^{*}y^{*}h^0(\operatorname {\mathrm {at}}_{\mathcal {E}})(m) = -\sum dx_j^{\prime }\otimes \varphi (t^{*}n_j^{\prime })$
. Pulling back along g gives
The morphism
![]() $\tau ^{\prime }_{\varphi }:\operatorname {Coker}(s^{*}\Omega _Y\oplus t^{*}\Omega _Y \to \Omega _Z)\mid _T\to \Omega _{\overline {T}/T}\mid _T=I$
sends
$\tau ^{\prime }_{\varphi }:\operatorname {Coker}(s^{*}\Omega _Y\oplus t^{*}\Omega _Y \to \Omega _Z)\mid _T\to \Omega _{\overline {T}/T}\mid _T=I$
sends
![]() $dx$
to
$dx$
to
![]() $df(x)$
, where
$df(x)$
, where
![]() $df:\Omega _Z\to I$
is the derivation describing f as a deformation of e (s.t.
$df:\Omega _Z\to I$
is the derivation describing f as a deformation of e (s.t.
![]() $f=e+I\otimes e + df:e^{-1}\mathcal {O}_Z\to \mathcal {O}_T\oplus I$
). In conclusion, we get that the composition is given by the map
$f=e+I\otimes e + df:e^{-1}\mathcal {O}_Z\to \mathcal {O}_T\oplus I$
). In conclusion, we get that the composition is given by the map
![]() $g^{*}n\mapsto \sum -df(x_i)\otimes f^{*}\varphi (n_i)$
if
$g^{*}n\mapsto \sum -df(x_i)\otimes f^{*}\varphi (n_i)$
if
![]() $s^{*}n=\sum x_i t^{*}n_i$
. However, we have the automorphism
$s^{*}n=\sum x_i t^{*}n_i$
. However, we have the automorphism
![]() $\gamma _{\varphi }$
of
$\gamma _{\varphi }$
of
![]() $\overline {E}$
given by the composition
$\overline {E}$
given by the composition
![]() $\overline {E}\simeq f^{*}t^{*}E_Y\xrightarrow {f^{*}\varphi }f^{*}s^{*}E_Y\simeq \overline {E}$
. We compute
$\overline {E}\simeq f^{*}t^{*}E_Y\xrightarrow {f^{*}\varphi }f^{*}s^{*}E_Y\simeq \overline {E}$
. We compute
whenever
![]() $s^{*}n=\sum x_i t^{*}n_i$
. Since
$s^{*}n=\sum x_i t^{*}n_i$
. Since
![]() $\varphi $
restricts to the identity automorphism on T, we know that
$\varphi $
restricts to the identity automorphism on T, we know that
![]() $\gamma _{\varphi }$
is of the form
$\gamma _{\varphi }$
is of the form
![]() $\operatorname {\mathrm {id}}_{\overline {E}}+\rho $
, where
$\operatorname {\mathrm {id}}_{\overline {E}}+\rho $
, where
![]() $\rho :E\to I\otimes E$
is a morphism. We claim that
$\rho :E\to I\otimes E$
is a morphism. We claim that
![]() $\rho (g^{*}n) = dx_i\otimes f^{*}\varphi (t^{*}n_i)$
whenever
$\rho (g^{*}n) = dx_i\otimes f^{*}\varphi (t^{*}n_i)$
whenever
![]() $s^{*}n=\sum x_i t^{*}n_i$
. But we have
$s^{*}n=\sum x_i t^{*}n_i$
. But we have
Lemma 6.14. In the situation of Lemma 6.5, suppose that
![]() $E\in D^{\leq 0}_{qcoh}(\mathcal {Y})$
. Then the composition
$E\in D^{\leq 0}_{qcoh}(\mathcal {Y})$
. Then the composition
![]() $s^{*}y^{*}E\xrightarrow {s^{*}y^{*}\operatorname {\mathrm {at}}_E} s^{*}y^{*}L_{\mathcal {Y}}[1]\otimes s^{*}y^{*}E\to s^{*}y^{*}h^{1}(L_{\mathcal {Y}})\otimes s^{*}y^{*}E$
agrees up to natural isomorphisms with the connecting homomorphism
$s^{*}y^{*}E\xrightarrow {s^{*}y^{*}\operatorname {\mathrm {at}}_E} s^{*}y^{*}L_{\mathcal {Y}}[1]\otimes s^{*}y^{*}E\to s^{*}y^{*}h^{1}(L_{\mathcal {Y}})\otimes s^{*}y^{*}E$
agrees up to natural isomorphisms with the connecting homomorphism
![]() $\delta $
, obtained by applying the Snake Lemma to the following diagram:
$\delta $
, obtained by applying the Snake Lemma to the following diagram:
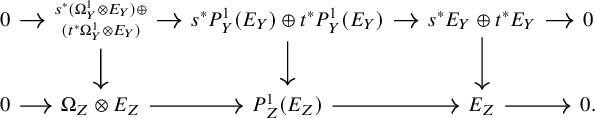
Proof. Let
![]() $R:=P_{k}(\mathcal {O}_Z)$
and
$R:=P_{k}(\mathcal {O}_Z)$
and
![]() $Q=P_{k}(\mathcal {O}_Y)$
be the standard simplicial resolutions and
$Q=P_{k}(\mathcal {O}_Y)$
be the standard simplicial resolutions and
![]() $s_R^{*}$
and
$s_R^{*}$
and
![]() $t_R^{*}$
the pullback functors from Q-modules to R-modules induced by s and t, respectively. Then, we have a commutative diagram of R-modules
$t_R^{*}$
the pullback functors from Q-modules to R-modules induced by s and t, respectively. Then, we have a commutative diagram of R-modules
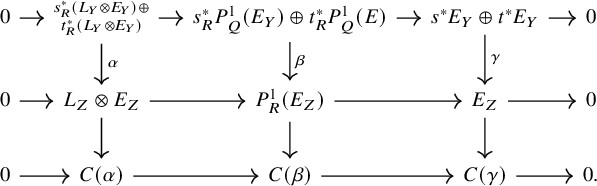
By the construction of the Atiyah class, we have natural isomorphisms
![]() $C(\alpha )\simeq s^{*}y^{*}L_{\mathcal {Y}}[1]\otimes E$
and
$C(\alpha )\simeq s^{*}y^{*}L_{\mathcal {Y}}[1]\otimes E$
and
![]() $C(\gamma )\simeq s^{*}y^{*}E[1]$
with respect to which the connecting map associated to the lower row is naturally identified with
$C(\gamma )\simeq s^{*}y^{*}E[1]$
with respect to which the connecting map associated to the lower row is naturally identified with
![]() $s^{*}y^{*}\operatorname {\mathrm {at}}_E[1]$
in
$s^{*}y^{*}\operatorname {\mathrm {at}}_E[1]$
in
![]() $D^{\Delta }(R)$
. The diagram maps to the similar diagram of
$D^{\Delta }(R)$
. The diagram maps to the similar diagram of
![]() $\mathcal {O}_Z$
-modules
$\mathcal {O}_Z$
-modules
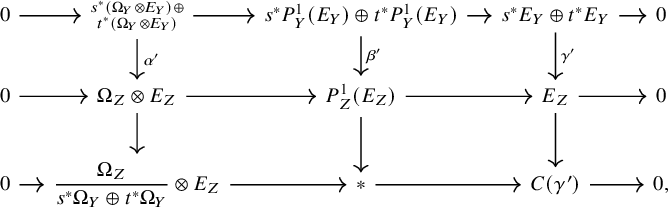
where the last row is obtained by taking cones of the vertical morphisms and then pushing out along
![]() $C(\alpha ')\to \Omega _Z/(s^{*}\Omega _Y\oplus t^{*}\Omega _Y) \otimes E_Z$
. The morphism
$C(\alpha ')\to \Omega _Z/(s^{*}\Omega _Y\oplus t^{*}\Omega _Y) \otimes E_Z$
. The morphism
![]() $C(\alpha )\to \Omega _Z/(s^{*}\Omega _Y\oplus t^{*}\Omega _Y)\otimes E_Z$
here is identified with the truncation morphism
$C(\alpha )\to \Omega _Z/(s^{*}\Omega _Y\oplus t^{*}\Omega _Y)\otimes E_Z$
here is identified with the truncation morphism
![]() $L_{\mathcal {Y}}[1]\to h^1(L_{\mathcal {Y}})$
tensored with
$L_{\mathcal {Y}}[1]\to h^1(L_{\mathcal {Y}})$
tensored with
![]() $E_Z$
. By pulling back the lower row along the natural map
$E_Z$
. By pulling back the lower row along the natural map
![]() $s^{*}y^{*}E[1]\to C(\gamma ')$
obtained from the diagonal map
$s^{*}y^{*}E[1]\to C(\gamma ')$
obtained from the diagonal map
![]() $s^{*}y^{*}E\to s^{*}E_Y\oplus t^{*}E_Y$
, we get an extension
$s^{*}y^{*}E\to s^{*}E_Y\oplus t^{*}E_Y$
, we get an extension
That the induced connecting homomorphism agrees with the one coming from the Snake Lemma follows from Lemma 6.15.
Lemma 6.15. Suppose that we have a commutative diagram in an abelian category with exact rows
Form the exact sequence
and let
![]() $j:C(\alpha )\to \operatorname {Coker}(\alpha )$
and
$j:C(\alpha )\to \operatorname {Coker}(\alpha )$
and
![]() $i:\operatorname {\mathrm {Ker}}(\gamma )[1]\to C(\gamma )$
denote the natural maps. Then the connecting homomorphism associated to the sequence of complexes of A-modules
$i:\operatorname {\mathrm {Ker}}(\gamma )[1]\to C(\gamma )$
denote the natural maps. Then the connecting homomorphism associated to the sequence of complexes of A-modules
is exactly minus the shift by
![]() $1$
of the connecting morphism
$1$
of the connecting morphism
![]() $\delta :\operatorname {\mathrm {Ker}}(\gamma )\to \operatorname {Coker}(\alpha )$
in the Snake Lemma.
$\delta :\operatorname {\mathrm {Ker}}(\gamma )\to \operatorname {Coker}(\alpha )$
in the Snake Lemma.
Proof. One checks by a direct computation that M is just the cone over
![]() $\delta $
with the two maps being the canonical inclusion and projection. It follows by the usual considerations of mapping cones that the connecting morphism of the sequence
$\delta $
with the two maps being the canonical inclusion and projection. It follows by the usual considerations of mapping cones that the connecting morphism of the sequence
![]() $j_*i^{*}\underline {C}$
is
$j_*i^{*}\underline {C}$
is
![]() $-\delta $
.
$-\delta $
.
Remark 6.16. To conclude, we point out that the conclusions of §6.3–§6.5 still hold when
![]() $\mathcal {M}$
is open in a moduli stack of perfect complexes, and
$\mathcal {M}$
is open in a moduli stack of perfect complexes, and
![]() $\mathcal {E}$
is the universal complex, using the results of [Reference Huybrechts and Thomas6]. We assume here that the complexes being parametrized have vanishing negative
$\mathcal {E}$
is the universal complex, using the results of [Reference Huybrechts and Thomas6]. We assume here that the complexes being parametrized have vanishing negative
![]() $\operatorname {\mathrm {Ext}}$
-groups universally on
$\operatorname {\mathrm {Ext}}$
-groups universally on
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
The arguments of 6.3 and 6.4 go through with Theorem 3.3 and Corollary 3.4 of [Reference Huybrechts and Thomas6] in place of Remark 6.7 and Remark 6.8, respectively. The arguments of 6.5 go through unchanged for complexes.
Competing interest
The author has no competing interest to declare.
Funding statement
This research was supported by the Research Council of Norway grant number 302277 - ‘Orthogonal gauge duality and non-commutative geometry’.
















