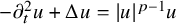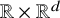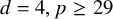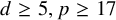1 Introduction
In this paper, we consider the defocusing nonlinear wave equation
where
![]() $u:\mathbb {R}^{1+d}\to \mathbb {C}$
is the unknown field,
$u:\mathbb {R}^{1+d}\to \mathbb {C}$
is the unknown field,
![]() $ \Box =\partial ^{\alpha }\partial _{\alpha }=-\partial _t^2+\sum _{i=1}^d\partial _i^2$
is the d’Alembertian operatorFootnote 1 on Minkowski spacetime
$ \Box =\partial ^{\alpha }\partial _{\alpha }=-\partial _t^2+\sum _{i=1}^d\partial _i^2$
is the d’Alembertian operatorFootnote 1 on Minkowski spacetime
![]() $\mathbb {R}^{1+d}$
with the standard Minkowski metric
$\mathbb {R}^{1+d}$
with the standard Minkowski metric
and we assume
![]() $p\in 2\mathbb {Z}_{+}+1$
for simplicity.
$p\in 2\mathbb {Z}_{+}+1$
for simplicity.
Given smooth initial data
![]() $(u|_{t=0}, \partial _tu|_{t=0})$
, there exists a local smooth solution on the maximal existence of interval
$(u|_{t=0}, \partial _tu|_{t=0})$
, there exists a local smooth solution on the maximal existence of interval
![]() $[0, T)$
;
$[0, T)$
;
![]() $T<+\infty $
if and only if
$T<+\infty $
if and only if
![]() $\limsup _{t\uparrow T}\|u(t)\|_{L^\infty }=+\infty $
, see [Reference Sogge68, Reference Luk45]; moreover, there holds the energy conservation
$\limsup _{t\uparrow T}\|u(t)\|_{L^\infty }=+\infty $
, see [Reference Sogge68, Reference Luk45]; moreover, there holds the energy conservation
The class of solutions to (1.1) is invariant under the scaling
This scaling symmetry preserves the critical norm invariant, i.e.,
We can split the range of parameters
![]() $(d,p)$
into three cases accordingly:
$(d,p)$
into three cases accordingly:
-
• Subcritical case:
 $s_c<1 \Longleftrightarrow d\leq 2$
or
$s_c<1 \Longleftrightarrow d\leq 2$
or
 $p<1+4/(d-2)$
for
$p<1+4/(d-2)$
for
 $d\geq 3$
.
$d\geq 3$
. -
• Critical case:
 $s_c=1 \Longleftrightarrow p=1+4/(d-2)$
and
$s_c=1 \Longleftrightarrow p=1+4/(d-2)$
and
 $d\geq 3$
.
$d\geq 3$
. -
• Supercritical case:
 $s_c>1 \Longleftrightarrow p>1+4/(d-2)$
and
$s_c>1 \Longleftrightarrow p>1+4/(d-2)$
and
 $d\geq 3$
.
$d\geq 3$
.
For the subcritical case, the global well-posedness and propagation of regularity dated back to Jörgens [Reference Jörgens31] for
![]() $d=3$
; see also [Reference Ginibre and Velo19, Reference Ginibre and Velo20] for the global well-posedness within the energy class
$d=3$
; see also [Reference Ginibre and Velo19, Reference Ginibre and Velo20] for the global well-posedness within the energy class
![]() $H^1\times L^2$
for all dimensions; the propagation of regularity holds at least for
$H^1\times L^2$
for all dimensions; the propagation of regularity holds at least for
![]() $d\leq 9$
[Reference Brenner and von Wahl3]. The critical case is much more difficult. The global regularity result was obtained firstly in [Reference Struwe71] for
$d\leq 9$
[Reference Brenner and von Wahl3]. The critical case is much more difficult. The global regularity result was obtained firstly in [Reference Struwe71] for
![]() $d=3$
and spherically symmetric initial data, and then extended to
$d=3$
and spherically symmetric initial data, and then extended to
![]() $d\leq 9$
for general smooth data in [Reference Grillakis21, Reference Grillakis22, Reference Shatah and Struwe66], and all dimensions in [Reference Shatah and Struwe67] (in the energy class
$d\leq 9$
for general smooth data in [Reference Grillakis21, Reference Grillakis22, Reference Shatah and Struwe66], and all dimensions in [Reference Shatah and Struwe67] (in the energy class
![]() $H^1\times L^2$
). For the long-time behavior of these global solutions, we refer to [Reference Yang75] and references therein.
$H^1\times L^2$
). For the long-time behavior of these global solutions, we refer to [Reference Yang75] and references therein.
For the supercritical case, it is known that the Cauchy problem is ill-posed in some low regularity spaces [Reference Christ, Colliander and Tao6], or even in the energy class [Reference Ibrahim, Majdoub and Masmoudi26], despite the global existence of weak solutions [Reference Strauss70], as well as the global well-posedness with scattering for small smooth data [Reference Lindblad and Sogge44]. The global well-posedness for general smooth data is a long-standing open problem [Reference Bourgain2, Reference Tao72]. In the breakthrough work [Reference Merle, Raphaël, Rodnianski and Szeftel51], Merle, Raphaël, Rodnianski and Szeftel construct radial and asymptotically self-similar blow-up solutions for the energy supercritical defocusing nonlinear Schrödinger equations (NLS). The goal of this paper is to extend a similar blow-up result for NLS to the defocusing supercritical wave equation.
Before stating our theorem, we recall Tao’s blow-up result [Reference Tao73] for the defocusing nonlinear wave system of the form
![]() $\Box u=(\nabla _{\mathbb {R}^m}F)(u)$
, where
$\Box u=(\nabla _{\mathbb {R}^m}F)(u)$
, where
![]() $u:\mathbb {R}^{1+d}\to \mathbb {R}^m$
is vector-valued, and
$u:\mathbb {R}^{1+d}\to \mathbb {R}^m$
is vector-valued, and
![]() $F:\mathbb {R}^m\to \mathbb {R}$
is a smooth potential which is positive and homogeneous of order
$F:\mathbb {R}^m\to \mathbb {R}$
is a smooth potential which is positive and homogeneous of order
![]() $p+1$
outside of the unit ball for some
$p+1$
outside of the unit ball for some
![]() $p>1$
(letting
$p>1$
(letting
![]() $m=2$
and
$m=2$
and
![]() $F(u)=|u|^{p+1}/(p+1)$
we recover (1.1)). Tao [Reference Tao73] proved that for any supercritical
$F(u)=|u|^{p+1}/(p+1)$
we recover (1.1)). Tao [Reference Tao73] proved that for any supercritical
![]() $(d,p)$
, and sufficiently large positive integer m, there exists a defocusing
$(d,p)$
, and sufficiently large positive integer m, there exists a defocusing
![]() $F: \mathbb {R}^m\to \mathbb {R}$
such that the system
$F: \mathbb {R}^m\to \mathbb {R}$
such that the system
![]() $\Box u=(\nabla _{\mathbb {R}^m}F)(u)$
has no global smooth solution for some smooth compactly supported initial data. A similar result for the defocusing Schrödinger system was obtained in [Reference Tao74].
$\Box u=(\nabla _{\mathbb {R}^m}F)(u)$
has no global smooth solution for some smooth compactly supported initial data. A similar result for the defocusing Schrödinger system was obtained in [Reference Tao74].
1.1 Main results
Roughly speaking, we prove that the defocusing supercritical nonlinear complex-valued wave equation for
![]() $d\ge 4$
admits finite time blow-up solutions arising from smooth initial data. The leading order term of blow-up solution is given by a self-similar blow-up solution of the relativistic compressible Euler equation, which is stated here as Assumption 1 (in Section 2). In our companion paper [Reference Shao, Wei and Zhang65], we have verified Assumption 1 for some
$d\ge 4$
admits finite time blow-up solutions arising from smooth initial data. The leading order term of blow-up solution is given by a self-similar blow-up solution of the relativistic compressible Euler equation, which is stated here as Assumption 1 (in Section 2). In our companion paper [Reference Shao, Wei and Zhang65], we have verified Assumption 1 for some
![]() $(d,p)$
.
$(d,p)$
.
Theorem 1.1. Let
![]() $d\in \mathbb {Z}\cap [4,+\infty )$
and
$d\in \mathbb {Z}\cap [4,+\infty )$
and
![]() $p\in 2\mathbb {Z}_{+}+1$
be such thatFootnote 2
$p\in 2\mathbb {Z}_{+}+1$
be such thatFootnote 2
![]() $k>\ell +\sqrt \ell $
, where
$k>\ell +\sqrt \ell $
, where
![]() $k:=d-1$
and
$k:=d-1$
and
![]() $\ell :=1+4/(p-1)$
. Assume that there exists
$\ell :=1+4/(p-1)$
. Assume that there exists
![]() $\beta \in (1, k/(\ell +\sqrt \ell ))$
such that Assumption 1 holds. Then there exist compactly supported smooth functions
$\beta \in (1, k/(\ell +\sqrt \ell ))$
such that Assumption 1 holds. Then there exist compactly supported smooth functions
![]() $u_0, u_1:\mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
such that there is no global smooth solution
$u_0, u_1:\mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
such that there is no global smooth solution
![]() $u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
to the defocusing nonlinear wave equation (1.1) with initial data
$u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
to the defocusing nonlinear wave equation (1.1) with initial data
![]() $u(0)=u_0$
,
$u(0)=u_0$
,
![]() $\partial _t u(0)=u_1$
.
$\partial _t u(0)=u_1$
.
Corollary 1.2. If
![]() $d=4$
,
$d=4$
,
![]() $p\in (2\mathbb {Z}+1)\cap [29,+\infty )$
or
$p\in (2\mathbb {Z}+1)\cap [29,+\infty )$
or
![]() $d\geq 5, p\in (2\mathbb {Z}+1)\cap [17,+\infty )$
, then there exist compactly supported smooth functions
$d\geq 5, p\in (2\mathbb {Z}+1)\cap [17,+\infty )$
, then there exist compactly supported smooth functions
![]() $u_0, u_1:\mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
such that there is no global smooth solution
$u_0, u_1:\mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
such that there is no global smooth solution
![]() $u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
to the defocusing nonlinear wave equation (1.1) with initial data
$u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {R}^2(=\mathbb {C})$
to the defocusing nonlinear wave equation (1.1) with initial data
![]() $u(0)=u_0$
,
$u(0)=u_0$
,
![]() $\partial _t u(0)=u_1$
.
$\partial _t u(0)=u_1$
.
Several remarks are in order.
-
1. For the blow-up solution u we construct in Theorem 1.1, if u blows up at time
 $T_*\in (0, +\infty )$
, then according to our construction, we have the blow-up speed As
$T_*\in (0, +\infty )$
, then according to our construction, we have the blow-up speed As $$ \begin{align*} \|u(t,\cdot)\|_{L^\infty}\gtrsim(T_*-t)^{-\frac{2\beta}{p-1}},\quad \|(u(t),\partial_tu(t))\|_{\dot{H}_x^{s_c}\times\dot{H}_x^{s_c-1}}\gtrsim (T_*-t)^{(1-\beta)\frac d2}. \end{align*} $$
$$ \begin{align*} \|u(t,\cdot)\|_{L^\infty}\gtrsim(T_*-t)^{-\frac{2\beta}{p-1}},\quad \|(u(t),\partial_tu(t))\|_{\dot{H}_x^{s_c}\times\dot{H}_x^{s_c-1}}\gtrsim (T_*-t)^{(1-\beta)\frac d2}. \end{align*} $$
 $\beta>1$
, our solution is unbounded in the critical space. This is compatible with the results in the literature, which state that the solutions for the supercritical defocusing wave equation that are bounded in the critical space
$\beta>1$
, our solution is unbounded in the critical space. This is compatible with the results in the literature, which state that the solutions for the supercritical defocusing wave equation that are bounded in the critical space
 $\dot {H}_x^{s_c}\times \dot {H}_x^{s_c-1}$
must be global and scattering (at least for real-valued solutions and some supercritical
$\dot {H}_x^{s_c}\times \dot {H}_x^{s_c-1}$
must be global and scattering (at least for real-valued solutions and some supercritical
 $(d,p)$
, see [Reference Bulut4, Reference Bulut5, Reference Duyckaerts and Yang18, Reference Killip and Visan35, Reference Killip and Visan36]).
$(d,p)$
, see [Reference Bulut4, Reference Bulut5, Reference Duyckaerts and Yang18, Reference Killip and Visan35, Reference Killip and Visan36]).
-
2. As in the recent breakthrough work by Merle-Raphaël-Rodnianski-Szeftel [Reference Merle, Raphaël, Rodnianski and Szeftel51, Reference Merle, Raphaël, Rodnianski and Szeftel52, Reference Merle, Raphaël, Rodnianski and Szeftel53], the heart of proof of Theorem 1.1 is to study (1.1) in its hydrodynamical formulation, i.e., with respect to its phase and modulus variables, i.e. (2.1). After introducing a front re-normalization (2.2), (2.1) becomes (2.3). Taking the formal limit
 $b\to 0$
, we reveal the underlying relativistic compressible Euler dynamics (2.6). The relativistic Euler dynamics provides us with a self-similar blow-up solution, which has been constructed in our companion paper [Reference Shao, Wei and Zhang65] and which, in turn, acts as the leading order term of the blow-up solution of the defocusing supercritical wave equation (1.1).
$b\to 0$
, we reveal the underlying relativistic compressible Euler dynamics (2.6). The relativistic Euler dynamics provides us with a self-similar blow-up solution, which has been constructed in our companion paper [Reference Shao, Wei and Zhang65] and which, in turn, acts as the leading order term of the blow-up solution of the defocusing supercritical wave equation (1.1). -
3. In the proof, we first construct a good approximate solution, then solve the perturbation equation backward in time. This method is quite different from [Reference Merle, Raphaël, Rodnianski and Szeftel51], and simplifies our proof greatly. Unlike [Reference Merle, Raphaël, Rodnianski and Szeftel51], we do not need to analyze the stability of the linearized operator near the leading order profile constructed in [Reference Shao, Wei and Zhang65], hence we only use less information of the leading order profile (see Assumption 1). On the other hand, in [Reference Merle, Raphaël, Rodnianski and Szeftel51], the initial data for blow-up form a finite co-dimensional manifold in the class of radial smooth fast-decay functions, we only construct the blow-up solution for one initial data
 $(u_0, u_1)$
in Theorem 1.1. We believe that the blow-up should hold for a large class of initial data, just as in [Reference Merle, Raphaël, Rodnianski and Szeftel51]. This is left to the future work.
$(u_0, u_1)$
in Theorem 1.1. We believe that the blow-up should hold for a large class of initial data, just as in [Reference Merle, Raphaël, Rodnianski and Szeftel51]. This is left to the future work. -
4. To prove Corollary 1.2, we just need to verify Assumption 1, which is related to the existence of a smooth global solution to a specific ODE (2.8). If
 $d=4, p\geq 29$
or
$d=4, p\geq 29$
or
 $d=5, p\geq 17$
, Assumption 1 is verified in our companion paper [Reference Shao, Wei and Zhang65]. As a consequence, if one can find some other methods to verify Assumption 1 for smaller p, then one can also get the blow-up for that smaller p. The case
$d=5, p\geq 17$
, Assumption 1 is verified in our companion paper [Reference Shao, Wei and Zhang65]. As a consequence, if one can find some other methods to verify Assumption 1 for smaller p, then one can also get the blow-up for that smaller p. The case
 $d>5$
follows from the result for
$d>5$
follows from the result for
 $d=5$
and truncation, see Subsection 2.5.
$d=5$
and truncation, see Subsection 2.5. -
5. We emphasize that if Assumption 1 is valid, then we must have
 $d>\beta (\ell +\sqrt \ell )+1$
, where
$d>\beta (\ell +\sqrt \ell )+1$
, where
 $\ell :=1+4/(p-1)>1$
. Using
$\ell :=1+4/(p-1)>1$
. Using
 $\beta>1$
, we get
$\beta>1$
, we get
 $d>3$
. As a result, the case of
$d>3$
. As a result, the case of
 $d=3$
is not amenable to our analysis at present, and the existence of blow-up solutions for
$d=3$
is not amenable to our analysis at present, and the existence of blow-up solutions for
 $d=3$
remains open. We point out that similar situation happens in [Reference Merle, Raphaël, Rodnianski and Szeftel51], where the construction fails for
$d=3$
remains open. We point out that similar situation happens in [Reference Merle, Raphaël, Rodnianski and Szeftel51], where the construction fails for
 $3$
-D and
$3$
-D and
 $4$
-D defocusing supercritical NLS.
$4$
-D defocusing supercritical NLS. -
6. In this work, we can only construct the blow-up for the complex-valued solution. The blow-up for the scalar defocusing supercritical wave equation remains open at this point. We guess that the same blow-up result should hold for the scalar nonlinear wave equation, at least for
 $(d,p)$
satisfying the same hypothesis as in Theorem 1.1.
$(d,p)$
satisfying the same hypothesis as in Theorem 1.1. -
7. In this paper, we initiate our exploration of complex-valued blow-up solutions by employing the modulus-phase decomposition
 $u=w \mathrm {e}^{\mathrm {i}\Phi }$
, as detailed in Section 2. For the
$u=w \mathrm {e}^{\mathrm {i}\Phi }$
, as detailed in Section 2. For the
 $\mathbb {R}$
-valued problem, an analogous approach appears promising. Specifically, we propose a decomposition of the form
$\mathbb {R}$
-valued problem, an analogous approach appears promising. Specifically, we propose a decomposition of the form
 $u=wf(\Phi )$
, where
$u=wf(\Phi )$
, where
 $f:\mathbb {R}\to \mathbb {R}^+$
is an unknown real-valued function. Under this framework, the problem reduces to solving the following system of equations: When compared with (2.1), the above system exhibits a significantly higher level of complexity. Consequently, its thorough investigation is deferred to future work.
$f:\mathbb {R}\to \mathbb {R}^+$
is an unknown real-valued function. Under this framework, the problem reduces to solving the following system of equations: When compared with (2.1), the above system exhibits a significantly higher level of complexity. Consequently, its thorough investigation is deferred to future work. $$\begin{align*}2\partial^\alpha w\partial_\alpha\Phi+w\Box \Phi=0,\quad f"(\Phi)=-f(\Phi)^p,\quad \Box w=f(\Phi)^{p-1}\left(w^p+w\partial^\alpha\Phi\partial_\alpha\Phi\right).\end{align*}$$
$$\begin{align*}2\partial^\alpha w\partial_\alpha\Phi+w\Box \Phi=0,\quad f"(\Phi)=-f(\Phi)^p,\quad \Box w=f(\Phi)^{p-1}\left(w^p+w\partial^\alpha\Phi\partial_\alpha\Phi\right).\end{align*}$$
The road map of the proof of Theorem 1.1 and Corollary 1.2 can be found in Section 2. The proof is based on Propositions 2.4, 2.7 and 2.8. Our starting point is to introduce a front re-normalization (2.2), relying on a constant
![]() $b>0$
; taking the limit
$b>0$
; taking the limit
![]() $b\to 0$
, the defocusing wave equation becomes the relativistic compressible Euler equations.
$b\to 0$
, the defocusing wave equation becomes the relativistic compressible Euler equations.
We first write the desired solution to (1.1) in the form of a power series (see (2.4)) with respect to the constant
![]() $b>0$
. The non-degeneracy of the leading order approximation allows us to solve all high-order approximations
$b>0$
. The non-degeneracy of the leading order approximation allows us to solve all high-order approximations
![]() $(\rho _n, \phi _n)$
, which is exactly the purpose of Proposition 2.4. The proof of Proposition 2.4 is rather technical and can be found in Section 5. One of the key ingredients used is the existence of smooth solutions to the second order ODEs having singular points with a parameter
$(\rho _n, \phi _n)$
, which is exactly the purpose of Proposition 2.4. The proof of Proposition 2.4 is rather technical and can be found in Section 5. One of the key ingredients used is the existence of smooth solutions to the second order ODEs having singular points with a parameter
![]() $\lambda $
, see Appendix B.
$\lambda $
, see Appendix B.
Since we do not have enough information on
![]() $(\rho _n, \phi _n)$
, especially the estimate uniform in n, we may not have the convergence of the formal series (2.4). To overcome this drawback, we truncate
$(\rho _n, \phi _n)$
, especially the estimate uniform in n, we may not have the convergence of the formal series (2.4). To overcome this drawback, we truncate
![]() $(\rho _n, \phi _n)$
in the form of (2.23), and in Proposition 2.7 we prove that the truncated solution is a good approximate solution to the defocusing wave equation. The proof of Proposition 2.7 can be found in Section 3.
$(\rho _n, \phi _n)$
in the form of (2.23), and in Proposition 2.7 we prove that the truncated solution is a good approximate solution to the defocusing wave equation. The proof of Proposition 2.7 can be found in Section 3.
Finally, we construct a solution to (1.1) near the truncated approximation solution. This is exactly what Proposition 2.8 says. The proof of Proposition 2.8 can be found in Section 4, where we use the energy method to solve the wave equation in a time-backward direction, and we need to use a technical truncation to avoid the singularity at blow-up time. Such method of solving backward in time has been used in [Reference Krieger, Schlag and Tataru41, Reference Krieger, Schlag and Tataru42, Reference Perelman60]. Let’s emphasize that this part does not depend at all on our method of constructing the approximate solutions, and it includes the case
![]() $d=3$
and does not require Assumption 1 or the spherical symmetry of the approximate solutions either.
$d=3$
and does not require Assumption 1 or the spherical symmetry of the approximate solutions either.
1.2 Blow-up phenomenon for related models
Let’s review some important results on the blow-up for other related equations.
It is more common to observe the blow-up phenomenon for the focusing nonlinear wave equation, i.e.,
In fact, the spatial independent function
![]() $u(t)=C_p(T-t)^{-2/(p-1)}$
, where
$u(t)=C_p(T-t)^{-2/(p-1)}$
, where
![]() $C_p^{p-1}=2(p+1)/(p-1)^2$
, gives a blow-up solution to (1.4). This ODE-type solution can be further truncated to a smooth compactly supported blow-up solution to (1.4) by using the finite speed of propagation [Reference Alinhac1, Reference John30, Reference Levine43]. We will use similar ideas to prove Corollary 1.2 for the case
$C_p^{p-1}=2(p+1)/(p-1)^2$
, gives a blow-up solution to (1.4). This ODE-type solution can be further truncated to a smooth compactly supported blow-up solution to (1.4) by using the finite speed of propagation [Reference Alinhac1, Reference John30, Reference Levine43]. We will use similar ideas to prove Corollary 1.2 for the case
![]() $d>5$
. See also [Reference Donninger12, Reference Duyckaerts, Kenig and Merle15, Reference Duyckaerts, Kenig and Merle16, Reference Duyckaerts and Yang18, Reference Jendrej27, Reference Kenig32, Reference Kenig and Merle34, Reference Krieger and Schlag40, Reference Krieger, Schlag and Tataru42, Reference Martel, Yvan and Merle46, Reference Merle and Zaag58] for the construction and classification of blow-up (or global) solutions as well as recent breakthrough [Reference Duyckaerts, Jia, Kenig and Merle13, Reference Duyckaerts, Kenig and Merle17, Reference Jendrej and Lawrie29] on the soliton resolution conjecture.
$d>5$
. See also [Reference Donninger12, Reference Duyckaerts, Kenig and Merle15, Reference Duyckaerts, Kenig and Merle16, Reference Duyckaerts and Yang18, Reference Jendrej27, Reference Kenig32, Reference Kenig and Merle34, Reference Krieger and Schlag40, Reference Krieger, Schlag and Tataru42, Reference Martel, Yvan and Merle46, Reference Merle and Zaag58] for the construction and classification of blow-up (or global) solutions as well as recent breakthrough [Reference Duyckaerts, Jia, Kenig and Merle13, Reference Duyckaerts, Kenig and Merle17, Reference Jendrej and Lawrie29] on the soliton resolution conjecture.
Other related models such as the nonlinear Schrödinger equation, see [Reference Kenig and Merle33, Reference Merle and Raphaël48, Reference Merle, Raphaël and Rodnianski50, Reference Merle, Raphaël, Rodnianski and Szeftel51, Reference Merle, Raphaël and Szeftel54, Reference Merle, Raphaël and Szeftel55, Reference Perelman59, Reference Perelman61]; see [Reference Duyckaerts, Jia, Kenig and Merle14, Reference Krieger and Miao38, Reference Krieger, Miao and Schlag39, Reference Krieger, Schlag and Tataru41, Reference Raphaël and Rodnianski62, Reference Rodnianski and Sterbenz64] for the wave map; see [Reference Merle, Raphaël and Rodnianski49, Reference Perelman60] for the Schrödinger maps; see [Reference Collot, Raphaël and Szeftel7, Reference Collot, Raphaël and Szeftel8, Reference Cortázar, del Pino and Musso9, Reference del Pino, Musso and Wei11, Reference Harada23, Reference Matano and Merle47, Reference Merle, Raphaël and Szeftel56, Reference Merle and Zaag57] for the semilinear heat equation and [Reference Dávila, del Pino and Wei10, Reference Jendrej and Lawrie28, Reference Kim and Merle37, Reference Raphaël and Schweyer63] for the harmonic heat flow.
1.3 Notations and conventions
Unless stated otherwise, we adopt the following notations, abbreviations, and conventions:
-
• Constants:
 $\mathrm i=\sqrt {-1}$
is the imaginary unit,
$\mathrm i=\sqrt {-1}$
is the imaginary unit,
 $\mathrm e$
is the base of the natural logarithm.
$\mathrm e$
is the base of the natural logarithm. -
• For any
 $a\in \mathbb {R}$
, we denote
$a\in \mathbb {R}$
, we denote
 $\mathbb {Z}_{\geq a}:=\mathbb {Z}\cap [a, +\infty )$
and
$\mathbb {Z}_{\geq a}:=\mathbb {Z}\cap [a, +\infty )$
and
 $\mathbb {Z}_{>a}:=\mathbb {Z}\cap (a, +\infty )$
. Moreover, we denote
$\mathbb {Z}_{>a}:=\mathbb {Z}\cap (a, +\infty )$
. Moreover, we denote
 $\mathbb {Z}_+:=\mathbb {Z}_{\geq 1}$
. Similarly,
$\mathbb {Z}_+:=\mathbb {Z}_{\geq 1}$
. Similarly,
 $\mathbb {R}_{\geq 0}:=\mathbb {R}\cap [0, +\infty )$
.
$\mathbb {R}_{\geq 0}:=\mathbb {R}\cap [0, +\infty )$
. -
• Greek indices run from
 $0$
to d, where
$0$
to d, where
 $d\in \mathbb {Z}_{\geq 2}$
is the spatial dimension, Latin indices run from
$d\in \mathbb {Z}_{\geq 2}$
is the spatial dimension, Latin indices run from
 $1$
to d, and we use the Einstein’s summation convention: repeated indices appearing once upstairs and once downstairs are summed over their range.
$1$
to d, and we use the Einstein’s summation convention: repeated indices appearing once upstairs and once downstairs are summed over their range. -
•
 $(t,x)=(t, x_1, \cdots , x_d)$
denotes coordinates in spacetime,
$(t,x)=(t, x_1, \cdots , x_d)$
denotes coordinates in spacetime,
 $r=|x|=(\sum _{j=1}^dx_j^2)^{1/2}$
. We write
$r=|x|=(\sum _{j=1}^dx_j^2)^{1/2}$
. We write
 $\partial _{0}=-\partial ^0=\partial _t=\frac {\partial }{\partial t}$
,
$\partial _{0}=-\partial ^0=\partial _t=\frac {\partial }{\partial t}$
,
 $\partial _{j}=\partial ^j=\partial _{x_j}=\frac {\partial }{\partial x_j}$
for
$\partial _{j}=\partial ^j=\partial _{x_j}=\frac {\partial }{\partial x_j}$
for
 $j\in \mathbb {Z}\cap [1,d]$
,
$j\in \mathbb {Z}\cap [1,d]$
,
 $\Box =\partial ^\alpha \partial _\alpha =-\partial _t^2+\sum _{j=1}^d\partial _j^2$
and
$\Box =\partial ^\alpha \partial _\alpha =-\partial _t^2+\sum _{j=1}^d\partial _j^2$
and
 $\Delta =\sum _{j=1}^d\partial _j^2$
, then
$\Delta =\sum _{j=1}^d\partial _j^2$
, then
 $\Box =-\partial _t^2+\Delta $
.
$\Box =-\partial _t^2+\Delta $
. -
• We denote
 $\ell :=1+4/(p-1)>1$
,
$\ell :=1+4/(p-1)>1$
,
 $k:=d-1\in \mathbb {Z}_{+}$
and
$k:=d-1\in \mathbb {Z}_{+}$
and
 $\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
.
$\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
. -
• For a (vector-valued) differentiable function
 $f=f(t,x)$
, we denote and
$f=f(t,x)$
, we denote and $$ \begin{align*} Df:=(\partial_tf, \partial_1f, \partial_2f,\cdots, \partial_df) &\quad\text{and}\quad D_xf:=(\partial_1f, \partial_2f,\cdots, \partial_df)=\nabla_x f, \end{align*} $$
$$ \begin{align*} Df:=(\partial_tf, \partial_1f, \partial_2f,\cdots, \partial_df) &\quad\text{and}\quad D_xf:=(\partial_1f, \partial_2f,\cdots, \partial_df)=\nabla_x f, \end{align*} $$
 $|Df|:=(|\partial _tf|^2+\sum _{j=1}^d|\partial _jf|^2)^{1/2}$
,
$|Df|:=(|\partial _tf|^2+\sum _{j=1}^d|\partial _jf|^2)^{1/2}$
,
 $|D_xf|:=(\sum _{j=1}^d|\partial _jf|^2)^{1/2}$
. For all
$|D_xf|:=(\sum _{j=1}^d|\partial _jf|^2)^{1/2}$
. For all
 $j\in \mathbb {Z}_{+}$
we denote
$j\in \mathbb {Z}_{+}$
we denote
 $D^jf:=DD^{j-1}f$
,
$D^jf:=DD^{j-1}f$
,
 $D_x^jf:=D_xD_x^{j-1}f$
,
$D_x^jf:=D_xD_x^{j-1}f$
,
 $D^0f=D_x^0f=f$
, noting that
$D^0f=D_x^0f=f$
, noting that
 $D^{j-1}f$
and
$D^{j-1}f$
and
 $D_x^{j-1}f$
are again vector-valued functions; moreover,
$D_x^{j-1}f$
are again vector-valued functions; moreover,
 $D^{\leq 1}f:=(f, Df)$
.
$D^{\leq 1}f:=(f, Df)$
.
-
• For
 $(t,x)\in [0, T)\times \mathbb {R}^d$
, we let
$(t,x)\in [0, T)\times \mathbb {R}^d$
, we let
 $\tau :=-\ln (T-t)$
and
$\tau :=-\ln (T-t)$
and
 $Z:=|x|/(T-t)\in [0, +\infty )$
.
$Z:=|x|/(T-t)\in [0, +\infty )$
. -
• For
 $N\geq 0$
,
$N\geq 0$
,
 $H_x^N$
denotes the inhomogeneous Sobolev space with the norm
$H_x^N$
denotes the inhomogeneous Sobolev space with the norm
 $\|\cdot \|_{H_x^N}$
with respect to the spatial variables and
$\|\cdot \|_{H_x^N}$
with respect to the spatial variables and
 $\dot H_x^N$
denotes the homogeneous Sobolev space with the norm
$\dot H_x^N$
denotes the homogeneous Sobolev space with the norm
 $\|\cdot \|_{\dot H_x^N}$
. Moreover, we denote
$\|\cdot \|_{\dot H_x^N}$
. Moreover, we denote
 $L_x^2:=H_x^0$
.
$L_x^2:=H_x^0$
. -
• A function space is a linear vector space if it is closed under addition and multiplication by a constant. A function space is a ring (algebra) if it contains all the constant functions and is closed under addition and multiplication. Then a ring is also a linear vector space.
2 A roadmap of the proof
We introduce the modulus-phase decomposition
![]() $u=w \mathrm {e}^{\mathrm {i}\Phi }$
, with
$u=w \mathrm {e}^{\mathrm {i}\Phi }$
, with
![]() $w:\mathbb {R}^{1+d}\to \mathbb {R}_{>0}$
and
$w:\mathbb {R}^{1+d}\to \mathbb {R}_{>0}$
and
![]() $\Phi :\mathbb {R}^{1+d}\to \mathbb {R}$
. Then
$\Phi :\mathbb {R}^{1+d}\to \mathbb {R}$
. Then
and (1.1) becomes
Let
![]() $b>0$
be a positive constant. We re-normalize according to
$b>0$
be a positive constant. We re-normalize according to
then (2.1) becomes
We seek solutions
![]() $(\rho , \phi )$
to (2.3) in the form of
$(\rho , \phi )$
to (2.3) in the form of
 $$ \begin{align} \rho(t,x)=\sum_{n=0}^{\infty}\rho_n(t,x) b^n,\qquad \phi(t,x)=\sum_{n=0}^\infty \phi_n(t,x)b^n. \end{align} $$
$$ \begin{align} \rho(t,x)=\sum_{n=0}^{\infty}\rho_n(t,x) b^n,\qquad \phi(t,x)=\sum_{n=0}^\infty \phi_n(t,x)b^n. \end{align} $$
Plugging (2.4) into (2.3), we obtain the following recurrence relation for
![]() $n\in \mathbb {Z}_{\geq 0}$
:
$n\in \mathbb {Z}_{\geq 0}$
:
 $$ \begin{align} \begin{aligned} \Box\rho_{n-1}&=\sum_{n_1+n_2+\cdots+n_p=n}\rho_{n_1}\rho_{n_2}\cdots\rho_{n_p}+ \sum_{n_1+n_2+n_3=n}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3},\\ 0&=2\sum_{n_1+n_2=n}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}+\sum_{n_1+n_2=n}\rho_{n_1}\Box\phi_{n_2}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Box\rho_{n-1}&=\sum_{n_1+n_2+\cdots+n_p=n}\rho_{n_1}\rho_{n_2}\cdots\rho_{n_p}+ \sum_{n_1+n_2+n_3=n}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3},\\ 0&=2\sum_{n_1+n_2=n}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}+\sum_{n_1+n_2=n}\rho_{n_1}\Box\phi_{n_2}, \end{aligned} \end{align} $$
where we have used the convention that
![]() $\rho _{-n'}=\phi _{-n'}=0$
for all
$\rho _{-n'}=\phi _{-n'}=0$
for all
![]() $n'\in \mathbb {Z}_{+}$
. Here (2.4) is only a formal expansion and we will use cutoff functions to construct approximate solutions. Here b plays the role of deriving recurrence relation (2.5), the smallness lies in the functions
$n'\in \mathbb {Z}_{+}$
. Here (2.4) is only a formal expansion and we will use cutoff functions to construct approximate solutions. Here b plays the role of deriving recurrence relation (2.5), the smallness lies in the functions
![]() $\rho _n,\phi _n$
as
$\rho _n,\phi _n$
as
![]() $t\uparrow T$
rather than
$t\uparrow T$
rather than
![]() $b^n$
. We will not let
$b^n$
. We will not let
![]() $b\downarrow 0$
, in fact, we will fix
$b\downarrow 0$
, in fact, we will fix
![]() $b=1$
.
$b=1$
.
2.1 The leading order term of the blow-up solution
Letting
![]() $n=0$
in (2.5), we know that
$n=0$
in (2.5), we know that
![]() $(\rho _0,\phi _0)$
satisfies the systemFootnote 3
$(\rho _0,\phi _0)$
satisfies the systemFootnote 3
For any
![]() $\beta>1$
, the system (2.6) is invariant under the scaling
$\beta>1$
, the system (2.6) is invariant under the scaling
We seek radially symmetric self-similar blow-up solutions to (2.6) of the form
where
![]() $T>0$
is the blow-up time and
$T>0$
is the blow-up time and
![]() $\beta>1$
is a constant.Footnote 4 Let
$\beta>1$
is a constant.Footnote 4 Let
![]() $v=\partial _r\phi _0/\partial _t\phi _0$
, then
$v=\partial _r\phi _0/\partial _t\phi _0$
, then
![]() $v=v(Z)$
solves the ODEFootnote 5
$v=v(Z)$
solves the ODEFootnote 5
 $$ \begin{align} &\Delta_Z(Z,v){\mathrm dv}/{\mathrm dZ}=\Delta_v(Z,v),\quad \Delta_v(Z,v):=(1-v^2)[\beta\ell(1-v^2)Z-kv(1-Zv)], \nonumber\\ &\Delta_Z(Z,v):=Z\left[(1-Zv)^2-\ell(v-Z)^2\right],\end{align} $$
$$ \begin{align} &\Delta_Z(Z,v){\mathrm dv}/{\mathrm dZ}=\Delta_v(Z,v),\quad \Delta_v(Z,v):=(1-v^2)[\beta\ell(1-v^2)Z-kv(1-Zv)], \nonumber\\ &\Delta_Z(Z,v):=Z\left[(1-Zv)^2-\ell(v-Z)^2\right],\end{align} $$
where
![]() $\ell :=1+4/(p-1)>1$
and
$\ell :=1+4/(p-1)>1$
and
![]() $k:=d-1\in \mathbb {Z}_{\geq 1}$
. See Subsection A.1 for the derivation of (2.8).
$k:=d-1\in \mathbb {Z}_{\geq 1}$
. See Subsection A.1 for the derivation of (2.8).
Recall the following fact from [Reference Shao, Wei and Zhang65] (recalling footnote 4).
Lemma 2.1 ([Reference Shao, Wei and Zhang65], Lemma 2.1).
If
![]() $v(Z):[0,1]\to (-1,1)$
is a
$v(Z):[0,1]\to (-1,1)$
is a
![]() $C^1$
solution to (2.8) with
$C^1$
solution to (2.8) with
![]() $v(0)=0$
and
$v(0)=0$
and
![]() $\ell>1, \beta >0, k>0$
, then
$\ell>1, \beta >0, k>0$
, then
![]() $k>\beta (\ell +\sqrt {\ell })$
.
$k>\beta (\ell +\sqrt {\ell })$
.
As a consequence, it is natural to restrict the parameters
![]() $(k,\ell ,\beta )$
in the following range:
$(k,\ell ,\beta )$
in the following range:
Assumption 1. There exists a smooth function
![]() $v=v(Z)\in (-1,1)$
defined on
$v=v(Z)\in (-1,1)$
defined on
![]() $Z\in [0,+\infty )$
solving the ODE (2.8) with
$Z\in [0,+\infty )$
solving the ODE (2.8) with
![]() $v(0)=0$
and
$v(0)=0$
and
![]() $v\in C_{\operatorname {o}}^{\infty }([0,+\infty ))$
.
$v\in C_{\operatorname {o}}^{\infty }([0,+\infty ))$
.
Here we define (with
![]() $\mathbb {R}_{\geq 0}:=[0,+\infty ) $
)
$\mathbb {R}_{\geq 0}:=[0,+\infty ) $
)
Then
![]() $C_{\text {e}}^\infty (\mathbb {R}_{\geq 0}) $
is a ring and
$C_{\text {e}}^\infty (\mathbb {R}_{\geq 0}) $
is a ring and
![]() $C_{\text {o}}^\infty (\mathbb {R}_{\geq 0}) $
is a linear vector space.
$C_{\text {o}}^\infty (\mathbb {R}_{\geq 0}) $
is a linear vector space.
Remark 2.2. Under Assumption 1 and (2.9), we can show that the solution
![]() $v(Z)$
satisfies
$v(Z)$
satisfies
-
•
 $v(Z)<Z$
and
$v(Z)<Z$
and
 $Zv(Z)<1$
for all
$Zv(Z)<1$
for all
 $Z\in (0,+\infty )$
.
$Z\in (0,+\infty )$
. -
•
 $\Delta _Z(Z, v(Z))>0$
for
$\Delta _Z(Z, v(Z))>0$
for
 $Z\in (0, Z_1)$
and
$Z\in (0, Z_1)$
and
 $\Delta _Z(Z, v(Z))<0$
for
$\Delta _Z(Z, v(Z))<0$
for
 $Z\in (Z_1, +\infty )$
, where
$Z\in (Z_1, +\infty )$
, where
 $Z_1=\frac {k}{\sqrt {\ell }(k-\beta (\ell -1))}>0$
.
$Z_1=\frac {k}{\sqrt {\ell }(k-\beta (\ell -1))}>0$
. -
• Let
 $\Delta _0(Z):=\Delta _Z(Z, v(Z))$
for
$\Delta _0(Z):=\Delta _Z(Z, v(Z))$
for
 $Z\in [0,+\infty )$
, then
$Z\in [0,+\infty )$
, then
 $\Delta _0'(Z_1)\neq 0$
.
$\Delta _0'(Z_1)\neq 0$
.
See Subsection A.2 for the proof.
In view of Assumption 1, we can define that for
![]() $Z\in [0,+\infty )$
$Z\in [0,+\infty )$
 $$ \begin{align} \begin{aligned} \widehat\phi_0(Z)&:=\frac1{\beta-1}\exp\left((\beta-1)\int_0^Z\frac{v(s)}{1-sv(s)}\,\mathrm ds\right),\\\widehat\rho_0(Z)&:=\frac{(\beta-1)^{\frac{2}{p-1}}\widehat\phi_0(Z)^{\frac{2}{p-1}}(1-v(Z)^2)^{\frac{1}{p-1}}} {(1-Zv(Z))^{\frac{2}{p-1}}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \widehat\phi_0(Z)&:=\frac1{\beta-1}\exp\left((\beta-1)\int_0^Z\frac{v(s)}{1-sv(s)}\,\mathrm ds\right),\\\widehat\rho_0(Z)&:=\frac{(\beta-1)^{\frac{2}{p-1}}\widehat\phi_0(Z)^{\frac{2}{p-1}}(1-v(Z)^2)^{\frac{1}{p-1}}} {(1-Zv(Z))^{\frac{2}{p-1}}}. \end{aligned} \end{align} $$
Then
![]() $\widehat \phi _0(Z)>0$
,
$\widehat \phi _0(Z)>0$
,
![]() $\widehat \rho _0(0)=1$
and
$\widehat \rho _0(0)=1$
and
![]() $\widehat \rho _0(Z)>0$
for all
$\widehat \rho _0(Z)>0$
for all
![]() $Z\in [0,+\infty )$
. As a consequence,
$Z\in [0,+\infty )$
. As a consequence,
![]() $(\phi _0, \rho _0)$
defined by (2.7) solves (2.6) (see Lemma A.1), and
$(\phi _0, \rho _0)$
defined by (2.7) solves (2.6) (see Lemma A.1), and
![]() $\widehat \phi _0,\ \widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty )) $
(see Lemma A.6). This is the leading order term of our blow-up solution
$\widehat \phi _0,\ \widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty )) $
(see Lemma A.6). This is the leading order term of our blow-up solution
![]() $(\rho ,\phi )$
to (2.3).
$(\rho ,\phi )$
to (2.3).
2.2 Solving
 $(\rho _n, \phi _n)$
for
$(\rho _n, \phi _n)$
for
 $n\in \mathbb {Z}_{\geq 1}$
$n\in \mathbb {Z}_{\geq 1}$
In Subsection 2.1, under Assumption 1, we construct the leading order blow-up solution
![]() $(\rho _0, \phi _0)$
. In view of the expansion (2.4), we construct
$(\rho _0, \phi _0)$
. In view of the expansion (2.4), we construct
![]() $(\rho _n, \phi _n)$
for
$(\rho _n, \phi _n)$
for
![]() $n\in \mathbb {Z}_{\geq 1}$
. We rewrite the recurrence relation (2.5) for
$n\in \mathbb {Z}_{\geq 1}$
. We rewrite the recurrence relation (2.5) for
![]() $n\in \mathbb {Z}_{\geq 1}$
as
$n\in \mathbb {Z}_{\geq 1}$
as
 $$ \begin{align} \notag&(p\rho_0^{p-1}+\partial^\alpha\phi_0\partial_\alpha\phi_0)\rho_n+2\rho_0\partial^\alpha\phi_0\partial_\alpha\phi_n\\& \quad =\Box\rho_{n-1} -\sum_{\substack{n_1+\cdots+n_p=n\\ n_1, \cdots, n_p\leq n-1}}\rho_{n_1}\cdots\rho_{n_p}-\sum_{\substack{n_1+n_2+n_3=n\\ n_1, n_2, n_3\leq n-1}}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3}=:F_n,\end{align} $$
$$ \begin{align} \notag&(p\rho_0^{p-1}+\partial^\alpha\phi_0\partial_\alpha\phi_0)\rho_n+2\rho_0\partial^\alpha\phi_0\partial_\alpha\phi_n\\& \quad =\Box\rho_{n-1} -\sum_{\substack{n_1+\cdots+n_p=n\\ n_1, \cdots, n_p\leq n-1}}\rho_{n_1}\cdots\rho_{n_p}-\sum_{\substack{n_1+n_2+n_3=n\\ n_1, n_2, n_3\leq n-1}}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3}=:F_n,\end{align} $$
 $$ \begin{align} \notag&\rho_0\Box\phi_n+2\partial^\alpha\rho_0\partial_\alpha\phi_n+2\partial^\alpha\phi_0\partial_\alpha\rho_n+\Box\phi_0\rho_n \\&\quad =-2\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq n-1}}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}-\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq n-1}}\rho_{n_1}\Box\phi_{n_2}=:G_n. \end{align} $$
$$ \begin{align} \notag&\rho_0\Box\phi_n+2\partial^\alpha\rho_0\partial_\alpha\phi_n+2\partial^\alpha\phi_0\partial_\alpha\rho_n+\Box\phi_0\rho_n \\&\quad =-2\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq n-1}}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}-\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq n-1}}\rho_{n_1}\Box\phi_{n_2}=:G_n. \end{align} $$
Using the equations for
![]() $(\rho _0, \phi _0)$
given by (2.6), the above recurrence relation becomes
$(\rho _0, \phi _0)$
given by (2.6), the above recurrence relation becomes
By (2.15), we have
 $$ \begin{align} \rho_n=\frac{\rho_0^{1-p}F_n}{p-1}-\frac2{p-1}\rho_0^{2-p}\partial^\alpha\phi_0\partial_\alpha\phi_n. \end{align} $$
$$ \begin{align} \rho_n=\frac{\rho_0^{1-p}F_n}{p-1}-\frac2{p-1}\rho_0^{2-p}\partial^\alpha\phi_0\partial_\alpha\phi_n. \end{align} $$
Substituting the above identity into (2.16), we obtain the following linear equation for
![]() $\phi _n$
:
$\phi _n$
:
 $$ \begin{align} \partial^\alpha\left(\rho_0^2\partial_\alpha\phi_n-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi_n\right)=\rho_0G_n-\frac2{p-1}\partial^\alpha\left(\rho_0^{2-p}\partial_\alpha\phi_0 F_n\right)=:H_n. \end{align} $$
$$ \begin{align} \partial^\alpha\left(\rho_0^2\partial_\alpha\phi_n-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi_n\right)=\rho_0G_n-\frac2{p-1}\partial^\alpha\left(\rho_0^{2-p}\partial_\alpha\phi_0 F_n\right)=:H_n. \end{align} $$
We introduce the linearized operator
 $$ \begin{align} \mathscr{L}(\phi):=\partial^\alpha\left(\rho_0^2\partial_\alpha\phi-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi\right),\qquad \phi=\phi(t,x)=\phi(t,r). \end{align} $$
$$ \begin{align} \mathscr{L}(\phi):=\partial^\alpha\left(\rho_0^2\partial_\alpha\phi-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi\right),\qquad \phi=\phi(t,x)=\phi(t,r). \end{align} $$
Then our aim is to solve inductively
![]() $\mathscr {L}(\phi _n)=H_n$
for each
$\mathscr {L}(\phi _n)=H_n$
for each
![]() $n\geq 1$
.
$n\geq 1$
.
Indeed, we can show that
![]() $\mathscr {L}$
is surjective in some well-chosen functional spaces and then we solve
$\mathscr {L}$
is surjective in some well-chosen functional spaces and then we solve
![]() $\mathscr {L}(\phi _n)=H_n$
in these spaces. Letting
$\mathscr {L}(\phi _n)=H_n$
in these spaces. Letting
![]() $\tau =\ln \frac 1{T-t}$
, we define (here
$\tau =\ln \frac 1{T-t}$
, we define (here
![]() $C_{\text {e}}^\infty ([0,+\infty )) $
is defined in (2.10))
$C_{\text {e}}^\infty ([0,+\infty )) $
is defined in (2.10))
 $$ \begin{align} {\mathscr X}_0&:=\left\{f(t,x)=\sum_{j=0}^n f_j(Z)\tau^j: n\in\mathbb{Z}_{\geq 0}, f_j\in C_{\text{e}}^\infty([0,+\infty))\ \ \forall\ j\in\mathbb{Z}\cap[0,n]\right\}, \end{align} $$
$$ \begin{align} {\mathscr X}_0&:=\left\{f(t,x)=\sum_{j=0}^n f_j(Z)\tau^j: n\in\mathbb{Z}_{\geq 0}, f_j\in C_{\text{e}}^\infty([0,+\infty))\ \ \forall\ j\in\mathbb{Z}\cap[0,n]\right\}, \end{align} $$
Then
![]() ${\mathscr X}_0$
is a ring (using that
${\mathscr X}_0$
is a ring (using that
![]() $\{f(t,x)=f(Z)\tau ^j:f_j\in C_{\text {e}}^\infty ([0,+\infty )),\ j\in \mathbb {Z}_{\geq 0}\} $
is closed under multiplication) and
$\{f(t,x)=f(Z)\tau ^j:f_j\in C_{\text {e}}^\infty ([0,+\infty )),\ j\in \mathbb {Z}_{\geq 0}\} $
is closed under multiplication) and
![]() ${\mathscr X}_\lambda $
is a linear vector space.
${\mathscr X}_\lambda $
is a linear vector space.
We have the following properties for the functional spaces
![]() ${\mathscr X}_\lambda $
.
${\mathscr X}_\lambda $
.
Lemma 2.3.
-
(i) Let
 $\lambda ,\mu \in \mathbb {C}$
,
$\lambda ,\mu \in \mathbb {C}$
,
 $f\in {\mathscr X}_\lambda , g\in {\mathscr X}_\mu $
. Then
$f\in {\mathscr X}_\lambda , g\in {\mathscr X}_\mu $
. Then
 $\partial _t f\in {\mathscr X}_{\lambda -1}$
,
$\partial _t f\in {\mathscr X}_{\lambda -1}$
,
 $\Delta f\in {\mathscr X}_{\lambda -2}$
,
$\Delta f\in {\mathscr X}_{\lambda -2}$
,
 $\Box f\in {\mathscr X}_{\lambda -2}$
,
$\Box f\in {\mathscr X}_{\lambda -2}$
,
 $fg\in {\mathscr X}_{\lambda +\mu }$
,
$fg\in {\mathscr X}_{\lambda +\mu }$
,
 $\partial ^\alpha f\partial _\alpha g\in {\mathscr X}_{\lambda +\mu -2}$
, and
$\partial ^\alpha f\partial _\alpha g\in {\mathscr X}_{\lambda +\mu -2}$
, and
 $\partial ^\alpha (f\partial _\alpha g)\in {\mathscr X}_{\lambda +\mu -2}$
.
$\partial ^\alpha (f\partial _\alpha g)\in {\mathscr X}_{\lambda +\mu -2}$
. -
(ii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda>j+\mu $
. If
$\lambda>j+\mu $
. If
 $f\in {\mathscr X}_\lambda $
, then
$f\in {\mathscr X}_\lambda $
, then
 $(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
, where
$(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
, where
 $\mathcal C$
is the light cone
$\mathcal C$
is the light cone
 $\mathcal C:=\left \{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\right \}$
.
$\mathcal C:=\left \{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\right \}$
. -
(iii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda \geq j+\mu $
. If
$\lambda \geq j+\mu $
. If
 $f(t,x)=(T-t)^\lambda \widehat f(Z)$
for some
$f(t,x)=(T-t)^\lambda \widehat f(Z)$
for some
 $\widehat f\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, then
$\widehat f\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, then
 $(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
.
$(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
.
The proof of Lemma 2.3 can be found in Subsection 5.1.
Proposition 2.4. The linear operator
![]() $\mathscr {L}:{\mathscr X}_{\lambda }\to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
$\mathscr {L}:{\mathscr X}_{\lambda }\to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
![]() $\lambda \in \mathbb {C}$
, where
$\lambda \in \mathbb {C}$
, where
![]() $\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
.
$\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
.
See Section 5 for the proof of Proposition 2.4.
Let
Recall from (2.7) that
As
![]() $\widehat \phi _0(Z), \widehat \rho _0(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, by (2.20), (2.21) we have
$\widehat \phi _0(Z), \widehat \rho _0(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, by (2.20), (2.21) we have
![]() $\phi _0\in {\mathscr X}_{\lambda _0}$
and
$\phi _0\in {\mathscr X}_{\lambda _0}$
and
![]() $\rho _0\in {\mathscr X}_{\mu _0}$
. Similarly, for
$\rho _0\in {\mathscr X}_{\mu _0}$
. Similarly, for
![]() $ a\in \mathbb {R}$
we have
$ a\in \mathbb {R}$
we have
![]() $\rho _0(t,r)^a=(T-t)^{a\mu _0}\widehat \rho _0(Z)^a $
and
$\rho _0(t,r)^a=(T-t)^{a\mu _0}\widehat \rho _0(Z)^a $
and
![]() $\widehat \rho _0(Z)^a\in C_{\text {e}}^\infty ([0,+\infty ))$
, then
$\widehat \rho _0(Z)^a\in C_{\text {e}}^\infty ([0,+\infty ))$
, then
![]() $\rho _0^a\in {\mathscr X}_{a\mu _0}$
. Moreover,
$\rho _0^a\in {\mathscr X}_{a\mu _0}$
. Moreover,
![]() $\widehat \phi _0(Z), \widehat \rho _0(Z)$
are real-valued, so are
$\widehat \phi _0(Z), \widehat \rho _0(Z)$
are real-valued, so are
![]() $\phi _0$
,
$\phi _0$
,
![]() $\rho _0$
.
$\rho _0$
.
Lemma 2.5. Assume that
![]() $n\in \mathbb {Z}_{\geq 1}$
,
$n\in \mathbb {Z}_{\geq 1}$
,
![]() $\phi _j\in {\mathscr X}_{\lambda _j}$
,
$\phi _j\in {\mathscr X}_{\lambda _j}$
,
![]() $\rho _j\in {\mathscr X}_{\mu _j}$
are are real-valued for
$\rho _j\in {\mathscr X}_{\mu _j}$
are are real-valued for
![]() $j\in \mathbb {Z}\cap [0, n-1]$
. Let
$j\in \mathbb {Z}\cap [0, n-1]$
. Let
![]() $F_n$
,
$F_n$
,
![]() $G_n$
be defined in (2.13), (2.14). Then there exist real-valued
$G_n$
be defined in (2.13), (2.14). Then there exist real-valued
![]() $\phi _n\in {\mathscr X}_{\lambda _n}$
and
$\phi _n\in {\mathscr X}_{\lambda _n}$
and
![]() $\rho _n\in {\mathscr X}_{\mu _n}$
such that (2.15) and (2.16) hold.
$\rho _n\in {\mathscr X}_{\mu _n}$
such that (2.15) and (2.16) hold.
Proof. By Lemma 2.3 (i) and the definition of
![]() $F_n$
, we have
$F_n$
, we have
![]() $F_n\in {\mathscr X}_{\mu _{n-1}-2}$
, where we have used the fact that
$F_n\in {\mathscr X}_{\mu _{n-1}-2}$
, where we have used the fact that
![]() $\mu _{n_1}+\cdots +\mu _{n_p}=\mu _{n-1}-2$
if
$\mu _{n_1}+\cdots +\mu _{n_p}=\mu _{n-1}-2$
if
![]() $n_1+\cdots +n_p=n$
and
$n_1+\cdots +n_p=n$
and
![]() $\mu _{n_1}+\lambda _{n_2}+\lambda _{n_3}-2=\mu _{n-1}-2$
if
$\mu _{n_1}+\lambda _{n_2}+\lambda _{n_3}-2=\mu _{n-1}-2$
if
![]() $n_1+n_2+n_3=n$
. Using Lemma 2.3 (i) and the definition of
$n_1+n_2+n_3=n$
. Using Lemma 2.3 (i) and the definition of
![]() $G_n$
, we have
$G_n$
, we have
![]() $G_n\in {\mathscr X}_{(2n-1)(\beta -1)-2\beta /(p-1)-2}$
, where we have used the fact that
$G_n\in {\mathscr X}_{(2n-1)(\beta -1)-2\beta /(p-1)-2}$
, where we have used the fact that
![]() $\mu _{n_1}+\lambda _{n_2}-2=(2n-1)(\beta -1)-2\beta /(p-1)-2$
if
$\mu _{n_1}+\lambda _{n_2}-2=(2n-1)(\beta -1)-2\beta /(p-1)-2$
if
![]() $n_1+n_2=n$
. It follows from Lemma 2.3 (i) that
$n_1+n_2=n$
. It follows from Lemma 2.3 (i) that
![]() $\rho _0G_n\in {\mathscr X}_{\mu _0+(2n-1)(\beta -1)-2\beta /(p-1)-2}={\mathscr X}_{2n(\beta -1)-\beta \ell -1}$
(recall that
$\rho _0G_n\in {\mathscr X}_{\mu _0+(2n-1)(\beta -1)-2\beta /(p-1)-2}={\mathscr X}_{2n(\beta -1)-\beta \ell -1}$
(recall that
![]() $\rho _0\in {\mathscr X}_{\mu _0}$
,
$\rho _0\in {\mathscr X}_{\mu _0}$
,
![]() $\ell =1+\frac {4}{p-1}$
). Since
$\ell =1+\frac {4}{p-1}$
). Since
![]() $\rho _0^{2-p}\in {\mathscr X}_{(2-p)\mu _0}$
,
$\rho _0^{2-p}\in {\mathscr X}_{(2-p)\mu _0}$
,
![]() $F_n\in {\mathscr X}_{\mu _{n-1}-2}$
, by Lemma 2.3 (i) we get
$F_n\in {\mathscr X}_{\mu _{n-1}-2}$
, by Lemma 2.3 (i) we get
![]() $\rho _0^{2-p}F_n\in {\mathscr X}_{\mu _{n-1}-2+(2-p)\mu _0}$
, then by
$\rho _0^{2-p}F_n\in {\mathscr X}_{\mu _{n-1}-2+(2-p)\mu _0}$
, then by
![]() $\phi _0\in {\mathscr X}_{\lambda _0}$
we have
$\phi _0\in {\mathscr X}_{\lambda _0}$
we have
Hence by the definition of
![]() $H_n$
in (2.18), we have
$H_n$
in (2.18), we have
![]() $H_n\in {\mathscr X}_{2n(\beta -1)-\beta \ell -1}={\mathscr X}_{\lambda _n-\gamma }$
(recall that
$H_n\in {\mathscr X}_{2n(\beta -1)-\beta \ell -1}={\mathscr X}_{\lambda _n-\gamma }$
(recall that
![]() $\gamma =\beta (\ell -1)+2$
). Moreover,
$\gamma =\beta (\ell -1)+2$
). Moreover,
![]() $F_n, G_n, H_n$
are real-valued.
$F_n, G_n, H_n$
are real-valued.
By Proposition 2.4, there exists (real-valued)
![]() $\phi _n\in {\mathscr X}_{\lambda _n}$
such that
$\phi _n\in {\mathscr X}_{\lambda _n}$
such that
![]() $\mathscr {L}(\phi _n)=H_n$
(otherwise take
$\mathscr {L}(\phi _n)=H_n$
(otherwise take
![]() $\operatorname {Re}\phi _n$
), then (2.18) holds. Let
$\operatorname {Re}\phi _n$
), then (2.18) holds. Let
![]() $\rho _n$
be defined by (2.17). Then
$\rho _n$
be defined by (2.17). Then
![]() $\rho _n$
is real-valued. Moreover, using (i) of Lemma 2.3,
$\rho _n$
is real-valued. Moreover, using (i) of Lemma 2.3,
![]() $\rho _0^{1-p}\in {\mathscr X}_{(1-p)\mu _0}$
,
$\rho _0^{1-p}\in {\mathscr X}_{(1-p)\mu _0}$
,
![]() $\rho _0^{2-p}\in {\mathscr X}_{(2-p)\mu _0}$
,
$\rho _0^{2-p}\in {\mathscr X}_{(2-p)\mu _0}$
,
![]() $F_n\in {\mathscr X}_{\mu _{n-1}-2}$
,
$F_n\in {\mathscr X}_{\mu _{n-1}-2}$
,
![]() $\phi _0\in {\mathscr X}_{\lambda _0}$
and
$\phi _0\in {\mathscr X}_{\lambda _0}$
and
![]() $\phi _n\in {\mathscr X}_{\lambda _n}$
, we have
$\phi _n\in {\mathscr X}_{\lambda _n}$
, we have
hence
![]() $\rho _n\in {\mathscr X}_{\mu _n}$
. Now (2.15) follows from (2.17), and (2.16) follows from (2.17) and (2.18).
$\rho _n\in {\mathscr X}_{\mu _n}$
. Now (2.15) follows from (2.17), and (2.16) follows from (2.17) and (2.18).
As
![]() $\phi _0\in {\mathscr X}_{\lambda _0}$
,
$\phi _0\in {\mathscr X}_{\lambda _0}$
,
![]() $\rho _0\in {\mathscr X}_{\mu _0}$
and
$\rho _0\in {\mathscr X}_{\mu _0}$
and
![]() $\phi _0$
,
$\phi _0$
,
![]() $\rho _0$
are real-valued, by Lemma 2.5 and the induction, we have the following result.
$\rho _0$
are real-valued, by Lemma 2.5 and the induction, we have the following result.
Proposition 2.6. Let
![]() $\phi _0$
,
$\phi _0$
,
![]() $\rho _0$
be defined in (2.7). For each
$\rho _0$
be defined in (2.7). For each
![]() $n\in \mathbb {Z}_{\geq 1}$
, there exist real-valued
$n\in \mathbb {Z}_{\geq 1}$
, there exist real-valued
![]() $\phi _n\in {\mathscr X}_{\lambda _n}$
and
$\phi _n\in {\mathscr X}_{\lambda _n}$
and
![]() $\rho _n\in {\mathscr X}_{\mu _n}$
such that (2.15) and (2.16) hold with
$\rho _n\in {\mathscr X}_{\mu _n}$
such that (2.15) and (2.16) hold with
![]() $F_n$
,
$F_n$
,
![]() $G_n$
defined in (2.13), (2.14). Hence, (2.5) holds for
$G_n$
defined in (2.13), (2.14). Hence, (2.5) holds for
![]() $n\in \mathbb {Z}_{\geq 0}$
.
$n\in \mathbb {Z}_{\geq 0}$
.
Now we briefly explain the ideas in the proof of Proposition 2.4. In the proof of Lemma 2.5, we see that we only need to use the surjectivity of
![]() $\mathscr {L}$
from
$\mathscr {L}$
from
![]() ${\mathscr X}_{\lambda }$
to
${\mathscr X}_{\lambda }$
to
![]() ${\mathscr X}_{\lambda -\gamma }$
for
${\mathscr X}_{\lambda -\gamma }$
for
![]() $\lambda \in \{\lambda _n:n\in \mathbb {Z}_{+}\}$
. However, this is not easy to solve the equation
$\lambda \in \{\lambda _n:n\in \mathbb {Z}_{+}\}$
. However, this is not easy to solve the equation
![]() $\mathscr {L} f=g$
for
$\mathscr {L} f=g$
for
![]() $f\in {\mathscr X}_{\lambda }$
even in the simplest case
$f\in {\mathscr X}_{\lambda }$
even in the simplest case
![]() $g=(T-t)^{\lambda -\gamma }\widehat g(Z)\in {\mathscr X}_{\lambda -\gamma }$
for some
$g=(T-t)^{\lambda -\gamma }\widehat g(Z)\in {\mathscr X}_{\lambda -\gamma }$
for some
![]() $\widehat g\in C_{\text {e}}^\infty ([0, +\infty ))$
(without the logarithm correction
$\widehat g\in C_{\text {e}}^\infty ([0, +\infty ))$
(without the logarithm correction
![]() $\tau ^j$
for
$\tau ^j$
for
![]() $j\in \mathbb {Z}_{+}$
), in which process we need to check a non-degenerate property (nonzero of Wronski defined in (5.32)) on the coefficients of
$j\in \mathbb {Z}_{+}$
), in which process we need to check a non-degenerate property (nonzero of Wronski defined in (5.32)) on the coefficients of
![]() $\mathscr {L}_\lambda $
(defined in (5.23)), and it is difficult to check that all
$\mathscr {L}_\lambda $
(defined in (5.23)), and it is difficult to check that all
![]() $\lambda _n$
satisfy the non-degenerate property, even for one
$\lambda _n$
satisfy the non-degenerate property, even for one
![]() $\lambda _{n_0}$
. To overcome this drawback, we solve the equation for all
$\lambda _{n_0}$
. To overcome this drawback, we solve the equation for all
![]() $\lambda \in \mathbb {C}$
, not merely for those
$\lambda \in \mathbb {C}$
, not merely for those
![]() $\lambda \in \{\lambda _n:n\in \mathbb {Z}_{+}\}$
. It turns out that the non-degenerate property holds for all but countably many
$\lambda \in \{\lambda _n:n\in \mathbb {Z}_{+}\}$
. It turns out that the non-degenerate property holds for all but countably many
![]() $\lambda \in \mathbb {C}$
(these
$\lambda \in \mathbb {C}$
(these
![]() $\lambda $
are “bad” in some sense) and the solution depends analytically on
$\lambda $
are “bad” in some sense) and the solution depends analytically on
![]() $\lambda $
. In this way, we can show that the solution
$\lambda $
. In this way, we can show that the solution
![]() $f=f(\cdot ;\lambda )$
is a meromorphic function on
$f=f(\cdot ;\lambda )$
is a meromorphic function on
![]() $\lambda $
. For those countably many
$\lambda $
. For those countably many
![]() $\lambda \in \mathbb {C}$
not satisfying the non-degenerate property, the analytic property of f allows us to introduce a logarithm correction to solve the corresponding equation for “bad”
$\lambda \in \mathbb {C}$
not satisfying the non-degenerate property, the analytic property of f allows us to introduce a logarithm correction to solve the corresponding equation for “bad”
![]() $\lambda $
. See Section 5 and Appendix B for details.
$\lambda $
. See Section 5 and Appendix B for details.
2.3 The approximate solution
Let
![]() $(\rho _n,\phi _n)\in {\mathscr X}_{\mu _n}\times {\mathscr X}_{\lambda _n} (n\in \mathbb {Z}_{\geq 0})$
be given by Proposition 2.6. We fix a bump function
$(\rho _n,\phi _n)\in {\mathscr X}_{\mu _n}\times {\mathscr X}_{\lambda _n} (n\in \mathbb {Z}_{\geq 0})$
be given by Proposition 2.6. We fix a bump function
![]() $\eta \in C_c^\infty (\mathbb {R};[0,1])$
such that
$\eta \in C_c^\infty (\mathbb {R};[0,1])$
such that
![]() $\eta |_{[0,1]}=1$
and
$\eta |_{[0,1]}=1$
and
![]() $\eta |_{[2,+\infty )}=0$
.
$\eta |_{[2,+\infty )}=0$
.
Proposition 2.7. Let
![]() $T=b=1$
. There exist
$T=b=1$
. There exist
![]() $N_0\in \mathbb {Z}_+$
,
$N_0\in \mathbb {Z}_+$
,
![]() $c_0\in (0,T)$
and a sequence
$c_0\in (0,T)$
and a sequence
![]() $\{T_n\}_{n\geq 0}$
such that
$\{T_n\}_{n\geq 0}$
such that
![]() $T_n=T$
for
$T_n=T$
for
![]() $0\leq n<N_0$
,
$0\leq n<N_0$
,
![]() $0<T_n\leq T_{n-1}/4$
for all
$0<T_n\leq T_{n-1}/4$
for all
![]() $n\geq N_0$
, and for functionsFootnote 6
$n\geq N_0$
, and for functionsFootnote 6
 $$ \begin{align} \rho_*(t,x)&:=\sum_{n=0}^\infty \eta\left(\frac{T-t}{T_n}\right)\rho_n(t,x)b^n,\quad \phi_*(t,x):=\sum_{n=0}^\infty \eta\left(\frac{T-t}{T_n}\right)\phi_n(t,x)b^n,\end{align} $$
$$ \begin{align} \rho_*(t,x)&:=\sum_{n=0}^\infty \eta\left(\frac{T-t}{T_n}\right)\rho_n(t,x)b^n,\quad \phi_*(t,x):=\sum_{n=0}^\infty \eta\left(\frac{T-t}{T_n}\right)\phi_n(t,x)b^n,\end{align} $$
defined on
![]() $(t,x)\in [0,T)\times \mathbb {R}^d$
we have
$(t,x)\in [0,T)\times \mathbb {R}^d$
we have
2.4 Solving nonlinear wave equation
Proposition 2.8. Assume that
![]() $T=1$
,
$T=1$
,
![]() $w_*\in C^\infty (\mathcal C),\Phi _*\in C^\infty (\mathcal C)$
satisfy
$w_*\in C^\infty (\mathcal C),\Phi _*\in C^\infty (\mathcal C)$
satisfy
for some
![]() $c_0\in (0,T)=(0,1)$
. Suppose that (2.27) holds for
$c_0\in (0,T)=(0,1)$
. Suppose that (2.27) holds for
![]() $E_*$
,
$E_*$
,
![]() $J_*$
defined as
$J_*$
defined as
Then there exist
![]() $c_1\in (0,c_0)$
and
$c_1\in (0,c_0)$
and
![]() $u\in C^2((T-c_1,T)\times \mathbb {R}^d;\mathbb {C})$
such that
$u\in C^2((T-c_1,T)\times \mathbb {R}^d;\mathbb {C})$
such that
![]() $u(t,\cdot ),\partial _tu(t,\cdot )\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
for
$u(t,\cdot ),\partial _tu(t,\cdot )\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
for
![]() $t\in (T-c_1,T),$
$t\in (T-c_1,T),$
![]() $\Box u=|u|^{p-1}u$
for
$\Box u=|u|^{p-1}u$
for
![]() $t\in (T-c_1,T), |x|\leq T-t$
, and
$t\in (T-c_1,T), |x|\leq T-t$
, and
for some constant
![]() $C>0$
.
$C>0$
.
In fact,
![]() $u=(1+h) w_*\mathrm e^{\text {i}\Phi _*}$
,
$u=(1+h) w_*\mathrm e^{\text {i}\Phi _*}$
,
![]() $h=O((T-t)^{\lambda })$
,
$h=O((T-t)^{\lambda })$
,
![]() $ \forall \ \lambda>0$
. To prove Proposition 2.8, it suffices to solve the equation for h (see (4.1)) and prove that h is small. In view of the singularity of (4.1) at blow-up time T, we take a sequence
$ \forall \ \lambda>0$
. To prove Proposition 2.8, it suffices to solve the equation for h (see (4.1)) and prove that h is small. In view of the singularity of (4.1) at blow-up time T, we take a sequence
![]() $\varepsilon _n\downarrow 0$
and then we solve (4.1) (with technical truncation) with zero initial data at
$\varepsilon _n\downarrow 0$
and then we solve (4.1) (with technical truncation) with zero initial data at
![]() $T-\varepsilon _n$
in a backward direction. We denote the solution for each
$T-\varepsilon _n$
in a backward direction. We denote the solution for each
![]() $n\in \mathbb {Z}_{+}$
by
$n\in \mathbb {Z}_{+}$
by
![]() $h_n$
. Using energy estimates and a bootstrap argument, we can show that
$h_n$
. Using energy estimates and a bootstrap argument, we can show that
![]() $h_n$
lives in an interval with a positive lower bound independent of
$h_n$
lives in an interval with a positive lower bound independent of
![]() $n\in \mathbb {Z}_{+}$
. Taking the limit
$n\in \mathbb {Z}_{+}$
. Taking the limit
![]() $n\to \infty $
we get a desired solution to (4.1) (in the light cone). See Section 4 for details.
$n\to \infty $
we get a desired solution to (4.1) (in the light cone). See Section 4 for details.
2.5 Proof of main results
Let’s begin with the proof of Theorem 1.1.
Proof of Theorem 1.1.
Let
![]() $T=b=1$
and
$T=b=1$
and
![]() $(\rho _*, \phi _*)\in C^\infty (\mathcal C)$
,
$(\rho _*, \phi _*)\in C^\infty (\mathcal C)$
,
![]() $c_0\in (0,T)$
be given by Proposition 2.7, and
$c_0\in (0,T)$
be given by Proposition 2.7, and
![]() $w_*=\rho _*$
,
$w_*=\rho _*$
,
![]() $\Phi _*=\phi _*$
. Then
$\Phi _*=\phi _*$
. Then
![]() $w_*, \Phi _*\in C^\infty (\mathcal C)$
, (2.28) is equivalent to (2.25), (2.29) is equivalent to (2.26). The definitions of
$w_*, \Phi _*\in C^\infty (\mathcal C)$
, (2.28) is equivalent to (2.25), (2.29) is equivalent to (2.26). The definitions of
![]() $E_*$
,
$E_*$
,
![]() $J_*$
in (2.24) and (2.30) are the same, and (2.27) also follows from Proposition 2.7. It follows from Proposition 2.8 that there exist
$J_*$
in (2.24) and (2.30) are the same, and (2.27) also follows from Proposition 2.7. It follows from Proposition 2.8 that there exist
![]() $c_1\in (0,c_0)\subset (0,1)$
,
$c_1\in (0,c_0)\subset (0,1)$
,
![]() $\widetilde u\in C^2((T-c_1,T)\times \mathbb {R}^d;\mathbb {C})$
such that
$\widetilde u\in C^2((T-c_1,T)\times \mathbb {R}^d;\mathbb {C})$
such that
![]() $\widetilde u(t,\cdot ),\partial _t\widetilde u(t,\cdot )\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
for
$\widetilde u(t,\cdot ),\partial _t\widetilde u(t,\cdot )\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
for
![]() $t\in (T-c_1,T),$
$t\in (T-c_1,T),$
![]() $\Box \widetilde u=|\widetilde u|^{p-1}\widetilde u$
for
$\Box \widetilde u=|\widetilde u|^{p-1}\widetilde u$
for
![]() $t\in (T-c_1,T), |x|\leq T-t$
, and
$t\in (T-c_1,T), |x|\leq T-t$
, and
for some constant
![]() $ C_1>0$
. Choose initial data
$ C_1>0$
. Choose initial data
![]() $u_0, u_1: \mathbb {R}^d\to \mathbb {C}$
such that
$u_0, u_1: \mathbb {R}^d\to \mathbb {C}$
such that
Then
![]() $u_0,u_1\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
. Moreover, let
$u_0,u_1\in C_c^{\infty }(\mathbb {R}^d;\mathbb {C})$
. Moreover, let
![]() $u_*(t,x)=\widetilde u(t+T-c_1/2,x)$
for
$u_*(t,x)=\widetilde u(t+T-c_1/2,x)$
for
![]() $t\in (-c_1/2,c_1/2)$
,
$t\in (-c_1/2,c_1/2)$
,
![]() $x\in \mathbb {R}^d$
then
$x\in \mathbb {R}^d$
then
![]() $u_*(0,x)=u_0(x)$
,
$u_*(0,x)=u_0(x)$
,
![]() $\partial _t u_*(0,x)=u_1(x)$
and
$\partial _t u_*(0,x)=u_1(x)$
and
![]() $\Box u_*=| u_*|^{p-1} u_*$
for
$\Box u_*=| u_*|^{p-1} u_*$
for
![]() $t\in [0,c_1/2), |x|\leq c_1/2-t$
. Suppose for contradiction that Theorem 1.1 fails for this initial data
$t\in [0,c_1/2), |x|\leq c_1/2-t$
. Suppose for contradiction that Theorem 1.1 fails for this initial data
![]() $u_0, u_1$
, then there exists a smooth function
$u_0, u_1$
, then there exists a smooth function
![]() $u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {C}$
such that
$u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {C}$
such that
![]() $\Box u=|u|^{p-1}u$
and
$\Box u=|u|^{p-1}u$
and
![]() $u(0, x)=u_0(x), \partial _tu(0, x)=u_1(x)$
for all
$u(0, x)=u_0(x), \partial _tu(0, x)=u_1(x)$
for all
![]() $x\in \mathbb {R}^d$
. Finite speed of propagation shows that
$x\in \mathbb {R}^d$
. Finite speed of propagation shows that
![]() $u= u_*$
in the region
$u= u_*$
in the region
![]() $\{(t,x)\in [0, c_1/2)\times \mathbb {R}^d: |x|\leq c_1/2-t\}$
. Hence by (2.32) we have
$\{(t,x)\in [0, c_1/2)\times \mathbb {R}^d: |x|\leq c_1/2-t\}$
. Hence by (2.32) we have
On the other hand, since u is smooth on
![]() $[0, +\infty )\times \mathbb {R}^d$
, we have
$[0, +\infty )\times \mathbb {R}^d$
, we have
![]() $|u(t,x)|\leq C$
for all
$|u(t,x)|\leq C$
for all
![]() $|x|\leq 2T$
and
$|x|\leq 2T$
and
![]() $t\in [0, c_1/2]$
, where
$t\in [0, c_1/2]$
, where
![]() $C>0$
is a constant. This reaches a contradiction.
$C>0$
is a constant. This reaches a contradiction.
The following result was proved in [Reference Shao, Wei and Zhang65] Theorem 2.2 and Lemma A.7 (
![]() $ \beta>\ell +1$
in [Reference Shao, Wei and Zhang65] is equivalent to
$ \beta>\ell +1$
in [Reference Shao, Wei and Zhang65] is equivalent to
![]() $\beta>1$
in this paper, recalling footnote 4).
$\beta>1$
in this paper, recalling footnote 4).
Lemma 2.9. There exist
![]() $\ell ^*(3)=\frac {76-4\sqrt {154}}{23}\in (\frac {8}{7},\frac {7}{6})$
and
$\ell ^*(3)=\frac {76-4\sqrt {154}}{23}\in (\frac {8}{7},\frac {7}{6})$
and
![]() $\ell _1(4)\in (5/4,4/3) $
such that if
$\ell _1(4)\in (5/4,4/3) $
such that if
Then there exists
![]() $\beta \in (1, k/(\ell +\sqrt \ell ))$
Footnote 7such that Assumption 1 holds for
$\beta \in (1, k/(\ell +\sqrt \ell ))$
Footnote 7such that Assumption 1 holds for
![]() $d=k+1$
.
$d=k+1$
.
Proof of Corollary 1.2.
Let
![]() $T=1$
. If
$T=1$
. If
![]() $d=4$
,
$d=4$
,
![]() $k=3$
,
$k=3$
,
![]() $p\geq 29$
,
$p\geq 29$
,
![]() $\ell =1+\frac {4}{p-1}$
, then
$\ell =1+\frac {4}{p-1}$
, then
![]() $1<\ell \leq 1+\frac {4}{29-1}=\frac {8}{7}<\ell ^*(3)$
. If
$1<\ell \leq 1+\frac {4}{29-1}=\frac {8}{7}<\ell ^*(3)$
. If
![]() $d=5$
,
$d=5$
,
![]() $k=4$
,
$k=4$
,
![]() $p\geq 17$
,
$p\geq 17$
,
![]() $\ell =1+\frac {4}{p-1}$
, then
$\ell =1+\frac {4}{p-1}$
, then
![]() $1<\ell \leq 1+\frac {4}{17-1}=\frac {5}{4}<\ell _1(4)$
. Thus, if
$1<\ell \leq 1+\frac {4}{17-1}=\frac {5}{4}<\ell _1(4)$
. Thus, if
![]() $d=4$
,
$d=4$
,
![]() $p\geq 29$
or
$p\geq 29$
or
![]() $d=5$
,
$d=5$
,
![]() $p\geq 17$
, then (2.33) holds for
$p\geq 17$
, then (2.33) holds for
![]() $k=d-1$
,
$k=d-1$
,
![]() $\ell =1+\frac {4}{p-1}$
and the result follows from Theorem 1.1.
$\ell =1+\frac {4}{p-1}$
and the result follows from Theorem 1.1.
The remaining case is
![]() $d>5$
,
$d>5$
,
![]() $p\geq 17$
. Then Assumption 1 holds with d replaced by
$p\geq 17$
. Then Assumption 1 holds with d replaced by
![]() $d'=5$
. By the proof of Theorem 1.1, there exists
$d'=5$
. By the proof of Theorem 1.1, there exists
![]() $c_1\in (0,1)$
,
$c_1\in (0,1)$
,
![]() $\widetilde u\in C^2((T-c_1,T)\times \mathbb {R}^5;\mathbb {C})$
such that
$\widetilde u\in C^2((T-c_1,T)\times \mathbb {R}^5;\mathbb {C})$
such that
![]() $\widetilde u(t,\cdot ),\partial _t\widetilde u(t,\cdot )\in C_c^{\infty }(\mathbb {R}^5;\mathbb {C})$
for
$\widetilde u(t,\cdot ),\partial _t\widetilde u(t,\cdot )\in C_c^{\infty }(\mathbb {R}^5;\mathbb {C})$
for
![]() $t\in (T-c_1,T),$
$t\in (T-c_1,T),$
![]() $\Box \widetilde u=|\widetilde u|^{p-1}\widetilde u$
for
$\Box \widetilde u=|\widetilde u|^{p-1}\widetilde u$
for
![]() $t\in (T-c_1,T), |x|\leq T-t$
, and (2.32) holds for some constant
$t\in (T-c_1,T), |x|\leq T-t$
, and (2.32) holds for some constant
![]() $ C_1>0$
. Choose initial data
$ C_1>0$
. Choose initial data
![]() $u_0, u_1: \mathbb {R}^d\to \mathbb {C}$
such that
$u_0, u_1: \mathbb {R}^d\to \mathbb {C}$
such that
for all
![]() $x=(x_1,\cdots ,x_d)\in \mathbb {R}^d$
. Then
$x=(x_1,\cdots ,x_d)\in \mathbb {R}^d$
. Then
![]() $u_0,u_1\in C_c^{\infty }(\mathbb {R}^d;\mathcal C)$
. Moreover, let
$u_0,u_1\in C_c^{\infty }(\mathbb {R}^d;\mathcal C)$
. Moreover, let
![]() $u_*(t,x)=\eta (|x|)\widetilde u(t+T-c_1/2,x_1,\cdots ,x_5)$
for
$u_*(t,x)=\eta (|x|)\widetilde u(t+T-c_1/2,x_1,\cdots ,x_5)$
for
![]() $t\in (-c_1/2,c_1/2)$
,
$t\in (-c_1/2,c_1/2)$
,
![]() $x=(x_1,\cdots ,x_d)\in \mathbb {R}^d$
. Then
$x=(x_1,\cdots ,x_d)\in \mathbb {R}^d$
. Then
![]() $u_*(0,x)=u_0(x)$
,
$u_*(0,x)=u_0(x)$
,
![]() $\partial _t u_*(0,x)=u_1(x)$
and
$\partial _t u_*(0,x)=u_1(x)$
and
![]() $\Box u_*=| u_*|^{p-1} u_*$
for
$\Box u_*=| u_*|^{p-1} u_*$
for
![]() $t\in [0,c_1/2), |x|\leq c_1/2-t$
. Here we used that
$t\in [0,c_1/2), |x|\leq c_1/2-t$
. Here we used that
![]() $\eta (|x|)=1 $
for
$\eta (|x|)=1 $
for
![]() $|x|\leq 1$
and that if
$|x|\leq 1$
and that if
![]() $t\in [0,c_1/2), |x|\leq c_1/2-t$
then
$t\in [0,c_1/2), |x|\leq c_1/2-t$
then
![]() $|x|\leq c_1/2<1$
. Suppose for contradiction that Corollary 1.2 fails for this kind of initial data
$|x|\leq c_1/2<1$
. Suppose for contradiction that Corollary 1.2 fails for this kind of initial data
![]() $u_0, u_1$
, then there exists a smooth function
$u_0, u_1$
, then there exists a smooth function
![]() $u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {C}$
such that
$u: [0,+\infty )\times \mathbb {R}^d\to \mathbb {C}$
such that
![]() $\Box u=|u|^{p-1}u$
and
$\Box u=|u|^{p-1}u$
and
![]() $u(0, x)=u_0(x), \partial _tu(0, x)=u_1(x)$
for all
$u(0, x)=u_0(x), \partial _tu(0, x)=u_1(x)$
for all
![]() $x\in \mathbb {R}^d$
, and we can get a contradiction as in the proof of Theorem 1.1.
$x\in \mathbb {R}^d$
, and we can get a contradiction as in the proof of Theorem 1.1.
3 The approximate solution
In this section, we prove Proposition 2.7, i.e., the construction of the approximate solution.
3.1 Construction of the approximate solution
Let
![]() $T=b=1$
and
$T=b=1$
and
![]() $(\rho _n,\phi _n)\in {\mathscr X}_{\mu _n}\times {\mathscr X}_{\lambda _n} (n\in \mathbb {Z}_{\geq 0})$
be given by Proposition 2.6. For
$(\rho _n,\phi _n)\in {\mathscr X}_{\mu _n}\times {\mathscr X}_{\lambda _n} (n\in \mathbb {Z}_{\geq 0})$
be given by Proposition 2.6. For
![]() $N\in \mathbb {Z}_+$
and
$N\in \mathbb {Z}_+$
and
![]() $(t,x)\in [0,T)\times \mathbb {R}^d$
, let
$(t,x)\in [0,T)\times \mathbb {R}^d$
, let
 $$ \begin{align*} &\rho_{(N)}(t,x):=\sum_{n=0}^{N}\rho_n(t,x) b^n,\qquad \phi_{(N)}(t,x):=\sum_{n=0}^N \phi_n(t,x)b^n,\\ &E_N:=\rho_{(N)}^{p}+\rho_{(N)}\partial^{\alpha}\phi_{(N)}\partial_{\alpha}\phi_{(N)}-b\Box\rho_{(N)},\\ &J_N:= 2\partial^{\alpha}\rho_{(N)}\partial_{\alpha}\phi_{(N)}+\rho_{(N)}\Box\phi_{(N)}. \end{align*} $$
$$ \begin{align*} &\rho_{(N)}(t,x):=\sum_{n=0}^{N}\rho_n(t,x) b^n,\qquad \phi_{(N)}(t,x):=\sum_{n=0}^N \phi_n(t,x)b^n,\\ &E_N:=\rho_{(N)}^{p}+\rho_{(N)}\partial^{\alpha}\phi_{(N)}\partial_{\alpha}\phi_{(N)}-b\Box\rho_{(N)},\\ &J_N:= 2\partial^{\alpha}\rho_{(N)}\partial_{\alpha}\phi_{(N)}+\rho_{(N)}\Box\phi_{(N)}. \end{align*} $$
It follows from (2.5) that
 $$ \begin{align*} E_{N}(t,x)=\sum_{n=N+1}^{pN}E_{N,n}(t,x) b^n,\qquad J_{N}(t,x)=\sum_{n=N+1}^{2N} J_{N,n}(t,x)b^n \end{align*} $$
$$ \begin{align*} E_{N}(t,x)=\sum_{n=N+1}^{pN}E_{N,n}(t,x) b^n,\qquad J_{N}(t,x)=\sum_{n=N+1}^{2N} J_{N,n}(t,x)b^n \end{align*} $$
with
 $$ \begin{align*} E_{N,n}&:=\sum_{\substack{n_1+\cdots+n_p=n\\ n_1, \cdots, n_p\leq N}}\rho_{n_1}\rho_{n_2}\cdots\rho_{n_p}+\sum_{\substack{n_1+n_2+n_3=n\\ n_1, n_2, n_3\leq N}}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3}-\Box\rho_{N}\mathbf{1}_{n=N+1},\\ J_{N,n}&:=2\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq N}}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}+\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq N}}\rho_{n_1}\Box\phi_{n_2}. \end{align*} $$
$$ \begin{align*} E_{N,n}&:=\sum_{\substack{n_1+\cdots+n_p=n\\ n_1, \cdots, n_p\leq N}}\rho_{n_1}\rho_{n_2}\cdots\rho_{n_p}+\sum_{\substack{n_1+n_2+n_3=n\\ n_1, n_2, n_3\leq N}}\rho_{n_1}\partial^\alpha\phi_{n_2}\partial_\alpha\phi_{n_3}-\Box\rho_{N}\mathbf{1}_{n=N+1},\\ J_{N,n}&:=2\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq N}}\partial^\alpha\rho_{n_1}\partial_\alpha\phi_{n_2}+\sum_{\substack{n_1+n_2=n\\ n_1, n_2\leq N}}\rho_{n_1}\Box\phi_{n_2}. \end{align*} $$
Then
![]() $E_{N,n}\in \mathscr {X}_{2n(\beta -1)-2p\beta /(p-1)}$
,
$E_{N,n}\in \mathscr {X}_{2n(\beta -1)-2p\beta /(p-1)}$
,
![]() $J_{N,n}\in \mathscr {X}_{(2n-1)(\beta -1)-2\beta /(p-1)-2}=\mathscr {X}_{(2n+1)(\beta -1)-2p\beta /(p-1)}$
. Here the proof is similar to Lemma 2.5.
$J_{N,n}\in \mathscr {X}_{(2n-1)(\beta -1)-2\beta /(p-1)-2}=\mathscr {X}_{(2n+1)(\beta -1)-2p\beta /(p-1)}$
. Here the proof is similar to Lemma 2.5.
Take
![]() $N_0\in \mathbb {Z}_+$
such that
$N_0\in \mathbb {Z}_+$
such that
![]() $2N_0(\beta -1)-2p\beta /(p-1)>3 $
. We fix such
$2N_0(\beta -1)-2p\beta /(p-1)>3 $
. We fix such
![]() $N_0$
(which is the same as the one in Proposition 2.7) and a non-decreasing sequence
$N_0$
(which is the same as the one in Proposition 2.7) and a non-decreasing sequence
![]() $\{k_N\}_{N\in \mathbb {Z}_{\geq N_0}}\subset \mathbb {Z}_+$
such that
$\{k_N\}_{N\in \mathbb {Z}_{\geq N_0}}\subset \mathbb {Z}_+$
such that
Then by Lemma 2.3 (ii), we have
![]() $(T-t)^{-2k_N}(D^jE_{N},D^jJ_{N})\in L^{\infty }(\mathcal C) $
for
$(T-t)^{-2k_N}(D^jE_{N},D^jJ_{N})\in L^{\infty }(\mathcal C) $
for
![]() $0\leq j\leq k_N$
,
$0\leq j\leq k_N$
,
![]() $N\geq N_0$
. Or equivalently, for each
$N\geq N_0$
. Or equivalently, for each
![]() $N\in \mathbb {Z}\cap [N_0,+\infty )$
there is a constant
$N\in \mathbb {Z}\cap [N_0,+\infty )$
there is a constant
![]() $A_N>0$
satisfying
$A_N>0$
satisfying
In fact for every fixed
![]() $n>d/2$
, we can use
$n>d/2$
, we can use
![]() $(\rho _{(N)},\phi _{(N)})$
as an approximate solution for N large enough (but fixed) to construct blow-up solutions of
$(\rho _{(N)},\phi _{(N)})$
as an approximate solution for N large enough (but fixed) to construct blow-up solutions of
![]() $H^n$
regularity. But to obtain a blow-up solution of
$H^n$
regularity. But to obtain a blow-up solution of
![]() $C^{\infty }$
initial data, we need to sum all the
$C^{\infty }$
initial data, we need to sum all the
![]() $(\rho _{n},\phi _{n}) $
with truncation as in (2.23). Note that for
$(\rho _{n},\phi _{n}) $
with truncation as in (2.23). Note that for
![]() $T-t\in [2T_{N+1},T_N] $
, we have
$T-t\in [2T_{N+1},T_N] $
, we have
![]() $E_{*}(t,x)=E_{N}(t,x) $
and
$E_{*}(t,x)=E_{N}(t,x) $
and
![]() $J_{*}(t,x)=J_{N}(t,x) $
. The following result extends the above estimate to the case
$J_{*}(t,x)=J_{N}(t,x) $
. The following result extends the above estimate to the case
![]() $T-t\in [T_{N+1},T_N]$
(with a possible different
$T-t\in [T_{N+1},T_N]$
(with a possible different
![]() $A_N$
).
$A_N$
).
Lemma 3.1. Let
![]() $T=b=1$
. Then there exists a sequence
$T=b=1$
. Then there exists a sequence
![]() $\{A_N\}_{N\in \mathbb {Z}_{\geq N_0-1}}$
such that for all
$\{A_N\}_{N\in \mathbb {Z}_{\geq N_0-1}}$
such that for all
![]() $\{T_n\}_{n\in \mathbb {Z}_{\geq 0}}$
satisfying
$\{T_n\}_{n\in \mathbb {Z}_{\geq 0}}$
satisfying
![]() $T_n=T$
for
$T_n=T$
for
![]() $0\leq n<N_0$
,
$0\leq n<N_0$
,
![]() $0<T_n\leq T_{n-1}/4$
for all
$0<T_n\leq T_{n-1}/4$
for all
![]() $n\geq N_0$
, if we define
$n\geq N_0$
, if we define
![]() $ \rho _*$
,
$ \rho _*$
,
![]() $ \phi _*$
,
$ \phi _*$
,
![]() $E_*$
,
$E_*$
,
![]() $J_*$
by (2.23), (2.24), then for
$J_*$
by (2.23), (2.24), then for
![]() $j\in \mathbb {Z}\cap [0,k_N]$
we have
$j\in \mathbb {Z}\cap [0,k_N]$
we have
Lemma 3.2. Let
![]() $T=b=1$
. There exists a sequence
$T=b=1$
. There exists a sequence
![]() $\{\widetilde {T}_n\}_{n\geq 0}$
satisfying
$\{\widetilde {T}_n\}_{n\geq 0}$
satisfying
such that for every sequence
![]() $\{{T}_n\}_{n\geq 0}$
with
$\{{T}_n\}_{n\geq 0}$
with
![]() ${T}_n=T$
for
${T}_n=T$
for
![]() $0\leq n<N_0$
and
$0\leq n<N_0$
and
![]() $0<{T}_n\leq \min (\widetilde T_n, T_{n-1}/4)$
for
$0<{T}_n\leq \min (\widetilde T_n, T_{n-1}/4)$
for
![]() $n\geq N_0$
, for
$n\geq N_0$
, for
![]() $ \rho _*$
,
$ \rho _*$
,
![]() $ \phi _*$
defined in (2.23), we have
$ \phi _*$
defined in (2.23), we have
Lemma 3.3. Let
![]() $T=1$
. There exists
$T=1$
. There exists
![]() $\widetilde {c}\in (0,T)$
such that
$\widetilde {c}\in (0,T)$
such that
Let’s first prove Proposition 2.7 by admitting Lemma 3.1
![]() $\sim $
Lemma 3.3 for the moment.
$\sim $
Lemma 3.3 for the moment.
Proof of Proposition 2.7.
Step 1. Construction of the sequence
![]() $\{{T}_n\}_{n\geq 0}$
. Let
$\{{T}_n\}_{n\geq 0}$
. Let
![]() $A_N>0$
be given by Lemma 3.1 and the sequence
$A_N>0$
be given by Lemma 3.1 and the sequence
![]() $\{\widetilde {T}_n\}_{n\geq 0}$
be given by Lemma 3.2. Let
$\{\widetilde {T}_n\}_{n\geq 0}$
be given by Lemma 3.2. Let
![]() ${T}_n=T$
for
${T}_n=T$
for
![]() $0\leq n<N_0$
and
$0\leq n<N_0$
and
![]() $T_n=\min (\widetilde {T}_n,A_n^{-1/k_n},T_{n-1}/4)$
for
$T_n=\min (\widetilde {T}_n,A_n^{-1/k_n},T_{n-1}/4)$
for
![]() $n\geq N_0$
. Then
$n\geq N_0$
. Then
![]() $0<{T}_n\leq {T}_{n-1}/4$
,
$0<{T}_n\leq {T}_{n-1}/4$
,
![]() $T_n\leq \widetilde {T}_n$
,
$T_n\leq \widetilde {T}_n$
,
![]() $A_n{T}_n^{k_n}\leq 1$
, for all
$A_n{T}_n^{k_n}\leq 1$
, for all
![]() $n\geq N_0$
, and
$n\geq N_0$
, and
![]() $\lim \limits _{N\to +\infty }T_N=0$
. So, there hold (3.2) for
$\lim \limits _{N\to +\infty }T_N=0$
. So, there hold (3.2) for
![]() $j\in \mathbb {Z}\cap [0,k_N]$
, (3.3), (3.4), and (3.5) with
$j\in \mathbb {Z}\cap [0,k_N]$
, (3.3), (3.4), and (3.5) with
![]() $\widetilde {c}\in (0,T)$
given by Lemma 3.3.
$\widetilde {c}\in (0,T)$
given by Lemma 3.3.
Step 2. Proof of (2.25). As
![]() $ \beta>1$
,
$ \beta>1$
,
![]() $(T-t)^{\beta -1}\in L^\infty (\mathcal C)$
, we get by (3.3) that
$(T-t)^{\beta -1}\in L^\infty (\mathcal C)$
, we get by (3.3) that
 $$ \begin{align*} &(T-t)^{\beta-1+j}D^j(\phi_*-\phi_0)=(T-t)^{\beta-1}(T-t)^{j}D^j(\phi_*-\phi_0)\in L^\infty(\mathcal C),\quad \forall\ j\in\mathbb{Z}_{\geq0},\\ &(T-t)^{\frac{2\beta}{p-1}+j}D^j(\rho_*-\rho_0)=(T-t)^{\beta-1}(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}D^j(\rho_*-\rho_0)\in L^\infty(\mathcal C),\quad \forall\ j\in\mathbb{Z}_{\geq0}, \end{align*} $$
$$ \begin{align*} &(T-t)^{\beta-1+j}D^j(\phi_*-\phi_0)=(T-t)^{\beta-1}(T-t)^{j}D^j(\phi_*-\phi_0)\in L^\infty(\mathcal C),\quad \forall\ j\in\mathbb{Z}_{\geq0},\\ &(T-t)^{\frac{2\beta}{p-1}+j}D^j(\rho_*-\rho_0)=(T-t)^{\beta-1}(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}D^j(\rho_*-\rho_0)\in L^\infty(\mathcal C),\quad \forall\ j\in\mathbb{Z}_{\geq0}, \end{align*} $$
which, along with with (3.4), implies (2.25).
Step 3. Proof of (2.26). By (3.3), we have (for some
![]() $ C_1>0$
)
$ C_1>0$
)
Now we take
![]() $c_0\in (0,T)$
such that
$c_0\in (0,T)$
such that
![]() $c_0+c_0^{\beta -1}C_1\leq \widetilde {c}$
, where the existence of such a
$c_0+c_0^{\beta -1}C_1\leq \widetilde {c}$
, where the existence of such a
![]() $c_0$
is ensured by
$c_0$
is ensured by
![]() $\beta>1$
and
$\beta>1$
and
![]() $ \widetilde {c}>0$
. Then for
$ \widetilde {c}>0$
. Then for
![]() $(t,x)\in \mathcal C, T-t<c_0$
, we get by (3.5) that (as
$(t,x)\in \mathcal C, T-t<c_0$
, we get by (3.5) that (as
![]() $T-t>0$
)
$T-t>0$
)
 $$ \begin{align*} (T-t)^{\beta}(\partial_t\phi_*-|D_x\phi_*|) \geq& (T-t)^{\beta}(\partial_t\phi_0-|D_x\phi_0|)-(T-t)^{\beta}(|\partial_t(\phi_*-\phi_0)|+|D_x(\phi_*-\phi_0)|)\\ \geq& \widetilde{c}-(T-t)^{\beta-1}C_1\geq \widetilde{c}-c_0^{\beta-1}C_1\geq c_0, \end{align*} $$
$$ \begin{align*} (T-t)^{\beta}(\partial_t\phi_*-|D_x\phi_*|) \geq& (T-t)^{\beta}(\partial_t\phi_0-|D_x\phi_0|)-(T-t)^{\beta}(|\partial_t(\phi_*-\phi_0)|+|D_x(\phi_*-\phi_0)|)\\ \geq& \widetilde{c}-(T-t)^{\beta-1}C_1\geq \widetilde{c}-c_0^{\beta-1}C_1\geq c_0, \end{align*} $$
and
Step 4. Proof of (2.27). We fix
![]() $ \lambda>0$
,
$ \lambda>0$
,
![]() $j\in \mathbb {Z}_{\geq 0} $
. As
$j\in \mathbb {Z}_{\geq 0} $
. As
![]() $\lim \limits _{N\to +\infty }k_N=+\infty $
, there exists
$\lim \limits _{N\to +\infty }k_N=+\infty $
, there exists
![]() $N_1\in \mathbb {Z}_{\geq N_0}$
such that
$N_1\in \mathbb {Z}_{\geq N_0}$
such that
![]() $ k_N>\lambda +j$
for
$ k_N>\lambda +j$
for
![]() $N\in \mathbb {Z}_{\geq N_1}$
. Then by (3.2) and
$N\in \mathbb {Z}_{\geq N_1}$
. Then by (3.2) and
![]() $A_n{T}_n^{k_n}\leq 1$
, we have
$A_n{T}_n^{k_n}\leq 1$
, we have
for
![]() $T-t\in [T_{N+1},T_N]$
,
$T-t\in [T_{N+1},T_N]$
,
![]() $(t,x)\in \mathcal C$
,
$(t,x)\in \mathcal C$
,
![]() $N\in \mathbb {Z}_{\geq N_1}$
. As
$N\in \mathbb {Z}_{\geq N_1}$
. As
![]() $\lim _{N\to +\infty }T_N=0$
, we have
$\lim _{N\to +\infty }T_N=0$
, we have
As
![]() $\rho _*, \phi _*\in C^\infty ([0, T)\times \mathbb {R}^d)$
(see footnote 6), we have
$\rho _*, \phi _*\in C^\infty ([0, T)\times \mathbb {R}^d)$
(see footnote 6), we have
![]() $E_*, J_*\in C^\infty ([0,T)\times \mathbb {R}^d)$
by (2.24). Thus, there exists a constant
$E_*, J_*\in C^\infty ([0,T)\times \mathbb {R}^d)$
by (2.24). Thus, there exists a constant
![]() $ C(j,T_{N_1})>0$
such that
$ C(j,T_{N_1})>0$
such that
Then (recall that
![]() $\mathcal C=\left \{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\right \}$
)
$\mathcal C=\left \{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\right \}$
)
3.2 Proof of main lemmas
We define the following auxiliary spaces
 $$ \begin{align} {\mathscr X}_{\lambda}^*&:=\left\{f(t,x,s)=\sum_{j=0}^n f_j(t,x)\eta_j\left(\frac{T-t}{s}\right): n\in\mathbb{Z}_{\geq 0}, f_j\in {\mathscr X}_{\lambda}, \eta_j\in\mathscr Y_0,\ \forall\ j\right\}. \end{align} $$
$$ \begin{align} {\mathscr X}_{\lambda}^*&:=\left\{f(t,x,s)=\sum_{j=0}^n f_j(t,x)\eta_j\left(\frac{T-t}{s}\right): n\in\mathbb{Z}_{\geq 0}, f_j\in {\mathscr X}_{\lambda}, \eta_j\in\mathscr Y_0,\ \forall\ j\right\}. \end{align} $$
Note that
![]() $ \eta \in \mathscr Y_0$
,
$ \eta \in \mathscr Y_0$
,
![]() $ \mathscr Y_0$
is a ring, and
$ \mathscr Y_0$
is a ring, and
![]() $ {\mathscr X}_{\lambda }^*$
is a linear vector space.
$ {\mathscr X}_{\lambda }^*$
is a linear vector space.
Lemma 3.4.
-
(i) Let
 $\lambda ,\mu \in \mathbb {C}$
,
$\lambda ,\mu \in \mathbb {C}$
,
 $f\in {\mathscr X}_\lambda ^*, g\in {\mathscr X}_\mu ^*$
. Then
$f\in {\mathscr X}_\lambda ^*, g\in {\mathscr X}_\mu ^*$
. Then
 $\Box f\in {\mathscr X}_{\lambda -2}^*$
,
$\Box f\in {\mathscr X}_{\lambda -2}^*$
,
 $fg\in {\mathscr X}_{\lambda +\mu }^*$
,
$fg\in {\mathscr X}_{\lambda +\mu }^*$
,
 $\partial ^\alpha f\partial _\alpha g\in {\mathscr X}_{\lambda +\mu -2}^*$
.
$\partial ^\alpha f\partial _\alpha g\in {\mathscr X}_{\lambda +\mu -2}^*$
. -
(ii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda>j+\mu $
. If
$\lambda>j+\mu $
. If
 $f\in {\mathscr X}_\lambda ^*$
, then
$f\in {\mathscr X}_\lambda ^*$
, then
 $(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C\times (0,1])$
.
$(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C\times (0,1])$
.
Here the operators
![]() $\Box $
,
$\Box $
,
![]() $\partial _\alpha $
and D are only acted on
$\partial _\alpha $
and D are only acted on
![]() $(t,x)$
and not on s.
$(t,x)$
and not on s.
Lemma 3.5.
-
(i) Let
 $\lambda ,\mu \in \mathbb {C}$
,
$\lambda ,\mu \in \mathbb {C}$
,
 $f\in {\mathscr X}_\lambda ^*, g\in {\mathscr X}_\mu ^*$
. Then
$f\in {\mathscr X}_\lambda ^*, g\in {\mathscr X}_\mu ^*$
. Then
 $\Delta f\in {\mathscr X}_{\lambda -2}^*$
,
$\Delta f\in {\mathscr X}_{\lambda -2}^*$
,
 $\partial _t f\in {\mathscr X}_{\lambda -1}^*$
,
$\partial _t f\in {\mathscr X}_{\lambda -1}^*$
,
 $fg\in {\mathscr X}_{\lambda +\mu }^*$
.
$fg\in {\mathscr X}_{\lambda +\mu }^*$
. -
(ii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda>j+\mu $
. If
$\lambda>j+\mu $
. If
 $f\in {\mathscr X}_\lambda ^*$
, then
$f\in {\mathscr X}_\lambda ^*$
, then
 $(T-t)^{-\mu }D_x^jf\in L^\infty (\mathcal C\times (0,1])$
.
$(T-t)^{-\mu }D_x^jf\in L^\infty (\mathcal C\times (0,1])$
.
Proof. By the definition of
![]() ${\mathscr X}_{\lambda }^*$
, it suffices to prove the result for
${\mathscr X}_{\lambda }^*$
, it suffices to prove the result for
![]() $f(t,x,s)=f_1(t,x)\eta _1\big (\frac {T-t}{s}\big )$
,
$f(t,x,s)=f_1(t,x)\eta _1\big (\frac {T-t}{s}\big )$
,
![]() $g(t,x,s)=g_1(t,x)\widetilde {\eta }_1\big (\frac {T-t}{s}\big )$
for some
$g(t,x,s)=g_1(t,x)\widetilde {\eta }_1\big (\frac {T-t}{s}\big )$
for some
![]() $f_1\in {\mathscr X}_{\lambda }, g_1\in {\mathscr X}_\mu $
,
$f_1\in {\mathscr X}_{\lambda }, g_1\in {\mathscr X}_\mu $
,
![]() $\eta _1,\widetilde {\eta }_1\in \mathscr Y_0$
.
$\eta _1,\widetilde {\eta }_1\in \mathscr Y_0$
.
In this case,
![]() $\Delta f(t,x,s)=\Delta f_1(t,x)\eta _1\big (\frac {T-t}{s}\big )$
. By Lemma 2.3 (i), we have
$\Delta f(t,x,s)=\Delta f_1(t,x)\eta _1\big (\frac {T-t}{s}\big )$
. By Lemma 2.3 (i), we have
![]() $\Delta f_1\in {\mathscr X}_{\lambda -2},$
thus
$\Delta f_1\in {\mathscr X}_{\lambda -2},$
thus
![]() $\Delta f\in {\mathscr X}_{\lambda -2}^*$
. We also have
$\Delta f\in {\mathscr X}_{\lambda -2}^*$
. We also have
with
![]() $ \eta _2(z)=-z\eta _1'(z)\in \mathscr Y_0$
(as
$ \eta _2(z)=-z\eta _1'(z)\in \mathscr Y_0$
(as
![]() $\eta _2=0 $
,
$\eta _2=0 $
,
![]() $\eta _2'=0 $
in
$\eta _2'=0 $
in
![]() $[0,1]\cup [2,+\infty ) $
). By Lemma 2.3 (i), we have
$[0,1]\cup [2,+\infty ) $
). By Lemma 2.3 (i), we have
![]() $\partial _t f_1\in {\mathscr X}_{\lambda -1}, (T-t)^{-1} \in {\mathscr X}_{-1}, (T-t)^{-1} f_1\in {\mathscr X}_{\lambda -1},$
thus
$\partial _t f_1\in {\mathscr X}_{\lambda -1}, (T-t)^{-1} \in {\mathscr X}_{-1}, (T-t)^{-1} f_1\in {\mathscr X}_{\lambda -1},$
thus
![]() $\partial _t f\in {\mathscr X}_{\lambda -1}^*$
.
$\partial _t f\in {\mathscr X}_{\lambda -1}^*$
.
In this case,
![]() $(fg)(t,x,s)=(f_1g_1)(t,x)(\eta _1\widetilde {\eta }_1)\big (\frac {T-t}{s}\big )$
. By Lemma 2.3 (i), we have
$(fg)(t,x,s)=(f_1g_1)(t,x)(\eta _1\widetilde {\eta }_1)\big (\frac {T-t}{s}\big )$
. By Lemma 2.3 (i), we have
![]() $f_1g_1\in {\mathscr X}_{\lambda +\mu },$
as
$f_1g_1\in {\mathscr X}_{\lambda +\mu },$
as
![]() $\mathscr Y_0$
is a ring we have
$\mathscr Y_0$
is a ring we have
![]() $\eta _1\widetilde {\eta }_1\in \mathscr Y_0$
, thus
$\eta _1\widetilde {\eta }_1\in \mathscr Y_0$
, thus
![]() $fg\in {\mathscr X}_{\lambda +\mu }^*$
. This completes the proof of (i).
$fg\in {\mathscr X}_{\lambda +\mu }^*$
. This completes the proof of (i).
Assume that
![]() $\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
$\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
![]() $\alpha _1+\cdots +\alpha _d=j$
, then we have
$\alpha _1+\cdots +\alpha _d=j$
, then we have
Then (ii) follows from Lemma 2.3 (ii) and
![]() $ \eta _{1}\in L^{\infty }([0,+\infty ))$
.
$ \eta _{1}\in L^{\infty }([0,+\infty ))$
.
Proof of Lemma 3.4.
By Lemma 3.5 (i), we have
![]() $fg\in {\mathscr X}_{\lambda +\mu }^*$
,
$fg\in {\mathscr X}_{\lambda +\mu }^*$
,
![]() $\Delta f\in {\mathscr X}_{\lambda -2}^*$
,
$\Delta f\in {\mathscr X}_{\lambda -2}^*$
,
![]() $\partial _t f\in {\mathscr X}_{\lambda -1}^*$
,
$\partial _t f\in {\mathscr X}_{\lambda -1}^*$
,
![]() $\partial _t^2 f\in {\mathscr X}_{\lambda -2}^*$
, thus
$\partial _t^2 f\in {\mathscr X}_{\lambda -2}^*$
, thus
![]() $\Box f=-\partial _t^2f+\Delta f\in {\mathscr X}_{\lambda -2}^*$
. As a consequence, we have
$\Box f=-\partial _t^2f+\Delta f\in {\mathscr X}_{\lambda -2}^*$
. As a consequence, we have
![]() $\Box (fg)\in \mathscr {X}_{(\lambda +\mu )-2}^* $
,
$\Box (fg)\in \mathscr {X}_{(\lambda +\mu )-2}^* $
,
![]() $(\Box f)g\in \mathscr {X}_{(\lambda -2)+\mu }^*$
,
$(\Box f)g\in \mathscr {X}_{(\lambda -2)+\mu }^*$
,
![]() $f\Box g\in \mathscr {X}_{\lambda +(\mu -2)}^* $
, hence
$f\Box g\in \mathscr {X}_{\lambda +(\mu -2)}^* $
, hence
![]() $\partial ^\alpha f\partial _\alpha g=(\Box (fg)-(\Box f)g-f\Box g)/2\in \mathscr {X}_{\lambda +\mu -2}^*$
.
$\partial ^\alpha f\partial _\alpha g=(\Box (fg)-(\Box f)g-f\Box g)/2\in \mathscr {X}_{\lambda +\mu -2}^*$
.
Assume that
![]() $\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
$\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
![]() $\alpha _0+\cdots +\alpha _d=j$
. By Lemma 3.5 (i), we have
$\alpha _0+\cdots +\alpha _d=j$
. By Lemma 3.5 (i), we have
![]() $\partial _t^{\alpha _0} f\in {\mathscr X}_{\lambda -\alpha _0}^*$
. Then by Lemma 3.5 (ii) and
$\partial _t^{\alpha _0} f\in {\mathscr X}_{\lambda -\alpha _0}^*$
. Then by Lemma 3.5 (ii) and
![]() $\lambda -\alpha _0>j'+\mu $
(here
$\lambda -\alpha _0>j'+\mu $
(here
![]() $j'=\alpha _1+\cdots +\alpha _d=j-\alpha _0$
), we have
$j'=\alpha _1+\cdots +\alpha _d=j-\alpha _0$
), we have
This completes the proof.
Now we are in a position to prove Lemma 3.1.
Proof of Lemma 3.1.
For
![]() $t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
and
$t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
and
![]() $N\in \mathbb {Z}_{\geq 0}$
, let
$N\in \mathbb {Z}_{\geq 0}$
, let
 $$ \begin{align*} &\rho_{N*}(t,x,s):=\sum_{n=0}^{N}\rho_n(t,x) b^n+\eta\left(\frac{T-t}{s}\right)\rho_{N+1}(t,x) b^{N+1},\\ & \phi_{N*}(t,x,s):=\sum_{n=0}^N \phi_n(t,x)b^n+\eta\left(\frac{T-t}{s}\right)\phi_{N+1}(t,x) b^{N+1}. \end{align*} $$
$$ \begin{align*} &\rho_{N*}(t,x,s):=\sum_{n=0}^{N}\rho_n(t,x) b^n+\eta\left(\frac{T-t}{s}\right)\rho_{N+1}(t,x) b^{N+1},\\ & \phi_{N*}(t,x,s):=\sum_{n=0}^N \phi_n(t,x)b^n+\eta\left(\frac{T-t}{s}\right)\phi_{N+1}(t,x) b^{N+1}. \end{align*} $$
Then by (2.23), for all
![]() $N\in \mathbb {Z}_{\geq N_0-1}$
, we have
$N\in \mathbb {Z}_{\geq N_0-1}$
, we have
Let
Then by (2.24), for all
![]() $N\in \mathbb {Z}_{\geq N_0-1}$
, we have
$N\in \mathbb {Z}_{\geq N_0-1}$
, we have
Now (3.2) is reduced to the proof of
For
![]() $t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
, let
$t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
, let
 $$ \begin{align*} &\rho_{N,n}(t,x,s):=\left\{\begin{array}{ll} \rho_{n}(t,x) & n\in\mathbb{Z}\cap[0,N] \\ \rho_{n}^*(t,x,s) &n=N+1 \\ 0 & n\in\mathbb{Z}_{\geq N+2} \end{array} \right.,\\ &\phi_{N,n}(t,x,s):=\left\{\begin{array}{ll} \phi_{n}(t,x) & n\in\mathbb{Z}\cap[0,N] \\ \phi_{n}^*(t,x,s) &n=N+1 \\ 0 & n\in\mathbb{Z}_{\geq N+2} \end{array} \right.. \end{align*} $$
$$ \begin{align*} &\rho_{N,n}(t,x,s):=\left\{\begin{array}{ll} \rho_{n}(t,x) & n\in\mathbb{Z}\cap[0,N] \\ \rho_{n}^*(t,x,s) &n=N+1 \\ 0 & n\in\mathbb{Z}_{\geq N+2} \end{array} \right.,\\ &\phi_{N,n}(t,x,s):=\left\{\begin{array}{ll} \phi_{n}(t,x) & n\in\mathbb{Z}\cap[0,N] \\ \phi_{n}^*(t,x,s) &n=N+1 \\ 0 & n\in\mathbb{Z}_{\geq N+2} \end{array} \right.. \end{align*} $$
where
As
![]() $\rho _n\in {\mathscr X}_{\mu _n}$
,
$\rho _n\in {\mathscr X}_{\mu _n}$
,
![]() $\phi _n\in {\mathscr X}_{\lambda _n}$
for all
$\phi _n\in {\mathscr X}_{\lambda _n}$
for all
![]() $n\in \mathbb {Z}_{\geq 0}$
, we have
$n\in \mathbb {Z}_{\geq 0}$
, we have
![]() $\rho _n^*,\rho _{N,n}\in {\mathscr X}_{\mu _n}^*$
,
$\rho _n^*,\rho _{N,n}\in {\mathscr X}_{\mu _n}^*$
,
![]() $\phi _n^*,\phi _{N,n}\in {\mathscr X}_{\lambda _n}^*$
for all
$\phi _n^*,\phi _{N,n}\in {\mathscr X}_{\lambda _n}^*$
for all
![]() $n,N\in \mathbb {Z}_{\geq 0}$
. For
$n,N\in \mathbb {Z}_{\geq 0}$
. For
![]() $t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
and
$t\in [0, T), x\in \mathbb {R}^d, s\in (0,+\infty )$
and
![]() $N\in \mathbb {Z}_{\geq 0}$
, we have
$N\in \mathbb {Z}_{\geq 0}$
, we have
 $$ \begin{align*} \rho_{N*}(t,x,s):=\sum_{n=0}^{N+1}\rho_{N,n}(t,x,s) b^n,\quad \phi_{N*}(t,x,s):=\sum_{n=0}^{N+1}\phi_{N,n}(t,x,s)b^n. \end{align*} $$
$$ \begin{align*} \rho_{N*}(t,x,s):=\sum_{n=0}^{N+1}\rho_{N,n}(t,x,s) b^n,\quad \phi_{N*}(t,x,s):=\sum_{n=0}^{N+1}\phi_{N,n}(t,x,s)b^n. \end{align*} $$
Then by (3.9), (2.5) and
![]() $\rho _{N,n}(t,x,s)=\rho _{n}(t,x) $
for
$\rho _{N,n}(t,x,s)=\rho _{n}(t,x) $
for
![]() $n\in \mathbb {Z}\cap [0,N] $
, we have
$n\in \mathbb {Z}\cap [0,N] $
, we have
 $$ \begin{align} E_{N*}(t,x,s)=\sum_{n=N+1}^{p(N+1)}E_{N,n}^*(t,x,s) b^n,\quad J_{N*}(t,x,s)=\sum_{n=N+1}^{2(N+1)} J_{N,n}^*(t,x,s)b^n, \end{align} $$
$$ \begin{align} E_{N*}(t,x,s)=\sum_{n=N+1}^{p(N+1)}E_{N,n}^*(t,x,s) b^n,\quad J_{N*}(t,x,s)=\sum_{n=N+1}^{2(N+1)} J_{N,n}^*(t,x,s)b^n, \end{align} $$
with (note that
![]() $\rho _{N,n}(t,x,s)=0$
for
$\rho _{N,n}(t,x,s)=0$
for
![]() $n\in \mathbb {Z}_{\geq N+2} $
)
$n\in \mathbb {Z}_{\geq N+2} $
)
 $$ \begin{align*} E_{N,n}^*&=\sum_{n_1+\cdots+n_p=n}\rho_{N,n_1}\rho_{N,n_2}\cdots\rho_{N,n_p}+\sum_{n_1+n_2+n_3=n}\rho_{N,n_1}\partial^\alpha\phi_{N,n_2}\partial_\alpha\phi_{N,n_3}-\Box\rho_{N,n-1},\\ J_{N,n}^*&=2\sum_{n_1+n_2=n}\partial^\alpha\rho_{N,n_1}\partial_\alpha\phi_{N,n_2}+\sum_{n_1+n_2=n}\rho_{N,n_1}\Box\phi_{N,n_2}. \end{align*} $$
$$ \begin{align*} E_{N,n}^*&=\sum_{n_1+\cdots+n_p=n}\rho_{N,n_1}\rho_{N,n_2}\cdots\rho_{N,n_p}+\sum_{n_1+n_2+n_3=n}\rho_{N,n_1}\partial^\alpha\phi_{N,n_2}\partial_\alpha\phi_{N,n_3}-\Box\rho_{N,n-1},\\ J_{N,n}^*&=2\sum_{n_1+n_2=n}\partial^\alpha\rho_{N,n_1}\partial_\alpha\phi_{N,n_2}+\sum_{n_1+n_2=n}\rho_{N,n_1}\Box\phi_{N,n_2}. \end{align*} $$
By Lemma 3.4 (i), we have
![]() $E_{N,n}^*\in \mathscr {X}_{2n(\beta -1)-2p\beta /(p-1)}^*$
,
$E_{N,n}^*\in \mathscr {X}_{2n(\beta -1)-2p\beta /(p-1)}^*$
,
![]() ${ J_{N,n}^*}\in \mathscr {X}_{(2n+1)(\beta -1)-2p\beta /(p-1)}^*$
, where we have used the facts that
${ J_{N,n}^*}\in \mathscr {X}_{(2n+1)(\beta -1)-2p\beta /(p-1)}^*$
, where we have used the facts that
![]() $\mu _{n_1}+\cdots +\mu _{n_p}=\mu _{n-1}-2$
if
$\mu _{n_1}+\cdots +\mu _{n_p}=\mu _{n-1}-2$
if
![]() $n_1+\cdots +n_p=n$
,
$n_1+\cdots +n_p=n$
,
![]() $\mu _{n_1}+\lambda _{n_2}+\lambda _{n_3}-2=\mu _{n-1}-2=2n(\beta -1)-2p\beta /(p-1)$
if
$\mu _{n_1}+\lambda _{n_2}+\lambda _{n_3}-2=\mu _{n-1}-2=2n(\beta -1)-2p\beta /(p-1)$
if
![]() $n_1+n_2+n_3=n$
and
$n_1+n_2+n_3=n$
and
![]() $\mu _{n_1}+\lambda _{n_2}-2=(2n-1)(\beta -1)-2\beta /(p-1)-2=(2n+1)(\beta -1)-2p\beta /(p-1)$
if
$\mu _{n_1}+\lambda _{n_2}-2=(2n-1)(\beta -1)-2\beta /(p-1)-2=(2n+1)(\beta -1)-2p\beta /(p-1)$
if
![]() $n_1+n_2=n$
.
$n_1+n_2=n$
.
If
![]() $n\geq N+1$
and
$n\geq N+1$
and
![]() $j\in \mathbb {Z}\cap [0,k_N]$
, then we get by (3.1) that
$j\in \mathbb {Z}\cap [0,k_N]$
, then we get by (3.1) that
 $$ \begin{align*} &(2n+1)(\beta-1)-2p\beta/(p-1)-j>2n(\beta-1)-2p\beta/(p-1)-j\\ &>2N(\beta-1)-2p\beta/(p-1)-j>3k_N-j\geq 2k_N. \end{align*} $$
$$ \begin{align*} &(2n+1)(\beta-1)-2p\beta/(p-1)-j>2n(\beta-1)-2p\beta/(p-1)-j\\ &>2N(\beta-1)-2p\beta/(p-1)-j>3k_N-j\geq 2k_N. \end{align*} $$
Thus, by Lemma 3.4 (ii), we have
![]() $(T-t)^{-2k_N}D^jE_{N,n}^*\in L^\infty (\mathcal C\times (0,1])$
for
$(T-t)^{-2k_N}D^jE_{N,n}^*\in L^\infty (\mathcal C\times (0,1])$
for
![]() $n\in \mathbb {Z}\cap [N+1,p(N+1)]$
, and
$n\in \mathbb {Z}\cap [N+1,p(N+1)]$
, and
![]() $(T-t)^{-2k_N}D^jJ_{N,n}^*\in L^\infty (\mathcal C\times (0,1])$
for
$(T-t)^{-2k_N}D^jJ_{N,n}^*\in L^\infty (\mathcal C\times (0,1])$
for
![]() $n\in \mathbb {Z}\cap [N+1,2(N+1)]$
, which along with (3.12) implies (3.10).
$n\in \mathbb {Z}\cap [N+1,2(N+1)]$
, which along with (3.12) implies (3.10).
Next we prove Lemma 3.2.
Proof of Lemma 3.2.
For
![]() $(t,x)\in [0,T)\times \mathbb {R}^d$
, and any fixed
$(t,x)\in [0,T)\times \mathbb {R}^d$
, and any fixed
![]() $\{T_n\}_{n\geq 0}$
satisfying
$\{T_n\}_{n\geq 0}$
satisfying
![]() $T_n=T$
for
$T_n=T$
for
![]() $0\leq n<N_0$
and
$0\leq n<N_0$
and
![]() $0<T_n\le T_{n-1}/4$
for
$0<T_n\le T_{n-1}/4$
for
![]() $n\ge N_0$
, we define
$n\ge N_0$
, we define
![]() $\rho _{*}, \phi _*$
by (2.23), then (
$\rho _{*}, \phi _*$
by (2.23), then (
![]() $ (\rho _n^*,\phi _n^*)$
is defined in (3.11))
$ (\rho _n^*,\phi _n^*)$
is defined in (3.11))
 $$ \begin{align*} &\rho_{*}(t,x)=\sum_{n=0}^{\infty}\rho_n^*(t,x,T_n) b^n, \quad \phi_{*}(t,x)=\sum_{n=0}^{\infty} \phi_n^*(t,x,T_n)b^n,\\ &(\rho_{*}-\rho_0)(t,x)=\sum_{n=1}^{\infty}\rho_n^*(t,x,T_n) b^n,\quad (\phi_{*}-\phi_{0})(t,x)=\sum_{n=1}^{\infty} \phi_n^*(t,x,T_n)b^n. \end{align*} $$
$$ \begin{align*} &\rho_{*}(t,x)=\sum_{n=0}^{\infty}\rho_n^*(t,x,T_n) b^n, \quad \phi_{*}(t,x)=\sum_{n=0}^{\infty} \phi_n^*(t,x,T_n)b^n,\\ &(\rho_{*}-\rho_0)(t,x)=\sum_{n=1}^{\infty}\rho_n^*(t,x,T_n) b^n,\quad (\phi_{*}-\phi_{0})(t,x)=\sum_{n=1}^{\infty} \phi_n^*(t,x,T_n)b^n. \end{align*} $$
Recall that
![]() $\rho _n^*\in {\mathscr X}_{\mu _n}^*$
and
$\rho _n^*\in {\mathscr X}_{\mu _n}^*$
and
![]() $\phi _n^*\in {\mathscr X}_{\lambda _n}^*$
for all
$\phi _n^*\in {\mathscr X}_{\lambda _n}^*$
for all
![]() $n\in \mathbb {Z}_{\geq 0}$
. By (2.22), we have
$n\in \mathbb {Z}_{\geq 0}$
. By (2.22), we have
 $$ \begin{align*} \lambda_n-j&=(2n-1)(\beta-1)-j>(n-1)(\beta-1)-j,\quad \forall\ n\in\mathbb{Z}_{+},\\ \mu_n-j&=2n(\beta-1)-\frac{2\beta}{p-1}-j>n(\beta-1)-\frac{2\beta}{p-1}-j,\quad \forall\ n\in\mathbb{Z}_{+}. \end{align*} $$
$$ \begin{align*} \lambda_n-j&=(2n-1)(\beta-1)-j>(n-1)(\beta-1)-j,\quad \forall\ n\in\mathbb{Z}_{+},\\ \mu_n-j&=2n(\beta-1)-\frac{2\beta}{p-1}-j>n(\beta-1)-\frac{2\beta}{p-1}-j,\quad \forall\ n\in\mathbb{Z}_{+}. \end{align*} $$
Thus, by Lemma 3.4 (ii), for any
![]() $j,n\in \mathbb {Z}_{\geq 0}$
, there exists a constant
$j,n\in \mathbb {Z}_{\geq 0}$
, there exists a constant
![]() $B_{n,j}>0$
, which is independent of the sequence
$B_{n,j}>0$
, which is independent of the sequence
![]() $\{T_n\}_{n\geq 0}$
, such that for all
$\{T_n\}_{n\geq 0}$
, such that for all
![]() $(t,x)\in \mathcal C$
, we have
$(t,x)\in \mathcal C$
, we have
which gives (recalling that
![]() $\eta ((T-t)/T_n))\neq 0$
implies
$\eta ((T-t)/T_n))\neq 0$
implies
![]() $T-t\leq 2T_n$
)
$T-t\leq 2T_n$
)
Let
![]() $\widetilde {T}_n:=T$
for
$\widetilde {T}_n:=T$
for
![]() $0\leq n<N_0$
and for
$0\leq n<N_0$
and for
![]() $n\geq N_0$
we let
$n\geq N_0$
we let
Now we prove that
![]() $\{\widetilde T_n\}_{n\ge 0}$
is a desired sequence for Lemma 3.2.
$\{\widetilde T_n\}_{n\ge 0}$
is a desired sequence for Lemma 3.2.
Let
![]() $\{T_n\}_{n\geq 0}$
be such that
$\{T_n\}_{n\geq 0}$
be such that
![]() $T_n=T$
for
$T_n=T$
for
![]() $0\le n<N_0$
and
$0\le n<N_0$
and
![]() $0<T_n\leq \min (\widetilde T_n, T_{n-1}/4)$
for
$0<T_n\leq \min (\widetilde T_n, T_{n-1}/4)$
for
![]() $n\geq N_0$
. Then
$n\geq N_0$
. Then
![]() $\widetilde {B}_{n}(2\widetilde {T}_n)^{(n-1)(\beta -1)}\leq 1 $
for
$\widetilde {B}_{n}(2\widetilde {T}_n)^{(n-1)(\beta -1)}\leq 1 $
for
![]() $n\geq N_0$
. Fix
$n\geq N_0$
. Fix
![]() $j\in \mathbb {Z}_{\geq 0}$
. For any
$j\in \mathbb {Z}_{\geq 0}$
. For any
![]() $(t,x)\in \mathcal C$
, we have
$(t,x)\in \mathcal C$
, we have
 $$ \begin{align*} &(T-t)^{j}|D^j(\phi_*-\phi_0)(t,x)|+(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}|D^j(\rho_*-\rho_0)(t,x)|\\&\quad\leq \sum_{n=1}^{\infty}\left((T-t)^{j}|D^j\phi_n^*(t,x,T_n)|+(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}|D^j\rho_n^*(t,x,T_n)|\right)\\&\quad\leq \sum_{n=1}^{\infty}B_{n,j}(2T_n)^{(n-1)(\beta-1)}\leq \sum_{n=1}^{\infty}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}\\&\quad\leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+\sum_{n=N_0+j}^{\infty}2^{-n}\widetilde{B}_{n}(2\widetilde{T}_n)^{(n-1)(\beta-1)}\\&\quad\leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+\sum_{n=N_0+j}^{\infty}2^{-n} \leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+1, \end{align*} $$
$$ \begin{align*} &(T-t)^{j}|D^j(\phi_*-\phi_0)(t,x)|+(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}|D^j(\rho_*-\rho_0)(t,x)|\\&\quad\leq \sum_{n=1}^{\infty}\left((T-t)^{j}|D^j\phi_n^*(t,x,T_n)|+(T-t)^{\frac{2\beta}{p-1}+j-\beta+1}|D^j\rho_n^*(t,x,T_n)|\right)\\&\quad\leq \sum_{n=1}^{\infty}B_{n,j}(2T_n)^{(n-1)(\beta-1)}\leq \sum_{n=1}^{\infty}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}\\&\quad\leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+\sum_{n=N_0+j}^{\infty}2^{-n}\widetilde{B}_{n}(2\widetilde{T}_n)^{(n-1)(\beta-1)}\\&\quad\leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+\sum_{n=N_0+j}^{\infty}2^{-n} \leq \sum_{n=1}^{N_0+j-1}B_{n,j}(2\widetilde{T}_n)^{(n-1)(\beta-1)}+1, \end{align*} $$
which implies (3.3), as the right hand side is a finite constant independent of
![]() $(t,x)\in \mathcal C$
.
$(t,x)\in \mathcal C$
.
Finally, we prove Lemma 3.3.
Proof of Lemma 3.3.
By (2.7), Lemma A.6 and Lemma 2.3 (iii), we obtain (3.4). It suffices to prove (3.5). By (2.7), we have
It follows from (2.12) that
 $$ \begin{align} \widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\quad Z\widehat\phi_0'(Z)+(\beta-1)\widehat\phi_0(Z)=\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}. \end{align} $$
$$ \begin{align} \widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\quad Z\widehat\phi_0'(Z)+(\beta-1)\widehat\phi_0(Z)=\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}. \end{align} $$
Hence,
 $$ \begin{align} (T-t)^\beta\left(\partial_t\phi_0-|D_x\phi_0|\right)=(\beta-1)\frac{\widehat\phi_0(Z)(1-{|v(Z)|})}{1-Zv(Z)}. \end{align} $$
$$ \begin{align} (T-t)^\beta\left(\partial_t\phi_0-|D_x\phi_0|\right)=(\beta-1)\frac{\widehat\phi_0(Z)(1-{|v(Z)|})}{1-Zv(Z)}. \end{align} $$
Since
![]() $\beta>1$
,
$\beta>1$
,
![]() $\widehat \phi _0(Z)>0, v(Z)\in (-1,1), Zv(Z)<1$
for all
$\widehat \phi _0(Z)>0, v(Z)\in (-1,1), Zv(Z)<1$
for all
![]() $Z\in [0,+\infty )$
and
$Z\in [0,+\infty )$
and
![]() $\widehat \phi _0, v\in C^\infty ([0,+\infty ))$
, we know that the right hand side of (3.14) is strictly positive and continuous. Thus, there exists
$\widehat \phi _0, v\in C^\infty ([0,+\infty ))$
, we know that the right hand side of (3.14) is strictly positive and continuous. Thus, there exists
![]() $\widetilde c_1\in (0, T)$
such that
$\widetilde c_1\in (0, T)$
such that
 $$ \begin{align*} \inf_{Z\in[0,2]}(\beta-1)\frac{\widehat\phi_0(Z)(1-{|v(Z)|})}{1-Zv(Z)}>\widetilde c_1. \end{align*} $$
$$ \begin{align*} \inf_{Z\in[0,2]}(\beta-1)\frac{\widehat\phi_0(Z)(1-{|v(Z)|})}{1-Zv(Z)}>\widetilde c_1. \end{align*} $$
On the other hand, by (2.7), we have
![]() $(T-t)^{2\beta /(p-1)}\rho _0=\widehat \rho _0(Z)$
. As
$(T-t)^{2\beta /(p-1)}\rho _0=\widehat \rho _0(Z)$
. As
![]() $\widehat \rho (Z)>0$
and
$\widehat \rho (Z)>0$
and
![]() $\widehat \rho \in C([0,+\infty ))$
, there exists
$\widehat \rho \in C([0,+\infty ))$
, there exists
![]() $\widetilde c_2\in (0, T)$
such that
$\widetilde c_2\in (0, T)$
such that
![]() $\inf _{Z\in [0,2]}\widehat \rho _0(Z)>\widetilde c_2$
. As a consequence, letting
$\inf _{Z\in [0,2]}\widehat \rho _0(Z)>\widetilde c_2$
. As a consequence, letting
![]() $\widetilde c:=\min (\widetilde c_1, \widetilde c_2)\in (0, T)$
, we have (3.5).
$\widetilde c:=\min (\widetilde c_1, \widetilde c_2)\in (0, T)$
, we have (3.5).
4 The blow-up solution of nonlinear wave equation
Fix
![]() $T=1$
. Recall that
$T=1$
. Recall that
![]() $\mathcal C=\{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\}$
. Let
$\mathcal C=\{(t,x)\in [0, T)\times \mathbb {R}^d: |x|<2(T-t)\}$
. Let
![]() $w_*\in C^\infty (\mathcal C;\mathbb {R}), \Psi _*\in C^\infty (\mathcal C;\mathbb {R})$
be such that both (2.28) and (2.29) hold; moreover, (2.27) also holds for
$w_*\in C^\infty (\mathcal C;\mathbb {R}), \Psi _*\in C^\infty (\mathcal C;\mathbb {R})$
be such that both (2.28) and (2.29) hold; moreover, (2.27) also holds for
![]() $E_*, J_*$
defined by (2.30).
$E_*, J_*$
defined by (2.30).
4.1 Derivation of the error equation
We construct a blow-up solution u to
![]() $\Box u=|u|^{p-1}u$
of the form
$\Box u=|u|^{p-1}u$
of the form
![]() $u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, where h is complex-valued. First of all, we deduce the equation for the error h.
$u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, where h is complex-valued. First of all, we deduce the equation for the error h.
Lemma 4.1. Assume that
![]() $u=(1+h)w_*\operatorname {e}^{\operatorname {i}\Phi _*}$
solves
$u=(1+h)w_*\operatorname {e}^{\operatorname {i}\Phi _*}$
solves
![]() $\Box u=|u|^{p-1}u$
. Then h satisfies
$\Box u=|u|^{p-1}u$
. Then h satisfies
where
![]() $h_{\operatorname {r}}=\mathrm {Re}\,h=(h+\bar h)/2$
and
$h_{\operatorname {r}}=\mathrm {Re}\,h=(h+\bar h)/2$
and
The converse is also true.
Proof. This is a brute force computation. If
![]() $u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, then for any
$u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, then for any
![]() $\alpha \in \mathbb {Z}\cap [0, d]$
, we have
$\alpha \in \mathbb {Z}\cap [0, d]$
, we have
Hence,

By the definition of
![]() $\varphi _1$
, we have
$\varphi _1$
, we have
![]() $1+(p-1)h_{\text {r}}+h+\varphi _1(h)=(1+h)|1+h|^{p-1}$
. Thus,
$1+(p-1)h_{\text {r}}+h+\varphi _1(h)=(1+h)|1+h|^{p-1}$
. Thus,
 $$ \begin{align*} &\Box u=|u|^{p-1}u\Longleftrightarrow\Box h+2\text{i}\partial^\alpha\Phi_*\partial_\alpha h+2\frac{\partial^\alpha w_*}{w_*}\partial_\alpha h+(1+h)\left(w_*^{p-1}+\frac{\text{i} J_*-E_*}{w_*}\right)\\ &\qquad\qquad\qquad\qquad\qquad\qquad =\big(1+(p-1)h_{\text{r}}+h+\varphi_1(h)\big)w_*^{p-1}\\ &\Longleftrightarrow\Box h+2\text{i}\partial^\alpha\Phi_*\partial_\alpha h+2\frac{\partial^\alpha w_*}{w_*}\partial_\alpha h-(p-1)w_*^{p-1}h_{\text{r}}=w_*^{p-1}\varphi_1(h)+\frac{E_*-\text{i} J_*}{w_*}(1+h). \end{align*} $$
$$ \begin{align*} &\Box u=|u|^{p-1}u\Longleftrightarrow\Box h+2\text{i}\partial^\alpha\Phi_*\partial_\alpha h+2\frac{\partial^\alpha w_*}{w_*}\partial_\alpha h+(1+h)\left(w_*^{p-1}+\frac{\text{i} J_*-E_*}{w_*}\right)\\ &\qquad\qquad\qquad\qquad\qquad\qquad =\big(1+(p-1)h_{\text{r}}+h+\varphi_1(h)\big)w_*^{p-1}\\ &\Longleftrightarrow\Box h+2\text{i}\partial^\alpha\Phi_*\partial_\alpha h+2\frac{\partial^\alpha w_*}{w_*}\partial_\alpha h-(p-1)w_*^{p-1}h_{\text{r}}=w_*^{p-1}\varphi_1(h)+\frac{E_*-\text{i} J_*}{w_*}(1+h). \end{align*} $$
This completes the proof of Lemma 4.1.
We fix a bump function
![]() $\xi \in C_c^\infty (\mathbb {R};[0,1])$
such that
$\xi \in C_c^\infty (\mathbb {R};[0,1])$
such that
![]() $\operatorname {supp}\xi \subset [-1,1]$
and
$\operatorname {supp}\xi \subset [-1,1]$
and
![]() $\xi _{[0,4/5]}=1$
. We define the vector fields
$\xi _{[0,4/5]}=1$
. We define the vector fields
![]() $X, Y$
byFootnote 8
$X, Y$
byFootnote 8
 $$ \begin{align} X(t,x):=D\Phi_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right),\quad Y(t,x):=\frac{Dw_*(t,x)}{w_*(t,x)}\xi\left(\frac{3|x|}{5(T-t)}\right) \end{align} $$
$$ \begin{align} X(t,x):=D\Phi_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right),\quad Y(t,x):=\frac{Dw_*(t,x)}{w_*(t,x)}\xi\left(\frac{3|x|}{5(T-t)}\right) \end{align} $$
for
![]() $(t, x)\in [0, T)\times \mathbb {R}^d$
. We also define the functions on
$(t, x)\in [0, T)\times \mathbb {R}^d$
. We also define the functions on
![]() $[0, T)\times \mathbb {R}^d$
by
$[0, T)\times \mathbb {R}^d$
by
 $$ \begin{align} V_*(t,x):=(p-1)w_*^{p-1}(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right),\quad N_*(t,x):=\frac{E_*-\operatorname{i}J_*}{w_*}(t,x)\xi\left(\frac{3|x|}{4(T-t)}\right). \end{align} $$
$$ \begin{align} V_*(t,x):=(p-1)w_*^{p-1}(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right),\quad N_*(t,x):=\frac{E_*-\operatorname{i}J_*}{w_*}(t,x)\xi\left(\frac{3|x|}{4(T-t)}\right). \end{align} $$
Then
![]() $X, Y\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {R}^{d+1})$
and
$X, Y\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {R}^{d+1})$
and
![]() $V_*\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {R}), N_*\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {C})$
. Moreover, we have
$V_*\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {R}), N_*\in C^\infty ([0, T)\times \mathbb {R}^d; \mathbb {C})$
. Moreover, we have
Let
![]() $c_0\in (0, T)$
satisfy (2.29). Let
$c_0\in (0, T)$
satisfy (2.29). Let
![]() $\mathcal C_1:=\{(t,x)\in [T-c_0, T)\times \mathbb {R}^d: |x|\leq 4(T-t)/3\}\subset \mathcal C$
. Using (2.28), (2.29) and (2.27), we have
$\mathcal C_1:=\{(t,x)\in [T-c_0, T)\times \mathbb {R}^d: |x|\leq 4(T-t)/3\}\subset \mathcal C$
. Using (2.28), (2.29) and (2.27), we have
![]() $X_0(t,x)>0, V_*(t,x)>0$
for all
$X_0(t,x)>0, V_*(t,x)>0$
for all
![]() $(t,x)\in \mathcal C_1$
. The following lemma gives more useful properties.
$(t,x)\in \mathcal C_1$
. The following lemma gives more useful properties.
Lemma 4.2. There exists a constant
![]() $M>0$
such that
$M>0$
such that
 $$ \begin{align} &(T-t)\left(\frac{|DX|}{X_0}+|Y|+\frac{|DV_*|}{V_*}\right)\leq M, \end{align} $$
$$ \begin{align} &(T-t)\left(\frac{|DX|}{X_0}+|Y|+\frac{|DV_*|}{V_*}\right)\leq M, \end{align} $$
on
![]() $\mathcal C_1$
. Moreover, for any
$\mathcal C_1$
. Moreover, for any
![]() $j\in \mathbb {Z}_{\geq 0}$
,
$j\in \mathbb {Z}_{\geq 0}$
,
For any
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda>0$
, there exists a constant
$\lambda>0$
, there exists a constant
![]() $M_{j,\lambda }>0$
such that
$M_{j,\lambda }>0$
such that
Proof. On
![]() $\mathcal C_1$
, we have
$\mathcal C_1$
, we have
By (2.28), we have
![]() $(T-t)^{\beta }X_0=(T-t)^{\beta }\partial _t\Phi _*\in L^\infty (\mathcal C_1)$
and
$(T-t)^{\beta }X_0=(T-t)^{\beta }\partial _t\Phi _*\in L^\infty (\mathcal C_1)$
and
![]() $(T-t)^{2\beta }V_*\in L^\infty (\mathcal C_1)$
. By (2.29), we have
$(T-t)^{2\beta }V_*\in L^\infty (\mathcal C_1)$
. By (2.29), we have
![]() $(T-t)^\beta X_0=(T-t)^{\beta }\partial _t\Phi _*\geq c_0, (T-t)^{2\beta }V_*=(p-1)(T-t)^{2\beta }w_*^{p-1}\geq (p-1)c_0^{p-1}$
on
$(T-t)^\beta X_0=(T-t)^{\beta }\partial _t\Phi _*\geq c_0, (T-t)^{2\beta }V_*=(p-1)(T-t)^{2\beta }w_*^{p-1}\geq (p-1)c_0^{p-1}$
on
![]() $\mathcal C_1$
. This proves (4.6).
$\mathcal C_1$
. This proves (4.6).
It follows from (2.28) that
![]() $(T-t)^{\beta +1}|DX|=(T-t)^{\beta +1}|D^2\Phi _*|\in L^\infty (\mathcal C_1)$
, hence by
$(T-t)^{\beta +1}|DX|=(T-t)^{\beta +1}|D^2\Phi _*|\in L^\infty (\mathcal C_1)$
, hence by
![]() $(T-t)^\beta X_0\geq c_0$
on
$(T-t)^\beta X_0\geq c_0$
on
![]() $\mathcal C_1$
, we have
$\mathcal C_1$
, we have
![]() $(T-t)|DX|/X_0\in L^\infty (\mathcal C_1)$
. Similarly, by using (2.28) and (4.6), we get
$(T-t)|DX|/X_0\in L^\infty (\mathcal C_1)$
. Similarly, by using (2.28) and (4.6), we get
![]() $(T-t)(|Y|+|DV_*|/V_*)\in L^\infty (\mathcal C_1)$
. This proves (4.5).
$(T-t)(|Y|+|DV_*|/V_*)\in L^\infty (\mathcal C_1)$
. This proves (4.5).
Next we prove (4.7) and (4.8). Recall the product rule: for smooth
![]() $f,g$
and
$f,g$
and
![]() $(\alpha _0, \alpha _1,\cdots , \alpha _d)\in \mathbb {Z}_{\geq 0}^{d+1}$
, we have (see [Reference Hardy24])
$(\alpha _0, \alpha _1,\cdots , \alpha _d)\in \mathbb {Z}_{\geq 0}^{d+1}$
, we have (see [Reference Hardy24])
 $$ \begin{align*} \frac{\partial^{\alpha_0+\alpha_1+\cdots+\alpha_d}}{\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}}(fg)= &\sum_{j=0}^{\alpha_0}\sum_{j_1=0}^{\alpha_1}\cdots\sum_{j_d=0}^{\alpha_d}\binom{\alpha_0}{j_0}\binom{\alpha_1}{j_1}\cdots\binom{\alpha_d}{j_d}\\ &\qquad\qquad\times\frac{\partial^{j_0+j_1+\cdots+j_d}f}{\partial_t^{j_0}\partial_{x_1}^{j_1}\cdots\partial_{x_d}^{j_d}}\cdot \frac{\partial^{\alpha_0-j_0+\alpha_1-j_1+\cdots+\alpha_d-j_d}g}{\partial_t^{\alpha_0-j_0}\partial_{x_1}^{\alpha_1-j_1}\cdots\partial_{x_d}^{\alpha_d-j_d}}. \end{align*} $$
$$ \begin{align*} \frac{\partial^{\alpha_0+\alpha_1+\cdots+\alpha_d}}{\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}}(fg)= &\sum_{j=0}^{\alpha_0}\sum_{j_1=0}^{\alpha_1}\cdots\sum_{j_d=0}^{\alpha_d}\binom{\alpha_0}{j_0}\binom{\alpha_1}{j_1}\cdots\binom{\alpha_d}{j_d}\\ &\qquad\qquad\times\frac{\partial^{j_0+j_1+\cdots+j_d}f}{\partial_t^{j_0}\partial_{x_1}^{j_1}\cdots\partial_{x_d}^{j_d}}\cdot \frac{\partial^{\alpha_0-j_0+\alpha_1-j_1+\cdots+\alpha_d-j_d}g}{\partial_t^{\alpha_0-j_0}\partial_{x_1}^{\alpha_1-j_1}\cdots\partial_{x_d}^{\alpha_d-j_d}}. \end{align*} $$
Hence,
 $$ \begin{align} |D^n(fg)|&\lesssim_n\sum_{j=0}^n|D^jf||D^{n-j}g|,\quad |D_x^n(fg)|\lesssim_n\sum_{j=0}^n|D_x^jf||D_x^{n-j}g|,\quad \forall\ n\in\mathbb{Z}_{\geq 0}, \end{align} $$
$$ \begin{align} |D^n(fg)|&\lesssim_n\sum_{j=0}^n|D^jf||D^{n-j}g|,\quad |D_x^n(fg)|\lesssim_n\sum_{j=0}^n|D_x^jf||D_x^{n-j}g|,\quad \forall\ n\in\mathbb{Z}_{\geq 0}, \end{align} $$
 $$ \begin{align} |gD^nf|&\lesssim_n |D^n(fg)|+\sum_{j=0}^{n-1}|D^jf||D^{n-j}g|,\quad\forall\ n\in\mathbb{Z}_{+}. \end{align} $$
$$ \begin{align} |gD^nf|&\lesssim_n |D^n(fg)|+\sum_{j=0}^{n-1}|D^jf||D^{n-j}g|,\quad\forall\ n\in\mathbb{Z}_{+}. \end{align} $$
As
![]() $X=D\Phi _*$
on
$X=D\Phi _*$
on
![]() $\mathcal C_1$
, we get by (2.28) that
$\mathcal C_1$
, we get by (2.28) that
Now we use the induction argument to prove that
By (4.5), we know that (4.13) holds for
![]() $j=0$
. Assume that (4.13) holds for all
$j=0$
. Assume that (4.13) holds for all
![]() $j\in \mathbb {Z}\cap [0, n-1]$
for some
$j\in \mathbb {Z}\cap [0, n-1]$
for some
![]() $n\in \mathbb {Z}_{+}$
. Note that
$n\in \mathbb {Z}_{+}$
. Note that
![]() $Dw_*=w_*Y$
on
$Dw_*=w_*Y$
on
![]() $\mathcal C_1$
, hence by (4.11) we have
$\mathcal C_1$
, hence by (4.11) we have
 $$\begin{align*}|w_*D^nY|\lesssim_n|D^n(Dw_*)|+\sum_{j=1}^{n}|D^jw_*||D^{n-j}Y|\quad\text{on}\quad \mathcal C_1.\end{align*}$$
$$\begin{align*}|w_*D^nY|\lesssim_n|D^n(Dw_*)|+\sum_{j=1}^{n}|D^jw_*||D^{n-j}Y|\quad\text{on}\quad \mathcal C_1.\end{align*}$$
Using (2.29), (2.28) and the induction assumption, we obtain
 $$ \begin{align*} &(T-t)^{1+n}|D^nY|\leq \frac1{c_0}(T-t)^{1+n+\frac{2\beta}{p-1}}|w_*D^nY|\\& \quad\lesssim_n (T-t)^{1+n+\frac{2\beta}{p-1}}|D^{1+n}w_*|+\sum_{j=1}^{n}(T-t)^{\frac{2\beta}{p-1}+j}|D^jw_*|(T-t)^{1+n-j}|D^{n-j}Y|\in L^\infty(\mathcal C_1). \end{align*} $$
$$ \begin{align*} &(T-t)^{1+n}|D^nY|\leq \frac1{c_0}(T-t)^{1+n+\frac{2\beta}{p-1}}|w_*D^nY|\\& \quad\lesssim_n (T-t)^{1+n+\frac{2\beta}{p-1}}|D^{1+n}w_*|+\sum_{j=1}^{n}(T-t)^{\frac{2\beta}{p-1}+j}|D^jw_*|(T-t)^{1+n-j}|D^{n-j}Y|\in L^\infty(\mathcal C_1). \end{align*} $$
This proves (4.13).
Now we prove that
By (2.28), we know that (4.14) holds for
![]() $m=1$
. We assume that (4.14) holds for
$m=1$
. We assume that (4.14) holds for
![]() $m-1$
, where
$m-1$
, where
![]() $m\in \mathbb {Z}\cap [2,+\infty )$
. By (4.10), for
$m\in \mathbb {Z}\cap [2,+\infty )$
. By (4.10), for
![]() $j\in \mathbb {Z}_{\geq 0}$
we have
$j\in \mathbb {Z}_{\geq 0}$
we have
 $$ \begin{align*} \left|D^j(w_*^m)\right|=\left|D^j(w_*^{m-1}w_*)\right|\lesssim_j \sum_{i=0}^j\left|D^i(w_*^{m-1})\right|\left|D^{j-i}w_*\right|, \end{align*} $$
$$ \begin{align*} \left|D^j(w_*^m)\right|=\left|D^j(w_*^{m-1}w_*)\right|\lesssim_j \sum_{i=0}^j\left|D^i(w_*^{m-1})\right|\left|D^{j-i}w_*\right|, \end{align*} $$
which gives
 $$ \begin{align*} (T-t)^{\frac{2\beta}{p-1}m+j}\left|D^j(w_*^m)\right|&\lesssim_j\sum_{i=0}^j(T-t)^{\frac{2\beta}{p-1}(m-1)+i}\left|D^i(w_*^{m-1})\right|(T-t)^{\frac{2\beta}{p-1}+j-i}\left|D^{j-i}w_*\right|\\ &\in L^\infty(\mathcal C_1). \end{align*} $$
$$ \begin{align*} (T-t)^{\frac{2\beta}{p-1}m+j}\left|D^j(w_*^m)\right|&\lesssim_j\sum_{i=0}^j(T-t)^{\frac{2\beta}{p-1}(m-1)+i}\left|D^i(w_*^{m-1})\right|(T-t)^{\frac{2\beta}{p-1}+j-i}\left|D^{j-i}w_*\right|\\ &\in L^\infty(\mathcal C_1). \end{align*} $$
By the induction argument, we have (4.14). Letting
![]() $m=p-1$
in (4.14), we get (using (4.9))
$m=p-1$
in (4.14), we get (using (4.9))
Finally, we estimate
![]() $N_*$
. Let
$N_*$
. Let
![]() $\widetilde \xi (t,x):=\xi (3|x|/(4(T-t)))$
. Then by Lemma 2.3 (iii), we have
$\widetilde \xi (t,x):=\xi (3|x|/(4(T-t)))$
. Then by Lemma 2.3 (iii), we have
![]() $(T-t)^{j}D^j\widetilde \xi \in L^\infty (\mathcal C)$
. Let
$(T-t)^{j}D^j\widetilde \xi \in L^\infty (\mathcal C)$
. Let
![]() $\widetilde N_*:=(E_*-\text {i} J_*)\widetilde \xi $
, then
$\widetilde N_*:=(E_*-\text {i} J_*)\widetilde \xi $
, then
![]() $N_*=\widetilde N_*/w_*$
. By (4.10), we have
$N_*=\widetilde N_*/w_*$
. By (4.10), we have
 $$ \begin{align*} \left|D^j\widetilde N_*\right|\lesssim_j \sum_{i=0}^j\left|D^i(E_*-\text{i} J_*)\right|\left|D^{j-i}\widetilde \xi\right|, \end{align*} $$
$$ \begin{align*} \left|D^j\widetilde N_*\right|\lesssim_j \sum_{i=0}^j\left|D^i(E_*-\text{i} J_*)\right|\left|D^{j-i}\widetilde \xi\right|, \end{align*} $$
hence by (2.27), for all
![]() $\lambda>0$
and
$\lambda>0$
and
![]() $j\in \mathbb {Z}_{\geq 0}$
we have
$j\in \mathbb {Z}_{\geq 0}$
we have
 $$ \begin{align} (T-t)^{-\lambda}\left|D^j\widetilde N_*\right|\lesssim_j\sum_{i=0}^j(T-t)^{-(\lambda+j-i)}\left|D^i(E_*-\text{i} J_*)\right|(T-t)^{j-i}\left|D^{j-i}\widetilde \xi\right|\in L^\infty(\mathcal C). \end{align} $$
$$ \begin{align} (T-t)^{-\lambda}\left|D^j\widetilde N_*\right|\lesssim_j\sum_{i=0}^j(T-t)^{-(\lambda+j-i)}\left|D^i(E_*-\text{i} J_*)\right|(T-t)^{j-i}\left|D^{j-i}\widetilde \xi\right|\in L^\infty(\mathcal C). \end{align} $$
Now we use the induction argument to prove that
For
![]() $j=0$
, (4.17) follows from (4.16) and (2.29). Assume that (4.17) holds for all
$j=0$
, (4.17) follows from (4.16) and (2.29). Assume that (4.17) holds for all
![]() $j\in \mathbb {Z}\cap [0, n-1]$
for some
$j\in \mathbb {Z}\cap [0, n-1]$
for some
![]() $n\in \mathbb {Z}_{+}$
. As
$n\in \mathbb {Z}_{+}$
. As
![]() $\widetilde N_*=w_*N_*$
, we get by (4.11) that
$\widetilde N_*=w_*N_*$
, we get by (4.11) that
 $$\begin{align*}\left|w_*D^nN_*\right|\lesssim_n \left|D^n\widetilde N_*\right|+\sum_{j=1}^{n}|D^jw_*||D^{n-j}N_*|\quad\text{on}\quad \mathcal C_1.\end{align*}$$
$$\begin{align*}\left|w_*D^nN_*\right|\lesssim_n \left|D^n\widetilde N_*\right|+\sum_{j=1}^{n}|D^jw_*||D^{n-j}N_*|\quad\text{on}\quad \mathcal C_1.\end{align*}$$
Using (2.27), (2.28), (2.29) and the induction assumption, for any
![]() $\lambda>0$
we obtain
$\lambda>0$
we obtain
 $$ \begin{align*} &(T-t)^{-\lambda}|D^nN_*|\leq \frac1{c_0}(T-t)^{-\lambda+\frac{2\beta}{p-1}}\left|w_*D^nN_*\right|\\ \lesssim_n& (T-t)^{\frac{2\beta}{p-1}}(T-t)^{-\lambda}\left|D^n\widetilde N_*\right|+\sum_{j=1}^{n}(T-t)^{\frac{2\beta}{p-1}+j}\left|D^jw_*\right|(T-t)^{-(\lambda+j)}\left|D^{n-j}N_*\right| \in L^\infty(\mathcal C_1). \end{align*} $$
$$ \begin{align*} &(T-t)^{-\lambda}|D^nN_*|\leq \frac1{c_0}(T-t)^{-\lambda+\frac{2\beta}{p-1}}\left|w_*D^nN_*\right|\\ \lesssim_n& (T-t)^{\frac{2\beta}{p-1}}(T-t)^{-\lambda}\left|D^n\widetilde N_*\right|+\sum_{j=1}^{n}(T-t)^{\frac{2\beta}{p-1}+j}\left|D^jw_*\right|(T-t)^{-(\lambda+j)}\left|D^{n-j}N_*\right| \in L^\infty(\mathcal C_1). \end{align*} $$
This proves (4.17) for
![]() $j=n$
. By induction, we have (4.17), which is equivalent to (4.8).
$j=n$
. By induction, we have (4.17), which is equivalent to (4.8).
Taking
![]() $\lambda =1$
in (4.8), we get
$\lambda =1$
in (4.8), we get
Therefore, (4.7) follows from (4.12), (4.13), (4.15) and (4.18).
4.2 Energy estimates for the linearized wave equation
Lemma 4.3. Let
![]() $T_*\in (0, c_0)$
and
$T_*\in (0, c_0)$
and
![]() $h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
$h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
![]() $t\in [T-T_*, T)$
. We define the linear operator
$t\in [T-T_*, T)$
. We define the linear operator
where
![]() $h_{\operatorname {r}}=(h+\bar h)/2$
and energy functionals
$h_{\operatorname {r}}=(h+\bar h)/2$
and energy functionals
Then there exist positive constants
![]() $M_1>1$
and
$M_1>1$
and
![]() $\{C_j\}_{j\in \mathbb {Z}_{\geq 0}}$
such that
$\{C_j\}_{j\in \mathbb {Z}_{\geq 0}}$
such that
 $$ \begin{align} \sqrt{E_j[h](t)}\leq C_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{\left\|D_x^i\mathcal Lh(s)\right\|_{L^2}}{(T-s)^{(j-i)\beta}}\mathrm ds,\quad\forall\ t\in[T-T_*, T),\ \forall\ j\in\mathbb{Z}_{\geq 0}. \end{align} $$
$$ \begin{align} \sqrt{E_j[h](t)}\leq C_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{\left\|D_x^i\mathcal Lh(s)\right\|_{L^2}}{(T-s)^{(j-i)\beta}}\mathrm ds,\quad\forall\ t\in[T-T_*, T),\ \forall\ j\in\mathbb{Z}_{\geq 0}. \end{align} $$
Proof. Let
![]() $T_*\in (0, c_0)$
and
$T_*\in (0, c_0)$
and
![]() $h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
$h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
We define the energy momentum tensor
![]() $T[h]$
by
$T[h]$
by
where we have used the Einstein’s convention in
![]() $\partial ^\alpha h\overline {\partial _\alpha h}$
. Then we have
$\partial ^\alpha h\overline {\partial _\alpha h}$
. Then we have
We define
Let’s first claim that there exists a constant
![]() $\widetilde c_0>0$
such that
$\widetilde c_0>0$
such that
and there exists a constant
![]() $C_*>0$
such that
$C_*>0$
such that
and moreover, for all
![]() $j\in \mathbb {Z}_{\geq 0}$
,
$j\in \mathbb {Z}_{\geq 0}$
,
 $$ \begin{align} \left\|D_x^j(\mathcal LD_xh-D_x\mathcal Lh)\right\|_{L_x^2}\lesssim_j \sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}\quad\forall\ t\in[T-T_*, T), \end{align} $$
$$ \begin{align} \left\|D_x^j(\mathcal LD_xh-D_x\mathcal Lh)\right\|_{L_x^2}\lesssim_j \sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}\quad\forall\ t\in[T-T_*, T), \end{align} $$
where the implicit constants only depend on
![]() $X, Y, V_*, N_*$
(and they are independent of h).
$X, Y, V_*, N_*$
(and they are independent of h).
Now we prove (4.22) by the induction argument. We first consider
![]() $j=0$
. For all
$j=0$
. For all
![]() $t\in [T-T_*, T)$
, by (4.24),
$t\in [T-T_*, T)$
, by (4.24),
![]() $X^0=-X_0$
,
$X^0=-X_0$
,
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
, (4.26) and (4.6), we have
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
, (4.26) and (4.6), we have
 $$ \begin{align} E_0[h](t)\leq \int_{\mathbb{R}^d}\frac{-P_0^X[h](t,x)}{\widetilde c_0X_0(t,x)}\,\mathrm dx\leq \frac{M}{\widetilde c_0}(T-t)^{\beta}\int_{\mathbb{R}^d}-P_0^X[h](t,x)\,\mathrm dx. \end{align} $$
$$ \begin{align} E_0[h](t)\leq \int_{\mathbb{R}^d}\frac{-P_0^X[h](t,x)}{\widetilde c_0X_0(t,x)}\,\mathrm dx\leq \frac{M}{\widetilde c_0}(T-t)^{\beta}\int_{\mathbb{R}^d}-P_0^X[h](t,x)\,\mathrm dx. \end{align} $$
Let
By the divergence theorem (recall that
![]() $\partial ^0=-\partial _0=-\partial _t$
), we get
$\partial ^0=-\partial _0=-\partial _t$
), we get
Using (4.27), (4.24) and Cauchy’s inequality, we obtain
 $$ \begin{align*} &\left|\frac{\mathrm d}{\mathrm dt}\widetilde E_0[h](t)\right|\leq C_*(T-t)^{-\beta}\left((T-t)^{-1}E_0[h](t)+\sqrt{E_0[h](t)}\|\mathcal Lh(t)\|_{L_x^2}\right),\quad\forall\ t\in[T-T_*, T). \end{align*} $$
$$ \begin{align*} &\left|\frac{\mathrm d}{\mathrm dt}\widetilde E_0[h](t)\right|\leq C_*(T-t)^{-\beta}\left((T-t)^{-1}E_0[h](t)+\sqrt{E_0[h](t)}\|\mathcal Lh(t)\|_{L_x^2}\right),\quad\forall\ t\in[T-T_*, T). \end{align*} $$
Hence, by (4.29) and
![]() $h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
, for all
$h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
, for all
![]() $t\in [T-T_*, T)$
we have
$t\in [T-T_*, T)$
we have
 $$ \begin{align*} E_0[h](t)&\leq \frac M{\widetilde c_0}(T-t)^\beta\widetilde E_0[h](t)\leq \frac M{\widetilde c_0}(T-t)^\beta\int_t^T\left|\frac{\mathrm d}{\mathrm dt}\widetilde E_0[h](s)\right|\,\mathrm ds\\&\leq \frac{MC_*}{\widetilde c_0}(T-t)^\beta\int_t^T(T-s)^{-\beta}\left((T-s)^{-1}E_0[h](s)+\sqrt{E_0[h](s)}\|\mathcal Lh(s)\|_{L_x^2}\right)\,\mathrm ds. \end{align*} $$
$$ \begin{align*} E_0[h](t)&\leq \frac M{\widetilde c_0}(T-t)^\beta\widetilde E_0[h](t)\leq \frac M{\widetilde c_0}(T-t)^\beta\int_t^T\left|\frac{\mathrm d}{\mathrm dt}\widetilde E_0[h](s)\right|\,\mathrm ds\\&\leq \frac{MC_*}{\widetilde c_0}(T-t)^\beta\int_t^T(T-s)^{-\beta}\left((T-s)^{-1}E_0[h](s)+\sqrt{E_0[h](s)}\|\mathcal Lh(s)\|_{L_x^2}\right)\,\mathrm ds. \end{align*} $$
By Grönwall’s lemma, we have
 $$ \begin{align*} \sqrt{E_0[h](t)}\leq\frac{MC_*}{2\widetilde c_0}\int_t^T\left(\frac{T-t}{T-s}\right)^{\frac{MC_0/\widetilde c_0+\beta}{2}}\|\mathcal Lh(s)\|_{L_x^2}\,\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align*} $$
$$ \begin{align*} \sqrt{E_0[h](t)}\leq\frac{MC_*}{2\widetilde c_0}\int_t^T\left(\frac{T-t}{T-s}\right)^{\frac{MC_0/\widetilde c_0+\beta}{2}}\|\mathcal Lh(s)\|_{L_x^2}\,\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align*} $$
Letting
![]() $M_1:=\frac {MC_*/\widetilde c_0+\beta }{2}>0$
, we know that (4.22) holds for
$M_1:=\frac {MC_*/\widetilde c_0+\beta }{2}>0$
, we know that (4.22) holds for
![]() $j=0$
.
$j=0$
.
Let
![]() $n\in \mathbb {Z}_{+}$
. We assume that (4.22) holds for all
$n\in \mathbb {Z}_{+}$
. We assume that (4.22) holds for all
![]() $j\in \mathbb {Z}\cap [0,n-1]$
. Then by (4.22) for
$j\in \mathbb {Z}\cap [0,n-1]$
. Then by (4.22) for
![]() $j=n-1$
and (4.28), for
$j=n-1$
and (4.28), for
![]() $t\in [T-T_*, T)$
we have (also using (4.20) and (4.21))
$t\in [T-T_*, T)$
we have (also using (4.20) and (4.21))
 $$ \begin{align*} &\sqrt{E_n[h](t)}=\sqrt{E_{n-1}[D_xh](t)}\lesssim_n\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^{n-1}\frac{\|D_x^j\mathcal LD_xh(s)\|_{L_x^2}}{(T-s)^{(n-1-j)\beta}}\,\mathrm ds\\&\quad\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^{n-1}\frac{\|D_x^{j+1}\mathcal Lh(s)\|_{L_x^2}+\sum_{i=0}^j(T-s)^{-\beta-1+i-j}\sqrt{E_i[h](s)}}{(T-s)^{(n-1-j)\beta}}\,\mathrm ds\\&\quad\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=1}^{n}\frac{\|D_x^{j}\mathcal Lh(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\,\mathrm ds+I_n(t), \end{align*} $$
$$ \begin{align*} &\sqrt{E_n[h](t)}=\sqrt{E_{n-1}[D_xh](t)}\lesssim_n\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^{n-1}\frac{\|D_x^j\mathcal LD_xh(s)\|_{L_x^2}}{(T-s)^{(n-1-j)\beta}}\,\mathrm ds\\&\quad\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^{n-1}\frac{\|D_x^{j+1}\mathcal Lh(s)\|_{L_x^2}+\sum_{i=0}^j(T-s)^{-\beta-1+i-j}\sqrt{E_i[h](s)}}{(T-s)^{(n-1-j)\beta}}\,\mathrm ds\\&\quad\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=1}^{n}\frac{\|D_x^{j}\mathcal Lh(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\,\mathrm ds+I_n(t), \end{align*} $$
where
 $$ \begin{align*} I_n(t):=\sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}(T-s)^{-1+i-j-(n-j)\beta}\sqrt{E_i[h](s)}\,\mathrm ds. \end{align*} $$
$$ \begin{align*} I_n(t):=\sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}(T-s)^{-1+i-j-(n-j)\beta}\sqrt{E_i[h](s)}\,\mathrm ds. \end{align*} $$
For
![]() $T-T_*\leq t<s<T$
,
$T-T_*\leq t<s<T$
,
![]() $j\geq i\geq 0$
we have
$j\geq i\geq 0$
we have
![]() $0<T-s<T_*<c_0<T=1$
and
$0<T-s<T_*<c_0<T=1$
and
![]() $ (T-s)^{-1+i-j-(n-j)\beta }=(T-s)^{-1-(n-i)\beta +(j-i)(\beta -1)}\leq (T-s)^{-1-(n-i)\beta }$
(as
$ (T-s)^{-1+i-j-(n-j)\beta }=(T-s)^{-1-(n-i)\beta +(j-i)(\beta -1)}\leq (T-s)^{-1-(n-i)\beta }$
(as
![]() $ \beta>1$
). Then
$ \beta>1$
). Then
 $$ \begin{align*} &I_n(t)\leq n\sum_{i=0}^{n-1}\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}(T-s)^{-1-(n-i)\beta}\sqrt{E_i[h](s)}\,\mathrm ds. \end{align*} $$
$$ \begin{align*} &I_n(t)\leq n\sum_{i=0}^{n-1}\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}(T-s)^{-1-(n-i)\beta}\sqrt{E_i[h](s)}\,\mathrm ds. \end{align*} $$
Using the induction assumption and Fubini’s theorem, we have
 $$ \begin{align*} I_n(t)&\lesssim_n\sum_{i=0}^{n-1}\sum_{j=0}^i \int_t^T\frac{\left((T-t)/(T-s)\right)^{M_1}}{(T-s)^{1+(n-i)\beta}} \int_s^T\left(\frac{T-s}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\,\mathrm d\tau\,\mathrm ds\\&=\sum_{i=0}^{n-1}\sum_{j=0}^i\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\int_t^\tau\frac{\mathrm ds}{(T-s)^{1+(n-i)\beta}}\,\mathrm d\tau\\&\leq\sum_{i=0}^{n-1}\sum_{j=0}^i\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\frac{1}{(T-\tau)^{(n-i)\beta}}\,\mathrm d\tau\\&\leq n\sum_{j=0}^{n-1}\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(n-j)\beta}}\,\mathrm d\tau. \end{align*} $$
$$ \begin{align*} I_n(t)&\lesssim_n\sum_{i=0}^{n-1}\sum_{j=0}^i \int_t^T\frac{\left((T-t)/(T-s)\right)^{M_1}}{(T-s)^{1+(n-i)\beta}} \int_s^T\left(\frac{T-s}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\,\mathrm d\tau\,\mathrm ds\\&=\sum_{i=0}^{n-1}\sum_{j=0}^i\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\int_t^\tau\frac{\mathrm ds}{(T-s)^{1+(n-i)\beta}}\,\mathrm d\tau\\&\leq\sum_{i=0}^{n-1}\sum_{j=0}^i\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(i-j)\beta}}\frac{1}{(T-\tau)^{(n-i)\beta}}\,\mathrm d\tau\\&\leq n\sum_{j=0}^{n-1}\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^j\mathcal Lh(\tau)\|_{L_x^2}}{(T-\tau)^{(n-j)\beta}}\,\mathrm d\tau. \end{align*} $$
Therefore, we obtain (4.22) for
![]() $j=n$
. This proves (4.22) for all
$j=n$
. This proves (4.22) for all
![]() $j\in \mathbb {Z}_{\geq 0}$
.
$j\in \mathbb {Z}_{\geq 0}$
.
Thus, it remains to prove (4.26), (4.27) and (4.28). We start with
 $$\begin{align*}P_0^X[h]=T[h]_{0\nu}X^\nu=T[h]_{00}X^0+\sum_{i=1}^dT[h]_{0i}X^i.\end{align*}$$
$$\begin{align*}P_0^X[h]=T[h]_{0\nu}X^\nu=T[h]_{00}X^0+\sum_{i=1}^dT[h]_{0i}X^i.\end{align*}$$
On
![]() $\mathcal C_*\subset \mathcal C_1$
, by (4.2), we have
$\mathcal C_*\subset \mathcal C_1$
, by (4.2), we have
![]() $-X^0=X_0=\partial _t\Phi _*$
and
$-X^0=X_0=\partial _t\Phi _*$
and
![]() $X^i=X_i=\partial _i\Phi _*$
for
$X^i=X_i=\partial _i\Phi _*$
for
![]() $i\in \mathbb {Z}\cap [1,d]$
, hence by (4.23) and Cauchy’s inequality,
$i\in \mathbb {Z}\cap [1,d]$
, hence by (4.23) and Cauchy’s inequality,
 $$ \begin{align*} \left|\sum_{i=1}^dT[h]_{0i}X^i\right|&\leq\sum_{i=1}^d|\partial_th||\partial_ih||\partial_i\Phi_*|\leq |\partial_th||D_xh||D_x\Phi_*|\leq \frac{|\partial_th|^2+|D_xh|^2}{2}|D_x\Phi_*|\\ &\leq T[h]_{00}|D_x\Phi_*|. \end{align*} $$
$$ \begin{align*} \left|\sum_{i=1}^dT[h]_{0i}X^i\right|&\leq\sum_{i=1}^d|\partial_th||\partial_ih||\partial_i\Phi_*|\leq |\partial_th||D_xh||D_x\Phi_*|\leq \frac{|\partial_th|^2+|D_xh|^2}{2}|D_x\Phi_*|\\ &\leq T[h]_{00}|D_x\Phi_*|. \end{align*} $$
On the other hand, by (2.28) and (2.29), there exists a constant
![]() $\widetilde c_0\in (0,1)$
such that
$\widetilde c_0\in (0,1)$
such that
Thus, we have
![]() $|X|\leq |\partial _t\Phi _*|+|D_x\Phi _*|\leq 2\partial _t\Phi _*=2X_0 $
and
$|X|\leq |\partial _t\Phi _*|+|D_x\Phi _*|\leq 2\partial _t\Phi _*=2X_0 $
and
 $$\begin{align*}\left|\sum_{i=1}^dT[h]_{0i}X^i\right|\leq T[h]_{00}|D_x\Phi_*|\leq T[h]_{00}(1-\widetilde c_0)\partial_t\Phi_*=T[h]_{00}(1-\widetilde c_0)X_0,\end{align*}$$
$$\begin{align*}\left|\sum_{i=1}^dT[h]_{0i}X^i\right|\leq T[h]_{00}|D_x\Phi_*|\leq T[h]_{00}(1-\widetilde c_0)\partial_t\Phi_*=T[h]_{00}(1-\widetilde c_0)X_0,\end{align*}$$
hence
This proves (4.26).
As for (4.27), we compute
 $$ \begin{align*} \partial^\mu T[h]_{\mu\nu}&=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)+\operatorname{Re}\left(\partial_\mu h\partial^\mu\overline{\partial_\nu h}\right)-\frac12\partial_\nu\left(\partial^\alpha h\overline{\partial_\alpha h}+V_*h_{\text{r}}^2\right)\\ &=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)+\frac12\operatorname{Re}\partial_\nu\left(\partial_\mu h\overline{\partial^\mu h}\right)-\frac12\partial_\nu\left(\partial^\alpha h\overline{\partial_\alpha h}\right)-h_{\text{r}}\partial_\nu h_{\text{r}}V_*-\frac12 h_{\text{r}}^2\partial_\nu V_*\\ &=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)-h_{\text{r}}\partial_\nu h_{\text{r}}V_*-\frac12 h_{\text{r}}^2\partial_\nu V_* \end{align*} $$
$$ \begin{align*} \partial^\mu T[h]_{\mu\nu}&=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)+\operatorname{Re}\left(\partial_\mu h\partial^\mu\overline{\partial_\nu h}\right)-\frac12\partial_\nu\left(\partial^\alpha h\overline{\partial_\alpha h}+V_*h_{\text{r}}^2\right)\\ &=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)+\frac12\operatorname{Re}\partial_\nu\left(\partial_\mu h\overline{\partial^\mu h}\right)-\frac12\partial_\nu\left(\partial^\alpha h\overline{\partial_\alpha h}\right)-h_{\text{r}}\partial_\nu h_{\text{r}}V_*-\frac12 h_{\text{r}}^2\partial_\nu V_*\\ &=\operatorname{Re}\left(\Box h\overline{\partial_\nu h}\right)-h_{\text{r}}\partial_\nu h_{\text{r}}V_*-\frac12 h_{\text{r}}^2\partial_\nu V_* \end{align*} $$
for
![]() $\nu \in \mathbb {Z}\cap [0,d]$
. Hence,
$\nu \in \mathbb {Z}\cap [0,d]$
. Hence,
 $$ \begin{align*} \partial^\mu P_\mu^X[h]&=T[h]_{\mu\nu}\partial^\mu X^\nu+(\partial^\mu T[h]_{\mu\nu})X^\nu\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box hX^\nu\overline{\partial_\nu h}\right)-h_{\text{r}}X^\nu\partial_\nu h_{\text r}V_*-\frac12h_{\text{r}}^2X^\nu\partial_\nu V_*\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box h\overline{Xh}\right)-V_*h_{\text r}Xh_{\text r}-\frac12h_{\text r}^2XV_*, \end{align*} $$
$$ \begin{align*} \partial^\mu P_\mu^X[h]&=T[h]_{\mu\nu}\partial^\mu X^\nu+(\partial^\mu T[h]_{\mu\nu})X^\nu\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box hX^\nu\overline{\partial_\nu h}\right)-h_{\text{r}}X^\nu\partial_\nu h_{\text r}V_*-\frac12h_{\text{r}}^2X^\nu\partial_\nu V_*\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box h\overline{Xh}\right)-V_*h_{\text r}Xh_{\text r}-\frac12h_{\text r}^2XV_*, \end{align*} $$
where we have used the fact that
![]() $X^\nu $
is real-valued for
$X^\nu $
is real-valued for
![]() $\nu \in \mathbb {Z}\cap [0, d]$
,
$\nu \in \mathbb {Z}\cap [0, d]$
,
![]() $Xh=X^\nu \partial _\nu h$
and we define
$Xh=X^\nu \partial _\nu h$
and we define
Hence, it follows from (4.19) that
 $$ \begin{align} \partial^\mu P_\mu^X[h]&=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box h\overline{Xh}\right)-V_*h_{\text r}Xh_{\text r}-\frac12h_{\text r}^2XV_*\nonumber\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}-\frac12h_{\text r}^2XV_*+\operatorname{Re}\left(\mathcal Lh\overline{Xh}\right)-2\operatorname{Re}\left(Yh\overline{Xh}\right). \end{align} $$
$$ \begin{align} \partial^\mu P_\mu^X[h]&=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}+\operatorname{Re}\left(\Box h\overline{Xh}\right)-V_*h_{\text r}Xh_{\text r}-\frac12h_{\text r}^2XV_*\nonumber\\ &=T[h]_{\mu\nu}(\pi^X)^{\mu\nu}-\frac12h_{\text r}^2XV_*+\operatorname{Re}\left(\mathcal Lh\overline{Xh}\right)-2\operatorname{Re}\left(Yh\overline{Xh}\right). \end{align} $$
By (4.23), we have
![]() $|T[h]_{\mu \nu }|\leq T[h]_{00}$
for all
$|T[h]_{\mu \nu }|\leq T[h]_{00}$
for all
![]() $\mu ,\nu \in \mathbb {Z}\cap [0,d]$
and
$\mu ,\nu \in \mathbb {Z}\cap [0,d]$
and
![]() $|Dh|^2\leq 2T[h]_{00}$
. Thus, by (4.31),
$|Dh|^2\leq 2T[h]_{00}$
. Thus, by (4.31),
![]() $|X|\leq 2 X_0$
, (4.5) and (4.6), on
$|X|\leq 2 X_0$
, (4.5) and (4.6), on
![]() $\mathcal C_*$
we have (note that
$\mathcal C_*$
we have (note that
![]() $|XV_*|\leq |X||DV_*|$
,
$|XV_*|\leq |X||DV_*|$
,
![]() $|Xh|\leq |X||Dh|$
,
$|Xh|\leq |X||Dh|$
,
![]() $|Yh|\leq |Y||Dh|$
, see footnote 8)
$|Yh|\leq |Y||Dh|$
, see footnote 8)
 $$ \begin{align*} \left|\partial^\mu P_\mu^X[h]\right|&\lesssim T[h]_{00}|DX|+T[h]_{00}X_0\frac{|DV_*|}{V_*}+|\mathcal Lh||X||Dh|+|Y||Dh||X||Dh|\\ &\lesssim T[h]_{00}(T-t)^{-1}X_0+|\mathcal Lh|X_0\sqrt{T[h]_{00}}\\ &\lesssim (T-t)^{-\beta}\left((T-t)^{-1}T[h]_{00}+\sqrt{T[h]_{00}}|\mathcal Lh|\right), \end{align*} $$
$$ \begin{align*} \left|\partial^\mu P_\mu^X[h]\right|&\lesssim T[h]_{00}|DX|+T[h]_{00}X_0\frac{|DV_*|}{V_*}+|\mathcal Lh||X||Dh|+|Y||Dh||X||Dh|\\ &\lesssim T[h]_{00}(T-t)^{-1}X_0+|\mathcal Lh|X_0\sqrt{T[h]_{00}}\\ &\lesssim (T-t)^{-\beta}\left((T-t)^{-1}T[h]_{00}+\sqrt{T[h]_{00}}|\mathcal Lh|\right), \end{align*} $$
which gives (4.27).
Finally, we prove (4.28). By (4.19), we have
Let
![]() $j\in \mathbb {Z}_{\geq 0}$
, by (4.10) and (4.7), for any
$j\in \mathbb {Z}_{\geq 0}$
, by (4.10) and (4.7), for any
![]() $t\in [T-T_*, T)$
we have
$t\in [T-T_*, T)$
we have
 $$ \begin{align*} \|D_x^j(D_xX^{\alpha}\partial_{\alpha}h)(t)\|_{L_x^2}&\lesssim_j\sum_{i=0}^j\|D_x^{j-i}D_xX(t)\|_{L_x^\infty}\|DD_x^{i}h(t)\|_{L_x^2}\\ &\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
$$ \begin{align*} \|D_x^j(D_xX^{\alpha}\partial_{\alpha}h)(t)\|_{L_x^2}&\lesssim_j\sum_{i=0}^j\|D_x^{j-i}D_xX(t)\|_{L_x^\infty}\|DD_x^{i}h(t)\|_{L_x^2}\\ &\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
Similarly, we have (recalling
![]() $\beta>1$
)
$\beta>1$
)
 $$ \begin{align*} \|D_x^j(D_xY^{\alpha}\partial_{\alpha}h)(t)\|_{L_x^2}\lesssim_j \sum_{i=0}^j(T-t)^{-2+i-j}\sqrt{E_i[h](t)}\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
$$ \begin{align*} \|D_x^j(D_xY^{\alpha}\partial_{\alpha}h)(t)\|_{L_x^2}\lesssim_j \sum_{i=0}^j(T-t)^{-2+i-j}\sqrt{E_i[h](t)}\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
 $$ \begin{align*} \|D_x^j(D_xV_*\cdot h_r)\|_{L_x^2}&\lesssim_j\sum_{i=0}^j\|D_x^{j-i+1}V_*/\sqrt{V_*}\|_{L_x^\infty}\|\sqrt{V_*}D_x^ih_{\text{r}}\|_{L_x^2}\\ &\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
$$ \begin{align*} \|D_x^j(D_xV_*\cdot h_r)\|_{L_x^2}&\lesssim_j\sum_{i=0}^j\|D_x^{j-i+1}V_*/\sqrt{V_*}\|_{L_x^\infty}\|\sqrt{V_*}D_x^ih_{\text{r}}\|_{L_x^2}\\ &\lesssim_j\sum_{i=0}^j(T-t)^{-\beta-1+i-j}\sqrt{E_i[h](t)}. \end{align*} $$
Hence, we get (4.28).
4.3 Solving the error equation
Lemma 4.4. There exists a constant
![]() $c_2\in (0, c_0)$
that depends only on
$c_2\in (0, c_0)$
that depends only on
![]() $X, Y, V_*, N_*$
such that for any
$X, Y, V_*, N_*$
such that for any
![]() $f\in C^\infty _c([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
satisfying
$f\in C^\infty _c([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
satisfying
![]() $|D_x^jf|\leq |D_x^j N_*|$
for all
$|D_x^jf|\leq |D_x^j N_*|$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
, there is a solution
$j\in \mathbb {Z}_{\geq 0}$
, there is a solution
![]() $h\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
to the error equation
$h\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
to the error equation
Moreover,
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
![]() $t\in [T-c_2, T)$
, and there exists a constant
$t\in [T-c_2, T)$
, and there exists a constant
![]() $C_{\Box }>0$
that depends only on
$C_{\Box }>0$
that depends only on
![]() $X, Y, V_*, N_*$
(
$X, Y, V_*, N_*$
(
![]() $C_{\Box }$
does not depend on f) such that
$C_{\Box }$
does not depend on f) such that
and for any
![]() $j\in \mathbb {Z}_{\geq 0}$
,
$j\in \mathbb {Z}_{\geq 0}$
,
![]() $\lambda>0$
, there exists a constant
$\lambda>0$
, there exists a constant
![]() $C_{j,\lambda }>0$
that depends only on
$C_{j,\lambda }>0$
that depends only on
![]() $X, Y, V_*, N_*$
(
$X, Y, V_*, N_*$
(
![]() $C_{j,\lambda }$
does not depend on f) such that
$C_{j,\lambda }$
does not depend on f) such that
The proof is based on the following lemma.
Lemma 4.5. Let
![]() $f\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
$f\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
![]() $|D_x^jf|\leq |D_x^jN_*|$
for all
$|D_x^jf|\leq |D_x^jN_*|$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
. Let
$j\in \mathbb {Z}_{\geq 0}$
. Let
![]() $T_*\in (0, c_0)$
. Assume that
$T_*\in (0, c_0)$
. Assume that
![]() $h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
solves (4.32) on
$h\in C_c^\infty ([T-T_*, T)\times \mathbb {R}^d;\mathbb {C})$
solves (4.32) on
![]() $[T-T_*, T)\times \mathbb {R}^d$
; moreover,
$[T-T_*, T)\times \mathbb {R}^d$
; moreover,
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
![]() $t\in [T-T_*, T)$
and
$t\in [T-T_*, T)$
and
Then there exists a constant
![]() $C_{\Box }>0$
that depends only on
$C_{\Box }>0$
that depends only on
![]() $X, Y, V_*, N_*$
(
$X, Y, V_*, N_*$
(
![]() $C_{\Box }$
does not depend on
$C_{\Box }$
does not depend on
![]() $f, T_*$
) such that
$f, T_*$
) such that
and for any
![]() $j\in \mathbb {Z}_{\geq 0}$
,
$j\in \mathbb {Z}_{\geq 0}$
,
![]() $\lambda>0$
, there exists a constant
$\lambda>0$
, there exists a constant
![]() $C_{j,\lambda }>0$
that depends only on
$C_{j,\lambda }>0$
that depends only on
![]() $X, Y, V_*, N_*$
(
$X, Y, V_*, N_*$
(
![]() $C_{j,\lambda }$
does not depend on
$C_{j,\lambda }$
does not depend on
![]() $f, T_*$
) such that
$f, T_*$
) such that
Now we present the proof of Lemma 4.4
Proof of Lemma 4.4.
Let
![]() $f\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
$f\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
be such that
![]() $|D_x^jf|\leq |D_x^jN_*|$
for all
$|D_x^jf|\leq |D_x^jN_*|$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
. We assume that
$j\in \mathbb {Z}_{\geq 0}$
. We assume that
![]() $\varepsilon \in (0, c_0)$
satisfies
$\varepsilon \in (0, c_0)$
satisfies
![]() $f(t,x)=0$
for all
$f(t,x)=0$
for all
![]() $(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
. By the standard local well-posedness theory (Theorem 6.4.11 in [Reference Hörmander25]), there is a unique local solution
$(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
. By the standard local well-posedness theory (Theorem 6.4.11 in [Reference Hörmander25]), there is a unique local solution
![]() $h\in C^\infty ((T-T_+, T)\times \mathbb {R}^d;\mathbb {C})$
to (4.32) with
$h\in C^\infty ((T-T_+, T)\times \mathbb {R}^d;\mathbb {C})$
to (4.32) with
![]() $(h, \partial _th)|_{t=T-\varepsilon /2}=(0, 0)$
, where
$(h, \partial _th)|_{t=T-\varepsilon /2}=(0, 0)$
, where
![]() $\varepsilon <T_+\leq c_0$
corresponds to the left life span of h; moreover, if
$\varepsilon <T_+\leq c_0$
corresponds to the left life span of h; moreover, if
![]() $T_+<c_0$
, then
$T_+<c_0$
, then
By the uniqueness and
![]() $f(t,x)=0$
for all
$f(t,x)=0$
for all
![]() $(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
, we have
$(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
, we have
![]() $h(t,x)=0$
for all
$h(t,x)=0$
for all
![]() $(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
. Moreover, by
$(t,x)\in (T-\varepsilon , T)\times \mathbb {R}^d$
. Moreover, by
![]() $|f|\leq |N_*|$
, (4.4) and the finite speed of propagation, we have
$|f|\leq |N_*|$
, (4.4) and the finite speed of propagation, we have
Let
![]() $c_2\in (0, c_0)$
be such that
$c_2\in (0, c_0)$
be such that
![]() $C_{0,2\beta }\cdot c_2<1/2$
, where
$C_{0,2\beta }\cdot c_2<1/2$
, where
![]() $C_{0,2\beta }>0$
is given by (4.37). Note that
$C_{0,2\beta }>0$
is given by (4.37). Note that
![]() $c_2$
is independent of f and
$c_2$
is independent of f and
![]() $T_*$
. We claim that
$T_*$
. We claim that
![]() $T_+\geq c_2$
. We assume in contrary that
$T_+\geq c_2$
. We assume in contrary that
![]() $\varepsilon <T_+<c_2$
. Let
$\varepsilon <T_+<c_2$
. Let
Then
![]() $(0,\varepsilon )\subset {\mathscr {E}}$
. Let
$(0,\varepsilon )\subset {\mathscr {E}}$
. Let
![]() $T_s:=\sup {\mathscr {E}}\in [\varepsilon , T_+]$
. By (4.38), we have
$T_s:=\sup {\mathscr {E}}\in [\varepsilon , T_+]$
. By (4.38), we have
![]() $T_s<T_+$
, hence
$T_s<T_+$
, hence
![]() $T_s\in \mathscr {E}$
and
$T_s\in \mathscr {E}$
and
![]() $T_s<T_+<c_2$
. By (4.37), we have
$T_s<T_+<c_2$
. By (4.37), we have
for all
![]() $t\in [T-T_s, T)\subset [T-c_2, T)$
. Thus, by the continuity we have
$t\in [T-T_s, T)\subset [T-c_2, T)$
. Thus, by the continuity we have
![]() $T_s+\delta \in \mathscr {E}$
for some
$T_s+\delta \in \mathscr {E}$
for some
![]() $\delta>0$
. This contradicts with
$\delta>0$
. This contradicts with
![]() $T_s=\sup \mathscr {E}$
. Therefore,
$T_s=\sup \mathscr {E}$
. Therefore,
![]() $T_+\geq c_2$
and
$T_+\geq c_2$
and
![]() $\|h(t,\cdot )\|_{L^\infty (\mathbb {R}^d)}\leq (T-t)^{2\beta -1}$
for all
$\|h(t,\cdot )\|_{L^\infty (\mathbb {R}^d)}\leq (T-t)^{2\beta -1}$
for all
![]() $t\in [T-c_2, T)$
. Now Lemma 4.5 (letting
$t\in [T-c_2, T)$
. Now Lemma 4.5 (letting
![]() $T_*=c_2$
) implies Lemma 4.4.
$T_*=c_2$
) implies Lemma 4.4.
Let’s complete the proof of Lemma 4.5.
Proof of Lemma 4.5.
Assume that h solves (4.32). Then (
![]() $\mathcal L$
is defined in (4.19))
$\mathcal L$
is defined in (4.19))
We claim that for each
![]() $j\in \mathbb {Z}_{\geq 0}$
, there exists a constant
$j\in \mathbb {Z}_{\geq 0}$
, there exists a constant
![]() $\widetilde C_j>0$
such that
$\widetilde C_j>0$
such that
 $$ \begin{align} \sqrt{E_j[h](t)}\leq \widetilde C_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{\left\|D_x^i f(s)\right\|_{L_x^2}}{(T-s)^{(j-i)\beta}}\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align} $$
$$ \begin{align} \sqrt{E_j[h](t)}\leq \widetilde C_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{\left\|D_x^i f(s)\right\|_{L_x^2}}{(T-s)^{(j-i)\beta}}\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align} $$
By the definition of
![]() $\varphi _1$
, we know that
$\varphi _1$
, we know that
![]() $\varphi _1$
is a polynomial on
$\varphi _1$
is a polynomial on
![]() $(h, \overline {h})$
of the form
$(h, \overline {h})$
of the form
![]() $\varphi _1=\sum _{2\leq i+j\leq p}c_{i,j}h^i\overline {h}^j$
, with
$\varphi _1=\sum _{2\leq i+j\leq p}c_{i,j}h^i\overline {h}^j$
, with
![]() $c_{i,j}\in \mathbb {R}$
, thus
$c_{i,j}\in \mathbb {R}$
, thus
Hence,
![]() $\operatorname {supp}_x\varphi _1(h)(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
$\operatorname {supp}_x\varphi _1(h)(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
for all
![]() $t\in [T-T_*, T)$
. For
$t\in [T-T_*, T)$
. For
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $t\in [T-T_*, T)$
, by (4.10), (4.7) and Poincaré’s inequality, we have
$t\in [T-T_*, T)$
, by (4.10), (4.7) and Poincaré’s inequality, we have
 $$ \begin{align*} \left\|D_x^j(V_*\varphi_1(h))(t)\right\|_{L_x^2}&\lesssim_j \sum_{i=0}^j\|D_x^{j-i}V_*(t)\|_{L_x^\infty}\|D_x^i\varphi_1(h)(t)\|_{L_x^2}\\ &\lesssim_j \sum_{i=0}^j(T-t)^{-(2\beta+j-i)}(T-t)^{j-i}\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\\&\lesssim_j (T-t)^{-2\beta}\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\end{align*} $$
$$ \begin{align*} \left\|D_x^j(V_*\varphi_1(h))(t)\right\|_{L_x^2}&\lesssim_j \sum_{i=0}^j\|D_x^{j-i}V_*(t)\|_{L_x^\infty}\|D_x^i\varphi_1(h)(t)\|_{L_x^2}\\ &\lesssim_j \sum_{i=0}^j(T-t)^{-(2\beta+j-i)}(T-t)^{j-i}\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\\&\lesssim_j (T-t)^{-2\beta}\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\end{align*} $$
Using the classical product estimate,
and (4.35), we infer
 $$ \begin{align*} &\|D_x^n(h^i\overline{h}^j)\|_{L_x^2}\lesssim_{n,i,j} \|h\|_{L_x^\infty}^{i+j-1}\|D_x^nh\|_{L_x^2},\quad\forall\ n,i,j\in\mathbb{Z}_{\geq0},\ i+j\geq2,\\ &\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\lesssim_j\left(\|h(t)\|_{L_x^\infty}+\|h(t)\|_{L_x^\infty}^{p-1}\right)\|D_x^jh(t)\|_{L_x^2}\lesssim_j (T-t)^{2\beta-1}\|D_x^jh(t)\|_{L_x^2}, \\ &\left\|D_x^j(V_*\varphi_1(h))(t)\right\|_{L_x^2}\lesssim_j(T-t)^{-2\beta} (T-t)^{2\beta-1}\|D_x^jh(t)\|_{L_x^2}=(T-t)^{-1}\|D_x^jh(t)\|_{L_x^2}; \end{align*} $$
$$ \begin{align*} &\|D_x^n(h^i\overline{h}^j)\|_{L_x^2}\lesssim_{n,i,j} \|h\|_{L_x^\infty}^{i+j-1}\|D_x^nh\|_{L_x^2},\quad\forall\ n,i,j\in\mathbb{Z}_{\geq0},\ i+j\geq2,\\ &\|D_x^j\varphi_1(h)(t)\|_{L_x^2}\lesssim_j\left(\|h(t)\|_{L_x^\infty}+\|h(t)\|_{L_x^\infty}^{p-1}\right)\|D_x^jh(t)\|_{L_x^2}\lesssim_j (T-t)^{2\beta-1}\|D_x^jh(t)\|_{L_x^2}, \\ &\left\|D_x^j(V_*\varphi_1(h))(t)\right\|_{L_x^2}\lesssim_j(T-t)^{-2\beta} (T-t)^{2\beta-1}\|D_x^jh(t)\|_{L_x^2}=(T-t)^{-1}\|D_x^jh(t)\|_{L_x^2}; \end{align*} $$
Similarly, by (4.7) and Poincaré’s inequality, we have
Therefore, for each
![]() $j\in \mathbb {Z}_{\geq 0}$
, there holds
$j\in \mathbb {Z}_{\geq 0}$
, there holds
By (4.43), (4.22), for any
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $t\in [T-T_*, T)$
we have
$t\in [T-T_*, T)$
we have
 $$ \begin{align} \sqrt{E_j[h](t)}&\lesssim_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{(T-s)^{-1}\|D_x^ih(s)\|_{L_x^2}+\|D_x^if(s)\|_{L_x^2}}{(T-s)^{(j-i)\beta}}\mathrm ds. \end{align} $$
$$ \begin{align} \sqrt{E_j[h](t)}&\lesssim_j\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{i=0}^j\frac{(T-s)^{-1}\|D_x^ih(s)\|_{L_x^2}+\|D_x^if(s)\|_{L_x^2}}{(T-s)^{(j-i)\beta}}\mathrm ds. \end{align} $$
It follows from Poincaré’s inequality and
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
that
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
that
Here we also used the definitions of
![]() $E_0$
and
$E_0$
and
![]() $E_j$
in (4.20) and (4.21). Next we use the induction argument to prove (4.40).
$E_j$
in (4.20) and (4.21). Next we use the induction argument to prove (4.40).
For
![]() $j=0$
, by (4.44) and (4.45), there exists a constant
$j=0$
, by (4.44) and (4.45), there exists a constant
![]() $C_0'>0$
satisfying
$C_0'>0$
satisfying
 $$ \begin{align*} \sqrt{E_0[h](t)}\leq C_0'\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\left(\sqrt{E_0[h](s)}+\|f(s)\|_{L_x^2}\right)\,\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align*} $$
$$ \begin{align*} \sqrt{E_0[h](t)}\leq C_0'\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\left(\sqrt{E_0[h](s)}+\|f(s)\|_{L_x^2}\right)\,\mathrm ds,\quad\forall\ t\in[T-T_*, T). \end{align*} $$
By Grönwall’s lemma, we get
 $$ \begin{align*} (T-t)^{-M_1}\sqrt{E_0[h](t)}&\leq C_0'\int_t^T(T-s)^{-M_1}\text{e}^{C_0'(s-t)}\|f(s)\|_{L_x^2}\,\mathrm ds\\ &\leq C_0'\text{e}^{C_0'T}\int_t^T(T-s)^{-M_1}\|f(s)\|_{L_x^2}\,\mathrm ds \end{align*} $$
$$ \begin{align*} (T-t)^{-M_1}\sqrt{E_0[h](t)}&\leq C_0'\int_t^T(T-s)^{-M_1}\text{e}^{C_0'(s-t)}\|f(s)\|_{L_x^2}\,\mathrm ds\\ &\leq C_0'\text{e}^{C_0'T}\int_t^T(T-s)^{-M_1}\|f(s)\|_{L_x^2}\,\mathrm ds \end{align*} $$
for all
![]() $t\in [T-T_*, T)$
. This proves (4.40) for
$t\in [T-T_*, T)$
. This proves (4.40) for
![]() $j=0$
. Let
$j=0$
. Let
![]() $n\in \mathbb {Z}_{+}$
, assume that (4.40) holds for
$n\in \mathbb {Z}_{+}$
, assume that (4.40) holds for
![]() $j\in \mathbb {Z}\cap [0, n-1]$
. By (4.20), (4.21) and
$j\in \mathbb {Z}\cap [0, n-1]$
. By (4.20), (4.21) and
![]() $ \beta>1$
, we have
$ \beta>1$
, we have
for
![]() $ s\in [T-T_*, T)$
. Then by (4.44) for
$ s\in [T-T_*, T)$
. Then by (4.44) for
![]() $j=n$
, (4.45) for
$j=n$
, (4.45) for
![]() $j=i<n$
, and the induction assumption, we have (as
$j=i<n$
, and the induction assumption, we have (as
![]() $0<T-t\leq T_*<c_0<1$
)
$0<T-t\leq T_*<c_0<1$
)
 $$ \begin{align*} \sqrt{E_n[h](t)}&\lesssim_n\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\left(\|D_x^nf(s)\|_{L_x^2}+\sum_{j=0}^{n-1}\frac{\sqrt{E_j[h](s)}+\|D_x^jf(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\right)\,\mathrm ds\\ &\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^n\frac{\|D_x^jf(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\,\mathrm ds+I_n(t), \end{align*} $$
$$ \begin{align*} \sqrt{E_n[h](t)}&\lesssim_n\int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\left(\|D_x^nf(s)\|_{L_x^2}+\sum_{j=0}^{n-1}\frac{\sqrt{E_j[h](s)}+\|D_x^jf(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\right)\,\mathrm ds\\ &\lesssim_n \int_t^T\left(\frac{T-t}{T-s}\right)^{M_1}\sum_{j=0}^n\frac{\|D_x^jf(s)\|_{L_x^2}}{(T-s)^{(n-j)\beta}}\,\mathrm ds+I_n(t), \end{align*} $$
where
 $$ \begin{align*} I_n(t)&:=\sum_{j=0}^{n-1}\int_t^T\frac{\big((T-t)/(T-s)\big)^{M_1}}{(T-s)^{(n-j)\beta}}\int_s^T\left(\frac{T-s}{T-\tau}\right)^{M_1}\sum_{i=0}^j\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\,\mathrm d\tau\,\mathrm ds\\ &=\sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\int_t^{\tau}\frac{\mathrm ds}{(T-s)^{(n-j)\beta}}\,\mathrm d\tau\\ &\leq \sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\frac{1}{(T-\tau)^{(n-j)\beta}}\,\mathrm d\tau\\ &\leq n\sum_{i=0}^{n-1}\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(n-i)\beta}}\,\mathrm d\tau.\end{align*} $$
$$ \begin{align*} I_n(t)&:=\sum_{j=0}^{n-1}\int_t^T\frac{\big((T-t)/(T-s)\big)^{M_1}}{(T-s)^{(n-j)\beta}}\int_s^T\left(\frac{T-s}{T-\tau}\right)^{M_1}\sum_{i=0}^j\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\,\mathrm d\tau\,\mathrm ds\\ &=\sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\int_t^{\tau}\frac{\mathrm ds}{(T-s)^{(n-j)\beta}}\,\mathrm d\tau\\ &\leq \sum_{j=0}^{n-1}\sum_{i=0}^j\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(j-i)\beta}}\frac{1}{(T-\tau)^{(n-j)\beta}}\,\mathrm d\tau\\ &\leq n\sum_{i=0}^{n-1}\int_t^T\left(\frac{T-t}{T-\tau}\right)^{M_1}\frac{\|D_x^if(\tau)\|_{L_x^2}}{(T-\tau)^{(n-i)\beta}}\,\mathrm d\tau.\end{align*} $$
Thus, (4.40) holds for
![]() $j=n$
. Therefore, by the the induction, (4.40) holds for all
$j=n$
. Therefore, by the the induction, (4.40) holds for all
![]() $j\in \mathbb {Z}_{\geq 0}$
.
$j\in \mathbb {Z}_{\geq 0}$
.
As
![]() $|D_x^jf|\leq |D_x^jN_*|$
for all
$|D_x^jf|\leq |D_x^jN_*|$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
, by (4.4) and (4.8), for all
$j\in \mathbb {Z}_{\geq 0}$
, by (4.4) and (4.8), for all
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda>0$
there exists a constant
$\lambda>0$
there exists a constant
![]() $\widetilde M_{j,\lambda }>0$
which is independent of f and
$\widetilde M_{j,\lambda }>0$
which is independent of f and
![]() $T_*$
such that
$T_*$
such that
![]() $\|D_x^jf(t)\|_{L^2}\leq \widetilde M_{j,\lambda }(T-t)^\lambda $
for all
$\|D_x^jf(t)\|_{L^2}\leq \widetilde M_{j,\lambda }(T-t)^\lambda $
for all
![]() $t\in [T-T_*, T)$
. Using (4.40), (4.21) and (4.45), for all
$t\in [T-T_*, T)$
. Using (4.40), (4.21) and (4.45), for all
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda>0$
there exists a constant
$\lambda>0$
there exists a constant
![]() $M_{j,\lambda }'>0$
independent of f and
$M_{j,\lambda }'>0$
independent of f and
![]() $T_*$
(depending on
$T_*$
(depending on
![]() $\widetilde M_{j,\lambda '} $
for some
$\widetilde M_{j,\lambda '} $
for some
![]() $\lambda '>\lambda $
) such that
$\lambda '>\lambda $
) such that
By Sobolev’s embedding theorem (
![]() $H_x^d(\mathbb {R}^d)\hookrightarrow L_x^\infty (\mathbb {R}^d)$
), we have (4.37). It remains to prove (4.36). By (4.41), (4.35), (4.32), (4.37), (4.7) (
$H_x^d(\mathbb {R}^d)\hookrightarrow L_x^\infty (\mathbb {R}^d)$
), we have (4.37). It remains to prove (4.36). By (4.41), (4.35), (4.32), (4.37), (4.7) (
![]() $j=0$
) and (4.8) (
$j=0$
) and (4.8) (
![]() $j=0, \lambda =1$
), we know that there there exist constants
$j=0, \lambda =1$
), we know that there there exist constants
![]() $ C_2'>0, C_3'>0$
such that
$ C_2'>0, C_3'>0$
such that
on
![]() $[T-T_*, T)\times \mathbb {R}^d$
, which implies (4.36).
$[T-T_*, T)\times \mathbb {R}^d$
, which implies (4.36).
4.4 Solving nonlinear wave equation
Proof of Proposition 2.8.
Let
![]() $\xi _1=1-\xi $
, then
$\xi _1=1-\xi $
, then
![]() $\xi _1|_{[0,4/5]}=0, \xi _1|_{[1,+\infty )}=1$
. Let
$\xi _1|_{[0,4/5]}=0, \xi _1|_{[1,+\infty )}=1$
. Let
Then for each
![]() $n\in \mathbb {Z}_{+}$
, we have
$n\in \mathbb {Z}_{+}$
, we have
![]() $f_n\in C^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
and
$f_n\in C^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
and
![]() $\operatorname {supp}f_n\subset \{(t,x)\in [T-c_0, T-4\varepsilon _n/5]\times \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
, hence
$\operatorname {supp}f_n\subset \{(t,x)\in [T-c_0, T-4\varepsilon _n/5]\times \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
, hence
![]() $f_n\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
; as
$f_n\in C_c^\infty ([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
; as
![]() $f_n$
equals to
$f_n$
equals to
![]() $N_*$
multiplied by a function in t that takes values in
$N_*$
multiplied by a function in t that takes values in
![]() $[0, 1]$
, we have
$[0, 1]$
, we have
![]() $|D_x^jf_n|\leq |D_x^jN_*|$
for all
$|D_x^jf_n|\leq |D_x^jN_*|$
for all
![]() $j\in \mathbb {Z}_{+}$
. By Lemma 4.4, for each
$j\in \mathbb {Z}_{+}$
. By Lemma 4.4, for each
![]() $n\in \mathbb {Z}_{+}$
, there exists
$n\in \mathbb {Z}_{+}$
, there exists
![]() $h_n\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
satisfying
$h_n\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
satisfying
 $$ \begin{align} \Box h_n+2\text{i} Xh_n+2Yh_n-V_*(h_n)_{\text{r}}-\frac1{p-1}V_*\varphi_1(h_n)-N_*h_n=f_n=N_*\xi_1\left(\frac{T-t}{\varepsilon_n}\right) \end{align} $$
$$ \begin{align} \Box h_n+2\text{i} Xh_n+2Yh_n-V_*(h_n)_{\text{r}}-\frac1{p-1}V_*\varphi_1(h_n)-N_*h_n=f_n=N_*\xi_1\left(\frac{T-t}{\varepsilon_n}\right) \end{align} $$
on
![]() $[T-c_2, T)\times \mathbb {R}^d$
. Moreover, for
$[T-c_2, T)\times \mathbb {R}^d$
. Moreover, for
![]() $n\in \mathbb {Z}_{+}$
, we have
$n\in \mathbb {Z}_{+}$
, we have
and for
![]() $j\in \mathbb {Z}_{\geq 0},\lambda>0$
we have
$j\in \mathbb {Z}_{\geq 0},\lambda>0$
we have
where
![]() $C_\Box $
and
$C_\Box $
and
![]() $C_{j,\lambda }$
are given by Lemma 4.4. By
$C_{j,\lambda }$
are given by Lemma 4.4. By
![]() $h_n\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
, (4.47), (4.48), (4.49) and the Arzelà–Ascoli theorem, there exists a subsequence of
$h_n\in C_c^\infty ([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
, (4.47), (4.48), (4.49) and the Arzelà–Ascoli theorem, there exists a subsequence of
![]() $\{h_n\}_{n=1}^\infty $
, which is still denoted by
$\{h_n\}_{n=1}^\infty $
, which is still denoted by
![]() $\{h_n\}_{n=1}^\infty $
Footnote 9, such that
$\{h_n\}_{n=1}^\infty $
Footnote 9, such that
![]() $h_n\to h$
in
$h_n\to h$
in
![]() $C^1([T-c_0, T)\times \mathbb {R}^d)$
for some
$C^1([T-c_0, T)\times \mathbb {R}^d)$
for some
![]() $h\in C^1([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
and (here
$h\in C^1([T-c_0, T)\times \mathbb {R}^d;\mathbb {C})$
and (here
![]() $D^{\leq 1}f:=(f,Df)$
)
$D^{\leq 1}f:=(f,Df)$
)
Letting
![]() $j=2$
,
$j=2$
,
![]() $\lambda =1$
in (4.49), by (4.50) and the Gagliardo–Nirenberg inequality, we have
$\lambda =1$
in (4.49), by (4.50) and the Gagliardo–Nirenberg inequality, we have
for some constant
![]() $\widetilde C_0>0$
which is independent of
$\widetilde C_0>0$
which is independent of
![]() $n\in \mathbb {Z}_{+}$
. Letting
$n\in \mathbb {Z}_{+}$
. Letting
![]() $j=0$
and
$j=0$
and
![]() $\lambda =1$
in (4.49), by the definition of
$\lambda =1$
in (4.49), by the definition of
![]() $\varphi _1$
, there exists a constant
$\varphi _1$
, there exists a constant
![]() $\widetilde C_1>0$
such that for all
$\widetilde C_1>0$
such that for all
![]() $n\in \mathbb {Z}_+$
and
$n\in \mathbb {Z}_+$
and
![]() $(t,x)\in [T-c_2, T)\times \mathbb {R}^d$
, we have
$(t,x)\in [T-c_2, T)\times \mathbb {R}^d$
, we have
Combining this with (4.46), (4.49), (4.7) (
![]() $j=0$
), and (4.8) (
$j=0$
), and (4.8) (
![]() $j=0, \lambda =1$
), we know that there exist constants
$j=0, \lambda =1$
), we know that there exist constants
![]() $\widetilde C_2>0, \widetilde C_3>0$
such that for all
$\widetilde C_2>0, \widetilde C_3>0$
such that for all
![]() $n\in \mathbb {Z}_{+}$
, we haveFootnote 10
$n\in \mathbb {Z}_{+}$
, we haveFootnote 10
 $$ \begin{align*} |\Box h_{n}-\Box h_{n+1}|&\leq \widetilde C_2(T-t)^{-2\beta}\left|D^{\leq 1}(h_n-h_{n+1})\right|+\widetilde C_2\varepsilon_n\\ &\overset{(4.49)}{\underset{(4.50)}{\leq}}\widetilde C_2(T-t)^{-2\beta}\min\left(2^{-n}, 2(C_{0, 4\beta}+C_{1,4\beta})(T-t)^{4\beta}\right)+\widetilde C_2\varepsilon_n\\ &\leq \widetilde C_3(2^{-n/2}+\varepsilon_n) \end{align*} $$
$$ \begin{align*} |\Box h_{n}-\Box h_{n+1}|&\leq \widetilde C_2(T-t)^{-2\beta}\left|D^{\leq 1}(h_n-h_{n+1})\right|+\widetilde C_2\varepsilon_n\\ &\overset{(4.49)}{\underset{(4.50)}{\leq}}\widetilde C_2(T-t)^{-2\beta}\min\left(2^{-n}, 2(C_{0, 4\beta}+C_{1,4\beta})(T-t)^{4\beta}\right)+\widetilde C_2\varepsilon_n\\ &\leq \widetilde C_3(2^{-n/2}+\varepsilon_n) \end{align*} $$
on
![]() $[T-c_2, T)\times \mathbb {R}^d$
. Hence, by (4.50) and (4.51) we know that
$[T-c_2, T)\times \mathbb {R}^d$
. Hence, by (4.50) and (4.51) we know that
![]() $\{h_n\}_{n=1}^\infty $
is Cauchy in
$\{h_n\}_{n=1}^\infty $
is Cauchy in
![]() $C^2([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
, hence
$C^2([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
, hence
![]() $h\in C^2([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
and
$h\in C^2([T-c_2, T)\times \mathbb {R}^d;\mathbb {C})$
and
![]() $h_n\to h$
in
$h_n\to h$
in
![]() $C^2$
. Moreover, by (4.49), (4.50) and the Gagliardo–Nirenberg inequality we know that
$C^2$
. Moreover, by (4.49), (4.50) and the Gagliardo–Nirenberg inequality we know that
![]() $\{D_x^jD^{\leq 1}h_n\}$
is Cauchy in
$\{D_x^jD^{\leq 1}h_n\}$
is Cauchy in
![]() $L^\infty ([T-c_2, T)\times \mathbb {R}^d)$
for all
$L^\infty ([T-c_2, T)\times \mathbb {R}^d)$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
. Hence (also using (4.47))
$j\in \mathbb {Z}_{\geq 0}$
. Hence (also using (4.47))
![]() $h(t,\cdot ), \partial _th(t,\cdot )\in C_c^\infty (\mathbb {R}^d)$
with
$h(t,\cdot ), \partial _th(t,\cdot )\in C_c^\infty (\mathbb {R}^d)$
with
![]() $\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
. Moreover, h solves the equation (as
$\operatorname {supp}_xh(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 4(T-t)/3\}$
. Moreover, h solves the equation (as
![]() $f_n\to N_*$
)
$f_n\to N_*$
)
By (4.49), we have
Let
![]() $c_1\in (0,c_2)\subset (0, T)$
be such that
$c_1\in (0,c_2)\subset (0, T)$
be such that
![]() $C_{0, 1}c_1<1/2$
, hence
$C_{0, 1}c_1<1/2$
, hence
![]() $|h(t,x)|<1/2$
for all
$|h(t,x)|<1/2$
for all
![]() $(t,x)\in [T-c_1, T)\times \mathbb {R}^d$
. Let
$(t,x)\in [T-c_1, T)\times \mathbb {R}^d$
. Let
 $$ \begin{align*}u(t,x):=(1+h(t,x))w_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right)\exp\left(\text{i}\Phi_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right)\right)\end{align*} $$
$$ \begin{align*}u(t,x):=(1+h(t,x))w_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right)\exp\left(\text{i}\Phi_*(t,x)\xi\left(\frac{3|x|}{5(T-t)}\right)\right)\end{align*} $$
for
![]() $(t,x)\in [T-c_1, T)\times \mathbb {R}^d$
. Then
$(t,x)\in [T-c_1, T)\times \mathbb {R}^d$
. Then
![]() $u\in C^2([T-c_1, T)\times \mathbb {R}^d;\mathbb {C})$
with
$u\in C^2([T-c_1, T)\times \mathbb {R}^d;\mathbb {C})$
with
![]() $u(t,\cdot ), \partial _tu(t,\cdot )\in C_c^\infty (\mathbb {R}^d)$
and
$u(t,\cdot ), \partial _tu(t,\cdot )\in C_c^\infty (\mathbb {R}^d)$
and
![]() $\operatorname {supp}_xu(t,\cdot ), \operatorname {supp}_x\partial _tu(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 5(T-t)/3\}$
for
$\operatorname {supp}_xu(t,\cdot ), \operatorname {supp}_x\partial _tu(t,\cdot )\subset \{x\in \mathbb {R}^d: |x|\leq 5(T-t)/3\}$
for
![]() $t\in [T-c_1, T)$
. Moreover, on
$t\in [T-c_1, T)$
. Moreover, on
![]() $\mathcal C_0:=\{(t,x)\in (T-c_1, T)\times \mathbb {R}^d: |x|\leq T-t\}$
we have
$\mathcal C_0:=\{(t,x)\in (T-c_1, T)\times \mathbb {R}^d: |x|\leq T-t\}$
we have
![]() $u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, and by (4.2), (4.3) and (4.52), we know that h satisfies (4.1) on
$u=(1+h)w_*\text {e}^{\text {i}\Phi _*}$
, and by (4.2), (4.3) and (4.52), we know that h satisfies (4.1) on
![]() $\mathcal C_0$
, hence by Lemma 4.1 we know that
$\mathcal C_0$
, hence by Lemma 4.1 we know that
![]() $\Box u=|u|^{p-1}u$
on
$\Box u=|u|^{p-1}u$
on
![]() $\mathcal C_0$
. Finally, by
$\mathcal C_0$
. Finally, by
![]() $|h|<1/2$
, (2.28) (for
$|h|<1/2$
, (2.28) (for
![]() $j=0$
) and (2.29) we have (2.31) on
$j=0$
) and (2.29) we have (2.31) on
![]() $\mathcal C_0$
.
$\mathcal C_0$
.
This completes the proof of Proposition 2.8.
5 The linearized operator
 $\mathscr {L}$
$\mathscr {L}$
5.1 Functional spaces
In this subsection, we define some functional spaces consisting of smooth functions. Let
![]() $I\subset [0,+\infty )$
be an interval. We denote
$I\subset [0,+\infty )$
be an interval. We denote
![]() $I^2:=\{x^2: x\in I\}$
andFootnote 11
$I^2:=\{x^2: x\in I\}$
andFootnote 11
Then
![]() $ C_{\text {e}}^\infty (I)$
is a ring, and
$ C_{\text {e}}^\infty (I)$
is a ring, and
![]() $ C_{\text {o}}^\infty (I)$
is a linear vector space. Note that when
$ C_{\text {o}}^\infty (I)$
is a linear vector space. Note that when
![]() $I=[0,+\infty )$
, the definitions in (5.1), (5.2) are the same as in (2.10), (2.11). For example, we have
$I=[0,+\infty )$
, the definitions in (5.1), (5.2) are the same as in (2.10), (2.11). For example, we have
![]() $f(Z)=Z\in C_{\text {o}}^\infty ([0,+\infty ))\setminus C_{\text {e}}^\infty ([0,+\infty ))$
and
$f(Z)=Z\in C_{\text {o}}^\infty ([0,+\infty ))\setminus C_{\text {e}}^\infty ([0,+\infty ))$
and
![]() $f(Z)=Z^2\in C_{\text {e}}^\infty ([0,+\infty ))\setminus C_{\text {o}}^\infty ([0,+\infty ))$
.
$f(Z)=Z^2\in C_{\text {e}}^\infty ([0,+\infty ))\setminus C_{\text {o}}^\infty ([0,+\infty ))$
.
Lemma 5.1. Let
![]() $f\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
. Define
$f\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
. Define
![]() $F(x)=f(|x|)$
for
$F(x)=f(|x|)$
for
![]() $x\in \mathbb {R}^d$
, then
$x\in \mathbb {R}^d$
, then
![]() $F\in C^\infty (\mathbb {R}^d)$
.
$F\in C^\infty (\mathbb {R}^d)$
.
Proof. As
![]() $f\in C_{\text {e}}^\infty ([0,+\infty ))$
, there exists a function
$f\in C_{\text {e}}^\infty ([0,+\infty ))$
, there exists a function
![]() $\widetilde f\in C^\infty ([0,+\infty ))$
such that
$\widetilde f\in C^\infty ([0,+\infty ))$
such that
![]() $f(Z)=\widetilde f(Z^2)$
for all
$f(Z)=\widetilde f(Z^2)$
for all
![]() $Z\in [0,+\infty )$
, hence
$Z\in [0,+\infty )$
, hence
![]() $F(x)=\widetilde f(|x|^2)$
for all
$F(x)=\widetilde f(|x|^2)$
for all
![]() $x\in \mathbb {R}^d$
. The smoothness of F follows from the smoothness of
$x\in \mathbb {R}^d$
. The smoothness of F follows from the smoothness of
![]() $\widetilde f$
and
$\widetilde f$
and
![]() $x\mapsto |x|^2$
.
$x\mapsto |x|^2$
.
We also have the following fundamental properties. Let
![]() $I\subset [0,+\infty )$
be an interval, then
$I\subset [0,+\infty )$
be an interval, then
Moreover, if
![]() $\Omega \subset \mathbb {C}$
is open,
$\Omega \subset \mathbb {C}$
is open,
![]() $\varphi \in C^\infty (\Omega ;\mathbb {C})$
(not necessary to be holomorphic), and
$\varphi \in C^\infty (\Omega ;\mathbb {C})$
(not necessary to be holomorphic), and
![]() $f\in C_{\text {e}}^\infty (I)$
with
$f\in C_{\text {e}}^\infty (I)$
with
![]() $f(Z)\in \Omega $
for all
$f(Z)\in \Omega $
for all
![]() $Z\in I$
, then the composition
$Z\in I$
, then the composition
![]() $\varphi \circ f\in C_{\text {e}}^\infty (I)$
. In particular,
$\varphi \circ f\in C_{\text {e}}^\infty (I)$
. In particular,
Lemma 5.2. If
![]() $ f\in {\mathscr X}_0$
, then
$ f\in {\mathscr X}_0$
, then
![]() $\partial _\tau f, Z\partial _Z f, \partial _Z^2 f, \partial _Z f/Z\in {\mathscr X}_0$
.
$\partial _\tau f, Z\partial _Z f, \partial _Z^2 f, \partial _Z f/Z\in {\mathscr X}_0$
.
Proof. By the definition of
![]() ${\mathscr X}_0$
in (2.20), it suffices to prove the result for
${\mathscr X}_0$
in (2.20), it suffices to prove the result for
![]() $f=\widehat f(Z)\tau ^n$
for some
$f=\widehat f(Z)\tau ^n$
for some
![]() $\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
and some
$\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
and some
![]() $n\in \mathbb {Z}_{\geq 0}$
.
$n\in \mathbb {Z}_{\geq 0}$
.
As
![]() $\partial _\tau f=n\widehat f(Z)\tau ^{n-1}$
, we have
$\partial _\tau f=n\widehat f(Z)\tau ^{n-1}$
, we have
![]() $\partial _\tau f\in {\mathscr X}_0$
(
$\partial _\tau f\in {\mathscr X}_0$
(
![]() $\partial _\tau f=0$
for
$\partial _\tau f=0$
for
![]() $n=0$
).
$n=0$
).
Note that
![]() $Z\partial _Z f=Z\widehat f'(Z)\tau ^n, \partial _Z^2 f=\widehat f"(Z)\tau ^n, \partial _Z f/Z=\frac {1}{Z}\widehat f'(Z)\tau ^n$
. As
$Z\partial _Z f=Z\widehat f'(Z)\tau ^n, \partial _Z^2 f=\widehat f"(Z)\tau ^n, \partial _Z f/Z=\frac {1}{Z}\widehat f'(Z)\tau ^n$
. As
![]() $\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
, by (5.3) we have
$\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
, by (5.3) we have
![]() $\widehat f'\in C^\infty _{\text {o}}([0,+\infty ))$
, then by the definitions of
$\widehat f'\in C^\infty _{\text {o}}([0,+\infty ))$
, then by the definitions of
![]() $C^\infty _{\text {e}}([0,+\infty ))$
and
$C^\infty _{\text {e}}([0,+\infty ))$
and
![]() $C^\infty _{\text {o}}([0,+\infty ))$
we have
$C^\infty _{\text {o}}([0,+\infty ))$
we have
![]() $Z\widehat f'(Z),\frac {1}{Z}\widehat f'(Z)\in C^\infty _{\text {e}}([0,+\infty ))$
, by (5.4) we have
$Z\widehat f'(Z),\frac {1}{Z}\widehat f'(Z)\in C^\infty _{\text {e}}([0,+\infty ))$
, by (5.4) we have
![]() $\widehat f"\in C^\infty _{\text {e}}([0,+\infty ))$
. Thus,
$\widehat f"\in C^\infty _{\text {e}}([0,+\infty ))$
. Thus,
![]() $Z\partial _Z f$
,
$Z\partial _Z f$
,
![]() $\partial _Z^2 f$
,
$\partial _Z^2 f$
,
![]() $\partial _Z f/Z\in {\mathscr X}_0$
.
$\partial _Z f/Z\in {\mathscr X}_0$
.
Now we prove Lemma 2.3.
Proof.
-
(i) Let
 $f(t,x)=(T-t)^\lambda \widehat f(\tau , Z)$
for some
$f(t,x)=(T-t)^\lambda \widehat f(\tau , Z)$
for some
 $\widehat f\in {\mathscr X}_0$
and
$\widehat f\in {\mathscr X}_0$
and
 $g(t,x)=(T-t)^\mu \widehat g(\tau , Z)$
for some
$g(t,x)=(T-t)^\mu \widehat g(\tau , Z)$
for some
 $\widehat g\in {\mathscr X}_0$
. Then
$\widehat g\in {\mathscr X}_0$
. Then
 $(fg)(t,x)=(T-t)^{\lambda +\mu }(\widehat f\widehat g)(\tau , Z)$
. As
$(fg)(t,x)=(T-t)^{\lambda +\mu }(\widehat f\widehat g)(\tau , Z)$
. As
 ${\mathscr X}_0 $
is a ring, we have
${\mathscr X}_0 $
is a ring, we have
 $\widehat f\widehat g\in {\mathscr X}_0$
and then
$\widehat f\widehat g\in {\mathscr X}_0$
and then
 $fg\in {\mathscr X}_{\lambda +\mu }$
. It is direct to check that Since
$fg\in {\mathscr X}_{\lambda +\mu }$
. It is direct to check that Since $$ \begin{align*} \partial_t f=(T-t)^{\lambda-1}\left(\partial_\tau+Z\partial_Z-\lambda\right)\widehat f,\quad \Delta f=(T-t)^{\lambda-2}\left(\partial_Z^2+(k/Z)\partial_Z\right)\widehat f. \end{align*} $$
$$ \begin{align*} \partial_t f=(T-t)^{\lambda-1}\left(\partial_\tau+Z\partial_Z-\lambda\right)\widehat f,\quad \Delta f=(T-t)^{\lambda-2}\left(\partial_Z^2+(k/Z)\partial_Z\right)\widehat f. \end{align*} $$
 $\widehat f\in {\mathscr X}_0$
, by Lemma 5.2 we have
$\widehat f\in {\mathscr X}_0$
, by Lemma 5.2 we have
 $\partial _\tau \widehat f, Z\partial _Z\widehat f, \partial _Z^2\widehat f, \partial _Z\widehat f/Z\in {\mathscr X}_0$
, which gives Thus,
$\partial _\tau \widehat f, Z\partial _Z\widehat f, \partial _Z^2\widehat f, \partial _Z\widehat f/Z\in {\mathscr X}_0$
, which gives Thus, $$\begin{align*}\left(\partial_\tau+Z\partial_Z-\lambda\right)\widehat f\in{\mathscr X}_0,\quad \left(\partial_Z^2+(k/Z)\partial_Z\right)\widehat f\in{\mathscr X}_0.\end{align*}$$
$$\begin{align*}\left(\partial_\tau+Z\partial_Z-\lambda\right)\widehat f\in{\mathscr X}_0,\quad \left(\partial_Z^2+(k/Z)\partial_Z\right)\widehat f\in{\mathscr X}_0.\end{align*}$$
 $\partial _t f\in {\mathscr X}_{\lambda -1}$
,
$\partial _t f\in {\mathscr X}_{\lambda -1}$
,
 $\Delta f\in {\mathscr X}_{\lambda -2}$
. As a consequence, we have
$\Delta f\in {\mathscr X}_{\lambda -2}$
. As a consequence, we have
 $\partial _t^2 f\in {\mathscr X}_{\lambda -2}$
,
$\partial _t^2 f\in {\mathscr X}_{\lambda -2}$
,
 $\Box f=-\partial _t^2 f+\Delta f\in {\mathscr X}_{\lambda -2}$
and (also using
$\Box f=-\partial _t^2 f+\Delta f\in {\mathscr X}_{\lambda -2}$
and (also using
 $fg\in {\mathscr X}_{\lambda +\mu } $
for
$fg\in {\mathscr X}_{\lambda +\mu } $
for
 $ f\in {\mathscr X}_{\lambda }$
,
$ f\in {\mathscr X}_{\lambda }$
,
 $ g\in {\mathscr X}_{\mu }$
) hence,
$ g\in {\mathscr X}_{\mu }$
) hence, $$\begin{align*}\Box(fg)\in{\mathscr X}_{(\lambda+\mu)-2}, \quad (\Box f)g\in{\mathscr X}_{(\lambda-2)+\mu}, \quad f\Box g\in{\mathscr X}_{\lambda+(\mu-2)},\end{align*}$$
$$\begin{align*}\Box(fg)\in{\mathscr X}_{(\lambda+\mu)-2}, \quad (\Box f)g\in{\mathscr X}_{(\lambda-2)+\mu}, \quad f\Box g\in{\mathscr X}_{\lambda+(\mu-2)},\end{align*}$$
 $$ \begin{align*} &\partial^\alpha f\partial_\alpha g=[\Box(fg)-(\Box f)g-f\Box g]/2\in{\mathscr X}_{\lambda+\mu-2},\\ & \partial^\alpha(f\partial_\alpha g)=\partial^\alpha f\partial_\alpha g+f\Box g\in{\mathscr X}_{\lambda+\mu-2}. \end{align*} $$
$$ \begin{align*} &\partial^\alpha f\partial_\alpha g=[\Box(fg)-(\Box f)g-f\Box g]/2\in{\mathscr X}_{\lambda+\mu-2},\\ & \partial^\alpha(f\partial_\alpha g)=\partial^\alpha f\partial_\alpha g+f\Box g\in{\mathscr X}_{\lambda+\mu-2}. \end{align*} $$
-
(iii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda \geq j+\mu $
. Let
$\lambda \geq j+\mu $
. Let
 $f(t,x)=(T-t)^\lambda \widehat f(Z)$
for some
$f(t,x)=(T-t)^\lambda \widehat f(Z)$
for some
 $\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
. Assume that
$\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
. Assume that
 $\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
$\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
 $\alpha _0+\cdots +\alpha _d=j$
. We only need to prove that (5.11)Let
$\alpha _0+\cdots +\alpha _d=j$
. We only need to prove that (5.11)Let $$ \begin{align} (T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}f\in L^\infty(\mathcal C). \end{align} $$
$$ \begin{align} (T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}f\in L^\infty(\mathcal C). \end{align} $$
 $\widetilde f(x):=\widehat f(|x|)$
for
$\widetilde f(x):=\widehat f(|x|)$
for
 $x\in \mathbb {R}^d$
, then by Lemma 5.1 we have
$x\in \mathbb {R}^d$
, then by Lemma 5.1 we have
 $\widetilde f\in C^\infty (\mathbb {R}^d)$
. Let
$\widetilde f\in C^\infty (\mathbb {R}^d)$
. Let
 $j'=\alpha _1+\cdots +\alpha _d\in \mathbb {Z}\cap [0,j]$
, and we let Then
$j'=\alpha _1+\cdots +\alpha _d\in \mathbb {Z}\cap [0,j]$
, and we let Then $$\begin{align*}f_\alpha:=(-(\lambda-j')+x\cdot\nabla_x)(-(\lambda-j'-1)+x\cdot\nabla_x)\cdots(-(\lambda-j+1)+x\cdot\nabla_x)\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f.\end{align*}$$
$$\begin{align*}f_\alpha:=(-(\lambda-j')+x\cdot\nabla_x)(-(\lambda-j'-1)+x\cdot\nabla_x)\cdots(-(\lambda-j+1)+x\cdot\nabla_x)\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f.\end{align*}$$
 $f_\alpha \in C^\infty (\mathbb {R}^d)$
and one can check by direct computation that As
$f_\alpha \in C^\infty (\mathbb {R}^d)$
and one can check by direct computation that As $$\begin{align*}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}f(t,x)=(T-t)^{\lambda-j}f_\alpha(x/(T-t)),\quad \forall\ (t,x)\in[0, T)\times\mathbb{R}^d.\end{align*}$$
$$\begin{align*}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}f(t,x)=(T-t)^{\lambda-j}f_\alpha(x/(T-t)),\quad \forall\ (t,x)\in[0, T)\times\mathbb{R}^d.\end{align*}$$
 $|x/(T-t)|<2$
for
$|x/(T-t)|<2$
for
 $(t,x)\in \mathcal C$
and
$(t,x)\in \mathcal C$
and
 $\lambda -j-\mu \geq 0$
, we have (5.11).
$\lambda -j-\mu \geq 0$
, we have (5.11).
-
(ii) Let
 $\lambda ,\mu \in \mathbb {R}$
and
$\lambda ,\mu \in \mathbb {R}$
and
 $j\in \mathbb {Z}_{\geq 0}$
be such that
$j\in \mathbb {Z}_{\geq 0}$
be such that
 $\lambda> j+\mu $
. By the definitions of
$\lambda> j+\mu $
. By the definitions of
 ${\mathscr X}_0$
and
${\mathscr X}_0$
and
 ${\mathscr X}_\lambda $
, it suffices to prove
${\mathscr X}_\lambda $
, it suffices to prove
 $(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
for
$(T-t)^{-\mu }D^jf\in L^\infty (\mathcal C)$
for
 $f(t,x)=(T-t)^\lambda \widehat f(Z)\tau ^n$
for some
$f(t,x)=(T-t)^\lambda \widehat f(Z)\tau ^n$
for some
 $\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
and some
$\widehat f\in C^\infty _{\text {e}}([0,+\infty ))$
and some
 $n\in \mathbb {Z}_{\geq 0}$
. Let
$n\in \mathbb {Z}_{\geq 0}$
. Let
 $P(\tau ):=\tau ^n$
and
$P(\tau ):=\tau ^n$
and
 $\widetilde P(t):=P(\tau )=P(-\ln (T-t))$
. Then by the induction, for any
$\widetilde P(t):=P(\tau )=P(-\ln (T-t))$
. Then by the induction, for any
 $i\in \mathbb {Z}_{\geq 0}$
, there is a polynomial
$i\in \mathbb {Z}_{\geq 0}$
, there is a polynomial
 $P_i(\tau )$
such that
$P_i(\tau )$
such that
 $\widetilde P^{(i)}(t)=(T-t)^{-i}P_i(\tau )$
. Hence, (5.12)Let
$\widetilde P^{(i)}(t)=(T-t)^{-i}P_i(\tau )$
. Hence, (5.12)Let $$ \begin{align} (T-t)^{i+\varepsilon}\widetilde P^{(i)}(t)\in L^\infty([0,T)),\quad\forall\ i\in\mathbb{Z}_{\geq 0},\ \forall\ \varepsilon>0. \end{align} $$
$$ \begin{align} (T-t)^{i+\varepsilon}\widetilde P^{(i)}(t)\in L^\infty([0,T)),\quad\forall\ i\in\mathbb{Z}_{\geq 0},\ \forall\ \varepsilon>0. \end{align} $$
 $\widetilde f(t,x):=(T-t)^\lambda \widehat f(Z)$
for
$\widetilde f(t,x):=(T-t)^\lambda \widehat f(Z)$
for
 $(t,x)\in [0,T)\times \mathbb {R}^d$
, then
$(t,x)\in [0,T)\times \mathbb {R}^d$
, then
 $f(t,x)=\widetilde f(t,x)\widetilde P(t)$
for
$f(t,x)=\widetilde f(t,x)\widetilde P(t)$
for
 $(t,x)\in [0,T)\times \mathbb {R}^d$
, and by (iii) we have (5.13)Assume that
$(t,x)\in [0,T)\times \mathbb {R}^d$
, and by (iii) we have (5.13)Assume that $$ \begin{align} (T-t)^{i-\lambda}D^i\widetilde f\in L^\infty(\mathcal C),\quad \forall\ i\in\mathbb{Z}_{\geq 0}. \end{align} $$
$$ \begin{align} (T-t)^{i-\lambda}D^i\widetilde f\in L^\infty(\mathcal C),\quad \forall\ i\in\mathbb{Z}_{\geq 0}. \end{align} $$
 $\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
$\alpha _0,\alpha _1,\cdots ,\alpha _d\in \mathbb {Z}_{\geq 0}$
are such that
 $\alpha _0+\cdots +\alpha _d=j$
. It suffices to prove (5.14)By Leibnitz’s product rule, we have
$\alpha _0+\cdots +\alpha _d=j$
. It suffices to prove (5.14)By Leibnitz’s product rule, we have $$ \begin{align} (T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}(\widetilde f(t,x)\widetilde P(t))\in L^\infty(\mathcal C). \end{align} $$
Then (5.14) follows from
$$ \begin{align} (T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}(\widetilde f(t,x)\widetilde P(t))\in L^\infty(\mathcal C). \end{align} $$
Then (5.14) follows from $$ \begin{align*} &(T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}(\widetilde f(t,x)\widetilde P(t))\\&\quad =(T-t)^{-\mu}\sum_{i=0}^{\alpha_0}\binom{\alpha_0}{i}\widetilde P^{(i)}(t)\partial_t^{\alpha_0-i}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f(t,x)\\&\quad =\sum_{i=0}^{\alpha_0}\binom{\alpha_0}{i}(T-t)^{\lambda-j-\mu+i}\widetilde P^{(i)}(t)\cdot(T-t)^{j-i-\lambda}\partial_t^{\alpha_0-i}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f(t,x). \end{align*} $$
$$ \begin{align*} &(T-t)^{-\mu}\partial_t^{\alpha_0}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}(\widetilde f(t,x)\widetilde P(t))\\&\quad =(T-t)^{-\mu}\sum_{i=0}^{\alpha_0}\binom{\alpha_0}{i}\widetilde P^{(i)}(t)\partial_t^{\alpha_0-i}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f(t,x)\\&\quad =\sum_{i=0}^{\alpha_0}\binom{\alpha_0}{i}(T-t)^{\lambda-j-\mu+i}\widetilde P^{(i)}(t)\cdot(T-t)^{j-i-\lambda}\partial_t^{\alpha_0-i}\partial_{x_1}^{\alpha_1}\cdots\partial_{x_d}^{\alpha_d}\widetilde f(t,x). \end{align*} $$
 $\lambda -j-\mu>0$
, (5.12) and (5.13).
$\lambda -j-\mu>0$
, (5.12) and (5.13).
This completes the proof of Lemma 2.3.
5.2
 $\mathscr {L}$
acting on
$\mathscr {L}$
acting on
 ${\mathscr X}_\lambda $
${\mathscr X}_\lambda $
Let’s first compute the linear operator
![]() $\mathscr {L}_\lambda $
induced by
$\mathscr {L}_\lambda $
induced by
![]() $\mathscr {L}$
acting on
$\mathscr {L}$
acting on
![]() ${\mathscr X}_\lambda $
. The following lemma relies highly on the properties of the leading order profile
${\mathscr X}_\lambda $
. The following lemma relies highly on the properties of the leading order profile
![]() $(\rho _0,\phi _0)$
. For readers’ convenience, we recall some notations. The linear operator
$(\rho _0,\phi _0)$
. For readers’ convenience, we recall some notations. The linear operator
![]() $\mathscr L$
is defined in (2.19):
$\mathscr L$
is defined in (2.19):
 $$\begin{align*}\mathscr{L}(\phi):=\partial^\alpha\left(\rho_0^2\partial_\alpha\phi-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi\right),\quad\phi=\phi(t,x)=\phi(t,r),\end{align*}$$
$$\begin{align*}\mathscr{L}(\phi):=\partial^\alpha\left(\rho_0^2\partial_\alpha\phi-\frac4{p-1}\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\phi\right),\quad\phi=\phi(t,x)=\phi(t,r),\end{align*}$$
where according to (2.7),
By (3.13),
![]() $\widehat \phi _0$
satisfies
$\widehat \phi _0$
satisfies
 $$\begin{align*}\widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\quad Z\widehat\phi_0'(Z)+(\beta-1)\widehat\phi_0(Z)=\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)},\end{align*}$$
$$\begin{align*}\widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\quad Z\widehat\phi_0'(Z)+(\beta-1)\widehat\phi_0(Z)=\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)},\end{align*}$$
and
![]() $\widehat \rho _0$
is defined by (2.12):
$\widehat \rho _0$
is defined by (2.12):
 $$ \begin{align*} \widehat\rho_0(Z):=\frac{(\beta-1)^{\frac{2}{p-1}}\widehat\phi_0(Z)^{\frac{2}{p-1}}(1-v(Z)^2)^{\frac{1}{p-1}}} {(1-Zv(Z))^{\frac{2}{p-1}}}. \end{align*} $$
$$ \begin{align*} \widehat\rho_0(Z):=\frac{(\beta-1)^{\frac{2}{p-1}}\widehat\phi_0(Z)^{\frac{2}{p-1}}(1-v(Z)^2)^{\frac{1}{p-1}}} {(1-Zv(Z))^{\frac{2}{p-1}}}. \end{align*} $$
Lemma 5.3. There exist real-valued
![]() $A_0,\widetilde B_0, D_1, D_2\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
and
$A_0,\widetilde B_0, D_1, D_2\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
and
![]() $\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
with
$\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
with
 $$ \begin{align} A_0(Z)=\widehat\rho_0(Z)^2\frac{(1-Zv(Z))^2-\ell(v(Z)-Z)^2}{1-v(Z)^2}=\widehat\rho_0(Z)^2\frac{\Delta_Z(Z, v(Z))}{Z(1-v(Z)^2)}, \end{align} $$
$$ \begin{align} A_0(Z)=\widehat\rho_0(Z)^2\frac{(1-Zv(Z))^2-\ell(v(Z)-Z)^2}{1-v(Z)^2}=\widehat\rho_0(Z)^2\frac{\Delta_Z(Z, v(Z))}{Z(1-v(Z)^2)}, \end{align} $$
such that if we define
and
then there hold (here
![]() $\mathscr {L}$
is defined in (2.19) and
$\mathscr {L}$
is defined in (2.19) and
![]() $\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
)
$\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
)
and
Proof. We first consider the functions in the form of
![]() $(T-t)^{\lambda } f(\tau , Z)$
, where f is a smooth function and
$(T-t)^{\lambda } f(\tau , Z)$
, where f is a smooth function and
Let
![]() $\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
, and let
$\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
, and let
![]() $f=f(\tau , Z)$
and
$f=f(\tau , Z)$
and
![]() $\lambda \in \mathbb {C}$
. Now we compute
$\lambda \in \mathbb {C}$
. Now we compute
![]() $\mathscr {L}\big ((T-t)^\lambda f\big )$
.
$\mathscr {L}\big ((T-t)^\lambda f\big )$
.
We will use the following identities: for
![]() $\lambda ,\mu \in \mathbb {C}, f=f(\tau , Z), g=g(\tau , Z)$
,
$\lambda ,\mu \in \mathbb {C}, f=f(\tau , Z), g=g(\tau , Z)$
,
 $$ \begin{align} &\partial^\alpha\left((T-t)^\lambda f\right)\partial_\alpha\left((T-t)^\mu g\right)\nonumber\\&\quad=(T-t)^{\lambda+\mu-2}\Big[-(\partial_\tau f+Z\partial_Z f-\lambda f) (\partial_\tau g+Z\partial_Zg-\mu g)+\partial_Z f\partial_Zg\Big], \end{align} $$
$$ \begin{align} &\partial^\alpha\left((T-t)^\lambda f\right)\partial_\alpha\left((T-t)^\mu g\right)\nonumber\\&\quad=(T-t)^{\lambda+\mu-2}\Big[-(\partial_\tau f+Z\partial_Z f-\lambda f) (\partial_\tau g+Z\partial_Zg-\mu g)+\partial_Z f\partial_Zg\Big], \end{align} $$
 $$ \begin{align}&\partial^\alpha\left((T-t)^\lambda f\partial_\alpha\left((T-t)^\mu g\right)\right)=(T-t)^{\lambda+\mu-2}\Big[-\big(\partial_\tau+Z\partial_Z-(\lambda+\mu-1)\big)\big(f(\partial_\tau g\nonumber \\&\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad + Z\partial_Zg-\mu g)\big)+(\partial_Z+k/Z)(f\partial_Zg)\Big]. \end{align} $$
$$ \begin{align}&\partial^\alpha\left((T-t)^\lambda f\partial_\alpha\left((T-t)^\mu g\right)\right)=(T-t)^{\lambda+\mu-2}\Big[-\big(\partial_\tau+Z\partial_Z-(\lambda+\mu-1)\big)\big(f(\partial_\tau g\nonumber \\&\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad\qquad + Z\partial_Zg-\mu g)\big)+(\partial_Z+k/Z)(f\partial_Zg)\Big]. \end{align} $$
Readers can check (5.21) and (5.22) by using direct computation.
By (2.7), (5.22) and
![]() $\gamma =4\beta /(p-1)+2$
, we have
$\gamma =4\beta /(p-1)+2$
, we have
 $$ \begin{align*} \partial^\alpha\left(\rho_0^2\partial_\alpha\left((T-t)^\lambda f\right)\right)&=(T-t)^{\lambda-\gamma}\big\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(\partial_\tau+Z\partial_Z-\lambda)f\right]\\& \quad +\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\big\}. \end{align*} $$
$$ \begin{align*} \partial^\alpha\left(\rho_0^2\partial_\alpha\left((T-t)^\lambda f\right)\right)&=(T-t)^{\lambda-\gamma}\big\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(\partial_\tau+Z\partial_Z-\lambda)f\right]\\& \quad +\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\big\}. \end{align*} $$
It follows from (3.13) that
 $$ \begin{align*} -(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(\partial_\tau+Z\partial_Z-\lambda)f+\partial_Z\widehat\phi_0\partial_Zf&=\frac{(\beta-1)\widehat\phi_0}{1-Zv(Z)}\big(-\partial_\tau+(v-Z)\partial_Z+\lambda\big)f\\&=:g(\tau, Z), \end{align*} $$
$$ \begin{align*} -(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(\partial_\tau+Z\partial_Z-\lambda)f+\partial_Z\widehat\phi_0\partial_Zf&=\frac{(\beta-1)\widehat\phi_0}{1-Zv(Z)}\big(-\partial_\tau+(v-Z)\partial_Z+\lambda\big)f\\&=:g(\tau, Z), \end{align*} $$
and then
![]() $\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\left ((T-t)^\lambda f\right )=(T-t)^{\lambda -\beta -1}g(\tau , Z)$
. By (2.7) and (5.22), we have
$\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\left ((T-t)^\lambda f\right )=(T-t)^{\lambda -\beta -1}g(\tau , Z)$
. By (2.7) and (5.22), we have
 $$ \begin{align*} \partial^\alpha&\left(\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\left((T-t)^\lambda f\right)\right)=\partial^\alpha\left((T-t)^{\mu}\widehat\rho_0^{3-p}g\partial_\alpha\left((T-t)^{1-\beta}\widehat\phi_0\right)\right)\\&=(T-t)^{\lambda-\gamma}\Big\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0^{3-p}g\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)\right]\\&\qquad\qquad\qquad+(\partial_Z+k/Z)\left(\widehat\rho_0^{3-p}g\partial_Z\widehat\phi_0\right)\Big\}, \end{align*} $$
$$ \begin{align*} \partial^\alpha&\left(\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\left((T-t)^\lambda f\right)\right)=\partial^\alpha\left((T-t)^{\mu}\widehat\rho_0^{3-p}g\partial_\alpha\left((T-t)^{1-\beta}\widehat\phi_0\right)\right)\\&=(T-t)^{\lambda-\gamma}\Big\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0^{3-p}g\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)\right]\\&\qquad\qquad\qquad+(\partial_Z+k/Z)\left(\widehat\rho_0^{3-p}g\partial_Z\widehat\phi_0\right)\Big\}, \end{align*} $$
where
![]() $\mu =-\frac {2\beta }{p-1}(3-p)+\lambda -\beta -1$
satisfies
$\mu =-\frac {2\beta }{p-1}(3-p)+\lambda -\beta -1$
satisfies
![]() $\mu +(1-\beta )-2=\lambda -\gamma $
. By (2.12) and (3.13),
$\mu +(1-\beta )-2=\lambda -\gamma $
. By (2.12) and (3.13),
 $$ \begin{align*} \widehat\rho_0(Z)^{3-p}\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)&=\widehat\rho_0(Z)^2\widehat\rho_0(Z)^{1-p}\frac{(\beta-1)^2\widehat\phi_0(Z)^2}{(1-Zv(Z))^2}=\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2},\\ \widehat\rho_0(Z)^{3-p}\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}\partial_Z\widehat\phi_0&=\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}, \end{align*} $$
$$ \begin{align*} \widehat\rho_0(Z)^{3-p}\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)&=\widehat\rho_0(Z)^2\widehat\rho_0(Z)^{1-p}\frac{(\beta-1)^2\widehat\phi_0(Z)^2}{(1-Zv(Z))^2}=\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2},\\ \widehat\rho_0(Z)^{3-p}\frac{(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)}\partial_Z\widehat\phi_0&=\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}, \end{align*} $$
thus
 $$ \begin{align*} \widehat\rho_0^{3-p}g\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)&=\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f,\\ \widehat\rho_0^{3-p}g\partial_Z\widehat\phi_0&=\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f. \end{align*} $$
$$ \begin{align*} \widehat\rho_0^{3-p}g\big(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0\big)&=\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f,\\ \widehat\rho_0^{3-p}g\partial_Z\widehat\phi_0&=\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f. \end{align*} $$
Therefore,
 $$ \begin{align*} &\partial^\alpha\left(\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\left((T-t)^\lambda f\right)\right)\\& \quad =(T-t)^{\lambda-\gamma}\Bigg\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\\&\qquad\qquad\qquad+\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\Bigg\}. \end{align*} $$
$$ \begin{align*} &\partial^\alpha\left(\rho_0^{3-p}\partial_\alpha\phi_0\partial^{\widetilde\alpha}\phi_0\partial_{\widetilde\alpha}\left((T-t)^\lambda f\right)\right)\\& \quad =(T-t)^{\lambda-\gamma}\Bigg\{-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\\&\qquad\qquad\qquad+\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\Bigg\}. \end{align*} $$
Finally, recall that
![]() $ \mathscr {L}(\phi )=\partial ^\alpha \left (\rho _0^2\partial _\alpha \phi -\frac 4{p-1}\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi \right )$
,
$ \mathscr {L}(\phi )=\partial ^\alpha \left (\rho _0^2\partial _\alpha \phi -\frac 4{p-1}\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi \right )$
,
![]() $\frac 4{p-1}=\ell -1$
, we obtain
$\frac 4{p-1}=\ell -1$
, we obtain
 $$ \begin{align*} \mathscr{L}\big((T-t)^\lambda f\big)=(T-t)^{\lambda-\gamma}\Bigg\{&-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(\partial_\tau+Z\partial_Z-\lambda)f\right]\\&+\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\\&+(\ell-1)\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\\&-(\ell-1)\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\Bigg\}. \end{align*} $$
$$ \begin{align*} \mathscr{L}\big((T-t)^\lambda f\big)=(T-t)^{\lambda-\gamma}\Bigg\{&-\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(\partial_\tau+Z\partial_Z-\lambda)f\right]\\&+\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\\&+(\ell-1)\big(\partial_\tau+Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\\&-(\ell-1)\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big(-\partial_\tau+(v(Z)-Z)\partial_Z+\lambda\big)f\right]\Bigg\}. \end{align*} $$
For any
![]() $\lambda \in \mathbb {C}$
, we define a linear operator
$\lambda \in \mathbb {C}$
, we define a linear operator
![]() $\mathscr {L}_\lambda $
by
$\mathscr {L}_\lambda $
by
 $$ \begin{align} (\mathscr{L}_\lambda f)(Z):=&-\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(Z\partial_Z-\lambda)f\right]+\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\nonumber\\&+(\ell-1)\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big((v(Z)-Z)\partial_Z+\lambda\big)f\right]\nonumber\\&-(\ell-1)\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big((v(Z)-Z)\partial_Z+\lambda\big)f\right], \end{align} $$
$$ \begin{align} (\mathscr{L}_\lambda f)(Z):=&-\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left[\widehat\rho_0(Z)^2(Z\partial_Z-\lambda)f\right]+\left(\partial_Z+k/Z\right)\left(\widehat\rho_0(Z)^2\partial_Zf\right)\nonumber\\&+(\ell-1)\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left[\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\big((v(Z)-Z)\partial_Z+\lambda\big)f\right]\nonumber\\&-(\ell-1)\left(\partial_Z+\frac kZ\right)\left[\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\big((v(Z)-Z)\partial_Z+\lambda\big)f\right], \end{align} $$
where
![]() $f=f(Z)$
depends only on
$f=f(Z)$
depends only on
![]() $Z\in [0,+\infty )$
(not on
$Z\in [0,+\infty )$
(not on
![]() $ \tau $
). Assume that
$ \tau $
). Assume that
![]() $f=f(Z)=f(Z; \lambda )$
satisfies
$f=f(Z)=f(Z; \lambda )$
satisfies
![]() $(\mathscr {L}_\lambda f)(Z)=g(Z)=g(Z; \lambda )$
, then (here
$(\mathscr {L}_\lambda f)(Z)=g(Z)=g(Z; \lambda )$
, then (here
![]() $\mathscr {L}$
and
$\mathscr {L}$
and
![]() $\mathscr {L}_\lambda $
do not act on
$\mathscr {L}_\lambda $
do not act on
![]() $ \lambda $
)
$ \lambda $
)
Now it is enough to prove that
![]() $\mathscr {L}_\lambda $
defined in (5.23) can be written in the form of (5.16) with
$\mathscr {L}_\lambda $
defined in (5.23) can be written in the form of (5.16) with
![]() $B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)$
,
$B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)$
,
![]() $D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)$
and
$D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)$
and
![]() $A_0(Z),\widetilde B_0(Z),D_1(Z), D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
,
$A_0(Z),\widetilde B_0(Z),D_1(Z), D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
,
![]() $\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
satisfying (5.15), (5.17), (5.18), (5.19).
$\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
satisfying (5.15), (5.17), (5.18), (5.19).
Comparing the coefficients of
![]() $ \partial _Z^j$
(
$ \partial _Z^j$
(
![]() $j=0,1,2$
) in (5.23) and (5.16), we find
$j=0,1,2$
) in (5.23) and (5.16), we find
 $$ \begin{align*} A_0(Z)&=\widehat\rho_0(Z)^2(1-Z^2)+(\ell-1)\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}Z(v(Z)-Z)-(\ell-1)\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}(v(Z)-Z)\\&=\widehat\rho_0(Z)^2\left((1-Z^2)-(\ell-1)\frac{(v(Z)-Z)^2}{1-v(Z)^2}\right)=\widehat\rho_0(Z)^2\frac{(1-Zv(Z))^2-\ell(v(Z)-Z)^2}{1-v(Z)^2},\\B_0(Z;\lambda)&=-Z^2\partial_Z(\widehat\rho_0^2)-Z\widehat\rho_0^2+\lambda Z\widehat\rho_0^2+(\lambda-\gamma+1)Z\widehat\rho_0^2+\partial_Z(\widehat\rho_0^2)+(k/Z)\widehat\rho_0^2\\&\quad+(\ell-1)Z\partial_Z\left(\frac{\widehat\rho_0^2}{1-v^2}\right)(v-Z)+\frac{(\ell-1)\widehat\rho_0^2}{1-v^2}\big(Zv'-Z-(\lambda-\gamma+1)(v-Z)+\lambda Z\big)\\&\quad-(\ell-1)\partial_Z\left(\frac{\widehat\rho_0^2v}{1-v^2}\right)(v-Z)-(\ell-1)\frac{\widehat\rho_0^2v}{1-v^2}\big(v'-1+(k/Z)(v-Z)+\lambda\big),\\D_0(Z;\lambda)&=-\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left(-\lambda\widehat\rho_0(Z)^2\right)+(\ell-1)\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left(\lambda\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\right)\\&\quad-(\ell-1)\left(\partial_Z+\frac kZ\right)\left(\lambda\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\right). \end{align*} $$
$$ \begin{align*} A_0(Z)&=\widehat\rho_0(Z)^2(1-Z^2)+(\ell-1)\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}Z(v(Z)-Z)-(\ell-1)\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}(v(Z)-Z)\\&=\widehat\rho_0(Z)^2\left((1-Z^2)-(\ell-1)\frac{(v(Z)-Z)^2}{1-v(Z)^2}\right)=\widehat\rho_0(Z)^2\frac{(1-Zv(Z))^2-\ell(v(Z)-Z)^2}{1-v(Z)^2},\\B_0(Z;\lambda)&=-Z^2\partial_Z(\widehat\rho_0^2)-Z\widehat\rho_0^2+\lambda Z\widehat\rho_0^2+(\lambda-\gamma+1)Z\widehat\rho_0^2+\partial_Z(\widehat\rho_0^2)+(k/Z)\widehat\rho_0^2\\&\quad+(\ell-1)Z\partial_Z\left(\frac{\widehat\rho_0^2}{1-v^2}\right)(v-Z)+\frac{(\ell-1)\widehat\rho_0^2}{1-v^2}\big(Zv'-Z-(\lambda-\gamma+1)(v-Z)+\lambda Z\big)\\&\quad-(\ell-1)\partial_Z\left(\frac{\widehat\rho_0^2v}{1-v^2}\right)(v-Z)-(\ell-1)\frac{\widehat\rho_0^2v}{1-v^2}\big(v'-1+(k/Z)(v-Z)+\lambda\big),\\D_0(Z;\lambda)&=-\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left(-\lambda\widehat\rho_0(Z)^2\right)+(\ell-1)\big(Z\partial_Z-(\lambda-\gamma+1)\big)\left(\lambda\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\right)\\&\quad-(\ell-1)\left(\partial_Z+\frac kZ\right)\left(\lambda\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\right). \end{align*} $$
Then (5.23) and (5.16) are equivalent and
![]() $A_0$
satisfies (5.15).
$A_0$
satisfies (5.15).
By the expression of
![]() $ B_0(Z;\lambda ) $
, we have
$ B_0(Z;\lambda ) $
, we have
![]() $B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)$
with
$B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)$
with
 $$ \begin{align*} \widehat B_0(Z)&=2Z\widehat\rho_0^2+\frac{(\ell-1)\widehat\rho_0^2}{1-v^2}(2Z-v)-\frac{(\ell-1)\widehat\rho_0^2v}{1-v^2} =\frac{2\widehat\rho_0^2}{1-v^2}\big(Z(1-v^2)+(\ell-1)(Z-v)\big).\\\widetilde{B}_0(Z)&= k\widehat \rho_0^2+(1-Z^2)Z\partial_Z(\widehat\rho_0^2)-\gamma Z^2\widehat\rho_0^2+(\ell-1)(v-Z)\bigg[Z^2\partial_Z\left(\frac{\widehat\rho_0^2}{1-v^2}\right)-Z\partial_Z\left(\frac{\widehat\rho_0^2v}{1-v^2}\right)\bigg]\\&\quad+(\ell-1)\frac{\widehat\rho_0^2}{1-v^2}\left(Z(Z-v)v'+(k+\gamma)Zv-\gamma Z^2-kv^2\right). \end{align*} $$
$$ \begin{align*} \widehat B_0(Z)&=2Z\widehat\rho_0^2+\frac{(\ell-1)\widehat\rho_0^2}{1-v^2}(2Z-v)-\frac{(\ell-1)\widehat\rho_0^2v}{1-v^2} =\frac{2\widehat\rho_0^2}{1-v^2}\big(Z(1-v^2)+(\ell-1)(Z-v)\big).\\\widetilde{B}_0(Z)&= k\widehat \rho_0^2+(1-Z^2)Z\partial_Z(\widehat\rho_0^2)-\gamma Z^2\widehat\rho_0^2+(\ell-1)(v-Z)\bigg[Z^2\partial_Z\left(\frac{\widehat\rho_0^2}{1-v^2}\right)-Z\partial_Z\left(\frac{\widehat\rho_0^2v}{1-v^2}\right)\bigg]\\&\quad+(\ell-1)\frac{\widehat\rho_0^2}{1-v^2}\left(Z(Z-v)v'+(k+\gamma)Zv-\gamma Z^2-kv^2\right). \end{align*} $$
By the expression of
![]() $ D_0(Z;\lambda )$
, we have
$ D_0(Z;\lambda )$
, we have
![]() $D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)$
with
$D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)$
with
 $$ \begin{align*} D_1(Z)=&\big(Z\partial_Z+\gamma-1\big)\left(\widehat\rho_0(Z)^2\right)+(\ell-1)\big(Z\partial_Z+\gamma-1\big)\left(\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\right)\\ &-(\ell-1)\left(\partial_Z+\frac kZ\right)\left(\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\right),\\ D_2(Z)=&-\widehat\rho_0(Z)^2-(\ell-1)\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}=-\widehat\rho_0(Z)^2\frac{\ell-v(Z)^2}{1-v(Z)^2}. \end{align*} $$
$$ \begin{align*} D_1(Z)=&\big(Z\partial_Z+\gamma-1\big)\left(\widehat\rho_0(Z)^2\right)+(\ell-1)\big(Z\partial_Z+\gamma-1\big)\left(\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}\right)\\ &-(\ell-1)\left(\partial_Z+\frac kZ\right)\left(\frac{\widehat\rho_0(Z)^2v(Z)}{1-v(Z)^2}\right),\\ D_2(Z)=&-\widehat\rho_0(Z)^2-(\ell-1)\frac{\widehat\rho_0(Z)^2}{1-v(Z)^2}=-\widehat\rho_0(Z)^2\frac{\ell-v(Z)^2}{1-v(Z)^2}. \end{align*} $$
It remains to prove that
![]() $A_0(Z),\widetilde B_0(Z),D_1(Z), D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
,
$A_0(Z),\widetilde B_0(Z),D_1(Z), D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
,
![]() $\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
and (5.17), (5.18), (5.19).
$\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
and (5.17), (5.18), (5.19).
By Lemma A.6 we have
![]() $\widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty )), v\in C_{\text {o}}^\infty ([0,+\infty ))$
; by (5.5) and (5.6) we have
$\widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty )), v\in C_{\text {o}}^\infty ([0,+\infty ))$
; by (5.5) and (5.6) we have
![]() $\widehat \rho _0^2\in C_{\text {e}}^\infty ([0,+\infty ))$
,
$\widehat \rho _0^2\in C_{\text {e}}^\infty ([0,+\infty ))$
,
![]() $(v(Z)-Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
and
$(v(Z)-Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
and
![]() $1-v(Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
; by (5.6) we have
$1-v(Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
; by (5.6) we have
![]() $Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, hence
$Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, hence
![]() $1-Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, then using (5.5) we get
$1-Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
, then using (5.5) we get
![]() $(1-Zv(Z))^2\in C_{\text {e}}^\infty ([0,+\infty ))$
. Therefore, by
$(1-Zv(Z))^2\in C_{\text {e}}^\infty ([0,+\infty ))$
. Therefore, by
![]() $v\in (-1, 1)$
(see Assumption 1), (5.8) and (5.15) we have
$v\in (-1, 1)$
(see Assumption 1), (5.8) and (5.15) we have
![]() $A_0(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
.
$A_0(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
.
Similarly, by Lemma A.6 and (5.3)–(5.8) we have
![]() $\widehat B_0(Z)\in C_{\text {o}}^\infty ([0,+\infty ))$
and
$\widehat B_0(Z)\in C_{\text {o}}^\infty ([0,+\infty ))$
and
![]() $\widetilde B_0(Z)$
,
$\widetilde B_0(Z)$
,
![]() $D_1(Z)$
,
$D_1(Z)$
,
![]() $D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
.
$D_2(Z)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
.
It follows from
![]() $\widehat \rho _0(0)=1$
and
$\widehat \rho _0(0)=1$
and
![]() $v(0)=0$
that
$v(0)=0$
that
![]() $A_0(0)=1$
. By Remark 2.2 and
$A_0(0)=1$
. By Remark 2.2 and
![]() $\widehat \rho _0(Z)>0$
for all
$\widehat \rho _0(Z)>0$
for all
![]() $Z\in [0,+\infty )$
, we have
$Z\in [0,+\infty )$
, we have
![]() $A_0(Z_1)=0$
and (5.18). Let
$A_0(Z_1)=0$
and (5.18). Let
![]() $\Delta _0(Z)=\Delta _Z(Z, v(Z))$
, then by
$\Delta _0(Z)=\Delta _Z(Z, v(Z))$
, then by
![]() $\Delta _0(Z_1)=0$
and Remark 2.2,
$\Delta _0(Z_1)=0$
and Remark 2.2,
![]() $A_0'(Z_1)=\widehat \rho _0(Z_1)^2\Delta _0'(Z_1)/(Z_1(1-v(Z_1)^2))\neq 0$
. This along with
$A_0'(Z_1)=\widehat \rho _0(Z_1)^2\Delta _0'(Z_1)/(Z_1(1-v(Z_1)^2))\neq 0$
. This along with
![]() $A_0(Z_1)<A_0(Z)$
for all
$A_0(Z_1)<A_0(Z)$
for all
![]() $Z\in [0, Z_1)$
implies
$Z\in [0, Z_1)$
implies
![]() $A_0'(Z_1)< 0$
. So we have (5.17).
$A_0'(Z_1)< 0$
. So we have (5.17).
As
![]() $v(Z)\in (0, 1)$
,
$v(Z)\in (0, 1)$
,
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z>0$
(see Remark 2.2) and
$Z>0$
(see Remark 2.2) and
![]() $\widehat \phi _0(Z)>0$
for all
$\widehat \phi _0(Z)>0$
for all
![]() $Z\in [0,+\infty )$
, we have
$Z\in [0,+\infty )$
, we have
![]() $\widehat B_0(Z)>0$
for all
$\widehat B_0(Z)>0$
for all
![]() $Z>0$
; as
$Z>0$
; as
![]() $\widehat \rho _0(0)=1$
and
$\widehat \rho _0(0)=1$
and
![]() $v(0)=0$
we have
$v(0)=0$
we have
![]() $\widetilde B_0(0)=k\in \mathbb {Z}_{+} $
. This proves (5.19).
$\widetilde B_0(0)=k\in \mathbb {Z}_{+} $
. This proves (5.19).
Next we compute the dual operator of
![]() $\mathscr {L}_\lambda $
. For any
$\mathscr {L}_\lambda $
. For any
![]() $\lambda \in \mathbb {C}$
, we define an operator
$\lambda \in \mathbb {C}$
, we define an operator
![]() $\mathscr {L}_\lambda ^*$
, called the dual operator of
$\mathscr {L}_\lambda ^*$
, called the dual operator of
![]() $\mathscr {L}_\lambda $
, by
$\mathscr {L}_\lambda $
, by
Lemma 5.4. For any
![]() $\lambda \in \mathbb {C}$
, we have
$\lambda \in \mathbb {C}$
, we have
![]() $\mathscr {L}_\lambda ^*=\mathscr {L}_{-\lambda +\gamma -k-2}$
.
$\mathscr {L}_\lambda ^*=\mathscr {L}_{-\lambda +\gamma -k-2}$
.
Proof. By the definition (5.25), it is enough to prove that
for all
![]() $\lambda \in \mathbb {C}$
and
$\lambda \in \mathbb {C}$
and
![]() $f,g\in C_c^\infty ((0,+\infty ))$
. We fix
$f,g\in C_c^\infty ((0,+\infty ))$
. We fix
![]() $\lambda \in \mathbb {C}$
and
$\lambda \in \mathbb {C}$
and
![]() $f,g\in C_c^\infty ((0,+\infty ))$
. Let
$f,g\in C_c^\infty ((0,+\infty ))$
. Let
recalling
![]() $Z=|x|/(T-t)$
. Then by Lemma 5.3, we have
$Z=|x|/(T-t)$
. Then by Lemma 5.3, we have
![]() $\mathscr {L}\widetilde {f}(t,x)=(T-t)^{\lambda -\gamma }(\mathscr {L}_\lambda f)(Z) $
and
$\mathscr {L}\widetilde {f}(t,x)=(T-t)^{\lambda -\gamma }(\mathscr {L}_\lambda f)(Z) $
and
![]() $\mathscr {L}\widetilde {g}(t,x)=(T-t)^{-\lambda -k-2}(\mathscr {L}_{-\lambda +\gamma -k-2} g)(Z) $
, thus
$\mathscr {L}\widetilde {g}(t,x)=(T-t)^{-\lambda -k-2}(\mathscr {L}_{-\lambda +\gamma -k-2} g)(Z) $
, thus
![]() $(\mathscr {L}\widetilde {f}\cdot \widetilde {g})(t,x)=(T-t)^{-k-2}(\mathscr {L}_\lambda f)(Z)g(Z) $
, and
$(\mathscr {L}\widetilde {f}\cdot \widetilde {g})(t,x)=(T-t)^{-k-2}(\mathscr {L}_\lambda f)(Z)g(Z) $
, and
![]() $(\widetilde {f}\cdot \mathscr {L}\widetilde {g})(t,x)=(T-t)^{-k-2}f(Z)(\mathscr {L}_{-\lambda +\gamma -k-2} g)(Z)$
. Recall that
$(\widetilde {f}\cdot \mathscr {L}\widetilde {g})(t,x)=(T-t)^{-k-2}f(Z)(\mathscr {L}_{-\lambda +\gamma -k-2} g)(Z)$
. Recall that
![]() $d=k+1$
,
$d=k+1$
,
![]() $ Z=|x|/(T-t)$
, then we have (here
$ Z=|x|/(T-t)$
, then we have (here
![]() $|S^k| $
is the area of the unit sphere
$|S^k| $
is the area of the unit sphere
![]() $S^k$
in
$S^k$
in
![]() $\mathbb {R}^d=\mathbb {R}^{k+1}$
)
$\mathbb {R}^d=\mathbb {R}^{k+1}$
)
 $$ \begin{align*} &\int_{\mathbb{R}^d}(\mathscr{L}\widetilde{f}\cdot\widetilde{g})(t,x)dx=(T-t)^{-1}|S^k|\int_0^\infty(\mathscr{L}_\lambda f)(Z)g(Z)Z^k\,\mathrm{d}Z,\\ &\int_{\mathbb{R}^d}(\widetilde{f}\cdot\mathscr{L}\widetilde{g})(t,x)dx=(T-t)^{-1}|S^k|\int_0^\infty f(Z)(\mathscr{L}_{-\lambda+\gamma-k-2} g)(Z)Z^k\,\mathrm{d}Z, \end{align*} $$
$$ \begin{align*} &\int_{\mathbb{R}^d}(\mathscr{L}\widetilde{f}\cdot\widetilde{g})(t,x)dx=(T-t)^{-1}|S^k|\int_0^\infty(\mathscr{L}_\lambda f)(Z)g(Z)Z^k\,\mathrm{d}Z,\\ &\int_{\mathbb{R}^d}(\widetilde{f}\cdot\mathscr{L}\widetilde{g})(t,x)dx=(T-t)^{-1}|S^k|\int_0^\infty f(Z)(\mathscr{L}_{-\lambda+\gamma-k-2} g)(Z)Z^k\,\mathrm{d}Z, \end{align*} $$
for all
![]() $t\in [0, T)$
. Thus, it is enough to prove that
$t\in [0, T)$
. Thus, it is enough to prove that
Let
![]() $ \mathcal {J}:=\mathscr {L}\widetilde {f}\cdot \widetilde {g}-\widetilde {f}\cdot \mathscr {L}\widetilde {g}$
. Then (5.27) is further reduced to
$ \mathcal {J}:=\mathscr {L}\widetilde {f}\cdot \widetilde {g}-\widetilde {f}\cdot \mathscr {L}\widetilde {g}$
. Then (5.27) is further reduced to
By the definition of
![]() $\mathscr {L} $
in (2.19), we can write
$\mathscr {L} $
in (2.19), we can write
![]() $ \mathcal {J}$
in the divergence form
$ \mathcal {J}$
in the divergence form
![]() $ \mathcal {J}=\partial ^\alpha P_{\alpha }$
with
$ \mathcal {J}=\partial ^\alpha P_{\alpha }$
with
Let
![]() $E(t):=\int _{\mathbb {R}^d}P_0(t,x)\,\mathrm dx$
for
$E(t):=\int _{\mathbb {R}^d}P_0(t,x)\,\mathrm dx$
for
![]() $t\in [0, T)$
. By the divergence theorem (recalling
$t\in [0, T)$
. By the divergence theorem (recalling
![]() $\partial ^0=-\partial _0=-\partial _t$
and the fact that
$\partial ^0=-\partial _0=-\partial _t$
and the fact that
![]() $\operatorname {supp}_xP_\alpha (t,\cdot )$
is compact for each t and
$\operatorname {supp}_xP_\alpha (t,\cdot )$
is compact for each t and
![]() $\alpha $
), we have
$\alpha $
), we have
Thus, it is enough to prove that
![]() $E(t)$
is constant in t. We can write
$E(t)$
is constant in t. We can write
![]() $P_0=P_{0,1}-\frac 4{p-1}P_{0,2}$
with
$P_0=P_{0,1}-\frac 4{p-1}P_{0,2}$
with
As
![]() $\widetilde {f}(t,x)=(T-t)^{\lambda }f(Z) $
,
$\widetilde {f}(t,x)=(T-t)^{\lambda }f(Z) $
,
![]() $\widetilde {g}(t,x)=(T-t)^{-\lambda +\gamma -k-2}g(Z) $
, we have
$\widetilde {g}(t,x)=(T-t)^{-\lambda +\gamma -k-2}g(Z) $
, we have
 $$ \begin{align*} &\partial_t\widetilde{f}(t,x)=(T-t)^{\lambda-1}f_1(Z)\text{ with } f_1(Z):=-\lambda f(Z)+Zf'(Z),\\& \partial_t\widetilde{g}(t,x)=(T-t)^{-\lambda+\gamma-k-3}g_1(Z)\text{ with } g_1(Z):=-(-\lambda+\gamma-k-2)g(Z)+Zg'(Z). \end{align*} $$
$$ \begin{align*} &\partial_t\widetilde{f}(t,x)=(T-t)^{\lambda-1}f_1(Z)\text{ with } f_1(Z):=-\lambda f(Z)+Zf'(Z),\\& \partial_t\widetilde{g}(t,x)=(T-t)^{-\lambda+\gamma-k-3}g_1(Z)\text{ with } g_1(Z):=-(-\lambda+\gamma-k-2)g(Z)+Zg'(Z). \end{align*} $$
Then by (2.7),
![]() $\gamma =\frac {4\beta }{p-1}+2 $
and
$\gamma =\frac {4\beta }{p-1}+2 $
and
![]() $d=k+1$
, we get
$d=k+1$
, we get
 $$ \begin{align*} P_{0,1}(t,x)&=(T-t)^{-\frac{4\beta}{p-1}+\gamma-k-3}\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]\\&=(T-t)^{-d}\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]. \end{align*} $$
$$ \begin{align*} P_{0,1}(t,x)&=(T-t)^{-\frac{4\beta}{p-1}+\gamma-k-3}\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]\\&=(T-t)^{-d}\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]. \end{align*} $$
As
![]() $\widetilde {f}(t,x)=(T-t)^{\lambda }f(Z) $
,
$\widetilde {f}(t,x)=(T-t)^{\lambda }f(Z) $
,
![]() $\widetilde {g}(t,x)=(T-t)^{-\lambda +\gamma -k-2}g(Z) $
, we get by (2.7) and (5.21) that
$\widetilde {g}(t,x)=(T-t)^{-\lambda +\gamma -k-2}g(Z) $
, we get by (2.7) and (5.21) that
where
 $$ \begin{align*} &f_2:=-(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(Z\partial_Z-\lambda)f+\partial_Z\widehat\phi_0\partial_Zf,\\ &g_2:=-(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(Z\partial_Z+\lambda-\gamma+k+2)g+\partial_Z\widehat\phi_0\partial_Zg. \end{align*} $$
$$ \begin{align*} &f_2:=-(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(Z\partial_Z-\lambda)f+\partial_Z\widehat\phi_0\partial_Zf,\\ &g_2:=-(Z\partial_Z\widehat\phi_0-(1-\beta)\widehat\phi_0)(Z\partial_Z+\lambda-\gamma+k+2)g+\partial_Z\widehat\phi_0\partial_Zg. \end{align*} $$
Then by (2.7), (A.2) and
![]() $\gamma =\frac {4\beta }{p-1}+2=\frac {2(3-p)\beta }{p-1}+2\beta +2 $
,
$\gamma =\frac {4\beta }{p-1}+2=\frac {2(3-p)\beta }{p-1}+2\beta +2 $
,
![]() $d=k+1$
, we have
$d=k+1$
, we have
 $$ \begin{align*} &P_{0,2}(t,x)\\& \quad =(T-t)^{-\frac{2(3-p)\beta}{p-1}-2\beta+\gamma-k-3}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)] \\& \quad =(T-t)^{-d}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)]. \end{align*} $$
$$ \begin{align*} &P_{0,2}(t,x)\\& \quad =(T-t)^{-\frac{2(3-p)\beta}{p-1}-2\beta+\gamma-k-3}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)] \\& \quad =(T-t)^{-d}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)]. \end{align*} $$
As
![]() $P_0=P_{0,1}-\frac 4{p-1}P_{0,2}$
, we have
$P_0=P_{0,1}-\frac 4{p-1}P_{0,2}$
, we have
![]() $P_{0}(t,x)=(T-t)^{-d}H(Z) $
with
$P_{0}(t,x)=(T-t)^{-d}H(Z) $
with
 $$ \begin{align*} H(Z)&:=\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]\\&\quad-\frac4{p-1}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)]. \end{align*} $$
$$ \begin{align*} H(Z)&:=\widehat\rho_0(Z)^2[f_1(Z)g(Z)-f(Z)g_1(Z)]\\&\quad-\frac4{p-1}\widehat\rho_0(Z)^{3-p}[(\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)] [f_2(Z)g(Z)-f(Z)g_2(Z)]. \end{align*} $$
Then by
![]() $d=k+1$
,
$d=k+1$
,
![]() $ Z=|x|/(T-t)$
, we have
$ Z=|x|/(T-t)$
, we have
![]() $E(t)=\int _{\mathbb {R}^d}P_0(t,x)\,\mathrm dx=|S^k|\int _0^\infty H(Z)Z^k\,\mathrm {d}Z$
, which is constant in t. By (5.29), we have (5.28), thus (5.27) and (5.26).
$E(t)=\int _{\mathbb {R}^d}P_0(t,x)\,\mathrm dx=|S^k|\int _0^\infty H(Z)Z^k\,\mathrm {d}Z$
, which is constant in t. By (5.29), we have (5.28), thus (5.27) and (5.26).
5.3 Surjection of
 $\mathscr {L}$
$\mathscr {L}$
This subsection is devoted to the proof of Proposition 2.4, i.e.,
![]() $\mathscr {L}:{\mathscr X}_\lambda \to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
$\mathscr {L}:{\mathscr X}_\lambda \to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
![]() $\lambda \in \mathbb {C}$
. For this, it suffices to show that
$\lambda \in \mathbb {C}$
. For this, it suffices to show that
Lemma 5.5. If
![]() $R\in (k,+\infty )$
, then the linear operator
$R\in (k,+\infty )$
, then the linear operator
![]() $\mathscr {L}:{\mathscr X}_\lambda \to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
$\mathscr {L}:{\mathscr X}_\lambda \to {\mathscr X}_{\lambda -\gamma }$
is surjective for all
![]() $\lambda \in B_R:=\{\lambda \in \mathbb {C}:|\lambda |<R\}$
, where
$\lambda \in B_R:=\{\lambda \in \mathbb {C}:|\lambda |<R\}$
, where
![]() $\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
.
$\gamma :=4\beta /(p-1)+2=\beta (\ell -1)+2$
.
From here until the end of this section, we fix an
![]() $R\in (k,+\infty )$
.
$R\in (k,+\infty )$
.
We consider functions depending analytically on a complex number
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $I\subset [0,+\infty )$
be an interval and let
$I\subset [0,+\infty )$
be an interval and let
![]() $\Omega \subset \mathbb {C}$
be an open set. We define
$\Omega \subset \mathbb {C}$
be an open set. We define
 $$ \begin{align*} \operatorname{Hol}(\Omega)&:=\{\text{all holomorphic function on }\Omega\},\\ \mathcal{H}_I(\Omega)&:=\left\{f=f(Z;\lambda)\in C^\infty(I\times\Omega;\mathbb{C}): f(Z;\cdot)\in\operatorname{Hol}(\Omega)\text{ for all }Z\in I\right\},\\ \mathcal H_I^{\text{e}}(\Omega)&:=\{f\in C^\infty(I\times\Omega):\exists\ \widetilde{f}\in\mathcal H_{I^2}(\Omega),\text{ s.t. }f(Z;\lambda)=\widetilde f(Z^2;\lambda) \quad \forall\ Z\in I,\ \lambda\in \Omega\}. \end{align*} $$
$$ \begin{align*} \operatorname{Hol}(\Omega)&:=\{\text{all holomorphic function on }\Omega\},\\ \mathcal{H}_I(\Omega)&:=\left\{f=f(Z;\lambda)\in C^\infty(I\times\Omega;\mathbb{C}): f(Z;\cdot)\in\operatorname{Hol}(\Omega)\text{ for all }Z\in I\right\},\\ \mathcal H_I^{\text{e}}(\Omega)&:=\{f\in C^\infty(I\times\Omega):\exists\ \widetilde{f}\in\mathcal H_{I^2}(\Omega),\text{ s.t. }f(Z;\lambda)=\widetilde f(Z^2;\lambda) \quad \forall\ Z\in I,\ \lambda\in \Omega\}. \end{align*} $$
Then
![]() $ \operatorname {Hol}(\Omega )$
,
$ \operatorname {Hol}(\Omega )$
,
![]() $ \mathcal H_I(\Omega )$
,
$ \mathcal H_I(\Omega )$
,
![]() $ \mathcal H_I^{\text {e}}(\Omega )$
are rings. Moreover, we have
$ \mathcal H_I^{\text {e}}(\Omega )$
are rings. Moreover, we have
The proof of Lemma 5.5 is based on the following result, which will be proved in next subsection.
Lemma 5.6. There exists
![]() $ \varphi \in \operatorname {Hol}(B_R)\setminus \{0\}$
such that if
$ \varphi \in \operatorname {Hol}(B_R)\setminus \{0\}$
such that if
![]() $g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, then there exists
$g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, then there exists
![]() $f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
$\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
![]() $(0,+\infty )$
(for all
$(0,+\infty )$
(for all
![]() $ \lambda \in B_R$
).
$ \lambda \in B_R$
).
Proof of Lemma 5.5.
We first prove that
![]() $\mathscr {L}$
maps
$\mathscr {L}$
maps
![]() ${\mathscr X}_\lambda $
to
${\mathscr X}_\lambda $
to
![]() ${\mathscr X}_{\lambda -\gamma }$
.
${\mathscr X}_{\lambda -\gamma }$
.
Recall that
![]() $\mathscr {L}(\phi )=\partial ^\alpha \left (\rho _0^2\partial _\alpha \phi -\frac 4{p-1}\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi \right )$
,
$\mathscr {L}(\phi )=\partial ^\alpha \left (\rho _0^2\partial _\alpha \phi -\frac 4{p-1}\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi \right )$
,
![]() $\rho _0^2\in {\mathscr X}_{2\mu _0}$
,
$\rho _0^2\in {\mathscr X}_{2\mu _0}$
,
![]() $\rho _0^{3-p}\in {\mathscr X}_{(3-p)\mu _0}$
,
$\rho _0^{3-p}\in {\mathscr X}_{(3-p)\mu _0}$
,
![]() $\phi _0\in {\mathscr X}_{\lambda _0}$
,
$\phi _0\in {\mathscr X}_{\lambda _0}$
,
![]() $\lambda _0=1-\beta $
,
$\lambda _0=1-\beta $
,
![]() $\mu _0=-\frac {2\beta }{p-1}$
(see (2.22)) and
$\mu _0=-\frac {2\beta }{p-1}$
(see (2.22)) and
![]() $\gamma =4\beta /(p-1)+2$
. If
$\gamma =4\beta /(p-1)+2$
. If
![]() $ \phi \in {\mathscr X}_\lambda $
, by Lemma 2.3 (i), we have
$ \phi \in {\mathscr X}_\lambda $
, by Lemma 2.3 (i), we have
![]() $\partial ^\alpha (\rho _0^2\partial _\alpha \phi )\in {\mathscr X}_{\lambda -\gamma }$
,
$\partial ^\alpha (\rho _0^2\partial _\alpha \phi )\in {\mathscr X}_{\lambda -\gamma }$
,
![]() $\partial ^\alpha (\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi )\in {\mathscr X}_{\lambda -\gamma }$
, where we have used that
$\partial ^\alpha (\rho _0^{3-p}\partial _\alpha \phi _0\partial ^{\widetilde \alpha }\phi _0\partial _{\widetilde \alpha }\phi )\in {\mathscr X}_{\lambda -\gamma }$
, where we have used that
![]() $\lambda +2\mu _{0}-2=\lambda -\gamma =\lambda +\lambda _0-2+(3-p)\mu _0+\lambda _0-2$
, thus
$\lambda +2\mu _{0}-2=\lambda -\gamma =\lambda +\lambda _0-2+(3-p)\mu _0+\lambda _0-2$
, thus
![]() $ \mathscr {L}(\phi )\in {\mathscr X}_{\lambda -\gamma } $
.
$ \mathscr {L}(\phi )\in {\mathscr X}_{\lambda -\gamma } $
.
Now we prove that
![]() $\mathscr {L}$
is surjective. By the definitions of
$\mathscr {L}$
is surjective. By the definitions of
![]() ${\mathscr X}_0$
and
${\mathscr X}_0$
and
![]() ${\mathscr X}_\lambda $
, it suffices to prove that for every
${\mathscr X}_\lambda $
, it suffices to prove that for every
![]() $g\in C^\infty _{\text {e}}([0,+\infty ))$
,
$g\in C^\infty _{\text {e}}([0,+\infty ))$
,
![]() $n\in \mathbb {Z}_{\geq 0}$
and
$n\in \mathbb {Z}_{\geq 0}$
and
![]() $\lambda _*\in B_R$
, there exists
$\lambda _*\in B_R$
, there exists
![]() $F_n\in {\mathscr X}_{\lambda _*}$
such that
$F_n\in {\mathscr X}_{\lambda _*}$
such that
![]() $\mathscr {L} F_n(t,x)=(T-t)^{\lambda _*-\gamma } g(Z)\tau ^n/n!$
. Now we fix
$\mathscr {L} F_n(t,x)=(T-t)^{\lambda _*-\gamma } g(Z)\tau ^n/n!$
. Now we fix
![]() $g\in C_{\text {e}}^\infty ([0,+\infty ))$
and
$g\in C_{\text {e}}^\infty ([0,+\infty ))$
and
![]() $\lambda _*\in B_R$
.
$\lambda _*\in B_R$
.
By Lemma 5.6, there exist
![]() $ \varphi \in \operatorname {Hol}(B_R)\setminus \{0\}$
and a function
$ \varphi \in \operatorname {Hol}(B_R)\setminus \{0\}$
and a function
![]() $f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f(Z;\lambda )=\varphi (\lambda )g(Z)$
for
$\mathscr {L}_\lambda f(Z;\lambda )=\varphi (\lambda )g(Z)$
for
![]() $Z\in (0,+\infty )$
,
$Z\in (0,+\infty )$
,
![]() $ \lambda \in B_R$
. As
$ \lambda \in B_R$
. As
![]() $f\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
there exists
$f\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
there exists
![]() $\widetilde {f}\in \mathcal H_{[0,+\infty )}(B_R)$
such that
$\widetilde {f}\in \mathcal H_{[0,+\infty )}(B_R)$
such that
![]() $f(Z;\lambda )=\widetilde {f}(Z^2;\lambda )$
for
$f(Z;\lambda )=\widetilde {f}(Z^2;\lambda )$
for
![]() $Z\in [0,+\infty )$
,
$Z\in [0,+\infty )$
,
![]() $ \lambda \in B_R$
. As
$ \lambda \in B_R$
. As
![]() $\lambda _*\in B_R$
, there exist
$\lambda _*\in B_R$
, there exist
![]() $\delta _*>0$
and
$\delta _*>0$
and
![]() $m_*\in \mathbb {Z}_{\geq 0}$
such that
$m_*\in \mathbb {Z}_{\geq 0}$
such that
![]() $B_{2\delta _*}(\lambda _*)\subset B_R$
and
$B_{2\delta _*}(\lambda _*)\subset B_R$
and
Here
![]() $B_{2\delta _*}(\lambda _*):=\{\lambda \in \mathbb {C}:|\lambda -\lambda _*|<2\delta _*\}$
and we have used the fact that if
$B_{2\delta _*}(\lambda _*):=\{\lambda \in \mathbb {C}:|\lambda -\lambda _*|<2\delta _*\}$
and we have used the fact that if
![]() $\varphi \in \operatorname {Hol}(\Omega )\setminus \{0\}$
, then the zero set
$\varphi \in \operatorname {Hol}(\Omega )\setminus \{0\}$
, then the zero set
![]() $\mathcal Z(\varphi ):=\{\lambda \in \Omega :\varphi (\lambda )=0\}$
is discrete.
$\mathcal Z(\varphi ):=\{\lambda \in \Omega :\varphi (\lambda )=0\}$
is discrete.
Let
![]() $\widetilde F({Z};\lambda ):=\widetilde f({Z};\lambda )/\widetilde \varphi (\lambda )$
,
$\widetilde F({Z};\lambda ):=\widetilde f({Z};\lambda )/\widetilde \varphi (\lambda )$
,
![]() $F(Z;\lambda ):=\widetilde F(Z^2;\lambda )$
for
$F(Z;\lambda ):=\widetilde F(Z^2;\lambda )$
for
![]() $Z\in [0,+\infty )$
,
$Z\in [0,+\infty )$
,
![]() $ \lambda \in B_R$
. Then
$ \lambda \in B_R$
. Then
![]() $\widetilde F\in \mathcal H_{[0,+\infty )}(\Omega _*)$
,
$\widetilde F\in \mathcal H_{[0,+\infty )}(\Omega _*)$
,
![]() $F\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(\Omega _*)$
,
$F\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(\Omega _*)$
,
![]() $F(Z;\lambda )=f(Z;\lambda )/\widetilde \varphi (\lambda )$
, and
$F(Z;\lambda )=f(Z;\lambda )/\widetilde \varphi (\lambda )$
, and
By Lemma 5.3, we have
for all
![]() $\lambda \in \Omega _*$
and
$\lambda \in \Omega _*$
and
![]() $Z\in (0, +\infty )$
. Let
$Z\in (0, +\infty )$
. Let
Then
![]() $F_*,G\in C^{\infty }([0,T)\times \mathbb {R}^d\times \Omega _*) $
(as
$F_*,G\in C^{\infty }([0,T)\times \mathbb {R}^d\times \Omega _*) $
(as
![]() $Z^2=|x|^2/(T-t)^2$
is smooth on
$Z^2=|x|^2/(T-t)^2$
is smooth on
![]() $[0,T)\times \mathbb {R}^d $
) and
$[0,T)\times \mathbb {R}^d $
) and
![]() $ \mathscr {L} F_*(t,x;\lambda )=G(t,x;\lambda )$
on
$ \mathscr {L} F_*(t,x;\lambda )=G(t,x;\lambda )$
on
![]() $[0,T)\times \mathbb {R}^d\times \Omega _* $
(the case
$[0,T)\times \mathbb {R}^d\times \Omega _* $
(the case
![]() $Z=0$
follows by continuity).
$Z=0$
follows by continuity).
Recall that
![]() $ \tau =\ln \frac {1}{T-t}$
and then
$ \tau =\ln \frac {1}{T-t}$
and then
 $$ \begin{align*} G(t,x;\lambda)=(T-t)^{\lambda_*-\gamma}\mathrm{e}^{-(\lambda-\lambda_*)\tau}(\lambda-\lambda_*)^{m_*}g(Z)=\sum_{n=0}^{\infty}(T-t)^{\lambda_*-\gamma}\frac{(-\tau)^n}{n!}(\lambda-\lambda_*)^{m_*+n}g(Z) \end{align*} $$
$$ \begin{align*} G(t,x;\lambda)=(T-t)^{\lambda_*-\gamma}\mathrm{e}^{-(\lambda-\lambda_*)\tau}(\lambda-\lambda_*)^{m_*}g(Z)=\sum_{n=0}^{\infty}(T-t)^{\lambda_*-\gamma}\frac{(-\tau)^n}{n!}(\lambda-\lambda_*)^{m_*+n}g(Z) \end{align*} $$
locally uniformly on
![]() $[0,T)\times \mathbb {R}^d\times B_{\delta _*}(\lambda _*)$
. By Cauchy’s integration formula (Theorem 4.4 in Chapter 2 of [Reference Stein and Shakarchi69]), we have (for
$[0,T)\times \mathbb {R}^d\times B_{\delta _*}(\lambda _*)$
. By Cauchy’s integration formula (Theorem 4.4 in Chapter 2 of [Reference Stein and Shakarchi69]), we have (for
![]() $n\in \mathbb {Z}_{\geq 0}$
)
$n\in \mathbb {Z}_{\geq 0}$
)
 $$ \begin{align*} (T-t)^{\lambda_*-\gamma} g(Z)\frac{\tau^n}{n!}&=\frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{G(t,x;\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\&= \frac{\delta_*^{-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}G(t,x;\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{-\text{i} (m_*+n)\theta}\,\mathrm d\theta. \end{align*} $$
$$ \begin{align*} (T-t)^{\lambda_*-\gamma} g(Z)\frac{\tau^n}{n!}&=\frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{G(t,x;\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\&= \frac{\delta_*^{-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}G(t,x;\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{-\text{i} (m_*+n)\theta}\,\mathrm d\theta. \end{align*} $$
Now let (for
![]() $n\in \mathbb {Z}_{\geq 0}$
)
$n\in \mathbb {Z}_{\geq 0}$
)
 $$ \begin{align*} F_n(t,x)&:=\frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{F_*(t,x;\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\&= \frac{\delta_*^{-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}F_*(t,x;\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{-\text{i} (m_*+n)\theta}\,\mathrm d\theta. \end{align*} $$
$$ \begin{align*} F_n(t,x)&:=\frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{F_*(t,x;\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\&= \frac{\delta_*^{-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}F_*(t,x;\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{-\text{i} (m_*+n)\theta}\,\mathrm d\theta. \end{align*} $$
Then
![]() $F_n\in C^{\infty }([0,T)\times \mathbb {R}^d) $
and
$F_n\in C^{\infty }([0,T)\times \mathbb {R}^d) $
and
![]() $\mathscr {L} F_n(t,x)=(T-t)^{\lambda _*-\gamma } g(Z)\tau ^n/n!$
. It remains to prove that
$\mathscr {L} F_n(t,x)=(T-t)^{\lambda _*-\gamma } g(Z)\tau ^n/n!$
. It remains to prove that
![]() $F_n\in {\mathscr X}_{\lambda _*}$
.
$F_n\in {\mathscr X}_{\lambda _*}$
.
As
![]() $ \tau =\ln \frac {1}{T-t}$
,
$ \tau =\ln \frac {1}{T-t}$
,
![]() $ F_*(t,x;\lambda )=(T-t)^{\lambda }\widetilde F(Z^2;\lambda )$
then
$ F_*(t,x;\lambda )=(T-t)^{\lambda }\widetilde F(Z^2;\lambda )$
then
 $$ \begin{align*} F_*(t,x;\lambda)=(T-t)^{\lambda_*}\mathrm{e}^{-(\lambda-\lambda_*)\tau}\widetilde F(Z^2;\lambda)=\sum_{j=0}^{\infty}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}(\lambda-\lambda_*)^{j}\widetilde F(Z^2;\lambda), \end{align*} $$
$$ \begin{align*} F_*(t,x;\lambda)=(T-t)^{\lambda_*}\mathrm{e}^{-(\lambda-\lambda_*)\tau}\widetilde F(Z^2;\lambda)=\sum_{j=0}^{\infty}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}(\lambda-\lambda_*)^{j}\widetilde F(Z^2;\lambda), \end{align*} $$
locally uniformly on
![]() $[0,T)\times \mathbb {R}^d\times B_{\delta _*}(\lambda _*)$
, so we have
$[0,T)\times \mathbb {R}^d\times B_{\delta _*}(\lambda _*)$
, so we have
 $$ \begin{align*} F_n(t,x)&=\sum_{j=0}^{\infty}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}F_{n,j}(Z^2),\qquad\text{where}\\ F_{n,j}(\widetilde{Z})&:= \frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{(\lambda-\lambda_*)^{j}\widetilde F(\widetilde{Z};\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\ &=\frac{\delta_*^{j-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}\widetilde F(\widetilde{Z};\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{\text{i} (j-m_*-n)\theta}\,\mathrm d\theta. \end{align*} $$
$$ \begin{align*} F_n(t,x)&=\sum_{j=0}^{\infty}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}F_{n,j}(Z^2),\qquad\text{where}\\ F_{n,j}(\widetilde{Z})&:= \frac{(-1)^n}{2\pi\text{i}}\oint_{|\lambda-\lambda_*|=\delta_*}\frac{(\lambda-\lambda_*)^{j}\widetilde F(\widetilde{Z};\lambda)}{(\lambda-\lambda_*)^{m_*+n+1}}\,\mathrm d\lambda\\ &=\frac{\delta_*^{j-m_*-n}}{2\pi(-1)^n}\int_0^{2\pi}\widetilde F(\widetilde{Z};\lambda_*+\delta_*\mathrm{e}^{\text{i} \theta})\mathrm{e}^{\text{i} (j-m_*-n)\theta}\,\mathrm d\theta. \end{align*} $$
As
![]() $\widetilde F\in \mathcal H_{[0,+\infty )}(\Omega _*)\subset C^{\infty }([0,+\infty )\times \Omega _*)$
, we have
$\widetilde F\in \mathcal H_{[0,+\infty )}(\Omega _*)\subset C^{\infty }([0,+\infty )\times \Omega _*)$
, we have
![]() $F_{n,j}\in C^\infty ([0,+\infty ))$
,
$F_{n,j}\in C^\infty ([0,+\infty ))$
,
![]() $Z\mapsto F_{n,j}(Z^2)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
for every
$Z\mapsto F_{n,j}(Z^2)\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
for every
![]() $n,j\in \mathbb {Z}_{\geq 0}$
; moreover by Cauchy’s theorem (Corollary 2.3 in Chapter 2 of [Reference Stein and Shakarchi69]), we have
$n,j\in \mathbb {Z}_{\geq 0}$
; moreover by Cauchy’s theorem (Corollary 2.3 in Chapter 2 of [Reference Stein and Shakarchi69]), we have
![]() $F_{n,j}=0 $
for
$F_{n,j}=0 $
for
![]() $j>m_*+n$
,
$j>m_*+n$
,
![]() $n,j\in \mathbb {Z}_{\geq 0}$
. Thus,
$n,j\in \mathbb {Z}_{\geq 0}$
. Thus,
 $$ \begin{align*}F_n(t,x)=\sum_{j=0}^{m_*+n}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}F_{n,j}(Z^2) \in {\mathscr X}_{\lambda_*}.\end{align*} $$
$$ \begin{align*}F_n(t,x)=\sum_{j=0}^{m_*+n}(T-t)^{\lambda_*}\frac{(-\tau)^j}{j!}F_{n,j}(Z^2) \in {\mathscr X}_{\lambda_*}.\end{align*} $$
This completes the proof of Lemma 5.5.
5.4 Solvability of
 $\mathscr {L}_\lambda $
$\mathscr {L}_\lambda $
In this subsection, we prove Lemma 5.6.
Lemma 5.7. For
![]() $g\in C_{\operatorname {e}}^{\infty }([0, Z_1))$
, there exists
$g\in C_{\operatorname {e}}^{\infty }([0, Z_1))$
, there exists
![]() $F=F(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
satisfying
$F=F(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
satisfying
![]() $\mathscr {L}_\lambda F=g$
on
$\mathscr {L}_\lambda F=g$
on
![]() $(0,Z_1)$
and
$(0,Z_1)$
and
![]() $F(0;\lambda )=1$
for all
$F(0;\lambda )=1$
for all
![]() $\lambda \in B_R$
.
$\lambda \in B_R$
.
Proof. By Lemma 5.3, we have
![]() $\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
and
$\widehat B_0\in C_{\operatorname {o}}^\infty ([0,+\infty ))$
and
![]() $A_0$
,
$A_0$
,
![]() $\widetilde B_0$
,
$\widetilde B_0$
,
![]() $D_1$
,
$D_1$
,
![]() $D_2\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
. Thus, there exist
$D_2\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
. Thus, there exist
![]() $\widetilde {A}_0,B_1,B_2,\widetilde {D}_1,\widetilde {D}_2\in C^\infty ([0,+\infty ))$
such that
$\widetilde {A}_0,B_1,B_2,\widetilde {D}_1,\widetilde {D}_2\in C^\infty ([0,+\infty ))$
such that
![]() $A_0(Z)=\widetilde {A}_0(Z^2), \widetilde B_0(Z)=B_1(Z^2), \widehat B_0(Z)=ZB_2(Z^2), D_1(Z)=\widetilde {D}_1(Z^2), D_2(Z)=\widetilde {D}_2(Z^2)$
. Then
$A_0(Z)=\widetilde {A}_0(Z^2), \widetilde B_0(Z)=B_1(Z^2), \widehat B_0(Z)=ZB_2(Z^2), D_1(Z)=\widetilde {D}_1(Z^2), D_2(Z)=\widetilde {D}_2(Z^2)$
. Then
![]() $B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)=Z^{-1} B_1(Z^2)+\lambda Z B_2(Z^2)$
,
$B_0(Z;\lambda )=Z^{-1}\widetilde B_0(Z)+\lambda \widehat B_0(Z)=Z^{-1} B_1(Z^2)+\lambda Z B_2(Z^2)$
,
![]() $D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)=\lambda \widetilde {D}_1(Z^2)+\lambda ^2\widetilde {D}_2(Z^2)$
. Let
$D_0(Z;\lambda )=\lambda D_1(Z)+\lambda ^2D_2(Z)=\lambda \widetilde {D}_1(Z^2)+\lambda ^2\widetilde {D}_2(Z^2)$
. Let
![]() $\widetilde {Z}:=Z^2$
. Then for
$\widetilde {Z}:=Z^2$
. Then for
![]() $ f(Z)=\widetilde {f}(Z^2)=\widetilde {f}(\widetilde {Z})$
, we have
$ f(Z)=\widetilde {f}(Z^2)=\widetilde {f}(\widetilde {Z})$
, we have
![]() $ f'(Z)=2Z\widetilde {f}'(\widetilde {Z})$
,
$ f'(Z)=2Z\widetilde {f}'(\widetilde {Z})$
,
![]() $ f"(Z)=2\widetilde {f}'(\widetilde {Z})+4Z^2\widetilde {f}"(\widetilde {Z})$
, and by (5.16),
$ f"(Z)=2\widetilde {f}'(\widetilde {Z})+4Z^2\widetilde {f}"(\widetilde {Z})$
, and by (5.16),
 $$ \begin{align*} &(\mathscr{L}_\lambda f)(Z)=A_0(Z)f"(Z)+B_0(Z;\lambda)f'(Z)+D_0(Z;\lambda)f(Z)\\& \quad =\widetilde{A}_0(Z^2)[2\widetilde{f}'(\widetilde{Z})+4Z^2\widetilde{f}"(\widetilde{Z})]+[Z^{-1} B_1(Z^2)+\lambda Z B_2(Z^2)]\cdot2Z\widetilde{f}'(\widetilde{Z})\\& \qquad + [\lambda \widetilde{D}_1(Z^2)+\lambda^2\widetilde{D}_2(Z^2)]\widetilde{f}(\widetilde{Z})\\& \quad =4\widetilde{Z}\widetilde{A}_0(\widetilde{Z})\widetilde{f}"(\widetilde{Z})+2[\widetilde{A}_0(\widetilde{Z})+B_1(\widetilde{Z})+\lambda \widetilde{Z} B_2(\widetilde{Z})]\widetilde{f}'(\widetilde{Z})+ [\lambda \widetilde{D}_1(\widetilde{Z})+\lambda^2\widetilde{D}_2(\widetilde{Z})]\widetilde{f}(\widetilde{Z}). \end{align*} $$
$$ \begin{align*} &(\mathscr{L}_\lambda f)(Z)=A_0(Z)f"(Z)+B_0(Z;\lambda)f'(Z)+D_0(Z;\lambda)f(Z)\\& \quad =\widetilde{A}_0(Z^2)[2\widetilde{f}'(\widetilde{Z})+4Z^2\widetilde{f}"(\widetilde{Z})]+[Z^{-1} B_1(Z^2)+\lambda Z B_2(Z^2)]\cdot2Z\widetilde{f}'(\widetilde{Z})\\& \qquad + [\lambda \widetilde{D}_1(Z^2)+\lambda^2\widetilde{D}_2(Z^2)]\widetilde{f}(\widetilde{Z})\\& \quad =4\widetilde{Z}\widetilde{A}_0(\widetilde{Z})\widetilde{f}"(\widetilde{Z})+2[\widetilde{A}_0(\widetilde{Z})+B_1(\widetilde{Z})+\lambda \widetilde{Z} B_2(\widetilde{Z})]\widetilde{f}'(\widetilde{Z})+ [\lambda \widetilde{D}_1(\widetilde{Z})+\lambda^2\widetilde{D}_2(\widetilde{Z})]\widetilde{f}(\widetilde{Z}). \end{align*} $$
Let
Then we get
Let
![]() $I_1=[0,Z_1^2)$
. As
$I_1=[0,Z_1^2)$
. As
![]() $\widetilde {A}_0,B_1,B_2,\widetilde {D}_1,\widetilde {D}_2\in C^\infty ([0,+\infty ))$
, we have
$\widetilde {A}_0,B_1,B_2,\widetilde {D}_1,\widetilde {D}_2\in C^\infty ([0,+\infty ))$
, we have
![]() $\widetilde {A}\in C^\infty (I_1)$
,
$\widetilde {A}\in C^\infty (I_1)$
,
![]() $\widetilde {B}, \widetilde {D}\in \mathcal H_{I_1}(\mathbb {C})$
, and
$\widetilde {B}, \widetilde {D}\in \mathcal H_{I_1}(\mathbb {C})$
, and
![]() $\widetilde {A}'(0)=4\widetilde {A}_0(0)=4{A}_0(0)=4\neq 0$
(using (5.17)). By (5.18), we have
$\widetilde {A}'(0)=4\widetilde {A}_0(0)=4{A}_0(0)=4\neq 0$
(using (5.17)). By (5.18), we have
![]() $\widetilde {A}_0(Z^2)=A_0(Z)>0$
for
$\widetilde {A}_0(Z^2)=A_0(Z)>0$
for
![]() $Z\in [0,Z_1)$
. Thus,
$Z\in [0,Z_1)$
. Thus,
![]() $\widetilde {A}(\widetilde {Z})=4\widetilde {Z}\widetilde {A}_0(\widetilde {Z})=0$
has a unique solution
$\widetilde {A}(\widetilde {Z})=4\widetilde {Z}\widetilde {A}_0(\widetilde {Z})=0$
has a unique solution
![]() $\widetilde {Z}=0 $
in
$\widetilde {Z}=0 $
in
![]() $I_1=[0,Z_1^2)$
.
$I_1=[0,Z_1^2)$
.
Moreover, we have
![]() $\widetilde {B}(\widetilde {Z};\lambda )=\widetilde B_1(\widetilde {Z})+\lambda \widetilde {B}_2(\widetilde {Z})$
, where
$\widetilde {B}(\widetilde {Z};\lambda )=\widetilde B_1(\widetilde {Z})+\lambda \widetilde {B}_2(\widetilde {Z})$
, where
![]() $\widetilde {B}_1(\widetilde {Z}):=2[\widetilde {A}_0(\widetilde {Z})+B_1(\widetilde {Z})], \widetilde {B}_2(\widetilde {Z}):=2\widetilde {Z}B_2(\widetilde {Z})$
, then
$\widetilde {B}_1(\widetilde {Z}):=2[\widetilde {A}_0(\widetilde {Z})+B_1(\widetilde {Z})], \widetilde {B}_2(\widetilde {Z}):=2\widetilde {Z}B_2(\widetilde {Z})$
, then
![]() $\widetilde B_1(0)=2[\widetilde {A}_0(0)+B_1(0)]=2[{A}_0(0)+\widetilde B_0(0)] =2(1+k)>0$
(using (5.17) and (5.19)) and
$\widetilde B_1(0)=2[\widetilde {A}_0(0)+B_1(0)]=2[{A}_0(0)+\widetilde B_0(0)] =2(1+k)>0$
(using (5.17) and (5.19)) and
![]() $\widetilde {B}_2(0)=0$
. As a consequence, for any
$\widetilde {B}_2(0)=0$
. As a consequence, for any
![]() $\lambda \in \mathbb {C}$
and
$\lambda \in \mathbb {C}$
and
![]() $n\in \mathbb {Z}_{\geq 0}$
we have
$n\in \mathbb {Z}_{\geq 0}$
we have
![]() $n\widetilde {A}'(0)+\widetilde {B}(0;\lambda )=4n+2(1+k)\neq 0$
. As
$n\widetilde {A}'(0)+\widetilde {B}(0;\lambda )=4n+2(1+k)\neq 0$
. As
![]() $g\in C_{\operatorname {e}}^{\infty }([0, Z_1))$
, there exists
$g\in C_{\operatorname {e}}^{\infty }([0, Z_1))$
, there exists
![]() $\widetilde {g}\in C^{\infty }([0,Z_1^2))$
such that
$\widetilde {g}\in C^{\infty }([0,Z_1^2))$
such that
![]() $g(Z)=\widetilde {g}(Z^2)$
. By Proposition B.4, there exists
$g(Z)=\widetilde {g}(Z^2)$
. By Proposition B.4, there exists
![]() $\widetilde F=\widetilde F(\widetilde {Z};\lambda )\in \mathcal H_{I_1}(B_R)$
satisfying
$\widetilde F=\widetilde F(\widetilde {Z};\lambda )\in \mathcal H_{I_1}(B_R)$
satisfying
where the prime
![]() $'$
denotes the derivative with respect to
$'$
denotes the derivative with respect to
![]() $\widetilde {Z}$
. Now we define
$\widetilde {Z}$
. Now we define
then
![]() $F\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
,
$F\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
,
![]() $F(0;\lambda )=\widetilde F(0;\lambda )=1$
and
$F(0;\lambda )=\widetilde F(0;\lambda )=1$
and
![]() $\mathscr {L}_\lambda F=g$
in
$\mathscr {L}_\lambda F=g$
in
![]() $(0, Z_1)$
by recalling (5.30).
$(0, Z_1)$
by recalling (5.30).
In view of Lemma 5.3 and Proposition B.4, we let
By
![]() $B_0(Z_1;\lambda )=Z_1^{-1}\widetilde B_0(Z_1)+\lambda \widehat B_0(Z_1)$
and
$B_0(Z_1;\lambda )=Z_1^{-1}\widetilde B_0(Z_1)+\lambda \widehat B_0(Z_1)$
and
![]() $\widehat B_0(Z_1)>0$
, we know that
$\widehat B_0(Z_1)>0$
, we know that
![]() $\Lambda _*\subset \mathbb {C}$
is a non-empty (countable) discrete set.
$\Lambda _*\subset \mathbb {C}$
is a non-empty (countable) discrete set.
Lemma 5.8. There exists a nonzero polynomial
![]() $ \psi _1(\lambda )$
satisfying
$ \psi _1(\lambda )$
satisfying
![]() $\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
such that for
$\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
such that for
![]() $g\in C^{\infty }((0, +\infty ))$
, there exists a function
$g\in C^{\infty }((0, +\infty ))$
, there exists a function
![]() $F=F(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
satisfying
$F=F(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
satisfying
![]() $\mathscr {L}_\lambda F=\psi _1(\lambda )\cdot g$
on
$\mathscr {L}_\lambda F=\psi _1(\lambda )\cdot g$
on
![]() $(0, +\infty )$
and
$(0, +\infty )$
and
![]() $F(Z_1;\lambda )=\psi _1(\lambda )$
for all
$F(Z_1;\lambda )=\psi _1(\lambda )$
for all
![]() $\lambda \in B_R$
.
$\lambda \in B_R$
.
Proof. By Lemma 5.3, we have
![]() $A_0(Z_1)=0$
,
$A_0(Z_1)=0$
,
![]() $A_0'(Z_1)\neq 0$
,
$A_0'(Z_1)\neq 0$
,
![]() $\widehat B_0(Z_1)>0$
and
$\widehat B_0(Z_1)>0$
and
![]() $Z_1$
is the unique solution of
$Z_1$
is the unique solution of
![]() $A_0(Z)=0$
in
$A_0(Z)=0$
in
![]() $(0, +\infty ) $
. Hence Lemma 5.8 follows from Proposition B.4.
$(0, +\infty ) $
. Hence Lemma 5.8 follows from Proposition B.4.
Taking
![]() $g=0$
in Lemma 5.7 we know that there exists
$g=0$
in Lemma 5.7 we know that there exists
![]() $\Psi _1=\Psi _1(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
satisfying
$\Psi _1=\Psi _1(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
satisfying
![]() $\mathscr {L}_\lambda \Psi _1=0$
on
$\mathscr {L}_\lambda \Psi _1=0$
on
![]() $(0,Z_1)$
and
$(0,Z_1)$
and
![]() $\Psi _1(0;\lambda )=1$
for all
$\Psi _1(0;\lambda )=1$
for all
![]() $\lambda \in B_R$
. Taking
$\lambda \in B_R$
. Taking
![]() $g=0$
in Lemma 5.8 we know that there exists
$g=0$
in Lemma 5.8 we know that there exists
![]() $\Psi _2=\Psi _2(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
satisfying
$\Psi _2=\Psi _2(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
satisfying
![]() $\mathscr {L}_\lambda \Psi _2=0$
on
$\mathscr {L}_\lambda \Psi _2=0$
on
![]() $(0, +\infty )$
and
$(0, +\infty )$
and
![]() $\Psi _2(Z_1;\lambda )=\psi _1(\lambda )$
for all
$\Psi _2(Z_1;\lambda )=\psi _1(\lambda )$
for all
![]() $\lambda \in B_R$
. We define the Wronski
$\lambda \in B_R$
. We define the Wronski
where the prime
![]() $'$
denotes the derivative with respect to Z. Then we have
$'$
denotes the derivative with respect to Z. Then we have
Lemma 5.9. Fix
![]() $Z_0\in (0,Z_1)$
. Let
$Z_0\in (0,Z_1)$
. Let
![]() $\psi _2(\lambda ):=W(Z_0;\lambda )$
for all
$\psi _2(\lambda ):=W(Z_0;\lambda )$
for all
![]() $\lambda \in B_R$
and
$\lambda \in B_R$
and
![]() $\lambda _0^*:=\gamma -k-2$
. Then
$\lambda _0^*:=\gamma -k-2$
. Then
![]() $\psi _2\in \operatorname {Hol}(B_R)$
,
$\psi _2\in \operatorname {Hol}(B_R)$
,
![]() $0<-\lambda _0^*<k<R$
and
$0<-\lambda _0^*<k<R$
and
![]() $\psi _2(\lambda _0^*)\neq 0$
.
$\psi _2(\lambda _0^*)\neq 0$
.
Proof. As
![]() $\Psi _1(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
,
$\Psi _1(Z;\lambda )\in \mathcal H_{[0, Z_1)}^{\operatorname {e}}(B_R)$
,
![]() $\Psi _2(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
, by (5.32) we have
$\Psi _2(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
, by (5.32) we have
![]() $W(Z;\lambda )\in \mathcal H_{(0, Z_1)}(B_R)$
, then by
$W(Z;\lambda )\in \mathcal H_{(0, Z_1)}(B_R)$
, then by
![]() $Z_0\in (0,Z_1)$
we have
$Z_0\in (0,Z_1)$
we have
![]() $\psi _2(\lambda )=W(Z_0;\lambda )\in \operatorname {Hol}(B_R)$
. As
$\psi _2(\lambda )=W(Z_0;\lambda )\in \operatorname {Hol}(B_R)$
. As
![]() $\beta>0$
,
$\beta>0$
,
![]() $\ell>1$
,
$\ell>1$
,
![]() $\gamma =\beta (\ell -1)+2$
,
$\gamma =\beta (\ell -1)+2$
,
![]() $\lambda _0^*=\gamma -k-2$
, we get by (2.9) that
$\lambda _0^*=\gamma -k-2$
, we get by (2.9) that
and
![]() $R>k>k-\beta (\ell -1)=-\lambda _0^*>0$
, then
$R>k>k-\beta (\ell -1)=-\lambda _0^*>0$
, then
![]() $\lambda _0^*\in B_R$
. It remains to prove that
$\lambda _0^*\in B_R$
. It remains to prove that
![]() $\psi _2(\lambda _0^*)\neq 0$
.
$\psi _2(\lambda _0^*)\neq 0$
.
We consider the dual
![]() $\mathscr {L}_0^*$
of
$\mathscr {L}_0^*$
of
![]() $\mathscr {L}_0$
, defined by (5.25). On one hand, we get by Lemma 5.4 that
$\mathscr {L}_0$
, defined by (5.25). On one hand, we get by Lemma 5.4 that
On the other hand, by (recalling that
![]() $D_0(\cdot ;0)=0$
)
$D_0(\cdot ;0)=0$
)
and (5.25), we compute that
Comparing the coefficients of
![]() $\partial _Z$
in (5.35) and (5.36), we obtain
$\partial _Z$
in (5.35) and (5.36), we obtain
 $$ \begin{align*} Z^{-1}\widetilde B_0(Z)+\lambda_0^*\widehat B_0(Z)&=B_0(Z;\lambda_0^*)=[2\partial_Z(Z^kA_0)(Z)-Z^{k-1}\widetilde B_0(Z)]/{Z^k}\\ &={2k}{Z}^{-1}A_0(Z)+2A_0'(Z)-Z^{-1}\widetilde B_0(Z) \end{align*} $$
$$ \begin{align*} Z^{-1}\widetilde B_0(Z)+\lambda_0^*\widehat B_0(Z)&=B_0(Z;\lambda_0^*)=[2\partial_Z(Z^kA_0)(Z)-Z^{k-1}\widetilde B_0(Z)]/{Z^k}\\ &={2k}{Z}^{-1}A_0(Z)+2A_0'(Z)-Z^{-1}\widetilde B_0(Z) \end{align*} $$
for all
![]() $Z\in (0,+\infty )$
. Letting
$Z\in (0,+\infty )$
. Letting
![]() $Z=Z_1$
, we get(as
$Z=Z_1$
, we get(as
![]() $A_0(Z_1)=0$
, see (5.17))
$A_0(Z_1)=0$
, see (5.17))
For any
![]() $n\in \mathbb {Z}_{\geq 0}$
, by (5.37), (5.17), (5.19) and
$n\in \mathbb {Z}_{\geq 0}$
, by (5.37), (5.17), (5.19) and
![]() $\lambda _0^*<0$
(i.e. (5.34)), we have
$\lambda _0^*<0$
(i.e. (5.34)), we have
 $$ \begin{align} \begin{aligned} nA_0'(Z_1)+B_0(Z_1;\lambda_0^*)&=nA_0'(Z_1)+Z_1^{-1}\widetilde B_0(Z_1)+\lambda_0^*\widehat B_0(Z_1)\\ &=(n+1)A_0'(Z_1)+{\lambda_0^*}\widehat B_0(Z_1)/{2}<0, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} nA_0'(Z_1)+B_0(Z_1;\lambda_0^*)&=nA_0'(Z_1)+Z_1^{-1}\widetilde B_0(Z_1)+\lambda_0^*\widehat B_0(Z_1)\\ &=(n+1)A_0'(Z_1)+{\lambda_0^*}\widehat B_0(Z_1)/{2}<0, \end{aligned} \end{align} $$
It follows from (5.31) and (5.38) that
![]() $\lambda _0^*\notin \Lambda _*$
. Then by
$\lambda _0^*\notin \Lambda _*$
. Then by
![]() $\lambda _0^*\in B_R$
and Lemma 5.8, we have
$\lambda _0^*\in B_R$
and Lemma 5.8, we have
![]() $\psi _1(\lambda _0^*)\neq 0$
. Let
$\psi _1(\lambda _0^*)\neq 0$
. Let
![]() $f_1=\Psi _1(\cdot ;\lambda _0^*)$
and
$f_1=\Psi _1(\cdot ;\lambda _0^*)$
and
![]() $f_2=\Psi _2(\cdot ;\lambda _0^*)$
, then
$f_2=\Psi _2(\cdot ;\lambda _0^*)$
, then
![]() $f_1\in C_{\text {e}}^\infty ([0,Z_1))$
,
$f_1\in C_{\text {e}}^\infty ([0,Z_1))$
,
![]() $f_2\in C^\infty ((0,+\infty ))$
and
$f_2\in C^\infty ((0,+\infty ))$
and
![]() $(\mathscr {L}_{\lambda _0^*}f_j)(Z)=0$
for
$(\mathscr {L}_{\lambda _0^*}f_j)(Z)=0$
for
![]() $Z\in (0, Z_1)$
,
$Z\in (0, Z_1)$
,
![]() $j\in \{1, 2\}$
. By (5.35) and (5.36), we get
$j\in \{1, 2\}$
. By (5.35) and (5.36), we get
By
![]() $f_1,A_0,\widetilde B_0\in C_{\text {e}}^\infty ([0,Z_1))$
,
$f_1,A_0,\widetilde B_0\in C_{\text {e}}^\infty ([0,Z_1))$
,
![]() $k\geq 3$
we have
$k\geq 3$
we have
![]() $[\partial _Z(Z^kA_0f_1)(Z)-Z^{k-1}\widetilde B_0(Z)f_1(Z)]|_{Z=0}=0$
, so
$[\partial _Z(Z^kA_0f_1)(Z)-Z^{k-1}\widetilde B_0(Z)f_1(Z)]|_{Z=0}=0$
, so
For
![]() $f_2$
, since
$f_2$
, since
![]() $A_0(Z_1)=0$
(see (5.17)), we have
$A_0(Z_1)=0$
(see (5.17)), we have
 $$ \begin{align} &\partial_Z(Z^kA_0f_2)(Z)-Z^{k-1}\widetilde B_0(Z)f_2(Z)=[\partial_Z(Z^kA_0f_2)(Z)-Z^{k-1}\widetilde B_0(Z)f_2(Z)]|_{Z=Z_1}\notag\\& \quad =Z_1^kA_0'(Z_1)f_2(Z_1)-Z_1^{k-1}\widetilde B_0(Z_1)f_2(Z_1)=Z_1^k(A_0'(Z_1)-Z_1^{-1}\widetilde B_0(Z_1))\psi_1(\lambda_0^*)=:C' \end{align} $$
$$ \begin{align} &\partial_Z(Z^kA_0f_2)(Z)-Z^{k-1}\widetilde B_0(Z)f_2(Z)=[\partial_Z(Z^kA_0f_2)(Z)-Z^{k-1}\widetilde B_0(Z)f_2(Z)]|_{Z=Z_1}\notag\\& \quad =Z_1^kA_0'(Z_1)f_2(Z_1)-Z_1^{k-1}\widetilde B_0(Z_1)f_2(Z_1)=Z_1^k(A_0'(Z_1)-Z_1^{-1}\widetilde B_0(Z_1))\psi_1(\lambda_0^*)=:C' \end{align} $$
for all
![]() $Z\in (0, Z_1)$
, where we have used
$Z\in (0, Z_1)$
, where we have used
![]() $f_2(Z_1)=\Psi _2(Z_1;\lambda _0^*)=\psi _1(\lambda _0^*)$
(recalling Lemma 5.8). Moreover, by (5.37),
$f_2(Z_1)=\Psi _2(Z_1;\lambda _0^*)=\psi _1(\lambda _0^*)$
(recalling Lemma 5.8). Moreover, by (5.37),
![]() $\lambda _0^*<0$
(in (5.34)) and
$\lambda _0^*<0$
(in (5.34)) and
![]() $\widehat B_0(Z_1)>0$
(in (5.19)), we have
$\widehat B_0(Z_1)>0$
(in (5.19)), we have
![]() $A_0'(Z_1)-Z_1^{-1}\widetilde B_0(Z_1)={\lambda _0^*}\widehat B_0(Z_1)/{2}<0$
, then by
$A_0'(Z_1)-Z_1^{-1}\widetilde B_0(Z_1)={\lambda _0^*}\widehat B_0(Z_1)/{2}<0$
, then by
![]() $\psi _1(\lambda _0^*)\neq 0$
we have
$\psi _1(\lambda _0^*)\neq 0$
we have
![]() $C'\neq 0$
. We claim that
$C'\neq 0$
. We claim that
Indeed, if
![]() $f_1(Z^*)=0$
for some
$f_1(Z^*)=0$
for some
![]() $Z^*\in (0, Z_1)$
, by the uniqueness of solutions to (5.39) in
$Z^*\in (0, Z_1)$
, by the uniqueness of solutions to (5.39) in
![]() $(0, Z_1)$
with
$(0, Z_1)$
with
![]() $f_1(Z^*)=0$
, we have
$f_1(Z^*)=0$
, we have
![]() $f_1(Z)=0$
for all
$f_1(Z)=0$
for all
![]() $Z\in (0, Z_1)$
, which contradicts with
$Z\in (0, Z_1)$
, which contradicts with
![]() $1=f_1(0)=\lim _{Z\to 0+}f_1(Z)$
. This proves (5.41). As
$1=f_1(0)=\lim _{Z\to 0+}f_1(Z)$
. This proves (5.41). As
![]() $f_1=\Psi _1(\cdot ;\lambda _0^*)$
,
$f_1=\Psi _1(\cdot ;\lambda _0^*)$
,
![]() $f_2=\Psi _2(\cdot ;\lambda _0^*)$
, by (5.32), (5.39), (5.40), (5.41) and
$f_2=\Psi _2(\cdot ;\lambda _0^*)$
, by (5.32), (5.39), (5.40), (5.41) and
![]() $C'\neq 0$
, we have
$C'\neq 0$
, we have
 $$ \begin{align*} &Z^kA_0(Z)W(Z;\lambda_0^*)=Z^kA_0(Z)[f_1(Z)f_2'(Z)-f_1'(Z)f_2(Z)]\\&\quad=f_1(Z)\partial_Z(Z^kA_0f_2)(Z)-\partial_Z(Z^kA_0f_1)(Z)f_2(Z)\\&\quad=f_1(Z)[Z^{k-1}\widetilde B_0(Z)f_2(Z)+C']-Z^{k-1}\widetilde B_0(Z)f_1(Z)f_2(Z)=C'f_1(Z)\neq0, \end{align*} $$
$$ \begin{align*} &Z^kA_0(Z)W(Z;\lambda_0^*)=Z^kA_0(Z)[f_1(Z)f_2'(Z)-f_1'(Z)f_2(Z)]\\&\quad=f_1(Z)\partial_Z(Z^kA_0f_2)(Z)-\partial_Z(Z^kA_0f_1)(Z)f_2(Z)\\&\quad=f_1(Z)[Z^{k-1}\widetilde B_0(Z)f_2(Z)+C']-Z^{k-1}\widetilde B_0(Z)f_1(Z)f_2(Z)=C'f_1(Z)\neq0, \end{align*} $$
for all
![]() $Z\in (0, Z_1)$
. Thus,
$Z\in (0, Z_1)$
. Thus,
![]() $W(Z;\lambda _0^*)\neq 0 $
for all
$W(Z;\lambda _0^*)\neq 0 $
for all
![]() $Z\in (0, Z_1)$
, and
$Z\in (0, Z_1)$
, and
![]() $\psi _2(\lambda _0^*)=W(Z_0;\lambda _0^*)\neq 0$
.
$\psi _2(\lambda _0^*)=W(Z_0;\lambda _0^*)\neq 0$
.
Now we fix
![]() $Z_0\in (0,Z_1)$
,
$Z_0\in (0,Z_1)$
,
![]() $\psi _2(\lambda )=W(Z_0;\lambda )$
,
$\psi _2(\lambda )=W(Z_0;\lambda )$
,
![]() $\lambda _0^*:=\gamma -k-2$
. Let
$\lambda _0^*:=\gamma -k-2$
. Let
![]() $ \psi _1(\lambda )$
be given by Lemma 5.8 and
$ \psi _1(\lambda )$
be given by Lemma 5.8 and
![]() $\varphi (\lambda ):=\psi _1(\lambda )\psi _2(\lambda )$
for all
$\varphi (\lambda ):=\psi _1(\lambda )\psi _2(\lambda )$
for all
![]() $\lambda \in B_R$
. Let
$\lambda \in B_R$
. Let
![]() $g\in C_{\text {e}}^\infty ([0,+\infty ))$
, we need to prove that there exists a function
$g\in C_{\text {e}}^\infty ([0,+\infty ))$
, we need to prove that there exists a function
![]() $f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
$\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
![]() $(0,+\infty )$
.
$(0,+\infty )$
.
We first consider the case when g is supported near
![]() $Z=0$
.
$Z=0$
.
Lemma 5.10. Assume that
![]() $g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
satisfies
$g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
satisfies
![]() $\operatorname {supp}g\subset [0, Z_1)$
, then there exists a function
$\operatorname {supp}g\subset [0, Z_1)$
, then there exists a function
![]() $f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
$\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
![]() $(0,+\infty )$
.
$(0,+\infty )$
.
Proof. By Lemma 5.7, there exists
![]() $f_0\in \mathcal H_{[0, Z_1)}^{\text e}(B_R)$
such that
$f_0\in \mathcal H_{[0, Z_1)}^{\text e}(B_R)$
such that
![]() $\mathscr {L}_\lambda f_0=g$
on
$\mathscr {L}_\lambda f_0=g$
on
![]() $(0, Z_1)$
with
$(0, Z_1)$
with
![]() $f_0(0;\lambda )=1$
for all
$f_0(0;\lambda )=1$
for all
![]() $\lambda \in B_R$
. We assume that
$\lambda \in B_R$
. We assume that
![]() $\operatorname {supp}g\subset [0,\delta )$
for some
$\operatorname {supp}g\subset [0,\delta )$
for some
![]() $\delta \in (0, Z_1)$
, then
$\delta \in (0, Z_1)$
, then
![]() $(\mathscr {L}_\lambda f_0)(Z)=0$
for
$(\mathscr {L}_\lambda f_0)(Z)=0$
for
![]() $Z\in [\delta , Z_1)$
. For
$Z\in [\delta , Z_1)$
. For
![]() $\lambda \in B_R$
, let
$\lambda \in B_R$
, let
Then
![]() $C_1, C_2$
are holomorphic functions on
$C_1, C_2$
are holomorphic functions on
![]() $B_R$
and for all
$B_R$
and for all
![]() $\lambda \in B_R$
there holds
$\lambda \in B_R$
there holds
 $$ \begin{align*}&W(\delta;\lambda)f_0(\delta;\lambda)=C_1(\lambda)\Psi_1(\delta;\lambda)+C_2(\lambda)\Psi_2(\delta;\lambda),\\& W(\delta;\lambda)f_0'(\delta;\lambda)=C_1(\lambda)\Psi_1'(\delta;\lambda)+C_2(\lambda)\Psi_2'(\delta;\lambda).\end{align*} $$
$$ \begin{align*}&W(\delta;\lambda)f_0(\delta;\lambda)=C_1(\lambda)\Psi_1(\delta;\lambda)+C_2(\lambda)\Psi_2(\delta;\lambda),\\& W(\delta;\lambda)f_0'(\delta;\lambda)=C_1(\lambda)\Psi_1'(\delta;\lambda)+C_2(\lambda)\Psi_2'(\delta;\lambda).\end{align*} $$
By the uniqueness of the solution on
![]() $[\delta , Z_1)$
, we have
$[\delta , Z_1)$
, we have
For
![]() $\lambda \in B_R$
, let
$\lambda \in B_R$
, let
 $$\begin{align*}f_*(Z;\lambda):=\begin{cases} W(\delta;\lambda)f_0(Z;\lambda)-C_1(\lambda)\Psi_1(Z;\lambda) & \text{if }Z\in [0, Z_1),\\ C_2(\lambda)\Psi_2(Z;\lambda) & \text{if }Z\in[\delta, +\infty). \end{cases}\end{align*}$$
$$\begin{align*}f_*(Z;\lambda):=\begin{cases} W(\delta;\lambda)f_0(Z;\lambda)-C_1(\lambda)\Psi_1(Z;\lambda) & \text{if }Z\in [0, Z_1),\\ C_2(\lambda)\Psi_2(Z;\lambda) & \text{if }Z\in[\delta, +\infty). \end{cases}\end{align*}$$
Then
![]() $f_*\in \mathcal H_{[0,+\infty )}^{\text e}(B_R)$
and
$f_*\in \mathcal H_{[0,+\infty )}^{\text e}(B_R)$
and
![]() $\mathscr {L}_\lambda f_*=W(\delta ;\lambda )\cdot g$
on
$\mathscr {L}_\lambda f_*=W(\delta ;\lambda )\cdot g$
on
![]() $(0,+\infty )$
. By (5.33), we have
$(0,+\infty )$
. By (5.33), we have
![]() $W(Z;\lambda )=W(Z_0;\lambda )\mathrm {e}^{- A_*(Z;\lambda )}=\psi _2(\lambda )\mathrm {e}^{- A_*(Z;\lambda )}$
with
$W(Z;\lambda )=W(Z_0;\lambda )\mathrm {e}^{- A_*(Z;\lambda )}=\psi _2(\lambda )\mathrm {e}^{- A_*(Z;\lambda )}$
with
![]() $A_*(Z;\lambda ):=\int _{Z_0}^Z\frac {B_0(Z;\lambda )}{A_0(Z)}\mathrm {d}Z\in \mathcal H_{(0,Z_1)}(B_R) $
(using Lemma 5.3). Recall that
$A_*(Z;\lambda ):=\int _{Z_0}^Z\frac {B_0(Z;\lambda )}{A_0(Z)}\mathrm {d}Z\in \mathcal H_{(0,Z_1)}(B_R) $
(using Lemma 5.3). Recall that
![]() $\varphi =\psi _1\psi _2$
,
$\varphi =\psi _1\psi _2$
,
![]() $ \psi _1$
is a polynomial, then
$ \psi _1$
is a polynomial, then
![]() $\varphi (\lambda )=\psi _1(\lambda )W(\delta ;\lambda )\mathrm {e}^{A_*(\delta ;\lambda )} $
, and the result follows by taking
$\varphi (\lambda )=\psi _1(\lambda )W(\delta ;\lambda )\mathrm {e}^{A_*(\delta ;\lambda )} $
, and the result follows by taking
![]() $ f(Z;\lambda ):=\psi _1(\lambda )\mathrm {e}^{A_*(\delta ;\lambda )}f_*(Z;\lambda )$
for
$ f(Z;\lambda ):=\psi _1(\lambda )\mathrm {e}^{A_*(\delta ;\lambda )}f_*(Z;\lambda )$
for
![]() $Z\in [0, +\infty ),\lambda \in B_R$
.
$Z\in [0, +\infty ),\lambda \in B_R$
.
Now we consider the case when g is supported away from
![]() $Z=0$
.
$Z=0$
.
Lemma 5.11. Assume that
![]() $g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
satisfies
$g\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
satisfies
![]() $\operatorname {supp}g\subset (0, +\infty )$
, then there exists a function
$\operatorname {supp}g\subset (0, +\infty )$
, then there exists a function
![]() $f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f=f(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
$\mathscr {L}_\lambda f(\cdot ;\lambda )=\varphi (\lambda )\cdot g$
on
![]() $(0,+\infty )$
.
$(0,+\infty )$
.
Proof. By Lemma 5.8, there exists
![]() $f_0=f_0(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
such that
$f_0=f_0(Z;\lambda )\in \mathcal H_{(0,+\infty )}(B_R)$
such that
![]() $\mathscr {L}_\lambda f_0=\psi _1(\lambda )\cdot g$
on
$\mathscr {L}_\lambda f_0=\psi _1(\lambda )\cdot g$
on
![]() $(0, +\infty )$
. We assume that
$(0, +\infty )$
. We assume that
![]() $\operatorname {supp} g\subset (\delta , +\infty )$
for some
$\operatorname {supp} g\subset (\delta , +\infty )$
for some
![]() $\delta \in (0, Z_1)$
, then
$\delta \in (0, Z_1)$
, then
![]() $(\mathscr {L}_\lambda f_0)(Z)=0$
for
$(\mathscr {L}_\lambda f_0)(Z)=0$
for
![]() $Z\in (0,\delta ]$
. For
$Z\in (0,\delta ]$
. For
![]() $\lambda \in B_R$
, let
$\lambda \in B_R$
, let
![]() $C_1(\lambda ), C_2(\lambda )$
be defined by (5.42) and (5.43) respectively. For the same reason as in the proof of Lemma 5.10, we have
$C_1(\lambda ), C_2(\lambda )$
be defined by (5.42) and (5.43) respectively. For the same reason as in the proof of Lemma 5.10, we have
For
![]() $\lambda \in B_R$
, let
$\lambda \in B_R$
, let
 $$\begin{align*}f_*(Z;\lambda):=\begin{cases} W(\delta;\lambda)f_0(Z;\lambda)-C_2(\lambda)\Psi_2(Z;\lambda) & \text{if }Z\in (0, +\infty),\\ C_1(\lambda)\Psi_1(Z;\lambda) & \text{if }Z\in[0,\delta]. \end{cases}\end{align*}$$
$$\begin{align*}f_*(Z;\lambda):=\begin{cases} W(\delta;\lambda)f_0(Z;\lambda)-C_2(\lambda)\Psi_2(Z;\lambda) & \text{if }Z\in (0, +\infty),\\ C_1(\lambda)\Psi_1(Z;\lambda) & \text{if }Z\in[0,\delta]. \end{cases}\end{align*}$$
Then
![]() $f_*\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
and
$f_*\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
and
![]() $\mathscr {L}_\lambda f_*=W(\delta ;\lambda )\psi _1(\lambda )\cdot g$
on
$\mathscr {L}_\lambda f_*=W(\delta ;\lambda )\psi _1(\lambda )\cdot g$
on
![]() $(0,+\infty )$
. As in the proof of Lemma 5.10, we have
$(0,+\infty )$
. As in the proof of Lemma 5.10, we have
![]() $\varphi (\lambda )=\psi _1(\lambda )W(\delta ;\lambda )\mathrm {e}^{A_*(\delta ;\lambda )} $
and
$\varphi (\lambda )=\psi _1(\lambda )W(\delta ;\lambda )\mathrm {e}^{A_*(\delta ;\lambda )} $
and
![]() $A_*(Z;\lambda )\in \mathcal H_{(0,Z_1)}(B_R) $
, then the result follows by taking
$A_*(Z;\lambda )\in \mathcal H_{(0,Z_1)}(B_R) $
, then the result follows by taking
![]() $ f(Z;\lambda ):=\mathrm {e}^{A_*(\delta ;\lambda )}f_*(Z;\lambda )$
for
$ f(Z;\lambda ):=\mathrm {e}^{A_*(\delta ;\lambda )}f_*(Z;\lambda )$
for
![]() $Z\in [0, +\infty ),\lambda \in B_R$
.
$Z\in [0, +\infty ),\lambda \in B_R$
.
Now we are in a position to prove Lemma 5.6.
Proof of Lemma 5.6.
We fix
![]() $Z_0\in (0,Z_1)$
,
$Z_0\in (0,Z_1)$
,
![]() $\psi _2(\lambda )=W(Z_0;\lambda )$
,
$\psi _2(\lambda )=W(Z_0;\lambda )$
,
![]() $\lambda _0^*:=\gamma -k-2$
. Let
$\lambda _0^*:=\gamma -k-2$
. Let
![]() $ \psi _1(\lambda )$
be given by Lemma 5.8 and
$ \psi _1(\lambda )$
be given by Lemma 5.8 and
![]() $\varphi (\lambda ):=\psi _1(\lambda )\psi _2(\lambda )$
for all
$\varphi (\lambda ):=\psi _1(\lambda )\psi _2(\lambda )$
for all
![]() $\lambda \in B_R$
. By Lemma 5.9, we have
$\lambda \in B_R$
. By Lemma 5.9, we have
![]() $\lambda _0^*\in B_R$
and
$\lambda _0^*\in B_R$
and
![]() $\psi _2\in \operatorname {Hol}(B_R)\setminus \{0\}$
. By Lemma 5.8 we have
$\psi _2\in \operatorname {Hol}(B_R)\setminus \{0\}$
. By Lemma 5.8 we have
![]() $\psi _1\in \operatorname {Hol}(B_R)\setminus \{0\}$
. Thus,
$\psi _1\in \operatorname {Hol}(B_R)\setminus \{0\}$
. Thus,
![]() $\varphi =\psi _1\psi _2\in \operatorname {Hol}(B_R)\setminus \{0\}$
.
$\varphi =\psi _1\psi _2\in \operatorname {Hol}(B_R)\setminus \{0\}$
.
Let
![]() $\zeta \in C^\infty (\mathbb {R};[0,1])$
satisfy
$\zeta \in C^\infty (\mathbb {R};[0,1])$
satisfy
![]() $\operatorname {supp}\zeta \subset (Z_1/2, +\infty )$
and
$\operatorname {supp}\zeta \subset (Z_1/2, +\infty )$
and
![]() $\zeta (Z)=1$
for
$\zeta (Z)=1$
for
![]() $Z\in [3Z_1/4, +\infty )$
. Let
$Z\in [3Z_1/4, +\infty )$
. Let
![]() $g_1(Z)=g(Z)(1-\zeta (Z)), g_2(Z)=g(Z){\zeta }(Z)$
for all
$g_1(Z)=g(Z)(1-\zeta (Z)), g_2(Z)=g(Z){\zeta }(Z)$
for all
![]() $Z\in [0,+\infty )$
. Then
$Z\in [0,+\infty )$
. Then
By Lemma 5.10, there exists
![]() $f_1=f_1(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f_1=f_1(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f_1=\varphi (\lambda )g_1$
on
$\mathscr {L}_\lambda f_1=\varphi (\lambda )g_1$
on
![]() $(0,+\infty )$
. By Lemma 5.11, there exists
$(0,+\infty )$
. By Lemma 5.11, there exists
![]() $f_2=f_2(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
$f_2=f_2(Z;\lambda )\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
such that
![]() $\mathscr {L}_\lambda f_2=\varphi (\lambda )g_2$
on
$\mathscr {L}_\lambda f_2=\varphi (\lambda )g_2$
on
![]() $(0,+\infty )$
. Let
$(0,+\infty )$
. Let
![]() $f=f_1+f_2$
, then
$f=f_1+f_2$
, then
![]() $f\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
satisfies
$f\in \mathcal H_{[0,+\infty )}^{\operatorname {e}}(B_R)$
satisfies
![]() $\mathscr {L}_\lambda f=\varphi (\lambda )g$
on
$\mathscr {L}_\lambda f=\varphi (\lambda )g$
on
![]() $(0,+\infty )$
.
$(0,+\infty )$
.
A The derivation and properties of ODE (2.8)
A.1 The derivation of ODE (2.8)
Lemma A.1. Let
![]() $\beta>1$
and
$\beta>1$
and
![]() $v=v(Z)\in C^\infty ([0, +\infty );(-1, 1))$
be given by Assumption 1. We define
$v=v(Z)\in C^\infty ([0, +\infty );(-1, 1))$
be given by Assumption 1. We define
![]() $\widehat \phi _0(Z), \widehat \rho _0(Z)$
according to (2.12) and we define
$\widehat \phi _0(Z), \widehat \rho _0(Z)$
according to (2.12) and we define
![]() $\phi _0(t,x),\rho _0(t,x)$
by (2.7). Then
$\phi _0(t,x),\rho _0(t,x)$
by (2.7). Then
![]() $(\phi _0,\rho _0)$
solves the leading order equation (2.6).
$(\phi _0,\rho _0)$
solves the leading order equation (2.6).
Proof. Recall that
![]() $Z=r/(T-t)$
with
$Z=r/(T-t)$
with
![]() $r=|x|$
, we know that
$r=|x|$
, we know that
![]() $\phi _0=\phi _0(t,r)$
and
$\phi _0=\phi _0(t,r)$
and
![]() $\rho _0=\rho _0(t,r)$
are radially symmetric. Hence, (2.6) is equivalent to
$\rho _0=\rho _0(t,r)$
are radially symmetric. Hence, (2.6) is equivalent to
where
![]() $k=d-1\in \mathbb {Z}_{\geq 1}$
. It follows from (2.7) that
$k=d-1\in \mathbb {Z}_{\geq 1}$
. It follows from (2.7) that
where the prime
![]() $'$
stands for the derivative with respect to Z. By (2.12), we have
$'$
stands for the derivative with respect to Z. By (2.12), we have
 $$ \begin{align} \widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)}\Longleftrightarrow\big((\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)\big)v(Z)=\widehat\phi_0'(Z), \end{align} $$
$$ \begin{align} \widehat\phi_0'(Z)=\frac{(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)}\Longleftrightarrow\big((\beta-1)\widehat\phi_0(Z)+Z\widehat\phi_0'(Z)\big)v(Z)=\widehat\phi_0'(Z), \end{align} $$
thus
 $$\begin{align*}\partial_t\phi_0(t,x)=\frac{(T-t)^{-\beta}(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)},\qquad \partial_r\phi_0(t,x)=\frac{(T-t)^{-\beta}(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\end{align*}$$
$$\begin{align*}\partial_t\phi_0(t,x)=\frac{(T-t)^{-\beta}(\beta-1)\widehat\phi_0(Z)}{1-Zv(Z)},\qquad \partial_r\phi_0(t,x)=\frac{(T-t)^{-\beta}(\beta-1)\widehat\phi_0(Z)v(Z)}{1-Zv(Z)},\end{align*}$$
and then we have
 $$\begin{align*}|\partial_t\phi_0|^2-|\partial_r\phi_0|^2=\frac{(T-t)^{-2\beta}(\beta-1)^2\widehat\phi_0(Z)^2(1-v(Z)^2)}{(1-Zv(Z))^2}.\end{align*}$$
$$\begin{align*}|\partial_t\phi_0|^2-|\partial_r\phi_0|^2=\frac{(T-t)^{-2\beta}(\beta-1)^2\widehat\phi_0(Z)^2(1-v(Z)^2)}{(1-Zv(Z))^2}.\end{align*}$$
Using (2.7) and (2.12) for
![]() $\rho _0$
and
$\rho _0$
and
![]() $\widehat \rho _0$
, we obtain the first equation in (A.1).
$\widehat \rho _0$
, we obtain the first equation in (A.1).
Now we define
 $$ \begin{align} \ell=\frac4{p-1}+1>1,\quad \widetilde\phi_0(Z):=\frac{\widehat\phi_0(Z)^\ell(1-v(Z)^2)^{\frac{2}{p-1}}}{(1-Zv(Z))^\ell}=\frac{\widehat\phi_0(Z)^\ell(1-v(Z)^2)^{\frac{\ell-1}{2}}}{(1-Zv(Z))^\ell}>0. \end{align} $$
$$ \begin{align} \ell=\frac4{p-1}+1>1,\quad \widetilde\phi_0(Z):=\frac{\widehat\phi_0(Z)^\ell(1-v(Z)^2)^{\frac{2}{p-1}}}{(1-Zv(Z))^\ell}=\frac{\widehat\phi_0(Z)^\ell(1-v(Z)^2)^{\frac{\ell-1}{2}}}{(1-Zv(Z))^\ell}>0. \end{align} $$
Then we compute that
 $$ \begin{align*} \rho_0^2\partial_t\phi_0(t,x)&=(T-t)^{-\beta\ell}(\beta-1)^\ell\widetilde\phi_0(Z),\\ \rho_0^2\partial_r\phi_0(t,x)&=(T-t)^{-\beta\ell}(\beta-1)^\ell\widetilde\phi_0(Z)v(Z),\\ \partial_t(\rho_0^2\partial_t\phi_0)(t,x)&= (T-t)^{-\beta\ell-1}(\beta-1)^\ell\big(\beta\ell\widetilde\phi_0(Z)+Z\widetilde\phi_0'(Z)\big),\\ \partial_r(\rho_0^2\partial_r\phi_0)(t,x)&=(T-t)^{-\beta\ell-1}(\beta-1)^\ell(\widetilde\phi_0 v)'(Z),\\ \frac{k}{r}\rho_0^2\partial_r\phi_0(t,x)&=(T-t)^{-\beta\ell-1}(\beta-1)^\ell\frac{k}{Z}(\widetilde\phi_0 v)(Z). \end{align*} $$
$$ \begin{align*} \rho_0^2\partial_t\phi_0(t,x)&=(T-t)^{-\beta\ell}(\beta-1)^\ell\widetilde\phi_0(Z),\\ \rho_0^2\partial_r\phi_0(t,x)&=(T-t)^{-\beta\ell}(\beta-1)^\ell\widetilde\phi_0(Z)v(Z),\\ \partial_t(\rho_0^2\partial_t\phi_0)(t,x)&= (T-t)^{-\beta\ell-1}(\beta-1)^\ell\big(\beta\ell\widetilde\phi_0(Z)+Z\widetilde\phi_0'(Z)\big),\\ \partial_r(\rho_0^2\partial_r\phi_0)(t,x)&=(T-t)^{-\beta\ell-1}(\beta-1)^\ell(\widetilde\phi_0 v)'(Z),\\ \frac{k}{r}\rho_0^2\partial_r\phi_0(t,x)&=(T-t)^{-\beta\ell-1}(\beta-1)^\ell\frac{k}{Z}(\widetilde\phi_0 v)(Z). \end{align*} $$
Therefore, the second equation in (A.1) is equivalent to
Recall from (A.3) and (A.4) that
 $$ \begin{align*} \frac{\widetilde\phi_0'}{\widetilde\phi_0} &=\ell\frac{\widehat\phi_0'}{\widehat\phi_0}-(\ell-1)\frac{vv'}{1-v^2}+\ell\frac{v+Zv'}{1-Zv}\\ &=\ell\frac{(\beta-1)v}{1-Zv}+\ell\frac{v}{1-Zv}-(\ell-1)\frac{vv'}{1-v^2}+\ell\frac{Zv'}{1-Zv}\\ &=\frac{\beta\ell v}{1-Zv}+\frac{vv'}{1-v^2}+\frac{\ell(Z-v)v'}{(1-v^2)(1-Zv)}, \end{align*} $$
$$ \begin{align*} \frac{\widetilde\phi_0'}{\widetilde\phi_0} &=\ell\frac{\widehat\phi_0'}{\widehat\phi_0}-(\ell-1)\frac{vv'}{1-v^2}+\ell\frac{v+Zv'}{1-Zv}\\ &=\ell\frac{(\beta-1)v}{1-Zv}+\ell\frac{v}{1-Zv}-(\ell-1)\frac{vv'}{1-v^2}+\ell\frac{Zv'}{1-Zv}\\ &=\frac{\beta\ell v}{1-Zv}+\frac{vv'}{1-v^2}+\frac{\ell(Z-v)v'}{(1-v^2)(1-Zv)}, \end{align*} $$
hence (A.5) is equivalent to
 $$ \begin{align*} \beta\ell-v'-\frac{kv}{Z}=(v-Z)\frac{\widetilde\phi_0'}{\widetilde\phi_0} =\frac{\beta\ell v(v-Z)}{1-Zv}+\frac{v(v-Z)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)}, \end{align*} $$
$$ \begin{align*} \beta\ell-v'-\frac{kv}{Z}=(v-Z)\frac{\widetilde\phi_0'}{\widetilde\phi_0} =\frac{\beta\ell v(v-Z)}{1-Zv}+\frac{v(v-Z)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)}, \end{align*} $$
or equivalently,
 $$ \begin{align*} \beta\ell-\frac{\beta\ell v(v-Z)}{1-Zv}-\frac{kv}{Z} &=v'+\frac{v(v-Z)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)},\\\frac{\beta\ell(1-v^2)}{1-Zv}-\frac{kv}{Z} &=\frac{(1-Zv)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)}, \end{align*} $$
$$ \begin{align*} \beta\ell-\frac{\beta\ell v(v-Z)}{1-Zv}-\frac{kv}{Z} &=v'+\frac{v(v-Z)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)},\\\frac{\beta\ell(1-v^2)}{1-Zv}-\frac{kv}{Z} &=\frac{(1-Zv)v'}{1-v^2}-\frac{\ell(v-Z)^2v'}{(1-v^2)(1-Zv)}, \end{align*} $$
which is a direct consequence of (2.8).
A.2 Properties of solutions to ODE (2.8)
In this part, we prove Remark 2.2.
Lemma A.2. Under Assumption 1, we have
![]() $v(Z_1)=v_1$
, where
$v(Z_1)=v_1$
, where
 $$ \begin{align} Z_1=\frac{k}{\sqrt{\ell}(k-\beta(\ell-1))},\qquad v_1=\frac{\beta\sqrt{\ell}}{k-\beta\ell}. \end{align} $$
$$ \begin{align} Z_1=\frac{k}{\sqrt{\ell}(k-\beta(\ell-1))},\qquad v_1=\frac{\beta\sqrt{\ell}}{k-\beta\ell}. \end{align} $$
Proof. We define a function
![]() $F_0\in C^\infty ([0, +\infty ))$
by
$F_0\in C^\infty ([0, +\infty ))$
by
Then
![]() $F_0(0)=1$
and
$F_0(0)=1$
and
![]() $F_0(1)=(\sqrt \ell -1)(v(1)-1)<0$
, where we have used that
$F_0(1)=(\sqrt \ell -1)(v(1)-1)<0$
, where we have used that
![]() $v(1)\in (-1, 1)$
, recalling Assumption 1. By the intermediate value theorem, there exists
$v(1)\in (-1, 1)$
, recalling Assumption 1. By the intermediate value theorem, there exists
![]() $Z_0\in (0,1)$
such that
$Z_0\in (0,1)$
such that
![]() $F_0(Z_0)=0$
. Thus,
$F_0(Z_0)=0$
. Thus,
![]() $\Delta _Z(Z_0, v(Z_0))=Z_0F_0(Z_0)\big (1-Z_0v(Z_0)-\sqrt \ell (v(Z_0)-Z_0)\big )=0$
. Then we have
$\Delta _Z(Z_0, v(Z_0))=Z_0F_0(Z_0)\big (1-Z_0v(Z_0)-\sqrt \ell (v(Z_0)-Z_0)\big )=0$
. Then we have
![]() $\Delta _v(Z_0, v(Z_0))=\Delta _Z(Z_0, v(Z_0))v'(Z_0)=0$
, i.e.,
$\Delta _v(Z_0, v(Z_0))=\Delta _Z(Z_0, v(Z_0))v'(Z_0)=0$
, i.e.,
![]() $\Delta _v(Z_0, v(Z_0))=\Delta _Z(Z_0, v(Z_0))=0$
. On the other hand, it is direct to check that
$\Delta _v(Z_0, v(Z_0))=\Delta _Z(Z_0, v(Z_0))=0$
. On the other hand, it is direct to check that
where
![]() $Z_1, v_1$
are given by (A.6). Moreover, it follows from (2.9) that
$Z_1, v_1$
are given by (A.6). Moreover, it follows from (2.9) that
![]() $0<v_1<Z_1<1$
. Hence, we must have
$0<v_1<Z_1<1$
. Hence, we must have
![]() $(Z_0, v(Z_0))=(Z_1, v_1)$
, which implies that
$(Z_0, v(Z_0))=(Z_1, v_1)$
, which implies that
![]() $v(Z_1)=v_1$
.
$v(Z_1)=v_1$
.
Lemma A.3. Under Assumption 1, let
![]() $\Delta _0(Z):=\Delta _Z(Z, v(Z))$
for
$\Delta _0(Z):=\Delta _Z(Z, v(Z))$
for
![]() $Z\in [0, +\infty )$
, then we have
$Z\in [0, +\infty )$
, then we have
![]() $\Delta _0(Z)>0$
for
$\Delta _0(Z)>0$
for
![]() $Z\in (0, Z_1)$
,
$Z\in (0, Z_1)$
,
![]() $\Delta _0(Z)<0$
for
$\Delta _0(Z)<0$
for
![]() $Z\in (Z_1, +\infty )$
and
$Z\in (Z_1, +\infty )$
and
![]() $\Delta _0'(Z_1)\neq 0$
.
$\Delta _0'(Z_1)\neq 0$
.
Proof. By the definition of
![]() $\Delta _0(Z)$
, we have
$\Delta _0(Z)$
, we have
![]() $\Delta _0\in C^\infty ([0, +\infty ))$
and (see (2.8))
$\Delta _0\in C^\infty ([0, +\infty ))$
and (see (2.8))
where
![]() $F_0\in C^\infty ([0, +\infty ))$
is defined by (A.7) and
$F_0\in C^\infty ([0, +\infty ))$
is defined by (A.7) and
![]() $\widetilde F_0\in C^\infty ([0, +\infty ))$
is defined by
$\widetilde F_0\in C^\infty ([0, +\infty ))$
is defined by
If
![]() $\Delta _0(Z_*)=0$
for some
$\Delta _0(Z_*)=0$
for some
![]() $Z_*\in (0, +\infty )$
, then
$Z_*\in (0, +\infty )$
, then
![]() $\Delta _v(Z_*, v(Z_*))=\Delta _0(Z_*)v'(Z_*)=0$
, and by (A.8) we obtain
$\Delta _v(Z_*, v(Z_*))=\Delta _0(Z_*)v'(Z_*)=0$
, and by (A.8) we obtain
![]() $Z_*=Z_1$
, hence (using Lemma A.2, (A.8) and (A.9))
$Z_*=Z_1$
, hence (using Lemma A.2, (A.8) and (A.9))
Now we prove that
![]() $\Delta _0'(Z_1)\neq 0$
. By the proof of Lemma A.2, we have
$\Delta _0'(Z_1)\neq 0$
. By the proof of Lemma A.2, we have
![]() $F_0(Z_1)=0$
. Then by (A.7) and (A.10), we have
$F_0(Z_1)=0$
. Then by (A.7) and (A.10), we have
![]() $\widetilde F_0(Z_1)=2(1-Z_1v(Z_1))>0$
. Thus (using (A.9)),
$\widetilde F_0(Z_1)=2(1-Z_1v(Z_1))>0$
. Thus (using (A.9)),
![]() $\Delta _0'(Z_1)=Z_1F_0'(Z_1)\widetilde F_0(Z_1) $
. Assume on the contrary that
$\Delta _0'(Z_1)=Z_1F_0'(Z_1)\widetilde F_0(Z_1) $
. Assume on the contrary that
![]() $\Delta _0'(Z_1)=0$
, then
$\Delta _0'(Z_1)=0$
, then
![]() $F_0'(Z_1)=0$
.
$F_0'(Z_1)=0$
.
Let
![]() $\Delta _1(Z):=\Delta _v(Z, v(Z))$
. Then (2.8) becomes
$\Delta _1(Z):=\Delta _v(Z, v(Z))$
. Then (2.8) becomes
![]() $\Delta _0(Z)v'(Z)=\Delta _1(Z)$
. Taking derivative with respect to Z at
$\Delta _0(Z)v'(Z)=\Delta _1(Z)$
. Taking derivative with respect to Z at
![]() $Z=Z_1$
on both sides, we obtain(using
$Z=Z_1$
on both sides, we obtain(using
![]() $\Delta _0(Z_1)=0$
)
$\Delta _0(Z_1)=0$
)
![]() $\Delta _1'(Z_1)=\Delta _0'(Z_1)v'(Z_1)=0$
and
$\Delta _1'(Z_1)=\Delta _0'(Z_1)v'(Z_1)=0$
and
![]() $\Delta _1(Z_1)=0$
. By (2.8), we have
$\Delta _1(Z_1)=0$
. By (2.8), we have
![]() $\Delta _1(Z)=F_1(Z)\widetilde F_1(Z)$
with
$\Delta _1(Z)=F_1(Z)\widetilde F_1(Z)$
with
![]() $F_1(Z):=Z-g_1(v(Z)) $
,
$F_1(Z):=Z-g_1(v(Z)) $
,
![]() $\widetilde F_1(Z):=(1-v(Z)^2)(\beta \ell +(k-\beta \ell )v(Z)^2) $
,
$\widetilde F_1(Z):=(1-v(Z)^2)(\beta \ell +(k-\beta \ell )v(Z)^2) $
,
![]() $g_1(v):=kv/(\beta \ell +(k-\beta \ell )v^2) $
(note that
$g_1(v):=kv/(\beta \ell +(k-\beta \ell )v^2) $
(note that
![]() $0<\beta \ell <k$
using (2.9)). As
$0<\beta \ell <k$
using (2.9)). As
![]() $v(Z_1)\in (-1,1)$
, we have
$v(Z_1)\in (-1,1)$
, we have
![]() $\widetilde F_1(Z_1)>0$
, then by
$\widetilde F_1(Z_1)>0$
, then by
![]() $\Delta _1'(Z_1)=0$
and
$\Delta _1'(Z_1)=0$
and
![]() $\Delta _1(Z_1)=0$
we have
$\Delta _1(Z_1)=0$
we have
![]() $F_1(Z_1)=0$
,
$F_1(Z_1)=0$
,
![]() $\Delta _1'(Z_1)=F_1'(Z_1)\widetilde F_1(Z_1)=0$
and
$\Delta _1'(Z_1)=F_1'(Z_1)\widetilde F_1(Z_1)=0$
and
![]() $F_1'(Z_1)=0$
. Thus,
$F_1'(Z_1)=0$
. Thus,
![]() $0=1-g_1'(v(Z_1))v'(Z_1)=1-g_1'(v_1)v'(Z_1) $
(using Lemma A.2).
$0=1-g_1'(v(Z_1))v'(Z_1)=1-g_1'(v_1)v'(Z_1) $
(using Lemma A.2).
Similarly, by (A.7), we have
![]() $F_0(Z)=F_2(Z)\widetilde F_2(Z)$
with
$F_0(Z)=F_2(Z)\widetilde F_2(Z)$
with
![]() $F_2(Z):=g_2(v(Z))-Z $
,
$F_2(Z):=g_2(v(Z))-Z $
,
![]() $\widetilde F_2(Z):=v(Z)+\ell $
,
$\widetilde F_2(Z):=v(Z)+\ell $
,
![]() $g_2(v):=(1+\sqrt \ell v)/(v+\sqrt \ell ) $
, and
$g_2(v):=(1+\sqrt \ell v)/(v+\sqrt \ell ) $
, and
![]() $\widetilde F_2(Z_1)>0$
. Thus,
$\widetilde F_2(Z_1)>0$
. Thus,
![]() $F_2(Z_1)=0$
,
$F_2(Z_1)=0$
,
![]() $F_2'(Z_1)=0$
(using
$F_2'(Z_1)=0$
(using
![]() $F_0(Z_1)= F_0'(Z_1)=0$
) and
$F_0(Z_1)= F_0'(Z_1)=0$
) and
![]() $0=g_2'(v_1)v'(Z_1)-1$
.
$0=g_2'(v_1)v'(Z_1)-1$
.
Now we have
![]() $1=g_1'(v_1)v'(Z_1)=g_2'(v_1)v'(Z_1)$
and
$1=g_1'(v_1)v'(Z_1)=g_2'(v_1)v'(Z_1)$
and
![]() $g_1'(v_1)=g_2'(v_1) $
. On the other hand,
$g_1'(v_1)=g_2'(v_1) $
. On the other hand,
 $$ \begin{align*} g_1(v)-g_2(v)&=\frac{kv}{\beta \ell+(k-\beta \ell)v^2}-\frac{1+\sqrt\ell v}{v+\sqrt\ell}= \frac{(1-v^2)(kv\sqrt\ell-\beta \ell(1+\sqrt\ell v)}{(\beta \ell+(k-\beta \ell)v^2)(v+\sqrt\ell)}\\ &=\frac{(1-v^2)(k-\beta \ell)\sqrt\ell(v-v_1)}{(\beta \ell+(k-\beta \ell)v^2)(v+\sqrt\ell)}, \end{align*} $$
$$ \begin{align*} g_1(v)-g_2(v)&=\frac{kv}{\beta \ell+(k-\beta \ell)v^2}-\frac{1+\sqrt\ell v}{v+\sqrt\ell}= \frac{(1-v^2)(kv\sqrt\ell-\beta \ell(1+\sqrt\ell v)}{(\beta \ell+(k-\beta \ell)v^2)(v+\sqrt\ell)}\\ &=\frac{(1-v^2)(k-\beta \ell)\sqrt\ell(v-v_1)}{(\beta \ell+(k-\beta \ell)v^2)(v+\sqrt\ell)}, \end{align*} $$
here we used (A.6), thus
 $$ \begin{align*} g_1'(v_1)-g_2'(v_1)&=\frac{(1-v_1^2)(k-\beta \ell)\sqrt\ell}{(\beta \ell+(k-\beta \ell)v_1^2)(v_1+\sqrt\ell)}>0, \end{align*} $$
$$ \begin{align*} g_1'(v_1)-g_2'(v_1)&=\frac{(1-v_1^2)(k-\beta \ell)\sqrt\ell}{(\beta \ell+(k-\beta \ell)v_1^2)(v_1+\sqrt\ell)}>0, \end{align*} $$
which is a contradiction. Therefore,
![]() $\Delta _0'(Z_1)\neq 0$
.
$\Delta _0'(Z_1)\neq 0$
.
By
![]() $F_0(0)=\widetilde F_0(0)=1>0$
, (A.9), and (A.11), we have
$F_0(0)=\widetilde F_0(0)=1>0$
, (A.9), and (A.11), we have
![]() $\Delta _0(Z)>0$
for
$\Delta _0(Z)>0$
for
![]() $Z\in (0, Z_1)$
. Finally, using
$Z\in (0, Z_1)$
. Finally, using
![]() $\Delta _0'(Z_1)\neq 0$
and (A.11), we have
$\Delta _0'(Z_1)\neq 0$
and (A.11), we have
![]() $\Delta _0'(Z_1)<0$
and
$\Delta _0'(Z_1)<0$
and
![]() $\Delta _0(Z)<0$
for all
$\Delta _0(Z)<0$
for all
![]() $Z\in (Z_1, +\infty )$
.
$Z\in (Z_1, +\infty )$
.
To finish the proof of Remark 2.2, it remains to show that
![]() $v(Z)<Z$
and
$v(Z)<Z$
and
![]() $Zv(Z)<1$
for all
$Zv(Z)<1$
for all
![]() $Z\in (0, +\infty )$
. We use the barrier function method. For any
$Z\in (0, +\infty )$
. We use the barrier function method. For any
![]() $V\in C^1((0, +\infty ))$
, we define
$V\in C^1((0, +\infty ))$
, we define
Then
![]() $\mathscr Av=0$
if v is given by Assumption 1.
$\mathscr Av=0$
if v is given by Assumption 1.
Lemma A.4. Under Assumption 1, we have
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z\in (0, +\infty )$
.
$Z\in (0, +\infty )$
.
Proof. Since
![]() $v(Z)\in (-1, 1)$
for all
$v(Z)\in (-1, 1)$
for all
![]() $Z\in (0, +\infty )$
by Assumption 1, it suffices to prove
$Z\in (0, +\infty )$
by Assumption 1, it suffices to prove
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z\in (0, 1)$
. We first show that
$Z\in (0, 1)$
. We first show that
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z\in (Z_1, 1)$
. By (A.9),
$Z\in (Z_1, 1)$
. By (A.9),
![]() $F_0(0)=1, F_0(Z_1)=0$
and (A.11), we have
$F_0(0)=1, F_0(Z_1)=0$
and (A.11), we have
As
![]() $F_0(1)<0$
and
$F_0(1)<0$
and
![]() $Z_1\in (0,1)$
, we have
$Z_1\in (0,1)$
, we have
![]() $F_0(Z)<0$
for all
$F_0(Z)<0$
for all
![]() $Z\in (Z_1, 1)$
, hence
$Z\in (Z_1, 1)$
, hence
 $$\begin{align*}v(Z)<\frac{\sqrt\ell Z-1}{\sqrt{\ell}-Z}<Z,\quad\forall\ Z\in(Z_1, 1).\end{align*}$$
$$\begin{align*}v(Z)<\frac{\sqrt\ell Z-1}{\sqrt{\ell}-Z}<Z,\quad\forall\ Z\in(Z_1, 1).\end{align*}$$
Next we prove that
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z\in (0, Z_1)$
. Let
$Z\in (0, Z_1)$
. Let
![]() $V_1(Z):=Z$
for all
$V_1(Z):=Z$
for all
![]() $Z\in [0, +\infty )$
, then we have
$Z\in [0, +\infty )$
, then we have
where we have used
![]() $\beta \ell -k-1<0$
, which follows from (2.9). On the other hand, letting
$\beta \ell -k-1<0$
, which follows from (2.9). On the other hand, letting
![]() $Z\to 0+$
in
$Z\to 0+$
in
![]() $\mathrm dv/\mathrm dZ=\Delta _v(Z, v(Z))/\Delta _Z(Z,v(Z))$
, by L’Hôpital’s rule, we have
$\mathrm dv/\mathrm dZ=\Delta _v(Z, v(Z))/\Delta _Z(Z,v(Z))$
, by L’Hôpital’s rule, we have
hence
![]() $v'(0)=\beta \ell /(k+1)<1=V_1'(0)$
. As
$v'(0)=\beta \ell /(k+1)<1=V_1'(0)$
. As
![]() $v(0)=0=V_1(0)$
, there exists
$v(0)=0=V_1(0)$
, there exists
![]() $\delta \in (0, Z_1)$
such that
$\delta \in (0, Z_1)$
such that
![]() $v(Z)<V_1(Z)$
for all
$v(Z)<V_1(Z)$
for all
![]() $Z\in (0, \delta )$
. Assume for contradiction that
$Z\in (0, \delta )$
. Assume for contradiction that
![]() $Z_*\in (0, Z_1)\subset (0, 1)$
satisfies
$Z_*\in (0, Z_1)\subset (0, 1)$
satisfies
![]() $v(Z)<V_1(Z)$
for all
$v(Z)<V_1(Z)$
for all
![]() $Z\in (0, Z_*)$
and
$Z\in (0, Z_*)$
and
![]() $v(Z_*)=V_1(Z_*)=Z_*$
, then
$v(Z_*)=V_1(Z_*)=Z_*$
, then
![]() $v'(Z_*)\geq V_1'(Z_*)$
. Thus, by
$v'(Z_*)\geq V_1'(Z_*)$
. Thus, by
![]() $\Delta _Z(Z_*, V_1(Z_*))=\Delta _Z(Z_*, v(Z_*))=Z_*(1-Z_*^2)^2>0$
, we have
$\Delta _Z(Z_*, V_1(Z_*))=\Delta _Z(Z_*, v(Z_*))=Z_*(1-Z_*^2)^2>0$
, we have
 $$ \begin{align*} (\mathscr AV_1)(Z_*)&=-\Delta_Z(Z_*, V_1(Z_*))V_1'(Z_*)+\Delta_v(Z_*, V_1(Z_*))\\ &\geq -\Delta_Z(Z_*, v(Z_*))v'(Z_*)+\Delta_v(Z_*, v(Z_*))=(\mathscr Av)(Z_*)=0, \end{align*} $$
$$ \begin{align*} (\mathscr AV_1)(Z_*)&=-\Delta_Z(Z_*, V_1(Z_*))V_1'(Z_*)+\Delta_v(Z_*, V_1(Z_*))\\ &\geq -\Delta_Z(Z_*, v(Z_*))v'(Z_*)+\Delta_v(Z_*, v(Z_*))=(\mathscr Av)(Z_*)=0, \end{align*} $$
which contradicts with (A.13). Therefore, we have
![]() $v(Z)<V_1(Z)=Z$
for all
$v(Z)<V_1(Z)=Z$
for all
![]() $Z\in (0, Z_1)$
.
$Z\in (0, Z_1)$
.
Finally, by
![]() $v(Z_1)=v_1<Z_1<1$
, we obtain
$v(Z_1)=v_1<Z_1<1$
, we obtain
![]() $v(Z)<Z$
for all
$v(Z)<Z$
for all
![]() $Z\in (0, 1)$
.
$Z\in (0, 1)$
.
Lemma A.5. Under Assumption 1, we have
![]() $v(Z)<1/Z$
for all
$v(Z)<1/Z$
for all
![]() $Z\in (0, +\infty )$
.
$Z\in (0, +\infty )$
.
Proof. Since
![]() $v(Z)\in (-1, 1)$
for all
$v(Z)\in (-1, 1)$
for all
![]() $Z\in (0, +\infty )$
by Assumption 1, it suffices to prove
$Z\in (0, +\infty )$
by Assumption 1, it suffices to prove
![]() $v(Z)<1/Z$
for all
$v(Z)<1/Z$
for all
![]() $Z\in (1, +\infty )$
. Let
$Z\in (1, +\infty )$
. Let
![]() $V_2(Z):=1/Z$
for
$V_2(Z):=1/Z$
for
![]() $Z\in (0, +\infty )$
, then we have
$Z\in (0, +\infty )$
, then we have
where we have used
![]() $\beta>1$
by (2.9). As
$\beta>1$
by (2.9). As
![]() $v(Z_1)=v_1<1=V_2(Z_1)$
, there exists
$v(Z_1)=v_1<1=V_2(Z_1)$
, there exists
![]() $\delta>0$
such that
$\delta>0$
such that
![]() $v(Z)<V_2(Z)$
for
$v(Z)<V_2(Z)$
for
![]() $Z\in [Z_1, Z_1+\delta )$
. Assume for contradiction that
$Z\in [Z_1, Z_1+\delta )$
. Assume for contradiction that
![]() $Z^*\in (1, +\infty )$
satisfies
$Z^*\in (1, +\infty )$
satisfies
![]() $v(Z)<V_2(Z)$
for all
$v(Z)<V_2(Z)$
for all
![]() $Z\in (Z_1, Z^*)$
and
$Z\in (Z_1, Z^*)$
and
![]() $v(Z^*)=V_2(Z^*)$
, then
$v(Z^*)=V_2(Z^*)$
, then
![]() $v'(Z^*)\geq V_2'(Z^*)$
. Thus, by
$v'(Z^*)\geq V_2'(Z^*)$
. Thus, by
![]() $\Delta _Z(Z^*, V_2(Z^*))=\Delta _Z(Z^*, v(Z^*))=-\ell (1-Z_*^2)^2/Z_*<0$
, we have
$\Delta _Z(Z^*, V_2(Z^*))=\Delta _Z(Z^*, v(Z^*))=-\ell (1-Z_*^2)^2/Z_*<0$
, we have
 $$ \begin{align*} (\mathscr AV_2)(Z^*)&=-\Delta_Z(Z^*, V_2(Z^*))V_2'(Z^*)+\Delta_v(Z^*, V_2(Z^*))\\ &\leq-\Delta_Z(Z^*, v(Z^*))v'(Z^*)+\Delta_v(Z^*, v(Z^*))=(\mathscr Av)(Z^*)=0, \end{align*} $$
$$ \begin{align*} (\mathscr AV_2)(Z^*)&=-\Delta_Z(Z^*, V_2(Z^*))V_2'(Z^*)+\Delta_v(Z^*, V_2(Z^*))\\ &\leq-\Delta_Z(Z^*, v(Z^*))v'(Z^*)+\Delta_v(Z^*, v(Z^*))=(\mathscr Av)(Z^*)=0, \end{align*} $$
which contradicts with (A.14). Therefore,
![]() $v(Z)<V_2(Z)=1/Z$
for all
$v(Z)<V_2(Z)=1/Z$
for all
![]() $Z\in (1,+\infty )$
.
$Z\in (1,+\infty )$
.
The proof of Remark 2.2 is completed now. To conclude this appendix, we prove that
![]() $\widehat \phi _0, \widehat \rho _0\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, where
$\widehat \phi _0, \widehat \rho _0\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
, where
![]() $\widehat \phi _0$
and
$\widehat \phi _0$
and
![]() $\widehat \rho _0$
are defined by (2.12).
$\widehat \rho _0$
are defined by (2.12).
Lemma A.6. Let
![]() $v\in C_{\operatorname {o}}^\infty ([0, +\infty ))$
be given by Assumption 1, and define
$v\in C_{\operatorname {o}}^\infty ([0, +\infty ))$
be given by Assumption 1, and define
![]() $\widehat \phi _0, \widehat \rho _0$
by (2.12). Then we have
$\widehat \phi _0, \widehat \rho _0$
by (2.12). Then we have
![]() $\widehat \phi _0, \widehat \rho _0\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
.
$\widehat \phi _0, \widehat \rho _0\in C_{\operatorname {e}}^\infty ([0,+\infty ))$
.
Proof. We first claim that
 $$ \begin{align} f\in C_{\text{o}}^\infty([0, +\infty))\Longrightarrow F(Z):=\int_0^Zf(s)\,\mathrm ds\in C_{\text{e}}^\infty([0, +\infty)). \end{align} $$
$$ \begin{align} f\in C_{\text{o}}^\infty([0, +\infty))\Longrightarrow F(Z):=\int_0^Zf(s)\,\mathrm ds\in C_{\text{e}}^\infty([0, +\infty)). \end{align} $$
Now we prove that
![]() $\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
. By
$\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
. By
![]() $v\in C_{\text {o}}^\infty ([0, +\infty ))$
, we have
$v\in C_{\text {o}}^\infty ([0, +\infty ))$
, we have
![]() $1-Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
. Since
$1-Zv(Z)\in C_{\text {e}}^\infty ([0,+\infty ))$
. Since
![]() $Zv(Z)<1$
for all
$Zv(Z)<1$
for all
![]() $Z\in [0,+\infty )$
by Lemma A.5, it follows from (5.8) that
$Z\in [0,+\infty )$
by Lemma A.5, it follows from (5.8) that
![]() $0<\frac 1{1-Zv(Z)}\in C_{\text {e}}^\infty ([0,+\infty ))$
, hence by
$0<\frac 1{1-Zv(Z)}\in C_{\text {e}}^\infty ([0,+\infty ))$
, hence by
![]() $v\in C_{\text {o}}^\infty ([0, +\infty ))$
and (5.7) we have
$v\in C_{\text {o}}^\infty ([0, +\infty ))$
and (5.7) we have
![]() $\frac {v(Z)}{1-Zv(Z)}\in C_{\text {o}}^\infty ([0, +\infty ))$
, then by (A.15) we obtain
$\frac {v(Z)}{1-Zv(Z)}\in C_{\text {o}}^\infty ([0, +\infty ))$
, then by (A.15) we obtain
 $$\begin{align*}(\beta-1)\int_0^Z \frac{v(s)}{1-sv(s)}\,\mathrm ds\in C_{\text{e}}^\infty([0, +\infty)).\end{align*}$$
$$\begin{align*}(\beta-1)\int_0^Z \frac{v(s)}{1-sv(s)}\,\mathrm ds\in C_{\text{e}}^\infty([0, +\infty)).\end{align*}$$
Thus, by (5.9) and (2.12) we have
![]() $\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
.
$\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
.
As for
![]() $\widehat \rho _0$
, by
$\widehat \rho _0$
, by
![]() $0<\frac 1{1-Zv(Z)}\in C_{\text {e}}^\infty ([0,+\infty ))$
, and (5.10), we have
$0<\frac 1{1-Zv(Z)}\in C_{\text {e}}^\infty ([0,+\infty ))$
, and (5.10), we have
![]() $1/{(1-Zv(Z))^{\frac 2{p-1}}}\in C_{\text {e}}^\infty ([0,+\infty )).$
Similarly, using
$1/{(1-Zv(Z))^{\frac 2{p-1}}}\in C_{\text {e}}^\infty ([0,+\infty )).$
Similarly, using
![]() $\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
and
$\widehat \phi _0\in C_{\text {e}}^\infty ([0,+\infty ))$
and
![]() $\widehat \phi _0(Z)>0$
for all
$\widehat \phi _0(Z)>0$
for all
![]() $Z\in [0, +\infty )$
, we get
$Z\in [0, +\infty )$
, we get
![]() $\widehat \phi _0(Z)^{2/(p-1)}\in C_{\text {e}}^\infty ([0,+\infty ))$
. It follows from
$\widehat \phi _0(Z)^{2/(p-1)}\in C_{\text {e}}^\infty ([0,+\infty ))$
. It follows from
![]() $1-v(Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
,
$1-v(Z)^2\in C_{\text {e}}^\infty ([0,+\infty ))$
,
![]() $v(Z)\in (-1, 1)$
for all
$v(Z)\in (-1, 1)$
for all
![]() $Z\in [0, +\infty )$
and (5.10) that
$Z\in [0, +\infty )$
and (5.10) that
![]() $(1-v(Z)^2)^{\frac 1{p-1}}\in C_{\text {e}}^\infty ([0,+\infty )).$
Therefore, by (2.12) and (5.5), we have
$(1-v(Z)^2)^{\frac 1{p-1}}\in C_{\text {e}}^\infty ([0,+\infty )).$
Therefore, by (2.12) and (5.5), we have
![]() $\widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty ))$
.
$\widehat \rho _0\in C_{\text {e}}^\infty ([0,+\infty ))$
.
Finally, it suffices to show the claim (A.15). By (2.11), there exists
![]() $\widetilde f\in C^\infty ([0, +\infty ))$
such that
$\widetilde f\in C^\infty ([0, +\infty ))$
such that
![]() $f(Z)=Z\widetilde f(Z^2)$
for all
$f(Z)=Z\widetilde f(Z^2)$
for all
![]() $Z\in [0, +\infty )$
. Let
$Z\in [0, +\infty )$
. Let
 $$\begin{align*}\widetilde F(Z):=\frac12\int_0^Z\widetilde f(s)\,\mathrm ds,\quad\forall\ Z\in[0, +\infty),\end{align*}$$
$$\begin{align*}\widetilde F(Z):=\frac12\int_0^Z\widetilde f(s)\,\mathrm ds,\quad\forall\ Z\in[0, +\infty),\end{align*}$$
then
![]() $\widetilde F\in C^\infty ([0, +\infty ))$
. Moreover, we have
$\widetilde F\in C^\infty ([0, +\infty ))$
. Moreover, we have
 $$\begin{align*}F(Z)=\int_0^Zf(s)\,\mathrm ds=\int_0^Z s\widetilde f(s^2)\,\mathrm ds=\frac12\int_0^{Z^2}\widetilde f(s)\,\mathrm ds=\widetilde F(Z^2),\quad\forall\ Z\in[0, +\infty).\end{align*}$$
$$\begin{align*}F(Z)=\int_0^Zf(s)\,\mathrm ds=\int_0^Z s\widetilde f(s^2)\,\mathrm ds=\frac12\int_0^{Z^2}\widetilde f(s)\,\mathrm ds=\widetilde F(Z^2),\quad\forall\ Z\in[0, +\infty).\end{align*}$$
Hence by (2.10), we have
![]() $F\in C_{\text {e}}^\infty ([0,+\infty ))$
.
$F\in C_{\text {e}}^\infty ([0,+\infty ))$
.
B Linear ODEs with singular points
In this appendix, we establish the well-posedness theory for a class of second order linear ODEs with singular points.
First of all, we introduce a preliminary lemma, which ensures that the functions we are considering are smooth in the sense of multi-variable functions. Let
![]() $I\subset \mathbb {R}$
be an interval and let
$I\subset \mathbb {R}$
be an interval and let
![]() $\Omega \subset \mathbb {C}$
be an open subset. We define
$\Omega \subset \mathbb {C}$
be an open subset. We define
 $$ \begin{align} \mathcal H_I^{0}(\Omega)&:=\big\{x=x(t;\lambda)\in C(I\times\Omega;\mathbb{C}): x(\cdot;\lambda)\in C^\infty(I) \text{ for all }\lambda\in\Omega,\nonumber \\&\qquad x(t;\cdot)\in\operatorname{Hol}(\Omega) \text{ for all }t\in I \text{ and }\partial_t^jx\in L^\infty(I\times\Omega)\text{ for all }j\in\mathbb{Z}_{\geq 0}\big\}, \end{align} $$
$$ \begin{align} \mathcal H_I^{0}(\Omega)&:=\big\{x=x(t;\lambda)\in C(I\times\Omega;\mathbb{C}): x(\cdot;\lambda)\in C^\infty(I) \text{ for all }\lambda\in\Omega,\nonumber \\&\qquad x(t;\cdot)\in\operatorname{Hol}(\Omega) \text{ for all }t\in I \text{ and }\partial_t^jx\in L^\infty(I\times\Omega)\text{ for all }j\in\mathbb{Z}_{\geq 0}\big\}, \end{align} $$
Then
![]() $ \operatorname {Hol}(\Omega )$
,
$ \operatorname {Hol}(\Omega )$
,
![]() $ \mathcal H_I^{0}(\Omega )$
,
$ \mathcal H_I^{0}(\Omega )$
,
![]() $ \mathcal H_I(\Omega )$
are rings and the definitions in (B.1), (B.3) are the same as in section 5.3. This appendix is only used in the proof of Lemma 5.6, which does not require the definition of Z in
$ \mathcal H_I(\Omega )$
are rings and the definitions in (B.1), (B.3) are the same as in section 5.3. This appendix is only used in the proof of Lemma 5.6, which does not require the definition of Z in
![]() $Z=|x|/(T-t)$
.
$Z=|x|/(T-t)$
.
So, with abuse of notation, we replace Z by t and use x to denote a general function of
![]() $(t;\lambda )$
. We stress that here
$(t;\lambda )$
. We stress that here
![]() $(t,x)$
has nothing to do with the coordinates in
$(t,x)$
has nothing to do with the coordinates in
![]() $\mathbb {R}^{1+d}$
.
$\mathbb {R}^{1+d}$
.
Lemma B.1. Let
![]() $I\subset \mathbb {R}$
be an interval and
$I\subset \mathbb {R}$
be an interval and
![]() $\Omega \subset \mathbb {C}$
be an open subset. Then
$\Omega \subset \mathbb {C}$
be an open subset. Then
![]() $\mathcal H_I^0(\Omega )\subset \mathcal H_I(\Omega )$
.
$\mathcal H_I^0(\Omega )\subset \mathcal H_I(\Omega )$
.
Proof. Let
![]() $x=x(t;\lambda )\in \mathcal H_I^0(\Omega )$
. Pick
$x=x(t;\lambda )\in \mathcal H_I^0(\Omega )$
. Pick
![]() $\lambda _0\in \Omega $
and let
$\lambda _0\in \Omega $
and let
![]() $r\in (0,1)$
be such that
$r\in (0,1)$
be such that
![]() $B_r(\lambda _0):=\{\lambda \in \mathbb {C}:|\lambda -\lambda _0|<r\}\subset \Omega $
. By Cauchy’s integration formula (Theorem 4.4 in Chapter 2 of [Reference Stein and Shakarchi69]), for any
$B_r(\lambda _0):=\{\lambda \in \mathbb {C}:|\lambda -\lambda _0|<r\}\subset \Omega $
. By Cauchy’s integration formula (Theorem 4.4 in Chapter 2 of [Reference Stein and Shakarchi69]), for any
![]() $t\in I, \lambda \in \Omega $
we have
$t\in I, \lambda \in \Omega $
we have
 $$ \begin{align} x(t;\lambda)=\sum_{k=0}^\infty x_k(t)(\lambda-\lambda_0)^k, \end{align} $$
$$ \begin{align} x(t;\lambda)=\sum_{k=0}^\infty x_k(t)(\lambda-\lambda_0)^k, \end{align} $$
where
 $$ \begin{align} x_k(t)=\frac1{2\pi\text{i}}\int_{|\lambda-\lambda_0|=r}\frac{x(t;\lambda)}{(\lambda-\lambda_0)^{k+1}}\,\mathrm d\lambda=\frac{r^{-k}}{2\pi}\int_0^{2\pi}x\left(t;\lambda_0+re^{\text{i}\theta}\right)e^{-\text{i} k\theta}\,\mathrm d\theta \end{align} $$
$$ \begin{align} x_k(t)=\frac1{2\pi\text{i}}\int_{|\lambda-\lambda_0|=r}\frac{x(t;\lambda)}{(\lambda-\lambda_0)^{k+1}}\,\mathrm d\lambda=\frac{r^{-k}}{2\pi}\int_0^{2\pi}x\left(t;\lambda_0+re^{\text{i}\theta}\right)e^{-\text{i} k\theta}\,\mathrm d\theta \end{align} $$
for all
![]() $t\in I, k\in \mathbb {Z}_{\geq 0}$
. Since
$t\in I, k\in \mathbb {Z}_{\geq 0}$
. Since
![]() $x(\cdot ;\lambda )\in C^\infty (I)$
for all
$x(\cdot ;\lambda )\in C^\infty (I)$
for all
![]() $\lambda \in \Omega $
and
$\lambda \in \Omega $
and
![]() $\partial _t^jx\in L^\infty (I\times \Omega )$
, by (B.5) and the dominated convergence theorem, we have
$\partial _t^jx\in L^\infty (I\times \Omega )$
, by (B.5) and the dominated convergence theorem, we have
![]() $x_k\in C^\infty (I)$
and
$x_k\in C^\infty (I)$
and
Using (B.6), we know that
![]() $\sum _{k=0}^\infty x_k^{(j)}(t)\partial _\lambda ^\alpha ((\lambda -\lambda _0)^k)$
is uniformly absolutely convergent on
$\sum _{k=0}^\infty x_k^{(j)}(t)\partial _\lambda ^\alpha ((\lambda -\lambda _0)^k)$
is uniformly absolutely convergent on
![]() $I\times B_{r/2}(\lambda _0)$
for all
$I\times B_{r/2}(\lambda _0)$
for all
![]() $j\in \mathbb {Z}_{\geq 0}$
and
$j\in \mathbb {Z}_{\geq 0}$
and
![]() $\alpha \in (\mathbb {Z}_{\geq 0})^2$
, hence (B.4) implies that
$\alpha \in (\mathbb {Z}_{\geq 0})^2$
, hence (B.4) implies that
![]() $x\in C^\infty (I\times B_{r/2}(\lambda _0))$
. Since
$x\in C^\infty (I\times B_{r/2}(\lambda _0))$
. Since
![]() $\lambda _0\in \Omega $
is arbitrary, we have
$\lambda _0\in \Omega $
is arbitrary, we have
![]() $x\in C^\infty (I\times \Omega )$
. Hence
$x\in C^\infty (I\times \Omega )$
. Hence
![]() $x\in \mathcal {H}_I(\Omega )$
.
$x\in \mathcal {H}_I(\Omega )$
.
Remark B.2. As smoothness is a local property, we have
![]() $\mathcal {H}_{I,\text {loc}}^0(\Omega )\subset \mathcal H_I(\Omega )$
, where
$\mathcal {H}_{I,\text {loc}}^0(\Omega )\subset \mathcal H_I(\Omega )$
, where
Moreover, we have
![]() $\mathcal H_I(\Omega )\subset \mathcal H_{I,\text {loc}}^0(\Omega ')$
for any open subset
$\mathcal H_I(\Omega )\subset \mathcal H_{I,\text {loc}}^0(\Omega ')$
for any open subset
![]() $\Omega '\subset \subset \Omega $
(i.e. there exists a compact set K such that
$\Omega '\subset \subset \Omega $
(i.e. there exists a compact set K such that
![]() $\Omega '\subset K\subset \Omega $
).
$\Omega '\subset K\subset \Omega $
).
Lemma B.3. Let
![]() $I\subset \mathbb {R}$
be an interval and let
$I\subset \mathbb {R}$
be an interval and let
![]() $A(t)\in C^\infty (I; \mathbb {C})$
be such that
$A(t)\in C^\infty (I; \mathbb {C})$
be such that
![]() $A(t)=0$
has a unique solution
$A(t)=0$
has a unique solution
![]() $t=t_0$
in I
Footnote 12 with
$t=t_0$
in I
Footnote 12 with
![]() $A'(t_0)\neq 0$
. Let
$A'(t_0)\neq 0$
. Let
![]() $\Omega \subset \mathbb {C}$
be an open subset and let
$\Omega \subset \mathbb {C}$
be an open subset and let
![]() $B(t;\lambda ), D(t;\lambda )\in C^\infty (I\times \Omega ;\mathbb {C})$
be such that
$B(t;\lambda ), D(t;\lambda )\in C^\infty (I\times \Omega ;\mathbb {C})$
be such that
![]() $B, D\in \mathcal H_{I,\operatorname {loc}}^0(\Omega )$
, which implies
$B, D\in \mathcal H_{I,\operatorname {loc}}^0(\Omega )$
, which implies
 $$ \begin{align*} N_0^*:=\sup_{\lambda\in\Omega}\left(\max\left\{3, -\operatorname{Re}\left(\frac{B(t_0;\lambda)}{A'(t_0)}\right)+1\right\}\right)<+\infty. \end{align*} $$
$$ \begin{align*} N_0^*:=\sup_{\lambda\in\Omega}\left(\max\left\{3, -\operatorname{Re}\left(\frac{B(t_0;\lambda)}{A'(t_0)}\right)+1\right\}\right)<+\infty. \end{align*} $$
Then there exists
![]() $N_0>N_0^*$
such that for all
$N_0>N_0^*$
such that for all
![]() $N\in \mathbb {Z}\cap (N_0, +\infty )$
, if
$N\in \mathbb {Z}\cap (N_0, +\infty )$
, if
![]() $f\in \mathcal {H}_{I,\operatorname {loc}}^0(\Omega )$
is such that
$f\in \mathcal {H}_{I,\operatorname {loc}}^0(\Omega )$
is such that
then the linear ODE (here the prime
![]() $'$
refers to the derivative with respect to t)
$'$
refers to the derivative with respect to t)
has a (complex-valued) smooth solution
![]() $x(t;\lambda )$
on
$x(t;\lambda )$
on
![]() $I\times \Omega $
such that
$I\times \Omega $
such that
![]() $x\in \mathcal H_{I}(\Omega )$
.
$x\in \mathcal H_{I}(\Omega )$
.
Proof. Without loss of generality, we assume that
![]() $t_0=0\in {I}$
, and there exists
$t_0=0\in {I}$
, and there exists
![]() $\delta _0\in (0, 1)$
such that
$\delta _0\in (0, 1)$
such that
![]() $I_0=[-\delta _0, \delta _0]\subset I$
or
$I_0=[-\delta _0, \delta _0]\subset I$
or
![]() $I_0=[0, \delta _0]= I\cap [-\delta _0, \delta _0]$
.
$I_0=[0, \delta _0]= I\cap [-\delta _0, \delta _0]$
.
Step 1. Existence of a
![]() $C^2$
local solution. We define the Banach space
$C^2$
local solution. We define the Banach space
where
![]() $N\geq 3$
is an integer, with the norm
$N\geq 3$
is an integer, with the norm
![]() $\|y\|_{Y_N}:=\left \|{y(t;\lambda )}/{|t|^N}\right \|_{L^\infty (I_0\times \Omega )}\kern-1pt.$
$\|y\|_{Y_N}:=\left \|{y(t;\lambda )}/{|t|^N}\right \|_{L^\infty (I_0\times \Omega )}\kern-1pt.$
We define a linear operator
![]() $\mathcal T_N: Y_N\to Y_N$
by
$\mathcal T_N: Y_N\to Y_N$
by
 $$\begin{align*}(\mathcal T_Ny)(t;\lambda):=\int_0^t\left(\frac{B(s;\lambda)}{A(s)}y(s;\lambda)+\frac{D(s;\lambda)}{A(s)}\int_0^sy(\tau;\lambda)\,\mathrm d\tau\right)\,\mathrm ds, \qquad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega.\end{align*}$$
$$\begin{align*}(\mathcal T_Ny)(t;\lambda):=\int_0^t\left(\frac{B(s;\lambda)}{A(s)}y(s;\lambda)+\frac{D(s;\lambda)}{A(s)}\int_0^sy(\tau;\lambda)\,\mathrm d\tau\right)\,\mathrm ds, \qquad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega.\end{align*}$$
By the hypotheses on the coefficients
![]() $A, B, D$
, we have
$A, B, D$
, we have
 $$ \begin{align} M:=\sup_{s\in I_0}\left|\frac s{A(s)}\right|+\sup_{s\in I_0,\lambda\in\Omega}\left|\frac{s B(s;\lambda)}{A(s)}\right|+\sup_{s\in I_0,\lambda\in\Omega}\left|\frac{s D(s;\lambda)}{A(s)}\right|\in (0, +\infty). \end{align} $$
$$ \begin{align} M:=\sup_{s\in I_0}\left|\frac s{A(s)}\right|+\sup_{s\in I_0,\lambda\in\Omega}\left|\frac{s B(s;\lambda)}{A(s)}\right|+\sup_{s\in I_0,\lambda\in\Omega}\left|\frac{s D(s;\lambda)}{A(s)}\right|\in (0, +\infty). \end{align} $$
Hence, for all
![]() $t\in I_0\subset [-1,1]$
and for all
$t\in I_0\subset [-1,1]$
and for all
![]() $\lambda \in \mathbb {C}$
we have
$\lambda \in \mathbb {C}$
we have
 $$ \begin{align*} \left|(\mathcal T_Ny)(t;\lambda)\right|&=\left|\int_0^t\left(\frac{s B(s;\lambda)}{A(s)}\frac{y(s;\lambda)}{s^N}s^{N-1}+\frac{s D(s;\lambda)}{A(s)}\frac1s\int_0^s\frac{y(\tau;\lambda)}{\tau^N}\tau^N\,\mathrm d\tau\right)\,\mathrm ds\right|\\ &\leq \frac{M}{N}|t|^N\|y\|_{Y_N}, \end{align*} $$
$$ \begin{align*} \left|(\mathcal T_Ny)(t;\lambda)\right|&=\left|\int_0^t\left(\frac{s B(s;\lambda)}{A(s)}\frac{y(s;\lambda)}{s^N}s^{N-1}+\frac{s D(s;\lambda)}{A(s)}\frac1s\int_0^s\frac{y(\tau;\lambda)}{\tau^N}\tau^N\,\mathrm d\tau\right)\,\mathrm ds\right|\\ &\leq \frac{M}{N}|t|^N\|y\|_{Y_N}, \end{align*} $$
which gives
We also define an operator
![]() $\mathcal F_N:Y_N\to Y_N$
by
$\mathcal F_N:Y_N\to Y_N$
by
 $$\begin{align*}(\mathcal F_Nf)(t;\lambda):=\int_0^t\frac{f(s;\lambda)}{A(s)}\,\mathrm ds, \qquad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega.\end{align*}$$
$$\begin{align*}(\mathcal F_Nf)(t;\lambda):=\int_0^t\frac{f(s;\lambda)}{A(s)}\,\mathrm ds, \qquad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega.\end{align*}$$
Using (B.9), we know that
![]() $\mathcal F_N:Y_N\to Y_N$
is a bounded linear operator with
$\mathcal F_N:Y_N\to Y_N$
is a bounded linear operator with
![]() $\left \|\mathcal F_Nf\right \|_{Y_N}\leq \frac {M}{N}\|f\|_{Y_N}$
for all
$\left \|\mathcal F_Nf\right \|_{Y_N}\leq \frac {M}{N}\|f\|_{Y_N}$
for all
![]() $f\in Y_N$
. Now we take
$f\in Y_N$
. Now we take
![]() $N_0\in \mathbb {Z}$
such that
$N_0\in \mathbb {Z}$
such that
![]() $N_0>N_0^*+2M$
. For any
$N_0>N_0^*+2M$
. For any
![]() $N\in \mathbb {Z}\cap (N_0, +\infty )$
, by (B.10) we know that
$N\in \mathbb {Z}\cap (N_0, +\infty )$
, by (B.10) we know that
![]() $\|\mathcal T_N\|_{Y_N\to Y_N}\leq 1/2$
, hence
$\|\mathcal T_N\|_{Y_N\to Y_N}\leq 1/2$
, hence
![]() $\operatorname {id}+\mathcal {T}_N:Y_N\to Y_N$
is invertible, then
$\operatorname {id}+\mathcal {T}_N:Y_N\to Y_N$
is invertible, then
![]() $(\operatorname {id}+\mathcal T_N)^{-1}\mathcal F_N: Y_N\to Y_N$
is a bounded linear operator with
$(\operatorname {id}+\mathcal T_N)^{-1}\mathcal F_N: Y_N\to Y_N$
is a bounded linear operator with
For any
![]() $N\in \mathbb {Z}\cap (N_0, +\infty )$
, given
$N\in \mathbb {Z}\cap (N_0, +\infty )$
, given
![]() $f\in \mathcal {H}_{I,\text {loc}}^0(\Omega )$
satisfying (B.7) (then
$f\in \mathcal {H}_{I,\text {loc}}^0(\Omega )$
satisfying (B.7) (then
![]() $f\in Y_N$
), we define
$f\in Y_N$
), we define
 $$ \begin{align*}y=(\operatorname{id}+\mathcal T_N)^{-1}\mathcal F_Nf\in Y_N,\quad x(t;\lambda)=\int_0^ty(s;\lambda)\,\mathrm ds,\ \forall\ t\in I_0,\ \forall\ \lambda\in\Omega,\end{align*} $$
$$ \begin{align*}y=(\operatorname{id}+\mathcal T_N)^{-1}\mathcal F_Nf\in Y_N,\quad x(t;\lambda)=\int_0^ty(s;\lambda)\,\mathrm ds,\ \forall\ t\in I_0,\ \forall\ \lambda\in\Omega,\end{align*} $$
then
![]() $x\in C(I_0\times \Omega )$
,
$x\in C(I_0\times \Omega )$
,
![]() $x(\cdot ;\lambda )\in C^1(I_0)$
for all
$x(\cdot ;\lambda )\in C^1(I_0)$
for all
![]() $\lambda \in \Omega $
,
$\lambda \in \Omega $
,
![]() $x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
$x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
![]() $t\in I_0$
,
$t\in I_0$
,
 $$\begin{align*}x'(t;\lambda)=\int_0^t\left(-\frac{B(\tau;\lambda)}{A(\tau)}x'(\tau;\lambda)-\frac{D(\tau;\lambda)}{A(\tau)}x(\tau;\lambda)+ \frac{f(\tau;\lambda)}{A(\tau)}\right)\,\mathrm d\tau, \quad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega,\end{align*}$$
$$\begin{align*}x'(t;\lambda)=\int_0^t\left(-\frac{B(\tau;\lambda)}{A(\tau)}x'(\tau;\lambda)-\frac{D(\tau;\lambda)}{A(\tau)}x(\tau;\lambda)+ \frac{f(\tau;\lambda)}{A(\tau)}\right)\,\mathrm d\tau, \quad \forall\ t\in I_0,\ \forall\ \lambda\in\Omega,\end{align*}$$
and
![]() $x'(t;\lambda )=y(t;\lambda )$
,
$x'(t;\lambda )=y(t;\lambda )$
,
![]() $x(t;\lambda )=\int _0^tx'(s;\lambda )\,\mathrm ds$
for
$x(t;\lambda )=\int _0^tx'(s;\lambda )\,\mathrm ds$
for
![]() $t\in I_0$
and
$t\in I_0$
and
![]() $\lambda \in \Omega $
. Moreover, we have (recalling
$\lambda \in \Omega $
. Moreover, we have (recalling
![]() $t_0=0$
)
$t_0=0$
)
On the other hand, since
![]() $x'(t;\lambda )=\int _0^t X(s;\lambda )\,\mathrm ds$
for
$x'(t;\lambda )=\int _0^t X(s;\lambda )\,\mathrm ds$
for
![]() $t\in I_0, \lambda \in \Omega $
, where
$t\in I_0, \lambda \in \Omega $
, where
 $$ \begin{align*} X(s;\lambda)&:=-\frac{B(s;\lambda)}{A(s)}x'(s;\lambda)-\frac{D(s;\lambda)}{A(s)}x(s;\lambda)+\frac{f(s;\lambda)}{A(s)}\\ &=-\frac{sB(s;\lambda)}{A(s)}\frac{x'(s;\lambda)}{s^N}s^{N-1}-\frac{sD(s;\lambda)}{A(s)}\frac{x(s;\lambda)}{s^{N+1}}s^N+ \frac{s}{A(s)}\frac{f(s;\lambda)}{s^N}s^{N-1} \end{align*} $$
$$ \begin{align*} X(s;\lambda)&:=-\frac{B(s;\lambda)}{A(s)}x'(s;\lambda)-\frac{D(s;\lambda)}{A(s)}x(s;\lambda)+\frac{f(s;\lambda)}{A(s)}\\ &=-\frac{sB(s;\lambda)}{A(s)}\frac{x'(s;\lambda)}{s^N}s^{N-1}-\frac{sD(s;\lambda)}{A(s)}\frac{x(s;\lambda)}{s^{N+1}}s^N+ \frac{s}{A(s)}\frac{f(s;\lambda)}{s^N}s^{N-1} \end{align*} $$
for
![]() $s\in I_0\setminus \{0\}$
and
$s\in I_0\setminus \{0\}$
and
![]() $\lambda \in \Omega $
, thus there exists a constant
$\lambda \in \Omega $
, thus there exists a constant
![]() $C>0$
such that we have
$C>0$
such that we have
![]() $|X(s;\lambda )|\leq C|s|^{N-1}$
for
$|X(s;\lambda )|\leq C|s|^{N-1}$
for
![]() $s\in I_0\setminus \{0\}, \lambda \in \Omega $
. As
$s\in I_0\setminus \{0\}, \lambda \in \Omega $
. As
![]() $N>1$
, we know that
$N>1$
, we know that
![]() $x'(\cdot ;\lambda )\in C^1(I_0)$
(thus
$x'(\cdot ;\lambda )\in C^1(I_0)$
(thus
![]() $x(\cdot ;\lambda )\in C^2(I_0)$
) and
$x(\cdot ;\lambda )\in C^2(I_0)$
) and
![]() $x"(0;\lambda )=0$
for
$x"(0;\lambda )=0$
for
![]() $\lambda \in \Omega $
. Hence, x solves (B.8) on
$\lambda \in \Omega $
. Hence, x solves (B.8) on
![]() $(t,\lambda )\in I_0\times \mathbb {C}$
. We also have
$(t,\lambda )\in I_0\times \mathbb {C}$
. We also have
Step 2. Smoothness of the
![]() $C^2$
local solution. In this step, we show that
$C^2$
local solution. In this step, we show that
![]() $x(\cdot ;\lambda )\in C^\infty (I_0)$
for any
$x(\cdot ;\lambda )\in C^\infty (I_0)$
for any
![]() $\lambda \in \Omega $
. By standard ODE theory, we have
$\lambda \in \Omega $
. By standard ODE theory, we have
![]() $x(\cdot ;\lambda )\in C^\infty (I_0\setminus \{0\})$
for all
$x(\cdot ;\lambda )\in C^\infty (I_0\setminus \{0\})$
for all
![]() $\lambda \in \Omega $
. We claim that for any
$\lambda \in \Omega $
. We claim that for any
![]() $k\in \mathbb {Z}\cap [0, N]$
, there exists a constant
$k\in \mathbb {Z}\cap [0, N]$
, there exists a constant
![]() $C_k>0$
such that
$C_k>0$
such that
We use the induction. By (B.11) and (B.12), we know that (B.13) holds for
![]() $k\in \{0,1,2\}$
. Assume that for some
$k\in \{0,1,2\}$
. Assume that for some
![]() $K\in \mathbb {Z}\cap [1, N-1]$
, (B.13) holds for all
$K\in \mathbb {Z}\cap [1, N-1]$
, (B.13) holds for all
![]() $k\in \mathbb {Z}\cap [0, K]$
. Now we prove that (B.13) holds for
$k\in \mathbb {Z}\cap [0, K]$
. Now we prove that (B.13) holds for
![]() $k=K+1$
. By our induction hypotheses,
$k=K+1$
. By our induction hypotheses,
![]() $x(\cdot ;\lambda )\in C^{(K)}(I_0)$
and
$x(\cdot ;\lambda )\in C^{(K)}(I_0)$
and
![]() $x^{(K+1)}(0;\lambda )=\lim _{t\to 0}(x^{(K)}(t;\lambda )/t)=0$
for all
$x^{(K+1)}(0;\lambda )=\lim _{t\to 0}(x^{(K)}(t;\lambda )/t)=0$
for all
![]() $\lambda \in \Omega $
. For
$\lambda \in \Omega $
. For
![]() $t\in I_0\setminus \{0\}$
, taking derivative
$t\in I_0\setminus \{0\}$
, taking derivative
![]() $K-1$
times on both sides of (B.8) with respect to t, we obtain
$K-1$
times on both sides of (B.8) with respect to t, we obtain
 $$ \begin{align} A(t)x^{(K+1)}(t;\lambda)+\sum_{j=0}^{K}A_{j, K}(t;\lambda)x^{(j)}(t;\lambda)=f^{(K-1)}(t;\lambda),\quad \forall\ t\in I_0\setminus\{0\},\ \forall\ \lambda\in\Omega, \end{align} $$
$$ \begin{align} A(t)x^{(K+1)}(t;\lambda)+\sum_{j=0}^{K}A_{j, K}(t;\lambda)x^{(j)}(t;\lambda)=f^{(K-1)}(t;\lambda),\quad \forall\ t\in I_0\setminus\{0\},\ \forall\ \lambda\in\Omega, \end{align} $$
where
![]() $A_{j,K}$
’s are linear combinations of
$A_{j,K}$
’s are linear combinations of
![]() $A, B, D$
and their derivatives, hence
$A, B, D$
and their derivatives, hence
![]() $A_{j,K}(t;\lambda )\in C^\infty (I\times \Omega )\cap L^\infty (I_0\times \Omega )$
for all
$A_{j,K}(t;\lambda )\in C^\infty (I\times \Omega )\cap L^\infty (I_0\times \Omega )$
for all
![]() $j\in \mathbb {Z}\cap [0, K]$
.Footnote 13 As
$j\in \mathbb {Z}\cap [0, K]$
.Footnote 13 As
![]() $f\in \mathcal H_{I,\text {loc}}^0(\Omega )$
satisfies (B.7), we haveFootnote 14
$f\in \mathcal H_{I,\text {loc}}^0(\Omega )$
satisfies (B.7), we haveFootnote 14
![]() $f^{(k)}(t;\lambda )/|t|^{N-k}\in L^\infty (I_0\times \Omega )$
for all
$f^{(k)}(t;\lambda )/|t|^{N-k}\in L^\infty (I_0\times \Omega )$
for all
![]() $k\in \mathbb {Z}\cap [0, N]$
. Therefore,
$k\in \mathbb {Z}\cap [0, N]$
. Therefore,
 $$\begin{align*}\frac{\left|x^{(K+1)}(t;\lambda)\right|}{|t|^{N-K}}=\frac{|t|}{|A(t)|}\frac{\left|f^{(K-1)}(t;\lambda)-\sum_{j=0}^{K}A_{j, K}(t;\lambda)x^{(j)}(t;\lambda)\right|}{|t|^{N-(K-1)}}\in L^\infty(I_0\times\Omega).\end{align*}$$
$$\begin{align*}\frac{\left|x^{(K+1)}(t;\lambda)\right|}{|t|^{N-K}}=\frac{|t|}{|A(t)|}\frac{\left|f^{(K-1)}(t;\lambda)-\sum_{j=0}^{K}A_{j, K}(t;\lambda)x^{(j)}(t;\lambda)\right|}{|t|^{N-(K-1)}}\in L^\infty(I_0\times\Omega).\end{align*}$$
This proves (B.13) for
![]() $k=K+1$
. Hence, (B.13) holds by the induction and thus
$k=K+1$
. Hence, (B.13) holds by the induction and thus
![]() $x(\cdot ;\lambda )\in C^N(I_0)$
for all
$x(\cdot ;\lambda )\in C^N(I_0)$
for all
![]() $\lambda \in \Omega $
and
$\lambda \in \Omega $
and
Next we claim that for
![]() $k\in \mathbb {Z}\cap [N,+\infty )$
we have
$k\in \mathbb {Z}\cap [N,+\infty )$
we have
By (B.13), we know that (B.16) holds for
![]() $k=N$
. Assume that for some
$k=N$
. Assume that for some
![]() $k\in \mathbb {Z}_{\geq N}$
we have
$k\in \mathbb {Z}_{\geq N}$
we have
For
![]() $t\in I_0\setminus \{0\}$
and
$t\in I_0\setminus \{0\}$
and
![]() $\lambda \in \Omega $
, by (B.14) for
$\lambda \in \Omega $
, by (B.14) for
![]() $K=k+1$
and footnote 13 we have
$K=k+1$
and footnote 13 we have
 $$ \begin{align} &F_k(t;\lambda):=f^{(k)}(t;\lambda)-\sum_{j=0}^{k}A_{j, k+1}(t;\lambda)x^{(j)}(t;\lambda). \end{align} $$
$$ \begin{align} &F_k(t;\lambda):=f^{(k)}(t;\lambda)-\sum_{j=0}^{k}A_{j, k+1}(t;\lambda)x^{(j)}(t;\lambda). \end{align} $$
Then by
![]() $f\in \mathcal H_{I_0}^0(\Omega )$
, (B.15) and (B.17) we have
$f\in \mathcal H_{I_0}^0(\Omega )$
, (B.15) and (B.17) we have
![]() $\sup _{t\in I_0\setminus \{0\},\lambda \in \Omega }|F_k(t;\lambda )|<+\infty $
. Let
$\sup _{t\in I_0\setminus \{0\},\lambda \in \Omega }|F_k(t;\lambda )|<+\infty $
. Let
![]() $\widetilde A(t):=\int _0^1A'(ts)\,\mathrm ds$
and
$\widetilde A(t):=\int _0^1A'(ts)\,\mathrm ds$
and
![]() $\widetilde B(t;\lambda ):=B(t;\lambda )-\frac {B(0;\lambda )}{A'(0)}\widetilde A(t)$
for
$\widetilde B(t;\lambda ):=B(t;\lambda )-\frac {B(0;\lambda )}{A'(0)}\widetilde A(t)$
for
![]() $t\in I_0, \lambda \in \Omega $
, then
$t\in I_0, \lambda \in \Omega $
, then
![]() $\widetilde B(0;\lambda )=0$
,
$\widetilde B(0;\lambda )=0$
,
![]() $\widetilde A\in C^{\infty }(I_0)$
,
$\widetilde A\in C^{\infty }(I_0)$
,
![]() $\widetilde B\in C(I_0\times \Omega )$
for
$\widetilde B\in C(I_0\times \Omega )$
for
![]() $\lambda \in \Omega $
,
$\lambda \in \Omega $
,
![]() $\partial _t\widetilde B\in L^{\infty }(I_0\times \Omega ) $
and
$\partial _t\widetilde B\in L^{\infty }(I_0\times \Omega ) $
and
![]() $\widetilde A(t)={A(t)}/{t}$
for
$\widetilde A(t)={A(t)}/{t}$
for
![]() $ t\in I_0\setminus \{0\}$
. Thus,
$ t\in I_0\setminus \{0\}$
. Thus,
![]() $\widetilde B(t;\lambda )/t\in L^{\infty }(I_0\times \Omega )$
and
$\widetilde B(t;\lambda )/t\in L^{\infty }(I_0\times \Omega )$
and
![]() $\widetilde B(t;\lambda )/A(t)\in L^{\infty }(I_0\times \Omega )$
(using (B.9)).
$\widetilde B(t;\lambda )/A(t)\in L^{\infty }(I_0\times \Omega )$
(using (B.9)).
Let
![]() $\eta (t;\lambda ):=|t|^{\frac {B(0;\lambda )}{A'(0)}}\exp \left (\int _0^t\frac {\widetilde B(s;\lambda )}{A(s)}\,\mathrm ds\right ) $
then (here
$\eta (t;\lambda ):=|t|^{\frac {B(0;\lambda )}{A'(0)}}\exp \left (\int _0^t\frac {\widetilde B(s;\lambda )}{A(s)}\,\mathrm ds\right ) $
then (here
![]() $\eta $
is different from the one in (2.23))
$\eta $
is different from the one in (2.23))
for some constant
![]() $C_\eta>0$
. We also have
$C_\eta>0$
. We also have
![]() $\eta \in C^\infty ((I_0\setminus \{0\})\times \Omega ;\mathbb {C}\setminus \{0\})$
and
$\eta \in C^\infty ((I_0\setminus \{0\})\times \Omega ;\mathbb {C}\setminus \{0\})$
and
 $$ \begin{align*} \frac{\eta'(t;\lambda)}{\eta(t;\lambda)}=\frac{\widetilde B(t;\lambda)}{A(t)}+\frac{B(0;\lambda)}{A'(0)t}=\frac{ B(t;\lambda)}{A(t)}-\frac{B(0;\lambda)}{A'(0)}\frac{\widetilde A(t)}{A(t)}+\frac{B(0;\lambda)}{A'(0)t}=\frac{ B(t;\lambda)}{A(t)},\quad \forall\ t\in I_0\setminus\{0\}. \end{align*} $$
$$ \begin{align*} \frac{\eta'(t;\lambda)}{\eta(t;\lambda)}=\frac{\widetilde B(t;\lambda)}{A(t)}+\frac{B(0;\lambda)}{A'(0)t}=\frac{ B(t;\lambda)}{A(t)}-\frac{B(0;\lambda)}{A'(0)}\frac{\widetilde A(t)}{A(t)}+\frac{B(0;\lambda)}{A'(0)t}=\frac{ B(t;\lambda)}{A(t)},\quad \forall\ t\in I_0\setminus\{0\}. \end{align*} $$
Here we used
![]() $\widetilde A(t)={A(t)}/{t}$
. It follows from (B.18) that
$\widetilde A(t)={A(t)}/{t}$
. It follows from (B.18) that
By (B.14) for
![]() $K=k$
and (B.15), (B.17), we have
$K=k$
and (B.15), (B.17), we have
![]() $A(t)x^{(k+1)}(t;\lambda )\in L^\infty ((I_0\setminus \{0\})\times \Omega )$
; using (B.20),
$A(t)x^{(k+1)}(t;\lambda )\in L^\infty ((I_0\setminus \{0\})\times \Omega )$
; using (B.20),
![]() $|A(t)|\sim |t|$
as
$|A(t)|\sim |t|$
as
![]() $t\to 0$
and
$t\to 0$
and
we have
hence
 $$\begin{align*}A(t)^k\eta(t;\lambda)x^{(k+1)}(t;\lambda)=\int_0^tA(s)^{k-1}\eta(s;\lambda)F_k(s;\lambda)\,\mathrm ds,\qquad\forall\ t\in I_0\setminus\{0\},\ \forall\ \lambda\in\Omega.\end{align*}$$
$$\begin{align*}A(t)^k\eta(t;\lambda)x^{(k+1)}(t;\lambda)=\int_0^tA(s)^{k-1}\eta(s;\lambda)F_k(s;\lambda)\,\mathrm ds,\qquad\forall\ t\in I_0\setminus\{0\},\ \forall\ \lambda\in\Omega.\end{align*}$$
As a consequence, we have
 $$ \begin{align*} \left|x^{(k+1)}(t;\lambda)\right|=\frac{\left|\int_0^tA(s)^{k-1}\eta(s;\lambda)F_k(s;\lambda)\,\mathrm ds\right|}{|A(t)|^k|\eta(t;\lambda)|}\leq C_{k+1}\frac{\int_0^{|t|}s^{k-1}s^{\operatorname{Re}(B(0;\lambda)/A'(0))}\,\mathrm ds}{|t|^k|t|^{\operatorname{Re}(B(0;\lambda)/A'(0))}}\leq \widetilde C_{k+1} \end{align*} $$
$$ \begin{align*} \left|x^{(k+1)}(t;\lambda)\right|=\frac{\left|\int_0^tA(s)^{k-1}\eta(s;\lambda)F_k(s;\lambda)\,\mathrm ds\right|}{|A(t)|^k|\eta(t;\lambda)|}\leq C_{k+1}\frac{\int_0^{|t|}s^{k-1}s^{\operatorname{Re}(B(0;\lambda)/A'(0))}\,\mathrm ds}{|t|^k|t|^{\operatorname{Re}(B(0;\lambda)/A'(0))}}\leq \widetilde C_{k+1} \end{align*} $$
for all
![]() $t\in I_0\setminus \{0\}$
and
$t\in I_0\setminus \{0\}$
and
![]() $\lambda \in \Omega $
, where
$\lambda \in \Omega $
, where
![]() $C_{k+1}>0$
and
$C_{k+1}>0$
and
![]() $\widetilde C_{k+1}>0$
are constants. Here we have used
$\widetilde C_{k+1}>0$
are constants. Here we have used
![]() $k+\inf _{\lambda \in \Omega }\operatorname {Re}(B(0;\lambda )/A'(0))>0$
, which follows from (B.21). This proves (B.16).
$k+\inf _{\lambda \in \Omega }\operatorname {Re}(B(0;\lambda )/A'(0))>0$
, which follows from (B.21). This proves (B.16).
Next we use once again the induction to prove that
We know from (B.13) that (B.22) holds for
![]() $k\leq N$
. Now we assume that for some
$k\leq N$
. Now we assume that for some
![]() $k\in \mathbb {Z}_{\geq N}$
, (B.22) holds for
$k\in \mathbb {Z}_{\geq N}$
, (B.22) holds for
![]() $0, 1,\cdots , k$
. Then by (B.19), we have
$0, 1,\cdots , k$
. Then by (B.19), we have
![]() $F_k(\cdot ;\lambda )\in C(I_0)$
, by (B.16) with k replaced by
$F_k(\cdot ;\lambda )\in C(I_0)$
, by (B.16) with k replaced by
![]() $k+2$
and
$k+2$
and
![]() $A(0)=0$
we have
$A(0)=0$
we have
![]() $\lim _{t\to 0}A(t)x^{(k+2)}(t;\lambda )=0$
, and by (B.18) we have
$\lim _{t\to 0}A(t)x^{(k+2)}(t;\lambda )=0$
, and by (B.18) we have
where we have used
![]() $kA'(0)+B(0;\lambda )\neq 0$
, which follows from
$kA'(0)+B(0;\lambda )\neq 0$
, which follows from
![]() $k>-\inf _{\lambda \in \Omega }\operatorname {Re}(B(0;\lambda )/A'(0))$
(see (B.21)). Finally, we get by L’Hôpital’s rule that
$k>-\inf _{\lambda \in \Omega }\operatorname {Re}(B(0;\lambda )/A'(0))$
(see (B.21)). Finally, we get by L’Hôpital’s rule that
This proves (B.22) for
![]() $k+1$
. Then (B.22) holds for all
$k+1$
. Then (B.22) holds for all
![]() $k\in \mathbb {Z}_{\geq N}$
by the induction. Hence,
$k\in \mathbb {Z}_{\geq N}$
by the induction. Hence,
![]() $x(\cdot ;\lambda )\in C^\infty (I_0)$
for all
$x(\cdot ;\lambda )\in C^\infty (I_0)$
for all
![]() $\lambda \in \Omega $
. Moreover, combining (B.15) and (B.16) gives that
$\lambda \in \Omega $
. Moreover, combining (B.15) and (B.16) gives that
Step 3.
![]() $x\in C^\infty (I_0\times \Omega )$
. Recall that
$x\in C^\infty (I_0\times \Omega )$
. Recall that
![]() $x\in C(I_0\times \Omega )$
satisfies
$x\in C(I_0\times \Omega )$
satisfies
![]() $x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
$x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
![]() $t\in I_0$
(in Step 1) and
$t\in I_0$
(in Step 1) and
![]() $x(\cdot ;\lambda )\in C^\infty (I_0)$
for all
$x(\cdot ;\lambda )\in C^\infty (I_0)$
for all
![]() $\lambda \in \Omega $
(in Step 2). Using (B.23) we have
$\lambda \in \Omega $
(in Step 2). Using (B.23) we have
![]() $x\in \mathcal H_{I_0}^0(\Omega )$
. Then Lemma B.1 implies that
$x\in \mathcal H_{I_0}^0(\Omega )$
. Then Lemma B.1 implies that
![]() $x\in C^\infty (I_0\times \Omega )$
.
$x\in C^\infty (I_0\times \Omega )$
.
Step 4. Extension of the smooth local solution. For any fixed
![]() $\lambda \in \Omega $
, we have constructed a local solution
$\lambda \in \Omega $
, we have constructed a local solution
![]() $x_L(\cdot ;\lambda )\in C^\infty (I_0)$
of (B.8) on
$x_L(\cdot ;\lambda )\in C^\infty (I_0)$
of (B.8) on
![]() $I_0\subset I$
. Moreover, we have
$I_0\subset I$
. Moreover, we have
![]() $x_L\in C^\infty (I_0\times \Omega )$
and
$x_L\in C^\infty (I_0\times \Omega )$
and
![]() $x_L(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
$x_L(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
![]() $t\in I_0$
. By standard ODE theory, the initial value problem
$t\in I_0$
. By standard ODE theory, the initial value problem
 $$\begin{align*}\begin{cases} x"(t;\lambda)+\frac{B(t;\lambda)}{A(t)}x'(t;\lambda)+\frac{D(t;\lambda)}{A(t)}x(t;\lambda)=\frac{f(t;\lambda)}{A(t)},\\ x(\delta_0/2;\lambda)=x_L(\delta_0/2;\lambda), x'(\delta_0/2;\lambda)=x_L'(\delta_0/2;\lambda) \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} x"(t;\lambda)+\frac{B(t;\lambda)}{A(t)}x'(t;\lambda)+\frac{D(t;\lambda)}{A(t)}x(t;\lambda)=\frac{f(t;\lambda)}{A(t)},\\ x(\delta_0/2;\lambda)=x_L(\delta_0/2;\lambda), x'(\delta_0/2;\lambda)=x_L'(\delta_0/2;\lambda) \end{cases}\end{align*}$$
has a unique solution
![]() $x=x(t;\lambda )$
on
$x=x(t;\lambda )$
on
![]() $((0, +\infty )\cap I)\times \Omega $
and
$((0, +\infty )\cap I)\times \Omega $
and
![]() $x\in C^\infty (((0, +\infty )\cap I)\times \Omega )$
. Moreover, by the analytic dependence on parameters (Lemma B.5), we have
$x\in C^\infty (((0, +\infty )\cap I)\times \Omega )$
. Moreover, by the analytic dependence on parameters (Lemma B.5), we have
![]() $x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
$x(t;\cdot )\in \operatorname {Hol}(\Omega )$
for all
![]() $t\in (0, +\infty )\cap I$
. Hence,
$t\in (0, +\infty )\cap I$
. Hence,
![]() $x_L$
can be extended to be a smooth solution of (B.8) on
$x_L$
can be extended to be a smooth solution of (B.8) on
![]() $((0, +\infty )\cap I)\times \Omega $
; Similarly we can extend
$((0, +\infty )\cap I)\times \Omega $
; Similarly we can extend
![]() $x_L$
on the negative direction (for the case
$x_L$
on the negative direction (for the case
![]() $I_0=[-\delta _0,\delta _0]$
). And for the extended solution x, we have
$I_0=[-\delta _0,\delta _0]$
). And for the extended solution x, we have
![]() $x\in \mathcal H_I(\Omega )$
.
$x\in \mathcal H_I(\Omega )$
.
Proposition B.4. Let
![]() $I\subset \mathbb {R}$
be an interval. Let
$I\subset \mathbb {R}$
be an interval. Let
![]() $A(t)\in C^\infty (I;\mathbb {C})$
be such that
$A(t)\in C^\infty (I;\mathbb {C})$
be such that
![]() $A(t)=0$
has a unique solution
$A(t)=0$
has a unique solution
![]() $t=t_0$
in I with
$t=t_0$
in I with
![]() $A'(t_0)\neq 0$
. Let
$A'(t_0)\neq 0$
. Let
![]() $B(t;\lambda ), D(t;\lambda )\in \mathcal H_I(\mathbb {C})$
. Assume that
$B(t;\lambda ), D(t;\lambda )\in \mathcal H_I(\mathbb {C})$
. Assume that
![]() $B(t;\lambda )=\widetilde B(t)+\lambda \widehat B(t)$
for
$B(t;\lambda )=\widetilde B(t)+\lambda \widehat B(t)$
for
![]() $t\in I$
and
$t\in I$
and
![]() $\lambda \in \mathbb {C}$
, where
$\lambda \in \mathbb {C}$
, where
![]() $\widetilde B, \widehat B\in C^\infty (I;\mathbb {C})$
. Suppose that
$\widetilde B, \widehat B\in C^\infty (I;\mathbb {C})$
. Suppose that
We define
Then
![]() $\Lambda _*\subset \mathbb {C}$
is a (probably empty) discrete set. Let
$\Lambda _*\subset \mathbb {C}$
is a (probably empty) discrete set. Let
![]() $R\in (0,+\infty )$
. There exists a nonzero polynomial
$R\in (0,+\infty )$
. There exists a nonzero polynomial
![]() $ \psi _1(\lambda )$
satisfying
$ \psi _1(\lambda )$
satisfying
![]() $\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
such that for every
$\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
such that for every
![]() $f(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
, the inhomogeneous ODE
$f(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
, the inhomogeneous ODE
 $$ \begin{align} \begin{cases} A(t)x"(t;\lambda)+B(t;\lambda)x'(t;\lambda)+D(t;\lambda)x(t;\lambda)=\psi_1(\lambda)f(t;\lambda),\quad t\in I, \lambda\in B_R,\\ x(t_0;\lambda)=\psi_1(\lambda),\quad \lambda\in B_R, \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} A(t)x"(t;\lambda)+B(t;\lambda)x'(t;\lambda)+D(t;\lambda)x(t;\lambda)=\psi_1(\lambda)f(t;\lambda),\quad t\in I, \lambda\in B_R,\\ x(t_0;\lambda)=\psi_1(\lambda),\quad \lambda\in B_R, \end{cases} \end{align} $$
where the prime
![]() $'$
refers to the derivative with respect to
$'$
refers to the derivative with respect to
![]() $t\in I$
, has a solution
$t\in I$
, has a solution
![]() $x=x(t;\lambda )\in \mathcal H_I(B_R)$
. Moreover, if
$x=x(t;\lambda )\in \mathcal H_I(B_R)$
. Moreover, if
![]() $\widehat B(t_0)=0$
, then
$\widehat B(t_0)=0$
, then
![]() $ \psi _1(\lambda )=1$
.
$ \psi _1(\lambda )=1$
.
Proof. We first show that
![]() $\Lambda _*$
is a discrete set. If
$\Lambda _*$
is a discrete set. If
![]() $\widehat B(t_0)\neq 0$
, then
$\widehat B(t_0)\neq 0$
, then
![]() $\Lambda _*=\{-nA'(t_0)/\widehat B(t_0)-\widetilde B(t_0)/\widehat B(t_0): n\in \mathbb {Z}_{\geq 0}\}$
, hence
$\Lambda _*=\{-nA'(t_0)/\widehat B(t_0)-\widetilde B(t_0)/\widehat B(t_0): n\in \mathbb {Z}_{\geq 0}\}$
, hence
![]() $\Lambda _*$
is a discrete set. If
$\Lambda _*$
is a discrete set. If
![]() $\widehat B(t_0)= 0$
, then
$\widehat B(t_0)= 0$
, then
![]() $\lambda _*\in \Lambda _*$
if and only if
$\lambda _*\in \Lambda _*$
if and only if
![]() $0=nA'(t_0)+B(t_0;\lambda _*)=nA'(t_0)+\widetilde B(t_0)=0$
for some
$0=nA'(t_0)+B(t_0;\lambda _*)=nA'(t_0)+\widetilde B(t_0)=0$
for some
![]() $n\in \mathbb {Z}_{\geq 0}$
, which implies that
$n\in \mathbb {Z}_{\geq 0}$
, which implies that
![]() $-\widetilde B(t_0)/A'(t_0)\in \mathbb {Z}_{\geq 0}$
, and this is a contradiction with our assumption (B.24). As a consequence, if
$-\widetilde B(t_0)/A'(t_0)\in \mathbb {Z}_{\geq 0}$
, and this is a contradiction with our assumption (B.24). As a consequence, if
![]() $\widehat B(t_0)=0$
(and
$\widehat B(t_0)=0$
(and
![]() $-\widetilde B(t_0)/A'(t_0)\notin \mathbb {Z}_{\geq 0}$
), then
$-\widetilde B(t_0)/A'(t_0)\notin \mathbb {Z}_{\geq 0}$
), then
![]() $\Lambda _*=\emptyset $
.
$\Lambda _*=\emptyset $
.
Next, we construct
![]() $ \psi _1(\lambda )$
. Let
$ \psi _1(\lambda )$
. Let
![]() $N_0$
be given by Lemma B.3 (for
$N_0$
be given by Lemma B.3 (for
![]() $\Omega =B_R$
) and fix an integer
$\Omega =B_R$
) and fix an integer
![]() $N>\max \{N_0+1,-\inf _{\lambda \in B_R}\operatorname {Re}\left (B(t_0;\lambda )/A'(t_0)\right )+1\}$
. Let
$N>\max \{N_0+1,-\inf _{\lambda \in B_R}\operatorname {Re}\left (B(t_0;\lambda )/A'(t_0)\right )+1\}$
. Let
![]() $ \psi _1(\lambda ):=1$
for the case
$ \psi _1(\lambda ):=1$
for the case
![]() $\widehat B(t_0)=0$
and
$\widehat B(t_0)=0$
and
![]() $ \psi _1(\lambda ):=\prod _{j=0}^{N-1}\big (jA'(t_0)+B(t_0,\lambda )\big )$
for the case
$ \psi _1(\lambda ):=\prod _{j=0}^{N-1}\big (jA'(t_0)+B(t_0,\lambda )\big )$
for the case
![]() $\widehat B(t_0)\neq 0$
.
$\widehat B(t_0)\neq 0$
.
Claim 1.
![]() $ \psi _1(\lambda )$
is a nonzero polynomial. If
$ \psi _1(\lambda )$
is a nonzero polynomial. If
![]() $\widehat B(t_0)=0$
, then
$\widehat B(t_0)=0$
, then
![]() $ \psi _1(\lambda )\equiv 1$
is a polynomial of degree
$ \psi _1(\lambda )\equiv 1$
is a polynomial of degree
![]() $0$
; if
$0$
; if
![]() $\widehat B(t_0)\neq 0$
, as
$\widehat B(t_0)\neq 0$
, as
![]() $ B(t_0,\lambda )=\widetilde B(t_0)+\lambda \widehat B(t_0)$
, then
$ B(t_0,\lambda )=\widetilde B(t_0)+\lambda \widehat B(t_0)$
, then
![]() $ \psi _1(\lambda )$
is a polynomial of degree N.
$ \psi _1(\lambda )$
is a polynomial of degree N.
Claim 2.
![]() $\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
. If
$\{\lambda \in B_R: \psi _1(\lambda )=0\}=\Lambda _*\cap B_R$
. If
![]() $\widehat B(t_0)=0$
, then
$\widehat B(t_0)=0$
, then
![]() $\{\lambda \in B_R: \psi _1(\lambda )=0\}=\emptyset =\Lambda _*=\Lambda _*\cap B_R$
. For the case
$\{\lambda \in B_R: \psi _1(\lambda )=0\}=\emptyset =\Lambda _*=\Lambda _*\cap B_R$
. For the case
![]() $\widehat B(t_0)\neq 0$
, if
$\widehat B(t_0)\neq 0$
, if
![]() $\psi _1(\lambda )=0 $
then
$\psi _1(\lambda )=0 $
then
![]() $jA'(t_0)+B(t_0,\lambda )=0$
for some
$jA'(t_0)+B(t_0,\lambda )=0$
for some
![]() $j\in \mathbb {Z}\cap [0,N-1]$
and
$j\in \mathbb {Z}\cap [0,N-1]$
and
![]() $\lambda \in \Lambda _*$
, thus
$\lambda \in \Lambda _*$
, thus
![]() $\{\lambda \in B_R: \psi _1(\lambda )=0\}\subseteq \Lambda _*\cap B_R$
. On the other hand, if
$\{\lambda \in B_R: \psi _1(\lambda )=0\}\subseteq \Lambda _*\cap B_R$
. On the other hand, if
![]() $\lambda _0\in \Lambda _*\cap B_R$
(and
$\lambda _0\in \Lambda _*\cap B_R$
(and
![]() $\widehat B(t_0)\neq 0$
), then
$\widehat B(t_0)\neq 0$
), then
![]() $nA'(t_0)+B(t_0;\lambda _0)=0$
for some
$nA'(t_0)+B(t_0;\lambda _0)=0$
for some
![]() $n\in \mathbb {Z}_{\geq 0}$
, and
$n\in \mathbb {Z}_{\geq 0}$
, and
![]() $n=-B(t_0;\lambda _0)/A'(t_0)\leq -\inf _{\lambda \in B_R}\operatorname {Re}\left (B(t_0;\lambda )/A'(t_0)\right )<N-1$
, thus
$n=-B(t_0;\lambda _0)/A'(t_0)\leq -\inf _{\lambda \in B_R}\operatorname {Re}\left (B(t_0;\lambda )/A'(t_0)\right )<N-1$
, thus
![]() $n\in \mathbb {Z}\cap [0,N-1]$
and
$n\in \mathbb {Z}\cap [0,N-1]$
and
![]() $\psi _1(\lambda _0)=0 $
. So
$\psi _1(\lambda _0)=0 $
. So
![]() $\Lambda _*\cap B_R\subseteq \{\lambda \in B_R: \psi _1(\lambda )=0\}$
.
$\Lambda _*\cap B_R\subseteq \{\lambda \in B_R: \psi _1(\lambda )=0\}$
.
It remains to construct
![]() $x(t;\lambda )$
. For any
$x(t;\lambda )$
. For any
![]() $n\in \mathbb {Z}\cap [0, N]$
and
$n\in \mathbb {Z}\cap [0, N]$
and
![]() $\lambda \in \mathbb {C}$
, let
$\lambda \in \mathbb {C}$
, let
![]() $ \psi _{1,n}(\lambda ):=1$
for the case
$ \psi _{1,n}(\lambda ):=1$
for the case
![]() $\widehat B(t_0)=0$
and
$\widehat B(t_0)=0$
and
![]() $ \psi _{1,n}(\lambda ):=\prod _{j=n}^{N-1}\big (jA'(t_0)+B(t_0,\lambda )\big )$
(here
$ \psi _{1,n}(\lambda ):=\prod _{j=n}^{N-1}\big (jA'(t_0)+B(t_0,\lambda )\big )$
(here
![]() $\psi _{1, N}(\lambda ):=1$
) for the case
$\psi _{1, N}(\lambda ):=1$
) for the case
![]() $\widehat B(t_0)\neq 0$
. Then
$\widehat B(t_0)\neq 0$
. Then
![]() $ \psi _{1}(\lambda )=\psi _{1,0}(\lambda )$
for all
$ \psi _{1}(\lambda )=\psi _{1,0}(\lambda )$
for all
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
Claim 3. If
![]() $n\in \mathbb {Z}\cap [0,N]$
,
$n\in \mathbb {Z}\cap [0,N]$
,
![]() $g(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
,
$g(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
,
![]() $ \partial _t^ig(t_0;\lambda )=0$
for
$ \partial _t^ig(t_0;\lambda )=0$
for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i<n$
. Then
$0\leq i<n$
. Then
has a solution
![]() $y=y(t;\lambda )\in \mathcal H_I(B_R)$
.
$y=y(t;\lambda )\in \mathcal H_I(B_R)$
.
Let
![]() $g(t;\lambda )=f(t;\lambda )-D(t;\lambda )$
,
$g(t;\lambda )=f(t;\lambda )-D(t;\lambda )$
,
![]() $n=0$
, then by Claim 3, (B.27) has a solution
$n=0$
, then by Claim 3, (B.27) has a solution
![]() $y=y(t;\lambda )\in \mathcal H_I(B_R)$
with
$y=y(t;\lambda )\in \mathcal H_I(B_R)$
with
![]() $n=0$
.
$n=0$
.
![]() $x(t;\lambda )=y(t;\lambda )+\psi _{1}(\lambda )\in \mathcal H_I(B_R)$
solves (B.26) (using
$x(t;\lambda )=y(t;\lambda )+\psi _{1}(\lambda )\in \mathcal H_I(B_R)$
solves (B.26) (using
![]() $ \psi _{1}(\lambda )=\psi _{1,0}(\lambda )$
).
$ \psi _{1}(\lambda )=\psi _{1,0}(\lambda )$
).
It remains to prove Claim 3. We use the (backward) induction. We need to prove that:
-
(i) Claim 3 holds for
 $n=N$
;
$n=N$
; -
(ii) if
 $j\in \mathbb {Z}\cap [0,N-1]$
, Claim 3 holds for
$j\in \mathbb {Z}\cap [0,N-1]$
, Claim 3 holds for
 $n=j+1$
, then Claim 3 holds for
$n=j+1$
, then Claim 3 holds for
 $n=j$
.
$n=j$
.
Proof of (i). As
![]() $g\in \mathcal H_I(\mathbb {C})\subset \mathcal H_{I,\text {loc}}^0(B_R)$
,
$g\in \mathcal H_I(\mathbb {C})\subset \mathcal H_{I,\text {loc}}^0(B_R)$
,
![]() $n=N$
, by Taylor’s theorem with integral remainders, we have
$n=N$
, by Taylor’s theorem with integral remainders, we have
![]() $g(t;\lambda )/|t-t_0|^{N}\in L^\infty _{\text {loc}}(I\times \mathbb {C})$
, and we also have
$g(t;\lambda )/|t-t_0|^{N}\in L^\infty _{\text {loc}}(I\times \mathbb {C})$
, and we also have
![]() $ \psi _{1,n}(\lambda )=\psi _{1,N}(\lambda )=1$
. Then the result follows from Lemma B.3.
$ \psi _{1,n}(\lambda )=\psi _{1,N}(\lambda )=1$
. Then the result follows from Lemma B.3.
Proof of (ii). We fix
![]() $j\in \mathbb {Z}\cap [0,N-1]$
and assume
$j\in \mathbb {Z}\cap [0,N-1]$
and assume
![]() $g(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
,
$g(t;\lambda )\in \mathcal H_I(\mathbb {C}) $
,
![]() $ \partial _t^ig(t_0;\lambda )=0$
for
$ \partial _t^ig(t_0;\lambda )=0$
for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i<j$
. For
$0\leq i<j$
. For
![]() $t\in I, \lambda \in \mathbb {C}$
, let
$t\in I, \lambda \in \mathbb {C}$
, let
![]() $x_j(t):=(t-t_0)^{j+1}$
,
$x_j(t):=(t-t_0)^{j+1}$
,
![]() $y_j(t;\lambda ):=A(t)x_j"(t)+B(t;\lambda )x_j'(t)+D(t;\lambda )x_j(t)$
, then
$y_j(t;\lambda ):=A(t)x_j"(t)+B(t;\lambda )x_j'(t)+D(t;\lambda )x_j(t)$
, then
![]() $x_j\in C^{\infty }(I)$
,
$x_j\in C^{\infty }(I)$
,
![]() $x_j(t_0)=0$
,
$x_j(t_0)=0$
,
![]() $y_j(t;\lambda )\in \mathcal H_I(\mathbb {C})$
, and
$y_j(t;\lambda )\in \mathcal H_I(\mathbb {C})$
, and
By Taylor’s formula, we have
![]() $\partial _t^iy_j(t_0;\lambda )=0$
for
$\partial _t^iy_j(t_0;\lambda )=0$
for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i<j$
and
$0\leq i<j$
and
 $$ \begin{align*} \partial_t^jy_j(t_0;\lambda)&=j!\lim_{t\to t_0}\frac{y_j(t;\lambda)}{(t-t_0)^j}=j!\lim_{t\to t_0}j(j+1)\frac{A(t)}{t-t_0}+j!B(t_0;\lambda)(j+1)\\&=j!j(j+1)A'(t_0)+(j+1)!B(t_0;\lambda)=(j+1)!(jA'(t_0)+B(t_0;\lambda)). \end{align*} $$
$$ \begin{align*} \partial_t^jy_j(t_0;\lambda)&=j!\lim_{t\to t_0}\frac{y_j(t;\lambda)}{(t-t_0)^j}=j!\lim_{t\to t_0}j(j+1)\frac{A(t)}{t-t_0}+j!B(t_0;\lambda)(j+1)\\&=j!j(j+1)A'(t_0)+(j+1)!B(t_0;\lambda)=(j+1)!(jA'(t_0)+B(t_0;\lambda)). \end{align*} $$
For the case of
![]() $\widehat B(t_0)\neq 0$
, let
$\widehat B(t_0)\neq 0$
, let
![]() $a_j=(j+1)!$
,
$a_j=(j+1)!$
,
![]() $b_j(\lambda )=jA'(t_0)+B(t_0;\lambda )$
then
$b_j(\lambda )=jA'(t_0)+B(t_0;\lambda )$
then
![]() $a_j\neq 0$
,
$a_j\neq 0$
,
![]() $b_j\in \operatorname {Hol}(\mathbb {C})$
. As
$b_j\in \operatorname {Hol}(\mathbb {C})$
. As
![]() $ \psi _{1,n}(\lambda )=\prod _{j=n}^{N-1}\big (jA'(t_0)+B(t_0;\lambda )\big )$
for
$ \psi _{1,n}(\lambda )=\prod _{j=n}^{N-1}\big (jA'(t_0)+B(t_0;\lambda )\big )$
for
![]() $n\in \mathbb {Z}\cap [0,N]$
we have
$n\in \mathbb {Z}\cap [0,N]$
we have
![]() $ \psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
and
$ \psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
and
![]() $ \partial _t^jy_j(t_0;\lambda )=(j+1)!(jA'(t_0)+B(t_0;\lambda ))=a_jb_j(\lambda )$
for all
$ \partial _t^jy_j(t_0;\lambda )=(j+1)!(jA'(t_0)+B(t_0;\lambda ))=a_jb_j(\lambda )$
for all
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
For the case of
![]() $\widehat B(t_0)=0$
, we have
$\widehat B(t_0)=0$
, we have
![]() $jA'(t_0)+B(t_0,\lambda )=jA'(t_0)+\widetilde B(t_0)\neq 0$
(using (B.24)). Let
$jA'(t_0)+B(t_0,\lambda )=jA'(t_0)+\widetilde B(t_0)\neq 0$
(using (B.24)). Let
![]() $a_j=(j+1)!(jA'(t_0)+\widetilde B(t_0))$
,
$a_j=(j+1)!(jA'(t_0)+\widetilde B(t_0))$
,
![]() $b_j(\lambda )=1$
then
$b_j(\lambda )=1$
then
![]() $a_j\neq 0$
,
$a_j\neq 0$
,
![]() $b_j\in \operatorname {Hol}(\mathbb {C})$
,
$b_j\in \operatorname {Hol}(\mathbb {C})$
,
![]() $\partial _t^jy_j(t_0;\lambda )=a_j=a_jb_j $
. As
$\partial _t^jy_j(t_0;\lambda )=a_j=a_jb_j $
. As
![]() $ \psi _{1,n}(\lambda )=1$
for
$ \psi _{1,n}(\lambda )=1$
for
![]() $n\in \mathbb {Z}\cap [0,N]$
we have
$n\in \mathbb {Z}\cap [0,N]$
we have
![]() $\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
for all
$\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
for all
![]() $\lambda \in \mathbb {C}$
.
$\lambda \in \mathbb {C}$
.
Thus, we always have
![]() $a_j\neq 0$
,
$a_j\neq 0$
,
![]() $b_j\in \operatorname {Hol}(\mathbb {C})$
,
$b_j\in \operatorname {Hol}(\mathbb {C})$
,
![]() $\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
,
$\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
,
![]() $ \partial _t^jy_j(t_0;\lambda )=a_jb_j(\lambda )$
.
$ \partial _t^jy_j(t_0;\lambda )=a_jb_j(\lambda )$
.
For
![]() $t\in I, \lambda \in \mathbb {C}$
, let
$t\in I, \lambda \in \mathbb {C}$
, let
![]() $\widetilde g(t;\lambda ):=b_j(\lambda )g(t;\lambda )-\partial _t^jg(t_0;\lambda )\cdot y_j(t;\lambda )/a_j $
then
$\widetilde g(t;\lambda ):=b_j(\lambda )g(t;\lambda )-\partial _t^jg(t_0;\lambda )\cdot y_j(t;\lambda )/a_j $
then
![]() $\widetilde g\in \mathcal H_I(\mathbb {C})$
,Footnote 15 and
$\widetilde g\in \mathcal H_I(\mathbb {C})$
,Footnote 15 and
![]() $\partial _t^j\widetilde g(t_0;\lambda )=0$
. As
$\partial _t^j\widetilde g(t_0;\lambda )=0$
. As
![]() $ \partial _t^ig(t_0;\lambda )=0$
,
$ \partial _t^ig(t_0;\lambda )=0$
,
![]() $\partial _t^iy_j(t_0;\lambda )=0$
for
$\partial _t^iy_j(t_0;\lambda )=0$
for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i<j$
, we have
$0\leq i<j$
, we have
![]() $ \partial _t^i\widetilde g(t_0;\lambda )=0$
, for
$ \partial _t^i\widetilde g(t_0;\lambda )=0$
, for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i<j$
. Thus,
$0\leq i<j$
. Thus,
![]() $ \partial _t^i\widetilde g(t_0;\lambda )=0$
, for
$ \partial _t^i\widetilde g(t_0;\lambda )=0$
, for
![]() $i\in \mathbb {Z}$
,
$i\in \mathbb {Z}$
,
![]() $0\leq i\leq j$
.
$0\leq i\leq j$
.
By the induction assumption (for
![]() $n=j+1$
), there exists
$n=j+1$
), there exists
![]() $\widetilde y(t;\lambda )\in \mathcal H_I(B_R)$
such that
$\widetilde y(t;\lambda )\in \mathcal H_I(B_R)$
such that
For all
![]() $t\in I, \lambda \in B_R$
, let
$t\in I, \lambda \in B_R$
, let
![]() $ y(t;\lambda ):=\widetilde y(t;\lambda )+\psi _{1,j+1}(\lambda )\partial _t^jg(t_0;\lambda )\cdot x_j(t)/a_j$
, then
$ y(t;\lambda ):=\widetilde y(t;\lambda )+\psi _{1,j+1}(\lambda )\partial _t^jg(t_0;\lambda )\cdot x_j(t)/a_j$
, then
![]() $y\in \mathcal H_I(B_R)$
,
$y\in \mathcal H_I(B_R)$
,
![]() $y(t_0;\lambda )=0 $
and
$y(t_0;\lambda )=0 $
and
 $$ \begin{align*} &A(t) y"(t;\lambda)+B(t;\lambda) y'(t;\lambda)+D(t;\lambda) y(t;\lambda)\\&\quad =\psi_{1,j+1}(\lambda)\widetilde g(t;\lambda)+\psi_{1,j+1}(\lambda)\partial_t^jg(t_0;\lambda)\cdot y_j(t;\lambda)/a_j=\psi_{1,j+1}(\lambda)b_j(\lambda)g(t;\lambda)=\psi_{1,j}(\lambda)g(t;\lambda), \end{align*} $$
$$ \begin{align*} &A(t) y"(t;\lambda)+B(t;\lambda) y'(t;\lambda)+D(t;\lambda) y(t;\lambda)\\&\quad =\psi_{1,j+1}(\lambda)\widetilde g(t;\lambda)+\psi_{1,j+1}(\lambda)\partial_t^jg(t_0;\lambda)\cdot y_j(t;\lambda)/a_j=\psi_{1,j+1}(\lambda)b_j(\lambda)g(t;\lambda)=\psi_{1,j}(\lambda)g(t;\lambda), \end{align*} $$
where we have used
![]() $y_j(t;\lambda )=A(t)x_j"(t)+B(t;\lambda )x_j'(t)+D(t;\lambda )x_j(t)$
,
$y_j(t;\lambda )=A(t)x_j"(t)+B(t;\lambda )x_j'(t)+D(t;\lambda )x_j(t)$
,
![]() $\widetilde g(t;\lambda )+\partial _t^jg(t_0;\lambda )\cdot y_j(t;\lambda )/a_j =b_j(\lambda )g(t;\lambda )$
and
$\widetilde g(t;\lambda )+\partial _t^jg(t_0;\lambda )\cdot y_j(t;\lambda )/a_j =b_j(\lambda )g(t;\lambda )$
and
![]() $\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
. Thus,
$\psi _{1,j}(\lambda )=b_j(\lambda )\psi _{1,j+1}(\lambda )$
. Thus,
![]() $y\in \mathcal H_I(B_R)$
solves (B.27) for
$y\in \mathcal H_I(B_R)$
solves (B.27) for
![]() $n=j$
. This completes the proof.
$n=j$
. This completes the proof.
In the end of this appendix, we prove the analytic dependence on parameters of solutions to linear regular ODEs. The following lemma has been used in Step 4 of the proof of Lemma B.3, to show that the extended smooth solution is analytic with respect to the parameter
![]() $\lambda $
.
$\lambda $
.
Lemma B.5. Let
![]() $\Omega \subset \mathbb {C}$
be an open set and
$\Omega \subset \mathbb {C}$
be an open set and
![]() $I\subset \mathbb {R}$
. Let
$I\subset \mathbb {R}$
. Let
![]() $p(t;\lambda ), q(t;\lambda ), f(t;\lambda )\in C^\infty (I\times \Omega ;\mathbb {C})$
be such that
$p(t;\lambda ), q(t;\lambda ), f(t;\lambda )\in C^\infty (I\times \Omega ;\mathbb {C})$
be such that
![]() $p(t;\cdot ), q(t;\cdot ), f(t;\cdot )$
are analytic on
$p(t;\cdot ), q(t;\cdot ), f(t;\cdot )$
are analytic on
![]() $\Omega $
for each
$\Omega $
for each
![]() $t\in I$
. Let
$t\in I$
. Let
![]() $x_0(\lambda ), x_1(\lambda )$
be two analytic functions on
$x_0(\lambda ), x_1(\lambda )$
be two analytic functions on
![]() $\Omega $
and let
$\Omega $
and let
![]() $t_0\in I$
. For each
$t_0\in I$
. For each
![]() $\lambda \in \Omega $
, let
$\lambda \in \Omega $
, let
![]() $x(t;\lambda ) (t\in I)$
be the unique smooth solution to the initial value problem
$x(t;\lambda ) (t\in I)$
be the unique smooth solution to the initial value problem
where the prime
![]() $'$
refers to the derivative with respect to
$'$
refers to the derivative with respect to
![]() $t\in I$
. Then for each
$t\in I$
. Then for each
![]() $t\in I$
, the function
$t\in I$
, the function
![]() $\lambda \in \Omega \mapsto x(t;\lambda )$
is analytic.
$\lambda \in \Omega \mapsto x(t;\lambda )$
is analytic.
Proof. By the standard ODE theory, we know that
![]() $x\in C^\infty (I\times \Omega )$
. For any complex function
$x\in C^\infty (I\times \Omega )$
. For any complex function
![]() $\varphi =\varphi (\lambda ):\mathbb {C}\to \mathbb {C}$
of class
$\varphi =\varphi (\lambda ):\mathbb {C}\to \mathbb {C}$
of class
![]() $C^1$
seen as a function on
$C^1$
seen as a function on
![]() $\mathbb {R}^2$
, we can define the Wirtinger derivatives
$\mathbb {R}^2$
, we can define the Wirtinger derivatives
Now it suffices to show that
![]() $\partial _{\bar \lambda }x(t;\lambda )=0$
for all
$\partial _{\bar \lambda }x(t;\lambda )=0$
for all
![]() $(t, \lambda )\in I\times \Omega $
. Since
$(t, \lambda )\in I\times \Omega $
. Since
![]() $x\in C^\infty (I\times \Omega )$
, the derivative with respect to t and
$x\in C^\infty (I\times \Omega )$
, the derivative with respect to t and
![]() $\partial _{\bar \lambda }$
are commutable. By the analyticity of coefficients and the initial data, we know that
$\partial _{\bar \lambda }$
are commutable. By the analyticity of coefficients and the initial data, we know that
![]() $\partial _{\bar \lambda }x$
satisfies
$\partial _{\bar \lambda }x$
satisfies
By the uniqueness, we have
![]() $\partial _{\bar \lambda }x(t;\lambda )=0$
for all
$\partial _{\bar \lambda }x(t;\lambda )=0$
for all
![]() $(t, \lambda )\in I\times \Omega $
.
$(t, \lambda )\in I\times \Omega $
.
Acknowledgments
We would like to warmly thank the anonymous referee who gave many insightful comments and helpful suggestions that substantially improved the manuscript.
Competing interest
The authors have no competing interests to declare.
Financial support
D. Wei is partially supported by the National Key R&D Program of China under the grant 2021YFA1001500. Z. Zhang is partially supported by NSF of China under Grant 12288101.