Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T02:34:35.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Some dependence results between the spreading speed and the coefficients of the space–time periodic Fisher–KPP equation

Published online by Cambridge University Press:  28 February 2011

GRÉGOIRE NADIN
GRÉGOIRE NADIN*
Affiliation:
CNRS, UMR 7598, Laboratoire Jacques-Louis Lions, F-75005 Paris, France email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

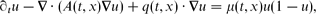We investigate in this paper the dependence relation between the space–time periodic coefficients A, q and μ of the reaction–diffusion equation and the spreading speed of the solutions of the Cauchy problem associated with compactly supported initial data. We prove in particular that (1) taking the spatial or temporal average of μ decreases the minimal speed, (2) if μ is not constant with respect to x, then increasing the amplitude of the diffusion matrix A does not necessarily increase the minimal speed and (3) if A = IN, μ is a constant, then the introduction of a space periodic drift term q = ∇Q decreases the minimal speed. In order to prove these results, we use a variational characterisation of the spreading speed that involves a family of periodic principal eigenvalues associated with the linearisation of the equation near zero. We are thus back to the investigation of the dependence relation between this family of eigenvalues and the coefficients.

Keywords

Eigenvalue optimizationreaction-diffusion equationsspreading propertiesspace-time periodic parabolic equations
Type
Papers
Information
European Journal of Applied Mathematics , Volume 22 , Issue 2 , April 2011 , pp. 169 - 185
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aronson, D. G. & Weinberger, H. F. (1978) Multidimensional nonlinear diffusions arising in population genetics. Adv. Math. 30, 33–76.CrossRefGoogle Scholar
[2]Audoly, B., Berestycki, H. & Pomeau, Y. (2000) Réaction diffusion en écoulement stationnaire rapide. C. R. Acad. Sci., Paris 328, 255–262.Google Scholar
[3]Berestycki, H. & Hamel, F. (2002) Front propagation in periodic excitable media. Commun. Pure Appl. Math. 55, 949–1032.Google Scholar
[4]Berestycki, H., Hamel, F. & Nadin, G. (2008) Asymptotic spreading in heterogeneous diffusive excitable media. J. Funct. Anal. 255 (9), 2146–2189.CrossRefGoogle Scholar
[5]Berestycki, H., Hamel, F. & Nadirashvili, N. (2005a) Elliptic eigenvalue problems with large drift and applications to nonlinear propagation phenomena. Commun. Math. Phys. 253, 451–480.Google Scholar
[6]Berestycki, H., Hamel, F. & Nadirashvili, N. (2005b) The speed of propagation for KPP-type problems. I. Periodic framework. J. Eur. Math. Soc. 7, 173–213.CrossRefGoogle Scholar
[7]Berestycki, H., Hamel, F. & Roques, L. (2005a) Analysis of the periodically fragmented environment model. I. Species persistence. J. Math. Biol. 51, 75–113.CrossRefGoogle ScholarPubMed
[8]Berestycki, H., Hamel, F. & Roques, L. (2005b) Analysis of the periodically fragmented environment model. II. Biological invasions and pulsating travelling fronts. J. Math. Pures Appl. 84, 1101–1146.CrossRefGoogle Scholar
[9]El Smaily, M. (2008) Équations de Réaction-Diffusion dans des Milieux Hétérogènes Non-Bornés, PhD thesis, Section 2.7.Google Scholar
[10]El Smaily, M. & Kirsch, S. (2011) The speed of propagation for KPP reaction-diffusion equations within large drift. Adv. in Diff, Eq. 16 (3–4), 361–400.Google Scholar
[11]Fisher, R. A. (1937) The advance of advantageous genes. Ann. Eugenics 7, 335–369.CrossRefGoogle Scholar
[12]Freidlin, M. (1984) On wave front propagation in periodic media. In: Pinsky, M. (editor), Stochastic Analysis and Applications (Advances in Probability and Related Topics), Vol. 7, Marcel Dekker, New York, NY, pp. 147–166.Google Scholar
[13]Freidlin, M. & Gartner, J. (1979) On the propagation of concentration waves in periodic and random media. Sov. Math. Dokl. 20, 1282–1286.Google Scholar
[14]Hamel, F., Roques, L. & Fayard, J. (2010) Spreading speeds in slowly oscillating environments. Bull. Math. Biol. 72, 1166–1195.CrossRefGoogle ScholarPubMed
[15]Hamel, F., Nadin, G. & Roques, L. (to appear) A viscosity solution method for the spreading speed formula in slowly varying media. Indiana Univ. Math. J.Google Scholar
[16]Heinze, S. (2005) Large convection limits for KPP fronts. (Max Planck Institute for Mathematics, Bonn, Germany) (Preprint No. 21).Google Scholar
[17]Kiselev, A. & Ryzhik, L. (2001) Enhancement of the traveling front speeds in reaction-diffusion equations with advection. Ann. Inst. H. Poincaré Anal. Non Linéaire 18, 309–358.CrossRefGoogle Scholar
[18]Kolmogorov, A. N., Petrovsky, I. G. & Piskunov, N. S. (1937) Etude de l équation de la diffusion avec croissance de la quantité de matière et son application à un problème biologique. Bulletin Université d'Etat à Moscou (Bjul. Moskowskogo Gos. Univ.), pp. 1–26.Google Scholar
[19]Nadin, G. (2009a) The principal eigenvalue of a space-time periodic parabolic operator. Ann. Mat. Pura Appl. 4, 269–295.CrossRefGoogle Scholar
[20]Nadin, G. (2009b) Traveling fronts in space-time periodic media. J. Math. Pures Appl. 92, 232–262.Google Scholar
[21]Nadin, G. (2009c) The effect of the Schwarz rearrangement on the periodic principal eigenvalue of a nonsymmetric operator. SIAM J. Math. Anal. 4, 2388–2406.Google Scholar
[22]Nolen, J., Rudd, M. & Xin, J. (2005) Existence of KPP fronts in spatially-temporally periodic advection and variational principle for propagation speeds. Dyn. PDE 2 (1), 1–24.Google Scholar
[23]Nolen, J. & Xin, J. (2005) Existence of KPP -type fronts in space-time periodic shear flows and a study of minimal speeds based on variational principle. Disc. Cont. Dyn. Syst. 13 (5), 1217–1234.Google Scholar
[24]Nolen, J. & Xin, J. (2009) KPP fronts in 1D random drift. Disc. Cont. Dyn. Syst. B 11 (2), 421–442.Google Scholar
[25]Papanicolaou, G. & Xin, X. (1991) Mathematical biology. J. Stat. Phys. 63, 915–932.CrossRefGoogle Scholar
[26]Ryzhik, L. & Zlatos, A. (2007) KPP pulsating front speed-up by flows. Commun. Math. Sci. 5, 575–593.CrossRefGoogle Scholar
[27]Weinberger, H. (2002) On spreading speed and travelling waves for growth and migration models in a periodic habitat. J. Math. Biol. 45, 511–548.CrossRefGoogle Scholar
[28]Xin, J. (1992) Existence of planar flame fronts in convective-diffusive periodic media. Arch. Ration. Mech. Anal. 121, 205–233.CrossRefGoogle Scholar
[29]Zlatos, A. (2009) Sharp asymptotics for kpp pulsating front speed-up and diffusion enhancement by flows. Arch. Ration. Mech. Anal. 195 (2), 441–453.CrossRefGoogle Scholar
[30]Zlatos, A. Reaction-diffusion front speed enhancement by flows (preprint).Google Scholar