Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T07:20:05.779Z Has data issue: false hasContentIssue false
  • English
  • Français

The large-time asymptotic solution of the mKdV equation

Published online by Cambridge University Press:  04 June 2015

J. A. LEACH  and
ANDREW P. BASSOM
J. A. LEACH
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham, B15 2TT, UK email: [email protected]
ANDREW P. BASSOM
Affiliation:
School of Mathematics & Statistics, The University of Western Australia, Crawley WA 6009, Australia email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, an initial-value problem for the modified Korteweg-de Vries (mKdV) equation is addressed. Previous numerical simulations of the solution of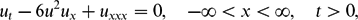

\[ u_{t} - 6u^{2} u_{x}+u_{xxx}=0, \quad -\infty<x<\infty, \quad t>0, \]
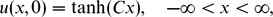where x and t represent dimensionless distance and time respectively, have considered the evolution when the initial data is given by
\[ u(x,0)=\tanh ( Cx ), \quad -\infty<x<\infty, \]
for C constant. These computations suggest that kink and soliton structures develop from this initial profile and here the method of matched asymptotic coordinate expansions is used to obtain the complete large-time structure of the solution in the particular case C = 1/3. The technique is able to confirm some of the numerical predictions, but also forms a basis that could be easily extended to account for other initial conditions and other physically significant equations. Not only can the details of the relevant long-time structure be determined but rates of convergence of the solution of the initial-value problem be predicted.

Keywords

Asymptotic methodslarge time solutionsolitons and kinks
Type
Papers
Information
European Journal of Applied Mathematics , Volume 26 , Issue 6 , December 2015 , pp. 931 - 943
Copyright
Copyright © Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Chanteur, G. & Raadu, M. (1987) Formation of shocklike modified Korteweg-de Vries solitions: Application to double layers. Phys. Fluids 30, 2708–2719.CrossRefGoogle Scholar
[2]Gardner, L. R. T., Gardner, G. A. & Geyikli, T. (1995) Solitary wave solutions of the MKdV− equation. Comput. Methods Appl. Mech. Engrg. 124, 321–333.CrossRefGoogle Scholar
[3]Kamchatnov, A. M., Kuo, Y.-H., Lin, T.-C., Horng, T.-L., Gou, S.-C., Clift, R., El, G. A. & Grimshaw, R. H. J. (2012) Undular bore theory for the Gardner equation. Phys. Rev. E 86, 036605-1-23.Google Scholar
[4]Kotlyarov, V. & Minakov, A. (2010) Riemann-Hilbert problem to the modified Korteveg-de Vries equation: Long-time dynamics of the steplike initial data. J. Math. Phys. 51, 093506-1-31.CrossRefGoogle Scholar
[5]Kruskal, M. D. (1962) Asymptotology in Mathematical Models in Physical Sciences, S. Drobot and P. A. Viebrock (editors), Proceedings of the Conference at the University of Notre Dame, Prentice-Hall, Englewood Cliffs, NJ, 1963, pp. 17–48.Google Scholar
[6]Leach, J. A. & Needham, D. J. (2003) The large-time development of the solution to an initial-value problem for the Korteweg-de Vries equation. I. Initial data has a discontinuous expansive step. Nonlinearity 21, 2391–2408.CrossRefGoogle Scholar
[7]Leach, J. A. & Needham, D. J. (2003) Matched Asymptotic Expansions in Reaction-Diffusion Theory, London, Springer Monographs in Mathematics.Google Scholar
[8]Leach, J. A. & Needham, D. J. (2009) The evolution of travelling wave-fronts in a hyperbolic Fisher model. III. The initial-value problem when the initial data has exponential decay rates. IMA J. Appl. Math. 74, 870–903.CrossRefGoogle Scholar
[9]Marchant, T. R. (2008) Undular bores and the initial-boundary value problem for the modified Korteweg-de Vries equation. Wave Motion 45, 540–555.CrossRefGoogle Scholar