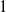1. Introduction
In the Euclidean setting, the Benamou–Brenier [Reference Benamou and Brenier5] formulation of the distance on the space
![]() $\mathscr{P}_2(\mathbb{R}^d)$
known as 2-Wasserstein or Kantorovich–Rubinstein distance is given by the minimisation problem
$\mathscr{P}_2(\mathbb{R}^d)$
known as 2-Wasserstein or Kantorovich–Rubinstein distance is given by the minimisation problem
for every
![]() $\mu _0,\mu _1 \in \mathscr{P}_2(\mathbb{R}^d)$
. The Partial Differential Equation (PDE) constraint is called continuity equation (we write
$\mu _0,\mu _1 \in \mathscr{P}_2(\mathbb{R}^d)$
. The Partial Differential Equation (PDE) constraint is called continuity equation (we write
![]() $(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
when
$(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
when
![]() $(\boldsymbol{\mu },\boldsymbol{\nu })$
is a solution). Over the years, the Benamou–Brenier formula (1.1) has revealed significant connections between the theory of optimal transport and different fields of mathematics, including partial differential equations [Reference Jordan, Kinderlehrer and Otto29], functional inequalities [Reference Otto and Villani35], and the novel notion of Lott–Sturm–Villani’s synthetic Ricci curvature bounds for metric measure spaces [Reference Lott and Villani30, Reference Lott and Villani31, Reference Sturm36, Reference Sturm37]. Inspired by the dynamical formulation (1.1), in independent works, Maas [Reference Maas32] (in the setting of Markov chains) and Mielke [Reference Mielke33] (in the context of reaction-diffusion systems) introduced a notion of optimal transport in discrete settings structured as a dynamical formulation à la Benamou–Brenier as in (1.1). One of the features of this discretisation procedure is the replacement of the continuity equation with a discrete counterpart: when working on a (finite) graph
$(\boldsymbol{\mu },\boldsymbol{\nu })$
is a solution). Over the years, the Benamou–Brenier formula (1.1) has revealed significant connections between the theory of optimal transport and different fields of mathematics, including partial differential equations [Reference Jordan, Kinderlehrer and Otto29], functional inequalities [Reference Otto and Villani35], and the novel notion of Lott–Sturm–Villani’s synthetic Ricci curvature bounds for metric measure spaces [Reference Lott and Villani30, Reference Lott and Villani31, Reference Sturm36, Reference Sturm37]. Inspired by the dynamical formulation (1.1), in independent works, Maas [Reference Maas32] (in the setting of Markov chains) and Mielke [Reference Mielke33] (in the context of reaction-diffusion systems) introduced a notion of optimal transport in discrete settings structured as a dynamical formulation à la Benamou–Brenier as in (1.1). One of the features of this discretisation procedure is the replacement of the continuity equation with a discrete counterpart: when working on a (finite) graph
![]() $(\mathcal{X},\mathcal{E})$
(resp. vertices and edges), the discrete continuity equation reads
$(\mathcal{X},\mathcal{E})$
(resp. vertices and edges), the discrete continuity equation reads
where
![]() $(m_t,J_t)$
corresponds to discrete masses and fluxes (s.t.
$(m_t,J_t)$
corresponds to discrete masses and fluxes (s.t.
![]() $J_t(x,y) = -J_t(y,x)$
). Maas’ proposed distance
$J_t(x,y) = -J_t(y,x)$
). Maas’ proposed distance
![]() $\mathcal{W}$
[Reference Maas32] is obtained by minimising, under the above constraint, a discrete analogue of the Benamou–Brenier action functional with reference measure
$\mathcal{W}$
[Reference Maas32] is obtained by minimising, under the above constraint, a discrete analogue of the Benamou–Brenier action functional with reference measure
![]() $\pi \in \mathscr{P}(\mathcal{X})$
and weight function
$\pi \in \mathscr{P}(\mathcal{X})$
and weight function
![]() $\omega \in \mathbb{R}^{\mathcal{E}}_+$
, of the form
$\omega \in \mathbb{R}^{\mathcal{E}}_+$
, of the form
and where
![]() $\theta _{\log }(a,b) \,:\!=\, \int _0^1 a^s b^{1-s}{\, \mathrm{d}} s$
denotes the
$\theta _{\log }(a,b) \,:\!=\, \int _0^1 a^s b^{1-s}{\, \mathrm{d}} s$
denotes the
![]() $1$
-homogeneous, positive mean called logarithmic mean. With this particular choice of the mean, it was proved [Reference Maas32], [Reference Mielke33] (see also [Reference Chow, Huang, Li and Zhou6]) that the discrete heat flow coincides with the gradient flow of the relative entropy with respect to the discrete distance
$1$
-homogeneous, positive mean called logarithmic mean. With this particular choice of the mean, it was proved [Reference Maas32], [Reference Mielke33] (see also [Reference Chow, Huang, Li and Zhou6]) that the discrete heat flow coincides with the gradient flow of the relative entropy with respect to the discrete distance
![]() $\mathcal{W}$
. In discrete settings, the equivalence between static and dynamical optimal transport breaks down, and the latter stands out in applications to evolution equations, discrete Ricci curvature and functional inequalities [Reference Erbar, Henderson, Menz and Tetali9, Reference Erbar and Maas15, Reference Mielke34, Reference Erbar and Maas16, Reference Erbar, Maas and Tetali11, Reference Fathi and Maas18, Reference Erbar and Fathi14]. Subsequently, several contributions have been devoted to the study of the scaling behaviour of discrete transport problems, in the setting of discrete-to-continuum approximation problems. The first convergence results were obtained in [Reference Gigli and Maas21] for symmetric grids on a
$\mathcal{W}$
. In discrete settings, the equivalence between static and dynamical optimal transport breaks down, and the latter stands out in applications to evolution equations, discrete Ricci curvature and functional inequalities [Reference Erbar, Henderson, Menz and Tetali9, Reference Erbar and Maas15, Reference Mielke34, Reference Erbar and Maas16, Reference Erbar, Maas and Tetali11, Reference Fathi and Maas18, Reference Erbar and Fathi14]. Subsequently, several contributions have been devoted to the study of the scaling behaviour of discrete transport problems, in the setting of discrete-to-continuum approximation problems. The first convergence results were obtained in [Reference Gigli and Maas21] for symmetric grids on a
![]() $d$
-dimensional torus, and by [Reference Trillos20] in a stochastic setting. In both cases, the authors obtained convergence of the discrete distances towards
$d$
-dimensional torus, and by [Reference Trillos20] in a stochastic setting. In both cases, the authors obtained convergence of the discrete distances towards
![]() $\mathbb{W}_2$
in the limit of the discretisation getting finer and finer.
$\mathbb{W}_2$
in the limit of the discretisation getting finer and finer.
Nonetheless, it turned out that the geometry of the graph plays a crucial role in the game. A general result was obtained in [Reference Gladbach, Kopfer and Maas24], where it is proved that the convergence of discrete distances associated with finite-volume partitions with vanishing size to the
![]() $2$
-Wasserstein space is substantially equivalent to an asymptotic isotropy condition on the mesh. The first complete characterisation of limits of transport costs on periodic graphs (Figure 1) in arbitrary dimension for general action functionals (not necessarily quadratic) was established in [Reference Gladbach, Kopfer, Maas and Portinale22, Reference Gladbach, Kopfer, Maas and Portinale23]: in this setting, the limit action functional (more precisely, the energy density) can be explicitly characterised in terms of a cell formula, which is a finite-dimensional constrained minimisation problem depending on the initial graph and the cost function at the discrete level. The action functionals considered in [Reference Gladbach, Kopfer, Maas and Portinale23] are of the form
$2$
-Wasserstein space is substantially equivalent to an asymptotic isotropy condition on the mesh. The first complete characterisation of limits of transport costs on periodic graphs (Figure 1) in arbitrary dimension for general action functionals (not necessarily quadratic) was established in [Reference Gladbach, Kopfer, Maas and Portinale22, Reference Gladbach, Kopfer, Maas and Portinale23]: in this setting, the limit action functional (more precisely, the energy density) can be explicitly characterised in terms of a cell formula, which is a finite-dimensional constrained minimisation problem depending on the initial graph and the cost function at the discrete level. The action functionals considered in [Reference Gladbach, Kopfer, Maas and Portinale23] are of the form
where we used the Lebesgue decomposition
and where the energy density
![]() $f: \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
is some given convex, lower semicontinuous function with at least linear growth, i.e. satisfying
$f: \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
is some given convex, lower semicontinuous function with at least linear growth, i.e. satisfying
whereas
![]() $f^\infty$
denotes its recession function (see (2.2) for the precise definition). The choice
$f^\infty$
denotes its recession function (see (2.2) for the precise definition). The choice
![]() $f(\rho, j) \,:\!=\, |j|^2/\rho$
corresponds to the
$f(\rho, j) \,:\!=\, |j|^2/\rho$
corresponds to the
![]() $\mathbb{W}_2$
distance. At the discrete level, on a locally finite connected graph
$\mathbb{W}_2$
distance. At the discrete level, on a locally finite connected graph
![]() $(\mathcal{X}, \mathcal{E})$
embedded in
$(\mathcal{X}, \mathcal{E})$
embedded in
![]() $\mathbb{R}^d$
, the natural counterpart is represented by action functionals of the form
$\mathbb{R}^d$
, the natural counterpart is represented by action functionals of the form
for a given lower semicontinuous, convex, and local cost function
![]() $F$
, which also has at least linear growth with respect to the second variable (see (2.8) for the precise definition).
$F$
, which also has at least linear growth with respect to the second variable (see (2.8) for the precise definition).
The main result in [Reference Gladbach, Kopfer, Maas and Portinale23] is the
![]() $\Gamma$
-convergence for constrained functionals as in (1.4), after a suitable rescaling of the graph
$\Gamma$
-convergence for constrained functionals as in (1.4), after a suitable rescaling of the graph
![]() $\mathcal{X}_{\varepsilon } \,:\!=\, \varepsilon \mathcal{X}$
,
$\mathcal{X}_{\varepsilon } \,:\!=\, \varepsilon \mathcal{X}$
,
![]() $\mathcal{E}_{\varepsilon } \,:\!=\, \varepsilon \mathcal{E}$
, and of the cost
$\mathcal{E}_{\varepsilon } \,:\!=\, \varepsilon \mathcal{E}$
, and of the cost
![]() $F_{\varepsilon }$
(and associated action
$F_{\varepsilon }$
(and associated action
![]() $\mathcal{A}_{\varepsilon }$
), in the framework of
$\mathcal{A}_{\varepsilon }$
), in the framework of
![]() $\mathbb{Z}^d$
-periodic graphs. In particular, the limit action is of the form (1.2), where the energy density
$\mathbb{Z}^d$
-periodic graphs. In particular, the limit action is of the form (1.2), where the energy density
![]() $f=f_{\mathrm{hom}}$
is given in terms of a cell formula, explicitly reading
$f=f_{\mathrm{hom}}$
is given in terms of a cell formula, explicitly reading
where
![]() ${\mathsf{Rep}}(\rho, j)$
denotes the set of discrete representatives of
${\mathsf{Rep}}(\rho, j)$
denotes the set of discrete representatives of
![]() $\rho$
and
$\rho$
and
![]() $j$
, given by all
$j$
, given by all
![]() $\mathbb{Z}^d$
-periodic functions
$\mathbb{Z}^d$
-periodic functions
![]() $m: \mathcal{X} \to \mathbb{R}_+$
with
$m: \mathcal{X} \to \mathbb{R}_+$
with
and all
![]() $\mathbb{Z}^d$
-periodic anti-symmetric discrete vector fields
$\mathbb{Z}^d$
-periodic anti-symmetric discrete vector fields
![]() $J: \mathcal{E} \to \mathbb{R}$
with zero discrete divergence and with effective flux equal to
$J: \mathcal{E} \to \mathbb{R}$
with zero discrete divergence and with effective flux equal to
![]() $j$
, i.e.,
$j$
, i.e.,
 \begin{align} \mathsf{div}\, J(x) \,:\!=\, \sum _{y \sim x} J(x,y) = 0 \quad \forall x \in \mathcal{X} \quad \text{ and }\quad \mathsf{Eff} (J) \,:\!=\, \frac 12 \sum _{\substack{(x,y) \in \mathcal{E} \\ x \in [0,1)^d} } J(x,y) (y-x) = j . \quad \end{align}
\begin{align} \mathsf{div}\, J(x) \,:\!=\, \sum _{y \sim x} J(x,y) = 0 \quad \forall x \in \mathcal{X} \quad \text{ and }\quad \mathsf{Eff} (J) \,:\!=\, \frac 12 \sum _{\substack{(x,y) \in \mathcal{E} \\ x \in [0,1)^d} } J(x,y) (y-x) = j . \quad \end{align}
The result covers several examples, both for what concerns the geometric properties of the graph (such as isotropic meshes of
![]() $\mathbb T^d$
, or the simple nearest-neighbour interaction on the symmetric grid) as well as the choice of the cost functionals (including discretisation of
$\mathbb T^d$
, or the simple nearest-neighbour interaction on the symmetric grid) as well as the choice of the cost functionals (including discretisation of
![]() $p$
-Wasserstein distances in arbitrary dimension and flow-based models, i.e. when
$p$
-Wasserstein distances in arbitrary dimension and flow-based models, i.e. when
![]() $F$
– or
$F$
– or
![]() $f$
– does not depend on the first variable).
$f$
– does not depend on the first variable).

Figure 1.
Example of
![]() $\mathbb{Z}^d$
-periodic graph embedded in
$\mathbb{Z}^d$
-periodic graph embedded in
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
As a consequence of this
![]() $\Gamma$
-convergence (in time-space) and a compactness result for curves of measures with bounded action [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], one obtains as a corollary [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.10] that, under the stronger assumption of superlinear growth on
$\Gamma$
-convergence (in time-space) and a compactness result for curves of measures with bounded action [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], one obtains as a corollary [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.10] that, under the stronger assumption of superlinear growth on
![]() $F$
, also the corresponding discrete boundary-value problems (i.e. the associated squared distances, in the case of the quadratic Wasserstein problems)
$F$
, also the corresponding discrete boundary-value problems (i.e. the associated squared distances, in the case of the quadratic Wasserstein problems)
![]() $\Gamma$
-converge to the corresponding continuous one, namely
$\Gamma$
-converge to the corresponding continuous one, namely
![]() ${\mathcal{MA}}_{\varepsilon } \stackrel{\Gamma }{\to }{\mathbb{MA}}_{\mathrm{hom}}$
(with respect to the weak topology), where
${\mathcal{MA}}_{\varepsilon } \stackrel{\Gamma }{\to }{\mathbb{MA}}_{\mathrm{hom}}$
(with respect to the weak topology), where
are the minimal discrete and homogenised action functionals, respectively. The superlinear growth condition, at the continuous level, is a reinforcement of the condition (1.3) and assumes the existence of a function
![]() $\theta :[0,\infty ) \to [0,\infty )$
with
$\theta :[0,\infty ) \to [0,\infty )$
with
![]() $\lim _{t \to \infty } \frac{\theta (t)}{t} = \infty$
and a constant
$\lim _{t \to \infty } \frac{\theta (t)}{t} = \infty$
and a constant
![]() $C \in \mathbb{R}$
such that
$C \in \mathbb{R}$
such that
In particular, this forces every
![]() $(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
with finite action to satisfy
$(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
with finite action to satisfy
![]() $\boldsymbol{\nu } \ll \boldsymbol{\mu } + \mathscr{L}^{\,d+1}$
[[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 6.1], and it ensures compactness in
$\boldsymbol{\nu } \ll \boldsymbol{\mu } + \mathscr{L}^{\,d+1}$
[[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 6.1], and it ensures compactness in
![]() $\mathcal{C}_{\mathrm{KR}} \bigl ([0,1];\, \mathcal{M}_+({\mathbb{T}}^d) \bigr )$
[[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], i.e. with respect to the time-uniform convergence in the Kantorovich–Rubinstein norm (recall that the KR norm metrises weak convergence on
$\mathcal{C}_{\mathrm{KR}} \bigl ([0,1];\, \mathcal{M}_+({\mathbb{T}}^d) \bigr )$
[[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], i.e. with respect to the time-uniform convergence in the Kantorovich–Rubinstein norm (recall that the KR norm metrises weak convergence on
![]() $\mathcal{M}_+({\mathbb{T}}^d)$
, see [[Reference Gladbach, Kopfer, Maas and Portinale23], Appendix A]). This compactness property makes the proof of the convergence
$\mathcal{M}_+({\mathbb{T}}^d)$
, see [[Reference Gladbach, Kopfer, Maas and Portinale23], Appendix A]). This compactness property makes the proof of the convergence
![]() ${\mathcal{MA}}_{\varepsilon } \stackrel{\Gamma }{\to }{\mathbb{MA}}_{\mathrm{hom}}$
an easy corollary of the convergence of the time-space energies.
${\mathcal{MA}}_{\varepsilon } \stackrel{\Gamma }{\to }{\mathbb{MA}}_{\mathrm{hom}}$
an easy corollary of the convergence of the time-space energies.
Without the assumption of superlinear growth the situation is much more subtle: in particular, the lower semicontinuity of
![]() $\mathbb{MA}$
obtained minimising the functional
$\mathbb{MA}$
obtained minimising the functional
![]() $\mathbb{A}$
associated to a function
$\mathbb{A}$
associated to a function
![]() $f$
satisfying only (1.3) is not trivial. This is due to the fact that, in this framework, being a solution to
$f$
satisfying only (1.3) is not trivial. This is due to the fact that, in this framework, being a solution to
![]() $\mathsf{CE}$
with bounded action only ensures bounds for
$\mathsf{CE}$
with bounded action only ensures bounds for
![]() $\boldsymbol{\mu } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
, which does not suffice to pass to the limit in the constraint given by the boundary conditions: jumps may occur at
$\boldsymbol{\mu } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
, which does not suffice to pass to the limit in the constraint given by the boundary conditions: jumps may occur at
![]() $t \in \{ 0,1\}$
in the limit. Therefore, when the cost
$t \in \{ 0,1\}$
in the limit. Therefore, when the cost
![]() $F$
grows linearly (linear bounds from both below and above), the scaling behaviour of the discrete boundary-value problems
$F$
grows linearly (linear bounds from both below and above), the scaling behaviour of the discrete boundary-value problems
![]() ${\mathcal{MA}}_{\varepsilon }$
, as well as the lower semicontinuity of
${\mathcal{MA}}_{\varepsilon }$
, as well as the lower semicontinuity of
![]() $\mathbb{MA}$
, cannot be understood with the techniques utilised in [Reference Gladbach, Kopfer, Maas and Portinale23]. The main goal of this work is, thus, to provide discrete-to-continuum results for
$\mathbb{MA}$
, cannot be understood with the techniques utilised in [Reference Gladbach, Kopfer, Maas and Portinale23]. The main goal of this work is, thus, to provide discrete-to-continuum results for
![]() ${\mathcal{MA}}_{\varepsilon }$
for cost functionals with linear growth, as well as for every flow-based type of cost, i.e.
${\mathcal{MA}}_{\varepsilon }$
for cost functionals with linear growth, as well as for every flow-based type of cost, i.e.
![]() $F(m,J) = F(J)$
. With similar arguments, we can also show the lower semicontinuity of
$F(m,J) = F(J)$
. With similar arguments, we can also show the lower semicontinuity of
![]() $\mathbb{MA}$
for a general energy density
$\mathbb{MA}$
for a general energy density
![]() $f$
under the same assumptions, see Section 3.3.
$f$
under the same assumptions, see Section 3.3.
Theorem 1.1 (Main result). Assume that either
![]() $F$
satisfies the linear growth condition, i.e.
$F$
satisfies the linear growth condition, i.e.
 \begin{align*} F(m,J) \leq C \Bigg ( 1 + \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x| \leq R } } |J(x,y)| + \sum _{ \substack{ x\in \mathcal{X}\\ |x| \leq R }} m(x) \Bigg ) \end{align*}
\begin{align*} F(m,J) \leq C \Bigg ( 1 + \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x| \leq R } } |J(x,y)| + \sum _{ \substack{ x\in \mathcal{X}\\ |x| \leq R }} m(x) \Bigg ) \end{align*}
for some constant
![]() $C\lt \infty$
and some
$C\lt \infty$
and some
![]() $R \gt 0$
, or that
$R \gt 0$
, or that
![]() $F$
does not depend on the
$F$
does not depend on the
![]() $m$
-variable (flow-based type). Then, as
$m$
-variable (flow-based type). Then, as
![]() $\varepsilon \to 0$
, the discrete functionals
$\varepsilon \to 0$
, the discrete functionals
![]() ${\mathcal{MA}}_{\varepsilon }$
${\mathcal{MA}}_{\varepsilon }$
![]() $\Gamma$
-converge to the continuous functional
$\Gamma$
-converge to the continuous functional
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
with respect to weak convergence.
${\mathbb{MA}}_{\mathrm{hom}}$
with respect to weak convergence.
The contribution of this paper is twofold. On one side, thanks to our main result, we can now include important examples, such as the
![]() $\mathbb{W}_1$
distance and related approximations, see in particular Section 4 for some explicit computations of the cell formula, including the equivalence between static and dynamical formulations (4.3), as well as some simulations. As typical in this discrete-to-continuum framework, also for
$\mathbb{W}_1$
distance and related approximations, see in particular Section 4 for some explicit computations of the cell formula, including the equivalence between static and dynamical formulations (4.3), as well as some simulations. As typical in this discrete-to-continuum framework, also for
![]() $\mathbb{W}_1$
-type problems, the geometry of the graph plays an important role in the homogenised norm obtained in the limit, giving rise to a whole class of crystalline norms, see Proposition 4.4 as well as Figure 2. On the other hand, this work provides ideas and techniques on how to handle the presence of singularities/jumps in the framework of curves of measures which are only of bounded variation, which is of independent interest.
$\mathbb{W}_1$
-type problems, the geometry of the graph plays an important role in the homogenised norm obtained in the limit, giving rise to a whole class of crystalline norms, see Proposition 4.4 as well as Figure 2. On the other hand, this work provides ideas and techniques on how to handle the presence of singularities/jumps in the framework of curves of measures which are only of bounded variation, which is of independent interest.
Related literature. In their seminal work [Reference Jordan, Kinderlehrer and Otto29], Jordan, Kinderlehrer, and Otto showed that the heat flow in
![]() $\mathbb{R}^d$
can be seen as the gradient flow of the relative entropy with respect to the
$\mathbb{R}^d$
can be seen as the gradient flow of the relative entropy with respect to the
![]() $2$
-Wasserstein distance. In the same spirit, a discrete counterpart was proved in [Reference Maas32] and [Reference Mielke33], independently, for the discrete heat flow and discrete relative entropy on Markov chains. In [Reference Forkert, Maas and Portinale19], the authors proved the evolutionary
$2$
-Wasserstein distance. In the same spirit, a discrete counterpart was proved in [Reference Maas32] and [Reference Mielke33], independently, for the discrete heat flow and discrete relative entropy on Markov chains. In [Reference Forkert, Maas and Portinale19], the authors proved the evolutionary
![]() $\Gamma$
-convergence of the discrete gradient-flow structures associated with finite-volume partitions and discrete Fokker–Planck equations, generalising a previous result obtained in [Reference Disser and Liero8] in the setting of isotropic, one-dimensional meshes. Similar results were later obtained in [Reference Hraivoronska and Tse26], [Reference Hraivoronska, Schlichting and Tse27] for the study of the limiting behaviour of random walks on tessellations in the diffusive limit. Generalised gradient-flow structures associated to jump processes and approximation results of nonlocal- and local-interaction equations have been studied in a series of works [Reference Esposito, Patacchini, Schlichting and Slepcev12], [Reference Esposito, Patacchini and Schlichting13], [Reference Esposito, Heinze, Pietschmann and Schlichting10]. Recently, [Reference Esposito and Mikolás17] considered the more general setting where the graph also depends on time.
$\Gamma$
-convergence of the discrete gradient-flow structures associated with finite-volume partitions and discrete Fokker–Planck equations, generalising a previous result obtained in [Reference Disser and Liero8] in the setting of isotropic, one-dimensional meshes. Similar results were later obtained in [Reference Hraivoronska and Tse26], [Reference Hraivoronska, Schlichting and Tse27] for the study of the limiting behaviour of random walks on tessellations in the diffusive limit. Generalised gradient-flow structures associated to jump processes and approximation results of nonlocal- and local-interaction equations have been studied in a series of works [Reference Esposito, Patacchini, Schlichting and Slepcev12], [Reference Esposito, Patacchini and Schlichting13], [Reference Esposito, Heinze, Pietschmann and Schlichting10]. Recently, [Reference Esposito and Mikolás17] considered the more general setting where the graph also depends on time.
2. General framework: continuous and discrete transport problems
In this section, we first introduce the general class of problems at the continuous level we are interested in, discussing main properties and known results. We then move to the discrete, periodic framework in the spirit of [Reference Gladbach, Kopfer, Maas and Portinale23], summarise the known convergence results and discuss the open problems we want to treat in this work. In contrast with [Reference Gladbach, Kopfer, Maas and Portinale23], for the sake of the exposition we restrict our analysis to the time interval
![]() $\mathcal{I} \,:\!=\, (0,1)$
. Nonetheless, our main results easily extend to a general bounded, open interval
$\mathcal{I} \,:\!=\, (0,1)$
. Nonetheless, our main results easily extend to a general bounded, open interval
![]() $\mathcal{I} \subset \mathbb{R}$
.
$\mathcal{I} \subset \mathbb{R}$
.
2.1. The continuous setting: transport problems on the torus
We start by recalling the definition of solutions to the continuity equation on
![]() $\mathbb{T}^d$
.
$\mathbb{T}^d$
.
Definition 2.1
(Continuity equation). A pair of measures
![]() $(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathcal{M}_+\big ((0,1) \times{\mathbb{T}}^d\big ) \times \mathcal{M}^d\big ((0,1) \times{\mathbb{T}}^d\big )$
is said to be a solution to the continuity equation
$(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathcal{M}_+\big ((0,1) \times{\mathbb{T}}^d\big ) \times \mathcal{M}^d\big ((0,1) \times{\mathbb{T}}^d\big )$
is said to be a solution to the continuity equation
if, for all functions
![]() $\varphi \in \mathcal{C}_c^1\big ((0,1)\times{\mathbb{T}^d}\big )$
, the identity
$\varphi \in \mathcal{C}_c^1\big ((0,1)\times{\mathbb{T}^d}\big )$
, the identity
holds. We use the notation
![]() $(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE}$
.
$(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE}$
.
Throughout the whole paper, we consider energy densities
![]() $f$
with the following properties.
$f$
with the following properties.
Assumption 2.2.
Let
![]() $f : \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
be a lower semicontinuous and convex function, whose domain
$f : \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
be a lower semicontinuous and convex function, whose domain
![]() $\mathsf{D}(f)$
has nonempty interior. We assume that there exist constants
$\mathsf{D}(f)$
has nonempty interior. We assume that there exist constants
![]() $c \gt 0$
and
$c \gt 0$
and
![]() $C \lt \infty$
such that the (at least) linear growth condition
$C \lt \infty$
such that the (at least) linear growth condition
holds for all
![]() $\rho \in \mathbb{R}_+$
and
$\rho \in \mathbb{R}_+$
and
![]() $j \in \mathbb{R}^d$
.
$j \in \mathbb{R}^d$
.
The corresponding recession function
![]() $f^\infty : \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
is defined by
$f^\infty : \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R} \cup \{+\infty \}$
is defined by
for every
![]() $(\rho _0, j_0) \in \mathsf{D}(f)$
. It is well established that the function
$(\rho _0, j_0) \in \mathsf{D}(f)$
. It is well established that the function
![]() $f^\infty$
is lower semicontinuous, convex, and it satisfies the inequality
$f^\infty$
is lower semicontinuous, convex, and it satisfies the inequality
see [Reference Ambrosio, Fusco and Pallara1, Section 2.6].
Let
![]() $\mathscr{L}^{\,d+1}$
denote the Lebesgue measure on
$\mathscr{L}^{\,d+1}$
denote the Lebesgue measure on
![]() $(0,1) \times{\mathbb{T}}^d$
. For
$(0,1) \times{\mathbb{T}}^d$
. For
![]() $\boldsymbol{\mu } \in \mathcal{M}_+\big ( (0,1) \times{\mathbb{T}}^d\big )$
and
$\boldsymbol{\mu } \in \mathcal{M}_+\big ( (0,1) \times{\mathbb{T}}^d\big )$
and
![]() $\boldsymbol{\nu } \in \mathcal{M}^d\big ( (0,1) \times{\mathbb{T}}^d\big )$
, we write their Lebesgue decompositions as
$\boldsymbol{\nu } \in \mathcal{M}^d\big ( (0,1) \times{\mathbb{T}}^d\big )$
, we write their Lebesgue decompositions as
for some
![]() $\rho \in L_+^1\big ( (0,1) \times{\mathbb{T}}^d \big )$
and
$\rho \in L_+^1\big ( (0,1) \times{\mathbb{T}}^d \big )$
and
![]() $j \in L^1\big ( (0,1) \times{\mathbb{T}}^d; \mathbb{R}^d\big )$
. Given these decompositions, there always exists a measure
$j \in L^1\big ( (0,1) \times{\mathbb{T}}^d; \mathbb{R}^d\big )$
. Given these decompositions, there always exists a measure
![]() $\boldsymbol{\sigma } \in \mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}}^d\bigr )$
such that
$\boldsymbol{\sigma } \in \mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}}^d\bigr )$
such that
for some
![]() $\rho ^\perp \in L_+^1(\boldsymbol{\sigma })$
and
$\rho ^\perp \in L_+^1(\boldsymbol{\sigma })$
and
![]() $j^\perp \in L^1(\boldsymbol{\sigma };\mathbb{R}^d)$
(take for example
$j^\perp \in L^1(\boldsymbol{\sigma };\mathbb{R}^d)$
(take for example
![]() $\boldsymbol{\sigma } \,:\!=\, |\boldsymbol{\mu }^\perp | + |\boldsymbol{\nu }^\perp |$
).
$\boldsymbol{\sigma } \,:\!=\, |\boldsymbol{\mu }^\perp | + |\boldsymbol{\nu }^\perp |$
).
Definition 2.3 (Action functionals). We define the action functionals by
 \begin{align*} &{\mathbb{A}} : \mathcal{M}_+\big ( (0,1) \times{\mathbb{T}^d} \big ) \times \mathcal{M}^d\big ( (0,1) \times{\mathbb{T}}^d\big ) \to \mathbb{R} \cup \{ +\infty \}, \\ &{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \,:\!=\, \int _{(0,1) \times{\mathbb{T}^d}} f \big ( \rho, j \big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{ (0,1) \times{\mathbb{T}^d}} f^\infty \big ( \rho ^\perp, j^\perp \big ){\, \mathrm{d}} \boldsymbol{\sigma }, \\ &{\mathbb{A}}(\boldsymbol{\mu }) \,:\!=\, \inf _{\boldsymbol{\nu }} \left \{{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \} . \end{align*}
\begin{align*} &{\mathbb{A}} : \mathcal{M}_+\big ( (0,1) \times{\mathbb{T}^d} \big ) \times \mathcal{M}^d\big ( (0,1) \times{\mathbb{T}}^d\big ) \to \mathbb{R} \cup \{ +\infty \}, \\ &{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \,:\!=\, \int _{(0,1) \times{\mathbb{T}^d}} f \big ( \rho, j \big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{ (0,1) \times{\mathbb{T}^d}} f^\infty \big ( \rho ^\perp, j^\perp \big ){\, \mathrm{d}} \boldsymbol{\sigma }, \\ &{\mathbb{A}}(\boldsymbol{\mu }) \,:\!=\, \inf _{\boldsymbol{\nu }} \left \{{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \} . \end{align*}
Remark 2.4. This definition does not depend on the choice of
![]() $\boldsymbol{\sigma }$
, due to the
$\boldsymbol{\sigma }$
, due to the
![]() $1$
-homogeneity of
$1$
-homogeneity of
![]() $f^\infty$
. As
$f^\infty$
. As
![]() $f(\rho, j) \geq - C(1+\rho )$
and
$f(\rho, j) \geq - C(1+\rho )$
and
![]() $f^\infty (\rho, j) \geq - C \rho$
from (2.1) and (2.3), the fact that
$f^\infty (\rho, j) \geq - C \rho$
from (2.1) and (2.3), the fact that
![]() $\boldsymbol{\mu }\bigl ((0,1) \times{\mathbb{T}^d} \bigr ) \lt \infty$
ensures that
$\boldsymbol{\mu }\bigl ((0,1) \times{\mathbb{T}^d} \bigr ) \lt \infty$
ensures that
![]() ${\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu })$
is well defined in
${\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu })$
is well defined in
![]() $\mathbb{R} \cup \{ + \infty \}$
.
$\mathbb{R} \cup \{ + \infty \}$
.
The natural setting to work in is the space
![]() $\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
of the curves of measures
$\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
of the curves of measures
![]() $\boldsymbol{\mu } : (0,1) \to \mathcal{M}_+({\mathbb{T}^d})$
such that the
$\boldsymbol{\mu } : (0,1) \to \mathcal{M}_+({\mathbb{T}^d})$
such that the
![]() $\mathrm{BV}$
-seminorm
$\mathrm{BV}$
-seminorm
![]() $\| \boldsymbol{\mu } \| = \|\boldsymbol{\mu } \|_{\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )}$
defined by
$\| \boldsymbol{\mu } \| = \|\boldsymbol{\mu } \|_{\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )}$
defined by
is finite. Note that, by the trace theorem in BV, curves of measures in
![]() $\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
have a well-defined trace at
$\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
have a well-defined trace at
![]() $t = 0$
and
$t = 0$
and
![]() $t=1$
. As shown in [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma3.13], any solution
$t=1$
. As shown in [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma3.13], any solution
![]() $(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE}$
can be disintegrated as
$(\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE}$
can be disintegrated as
![]() ${\, \mathrm{d}} \boldsymbol{\mu }(t,x) ={\, \mathrm{d}} \mu _t(x){\, \mathrm{d}} t$
for some measurable curve
${\, \mathrm{d}} \boldsymbol{\mu }(t,x) ={\, \mathrm{d}} \mu _t(x){\, \mathrm{d}} t$
for some measurable curve
![]() $t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}}^d)$
with finite constant mass. If
$t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}}^d)$
with finite constant mass. If
![]() ${\mathbb{A}}(\boldsymbol{\mu }) \lt \infty$
, then this curve belongs to
${\mathbb{A}}(\boldsymbol{\mu }) \lt \infty$
, then this curve belongs to
![]() $\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
and
$\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
and
2.2. Boundary conditions and lower semicontinuity
Define the minimal homogenised action for
![]() $\mu _0,\mu _1\in \mathcal{M}_+({\mathbb{T}^d})$
with
$\mu _0,\mu _1\in \mathcal{M}_+({\mathbb{T}^d})$
with
![]() $\mu _0({\mathbb{T}^d}) = \mu _1({\mathbb{T}^d})$
as
$\mu _0({\mathbb{T}^d}) = \mu _1({\mathbb{T}^d})$
as
Note that, in general,
![]() $\mathbb{MA}$
may be infinite (although the measures have equal masses). Despite the lower semicontinuity property of
$\mathbb{MA}$
may be infinite (although the measures have equal masses). Despite the lower semicontinuity property of
![]() $\mathbb{A}$
(cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 3.14]), the lower semicontinuity of
$\mathbb{A}$
(cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 3.14]), the lower semicontinuity of
![]() $\mathbb{MA}$
with respect to the natural weak topology of
$\mathbb{MA}$
with respect to the natural weak topology of
![]() $\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
is, in general, nontrivial. More precisely, it is a challenging question to prove (or disprove) that for any two sequences
$\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
is, in general, nontrivial. More precisely, it is a challenging question to prove (or disprove) that for any two sequences
![]() $\mu _0^n$
,
$\mu _0^n$
,
![]() $\mu _1^n \in \mathcal{M}_+({\mathbb{T}^d})$
, such that
$\mu _1^n \in \mathcal{M}_+({\mathbb{T}^d})$
, such that
![]() $\mu _i^n \to \mu _i$
weakly in
$\mu _i^n \to \mu _i$
weakly in
![]() $\mathcal{M}_+({\mathbb{T}^d})$
as
$\mathcal{M}_+({\mathbb{T}^d})$
as
![]() $n \to \infty$
for
$n \to \infty$
for
![]() $i=0,1$
, the inequality
$i=0,1$
, the inequality
holds. In this work, we provide a positive answer in the case when
![]() $f$
has linear growth or it is flow-based (i.e. it does not depend on the first variable), see Remark 3.14 and Proposition 3.15 below. First, we discuss the main challenges and the setup where the lower semicontinuity is already known to hold.
$f$
has linear growth or it is flow-based (i.e. it does not depend on the first variable), see Remark 3.14 and Proposition 3.15 below. First, we discuss the main challenges and the setup where the lower semicontinuity is already known to hold.
Remark 2.5
(Lack of compatible compactness). We know from [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 3.14] that
![]() $(\boldsymbol{\mu },\boldsymbol{\nu }) \mapsto{\mathbb{A}}(\boldsymbol{\mu },\boldsymbol{\nu })$
and
$(\boldsymbol{\mu },\boldsymbol{\nu }) \mapsto{\mathbb{A}}(\boldsymbol{\mu },\boldsymbol{\nu })$
and
![]() $\boldsymbol{\mu } \mapsto{\mathbb{A}}(\boldsymbol{\mu })$
are lower semicontinuous w.r.t. the weak topology. Moreover, if
$\boldsymbol{\mu } \mapsto{\mathbb{A}}(\boldsymbol{\mu })$
are lower semicontinuous w.r.t. the weak topology. Moreover, if
![]() $\boldsymbol{\mu }^n$
is a sequence with
$\boldsymbol{\mu }^n$
is a sequence with
then
![]() $\boldsymbol{\mu }^n$
is weakly compact and any limit
$\boldsymbol{\mu }^n$
is weakly compact and any limit
![]() $\boldsymbol{\mu }$
belongs to
$\boldsymbol{\mu }$
belongs to
![]() $\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
. This can be proved as in [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4]. Nonetheless, this property does not ensure the lower semicontinuity of
$\mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
. This can be proved as in [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4]. Nonetheless, this property does not ensure the lower semicontinuity of
![]() $\mathbb{MA}$
because weak convergence does not preserve the boundary conditions (at time
$\mathbb{MA}$
because weak convergence does not preserve the boundary conditions (at time
![]() $t=0$
and
$t=0$
and
![]() $t=1$
). For similar issues in the setting of functionals of
$t=1$
). For similar issues in the setting of functionals of
![]() $\mathbb{R}^d$
-valued curves with bounded variations and their minimisation, see e.g. [Reference Amar and Vitali2].
$\mathbb{R}^d$
-valued curves with bounded variations and their minimisation, see e.g. [Reference Amar and Vitali2].
Remark 2.6
(Superlinear growth). Under the strengthened assumption of superlinear growth on
![]() $f$
(with respect to the momentum variable), it is possible to prove the lower semicontinuity property (2.5), in the same way as in the proof of the discrete-to-continuum
$f$
(with respect to the momentum variable), it is possible to prove the lower semicontinuity property (2.5), in the same way as in the proof of the discrete-to-continuum
![]() $\Gamma$
-convergence of boundary-value problems of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.10]. More precisely, we say that
$\Gamma$
-convergence of boundary-value problems of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.10]. More precisely, we say that
![]() $f$
is of superlinear growth if there exists a function
$f$
is of superlinear growth if there exists a function
![]() $\theta :[0,\infty ) \to [0,\infty )$
with
$\theta :[0,\infty ) \to [0,\infty )$
with
![]() $\lim _{t \to \infty } \frac{\theta (t)}{t} = \infty$
and a constant
$\lim _{t \to \infty } \frac{\theta (t)}{t} = \infty$
and a constant
![]() $C \in \mathbb{R}$
such that
$C \in \mathbb{R}$
such that
Arguing as in [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 5.6], one shows that any function of superlinear growth must satisfy the growth condition given by Assumption 2.2. Moreover, in this case, the recession function satisfies
![]() $f^\infty (0,j)=+\infty$
, for every
$f^\infty (0,j)=+\infty$
, for every
![]() $j \neq 0$
. See [[Reference Gladbach, Kopfer, Maas and Portinale23], Examples 5.7 & 5.8] for some examples belonging to this class. By arguing similarly as in the proof of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], assuming superlinear growth one can show that if
$j \neq 0$
. See [[Reference Gladbach, Kopfer, Maas and Portinale23], Examples 5.7 & 5.8] for some examples belonging to this class. By arguing similarly as in the proof of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.9], assuming superlinear growth one can show that if
![]() $\boldsymbol{\mu }^n$
is a sequence with bounded action
$\boldsymbol{\mu }^n$
is a sequence with bounded action
![]() ${\mathbb{A}}(\boldsymbol{\mu }^n)$
and bounded total mass
${\mathbb{A}}(\boldsymbol{\mu }^n)$
and bounded total mass
![]() $\boldsymbol{\mu }^n \bigl ((0,1) \times{\mathbb{T}}^d \bigr )$
, then, up to a (non-relabelled) subsequence, we have
$\boldsymbol{\mu }^n \bigl ((0,1) \times{\mathbb{T}}^d \bigr )$
, then, up to a (non-relabelled) subsequence, we have
![]() $\boldsymbol{\mu }^n \to \boldsymbol{\mu }$
in
$\boldsymbol{\mu }^n \to \boldsymbol{\mu }$
in
![]() $\mathcal{M}_+((0,1)\times{\mathbb{T}^d})$
and
$\mathcal{M}_+((0,1)\times{\mathbb{T}^d})$
and
![]() $\mu _t^n \to \mu _t$
in
$\mu _t^n \to \mu _t$
in
![]() $\mathrm{KR}$
norm uniformly in
$\mathrm{KR}$
norm uniformly in
![]() $t \in (0,1)$
, with limit curve
$t \in (0,1)$
, with limit curve
![]() $\boldsymbol{\mu } \in W_{\mathrm{KR}}^{1,1}((0,1); \mathcal{M}_+({\mathbb{T}^d}))$
. Using this fact, it is clear that the problem of “jumps” in the limit explained in Remark 2.5 does not occur, and the lower semicontinuity (2.5) directly follows from the lower semicontinuity of
$\boldsymbol{\mu } \in W_{\mathrm{KR}}^{1,1}((0,1); \mathcal{M}_+({\mathbb{T}^d}))$
. Using this fact, it is clear that the problem of “jumps” in the limit explained in Remark 2.5 does not occur, and the lower semicontinuity (2.5) directly follows from the lower semicontinuity of
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
Remark 2.7.
(Nonnegativity) Without loss of generality, we can assume that
![]() $f \geq 0$
. Indeed, thanks to the linear growth assumption 2.2, we can define a new function
$f \geq 0$
. Indeed, thanks to the linear growth assumption 2.2, we can define a new function
which is now nonnegative and with (at least) linear growth. Furthermore, we can compute the recess
![]() $\widetilde f^\infty$
and from the definition we see that
$\widetilde f^\infty$
and from the definition we see that
Denote by
![]() $\widetilde{\mathbb{A}}$
the action functional obtained by replacing
$\widetilde{\mathbb{A}}$
the action functional obtained by replacing
![]() $f$
with
$f$
with
![]() $\widetilde f$
. Thanks to (2.6), (2.7), we have that
$\widetilde f$
. Thanks to (2.6), (2.7), we have that
 \begin{align*} \widetilde{\mathbb{A}}(\boldsymbol{\mu }) \,:\!=\, &\inf _{\boldsymbol{\nu }} \left \{ \widetilde{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \}\\ = &\inf _{\boldsymbol{\nu }} \left \{{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \} + C(\boldsymbol{\mu }\big ( (0,1) \times{\mathbb{T}}^d\big )+1). \end{align*}
\begin{align*} \widetilde{\mathbb{A}}(\boldsymbol{\mu }) \,:\!=\, &\inf _{\boldsymbol{\nu }} \left \{ \widetilde{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \}\\ = &\inf _{\boldsymbol{\nu }} \left \{{\mathbb{A}}(\boldsymbol{\mu }, \boldsymbol{\nu }) \, : \, (\boldsymbol{\mu }, \boldsymbol{\nu }) \in \mathsf{CE} \right \} + C(\boldsymbol{\mu }\big ( (0,1) \times{\mathbb{T}}^d\big )+1). \end{align*}
It follows that the corresponding boundary value problems are given by
Therefore, the (weak) lower semicontinuity for
![]() $\widetilde{\mathbb{MA}}$
is equivalent to that of
$\widetilde{\mathbb{MA}}$
is equivalent to that of
![]() $\mathbb{MA}$
.
$\mathbb{MA}$
.
2.3. The discrete framework: transport problems on periodic graphs
We recall the framework of [Reference Gladbach, Kopfer, Maas and Portinale23]: let
![]() $(\mathcal{X}, \mathcal{E})$
be a locally finite and
$(\mathcal{X}, \mathcal{E})$
be a locally finite and
![]() $\mathbb{Z}^d$
-periodic connected graph of bounded degree. We encode the set of vertices as
$\mathbb{Z}^d$
-periodic connected graph of bounded degree. We encode the set of vertices as
![]() $\mathcal{X} = \mathbb{Z}^d \times{V}$
, where
$\mathcal{X} = \mathbb{Z}^d \times{V}$
, where
![]() $V$
is a finite set, and we use coordinates
$V$
is a finite set, and we use coordinates
![]() $x = (x_{\mathsf{z}}, x_{\mathsf{v}}) \in \mathcal{X}$
. The set of edges
$x = (x_{\mathsf{z}}, x_{\mathsf{v}}) \in \mathcal{X}$
. The set of edges
![]() $\mathcal{E} \subseteq \mathcal{X} \times \mathcal{X}$
is symmetric and
$\mathcal{E} \subseteq \mathcal{X} \times \mathcal{X}$
is symmetric and
![]() $\mathbb{Z}^d$
-periodic, and we use the notation
$\mathbb{Z}^d$
-periodic, and we use the notation
![]() $x \sim y$
whenever
$x \sim y$
whenever
![]() $(x,y) \in \mathcal{E}$
. Let
$(x,y) \in \mathcal{E}$
. Let
![]() $R_0 \,:\!=\, \max _{(x,y) \in \mathcal{E}} | x_{\mathsf{z}} - y_{\mathsf{z}}|_{\infty }$
be the maximal edge length in the supremum norm
$R_0 \,:\!=\, \max _{(x,y) \in \mathcal{E}} | x_{\mathsf{z}} - y_{\mathsf{z}}|_{\infty }$
be the maximal edge length in the supremum norm
![]() $|\cdot |_{\infty }$
on
$|\cdot |_{\infty }$
on
![]() $\mathbb{R}^d$
. We use the notation
$\mathbb{R}^d$
. We use the notation
![]() ${\mathcal{X}^Q} \,:\!=\, \{ x \in \mathcal{X} \, : \, x_{\mathsf{z}} = 0 \}$
and
${\mathcal{X}^Q} \,:\!=\, \{ x \in \mathcal{X} \, : \, x_{\mathsf{z}} = 0 \}$
and
![]() $ \mathcal{E}^Q \,:\!=\, \big \{ (x, y) \in \mathcal{E} \, : \, x_{\mathsf{z}} = 0 \big \}.$
For a discussion concerning abstract and embedded graphs, see [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 2.2].
$ \mathcal{E}^Q \,:\!=\, \big \{ (x, y) \in \mathcal{E} \, : \, x_{\mathsf{z}} = 0 \big \}.$
For a discussion concerning abstract and embedded graphs, see [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 2.2].
In what follows, we denote by
![]() $\mathbb{R}^{\mathcal{X}}_+$
the set of functions
$\mathbb{R}^{\mathcal{X}}_+$
the set of functions
![]() $m \colon \mathcal{X} \to \mathbb{R}_+$
and by
$m \colon \mathcal{X} \to \mathbb{R}_+$
and by
![]() $\mathbb{R}^{\mathcal{E}}_a$
the set of anti-symmetric functions
$\mathbb{R}^{\mathcal{E}}_a$
the set of anti-symmetric functions
![]() $J \colon \mathcal{E} \to \mathbb{R}$
, that is, such that
$J \colon \mathcal{E} \to \mathbb{R}$
, that is, such that
![]() $J(x,y) = -J(y,x)$
. The elements of
$J(x,y) = -J(y,x)$
. The elements of
![]() $\mathbb{R}^{\mathcal{E}}_a$
will often be called (discrete) vector fields.
$\mathbb{R}^{\mathcal{E}}_a$
will often be called (discrete) vector fields.
Assumption 2.8 (Admissible cost function). The function
![]() $F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
is assumed to have the following properties:
$F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
is assumed to have the following properties:
-
(a)
 $F$
is convex and lower semicontinuous.
$F$
is convex and lower semicontinuous.
-
(b)
 $F$
is local, meaning that, for some number
$F$
is local, meaning that, for some number
 $R_1 \lt \infty$
, we have
$R_1 \lt \infty$
, we have
 $F(m,J) = F(m',J')$
whenever
$F(m,J) = F(m',J')$
whenever
 $m, m' \in \mathbb{R}_+^{\mathcal{X}}$
and
$m, m' \in \mathbb{R}_+^{\mathcal{X}}$
and
 $J, J' \in \mathbb{R}_a^{\mathcal{E}}$
agree within a ball of radius
$J, J' \in \mathbb{R}_a^{\mathcal{E}}$
agree within a ball of radius
 $R_1$
, i.e.
$R_1$
, i.e.
 \begin{align*} m(x) & = m'(x) && \text{for all } x \in \mathcal{X} \text{ with } |x_{\mathsf{z}}|_{\infty } \leq R_1, \quad and \\ J(x,y) & = J'(x,y) && \text{for all } (x,y) \in \mathcal{E} \text{ with } |x_{\mathsf{z}}|_{\infty }, |y_{\mathsf{z}}|_{\infty } \leq R_1 . \end{align*}
\begin{align*} m(x) & = m'(x) && \text{for all } x \in \mathcal{X} \text{ with } |x_{\mathsf{z}}|_{\infty } \leq R_1, \quad and \\ J(x,y) & = J'(x,y) && \text{for all } (x,y) \in \mathcal{E} \text{ with } |x_{\mathsf{z}}|_{\infty }, |y_{\mathsf{z}}|_{\infty } \leq R_1 . \end{align*}
-
(c)
 $F$
is of at least linear growth, i.e. there exist
$F$
is of at least linear growth, i.e. there exist
 $c \gt 0$
and
$c \gt 0$
and
 $C \lt \infty$
such that
(2.8)for any
$C \lt \infty$
such that
(2.8)for any \begin{align} F(m,J) \geq c \sum _{ (x, y) \in \mathcal{E}^Q } |J(x,y)| - C \Bigg ( 1 + \sum _{\substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R_{\mathrm{max}} }} m(x) \Bigg ) \end{align}
\begin{align} F(m,J) \geq c \sum _{ (x, y) \in \mathcal{E}^Q } |J(x,y)| - C \Bigg ( 1 + \sum _{\substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R_{\mathrm{max}} }} m(x) \Bigg ) \end{align}
 $m \in \mathbb{R}_+^{\mathcal{X}}$
and
$m \in \mathbb{R}_+^{\mathcal{X}}$
and
 $J \in \mathbb{R}_a^{\mathcal{E}}$
. Here,
$J \in \mathbb{R}_a^{\mathcal{E}}$
. Here,
 $R_{\mathrm{max}} \,:\!=\, \max \{R_0, R_1\}$
.
$R_{\mathrm{max}} \,:\!=\, \max \{R_0, R_1\}$
.
-
(d) There exist a
 $\mathbb{Z}^d$
-periodic function
$\mathbb{Z}^d$
-periodic function
 $m^\circ \in \mathbb{R}_+^{\mathcal{X}}$
and a
$m^\circ \in \mathbb{R}_+^{\mathcal{X}}$
and a
 $\mathbb{Z}^d$
-periodic and divergence-free vector field
$\mathbb{Z}^d$
-periodic and divergence-free vector field
 $J^\circ \in \mathbb{R}_a^{\mathcal{E}}$
such that
$J^\circ \in \mathbb{R}_a^{\mathcal{E}}$
such that
 \begin{align*} ( m^\circ, J^\circ ) \in \mathsf{D}(F)^\circ . \end{align*}
\begin{align*} ( m^\circ, J^\circ ) \in \mathsf{D}(F)^\circ . \end{align*}
Remark 2.9. Important examples that satisfy the growth condition (2.8) are of the form
where
![]() $1 \leq p \lt \infty$
, the constants
$1 \leq p \lt \infty$
, the constants
![]() $q_{xy}, q_{yx} \gt 0$
are fixed parameters defined for
$q_{xy}, q_{yx} \gt 0$
are fixed parameters defined for
![]() $(x,y)\in \mathcal{E}^Q$
, and
$(x,y)\in \mathcal{E}^Q$
, and
![]() $\Lambda$
is a suitable mean. Functions of this type naturally appear in discretisations of Wasserstein gradient-flow structures [Reference Maas32], [Reference Mielke33], [Reference Chow, Huang, Li and Zhou6], see also [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark2.6].
$\Lambda$
is a suitable mean. Functions of this type naturally appear in discretisations of Wasserstein gradient-flow structures [Reference Maas32], [Reference Mielke33], [Reference Chow, Huang, Li and Zhou6], see also [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark2.6].
The rescaled graph. Let
![]() ${\mathbb{T}}_{\varepsilon }^d = (\varepsilon \mathbb{Z} / \mathbb{Z})^d$
be the discrete torus of mesh size
${\mathbb{T}}_{\varepsilon }^d = (\varepsilon \mathbb{Z} / \mathbb{Z})^d$
be the discrete torus of mesh size
![]() $\varepsilon \in 1/\mathbb{N}$
. We denote by
$\varepsilon \in 1/\mathbb{N}$
. We denote by
![]() $[\varepsilon z]$
for
$[\varepsilon z]$
for
![]() $z \in \mathbb{Z}^d$
the corresponding equivalence classes. Equivalently,
$z \in \mathbb{Z}^d$
the corresponding equivalence classes. Equivalently,
![]() ${\mathbb{T}}_{\varepsilon }^d = \varepsilon \mathbb{Z}_{\varepsilon }^d$
where
${\mathbb{T}}_{\varepsilon }^d = \varepsilon \mathbb{Z}_{\varepsilon }^d$
where
![]() $\mathbb{Z}_{\varepsilon }^d = \big (\mathbb{Z} / \tfrac 1\varepsilon \mathbb{Z} \big )^d$
. The rescaled graph
$\mathbb{Z}_{\varepsilon }^d = \big (\mathbb{Z} / \tfrac 1\varepsilon \mathbb{Z} \big )^d$
. The rescaled graph
![]() $(\mathcal{X}_{\varepsilon }, \mathcal{E}_{\varepsilon })$
is defined as
$(\mathcal{X}_{\varepsilon }, \mathcal{E}_{\varepsilon })$
is defined as
where for
![]() $\bar z \in \mathbb{Z}_{\varepsilon }^d$
,
$\bar z \in \mathbb{Z}_{\varepsilon }^d$
,
For
![]() $x = \big ([\varepsilon z], v\big ) \in \mathcal{X}_{\varepsilon }$
, we write
$x = \big ([\varepsilon z], v\big ) \in \mathcal{X}_{\varepsilon }$
, we write
The equivalence relation
![]() $\sim$
on
$\sim$
on
![]() $\mathcal{X}$
is equivalently defined on
$\mathcal{X}$
is equivalently defined on
![]() $\mathcal{X}_{\varepsilon }$
by means of
$\mathcal{X}_{\varepsilon }$
by means of
![]() $\mathcal{E}_{\varepsilon }$
. Hereafter, we always assume that
$\mathcal{E}_{\varepsilon }$
. Hereafter, we always assume that
![]() $\varepsilon R_0 \lt \frac 12$
.
$\varepsilon R_0 \lt \frac 12$
.
The rescaled energies. Let
![]() $F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{ + \infty \}$
be a cost function satisfying Assumption 2.8. For
$F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{ + \infty \}$
be a cost function satisfying Assumption 2.8. For
![]() $\varepsilon \gt 0$
satisfying the conditions above, we can define a corresponding energy functional
$\varepsilon \gt 0$
satisfying the conditions above, we can define a corresponding energy functional
![]() $\mathcal{F}_{\varepsilon }$
in the rescaled periodic setting: following [Reference Gladbach, Kopfer, Maas and Portinale23], for
$\mathcal{F}_{\varepsilon }$
in the rescaled periodic setting: following [Reference Gladbach, Kopfer, Maas and Portinale23], for
![]() $\bar z \in \mathbb{Z}_{\varepsilon }^d$
, each function
$\bar z \in \mathbb{Z}_{\varepsilon }^d$
, each function
![]() $\psi : \mathcal{X}_{\varepsilon } \to \mathbb{R}$
induces a
$\psi : \mathcal{X}_{\varepsilon } \to \mathbb{R}$
induces a
![]() $\frac{1}{\varepsilon }\mathbb{Z}^d$
-periodic function
$\frac{1}{\varepsilon }\mathbb{Z}^d$
-periodic function
Similarly, each function
![]() $J : \mathcal{E}_{\varepsilon } \to \mathbb{R}$
induces a
$J : \mathcal{E}_{\varepsilon } \to \mathbb{R}$
induces a
![]() $\frac{1}{\varepsilon }\mathbb{Z}^d$
-periodic function
$\frac{1}{\varepsilon }\mathbb{Z}^d$
-periodic function
Definition 2.10 (Discrete energy functional). The rescaled energy is defined by
Remark 2.11. As observed in [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 2.8], the value
![]() $\mathcal{F}_{\varepsilon }(m,J)$
is well defined as an element in
$\mathcal{F}_{\varepsilon }(m,J)$
is well defined as an element in
![]() $\mathbb{R} \cup \{ + \infty \}$
. Indeed, the condition (2.8) yields
$\mathbb{R} \cup \{ + \infty \}$
. Indeed, the condition (2.8) yields
 \begin{align*} \mathcal{F}_{\varepsilon }( m, J ) = \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d F\bigg ( \frac{\tau _{\varepsilon }^z m}{\varepsilon ^d}, \frac{\tau _{\varepsilon }^z J}{\varepsilon ^{d-1}} \bigg ) & \geq - C \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \Bigg ( 1 + \sum _{\substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R_{\mathrm{max}} }} \frac{\tau _{\varepsilon }^z m(x)}{\varepsilon ^d} \Bigg ) \\& \geq - C \bigg ( 1 + (2R_{\mathrm{max}} + 1)^d \sum _{x \in \mathcal{X}_{\varepsilon }} m(x) \bigg ) \gt - \infty . \end{align*}
\begin{align*} \mathcal{F}_{\varepsilon }( m, J ) = \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d F\bigg ( \frac{\tau _{\varepsilon }^z m}{\varepsilon ^d}, \frac{\tau _{\varepsilon }^z J}{\varepsilon ^{d-1}} \bigg ) & \geq - C \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \Bigg ( 1 + \sum _{\substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R_{\mathrm{max}} }} \frac{\tau _{\varepsilon }^z m(x)}{\varepsilon ^d} \Bigg ) \\& \geq - C \bigg ( 1 + (2R_{\mathrm{max}} + 1)^d \sum _{x \in \mathcal{X}_{\varepsilon }} m(x) \bigg ) \gt - \infty . \end{align*}
Definition 2.12
(Discrete continuity equation). A pair
![]() $({\boldsymbol{m}}, \boldsymbol{J})$
is said to be a solution to the discrete continuity equation if
$({\boldsymbol{m}}, \boldsymbol{J})$
is said to be a solution to the discrete continuity equation if
![]() ${\boldsymbol{m}} : (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
is continuous,
${\boldsymbol{m}} : (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
is continuous,
![]() $\boldsymbol{J} : (0,1) \to \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
is Borel measurable, and
$\boldsymbol{J} : (0,1) \to \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
is Borel measurable, and
holds for all
![]() $x \in \mathcal{X}_{\varepsilon }$
in the sense of distributions. We use the notation
$x \in \mathcal{X}_{\varepsilon }$
in the sense of distributions. We use the notation
Remark 2.13. We may write (2.9) as
![]() $ \partial _t m_t + \mathsf{div} J_t = 0$
using the discrete divergence operator, given by
$ \partial _t m_t + \mathsf{div} J_t = 0$
using the discrete divergence operator, given by
The proof of the following lemma can be found in [Reference Gladbach, Kopfer, Maas and Portinale23].
Lemma 2.14 (Mass preservation). Let
![]() $({\boldsymbol{m}}, \boldsymbol{J}) \in \mathcal{CE}_{\varepsilon }$
. Then we have
$({\boldsymbol{m}}, \boldsymbol{J}) \in \mathcal{CE}_{\varepsilon }$
. Then we have
![]() $m_s(\mathcal{X}_{\varepsilon }) = m_t(\mathcal{X}_{\varepsilon })$
for all
$m_s(\mathcal{X}_{\varepsilon }) = m_t(\mathcal{X}_{\varepsilon })$
for all
![]() $s, t \in (0,1)$
.
$s, t \in (0,1)$
.
We are now ready to define one of the main objects in this paper.
Definition 2.15
(Discrete action functional). For any continuous function
![]() ${\boldsymbol{m}}: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
such that
${\boldsymbol{m}}: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
such that
![]() $t \mapsto \sum _{x \in \mathcal{X}_{\varepsilon }} m_t(x) \in L^1\bigl ((0,1)\bigr )$
and any Borel measurable function
$t \mapsto \sum _{x \in \mathcal{X}_{\varepsilon }} m_t(x) \in L^1\bigl ((0,1)\bigr )$
and any Borel measurable function
![]() $\boldsymbol{J}: (0,1) \to \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
, we define
$\boldsymbol{J}: (0,1) \to \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
, we define
Furthermore, we set
Arguing as in Remark 2.11, one can show [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark2.13] that
![]() $\mathcal{A}_{\varepsilon }({\boldsymbol{m}}, \boldsymbol{J})$
is well defined as an element in
$\mathcal{A}_{\varepsilon }({\boldsymbol{m}}, \boldsymbol{J})$
is well defined as an element in
![]() $\mathbb{R} \cup \{ + \infty \}$
, as a consequence of the growth condition (2.8).
$\mathbb{R} \cup \{ + \infty \}$
, as a consequence of the growth condition (2.8).
Definition 2.16
(Minimal discrete action functional). For any pair of boundary data
![]() $m_0$
,
$m_0$
,
![]() $m_1 \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
, we define the associated discrete boundary value problem as
$m_1 \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
, we define the associated discrete boundary value problem as
The aim of this work is to study the asymptotic behaviour of the energies
![]() ${\mathcal{MA}}_{\varepsilon }$
as
${\mathcal{MA}}_{\varepsilon }$
as
![]() $\varepsilon \to 0$
under the Assumption 2.8.
$\varepsilon \to 0$
under the Assumption 2.8.
3. Statement and proof of the main result
In this paper, we extend the
![]() $\Gamma$
-convergence result for the functionals
$\Gamma$
-convergence result for the functionals
![]() ${\mathcal{MA}}_{\varepsilon }$
towards
${\mathcal{MA}}_{\varepsilon }$
towards
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
, proved in [Reference Gladbach, Kopfer, Maas and Portinale23] for superlinear cost functionals, to two cases: under the assumption of linear growth (bound both from below and above) and when the function
${\mathbb{MA}}_{\mathrm{hom}}$
, proved in [Reference Gladbach, Kopfer, Maas and Portinale23] for superlinear cost functionals, to two cases: under the assumption of linear growth (bound both from below and above) and when the function
![]() $F$
does not depend on
$F$
does not depend on
![]() $\rho$
.
$\rho$
.
Assumption 3.1 (Linear growth). We say that a function
![]() $F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
has linear growth if it satisfies
$F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
has linear growth if it satisfies
 \begin{align*} F(m,J) \leq C \Bigg ( 1 + \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } |J(x,y)| + \sum _{ \substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R }} m(x) \Bigg ) \end{align*}
\begin{align*} F(m,J) \leq C \Bigg ( 1 + \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } |J(x,y)| + \sum _{ \substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R }} m(x) \Bigg ) \end{align*}
for some constant
![]() $C\lt \infty$
and some
$C\lt \infty$
and some
![]() $R \gt 0$
.
$R \gt 0$
.
Assumption 3.2 (Flow-based). We say that a function
![]() $F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
is of flow-based type if it depends only on the the second variable, i.e. (with a slight abuse of notation)
$F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
is of flow-based type if it depends only on the the second variable, i.e. (with a slight abuse of notation)
![]() $F(m,J) = F(J)$
, for some
$F(m,J) = F(J)$
, for some
![]() $F: \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{ +\infty \}$
.
$F: \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{ +\infty \}$
.
Similarly, we say that
![]() $f:\mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}$
is of flow-based type if it does not depend on the
$f:\mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}$
is of flow-based type if it does not depend on the
![]() $\rho$
variable, i.e.
$\rho$
variable, i.e.
![]() $f(\rho, j) = f(j)$
. In this case, the problem simplifies significantly, and the dynamical variational problem described in (2.4) admits an equivalent, static formulation (see (3.23)).
$f(\rho, j) = f(j)$
. In this case, the problem simplifies significantly, and the dynamical variational problem described in (2.4) admits an equivalent, static formulation (see (3.23)).
Remark 3.3 (Linear growth vs Lipschitz). While working with convex functions, to assume a linear growth condition (from above) is essentially equivalent to require Lipschitz continuity with respect to the second variable.
Lemma 3.4 (Lipschitz continuity). Let
![]() $f: \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}$
be a function, convex in the second variable. Let
$f: \mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}$
be a function, convex in the second variable. Let
![]() $C \gt 0$
. Then the following are equivalent:
$C \gt 0$
. Then the following are equivalent:
-
1. For every
 $\rho \in \mathbb{R}_+$
and
$\rho \in \mathbb{R}_+$
and
 $j \in \mathbb{R}^d$
the inequality
$j \in \mathbb{R}^d$
the inequality
 $f(\rho, j) \le C(1+ \rho + \lvert j\rvert )$
holds.
$f(\rho, j) \le C(1+ \rho + \lvert j\rvert )$
holds.
-
2. For every
 $\rho \in \mathbb{R}_+$
, the function
$\rho \in \mathbb{R}_+$
, the function
 $f(\rho, \cdot ) : \mathbb{R}^d \to \mathbb{R}_+$
is Lipschitz continuous (uniformly in
$f(\rho, \cdot ) : \mathbb{R}^d \to \mathbb{R}_+$
is Lipschitz continuous (uniformly in
 $\rho$
) with constant
$\rho$
) with constant
 $C$
, and the inequality
$C$
, and the inequality
 $f(\rho, 0) \le C(1+ \rho )$
holds.
$f(\rho, 0) \le C(1+ \rho )$
holds.
In the very same spirit, one can show the analogous result at the discrete level.
Lemma 3.5 (Lipschitz continuity II). Let
![]() $F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
be convex in the second variable. Let
$F : \mathbb{R}_+^{\mathcal{X}} \times \mathbb{R}_a^{\mathcal{E}} \to \mathbb{R} \cup \{+\infty \}$
be convex in the second variable. Let
![]() $C,R \gt 0$
. Then the following are equivalent:
$C,R \gt 0$
. Then the following are equivalent:
-
1.
 $F$
is of linear growth, in the sense of Assumption 3.1
, with the same constants
$F$
is of linear growth, in the sense of Assumption 3.1
, with the same constants
 $C$
and
$C$
and
 $R$
.
$R$
. -
2. For every
 $m \in \mathbb{R}_+^{\mathcal{X}}$
, we have that
as well as that
$m \in \mathbb{R}_+^{\mathcal{X}}$
, we have that
as well as that \begin{align*} F(m,0) \leq C \bigg ( 1 + \sum _{ \substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R }} m(x) \bigg ), \end{align*}
\begin{align*} F(m,0) \leq C \bigg ( 1 + \sum _{ \substack{ x\in \mathcal{X}\\ |x_{\mathsf{z}}|_{\infty } \leq R }} m(x) \bigg ), \end{align*}
 $F$
is Lipschitz continuous with constant
$F$
is Lipschitz continuous with constant
 $C$
in the second variable, in the sense that
(3.1)for every
$C$
in the second variable, in the sense that
(3.1)for every \begin{align} \left | F(m,J_1) - F(m,J_2) \right | \leq C \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } |J_1(x,y)- J_2(x,y)|, \end{align}
\begin{align} \left | F(m,J_1) - F(m,J_2) \right | \leq C \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } |J_1(x,y)- J_2(x,y)|, \end{align}
 $J_1, J_2 \in \mathbb{R}_a^{\mathcal{E}}$
.
$J_1, J_2 \in \mathbb{R}_a^{\mathcal{E}}$
.
Proof of Lemma
3.4. Let us assume the first condition and fix
![]() $\rho \in \mathbb{R}_+$
as well as
$\rho \in \mathbb{R}_+$
as well as
![]() $j_1,j_2 \in \mathbb{R}^d$
. It follows from the convexity in the second variable that the function
$j_1,j_2 \in \mathbb{R}^d$
. It follows from the convexity in the second variable that the function
is convex. In particular, the inequalities
hold for every
![]() $t \ge 1$
. Letting
$t \ge 1$
. Letting
![]() $t \to \infty$
, we thus find
$t \to \infty$
, we thus find
and, by arbitrariness of the arguments, the claimed Lipschitz continuity. The fact that
![]() $f(\rho, 0) \le C(1+ \rho )$
trivially follows from the first condition.
$f(\rho, 0) \le C(1+ \rho )$
trivially follows from the first condition.
Conversely, if the second condition holds, we necessarily have
for every
![]() $\rho \in \mathbb{R}_+$
and
$\rho \in \mathbb{R}_+$
and
![]() $j \in \mathbb{R}^d$
, which is precisely the first condition in the statement.
$j \in \mathbb{R}^d$
, which is precisely the first condition in the statement.
Let us recall the homogenised energy density
![]() $f_{\mathrm{hom}}$
, which describes the limit energy and is given by a cell formula. For given
$f_{\mathrm{hom}}$
, which describes the limit energy and is given by a cell formula. For given
![]() $\rho \geq 0$
and
$\rho \geq 0$
and
![]() $j \in \mathbb{R}^d$
,
$j \in \mathbb{R}^d$
,
![]() $f_{\mathrm{hom}}(\rho, j)$
is obtained by minimising over the unit cube the cost among functions
$f_{\mathrm{hom}}(\rho, j)$
is obtained by minimising over the unit cube the cost among functions
![]() $m$
and vector fields
$m$
and vector fields
![]() $J$
representing
$J$
representing
![]() $\rho$
and
$\rho$
and
![]() $j$
. More precisely, the function
$j$
. More precisely, the function
![]() $f_{\mathrm{hom}}:\mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}_+$
is given by
$f_{\mathrm{hom}}:\mathbb{R}_+ \times \mathbb{R}^d \to \mathbb{R}_+$
is given by
where the set of representatives
![]() ${\mathsf{Rep}}(\rho, j)$
consists of all
${\mathsf{Rep}}(\rho, j)$
consists of all
![]() $\mathbb{Z}^d$
-periodic functions
$\mathbb{Z}^d$
-periodic functions
![]() $m: \mathcal{X} \to \mathbb{R}_+$
and all
$m: \mathcal{X} \to \mathbb{R}_+$
and all
![]() $\mathbb{Z}^d$
-periodic anti-symmetric discrete vector fields
$\mathbb{Z}^d$
-periodic anti-symmetric discrete vector fields
![]() $J : \mathcal{E} \to \mathbb{R}$
satisfying
$J : \mathcal{E} \to \mathbb{R}$
satisfying
The set of representatives is nonempty for every choice of
![]() $\rho$
and
$\rho$
and
![]() $j$
by [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.5 (iv)]. In the case of embedded graphs, the definition of effective flux coincides with the one provided in the introduction (cfr. (3.2)), see [[Reference Gladbach, Kopfer, Maas and Portinale23], Proposition 9.1].
$j$
by [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.5 (iv)]. In the case of embedded graphs, the definition of effective flux coincides with the one provided in the introduction (cfr. (3.2)), see [[Reference Gladbach, Kopfer, Maas and Portinale23], Proposition 9.1].
Remark 3.6. It is not hard to show that if
![]() $F$
is of linear growth, then
$F$
is of linear growth, then
![]() $f_{\mathrm{hom}}$
is also of linear growth (and therefore, in view of Lemma 3.4, it is Lipschitz in the second variable uniformly w.r.t. the first one), see e.g. [Reference Gladbach, Maas and Portinale25].
$f_{\mathrm{hom}}$
is also of linear growth (and therefore, in view of Lemma 3.4, it is Lipschitz in the second variable uniformly w.r.t. the first one), see e.g. [Reference Gladbach, Maas and Portinale25].
We denote by
![]() ${\mathbb{A}}_{\mathrm{hom}}$
and
${\mathbb{A}}_{\mathrm{hom}}$
and
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
the action functionals corresponding to the choice
${\mathbb{MA}}_{\mathrm{hom}}$
the action functionals corresponding to the choice
![]() $f=f_{\mathrm{hom}}$
. In order to talk about
$f=f_{\mathrm{hom}}$
. In order to talk about
![]() $\Gamma$
-convergence, we need to specificy which type of discrete-to-continuum topology/convergence we adopt (in the same spirit of [Reference Gladbach, Kopfer, Maas and Portinale23]).
$\Gamma$
-convergence, we need to specificy which type of discrete-to-continuum topology/convergence we adopt (in the same spirit of [Reference Gladbach, Kopfer, Maas and Portinale23]).
Definition 3.7
(Embedding). For
![]() $\varepsilon \gt 0$
and
$\varepsilon \gt 0$
and
![]() $z \in \mathbb{R}^d$
, let
$z \in \mathbb{R}^d$
, let
![]() $Q_{\varepsilon }^z \,:\!=\, \varepsilon z + [0, \varepsilon )^d \subseteq{\mathbb{T}}^d$
denote the projection of the cube with side length
$Q_{\varepsilon }^z \,:\!=\, \varepsilon z + [0, \varepsilon )^d \subseteq{\mathbb{T}}^d$
denote the projection of the cube with side length
![]() $\varepsilon$
based at
$\varepsilon$
based at
![]() $\varepsilon z$
to the quotient
$\varepsilon z$
to the quotient
![]() ${\mathbb{T}}^d = \mathbb{R}^d/\mathbb{Z}^d$
. For
${\mathbb{T}}^d = \mathbb{R}^d/\mathbb{Z}^d$
. For
![]() $m \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
and
$m \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
and
![]() $J \in \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
, we define
$J \in \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
, we define
![]() $\iota _{\varepsilon } m \in \mathcal{M}_+({\mathbb{T}^d})$
and
$\iota _{\varepsilon } m \in \mathcal{M}_+({\mathbb{T}^d})$
and
![]() $\iota _{\varepsilon } J \in \mathcal{M}^d({\mathbb{T}}^d)$
by
$\iota _{\varepsilon } J \in \mathcal{M}^d({\mathbb{T}}^d)$
by
With a slight abuse of notation, given
![]() ${\boldsymbol{m}}: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
we also write
${\boldsymbol{m}}: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
we also write
![]() $\iota _{\varepsilon }{\boldsymbol{m}} \in \mathcal{M}_+\bigl ((0,1) \times{\mathbb{T}^d} \bigr )$
for the continuous space-time measure with time disintegration given by
$\iota _{\varepsilon }{\boldsymbol{m}} \in \mathcal{M}_+\bigl ((0,1) \times{\mathbb{T}^d} \bigr )$
for the continuous space-time measure with time disintegration given by
![]() $t \mapsto \iota _{\varepsilon } m_t$
. Moreover, for a given sequence of nonnegative discrete measures
$t \mapsto \iota _{\varepsilon } m_t$
. Moreover, for a given sequence of nonnegative discrete measures
![]() $m^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
, we write
$m^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
, we write
Similarly, for
![]() ${\boldsymbol{m}}^{\varepsilon }: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
we write
${\boldsymbol{m}}^{\varepsilon }: (0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
we write
![]() ${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu } \in \mathcal{M}_+\bigl ((0,1) \times{\mathbb{T}^d} \bigr )$
with an analogous meaning. Similar notation is used for (Borel, possibly discontinuous) curves of fluxes
${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu } \in \mathcal{M}_+\bigl ((0,1) \times{\mathbb{T}^d} \bigr )$
with an analogous meaning. Similar notation is used for (Borel, possibly discontinuous) curves of fluxes
![]() $\boldsymbol{J} : (0,1) \to \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
and convergent sequences of (curves of) fluxes.
$\boldsymbol{J} : (0,1) \to \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
and convergent sequences of (curves of) fluxes.
Remark 3.8
(Preservation of the continuity equation). The definition of this embedding for masses and fluxes ensures that solutions to the discrete continuity equation are mapped to solutions of
![]() $\mathsf{CE}$
, cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.9].
$\mathsf{CE}$
, cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.9].
We are ready to state our main result.
Theorem 3.9 (Main result). Let
![]() $(\mathcal{X},\mathcal{E},F)$
be as described in Section
2.2
and Assumption 2.8
. Assume that
$(\mathcal{X},\mathcal{E},F)$
be as described in Section
2.2
and Assumption 2.8
. Assume that
![]() $F$
is either of flow-based type (Assumption 3.2) or with linear growth (Assumption 3.1). Then, in either case, the functionals
$F$
is either of flow-based type (Assumption 3.2) or with linear growth (Assumption 3.1). Then, in either case, the functionals
![]() ${\mathcal{MA}}_{\varepsilon }$
${\mathcal{MA}}_{\varepsilon }$
![]() $\Gamma$
-convergence to
$\Gamma$
-convergence to
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
as
${\mathbb{MA}}_{\mathrm{hom}}$
as
![]() $\varepsilon \rightarrow 0$
with respect to the weak topology of
$\varepsilon \rightarrow 0$
with respect to the weak topology of
![]() $\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
. More precisely, we have
$\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
. More precisely, we have
-
(1) Liminf inequality : For any sequences
 $m_0^{\varepsilon },m_1^{\varepsilon } \in \mathcal{M}_+(\mathcal{X}_{\varepsilon })$
such that
$m_0^{\varepsilon },m_1^{\varepsilon } \in \mathcal{M}_+(\mathcal{X}_{\varepsilon })$
such that
 $m_i^{\varepsilon } \to \mu _i$
weakly in
$m_i^{\varepsilon } \to \mu _i$
weakly in
 $\mathcal{M}_+({\mathbb{T}^d})$
for
$\mathcal{M}_+({\mathbb{T}^d})$
for
 $i=\,0,1$
, we have that
$i=\,0,1$
, we have that
 \begin{align*} \liminf _{\varepsilon \rightarrow 0}{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon }) \geq{\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) . \end{align*}
\begin{align*} \liminf _{\varepsilon \rightarrow 0}{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon }) \geq{\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) . \end{align*}
-
(2) Limsup inequality : For any
 $\mu _0,\mu _1 \in \mathcal{M}_+({\mathbb{T}}^d)$
, there exist sequences
$\mu _0,\mu _1 \in \mathcal{M}_+({\mathbb{T}}^d)$
, there exist sequences
 $m_0^{\varepsilon }, m_1^{\varepsilon } \in \mathcal{M}_+(\mathcal{X}_{\varepsilon })$
such that
$m_0^{\varepsilon }, m_1^{\varepsilon } \in \mathcal{M}_+(\mathcal{X}_{\varepsilon })$
such that
 $m_i^{\varepsilon } \to \mu _i$
weakly in
$m_i^{\varepsilon } \to \mu _i$
weakly in
 $\mathcal{M}_+({\mathbb{T}^d})$
for
$\mathcal{M}_+({\mathbb{T}^d})$
for
 $i=0,1$
, and
$i=0,1$
, and
 \begin{align*} \limsup _{\varepsilon \rightarrow 0}{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon }, m_1^{\varepsilon }) \leq{\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) . \end{align*}
\begin{align*} \limsup _{\varepsilon \rightarrow 0}{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon }, m_1^{\varepsilon }) \leq{\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) . \end{align*}
Remark 3.10 (Convergence of the actions and superlinear regime). The
![]() $\Gamma$
-convergence of the energies
$\Gamma$
-convergence of the energies
![]() $\mathcal{A}_{\varepsilon }$
towards
$\mathcal{A}_{\varepsilon }$
towards
![]() ${\mathbb{A}}_{\mathrm{hom}}$
under Assumption 2.8 is the main result of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.1]. Related to it, similarly as discussed in Remark 2.6
, the superlinear case [[Reference Gladbach, Kopfer, Maas and Portinale23], Assumption 5.5], not included in the statement, has already been proved in [Reference Gladbach, Kopfer, Maas and Portinale23], and it follows directly from the aforementioned convergence
${\mathbb{A}}_{\mathrm{hom}}$
under Assumption 2.8 is the main result of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.1]. Related to it, similarly as discussed in Remark 2.6
, the superlinear case [[Reference Gladbach, Kopfer, Maas and Portinale23], Assumption 5.5], not included in the statement, has already been proved in [Reference Gladbach, Kopfer, Maas and Portinale23], and it follows directly from the aforementioned convergence
![]() $\mathcal{A}_{\varepsilon } \xrightarrow{\Gamma }{\mathbb{A}}_{\mathrm{hom}}$
and a strong compactness result which holds in such a framework, see in particular [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorems 5.9 & 5.10]. Without the superlinear growth assumption, the proof is much more involved and requires extra work and new ideas, which are the main contribution of this paper.
$\mathcal{A}_{\varepsilon } \xrightarrow{\Gamma }{\mathbb{A}}_{\mathrm{hom}}$
and a strong compactness result which holds in such a framework, see in particular [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorems 5.9 & 5.10]. Without the superlinear growth assumption, the proof is much more involved and requires extra work and new ideas, which are the main contribution of this paper.
Remark 3.11 (Compactness under linear growth from below). Just assuming Assumption 2.8
, the following compactness result for sequences of bounded action was proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4]: if
![]() ${\boldsymbol{m}}^{\varepsilon }:(0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
is such that
${\boldsymbol{m}}^{\varepsilon }:(0,1) \to \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
is such that
then there exists a curve
![]() $\boldsymbol{\mu }= \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
such that, up to a (non-relabelled) subsequence, we have
$\boldsymbol{\mu }= \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
such that, up to a (non-relabelled) subsequence, we have
for a.e.
![]() $t \in (0,1)$
. This is going to be an important tool in the proof of our main result.
$t \in (0,1)$
. This is going to be an important tool in the proof of our main result.
3.1. Proof of the limsup inequality
In this section, we prove the limsup inequality in Theorem3.9. This proof does not require Assumption 3.1 or Assumption 3.2, but rather a weaker hypothesis, which is satisfied under either of the two assumptions.
Proposition 3.12 (
![]() $\Gamma$
-limsup). Let
$\Gamma$
-limsup). Let
![]() $\mu _0, \mu _1$
be nonnegative measures on
$\mu _0, \mu _1$
be nonnegative measures on
![]() ${\mathbb{T}}^d$
. Assume that there exists a
${\mathbb{T}}^d$
. Assume that there exists a
![]() $\mathbb{Z}^d$
-periodic and divergence-free vector field
$\mathbb{Z}^d$
-periodic and divergence-free vector field
![]() $\bar J \in \mathbb{R}_a^{\mathcal{X}}$
such that
$\bar J \in \mathbb{R}_a^{\mathcal{X}}$
such that
 \begin{align} F(m,\bar J) \le C \Biggl (1 + \sum _{\substack{x \in \mathcal X \\ \lvert x\rvert _{\infty } \le R}} m(x)\Biggr ), \qquad m \in \mathbb{R}^{\mathcal{X}}_+, \end{align}
\begin{align} F(m,\bar J) \le C \Biggl (1 + \sum _{\substack{x \in \mathcal X \\ \lvert x\rvert _{\infty } \le R}} m(x)\Biggr ), \qquad m \in \mathbb{R}^{\mathcal{X}}_+, \end{align}
for some finite constants
![]() $C$
and
$C$
and
![]() $R$
. Then there exist two sequences
$R$
. Then there exist two sequences
![]() $(m_0^{\varepsilon })_{\varepsilon \gt 0}$
and
$(m_0^{\varepsilon })_{\varepsilon \gt 0}$
and
![]() $(m_1^{\varepsilon })_{\varepsilon \gt 0}$
in
$(m_1^{\varepsilon })_{\varepsilon \gt 0}$
in
![]() $\mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
such that
$\mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
such that
![]() $m_i^{\varepsilon } \to \mu _i$
weakly in
$m_i^{\varepsilon } \to \mu _i$
weakly in
![]() $\mathcal{M}_+({\mathbb{T}}^d)$
for
$\mathcal{M}_+({\mathbb{T}}^d)$
for
![]() $i=0,1$
and
$i=0,1$
and
Proof. We may and will assume that
![]() ${\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) \lt \infty$
. We also claim that it suffices to prove the statement with
${\mathbb{MA}}_{\mathrm{hom}}(\mu _0,\mu _1) \lt \infty$
. We also claim that it suffices to prove the statement with
![]() ${\mathbb{MA}}(\mu _0,\mu _1)+1/k$
in place of the right-hand side of (3.4) for every
${\mathbb{MA}}(\mu _0,\mu _1)+1/k$
in place of the right-hand side of (3.4) for every
![]() $k \in \mathbb{N}_1$
. Indeed, assume that we know of the existence of sequences
$k \in \mathbb{N}_1$
. Indeed, assume that we know of the existence of sequences
![]() $(m_i^{\varepsilon, k})_{\varepsilon }$
such that
$(m_i^{\varepsilon, k})_{\varepsilon }$
such that
![]() $m_i^{\varepsilon, k} \to \mu _i$
and
$m_i^{\varepsilon, k} \to \mu _i$
and
for every
![]() $k \in \mathbb{N}_1$
. Since
$k \in \mathbb{N}_1$
. Since
![]() ${\mathbb{T}}^d$
is compact, the weak convergence is equivalent to convergence in the Kantorovich–Rubinstein norm. Hence, for every
${\mathbb{T}}^d$
is compact, the weak convergence is equivalent to convergence in the Kantorovich–Rubinstein norm. Hence, for every
![]() $k$
, we can find
$k$
, we can find
![]() $\varepsilon _k$
such that when
$\varepsilon _k$
such that when
![]() $\varepsilon \le \varepsilon _k$
,
$\varepsilon \le \varepsilon _k$
,
We can also assume that
![]() $\varepsilon _{k+1} \le \frac{\varepsilon _k}{2}$
, for every
$\varepsilon _{k+1} \le \frac{\varepsilon _k}{2}$
, for every
![]() $k$
. It now suffices to set
$k$
. It now suffices to set
for every
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $i=0,1$
to get
$i=0,1$
to get
as well as
The claim is proved, since
![]() $k_{\varepsilon } \to _{\varepsilon } \infty$
, as can be readily verified.
$k_{\varepsilon } \to _{\varepsilon } \infty$
, as can be readily verified.
Thus, let us now choose
![]() $k$
and keep it fixed. By definition of
$k$
and keep it fixed. By definition of
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
, there exists
${\mathbb{MA}}_{\mathrm{hom}}$
, there exists
![]() $\boldsymbol{\mu } = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
with
$\boldsymbol{\mu } = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
with
![]() $\boldsymbol{\mu }_{t=0} = \mu _0, \boldsymbol{\mu }_{t=1} = \mu _1$
and such that
$\boldsymbol{\mu }_{t=0} = \mu _0, \boldsymbol{\mu }_{t=1} = \mu _1$
and such that
Recall from Remark 3.10 that
![]() $\mathcal{A}_{\varepsilon } \xrightarrow{\Gamma }{\mathbb{A}}_{\mathrm{hom}}$
; in particular, there exists a recovery sequence
$\mathcal{A}_{\varepsilon } \xrightarrow{\Gamma }{\mathbb{A}}_{\mathrm{hom}}$
; in particular, there exists a recovery sequence
![]() $({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
such that
$({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
such that
![]() ${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly and
${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly and
We shall prove that
![]() $\|{\iota _{\varepsilon } m_t^{\varepsilon } - \mu _t}\|_{\mathrm{KR}({\mathbb{T}}^d)} \to 0$
in (
$\|{\iota _{\varepsilon } m_t^{\varepsilon } - \mu _t}\|_{\mathrm{KR}({\mathbb{T}}^d)} \to 0$
in (
![]() $\mathscr{L}^1$
-)measure or, equivalently, that
$\mathscr{L}^1$
-)measure or, equivalently, that
In order to do this, assume by contradiction that there exists a subsequence such that
for some
![]() $\delta \gt 0$
. Up to possibly extracting a further subsequence, it can be easily checked that the hypotheses of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4] are satisfied (cfr. Remark 3.11); hence, there exists a further (not relabelled) subsequence such that, for almost every
$\delta \gt 0$
. Up to possibly extracting a further subsequence, it can be easily checked that the hypotheses of [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4] are satisfied (cfr. Remark 3.11); hence, there exists a further (not relabelled) subsequence such that, for almost every
![]() $t \in (0,1)$
,
$t \in (0,1)$
,
![]() $m_t^{\varepsilon _n} \to \mu _t$
weakly and thus
$m_t^{\varepsilon _n} \to \mu _t$
weakly and thus
![]() $\|{\iota _{\varepsilon _n}m_t^{\varepsilon _n} - \mu _t}\|_{\mathrm{KR}({\mathbb{T}}^d)} \to 0$
. The dominated convergence theorem yields an absurd.
$\|{\iota _{\varepsilon _n}m_t^{\varepsilon _n} - \mu _t}\|_{\mathrm{KR}({\mathbb{T}}^d)} \to 0$
. The dominated convergence theorem yields an absurd.
From (3.5) we deduce that for every
![]() $T \in (0,1/2)$
there exists a sequence of times
$T \in (0,1/2)$
there exists a sequence of times
![]() $(a_{\varepsilon }^T)_{\varepsilon } \subseteq (0,T)$
such that
$(a_{\varepsilon }^T)_{\varepsilon } \subseteq (0,T)$
such that
With a diagonal argument, we find a sequence
![]() $(a_{\varepsilon })_{\varepsilon } \subseteq (0,1/2)$
such that
$(a_{\varepsilon })_{\varepsilon } \subseteq (0,1/2)$
such that
Similarly, we can find another sequence
![]() $(b_{\varepsilon })_{\varepsilon } \subseteq (1/2,1)$
such that
$(b_{\varepsilon })_{\varepsilon } \subseteq (1/2,1)$
such that
We claim the sought recovery sequences is provided by
![]() $m_0^{\varepsilon } \,:\!=\, m^{\varepsilon }_{a_{\varepsilon }}$
and
$m_0^{\varepsilon } \,:\!=\, m^{\varepsilon }_{a_{\varepsilon }}$
and
![]() $m_1^{\varepsilon } \,:\!=\, m_{b_{\varepsilon }}^{\varepsilon }$
. In order to show this, let us define
$m_1^{\varepsilon } \,:\!=\, m_{b_{\varepsilon }}^{\varepsilon }$
. In order to show this, let us define
![]() $\widehat J^{\varepsilon } : \mathcal{E}_{\varepsilon } \to \mathbb{R}$
via the formulaFootnote
1
(recall the assumption (3.3))
$\widehat J^{\varepsilon } : \mathcal{E}_{\varepsilon } \to \mathbb{R}$
via the formulaFootnote
1
(recall the assumption (3.3))
so that
![]() $\widehat J^{\varepsilon }$
is divergence-free. Now define
$\widehat J^{\varepsilon }$
is divergence-free. Now define
 \begin{align*} \widetilde m^{\varepsilon }_t \,:\!=\, \begin{cases} m^{\varepsilon }_{a_{\varepsilon }} &\text{if } t \in [0,a_{\varepsilon }) \\ m^{\varepsilon }_t &\text{if } t \in [a_{\varepsilon },b_{\varepsilon }] \\ m^{\varepsilon }_{b_{\varepsilon }} &\text{if } t \in (b_{\varepsilon },1] \end{cases} \quad \text{ and }\quad \widetilde J^{\varepsilon }_t \,:\!=\, \begin{cases} \widehat J^{\varepsilon } &\text{if } t \in [0,a_{\varepsilon }) \\ J^{\varepsilon }_t &\text{if } t \in [a_{\varepsilon },b_{\varepsilon }] \\ \widehat J^{\varepsilon } &\text{if } t \in (b_{\varepsilon },1] \end{cases} . \end{align*}
\begin{align*} \widetilde m^{\varepsilon }_t \,:\!=\, \begin{cases} m^{\varepsilon }_{a_{\varepsilon }} &\text{if } t \in [0,a_{\varepsilon }) \\ m^{\varepsilon }_t &\text{if } t \in [a_{\varepsilon },b_{\varepsilon }] \\ m^{\varepsilon }_{b_{\varepsilon }} &\text{if } t \in (b_{\varepsilon },1] \end{cases} \quad \text{ and }\quad \widetilde J^{\varepsilon }_t \,:\!=\, \begin{cases} \widehat J^{\varepsilon } &\text{if } t \in [0,a_{\varepsilon }) \\ J^{\varepsilon }_t &\text{if } t \in [a_{\varepsilon },b_{\varepsilon }] \\ \widehat J^{\varepsilon } &\text{if } t \in (b_{\varepsilon },1] \end{cases} . \end{align*}
It is readily verified that
![]() $(\widetilde{\boldsymbol{m}}^{\varepsilon }, \widetilde{\boldsymbol{J}}^{\varepsilon })$
solves the continuity equation for every
$(\widetilde{\boldsymbol{m}}^{\varepsilon }, \widetilde{\boldsymbol{J}}^{\varepsilon })$
solves the continuity equation for every
![]() $\varepsilon$
. Therefore,
$\varepsilon$
. Therefore,
 \begin{align} {\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon }) &\leq \mathcal{A}_{\varepsilon }(\widetilde{\boldsymbol{m}}^{\varepsilon },\widetilde{\boldsymbol{J}}^{\varepsilon }) = \int _0^1 \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } \widetilde m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } \widetilde J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\\ &= \int _0^{a_{\varepsilon }} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }}{\varepsilon ^d}, \bar J \right ) \,{\, \mathrm{d}} t + \int _{a_{\varepsilon }}^{b_{\varepsilon }} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\nonumber \\ &\quad + \int _{b_{\varepsilon }}^1 \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon }}{\varepsilon ^d}, \bar J \right ) \,{\, \mathrm{d}} t\nonumber \\ & =: I_1 + I_2 + I_3.\nonumber \end{align}
\begin{align} {\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon }) &\leq \mathcal{A}_{\varepsilon }(\widetilde{\boldsymbol{m}}^{\varepsilon },\widetilde{\boldsymbol{J}}^{\varepsilon }) = \int _0^1 \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } \widetilde m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } \widetilde J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\\ &= \int _0^{a_{\varepsilon }} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }}{\varepsilon ^d}, \bar J \right ) \,{\, \mathrm{d}} t + \int _{a_{\varepsilon }}^{b_{\varepsilon }} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\nonumber \\ &\quad + \int _{b_{\varepsilon }}^1 \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon }}{\varepsilon ^d}, \bar J \right ) \,{\, \mathrm{d}} t\nonumber \\ & =: I_1 + I_2 + I_3.\nonumber \end{align}
The first and last integral can be estimated using the assumption (3.3). Indeed,
 \begin{align*} I_1+I_3 &\le C \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \Biggl ((a_{\varepsilon }+1-b_{\varepsilon }) \varepsilon ^d + \sum _{\substack{x \in \mathcal X \\ |x_{\mathsf{z}}|_{\infty } \le R}} \left ( a_{\varepsilon } (\tau ^z_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon })(x) + (1-b_{\varepsilon }) (\tau ^z_{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon })(x) \right )\Biggr ) \\ &\le C \left ( (a_{\varepsilon }+1-b_{\varepsilon }) + (2R+1)^d \sum _{x \in \mathcal{X}_{\varepsilon }} \left (a_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }(x) + (1-b_{\varepsilon }) m_{b_{\varepsilon }}^{\varepsilon }(x)\right ) \right ) \\ &= C \left ( (a_{\varepsilon }+1-b_{\varepsilon }) + (2R+1)^d \left (a_{\varepsilon } \iota _{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }({\mathbb{T}}^d) + (1-b_{\varepsilon })\iota _{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon }({\mathbb{T}}^d)\right ) \right ), \end{align*}
\begin{align*} I_1+I_3 &\le C \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \Biggl ((a_{\varepsilon }+1-b_{\varepsilon }) \varepsilon ^d + \sum _{\substack{x \in \mathcal X \\ |x_{\mathsf{z}}|_{\infty } \le R}} \left ( a_{\varepsilon } (\tau ^z_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon })(x) + (1-b_{\varepsilon }) (\tau ^z_{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon })(x) \right )\Biggr ) \\ &\le C \left ( (a_{\varepsilon }+1-b_{\varepsilon }) + (2R+1)^d \sum _{x \in \mathcal{X}_{\varepsilon }} \left (a_{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }(x) + (1-b_{\varepsilon }) m_{b_{\varepsilon }}^{\varepsilon }(x)\right ) \right ) \\ &= C \left ( (a_{\varepsilon }+1-b_{\varepsilon }) + (2R+1)^d \left (a_{\varepsilon } \iota _{\varepsilon } m_{a_{\varepsilon }}^{\varepsilon }({\mathbb{T}}^d) + (1-b_{\varepsilon })\iota _{\varepsilon } m_{b_{\varepsilon }}^{\varepsilon }({\mathbb{T}}^d)\right ) \right ), \end{align*}
and in the limit we find
As for the second integral, thanks to Assumption 2.8(c) we have that
 \begin{align} I_2 - \mathcal A_{\varepsilon }({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon }) &= - \int _{(0,a_{\varepsilon })\cup (b_{\varepsilon },1)} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\\ &\le C' \left ((a_{\varepsilon }+1-b_{\varepsilon })+(2R_{\mathrm{max}}+1)^d \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon }\left (\left ((0,a_{\varepsilon })\cup (b_{\varepsilon },1)\right ) \times{\mathbb{T}}^d\right ) \right ) .\nonumber \end{align}
\begin{align} I_2 - \mathcal A_{\varepsilon }({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon }) &= - \int _{(0,a_{\varepsilon })\cup (b_{\varepsilon },1)} \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F\left ( \frac{\tau ^z_{\varepsilon } m_t^{\varepsilon }}{\varepsilon ^d}, \frac{\tau ^z_{\varepsilon } J^{\varepsilon }_t}{\varepsilon ^{d-1}} \right ) \,{\, \mathrm{d}} t\\ &\le C' \left ((a_{\varepsilon }+1-b_{\varepsilon })+(2R_{\mathrm{max}}+1)^d \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon }\left (\left ((0,a_{\varepsilon })\cup (b_{\varepsilon },1)\right ) \times{\mathbb{T}}^d\right ) \right ) .\nonumber \end{align}
Since
![]() $(\iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon })_{\varepsilon }$
converges weakly, for every
$(\iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon })_{\varepsilon }$
converges weakly, for every
![]() $a, b \in (0,1)$
, we have that
$a, b \in (0,1)$
, we have that
 \begin{align*} \limsup _{\varepsilon \to 0} \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } \left ( \left ( (0,a_{\varepsilon })\cup (b_{\varepsilon },1) \right ) \times{\mathbb{T}}^d \right ) &\leq \limsup _{\varepsilon \to 0} \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } \left ( \big ( (0,a] \cup [b,1) \big ) \times{\mathbb{T}^d} \right ) \\ &\leq \boldsymbol{\mu } \left ( \big ( (0,a] \cup [b,1) \big ) \times{\mathbb{T}^d} \right ) . \end{align*}
\begin{align*} \limsup _{\varepsilon \to 0} \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } \left ( \left ( (0,a_{\varepsilon })\cup (b_{\varepsilon },1) \right ) \times{\mathbb{T}}^d \right ) &\leq \limsup _{\varepsilon \to 0} \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } \left ( \big ( (0,a] \cup [b,1) \big ) \times{\mathbb{T}^d} \right ) \\ &\leq \boldsymbol{\mu } \left ( \big ( (0,a] \cup [b,1) \big ) \times{\mathbb{T}^d} \right ) . \end{align*}
Using the fact that the previous estimate holds for every
![]() $a,b \in (0,1)$
, we obtain that
$a,b \in (0,1)$
, we obtain that
This, together with the estimate obtained in (3.8), gives us the inequality
In conclusion, from (3.6), (3.7), and (3.9), we find
which is sought upper bound.
3.2. Proof of the liminf inequality
In this section, we provide the proof of the liminf inequality in Theorem3.9. Let
![]() $m_0^{\varepsilon }$
,
$m_0^{\varepsilon }$
,
![]() $m_1^{\varepsilon }$
be sequences of measures weakly converging to
$m_1^{\varepsilon }$
be sequences of measures weakly converging to
![]() $\mu _0$
,
$\mu _0$
,
![]() $\mu _1$
, respectively. We want to show that
$\mu _1$
, respectively. We want to show that
Without loss of generality, we will assume that the limit inferior in the latter is a true finite limit, and that
![]() $m_0^{\varepsilon }(\mathcal{X}_{\varepsilon })=m_1^{\varepsilon }(\mathcal{X}_{\varepsilon })$
for every
$m_0^{\varepsilon }(\mathcal{X}_{\varepsilon })=m_1^{\varepsilon }(\mathcal{X}_{\varepsilon })$
for every
![]() $\varepsilon \gt 0$
.
$\varepsilon \gt 0$
.
We split the proof into two parts: first for
![]() $F$
with linear growth and then for
$F$
with linear growth and then for
![]() $F$
of flow-based type, respectively Assumption 3.1 and Assumption 3.2.
$F$
of flow-based type, respectively Assumption 3.1 and Assumption 3.2.
3.2.1. Case 1: F with linear growth
Assume that
![]() $F$
satisfies Assumption 3.1. Recall that, as a consequence of Lemma 3.5,
$F$
satisfies Assumption 3.1. Recall that, as a consequence of Lemma 3.5,
![]() $F$
is Lipschitz continuous as well, in the sense of (3.1).
$F$
is Lipschitz continuous as well, in the sense of (3.1).
Proof of the liminf inequality (linear growth). With a very similar argument as the one provided by Remark 2.7 in the continuous setting, we can with no loss of generality assume that
![]() $F$
is nonnegative. Let
$F$
is nonnegative. Let
![]() $({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
be approximate optimal solutions associated to
$({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
be approximate optimal solutions associated to
![]() ${\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon })$
, i.e. such that
${\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon })$
, i.e. such that
As usual, we write
![]() ${\, \mathrm{d}}{\boldsymbol{m}}^{\varepsilon } (t,x) = m_t^{\varepsilon }({\, \mathrm{d}} x){\, \mathrm{d}} t$
for some measurable curve
${\, \mathrm{d}}{\boldsymbol{m}}^{\varepsilon } (t,x) = m_t^{\varepsilon }({\, \mathrm{d}} x){\, \mathrm{d}} t$
for some measurable curve
![]() $t \mapsto m_t^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
of constant, finite mass. By compactness (Remark 3.11), we know that up to a further non-relabelled subsequence,
$t \mapsto m_t^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
of constant, finite mass. By compactness (Remark 3.11), we know that up to a further non-relabelled subsequence,
![]() ${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly in
${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly in
![]() $\mathcal{M}_+\big ((0,1)\times{\mathbb{T}^d} \big )$
with
$\mathcal{M}_+\big ((0,1)\times{\mathbb{T}^d} \big )$
with
![]() $\boldsymbol{\mu } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
. Due to the lack of continuity of the trace operators in
$\boldsymbol{\mu } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
. Due to the lack of continuity of the trace operators in
![]() $\mathrm{BV}$
, a priori we cannot conclude that
$\mathrm{BV}$
, a priori we cannot conclude that
![]() $\boldsymbol{\mu }_{t=0} = \mu _0$
and
$\boldsymbol{\mu }_{t=0} = \mu _0$
and
![]() $\boldsymbol{\mu }_{t=1} = \mu _1$
. In other words, there might be a “jump” in the limit as
$\boldsymbol{\mu }_{t=1} = \mu _1$
. In other words, there might be a “jump” in the limit as
![]() $\varepsilon \to 0$
at the boundary of
$\varepsilon \to 0$
at the boundary of
![]() $(0,1)$
. In order to take care of this problem, we rescale our measures
$(0,1)$
. In order to take care of this problem, we rescale our measures
![]() ${\boldsymbol{m}}^{\varepsilon }$
in time, so as to be able to “see” the jump in the interior of
${\boldsymbol{m}}^{\varepsilon }$
in time, so as to be able to “see” the jump in the interior of
![]() $(0,1)$
.
$(0,1)$
.
To this purpose, for
![]() $\delta \in (0,1/2)$
, we define
$\delta \in (0,1/2)$
, we define
![]() $\mathcal{I}_\delta \,:\!=\, (\delta, 1-\delta )$
and
$\mathcal{I}_\delta \,:\!=\, (\delta, 1-\delta )$
and
![]() ${\boldsymbol{m}}^{\varepsilon, \delta } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
as
${\boldsymbol{m}}^{\varepsilon, \delta } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
as
 \begin{align} m_t^{\varepsilon, \delta } \,:\!=\, \begin{cases} m_0^{\varepsilon } &\text{if } t \in (0,\delta ] \\ m_{\frac{t-\delta }{1-2\delta }}^{\varepsilon } &\text{if } t \in \mathcal{I}_\delta \\ m_1^{\varepsilon } &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}}{\boldsymbol{m}}^{\varepsilon, \delta }(t,x) \,:\!=\, m_t^{\varepsilon, \delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align}
\begin{align} m_t^{\varepsilon, \delta } \,:\!=\, \begin{cases} m_0^{\varepsilon } &\text{if } t \in (0,\delta ] \\ m_{\frac{t-\delta }{1-2\delta }}^{\varepsilon } &\text{if } t \in \mathcal{I}_\delta \\ m_1^{\varepsilon } &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}}{\boldsymbol{m}}^{\varepsilon, \delta }(t,x) \,:\!=\, m_t^{\varepsilon, \delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align}
By construction, the convergence of the boundary data, and the fact that, by assumption,
![]() ${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly, it is straightforward to see that
${\boldsymbol{m}}^{\varepsilon } \to \boldsymbol{\mu }$
weakly, it is straightforward to see that
![]() ${\boldsymbol{m}}^{\varepsilon, \delta } \to \widehat{\boldsymbol{\mu }}^\delta$
weakly, where
${\boldsymbol{m}}^{\varepsilon, \delta } \to \widehat{\boldsymbol{\mu }}^\delta$
weakly, where
 \begin{align} \widehat \mu _t^\delta \,:\!=\, \begin{cases} \mu _0 &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }} &\text{if } t \in \mathcal{I}_\delta \\ \mu _1 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \widehat{\boldsymbol{\mu }}^\delta (t,x) \,:\!=\, \widehat \mu _t^\delta ({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align}
\begin{align} \widehat \mu _t^\delta \,:\!=\, \begin{cases} \mu _0 &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }} &\text{if } t \in \mathcal{I}_\delta \\ \mu _1 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \widehat{\boldsymbol{\mu }}^\delta (t,x) \,:\!=\, \widehat \mu _t^\delta ({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align}
Note that the rescaled curve
![]() $t \mapsto \widehat \mu _t^\delta$
might have discontinuities at
$t \mapsto \widehat \mu _t^\delta$
might have discontinuities at
![]() $t=\delta$
and
$t=\delta$
and
![]() $t= 1-\delta$
, which correspond to the possible jumps in the limit as
$t= 1-\delta$
, which correspond to the possible jumps in the limit as
![]() $\varepsilon \to 0$
for
$\varepsilon \to 0$
for
![]() ${\boldsymbol{m}}^{\varepsilon }$
at
${\boldsymbol{m}}^{\varepsilon }$
at
![]() $\{0,1\}$
. Nevertheless,
$\{0,1\}$
. Nevertheless,
![]() $\widehat{\boldsymbol{\mu }}^\delta$
is a competitor for
$\widehat{\boldsymbol{\mu }}^\delta$
is a competitor for
![]() ${\mathbb{MA}}(\mu _0,\mu _1)$
, which, by the
${\mathbb{MA}}(\mu _0,\mu _1)$
, which, by the
![]() $\Gamma$
-convergence of
$\Gamma$
-convergence of
![]() $\mathcal{A}_{\varepsilon }$
towards
$\mathcal{A}_{\varepsilon }$
towards
![]() ${\mathbb{A}}_{\mathrm{hom}}$
(Remark 3.10), ensures that
${\mathbb{A}}_{\mathrm{hom}}$
(Remark 3.10), ensures that
We are left with estimating from above the left-hand side of the latter displayed equation. To do so, we seek a suitable curve of discrete vector fields
![]() $\boldsymbol{J}^{\varepsilon, \delta }$
with
$\boldsymbol{J}^{\varepsilon, \delta }$
with
![]() $({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) \in \mathcal{CE}_{\varepsilon }$
and having an action
$({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) \in \mathcal{CE}_{\varepsilon }$
and having an action
![]() $\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon, \delta },\boldsymbol{J}^{\varepsilon, \delta })$
comparable with
$\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon, \delta },\boldsymbol{J}^{\varepsilon, \delta })$
comparable with
![]() $\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon })$
for small
$\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon },\boldsymbol{J}^{\varepsilon })$
for small
![]() $\delta \gt 0$
. We set
$\delta \gt 0$
. We set
 \begin{align*} J_t^{\varepsilon, \delta } \,:\!=\, \begin{cases} 0 &\text{if } t \in (0,\delta ] \\ \frac{1}{1-2\delta } J_{\frac{t-\delta }{1-2\delta }}^{\varepsilon } &\text{if } t \in \mathcal{I}_\delta \\ 0 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \boldsymbol{J}^{\varepsilon, \delta }(t,x) \,:\!=\, J_t^{\varepsilon, \delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
\begin{align*} J_t^{\varepsilon, \delta } \,:\!=\, \begin{cases} 0 &\text{if } t \in (0,\delta ] \\ \frac{1}{1-2\delta } J_{\frac{t-\delta }{1-2\delta }}^{\varepsilon } &\text{if } t \in \mathcal{I}_\delta \\ 0 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \boldsymbol{J}^{\varepsilon, \delta }(t,x) \,:\!=\, J_t^{\varepsilon, \delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
We claim that
![]() $ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
and
$ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
and
where
![]() $C(F) \in \mathbb{R}_+$
only depends on
$C(F) \in \mathbb{R}_+$
only depends on
![]() $F$
(specifically on the constants in Assumption 2.8 and Assumption 3.1). This would suffice to conclude the proof of the sought liminf inequality. Indeed, from (3.11) and (3.15), we infer
$F$
(specifically on the constants in Assumption 2.8 and Assumption 3.1). This would suffice to conclude the proof of the sought liminf inequality. Indeed, from (3.11) and (3.15), we infer
 \begin{align*} \liminf _{\varepsilon \to 0} &{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon }, m_1^{\varepsilon }) = \liminf _{\varepsilon \to 0} \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \\ &\geq \frac{1}{1+C(F)\delta } \liminf _{\varepsilon \to 0} \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) - \frac{C(F) \delta }{1+C(F)\delta } \Big ( 1 + \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } ((0,1) \times{\mathbb{T}^d}) \Big ) \end{align*}
\begin{align*} \liminf _{\varepsilon \to 0} &{\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon }, m_1^{\varepsilon }) = \liminf _{\varepsilon \to 0} \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \\ &\geq \frac{1}{1+C(F)\delta } \liminf _{\varepsilon \to 0} \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) - \frac{C(F) \delta }{1+C(F)\delta } \Big ( 1 + \iota _{\varepsilon }{\boldsymbol{m}}^{\varepsilon } ((0,1) \times{\mathbb{T}^d}) \Big ) \end{align*}
which, combined with (3.14), yields
for any
![]() $\delta \in (0,1/2)$
. We conclude by letting
$\delta \in (0,1/2)$
. We conclude by letting
![]() $\delta \to 0$
.
$\delta \to 0$
.
We are left with the proof of
![]() $ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
and of the claim (3.15).
$ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
and of the claim (3.15).
Proof of
![]() $ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
. Let us fix
$ ({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta } ) \in \mathcal{CE}_{\varepsilon }$
. Let us fix
![]() $x \in \mathcal{X}_{\varepsilon }$
and
$x \in \mathcal{X}_{\varepsilon }$
and
![]() $\varphi \in C^1_c \bigl ((0,1)\bigr )$
. Set
$\varphi \in C^1_c \bigl ((0,1)\bigr )$
. Set
![]() $\widetilde \varphi : = \varphi \circ r_\delta$
, with
$\widetilde \varphi : = \varphi \circ r_\delta$
, with
![]() $r_\delta (s) \,:\!=\,(1-2\delta )s+\delta$
. We have
$r_\delta (s) \,:\!=\,(1-2\delta )s+\delta$
. We have
 \begin{align} \int _0^1 \partial _t \varphi m_t^{\varepsilon, \delta }(x){\, \mathrm{d}} t &= \int _0^\delta \partial _t \varphi \, m_0^{\varepsilon }(x){\, \mathrm{d}} t + \int _{1-\delta }^1 \partial _t \varphi \, m_1^{\varepsilon }(x){\, \mathrm{d}} t + \int _{\mathcal{I}_\delta } \partial _t \varphi \, m_{r_\delta ^{-1}(t)}^{\varepsilon }(x){\, \mathrm{d}} t \\ &= \varphi (\delta ) \, m_0^{\varepsilon }(x) - \varphi (1-\delta ) \, m_1^{\varepsilon }(x) + (1-2\delta )\int _0^1 (\partial _t \varphi ) \circ r_\delta \, m_s^{\varepsilon }(x){\, \mathrm{d}} s \nonumber \\ &= \widetilde \varphi (0) \, m_0^{\varepsilon }(x) - \widetilde \varphi (1) \, m_1^{\varepsilon }(x) + \int _0^1 \partial _s \widetilde \varphi \, m_s^{\varepsilon }(x){\, \mathrm{d}} s \nonumber \\ &= \int _0^1 \widetilde \varphi \, \sum _{y \sim x} J_s^{\varepsilon }(x,y){\, \mathrm{d}} s = \frac{1}{1-2\delta } \int _{\mathcal{I}_\delta } \varphi \, \sum _{y \sim x} J^{\varepsilon }_{r_\delta ^{-1}(t)}(x,y){\, \mathrm{d}} t \nonumber \\ &= \int _0^1 \varphi \sum _{y \sim x} J^{\varepsilon, \delta }_t(x,y){\, \mathrm{d}} t, \nonumber \end{align}
\begin{align} \int _0^1 \partial _t \varphi m_t^{\varepsilon, \delta }(x){\, \mathrm{d}} t &= \int _0^\delta \partial _t \varphi \, m_0^{\varepsilon }(x){\, \mathrm{d}} t + \int _{1-\delta }^1 \partial _t \varphi \, m_1^{\varepsilon }(x){\, \mathrm{d}} t + \int _{\mathcal{I}_\delta } \partial _t \varphi \, m_{r_\delta ^{-1}(t)}^{\varepsilon }(x){\, \mathrm{d}} t \\ &= \varphi (\delta ) \, m_0^{\varepsilon }(x) - \varphi (1-\delta ) \, m_1^{\varepsilon }(x) + (1-2\delta )\int _0^1 (\partial _t \varphi ) \circ r_\delta \, m_s^{\varepsilon }(x){\, \mathrm{d}} s \nonumber \\ &= \widetilde \varphi (0) \, m_0^{\varepsilon }(x) - \widetilde \varphi (1) \, m_1^{\varepsilon }(x) + \int _0^1 \partial _s \widetilde \varphi \, m_s^{\varepsilon }(x){\, \mathrm{d}} s \nonumber \\ &= \int _0^1 \widetilde \varphi \, \sum _{y \sim x} J_s^{\varepsilon }(x,y){\, \mathrm{d}} s = \frac{1}{1-2\delta } \int _{\mathcal{I}_\delta } \varphi \, \sum _{y \sim x} J^{\varepsilon }_{r_\delta ^{-1}(t)}(x,y){\, \mathrm{d}} t \nonumber \\ &= \int _0^1 \varphi \sum _{y \sim x} J^{\varepsilon, \delta }_t(x,y){\, \mathrm{d}} t, \nonumber \end{align}
where, in the fourth equality, we used that
![]() $({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
.
$({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
.
Proof of the action estimate. Define
![]() $r_\delta (s) \,:\!=\,(1-2\delta )s+\delta$
. Note that, by construction, for
$r_\delta (s) \,:\!=\,(1-2\delta )s+\delta$
. Note that, by construction, for
![]() $(t,(x,y)) \in \mathcal{I}_\delta \times \mathcal{E}_{\varepsilon }$
,
$(t,(x,y)) \in \mathcal{I}_\delta \times \mathcal{E}_{\varepsilon }$
,
On the other hand, for
![]() $(t,(x,y)) \in \big ( (0,\delta ] \cup [1-\delta, 1) \big ) \times \mathcal{E}_{\varepsilon }$
, we have that
$(t,(x,y)) \in \big ( (0,\delta ] \cup [1-\delta, 1) \big ) \times \mathcal{E}_{\varepsilon }$
, we have that
 \begin{align*} m_t^{\varepsilon, \delta }(x) = \begin{cases} m_0^{\varepsilon }(x) &\text{if } t \in (0,\delta ] \\ m_1^{\varepsilon }(x) &\text{if } t \in [1-\delta, 1) \end{cases} \quad \text{ and }\quad J_t^{\varepsilon, \delta }(x,y) = 0 . \end{align*}
\begin{align*} m_t^{\varepsilon, \delta }(x) = \begin{cases} m_0^{\varepsilon }(x) &\text{if } t \in (0,\delta ] \\ m_1^{\varepsilon }(x) &\text{if } t \in [1-\delta, 1) \end{cases} \quad \text{ and }\quad J_t^{\varepsilon, \delta }(x,y) = 0 . \end{align*}
It follows that the action of
![]() $({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta })$
is given by
$({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta })$
is given by
where we used the notation
Using Assumption 3.1, we see that, for
![]() $i=0,1$
,
$i=0,1$
,
and, by the Lipschitz continuity exhibited in Lemma 3.5, we also infer that
 \begin{align*} \mathcal{A}_{\varepsilon }^{\mathcal{I}_\delta }({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) &\leq (1-2\delta ) \left (\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) + C \Big (\frac 1{1-2\delta }-1 \Big ) \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } \int _0^1 \frac{\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}}{\, \mathrm{d}} t \right ) \\ &\le (1-2\delta ) \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) + 2 \delta C (2R+1)^d \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ (x,y) \in \mathcal{E}^Q } \int _0^1 \frac{\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}}{\, \mathrm{d}} t . \end{align*}
\begin{align*} \mathcal{A}_{\varepsilon }^{\mathcal{I}_\delta }({\boldsymbol{m}}^{\varepsilon, \delta }, \boldsymbol{J}^{\varepsilon, \delta }) &\leq (1-2\delta ) \left (\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) + C \Big (\frac 1{1-2\delta }-1 \Big ) \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ \substack{ (x,y) \in \mathcal{E} \\ |x_{\mathsf{z}}|_{\infty } \leq R } } \int _0^1 \frac{\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}}{\, \mathrm{d}} t \right ) \\ &\le (1-2\delta ) \mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) + 2 \delta C (2R+1)^d \sum _{z \in \mathbb{Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ (x,y) \in \mathcal{E}^Q } \int _0^1 \frac{\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}}{\, \mathrm{d}} t . \end{align*}
Since we assumed
![]() $F$
to be nonnegative, we can estimate
$F$
to be nonnegative, we can estimate
and, using (2.8),
 \begin{equation*} \sum _{z \in \mathbb {Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ (x,y) \in \mathcal {E}^Q } \int _0^1 \frac {\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}} {\, \mathrm {d}} t \le \frac {1}{c} \mathcal {A}_{\varepsilon }({\boldsymbol {m}}^{\varepsilon }, \boldsymbol {J}^{\varepsilon }) + \frac {C}{c} \left ( 1 + (1+2R_{\mathrm {max}})^d \| {\iota _{\varepsilon } {\boldsymbol {m}}^{\varepsilon }}\|_{\mathrm {TV}} \right ) . \end{equation*}
\begin{equation*} \sum _{z \in \mathbb {Z}_{\varepsilon }^d} \varepsilon ^d \sum _{ (x,y) \in \mathcal {E}^Q } \int _0^1 \frac {\lvert \tau _{\varepsilon }^z J^{\varepsilon }_t(x,y)\rvert }{\varepsilon ^{d-1}} {\, \mathrm {d}} t \le \frac {1}{c} \mathcal {A}_{\varepsilon }({\boldsymbol {m}}^{\varepsilon }, \boldsymbol {J}^{\varepsilon }) + \frac {C}{c} \left ( 1 + (1+2R_{\mathrm {max}})^d \| {\iota _{\varepsilon } {\boldsymbol {m}}^{\varepsilon }}\|_{\mathrm {TV}} \right ) . \end{equation*}
3.2.2. Case 2: F is flow-based
In this section, we show (3.10) in the case where
![]() $F$
(and hence
$F$
(and hence
![]() $f_{\mathrm{hom}}$
) is of flow-based type, i.e. it satisfies Assumption 3.2. We start by observing that, in this particular setting, both the discrete and the continuous formulations of the boundary-value problems admit an equivalent, static formulation.
$f_{\mathrm{hom}}$
) is of flow-based type, i.e. it satisfies Assumption 3.2. We start by observing that, in this particular setting, both the discrete and the continuous formulations of the boundary-value problems admit an equivalent, static formulation.
Let
![]() $(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
and consider the Lebesgue decomposition
$(\boldsymbol{\mu },\boldsymbol{\nu }) \in \mathsf{CE}$
and consider the Lebesgue decomposition
We know that every solution to the continuity equation can be disintegrated in the form
![]() $\boldsymbol{\mu }({\, \mathrm{d}} t,{\, \mathrm{d}} x) = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t$
for some measurable curve
$\boldsymbol{\mu }({\, \mathrm{d}} t,{\, \mathrm{d}} x) = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t$
for some measurable curve
![]() $t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}^d})$
of constant, finite mass. If
$t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}^d})$
of constant, finite mass. If
![]() $f$
is a function as in Assumption 2.2 that further does not depend on
$f$
is a function as in Assumption 2.2 that further does not depend on
![]() $\rho$
, then Jensen’s inequality yields
$\rho$
, then Jensen’s inequality yields
In order to take care of the singular part, consider the disintegration of
![]() $\boldsymbol{\sigma }$
with respect to the projection map
$\boldsymbol{\sigma }$
with respect to the projection map
![]() $\pi :(t,x) \mapsto x$
, in the form
$\pi :(t,x) \mapsto x$
, in the form
for some measurable
![]() $x \mapsto \sigma ^x \in \mathscr{P}\big ( (0,1) \big )$
. Due to the convexity of
$x \mapsto \sigma ^x \in \mathscr{P}\big ( (0,1) \big )$
. Due to the convexity of
![]() $f^\infty$
, by Jensen’s inequality we also obtain
$f^\infty$
, by Jensen’s inequality we also obtain
Now, we define the new space-time measures
 \begin{align} \begin{split} \widetilde{\boldsymbol{\mu }} \,:\!=\, \widetilde \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \quad \text{and} \quad \widetilde{\boldsymbol{\nu }} \,:\!=\, \widehat j \mathscr{L}^{\,d+1} + \widehat j^\perp{\, \mathrm{d}} t \otimes \pi _{\#}\boldsymbol{\sigma }, \quad \text{where} \\ \widetilde \mu _t\,:\!=\, \mu _0 + t (\mu _1 - \mu _0), \quad \widehat j(x) \,:\!=\, \int _0^1 j_t(x){\, \mathrm{d}} t, \quad \text{and} \ \ \widehat j^\perp (x) \,:\!=\, \int j^\perp{\, \mathrm{d}} \sigma ^x, \end{split} \end{align}
\begin{align} \begin{split} \widetilde{\boldsymbol{\mu }} \,:\!=\, \widetilde \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \quad \text{and} \quad \widetilde{\boldsymbol{\nu }} \,:\!=\, \widehat j \mathscr{L}^{\,d+1} + \widehat j^\perp{\, \mathrm{d}} t \otimes \pi _{\#}\boldsymbol{\sigma }, \quad \text{where} \\ \widetilde \mu _t\,:\!=\, \mu _0 + t (\mu _1 - \mu _0), \quad \widehat j(x) \,:\!=\, \int _0^1 j_t(x){\, \mathrm{d}} t, \quad \text{and} \ \ \widehat j^\perp (x) \,:\!=\, \int j^\perp{\, \mathrm{d}} \sigma ^x, \end{split} \end{align}
and note that
![]() $(\widetilde{\boldsymbol{\mu }}, \widetilde{\boldsymbol{\nu }}) \in \mathsf{CE}$
. By (3.18) and (3.19), we, therefore, have
$(\widetilde{\boldsymbol{\mu }}, \widetilde{\boldsymbol{\nu }}) \in \mathsf{CE}$
. By (3.18) and (3.19), we, therefore, have
We need to be careful here: the decomposition of
![]() $\widetilde{\boldsymbol{\nu }}$
in (3.20) may not be a Lebesgue decomposition, in the sense that
$\widetilde{\boldsymbol{\nu }}$
in (3.20) may not be a Lebesgue decomposition, in the sense that
![]() ${\, \mathrm{d}} t \otimes \pi _\# \boldsymbol{\sigma }$
can have a nonzero absolutely continuous part. Let
${\, \mathrm{d}} t \otimes \pi _\# \boldsymbol{\sigma }$
can have a nonzero absolutely continuous part. Let
![]() $\widetilde \sigma \in \mathcal{M}_+({\mathbb{T}^d})$
be singular w.r.t.
$\widetilde \sigma \in \mathcal{M}_+({\mathbb{T}^d})$
be singular w.r.t.
![]() $\mathscr{L}^d$
and such that
$\mathscr{L}^d$
and such that
![]() $\mu _0,\mu _1, \pi _\# \boldsymbol{\sigma } \ll \mathscr{L}^d + \widetilde \sigma$
. We can write the Lebesgue decompositions
$\mu _0,\mu _1, \pi _\# \boldsymbol{\sigma } \ll \mathscr{L}^d + \widetilde \sigma$
. We can write the Lebesgue decompositions
If we write
for some functions
![]() $\alpha, \beta :{\mathbb{T}^d} \to \mathbb{R}_+$
, then
$\alpha, \beta :{\mathbb{T}^d} \to \mathbb{R}_+$
, then
The inequality (3.21) becomes, recalling that
![]() $f^\infty$
is
$f^\infty$
is
![]() $1$
-homogeneous,
$1$
-homogeneous,
At this point, we need a lemma.
Lemma 3.13.
For every
![]() $j_1,j_2 \in \mathbb{R}^d$
, we have that
$j_1,j_2 \in \mathbb{R}^d$
, we have that
![]() $ f(j_1+j_2) \le f(j_1) + f^\infty (j_2)$
.
$ f(j_1+j_2) \le f(j_1) + f^\infty (j_2)$
.
Proof. Let
![]() $g \le f$
be a convex and Lipschitz continuous function. By convexity, for every
$g \le f$
be a convex and Lipschitz continuous function. By convexity, for every
![]() $\epsilon \in (0,1)$
, we have
$\epsilon \in (0,1)$
, we have
Let
![]() $j_0 \in \mathsf{D}(f)$
. By the Lipschitz continuity of
$j_0 \in \mathsf{D}(f)$
. By the Lipschitz continuity of
![]() $g$
,
$g$
,
and, since
![]() $g \le f$
,
$g \le f$
,
As we let
![]() $\epsilon \to 0$
, we find
$\epsilon \to 0$
, we find
Since
![]() $f$
is convex and lower semicontinuous, we conclude by an approximation argument.
$f$
is convex and lower semicontinuous, we conclude by an approximation argument.
Applying this lemma with
![]() $j_1 = \widehat j(x)$
and
$j_1 = \widehat j(x)$
and
![]() $j_2 = \alpha \widehat j^\perp (x)$
for every
$j_2 = \alpha \widehat j^\perp (x)$
for every
![]() $x \in{\mathbb{T}^d}$
, (3.22) finally becomes
$x \in{\mathbb{T}^d}$
, (3.22) finally becomes
In other words, we have shown that an optimal curve
![]() $\boldsymbol{\mu }$
between two given boundary data is always given by the affine interpolation (and a constant-in-time flux). We conclude that
$\boldsymbol{\mu }$
between two given boundary data is always given by the affine interpolation (and a constant-in-time flux). We conclude that
 \begin{align} &{\mathbb{MA}}(\mu _0,\mu _1) ={\mathbb{A}}(\boldsymbol{\widetilde \mu })\\ &\qquad = \inf _\nu \left \{ \int _{{\mathbb{T}^d}} f(\widetilde j){\, \mathrm{d}} x + \int _{{\mathbb{T}^d}} f^\infty (\widetilde j^\perp ){\, \mathrm{d}} \widetilde \sigma \, : \, \nu = \widetilde j \mathscr{L}^d + \widetilde j^\perp \widetilde \sigma, \ \mathscr{L}^d \perp \widetilde \sigma \ \ \text{and} \ \ \nabla \cdot \nu = \mu _0 - \mu _1 \right \}\nonumber . \end{align}
\begin{align} &{\mathbb{MA}}(\mu _0,\mu _1) ={\mathbb{A}}(\boldsymbol{\widetilde \mu })\\ &\qquad = \inf _\nu \left \{ \int _{{\mathbb{T}^d}} f(\widetilde j){\, \mathrm{d}} x + \int _{{\mathbb{T}^d}} f^\infty (\widetilde j^\perp ){\, \mathrm{d}} \widetilde \sigma \, : \, \nu = \widetilde j \mathscr{L}^d + \widetilde j^\perp \widetilde \sigma, \ \mathscr{L}^d \perp \widetilde \sigma \ \ \text{and} \ \ \nabla \cdot \nu = \mu _0 - \mu _1 \right \}\nonumber . \end{align}
We refer to the latter expression as the static formulation of the boundary value problem described by
![]() ${\mathbb{MA}}(\mu _0,\mu _1)$
(in the case when
${\mathbb{MA}}(\mu _0,\mu _1)$
(in the case when
![]() $f$
is of flow-based type).
$f$
is of flow-based type).
Remark 3.14. Using this equivalence, the lower semicontinuity of
![]() $\mathbb{MA}$
directly follows from the semicontinuity of
$\mathbb{MA}$
directly follows from the semicontinuity of
![]() $\mathbb{A}$
given by [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 3.14].
$\mathbb{A}$
given by [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 3.14].
Arguing in a similar way (in fact, via an even simpler argument, due to the lack of singularities), we obtain a static formulation of the discrete transport problem in terms of a discrete divergence equation, when
![]() $F(m,J)=F(J)$
. Precisely, in this case we obtain
$F(m,J)=F(J)$
. Precisely, in this case we obtain
The sought
![]() $\Gamma$
-liminf inequality easily follows from such static formulations.
$\Gamma$
-liminf inequality easily follows from such static formulations.
Proof of the liminf inequality (flow-based type). Let
![]() $m_0^{\varepsilon }$
,
$m_0^{\varepsilon }$
,
![]() $m_1^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
be sequences of discrete nonnegative measures that converge weakly (via
$m_1^{\varepsilon } \in \mathbb{R}_+^{\mathcal{X}_{\varepsilon }}$
be sequences of discrete nonnegative measures that converge weakly (via
![]() $\iota _{\varepsilon }$
in the usual sense) to
$\iota _{\varepsilon }$
in the usual sense) to
![]() $\mu _0$
,
$\mu _0$
,
![]() $\mu _1$
, and such that
$\mu _1$
, and such that
![]() $m_0^{\varepsilon }(\mathcal{X}_{\varepsilon }) = m_1^{\varepsilon }(\mathcal{X}_{\varepsilon })$
for every
$m_0^{\varepsilon }(\mathcal{X}_{\varepsilon }) = m_1^{\varepsilon }(\mathcal{X}_{\varepsilon })$
for every
![]() $\varepsilon \gt 0$
. Let
$\varepsilon \gt 0$
. Let
![]() $({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
be (almost-)optimal solutions associated with
$({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \in \mathcal{CE}_{\varepsilon }$
be (almost-)optimal solutions associated with
![]() ${\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon })$
, namely
${\mathcal{MA}}_{\varepsilon }(m_0^{\varepsilon },m_1^{\varepsilon })$
, namely
Consider the discrete equivalent of the measure constructed in (3.20), namely
which still solves the continuity equation. By applying Jensen’s inequality, the convexity of
![]() $F$
ensures that
$F$
ensures that
Thus
![]() $\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \ge \mathcal{A}_{\varepsilon }(\widetilde{\boldsymbol{m}}^{\varepsilon })$
. Note that, by construction,
$\mathcal{A}_{\varepsilon }({\boldsymbol{m}}^{\varepsilon }, \boldsymbol{J}^{\varepsilon }) \ge \mathcal{A}_{\varepsilon }(\widetilde{\boldsymbol{m}}^{\varepsilon })$
. Note that, by construction,
![]() $\widetilde{\boldsymbol{m}}^{\varepsilon } \to \widetilde{\boldsymbol{\mu }}$
weakly, where
$\widetilde{\boldsymbol{m}}^{\varepsilon } \to \widetilde{\boldsymbol{\mu }}$
weakly, where
Hence, from (3.24), (3.25), and the
![]() $\Gamma$
-convergence of
$\Gamma$
-convergence of
![]() $\mathcal{A}_{\varepsilon }$
to
$\mathcal{A}_{\varepsilon }$
to
![]() ${\mathbb{A}}_{\mathrm{hom}}$
(cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.1]), we infer that
${\mathbb{A}}_{\mathrm{hom}}$
(cfr. [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.1]), we infer that
which concludes the proof of the liminf inequality.
3.3. About the lower semicontinuity of
 $\mathbb{MA}$
$\mathbb{MA}$
In view of our main result, whenever
![]() $F$
satisfies either Assumption 3.1 or Assumption 3.2, the limit boundary-value problem
$F$
satisfies either Assumption 3.1 or Assumption 3.2, the limit boundary-value problem
![]() ${\mathbb{MA}}_{\mathrm{hom}}(\cdot, \cdot )$
is necessarily jointly lower semicontinuous with respect to the weak topology on
${\mathbb{MA}}_{\mathrm{hom}}(\cdot, \cdot )$
is necessarily jointly lower semicontinuous with respect to the weak topology on
![]() $\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
. This indeed follows from the general fact that any
$\mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
. This indeed follows from the general fact that any
![]() $\Gamma$
-limit with respect to a given topology is always lower semicontinuous with respect to that same topology. Using a very similar proof to that of the
$\Gamma$
-limit with respect to a given topology is always lower semicontinuous with respect to that same topology. Using a very similar proof to that of the
![]() $\Gamma$
-liminf inequality, we can actually show that, if
$\Gamma$
-liminf inequality, we can actually show that, if
![]() $f$
is with linear growth or it is of flow-based type, then the associated
$f$
is with linear growth or it is of flow-based type, then the associated
![]() $\mathbb{MA}$
is always lower semicontinuous (even if, a priori,
$\mathbb{MA}$
is always lower semicontinuous (even if, a priori,
![]() $f$
is not of the form
$f$
is not of the form
![]() $f=f_{\mathrm{hom}}$
), thus providing a positive answer in this framework to the validity of (2.5). In the flow-based setting, this fact has been observed in Remark 3.14.
$f=f_{\mathrm{hom}}$
), thus providing a positive answer in this framework to the validity of (2.5). In the flow-based setting, this fact has been observed in Remark 3.14.
Proposition 3.15.
Assume that
![]() $f$
is with linear growth, namely it satisfies one of the two equivalent conditions appearing in Lemma 3.4
, and assume that
$f$
is with linear growth, namely it satisfies one of the two equivalent conditions appearing in Lemma 3.4
, and assume that
![]() $(\mu _0^n$
,
$(\mu _0^n$
,
![]() $\mu _1^n) \to (\mu _0$
,
$\mu _1^n) \to (\mu _0$
,
![]() $\mu _1) \in \mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
weakly. Then:
$\mu _1) \in \mathcal{M}_+({\mathbb{T}^d}) \times \mathcal{M}_+({\mathbb{T}^d})$
weakly. Then:
The proof goes along the same line of the proof of the
![]() $\Gamma$
-liminf inequality for discrete energies
$\Gamma$
-liminf inequality for discrete energies
![]() $F$
with linear growth. We sketch it here and add details whenever we encounter nontrivial differences between the two proofs.
$F$
with linear growth. We sketch it here and add details whenever we encounter nontrivial differences between the two proofs.
Proof. Let
![]() $(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n) \in \mathsf{CE}$
be (almost-)optimal solutions associated to
$(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n) \in \mathsf{CE}$
be (almost-)optimal solutions associated to
![]() ${\mathbb{MA}}(\mu _0^n,\mu _1^n)$
, i.e.
${\mathbb{MA}}(\mu _0^n,\mu _1^n)$
, i.e.
With no loss of generality, we can assume
![]() $\sup _n{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) \lt \infty$
and that the limits inferior are true limits. By the compactness of Remark 2.5, we know that, up to a non-relabelled subsequence,
$\sup _n{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) \lt \infty$
and that the limits inferior are true limits. By the compactness of Remark 2.5, we know that, up to a non-relabelled subsequence,
![]() $\boldsymbol{\mu }^n \to \boldsymbol{\mu }$
weakly in
$\boldsymbol{\mu }^n \to \boldsymbol{\mu }$
weakly in
![]() $\mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}^d} \bigr )$
. Moreover, we also have
$\mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}^d} \bigr )$
. Moreover, we also have
![]() ${\, \mathrm{d}} \boldsymbol{\mu }(t,x) = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
for some measurable curve
${\, \mathrm{d}} \boldsymbol{\mu }(t,x) = \mu _t({\, \mathrm{d}} x){\, \mathrm{d}} t \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
for some measurable curve
![]() $t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}^d})$
of constant, finite mass. Once again, due to the lack of continuity of the trace operators in
$t \mapsto \mu _t \in \mathcal{M}_+({\mathbb{T}^d})$
of constant, finite mass. Once again, due to the lack of continuity of the trace operators in
![]() $\mathrm{BV}$
, we cannot ensure that
$\mathrm{BV}$
, we cannot ensure that
![]() $\boldsymbol{\mu }_{t=0} = \mu _0$
and
$\boldsymbol{\mu }_{t=0} = \mu _0$
and
![]() $\boldsymbol{\mu }_{t=1} = \mu _1$
. To solve this issue, we rescale our measures
$\boldsymbol{\mu }_{t=1} = \mu _1$
. To solve this issue, we rescale our measures
![]() $\boldsymbol{\mu }^n$
in time in the same spirit as in (3.12). For a given
$\boldsymbol{\mu }^n$
in time in the same spirit as in (3.12). For a given
![]() $\delta \gt 0$
, we define
$\delta \gt 0$
, we define
![]() $\mathcal{I}_\delta \,:\!=\, (\delta, 1-\delta )$
and
$\mathcal{I}_\delta \,:\!=\, (\delta, 1-\delta )$
and
![]() $\boldsymbol{\mu }^{n,\delta } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
as
$\boldsymbol{\mu }^{n,\delta } \in \mathrm{BV}_{\mathrm{KR}}\bigl ((0,1); \mathcal{M}_+({\mathbb{T}^d})\bigr )$
as
 \begin{align*} \mu _t^{n,\delta } \,:\!=\, \begin{cases} \mu _0^n &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }}^n &\text{if } t \in \mathcal{I}_\delta \\ \mu _1^n &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \boldsymbol{\mu }^{n,\delta }(t,x) \,:\!=\, \mu _t^{n,\delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
\begin{align*} \mu _t^{n,\delta } \,:\!=\, \begin{cases} \mu _0^n &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }}^n &\text{if } t \in \mathcal{I}_\delta \\ \mu _1^n &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \boldsymbol{\mu }^{n,\delta }(t,x) \,:\!=\, \mu _t^{n,\delta }({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
By construction, it is not hard to see that
![]() $\boldsymbol{\mu }^{n,\delta } \to \widehat{\boldsymbol{\mu }}^\delta$
weakly, where
$\boldsymbol{\mu }^{n,\delta } \to \widehat{\boldsymbol{\mu }}^\delta$
weakly, where
 \begin{align*} \widehat \mu _t^\delta \,:\!=\, \begin{cases} \mu _0 &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }} &\text{if } t \in \mathcal{I}_\delta \\ \mu _1 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \widehat{\boldsymbol{\mu }}^\delta (t,x) \,:\!=\, \widehat \mu _t^\delta ({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
\begin{align*} \widehat \mu _t^\delta \,:\!=\, \begin{cases} \mu _0 &\text{if } t \in (0,\delta ] \\ \mu _{\frac{t-\delta }{1-2\delta }} &\text{if } t \in \mathcal{I}_\delta \\ \mu _1 &\text{if } t \in [1-\delta, 1) \end{cases}, \quad{\, \mathrm{d}} \widehat{\boldsymbol{\mu }}^\delta (t,x) \,:\!=\, \widehat \mu _t^\delta ({\, \mathrm{d}} x){\, \mathrm{d}} t . \end{align*}
We stress that, as in (3.13), the rescaled curve
![]() $t \mapsto \widehat \mu _t^\delta$
could have discontinuities at
$t \mapsto \widehat \mu _t^\delta$
could have discontinuities at
![]() $t=\delta$
and
$t=\delta$
and
![]() $t= 1-\delta$
, corresponding to the possible jumps in the limit as
$t= 1-\delta$
, corresponding to the possible jumps in the limit as
![]() $n \to \infty$
for
$n \to \infty$
for
![]() $\boldsymbol{\mu }^n$
at
$\boldsymbol{\mu }^n$
at
![]() $\{0,1\}$
. Nevertheless,
$\{0,1\}$
. Nevertheless,
![]() $\widehat{\boldsymbol{\mu }}^\delta$
is a competitor for
$\widehat{\boldsymbol{\mu }}^\delta$
is a competitor for
![]() ${\mathbb{MA}}(\mu _0,\mu _1)$
, which, by lower semicontinuity of
${\mathbb{MA}}(\mu _0,\mu _1)$
, which, by lower semicontinuity of
![]() $\mathbb{A}$
, ensures that
$\mathbb{A}$
, ensures that
In order to estimate the left-hand side of the latter displayed equation, we seek a suitable vector meausure
![]() $\boldsymbol{\nu }^{n,\delta }$
so that
$\boldsymbol{\nu }^{n,\delta }$
so that
![]() $(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) \in \mathsf{CE}$
and whose action
$(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) \in \mathsf{CE}$
and whose action
![]() ${\mathbb{A}}(\boldsymbol{\mu }^{n,\delta },\boldsymbol{\nu }^{n,\delta })$
is comparable with
${\mathbb{A}}(\boldsymbol{\mu }^{n,\delta },\boldsymbol{\nu }^{n,\delta })$
is comparable with
![]() ${\mathbb{A}}(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n)$
for small
${\mathbb{A}}(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n)$
for small
![]() $\delta \gt 0$
.
$\delta \gt 0$
.
It is useful to introduce the following notation: for
![]() $\delta \in (0,1/2)$
,
$\delta \in (0,1/2)$
,
Define
![]() $\widehat \iota _\delta : \mathcal{M}^d(\mathcal{I}_\delta \times{\mathbb{T}^d}) \to \mathcal{M}^d\bigl ((0,1)\times{\mathbb{T}^d}\bigr )$
as the natural embedding obtained by extending to
$\widehat \iota _\delta : \mathcal{M}^d(\mathcal{I}_\delta \times{\mathbb{T}^d}) \to \mathcal{M}^d\bigl ((0,1)\times{\mathbb{T}^d}\bigr )$
as the natural embedding obtained by extending to
![]() $0$
any measure outside
$0$
any measure outside
![]() $\mathcal{I}_\delta$
, and set
$\mathcal{I}_\delta$
, and set
The proof that
![]() $( \boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta } ) \in \mathsf{CE}$
works as in (3.16). In the same spirit as in (3.15), we claim that
$( \boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta } ) \in \mathsf{CE}$
works as in (3.16). In the same spirit as in (3.15), we claim that
where
![]() $C(f) \in \mathbb{R}_+$
only depends on
$C(f) \in \mathbb{R}_+$
only depends on
![]() $f$
. The combination of (3.26), (3.27) and (3.28), and the arbitrariness of
$f$
. The combination of (3.26), (3.27) and (3.28), and the arbitrariness of
![]() $\delta$
would then suffice to conclude the proof.
$\delta$
would then suffice to conclude the proof.
We are left with the proof of the claim (3.28), which is a bit more involved, compared to that of (3.15), due to the presence of the singular part at the continuous level. We need the following.
Lemma 3.16. Let
![]() $\boldsymbol{\sigma } \in \mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}}^d \bigr )$
be a singular measure with respect to
$\boldsymbol{\sigma } \in \mathcal{M}_+\bigl ( (0,1) \times{\mathbb{T}}^d \bigr )$
be a singular measure with respect to
![]() $\mathscr{L}^{\,d+1}$
. Then, the measure
$\mathscr{L}^{\,d+1}$
. Then, the measure
![]() $(R_\delta )_{\#} \boldsymbol{\sigma } \in \mathcal{M}_+ (\mathcal{I}_\delta \times{\mathbb{T}^d})$
is also singular with respect to
$(R_\delta )_{\#} \boldsymbol{\sigma } \in \mathcal{M}_+ (\mathcal{I}_\delta \times{\mathbb{T}^d})$
is also singular with respect to
![]() $\mathscr{L}^{\,d+1}$
. Moreover, for every measure
$\mathscr{L}^{\,d+1}$
. Moreover, for every measure
![]() $\boldsymbol{\xi } = f \mathscr{L}^{\,d+1} + f^\perp \boldsymbol{\sigma } \in \mathcal{M}^n((0,1) \times{\mathbb{T}^d})$
, we have the decomposition
$\boldsymbol{\xi } = f \mathscr{L}^{\,d+1} + f^\perp \boldsymbol{\sigma } \in \mathcal{M}^n((0,1) \times{\mathbb{T}^d})$
, we have the decomposition
where the respective densities are given by the formulas
Proof. By assumption,
![]() $\boldsymbol{\sigma }$
is singular with respect to
$\boldsymbol{\sigma }$
is singular with respect to
![]() $\mathscr{L}^{\,d+1}$
, which means there exists a set
$\mathscr{L}^{\,d+1}$
, which means there exists a set
![]() $A \subset (0,1) \times{\mathbb{T}^d}$
such that
$A \subset (0,1) \times{\mathbb{T}^d}$
such that
![]() $\mathscr{L}^{\,d+1}(A) = 0 = \boldsymbol{\sigma }(A^c)$
. By the very definition of push-forward and the bijectivity of
$\mathscr{L}^{\,d+1}(A) = 0 = \boldsymbol{\sigma }(A^c)$
. By the very definition of push-forward and the bijectivity of
![]() $R_\delta$
, we then have that
$R_\delta$
, we then have that
whereas, by the scaling properties of the Lebesgue measure, we have that
![]() $\mathscr{L}^{\,d+1}(R_\delta (A)) = (1-2\delta ) \mathscr{L}^{\,d+1}(A) = 0$
, which shows the claimed singularity. The second part of the lemma follows from the fact that
$\mathscr{L}^{\,d+1}(R_\delta (A)) = (1-2\delta ) \mathscr{L}^{\,d+1}(A) = 0$
, which shows the claimed singularity. The second part of the lemma follows from the fact that
![]() $(R_\delta )_{\#} \mathscr{L}^{\,d+1} = (1-2\delta )^{-1} \mathscr{L}^{\,d+1}$
and the following statement: for every
$(R_\delta )_{\#} \mathscr{L}^{\,d+1} = (1-2\delta )^{-1} \mathscr{L}^{\,d+1}$
and the following statement: for every
![]() $\boldsymbol{\xi }' = f' \boldsymbol{\sigma }'$
with
$\boldsymbol{\xi }' = f' \boldsymbol{\sigma }'$
with
![]() $\boldsymbol{\sigma }' \in \mathcal{M}_+((0,1) \times{\mathbb{T}^d})$
, we claim that
$\boldsymbol{\sigma }' \in \mathcal{M}_+((0,1) \times{\mathbb{T}^d})$
, we claim that
Indeed, by definition of push-forward, we have for every test function
![]() $\varphi \in C_b$
$\varphi \in C_b$
which indeed shows (3.29).
Let
be Lebesgue decompositions. We apply Lemma 3.16 to both
![]() $\boldsymbol{\mu }^n$
and
$\boldsymbol{\mu }^n$
and
![]() $\boldsymbol{\nu }^n$
and find that, on
$\boldsymbol{\nu }^n$
and find that, on
![]() $\mathcal{I}_\delta \times{\mathbb{T}^d}$
, we have
$\mathcal{I}_\delta \times{\mathbb{T}^d}$
, we have
with
![]() $(R_\delta )_{\#} \boldsymbol{\sigma }$
singular with respect to
$(R_\delta )_{\#} \boldsymbol{\sigma }$
singular with respect to
![]() $\mathscr{L}^{\,d+1}$
and
$\mathscr{L}^{\,d+1}$
and
 \begin{align} \rho ^{n,\delta }(t,x) &= \big ( \rho ^n \circ R_\delta ^{-1} \big ) (t,x), \qquad &&\rho ^{n, \delta, \perp }(t,x) = (1-2\delta ) \big ( \rho ^{n,\perp } \circ R_\delta ^{-1} \big ) (t,x), \\ j^{n,\delta }(t,x) &= \frac 1{1-2\delta } \big ( j^n \circ R_\delta ^{-1} \big ) (t,x), \qquad &&j^{n, \delta, \perp }(t,x) = \big ( j^{n,\perp } \circ R_\delta ^{-1} \big ) .\nonumber \end{align}
\begin{align} \rho ^{n,\delta }(t,x) &= \big ( \rho ^n \circ R_\delta ^{-1} \big ) (t,x), \qquad &&\rho ^{n, \delta, \perp }(t,x) = (1-2\delta ) \big ( \rho ^{n,\perp } \circ R_\delta ^{-1} \big ) (t,x), \\ j^{n,\delta }(t,x) &= \frac 1{1-2\delta } \big ( j^n \circ R_\delta ^{-1} \big ) (t,x), \qquad &&j^{n, \delta, \perp }(t,x) = \big ( j^{n,\perp } \circ R_\delta ^{-1} \big ) .\nonumber \end{align}
Further consider the Lebesgue decompositions
for some
![]() $\sigma _1,\sigma _2 \in \mathcal{M}_+({\mathbb{T}}^d)$
singular w.r.t.
$\sigma _1,\sigma _2 \in \mathcal{M}_+({\mathbb{T}}^d)$
singular w.r.t.
![]() $\mathscr{L}^d$
. The action of
$\mathscr{L}^d$
. The action of
![]() $(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta })$
is given byFootnote
2
$(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta })$
is given byFootnote
2
where we used the notation
Making use of the formulas (3.30) and the homogeneity of
![]() $f^\infty$
, we find
$f^\infty$
, we find
 \begin{align} {\mathbb{A}}^{\mathcal{I}_\delta }&(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) = (1-2\delta ) \int _{(0,1) \times{\mathbb{T}^d}} f\Big ( \rho ^n, \frac{j^n}{1-2\delta } \Big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} f^\infty \big ( (1-2\delta ) \rho ^{n,\perp }, j^{n,\perp } \big ){\, \mathrm{d}} \boldsymbol{\sigma } \\ &\qquad = (1-2\delta ) \bigg ( \int _{(0,1) \times{\mathbb{T}^d}} f\Big ( \rho ^n, \frac{j^n}{1-2\delta } \Big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} f^\infty \Big ( \rho ^{n,\perp }, \frac{j^{n,\perp }}{1-2\delta } \Big ){\, \mathrm{d}} \boldsymbol{\sigma } \bigg ) .\nonumber \end{align}
\begin{align} {\mathbb{A}}^{\mathcal{I}_\delta }&(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) = (1-2\delta ) \int _{(0,1) \times{\mathbb{T}^d}} f\Big ( \rho ^n, \frac{j^n}{1-2\delta } \Big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} f^\infty \big ( (1-2\delta ) \rho ^{n,\perp }, j^{n,\perp } \big ){\, \mathrm{d}} \boldsymbol{\sigma } \\ &\qquad = (1-2\delta ) \bigg ( \int _{(0,1) \times{\mathbb{T}^d}} f\Big ( \rho ^n, \frac{j^n}{1-2\delta } \Big ){\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} f^\infty \Big ( \rho ^{n,\perp }, \frac{j^{n,\perp }}{1-2\delta } \Big ){\, \mathrm{d}} \boldsymbol{\sigma } \bigg ) .\nonumber \end{align}
Furthermore, it follows from the linear growth assumption that, for
![]() $i=0,1$
,
$i=0,1$
,
as well as, by (3.31), the nonnegativity of
![]() $f$
, and Assumption 2.2,
$f$
, and Assumption 2.2,
 \begin{align*}{\mathbb{A}}^{\mathcal{I}_\delta }(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) &\leq{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) + 2\delta (\mathrm{Lip} f ) \bigg ( \int _{(0,1) \times{\mathbb{T}^d}} | j^n |{\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} | j^{n,\perp } |{\, \mathrm{d}} \boldsymbol{\sigma } \bigg ) \\ &\leq{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) + \frac{2 \delta (\mathrm{Lip} f)}{c} \bigg ({\mathbb{A}}(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n) + C(1+\|\boldsymbol{\mu }^n\|_{\mathrm{TV}}) \bigg ) . \end{align*}
\begin{align*}{\mathbb{A}}^{\mathcal{I}_\delta }(\boldsymbol{\mu }^{n,\delta }, \boldsymbol{\nu }^{n,\delta }) &\leq{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) + 2\delta (\mathrm{Lip} f ) \bigg ( \int _{(0,1) \times{\mathbb{T}^d}} | j^n |{\, \mathrm{d}} \mathscr{L}^{\,d+1} + \int _{(0,1) \times{\mathbb{T}^d}} | j^{n,\perp } |{\, \mathrm{d}} \boldsymbol{\sigma } \bigg ) \\ &\leq{\mathbb{A}}(\boldsymbol{\mu }^n, \boldsymbol{\nu }^n) + \frac{2 \delta (\mathrm{Lip} f)}{c} \bigg ({\mathbb{A}}(\boldsymbol{\mu }^n,\boldsymbol{\nu }^n) + C(1+\|\boldsymbol{\mu }^n\|_{\mathrm{TV}}) \bigg ) . \end{align*}
We thus conclude (3.28).
4. Analysis of the cell problem with examples
This section is devoted to the characterisation and illustration of
![]() $f_{\mathrm{hom}}$
in the case where the function
$f_{\mathrm{hom}}$
in the case where the function
![]() $F$
is of the form
$F$
is of the form
for some strictly positive function
![]() $\alpha : \mathcal{E}^Q \ni (x,y) \mapsto \alpha _{xy}\gt 0$
. A natural problem of interest is to determine whether/when the
$\alpha : \mathcal{E}^Q \ni (x,y) \mapsto \alpha _{xy}\gt 0$
. A natural problem of interest is to determine whether/when the
![]() $\Gamma$
-limit
$\Gamma$
-limit
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
can be the
${\mathbb{MA}}_{\mathrm{hom}}$
can be the
![]() $W_1$
-distance. The analogous problem for the
$W_1$
-distance. The analogous problem for the
![]() $W_2$
-distance has been extensively studied in [Reference Gladbach, Kopfer and Maas24] and [Reference Gladbach, Kopfer, Maas and Portinale23] in the case where the graph stucture is associated with finite-volume partitions.
$W_2$
-distance has been extensively studied in [Reference Gladbach, Kopfer and Maas24] and [Reference Gladbach, Kopfer, Maas and Portinale23] in the case where the graph stucture is associated with finite-volume partitions.
4.1. Discrete
 $1$
-Wasserstein distance
$1$
-Wasserstein distance
We start the analysis of this special setting by observing that, in this case, the discrete functional
![]() ${\mathcal{MA}}_{\varepsilon }$
actually coincides with the
${\mathcal{MA}}_{\varepsilon }$
actually coincides with the
![]() $\mathbb{W}_1$
distance associated to a natural induced metric structure. In order to prove this fact, we first define
$\mathbb{W}_1$
distance associated to a natural induced metric structure. In order to prove this fact, we first define
![]() $\widetilde \alpha ^{\varepsilon } : \mathcal{E}_{\varepsilon } \to \mathbb{R}_+$
as the unique function such that
$\widetilde \alpha ^{\varepsilon } : \mathcal{E}_{\varepsilon } \to \mathbb{R}_+$
as the unique function such that
It is easy to check that this definition is well-posed and determines the value of
![]() $\widetilde \alpha _{xy}$
for every
$\widetilde \alpha _{xy}$
for every
![]() $(x,y) \in \mathcal{E}_{\varepsilon }$
. Further let
$(x,y) \in \mathcal{E}_{\varepsilon }$
. Further let
be the symmetrisation of
![]() $\widetilde \alpha ^{\varepsilon }$
. Given
$\widetilde \alpha ^{\varepsilon }$
. Given
![]() $J \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
, we can write
$J \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
, we can write
![]() $\mathcal{F}_{\varepsilon }(J)$
in terms of
$\mathcal{F}_{\varepsilon }(J)$
in terms of
![]() $\alpha ^{\varepsilon }$
. Precisely,
$\alpha ^{\varepsilon }$
. Precisely,
 \begin{align*} \mathcal{F}_{\varepsilon }(J) &= \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F \left ( \frac{\tau _{\varepsilon }^z J }{\varepsilon ^{d-1}} \right ) = \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d \sum _{(\widehat x, \widehat y) \in \mathcal{E}^Q } \alpha _{\widehat x \widehat y} \frac{ \lvert \tau ^z_{\varepsilon } J(\widehat x, \widehat y)\rvert }{\varepsilon ^{d-1}} \\ &= \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \sum _{(\widehat x, \widehat y) \in \mathcal{E}^Q} \tau ^z_{\varepsilon } \widetilde \alpha ^{\varepsilon }(\widehat x, \widehat y) \lvert \tau _{\varepsilon }^z J(\widehat x, \widehat y)\rvert = \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \widetilde \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert \\ &= \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert, \end{align*}
\begin{align*} \mathcal{F}_{\varepsilon }(J) &= \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d F \left ( \frac{\tau _{\varepsilon }^z J }{\varepsilon ^{d-1}} \right ) = \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \varepsilon ^d \sum _{(\widehat x, \widehat y) \in \mathcal{E}^Q } \alpha _{\widehat x \widehat y} \frac{ \lvert \tau ^z_{\varepsilon } J(\widehat x, \widehat y)\rvert }{\varepsilon ^{d-1}} \\ &= \sum _{z \in \mathbb{Z}^d_{\varepsilon }} \sum _{(\widehat x, \widehat y) \in \mathcal{E}^Q} \tau ^z_{\varepsilon } \widetilde \alpha ^{\varepsilon }(\widehat x, \widehat y) \lvert \tau _{\varepsilon }^z J(\widehat x, \widehat y)\rvert = \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \widetilde \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert \\ &= \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert, \end{align*}
where in the last passage we used that
![]() $\lvert J\rvert$
is symmetric. We define a distance on
$\lvert J\rvert$
is symmetric. We define a distance on
![]() $\mathcal{X}_{\varepsilon }$
given by
$\mathcal{X}_{\varepsilon }$
given by
One can easily show that
![]() $d_{\varepsilon }$
indeed defines a metric on
$d_{\varepsilon }$
indeed defines a metric on
![]() $\mathcal{X}_{\varepsilon }$
. In fact,
$\mathcal{X}_{\varepsilon }$
. In fact,
![]() $d_{\varepsilon }$
can be seen as a weighted graph distance.
$d_{\varepsilon }$
can be seen as a weighted graph distance.
Proposition 4.1.
For every
![]() $x,y \in \mathcal{X}_{\varepsilon }$
, we have
$x,y \in \mathcal{X}_{\varepsilon }$
, we have
 \begin{equation*} d_{\varepsilon }(x,y) = \inf \left \{ \sum _{i=0}^{k-1} 2 \alpha _{x_i x_{i+1}}^{\varepsilon } \, : \, x_0 = x, \, x_k = y, \, (x_i,x_{i+1}) \in \mathcal {E}_{\varepsilon } \ \, \, \forall i, \, k \in \mathbb {N} \right \} . \end{equation*}
\begin{equation*} d_{\varepsilon }(x,y) = \inf \left \{ \sum _{i=0}^{k-1} 2 \alpha _{x_i x_{i+1}}^{\varepsilon } \, : \, x_0 = x, \, x_k = y, \, (x_i,x_{i+1}) \in \mathcal {E}_{\varepsilon } \ \, \, \forall i, \, k \in \mathbb {N} \right \} . \end{equation*}
Proof. The inequality
![]() $\le$
directly follows by choosing unit fluxes along admissible paths: let
$\le$
directly follows by choosing unit fluxes along admissible paths: let
![]() $x_0=x,x_1,\dots, x_{k-1},x_k=y$
be a path, i.e.
$x_0=x,x_1,\dots, x_{k-1},x_k=y$
be a path, i.e.
![]() $(x_i,x_{i+1}) \in \mathcal{E}_{\varepsilon }$
for every
$(x_i,x_{i+1}) \in \mathcal{E}_{\varepsilon }$
for every
![]() $i = 0,1,\dots, k$
, and consider
$i = 0,1,\dots, k$
, and consider
which has divergence equal to
![]() $\delta _x-\delta _y$
. Then,
$\delta _x-\delta _y$
. Then,
 \begin{align*} d_{\varepsilon }(x,y) &={\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y) = \inf \left \{ \mathcal{F}_{\varepsilon }(J) \, : \, \mathsf{div} J = \delta _x-\delta _y \right \} \\ &= \inf \left \{ \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert \, : \, \mathsf{div} J = \delta _x-\delta _y \right \} \\ &\le \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J^P(x,y)\rvert \le \sum _{i=0}^{k-1} 2 \alpha _{x_i x_{i+1}}^{\varepsilon }, \end{align*}
\begin{align*} d_{\varepsilon }(x,y) &={\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y) = \inf \left \{ \mathcal{F}_{\varepsilon }(J) \, : \, \mathsf{div} J = \delta _x-\delta _y \right \} \\ &= \inf \left \{ \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J(x, y)\rvert \, : \, \mathsf{div} J = \delta _x-\delta _y \right \} \\ &\le \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \alpha ^{\varepsilon }_{xy} \lvert J^P(x,y)\rvert \le \sum _{i=0}^{k-1} 2 \alpha _{x_i x_{i+1}}^{\varepsilon }, \end{align*}
where in the last inequality we used that
![]() $\alpha ^{\varepsilon }$
is symmetric.
$\alpha ^{\varepsilon }$
is symmetric.
To prove the converse, let
![]() $\bar J \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
be an optimal flux for
$\bar J \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
be an optimal flux for
![]() ${\mathcal{MA}}_{\varepsilon }(\delta _x,\delta _y)$
, that is,
${\mathcal{MA}}_{\varepsilon }(\delta _x,\delta _y)$
, that is,
Since the graph
![]() $\mathcal{E}_{\varepsilon }$
is finite, in order for
$\mathcal{E}_{\varepsilon }$
is finite, in order for
![]() $\bar J$
to satisfy the divergence condition, there must exist a simple path
$\bar J$
to satisfy the divergence condition, there must exist a simple path
![]() $x_0 = x, x_1,\dots, x_k = y$
such that
$x_0 = x, x_1,\dots, x_k = y$
such that
![]() $(x_i,x_{i+1}) \in \mathcal{E}_{\varepsilon }$
and
$(x_i,x_{i+1}) \in \mathcal{E}_{\varepsilon }$
and
![]() $\bar J(x_i,x_{i+1}) \gt 0$
for every
$\bar J(x_i,x_{i+1}) \gt 0$
for every
![]() $i$
. Let
$i$
. Let
![]() $J^P$
be the associated vector field as in (4.2). Note that, for every
$J^P$
be the associated vector field as in (4.2). Note that, for every
![]() $\lambda \in \mathbb{R}$
, we have
$\lambda \in \mathbb{R}$
, we have
![]() $\mathsf{div} \bigl ((1-\lambda ) \bar J + \lambda J^P\bigr ) = \delta _x - \delta _y$
. Furthermore, the function
$\mathsf{div} \bigl ((1-\lambda ) \bar J + \lambda J^P\bigr ) = \delta _x - \delta _y$
. Furthermore, the function
is differentiable at
![]() $\lambda = 0$
, since
$\lambda = 0$
, since
![]() $(\bar J(x,y) = 0) \Rightarrow (J^P(x,y) = 0)$
. By optimality, the derivative at
$(\bar J(x,y) = 0) \Rightarrow (J^P(x,y) = 0)$
. By optimality, the derivative at
![]() $\lambda = 0$
must equal
$\lambda = 0$
must equal
![]() $0$
, i.e.
$0$
, i.e.
and, since
![]() $(J^P(x,y) \neq 0) \Rightarrow ({\textrm{sgn}}\, J^P(x,y) ={\textrm{sgn}}\, \bar J(x,y))$
, we have
$(J^P(x,y) \neq 0) \Rightarrow ({\textrm{sgn}}\, J^P(x,y) ={\textrm{sgn}}\, \bar J(x,y))$
, we have
 \begin{equation*} d_{\varepsilon }(x,y) = \sum _{(x,y) \in \mathcal {E}_{\varepsilon }} \alpha _{xy}^{\varepsilon } \lvert J^P(x,y)\rvert = 2\sum _{i=1}^k \alpha _{x_i x_{i+1}}^{\varepsilon }, \end{equation*}
\begin{equation*} d_{\varepsilon }(x,y) = \sum _{(x,y) \in \mathcal {E}_{\varepsilon }} \alpha _{xy}^{\varepsilon } \lvert J^P(x,y)\rvert = 2\sum _{i=1}^k \alpha _{x_i x_{i+1}}^{\varepsilon }, \end{equation*}
where, in the last equality, we used that the path is simple (and the symmetry of
![]() $\alpha ^{\varepsilon }$
). This shows the inequality
$\alpha ^{\varepsilon }$
). This shows the inequality
![]() $\geq$
and concludes the proof.
$\geq$
and concludes the proof.
Consider the
![]() $1$
-Wasserstein distance associted to
$1$
-Wasserstein distance associted to
![]() $d_{\varepsilon }$
, that is,
$d_{\varepsilon }$
, that is,
as well as, by Kantorovich duality,
for every
![]() $m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
.
$m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
.
Proposition 4.2.
For every
![]() $m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
, we have
$m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
, we have
Proof of ≥. Fix
![]() $m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
and set
$m_0,m_1 \in \mathscr{P}(\mathcal{X}_{\varepsilon })$
and set
![]() $m\,:\!=\, m_0-m_1$
. Let
$m\,:\!=\, m_0-m_1$
. Let
![]() $\bar J \in \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
be an optimal flux for
$\bar J \in \mathbb{R}_a^{\mathcal{E}_{\varepsilon }}$
be an optimal flux for
![]() ${\mathcal{MA}}_{\varepsilon }(m_0,m_1)$
, that is,
${\mathcal{MA}}_{\varepsilon }(m_0,m_1)$
, that is,
Let
![]() $\varphi : \mathcal{X}_{\varepsilon } \to \mathbb{R}$
be such that
$\varphi : \mathcal{X}_{\varepsilon } \to \mathbb{R}$
be such that
![]() $\mathrm{Lip}_{d_{\varepsilon }} \varphi \leq 1$
, i.e.
$\mathrm{Lip}_{d_{\varepsilon }} \varphi \leq 1$
, i.e.
![]() $ \left | \varphi (y) - \varphi (x) \right | \leq d_{\varepsilon }(x,y)$
for
$ \left | \varphi (y) - \varphi (x) \right | \leq d_{\varepsilon }(x,y)$
for
![]() $ x, y \in \mathcal{X}_{\varepsilon } .$
Then,
$ x, y \in \mathcal{X}_{\varepsilon } .$
Then,
 \begin{align*} \int _{\mathcal{X}_{\varepsilon }} \varphi{\, \mathrm{d}} m &= \int _{\mathcal{X}_{\varepsilon }} \varphi{\, \mathrm{d}} \mathsf{div} \bar J = \sum _{x \in \mathcal{X}_{\varepsilon }} \varphi (x) \sum _{y \sim x} \bar J(x,y) = \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \varphi (x) \big ( \bar J(x,y) - \bar J(y,x) \big )\\ &= \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \big ( \varphi (y) - \varphi (x) \big ) \bar J(x,y) \leq \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} d_{\varepsilon }(x,y) \lvert \bar J(x,y)\rvert . \end{align*}
\begin{align*} \int _{\mathcal{X}_{\varepsilon }} \varphi{\, \mathrm{d}} m &= \int _{\mathcal{X}_{\varepsilon }} \varphi{\, \mathrm{d}} \mathsf{div} \bar J = \sum _{x \in \mathcal{X}_{\varepsilon }} \varphi (x) \sum _{y \sim x} \bar J(x,y) = \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \varphi (x) \big ( \bar J(x,y) - \bar J(y,x) \big )\\ &= \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} \big ( \varphi (y) - \varphi (x) \big ) \bar J(x,y) \leq \frac 12 \sum _{(x,y) \in \mathcal{E}_{\varepsilon }} d_{\varepsilon }(x,y) \lvert \bar J(x,y)\rvert . \end{align*}
In order to conclude, we make the following crucial observation: as a consequence of the optimality of
![]() $\bar J$
, we claim that
$\bar J$
, we claim that
To this end, assume that
![]() $\bar J(x,y) \neq 0$
and consider an optimal
$\bar J(x,y) \neq 0$
and consider an optimal
![]() $J^{(x,y)}$
for
$J^{(x,y)}$
for
![]() $d_{\varepsilon }(x,y) ={\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y)$
. Note that, by construction,
$d_{\varepsilon }(x,y) ={\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y)$
. Note that, by construction,
which in turns also implies that
By optimality of
![]() $J^{(x,y)}$
, we have
$J^{(x,y)}$
, we have
whereas the optimality of
![]() $\bar J$
yields
$\bar J$
yields
 \begin{align*} \mathcal{F}_{\varepsilon } \bigl (\bar J + \bar J(x,y) \big ( J^{(x,y)} - \widetilde J \big )\bigr ) &= \sum _{(\widetilde x, \widetilde y) \in \mathcal{E}_{\varepsilon } \setminus \{(x,y), (y,x)\} } \alpha _{\widetilde x \widetilde y}^{\varepsilon } \lvert \bar J(\widetilde x, \widetilde y) + \bar J(x,y) J^{(x,y)}(\widetilde x, \widetilde y)\rvert \\ &\quad + \alpha _{xy}^{\varepsilon } \lvert \bar J(x,y) J^{(x,y)}(x,y)\rvert + \alpha _{yx}^{\varepsilon } \lvert \bar J(x,y) J^{(x,y)}(y,x)\rvert \\ &\ge \mathcal{F}_{\varepsilon }(\bar J) = \sum _{(\widetilde x, \widetilde y) \in \mathcal{E}_{\varepsilon }} \alpha _{\widetilde x\widetilde y}^{\varepsilon } \lvert \bar J(\widetilde x, \widetilde y)\rvert . \end{align*}
\begin{align*} \mathcal{F}_{\varepsilon } \bigl (\bar J + \bar J(x,y) \big ( J^{(x,y)} - \widetilde J \big )\bigr ) &= \sum _{(\widetilde x, \widetilde y) \in \mathcal{E}_{\varepsilon } \setminus \{(x,y), (y,x)\} } \alpha _{\widetilde x \widetilde y}^{\varepsilon } \lvert \bar J(\widetilde x, \widetilde y) + \bar J(x,y) J^{(x,y)}(\widetilde x, \widetilde y)\rvert \\ &\quad + \alpha _{xy}^{\varepsilon } \lvert \bar J(x,y) J^{(x,y)}(x,y)\rvert + \alpha _{yx}^{\varepsilon } \lvert \bar J(x,y) J^{(x,y)}(y,x)\rvert \\ &\ge \mathcal{F}_{\varepsilon }(\bar J) = \sum _{(\widetilde x, \widetilde y) \in \mathcal{E}_{\varepsilon }} \alpha _{\widetilde x\widetilde y}^{\varepsilon } \lvert \bar J(\widetilde x, \widetilde y)\rvert . \end{align*}
By applying the triangle inequality and simplifying the latter formula, we find
The combination of (4.5) and (4.6) implies
![]() $d_{\varepsilon }(x,y) = 2\alpha _{xy}^{\varepsilon }$
. With (4.4) at hand, we can write
$d_{\varepsilon }(x,y) = 2\alpha _{xy}^{\varepsilon }$
. With (4.4) at hand, we can write
and we conclude by arbitrariness of
![]() $\varphi$
.
$\varphi$
.
Proof of ≤. Let
![]() $\pi$
be such that
$\pi$
be such that
![]() $(e_i)_{\#} \pi = m_i$
for
$(e_i)_{\#} \pi = m_i$
for
![]() $i=0,1$
. Further, for every
$i=0,1$
. Further, for every
![]() $x,y \in \mathcal{X}_{\varepsilon }$
, let
$x,y \in \mathcal{X}_{\varepsilon }$
, let
![]() $J^{(x,y)} \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
be optimal for
$J^{(x,y)} \in \mathbb{R}^{\mathcal{E}_{\varepsilon }}_a$
be optimal for
![]() ${\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y)$
. It follows from a direct computation that the divergence of the asymmetric flux
${\mathcal{MA}}_{\varepsilon }(\delta _x, \delta _y)$
. It follows from a direct computation that the divergence of the asymmetric flux
is equal to
![]() $m_0 - m_1$
. Thus,
$m_0 - m_1$
. Thus,
and we conclude by arbitrariness of
![]() $\pi$
.
$\pi$
.
In view of the equality
![]() ${\mathcal{MA}}_{\varepsilon } = \mathbb{W}_{1,\varepsilon }$
, it is worth noting that for cost functions of the form (4.1) there are (at least) two different possible methods to show discrete-to-continuum limits for
${\mathcal{MA}}_{\varepsilon } = \mathbb{W}_{1,\varepsilon }$
, it is worth noting that for cost functions of the form (4.1) there are (at least) two different possible methods to show discrete-to-continuum limits for
![]() ${\mathcal{MA}}_{\varepsilon }$
. One such method is provided by the current work and makes use of the
${\mathcal{MA}}_{\varepsilon }$
. One such method is provided by the current work and makes use of the
![]() $\Gamma$
-convergence of
$\Gamma$
-convergence of
![]() $\mathcal{A}_{\varepsilon }$
to
$\mathcal{A}_{\varepsilon }$
to
![]() ${\mathbb{A}}_{\mathrm{hom}}$
proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4]. The convergence of the “weighted graph distance”
${\mathbb{A}}_{\mathrm{hom}}$
proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Theorem 5.4]. The convergence of the “weighted graph distance”
![]() $d_{\varepsilon }$
follows a posteriori. Another approach is to study directly the scaling limits of the distance
$d_{\varepsilon }$
follows a posteriori. Another approach is to study directly the scaling limits of the distance
![]() $d_{\varepsilon }$
as
$d_{\varepsilon }$
as
![]() $\varepsilon \to 0$
and, from that, infer the convergence of the associated
$\varepsilon \to 0$
and, from that, infer the convergence of the associated
![]() $1$
-Wasserstein distances, in a similar spirit as in [Reference Buttazzo, De Pascale and Fragalà4].
$1$
-Wasserstein distances, in a similar spirit as in [Reference Buttazzo, De Pascale and Fragalà4].
4.2. General properties of
 $f_{\mathrm{hom}}$
$f_{\mathrm{hom}}$
For
![]() $j \in \mathbb{R}^d$
, recall that
$j \in \mathbb{R}^d$
, recall that
where
![]() ${\mathsf{Rep}}(j)$
is the set of all
${\mathsf{Rep}}(j)$
is the set of all
![]() $\mathbb{Z}^d$
-periodic functions
$\mathbb{Z}^d$
-periodic functions
![]() $J \in \mathbb{R}^{\mathcal{E}}_a$
such that
$J \in \mathbb{R}^{\mathcal{E}}_a$
such that
As noted in [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.7], we may as well write
![]() $\min$
in place of
$\min$
in place of
![]() $\inf$
in (4.7).
$\inf$
in (4.7).
Our first observation is that, indeed, the homogenised density is a norm. This has already been proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Corollary 5.3]; for the sake of completeness, we provide here a simple proof in our setting.
Proposition 4.3.
The function
![]() $f_{\mathrm{hom}}$
is a norm.
$f_{\mathrm{hom}}$
is a norm.
Proof. Finiteness follows from the nonemptiness of the set of representatives proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Lemma 4.5]. To prove positiveness, take any
![]() $j \in \mathbb{R}^d$
and
$j \in \mathbb{R}^d$
and
![]() $J \in{\mathsf{Rep}}(j)$
. For every norm
$J \in{\mathsf{Rep}}(j)$
. For every norm
![]() $\|{\cdot }\|$
, we have
$\|{\cdot }\|$
, we have
The constant that multiplies
![]() $F(J)$
at the right-hand side is finite because every
$F(J)$
at the right-hand side is finite because every
![]() $\alpha _{xy}$
is strictly positive and the graph
$\alpha _{xy}$
is strictly positive and the graph
![]() $(\mathcal{X},\mathcal{E})$
is locally finite. Absolute homogeneity and the triangle inequality follow from the absolute homogeneity and subadditivity of
$(\mathcal{X},\mathcal{E})$
is locally finite. Absolute homogeneity and the triangle inequality follow from the absolute homogeneity and subadditivity of
![]() $F$
and the affinity of the constraints.
$F$
and the affinity of the constraints.
Hence,
![]() ${\mathbb{MA}}_{\mathrm{hom}}$
is always (i.e. for any choice of
${\mathbb{MA}}_{\mathrm{hom}}$
is always (i.e. for any choice of
![]() $(\alpha _{xy})_{x,y}$
and of the graph
$(\alpha _{xy})_{x,y}$
and of the graph
![]() $(\mathcal{X},\mathcal{E})$
) the
$(\mathcal{X},\mathcal{E})$
) the
![]() $W_1$
-distance w.r.t. some norm. However, the norm
$W_1$
-distance w.r.t. some norm. However, the norm
![]() $f_{\mathrm{hom}}$
can equal the
$f_{\mathrm{hom}}$
can equal the
![]() $2$
-norm
$2$
-norm
![]() $\lvert \cdot \rvert _2$
only in dimension
$\lvert \cdot \rvert _2$
only in dimension
![]() $d=1$
. In fact, the unit ball for
$d=1$
. In fact, the unit ball for
![]() $f_{\mathrm{hom}}$
has to be a polytope, namely the associated sphere is contained in the union of finitely many hyperplanes. These types of norms are also known as crystalline norms.
$f_{\mathrm{hom}}$
has to be a polytope, namely the associated sphere is contained in the union of finitely many hyperplanes. These types of norms are also known as crystalline norms.
Proposition 4.4.
The unit ball associated to the norm
![]() $f_{\mathrm{hom}}$
, namely
$f_{\mathrm{hom}}$
, namely
is the convex hull of finitely many points. In particular, the associated unit sphere is contained in the union of finitely many hyperplanes, i.e.
![]() $f_{\mathrm{hom}}$
is a crystalline norm.
$f_{\mathrm{hom}}$
is a crystalline norm.
Proof. Let
![]() $X$
be the vector space of all
$X$
be the vector space of all
![]() $\mathbb{Z}^d$
-periodic functions
$\mathbb{Z}^d$
-periodic functions
![]() $J \in \mathbb{R}^{\mathcal{E}}_a$
such that
$J \in \mathbb{R}^{\mathcal{E}}_a$
such that
![]() $\mathsf{div} J \equiv 0$
. The sublevel set
$\mathsf{div} J \equiv 0$
. The sublevel set
is clearly compact (due to the strict positivity of
![]() $(\alpha _{xy})_{x,y}$
) and can be written as finite intersection of half-spaces, namely
$(\alpha _{xy})_{x,y}$
) and can be written as finite intersection of half-spaces, namely
 \begin{equation*} X_1 = \bigcap _{r \in \{-1,1\}^{\mathcal {E}^Q} } \left \{ J \in X \, : \, \sum _{(x,y) \in \mathcal {E}^Q} \alpha _{xy} r_{xy} J(x,y) \le 1 \right \}. \end{equation*}
\begin{equation*} X_1 = \bigcap _{r \in \{-1,1\}^{\mathcal {E}^Q} } \left \{ J \in X \, : \, \sum _{(x,y) \in \mathcal {E}^Q} \alpha _{xy} r_{xy} J(x,y) \le 1 \right \}. \end{equation*}
Thus,
![]() $X_1$
is the convex hull of some finite set of points
$X_1$
is the convex hull of some finite set of points
![]() $A$
, that is,
$A$
, that is,
![]() $ X_1 ={\mathrm{conv}}(A)$
. Since
$ X_1 ={\mathrm{conv}}(A)$
. Since
![]() $f_{\mathrm{hom}}$
is defined as a minimum, we have
$f_{\mathrm{hom}}$
is defined as a minimum, we have
where the last equality is due to the linearity of
![]() $\mathsf{Eff}$
.
$\mathsf{Eff}$
.
4.3. Embedded graphs
To visualise some examples, we shall now focus on the case where
![]() $(\mathcal{X}, \mathcal{E})$
is embedded, in the sense that
$(\mathcal{X}, \mathcal{E})$
is embedded, in the sense that
![]() $V$
is a subset of
$V$
is a subset of
![]() $[0,1)^d$
, and we use the identification
$[0,1)^d$
, and we use the identification
![]() $(z,v) \equiv z+v$
(see also [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 2.2]). It has been proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Proposition 9.1] that, for embedded graphs, the identity
$(z,v) \equiv z+v$
(see also [[Reference Gladbach, Kopfer, Maas and Portinale23], Remark 2.2]). It has been proved in [[Reference Gladbach, Kopfer, Maas and Portinale23], Proposition 9.1] that, for embedded graphs, the identity
holds for every
![]() $\mathbb{Z}^d$
-periodic and divergence-free vector field
$\mathbb{Z}^d$
-periodic and divergence-free vector field
![]() $J \in \mathbb{R}^{\mathcal{E}}_a$
. In what follows, we also make the choice
$J \in \mathbb{R}^{\mathcal{E}}_a$
. In what follows, we also make the choice
4.3.1. One-dimensional case with nearest-neighbour interaction
Assume
![]() $d=1$
, let
$d=1$
, let
![]() $x_1 \lt x_2 \lt \cdots \lt x_k$
be an enumeration of
$x_1 \lt x_2 \lt \cdots \lt x_k$
be an enumeration of
![]() $V$
, and set
$V$
, and set
In other words, denoting
![]() $x_0 = x_k - 1$
and
$x_0 = x_k - 1$
and
![]() $x_{k+1} = x_1 + 1$
,
$x_{k+1} = x_1 + 1$
,
By rewriting (4.8) using (4.9), and by the definition of
![]() $f_{\mathrm{hom}}$
, we find
$f_{\mathrm{hom}}$
, we find
On the other hand, given
![]() $j \in \mathbb{R}^d$
, choose
$j \in \mathbb{R}^d$
, choose
This vector field is in
![]() ${\mathsf{Rep}}(j)$
because
${\mathsf{Rep}}(j)$
because
for every
![]() $i$
, and
$i$
, and
 \begin{align*} \mathsf{Eff}(J) &= \frac{1}{2} \sum _{i=1}^k \bigl ( J(x_i,x_{i+1})(x_{i+1}-x_i) + J(x_i,x_{i-1})(x_{i-1}-x_i) \bigr ) \\ &= \frac{j}{2} \sum _{i=1}^k \bigl ( \lvert x_{i+1} - x_i\rvert + \lvert x_i - x_{i-1}\rvert \bigr ) \\ &= \frac{j}{2} \bigl ( x_{k+1} - x_1 + x_k - x_0 \bigr ) \\ &= j. \end{align*}
\begin{align*} \mathsf{Eff}(J) &= \frac{1}{2} \sum _{i=1}^k \bigl ( J(x_i,x_{i+1})(x_{i+1}-x_i) + J(x_i,x_{i-1})(x_{i-1}-x_i) \bigr ) \\ &= \frac{j}{2} \sum _{i=1}^k \bigl ( \lvert x_{i+1} - x_i\rvert + \lvert x_i - x_{i-1}\rvert \bigr ) \\ &= \frac{j}{2} \bigl ( x_{k+1} - x_1 + x_k - x_0 \bigr ) \\ &= j. \end{align*}
A similar computation shows that
![]() $F(J) = \lvert j\rvert$
, from which
$F(J) = \lvert j\rvert$
, from which
![]() $f_{\mathrm{hom}}(j) = \lvert j\rvert$
.
$f_{\mathrm{hom}}(j) = \lvert j\rvert$
.

Figure 2.
Examples of graphs in
![]() $\mathbb{R}^2$
and corresponding unit balls for
$\mathbb{R}^2$
and corresponding unit balls for
![]() $f_{\mathrm{hom}}$
.
$f_{\mathrm{hom}}$
.
4.3.2. Cubic partition
Consider the case where
![]() $\mathcal{X} = \mathbb{Z}^d$
and
$\mathcal{X} = \mathbb{Z}^d$
and
It is a result of [[Reference Gladbach, Kopfer, Maas and Portinale23], Section 9.2] that
Notice that, in this case, the
![]() $2$
-norm is evaluated only at vectors on the coordinate axes. Therefore, the same result holds when
$2$
-norm is evaluated only at vectors on the coordinate axes. Therefore, the same result holds when
![]() $\alpha _{xy} = \frac{1}{2}\lvert x-y\rvert _p$
, for any
$\alpha _{xy} = \frac{1}{2}\lvert x-y\rvert _p$
, for any
![]() $p$
.
$p$
.
4.3.3. Graphs in
 $\mathbb{R}^2$
$\mathbb{R}^2$
A few other examples in dimension
![]() $d=2$
are shown in Figure 2: for each one, we display the graph and the unit ball in the corresponding norm
$d=2$
are shown in Figure 2: for each one, we display the graph and the unit ball in the corresponding norm
![]() $f_{\mathrm{hom}}$
. To algorithmically construct the unit balls, we solve the variational problem (4.7) for every
$f_{\mathrm{hom}}$
. To algorithmically construct the unit balls, we solve the variational problem (4.7) for every
![]() $j$
on a discretisation of the circle
$j$
on a discretisation of the circle
![]() $\mathbb S^1$
. In turn, this is achieved with the help of the Python library CVXPY [Reference Diamond and Boyd7], [Reference Agrawal, Verschueren, Diamond and Boyd3]. For visualisation, we make use of the library matplotlib [Reference Hunter28].
$\mathbb S^1$
. In turn, this is achieved with the help of the Python library CVXPY [Reference Diamond and Boyd7], [Reference Agrawal, Verschueren, Diamond and Boyd3]. For visualisation, we make use of the library matplotlib [Reference Hunter28].
Acknowledgements
The authors are very grateful to Jan Maas for his useful feedback on a preliminary version of this work. The authors also thank the anonymous reviewers for the careful reading of the manuscript and for useful suggestions. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper
Financial support
L.P. gratefully acknowledges fundings from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – GZ 2047/1, Projekt-ID 390685813. F.Q. gratefully acknowledges support from the Austrian Science Fund (FWF) project 10.55776/F65.
Competing interests
None.