Given an ergodic dynamical system (X,B,m, τ) and a probability measure μ on the integers, define for all f ∈ L1(X) The almost everywhere convergence of the convolution powers μnf(x) depends on the properties of μ. If μ has finite and then for all f ∈ Lp(X), 1< p < ∞, exists for a.e. x. However, if m2(μ) is finite and E(μ)≠0, then there exists E∈B such that a.e. and a.e. In the case when m2(μ) is infinite and E(μ)=0 we give examples for which we have divergence and other examples which show convergence is possible.

We present a class of S-unimodal maps having an invariant measure which is absolutely continuous with respect to Lebesgue measure. This measure can often be proved to be finite. We give an example of a map which has such a finite measure and for which the lim inf of the derivatives of the iterates of the map in the critical value is finite. It will be shown that all topologically conjugate non-flat S-unimodal maps have the same properties.

The pointwise spectral radii of irreducible matrices whose entries are polynomials with positive, integral coefficients are studied in this paper. Most results are derived in the case that the resulting algebraic function, the beta function of S. Tuncel, is in fact a polynomial. We show that the set of beta functions forms a semiring, and the spectral radius of a matrix of beta functions is again a beta function. We also show that the coefficients of a polynomial beta function p must be real algebraic integers, and p satisfies (after a change of variables if necessary) the inequality 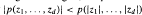for non-zero (and not all positive) complex numbers z1,…,zd. If 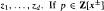and the ordered sequence of exponents appearing in p is of the form (m,m+1,…,M−,1,M) for some integers m and M, the same inequality is necessary and sufficient for p to be a beta function.

We study the properties of absolutely continuous invariant measures for one-dimensional transformations satisfying Schmitt's condition. We prove existence, constrictiveness of the induced Perron-Frobenius operator, openness of supports, estimate on a number of ergodic components, exponential decay of correlation, Bernoulli property, etc.

It is shown that three different notions of regularity for the stable foliation on the unit tangent bundle of a compact manifold of negative curvature are equivalent. Moreover if is a time-preserving conjugacy of geodesic flows of such manifolds M, N then the Lyapunov exponents at corresponding periodic points of the flows coincide. In particular Δ also preserves the Lebesgue measure class.

In this paper we consider almost everywhere convergence and divergence properties of various ergodic averages. A general method is given which can be used to construct averages for which a.e. convergence fails, and to show divergence (and in some cases ‘strong sweeping out’) for large classes of ergodic averages. We also show that there are sequences with the gaps between successive terms converging to zero, but such that the Cesaro averages obtained by sampling a flow along these sequences of times converge a.e. for all f∈L1(X).

For α ∈ (0, 1), let Γα denote the middle-α Cantor set contained in the interval [0,1]. Let denote the set of all t∈[−1,1] such that Γα ∩(Γα+t)is a single point. Both a geometric and a symbolic description of each is presented. The symbolic description of each will be as a shift invariant subset of the one-sided two shift that is determined by inequalities. An equivalence relation is defined on the one-sided two shift and then a linear order relation is defined on the equivalence classes. This order relation on the equivalence classes describes how the sets shrink as a decreases from ⅓ to 0.

The topological entropy of a transformation is expressed in terms of partitions of unity. The transverse entropy of a flow tangential to a foliation is defined and expresed in a similar way. The geometric entropy of a foliation of a Riemannian manifold is compared with the transverse entropy of its geodesic flow.

We study the spectrum of a transfer operator that gives a counterexample to the conjecture of Mayer. The effect of perturbations is considered.

Let T be the universal covering tree of a finite graph, G. By analogy with an open problem concerning negatively curved covering manifolds, Kaimanovich asked when two of the three natural measure classes on ∂T can coincide, the three measures being harmonic measure, the Patterson measure, and visibility measure. We provide an almost complete answer and discuss related issues. The answer is quite surprising in some cases.

We consider a compound central field in the Euclidean plane which is governed by a finite number of bell-shaped potential functions with finite range. The study of the qualitative behavior of the Hamilton flow in such a potential field can be reduced to that of the so-called perturbed billiards system. The main result in this paper is the construction of a symbolic dynamics of the Hamilton flow by using the perturbed billiards system provided that the energy E > 0 is small enough. We also try to show an analogue of the prime number theorem for the closed orbits of the flow following ideas presented by Morita and Parry and Pollicott.