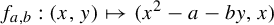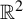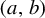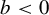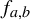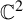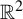1 Introduction and the main results
Consider the Hénon family
defined on
![]() ${\mathbb {R}}^2$
, where
${\mathbb {R}}^2$
, where
![]() $(a, b)\in {\mathbb {R}}\times {\mathbb {R}}^{\times }$
. Let
$(a, b)\in {\mathbb {R}}\times {\mathbb {R}}^{\times }$
. Let
![]() $\Omega (f_{a, b})$
be the non-wandering set of
$\Omega (f_{a, b})$
be the non-wandering set of
![]() $f_{a, b}$
. We say that
$f_{a, b}$
. We say that
![]() $f_{a, b}$
is a hyperbolic horseshoe on
$f_{a, b}$
is a hyperbolic horseshoe on
![]() ${\mathbb {R}}^2$
if
${\mathbb {R}}^2$
if
![]() $f_{a, b} : \Omega (f_{a, b}) \to \Omega (f_{a, b})$
is topologically conjugate to the full shift with two symbols and
$f_{a, b} : \Omega (f_{a, b}) \to \Omega (f_{a, b})$
is topologically conjugate to the full shift with two symbols and
![]() $\Omega (f_{a, b})$
is a hyperbolic set for
$\Omega (f_{a, b})$
is a hyperbolic set for
![]() $f_{a, b}$
. Denote by
$f_{a, b}$
. Denote by
![]() $h_{\mathrm {top}}(f_{a, b})$
the topological entropy of
$h_{\mathrm {top}}(f_{a, b})$
the topological entropy of
![]() $f_{a, b} : \Omega (f_{a, b}) \to \Omega (f_{a, b})$
. We know that
$f_{a, b} : \Omega (f_{a, b}) \to \Omega (f_{a, b})$
. We know that
![]() $0\leq h_{\mathrm {top}}(f_{a, b})\leq \log 2$
for any
$0\leq h_{\mathrm {top}}(f_{a, b})\leq \log 2$
for any
![]() $(a, b)\in {\mathbb {R}}\times {\mathbb {R}}^{\times }$
. Note also that if
$(a, b)\in {\mathbb {R}}\times {\mathbb {R}}^{\times }$
. Note also that if
![]() $f_{a, b}$
is a hyperbolic horseshoe, then
$f_{a, b}$
is a hyperbolic horseshoe, then
![]() $f_{a, b}$
attains the maximal entropy on
$f_{a, b}$
attains the maximal entropy on
![]() ${\mathbb {R}}^2$
, that is,
${\mathbb {R}}^2$
, that is,
![]() $h_{\mathrm {top}}(f_{a, b})=\log 2$
.
$h_{\mathrm {top}}(f_{a, b})=\log 2$
.
In [Reference Arai and IshiiAI], we have defined the hyperbolic horseshoe locus as
and the maximal entropy locus as
Let us set
![]() $\mathcal {H}_{{\mathbb {R}}}^{\pm }\equiv \mathcal {H}_{{\mathbb {R}}}\cap \{\pm b>0\}$
. Based on previous work [Reference Bedford and SmillieBSℝ2], it has been shown in [Reference Arai and IshiiAI] that there exists a real analytic function
$\mathcal {H}_{{\mathbb {R}}}^{\pm }\equiv \mathcal {H}_{{\mathbb {R}}}\cap \{\pm b>0\}$
. Based on previous work [Reference Bedford and SmillieBSℝ2], it has been shown in [Reference Arai and IshiiAI] that there exists a real analytic function
![]() $a_{\mathrm {tgc}} : {\mathbb {R}}^{\times } \to {\mathbb {R}}$
from the b-axis to the a-axis of the parameter space
$a_{\mathrm {tgc}} : {\mathbb {R}}^{\times } \to {\mathbb {R}}$
from the b-axis to the a-axis of the parameter space
![]() ${\mathbb {R}}\times {\mathbb {R}}^{\times }$
for the Hénon family
${\mathbb {R}}\times {\mathbb {R}}^{\times }$
for the Hénon family
![]() $f_{a, b}$
with
$f_{a, b}$
with
![]() $\lim _{b\to 0}a_{\mathrm {tgc}}(b)=2$
so that:
$\lim _{b\to 0}a_{\mathrm {tgc}}(b)=2$
so that:
-
•
 $(a, b)\in \mathcal {H}_{{\mathbb {R}}}$
if and only if
$(a, b)\in \mathcal {H}_{{\mathbb {R}}}$
if and only if
 $a>a_{\mathrm {tgc}}(b)$
;
$a>a_{\mathrm {tgc}}(b)$
; -
•
 $(a, b)\in \mathcal {M}_{{\mathbb {R}}}$
if and only if
$(a, b)\in \mathcal {M}_{{\mathbb {R}}}$
if and only if
 $a\geq a_{\mathrm {tgc}}(b)$
.
$a\geq a_{\mathrm {tgc}}(b)$
.
Moreover, it has been shown that:
-
• when
 $(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^+$
holds (that is,
$(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^+$
holds (that is,
 $a=a_{\mathrm {tgc}}(b)$
and
$a=a_{\mathrm {tgc}}(b)$
and
 $b>0$
),
$b>0$
),
 $f_{a, b}$
has exactly one orbit of homoclinic tangencies of
$f_{a, b}$
has exactly one orbit of homoclinic tangencies of
 $W^s(p_1)$
and
$W^s(p_1)$
and
 $W^u(p_1)$
;
$W^u(p_1)$
; -
• when
 $(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^-$
holds (that is,
$(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^-$
holds (that is,
 $a=a_{\mathrm {tgc}}(b)$
and
$a=a_{\mathrm {tgc}}(b)$
and
 $b<0$
),
$b<0$
),
 $f_{a, b}$
has exactly one orbit of heteroclinic tangencies of
$f_{a, b}$
has exactly one orbit of heteroclinic tangencies of
 $W^s(p_1)$
and
$W^s(p_1)$
and
 $W^u(p_3)$
,
$W^u(p_3)$
,
where
![]() $p_1$
(respectively
$p_1$
(respectively
![]() $p_3$
) is the unique saddle fixed point in the first (respectively third) quadrant. These results extend the previous assertions in [Reference Bedford and SmillieBSℝ2] for the case
$p_3$
) is the unique saddle fixed point in the first (respectively third) quadrant. These results extend the previous assertions in [Reference Bedford and SmillieBSℝ2] for the case
![]() $|b|<0.05$
to all
$|b|<0.05$
to all
![]() $b\ne 0$
. We note that their proofs (and the ones in [Reference Arai and IshiiAI] as well) rely on the profound theory of quasi-hyperbolicity [Reference Bedford and SmillieBSℂ8] combined with a detailed analysis of Hénon maps with maximal entropy [Reference Bedford and SmillieBSℝ1].
$b\ne 0$
. We note that their proofs (and the ones in [Reference Arai and IshiiAI] as well) rely on the profound theory of quasi-hyperbolicity [Reference Bedford and SmillieBSℂ8] combined with a detailed analysis of Hénon maps with maximal entropy [Reference Bedford and SmillieBSℝ1].
In their subsequent paper [Reference Bedford and SmillieBSℝ3], Bedford and Smillie classified the dynamics of
![]() $f_{a, b}$
in terms of a symbolic dynamics when
$f_{a, b}$
in terms of a symbolic dynamics when
![]() $(a, b)$
is close to the boundary
$(a, b)$
is close to the boundary
![]() $\partial \mathcal {H}_{{\mathbb {R}}}^+$
. However, their result holds only for
$\partial \mathcal {H}_{{\mathbb {R}}}^+$
. However, their result holds only for
![]() $0<b<0.4$
approximately because their construction is based on Yoccoz puzzle pieces for the complex one-dimensional map
$0<b<0.4$
approximately because their construction is based on Yoccoz puzzle pieces for the complex one-dimensional map
![]() $p(z)=z^2-1$
(see the last paragraph of [Reference Arai and IshiiAI, Appendix B]).
$p(z)=z^2-1$
(see the last paragraph of [Reference Arai and IshiiAI, Appendix B]).
The purpose of the current article is to generalize the results in [Reference Bedford and SmillieBSℝ3] for all
![]() $b\ne 0$
(including the case
$b\ne 0$
(including the case
![]() $b<0$
as well) by applying the new Markov-like partition constructed in [Reference Arai and IshiiAI]. To present our results, let us first recall that we have defined in [Reference Arai and IshiiAI] a neighborhood
$b<0$
as well) by applying the new Markov-like partition constructed in [Reference Arai and IshiiAI]. To present our results, let us first recall that we have defined in [Reference Arai and IshiiAI] a neighborhood
![]() $\mathcal {F}^{\pm }_{{\mathbb {R}}}$
of
$\mathcal {F}^{\pm }_{{\mathbb {R}}}$
of
![]() $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
so that
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
so that
![]() $f_{a, b}$
satisfies the crossed mapping condition with respect to a certain family of projective polydisks
$f_{a, b}$
satisfies the crossed mapping condition with respect to a certain family of projective polydisks
![]() $\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
for
$\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
for
![]() $(a, b)\in \mathcal {F}^{\pm }_{{\mathbb {R}}}$
(see [Reference Arai and IshiiAI, Theorem 2.12(iii)]). Moreover, their real sections
$(a, b)\in \mathcal {F}^{\pm }_{{\mathbb {R}}}$
(see [Reference Arai and IshiiAI, Theorem 2.12(iii)]). Moreover, their real sections
![]() $\mathcal {B}^{\pm }_i\cap {\mathbb {R}}^2$
cover the set
$\mathcal {B}^{\pm }_i\cap {\mathbb {R}}^2$
cover the set
![]() $K_{{\mathbb {R}}}$
of points in
$K_{{\mathbb {R}}}$
of points in
![]() ${\mathbb {R}}^2$
whose both forward and the backward orbits by
${\mathbb {R}}^2$
whose both forward and the backward orbits by
![]() $f_{a, b}$
are bounded. Let
$f_{a, b}$
are bounded. Let
![]() $a^{\pm }_{\mathrm {aprx}}$
be the piecewise linear function approximating
$a^{\pm }_{\mathrm {aprx}}$
be the piecewise linear function approximating
![]() $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
as in [Reference Arai and IshiiAI] and set
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
as in [Reference Arai and IshiiAI] and set
One can easily see that
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}\subset \mathcal {F}^{\pm }_{{\mathbb {R}}}$
. Moreover, in Appendix A, we show that
$\mathcal {E}^{\pm }_{{\mathbb {R}}}\subset \mathcal {F}^{\pm }_{{\mathbb {R}}}$
. Moreover, in Appendix A, we show that
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
$\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
![]() $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
(see Proposition A.1).
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
(see Proposition A.1).
Let
![]() $p_i\in {\mathbb {R}}^2$
be the unique saddle fixed point for
$p_i\in {\mathbb {R}}^2$
be the unique saddle fixed point for
![]() $i=1, 3$
and the unique saddle periodic point of period two for
$i=1, 3$
and the unique saddle periodic point of period two for
![]() $i=2, 4$
in the ith quadrant. In Theorem 4.3 (respectively Theorem 4.6), we obtain a partition of
$i=2, 4$
in the ith quadrant. In Theorem 4.3 (respectively Theorem 4.6), we obtain a partition of
![]() $K_{{\mathbb {R}}}\setminus (W^s(p_2)\cup W^s(p_4))$
(respectively
$K_{{\mathbb {R}}}\setminus (W^s(p_2)\cup W^s(p_4))$
(respectively
![]() $K_{{\mathbb {R}}}\setminus W^s(p_3)$
) into two parts, say, the left part and the right part for
$K_{{\mathbb {R}}}\setminus W^s(p_3)$
) into two parts, say, the left part and the right part for
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
(respectively for
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
(respectively for
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
). Figures 1 and 2 describe the shape of the partition pieces. This partition defines a coding with the alphabet
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
). Figures 1 and 2 describe the shape of the partition pieces. This partition defines a coding with the alphabet
![]() $\{L, R\}$
by assigning L to the left part and R to the right part. (Our coding is different from that in [Reference Bedford and SmillieBSℝ3] when
$\{L, R\}$
by assigning L to the left part and R to the right part. (Our coding is different from that in [Reference Bedford and SmillieBSℝ3] when
![]() $b>0$
is close to
$b>0$
is close to
![]() $0$
.) As pointed out in [Reference Bedford and SmillieBSℝ3], this coding has both advantages and disadvantages; an advantage is that it applies to Hénon maps degenerated from the horseshoe and a disadvantage is that the associated coding map is no more one-to-one.
$0$
.) As pointed out in [Reference Bedford and SmillieBSℝ3], this coding has both advantages and disadvantages; an advantage is that it applies to Hénon maps degenerated from the horseshoe and a disadvantage is that the associated coding map is no more one-to-one.

Figure 1
![]() $\{L, R\}$
-partition for
$\{L, R\}$
-partition for
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.

Figure 2
![]() $\{L, R\}$
-partition for
$\{L, R\}$
-partition for
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
Given a word w over an alphabet,
![]() $\overline {w}$
denotes either the left-infinite repetition
$\overline {w}$
denotes either the left-infinite repetition
![]() $\cdots www$
or the right-infinite repetition
$\cdots www$
or the right-infinite repetition
![]() $www \cdots $
(depending on the context). Let
$www \cdots $
(depending on the context). Let
![]() $\cdot $
be the ‘decimal point’ of a bi-infinite symbol sequence
$\cdot $
be the ‘decimal point’ of a bi-infinite symbol sequence
![]() $\cdots \varepsilon _{-1}\cdot \varepsilon _{0}\varepsilon _{1}\cdots $
. Our first main result concerns [Reference Bedford and SmillieBSℝ3, Theorem 1].
$\cdots \varepsilon _{-1}\cdot \varepsilon _{0}\varepsilon _{1}\cdots $
. Our first main result concerns [Reference Bedford and SmillieBSℝ3, Theorem 1].
Theorem 1.1. We have the following.
-
(1) When
 $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, there are at most two points in
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, there are at most two points in
 $K_{{\mathbb {R}}}\setminus (W^s(p_2)\cup W^s(p_4))$
with
$K_{{\mathbb {R}}}\setminus (W^s(p_2)\cup W^s(p_4))$
with
 $\{L, R\}$
-coding
$\{L, R\}$
-coding
 $\overline {R}L\cdot L\overline {R}\in \{L, R\}^{{\mathbb {Z}}}$
counted without multiplicity. Moreover:
$\overline {R}L\cdot L\overline {R}\in \{L, R\}^{{\mathbb {Z}}}$
counted without multiplicity. Moreover:-
(a)
 $f_{a, b}$
is a hyperbolic horseshoe on
$f_{a, b}$
is a hyperbolic horseshoe on
 ${\mathbb {R}}^2$
if and only if there are two such points;
${\mathbb {R}}^2$
if and only if there are two such points; -
(b)
 $f_{a, b}$
has a quadratic tangency but
$f_{a, b}$
has a quadratic tangency but
 $h_{\mathrm {top}}(f_{a, b})=\log 2$
if and only if there is one such point;
$h_{\mathrm {top}}(f_{a, b})=\log 2$
if and only if there is one such point; -
(c)
 $h_{\mathrm {top}}(f_{a, b})<\log 2$
if and only if there are no such points.
$h_{\mathrm {top}}(f_{a, b})<\log 2$
if and only if there are no such points.
-
-
(2) When
 $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, there are at most four points in
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, there are at most four points in
 $K_{{\mathbb {R}}}\setminus W^s(p_3)$
with
$K_{{\mathbb {R}}}\setminus W^s(p_3)$
with
 $\{L, R\}$
-coding
$\{L, R\}$
-coding
 $\overline {L}RR\cdot L\overline {R}\in \{L, R\}^{{\mathbb {Z}}}$
counted without multiplicity. Moreover:
$\overline {L}RR\cdot L\overline {R}\in \{L, R\}^{{\mathbb {Z}}}$
counted without multiplicity. Moreover:-
(a)
 $f_{a, b}$
is a hyperbolic horseshoe on
$f_{a, b}$
is a hyperbolic horseshoe on
 ${\mathbb {R}}^2$
if and only if there are four such points;
${\mathbb {R}}^2$
if and only if there are four such points; -
(b)
 $f_{a, b}$
has a quadratic tangency but
$f_{a, b}$
has a quadratic tangency but
 $h_{\mathrm {top}}(f_{a, b})=\log 2$
if and only if there are three such points;
$h_{\mathrm {top}}(f_{a, b})=\log 2$
if and only if there are three such points; -
(c)
 $h_{\mathrm {top}}(f_{a, b})<\log 2$
if and only if there are at most two such points.
$h_{\mathrm {top}}(f_{a, b})<\log 2$
if and only if there are at most two such points.
-
Obviously the map in either case (a) or (b) of Theorem 1.1 cannot be topologically conjugate to the map in case (c) because they have different values of topological entropy. M. Asaoka (private communication) pointed out that the map in case (b) is not expansive on its non-wandering set. Hence, the map in case (a) is not topologically conjugate to the map in case (b), that is, the map
![]() $f_{a, b}$
with
$f_{a, b}$
with
![]() $(a, b)\in \mathcal {H}_{{\mathbb {R}}}^{\pm }$
cannot be topologically conjugate to the map
$(a, b)\in \mathcal {H}_{{\mathbb {R}}}^{\pm }$
cannot be topologically conjugate to the map
![]() $f_{a, b}$
with
$f_{a, b}$
with
![]() $(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
$(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
We found that the paper [Reference Bedford and SmillieBSℝ3] does not contain a proof of its theorem 1 (which corresponds to our Theorem 1.1). Since our Theorem 1.1 originates from [Reference Bedford and SmillieBSℝ3, Theorem 1], we describe the proof of Theorem 1.1 in detail in §4.2. We also remark that the paper [Reference Bedford and SmillieBSℝ3] did not treat the case
![]() $b<0$
since their partition cannot directly apply to this case. Indeed, it can be shown that the number of points in
$b<0$
since their partition cannot directly apply to this case. Indeed, it can be shown that the number of points in
![]() $W^s(p_1)\cap W^u(p_3)$
having an appropriate
$W^s(p_1)\cap W^u(p_3)$
having an appropriate
![]() $\{L, R\}$
-coding with respect to the partition in [Reference Bedford and SmillieBSℝ3] is infinite and cannot provide a classification like [Reference Bedford and SmillieBSℝ3 Theorem 1] (see Remark 4.10).
$\{L, R\}$
-coding with respect to the partition in [Reference Bedford and SmillieBSℝ3] is infinite and cannot provide a classification like [Reference Bedford and SmillieBSℝ3 Theorem 1] (see Remark 4.10).
Next we analyze case (b) of Theorem 1.1 in detail. Denote by
![]() $\sigma : \{\alpha , \beta \}^{{\mathbb {Z}}}\to \{\alpha , \beta \}^{{\mathbb {Z}}}$
the shift map on the space of bi-infinite sequences with two symbols. Our second main result concerns [Reference Bedford and SmillieBSℝ3, Theorem 2].
$\sigma : \{\alpha , \beta \}^{{\mathbb {Z}}}\to \{\alpha , \beta \}^{{\mathbb {Z}}}$
the shift map on the space of bi-infinite sequences with two symbols. Our second main result concerns [Reference Bedford and SmillieBSℝ3, Theorem 2].
Theorem 1.2 We have the following.
-
(1) If
 $(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^+$
, then
$(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^+$
, then
 $f_{a, b} : \Omega (f_{a, b})\to \Omega (f_{a, b})$
is topologically conjugate to the factor map
$f_{a, b} : \Omega (f_{a, b})\to \Omega (f_{a, b})$
is topologically conjugate to the factor map
 $\sigma /_{\sim } : \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }\to \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }$
, where we define
$\sigma /_{\sim } : \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }\to \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }$
, where we define
 $\sim $
as
$\sim $
as  $$ \begin{align*}\sigma^n(\overline{\alpha}\beta\cdot \beta\beta\overline{\alpha})\sim \sigma^n(\overline{\alpha}\beta\cdot \alpha\beta\overline{\alpha})\end{align*} $$
$$ \begin{align*}\sigma^n(\overline{\alpha}\beta\cdot \beta\beta\overline{\alpha})\sim \sigma^n(\overline{\alpha}\beta\cdot \alpha\beta\overline{\alpha})\end{align*} $$
for all
 $n\in \mathbb {Z}.$
$n\in \mathbb {Z}.$
-
(2) If
 $(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^-$
, then
$(a, b)\in \partial \mathcal {H}_{{\mathbb {R}}}^-$
, then
 $f_{a, b} : \Omega (f_{a, b})\to \Omega (f_{a, b})$
is topologically conjugate to the factor map
$f_{a, b} : \Omega (f_{a, b})\to \Omega (f_{a, b})$
is topologically conjugate to the factor map
 $\sigma /_{\sim } : \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }\to \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }$
, where we define
$\sigma /_{\sim } : \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }\to \{\alpha , \beta \}^{{\mathbb {Z}}}/_{\sim }$
, where we define
 $\sim $
as for all
$\sim $
as for all $$ \begin{align*}\sigma^n(\overline{\beta}\alpha\cdot \beta\beta\overline{\alpha})\sim \sigma^n(\overline{\beta}\alpha\cdot \alpha\beta\overline{\alpha})\end{align*} $$
$$ \begin{align*}\sigma^n(\overline{\beta}\alpha\cdot \beta\beta\overline{\alpha})\sim \sigma^n(\overline{\beta}\alpha\cdot \alpha\beta\overline{\alpha})\end{align*} $$
 $n\in \mathbb {Z}.$
$n\in \mathbb {Z}.$
Note that, in [Reference Bedford and SmillieBSℝ3], the alphabet
![]() $\{a, b\}$
is used instead of {α, β}.
$\{a, b\}$
is used instead of {α, β}.
It would be interesting to generalize our results to:
-
(1) a real Hénon map on
 ${\mathbb {R}}^2$
, where
${\mathbb {R}}^2$
, where
 $(a, b)$
is taken near the boundary of a hyperbolic component (see [Reference AraiA1] for hyperbolic components in the real parameter space);
$(a, b)$
is taken near the boundary of a hyperbolic component (see [Reference AraiA1] for hyperbolic components in the real parameter space); -
(2) a complex Hénon map on
 ${\mathbb {C}}^2$
, where
${\mathbb {C}}^2$
, where
 $(a, b)$
is taken near the boundary of the complex horseshoe locus (compare [Reference Bedford and DujardinBD, Theorem 3.6] for a related result which claims that a topological horseshoe is a hyperbolic horseshoe in
$(a, b)$
is taken near the boundary of the complex horseshoe locus (compare [Reference Bedford and DujardinBD, Theorem 3.6] for a related result which claims that a topological horseshoe is a hyperbolic horseshoe in
 ${\mathbb {C}}^2$
).
${\mathbb {C}}^2$
).
The structure of this paper is as follows. In §2, we discuss some properties of symbolic dynamics associated with a family of boxes as well as its refinement. In §3, we characterize local stable/unstable manifolds in terms of the symbolic dynamics above. In §4, we construct the
![]() $\{L, R\}$
-partition and prove Theorem 1.1. In §5, we construct the
$\{L, R\}$
-partition and prove Theorem 1.1. In §5, we construct the
![]() $\{\alpha , \beta \}$
-partition and prove Theorem 1.2. Some statements in this article are proved by Arai [Reference AraiA2] with the help of computer assistance (see Appendix A for details).
$\{\alpha , \beta \}$
-partition and prove Theorem 1.2. Some statements in this article are proved by Arai [Reference AraiA2] with the help of computer assistance (see Appendix A for details).
2 Symbolic codings and refinements
In [Reference Arai and IshiiAI, §2.1], we constructed a complex neighborhood
![]() $\mathcal {F}^{\pm }$
of the boundary
$\mathcal {F}^{\pm }$
of the boundary
![]() $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
. When
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
. When
![]() $(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, we can regard
$(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, we can regard
![]() $f_{a, b}$
as a complex dynamical system defined on
$f_{a, b}$
as a complex dynamical system defined on
![]() ${\mathbb {C}}^2$
. Denote by
${\mathbb {C}}^2$
. Denote by
![]() $K_{a, b}$
the set of points in
$K_{a, b}$
the set of points in
![]() ${\mathbb {C}}^2$
whose both forward and backward orbits by
${\mathbb {C}}^2$
whose both forward and backward orbits by
![]() $f_{a, b}$
are bounded in
$f_{a, b}$
are bounded in
![]() ${\mathbb {C}}^2$
.
${\mathbb {C}}^2$
.
Let us write
![]() $\mathcal {F}^{\pm }_{{\mathbb {R}}}\equiv \mathcal {F}^{\pm }\cap {\mathbb {R}}^2$
. When
$\mathcal {F}^{\pm }_{{\mathbb {R}}}\equiv \mathcal {F}^{\pm }\cap {\mathbb {R}}^2$
. When
![]() $(a, b)\in \mathcal {F}^{\pm }_{{\mathbb {R}}}$
is a real parameter, the restriction
$(a, b)\in \mathcal {F}^{\pm }_{{\mathbb {R}}}$
is a real parameter, the restriction
![]() $f_{a, b}|_{{\mathbb {R}}^2} : {\mathbb {R}}^2\to {\mathbb {R}}^2$
is well defined. We denote it by
$f_{a, b}|_{{\mathbb {R}}^2} : {\mathbb {R}}^2\to {\mathbb {R}}^2$
is well defined. We denote it by
![]() $f_{{\mathbb {R}}}$
when we insist it has real dynamics and write
$f_{{\mathbb {R}}}$
when we insist it has real dynamics and write
![]() $K_{{\mathbb {R}}}\equiv K_{a, b}\cap {\mathbb {R}}^2$
.
$K_{{\mathbb {R}}}\equiv K_{a, b}\cap {\mathbb {R}}^2$
.
2.1 Symbolic codings
Given a finite set called an alphabet
![]() $\Sigma $
and a subset
$\Sigma $
and a subset
![]() $\mathfrak {T}\subset \Sigma \times \Sigma $
called the set of allowed transitions, we define
$\mathfrak {T}\subset \Sigma \times \Sigma $
called the set of allowed transitions, we define
and call its element a forward admissible sequence with respect to
![]() $\mathfrak {T}$
. Also we define
$\mathfrak {T}$
. Also we define
and call its element a backward admissible sequence with respect to
![]() $\mathfrak {T}$
. Finally, we set
$\mathfrak {T}$
. Finally, we set
and call its element a bi-infinite admissible sequence with respect to
![]() $\mathfrak {T}$
.
$\mathfrak {T}$
.
Below, we set
![]() ${\Sigma }^+\equiv \{0, 1, 2, 3\}$
and
${\Sigma }^+\equiv \{0, 1, 2, 3\}$
and
![]() ${\Sigma }^-\equiv \{0, 1, 2, 3, 4\}$
. Choose a subset of
${\Sigma }^-\equiv \{0, 1, 2, 3, 4\}$
. Choose a subset of
![]() ${\Sigma ^+\times \Sigma ^+}$
as
${\Sigma ^+\times \Sigma ^+}$
as
and a subset of
![]() $\Sigma ^-\times \Sigma ^-$
as
$\Sigma ^-\times \Sigma ^-$
as
We then write
![]() $\mathfrak {S}^{\pm }_{\mathrm {fwd}}\equiv \mathfrak {S}_{\mathrm {fwd}}(\mathfrak {T}^{\pm })$
,
$\mathfrak {S}^{\pm }_{\mathrm {fwd}}\equiv \mathfrak {S}_{\mathrm {fwd}}(\mathfrak {T}^{\pm })$
,
![]() $\mathfrak {S}^{\pm }_{\mathrm {bwd}}\equiv \mathfrak {S}_{\mathrm {bwd}}(\mathfrak {T}^{\pm })$
and
$\mathfrak {S}^{\pm }_{\mathrm {bwd}}\equiv \mathfrak {S}_{\mathrm {bwd}}(\mathfrak {T}^{\pm })$
and
![]() $\mathfrak {S}^{\pm }\equiv \mathfrak {S}(\mathfrak {T}^{\pm })$
.
$\mathfrak {S}^{\pm }\equiv \mathfrak {S}(\mathfrak {T}^{\pm })$
.
The transition diagram for
![]() $\mathfrak {S}^+$
(respectively
$\mathfrak {S}^+$
(respectively
![]() $\mathfrak {S}^-$
) is a directed graph whose vertex set is
$\mathfrak {S}^-$
) is a directed graph whose vertex set is
![]() $\Sigma ^+$
(respectively
$\Sigma ^+$
(respectively
![]() $\Sigma ^-$
) and the arrow set is
$\Sigma ^-$
) and the arrow set is
![]() $\mathfrak {T}^+$
(respectively
$\mathfrak {T}^+$
(respectively
![]() $\mathfrak {T}^-$
). See Figures 3 and 4.
$\mathfrak {T}^-$
). See Figures 3 and 4.

Figure 3 Transition diagram for
![]() $(a, b)\in \mathcal {F}^+_{{\mathbb {R}}}\cap \{b> 0\}$
.
$(a, b)\in \mathcal {F}^+_{{\mathbb {R}}}\cap \{b> 0\}$
.

Figure 4 Transition diagram for
![]() $(a, b)\in \mathcal {F}^-_{{\mathbb {R}}}\cap \{b< 0\}$
.
$(a, b)\in \mathcal {F}^-_{{\mathbb {R}}}\cap \{b< 0\}$
.
Let
![]() $D_u$
and
$D_u$
and
![]() $D_v$
be two topological disks in
$D_v$
be two topological disks in
![]() $\mathbb {C}$
. A projective polydisk (or a projective box, or simply a box)
$\mathbb {C}$
. A projective polydisk (or a projective box, or simply a box)
![]() $\mathcal {B}=D_u\times _{\mathrm {pr}}D_v$
is the product sets of
$\mathcal {B}=D_u\times _{\mathrm {pr}}D_v$
is the product sets of
![]() $D_u$
and
$D_u$
and
![]() $D_v$
with respect to certain projective coordinates in
$D_v$
with respect to certain projective coordinates in
![]() $\mathbb {C}^2$
(see [Reference IshiiI, §4.3] as well as [Reference Arai and IshiiAI, §2.2] for more detail).
$\mathbb {C}^2$
(see [Reference IshiiI, §4.3] as well as [Reference Arai and IshiiAI, §2.2] for more detail).
Definition 2.1. Let
![]() $\mathcal {B}=D_u\times _{\mathrm {pr}}D_v$
(respectively
$\mathcal {B}=D_u\times _{\mathrm {pr}}D_v$
(respectively
![]() $\mathcal {B}'=D^{\prime }_u\times _{\mathrm {pr}}D^{\prime }_v$
) be a projective polydisk, and let
$\mathcal {B}'=D^{\prime }_u\times _{\mathrm {pr}}D^{\prime }_v$
) be a projective polydisk, and let
![]() $\pi _u : \mathcal {B}\to D_u$
and
$\pi _u : \mathcal {B}\to D_u$
and
![]() $\pi _v : \mathcal {B}\to D_v$
(respectively
$\pi _v : \mathcal {B}\to D_v$
(respectively
![]() $\pi ^{\prime }_u : \mathcal {B}'\to D^{\prime }_u$
and
$\pi ^{\prime }_u : \mathcal {B}'\to D^{\prime }_u$
and
![]() ${\pi ^{\prime }_v : \mathcal {B}'\to D^{\prime }_v}$
) be the projections. We say that
${\pi ^{\prime }_v : \mathcal {B}'\to D^{\prime }_v}$
) be the projections. We say that
![]() $f : \mathcal {B} \cap f^{-1}(\mathcal {B}') \rightarrow \mathcal {B}'$
satisfies the crossed mapping condition (CMC) of degree d if it satisfies conditions (1) and (2) below, where
$f : \mathcal {B} \cap f^{-1}(\mathcal {B}') \rightarrow \mathcal {B}'$
satisfies the crossed mapping condition (CMC) of degree d if it satisfies conditions (1) and (2) below, where
![]() $\iota : \mathcal {B} \cap f^{-1}(\mathcal {B}') \rightarrow \mathcal {B}$
denotes the inclusion map.
$\iota : \mathcal {B} \cap f^{-1}(\mathcal {B}') \rightarrow \mathcal {B}$
denotes the inclusion map.
-
(1) The map
 $(\pi ^{\prime }_u \circ f, \pi _v \circ \iota ) : \mathcal {B} \cap f^{-1}(\mathcal {B}^{\prime }) \rightarrow D^{\prime }_u \times D_v$
is proper and degree d.
$(\pi ^{\prime }_u \circ f, \pi _v \circ \iota ) : \mathcal {B} \cap f^{-1}(\mathcal {B}^{\prime }) \rightarrow D^{\prime }_u \times D_v$
is proper and degree d. -
(2) The sets
 $\pi _u(\mathcal {B} \cap f^{-1}(\mathcal {B}'))$
and
$\pi _u(\mathcal {B} \cap f^{-1}(\mathcal {B}'))$
and
 $\pi ^{\prime }_v(\mathcal {B}' \cap f(\mathcal {B}))$
are relatively compact in
$\pi ^{\prime }_v(\mathcal {B}' \cap f(\mathcal {B}))$
are relatively compact in
 $D_u$
and
$D_u$
and
 $D^{\prime }_v$
, respectively.
$D^{\prime }_v$
, respectively.
See [Reference Arai and IshiiAI, Definition 2.11] as well as [Reference Ishii and SmillieIS, Definition 5.1] for the original definition.
Definition 2.2. A triple
![]() $(f_{a, b}, \{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}, \mathfrak {T}^{\pm })$
is said to satisfy the crossed mapping condition if
$(f_{a, b}, \{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}, \mathfrak {T}^{\pm })$
is said to satisfy the crossed mapping condition if
![]() $f_{a, b} : \mathcal {B}^{\pm }_i \cap f_{a, b}^{-1}(\mathcal {B}^{\pm }_j) \rightarrow \mathcal {B}^{\pm }_j$
satisfies the crossed mapping condition for all
$f_{a, b} : \mathcal {B}^{\pm }_i \cap f_{a, b}^{-1}(\mathcal {B}^{\pm }_j) \rightarrow \mathcal {B}^{\pm }_j$
satisfies the crossed mapping condition for all
![]() $(i, j) \in \mathfrak {T}^{\pm }$
.
$(i, j) \in \mathfrak {T}^{\pm }$
.
The next proposition is identical to [Reference Arai and IshiiAI, Theorem 2.12(iii)].
Theorem 2.3. For
![]() $(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, there is a family of projective polydisks
$(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, there is a family of projective polydisks
![]() $\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
in
$\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
in
![]() ${\mathbb {C}}^2$
so that the triple
${\mathbb {C}}^2$
so that the triple
![]() $(f_{a, b}, \{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}, \mathfrak {T}^{\pm })$
satisfies the crossed mapping condition.
$(f_{a, b}, \{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}, \mathfrak {T}^{\pm })$
satisfies the crossed mapping condition.
The next fact is proved in [Reference Arai and IshiiAI] and will be used later.
Lemma 2.4. We have:
-
(1)
 $\mathcal {B}^+_0{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_1{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\mathcal {B}^+_0{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_2{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\mathcal {B}^+_1{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_3{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\emptyset $
for
$\mathcal {B}^+_0{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_1{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\mathcal {B}^+_0{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_2{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\mathcal {B}^+_1{\kern-1pt}\cap{\kern-1pt} \mathcal {B}^+_3{\kern-1pt}\cap{\kern-1pt} K_{a, b}{\kern-1pt}={\kern-1pt}\emptyset $
for
 $(a, b){\kern-1pt}\in{\kern-1pt} \mathcal {F}^+\cap \{b{\kern-1pt}>{\kern-1pt}0\}$
;
$(a, b){\kern-1pt}\in{\kern-1pt} \mathcal {F}^+\cap \{b{\kern-1pt}>{\kern-1pt}0\}$
; -
(2)
 $\mathcal {B}^-_0\ \cap\ \mathcal {B}^-_1\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_0\ \cap\ \mathcal {B}^-_3\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_0\ \cap\ \mathcal {B}^-_4\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_1\ \cap\ \mathcal {B}^-_2\ \cap\ K_{a, b}= \mathcal {B}^-_1\cap \mathcal {B}^-_4\cap K_{a, b}=\mathcal {B}^-_2\cap \mathcal {B}^-_3\cap K_{a, b}=\emptyset $
for
$\mathcal {B}^-_0\ \cap\ \mathcal {B}^-_1\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_0\ \cap\ \mathcal {B}^-_3\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_0\ \cap\ \mathcal {B}^-_4\ \cap\ K_{a, b}\ =\ \mathcal {B}^-_1\ \cap\ \mathcal {B}^-_2\ \cap\ K_{a, b}= \mathcal {B}^-_1\cap \mathcal {B}^-_4\cap K_{a, b}=\mathcal {B}^-_2\cap \mathcal {B}^-_3\cap K_{a, b}=\emptyset $
for
 $(a, b)\in \mathcal {F}^-\cap \{b<0\}$
.
$(a, b)\in \mathcal {F}^-\cap \{b<0\}$
.
Proof. For claim (1), see the proof of [Reference Arai and IshiiAI, Lemma 3.4(i)]. For claim (2), see the proof of [Reference Arai and IshiiAI, Lemma 3.7(i)].
For
![]() $(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, define the orbit space of
$(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, define the orbit space of
![]() $f_{a, b}$
as
$f_{a, b}$
as
By [Reference Arai and IshiiAI, Proposition 3.1], we see that
 $$ \begin{align*} \bigcap_{n\in{\mathbb{Z}}}f^n\bigg(\bigcup_{i\in\Sigma^{\pm}}\mathcal{B}^{\pm}_i\bigg)=K_{a, b}.\end{align*} $$
$$ \begin{align*} \bigcap_{n\in{\mathbb{Z}}}f^n\bigg(\bigcup_{i\in\Sigma^{\pm}}\mathcal{B}^{\pm}_i\bigg)=K_{a, b}.\end{align*} $$
Therefore, the projection
can be defined.
Definition 2.5. A bi-infinite sequence
![]() $(i_n)_{n\in {\mathbb {Z}}}\in \mathfrak {S}^{\pm }$
is called a
$(i_n)_{n\in {\mathbb {Z}}}\in \mathfrak {S}^{\pm }$
is called a
![]() $\Sigma ^{\pm }$
-coding of
$\Sigma ^{\pm }$
-coding of
![]() $z_0\in K_{a, b}$
if it satisfies
$z_0\in K_{a, b}$
if it satisfies
![]() $\Phi ((i_n)_{n\in {\mathbb {Z}}}, (f^n(z_0))_{n\in {\mathbb {Z}}})=z_0$
.
$\Phi ((i_n)_{n\in {\mathbb {Z}}}, (f^n(z_0))_{n\in {\mathbb {Z}}})=z_0$
.
The next proposition is a restatement of [Reference Arai and IshiiAI, Propositions 3.3 and 3.6].
Proposition 2.6. Let
![]() $(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
. Then,
$(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
. Then,
![]() $\Phi : \Lambda ^{\pm }\to K_{a, b}$
is surjective.
$\Phi : \Lambda ^{\pm }\to K_{a, b}$
is surjective.
In particular, every point in
![]() $K_{a, b}$
has at least one
$K_{a, b}$
has at least one
![]() $\Sigma ^{\pm }$
-coding thanks to Proposition 2.6.
$\Sigma ^{\pm }$
-coding thanks to Proposition 2.6.
One can also show that the map
![]() $\Phi $
is almost injective. To do this, below we write
$\Phi $
is almost injective. To do this, below we write
![]() ${\mathcal {B}^{\pm }_i=D^{\pm }_{u, i}\times _{\mathrm {pr}}D^{\pm }_{v, i}}$
.
${\mathcal {B}^{\pm }_i=D^{\pm }_{u, i}\times _{\mathrm {pr}}D^{\pm }_{v, i}}$
.
Lemma 2.7. (Numerical Check 1)
Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, there exist projective polydisks
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, there exist projective polydisks
![]() $\mathcal {P}^+_{0, 3}$
,
$\mathcal {P}^+_{0, 3}$
,
![]() $\mathcal {P}^+_{1, 2}$
, and
$\mathcal {P}^+_{1, 2}$
, and
![]() $\mathcal {P}^+_{2, 3}$
so that:
$\mathcal {P}^+_{2, 3}$
so that:
-
(1)
 $\mathcal {P}^+_{0, 3}\supset \mathcal {B}^+_0\cap \mathcal {B}^+_3$
,
$\mathcal {P}^+_{0, 3}\supset \mathcal {B}^+_0\cap \mathcal {B}^+_3$
,
 $\mathcal {P}^+_{1, 2}\supset \mathcal {B}^+_1\cap \mathcal {B}^+_2$
, and
$\mathcal {P}^+_{1, 2}\supset \mathcal {B}^+_1\cap \mathcal {B}^+_2$
, and
 $\mathcal {P}^+_{2, 3}\supset \mathcal {B}^+_2\cap \mathcal {B}^+_3$
hold;
$\mathcal {P}^+_{2, 3}\supset \mathcal {B}^+_2\cap \mathcal {B}^+_3$
hold; -
(2)
 $f : \mathcal {P}^+_{0, 3}\ \cap\ f^{-1}(\mathcal {P}^+_{1, 2})\ \to\ \mathcal {P}^+_{1, 2}$
,
$f : \mathcal {P}^+_{0, 3}\ \cap\ f^{-1}(\mathcal {P}^+_{1, 2})\ \to\ \mathcal {P}^+_{1, 2}$
,
 $f : \mathcal {P}^+_{1, 2}\ \cap\ f^{-1}(\mathcal {P}^+_{0, 3})\ \to\ \mathcal {P}^+_{0, 3}$
, and
$f : \mathcal {P}^+_{1, 2}\ \cap\ f^{-1}(\mathcal {P}^+_{0, 3})\ \to\ \mathcal {P}^+_{0, 3}$
, and
 $f : \mathcal {P}^+_{2, 3}\ \cap\ f^{-1}(\mathcal {P}^+_{1, 2})\to \mathcal {P}^+_{1, 2}$
are crossed mappings of degree one.
$f : \mathcal {P}^+_{2, 3}\ \cap\ f^{-1}(\mathcal {P}^+_{1, 2})\to \mathcal {P}^+_{1, 2}$
are crossed mappings of degree one.
Proof. See Appendix A.
Lemma 2.8. (Numerical Check 2)
Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, there exist projective polydisks
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, there exist projective polydisks
![]() $\mathcal {P}^-_{0, 2}$
,
$\mathcal {P}^-_{0, 2}$
,
![]() $\mathcal {P}^-_{1, 3}$
,
$\mathcal {P}^-_{1, 3}$
,
![]() $\mathcal {P}^-_{2, 4}$
, and
$\mathcal {P}^-_{2, 4}$
, and
![]() $\mathcal {P}^-_{3, 4}$
so that:
$\mathcal {P}^-_{3, 4}$
so that:
-
(1)
 $\mathcal {P}^-_{0, 2}\supset \mathcal {B}^-_0\cap \mathcal {B}^-_2$
,
$\mathcal {P}^-_{0, 2}\supset \mathcal {B}^-_0\cap \mathcal {B}^-_2$
,
 $\mathcal {P}^-_{1, 3}\supset \mathcal {B}^-_1\cap \mathcal {B}^-_3$
,
$\mathcal {P}^-_{1, 3}\supset \mathcal {B}^-_1\cap \mathcal {B}^-_3$
,
 $\mathcal {P}^-_{2, 4}\supset \mathcal {B}^-_2\cap \mathcal {B}^-_4$
, and
$\mathcal {P}^-_{2, 4}\supset \mathcal {B}^-_2\cap \mathcal {B}^-_4$
, and
 $\mathcal {P}^-_{3, 4}\supset \mathcal {B}^-_3\cap \mathcal {B}^-_4$
hold;
$\mathcal {P}^-_{3, 4}\supset \mathcal {B}^-_3\cap \mathcal {B}^-_4$
hold; -
(2)
 $f : \mathcal {P}^-_{0, 2}\ \cap\ f^{-1}(\mathcal {P}^-_{2, 4})\ \to\ \mathcal {P}^-_{2, 4}$
,
$f : \mathcal {P}^-_{0, 2}\ \cap\ f^{-1}(\mathcal {P}^-_{2, 4})\ \to\ \mathcal {P}^-_{2, 4}$
,
 $f : \mathcal {P}^-_{1, 3}\ \cap\ f^{-1}(\mathcal {P}^-_{2, 4})\ \to\ \mathcal {P}^-_{2, 4}$
,
$f : \mathcal {P}^-_{1, 3}\ \cap\ f^{-1}(\mathcal {P}^-_{2, 4})\ \to\ \mathcal {P}^-_{2, 4}$
,
 $f : \mathcal {P}^-_{2, 4}\ \cap\ f^{-1}(\mathcal {P}^-_{3, 4})\to \mathcal {P}^-_{3, 4}$
, and
$f : \mathcal {P}^-_{2, 4}\ \cap\ f^{-1}(\mathcal {P}^-_{3, 4})\to \mathcal {P}^-_{3, 4}$
, and
 $f : \mathcal {P}^-_{3, 4}\cap f^{-1}(\mathcal {P}^-_{3, 4})\to \mathcal {P}^-_{3, 4}$
are crossed mappings of degree one.
$f : \mathcal {P}^-_{3, 4}\cap f^{-1}(\mathcal {P}^-_{3, 4})\to \mathcal {P}^-_{3, 4}$
are crossed mappings of degree one.
Proof. See Appendix A.
Proposition 2.9. We have the following.
-
(1) Let
 $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then,
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then,
 $1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for any
$1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for any
 $z\in K_{a, b}$
and moreover
$z\in K_{a, b}$
and moreover
 $\mathrm {card}(\Phi ^{-1}(z))= 1$
if and only if
$\mathrm {card}(\Phi ^{-1}(z))= 1$
if and only if
 $z\in K_{a, b}\setminus (V^s(p_2)\cup V^s(p_4))$
.
$z\in K_{a, b}\setminus (V^s(p_2)\cup V^s(p_4))$
. -
(2) Let
 $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then,
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then,
 $1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for any
$1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for any
 $z\in K_{a, b}$
and moreover
$z\in K_{a, b}$
and moreover
 $\mathrm {card}(\Phi ^{-1}(z))= 1$
if and only f
$\mathrm {card}(\Phi ^{-1}(z))= 1$
if and only f
 $z\in K_{a, b}\setminus V^s(p_3)$
.
$z\in K_{a, b}\setminus V^s(p_3)$
.
Probably Proposition 2.9 would hold for any
![]() $(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, but we restrict ourselves to
$(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}$
, but we restrict ourselves to
![]() $(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
which is sufficient for our purpose. The same would hold for Lemmas 2.10, 2.11, 3.1, and 3.2 below.
$(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
which is sufficient for our purpose. The same would hold for Lemmas 2.10, 2.11, 3.1, and 3.2 below.
To prove this proposition, we need to introduce a finite directed graph called the pairwise transition diagram for
![]() $\mathfrak {T}^{\pm }$
as follows. A vertex is an unordered pair
$\mathfrak {T}^{\pm }$
as follows. A vertex is an unordered pair
![]() $\{i, j\}\subset \Sigma ^{\pm }$
so that
$\{i, j\}\subset \Sigma ^{\pm }$
so that
![]() $\mathcal {B}^{\pm }_i\cap \mathcal {B}^{\pm }_j\cap K_{a, b}\ne \emptyset $
(see Lemma 2.4), and there is an arrow from
$\mathcal {B}^{\pm }_i\cap \mathcal {B}^{\pm }_j\cap K_{a, b}\ne \emptyset $
(see Lemma 2.4), and there is an arrow from
![]() $\{i, j\}$
to
$\{i, j\}$
to
![]() $\{i', j'\}$
if and only if both
$\{i', j'\}$
if and only if both
![]() $f : \mathcal {B}^{\pm }_i\cap f^{-1}(\mathcal {B}^{\pm }_{i'})\to \mathcal {B}^{\pm }_{i'}$
and
$f : \mathcal {B}^{\pm }_i\cap f^{-1}(\mathcal {B}^{\pm }_{i'})\to \mathcal {B}^{\pm }_{i'}$
and
![]() $f : \mathcal {B}^{\pm }_j\cap f^{-1}(\mathcal {B}^{\pm }_{j'})\to \mathcal {B}^{\pm }_{j'}$
are crossed mappings (by exchanging
$f : \mathcal {B}^{\pm }_j\cap f^{-1}(\mathcal {B}^{\pm }_{j'})\to \mathcal {B}^{\pm }_{j'}$
are crossed mappings (by exchanging
![]() $i'$
and
$i'$
and
![]() $j'$
, if necessary). See Figures 5 and 6.
$j'$
, if necessary). See Figures 5 and 6.

Figure 5 Pairwise transition diagram for
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.

Figure 6 Pairwise transition diagram for
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
Proof. We first prove case (1). Given a point
![]() $z\in K_{a, b}$
, let us consider the following condition (
$z\in K_{a, b}$
, let us consider the following condition (
![]() $\ast $
):
$\ast $
):
there exists
![]() $N\in \mathbb {Z}$
so that
$N\in \mathbb {Z}$
so that
![]() $f^N(z)\in \mathcal {B}^+_{i_N}\cap \mathcal {B}^+_{j_N}$
holds for some
$f^N(z)\in \mathcal {B}^+_{i_N}\cap \mathcal {B}^+_{j_N}$
holds for some
![]() $\{i_N, j_N\}\subset \Sigma ^+$
with
$\{i_N, j_N\}\subset \Sigma ^+$
with
![]() $i_N\ne j_N$
.
$i_N\ne j_N$
.
Suppose first the case that
![]() $z\in K_{a, b}$
does not satisfy condition (
$z\in K_{a, b}$
does not satisfy condition (
![]() $\ast $
). Since
$\ast $
). Since
![]() $K_{a, b}\subset \bigcup _{i\in \Sigma ^+}\mathcal {B}^+_i$
, this means that for any
$K_{a, b}\subset \bigcup _{i\in \Sigma ^+}\mathcal {B}^+_i$
, this means that for any
![]() $n\in \mathbb {Z}$
, there exists a unique
$n\in \mathbb {Z}$
, there exists a unique
![]() $i_n\in \Sigma ^+$
so that
$i_n\in \Sigma ^+$
so that
![]() $f^n(z)\in \mathcal {B}^+_{i_n}$
. This obviously implies that
$f^n(z)\in \mathcal {B}^+_{i_n}$
. This obviously implies that
![]() $\mathrm {card}(\Phi ^{-1}(z))=1$
.
$\mathrm {card}(\Phi ^{-1}(z))=1$
.
Suppose second the case that
![]() $z\in K_{a, b}$
satisfies condition (
$z\in K_{a, b}$
satisfies condition (
![]() $\ast $
). Since for every
$\ast $
). Since for every
![]() $z\in K_{a, b}$
, there exist at most two
$z\in K_{a, b}$
, there exist at most two
![]() $i\in \Sigma ^+$
so that
$i\in \Sigma ^+$
so that
![]() $z\in \mathcal {B}^+_i$
(see item (1) of Lemma 2.4), such a pair
$z\in \mathcal {B}^+_i$
(see item (1) of Lemma 2.4), such a pair
![]() $\{i_N, j_N\}$
is uniquely determined for a given N. We next observe that in the pairwise transition diagram, there exists exactly one out-going arrow from every vertex of the form
$\{i_N, j_N\}$
is uniquely determined for a given N. We next observe that in the pairwise transition diagram, there exists exactly one out-going arrow from every vertex of the form
![]() $\{i, j\}$
with
$\{i, j\}$
with
![]() $i\ne j$
(focus on bold arrows in Figure 5) and there are no arrows from such a vertex to a vertex of the form
$i\ne j$
(focus on bold arrows in Figure 5) and there are no arrows from such a vertex to a vertex of the form
![]() $\{k, k\}$
. This implies that there exists a unique path
$\{k, k\}$
. This implies that there exists a unique path
![]() $\{i_N, j_N\}\to \{i_{N+1}, j_{N+1}\}\to \cdots $
in the diagram starting from the vertex
$\{i_N, j_N\}\to \{i_{N+1}, j_{N+1}\}\to \cdots $
in the diagram starting from the vertex
![]() $\{i_N, j_N\}$
. Since this holds for every N appearing in condition (
$\{i_N, j_N\}$
. Since this holds for every N appearing in condition (
![]() $\ast $
), we conclude that
$\ast $
), we conclude that
![]() $\mathrm {card}(\Phi ^{-1}(z))=2$
. This together with the conclusion in the previous paragraph yields that
$\mathrm {card}(\Phi ^{-1}(z))=2$
. This together with the conclusion in the previous paragraph yields that
![]() $z\in K_{a, b}$
satisfies condition (
$z\in K_{a, b}$
satisfies condition (
![]() $\ast $
) if and only if
$\ast $
) if and only if
![]() $\mathrm {card}(\Phi ^{-1}(z))= 2$
.
$\mathrm {card}(\Phi ^{-1}(z))= 2$
.
Under condition (
![]() $\ast $
), we also observe that the path
$\ast $
), we also observe that the path
![]() $\{i_N, j_N\}\to \{i_{N+1}, j_{N+1}\}\to \cdots $
eventually falls into the cycle
$\{i_N, j_N\}\to \{i_{N+1}, j_{N+1}\}\to \cdots $
eventually falls into the cycle
![]() $\{0, 3\}\to \{1, 2\}\to \{0, 3\}\to \cdots $
of period
$\{0, 3\}\to \{1, 2\}\to \{0, 3\}\to \cdots $
of period
![]() $2$
. Now we apply Lemma 2.7. Since
$2$
. Now we apply Lemma 2.7. Since
![]() $\mathcal {P}^+_{0, 3}\supset \mathcal {B}^+_0\cap \mathcal {B}^+_3$
and
$\mathcal {P}^+_{0, 3}\supset \mathcal {B}^+_0\cap \mathcal {B}^+_3$
and
![]() $\mathcal {P}^+_{1, 2}\supset \mathcal {B}^+_1\cap \mathcal {B}^+_2$
hold by item (1) of Lemma 2.7, this implies that
$\mathcal {P}^+_{1, 2}\supset \mathcal {B}^+_1\cap \mathcal {B}^+_2$
hold by item (1) of Lemma 2.7, this implies that
![]() $f^n(z)$
eventually drops into either
$f^n(z)$
eventually drops into either
![]() $\mathcal {P}^+_{0, 3}$
or
$\mathcal {P}^+_{0, 3}$
or
![]() $\mathcal {P}^+_{1, 2}$
and stays there. By item (2) of Lemma 2.7, we see that
$\mathcal {P}^+_{1, 2}$
and stays there. By item (2) of Lemma 2.7, we see that
![]() $f^n(z)$
eventually belongs to either the local stable manifold of
$f^n(z)$
eventually belongs to either the local stable manifold of
![]() $p_2$
in
$p_2$
in
![]() $\mathcal {P}^+_{0, 3}$
or the local stable manifold of
$\mathcal {P}^+_{0, 3}$
or the local stable manifold of
![]() $p_4$
in
$p_4$
in
![]() $\mathcal {P}^+_{1, 2}$
. Therefore, we may conclude that
$\mathcal {P}^+_{1, 2}$
. Therefore, we may conclude that
![]() ${z\in V^s(p_2)\cup V^s(p_4)}$
. Conversely, suppose that
${z\in V^s(p_2)\cup V^s(p_4)}$
. Conversely, suppose that
![]() $z\in V^s(p_2)\cup V^s(p_4)$
. Since
$z\in V^s(p_2)\cup V^s(p_4)$
. Since
![]() $p_2\in \mathcal {B}^+_0\cap \mathcal {B}^+_3$
and
$p_2\in \mathcal {B}^+_0\cap \mathcal {B}^+_3$
and
![]() $p_4\in \mathcal {B}^+_1\cap \mathcal {B}^+_2$
, there exists
$p_4\in \mathcal {B}^+_1\cap \mathcal {B}^+_2$
, there exists
![]() $N\in \mathbb {Z}$
so that either
$N\in \mathbb {Z}$
so that either
![]() $f^N(z)\in \mathcal {B}^+_0\cap \mathcal {B}^+_3$
or
$f^N(z)\in \mathcal {B}^+_0\cap \mathcal {B}^+_3$
or
![]() $f^N(z)\in \mathcal {B}^+_1\cap \mathcal {B}^+_2$
holds. In particular, condition (
$f^N(z)\in \mathcal {B}^+_1\cap \mathcal {B}^+_2$
holds. In particular, condition (
![]() $\ast $
) is satisfied. Therefore, we conclude that
$\ast $
) is satisfied. Therefore, we conclude that
![]() $z\in K_{a, b}$
satisfies condition (
$z\in K_{a, b}$
satisfies condition (
![]() $\ast $
) if and only if
$\ast $
) if and only if
![]() $z\in V^s(p_2)\cup V^s(p_4)$
.
$z\in V^s(p_2)\cup V^s(p_4)$
.
The argument above obviously shows
![]() $1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for all
$1\leq \mathrm {card}(\Phi ^{-1}(z))\leq 2$
for all
![]() $z\in K_{a, b}$
. By combining the conclusions in the previous two paragraphs, we obtain
$z\in K_{a, b}$
. By combining the conclusions in the previous two paragraphs, we obtain
![]() $\mathrm {card}(\Phi ^{-1}(z))= 2$
if and only if
$\mathrm {card}(\Phi ^{-1}(z))= 2$
if and only if
![]() $z\in V^s(p_2)\cup V^s(p_4)$
, which proves case (1). The proof for case (2) is similarly obtained by using Lemma 2.8.
$z\in V^s(p_2)\cup V^s(p_4)$
, which proves case (1). The proof for case (2) is similarly obtained by using Lemma 2.8.
2.2 Refined codings
In what follows, it is essential to refine the boxes
![]() $\mathcal {B}^+_2$
,
$\mathcal {B}^+_2$
,
![]() $\mathcal {B}^-_2$
and
$\mathcal {B}^-_2$
and
![]() $\mathcal {B}^-_3$
.
$\mathcal {B}^-_3$
.
Lemma 2.10. (Numerical Check 3)
When
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, the crossed mapping
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, the crossed mapping
of degree two satisfies the off-criticality condition.
Proof. See Appendix A.
It then follows from [Reference IshiiI, Theorem 2.14] that the domain
consists of two connected components denoted as
![]() $\mathcal {B}^+_{2'}$
and
$\mathcal {B}^+_{2'}$
and
![]() $\mathcal {B}^+_{2"}$
with
$\mathcal {B}^+_{2"}$
with
![]() $p_4\in \mathcal {B}^+_{2'}$
. Moreover, both
$p_4\in \mathcal {B}^+_{2'}$
. Moreover, both
![]() $\mathcal {B}^+_{2'}$
and
$\mathcal {B}^+_{2'}$
and
![]() $\mathcal {B}^+_{2"}$
are biholomorphic to polydisks, and
$\mathcal {B}^+_{2"}$
are biholomorphic to polydisks, and
![]() $f^4 : \mathcal {B}^+_{2'}\to \mathcal {B}^+_2$
and
$f^4 : \mathcal {B}^+_{2'}\to \mathcal {B}^+_2$
and
![]() $f^4 : \mathcal {B}^+_{2"}\to \mathcal {B}^+_2$
are crossed mappings of degree one (see Step 5 of the proof of [Reference IshiiI, Theorem 2.14]).
$f^4 : \mathcal {B}^+_{2"}\to \mathcal {B}^+_2$
are crossed mappings of degree one (see Step 5 of the proof of [Reference IshiiI, Theorem 2.14]).
Lemma 2.11. (Numerical Check 4)
When
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, the crossed mapping
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, the crossed mapping
of degree two satisfies the off-criticality condition for
![]() $i=2, 3$
.
$i=2, 3$
.
Proof. See Appendix A.
Again, it then follows from [Reference IshiiI, Theorem 2.14] that the domain
consists of two connected components denoted as
![]() $\mathcal {B}^-_{i'}$
and
$\mathcal {B}^-_{i'}$
and
![]() $\mathcal {B}^-_{i"}$
for
$\mathcal {B}^-_{i"}$
for
![]() $i=2, 3$
with
$i=2, 3$
with
![]() $p_3\in \mathcal {B}^-_{3'}$
. Moreover, both
$p_3\in \mathcal {B}^-_{3'}$
. Moreover, both
![]() $\mathcal {B}^-_{i'}$
and
$\mathcal {B}^-_{i'}$
and
![]() $\mathcal {B}^-_{i"}$
are biholomorphic to polydisks, and
$\mathcal {B}^-_{i"}$
are biholomorphic to polydisks, and
![]() $f^2 : \mathcal {B}^-_{i'}\to \mathcal {B}^-_3$
and
$f^2 : \mathcal {B}^-_{i'}\to \mathcal {B}^-_3$
and
![]() ${f^2 : \mathcal {B}^-_{i"}\to \mathcal {B}^-_3}$
are crossed mappings of degree one. Note that, a priori, we are not able to distinguish the components
${f^2 : \mathcal {B}^-_{i"}\to \mathcal {B}^-_3}$
are crossed mappings of degree one. Note that, a priori, we are not able to distinguish the components
![]() $\mathcal {B}^-_{i'}$
and
$\mathcal {B}^-_{i'}$
and
![]() $\mathcal {B}^-_{i"}$
(modulo the condition
$\mathcal {B}^-_{i"}$
(modulo the condition
![]() $p_3\in \mathcal {B}^-_{3'}$
) until items (3) and (4) of Corollary 3.6, where we determine
$p_3\in \mathcal {B}^-_{3'}$
) until items (3) and (4) of Corollary 3.6, where we determine
![]() $\mathcal {B}^-_{i'}$
and
$\mathcal {B}^-_{i'}$
and
![]() $\mathcal {B}^-_{i"}$
so that
$\mathcal {B}^-_{i"}$
so that
![]() $\mathcal {B}^-_{i', {\mathbb {R}}}$
contains a curve
$\mathcal {B}^-_{i', {\mathbb {R}}}$
contains a curve
![]() $\gamma _{i, \mathrm {left}}$
on the ‘left’ and
$\gamma _{i, \mathrm {left}}$
on the ‘left’ and
![]() $\mathcal {B}^-_{i", {\mathbb {R}}}$
contains a curve
$\mathcal {B}^-_{i", {\mathbb {R}}}$
contains a curve
![]() $\gamma _{i, \mathrm {right}}$
on the ‘right’.
$\gamma _{i, \mathrm {right}}$
on the ‘right’.
It is useful to consider the corresponding refined symbolic dynamics as follows. We set
![]() $\widetilde {{\Sigma }}^+\equiv \{0, 1, 2', 2", 3\}$
and
$\widetilde {{\Sigma }}^+\equiv \{0, 1, 2', 2", 3\}$
and
![]() $\widetilde {{\Sigma }}^-\equiv \{0, 1, 2', 2", 3', 3", 4\}$
. Choose a subset of
$\widetilde {{\Sigma }}^-\equiv \{0, 1, 2', 2", 3', 3", 4\}$
. Choose a subset of
![]() $\widetilde {\Sigma }^+\times \widetilde {\Sigma }^+$
as
$\widetilde {\Sigma }^+\times \widetilde {\Sigma }^+$
as
and a subset of
![]() $\widetilde {\Sigma }^-\times \widetilde {\Sigma }^-$
as
$\widetilde {\Sigma }^-\times \widetilde {\Sigma }^-$
as
 $$ \begin{align*} \widetilde{\mathfrak{T}}^-\equiv\{(0, 0), (0, 2'), & (0, 2"), (1, 0), (1, 2'), (1, 2"), \\ & (2', 4), (2", 4), (3', 4), (3", 4), (4, 1), (4, 3'), (4, 3") \}. \end{align*} $$
$$ \begin{align*} \widetilde{\mathfrak{T}}^-\equiv\{(0, 0), (0, 2'), & (0, 2"), (1, 0), (1, 2'), (1, 2"), \\ & (2', 4), (2", 4), (3', 4), (3", 4), (4, 1), (4, 3'), (4, 3") \}. \end{align*} $$
We then write
![]() $\widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}\equiv \mathfrak {S}_{\mathrm {fwd}}(\widetilde {\mathfrak {T}}^{\pm })$
,
$\widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}\equiv \mathfrak {S}_{\mathrm {fwd}}(\widetilde {\mathfrak {T}}^{\pm })$
,
![]() $\widetilde {\mathfrak {S}}^{\pm }_{\mathrm {bwd}}\equiv \mathfrak {S}_{\mathrm {bwd}}(\widetilde {\mathfrak {T}}^{\pm })$
, and
$\widetilde {\mathfrak {S}}^{\pm }_{\mathrm {bwd}}\equiv \mathfrak {S}_{\mathrm {bwd}}(\widetilde {\mathfrak {T}}^{\pm })$
, and
![]() $\widetilde {\mathfrak {S}}^{\pm }\equiv \mathfrak {S}(\widetilde {\mathfrak {T}}^{\pm })$
.
$\widetilde {\mathfrak {S}}^{\pm }\equiv \mathfrak {S}(\widetilde {\mathfrak {T}}^{\pm })$
.
For
![]() $(a, b)\in \mathcal {F}_{{\mathbb {R}}}^{\pm }\cap \{b\ne 0\}$
, define the refined orbit space of
$(a, b)\in \mathcal {F}_{{\mathbb {R}}}^{\pm }\cap \{b\ne 0\}$
, define the refined orbit space of
![]() $f_{a, b}$
as
$f_{a, b}$
as
Since
![]() $\mathcal {B}^+_{2'}\cup \mathcal {B}^+_{2"}\subset \mathcal {B}^+_2$
and
$\mathcal {B}^+_{2'}\cup \mathcal {B}^+_{2"}\subset \mathcal {B}^+_2$
and
![]() $\mathcal {B}^-_{i'}\cup \mathcal {B}^-_{i"}\subset \mathcal {B}^-_i$
(
$\mathcal {B}^-_{i'}\cup \mathcal {B}^-_{i"}\subset \mathcal {B}^-_i$
(
![]() $i=2, 3$
) hold, we see that
$i=2, 3$
) hold, we see that
 $$ \begin{align*} \bigcap_{n\in{\mathbb{Z}}}f^n\bigg(\bigcup_{i\in\widetilde{\Sigma}^{\pm}}\mathcal{B}^{\pm}_i\bigg)\subset K_{a, b}.\end{align*} $$
$$ \begin{align*} \bigcap_{n\in{\mathbb{Z}}}f^n\bigg(\bigcup_{i\in\widetilde{\Sigma}^{\pm}}\mathcal{B}^{\pm}_i\bigg)\subset K_{a, b}.\end{align*} $$
Therefore, the projection
can be defined.
Definition 2.12. A bi-infinite sequence
![]() $(i_n)_{n\in {\mathbb {Z}}}\in \widetilde {\mathfrak {S}}^{\pm }$
is called a
$(i_n)_{n\in {\mathbb {Z}}}\in \widetilde {\mathfrak {S}}^{\pm }$
is called a
![]() $\widetilde {\Sigma }^{\pm }$
-coding of
$\widetilde {\Sigma }^{\pm }$
-coding of
![]() $z_0\in K_{a, b}$
if it satisfies
$z_0\in K_{a, b}$
if it satisfies
![]() $\widetilde {\Phi }((i_n)_{n\in {\mathbb {Z}}}, (f^n(z_0))_{n\in {\mathbb {Z}}})=z_0$
.
$\widetilde {\Phi }((i_n)_{n\in {\mathbb {Z}}}, (f^n(z_0))_{n\in {\mathbb {Z}}})=z_0$
.
3 Local stable/unstable manifolds
3.1 Dynamics in
 ${\mathbb {C}}^2$
${\mathbb {C}}^2$
For a real parameter
![]() $(a, b)\in \mathcal {F}_{{\mathbb {R}}}^{\pm }\cap \{b\ne 0\}$
, we let
$(a, b)\in \mathcal {F}_{{\mathbb {R}}}^{\pm }\cap \{b\ne 0\}$
, we let
![]() $p_i\in {\mathbb {R}}^2$
be either the unique saddle fixed point (for
$p_i\in {\mathbb {R}}^2$
be either the unique saddle fixed point (for
![]() $i=1, 3$
) or the unique saddle periodic point of period two (for
$i=1, 3$
) or the unique saddle periodic point of period two (for
![]() $i=2, 4$
) of
$i=2, 4$
) of
![]() $f_{{\mathbb {R}}}$
in the ith quadrant. For a complex parameter
$f_{{\mathbb {R}}}$
in the ith quadrant. For a complex parameter
![]() ${(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}}$
, denote again by
${(a, b)\in \mathcal {F}^{\pm }\cap \{b\ne 0\}}$
, denote again by
![]() $p_i\in {\mathbb {C}}^2$
its complex continuation. Let
$p_i\in {\mathbb {C}}^2$
its complex continuation. Let
![]() $V^{s/u}(p_i)$
be the complex stable/unstable manifold at
$V^{s/u}(p_i)$
be the complex stable/unstable manifold at
![]() $p_i$
. Denote by
$p_i$
. Denote by
![]() $V^{s/u}_{\mathrm {loc}}(p_i)_j$
the connected component of
$V^{s/u}_{\mathrm {loc}}(p_i)_j$
the connected component of
![]() $V^{u/s}(p_i) \cap \mathcal {B}_j^{\pm }$
containing
$V^{u/s}(p_i) \cap \mathcal {B}_j^{\pm }$
containing
![]() $p_i$
.
$p_i$
.
Recall that a bi-infinite
![]() $\mathfrak {T}^{\pm }$
-admissible sequence
$\mathfrak {T}^{\pm }$
-admissible sequence
![]() $I=(i_n)_{n\in {\mathbb {Z}}}\in \mathfrak {S}^{\pm }$
is a
$I=(i_n)_{n\in {\mathbb {Z}}}\in \mathfrak {S}^{\pm }$
is a
![]() $\Sigma ^{\pm }$
-coding of
$\Sigma ^{\pm }$
-coding of
![]() $z\in K_{a, b}$
if and only if
$z\in K_{a, b}$
if and only if
![]() $z\in \bigcap _{n\in \mathbb {Z}}f^{-n}(\mathcal {B}^{\pm }_{i_n})$
. Based on this observation, we define
$z\in \bigcap _{n\in \mathbb {Z}}f^{-n}(\mathcal {B}^{\pm }_{i_n})$
. Based on this observation, we define
for a forward
![]() $\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
$\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
![]() $I=(i_n)_{n\geq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}$
. We also define
$I=(i_n)_{n\geq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}$
. We also define
for a backward
![]() $\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
$\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
![]() $J=(j_n)_{n\leq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {bwd}}$
. Given a point
$J=(j_n)_{n\leq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {bwd}}$
. Given a point
![]() $z\in K_{a, b}$
, a forward
$z\in K_{a, b}$
, a forward
![]() $\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
$\widetilde {\mathfrak {T}}^{\pm }$
-admissible sequence
![]() $I=(i_n)_{n\geq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}$
is called a forward
$I=(i_n)_{n\geq 0}\in \widetilde {\mathfrak {S}}^{\pm }_{\mathrm {fwd}}$
is called a forward
![]() $\widetilde {\Sigma }^{\pm }$
-coding of z if z belongs to
$\widetilde {\Sigma }^{\pm }$
-coding of z if z belongs to
![]() $K^s_I$
.
$K^s_I$
.
We first characterize local stable manifolds in terms of forward
![]() $\widetilde {\Sigma }^{\pm }$
-coding.
$\widetilde {\Sigma }^{\pm }$
-coding.
Lemma 3.1. Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
 $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
 $V^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}$
.
$V^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}$
. -
(2)
 $V^s_{\mathrm {loc}}(p_4)_2$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_4)_2$
is a vertical disk of degree one in
 $\mathcal {B}^+_2$
and
$\mathcal {B}^+_2$
and
 $V^s_{\mathrm {loc}}(p_4)_2=K^s_{\overline {2'310}}$
.
$V^s_{\mathrm {loc}}(p_4)_2=K^s_{\overline {2'310}}$
. -
(3)
 $V^s_{\mathrm {loc}}(p_2)_0$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_2)_0$
is a vertical disk of degree one in
 $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
 $V^s_{\mathrm {loc}}(p_2)_0=K^s_{\overline {02'31}}$
.
$V^s_{\mathrm {loc}}(p_2)_0=K^s_{\overline {02'31}}$
. -
(4)
 $V^s_{\mathrm {loc}}(p_4)_1$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_4)_1$
is a vertical disk of degree one in
 $\mathcal {B}^+_1$
and
$\mathcal {B}^+_1$
and
 $V^s_{\mathrm {loc}}(p_4)_1=K^s_{\overline {102'3}}$
.
$V^s_{\mathrm {loc}}(p_4)_1=K^s_{\overline {102'3}}$
. -
(5)
 $V^s_{\mathrm {loc}}(p_2)_3$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_2)_3$
is a vertical disk of degree one in
 $\mathcal {B}^+_3$
and
$\mathcal {B}^+_3$
and
 $V^s_{\mathrm {loc}}(p_2)_3=K^s_{\overline {3102'}}$
.
$V^s_{\mathrm {loc}}(p_2)_3=K^s_{\overline {3102'}}$
. -
(6)
 $f^{-1}(V^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_2$
is a vertical disk of degree one in
$f^{-1}(V^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_2$
is a vertical disk of degree one in
 $\mathcal {B}^+_2$
. Moreover,
$\mathcal {B}^+_2$
. Moreover,
 $f^{-1}(V^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_2=K^s_{2"\overline {2'310}}$
.
$f^{-1}(V^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_2=K^s_{2"\overline {2'310}}$
.
Proof. Claim (1) follows from the fact that
![]() $f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one.
$f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one.
It follows from the definition of
![]() $\mathcal {B}^+_{2'}$
that
$\mathcal {B}^+_{2'}$
that
![]() $\bigcap _{n\geq 0}f^{-4n}(\mathcal {B}^+_{2'})\kern1.3pt{=}\kern1.3pt K^s_{\overline {2'310}}$
. Since
$\bigcap _{n\geq 0}f^{-4n}(\mathcal {B}^+_{2'})\kern1.3pt{=}\kern1.3pt K^s_{\overline {2'310}}$
. Since
![]() ${f^4 : \mathcal {B}^+_{2'}\kern1.3pt{\to}\kern1.3pt \mathcal {B}^+_2}$
is a crossed mapping of degree one,
${f^4 : \mathcal {B}^+_{2'}\kern1.3pt{\to}\kern1.3pt \mathcal {B}^+_2}$
is a crossed mapping of degree one,
![]() $\bigcap _{n\geq 0}f^{-4n}(\mathcal {B}^+_{2'})$
is a vertical disk of degree one in
$\bigcap _{n\geq 0}f^{-4n}(\mathcal {B}^+_{2'})$
is a vertical disk of degree one in
![]() $\mathcal {B}^+_2$
containing the fixed point
$\mathcal {B}^+_2$
containing the fixed point
![]() $p_4$
and hence is equal to
$p_4$
and hence is equal to
![]() $V^s_{\mathrm {loc}}(p_4)_2$
. This proves claim (2).
$V^s_{\mathrm {loc}}(p_4)_2$
. This proves claim (2).
Claim (3) follows from claim (2) and the fact that
![]() $f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_2)\to \mathcal {B}^+_2$
is a crossed mapping of degree one, claim (4) follows from claim (3) and the fact that
$f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_2)\to \mathcal {B}^+_2$
is a crossed mapping of degree one, claim (4) follows from claim (3) and the fact that
![]() $f : \mathcal {B}^+_1\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one, claim (5) follows from claim (4) and the fact that
$f : \mathcal {B}^+_1\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one, claim (5) follows from claim (4) and the fact that
![]() $f : \mathcal {B}^+_3\cap f^{-1}(\mathcal {B}^+_1)\to \mathcal {B}^+_1$
is a crossed mapping of degree one, and claim (6) follows from claim (2) and the fact that
$f : \mathcal {B}^+_3\cap f^{-1}(\mathcal {B}^+_1)\to \mathcal {B}^+_1$
is a crossed mapping of degree one, and claim (6) follows from claim (2) and the fact that
![]() $f : \mathcal {B}^+_{2"}\cap f^{-1}(\mathcal {B}^+_2)\to \mathcal {B}^+_2$
is a crossed mapping of degree one.
$f : \mathcal {B}^+_{2"}\cap f^{-1}(\mathcal {B}^+_2)\to \mathcal {B}^+_2$
is a crossed mapping of degree one.
Similarly, we have the following lemma.
Lemma 3.2. Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
 $\mathcal {B}^-_0$
and
$\mathcal {B}^-_0$
and
 $V^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}$
.
$V^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}$
. -
(2)
 $V^s_{\mathrm {loc}}(p_3)_3$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_3)_3$
is a vertical disk of degree one in
 $\mathcal {B}^-_3$
and
$\mathcal {B}^-_3$
and
 $V^s_{\mathrm {loc}}(p_3)_3=K^s_{\overline {3'4}}$
.
$V^s_{\mathrm {loc}}(p_3)_3=K^s_{\overline {3'4}}$
. -
(3)
 $V^s_{\mathrm {loc}}(p_3)_4$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_3)_4$
is a vertical disk of degree one in
 $\mathcal {B}^-_4$
and
$\mathcal {B}^-_4$
and
 $V^s_{\mathrm {loc}}(p_3)_4=K^s_{\overline {43'}}$
.
$V^s_{\mathrm {loc}}(p_3)_4=K^s_{\overline {43'}}$
. -
(4)
 $f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_2$
consists of two mutually disjoint vertical disks of degree one in
$f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_2$
consists of two mutually disjoint vertical disks of degree one in
 $\mathcal {B}^-_2$
denoted by
$\mathcal {B}^-_2$
denoted by
 $V_{2'}\subset \mathcal {B}^-_{2'}$
and
$V_{2'}\subset \mathcal {B}^-_{2'}$
and
 $V_{2"}\subset \mathcal {B}^-_{2"}$
. Moreover,
$V_{2"}\subset \mathcal {B}^-_{2"}$
. Moreover,
 $V_{2'}=K^s_{2'\overline {43'}}$
and
$V_{2'}=K^s_{2'\overline {43'}}$
and
 $V_{2"}=K^s_{2"\overline {43'}}$
.
$V_{2"}=K^s_{2"\overline {43'}}$
. -
(5)
 $f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_3$
consists of two mutually disjoint vertical disks of degree one in
$f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_3$
consists of two mutually disjoint vertical disks of degree one in
 $\mathcal {B}^-_3$
denoted by
$\mathcal {B}^-_3$
denoted by
 $V_{3'}\subset \mathcal {B}^-_{3'}$
and
$V_{3'}\subset \mathcal {B}^-_{3'}$
and
 $V_{3"}\subset \mathcal {B}^-_{3"}$
. Moreover,
$V_{3"}\subset \mathcal {B}^-_{3"}$
. Moreover,
 $V_{3'}=K^s_{3'\overline {43'}}$
and
$V_{3'}=K^s_{3'\overline {43'}}$
and
 $V_{3"}=K^s_{3"\overline {43'}}$
.
$V_{3"}=K^s_{3"\overline {43'}}$
. -
(6)
 $f^{-1}(V_{2'})\cap \mathcal {B}^-_1$
is a vertical disk of degree one in
$f^{-1}(V_{2'})\cap \mathcal {B}^-_1$
is a vertical disk of degree one in
 $\mathcal {B}^-_1$
. Moreover,
$\mathcal {B}^-_1$
. Moreover,
 $f^{-1}(V_{2'})\cap \mathcal {B}^-_1=K^s_{12'\overline {43'}}$
.
$f^{-1}(V_{2'})\cap \mathcal {B}^-_1=K^s_{12'\overline {43'}}$
. -
(7)
 $f^{-1}(V_{2'})\cap \mathcal {B}^-_0$
is a vertical disk of degree one in
$f^{-1}(V_{2'})\cap \mathcal {B}^-_0$
is a vertical disk of degree one in
 $\mathcal {B}^-_0$
. Moreover,
$\mathcal {B}^-_0$
. Moreover,
 $f^{-1}(V_{2'})\cap \mathcal {B}^-_0=K^s_{02'\overline {43'}}$
.
$f^{-1}(V_{2'})\cap \mathcal {B}^-_0=K^s_{02'\overline {43'}}$
.
Proof. Claim (1) follows from the fact that
![]() $f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one.
$f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one.
It follows from the definition of
![]() $\mathcal {B}^-_{3'}$
that
$\mathcal {B}^-_{3'}$
that
![]() $\bigcap _{n\geq 0}f^{-2n}(\mathcal {B}^-_{3'})=K^s_{\overline {3'4}}$
. Since
$\bigcap _{n\geq 0}f^{-2n}(\mathcal {B}^-_{3'})=K^s_{\overline {3'4}}$
. Since
![]() ${f^2 : \mathcal {B}^-_{3'}\to \mathcal {B}^-_3}$
is a crossed mapping of degree one,
${f^2 : \mathcal {B}^-_{3'}\to \mathcal {B}^-_3}$
is a crossed mapping of degree one,
![]() $\bigcap _{n\geq 0}f^{-2n}(\mathcal {B}^-_{3'})$
is a vertical disk of degree one in
$\bigcap _{n\geq 0}f^{-2n}(\mathcal {B}^-_{3'})$
is a vertical disk of degree one in
![]() $\mathcal {B}^-_3$
containing the fixed point
$\mathcal {B}^-_3$
containing the fixed point
![]() $p_3$
and hence is equal to
$p_3$
and hence is equal to
![]() $V^s_{\mathrm {loc}}(p_3)_3$
. This proves claim (2).
$V^s_{\mathrm {loc}}(p_3)_3$
. This proves claim (2).
Claim (3) follows from claim (2) and the fact that
![]() $f : \mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_3)\to \mathcal {B}^-_3$
is a crossed mapping of degree one. Claims (6) and (7) follow from the fact in claim (3) that
$f : \mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_3)\to \mathcal {B}^-_3$
is a crossed mapping of degree one. Claims (6) and (7) follow from the fact in claim (3) that
![]() $V_{2'}$
is a vertical disk of degree one in
$V_{2'}$
is a vertical disk of degree one in
![]() $\mathcal {B}^-_2$
and that
$\mathcal {B}^-_2$
and that
![]() $f : \mathcal {B}^-_1\cap f^{-1}(\mathcal {B}^-_2)\to \mathcal {B}^-_2$
and
$f : \mathcal {B}^-_1\cap f^{-1}(\mathcal {B}^-_2)\to \mathcal {B}^-_2$
and
![]() $f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_2)\to \mathcal {B}^-_2$
are crossed mappings of degree one.
$f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_2)\to \mathcal {B}^-_2$
are crossed mappings of degree one.
By Lemma 2.11 and claim (2), we see that
![]() $f^{-2}(V^s_{\mathrm {loc}}(p_3)_3)\cap \mathcal {B}^-_i$
consists of two mutually disjoint vertical disks of degree one in
$f^{-2}(V^s_{\mathrm {loc}}(p_3)_3)\cap \mathcal {B}^-_i$
consists of two mutually disjoint vertical disks of degree one in
![]() $\mathcal {B}^-_i$
for
$\mathcal {B}^-_i$
for
![]() $i=2, 3$
. Since we have
$i=2, 3$
. Since we have
![]() $f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_i=f^{-2}(V^s_{\mathrm {loc}}(p_3)_3)\cap \mathcal {B}^-_i$
, the first half of claims (4) and (5) follow. The second half of claims (4) and (5) easily follows from claim (3).
$f^{-1}(V^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_i=f^{-2}(V^s_{\mathrm {loc}}(p_3)_3)\cap \mathcal {B}^-_i$
, the first half of claims (4) and (5) follow. The second half of claims (4) and (5) easily follows from claim (3).
For
![]() $(a, b)\in \mathcal {F}^+\cap \{b\ne 0\}$
, we know that
$(a, b)\in \mathcal {F}^+\cap \{b\ne 0\}$
, we know that
![]() $f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one. Hence,
$f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one. Hence,
![]() $V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
![]() $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
![]() $V^u_{\mathrm {loc}}(p_1)_0$
is a horizontal disk of degree one in
$V^u_{\mathrm {loc}}(p_1)_0$
is a horizontal disk of degree one in
![]() $\mathcal {B}^+_0$
. For
$\mathcal {B}^+_0$
. For
![]() $(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
, we know that
$(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
, we know that
![]() $f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one. Hence,
$f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one. Hence,
![]() $V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
$V^s_{\mathrm {loc}}(p_1)_0$
is a vertical disk of degree one in
![]() $\mathcal {B}^-_0$
. The next fact is stated in [Reference Arai and IshiiAI, Proposition 3.10].
$\mathcal {B}^-_0$
. The next fact is stated in [Reference Arai and IshiiAI, Proposition 3.10].
Proposition 3.3. When
![]() $(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
,
$(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
,
![]() $V^u_{\mathrm {loc}}(p_3)_3$
is a horizontal disk of degree one in
$V^u_{\mathrm {loc}}(p_3)_3$
is a horizontal disk of degree one in
![]() $\mathcal {B}^-_3$
.
$\mathcal {B}^-_3$
.
Let
![]() $(a, b)\in \mathcal {F}^+\cap \{b\ne 0\}$
. For a forward admissible sequence of the form
$(a, b)\in \mathcal {F}^+\cap \{b\ne 0\}$
. For a forward admissible sequence of the form
![]() ${I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^+}$
, we define
${I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^+}$
, we define
and for a backward admissible sequence of the form
![]() $J=\overline {0}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^+$
, we define
$J=\overline {0}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^+$
, we define
Let
![]() $(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
. For a forward admissible sequence of the form
$(a, b)\in \mathcal {F}^-\cap \{b\ne 0\}$
. For a forward admissible sequence of the form
![]() ${I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^-}$
, we define
${I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^-}$
, we define
and for a backward admissible sequence of the form
![]() $J=\overline {43}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^-$
, we define
$J=\overline {43}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^-$
, we define
Remark 3.4. The set
![]() $K^u_J$
is all the points whose
$K^u_J$
is all the points whose
![]() $\Sigma ^{\pm }$
-coding is J, but we defined
$\Sigma ^{\pm }$
-coding is J, but we defined
![]() $V^u_J(a, b)^{\pm }$
as a piece of a certain local unstable manifold. Hence,
$V^u_J(a, b)^{\pm }$
as a piece of a certain local unstable manifold. Hence,
![]() $V^u_J(a, b)^{\pm }\subset K^u_J$
always holds but
$V^u_J(a, b)^{\pm }\subset K^u_J$
always holds but
![]() $V^u_J(a, b)^{\pm }$
is not necessarily equal to
$V^u_J(a, b)^{\pm }$
is not necessarily equal to
![]() $K^u_J$
. For example,
$K^u_J$
. For example,
![]() $K^u_{\overline {43}}$
consists of infinitely many mutually disjoint horizontal disks in
$K^u_{\overline {43}}$
consists of infinitely many mutually disjoint horizontal disks in
![]() $\mathcal {B}^-_3$
in the case of
$\mathcal {B}^-_3$
in the case of
![]() $b < 0$
. However,
$b < 0$
. However,
![]() $V^u_{\overline {43}}(a, b)^-$
is one of those disks. For the motivation of our definition, see Remark 4.10.
$V^u_{\overline {43}}(a, b)^-$
is one of those disks. For the motivation of our definition, see Remark 4.10.
3.2 Dynamics in
 ${\mathbb {R}}^2$
${\mathbb {R}}^2$
Let us assume that
![]() $(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
. We denote the real slice of
$(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
. We denote the real slice of
![]() $\mathcal {B}^{\pm }_i$
by
$\mathcal {B}^{\pm }_i$
by
![]() $\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\equiv \mathcal {B}^{\pm }_i\cap {\mathbb {R}}^2$
. A curve
$\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\equiv \mathcal {B}^{\pm }_i\cap {\mathbb {R}}^2$
. A curve
![]() $\gamma $
in
$\gamma $
in
![]() $\mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
is said to be horizontal (respectively vertical) if the projection
$\mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
is said to be horizontal (respectively vertical) if the projection
![]() $\pi _x : \gamma \to D_{x, {\mathbb {R}}}$
(respectively
$\pi _x : \gamma \to D_{x, {\mathbb {R}}}$
(respectively
![]() $\pi _y : \gamma \to D_{y, {\mathbb {R}}}$
) is a bijection, where
$\pi _y : \gamma \to D_{y, {\mathbb {R}}}$
) is a bijection, where
![]() $D_{x, {\mathbb {R}}}$
and
$D_{x, {\mathbb {R}}}$
and
![]() $D_{y, {\mathbb {R}}}$
are intervals so that
$D_{y, {\mathbb {R}}}$
are intervals so that
![]() $\mathcal {B}^{\pm }_{j, {\mathbb {R}}}=D_{x, {\mathbb {R}}}\times _{\mathrm {pr}}D_{y, {\mathbb {R}}}$
.
$\mathcal {B}^{\pm }_{j, {\mathbb {R}}}=D_{x, {\mathbb {R}}}\times _{\mathrm {pr}}D_{y, {\mathbb {R}}}$
.
Recall that
![]() $p_i$
is either the unique saddle fixed point (for
$p_i$
is either the unique saddle fixed point (for
![]() $i=1, 3$
) or the unique saddle periodic point of period two (for
$i=1, 3$
) or the unique saddle periodic point of period two (for
![]() $i=2, 4$
) in the ith quadrant. Denote by
$i=2, 4$
) in the ith quadrant. Denote by
![]() $W^{u/s}_{\mathrm {loc}}(p_i)_j$
the connected component of
$W^{u/s}_{\mathrm {loc}}(p_i)_j$
the connected component of
![]() $W^{u/s}(p_i) \cap \mathcal {B}_{j, {\mathbb {R}}}^{\pm }$
containing
$W^{u/s}(p_i) \cap \mathcal {B}_{j, {\mathbb {R}}}^{\pm }$
containing
![]() $p_i$
. We have
$p_i$
. We have
![]() $W^{u/s}_{\mathrm {loc}}(p_i)_j=V^{u/s}_{\mathrm {loc}}(p_i)_j\cap {\mathbb {R}}^2$
.
$W^{u/s}_{\mathrm {loc}}(p_i)_j=V^{u/s}_{\mathrm {loc}}(p_i)_j\cap {\mathbb {R}}^2$
.
Corollary 3.5. Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $W^s_{\mathrm {loc}}(p_1)_0$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_1)_0$
is a vertical curve in
 $\mathcal {B}^+_{0, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{0, {\mathbb {R}}}$
denoted by
 $\gamma^+_{0,\mathrm{right}}$
and
$\gamma^+_{0,\mathrm{right}}$
and
 $W^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}\cap {\mathbb {R}}^2$
. -
(2)
 $W^s_{\mathrm {loc}}(p_4)_2$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_4)_2$
is a vertical curve in
 $\mathcal {B}^+_{2, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{2, {\mathbb {R}}}$
denoted by
 $\gamma^+_{2,\mathrm{right}}$
and
$\gamma^+_{2,\mathrm{right}}$
and
 $W^s_{\mathrm {loc}}(p_4)_2\hspace{-1pt}= \hspace{-1pt}K^s_{\overline {2'310}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_4)_2\hspace{-1pt}= \hspace{-1pt}K^s_{\overline {2'310}}\cap {\mathbb {R}}^2$
. -
(3)
 $W^s_{\mathrm {loc}}(p_2)_0$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_2)_0$
is a vertical curve in
 $\mathcal {B}^+_{0, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{0, {\mathbb {R}}}$
denoted by
 $\gamma^+_{0,\mathrm{left}}$
and
$\gamma^+_{0,\mathrm{left}}$
and
 $W^s_{\mathrm {loc}}(p_2)_0=K^s_{\overline {02'31}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_2)_0=K^s_{\overline {02'31}}\cap {\mathbb {R}}^2$
. -
(4)
 $W^s_{\mathrm {loc}}(p_4)_1$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_4)_1$
is a vertical curve in
 $\mathcal {B}^+_{1, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{1, {\mathbb {R}}}$
denoted by
 $\gamma^+_{1,\mathrm{left}}$
and
$\gamma^+_{1,\mathrm{left}}$
and
 $W^s_{\mathrm {loc}}(p_4)_1=K^s_{\overline {102'3}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_4)_1=K^s_{\overline {102'3}}\cap {\mathbb {R}}^2$
. -
(5)
 $W^s_{\mathrm {loc}}(p_2)_3$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_2)_3$
is a vertical curve in
 $\mathcal {B}^+_{3, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{3, {\mathbb {R}}}$
denoted by
 $\gamma^+_{3,\mathrm{right}}$
and
$\gamma^+_{3,\mathrm{right}}$
and
 $W^s_{\mathrm {loc}}(p_2)_3= K^s_{\overline {3102'}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_2)_3= K^s_{\overline {3102'}}\cap {\mathbb {R}}^2$
. -
(6)
 $f^{-1}_{{\mathbb {R}}}(W^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_{2, {\mathbb {R}}}$
is a vertical curve in
$f^{-1}_{{\mathbb {R}}}(W^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_{2, {\mathbb {R}}}$
is a vertical curve in
 $\mathcal {B}^+_{2, {\mathbb {R}}}$
denoted by
$\mathcal {B}^+_{2, {\mathbb {R}}}$
denoted by
 $\gamma^+_{2,\mathrm{left}}$
and
$\gamma^+_{2,\mathrm{left}}$
and
 $f^{-1}_{{\mathbb {R}}}(W^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_{2, {\mathbb {R}}}=K^s_{2"\overline {2'310}}\cap {\mathbb {R}}^2$
.
$f^{-1}_{{\mathbb {R}}}(W^s_{\mathrm {loc}}(p_4)_2)\cap \mathcal {B}^+_{2, {\mathbb {R}}}=K^s_{2"\overline {2'310}}\cap {\mathbb {R}}^2$
.
Proof. This immediately follows from Lemma 3.1 by taking the real parts.
We also know that
![]() $V^u_{\mathrm {loc}}(p_1)_0$
is a horizontal disk of degree one in
$V^u_{\mathrm {loc}}(p_1)_0$
is a horizontal disk of degree one in
![]() $\mathcal {B}^+_0$
. Therefore,
$\mathcal {B}^+_0$
. Therefore,
![]() $W^u_{\mathrm {loc}}(p_1)_0$
is a horizontal curve in
$W^u_{\mathrm {loc}}(p_1)_0$
is a horizontal curve in
![]() $\mathcal {B}^+_{0, {\mathbb {R}}}$
.
$\mathcal {B}^+_{0, {\mathbb {R}}}$
.
When there are two mutually disjoint vertical curves in
![]() $\mathcal {B}^-_{i, {\mathbb {R}}}$
, we can distinguish the left one and the right one.
$\mathcal {B}^-_{i, {\mathbb {R}}}$
, we can distinguish the left one and the right one.
Corollary 3.6. Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $W^s_{\mathrm {loc}}(p_1)_0$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_1)_0$
is a vertical curve in
 $\mathcal {B}^-_{0, {\mathbb {R}}}$
denoted by
$\mathcal {B}^-_{0, {\mathbb {R}}}$
denoted by
 $\gamma^-_{0,\mathrm{right}}$
and
$\gamma^-_{0,\mathrm{right}}$
and
 $W^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}\cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_1)_0=K^s_{\overline {0}}\cap {\mathbb {R}}^2$
. -
(2)
 $W^s_{\mathrm {loc}}(p_3)_3$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_3)_3$
is a vertical curve in
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
denoted by
$\mathcal {B}^-_{3, {\mathbb {R}}}$
denoted by
 $\gamma^-_{3,\mathrm{left}}$
and
$\gamma^-_{3,\mathrm{left}}$
and
 $W^s_{\mathrm {loc}}(p_3)_3=K^s_{\overline {3'4}} \cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_3)_3=K^s_{\overline {3'4}} \cap {\mathbb {R}}^2$
. -
(3)
 $W^s_{\mathrm {loc}}(p_3)_4$
is a vertical curve in
$W^s_{\mathrm {loc}}(p_3)_4$
is a vertical curve in
 $\mathcal {B}^-_{4, {\mathbb {R}}}$
denoted by
$\mathcal {B}^-_{4, {\mathbb {R}}}$
denoted by
 $\gamma^-_{4,\mathrm{right}}$
and
$\gamma^-_{4,\mathrm{right}}$
and
 $W^s_{\mathrm {loc}}(p_3)_4=K^s_{\overline {43'}} \cap {\mathbb {R}}^2$
.
$W^s_{\mathrm {loc}}(p_3)_4=K^s_{\overline {43'}} \cap {\mathbb {R}}^2$
. -
(4)
 $f_{{\mathbb {R}}}^{-1}(W^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_{2, {\mathbb {R}}}$
consists of two mutually disjoint vertical curves in
$f_{{\mathbb {R}}}^{-1}(W^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_{2, {\mathbb {R}}}$
consists of two mutually disjoint vertical curves in
 $\mathcal {B}^-_{2, {\mathbb {R}}}$
; the left one is denoted by
$\mathcal {B}^-_{2, {\mathbb {R}}}$
; the left one is denoted by
 $\gamma^-_{2, \mathrm {left}}\subset \mathcal {B}^-_{2', {\mathbb {R}}}$
and the right one is denoted by
$\gamma^-_{2, \mathrm {left}}\subset \mathcal {B}^-_{2', {\mathbb {R}}}$
and the right one is denoted by
 $\gamma^-_{2, \mathrm {right}}\subset \mathcal {B}^-_{2", {\mathbb {R}}}$
. Moreover,
$\gamma^-_{2, \mathrm {right}}\subset \mathcal {B}^-_{2", {\mathbb {R}}}$
. Moreover,
 $\gamma^-_{2, \mathrm {left}}=K^s_{2'\overline {43'}} \cap {\mathbb {R}}^2$
and
$\gamma^-_{2, \mathrm {left}}=K^s_{2'\overline {43'}} \cap {\mathbb {R}}^2$
and
 $\gamma^-_{2, \mathrm {right}}=K^s_{2"\overline {43'}} \cap {\mathbb {R}}^2$
.
$\gamma^-_{2, \mathrm {right}}=K^s_{2"\overline {43'}} \cap {\mathbb {R}}^2$
. -
(5)
 $f_{{\mathbb {R}}}^{-1}(W^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_{3, {\mathbb {R}}}$
consists of two mutually disjoint vertical curves in
$f_{{\mathbb {R}}}^{-1}(W^s_{\mathrm {loc}}(p_3)_4)\cap \mathcal {B}^-_{3, {\mathbb {R}}}$
consists of two mutually disjoint vertical curves in
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
; the left one is denoted by
$\mathcal {B}^-_{3, {\mathbb {R}}}$
; the left one is denoted by
 $\gamma^-_{3, \mathrm {left}}\subset \mathcal {B}^-_{3', {\mathbb {R}}}$
and the right one is denoted by
$\gamma^-_{3, \mathrm {left}}\subset \mathcal {B}^-_{3', {\mathbb {R}}}$
and the right one is denoted by
 $\gamma^-_{3, \mathrm {right}}\subset \mathcal {B}^-_{3", {\mathbb {R}}}$
. Moreover,
$\gamma^-_{3, \mathrm {right}}\subset \mathcal {B}^-_{3", {\mathbb {R}}}$
. Moreover,
 $\gamma^-_{3, \mathrm {left}}=K^s_{3'\overline {43'}} \cap {\mathbb {R}}^2$
and
$\gamma^-_{3, \mathrm {left}}=K^s_{3'\overline {43'}} \cap {\mathbb {R}}^2$
and
 $\gamma^-_{3, \mathrm {right}}=K^s_{ 3"\overline {43'}} \cap {\mathbb {R}}^2$
.
$\gamma^-_{3, \mathrm {right}}=K^s_{ 3"\overline {43'}} \cap {\mathbb {R}}^2$
. -
(6)
 $f_{{\mathbb {R}}}^{-1}(\gamma^-_{2, \mathrm {left}})\cap \mathcal {B}^-_{1, {\mathbb {R}}}$
is a vertical curve in
$f_{{\mathbb {R}}}^{-1}(\gamma^-_{2, \mathrm {left}})\cap \mathcal {B}^-_{1, {\mathbb {R}}}$
is a vertical curve in
 $\mathcal {B}^-_{1, {\mathbb {R}}}$
denoted by
$\mathcal {B}^-_{1, {\mathbb {R}}}$
denoted by
 $\gamma^-_{1, \mathrm {left}}$
. Moreover,
$\gamma^-_{1, \mathrm {left}}$
. Moreover,
 $\gamma^-_{1, \mathrm {left}}=K^s_{12'\overline {43'}} \cap {\mathbb {R}}^2$
.
$\gamma^-_{1, \mathrm {left}}=K^s_{12'\overline {43'}} \cap {\mathbb {R}}^2$
. -
(7)
 $f_{{\mathbb {R}}}^{-1}(\gamma^-_{2, \mathrm {left}})\cap \mathcal {B}^-_{0, {\mathbb {R}}}$
is a vertical curve in
$f_{{\mathbb {R}}}^{-1}(\gamma^-_{2, \mathrm {left}})\cap \mathcal {B}^-_{0, {\mathbb {R}}}$
is a vertical curve in
 $\mathcal {B}^-_{0, {\mathbb {R}}}$
denoted by
$\mathcal {B}^-_{0, {\mathbb {R}}}$
denoted by
 $\gamma^-_{0, \mathrm {left}}$
. Moreover,
$\gamma^-_{0, \mathrm {left}}$
. Moreover,
 $\gamma^-_{0, \mathrm {left}}=K^s_{02'\overline {43'}} \cap {\mathbb {R}}^2$
.
$\gamma^-_{0, \mathrm {left}}=K^s_{02'\overline {43'}} \cap {\mathbb {R}}^2$
.
Proof. This immediately follows from Lemma 3.2 by taking the real parts.
Below, when the context is clear, we drop the superscript
![]() $\pm$
in
$\pm$
in
![]() $\gamma^\pm_{j,\mathrm{left}}$
and
$\gamma^\pm_{j,\mathrm{left}}$
and
![]() $\gamma^\pm_{j,\mathrm{right}}$
, and write
$\gamma^\pm_{j,\mathrm{right}}$
, and write
![]() $\gamma_{j,\mathrm{left}}$
and
$\gamma_{j,\mathrm{left}}$
and
![]() $\gamma_{j,\mathrm{right}}$
, respectively.
$\gamma_{j,\mathrm{right}}$
, respectively.
Since
![]() $p_3\in \gamma _{3, \mathrm {left}}$
, we have
$p_3\in \gamma _{3, \mathrm {left}}$
, we have
![]() $\gamma _{3, \mathrm {left}}=W^s_{\mathrm {loc}}(p_3)_3$
. We also know that
$\gamma _{3, \mathrm {left}}=W^s_{\mathrm {loc}}(p_3)_3$
. We also know that
![]() $V^u_{\mathrm {loc}}(p_3)_3$
is a horizontal disk of degree one in
$V^u_{\mathrm {loc}}(p_3)_3$
is a horizontal disk of degree one in
![]() $\mathcal {B}^-_3$
(see Proposition 3.3), and hence
$\mathcal {B}^-_3$
(see Proposition 3.3), and hence
![]() $W^u_{\mathrm {loc}}(p_3)_3$
is a horizontal curve in
$W^u_{\mathrm {loc}}(p_3)_3$
is a horizontal curve in
![]() $\mathcal {B}^-_{3, {\mathbb {R}}}$
.
$\mathcal {B}^-_{3, {\mathbb {R}}}$
.
Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. For a forward admissible sequence of the form
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. For a forward admissible sequence of the form
![]() $I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^+$
, we define
$I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^+$
, we define
and for a backward admissible sequence of the form
![]() $J=\overline {0}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^+$
, we define
$J=\overline {0}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^+$
, we define
Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. For a forward admissible sequence of the form
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. For a forward admissible sequence of the form
![]() $I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^-$
, we define
$I=i_0 i_1\cdots i_n\overline {0}\in \mathfrak {S}_{\mathrm {fwd}}^-$
, we define
and for a backward admissible sequence of the form
![]() $J=\overline {43}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^-$
, we define
$J=\overline {43}j_{-n}\cdots j_{-1}j_0\in \mathfrak {S}_{\mathrm {bwd}}^-$
, we define
As in [Reference Arai and IshiiAI, Definition 4.4],
![]() $W^u_{\overline {43}4124}(a, b)^-$
is decomposed into two parts: the ‘inner part’
$W^u_{\overline {43}4124}(a, b)^-$
is decomposed into two parts: the ‘inner part’
![]() $W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
and the ‘outer part’
$W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
and the ‘outer part’
![]() $W^u_{\overline {43}4124}(a, b)^-_{\mathrm {outer}}$
.
$W^u_{\overline {43}4124}(a, b)^-_{\mathrm {outer}}$
.
4 Dynamics near the boundary
 $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
4.1 The
 $\{L, R\}$
-coding
$\{L, R\}$
-coding
In this subsection, we define the
![]() $\{L, R\}$
-coding with respect to our box systems
$\{L, R\}$
-coding with respect to our box systems
![]() $\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
. We note that our partition to define the
$\{\mathcal {B}^{\pm }_i\}_{i\in \Sigma ^{\pm }}$
. We note that our partition to define the
![]() $\{L, R\}$
-coding is more involved than that given in [Reference Bedford and SmillieBSℝ3].
$\{L, R\}$
-coding is more involved than that given in [Reference Bedford and SmillieBSℝ3].
When
![]() $\gamma \subset \mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
is a vertical curve, the notion of left/right component of
$\gamma \subset \mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
is a vertical curve, the notion of left/right component of
![]() $\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma $
can be defined and denoted as
$\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma $
can be defined and denoted as
![]() $\mathrm {left}(\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma )$
and
$\mathrm {left}(\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma )$
and
![]() $\mathrm {right}(\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma )$
.
$\mathrm {right}(\mathcal {B}^{\pm }_{i, {\mathbb {R}}}\setminus \gamma )$
.
Propositions 4.1 and 4.4 will be crucial in the rest of this paper.
Proposition 4.1. Suppose that
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Let
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Let
![]() $z\in K_{{\mathbb {R}}}$
and let
$z\in K_{{\mathbb {R}}}$
and let
![]() $(i_n)_{n\geq 0}\in \mathfrak {S}^+_{\mathrm {fwd}}$
be its forward
$(i_n)_{n\geq 0}\in \mathfrak {S}^+_{\mathrm {fwd}}$
be its forward
![]() $\Sigma ^+$
-coding.
$\Sigma ^+$
-coding.
-
(1) If
 $i_0=0$
, then z belongs to the closure of
$i_0=0$
, then z belongs to the closure of
 $\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
.
$\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
. -
(2) If
 $i_0=1$
, then z belongs to the closure of
$i_0=1$
, then z belongs to the closure of
 $\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
.
$\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
. -
(3) If
 $i_0=2$
, then z belongs to the closure of
$i_0=2$
, then z belongs to the closure of
 $\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
.
$\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
. -
(4) If
 $i_0=3$
, then z belongs to the closure of
$i_0=3$
, then z belongs to the closure of
 $\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
.
$\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
.
Proof. Let
![]() $i_0=0$
and assume that z belongs to
$i_0=0$
and assume that z belongs to
![]() $\mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
. Since
$\mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
. Since
![]() $(i_n)_{n\geq 0}$
is admissible,
$(i_n)_{n\geq 0}$
is admissible,
![]() $i_1$
is either
$i_1$
is either
![]() $2$
or
$2$
or
![]() $3$
(but not
$3$
(but not
![]() $1$
). It follows that
$1$
). It follows that
![]() $f_{{\mathbb {R}}}(z)$
belongs to
$f_{{\mathbb {R}}}(z)$
belongs to
![]() $\mathrm {right}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
(compare [Reference Arai and IshiiAI, Lemma 4.7]) and
$\mathrm {right}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
(compare [Reference Arai and IshiiAI, Lemma 4.7]) and
![]() $i_1=2$
. Similarly, since
$i_1=2$
. Similarly, since
![]() $i_2$
is either
$i_2$
is either
![]() $2$
or
$2$
or
![]() $3$
(but not
$3$
(but not
![]() $0$
), it follows that
$0$
), it follows that
![]() $f_{{\mathbb {R}}}^2(z)$
belongs to
$f_{{\mathbb {R}}}^2(z)$
belongs to
![]() $\mathrm {right}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
and
$\mathrm {right}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
and
![]() $i_2=3$
. A similar argument shows that
$i_2=3$
. A similar argument shows that
![]() $f_{{\mathbb {R}}}^3(z)$
belongs to
$f_{{\mathbb {R}}}^3(z)$
belongs to
![]() $\mathrm {left}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
and
$\mathrm {left}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
and
![]() $i_3=1$
, and
$i_3=1$
, and
![]() $f_{{\mathbb {R}}}^4(z)$
belongs to
$f_{{\mathbb {R}}}^4(z)$
belongs to
![]() $\mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
and
$\mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
and
![]() $i_4=0$
. By repeating this, we see that
$i_4=0$
. By repeating this, we see that
![]() ${z\in K^s_{\overline {0231}}\cap {\mathbb {R}}^2}$
. Moreover, since
${z\in K^s_{\overline {0231}}\cap {\mathbb {R}}^2}$
. Moreover, since
![]() $\mathrm {right}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\subset \mathcal {B}^+_{2', {\mathbb {R}}}$
, we obtain
$\mathrm {right}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\subset \mathcal {B}^+_{2', {\mathbb {R}}}$
, we obtain
![]() $z\in K^s_{\overline {02'31}}\cap {\mathbb {R}}^2$
. It follows from Lemma 3.1(1) that
$z\in K^s_{\overline {02'31}}\cap {\mathbb {R}}^2$
. It follows from Lemma 3.1(1) that
![]() $z\in W^s_{\mathrm {loc}}(p_2)_0$
, which contradicts to the assumption that
$z\in W^s_{\mathrm {loc}}(p_2)_0$
, which contradicts to the assumption that
![]() $z\in \mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
. Hence, claim (1) of this proposition is proved. The proofs for the other cases are similar.
$z\in \mathrm {left}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
. Hence, claim (1) of this proposition is proved. The proofs for the other cases are similar.
To define the
![]() $\{L, R\}$
-partition, it is important to control the slopes of local stable manifolds. To obtain a simple criterion for estimates of the slopes, we employ the Poincaré metric and (vertical) Poincaré cone field (see [Reference IshiiI, Definition 2.5]). Let
$\{L, R\}$
-partition, it is important to control the slopes of local stable manifolds. To obtain a simple criterion for estimates of the slopes, we employ the Poincaré metric and (vertical) Poincaré cone field (see [Reference IshiiI, Definition 2.5]). Let
![]() $\mathcal {P}=D_x\times D_y$
be a polydisk, where
$\mathcal {P}=D_x\times D_y$
be a polydisk, where
![]() $D_x\subset \mathbb {C}$
is a round disk of radius
$D_x\subset \mathbb {C}$
is a round disk of radius
![]() $\delta>0$
and
$\delta>0$
and
![]() $D_y\subset \mathbb {C}$
is the round disk of radius
$D_y\subset \mathbb {C}$
is the round disk of radius
![]() $R>0$
. Take
$R>0$
. Take
![]() $0<r<R$
and set
$0<r<R$
and set
![]() $\mathcal {P}'=D_x\times D^{\prime }_y$
, where
$\mathcal {P}'=D_x\times D^{\prime }_y$
, where
![]() $D^{\prime }_y\subset \mathbb {C}$
is the round disk of radius r. Denote by
$D^{\prime }_y\subset \mathbb {C}$
is the round disk of radius r. Denote by
![]() $|v_x|_P$
(respectively
$|v_x|_P$
(respectively
![]() $|v_y|_P$
) the Poincaré metric in
$|v_y|_P$
) the Poincaré metric in
![]() $D_x$
(respectively
$D_x$
(respectively
![]() $D_y$
).
$D_y$
).
Let D be a vertical disk of degree one in
![]() $\mathcal {P}$
. It has been shown in [Reference IshiiI, Corollary 2.10] that every tangent vector
$\mathcal {P}$
. It has been shown in [Reference IshiiI, Corollary 2.10] that every tangent vector
![]() $v\in T_zD$
belongs to the vertical Poincaré cone at z:
$v\in T_zD$
belongs to the vertical Poincaré cone at z:
As in the example following [Reference IshiiI, Corollary 2.10], the condition
![]() $|v_y|_P\geq |v_x|_P$
is rewritten as
$|v_y|_P\geq |v_x|_P$
is rewritten as
 $$ \begin{align*}\frac{|v_y|_E}{|v_x|_E}\geq \frac{R^2-|y|^2}{\delta^2-|x|^2},\end{align*} $$
$$ \begin{align*}\frac{|v_y|_E}{|v_x|_E}\geq \frac{R^2-|y|^2}{\delta^2-|x|^2},\end{align*} $$
where
![]() $|v_x|_E$
(respectively
$|v_x|_E$
(respectively
![]() $|v_y|_E$
) denotes the Euclidean metric in
$|v_y|_E$
) denotes the Euclidean metric in
![]() $\mathbb {C}$
. Moreover, if we restrict z to
$\mathbb {C}$
. Moreover, if we restrict z to
![]() $\mathcal {P}'$
, the estimate above yields
$\mathcal {P}'$
, the estimate above yields
 $$ \begin{align*}\frac{|v_y|_E}{|v_x|_E}\geq \frac{R^2-r^2}{\delta^2}\end{align*} $$
$$ \begin{align*}\frac{|v_y|_E}{|v_x|_E}\geq \frac{R^2-r^2}{\delta^2}\end{align*} $$
for any
![]() $v\in T_{z'}D$
and any
$v\in T_{z'}D$
and any
![]() $z'\in \mathcal {P}'$
. Finally, let us replace
$z'\in \mathcal {P}'$
. Finally, let us replace
![]() $\mathcal {P}=D_x\times D_y$
by the projective polydisk
$\mathcal {P}=D_x\times D_y$
by the projective polydisk
![]() $D_x\times _{\mathrm {pr}}D_y$
, where the u-direction is
$D_x\times _{\mathrm {pr}}D_y$
, where the u-direction is
![]() $(1, 0)$
and the v-direction is
$(1, 0)$
and the v-direction is
![]() $(s, 1)$
with
$(s, 1)$
with
![]() $s\ne 0$
. The computation
$s\ne 0$
. The computation
 $$ \begin{align*} \begin{bmatrix} 1 & |s| \\[5pt] 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\[5pt] \frac{R^2-r^2}{\delta^2} \end{bmatrix}= \begin{bmatrix} \frac{\delta^2+|s|(R^2-r^2)}{\delta^2} \\[5pt] \frac{R^2-r^2}{\delta^2} \end{bmatrix} \end{align*} $$
$$ \begin{align*} \begin{bmatrix} 1 & |s| \\[5pt] 0 & 1 \end{bmatrix} \begin{bmatrix} 1 \\[5pt] \frac{R^2-r^2}{\delta^2} \end{bmatrix}= \begin{bmatrix} \frac{\delta^2+|s|(R^2-r^2)}{\delta^2} \\[5pt] \frac{R^2-r^2}{\delta^2} \end{bmatrix} \end{align*} $$
shows that the slope of
![]() $v\in T_{z'}D$
in modulus is estimated from below by
$v\in T_{z'}D$
in modulus is estimated from below by
 $$ \begin{align} \frac{R^2-r^2}{\delta^2+|s|(R^2-r^2)} \end{align} $$
$$ \begin{align} \frac{R^2-r^2}{\delta^2+|s|(R^2-r^2)} \end{align} $$
for any
![]() $z'\in \mathcal {P}'$
.
$z'\in \mathcal {P}'$
.
In the following lemma, a horizontal edge (respectively vertical edge) of a quadrilateral
![]() $\mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
in
$\mathcal {B}^{\pm }_{i, {\mathbb {R}}}$
in
![]() ${\mathbb {R}}^2$
is a connected component of the real part of
${\mathbb {R}}^2$
is a connected component of the real part of
![]() $D^{\pm }_{u, i}\times _{\mathrm {pr}} \partial D^{\pm }_{v, i}$
(respectively
$D^{\pm }_{u, i}\times _{\mathrm {pr}} \partial D^{\pm }_{v, i}$
(respectively
![]() $\partial D^{\pm }_{u, i}\times _{\mathrm {pr}} D^{\pm }_{v, i}$
). Given a closed interval
$\partial D^{\pm }_{u, i}\times _{\mathrm {pr}} D^{\pm }_{v, i}$
). Given a closed interval
![]() $I=[\alpha , \beta ]$
in the y-axis, we put
$I=[\alpha , \beta ]$
in the y-axis, we put
![]() $|I|=|\beta -\alpha |$
and let
$|I|=|\beta -\alpha |$
and let
![]() $D_I$
be the disk in the complex y-plane centered at
$D_I$
be the disk in the complex y-plane centered at
![]() $({\alpha +\beta})/{2}$
with radius
$({\alpha +\beta})/{2}$
with radius
![]() ${|I|}/{2}$
. As before, given a polydisk
${|I|}/{2}$
. As before, given a polydisk
![]() $\mathcal {P}_i$
, denote by
$\mathcal {P}_i$
, denote by
![]() $\mathcal {P}_{i, {\mathbb {R}}}$
its real part.
$\mathcal {P}_{i, {\mathbb {R}}}$
its real part.
Lemma 4.2. (Numerical Check 5)
Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
.
-
(1) One can find two concentric intervals
 $I_2=[y_2-R_2, y_2+R_2]$
and
$I_2=[y_2-R_2, y_2+R_2]$
and
 $I^{\prime }_2=[y_2-r_2, y_2+r_2]$
in the y-axis with
$I^{\prime }_2=[y_2-r_2, y_2+r_2]$
in the y-axis with
 $r_2<R_2$
and a disk
$r_2<R_2$
and a disk
 $D_2$
of radius
$D_2$
of radius
 $\delta _2>0$
so that:
$\delta _2>0$
so that:-
(a) a projective polydisk of the form
 $\mathcal {P}_2=D_2\times _{\mathrm {pr}} D_{I_2}$
contains
$\mathcal {P}_2=D_2\times _{\mathrm {pr}} D_{I_2}$
contains
 $p_2$
;
$p_2$
; -
(b)
 $f^2 : \mathcal {P}_2\cap f^{-2}(\mathcal {P}_2)\to \mathcal {P}_2$
is a crossed mapping of degree one;
$f^2 : \mathcal {P}_2\cap f^{-2}(\mathcal {P}_2)\to \mathcal {P}_2$
is a crossed mapping of degree one; -
(c)
 $\mathrm {pr}_y(\mathcal {B}^+_{0, {\mathbb {R}}}\cup \mathcal {B}^+_{3, {\mathbb {R}}})\subset I^{\prime }_2$
;
$\mathrm {pr}_y(\mathcal {B}^+_{0, {\mathbb {R}}}\cup \mathcal {B}^+_{3, {\mathbb {R}}})\subset I^{\prime }_2$
; -
(d)
 $\mathcal {P}_{2, {\mathbb {R}}}\cap \mathcal {B}^+_{i , {\mathbb {R}}}$
does not intersect the vertical edges of
$\mathcal {P}_{2, {\mathbb {R}}}\cap \mathcal {B}^+_{i , {\mathbb {R}}}$
does not intersect the vertical edges of
 $\mathcal {B}^+_{i, {\mathbb {R}}}$
for
$\mathcal {B}^+_{i, {\mathbb {R}}}$
for
 $i=0, 3$
;
$i=0, 3$
; -
(e) the slopes of the horizontal edges of
 $\mathcal {B}^+_{0, {\mathbb {R}}}$
and
$\mathcal {B}^+_{0, {\mathbb {R}}}$
and
 $\mathcal {B}^+_{3, {\mathbb {R}}}$
in modulus are bounded by from above, where
$\mathcal {B}^+_{3, {\mathbb {R}}}$
in modulus are bounded by from above, where $$ \begin{align*}\frac{R_2^2-r_2^2}{\delta_2^2+|s_2|(R_2^2-r_2^2)}\end{align*} $$
$$ \begin{align*}\frac{R_2^2-r_2^2}{\delta_2^2+|s_2|(R_2^2-r_2^2)}\end{align*} $$
 $(s_2, 1)$
is the v-direction in defining
$(s_2, 1)$
is the v-direction in defining
 $\mathcal {P}_2$
.
$\mathcal {P}_2$
.
-
-
(2) One can find two concentric intervals
 $I_4=[y_4-R_4, y_4+R_4]$
and
$I_4=[y_4-R_4, y_4+R_4]$
and
 $I^{\prime }_4=[y_4-r_4, y_4+r_4]$
in the y-axis with
$I^{\prime }_4=[y_4-r_4, y_4+r_4]$
in the y-axis with
 $r_4<R_4$
and a disk
$r_4<R_4$
and a disk
 $D_4$
of radius
$D_4$
of radius
 $\delta _4>0$
so that:
$\delta _4>0$
so that:-
(a) a projective polydisk of the form
 $\mathcal {P}_4=D_4\times _{\mathrm {pr}} D_{I_4}$
contains
$\mathcal {P}_4=D_4\times _{\mathrm {pr}} D_{I_4}$
contains
 $p_4$
;
$p_4$
; -
(b)
 $f^2 : \mathcal {P}_4\cap f^{-2}(\mathcal {P}_4)\to \mathcal {P}_4$
is a crossed mapping of degree one;
$f^2 : \mathcal {P}_4\cap f^{-2}(\mathcal {P}_4)\to \mathcal {P}_4$
is a crossed mapping of degree one; -
(c)
 $\mathrm {pr}_y(\mathcal {B}^+_{1, {\mathbb {R}}}\cup \mathcal {B}^+_{2, {\mathbb {R}}})\subset I^{\prime }_4$
;
$\mathrm {pr}_y(\mathcal {B}^+_{1, {\mathbb {R}}}\cup \mathcal {B}^+_{2, {\mathbb {R}}})\subset I^{\prime }_4$
; -
(d)
 $\mathcal {P}_{4, {\mathbb {R}}}\cap \mathcal {B}^+_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
$\mathcal {P}_{4, {\mathbb {R}}}\cap \mathcal {B}^+_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
 $\mathcal {B}^+_{i, {\mathbb {R}}}$
for
$\mathcal {B}^+_{i, {\mathbb {R}}}$
for
 $i=1, 2$
;
$i=1, 2$
; -
(e) the slopes of the horizontal edges of
 $\mathcal {B}^+_{1, {\mathbb {R}}}$
and
$\mathcal {B}^+_{1, {\mathbb {R}}}$
and
 $\mathcal {B}^+_{2, {\mathbb {R}}}$
in modulus are bounded by from above, where
$\mathcal {B}^+_{2, {\mathbb {R}}}$
in modulus are bounded by from above, where $$ \begin{align*} \frac{R_4^2-r_4^2}{\delta_4^2+|s_4|(R_4^2-r_4^2)} \end{align*} $$
$$ \begin{align*} \frac{R_4^2-r_4^2}{\delta_4^2+|s_4|(R_4^2-r_4^2)} \end{align*} $$
 $(s_4, 1)$
is the v-direction in defining
$(s_4, 1)$
is the v-direction in defining
 $\mathcal {P}_4$
.
$\mathcal {P}_4$
.
-
Proof. See Appendix A.

Figure 7 The polydisk
![]() $\mathcal {P}_2$
.
$\mathcal {P}_2$
.
Let
![]() $P^+_L$
be the union of
$P^+_L$
be the union of
![]() $\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
and
$\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)$
and
![]() $\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
. Let
$\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)$
. Let
![]() $P^+_R$
be the union of
$P^+_R$
be the union of
![]() $\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
and
$\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)$
and
![]() $\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
.
$\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)$
.
Theorem 4.3. For
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, the pair
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, the pair
![]() $\{P^+_L, P^+_R\}$
forms a partition for
$\{P^+_L, P^+_R\}$
forms a partition for
![]() $K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
, that is: (1)
$K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
, that is: (1)
![]() $P^+_L\cap P^+_R\cap K_{{\mathbb {R}}}=\emptyset $
and (2)
$P^+_L\cap P^+_R\cap K_{{\mathbb {R}}}=\emptyset $
and (2)
![]() $P^+_L\cup P^+_R\supset K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
.
$P^+_L\cup P^+_R\supset K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
.
Proof. Let
![]() $C_2$
be the real local stable manifold at
$C_2$
be the real local stable manifold at
![]() $p_2$
in the real part
$p_2$
in the real part
![]() $\mathcal {P}_{2, \mathbb {R}}$
. By Lemma 4.2(1)(b),
$\mathcal {P}_{2, \mathbb {R}}$
. By Lemma 4.2(1)(b),
![]() $C_2$
is a vertical curve connecting the upper boundary and the lower boundary of
$C_2$
is a vertical curve connecting the upper boundary and the lower boundary of
![]() ${\mathbb {R}}\times I_2$
so that it divides
${\mathbb {R}}\times I_2$
so that it divides
![]() ${\mathbb {R}}\times I_2$
into the left part and the right part. Note that
${\mathbb {R}}\times I_2$
into the left part and the right part. Note that
![]() ${C_2\cap \mathcal {P}_{2, \mathbb {R}}\ne \emptyset} $
by Lemma 4.2(1)(a). This together with Lemma 4.2(1)(d) yields that
${C_2\cap \mathcal {P}_{2, \mathbb {R}}\ne \emptyset} $
by Lemma 4.2(1)(a). This together with Lemma 4.2(1)(d) yields that
![]() $C_2$
intersects
$C_2$
intersects
![]() $\partial \mathcal {B}^+_{i, \mathbb {R}}$
only at its horizontal edges for
$\partial \mathcal {B}^+_{i, \mathbb {R}}$
only at its horizontal edges for
![]() $i=0, 3$
.
$i=0, 3$
.
However, thanks to the estimate in equation (4.1),
![]() $C_2$
intersects each of the horizontal edges exactly once by Lemma 4.2(1)(c) and (e). It follows that
$C_2$
intersects each of the horizontal edges exactly once by Lemma 4.2(1)(c) and (e). It follows that
![]() $C_2$
divides
$C_2$
divides
![]() $\mathcal {B}^+_{i, \mathbb {R}}$
(
$\mathcal {B}^+_{i, \mathbb {R}}$
(
![]() ${i=0, 3}$
) into two connected components, one is in the left part of
${i=0, 3}$
) into two connected components, one is in the left part of
![]() ${\mathbb {R}}\times I_2$
and the other is in the right part of
${\mathbb {R}}\times I_2$
and the other is in the right part of
![]() ${\mathbb {R}}\times I_2$
. By the uniqueness of the stable manifold
${\mathbb {R}}\times I_2$
. By the uniqueness of the stable manifold
![]() $W^s(p_2)$
, we see that
$W^s(p_2)$
, we see that
![]() $C_2\cap \mathcal {B}^+_{0, {\mathbb {R}}}= W^s_{\mathrm {loc}}(p_2)_0$
and
$C_2\cap \mathcal {B}^+_{0, {\mathbb {R}}}= W^s_{\mathrm {loc}}(p_2)_0$
and
![]() $C_2\cap \mathcal {B}^+_{3, {\mathbb {R}}}= W^s_{\mathrm {loc}}(p_2)_3$
. Therefore, it follows that
$C_2\cap \mathcal {B}^+_{3, {\mathbb {R}}}= W^s_{\mathrm {loc}}(p_2)_3$
. Therefore, it follows that
![]() $\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)\cap \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)=\emptyset $
. A similar argument with Lemma 4.2(2) shows that
$\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)\cap \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)=\emptyset $
. A similar argument with Lemma 4.2(2) shows that
![]() $\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\cap \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)=\emptyset $
. This together with
$\mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\cap \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)=\emptyset $
. This together with
![]() $\mathcal {B}^+_{0, {\mathbb {R}}}\cap \mathcal {B}^+_{2, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^+_{1, {\mathbb {R}}}\cap \mathcal {B}^+_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\emptyset $
(see item (1) of Lemma 2.4) yields item (1) of Theorem 4.3.
$\mathcal {B}^+_{0, {\mathbb {R}}}\cap \mathcal {B}^+_{2, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^+_{1, {\mathbb {R}}}\cap \mathcal {B}^+_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\emptyset $
(see item (1) of Lemma 2.4) yields item (1) of Theorem 4.3.
Take
![]() $z\in K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
. Since
$z\in K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
. Since
![]() $z\notin W^s(p_2)\cap W^s(p_4)$
, it does not belong to the boundary of the pieces in Proposition 4.1). Hence, there exists a
$z\notin W^s(p_2)\cap W^s(p_4)$
, it does not belong to the boundary of the pieces in Proposition 4.1). Hence, there exists a
![]() $\Sigma ^+$
-coding
$\Sigma ^+$
-coding
![]() ${(i_n)_{n\in \mathbb {Z}}\in \mathfrak {S}^+}$
of z by Proposition 2.6. Then, Proposition 4.1 yields that z belongs to either
${(i_n)_{n\in \mathbb {Z}}\in \mathfrak {S}^+}$
of z by Proposition 2.6. Then, Proposition 4.1 yields that z belongs to either
![]() $P^+_L$
or
$P^+_L$
or
![]() $P^+_R$
. This proves item (2) of Theorem 4.3.
$P^+_R$
. This proves item (2) of Theorem 4.3.
Therefore, this defines a unique
![]() $\{L, R\}$
-coding for every point in
$\{L, R\}$
-coding for every point in
![]() $K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
.
$K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
.
Proposition 4.4. Suppose that
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Let
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Let
![]() $z\in K_{{\mathbb {R}}}$
and let
$z\in K_{{\mathbb {R}}}$
and let
![]() $(i_n)_{n\geq 0}\in \mathfrak {S}^-_{\mathrm {fwd}}$
be its forward
$(i_n)_{n\geq 0}\in \mathfrak {S}^-_{\mathrm {fwd}}$
be its forward
![]() $\Sigma ^-$
-coding.
$\Sigma ^-$
-coding.
-
(1) If
 $i_0=0$
, then z belongs to the closure of
$i_0=0$
, then z belongs to the closure of
 $\mathrm {left}(\mathcal {B}^-_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_1)_0)$
.
$\mathrm {left}(\mathcal {B}^-_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_1)_0)$
. -
(2) If
 $i_0=1$
, then z belongs to the closure of
$i_0=1$
, then z belongs to the closure of
 $\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})$
.
$\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})$
. -
(3) If
 $i_0=2$
, then z belongs to the closure of
$i_0=2$
, then z belongs to the closure of
 $\mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})$
.
$\mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})$
. -
(4) If
 $i_0=3$
, then z belongs to the closure of
$i_0=3$
, then z belongs to the closure of
 $\mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
.
$\mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
. -
(5) If
 $i_0=4$
, then z belongs to the closure of
$i_0=4$
, then z belongs to the closure of
 $\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)$
.
$\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)$
.
Proof. The proof is similar to that of Proposition 4.1, and hence is omitted.
Lemma 4.5. (Numerical Check 6)
Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
.
-
(1) One can find two concentric intervals
 $I_3=[y_3-R_3, y_3+R_3]$
and
$I_3=[y_3-R_3, y_3+R_3]$
and
 $I^{\prime }_3=[y_3-r_3, y_3+r_3]$
in the y-axis with
$I^{\prime }_3=[y_3-r_3, y_3+r_3]$
in the y-axis with
 $r_3<R_3$
and a disk
$r_3<R_3$
and a disk
 $D_3$
of radius
$D_3$
of radius
 $\delta _3>0$
so that:
$\delta _3>0$
so that:-
(a) a projective polydisk of the form
 $\mathcal {P}_3=D_3\times _{\mathrm {pr}} D_{I_3}$
contains
$\mathcal {P}_3=D_3\times _{\mathrm {pr}} D_{I_3}$
contains
 $p_3$
;
$p_3$
; -
(b)
 $f : \mathcal {P}_3\cap f^{-1}(\mathcal {P}_3)\to \mathcal {P}_3$
is a crossed mapping of degree one;
$f : \mathcal {P}_3\cap f^{-1}(\mathcal {P}_3)\to \mathcal {P}_3$
is a crossed mapping of degree one; -
(c)
 $\mathrm {pr}_y(\mathcal {B}^-_{2, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}}\cup \mathcal {B}^-_{4, {\mathbb {R}}})\subset I^{\prime }_3$
;
$\mathrm {pr}_y(\mathcal {B}^-_{2, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}}\cup \mathcal {B}^-_{4, {\mathbb {R}}})\subset I^{\prime }_3$
; -
(d)
 $\mathcal {P}_{3, {\mathbb {R}}}\cap \mathcal {B}^-_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
$\mathcal {P}_{3, {\mathbb {R}}}\cap \mathcal {B}^-_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
 $\mathcal {B}^-_{i, {\mathbb {R}}}$
for
$\mathcal {B}^-_{i, {\mathbb {R}}}$
for
 $i=2, 3, 4$
;
$i=2, 3, 4$
; -
(e) the slopes of the horizontal edges of
 $\mathcal {B}^-_{2, {\mathbb {R}}}$
,
$\mathcal {B}^-_{2, {\mathbb {R}}}$
,
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
and
$\mathcal {B}^-_{3, {\mathbb {R}}}$
and
 $\mathcal {B}^-_{4, {\mathbb {R}}}$
in modulus are bounded byfrom above, where
$\mathcal {B}^-_{4, {\mathbb {R}}}$
in modulus are bounded byfrom above, where $$ \begin{align*}\frac{R_3^2-r_3^2}{\delta _3^2+|s_3|(R_3^2-r_3^2)}\end{align*} $$
$$ \begin{align*}\frac{R_3^2-r_3^2}{\delta _3^2+|s_3|(R_3^2-r_3^2)}\end{align*} $$
 $(s_3, 1)$
is the v-direction in defining
$(s_3, 1)$
is the v-direction in defining
 $\mathcal {P}_3$
.
$\mathcal {P}_3$
.
-
-
(2) One can find two concentric intervals
 $I_1=[y_1-R_1, y_1+R_1]$
and
$I_1=[y_1-R_1, y_1+R_1]$
and
 $I^{\prime }_1=[y_1-r_1, y_1+r_1]$
in the y-axis with
$I^{\prime }_1=[y_1-r_1, y_1+r_1]$
in the y-axis with
 $r_1<R_1$
and a disk
$r_1<R_1$
and a disk
 $D_1$
of radius
$D_1$
of radius
 $\delta _1>0$
so that:
$\delta _1>0$
so that:-
(a) a projective polydisk of the form
 $\mathcal {P}_1=D_1\times _{\mathrm {pr}} D_{I_1}$
does not contain
$\mathcal {P}_1=D_1\times _{\mathrm {pr}} D_{I_1}$
does not contain
 $p_3$
;
$p_3$
; -
(b)
 $f : \mathcal {P}_1\cap f^{-1}(\mathcal {P}_3)\to \mathcal {P}_3$
is a crossed mapping of degree one;
$f : \mathcal {P}_1\cap f^{-1}(\mathcal {P}_3)\to \mathcal {P}_3$
is a crossed mapping of degree one; -
(c)
 $\mathrm {pr}_y(\mathcal {B}^-_{1, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}})\subset I^{\prime }_1$
;
$\mathrm {pr}_y(\mathcal {B}^-_{1, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}})\subset I^{\prime }_1$
; -
(d)
 $\mathcal {P}_{1, {\mathbb {R}}}\cap \mathcal {B}^-_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
$\mathcal {P}_{1, {\mathbb {R}}}\cap \mathcal {B}^-_{i, {\mathbb {R}}}$
does not intersect the vertical edges of
 $\mathcal {B}^-_{i, {\mathbb {R}}}$
for
$\mathcal {B}^-_{i, {\mathbb {R}}}$
for
 $i=1, 3$
;
$i=1, 3$
; -
(e) the slopes of the horizontal edges of
 $\mathcal {B}^-_{1, {\mathbb {R}}}$
and
$\mathcal {B}^-_{1, {\mathbb {R}}}$
and
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
in modulus are bounded byfrom above, where
$\mathcal {B}^-_{3, {\mathbb {R}}}$
in modulus are bounded byfrom above, where $$ \begin{align*}\frac{R_1^2-r_1^2}{\delta _1^2+|s_1|(R_1^2-r_1^2)}\end{align*} $$
$$ \begin{align*}\frac{R_1^2-r_1^2}{\delta _1^2+|s_1|(R_1^2-r_1^2)}\end{align*} $$
 $(s_1, 1)$
is the v-direction in defining
$(s_1, 1)$
is the v-direction in defining
 $\mathcal {P}_1$
.
$\mathcal {P}_1$
.
-
Proof. See Appendix A.
As an immediate consequence of Lemma 2.11, we know that
![]() $f_{{\mathbb {R}}}^2(\mathcal {B}^-_{i', {\mathbb {R}}})$
and
$f_{{\mathbb {R}}}^2(\mathcal {B}^-_{i', {\mathbb {R}}})$
and
![]() $f_{{\mathbb {R}}}^2(\mathcal {B}^-_{i", {\mathbb {R}}})$
are connected components of
$f_{{\mathbb {R}}}^2(\mathcal {B}^-_{i", {\mathbb {R}}})$
are connected components of
![]() $f_{{\mathbb {R}}}(f_{{\mathbb {R}}}(\mathcal {B}^-_{i, {\mathbb {R}}})\cap \mathcal {B}^-_{4, {\mathbb {R}}}) \cap \mathcal {B}^-_{3, {\mathbb {R}}}$
for
$f_{{\mathbb {R}}}(f_{{\mathbb {R}}}(\mathcal {B}^-_{i, {\mathbb {R}}})\cap \mathcal {B}^-_{4, {\mathbb {R}}}) \cap \mathcal {B}^-_{3, {\mathbb {R}}}$
for
![]() $i=2, 3$
. Let
$i=2, 3$
. Let
![]() $P^-_L$
be the union of
$P^-_L$
be the union of
![]() $\mathrm {left}(f_{{\mathbb {R}}}^2(\mathcal {B}^-_{2', {\mathbb {R}}}\cup \mathcal {B}^-_{3', {\mathbb {R}}})\setminus \gamma _{3, \mathrm {right}})$
and
$\mathrm {left}(f_{{\mathbb {R}}}^2(\mathcal {B}^-_{2', {\mathbb {R}}}\cup \mathcal {B}^-_{3', {\mathbb {R}}})\setminus \gamma _{3, \mathrm {right}})$
and
![]() $\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)$
. Let
$\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)$
. Let
![]() $P^-_R$
be the union of
$P^-_R$
be the union of
![]() $\mathcal {B}^-_{0, {\mathbb {R}}}$
,
$\mathcal {B}^-_{0, {\mathbb {R}}}$
,
![]() $\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})$
,
$\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})$
,
![]() $\mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})$
, and
$\mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})$
, and
![]() $\mathrm {right}(f_{{\mathbb {R}}}^2(\mathcal {B}^-_{2", {\mathbb {R}}}\cup \mathcal {B}^-_{3", {\mathbb {R}}})\setminus \gamma _{3, \mathrm {left}})$
.
$\mathrm {right}(f_{{\mathbb {R}}}^2(\mathcal {B}^-_{2", {\mathbb {R}}}\cup \mathcal {B}^-_{3", {\mathbb {R}}})\setminus \gamma _{3, \mathrm {left}})$
.
Theorem 4.6. For
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, the pair
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, the pair
![]() $\{P^-_L, P^-_R\}$
forms a partition for
$\{P^-_L, P^-_R\}$
forms a partition for
![]() $K_{{\mathbb {R}}}\setminus W^s(p_3)$
, that is (1)
$K_{{\mathbb {R}}}\setminus W^s(p_3)$
, that is (1)
![]() $P^-_L\cap P^-_R\cap K_{{\mathbb {R}}}=\emptyset $
and (2)
$P^-_L\cap P^-_R\cap K_{{\mathbb {R}}}=\emptyset $
and (2)
![]() $P^-_L\cup P^-_R\supset K_{{\mathbb {R}}}\setminus W^s(p_3)$
.
$P^-_L\cup P^-_R\supset K_{{\mathbb {R}}}\setminus W^s(p_3)$
.
Proof. We proceed as in the proof of Theorem 4.3. First, it follows from Lemma 4.5 that
 $\mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}}){\kern2pt}\cap{\kern2pt} \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}}){\kern2pt}={\kern2pt}\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)){\kern2pt}\cap{\kern2pt} \mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})=\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4))\cap \mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}})=\emptyset $
. This together with
$\mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}}){\kern2pt}\cap{\kern2pt} \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}}){\kern2pt}={\kern2pt}\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)){\kern2pt}\cap{\kern2pt} \mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})=\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4))\cap \mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}})=\emptyset $
. This together with
![]() $\mathcal {B}^-_{0, {\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{0, {\mathbb {R}}}\cap \mathcal {B}^-_{4, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{1, {\mathbb {R}}}\cap \mathcal {B}^-_{4, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{2, {\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\emptyset $
(see item (2) of Lemma 2.4) yields item (1) of Theorem 4.6.
$\mathcal {B}^-_{0, {\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{0, {\mathbb {R}}}\cap \mathcal {B}^-_{4, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{1, {\mathbb {R}}}\cap \mathcal {B}^-_{4, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\mathcal {B}^-_{2, {\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}}\cap K_{{\mathbb {R}}}=\emptyset $
(see item (2) of Lemma 2.4) yields item (1) of Theorem 4.6.
The proof of item (2) of Theorem 4.6 is slightly different from that of item (2) of Theorem 4.3 since we replace
![]() $\mathcal {B}^-_{3, {\mathbb {R}}}$
by
$\mathcal {B}^-_{3, {\mathbb {R}}}$
by
![]() $f^2_{{\mathbb {R}}}(\mathcal {B}^-_{2', {\mathbb {R}}}\cup \mathcal {B}^-_{3', {\mathbb {R}}})$
and
$f^2_{{\mathbb {R}}}(\mathcal {B}^-_{2', {\mathbb {R}}}\cup \mathcal {B}^-_{3', {\mathbb {R}}})$
and
![]() $f^2_{{\mathbb {R}}}(\mathcal {B}^-_{2", {\mathbb {R}}}\cup \mathcal {B}^-_{3", {\mathbb {R}}})$
. Notice that we use
$f^2_{{\mathbb {R}}}(\mathcal {B}^-_{2", {\mathbb {R}}}\cup \mathcal {B}^-_{3", {\mathbb {R}}})$
. Notice that we use
![]() $\mathcal {B}^-_{i', {\mathbb {R}}}$
and
$\mathcal {B}^-_{i', {\mathbb {R}}}$
and
![]() $\mathcal {B}^-_{i", {\mathbb {R}}}$
(
$\mathcal {B}^-_{i", {\mathbb {R}}}$
(
![]() $i=2, 3$
) to define the partition
$i=2, 3$
) to define the partition
![]() $\{P^-_L, P^-_R\}$
, but we do not use
$\{P^-_L, P^-_R\}$
, but we do not use
![]() $\mathcal {B}^+_{2', {\mathbb {R}}}$
and
$\mathcal {B}^+_{2', {\mathbb {R}}}$
and
![]() $\mathcal {B}^+_{2", {\mathbb {R}}}$
to define the partition
$\mathcal {B}^+_{2", {\mathbb {R}}}$
to define the partition
![]() $\{P^+_L, P^+_R\}$
. Take any
$\{P^+_L, P^+_R\}$
. Take any
![]() $z\in K_{{\mathbb {R}}}\setminus W^s(p_3)$
. Then, it follows from Propositions 2.6 and 2.9(2) that z has a unique
$z\in K_{{\mathbb {R}}}\setminus W^s(p_3)$
. Then, it follows from Propositions 2.6 and 2.9(2) that z has a unique
![]() $\Sigma ^-$
-coding
$\Sigma ^-$
-coding
![]() $(i_n)_{n\in \mathbb {Z}}\in \mathfrak {S}^-$
. If
$(i_n)_{n\in \mathbb {Z}}\in \mathfrak {S}^-$
. If
![]() $i_0\ne 3$
, then Proposition 4.4(1), (2), (3), and (5) yield that z belongs to either
$i_0\ne 3$
, then Proposition 4.4(1), (2), (3), and (5) yield that z belongs to either
![]() $P^-_L$
or
$P^-_L$
or
![]() $P^-_R$
. So, suppose that
$P^-_R$
. So, suppose that
![]() $i_0=3$
. Then, the forward
$i_0=3$
. Then, the forward
![]() $\Sigma ^-$
-coding of
$\Sigma ^-$
-coding of
![]() $f_{{\mathbb {R}}}^{-2}(z)$
is either
$f_{{\mathbb {R}}}^{-2}(z)$
is either
![]() $243\cdots $
or
$243\cdots $
or
![]() $343\cdots $
. Hence,
$343\cdots $
. Hence,
![]() $f_{{\mathbb {R}}}^{-2}(z)\in (\mathcal {B}^-_{2, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}})\cap f_{{\mathbb {R}}}^{-1}(\mathcal {B}^-_{4, {\mathbb {R}}}\cap f_{{\mathbb {R}}}^{-1}(\mathcal {B}^-_{3, {\mathbb {R}}}))$
. It then follows that
$f_{{\mathbb {R}}}^{-2}(z)\in (\mathcal {B}^-_{2, {\mathbb {R}}}\cup \mathcal {B}^-_{3, {\mathbb {R}}})\cap f_{{\mathbb {R}}}^{-1}(\mathcal {B}^-_{4, {\mathbb {R}}}\cap f_{{\mathbb {R}}}^{-1}(\mathcal {B}^-_{3, {\mathbb {R}}}))$
. It then follows that
 $$ \begin{align} \nonumber K_{{\mathbb{R}}}\cap\mathcal{B}^-_{3, {\mathbb{R}}}&\subset (f_{{\mathbb{R}}}(f_{{\mathbb{R}}}(\mathcal{B}^-_{2, {\mathbb{R}}})\cap \mathcal{B}^-_{4, {\mathbb{R}}})\cap \mathcal{B}^-_{3, {\mathbb{R}}})\cup(f_{{\mathbb{R}}}(f_{{\mathbb{R}}}(\mathcal{B}^-_{3, {\mathbb{R}}})\cap \mathcal{B}^-_{4, {\mathbb{R}}})\cap \mathcal{B}^-_{3, {\mathbb{R}}}) \\ &= f_{{\mathbb{R}}}^2(\mathcal{B}^-_{2', {\mathbb{R}}}\cup \mathcal{B}^-_{3', {\mathbb{R}}})\cup f_{{\mathbb{R}}}^2(\mathcal{B}^-_{2", {\mathbb{R}}}\cup \mathcal{B}^-_{3", {\mathbb{R}}}). \end{align} $$
$$ \begin{align} \nonumber K_{{\mathbb{R}}}\cap\mathcal{B}^-_{3, {\mathbb{R}}}&\subset (f_{{\mathbb{R}}}(f_{{\mathbb{R}}}(\mathcal{B}^-_{2, {\mathbb{R}}})\cap \mathcal{B}^-_{4, {\mathbb{R}}})\cap \mathcal{B}^-_{3, {\mathbb{R}}})\cup(f_{{\mathbb{R}}}(f_{{\mathbb{R}}}(\mathcal{B}^-_{3, {\mathbb{R}}})\cap \mathcal{B}^-_{4, {\mathbb{R}}})\cap \mathcal{B}^-_{3, {\mathbb{R}}}) \\ &= f_{{\mathbb{R}}}^2(\mathcal{B}^-_{2', {\mathbb{R}}}\cup \mathcal{B}^-_{3', {\mathbb{R}}})\cup f_{{\mathbb{R}}}^2(\mathcal{B}^-_{2", {\mathbb{R}}}\cup \mathcal{B}^-_{3", {\mathbb{R}}}). \end{align} $$
Thanks to claim (4) of Proposition 4.4, we observe that
![]() $z\in (K_{{\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}})\setminus W^s(p_3)$
is a point in
$z\in (K_{{\mathbb {R}}}\cap \mathcal {B}^-_{3, {\mathbb {R}}})\setminus W^s(p_3)$
is a point in
![]() $\mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
. This together with the inclusion in equation (4.2) yields that z belongs to either
$\mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
. This together with the inclusion in equation (4.2) yields that z belongs to either
![]() $P^-_L$
or
$P^-_L$
or
![]() $P^-_R$
, and hence we have item (2) of Theorem 4.6.
$P^-_R$
, and hence we have item (2) of Theorem 4.6.
Therefore, this defines a unique
![]() $\{L, R\}$
-coding for every point in
$\{L, R\}$
-coding for every point in
![]() $K_{{\mathbb {R}}}\setminus W^s(p_3)$
.
$K_{{\mathbb {R}}}\setminus W^s(p_3)$
.
4.2 Proof of Theorem 1.1
Below,
![]() $\mathrm {card}(A)$
denotes the cardinality of A counted without multiplicity. The proof of Theorem 1.1 is based on the following two results from [Reference Arai and IshiiAI].
$\mathrm {card}(A)$
denotes the cardinality of A counted without multiplicity. The proof of Theorem 1.1 is based on the following two results from [Reference Arai and IshiiAI].
Theorem 4.7. [Reference Arai and IshiiAI, Theorem 5.1]
When
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, we have
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
, we have
![]() ${h_{\mathrm {top}}}(f_{{\mathbb {R}}})=\log 2$
if and only if
${h_{\mathrm {top}}}(f_{{\mathbb {R}}})=\log 2$
if and only if
![]() $\mathrm {card}(W_{31\overline {0}}^s(a, b)^+\cap W_{\overline {0}23}^u(a, b)^+)\geq 1$
. When
$\mathrm {card}(W_{31\overline {0}}^s(a, b)^+\cap W_{\overline {0}23}^u(a, b)^+)\geq 1$
. When
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, we have
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
, we have
![]() ${h_{\mathrm {top}}}(f_{{\mathbb {R}}})=\log 2$
if and only if
${h_{\mathrm {top}}}(f_{{\mathbb {R}}})=\log 2$
if and only if
![]() ${\mathrm {card}}(W_{41\overline {0}}^s(a, b)^-\cap W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}})\geq 1$
.
${\mathrm {card}}(W_{41\overline {0}}^s(a, b)^-\cap W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}})\geq 1$
.
Theorem 4.8. [Reference Arai and IshiiAI, Theorem 5.14]
When
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
,
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
,
![]() $f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
$f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
![]() ${\mathbb {R}}^2$
if and only if
${\mathbb {R}}^2$
if and only if
![]() $\mathrm {card}(W_{31\overline {0}}^s(a, b)^+\cap W_{\overline {0}23}^u(a, b)^+)=2$
. When
$\mathrm {card}(W_{31\overline {0}}^s(a, b)^+\cap W_{\overline {0}23}^u(a, b)^+)=2$
. When
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
,
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
,
![]() $f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
$f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
![]() ${\mathbb {R}}^2$
if and only if
${\mathbb {R}}^2$
if and only if
![]() $\mathrm {card}(W_{41\overline {0}}^s(a, b)^-\cap W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}})=2$
.
$\mathrm {card}(W_{41\overline {0}}^s(a, b)^-\cap W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}})=2$
.
Let us set
and
Note that we dropped ‘inner’ from
![]() $W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
in the definition above because the inner part and the outer part of
$W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
in the definition above because the inner part and the outer part of
![]() $W_{\overline {43}4124}^u(a, b)^-$
cannot be distinguished by the
$W_{\overline {43}4124}^u(a, b)^-$
cannot be distinguished by the
![]() $\Sigma ^-$
-coding. As an immediate consequence of Theorems 4.7 and 4.8, we have the following corollary.
$\Sigma ^-$
-coding. As an immediate consequence of Theorems 4.7 and 4.8, we have the following corollary.
Corollary 4.9. We have the following.
-
(1) Let
 $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have
 $\mathrm {card}(S(a, b)^+) \leq 2$
. Moreover:
$\mathrm {card}(S(a, b)^+) \leq 2$
. Moreover:-
(a)
 $f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
$f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
 ${\mathbb {R}}^2$
if and only if
${\mathbb {R}}^2$
if and only if
 $\mathrm {card}(S(a, b)^+)=2$
;
$\mathrm {card}(S(a, b)^+)=2$
; -
(b)
 $f_{{\mathbb {R}}}$
has a quadratic tangency but
$f_{{\mathbb {R}}}$
has a quadratic tangency but
 $h_{\mathrm {top}}(f_{{\mathbb {R}}})=\log 2$
if and only if
$h_{\mathrm {top}}(f_{{\mathbb {R}}})=\log 2$
if and only if
 $\mathrm {card}(S(a, b)^+)=1$
;
$\mathrm {card}(S(a, b)^+)=1$
; -
(c)
 $h_{\mathrm {top}}(f_{{\mathbb {R}}})<\log 2$
if and only if
$h_{\mathrm {top}}(f_{{\mathbb {R}}})<\log 2$
if and only if
 $\mathrm {card}(S(a, b)^+)=0$
.
$\mathrm {card}(S(a, b)^+)=0$
.
-
-
(2) Let
 $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have
 $\mathrm {card}(S(a, b)^-) \leq 4$
. Moreover:
$\mathrm {card}(S(a, b)^-) \leq 4$
. Moreover:-
(a)
 $f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
$f_{{\mathbb {R}}}$
is a hyperbolic horseshoe on
 ${\mathbb {R}}^2$
if and only if
${\mathbb {R}}^2$
if and only if
 ${\mathrm {card}}(S(a, b)^-)=4$
;
${\mathrm {card}}(S(a, b)^-)=4$
; -
(b)
 $f_{{\mathbb {R}}}$
has a quadratic tangency but
$f_{{\mathbb {R}}}$
has a quadratic tangency but
 $h_{\mathrm {top}}(f_{{\mathbb {R}}})=\log 2$
if and only if
$h_{\mathrm {top}}(f_{{\mathbb {R}}})=\log 2$
if and only if
 ${\mathrm {card}}(S(a, b)^-)=3$
;
${\mathrm {card}}(S(a, b)^-)=3$
; -
(c)
 $h_{\mathrm {top}}(f_{{\mathbb {R}}})<\log 2$
if and only if
$h_{\mathrm {top}}(f_{{\mathbb {R}}})<\log 2$
if and only if
 ${\mathrm {card}}(S(a, b)^-)\leq 2$
.
${\mathrm {card}}(S(a, b)^-)\leq 2$
.
-
Proof. The bound
![]() $\mathrm {card}(S(a, b)^+) \leq 2$
in case (1) follows from the fact that
$\mathrm {card}(S(a, b)^+) \leq 2$
in case (1) follows from the fact that
![]() $V_{31\overline {0}}^s(a, b)^+$
is a vertical disk of degree one in
$V_{31\overline {0}}^s(a, b)^+$
is a vertical disk of degree one in
![]() $\mathcal {B}^+_3$
and
$\mathcal {B}^+_3$
and
![]() $V_{\overline {0}23}^u(a, b)^+$
is a horizontal disk of degree two in
$V_{\overline {0}23}^u(a, b)^+$
is a horizontal disk of degree two in
![]() $\mathcal {B}^+_3$
. The bound
$\mathcal {B}^+_3$
. The bound
![]() $\mathrm {card}(S(a, b)^-) \leq 4$
in case (2) follows from the fact that
$\mathrm {card}(S(a, b)^-) \leq 4$
in case (2) follows from the fact that
![]() $V_{41\overline {0}}^s(a, b)^-$
is a vertical disk of degree one in
$V_{41\overline {0}}^s(a, b)^-$
is a vertical disk of degree one in
![]() $\mathcal {B}^-_4$
and
$\mathcal {B}^-_4$
and
![]() $V_{\overline {43}4124}^u(a, b)^-$
consists of two horizontal disks of degree two in
$V_{\overline {43}4124}^u(a, b)^-$
consists of two horizontal disks of degree two in
![]() $\mathcal {B}^-_4$
.
$\mathcal {B}^-_4$
.
Consider first the classification in case (2). If
![]() $W_{41\overline {0}}^s(a, b)^-$
intersects
$W_{41\overline {0}}^s(a, b)^-$
intersects
![]() $W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
, then it follows that
$W^u_{\overline {43}4124}(a, b)^-_{\mathrm {inner}}$
, then it follows that
![]() $W_{41\overline {0}}^s(a, b)^-$
intersects
$W_{41\overline {0}}^s(a, b)^-$
intersects
![]() $W^u_{\overline {43}4124}(a, b)^-_{\mathrm {outer}}$
exactly twice (see [Reference Arai and IshiiAI, Figure 25 as well as Definition 4.4]). Hence,
$W^u_{\overline {43}4124}(a, b)^-_{\mathrm {outer}}$
exactly twice (see [Reference Arai and IshiiAI, Figure 25 as well as Definition 4.4]). Hence,
Then, claim (a) follows from Theorem 4.8, claim (c) follows from Theorem 4.7 and that
![]() $(a, b)$
belongs to the closure of
$(a, b)$
belongs to the closure of
![]() $\mathcal {H}_{{\mathbb {R}}}^{\pm }$
if and only if
$\mathcal {H}_{{\mathbb {R}}}^{\pm }$
if and only if
![]() ${h_{\mathrm {top}}}(f_{a, b})=\log 2$
(see [Reference Arai and IshiiAI, Main Corollary]), and claim (b) follows from claims (a), (c), and that
${h_{\mathrm {top}}}(f_{a, b})=\log 2$
(see [Reference Arai and IshiiAI, Main Corollary]), and claim (b) follows from claims (a), (c), and that
![]() $\mathcal {H}_{{\mathbb {R}}}^{\pm }$
is open. Proof for the classification in case (1) is similar and hence omitted.
$\mathcal {H}_{{\mathbb {R}}}^{\pm }$
is open. Proof for the classification in case (1) is similar and hence omitted.
Thanks to this corollary, our task to finish the proof of Theorem 1.1 is to transfer the
![]() $\Sigma ^{\pm }$
-coding to the
$\Sigma ^{\pm }$
-coding to the
![]() $\{L, R\}$
-coding. Notice that the paper [Reference Bedford and SmillieBSℝ3] lacks a proof of its theorem 1 which corresponds to our Theorem 1.1.
$\{L, R\}$
-coding. Notice that the paper [Reference Bedford and SmillieBSℝ3] lacks a proof of its theorem 1 which corresponds to our Theorem 1.1.
Proof of Theorem 1.1(1)
For a point
![]() $z\in K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
, we consider the following conditions:
$z\in K_{{\mathbb {R}}}\setminus (W^s(p_2)\cap W^s(p_4))$
, we consider the following conditions:
-
(a) the
 $\Sigma ^+$
-coding of z exists and is
$\Sigma ^+$
-coding of z exists and is
 $\overline {0}2\cdot 31\overline {0}$
;
$\overline {0}2\cdot 31\overline {0}$
; -
(b)
 $f^{-2}(z)\in W^u_{\mathrm {loc}}(p_1)_0$
;
$f^{-2}(z)\in W^u_{\mathrm {loc}}(p_1)_0$
; -
(c)
 $f^2(z)\in W^s_{\mathrm {loc}}(p_1)_0$
;
$f^2(z)\in W^s_{\mathrm {loc}}(p_1)_0$
; -
(d) the
 $\{L, R\}$
-coding of z is
$\{L, R\}$
-coding of z is
 $\overline {R}L\cdot L\overline {R}$
.
$\overline {R}L\cdot L\overline {R}$
.
It is easy to see that
![]() $z\in S^+(a, b)$
if and only if z satisfies conditions (a), (b), and (c). Assume that condition (a) holds. Then, the forward
$z\in S^+(a, b)$
if and only if z satisfies conditions (a), (b), and (c). Assume that condition (a) holds. Then, the forward
![]() $\Sigma ^+$
-coding of
$\Sigma ^+$
-coding of
![]() $f^2(z)$
is
$f^2(z)$
is
![]() $\overline {0}\in \mathfrak {S}^+_{\mathrm {fwd}}$
. Since
$\overline {0}\in \mathfrak {S}^+_{\mathrm {fwd}}$
. Since
![]() $f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one, this yields condition (c) as in Corollary 3.5(1). Since the backward
$f : \mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_0)\to \mathcal {B}^+_0$
is a crossed mapping of degree one, this yields condition (c) as in Corollary 3.5(1). Since the backward
![]() $\Sigma ^+$
-coding of
$\Sigma ^+$
-coding of
![]() $f^{-2}(z)$
including the
$f^{-2}(z)$
including the
![]() $0$
th digit is
$0$
th digit is
![]() $\overline {0}\in \mathfrak {S}^+_{\mathrm {bwd}}$
, a similar argument yields condition (b). Therefore, it is sufficient to prove that condition (a) holds if and only if condition (d) holds. Note that
$\overline {0}\in \mathfrak {S}^+_{\mathrm {bwd}}$
, a similar argument yields condition (b). Therefore, it is sufficient to prove that condition (a) holds if and only if condition (d) holds. Note that
![]() $\overline {R}L\cdot L\overline {R} = \overline {R}L\cdot LR\overline {R}$
.
$\overline {R}L\cdot L\overline {R} = \overline {R}L\cdot LR\overline {R}$
.
(a) implies (d): Since
![]() $z\notin W^s(p_2)\cup W^s(p_4)$
, Proposition 4.1 and the definition of the partition
$z\notin W^s(p_2)\cup W^s(p_4)$
, Proposition 4.1 and the definition of the partition
![]() $\{P_L^+, P_R^+\}$
imply the following.
$\{P_L^+, P_R^+\}$
imply the following.
-
• If
 $i_0=0$
, then
$i_0=0$
, then
 $z\in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)\subset P_R^+$
.
$z\in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_0)\subset P_R^+$
. -
• If
 $i_0=1$
, then
$i_0=1$
, then
 $z\in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)\subset P_R^+$
.
$z\in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_1)\subset P_R^+$
. -
• If
 $i_0=2$
, then
$i_0=2$
, then
 $z\in \mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\subset P_L^+$
.
$z\in \mathrm {left}(\mathcal {B}^+_{2, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_4)_2)\subset P_L^+$
. -
• If
 $i_0=3$
, then
$i_0=3$
, then
 $z\in \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)\subset P_L^+$
.
$z\in \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_2)_3)\subset P_L^+$
.
Therefore, we replace the
![]() $0$
s and
$0$
s and
![]() $1$
s in
$1$
s in
![]() $\overline {0}2\cdot 31\overline {0}$
by R, and the
$\overline {0}2\cdot 31\overline {0}$
by R, and the
![]() $2$
s and
$2$
s and
![]() $3$
s in
$3$
s in
![]() $\overline {0}2\cdot 31\overline {0}$
by L to obtain
$\overline {0}2\cdot 31\overline {0}$
by L to obtain
![]() $\overline {R}L\cdot LR\overline {R}$
.
$\overline {R}L\cdot LR\overline {R}$
.
(d) implies (a): We note that z has a unique
![]() $\Sigma ^+$
-coding thanks to Proposition 2.6 and claim (1) of Proposition 2.9.
$\Sigma ^+$
-coding thanks to Proposition 2.6 and claim (1) of Proposition 2.9.
First consider the forward
![]() $\{L, R\}$
-coding
$\{L, R\}$
-coding
![]() $LR\overline {R}$
. By the definition of the
$LR\overline {R}$
. By the definition of the
![]() $\{L, R\}$
-partition, the
$\{L, R\}$
-partition, the
![]() $0$
th digit of the
$0$
th digit of the
![]() $\Sigma ^+$
-coding is either
$\Sigma ^+$
-coding is either
![]() $2$
or
$2$
or
![]() $3$
. There is no arrow from
$3$
. There is no arrow from
![]() $2$
to the R-side in the transition graph, but there is an arrow
$2$
to the R-side in the transition graph, but there is an arrow
![]() $3\to 1$
from
$3\to 1$
from
![]() $3$
to the R-side. Hence, the
$3$
to the R-side. Hence, the
![]() $0$
th digit of the
$0$
th digit of the
![]() $\Sigma ^+$
-coding is
$\Sigma ^+$
-coding is
![]() $3$
and the
$3$
and the
![]() $1$
st digit is
$1$
st digit is
![]() $1$
. Then, the only arrow from
$1$
. Then, the only arrow from
![]() $1$
to the R-side is
$1$
to the R-side is
![]() $1\to 0$
. By repeating this argument, we obtain
$1\to 0$
. By repeating this argument, we obtain
![]() $31\overline {0}$
as the forward
$31\overline {0}$
as the forward
![]() $\Sigma ^+$
-coding.
$\Sigma ^+$
-coding.
Next, consider the backward
![]() $\{L, R\}$
-coding
$\{L, R\}$
-coding
![]() $\overline {R}LL$
(including the
$\overline {R}LL$
(including the
![]() $0$
th digit). As discussed above, the
$0$
th digit). As discussed above, the
![]() $0$
th digit of the
$0$
th digit of the
![]() $\Sigma ^+$
-coding is
$\Sigma ^+$
-coding is
![]() $3$
. The only arrow in the transition graph from the L-side to
$3$
. The only arrow in the transition graph from the L-side to
![]() $3$
is
$3$
is
![]() $2\to 3$
, and hence the
$2\to 3$
, and hence the
![]() $-1$
th digit is
$-1$
th digit is
![]() $2$
. Then, there are two arrows
$2$
. Then, there are two arrows
![]() $0\to 2$
and
$0\to 2$
and
![]() $1\to 2$
from the R-side to
$1\to 2$
from the R-side to
![]() $2$
. There is no arrow from the R-side to
$2$
. There is no arrow from the R-side to
![]() $1$
, but there is an arrow
$1$
, but there is an arrow
![]() $1\to 2$
from the R-side. Hence, the
$1\to 2$
from the R-side. Hence, the
![]() $-2$
th digit of the
$-2$
th digit of the
![]() $\Sigma ^+$
-coding is
$\Sigma ^+$
-coding is
![]() $1$
. By repeating this argument, we obtain
$1$
. By repeating this argument, we obtain
![]() $\overline {0}23$
as the backward
$\overline {0}23$
as the backward
![]() $\Sigma ^+$
-coding including the
$\Sigma ^+$
-coding including the
![]() $0$
th digit.
$0$
th digit.
By combining the forward and the backward
![]() $\Sigma ^+$
-codings above, we obtain condition (a).
$\Sigma ^+$
-codings above, we obtain condition (a).
Proof of Theorem 1.1(2)
For a point
![]() $z\in K_{{\mathbb {R}}}\setminus W^s(p_3)$
, we consider the following conditions:
$z\in K_{{\mathbb {R}}}\setminus W^s(p_3)$
, we consider the following conditions:
-
(a) the
 $\Sigma ^-$
-coding of z exists and is
$\Sigma ^-$
-coding of z exists and is
 $\overline {43}412\cdot 41\overline {0}$
;
$\overline {43}412\cdot 41\overline {0}$
; -
(b)
 $f^{-4}(z)\in W^u_{\mathrm {loc}}(p_3)_3$
;
$f^{-4}(z)\in W^u_{\mathrm {loc}}(p_3)_3$
; -
(c)
 $f^2(z)\in W^s_{\mathrm {loc}}(p_1)_0$
;
$f^2(z)\in W^s_{\mathrm {loc}}(p_1)_0$
; -
(d) the
 $\{L, R\}$
-coding of z is
$\{L, R\}$
-coding of z is
 $\overline {L}RR\cdot L\overline {R}$
.
$\overline {L}RR\cdot L\overline {R}$
.
It is easy to see that
![]() $z\in S^-(a, b)$
if and only if z satisfies conditions (a), (b), and (c). Assume that condition (a) holds. Then, the forward
$z\in S^-(a, b)$
if and only if z satisfies conditions (a), (b), and (c). Assume that condition (a) holds. Then, the forward
![]() $\Sigma ^-$
-coding of
$\Sigma ^-$
-coding of
![]() $f^2(z)$
is
$f^2(z)$
is
![]() $\overline {0}\in \mathfrak {S}^-_{\mathrm {fwd}}$
. Since
$\overline {0}\in \mathfrak {S}^-_{\mathrm {fwd}}$
. Since
![]() $f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one, this yields condition (c) as in Corollary 3.6(1). Therefore, it is sufficient to prove that conditions (a) and (b) hold if and only if condition (d) holds. Note that
$f : \mathcal {B}^-_0\cap f^{-1}(\mathcal {B}^-_0)\to \mathcal {B}^-_0$
is a crossed mapping of degree one, this yields condition (c) as in Corollary 3.6(1). Therefore, it is sufficient to prove that conditions (a) and (b) hold if and only if condition (d) holds. Note that
![]() $\overline {L}RR\cdot L\overline {R} = \overline {LL}LRR\cdot LR\overline {R}$
.
$\overline {L}RR\cdot L\overline {R} = \overline {LL}LRR\cdot LR\overline {R}$
.
(a) and (b) imply (d): Since
![]() $z\notin W^s(p_3)$
, Proposition 4.4 and the definition of the partition
$z\notin W^s(p_3)$
, Proposition 4.4 and the definition of the partition
![]() $\{P_L^-, P_R^-\}$
imply the following.
$\{P_L^-, P_R^-\}$
imply the following.
-
• If
 $i_0=0$
, then
$i_0=0$
, then
 $z\in \mathrm {left}(\mathcal {B}^-_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_1)_0)\subset P_R^-$
.
$z\in \mathrm {left}(\mathcal {B}^-_{0, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_1)_0)\subset P_R^-$
. -
• If
 $i_0=1$
, then
$i_0=1$
, then
 $z\in \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})\subset P_R^-$
.
$z\in \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}}\setminus \gamma _{1, \mathrm {left}})\subset P_R^-$
. -
• If
 $i_0=2$
, then
$i_0=2$
, then
 $z\in \mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})\subset P_R^-$
.
$z\in \mathrm {right}(\mathcal {B}^-_{2, {\mathbb {R}}}\setminus \gamma _{2, \mathrm {left}})\subset P_R^-$
. -
• If
 $i_0=3$
, then
$i_0=3$
, then
 $z\in \mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
.
$z\in \mathrm {right}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {left}}) \cap \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}}\setminus \gamma _{3, \mathrm {right}})$
. -
• If
 $i_0=4$
, then
$i_0=4$
, then
 $z\in \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)\subset P_L^-$
.
$z\in \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}\setminus W^s_{\mathrm {loc}}(p_3)_4)\subset P_L^-$
.
Therefore, we replace the
![]() $0$
s,
$0$
s,
![]() $1$
s, and
$1$
s, and
![]() $2$
s in
$2$
s in
![]() $\overline {43}412\cdot 41\overline {0}$
by R, and the
$\overline {43}412\cdot 41\overline {0}$
by R, and the
![]() $4$
s in
$4$
s in
![]() $\overline {43}412\cdot 41\overline {0}$
by L to obtain
$\overline {43}412\cdot 41\overline {0}$
by L to obtain
![]() $\overline {L\ast }LRR\cdot LR\overline {R}$
.
$\overline {L\ast }LRR\cdot LR\overline {R}$
.
The problem here is that
![]() $\mathcal {B}^-_{3, {\mathbb {R}}}$
is divided into both a part of
$\mathcal {B}^-_{3, {\mathbb {R}}}$
is divided into both a part of
![]() $P^-_L$
and a part of
$P^-_L$
and a part of
![]() $P^-_R$
, and hence we need to determine the letters in the
$P^-_R$
, and hence we need to determine the letters in the
![]() $-(2n+4)$
th digits (
$-(2n+4)$
th digits (
![]() $n\geq 0$
) which are denoted by
$n\geq 0$
) which are denoted by
![]() $\ast $
above. Here, we claim that
$\ast $
above. Here, we claim that
holds for all
![]() $n\geq 0$
. Indeed, the case
$n\geq 0$
. Indeed, the case
![]() $n=0$
is identical to assumption (b) and we see that
$n=0$
is identical to assumption (b) and we see that
![]() $f_{{\mathbb {R}}}^{-(2(n+1)+4)}(z)=f_{{\mathbb {R}}}^{-2}(f_{{\mathbb {R}}}^{-(2n+4)}(z))\in f_{{\mathbb {R}}}^{-2}(W^u_{\mathrm {loc}}(p_3)_3)\subset W^u_{\mathrm {loc}}(p_3)_3$
, and hence equation (4.3) is proved. The claim in equation (4.3) together with case (4) of Proposition 4.4 implies that
$f_{{\mathbb {R}}}^{-(2(n+1)+4)}(z)=f_{{\mathbb {R}}}^{-2}(f_{{\mathbb {R}}}^{-(2n+4)}(z))\in f_{{\mathbb {R}}}^{-2}(W^u_{\mathrm {loc}}(p_3)_3)\subset W^u_{\mathrm {loc}}(p_3)_3$
, and hence equation (4.3) is proved. The claim in equation (4.3) together with case (4) of Proposition 4.4 implies that
![]() $f_{{\mathbb {R}}}^{-(2n+4)}(z)\in P_L^-$
(see Figure 8). Therefore, we conclude
$f_{{\mathbb {R}}}^{-(2n+4)}(z)\in P_L^-$
(see Figure 8). Therefore, we conclude
![]() $\ast =L$
and condition (d) follows.
$\ast =L$
and condition (d) follows.

Figure 8 The real box
![]() $\mathcal {B}^-_{3, {\mathbb {R}}}$
.
$\mathcal {B}^-_{3, {\mathbb {R}}}$
.
(d) implies (a): We note that z has a unique
![]() $\Sigma ^-$
-coding thanks to Proposition 2.6 and case (2) of Proposition 2.9. Then, the rest of the argument is similar to the proof of ‘(d) implies (a)’ in the case
$\Sigma ^-$
-coding thanks to Proposition 2.6 and case (2) of Proposition 2.9. Then, the rest of the argument is similar to the proof of ‘(d) implies (a)’ in the case
![]() $b>0$
, and hence is omitted.
$b>0$
, and hence is omitted.
(d) implies (b): A discussion similar to the previous paragraph yields that the only transition with
![]() $LRRL$
is
$LRRL$
is
![]() $4124$
. Therefore, the backward
$4124$
. Therefore, the backward
![]() $\Sigma ^-$
-coding of z including the
$\Sigma ^-$
-coding of z including the
![]() $0$
th digit is
$0$
th digit is
![]() $\overline {43}4124\in \mathfrak {S}^+_{\mathrm {bwd}}$
. Moreover, by case (3) of Proposition 4.4 and the definition of the partition piece
$\overline {43}4124\in \mathfrak {S}^+_{\mathrm {bwd}}$
. Moreover, by case (3) of Proposition 4.4 and the definition of the partition piece
![]() $P^-_L$
, we see that
$P^-_L$
, we see that
![]() $f_{{\mathbb {R}}}^{-(2n+4)}(z)\in f^2_{{\mathbb {R}}}(\mathcal {B}^-_{3', {\mathbb {R}}})$
. This yields
$f_{{\mathbb {R}}}^{-(2n+4)}(z)\in f^2_{{\mathbb {R}}}(\mathcal {B}^-_{3', {\mathbb {R}}})$
. This yields
![]() $f_{{\mathbb {R}}}^{-(2n+6)}(z)\in \mathcal {B}^-_{3', {\mathbb {R}}}$
for all
$f_{{\mathbb {R}}}^{-(2n+6)}(z)\in \mathcal {B}^-_{3', {\mathbb {R}}}$
for all
![]() $n\geq 0$
. Since
$n\geq 0$
. Since
![]() $f^2 : \mathcal {B}^-_{3'}\to \mathcal {B}^-_3$
is a crossed mapping of degree one, we have
$f^2 : \mathcal {B}^-_{3'}\to \mathcal {B}^-_3$
is a crossed mapping of degree one, we have
![]() $f_{{\mathbb {R}}}^{-(2n+6)}(z)\in W^u_{\mathrm {loc}}(p_3)_{p_3'}$
(compare item (2) of Corollary 3.6). Hence,
$f_{{\mathbb {R}}}^{-(2n+6)}(z)\in W^u_{\mathrm {loc}}(p_3)_{p_3'}$
(compare item (2) of Corollary 3.6). Hence,
![]() $f_{{\mathbb {R}}}^{-4}(z)\in f^2_{{\mathbb {R}}}(W^u_{\mathrm {loc}}(p_3)_{3'})= W^u_{\mathrm {loc}}(p_3)_3$
and claim (b) is proved.
$f_{{\mathbb {R}}}^{-4}(z)\in f^2_{{\mathbb {R}}}(W^u_{\mathrm {loc}}(p_3)_{3'})= W^u_{\mathrm {loc}}(p_3)_3$
and claim (b) is proved.
Remark 4.10
-
(a) When
 $b \kern1.3pt{<}\kern1.3pt 0$
, the crossed mapping
$b \kern1.3pt{<}\kern1.3pt 0$
, the crossed mapping
 $f^2 : \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4 \cap f^{-1}(\mathcal {B}^-_3))\to \mathcal {B}^-_3$
has degree two. Then the set
$f^2 : \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4 \cap f^{-1}(\mathcal {B}^-_3))\to \mathcal {B}^-_3$
has degree two. Then the set
 $K^u_{\overline {43}}$
consists of infinitely many horizontal disks in
$K^u_{\overline {43}}$
consists of infinitely many horizontal disks in
 $\mathcal {B}^-_3$
, and
$\mathcal {B}^-_3$
, and
 $K^u_{\overline {43}4124} \cap K^s_{41\overline {0}}$
consists of infinitely many points. Hence, we cannot classify the dynamics of the Hénon maps only by the number of points with the
$K^u_{\overline {43}4124} \cap K^s_{41\overline {0}}$
consists of infinitely many points. Hence, we cannot classify the dynamics of the Hénon maps only by the number of points with the
 $\Sigma ^-$
-coding
$\Sigma ^-$
-coding
 $\overline {43}412\cdot 41\overline {0}$
. In Corollary 4.9(2), we classify the dynamics by
$\overline {43}412\cdot 41\overline {0}$
. In Corollary 4.9(2), we classify the dynamics by
 $S(a, b)^-$
instead. Here,
$S(a, b)^-$
instead. Here,
 $S(a, b)^-$
is the number of intersection points of
$S(a, b)^-$
is the number of intersection points of
 $W^u_{\overline {43}4124}(a, b)^-$
and
$W^u_{\overline {43}4124}(a, b)^-$
and
 $W^s_{41\overline {0}}(a, b)^-$
, and
$W^s_{41\overline {0}}(a, b)^-$
, and
 $W^u_{\overline {43}4124}(a, b)^-$
is defined as a certain preimage of the local unstable manifold
$W^u_{\overline {43}4124}(a, b)^-$
is defined as a certain preimage of the local unstable manifold
 $W^u_{\overline {43}}(a, b)^-$
, one of the disks which
$W^u_{\overline {43}}(a, b)^-$
, one of the disks which
 $K^u_{\overline {43}}$
consists of.
$K^u_{\overline {43}}$
consists of. -
(b) Our goal was to classify the dynamics in terms of
 $\{ L, R \}$
-coding. Hence, our
$\{ L, R \}$
-coding. Hence, our
 $\{ L, R \}$
-partition must distinguish
$\{ L, R \}$
-partition must distinguish
 $W^u_{\overline {43}}(a, b)^-$
from the other horizontal disks in
$W^u_{\overline {43}}(a, b)^-$
from the other horizontal disks in
 $K^u_{\overline {43}}$
(more precisely, claim (d) must imply claim (a) in the proof of Theorem 1.1(2)). This is the reason why we refined the box
$K^u_{\overline {43}}$
(more precisely, claim (d) must imply claim (a) in the proof of Theorem 1.1(2)). This is the reason why we refined the box
 $\mathcal {B}^-_3$
into two parts
$\mathcal {B}^-_3$
into two parts
 $\mathcal {B}^-_{3^{\prime }}$
and
$\mathcal {B}^-_{3^{\prime }}$
and
 $\mathcal {B}^-_{3^{\prime \prime }}$
so that
$\mathcal {B}^-_{3^{\prime \prime }}$
so that
 $f^2 : \mathcal {B}^-_{3^{\prime }} \rightarrow \mathcal {B}^-_{3^{\prime }}$
has degree one and hence we have
$f^2 : \mathcal {B}^-_{3^{\prime }} \rightarrow \mathcal {B}^-_{3^{\prime }}$
has degree one and hence we have
 $K^u_{\overline {43^{\prime }}} = W^u_{\overline {43}}(a, b)^-$
.
$K^u_{\overline {43^{\prime }}} = W^u_{\overline {43}}(a, b)^-$
. -
(c) However, since
 $f : \mathcal {B}^{\pm }_0\cap f^{-1}(\mathcal {B}^{\pm }_0)\to \mathcal {B}^{\pm }_0$
is degree one,
$f : \mathcal {B}^{\pm }_0\cap f^{-1}(\mathcal {B}^{\pm }_0)\to \mathcal {B}^{\pm }_0$
is degree one,
 $K^{u/s}_{\overline {0}}$
are disks of degree one without any refinement.
$K^{u/s}_{\overline {0}}$
are disks of degree one without any refinement.
5 Dynamics at the boundary
 $\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
$\partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
The purpose of this section is to prove Theorem 1.2.
For simplicity, we write
![]() $\mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {left}})$
(
$\mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {left}})$
(
![]() $j = 0, 1, 2$
) and
$j = 0, 1, 2$
) and
![]() $\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {right}})$
(
$\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {right}})$
(
![]() $j = 2, 3$
) below. Let
$j = 2, 3$
) below. Let
![]() $\mathfrak {M}^+_1$
be the family of these sets. Similarly, we write
$\mathfrak {M}^+_1$
be the family of these sets. Similarly, we write
![]() $\mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {left}})$
(
$\mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {left}})$
(
![]() $j = 0, 1, 2, 3$
) and
$j = 0, 1, 2, 3$
) and
![]() $\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {right}})$
(
$\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {right}})$
(
![]() $j = 2, 3, 4$
) below. Let
$j = 2, 3, 4$
) below. Let
![]() $\mathfrak {M}^-_1$
be the family of these sets. We call the elements of
$\mathfrak {M}^-_1$
be the family of these sets. We call the elements of
![]() $\mathfrak {M}^{\pm }_1$
margins of
$\mathfrak {M}^{\pm }_1$
margins of
![]() $\mathcal {B}^{\pm }_{j, {\mathbb {R}}}$
.
$\mathcal {B}^{\pm }_{j, {\mathbb {R}}}$
.
5.1 Refined dynamics
We first refine local stable/unstable manifolds for our purpose. The proofs of the following lemmas are analogous to Lemmas 3.1 and 3.2, and hence are omitted.
Lemma 5.1. Let
![]() $(a, b) \in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b) \in \mathcal {E}^+_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $V^s_{\overline {0}}(a, b)^+$
is a vertical disk of degree one in
$V^s_{\overline {0}}(a, b)^+$
is a vertical disk of degree one in
 $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
 $V^s_{\overline {0}}(a, b)^+ = K^s_{\overline {0}}$
.
$V^s_{\overline {0}}(a, b)^+ = K^s_{\overline {0}}$
. -
(2)
 $V^s_{1 \overline {0}}(a, b)^+$
is a vertical disk of degree one in
$V^s_{1 \overline {0}}(a, b)^+$
is a vertical disk of degree one in
 $\mathcal {B}^+_1$
and
$\mathcal {B}^+_1$
and
 $V^s_{1 \overline {0}}(a, b)^+ = K^s_{1 \overline {0}}$
.
$V^s_{1 \overline {0}}(a, b)^+ = K^s_{1 \overline {0}}$
. -
(3)
 $V^s_{3 1 \overline {0}}(a, b)^+$
is a vertical disk of degree one in
$V^s_{3 1 \overline {0}}(a, b)^+$
is a vertical disk of degree one in
 $\mathcal {B}^+_3$
and
$\mathcal {B}^+_3$
and
 $V^s_{3 1 \overline {0}}(a, b)^+ = K^s_{3 1 \overline {0}}$
.
$V^s_{3 1 \overline {0}}(a, b)^+ = K^s_{3 1 \overline {0}}$
. -
(4)
 $V^u_{\overline {0}}(a, b)^+$
is a horizontal disk of degree one in
$V^u_{\overline {0}}(a, b)^+$
is a horizontal disk of degree one in
 $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
 $V^u_{\overline {0}}(a, b)^+ = K^u_{\overline {0}}$
.
$V^u_{\overline {0}}(a, b)^+ = K^u_{\overline {0}}$
. -
(5)
 $V^u_{\overline {0} 3}(a, b)^+$
is a horizontal disk of degree two in
$V^u_{\overline {0} 3}(a, b)^+$
is a horizontal disk of degree two in
 $\mathcal {B}^+_3$
and
$\mathcal {B}^+_3$
and
 $V^u_{\overline {0} 3}(a, b)^+ = K^u_{\overline {0} 3}$
.
$V^u_{\overline {0} 3}(a, b)^+ = K^u_{\overline {0} 3}$
. -
(6)
 $V^u_{\overline {0} 2}(a, b)^+$
is a horizontal disk of degree one in
$V^u_{\overline {0} 2}(a, b)^+$
is a horizontal disk of degree one in
 $\mathcal {B}^+_2$
and
$\mathcal {B}^+_2$
and
 $V^u_{\overline {0} 2}(a, b)^+ = K^u_{\overline {0} 2}$
.
$V^u_{\overline {0} 2}(a, b)^+ = K^u_{\overline {0} 2}$
. -
(7)
 $V^u_{\overline {0} 3 1}(a, b)^+$
is a horizontal disk of degree two in
$V^u_{\overline {0} 3 1}(a, b)^+$
is a horizontal disk of degree two in
 $\mathcal {B}^+_1$
and
$\mathcal {B}^+_1$
and
 $V^u_{\overline {0} 3 1}(a, b)^+ = K^u_{\overline {0} 3 1}$
.
$V^u_{\overline {0} 3 1}(a, b)^+ = K^u_{\overline {0} 3 1}$
. -
(8)
 $V^u_{\overline {0} 2 3}(a, b)^+$
is a horizontal disk of degree two in
$V^u_{\overline {0} 2 3}(a, b)^+$
is a horizontal disk of degree two in
 $\mathcal {B}^+_3$
and
$\mathcal {B}^+_3$
and
 $V^u_{\overline {0} 2 3}(a, b)^+ = K^u_{\overline {0} 2 3}$
.
$V^u_{\overline {0} 2 3}(a, b)^+ = K^u_{\overline {0} 2 3}$
. -
(9)
 $V^u_{\overline {0} 2 2}(a, b)^+$
is a horizontal disk of degree one in
$V^u_{\overline {0} 2 2}(a, b)^+$
is a horizontal disk of degree one in
 $\mathcal {B}^+_2$
and
$\mathcal {B}^+_2$
and
 $V^u_{\overline {0} 2 2}(a, b)^+ = K^u_{\overline {0} 2 2}$
.
$V^u_{\overline {0} 2 2}(a, b)^+ = K^u_{\overline {0} 2 2}$
. -
(10)
 $V^u_{\overline {0} 3 1 0}(a, b)^+$
is a horizontal disk of degree two in
$V^u_{\overline {0} 3 1 0}(a, b)^+$
is a horizontal disk of degree two in
 $\mathcal {B}^+_0$
and
$\mathcal {B}^+_0$
and
 $V^u_{\overline {0} 3 1 0}(a, b)^+ = K^u_{\overline {0} 3 1 0}$
.
$V^u_{\overline {0} 3 1 0}(a, b)^+ = K^u_{\overline {0} 3 1 0}$
.
Lemma 5.2. Let
![]() $(a, b) \in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b) \in \mathcal {E}^-_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $V^s_{\overline {0}}(a, b)^-$
is a vertical disk of degree one in
$V^s_{\overline {0}}(a, b)^-$
is a vertical disk of degree one in
 $\mathcal {B}^-_0$
and
$\mathcal {B}^-_0$
and
 $V^s_{\overline {0}}(a, b)^- = K^s_{\overline {0}}$
.
$V^s_{\overline {0}}(a, b)^- = K^s_{\overline {0}}$
. -
(2)
 $V^s_{1 \overline {0}}(a, b)^-$
is a vertical disk of degree one in
$V^s_{1 \overline {0}}(a, b)^-$
is a vertical disk of degree one in
 $\mathcal {B}^-_1$
and
$\mathcal {B}^-_1$
and
 $V^s_{1 \overline {0}}(a, b)^- = K^s_{1 \overline {0}}$
.
$V^s_{1 \overline {0}}(a, b)^- = K^s_{1 \overline {0}}$
. -
(3)
 $V^s_{4 1 \overline {0}}(a, b)^-$
is a vertical disk of degree one in
$V^s_{4 1 \overline {0}}(a, b)^-$
is a vertical disk of degree one in
 $\mathcal {B}^-_4$
and
$\mathcal {B}^-_4$
and
 $V^s_{4 1\overline {0}}(a, b)^- = K^s_{4 1 \overline {0}}$
.
$V^s_{4 1\overline {0}}(a, b)^- = K^s_{4 1 \overline {0}}$
. -
(4)
 $V^u_{\overline {43}}(a, b)^-$
is a horizontal disk of degree one in
$V^u_{\overline {43}}(a, b)^-$
is a horizontal disk of degree one in
 $\mathcal {B}^-_3$
and
$\mathcal {B}^-_3$
and
 $V^u_{\overline {43}}(a, b)^- \subset K^u_{\overline {43}}$
.
$V^u_{\overline {43}}(a, b)^- \subset K^u_{\overline {43}}$
. -
(5)
 $V^u_{\overline {43} 4}(a, b)^-$
is a horizontal disk of degree two in
$V^u_{\overline {43} 4}(a, b)^-$
is a horizontal disk of degree two in
 $\mathcal {B}^-_4$
and
$\mathcal {B}^-_4$
and
 $V^u_{\overline {43} 4}(a, b)^- \subset K^u_{\overline {43} 4}$
.
$V^u_{\overline {43} 4}(a, b)^- \subset K^u_{\overline {43} 4}$
. -
(6)
 $V^u_{\overline {43} 4 3}(a, b)^-$
consists of two mutually disjoint disks of degree one in
$V^u_{\overline {43} 4 3}(a, b)^-$
consists of two mutually disjoint disks of degree one in
 $\mathcal {B}^-_3$
. Moreover,
$\mathcal {B}^-_3$
. Moreover,
 $V^u_{\overline {43} 4 3}(a, b)^- \subset K^u_{\overline {43}}$
.
$V^u_{\overline {43} 4 3}(a, b)^- \subset K^u_{\overline {43}}$
. -
(7)
 $V^u_{\overline {43} 4 1}(a, b)^-$
is a horizontal disk of degree two in
$V^u_{\overline {43} 4 1}(a, b)^-$
is a horizontal disk of degree two in
 $\mathcal {B}^-_1$
and
$\mathcal {B}^-_1$
and
 $V^u_{\overline {43} 4 1}(a, b)^- \subset K^u_{\overline {43} 4 1}$
.
$V^u_{\overline {43} 4 1}(a, b)^- \subset K^u_{\overline {43} 4 1}$
. -
(8)
 $V^u_{\overline {43} 4 1 0}(a, b)^-$
is a horizontal disk of degree two in
$V^u_{\overline {43} 4 1 0}(a, b)^-$
is a horizontal disk of degree two in
 $\mathcal {B}^-_0$
and
$\mathcal {B}^-_0$
and
 $V^u_{\overline {43} 4 1 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0}$
.
$V^u_{\overline {43} 4 1 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0}$
. -
(9)
 $V^u_{\overline {43} 4 1 2}(a, b)^-$
consists of two mutually disjoint disks of degree one in
$V^u_{\overline {43} 4 1 2}(a, b)^-$
consists of two mutually disjoint disks of degree one in
 $\mathcal {B}^-_2$
. Moreover,
$\mathcal {B}^-_2$
. Moreover,
 $V^u_{\overline {43} 4 1 2}(a, b)^- \subset K^u_{\overline {43} 4 1 2}$
.
$V^u_{\overline {43} 4 1 2}(a, b)^- \subset K^u_{\overline {43} 4 1 2}$
. -
(10)
 $V^u_{\overline {43} 4 1 0 0}(a, b)^-$
is a horizontal disk of degree one in
$V^u_{\overline {43} 4 1 0 0}(a, b)^-$
is a horizontal disk of degree one in
 $\mathcal {B}^-_0$
and
$\mathcal {B}^-_0$
and
 $V^u_{\overline {43} 4 1 0 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0 0}$
.
$V^u_{\overline {43} 4 1 0 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0 0}$
. -
(11)
 $V^u_{\overline {43} 4 1 0 2}(a, b)^-$
consists of two mutually disjoint disks of degree one in
$V^u_{\overline {43} 4 1 0 2}(a, b)^-$
consists of two mutually disjoint disks of degree one in
 $\mathcal {B}^-_2$
. Moreover,
$\mathcal {B}^-_2$
. Moreover,
 $V^u_{\overline {43} 4 1 0 2}(a, b)^- \subset K^u_{\overline {43} 4 1 0 2}$
.
$V^u_{\overline {43} 4 1 0 2}(a, b)^- \subset K^u_{\overline {43} 4 1 0 2}$
. -
(12)
 $V^u_{\overline {43} 4 1 2 4}(a, b)^-$
consists of two mutually disjoint disks of degree two in
$V^u_{\overline {43} 4 1 2 4}(a, b)^-$
consists of two mutually disjoint disks of degree two in
 $\mathcal {B}^-_4$
. Moreover,
$\mathcal {B}^-_4$
. Moreover,
 $V^u_{\overline {43} 4 1 2 4}(a, b)^- \subset K^u_{\overline {43} 4 1 2 4}$
.
$V^u_{\overline {43} 4 1 2 4}(a, b)^- \subset K^u_{\overline {43} 4 1 2 4}$
.
The corollary below follows from Lemma 5.1 (see Figure 9).

Figure 9 The
![]() $\Sigma ^+$
-coding of pieces of stable/unstable manifolds for
$\Sigma ^+$
-coding of pieces of stable/unstable manifolds for
![]() $b>0$
.
$b>0$
.
Corollary 5.3. Let
![]() $(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $W^s_{\overline {0}}(a, b)^+$
is a vertical curve in
$W^s_{\overline {0}}(a, b)^+$
is a vertical curve in
 $\mathcal {B}^+_{0, {\mathbb {R}}}$
and
$\mathcal {B}^+_{0, {\mathbb {R}}}$
and
 $W^s_{\overline {0}}(a, b)^+ = K^s_{\overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{\overline {0}}(a, b)^+ = K^s_{\overline {0}} \cap {\mathbb {R}}^2$
. -
(2)
 $W^s_{1 \overline {0}}(a, b)^+$
is a vertical curve in
$W^s_{1 \overline {0}}(a, b)^+$
is a vertical curve in
 $\mathcal {B}^+_{1, {\mathbb {R}}}$
and
$\mathcal {B}^+_{1, {\mathbb {R}}}$
and
 $W^s_{1 \overline {0}}(a, b)^+ = K^s_{1 \overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{1 \overline {0}}(a, b)^+ = K^s_{1 \overline {0}} \cap {\mathbb {R}}^2$
. -
(3)
 $W^s_{3 1 \overline {0}}(a, b)^+$
is a vertical curve in
$W^s_{3 1 \overline {0}}(a, b)^+$
is a vertical curve in
 $\mathcal {B}^+_{3, {\mathbb {R}}}$
and
$\mathcal {B}^+_{3, {\mathbb {R}}}$
and
 $W^s_{3 1 \overline {0}}(a, b)^+ = K^s_{3 1 \overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{3 1 \overline {0}}(a, b)^+ = K^s_{3 1 \overline {0}} \cap {\mathbb {R}}^2$
. -
(4)
 $W^u_{\overline {0}}(a, b)^+$
is a horizontal curve in
$W^u_{\overline {0}}(a, b)^+$
is a horizontal curve in
 $\mathcal {B}^+_{0, {\mathbb {R}}}$
and
$\mathcal {B}^+_{0, {\mathbb {R}}}$
and
 $W^u_{\overline {0}}(a, b)^+ = K^u_{\overline {0}} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0}}(a, b)^+ = K^u_{\overline {0}} \cap {\mathbb {R}}^2$
. -
(5) The intersection of
 $W^u_{\overline {0} 3}(a, b)^+$
and
$W^u_{\overline {0} 3}(a, b)^+$
and
 $\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \overline {\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus W^s_{3 1 \overline {0}}(a, b)^+)}$
consists of two horizontal curves in
$\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \overline {\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus W^s_{3 1 \overline {0}}(a, b)^+)}$
consists of two horizontal curves in
 $\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \overline {\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus W^s_{3 1 \overline {0}}(a, b)^+)}$
and
$\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \overline {\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus W^s_{3 1 \overline {0}}(a, b)^+)}$
and
 $W^u_{\overline {0} 3}(a, b)^+ = K^u_{\overline {0} 3} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0} 3}(a, b)^+ = K^u_{\overline {0} 3} \cap {\mathbb {R}}^2$
. -
(6)
 $W^u_{\overline {0} 2}(a, b)^+$
is a horizontal curve in
$W^u_{\overline {0} 2}(a, b)^+$
is a horizontal curve in
 $\mathcal {B}^+_{2, {\mathbb {R}}}$
and
$\mathcal {B}^+_{2, {\mathbb {R}}}$
and
 $W^u_{\overline {0} 2}(a, b)^+ = K^u_{\overline {0} 2} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0} 2}(a, b)^+ = K^u_{\overline {0} 2} \cap {\mathbb {R}}^2$
. -
(7) The intersection of
 $W^u_{\overline {0} 3 1}(a, b)^+$
and
$W^u_{\overline {0} 3 1}(a, b)^+$
and
 $\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^+)}$
consists of two horizontal curves in
$\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^+)}$
consists of two horizontal curves in
 $\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^+)}$
and
$\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^+)}$
and
 $W^u_{\overline {0} 3 1}(a, b)^+\hspace{-1pt} =\hspace{-1pt} K^u_{\overline {0} 3 1} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0} 3 1}(a, b)^+\hspace{-1pt} =\hspace{-1pt} K^u_{\overline {0} 3 1} \cap {\mathbb {R}}^2$
. -
(8)
 $W^u_{\overline {0} 2 3}(a, b)^+$
is a horizontal curve in
$W^u_{\overline {0} 2 3}(a, b)^+$
is a horizontal curve in
 $\mathcal {B}^+_{3, {\mathbb {R}}}$
from its right boundary to itself. Moreover,
$\mathcal {B}^+_{3, {\mathbb {R}}}$
from its right boundary to itself. Moreover,
 $W^u_{\overline {0} 2 3}(a, b)^+ = K^u_{\overline {0} 2 3} \cap {\mathbb {R}}^2$
and this curve is tangent to
$W^u_{\overline {0} 2 3}(a, b)^+ = K^u_{\overline {0} 2 3} \cap {\mathbb {R}}^2$
and this curve is tangent to
 $W^s_{3 1 \overline {0}}(a, b)^+$
at just one point.
$W^s_{3 1 \overline {0}}(a, b)^+$
at just one point. -
(9)
 $W^u_{\overline {0} 2 2}(a, b)^+$
is a horizontal curve in
$W^u_{\overline {0} 2 2}(a, b)^+$
is a horizontal curve in
 $\mathcal {B}^+_{2, {\mathbb {R}}}$
and
$\mathcal {B}^+_{2, {\mathbb {R}}}$
and
 $W^u_{\overline {0} 2 2}(a, b)^+ = K^u_{\overline {0} 2 2} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0} 2 2}(a, b)^+ = K^u_{\overline {0} 2 2} \cap {\mathbb {R}}^2$
. -
(10) The intersection of
 $W^u_{\overline {0} 3 1 0}(a, b)^+$
and
$W^u_{\overline {0} 3 1 0}(a, b)^+$
and
 $\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^+)}$
consists of two horizontal curves in
$\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^+)}$
consists of two horizontal curves in
 $\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^+)}$
and
$\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^+)}$
and
 $W^u_{\overline {0} 3 1 0}(a, b)^+ = K^u_{\overline {0} 3 1 0} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {0} 3 1 0}(a, b)^+ = K^u_{\overline {0} 3 1 0} \cap {\mathbb {R}}^2$
.
Proof. The claims (1)–(4), (6), and (9) immediately follow from Lemma 5.1. Claim (8) follows from this lemma and the assumption that
![]() $W^u_{\overline {0}23}(a, b)^+$
is tangent to
$W^u_{\overline {0}23}(a, b)^+$
is tangent to
![]() $W^s_{31\overline {0}}(a, b)^+$
at just one point. Since
$W^s_{31\overline {0}}(a, b)^+$
at just one point. Since
![]() $W^u_{\overline {0}3}(a, b)^+$
is further out than
$W^u_{\overline {0}3}(a, b)^+$
is further out than
![]() $W^u_{\overline {0}23}(a, b)^+$
,
$W^u_{\overline {0}23}(a, b)^+$
,
![]() $W^u_{\overline {0}23}(a, b)^+$
intersects with
$W^u_{\overline {0}23}(a, b)^+$
intersects with
![]() $W^s_{31\overline {0}}(a, b)^+$
at distinct two points. This proves the claim (5). Claim (7) follows from claim (5), and claim (10) follows from claim (7).
$W^s_{31\overline {0}}(a, b)^+$
at distinct two points. This proves the claim (5). Claim (7) follows from claim (5), and claim (10) follows from claim (7).
Similarly, we have the corollary below from Lemma 5.2 (see Figure 10). The proof is analogous to that of Corollary 5.3, and hence is omitted.
Corollary 5.4. Let
![]() $(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
. Then, we have the following.
$(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
. Then, we have the following.
-
(1)
 $W^s_{\overline {0}}(a, b)^-$
is a vertical curve in
$W^s_{\overline {0}}(a, b)^-$
is a vertical curve in
 $\mathcal {B}^-_{0, {\mathbb {R}}}$
and
$\mathcal {B}^-_{0, {\mathbb {R}}}$
and
 $W^s_{\overline {0}}(a, b)^- = K^s_{\overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{\overline {0}}(a, b)^- = K^s_{\overline {0}} \cap {\mathbb {R}}^2$
. -
(2)
 $W^s_{1 \overline {0}}(a, b)^-$
is a vertical curve in
$W^s_{1 \overline {0}}(a, b)^-$
is a vertical curve in
 $\mathcal {B}^-_{1, {\mathbb {R}}}$
and
$\mathcal {B}^-_{1, {\mathbb {R}}}$
and
 $W^s_{1 \overline {0}}(a, b)^- = K^s_{1 \overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{1 \overline {0}}(a, b)^- = K^s_{1 \overline {0}} \cap {\mathbb {R}}^2$
. -
(3)
 $W^s_{4 1 \overline {0}}(a, b)^-$
is a vertical curve in
$W^s_{4 1 \overline {0}}(a, b)^-$
is a vertical curve in
 $\mathcal {B}^-_{4, {\mathbb {R}}}$
and
$\mathcal {B}^-_{4, {\mathbb {R}}}$
and
 $W^s_{4 1\overline {0}}(a, b)^- = K^s_{4 1 \overline {0}} \cap {\mathbb {R}}^2$
.
$W^s_{4 1\overline {0}}(a, b)^- = K^s_{4 1 \overline {0}} \cap {\mathbb {R}}^2$
. -
(4)
 $W^u_{\overline {43}}(a, b)^-$
is a horizontal curve in
$W^u_{\overline {43}}(a, b)^-$
is a horizontal curve in
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
and
$\mathcal {B}^-_{3, {\mathbb {R}}}$
and
 $W^u_{\overline {43}}(a, b)^- \subset K^u_{\overline {43}} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43}}(a, b)^- \subset K^u_{\overline {43}} \cap {\mathbb {R}}^2$
. -
(5) The intersection of
 $W^u_{\overline {43} 4}(a, b)^-$
and
$W^u_{\overline {43} 4}(a, b)^-$
and
 $\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} \setminus W^s_{4 1 \overline {0}}(a, b)^-)$
consists of two horizontal curves in
$\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} \setminus W^s_{4 1 \overline {0}}(a, b)^-)$
consists of two horizontal curves in
 $\mathcal {B}^-_{4, {\mathbb {R}}} {\kern-1pt}\setminus{\kern-1pt} \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} {\kern-1pt}\setminus{\kern-1pt} W^s_{4 1 \overline {0}}(a, b)^-)$
and
$\mathcal {B}^-_{4, {\mathbb {R}}} {\kern-1pt}\setminus{\kern-1pt} \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} {\kern-1pt}\setminus{\kern-1pt} W^s_{4 1 \overline {0}}(a, b)^-)$
and
 $W^u_{\overline {43} 4}(a, b)^- {\kern-1pt}\subset{\kern-1pt} K^u_{\overline {43} 4} {\kern-1pt}\cap{\kern-1pt} {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4}(a, b)^- {\kern-1pt}\subset{\kern-1pt} K^u_{\overline {43} 4} {\kern-1pt}\cap{\kern-1pt} {\mathbb {R}}^2$
.
Figure 10 The
 $\Sigma ^-$
-coding of pieces of stable/unstable manifolds for
$\Sigma ^-$
-coding of pieces of stable/unstable manifolds for
 $b<0$
.
$b<0$
. -
(6)
 $W^u_{\overline {43} 4 3}(a, b)^-$
consists of two mutually disjoint horizontal curves in
$W^u_{\overline {43} 4 3}(a, b)^-$
consists of two mutually disjoint horizontal curves in
 $\mathcal {B}^-_{3, {\mathbb {R}}}$
. Moreover,
$\mathcal {B}^-_{3, {\mathbb {R}}}$
. Moreover,
 $W^u_{\overline {43} 4 3}(a, b)^- \subset K^u_{\overline {43}} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 3}(a, b)^- \subset K^u_{\overline {43}} \cap {\mathbb {R}}^2$
. -
(7) The intersection of
 $W^u_{\overline {43} 4 1}(a, b)^-$
and
$W^u_{\overline {43} 4 1}(a, b)^-$
and
 $\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^-)}$
consists of two horizontal curves in
$\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^-)}$
consists of two horizontal curves in
 $\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^-)}$
and
$\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus W^s_{1 \overline {0}}(a, b)^-)}$
and
 $W^u_{\overline {43} 4 1}(a, b)^- \subset K^u_{\overline {43} 4 1} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 1}(a, b)^- \subset K^u_{\overline {43} 4 1} \cap {\mathbb {R}}^2$
. -
(8) The intersection of
 $W^u_{\overline {43} 4 1 0}(a, b)^-$
and
$W^u_{\overline {43} 4 1 0}(a, b)^-$
and
 $\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
consists of two horizontal curves in
$\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
consists of two horizontal curves in
 $\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
and
$\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
and
 $W^u_{\overline {43} 4 1 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 1 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0} \cap {\mathbb {R}}^2$
. -
(9)
 $W^u_{\overline {43} 4 1 2}(a, b)^-$
consists of two mutually disjoint horizontal curves in
$W^u_{\overline {43} 4 1 2}(a, b)^-$
consists of two mutually disjoint horizontal curves in
 $\mathcal {B}^-_{2, {\mathbb {R}}}$
. Moreover,
$\mathcal {B}^-_{2, {\mathbb {R}}}$
. Moreover,
 $W^u_{\overline {43} 4 1 2}(a, b)^- \subset K^u_{\overline {43} 4 1 2} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 1 2}(a, b)^- \subset K^u_{\overline {43} 4 1 2} \cap {\mathbb {R}}^2$
. -
(10) The intersection of
 $W^u_{\overline {43} 4 1 0 0}(a, b)^-$
and
$W^u_{\overline {43} 4 1 0 0}(a, b)^-$
and
 $\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
consists of two horizontal curves in
$\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
consists of two horizontal curves in
 $\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
and
$\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \overline {\mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus W^s_{\overline {0}}(a, b)^-)}$
and
 $W^u_{\overline {43} 4 1 0 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0 0} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 1 0 0}(a, b)^- \subset K^u_{\overline {43} 4 1 0 0} \cap {\mathbb {R}}^2$
. -
(11)
 $W^u_{\overline {43} 4 1 0 2}(a, b)^-$
consists of two mutually disjoint horizontal curves in
$W^u_{\overline {43} 4 1 0 2}(a, b)^-$
consists of two mutually disjoint horizontal curves in
 $\mathcal {B}^-_{2, {\mathbb {R}}}$
. Moreover,
$\mathcal {B}^-_{2, {\mathbb {R}}}$
. Moreover,
 $W^u_{\overline {43} 4 1 0 2}(a, b)^- \subset K^u_{\overline {43} 4 1 0 2} \cap {\mathbb {R}}^2$
.
$W^u_{\overline {43} 4 1 0 2}(a, b)^- \subset K^u_{\overline {43} 4 1 0 2} \cap {\mathbb {R}}^2$
. -
(12)
 $W^u_{\overline {43} 4 1 2 4}(a, b)^-$
consists of two mutually disjoint horizontal curves in
$W^u_{\overline {43} 4 1 2 4}(a, b)^-$
consists of two mutually disjoint horizontal curves in
 $\mathcal {B}^-_{4, {\mathbb {R}}}$
from the right boundary to itself and
$\mathcal {B}^-_{4, {\mathbb {R}}}$
from the right boundary to itself and
 $W^u_{\overline {43} 4 1 2 4}(a, b)^- \subset K^u_{\overline {43} 4 1 2 4} \cap {\mathbb {R}}^2$
. Moreover, the inner one of these two curves is
$W^u_{\overline {43} 4 1 2 4}(a, b)^- \subset K^u_{\overline {43} 4 1 2 4} \cap {\mathbb {R}}^2$
. Moreover, the inner one of these two curves is
 $W^u_{\overline {43} 4 1 2 4}(a, b)^-_{\mathrm {inner}}$
and this curve is tangent to
$W^u_{\overline {43} 4 1 2 4}(a, b)^-_{\mathrm {inner}}$
and this curve is tangent to
 $W^u_{4 1 \overline {0}}(a, b)^-$
at just one point.
$W^u_{4 1 \overline {0}}(a, b)^-$
at just one point.
The following definitions of pieces of stable/unstable manifolds are necessary to construct the
![]() $\{\alpha , \beta \}$
-partition for the proof of Theorem 1.2. First, we let
$\{\alpha , \beta \}$
-partition for the proof of Theorem 1.2. First, we let
![]() $(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
.
$(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
.
-
• We write
 $\gamma ^+_{0, \mathrm {right}}$
as
$\gamma ^+_{0, \mathrm {right}}$
as
 $W^s_{\overline {0}}(a, b)^+$
.
$W^s_{\overline {0}}(a, b)^+$
. -
• We write
 $\gamma ^+_{1, \mathrm {right}}$
as
$\gamma ^+_{1, \mathrm {right}}$
as
 $W^s_{1 \overline {0}}(a, b)^+$
.
$W^s_{1 \overline {0}}(a, b)^+$
. -
• We write
 $\gamma ^+_{3, \mathrm {left}}$
as
$\gamma ^+_{3, \mathrm {left}}$
as
 $W^s_{3 1 \overline {0}}(a, b)^+$
.
$W^s_{3 1 \overline {0}}(a, b)^+$
. -
• We write
 $\gamma ^+_{0, \mathrm {upper}}$
as
$\gamma ^+_{0, \mathrm {upper}}$
as
 $W^u_{\overline {0}}(a, b)^+$
.
$W^u_{\overline {0}}(a, b)^+$
. -
• We write
 $\gamma ^+_{3, \mathrm {upper}}$
(respectively
$\gamma ^+_{3, \mathrm {upper}}$
(respectively
 $\gamma ^+_{3, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^+_{3, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {0} 3}(a, b)^+ \cap (\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \gamma ^+_{3, \mathrm {left}}))$
.
$W^u_{\overline {0} 3}(a, b)^+ \cap (\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \gamma ^+_{3, \mathrm {left}}))$
. -
• We write
 $\gamma ^+_{2, \mathrm {upper}}$
(respectively
$\gamma ^+_{2, \mathrm {upper}}$
(respectively
 $\gamma ^+_{2, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^+_{2, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {0} 2}(a, b)^+ \cap \mathcal {B}^+_{2, {\mathbb {R}}}$
.
$W^u_{\overline {0} 2}(a, b)^+ \cap \mathcal {B}^+_{2, {\mathbb {R}}}$
. -
• We write
 $\gamma ^+_{1, \mathrm {upper}}$
(respectively
$\gamma ^+_{1, \mathrm {upper}}$
(respectively
 $\gamma ^+_{1, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^+_{1, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {0} 3 1}(a, b)^+ \cap (\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \gamma ^+_{1, \mathrm {right}}))$
.
$W^u_{\overline {0} 3 1}(a, b)^+ \cap (\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}} \setminus \gamma ^+_{1, \mathrm {right}}))$
. -
• We write
 $\gamma ^+_{3, \mathrm {inner}}$
as
$\gamma ^+_{3, \mathrm {inner}}$
as
 $W^u_{\overline {0} 2 3}(a, b)^+$
.
$W^u_{\overline {0} 2 3}(a, b)^+$
. -
• We write
 $\gamma ^+_{2, \mathrm {upper}}$
as
$\gamma ^+_{2, \mathrm {upper}}$
as
 $W^u_{\overline {0} 2 2}(a, b)^+$
.
$W^u_{\overline {0} 2 2}(a, b)^+$
. -
• We write
 $\gamma ^+_{0, \mathrm {lower}}$
as the lower connected component of
$\gamma ^+_{0, \mathrm {lower}}$
as the lower connected component of
 $W^u_{\overline {0} 3 1 0}(a, b)^+ \cap (\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \gamma ^+_{0, \mathrm {right}}))$
.
$W^u_{\overline {0} 3 1 0}(a, b)^+ \cap (\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \gamma ^+_{0, \mathrm {right}}))$
.
See Figure 11 for more details. Next, we let
![]() $(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
.
$(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
.
-
• We write
 $\gamma ^-_{0, \mathrm {right}}$
as
$\gamma ^-_{0, \mathrm {right}}$
as
 $W^s_{\overline {0}}(a, b)^-$
.
$W^s_{\overline {0}}(a, b)^-$
. -
• We write
 $\gamma ^-_{1, \mathrm {right}}$
as
$\gamma ^-_{1, \mathrm {right}}$
as
 $W^s_{1 \overline {0}}(a, b)^-$
.
$W^s_{1 \overline {0}}(a, b)^-$
. -
• We write
 $\gamma ^-_{4, \mathrm {left}}$
as
$\gamma ^-_{4, \mathrm {left}}$
as
 $W^s_{4 1 \overline {0}}(a, b)^-$
.
$W^s_{4 1 \overline {0}}(a, b)^-$
. -
• We write
 $\gamma ^-_{3, \mathrm {lower}}$
as
$\gamma ^-_{3, \mathrm {lower}}$
as
 $W^u_{\overline {43}}(a, b)^-$
.
$W^u_{\overline {43}}(a, b)^-$
. -
• We write
 $\gamma ^-_{4, \mathrm {upper}}$
(respectively
$\gamma ^-_{4, \mathrm {upper}}$
(respectively
 $\gamma ^-_{4, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^-_{4, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {43} 4}(a, b)^- \cap (\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \gamma ^-_{4, \mathrm {left}}))$
.
$W^u_{\overline {43} 4}(a, b)^- \cap (\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}} \setminus \gamma ^-_{4, \mathrm {left}}))$
. -
• We write
 $\gamma ^-_{3, \mathrm {upper}}$
(respectively
$\gamma ^-_{3, \mathrm {upper}}$
(respectively
 $\gamma ^-_{3, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^-_{3, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {43} 4 3}(a, b)^-$
.
$W^u_{\overline {43} 4 3}(a, b)^-$
. -
• We write
 $\gamma ^-_{1, \mathrm {upper}}$
(respectively
$\gamma ^-_{1, \mathrm {upper}}$
(respectively
 $\gamma ^-_{1, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
$\gamma ^-_{1, \mathrm {lower}}$
) as the upper (respectively lower) connected component of
 $W^u_{\overline {43} 4 1}(a, b)^- \cap (\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \gamma ^-_{1, \mathrm {right}}))$
.
$W^u_{\overline {43} 4 1}(a, b)^- \cap (\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}} \setminus \gamma ^-_{1, \mathrm {right}}))$
. -
• We write
 $\gamma ^-_{0, \mathrm {lower}}$
as the lower connected component of
$\gamma ^-_{0, \mathrm {lower}}$
as the lower connected component of
 $W^u_{\overline {43} 4 1 0}(a, b)^- \cap (\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \gamma ^-_{0, \mathrm {right}}))$
.
$W^u_{\overline {43} 4 1 0}(a, b)^- \cap (\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}} \setminus \gamma ^-_{0, \mathrm {right}}))$
. -
• We write
 $\gamma ^-_{2, \mathrm {lower}}$
as the lower connected component of
$\gamma ^-_{2, \mathrm {lower}}$
as the lower connected component of
 $W^u_{\overline {43} 4 1 2}(a, b)^- \cap \mathcal {B}^-_{2, {\mathbb {R}}}$
.
$W^u_{\overline {43} 4 1 2}(a, b)^- \cap \mathcal {B}^-_{2, {\mathbb {R}}}$
. -
• We write
 $\gamma ^-_{0, \mathrm {upper}}$
as the upper connected component of
$\gamma ^-_{0, \mathrm {upper}}$
as the upper connected component of
 $W^u_{\overline {43} 4 1 0 0}(a, b)^- \cap (\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \gamma ^-_{0, \mathrm {right}}))$
.
$W^u_{\overline {43} 4 1 0 0}(a, b)^- \cap (\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{0, {\mathbb {R}}} \setminus \gamma ^-_{0, \mathrm {right}}))$
. -
• We write
 $\gamma ^-_{2, \mathrm {upper}}$
as the upper connected component of
$\gamma ^-_{2, \mathrm {upper}}$
as the upper connected component of
 $W^u_{\overline {43} 4 1 0 2}(a, b)^- \cap \mathcal {B}^-_{2, {\mathbb {R}}}$
.
$W^u_{\overline {43} 4 1 0 2}(a, b)^- \cap \mathcal {B}^-_{2, {\mathbb {R}}}$
. -
• We write
 $\gamma ^-_{4, \mathrm {inner}}$
as
$\gamma ^-_{4, \mathrm {inner}}$
as
 $W^u_{\overline {43} 4 1 2 4}(a, b)^-_{\mathrm {inner}}$
.
$W^u_{\overline {43} 4 1 2 4}(a, b)^-_{\mathrm {inner}}$
.
See Figure 12 for more details.

Figure 11 Margins in
![]() $\mathfrak {M}^+_2$
.
$\mathfrak {M}^+_2$
.

Figure 12 Margins in
![]() $\mathfrak {M}^-_2$
.
$\mathfrak {M}^-_2$
.
5.2 The
 $\{\alpha , \beta \}$
-coding
$\{\alpha , \beta \}$
-coding
The purpose of this subsection is to define the
![]() $\{\alpha , \beta \}$
-coding. We basically follow the construction of
$\{\alpha , \beta \}$
-coding. We basically follow the construction of
![]() $B^a$
and
$B^a$
and
![]() $B^b$
in [Reference Bedford and SmillieBSℝ3, §6]. Hereafter, we always assume that
$B^b$
in [Reference Bedford and SmillieBSℝ3, §6]. Hereafter, we always assume that
![]() $(a, b) \in \partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
.
$(a, b) \in \partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
.
For
![]() $\gamma ^+_{j, \mathrm {left}}$
,
$\gamma ^+_{j, \mathrm {left}}$
,
![]() $\gamma ^+_{j, \mathrm {right}}$
,
$\gamma ^+_{j, \mathrm {right}}$
,
![]() $\gamma ^+_{j, \mathrm {upper}}$
,
$\gamma ^+_{j, \mathrm {upper}}$
,
![]() $\gamma ^+_{j, \mathrm {lower}}$
,
$\gamma ^+_{j, \mathrm {lower}}$
,
![]() $\gamma ^+_{j, \mathrm {inner}}$
given in the previous subsection, we set
$\gamma ^+_{j, \mathrm {inner}}$
given in the previous subsection, we set
![]() $\mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
$\mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
![]() $\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
$\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
![]() $\mathrm {upper}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
$\mathrm {upper}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
![]() $\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
$\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
,
![]() $\mathrm {inner}(\mathcal {B}^+_{j, {\mathbb {R}}}) \subset \mathcal {B}^+_{j, {\mathbb {R}}}$
as follows (see Figure 11).
$\mathrm {inner}(\mathcal {B}^+_{j, {\mathbb {R}}}) \subset \mathcal {B}^+_{j, {\mathbb {R}}}$
as follows (see Figure 11).
-
• We write
 $\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \gamma ^+_{3, \mathrm {left}})$
.
$\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}} \setminus \gamma ^+_{3, \mathrm {left}})$
. -
• We write
 $\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {right}})$
(
$\mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \gamma ^+_{j, \mathrm {right}})$
(
 $j = 0, 1$
).
$j = 0, 1$
). -
• We write
 $\mathrm {upper}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part further up than
$\mathrm {upper}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part further up than
 $\gamma ^+_{j, \mathrm {upper}}$
in either
$\gamma ^+_{j, \mathrm {upper}}$
in either
 $\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 0, 1)$
,
$\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 0, 1)$
,
 $\mathcal {B}^+_{j, {\mathbb {R}}} (j = 2)$
, or
$\mathcal {B}^+_{j, {\mathbb {R}}} (j = 2)$
, or
 $\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 3)$
.
$\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 3)$
. -
• We write
 $\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part lower than
$\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part lower than
 $\gamma ^+_{j, \mathrm {lower}}$
in either
$\gamma ^+_{j, \mathrm {lower}}$
in either
 $\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 0, 1)$
,
$\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 0, 1)$
,
 $\mathcal {B}^+_{j, {\mathbb {R}}} (j = 2)$
, or
$\mathcal {B}^+_{j, {\mathbb {R}}} (j = 2)$
, or
 $\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 3)$
.
$\mathcal {B}^+_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^+_{j, {\mathbb {R}}}) (j = 3)$
. -
• We write
 $\mathrm {inner}(\mathcal {B}^+_{3, {\mathbb {R}}})$
as the part further in than
$\mathrm {inner}(\mathcal {B}^+_{3, {\mathbb {R}}})$
as the part further in than
 $\gamma ^+_{3, \mathrm {inner}}$
in
$\gamma ^+_{3, \mathrm {inner}}$
in
 $\mathcal {B}^+_{3, {\mathbb {R}}}$
.
$\mathcal {B}^+_{3, {\mathbb {R}}}$
.
Let
![]() $\mathfrak {M}^+_2$
be the family of sets defined as above.
$\mathfrak {M}^+_2$
be the family of sets defined as above.
For
![]() $\gamma ^-_{j, \mathrm {left}}$
,
$\gamma ^-_{j, \mathrm {left}}$
,
![]() $\gamma ^-_{j, \mathrm {right}}$
,
$\gamma ^-_{j, \mathrm {right}}$
,
![]() $\gamma ^-_{j, \mathrm {upper}}$
,
$\gamma ^-_{j, \mathrm {upper}}$
,
![]() $\gamma ^-_{j, \mathrm {lower}}$
,
$\gamma ^-_{j, \mathrm {lower}}$
,
![]() $\gamma ^-_{j, \mathrm {inner}}$
given in the previous subsection, we set
$\gamma ^-_{j, \mathrm {inner}}$
given in the previous subsection, we set
![]() $\mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
$\mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
![]() $\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
$\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
![]() $\mathrm {upper}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
$\mathrm {upper}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
![]() $\mathrm {lower}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
$\mathrm {lower}(\mathcal {B}^-_{j, {\mathbb {R}}})$
,
![]() $\mathrm {inner}(\mathcal {B}^-_{j, {\mathbb {R}}}) \subset \mathcal {B}^-_{j, {\mathbb {R}}}$
as follows (see Figure 12).
$\mathrm {inner}(\mathcal {B}^-_{j, {\mathbb {R}}}) \subset \mathcal {B}^-_{j, {\mathbb {R}}}$
as follows (see Figure 12).
-
• We write
 $\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}} \setminus \gamma ^-_{4, \mathrm {left}})$
.
$\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}) \equiv \mathrm {left}(\mathcal {B}^-_{3, {\mathbb {R}}} \setminus \gamma ^-_{4, \mathrm {left}})$
. -
• We write
 $\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {right}})$
(
$\mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) \equiv \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \gamma ^-_{j, \mathrm {right}})$
(
 $j = 0, 1$
).
$j = 0, 1$
). -
• We write
 $\mathrm {upper}(\mathcal {B}^-_{j, {\mathbb {R}}})$
as the part further up than
$\mathrm {upper}(\mathcal {B}^-_{j, {\mathbb {R}}})$
as the part further up than
 $\gamma ^-_{j, \mathrm {upper}}$
in either
$\gamma ^-_{j, \mathrm {upper}}$
in either
 $\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 0, 1)$
,
$\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 0, 1)$
,
 $\mathcal {B}^-_{j, {\mathbb {R}}} (j = 2, 3)$
, or
$\mathcal {B}^-_{j, {\mathbb {R}}} (j = 2, 3)$
, or
 $\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 4)$
.
$\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 4)$
. -
• We write
 $\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part lower than
$\mathrm {lower}(\mathcal {B}^+_{j, {\mathbb {R}}})$
as the part lower than
 $\gamma ^-_{j, \mathrm {lower}}$
in either
$\gamma ^-_{j, \mathrm {lower}}$
in either
 $\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 0, 1)$
,
$\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {right}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 0, 1)$
,
 $\mathcal {B}^-_{j, {\mathbb {R}}} (j = 2, 3)$
, or
$\mathcal {B}^-_{j, {\mathbb {R}}} (j = 2, 3)$
, or
 $\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 4)$
.
$\mathcal {B}^-_{j, {\mathbb {R}}} \setminus \mathrm {left}(\mathcal {B}^-_{j, {\mathbb {R}}}) (j = 4)$
. -
• We write
 $\mathrm {inner}(\mathcal {B}^-_{4, {\mathbb {R}}})$
as the part further in than
$\mathrm {inner}(\mathcal {B}^-_{4, {\mathbb {R}}})$
as the part further in than
 $\gamma ^-_{4, \mathrm {inner}}$
in
$\gamma ^-_{4, \mathrm {inner}}$
in
 $\mathcal {B}^-_{4, {\mathbb {R}}}$
.
$\mathcal {B}^-_{4, {\mathbb {R}}}$
.
Let
![]() $\mathfrak {M}^-_2$
be the family of sets defined as above. We call the elements of
$\mathfrak {M}^-_2$
be the family of sets defined as above. We call the elements of
![]() $\mathfrak {M}^{\pm }_2$
the margins of
$\mathfrak {M}^{\pm }_2$
the margins of
![]() $\mathcal {B}^{\pm }_{j, {\mathbb {R}}}$
just like
$\mathcal {B}^{\pm }_{j, {\mathbb {R}}}$
just like
![]() $\mathfrak {M}^{\pm }_1$
.
$\mathfrak {M}^{\pm }_1$
.
We then construct the
![]() $\{\alpha , \beta \}$
-partition as described in Figures 13 and 14. Define
$\{\alpha , \beta \}$
-partition as described in Figures 13 and 14. Define
![]() $\mathcal {B}_{j, \alpha , \mathbb {R}}^{+}$
for
$\mathcal {B}_{j, \alpha , \mathbb {R}}^{+}$
for
![]() $j = 0$
and
$j = 0$
and
![]() $\mathcal {B}_{j, \beta , \mathbb {R}}^{+}$
for
$\mathcal {B}_{j, \beta , \mathbb {R}}^{+}$
for
![]() $j = 1, 2$
as
$j = 1, 2$
as
![]() $\mathcal {B}_{j, \mathbb {R}}^{+} \setminus (\mathrm {left}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {right}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {upper}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {lower}(\mathcal {B}_{j, \mathbb {R}}^{+}))$
. The set
$\mathcal {B}_{j, \mathbb {R}}^{+} \setminus (\mathrm {left}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {right}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {upper}(\mathcal {B}_{j, \mathbb {R}}^{+}) \cup \mathrm {lower}(\mathcal {B}_{j, \mathbb {R}}^{+}))$
. The set
![]() $\mathcal {B}_{3, \mathbb {R}}^{+} \setminus (\mathrm {left}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {right}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {upper}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {lower}(\mathcal {B}_{3, \mathbb {R}}^{+}))$
with one point
$\mathcal {B}_{3, \mathbb {R}}^{+} \setminus (\mathrm {left}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {right}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {upper}(\mathcal {B}_{3, \mathbb {R}}^{+}) \cup \mathrm {lower}(\mathcal {B}_{3, \mathbb {R}}^{+}))$
with one point
![]() $\star ^+$
being removed has two connected components. We let
$\star ^+$
being removed has two connected components. We let
![]() $\mathcal {B}^+_{3, \alpha , {\mathbb {R}}}$
be the upper one with
$\mathcal {B}^+_{3, \alpha , {\mathbb {R}}}$
be the upper one with
![]() $\star ^+$
being added, and let
$\star ^+$
being added, and let
![]() $\mathcal {B}^+_{3, \beta , {\mathbb {R}}}$
be the lower one with
$\mathcal {B}^+_{3, \beta , {\mathbb {R}}}$
be the lower one with
![]() $\star ^+$
being added.
$\star ^+$
being added.
Definition 5.5. We define
![]() $\mathcal {B}_{\alpha , \mathbb {R}}^{+} \equiv \mathcal {B}_{0, \alpha , \mathbb {R}}^{+} \cup \mathcal {B}_{3, \alpha , \mathbb {R}}^{+}$
and
$\mathcal {B}_{\alpha , \mathbb {R}}^{+} \equiv \mathcal {B}_{0, \alpha , \mathbb {R}}^{+} \cup \mathcal {B}_{3, \alpha , \mathbb {R}}^{+}$
and
![]() $\mathcal {B}_{\beta , \mathbb {R}}^{+} \equiv \mathcal {B}_{1, \beta , \mathbb {R}}^{+} \cup \mathcal {B}_{2, \beta , \mathbb {R}}^{+} \cup \mathcal {B}_{3, \beta , \mathbb {R}}^{+}$
.
$\mathcal {B}_{\beta , \mathbb {R}}^{+} \equiv \mathcal {B}_{1, \beta , \mathbb {R}}^{+} \cup \mathcal {B}_{2, \beta , \mathbb {R}}^{+} \cup \mathcal {B}_{3, \beta , \mathbb {R}}^{+}$
.

Figure 13 The
![]() $\{ \alpha , \beta \}$
-partition (
$\{ \alpha , \beta \}$
-partition (
![]() $b> 0$
).
$b> 0$
).

Figure 14 The
![]() $\{ \alpha , \beta \}$
-partition (
$\{ \alpha , \beta \}$
-partition (
![]() $b < 0$
).
$b < 0$
).
Similarly, define
![]() $\mathcal {B}_{j, \alpha , \mathbb {R}}^{-}$
for
$\mathcal {B}_{j, \alpha , \mathbb {R}}^{-}$
for
![]() $j = 0, 1$
and
$j = 0, 1$
and
![]() $\mathcal {B}_{j, \beta , \mathbb {R}}^{-}$
for
$\mathcal {B}_{j, \beta , \mathbb {R}}^{-}$
for
![]() $j = 2, 3$
as
$j = 2, 3$
as
![]() $\mathcal {B}_{j, \mathbb {R}}^{-} \setminus (\mathrm {left}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {right}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {upper}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {lower}(\mathcal {B}_{j, \mathbb {R}}^{-}))$
. The set
$\mathcal {B}_{j, \mathbb {R}}^{-} \setminus (\mathrm {left}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {right}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {upper}(\mathcal {B}_{j, \mathbb {R}}^{-}) \cup \mathrm {lower}(\mathcal {B}_{j, \mathbb {R}}^{-}))$
. The set
![]() $\mathcal {B}_{4, \mathbb {R}}^{-} \setminus (\mathrm {left}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {right}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {upper}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {lower}(\mathcal {B}_{4, \mathbb {R}}^{-}))$
with one point
$\mathcal {B}_{4, \mathbb {R}}^{-} \setminus (\mathrm {left}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {right}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {upper}(\mathcal {B}_{4, \mathbb {R}}^{-}) \cup \mathrm {lower}(\mathcal {B}_{4, \mathbb {R}}^{-}))$
with one point
![]() $\star ^-$
being removed has two connected components. We let
$\star ^-$
being removed has two connected components. We let
![]() $\mathcal {B}^-_{4, \alpha , {\mathbb {R}}}$
be the upper one with
$\mathcal {B}^-_{4, \alpha , {\mathbb {R}}}$
be the upper one with
![]() $\star ^-$
being added, and let
$\star ^-$
being added, and let
![]() $\mathcal {B}^-_{4, \beta , {\mathbb {R}}}$
be the lower one with
$\mathcal {B}^-_{4, \beta , {\mathbb {R}}}$
be the lower one with
![]() $\star ^-$
being added.
$\star ^-$
being added.
Definition 5.6. We define
![]() $\mathcal {B}_{\alpha , \mathbb {R}}^{-} \equiv \mathcal {B}_{0, \alpha , \mathbb {R}}^{-} \cup \mathcal {B}_{2, \alpha , \mathbb {R}}^{-} \cup \mathcal {B}_{4, \alpha , \mathbb {R}}^{-}$
and
$\mathcal {B}_{\alpha , \mathbb {R}}^{-} \equiv \mathcal {B}_{0, \alpha , \mathbb {R}}^{-} \cup \mathcal {B}_{2, \alpha , \mathbb {R}}^{-} \cup \mathcal {B}_{4, \alpha , \mathbb {R}}^{-}$
and
![]() $\mathcal {B}_{\beta , \mathbb {R}}^{-} \equiv \mathcal {B}_{1, \beta , \mathbb {R}}^{-} \cup \mathcal {B}_{3, \beta , \mathbb {R}}^{-} \cup \mathcal {B}_{4, \beta , \mathbb {R}}^{-}$
.
$\mathcal {B}_{\beta , \mathbb {R}}^{-} \equiv \mathcal {B}_{1, \beta , \mathbb {R}}^{-} \cup \mathcal {B}_{3, \beta , \mathbb {R}}^{-} \cup \mathcal {B}_{4, \beta , \mathbb {R}}^{-}$
.
The transitions between the margins can be described in the following two lemmas.
Lemma 5.7. The transitions between margins in
![]() $\mathfrak {M}^+_2$
are given by Figure 15. In this figure, for example,
$\mathfrak {M}^+_2$
are given by Figure 15. In this figure, for example,
![]() $\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}) \rightarrow \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
means
$\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}}) \rightarrow \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
means
![]() $f(\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}})) \cap \mathcal {B}^+_{1, {\mathbb {R}}} \subset \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
.
$f(\mathrm {left}(\mathcal {B}^+_{3, {\mathbb {R}}})) \cap \mathcal {B}^+_{1, {\mathbb {R}}} \subset \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
.

Figure 15 The transitions between margins in
![]() $\mathfrak {M}^+_2$
.
$\mathfrak {M}^+_2$
.
Lemma 5.8. The transitions between margins in
![]() $\mathfrak {M}^-_2$
are given by Figure 16. In this figure,
$\mathfrak {M}^-_2$
are given by Figure 16. In this figure,
![]() $\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}) \rightarrow \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}})$
means
$\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}}) \rightarrow \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}})$
means
![]() $f(\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}})) \cap \mathcal {B}^-_{1, {\mathbb {R}}} \subset \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}})$
.
$f(\mathrm {left}(\mathcal {B}^-_{4, {\mathbb {R}}})) \cap \mathcal {B}^-_{1, {\mathbb {R}}} \subset \mathrm {right}(\mathcal {B}^-_{1, {\mathbb {R}}})$
.

Figure 16 The transitions between margins in
![]() $\mathfrak {M}^-_2$
.
$\mathfrak {M}^-_2$
.
From these lemmas, we have the following proposition.
Proposition 5.9. For
![]() $(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
, we have
$(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
, we have
![]() $K_{{\mathbb {R}}} \subset \mathcal {B}^+_{\alpha , {\mathbb {R}}} \cup \mathcal {B}^+_{\beta , {\mathbb {R}}}$
.
$K_{{\mathbb {R}}} \subset \mathcal {B}^+_{\alpha , {\mathbb {R}}} \cup \mathcal {B}^+_{\beta , {\mathbb {R}}}$
.
Proof. Suppose
![]() $p \in K_{{\mathbb {R}}}$
. It suffices to show that
$p \in K_{{\mathbb {R}}}$
. It suffices to show that
for any
![]() $M \in \mathfrak {M}^+_2$
(compare Proposition 4.1). Here, we show this claim for
$M \in \mathfrak {M}^+_2$
(compare Proposition 4.1). Here, we show this claim for
![]() $M = \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
for example. We can also show this for another M similarly.
$M = \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
for example. We can also show this for another M similarly.
Take a point
![]() $p \in K_{{\mathbb {R}}}$
. Assume that the zeroth coordinate of the
$p \in K_{{\mathbb {R}}}$
. Assume that the zeroth coordinate of the
![]() $\Sigma ^+$
-coding of p is
$\Sigma ^+$
-coding of p is
![]() $1$
and
$1$
and
![]() $p \in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
. By the transitions between symbols, the first coordinate of the
$p \in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
. By the transitions between symbols, the first coordinate of the
![]() $\Sigma ^+$
-coding of p is either 0 or 2. Since
$\Sigma ^+$
-coding of p is either 0 or 2. Since
![]() $p \in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
, the first coordinate must be
$p \in \mathrm {right}(\mathcal {B}^+_{1, {\mathbb {R}}})$
, the first coordinate must be
![]() $0$
. Then, we have
$0$
. Then, we have
![]() $f(p) \in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
by Lemma 5.7. By chasing the orbit of p similarly, we can find that
$f(p) \in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
by Lemma 5.7. By chasing the orbit of p similarly, we can find that
![]() $f^{n_0}(p)$
belongs to
$f^{n_0}(p)$
belongs to
![]() $\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
and
$\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
and
![]() $f^n(p)$
also belongs to
$f^n(p)$
also belongs to
![]() $\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
for any
$\mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
for any
![]() $n> n_0$
. Therefore,
$n> n_0$
. Therefore,
![]() $f^{n_0}(p)$
lies on
$f^{n_0}(p)$
lies on
![]() $W^s_{\mathrm {loc}}(p_1)^+_0$
. This contradicts to the fact that
$W^s_{\mathrm {loc}}(p_1)^+_0$
. This contradicts to the fact that
![]() $f^{n_0}(p) \in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
.
$f^{n_0}(p) \in \mathrm {right}(\mathcal {B}^+_{0, {\mathbb {R}}})$
.
Proposition 5.10. For
![]() $(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
, we have
$(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
, we have
![]() $K_{{\mathbb {R}}} \subset \mathcal {B}^-_{\alpha , {\mathbb {R}}} \cup \mathcal {B}^-_{\beta , {\mathbb {R}}}$
.
$K_{{\mathbb {R}}} \subset \mathcal {B}^-_{\alpha , {\mathbb {R}}} \cup \mathcal {B}^-_{\beta , {\mathbb {R}}}$
.
Proof. The proof is similar to that of the previous proposition, and hence is omitted.
5.3 Proof of Theorem 1.2
In this subsection, we continue to assume that
![]() $(a, b) \in \partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
. Below, we write
$(a, b) \in \partial \mathcal {H}^{\pm }_{{\mathbb {R}}}$
. Below, we write
and
as the forward/backward filled Julia set of
![]() $f_{a, b}$
, respectively. We also write
$f_{a, b}$
, respectively. We also write
![]() $J_{\mathrm {fwd}} \equiv \partial K_{\mathrm {fwd}}$
and
$J_{\mathrm {fwd}} \equiv \partial K_{\mathrm {fwd}}$
and
![]() $J_{\mathrm {bwd}} \equiv \partial K_{\mathrm {bwd}}$
as the forward/backward Julia set, and let
$J_{\mathrm {bwd}} \equiv \partial K_{\mathrm {bwd}}$
as the forward/backward Julia set, and let
![]() $J \equiv J_{\mathrm {fwd}} \cap J_{\mathrm {bwd}}$
be the Julia set. By [Reference Arai and IshiiAI, Proposition 3.1], the filled Julia set
$J \equiv J_{\mathrm {fwd}} \cap J_{\mathrm {bwd}}$
be the Julia set. By [Reference Arai and IshiiAI, Proposition 3.1], the filled Julia set
![]() $K_{\mathrm {fwd}} \cap K_{\mathrm {bwd}}$
coincides with
$K_{\mathrm {fwd}} \cap K_{\mathrm {bwd}}$
coincides with
![]() $K \equiv K_{a, b}$
. Moreover, the filled Julia set is included in the real plane
$K \equiv K_{a, b}$
. Moreover, the filled Julia set is included in the real plane
![]() ${\mathbb {R}}^2$
and coincides with the Julia set J by [Reference Bedford, Lyubich and SmillieBLS, Theorem 10.1(4), (7)] since
${\mathbb {R}}^2$
and coincides with the Julia set J by [Reference Bedford, Lyubich and SmillieBLS, Theorem 10.1(4), (7)] since
![]() $h_{\mathrm {top}}(f) = \log {2}$
holds. Hence, we have
$h_{\mathrm {top}}(f) = \log {2}$
holds. Hence, we have
![]() ${J = K = K_{\mathbb {R}}}$
.
${J = K = K_{\mathbb {R}}}$
.
We write
![]() $\mathcal {B}^+_{{\mathbb {R}}}$
as the region in
$\mathcal {B}^+_{{\mathbb {R}}}$
as the region in
![]() ${\mathbb {R}}^2$
enclosed by the curves
${\mathbb {R}}^2$
enclosed by the curves
![]() $W^u_{\mathrm {loc}}(p_1)_0$
,
$W^u_{\mathrm {loc}}(p_1)_0$
,
![]() $\gamma ^+_{1, \mathrm {lower}}$
,
$\gamma ^+_{1, \mathrm {lower}}$
,
![]() $\gamma ^+_{2, \mathrm {lower}}$
,
$\gamma ^+_{2, \mathrm {lower}}$
,
![]() $\gamma ^+_{3, \mathrm {left}}$
,
$\gamma ^+_{3, \mathrm {left}}$
,
![]() $\gamma ^+_{3, \mathrm {upper}}$
,
$\gamma ^+_{3, \mathrm {upper}}$
,
![]() $\gamma ^+_{3, \mathrm {lower}}$
, and
$\gamma ^+_{3, \mathrm {lower}}$
, and
![]() $f^{-1}(W^s_{\mathrm {loc}}(p_1)_0)$
. Moreover, let
$f^{-1}(W^s_{\mathrm {loc}}(p_1)_0)$
. Moreover, let
![]() $\mathcal {B}^+_{\tilde {\alpha }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^+_{\alpha , {\mathbb {R}}})$
and
$\mathcal {B}^+_{\tilde {\alpha }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^+_{\alpha , {\mathbb {R}}})$
and
![]() ${\mathcal {B}^+_{\tilde {\beta }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^+_{\beta , {\mathbb {R}}})}$
. Also, we write
${\mathcal {B}^+_{\tilde {\beta }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^+_{\beta , {\mathbb {R}}})}$
. Also, we write
![]() $\mathcal {B}^-_{{\mathbb {R}}}$
as the region in
$\mathcal {B}^-_{{\mathbb {R}}}$
as the region in
![]() ${\mathbb {R}}^2$
enclosed by the curves
${\mathbb {R}}^2$
enclosed by the curves
![]() $W^u_{\mathrm {loc}}(p_3)_3$
,
$W^u_{\mathrm {loc}}(p_3)_3$
,
![]() $\gamma ^-_{0, \mathrm {upper}}$
,
$\gamma ^-_{0, \mathrm {upper}}$
,
![]() $\gamma ^-_{1, \mathrm {lower}}$
,
$\gamma ^-_{1, \mathrm {lower}}$
,
![]() $\gamma ^-_{2, \mathrm {upper}}$
,
$\gamma ^-_{2, \mathrm {upper}}$
,
![]() $\gamma ^-_{4, \mathrm {left}}$
,
$\gamma ^-_{4, \mathrm {left}}$
,
![]() $\gamma ^-_{4, \mathrm {upper}}$
,
$\gamma ^-_{4, \mathrm {upper}}$
,
![]() $\gamma ^-_{4, \mathrm {lower}}$
, and
$\gamma ^-_{4, \mathrm {lower}}$
, and
![]() $f^{-1}(W^s_{\mathrm {loc}}(p_1)_0)$
. Moreover, let
$f^{-1}(W^s_{\mathrm {loc}}(p_1)_0)$
. Moreover, let
![]() $\mathcal {B}^-_{\tilde {\alpha }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^-_{\alpha , {\mathbb {R}}})$
and
$\mathcal {B}^-_{\tilde {\alpha }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^-_{\alpha , {\mathbb {R}}})$
and
![]() $\mathcal {B}^-_{\tilde {\beta }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^-_{\beta , {\mathbb {R}}})$
. Then, the
$\mathcal {B}^-_{\tilde {\beta }, {\mathbb {R}}} = f^{-1}(\mathcal {B}^-_{\beta , {\mathbb {R}}})$
. Then, the
![]() $\{ \tilde {\alpha }, \tilde {\beta } \}$
-partition is described in Figure 17.
$\{ \tilde {\alpha }, \tilde {\beta } \}$
-partition is described in Figure 17.

Figure 17 The
![]() $\{ \tilde {\alpha }, \tilde {\beta } \}$
-partition.
$\{ \tilde {\alpha }, \tilde {\beta } \}$
-partition.
For any point
![]() $p \in J$
, the
$p \in J$
, the
![]() $\{ \tilde {\alpha }, \tilde {\beta } \}$
-coding of
$\{ \tilde {\alpha }, \tilde {\beta } \}$
-coding of
![]() $f^{-1}(p)$
coincides with the symbolic sequence obtained by replacing
$f^{-1}(p)$
coincides with the symbolic sequence obtained by replacing
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in the
$\beta $
in the
![]() $\{ \alpha , \beta \}$
-coding of p for
$\{ \alpha , \beta \}$
-coding of p for
![]() $\tilde {\alpha }$
and
$\tilde {\alpha }$
and
![]() $\tilde {\beta }$
, respectively.
$\tilde {\beta }$
, respectively.
From now, we assume that
![]() $(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
. The argument for the case
$(a, b) \in \partial \mathcal {H}^+_{{\mathbb {R}}}$
. The argument for the case
![]() $(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
is similar, and hence will be omitted.
$(a, b) \in \partial \mathcal {H}^-_{{\mathbb {R}}}$
is similar, and hence will be omitted.
For
![]() $p \in K$
, let
$p \in K$
, let
![]() $s^+(p)$
be the set of all
$s^+(p)$
be the set of all
![]() $\{ \alpha , \beta \}$
-codings of p, that is,
$\{ \alpha , \beta \}$
-codings of p, that is,
In the case that
![]() $p = f^n(\star ^+)$
for some
$p = f^n(\star ^+)$
for some
![]() $n \in {\mathbb {Z}}$
, we have
$n \in {\mathbb {Z}}$
, we have
![]() $s^+(p) = \{ \sigma ^n(\overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }), \sigma ^n(\overline {\alpha } \beta \cdot \beta \beta \overline {\alpha }) \}$
. However, if
$s^+(p) = \{ \sigma ^n(\overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }), \sigma ^n(\overline {\alpha } \beta \cdot \beta \beta \overline {\alpha }) \}$
. However, if
![]() $p \in J^{\prime } \equiv J \setminus \{ f^n(\star ^+) : n \in {\mathbb {Z}} \}$
, then
$p \in J^{\prime } \equiv J \setminus \{ f^n(\star ^+) : n \in {\mathbb {Z}} \}$
, then
![]() $s^+(p)$
consists of one point. Therefore,
$s^+(p)$
consists of one point. Therefore,
![]() $s^+ : p \mapsto s^+(p)$
is a map from J to
$s^+ : p \mapsto s^+(p)$
is a map from J to
![]() ${\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
, where
${\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
, where
![]() $\sim $
is the equivalence relation generated by
$\sim $
is the equivalence relation generated by
![]() $\sigma ^n(\overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }) \sim \sigma ^n(\overline {\alpha } \beta \cdot \beta \beta \overline {\alpha })$
,
$\sigma ^n(\overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }) \sim \sigma ^n(\overline {\alpha } \beta \cdot \beta \beta \overline {\alpha })$
,
![]() $n \in {\mathbb {Z}}$
.
$n \in {\mathbb {Z}}$
.
Proposition 5.11. The map
![]() $s^+: J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}}$
is continuous.
$s^+: J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}}$
is continuous.
Proof. The map
![]() $s^+$
is obviously continuous on
$s^+$
is obviously continuous on
![]() $J^{\prime }$
. We show that it is continuous on
$J^{\prime }$
. We show that it is continuous on
![]() $f^n(\star ^+)$
. The neighborhood basis for
$f^n(\star ^+)$
. The neighborhood basis for
![]() $s^+(f^n(\star ^+))$
according to the quotient topology is given by
$s^+(f^n(\star ^+))$
according to the quotient topology is given by
![]() ${\{ \ast \alpha ^N \beta \cdot ? \beta \alpha ^N \ast \}}_{N \geq 0}$
, where
${\{ \ast \alpha ^N \beta \cdot ? \beta \alpha ^N \ast \}}_{N \geq 0}$
, where
![]() $?$
is either
$?$
is either
![]() $\alpha $
or
$\alpha $
or
![]() $\beta $
, and
$\beta $
, and
![]() $\ast $
means any one-sided infinite sequence. Take any N. The map
$\ast $
means any one-sided infinite sequence. Take any N. The map
![]() $f^j$
is continuous for each
$f^j$
is continuous for each
![]() $j \in {\mathbb {Z}}$
such that
$j \in {\mathbb {Z}}$
such that
![]() $-N \leq j \leq N$
,
$-N \leq j \leq N$
,
![]() $j \neq 0$
. Hence, we can choose a neighborhood
$j \neq 0$
. Hence, we can choose a neighborhood
![]() $U_j$
of
$U_j$
of
![]() $f^{n+j}(\star ^+)$
such that
$f^{n+j}(\star ^+)$
such that
![]() $U_j \subset \mathcal {B}^+_{\alpha }$
if
$U_j \subset \mathcal {B}^+_{\alpha }$
if
![]() $-N \leq j \leq N$
,
$-N \leq j \leq N$
,
![]() $j \neq 0, \pm 1$
and
$j \neq 0, \pm 1$
and
![]() $U_j \subset \mathcal {B}^+_{\beta }$
if
$U_j \subset \mathcal {B}^+_{\beta }$
if
![]() $j = \pm 1$
. Then,
$j = \pm 1$
. Then,
![]() $U = \bigcap _{j \in {\mathbb {Z}}} f^{-j}(U_j)$
is a neighborhood of
$U = \bigcap _{j \in {\mathbb {Z}}} f^{-j}(U_j)$
is a neighborhood of
![]() $f^n(\star ^+)$
and satisfies
$f^n(\star ^+)$
and satisfies
![]() $p \in U \cap J \Rightarrow s^+(p) \in \{ \sigma ^n(\ast \alpha ^N \beta \cdot ? \beta \alpha ^N \ast ) \}$
.
$p \in U \cap J \Rightarrow s^+(p) \in \{ \sigma ^n(\ast \alpha ^N \beta \cdot ? \beta \alpha ^N \ast ) \}$
.
To prove Theorem 1.2 in the case
![]() $b> 0$
, it suffices to show that the continuous map
$b> 0$
, it suffices to show that the continuous map
![]() $s^+$
is bijective. In the rest this subsection, we will show its surjectivity and injectivity.
$s^+$
is bijective. In the rest this subsection, we will show its surjectivity and injectivity.
For each binomial number
![]() $0 \leq \theta \leq 1$
, we define a curve
$0 \leq \theta \leq 1$
, we define a curve
![]() $\tau ^s_{\theta }$
in
$\tau ^s_{\theta }$
in
![]() $\mathcal {B}^+_{{\mathbb {R}}}$
included in
$\mathcal {B}^+_{{\mathbb {R}}}$
included in
![]() $\overline {W^s(p_1)}$
as follows. For
$\overline {W^s(p_1)}$
as follows. For
![]() $\theta = 0, 1$
, let
$\theta = 0, 1$
, let
![]() $\tau ^s_0$
be the right-hand boundary of
$\tau ^s_0$
be the right-hand boundary of
![]() $\mathcal {B}^+_{{\mathbb {R}}}$
and let
$\mathcal {B}^+_{{\mathbb {R}}}$
and let
![]() $\tau ^s_1$
be its left-hand boundary.
$\tau ^s_1$
be its left-hand boundary.
Next, for a finite binomial
![]() $0 < \theta < 1$
, we define
$0 < \theta < 1$
, we define
![]() $\tau ^s_{\theta }$
inductively as follows. Assume that
$\tau ^s_{\theta }$
inductively as follows. Assume that
![]() $\tau ^s_{\theta }$
is already defined for a finite binomial
$\tau ^s_{\theta }$
is already defined for a finite binomial
![]() $0 < \theta \leq 1$
. Then, we let
$0 < \theta \leq 1$
. Then, we let
![]() $f^{-1}(\tau ^s_{\theta }) \cap \mathcal {B}^+_{\alpha , {\mathbb {R}}} = \tau ^s_{\theta / 2}$
and
$f^{-1}(\tau ^s_{\theta }) \cap \mathcal {B}^+_{\alpha , {\mathbb {R}}} = \tau ^s_{\theta / 2}$
and
![]() $f^{-1}(\tau ^s_{\theta }) \cap \mathcal {B}^+_{\beta , {\mathbb {R}}} = \tau ^s_{1 - \theta / 2}$
for
$f^{-1}(\tau ^s_{\theta }) \cap \mathcal {B}^+_{\beta , {\mathbb {R}}} = \tau ^s_{1 - \theta / 2}$
for
![]() $\theta ^{\prime } = {\theta }/{2}, 1 - {\theta }/{2}$
. However,
$\theta ^{\prime } = {\theta }/{2}, 1 - {\theta }/{2}$
. However,
![]() $\tau ^s_{1/2} = f^{-1}(\tau ^s_1)$
for
$\tau ^s_{1/2} = f^{-1}(\tau ^s_1)$
for
![]() $\theta ^{\prime } = \tfrac 12$
instead. The curve
$\theta ^{\prime } = \tfrac 12$
instead. The curve
![]() $\tau ^s_{\theta }$
is represented as two connected curves
$\tau ^s_{\theta }$
is represented as two connected curves
![]() $\tau ^s_{\theta ^{\prime } \pm }$
from the upper hand boundary of
$\tau ^s_{\theta ^{\prime } \pm }$
from the upper hand boundary of
![]() $\mathcal {B}^+_{{\mathbb {R}}}$
to its lower hand boundary, where
$\mathcal {B}^+_{{\mathbb {R}}}$
to its lower hand boundary, where
![]() $\tau ^s_{\theta ^{\prime } +}$
is left of
$\tau ^s_{\theta ^{\prime } +}$
is left of
![]() $\tau ^s_{\theta ^{\prime } -}$
. By definition,
$\tau ^s_{\theta ^{\prime } -}$
. By definition,
![]() $\tau ^s_{\theta }$
is included in
$\tau ^s_{\theta }$
is included in
![]() $W^s(p_1)$
for any finite binomial
$W^s(p_1)$
for any finite binomial
![]() $0 \leq \theta \leq 1$
. Also, for any point in
$0 \leq \theta \leq 1$
. Also, for any point in
![]() $W^s(p_1) \cap \mathcal {B}^+_{{\mathbb {R}}}$
, there is a unique finite binomial
$W^s(p_1) \cap \mathcal {B}^+_{{\mathbb {R}}}$
, there is a unique finite binomial
![]() $\theta $
such that the curve
$\theta $
such that the curve
![]() $\tau ^s_{\theta }$
passes that point.
$\tau ^s_{\theta }$
passes that point.
Finally, any infinite binomial
![]() $0 \leq \theta \leq 1$
can be represented as the limit of some sequence
$0 \leq \theta \leq 1$
can be represented as the limit of some sequence
![]() $(\theta _j)_j$
of finite binomials. Then, we have
$(\theta _j)_j$
of finite binomials. Then, we have
![]() $\tau ^s_{\theta _j} \subset f^{-1}(\mathcal {B}^+_i)$
for some preimage
$\tau ^s_{\theta _j} \subset f^{-1}(\mathcal {B}^+_i)$
for some preimage
![]() $f^{-1}(\mathcal {B}^+_i)$
and large j. For each j, the connected component
$f^{-1}(\mathcal {B}^+_i)$
and large j. For each j, the connected component
![]() $V_j$
of
$V_j$
of
![]() $W^s(p_1) \cap f^{-1}(\mathcal {B}^+_i)$
including
$W^s(p_1) \cap f^{-1}(\mathcal {B}^+_i)$
including
![]() $\tau ^s_{\theta _j}$
can be described as a graph of some holomorphic function since this component is a vertical disk of
$\tau ^s_{\theta _j}$
can be described as a graph of some holomorphic function since this component is a vertical disk of
![]() $f^{-1}(\mathcal {B}^+_i)$
. Since the sequence of these functions uniformly converges, its limit function is also holomorphic. Hence, the limit set V of
$f^{-1}(\mathcal {B}^+_i)$
. Since the sequence of these functions uniformly converges, its limit function is also holomorphic. Hence, the limit set V of
![]() $V_j$
is a graph of this holomorphic function, which implies V is a vertical disk of
$V_j$
is a graph of this holomorphic function, which implies V is a vertical disk of
![]() $f^{-1}(\mathcal {B}^+_i)$
. We let
$f^{-1}(\mathcal {B}^+_i)$
. We let
![]() $\tau ^s_{\theta }$
be the limit set of
$\tau ^s_{\theta }$
be the limit set of
![]() $\tau ^s_{\theta _j}$
. Then,
$\tau ^s_{\theta _j}$
. Then,
![]() $\tau ^s_{\theta }$
is a curve from the upper hand boundary of
$\tau ^s_{\theta }$
is a curve from the upper hand boundary of
![]() $\mathcal {B}^+_{{\mathbb {R}}}$
to its lower hand boundary, and it is included in V.
$\mathcal {B}^+_{{\mathbb {R}}}$
to its lower hand boundary, and it is included in V.
Remark 5.12. A finite binomial number
![]() $\theta $
has two infinite binomial representations (e.g.
$\theta $
has two infinite binomial representations (e.g.
![]() $0.1 = 0.0111\cdots = 0.1000\cdots $
). Each representation corresponds to each of the two curves
$0.1 = 0.0111\cdots = 0.1000\cdots $
). Each representation corresponds to each of the two curves
![]() $\tau ^s_{\theta \pm }$
of degree one, respectively (e.g.
$\tau ^s_{\theta \pm }$
of degree one, respectively (e.g.
![]() $\tau ^s_{0.0111\cdots } = \tau ^s_{0.1-}$
,
$\tau ^s_{0.0111\cdots } = \tau ^s_{0.1-}$
,
![]() $\tau ^s_{0.1000\cdots } = \tau ^s_{0.1+}$
). From now, we distinguish two infinite binomial representations of a finite binomial number if needed.
$\tau ^s_{0.1000\cdots } = \tau ^s_{0.1+}$
). From now, we distinguish two infinite binomial representations of a finite binomial number if needed.
For a point
![]() $p \in J^{\prime }$
, we choose
$p \in J^{\prime }$
, we choose
![]() $0 \leq \theta \leq 1$
so that
$0 \leq \theta \leq 1$
so that
![]() $\tau ^s_{\theta }$
passes p. Let
$\tau ^s_{\theta }$
passes p. Let
![]() $0. d_1 d_2 d_3 \cdots $
be the binomial representation of
$0. d_1 d_2 d_3 \cdots $
be the binomial representation of
![]() $\theta $
. By the definition of
$\theta $
. By the definition of
![]() $\tau ^s_{\theta }$
,
$\tau ^s_{\theta }$
,
![]() $d_j = 0$
if and only if
$d_j = 0$
if and only if
![]() $f^j(p) \in \mathcal {B}^+_{\alpha , {\mathbb {R}}}$
and
$f^j(p) \in \mathcal {B}^+_{\alpha , {\mathbb {R}}}$
and
![]() $d_j = 1$
if and only if
$d_j = 1$
if and only if
![]() $f^j(p) \in \mathcal {B}^+_{\beta , {\mathbb {R}}}$
for each
$f^j(p) \in \mathcal {B}^+_{\beta , {\mathbb {R}}}$
for each
![]() $j \geq 1$
. Hence, we have the following proposition.
$j \geq 1$
. Hence, we have the following proposition.
Proposition 5.13. The map
![]() $s^+ : J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
is surjective.
$s^+ : J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
is surjective.
Proof. Let
![]() $\mathcal {S}^{\prime } = {\{ \alpha , \beta \}}^{{\mathbb {Z}}} \setminus \bigcup _{j \in {\mathbb {Z}}} \sigma ^j \{ \overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }, \overline {\alpha } \beta \cdot \beta \beta \overline {\alpha } \}$
. It suffices to show that there exists a point
$\mathcal {S}^{\prime } = {\{ \alpha , \beta \}}^{{\mathbb {Z}}} \setminus \bigcup _{j \in {\mathbb {Z}}} \sigma ^j \{ \overline {\alpha } \beta \cdot \alpha \beta \overline {\alpha }, \overline {\alpha } \beta \cdot \beta \beta \overline {\alpha } \}$
. It suffices to show that there exists a point
![]() $p \in J^{\prime }$
for each
$p \in J^{\prime }$
for each
![]() $s \in \mathcal {S}^{\prime }$
with
$s \in \mathcal {S}^{\prime }$
with
![]() $s^+(p) = s$
. Take any
$s^+(p) = s$
. Take any
![]() $s = (s_j)_j \in \mathcal {S}^{\prime }$
. For each j, let
$s = (s_j)_j \in \mathcal {S}^{\prime }$
. For each j, let
![]() $d_j = 0$
if
$d_j = 0$
if
![]() $s_j = \alpha $
and
$s_j = \alpha $
and
![]() $d_j = 1$
if
$d_j = 1$
if
![]() $s_j = \beta $
, and consider a binomial number
$s_j = \beta $
, and consider a binomial number
![]() $\theta ^j = d_j. d_{j+1} d_{j+2} d_{j+3} \cdots $
. If we choose a point
$\theta ^j = d_j. d_{j+1} d_{j+2} d_{j+3} \cdots $
. If we choose a point
![]() $p_n \in \tau ^s_{\theta ^{-n}} \cap J$
for each
$p_n \in \tau ^s_{\theta ^{-n}} \cap J$
for each
![]() $n \in {\mathbb {Z}}$
, then the jth coordinate of the
$n \in {\mathbb {Z}}$
, then the jth coordinate of the
![]() $\{ \alpha , \beta \}$
-coding of
$\{ \alpha , \beta \}$
-coding of
![]() $f^n(p_n)$
is
$f^n(p_n)$
is
![]() $s_j$
for
$s_j$
for
![]() $j \geq -n$
. Since J is compact,
$j \geq -n$
. Since J is compact,
![]() $f^n(p_n) \in \tau ^s_{\theta ^0}$
has a cluster point
$f^n(p_n) \in \tau ^s_{\theta ^0}$
has a cluster point
![]() $p \in \tau ^s_{\theta ^0}$
. Here, if p is on the orbit of
$p \in \tau ^s_{\theta ^0}$
. Here, if p is on the orbit of
![]() $\star ^+$
, then we have
$\star ^+$
, then we have
![]() $s \in \mathcal {S}^{\prime }$
. Therefore, p belongs to
$s \in \mathcal {S}^{\prime }$
. Therefore, p belongs to
![]() $J^{\prime }$
and satisfies
$J^{\prime }$
and satisfies
![]() $s^+(p) = s$
.
$s^+(p) = s$
.
We can also construct a curve
![]() $\tau ^u_{\vartheta }$
included in
$\tau ^u_{\vartheta }$
included in
![]() $\overline {W^u(p_1)}$
for each binomial number
$\overline {W^u(p_1)}$
for each binomial number
![]() ${0 \leq \vartheta \leq 1}$
by a similar argument according to
${0 \leq \vartheta \leq 1}$
by a similar argument according to
![]() $\mathcal {B}^+_{\alpha , {\mathbb {R}}}$
,
$\mathcal {B}^+_{\alpha , {\mathbb {R}}}$
,
![]() $\mathcal {B}^+_{\beta , {\mathbb {R}}}$
instead of
$\mathcal {B}^+_{\beta , {\mathbb {R}}}$
instead of
![]() $\mathcal {B}^+_{\tilde {\alpha }, {\mathbb {R}}}$
,
$\mathcal {B}^+_{\tilde {\alpha }, {\mathbb {R}}}$
,
![]() $\mathcal {B}^+_{\tilde {\beta }, {\mathbb {R}}}$
. For a point
$\mathcal {B}^+_{\tilde {\beta }, {\mathbb {R}}}$
. For a point
![]() $p \in J^{\prime }$
, we choose
$p \in J^{\prime }$
, we choose
![]() $0 < \vartheta < 1$
so that
$0 < \vartheta < 1$
so that
![]() $\tau ^u_{\vartheta }$
passes p, and let
$\tau ^u_{\vartheta }$
passes p, and let
![]() $0. d_0 d_{-1} d_{-2} \cdots $
be the infinite binomial representation of
$0. d_0 d_{-1} d_{-2} \cdots $
be the infinite binomial representation of
![]() $\vartheta $
. Then,
$\vartheta $
. Then,
![]() $d_j = 0$
if and only if
$d_j = 0$
if and only if
![]() $f^j(p) \in \mathcal {B}^+_{\alpha , {\mathbb {R}}}$
and
$f^j(p) \in \mathcal {B}^+_{\alpha , {\mathbb {R}}}$
and
![]() $d_j = 1$
if and only if
$d_j = 1$
if and only if
![]() $f^j(p) \in \mathcal {B}^+_{\beta , {\mathbb {R}}}$
for each
$f^j(p) \in \mathcal {B}^+_{\beta , {\mathbb {R}}}$
for each
![]() $j \leq 0$
. Therefore, we have the following proposition.
$j \leq 0$
. Therefore, we have the following proposition.
Proposition 5.14. The map
![]() $s^+ : J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
is injective.
$s^+ : J \rightarrow {\{ \alpha , \beta \}}^{{\mathbb {Z}}} / {\sim }$
is injective.
Proof. It suffices to show that there exists at most one point
![]() $p \in J^{\prime }$
for any
$p \in J^{\prime }$
for any
![]() $s = (s_j)_j \in \mathcal {S}^{\prime }$
with
$s = (s_j)_j \in \mathcal {S}^{\prime }$
with
![]() $s^+(p) = s$
. Let
$s^+(p) = s$
. Let
![]() $d_j = 0$
if
$d_j = 0$
if
![]() $s_j = \alpha $
and
$s_j = \alpha $
and
![]() $d_j = 1$
if
$d_j = 1$
if
![]() $s_j = \beta $
for each
$s_j = \beta $
for each
![]() $j \in {\mathbb {Z}}$
, and consider two binomial numbers
$j \in {\mathbb {Z}}$
, and consider two binomial numbers
![]() $\theta = 0. d_1 d_2 d_3 \cdots $
and
$\theta = 0. d_1 d_2 d_3 \cdots $
and
![]() $\vartheta = 0. d_0 d_{-1} d_{-2} \cdots $
. Then,
$\vartheta = 0. d_0 d_{-1} d_{-2} \cdots $
. Then,
![]() $\theta $
corresponds to a curve
$\theta $
corresponds to a curve
![]() $\tau ^s_{\theta }$
(or one of
$\tau ^s_{\theta }$
(or one of
![]() $\tau ^s_{\theta \pm }$
), and
$\tau ^s_{\theta \pm }$
), and
![]() $\vartheta $
corresponds to a curve
$\vartheta $
corresponds to a curve
![]() $\tau ^u_{\vartheta }$
(or one of
$\tau ^u_{\vartheta }$
(or one of
![]() $\tau ^u_{\vartheta \pm }$
). We can obtain a point p with
$\tau ^u_{\vartheta \pm }$
). We can obtain a point p with
![]() $s^+(p) = s$
as an intersection point of
$s^+(p) = s$
as an intersection point of
![]() $\tau ^s_{\theta }$
and
$\tau ^s_{\theta }$
and
![]() $\tau ^u_{\vartheta }$
.
$\tau ^u_{\vartheta }$
.
The curve
![]() $\tau ^s_{\theta } \cap U^+$
is included in either
$\tau ^s_{\theta } \cap U^+$
is included in either
![]() $\mathcal {B}^+_0 \cup \mathcal {B}^+_1$
,
$\mathcal {B}^+_0 \cup \mathcal {B}^+_1$
,
![]() $\mathcal {B}^+_0 \cup \mathcal {B}^+_2$
, or
$\mathcal {B}^+_0 \cup \mathcal {B}^+_2$
, or
![]() $\mathcal {B}^+_3$
, and
$\mathcal {B}^+_3$
, and
![]() $\tau ^u_{\vartheta } \cap U^+$
is included in either
$\tau ^u_{\vartheta } \cap U^+$
is included in either
![]() $\mathcal {B}^+_0 \cup \mathcal {B}^+_3$
or
$\mathcal {B}^+_0 \cup \mathcal {B}^+_3$
or
![]() $\mathcal {B}^+_1 \cup \mathcal {B}^+_2 \cup \mathcal {B}^+_3$
. Hence,
$\mathcal {B}^+_1 \cup \mathcal {B}^+_2 \cup \mathcal {B}^+_3$
. Hence,
![]() $\tau ^s_{\theta } \cap \tau ^u_{\vartheta }$
is included in one of four boxes
$\tau ^s_{\theta } \cap \tau ^u_{\vartheta }$
is included in one of four boxes
![]() $\mathcal {B}^+_i$
(
$\mathcal {B}^+_i$
(
![]() $i = 0, 1, 2, 3$
). We can obtain
$i = 0, 1, 2, 3$
). We can obtain
![]() $\tau ^s_{\theta } \cap \mathcal {B}^+_i$
as the intersection of a vertical disk of degree one in
$\tau ^s_{\theta } \cap \mathcal {B}^+_i$
as the intersection of a vertical disk of degree one in
![]() $\mathcal {B}^+_i$
and
$\mathcal {B}^+_i$
and
![]() ${\mathbb {R}}^2$
, or as one of two branches of the intersection of a vertical disk of degree two in
${\mathbb {R}}^2$
, or as one of two branches of the intersection of a vertical disk of degree two in
![]() $\mathcal {B}^+_i$
and
$\mathcal {B}^+_i$
and
![]() ${\mathbb {R}}^2$
. Also, we can obtain
${\mathbb {R}}^2$
. Also, we can obtain
![]() $\tau ^u_{\vartheta } \cap \mathcal {B}^+_i$
as the intersection of a horizontal disk of degree one in
$\tau ^u_{\vartheta } \cap \mathcal {B}^+_i$
as the intersection of a horizontal disk of degree one in
![]() $\mathcal {B}^+_i$
and
$\mathcal {B}^+_i$
and
![]() ${\mathbb {R}}^2$
, or as one of two branches of the intersection of a horizontal disk of degree two in
${\mathbb {R}}^2$
, or as one of two branches of the intersection of a horizontal disk of degree two in
![]() $\mathcal {B}^+_i$
and
$\mathcal {B}^+_i$
and
![]() ${\mathbb {R}}^2$
. Therefore,
${\mathbb {R}}^2$
. Therefore,
![]() $\tau ^s_{\theta }$
and
$\tau ^s_{\theta }$
and
![]() $\tau ^u_{\vartheta }$
intersect at at most one point.
$\tau ^u_{\vartheta }$
intersect at at most one point.
Acknowledgements
Both authors thank Zin Arai in Tokyo Institute of Technology who performed computer-assisted proofs mentioned above. The second-named author is grateful to Kanae Hiraga for her visit to Kyushu University in 2022 which inspired him to employ the Poincaré metric in the argument presented just before Lemma 4.2. The second-named author is partially supported by JSPS KAKENHI Grant Numbers 18H01138, 20H01809, and 22H05107.
A Appendix. Computer-assisted proofs
In this appendix, we explain the proofs of Proposition A.1 and Lemmas 2.7, 2.8, 2.10, 2.11, 4.2, and 4.5. These proofs require computer-assistance, and are performed by Arai [Reference AraiA2]. Note that these lemmas concern only the real parameters
![]() $(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
, and hence the computational cost is not so high.
$(a, b)\in \mathcal {E}^{\pm }_{{\mathbb {R}}}$
, and hence the computational cost is not so high.
Proposition A.1. The locus
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
$\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
![]() $\partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
$\partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
Proof. When
![]() $(a, b)$
belongs to the left boundary of
$(a, b)$
belongs to the left boundary of
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}$
, we show that there exists a periodic point of period
$\mathcal {E}^{\pm }_{{\mathbb {R}}}$
, we show that there exists a periodic point of period
![]() $7$
in
$7$
in
![]() $\mathbb {C}^2\setminus \mathbb {R}^2$
by using the interval Krawczyk method (see [Reference Arai and IshiiAI, Theorem 2.12(i)]). This implies
$\mathbb {C}^2\setminus \mathbb {R}^2$
by using the interval Krawczyk method (see [Reference Arai and IshiiAI, Theorem 2.12(i)]). This implies
![]() $h_{\mathrm {top}}(f_{a, b})<\log 2$
by [Reference Bedford, Lyubich and SmillieBLS, Theorem 10.1]. When
$h_{\mathrm {top}}(f_{a, b})<\log 2$
by [Reference Bedford, Lyubich and SmillieBLS, Theorem 10.1]. When
![]() $(a, b)$
belongs to the right boundary of
$(a, b)$
belongs to the right boundary of
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}$
, we show that
$\mathcal {E}^{\pm }_{{\mathbb {R}}}$
, we show that
![]() $f_{a, b}$
is hyperbolic by using a technique in [Reference AraiA1] (see [Reference Arai and IshiiAI, Theorem 2.12(ii)]). These results together with [Reference Arai and IshiiAI, Main Theorem] yields that the locus
$f_{a, b}$
is hyperbolic by using a technique in [Reference AraiA1] (see [Reference Arai and IshiiAI, Theorem 2.12(ii)]). These results together with [Reference Arai and IshiiAI, Main Theorem] yields that the locus
![]() $\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
$\mathcal {E}^{\pm }_{{\mathbb {R}}}$
forms a neighborhood of
![]() $\partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
$\partial \mathcal {H}_{{\mathbb {R}}}^{\pm }$
.
Proof of Lemmas 2.7 and 2.8
For Lemma 2.7, we first choose appropriate topological disks
![]() $\widetilde {D}^+_{u, i}\subset D^+_{u, i}$
(
$\widetilde {D}^+_{u, i}\subset D^+_{u, i}$
(
![]() $i=0, 1, 2$
) and set
$i=0, 1, 2$
) and set
![]() $\mathcal {P}^+_{0, 3}\equiv \widetilde {D}^+_{u, 0}\times _{\mathrm {pr}}D^+_{v, 0}\subset \mathcal {B}^+_0$
,
$\mathcal {P}^+_{0, 3}\equiv \widetilde {D}^+_{u, 0}\times _{\mathrm {pr}}D^+_{v, 0}\subset \mathcal {B}^+_0$
,
![]() $\mathcal {P}^+_{1, 2}\equiv \widetilde {D}^+_{u, 1}\times _{\mathrm {pr}}D^+_{v, 1}\subset \mathcal {B}^+_1$
and
$\mathcal {P}^+_{1, 2}\equiv \widetilde {D}^+_{u, 1}\times _{\mathrm {pr}}D^+_{v, 1}\subset \mathcal {B}^+_1$
and
![]() $\mathcal {P}^+_{2, 3}\equiv \widetilde {D}^+_{u, 2}\times _{\mathrm {pr}}D^+_{v, 2}\subset \mathcal {B}^+_2$
so that conditions (1) and (2) in the lemma are satisfied.
$\mathcal {P}^+_{2, 3}\equiv \widetilde {D}^+_{u, 2}\times _{\mathrm {pr}}D^+_{v, 2}\subset \mathcal {B}^+_2$
so that conditions (1) and (2) in the lemma are satisfied.
For Lemma 2.8, we choose appropriate topological disks
![]() $\widetilde {D}^-_{u, i}\subset D^-_{u, i}$
(
$\widetilde {D}^-_{u, i}\subset D^-_{u, i}$
(
![]() $i=0, 1, 2, 3$
) and set
$i=0, 1, 2, 3$
) and set
![]() $\mathcal {P}^-_{0, 2}\equiv \widetilde {D}^-_{u, 0}\times _{\mathrm {pr}}D^-_{v, 0}\subset \mathcal {B}^-_0$
,
$\mathcal {P}^-_{0, 2}\equiv \widetilde {D}^-_{u, 0}\times _{\mathrm {pr}}D^-_{v, 0}\subset \mathcal {B}^-_0$
,
![]() $\mathcal {P}^-_{1, 3}\equiv \widetilde {D}^-_{u, 1}\times _{\mathrm {pr}}D^-_{v, 1}\subset \mathcal {B}^-_0$
,
$\mathcal {P}^-_{1, 3}\equiv \widetilde {D}^-_{u, 1}\times _{\mathrm {pr}}D^-_{v, 1}\subset \mathcal {B}^-_0$
,
![]() $\mathcal {P}^-_{2, 4}\equiv \widetilde {D}^-_{u, 2}\times _{\mathrm {pr}}D^-_{v, 2}\subset \mathcal {B}^-_0$
and
$\mathcal {P}^-_{2, 4}\equiv \widetilde {D}^-_{u, 2}\times _{\mathrm {pr}}D^-_{v, 2}\subset \mathcal {B}^-_0$
and
![]() $\mathcal {P}^-_{3, 4}\equiv \widetilde {D}^-_{u, 3}\times _{\mathrm {pr}}D^-_{v, 3}\subset \mathcal {B}^-_0$
so that conditions (1) and (2) in the lemma are satisfied.
$\mathcal {P}^-_{3, 4}\equiv \widetilde {D}^-_{u, 3}\times _{\mathrm {pr}}D^-_{v, 3}\subset \mathcal {B}^-_0$
so that conditions (1) and (2) in the lemma are satisfied.
Proof of Lemmas 2.10 and 2.11
Let
![]() $\pi _{u, i} : \mathcal {B}^{\pm }_i\to D^{\pm }_{u, i}$
be the projection given by
$\pi _{u, i} : \mathcal {B}^{\pm }_i\to D^{\pm }_{u, i}$
be the projection given by
![]() $\pi _{u, i}(u, v)=u$
and let
$\pi _{u, i}(u, v)=u$
and let
![]() $\iota _{v_0, i} : D_{u, i}\to \mathcal {B}^{\pm }_i$
be given by
$\iota _{v_0, i} : D_{u, i}\to \mathcal {B}^{\pm }_i$
be given by
![]() $\iota _{v_0, i}(u)=(u, v_0)$
for
$\iota _{v_0, i}(u)=(u, v_0)$
for
![]() $v_0\in D^{\pm }_{v, i}$
. The proof is similar to [Reference Arai and IshiiAI, Lemma 3.13] and goes as follows.
$v_0\in D^{\pm }_{v, i}$
. The proof is similar to [Reference Arai and IshiiAI, Lemma 3.13] and goes as follows.
Let
![]() $(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. For Lemma 2.10, we show the following claim by computer assistance. For every fixed
$(a, b)\in \mathcal {E}^+_{{\mathbb {R}}}$
. For Lemma 2.10, we show the following claim by computer assistance. For every fixed
![]() $v_0\in D_{v, 2}^+$
, we have
$v_0\in D_{v, 2}^+$
, we have
for
![]() $u\in D_{u, 2}^+$
with
$u\in D_{u, 2}^+$
with
![]() $\iota _{v_0, 2}(u)\in \mathcal {B}^+_2\cap f^{-1}(\mathcal {B}^+_3\cap f^{-1}(\mathcal {B}^+_1\cap f^{-1}(\mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_2))))$
.
$\iota _{v_0, 2}(u)\in \mathcal {B}^+_2\cap f^{-1}(\mathcal {B}^+_3\cap f^{-1}(\mathcal {B}^+_1\cap f^{-1}(\mathcal {B}^+_0\cap f^{-1}(\mathcal {B}^+_2))))$
.
Let
![]() $(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. For Lemma 2.11, we show the following claims by computer assistance.
$(a, b)\in \mathcal {E}^-_{{\mathbb {R}}}$
. For Lemma 2.11, we show the following claims by computer assistance.
-
(1) For every fixed
 $v_0\in D_{v, 2}^-$
, we have for
$v_0\in D_{v, 2}^-$
, we have for $$ \begin{align*} \frac{d}{du}\{\pi^-_{u, 3} \circ f^2\circ\iota_{v_0, 2}(u)\}\ne 0\end{align*} $$
$$ \begin{align*} \frac{d}{du}\{\pi^-_{u, 3} \circ f^2\circ\iota_{v_0, 2}(u)\}\ne 0\end{align*} $$
 $u\in D_{u, 2}^-$
with
$u\in D_{u, 2}^-$
with
 $\iota _{v_0, 2}(u)\in \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_2))$
.
$\iota _{v_0, 2}(u)\in \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_2))$
.
-
(2) For every fixed
 $v_0\in D_{v, 3}^-$
, we have for
$v_0\in D_{v, 3}^-$
, we have for $$ \begin{align*}\frac{d}{du}\{\pi^-_{u, 3} \circ f^2\circ\iota_{v_0, 3}(u)\}\ne 0\end{align*} $$
$$ \begin{align*}\frac{d}{du}\{\pi^-_{u, 3} \circ f^2\circ\iota_{v_0, 3}(u)\}\ne 0\end{align*} $$
 $u\in D_{u, 3}^-$
with
$u\in D_{u, 3}^-$
with
 $\iota _{v_0, 3}(u)\in \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_3))$
.
$\iota _{v_0, 3}(u)\in \mathcal {B}^-_3\cap f^{-1}(\mathcal {B}^-_4\cap f^{-1}(\mathcal {B}^-_3))$
.
Proof of Lemmas 4.2 and 4.5
We define the projective polydisk
![]() $\mathcal {P}_i=D_i\times _{\mathrm {pr}} D_{I_i}$
in claim (b) as follows. For
$\mathcal {P}_i=D_i\times _{\mathrm {pr}} D_{I_i}$
in claim (b) as follows. For
![]() $i=2, 3, 4$
, we first compute the stable direction at the saddle point
$i=2, 3, 4$
, we first compute the stable direction at the saddle point
![]() $p_i$
and define
$p_i$
and define
![]() $\pi _u$
to be the projection to this direction. We also define
$\pi _u$
to be the projection to this direction. We also define
![]() $\pi _v$
as the projection
$\pi _v$
as the projection
![]() $\mathrm {pr}_y$
orthogonal to the y-axis. We let
$\mathrm {pr}_y$
orthogonal to the y-axis. We let
![]() $D_i$
be a disk centered at
$D_i$
be a disk centered at
![]() $\pi _u(p_i)$
and determine its radius
$\pi _u(p_i)$
and determine its radius
![]() $\delta _i>0$
is determined so that claims (a) and (c) hold. For
$\delta _i>0$
is determined so that claims (a) and (c) hold. For
![]() $i=1$
, we approximately compute the tangential direction of
$i=1$
, we approximately compute the tangential direction of
![]() $W^s_{\mathrm {loc}}(p_3)_4$
at some
$W^s_{\mathrm {loc}}(p_3)_4$
at some
![]() $p\in W^s_{\mathrm {loc}}(p_3)_4\cap \mathcal {B}^-_{2, {\mathbb {R}}}$
and pull it back by f to define the direction of the projection
$p\in W^s_{\mathrm {loc}}(p_3)_4\cap \mathcal {B}^-_{2, {\mathbb {R}}}$
and pull it back by f to define the direction of the projection
![]() $\pi _u$
for
$\pi _u$
for
![]() $\mathcal {P}_1$
. We also define
$\mathcal {P}_1$
. We also define
![]() $\pi _v$
as the projection
$\pi _v$
as the projection
![]() $\mathrm {pr}_y$
orthogonal to the y-axis. We let
$\mathrm {pr}_y$
orthogonal to the y-axis. We let
![]() $D_1$
be a disk centered at
$D_1$
be a disk centered at
![]() $\pi _u(f^{-1}(p))$
and determine its radius
$\pi _u(f^{-1}(p))$
and determine its radius
![]() $\delta _1>0$
is determined so that claims (a) and (c) hold.
$\delta _1>0$
is determined so that claims (a) and (c) hold.