Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
RUDOLPH, DANIEL J.
2012.
Informal research statement.
Ergodic Theory and Dynamical Systems,
Vol. 32,
Issue. 2,
p.
323.


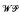 denote the class of transformations with the weak Pinsker property, and let [
denote the class of transformations with the weak Pinsker property, and let [