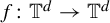1. Introduction
The Lyapunov exponents come from the study of differential equations in the thesis of Lyapunov [Reference Lyapunov14]. They were systematically introduced into ergodic theory by works of Furstenberg and Kesten [Reference Furstenberg and Kesten11] and Oseledets [Reference Oseledec18]. They are directly related to the expansion rates of the system and also to the positive metric entropy, using for example the Margulis–Ruelle inequality and the Pesin entropy formula. Ya. Pesin explored the concept of Lyapunov exponents developing a rich theory of non-uniformly hyperbolic systems, which are the systems with non-zero Lyapunov exponents.
However, in general, these systems are not robust: they do not form an open set. In the works [Reference Bochi3, Reference Bochi and Viana5], the authors show that if a non-uniformly hyperbolic system does not admit dominated splitting, it can be approximated by systems with zero Lyapunov exponents in
![]() $C^1$
topology. Usually, the presence of dominated decomposition guarantees higher regularity in
$C^1$
topology. Usually, the presence of dominated decomposition guarantees higher regularity in
![]() $C^1$
topology, see for example [Reference Saghin, Valenzuela-Henríquez and Vásquez21]. In the non-invertible setting, [Reference Andersson, Carrasco and Saghin1] showed the existence of
$C^1$
topology, see for example [Reference Saghin, Valenzuela-Henríquez and Vásquez21]. In the non-invertible setting, [Reference Andersson, Carrasco and Saghin1] showed the existence of
![]() $C^1$
open sets without dominated decomposition such that integrated Lyapunov exponents vary continuously with the dynamics in the
$C^1$
open sets without dominated decomposition such that integrated Lyapunov exponents vary continuously with the dynamics in the
![]() $C^1$
topology.
$C^1$
topology.
For a linear Anosov automorphism of the torus
![]() $A \colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
, the Lyapunov exponents are constant and indeed they are equal to the logarithm of the norm of eigenvalues of A. In general, Lyapunov exponents cannot be explicitly calculated. The regularity of Lyapunov exponents with respect to dynamics and invariant measures is a subtle question. Let us recall a flexibility conjecture by J. Bochi, A. Katok and F. Rodriguez Hertz. Let
$A \colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
, the Lyapunov exponents are constant and indeed they are equal to the logarithm of the norm of eigenvalues of A. In general, Lyapunov exponents cannot be explicitly calculated. The regularity of Lyapunov exponents with respect to dynamics and invariant measures is a subtle question. Let us recall a flexibility conjecture by J. Bochi, A. Katok and F. Rodriguez Hertz. Let
![]() $\operatorname {Diff}_m^{\infty } (M)$
be the set of m-preserving diffeomorphisms (volume preserving)
$\operatorname {Diff}_m^{\infty } (M)$
be the set of m-preserving diffeomorphisms (volume preserving)
![]() $f : M \rightarrow M$
of class
$f : M \rightarrow M$
of class
![]() $C^{\infty }$
.
$C^{\infty }$
.
Conjecture 1.1. [Reference Bochi, Katok and Rodriguez Hertz4]
Given a connected component
![]() $C \subset \operatorname {Diff}_m^{\infty } (M)$
and any list of numbers
$C \subset \operatorname {Diff}_m^{\infty } (M)$
and any list of numbers
![]() $\xi _1 \geq \cdots \geq \xi _d$
with
$\xi _1 \geq \cdots \geq \xi _d$
with
![]() $\sum _{i=1}^{d} \xi _i =0,$
there exists an ergodic diffeomorphism
$\sum _{i=1}^{d} \xi _i =0,$
there exists an ergodic diffeomorphism
![]() $f \in C$
such that
$f \in C$
such that
![]() $\xi _i, i=1, \ldots , d$
are the Lyapunov exponents with respect to
$\xi _i, i=1, \ldots , d$
are the Lyapunov exponents with respect to
![]() $m.$
$m.$
Moreover, in the setting of volume-preserving Anosov diffeomorphisms, they posed the following problem.
Problem 1. [Reference Bochi, Katok and Rodriguez Hertz4]
(Strong flexibility) Let
![]() $A \in SL(d, \mathbb {Z})$
be a hyperbolic linear transformation inducing conservative Anosov diffeomorphism
$A \in SL(d, \mathbb {Z})$
be a hyperbolic linear transformation inducing conservative Anosov diffeomorphism
![]() $F_A$
on
$F_A$
on
![]() $\mathbb {T}^d$
with Lyapunov exponents:
$\mathbb {T}^d$
with Lyapunov exponents:
![]() $\unicode{x3bb} _1 \geq \unicode{x3bb} _2 \cdots \geq \unicode{x3bb} _{u}> 0 > \unicode{x3bb} _{u+1} \geq \cdots \geq \unicode{x3bb} _d.$
Given any list of numbers
$\unicode{x3bb} _1 \geq \unicode{x3bb} _2 \cdots \geq \unicode{x3bb} _{u}> 0 > \unicode{x3bb} _{u+1} \geq \cdots \geq \unicode{x3bb} _d.$
Given any list of numbers
![]() $\xi _1 \geq \xi _2 \geq \cdots \geq \xi _u \geq \xi _{u+1} \geq \cdots \geq \xi _d$
such that:
$\xi _1 \geq \xi _2 \geq \cdots \geq \xi _u \geq \xi _{u+1} \geq \cdots \geq \xi _d$
such that:
-
(1)
 $\sum _{i=1}^{d} \xi _i = 0;$
$\sum _{i=1}^{d} \xi _i = 0;$
-
(2)
 $\sum _{i=1}^{u} \xi _i \leq \sum _{i=1}^{u} \unicode{x3bb} _i,$
$\sum _{i=1}^{u} \xi _i \leq \sum _{i=1}^{u} \unicode{x3bb} _i,$
does there exist a conservative Anosov diffeomorphism f homotopic to
![]() $F_A$
such that
$F_A$
such that
![]() $\{\xi _i\}$
is the list of all Lyapunov exponents with respect to volume measure?
$\{\xi _i\}$
is the list of all Lyapunov exponents with respect to volume measure?
In this work, we study a subset of transformations
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
homotopic to a linear Anosov automorphism
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
homotopic to a linear Anosov automorphism
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
, where f has some hyperbolicity (partial hyperbolicity or non-uniform hyperbolicity). See §2 for the definitions. In particular, we show that for a class of partially hyperbolic diffeomorphisms and homotopic to Anosov linear automorphism, not all lists of numbers can be realized as Lyapunov exponents. More precisely, in such a class of dynamics, we need the conditions (1) and (2) imposed in Problem 1.
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
, where f has some hyperbolicity (partial hyperbolicity or non-uniform hyperbolicity). See §2 for the definitions. In particular, we show that for a class of partially hyperbolic diffeomorphisms and homotopic to Anosov linear automorphism, not all lists of numbers can be realized as Lyapunov exponents. More precisely, in such a class of dynamics, we need the conditions (1) and (2) imposed in Problem 1.
This type of result also appears in [Reference Bochi, Katok and Rodriguez Hertz4, Reference Costa and Micena10, Reference Micena15–Reference Micena and Tahzibi17, Reference Saghin and Xia22]. In [Reference Micena and Tahzibi16], it has been proved that for any conservative partially hyperbolic systems in the torus
![]() ${\mathbb {T}}^3$
, the stable or unstable Lyapunov exponent is bounded by the stable or unstable Lyapunov exponent of its linearization. It is well worth mentioning that Carrasco and Saghin [Reference Carrasco and Saghin9] constructed a
${\mathbb {T}}^3$
, the stable or unstable Lyapunov exponent is bounded by the stable or unstable Lyapunov exponent of its linearization. It is well worth mentioning that Carrasco and Saghin [Reference Carrasco and Saghin9] constructed a
![]() $C^\infty $
and volume-preserving example on
$C^\infty $
and volume-preserving example on
![]() $\mathbb {T}^3$
that shows that the largest Lyapunov exponent of a diffeomorphism in the homotopy class of an Anosov linear automorphism of
$\mathbb {T}^3$
that shows that the largest Lyapunov exponent of a diffeomorphism in the homotopy class of an Anosov linear automorphism of
![]() $\mathbb {T}^3$
may be larger than the largest Lyapunov exponent of A. However, in their example, f does not admit a three-bundle partially hyperbolic splitting.
$\mathbb {T}^3$
may be larger than the largest Lyapunov exponent of A. However, in their example, f does not admit a three-bundle partially hyperbolic splitting.
We also mention that our results address (and give a negative answer in some special cases of derived from Anosov diffeomorhisms) a question in [Reference Carrasco and Saghin9]: Does there exist a derived from Anosov diffeomorphism f such that the sum of the positive Lyapunov exponents of f is larger than the sum of the positive Lyapunov exponents of its linear part?
2. Definitions and statements of results
Definition 2.1. Let M be a closed manifold. A diffeomorphism
![]() $f\colon M \rightarrow M$
is called a partially hyperbolic diffeomorphism if there is a suitable norm
$f\colon M \rightarrow M$
is called a partially hyperbolic diffeomorphism if there is a suitable norm
![]() $\|\cdot \|$
and the tangent bundle
$\|\cdot \|$
and the tangent bundle
![]() $TM$
admits a
$TM$
admits a
![]() $Df$
-invariant decomposition
$Df$
-invariant decomposition
![]() $TM = E^s \oplus E^c \oplus E^u$
such that for all unitary vectors
$TM = E^s \oplus E^c \oplus E^u$
such that for all unitary vectors
![]() $v^{\sigma } \in E^{\sigma }_x, \sigma \in \{s,c,u\}$
and every
$v^{\sigma } \in E^{\sigma }_x, \sigma \in \{s,c,u\}$
and every
![]() $x \in M$
, we have
$x \in M$
, we have
moreover,
Every diffeomorphism of the torus
![]() $\mathbb {T}^d$
induces an automorphism of the fundamental group and there exists a unique linear diffeomorphism
$\mathbb {T}^d$
induces an automorphism of the fundamental group and there exists a unique linear diffeomorphism
![]() $f_{\ast }$
which induces the same automorphism on
$f_{\ast }$
which induces the same automorphism on
![]() $\pi _1(\mathbb {T}^d).$
The diffeomorphism
$\pi _1(\mathbb {T}^d).$
The diffeomorphism
![]() $f_{\ast }$
is called linearization of
$f_{\ast }$
is called linearization of
![]() $f.$
$f.$
Anosov diffeomorphisms can be considered partially hyperbolic systems with
![]() $E^c = 0.$
However, in this paper, whenever we consider an Anosov diffeomorphism as a partially hyperbolic system, we mean that there exists a non-trivial (centre bundle) partially hyperbolic decomposition.
$E^c = 0.$
However, in this paper, whenever we consider an Anosov diffeomorphism as a partially hyperbolic system, we mean that there exists a non-trivial (centre bundle) partially hyperbolic decomposition.
Clearly, a partially hyperbolic diffeomorphism may have various partially hyperbolic invariant decompositions. We will consider several (non-necessarily disjoint) categories of partially hyperbolic diffeomorphisms indexed by the dimensions of invariant bundles.
More precisely, we say
![]() $f \in Ph_{(d_s, d_u)}(M)$
if f admits a partially hyperbolic decomposition with
$f \in Ph_{(d_s, d_u)}(M)$
if f admits a partially hyperbolic decomposition with
![]() $\dim (E^{\sigma }) = d_{\sigma }$
for
$\dim (E^{\sigma }) = d_{\sigma }$
for
![]() $ \sigma \in \{s, u\}.$
Clearly,
$ \sigma \in \{s, u\}.$
Clearly,
![]() $\dim (E^c) = \dim (M) - d_s - d_u.$
For instance, consider the cat map A on
$\dim (E^c) = \dim (M) - d_s - d_u.$
For instance, consider the cat map A on
![]() $\mathbb {T}^2$
induced by matrix
$\mathbb {T}^2$
induced by matrix
![]() $(\begin {smallmatrix} 2 & 1 \\ 1 & 1 \\ \end {smallmatrix} )$
, then
$(\begin {smallmatrix} 2 & 1 \\ 1 & 1 \\ \end {smallmatrix} )$
, then
![]() $A \times A$
is a partially hyperbolic (in fact, Anosov) diffeomorphism and belongs to
$A \times A$
is a partially hyperbolic (in fact, Anosov) diffeomorphism and belongs to
![]() $Ph_{(1, 1)} \cap Ph_{(2,1)} \cap Ph_{(1, 2)}.$
$Ph_{(1, 1)} \cap Ph_{(2,1)} \cap Ph_{(1, 2)}.$
Definition 2.2. Let
![]() $f\colon \mathbb {T}^d \rightarrow \mathbb {T}^d $
be a partially hyperbolic diffeomorphism, and f is called a derived from Anosov (DA) diffeomorphism if its linearization
$f\colon \mathbb {T}^d \rightarrow \mathbb {T}^d $
be a partially hyperbolic diffeomorphism, and f is called a derived from Anosov (DA) diffeomorphism if its linearization
![]() $f_{\ast }\colon \mathbb {T}^d \rightarrow \mathbb {T}^d $
is a linear Anosov automorphism.
$f_{\ast }\colon \mathbb {T}^d \rightarrow \mathbb {T}^d $
is a linear Anosov automorphism.
Definition 2.3. We say that the diffeomorphism
![]() $f\colon M\rightarrow M$
admits a dominated splitting if there is an invariant (by
$f\colon M\rightarrow M$
admits a dominated splitting if there is an invariant (by
![]() $Df$
) continuous decomposition
$Df$
) continuous decomposition
![]() $TM=E\oplus F$
and constants
$TM=E\oplus F$
and constants
![]() $0<\nu <1, C>0$
such that
$0<\nu <1, C>0$
such that
 $$ \begin{align*} \frac{\|Df^n|_{E(x)}\|}{\|Df^{-n}|_{F(f^n(n))}\|^{-1}}\leq C\nu^n\quad\text{for all } x\in M, n>0. \end{align*} $$
$$ \begin{align*} \frac{\|Df^n|_{E(x)}\|}{\|Df^{-n}|_{F(f^n(n))}\|^{-1}}\leq C\nu^n\quad\text{for all } x\in M, n>0. \end{align*} $$
Let us recall a simple version of the Oseledets’ theorem.
Theorem 2.4. [Reference Oseledec18]
Let
![]() $f\colon M\rightarrow M$
be a
$f\colon M\rightarrow M$
be a
![]() $C^1$
diffeomorphism, then there is a full probability Borelian set
$C^1$
diffeomorphism, then there is a full probability Borelian set
![]() $\mathcal {R}$
(this is,
$\mathcal {R}$
(this is,
![]() $\mu (\mathcal {R})=1$
for all f-invariant probability measure
$\mu (\mathcal {R})=1$
for all f-invariant probability measure
![]() $\mu $
) such that for each
$\mu $
) such that for each
![]() $x\in \mathcal {R}$
, there is a decomposition
$x\in \mathcal {R}$
, there is a decomposition
![]() $T_xM=E_1\oplus \cdots E_{k(x)}$
and constants
$T_xM=E_1\oplus \cdots E_{k(x)}$
and constants
![]() $\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _{k(x)}$
such that
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _{k(x)}$
such that
for all
![]() $v\in E_i$
. The
$v\in E_i$
. The
![]() $\unicode{x3bb} _i(x)$
is called a Lyapunov exponent. Moreover, for any
$\unicode{x3bb} _i(x)$
is called a Lyapunov exponent. Moreover, for any
![]() $ 1 \leq j \leq k(x) $
,
$ 1 \leq j \leq k(x) $
,

where
![]() $F_j = E_1 \oplus \cdots \oplus E_j$
and
$F_j = E_1 \oplus \cdots \oplus E_j$
and
![]() $d_i= \mathrm {dim} (E_i).$
$d_i= \mathrm {dim} (E_i).$
In this paper, when m refers to a measure, it stands for a fixed Lebesgue measure on
![]() $\mathbb {T}^d$
.
$\mathbb {T}^d$
.
2.1. Lyapunov exponents of partially hyperbolic diffeomorphisms
In our first main theorem, we prove that linear Anosov diffeomorphisms maximize (respectively minimize) the sum of unstable (respectively stable) Lyapunov exponents, in any homotopy path totally inside partially hyperbolic diffeomorphisms.
The notion of metric entropy appears naturally when dealing with Lyapunov exponents. For a partially hyperbolic diffeomorphism, it is possible to define entropy of an invariant measure along unstable foliation and there is variational principle results for such entropy. A u-maximal entropy measure is a measure which attains the supremum of unstable entropy among all invariant measures. See §3.2.1 and references for more details.
Theorem A. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
![]() $C^2$
volume-preserving DA diffeomorphism in
$C^2$
volume-preserving DA diffeomorphism in
![]() $Ph_{d_s, d_u}$
with linearization
$Ph_{d_s, d_u}$
with linearization
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
such that f and A are homotopic by a path fully contained in
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
such that f and A are homotopic by a path fully contained in
![]() $Ph_{d_s, d_u}({\mathbb {T}}^d)$
, then
$Ph_{d_s, d_u}({\mathbb {T}}^d)$
, then
 $$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x) \leq \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A) \,\,\,\, \text{and} \,\,\,\, \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(f, x) \geq \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(A), \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x) \leq \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A) \,\,\,\, \text{and} \,\,\,\, \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(f, x) \geq \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(A), \end{align*} $$
for m-almost every (a.e.)
![]() $x \in {\mathbb {T}}^d$
and, the first (respectively second) inequality is strict unless m is a measure of u-maximal entropy (respectively u-maximal for
$x \in {\mathbb {T}}^d$
and, the first (respectively second) inequality is strict unless m is a measure of u-maximal entropy (respectively u-maximal for
![]() $f^{-1}$
).
$f^{-1}$
).
This is related to the result of [Reference Micena and Tahzibi16]: let
![]() $f\colon \mathbb {T}^3 \rightarrow \mathbb {T}^3$
be a
$f\colon \mathbb {T}^3 \rightarrow \mathbb {T}^3$
be a
![]() $C^2$
conservative derived from Anosov partially hyperbolic diffeomorphism with linearization A. Then,
$C^2$
conservative derived from Anosov partially hyperbolic diffeomorphism with linearization A. Then,
![]() $\unicode{x3bb} ^u(x) \leq \unicode{x3bb} ^u(A)$
for almost every
$\unicode{x3bb} ^u(x) \leq \unicode{x3bb} ^u(A)$
for almost every
![]() $x.$
We recall that the authors used quasi-isometric property of unstable foliation for the three-dimensional derived from Anosov diffeomorphisms. They do not assume that f is in the same connected component of A.
$x.$
We recall that the authors used quasi-isometric property of unstable foliation for the three-dimensional derived from Anosov diffeomorphisms. They do not assume that f is in the same connected component of A.
Theorem B. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
![]() $C^2$
volume-preserving DA diffeomorphism in
$C^2$
volume-preserving DA diffeomorphism in
![]() $Ph_{d_s, d_u}$
with linearization
$Ph_{d_s, d_u}$
with linearization
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
belonging to
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
belonging to
![]() $Ph_{d_s, d_u}.$
Suppose that for
$Ph_{d_s, d_u}.$
Suppose that for
![]() $\sigma \in \{s, u\}$
, there is a
$\sigma \in \{s, u\}$
, there is a
![]() $(d - d_{\sigma })$
-dimensional subspace
$(d - d_{\sigma })$
-dimensional subspace
![]() $P_{\sigma } \subset \mathbb {R}^d, $
such that
$P_{\sigma } \subset \mathbb {R}^d, $
such that
![]() $\angle (E^{\sigma }_f(x), P_{\sigma })> \alpha > 0$
for all
$\angle (E^{\sigma }_f(x), P_{\sigma })> \alpha > 0$
for all
![]() $x \in \mathbb {R}^d$
(
$x \in \mathbb {R}^d$
(
![]() $E^{\sigma }_f$
stands for the lift of the bundles), then
$E^{\sigma }_f$
stands for the lift of the bundles), then
 $$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x) \leq \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A) \quad \text{and} \quad \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(f, x) \geq \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(A), \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x) \leq \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A) \quad \text{and} \quad \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(f, x) \geq \sum_{i = 1}^{d_s} \unicode{x3bb}^s_i(A), \end{align*} $$
for m-a.e.
![]() $x \in \mathbb {T}^d.$
$x \in \mathbb {T}^d.$
Observe that the assumption on the existence of
![]() $P_{\sigma }$
in the above theorem is a mild condition and is satisfied if the stable and unstable bundles of f do not vary too much. Indeed, we require that
$P_{\sigma }$
in the above theorem is a mild condition and is satisfied if the stable and unstable bundles of f do not vary too much. Indeed, we require that
![]() $\{ E^{\sigma }_f(x), x \in \mathbb {R}^d\}$
is not dense in the Grassmannian of
$\{ E^{\sigma }_f(x), x \in \mathbb {R}^d\}$
is not dense in the Grassmannian of
![]() $d_{\sigma }$
-dimensional subspaces.
$d_{\sigma }$
-dimensional subspaces.
2.2. Lyapunov exponents of non-uniformly Anosov systems
In this section, we deal with dynamics that are not necessarily partially hyperbolic. However, they enjoy some dominated splitting property: Oseledets’ splitting (stable/unstable) is dominated.
Definition 2.5. A
![]() $C^2$
-volume-preserving diffeomorphism f is called non-uniformly Anosov if it admits an f-invariant dominated decomposition
$C^2$
-volume-preserving diffeomorphism f is called non-uniformly Anosov if it admits an f-invariant dominated decomposition
![]() $TM= E \oplus F$
such that
$TM= E \oplus F$
such that
![]() $\unicode{x3bb} ^{F}_i(x)>0$
(all Lyapunov exponents along F) and
$\unicode{x3bb} ^{F}_i(x)>0$
(all Lyapunov exponents along F) and
![]() $\unicode{x3bb} ^{E}_i(x)<0$
(all Lyapunov exponents along E) for
$\unicode{x3bb} ^{E}_i(x)<0$
(all Lyapunov exponents along E) for
![]() $\mu $
-a.e x.
$\mu $
-a.e x.
In the next theorem, we compare Lyapunov exponents of a non-uniformly Anosov diffeomorphism with those of linear Anosov automorphism if they are homotopic. Observe that by definition, the number of negative (positive) Lyapunov exponents of a non-uniformly Anosov diffeomorphism is constant almost everywhere and coincides with the dimension of the bundles in the dominated splitting. However, the Lyapunov exponents may depend on the orbit, as we do not assume ergodicity. In fact, it is interesting to know whether, in general, all topologically transitive non-uniformly Anosov diffeomorphisms are ergodic or not. We conjecture that all topologically transitive non-uniformly Anosov diffeomorphisms are ergodic.
Let
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a linear Anosov diffeomorphism such that
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a linear Anosov diffeomorphism such that
![]() $T \mathbb {T}^d = E^s_{A} \oplus E^u_{A}.$
Denote by
$T \mathbb {T}^d = E^s_{A} \oplus E^u_{A}.$
Denote by
![]() $d_s =\mathrm {dim} (E^s_A)$
and
$d_s =\mathrm {dim} (E^s_A)$
and
![]() $d_u =\mathrm {dim}(E^u_A).$
After changing to an equivalent Riemannian norm, if necessary, there are
$d_u =\mathrm {dim}(E^u_A).$
After changing to an equivalent Riemannian norm, if necessary, there are
![]() $0<\unicode{x3bb} <1<\gamma $
such that
$0<\unicode{x3bb} <1<\gamma $
such that
![]() $\|A|_{E^s}\| \leq \unicode{x3bb} $
,
$\|A|_{E^s}\| \leq \unicode{x3bb} $
,
![]() $m(A|_{E^u}) \geq \gamma $
and
$m(A|_{E^u}) \geq \gamma $
and
![]() $E^s_A$
is orthogonal to
$E^s_A$
is orthogonal to
![]() $E^u_A.$
Indeed, to use fewer constants in the proofs, we assume that
$E^u_A.$
Indeed, to use fewer constants in the proofs, we assume that
![]() $E^u_i$
and
$E^u_i$
and
![]() $E^u_j, i \neq j$
are orthogonal, where
$E^u_j, i \neq j$
are orthogonal, where
![]() $E^u_i$
terms are generalized eigenspaces of A which coincide with the Oseledets decomposition. Recall that for a linear transformation T,
$E^u_i$
terms are generalized eigenspaces of A which coincide with the Oseledets decomposition. Recall that for a linear transformation T,
![]() $m(T):= \|T^{-1}\|^{-1}.$
We refer to
$m(T):= \|T^{-1}\|^{-1}.$
We refer to
![]() $\gamma , \unicode{x3bb} $
as rates of hyperbolicity of A. Observe that Lyapunov exponents of any diffeomorphism are independent of the choice of the equivalent norm.
$\gamma , \unicode{x3bb} $
as rates of hyperbolicity of A. Observe that Lyapunov exponents of any diffeomorphism are independent of the choice of the equivalent norm.
Theorem C. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
![]() $C^{2}$
conservative non-uniformly Anosov diffeomorphism with dominated decomposition
$C^{2}$
conservative non-uniformly Anosov diffeomorphism with dominated decomposition
![]() $TM=E\oplus F$
, homotopic to A such that:
$TM=E\oplus F$
, homotopic to A such that:
-
(1)
 $\mathrm {dim} (E) =d_s$
and
$\mathrm {dim} (E) =d_s$
and
 $\mathrm {dim} (F) =d_u;$
$\mathrm {dim} (F) =d_u;$
-
(2)
 $E(x)\cap E^u_A=\{0\}$
and
$E(x)\cap E^u_A=\{0\}$
and
 $F(x)\cap E^s_A=\{0\};$
$F(x)\cap E^s_A=\{0\};$
-
(3)
 $\|Df|_E\|<\gamma $
and
$\|Df|_E\|<\gamma $
and
 $m(Df|_F)>\unicode{x3bb} $
.
$m(Df|_F)>\unicode{x3bb} $
.
Suppose that the distributions E and F are integrable, then
![]() $\sum _{i=1}^{d_u}\unicode{x3bb} ^{F}_{i}(f,x)\leq \sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
and
$\sum _{i=1}^{d_u}\unicode{x3bb} ^{F}_{i}(f,x)\leq \sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
and
![]() $\sum _{i=1}^{d_s}\unicode{x3bb} ^{E}_i(f,x)\geq \sum _{i=1}^{d_s} \unicode{x3bb} _i^s(A)$
for Lebesgue-a.e.
$\sum _{i=1}^{d_s}\unicode{x3bb} ^{E}_i(f,x)\geq \sum _{i=1}^{d_s} \unicode{x3bb} _i^s(A)$
for Lebesgue-a.e.
![]() $x\in {\mathbb {T}}^d$
.
$x\in {\mathbb {T}}^d$
.
Let us comment on the hypotheses: the first and second one ask for some compatibility of invariant bundles and the third one asks that any possible expansion in the dominated bundle E is less than the expansion rate of A and similarly any possible contraction in the dominating bundle F is weaker than the contraction rate of
![]() $A.$
$A.$
Bonatti and Viana [Reference Bonatti and Viana6] constructed the first examples of robustly transitive diffeomorphisms that are not partially hyperbolic, which was later generalized in higher dimensions by [Reference Tahzibi23]. Those classes of examples satisfy the hypotheses of the above theorem.
Theorem 2.6. [Reference Bonatti and Viana6, Reference Buzzi and Fisher8, Reference Tahzibi23]
There is an open set
![]() $\mathcal {U}\subset \operatorname {Diff}^1_m({\mathbb {T}}^d)$
such that any
$\mathcal {U}\subset \operatorname {Diff}^1_m({\mathbb {T}}^d)$
such that any
![]() $C^2$
-diffeomorphism in
$C^2$
-diffeomorphism in
![]() $\mathcal {U}$
satisfies all hypotheses of Theorem C and the bundles E and F are integrable.
$\mathcal {U}$
satisfies all hypotheses of Theorem C and the bundles E and F are integrable.
In the above theorem, the integrability of invariant subbundles E and F is proved in [Reference Buzzi and Fisher8].
2.3. Regularity of foliations
Any partially hyperbolic diffeomorphism admits invariant stable and unstable foliations. As the proofs of our main results are based on the regularity of such foliations, we need to recall some basic definitions and results in this subsection. Consider
![]() ${\mathcal {F}}$
a foliation in M, B a
${\mathcal {F}}$
a foliation in M, B a
![]() ${\mathcal {F}}$
-foliated box and m the Lebesgue measure in M. Denote by
${\mathcal {F}}$
-foliated box and m the Lebesgue measure in M. Denote by
![]() $\mathrm {Vol}_{L_x}$
the Lebesgue measure of leaf
$\mathrm {Vol}_{L_x}$
the Lebesgue measure of leaf
![]() $L_x$
and
$L_x$
and
![]() $m_{L_x}$
the disintegration of the Lebesgue measure m along the leaf
$m_{L_x}$
the disintegration of the Lebesgue measure m along the leaf
![]() $L_x$
. The disintegrated measures are in fact a projective class of measures. However, whenever we fix a compact foliated box B, then we can use the Rohlin disintegration theorem for the normalized restriction of m on B to get probability conditional measures. So in what follows, after fixing a foliated box B by
$L_x$
. The disintegrated measures are in fact a projective class of measures. However, whenever we fix a compact foliated box B, then we can use the Rohlin disintegration theorem for the normalized restriction of m on B to get probability conditional measures. So in what follows, after fixing a foliated box B by
![]() $m_{L_x}$
and
$m_{L_x}$
and
![]() $\mathrm {Vol}_{L_x}$
, we understand probability measures whose support is inside the plaque of
$\mathrm {Vol}_{L_x}$
, we understand probability measures whose support is inside the plaque of
![]() $L_x$
which contains
$L_x$
which contains
![]() $x \in B$
and is inside B.
$x \in B$
and is inside B.
Definition 2.7. We say that the foliation
![]() ${\mathcal {F}}$
is upper leafwise absolutely continuous if for any foliated box B,
${\mathcal {F}}$
is upper leafwise absolutely continuous if for any foliated box B,
![]() $m_{L_x}\!\ll \mathrm {Vol}_{L_x}$
for m-a.e.
$m_{L_x}\!\ll \mathrm {Vol}_{L_x}$
for m-a.e.
![]() $x\in B$
. Equivalently, if given a set
$x\in B$
. Equivalently, if given a set
![]() $Z\subset B$
such that
$Z\subset B$
such that
![]() $\mathrm {Vol}_{L_x}(Z\cap L_x)=0$
for m-a.e.
$\mathrm {Vol}_{L_x}(Z\cap L_x)=0$
for m-a.e.
![]() $x \in B$
, then
$x \in B$
, then
![]() $m(Z)=0$
.
$m(Z)=0$
.
Definition 2.8. We say that the foliation
![]() ${\mathcal {F}}$
is lower leafwise absolutely continuous if
${\mathcal {F}}$
is lower leafwise absolutely continuous if
![]() $\mathrm {Vol}_{L_x}\!\ll m_{L_x}$
for m-a.e.
$\mathrm {Vol}_{L_x}\!\ll m_{L_x}$
for m-a.e.
![]() $x\in B$
. Equivalently, if given a set
$x\in B$
. Equivalently, if given a set
![]() $Z\subset B$
such that
$Z\subset B$
such that
![]() $m(Z)=0$
, then
$m(Z)=0$
, then
![]() $\mathrm {Vol}_{L_x}(Z\cap L_x)=0$
for m-a.e.
$\mathrm {Vol}_{L_x}(Z\cap L_x)=0$
for m-a.e.
![]() $x \in B$
.
$x \in B$
.
Definition 2.9. We say that the foliation
![]() ${\mathcal {F}}$
is leafwise absolutely continuous if
${\mathcal {F}}$
is leafwise absolutely continuous if
![]() $\mathrm {Vol}_{L_x}\!\sim m_{L_x}$
(this is,
$\mathrm {Vol}_{L_x}\!\sim m_{L_x}$
(this is,
![]() $m_{L_x}\!\ll \mathrm {Vol}_{L_x}$
and
$m_{L_x}\!\ll \mathrm {Vol}_{L_x}$
and
![]() $\mathrm {Vol}_{L_x}\!\ll m_{L_x}$
) for m-a.e.
$\mathrm {Vol}_{L_x}\!\ll m_{L_x}$
) for m-a.e.
![]() $x\in B$
.
$x\in B$
.
Proposition 2.10. [Reference Brin and Pesin7]
If
![]() $f\colon M\rightarrow M$
is a
$f\colon M\rightarrow M$
is a
![]() $C^2$
partially hyperbolic diffeomorphism, then the foliations
$C^2$
partially hyperbolic diffeomorphism, then the foliations
![]() $W^s$
and
$W^s$
and
![]() $W^u$
are leafwise absolutely continuous.
$W^u$
are leafwise absolutely continuous.
We also mention the result of Ya. Pesin for non-uniformly hyperbolic systems, see [Reference Barreira and Pesin2, Theorem 4.3.1], which shows absolute continuity of local Pesin laminations.
3. Proof of results
Theorems A and B are obtained by the following result.
Theorem 3.1. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
![]() $C^2$
volume-preserving partially hyperbolic diffeomorphism such that there are closed non-degenerate
$C^2$
volume-preserving partially hyperbolic diffeomorphism such that there are closed non-degenerate
![]() $d_u$
-forms and
$d_u$
-forms and
![]() $d_s$
-forms on
$d_s$
-forms on
![]() $E^u$
and
$E^u$
and
![]() $E^s$
, respectively. Suppose that A, the linearization of f, is partially hyperbolic and
$E^s$
, respectively. Suppose that A, the linearization of f, is partially hyperbolic and
![]() $\mathrm {dim} E^{\sigma }_f=\mathrm {dim} E^{\sigma }_A$
,
$\mathrm {dim} E^{\sigma }_f=\mathrm {dim} E^{\sigma }_A$
,
![]() $\sigma \in \{s,c,u\}$
, then
$\sigma \in \{s,c,u\}$
, then

for m-a.e.
![]() $x\in {\mathbb {T}}^d$
.
$x\in {\mathbb {T}}^d$
.
For the proof of this theorem, we use a result of Saghin [Reference Saghin20]. Let
![]() $f\colon M\rightarrow M$
be a diffeomorphism and W an f-invariant foliation on M, that is,
$f\colon M\rightarrow M$
be a diffeomorphism and W an f-invariant foliation on M, that is,
![]() $f(W(x))=W(f(x))$
, and
$f(W(x))=W(f(x))$
, and
![]() $B_r(x,f)$
be the ball of the leaf
$B_r(x,f)$
be the ball of the leaf
![]() $W(x)$
with radius r centred at x. We say that
$W(x)$
with radius r centred at x. We say that
is the volume growth rate of the foliation at x and
is the volume growth rate of W. Here, Vol stands for the
![]() $\mathrm {Vol}_{W}$
which is the induced volume to the leaves of W. We use this notation throughout the paper except when it may create confusion.
$\mathrm {Vol}_{W}$
which is the induced volume to the leaves of W. We use this notation throughout the paper except when it may create confusion.
When f is a partially hyperbolic diffeomorphism, we denote by
![]() $\chi _u(f)$
the volume growth of unstable foliation
$\chi _u(f)$
the volume growth of unstable foliation
![]() $W^u$
.
$W^u$
.
Theorem 3.2. [Reference Saghin20]
Let
![]() $f\colon M\rightarrow M$
be a
$f\colon M\rightarrow M$
be a
![]() $C^1$
partially hyperbolic diffeomorphism such that there is a closed non-degenerate
$C^1$
partially hyperbolic diffeomorphism such that there is a closed non-degenerate
![]() $d_u$
-form on the unstable bundle
$d_u$
-form on the unstable bundle
![]() $E^u$
, then
$E^u$
, then
![]() $\chi _u(f)=\log sp(f_{*,d_u})$
, where
$\chi _u(f)=\log sp(f_{*,d_u})$
, where
![]() $f_{*,d_u}$
is the induced map in the
$f_{*,d_u}$
is the induced map in the
![]() $d_u$
-cohomology of De Rham.
$d_u$
-cohomology of De Rham.
Proposition 3.3. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a
![]() $C^1$
partially hyperbolic diffeomorphism admitting a closed non-degenerate
$C^1$
partially hyperbolic diffeomorphism admitting a closed non-degenerate
![]() $d_u$
-form on the unstable bundle
$d_u$
-form on the unstable bundle
![]() $E^u$
. For fixed
$E^u$
. For fixed
![]() ${x\in {\mathbb {T}}^d, r>0}$
, the balls
${x\in {\mathbb {T}}^d, r>0}$
, the balls
![]() $B_r(x,f)\subset W^u(x,f)$
and
$B_r(x,f)\subset W^u(x,f)$
and
![]() $B_r(x,A)\subset W^u(x,A)$
satisfy the following. Given
$B_r(x,A)\subset W^u(x,A)$
satisfy the following. Given
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $n_0 \in \mathbb {N}$
such that if
$n_0 \in \mathbb {N}$
such that if
![]() $n>n_0$
, we have
$n>n_0$
, we have
Proof. By Theorem 3.2, we have that
that is,
therefore, given
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $n_0$
such that if
$n_0$
such that if
![]() $n>n_0$
,
$n>n_0$
,
Then,
Proof of Theorem 3.1
We prove the statement for the sum of unstable exponents. One may repeat the argument for
![]() $f^{-1}$
to obtain the claim for stable exponents.
$f^{-1}$
to obtain the claim for stable exponents.
Suppose by contradiction that there is a positive volume set
![]() $Z\subset \mathcal {R} \subset {\mathbb {T}}^d$
, (where
$Z\subset \mathcal {R} \subset {\mathbb {T}}^d$
, (where
![]() $\mathcal {R}$
is the set of points satisfying Oseledets’ theorem as stated in Theorem 2.4) such that for all
$\mathcal {R}$
is the set of points satisfying Oseledets’ theorem as stated in Theorem 2.4) such that for all
![]() $x\in Z$
, we have
$x\in Z$
, we have
![]() $\sum _{i=1}^{d_u}\unicode{x3bb} ^u_i(f,x)>\sum _{i=1}^{d_u}\unicode{x3bb} ^u_i(A)$
.
$\sum _{i=1}^{d_u}\unicode{x3bb} ^u_i(f,x)>\sum _{i=1}^{d_u}\unicode{x3bb} ^u_i(A)$
.
For
![]() $q\in {\mathbb {N}}\setminus \{0\}$
, we define the set
$q\in {\mathbb {N}}\setminus \{0\}$
, we define the set

Since
![]() $\bigcup _{q=1}^{\infty }Z_q=Z$
, there is a q such that
$\bigcup _{q=1}^{\infty }Z_q=Z$
, there is a q such that
![]() $m(Z_q)>0$
. For any
$m(Z_q)>0$
. For any
![]() $x\in Z_q$
, we have
$x\in Z_q$
, we have

So, there is
![]() $n_0$
such that for
$n_0$
such that for
![]() $n\geq n_0$
, we have
$n\geq n_0$
, we have

So we get

By this fact, for each
![]() $n>0$
, we define the set
$n>0$
, we define the set

So, there is
![]() $N>0$
with
$N>0$
with
![]() $m(Z_{q,N})>0$
.
$m(Z_{q,N})>0$
.
Now for any
![]() $x\in {\mathbb {T}}^d$
, let
$x\in {\mathbb {T}}^d$
, let
![]() $B_x$
be a foliated box of
$B_x$
be a foliated box of
![]() $W^u_{f}$
around x. By compactness, we can take a finite cover
$W^u_{f}$
around x. By compactness, we can take a finite cover
![]() $\{B_{x_i}\}_{i=1}^{j}$
of
$\{B_{x_i}\}_{i=1}^{j}$
of
![]() ${\mathbb {T}}^d$
. As
${\mathbb {T}}^d$
. As
![]() $W^u_f$
is absolutely continuous [Reference Brin and Pesin7], there is i and
$W^u_f$
is absolutely continuous [Reference Brin and Pesin7], there is i and
![]() $x\in B_{x_i}$
such that
$x\in B_{x_i}$
such that
![]() $\mathrm {Vol}_ W^u(f)(B_{x_i}\cap W^u_{f}(x)\cap Z_{q,N})>0$
.
$\mathrm {Vol}_ W^u(f)(B_{x_i}\cap W^u_{f}(x)\cap Z_{q,N})>0$
.
Consider
![]() $B_r(x)\subset W^u_f(x)$
satisfying
$B_r(x)\subset W^u_f(x)$
satisfying
![]() $ {\mathrm {Vol}_{W^u(f)}(B_r(x)\cap Z_{q,N})>0}$
. By Proposition 3.3, there is
$ {\mathrm {Vol}_{W^u(f)}(B_r(x)\cap Z_{q,N})>0}$
. By Proposition 3.3, there is
![]() $K(\epsilon ) \in \mathbb {N}$
such that for all
$K(\epsilon ) \in \mathbb {N}$
such that for all
![]() $k \geq K(\epsilon )$
,
$k \geq K(\epsilon )$
,
 $$ \begin{align} \mathrm{Vol}_{W^u(f)}(f^k(B_r(x)))&\leq (1+\epsilon)^k\mathrm{Vol}_{W^u(A)}(A^k(B_r(x)))\nonumber\\&\leq(1+\epsilon)^k e^{k\sum\unicode{x3bb}^u_i(A)}\mathrm{Vol}_{W^u(A)}(B_r(x)). \end{align} $$
$$ \begin{align} \mathrm{Vol}_{W^u(f)}(f^k(B_r(x)))&\leq (1+\epsilon)^k\mathrm{Vol}_{W^u(A)}(A^k(B_r(x)))\nonumber\\&\leq(1+\epsilon)^k e^{k\sum\unicode{x3bb}^u_i(A)}\mathrm{Vol}_{W^u(A)}(B_r(x)). \end{align} $$
However, for
![]() $k\geq N$
,
$k\geq N$
,

Taking
![]() $\epsilon < {1}/{q},$
for large enough k, the inequalities in equations (3.1) and (3.2) give a contradiction.
$\epsilon < {1}/{q},$
for large enough k, the inequalities in equations (3.1) and (3.2) give a contradiction.
3.1. Proof of Theorem B
We use Theorem 3.1 and the following proposition to conclude the proof of Theorem B.
Proposition 3.4. Let W be a foliation in
![]() ${\mathbb {R}}^d$
of dimension
${\mathbb {R}}^d$
of dimension
![]() $d_u$
. If there is a (
$d_u$
. If there is a (
![]() $d\text {--}d_u$
)-plane P in
$d\text {--}d_u$
)-plane P in
![]() ${\mathbb {R}}^d$
such that
${\mathbb {R}}^d$
such that
![]() $\angle (T_xW,P)>\alpha >0$
for all
$\angle (T_xW,P)>\alpha >0$
for all
![]() $x\in {\mathbb {R}}^d$
, then there is a
$x\in {\mathbb {R}}^d$
, then there is a
![]() $d_u$
-form
$d_u$
-form
![]() $\omega $
which is closed and non-degenerate on W.
$\omega $
which is closed and non-degenerate on W.
Proof. Let B be the orthogonal complement of P, there is always a closed and non-degenerate form in B, in fact, just take the volume form
![]() $\omega =dx_1\wedge dx_2\wedge \cdots \wedge dx_{d_u}$
which is non-degenerate in B and
$\omega =dx_1\wedge dx_2\wedge \cdots \wedge dx_{d_u}$
which is non-degenerate in B and
![]() $\omega $
is closed. Note that
$\omega $
is closed. Note that
![]() $\omega $
is degenerate only in
$\omega $
is degenerate only in
![]() $B^{\bot }=P$
and by hypothesis,
$B^{\bot }=P$
and by hypothesis,
![]() $\angle (T_xW,P)>\alpha >0$
. So,
$\angle (T_xW,P)>\alpha >0$
. So,
![]() $\omega $
is closed and non-degenerate in
$\omega $
is closed and non-degenerate in
![]() $T_xW$
for all
$T_xW$
for all
![]() $x\in {\mathbb {R}}^d$
.
$x\in {\mathbb {R}}^d$
.
Corollary 3.5. If
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
is a linear partially hyperbolic diffeomorphism and f is a
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
is a linear partially hyperbolic diffeomorphism and f is a
![]() $C^2$
conservative diffeomorphism which is a small
$C^2$
conservative diffeomorphism which is a small
![]() $C^1$
-perturbation of A, then
$C^1$
-perturbation of A, then
![]() $\sum _{i=1}^{d_u}\unicode{x3bb} _i^u(f,x)\leq \sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
and
$\sum _{i=1}^{d_u}\unicode{x3bb} _i^u(f,x)\leq \sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
and
![]() $\sum _{i=1}^{d_s}\unicode{x3bb} _i^s(f,x)\geq \sum _{i=1}^{d_s} \unicode{x3bb} _i^s(A)$
for Lebesgue-a.e.
$\sum _{i=1}^{d_s}\unicode{x3bb} _i^s(f,x)\geq \sum _{i=1}^{d_s} \unicode{x3bb} _i^s(A)$
for Lebesgue-a.e.
![]() ${x\in {\mathbb {T}}^d}$
.
${x\in {\mathbb {T}}^d}$
.
3.2. Proof of Theorem A
From [Reference Roldan19, Proposição 3.1.2], we have the following proposition.
Proposition 3.6. [Reference Roldan19]
Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a partially hyperbolic diffeomorphism homotopic to a linear Anosov diffeomorphism A such that:
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a partially hyperbolic diffeomorphism homotopic to a linear Anosov diffeomorphism A such that:
-
(a) each element of the homotopic path is a partially hyperbolic diffeomorphism;
-
(b) if
 $f_1$
and
$f_1$
and
 $f_2$
are two elements of the homotopic path, then
$f_2$
are two elements of the homotopic path, then
 $\mathrm {dim} E^{\sigma }(f_1)=\mathrm {dim} E^{\sigma }(f_2)$
,
$\mathrm {dim} E^{\sigma }(f_1)=\mathrm {dim} E^{\sigma }(f_2)$
,
 $\sigma \in \{s,c,u\},$
$\sigma \in \{s,c,u\},$
then there exists a closed non-degenerate
![]() $d_u$
-form on
$d_u$
-form on
![]() $W^u(f)$
.
$W^u(f)$
.
By the proposition above, f has a
![]() $d_u$
closed and non-degenerate form on
$d_u$
closed and non-degenerate form on
![]() $W^u$
, using the inverse
$W^u$
, using the inverse
![]() $f^{-1}$
, we get a
$f^{-1}$
, we get a
![]() $d_s$
closed and non-degenerate form on
$d_s$
closed and non-degenerate form on
![]() $W^s$
. By Theorem 3.1, we conclude the first part of Theorem A. In the next subsection, we complete the proof.
$W^s$
. By Theorem 3.1, we conclude the first part of Theorem A. In the next subsection, we complete the proof.
3.2.1. Maximizing measures
In this section, we prove the last part of Theorem A. We write all proofs for the unstable bundle.
First, we recall the definition of topological and metric entropy along an expanding foliation. In [Reference Hu, Hua and Wu13], the authors define the notion of topological and metric entropy along unstable foliation and prove the variational principle.
Let
![]() $f\colon M\rightarrow M$
be a
$f\colon M\rightarrow M$
be a
![]() $C^1$
-partially hyperbolic diffeomorphism and
$C^1$
-partially hyperbolic diffeomorphism and
![]() $\mu $
is an f-invariant probability measure. For a partition
$\mu $
is an f-invariant probability measure. For a partition
![]() $\alpha $
of M, denote
$\alpha $
of M, denote
![]() $\alpha _0^{n-1}=\bigvee _{i=0}^{n-1}f^{-i}\alpha $
and by
$\alpha _0^{n-1}=\bigvee _{i=0}^{n-1}f^{-i}\alpha $
and by
![]() $\alpha (x)$
the element of
$\alpha (x)$
the element of
![]() $\alpha $
containing x. Given
$\alpha $
containing x. Given
![]() $\varepsilon>0$
, let
$\varepsilon>0$
, let
![]() $\mathcal {P}=\mathcal {P}_{\varepsilon }$
denote the set of finite measurable partitions of M whose elements have diameters smaller than or equal to
$\mathcal {P}=\mathcal {P}_{\varepsilon }$
denote the set of finite measurable partitions of M whose elements have diameters smaller than or equal to
![]() $\varepsilon $
. For each
$\varepsilon $
. For each
![]() $\alpha \in \mathcal {P}$
, we define a partition
$\alpha \in \mathcal {P}$
, we define a partition
![]() $\eta $
such that
$\eta $
such that
![]() $\eta (x)=\alpha (x)\cap W^u_\mathrm{loc}(x)$
for each
$\eta (x)=\alpha (x)\cap W^u_\mathrm{loc}(x)$
for each
![]() $x \in M$
, where
$x \in M$
, where
![]() $W^u_\mathrm{loc}(x)$
denotes the local unstable manifold at x whose size is greater than the diameter
$W^u_\mathrm{loc}(x)$
denotes the local unstable manifold at x whose size is greater than the diameter
![]() $\varepsilon $
of
$\varepsilon $
of
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\mathcal {P}^u=\mathcal {P}^u_{\varepsilon }$
denote the set of partitions
$\mathcal {P}^u=\mathcal {P}^u_{\varepsilon }$
denote the set of partitions
![]() $\eta $
obtained in this way. We define the conditional entropy of
$\eta $
obtained in this way. We define the conditional entropy of
![]() $\alpha $
given
$\alpha $
given
![]() $\eta $
with respect to
$\eta $
with respect to
![]() $\mu $
by
$\mu $
by
where
![]() $\mu ^{\eta }_{x}$
refer to the disintegration of
$\mu ^{\eta }_{x}$
refer to the disintegration of
![]() $\mu $
along
$\mu $
along
![]() $\eta $
.
$\eta $
.
Definition 3.7. The conditional entropy of f with respect to a measurable partition
![]() $\alpha $
given
$\alpha $
given
![]() $\eta \in \mathcal {P}^u$
is defined as
$\eta \in \mathcal {P}^u$
is defined as
The conditional entropy of f given
![]() $\eta \in \mathcal {P}^u$
is defined as
$\eta \in \mathcal {P}^u$
is defined as
and the unstable metric entropy of f is defined as
Now, we go to define the unstable topological entropy.
We denote by
![]() $\rho ^u$
the metric induced by the Riemannian structure on the unstable manifold and let
$\rho ^u$
the metric induced by the Riemannian structure on the unstable manifold and let
![]() $\rho ^u_n(x,y)=\max _{0\leq j\leq n-1}\rho ^u(f^j(x),f^j(y))$
. Let
$\rho ^u_n(x,y)=\max _{0\leq j\leq n-1}\rho ^u(f^j(x),f^j(y))$
. Let
![]() $W^u(x,\delta )$
be the open ball inside
$W^u(x,\delta )$
be the open ball inside
![]() $W^u(x)$
centred at x of radius
$W^u(x)$
centred at x of radius
![]() $\delta $
with respect to the metric
$\delta $
with respect to the metric
![]() $\rho ^u$
. Let
$\rho ^u$
. Let
![]() $N^u(f,\epsilon ,n,x,\delta )$
be the maximal number of points in
$N^u(f,\epsilon ,n,x,\delta )$
be the maximal number of points in
![]() $\overline {W^u(x,\delta )}$
with pairwise
$\overline {W^u(x,\delta )}$
with pairwise
![]() $\rho ^u_ n$
-distances at least
$\rho ^u_ n$
-distances at least
![]() $\epsilon $
. We call such a set an
$\epsilon $
. We call such a set an
![]() $(n,\epsilon ) u$
-separated set of
$(n,\epsilon ) u$
-separated set of
![]() $\overline {W^u(x,\delta )}$
.
$\overline {W^u(x,\delta )}$
.
Definition 3.8. The unstable topological entropy of f on M is defined by
where
Let
![]() $\mathcal {M}_f(M)$
and
$\mathcal {M}_f(M)$
and
![]() $\mathcal {M}_f^e(M)$
denote the set of all f-invariant and ergodic probability measures on M, respectively.
$\mathcal {M}_f^e(M)$
denote the set of all f-invariant and ergodic probability measures on M, respectively.
Theorem 3.9. [Reference Hu, Hua and Wu13]
Let
![]() $f\colon M\rightarrow M$
be a
$f\colon M\rightarrow M$
be a
![]() $C^1$
-partially hyperbolic diffeomorphism. Then,
$C^1$
-partially hyperbolic diffeomorphism. Then,
Moreover,
Furthermore, the authors proved that unstable topological entropy coincides with unstable volume growth.
Theorem 3.10. [Reference Hu, Hua and Wu13]
Unstable topological entropy coincides with unstable volume growth, i.e.
![]() $h^u_{\mathrm {top}}(f)=\chi _u(f)$
.
$h^u_{\mathrm {top}}(f)=\chi _u(f)$
.
As in the hypotheses of Theorem A, the diffeomorphisms f and A are homotopic, so using Theorem 3.2, we have
Thus,
 $$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x)=h^u_m(f)\leq h^u_{\mathrm{top}}(f)=h^u_{\mathrm{top}}(A)= \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A). \end{align*} $$
$$ \begin{align*} \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(f, x)=h^u_m(f)\leq h^u_{\mathrm{top}}(f)=h^u_{\mathrm{top}}(A)= \sum_{i = 1}^{d_u} \unicode{x3bb}^u_i(A). \end{align*} $$
Then we conclude that
![]() $h^u_m(f)= h^u_{\mathrm {top}}(f)$
.
$h^u_m(f)= h^u_{\mathrm {top}}(f)$
.
3.3. Proof of Theorem C
We remember that
![]() $A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
is a linear Anosov diffeomorphism and
$A\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
is a linear Anosov diffeomorphism and
![]() $0<\unicode{x3bb} <1<\gamma $
are rates for hyperbolicity,
$0<\unicode{x3bb} <1<\gamma $
are rates for hyperbolicity,
![]() $d_s =\mathrm {dim} (E^s_A)$
and
$d_s =\mathrm {dim} (E^s_A)$
and
![]() ${d_u =\mathrm {dim} (E^u_A).}$
Let
${d_u =\mathrm {dim} (E^u_A).}$
Let
![]() $W^s_A, W^u_A$
be the stable and unstable foliation of A and by
$W^s_A, W^u_A$
be the stable and unstable foliation of A and by
![]() $\widetilde {W}^{s}_A$
,
$\widetilde {W}^{s}_A$
,
![]() $\widetilde {W}^{u}_A$
, we denote their lifts to the universal cover
$\widetilde {W}^{u}_A$
, we denote their lifts to the universal cover
![]() $\mathbb {R}^d$
. These foliations are stable and unstable foliations of
$\mathbb {R}^d$
. These foliations are stable and unstable foliations of
![]() $\widetilde {A}$
which is a lift of A. We use ‘
$\widetilde {A}$
which is a lift of A. We use ‘
![]() $\sim $
’ for objects in the universal cover. The norm and distance on
$\sim $
’ for objects in the universal cover. The norm and distance on
![]() $\mathbb {R}^d$
are the lift of adapted norm and corresponding distance where the hyperbolicity conditions of A are satisfied, see §2.2 before the announcement of Theorem C.
$\mathbb {R}^d$
are the lift of adapted norm and corresponding distance where the hyperbolicity conditions of A are satisfied, see §2.2 before the announcement of Theorem C.
Similar to [Reference Hammerlindl12, Proposition 2.5 and Corollary 2.6], we show the following proposition.
Proposition 3.11. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a diffeomorphism that admits a dominated splitting
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a diffeomorphism that admits a dominated splitting
![]() $TM=E\oplus F$
with
$TM=E\oplus F$
with
![]() $\|Df|_E\|\leq \hat {\gamma }<\gamma $
and
$\|Df|_E\|\leq \hat {\gamma }<\gamma $
and
![]() $m(Df|_F) \geq \hat {\unicode{x3bb} }>\unicode{x3bb} $
, homotopic to A such that
$m(Df|_F) \geq \hat {\unicode{x3bb} }>\unicode{x3bb} $
, homotopic to A such that
![]() $\mathrm {dim} (E) =d_s$
and
$\mathrm {dim} (E) =d_s$
and
![]() $\mathrm {dim} (F) =d_u.$
Suppose that the distributions E and F are integrable, and denote by
$\mathrm {dim} (F) =d_u.$
Suppose that the distributions E and F are integrable, and denote by
![]() $\mathcal {E}$
and
$\mathcal {E}$
and
![]() $\mathcal {F}$
their respective tangent foliations, then there is
$\mathcal {F}$
their respective tangent foliations, then there is
![]() $R>0$
such that:
$R>0$
such that:
-
•
 $\mathcal {E}(x)\subset B_{R}(\widetilde {W}^{s}_A(x))$
;
$\mathcal {E}(x)\subset B_{R}(\widetilde {W}^{s}_A(x))$
; -
•
 $\mathcal {F}(x)\subset B_{R}(\widetilde {W}^{u}_A(x))$
,
$\mathcal {F}(x)\subset B_{R}(\widetilde {W}^{u}_A(x))$
,
where
![]() $B_{R}(\widetilde {W}^{s}_A(x)) \subset \mathbb {R}^d$
is the set of points which are at distance R from
$B_{R}(\widetilde {W}^{s}_A(x)) \subset \mathbb {R}^d$
is the set of points which are at distance R from
![]() $W^s_A(x)$
. Use a similar definition for
$W^s_A(x)$
. Use a similar definition for
![]() $B_{R}(\widetilde {W}^{u}_A(x)).$
$B_{R}(\widetilde {W}^{u}_A(x)).$
Corollary 3.12. Fixing
![]() $x \in \mathbb {R}^n$
, if
$x \in \mathbb {R}^n$
, if
![]() $ \|x-y\|\rightarrow \infty $
and
$ \|x-y\|\rightarrow \infty $
and
![]() $y\in \mathcal {E}(x)$
, then
$y\in \mathcal {E}(x)$
, then
![]() $({x-y})/{\|x-y\|}\rightarrow \widetilde {E}^{s}_A(x)$
uniformly. More precisely, for
$({x-y})/{\|x-y\|}\rightarrow \widetilde {E}^{s}_A(x)$
uniformly. More precisely, for
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $M>0$
such that if
$M>0$
such that if
![]() $x\in {\mathbb {R}}^d$
,
$x\in {\mathbb {R}}^d$
,
![]() $y\in \mathcal {E}(x)$
and
$y\in \mathcal {E}(x)$
and
![]() $\|x-y\|>M$
, then
$\|x-y\|>M$
, then
where
![]() $\pi _A^{s}$
is the orthogonal projection on the subspace
$\pi _A^{s}$
is the orthogonal projection on the subspace
![]() $E^s_A$
along
$E^s_A$
along
![]() $E^u_A$
, and
$E^u_A$
, and
![]() $\pi _A^{u}$
is the projection on the subspace
$\pi _A^{u}$
is the projection on the subspace
![]() $E^{u}_A$
along
$E^{u}_A$
along
![]() $E^s_A.$
$E^s_A.$
Analogous statements hold for
![]() $\mathcal {F}$
. The following proposition is a topological remark (see [Reference Hammerlindl12]) and comes from the fact that f and A are homotopic and A is not singular.
$\mathcal {F}$
. The following proposition is a topological remark (see [Reference Hammerlindl12]) and comes from the fact that f and A are homotopic and A is not singular.
Proposition 3.13. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a homeomorphism with linearization A, then for each
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
be a homeomorphism with linearization A, then for each
![]() $k \in {\mathbb {Z}}$
and
$k \in {\mathbb {Z}}$
and
![]() $C>1$
, there is an
$C>1$
, there is an
![]() $M>0$
such that for all
$M>0$
such that for all
![]() $x,y\in {\mathbb {R}}^d$
,
$x,y\in {\mathbb {R}}^d$
,
 $$ \begin{align*} \|x-y\|>M \Rightarrow \frac{1}{C}<\frac{\|\tilde{f}^k(x)-\tilde{f}^k(y)\|}{\|\tilde{A}^k(x)-\tilde{A}^k(y)\|}<C. \end{align*} $$
$$ \begin{align*} \|x-y\|>M \Rightarrow \frac{1}{C}<\frac{\|\tilde{f}^k(x)-\tilde{f}^k(y)\|}{\|\tilde{A}^k(x)-\tilde{A}^k(y)\|}<C. \end{align*} $$
More generally, for each
![]() $k\in {\mathbb {Z}}$
,
$k\in {\mathbb {Z}}$
,
![]() $C>1$
and any linear projection
$C>1$
and any linear projection
![]() $\pi \colon {\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$
, with A-invariant image, there is
$\pi \colon {\mathbb {R}}^d\rightarrow {\mathbb {R}}^d$
, with A-invariant image, there is
![]() $M> 0$
such that for
$M> 0$
such that for
![]() $x,y\in {\mathbb {R}}^d$
, with
$x,y\in {\mathbb {R}}^d$
, with
![]() $\|x-y\|>M$
,
$\|x-y\|>M$
,
 $$ \begin{align*} \frac{1}{C}<\frac{\|\pi(\tilde{f}^k(x)-\tilde{f}^k(y))\|}{\|\pi(\tilde{A}^k(x)-\tilde{A}^k(y))\|}<C. \end{align*} $$
$$ \begin{align*} \frac{1}{C}<\frac{\|\pi(\tilde{f}^k(x)-\tilde{f}^k(y))\|}{\|\pi(\tilde{A}^k(x)-\tilde{A}^k(y))\|}<C. \end{align*} $$
Proof of Proposition 3.11
To prove the first claim (the second one is similar), it is enough to show that
![]() $\|\pi ^u_A(x-y)\|$
is uniformly bounded for all
$\|\pi ^u_A(x-y)\|$
is uniformly bounded for all
![]() $y\in \mathcal {E}(x)$
. Let
$y\in \mathcal {E}(x)$
. Let
![]() $C>1$
close enough to
$C>1$
close enough to
![]() $1$
such that
$1$
such that
![]() $C \hat {\gamma } < \gamma $
and
$C \hat {\gamma } < \gamma $
and
![]() $1 < {\gamma }/{C}.$
Put
$1 < {\gamma }/{C}.$
Put
![]() $k=1$
and C chosen as above in Proposition 3.13, and get appropriate M. By contradiction, suppose that
$k=1$
and C chosen as above in Proposition 3.13, and get appropriate M. By contradiction, suppose that
![]() $\|\pi ^u_A(x-y)\|$
is not bounded. So, there is
$\|\pi ^u_A(x-y)\|$
is not bounded. So, there is
![]() $y\in \mathcal {E}(x)$
with
$y\in \mathcal {E}(x)$
with
![]() $\|\pi ^u_A(x-y)\|>M$
and consequently,
$\|\pi ^u_A(x-y)\|>M$
and consequently,
which implies that we can use induction and for any
![]() $n \geq 1$
, obtain
$n \geq 1$
, obtain
Finally, there is a constant
![]() $\eta> 0$
such that
$\eta> 0$
such that
Now consider a smooth curve
![]() $\alpha \colon [a,b]\rightarrow \mathcal {E}(x)$
with
$\alpha \colon [a,b]\rightarrow \mathcal {E}(x)$
with
![]() $\alpha (a)=x$
and
$\alpha (a)=x$
and
![]() $\alpha (b)=y$
whose length is
$\alpha (b)=y$
whose length is
![]() $d_{\mathcal {E}}(x,y)$
. Then,
$d_{\mathcal {E}}(x,y)$
. Then,
 $$ \begin{align*} \|\tilde{f}^{n}(x)-\tilde{f}^{n}(y)\|&\leq d_{\mathcal{E}}(\tilde{f}^{n}(x),\tilde{f}^{n}(y))\leq l(\tilde{f}^{n}(\alpha(t))) =\int_a^b\bigg\|\frac{d}{dt}(\tilde{f}^{n}(\alpha(t))\bigg\|\,dt\\ &\leq \int_a^b\|D\tilde{f}^{n}|_{W^{cs}}\|\cdot\|(\alpha'(t))\|\,dt< \int_a^b\hat{\gamma}^{n} \|\alpha'(t)\|\,dt, \end{align*} $$
$$ \begin{align*} \|\tilde{f}^{n}(x)-\tilde{f}^{n}(y)\|&\leq d_{\mathcal{E}}(\tilde{f}^{n}(x),\tilde{f}^{n}(y))\leq l(\tilde{f}^{n}(\alpha(t))) =\int_a^b\bigg\|\frac{d}{dt}(\tilde{f}^{n}(\alpha(t))\bigg\|\,dt\\ &\leq \int_a^b\|D\tilde{f}^{n}|_{W^{cs}}\|\cdot\|(\alpha'(t))\|\,dt< \int_a^b\hat{\gamma}^{n} \|\alpha'(t)\|\,dt, \end{align*} $$
implies that
Equations (3.3) and (3.4) and
![]() ${\gamma }/{C}> \hat {\gamma }$
give us a contradiction when n is large enough.
${\gamma }/{C}> \hat {\gamma }$
give us a contradiction when n is large enough.
Proposition 3.14. Let
![]() $f\colon M\rightarrow M$
be a
$f\colon M\rightarrow M$
be a
![]() $C^2$
conservative non-uniformly Anosov diffeomorphism with
$C^2$
conservative non-uniformly Anosov diffeomorphism with
![]() $TM = E \oplus F$
. If the distribution E is integrable, then the respective foliation
$TM = E \oplus F$
. If the distribution E is integrable, then the respective foliation
![]() $\mathcal {E}$
is upper leafwise absolutely continuous.
$\mathcal {E}$
is upper leafwise absolutely continuous.
Let
![]() $\mathcal {R}$
be the regular set in Pesin sense such that
$\mathcal {R}$
be the regular set in Pesin sense such that
![]() $m(\mathcal {R}) = 1$
and
$m(\mathcal {R}) = 1$
and
![]() $\mathcal {R} = \bigcup _{l=1}^{\infty } \mathcal {R}_l$
is the union of Pesin’s block where
$\mathcal {R} = \bigcup _{l=1}^{\infty } \mathcal {R}_l$
is the union of Pesin’s block where
![]() $m(\mathcal {R}_l) \rightarrow 1, \mathcal {R}_l \subset \mathcal {R}_{l+1}.$
Moreover, the size of Pesin stable manifolds of points in
$m(\mathcal {R}_l) \rightarrow 1, \mathcal {R}_l \subset \mathcal {R}_{l+1}.$
Moreover, the size of Pesin stable manifolds of points in
![]() $\mathcal {R}_l$
is larger than some positive constant
$\mathcal {R}_l$
is larger than some positive constant
![]() $r_l.$
In general,
$r_l.$
In general,
![]() $r_l \rightarrow 0$
when
$r_l \rightarrow 0$
when
![]() $l \rightarrow \infty .$
We use an absolute continuity result due to Pesin [Reference Barreira and Pesin2, Theorem 4.3.1] which essentially shows the absolute continuity of Pesin’s stable laminations in each block.
$l \rightarrow \infty .$
We use an absolute continuity result due to Pesin [Reference Barreira and Pesin2, Theorem 4.3.1] which essentially shows the absolute continuity of Pesin’s stable laminations in each block.
Proof of Proposition 3.14
Suppose by contraction that
![]() $\mathcal {E}$
is not upper leafwise absolutely continuous. So, there exist a foliated box B and a set
$\mathcal {E}$
is not upper leafwise absolutely continuous. So, there exist a foliated box B and a set
![]() $Z\subset B$
with
$Z\subset B$
with
![]() $\mathrm {Vol}_{\mathcal {E}}(Z\cap \mathcal {E}(x))=0$
for m-a.e.
$\mathrm {Vol}_{\mathcal {E}}(Z\cap \mathcal {E}(x))=0$
for m-a.e.
![]() $x \in B$
and
$x \in B$
and
![]() $m(Z)>0$
. There exists
$m(Z)>0$
. There exists
![]() $l \geq 1$
such that
$l \geq 1$
such that
![]() $m(Z \cap \mathcal {R}_l)> 0.$
Take a Lebesgue density point
$m(Z \cap \mathcal {R}_l)> 0.$
Take a Lebesgue density point
![]() $z\in Z\cap \mathcal {R}_l$
such that for V a small neighbourhood of z, we have
$z\in Z\cap \mathcal {R}_l$
such that for V a small neighbourhood of z, we have
![]() $m(Z \cap \mathcal {R}_l \cap V)> 0.$
$m(Z \cap \mathcal {R}_l \cap V)> 0.$
As Pesin stable manifolds are contained in the leaves of
![]() $\mathcal {E}$
, our assumption
$\mathcal {E}$
, our assumption
![]() $\mathrm {Vol}_{\mathcal {E}}(Z\cap \mathcal {E}(x))=0$
and upper leafwise absolute continuity of stable manifolds imply that Z has zero measure with respect to conditional measures of m along Pesin stable manifolds in
$\mathrm {Vol}_{\mathcal {E}}(Z\cap \mathcal {E}(x))=0$
and upper leafwise absolute continuity of stable manifolds imply that Z has zero measure with respect to conditional measures of m along Pesin stable manifolds in
![]() $\mathcal {R}_l$
.) Hence,
$\mathcal {R}_l$
.) Hence,
![]() $m(Z \cap \mathcal {R}_l \cap V) = 0$
, which is a contradiction.
$m(Z \cap \mathcal {R}_l \cap V) = 0$
, which is a contradiction.
Fix
![]() $x\in \mathbb {R}^n$
and denote by
$x\in \mathbb {R}^n$
and denote by
![]() $U_r\subset \widetilde {W}^u_A (x)$
the ball of radius r with centre x.
$U_r\subset \widetilde {W}^u_A (x)$
the ball of radius r with centre x.
Proposition 3.15. Let
![]() $f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
as in Theorem C, then given
$f\colon {\mathbb {T}}^d\rightarrow {\mathbb {T}}^d$
as in Theorem C, then given
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $r_0>0$
and a constant
$r_0>0$
and a constant
![]() $C_0>0$
such that
$C_0>0$
such that
for all
![]() $n>0$
and
$n>0$
and
![]() $r \geq r_0$
, where
$r \geq r_0$
, where
![]() $\pi _z$
is the orthogonal projection from
$\pi _z$
is the orthogonal projection from
![]() $\mathcal {F}(z)$
to
$\mathcal {F}(z)$
to
![]() $\widetilde {W}_A^u(z)$
(along
$\widetilde {W}_A^u(z)$
(along
![]() $\widetilde {E}_A^s$
) for any
$\widetilde {E}_A^s$
) for any
![]() $z \in \mathbb {R}^n$
.
$z \in \mathbb {R}^n$
.
Proof of Proposition 3.15
We prove the following claims.
Claim 1. For
![]() $z\in {\mathbb {R}}^d$
, the orthogonal projection
$z\in {\mathbb {R}}^d$
, the orthogonal projection
![]() $\pi _z\colon \mathcal {F}(z)\rightarrow \widetilde {W}^u_A(z)$
is a uniform bi-Lipschitz diffeomorphism.
$\pi _z\colon \mathcal {F}(z)\rightarrow \widetilde {W}^u_A(z)$
is a uniform bi-Lipschitz diffeomorphism.
Proof of Claim 1
By item (2) of Theorem C and continuity of E and F, there is
![]() $\alpha>0$
such that the angle
$\alpha>0$
such that the angle
![]() $\angle (E,E^u_A)>\alpha $
and
$\angle (E,E^u_A)>\alpha $
and
![]() $\angle (F, E^s_A)>\alpha .$
So
$\angle (F, E^s_A)>\alpha .$
So
![]() $\widetilde {W}_A^s$
is uniformly transversal to the foliation
$\widetilde {W}_A^s$
is uniformly transversal to the foliation
![]() $\mathcal {F}$
and there is
$\mathcal {F}$
and there is
![]() $\beta>0$
such that
$\beta>0$
such that
for any
![]() $x\in \mathcal {F}(z)$
and
$x\in \mathcal {F}(z)$
and
![]() $v\in T_x\mathcal {F}(z)$
. This implies that
$v\in T_x\mathcal {F}(z)$
. This implies that
![]() $\mathrm {Jac} \pi _z(x)\neq 0$
. By the inverse function theorem, for each
$\mathrm {Jac} \pi _z(x)\neq 0$
. By the inverse function theorem, for each
![]() $x\in \mathcal {F}(z)$
, there is a ball
$x\in \mathcal {F}(z)$
, there is a ball
![]() $B(x, \delta )\subset \mathcal {F}(z)$
such that
$B(x, \delta )\subset \mathcal {F}(z)$
such that
![]() $\pi _z|_{B(x, \delta )}$
is a diffeomorphism. In fact, from the proof of the inverse function theorem and equation (3.5),
$\pi _z|_{B(x, \delta )}$
is a diffeomorphism. In fact, from the proof of the inverse function theorem and equation (3.5),
![]() $\delta $
can be taken independent of x. Again, by equation (3.5), there is
$\delta $
can be taken independent of x. Again, by equation (3.5), there is
![]() $\varepsilon>0$
, independent of x such that
$\varepsilon>0$
, independent of x such that
![]() $B(\pi _z(x), \varepsilon )\subset \pi _z(B(x, \delta ))$
. To prove that
$B(\pi _z(x), \varepsilon )\subset \pi _z(B(x, \delta ))$
. To prove that
![]() $\pi _z$
is surjective, we show that
$\pi _z$
is surjective, we show that
![]() $\pi _z(\mathcal {F}(z))$
is an open and closed subset. As
$\pi _z(\mathcal {F}(z))$
is an open and closed subset. As
![]() $\pi _z$
is a local homeomorphism, then
$\pi _z$
is a local homeomorphism, then
![]() $\pi _z(\mathcal {F}(z))$
is open. To verify that it is also closed, let
$\pi _z(\mathcal {F}(z))$
is open. To verify that it is also closed, let
![]() $y_n\in \pi _z(\mathcal {F}(z))$
be a sequence converging to y, and hence there is
$y_n\in \pi _z(\mathcal {F}(z))$
be a sequence converging to y, and hence there is
![]() $n_0$
large enough such that
$n_0$
large enough such that
![]() $y\in B(\varepsilon ,y_{n_0})$
and, therefore,
$y\in B(\varepsilon ,y_{n_0})$
and, therefore,
![]() $y\in {\pi _z}(\mathcal {F}(z))$
. So,
$y\in {\pi _z}(\mathcal {F}(z))$
. So,
![]() $\pi _z$
is surjective. Moreover,
$\pi _z$
is surjective. Moreover,
![]() $\pi _z$
is a covering map and injectivity follows from the fact that any covering map from a path-connected space to a simply connected space is a homeomorphism.
$\pi _z$
is a covering map and injectivity follows from the fact that any covering map from a path-connected space to a simply connected space is a homeomorphism.
Let us prove that
![]() $\pi _z$
is bi-Lipschitz. In fact,
$\pi _z$
is bi-Lipschitz. In fact,
Let us show that
![]() $\pi _z^{-1}$
is also Lipschitz. This is immediate from equation (3.5). Indeed, let
$\pi _z^{-1}$
is also Lipschitz. This is immediate from equation (3.5). Indeed, let
![]() $[x,y]$
be the line segment in
$[x,y]$
be the line segment in
![]() $\widetilde {W}^u_A (z)$
connecting x to
$\widetilde {W}^u_A (z)$
connecting x to
![]() $y,$
so the set
$y,$
so the set
![]() $\pi _z^{-1}([x,y])=\Gamma $
is a smooth curve connecting the points
$\pi _z^{-1}([x,y])=\Gamma $
is a smooth curve connecting the points
![]() $\pi _z^{-1}(x)$
and
$\pi _z^{-1}(x)$
and
![]() $\pi _z^{-1}(y)$
in
$\pi _z^{-1}(y)$
in
![]() $\mathcal {F}(z)$
. So,
$\mathcal {F}(z)$
. So,
 $$ \begin{align*} d_{\mathcal{F}}(\pi_z^{-1}(x),\pi_z^{-1}(y))\leq \mathrm{length}\,(\Gamma)=\int_{[x,y]}|d\pi_z^{-1}(t)|\,dt\leq \frac{1}{\beta}\|x-y\|.\\[-42pt] \end{align*} $$
$$ \begin{align*} d_{\mathcal{F}}(\pi_z^{-1}(x),\pi_z^{-1}(y))\leq \mathrm{length}\,(\Gamma)=\int_{[x,y]}|d\pi_z^{-1}(t)|\,dt\leq \frac{1}{\beta}\|x-y\|.\\[-42pt] \end{align*} $$
Claim 2. Given
![]() $\varepsilon>0$
, there is
$\varepsilon>0$
, there is
![]() $r_0> 0$
such that
$r_0> 0$
such that
![]() $\tilde {f}^n(\pi _x^{-1}(U_r)) \subset \pi _{\tilde {f}^n(x)}^{-1}(U_{r, n})$
for every
$\tilde {f}^n(\pi _x^{-1}(U_r)) \subset \pi _{\tilde {f}^n(x)}^{-1}(U_{r, n})$
for every
![]() $r \geq r_0$
and
$r \geq r_0$
and
![]() $n \geq 1,$
where
$n \geq 1,$
where
![]() $U_{r, n} \subset \widetilde {W}_A^u (\tilde {f}^n(x))$
is a
$U_{r, n} \subset \widetilde {W}_A^u (\tilde {f}^n(x))$
is a
![]() $d_u$
-dimensional ellipsoid with volume bounded above by
$d_u$
-dimensional ellipsoid with volume bounded above by
![]() $(1+\epsilon )^{nd_u} \mathrm {Vol}_{\tilde {W}_A^u}(A^n(U_r)).$
$(1+\epsilon )^{nd_u} \mathrm {Vol}_{\tilde {W}_A^u}(A^n(U_r)).$
Proof. Let
![]() $ r \geq r_0 := ({2R+2K})/{\varepsilon m(A|_{E^u})}$
, where R comes from Proposition 3.11 and
$ r \geq r_0 := ({2R+2K})/{\varepsilon m(A|_{E^u})}$
, where R comes from Proposition 3.11 and
![]() $\|\tilde {f}- \tilde {A}\|_{\infty } \leq K.$
We prove that
$\|\tilde {f}- \tilde {A}\|_{\infty } \leq K.$
We prove that
where
![]() $U_{r,1} \subset \widetilde {W}^u_A(\tilde {f}(x))$
is obtained from
$U_{r,1} \subset \widetilde {W}^u_A(\tilde {f}(x))$
is obtained from
![]() $\tilde {A}(U_r)$
by first applying a homothety of ratio
$\tilde {A}(U_r)$
by first applying a homothety of ratio
![]() $(1+\epsilon )$
centred at
$(1+\epsilon )$
centred at
![]() $\tilde {A}(x)$
and then translating by
$\tilde {A}(x)$
and then translating by
![]() $\tilde {f}(x) - \tilde {A}(x)$
. Observe that
$\tilde {f}(x) - \tilde {A}(x)$
. Observe that
![]() $U_{r, 1}$
is an ellipsoid inside the affine
$U_{r, 1}$
is an ellipsoid inside the affine
![]() $d_u$
dimensional subspace passing through
$d_u$
dimensional subspace passing through
![]() $\tilde {f}(x).$
Take any y on the boundary of
$\tilde {f}(x).$
Take any y on the boundary of
![]() $U_r$
. Let
$U_r$
. Let
![]() $z:=\pi _{\tilde {f}(x)}(\tilde {f}(\pi _x^{-1}(y))) \in \widetilde {W}^u_A(\tilde {f}(x))$
. On the one hand, we have
$z:=\pi _{\tilde {f}(x)}(\tilde {f}(\pi _x^{-1}(y))) \in \widetilde {W}^u_A(\tilde {f}(x))$
. On the one hand, we have
On the other hand,
 $$ \begin{align} \| z - \tilde{A}(y) \| &\leq \|z - \tilde{f}(\pi_x^{-1}(y))\| + \| \tilde{f}(\pi_x^{-1}(y))-\tilde{A}(\pi_x^{-1}(y)) \| \nonumber\\ &\quad+ \| \tilde{A}(\pi_x^{-1}(y)) - \tilde{A}(y) \| \nonumber\\ & \leq 2R+K. \end{align} $$
$$ \begin{align} \| z - \tilde{A}(y) \| &\leq \|z - \tilde{f}(\pi_x^{-1}(y))\| + \| \tilde{f}(\pi_x^{-1}(y))-\tilde{A}(\pi_x^{-1}(y)) \| \nonumber\\ &\quad+ \| \tilde{A}(\pi_x^{-1}(y)) - \tilde{A}(y) \| \nonumber\\ & \leq 2R+K. \end{align} $$
In the above inequalities, we have used Proposition 3.11 two times to get
(observe that
![]() $y - \pi _x^{-1}(y)$
belongs to the stable subspace of A) and finally
$y - \pi _x^{-1}(y)$
belongs to the stable subspace of A) and finally
Now, putting the inequalities in equations (3.7) and (3.8) together, we get
Observe that
![]() $\tilde {A}(y) + \tilde {f}(x)- \tilde {A}(x)$
is the translation of the
$\tilde {A}(y) + \tilde {f}(x)- \tilde {A}(x)$
is the translation of the
![]() $\tilde {A}(y)$
and belongs to
$\tilde {A}(y)$
and belongs to
![]() $\widetilde {W}_A^u(\tilde {f}(x)).$
Indeed,
$\widetilde {W}_A^u(\tilde {f}(x)).$
Indeed,
![]() $\tilde {A}(y)- \tilde {A}(x)$
is a vector which belongs to the unstable bundle of
$\tilde {A}(y)- \tilde {A}(x)$
is a vector which belongs to the unstable bundle of
![]() $\tilde {A}$
and we identify the unstable bundle at
$\tilde {A}$
and we identify the unstable bundle at
![]() $\tilde {f}(x)$
with the corresponding affine subspace of
$\tilde {f}(x)$
with the corresponding affine subspace of
![]() $\mathbb {R}^n$
passing through
$\mathbb {R}^n$
passing through
![]() $\tilde {f}(x)$
. Now, as the distance between
$\tilde {f}(x)$
. Now, as the distance between
![]() $(1+\epsilon ) \tilde {A}(U_r) $
and
$(1+\epsilon ) \tilde {A}(U_r) $
and
![]() $ \tilde {A}(U_r)$
is
$ \tilde {A}(U_r)$
is
![]() $ \epsilon r m(\tilde {A}|_{E^u}) \geq 2R + 2K$
(by the choice of r), we conclude that z belongs to the ellipsoid
$ \epsilon r m(\tilde {A}|_{E^u}) \geq 2R + 2K$
(by the choice of r), we conclude that z belongs to the ellipsoid
![]() $U_{r, 1} :=(\tilde {f}(x)- \tilde {A}(x)) + (1+\epsilon ) \tilde {A}(U_r)$
which proves equation (3.6). Moreover, observe that
$U_{r, 1} :=(\tilde {f}(x)- \tilde {A}(x)) + (1+\epsilon ) \tilde {A}(U_r)$
which proves equation (3.6). Moreover, observe that
![]() $\mathrm {Vol}_{\widetilde {W}^u_A} (U_{r, 1}) =(1+\epsilon )^{d_u} \mathrm {Vol}_{\widetilde {W}^u_A}(\tilde {A}(U_r)) = (1+\epsilon )^{d_u} e^{\sum _{i=1}^{d_u} \unicode{x3bb} ^u_i(A)} \mathrm {Vol}_{\widetilde {W}^u_A} (U_r).$
$\mathrm {Vol}_{\widetilde {W}^u_A} (U_{r, 1}) =(1+\epsilon )^{d_u} \mathrm {Vol}_{\widetilde {W}^u_A}(\tilde {A}(U_r)) = (1+\epsilon )^{d_u} e^{\sum _{i=1}^{d_u} \unicode{x3bb} ^u_i(A)} \mathrm {Vol}_{\widetilde {W}^u_A} (U_r).$

Figure 1 Volume comparison.
Now we apply again
![]() $\tilde {f}$
and obtain
$\tilde {f}$
and obtain
As the distance between
![]() $\tilde {A}(U_{r, 1})$
and
$\tilde {A}(U_{r, 1})$
and
![]() $(1+\epsilon )\tilde {A}(U_{r, 1})$
is larger than
$(1+\epsilon )\tilde {A}(U_{r, 1})$
is larger than
![]() $\varepsilon r m(\tilde {A}|_{E^u})$
, similarly as above, we obtain
$\varepsilon r m(\tilde {A}|_{E^u})$
, similarly as above, we obtain
where
![]() $U_{r, 2}$
is a translation of
$U_{r, 2}$
is a translation of
![]() $(1+\varepsilon )^2 \tilde {A}^2(U_r).$
In fact, inductively, we obtain
$(1+\varepsilon )^2 \tilde {A}^2(U_r).$
In fact, inductively, we obtain
where
![]() $U_{r, n+1}$
is an ellipsoid with volume less than
$U_{r, n+1}$
is an ellipsoid with volume less than
![]() $(1+\varepsilon )^{(n+1)d_u} e^{(n+1) \sum _{i=1}^{d_u} \unicode{x3bb} ^u_i(A)} \mathrm {Vol}_{\tilde {W}_A^u} (U_r).$
The last inclusion in equation (3.9) follows using the same arguments as above to prove equation (3.6) substituting the ball
$(1+\varepsilon )^{(n+1)d_u} e^{(n+1) \sum _{i=1}^{d_u} \unicode{x3bb} ^u_i(A)} \mathrm {Vol}_{\tilde {W}_A^u} (U_r).$
The last inclusion in equation (3.9) follows using the same arguments as above to prove equation (3.6) substituting the ball
![]() $U_r$
by the ellipsoid
$U_r$
by the ellipsoid
![]() $U_{r, n}.$
$U_{r, n}.$
By Claim 1, for all
![]() $x\in M$
, we have
$x\in M$
, we have
![]() $|\mathrm {Jac}\, \pi ^{-1}_x|$
is uniformly bounded and, consequently, there is a constant
$|\mathrm {Jac}\, \pi ^{-1}_x|$
is uniformly bounded and, consequently, there is a constant
![]() $C_0>0$
such that
$C_0>0$
such that
It concludes the proof of the Proposition 3.15 (see Figure 1).
Proof of Theorem C
Suppose by contradiction that there is a positive volume set
![]() $Z\subset {\mathbb {T}}^d$
such that
$Z\subset {\mathbb {T}}^d$
such that
![]() $\sum _{i=1}^{d_u}\unicode{x3bb} _i^{cu}(f,x)>\sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
for any
$\sum _{i=1}^{d_u}\unicode{x3bb} _i^{cu}(f,x)>\sum _{i=1}^{d_u}\unicode{x3bb} _i^u(A)$
for any
![]() $x\in Z$
.
$x\in Z$
.
Let
![]() $P\colon {\mathbb {R}}^d\rightarrow {\mathbb {T}}^d$
be the covering map,
$P\colon {\mathbb {R}}^d\rightarrow {\mathbb {T}}^d$
be the covering map,
![]() $D\subset {\mathbb {R}}^d$
a fundamental domain and
$D\subset {\mathbb {R}}^d$
a fundamental domain and
![]() ${\widetilde {Z}=P^{-1}(Z)\cap D}$
. We have
${\widetilde {Z}=P^{-1}(Z)\cap D}$
. We have
![]() $\mathrm {Vol}(\widetilde {Z})>0$
.
$\mathrm {Vol}(\widetilde {Z})>0$
.
For each
![]() $q\in {\mathbb {N}}\setminus \{0\}$
, we define the set
$q\in {\mathbb {N}}\setminus \{0\}$
, we define the set

We have
![]() $\bigcup _{q=1}^{\infty }Z_q=\widetilde {Z}$
, and thus there is q such that
$\bigcup _{q=1}^{\infty }Z_q=\widetilde {Z}$
, and thus there is q such that
![]() $m(Z_q)>0$
. For each
$m(Z_q)>0$
. For each
![]() $x\in Z_q$
, it follows that
$x\in Z_q$
, it follows that

So there is
![]() $n_0$
such that for
$n_0$
such that for
![]() $n\geq n_0$
, we have
$n\geq n_0$
, we have

This implies that

For every
![]() $n>0$
, we define
$n>0$
, we define

There is
![]() $N>0$
with
$N>0$
with
![]() $\mathrm {Vol}(Z_{q,N})>0$
.
$\mathrm {Vol}(Z_{q,N})>0$
.
For each
![]() $x\in D$
, consider
$x\in D$
, consider
![]() $B_x\subset {\mathbb {R}}^d$
a foliated box of
$B_x\subset {\mathbb {R}}^d$
a foliated box of
![]() $\mathcal {F}.$
By compactness, there is finite cover
$\mathcal {F}.$
By compactness, there is finite cover
![]() $\{B_{x_i}\}_{i=1}^{j}$
covering
$\{B_{x_i}\}_{i=1}^{j}$
covering
![]() $\overline {D}.$
Since
$\overline {D}.$
Since
![]() $W^{cu}_f$
is absolutely continuous and the covering map is smooth, then
$W^{cu}_f$
is absolutely continuous and the covering map is smooth, then
![]() $\mathcal {F}$
is absolutely continuous, and thus there is some i and
$\mathcal {F}$
is absolutely continuous, and thus there is some i and
![]() $p\in B_{x_i}$
such that
$p\in B_{x_i}$
such that
![]() $\mathrm {Vol}_{\mathcal {F}}(B_{x_i}\cap \mathcal {F}(p)\cap Z_{q,N})>0$
.
$\mathrm {Vol}_{\mathcal {F}}(B_{x_i}\cap \mathcal {F}(p)\cap Z_{q,N})>0$
.
There is a set
![]() $\pi _p^{-1}(U_r)\subset \mathcal {F}(p)$
, where
$\pi _p^{-1}(U_r)\subset \mathcal {F}(p)$
, where
![]() $\pi _p^{-1}(U_r)$
is as in Proposition 3.15 containing p and r is large enough such that
$\pi _p^{-1}(U_r)$
is as in Proposition 3.15 containing p and r is large enough such that
![]() $\mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)\cap Z_{q,N})>0.$
Let
$\mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)\cap Z_{q,N})>0.$
Let
![]() $\alpha>0$
be such that
$\alpha>0$
be such that
![]() $\mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)\cap Z_{q,N})=\alpha \mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)),$
and by Proposition 3.15, we have
$\mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)\cap Z_{q,N})=\alpha \mathrm {Vol}_{\mathcal {F}}(\pi _p^{-1}(U_r)),$
and by Proposition 3.15, we have
However,

Equations (3.10) and (3.11) give us a contradiction when n is large enough, and thus prove Theorem C.
Acknowledgements
J.S.C. was supported by CAPES-PROEX and CNPq process 141224/2013-4. A.T. was supported by the FAPESP thematic project 2017/06463-3 and the CNPq productivity fellowship.