Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hamenstädt, Ursula
1994.
Regularity at infinity of compact negatively curved manifolds.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 3,
p.
493.
Ledrappier, François
1995.
Proceedings of the International Congress of Mathematicians.
p.
1195.
Hamenstädt, Ursula
1995.
Invariant two-forms for geodesic flows.
Mathematische Annalen,
Vol. 301,
Issue. 1,
p.
677.
Hasselblatt, Boris
2002.
Vol. 1,
Issue. ,
p.
239.
MERRY, WILL J.
and
PATERNAIN, GABRIEL P.
2010.
STABILITY OF ANOSOV HAMILTONIAN STRUCTURES.
Journal of Topology and Analysis,
Vol. 02,
Issue. 04,
p.
419.
Foulon, Patrick
and
Hasselblatt, Boris
2013.
Contact Anosov flows on hyperbolic 3–manifolds.
Geometry & Topology,
Vol. 17,
Issue. 2,
p.
1225.
Butt, Karen
2024.
Approximate rigidity of the marked length spectrum.
Mathematics Research Reports,
Vol. 4,
Issue. ,
p.
63.


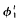 (resp.
(resp. 