Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fu, Jianxun
and
Yang, Fei
2015.
On the dynamics of a family of singularly perturbed rational maps.
Journal of Mathematical Analysis and Applications,
Vol. 424,
Issue. 1,
p.
104.
Xiao, Yingqing
and
Yang, Fei
2017.
Singular Perturbations with Multiple Poles of the Simple Polynomials.
Qualitative Theory of Dynamical Systems,
Vol. 16,
Issue. 3,
p.
731.
LU, ZHIXING
SUN, YUANYUAN
and
HU, XIAOPENG
2017.
PERIOD REGION DISTRIBUTIONS OF MCMULLEN FAMILY M SETS.
Fractals,
Vol. 25,
Issue. 04,
p.
1740012.
XIAO, YINGQING
and
YANG, FEI
2017.
Singular perturbations of the unicritical polynomials with two parameters.
Ergodic Theory and Dynamical Systems,
Vol. 37,
Issue. 6,
p.
1997.
Gao, Yan
Zeng, Jinsong
and
Zhao, Suo
2017.
A characterization of Sierpiński carpet rational maps.
Discrete & Continuous Dynamical Systems - A,
Vol. 37,
Issue. 9,
p.
5049.
Yang, Fei
2017.
A criterion to generate carpet Julia sets.
Proceedings of the American Mathematical Society,
Vol. 146,
Issue. 5,
p.
2129.
Hu, Jun
and
Etkin, Arkady
2020.
Julia Sets of Cubic Rational Maps with Escaping Critical Points.
Arnold Mathematical Journal,
Vol. 6,
Issue. 3-4,
p.
431.
Wang, Youming
and
Yang, Fei
2020.
Julia sets as buried Julia components.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 10,
p.
7287.
Fu, Yuming
and
Yang, Fei
2020.
Area and Hausdorff dimension of Sierpiński carpet Julia sets.
Mathematische Zeitschrift,
Vol. 294,
Issue. 3-4,
p.
1441.
Yang, Fei
2021.
Cantor Julia sets with Hausdorff dimension two.
International Mathematics Research Notices,
Vol. 2021,
Issue. 7,
p.
4994.
Wang, Youming
Zhan, Guoping
and
Liao, Liangwen
2022.
Buried Julia Components and Julia Sets.
Qualitative Theory of Dynamical Systems,
Vol. 21,
Issue. 1,
Hu, Jun
and
Etkin, Arkady
2022.
Cubic Rational Maps with Escaping Critical Points, Part I: Julia Set Dichotomy in the Case of an Attracting Fixed Point.
Qualitative Theory of Dynamical Systems,
Vol. 21,
Issue. 3,
Boyd, Suzanne
and
Mitchell, Alexander J.
2023.
The Boundedness Locus and Baby Mandelbrot Sets for Some Generalized McMullen Maps.
International Journal of Bifurcation and Chaos,
Vol. 33,
Issue. 09,
Xiao, Yingqing
and
Yang, Fei
2024.
Disconnected Julia sets as buried Julia components.
Mathematische Zeitschrift,
Vol. 308,
Issue. 4,
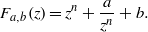 $$\begin{eqnarray*}{F}_{a, b} (z)= {z}^{n} + \frac{a}{{z}^{n} } + b.\end{eqnarray*}$$
$$\begin{eqnarray*}{F}_{a, b} (z)= {z}^{n} + \frac{a}{{z}^{n} } + b.\end{eqnarray*}$$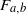 ${F}_{a, b} $ according to the dynamical behavior of the orbits of its free critical points.
${F}_{a, b} $ according to the dynamical behavior of the orbits of its free critical points.