Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T09:40:35.103Z Has data issue: false hasContentIssue false
  • English
  • Français

Lorenz-like flows: exponential decay of correlations for the Poincaré map, logarithm law, quantitative recurrence

Published online by Cambridge University Press:  11 December 2009

S. GALATOLO  and
MARIA JOSÉ PACIFICO
S. GALATOLO
Affiliation:
Dipartimento di Matematica Applicata via Buonarroti 1, 56100, Pisa, Italia (email: [email protected])
MARIA JOSÉ PACIFICO
Affiliation:
Instituto de Matemática, Universidade Federal do Rio de Janeiro, C. P. 68.530, 21.945-970 Rio de Janeiro, Brazil (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we prove that the Poincaré map associated to a Lorenz-like flow has exponential decay of correlations with respect to Lipschitz observables. This implies that the hitting time associated to the flow satisfies a logarithm law. The hitting time τr(x,x0) is the time needed for the orbit of a point x to enter a ball Br(x0) centered at x0, with small radius r, for the first time. 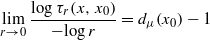As the radius of the ball decreases to 0 its asymptotic behavior is a power law whose exponent is related to the local dimension of the physical measure at x0: for each x0 such that the local dimension dμ (x0) exists, holds for μ almost each x. In a similar way, it is possible to consider a quantitative recurrence indicator quantifying the speed of an orbit to come back to its starting point. Similar results hold for this recurrence indicator.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 6 , December 2010 , pp. 1703 - 1737
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Afraimovich, V. S., Bykov, V. V. and Shil’nikov, L. P.. On the appearance and structure of the Lorenz attractor. Dokl. Acad. Sci. USSR 234 (1977), 336–339.Google Scholar
[2]Afraimovich, V. S., Chernov, N. I. and Sataev, E. A.. Statistical properties of 2-D generalized hyperbolic attractors. Chaos 5(1) (1995), 238–252.CrossRefGoogle ScholarPubMed
[3]Ambrosio, L. and Gigli, N.. Savarè, Gradient Flows: in Metric Spaces and in the Space of Probability Measures. Birkhäuser, Basle, 2005.Google Scholar
[4]Araujo, V., Pacifico, M. J., Pujals, E. and Viana, M.. Singular-hyperbolic attractors are chaotic. Trans. Amer. Math. Soc. 361 (2009), 2431–2485.CrossRefGoogle Scholar
[5]Araujo, V. and Pacifico, M. J.. Three dimensional flows. XXV Brazilian Mathematical Colloquium (Rio de Janeiro, July 2005). Instituto Nacional de Matemtica Pura e Aplicada, Rio de Janeiro, 2007.Google Scholar
[6]Athreya, J. S. and Margulis, G. A.. Logarithm laws for unipotent flows, I. Preprint, 2008, arXiv: 0811.2806.Google Scholar
[7]Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219 (2001), 443–463.CrossRefGoogle Scholar
[8]Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product struture of hyperbolic measures. Ann. of Math. 149 (1999), 755–783.CrossRefGoogle Scholar
[9]Boshernitzan, M. D.. Quantitative recurrence results. Invent. Math. 113 (1993), 617–631.CrossRefGoogle Scholar
[10]Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopedia of Mathematical Sciences, 102). Springer, Berlin, 2005.Google Scholar
[11]Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms, 2nd edn(Lecture Notes in Mathematics, 470). Springer, Berlin, 2008.CrossRefGoogle Scholar
[12]Bunimovich, L. A.. Statistical properties of Lorenz attractors. Nonlinear Dynamics and Turbulence. Pitman, Boston, MA, 1983, pp. 71–92.Google Scholar
[13]Dolgopyat, D.. Limit theorems for partially hyperbolic systems. Trans. Amer. Math. Soc. 356 (2004), 1637–1689.CrossRefGoogle Scholar
[14]Galatolo, S.. Hitting time and dimension in axiom A systems, generic interval exchanges and an application to Birkoff sums. J. Stat. Phys. 123 (2006), 111–124.CrossRefGoogle Scholar
[15]Galatolo, S.. Dimension and hitting time in rapidly mixing systems. Math. Res. Lett. 14(5–6) (2007), 797–805.CrossRefGoogle Scholar
[16]Galatolo, S. and Kim, D. H.. The dynamical Borel–Cantelli lemma and the waiting time problems. Indag. Math. (N.S.) 18(3) (2007), 421–434.CrossRefGoogle Scholar
[17]Galatolo, S. and Peterlongo, P.. Long hitting time, slow decay of correlations and arithmetical properties. 2008, arXiv: 0801.3109v2.Google Scholar
[18]Guckenheimer, J. and Williams, R. F.. Structural stability of Lorenz attractors. Publ. Math. Inst. Hautes Études Sci. 50 (1979), 59–72.CrossRefGoogle Scholar
[19]Hill, R. and Velani, S.. The ergodic theory of shrinking targets. Invent. Math. 119 (1995), 175–198.CrossRefGoogle Scholar
[20]Kim, D. H. and Seo, B. K.. The waiting time for irrational rotations. Nonlinearity 16 (2003), 1861–1868.CrossRefGoogle Scholar
[21]Kim, D. H. and Marmi, S.. The recurrence time for interval exchange maps. Nonlinearity 21 (2008), 2201–2210.CrossRefGoogle Scholar
[22]Kleinbock, D. Y. and Margulis, G. A.. Logarithm laws for flows on homogeneous spaces. Invent. Math. 138 (1999), 451–494.CrossRefGoogle Scholar
[23]Kontoyiannis, I.. Asymptotic recurrence and waiting times for stationary processes. J. Theoret. Probab. 11 (1998), 795–811.CrossRefGoogle Scholar
[24]Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc 186 (1973), 481–488.CrossRefGoogle Scholar
[25]Liverani, C.. Invariant measures and their properties. A functional analytic point of view. Dynamical Systems. Part II: Topological Geometrical and Ergodic Properties of Dynamics. Pubblicazioni della Classe di Scienze, Scuola Normale Superiore, Pisa. Centro di Ricerca Matematica ‘Ennio De Giorgi’, 2004.Google Scholar
[26]Lorenz, E. N.. Deterministic nonperiodic flow. J. Atmospheric Sci. 20 (1963), 130–141.2.0.CO;2>CrossRefGoogle Scholar
[27]Lorenz, E. N.. On the prevalence of aperiodicity in simple systems. Global Analysis. Eds. Grmela, hl and Marsden, J.. Springer, New York, 1979, pp. 53–75.CrossRefGoogle Scholar
[28]Luzzatto, S., Melbourne, I. and Paccaut, F.. The Lorenz attractor is mixing. Comm. Math. Phys. 260 (2005), 393–401.CrossRefGoogle Scholar
[29]Maucourant, F.. Dynamical Borel–Cantelli lemma for hyperbolic spaces. Israel J. Math. 152 (2006), 143–155.CrossRefGoogle Scholar
[30]MacKay, R. S.. A steady mixing flow with no-slip boundaries?Chaos, Complexity and Transport. Eds. Chandre, C., Leoncini, X. and Zaslavsky, G. M.. World Scientific, Singapore, 2008, pp. 55–68.CrossRefGoogle Scholar
[31]Masur, H.. Logarithmic law for geodesics in moduli spaces. Contemp. Math. 150 (1993), 229–245.CrossRefGoogle Scholar
[32]Palis, J. and de Melo, W.. Geometric Theory of Dynamical Systems. Springer, Berlin, 1982.CrossRefGoogle Scholar
[33]Pesin, Y.. Dimension theory in dynamical systems. Chicago Lectures in Math. (1997).Google Scholar
[34]Saussol, B.. Recurrence rate in rapidly mixing dynamical systems. Discrete Contin. Dyn. Syst. Ser. A 15 (2006), 259–267.CrossRefGoogle Scholar
[35]Saussol, B., Troubetzkoy, S. and Vaienti, S.. Recurrence, dimensions and Lyapunov exponents. J. Stat. Phys. 106 (2002), 623–634.CrossRefGoogle Scholar
[36]Shields, P.. Waiting times: positive and negative results on the Wyner–Ziv problem. J. Theoret. Probab. 6(3) (1993), 499–519.CrossRefGoogle Scholar
[37]Sullivan, D.. Disjoint spheres, approximation by imaginary quadratic numbers, and the logarithm law for geodesics. Acta Math. 149 (1982), 215–237.CrossRefGoogle Scholar
[38]Sternberg, E.. On the structure of local homeomorphisms of euclidean n-space-II. Amer. J. Math. 80 (1958), 623–631.CrossRefGoogle Scholar
[39]Steinberger, T.. Local dimension of ergodic measures for two-dimensional Lorenz transformations. Ergod. Th. & Dynam. Sys. 20 (2000), 911–923.CrossRefGoogle Scholar
[40]Tseng, J.. On circle rotations and shrinking target properties. Discrete Contin. Dyn. Syst. 20(4) (2008), 1111–1122.CrossRefGoogle Scholar
[41]Tucker, W.. A rigorous ODE solver and Smale’s 14th problem. Found. Comput. Math. 2(1) (2002), 53–117.CrossRefGoogle Scholar
[42]Tucker, W.. The Lorenz attractor exists. C. R. Acad. Sci. Paris Ser. I 328 (1999), 1197–1202.CrossRefGoogle Scholar
[43]Viana, M.. Stochastic Dynamics of Deterministic Systems (Brazilian Mathematical Colloquium, 21). Instituto Nacional de Matemtica Pura e Aplicada, Rio de Janeiro, 1997.Google Scholar
[44]Young, L.-S.. Dimension, entropy and Liapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 1230–1237.CrossRefGoogle Scholar