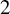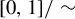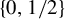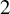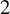1 Introduction
Our goal in this paper is to study skew products over irrational rotations on the circle and to explore relationships to laminations on infinite type surfaces. In particular, we prove that specific orbits are dense in a collection of skew product transformations. We use this to show that certain laminations on infinite type surfaces have dense boundary leaves. Finally, we use this to construct certain rays on infinite type surfaces with exotic properties, which are relevant to the study of Bavard and Walker’s loop graphs.
We consider the circle
$S^1$
as the closed unit interval
$[0,1]$
with
$0$
and
$1$
identified. For a number
$\alpha \in [0,1)$
, we define the rotation
$t=t_\alpha :S^1\to S^1$
by
$t(x)=x+\alpha $
modulo 1. We define the function
$f:S^1\to \mathbb R$
by
$f=\chi _{[0,1/2)} -\chi _{[1/2,1)}$
, where
$\chi _E$
denotes the characteristic function of the set E in question. We define a resulting skew product transformation
$T=T_\alpha :S^1\times \mathbb Z \to S^1\times \mathbb Z$
by
We endow
$\mathbb Z$
with the discrete topology and
$S^1\times \mathbb Z$
with the resulting product topology. We consider the continued fraction expansion for
$\alpha $
,
$$ \begin{align*} \alpha=[0;a_1,a_2,\ldots] = \frac{1}{a_1 + \frac{1}{a_2 + \frac{1}{a_3 + \cdots}}}.\end{align*} $$
We prove the following theorem.
Theorem 1.1. Suppose that the continued fraction expansion
$\alpha =[0;a_1,a_2,\ldots ]$
satisfies that
$a_1\geq 5$
is odd and
$a_n\geq 6$
is even for every
$n>1$
. Then, for any
$s\in \mathbb Z$
, the (forward) orbit
$\{T^n(1/2,s)\}_{n=0}^\infty $
is dense in
$S^1\times \mathbb Z$
.
Note that for any
$n\geq 0$
,
$T^n(x,s)=(t^nx, s+S_n(x))$
, where
$S_n(x)=\sum _{i=0}^{n-1} f(t^i x)$
is the nth Birkhoff sum for x. For any
$m\in \mathbb Z$
, we consider the set 
of times n at which
$S_n(x)$
is equal to m. Denote by
$k+\Sigma (x,m)$
the set above translated by
$k\in \mathbb Z$
. The following corollary, when
$k=0$
, is a restatement of Theorem 1.1. The general case, which is useful for our applications, also quickly follows from Theorem 1.1; see the next section for its proof.
Corollary 1.2. Suppose that the continued fraction expansion
$\alpha =[0;a_1,a_2,\ldots ]$
satisfies that
$a_1\geq 5$
is odd and
$a_n\geq 6$
is even for every
$n>1$
. Then, for any
$k,m\in \mathbb Z$
, the partial orbit
$\{t^n(1/2)\}_{n\in k+\Sigma (1/2,m)}$
is dense in
$S^1$
.
In particular, for any
$m\in \mathbb Z$
, there are infinitely many
$n\ge 0$
with
$S_n(1/2)=m$
. In contrast, it is shown in [Reference Boshernitzan and Ralston6, Theorem 1] (by the characterization of
$\mathcal H_{2}$
) that
$S_n(1/2)<0$
for all
$n\ge 1$
if
$\alpha =[0; a_1,a_2,\ldots ]$
with
$a_i$
even for all i odd. In addition, for almost every
$\alpha $
, there is an uncountable set (with Hausdorff dimension equal to some constant
$c\in (0,1)$
independent of
$\alpha $
) of initial points
$x\in [0,1)$
with
$S_n(x)\le 0$
for all
$n\ge 1$
[Reference Ralston8].
We use our results above to construct examples of interesting laminations and rays on infinite type surfaces. For the first statement, recall that a complete hyperbolic surface X is of the first kind if it is equal to its convex core. A geodesic lamination
$\Lambda $
on X is topologically transitive if it contains a leaf which is dense in
$\Lambda $
.
Theorem 1.3. Let S be any orientable infinite type surface with at least one isolated puncture. Then, there is a hyperbolic surface X of the first kind homeomorphic to S, and a geodesic lamination
$\Lambda $
on X, such that
$\Lambda $
is topologically transitive, with infinitely many leaves which are not dense in
$\Lambda $
.
For our second application, we consider the loop graph
$L(S;p)$
of an infinite type surface S with an isolated puncture p, defined by Bavard in [Reference Bavard2] and studied further by Bavard and Walker in [Reference Bavard and Walker4, Reference Bavard and Walker5]. The vertices of
$L(S;p)$
are the simple, essential loops on S asymptotic to p on both ends, considered up to isotopy. Two isotopy classes are joined by an edge when the corresponding isotopy classes can be realized disjointly. The graph
$L(S;p)$
is Gromov-hyperbolic and of infinite diameter [Reference Bavard and Walker5]; see also [Reference Aramayona, Fossas and Parlier1]. Bavard and Walker [Reference Bavard and Walker5] identified the points on the Gromov boundary of
$L(S;p)$
with cliques of the so-called high-filling rays. As a related notion, a
$2$
-filling ray
$\ell $
on S is a kind of fake boundary point for
$L(S;p)$
. Namely, such a ray is asymptotic to p, and intersects every loop on S, so that it has strong filling properties similar to high-filling rays, but it is not high-filling. See §3 for the precise definitions.
Bavard and Walker asked in [Reference Bavard and Walker4, Question 2.7.7] whether
$2$
-filling rays exist, for instance, when S is the plane minus a Cantor set. This was answered affirmatively by the authors in [Reference Chen and Rasmussen7]. Such
$2$
-filling rays always come organized into families of mutually disjoint
$2$
-filling rays called cliques. The authors showed that the cliques can have any finite cardinality in [Reference Chen and Rasmussen7, Theorem 5.1], and asked whether such cliques can be infinite [Reference Chen and Rasmussen7, Question 5.7]. We answer this question affirmatively in Theorem 1.4 below for any infinite type surface S with an isolated puncture. In particular,
$2$
-filling rays exist on all such surfaces. The analogous problem about the size of cliques of high-filling rays has been solved by methods different from our dynamical approach: such a clique can be of any finite cardinality on any infinite type surface S with an isolated puncture by [Reference Bavard and Walker4, Theorem 8.1.3], and it can also be infinite at least when S is the plane minus a Cantor set by [Reference Bavard3].
Theorem 1.4. Let S be an orientable infinite type surface with at least one isolated puncture p. Then, there exists an infinite clique of
$2$
-filling rays on S based at p.
It is an open problem to describe the boundaries of the loop graphs
$L(S;p)$
as spaces of geodesic laminations. The authors believe that solving this problem would lead to significantly better understanding of the graphs
$L(S;p)$
. The existence of exotic laminations and rays as constructed in Theorems 1.3 and 1.4 and in [Reference Chen and Rasmussen7] point to the difficulty of solving this problem and to the complexity of the graphs
$L(S;p)$
. It would be interesting to use skew products to construct other interesting laminations and mapping classes of infinite type surfaces.
2 Proof of Theorem 1.1
We choose
$\alpha =[0;a_1,a_2,\ldots ]$
satisfying the conditions of Theorem 1.1; that is,
$a_1\geq 5$
is odd and
$a_i\geq 6$
is even for every
$i\geq 2$
. Furthermore, we set
$\alpha _1=\alpha $
and for
$i\geq 2$
,
$$ \begin{align} \alpha_i = [0;a_i-1, a_{i+1}, a_{i+2}, \ldots]. \end{align} $$
Let
$$ \begin{align*} G(x) = \frac{1}{x} - \bigg\lfloor \frac{1}{x}\bigg\rfloor \end{align*} $$
be the Gauss transformation. Then,
$\alpha _{i+1} = G(\alpha _i) / (1-G(\alpha _i))$
.
Our method of proof considers first return maps to certain subintervals, which shares some similarity with the renormalization procedure used in related work; see [Reference Ralston8] for instance, which also gives insights about the behavior of other orbits.
We will compute a sequence of nested intervals
$[0,1)=I_1 \supset I_2 \supset I_3 \supset \cdots $
each centered at
$1/2$
and the first return maps to
$I_i$
. Let
$$ \begin{align*} k_i:I_i \to \mathbb N, \ \ \ k_i(x) = \inf\{k> 0 : t^kx \in I_i\} \end{align*} $$
be the first return time to
$I_i$
and
$$ \begin{align*} \overline{t}_i:I_i \to I_i, \ \ \ \overline{t}_i(x) = t^{k_i(x)}(x) \end{align*} $$
be the first return map. Our construction guarantees the following properties, which we will verify later.
-
(1)
$\overline {t}_i$
is rotation by
$(-1)^{i+1}\alpha _i$
(rescaled by the length of
$I_i$
). -
(2) Moreover, we compute the induced Birkhoff sums
that is,
$$ \begin{align*} \overline{f}_i:I_i \to \mathbb Z, \ \ \ \overline{f}_i(x) = \sum_{j=0}^{k_i(x) - 1} f(t^jx); \end{align*} $$
$\overline {f}_i$
records the Birkhoff sum accumulated before a point in
$I_i$
returns to
$I_i$
under iteration of t. Then, by our construction,
$\overline {f}_i$
will be equal to
$+1$
on the sub-interval of points to the left of
$1/2$
and
$-1$
on the sub-interval of points to the right of
$1/2$
.
Theorem 1.1 is a consequence of the following, seemingly weaker proposition.
Proposition 2.1. There is a sequence of intervals
$[0,1)=I_1\supset I_2\supset I_3\supset \cdots $
such that:
-
(1)
$I_i$
contains
$1/2$
for each i and is symmetric about
$1/2$
for each i; -
(2) for each
$i\geq 1$
, the interval
$I_{i+1}$
has length
$|I_{i+1}|\le \alpha _{i}|I_{i}|$
; -
(3) for each
$i\geq 2$
, after rescaling
$I_i$
by
$1/|I_i|$
, the function
$\overline {f}_i(x)$
is equal to
$\chi _{[0,1/2)} - \chi _{[1/2,1)}$
; -
(4) for any i and for any
$m\in \mathbb Z$
, there exists an orbit point
$t^k(1/2) \in I_i$
for some
$k\in \mathbb Z_+$
, with
$S_k(1/2)=m$
.
Proof of Theorem 1.1 assuming Proposition 2.1
First, we improve item (4) to the following claim: for any
$m\in \mathbb Z$
, there exist orbit points
$t^k(1/2)$
in
$I_i$
to the right of
$1/2$
with
$S_k(1/2)=m$
and similarly there exist points
$t^k(1/2)$
to the left of
$1/2$
with
$S_k(1/2)=m$
,
$k\in \mathbb Z_+$
. We focus on the case of finding points to the right of
$1/2$
, as the other case is analogous.
Choose i odd, so that the first return to
$I_i$
is rotation by
$\alpha _i=[0;a_{i}-1,a_{i+1},a_{i+2},\ldots ]$
. For any
$m\in \mathbb Z$
, there is some
$k\in \mathbb Z_+$
such that
$t^k(1/2)\in I_{i+1}$
with
$S_k(1/2)=m$
. If
$t^k(1/2)$
lies to the right of
$1/2$
, then there is nothing to show. Otherwise, since
$a_i-1 \geq 5$
, the length of
$I_{i+1}$
is at most
$\alpha _{i}|I_i|$
, and
$t^k(1/2)$
lies in
$I_{i+1}$
, we have that
$\overline {t}_i(t^k(1/2)) , \overline {t}_i^2(t^k(1/2)) \in I_i$
both lie to the right of
$1/2$
. Now we compute the Birkhoff sum at
$\overline {t}_i^2(t^k(1/2))$
. Let
$$ \begin{align*} l=k_i(t^k(1/2)) + k_i(\overline{t}_i(t^k(1/2))) \end{align*} $$
be the second return time of
$t^k(1/2)$
to
$I_i$
. Then by item (3), we have
$$ \begin{align*} S_{k+l}(1/2) &= S_k(1/2) + \overline{f}_i(t^k(1/2)) + \overline{f}_i(\overline{t}_i(t^k(1/2)))\\ &= S_k(1/2)+1+(-1)= S_k(1/2) = m. \end{align*} $$
That is, the point
$t^{k+l}(1/2)=\overline {t}_i^2(t^k(1/2)) \in I_i$
justifies the claim.
Now the theorem follows from this claim. By Proposition 2.1, the closure of the orbit of
$(1/2,0)$
contains
$\{1/2\}\times \mathbb Z$
. By the claim, for any
$m\in \mathbb Z$
, we may choose points
$t^k(1/2)$
arbitrarily close to
$1/2$
and to the right with
$S_k(1/2)=m$
. Consider any
$\epsilon \in (0,1/2)$
and a point
$(x,m)\in S^1 \times \mathbb Z$
. We want to show that for any
$s\in \mathbb Z$
, the orbit of
$(1/2,s)$
contains a point in
$[x,x+\epsilon )\times \{m\}$
. Since
$\alpha $
is irrational, the rotation t is minimal and there exists
$k\geq 0$
with
$t^k (1/2) \in [x,x+{\epsilon }/{2})$
. Suppose that
$S_k(1/2)=N$
. The functions
$\{f\circ t^i\}_{i=0}^k$
are individually constant on a short interval that has
$1/2$
as its left endpoint, so there is
$0<\delta <\epsilon /2$
such that any point
$y \in [1/2,1/2 + \delta )$
satisfies
$S_k(y)=S_k(1/2)=N$
. By the claim, we can choose
$l \geq 0$
such that
$$ \begin{align*} T^l(1/2,s) = (t^l(1/2), S_l(1/2))\in \big[\tfrac{1}{2},\tfrac{1}{2}+\delta\big) \times \{m-s-N\}. \end{align*} $$
Then,
$$ \begin{align*} T^{l+k}(1/2,s) = (t^{l+k}(1/2), s+S_l(1/2) + S_k(t^l(1/2))). \end{align*} $$
As
$t^l(1/2)\in [1/2,1/2+\delta )$
and
$t^k(1/2)\in [x,x+\epsilon /2)$
, we have
$$ \begin{align*} t^{l+k}(1/2)=t^k(t^{l}(1/2))\in [t^k(1/2), t^k(1/2)+\delta)\subset [x,x+\epsilon). \end{align*} $$
In addition,
$S_k(t^l(1/2))=N$
by our choice of
$\delta $
. It follows that
$s+S_l(1/2) + S_k(t^l(1/2))=s+(m-s-N)+N=m$
and
$T^{l+k}(1/2,s)\in [x,x+\epsilon )\times \{m\}$
, as desired.
Now we deduce Corollary 1.2 from Theorem 1.1.
Proof of Corollary 1.2
Theorem 1.1 is equivalent to the following major case of Corollary 1.2: for any
$m\in \mathbb Z$
, the partial orbit
$\{t^n(1/2)\}_{n\in \Sigma (1/2,m)}$
is dense in
$S^1$
. For the general case, for an arbitrary
$k\in \mathbb Z$
, we are interested in the density of the orbit points
$t^{n+k}(1/2)$
with
$n\in \Sigma (1/2,m)$
, that is, the image of the partial orbit
$\{t^n(1/2)\}_{n\in \Sigma (1/2,m)}$
under the rotation
$t^k$
. Such a partial orbit is also dense in
$S^1$
.
It remains to find the intervals
$I_i$
and prove Proposition 2.1. For this, we proceed by induction. To construct
$I_{i+1}$
based on
$J=I_i$
and its first return map, the inductive step fits into the following setup.
Assumption 2.2.
-
• We have chosen an interval
$J\subset [0,1)$
which contains
$1/2$
and is centered at
$1/2$
. -
• After scaling J by
$1/|J|$
to unit length, the first return map to J, which we denote by
$t_J$
, is a rotation by a number
$\beta =\pm [0;b,\ldots ]$
with
$b\geq 5$
odd (so
$|\beta |<1/5$
).
We construct a sub-interval
$J^{\mathrm {new}}$
of J that is centered at
$1/2$
with well-understood first return map among other properties. We describe the construction below in Lemmas 2.5 and 2.8, depending on the sign of
$\beta $
.
In the discussion below, we frequently look at different left-closed and right-open sub-intervals of
$[0,1)$
centered at
$1/2$
and rescale them to length
$1$
. To avoid confusion due to different scales, we use the following convention.
Convention 2.3. For a sub-interval J of
$[0,1)$
centered at
$1/2$
, we abuse notation and let
$J:[0,1)\to J$
be the unique affine homeomorphism fixing
$1/2$
. Then, for any
$x\in (0,1)$
,
$J(x)$
is the point at distance x from the left endpoint of J after rescaling J to unit length. Similarly,
$J[a,b)$
is the sub-interval of J corresponding to the interval
$[a,b)\subset [0,1)$
after rescaling J to unit length.
2.1 First case:
$\beta> 0$
We first consider the case
$\beta>0$
and introduce some notation to state the inductive construction in Lemma 2.5. Note that the first coefficient
$b=\lfloor 1/\beta \rfloor $
. We partition J into sub-intervals
$$ \begin{align*} J_0 = J[0,\beta), \ J_1 = J[\beta, 2\beta), \ \ldots, \ J_{b-1} = J[(b - 1)\beta, b\beta), \ J_{b} = J[b\beta, 1), \end{align*} $$
each of which has length
$\beta |J|$
except for
$J_{b}$
, which has length
$\beta G(\beta )|J|$
, where
$G(x) = 1/x - \lfloor 1/x \rfloor $
as before. For a point
$x\in J$
, we have
$t_J(x)=t^{k(x)}(x)$
, where
$k(x) = \inf \{k{\kern-1pt}>{\kern-1pt} 0 : t^kx {\kern-1pt}\in{\kern-1pt} J\}$
, and by our induction hypothesis,
$t_J(J(x))=J(x{\kern-1pt}+{\kern-1pt}\beta \,\mod 1)$
and
${t_J(J_i)=J_{i+1}}$
for all
$0\le i<b-1$
. We consider the orbit of
$x\in J$
under t before its first return to J, and record the sequence of values of f along this orbit, namely
$$ \begin{align*} \mathcal F(x) = \{ f(x), f(t(x)), \ldots, f(t^{k(x)-1}(x))\}. \end{align*} $$
This is equivalent to recording the sequence of partial sums
$\mathcal {S}(x)=\{S_i(x)\}_{i=1}^{k(x)}$
with 
. The partial sums keep track of the increment in the second coordinate (compared with
$(x,m)$
) along the orbit of
$(x,m)$
under T in the skew product:
$$ \begin{align*} \{(x,m),\ T(x,m)=(tx, m+fx), \ \ldots, \ T^{k(x)}(x,m)=(t^{k(x)}x, \ m+S_{k(x)}(x))\}. \end{align*} $$
Finally, we set
$\Sigma (x) = S_{k(x)}(x)$
, which is the total sum of the sequence
$\mathcal {F}(x)$
. We use
$\mathcal {F}_1\cdot \mathcal {F}_2$
to denote the concatenation of two sequences
$\mathcal {F}_1$
and
$\mathcal {F}_2$
.
Here are our remaining assumptions for the case
$\beta>0$
in addition to Assumption 2.2.
Assumption 2.4. There are sequences
$\mathcal F_+$
,
$\mathcal F_-$
, and
$\mathcal F_0$
with total sums
$1$
,
$-1$
, and
$0$
, respectively, such that:
-
• whenever
$x\in J[0,1/2)$
, we have
$\mathcal F(x) = \mathcal F_+$
; -
• whenever
$x\in J[1/2, 1 - \beta )$
, we have
$\mathcal F(x) = \mathcal F_-$
; -
• whenever
$x\in J[1-\beta ,1)$
, we have
$\mathcal F(x) = \mathcal F_- \cdot \mathcal F_0$
.
Here, we allow
$\mathcal F_0$
to be an empty sequence.
As a consequence of the assumptions above, the sequence
$\mathcal {S}(x)$
must be the sequence of partial sums for
$\mathcal F_+$
,
$\mathcal F_-$
, or
$\mathcal F_+\cdot \mathcal {F}_0$
depending on the location of x as above. Denote the partial sum sequences of
$\mathcal F_+$
and
$\mathcal F_-$
by
$\mathcal S_+$
and
$\mathcal {S}_-$
, and denote the total sums of
$\mathcal F_+$
,
$\mathcal F_-$
,
$\mathcal {F}_0$
as
$\Sigma _+, \Sigma _-, \Sigma _0$
. The assumptions above imply
$\Sigma _+=1$
,
$\Sigma _-=-1$
, and
$\Sigma _0=0$
.
We record the maximum and minimum over each sequence of partial sums, that is,
Our aim is to find a sub-interval
$J^{\mathrm {new}} \subset J$
containing and centered at
$1/2$
, for which the first return to
$J^{\mathrm {new}}$
, rescaled by
$1/|J^{\mathrm {new}}|$
, is a rotation by a new number
$\beta ^{\mathrm {new}} = -[0;c,\ldots ]$
with
$c\geq 3$
determined by
$\beta $
explicitly as in Lemma 2.5 below. Moreover, for
$x\in J^{\mathrm {new}}$
, denote the first return time to
$J^{\mathrm {new}}$
as
$$ \begin{align*} k^{\mathrm{new}}(x)=\inf \{k> 0 : t^k(x) \in J^{\mathrm{new}}\} \end{align*} $$
and consider, as before, the sequence of f-values
Let
$\mathcal S^{\mathrm {new}}(x)$
be the sequence of partial sums associated to
$\mathcal F^{\mathrm {new}}(x)$
, and let
$\Sigma ^{\mathrm {new}}(x) = S_{k^{\mathrm {new}}(x)}(x)$
be the total sum.
The following lemma shows how we construct the sub-interval
$J^{\mathrm {new}}$
and the nice properties guaranteed by the construction.
Lemma 2.5. Suppose there is a sub-interval
$J\subset [0,1)$
with first return map
$t_J$
satisfying Assumptions 2.2 and 2.4 with
$\beta =[0;b,c+1,\ldots ]>0$
, where
$c\ge 3$
. Denote
$b = 2n+1$
with
$n\geq 1$
. Then, the sub-interval
$J^{\mathrm {new}}\subset J$
, given by
has the following properties.
-
(1)
$J^{\mathrm {new}} $
is symmetric about
$1/2$
of length
$\beta (1-G(\beta ))|J|$
. -
(2)
$J^{\mathrm {new}}$
is a sub-interval of
$J_n$
, the right endpoints of
$J^{\mathrm {new}}$
and
$J_n$
are the same, and the left endpoint of
$J^{\mathrm {new}}$
has distance
$\beta G(\beta )|J|=|J_b|$
from the left endpoint of
$J_n$
. -
(3) The image of
$J_n\setminus J^{\mathrm {new}}$
under
$n+1$
iterations of
$t_J$
is
$J_b$
. -
(4) Re-scaling by
$1/|J^{\mathrm {new}}|$
, the first return map to
$J^{\mathrm {new}}$
is rotation by -
(5) There are sequences
satisfying:-
• whenever
$x\in J^{\mathrm {new}}[0,\beta ^{\mathrm {new}})$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_+^{\mathrm {new}} \mathcal F_0^{\mathrm {new}}$
; -
• whenever
$x\in J^{\mathrm {new}}[\beta ^{\mathrm {new}}, 1/2)$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_+^{\mathrm {new}}$
; -
• whenever
$x\in J^{\mathrm {new}}[1/2, 1)$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_-^{\mathrm {new}}$
.
Moreover,
$\mathcal F_+^{\mathrm {new}}, \mathcal F_-^{\mathrm {new}}, \mathcal F_0^{\mathrm {new}}$
have total sums
$1,-1,0$
, respectively. -
Proof. Item (1) is immediate. To see item (2), note that
$1/2$
lies in the interval
$J_n = J[n\beta , (n+1)\beta )$
and its distances to the endpoints are
$$ \begin{align*} \big(\tfrac12 - n\beta\big)|J| &= \tfrac12(1-2n\beta)|J| = \tfrac12 \beta|J|(1 + G(\beta)) \quad\text{and}\quad \big((n+1)\beta-\tfrac12\big)|J|\\&=\tfrac12 \beta|J|(1 - G(\beta)). \end{align*} $$
Since
$t_J$
is rotation by
$\beta |J|=|J_i|$
for
$i<b$
and
$t_J(J_i)=J_{i+1}$
for any
$i<b-1$
, item (3) easily follows; see Figure 1.
Figure 1 The decomposition of J into intervals
$J_i$
when
$b=2n+1=5$
for
$n=2$
and the orbit of
$J^{\mathrm {new}}$
under iterations of
$t_J$
, for
$\beta>0$
.
Now we analyze the first return map. After scaling by
$1/|J_n|=1/\beta $
, the first return map to
$J_n$
is rotation by
$(b\beta -1)/\beta =-G(\beta )$
. Therefore, by restricting to the further sub-interval
$J^{\mathrm {new}}$
and rescaling by
$1/|J^{\mathrm {new}}|$
, one can check that the first return map to
$J^{\mathrm {new}}$
is rotation by
$\beta ^{\mathrm {new}} =-G(\beta )/(1-G(\beta ))$
. This is essentially a simple case of Rauzy–Veech induction. See the next several paragraphs for more details. A direct computation verifies item (4), that is,
$$ \begin{align*} \beta^{\mathrm{new}} = -G(\beta) / (1-G(\beta))=-[0; c,\ldots]. \end{align*} $$
Next we compute the sequences
$\mathcal F_+^{\mathrm {new}}, \mathcal F_-^{\mathrm {new}}, \mathcal F_0^{\mathrm {new}}$
. Note that by item (2),
$t_J^k(J^{\mathrm {new}})$
is a sub-interval of
$J_{n+k}$
sharing its right endpoint for
$0\le k\le n$
and
$t_J^k(J^{\mathrm {new}})$
is a sub-interval of
$J_{k-(n+1)}$
sharing its left endpoint for
$n+1\le k\le 3n+1$
; see Figure 1.
In particular,
$t_J^{2n+1}(J^{\mathrm {new}})$
lies in
$J_n$
sharing its left endpoint, and we observe that this completes the first return to
$J^{\mathrm {new}}$
by
$t_J^{2n+1}$
for
$x\in J^{\mathrm {new}}[\beta ^{\mathrm {new}}, 1)$
. Counting for which
$0\le k\le 2n$
, we have
$t_J^{k}(x)$
on the left or right of
$J(1/2)$
, we observe that, for
$x\in J^{\mathrm {new}}[\beta ^{\mathrm {new}},1/2)$
, the sequence
$\mathcal F^{\mathrm {new}}(x)$
is equal to
$\mathcal F_+^{\mathrm {new}}$
defined as in item (5), that is,
$$ \begin{align*} \mathcal F_+^{\mathrm{new}}= \mathcal F_+ \cdot \mathcal F_-^n \cdot \mathcal F_0 \cdot \mathcal F_+^n; \end{align*} $$
and for
$x\in J^{\mathrm {new}}[1/2,1)$
, the sequence
$\mathcal F^{\mathrm {new}}(x)$
is equal to
$\mathcal F_-^{\mathrm {new}}$
as in item (5), that is,
$$ \begin{align*} \mathcal F_-^{\mathrm{new}} = \mathcal F_-^{n+1} \cdot \mathcal F_0 \cdot \mathcal F_+^n. \end{align*} $$
In contrast, any
$x\in J^{\mathrm {new}}[0,\beta ^{\mathrm {new}})$
also returns to
$J_n$
for the first time via
$t_J^{2n+1}$
, but lands in
$J_n\setminus J^{\mathrm {new}}=t_J^{2n+1}(J^{\mathrm {new}}[0,\beta ^{\mathrm {new}}))$
. After another
$2n+2$
iterations of
$t_J$
, x finally returns to
$J^{\mathrm {new}}$
and the additional sequence of f-values is
$\mathcal F_0^{\mathrm {new}}$
as in item (5), that is,
$$ \begin{align*} \mathcal F_0^{\mathrm{new}} =\mathcal F_+ \cdot \mathcal F_-^{n+1}\cdot \mathcal F_0 \cdot \mathcal F_+^n. \end{align*} $$
Indeed, after the first return to
$J_n$
(that is,
$2n+1$
iterations of
$t_J$
), x lands to the right of
$1/2$
for the next
$n+1$
iterations of
$t_J$
in J rather than n times as before, since
$t_J^{n+1}(J_n\setminus J^{\mathrm {new}})=J_b$
. Finally, the last
$n+1$
iterations take such x back to
$J^{\mathrm {new}}$
and x stays on the left of
$1/2$
until it is back.
Therefore, for
$x\in J^{\mathrm {new}}[0,\beta ^{\mathrm {new}})$
, we see that
$\mathcal F^{\mathrm {new}}(x)$
is the concatenation
$\mathcal F_+^{\mathrm {new}} \cdot \mathcal F_0^{\mathrm {new}}$
as claimed in item (5). The computations above in these three cases together verify item (5), where the total sums of the sequences
$\mathcal F_+^{\mathrm {new}}, \mathcal F_-^{\mathrm {new}}, \mathcal F_0^{\mathrm {new}}$
are
$1,-1, 0$
, respectively, as an immediate corollary of the expressions in item (5) and the total sums of
$\mathcal F_+, \mathcal F_-, \mathcal F_0$
given in Assumption 2.4.
Now, consider the partial sum sequences
$\mathcal S_+^{\mathrm {new}}$
and
$\mathcal S_-^{\mathrm {new}}$
for the sequences
$\mathcal F_+^{\mathrm {new}}$
and
$\mathcal F_-^{\mathrm {new}}$
, respectively. We estimate the upper and lower bounds of these partial sum sequences:
Lemma 2.6. For the sequences
$\mathcal F_+^{\mathrm {new}}$
,
$\mathcal F_-^{\mathrm {new}}$
and the integer n defined as in Lemma 2.5, assuming the total sums of
$\mathcal F_+$
,
$\mathcal F_-$
, and
$\mathcal F_0$
to be
$1, -1, 0$
, respectively, as in Assumption 2.4, and assuming
$n\ge 2$
(that is,
$b\ge 5$
), we have:
-
•
$M_+^{\mathrm {new}} \geq M_+$
; -
•
$m_+^{\mathrm {new}} \leq m_- - (n-2)$
; -
•
$M_-^{\mathrm {new}} \geq M_-$
; -
•
$m_-^{\mathrm {new}} \leq m_- - n$
.
Proof. These easily follow by inspection and the fact that
$\Sigma _+ = +1, \Sigma _- = -1$
. As
$\mathcal F^{\mathrm {new}} _+$
starts with the sequence
$\mathcal F_+$
, we note that
$\mathcal S_+$
is a prefix of the sequence
$\mathcal S^{\mathrm {new}}_+$
, which verifies the first bullet. The third bullet follows similarly.
For the second bullet, consider the expression
$$ \begin{align*}\mathcal F^{\mathrm{new}}_+=(\mathcal{F}_+ \cdot \mathcal{F}_-^{n-1})\cdot\mathcal F_- \cdot(\mathcal F_0 \cdot \mathcal F_+^n).\end{align*} $$
The sequence
$\mathcal F_+ \cdot \mathcal F_-^{n-1}$
has total sum
$\Sigma _+ + (n-1)\Sigma _-=-(n-2)$
, so for the subsequence
$\mathcal F_-$
after these terms, its partial sum sequence
$\mathcal {S}_-$
shifted by
$-(n-2)$
appears as a subsequence of
$\mathcal S^{\mathrm {new}}_-$
, which implies the second bullet.
The last bullet can be shown analogously, as the sequence
$\mathcal F^{\mathrm {new}}_-$
starts with
$(\mathcal F_-)^n\cdot \mathcal F_-$
, where the part in parentheses has total sum
$n\Sigma _-=-n$
.
2.2 Second case:
$\beta < 0$
We now consider the case
$\beta < 0$
. Denote
$\gamma = -\beta $
. Then, the first return map to J is
$t_J(J(x))=J(x-\gamma \,\mod 1)$
. The case here is essentially just mirroring the case above, as now we are rotating to the left. For clarity, we include some details below. Define the sequences
$\mathcal F(x)$
and
$\mathcal S(x)$
as before for any
$x\in J$
and let
$\Sigma (x)$
be the total sum of
$\mathcal F(x)$
. Here are the remaining assumptions for the case
$\beta <0$
.
Assumption 2.7. There are sequences
$\mathcal F_+,\mathcal F_-,\mathcal F_0$
with total sums
$\Sigma _+=1,\Sigma _-=-1, \Sigma _0=0$
, respectively, such that:
-
• for
$x\in J[0,\gamma )$
, we have
$\mathcal F(x) = \mathcal F_+ \cdot \mathcal F_0$
; -
• for
$x\in J[\gamma ,1/2)$
, we have
$\mathcal F(x) = \mathcal F_+$
; -
• for
$x\in J[1/2,1)$
, we have
$\mathcal F(x) = \mathcal F_-$
.
We denote the first coefficient by
$b=\lfloor 1 / \gamma \rfloor $
, and express it as
$b=2n+1$
for some
$n\geq 2$
. We again partition J into intervals
$$ \begin{align*} J_0 = J[1-\gamma, 1), J_1 = J[1-2\gamma, 1-\gamma), \ldots, J_b = J[0, 1-b\gamma), \end{align*} $$
and we have
$t_J(J_i)=J_{i+1}$
for
$0\le i < b-1$
. The interval
$J_b$
has length
$\gamma G(\gamma )$
.
Our aim is again to find a sub-interval
$J^{\mathrm {new}} \subset J$
containing
$1/2$
and symmetric about
$1/2$
, for which the first return to
$J^{\mathrm {new}}$
inherits nice properties regarding the sequence
$\mathcal F^{\mathrm {new}}(x)$
of f-values and the sequence
$\mathcal S^{\mathrm {new}}(x)$
of partial sums, defined just as in the previous case.
Lemma 2.8. Suppose there is a sub-interval
$J\subset [0,1)$
with first return map
$t_J$
satisfying Assumptions 2.2 and 2.7 with
$\beta =-\gamma =-[0;b,c+1,\ldots ]<0$
, where
$c\ge 3$
. Denote
$b = 2n+1$
with
$n\geq 1$
. Then, with notation as above, the sub-interval
$J^{\mathrm {new}}\subset J$
, given by
has the following properties.
-
(1)
$J^{\mathrm {new}} $
is symmetric about
$1/2$
of length
$\gamma (1-G(\gamma ))|J|$
. -
(2)
$J^{\mathrm {new}}$
is a sub-interval of
$J_n$
, the left endpoints of
$J^{\mathrm {new}}$
and
$J_n$
are the same, and the right endpoint of
$J^{\mathrm {new}}$
has distance
$\gamma G(\gamma )|J|=|J_b|$
from the right endpoint of
$J_n$
. -
(3) The image of
$J_n\setminus J^{\mathrm {new}}$
under
$n+1$
iterations of
$t_J$
is
$J_b$
. -
(4) Re-scaling by
$1/|J^{\mathrm {new}}|$
, the first return map to
$J^{\mathrm {new}}$
is rotation by -
(5) There are sequences
with total sums
$1,-1, 0$
, respectively, satisfying:
-
• whenever
$x\in J^{\mathrm {new}}[0,1/2)$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_+^{\mathrm {new}}$
; -
• whenever
$x\in J^{\mathrm {new}}[1/2, 1-\beta ^{\mathrm {new}})$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_-^{\mathrm {new}}$
; -
• whenever
$x\in J^{\mathrm {new}}[1-\beta ^{\mathrm {new}}, 1)$
, we have
$\mathcal F^{\mathrm {new}}(x) = \mathcal F_-^{\mathrm {new}} \mathcal F_0^{\mathrm {new}}$
.
-
Proof. The proof is almost the same as that of Lemma 2.5, by symmetry; see Figure 2. So we just summarize a few key points below.
Figure 2 The decomposition of J into intervals
$J_i$
when
$b=2n+1=5$
for
$n=2$
and the orbit of
$J^{\mathrm {new}}$
under iterations of
$t_J$
, for
$\beta <0$
.
Items (1)–(3) are just direct computations as before, noting that
$1/2$
lies in the interval
$J_n$
, but
$|J_b|$
-closer to its left endpoint this time.
As in the previous case, after scaling by
$1/|J_n|=1/\gamma $
, the first return map to
$J_n$
is rotation by
$(1-b\gamma )/\gamma =G(\gamma )$
, which is now positive. Thus, by restricting further to the sub-interval
$J^{\mathrm {new}}$
and rescaling by
$1/|J^{\mathrm {new}}|$
instead, the first return to
$J^{\mathrm {new}}$
is rotation by
$\beta ^{\mathrm {new}}= G(\gamma ) / (1-G(\gamma ))$
as in item (4).
Item (5) follows by an analysis of first returns to
$J^{\mathrm {new}}$
, which is just mirroring the case of
$\beta>0$
: the interval
$t_J^{2n+1}(J^{\mathrm {new}})$
lies in
$J_n$
sharing the right endpoint, completing the first return to
$J^{\mathrm {new}}$
for all
$x\in J^{\mathrm {new}}[0,1-\beta ^{\mathrm {new}})$
, and the sequence of f-values depends on whether x lies on the left or right of
$1/2$
, which only changes the first term (
$\mathcal F_\pm $
) in the concatenation. For those
$x\in J^{\mathrm {new}}[1-\beta ^{\mathrm {new}},1)$
, it takes another
$2n+2$
iterations of
$t_J$
to return to
$J^{\mathrm {new}}$
, resulting in the additional sequence
$\mathcal {F}_0^{\mathrm {new}}$
.
As before, for the partial sum sequences
$\mathcal S_+$
and
$\mathcal S_-$
, denote
and similarly for the partial sum sequences
$\mathcal S^{\mathrm {new}}_+$
and
$\mathcal S^{\mathrm {new}}_-$
by adding superscripts everywhere in the above equations.
The proof of the following lemma is similar to that of Lemma 2.6, using the expressions for
$\mathcal F_+^{\mathrm {new}}$
and
$\mathcal F_-^{\mathrm {new}}$
in Lemma 2.8.
Lemma 2.9. For the sequences
$\mathcal F_+^{\mathrm {new}}$
,
$\mathcal F_-^{\mathrm {new}}$
, and the integer n defined as in Lemma 2.8, assuming the total sums of
$\mathcal F_+$
,
$\mathcal F_-$
, and
$\mathcal F_0$
to be
$1, -1, 0$
, respectively, as in Assumption 2.7, and assuming
$n\ge 2$
, we have:
-
•
$M_+^{\mathrm {new}} \geq M_+ + n$
; -
•
$m_+^{\mathrm {new}} \leq m_+$
; -
•
$M_-^{\mathrm {new}} \geq M_+ + (n-2)$
; -
•
$m_-^{\mathrm {new}} \leq m_-$
.
2.3 The end of the proof
Finally, we can prove Proposition 2.1.
Proof of Proposition 2.1
We inductively construct
$I_i$
and check the first three items as follows. For the base case
$i=1$
, set
$I_1=[0,1)$
and
$\beta _1=\alpha $
. Then the three items are either obvious or vacuous. Since the first coefficient of
$\alpha $
is odd, Assumptions 2.2 and 2.4 hold for the rotation
$t_J=t$
on
$J=I_1$
, where
$\mathcal {F}_+=\{1\}$
,
$\mathcal {F}_-=\{-1\}$
, and
$\mathcal {F}_0=\emptyset $
is the empty sequence. By Lemma 2.5, we have a sub-interval 
symmetric about
$1/2$
of length less than
$\alpha _1|I_1|$
, for which the first return map is rotation by
$\beta ^{\mathrm {new}}=-\alpha _2$
, where
$\alpha _2$
is defined in equation (2.1).
Note that the first return map on
$I_2$
with the sequences
$\mathcal {F}^{\mathrm {new}}_+$
,
$\mathcal {F}^{\mathrm {new}}_-$
, and
$\mathcal {F}^{\mathrm {new}}_0$
from Lemma 2.5 satisfies Assumptions 2.2 and 2.7. Thus, Lemma 2.8 produces a sub-interval
$I_3$
symmetric about
$1/2$
of length less than
$\alpha _2|I_2|$
, for which the first return map is rotation by
$\alpha _3$
, with new sequences of f-values satisfying Assumptions 2.2 and 2.4.
We continue this process to define
$I_i$
inductively, alternating between applications of Lemmas 2.5 and 2.8 to
$I_i$
with i odd and even, respectively. Namely, given
$I_i$
and
$\alpha _i$
, define
$I_{i+1}=I_i^{\mathrm {new}}$
and
$\alpha _{i+1}=\alpha _i^{\mathrm {new}}$
. Item (5) in Lemmas 2.5 and 2.8 ensures item (3) in Proposition 2.1.
Define inductively
$\mathcal {F}_+^i$
,
$\mathcal {F}_-^i$
,
$\mathcal {F}_0^i$
as the sequences of f-values for first returns to
$I_i$
, using
$\mathcal F_\pm ^{i+1}=(\mathcal F_\pm ^i)^{\mathrm {new}}$
and similarly for
$\mathcal F_0^{i+1}$
. Let
$\mathcal S_\pm ^i$
be the sequences of partial sums of
$\mathcal {F}_\pm ^i$
. Let
$M_\pm ^i$
and
$m_\pm ^i$
be the bounds on the partial sums
$\mathcal S_\pm ^i$
estimated in Lemmas 2.6 and 2.9.
Finally, we prove item (4). We first prove below that there are points
$t^k(1/2)\in I_1$
in the forward orbit of
$1/2$
with
$S_k(1/2)$
equal to any given integer m. We will explain at the end how to find such points in
$I_j$
for any
$j\in \mathbb Z_+$
instead of
$I_1$
. Note that the sequence
$\mathcal S_-^i$
consists exactly of the Birkhoff sums of
$1/2$
that occur before
$1/2$
returns to
$I_i$
for the first time. We have
$M_-^i = \max \mathcal S_-^i$
and
$m_-^i = \min \mathcal S_-^i$
. Thus, it suffices to prove that
$M_-^i\to +\infty $
and
$m_-^i\to -\infty $
as
$i\to \infty $
.
Since the first coefficient
$a_i-1$
(or
$a_1$
when
$i=1$
) of
$\alpha _i$
is odd and at least
$5$
by assumption, 
(and 
). We have
$m_-^{2i}\le m_-^{2i-1}-n_{2i-1}\le m_-^{2i-1}-2$
by Lemma 2.6 and
$m_-^{2i+1}\le m_-^{2i}$
by Lemma 2.9. It follows that
$m_-^{i+2}\le m_-^i-2$
for all i and hence
$\lim m_-^i=-\infty $
. For a similar reason,
$\lim M_+^i=+\infty $
, which we now use to deduce that
$\lim M_-^i=+\infty $
. In fact, we have
$M_-^{2i+2}\ge M_-^{2i+1}\ge M_+^{2i}{\kern-1pt}+{\kern-1pt}(n_{2i}{\kern-1pt}-{\kern-1pt}2){\kern-1pt}\ge{\kern-1pt} M_+^{2i}$
by Lemmas 2.6 and 2.9. Thus,
$\lim M_-^i{\kern-1pt}={\kern-1pt}+\infty $
and
$\lim m_-^i{\kern-1pt}={\kern-1pt}-\infty $
as claimed.
The proof above works in the same way after replacing
$\alpha $
by
$\alpha _j$
,
$I_1$
by
$I_j$
, f by
$\overline {f}_j$
, and t by
$\overline {t}_j$
for any
$j\in \mathbb Z_+$
. That is, there is
$k\in \mathbb Z_+$
such that
$\overline {t}^k_j(1/2)\in I_j$
with
$\overline {t}_j$
-Birkhoff sum equal to m. As
$\overline {t}_j$
is the first return map to
$I_j$
, such a point in
$I_j$
is also in the forward orbit of
$1/2$
under t, and its
$\overline {t}_j$
-Birkhoff sum is equal to the corresponding t-Birkhoff sum, which completes the proof.
The same method can be used to study the Birkhoff sum along other orbits. We give a sketch for one explicit example below, which we use later to find a leaf that is not dense in Theorem 1.3.
Example 2.10. Fix
$m{\kern-1pt}\ge{\kern-1pt} 2$
. Let
$\alpha =[0; 2m{\kern-1pt}+{\kern-1pt}1, 2m{\kern-1pt}+{\kern-1pt}2, 2m{\kern-1pt}+{\kern-1pt}2, \ldots ]$
(that is,
$a_1=2m+1$
and
$a_n=2m+2$
for all
$n\ge 2$
), which satisfies the assumption of Theorem 1.1. We consider the orbit of
$x=(1+\alpha )/2$
and claim that
$S_n(x)\le 0$
for all
$n\in \mathbb Z$
. Here, we set
$S_0(x)=0$
and
$S_{-n}(x)=-\sum _{k=1}^n f(t^{-k}(x))$
for any
$n>0$
so that
$T^n(x,s)=(t^n(x), s+S_n(x))$
for all
$n\in \mathbb Z$
. The claim implies that the (forward and backward) orbit of
$(x,0)$
under iterations of T always has non-positive second coordinate.
We sketch a proof of the claim. First, note that we can take care of the backward orbit by symmetry. In fact, for our particular x, we have
$t^{-(n+1)}(x)=1-t^n(x)$
for all
$n>0$
, that is, the backward orbit (starting at
$t^{-1}(x)=(1-\alpha )/2$
) and the forward orbit (starting at x) are symmetric around
$1/2$
, and thus the sequences of f-values along the forward and backward orbits differ by a negative sign. It follows that
$S_{-n}(x)=S_n(x)$
for all
$n\in \mathbb Z_+$
. So it suffices to check that
$\max _{n\ge 1} S_n(x)\le 0$
.
To compute
$S_n(x)$
with
$n>0$
, we use the same renormalization procedure with the nested intervals
$I_1\supset I_2\supset \cdots $
as above. Let
$\mathcal F^i_{\pm }$
and
$\mathcal F^i_{0}$
(respectively
$\mathcal S^i_{\pm }$
and
$\mathcal S^i_{0}$
) be the sequence of f-values (respectively partial sums) defined inductively as in the proof above. Let
$M^i_{\pm }=\max \mathcal S^i_{\pm }$
and
$M^i_0=\max \mathcal S^i_0$
. A direct computation shows that
$t^m(x)=1-\tfrac 12\alpha G(\alpha )$
and
$t^{2m+1}(x)=(m+1)\alpha -\tfrac 12\alpha G(\alpha )$
, so the forward orbit enters
$I_2$
for the first time after
$2m+1$
iterations of t. In
$I_2$
-coordinates, we have
$t^{2m+1}(x)=I_2(y)$
with
$$ \begin{align*}y=\frac{[(m+1)\alpha - {1}/{2} \alpha G(\alpha)] - [m\alpha+\alpha G(\alpha)]}{\alpha (1-G(\alpha))}=\frac{\alpha - {3}/{2} \alpha G(\alpha)}{\alpha (1-G(\alpha))} = 1 - \frac{1}{2}\beta,\end{align*} $$
where
$\beta =G(\alpha )/(1-G(\alpha ))$
and the first return map
$\bar {t}_2:I_2\to I_2$
is rotation by
$-\beta $
in
$I_2$
-coordinates by Lemma 2.5. Our choice of
$\alpha $
makes
$\beta =\alpha $
. Then, applying the first return map
$\bar {t}_2$
another m times, we arrive at
$I_2(1-(m+1/2)\beta )$
, at which point we land in
$I_3$
for the first time. In
$I_3$
-coordinates, this is
$I_3(z)$
with
$$ \begin{align*}z = \frac{[1 - (m+1/2)\beta] - [1 - (m+1)\beta]}{\beta(1-G(\beta))} = \frac{1}{2}(1+\gamma),\end{align*} $$
where
$\gamma = G(\beta )/(1-G(\beta ))$
. Noting that
$\gamma =\beta =\alpha $
by our choice of
$\alpha $
, we see
$z=x$
, so we are now exactly at
$I_3(x)$
, and the first return map to
$I_3$
is rotation by
$\gamma =\alpha $
in
$I_3$
-coordinates by Lemma 2.8. Thus, from here on, the analysis repeats. It follows that the sequence of f-values along the forward orbit is given by
$$ \begin{align} [(\mathcal F^1_-)^{m+1}\cdot (\mathcal F^1_+)^{m} \cdot (\mathcal F^2_-)^{m}]\cdot [(\mathcal F^3_-)^{m+1}\cdot (\mathcal F^3_+)^{m} \cdot (\mathcal F^4_-)^{m}]\cdots \end{align} $$
The Birkhoff sums are the partial sums of this sequence, and to analyze them, we compute
$M_{\pm }^k$
and
$M_0^k$
for all
$k\ge 1$
. The idea of the computation is similar to the proof of Lemmas 2.6 and 2.9, which yields the following recursive formulas for our particular
$\alpha $
:
$$ \begin{align*}M^{2k}_+=M^{2k-1}_+,\quad M^{2k}_-=M^{2k-1}_-,\quad M^{2k}_0=M^{2k-1}_+,\end{align*} $$
and
$$ \begin{align*}M^{2k+1}_+=M^{2k}_0+m+1,\quad M^{2k+1}_-=M^{2k}_0+m-1,\quad M^{2k+1}_0=M^{2k}_0+m,\end{align*} $$
for all
$k\ge 1$
. Then, by induction, we have
$$ \begin{align*}M^{2k-1}_+=(m+1)k-m, \quad M^{2k-1}_-=(m+1)k-m-2, \quad M^{2k-1}_0=(m+1)k-m-1\end{align*} $$
for all
$k\ge 2$
, and
$$ \begin{align*}M^{2k}_+=(m+1)k-m,\quad M^{2k}_-=(m+1)k-m-2,\quad M^{2k}_0=(m+1)k-m\end{align*} $$
for all
$k\ge 1$
. Now by examining the sequence in equation (2.2) bracket by bracket, it is straightforward to check that
$\max _{n\ge 1} S_n(x)=-1$
.
3 Background on laminations and rays
We recall some background on geodesic laminations and geodesic rays on hyperbolic surfaces. Let X be a complete oriented hyperbolic surface without boundary. We will typically consider the case that X is of the first kind. This means that the limit set of
$\pi _1(X)$
acting on the universal cover
$\widetilde X \cong \mathbb {H}^2$
is the entire Gromov boundary
$\partial X\cong S^1$
. A geodesic lamination
$\Lambda $
on X is a closed subset of X consisting of pairwise disjoint, simple, complete geodesics. Each such complete geodesic is called a leaf of
$\Lambda $
.
In §4, we will construct laminations on hyperbolic surfaces using train tracks, weight systems, and foliated rectangles. Here is the necessary background. A train track
$\tau $
on X is a locally finite graph embedded on X with the following additional structure. At any vertex v of
$\tau $
, the set
$\mathcal B(v)$
of edges incident to v has a circular order induced from the orientation of X. We have a partition of
$\mathcal B(v)$
into a pair of non-empty sets
$\mathcal B_i(v)$
and
$\mathcal B_o(v)$
, which we call incoming and outgoing, respectively, such that the total order defined by any
$g\in \mathcal B_o(v)$
(respectively
$g\in \mathcal B_i(v)$
) restricts to the same order on
$\mathcal B_i(v)$
(respectively
$\mathcal B_o(v)$
) independent of g. For
$e,f \in \mathcal B_i(v)$
, we write
$e<f$
if and only if
$(e,f,g)$
is counterclockwise at v for any
$g\in \mathcal B_o(v)$
. For
$e,f \in \mathcal B_o(v)$
, we write
$e<f$
if and only if
$(e,f,g)$
is clockwise at v for any
$g\in \mathcal B_i(v)$
. The edges of
$\tau $
are called branches and the vertices of
$\tau $
are called switches. A train path t on
$\tau $
is a finite or infinite path immersed in
$\tau $
with the property that at every switch v, t enters v through
$\mathcal B_i(v)$
and exits v through
$\mathcal B_o(v)$
, or vice versa.
A weight system on
$\tau $
is a function
$w:\mathcal B(\tau )\to \mathbb R_+$
satisfying the switch equations: for any switch v of
$\tau $
, we have
$$ \begin{align*} \sum_{e\in \mathcal B_i(v)} w(e) = \sum_{f\in \mathcal B_o(v)} w(f). \end{align*} $$
Associated to the pair
$(\tau ,w)$
, we construct the following union of foliated rectangles. For each
$b\in \mathcal B(\tau )$
, we assign a rectangle
$R(b)=[0,w(b)]\times [0,1]$
. We glue the rectangles at each switch v as follows. For any switch v of
$\tau $
, we consider the interval
$I(v)=[0,\ell ]$
, where
$$ \begin{align*} \ell = \sum_{b\in \mathcal B_i(v)} w(b) = \sum_{b \in \mathcal B_o(v)} w(b). \end{align*} $$
Suppose that
$b_1<\cdots <b_n$
are the outgoing branches at v. Then,
$I(v)$
is divided into consecutive closed intervals
$I_1,\ldots ,I_n$
of lengths
$w(b_1),\ldots ,w(b_n)$
, respectively, where
$0\in I_1$
and the intervals
$I_i$
overlap only on their boundaries. Then, we glue
$[0,w(b_i)]\times \{0\}\subset R(b_i)$
via an orientation-preserving isometry to the interval
$I_i$
. Similarly,
$I(v)$
is also divided into intervals
$J_1,\ldots ,J_m$
of lengths
$w(c_1),\ldots ,w(c_m)$
, where
$c_1,\ldots ,c_m$
are the incoming branches at v. Then, we glue
$[0,w(c_j)]\times \{1\}\subset R(c_j)$
to
$J_j$
via an orientation-preserving isometry. The union of foliated rectangles
$\mathcal F$
for
$(\tau ,w)$
is the quotient of the disjoint union of the rectangles
$R(b)$
and intervals
$I(v)$
by these gluing relations.
Each rectangle
$R(b)$
of
$\mathcal F$
is foliated by the vertical segments
$\{v\}\times [0,1]$
for
$v\in [0,w(b)]$
. This endows
$\mathcal F$
with the structure of a singular foliation. The singularities are the points where at least three rectangles of
$\mathcal F$
meet. In fact, at most four rectangles can meet, in which case, we have two rectangles on both sides of an interval
$I(v)$
. By thickening
$I(v)$
to a rectangle, we assume exactly three rectangles meet at each singularity. A leaf
$\ell $
of
$\mathcal F$
is an embedding of
$\mathbb R$
into
$\mathcal F$
that is the union of a sequence
$$ \begin{align*} \ldots \sigma_{-1} \sigma_0 \sigma_1\ldots \end{align*} $$
of vertical line segments
$\sigma _i = \{v_i\}\times [0,1]\subset R(b_i)$
with consecutive segments meeting at endpoints, and which satisfies the following conditions. First, we require that
$\ldots b_{-1}b_0b_1\ldots $
is a train path of
$\tau $
. Second, we have an additional requirement when the leaf contains at least two singularities, which we now describe. Given an orientation of a leaf
$\ell $
, singularities on
$\ell $
fall into two types, merging or splitting; see Figure 3. Moreover, singularities along
$\ell $
must alternate between the two types as they arise from gluing of rectangles. At a merging singularity, there are two possible local pictures of
$\ell $
, namely merging from the left or right branch. Similarly, at a splitting singularity,
$\ell $
splits to the left or right branch. For a leaf
$\ell $
containing at least two singularities, we require a choice of left or right: either
$\ell $
always merges from the left and splits to the left, or it always merges from the right and splits to the right; see Figure 3.
Figure 3 Left, two singular leaves that split after passing through a splitting singularity; middle, two singular leaves that merge after passing through a merging singularity; right, a singular leaf (indicated by the arrows) passes through three singularities and always splits to the left and merges from the left.
A leaf will be called singular if it contains a singularity and non-singular otherwise. We will use unions of foliated rectangles in §4 to construct geodesic laminations on hyperbolic surfaces.
Finally, suppose that X has an isolated puncture p. A ray
$\ell $
is any complete simple geodesic asymptotic to p on at least one end. The ray
$\ell $
is a loop if it is asymptotic to p on both ends. A ray is filling if it intersects every loop based at p. Denote by
$\mathcal R(X;p)$
the graph whose vertices are the rays based at p, and whose edges join pairs of rays that are disjoint. By [Reference Bavard and Walker5], the graph
$\mathcal R(X;p)$
consists of uncountably many connected components. Among these components, exactly one is of infinite diameter and Gromov hyperbolic. The remaining components are cliques of rays. These cliques consist of pairwise disjoint rays, each of which intersects every ray not lying in the clique. A ray in such a clique connected component is called high filling. The set of cliques of high-filling rays is identified with the Gromov boundary
$\partial \mathcal R(X;p)$
[Reference Bavard and Walker5, Theorem 6.3.1]. If a ray is filling but not high filling, then it is called
$2$
-filling [Reference Bavard and Walker5, Lemma 5.6.4]. Thus, there is a trichotomy: a ray is either not filling,
$2$
-filling, or high filling. As such,
$2$
-filling rays can be thought of as fake boundary points for the graph
$\mathcal R(X;p)$
, with properties mimicking those of high-filling rays. Finally, note that a priori, the graph
$\mathcal R(X;p)$
depends on the particular hyperbolic metric X. However, if Y is a different complete hyperbolic surface of the first kind homeomorphic to X, then there is a natural bijection between the rays on X based at p and the rays on Y based at p; see the end of Part 1 in [Reference Bavard and Walker5]. This bijection preserves the property of a ray being a loop,
$2$
-filling, high filling, etc. Hence, we may actually define 
, where S is the underlying topological surface to X, and the graph
$\mathcal R(S;p)$
is well defined independent of a particular hyperbolic metric of the first kind on S. When S is the plane minus a Cantor set, then
$2$
-filling rays exist, and the construction can be applied to many other surfaces of infinite type [Reference Chen and Rasmussen7]. Theorem 1.4 now confirms their existence on any infinite type surface with at least one isolated puncture.
4 Laminations
We consider the train track
$\tau $
illustrated in Figure 4. The weights of three branches are labeled for some
$\alpha \in (0,1)$
. The weights of the other branches are determined by these via the switch equations. Associated to these weights on
$\tau $
, we construct the standard union of foliated rectangles F. There is a single branch of weight
$1$
in
$\tau $
, which gives rise to a rectangle R of F.
Figure 4 A weighted train track
$\tau $
. The second return map to a horizontal interval in the rectangle R of the union of foliated rectangles F is a rotation by
$\alpha $
.
The train track
$\tau $
has an infinite cyclic cover
$\widetilde \tau $
which is pictured in Figure 5. The weights on
$\tau $
pull back to weights on
$\widetilde \tau $
, some of which are labeled in Figure 5.
Figure 5 The infinite cyclic cover
$\widetilde \tau $
of
$\tau $
.
We consider the union of foliated rectangles
$\widetilde F$
for
$\widetilde \tau $
with the described weights; see Figure 6. Then,
$\widetilde F$
is an infinite cyclic cover of F. The branches of
$\widetilde \tau $
of weight
$1$
give rise to a sequence of rectangles
$\ldots , R_{-1}, R_0, R_1,\ldots $
in
$\widetilde F$
, which are indexed by
$\mathbb Z$
and cover the rectangle R of F corresponding to the branch of
$\tau $
with weight
$1$
. We choose the numbering so that there is a rectangle joining
$R_i$
to
$R_{i+1}$
and a rectangle joining
$R_i$
to
$R_{i-1}$
for each i, both with width
$1/2$
. For the rectangle of width
$1/2$
joining
$R_i$
and
$R_{i+1}$
, one of its boundary leaves (the lower boundary in Figure 6) extends to a singular leaf
$\ell _i$
in
$\tilde F$
passing through the singularities
$s_i$
and
$s_{i+1}$
. The leaves
$\ell _{i-1}$
and
$\ell _i$
share a ray
$r_i$
starting at
$s_i$
. The following consequence of Corollary 1.2 is crucial to our construction of an infinite clique of
$2$
-filling rays.
Figure 6 Part of the union of foliated rectangles
$\widetilde {F}$
.
Lemma 4.1. Suppose that
$\alpha \in (0,1)$
satisfies the conditions of Theorem 1.1. Then, for each i, the ray
$r_i$
of
$\widetilde F$
is dense in
$\widetilde F$
, and hence so is the singular leaf
$\ell _i$
.
Proof. To prove this, we parameterize the disjoint union
$\bigcup _{i\in \mathbb Z} R_i$
by
$[0,1]^2 \times \mathbb Z$
, where
$R_i$
is isometrically identified with the unit square
$[0,1]^2$
and the leaves of
$\widetilde F$
intersect the rectangles
$[0,1]^2$
in vertical segments
$\{x\}\times [0,1]$
. We further choose the orientation on the vertical segments such that the singularity
$s_i$
is given by
$(1/2, 0, i)$
in these coordinates and each
$r_i$
starts from
$s_i$
by going upward; see Figure 6.
After
$r_i$
passes through
$R_i$
for the first time, it travels downward in
$R_i$
along the vertical segment with coordinate
$(1-\alpha )-1/2 = 1/2-\alpha $
, since
$\alpha <1/2$
as in Theorem 1.1. Thus,
$r_i$
passes through
$(1/2-\alpha ,0,i)$
to exit
$R_i$
. At this point,
$r_i$
will enter
$R_{i-1}$
since
$1/2-\alpha <1/2$
, and it travels upward starting at
$(1-1/2+\alpha ,0,i-1)=(1/2+\alpha, 0,i-1)$
.
In general, if at some point the ray
$r_i$
is traveling upward in some
$R_j$
along the vertical segment with coordinate
$x\in (0,1)$
, it hits the top of
$R_j$
and then starts to travel downward in
$R_j$
along
$\{b(x)\}\times [0,1]$
, where
$$ \begin{align*}b(x)=\begin{cases} 1-\alpha-x & \text{if } x<1-\alpha,\\ 2-\alpha-x & \text{if } x>1-\alpha. \end{cases}\end{align*} $$
Note that
$b(x)=1-t(x)$
, where
$t=t_\alpha $
is the rotation by
$\alpha $
as in §1, that is,
$t(x)\in (0,1)$
is the fractional part of
$x+\alpha $
. At this point,
$r_i$
exits
$R_j$
at
$(b(x),0,j)$
and enters
$R_{j'}$
with
$j'=j+1$
if
$b(x)>1/2$
and
$j'=j-1$
if
$b(x)<1/2$
. That is,
${j'=j+f(t(x))}$
for the function
$f=\chi _{[0,1/2)}-\chi _{[1/2,1)}$
as in the definition of the transformation T in Theorem 1.1. Moreover,
$r_i$
enters
$R_{j'}$
by traveling upward along the vertical segment with coordinate
$1-b(x)=t(x)$
.
In the calculations above, we ignored all boundary cases since we only care about
$x=t^n(1/2)$
for some
$n\ge 0$
and
$\alpha $
is irrational.
It follows from the analysis above that
$r_i$
visits the nth rectangle with entry point
$$ \begin{align*} \bigg(t^{n-1}(1/2), 0, i + \sum_{j=1}^{n-1}f(t^j(1/2))\bigg). \end{align*} $$
The sum
$\sum _{j=1}^{n-1} f(t^j(1/2))$
is equal to
$S_{n}(1/2) - f(1/2)=S_{n}(1/2)+1$
, where
$S_n$
is the nth Birkhoff sum defined in §1. Thus,
$r_i$
contains the points
$(t^{n-1}(1/2),0, i+1 + S_{n}(1/2))$
for
$n\geq 1$
, and the pairs
$(t^{n-1}(1/2), i+1 +S_{n}(1/2))$
are dense in
$[0,1]\times \mathbb Z$
by Corollary 1.2. To see the last claim, note that for each
$m\in \mathbb Z$
, the set of
$n\ge 0$
with
$i+1+S_{n}(1/2)=m$
is
$\Sigma (1/2,m-i-1)$
, so the pairs above contain
$(t^{n}(1/2), m)$
for all
$n\in \Sigma (1/2,m-i-1)-1$
except possibly
$n=0$
, and the first coordinates of such pairs are dense by Corollary 1.2. This proves that
$r_i$
is dense in
$R_m$
for any
$m\in \mathbb Z$
and hence dense in the whole foliation
$\widetilde F$
. This completes the proof of Lemma 4.1.
We now define a geodesic lamination on an infinite type hyperbolic surface. The track
$\widetilde \tau $
may be folded to yield the train track
$\hat \tau $
pictured on the left of Figure 7. The track
$\hat \tau $
is carried by another track
$\sigma $
shown on the right of Figure 7, which can in turn be embedded in any infinite type surface
$\Sigma $
with at least one isolated puncture p as we explain below; see the left of Figure 8.
Figure 7 Left, the track
$\hat \tau $
obtained by folding
$\widetilde \tau $
; middle, another embedding of
$\widetilde \tau $
that spirals; right, the track
$\sigma $
obtained by collapsing parallel branches.
Figure 8 Left, the track
$\sigma $
obtained by embedding
$\hat \tau $
on an infinite type surface
$\Sigma $
and collapsing parallel branches. Right, the non-filling ray
$R_\infty $
on
$\Sigma $
.
On the left of Figure 8, every tiny black disk represents a subsurface of
$\Sigma $
with a single boundary component, corresponding to the boundary of the black disk. We require each such subsurface to have either positive genus or at least two punctures. Furthermore, in
$\Sigma $
, the border line pictured on the left of Figure 8 is glued to itself by a reflection across the central vertical line, so that
$\Sigma $
has no boundary. With this identification, each dotted horizontal line segment represents an essential simple closed curve
$\gamma _i$
on
$\Sigma $
. Thus, the surface
$\Sigma $
with the black disks removed is a flute surface
$\Sigma '$
. Any infinite-type surface without boundary and with at least one isolated puncture can be realized this way by appropriately choosing the topological type of the subsurfaces represented by the black disks.
Lemma 4.2. For any orientable surface S of infinite type with at least one isolated puncture p, there is a sequence of surfaces
$\{D_i\}_{i\ge 1}$
each with one boundary component and either positive genus or at least two punctures, so that the surface
$(\Sigma ,p)$
above with the black disks homeomorphic to the surfaces
$D_i$
is homeomorphic to
$(S,p)$
.
Proof. Recall the classification of (possibly non-compact) orientable surfaces without boundary [Reference Richards9]. Each surface S has a space of ends E, which is totally disconnected, compact, and metrizable. The non-planar ends form a closed subset
$E_g\subset E$
, which is non-empty if and only if S has infinite genus. Then the classification states that two surfaces are homeomorphic if and only if they have the same genus (possibly infinite) and the pairs of spaces of ends
$(E,E_g)$
are homeomorphic. Moreover, given any pair
$(E,E_g)$
with E totally disconnected, compact, and metrizable and
$E_g\subset E$
closed, and given
$n\in \mathbb Z_{\ge 0}\cup \{\infty \}$
so that
$n<\infty $
if and only if
$E_g=\emptyset $
, there is an orientable surface S with genus n and spaces of ends homeomorphic to
$(E,E_g)$
. We say S is of infinite type if either E is an infinite set or
$E_g$
is non-empty.
Consider any S of infinite type with an isolated puncture p, and denote its space of ends by E. Since p is isolated,
$E\setminus \{p\}$
is clopen. There are two cases.
(1) Suppose E is infinite. Then, there is an accumulation point
$x\in E$
and a sequence of nested clopen neighborhoods
$E\setminus \{p\}=V_1\supset V_2\supset \cdots $
of x with
$\bigcap _i V_i=\{x\}$
. Up to relabeling, we may assume that 
contains at least two points for all
$i\ge 1$
. For each
$i\ge 1$
, there is a surface
$S_i$
with space of ends homeomorphic to
$(U_i, U_i\cap E_g)$
. Moreover, if
$U_i\cap E_g=\emptyset $
, then we can choose
$S_i$
to have any genus
$n_i\in \mathbb Z_{\ge 0}$
, which we now specify. If S has finite genus, we may choose the numbers
$n_i$
so that
$\sum n_i$
is equal to the genus of S. If S has infinite genus, for each i with
$U_i\cap E_g= \emptyset $
, we choose
$n_i=0$
if x is planar and
$n_i>0$
if x is non-planar. Let
$D_i$
be
$S_i$
with an open disk removed. Then, each
$D_i$
either has positive genus or has at least two punctures. Choose the black disks in the construction of our surface
$\Sigma $
above to be homeomorphic to the surfaces
$D_i$
. Then,
$(\Sigma ,p)$
is homeomorphic to
$(S,p)$
by the classification of surfaces.
(2) Suppose E is finite. Then,
$E_g$
must be non-empty for S to be of infinite type. Then,
$E=E_g\sqcup E'\sqcup \{p\}$
, where
$E'$
consists of planar ends other than p. For
$1\le i\le |E_g|-1$
, let
$S_i$
be the surface of infinite genus and exactly one (non-planar) end, that is, the Loch Ness monster. For
$i=|E_g|$
, let
$S_i$
be the surface of genus one with
$|E'|$
punctures. For
$i>|E_g|$
, let
$S_i$
be the torus. Now for each
$i\in \mathbb Z_+$
, let
$D_i$
be
$S_i$
with an open disk removed. Choose the black disks in the construction of our surface
$\Sigma $
above to be homeomorphic to the surfaces
$D_i$
. Then,
$\Sigma $
has infinite genus and has the same pair of spaces of ends as S, so again
$(\Sigma ,p)$
is homeomorphic to
$(S,p)$
by the classification of surfaces.
The simple closed curves
$\{\gamma _i\}_{i\ge 0}$
cut
$\Sigma '$
into an infinite sequence of finite type subsurfaces
$\{\Sigma _i\}_{i\ge 0}$
. For each
$i\ge 1$
(respectively
$i=0$
), the surface
$\Sigma _i$
is bounded by two (respectively one) curves
$\gamma _i$
together with
$7$
(respectively
$2$
) boundary components of black disks (respectively and a puncture p). Thus, each
$\Sigma _i$
admits a complete hyperbolic structure with geodesic boundary components all of length
$1$
. In the following, we choose the metric on
$\Sigma _i$
with the additional property that the (finitely many) train paths in
$\sigma \cap \Sigma _i$
have lengths bounded above independent of i, which can be done for instance by making
$\Sigma _i$
(
$i\ge 1$
) all isometric under the obvious translation in Figure 8. Since each black disk represents a surface with positive genus or at least two punctures, it admits a hyperbolic structure of the first kind so that the boundary is a geodesic of length
$1$
. Hence, by gluing, we can endow
$\Sigma $
with a complete hyperbolic metric of the first kind so that:
-
(1) each
$\gamma _i$
is a closed geodesic of length
$1$
; -
(2) the train paths in
$\sigma \cap \Sigma _i$
have lengths bounded above independent of i.
Let
$\widetilde \Sigma \cong \mathbb {H}^2$
be the universal cover of
$\Sigma $
. Consider the preimage
$\widetilde \sigma $
of
$\sigma $
and the collection
$\mathcal L$
of lifts of all curves
$\gamma _i$
to
$\widetilde \Sigma $
. We notice the following fact.
Lemma 4.3. For the choice of hyperbolic metric on
$\Sigma $
above, there are uniform constants
$K,C>0$
such that any bi-infinite train path of
$\widetilde \sigma $
is a
$(K,C)$
-quasi-geodesic. In particular, it limits to two distinct points on the Gromov boundary
$\partial \widetilde \Sigma $
.
Proof. We show this by looking at the intersections with lines in
$\mathcal L$
. Each lift of
$\gamma _i$
is a bi-infinite geodesic in
$\mathcal L$
. Note that there is a lower bound on the distance between any two lines of
$\mathcal L$
by the collar lemma since the curves
$\gamma _i$
have bounded length. Moreover, the segment between any two consecutive intersections of the train path with
$\mathcal L$
is a lift of a train path in
$\sigma \cap \Sigma _i$
for some i, and thus its length is bounded above by a uniform constant due to our choice of metric.
We claim that any train path of
$\widetilde \sigma $
with endpoints on two lines of
$\mathcal L$
is not homotopic, relative to endpoints, into a line in
$\mathcal L$
. Given the claim, any bi-infinite train path of
$\widetilde \sigma $
intersects a bi-infinite non-backtracking sequence of geodesics in
$\mathcal L$
at a uniformly bounded linear rate, from which the lemma follows.
The claim above follows from the observations below. There are only two homeomorphism classes of pairs
$(\Sigma _i, \Sigma _i \cap \sigma )$
. Moreover, in each track
$\Sigma _i \cap \sigma $
, there are finitely many train paths. Finally, by the choice of curves
$\gamma _i$
, no train path of
$\Sigma _i \cap \sigma $
is homotopic into
$\partial \Sigma _i$
via a homotopy keeping the endpoints of the train path on the boundary, and no two distinct train paths of
$\Sigma _i \cap \sigma $
are homotopic via such a homotopy.
Consequently, any bi-infinite train path t of
$\widetilde \sigma $
may be straightened to a geodesic
$\alpha $
in
$\partial \widetilde \Sigma $
with the same endpoints on the Gromov boundary. Moreover, the proof above implies that the sequences of lines in
$\mathcal L$
intersecting
$\alpha $
and t, respectively, are identical. In addition, the intersections with
$\mathcal L$
cut both
$\alpha $
and t into segments of length bounded above and below by uniform constants. We also see from the last observation made in the proof above that if
$t_1,t_2$
are train paths in
$\widetilde \sigma $
such that
$t_i$
joins a line
$L_i \in \mathcal L$
to a line
$L_i' \in \mathcal L$
, then
$t_1$
and
$t_2$
are equal if and only if
$L_1=L_2$
and
$L_1'=L_2'$
. The following lemmas can be deduced from these facts.
Lemma 4.4. Let
$\{t_i\}_{i=1}^\infty $
be bi-infinite train paths of
$\widetilde \sigma $
straightening to geodesics
$\{\alpha _i\}_{i=1}^\infty $
of
$\widetilde \Sigma $
. If
$\alpha $
is a geodesic of
$\widetilde \Sigma $
such that
$\alpha _i\to \alpha $
, then
$\alpha $
intersects infinitely many lines in
$\mathcal L$
at each end.
Proof. Suppose this is not the case. Then one end of
$\alpha $
projects to a geodesic ray in
$\Sigma $
disjoint from the curves
$\gamma _j$
. Note that each
$\alpha _i$
projected to
$\Sigma $
is disjoint from the boundary curve of each black disk in Figure 8. Hence, the limiting ray above is also disjoint from such boundary components. So the ray must be trapped in some
$\Sigma _j$
. This implies that there is an arbitrarily long geodesic segment
$\beta _i$
inside
$\Sigma _j$
in the projection of
$\alpha _i$
for i sufficiently large. This contradicts the observation we made above, that
$\alpha _i$
is divided by
$\mathcal L$
into segments of uniformly bounded length.
Lemma 4.5. Let
$\{t_i\}_{i=1}^\infty $
be bi-infinite train paths of
$\widetilde \sigma $
straightening to geodesics
$\{\alpha _i\}_{i=1}^\infty $
of
$\widetilde \Sigma $
. Suppose that
$\alpha $
is a geodesic of
$\widetilde \Sigma $
. Then,
$\alpha _i\to \alpha $
if and only if
$\alpha $
is also carried by
$\widetilde \sigma $
and for any finite sub-path s of the train path t defining
$\alpha $
, s is contained in
$t_i$
for all large enough i. In particular, the set of geodesics carried by
$\widetilde \sigma $
is closed in the space of geodesics of
$\widetilde \Sigma $
.
Proof. We only focus on the less obvious direction: if
$\alpha _i$
converges to a geodesic
$\alpha $
, then
$\alpha $
is carried by
$\widetilde \sigma $
and for any finite sub-path s of the train path t defining
$\alpha $
, s is contained in
$t_i$
for all large enough i.
Each
$\alpha _i$
intersects a bi-infinite sequence of lines in
$\mathcal L$
. By Lemma 4.4 and the fact that intersection is an open condition, these sequences (with an appropriate choice of the
$0$
th term) are pointwise eventually constant, with the limiting sequence equal to the lines in
$\mathcal L$
intersecting
$\alpha $
. As each straightening
$\alpha _i$
intersects the same sequence of lines in
$\mathcal L$
as the corresponding train path
$t_i$
does, the limiting sequence above determines a train path t carrying
$\alpha $
with the desired properties.
Lemma 4.6. Let s and t be bi-infinite train paths of
$\widetilde \sigma $
straightening to geodesics
$\beta $
and
$\alpha $
. Then,
$\beta $
and
$\alpha $
share an endpoint
$q \in \partial \widetilde \Sigma $
if and only if s and t share an infinite train path limiting to q.
Proof. We again focus on the less obvious direction: if
$\beta $
and
$\alpha $
share an endpoint
$q \in \partial \widetilde \Sigma $
, then s and t share an infinite train path limiting to q. As in the proof above,
$\alpha $
intersects the same bi-infinite sequence of lines in
$\mathcal L$
as t does. Note that the endpoints of these lines must converge to q since lines in
$\mathcal L$
are at distances uniformly bounded away from zero. This implies that this sequence of lines would eventually all intersect the ray in
$\beta $
limiting to q, and vice versa. It easily follows that s and t intersect the same sequence of lines in
$\mathcal L$
at one end, determining the desired infinite train path.
Now we define a geodesic lamination on
$\Sigma $
as follows. Recall that the weights on
$\tau $
induce weights on
$\widetilde {\tau }$
. Via the union of foliated rectangles construction, the leaves of the rectangles glue to a set of train paths on
$\widetilde {\tau }$
and they correspond to a set
$\widetilde {\mathcal T}$
of train paths on
$\sigma $
via the carrying map. Finally, we consider the train path
$t_*$
in
$\sigma $
which passes through each surface
$\Sigma _i$
(
$i>0$
) exactly twice and never returns. This is the train path parallel to the border line on the left side of Figure 8. We define 
, a set of train paths on
$\sigma $
. By Lemma 4.3, we may straighten the train paths in
$\mathcal S$
to geodesics. Denote the resulting set of geodesics by
$\Lambda $
. Since the train paths in
$\mathcal S$
do not cross, neither do the geodesics of
$\Lambda $
.
Lemma 4.7. The set of geodesics
$\Lambda $
is closed as a subset of
$\Sigma $
. Therefore, it is a geodesic lamination on
$\Sigma $
.
We postpone the proof of Lemma 4.7 and first discuss the train paths in
$\mathcal S$
in more detail. Any non-singular leaf of
$\widetilde F$
uniquely determines a train path in
$\sigma $
, and it is determined by any segment of the leaf contained in a foliated rectangle of
$\widetilde F$
. Now we describe train paths of
$\widetilde {\mathcal T}$
corresponding to singular leaves of
$\widetilde {F}$
. Note that there is a sequence of quadrilaterals
$Q_i$
in the complement of the train track
$\sigma $
; see the left of Figure 8. In each
$Q_i$
,
$i\ge 1$
, a pair of singularities
$\mathfrak s_i$
and
$\mathfrak s_{-i}$
sit at the two opposite horizontal corners, corresponding to the singularities
$s_i$
and
$s_{-i+1}$
in Figure 6. For each
$i \in \mathbb Z_+$
, there is a unique singular leaf
$\ell _i$
containing
$\mathfrak s_i$
and
$\mathfrak s_{i+1}$
, and a unique singular leaf
$\ell _{-i}$
containing
$\mathfrak s_{-i}$
and
$\mathfrak s_{-i-1}$
. Moreover, there is a singular leaf
$\ell _0$
containing
$\mathfrak s_{-1}$
and
$\mathfrak s_1$
. Thus, we have a collection
$\ldots , \ell _{-1}, \ell _0, \ell _1, \ldots $
of singular leaves of
$\widetilde F$
indexed by the integers, corresponding to those investigated in Lemma 4.1. This gives rise to a collection
$\ldots , t_{-1}, t_0,t_1,\ldots $
of train paths in
$\mathcal S$
. Note that for each
$i\in \mathbb Z$
,
$\ell _i$
shares a ray with
$\ell _{i-1}$
and
$\ell _{i+1}$
, respectively, so that
$t_i$
shares a half-infinite sub-train-path with
$t_{i-1}$
and
$t_{i+1}$
, respectively.
For each i, the train path
$t_i$
gives rise to a leaf
$L_i$
of
$\Lambda $
, corresponding to the leaf
$\ell _i$
in
$\widetilde {F}$
studied in Lemma 4.1.
Proof of Lemma 4.7
Lift
$\Lambda $
to a set of geodesics
$\widetilde {\Lambda }$
on
$\widetilde \Sigma $
. Let
$\unicode{x3bb} _1,\unicode{x3bb} _2,\ldots $
be geodesics in
$\widetilde {\Lambda }$
converging to the geodesic
$\unicode{x3bb} $
. By Lemma 4.5,
$\unicode{x3bb} $
is carried by
$\widetilde \sigma $
. Let t be a train path of
$\widetilde \sigma $
straightening to
$\unicode{x3bb} $
. If t projects to
$t_*$
in
$\Sigma $
, then
$\unicode{x3bb} $
is in
$\widetilde \Lambda $
by definition. Otherwise, t passes through some branch b on the boundary of a quadrilateral in the complement of
$\widetilde \sigma $
. Hence,
$t_i$
passes through b for i sufficiently large. Without loss of generality, we assume that
$t_i$
passes through b for every i.
Lift
$\widetilde F$
to a foliation of a subset of
$\widetilde \Sigma $
. Then, for each i,
$t_i$
is the train path defined by a (possibly singular) leaf of
$\widetilde F$
. That is, after collapsing the rectangles of
$\widetilde F$
to branches, and composing with the carrying map to
$\widetilde \sigma $
, we obtain
$t_i$
. Thus, for each
$t_i$
, there is a unique vertical line segment
$u_i$
in the rectangle
$R(b)$
which the leaf corresponding to
$t_i$
passes through. Up to passing to a subsequence, the segments
$u_i$
converge to a vertical segment u in
$R(b)$
, and we may further assume all segments
$u_i$
lie on the same side of u, say the left side (for a chosen orientation of u). Let
$r_i$
be the (possibly singular) leaf defining
$t_i$
(which passes through
$u_i$
). Furthermore, let r be the (possibly singular) leaf which passes through u, and, when given the orientation induced by u, merges from or splits into the left rectangle at every singularity that it passes through (if there are indeed any such singularities). Then,
$u_i$
converges to u, since for any finite sequence of rectangles that u passes through,
$u_i$
also passes through the same sequence for i sufficiently large. Hence,
$t_i$
converges to the train path defined by u, which is therefore equal to t. In particular,
$\unicode{x3bb} $
is a leaf of
$\widetilde \Lambda $
.
The following lemma is the key to obtain our infinite clique of
$2$
-filling rays.
Lemma 4.8. The complementary component to
$\Lambda $
containing p is a once-punctured ideal polygon with countably infinitely many ends, exactly one of which is the limit of the others. The sides of the ideal polygon are the leaves
$\{L_i\}_{i\in \mathbb Z}$
.
To prove Lemma 4.8, we look at some particular rays, which we denote as
$R_i$
with
$i \in \mathbb Z\cup \{\infty \}$
. We apologize for reusing the notation and warn the reader not to confuse them with the rectangles
$R_i$
discussed earlier (which play no role in the rest of the paper).
First, we define a ray
$R_\infty $
with one end at the isolated puncture p. This is the geodesic ray pictured on the right of Figure 8. It is non-proper and not filling (as defined at the end of §3). Observe that it is disjoint from
$\Lambda $
.
We also define a sequence of geodesic rays
$R_i$
for
$i\in \mathbb Z \setminus \{0\}$
as follows. The ray
$R_i$
is obtained by following
$R_\infty $
until it enters the quadrilateral
$Q_i$
with ends corresponding to the singularities
$\mathfrak s_{\pm i}$
. Thereafter, it passes through
$\mathfrak s_i$
and follows the common half-infinite sub-train-path of
$t_{i-1}$
and
$t_i$
(if
$i>0$
) or of
$t_i$
and
$t_{i+1}$
(if
$i<0$
). The path just described may be homotoped to be simple and disjoint from any given leaf of
$\Lambda $
, and furthermore, none of its arcs in a component of
$\Sigma \setminus \sqcup _i \gamma _i$
is homotopic into the boundary. Hence, the path may be straightened to a geodesic ray
$R_i$
; see Figure 9.
Figure 9 The rays
$R_i$
and
$R_\infty $
. They enter the union of foliated rectangles at a cusp and thereafter follow a leaf of the corresponding singular foliation (the dotted lines in the figure). For ease of presentation, the picture has been ‘unwrapped’ before being embedded into
$\Sigma $
.
Now, we prove Lemma 4.8.
Proof. Recall that the surfaces
$\Sigma _j$
are the complementary subsurfaces of the dotted curves
$\gamma _j$
and black disks in Figure 8. We see that for
$i\gg 0$
or
$i\ll 0$
,
$R_i$
and
$R_\infty $
pass through many of the surfaces
$\Sigma _j$
in the same order, and in each such
$\Sigma _j$
, the arcs of
$R_i$
and
$R_\infty $
are homotopic, keeping endpoints on the boundary. Hence, we have
$R_i\to R_\infty $
as
$i\to \infty $
and as
$i\to -\infty $
. Furthermore,
$R_i$
is asymptotic to
$L_i$
and
$L_{i-1}$
if
$i>0$
, and
$R_i$
is asymptotic to
$L_i$
and
$L_{i+1}$
if
$i<0$
. Finally, the rays
$R_i$
occur in the order
$$ \begin{align*} R_\infty < \cdots < R_2 < R_1 < R_{-1} < R_{-2} < \cdots < R_\infty \end{align*} $$
in the circular order on geodesics asymptotic to p.
Lift
$R_\infty $
to a ray
$\widetilde {R}_\infty $
in the universal cover
$\widetilde \Sigma $
. Then,
$\widetilde {R}_\infty $
has one endpoint at a lift
$\widetilde p$
of p on
$\partial \widetilde \Sigma $
and the other endpoint at a point
$z\in \partial \widetilde \Sigma $
. Let g be a generator of the cyclic subgroup of
$\pi _1(\Sigma )$
fixing
$\widetilde p$
. There is a unique lift
$\widetilde {R}_i$
of
$R_i$
based at
$\widetilde p$
, between
$\widetilde {R}_\infty $
and
$g\cdot \widetilde {R}_\infty $
. Up to replacing g by
$g^{-1}$
, we see that
$\widetilde {R}_i \to g\widetilde {R}_\infty $
as
$i\to +\infty $
and
$\widetilde {R}_i \to \widetilde {R}_\infty $
as
$i\to -\infty $
. Moreover, there is a lift
$\widetilde {L}_i$
for
$i\in \mathbb Z$
such that:
-
•
$\widetilde {L}_0, \widetilde {R}_{-1}, \widetilde {R}_1$
are the sides of an ideal triangle; -
•
$\widetilde {L}_i, \widetilde {R}_i, \widetilde {R}_{i+1}$
are the sides of an ideal triangle for
$i>0$
; -
•
$\widetilde {L}_i, \widetilde {R}_i, \widetilde {R}_{i-1}$
are the sides of an ideal triangle for
$i<0$
.
Consequently,
$\widetilde {R}_\infty $
,
$g\widetilde {R}_\infty $
, and the geodesics
$\widetilde {L}_i$
form the sides of a polygon with countably infinitely many ends. Each of these ends is isolated except z and
$gz$
, which are limits of the others. After quotienting by g, we obtain a once-punctured ideal polygon with a countable set of ends, exactly one of which is the limit of the others, as claimed.
Finally, we prove Theorems 1.3 and 1.4.
Proof of Theorem 1.4
By Lemma 4.2, any infinite type surface S with at least one isolated puncture p is homeomorphic to our surface
$\Sigma $
by a suitable choice in the construction. Construct the lamination
$\Lambda $
and use the notation as above. We see from Lemma 4.8 that every simple ray based at p, except
$R_i$
for
$i\in \{\infty \}\cup \mathbb Z \setminus \{0\}$
, intersects
$L_i$
for some
$i\in \mathbb Z$
. Moreover,
$L_i$
has a half leaf asymptotic to
$R_i$
, and this half leaf is dense in
$\Lambda $
by Lemma 4.1. Hence, each
$R_i$
accumulates onto
$\Lambda $
. Thus, every simple ray based at p, not contained in
$\{R_i\}_{i\in \{\infty \}\cup \mathbb Z \setminus \{0\}}$
, intersects
$R_i$
for every
$i\in \mathbb Z\setminus \{0\}$
. Thus, each ray
$R_i$
is
$2$
-filling, only disjoint from one non-filling long ray
$R_\infty $
, and
$\{R_i\}_{i\in \mathbb Z \setminus \{0\}}$
is an infinite clique of
$2$
-filling rays.
Proof of Theorem 1.3
Let
$S=\Sigma $
with the hyperbolic structure and lamination
$\Lambda $
as above. In the construction of
$\Lambda $
, choose
$\alpha =[0;2m+1,2m+2,2m+2,\ldots ]$
as in Example 2.10 for some
$m\ge 2$
, which satisfies the assumptions of Theorem 1.1. Each leaf
$L_i$
described above is dense in
$\Lambda $
by Lemma 4.1, so
$\Lambda $
is topologically transitive. However, the full orbit we examined in Example 2.10 has (forward and backward) Birkhoff sum always non-positive, so the corresponding leaf misses infinitely many rectangles, and thus it is not dense. There is an obvious
$\mathbb Z$
action on
$\widetilde F$
in Figure 6. It is straightforward to see that the
$\mathbb Z$
-orbit of this leaf yields infinitely many distinct non-dense leaves, which completes our proof.
Acknowledgments
We owe a debt of gratitude to Jon Chaika for teaching us and suggesting the method used in this paper for studying irrational rotations. We also thank the anonymous referee for their careful reading of the paper and suggestions. The second author was partially funded by NSF grant DMS-2202986.
Open access
