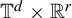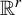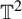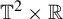1. Introduction
Let
![]() $\mathbb {T}=\mathbb {R}/\mathbb {Z}$
denote the torus, parameterized by
$\mathbb {T}=\mathbb {R}/\mathbb {Z}$
denote the torus, parameterized by
![]() $[0,1)$
. Given an irrational vector
$[0,1)$
. Given an irrational vector
![]() $\alpha =(\alpha _{1},\ldots , \alpha _d)\in \mathbb {R}^d$
, let
$\alpha =(\alpha _{1},\ldots , \alpha _d)\in \mathbb {R}^d$
, let
![]() $T_{\alpha }:\mathbb {T}^{d}\to \mathbb {T}^{d}$
denote the translation by
$T_{\alpha }:\mathbb {T}^{d}\to \mathbb {T}^{d}$
denote the translation by
![]() $\alpha $
on
$\alpha $
on
![]() $\mathbb {T}^d$
given by
$\mathbb {T}^d$
given by
![]() $x\mapsto x+\alpha $
(mod 1). Given an observable
$x\mapsto x+\alpha $
(mod 1). Given an observable
![]() $A(\cdot )$
on
$A(\cdot )$
on
![]() $\mathbb {R}^r$
, the cylindrical cascade above
$\mathbb {R}^r$
, the cylindrical cascade above
![]() $T_{\alpha }$
relative to
$T_{\alpha }$
relative to
![]() $A(\cdot )$
will be denoted by
$A(\cdot )$
will be denoted by
 $$ \begin{align*} \begin{aligned} W_{\alpha,A}\,:\,\mathbb{T}^{d}\times \mathbb{R}^{r} &\to \mathbb{T}^{d}\times \mathbb{R}^{r}, \\ (x,y) &\mapsto (x+\alpha,y+A(x)).\\ \end{aligned}\\[-20pt] \end{align*} $$
$$ \begin{align*} \begin{aligned} W_{\alpha,A}\,:\,\mathbb{T}^{d}\times \mathbb{R}^{r} &\to \mathbb{T}^{d}\times \mathbb{R}^{r}, \\ (x,y) &\mapsto (x+\alpha,y+A(x)).\\ \end{aligned}\\[-20pt] \end{align*} $$
The dynamics of
![]() $W_{\alpha ,A}$
are closely related to the Birkhoff sum of A, denoted by
$W_{\alpha ,A}$
are closely related to the Birkhoff sum of A, denoted by
![]() $A_N(\cdot )$
, by the expression
$A_N(\cdot )$
, by the expression
where
![]() $A_N(\cdot )$
is defined as
$A_N(\cdot )$
is defined as
 $$ \begin{align}A_N(x)= \begin{cases} \begin{aligned} &\sum_{n=0}^{N-1}A(T_{\alpha}^n x), \ \ \quad N\ge 1,\\ -&\sum_{n=1}^{-N}A(T_{\alpha}^{-n} x), \quad N\le -1,\\ &0, \quad\quad\qquad\qquad N=0. \end{aligned} \end{cases} \end{align} $$
$$ \begin{align}A_N(x)= \begin{cases} \begin{aligned} &\sum_{n=0}^{N-1}A(T_{\alpha}^n x), \ \ \quad N\ge 1,\\ -&\sum_{n=1}^{-N}A(T_{\alpha}^{-n} x), \quad N\le -1,\\ &0, \quad\quad\qquad\qquad N=0. \end{aligned} \end{cases} \end{align} $$
When
![]() $\alpha $
is Diophantine and A is smooth, the linear cohomological equation
$\alpha $
is Diophantine and A is smooth, the linear cohomological equation
![]() $A(x)-\int _{\mathbb {T}^d} A(u)\,du=-B(x+\alpha )+B(x)$
has a smooth solution B, and thus
$A(x)-\int _{\mathbb {T}^d} A(u)\,du=-B(x+\alpha )+B(x)$
has a smooth solution B, and thus
![]() $W_{\alpha ,A}$
is smoothly conjugated to the translation
$W_{\alpha ,A}$
is smoothly conjugated to the translation
![]() $W_{\alpha ,\int _{\mathbb {T}^d}A}$
. In this paper, we have examples where A is some indicator function and
$W_{\alpha ,\int _{\mathbb {T}^d}A}$
. In this paper, we have examples where A is some indicator function and
![]() $\alpha $
is Liouville.
$\alpha $
is Liouville.
The cascade
![]() $W_{\alpha ,A}$
can be seen as a random walk on the fiber
$W_{\alpha ,A}$
can be seen as a random walk on the fiber
![]() $\mathbb {R}^r$
driven by the translation
$\mathbb {R}^r$
driven by the translation
![]() $T_{\alpha }$
on the base
$T_{\alpha }$
on the base
![]() $\mathbb {T}^d$
, so it is natural to study its recurrence and ergodicity. For the walk
$\mathbb {T}^d$
, so it is natural to study its recurrence and ergodicity. For the walk
![]() $W_{\alpha , A}$
to be recurrent, the zero mean condition
$W_{\alpha , A}$
to be recurrent, the zero mean condition
![]() $\int _{\mathbb {T}^d}A=0$
(as vectors) is necessary, since, otherwise,
$\int _{\mathbb {T}^d}A=0$
(as vectors) is necessary, since, otherwise,
![]() $A_N$
goes to infinity by the ergodic theorem. In fact, Atkinson [Reference Atkinson2] showed that zero mean is also a sufficient condition for recurrence when
$A_N$
goes to infinity by the ergodic theorem. In fact, Atkinson [Reference Atkinson2] showed that zero mean is also a sufficient condition for recurrence when
![]() $r=1$
. For ergodicity, the case of one-dimensional rotations (
$r=1$
. For ergodicity, the case of one-dimensional rotations (
![]() $d=r=1$
) is well studied, and the ergodicity is often proved by the Denjoy–Koksma inequality and the essential values criterion (see definition below) [Reference Conze4, Reference Conze and Piękniewska6, Reference Frączek and Lemańczyk10, Reference Oren14].
$d=r=1$
) is well studied, and the ergodicity is often proved by the Denjoy–Koksma inequality and the essential values criterion (see definition below) [Reference Conze4, Reference Conze and Piękniewska6, Reference Frączek and Lemańczyk10, Reference Oren14].
In higher dimensions, the difficulty comes from the lack of the Denjoy–Koksma inequality for
![]() $d\ge 2$
(see [Reference Yoccoz16, Appendix 1, p. 215]). In the case where the fiber is
$d\ge 2$
(see [Reference Yoccoz16, Appendix 1, p. 215]). In the case where the fiber is
![]() $\mathbb {R}^r$
, only recurrent and transient examples are known when the base dimension
$\mathbb {R}^r$
, only recurrent and transient examples are known when the base dimension
![]() $d=2$
and the components of A are (zero-mean) indicator functions of polytopes for
$d=2$
and the components of A are (zero-mean) indicator functions of polytopes for
![]() $r>1$
(see [Reference Chevallier and Conze3]). More specifically, Chevallier and Conze [Reference Chevallier and Conze3] showed that, for the walk of any base space to be recurrent, a sufficient condition is that the Birkhoff sums of
$r>1$
(see [Reference Chevallier and Conze3]). More specifically, Chevallier and Conze [Reference Chevallier and Conze3] showed that, for the walk of any base space to be recurrent, a sufficient condition is that the Birkhoff sums of
![]() $A_i$
grow more slowly than
$A_i$
grow more slowly than
![]() $\mathcal {O}(n^{1/r})$
along some subsequence
$\mathcal {O}(n^{1/r})$
along some subsequence
![]() $N_n$
for most starting points. By using the
$N_n$
for most starting points. By using the
![]() $L^2$
-estimation of the ergodic deviations of A, they showed that, for almost every translation vector
$L^2$
-estimation of the ergodic deviations of A, they showed that, for almost every translation vector
![]() $\alpha $
, the walk
$\alpha $
, the walk
![]() $W_{\alpha ,A}$
is recurrent for polytopes. For integer-valued cocyles, Conze and Fraczek [Reference Conze and Frączek5] constructed examples of ergodic skew products for rotations of bounded type in the case of
$W_{\alpha ,A}$
is recurrent for polytopes. For integer-valued cocyles, Conze and Fraczek [Reference Conze and Frączek5] constructed examples of ergodic skew products for rotations of bounded type in the case of
![]() $\mathbb {T}^2\times \mathbb {Z}^2$
, where they took advantage of the recurrence of the cocycle from [Reference Chevallier and Conze3] and the boundedness of the rotations instead of the Denjoy–Koksma inequality. We refer the reader to the survey [Reference Dolgopyat and Fayad7] for a more comprehensive discussion about the recurrence and ergodicity of cylindrical cascades.
$\mathbb {T}^2\times \mathbb {Z}^2$
, where they took advantage of the recurrence of the cocycle from [Reference Chevallier and Conze3] and the boundedness of the rotations instead of the Denjoy–Koksma inequality. We refer the reader to the survey [Reference Dolgopyat and Fayad7] for a more comprehensive discussion about the recurrence and ergodicity of cylindrical cascades.
The ergodicity of the walk
![]() $W_{\alpha ,A}$
can be established if the sums
$W_{\alpha ,A}$
can be established if the sums
![]() $A_{N_n}$
are increasingly well distributed over
$A_{N_n}$
are increasingly well distributed over
![]() $\mathbb {R}^r$
along some subsequence
$\mathbb {R}^r$
along some subsequence
![]() ${N}_{n}$
, while the translation
${N}_{n}$
, while the translation
![]() $T^{N_n}_{\alpha }$
stays close to identity. This idea gives rise to the notion of essential values [Reference Schmidt15], which is the major tool for our construction of ergodic examples of
$T^{N_n}_{\alpha }$
stays close to identity. This idea gives rise to the notion of essential values [Reference Schmidt15], which is the major tool for our construction of ergodic examples of
![]() $W_{\alpha ,A}$
.
$W_{\alpha ,A}$
.
Definition 1.1.
![]() $a\in \mathbb {R}^{r}$
is called an essential value of A if, for each measurable set
$a\in \mathbb {R}^{r}$
is called an essential value of A if, for each measurable set
![]() $S\in \mathbb {T}^{d}$
of positive measure, for each
$S\in \mathbb {T}^{d}$
of positive measure, for each
![]() $\epsilon>0$
there exists
$\epsilon>0$
there exists
![]() $N\in \mathbb {Z}$
such that
$N\in \mathbb {Z}$
such that
The following lemma characterizes the set of all essential values of A, denoted by
![]() $E(A)$
, and gives a criterion for ergodicity.
$E(A)$
, and gives a criterion for ergodicity.
Lemma 1.2. [Reference Aaronson1, Reference Schmidt15]
-
(1)
 $E(A)$
is a closed subgroup of
$E(A)$
is a closed subgroup of
 $\mathbb {R}^{r}$
.
$\mathbb {R}^{r}$
. -
(2)
 $E(A)=\mathbb {R}^{r}$
if and only if
$E(A)=\mathbb {R}^{r}$
if and only if
 $W_{\alpha ,A}$
is ergodic.
$W_{\alpha ,A}$
is ergodic. -
(3) If A is integer valued and
 $E(A)=\mathbb {Z}^{r}$
, then
$E(A)=\mathbb {Z}^{r}$
, then
 $W_{\alpha ,A}$
is ergodic in
$W_{\alpha ,A}$
is ergodic in
 $\mathbb {T}^{d}\times \mathbb {Z}^{r}$
.
$\mathbb {T}^{d}\times \mathbb {Z}^{r}$
.
In this paper, we develop the ideas introduced by Fayad [Reference Fayad9] to recover Denjoy–Koksma-type inequalities for Liouville rotations. By combining these with several classical results from number theory for Diophantine approximations, we establish the essential value criterion to obtain the ergodicity of the walk
![]() $W_{\alpha ,A}$
.
$W_{\alpha ,A}$
.
Given a vector
![]() $L=(l,l')\in (0,1]^2$
, denote by
$L=(l,l')\in (0,1]^2$
, denote by
![]() $B_{L}$
the rectangle
$B_{L}$
the rectangle
![]() $[0,l]\times [0,l']\subset \mathbb {T}^2$
, and denote by
$[0,l]\times [0,l']\subset \mathbb {T}^2$
, and denote by
![]() $Vol(B_{L})$
its volume (area)
$Vol(B_{L})$
its volume (area)
![]() $ll'$
. We prove the following theorem.
$ll'$
. We prove the following theorem.
Theorem 1.3. For almost every
![]() $L=(l,l')\in (0,1]^2$
, there exists a
$L=(l,l')\in (0,1]^2$
, there exists a
![]() $G_{\delta }$
-dense set of
$G_{\delta }$
-dense set of
![]() $\alpha =(\alpha _{1},{\alpha }_{2}) \in \mathbb {R}^{2}-\mathbb {Q}^{2}$
such that the cylindrical cascade
$\alpha =(\alpha _{1},{\alpha }_{2}) \in \mathbb {R}^{2}-\mathbb {Q}^{2}$
such that the cylindrical cascade
![]() $W_{\alpha ,A}$
constructed over the zero-mean indicator function
$W_{\alpha ,A}$
constructed over the zero-mean indicator function
![]() $A(\cdot )=\chi _{B_{L}}(\cdot )-Vol(B_{L})$
is ergodic.
$A(\cdot )=\chi _{B_{L}}(\cdot )-Vol(B_{L})$
is ergodic.
We also give examples for the case of
![]() $\mathbb {T}^{2}\times \mathbb {R}^{2}$
, with more restrictions for the second rectangle. Given two pairs of lengths
$\mathbb {T}^{2}\times \mathbb {R}^{2}$
, with more restrictions for the second rectangle. Given two pairs of lengths
![]() $(l_{1},l^{\prime }_{1})$
,
$(l_{1},l^{\prime }_{1})$
,
![]() $(l_{2},l^{\prime }_{2})$
, define the corresponding rectangles
$(l_{2},l^{\prime }_{2})$
, define the corresponding rectangles
![]() $B_{1}=[0,l_{1}]\times [0, l^{\prime }_{1}]$
and
$B_{1}=[0,l_{1}]\times [0, l^{\prime }_{1}]$
and
![]() $B_{2}=[0,l_{2}]\times [0,l^{\prime }_{2}]$
and the zero-mean indicator functions
$B_{2}=[0,l_{2}]\times [0,l^{\prime }_{2}]$
and the zero-mean indicator functions
 $$ \begin{align} \begin{cases} A^{(1)}(\cdot)= \chi_{B_{1}}(\cdot)-\mathrm{vol}(B_{1}),\\ A^{(2)}(\cdot)= \chi_{B_{2}}(\cdot)-\mathrm{vol}(B_{2}).\\ \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} A^{(1)}(\cdot)= \chi_{B_{1}}(\cdot)-\mathrm{vol}(B_{1}),\\ A^{(2)}(\cdot)= \chi_{B_{2}}(\cdot)-\mathrm{vol}(B_{2}).\\ \end{cases} \end{align} $$
Then we have the following result for the
![]() $\mathbb {R}^{2}$
case.
$\mathbb {R}^{2}$
case.
Theorem 1.4. For almost every
![]() $(l_{1},l^{\prime }_{1})\in (0,1]^2$
, there exist
$(l_{1},l^{\prime }_{1})\in (0,1]^2$
, there exist
![]() $G_{\delta }$
-dense sets of
$G_{\delta }$
-dense sets of
![]() $(0,1]$
of
$(0,1]$
of
![]() $l_{2}$
and
$l_{2}$
and
![]() $l^{\prime }_{2}$
, and a
$l^{\prime }_{2}$
, and a
![]() $G_{\delta }$
-dense set of
$G_{\delta }$
-dense set of
![]() $\alpha =(\alpha _{1},\alpha _{2}) \in \mathbb {R}^{2}-\mathbb {Q}^{2}$
, such that the cylindrical cascade
$\alpha =(\alpha _{1},\alpha _{2}) \in \mathbb {R}^{2}-\mathbb {Q}^{2}$
, such that the cylindrical cascade
![]() $W_{\alpha ,A}$
constructed over
$W_{\alpha ,A}$
constructed over
![]() $A(\cdot )=(A^{(1)}(\cdot ),A^{(2)}(\cdot ))$
(as defined in (1.3)) is ergodic.
$A(\cdot )=(A^{(1)}(\cdot ),A^{(2)}(\cdot ))$
(as defined in (1.3)) is ergodic.
It is not hard to see that by restricting the vector function
![]() $A(\cdot )$
in Theorem 1.4 to its first coordinate
$A(\cdot )$
in Theorem 1.4 to its first coordinate
![]() $A^{(1)}$
we obtain Theorem 1.3 as a corollary. In this paper, we prove Theorem 1.4 in detail and keep Theorem 1.3 as its corollary.
$A^{(1)}$
we obtain Theorem 1.3 as a corollary. In this paper, we prove Theorem 1.4 in detail and keep Theorem 1.3 as its corollary.
Using our method, higher-dimensional counterparts in
![]() $\mathbb {T}^d\times \mathbb {R}^r$
can be obtained by requiring that the lengths of additional sides of the higher-dimensional boxes are Liouville when
$\mathbb {T}^d\times \mathbb {R}^r$
can be obtained by requiring that the lengths of additional sides of the higher-dimensional boxes are Liouville when
![]() $d>2$
or
$d>2$
or
![]() $r>1$
, and by applying the subgroup property of the essential values (point 2 of Lemma 1.2). Ergodic examples using polytopes in
$r>1$
, and by applying the subgroup property of the essential values (point 2 of Lemma 1.2). Ergodic examples using polytopes in
![]() $\mathbb {T}^d$
,
$\mathbb {T}^d$
,
![]() $d\ge 2,$
are more delicate due to their inclined sides, and their constructions are still in progress. Although Liouville conditions are needed with our method, ergodicity of the walk is expected for typical polytopes and typical translation vectors, due to the slow divergence rate of the Birkhoff sums of A.
$d\ge 2,$
are more delicate due to their inclined sides, and their constructions are still in progress. Although Liouville conditions are needed with our method, ergodicity of the walk is expected for typical polytopes and typical translation vectors, due to the slow divergence rate of the Birkhoff sums of A.
2. Arithmetic notation
Let x be a real number.
-
(1) Denote by
 $[x]$
the integer part of x.
$[x]$
the integer part of x. -
(2) Denote by
 $\{x\}$
the signed distance of the x to the closest integer: that is,
$\{x\}$
the signed distance of the x to the closest integer: that is,
 $\{x\}=x-n$
, where n is the only integer such that
$\{x\}=x-n$
, where n is the only integer such that
 $x-n\in [-1/2,1/2)$
.
$x-n\in [-1/2,1/2)$
. -
(3) Denote by
 $\lVert x \rVert = |\{x\}|$
the distance of x to the closest integer.
$\lVert x \rVert = |\{x\}|$
the distance of x to the closest integer.
3. Lemmas
Our construction is based on the approximation of the rectangle by small rational rectangles that tile the torus and the approximation of the translation vector by their vertices. We begin with the following observation.
Lemma 3.1. Let v denote the rational vector
![]() $(p/q,p'/q')$
on
$(p/q,p'/q')$
on
![]() $\mathbb {T}^2$
, where the coordinates are in reduced forms, that is,
$\mathbb {T}^2$
, where the coordinates are in reduced forms, that is,
![]() $(p,q)=1$
and
$(p,q)=1$
and
![]() $(p',q')=1$
. If, in addition, we have that
$(p',q')=1$
. If, in addition, we have that
![]() $(q, q')=1$
, then the following identity holds for any
$(q, q')=1$
, then the following identity holds for any
![]() $r\in \mathbb {Z}$
: that is,
$r\in \mathbb {Z}$
: that is,
 $$ \begin{align} \{mv \ |\ {r\le m\le r+qq'-1}\}=\bigg\{ \bigg(\frac{i}{q},\frac{j}{q'}\bigg)\ \bigg|\ 0\le i\le q-1, \ 0\le j \le q'-1\bigg\}. \end{align} $$
$$ \begin{align} \{mv \ |\ {r\le m\le r+qq'-1}\}=\bigg\{ \bigg(\frac{i}{q},\frac{j}{q'}\bigg)\ \bigg|\ 0\le i\le q-1, \ 0\le j \le q'-1\bigg\}. \end{align} $$
Remark 3.2. This lemma states that the orbit of length
![]() $qq'$
of the translations by v in
$qq'$
of the translations by v in
![]() $\mathbb {T}^2$
coincides with the vertices of the tiling of
$\mathbb {T}^2$
coincides with the vertices of the tiling of
![]() $\mathbb {T}^2$
by rectangles of side lengths
$\mathbb {T}^2$
by rectangles of side lengths
![]() $1/q$
and
$1/q$
and
![]() $1/q'$
.
$1/q'$
.
Proof. Because the cardinalities of the two sets are both
![]() $qq'$
, it is enough to show that, for
$qq'$
, it is enough to show that, for
![]() $r\le m, n \le r+qq'-1$
,
$r\le m, n \le r+qq'-1$
,
Note that
![]() $mv=nv$
in
$mv=nv$
in
![]() $\mathbb {T}^2$
is equivalent to
$\mathbb {T}^2$
is equivalent to
Because p and q are relatively prime, q divides
![]() $m-n$
, and, similarly,
$m-n$
, and, similarly,
![]() $q'$
divides
$q'$
divides
![]() $m-n$
. Note that q and
$m-n$
. Note that q and
![]() $q'$
are also relatively prime, so we have that
$q'$
are also relatively prime, so we have that
![]() $qq'$
divides
$qq'$
divides
![]() $m-n$
, which is only possible when
$m-n$
, which is only possible when
![]() $m=n$
, since
$m=n$
, since
![]() $|m-n|\le qq'-1$
.
$|m-n|\le qq'-1$
.
Our idea is to approximate the irrational translation vector
![]() $\alpha $
by rational vectors. First, we tile the torus
$\alpha $
by rational vectors. First, we tile the torus
![]() $\mathbb {T}^2$
by disjoint rectangles of side lengths
$\mathbb {T}^2$
by disjoint rectangles of side lengths
![]() $1/q$
and
$1/q$
and
![]() $1/q'$
: that is,
$1/q'$
: that is,
 $$ \begin{align} \mathbb{T}^2=\bigcup_{\substack{0\le i\le q-1\\ 0\le j\le q'-1}} R^{i,j}, \end{align} $$
$$ \begin{align} \mathbb{T}^2=\bigcup_{\substack{0\le i\le q-1\\ 0\le j\le q'-1}} R^{i,j}, \end{align} $$
where
![]() $R^{i,j}$
is the rectangle
$R^{i,j}$
is the rectangle
![]() $[i/q,(i+1)/q)\times [j/q',(j+1)/q')$
.
$[i/q,(i+1)/q)\times [j/q',(j+1)/q')$
.
Note that if the translation vector
![]() $\alpha $
is close to the rational vector
$\alpha $
is close to the rational vector
![]() $(p/q,p'/q')$
, then the above lemma implies that, starting from the origin, the orbit
$(p/q,p'/q')$
, then the above lemma implies that, starting from the origin, the orbit
![]() $\{m\alpha \}$
of length
$\{m\alpha \}$
of length
![]() $qq'$
visits a close neighborhood of every vertex of the tiling by
$qq'$
visits a close neighborhood of every vertex of the tiling by
![]() $R^{i,j}$
exactly once.
$R^{i,j}$
exactly once.
By approximating the rectangle
![]() $B_{L}=[0,l]\times [0,l']$
by a union of
$B_{L}=[0,l]\times [0,l']$
by a union of
![]() $R^{i,j}$
, we can control precisely the number of points in the orbit
$R^{i,j}$
, we can control precisely the number of points in the orbit
![]() $\{x+m\alpha \}$
that lie inside
$\{x+m\alpha \}$
that lie inside
![]() $B_{L}$
at special times. Specifically, we can compute the Birkhoff sums for
$B_{L}$
at special times. Specifically, we can compute the Birkhoff sums for
![]() $A=\chi _{B_L}-\text {Vol}(B_L)$
as follows.
$A=\chi _{B_L}-\text {Vol}(B_L)$
as follows.
Let
where
![]() $\delta =\{ql\}$
,
$\delta =\{ql\}$
,
![]() $\delta '=\{q'l'\}$
, and let
$\delta '=\{q'l'\}$
, and let
where
![]() $\eta =\{q\alpha _1\}$
,
$\eta =\{q\alpha _1\}$
,
![]() $\eta '=\{q'\alpha _2\}$
.
$\eta '=\{q'\alpha _2\}$
.
When
![]() $\eta ,\eta '$
is small compared with
$\eta ,\eta '$
is small compared with
![]() $\delta , \delta '$
, that is,
$\delta , \delta '$
, that is,
![]() $\alpha $
Liouville enough, we have the following expressions for the Birkhoff sums.
$\alpha $
Liouville enough, we have the following expressions for the Birkhoff sums.
Lemma 3.3. Denote
![]() $N=qq'$
, and suppose that
$N=qq'$
, and suppose that
![]() $|\delta |$
and
$|\delta |$
and
![]() $|\delta '|$
are smaller than
$|\delta '|$
are smaller than
![]() $1/4$
. Let
$1/4$
. Let
![]() $\tilde {\delta }\in [|\delta |, 1/4)$
and
$\tilde {\delta }\in [|\delta |, 1/4)$
and
![]() $\tilde {\delta '}\in [|\delta '|, 1/4)$
. If, for
$\tilde {\delta '}\in [|\delta '|, 1/4)$
. If, for
![]() $\tilde {\delta }$
and
$\tilde {\delta }$
and
![]() $\tilde {\delta '}$
, there exists a non-zero integer K such that
$\tilde {\delta '}$
, there exists a non-zero integer K such that
then there exists a set
![]() $\mathcal {F}\subset \mathbb {T}^2$
of measure
$\mathcal {F}\subset \mathbb {T}^2$
of measure
![]() $(1-4\tilde {\delta })(1-4\tilde {\delta '})$
such that, for every
$(1-4\tilde {\delta })(1-4\tilde {\delta '})$
such that, for every
![]() $x\in \mathcal {F}$
and every k between
$x\in \mathcal {F}$
and every k between
![]() $0$
and K (possibly negative), the Birkhoff sum
$0$
and K (possibly negative), the Birkhoff sum
![]() $A_{kN}(x)$
has the form
$A_{kN}(x)$
has the form
Proof. Define
![]() $\mathcal {F}$
to be the set of points that are not
$\mathcal {F}$
to be the set of points that are not
![]() $2\tilde {\delta } $
-close to the boundaries of any
$2\tilde {\delta } $
-close to the boundaries of any
![]() $R^{i,j}$
, in the following sense: that is,
$R^{i,j}$
, in the following sense: that is,
 $$ \begin{align} \mathcal{F}=\bigcup_{\substack{0\le i\le q-1\\ 0\le j\le q'-1}} \left\{(x_1,x_2)\in \mathbb{T}^2 \left| \ \begin{aligned} &(i+2\tilde{\delta})/q \le x_1\le (i+1-2\tilde{\delta})/q,\\ &(j+2\tilde{\delta})/q'\le x_2\le (j+1-2\tilde{\delta})/q' \end{aligned}\right. \right\}\!. \end{align} $$
$$ \begin{align} \mathcal{F}=\bigcup_{\substack{0\le i\le q-1\\ 0\le j\le q'-1}} \left\{(x_1,x_2)\in \mathbb{T}^2 \left| \ \begin{aligned} &(i+2\tilde{\delta})/q \le x_1\le (i+1-2\tilde{\delta})/q,\\ &(j+2\tilde{\delta})/q'\le x_2\le (j+1-2\tilde{\delta})/q' \end{aligned}\right. \right\}\!. \end{align} $$
Remark. More precisely it should be called ‘
![]() $2(\tilde {\delta },\tilde {\delta }')$
-close’, but, since
$2(\tilde {\delta },\tilde {\delta }')$
-close’, but, since
![]() $\tilde {\delta }$
and
$\tilde {\delta }$
and
![]() $\tilde {\delta }'$
always come together, we use the notation ‘
$\tilde {\delta }'$
always come together, we use the notation ‘
![]() $\tilde {\delta }$
-close’ to be more concise.
$\tilde {\delta }$
-close’ to be more concise.
![]() $\mathcal {F}$
is the disjoint union of
$\mathcal {F}$
is the disjoint union of
![]() $qq'$
rectangles, and each of them is of measure
$qq'$
rectangles, and each of them is of measure
![]() $(1-4\tilde {\delta }) (1-4\tilde {\delta })/(qq')$
, so the measure of
$(1-4\tilde {\delta }) (1-4\tilde {\delta })/(qq')$
, so the measure of
![]() $\mathcal {F}$
is
$\mathcal {F}$
is
![]() $(1-4\tilde {\delta })(1-4\tilde {\delta })$
.
$(1-4\tilde {\delta })(1-4\tilde {\delta })$
.
Note that, for
![]() $|m|\le |K|N$
,
$|m|\le |K|N$
,
![]() $m\alpha $
is
$m\alpha $
is
![]() $\tilde {\delta }-$
close to
$\tilde {\delta }-$
close to
![]() $m(p/q,p'/q')$
: that is,
$m(p/q,p'/q')$
: that is,
 $$ \begin{align} |m\alpha_1-mp/q| &\le|m||\eta|/q \le \tilde{\delta}/q,\nonumber\\ |m\alpha_2-mp'/q'| &\le |m||\eta'|/q'\le \tilde{\delta}/q'. \end{align} $$
$$ \begin{align} |m\alpha_1-mp/q| &\le|m||\eta|/q \le \tilde{\delta}/q,\nonumber\\ |m\alpha_2-mp'/q'| &\le |m||\eta'|/q'\le \tilde{\delta}/q'. \end{align} $$
Starting from a point x in
![]() $\mathcal {F}$
, since the points in
$\mathcal {F}$
, since the points in
![]() $\mathcal {F}$
are
$\mathcal {F}$
are
![]() $2\tilde {\delta }$
-away from the boundaries of
$2\tilde {\delta }$
-away from the boundaries of
![]() $R^{i,j}$
, the orbit
$R^{i,j}$
, the orbit
![]() $\{x+m\alpha \ | \ |m| \le |K|N-1\}$
stays
$\{x+m\alpha \ | \ |m| \le |K|N-1\}$
stays
![]() $\tilde {\delta }$
-away from the boundaries of
$\tilde {\delta }$
-away from the boundaries of
![]() $R^{i,j}$
. By Lemma 3.1, for
$R^{i,j}$
. By Lemma 3.1, for
![]() $|k|\le |K|-1$
, the orbit
$|k|\le |K|-1$
, the orbit
![]() $\{x+m\alpha | \ kN\le m \le (k+1)N-1\}$
visits each
$\{x+m\alpha | \ kN\le m \le (k+1)N-1\}$
visits each
![]() $R^{i,j}$
exactly once and stays
$R^{i,j}$
exactly once and stays
![]() $\tilde {\delta }$
-away from the boundaries of the small rectangles in the tiling.
$\tilde {\delta }$
-away from the boundaries of the small rectangles in the tiling.
Since
![]() $\tilde {\delta }>|\delta |$
and
$\tilde {\delta }>|\delta |$
and
![]() $\tilde {\delta '}>|\delta '|$
, our target rectangle
$\tilde {\delta '}>|\delta '|$
, our target rectangle
![]() $B_L$
contains the center parts of
$B_L$
contains the center parts of
![]() $bb'$
small rectangles, and the orbit visits
$bb'$
small rectangles, and the orbit visits
![]() $B_L bb'$
times within a time range of N. Therefore, for
$B_L bb'$
times within a time range of N. Therefore, for
![]() $0\le k\le |K|$
,
$0\le k\le |K|$
,
 $$ \begin{align} A_{kN}(x) &=kA_N(x)\nonumber\\ &=k(bb'-qq'll')\nonumber\\ &=k(bb'-(b+\delta)(b'+\delta'))\nonumber\\ &=-k(b\delta'+b'\delta+\delta\delta'). \end{align} $$
$$ \begin{align} A_{kN}(x) &=kA_N(x)\nonumber\\ &=k(bb'-qq'll')\nonumber\\ &=k(bb'-(b+\delta)(b'+\delta'))\nonumber\\ &=-k(b\delta'+b'\delta+\delta\delta'). \end{align} $$
In view of the negative sign in the definition of
![]() $A_N(x)$
for
$A_N(x)$
for
![]() $N<0$
in (1.1), the above identity holds for
$N<0$
in (1.1), the above identity holds for
![]() $-|K|<k<0$
with the same argument.
$-|K|<k<0$
with the same argument.
If we can show that
![]() $A_N(x)$
becomes increasingly small for sequences of q and
$A_N(x)$
becomes increasingly small for sequences of q and
![]() $q'$
, then, by choosing K increasingly large for Liouville translation vector
$q'$
, then, by choosing K increasingly large for Liouville translation vector
![]() $\alpha $
, the sequence
$\alpha $
, the sequence
![]() $\{A_{kN}\}_{0\le k\le K-1}$
can be increasingly well distributed in
$\{A_{kN}\}_{0\le k\le K-1}$
can be increasingly well distributed in
![]() $\mathbb {R}$
. The following lemma states that this is indeed the case for generic
$\mathbb {R}$
. The following lemma states that this is indeed the case for generic
![]() $L=(l,l')\in \mathbb {T}^2$
.
$L=(l,l')\in \mathbb {T}^2$
.
Lemma 3.4. For almost every
![]() $(l,l')\in (0,1]^2$
, there exist two sequences
$(l,l')\in (0,1]^2$
, there exist two sequences
![]() $\{q_{n}\}_{n\in \mathbb {N}}\text { and } \{q^{\prime }_{n}\}_{n\in \mathbb {N}} $
such that the following properties hold.
$\{q_{n}\}_{n\in \mathbb {N}}\text { and } \{q^{\prime }_{n}\}_{n\in \mathbb {N}} $
such that the following properties hold.
-
(1)
 $q_{n},q^{\prime }_{n}\rightarrow \infty $
, as
$q_{n},q^{\prime }_{n}\rightarrow \infty $
, as
 $n\rightarrow \infty $
.
$n\rightarrow \infty $
. -
(2)
 $q_n$
and
$q_n$
and
 $q^{\prime }_n$
are relatively prime, that is
$q^{\prime }_n$
are relatively prime, that is
 $(q_n,q^{\prime }_n)=1$
,
$(q_n,q^{\prime }_n)=1$
,
 $\text { for all } n\in \mathbb {N}$
.
$\text { for all } n\in \mathbb {N}$
. -
(3) We have
(3.11)where $$ \begin{align} \frac{l}{2(\ln q_{n})^{2}} \leq \vert b^{\prime}_{n}(q_{n}l-b_{n})+b_{n}(q^{\prime}_{n}l'-b^{\prime}_{n})\vert \leq \frac{2}{(\ln\ln\ln q_{n})^{1/2}}, \end{align} $$
$$ \begin{align} \frac{l}{2(\ln q_{n})^{2}} \leq \vert b^{\prime}_{n}(q_{n}l-b_{n})+b_{n}(q^{\prime}_{n}l'-b^{\prime}_{n})\vert \leq \frac{2}{(\ln\ln\ln q_{n})^{1/2}}, \end{align} $$
 $b_{n}$
and
$b_{n}$
and
 $b^{\prime }_{n}$
are the closest integers to
$b^{\prime }_{n}$
are the closest integers to
 $q_{n}l$
and
$q_{n}l$
and
 $q^{\prime }_{n}l'$
.
$q^{\prime }_{n}l'$
.
-
(4)
 $q^{\prime }_{n}$
and
$q^{\prime }_{n}$
and
 $q_{n}$
are approximately of the same magnitude: that is, (3.12)
$q_{n}$
are approximately of the same magnitude: that is, (3.12) $$ \begin{align} \frac{q_{n}}{(\ln q_{n})^2}\le q^{\prime}_{n}\le q_{n}(\ln \ln \ln q_{n})^{{1}/{2}}. \end{align} $$
$$ \begin{align} \frac{q_{n}}{(\ln q_{n})^2}\le q^{\prime}_{n}\le q_{n}(\ln \ln \ln q_{n})^{{1}/{2}}. \end{align} $$
-
(5) The next two inequalities follow from the proof of (3.11). We record them here for later use.
(3.13)and $$ \begin{align} \| q_{n}l \| \leq \frac{1}{q_{n}\ln \ln \ln q_{n}} \end{align} $$
(3.14)
$$ \begin{align} \| q_{n}l \| \leq \frac{1}{q_{n}\ln \ln \ln q_{n}} \end{align} $$
(3.14) $$ \begin{align} \| q^{\prime}_{n}l' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}. \end{align} $$
$$ \begin{align} \| q^{\prime}_{n}l' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}. \end{align} $$
Lemma 3.4 states that the Birkhoff sums for A can indeed be small along the subsequence
![]() $q_n q^{\prime }_n$
, while the coprime condition between
$q_n q^{\prime }_n$
, while the coprime condition between
![]() $q_n$
and
$q_n$
and
![]() $q^{\prime }_n$
is satisfied. When the fiber is of higher dimensions,
$q^{\prime }_n$
is satisfied. When the fiber is of higher dimensions,
![]() $\mathbb {R}^2$
for example, we need similar bounds for the second rectangle, but, to approximate the essential values along two axes, we need the magnitude of the Birkhoff sums for the second rectangle to alternate between large and small relative to the Birkhoff sums of the first rectangle. This can be achieved by restricting the length of the second rectangle in a
$\mathbb {R}^2$
for example, we need similar bounds for the second rectangle, but, to approximate the essential values along two axes, we need the magnitude of the Birkhoff sums for the second rectangle to alternate between large and small relative to the Birkhoff sums of the first rectangle. This can be achieved by restricting the length of the second rectangle in a
![]() $G_{\delta }$
-dense set, as stated in the next lemma.
$G_{\delta }$
-dense set, as stated in the next lemma.
Lemma 3.5. For almost every
![]() $l_{1},l^{\prime }_{1}\in (0,1]$
, there exist
$l_{1},l^{\prime }_{1}\in (0,1]$
, there exist
![]() $l_{2},l^{\prime }_{2}\in (0,1]$
(each belonging to a
$l_{2},l^{\prime }_{2}\in (0,1]$
(each belonging to a
![]() $G_{\delta }$
-dense set of (0,1]) such that, for the two sequences
$G_{\delta }$
-dense set of (0,1]) such that, for the two sequences
![]() $\{q_{n}\}_{n\in \mathbb {N}}$
,
$\{q_{n}\}_{n\in \mathbb {N}}$
,
![]() $\{q^{\prime }_{n}\}_{n\in \mathbb {N}}$
defined as in Lemma 3.4,
$\{q^{\prime }_{n}\}_{n\in \mathbb {N}}$
defined as in Lemma 3.4,
and
 $$ \begin{align} \frac{1}{4(\ln \ln \ln q_{2n+1})^{1/4}}&\leq \lvert q^{\prime}_{2n+1}(q_{2n+1}l_{2}-r_{2n+1})+q_{2n+1}(q^{\prime}_{2n+1}l^{\prime}_{2}-r^{\prime}_{2n+1}) \rvert\nonumber\\ &\leq \frac{3}{2(\ln \ln \ln q_{2n+1})^{1/4}}, \end{align} $$
$$ \begin{align} \frac{1}{4(\ln \ln \ln q_{2n+1})^{1/4}}&\leq \lvert q^{\prime}_{2n+1}(q_{2n+1}l_{2}-r_{2n+1})+q_{2n+1}(q^{\prime}_{2n+1}l^{\prime}_{2}-r^{\prime}_{2n+1}) \rvert\nonumber\\ &\leq \frac{3}{2(\ln \ln \ln q_{2n+1})^{1/4}}, \end{align} $$
where
![]() $r_{n}$
and
$r_{n}$
and
![]() $r^{\prime }_{n}$
are, respectively, the closest integer to
$r^{\prime }_{n}$
are, respectively, the closest integer to
![]() $q_{n}l_{2}$
and
$q_{n}l_{2}$
and
![]() $q^{\prime }_{n}l^{\prime }_{2}$
. Moreover, the inequalities above still hold if the sum in the middle is replaced by one of its summands.
$q^{\prime }_{n}l^{\prime }_{2}$
. Moreover, the inequalities above still hold if the sum in the middle is replaced by one of its summands.
Lemma 3.4 is the key to our construction of ergodic examples on
![]() $\mathbb {T}^2\times \mathbb {R}$
, where the main difficulty is the coprime condition between
$\mathbb {T}^2\times \mathbb {R}$
, where the main difficulty is the coprime condition between
![]() $q_n$
and
$q_n$
and
![]() $q^{\prime }_n$
. If we do not require the coprime condition, Lemma 3.4 can be easily obtained by using the classical version of Khintchine’s divergence theorem for Diophantine approximations and the Dirichlet principle (the pigeonhole principle). We dedicate the last section of our paper to its proof, together with the proof of Lemma 3.5.
$q^{\prime }_n$
. If we do not require the coprime condition, Lemma 3.4 can be easily obtained by using the classical version of Khintchine’s divergence theorem for Diophantine approximations and the Dirichlet principle (the pigeonhole principle). We dedicate the last section of our paper to its proof, together with the proof of Lemma 3.5.
4. Proof of the theorems using the lemmas
For every pair of
![]() $q_{n}$
,
$q_{n}$
,
![]() $q^{\prime }_{n}$
in Lemmas 3.4 and 3.5, we tile
$q^{\prime }_{n}$
in Lemmas 3.4 and 3.5, we tile
![]() $\mathbb {T}^2$
by corresponding small rectangles
$\mathbb {T}^2$
by corresponding small rectangles
where
![]() $0\le i\le q_{n}-1, \ 0\le j\le q^{\prime }_{n}-1$
.
$0\le i\le q_{n}-1, \ 0\le j\le q^{\prime }_{n}-1$
.
We first prove the inequality of the essential value criterion (1.2) for special rectangles
![]() $R^{i,j}_n$
, which then naturally generalizes to positive measure sets.
$R^{i,j}_n$
, which then naturally generalizes to positive measure sets.
Lemma 4.1. For the irrationals
![]() $l_{1},l^{\prime }_{1},l_{2},l^{\prime }_{2}$
and the sequences
$l_{1},l^{\prime }_{1},l_{2},l^{\prime }_{2}$
and the sequences
![]() $\{q_{n}\}$
,
$\{q_{n}\}$
,
![]() $\{q^{\prime }_{n}\}$
in Lemma 3.5, there exists a
$\{q^{\prime }_{n}\}$
in Lemma 3.5, there exists a
![]() $G_{\delta }$
-dense set S of
$G_{\delta }$
-dense set S of
![]() $\alpha $
in
$\alpha $
in
![]() $[0,1)^{2}$
with following property.
$[0,1)^{2}$
with following property.
For every
![]() $\alpha \in S$
, every
$\alpha \in S$
, every
![]() $ a\in \mathbb {R}$
and every
$ a\in \mathbb {R}$
and every
![]() $\epsilon>0$
, there exist infinitely many n, and
$\epsilon>0$
, there exist infinitely many n, and
![]() $N=N(\alpha , a, \epsilon , n)\in \mathbb {N}^{*}$
, such that, for every rectangle
$N=N(\alpha , a, \epsilon , n)\in \mathbb {N}^{*}$
, such that, for every rectangle
![]() $R_{n}^{i,j}$
defined in (4.1),
$R_{n}^{i,j}$
defined in (4.1),
 $$ \begin{align} \mu (R_{n}^{i,j} \cap T_{\alpha}^{-N}R_{n}^{i,j} \cap [ \vert A_{N}(\cdot)-(a,0) \vert < \epsilon])>\frac{1}{2q_{n}q^{\prime}_{n}}, \end{align} $$
$$ \begin{align} \mu (R_{n}^{i,j} \cap T_{\alpha}^{-N}R_{n}^{i,j} \cap [ \vert A_{N}(\cdot)-(a,0) \vert < \epsilon])>\frac{1}{2q_{n}q^{\prime}_{n}}, \end{align} $$
and the same inequality holds with a different n and N if we change
![]() $(a,0)$
to
$(a,0)$
to
![]() $(0,a)$
.
$(0,a)$
.
Proof. By choosing a subsequence of n, we can assume that
The set S and its density. Consider the subsets of
![]() $\mathbb {T}^2$
for the choices of
$\mathbb {T}^2$
for the choices of
![]() $\alpha =(\alpha _1, \alpha _2)$
given by
$\alpha =(\alpha _1, \alpha _2)$
given by
 $$ \begin{align} S=\bigcap_{m\ge 1}\bigcup_{n\ge m} \bigg(&\bigcup_{\substack{0\le p_n\le q_n-1\:\\(p_{n},q_{n})=1}} \bigg(\frac{p_{n}}{q_{n}}-\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}},\frac{p_{n}}{q_{n}}+\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}}\bigg)\nonumber\\ &\times \bigcup_{\substack{0\le p^{\prime}_n\le q^{\prime}_n-1:\\(p^{\prime}_{n},q^{\prime}_{n})=1}} \bigg(\frac{p^{\prime}_{n}}{q^{\prime}_{n}}-\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}},\frac{p^{\prime}_{n}}{q^{\prime}_{n}}+\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}}\bigg) \bigg). \end{align} $$
$$ \begin{align} S=\bigcap_{m\ge 1}\bigcup_{n\ge m} \bigg(&\bigcup_{\substack{0\le p_n\le q_n-1\:\\(p_{n},q_{n})=1}} \bigg(\frac{p_{n}}{q_{n}}-\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}},\frac{p_{n}}{q_{n}}+\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}}\bigg)\nonumber\\ &\times \bigcup_{\substack{0\le p^{\prime}_n\le q^{\prime}_n-1:\\(p^{\prime}_{n},q^{\prime}_{n})=1}} \bigg(\frac{p^{\prime}_{n}}{q^{\prime}_{n}}-\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}},\frac{p^{\prime}_{n}}{q^{\prime}_{n}}+\frac{1}{n (\ln q_n)^{2}q_{n}^2q^{\prime}_{n}}\bigg) \bigg). \end{align} $$
The set above is clearly a
![]() $G_{\delta }$
set. It remains to show that S is a dense set in
$G_{\delta }$
set. It remains to show that S is a dense set in
![]() $\mathbb {T}^2$
. Note that
$\mathbb {T}^2$
. Note that
![]() $(\alpha _1,\alpha _2)\in S$
if and only if there exists a subsequence of n, denoted by
$(\alpha _1,\alpha _2)\in S$
if and only if there exists a subsequence of n, denoted by
![]() $n_k$
, and two corresponding sequences of
$n_k$
, and two corresponding sequences of
![]() $p_{n_k}$
and
$p_{n_k}$
and
![]() $p^{\prime }_{n_k}$
, that are relatively prime to
$p^{\prime }_{n_k}$
, that are relatively prime to
![]() $q_{n_k}$
and
$q_{n_k}$
and
![]() $q^{\prime }_{n_k}$
, respectively, such that, for every k,
$q^{\prime }_{n_k}$
, respectively, such that, for every k,
 $$ \begin{align} &\bigg\vert \alpha_{1}-\frac{p_{n_k}}{q_{n_k}}\bigg\vert< \frac{1}{{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}}, \nonumber\\ &\bigg| \alpha_{2}-\frac{p^{\prime}_{n_k}}{q^{\prime}_{n_k}}\bigg|< \frac{1}{{n_k} (\ln q_{n_k})^{2}q_{n_k}q^{\prime 2}_{n_k}}. \end{align} $$
$$ \begin{align} &\bigg\vert \alpha_{1}-\frac{p_{n_k}}{q_{n_k}}\bigg\vert< \frac{1}{{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}}, \nonumber\\ &\bigg| \alpha_{2}-\frac{p^{\prime}_{n_k}}{q^{\prime}_{n_k}}\bigg|< \frac{1}{{n_k} (\ln q_{n_k})^{2}q_{n_k}q^{\prime 2}_{n_k}}. \end{align} $$
To see that S is dense, we will show that we can approximate any point in
![]() $\mathbb {T}^2$
well enough. Note that, for any given
$\mathbb {T}^2$
well enough. Note that, for any given
![]() $\epsilon>0$
, there exists M depending on
$\epsilon>0$
, there exists M depending on
![]() $\epsilon $
such that, for every
$\epsilon $
such that, for every
![]() $q_{n}\ge M$
and
$q_{n}\ge M$
and
![]() $q^{\prime }_{n}\ge M$
and every point
$q^{\prime }_{n}\ge M$
and every point
![]() $(\gamma ,\gamma ')$
in
$(\gamma ,\gamma ')$
in
![]() $\mathbb {T}^2$
, there exists
$\mathbb {T}^2$
, there exists
![]() $p_{n}$
coprime to
$p_{n}$
coprime to
![]() $q_{n}$
and
$q_{n}$
and
![]() $p^{\prime }_{n}$
coprime to
$p^{\prime }_{n}$
coprime to
![]() $q^{\prime }_{n}$
, with the property that
$q^{\prime }_{n}$
, with the property that
This is possible because the bound on the gaps between two consecutive totatives of a given number M is of order
![]() $o(M)$
(see [Reference Montgomery and Vaughan13]). Now fix
$o(M)$
(see [Reference Montgomery and Vaughan13]). Now fix
![]() $n_0$
and
$n_0$
and
![]() $p_{n_0}$
,
$p_{n_0}$
,
![]() $p^{\prime }_{n_0}$
such that inequality (4.6) holds and assume that
$p^{\prime }_{n_0}$
such that inequality (4.6) holds and assume that
![]() $n_0$
is large enough so that
$n_0$
is large enough so that
 $$ \begin{align} \frac{1}{{n_0} (\ln q_{n_0})^{2}q_{n_0}^2q^{\prime}_{n_0}}<\epsilon/2. \end{align} $$
$$ \begin{align} \frac{1}{{n_0} (\ln q_{n_0})^{2}q_{n_0}^2q^{\prime}_{n_0}}<\epsilon/2. \end{align} $$
Starting with
![]() $k=0$
, by replacing
$k=0$
, by replacing
![]() $\epsilon $
with
$\epsilon $
with
![]() $\epsilon _k= {1}/{{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime }_{n_k}}$
and replacing
$\epsilon _k= {1}/{{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime }_{n_k}}$
and replacing
![]() $\gamma $
with
$\gamma $
with
![]() ${p_{n_k}}/{q_{n_k}}$
in the argument for (4.6), we can inductively show the existence of
${p_{n_k}}/{q_{n_k}}$
in the argument for (4.6), we can inductively show the existence of
![]() $n_{k+1}$
such that the sequence of the intervals
$n_{k+1}$
such that the sequence of the intervals
 $$ \begin{align*} \bigg[\frac{p_{n_k}}{q_{n_k}}-\frac{1}{2{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}},\frac{p_{n_k}}{q_{n_k}}+\frac{1}{2{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}}\bigg] \end{align*} $$
$$ \begin{align*} \bigg[\frac{p_{n_k}}{q_{n_k}}-\frac{1}{2{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}},\frac{p_{n_k}}{q_{n_k}}+\frac{1}{2{n_k} (\ln q_{n_k})^{2}q_{n_k}^2q^{\prime}_{n_k}}\bigg] \end{align*} $$
are nested. A similar result holds for the second coordinate. This proves the existence of
![]() $(\alpha _1,\alpha _2)\in [0,1)^2$
such that (4.5) holds with the coprime pairs
$(\alpha _1,\alpha _2)\in [0,1)^2$
such that (4.5) holds with the coprime pairs
![]() $(p_{n_0},q_{n_0})$
and
$(p_{n_0},q_{n_0})$
and
![]() $(p^{\prime }_{n_0},q^{\prime }_{n_0})$
. By inequality (4.7),
$(p^{\prime }_{n_0},q^{\prime }_{n_0})$
. By inequality (4.7),
Combining the inequality above with (4.6) for
![]() $n=n_0$
gives
$n=n_0$
gives
Hence, S is dense in
![]() $\mathbb {T}^2$
.
$\mathbb {T}^2$
.
Preparation work. We need to show that there are different orders of magnitude for Birkhoff sums
![]() $A^{(1)}_N$
and
$A^{(1)}_N$
and
![]() $A^{(2)}_N$
along rigidity sequences .
$A^{(2)}_N$
along rigidity sequences .
We proceed with the essential value argument. For every
![]() $\alpha \in S$
, we can find a subsequence of n, and corresponding coprime numerators, such that (4.5) hold. For simplicity, we still denote the index by n.
$\alpha \in S$
, we can find a subsequence of n, and corresponding coprime numerators, such that (4.5) hold. For simplicity, we still denote the index by n.
For
![]() $M_n=\sqrt {n} (\ln q_n)^{2}q_{n}q^{\prime }_{n}$
, and for every
$M_n=\sqrt {n} (\ln q_n)^{2}q_{n}q^{\prime }_{n}$
, and for every
![]() $0\le m\le M_n$
(here we use weak inequalities to make writing easier),
$0\le m\le M_n$
(here we use weak inequalities to make writing easier),
 $$ \begin{align} \begin{aligned} \bigg|m\alpha_{1}-m\frac{p_{n}}{q_{n}}\bigg|&=m\bigg|\alpha_{1}-\frac{p_{n}}{q_{n}}\bigg|\le \frac{1}{\sqrt{n}q_{n}} \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bigg|m\alpha_{1}-m\frac{p_{n}}{q_{n}}\bigg|&=m\bigg|\alpha_{1}-\frac{p_{n}}{q_{n}}\bigg|\le \frac{1}{\sqrt{n}q_{n}} \end{aligned} \end{align} $$
and
 $$ \begin{align} \begin{aligned} \bigg|m\alpha_{2}-m\frac{p^{\prime}_{n}}{q^{\prime}_{n}}\bigg|&=m\bigg|\alpha_{2}-\frac{p^{\prime}_{n}}{q^{\prime}_{n}}\bigg|\leq \frac{1}{\sqrt{n}q^{\prime}_{n}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \bigg|m\alpha_{2}-m\frac{p^{\prime}_{n}}{q^{\prime}_{n}}\bigg|&=m\bigg|\alpha_{2}-\frac{p^{\prime}_{n}}{q^{\prime}_{n}}\bigg|\leq \frac{1}{\sqrt{n}q^{\prime}_{n}}. \end{aligned} \end{align} $$
For any
![]() $i,j \in \mathbb {N}$
, denote by
$i,j \in \mathbb {N}$
, denote by
![]() $\mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
the set of points
$\mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
the set of points
![]() $(x_{1},x_{2})$
satisfying
$(x_{1},x_{2})$
satisfying
and
 $$ \begin{align} \frac{2}{\sqrt{n}q^{\prime}_{n}}+\frac{j}{q^{\prime}_{n}}\leq x_{2} \leq \frac{j+1}{q^{\prime}_{n}} -\frac{2}{\sqrt{n}q^{\prime}_{n}}. \end{align} $$
$$ \begin{align} \frac{2}{\sqrt{n}q^{\prime}_{n}}+\frac{j}{q^{\prime}_{n}}\leq x_{2} \leq \frac{j+1}{q^{\prime}_{n}} -\frac{2}{\sqrt{n}q^{\prime}_{n}}. \end{align} $$
Then the Haar measure of the set
![]() $\mathcal {F}_{i,j}$
has the lower bound
$\mathcal {F}_{i,j}$
has the lower bound
 $$ \begin{align} \mu \{\mathcal{F}_{i,j}(q_{n},q^{\prime}_{n})\}&\geq \bigg(1-\frac{4}{\sqrt{n}}\bigg)\bigg(1-\frac{4}{\sqrt{n}}\bigg)\frac{1}{q_{n}q^{\prime}_{n}} \end{align} $$
$$ \begin{align} \mu \{\mathcal{F}_{i,j}(q_{n},q^{\prime}_{n})\}&\geq \bigg(1-\frac{4}{\sqrt{n}}\bigg)\bigg(1-\frac{4}{\sqrt{n}}\bigg)\frac{1}{q_{n}q^{\prime}_{n}} \end{align} $$
 $$ \begin{align} &\geq \frac{3}{4}\frac{1}{q^{\prime}_{n}q_{n}} \end{align} $$
$$ \begin{align} &\geq \frac{3}{4}\frac{1}{q^{\prime}_{n}q_{n}} \end{align} $$
for
![]() $n\ge 32^2$
.
$n\ge 32^2$
.
Let
 $$ \begin{align*} l_{1}=\frac{b_{n}+\delta_{n}}{q_{n}} \quad \mathrm{and} \quad l^{\prime}_1=\frac{b^{\prime}_{n}+\delta^{\prime}_{n}}{q^{\prime}_{n}}. \end{align*} $$
$$ \begin{align*} l_{1}=\frac{b_{n}+\delta_{n}}{q_{n}} \quad \mathrm{and} \quad l^{\prime}_1=\frac{b^{\prime}_{n}+\delta^{\prime}_{n}}{q^{\prime}_{n}}. \end{align*} $$
We now want to apply Lemma 3.3 to the first rectangle
![]() $B_1$
, with
$B_1$
, with
![]() $\tilde {\delta }_n=\tilde {\delta }_n'={1}/{\sqrt {n}}$
,
$\tilde {\delta }_n=\tilde {\delta }_n'={1}/{\sqrt {n}}$
,
![]() $K_n=\sqrt {n}(\ln q_n)^2$
and
$K_n=\sqrt {n}(\ln q_n)^2$
and
![]() $N_n=q_n q^{\prime }_n$
. The inequalities (4.8) and (4.9) show that
$N_n=q_n q^{\prime }_n$
. The inequalities (4.8) and (4.9) show that
 $$ \begin{align*} |\eta_n|=\|q_n \alpha_1\|\le \frac{1}{{n}(\ln q_n)^2 q_n q^{\prime}_n}=\frac{\tilde{\delta}_n}{K_n N_n} \end{align*} $$
$$ \begin{align*} |\eta_n|=\|q_n \alpha_1\|\le \frac{1}{{n}(\ln q_n)^2 q_n q^{\prime}_n}=\frac{\tilde{\delta}_n}{K_n N_n} \end{align*} $$
and
 $$ \begin{align*} |\eta^{\prime}_n|=\|q^{\prime}_n \alpha_1\| \le \frac{1}{{n}(\ln q_n)^2 q_n q^{\prime}_n}=\frac{\tilde{\delta}^{\prime}_n}{K_n N_n}. \end{align*} $$
$$ \begin{align*} |\eta^{\prime}_n|=\|q^{\prime}_n \alpha_1\| \le \frac{1}{{n}(\ln q_n)^2 q_n q^{\prime}_n}=\frac{\tilde{\delta}^{\prime}_n}{K_n N_n}. \end{align*} $$
By inequalities (3.13) and (3.14), and recalling the assumption (4.3) that
![]() $q_n$
is large, we have that
$q_n$
is large, we have that
and
Hence, by applying Lemma 3.3 to
![]() $A^{(1)}$
for
$A^{(1)}$
for
![]() $x\in \mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
,
$x\in \mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
,
Thus, from (3.11),
 $$ \begin{align*} | A^{(1)}_{N_{n}}(x)| &=| b_{n}b^{\prime}_{n}-q_{n}q^{\prime}_{n}l_{1}l^{\prime}_1| \\ &=| b_{n}b^{\prime}_{n}-(b_{n}+\delta_{n})(b^{\prime}_{n}+\delta^{\prime}_{n})| \\ &\le 2| b_{n}\delta^{\prime}_{n}+ b^{\prime}_{n}\delta_{n}| \\ &\le 2\times\text{ right-hand side of (3.11)} \\&= \frac{4}{(\ln \ln \ln q_n)^{1/2}} \end{align*} $$
$$ \begin{align*} | A^{(1)}_{N_{n}}(x)| &=| b_{n}b^{\prime}_{n}-q_{n}q^{\prime}_{n}l_{1}l^{\prime}_1| \\ &=| b_{n}b^{\prime}_{n}-(b_{n}+\delta_{n})(b^{\prime}_{n}+\delta^{\prime}_{n})| \\ &\le 2| b_{n}\delta^{\prime}_{n}+ b^{\prime}_{n}\delta_{n}| \\ &\le 2\times\text{ right-hand side of (3.11)} \\&= \frac{4}{(\ln \ln \ln q_n)^{1/2}} \end{align*} $$
and, similarly,
Therefore, for
![]() $x\in \mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
,
$x\in \mathcal {F}_{i,j}(q_{n},q^{\prime }_{n})$
,
Inequality (4.16) means that we can approximate the interval
![]() $[-\sqrt {2n}, \sqrt {2n}]$
with a precision of
$[-\sqrt {2n}, \sqrt {2n}]$
with a precision of
![]() $1/ (\ln \ln \ln q_n)^{1/2}$
by multiplying
$1/ (\ln \ln \ln q_n)^{1/2}$
by multiplying
![]() $A^{(1)}_{N_n}$
by a coefficient smaller than
$A^{(1)}_{N_n}$
by a coefficient smaller than
![]() $\sqrt {2n}(\ln q_n)^2$
, which is used to obtain (4.19).
$\sqrt {2n}(\ln q_n)^2$
, which is used to obtain (4.19).
For the second rectangle
![]() $B_2$
, by (3.15) and (3.16) for individual summands (see the comment at the end of Lemma 3.5), and using the more strict bound (3.16) and the assumption (4.3) that
$B_2$
, by (3.15) and (3.16) for individual summands (see the comment at the end of Lemma 3.5), and using the more strict bound (3.16) and the assumption (4.3) that
![]() $q_n$
is large, we obtain similar inequalities to (4.14) and (4.15): that is,
$q_n$
is large, we obtain similar inequalities to (4.14) and (4.15): that is,
 $$ \begin{align*} \|q_{n} l_2\|\le \frac{3}{2 q^{\prime}_n(\ln\ln\ln q_n)^{{1}/{4}}}< \frac{1}{\sqrt{n}}=\tilde{\delta}_n \end{align*} $$
$$ \begin{align*} \|q_{n} l_2\|\le \frac{3}{2 q^{\prime}_n(\ln\ln\ln q_n)^{{1}/{4}}}< \frac{1}{\sqrt{n}}=\tilde{\delta}_n \end{align*} $$
and
Therefore, we can apply Lemma (3.3) to
![]() $A^{(2)}$
, and we obtain the estimation
$A^{(2)}$
, and we obtain the estimation
Argument for the case of
![]() $(a,0)$
. For
$(a,0)$
. For
![]() $a\in \mathbb {R}$
and
$a\in \mathbb {R}$
and
![]() $\epsilon>0$
, by (4.16) and (4.17), we can first choose n large enough, and then
$\epsilon>0$
, by (4.16) and (4.17), we can first choose n large enough, and then
![]() $K_{2n}=K_{2n}(a, \epsilon )$
with
$K_{2n}=K_{2n}(a, \epsilon )$
with
![]() $|K_{2n}| \leq \sqrt {2n}(\ln q_{2n})^{2}$
such that
$|K_{2n}| \leq \sqrt {2n}(\ln q_{2n})^{2}$
such that
 $$ \begin{align} | K_{2n}A^{(2)}_{N_{2n}}(x) | \le \frac{3\sqrt{2n}(\ln q_{2n})^{2}}{(\ln q_{2n})^{3}} \leq \frac{3\sqrt{2n}}{\ln q_{2n}}\le \frac{3\sqrt{2n}}{2n}\le \frac{1}{\sqrt{2}}\epsilon, \end{align} $$
$$ \begin{align} | K_{2n}A^{(2)}_{N_{2n}}(x) | \le \frac{3\sqrt{2n}(\ln q_{2n})^{2}}{(\ln q_{2n})^{3}} \leq \frac{3\sqrt{2n}}{\ln q_{2n}}\le \frac{3\sqrt{2n}}{2n}\le \frac{1}{\sqrt{2}}\epsilon, \end{align} $$
where we use that
![]() $\ln q_n\ge n$
, which follows from assumption (4.3) at the beginning of the proof.
$\ln q_n\ge n$
, which follows from assumption (4.3) at the beginning of the proof.
Finally, by combining the two inequalities above, for
![]() $N=K_{2n}N_{2n}=K_{2n}q_{2n}q^{\prime }_{2n}$
,
$N=K_{2n}N_{2n}=K_{2n}q_{2n}q^{\prime }_{2n}$
,
![]() $x\in \mathcal {F}_{i,j}(q_{2n},q_{2n}')\subset R^{i,j}_{2n}$
, we get
$x\in \mathcal {F}_{i,j}(q_{2n},q_{2n}')\subset R^{i,j}_{2n}$
, we get
which implies that
So
 $$ \begin{align} &\mathcal{F}_{i,j}(q_{2n},q_{2n}') \cap T_{\alpha}^{-N}(\mathcal{F}_{i,j}(q_{2n},q_{2n}')\nonumber\\ &\quad\subset \ T_{\alpha}^{-N}(R^{i,j}_{2n})\cap R_{2n}^{i,j}\cap \{x\in [0,1)^{2}, | A_{N}(x)-(a,0)|\}\leq \epsilon \}. \end{align} $$
$$ \begin{align} &\mathcal{F}_{i,j}(q_{2n},q_{2n}') \cap T_{\alpha}^{-N}(\mathcal{F}_{i,j}(q_{2n},q_{2n}')\nonumber\\ &\quad\subset \ T_{\alpha}^{-N}(R^{i,j}_{2n})\cap R_{2n}^{i,j}\cap \{x\in [0,1)^{2}, | A_{N}(x)-(a,0)|\}\leq \epsilon \}. \end{align} $$
Note that N is a multiple of
![]() $q_{2n}q^{\prime }_{2n}$
, so at time N the rational vector
$q_{2n}q^{\prime }_{2n}$
, so at time N the rational vector
![]() $N(q_{2n}, q^{\prime }_{2n})$
returns to the origin. Because
$N(q_{2n}, q^{\prime }_{2n})$
returns to the origin. Because
![]() $N(q_{2n}, q^{\prime }_{2n})$
approximates
$N(q_{2n}, q^{\prime }_{2n})$
approximates
![]() $N\alpha $
really well, by inequality (4.8) and (4.9),
$N\alpha $
really well, by inequality (4.8) and (4.9),
 $$ \begin{align*} \mu ( \mathcal{F}_{i,j}(q_{2n},q_{2n}')\cap T_{\alpha}^{-N}( \mathcal{F}_{i,j}(q_{2n},q_{2n}')))&\geq \bigg(1-\frac{1}{\sqrt{2n}}\bigg)\bigg(1-\frac{1}{\sqrt{2n}}\bigg)\mu ( \mathcal{F}_{i,j}(q_{2n},q_{2n}')), \\ &\geq \frac{1}{2q_{2n}q_{2n}'}>0. \end{align*} $$
$$ \begin{align*} \mu ( \mathcal{F}_{i,j}(q_{2n},q_{2n}')\cap T_{\alpha}^{-N}( \mathcal{F}_{i,j}(q_{2n},q_{2n}')))&\geq \bigg(1-\frac{1}{\sqrt{2n}}\bigg)\bigg(1-\frac{1}{\sqrt{2n}}\bigg)\mu ( \mathcal{F}_{i,j}(q_{2n},q_{2n}')), \\ &\geq \frac{1}{2q_{2n}q_{2n}'}>0. \end{align*} $$
Argument for the case of
![]() $(0,a)$
. In the case of
$(0,a)$
. In the case of
![]() $(0,a)$
, we can use the odd terms
$(0,a)$
, we can use the odd terms
![]() $2n+1$
and repeat the argument above. Note that
$2n+1$
and repeat the argument above. Note that
![]() $A^{(2)}_{N_{2n+1}}$
is of order
$A^{(2)}_{N_{2n+1}}$
is of order
![]() $(\ln \ln \ln q_{2n+1})^{1/4}$
, while
$(\ln \ln \ln q_{2n+1})^{1/4}$
, while
![]() $A^{(1)}_{N_{2n+1}}$
is of order
$A^{(1)}_{N_{2n+1}}$
is of order
![]() $(\ln \ln \ln q_{2n+1})^{1/2}$
. Therefore, we can approximate any point in the interval
$(\ln \ln \ln q_{2n+1})^{1/2}$
. Therefore, we can approximate any point in the interval
![]() $[-\sqrt {2n+1}, \sqrt {2n+1}]$
with a precision of
$[-\sqrt {2n+1}, \sqrt {2n+1}]$
with a precision of
![]() $1/ (\ln \ln \ln q_{2n+1})^{1/4}$
after multiplying
$1/ (\ln \ln \ln q_{2n+1})^{1/4}$
after multiplying
![]() $A^{(2)}_{N_{2n+1}}$
by a coefficient
$A^{(2)}_{N_{2n+1}}$
by a coefficient
![]() $K_{2n+1}$
smaller than
$K_{2n+1}$
smaller than
![]() $\sqrt {2n+1}(\ln \ln \ln q_{2n+1})^{1/4}$
, while
$\sqrt {2n+1}(\ln \ln \ln q_{2n+1})^{1/4}$
, while
![]() $K_{2n+1}A^{(1)}_{N_{2n+1}}$
is still small and of order
$K_{2n+1}A^{(1)}_{N_{2n+1}}$
is still small and of order
![]() $1/ (\ln \ln \ln q_{2n+1})^{1/4}$
. This gives two inequalities similar to (4.19) and (4.20), and the same argument for positive measure at time
$1/ (\ln \ln \ln q_{2n+1})^{1/4}$
. This gives two inequalities similar to (4.19) and (4.20), and the same argument for positive measure at time
![]() $2n+1$
follows through.
$2n+1$
follows through.
This finishes the proof of Lemma 4.1.
Corollary 4.2. For almost every
![]() $l_{1},l^{\prime }_{1} \in (0,1]$
, a
$l_{1},l^{\prime }_{1} \in (0,1]$
, a
![]() $G_{\delta }$
-dense set of
$G_{\delta }$
-dense set of
![]() $l_{2},l^{\prime }_{2}\in (0,1]$
and a
$l_{2},l^{\prime }_{2}\in (0,1]$
and a
![]() $G_{\delta }$
-dense set of
$G_{\delta }$
-dense set of
![]() $\alpha =(\alpha _{1},{\alpha }_{2}) \in [0,1)^{2}$
, we have
$\alpha =(\alpha _{1},{\alpha }_{2}) \in [0,1)^{2}$
, we have
![]() $E(A)=\mathbb {R}^2$
.
$E(A)=\mathbb {R}^2$
.
Proof. By Theorem 1.2, it suffices to prove that a similar conclusion in Lemma 4.1 holds after we substitute
![]() $R_{n}^{i,j}$
by any set B of positive measure. In fact, for any positive measure set B, there exists n large enough, such that
$R_{n}^{i,j}$
by any set B of positive measure. In fact, for any positive measure set B, there exists n large enough, such that
 $$ \begin{align} \mu (R^{i,j}_{n}\cap B)> \frac{7}{8}\frac{1}{q_{n}'q_{n}} \end{align} $$
$$ \begin{align} \mu (R^{i,j}_{n}\cap B)> \frac{7}{8}\frac{1}{q_{n}'q_{n}} \end{align} $$
for some
![]() $0\leq i\leq q_{n}-1$
and
$0\leq i\leq q_{n}-1$
and
![]() $0\leq j\leq q_{n}'-1$
, and thus we can expect a slightly weaker lower bound for a general positive measure set B.
$0\leq j\leq q_{n}'-1$
, and thus we can expect a slightly weaker lower bound for a general positive measure set B.
For given
![]() $a\in \mathbb {R}$
,
$a\in \mathbb {R}$
,
![]() $\epsilon>0$
, choose n large enough such that inequality(4.23) holds, and denote
$\epsilon>0$
, choose n large enough such that inequality(4.23) holds, and denote
![]() $N=N(a,\epsilon )=K_{2n} N_{2n}=K_{2n}q_{2n}'q_{2n}$
, as in Lemma 4.1. By inequality(4.21),
$N=N(a,\epsilon )=K_{2n} N_{2n}=K_{2n}q_{2n}'q_{2n}$
, as in Lemma 4.1. By inequality(4.21),
Now, with standard measure computations, we are ready to show the desired bound
Let
![]() $\mathcal {X}=T_{\alpha }^{-N}(B\cap R^{i,j}_{2n})\cap (B\cap R^{i,j}_{2n})$
. Then we have the following bound for
$\mathcal {X}=T_{\alpha }^{-N}(B\cap R^{i,j}_{2n})\cap (B\cap R^{i,j}_{2n})$
. Then we have the following bound for
![]() $\mu (\mathcal {X})$
: that is,
$\mu (\mathcal {X})$
: that is,
 $$ \begin{align*} \mu (\mathcal{X})&=\mu (T_{\alpha}^{-N}(B\cap R^{i,j}_{2n})\cap (B\cap R^{i,j}_{2n})) \\ &=\mu (T_{\alpha}^{-N}(B\cap R^{i,j}_{2n}))+ \mu(B\cap R^{i,j}_{2n})-\mu(T_{\alpha}^{-N}(B\cap R^{i,j}_{2n})\cup (B\cap R^{i,j}_{2n})) \\ &\geq 2 \mu (B\cap R^{i,j}_{2n})-\mu(T_{\alpha}^{-N}(R_{2n}^{i,j})\cup R^{i,j}_{2n}) \\ & \geq \tfrac{7}{4}\mu (R_{2n}^{i,j})-\tfrac{5}{4}\mu(R_{2n}^{i,j}) \\ &=\tfrac{1}{2}\mu(R_{2n}^{i,j}), \end{align*} $$
$$ \begin{align*} \mu (\mathcal{X})&=\mu (T_{\alpha}^{-N}(B\cap R^{i,j}_{2n})\cap (B\cap R^{i,j}_{2n})) \\ &=\mu (T_{\alpha}^{-N}(B\cap R^{i,j}_{2n}))+ \mu(B\cap R^{i,j}_{2n})-\mu(T_{\alpha}^{-N}(B\cap R^{i,j}_{2n})\cup (B\cap R^{i,j}_{2n})) \\ &\geq 2 \mu (B\cap R^{i,j}_{2n})-\mu(T_{\alpha}^{-N}(R_{2n}^{i,j})\cup R^{i,j}_{2n}) \\ & \geq \tfrac{7}{4}\mu (R_{2n}^{i,j})-\tfrac{5}{4}\mu(R_{2n}^{i,j}) \\ &=\tfrac{1}{2}\mu(R_{2n}^{i,j}), \end{align*} $$
where the inequality
![]() $\mu (T_{\alpha }^{-N}(R_{2n}^{i,j})\cup R^{i,j}_{2n})\le \tfrac 54\mu (R_{2n}^{i,j})$
comes from the fact that
$\mu (T_{\alpha }^{-N}(R_{2n}^{i,j})\cup R^{i,j}_{2n})\le \tfrac 54\mu (R_{2n}^{i,j})$
comes from the fact that
![]() $T^{-N}_{\alpha }$
is close to identity, as
$T^{-N}_{\alpha }$
is close to identity, as
![]() $q_{2n}q^{\prime }_{2n}$
divides N(see (4.5)).
$q_{2n}q^{\prime }_{2n}$
divides N(see (4.5)).
Denote
![]() $\mathcal {Y}=\mathcal {F}_{i,j}(q_{2n},q_{2n}')$
. Note that
$\mathcal {Y}=\mathcal {F}_{i,j}(q_{2n},q_{2n}')$
. Note that
![]() $\mathcal {X}$
and
$\mathcal {X}$
and
![]() $\mathcal {Y}$
are both subsets of
$\mathcal {Y}$
are both subsets of
![]() $R^{i,j}_{2n}$
. By using the lower bound (4.12) of
$R^{i,j}_{2n}$
. By using the lower bound (4.12) of
![]() $\mu (\mathcal {Y})$
,
$\mu (\mathcal {Y})$
,
 $$ \begin{align*} \mu (\mathcal{X} \cap \mathcal{Y}) & =\mu(\mathcal{X})+\mu(\mathcal{Y})-\mu(\mathcal{X} \cup \mathcal{Y}) \\ & \geq \tfrac{1}{2}\mu(R_{2n}^{i,j})+\tfrac{3}{4}\mu(R_{2n}^{i,j})-\mu(R_{2n}^{i,j}) \\ & \geq \tfrac{1}{4}\mu (R_{2n}^{i,j}). \end{align*} $$
$$ \begin{align*} \mu (\mathcal{X} \cap \mathcal{Y}) & =\mu(\mathcal{X})+\mu(\mathcal{Y})-\mu(\mathcal{X} \cup \mathcal{Y}) \\ & \geq \tfrac{1}{2}\mu(R_{2n}^{i,j})+\tfrac{3}{4}\mu(R_{2n}^{i,j})-\mu(R_{2n}^{i,j}) \\ & \geq \tfrac{1}{4}\mu (R_{2n}^{i,j}). \end{align*} $$
Finally, we obtain the bound
This proves that, for every
![]() $a\in \mathbb {R}$
,
$a\in \mathbb {R}$
,
![]() $(a,0)\in E(A)$
. Similarly, we can prove that
$(a,0)\in E(A)$
. Similarly, we can prove that
![]() $(0,a)$
belongs to
$(0,a)$
belongs to
![]() $E(A)$
. By the subgroup property of essential value in Theorem 1.2, we have
$E(A)$
. By the subgroup property of essential value in Theorem 1.2, we have
![]() $E(A)=\mathbb {R}^2$
.
$E(A)=\mathbb {R}^2$
.
Corollary 4.3. By restricting the above discussions to the first coordinate of
![]() $A^{(1)}$
, it is easy to see that, in the case of
$A^{(1)}$
, it is easy to see that, in the case of
![]() $\mathbb {T}^2\times \mathbb {R}$
, for almost every
$\mathbb {T}^2\times \mathbb {R}$
, for almost every
![]() $l_{1},l^{\prime }_{1} \in (0,1]$
, there exists a
$l_{1},l^{\prime }_{1} \in (0,1]$
, there exists a
![]() $G_{\delta }$
dense set of
$G_{\delta }$
dense set of
![]() $\alpha =(\alpha _{1},{\alpha }_{2}) \in [0,1)^{2}$
, and we have
$\alpha =(\alpha _{1},{\alpha }_{2}) \in [0,1)^{2}$
, and we have
![]() ${E(A^{(1)})=\mathbb {R}}$
.
${E(A^{(1)})=\mathbb {R}}$
.
5. Proofs of Lemmas 3.4 and 3.5
We can see that the coprime condition is essential for Lemma 3.1, and, to achieve it, we need a stronger version of Khintchine’s divergence theorem that allows us to impose prime conditions for the denominators. We could also use the solved Duffin–Schaeffer conjecture [Reference Koukoulopoulos and Maynard11], but a weaker version in their original paper suffices.
Lemma 5.1. [Reference Duffin and Schaeffer8, Theorem 1]
If there exists a function
![]() $\psi :\mathbb {N}\rightarrow \mathbb {R}_{+}$
such that
$\psi :\mathbb {N}\rightarrow \mathbb {R}_{+}$
such that
-
(i)
 $\sum \psi (q)=\infty $
, and
$\sum \psi (q)=\infty $
, and -
(ii) there exists a strictly positive constant,
 $ c$
, such that the inequality
$ c$
, such that the inequality  $$ \begin{align*} \quad \sum_{q=1}^{n}\frac{\psi (q) \varphi (q)}{q}> c \sum_{q=1}^{n}\psi(q)\end{align*} $$
$$ \begin{align*} \quad \sum_{q=1}^{n}\frac{\psi (q) \varphi (q)}{q}> c \sum_{q=1}^{n}\psi(q)\end{align*} $$
holds for infinitely many n, where
 $\varphi (q)$
is Euler’s totient function,
$\varphi (q)$
is Euler’s totient function,
then, for almost every
![]() $l \in \mathbb {R}$
, there exist infinitely many pairs of integers
$l \in \mathbb {R}$
, there exist infinitely many pairs of integers
![]() $(b,q)$
such that
$(b,q)$
such that
With the help of Lemma 5.1, we can restrict the approximation of
![]() $l \in \mathbb {R}$
by rationals with prime denominators, as shown in the next lemma.
$l \in \mathbb {R}$
by rationals with prime denominators, as shown in the next lemma.
Corollary 5.2. For almost every
![]() $l\in \mathbb {R}$
, there exist infinitely many pairs of integers
$l\in \mathbb {R}$
, there exist infinitely many pairs of integers
![]() $(b,q)$
such that q is prime and
$(b,q)$
such that q is prime and
Proof. Define
 $$ \begin{align*} \psi(q)= \begin{cases} 1/(q\ln \ln \ln q) &\text{if }q\text{ is prime and }\ln \ln \ln q\ge 1, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \psi(q)= \begin{cases} 1/(q\ln \ln \ln q) &\text{if }q\text{ is prime and }\ln \ln \ln q\ge 1, \\ 0 & \text{otherwise.} \end{cases} \end{align*} $$
It suffices to check that conditions (i) and (ii) of Lemma 5.1 are satisfied for
![]() $\psi (q)$
.
$\psi (q)$
.
Note that, if q is prime, we have
![]() $\varphi (q)=q-1$
(where
$\varphi (q)=q-1$
(where
![]() $\varphi $
is Euler’s totient function). Then
$\varphi $
is Euler’s totient function). Then
![]() $\varphi (q)/q\geq 1/2$
, and condition (ii) of Lemma 5.1 is satisfied.
$\varphi (q)/q\geq 1/2$
, and condition (ii) of Lemma 5.1 is satisfied.
For condition (i), by the inequality of the sum of the reciprocals of primes
 $$ \begin{align} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\frac{1}{q} \geq \ln \ln (n+1)-\ln (\pi^{2}/6), \end{align} $$
$$ \begin{align} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\frac{1}{q} \geq \ln \ln (n+1)-\ln (\pi^{2}/6), \end{align} $$
we have
 $$ \begin{align*} \begin{aligned} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\psi(q) &\geq \frac{1}{\ln \ln \ln n} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\frac{1}{q}\\ &\mathop{\geq}\limits_{(5.2)} \frac{\ln \ln (n+1)-\ln (\pi^{2}/6)}{\ln\ln\ln n} \to \infty \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\psi(q) &\geq \frac{1}{\ln \ln \ln n} \sum\limits_{\substack{q \leq n \\ q \; \text{prime}}}\frac{1}{q}\\ &\mathop{\geq}\limits_{(5.2)} \frac{\ln \ln (n+1)-\ln (\pi^{2}/6)}{\ln\ln\ln n} \to \infty \end{aligned} \end{align*} $$
as
![]() $\ n\rightarrow \infty $
, and thus condition (i) is also satisfied.
$\ n\rightarrow \infty $
, and thus condition (i) is also satisfied.
Now we proceed with the proof of Lemma 3.4.
Proof of properties (1) and (5) of Lemma 3.4
By Corollary 5.2, we have that, for almost every
![]() $l\in (0,1]$
, there exists an increasing sequence of prime numbers
$l\in (0,1]$
, there exists an increasing sequence of prime numbers
![]() $\{q_{n}\}$
such that
$\{q_{n}\}$
such that
![]() $q_n\rightarrow \infty $
as
$q_n\rightarrow \infty $
as
![]() $n\rightarrow \infty $
and
$n\rightarrow \infty $
and
This shows inequality (3.13) in property (5) of Lemma 3.4. By choosing a subsequence of
![]() $q_n$
, we can assume that
$q_n$
, we can assume that
![]() $q_{n}\geq n^{2}$
and
$q_{n}\geq n^{2}$
and
![]() $\ln \ln \ln q_n\ge 1$
. By Dirichlet’s principle (the pigeonhole principle), if we divide the interval
$\ln \ln \ln q_n\ge 1$
. By Dirichlet’s principle (the pigeonhole principle), if we divide the interval
![]() $[0,1]$
into m segments of equal length, then, for
$[0,1]$
into m segments of equal length, then, for
![]() $m+1$
points, two of them must lie in the same segment. Thus, for every
$m+1$
points, two of them must lie in the same segment. Thus, for every
![]() $l' \in [0,1]$
, for all
$l' \in [0,1]$
, for all
![]() $ n\in \mathbb {N}$
, there exists
$ n\in \mathbb {N}$
, there exists
![]() $ q^{\prime }_{n}\in \mathbb {N}$
such that
$ q^{\prime }_{n}\in \mathbb {N}$
such that
and
This is inequality (3.14) in property (5) of Lemma 3.4. By Khintchine’s convergence theorem (see, for example, [Reference Lang12, Ch. II, Theorem 4]), for almost every
![]() $l'\in (0,1]$
, there exists a constant
$l'\in (0,1]$
, there exists a constant
![]() $C(l')$
such that
$C(l')$
such that
![]() $\|kl'\|\ge C(l')/k^2$
for all
$\|kl'\|\ge C(l')/k^2$
for all
![]() $k\in \mathbb {N}$
, and hence inequality (5.5) implies that
$k\in \mathbb {N}$
, and hence inequality (5.5) implies that
![]() $q^{\prime }_n\rightarrow \infty $
as
$q^{\prime }_n\rightarrow \infty $
as
![]() $n\rightarrow \infty $
for almost every
$n\rightarrow \infty $
for almost every
![]() $l'\in (0,1]$
. This proves property (1) of Lemma 3.4.
$l'\in (0,1]$
. This proves property (1) of Lemma 3.4.
Proof of the right-hand side of (3.11)
Combining (5.3) and (5.5) gives
Since
![]() $b_n$
,
$b_n$
,
![]() $b^{\prime }_n$
are, respectively, the closest integers to
$b^{\prime }_n$
are, respectively, the closest integers to
![]() $q_n l$
and
$q_n l$
and
![]() $q^{\prime }_n l'$
for
$q^{\prime }_n l'$
for
![]() $l,l'\in (0,1]$
, we have
$l,l'\in (0,1]$
, we have
![]() $b_n\le q_n$
and
$b_n\le q_n$
and
![]() $b^{\prime }_n\le q^{\prime }_n$
, and thus we obtain the right-hand side of (3.11) from the inequality above.
$b^{\prime }_n\le q^{\prime }_n$
, and thus we obtain the right-hand side of (3.11) from the inequality above.
Proof of property (2) of Lemma 3.4
Given
![]() $l\in (0,1]$
and the sequence of prime numbers
$l\in (0,1]$
and the sequence of prime numbers
![]() $q_n$
as in the proof of property (1), we show that, for almost every
$q_n$
as in the proof of property (1), we show that, for almost every
![]() $l' \in (0,1]$
and any infinite sequence of
$l' \in (0,1]$
and any infinite sequence of
![]() $q^{\prime }_n$
such that (5.5) hold, we have
$q^{\prime }_n$
such that (5.5) hold, we have
![]() $(q_{n},q^{\prime }_{n})= 1$
when n is large enough. Then property (2) follows by choosing a subsequence of n.
$(q_{n},q^{\prime }_{n})= 1$
when n is large enough. Then property (2) follows by choosing a subsequence of n.
Define
 $$ \begin{align*} G_{n,k}=\bigg\{l' \in [0,1]\ \bigg|\ \| kl' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}} \bigg\} \end{align*} $$
$$ \begin{align*} G_{n,k}=\bigg\{l' \in [0,1]\ \bigg|\ \| kl' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}} \bigg\} \end{align*} $$
and
where
denotes the set of k’s that violates the coprime condition. Note that, when
![]() $l'$
does not belong to
$l'$
does not belong to
![]() $G_n$
, the corresponding
$G_n$
, the corresponding
![]() $q^{\prime }_{n}$
that solves (5.4) and (5.5) is coprime to
$q^{\prime }_{n}$
that solves (5.4) and (5.5) is coprime to
![]() $q_n$
, so it suffices to show that almost every
$q_n$
, so it suffices to show that almost every
![]() $l'$
belongs to at most finitely many
$l'$
belongs to at most finitely many
![]() $G_n$
.
$G_n$
.
Since
![]() $q_n$
is prime, if
$q_n$
is prime, if
![]() $(k,q_{n})\neq 1$
, then
$(k,q_{n})\neq 1$
, then
![]() $(k,q_{n})=q_{n}$
and
$(k,q_{n})=q_{n}$
and
![]() $q_{n}\mid k$
. So
$q_{n}\mid k$
. So
Thus,
 $$ \begin{align*}\begin{aligned} \mu(G_{n})&\le \sum_{k\in S_n}\mu(G_{n,k})\\ &\leq \#S_n\cdot\frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}\\ &\leq\frac{ (\ln \ln \ln q_{n})^{1/2}}{q_{n}(\ln \ln \ln q_{n})^{1/2}}\\ &\leq \frac{1}{n^{2}}\\ \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} \mu(G_{n})&\le \sum_{k\in S_n}\mu(G_{n,k})\\ &\leq \#S_n\cdot\frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}\\ &\leq\frac{ (\ln \ln \ln q_{n})^{1/2}}{q_{n}(\ln \ln \ln q_{n})^{1/2}}\\ &\leq \frac{1}{n^{2}}\\ \end{aligned} \end{align*} $$
and
 $$ \begin{align*} \sum_{n=1}^{\infty} \mu (G_{n})\leq \sum_{n=1}^{\infty}\frac{1}{n^{2}}<\infty. \end{align*} $$
$$ \begin{align*} \sum_{n=1}^{\infty} \mu (G_{n})\leq \sum_{n=1}^{\infty}\frac{1}{n^{2}}<\infty. \end{align*} $$
By the Borel–Cantelli lemma, almost every
![]() $l' \in (0,1]$
belongs to at most finitely many
$l' \in (0,1]$
belongs to at most finitely many
![]() $G_n$
, which proves the coprime condition.
$G_n$
, which proves the coprime condition.
To prove the left-hand side of (3.11), it suffices to show that the two signed distances,
![]() $q_nl-b_n$
and
$q_nl-b_n$
and
![]() $q^{\prime }_nl-b^{\prime }_n$
, can be of the same sign infinitely many times, and that the lower bound holds for one of the distances. First, we introduce a lemma about the asymptotic estimation of the number of solutions to the approximation inequality.
$q^{\prime }_nl-b^{\prime }_n$
, can be of the same sign infinitely many times, and that the lower bound holds for one of the distances. First, we introduce a lemma about the asymptotic estimation of the number of solutions to the approximation inequality.
Lemma 5.3. [Reference Lang12, Ch. II, Theorem 7]
Let
![]() $\phi :\mathbb {N}\rightarrow [0,1]$
be a decreasing function such that
$\phi :\mathbb {N}\rightarrow [0,1]$
be a decreasing function such that
![]() $\sum _{k=1}^{\infty }\phi (k)$
diverges. For each positive integer N and irrational number l, let
$\sum _{k=1}^{\infty }\phi (k)$
diverges. For each positive integer N and irrational number l, let
 $$ \begin{align*}\Phi(N)=\sum _{k=1}^{N}\phi(k),\end{align*} $$
$$ \begin{align*}\Phi(N)=\sum _{k=1}^{N}\phi(k),\end{align*} $$
and let
![]() $\unicode{x3bb} (l, N)$
denote the number of solutions in integers b and q of the inequalities
$\unicode{x3bb} (l, N)$
denote the number of solutions in integers b and q of the inequalities
Then, for almost every
![]() $l\in \mathbb {R}$
,
$l\in \mathbb {R}$
,
Therefore, for almost every
![]() $l\in \mathbb {R}$
, the number of solutions
$l\in \mathbb {R}$
, the number of solutions
![]() $(b,q)$
for the above inequality is infinite.
$(b,q)$
for the above inequality is infinite.
Proof of the left-hand side of (3.11)
By choosing a subsequence, we can assume that
![]() $q_{n}\geq 2 q_{n-1}$
, and, without loss of generality, we can also assume that
$q_{n}\geq 2 q_{n-1}$
, and, without loss of generality, we can also assume that
![]() $q_{n}l -b_{n}$
is positive for all n, that is,
$q_{n}l -b_{n}$
is positive for all n, that is,
We show that, for almost every
![]() $l'\in (0,1]$
, there exist infinitely many pairs
$l'\in (0,1]$
, there exist infinitely many pairs
![]() $(b^{\prime }_{n},q^{\prime }_{n})$
such that
$(b^{\prime }_{n},q^{\prime }_{n})$
such that
![]() $ q^{\prime }_{n}l' -b^{\prime }_{n}$
are positive and smaller than
$ q^{\prime }_{n}l' -b^{\prime }_{n}$
are positive and smaller than
![]() $1/ (q_{n}\ln \ln \ln q_{n})$
.
$1/ (q_{n}\ln \ln \ln q_{n})$
.
Define
![]() $Q_0=q_0=0$
,
$Q_0=q_0=0$
,
![]() $Q_n={q_{n}(\ln \ln \ln q_{n})^{1/2}}$
for
$Q_n={q_{n}(\ln \ln \ln q_{n})^{1/2}}$
for
![]() $n\ge 1$
.
$n\ge 1$
.
Define
![]() $\phi :\mathbb {N}^*\rightarrow (0,1]$
by
$\phi :\mathbb {N}^*\rightarrow (0,1]$
by
Then
![]() $\phi (k)$
is decreasing. Note that
$\phi (k)$
is decreasing. Note that
 $$ \begin{align*} \sum _{k=1}^{Q_n}\phi(k)=\sum_{i=1}^{n}\bigg(1-\frac{q_{i-1}(\ln \ln \ln q_{i-1})^{1/2}}{q_{i}(\ln \ln \ln q_{i})^{1/2}}\bigg )\ge \frac{n}{2}, \end{align*} $$
$$ \begin{align*} \sum _{k=1}^{Q_n}\phi(k)=\sum_{i=1}^{n}\bigg(1-\frac{q_{i-1}(\ln \ln \ln q_{i-1})^{1/2}}{q_{i}(\ln \ln \ln q_{i})^{1/2}}\bigg )\ge \frac{n}{2}, \end{align*} $$
so
![]() $\sum \phi (k) $
diverges. By Lemma 5.3, for almost every
$\sum \phi (k) $
diverges. By Lemma 5.3, for almost every
![]() $l'\in (0,1]$
, the number of pairs of solutions
$l'\in (0,1]$
, the number of pairs of solutions
![]() $(b',q')$
such that
$(b',q')$
such that
is infinite. It is enough to note that
![]() $0<q'l-b'<\phi (q')$
means that
$0<q'l-b'<\phi (q')$
means that
for some n. These solutions can be indexed by a subsequence of n, and we omit the subindex and still denote them by
![]() $(b^{\prime }_n, q^{\prime }_n)$
.
$(b^{\prime }_n, q^{\prime }_n)$
.
This shows that there are infinitely many n’s such that
![]() $q_{n}l -b_{n}$
and
$q_{n}l -b_{n}$
and
![]() $q^{\prime }_{n}l' -b^{\prime }_{n}$
have the same sign.
$q^{\prime }_{n}l' -b^{\prime }_{n}$
have the same sign.
It remains to show the lower bound for one of the distances. Here, we show it for
![]() $b_n|q^{\prime }_n l'-b^{\prime }_n|$
. By Khintchine’s convergence theorem, for almost every
$b_n|q^{\prime }_n l'-b^{\prime }_n|$
. By Khintchine’s convergence theorem, for almost every
![]() $l'\in (0,1]$
,
$l'\in (0,1]$
,
for all k large enough (depending on
![]() $l'$
). By the inequality
$l'$
). By the inequality
![]() $q^{\prime }_{n}\leq q_{n}(\ln \ln \ln q_{n})^{1/2}$
,
$q^{\prime }_{n}\leq q_{n}(\ln \ln \ln q_{n})^{1/2}$
,
 $$ \begin{align} \| q^{\prime}_{n}l' \|\geq \frac{1}{q^{\prime}_n(\ln q^{\prime}_n)^{3/2}} \geq \frac{1}{q_{n}(\ln q_{n})^{2}} \end{align} $$
$$ \begin{align} \| q^{\prime}_{n}l' \|\geq \frac{1}{q^{\prime}_n(\ln q^{\prime}_n)^{3/2}} \geq \frac{1}{q_{n}(\ln q_{n})^{2}} \end{align} $$
for all n large enough, which gives the desired lower bound
Proof of property (4) of Lemma 3.4
The upper bound (5.4) for
![]() $q^{\prime }_{n}$
gives the right-hand side of property 4. The two inequalities (5.5) and (5.6) give that
$q^{\prime }_{n}$
gives the right-hand side of property 4. The two inequalities (5.5) and (5.6) give that
 $$ \begin{align*} \frac{1}{q^{\prime}_n(\ln q^{\prime}_n)^{3/2}}\le \| q^{\prime}_{n}l' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}. \end{align*} $$
$$ \begin{align*} \frac{1}{q^{\prime}_n(\ln q^{\prime}_n)^{3/2}}\le \| q^{\prime}_{n}l' \| \leq \frac{1}{q_{n}(\ln \ln \ln q_{n})^{1/2}}. \end{align*} $$
Using again the bound (5.4), we have that
Proof of Lemma 3.5
Similarly to the set of (4.4), we can prove that there exists a
![]() $G_\delta $
set of
$G_\delta $
set of
![]() $l_2$
(also of
$l_2$
(also of
![]() $l^{\prime }_2)$
such that there exists a subsequence of n where
$l^{\prime }_2)$
such that there exists a subsequence of n where
and
and
![]() $l^{\prime }_{2}$
such that
$l^{\prime }_{2}$
such that
and
This shows that the individual terms in the sum in inequalities (3.15) and (3.16) satisfy the given bounds, and thus the final remark of Lemma 3.5 is proved. The above choice of
![]() $l_2$
(and
$l_2$
(and
![]() $l_2'$
) forms a dense set of
$l_2'$
) forms a dense set of
![]() $(0,1]$
, as we can approximate any given number well enough by a rational with a denominator that is large enough. From inequalities (5.7) and (5.9), we have the existence of
$(0,1]$
, as we can approximate any given number well enough by a rational with a denominator that is large enough. From inequalities (5.7) and (5.9), we have the existence of
![]() $r_{2n}$
and
$r_{2n}$
and
![]() $r^{\prime }_{2n}$
such that
$r^{\prime }_{2n}$
such that
 $$ \begin{align*} \frac{1}{4(\ln q_{2n})^{3}}&\leq \frac{1}{2(\ln q_{2n})^{3}}-\frac{1}{4(\ln q_{2n})^{3}} \\ &\leq \lvert q^{\prime}_{2n}(q_{2n}l_{2}-r_{2n})+q_{2n}(q^{\prime}_{2n}l^{\prime}_{2}-r^{\prime}_{2n}) \rvert\\ &\leq \frac{1}{(\ln q_{2n})^{3}}+\frac{1}{4(\ln q_{2n})^{3}}\\ &\leq \frac{3}{2(\ln q_{2n})^{3}}. \end{align*} $$
$$ \begin{align*} \frac{1}{4(\ln q_{2n})^{3}}&\leq \frac{1}{2(\ln q_{2n})^{3}}-\frac{1}{4(\ln q_{2n})^{3}} \\ &\leq \lvert q^{\prime}_{2n}(q_{2n}l_{2}-r_{2n})+q_{2n}(q^{\prime}_{2n}l^{\prime}_{2}-r^{\prime}_{2n}) \rvert\\ &\leq \frac{1}{(\ln q_{2n})^{3}}+\frac{1}{4(\ln q_{2n})^{3}}\\ &\leq \frac{3}{2(\ln q_{2n})^{3}}. \end{align*} $$
Similarly, from inequalities (5.8) and (5.10), we have the existence of
![]() $r_{2n+1}$
and
$r_{2n+1}$
and
![]() $r^{\prime }_{2n+1}$
such that
$r^{\prime }_{2n+1}$
such that
 $$ \begin{align*} \frac{1}{4(\ln \ln \ln q_{2n+1})^{1/4}} &\leq \lvert q^{\prime}_{2n+1}(q_{2n+1}l_{2}-r_{2n+1})+q_{2n+1}(q^{\prime}_{2n+1}l^{\prime}_{2}-r^{\prime}_{2n+1}) \rvert \\ &\leq \frac{3}{2(\ln \ln \ln q_{2n+1})^{1/4}}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} \frac{1}{4(\ln \ln \ln q_{2n+1})^{1/4}} &\leq \lvert q^{\prime}_{2n+1}(q_{2n+1}l_{2}-r_{2n+1})+q_{2n+1}(q^{\prime}_{2n+1}l^{\prime}_{2}-r^{\prime}_{2n+1}) \rvert \\ &\leq \frac{3}{2(\ln \ln \ln q_{2n+1})^{1/4}}.\\[-3.5pc] \end{align*} $$
Acknowledgements
The authors would like to thank Bassam Fayad for suggesting the problem and for inspiring discussions. The second author was partially supported by the Swiss National Science Foundation through Grant No. 213663. The second author would also like to thank his wife Yangyang Cheng for her constant support. Finally, we would like to thank the referee for all the helpful comments that make the exposition clearer.