Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Day, Richard H.
and
Shafer, Wayne
1987.
Ergodic fluctuations in deterministic economic models.
Journal of Economic Behavior & Organization,
Vol. 8,
Issue. 3,
p.
339.
Góra, P.
and
Boyarsky, A.
1990.
Absolutely continuous invariant measures for the family of maps x → rxe-bxwith application to the Belousov-Zhabotinski reaction.
Dynamics and Stability of Systems,
Vol. 5,
Issue. 2,
p.
65.
Day, Richard H.
and
Pianigiani, Giulio
1991.
Statistical dynamics and economics.
Journal of Economic Behavior & Organization,
Vol. 16,
Issue. 1-2,
p.
37.
Keller, Gerhard
and
Nowicki, Tomasz
1992.
Spectral theory, zeta functions and the distribution of periodic points for Collet-Eckmann maps.
Communications in Mathematical Physics,
Vol. 149,
Issue. 1,
p.
31.
Rychlik, Marek
and
Sorets, Eugene
1992.
Regularity and other properties of absolutely continuous invariant measures for the quadratic family.
Communications in Mathematical Physics,
Vol. 150,
Issue. 2,
p.
217.
Chernov, N. I.
1995.
Limit theorems and Markov approximations for chaotic dynamical systems.
Probability Theory and Related Fields,
Vol. 101,
Issue. 3,
p.
321.
Denker, Manfred
Przytycki, Feliks
and
Urbański, Mariusz
1996.
On the transfer operator for rational functions on the Riemann sphere.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 2,
p.
255.


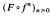 , where
, where 