Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-28T10:42:00.578Z Has data issue: false hasContentIssue false
  • English
  • Français

On sums of indicator functions in dynamical systems

Published online by Cambridge University Press:  13 October 2009

OLIVIER DURIEU  and
DALIBOR VOLNÝ
OLIVIER DURIEU
Affiliation:
Laboratoire de Mathématiques Raphaël Salem, UMR 6085 CNRS-Université de Rouen, France (email: [email protected], [email protected])
DALIBOR VOLNÝ
Affiliation:
Laboratoire de Mathématiques Raphaël Salem, UMR 6085 CNRS-Université de Rouen, France (email: [email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are interested in the limit theorem question for sums of indicator functions. We show that in every invertible ergodic dynamical system, for every increasing sequence (an)n∈ℕ⊂ℝ+ such that an↗∞ and an/n→0 as n→∞, there exists a dense Gδ of measurable sets A such that the sequence of the distributions of the partial sums 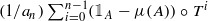is dense in the set of the probability measures on ℝ.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 5 , October 2010 , pp. 1419 - 1430
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Burton, R. and Denker, M.. On the central limit theorem for dynamical systems. Trans. Amer. Math. Soc. 302(2) (1987), 715–726.CrossRefGoogle Scholar
[2]Dehling, H., Durieu, O. and Volný, D.. New techniques for empirical processes of dependent data. Stochastic Process. Appl. to appear. ArXiv: 0806.2941.Google Scholar
[3]del Junco, A. and Rosenblatt, J.. Counterexamples in ergodic theory and number theory. Math. Ann. 245(3) (1979), 185–197.CrossRefGoogle Scholar
[4]Dudley, R. M.. Real Analysis and Probability (Cambridge Studies in Advanced Mathematics, 74). Cambridge University Press, Cambridge, 2002, Revised reprint of the 1989 original.CrossRefGoogle Scholar
[5]Durieu, O. and Volný, D.. An indicator function limit theorem in dynamical systems. Preprint. ArXiv: 0810.2452.Google Scholar
[6]Liardet, P. and Volný, D.. Sums of continuous and differentiable functions in dynamical systems. Israel J. Math. 98 (1997), 29–60.CrossRefGoogle Scholar
[7]Volný, D.. On limit theorems and category for dynamical systems. Yokohama Math. J. 38(1) (1990), 29–35.Google Scholar