Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
van Strien, Sebastian
and
Vargas, Edson
2004.
Real bounds, ergodicity and negative Schwarzian for multimodal maps.
Journal of the American Mathematical Society,
Vol. 17,
Issue. 4,
p.
749.
Shen, WeiXiao
2009.
Decay of geometry for unimodal maps: The C2 case.
Science Bulletin,
Vol. 54,
Issue. 11,
p.
1859.
Yu, Zhiheng
and
Liu, Liu
2019.
Complexity in iteration of polynomials.
Aequationes mathematicae,
Vol. 93,
Issue. 5,
p.
985.
Yang, Lili
and
Yu, Zhiheng
2022.
The order structure of forts iterated by quadratic polynomials.
Aequationes mathematicae,
Vol. 96,
Issue. 3,
p.
515.


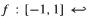 with finitely many non-flat critical points of turning type and we prove that any minimal set of
with finitely many non-flat critical points of turning type and we prove that any minimal set of 