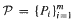Let Ω be a bounded region in Rn and let be a partition of Ω into a finite number of subsets having piecewise 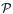C2 boundaries. The boundaries may contain cusps. Let τ: Ω → Ω be piecewise C2 on and expanding in the sense that there exists α > 1 such that for any 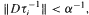i = 1, 2,…,m, where 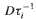is the derivative matrix of 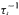and ‖·‖ is the euclidean matrix norm. The main result provides a lower bound on α which guarantees the existence of an absolutely continuous invariant measure for τ.

We prove that those non-uniformly hyperbolic maps and flows (with singularities) that enjoy the K-property are also Bernoulli. In particular, many billiard systems, including those systems of hard balls and stadia that have the K-property, and hyperbolic billiards, such as the Lorentz gas in any dimension, are Bernoulli. We obtain the Bernoulli property for both the billiard flows and the associated maps on the boundary of the phase space.

In this paper we study expansive automorphisms of compact 0-dimensional abelian groups. Our main result is the complete algebraic and topological classification of the transitive expansive automorpisms for which the maximal order of the elements is p2 for a prime p. This yields a classification of the transitive expansive automorphisms with topological entropy log p2. Finally, we prove a necessary and sufficient condition for an expansive automorphism to be conjugated, topologically and algebraically, to a shift over a finite group.

This paper represents a contribution to the variational approach to the understanding of the dynamics of exact area-preserving monotone twist maps of the annulus, currently known as the Aubry–Mather theory. The method introduced by Mather to construct invariant measures of Denjoy type is extended to produce almost-periodic measures, having arbitrary rationally independent frequencies, and positive entropy measures, supported within the gaps of Aubry–Mather sets which do not lie on invariant curves. This extension is based on a generalized version of the Percival's Lagrangian and on a new minimization procedure, which also gives a simplified proof of the basic existence theorem for the Aubry–Mather sets.

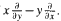We provide an algorithm to compute the first non-zero derivative of the return map r ↦ L(r, ε) of a planar vector field which is a polynomial perturbation of . It yields a new method for finding the centre conditions in the case of a homogeneous perturbative part.

Let T be an ergodic automorphism defined on a standard Borel probability space for which T and T−1 are isomorphic. We investigate the form of the conjugating automorphism. It is well known that if T is ergodic having a discrete spectrum and S is the conjugation between T and T−1, i.e. S satisfies TS = ST−1 then S2 = I the identity automorphism. We show that this result remains true under the weaker assumption that T has a simple spectrum. If T has the weak closure property and is isomorphic to its inverse, it is shown that the conjugation S satisfies S4 = I. Finally, we construct an example to show that the conjugation need not be an involution in this case. The example we construct, in addition to having the weak closure property, is of rank two, rigid and simple for all orders with a singular spectrum of multiplicity equal to two.

We study the pressure function for critically finite polynomials and analyze the case when this function fails to be real analytic.

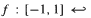We consider a C2 non-renormalizable polymodal map with finitely many non-flat critical points of turning type and we prove that any minimal set of f has zero Lebesgue measure.

We give some topological ergodic theorems inspired by the Wiener-Wintner ergodic theorem. These theorems are used to give results for uniquely ergodic transformations and to study unique equilibrium states for shift maps. These latter results give random L2 ergodic theorems for a finite set of commuting measure-preserving transformations.