Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-30T23:47:02.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Integer Cantor sets and an order-two ergodic theorem

Published online by Cambridge University Press:  19 September 2008

Albert M. Fisher
Albert M. Fisher
Affiliation:
University of Göttingen, Lotzestr. 13, D3400 Göttingen, Germany
Get access Rights & Permissions [Opens in a new window]

Abstract

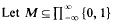Let denote the orbit closure, under the left shift σ, of the sequence… (all zeroes)… 101000101000000000101 … corresponding to the integer Cantor set 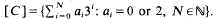. We prove that with respect to the infinite invariant measure ρ, which is the unique normalized non-atomic invariant measure on M, for every f ∈ L1(M, ρ), for ρ-a.e. x∈ M

where d = log 2/log 3, and c is the almost-sure value of the right-hand order-two density of the middle-third Cantor set. The proof uses renormalization to a scaling flow, plus identification of (M, σ) as a tower over the Kakutani-von Neumann dyadic odometer.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 13 , Issue 1 , March 1993 , pp. 45 - 64
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Aa 1]Aaronson, J.. Rational ergodicity and a metric invariant for Markov shifts. Israel J. M. 27 (1977), 93–123.CrossRefGoogle Scholar
[Aa 2]Aaronson, J.. On the ergodic theory of non-integrable functions and infinite measure spaces. Israel J. M. 27 (1977), 163–173.CrossRefGoogle Scholar
[Aa3]Aaronson, J.. On the pointwise behaviour of transformations preserving infinite measures. Israel J. M. 32 (1979), 67–82.CrossRefGoogle Scholar
[Aa 4]Aaronson, J.. The asymptotic distributional behaviour of transformations preserving infinite measures. J. D'Anal. Math. 39 (1981), 203–234.CrossRefGoogle Scholar
[Aa 5]Aaronson, J.. The intrinsic normalizing constants of transformations preserving infinite measures. J. D'Anal. Math. 49 (1987), 239–270.CrossRefGoogle Scholar
[Aa6]Aaronson, J.. Rational ergodicity, bounded rational ergodicity and some continuous measures on the circle. Israel U. M. 33 (1979), 181–197.CrossRefGoogle Scholar
[Aa-De 1]Aaronson, J. & Denker, M.. Upper bounds for ergodic sums of infinite measures preserving transformations. Trans. Amer. Math. Soc. 319 (1990), 101–138.CrossRefGoogle Scholar
[Aa-De 2]Aaronson, J. & Denker, M.. Lower bounds for partial sums of certain positive stationary processes. In: Almost Everywhere Convergence. Proceedings. Edgar, G. A. and Sucheston, L., eds. Academic, New York, 1989, pp 1–9.Google Scholar
[Aa-De-Fi]Aaronson, J., Denker, M. & Fisher, A. M.. Second order ergodic theorems for ergodic transformations of infinite measure spaces. Proc. Amer. Math. Soc. 144 No. 1 (1992), 115–128.CrossRefGoogle Scholar
[Aa-S]Aaronson, J. & Sullivan, D.. Rational ergodicity of geodesic flows. Ergod. Th. & Dynam. Sys. 4 (1984), 165–178.CrossRefGoogle Scholar
[Be-Fi]Bedford, T. & Fisher, A. M.. Analogues of the Lebesgue density theorem for fractal subsets of the reals and integers. Proc. London Math. Soc. 64 (1992), 95–124.CrossRefGoogle Scholar
[Bo]Bowen, R.. On axiom A diffeomorphisms. Conf. Board Math. Sci. 35 (1978), American Math. Soc., Providence RI, 1978.Google Scholar
[Fa]Falconer, K. J.. The geometry of fractal sets. Cambridge University Press, New York/Cambridge, 1985.CrossRefGoogle Scholar
[Fi 1]Fisher, A. M.. Convex-invariant means and a pathwise Central Limit Theorem. Adv. Math. 63 (1987), 213–246.CrossRefGoogle Scholar
[Fi 2]Fisher, A. M.. A pathwise Central Limit Theorem for random walks. Ann. Prob. to appear.Google Scholar
[Fi 3]Fisher, A. M.. Analogues of geodesic and horocycle flows for certain fractal sets. In preparation.Google Scholar
[Ha-I-K]Hajian, A., Ito, Y. & Kakutani, S.. Kakutani, S.: Selected Papers. Vol. 2. Birkhäuser, Boston-Basel, 1986.Google Scholar
[Ho]Hopf, E.. Ergodentheorie. Chelsea, New York, 1948.Google Scholar
[L-M]Ledrappier, F. & Misiurewicz, M.. Dimension of invariant measures for maps with exponent zero. Ergod. Th. & Dynam. Sys. 5 (1985), 595–610.CrossRefGoogle Scholar
[M]Marcus, B.. Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. Math. 105 (1977), 81–105.CrossRefGoogle Scholar
[T]Taqqu, M. S.. A biliographical guide to self-similar processes and long-range dependence. In: Dependence in Probability and Statistics. Eberlein, E. and Taqqu, M. S., eds. Birkhäuser, Boston-Basel, 1986, pp. 137–162.CrossRefGoogle Scholar
[V]Vervaat, W. V.. Sample path properties of self-similar processes with stationary increments. Ann. Prob. 13 (1985), 1–27.CrossRefGoogle Scholar
[W]Widder, D. V.. An Introduction to Transform Theory. Academic Press, New York-London, 1971.Google Scholar
[Y]S, L.. Young. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–124.Google Scholar