Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:38:52.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Hierarchies of chaotic maps on continua

Published online by Cambridge University Press:  13 August 2013

LOGAN HOEHN  and
CHRISTOPHER MOURON
LOGAN HOEHN
Affiliation:
Department of Mathematics, University of Alabama at Birmingham, 1300 University Boulevard, Birmingham, AL 35294, USA Department of Mathematics, Nipissing University, 100 College Drive, Box 5002, North Bay, ON, Canada P1B 8L7 email [email protected]
CHRISTOPHER MOURON
Affiliation:
Department of Mathematics and Computer Science, Rhodes College, Memphis, TN 38112, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

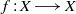Let $f: X\longrightarrow X$ be a map of a continuum. In this paper we examine the following dynamical conditions on 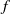$f$: (1) 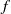$f$ is continuum-wise fully expansive; (2) 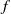$f$ is weakly continuum-wise fully expansive; (3) 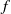$f$ is mixing; (4) 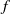$f$ is weakly mixing. We first show that (1) implies (2), (2) implies (3) and (3) implies (4). Then we investigate what topological conditions will force the reverse implications to hold and give examples of when the reverse conditions do not hold. In particular, a map of the universal dendrite is given that is weakly mixing but not mixing.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 6 , December 2014 , pp. 1897 - 1913
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Charatonik, J.. Monotone mappings of universal dendrites. Topology Appl. 38 (2) (1991), 163–187.Google Scholar
Dirbak, M., Snoha, L. and Spitalsky, V.. Dynamical consequences of a free interval: minimality, transitivity, mixing and topological entropy. Preprint, arXiv:1112.1191.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Haranczyk, G., Kwietniak, D. and Oprocha, P.. A note on transitivity, sensitivity and chaos for graph maps. J. Difference Equ. Appl. 17 (10) (2011), 1549–1553.Google Scholar
Lau, K. and Zame, A.. On weak mixing of cascades. Math. Systems Theory 6 (1972/73), 307–311.Google Scholar
Rogers, J. T.. Rotations of simply-connected regions and circle-like continua. Continuum Theory and Dynamical Systems (Arcata, CA, 1989) (Contemporary Mathematics, 117). American Mathematical Society, Providence, RI, 1991, pp. 139–148.CrossRefGoogle Scholar
Wazewski, T.. Sur les courbes de Jordan ne renfermant aucune courbe simple fermée de Jordan. Ann. Sot. Pofon. Math. 2 (1923), 49–170.Google Scholar