Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T00:46:43.432Z Has data issue: false hasContentIssue false
  • English
  • Français

Epsilon-hypercyclic operators

Published online by Cambridge University Press:  04 November 2009

CATALIN BADEA ,
SOPHIE GRIVAUX  and
VLADIMIR MÜLLER
CATALIN BADEA
Affiliation:
Laboratoire Paul Painlevé, UMR CNRS 8524, Université Lille 1, 59655 Villeneuve d’Ascq Cedex, France (email: [email protected], [email protected])
SOPHIE GRIVAUX
Affiliation:
Laboratoire Paul Painlevé, UMR CNRS 8524, Université Lille 1, 59655 Villeneuve d’Ascq Cedex, France (email: [email protected], [email protected])
VLADIMIR MÜLLER
Affiliation:
Institute of Mathematics AV CR, Zitna 25, 115 67 Prague 1, Czech Republic (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a separable infinite-dimensional Banach space, and T a bounded linear operator on X; T is hypercyclic if there is a vector x in X with dense orbit under the action of T. For a fixed ε∈(0,1), we say that T is ε-hypercyclic if there exists a vector x in X such that for every non-zero vector y∈X there exists an integer n with 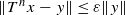. The main result of this paper is a construction of a bounded linear operator T on the Banach space ℓ1 which is ε-hypercyclic without being hypercyclic. This answers a question from V. Müller [Three problems, Mini-Workshop: Hypercyclicity and linear chaos, organized by T. Bermudez, G. Godefroy, K.-G. Grosse-Erdmann and A. Peris. Oberwolfach Rep.3 (2006), 2227–2276].

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 6 , December 2010 , pp. 1597 - 1606
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bayart, F. and Grivaux, S.. Frequently hypercylic operators. Trans. Amer. Math. Soc. 358 (2006), 5083–5117.CrossRefGoogle Scholar
[2]Bayart, F. and Matheron, É.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179). Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
[3]Bayart, F. and Matheron, É.. (Non)-weakly mixing operators and hypercyclicity sets. Ann. Inst. Fourier to appear.Google Scholar
[4]Bourdon, P. and Feldman, N.. Somewhere dense orbits are everywhere dense. Indiana Univ. Math. J. 52 (2003), 811–819.CrossRefGoogle Scholar
[5]Chan, K. and Sanders, R.. A weakly hypercyclic operator that is not norm hypercyclic. J. Operator Theory 52 (2004), 39–59.Google Scholar
[6]Costakis, G.. On a conjecture of D. Herrero concerning hypercyclic operators. C. R. Math. Acad. Sci. Paris 330 (2000), 179–182.CrossRefGoogle Scholar
[7]Feldman, N.. Perturbations of hypercyclic vectors. J. Math. Anal. Appl. 273 (2002), 67–74.CrossRefGoogle Scholar
[8]Grosse-Erdmann, K.-G. and Peris, A.. Frequently dense orbits. C. R. Math. Acad. Sci. Paris 341 (2005), 123–128.CrossRefGoogle Scholar
[9]Müller, V.. Three problems, Mini-Workshop: Hypercyclicity and linear chaos, organized by T. Bermudez, G. Godefroy, K.-G. Grosse-Erdmann and A. Peris. Oberwolfach Rep. 3 (2006), 2227–2276.Google Scholar
[10]Peris, A.. Multi-hypercyclic operators are hypercyclic. Math. Z. 236 (2001), 779–786.CrossRefGoogle Scholar
[11]Rolewicz, S.. On orbits of elements. Studia Math. 32 (1969), 17–22.CrossRefGoogle Scholar