Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T07:02:44.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Distribution of approximants and geodesic flows

Published online by Cambridge University Press:  03 June 2013

ALBERT M. FISHER  and
THOMAS A. SCHMIDT
ALBERT M. FISHER
Affiliation:
Dept Mat IME-USP, Caixa Postal 66281, CEP 05315-970 São Paulo, Brazil email [email protected]
THOMAS A. SCHMIDT
Affiliation:
Oregon State University, Corvallis, OR 97331, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a new proof of Moeckel’s result that for any finite index subgroup of the modular group, almost every real number has its regular continued fraction approximants equidistributed into the cusps of the subgroup according to the weighted cusp widths. Our proof uses a skew product over a cross-section for the geodesic flow on the modular surface. Our techniques show that the same result holds true for approximants found by Nakada’s $\alpha $-continued fractions, and also that the analogous result holds for approximants that are algebraic numbers given by any of Rosen’s 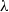$\lambda $-continued fractions, related to the infinite family of Hecke triangle Fuchsian groups.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 6 , December 2014 , pp. 1832 - 1848
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. L. and Flatto, L.. Geodesic flows, interval maps and symbolic dynamics. Bull. Amer. Math. Soc. 25 (1991), 229–334.CrossRefGoogle Scholar
Arnoux, P. and Hubert, P.. Fractions continues sur les surfaces de Veech. J. Anal. Math. 81 (2000), 35–64.Google Scholar
Arnoux, P.. Le codage du flot géodésique sur la surface modulaire. Enseign. Math. 40 (1994), 29–48.Google Scholar
Artin, E.. Ein mechanisches System mit quasiergodischen Bahnen. Abh. Math. Semin. Univ. Hambg. 3 (1924), 170–175; reproduced in Collected Papers. Springer, New York, 1982, pp. 499–505.Google Scholar
Arnoux, P. and Schmidt, T. A.. Veech surfaces with nonperiodic directions in the trace field. J. Mod. Dyn. 3 (4) (2009), 611–629.Google Scholar
Arnoux, P. and Schmidt, T. A.. Cross sections for geodesic flows and $\alpha $-continued fractions. Nonlinearity 26 (2013), 711–726.CrossRefGoogle Scholar
Burton, R. M., Kraaikamp, C. and Schmidt, T. A.. Natural extensions for the Rosen fractions. Trans. Amer. Math. Soc. 352 (3) (2000), 1277–1298.CrossRefGoogle Scholar
Bogomolny, E. and Schmit, C.. Multiplicities of periodic orbit lengths for non-arithmetic models. J. Phys. A: Math. Gen. 37 (2004), 4501–4526.Google Scholar
Chang, C.-H. and Mayer, D.. Thermodynamic formalism and Selberg’s zeta function for modular groups. Regul. Chaotic Dyn. 5 (3) (2000), 281–312.CrossRefGoogle Scholar
Dajani, K., Kraaikamp, C. and Steiner, W.. Metrical theory for $\alpha $-Rosen fractions. J. Eur. Math. Soc. (JEMS) 11 (6) (2009), 1259–1283.Google Scholar
Dani, S. G. and Smillie, J.. Uniform distribution of horocycle orbits for Fuchsian groups. Duke Math. J. 51 (1) (1984), 185–194.Google Scholar
Gröchenig, K. and Haas, A.. Backward continued fractions, Hecke groups and invariant measures for transformations of the interval. Ergod. Th. & Dynam. Sys. 16 (6) (1996), 1241–1274.Google Scholar
Hedlund, G. A.. A metrically transitive group defined by the modular groups. Amer. J. Math. 57 (3) (1935), 668–678.Google Scholar
Hedlund, G. A.. Fuchsian groups and transitive horocycles. Duke Math. J. 2 (1936), 530–542.Google Scholar
Hanson, E., Merberg, A., Towse, C. and Yudovina, E.. Generalized continued fractions and orbits under the action of Hecke triangle groups. Acta Arith. 134 (4) (2008), 337–348.Google Scholar
Hopf, E.. Ergodic theory and the geodesic flow on surfaces of constant negative curvature. Bull. Amer. Math. Soc. 77 (1971), 863–877.Google Scholar
Jager, H. and Liardet, P.. Distributions arithmétiques des dénominateurs de convergents de fractions continues. Indag. Math. 50 (2) (1988), 181–197.Google Scholar
Kraaikamp, C., Schmidt, T. A. and Steiner, W.. Natural extensions and entropy of $\alpha $-continued fractions. Nonlinearity 25 (2012), 2207–2243.Google Scholar
Katok, S. and Ugarcovici, I.. Symbolic dynamics for the modular surface and beyond. Bull. Amer. Math. Soc. 44 (1) (2007), 87–132.CrossRefGoogle Scholar
Lehner, J.. A Short Course in Automorphic Functions. Holt, Rinehart and Winston, New York, 1966.Google Scholar
Leutbecher, A.. Über die Heckeschen Gruppen $\mathfrak{G}(\lambda )$. Abh. Math. Semin. Univ. Hambg. 31 (1967), 199–205.Google Scholar
Manning, A.. Dynamics of geodesic and horocycle flows on surfaces of constant negative curvature. Ergodic Theory, Symbolic Dynamics, and Hyperbolic Spaces (Trieste, 1989). Oxford University Press, New York, 1991, pp. 71–91.Google Scholar
Mayer, D. and Mühlenbruch, T.. Nearest ${\lambda }_{q} $-multiple fractions. Spectrum and Dynamics (CRM Proceedings & Lecture Notes, 52). American Mathematical Society, Providence, RI, 2010, pp. 147–184.Google Scholar
Moeckel, R.. Geodesics on modular surfaces and continued fractions. Ergod. Th. & Dynam. Sys. 2 (1982), 69–83.CrossRefGoogle Scholar
Mayer, D. and Strömberg, F.. Symbolic dynamics for the geodesic flow on Hecke surfaces. J. Mod. Dyn. 2 (4) (2008), 581–627.Google Scholar
Nakada, H.. Metrical theory for a class of continued fraction transformations and their natural extensions. Tokyo J. Math. 4 (2) (1981), 399–426.Google Scholar
Nakanishi, T.. A remark on R. Moeckel’s paper: Geodesics on modular surfaces and continued fractions. Ergod. Th. & Dynam. Sys. 9 (3) (1989), 511–514.Google Scholar
Nakada, H.. On the Lenstra constant associated to the Rosen continued fractions. J. Eur. Math. Soc. (JEMS) 12 (1) (2010), 55–70.Google Scholar
Nakada, H., Ito, S. and Tanaka, S.. On the invariant measure for the transformations associated with some real continued-fractions. Keio Engrg. Rep. 30 (13) (1977), 159–175.Google Scholar
Pollicott, M.. Dynamical zeta functions. Integers 11B (2011), article no. A11.Google Scholar
Rosen, D.. A class of continued fractions associated with certain properly discontinuous groups. Duke Math. J. 21 (1954), 549–563.Google Scholar
Series, C.. The modular surface and continued fractions. J. Lond. Math. Soc. 31 (1985), 69–80.Google Scholar
Sheingorn, M.. Continued fractions and congruence subgroup geodesics. Number Theory with an Emphasis on the Markoff Spectrum (Provo, UT, 1991) (Lecture Notes in Pure and Applied Mathematics, 147). Dekker, New York, 1993, pp. 239–254.Google Scholar
Schmidt, T. A. and Sheingorn, M.. Length spectra of the Hecke triangle groups. Math. Z. 220 (3) (1995), 369–397.CrossRefGoogle Scholar
Smillie, J. and Ulcigrai, C.. Geodesic flow on the Teichmüller disk of the regular octagon, cutting sequences and octagon continued fractions maps. Dynamical Numbers – Interplay between Dynamical Systems and Number Theory (Contemporary Mathematics, 532). American Mathematical Society, Providence, RI, 2010, pp. 29–65.Google Scholar
Smillie, J. and Ulcigrai, C.. Beyond Sturmian sequences: coding linear trajectories in the regular octagon. Proc. Lond. Math. Soc. (3) 102 (2) (2011), 291–340.Google Scholar
Veech, W. A.. The metric theory of interval exchange transformations I, II, III. Amer. J. Math. 106 (1984), 1331–1422.Google Scholar