Published online by Cambridge University Press: 05 July 2013
In this paper we consider a filtered chain complex 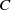 $C$ and its differential given by a connection matrix
$C$ and its differential given by a connection matrix 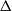 $\Delta $ which determines an associated spectral sequence
$\Delta $ which determines an associated spectral sequence 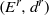 $({E}^{r} , {d}^{r} )$. We present an algorithm which sweeps the connection matrix in order to span the modules
$({E}^{r} , {d}^{r} )$. We present an algorithm which sweeps the connection matrix in order to span the modules 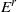 ${E}^{r} $ in terms of bases of
${E}^{r} $ in terms of bases of 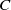 $C$ and gives the differentials
$C$ and gives the differentials 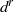 ${d}^{r} $. In this process a sequence of similar connection matrices and associated transition matrices are produced. This algebraic procedure can be viewed as a continuation, where the transition matrices give information about the bifurcation behavior. We introduce directed graphs, called flow and bifurcation schematics, that depict bifurcations that could occur if the sequence of connection matrices and transition matrices were realized in a continuation of a Morse decomposition, and we present a dynamic interpretation theorem that provides conditions on a parameterized family of flows under which such a continuation could occur.
${d}^{r} $. In this process a sequence of similar connection matrices and associated transition matrices are produced. This algebraic procedure can be viewed as a continuation, where the transition matrices give information about the bifurcation behavior. We introduce directed graphs, called flow and bifurcation schematics, that depict bifurcations that could occur if the sequence of connection matrices and transition matrices were realized in a continuation of a Morse decomposition, and we present a dynamic interpretation theorem that provides conditions on a parameterized family of flows under which such a continuation could occur.