Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-24T17:58:42.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Combable functions, quasimorphisms, and the central limit theorem

Published online by Cambridge University Press:  04 November 2009

DANNY CALEGARI  and
KOJI FUJIWARA
DANNY CALEGARI
Affiliation:
Department of Mathematics, Caltech, Pasadena CA, 91125, USA (email: [email protected])
KOJI FUJIWARA
Affiliation:
Graduate School of Information Science, Tohoku University, Sendai, Japan (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A function on a discrete group is weakly combable if its discrete derivative with respect to a combing can be calculated by a finite-state automaton. A weakly combable function is bicombable if it is Lipschitz in both the left- and right-invariant word metrics. Examples of bicombable functions on word-hyperbolic groups include:

  1. (1) homomorphisms to ℤ;

  2. (2) word length with respect to a finite generating set;

  3. (3) most known explicit constructions of quasimorphisms (e.g. the Epstein–Fujiwara counting quasimorphisms).

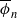We show that bicombable functions on word-hyperbolic groups satisfy a central limit theorem: if is the value of ϕ on a random element of word length n (in a certain sense), there are E and σ for which there is convergence in the sense of distribution 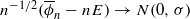, where N(0,σ) denotes the normal distribution with standard deviation σ. As a corollary, we show that if S1 and S2 are any two finite generating sets for G, there is an algebraic number λ1,2 depending on S1 and S2 such that almost every word of length n in the S1 metric has word length n⋅λ1,2 in the S2 metric, with error of size .

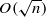Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 5 , October 2010 , pp. 1343 - 1369
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bavard, C.. Longeur stable des commutateurs. Enseign. Math. 37 (1991), 109–150.Google Scholar
[2]Berman, A. and Plemmons, R.. Nonnegative Matrices in the Mathematical Sciences. Academic Press, New York, 1979.Google Scholar
[3]Brooks, R.. Some remarks on bounded cohomology. Riemann Surfaces and Related Topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, NY, 1978) (Annals of Mathematics Studies, 97). Princeton University Press, Princeton, NJ, 1981, pp. 53–63.Google Scholar
[4]Calegari, D.. scl (MSJ Memoirs, 20). Mathematical Society of Japan, Tokyo, 2009.CrossRefGoogle Scholar
[5]Cannon, J.. The combinatorial structure of cocompact discrete hyperbolic groups. Geom. Dedicata 16(2) (1984), 123–148.CrossRefGoogle Scholar
[6]Coornaert, M.. Mesures de Patterson–Sullivan sur le bord d’un espace hyperbolique au sens de Gromov. Pacific J. Math. 159 (1993), 241–270.CrossRefGoogle Scholar
[7]Coornaert, M. and Papadopoulos, A.. Symbolic Dynamics and Hyperbolic Groups (Lecture Notes in Mathematics, 1539). Springer, Berlin, 1993.Google Scholar
[8]Coornaert, M. and Papadopoulos, A.. Symbolic coding for the geodesic flow associated to a word hyperbolic group. Manuscripta Math. 109 (2002), 465–492.Google Scholar
[9]Dehn, M.. Papers on group theory and topology. Translated from the German and with introductions and an appendix by John Stillwell. Springer, New York, 1987.Google Scholar
[10]Epstein, D., Cannon, J., Holt, D., Levy, S., Paterson, M. and Thurston, W.. Word Processing in Groups. Jones and Bartlett Publishers, Boston, MA, 1992.CrossRefGoogle Scholar
[11]Epstein, D. and Fujiwara, K.. The second bounded cohomology of word-hyperbolic groups. Topology 36 (1997), 1275–1289.CrossRefGoogle Scholar
[12]Grinstead, C. and Snell, J.. Introduction to Probability. American Mathematical Society Publications, Providence, RI, 1997.Google Scholar
[13]Gromov, M.. Hyperbolic groups. Essays in Group Theory (Mathematical Sciences Research Institute Publications, 8). Springer, New York, 1987, pp. 75–263.CrossRefGoogle Scholar
[14]Horsham, M. and Sharp, R.. Lengths, quasi-morphisms and statistics for free groups. Spectral Analysis in Geometry and Number Theory (Dedicated to Toshikazu Sunada on the occasion of his 60th birthday) (Contemporary Mathematics, 484). American Mathematical Society, Providence, RI, 2009, pp. 219–237.Google Scholar
[15]Kaimanovich, V., Kapovich, I. and Schupp, P.. The subadditive ergodic theorem and generic stretching factors for free group automorphisms. Israel J. Math. 157 (2007), 1–46.Google Scholar
[16]Kemeny, J. and Snell, L.. Finite Markov Chains (University Series in Undergraduate Mathematics). Van Nostrand, Princeton, NJ, 1960.Google Scholar
[17]Markov, A.. Extension of Limit Theorems of Probability Theory to a Sum of Variables Connected in a Chain, republished as Appendix B in Dynamic Probabilistic Systems, Vol. I: Markov Models (Series in Decision and Control, by Richard A. Howard). John Wiley and Sons, 1971.Google Scholar
[18]Matsumoto, S.. Private communication, 2008.Google Scholar
[19]Picaud, J.-C.. Cohomologie bornée des surfaces et courants géodésiques. Bull. Soc. Math. France 125 (1997), 115–142.Google Scholar
[20]Pollicott, M. and Yuri, M.. Dynamical Systems and Ergodic Theory (London Mathematical Society Student Texts, 40). Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
[21]Rees, S.. Hairdressing in groups: a survey of combings and formal languages. Geom. Topol. Monogr. 1 (1998), 493–509.Google Scholar
[22]Rivin, I.. Growth in free groups (and other stories). Preprint, 1999, math.CO/9911076.Google Scholar
[23]Romanovskii, V.. Discrete Markov chains. Wolters-Noordhoff Publishing, Groningen, 1970 (translated from the Russian by E. Seneta).Google Scholar
[24]Sarnak, P.. Private communication, 2008.Google Scholar
[25]Sharp, R.. Local limit theorems for free groups. Math. Ann. 321 (2001), 889–904.Google Scholar