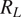Impact Statement
Clustering algorithms are unsupervised machine learning methods that are used across many areas of data science. The use of such methods can automate the identification of certain features, thus allowing for the analysis of very large datasets. Here, we show that a particular clustering algorithm called hierarchical density-based spatial clustering of applications with noise (HDBSCAN) can be used to automatically identify thermohaline staircases in hydrographic profiles from the Arctic Ocean. Compared to previous detection methods, HDBSCAN has the advantages of requiring minimal prior knowledge and of automatically connecting individual staircase “steps” across different hydrographic profiles. We expect that this method could be applied to many similar datasets, offering a straightforward way to identify and track layers in thermohaline staircases across the world’s oceans.
1. Introduction
Thermohaline staircases, formed by differential diffusion rates of heat and salt, appear as a series of vertically well-mixed horizontal layers, each separated by thin, strongly stratified interfaces. These structures have been observed throughout the world’s oceans (van der Boog et al., Reference van der Boog, Dijkstra, Pietrzak and Katsman2021a) as well as in saline lakes (Newman, Reference Newman1976), while related double-diffusive staircases are thought to occur in gas giants such as Jupiter and Saturn (André et al., Reference André, Barker and Mathis2017; Pontin et al., Reference Pontin, Barker, Hollerbach, André and Mathis2021). In particular, they are well known to occur in the Arctic Ocean (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022; Ménesguen et al., Reference Ménesguen, Lique and Caspar-Cohen2022). Around 250 to 800 meters below the surface of the Arctic Ocean, there is a layer of water originating from the Atlantic, which is warmer and saltier than the topmost layer that is in contact with the sea ice above (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008). The core of the Atlantic water (AW) is defined as the maximum subsurface temperature and is generally at a depth of 400 m in the Canada Basin. Above this depth, in a region in which both temperature and salinity increase downwards, lie the lower halocline waters (LHW), where the staircases are found (Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022).
Two-thirds of the world’s oceans are alpha oceans, which are stratified by temperature, with the warmest waters at the surface and colder waters at depth (Stewart and Haine, Reference Stewart and Haine2016). This is in contrast to the 15% that are beta oceans, the only regions where sea ice can form over deep water, such as the Arctic, which are primarily stratified by salinity, and therefore, the warm, salty AW is stable at depth (Carmack, Reference Carmack2007). The remaining oceans are called “transition zone oceans” (Stewart and Haine, Reference Stewart and Haine2016). While Arctic sea ice has been steadily disappearing (Comiso et al., Reference Comiso, Parkinson, Gersten and Stock2008), the density stratification above the AW core has historically been strong enough to insulate surface waters from the warmth at depth (Shibley et al., Reference Shibley, Timmermans, Carpenter and Toole2017). However, the lower sections of Arctic staircases have been disappearing in recent years (Ménesguen et al., Reference Ménesguen, Lique and Caspar-Cohen2022). Many works have noted that the AW contains enough heat to melt all Arctic sea ice, if it were somehow able to reach the surface (Maykut and Untersteiner, Reference Maykut and Untersteiner1971; Turner, Reference Turner2010; Stranne et al., Reference Stranne, Mayer, Weber, Ruddick, Jakobsson, Jerram, Weidner, Nilsson and Gårdfeldt2017; Shibley et al., Reference Shibley, Timmermans and Stranne2020). Given their potential role in modulating the Arctic climate, it is important to be able to accurately identify thermohaline staircases in observations to monitor changes.
The first recorded observation of thermohaline staircases in the Arctic Ocean was made in 1969 at Ice Island T-3 (Neal et al., Reference Neal, Neshyba and Denner1969). This iceberg, located somewhat northeast of the Canada Basin (often defined as 72–84°N, 130–155°W, see, e.g., Peralta-Ferriz and Woodgate, Reference Peralta-Ferriz and Woodgate2015), was the site of dozens of hydrographic profiles that contain clearly visible staircases (Neshyba et al., Reference Neshyba, Neal and Denner1971, Reference Neshyba, Neal and Denner1972; Neal and Neshyba, Reference Neal and Neshyba1973). Subsequent observations indicate that the staircases have been a consistent feature of the Canada Basin, including from data collected during the Arctic Internal Wave Experiment (AIWEX) (Padman and Dillon, Reference Padman and Dillon1987, Reference Padman and Dillon1988, Reference Padman and Dillon1989) and the Surface Heat Budget of the Arctic (SHEBA) experiment (Shaw and Stanton, Reference Shaw and Stanton2014). The frequency of such observations increased dramatically in 2004, when the introduction of autonomous ice-tethered profilers (ITPs) made possible the continuous, year-round sampling of the Arctic Ocean water column (Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011).
Although many early studies identified staircases by visual inspection, the recent increase in available data has spurred researchers to turn to algorithmic approaches. Here, we detail several previous studies whose foundational work was critical in the development of the current study. All of these studies used a similar approach to detect data points that fall within some well-mixed layer (henceforth for brevity simply “layer”) on a profile-by-profile basis. Timmermans et al. (Reference Timmermans, Toole, Krishfield and Winsor2008) defined a point in a hydrographic profile to be detected within a layer when the local vertical potential temperature gradient
$ \partial \theta /\partial z $
is below
$ 0.005{}^{\circ}\mathrm{C}\;{\mathrm{m}}^{-1} $
, roughly an order of magnitude smaller than the overall gradient for a typical profile. Shibley et al. (Reference Shibley, Timmermans, Carpenter and Toole2017) extended the automated detection method of Timmermans et al. (Reference Timmermans, Toole, Krishfield and Winsor2008) by including two additional conditions: (1) For each experiment, they visually determined different threshold values on both
$ \partial \theta /\partial z $
and on the temperature difference between neighboring points and (2) after then running the detection method, those authors only considered staircases that consisted of at least three layers. van der Boog et al. (Reference van der Boog, Otto Koetsier, Dijkstra, Pietrzak and Katsman2021b) developed a similar staircase detection algorithm, but chose threshold values of vertical density gradients that were expected to be applicable to staircases in all of the world’s oceans, not just the Arctic. Specifically, they set a vertical gradient threshold of
$ \partial {\sigma}_1/\partial p\le 0.0005\mathrm{kg}\;{\mathrm{m}}^{-3}\;{\mathrm{dbar}}^{-1} $
, where
$ {\sigma}_1 $
is the density anomaly referenced to
$ 1000 $
dbar. Then, from the subset of data that meets that condition, only mixed layers with a maximum variation of density anomaly of
$ 0.005\;\mathrm{kg}\;{\mathrm{m}}^{-3} $
or less, and whose neighboring interfaces had thicknesses of 30 dbar or less, were considered. Lu et al. (Reference Lu, Guo, Zhou, Song and Huang2022) defined the intersections between layers and interfaces as locations where the difference in the potential temperature gradient between two neighboring points is greater than
$ 0.003\;{}^{\circ}\mathrm{C}\;{\mathrm{m}}^{-1} $
, then disregarded the points within the interfaces. After performing this detection, Lu et al. (Reference Lu, Guo, Zhou, Song and Huang2022) then made cross-profile connections with the layer points that remained, following the work of Padman and Dillon (Reference Padman and Dillon1988), and used valleys in histograms of salinity to guide their choice of boundaries between layers, some of which were manually adjusted. We find it useful to distinguish between these two steps: the detection of points within layers for each profile and the connection of these points to those in other profiles that are within the same layer. Many previous studies did not describe a connection method because it was not needed for their ends; we use this framing to call attention to the novel aspects of our contribution.
All of the above techniques first detect a subset of the data points that are likely within layers based on vertical gradient thresholds. This approach requires sufficient knowledge of the staircases properties to select appropriate thresholds, as well as data with sufficient vertical resolution to accurately estimate the gradients. The connection algorithm Lu et al. (Reference Lu, Guo, Zhou, Song and Huang2022) describe, after its completion, still requires some amount of manual intervention to produce a final dataset of staircase layers. A commonality of all of these approaches is that they are purpose-built for the task of detecting staircases in specific contexts. These factors motivate the search for a more general approach to detect and connect thermohaline layers across different profiles, which could offer advantages such as greater scalability and applicability as well as more ready reproducibility, all of which would accelerate the pace of research on these important structures.
Many studies, notably Timmermans et al. (Reference Timmermans, Toole, Krishfield and Winsor2008), have observed that a collection of profiles that includes well-mixed layers, such as density staircases, is associated with clustered patterns when plotted in temperature-salinity (T–S) space (Schmitt et al., Reference Schmitt, Perkins, Boyd and Stalcup1987; Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011; Yu et al., Reference Yu, Bosse, Fer, Orvik, Bruvik, Hessevik and Kvalsund2017; Bebieva and Timmermans, Reference Bebieva and Timmermans2019). This clustering indicates that layers are thin sheets, extending laterally for hundreds of kilometers (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022). These patterns occur where a staircase is present because all data points within a particular layer have approximately the same temperature and salinity values as other observations from the same layer, regardless of their vertical position within the layer. This fact suggests that staircases could be detected by directly identifying clusters in T–S space. Clustering algorithms are a type of unsupervised machine learning and have been previously used in a variety of different oceanographic applications (Sonnewald et al., Reference Sonnewald, Lguensat, Jones, Dueben, Brajard and Balaji2021). Examples include grouping observations from freely drifting instruments in the Nordic Seas (Koszalka and LaCasce, Reference Koszalka and LaCasce2010), studying surface wave variability in the North Atlantic (Espejo et al., Reference Espejo, Camus, Losada and Méndez2014), classifying the heat content of hydrographic profiles (Maze et al., Reference Maze2017), resolving trapping in mesoscale eddies (Ma et al., Reference Ma, Li, Yang, Yang and Chen2019), defining spatial regions for Southern Ocean temperature profiles (Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019), detecting ENSO events (Houghton and Wilson, Reference Houghton and Wilson2020), finding hot spots for mixing in the Southern Ocean (Rosso et al., Reference Rosso, Mazloff, Talley, Purkey, Freeman and Maze2020), and identifying shifts in the North Atlantic circulation (Desbruyères et al., Reference Desbruyères, Chafik and Maze2021). However, to the best of our knowledge, they have never before been used to identify thermohaline staircases.
Here, we apply a method based on the hierarchical density-based spatial clustering of applications with noise (HDBSCAN) algorithm (Campello et al., Reference Campello, Moulavi and Sander2013) to both detect and connect thermohaline staircases across Arctic hydrographic profiles. This method has several advantages. It detects and automatically connects staircase layers across large hydrographic datasets in one step. In the past, HDBSCAN has been successfully applied to datasets with a number of points that were an order of magnitude larger than in this study, suggesting the application we present here could be scaled to accommodate more data (Logan and Fotopoulou, Reference Logan and Fotopoulou2020). Also, it does not consider profiles individually and therefore, does not require that each profile have fine vertical resolution. Our implementation of this algorithm does require knowledge of the typical layer thickness and the expected global salinity range of the staircase; however, as we will show, this is a more flexible requirement compared to determining threshold gradients. Most importantly, it exhibits excellent performance producing a final, connected dataset of layers to which no subsequent adjustments need to be made, and is thus suitable for application to datasets with a large number of points as well as being more easily reproducible. The purpose of this paper is to present this method, and so we will note possible implications of our results but will not explore them in great detail.
The structure of this paper is as follows. First, in Section 2, we introduce and explain our choice of the datasets used in our analysis. In Section 3, we introduce HDBSCAN and describe how we use it to identify staircases and how we choose the input parameters. Then, in Section 4, we apply this method to data from two different ITP experiments, focusing on results that reproduce those from the studies of Timmermans et al. (Reference Timmermans, Toole, Krishfield and Winsor2008) and Lu et al. (Reference Lu, Guo, Zhou, Song and Huang2022), hereafter denoted as T08 and L22, respectively. Finally, in Section 5, we use the comparison between our results and those of T08 and L22 to evaluate the performance of the clustering algorithm and give recommendations on when and how it can be best used to identify staircases.
2. Data
ITPs are automated, vertically profiling instruments that are connected via a wire cable to a surface buoy on an ice floe (Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011). The wire extends from the surface, through the ice, down to depths of 500–800 m. The profiler travels up and down the wire roughly two to three times a day, collecting high-resolution (~25 cm) measurements of salinity, temperature, and pressure with a salinity precision of
$ \pm 0.005 $
g/kg and a temperature precision of
$ \pm 0.001\;{}^{\circ}\mathrm{C} $
(Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Shibley et al., Reference Shibley, Timmermans, Carpenter and Toole2017; Bebieva and Timmermans, Reference Bebieva and Timmermans2019). Each traverse, alternating up or down, is recorded as a separate profile.
In this paper, data from two different ITP experiments, ITP2 and ITP3, are analyzed; see Table 1 for a summary. Because the measuring instruments are located at the top of the profiler, we use only the up-going profiles in order to avoid the known distortion caused by the wake of the profiling unit in the down-going profiles (Shibley et al., Reference Shibley, Timmermans, Carpenter and Toole2017). Figure 1 shows the locations of all up-going profiles for each of the two ITP experiments. We choose to analyze ITP2 and ITP3, in particular, to reproduce several results of T08 and L22, respectively.
Table 1. Details of the ice-tethered profilers (ITPs) used in this study
a The maximum distance between any two, not necessarily consecutive, profiles.
Figure 1. A map showing the locations of all profiles used from ITPs 2 and 3, showing the whole Arctic in (a) and a zoomed-in view in (b). The red box designates the Canada Basin as defined by Peralta-Ferriz and Woodgate (Reference Peralta-Ferriz and Woodgate2015).
At this point, we note some choices in the study relative to those of T08 and L22. Here, we choose to work with pressure, a directly measured quantity, while both of those studies use depth, which is derived from pressure; as the conversion between pressure and depth is linear, this difference does not affect our results or comparisons. Also note that although both of those earlier studies use potential temperature
$ \theta $
, we choose instead to use conservative temperature
$ \Theta $
, as recommended by TEOS-10 (McDougall and Barker, Reference McDougall and Barker2011). For the range of temperatures and salinities in the data we analyze, the difference
$ \mid \theta -\Theta \mid $
is a systematic shift that is always less than 0.05 °C. Because this shift is relatively constant, our results are not sensitive to this choice. Furthermore, TEOS-10 recommends using absolute salinity
$ {S}_A $
over practical salinity
$ {S}_P $
. Our results do not change significantly using one versus the other (see Supplementary Material), so we choose to use
$ {S}_P $
to make direct comparisons to the salinity ranges used by T08 and L22.
Staircases are only found in certain vertical ranges of the water column. However, as noted by L22, the salinity values of the layers are much more consistent across different profiles than their pressure or temperature characteristics, so we focus our analyses on a specific salinity range for each ITP. An appropriate range can be estimated by inspection of a few individual profiles or from general knowledge of the salinity range of staircases in the region. The bounds of this range need not be precise, but choosing a range that is too small will potentially miss layers. Running the algorithm on a liberally large range to capture all potential layers will take longer and may also return some clusters that do not correspond to meaningful thermohaline staircase layers. However, in Section 3.3, we detail a process of identifying erroneous clusters. For easier comparison, we choose salinity ranges used in past work, namely, 34.05–34.75 g/kg for ITP2 following T08 and 34.21–34.82 g/kg for ITP3 following L22.
As discussed in more detail below, the clustering algorithm does not distinguish between the different times and locations at which different profiles were taken. It follows that a dataset to be analyzed should not span larger temporal or spatial scales than the scales the staircases are known to be coherent across. T08, who analyzed much of the same data we do, found staircases that spanned the entire Canada Basin (approximately 800 km) and lasted at least 2 years. We define the longest span as the maximum distance between any two, not necessarily consecutive, profiles. We find the longest span (
$ \le 441 $
km) and duration (
$ \le 382 $
days) of the two ITPs we analyzed (see Table 1) are indeed smaller than the expected staircase coherence scales.
3. Methods
3.1. The HDBSCAN clustering algorithm
To identify T–S clusters as evidence for staircases within the ITP data, we use the HDBSCAN algorithm, which clusters data based on the relative densities in different regions. Algorithm-identified clusters in the ITP data are expected to correspond to staircase layers, with some exceptions, as detailed in Section 3.3. While Campello et al. (Reference Campello, Moulavi and Sander2013) present the algorithm in full detail, here we briefly review its general principles.
In the context of density-based clustering algorithms, the term “density” refers to a measure of the relative number of data points in a certain region of parameter space. HDBSCAN estimates the density of a region based on the distances between points and a number of their nearest neighbors, creating a hierarchy of clusterings from which it chooses the most prominent. First, it calculates the “core distance”
$ \varepsilon $
for each point as the minimum radius of a circle needed to encompass its
$ {m}_{pts} $
nearest neighbors. The inverse of
$ \varepsilon $
represents density; when it is small, points are close together and when it is large, points are spread out. HDBSCAN then creates a hierarchy of clusterings, starting with the largest
$ \varepsilon $
and working down. For each value
$ {\varepsilon}_0 $
, it first detects the level-set of non-noise points, where
$ \varepsilon \le {\varepsilon}_0 $
, then connects points together in the same cluster if they are within a distance of
$ \varepsilon $
.
As the value of
$ {\varepsilon}_0 $
decreases, a particular cluster may change by shrinking, splitting, or disappearing entirely. Having built this hierarchy tree, HDBSCAN can then select clusters at the ends of branches even though different branches may terminate at very different values of
$ {\varepsilon}_0 $
. However, when the data are particularly noisy, just before crossing the
$ {\varepsilon}_0 $
threshold where a cluster would disappear, it may split into many small, spurious clusters. To avoid including these artifacts in the final result, the algorithm ignores all clusters with fewer than
$ {m}_{clSize} $
number of points. The recommendation of the authors of HDBSCAN and the default behavior of the “hdbscan” Python package is to set
$ {m}_{clSize}={m}_{pts} $
(Campello et al., Reference Campello, Moulavi and Sander2013; Moulavi et al., Reference Moulavi, Jaskowiak, Campello, Zimek and Sander2014), giving one input parameter which controls both how the core distance is calculated and the minimum points per cluster. While there are other optional input parameters for HDBSCAN (see Supplementary Material), the results we obtained using the default settings were satisfactory, so we did not investigate their effects.
We choose HDBSCAN over other types of clustering algorithms for several reasons. Many previous oceanographic studies used partitioning algorithms such as k-means (Koszalka and LaCasce, Reference Koszalka and LaCasce2010; Espejo et al., Reference Espejo, Camus, Losada and Méndez2014; Houghton and Wilson, Reference Houghton and Wilson2020) or Gaussian mixture models (Maze et al., Reference Maze2017; Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019; Rosso et al., Reference Rosso, Mazloff, Talley, Purkey, Freeman and Maze2020; Desbruyères et al., Reference Desbruyères, Chafik and Maze2021); however, partitioning algorithms require one to specify the number of clusters a priori, which is not known for our application. The first reason for choosing HDBSCAN is that it does not have this requirement (Ester et al., Reference Ester, Kriegel, Sander and Xu1996; Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019). Second, HDBSCAN allows points that lie outside a cluster to be categorized as “noise.” In our case, this is important because points in an interface between layers should not be assigned to any cluster. Third, unlike DBSCAN, which uses the same threshold
$ {\varepsilon}_0 $
for all clusters throughout the domain (Ester et al., Reference Ester, Kriegel, Sander and Xu1996; Campello et al., Reference Campello, Moulavi and Sander2013), HDBSCAN creates a hierarchy of clusterings with different
$ {\varepsilon}_0 $
and can, therefore, correctly identify clusters that vary significantly in both the number of points per cluster and the densities of points within the clusters (McInnes et al., Reference McInnes, Healy and Astels2017). Fourth, HDBSCAN can correctly identify arbitrarily shaped clusters, whereas partitioning algorithms like k-means generally find center-defined clusters, which, because points are assigned to clusters based on their distance from the cluster’s center point, are only equipped to find globular or convex clusters (Ester et al., Reference Ester, Kriegel, Sander and Xu1996; Hinneburg and Keim, Reference Hinneburg and Keim2003). This is important because the shapes of clusters associated with thermohaline staircases are not necessarily globular. Lastly, HDBSCAN requires only one input parameter
$ \left({m}_{pts}\right) $
to be specified, reducing the number of choices to be made before each run of the algorithm. Further, we determine the value of
$ {m}_{pts} $
systematically, as explained below.
Having chosen a clustering algorithm, we now turn to specifying the two-dimensional space within which the clustering algorithm will operate. Figure 2(a) shows data from ITP2 in Θ–SP space, where discrete groups of points associated with individual layers and spanning multiple profiles are apparent; these are colored according to their eventual partitioning into clusters. Note the occurrence of occasional gaps in
$ \Theta $
values, seen in the salinity ranges 34.16–34.30 and 34.65–34.74 g/kg. These result from the uneven spatial coverage of the meandering drift path of the ITPs (see Figure 1) together with the tendency for the temperature to vary more horizontally within a particular layer than salinity (Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022). In order to avoid HDBSCAN splitting such groups of points into multiple clusters for the same layer, for each temperature profile
$ \Theta (z) $
, we define the local anomaly as
$$ {\Theta}^{\prime }(z)=\Theta (z)-\frac{1}{\mathrm{\ell}}{\int}_{z-\mathrm{\ell}/2}^{z+\mathrm{\ell}/2}\Theta \left({z}^{\prime}\right)d{z}^{\prime }, $$
where
$ \mathrm{\ell} $
is the width of a rectangular moving average window. Presenting the ITP2 data in
$ {\Theta}^{\prime}\hbox{--} {S}_P $
space rather than
$ \Theta \hbox{--} {S}_P $
space, as in Figure 2(c), leads to groups that are more centered around zero along the temperature axis, without notable gaps. We choose to work in this space as it will allow HDBSCAN to group points more accurately. We also confirmed the difference between using
$ \Theta $
or
$ \theta $
and
$ {S}_P $
or
$ {S}_A $
did not significantly affect the results. Finally, we mention that HDBSCAN is sensitive to the aspect ratio of the axes; however, because the results were found to be satisfactory, we did not investigate this dependency.
Figure 2. Results from the clustering algorithm with
$ {m}_{pts}=170 $
and
$ \mathrm{\ell}=100 $
dbar run on 53,042 data points in the salinity range 34.05–34.75 g/kg from all up-going ITP2 profiles. (a) The data in
$ \Theta $
–
$ {S}_P $
space with dashed lines of constant potential density anomaly (
$ \mathrm{kg}\;{\mathrm{m}}^{-3} $
) referenced to the surface. The red box bounds the clusters marked in panels (b) and (d). (b) Profiles 183, 185, and 187 from ITP2 in a limited pressure range to show detail. Each profile is offset in
$ {S}_P $
for clarity. (c) The spatial arrangement used as input for the algorithm where the gray points are noise and each color-marker combination indicates a cluster. The same color-marker combinations are used in each panel, and the markers in panels (c) and (d) are at the cluster average for each axis. (d) A subset of the data in
$ \alpha \Theta $
–
$ \beta {S}_P $
space with the linear regression line and inverse slope (
$ {R}_L $
) noted for each individual cluster and with dashed lines of slope
$ \alpha \Theta /\beta {S}_P=1 $
.
3.2. Selecting values of input parameters
It remains to choose values for the method parameters. The HDBSCAN algorithm is deterministic; that is, given the same arrangement of input data and the same value of the
$ {m}_{pts} $
parameter, it will find the same clusters every time. The exact arrangement of data in
$ {\Theta}^{\prime } $
–
$ {S}_P $
space that we feed into the algorithm depends on three factors: (1) the set of profiles that we include, (2) the salinity range that we decide to analyze, and (3) the window width
$ \mathrm{\ell} $
used to calculate the local anomaly of conservative temperature
$ {\Theta}^{\prime } $
in Equation (3.1). We discussed our method of selecting the profiles and salinity range previously in Section 2. Here, we explain how we select values for
$ \mathrm{\ell} $
and
$ {m}_{pts} $
.
The results of a clustering algorithm can be judged on the basis of either external or internal validation. External validation methods involve comparing the clustering results to an external “ground truth,” while internal validation methods use the data themselves to provide a measure of quality for the clustering (Moulavi et al., Reference Moulavi, Jaskowiak, Campello, Zimek and Sander2014). In this application, external validation would require detailed labeling, indicating to which layer, if any, each individual point belongs. Such labels could be determined by a separate method; however, we aim for this method to be broadly applicable to more than just reproducing previous results. Therefore, we tune our selection of
$ \mathrm{\ell} $
and
$ {m}_{pts} $
using density-based clustering validation (DBCV) (Moulavi et al., Reference Moulavi, Jaskowiak, Campello, Zimek and Sander2014) as an internal validation. DBCV considers good clustering solutions to be those in which the lowest-density regions within the clusters are still denser than the highest-density regions of the surrounding noise points. It bases the density estimates on the so-called “mutual reachability distance,” defined for each pair of points to be the maximum
$ \varepsilon $
of either point or the distance between the two, whichever is largest. For more details, see Moulavi et al. (Reference Moulavi, Jaskowiak, Campello, Zimek and Sander2014).
To evaluate algorithm performance, we performed a parameter sweep through different values of
$ \mathrm{\ell} $
and
$ {m}_{pts} $
, and present the number of clusters found together with the DBCV scores in Figure 3. For the
$ \mathrm{\ell} $
dependence, see Figure 3(a), we find a downward trend in the number of clusters as
$ \mathrm{\ell} $
increases. DBCV scores tend to be larger in the middle of the
$ \mathrm{\ell} $
range, with the highest score occurring for
$ \mathrm{\ell}=100 $
dbar. We may also note that the choice of
$ \mathrm{\ell} $
shapes a large-scale feature of the
$ {\Theta}^{\prime } $
–
$ {S}_P $
plots. In Figure 2(c), a zig-zag pattern of increasing, rapidly decreasing, and then increasing again
$ {\Theta}^{\prime } $
is seen in the range of
$ {S}_P\approx 34.63 $
–34.72 g/kg. This pattern is due to the presence of the AW subsurface temperature maximum in
$ \Theta $
profiles; it disappears when
$ \mathrm{\ell} $
is small while becoming more exaggerated for larger
$ \mathrm{\ell} $
(see Supplementary Material). Based upon previous studies of staircases in the Canada Basin during this time period (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022), we estimated the typical layer thickness to be 5 m in height or 5 dbar in pressure, though we found similar results for estimates of 0.5–7.5 dbar (see Supplementary Material). The choice
$ \mathrm{\ell}=100 $
dbar, where the largest DBCV score occurs, thus corresponds to approximately 20 times the typical layer thickness. This value is found to be large enough that the staircases are completely smoothed out yet small enough that the features outside the analyzed pressure range do not significantly affect the moving average.
Figure 3. A parameter sweep showing the number of clusters found (solid lines) and DBCV (dashed lines) in ITP2 as a function of (a) 27 different values of
$ \mathrm{\ell} $
with
$ {m}_{pts}=170 $
and (b) 44 different values of
$ {m}_{pts} $
with
$ \mathrm{\ell}=100 $
dbar.
We now turn to
$ {m}_{pts} $
, which under the default settings of HDBSCAN, sets the minimum number of points in a cluster (Campello et al., Reference Campello, Moulavi and Sander2013). If the value of
$ {m}_{pts} $
is too small, the algorithm may erroneously split a cluster that represents one layer into multiple, smaller clusters, while a too-large value of
$ {m}_{pts} $
would lead to the incorrect grouping of multiple discrete layers into a single cluster. Note that this upper bound on a reasonable
$ {m}_{pts} $
depends greatly on the number of data points given to the algorithm the more data points the algorithm is given, the higher the value of
$ {m}_{pts} $
can reasonably be set. In the parameter sweep of Figure 3(b), we find the number of clusters decreases rapidly until
$ {m}_{pts}\approx 60 $
, then decreases at a much slower rate, while the highest DBCV scores occur for intermediate values of
$ {m}_{pts} $
. As with
$ \mathrm{\ell} $
, we choose the value of
$ {m}_{pts} $
having the highest DBCV score. For ITP2, this led to our selection of
$ {m}_{pts}=170 $
.
Running HDBSCAN on ITP2 using the procedure outlined above with the choices
$ \mathrm{\ell}=100 $
and
$ {m}_{pts}=170 $
leads to the clusters presented in Figure 2. Following the same parameter selection process for ITP3, we obtain the values
$ \mathrm{\ell}=100 $
dbar and
$ {m}_{pts}=580 $
(see Supplementary Material). Table 2 summarizes our input parameter choices and the resulting number of clusters and DBCV values for both ITP2 and ITP3.
Table 2. The values of parameters used to run the clustering algorithm over both datasets
1 The first number is the total number of clusters found by the algorithm. The second is the number of clusters that were neither outliers in
$ I{R}_{S_P} $
nor
$ {R}_L $
.
3.3. Evaluating the clustering algorithm results
The DBCV score gives a measure of quality for the clusters in terms of their densities of points relative to the surrounding noise. However, DBCV does not take into account the properties of the clusters that we expect from the physical situation of staircases, such as their spans in
$ \Theta $
and
$ {S}_P $
or how far they are from neighboring clusters. We, therefore, present two metrics to help predict whether each cluster will accurately represent what we expect from layers within staircases: the lateral density ratio
$ {R}_L $
and the normalized inter-cluster range
$ IR $
.
The relative strength of horizontal variations in salinity and temperature along the
$ i $
th layer is described by the lateral density ratio
$$ {R}_L^i=\frac{\beta \Delta {S}_P}{\alpha \Delta \Theta}, $$
where
$ \beta ={\rho}^{-1}\partial \rho /\partial {S}_P $
is the haline contraction coefficient,
$ \alpha =-{\rho}^{-1}\partial \rho /\mathrm{\partial \Theta } $
is the thermal expansion coefficient, and
$ \Delta {S}_P $
and
$ \Delta \Theta $
are the variations in salinity and temperature, respectively, along a particular layer (Radko, Reference Radko2013; Bebieva and Timmermans, Reference Bebieva and Timmermans2019). We estimate
$ {R}_L $
by finding the inverse slope of the best-fit line through each cluster in
$ \alpha \Theta $
–
$ \beta {S}_P $
space (see Figure 2(d)) (Chen, Reference Chen1995; Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008). These lines are found using Orthogonal Distance Regression, which is more suitable than ordinary least squares in our case due to the presence of variability along both the
$ \alpha \Theta $
and
$ \beta {S}_P $
axes (Winton, Reference Winton2011); however, both methods yield similar results (not shown).
$ {R}_L $
quantifies the relative importance of
$ {S}_P $
and
$ \Theta $
for the density of that layer (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Bebieva and Timmermans, Reference Bebieva and Timmermans2019) and is known to be directly related to the ratio of the vertical fluxes of salinity and heat within a staircase (Bebieva and Timmermans, Reference Bebieva and Timmermans2019). Note that the lateral density ratio
$ {R}_L $
is distinct from the density ratio,
$ {R}_{\rho } $
, which is defined using the same Equation (3.2) but with
$ \Delta {S}_P $
and
$ \Delta \Theta $
taken in the vertical direction (Shibley et al., Reference Shibley, Timmermans, Carpenter and Toole2017). The relative constancy of
$ {R}_L $
values across time and space has been interpreted as reflecting the remarkable degree of lateral coherence of staircase layers (Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011). The values of
$ {R}_L $
have also been shown to be remarkably similar across neighboring layers (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008). Therefore, if a value of
$ {R}_L $
lies significantly outside of the general range of its neighbors, the cluster either reflects the erroneous grouping of multiple layers into a single cluster, or else a physical merging or splitting of layers, as discussed in Section 4.2.
We also define a measure of the relative spread of a variable, such as temperature or salinity, within a cluster in comparison with the differences between adjacent clusters. Ordering the clusters sequentially in density, the normalized inter-cluster range for the ith cluster is given by
$$ {IR}_v^i=\frac{v_{max}^i-{v}_{min}^i}{\min \left(|{\overline{v}}^i-{\overline{v}}^{i-1}|,|{\overline{v}}^i-{\overline{v}}^{i+1}|\right)}, $$
where
$ i-1 $
and
$ i+1 $
denote the adjacent clusters to either side,
$ v $
is the variable of interest (i.e., pressure,
$ \Theta $
, or
$ {S}_P $
),
$ {v}_{max}^i $
and
$ {v}_{min}^i $
are the maximum and minimum values of the variable
$ v $
within cluster
$ i $
, and
$ {\overline{v}}^i $
denotes the mean value of
$ v $
for cluster
$ i $
. The numerator is the span between the maximum
$ {v}_{max}^i $
and minimum
$ {v}_{min}^i $
within cluster
$ i $
. The denominator is the span between the mean of that cluster
$ {\overline{v}}^i $
and the mean of either the cluster above or below, whichever is smaller. For clusters at either end of the variable space, we take the denominator to be the span between the mean of the ith cluster and that of its single neighbor.
The inter-cluster range
$ {IR}_v $
, therefore, quantifies the range of a given variable,
$ v $
, within a cluster in comparison with the range to the nearest neighboring cluster. For a staircase, the salinity values within one layer are generally well separated from the salinity values of the neighboring layers (Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022). Therefore, we expect that the clusters with large
$ {IR}_{S_P} $
could represent a part of a single layer that was erroneously divided into multiple clusters by the algorithm or entirely different physical features, as discussed in Section 4.3.
In order to evaluate clusterings, we choose a method to detect outliers in both
$ {IR}_{S_P} $
and
$ {R}_L $
. We define outliers as points more than two standard deviations from the mean or equivalently with a z-score greater than 2 (approximately corresponding to a p-value of 0.05 for a two-tailed test). More sophisticated outlier detection methods exist, and while this approach is not guaranteed to find all erroneous clusters, outliers in
$ {IR}_{S_P} $
and
$ {R}_L $
give us an indication, based on simple and measurable physical characteristics, of particular clusters that may not represent a single, full layer and which therefore require closer inspection. Although such outliers could be manually adjusted to better capture single, complete layers, we disregard them when calculating statistics and trends.
4. Results
Now, having presented the HDBSCAN clustering algorithm, our process of selecting
$ \mathrm{\ell} $
and
$ {m}_{pts}, $
and metrics to identify erroneous clustering, we apply this method to data from ITP2 and ITP3.
4.1. Properties of detected layers
As a starting point, we examine the average value of pressure,
$ \Theta $
, or
$ {S}_P $
for each cluster found from profiles collected by ITP3. Inspired by L22, we plot those values over time in Figure 4. We find that the clustering algorithm is capable of tracking individual layers across hundreds of profiles collected along the 2541 km-long track traced by ITP3 over 382 days. A pattern emerges where the pressures of individual layers appear to have more variability than temperature and salinity, consistent with T08. Moreover, we find that salinity variations within a layer are smaller than the salinity differences between two neighboring layers, while the opposite is true for pressure and temperature (similar to L22; see their Figure 3). We find similar results for ITP2 (see Supplementary Material).
Figure 4. The average (a) pressure, (b)
$ \Theta $
, and (c)
$ {S}_P $
for the points within each cluster for each profile (profile cluster average, PCA) across time. The clustering algorithm was run with
$ {m}_{pts}=580 $
and
$ \mathrm{\ell}=100 $
dbar on 678,575 data points in the salinity range of 34.21–34.82 g/kg from all up-going ITP3 profiles.
More quantitatively, we find differences in salinity between clusters are approximately seven times larger than variations within a cluster. That is, we compute the standard deviation of salinity within each cluster and find that the median is
$ 2.2 $
mg/kg, while the median absolute difference between the average salinity of adjacent clusters is
$ 15.4 $
mg/kg. This is in agreement with L22, who found inter-layer salinity differences to be an order of magnitude larger than variations within a layer. Furthermore, the median normalized inter-cluster ranges (Equation (3.3)) in Table 3 quantitatively confirms the qualitative patterns noted by T08 and L22 as
$ {\hat{IR}}_p $
,
$ {\hat{IR}}_{\Theta}>1 $
and
$ {\hat{IR}}_{S_P}<1 $
for both ITPs, where
$ \hat{.} $
indicates the median. Table 3 also contains the median of the differences between neighboring cluster averages of temperature,
$ \hat{\Delta \Theta} $
, and salinity,
$ \hat{\Delta {S}_P} $
, for both ITPs. For ITP3, these values of 0.048 °C and 15.4 mg/kg match those of L22, which are 0.05 °C and 17 mg/kg. They also agree with T08, who reported the difference in temperature and salinity across interfaces to be
$ \delta \theta \approx 0.04{}^{\circ} $
C and
$ \delta S\approx 14 $
mg/kg.
Table 3. The median normalized inter-cluster ranges and differences between average values of adjacent clusters for ITP2 and ITP3 calculated after removing outliers with z-score
$ >2 $
in the respective variable
4.2. Outliers and splitting/merging layers
As discussed previously in Section 3.3, outliers have been identified in the inter-cluster salinity range
$ {IR}_{S_P} $
as well as the lateral density ratio
$ {R}_L $
. Figure 5 shows
$ {IR}_{S_P} $
and
$ {R}_L $
for both ITPs with outliers indicated by red circles. We find that these outliers can either be due to erroneous clustering or indicate the presence of different physical features, such as the splitting or merging of thermohaline staircase layers, which is a well-known phenomenon (Neshyba et al., Reference Neshyba, Neal and Denner1972; Padman and Dillon, Reference Padman and Dillon1988; Kimura et al., Reference Kimura, Nicholls and Venables2015).
Figure 5. The value of each cluster’s normalized inter-cluster range for salinity
$ {IR}_{S_P} $
in (a) and (c) and the lateral density ratio
$ {R}_L $
in (b) and (d) as a function of the cluster’s average pressure. The colors and markers for ITP2 in (a) and (b) are the same as the clustering shown in Figure 2 and for ITP3 in (c) and (d), they are the same as shown in Figure 4. Markers circled in red indicate outliers with a z-score greater than
$ 2 $
. (b) The solid curve is a second-degree polynomial fit (equation given by the annotation) for the non-outlier points from ITP2 and the dashed curve is the same for ITP3. (d) The solid curve is a second-degree polynomial fit (equation given by the annotation) for the non-outlier points from ITP3, and the dashed curve is the same for ITP2.
We can learn more about these features from the illustrative sets of particular salinity profiles from ITP2 presented in Figure 6. Both sets of profiles span less than a week, and we narrow the displayed pressure ranges so that the individual steps are visible. This figure shows that, overall, the algorithm captures the layered structure very well, marking points within interfaces as noise. Nevertheless, it is imperfect. Near layer boundaries, the algorithm sometimes includes points from an interface within a cluster, and sometimes neglects to include points within a layer. Additionally, as seen in the first profile of Figure 6(b) around 236 dbar, the algorithm can also miss layers entirely, especially when the layer is particularly thin and only present in a small number of profiles. Occasional issues such as these are to be expected with any automated detection method.
Figure 6. Individual
$ {S}_P $
profiles from ITP2, specifically chosen to show the examples of outlier clusters in
$ {IR}_{S_P} $
and
$ {R}_L $
highlighted by the bands of color. (a) Profiles 67, 69, 73, 75, 81, 83, 91, 93, 97, and 99 collected between August 31 and September 5, 2004. (b) Profiles 87, 89, 95, 97, 99, 101, 103, 105, 109, and 111 collected between September 3 and 7, 2004. The colors and markers are the same as the clustering shown in Figure 2. The gray dots are noise points, and the black lines show the profiles. Each profile is offset in
$ {S}_P $
for clarity.
Focusing on ITP2 as an example, we find two outliers in
$ {IR}_{S_P} $
marked by an orange 4-pointed star and a green “
$ \times $
” in Figure 5(a). We can track the same clusters in Figure 2(c), indicated by orange or green dots with a 4-pointed star or a “
$ \times $
” at the center of the cluster. They both have an average
$ {S}_P\approx 34.67 $
g/kg but are separated in
$ {\Theta}^{\prime } $
. A series of individual salinity profiles associated with these outliers over approximately 6 days is shown in Figure 6(a). We find that these outliers correspond to a relatively thick single layer that was erroneously split across two clusters by the algorithm. We attribute this erroneous splitting to the zig-zag pattern in
$ {\Theta}^{\prime } $
–
$ {S}_P $
space mentioned in Section 3.2 and note that it could be eliminated with a different selection of
$ \mathrm{\ell} $
. Although we can attribute these outliers in
$ {IR}_{S_P} $
to an artifact of the method, there are other instances where such outliers indicate the presence of physical features, as we will discuss in Section 4.3.
Next, we examine outliers in
$ {R}_L $
, defined in Equation (3.2), for ITP2, marked by red circles in Figure 5(b). These outliers correspond to clusters that appear to have multiple layers grouped together. For example, the outlier cluster marked by an orange half-circle in Figure 5(b) can be seen in Figure 2(c) spanning
$ {S}_P=34.054 $
–
$ 34.159 $
, a much wider range than any other cluster. Similarly, in Figure 2(c), the outlier cluster marked by a purple star spans
$ {S}_P=34.233 $
–
$ 34.261 $
and clearly encompasses what should be two distinct clusters. Some outliers in
$ {R}_L $
are the result of erroneously clustering multiple layers together. On the other hand, the particular feature of the outlier cluster marked by a teal “
$ \times $
,” centered around 232 dbar with
$ {R}_L=-12.7 $
in Figure 5(b), indicates splitting or merging. As highlighted in Figure 6(b), it typically spans multiple stair steps, but in the last few profiles, it only spans a single, larger step. This illustrates that we can use outliers in
$ {R}_L $
to identify clusters that are not single, complete layers and to find instances of potential splitting or merging.
4.3. Remnant intrusions revealed by temperature
Direct comparisons with other layer detection methods can also be used to identify interesting physical features. To demonstrate this, here we directly compare average layer characteristics computed by HDBSCAN to those reported by L22, both using data from ITP3. L22 used 758 profiles from ITP3, while we used all 766 available up-going profiles. Based on the gaps in Figure 3 of L22, we believe that the eight missing up-going profiles are from July 2006. Figure 7 shows the average
$ \Theta $
and
$ {S}_P $
for each cluster found in our study and by L22 based on the values in their Table A1 after converting
$ \theta $
to
$ \Theta $
. We initially find 43 clusters and, after eliminating outliers in
$ {IR}_{S_P} $
and
$ {R}_L $
as described in Section 3.3, we find 40 clusters. While L22 identified only 34 thermohaline layers, we find close agreement between those and the clusters we found for
$ {S}_P\lesssim 34.74 $
g/kg. Below where this salinity occurs in the water column, we find five more clusters than L22.
Figure 7. The average
$ \Theta $
and
$ {S}_P $
for the 34 layers found by Lu et al. (Reference Lu, Guo, Zhou, Song and Huang2022) in black dots and for the 43 layers found in our study using data from ITP3 and the same colors and markers as in Figure 4. Clusters circled in red are outliers in either
$ {IR}_{S_P} $
or
$ {R}_L $
.
The differences between these two results appear to be related to the presence of remnant intrusions, which display features of both staircase layers and intrusions and are thought to represent an intermediate stage in staircase formation. Such features are known to appear near the bottom of staircases around the AW core and have been analyzed in detail by Bebieva and Timmermans (Reference Bebieva and Timmermans2019). They are characterized by homogeneous salinity, which leads the method of L22 to treat them as single layers. However, they have a temperature structure that is inverted (warmer above colder) compared to the typical gradient within a thermohaline staircase. The warm and cold sections are distinct enough for the clustering algorithm to split the structure into multiple clusters, each of which is homogeneous in salinity and relatively homogeneous in temperature. Figure 8 highlights an example of a remnant intrusion where the method of L22 gives results that differ from ours; the layer spanning approximately 320–340 dbar is constant in
$ {S}_P $
, but decreases in
$ \Theta $
with depth and is divided into two clusters using the clustering method. These two clusters can be found in Figure 5(c), indicated by the blue “Y” centered around 337 dbar with
$ {IR}_{S_P}=23.8 $
and the orange “
$ + $
” centered around 348 dbar with
$ {IR}_{S_P}=79.3 $
.
Figure 8. Individual profiles 313, 315, 317, 319, and 321 from ITP3, collected between November 10 and 12, 2005, specifically chosen to show the example of a temperature inversion highlighted by the bands of color. The colors and markers of the individual points are the same as the clustering shown in Figures 4 and 7. The gray dots are noise points. The black lines on the left of each pair are the
$ {S}_P $
profiles, while the red lines on the right are for
$ \Theta $
. Each profile is offset in both
$ {S}_P $
and
$ \Theta $
for clarity.
Such remnant intrusions exist between the active intrusions of the AW core and the staircase layers of the LHW. Staircases may be formed from intrusions, but such features have distinctly different patterns of heat and salt flux from double-diffusively driven staircases (Bebieva and Timmermans, Reference Bebieva and Timmermans2019). The disagreement between our results and those of L22 highlights the difficulty of detecting remnant intrusions. While neither method is designed to automatically distinguish between these and staircase layers, the method presented here offers the opportunity to identify them when evaluating outlier clusters. Moreover, although Table 3 supports the suggestion by L22 that salinity is the most appropriate variable by which to identify staircase layers, having shown that a layer identified by L22 is, in fact, a remnant intrusion illustrates why it remains important to consider temperature as well.
4.4. Dependence of
$ {R}_L $
on pressure
Lastly, we revisit Figure 5(b,d), where the distribution of points suggests a dependence of
$ {R}_L $
on pressure. This is in contrast to previous studies which have found a constant
$ {R}_L $
for the depth range we analyze (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011; Bebieva and Timmermans, Reference Bebieva and Timmermans2019). For ITP2 in panel (b), after removing the five outliers indicated across panels (a) and (b), we use a second-degree polynomial fit to find
$ {R}_L=-3.81\times {10}^{-4}{p}^2+0.24p-39.85 $
, where
$ p $
is pressure, with a coefficient of determination
$ {R}^2=0.67 $
. For ITP3 in panel (d), we remove the three outliers in panels (c) and (d), and then find quite a similar dependence of
$ {R}_L=-3.38\times {10}^{-4}{p}^2+0.24p-43.29 $
with a coefficient of determination
$ {R}^2=0.84 $
. Comparing these two curves in Figure 5(b,d), we find most of the difference can be explained by a downward shift of roughly 20 dbar in the upper water column to 50 dbar in the lower water column from ITP2 to ITP3. Note that a second-degree polynomial was chosen here as a simple parametric model to capture the apparent non-linear dependence of that
$ {R}_L $
on pressure.
By contrast, T08 concluded there was no vertical dependence of
$ {R}_L $
. They analyzed data from ITP1 through ITP6, which sampled the Canada Basin during the period from 2004 to 2007, and found a constant value of
$ {R}_L=-3.7\pm 0.9 $
. Their Figure 6(a) shows five values of
$ {R}_L $
for ITP2 that range from −3.5 to −3.0. While Bebieva and Timmermans (Reference Bebieva and Timmermans2019) found that
$ {R}_L $
changes below the depth of the temperature maximum, those authors also found in their Figure 3(b) that
$ {R}_L $
is constant in the depth range we consider in this study. Additionally, the presence of remnant intrusions does not explain the difference in our results, as the pressure dependence of
$ {R}_L $
is evident in the upper part of the water column where they are absent. Although we find that
$ {R}_L $
depends on pressure, our results agree with those of T08 on the magnitude of
$ {R}_L $
, as we find the mean value for all non-outlier clusters of ITP2 to be
$ -3.55 $
with a standard deviation of
$ 2.24 $
, and so we compare more of our results to those of T08.
We reproduce several of the figures from T08 in Figure 2. The combinations of color and markers for the clusters are the same in Figures 2, 5, and 6. In Figure 2(a), we plot data from ITP2 in
$ \Theta $
–
$ {S}_P $
space, reproducing Figure 5(a) from T08. Those authors noted that points from each particular layer clustered along lines in
$ \Theta $
–
$ {S}_P $
space that cross isopycnals, and when we mark the clusters found by the algorithm, those layers become visually distinct. Figure 2(b) shows profile 185 in the same depth range as Figure 4 from T08, plus the up-going profiles taken by ITP2 immediately before and after. This illustrates that the clustering algorithm is indeed marking points within those particular layers as in the same cluster and points within interfaces as noise. It also shows that the clustering algorithm tracks the same layers across neighboring profiles even though the pressure at which those layers are found varies. Figure 2(c) shows the ITP2 data on the axes used by the clustering algorithm. In Figure 2(d), we plot the clusters bounded by the box in Figure 2(a) in
$ \alpha \Theta $
–
$ \beta {S}_P $
space, reproducing Figure 6(a) from T08. The dashed lines of slope 1 correspond to isopycnals as
$ \Delta \rho =-\alpha \Delta \Theta +\beta {S}_P $
. Overall, the panels in Figure 2 are close visual matches for those particular figures in T08.
After examining the differences between the two in detail (see Supplementary Material), it remains unclear why the values of
$ {R}_L $
we found for clusters in ITP2 data differ from T08. However, we believe that the quantitative agreement in magnitude for the values of
$ {R}_L $
and the qualitative match between the clustering results and the features in Figure 2 show that the clustering method reproduces those results from T08. Overall, these findings suggest that the clustering algorithm is indeed revealing a dependence of
$ {R}_L $
on pressure in the data we analyzed from ITP2 and ITP3. Since
$ {R}_L $
is directly related to the ratio of the vertical derivatives of the vertical fluxes of salinity and heat within a staircase (Bebieva and Timmermans, Reference Bebieva and Timmermans2019), this could indicate a pressure dependence of that ratio.
5. Discussion
In this paper, we have presented a method based on the HDBSCAN clustering algorithm to both detect and connect well-mixed layers in thermohaline staircases across Arctic Ocean hydrographic data. HDBSCAN has previously been successfully applied to sets with millions of data points (Logan and Fotopoulou, Reference Logan and Fotopoulou2020). As the comparison with results from previous studies was favorable, this suggests that this method may produce trustworthy results when applied to datasets with larger numbers of points. This study contributes to a growing set of examples of clustering algorithms being used in oceanography (e.g., Koszalka and LaCasce, Reference Koszalka and LaCasce2010; Espejo et al., Reference Espejo, Camus, Losada and Méndez2014; Maze et al., Reference Maze2017; Jones et al., Reference Jones, Holt, Meijers and Shuckburgh2019; Ma et al., Reference Ma, Li, Yang, Yang and Chen2019; Houghton and Wilson, Reference Houghton and Wilson2020; Rosso et al., Reference Rosso, Mazloff, Talley, Purkey, Freeman and Maze2020, Desbruyères et al., Reference Desbruyères, Chafik and Maze2021, Sonnewald et al., Reference Sonnewald, Lguensat, Jones, Dueben, Brajard and Balaji2021). The continued and extended use of clustering algorithms in oceanography and related fields is an important development since discovering and detecting features in all manner of datasets becomes more challenging as they grow ever larger.
Special attention was given herein to the identification of outliers using parameters output by the method itself. We found that clusters which are outliers in the lateral density ratio
$ {R}_L $
often indicate multiple layers that are erroneously clustered together, but can also highlight potential instances of layer splitting or merging. By introducing the normalized inter-cluster range
$ {IR}_v $
, we quantitatively showed that the pressure and temperature values vary more within a layer than the difference between the values of neighboring layers, while the opposite is true for salinity. Because we know that the practical salinity
$ {S}_P $
values in a particular layer are well separated from those of neighboring layers, we identified clusters with notably large values of
$ {IR}_{S_P} $
as likely to be either only part of a layer that was erroneously split by the algorithm or a remnant intrusion. This study also suggests that there may be a pressure dependence of the lateral density ratio
$ {R}_L $
, seen in both ITP2 and ITP3. The reasons for this dependence are unclear and are worthy of further study. Following the model presented by Bebieva and Timmermans (Reference Bebieva and Timmermans2019), the ratio of vertical fluxes of heat and salt could be recalculated using this more complex vertical dependence of
$ {R}_L $
. This could then be compared to simulations (Yang et al., Reference Yang, Verzicco, Lohse and Caulfield2022) and parameterizations (Radko et al., Reference Radko, Bulters, Flanagan and Campin2014; Shibley and Timmermans, Reference Shibley and Timmermans2019) of the flux ratio in other models. However, in order to verify these with observations, vertical resolution fine enough to resolve the interfaces between layers, that is, finer than provided by ITPs, would be needed.
The method we presented here has certain advantages in particular circumstances. For example, all of the other methods referred to herein (Timmermans et al., Reference Timmermans, Toole, Krishfield and Winsor2008; Shibley et al., Reference Shibley, Timmermans, Carpenter and Toole2017; van der Boog et al., Reference van der Boog, Otto Koetsier, Dijkstra, Pietrzak and Katsman2021b; Lu et al., Reference Lu, Guo, Zhou, Song and Huang2022) require setting one or multiple thresholds on gradients in temperature, salinity, or density which are used to identify sections of profiles where layers may be present. However, choosing reasonable values for these thresholds requires precise prior knowledge of the staircase properties, which may not be available before identifying staircases in that particular region and time period. The method presented here requires the selection of a salinity range in which to search and an estimate of the typical layer thickness, which can be determined from a brief look at a dataset or from previous studies. To evaluate the clusters, a selection of an outlier detection method is required. In addition, while the other techniques require resolution high enough to resolve small-scale vertical gradients, the method presented here—which does not distinguish between individual profiles—only requires that a sufficient number of data points be available in order to detect clusters. Therefore, this technique could potentially find staircases in datasets that have too low a resolution to resolve the steps in any particular profile. While, in this study, we use all data points available after filtering, we found that subsampling profiles to every second, third, or fourth point yielded similar results (not shown). Finally, the method automatically connects layers across profiles. While L22 used an automated connection method, it still required subsequent adjustments to the layers to be made manually. Consequently, the method presented here could be readily applied to datasets with larger numbers of points and used to examine the large-scale, lateral properties of coherent layers in thermohaline staircases.
The clustering algorithm has several limitations. It cannot be used to examine sets of profiles spanning temporal or spatial scales larger than those on which stairs are known to be coherent. This method considers all profiles simultaneously, and it is not applicable to identifying stair steps in datasets of independent individual profiles. While this method could be applied on a profile-by-profile basis, each profile would require a separate selection of
$ {m}_{pts} $
, which itself becomes highly sensitive with a small number of points to cluster. Moreover, as the clustering algorithm does not consider profiles individually, it may miss layers that are only present in a small number of profiles, as may occur especially for layers that split or merge. Finally, although the clustering method captures the overall structure of the staircase layers well, it sometimes miscategorizes points, especially near the boundaries between layers and interfaces.
The method presented here could be used in conjunction with other staircase detection methods. For example, if a different detection method were used to identify which data points in a collection of profiles are in layers, the clustering algorithm could be run on just the layer points to automatically connect the layers across profiles. Additionally, the clustering algorithm could be used on a large collection of datasets to identify which subsets contain staircases; then, a more specifically tuned staircase detection method could be used on just that subset, reducing the amount of time-consuming analysis.
Because the method can be scaled to datasets with a larger number of points, a natural extension would be to apply it to a dataset with profiles from many ITPs. Furthermore, although we have focused on identifying upper-ocean Arctic thermohaline staircases, it could also be useful in other oceanic regimes. Staircases with steps on the order of 50 m thick have been observed in the Arctic between depths of 2000–3000 m (Timmermans et al., Reference Timmermans, Garrett and Carmack2003), much deeper than ITPs measure, while the Argo network of autonomous profiling floats has captured staircases in regions all over the world (van der Boog et al., Reference van der Boog, Dijkstra, Pietrzak and Katsman2021a). Since this method does not assume a consistent vertical resolution across the profiles, it could be run on a mix of data from different types of instruments, assuming they operated within the same region and time period. This method could also be adjusted to identify other structures that appear in
$ \Theta $
–
$ S $
space, such as different types of layers or water masses, or even structures that can appear in different spaces, such as
$ \Theta $
–
$ {\mathrm{O}}_2 $
(Rosso et al., Reference Rosso, Mazloff, Talley, Purkey, Freeman and Maze2020). On the technical side, another topic of future study would be to adapt this method to automatically distinguish between well-mixed layers and intrusions. However, when using this clustering algorithm to specifically search for staircase layers, we recommend avoiding the bottom of the thermocline around the AW core, where remnant intrusions are known to appear (Bebieva and Timmermans, Reference Bebieva and Timmermans2019). Finally, there may be methods other than the DBCV validation process used herein that may be better able to guide the choice of parameters, potentially improving the detection fidelity.
Acknowledgements
We acknowledge fruitful discussions with Maike Sonnewald and Carine van der Boog. M.G.S. acknowledges fruitful discussions that occurred during the Kavli Institute of Theoretical Physics program on Layering in Atmospheres, Oceans and Plasmas (supported by the National Science Foundation under grant no. NSF PHY-1748958). E.R. is grateful to the researchers, staff, and students of the Centre for Earth Observation Science for the support received during the preparation of this manuscript. J. M. L. thanks the Department of Physics at the University of Toronto, where he was a visiting scientist during the time this work was carried out.
Author contribution
Conceptualization: M.G.S., N.G., E.R., J.M.L.; data curation: M.G.S.; formal analysis: M.G.S.; funding acquisition: N.G.; investigation: M.G.S.; methodology: M.G.S.; software: M.G.S.; supervision: N.G., E.R., J.M.L.; validation: M.G.S., N.G., E.R., J.M.L.; visualization: M.G.S.; writing – original draft: M.G.S.; writing – review & editing: M.G.S., N.G., E.R., J.M.L.; All authors approved the final submitted draft.
Competing interest
The authors declare none.
Data availability statement
Replication code can be found on Zenodo: https://zenodo.org/doi/10.5281/zenodo.8029947. The Ice-Tethered Profiler data were collected and made available by the Ice-Tethered Profiler Program (Toole et al., Reference Toole, Krishfield, Timmermans and Proshutinsky2011; Krishfield et al., Reference Krishfield, Toole and Timmermans2008) based at the Woods Hole Oceanographic Institution (https://www2.whoi.edu/site/itp/).
Ethics statement
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Funding statement
M.G.S. and N.G. were supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) (funding reference numbers RGPIN-2015-03684 and RGPIN-2022-04560). J.M.L. was supported by grant number 2049521 from the Physical Oceanography program of the United States National Science Foundation. ER was supported by the NSERC Postdoctoral Fellowship award, the NSERC Canada-150 Chair (Award G00321321), and the NSERC Discovery Grant (funding reference number RGPIN-2024-05545).
Supplementary material
The supplementary material for this article can be found at http://doi.org/10.1017/eds.2024.13.
Open access
