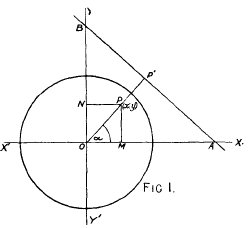
It is evident that if MCA1 = MBC the point M lies on the circle O, which touches AC at C and passes through B. Again, if we take two equal and opposite pencils A(BIMC) and C(A1EMb) we know that their intersections lie on an hyperbola, and observe that when AI is the bisector of A its corresponding ray CE of the second pencil is parallel to it. This gives the direction of the asymptotes; the second asymptote will be parallel to the external bisector of A. The conic is therefore a rectangular hyperbola. When the ray of the first pencil coincides with AC1 the ray of the second corresponding to it will make with CA an angle equal to A, it is therefore parallel to AB, and the point of intersection is C; hence the second ray ab is a tangent at C, similarly BA is a tangent at A; therefore AC passes through the centre of the conic, and B′ is the centre. The point M where this conic cuts O is the required point M. Denote this hyperbola by γ, then on repeating this construction at B we get a second hyperbola β cutting the circle O1 at M1, which makes angle M1BA2 = M1AC = M1CB. (See Fig. on p. 157.)