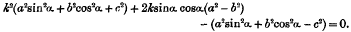The necessary and sufficient condition that two generators of the  should be at right angles is that their point of intersection should lie on the director sphere x2 + y2 + z2- = a2 + b2 – c2. Let a2 + b2 – c2 = r2 and a2 > b2. Then if r2 > a2, b2 > c2, and in this case the curve of intersection of the H1 and sphere consists of two closed ovals lying on opposite sides of the plane XOY. Thus every generator of the H1 meets the sphere in two real points. This result is easy to obtain analytically. For the generator
should be at right angles is that their point of intersection should lie on the director sphere x2 + y2 + z2- = a2 + b2 – c2. Let a2 + b2 – c2 = r2 and a2 > b2. Then if r2 > a2, b2 > c2, and in this case the curve of intersection of the H1 and sphere consists of two closed ovals lying on opposite sides of the plane XOY. Thus every generator of the H1 meets the sphere in two real points. This result is easy to obtain analytically. For the generator
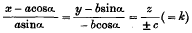
meets the sphere in points given by