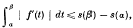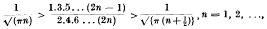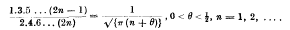Research Article
A bilinear transformation
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 1-7
-
- Article
-
- You have access
- Export citation
A criterion for differentiability
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 8-11
-
- Article
-
- You have access
- Export citation
A note on rectifiable curves
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 12-14
-
- Article
-
- You have access
- Export citation
A remark about canonical forms
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 15
-
- Article
-
- You have access
- Export citation
A generalisation of Dirichlet's multiple integral
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 16-18
-
- Article
-
- You have access
- Export citation
On Wallis' formula
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 19-21
-
- Article
-
- You have access
- Export citation
Obituary
Miss C. M. Hamill
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 22-25
-
- Article
-
- You have access
- Export citation
Horatio S. Carslaw
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 26
-
- Article
-
- You have access
- Export citation
John Mackie
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 27-28
-
- Article
-
- You have access
- Export citation
W. M. H. Greaves
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 28-30
-
- Article
-
- You have access
- Export citation
Alexander D. Russell
-
- Published online by Cambridge University Press:
- 31 October 2008, p. 32
-
- Article
-
- You have access
- Export citation
Archibald R. Richardson
-
- Published online by Cambridge University Press:
- 31 October 2008, pp. 31-32
-
- Article
-
- You have access
- Export citation